PSEB 11th Class Physics Important Questions Chapter 7 System of Particles and Rotational Motion

Punjab State Board PSEB 11th Class Physics Important Questions Chapter 7 System of Particles and Rotational Motion Important Questions and Answers.

PSEB 11th Class Physics Important Questions Chapter 7 System of Particles and Rotational Motion

very short answer type questions

Question 1.
(n – 1) equal point masses each of mass m are placed at the vertices of a regular n-polygon. The vacant vertex has a position vector \(\vec{a}\) with respect to the centre of the polygon. Find the position vector of centre of mass. (NCERT Exemplar)
Solution
Suppose, \(\vec{b}\) be the position vector of centre of mass of regular n-polygon. As (n – 1) equal point masses each of mass m are placed at (n – 1) vertices of regular polygon, therefore
\(\frac{(n-1) m b+m a}{(n-1+1) m}\) = 0
⇒ (n – 1)mb + ma = 0
⇒ b = \(\frac{-a}{(n-1)}\)

Question 2.
If net torque on a rigid body is zero, does it linear momentum necessary remain conserved?
Answer:
The linear momentum remain conserved if the net force on the system is zero.

Question 3.
When is a body lying in a gravitation field in stable equilibrium?
Answer:
A body in a gravitation field will be in stable equilibrium, if the vertical line through its centre of gravity passes through the base of the body.

Question 4.
Is centre of mass and centre of gravity body always coincide?
Ans.
No, if the body is large such that g varies from one point to another, then centre of gravity is offset from centre of mass.
But for small bodies, centre of mass and centre of gravity lies at their geometrical centres.

Question 5.
Why is moment of inertia also called rotational inertia?
Answer:
The moment of inertia gives a measure of inertia in rotational motion. So, it is also called rotational inertia.

Question 6.
In a flywheel, most of the mass is concentrated at the rim. Explain why?
Answer:
Concentration of mass at the rim increases the moment of inertia and thereby brings uniform motion.

Question 7.
Does the radius of gyration depend upon the speed of rotation of the body?
Answer:
No, it depends only on the distribution of mass of the body.

Question 8.
Can the mass of body be taken to be concentrated at its centre of mass for the purpose of calculating its rotational inertia?
Answer:
No, the moment of inertia greatly depends on the distribution of mass about the axis of rotation.

Short answer type questions

Question 1.
Does angular momentum of a body in translatory motion is zero?
Solution:
Angular momentum of a body is measured with respect to certain origin.

So, a body in translatory motion can have angular momentum.
It will be zero, if origin lies on the line of motion of particle.

Question 2.
Figure shows momentum versus time graph for a particle moving along x – axis. In which region, force on the particle is large. Why?

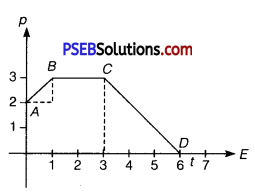
Solution:
Net force is given by F = \(\frac{d p}{d t}\)
Also, rate of change of momentum = slope of graph.
As from graph, slope AB = slope CD
And slope (BC) = slope (DE) = 0
So, force acting on the particle is equal in regions AB and CD and in regions BC and DE (which is zero).

Question 3.
Two cylindrical hollow drums of radii R and 2J2, and of a common height h, are rotating with angular velocities ω (anti-clockwise) and ω (clockwise), respectively.
Their axes, fixed are parallel and in a horizontal plane separated by (3R + δ). They are now brought in contact (δ → 0).
(i) Show the frictional forces just after contact.
(ii) Identify forces and torques external to the system just after contact.
(iii) What would be the ratio of final angular velocities when friction ceases? (NCERT Exemplar)
Solution:

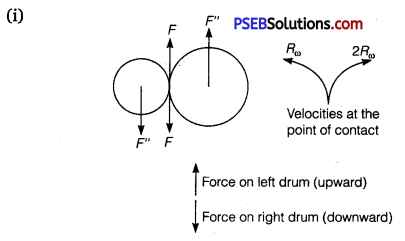
(ii) F’ = F = F” where F and F” are external forces through support.
F_net = 0
External torque = F x 3 R, anti-clockwise.

(iii) Let ω₁ and ω₂ be final angular velocities (anti-clockwise and clockwise respectively).
Finally, there will be no friction.
Hence, Rω₁ = 2Rω₂ ⇒ \(\frac{\omega_{1}}{\omega_{2}}\) = 2

Question 4.
Angular momentum of a system is conserved if its M.I. is changed. Is its rotational K. E. also conserved?
Solution:
Kinetic energy of rotation = \(\frac{1}{2}\)Iω² = \(\frac{1}{2}\) (Iω)ω = \(\frac{1}{2}\)Lω

L = Iω is constant, if moment of inertia (I) of the system changes. It means as I changes, then ω also changes.
Hence K.E. of rotation also changes with the change in I. In other words, rotational K.E. is not conserved.

Question 5.
How much fraction of the kinetic energy of rolling is purely
(i) translational, (ii) rotational.
Solution:

Question 6.
Listening to the discussion on causes of pollution and due to which temperature on earth is rising, increase in temperature leads to melting of polar ice, Meenu realised that if each one of us contributed to create pollution free environment, then even small efforts can lead to big results. So, she decided to lead the step and instead of going to school by her car, she joined school bus and also asked her father to go to office using car pool.
(i) What do you think is mainly responsible for global warming?
(ii) If the ice on polar caps of the earth melts due to pollution, how will it affect the duration of the day?
Explain.
(iii) What values does Meenu show?
Answer:
(i) Pollution created by the people of world is the main cause of global warming.
(ii) Earth rotates about its polar axis. When ice of polar caps of earth melts, mass concentrated near the axis of rotation spreads out, therefore moment of inertia, I increases.
As no external torque acts,
∴ L = I = Iω = (\(\frac{2 \pi}{T}\)) = Constant
With increase of I, T will increase i.e., length of day will also increase,
(iii) Meenu is considerate towards environment and her thought of leading the steps to reduce pollution is commendable.

Question 7.
Explain how a cat is able to land on its feet after a fall taking the advantage of principle of conservation of angular momentum?
Answer:
When a cat falls to ground from a height, it stretches its body alongwith the tail so that its moment of inertia becomes high. Since, la is to remain constant, the value of angular speed a decreases and therefore the cat is able to’ land on the ground gently.

Question 8.
A uniform disc of radius R is resting on a table on its rim. The coefficient of friction between disc and table is μ (figure). Now, the disc is pulled with a force \(\overrightarrow{\boldsymbol{F}}\) as shown in the figure. What is the maximum value of \(\overrightarrow{\boldsymbol{F}}\) for which the disc rolls without slipping? (NCERT Exemplar)

Solution:
Let the acceleration of the centre of mass of disc be a, then
Ma = F – f
The angular acceleration of the disc is a = a/R (if there is no sliding).
Then, (\(\frac{1}{2}\)MR²)α = Rf
⇒ Ma = 2f
Thus, f =F/3. Since, there is no sliding.
⇒ f ≤ μ mg ⇒ F ≤ 3μ Mg

Question 9.
Two equal and opposite forces act on a rigid body. Under what condition will the body (i) rotate (ii) not rotate?
Answer:
(i) Two equal and opposite forces acting on a rigid body such that their lines of action do not coincide, constitute a couple. This couple produces the turning effect on the body. Hence, the rigid body will rotate.

(ii) If two equal and opposite forces act in such a way that their lines of action coincide, then these forces cancel out the effect of each other. Hence, the body will not rotate.

Long answer type questions

Question 1.
Find position of centre of mass of a semicircular disc of radius r. (NCERT Exemplar)
Solution:
As semicircular disc is symmetrical about its one of diameter, we take axes as shown. So, now we only have to calculate Y_CM (As X_CM is zero by symmetry and choice of origin).

Now, for a small element OAB, as element is small and it can be treated as a triangle so,
Area of sector OAB = \(\frac{1}{2}\) x r x rdθ
Height of triangle = r
Base of triangle = AB = rdθ
So, its mass dm = \(\frac{1}{2}\)r² dθ.ρ [∵ ρ = \(\frac{\text { mass }}{\text { area }}\)]
As centre of mass of a triangle is at a distance of \(\frac{2}{3}\) from its vertex (at centroid, intersection of medians). So, y = \(\frac{2}{3}\)rsinθ (location of CM of small sector AOB).


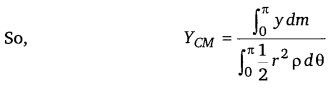
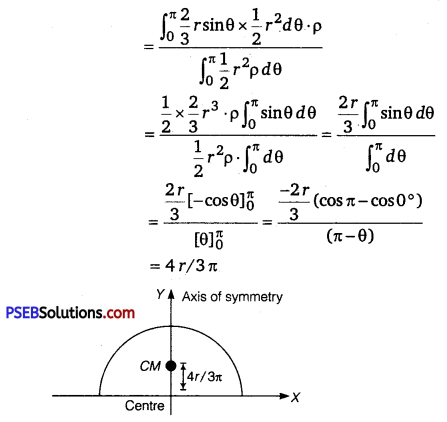
So, CM of disc is at a distance of \(\frac{4 r}{3 \pi}\)from its centre on its axis of symmetry.

Question 2.
Obtain an expression for linear acceleration of a cylinder rolling down an inclined plane and hence find the condition for the cylinder to roll down the inclined plane without slipping.
Solution:
When a cylinder rolls down on an inclind plane, then forces involved are (i) Weight mg (ii) Normal reaction N (iii) Friction f
From free body diagam,

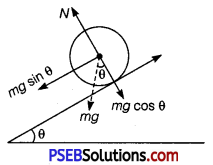
From free body diagram,
N – mg cos θ = 0
or N = mg cosθ
Also, if a = acceleration of centre of mass down the plane, then
F_net = ma = mgsin θ – f …………… (i)
As friction produces torque necessary for rotation,
τ = Iα = f R