Punjab State Board PSEB 11th Class Physics Important Questions Chapter 9 Mechanical Properties of Solids Important Questions and Answers.
PSEB 11th Class Physics Important Questions Chapter 9 Mechanical Properties of Solids
Very Short Answer Type Questions
Question 1.
Two identical solid balls, one of ivory and the other of wet clay, are dropped from the same height on the floor. Which will rise to a greater height after striking the floor and why?
Answer:
The ball of ivory will rise to a greater height because ivory is more elastic than wet-clay.
Question 2.
Is it possible to double the length of a metallic wire by applying a force over it?
Answer:
No, it is not possible because, within elastic limit, strain is only order of 10-3, wires actually break much before it is stretched to double the length.
Question 3.
Is stress a vector quantity? (NCERT Exemplar)
Stress = \(\frac{\text { Magnitude of internal reaction force }}{\text { Area of cross – section }}\)
Therefore, stress is a scalar quantity, not a vector quantity.
![]()
Question 4.
What does the slope of stress versus strain graph indicate?
Answer:
The slope of stress (on y-axis) and strain (on x-axis) gives modulus of elasticity.
The slope of stress (on x-axis) and strain (on y-axis) gives the reciprocal of modulus of elasticity.
Question 5.
Stress and pressure are both forces per unit area. Then in what respect does stress differ from pressure?
Answer:
Pressure is an external force per unit area, while stress is the internal restoring force which comes into play in a deformed body acting transversely per unit area of a body.
Question 6.
What is the Young’s modulus for a perfect rigid body?
Solution:
Young’s modulus (Y) = \(\frac{F}{A} \times \frac{l}{\Delta l}\)
For a perfectly rigid body, change in length Δl = 0
∴ Y = \(\frac{F}{A} \times \frac{l}{0}\) = ∞
Therefore, Young’s modulus for a perfectly rigid body is ∞.
Question 7.
What is Bulk modulus for a perfectly rigid body?
Solution:
Bulk modulus (B) = \(\frac{p}{\Delta V / V}=\frac{p V}{\Delta V}\)
For perfectly rigid body, change in volume ΔV = 0
∴ B = \(\frac{p V}{0}\) = ∞
Therefore, Bulk modulus for a perfectly rigid body is ∞.
![]()
Short Answer Type Questions
Question 1.
Explain why steel is more elastic than rubber?
Solution:
Consider two pieces of wires, one of steel and the other of rubber. Suppose both are of equal length (L) and of equal area of cross-section (a). Let each be stretched by equal forces, each being equal to F. We find that the change in length of the rubber wire (lr) is more than that of the steel (ls)i.e.,lr>ls.
If Ys and Yr are the Young’s moduli of steel and rubber respectively, then from the definition of Young’s modulus,
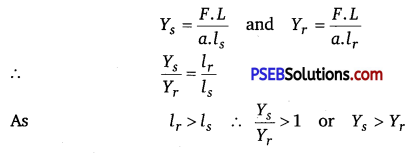
i. e,, the Young’s modulus of steel is more than that of rubber. Hence steel is more elastic than rubber.
Or
Any material which offers more opposition to the deforming force to change its configuration is more elastic.
Question 2.
Elasticity is said to be internal property of matter. Explain.
Answer:
When a deforming force acts on a body, the atoms of the substance get displaced from their original positions. Due to this, the configuration of the body (substance) changes. The moment, the deforming force is removed, the atoms return to their original positions and hence, the substance or body regains its original configuration. That is why, elasticity is said to be internal property of matter.
Question 3.
A wire elongates by l mm when a load W is hanged from it. If the wire goes over a pulley and two weights W each are hung at the two ends, then what will be the elongation of the wire in mm?
Solution:
According to Hooke’s law,
Modulus of elasticity, E = \(\frac{W}{A} \times \frac{L}{l}\)
where, L = original length of the wire
A- cross-sectional area of the wire
Elongation, l = \(\frac{W L}{A E}\) ………………………… (i)
On either side of the wire, tension is W and length is L/2.
Δl = \(\frac{W L / 2}{A E}=\frac{W L}{2 A E}=\frac{l}{2}\) [from eq.(i)]
Total elongation in the wire = \(\frac{l}{2}+\frac{l}{2}\) = l
![]()
Question 4.
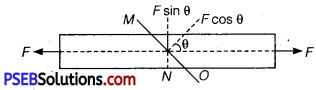
A bar of cross-section A is subjected to equal and opposite tensile forces at its, ends. Consider a plane section of the bar whose normal makes an angle θ with the axis of the bar.
(i) What is the tensile stress on this plane?
(ii) What is the shearing stress on this plane?
(iii) For what value of θ is the tensile stress maximum?
(iv) For what value of θ is the shearing stress maximum?
Solution:
(i) The resolved part of F along the normal is the tensile force on this plane and the resolved part parallel to the plane is the shearing force on the plane.
∵ Area of MO plane section = A sec θ
Tensile stress = \(\frac{\text { Force }}{\text { Area }}=\frac{F \cos \theta}{A \sec \theta}=\frac{F}{A} \cos ^{2} \theta\)
= [ ∵ sec θ = \(\frac{1}{\cos \theta}\)]
(ii) Shearing stress applied on the top face
So, F = F sinθ
Shearing stress = \(\frac{\text { Force }}{\text { Area }}=\frac{F \sin \theta}{A \sec \theta}\)
= \(\frac{F}{A}\) sinθcosθ
= \(\frac{F}{2 A} \sin 2 \theta\) [∵ sin 2θ = 2sinθcosθ]
(iii) Tensile stress will be maximum when cos2θ is maximum i.e., cosθ = 1 or θ=0°.
(iv) Shearing stress will be maximum when sin20 is maximum i.e., sin2θ = 1 or 2θ = 90° or θ = 45°.
Question 5.
What is an elastomer? What are their special features?
Answer:
Elastomers are those substances which can be stretched to cause large strains.Substances like tissue of aorta, rubber etc., are elastomers.
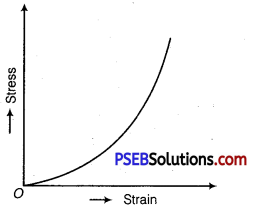
The stress-strain curve for an elastomer is shown in figure. Although elastic region is very large but the materials does not obey Hooke’s law over most of the region. Moreover, there is no well-defined plastic region.
Question 6.
The Young’s modulus for steel is much more than that for rubber. For the same longitudinal strain, which one will have greater tensile stress? (NCERT Exemplar)
Solution:
Young’s modulus (Y) = \( \frac{\text { Stress }}{\text { Longitudinal strain }}\)
For same longitudinal strain, Y ∝ stress

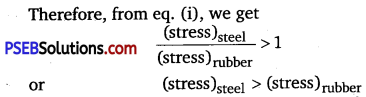
Question 7.
Why are the springs made of steel and not of copper?
Answer:
A spring will be better one if a large restoring force is set up in it on being deformed, which in turn depends upon the elasticity of the material of the spring. Since the Young’s modulus of elasticity of steel is more than that of copper, hence, steel is preferred in making the springs.
![]()
Question 8.
Identical springs of steel and copper are equally stretched. On which, more work will have to be done? (NCERT Exemplar)
Solution:
Work done in stretching a wire is given by
W =- \(\frac{1}{2}\) F x Δl
As springs of steel and copper are equally stretched.
Therefore, for same force (F).
W ∝ Δl …………………………………… (i)
Young’s modulus (Y) = \(\frac{F}{A} \times \frac{l}{\Delta l}\)
or Δl = \(\frac{F}{A} \times \frac{l}{Y}\)
As both spring are identical,
∴ Δl ∝ \(\frac{1}{Y}\) …………………………………. (ii)
From eqs. (i) and (ii), we get W ∝ \(\frac{1}{Y}\) .
∴ \(\frac{W_{\text {steel }}}{W_{\text {copper }}}=\frac{Y_{\text {copper }}}{Y_{\text {steel }}}<1\)
[as Ysteel > Ycopper]
or Wsteel < WCopper
Therefore, more work will be done for stretching copper spring.
Long Answer Type Questions
Question 1.
A steel wire of length 21 and cross-sectional area A is stretched within elastic limit as shown in figure. Calculate the strain and stress in the wire.
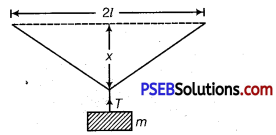
Solution:
Total length L =21. Increase in length of the wire, when it is stretched from its mid-point.
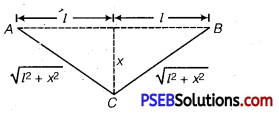
From Pythagoras theorem, BC2 =l2 + x2
BC= \(\sqrt{l^{2}+x^{2}}\)
Similarly, AC = \(\sqrt{l^{2}+x^{2}}\)

Since x<< l, so using Binomial expansion, we have
\(\left(1+\frac{x^{2}}{l^{2}}\right)^{1 / 2}=\left(1+\frac{x^{2}}{2 l^{2}}\right)\)
[Neglecting terms containing higher powers of x]
∴ ΔL = 2l\(\left(1+\frac{x^{2}}{2 l^{2}}\right)-2 l=\frac{x^{2}}{l}\)
Hence Strain = \(\frac{\Delta L}{L}=\frac{x^{2}}{l \times 2 l}=\frac{x^{2}}{2 l^{2}}\)
Stress = \(\frac{F}{A}=\frac{\text { Tension }}{\text { Area }} \)
So, area of cross section of wire having radius r is πr²
Stress = \(\frac{T}{\pi r^{2}}\)
![]()
Question 2.
Consider a long steel bar unde a tensile stress due to forces F acting at the edges along the length of the bar (figure). Consider a plane making an angle θ with the length. What are the tensile and shearing stresses on this plane?
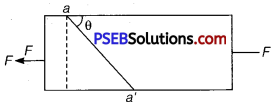
(a) For what angle is the tensile stress a maximum?
(b) For what angle is the shearing stress a maximum? (NCERT Exemplar)
Solution:
Consider the adjacent diagram.
Let the cross-sectional area of the bar be A. Consider the equilibrium of the plane aa’.
A force F must be acting on this plane making an angle \(\frac{\pi}{2}\) – θ with the normal ON. Resolving F into components, along the plane (FP) and normal to the plane.
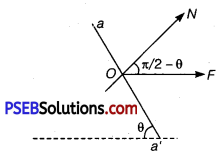
FP = F cosθ
FN = Fsinθ
Let the area of the face aa’ be A’, then
\(\frac{A}{A^{\prime}}\) = sinθ’
∴ A’= \(\frac{A}{\sin \theta}\)

(a) For tensile stress to be maximum, sin2θ =1
⇒ sinθ = 1
⇒ θ = \(\frac{\pi}{2}\)
(b) For shearing stress to be maximum,
sin 2θ = 1
⇒ 2θ = \(\frac{\pi}{2}\)
⇒ θ = \(\frac{\pi}{4}\)
