Punjab State Board PSEB 11th Class Physics Book Solutions Chapter 9 Mechanical Properties of Solids Textbook Exercise Questions and Answers.
PSEB Solutions for Class 11 Physics Chapter 9 Mechanical Properties of Solids
PSEB 11th Class Physics Guide Mechanical Properties of Solids Textbook Questions and Answers
Question 1.
A steel wire of length 4.7 m and cross-sectional area 3.0 x 10-5 m2 stretches by the same amount as a copper wire of length 3.5 m and cross-sectional area of 4.0 x 10-5 m2 under a given load. What is the ratio of the Young’s modulus of steel to that of copper?
Solution:
Given, length of the steel wire, L1 = 4.7 m
Area of cross-section of the steel wire,A1 = 3.0 x 10-5 m2
Length of the copper wire, L2 = 3.5 m
Area of cross-section of the copper wire, A2 = 4.0 x 10-5 m2
Change in length = ΔL1 = ΔL2 = ΔL
Force applied in both the cases = F
Young’s modulus of the steel wire,
Y1 = \(\frac{F_{1}}{A_{1}} \times \frac{L_{1}}{\Delta L_{1}} \)
= \(\frac{F \times 4.7}{3.0 \times 10^{-5} \times \Delta L} \) ………………………………. (i)
Young’s modulus of the copper wire,
Y2 = \(\frac{F_{2}}{A_{2}} \times \frac{L_{2}}{\Delta L_{2}}=\frac{F \times 3.5}{4.0 \times 10^{-5} \times \Delta L}\) ………………………………. (ii)
Dividing eq. (i) by eq. (ii), we get:
\(\frac{Y_{1}}{Y_{2}}=\frac{4.7 \times 4.0 \times 10^{-5}}{3.0 \times 10^{-5} \times 3.5}\) = 1.79:1
The ratio of Young’s modulus of steel to that of copper is 1.79: 1.
![]()
Question 2.
Figure given below shows the strain-stress curve for a given material. What are (a) Young’s modulus and (b) approximate yield strengths for this material?
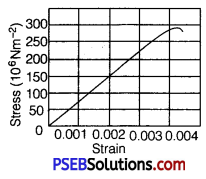
Solution:
(a) It is clear from the given graph that for stress 150 x 106 N/m2, strain is 0.002.
∴ Young s modulus, Y = \(\frac{\text { Stress }}{\text { Strain }}\)
= \(\frac{150 \times 10^{6}}{0.002}\) = 7.5 x 1010 N/m2
Hence, Young’s modulus for the given material is 7.5 x1010 N/m2
(b) The yield strength of a material is the maximum stress that the material can sustain without crossing the elastic limit. It is clear from the given graph that the approximate yield strength of this material is 300 x 106 N/m2 or 3 x 108 N/m2.
Question 3.
The stress-strain graphs for materials A and B are shown in figure given below.
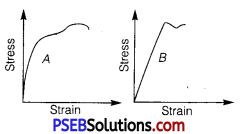
The graphs are drawn to the same scale.
(a) Which of the materials has the greater Young’s modulus?
(b) Which of the two is the stronger material?
Solution:
(a) A, for a given strain, the stress for material A is more than it is for > material B, as shown in the two graphs.
Young’s modulus = \(\frac{\text { Stress }}{\text { Strain }}\)
For a given strain, if the stress for a material is more, then Young’s modulus is also greater for that material. Therefore, Young’s modulus for material A is greater than it is for material B.
(b) A, the amount of stress required for fracturing a material, corresponding to its fracture point, gives the strength of that material. Fracture point is the extreme point in a stress-strain curve. It can be observed that material A can withstand more strain than material B. Hence, material A is stronger than material B.
Question 4.
Read the following two statements below carefully and state, with reasons, if it is true or false.
(a) The Young’s modulus of rubber is greater than that of steel;
(b) The stretching of a coil is determined by its shear modulus.
Solution:
(a) False.
Reason: For a given stress, the strain in rubber is more than it is in steel.
Young’s modulus, Y = \(\frac{\text { Stress }}{\text { Strain }} \)
For a constant stress Y ∝ \(\frac{1}{\text { Strain }}\)
Hence, Young’s modulus for rubber is less than it is for steel.
(b) True.
Reason: Shear modulus is the ratio of the applied stress to the change in the shape of a body. The stretching of a coil changes its shape. Hence, shear modulus of elasticity is involved in this process.
![]()
Question 5.
Two wires of diameter 0.25 cm, one made of steel and the other made of brass are loaded as shown in figure given below. The unloaded length of steel wire is 1.5 m and that of brass wire is 1.0 m.
Compute the elongations of the steel and the brass wires.
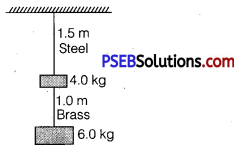
Solution:
Given, diameter of the wires, d = 0.25 cm
Hence, the radius of the wires, r = \(\frac{d}{2} \) = 0.125cm = 0.125 x 10-2m
Length of the steel wire, L1 = 1.5 m
Length of the brass wire, L2 = 1.0 m
Total force exerted on the steel wire,
F1 = (4 +6)g= 10×9.8 = 98N .
Young’s modulus for steel
Y1 = \(\frac{\left(\frac{F_{1}}{A_{1}}\right)}{\left(\frac{\Delta L_{1}}{L_{1}}\right)} \)
where, ΔL1 = Change in the length of the steel wire
A1 = Area of cross-section of the steel wire = πr²1
Young’s modulus of steel, Y1 = 2.0 x 1011 Pa
∴ ΔL1 = \(\frac{F_{1} \times L_{1}}{A_{1} \times Y_{1}}=\frac{F_{1} \times L_{1}}{\pi r_{1}^{2} \times Y_{1}}\)
= \(\frac{98 \times 1.5}{3.14\left(0.125 \times 10^{-2}\right)^{2} \times 2 \times 10^{11}}\)
= 1.5 x 10-4 m
Total force on the brass wire
F2 =6 x 9.8=58.8N
Young’s modulus for brass
Y2 = \(\frac{\left(\frac{F_{2}}{A_{2}}\right)}{\left(\frac{\Delta L_{2}}{L_{2}}\right)}\)
where, ΔL2 = Change in length of the steel wire
A2 = Area of cross-section of the brass wire
∴ ΔL2 = \(\frac{F_{2} \times L_{2}}{A_{2} \times Y_{2}}=\frac{F_{2} \times L_{2}}{\pi r_{2}^{2} \times Y_{2}}\)
= \(\frac{58.8 \times 1.0}{3.14 \times\left(0.125 \times 10^{-2}\right)^{2} \times\left(0.91 \times 10^{11}\right)}\)
= 1.3 x 10-4 m
Hence, elongation of the steel wire =1.49 x 10-4 m
and elongation of the brass wire = 1.3 x 10-4 m
Question 6.
The edge of an aluminium cube is 10 cm long. One face of the cube is firmly fixed to a vertical wall. A mass of 100 kg Is the attached to the opposite face of the cube. The shear modulus of aluminium is 25 GPa. What is the vertical deflection of this face?
Solution:
Given, edge of the aluminium cube, L = 10cm = 0.1 m
The mass attached to the cube, m =100 kg
Shear modulus (ri) of aluminium = 25GPa =25 x 109 Pa
Shear modulus, η = \(\frac{\text { Shear stress }}{\text { Shear strain }}=\frac{\frac{F}{A}}{\frac{\Delta L}{L}}\)
where, F = Applied force = mg = 100 x 9.8 = 980 N
A = Area of one of the faces of the cube = 0.1 x 0.1 = 0.01 m2
ΔL = Vertical deflection of the cube
ΔL = \(\frac{F L}{A \eta}=\frac{980 \times 0.1}{10^{-2} \times\left(25 \times 10^{9}\right)}\)
= 3.92 x 10-7 m
The vertical deflection of this face of the cube is 3.92 x 10-7 m.
Question 7.
Four identical tblloW cylindrical columns of mild steel support a big structure of mass’50,000 kg. The inner and outer radii of each column are 30 cm and 60 cm respectively. Assuming the load distribution to be uniform, calculate the compressional strain of each column.
Solution:
Given, mass of the big structure, M = 50000 kg
Inner radius of the column, r = 30 cm = 0.3 m
Outer radius of the column, R = 60 cm = 0.6 m
Young’s modulus of steel, Y = 2 x 1011 Pa
Total force exerted, F =Mg = 50000 x 9.8N
Stress = Force exerted on a single column = \(\frac{50000 \times 9.8}{4}\) = 122500 N
Young’s modulus, Y = \(\frac{\text { Stress }}{\text { Strain }} \)
Strain = \(\frac{F}{\frac{A}{Y}} \)
where, Area, A = π(R2 – r2) = π[(0.6)2 – (0.3)2]
Strain = \(\frac{122500}{3.14\left[(0.6)^{2}-(0.3)^{2}\right] \times 2 \times 10^{11}}\) = 7.22 x 10-7
Hence, the compressional strain of each column is 7.22 x 10-7.
∴Compressional strain of all columns is given by
= 7.22 x 10 -7 x 4 = 2.88 x 10-6.
![]()
Question 8.
A piece of copper having a rectangular cross-section of 15.2 minxes 19.2 mm is pulled in tension with 44,500 N force, producing only elastic deformation. Calculate the resulting strain?
Solution:
Given, cross-section area.of copper piece (A) = 15.2 mm x 19.1 mm
= (15.2 x 19.1) x 10 -6m2
Force applied (F) = 44500 N
Young’s modulus (Y) =1.1 x 1011 Nm-2
Young s modulus (Y) = \(=\frac{\text { Longitudinal stress }}{\text { Longitudinal strain }}\)
or Longitudinal strain = \(\frac{\text { Longitudinal stress }}{\text { Young’s modulus }}\)
Young’s modulus
= \(\frac{(F / A)}{Y}=\frac{F}{A Y}\)
= \(\frac{44500}{15.2 \times 19.1 \times 10^{-6} \times 1.1 \times 10^{11}}\)
= 0.0013934.
Question 9.
A steel cable with a radius of 1.5 cm supports a chairlift at a ski area. If the maximum stress is not to exceed 108 Nm -2, what is the maximum load the cable can support?
Solution:
Radius of the steel cable, r = 1.5cm = 0.015m
Maximum allowable stress = 108 N m-2
Maximum stress = \(\frac{\text { Maximum force }}{\text { Area of cross – section }} \)
∴ Maximum force = Maximum stress x Area of cross – section
= 108 x π (0.015)2
= 7.065 x 104 N
Hence, the cable can support the maximum load of 7.065 x 104 N.
Question 10.
A rigid bar of mass 15 kg is supported symmetrically by three wires each 2.0 m long. Those at each mid are of copper and the middle one is of iron. Determine the ratio of their diameters if each is to have the same tension.
Solution:
The tension force acting on each wire is the same. Thus, the extension in each case is the same. Since the wires are of the same length, the strain will also be the same.
The relation for Young’s modulus is given as:
Y = \(\frac{\text { Stress }}{\text { Strain }}=\frac{\frac{F}{A}}{\text { Strain }}=\frac{\frac{4 F}{\pi d^{2}}}{\text { Strain }}\) ……………………………. (i)
where, F = Tension force
A = Area of cross-section
d = Diameter of the wire
It can be inferred from equation (i) that Y ∝ \(\frac{1}{d^{2}}\)
Young’s modulus for iron, Y1 = 190 x 109 Pa
Diameter of the iron wire = d1
Young’s modulus for copper, Y2 = 110 x 109 Pa
Diameter of the copper wire = d2
Therefore, the ratio of their diameters is given as:
\(\frac{d_{2}}{d_{1}}=\sqrt{\frac{Y_{1}}{Y_{2}}}=\sqrt{\frac{190 \times 10^{9}}{110 \times 10^{9}}}=\sqrt{\frac{19}{11}}\)
= 1.31:11.
![]()
Question 11.
A 14.5 kg mass, fastened to the end of a steel wire of unstretched length 1.0 m, is whirled in a vertical circle with an angular velocity of 2 rev/s at the bottom of the circle.
The cross-sectional area of the wire is 0.065 cm2. Calculate the elongation of the wire when the mass is at the lowest point of its path.
Solution:
Given, mass, m = 14.5kg
Length of the steel wire, l = 1.0 m
Angular velocity, ω = 2 rev / s
Cross-sectional area of the wire, a = 0.065cm2 = 0.065 x 10-4 m2
Let δl be died elongation of the wire when the mass is at the lowest point of its path.
When the mass is placed at the position of the vertical circle, the total force on the mass is :
F = mg+mlω2 ,
= 14.5 x 9.8 +14.5x 1 x (2)2 = 200.1 N
Young’s modulus = \(\frac{\text { Stress }}{\text { Strain }} \)
Y = \(\frac{\frac{F}{A}}{\frac{\Delta l}{l}}=\frac{F}{A} \cdot \frac{l}{\Delta l}\)
∴ Δl = \(\frac{F l}{A Y}\)
Young’s modulus for steel = 2 x 1011 Pa
∴ Δl = \(\frac{200.1 \times 1}{0.065 \times 10^{-4} \times 2 \times 10^{11}} \) = 1539.23 x 10-7
= 1.539 x 10-4
Hence, the elongation of the wire is 1.539 x 10-4 m.
Question 12.
Compute the bulk modulus of water from the following data: Initial volume =100.0 litre, Pressure increase =100.0atm (1 atm = 1.013 x 105 Pa), Final volume = 100.5 litre. Compare the bulk modulus of water with that of air (at constant temperature). Explain in simple terms why the ratio is so large.
Solution:
Initial volume, V1 = 100.0 l x 10-3 m3
Final volume, V2 = 100.5l = 100.5 x 10-3 m-3
Increase in volume, V = V2 — V1 = 0.5 x 10-3 m3
Increase in pressure, Δp =100.0 atm = 100 x 1.013 x 105 Pa
Bulk modulus = \( \frac{\Delta p}{\frac{\Delta V}{V_{1}}}=\frac{\Delta p \times V_{1}}{\Delta V}\)
= \(\frac{100 \times 1.013 \times 10^{5} \times 100 \times 10^{-3}}{0.5 \times 10^{-3}}\) = 2.206 x 109 Pa
Bulk modulus of air = 1.0 x 105 Pa
∴ \(\frac{\text { Bulk modulus of water }}{\text { Bulk modulus of air }}=\frac{2.026 \times 10^{9}}{1.0 \times 10^{5}}\)
= 2.026 x 104
This ratio is very high because air is more compressible than water.
Question 13.
What is the density of water at a depth where pressure is 80.0 atm, given that its density at the surface is 103 x 103 kgm-3?
Solution:
Let the given depth be h.
Pressure at the given depth, p = 80.0 atm = 80 x 1.01 x 105 Pa
Density of water at the surface, ρ1 = 1.03 x 103 kg m-3
Let ρ2 be the density of water at the depth h.
Let V1 be the volume of water of mass m at the surface.
Let V2 be the volumé of water of mass m at the depth h.
Let ΔV be the change in volume.
ΔV = V1 – V2 = \(m\left(\frac{1}{\rho_{1}}-\frac{1}{\rho_{2}}\right)\)
∴ Volumetric strain= \(\frac{\Delta V}{V_{1}}=m\left(\frac{1}{\rho_{1}}-\frac{1}{\rho_{2}}\right) \times \frac{\rho_{1}}{m}\)
∴ \(\frac{\Delta V}{V_{1}}=1-\frac{\rho_{1}}{\rho_{2}}\) ………………………………. (i)
Bulk modulus, B = \(\frac{p V_{1}}{\Delta V}\)
\(\frac{\Delta V}{V_{1}}=\frac{p}{B}\)
Compressibility of water = \(\frac{1}{B}=45.8 \times 10^{-11} \mathrm{~Pa}^{-1}\)
∴ \(\frac{\Delta V}{V_{1}}=80 \times 1.013 \times 10^{5} \times 45.8 \times 10^{-11}\) = 3.71 x 10-3 ………….(ii)
From equations (i) and (ii), we get
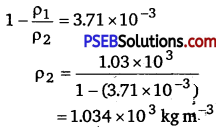
Therefore, the density of water at the given depth (h) is 1.034 x 103 kg m-3.
![]()
Question 14.
Compute the fractional change in volume of a glass slab, when subjected to a hydraulic pressure of 10 atm.
Solution:
Hydraulic pressure exerted on the glass slab, p = 10 atm = 10 x 1.013 x 105 Pa
Bulk modulus of glass, B = 37 x 109 Nm-2
Bulk modulus, B = \(\frac{p}{\frac{\Delta V}{V}}\)
where, \(\frac{\Delta V}{V}\) = Fractional change in volume
∴ \(\frac{\Delta V}{V}=\frac{p}{B}=\frac{10 \times 1.013 \times 10^{5}}{37 \times 10^{9}}\)
= 2.73 x 10-5
Hence, the fractional change in the volume of the glass slab is
2.73 x 10-5 = 2.73 x 10-3% = 0.0027%
Question 15.
Determine the volume contraction of a solid copper cube, 10 cm on an edge, when subjected to a hydraulic pressure of 7.0x 106 Pa.
Solution:
Length of an edge of the solid copper cube, l =10 cm = 0.1 m
Hydraulic pressure, p = 7.0 x 106 Pa
Bulk modulus of copper, B = 140 x 109 Pa
Bulk modulus, B = \(\frac{P}{\frac{P}{\Delta V}}\)
where, \(\frac{\Delta V}{V}\) = Volumetric strain
ΔV = Change in volume
V =,Original volume
ΔV = \(\frac{p V}{B}\)
Original volume of the cube, V = l3

Therefore, the volume contraction of the solid copper cube is 0.05 cm3.
Question 16.
How much should the pressure on a litre of water be changed to compress by 0.10%?
Solution:
Volume of water, V =1 L
It is given that water is to be compressed by 0.10%.
∴ Fractional change, \(\frac{\Delta V}{V}=\frac{0.1}{100 \times 1}=10^{-3}\)
Bulk modulus, B = \(\frac{p}{\frac{\Delta V}{V}}\)
p = B x \( \frac{\Delta V}{V}\)
Bulk modulus of water, B = 2.2 x 109 Nm-2
p = 22 x 109 x 10-3
=2.2 x 106 Nm-2
Therefore, the pressure on water should be 2.2 x 106 Nm-2.
![]()
Additional Exercises
Question 17.
Anvils made of single crystals of diamond, with the shape as shown in figure given below, are used to investigate behaviour of materials under very high pressures. Flat faces at the narrow end of the anvil have a diameter of 0.50 mm, and the wide ends are subjected to a compressional force of 50,000 N. What is the pressure at the tip of the anvil?
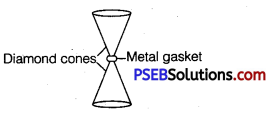
Solution:
Diameter of the cones at the narrow ends, d = 0.50 mm = 0.5 x 10-3m
radius, r = \( \frac{d}{2}\) = 0.25 x 10-3 m
Compressional force, F = 50000 N
Pressure at the tip of the anvil,
p = \(\frac{\text { Force }}{\text { Area }}=\frac{F}{\pi r^{2}}\)
= \(\frac{50000}{3.14 \times\left(0.25 \times 10^{-3}\right)^{2}}\)
= 2.55 x 1011 Pa
Therefore, the pressure at the tip of the anvil is 2.55 x 1011 Pa.
Question 18.
A rod of length 1.05 m having negligible mass is supported at its ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in figure given below. The cross-sectional areas of wires A and B are 1.0 mm2 and 2.0mm2, respectively. At what point along the rod should a mass m he suspended in order to produce (a) equal stresses and (b) equal strains in both steel and aluminium wires.
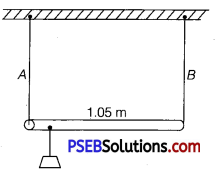
Solution:
Given, cross-sectional area of wire A, a1 = 1.0 mm2 = 1.0 x 10-6 m2
Cross-sectional area of wire B, a2 = 2.0 mm2 = 2.0 x 10-6 m2
Young’s modulus for steel, Y1 = 2 x 1011 Nm-2
Young’s modulus for aluminium, Y2 = 7.0 x 1010 Nm-2
Let a small mass m be suspended to the rod at a distance y from the end where wire A is attached.
Stress in the wire = \(\frac{\text { Force }}{\text { Area }}=\frac{F}{a}\)
If the two wires have equal stresses, then,
\( \frac{F_{1}}{a_{1}}=\frac{F_{2}}{a_{2}}\)
where, F1 = Force exerted on the steel wire
F2 = Force exerted on the aluminium wire
\(\frac{F_{1}}{F_{2}}=\frac{a_{1}}{a_{2}}=\frac{1}{2}\) …………………………. (i)
The situation is shown in the following figure.
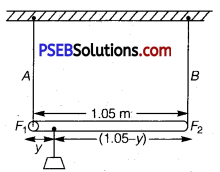
Taking torque about the point of suspension, we have
F1y = F2(1.05— y)
\(\frac{F_{1}}{F_{2}}=\frac{(1.05-y)}{y}\) ……………………….(ii)
Using equations (i) and (ii), we can write

In order to produce an equal stress in the two wires, the mass should be suspended at a distance of 0.7 m from the end where wire A is attached.
(b) Young s modulus = \(\frac{\text { Stress }}{\text { Strain }} \)
Strain = \(\frac{\text { Stress }}{\text { Young’s modulus }}=\frac{\frac{F}{a}}{Y}\)
If the strain in the two wires is equal, then,
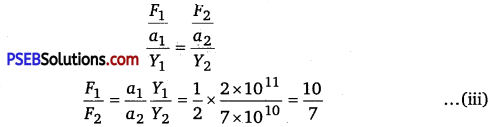
Taking torque about the point where mass m, is suspended at a distance y1 from the side where wire A attached, we get
F1y1 =F2(1.05-y1)
\(\frac{F_{1}}{F_{2}}=\frac{\left(1.05-y_{1}\right)}{y_{1}}\) ……………………………. (iv)
Using equations (iii) and (iv), we get
\(\frac{\left(1.05-y_{1}\right)}{y_{1}}=\frac{10}{7}\)
7(1.05 – y1) = 10 y1
⇒ 17 y1 = 7.35
y1 = 0.432 m
In order to produce an equal strain in the two wires, the mass should be suspended at a distance of 0.432 m from the end where wire A is attached.
![]()
Question 19.
A mild steel wire of length 1.0 m and cross-sectional area 0.50 x 10-2 cm2 is stretched, well within its elastic limit, horizontally between two pillars. A mass of 100 g is suspended from the mid-point of the wire. Calculate the depression at the mid-point.
Solution:

Length of the steel wire = 1.0 m
Area of cross-section, A = 0.50 x 10-2 cm2 = 0.50 x 10-6 m2
A mass 100 g is suspended from its mid-point.
m = 100 g = 0.1kg
Hence, the wire dips, as shown in the given figure.
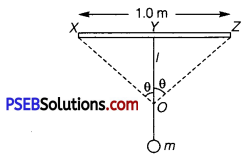
Original length = XZ
Depression = l
The length after mass m, is attached to the wire = XO +OZ
Increase in the length of the wire:
Δl = (XO + OZ)-XZ
Where

Expanding and neglecting higher terms, we get:
Δl = \(\frac{l^{2}}{0.5}\)
Strain = \(\frac{\text { Increase in length }}{\text { Original length }}\)
Let T be the tension in the wire.
∴ mg = 2Tcos θ
Using the figure, it can be written as
Cos θ = \(\frac{l}{\left[(0.5)^{2}+l^{2}\right]^{\frac{1}{2}}}=\frac{l}{(0.5)\left[1+\left(\frac{l}{0.5}\right)^{2}\right]^{\frac{1}{2}}}\)
Expanding the expression and eliminating the higher terms, we get
Cos θ = \(\frac{l}{(0.5)\left(1+\frac{l^{2}}{2(0.5)^{2}}\right)}\)
\(\left(1+\frac{l^{2}}{2(0.5)^{2}}\right)\) ≈ 1 for small l

Hence, the depression at the mid-point is 0.0107 m.
Question 20.
Two strips of metal are riveted together at their ends by four rivets, each of diameter 6.0 mm. What is the maximum tension’ that can be exerted by the riveted strip if the shearing stress on the rivet is not to exceed 6.9 x 107 Pa?
Assume that each rivet is to carry one-quarter of the load.
Solution:
Diameter of the metal strip, d = 6.0 mm = 6.0 x 10-3 m
Radius, r = \(\frac{d}{2}\) = 3.0 x 10-3 m
Maximum shearing stress = 6.9 x 107 Pa
Maximum stress = \(\frac{\text { Maximum load or force }}{\text { Area }}\)
Maximum force = Maximum stress x Area
= 6.9 x 107 x π x (r)2
= 6.9 x 107 x 3.14 x (3 x10-3)2
= 1949.94 N
Each rivet carries one quarter of the load.
∴ Maximum tension on each rivet = 4 x 1949.94 = 7799.76 N.
![]()
Question 21.
The Marina trench is located in the Pacific Ocean, and at one place it is nearly eleven km beneath the surface of the water. The water pressure at the bottom of the trench is about 1.1 x 108 Pa. A steel ball of initial volume 0.32m is dropped into the ocean and falls to the bottom of the trench. What is the change in the volume of the ball when it reaches to the bottom?
Solution:
Water pressure at the bottom, p = 1.1 x 108 Pa
Initial volume of the steel ball, V = 0.32 m3
Bulk modulus of steel, B = 1.6 x 1011 Nm-2
The ball falls at the bottom of the Pacific Ocean, which is 11 km beneath the surface.
Let the change in the volume of the ball on reaching the bottom of the trench be ΔV.
Bulk modulus, B = \( \frac{p}{\frac{\Delta V}{V}}\)
ΔV = \(\frac{p V}{B}=\frac{1.1 \times 10^{8} \times 0.32}{1.6 \times 10^{11}}\)
= 2.2 x 10-4 m3
Therefore, the change in volume of the ball on reaching the bottom of the trench is 2.2 x 10-4 m3.
