PSEB 11th Class Physics Important Questions Chapter 8 Gravitation

Punjab State Board PSEB 11th Class Physics Important Questions Chapter 8 Gravitation Important Questions and Answers.

PSEB 11th Class Physics Important Questions Chapter 8 Gravitation

Very Short Answer Type Questions

Question 1.
By which law is the Kepler’s law of areas identical?
Answer:
The law of conservation of angular momentum.

Question 2.
Draw areal velocity versus time graph for mars. (NCERT Exemplar)
Answer:
Areal velocity of planet revolving around the Sun is constant with time (Kepler’s second law).

Question 3.
At what factor between the two particles gravitational force does not depend?
Answer:
Gravitational force does not depend upon the medium between the two particles.

Question 4.
Two particles of masses m₁ and m₂ attract each other gravitationally and are set in motion under the influence of the gravitational force? Will the centre of mass move?
Answer:
Since the gravitational force is an internal force, therefore the centre of mass would not move.

Question 5.
Work done in moving a particle round a closed path under the action of gravitation force is zero. Why?
Answer:
Gravitational force is a conservative force which means that work done by it, is independent of path followed.

Question 6.
What would happen if the force of gravity were to disappear suddenly?
Answer:
The universe would collapse. We would be thrown away because of the centrifugal force. Eating, drinking and in fact all activities would become impossible.

Question 7.
Why a body weighs more at poles and less at equator?
Answer:
The value of g is more at poles than at the equator. Therefore, a body weighs more at poles than at equator.

Question 8.
Give a method for the determination of the mass of the moon.
Solution:
Soli By making use of the relation, gm = \(\frac{G M_{m}}{R_{m}^{2}} \)

Short Answer Type Questions

Question 1.
A planet moving along an elliptical orbit is closest to the Sim at a distance r₁ and farthest away at a distance of r₂.
If v₁ and v₂ are the linear velocities at these points respectively, then find the ratio \(\frac{v_{1}}{v_{2}}\).
Solution:
From the law of conservation of angular momentum
mr₁v₁ = mr₂v₂
⇒ r₁v₁ = r₂v₂ or
\(\frac{v_{1}}{v_{2}}=\frac{r_{2}}{r_{1}}\)

Question 2.
A mass M is broken into two parts, m and (M – m). How is m related to M so that the gravitational force between two parts is maximum?
Solution:
Let =m,m₂ =M – m
F = G\(\frac{m(M-m)}{r^{2}}=\frac{G}{r^{2}}\left(M m-m^{2}\right)\)
Differentiating w.r:t. m, \(\frac{d F}{d m}=\frac{G}{r^{2}}(M-2 m)\)
For F to be maximum, \(\frac{d F}{d m}\) = 0

m₁ = m₂ = M/2

Question 3.
Two stationary particles of masses M₁ and M₂ are a distance d apart. A third particle lying on the line joining the particles, experiences no resultant gravitational force. What is the distance of this particle from M₁?
Solution:
The force on m towards Mi is F =G \(\frac{M_{1} m}{r^{2}}\)
The force on m towards Mi is F = G \(\frac{M_{2} m}{(d-r)^{2}} \)

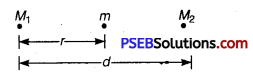
Equating two forces, we have

So, distance of an particle from m is . r = d
r = d \(\left(\frac{\sqrt{M_{1}}}{\sqrt{M_{1}}+\sqrt{M_{2}}}\right)\).

Question 4.
Aspherical planet has mass M_p and clinometer D_p. A particle of mass m falling freely near the surface of this planet will experience an acceleration due to gravity, equal to whom?
Solution:
Force is given by
F = \(-\frac{G M m}{R^{2}}=\frac{G M_{p} m}{\left(D_{P} / 2\right)^{2}}=\frac{4 G M_{P} m}{D_{P}^{2}}\)
\(\frac{F}{m}=\frac{4 G M_{P}}{D_{P}^{2}}\)

Question 5.
What is the gravitational potential energy of a body at height h from the Earth surface?
Solution:
Gravitational potential energy, i. e.,
U_h = \(-\frac{G M m}{R+h}=-\frac{g R^{2} m}{R+h}\)
[where g = \(\frac{G M}{R^{2}}\) ]
= – \(\frac{g R^{2} m}{R\left(1+\frac{h}{R}\right)}=-\frac{m g R}{1+\frac{h}{R}}\)
.
Question 6.
An artificial satellite is moving in a circular orbit around the Earth with a speed equal to half the magnitude of escape velocity from Earth.
Determine
(i) the height of satellite above Earth’s surface.
(ii) if the satellite is suddenly stopped, find the speed with
which the satellite will hit the Earth’s surface after falling down.
Solution:
Escape velocity = \(\sqrt{2 g R}\), where g is acceleration due to gravity on surface of Earth and R the radius of Earth.
Orbital velocity = \(\frac{1}{2} v_{e}=\frac{1}{2} \sqrt{2 g R}=\sqrt{\frac{g R}{2}} \) …………………. (i)

(i) If h is the height of satellite above Earth

h=R
(ii) If the satellite is stopped in orbit, the kinetic energy is zero and its
potential energy is – \(\frac{G M m}{2 R}\)
Total energy =-\(\frac{G M m}{2 R}\)

Let v be its velocity when it reaches the Earth.
Hence the kinetic energy = \(\frac{1}{2} m v^{2}\)
Potential energy = – \(\frac{G M m}{2 R}\)

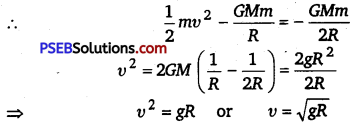
Question 7.
Why do different planets have different escape velocities?
Solution:
Escape velocity, v = \(\sqrt{2 g R}=\sqrt{\frac{2 G M}{R}}\)
Thus escape velocity of a planet depends upon (i) its mass (M) and
(ii) its size (R).
As different planets have different masses and sizes, so they have different escape velocities.

Question 8.
Under what circumstances would your weight become zero?
Answer:
The weight will become zero under the following circumstances
(i) during free fall
(ii) at the centre of the Earth
(iii) in an artificial satellite
(iv) at a point where gravitational pull of Earth is equal to the gravitational pull of the Moon.

Long Answer Type Questions

Question 1.
A mass m is placed at P, a distance h along the normal through the centre O of a thin circular ring of mass M and radius r. If the mass is removed further away such that OP becomes 2h, by what factor the force of gravitation will decrease, if h = r? (NCERT Exemplar)

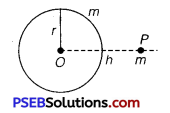
Solution:
Consider a small element of the ring of mass dM, gravitational force between dM and m, distance x apart in figure i.e.,
dF = \(\frac{G(d m) m}{x^{2}}\)

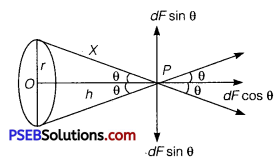
dF can be resolved into two rectangular components.
(i) dF cos θ along PO and
(ii) dF sinθ perpendicular to PO (given figure)
The total force (F) between the ring and mass (m) can be obtained by integrating the effects of all the elements forming the ring, whereas all the components perpendicular to PO cancel out i.e., ∫dFsinθ=O, the component along PO add together to give F i.e.,

Question 2.
A satellite is to be placed in equatorial geostationary orbit around the Earth for communication.
(i) Calculate height of such a satellite.
(ii) Find out the minimum number of satellites that are needed to cover entire Earth so that at least one of satellite is visible from any point on the equator.
[M = 6 x 10 ²⁴ kg, R = 6400 km, T = 24 h, G = 6.67 x 10^-11SI (NCERT Exemplar)
Solution:
(i) As, according co Kepler’s third law, we get
T² = \(\frac{4 \pi^{2} r^{3}}{G M}\)
⇒ r = \( \left(\frac{G M T^{2}}{4 \pi^{2}}\right)^{1 / 3}\)

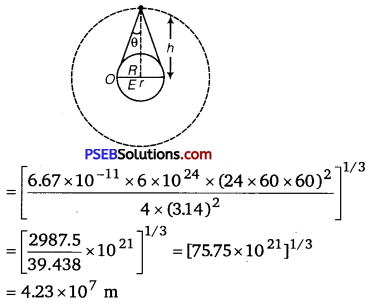
As we known =R +h
h=r-R
h=4.23 x 10⁷ m – 6.4 x 10⁶ m
h = 3.59 x 10⁷ m

(ii) In ΔOES,cos θ = \(\frac{O A}{O S}=\frac{R}{R+h}\)
= \(\frac{1}{\left(1+\frac{h}{R}\right)}\)
= \(\frac{1}{(1+5.609)}\)
=0.1513
(as,\(\frac{h}{R}=\frac{3.59 \times 10^{7} \mathrm{~m}}{6.4 \times 10^{6} \mathrm{~m}}\) = 5.609)
where, θ ≈ 81° or 2θ = 162°
Number of satellites required to cover entire the Earth.
= \(\frac{360^{\circ}}{162^{\circ}}=2.2\) ≈ 3.