PSEB 12th Class Chemistry Solutions Chapter 4 Chemical Kinetics

Punjab State Board PSEB 12th Class Chemistry Book Solutions Chapter 4 Chemical Kinetics Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Chemistry Chapter 4 Chemical Kinetics

PSEB 12th Class Chemistry Guide Chemical Kinetics InText Questions and Answers

Question 1.
From the rate expression for the following reactions, determine their order of reaction and the dimensions of the rate constants.
(i) 3 NO(g) → N₂O(g) Rate = k[NO]²
(ii) H₂O₂ (aq) +3I^– (aq) + 2H⁺ → 2H₂O (l) + \(\mathbf{I}_{3}^{-}\)
Rate = k[H₂O₂] [I^–]
(iii) CH₃CHO(g) → CH₄(g) + CO(g) Rate = k [CH₃CHO]^3/2
(iv) C₂H₅Cl(g) → C₂H₄(g) + HCl (g) Rate = k [C₂H₅Cl]
Solution:
(i) Given, rate = k [NO]²
Therefore, order of the reaction = 2
Dimension of rate constant (k) = \(\frac{\text { Rate }}{[\mathrm{NO}]^{2}}\)
= \(\frac{m o l L^{-1} s^{-1}}{\left(m o l L^{-1}\right)^{2}}\)
= \(\frac{\mathrm{mol} \mathrm{L}^{-1} \mathrm{~s}^{-1}}{\mathrm{~mol}^{2} \mathrm{~L}^{-2}}\)
= L mol^-1 s^-1

(ii) Given, rate = k [H₂O₂] [I^– ]
Therefore, order of the reaction = 2
Dimension of k = \(\frac{\text { Rate }}{\left[\mathrm{H}_{2} \mathrm{O}_{2}\right]\left[\mathrm{I}^{-}\right]}\)
= \(\frac{\mathrm{mol} \mathrm{L}^{-1} \mathrm{~s}^{-1}}{\left(\mathrm{~mol} \mathrm{~L}^{-1}\right)\left(\mathrm{mol} \mathrm{L}^{-1}\right)}\)
= L mol^-1 s^-1

(iii) Given rate = k[CH₃CHO]^3/2
Therefore, order of the reaction = \(\frac{3}{2}\)
Dimension of k = \(\frac{\text { Rate }}{\left[\mathrm{CH}_{3} \mathrm{CHO}\right]^{3 / 2}}\)

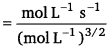
= \(\frac{\text { mol L }^{-1} \mathrm{~s}^{-1}}{\mathrm{~mol}^{\frac{3}{2}} \mathrm{~L}^{-\frac{3}{2}}}\)
= mol ^-1/2L^1/2 s^-1

(iv) Given, rate = k [C₂H₅Cl]
Therefore, order of the reaction = 1
Dimension of k = \(\frac{\text { Rate }}{\left[\mathrm{C}_{2} \mathrm{H}_{5} \mathrm{Cl}\right]}\)
= \(\frac{\mathrm{mol} \mathrm{L}^{-1} \mathrm{~s}^{-1}}{\mathrm{~mol} \mathrm{~L}^{-1}}\) = s^-1

Question 2.
For the reaction:
2A + B → A₂B
the rate = k[A] [B]² with k = 2.0 x 10^-6 mol^-2L²s^-1. Calculate the initial rate of the reaction when [A] = 0.1 mol L^-1, [B] = 0.2 mol L^-1. Calculate the rate of reaction after [A] is reduced to 0.06 mol L^-1.
Solution:
The initial rate of the reaction is
Rate = k [A][B]²
= (2.0 × 10^-6 mol^-2 L² s^-1) (0.1 mol L^-11) (0.2 mol L^-1 )²
= 8.0 × 10^-9 mol L^-1 s^-1
When [A] is reduced from 0.1 mol L^-1 to 0.06 molL^-1, the concentration of A reacted = (0.1 – 0.06) mol L^-1 = 0.04 mol L^-1 Therefore, concentration of B reacted
= \(\frac{1}{2}\) × 0.04 mol L^-1 = 0.02 mol L^-1
Then, concentration of B available, [B] = (0.2 -0.02) mol L^-1
= 0.18 mol L^-1
After [A] is reduced to 0.06 mol L^-1, the rate of the reaction is given by,
Rate = k [A][B]²
= (2.0 × 10^-6 mol^-2 L² s^-1) (0.06 mol L^-1) (0.18 mol L^-1)²
= 3.89 × 10^-9 mol L^-1 s^-1

Question 3.
The decomposition of NH₃ on platinum surface is zero order reaction. What are the rates of production of N₂ and H₂ if k = 2.5 x 10^-4 mol^-1 L s^-1?
Solution:
The decomposition of NH₃ on platinum surface is represented by the following equation

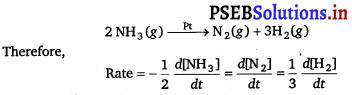
For zero order reaction, rate = k
∴ \(-\frac{1}{2} \frac{d\left[\mathrm{NH}_{3}\right]}{d t}=\frac{d\left[\mathrm{~N}_{2}\right]}{d t}=\frac{1}{3} \frac{d\left[\mathrm{H}_{2}\right]}{d t}\)
= 2.5 × 10^-4 mol L^-1 s^-1
Therefore, the rate of production of N₂
\(\frac{d\left[\mathrm{~N}_{2}\right]}{d t}\) = 2.5 × 10^-4 mol L^-1 s^-1
The rate of production of H₂
\(\frac{d\left[\mathrm{H}_{2}\right]}{d t}\) = 3 × 2.5 × 10^-4 mol L^-1 s^-1
= 7.5 × 10^-4 mol L^-1 s^-1

Question 4.
The decomposition of dimethyl ether leads to the formation of CH₄, H₂ and CO and the reaction rate is given by
Rate = k [CH₃OCH₃]^3/2
The rate of reaction is followed by increase in pressure in a closed vessel, so the rate can also be expressed in terms of the partial pressure of dimethyl ether, i.e.,
Rate = k(PCH_3OCH3 )^3/2
If the pressure is measured in bar and time in minutes, then what are the units of rate and rate constants?
Solution:
If the pressure is measured in bar and time in minutes, then
Unit of rate = bar min^-1
Rate = k(PCH_3OCH3 )^3/2
⇒ k = \(\frac{\text { Rate }}{\left(p_{\mathrm{CH}_{3} \mathrm{OCH}_{3}}\right)^{3 / 2}}\)
=

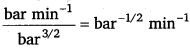
Question 5.
Mention the factors that affect the rate of a chemical reaction.
Answer:
The factors that affect the rate of a chemical reaction are as follows :
(i) Nature of reactants: Ionic substances react more rapidly than covalent compounds because ions produced after dissociation are immediately available for reaction.

(ii) Concentration of reactants: Rate of a chemical reaction is direcdy proportional to the concentration of reactants.

(iii) Temperature: Generally rate of a reaction increases on increasing the temperature.

(iv) Presence of catalyst: In presence of catalyst, the rate of reaction generally increase and the equilibrium state is attained quickly in reversible reactions.

(v) Surface area of the reactants: Rate of reaction increases with increase in surface area of the reactants. That is why powdered form of reactants is preffered than their granular form.

Question 6.
A reaction is second order with respect to a reactant. How is the rate of reaction affected if the concentration of the reactant is (i) doubled (ii) reduced to half?
Solution:
Let the concentration of the reactant be [A] = a
Rate of reaction, R = k [A]² = ka²
(i) If the concentration of the reactant is doubled, i.e. [A] = 2a, then the rate of the reaction would be
R’ = k (2a)²
= 4ka² = 4R
Therefore, the rate of the reaction would increase by 4 times.

Question 7.
What is the effect of temperature on the rate constant of a reaction? How can this effect of temperature on rate constant be represented quantitatively?
Answer:
The rate constant is nearly doubled with a rise in temperature by 10° for a chemical reaction.

The temperature effect on the rate constant can be represented quantitatively by Arrhenius equation, k = Ae^-E_a/RT

Where, k is the rate constant, A is the Arrhenius factor or the frequency factor, R is the gas constant, T is the temperature, and E_a is the energy of activation for the reaction.

Question 8.
In a pseudo first order hydrolysis of ester in water, the following results were obtained:

t/s	0	30	60	90
[Ester]/molL-1	0.55	0.31	0.17	0.085

(i) Calculate the average rate of reaction between the time interval 30 to 60 seconds.
(ii) Calculate the pseudo first order rate constant for the hydrolysis of ester.
Solution:
(i) Average rate of reaction between the time interval, 30 to 60 seconds
= \(\frac{d[\text { Ester }]}{d t}\)
= \(\frac{0.31-0.17}{60-30}\)
= \(\frac{0.14}{30}\)
= 4.67 × 10^-3 mol L^-1 s^-1

Question 9.
A reaction is first order in A and second order in B.
(i) Write the differential rate equation.
(ii) How is the rate affected on increasing the concentration of B three times?
(iii) How is the rate affected when the concentrations of both A and B are doubled?
Solution:
(i) The differential rate equation will be
– \(\frac{d[\mathrm{R}]}{d t}\) = k[A][B]²

(ii) If the concentration of B is increased three times, then
– \(\frac{d[\mathrm{R}]}{d t}\) = k[A][3B]²
= 9.k [A][B]²
Therefore, the rate of reaction will increase 9 times.

(iii) When the concentrations of both A and B are doubled,
– \(\frac{d[\mathrm{R}]}{d t}\) = k[2A][2B]²
= 8.k [A] [B]²
Therefore, the rate of reaction will increase 8 times.

Question 10.
In a reaction between A and B, the initial rate of reaction (r₀) was measured for different initial concentrations of A and B as given below:

A/mol L-1	0.20	0.20	0.40
B/mol L-1	0.30	0.10	0.05
r0/mol L-1 s-1	5.07 × 10-5	5.07 × 105	1.43 × 10-4

What is the order of the reaction with respect to A and B?
Solution:
Let the order of the reaction with respect to A be x and with respect to B be y.
Therefore
r₀ = k [A]^x [B]^y
5.07 × 10^-5 = k[0.20]^x [0.30]^y …………. (i)
5.07 × 10^-5 = k[0.20]^x [0.10]^y …………. (ii)
1.43 × 10^-4 = k[0.40]^x [0.05]^y ……….. (iii)

Hence, the order of the reaction with respect to A is 1.5 and with respect to B is 0.

Question 11.
The following results have been obtained during the kinetic studies of the reaction:
2A + B → C + D

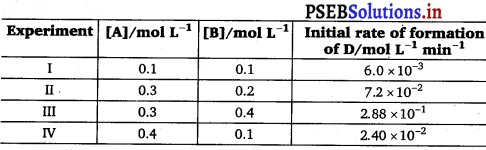
Determine the rate law and the rate constant for the reaction.
Solution:
Let the order of the-reaction with respect to A be x and with respect to B be y.
Therefore, rate of the reaction is given by,
Rate = k [A]^x [B]^y According to the question,
6.0 × 10^-3; = k[0.1]^x [0.1]^y …………. (i)
7.2 × 10^-2 = k[0.3]^x [0.2]^y …………… (ii)
2.88 × 10^-1 = k[0.3]^x [0.4]^y ………….. (iii)
2.40 × 10^-2 = k[0.4]^x [0.1]^y …………… (iv)
Dividing equation (iv) by (i), we get

Question 12.
The reaction between A and B is first order with respect to A and zero order with respect to B. Fill in the blanks in the following table:

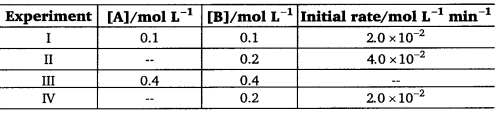
Solution:
The given reaction is of the first order with respect to A and of zero order with respect to B.
Therefore, the rate of the reaction is given by,
Rate = k[A]¹[B]⁰
⇒ Rate = fc[A]
From experiment I, we get
2.0 × 10^-2 molL^-1 min^-1 = k(0.1 molL^-1)
⇒ k = 0.2 min^-1

From experiment II, we get
4.0 × 10^-2 molL^-1 min^-1 = 0.2 min^-1 [A]
⇒ [A] = 0.2 mol L^-1

From experiment III, we get
Rate = 0.2 min^-1; × 0.4 mol L^-1
= 0.08 mol L^-1 min^-1

From experiment IV, we get
2.0 × 10^-2 molL^-1 min^-1 = 0.2 min^-1 [A]
⇒ [A] = 0.1 mol L^-1

Question 13.
Calculate the half-life of a first order reaction from their rate constants given below:
(i) 200 s^-1
(ii) 2 min^-1
(iii) 4 years^-1
Solution:
Half life period for first order reaction, t_1/2 = \(\)
(i) t_1/2 = \(\frac{0.693}{200 \mathrm{~s}^{-1}}\) = 0.347 × 10^-2 s
= 3.47 × 10^-3 s
(ii) t_1/2 = \(\frac{0.693}{2 \min ^{-1}}\) = 0.35 mm
(iii) t_1/2 = \(\frac{0.693}{4 \text { years }^{-1}}\)= 0.173 years 4 years-1

Question 14.
The half-life for radioactive decay of ¹⁴C is 5730 years. An archaeological artifact containing wood had only 80% of the ¹⁴C found in a living tree. Estimate the age of the sample.
Solution:
Decay constant (k) = \(\frac{0.693}{t_{1 / 2}}\)
\(\frac{0.693}{5730}\) = years ^-1
Radioactive decay follows first order kinetics
t = \(\frac{2.303}{k}\) = log\(\frac{[R]_{0}}{[R]}\)
= \(\frac{\frac{2.303}{0.693}}{5730}\) × log \(\frac{100}{80}\)
= 1845 years
Hence, the age of the sample is 1845 years.

Question 15.
The experimental data for decomposition of N₂0₅
[2N₂O₅ → 4NO₂ + O₂]
in gas phase at 318K are given below:

(i) Plot [N₂O₅] against t.
(ii) Find the half-life period for the reaction.
(iii) Draw a graph between log [N₂O₅ ] and t.
(iv) What is the rate law?
(v) Calculate the rate constant
(vi) Calculate the half-life period from k and compare it with (ii).
Solution:
(i) The plot of [N₂O₅] against time is given below:

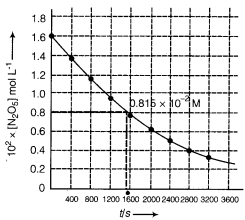
(ii) Initial concentration of N₂O₅ = 1.63 x 10^-2 M
Half of this concentration = 0.815 x 10^-2 M
Time corresponding to this concentration = 1440 s
Hence t_1/2 = 1440 s

(iii) For graph between log[N₂O₅] and time, we first find the values of log[N₂O₅]

Time (s)	102 × [N2O5] mol L-1	log [N2O5]
0	1.63	-1.79
400	1.36	-1.87
800	1.14	-1.94
1200	0.93	-2.03
1600	0.78	-2.11
2000	0.64	-2.19
2400	0.53	-2.28
2800	0.43	-2.37
3200	0.35	-2.46

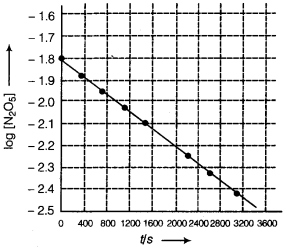
(iv) The given reaction is of the first order as the plot, log [N₂0₅] v/s t, is a straight line. Therefore, the rate law of the reaction is
Rate = k [N₂O₅]

(v) From the plot, log [N₂O₅] v/s t, we get
Slope = \(\frac{-2.46-(-1.79)}{3200-0}\)
= \(\frac{-0.67}{3200}\)
Again, slope of the line of the plot log [N₂O₅] v/s t is given by
– \(\frac{k}{2.303}\)
Therefore we get
\(-\frac{k}{2.303}=-\frac{0.67}{3200}\)
k = \(\frac{0.67 \times 2.303}{3200}\)
= 4.82 × 10^-4s^-1

(vi) Half-life period (t_1/2) = \(\)
= \(\frac{0.693}{4.82 \times 10^{-4} \mathrm{~s}^{-1}}\) = 1438 s
Half-life period (t_1/2) is calculated from the formula and slopes are approximately the same.

Question 16.
The rate constant for a first order reaction is 60 s^-1. How much time will it take to reduce the initial concentration of the reactant to its 1/16^th value?
Solution:
For first order reaction
t = \(\frac{2.303}{k}\) log \(\frac{1}{(a-x)}\) …………. (i)
Given (a – x) = \(\frac{1}{16}\); k= 60 s^-1
Placing the values in equation (i)
t = \(\frac{2.303}{60 \mathrm{~s}^{-1}}\) log \(\frac{a \times 16}{a}\)
= \(\frac{2.303}{60 \mathrm{~s}^{-1}}\) log16 \(\frac{2.303}{60 \mathrm{~s}^{-1}}\) × 4 log 2
= \(\frac{2.303}{60 \mathrm{~s}^{-1}}\) × 4 × 0.3010
= 4.6 × 10^-2s
Hence, the required time is 4.6 × 10^-2 s.

Question 17.
During nuclear explosion, one of the products is ⁹⁰Sr with half-life of 28.1 years. If 1μ g of ⁹⁰Sr was absorbed in the bones of a newly born baby instead of calcium, how much of it will remain after 10 years and 60 years if it is not lost metabolically.
Solution:
As radioactive disintegration follows first order kinetics,
∴ Decay constant of ⁹⁰Sr, k = \(\frac{0.693}{t_{1 / 2}}\)
= \(\frac{0.693}{28.1 \mathrm{y}}\) = 2.466 × 10^-2y^-1

To calculate the amount left after 10 years
[R]₀ = 1μg, t = 10 years, k = 2.466 × 10^-2y^-1,[R] =?
k = \(\frac{2.303}{t}\) log \(\frac{[R]_{0}}{[R]}\)
2.466 × 10^-2 = \(\frac{2.303}{10}\) log \(\frac{1}{[R]}\)
or log[R] = – 0.1071
or [Rl = Antilog \(\overline{1}\).8929 = 0.78 14 μg

To calculate the amount left after 60 years
2.466 × 10^-2 = \(\frac{2.303}{60}\) log \(\frac{1}{[R]}\)
or log[R] = – 0.6425
or [R] = Antilog \(\overline{1}\).3575 = 0.2278 μg

Question 18.
For a first order reaction, show that time required for 99% completion is twice the time required for the completion of 90% of reaction.
Solution:
For a first order reaction, the time required for 99% completion is

Therefore, t₁ = 2t₂
Hence, the time required for 99% completion of a first order reaction is twice the time required for the completion of 90% of the reaction.

Question 19.
A first order reaction takes 40 min for 30% decomposition.
Calculate t_1/2
Solution:
Given, t = 40 min,
For a first order reaction,

Question 20.
For the decomposition of azoisopropane to hexane and nitrogen at 543 K, the following data are obtained.

t (sec)	P(mm of Hg)
0	35.0
360	54.0
720	63.0

Calculate the rate constant.
Solution:
The decomposition of azoisopropane to hexane and nitrogen at 543 K is represented by the following equation:

Hence, the average value of rate constant
k = \(\frac{\left(2.175 \times 10^{-3}\right)+\left(2.235 \times 10^{-3}\right)}{2} s^{-1}\)
= 2.21 × 10^-3s^-1

Question 21.
The following data were obtained during the first order thermal decomposition of SO₂Cl₂ at a constant volume.
SO₂Cl₂(g) → SO₂(g) + Cl₂(g)

Experiment	Time/s-1	Total pressure/atm
1	0	0.5
2	100	0.6

Calculate the rate of the reaction when total pressure is 0.65 atm.
Solution:
The first order thermal decomposition of SO₂cl₂ at a constant volume is represented by the following equation:

= 2.23 × 10^-3s^-1

When P_t = 0.65 atm,
P₀ + p = 0.65
⇒ p = 0.65 – P₀
= 0.65 – 0.5
= 0.15 atm
Pressure of SO₂Cl₂ at time t (P_SO2Cl2 SO₂Cl₂
= P₀ – P
= 0.5 – 0.15
= 0.35 atm

Therefore, the rate of equation, when total pressure is 0.65 atm, is given by,
Rate = k × (P_SO2Cl2 SO₂Cl₂)
= (2.23 × 10^-3 s^-1) (0.35 atm)
= 7.8 × 10^-5 atm s^-1

Question 22.
The rate constant for the decomposition of N₂O₅ at various temperatures is given below:

Draw a graph between In k and 1/T and calculate the values of A and E_a.
Predict the rate constant at 30° and 50°C.
Solution:
To draw the plot of log k versus 1/T, we can rewrite the given data as follows:

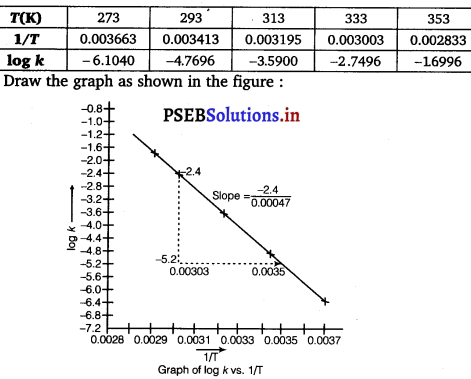
From graph, we find
Slope = \(\frac{-2.4}{0.00047}\) = 5106.38
E_a = – Slope × 2.303 × R
= – (- 5106.38) × 2.303 × 8.314
= 97772.58 J mol^-1
= 97.77258 kJ mol^-1

We know that,
log k = log A – \(\frac{E_{a}}{2.303 R T}\)
log k = log \(\left[-\frac{E_{a}}{2.303 R}\right] \frac{1}{T}\) = log A
Compare it with y = mx + c (which is equation of line in intercept form)
log A = value of intercept on y-axis i.e.
on log k-axis [y₂ – y₁ = -1 – (-7.2)]
= (-1 + 7.2) = 6.2 ,
log A = 6.2
A = Antilog 6.2
= 1.585 × 10⁶ s^-1
The values of rate constant k can be found from graph as follows:

We can also calculate the value of A from the following formula
log k = log A = \(\frac{E_{a}}{2.303 R T}\)

Question 23.
The rate constant for the decomposition of hydrocarbons is 2.418 × 10^-5 s^-1 at 546 K. If the energy of activation is 179.9 kJ/mol, what will be the value of pre-exponential factor.
Solution:
Given, k = 2.418 × 10^-5s^-1, T = 546 K
E_a = 179.9 kJ mol^-1 = 179.9 × 10³ J mol^-1
According to the Arrhenius equation,
k = Ae^-Ea/RT
ln k = ln A – \(\frac{E_{a}}{R T}\)
log k = log A – \(\frac{E_{a}}{2.303 R T}\)
log A = log K + \(\frac{E_{a}}{2.303 R T}\)
= log(2.418 × 10¹⁵s^-1) + \(\frac{179.9 \times 10^{3} \mathrm{~J} \mathrm{~mol}^{-1}}{2.303 \times 8.314 \mathrm{Jk}^{-1} \mathrm{~mol}^{-1} \times 546 \mathrm{~K}}\)
= (0.3835 – 5) +17.2082 = 12.5917
Therefore, A = antilog (12.5917) = 3.9 × 10¹²s^-1

Question 24.
Consider a certain reaction A → Products with k = 2.0 × 10^-2s^-1 Calculate the concentration of A remaining after 100 s if the initial concentration of A is 1.0 mol L^-1.
Solution:
Given, k = 2.0 x 10^-2s^-1, t = 100 s, [A]₀ = 1.0 mol L^-1
Since, the unit of k is s^-1, the given reaction is a first order reaction.

Question 25.
Sucrose decomposes in acid solution into glucose and fructose according to the first order rate law, with t_1/2 =3.00 hours. What fraction of sample of sucrose remains after 8 hours?
Solution:
For a first order reaction,

= 0.158 M
Hence, the fraction of sample of sucrose that remains after 8 hours is 0.158 M.

Question 26.
The decomposition of hydrocarbon follows the equation k = (45 × 10¹¹ s¹)e^-28000k/T
Calculate E_a.
Solution:
The given equation is
k = (45 × 10¹¹ s¹)e^-28000k/T …(i)
Arrhenius equation is given by,
k = Ae^E_a/RT …(ii)
From equation (i) and (ii), we get
\(\frac{E_{a}}{R T}\) = \(\frac{28000 \mathrm{~K}}{T}\)
⇒ E_a = R × 28000 K
= 8.314 J K^-1 mol^-1 × 28000 K
= 232792 J mol^-1
= 232.792 kJ mol^-1

Question 27.
The rate constant for the first order decomposition of H₂O₂ is given by the following equation :
log k = 14.34 – 1.25 × 10⁴ K/T
Calculate E_a for this reaction and at what temperature will its half-period be 256 minutes?
Solution:
Arrhenius equation is given by,
k = Ae^-E_a/RT
⇒ log k = log A – \(\frac{E_{a}}{2.303 \mathrm{RT}}\) …(i)
log k = 14.34 – 1.25 × 10⁴ K/T …(ii)
From equation (i) and (ii), we get
\(\frac{E_{a}}{2.303 \mathrm{RT}}\) = \(\frac{1.25 \times 10^{4} \mathrm{~K}}{T}\)
⇒ E_a = 1.25 × 10⁴K × 2.303 × R
= 1.25 × 10⁴K × 2.303 × 8.314 J K^-1 mol^-1
= 239339.3 J mol^-1
= 239.34 kJ mol^-1
Also, when t_1/2 = 256 minutes,
For first order reaction
k = \(\frac{0.693}{t_{1 / 2}}\)
= \(\frac{0.693}{256}\)
= 2.707 × 10^-13 min^-1
= 4.51 × 10^-5 s^-1
According to Arrhenius theory,
log k = 14.34 – 1.25 × 10^,4K/T

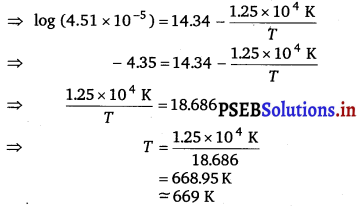
Question 28.
The decomposition of A into product has value of & as 45 × 10³ s^-1 at 10°C and energy of activation 60 kJ mol^-1. At what temperature would k be 1.5 × 10⁴ s^-1.
Solution:
From Arrhenius equation, we get
\(\log \frac{k_{2}}{k_{1}}\) = \(\frac{E_{a}}{2.303 \mathrm{R}}\left(\frac{T_{2}-T_{1}}{T_{1} T_{2}}\right)\)
Also, k₁ = 4.5 × 10³ s^-1
T₁ = 273 + 10 = 283k
k₂ = 1.5 × 10⁴ s^-1
E_a = 60 kJmol^-1 = 6.0 × 10⁴ Jmol^-1

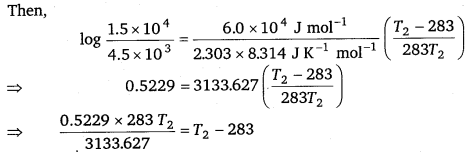
⇒ 0.0472T₂ = T₂ – 283
⇒ 0.9528T₂ = 283
⇒ T₂ = 297.019 K
= 297K = (297 – 273)⁰C
= 24⁰C
Hence, k would be 1.5 × 10⁴ s^-1 at 24⁰C.

Question 29.
The time required for 10% completion of a first order reaction at 298 K is equal to that required for its 25% completion at 308 K. If the value of A is 4 × 10¹⁰ s^-1. Calculate k at 318 K and E_a.
Solution:
For a first order reaction,

To calculate k at 318 K,
It is given that, A = 4 × 10¹⁰ s^-1, T = 318 K
Again, from Arrhenius equation, we get
log k = log A – \(\frac{E_{a}}{2.303 \mathrm{RT}}\)
= log (4 × 10¹⁰) – \(\frac{76.64 \times 10^{3}}{2.303 \times 8.314 \times 318}\)
= (0.6021 + 10) – 12.5870 = -1.9849 k
k = Antilog (-1.9849)
= Antilog (2.0151) = 1.035 × 10^-2s^-1
E_a = 76.640 kJ mol^-1
E_a = 76.640 kJmol^-1
k = 1.035 × 10^-2s^-1

Question 30.
The rate of a reaction quadruples when the temperature changes from 293 K to 313 K. Calculate the energy of activation of the reaction assuming that it does not change with temperature.
Solution:
Given, k₂ = 4k₁, T₁ = 293 K, T₂ = 313 K
From Arrhenius equation, we get

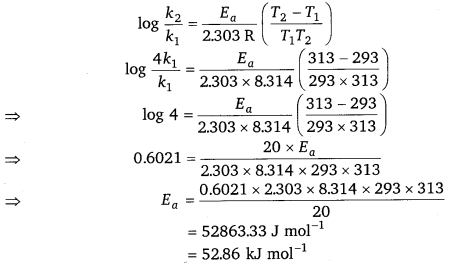
Hence, the required energy of activation is 52.86 kJ mol^-1

Chemistry Guide for Class 12 PSEB Chemical Kinetics Textbook Questions and Answers

Question 1.
For the reaction R → P, the concentration of a reactant changes from 0.03 M to 0.02 M in 25 minutes. Calculate the average rate of reaction using units of time both in minutes and seconds.
Solution:

Question 2.
In a reaction, 2A → Products, the concentration of A decreases from 0.5 mol L^-1 to 0.4 mol L^-1 in 10 minutes. Calculate the rate during this interval?
Solution:
Rate of reaction = Rate of disappearance of A = – \(\frac{1}{2} \frac{\Delta[A]}{\Delta t}\)
= – \(\frac{1}{2} \frac{[A]_{2}-[A]_{1}}{t_{2}-t_{1}}\)
= – \(\frac{1}{2} \frac{(0.4-0.5) \mathrm{mol} \mathrm{L}^{-1}}{10 \mathrm{~min}}\)
= – \(\frac{1}{2} \frac{-0.1}{10}\)
= 0.005 mol L^-1 min^-1
= 5 × 10^-3 M min^-1

Question 3.
For a reaction, A + B → Product; the rate law is given by,
r = k [A]^1/2 [B]². What is the order of the reaction?
Solution:
The order of the reaction = \(\frac{1}{2}\) + 2
= 2\(\frac{1}{2}\) = 2.5

Question 4.
The conversion of molecules X to Y follows second order kinetics. If concentration of X is increased to three times how will it affect the rate of formation of Y? ‘
Solution:
The reaction X → Y follows second order kinetics.
Therefore, the rate equation for this reaction will be:
Rate (r) = k[X]² = k × X² …………. (i)
If the concentration of X is increased to three times, then
Rate (r’) = fc(3X)² = k × 9X² ………….. (ii)
Dividing eq. (ii) by eq. (i)
\(\frac{r^{\prime}}{r}=\frac{k \times 9 X^{2}}{k \times X^{2}}\) = 9
It means that the rate of formation of Y will increase by nine times.

Question 5.
A first order reaction has a rate constant 1.15 × 10^-3s^-1. How long will 5 g of this reactant take to reduce to 3 g?
Solution:
Initial amount [R]₀ = 5 g
Final amount [R] = 3 g
Rate constant (k) = 1.15 × 10^-3s^-1
We know that for a 1^st order reaction,

= 444.38 s
= 444 s

Question 6.
Time required to decompose SO₂Cl₂ to half of its initial amount is 60 minutes. If the decomposition is a first order reaction, calculate the rate constant of the reaction.
Solution:
We know that for a 1^st order reaction,
t_1/2 = \(\frac{0.693}{k}\)
> k = \(\frac{0.693}{t_{1 / 2}}\)
= \(\frac{0.693}{60 \mathrm{~min}}\) = \(\frac{0.693}{(60 \times 60) \mathrm{s}}\)
or k = 1.925 × 10^-4 s^-1]

Question 7.
What will be the effect of temperature on rate constant?
Answer:
The rate constant of a reaction is nearly doubled with a 10° rise in temperature. However, the exact dependence of the rate of a chemical reaction on temperature is given by Arrhenius equation,
k = Ae^-Ea/RT
Where, A is the Arrhenius factor or the frequency factor, T is the temperature, R is the gas constant, E_a is the activation energy.

Question 8.
The rate of the chemical reaction doubles for an increase of 10 K in absolute temperature from 298 K. Calculate E_a.
Solution:
Given, T₁ = 298 K
∴ T₂ = (298 + 10)K = 308K
We also know that the rate of the reaction doubles when temperature is increased by 10°.
Therefore, let us take the value of k₁ = k and that of k₂ = 2k
Also, R =8.314 JK^-1 mol^-1
Now, substituting these values in the equation:

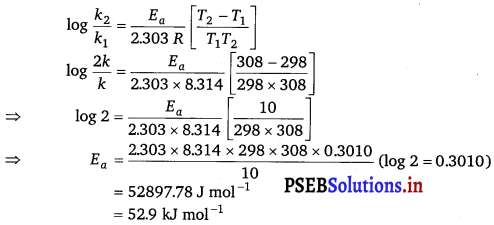
Question 9.
The activation energy for the reaction
2HI (g) → H₂ + I₂(g)
is 209.5 kJ mol^-1 at 58IK. Calculate the fraction of molecules of reactants having energy equal to or greater than activation energy?
Solution:
Fraction of molecules of reactants (x) having energy equal to or greater than activation energy may be calculated as follows
or log x = \(\frac{-E_{a}}{R T}\) or log x = –\(\frac{E_{a}}{2.303 R T}\)
or log x = – \(\frac{209.5 \times 10^{3}}{2.303 \times 8.314 \times 581}\)
= -18.8323
x = Antilog (-18.8323) = Antilog (\(\overline{19}\).1677)
= 1.471 × 10^-19
Hence, fraction of molecules of reactants having energy equal to or greater than activation energy = 1.471 × 10^-19