Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 12 Linear Programming Ex 12.1 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 12 Maths Chapter 12 Linear Programming Ex 12.1
Direction (1 – 6): Solve the following linear programming problems graphically.
Question 1.
Maximise Z = 3x + 4y
subject to the constraints : x + y ≤ 4, x ≥ 0, y ≥ 0.
Solution.
The feasible region determined by the constraints, x + y ≤ 4, x ≥ 0, y ≥ 0, is as follows.
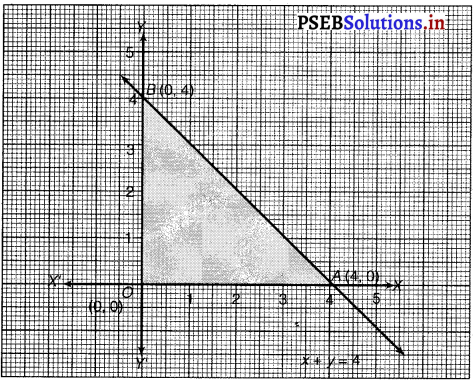
The corner points of the feasible region are 0 (0, 0), A (4, 0) and B (0, 4).

Therefore, the maximum value of Z is 16 at the point B(0, 4).
![]()
Question 2.
Minimise Z = – 3x + 4y
Subject to x + 2y ≤ 8, 3x + 2y ≤ 12, x ≥ 0, y ≥ 0
Solution.
The feasible region determined by the system of constraints, x + 2y ≤ 8, 3x + 2y ≤ 12, x ≥ 0 and y ≥ 0 is as follows.
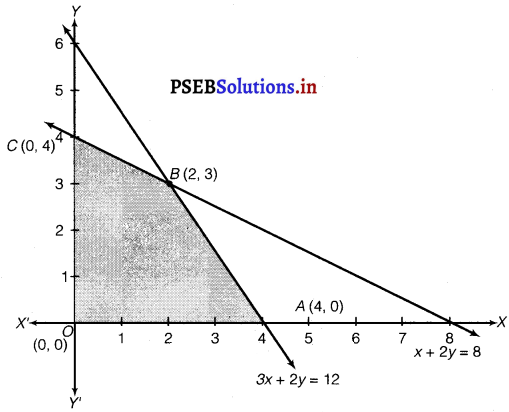
The comer points of the feasible region are O (0, 0), A (4, 0), B (2, 3) and C (0, 4).
The values of Z at these comer points are as follows

Therefore, the minimum value of Z is – 12 at the point (4, 0).
![]()
Question 3.
Maximise Z = 5x + 3y
subject to 3x + 5y ≤ 15, 5x + 2y ≤ 10, x ≥ 0, y ≥ 0.
Solution.
The feasible region determined by the system of constraints, 3 + 5y ≤ 15, 5x + 2y ≤ 10, x ≥ 0 and y ≥ 0 are as follows.
The corner points of the feasible region are O (0, 0), A (2, 0), B (0, 3) and C (\(\frac{20}{19}\), \(\frac{45}{19}\))
The values of Z at these comer points are as follows.
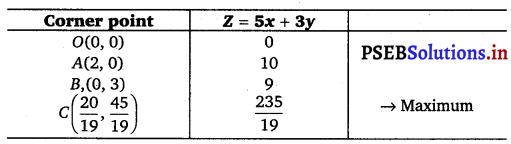
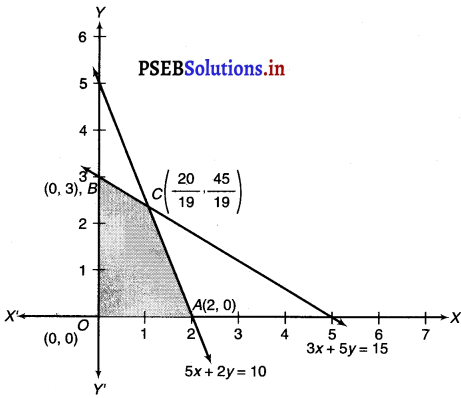
Therefore, the maximum value of Z is \(\frac{235}{19}\) at the point (\(\frac{20}{19}\), \(\frac{45}{19}\)).
![]()
Question 4.
Minimise Z = 3x + 5y
such that x + 3y ≥ 3, x + y ≥ 2, x, y ≥ 0.
Solution.
The feasible region determined by the system of constraints, x + 3y ≥ 3, x + y ≥ 2 and x, y ≥ 0 is as follows
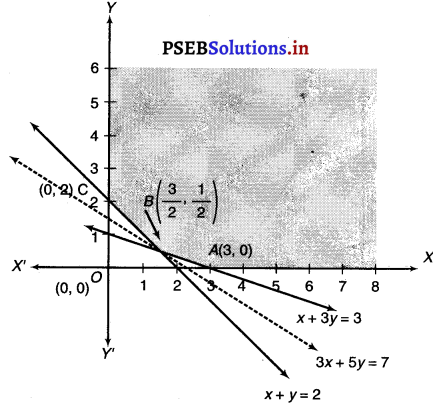
It can be seen that the feasible region is unbounded.
The corner points of the feasile region are A (3, 0), (\(\frac{3}{2}\), \(\frac{1}{2}\)) and C (0, 2)
The values of Z at these comer points are as follows

As the feasible region is unbounded, therefore, 7 may or may not be the minimum value of Z.
For this, we draw the graph of the inequality, 3x + 5y < 7 and check whether the resulting half plane has points in common with the feasible region or not.
It can be seen that the feasible region has no common point with 3x + 5y < 7.
Therefore, the minimum value of Z is 7 at (\(\frac{3}{2}\), \(\frac{1}{2}\)).
![]()
Question 5.
Maximise Z = 3x + 2y subject to x + 2y ≤ 10, 3x + y ≤ 15, x, y ≥ 0.
Solution. T
he feasible region determined by the constraints, x + 2y ≤ 10, 3x + y ≤ 15, x ≥ 0 and y ≥ 0 is as follows.
The corner points of the feasible region are A(5, 0) B(4, 3) and C(0, 5).
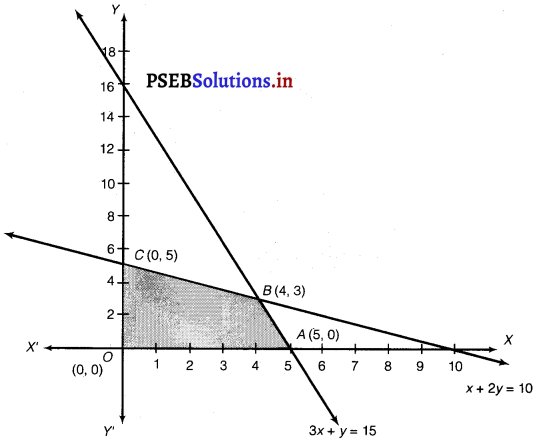
The values of Z at these comer points are as follows.

Therefore, the maximum value of Z is 18 at the point B(4, 3).
![]()
Question 6.
Minimise Z = x + 2y subject to 2x + y ≥ 3, x + 2y ≥ 6, x, y ≥ 0.
Solution.
The feasible region determined by the constraints, 2x + y ≥ 3, x + 2y ≥ 6, x ≥ 0 and y ≥ 0 is as follows.
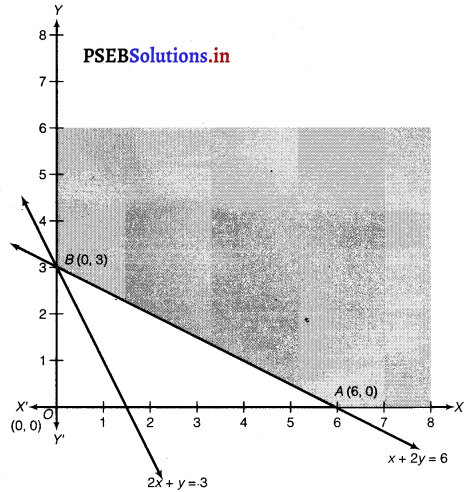
The corner points of the feasible region are A(6, 0) and B(0, 3).
The values of Z at these comer points are as follows

Comer point Z = x + 2y.
It can be seen that the value of Z at points A and B is same.
If we take any other point such as (2, 2) on line x + 2y = 6, then Z = 6.
Thus, the minimum value of Z occurs for more than 2 points.
Therefore, the value of Z is minimum at every point on the line, x + 2y = 6.
![]()
Direction (7 – 10): Show that the minimum of Z occurs at more than two points.
Question 7.
Minimise and Maximise Z = 5x + 110y subject to x + 2y ≤ 120, x + y ≥ 60, x – 2y ≥ 0, x, y ≥ 0.
Solution.
The feasible region determined by the constraints, x + 2y ≤ 120, x + y ≥ 60, x – 2y ≥ 0, x ≥ 0, and y ≥ 0 is as follows
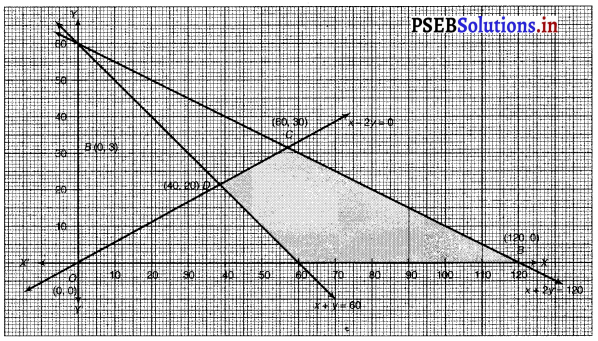
The corner points of the feasible region are A (60, 0), B (120, 0), C (60, 30) and D (40, 20).
The values of Z at the corner points are as follows

The minimum value of Z is 300 at (60, 0) and the maximum value of Z is 600 at all the points on the line segment joining (120, 0) and (60, 30).
![]()
Question 8.
Minimise and maximise Z = x + 2y subject to x + 2y ≥ 100, 2x – y ≤ 0, 2x + y ≤ 200; x, y ≥ 0. Solution. The feasible region determined by the constraints, x + 2y ≥ 100, 2x – y ≤ 0,2x + y ≤ 200, x > 0 and y ≥ 0 is as follows
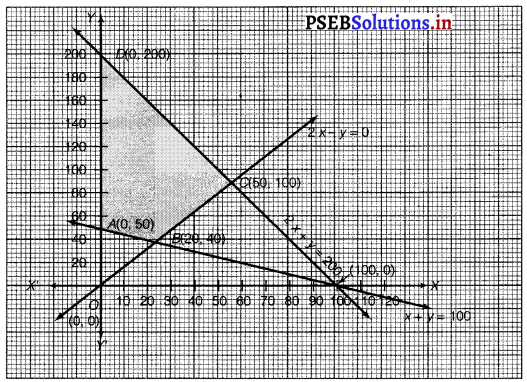
The comer points of the feasible region are A (0, 50), B (20, 40), C (50, 100) and D (0, 200).
The values of Z at the corner points are as follows

The minimum value of Z is 400 at (0, 200) and the maximum value of Z is 100 at all the points on the line segment joining (0, 50) and (20, 40).
![]()
Question 9.
Maximise Z = – x + 2y,
subject to the constraints : x ≥ 3, x + y ≥ 5, x + 2y ≥ 6, y ≥ 0.
Solution.
The feasible region determined by the constraints, x ≥ 3, x + y ≥ 5, x + 2y ≥ 6 and y ≥ 0 is as given below
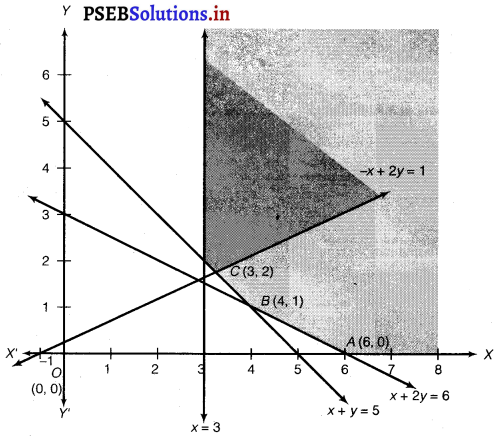
It can be seen that the feasible region is unbounded
The values of Z at corner points A(6,0), B(4,1) and C(3,2) are as follows.
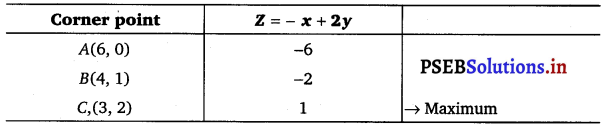
As the feasible region is unbounded, therefore, Z = 1 may or may not be the maximum value.
For this, we graph the inequality, – x + 2y > 1 and check whether the resulting half plane has points in common with the feasible region or not. The resulting feasible reason has points in common with the feasible region.
Therefore, Z = 1 is not the maximum value. Hence, Z has no maximum value.
![]()
Question 10.
Maximise Z = x + y,
subject to x – y ≤ – 1, – x + y ≤ 0, x, y ≥ 0.
Solution.
The region determined by the constraints, x – y ≤ – 1, – x + y ≤ 0, x, y ≥ 0 is as follows.
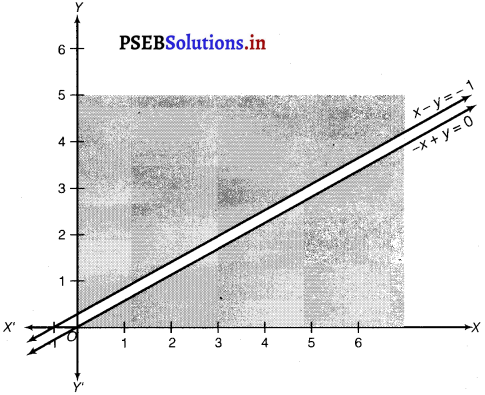
There is no feasible region and thus, Z has no maximum value.
