PSEB 12th Class Maths Solutions Chapter 3 Matrices Miscellaneous Exercise

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 3 Matrices Miscellaneous Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 3 Matrices Miscellaneous Exercise

Question 1.
Let A = \(\left[\begin{array}{ll}
0 & 1 \\
0 & 0
\end{array}\right]\), show that (aI + bA)ⁿ = aⁿI + na^{n – 1}bA, where I is the identity matrix of order 2 and n ∈ N.
Solution.
It is given that A = \(\left[\begin{array}{ll}
0 & 1 \\
0 & 0
\end{array}\right]\)
To show:
P(n): {aI + bA)ⁿ =(aI + bA)ⁿ = aⁿI + na^{n – 1}bA, n ∈ N.
We shall prove that the result by using the principle of mathematical induction.
For n = 1, we have
P(1): (aI + bA) = aI + ba°A = aI + bA
Therefore, the result is true for n = 1.
Let the result be true for n = k.
That is, P(k): (aI + bA)^k = a^kI = ka^{k – 1} bA
Now, we prove that the result is true for n = k +1.
Consider
(aI + bA)^{k + 1} = (aI + bA)^k (aI + bA)
(∵ a^{x + y} = a^x x a^y)
= (a^kI + ka^{k – 1}bA) (aI + bA)
= a^{k + 1} I + ka^kbAI + a^kbIA + ka^{k – 1} b²A²
= a^{k + 1}I + (k + 1)a^kbA + ka^{k – 1}b²A²

Now, A² = \(\left[\begin{array}{ll}
0 & 1 \\
0 & 0
\end{array}\right]\left[\begin{array}{ll}
0 & 1 \\
0 & 0
\end{array}\right]=\left[\begin{array}{ll}
0 & 0 \\
0 & 0
\end{array}\right]\) = 0

From Eq. (i) we have,
(aI + bA)^{k + 1} = a^{k + 1}I + (k + 1)a^kbA + 0
= a^{k + 1}I + (k + 1)a^kbA

Therefore, the result is true for n = k + 1.
Thus, by the principle of mathematical induction, we have
(aI + bA)ⁿ = aⁿI + na^{n – 1}bA, where A = \(\left[\begin{array}{ll}
0 & 1 \\
0 & 0
\end{array}\right]\) n ∈ N.

Question 2.
If A = \(\left[\begin{array}{lll}
1 & 1 & 1 \\
1 & 1 & 1 \\
1 & 1 & 1
\end{array}\right]\), prove that Aⁿ = \(\left[\begin{array}{lll}
3^{n-1} & 3^{n-1} & 3^{n-1} \\
3^{n-1} & 3^{n-1} & 3^{n-1} \\
3^{n-1} & 3^{n-1} & 3^{n-1}
\end{array}\right]\), n ∈ N.
Solution.
It is given that A = \(\left[\begin{array}{lll}
1 & 1 & 1 \\
1 & 1 & 1 \\
1 & 1 & 1
\end{array}\right]\)
To show:
P(n) = Aⁿ = \(\left[\begin{array}{lll}
3^{n-1} & 3^{n-1} & 3^{n-1} \\
3^{n-1} & 3^{n-1} & 3^{n-1} \\
3^{n-1} & 3^{n-1} & 3^{n-1}
\end{array}\right]\), n ∈ N

We shall prove the result by using the principle of mathematical induction.
For n= 1, we have
P(1) = \(\left[\begin{array}{lll}
3^{1-1} & 3^{1-1} & 3^{1-1} \\
3^{1-1} & 3^{1-1} & 3^{1-1} \\
3^{1-1} & 3^{1-1} & 3^{1-1}
\end{array}\right]=\left[\begin{array}{lll}
3^{0} & 3^{0} & 3^{0} \\
3^{0} & 3^{0} & 3^{0} \\
3^{0} & 3^{0} & 3^{0}
\end{array}\right]=\left[\begin{array}{lll}
1 & 1 & 1 \\
1 & 1 & 1 \\
1 & 1 & 1
\end{array}\right]\) = A
Therefore, the result is true for n = 1.
Let the result be true for n = k.
i.e., P(k) = A^k = \(\left[\begin{array}{lll}
3^{k-1} & 3^{k-1} & 3^{k-1} \\
3^{k-1} & 3^{k-1} & 3^{k-1} \\
3^{k-1} & 3^{k-1} & 3^{k-1}
\end{array}\right]\)
Now, we prove that the result is true for n = k + 1.
Now, A^{k + 1} = A . A^k
= \(\left[\begin{array}{lll}
1 & 1 & 1 \\
1 & 1 & 1 \\
1 & 1 & 1
\end{array}\right]\left[\begin{array}{lll}
3^{k-1} & 3^{k-1} & 3^{k-1} \\
3^{k-1} & 3^{k-1} & 3^{k-1} \\
3^{k-1} & 3^{k-1} & 3^{k-1}
\end{array}\right]\)

= \(\left[\begin{array}{lll}
3 \cdot 3^{k-1} & 3 \cdot 3^{k-1} & 3 \cdot 3^{k-1} \\
3 \cdot 3^{k-1} & 3 \cdot 3^{k-1} & 3 \cdot 3^{k-1} \\
3 \cdot 3^{k-1} & 3 \cdot 3^{k-1} & 3 \cdot 3^{k-1}
\end{array}\right]=\left[\begin{array}{lll}
3^{(k+1)-1} & 3^{(k+1)-1} & 3^{(k+1)-1} \\
3^{(k+1)-1} & 3^{(k+1)-1} & 3^{(k+1)-1} \\
3^{(k+1)-1} & 3^{(k+1)-1} & 3^{(k+1)-1}
\end{array}\right]\)

Therefore, the result is true for n = k + 1.
Thus, by the principle of mathematical induction, we have
Aⁿ = \(\left[\begin{array}{lll}
3^{n-1} & 3^{n-1} & 3^{n-1} \\
3^{n-1} & 3^{n-1} & 3^{n-1} \\
3^{n-1} & 3^{n-1} & 3^{n-1}
\end{array}\right]\), n ∈ N.

Question 3.
If A = \(\left[\begin{array}{rr}
3 & -4 \\
1 & -1
\end{array}\right]\), then prove Aⁿ = \(\left[\begin{array}{cc}
1+2 n & -4 n \\
n & 1-2 n
\end{array}\right]\), where n is any positive integer.
Solution.
It is given that A = \(\left[\begin{array}{rr}
3 & -4 \\
1 & -1
\end{array}\right]\)

To prove:
P(n) : Aⁿ = \(\left[\begin{array}{cc}
1+2 n & -4 n \\
n & 1-2 n
\end{array}\right]\), n ∈ N
We shall prove that result by using the principle of mathematical induction.
For n = 1, we have
P(1) : A¹ = \(\left[\begin{array}{cc}
1+2 & -4 \\
1 & 1-2
\end{array}\right]=\left[\begin{array}{cc}
3 & -4 \\
1 & -1
\end{array}\right]\) = A

Therefore, the result is true for n = 1.
Let the result be true for n = k.

i.e., p(k) = A^k = \(\left[\begin{array}{cc}
1+2 k & -4 k \\
k & 1-2 k
\end{array}\right]\), n ∈ N

Now, we prove that the result is true for n = k +1.
Consider A^k+1 = A^k . A

Therefore, the result is true for n = k +1.
Thus, by the principle of mathematical induction, we have

Aⁿ = \(\left[\begin{array}{cc}
1+2 n & -4 n \\
n & 1-2 n
\end{array}\right]\), n ∈ N.

Question 4.
If A and B are symmetric matrices, prove that AB – BA is a skew symmetric matrix.
Solution.
It is given that A and B are symmetric matrices. Therefore, we have
A’ = A and B’ = B …………..(i)
Now, (AB – BA)’ = (AB)’ – (BA)’ [(A -B)’ = A’ – B’]
= B’A’ – A’B’ [(AB)’ = B’A’]
= BA – AB [UsingEq. (i)]
= – (AB – BA)
∴ (AB – BA)’ = – (AB – BA)
Thus, (AB – BA) is a skew symmetric matrix.

Question 5.
Show that the matrix B’ AB is symmetric or skew symmetric according as A is symmetric or skew symmetric.
Solution.
We suppose that A is a symmetric matrix, then A’ = A ………… (i)
Consider
(B’ABX = {B’ (AB)}’
= (AB)’ (B’)’ [(AB)’ = B’A’]
= B’A'(B) [∵ (B’)’ = B]
= B'(A’B)
= B'(AB) [Using Eq. (i)]
∴ (B’AB)’ = B’ AB
Thus, if A is a symmetric matrix, then B’AB is a symmetric matrix.
Now, we suppose that A is a skew symmetric matrix.
Then, A’ = – A
Consider
(B’AB)’ = [B’ (AB)]’ = (AB)’ (B’ )’ [∵ (AB)’ = B’A’ and (A’)’ = A]
= (B’A’)B = B’ (-A)B
= – B’AB
∴ (B’ AB)’ = – B’ AB
Thus, if A is a skew-symmetric matrix, then B’ AB is a skew symmetric matrix.
Hence, if A is a symmetric or skew symmetric matrix, then B’AB is a symmetric or skew symmetric matrix accordingly.

Question 6.
Find the values of x, y and z if the matrix A = \(\left[\begin{array}{ccc}
0 & 2 y & z \\
x & y & -z \\
x & -y & z
\end{array}\right]\) satisfy the equation A’ A = I.
Solution.
Given, A’A = I

On comparing the corresponding elements, we have
2x² = 1,
⇒ x² = \(\frac{1}{2}\),
⇒ x = ± \(\frac{1}{\sqrt{2}}\)

6y² = 1,
⇒ y² = \(\frac{1}{6}\),
⇒ y = ± \(\frac{1}{\sqrt{6}}\)

3z² = 1
⇒ z² = \(\frac{1}{3}\)
⇒ z = ± \frac{1}{\sqrt{3}}\(\).

Question 7.
For what values of x:[1 2 1] \(\left[\begin{array}{lll}
1 & 2 & 0 \\
2 & 0 & 1 \\
1 & 0 & 2
\end{array}\right]\left[\begin{array}{l}
0 \\
2 \\
x
\end{array}\right]\) = 0?
Solution.
We have [1 2 1] \(\left[\begin{array}{lll}
1 & 2 & 0 \\
2 & 0 & 1 \\
1 & 0 & 2
\end{array}\right]\left[\begin{array}{l}
0 \\
2 \\
x
\end{array}\right]\) = 0
⇒ [1 + 4 + 1 2 + 0 + 0 0 + 2 + 2] \(\left[\begin{array}{l}
0 \\
2 \\
x
\end{array}\right]\) = 0

⇒ [6 2 4] \(\left[\begin{array}{l}
0 \\
2 \\
x
\end{array}\right]\) = 0
⇒ [6(0) + 2(2) + 4(x)]= 0
[4 + 4x] = [0]
∴ 4 + 4x = 0
⇒ x = – 1
Thus, the required value of x is – 1.

Question 8.
If A = \(\left[\begin{array}{cc}
3 & 1 \\
-1 & 2
\end{array}\right]\) show that A² – 5A + 7I = 0.
Solution.
k is given that A = \(\left[\begin{array}{cc}
3 & 1 \\
-1 & 2
\end{array}\right]\)

Question 9.
Find x, if [x – 5 – 1] \(\left[\begin{array}{lll}
1 & 0 & 2 \\
0 & 2 & 1 \\
2 & 0 & 3
\end{array}\right]\left[\begin{array}{c}
x \\
4 \\
1
\end{array}\right]\) = 0.
Solution.
[x – 5 – 1] \(\left[\begin{array}{lll}
1 & 0 & 2 \\
0 & 2 & 1 \\
2 & 0 & 3
\end{array}\right]\left[\begin{array}{c}
x \\
4 \\
1
\end{array}\right]\)

⇒ [x + 0 – 2 0 – 10 + 0 2x – 5 – 3] \(\left[\begin{array}{l}
x \\
4 \\
1
\end{array}\right]\) = 0
⇒ [x – 2 -10 2x – 8] \(\left[\begin{array}{l}
x \\
4 \\
1
\end{array}\right]\) = 0

⇒ [x(x – 2) – 40 + 2x – 8] = 0
⇒ [x² – 2x – 40 + 2x – 8] = 0
⇒ [x² – 48] = [0]
⇒ x² – 48 = 0
⇒ x² = 48
⇒ x = ± 4√3.

Question 10.
A manufacturer produces three products x, y, z which he sells in two markets.
Annual sales are indicated below

(a) If unit sale prices of x, y and z are ₹ 2.50, ₹ 1.50 and ₹ 1.00, respectively, then find the total revenue In each market with the help of matrix algebra.
(b) If the unit costs of the above three commodities are ₹ 2.00, ₹ 1.00 and 50 paise respectively. Find the gross profit.
Solution.
(a) The unit sale prices of x, y and z are respectively given as ₹ 2.50, ₹ 1.50, and ₹ 1.00.
Consequently, the total revenue in market I can be represented in the form of a matrix as
[10000 2000 18000] \(\left[\begin{array}{l}
2.50 \\
1.50 \\
1.00
\end{array}\right]\)
= 10000 × 2.50 + 2000 × 1.50 + 18000 × 1.00
= 25000 +3000 + 18000 = 46000
The total revenue in market II can be represented in the form of a matrix as
[6000 2000 8000] \(\left[\begin{array}{l}
2.50 \\
1.50 \\
1.00
\end{array}\right]\)
= 6000 × 2.50 + 20000 × 1.50 + 8000 × 1.00
= 15000 + 30000 + 8000 = 53000
Therefore, the total revenue in market I is ₹ 46000 and the same in market II is ₹ 53000.

(b) The unit cost prices of x, y, and z are respectively given as 2.00, U.00, and 50 paise.
Consequently, the total cost prices of all the products in market I can be represented in the form of a matrix as
[10000 2000 18000] \(\left[\begin{array}{l}
2.00 \\
1.00 \\
0.50
\end{array}\right]\)
= 10000 × 2.00 + 2000 × 1.00 + 18000 × 0.50
= 20000 + 2000 + 9000 = 31000
Since the total revenue in market I is ₹ 46000, the gross profit in this market is (₹ 46000 – ₹ 31000) = ₹ 15000.
The total cost prices of all the products in market Il can be represented in the form of a matrix as
[6000 20000 8000] \(\left[\begin{array}{l}
2.00 \\
1.00 \\
0.50
\end{array}\right]\)
= 6000 × 2.00 + 20000 × 1.00 + 8000 × 0.50
= 12000 + 20000 + 4000 = 36000
Since the total revenue in market is ₹ 53000, the gross profit in this market is ( 53000 – 36000) = 17000.
Total gross profit = ₹ (15000 + 17000) = ₹ 32000.

Question 11.
Find the matrix X so that X \(\left[\begin{array}{lll}
1 & 2 & 3 \\
4 & 5 & 6
\end{array}\right]\) = \(\left[\begin{array}{ccc}
-7 & -8 & -9 \\
2 & 4 & 6
\end{array}\right]\)
Solution.
It is given that

\(\left[\begin{array}{lll}
1 & 2 & 3 \\
4 & 5 & 6
\end{array}\right]\) = \(\left[\begin{array}{ccc}
-7 & -8 & -9 \\
2 & 4 & 6
\end{array}\right]\)

The matrix given on the R.H.S. of the equation is a 2 × 3 matrix and the one given on the L.H.S. of the equation is a 2 × 3 matrix. Therefore, X has to be a 2 × 2 matrix.
Now, let x = \(\left[\begin{array}{ll}
a & c \\
b & d
\end{array}\right]\)
Therefore, we have

\(\left[\begin{array}{ll}
a & c \\
b & d
\end{array}\right]\left[\begin{array}{lll}
1 & 2 & 3 \\
4 & 5 & 6
\end{array}\right]=\left[\begin{array}{ccc}
-7 & -8 & -9 \\
2 & 4 & 6
\end{array}\right]\)

⇒ \(\left[\begin{array}{ccc}
a+4 c & 2 a+5 c & 3 a+6 c \\
b+4 d & 2 b+5 d & 3 b+6 d
\end{array}\right]=\left[\begin{array}{ccc}
-7 & -8 & -9 \\
2 & 4 & 6
\end{array}\right]\)

On equating the corresponding elements of the two matrices, we have
a + 4c = – 7,
b + 4d = 2,

2a + 5c = – 8,
2b + 5d = 4,

3a + 6c = – 9,
3b + 6d = 6

Now, a + 4c = – 7
⇒ a = – 7 – 4c

∴ 2a + 5c = – 8
⇒ – 14 – 8c + 5c = – 8
⇒ – 3c = 6
⇒ c = – 2
∴ a = – 7 – 4(- 2)
= – 7 + 8 = 1

Now, b + 4d = 2
⇒ b = 2 – 4d
∴ 2b + 5d = 4
⇒ 4 – 8d + 5d = 4
⇒ – 3d = 0
⇒ d = 0.
Thus, a = 1, b = 2, c = – 2, d = 0
Hence, the required matrix X is \(\left[\begin{array}{cc}
1 & -2 \\
2 & 0
\end{array}\right]\).

Question 12.
If A and B are square matrices of the same order such that AB = BA, then prove by induction that AB” = B” A. Further, provethat(AB)” =A”B” for all n ∈ N.
Solution.
A and B are square matrices of the same order such that AB = BA.
To prove:
P(n): ABⁿ = BⁿA, n e N
For n = 1,we have P(1): AB = BA (Given)
AB¹ = B¹A
Therefore, the result is true for n = 1.
Let the result be true for n = k.
P(k): AB^k = B^kA ………….(i)
Now, we prove that the result is true for n = k + 1.
AB^{k + 1} = AB^k . B = (B^kA)B [From Eq. (j)]
= B^k (AB) [By associative law]
= B^k (BA) [: AB = BA (Given)]
= (B^kB)A [By associative law]
= B^{k + 1} A
Therefore, the result is true for n = k + 1.
Thus, by the principle of mathematical induction, we have
ABⁿ = BⁿA, n e N.
Now, we prove that (AB)ⁿ = AⁿBⁿ for all n ∈ N
For n = 1, we have
(AB)¹ = A¹B¹ = AB
Therefore, the result is true for n = 1.
Let the result be true for n = k.
(AB)^k = A^kB^k …………….(ii)
Now, we prove that the result is true for n = k + 1.
(AB)^{k + 1} = (AB)^k . (AB)
= (A^kB^k).(AB)
= A^k(B^kA)B
= A^k(AB^k)B
= (A^kA).(B^kB)
= A^{k + 1}B^{k + 1}
Therefore, the result is true for n = k +1.
Thus, by the principle of mathematical induction, we have (AB)ⁿ = AⁿBⁿ, for all natural numbers.

Direction (13 – 15) Choose the correct answer in the following questions.

Question 13.
If A = \(\left[\begin{array}{cc}
\alpha & \beta \\
\gamma & -\alpha
\end{array}\right]\) is such that A² = I, then
(A) 1 + α² + βγ = 0
(C) 1 – α² – βγ = 0
(B) 1 – α² + βγ = 0
(D) 1 + α² – βγ = 0
Solution.
We have, A = \(\left[\begin{array}{cc}
\alpha & \beta \\
\gamma & -\alpha
\end{array}\right]\)

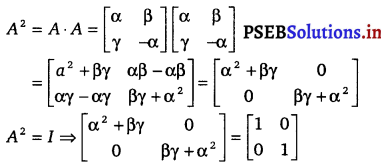
On comparing the corresponding elements, we have
α² + βγ = 1
α² + βγ – 1 = 0
1 – α² – βγ = 0
Hence, the correct answer is (C).

Question 14.
If the matrix A is both symmetric and skew symmetric, then
(A) A is a diagonal matrix
(B) A is a zero matrix
(C) A is a square matrix
(D) None of these
Solution.
If A is both symmetric and skew symmetric matrix, then we should have
A’ = A and A’ = – A
⇒ A = – A
⇒ A + A = 0
⇒ 2A = 0 A = 0
Therefore, A is a zero matrix.
Hence, the correct answer is (B).

Question 15.
If A is square matrix such that A² = A, then (I + A)³ – 7A is equal to
(A) A
(B) I – A
(C) I
(D)3A
Solution.
(I + A)³ – 7A = I³ + A³ + 3I²A + 3A²I – 7A
= I + A³ + 3A + 3A² – 7A
= I + A² . A + 3A + 3A – 7A [∵ A² = A (given)]
= I + A.A – A
= I + A² – A
I + A – A = 1
∴ (I + A)³ – 7A = 1
Hence, the correct answer is (C).