PSEB 12th Class Maths Solutions Chapter 4 Determinants Ex 4.2

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 4 Determinants Ex 4.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 4 Determinants Ex 4.2

Direction (1 – 5): Using the property of determinants and without expanding.

Question 1.
\(\left|\begin{array}{lll}
x & a & x+a \\
y & b & y+b \\
z & c & z+c
\end{array}\right|\) = 0
Solution.
We have, \(\left|\begin{array}{lll}
x & a & x+a \\
y & b & y+b \\
z & c & z+c
\end{array}\right|=\left|\begin{array}{lll}
x & a & a \\
y & b & b \\
z & c & c
\end{array}\right|\) = 0 [applying C₃ → C₃ – C₁]

[Since, the two columns of the determinants are identical.]

Question 2.
\(\left|\begin{array}{lll}
a-b & b-c & c-a \\
b-c & c-a & a-b \\
c-a & a-b & b-c
\end{array}\right|\) = 0
Solution.
∆ = \(\left|\begin{array}{lll}
a-b & b-c & c-a \\
b-c & c-a & a-b \\
c-a & a-b & b-c
\end{array}\right|\)

[applying R₁ → R + R₂]

∆ = \(\left|\begin{array}{ccc}
a-c & b-a & c-b \\
b-c & c-a & a-b \\
-(a-c) & -(b-a) & -(c-b)
\end{array}\right|=-\begin{array}{ccc}
a-c & b-a & c-b \\
b-c & c-a & a-b \\
a-c & b-a & c-b
\end{array} \mid\) = 0
[Since the two rows R₁ and R₃ are identical].

Question 3.
\(\left|\begin{array}{lll}
2 & 7 & 65 \\
3 & 8 & 75 \\
5 & 9 & 86
\end{array}\right|\) = 0
Solution.
\(\left|\begin{array}{lll}
2 & 7 & 65 \\
3 & 8 & 75 \\
5 & 9 & 86
\end{array}\right|=\left|\begin{array}{lll}
2 & 7 & 2 \\
3 & 8 & 3 \\
5 & 9 & 5
\end{array}\right|\) = 0 (applying C₃ → C₃ – 9 C₂)
[Since, two columns are identical]

Question 4.
\(\left|\begin{array}{lll}
1 & b c & a(b+c) \\
1 & c a & b(c+a) \\
1 & a b & c(a+b)
\end{array}\right|\) = 0
Solution.
∆ = \(\left|\begin{array}{lll}
1 & b c & a(b+c) \\
1 & c a & b(c+a) \\
1 & a b & c(a+b)
\end{array}\right|\)

∆ = \(\left|\begin{array}{lll}
1 & b c & a b+b c+c a \\
1 & c a & a b+b c+c a \\
1 & a b & a b+b c+c a
\end{array}\right|\) (applying C₃ → C₃ – 9 C₂)

On taking (ab + bc + ca) common from C₃, we have

∆ = (ab + bc + ca) \(\left|\begin{array}{ccc}
1 & b c & 1 \\
1 & c a & 1 \\
1 & a b & 1
\end{array}\right|\)
= 0 × (ab + bc + ca) = 0
[Since, two columns C₁ and C₃ are identical]

Question 5.
\(\left|\begin{array}{lll}
b+c & q+r & y+z \\
c+a & r+p & z+x \\
a+b & p+q & x+y
\end{array}\right|=2\left|\begin{array}{lll}
a & p & x \\
b & q & y \\
c & r & z
\end{array}\right|\)
solution.

Direction (6 – 14): By using properties of determinants.

Question 6.
\(\left|\begin{array}{ccc}
0 & a & -b \\
-a & 0 & -c \\
b & c & 0
\end{array}\right|\) = 0
Solution.
We have, ∆ = \(\left|\begin{array}{ccc}
0 & a & -b \\
-a & 0 & -c \\
b & c & 0
\end{array}\right|\)

∆ = \(=\frac{1}{c}\left|\begin{array}{ccc}
0 & a c & -b c \\
-a & 0 & -c \\
b & c & 0
\end{array}\right|\) (applying R₁ → cR₁)

∆ = \(\frac{1}{c}\left|\begin{array}{ccc}
a b & a c & 0 \\
-a & 0 & -c \\
b & c & 0
\end{array}\right|=\frac{a}{c}\left|\begin{array}{ccc}
b & c & 0 \\
-a & 0 & -c \\
b & c & 0
\end{array}\right|\) = 0
(applying R₁ → R₁ – bR₂)
[Since, the two rows R₁ and R₃ are identical].

Question 7.
\(\left|\begin{array}{ccc}
-a^{2} & a b & a c \\
b a & -b^{2} & b c \\
c a & c b & -c^{2}
\end{array}\right|\) = 4 a² b² c²
Solution.

[Applying R₂ → R₂ + R₁ and R₃ R₃ + R₁], we have

∆ = a² b² c² \(\left|\begin{array}{ccc}
-1 & 1 & 1 \\
0 & 0 & 2 \\
0 & 2 & 0
\end{array}\right|\)

= a² b² c² \(\left|\begin{array}{ll}
0 & 2 \\
2 & 0
\end{array}\right|\)
= a² b² c² (0 – 4)
= 4 a² b² c² = R.H.S.

Question 8.
(i) \(\left|\begin{array}{lll}
1 & a & a^{2} \\
1 & b & b^{2} \\
1 & c & c^{2}
\end{array}\right|\) = (a – b) (b – c) (c – a)

(ii) \(\left|\begin{array}{ccc}
1 & 1 & 1 \\
a & b & c \\
a^{3} & b^{3} & c^{3}
\end{array}\right|\) = (a – b) (b – c) (c – a) (a + b + c)
Solution.
(i)

By expanding along C₁, we have

∆ = (a – b) (b – c) (c – a) \(\left|\begin{array}{cc}
0 & -1 \\
1 & b+c
\end{array}\right|\)
= (a – b) (b – c) (c – a)

(ii) Let ∆ = \(\left|\begin{array}{ccc}
1 & 1 & 1 \\
a & b & c \\
a^{3} & b^{3} & c^{3}
\end{array}\right|\)
Applying C₁ → C₁ – C₃, C₂ → C₂ – C₃, we have

By expanding along C₁, we have
∆ = (a – b) (b – c) (c – a) (a + b + c) (- 1) \(\left|\begin{array}{cc}
0 & 1 \\
1 & c
\end{array}\right|\)
= (a – b) (b – c) (c – a) (a + b + c)

Question 9.
\(\left|\begin{array}{lll}
x & x^{2} & y z \\
y & y^{2} & z x \\
z & z^{2} & x y
\end{array}\right|\) = (x – y) (y – z) (z – x) (xy + yz + zx)
Solution.
L.H.S = \(\mid \begin{array}{lll}
x & x^{2} & y z \\
y & y^{2} & z x \\
z & z^{2} & x y
\end{array}\)

Applying R₂ → R₂ – R₁ and R₃ → R₃ – R₁, we have

∆ = \(\left|\begin{array}{ccc}
x & x^{2} & y z \\
y-x & y^{2}-x^{2} & z x-y z \\
z-x & z^{2}-x^{2} & x y-y z
\end{array}\right|\)

= (x – y) (z – x) (z – y) [(- xz – yz) + (- x² – xy + x²)]
= – (x – y) (z – x) (z – y) (xy + yz + zx)
= (x – y) (y – z) (z – x) (xy + yz + zx) = R.H.S.
Hence, the given result is proved.

Question 10.
(i) \(\left|\begin{array}{ccc}
x+4 & 2 x & 2 x \\
2 x & x+4 & 2 x \\
2 x & 2 x & x+4
\end{array}\right|\) = (5x + 4) (4 – x)²

(ii) \(\left|\begin{array}{ccc}
y+k & y & y \\
y & y+k & y \\
y & y & y+k
\end{array}\right|\) = k² (3y + k)
Solution.
(i)

= (5x + 4)(4 – x) (4 – x) \(\left|\begin{array}{ccc}
1 & 0 & 0 \\
2 x & 1 & 0 \\
2 x & 0 & 1
\end{array}\right|\)
By expanding along C₃, have
∆ = (5x + 4) (4 – x)² \(\left|\begin{array}{cc}
1 & 0 \\
2 x & 1
\end{array}\right|\)
= (5x + 4) (4 – x)²
Hence, the given result is proved.

(ii)

Question 11.
(i) \(\left|\begin{array}{ccc}
a-b-c & 2 a & 2 a \\
2 b & b-c-a & 2 b \\
2 c & 2 c & c-a-b
\end{array}\right|\) = (a + b + c)²

(ii) \(\left|\begin{array}{ccc}
x+y+2 z & x & y \\
z & y+z+2 x & y \\
z & x & z+x+2 y
\end{array}\right|\) = 2(x + y + z)²
Solution.
(i) Let ∆ = \(\left|\begin{array}{ccc}
a-b-c & 2 a & 2 a \\
2 b & b-c-a & 2 b \\
2 c & 2 c & c-a-b
\end{array}\right|\)

Applying R₁ → R₁ + R₂ + R₃, we have
∆ = \(\left|\begin{array}{ccc}
a+b+c & a+b+c & a+b+c \\
2 b & b-c-a & 2 b \\
2 c & 2 c & c-a-b
\end{array}\right|\)

= (a + b + c) \(\left|\begin{array}{ccc}
1 & 1 & 1 \\
2 b & b-c-a & 2 b \\
2 c & 2 c & c-a-b
\end{array}\right|\) (Taking out (a + b+ c) common from R₁)

Applying C₂ → C₂ – C₁ and C₃ → C₃ – C₁, we have
∆ = (a + b + c) \(\left|\begin{array}{ccc}
1 & 0 & 0 \\
2 b & -(a+b+c) & 0 \\
2 c & 0 & -(a+b+c)
\end{array}\right|\)

= (a + b + c)³ \(\left|\begin{array}{ccc}
1 & 0 & 0 \\
2 b & -1 & 0 \\
2 c & 0 & -1
\end{array}\right|\)

By expanding along C₃, we have
∆ = (a + b + c)³ (- 1) (- 1) = (a + b + c)³
Hence, the given result is proved.

(ii)

By expanding along R₃, we have
= 2(x + y+ z)² (1)(1 – 0) = 2(x + y+ z)³
Hence, the given result is proved.

Question 12.
\(\left|\begin{array}{ccc}
1 & x & x^{2} \\
x^{2} & 1 & x \\
x & x^{2} & 1
\end{array}\right|\) = (1 – x³)²
Solution.
∆ = \(\left|\begin{array}{ccc}
1 & x & x^{2} \\
x^{2} & 1 & x \\
x & x^{2} & 1
\end{array}\right|\)

Applying R₁ → R₁ + R₂ + R₃, we have

Question 13.
\(\left|\begin{array}{ccc}
1+a^{2}-b^{2} & 2 a b & -2 b \\
2 a b & 1-a^{2}+b^{2} & 2 a \\
2 b & -2 a & 1-a^{2}-b^{2}
\end{array}\right|\) = (1 + a² + b²)³
Solution.
Let ∆ = \(\left|\begin{array}{ccc}
1+a^{2}-b^{2} & 2 a b & -2 b \\
2 a b & 1-a^{2}+b^{2} & 2 a \\
2 b & -2 a & 1-a^{2}-b^{2}
\end{array}\right|\)

Applying R₁ → R₁ + bR₂ and R₂ → R₂ – aR₃

∆ = \(\left|\begin{array}{ccc}
1+a^{2}+b^{2} & 0 & -b\left(1+a^{2}+b^{2}\right) \\
0 & 1+a^{2}+b^{2} & a\left(1+a^{2}+b^{2}\right) \\
2 b & -2 a & 1-a^{2}-b^{2}
\end{array}\right|\)

= (1 + a² + b²)² \(\left|\begin{array}{ccc}
1 & 0 & -b \\
0 & 1 & a \\
2 b & -2 a & 1-a^{2}-b^{2}
\end{array}\right|\)

By expanding along R₁, we have
∆ = (1 + a² + b²)² \(\left[(1)\left|\begin{array}{cc}
1 & a \\
-2 a & 1-a^{2}-b^{2}
\end{array}\right|-b\left|\begin{array}{cc}
0 & 1 \\
2 b & -2 a
\end{array}\right|\right]\)

= (1 + a² + b²)² [1 – a² – b² + 2a² – b(- 2b)]
= (1 + a² + b²)² (1 + a² + b²)
= (1 + a² + b²)³

Hence, the given result is proved.

Question 14.
\(\left|\begin{array}{ccc}
a^{2}+1 & a b & a c \\
a b & b^{2}+1 & b c \\
c a & c b & c^{2}+1
\end{array}\right|\) = 1 + a² + b² + c²
Solution.

By expanding along R₃, we have
∆ = \(-1\left|\begin{array}{cc}
b^{2} & c^{2} \\
1 & 0
\end{array}\right|+1\left|\begin{array}{cc}
a^{2}+1 & b^{2} \mid \\
-1 & 1
\end{array}\right|\)

= – 1(- c²) + (a² + 1 + b²)
= 1 + a² + b² + c²

Direction (15 – 16): Choose the correct answer in the following questions.

Question 15.
Let A be a square matrix of order 3 × 3 then |KA| is equal to
(A) k |A|
(B) k² |A|
(C) k³ |A|
(D) 3k |A|
Solution.
A is a square matrix of order 3 × 3. (Given)

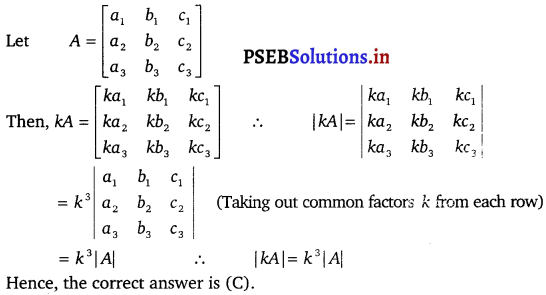
Question 16.
Which of the following is correct?
(A) Determinant is a square matrix.
(B) Determinant is a number associated to a matrix.
(C) Determinant is a number associated to a square matrix.
(D) None of these
Solution.
We know that to every square matrix, A [a_ij] of order n. We can associate a number called the determinant of square matrix A, where a_ij = (i, j)th element of A.
Thus, the determinant is a number associated to a square matrix. Hence, the correct answer is (C).