PSEB 12th Class Maths Solutions Chapter 4 Determinants Ex 4.6

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 4 Determinants Ex 4.6 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 4 Determinants Ex 4.6

Direction (1 – 4): Examine the consistency of the following system of equations.

Question 1.
x + 2y = 2, 2x + 3y = 3.
Solution.
The given system of equations is
x + 2y = 2
2x + 3y = 3
The given system of equations can be written in the form of AX = B,
where
A = \(\left[\begin{array}{ll}
1 & 2 \\
2 & 3
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) and B = \(\left[\begin{array}{l}
2 \\
3
\end{array}\right]\)

Now, |A| = 1(3) – 2(2) = 3 – 4 = – 1 ≠ 0
So, A is non-singular. Therefore, A^-1 exists.
Hence, the given system of equations is consistent.

Question 2.
2x – y = 5, x + y = 4.
Solution.
The given system of equations is
2x – y = 5
x + y = 4
The given system of equations can be written in the form of AX = B, where
A = \(\left[\begin{array}{cc}
2 & -1 \\
1 & 1
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) and B = \(\left[\begin{array}{l}
5 \\
4
\end{array}\right]\)
Now, |A| = 2(1) – (- 1) = 2 + 1 = 3 ≠ 0.
So, A is non-singular. Therefore, A^-1 exists.
Hence, the given system of equations is consistent.

Question 3.
x + 3y = 5, 2x + 6y = 8
Solution.
The given system of equations is
x + 3y = 5
2x + 6y = 8
The given system of equations can be written in the form of AX = B, where
A = \(\left[\begin{array}{ll}
1 & 3 \\
2 & 6
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) and B = \(\left[\begin{array}{l}
5 \\
8
\end{array}\right]\).
Now, |A| = 1(6) – 3(2) = 6 – 6 = 0
So, A is a singular matrix.
Now, (adj A) = \(\left[\begin{array}{rr}
6 & -3 \\
-2 & 1
\end{array}\right]\)
(adj A) B = \(\left[\begin{array}{cc}
6 & -3 \\
-2 & 1
\end{array}\right]\left[\begin{array}{l}
5 \\
8
\end{array}\right]\)
= \(\left[\begin{array}{c}
30-24 \\
-10+8
\end{array}\right]=\left[\begin{array}{c}
6 \\
-2
\end{array}\right]\) ≠ 0.
Thus, the solution of given system of equations does not exist.
Hence, tne system or equations is inconsistent.

Question 4.
x + y + z = 1, 2x + 3y + 2z = 2, ax + ay + 2az = 4.
Solution.
The given system of equations is
x + y + z = 1
2x + 63y + 2z = 2
czx + ay + 2az = 4
This system of equations can be written in the form of AX = B, where
A = \(\left[\begin{array}{ccc}
1 & 1 & 1 \\
2 & 3 & 2 \\
a & a & 2 a
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) and B = \(\left[\begin{array}{l}
1 \\
2 \\
4
\end{array}\right]\)
Now, |A| = 1(6a – 2a) – 1 (4a – 2a) + 1 (2a – 3a)
= 4a – 2a – a
= 4a – 3a = a ≠ 0.
So, A is non-singular. Therefore, A^-1 exists.
Hence, the given system of equations is consistent.

Question 5.
3x – y – 2z = 2, 2y – z = – 1, 3x – 5y = 3.
Solution.
The given system of equations is
3x – y – 2z = 2
2y – z = – 1
3x – 5y = 3
This system of equations can be written in the form of AX = B, where
A = \(\left[\begin{array}{ccc}
3 & -1 & -2 \\
0 & 2 & -1 \\
3 & -5 & 0
\end{array}\right]\), X = \(=\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) and B = \(\left[\begin{array}{c}
2 \\
-1 \\
3
\end{array}\right]\)
Now, |A| = 3(0 – 5) – 0 + 3(1 + 4)
= – 15 + 15 = 0
So, A is a singular matrix.
Now, (adj A ) = \(\left[\begin{array}{ccc}
-5 & 10 & 5 \\
-3 & 6 & 3 \\
-6 & 12 & 6
\end{array}\right]\)

(adj A) B = \(\left[\begin{array}{ccc}
-5 & 10 & 5 \\
-3 & 6 & 3 \\
-6 & 12 & 6
\end{array}\right]\left[\begin{array}{r}
2 \\
-1 \\
3
\end{array}\right]\)

= \(\left[\begin{array}{c}
-10-10+15 \\
-6-6+9 \\
-12-12+18
\end{array}\right]=\left[\begin{array}{c}
-5 \\
-3 \\
-6
\end{array}\right] \neq 0\)

Thus, the solution of the given system of equations does not exist.
Hence, the system of the equations is inconsistent.

Question 6.
5x – y + 4z = 5, 2x + 3y + 5z = 2, 5x – 2y + 6z = – 1.
Solution.
The given system of equations is
5x – y + 4z = 5
2x + 3y + 5z =2
5x – 2y + 6z = – 1
This system of equations can be written in the form of AX = B, where
A = \(\left[\begin{array}{rrr}
5 & -1 & 4 \\
2 & 3 & 5 \\
5 & -2 & 6
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) and B = \(\left[\begin{array}{c}
5 \\
2 \\
-1
\end{array}\right]\)
5 -2 6 z -1
Now, |A| = 5(18 + 10) + 1 (12 – 25) + 4(- 4 – 15)
= 5 (28) + 1 (- 13) + 4 (- 19)
= 140 – 13 – 76 = 51 ≠ 0
So, A is non-singular. Therefore, A’ exists.
Hence, the given system of equations is consistent.

Direction (7 – 14): Solve the system of linear equations, using matrix method.

Question 7.
5x + 2y = 4, 7x + 3y = 5.
Solution.
The given system of equations can be written in the form of AX = B,
where
A = \(\left[\begin{array}{ll}
5 & 2 \\
7 & 3
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) and B = \(\left[\begin{array}{l}
4 \\
5
\end{array}\right]\)
Now, |A| = 15 – 14 = 1 ≠ 0.
Thus, A is non-singular. Therefore, its inverse exists.
Cofactors of A are
A₁₁ = 3,
A₁₂ = – 7,
A₂₁ = – 2,
A₂₂ = 5

Question 8.
2x – y = – 2, 3x + 4y = 3
Solution.
The given system of equations can be written in the form of AX = B,
where
A = \(\left[\begin{array}{rr}
2 & -1 \\
3 & 4
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) and B = \(\left[\begin{array}{r}
-2 \\
3
\end{array}\right]\).
Now, |A| = 8 + 3 = 11 ≠ 0
Thus, A is non-singular. Therefore, its inverse exists.
Cofactors of A are
A₁₁ = 4,
A₁₂ = – 3,
A₂₁ = 1,
A₂₂ = 2

Question 9.
4x – 3y = 3, 3x – 5y = 7.
Solution.
The given system of equations can be written in the form of AX = B, where
A = \(\left[\begin{array}{cc}
4 & -3 \\
3 & -5
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) and B = \(\left[\begin{array}{l}
3 \\
7
\end{array}\right]\)
Now, |A| = – 20 + 9 = – 11 ≠ 0.
Thus, A is non-singular. Therefore, its inverse exists.
Determinants 179
Cofactors of A are
A₁₁ = – 5,
A₁₂ = – 3,
A₂₁ = 3,
A₂₂ = 4

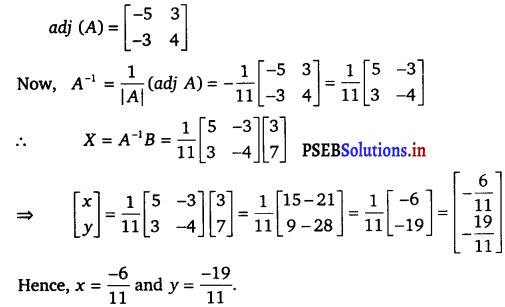
Question 10.
5x + 2y = 3, 3x + 2y = 5.
Solution.
The given system of equations can be written in the form of AX = B,
where
A = \(\left[\begin{array}{ll}
5 & 2 \\
3 & 2
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) and B = \(\).
Now, |A| = 10 – 6 = 4 ≠ 0
Thus, A is non-singular. Therefore, its inverse exists.
Cofactors of A are
A₁₁ = 2,
A₁₂ = – 3,
A₂₁ = – 2,
A₂₂ = 5

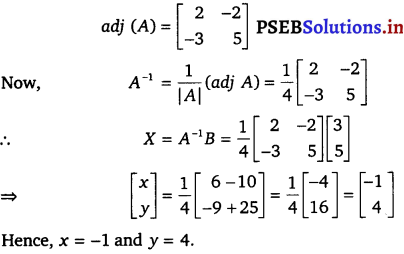
Question 11.
2x + y + z = 1, x – 2y – z = \(\frac{3}{2}\), 3y – 5z = 9.
Solution.
The given system of equations can be written in the form of AX = B, where
A = \(\left[\begin{array}{rrr}
2 & 1 & 1 \\
1 & -2 & -1 \\
0 & 3 & -5
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) and B = \(\left[\begin{array}{l}
1 \\
\frac{3}{2} \\
9
\end{array}\right]\)

Now, |A| = 2(10 + 3) – 1 (- 5 – 3) + 0
= 2 (13) – 1 (- 8) = 26 + 8 = 34 ≠ 0
Thus, A is non-singular. Therefore, its inverse exists.
Cofactors of A are
A₁₁ = 13,
A₁₂ = 5,
A₁₃ = 3
A₂₁ = 8,
A₂₂ = – 10,
A₂₃ = – 6
A₃₁ = 1,
A₃₂ = 3,
A₃₃ = – 5

Question 12.
x – y + z = 4, 2x + y – 3z = 0, x + y + z = 2.
Solution.
The given system of equations can be written in the form of AX = B,
where
A = \(\left[\begin{array}{ccc}
1 & -1 & 1 \\
2 & 1 & -3 \\
1 & 1 & 1
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) and B = \(\left[\begin{array}{l}
4 \\
0 \\
2
\end{array}\right]\)
Now |A| = 1 (1 + 3) + 1 (2 + 3) + 1 (2 – 1)
= 4 + 5 + 1 = 10 ≠ 0
Thus, A is non-singular. Therefore, its inverse exists.
Cofactors of A are
A₁₁ = 4,
A₁₂ = – 5,
A₁₃ = 1
A₂₁ = 2,
A₂₂ = 0,
A₂₃ = – 2
A₃₁ = 2,
A₃₂ = 5,
A₃₃ = 3

∴ adj (A) = \(\left[\begin{array}{rrr}
4 & 2 & 2 \\
-5 & 0 & 5 \\
1 & -2 & 3
\end{array}\right]\)

Question 13.
2x + 3y + 3z = 5, x – 2y + z = – 4, 3x – y – 2z = 3.
Solution.
The given system of equations can be written in the form of AX = B,
where
A = \(\left[\begin{array}{rrr}
2 & 3 & 3 \\
1 & -2 & 1 \\
3 & -1 & -2
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) and B = \(\left[\begin{array}{r}
5 \\
-4 \\
3
\end{array}\right]\)
Now, |A| = 2(4 + 1) – 3 (- 2 – 3) + 3 (- 1 + 6)
= 2(5) – 3 (- 5) + 3(5)
= 10 + 15 + 15 =40 ≠ 0
Thus, A is non-singular. Therefore, its inverse exists.
Cofactors of A are
A₁₁ = 5,
A₁₂ = 5,
A₁₃ = 5,
A₂₁ = 3,
A₂₂ = – 13,
A₃₂ = 11
A₃₁ = 9,
A₃₂ = 1,
A₃₃ = – 7

Question 14.
x – y + 2z = 7, 3x + 4y – 5z = – 5, 2x – y + 3z = 12.
Solution.
The given system of equations can be written in the form of AK = B,
where
A = \(\left[\begin{array}{rrr}
1 & -1 & 2 \\
3 & 4 & -5 \\
2 & -1 & 3
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) and B = \(\left[\begin{array}{c}
7 \\
-5 \\
12
\end{array}\right]\)
Now, |A| = 1 (12 – 5) + 1 (9 + 10) + 2(- 3 – 8)
= 7 + 19 – 22 = 4 ≠ 0
Thus, A is non-singular. Therefore, its inverse exists.
Cofactors of A are
A₁₁ = 7,
A₁₂ = -19,
A₁₃ = -11
A₂₁ = 1,
A₂₂ = – 1,
A₂₃ = – 1
A₃₁ = – 3,
A₃₂ = 11,
A₃₃ = 7

Question 15.
If A = \(\) find A^-1. Using A^-1, solve the system of equations 2x – 3y + 5z = 11, 3x + 2y – 4z = – 5, x + y – 2z = – 3
Solution.
The given system of equations can be written in the form of AX = B, where
A = \(\left[\begin{array}{rrr}
2 & -3 & 5 \\
3 & 2 & -4 \\
1 & 1 & -2
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) and B = \(\left[\begin{array}{r}
11 \\
-5 \\
-3
\end{array}\right]\)
Now, |A| = 2(- 4 + 4) + 3(- 6 + 4) + 5 (3 – 2)
= 0 – 6 + 5 = – 1 ≠ 0
Thus, A is non-singular. Therefore, its inverse exists.
Cofactors of A are
A₁₁ = 0,
A₁₂ = 2,
A₁₃ = 1,
A₂₁ = – 1,
A₂₂ = – 9,
A₂₃ = – 5
A₃₁ = 2,
A₃₂ = 23,
A₃₃ = 13.

Question 16.
The cost of 4 kg onion, 3kg wheat and 2 kg rice is ₹ 60. The cost of 2kg onion, 4kg wheat and 6kg rice is ₹ 90. The cost of 6 kg onion, 2 kg wheat and 3 kg rice is ₹ 70. Find the cost of each item per kg by matrix method.
Solution.
Let the cost of onions, wheat and rice per kg be ₹ x, ₹ y and ₹ z respectively.
Then, the given situation can be represented by a system of equations as
4x + 3y + 2z = 60
2x + 4y + 6z = 90
6x + 2y + 3z = 70
This system of equations can be written in the form of AX = B, where
A = \(\left[\begin{array}{lll}
4 & 3 & 2 \\
2 & 4 & 6 \\
6 & 2 & 3
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) and B = \(\left[\begin{array}{l}
60 \\
90 \\
70
\end{array}\right]\)
∴ |A| = 4 (12 – 12) – 3 (6 – 36) + 2 (4 – 24)
= 0 + 90 – 40 = 50 ≠ 0
Thus, A is non-singular. Therefore its inverse exists.
Cofactors of A are
A₁₁ = 0,
A₁₂ = 30,
A₁₃ = – 20,
A₂₁ = – 5,
A₂₂ = 0,
A₂₃ = 10,
A₃₁ = 10,
A₃₂= – 20,
A₃₃ = 10.

∴ x = 5, y = 8 and z = 8.
Hence, the cost of onion is ₹ 5 per kg, the cost of wheat is ₹ 8 per kg and the cost of rice is ₹ 8 per kg.