PSEB 12th Class Maths Solutions Chapter 5 Continuity and Differentiability Ex 5.3

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 5 Continuity and Differentiability Ex 5.3 Textook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 5 Continuity and Differentiability Ex 5.3

Direction (1 – 15): Find \(\frac{d y}{d x}\) in the following :

Question 1.
2x + 3y = sin x
Solution.
Given, 2x + 3y = sin x
On differentiating w.r.t. x, we get
\(\frac{d}{d x}\) (2x + 3y) = \(\frac{d}{d x}\) (sin x)
⇒ \(\frac{d}{d x}\) (2x) + \(\frac{d}{d x}\) (3y) = cos x
⇒ 2 + 3 \(\frac{d y}{d x}\) = cos x dx
⇒ 3 \(\frac{d y}{d x}\) = cos x – 2
∴ \(\frac{d y}{d x}=\frac{\cos x-2}{3}\)

Question 2.
2x + 3y = sin y
Solution.
Given, 2x + 3y = sin y
On differentiating w.r.t. x, we get
\(\frac{d}{d x}\) (2x) + \(\frac{d}{d x}\) (3y) = \(\frac{d}{d x}\) (sin y)
⇒ 2 + 3 \(\frac{d y}{d x}\) = cos y \(\frac{d y}{d x}\)
⇒ 2 = (cos y – 3) \(\frac{d y}{d x}\)
∴ \(\frac{d y}{d x}\) = \(\frac{2}{\cos y-3}\)

Question 3.
ax + by² = cos y
Solution.
Given, ax + by² = cos y
On differentiating w.r.t. x, we get
\(\frac{d}{d x}\) (ax) + \(\frac{d}{d x}\) (y²) = \(\frac{d}{d x}\) (cos y)
⇒ a + b \(\frac{d}{d x}\) (y²) = \(\frac{d}{d x}\) (cos y) …………(i)
Using chain rule,
\(\frac{d}{d x}\) (y²) \(\frac{d y}{d x}\) and
\(\frac{d}{d x}\) (cos y) = – sin y \(\frac{d y}{d x}\) …………..(ii)
From (i) and (ii), we get
a + b × 2y \(\frac{d y}{d x}\) = – sin y \(\frac{d y}{d x}\)
⇒ (2by + sin y) \(\frac{d y}{d x}\) = – a
∴ \(\frac{d y}{d x}=\frac{-a}{2 b y+\sin y}\)

Question 4.
xy + y² = tanx + y
Solution.
Given, xy + y² = tanx + y
On differenating w.r.t. x, we get
\(\frac{d}{d x}\) (xy + y²) = \(\frac{d}{d x}\) (tanx + y)
⇒ \(\frac{d}{d x}\) (xy) + \(\frac{d}{d x}\) (y²) = \(\frac{d}{d x}\) (tanx) + \(\frac{d y}{d x}\)

⇒ [y . \(\frac{d}{d x}\) (x) + x . \(\frac{d y}{d x}\)] + 2y \(\frac{d y}{d x}\) = sec² x + \(\frac{d y}{d x}\)

⇒ y . 1 + x \(\frac{d y}{d x}\) + 2y \(\frac{d y}{d x}\) = sec² x + \(\frac{d y}{d x}\)

⇒ (x + 2y – 1) \(\frac{d y}{d x}\) = sec² x – y
∴ \(\frac{d y}{d x}=\frac{\sec ^{2} x-y}{(x+2 y-1)}\)

Question 5.
x² + xy + y² = 100
Sol.
Given, x² + xy + y² = 100
On differentiating w.r.t. x, we get
\(\frac{d}{d x}\) (x² + xy + y²) = \(\frac{d}{d x}\) (100)
⇒ \(\frac{d}{d x}\) (x²) + \(\frac{d}{d x}\) (xy) + \(\frac{d}{d x}\) (y²) = 0
⇒ 2x + [y . \(\frac{d}{d x}\) (x) + x . \(\frac{d y}{d x}\)] + 2y \(\frac{d y}{d x}\) = 0
⇒ 2x + y . 1 + x . \(\frac{d y}{d x}\) + 2y \(\frac{d y}{d x}\) = 0
⇒ 2x + y + (x + 2y) \(\frac{d y}{d x}\) = 0
⇒ \(\frac{d y}{d x}\) = – \(-\frac{2 x+y}{x+2 y}\)

Question 6.
x³ + x²y + xy² + y³ = 81
Solution.
Given, x³ + x²y + xy² + y³ = 81
On differentiating w.rt. x, we get
\(\frac{d}{d x}\) (x³ + x²y + xy² + y³) = \(\frac{d}{d x}\) (81)

⇒ \(\frac{d}{d x}\) (x³) + \(\frac{d}{d x}\) (x²y) + \(\frac{d}{d x}\) (xy²) + \(\frac{d}{d x}\) (y³) = 0

⇒ 3x² + [y \(\frac{d}{d x}\) x² + x² \(\frac{d y}{d x}\)] + [y² \(\frac{d}{d x}\) (x) + x \(\frac{d}{d x}\) (y²)] + 3 y² \(\frac{d}{d x}\) = 0

⇒ 3x² + [y . 2x + x² \(\frac{d y}{d x}\)] + [y² . 1 + x . 2y . \(\frac{d y}{d x}\)] + 3y² \(\frac{d y}{d x}\) = 0

⇒ (x² + 2xy + 3y²) \(\frac{d y}{d x}\) + (3x² + 2xy + y²)

∴ \(\frac{d y}{d x}=\frac{-\left(3 x^{2}+2 x y+y^{2}\right)}{\left(x^{2}+2 x y+3 y^{2}\right)}\)

Question 7.
sin² y + cos xy = k
Solution.
Given, sin² y + cos xy = k
On differentiating w.r.t. x, we get
⇒ \(\frac{d}{d x}\) (sin² y + cos xy) = \(\frac{d}{d x}\) (k)

⇒ \(\frac{d}{d x}\) (sin² y) + \(\frac{d}{d x}\) (cos xy) = 0 ……….(i)
Using chain rule, we get
\(\frac{d}{d x}\) (sin² y) = 2 sin y \(\frac{d}{d x}\) (sin y) = 2 sin y cos y \(\frac{d y}{d x}\) ………….(ii)

\(\frac{d}{d x}\) (cos xy) = – sin xy \(\frac{d}{d x}\) (xy) = – sin xy[y \(\frac{d}{d x}\) (x) + x \(\frac{d y}{d x}\)]

= – sin xy [y . 1 + x \(\frac{d y}{d x}\)] = – y sin xy – x sin xy \(\frac{d y}{d x}\) ………..(iii)
From Eq.s (i), (ii) and (iii), we get
2 sin y cos y \(\frac{d}{d x}\) – y sin xy – x sin xy \(\frac{d y}{d x}\) = 0
(2 sin y cos y – x sin xy) \(\frac{d y}{d x}\) = y sin xy
(sin 2y – x sin xy) \(\frac{d y}{d x}\) =y sin xy
∴ \(\frac{d y}{d x}\) = \(\frac{y \sin x y}{\sin 2 y-x \sin x y}\)

Question 8.
sin² x + cos² y = 1
Solution.
Given, sin² x + cos² y = 1
On differentiating w.r.t. x, we get
\(\frac{d}{d x}\) (sin² x + cos² y) = \(\frac{d}{d x}\) (1)
⇒ \(\frac{d}{d x}\) (sin² x) + \(\frac{d}{d x}\) (cos² y) = 0

⇒ 2 sin x . ⇒ (sin x) + 2 cos y . \(\frac{d}{d x}\) (cos y) = 0

⇒ 2 sin x cos x + 2 cos y (- sin y) . \(\frac{d y}{d x}\) = 0

⇒ sin 2x – sin 2y \(\frac{d y}{d x}\) = 0

∴ \(\frac{d y}{d x}=\frac{\sin 2 x}{\sin 2 y}\)

Question 9.
y = sin^-1 \(\left(\frac{2 x}{1+x^{2}}\right)\)
Solution.
Given, y = sin^-1 \(\left(\frac{2 x}{1+x^{2}}\right)\)
⇒ sin y = \(\left(\frac{2 x}{1+x^{2}}\right)\)
On differentiating w.r.t. x, we get
\(\frac{d}{d x}\) (sin y) = \(\frac{d}{d x}\) (\(\left(\frac{2 x}{1+x^{2}}\right)\))

cos y \(\frac{d y}{d x}\) = \(\frac{d}{d x}\) (\(\left(\frac{2 x}{1+x^{2}}\right)\)) …………(i)

The function \(\left(\frac{2 x}{1+x^{2}}\right)\) is of the form of \(f\frac{u}{v}\)

Therefore, by quotient rule, we get

Alternate method:
y = sin^-1 \(\left(\frac{2 x}{1+x^{2}}\right)\), put x = tan θ
θ = tan^-1 x
= sin^-1 \(\left(\frac{2 \tan \theta}{1+\tan ^{2} \theta}\right)\)
= sin^-1 sin 2θ
= 2θ = 2 tan^-1 x [∵ sin^-1 sin(θ) = θ]
∴ \(\frac{d y}{d x}=\frac{2}{1+x^{2}}\).

Question 10.
y = tan^-1 \(\left(\frac{3 x-x^{3}}{1-3 x^{2}}\right)\), \(-\frac{1}{\sqrt{3}}<x<\frac{1}{\sqrt{3}}\)
Solution.
Given, y = tan^-1 \(\left(\frac{3 x-x^{3}}{1-3 x^{2}}\right)\)

⇒ tan y = \(\left(\frac{3 x-x^{3}}{1-3 x^{2}}\right)\) …………(i)
It is known that, tan y = \(\frac{3 \tan \frac{y}{3}-\tan ^{3} \frac{y}{3}}{1-3 \tan ^{2} \frac{y}{3}}\) ………..(ii)
On comparing Eqs. (i) and (ii), we get

x = tan \(\frac{y}{3}\)

On differenating w.r.t x, we get

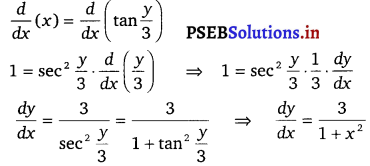
Question 11.
y = cos^-1 \(\left(\frac{1-x^{2}}{1+x^{2}}\right)\), 0 < x < 1
Solution.
Given, y = cos^-1 \(\left(\frac{1-x^{2}}{1+x^{2}}\right)\)
⇒ cos y = cos^-1 \(\left(\frac{1-x^{2}}{1+x^{2}}\right)\)

⇒ \(\frac{1-\tan ^{2} \frac{y}{2}}{1+\tan ^{2} \frac{y}{2}}=\frac{1-x^{2}}{1+x^{2}}\)

On comparing L.H.S. and R.H.S. of the above relationship, we get
tan \(\frac{y}{2}\) = x

On differentiating wr.t. x, we get

Question 12.
y = sin^-1 \(\left(\frac{1-x^{2}}{1+x^{2}}\right)\), 0 < x < 1
Solution.
Given, y = sin^-1 \(\left(\frac{1-x^{2}}{1+x^{2}}\right)\)

sin y = \(\left(\frac{1-x^{2}}{1+x^{2}}\right)\)

On differentiating wr.t. x, we get

\(\frac{d}{d x}\) (sin y) = \(\frac{d}{d x}\) \(\left(\frac{1-x^{2}}{1+x^{2}}\right)\)

Usin chain rule, we get

Question 13.
y = cos^-1 \(\left(\frac{2 x}{1+x^{2}}\right)\), – 1 < x < 1
Solution.
Given, y = cos^-1 \(\left(\frac{2 x}{1+x^{2}}\right)\)

cos y = \(\frac{2 x}{1+x^{2}\)

On differentiating wr.t. x, we get

Question 14.
y = sin^-1 \(\left(2 x \sqrt{1-x^{2}}\right)\), \(-\frac{1}{\sqrt{2}}<x<\frac{1}{\sqrt{2}}\)
Solution.
Given, y = sin^-1 \(\left(2 x \sqrt{1-x^{2}}\right)\), \(-\frac{1}{\sqrt{2}}<x<\frac{1}{\sqrt{2}}\)

⇒ sin y = 2x\(\sqrt{1-x^{2}}\)

On differentiating wr.t. x, we get

Question 15.
y = sec^-1 \(\left(\frac{1}{2 x^{2}-1}\right)\), 0 < x < \(\frac{1}{\sqrt{2}}\)
Solution.
Given, y = sec^-1 \(\left(\frac{1}{2 x^{2}-1}\right)\)
⇒ sec y = \(\frac{1}{2 x^{2}-1}\)
⇒ cos y = 2x² – 1
⇒ 2x² = 1 + cos y
⇒ 2x² = 2 cos² \(\frac{y}{2}\)
⇒ x = cos \(\frac{y}{2}\)
On differentiating wr.t. x, we get