PSEB 12th Class Maths Solutions Chapter 5 Continuity and Differentiability Ex 5.4

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 5 Continuity and Differentiability Ex 5.4 Textook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 5 Continuity and Differentiability Ex 5.4

Question 1.
\(\frac{e^{x}}{\sin x}\)

Solution.
Let y = \(\frac{e^{x}}{\sin x}\)

By using the quotient rule, we get

\(\frac{d y}{d x}\) = \(\frac{\sin x \frac{d}{d x}\left(e^{x}\right)-e^{x} \frac{d}{d x}(\sin x)}{\sin ^{2} x}\)

= \(\frac{\sin x \cdot\left(e^{x}\right)-e^{x} \cdot(\cos x)}{\sin ^{2} x}\)

= \(\frac{e^{x}(\sin x-\cos x)}{\sin ^{2} x}\), x ≠ nπ, n ∈ Z.

Question 2.
e^sin-1 x.
Solution.
Let y = e^sin-1 x
By using the chain rule, we get

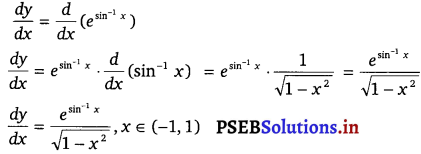
Question 3.
e^x3
Solution.
Let y = e^x3
By using the chain rule, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\) (e^x3)

= e^x3 . \(\frac{d}{d x}\) (x³)

= e^x3 . 3x²
= 3x² e^x3

Question 4.
sin(tan^-1 e^-x
Solution.
Let y = sin(tan^-1 e^-x
By using the chain rule, we get

Question 5.
log (cos e^x)
Solution.
Let y = log (cos e^x)
By using the chain rule, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\) [log (cos e^x)]

= \(\frac{1}{\cos e^{x}}\) . \(\frac{d}{d x}\) (cos e^x)

= \(\frac{1}{\cos e^{x}}\) . (- sin e^x) . \(\frac{d}{d x}\) (e^x)

= \(\frac{-\sin e^{x}}{\cos e^{x}}\) . e^x

= – e^x tan e^x, e^x ≠ (2n + 1) \(\frac{\pi}{2}\), n ∈ N.

Question 6.
\(e^{x}+e^{x^{2}}+\ldots+e^{x^{5}}\)
Solution.
\(e^{x}+e^{x^{2}}+\ldots+e^{x^{5}}\)
By using the chain rule, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\) (\(e^{x}+e^{x^{2}}+\ldots+e^{x^{5}}\))

= \(\frac{d}{d x}\) (e^x ) + \(\frac{d}{d x}\) (e^x2) + \(\frac{d}{d x}\) (e^x3) + \(\frac{d}{d x}\) (e^x4) + \(\frac{d}{d x}\) (e^x5)

= e^{x + [ex2 . \(\frac{d}{d x}\) (x2)] + [ ex3 . \(\frac{d}{d x}\) (x3)] + [ex4 . \(\frac{d}{d x}\) (x4)] + [ex5 . \(\frac{d}{d x}\) (x5)]}

= e^x + (e^x2 × 2x) + (e^x3 × 3x²) + (e^x4 × 4x³) + (e^x5 × 5x⁴)

= e^x + 2x e^x2 + 3x² e^x3 + 4x³ e^x4 + 5x⁴ e^x5

Question 7.
\(\sqrt{e^{\sqrt{x}}}\), x > 0
Solution.
Let y = \(\sqrt{e^{\sqrt{x}}}\)
Then, y² = e^√x
On differentiating w.r.t x, we get
y² = e^√x
⇒ 2y \(\frac{d y}{d x}\) = e^√x (√x)

⇒ 2y \(\frac{d y}{d x}\) = e^√x \(\frac{1}{2} \cdot \frac{1}{\sqrt{x}}\)

⇒ \(\frac{d y}{d x}=\frac{e^{\sqrt{x}}}{4 y \sqrt{x}}\)

⇒ \(\frac{d y}{d x}=\frac{e^{\sqrt{x}}}{4 \sqrt{e^{\sqrt{x}}} \sqrt{x}}\)

⇒ \(\frac{d y}{d x}=\frac{e^{\sqrt{x}}}{4 \sqrt{x e^{\sqrt{x}}}}\), x > 0

Question 8.
log (log x), x > 1
Solution.
Let y = log (log x)
By using the chain rule, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\) [log (log x)]
= \(\frac{1}{\log x} \cdot \frac{d}{d x}\) (log x)

= \(\frac{1}{\log x} \cdot \frac{1}{x}=\frac{1}{x \log x}\), x > 1.

Question 9.
\(\frac{\cos x}{\log x}\), x > 0
Solution.
Let y = \(\frac{\cos x}{\log x}\)
By using quotient rule, we get
\(\frac{d y}{d x}=\frac{\frac{d}{d x}(\cos x) \times \log x-\cos x \times \frac{d}{d x}(\log x)}{(\log x)^{2}}\)

= \(\frac{-\sin x \log x-\cos x \times \frac{1}{x}}{(\log x)^{2}}\)

= \(\frac{-[x \log x \sin x+\cos x]}{x(\log x)^{2}}\), x > 0.

Question 10.
cos (log x + e^x), x > 0
Solution.
Let y = cos (log x + e^x)
By using chain rule, we get
\(\frac{d y}{d x}\) = – sin (log x + e^x) + \(\frac{d}{d x}\) (log x + e^x)
= – sin (log x + e^x) . [\(\frac{d}{d x}\) (log x) + \(\frac{d}{d x}\) (e^x)]
= – sin (log x + e^x) . (\(\frac{1}{x}\) + e^x)
= – (\(\frac{1}{x}\) + e^x) sin (log x + e^x).