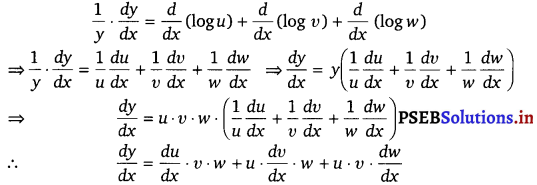PSEB 12th Class Maths Solutions Chapter 5 Continuity and Differentiability Ex 5.5

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 5 Continuity and Differentiability Ex 5.5 Textook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 5 Continuity and Differentiability Ex 5.5

DirectIon (1 – 11): Differentiate the following functions w.r.t. x:

Question 1.
cos x . cos 2x . cos 3x
Solution.
Let y = cos x . cos 2x . cos 3x
Taking logarithm on othsides, we get
log y = log(cos x . cos 2x . cos 3x)
⇒ log y = log (cos x) + log (cos 2x) + log (cos 3x)
On differentiating bothsides w.r.t x, we get
\(\frac{1}{y}\) . \(\frac{d y}{d x}\) = \(\frac{1}{\cos x}\) \(\frac{d}{d x}\) (cos x) + \(\frac{1}{\cos 2 x}\) . \(\frac{d}{d x}\) (cos 2x) + \(\frac{1}{\cos 3 x}\) . \(\frac{d}{d x}\) (cos 3x)

⇒ \(\frac{d y}{d x}\) = y \(\left[-\frac{\sin x}{\cos x}-\frac{\sin 2 x}{\cos 2 x} \cdot \frac{d}{d x}(2 x)-\frac{\sin 3 x}{\cos 3 x} \cdot \frac{d}{d x}(3 x)\right]\)

∴ \(\frac{d y}{d x}\) = – cos x . cos 2x . cos 3x [tan x + 2 tan 2x + 3 tan 3x]

Question 2.
\(\sqrt{\frac{(x-1)(x-2)}{(x-3)(x-4)(x-5)}}\)

Solution.
Let y = \(\sqrt{\frac{(x-1)(x-2)}{(x-3)(x-4)(x-5)}}\)

Taking logarithm on othsides, we get
log y = log \(\sqrt{\frac{(x-1)(x-2)}{(x-3)(x-4)(x-5)}}\)

⇒ log y = \(\frac{1}{2}\) log \(\sqrt{\frac{(x-1)(x-2)}{(x-3)(x-4)(x-5)}}\)

⇒ log y = \(\frac{1}{2}\) – [log {(x – 1) (x – 2)} – log {(x – 3) (x – 4) (x – 5)}]

⇒ log y = \(\frac{1}{2}\) [log (x – 1) + log (x – 2) – log (x – 3) – log (x – 4) – log (x – 5)]

On differentiating bothsides w.r.t x, we get

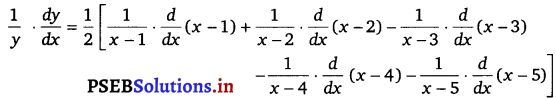
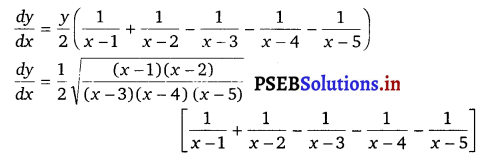
Question 3.
(log x)^{cos x}
Solution.
Let y = (log x)^{cos x}
On differentiating bothsides w.r.t x, we get

\(\frac{1}{y}\) . \(\frac{d y}{d x}\) = \(\frac{d}{d x}\) (cos x) × log(log x) + cos x × \(\frac{d}{d x}\) [log (log x)]

⇒ \(\frac{1}{y}\) . \(\frac{d y}{d x}\) = – sin x log (log x) + cos x × \(\frac{1}{\log x}\) . \(\frac{d}{d x}\) (log x)

⇒ \(\frac{d y}{d x}\) = y [- sin x log (log x) + \(\frac{\cos x}{\log x} \times \frac{1}{x}\)]

∴ \(\frac{d y}{d x}\) = (log x)^{cos x} [\(\frac{\cos x}{x \log x}\) – sin x log (log x)]

Question 4.
x^x – 2^{sin x}
Solution.
Let y = x^x – 2^{sin x}
Also, let x^x = u and 2^{sin x} = v
∴ y = u – v
⇒ \(\frac{d y}{d x}\) = \(\frac{d u}{d x}\) – \(\frac{d v}{d x}\)
Now, u = x^x
Taking lagarithm on bothsides, we get
log u = x log x
On differentiating bothsides w.r.t x, we get
\(\frac{1}{u}\) . \(\frac{d u}{d x}\) = [\(\frac{d}{d x}\) (x) × log x + x × \(\frac{d}{d x}\) (log x)]

⇒ \(\frac{d u}{d x}\) = u [1 × log x + x × \(\frac{1}{x}\)]

⇒ \(\frac{d u}{d x}\) = x^x (log x + 1)

⇒ \(\frac{d u}{d x}\) = x^x (1 + log x)
And, v = 2^{sin x}
Taking lagarithm on bothsides, we get
log v = sin x log 2
On differentiating bothsides w.r.t x, we get
\(\frac{1}{v}\) . \(\frac{d v}{d x}\) = log 2 . [\(\frac{d}{d x}\) (sin x)

⇒ \(\frac{d v}{d x}\) = v log 2 cos x

⇒ \(\frac{d v}{d x}\) = 2^{sin x} cos x log 2

⇒ \(\frac{d y}{d x}\) = x^x (1 + log x) – 2^{sin x} cos x log 2.

Question 5.
(x + 3)² . (x + 4)³ . (x + 5)⁴
Solution.
Let y = (x + 3)² . (x + 4)³ . (x + 5)⁴
Taking lagarithm on bothsides, we get
log y = log (x + 3)² + log (x + 4)³ + log (x + 5)⁴
log y = 2 log (x + 3) + 3 log (x + 4) + 4 log (x + 5)
On differentiating bothsides w.r.t x, we get
\(\frac{1}{y}\) . \(\frac{d y}{d x}\) = 2 . \(\frac{1}{x+3}\) . \(\frac{d}{d x}\) (x + 3) + 3 . \(\frac{1}{x+4}\) . \(\frac{d}{d x}\) (x + 4) + 4 . \(\frac{1}{x +5}\) \(\frac{d}{d x}\) (x + 5)

⇒ \(\frac{d y}{d x}\) = y \(\left[\frac{2}{x+3}+\frac{3}{x+4}+\frac{4}{x+5}\right]\)

⇒ \(\frac{d y}{d x}\) = (x + 3)² . (x + 4)³ . (x + 5)⁴ \(\left[\frac{2}{x+3}+\frac{3}{x+4}+\frac{4}{x+5}\right]\)

⇒ \(\frac{d y}{d x}\) = (x + 3)² + (x + 4)³ + (x + 5)⁴ . \(\left[\frac{2(x+4)(x+5)+3(x+3)(x+5)+4(x+3)(x+4)}{(x+3)(x+4)(x+5)}\right]\)

⇒ \(\frac{d y}{d x}\) = (x + 3) (x + 4)² (x + 5)³ . [2 (x² + 9x + 20) + 3 (x² + 8x + 15 + 4 (x² + 7x + 12)]

⇒ \(\frac{d y}{d x}\) = (x + 3) (x + 4)² (x + 5)³ . [2x² + 18x + 40 + 3x² + 24x + 45 + 4x² + 28x + 48]

∴ \(\frac{d y}{d x}\) = (x + 3) (x + 4)² (x + 5)³ (9x² + 70x + 133)

Question 6.
\(\left(x+\frac{1}{x}\right)^{x}+x^{\left(1+\frac{1}{x}\right)}\)
Solution.
Let y = \(\left(x+\frac{1}{x}\right)^{x}+x^{\left(1+\frac{1}{x}\right)}\)

Also, let u = \(\left(x+\frac{1}{x}\right)^{x}\) and v = \(x^{\left(x+\frac{1}{x}\right)}\)

∴ y = u + v
⇒ \(\frac{d y}{d x}\) = \(\frac{d u}{d x}\) + \(\frac{d v}{d x}\)
Then, u = \(\left(x+\frac{1}{x}\right)^{x}\)
⇒ log u = log \(\left(x+\frac{1}{x}\right)^{x}\)
⇒ log u = x log (x + \(\frac{1}{x}\)) (Taking log on bothsides)
On differentiating bothsides w.r.t x, we get

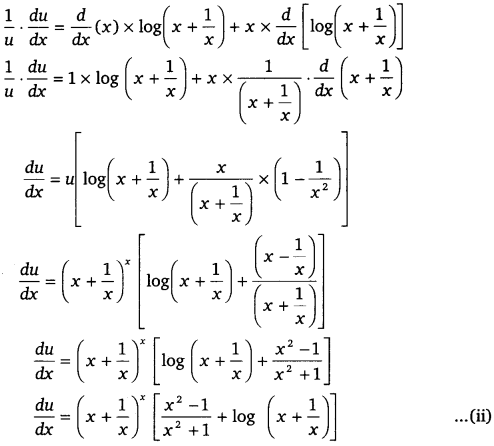
\(\frac{d y}{d x}\) = v \(\left(\frac{-\log x+x+1}{x^{2}}\right)\)

\(\frac{d y}{d x}\) = \(x^{\left(1+\frac{1}{x}\right)}\left(\frac{x+1-\log x}{x^{2}}\right)\) ………….(iii)

Therefore from eqs. (i), (ii) and (iii), we get

\(\frac{d y}{d x}\) = \(\left(x+\frac{1}{x}\right)^{x}\left[\frac{x^{2}-1}{x^{2}+1}+\log \left(x+\frac{1}{x}\right)\right]+x^{\left(1+\frac{1}{x}\right)}\left(\frac{x+1-\log x}{x^{2}}\right)\)

Question 7.
(log x)^x + x^{log x}
Solution.
Let y = (log x)^x + x^{log x}
Also, let u = (log x)^x and v = x^{log x}
∴ y = u + v
⇒ \(\frac{d y}{d x}\) = \(\frac{d u}{d x}\) + \(\frac{d v}{d x}\) ………….(i)
Then, u = (log x)^x
⇒ log u = log [(log x)^x]
(Taking log on bothsides)
⇒ log u = x log (log x)
On differentiating bothsides w.r.t x, we get

Again, v = x^{log x}
⇒ log v = log (x^{log x}) (Taking log on bothsides)
⇒ log v = log x log x
= (log x)²
On differentiating bothsides w.r.t x, we get
\(\frac{1}{v}\) \(\frac{d v}{d x}\) = \(\frac{d}{d x}\) [(log x)²]

⇒ \(\frac{1}{v}\) \(\frac{d v}{d x}\) = 2 (log x) . \(\frac{d}{d x}\) (log x)

⇒ \(\frac{d v}{d x}\) = 2v (log x) . \(\frac{1}{x}\)

⇒ \(\frac{d v}{d x}\) = 2x^{log x} \(\frac{\log x}{x}\)

⇒ \(\frac{d v}{d x}\) = 2x^{log x – 1} . log x
Therefore, from Eqs. (i), (ii) and (iii), we get

\(\frac{d y}{d x}\) = (log x)^{log x – 1} [1 + log x . log (log x)] + 2x^{log x – 1} . log x

Question 8.
(sin x)^x + sin^-1 √x
Solution.
Let y = (sin x)^x + sin^-1 √x
Also, let u = (sin x)^x and v = sin^-1 √x
⇒ y = u + v
⇒ \(\frac{d y}{d x}\) = \(\frac{d u}{d x}\) + \(\frac{d v}{d x}\) ………….(i)
Then, u = (sin x)^x
⇒ log u = log (sin x)^x (Taking log on bothsides)
log u = x log (sin x)
On differentiating bothsides w.r.t x, we get

Question 9.
x^{sin x} + (sin x)^{cos x}
Solution.
Let y = x^{sin x} + (sin x)^{cos x}
also, let u = x^{sin x} and v = (sin x)^{cos x}
⇒ y = u + v
⇒ \(\frac{d y}{d x}\) = \(\frac{d u}{d x}\) + \(\frac{d v}{d x}\)
Then, u = x^{sin x}
⇒ log u = log (x^{sin x}) (Taking log on bothsides)
⇒ log u = sin x log x
On differentiating bothsides w.r.t x, we get
\(\frac{1}{u}\) . \(\frac{d u}{d x}\) = \(\frac{d}{d x}\) (sin x) . log x + sin x . \(\frac{d}{d x}\) (log x)

⇒ \(\frac{d u}{d x}\) = u [cos x log x + sin x . \(\frac{1}{x}\)]

⇒ \(\frac{d u}{d x}\) = x^{sin x} [cos x log x + \(\frac{\sin x}{x}\)] …………..(ii)
Again, v = (sin x)^{cos x}
⇒ log v = log (sin x)^{cos x}
⇒ log v = cos x log (sin x)
On differentiating bothsides w.r.t x, we get
\(\frac{1}{v}\) . \(\frac{d v}{d x}\) = \(\frac{d}{d x}\) (cos x) × log(sin x) + cos x × \(\frac{d}{d x}\) [log(sin x)]

⇒ \(\frac{d v}{d x}\) = v[- sin x . log(sin x) + cos x . \(\frac{1}{\sin x} \cdot \frac{d}{d x}\) (sin x)]

⇒ \(\frac{d v}{d x}\) = (sin x)^{cos x} [- sin x log sin x + \(\frac{\cos x}{\sin x}\) cos x]

⇒ \(\frac{d v}{d x}\) = (sin x)^{cos x} [- sin x log . sin x + cot x cos x]

⇒ \(\frac{d v}{d x}\) = (sin x)^{cos x} [cot x cos x – sin x log sin x] ……………(iii)
Therefore, from Eqs. (i), (ii) and (iii), we get
\(\frac{d v}{d x}\) = x^{sin x} [cos x log x + \(\frac{\sin x}{x}\)] + (sin x)^{cos x} [cot x cos x – sin x log sin x]

Question 10.
x^{x cos x} + \(\frac{x^{2}+1}{x^{2}-1}\)
Solution.
Let y = x^{x cos x} + \(\frac{x^{2}+1}{x^{2}-1}\)
Also, let u = x^{cos x} and v = \(\frac{x^{2}+1}{x^{2}-1}\)
⇒ y = u + v
⇒ \(\frac{d y}{d x}\) = \(\frac{d u}{d x}\) + \(\frac{d v}{d x}\) …………..(i)
Then, u = x^{x cos x}
⇒ log u = log (x)^{x cos x} (Taking log on bothsides)
⇒ log u = x cos x log x
On differentiating bothsides w.r.t x, we get
\(\frac{1}{u}\) . \(\frac{d u}{d x}\) = \(\frac{d}{d x}\) (x) . cos x . log x + x . \(\frac{d}{d x}\) (cos x) . log x + x cos x . \(\frac{d}{d x}\) (log x)

⇒ \(\frac{d u}{d x}\) = u [1 . cos x . log x + x . (- sin x) log x + x cos x . \(\frac{1}{x}\)]

⇒ \(\frac{d u}{d x}\) = x^{x cos x} (cos x log x – x sin x log x + cos x)

\(\frac{d u}{d x}\) = x^{x cos x} [cos x (1 + log x) – x sin x log x] …………..(ii)

Again, v = \(\frac{x^{2}+1}{x^{2}-1}\)

⇒ log v = log(x² + 1) – log (x – 1) (Taking log on both sides)
On differentiating both sides w.r.t x, we get

Question 11.
(x cos x)^x + (x sin x)^{\(\frac{1}{x}\)}
Solution.
Let y = (x cos x)^x + (x sin x)^{\(\frac{1}{x}\)}
Also, let u = (x cos x)^x and v = (x sin x)^{\(\frac{1}{x}\)}
⇒ y = u + v
⇒ \(\frac{d y}{d x}\) = \(\frac{d u}{d x}\) + \(\frac{d v}{d x}\)
Then, u = (x cos x)^x
⇒ log u = log (x cos x)^x (Taking log on both sides)
⇒ log u = x log (x cos x)
⇒ log u = x[log x + log cos x]
⇒ log u = x log x + x log cos x
On differentiating both sides w.r.t x, we get

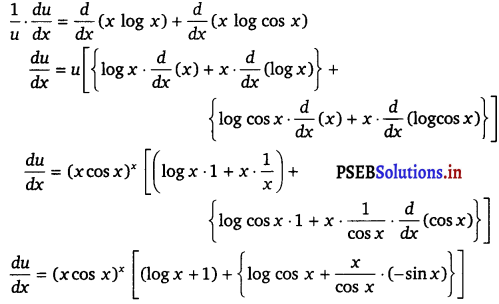
⇒ \(\frac{d u}{d x}\) = (x cos x)^x [(1 + log x) + (log cos x – x tan x)]
⇒ \(\frac{d u}{d x}\) = (x cos x)^x [1 – x tan x + (log x + log cos x)]
⇒ \(\frac{d u}{d x}\) = (x cos x)^x [1 – x tan x + log (x cos x)] …………..(ii)
Again, v = (x sin x)^{\(\frac{1}{x}\)}
⇒ log v = log (x sin x)^{\(\frac{1}{x}\)} (Taking log on both sides)
⇒ log v = \(\frac{1}{x}\) log (x sin x)
⇒ log v = \(\frac{1}{x}\) (log x + log sin x)
⇒ log v = \(\frac{1}{x}\) log x + \(\frac{1}{x}\) log sin x
On differentiating both sides w.r.t x, we get

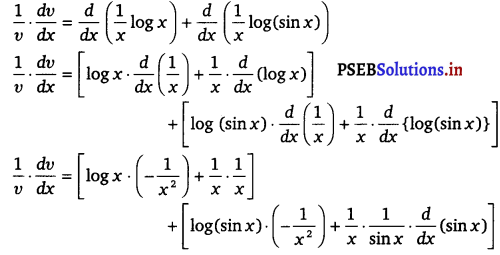
DIrectIon (12 – 15) : Find of the following functions:

Question 12.
x^y + y^x = 1
Solution.
Given, x^y + y^x = 1
Let x^y = u and y^x = v
Then, the function becomes u + v = 1
∴ \(\frac{d u}{d x}\) + \(\frac{d v}{d x}\) = 0
Now, u = x^y
⇒ log u = log(x^y) (Taking log on both sides)
⇒ log u = y log x
On differentiating both sides w.r.t. x, we get
\(\frac{1}{u}\) . \(\frac{d u}{d x}\) = log x \(\frac{d y}{d x}\) + y . \(\frac{d}{d x}\) (log x)

⇒ \(\frac{d u}{d x}\) = x^y [log x \(\frac{d y}{d x}\) + y . \(\frac{1}{x}\)]

⇒ \(\frac{d u}{d x}\) = x^y (log x \(\frac{d y}{d x}\) + \(\frac{y}{x}\)) …………(ii)

Again, v = y^x
⇒ log v = log y^x
⇒ log v = x log y
On differentiating both sides w.r.t. x, we get

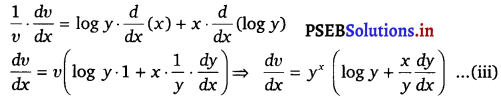
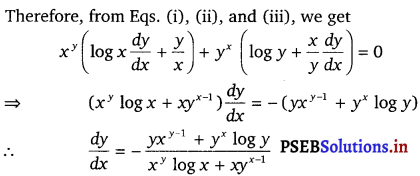
Question 13.
y^x = x^y
Solution.
Given, y^x = x^y
Taking logarithm on both sides , we get
log y^x = log x^y
⇒ x log y = y log x
On differentiating both sides w.r.t. x, we get

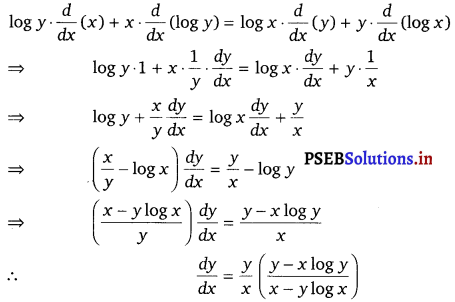
Question 14.
(cos x)^y = (cos y)^x
Solution.
Given, (cos x)^y = (cos y)^x
Taking logarithm on both sides , we get
⇒ log (cos x)^y = log (cos y)^x
⇒ y log (cos x) = x log (cos y)
On differentiating both sides w.r.t. x, we get
log cos x . \(\frac{d y}{d x}\) + y . \(\frac{d}{d x}\) (log cos x) = log cos y . \(\frac{d}{d x}\) (x) + x . \(\frac{d}{d x}\) (log cos y)

⇒ log cos x . \(\frac{d y}{d x}\) + \(\frac{y}{\cos x}\) (- sin x) = log cos y + \(\frac{x}{\cos y}\) (- sin y) . \(\frac{d y}{d x}\)

⇒ log cos x \(\frac{d y}{d x}\) – y tan x = log cos y – x tan y \(\frac{d y}{d x}\)

⇒ (log cos x + x tan y) \(\frac{d y}{d x}\) = y tan x + log cos y

∴ \(\frac{d y}{d x}=\frac{y \tan x+\log \cos y}{x \tan y+\log \cos x}\).

Question 15.
xy = e^{(x – y)}
Solution.
Given, xy = e^{(x – y)}
Taking logarithm on bothsides, we get
⇒ log (xy) = log (e^{(x – y)})
⇒ log x + log y = (x – y) log e
⇒ log x + log y = (x – y) × 1
⇒ log x + log y = x – y
On differentiating both sides w.r.t. x, we get
\(\frac{d}{d x}\) (log x) + \(\frac{d}{d x}\) (log y) = \(\frac{d}{d x}\) (x) – \(\frac{d y}{d x}\)

⇒ \(\frac{1}{x}\) + \(\frac{1}{y}\) . \(\frac{d y}{d x}\) = 1 – \(\frac{d y}{d x}\)

⇒ (1 + \(\frac{1}{y}\)) \(\frac{d y}{d x}\) = 1 – \(\frac{1}{x}\)

⇒ \(\left(\frac{y+1}{y}\right) \frac{d y}{d x}=\frac{x-1}{x}\)

⇒ \(\frac{d y}{d x}=\frac{y(x-1)}{x(y+1)}\)

Question 16.
Find the derivative of the function given by f(x) = (1 + x) (1 + x²) (1 + x⁴) (1 + x⁸) and hence find f(1).
Solution.
Given f(x) = (1 + x) (1 + x²) (1 + x⁴) (1 + x⁸)
Taking logarithm on both sides, we get
log f(x) = log (1 + x) + log (1 + x²) + log(1 + x⁴) + log (1 + x⁸)
On differentiating both sides w.r.t. x, we get
\(\) . \(\frac{d}{d x}\) [f(x)] = \(\frac{d}{d x}\) log (1 + x) + \(\frac{d}{d x}\) log (1 + x²) + log (1 + x⁴) + log (1 + x⁸)

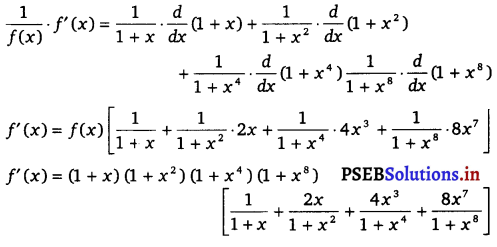
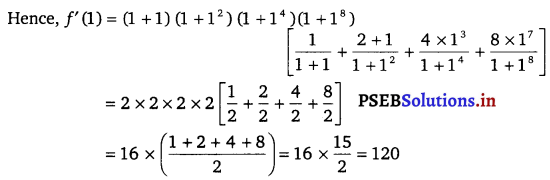
Question 17.
Differentiate(x² – 5x + 8) (x³ + 7x +9) in three ways mentioned below:
(i) By using product rule.
(ii) By expanding the product to obtain a single polynomial.
(iii) By logarithmic differentiation.
Do they all give the same answer?
Solution.
(i) Let y = (x² – 5x + 8) (x³ + 7x + 9)
Let x² – 5x + 8 = u and x³ + 7x + 9 = v
∴ y = uv
⇒ \(\frac{d y}{d x}\) = \(\frac{d u}{d x}\) . v + u . \(\frac{d v}{d x}\)

⇒ \(\frac{d y}{d x}\) = \(\frac{d}{d x}\) (x² – 5x + 8) . (x³ + 7x + 9) + (x² – 5x + 8) . \(\frac{d}{d x}\) (x³ + 7x + 9)

⇒ \(\frac{d y}{d x}\) = (2x – 5) (x³ + 7x + 9) + (x² – 5x + 8) (3x² + 7)

⇒ \(\frac{d y}{d x}\) = 2x (x³ + 7x + 9) – 5 (x³ + 7x + 9) + x² (3x² + 7) – 5x (3x² + 7) + 8 (3x² + 7)

⇒ \(\frac{d y}{d x}\) = (2x⁴ + 14x² + 18x) – 5x³ – 35x – 45 + (3x⁴ + 7x²) – 15x³ – 35x + 24x² + 56

∴ \(\frac{d y}{d x}\) = 5x⁴ – 20x³ + 45x² – 52x + 11

(ii) y = (x² – 5x + 8) (x³ + 7x + 9)
= x² (x³ +7x + 9) – 5x (x³ + 7x + 9) + 8(x³ + 7x + 9)
= x⁵ + 7x³ + 9x² – 5x⁴ – 35x² – 45x + 8x³ 56x + 72
= x⁵ – 5x⁴ + 15x³ – 26x² + 11x + 72
∴ \(\frac{d y}{d x}\) = \(\frac{d}{d x}\) (x⁵ – 5x⁴ + 15x³ – 26x² + 11x + 72)

= \(\frac{d}{d x}\) (x⁵ – \(\frac{d}{d x}\) (5x⁴) + 15 \(\frac{d}{d x}\) (x³ – 26 \(\frac{d}{d x}\) (x²) + 11 \(\frac{d}{d x}\) (x) + \(\frac{d}{d x}\) (72)

= 5x⁴ – 5 × 4x³ + 15 × 3x² – 26 × 2x + 11 × 1 + 0
= 5x⁴ – 20x³ + 45x² – 52x + 11

(iii) y = (x² – 5x + 8) (x³ + 7x + 9)
Taking logarithm on both sides, we get
log y = log (x² – 5x + 8) + log (x³ + 7x + 9)
On differentiating both sides w.r.t x, we get
\(\frac{1}{y}\) . \(\frac{d y}{d x}\) = \(\frac{d}{d x}\) log (x² – 5x + 8) + \(\frac{d}{d x}\) log (x³ + 7x + 9)

⇒ \(\frac{d y}{d x}\) = 2x (x³ + 7x + 9) -5 (x³ + 7x + 9) + 3x² (x² – 5x + 8) + 7 (x² – 5x + 8)

⇒ \(\frac{d y}{d x}\) = (2x⁴ + 14x² + 18x) – 5x³ – 35x – 45 + (3x⁴ – 15x³ + 24x²) + (7x² – 35x + 56)

⇒ \(\frac{d y}{d x}\) = 5x⁴ – 20x³ + 45x² – 52x + 11

From the above three observations, it can be concluded that all the results of \(\frac{d y}{d x}\) are same.

Question 18.
If u, v and w are functions of x, then show that
\(\frac{d}{d x}\) (u . v . w) = \(\frac{d u}{d x}\) v . w + u . \(\frac{d v}{d x}\) . w + u . v . \(\frac{d w}{d x}\)
in two ways-first by repeated application of product rule, second by logarithmic differentiation.
Solution.
Let y = u . v . w = u(v . w)
By applying product rule, we get
\(\frac{d y}{d x}\) = \(\frac{d u}{d x}\) (v . w) + u . \(\frac{d}{d x}\) (v . w)

\(\frac{d y}{d x}\) = \(\frac{d u}{d x}\) v . w + u [\(\frac{d v}{d x}\) . w + v . \(\frac{d w}{d x}\)] (Again, applying product rule)

\(\frac{d y}{d x}\) = \(\frac{d u}{d x}\) . v . w + u . \(\frac{d v}{d x}\) . w + u . v . \(\frac{d w}{d x}\)

By taking logarithm on both sides of the equation y = u u w, we get
log y = log u + log u + log w
On differentiating both sides w.r.t. x, we get