PSEB 12th Class Maths Solutions Chapter 5 Continuity and Differentiability Ex 5.7

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 5 Continuity and Differentiability Ex 5.7 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 5 Continuity and Differentiability Ex 5.7

Direction (1 – 10) : Find the second order derivatives of the following functions.

Question 1.
x² + 3x + 2
Solution.
Let y = x² + 3x + 2
Differentiating w.r.t. r, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\) (x²) + \(\frac{d}{d x}\) (3x) + \(\frac{d}{d x}\) (2)
= 2x + 3 + 0
= 2x + 3
Again, differentiating w.r.t. x, we get
\(\frac{d^{2} y}{d x^{2}}\) = \(\frac{d}{d x}\) (2x + 3)
= \(\frac{d}{d x}\) (2x) + \(\frac{d}{d x}\) (3)
= 2 + 0 = 2.

Question 2.
x²⁰
Sol.
Let y = x²⁰
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\) (x²⁰)
= 20 x¹⁹
Again, differentiating w.r.t. x, we get
\(\frac{d^{2} y}{d x^{2}}\) = \(\frac{d}{d x}\) (20 x¹⁹)
= 20 \(\frac{d}{d x}\) (x¹⁹)
= 20 × 19 × x¹⁸
= 380 × x¹⁸

Question 3.
x . cos x
Solution.
Let y = x cos x
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\) (x . cos x)
= cos x . \(\frac{d}{d x}\) (x) + x \(\frac{d}{d x}\) (cos x)
= cos x . 1 + x (- sin x)
= cos x – x sin x
Again, differentiating w.r.t. x, we get
\(\frac{d^{2} y}{d x^{2}}\) = \(\frac{d}{d x}\) [cos x – x sin x]
= \(\frac{d}{d x}\) (cos x ) – \(\frac{d}{d x}\) (x sin x)
= – sin x – [sin x . \(\frac{d}{d x}\) (x) + x . \(\frac{d}{d x}\) (sin x)]
= – sin x – (sin x + x cos x)
= – (x cos x + 2 sin x)

Question 4.
log x
Solution.
Let y = log x
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\) (log x) = \(\frac{1}{x}\)
Again, differentiating w.r.t. x, we get
\(\frac{d^{2} y}{d x^{2}}\) = \(\frac{d}{d x}\) (\(\frac{1}{x}\))
= \(\frac{-1}{x^{2}}\)

Question 5.
x³ log x
Solution.
Let y = x³ log x
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\) [x³ log x]
= log x . \(\frac{d}{d x}\) (x³) + x³ . \(\frac{d}{d x}\) (log x)
= log x . 3x² + x³ . \(\frac{1}{x}\)
= log x . 3x² + x²
= x² (1 + 3 log x)
Again, differentiating w.r.t. x, we get
\(\frac{d^{2} y}{d x^{2}}\) = \(\frac{d}{d x}\) [x² (1 + 3 log x)]
= (1 + 3 log x) . \(\frac{d}{d x}\) (x²) + x² \(\frac{d}{d x}\) (1 +3 log x)
= (1 + 3 log x) . 2x + x² . \(\frac{3}{x}\)
= 2x + 6x log x + 3x
= 5x + 6x log x
= x (5 + 6 log x)

Question 6.
e^x sin 5x
Solution.
Let y = e^x sin 5x
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\) (e^x sin 5x)
= sin 5x . \(\frac{d}{d x}\) (e^x) + e^x . cos 5x . \(\frac{d}{d x}\) (5x)
= e^x sin 5x + e^x cos 5x . 5
Again, differentiating w.r.t. x, we get
\(\frac{d^{2} y}{d x^{2}}\) = \(\frac{d}{d x}\) [e^x (sin 5x + 5 cos 5x)]
= (sin 5x + 5 cos 5x) . \(\frac{d}{d x}\) (e^x) + e^x . \(\frac{d}{d x}\) (sin 5x + 5 cos 5x)
= (sin 5x + 5 cos 5x) e^x + e^x [cos 5x . \(\frac{d}{d x}\) (5x) + 5 (- sin 5x) . \(\frac{d}{d x}\) (5x)]
= e^x (sin 5x + 5 cos 5x) + e^x (5 cos 5x – 25 sin 5x)
= e^x (10 cos 5x – 24 sin 5x)
= 2 e^x (5 cos 5x – 12 sin 5x)

Question 7.
e^6x cos 3x
Solution.
Let y = e^6x cos 3x
Differentiating w.r.t x, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\) (e^6x . cos 3x)

= cos 3x . e^6x \(\frac{d}{d x}\) (6x) + e^6x . (- sin 3x) . \(\frac{d}{d x}\) (3x)

= 6 e^6x cos 3x – 3 e^6x sin 3x …………….(i)
Again, differentiating w.r.t. x, we get
\(\frac{d^{2} y}{d x^{2}}\) = \(\frac{d}{d x}\) (6 e^6x cos 3x – 3 e^6x sin 3x)

= 6 . \(\frac{d}{d x}\) (e^6x cos 3x) – 3 \(\frac{d}{d x}\) (e^6x sin 3x)

= 6 . [6e^6x cos 3x – 3 e^6x sin 3x] – 3 . [sin 3x . \(\frac{d}{d x}\) (e^6x) + e^6x \(\frac{d}{d x}\) (sin 3x)]

36e^6x cos 3x – 18 e^6x sin 3x – 3 [sin 3x . e^6x . 6 + e^6x . cos 3x . 3] = 36 e^6x cos 3x – 18 e^6x sin 3x – 18 e^6x sin 3x – 9 e^6x cos 3x
= 27 e^6x cos 3x – 36 e^6x sin 3x
= 9 e^6x (3 cos 3x – 4 sin 3x)

Question 8.
tan^-1 x
Solution.
Let y = tan^-1 x
Differentiating w.r.t x, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\) (tan^-1 x)

= \(\frac{1}{1+x^{2}}\)

Again, differentiating w.r.t. x, we get
\(\frac{d^{2} y}{d x^{2}}\) = \(\frac{d}{d x}\) (\(\frac{1}{1+x^{2}}\))

= \(\frac{d}{d x}\) (1 + x²)^-1

= (- 1) (1 + x²)^-2 . \(\frac{d}{d x}\) (1 +x²)

= \(\frac{-1}{\left(1+x^{2}\right)^{2}}\) 2x

= \(\frac{-2 x}{\left(1+x^{2}\right)^{2}}\)

Question 9.
log (log x)
Solution.
Lety = log (log x)
Differentiating w.r.t x, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\) [log (log x)]

= \(\frac{1}{\log x}\) . \(\frac{d}{d x}\) (log x)

= \(\frac{1}{x \log x}\) = (x log x)^-1

Again, differentiating w.r.t. x, we get
\(\frac{d^{2} y}{d x^{2}}\) = \(\frac{d}{d x}\) (x log x)^-1

= (- 1) . (x log x)^-2 . \(\frac{d}{d x}\) (x log x)

= \(\frac{-1}{(x \log x)^{2}} \cdot\left[\log x \cdot \frac{d}{d x}(x)+x \cdot \frac{d}{d x}(\log x)\right]\)

= \(\frac{-1}{(x \log x)^{2}} \cdot\left[\log x \cdot 1+x \cdot \frac{1}{x}\right]=\frac{-(1+\log x)}{(x \log x)^{2}}\)

Question 10.
sin (log x)
Solution.
Let y = sin (log x)
Differentiating w.r.t x, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\) [sin (log x)]

= cos log x . \(\frac{d}{d x}\) (log x)

= \(\frac{\cos (\log x)}{x}\)

Again, differentiating w.r.t. x, we get
\(\frac{d^{2} y}{d x^{2}}\) = \(\frac{d}{d x}\) [latex]\frac{\cos (\log x)}{x}[/latex]

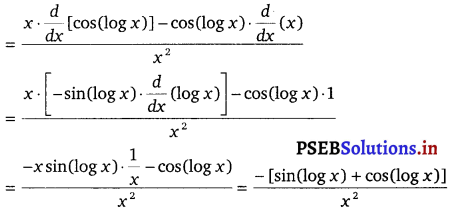
Question 11.
If y = 5 cos x – 3 sin x, prove that \(\frac{d^{2} y}{d x^{2}}\) = 0.
Solution.
Given, y = 5 cos x – 3sin x
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\) (5 cos x) – \(\frac{d}{d x}\) (3 sin x)
= 5 \(\frac{d}{d x}\) (cos x) – 3 \(\frac{d}{d x}\) (sin x)
= 5(- sin x) – 3 cos x
= – (5 sin x + 3 cos x)
Again, differentiating w.r.t. x, we get
\(\frac{d^{2} y}{d x^{2}}\) = \(\frac{d}{d x}\) [- (5 sin x + 3 cos x)]
= – [5 . \(\frac{d}{d x}\) (sin x) + 3 . \(\frac{d}{d x}\) (cos x)]
= – [5 cos x + 3 (- sin x)]
= – [5 cos x – 3 sin x] = – y
\(\frac{d^{2} y}{d x^{2}}\) + y = 0
∴ Hence proved.

Question 12.
If y = cos^-1 x, find \(\frac{d^{2} y}{d x^{2}}\) in terms of y alone.
Solution.
Given, y = cos^-1 x
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = \(\frac{d}{d x}\) (cos^-1 x)

= \(\frac{-1}{\sqrt{1-x^{2}}}=-\left(1-x^{2}\right)^{\frac{-1}{2}}\)

Again, differentiating w.r.t. x, we get

Question 13.
If y = 3 cos (log x) + 4 sin (log x), show that x²y₂ + xy₁ + y = 0.
Solution.
Given, y = 3 cos (log x) + 4 sin (log x), show that x²y₂ + xy₁ + y = 0.
Differentiating w.r.t. x, we get
\(\frac{d x}{d y}\) = y₁
= 3 . \(\frac{d}{d x}\) [cos (log x)] + 4 . \(\frac{d}{d x}\) [sin (log x)]

= 3 . [- sin(log x) . \(\frac{d}{d x}\) (log x)] + 4 . [cos (log x) . \(\frac{d}{d x}\) (log x)]

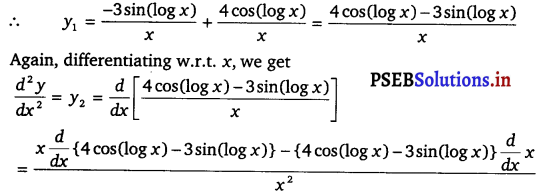
= – sin (log x) – 7 cos (log x) + 4 cos (log x) – 3 sin (log x) + 3 cos (log x) + 4 sin (log x)
= 0
Hence proved.

Question 14.
If y = A e^mx + B e^nx, show that \(\frac{d^{2} y}{d x^{2}}\) – (m + n) \(\frac{d y}{d x}\) + mny = 0.
Solution.
\(\frac{d y}{d x}\) = A . \(\frac{d}{d x}\) (e^mx) + B . \(\frac{d}{d x}\) (e^nx)

= A . e^mx . \(\frac{d}{d x}\) (mx) + B . e^nx . \(\frac{d}{d x}\) (nx)

= Ame^mx + Bne^nx

Again, differentiating w.r.t. x, we get
\(\frac{d^{2} y}{d x^{2}}\) = \(\frac{d}{d x}\) (Ame^mx + Bne^nx)

= Am . \(\frac{d}{d x}\) (e^mx) + Bn . \(\frac{d}{d x}\) (e^nx)

Am . e^mx . \(\frac{d}{d x}\) (mx) + Bne^nx \(\frac{d}{d x}\) (nx)

= Am² e^mx + Bn² e^nx

∴ \(\frac{d^{2} y}{d x^{2}}\) – (m + n) \(\frac{d y}{d x}\) + mny

= Am² e^mx + Bn² e^nx – (m + n) . (Ame^mx + Bne^nx) + mn (Ae^mx + Be^nx)

= Am² e^mx + Bn² e^nx – Am² e^mx – Bmne^nx – Amne^nx – Bn² e^nx + Amne^mx + Bmne^nx = 0

Hence proved.

Question 15.
If y = 500 e^7x + 600 e^-7x, show that \(\frac{d^{2} y}{d x^{2}}\) = 49y.
Solution.
Given, y = 500 e^7x + 600 e^-7x
Differentiating w.r.t. x, we get
\(\frac{d^{2} y}{d x^{2}}\) = 500 . \(\frac{d}{d x}\) (e^7x) + 600 . \(\frac{d}{d x}\) (e^-7x)

= 500 . e^7x \(\frac{d}{d x}\) (7x) + 600 . \(\frac{d}{d x}\) . (- 7x)

Again, differentiating w.r.t. x, we get

\(\frac{d^{2} y}{d x^{2}}\) = 3500 . \(\frac{d}{d x}\) (e^7x) – 4200 \(\frac{d}{d x}\) (e^-7x)

= 3500 . e^7x \(\frac{d}{d x}\) (7x) – 4200 . e^-7x \(\frac{d}{d x}\) (- 7x)

= 7 × 3500 . e^7x + 7 × 4200 . e^-7x
= 49 × 500 e^7x + 49 × 600 ^-7x
= 49 (500 e^7x + 600 e^-7x) = 49 y
Hence proved.

Question 16.
If e^y (x + 1) = 1, show that \(\frac{d^{2} y}{d x^{2}}=\left(\frac{d y}{d x}\right)^{2}\).
Solution.
Given, e^y (x + 1) = 1

e^y = \(\frac{1}{x+1}\)

Taking logarithm on both sides, we get
y = log \(\frac{1}{x+1}\)
Differentiating w.r.t. x, we get
\(\frac{d y}{d x}\) = (x + 1) \(\frac{d}{d x}\) \(\frac{1}{x+1}\)

= (x + 1) . \(\frac{-1}{(x+1)^{2}}=\frac{-1}{x+1}\)

Again, differentiating w.r.t. x, we get
\(\frac{d^{2} y}{d x^{2}}=-\frac{d}{d x}\left(\frac{1}{x+1}\right)\) = \(-\left[\frac{-1}{(x+1)^{2}}\right]=\frac{1}{(x+1)^{2}}\)

⇒ \(\frac{d^{2} y}{d x^{2}}=\left(\frac{-1}{x+1}\right)^{2}\)

⇒ \(\frac{d^{2} y}{d x^{2}}=\left(\frac{d y}{d x}\right)^{2}\)
Hence proved.

Question 17.
If y = (tan^-1 x)², show that (x² + 1)² y₂ + 2x (x² + 1) y₁ = 2.
Solution.
Given, y = (tan x)²
Differentiating w.r.t. x, we get
y₁ = 2 tan^-1 x \(\frac{d}{d x}\) (tan^-1 x)
⇒ y₁ = 2 tan^-1 . \(\frac{1}{1+x^{2}}\)

⇒ (1 + x²) y₁ = 2 tan^-1 x
Again, differentiating w.r.t. x, we get

(1 + x²) \(\frac{d y_{1}}{d x}\) + y₁ \(\frac{d}{d x}\) (1 + x²) = \(\frac{2}{1+x^{2}}\)

⇒ (1 + x²) y₂ + y₁ (0 + 2x) = \(\frac{2}{1+x^{2}}\)
[∵ \(\frac{d}{d x}\) (y₁) = y₁]

⇒ (1 + x²)² y₂ + 2x (1 + x²) y₁ = 2

Hence proved.