PSEB 12th Class Maths Solutions Chapter 6 Application of Derivatives Ex 6.5

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 6 Application of Derivatives Ex 6.5 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 6 Application of Derivatives Ex 6.5

Question 1.
Find the maximum and minimum values, if any, of the following functions given by
(i) = (2x – 1)² + 3
(ii) f(x) = 9x² + 12x + 2
(iii) f(x) = – (x – 1)² + 10
(iv) g(x) = x³ + 1
Solution.
(i) The given function is f(x) = (2x – 1)² + 3.
It can be observed that (2x – 1)² ≥ 0 for every x ∈ R.

Therefore, f(x) = (2x – 1)² + 3 ≥ 3 for every x ∈ R.
The minimum value of f is attained when 2x – 1 = 0
⇒ x = \(\frac{1}{2}\)
∴ Minimum value of f = f(\(\frac{1}{2}\))
= (2 . \(\frac{1}{2}\) – 1)² + 3 = 3
Hence, function f does not have a maximum value.

(ii) The given function is f(x) = 9x² + 12x + 2
= (3x + 2)² – 2
It can be observed that (3x + 2)² ≥ 0 for every x ∈ R.
Therefore, f(x) = (3x + 2)² – 2 ≥ – 2 for every x ∈ R.
The minimum value of f is attained when 3x +2 = 0
⇒ x = \(\frac{-2}{3}\)
∴ Minimum value of f = f(\(\frac{-2}{3}\))= (3 . (\(\frac{- 2}{3}\)) + 2)² – 2 = – 2.
Hence, function f does not have a maximum value.

(iii) The given function is f(x) = -(x – 1)² + 10.
It can be observed that (x – 1)² ≥ 0 for every x ∈ R.
Therefore, f(x) = – (x – 1)² + 10 ≤ 10 for every x ∈ R.
The minimum value off is attained when (x – 1) = 0
⇒ x = 1
∴ Minimum value of f = f(1) = -(1 – 1)² + 10 = 10
Hence, function f does not have a minimum value.

(iv) The given function is g(x) = x³ + 1.
We observe that the value of f(x) increases when the value of x increases and f(x) can be made as large as we please by giving large value to x. So, f(x) does not have the maximum value.
Similarly, f(x) can be made as small as we please by giving smaller values of x.
So, f(x) does not have the minimum value.

Question 2.
Find the maximum and minimum values, if any, of the following functions given by
(i) f(x) = |x + 2| – 1
(ii) g(x) = – |x + 1| + 3
(iii) h(x) = sin (2x) + 5
(iv) f(x) = |sin 4x| + 3|
(v) h(x) = x + 1, x e (-1, 1)
Solution.
(i) Given, f(x) = |x + 2 | – 1
We know that, | x + 2 | ≥ 0 for every x ∈ R.
Therefore, f(x) = |x + 2| – 1 ≥ – 1 for every x ∈ R.
The minimum value of / is attained when | x + 2| = 0
⇒ x = – 2
∴ Minimum value of f = f(- 2) = = |- 2 + 2| – 1 = – 1
Hence, function f does not have a maximum value.

(ii) Given, g(x) = – | x + 1| + 3
We know that -| x + 1| < 0 for every x ∈ R.
Therefore, g(x) = -|x + 1| + 3 ≤ 3 for every x ∈ R.
The maximum value of g is attained when |x + 1| = 0
⇒ x = – 1
∴ Maximum value of g = g(- 1) = -|- 1 + 1| + 3 = 3
Hence, function g does not have a minimum value.

(iii) Given, h(x) = sin 2x + 5
We know that, – 1 ≤ sin 2x ≤ 1
⇒ – 1 + 5 ≤ sin 2x + 5 ≤ 1 + 5
⇒ 4 ≤ sin 2x + 5 ≤ 6
Hence, the maximum and minimum values of h are 6 and 4, respectively.

(iv) Given,f(x) = |sin 4x + 3|
We know that, – 1 < sin 4x < 1
⇒ 2 ≤ sin 4x + 3 ≤ 4
2 ≤ |sin 4x + 3| ≤ 4
Hence, the maximum and minimum values of f are 4 and 2, respectively.

(v) h(x) = x + 1, x ∈ (- 1, 1)
Here, if a point x₀ is closest to – 1, then we find \(\frac{x_{0}}{2}\) + 1 < x₀ ∈ (- 1, 1).
Also, if x₁ is closest to 1, then
x₁ + 1 < \(\frac{x_{1}+1}{2}\) + 1 for all x₁ ∈ (- 1, 1).
Hence, function h(x) has neither maximum nor minimum value in (- 1, 1).

Question 3.
Find the local maxima and local minima, if any, of the following functions, Find also the local maximum and the local minimum values, as the case may be :
(i) f(x) = x²
(ii) g(x) = x³ – 3x
(iii) h(x) = sin x + cos x, 0 < x < \(\frac{\pi}{2}\)
(iv) f(x) = sin x – cos x, 0 < x < 2π
(v) f(x) = x³ – 6x² + 9x + 15
(vi) g(x) = \(\frac{x}{2}+\frac{2}{x}\), x > 0
(vii) g(x) = \(\frac{1}{x^{2}+2}\)
(viii) f(x) = \(x \sqrt{1-x}\), x > 0
Solution.
(i) Given, f(x) = x²
⇒ f'(x) = 2x
Now, f'(x) = 0
⇒ x = 0
Thus, x = 0 is the only critical point which could possibly be the point of local maxima or local minima of f.
We have f”(0) = 2, which is positive.
Therefore, by second derivative test, x = 0 is a point of local minima and local minimum value of f at x = 0 is f(0) = 0.

(ii) Given, g(x) = x³ – 3x
⇒ g'(x) = 3x² – 3
Now, g'(x) = 0
⇒ 3x² = 3
⇒ x = ± 1
∴ g'(x) = 6x
⇒ g'(1) = 6 > 0
⇒ g'(- 1) = – 6 > 0
By second derivative test x = 1 is a point of local minima and local minimum value of g at x = 1 is
g(1) = 1³ – 3
= 1 – 3 = – 2.
However, x = – 1 is a point of local maxima and local maximum value of g at x = – 1 is
g(- 1) = (- 1)³ – 3(- 1)
= – 1 + 3 = 2.

(iii) Given, h(x) = sinx + cos x, 0 < x < \(\frac{\pi}{2}\)
∴ h'(x) = – sin x – cos x = -(sin x + cos x)
h'(x) = 0
⇒ sin x = cos x
⇒ tan x = 1
⇒ x = \(\frac{\pi}{4}\) ∈ (0, \(\frac{\pi}{2}\))
h”(x) = – sin x – cos x
= – (sin x + cos x)
h(\(\frac{\pi}{4}\)) = – \(\left(\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}\right)=-\frac{2}{\sqrt{2}}=-\sqrt{2}<0\)
Therefore, by second derivative test, x = \(\frac{\pi}{4}\) is a point of local maxima and
and the local maximum value of h at x = \(\frac{\pi}{4}\) is h(\(\frac{\pi}{4}\)) = sin \(\frac{\pi}{4}\) + cos \(\frac{\pi}{4}\)
= \(\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}\) = √2.

(iv) f(x) = sin x – cos x, 0 < x < 2π
∴ f'(x) = cos x + sin x f'(x) = 0
⇒ cos x = – sin x ⇒ tan x = 1
⇒ x = \(\frac{3 \pi}{4}\), \(\frac{7 \pi}{4}\) ∈ (0, 2π)
f”(x) = – sin x + cos x f”(\(\frac{3 \pi}{4}\)) = \(-\sin \frac{3 \pi}{4}+\cos \frac{3 \pi}{4}=-\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}}=-\sqrt{2}>0\)

f”(\(\frac{7 \pi}{4}\)) = \(-\sin \frac{7 \pi}{4}+\cos \frac{7 \pi}{4}=\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}=\sqrt{2}>0\)

Therefore, by second derivative test, x = \(\frac{3 \pi}{4}\) is a point of local maxima and the local maximum value of f at x = \(\frac{3 \pi}{4}\) is
f(\(\frac{3 \pi}{4}\)) = sin \(\frac{3 \pi}{4}\) – cos \(\frac{3 \pi}{4}\)
= \(\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}\) = √2.

However, x = \(\frac{7 \pi}{4}\) is a point of local minima and the local minimum value of f at x = \(\frac{7 \pi}{4}\) is
f(\(\frac{7 \pi}{4}\)) = sin \(\frac{7 \pi}{4}\) – cos \(\frac{7 \pi}{4}\)
= \(-\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}}=-\sqrt{2}\)

(v) Given, f(x) = x³ – 6x² + 9x + 15
f'(x) = 3x² – 12x + 9
f'(x) = 0
⇒ 3(x² – 4x + 3) = 0
⇒ 3(x – 1) (x – 3) = 0
⇒ x = 1, 3
Now, f'(x) = 6x – 12 = 6 (x – 2)
f'(1) = 6(1 – 2) = – 6 < 0 ⇒ f'(3) = 6(3 – 2) = 6 > 0
Therefore, by second derivative test, x = 1 is a point of local maxima and the local maximum value of f at x = 1 is
f(1) = 1 – 6 + 9 + 15 = 19.
However, x = 3 is a point of local minima and the local minimum value of f at x = 3 is
f(3) = 27 – 54 + 27 + 15 = 15

(vi) Given, g(x) = \(\frac{x}{2}+\frac{2}{x}\), x > 0

∴ g'(x) = \(\frac{1}{2}-\frac{2}{x^{2}}\)

Now, g'(x) = 0 gives \(\frac{2}{x^{2}}=\frac{1}{2}\)
⇒ x² = 4
⇒ x = ± 2
Therefore, by second derivative test, x = 2 is a point of local minima and the local minimum value of g at x = 2 is
g(2) = \(\frac{2}{2}+\frac{2}{2}\) = 1 + 1 = 2.

(vii) Given, g(x) = \(\frac{1}{x^{2}+2}\)

∴ g'(x) = \(\frac{-(2 x)}{\left(x^{2}+2\right)^{2}}\)
Now, g'(x) = 0
⇒ \(\frac{-2 x}{\left(x^{2}+2\right)^{2}}\) = 0
⇒ x = 0
Now, for values close to x = 0 and to the left of 0, g’(x) > 0.
Also, for values close to x = 0 and to the right of 0, g’(x) < 0.
Therefore, by first derivative test, x = 0 is a point of local maxima and the local maximum value of g(0) is \(\frac{1}{0+2}=\frac{1}{2}\).

(viii) Given, f(x) = x\(\sqrt{1-x}\)

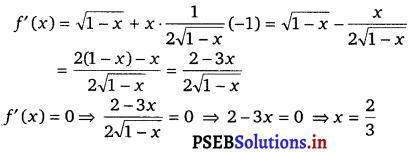
Therefore, by second derivative test, x = \(\frac{2}{3}\) is a point of local maxima and the local maximum value of f at x = \(\frac{2}{3}\) is
f(\(\frac{2}{3}\)) = \(\frac{2}{3} \sqrt{1-\frac{2}{3}}=\frac{2}{3} \sqrt{\frac{1}{3}}=\frac{2}{3 \sqrt{3}}=\frac{2 \sqrt{3}}{9}\).

Question 4.
Prove that the following functions do not have maxima or minima:
(i) f(x) = e^x
(ii) g(x) = log x
(iii) h(x) = x³ + x² + x + 1
Solution.
(i) Given function is f(x) = e^x
⇒ f'(x) = e^x
Now, if f'(x) = 0, then e^x = 0.
But, the exponential function can never assume 0 for any value of x. ,
Therefore, there does not exist c ∈ R such that f'(c) = 0.
Hence, function f does not have maxima or minima.

(ii) Given function is g(x) = log x
⇒ g'(x) = \(\frac{1}{x}\)
Since, log x is defined for a positive number x, g’ (x) > 0 for any x.
Therefore, there does not exist ce R such that g’ (c) = 0.
Hence, function g does not have maxima or minima.

(iii) Given function is h(x) = x³ + x² + x + 1
⇒ h'(x) = 3x + 2x + 1
Now, h(x) = 0
⇒ 3x² + 2x +1 = 0
⇒ x = \(\frac{-2 \pm 2 \sqrt{2} i}{6}=\frac{-1 \pm \sqrt{2} i}{3}\) ∉ R
Therefore, there does not exist c ∈ R such that h'(c) = 0.
Hence, function h does not have maxima or minima.

Question 5.
Find the absolute maximum value and the absolute minimum value of the following functions in the given intervals :
(i) f(x) = x³, x ∈ [- 2, 2]
(ii) f(x) = sin x + cos x, x ∈ [0, π]
(iii) f(x) = 4x – \(\frac{1}{2}\) x², x ∈ [- 2, \(\frac{9}{2}\)]
(iv) f(x) = (x – 1)² + 3, x ∈ [- 3, 1]
Solution.
(i) The given function is f(x) = x³
∴ f'(x) = 3x²
Now, f(x) = 0
⇒ x = 0
Then, we evaluate the value of f at critical point x = 0 and at end points of the interval [- 2, 2].
∴ f(0) = 0; f(- 2) = (- 2) 3 = – 8; 012f(2) = (2)³ – 8
Hence, we can conclude that the absolute maximum value of f on [- 2, 2] is 8 occurring at x = 2.
Also, the absolute minimum value of f on [- 2, 2] is – 8 occurring at x = – 2.

(ii) The given function is f(x) = sin x + cos x.
f'(x) = cos x – sin x
Now, f'(x) = 0
⇒ sin x = cos x
⇒ tan x = 1
⇒ x = \(\frac{\pi}{4}\)
Then, we evaluate the value of f at critical point x = \(\frac{\pi}{4}\) and at the end points of the interval [0, π].

∴ f(\(\frac{\pi}{4}\)) = sin \(\frac{\pi}{4}\) + cos \(\frac{\pi}{4}\)
= \(\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}+\frac{2}{\sqrt{2}}=\sqrt{2}\)

f(0) = sin 0 + cos 0 = 0 + 1 = 1
f(π) = sin π + cos π = 0 – 1 = – 1
Hence, we can conclude that the absolute maximum value of f on [0, π] is 2 occurring at x = \(\frac{\pi}{4}\) and the absolute minimum value of f on [0, π] is – 1 occurring at x = π.

(iii) The given function is f(x) = 4x – \(\frac{1}{2}\) x²
f(x) = 4 – \(\frac{1}{2}\) (2x) = 4 – x
Now, f'(x) = 0
⇒ x = 4
Then, we evaluate the value of f at critical point x = 4 and at the end [- 2, \(\frac{9}{2}\)]
∴ f(4) = 16 – \(\frac{1}{2}\) (16) = 16 – 8 = 8

f(- 2) = – 8 – \(\frac{1}{2}\) (4) = – 8 – 2 = – 10

f(\(\frac{1}{2}\)) = \(4\left(\frac{9}{2}\right)-\frac{1}{2}\left(\frac{9}{2}\right)^{2}=18-\frac{81}{8}\)

= 18 – 10.125 = 7.875
Hence, we can conclude that the absolute maximum value of f on is 8 occurring at x = 4 and the absolute minimum value of f on – 10 occurring at x = – 2.

(iv) The given function is f(x) = (x – 1)² + 3
∴ f'(x) = 2(x – 1)
Now, f'(x) = 0
⇒2 (x – 1) = 0
⇒ x = 1
Then, we evaluate the value of f at critical point x = 1 and at the end points of the interval [- 3, 1].
∴ f(1) = (1 – 1)² + 3 = 0 + 3 = 3;
f(- 3) = (- 3 – 1)² + 3 = 16 + 3 = 19
Hence, we can conclude that the absolute maximum value of / on [- 3, 1] is 19 occurring at x = – 3 and the minimum value of f on [- 3, 1] is 3 occurring at x = 1.

Question 6.
Find the maximum profit that a company can make, if the profit function is given by p(x) = 41 – 72x – 18x²
Solution.
The profit function is given as p(x) = 41 – 72x – 18x²
On differentiating both sides w.r.t. x, we get
p'(x) = – 72 – 36x = – 36 (2 + x)
Again, differentiating both sides w.r.t. x, wt ,et
p”(x) = – 36
For maxima or minima, put p(x) = 0
⇒ – 36 (2 + x) = 0
⇒ x + 2 = 0
⇒x = – 2
At x = – 2, p'(-2) = – 36 < 0
∴ x = – 2 is a point of maxima.
Maximum profit, p(- 2) = 41 – 72 (- 2) – 81 (- 2)²
= 41 + 144 – 72 = 113
Hence, the maximum profit that a company can make, is 113 units.

Question 7.
Find both the maximum value and the minimum value of 3x⁴ – 8x³ + 12x² – 48x + 25 on the interval [0, 3].
Solution.
Let f(x) = 3x⁴ – 8x³ + 12x² – 48x + 25
⇒ f'(x) = 12x³ – 24x² + 24x – 48
= 12 (x³ – 2x² + 2x – 4)
= 12 (x² (x – 2) + 2 (x – 2))
= 12(x – 2) (x² + 2)
For maxima or minima put f'(x) = 0
12(x – 2) (x² + 2) = 0
⇒ if x – 2 = 0 ⇒ x = 2 e [0, 3]
And if, x² + 2 = 0
⇒ x² = – 2
⇒x = √- 2
Hence, the only real root is x = 2 which is considered as critical point.
Now, we evaluate the value of f at critical point x = 2 and at the end point of the interval [0, 3].
At x = 2, f(2) = 3 × 2⁴ – 8 × 2³ + 12 × 2² – 48 × 2 + 25
= 48 – 64 + 48 – 96 + 25 = – 39

At x = 0, f(0) = 0 – 0 + 0 – 0 + 25 = 25
At x = 3, f(3) = 3 × 3⁴ – 8 × 3³ + 12 × 3² – 48 × 3 + 25
= 243 – 216 + 108 – 144 + 25 = 16
Hence, we can conclude that the absolute maximum value of f is 25 at x = 0 and the absolute minimum value of f is – 39 at x = 2.

Question 8.
At what points in the interval [0, 2π], does the function sin2x attain its maximum value?
Solution.
Let f(x) = sin 2x
⇒ f'(x) = 2 cos 2x
Now, f'(x) = 0
⇒ cos 2x = 0
⇒ 2x = \(\frac{\pi}{2}, \frac{3 \pi}{2}, \frac{5 \pi}{2}, \frac{7 \pi}{2}\)

⇒ x = \(\frac{\pi}{4}, \frac{3 \pi}{4}, \frac{5 \pi}{4}, \frac{7 \pi}{4}\)

Then, we evaluate the value off at critical points x = \(\frac{\pi}{4}, \frac{3 \pi}{4}, \frac{5 \pi}{4}, \frac{7 \pi}{4}\) and at the end points of the interval [0, 2π].
f(\(\frac{\pi}{4}\)) = sin \(\frac{\pi}{2}\) = 1;

f(\(\frac{3 \pi}{4}\)) = sin \(\frac{3 \pi}{2}\) = – 1;

f(\(\frac{5 \pi}{4}\)) = sin \(\frac{5 \pi}{2}\) = 1;

f(\(\frac{7 \pi}{4}\)) = sin \(\frac{7 \pi}{2}\) = – 1;

f(0) = sin 0 = 0;
f(2π) = sin 2π = 0
Hence, we can conclude that the absolute maximum value of f on [0, 2π] is occurring at x = \(\frac{\pi}{4}\) and x = \(\frac{5 \pi}{4}\).

Question 9.
What is the maximum value of the function sin x + cos x?
Solution.
Let f(x) = sin x + cos x
f”(x) = – sin x – cos x = – (sin x + cos x)
Now, f”(x) will be negative when (sin x + cos x) is positive i.e., when sin x and cos x are both positive.
Also, we know that, sin x and cos x both are positive in the first quadrant.
Then, f”(x) will be negative when x ∈ (0, \(\frac{\pi}{2}\))
Thus, we consider x = \(\frac{\pi}{4}\)

f”(\(\frac{\pi}{4}\)) = – (sin \(\frac{\pi}{4}\) + cos \(\frac{\pi}{4}\))

= –\(\left(\frac{2}{\sqrt{2}}\right)\) = – √2
∴ By second derivative test, f will be the maximum at x = \(\frac{\pi}{4}\) and the maximum value of f is
f(\(\frac{\pi}{4}\)) = sin \(\frac{\pi}{4}\) + cos \(\frac{\pi}{4}\)
= \(\frac{1}{\sqrt{2}} \times \frac{1}{\sqrt{2}}=\frac{2}{\sqrt{2}}=\sqrt{2}\).

Question 10.
Find the maximum value of 2x³ – 24x + 107in the interval [1, 3]. Find the maximum value of the same function in [- 3, – 1].
Solution.
Let f(x) = 2x³ – 24x + 107
⇒ f(x) = 6x² – 24
= 6(x² – 4)
Now, f'(x) = 0
⇒ 6 (x² – 4) = 0
⇒ x² = 4
⇒ x = ± 2
We first consider the interval [1, 3]
Then, we evaluate the value of f at the critical point x = 2 ∈ [1, 3] and at the end points of the interval [1, 3].
f(2) = 2(8) – 24(2) +107 = 16 – 48 +107 = 75
f(1) = 2(1)-24(1)+ 107 = 2 – 24 +107 = 85
f(3) = 2(27) – 24(3) +107 = 54 – 72 +107 = 89
Hence, the absolute maximum value of f(x) in the interval [1, 3] is 89 occurring at x = 3.
Next, we consider the interval [- 3, – 1],
Evaluate the value of f at the critical point x = – 2 ∈ [- 3, – 1] and at the end points of the interval [1, 3].
f(- 3) = 2(- 27) – 24(- 3) +107 = – 54 + 72 +107 = 125
f(- 1) = 2(- 1) – 24(- 1) + 107 = – 2 + 24 +107 = 129
f(- 2) = 2(- 8) – 24(- 2) + 107 = – 16 + 48 +107 = 139
Hence, the absolute maximum value of f(x) in the interval [- 3, – 1] is 139 occurring at x = – 2.

Question 11.
It is given that at x = 1, the function x⁴ – 62x² + ax + 9 attains its maximum value, on the interval [0, 2]. Find the value of a.
Solution.
Let f(x) = x⁴ – 62x² + ax + 9
f'(x) = 4x³ – 124x + a
It is given that function f attains its maximum value on the interval [0, 2] at x = 1.
∴ f'(1) = 0
⇒ 4 – 124 + a = 0
⇒ a = 120
Hence, the value of a is 120.

Question 12.
Find the maximum and minimum values of x + sin 2x on [0, 2π].
Solution.
Let f(x) = x + sin 2x
⇒ f'(x) = 1 + 2 cos 2x
Now, f'(x) = 0
⇒ cos 2x = – \(\frac{1}{2}\) = – cos \(\frac{\pi}{3}\)

= cos (π – \(\frac{\pi}{3}\))

= cos \(\frac{2 \pi}{3}\)

2x = 2n ± \(\frac{2 \pi}{3}\), n ∈ Z

x = nπ ± \(\frac{\pi}{3}\), n ∈ Z
⇒ x = \(\frac{\pi}{3}, \frac{2 \pi}{3}, \frac{4 \pi}{3}, \frac{5 \pi}{3}\) ∈[0, 2π]

Then, we evaluate the value of f at critical points x = \(\frac{\pi}{3}, \frac{2 \pi}{3}, \frac{4 \pi}{3}, \frac{5 \pi}{3}\) and at the end points of the interval [0, 2π],
∴ f(\(\frac{\pi}{3}\)) = \(\frac{\pi}{3}+\sin \frac{2 \pi}{3}=\frac{\pi}{3}+\frac{\sqrt{3}}{2}\);

f(\(\frac{2 \pi}{3}\)) = \(\frac{2 \pi}{3}+\sin \frac{4 \pi}{3}=\frac{2 \pi}{3}-\frac{\sqrt{3}}{2}\);

f(\(\frac{4 \pi}{3}\)) = \(\frac{4 \pi}{3}+\sin \frac{8 \pi}{3}=\frac{4 \pi}{3}+\frac{\sqrt{3}}{2}\);

f(\(\frac{5 \pi}{3}\)) = \(\frac{5 \pi}{3}+\sin \frac{10 \pi}{3}=\frac{5 \pi}{3}-\frac{\sqrt{3}}{2}\);
f(0) = 0 + sin 0 = 0;
f(2π) = 2π + sin 4π = 2π + 0 = 2π
Thus, maximum value is 2π at x = 2π and minimum value is 0 at x = 0.

Question 13.
Find two numbers whose sum is 24 and whose product is as large as possible.
Solution.
Let one number be x.
Then, the other number is (24 – x).
Let f(x) denote the product of the two numbers.
Thus, we have P(x) = x(24 – x) = 24x – x²
P'(x) = 24 – 2x;
P”(x) = – 2
Now, P’ (x) = 0
⇒ x =12
Also, P”(12) = – 2 < 0
By second derivative test, x = 12 is the point of local maxima of P.
Hence, the product of the number is the maximum when the numbers are 12 and 24 – 12 = 12.

Question14.
Find two positive numbers x and y such that x + y = 60 and xy³ is maximum.
Solution.
The two numbers are x and y such that x + y – 60
⇒ y = 60 – x
Let f(x) = xy³
⇒ f(x) = x(60 – x)³
⇒ f'(x) = (60 – x)³ – 3x (60 – x)²
= (60 – x)² [60 – x – 3x]
= (60 – x)² (60 – 4x)
Also, f(x) = – 2 (60 – x) (60 – 4x) – 4 (60 – x)²
= – 2 (60 – x) [60 – 4x + 2(60 – x)]
= – 2 (60 – x) (180 – 6x)
= -12(60 – x) (30 – x)
Now, f'(x) = 0
⇒ x = 60 or x = 15
When, x = 60 then, f”(x) = 0
When x = 15, then f'(x) – 12(60 – 15) (30 – 15) = – 12 × 45 × 15 < 0 .
∴ By second derivative test, x = 15 is a point of local maxima of f.
Thus, function xy³ is maximum when x = 15 and y = 60 -15 = 45.
Hence, the required numbers are 15 and 45.

Question 15.
Find two positive numbers x and y such that their sum is 35 and the product x²zy⁵ is a maximum.
Solution.
Let one number be x. Then, the other number is y = (35 – x).
Let P(x) = x²y⁵, then
P(x) = x² (35 – x)⁵
∴ P'(x) = 2x (35 – x)⁵ – 5x² (35 – x)⁴
= x (35 – x)⁴ [2(35 – x) – 5x]
= x (35 – x)⁴ (70 – 7x)
= 7x (35 – x)4^{4/sup> (10 – x)}

And p”(x) = 7(35 – x)⁴ (10 – x) + 7x [- (35 – x)⁴ – 4(35 – x)³ (10 – x)]
= 7 (35 – x)⁴ (10 – x) – 7x (35 – x)⁴ – 28x (35 – x)³ (10 – x)
= 7 (35 – x)³ [(35 – x)(10 – x) – x(35 – x) – 4x(10 – x)]
= 7 (35-x)³ [350 – 45x + x² – 35x + x² – 40x + 4x²]
= 7 (35 – x)³ (6x² – 120x + 350)
Now, P'(x) = 0
⇒ x = 0, x = 35, x = 10
When, x = 35, f'(x) = f(x) = 0 and y = 35 – 35 = 0.
This will make the product x²y⁵ equal to 0.
When x = 0, then y = 35 -0 = 35 and the product x2y2 will be 0.
∴ x = 0 and x = 35 cannot be the possible values of x.
When x = 10 then, we have
P'(x) = 7(35 – 10)³ (6 × 100 – 120 × 10 + 350)
= 7(25)³ (- 250) < 0
∴ By second derivative test, P(x) will be the maximum when x = 10 and y = 35 – 10 = 25.
Hence, the required numbers are 10 and 25.

Question 16.
Find two positive numbers whose sum is 16 and the sum of whose cubes is minimum.
Solution.
Let one number be x.
Then, the other number is (16 – x).
Let the sum of the cubes of these numbers be denoted by S(x). Then, S(x) = x3 + (16 -x)3
∴ S'(x) = 3x² – 3(16 – x)²;
S'(x) = 6x + 6(16 – x)
Now, S'(x) = 0
⇒ 3x² – 3(16 – x)² = 0
⇒ x² – (16 – x)² = 0
⇒ x² – 256 – x² + 32x = 0
⇒ x =\(\frac{256}{32}\) = 8
Now, S'(8) = 6(8) + 6(16 -8) = 48 + 48 = 96 > 0.
By second derivatives test, x = 8 is the point of local minima of S.
Hence, the sum of the cubes of the numbers is the minimum when the numbers are 8 and 16 – 8 = 8.

Question 17.
A square piece of tin of side 18 cm is to be made into a box without top, by cutting a square from each corner and folding up the flaps to form the box. What should be the side of the square to be cut off so that the volume of the box is the maximum possible?
Solution.

Let the side of the square to be cut-off be x cm (0 < x < 9).
Then, the length and the breadth of the box will be (18 – 2x) cm each and the height of the box is x cm.
Let V the volume of the open box formed by folding up the flaps, then
V = x (18 – 2x) (18 – 2x)
= 4x (9 – x)²
= 4x (81 + x² – 18x)
= 4(x³ – 18x² + 81x)
On differentiating twice w.r.t. x, we get
\(\frac{d V}{d x}\) = 4(3x² – 36x + 81)
= 12(x² – 12x+27)
and \(\frac{d^{2} V}{d x^{2}}\) = 12 (2x – 12) = 24 (x – 6)
For maxima put \(\frac{d V}{d x}\) = 0
⇒ 12(x – 12x + 27) = 0
⇒ x² – 12x + 27 = 0
⇒ (x – 3) (x – 9) = 0
⇒ x = 3, 9
But x = 9 is not possible,
∵ 2x = 2 × 9 = 18
Which is equal to side of square piece.
At x = 3,
\(\left(\frac{d^{2} V}{d x^{2}}\right)_{x=3}\) = 24 (3 – 6) = – 72 < 0

∴ By second derivative test, x = 5 is the point of maxima.
Hence, the side of the square to be cut-off to make the volume of the box maximum possible is 5 cm.

Question 18.
A rectangular sheet of tin 45cm by 24cm is to be made into a box without top, by cutting off square from each comer and folding up the flaps. What should be the side of the square to be cut off so that the volume of the box is the maximum possible?
Solution.

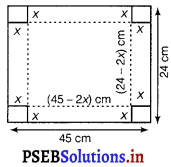
Let the side of the square to be cut off be x cm.
Then, the height of the box is x, the length is 45 – 2x and the breadth is 24 f'(x) 2x.
Let V be the corresponding volume of the box then,
V = x (24 – 2x) (45 – 2x)
V = x (4x² – 138x + 1080)
=4x³ – 138 x² + 1080x
On differentiating twice w.r.t. x,

\(\frac{d V}{d x}\) = 12x² – 276x + 1080

\(\frac{d^{2} V}{d x^{2}}\) = 24x – 276
For maxima put \(\frac{d V}{d x}\) = o
⇒ 12x² – 276x + 1080 = 0
⇒ x² – 23x + 90 = 0
= (x – 18) (x – 5) = 0
⇒ x = 5, 18
It is not possible to cut-off a square of side 18 cm from each corner of the rectangular sheet.
Thus, x cannot be equal to 18.
At x = 5,
\(\left(\frac{d^{2} V}{d x^{2}}\right)_{x=5}\) = 24 × 5 – 276
= 120 – 276
= – 156 < 0
∴ By second derivative test, x = 5 is the point of maxima.
Hence, the side of the square to be cut-off to make the volume of the box maximum possible is 5 cm.

Question 19.
Show that of all the rectangles inscribed in a given fixed circle, the square has the maximum area.
Solution.
Let a rectangle of length l and breadth b be inscribed in the given circle of radius a.
Then, the diagonal passes through the centre and is of length 2a cm.

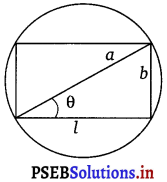
Now, by applying the Pythagoras theorem, we have (2 a)² = l² + b²
⇒ b² = 4 a² – l²
⇒ b = \(\sqrt{4 a^{2}-l^{2}}\)
∴ Area of rectangle, A = l \(\sqrt{4 a^{2}-l^{2}}\)

∴ By the second derivative test, when l = √2a then the area of the rectangle is the maximum.
Since, l = b = √2a, therefore the rectangle is a square.
Hence, it has been proved that of all the rectangles inscribed in the given fixed circle the square has the maximum area.

Question 20.
Show that th right circular cylinder of given surface and maximum volume Is such that its heigh is equal to the diameter of the base.
Solution.

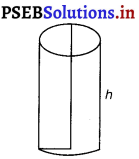
Let r and h be the radius and height of the cylinder, respectively.
Then, the surface area (S) of the cylinder is given by
S = 2πr² + 2πrh
⇒ h = \(\frac{S-2 \pi r^{2}}{2 \pi r}=\frac{S}{2 \pi}\left(\frac{1}{r}\right)-r\)

Let V be the volume of the cylinder. Then,

V = πr²h
= πr² \(\left[\frac{S}{2 \pi}\left(\frac{1}{r}\right)-r\right]=\frac{S r}{2}-\pi r^{3}\)

On differentiating w.r.t. x, we get
\(\frac{d V}{d r}=\frac{S}{2}-3 \pi r^{2}\)

For maxima or mmima put \(\frac{d V}{d r}\) = 0
\(\frac{S}{2}\) = 3πr²
r² = \(\frac{S}{6 \pi}\)

Now, \(\frac{d^{2} V}{d r^{2}}\) = – 6π \(\left(\sqrt{\frac{S}{6 \pi}}\right)\) < 0

∴ By second derivative test, the volume is the maximum when r² = \(\frac{S}{6 \pi}\).

Now, when r² = \(\frac{S}{6 \pi}\), then h = \(\frac{6 \pi r^{2}}{2 \pi}\left(\frac{1}{r}\right)\) – \(\frac{1}{r}\) = 3r – r = 2r.
Hence, the volume is the maximum when the height is twice the radius si.e., when the height is equal to the diameter.

Question 21.
Of all the closed cylindrical cans (right circular), of a given volume of 100 cubic cm, find the dimensions of the can which has the minimum surface area?
Solution.

 

Let r and h be the radius and height of the cylinder, respectively.
Then, volume (V) of the cylinder is given by
V = πr²h = 100
∴ h = \(\frac{100}{\pi r^{2}}\)
Surface area (S) of the cylinder is given by S = 2πr² + 2πrh = 2πr² + \(\frac{200}{r}\)
On differentiating w.r.t. x, we get h
∴ \(\frac{d S}{d r}\) = 4πr – \(\frac{200}{r^{2}}\)
Now, for maxima or minima put \(\frac{d S}{d r}\) = 0

⇒ 4πr = \(\frac{200}{r^{2}}\)

⇒ r³ = \(\frac{200}{4 \pi}=\frac{50}{\pi}\)

⇒ r = \(\left(\frac{50}{\pi}\right)^{\frac{1}{3}}\)

Again, differentiating w.r.t. x, we get.
\(\frac{d^{2} S}{d r^{2}}\) = 4π + \(\frac{400}{r^{3}}\)

Now, it is observed that when r = latex]\left(\frac{50}{\pi}\right)^{\frac{1}{3}}[/latex], \(\frac{d^{2} S}{d r^{2}}\) > 0.

∴ By second derivative test, the surface area is the minimum when the radius of the cylinder is \(\left(\frac{50}{\pi}\right)^{\frac{1}{3}}\) cm.

when r = \(\left(\frac{50}{\pi}\right)^{\frac{1}{3}}\), then h = \(\frac{100}{\pi\left(\frac{50}{\pi}\right)^{\frac{2}{3}}}=2\left(\frac{50}{\pi}\right)^{\frac{1}{3}}\) cm

Hence, the required dimensions of the can which has the minimum surface area, is given by radius = \(\left(\frac{50}{\pi}\right)^{\frac{1}{3}}\) cm and height = 2 \(\left(\frac{50}{\pi}\right)^{\frac{1}{3}}\) cm.

Question 22.
A wire of length 28 m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a circle. What should be the length of the two pieces so that the combined area of the square and the circle is minimum?
Solution.
Let a piece of length l be cut from the given wire to make a square.
Then, the other piece of wire to be made into a circle is of length (28 – l) m.
Now, side of square = \(\frac{l}{4}\)
Let r be the radius of the circle. Then, 2πr = 28 – l
The combined area of the square and the circle (A) is given by A = (side of the square)² + πr²

∴ By second derivative test, the area (A) is the minimum when l = \(\frac{112}{\pi+4}\)

Hence, the combined area is the minimum when the length of the wire in making the square is \(\frac{112}{\pi+4}\) cm while the length of the wire in making the circle is 28 – \(\frac{112}{\pi+4}=\frac{28 \pi}{\pi+4}\) cm.

Question 23.
Prove that the volume of the largest cone that can be inscribed in a sphere of radius R, is \(\frac{8}{27}\) of the volume of the sphere.
Solution.
Let r and h be the radius and height of the cone respectively inscribed in a sphere of radius R.
Let V be the volume of the cone.
Then, V = \(\frac{1}{3}\) πr²h
Height of the cone is given by h = R + AB
= R + \(\sqrt{R^{2}-r^{2}}\) [∵ ABC is right angled triangle]

For maxima put
\(\frac{d V}{d r}\) = 0

⇒ \(\frac{2}{3}\) πrR = \(\frac{3 \pi r^{3}-2 \pi r R^{2}}{3 \sqrt{R^{2}-r^{2}}}\)

⇒ 2R = \(\frac{3 r^{2}-2 R^{2}}{\sqrt{R^{2}-r^{2}}}\)

⇒ 2R \(\sqrt{R^{2}-r^{2}}\) = (3r² – 2R²)²
⇒ 4R² (R² – r²)
= (3r² – 2R²)²
⇒ 4R⁴ – 4R²r² = 9r⁴ + 4R⁴ – 12r²R²
⇒ 9r⁴ = 8R²r²
⇒ r² = \(\frac{8}{9}\) R²

∴ By second derivative test, the volume of the cone is the maximum when r² = \(\frac{8}{9}\) R².

When r² = \(\frac{8}{9}\) R², then
h = R + \(\sqrt{R^{2}-\frac{8}{9} R^{2}}=R+\sqrt{\frac{1}{9} R^{2}}=R+\frac{R}{3}=\frac{4}{3} R\)

Therefore, V = \(\frac{1}{3} \pi\left(\frac{8}{9} R^{2}\right)\left(\frac{4}{3} R\right)=\frac{8}{27}\left(\frac{4}{3} \pi R^{3}\right)\)

= \(\frac{8}{27}\) × (volume of the sphere)
Hence, the volume of the largest cone that can be inscribed in the sphere, is \(\frac{8}{27}\) of the volume of the sphere.

Question 24.
Show that the right circular cone of least curved surface and given volume has an altitude equal toJ time the radius of the base.
Solution.
Let r be the radius of the base, h be the height, V be the volume and S be the curved surface area of the cone.
Then, V = \(\frac{1}{3}\) πr²h
⇒ 3V = πr²h
⇒ 9V² = π² r⁴ h²
⇒ h² = \(\frac{9 V^{2}}{\pi^{2} r^{4}}\) ……………..(i)
And S = πrl
⇒ S = πr \(\sqrt{r^{2}+h^{2}}\) (∵ l = \(\sqrt{h^{2}+r^{2}}\))
⇒ S² = π² r² (r² + h²)
= π² r² (\(\frac{9 V^{2}}{\pi^{2} r^{4}}\) + r²) [Using Eq. (i)]

⇒ S² = \(\frac{9 V^{2}}{r^{2}}\) + π² r⁴ …………(ii)

Hence, S² and therefore S is minimum when 9V² = 2π²r⁶
On putting 9 V² = 2π²r⁶ in Eq. (i) we get
2π²r⁶ = π²r⁴h²
⇒ 2r² = h²
⇒ h = √2r
Hence, altitude of right circular cone is √2 times the radius of the base.

Question 25.
Show that the semi-vertical angle of the cone of the maximum volume and of given slant height is tan^-1 √2.
Solution.

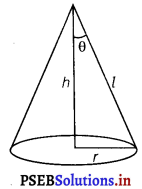
Let θ be the semi-vertical angle of the cone.
It is clear that θ ∈ [0, \(\frac{\pi}{2}\)]
Let r, h and l be the radius, height and the slant height of the cone, respectively.
The slant height of the cone is given as constant.
Now, r = l sin θ and h = l cos θ
The volume (V) of the cone is given by V = \(\frac{1}{3}\) πr² h
⇒ \(\frac{1}{3}\) π (l² sin² θ) (l cos θ)
= \(\frac{1}{3}\) π l² sin² θ cos θ
On differentiating w.r.t. θ, we get
∴ \(\frac{d V}{d \theta}\) = \(\frac{l^{2} \pi}{3}\) [sin² θ (- sin θ) + cos θ (2 sin θ cos θ)]

= \(\frac{l^{3} \pi}{3}[\) [- sin³ θ + 2sin θ cos² θ]

Again, differentiating w.r.t. θ, we get
\(\frac{d^{2} V}{d \theta^{2}}\) = \(\frac{l^{3} \pi}{3}\) [- 3 sin² θ cos θ + 2 cos³ θ – 4 sin² θ cos θ]

= \(\frac{l^{3} \pi}{3}\) [2 cos³ θ – 7 sin² θ cos θ]
For maxima put \(\frac{d V}{d \theta}\) = 0
⇒ sin³ θ = 2 sin θ cos θ v d0
⇒ tan² θ = 2
⇒ tan θ = √2
⇒ θ = tan^-1 √2
Now, when θ = tan^-1 √2, then tan² θ = 2 or sin² θ = 2 cos² θ
Then, we have

\(\frac{d^{2} V}{d \theta^{2}}\) = \(\frac{l^{3} \pi}{3}\) [2 cos³ θ – 14 cos³ θ]
= – 4πl³ cos³ θ < 0 for θ ∈ [0, \(\frac{\pi}{2}\)]

∴ By second derivative test, the volume (V) is the maximum when θ = tan^-1 √2.
Hence, for a given slant height, the semi-vertical angle of the cone of the maximum volume is tan^-1 √2.

Question 26.
Show that the semi-vertical angle of right circular cone of given surface area and maximum volume is sin^-1 (\(\frac{1}{3}\)).
Solution.
With usual notation, given that total surface area S = πrl + πr²

Direction (27 – 29): Choose the correct answer.

Question27.
The point on the curve x² = 2y which is nearest to the point (0, 5) is
(A) (2√2, 4)
(B) (2√2, 0)
(C) (0, 0)
(D) (2, 2)
Solution.
Let d be the distance of the point (x, y) on x² = 2y from the point (0, 5),
then
d = \(\sqrt{(x-0)^{2}+(y-5)^{2}}=\sqrt{x^{2}+(y-5)^{2}}\) ……………(i)

= \(\sqrt{2 y+(y-5)^{2}}\) [Putting x² = 2y]

= \(\sqrt{y^{2}-8 y+25}\)

= \(\sqrt{y^{2}-8 y+4^{2}+9}=\sqrt{(y-4)^{2}+9}\)

d is least when (y – 4)² = 0 i.e., when y = 4
when y = 4 then x² = 2 × 4
⇒ x = ± √8 = ± 2√2
∴ The points (2√2, 4) and (- 2√2, 4) on the given curve are nearest to the point (0, 5).
The correct answer is (A).

Question 28.
For all real values of x, the minimum value of \(\frac{1-x+x^{2}}{1+x+x^{2}}\) is
(A) 0
(B) 1
(C) 3
(D) \(\frac{1}{3}\)
Solution.

The correct answer is (D).

Question 29.
The maximum value of [x (x – 1) + 1]^{\(\frac{1}{3}\)},0 < x < 1 is
(A) \(\left(\frac{1}{3}\right)^{\frac{1}{3}}\)

(B) \(\frac{1}{2}\)

(C) 1
(D) 0
Solution.
Let f(x) = [x (x – 1) + 1]^{\(\frac{1}{3}\)}

∴ f'(x) = \(\frac{2 x-1}{3[x(x-1)+1]^{\frac{2}{3}}}\)

Now, f'(x) = 0
⇒ x = \(\frac{1}{2}\)
Then, we evaluate the value of f at critical point x = \(\frac{1}{2}\) and at the point of the interval [0, 1]
{i.e., at x = 0 and x = 1}.
f(0) = [0 (0 – 1) + 1]^{\(\frac{1}{3}\)} = 1;

f(1) = [1 (1 – 1) + 1]^{\(\frac{1}{3}\)} = 1

f(\(\frac{1}{2}\)) = \(\left[\frac{1}{2}\left(\frac{-1}{2}\right)+1\right]^{\frac{1}{3}}=\left(\frac{3}{4}\right)^{\frac{1}{3}}\)

Hence, we can conclude that the maximum value off in the interval [0, 1] is 1.
The correct answer is (C).