PSEB 12th Class Maths Solutions Chapter 7 Integrals Ex 7.9

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 7 Integrals Ex 7.9 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 7 Integrals Ex 7.9

Direction (1 – 20): Evaluate the definite integrals.

Question 1.
\(\int_{-1}^{1}\) (x + 1) dx
Solution.
Let I = \(\int_{-1}^{1}\) (x + 1) dx
∫ (x + 1) dx = \(\frac{x^{2}}{2}\) + x = F(x)
By second fundamental theorem of calculus, we get
I = F(1) – F(- 1)
= \(\left(\frac{1}{2}+1\right)-\left(\frac{1}{2}-1\right)\)

= \(\frac{1}{2}\) + 1 – \(\frac{1}{2}\) + 1 = 2.

Question 2.
\(\int_{2}^{3} \frac{1}{x}\) dx
Solution.
Let I = \(\int_{2}^{3} \frac{1}{x}\) dx
∫ \(\frac{1}{x}\) dx = log |x| = F(x)
By second fundamental theorem of calculus, we get
I = F(3) – F(2)
= log |3| – log |2| [∵ log(a) – log(b) = log (\(\frac{a}{b}\))]
= log \(\frac{3}{2}\)

Question 3.
\(\int_{1}^{2}\) (4x³ + 5x² + 6x + 9) dx
Solution.
Let I = \(\int_{1}^{2}\) (4x³ + 5x² + 6x + 9) dx
∫ (4x³ + 5x² + 6x + 9) dx = \(4\left(\frac{x^{4}}{4}\right)-5\left(\frac{x^{3}}{3}\right)+6\left(\frac{x^{2}}{2}\right)\) + 9(x)
= x⁴ – \(\frac{5 x^{3}}{3}\) + 3x² + 9x = F(x)
By second fundamental theorem of calculus, we get
I = F(2) – F(1)

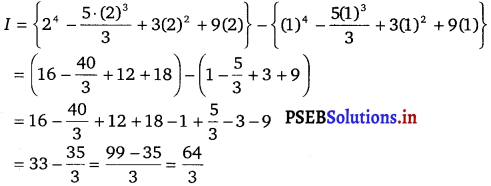
Question 4.
\(\int_{0}^{\frac{\pi}{4}}\) sin 2x dx
Solution.
Let I = \(\int_{0}^{\frac{\pi}{4}}\) sin 2x dx

∫ sin 2x dx = \(\left(\frac{-\cos 2 x}{2}\right)\) = F(x)
By second fundamental theorem of calculus, we get
I = F(\(\frac{\pi}{4}\)) – F(0)

= \(\frac{1}{2}\left[\cos 2\left(\frac{\pi}{4}\right)-\cos 0\right]\)

= – \(\frac{1}{2}\) [0 – 1]

= \(\frac{1}{2}\)

Question 5.
\(\int_{0}^{\frac{\pi}{2}}\) cos 2x dx
Solution.
Let I = \(\int_{0}^{\frac{\pi}{2}}\) cos 2x dx

∫ cos 2x = \(\left(\frac{\sin 2 x}{2}\right)\) = F(x)

By second fundamental theorem of calculus, we get
I = F(\(\frac{\pi}{4}\)) – F(0)

= \(\frac{1}{2}\) [sin 2(\(\frac{\pi}{2}\)) – sin 0]

= \(\frac{1}{2}\) [sin π – sin 0]

= \(\frac{1}{2}\) [0 – 0] = 0.

Question 6.
\(\int_{4}^{5}\) e^x dx
Solution.
Let I = \(\int_{4}^{5}\) e^x dx
∫ e^x dx = ex = F(x)
By second fundamental theorem of calculus, we get
I = F(5) – F(4)
= e⁵ – e⁴
= e⁴ (e – 1)

Question 7.
\(\int_{0}^{\frac{\pi}{4}}\) tan x dx
Sol.
Let I = \(\int_{0}^{\frac{\pi}{4}}\) tan x dx
∫ tan x dx = – log |cos x| =F(x)
By second fundamental theorem of calculus, we get
I = F(\(\frac{\pi}{4}\)) – F(0)

= – log |cos \(\frac{\pi}{4}\)| + log |cos 0|

= – log |\(\frac{1}{\sqrt{2}}\)| + log |1|

= – log \((2)^{-\frac{1}{2}}\)

= \(\frac{1}{2}\) log 2.

Question 8.
\(\int_{\frac{\pi}{6}}^{\frac{\pi}{4}}\) cosec x dx
Solution.
21et I = \(\int_{\frac{\pi}{6}}^{\frac{\pi}{4}}\) cosec x dx
∫ cosec x dx = log cosec x – cot x = F(x)
By second fundamental theorem of calculus, we get
I = F(\(\frac{\pi}{4}\)) – F(\(\frac{\pi}{6}\))

= log |cosec \(\frac{\pi}{4}\) – cot \(\frac{\pi}{4}\)| – log |cosec \(\frac{\pi}{6}\) – cot \(\frac{\pi}{6}\)|

= log |√2 – 1| – log |2 – √3|

= log \(\left(\frac{\sqrt{2}-1}{2-\sqrt{3}}\right)\)

Question 9.
\(\int_{0}^{1} \frac{d x}{\sqrt{1-x^{2}}}\)
Solution.
Let I = \(\int_{0}^{1} \frac{d x}{\sqrt{1-x^{2}}}\)

⇒ ∫ \(\frac{d x}{\sqrt{1-x^{2}}}\) = sin^-1 x = F(x)

By second fundamental theorem of calculus, we get
I = F(1) – F(0)
= sin^-1 (1) – sin^-1 (0)

= \(\frac{\pi}{2}\) – 0 = \(\frac{\pi}{2}\)

Question 10.
\(\int_{0}^{1} \frac{d x}{1+x^{2}}\)
Solution.
Let I = \(\int_{0}^{1} \frac{d x}{1+x^{2}}\)

∫ \(\frac{d x}{1+x^{2}}\) = tan^-1 x = F(x)
By second fundamental theorem of calculus, we get
I = F(1) – F(0)
= tan^-1 (1) – tan^-1 (0) = \(\frac{\pi}{4}\)

Question 11.
\(\int_{2}^{3} \frac{d x}{x^{2}-1}\)
Solution.

Question 12.
\(\cdot \int_{0}^{\frac{\pi}{2}}\) cos² x dx
Solution.
Let I = \(\cdot \int_{0}^{\frac{\pi}{2}}\) cos² x dx

Question 13.
\(\int_{2}^{3} \frac{x d x}{x^{2}+1}\)
Solution.
Let I = \(\int_{2}^{3} \frac{x d x}{x^{2}+1}\)

\(\int \frac{x}{x^{2}+1} d x=\frac{1}{2} \int \frac{2 x}{x^{2}+1} d x\)

= \(\frac{1}{2}\) log (1 + x²) = F(x)

By second fundamental theorem of calculus, we get

I = F(3) – F(2)
= \(\frac{1}{2}\) [log(1 +(3)²) – log(1 + (2)²)]

= \(\frac{1}{2}\) [log(10) – log(5)]

= \(\frac{1}{2}\) log (\(\frac{10}{5}\))

= \(\frac{1}{2}\) log 2

Question 14.
\(\int_{0}^{1} \frac{2 x+3}{5 x^{2}+1}\) dx
Solution.
Let I = \(\int_{0}^{1} \frac{2 x+3}{5 x^{2}+1}\) dx

Question 15.
\(\int_{0}^{1}\) x e^x2 dx
Solution.
Let I = \(\int_{0}^{1}\) x e^x2 dx
put x² = t
⇒ 2x dx = dt
As x → 0, t → 0 and as x → 1, t → 1
I = \(\frac{1}{2}\) \(\int_{0}^{1}\) e^t dt

⇒ \(\frac{1}{2}\) ∫ e^t dt = \(\frac{1}{2}\) e^t = F(t)

By second fundamental theorem of calculus, we get
I = F(1) – F(0)
= \(\frac{1}{2}\) e – \(\frac{1}{2}\) e⁰

= \(\frac{1}{2}\) (e – 1)

Question 16.
\(\int_{1}^{2} \frac{5 x^{2}}{x^{2}+4 x+3}\) dx
Solution.
Let I = \(\int_{1}^{2} \frac{5 x^{2}}{x^{2}+4 x+3}\) dx
Dividing 5x² by x² + 4x + 3, we get

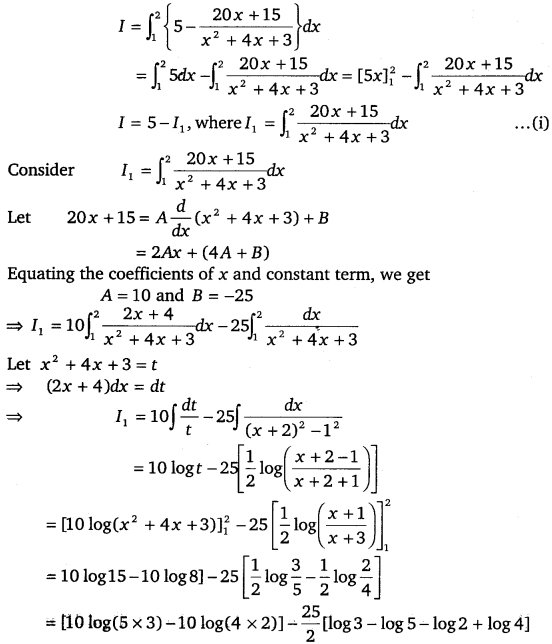
Question 17.
\(\int_{0}^{\frac{\pi}{4}}\) (2 sec² x + x³ + 2) dx
Solution.
Let I = \(\int_{0}^{\frac{\pi}{4}}\) (2 sec² x + x³ + 2) dx

∫ (2 sec² x + x³ + 2) dx = 2 tan x + \(\frac{x^{4}}{4}\) + 2x

By second fundamental theorem of calculus, we get

I = F(\(\frac{\pi}{4}\)) – F(0)

= \(\left\{\left(2 \tan \frac{\pi}{4}+\frac{1}{4}\left(\frac{\pi}{4}\right)^{4}+2\left(\frac{\pi}{4}\right)\right)\right\}\) – (2 tan 0 + 0 + 0)

= \(2 \tan \frac{\pi}{4}+\frac{\pi^{4}}{4^{5}}+\frac{\pi}{2}=2+\frac{\pi}{2}+\frac{\pi^{4}}{1024}\)

Question 18.
\(\int_{0}^{\pi}\) (sin² \(\frac{x}{2}\) – cos² \(\frac{x}{2}\)) dx
Solution.
Let I = \(\int_{0}^{\pi}\) (sin² \(\frac{x}{2}\) – cos² \(\frac{x}{2}\)) dx

= – \(\int_{0}^{\pi}\) (cos² \(\frac{x}{2}\) – sin² \(\frac{x}{2}\)) dx

= – \(\int_{0}^{\pi}\) cos x dx
∫ cos dx = sin x = F(x)
By second fundamental theorem of calculus, we get
I = F(π) – F(0)
= sin π – sin 0 = 0.

Question 19.
\(\int_{0}^{2} \frac{6 x+3}{x^{2}+4}\) dx
Solution.
Let I = \(\int_{0}^{2} \frac{6 x+3}{x^{2}+4}\) dx

Question 20.
\(\int_{0}^{1}\) (xe^x + sin \(\frac{\pi x}{4}\)) dx
Solution.
Let I = \(\int_{0}^{1}\) (xe^x + sin \(\frac{\pi x}{4}\)) dx

Question 21.
\(\int_{1}^{\sqrt{3}} \frac{d x}{1+x^{2}}\) equals
(A) \(\frac{\pi}{3}\)

(B) \(\frac{2 \pi}{3}\)

(C) \(\frac{\pi}{6}\)

(D) \(\frac{\pi}{12}\)
Solution.
Let I = \(\int_{1}^{\sqrt{3}} \frac{d x}{1+x^{2}}\)
= tan^-1 x = F(x)
By second fundamental theorem of calculus, we get
\(\int_{1}^{\sqrt{3}} \frac{d x}{1+x^{2}}\) = F(√3) – F(1)

= tan^-1 (√3) – tan^-1 (1)

= \(\frac{\pi}{3}-\frac{\pi}{4}=\frac{\pi}{12}\)

Hence, the correct answer is (D).

Question 22.
\(\int_{0}^{\frac{2}{3}} \frac{d x}{4+9 x^{2}}\) equals
(A) \(\frac{\pi}{6}\)

(B) \(\frac{\pi}{12}\)

(C) \(\frac{\pi}{24}\)

(D) \(\frac{\pi}{4}\)
Solution.

Hence, the correct answer is (C).