PSEB 12th Class Maths Solutions Chapter 9 Differential Equations Ex 9.4

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter Differential Equations Ex 9.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 9 Differential Equations Ex 9.4

Direction (1 -1 0): For each of the differential equations in given questions, find the general solution.

Question 1.
\(\frac{d y}{d x}=\frac{1-\cos x}{1+\cos x}\)
Solution.

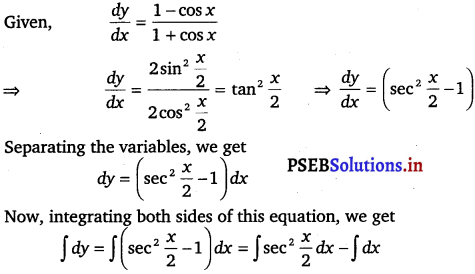
⇒ y = 2 tan \(\frac{x}{2}\) – x + C
This is the required general solution of the given differential equation.

Question 2.
\(\frac{d y}{d x}=\sqrt{4-y^{2}}\) (- 2 < y < 2)
Solution.
Given, \(\frac{d y}{d x}=\sqrt{4-y^{2}}\)
Separating the variables, we get
⇒ \(\frac{d y}{\sqrt{4-y^{2}}}\) = dx
⇒ sin^-1 \(\frac{y}{2}\) = x + C
Now, integrating both sides of this equation, we get
∫ \(\frac{d y}{\sqrt{4-y^{2}}}\) = ∫ dx
\(\frac{y}{2}\) = sin(x + C)
⇒ y = 2 sin (x + C)
This is the required general solution of the given differential equation.

Question 3.
\(\frac{d y}{d x}\) + y = 1 (y ≠ 1)
Solution.
Given, \(\frac{d y}{d x}\) + y = 1
⇒ dy + y dx = dx
⇒ dy = (1 – y) dx
Separating the variables, we get
⇒ \(\frac{d y}{1-y}\) = dx
Now, integrating both sides, we get
∫ \(\frac{d y}{1-y}\) = ∫ dx
⇒ log(l – y) = x + log C
⇒ – log C – log (1 – y) = x
⇒ log C(1 – y) = – x
⇒ C (1 – y) = e^-x
⇒ 1 – y = \(\frac{1}{C}\) e^-x
⇒ y = 1 – \(\frac{1}{C}\) e^-x
⇒ y = 1 + A e^-x (where A = Question )
This is the required general solution of the given differential equation.

Question 4.
sec² x tan y dx + sec² y tan x dy = 0
Solution.
Given, sec² x tan y dx + sec² y tan x dy = 0

⇒ \(\frac{\sec ^{2} x \tan y d x+\sec ^{2} y \tan x d y}{\tan x \tan y}\) = 0

⇒ \(\frac{\sec ^{2} x}{\tan x} d x+\frac{\sec ^{2} y}{\tan y} d y\) = 0

Integrating bothsides, we get

⇒ \(\int \frac{\sec ^{2} x}{\tan x} d x+\int \frac{\sec ^{2} y}{\tan y} d y\) = 0
⇒ log | tan x | + log | tan y | = log C
⇒ log | tan x tan y | = log C
⇒ tan x tan y = C
Which is the required solution, where x ≠ odd multiple of \(\frac{\pi}{2}\) and x ∈ R.

Question 5.
(e^x + e^{– x}) dy – (e^x – e^{– x}) dx = 0
Solution.
Given, (e^x + e^{– x}) dy – (e^x – e^{– x}) dx = 0
⇒ (e^x + e^{– x}) dy = (e^x – e^{– x}) dx
⇒ dy = \(\left[\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}\right]\) dx
Integrating both sides, we get
∫ dy = ∫ \(\left[\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}\right]\) dx + C

⇒ y = ∫ \(\left[\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}\right]\) dx + C …………….(i)

Let (e^x + e^{– x}) = t
Differentiating both sides w.r.t. x, we get
\(\frac{d}{d x}\) (e^x + e^{– x}) = \(\frac{d t}{d x}\)
⇒ e^x – e^{– x} = \(\frac{d t}{d x}\)
⇒ (e^x – e^{– x}) dx = dt
Substituting this value in equation (i), we get
y = ∫ \(\frac{1}{t}\) dt + C
⇒ y = log (t) + C
⇒ y = log (e^x + e^{– x}) + C
This is the required general solution of the given differential equation.

Question 6.
\(\frac{d y}{d x}\) = (1 + x²) (1 + y²)
Solution.
Given, \(\frac{d y}{d x}\) = (1 + x²) (1 + y²)
⇒ \(\frac{d y}{1+y^{2}}\) = (1 + x²) dx
Integrating both sides, we get
∫ \(\frac{d y}{1+y^{2}}\) = ∫ (1 + x²) dx
⇒ tan^-1 y = ∫ dx + ∫ x² dx
⇒ tan^-1 y = x + \(\frac{x^{3}}{3}\) + C
This is the required general solution of the given differential equation.

Question 7.
y log y dx – x dy = 0
Solution.
Given, y log y dx – x dy = 0
⇒ y log y dx = x dy
⇒ \(\frac{d y}{y \log y}=\frac{d x}{x}\)
Integrating both sides, we get
⇒ \(\int \frac{d y}{y \log y}=\int \frac{d x}{x}\)
Let log y = t
Differentiating w.r.t. y, we get
⇒ \(\frac{d}{d y}\) (log y) = \(\frac{d t}{d y}\)

⇒ \(\frac{1}{y}=\frac{d t}{d y}\)

⇒ \(\frac{1}{y}\) dy = dt
Substituting this value in equation (i), we get
\(\int \frac{d t}{t}=\int \frac{d x}{x}\)

⇒ log t = log x + log C
⇒ log (log y) = log Cx
⇒ log y = Cx
⇒ y = e^Cx

Question 8.
x⁵ \(\frac{d y}{d x}\) = – y⁵
Solution.

⇒ x^{– 4} + y^{– 4} = – 4 k
⇒ x^{– 4} + y^{– 4} = C (C = – 4k)
This is the required general solution of the given differential equation.

Question 9.
\(\frac{d y}{d x}\) = sin^{– 1} x
Solution.
Given, \(\frac{d y}{d x}\) = sin^{– 1} x
⇒ dy = sin^{– 1} x dx
Integrating both sides, we get
∫ dy = ∫ sin^{– 1} x dx
⇒ y = ∫ (sin^{– 1} x . 1) dx
⇒ y = sin^{– 1} x . ∫ (1) dx – ∫ \(\left[\left(\frac{d}{d x}\left(\sin ^{-1} x\right) \cdot \int(1) d x\right)\right]\) dx

⇒ y = sin^{– 1} x . x – ∫ \(\left(\frac{1}{\sqrt{1-x^{2}}} \cdot x\right)\) dx

⇒ y = x sin^{– 1} x + ∫ \(\frac{-x}{\sqrt{1-x^{2}}}\) dx
Let 1 – x² = t
Differentiating w.r.t x, we get
⇒ \(\frac{d}{d x}\) (1 – x²) = \(\frac{d t}{d x}\)
⇒ – 2x = \(\frac{d t}{d x}\)
⇒ x dx = – \(\frac{1}{2}\) dt
Substituting this value in equation (i), we get
y = x sin^-1 x + ∫ \(\frac{1}{2 \sqrt{t}}\) dt

⇒ y = x sin^-1 x + \(\frac{1}{2} \cdot \int(t)^{-\frac{1}{2}}\) dt

⇒ y = x sin^-1 x + \(\frac{1}{2} \cdot \frac{t^{\frac{1}{2}}}{\frac{1}{2}}\) + C

⇒ y = x sin^-1 x + √t + C

⇒ y = x sin^-1 x + √1 – x² + C

This is the required general solution of the given differential equation.

Question 10.
e^x tan y dx + (1 – e^x) sec² y dy = 0
Solution.
Given, e^x tan y dx + (1 – e^x) sec² y dy = 0
(1 – e^x)sec² y dy = – e^x tan y dx
Separating the variables, we get
\(\frac{\sec ^{2} y}{\tan y} d y=\frac{-e^{x}}{1-e^{x}} d x\) ………………(i)
Integrating both sides, we get
\(\int \frac{\sec ^{2} y}{\tan y} d y=\int \frac{-e^{x}}{1-e^{x}} d x\)
Let tan y = u
Differentiating w.r.t. y, we get

Substituting the value of \(\int \frac{\sec ^{2} y}{\tan y}\) dy and \(\int \frac{-e^{x}}{1-e^{x}}\) dx in equation (i), we get
⇒ log (tan y) = log(1 – e^x) + logC
⇒ log (tan y) = log [C(1 – e^x)]
⇒ tan y = C (1 – e^x)
This is the required general solution of the given differential equation.

Direction (11 – 14): For each of the differential equation in given questions, find a particular solution satisfying the given condition.
Question 11.
(x³ + x² + x + 1)\(\frac{d y}{d x}\) = 2x² + x y = 1 when x = 0.
Solution.

Question 12.
x (x² – 1) \(\frac{d y}{d x}\) = 1; y = 0 when x = 2
Solution.

Question 13.
cos (\(\frac{d y}{d x}\)) = a, (a ∈ R); y = 1 when x = 0
Solution.
Given, cos (\(\frac{d y}{d x}\)) = a
⇒ \(\frac{d y}{d x}\) = cos^-1 a
⇒ dy = cos^-1 a dx
Integrating both sides, we get
∫ dy = ∫ cos^-1 a dx
⇒ y = cos^-1 a . x + C
⇒ y = x cos^-1 a + C
Now, y = 1 when x = 0
⇒ 1 = 0 . cos^-1 a + C
⇒ C = 1
Substituting C = 1 in equation (i), we get
y = x cos^-1 a + C
⇒ \(\frac{y-1}{x}\) = cos^-1 a
⇒ cos (\(\frac{y-1}{x}\)) = a.

Question 14.
\(\frac{d y}{d x}\) = y tan x; y = 1 when x = 0
Solution.
Given, \(\frac{d y}{d x}\) = y tan x
⇒ \(\frac{d y}{y}\) = tan x dx
Integrating both sides, we get
∫ \(\frac{d y}{y}\) = ∫ tan x dx
⇒ log y = log (sec x) + log C
⇒ log y = log (C sec x)
⇒ y = C sec x
Now, y = 1 when x = 0
⇒ 1 + C × sec 0
⇒ 1 = C × 1
Substituting C = 1 in equation (j), we get
y = sec x

Question 15.
Find the equation of curve passing through the point (0, 0) and whose differential equation is y’ = e^x sin x.
Solution.
Differential equation is
y’ = e^x sin x or \(\frac{d y}{d x}\) = e^x sin x
∴ dy = e^x sin x dx
Integrating both sides, we get
∫ dy = ∫ e^x sin x dx
Integrating by parts taking e^x as the first function
y= e^x (- cos x) – ∫ e^x (- cos x) dx
= – e^x cos x + ∫ e^x cos x dx
Again integrating by parts taking e^x as first function
= – e^x cosx + e^x sin x – ∫ e^x sin x dx
or 2y = – e^x cos x + e^x sec + C
y = \(\frac{e^{x}}{2}\) (- cos x + sin x) + C ………….(i)
Put x = 0, y = 0
On substituting C = \(\frac{1}{2}\) in equation (i), we get
y = \(\frac{e^{x}}{2}\) (sin x – cos x) + \(\frac{1}{2}\)
⇒ 2y = e^x (sin x – cos x) + 1
⇒ 2y – 1 = e^x (sin x – cos x)
Hence, the required equation of the curve is 2y – 1 = e^x (sin x – cos x).

Question 16.
For the differential equation xy \(\frac{d y}{d x}\) = (x + 2)(y + 2), find the solution curve passing through the point (1, – 1).
Solution.
The differential equation is xy \(\frac{d y}{d x}\) = (x + 2) (y +2)
or xy dy = (x + 2) (y + 2) dx
Dividing by x (y +2)
\(\frac{y}{y+2} \frac{d y}{d x}=\frac{x+2}{x} d x\)
Integrating both sides, we get
\(\int y \frac{d y}{y+2}=\int \frac{x+2}{x} d x\)

\(\int \frac{y+2-2}{x+2} d y=\int\left(1+\frac{2}{x}\right) d x\) \(\int\left(1-\frac{2}{y+2}\right) d y=\int\left(1+\frac{2}{x}\right) d x\)

y – 2 log (y + 2) = x + 2 log x + C
y – x – C = log [x² (y + 2)²]
The curve passes through (1, -1)
∴ – 1 – 2 log 1 = 1 + 2 log 1 + C [∵ log 1 = 0]
– 1 = 1 + C
∴ C = – 2
Substituting C = – 2 in equation (i), we get
y – x + 2 = log [x² (y + 2)²]
This is the required solution of the given curve.

Question 17.
Find the equation of a curve passing through the point (0, -2) given that at any point (x, y) on the curve, the product of the slope of its tangents and y-coordinate of the point is equal to the x-coordinate of the point.
Sol.
Let x and y be the x-coordinate and y-coordinate of the curve respectively.
We know that the slope of a tangent to the curve in the coordinate axis is given by the \(\frac{d y}{d x}\).
According to the given information, we get
y . \(\frac{d y}{d x}\) = x dx
y dy = x dx
Integratin both sides, we get
∫ y dy = ∫ x dx
⇒ \(\frac{y^{2}}{2}=\frac{x^{2}}{2}\) + C
⇒ y² – x² = 2C …………..(i)
Now, the curve passes through the point (0, – 2).
∴ (- 2)² – 0² = 2C
⇒ 2C = 4
Substituting 2C = 4 in equation (i), we get
y² – x² = 4
This is the required equation of the curve.

Question 18.
At any point (x, y) of a curve, the slope of the tangent is twice the slope of the line segment joining the point of contact to the point (- 4, – 3). Find the equation of the curve given that it passes through (- 2, 1).
Solution.
It is given that (x, y) is the point of contact of the curve and its tangent.
The slope (m₁) of the line segment joining (x, y) and (- 4, – 3) is \(\frac{y+3}{x+4}\).
We know that the slope of the tangent to the curve is given by the relation, \(\frac{d y}{d x}\)
∴ slope (m₂) of the tangent = \(\frac{d y}{d x}\)
According to the question,
m₂ = 2m
⇒ \(\frac{d y}{d x}=\frac{2(y+3)}{x+4}\)

⇒ \(\frac{d y}{y+3}=\frac{2 d x}{x+4}\)

Integrating both sides, we get

\(\int \frac{d y}{y+3}=2 \int \frac{d y}{x+4}\)
⇒ log (y + 3) = 2log (x + 4) + log C
⇒ log (y + 3) = log C (x + 4)²
⇒ y + 3 = C (x + 4)² ………………(i)
This is the general equation of the curve.
It is given that it passes through point (- 2, 1)
⇒ 1 + 3 = C(- 2 + 4)²
⇒ 4 = 4C
⇒ C = 1
Substituting C = 1 in equation (i), we get
y + 3 = C(x + 4)
This is the required equation of the curve.

Question 19.
The volume of spherical balloon being inflated changes at a constant rate, If initially its radius is 3 units and after 3 seconds it is 6 units. Find the radius of balloon after t seconds.
Solution.
Let the rate of change of the volume of the balloon be k (where k is a constant).
⇒ \(\frac{d V}{d t}\) = k

⇒ \(\frac{d}{d t}\left(\frac{4}{3} \pi r^{3}\right)\) = k [Volume of sphere = \(\frac{4}{3}\) πr³]

⇒ \(\frac{4}{3}\) π . 3r² . \(\frac{d r}{d t}\) = k

⇒ 4πr² dr = k dt
Integrating both sides, we get
4π ∫ r² dr = k ∫ dt
⇒ 4π . \(\frac{r^{3}}{3}\) = kt + C
⇒ 4πr³ = 3 (kt + C) ……………(i)
Now, at t = 0, r = 3
⇒ 4π × 3³ = 3 (k × 0 + C)
⇒ 108 π = 3C
⇒ C = 36π
At t = 3, r = 6;
⇒ 4π × 6³ = 3(k × 3 + C)
⇒ 864π = 3 (3k + 36π)
⇒ 3k = – 288π – 36π = 252π
k = 84π
Substituting the values of k and C in equation (i), we get
4πr³ = 3 [84π + 36π]
⇒ 4πr³ = 4π (63t + 27)
⇒ r³ = (63t + 27)
⇒ r = (63π + 27)\(\frac{1}{3}\)
Thus, the radius of the balloon after t seconds is (63t + 27)\(\frac{1}{3}\).

Question 20.
In a bank, principal increases continuously at the rate of r% per year. Find the value of r if loo double itself in 10 years
Sol.
Let p, t and r represent the principal, time and rate of interest respectively.
It is given that the principal increases continuously at the rate r% per year.

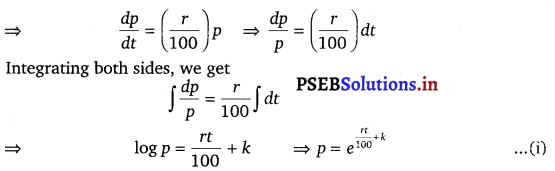
It is given that when t = 0, p = 100
⇒ 100 = e^k ………….(ii)
Now, if t = 10, then p = 2 × 100 = 200
Therefore, equation (i) becomes
200 = \(e^{\frac{r}{10}+k}\)
200 = \(e^{\frac{r}{10}}\) . e^k
⇒ 200 = \(e^{\frac{r}{10}}\) . 100 [From equation (ii)]
⇒ \(e^{\frac{r}{10}}\) = 2
⇒ \(\frac{r}{10}\) = log_e 2
⇒ \(\frac{r}{10}\) = 0.6931
⇒ r = 6.931
Hence, the value of r is 6.93%.

Question 21.
In a bank, principal increases continuously at the rate of 5% per year. An amount oR 1000 is deposited with this bank, how much will it worth after 10 years (e^0.5 = 1.648).
Solution.
Let p and t be the principal and time respectively.
It is given that the principal increases continuously at the rate of 5% per year.

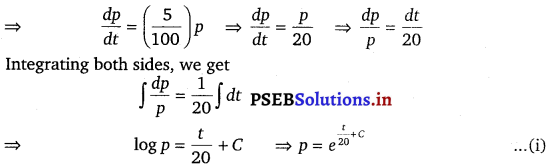
Now, if t = 0 then p = 1000
⇒ 1000 = e^c ………….(ii)
At t = 10, equation (i) becomes
⇒ p = \(e^{\frac{1}{2}+C}\)
⇒ p = e^0.5 x e^C
⇒ p = 1.648 × 1000
⇒ p = 1648
Hence, after lo years the amount will worth ₹ 1648.

Question 22.
In a culture, the bacteria count is 1,00,000. The number is increased by 10% in 2 hours. In how many hours will the count reach 2,00,000,11 the rate of growth of bacteria is proportional to the number present?
Solution.
Let y be the number of bacteria at any instant t.
It is given that the rate of growth of the bacteria is proportional to the number present.
∴ \(\frac{d y}{d t}\) ∝ y

\(\frac{d y}{d t}\) = ky (where k is a constant)

⇒ \(\frac{d y}{y}\) = k dt

Integrating both sides, we get
∫ \(\frac{d y}{y}\) = k ∫ dt
⇒ logy = kt + C
Let y₀ be the number of bacteria at t = 0.
log y₀ = C
Substituting the value of C in equation (i), we get
log y = kt + log y₀
⇒ log y – log y₀ = kt
log \(\left(\frac{y}{y_{0}}\right)\) = kt
⇒ kt = log \(\left(\frac{y}{y_{0}}\right)\) ………… (ii)

Also, it is given that the number of bacteria increases by 10% in 2 hours.
⇒ y = \(\frac{110}{100}\) y₀
⇒ \(\frac{y}{y_{0}}=\frac{11}{10}\) ………….(iii)
Substituting the value in equation (ii), we get

Question 23.
The general solution of the differential equation \(\frac{d y}{d x}\) = e^{x + y} is
(A) e^x + e^{– y} = C
(B) e^x + e^y = C
(C) e^{– x} + e^y = C
(D) e^{– x} + e^{– y} = C
Solution.
\(\frac{d y}{d x}\) = e^{x + y}
= e^x . e^y
∫ \(\frac{d y}{e^{y}}\) = e^x dx
e^{– y} dy = e^x dx
Integrating both sides, we get
⇒ ∫ e^{– y} dy = ∫ e^x dx
⇒ – e^{– y} = e^x + k
⇒ e^x + e^{– y} = – k
⇒ e^x + e^{– y} = C (C = – k)
Hence, the correct answer is (A).