Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 6 Triangles Ex 6.2 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 7 Maths Chapter 6 Triangles Ex 6.2
1. State, if a triangle is possible with the following angles.
Question (a).
35°, 70°, 65°
Answer:
No Reason :
Sum of three angles
= 35° + 70° + 65° = 170°
But, we know that sum of angles of a triangle is always 180°
∴ A triangle cannot have angles 35°, 70° and 90°.
Question (b).
70°, 50°, 60°
Answer:
Yes
Reason :
Sum of three angles
= 70° + 50° + 60°
= 180°
By angle sum property
∴ A triangle can have angles 70°, 50° and 60°.
Question (c).
90°, 80°, 20°
Answer:
No
Reason :
Sum of three angles
= 90° + 80° + 20°
=190°
But, we know that sum of angles of a triangle is always 180°
(Angle sum properly)
∴ A triangle cannot have angles 90°, 80° and 20°.
Question (d).
60°, 60°, 60°
Answer:
Yes
Reason :
Sum of three angles
= 60° + 60° + 60°
= 180°
by angle sum property.
∴ A triangle can have angles 60°, 60° and 60°.
![]()
Question (e).
90°, 90°, 90°
Answer:
No Reason :
Sum of three angles
= 90° + 90° + 90°
= 270°
But, we know that sum of angles of a triangle is always 180° (Angle sum properly)
∴ A triangle cannot have angles 90°, 90° and 90°.
2. Find the value of x in the following figures :
Question (i).
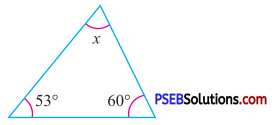
Answer:
By angle sum property of a triangle
x + 53° + 60° = 180°
x + 113° = 180°
x = 180° – 113°
x = 67°
Question (ii).
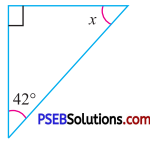
Answer:
By angle sum property of a triangle
90° + x + 42° = 180°
132° + x = 180°
x = 180° – 132°
x = 48°
Question (iii).
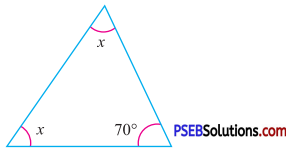
Answer:
By angle sum property of a triangle
x + x + 70° = 180°
2x + 70° = 180°
2x = 180° – 70°
2x = 110°
x = \(\frac{110^{\circ}}{2}\)
x = 55°
![]()
Question (iv).
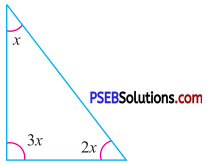
Answer:
By angle sum property of a triangle
x + 3x + 2x = 180°
6x = 180°
x = \(\frac{180^{\circ}}{6}\)
x = 30°
Question (v).
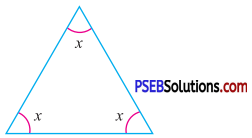
Answer:
By angle sum property of a triangle
x + x + x = 180°
3x = 180°
x = \(\frac{180^{\circ}}{3}\)
x = 60°
Question (vi).
Answer:
By angle sum property of a triangle
x – 5° + 60° + x + 5° = 180°
2x + 60° = 180°
2x = 180° – 60°
2x = 120°
x = \(\frac{120^{\circ}}{2}\)
x = 60°
3. Find the values of x and y in the following figures :
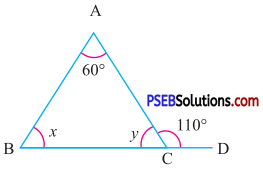
Question (i).
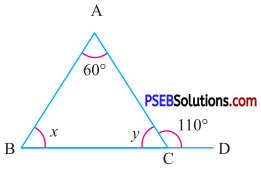
Answer:
Since in ΔABC, BC is produced to D
∴ 60° + x = 110°
(By exterior angle property)
x = 110°- 60°
x = 50° ………. (1)
Now, in ΔABC
60° + x + y = 180°
(By angle sum property of triangle)
60° + 50° + y = 180° [(By using (1)]
110° + y = 180°
y = 180° – 110°
y = 70°
Hence, x = 50°,
y = 70°
![]()
Question (ii).
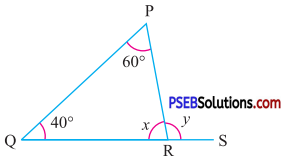
Answer:
In ΔPQR,
∠P + ∠Q + ∠R = 180°
60° + 40° + x = 180°
(By angle sum property of triangle)
100° + x = 180°
x = 180° – 100°
x = 80°
Now,in ΔPQR, QR is produced
∴ y = 60° + 40°
(By exterior angle property)
y = 100°
Hence, x = 80°,
y = 100°
Question (iii).
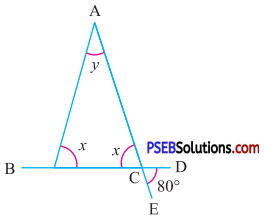
Answer:
∠ACB = ∠ECD
∴ x = 80°….(1)
(vertically opposite angles)
∠ACD + ∠ECD = 180° (Linear pair)
∴ ∠ACD + 80° = 180° [by using (1)]
∠ACD = 180°- 80°
∠ACD = 100° ….(2)
In ΔABC, BC is produced to D
∴ x + y = ∠ACD
(By exterior angle property)
80° + y = 100°
(By using (1) and (2))
y = 100° – 80°
y = 20°
Hence, x = 80° and y = 20°
Question (iv).
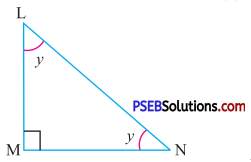
Answer:
By angle sum property of a triangle
∠L + ∠M + ∠N = 180°
y + 90° + y = 180°
2 y + 90° = 180°
2y = 180° – 90°
2y = 90°
y = \(\frac{90^{\circ}}{2}\)
y = 45°
Question (v).
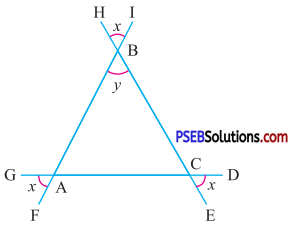
Answer:
∠ABC = ∠HBI
(Vertically opposite angles)
∴ y = x …(1)
∠BAC = ∠GAF
(Vertically opposite angles)
∴ ∠BAC = x ….(2)
∠ACB = ∠EFD
(Vertically opp. angles)
∠ACB = x …(3)
Now, in ΔABC
∠BAC + ∠ABC + ∠ACB = 180°
(By angle sum property of triangle)
x + x + x = 180°
[by using (1), (2) and (3)]
3x = 180°
x = \(\frac{180^{\circ}}{3}\)
x = 60°
y = x
= 60° (by using (1) and (4))
Hence, x = 60°, y = 60°
![]()
Question (vi).
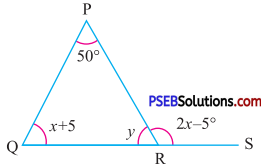
Answer:
In ΔPQR, QR is produced to S,
∴ 2x – 5° = 50° + x + 5°
(By exterior angle property.)
2x – 5°= 55° + x
2x – x = 55° + 5°
x = 60° ….(i)
Now, by angle sum property of a ΔPQR
50° + x + 5° + y = 180°
55° + 60° + y = 180°
115°+ y = 180°
y = 180° – 115°
y = 65°
Hence, x = 60° and y = 65°
4. The angles of a triangle are in the ratio 5:6:7. Find the measure of each of the angles.
Solution:
Let the measure of the given angles be
(5x)°, (6x)°, (7x)°
By angle sum property of a triangle
(5x)° + (6x)° + (7x)° = 180°
(18x)° = 180°
x = \(\frac{180^{\circ}}{18}\)
x = 10
Required angles
= (5 × 10)°, (6 × 10)°, (7 × 10)°
= 50°, 60°, 70°
5. One angle of a triangle is 60°. The other two angles are in the ratio 4 : 8. Find the angles.
Solution:
One angle of triangle = 60°
Let the other two angles be (4x)° and (8x)°
By angle sum property of a triangle
60° + (4x)° + (8x)° = 180°
60° + (12x)° = 180°
(12x)° = 180° – 60°
(12x)° = 120°
x = \(\frac{120^{\circ}}{12}\)
x = 10
Required angles = (4x)°, (8x)°
(4 × 10)°, (8 × 10)°
= 40°, 80°
![]()
6. In a triangle ABC, ZB = 50°, ∠C = 62°. Find ∠A.
Solution:
In a ΔABC, ∠B = 50°, ∠C = 62°
By angle sum property of a triangle
∠A + ∠B + ∠C = 180°
∠A + 50° + 62° = 180°
∠A + 112° = 180°
∠A = 180° – 112°
∠A = 68°
7. In a right angled triangle two acute angles are in the ratio 2 : 3. Find the angles.
Solution:
In a right angle triangle one angle = 90°
Let the other two angles be (2x)°, (3x)°
By angle sum property of a triangle.
90° + (2x)° + (3x)° = 180°
90° + (5x)° = 180°
(5x)° = 180° – 90°
(5x)° = 90°
x = \(\frac{90^{\circ}}{5}\)
x = 18
Required angles = (2x)°, (3x)°
= (2 × 18)°, (3 × 18)°
= 36°, 54°
8. Three angles of a triangle are (2x + 20)°, (x + 30)° and (2x – 10)°. Find the angles.
Solution:
Since, we know that the sum of angles of a triangle is always 180°
∴ (2x + 20)° + (x + 30)° + (2x – 10)° = 180°
(5x + 40)° = 180°
(5x)° = 180° – 40°
(5x)° = 140°
x = \(\frac{140^{\circ}}{5}\)
x = 28
Required angles
= (2x + 20)°, (2x + 30)° and (2x – 10)°
= (2 × 28 + 20)°, (28 + 30)° and (2 × 28 -10)°
= (56 + 20)°, (58)° and (56 – 10)°
= 76°, 58° and 46°
![]()
9. Multiple choice questions :
Question (i).
A triangle can have two …………….
(a) Acute angles
(b) Obtuse angles
(c) Right angles
(d) None of these.
Answer:
(a) Acute angles
Question (ii).
A triangle is possible with measure of angles
(a) 30°, 40°, 100°
(b) 60°, 60°, 70°
(c) 60°, 50°, 70°
(d) 90°, 89°, 92°
Answer:
(c) 60°, 50°, 70°
Question (iii).
One of the equal angles of an isosceles triangle is 45° then its third angle is
(a) 45°
(b) 60°
(c) 100°
(d) 90°
Answer:
(d) 90°
Question (iv).
The number of obtuse angles that a triangle can have
(a) 2
(b) 1
(c) 3
(d) 4.
Answer:
(b) 1
