Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 11 ਖੇਤਰਮਿਤੀ Ex 11.2 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 8 Maths Chapter 11 ਖੇਤਰਮਿਤੀ Exercise 11.2
ਪ੍ਰਸ਼ਨ 1.
ਇਕ ਮੇਜ਼ ਦੇ ਉੱਪਰੀ ਸ ਦਾ ਆਕਾਰ ਸਮਲੰਬ ਵਰਗਾ ਹੈ । ਜੇਕਰ ਸਮਾਂਤਰ ਭੁਜਾਵਾਂ 1 m ਅਤੇ 1.2 m ਹੈ ਅਤੇ ਇਹਨਾਂ ਸਮਾਂਤਰ ਭੁਜਾਵਾਂ ਦੇ ਵਿਚ ਦੂਰੀ 0.8 m ਹੈ, ਤਾਂ ਇਸਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਸਮਾਂਤਰ ਭੁਜਾਵਾਂ ਦੀ ਲੰਬਾਈ :
AB = 1.2 m ਅਤੇ
CD = 1 m
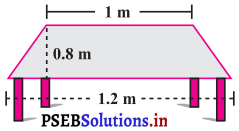
ਲੰਬ ਦੀ ਲੰਬਾਈ
= 0.8 m
∴ ਸਮਲੰਬ ਦਾ ਖੇਤਰਫਲ
= \(\frac{1}{2}\) × h (AB + CD)
= \(\frac{1}{2}\) × 0.8 (1 2 + 1.0)
= (0.4) (2.2) = 0.88 m2.
ਪ੍ਰਸ਼ਨ 2.
ਇਕ ਸਮਲੰਬ ਦਾ ਖੇਤਰਫਲ 34 cm2 ਹੈ ਅਤੇ ਇਸਦੀ ਉੱਚਾਈ 4 cm ਹੈ । ਸਮਾਂਤਰ ਭੁਜਾਵਾਂ ਵਿਚੋਂ ਇਕ ਦੀ ਲੰਬਾਈ 10 cm ਹੈ । ਦੂਸਰੀ ਸਮਾਂਤਰ ਭੁਜਾ ਦੀ ਲੰਬਾਈ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਪਹਿਲੀ ਸਮਾਂਤਰ ਭੁਜਾ ਦੀ ਲੰਬਾਈ = a = 10 cm
ਮੰਨ ਲਉ ਦੂਸਰੀ ਸਮਾਂਤਰ ਭੁਜਾ ਦੀ ਲੰਬਾਈ = b cm
ਸਮਲੰਬ ਦੀ ਉੱਚਾਈ = h= 4 cm
ਸਮਲੰਬ ਦਾ ਖੇਤਰਫਲ = 34 cm2
⇒ \(\frac{1}{2}\)h (a + b) = 34
⇒ \(\frac{1}{2}\) × 4 (10 + b) = 34
⇒ 2 (10 + b) = 34
⇒ 10 + b = \(\frac{34}{2}\) = 17
⇒ b = 17 – 10
⇒ b = 7 cm
∴ ਦੂਸਰੀ ਸਮਾਂਤਰ ਭੁਜਾ ਦੀ ਲੰਬਾਈ 7 cm ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 3.
ਇਕ ਸਮਲੰਬ ਦੇ ਆਕਾਰ ਦੇ ਖੇਤ ABCD ਦੀ ਵਾੜ ਦੀ ਲੰਬਾਈ 120 m ਹੈ । ਜੇ BC = 48 m, CD = 17 m ਅਤੇ D = 40 m ਹੈ, ਤਾਂ ਇਸ ਖੇਤ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ । ਭੁਜਾ AB ਸਮਾਂਤਰ ਭੁਜਾਵਾਂ AD ਅਤੇ BC’ਤੇ ਲੰਬ ਹੈ ।
ਹੱਲ:
ਸਮਲੰਬ ਦੇ ਵਾੜ ਦੀ ਲੰਬਾਈ = 120 m
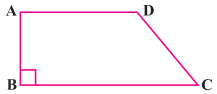
∴ ਸਮਲੰਬ ਦਾ ਪਰਿਮਾਪ = 120 m
⇒ AB + BC + CD + DA = 120
⇒ AB + 48 + 17 + 40 = 120
⇒ AB + 105 = 120
⇒ AB = 120 – 105 = 15 m
ਹੁਣ ਸਮਲੰਬ ਦਾ ਖੇਤਰਫਲ = \(\frac{1}{2}\) × (ਸਮਾਂਤਰ ਭੁਜਾਵਾਂ ਦਾ ਜੋੜ) × ਉੱਚਾਈ
= \(\frac{1}{2}\) × (48 + 40) × 15
= \(\frac{1}{2}\) × 88 × 15
= 44 × 15 = 660 m2.
ਪ੍ਰਸ਼ਨ 4.
ਇਕ ਚਤੁਰਭੁਜ ਆਕਾਰ ਦੇ ਖੇਤ ਦਾ ਵਿਕਰਨ 24 m ਹੈ ਅਤੇ ਬਾਕੀ ਸਨਮੁਖ ਸਿਖਰਾਂ ਤੋਂ ਇਸ ਦੇ ਵਿਕਰਨ ’ਤੇ ਖਿੱਚੇ ਗਏ ਲੰਬ 8 m ਅਤੇ 13 m ਹਨ । ਖੇਤ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨਿਆ ABCD ਇਕ ਚਤੁਰਭੁਜ ਦੇ ਅਕਾਰ ਦਾ ਖੇਤ ਹੈ ।
ਮੰਨ ਲਉ AC ਵਿਕਰਨ ਹੈ
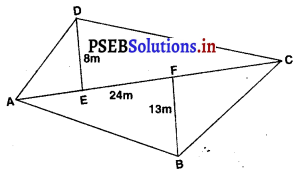
∴ ਖੇਤ △BCD ਦਾ ਖੇਤਰਫਲ = △ACD ਦਾ ਖੇਤਰਫਲ + △ACB ਦਾ ਖੇਤਰਫਲ
= \(\frac{1}{2}\) × AC × DE + \(\frac{1}{2}\) AC × BF
= \(\frac{1}{2}\) × 24 × 8 + \(\frac{1}{2}\) × 24 × 13
= 96 + 156
= 252 m2.
![]()
ਪ੍ਰਸ਼ਨ 5.
ਕਿਸੇ ਸਮਚਤੁਰਭੁਜ ਦੇ ਵਿਕਰਨ 7.5 cm ਅਤੇ 12 cm ਹੈ । ਇਸਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ ABCD ਇਕ ਸਮਚਤੁਰਭੁਜ ਹੈ ।
∴ ਇਸਦਾ ਪਹਿਲਾ ਵਿਕਰਨ AC = 7.5 cm
ਦੂਸਰਾ ਵਿਕਰਨ BD = 12 cm
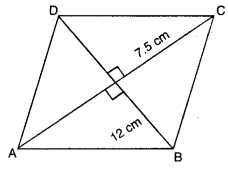
∴ ਸਮਚਤੁਰਭੁਜ ਦਾ ਖੇਤਰਫਲ = \(\frac{1}{2}\) × (ਪਹਿਲਾ ਵਿਕਰਨ) × (ਦੂਸਰਾ ਕਰਨ)
= \(\frac{1}{2}\) × 7.5 × 12
= 45.0 cm2.
ਪ੍ਰਸ਼ਨ 6.
ਇਕ ਸਮਚਤੁਰਭੁਜ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ਜਿਸਦੀ ਭੁਜਾ 6 cm ਅਤੇ ਸਿਖਰਲੰਬ 4 cm ਹੈ । ਜੇਕਰ ਇਕ ਵਿਕਰਨ ਦੀ ਲੰਬਾਈ 8 cm ਹੈ, ਤਾਂ ਦੂਸਫ਼ੇ ਵਿਕਰਨ ਦੀ ਲੰਬਾਈ ਪਤਾ
ਹੱਲ:
ਮੰਨ ਲਉ ABCD ਸਮਚਤੁਰਭੁਜ ਹੈ ।
ਸਮਚਤੁਰਭੁਜ ਦੀ ਭੁਜਾ = 6 cm
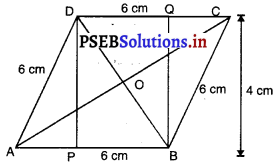
ਸਮਚਤੁਰਭੁਜ ਦਾ ਸਿਖਰਲੰਬ = h = 4 cm
∴ ਸਮਚਤੁਰਭੁਜ ABCD ਦਾ ਖੇਤਰਫਲ = △ABD ਦਾ ਖੇਤਰਫਲ + △BCD ਦਾ ਖੇਤਰਫਲ
= \(\frac{1}{2}\)(AB × DP) + \(\frac{1}{2}\)(DC × BQ)
= \(\frac{1}{2}\) × 6 + 4 + \(\frac{1}{2}\) × 6 × 4
= 12 + 12 = 24 cm2
∴ ਸਮਚਤੁਰਭੁਜ ਦਾ ਖੇਤਰਫਲ = 24 cm2
⇒ \(\frac{1}{2}\)(d1 × d2) = 24
⇒ d1 × d2 = 2(24)
⇒ 8 × d2 = 48
⇒ d = \(\frac{48}{8}\) = 6 cm
∴ ਦੂਸਰੇ ਵਿਕਰਨ ਦੀ ਲੰਬਾਈ = 6 cm
![]()
ਪ੍ਰਸ਼ਨ 7.
ਕਿਸੇ ਭਵਨ ਦੇ ਫਰਸ਼ ਤੇ ਸਮਚਤੁਰਭੁਜ ਦੇ ਆਕਾਰ ਦੀਆਂ 300 ਟਾਈਲਾਂ ਹਨ ਅਤੇ ਇਸ ਵਿਚ ਹਰੇਕ ਦਾ ਵਿਕਰਨ 45 cm ਅਤੇ 30 cm ਲੰਬਾਈ ਦੇ ਹਨ । ₹ 4 ਪ੍ਰਤੀ ਵਰਗ ਮੀਟਰ ਦੀ ਦਰ ਨਾਲ ਇਸ ਫਰਸ਼ ਨੂੰ ਪਾਲਿਸ਼ ਕਰਨ ਦਾ ਖ਼ਰਚ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ ABCD ਸਮਚਤੁਰਭੁਜ ਦੇ ਅਕਾਰ ਦੀਆਂ ਟਾਇਲਾਂ ਹਨ ।
∴ ਟਾਈਲਾਂ ਦਾ ਪਹਿਲਾ ਵਿਕਰਨ (d1) = 45 cm
ਟਾਈਲ ਦਾ ਦੂਸਰਾ ਵਿਕਰਨ (d2) = 30 cm
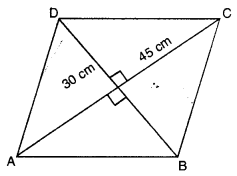
∴ ਸਮਚਤੁਰਭੁਜ ਅਕਾਰ ਦੀ ਟਾਈਲ ਦਾ ਖੇਤਰਫਲ
= \(\frac{1}{2}\) × d1 × d2
= \(\frac{1}{2}\) × 45 × 30
∴ 1 ਟਾਈਲ ਦਾ ਖੇਤਰਫਲ = 45 × 15 = 675 cm2
ਟਾਈਲਾਂ ਦੀ ਸੰਖਿਆ = 3000
∴ 3000 ਟਾਈਲਾਂ ਦਾ ਖੇਤਰਫਲ = 675 × 3000 cm2
= 2025000 cm2
ਫਰਸ਼ ਨੂੰ ਪਾਲਿਸ਼ ਕਰਨ ਦਾ ਖ਼ਰਚ = ₹ 4 ਪ੍ਰਤੀ m2
ਫਰਸ਼ ਦਾ ਖੇਤਰਫਲ = 2025000 cm2
= \(\frac{2025000}{10,000}\) m2
[∵ 1m =100 cm
∴ 1 m2 = 10000 cm2]
= 202.5 m2
∴ ਪਾਲਿਸ਼ ਦਾ ਕੁੱਲ ਖ਼ਰਚ = ₹ 4 × 202.5
= ₹ 810
ਪ੍ਰਸ਼ਨ 8.
ਮੋਹਨ ਇਕ ਸਮਲੰਬ ਦੇ ਆਕਾਰ ਦਾ ਖੇਤ ਖਰੀਦਣਾ ਚਾਹੁੰਦਾ ਹੈ । ਇਸ ਖੇਤ ਦੀ ਨਦੀ ਦੇ ਨਾਲ ਵਾਲੀ ਭੁਜਾ ਸੜਕ ਦੇ ਨਾਲ ਵਾਲੀ ਬਾਕੀ ਭੁਜਾ ਦੇ ਸਮਾਂਤਰ ਹੈ ਅਤੇ ਲੰਬਾਈ ਵਿਚ ਦੁੱਗਣੀ ਹੈ । ਜੇ ਇਸ ਖੇਤ ਦਾ ਖੇਤਰਫਲ 10500 m2 ਹੈ ਅਤੇ ਦੋ ਸਮਾਂਤਰ ਭੁਜਾਵਾਂ ਦੇ ਵਿੱਚਕਾਰਲੀ ਦੂਰੀ 100 m ਹੈ, ਤਾਂ ਨਦੀ ਦੇ ਨਾਲ ਵਾਲੀ ਭੁਜਾ ਪਤਾ ਕਰੋ ।
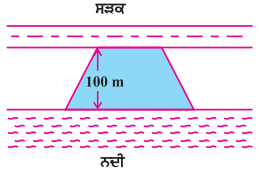
ਹੱਲ:
ਮੰਨ ਲਉ ਖੇਤ ਦੀ ਸੜਕ ਦੇ ਨਾਲ ਵਾਲੀ ਭੁਜਾ ਦੀ ਲੰਬਾਈ = x m
∴ ਖੇਤ ਦੀ ਨਦੀ ਦੇ ਨਾਲ ਵਾਲੀ ਭੁਜਾ ਦੀ ਲੰਬਾਈ = 2x m
ਦੋ ਭੁਜਾਵਾਂ ਦੇ ਵਿਚ ਦੀ ਲੰਬਵਤ ਦੂਰੀ
= 100 m
ਖੇਤ ਦਾ ਖੇਤਰਫਲ = 10500 m2
∴ ਸਮਲੰਬ ਅਕਾਰ ਦੇ ਖੇਤ ਦਾ ਖੇਤਰਫਲ
= 10500 m2
⇒ \(\frac{1}{2}\) × (ਸਮਾਂਤਰ ਭੁਜਾਵਾਂ ਦਾ ਜੋੜ) × ਲੰਬ ਦੂਰੀ
= 10500
⇒ \(\frac{1}{2}\)(1 + 25) × 100 = 10,500
⇒ \(\frac{3x}{2}\) = 105
⇒ 3x = 210
⇒ x = \(\frac{210}{3}\) = 70 m
∴ ਨਦੀ ਦੇ ਨਾਲ ਵਾਲੀ ਭੁਜਾ ਦੀ ਲੰਬਾਈ
= 2x
= 2 × 70 = 140 m
![]()
ਪ੍ਰਸ਼ਨ 9.
ਇਕ ਉੱਪਰ ਉੱਠੇ ਹੋਏ ਚਬੂਤਰੇ ਦੀ ਉੱਪਰਲੀ ਸੜਾ ਦਾ ਆਕਾਰ ਕੀ ਹੈ । ਜਿਸ ਤਰ੍ਹਾਂ ਕਿ ਚਿੱਤਰ ਵਿਚ ਦਰਸਾਇਆ ਗਿਆ ਹੈ । ਅੱਠ ਭੁਜੀ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।
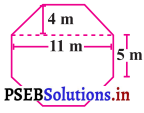
ਹੱਲ:
ਮੰਨ ਲਉ ABCDEFGH ਆਕ੍ਰਿਤੀ ਵਿਚ ਦਰਸਾਇਆ ਗਿਆ ਅੱਠਭੁਜੀ ਹੈ ।
ਅੱਠਭੁਜ ਦੀ ਹਰੇਕ ਭੁਜਾ = 5 m
ਹੁਣ, ਅੱਠਭੁਜ ABCDEFGH ਦਾ ਖੇਤਰਫਲ
= ਸਮਲੰਬ ABCD ਦਾ ਖੇਤਰਫਲ + ਆਇਤ ADE ਦਾ ਖੇਤਰਫਲ + ਸਮਲੰਬ HEFG ਦਾ ਖੇਤਰਫਲ
= \(\frac{1}{2}\)(BC + AD) BP + (AD × DE) + \(\frac{1}{2}\)(HE + GF) × GQ = \(\frac{1}{2}\)(11 + 5) × 4 + (11 × 5) + \(\frac{1}{2}\)(11 + 5) × 4
= (16 × 2) + (11 × 5) + (16 × 2)
= 32 + 55 + 32
= 119 m2
ਪ੍ਰਸ਼ਨ 10.
ਇਕ ਪੰਜਭੁਜ ਆਕਾਰ ਦਾ ਬਗੀਚਾ ਹੈ । ਜਿਸ ਤਰ੍ਹਾਂ ਕਿ ਚਿੱਤਰ ਵਿਚ ਦਰਸਾਇਆ ਗਿਆ ਹੈ । ਇਸਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰਨ ਦੇ ਲਈ ਜੋਤੀ ਅਤੇ ਕਵਿਤਾ ਨੇ ਇਸ ਨੂੰ ਦੋ ਵੱਖਵੱਖ ਤਰੀਕਿਆਂ ਨਾਲ ਵੰਡਿਆ । ਦੋਨੋਂ ਤਰੀਕਿਆਂ ਦਾ ਉਪਯੋਗ ਕਰਦੇ ਹੋਏ ਇਸ ਬਗੀਚੇ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ । ਕੀ ਤੁਸੀਂ ਇਸਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰਨ ਦੀ ਕੋਈ ਹੋਰ ਵਿਧੀ ਦੱਸ ਸਕਦੇ ਹੋ ?
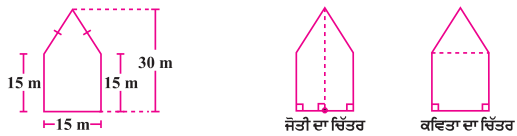
ਹੱਲ:
ਜੋਤੀ ਦੇ ਆਰੇਖ ਦੀ ਸਥਿਤੀ ਵਿਚ :
ਪੰਜਭੁਜ ਦੀ ਹਰੇਕ ਭੁਜਾ ਦੀ ਲੰਬਾਈ = 15 m
ਲੰਬ DP ਦੀ ਲੰਬਾਈ = 30 m
∴ ਪੰਜਭੁਜ ABCDE ਦਾ ਖੇਤਰਫਲ = 2 × ਸਮਲੰਬ APDE ਦਾ ਖੇਤਰਫਲ
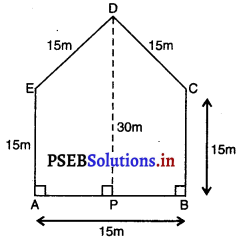
= 2 × (\(\frac{1}{2}\) ਸਮਾਂਤਰ ਭੁਜਾਵਾਂ ਦਾ ਯੋਗ ) × ਲੰਬੀ ਦੂਰੀ
= 2 × (\(\frac{1}{2}\)(30 + 15) × \(\frac{15}{2}\)]
= 45 × \(\frac{15}{2}\) = \(\frac{675}{2}\) m2 = 337.5m2
ਕਵਿਤਾ ਦੇ ਆਰੇਖ ਦੀ ਸਥਿਤੀ ਵਿਚ :
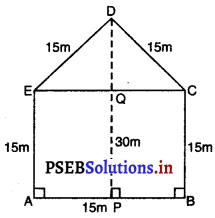
ਪੰਜਭੁਜ ABCDE = △DEC ਦਾ ਖੇਤਰਫਲ + ABCE ਦਾ ਖੇਤਰਫਲ
= \(\frac{1}{2}\) × EC × DQ + EA × AB
= \(\frac{1}{2}\) × 15 × 15 + 15 × 15
= \(\frac{225}{2}\) + \(\frac{225}{1}\)
= \(\frac{225+450}{2}\) = \(\frac{675}{2}\) m2 = 337.5 m2
![]()
ਪ੍ਰਸ਼ਨ 11.
ਨਾਲ ਦਿੱਤੇ ਫੋਟੋ ਫਰੇਮ ਦੇ ਚਿੱਤਰ ਦੀਆਂ ਬਾਹਰੀ ਅਤੇ ਅੰਦਰੂਨੀ ਮਾਪ ਕੁਮਵਾਰ 24 cm × 28 cm ਅਤੇ 16 cm × 20 cm ਹੈ । ਜੇਕਰ ਫਰੇਮ ਦੇ ਹਰੇਕ ਹਿੱਸੇ ਦੀ ਚੌੜਾਈ ਸਮਾਨ ਹੈ, ਤਾਂ ਹਰੇਕ ਹਿੱਸੇ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।
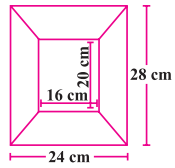
ਹੱਲ:
ਫੋਟੋ ਫਰੇਮ ਦੇ ਚਿੱਤਰ ਵਿਚ ਦਰਸਾਏ ਅਨੁਸਾਰ ਹੈ ।
ਫੋਟੋ ਫਰੇਮ ਵਿਚ ਸਮਲੰਬ ਆਕਾਰ ਦੇ ਚਾਰ ਖੰਡ ਹਨ !
ਅਰਥਾਤ ABCD, BEFC, EGHF ਅਤੇ GADH
ਇਨ੍ਹਾਂ ਚਾਰਾਂ ਭਾਗਾਂ ਵਿਚ, ਸਨਮੁੱਖ ਖੰਡ ਦੇ ਖੇਤਰਫਲ ਸਮਾਨ ਹਨ ।
ਅਰਥਾਤ ਖੰਡ ABCD ਦਾ ਖੇਤਰਫਲ = ਖੰਡ EGHF ਦਾ ਖੇਤਰਫਲ ਅਤੇ ਖੰਡ GADH ਦਾ ਖੇਤਰਫਲ = ਖੰਡ BEFC ਦਾ ਖੇਤਰਫਲ
ਹੁਣ, ਸਮਲੰਬ ABCD ਦਾ ਖੇਤਰਫਲ
= \(\frac{1}{2}\)(AB + CD) × (ਫਰੇਮ ਦੀ ਚੌੜਾਈ)
= \(\frac{1}{2}\)(24 + 16) × 4
= (40) × 2 = 80 cm2
∴ ਖੰਡ ABCD ਦਾ ਖੇਤਰਫਲ
= ਖੰਡ EGHF ਦਾ ਖੇਤਰਫਲ = 80 cm2 ਨਾਲ ਹੀ,
ਸਮਲੰਬ BEFC ਦਾ ਖੇਤਰਫਲ = \(\frac{1}{2}\) × (BE + CF) × ਫਰੇਮ ਦੀ ਚੌੜਾਈ
= \(\frac{1}{2}\)(28 + 20) × 4
= 48 × 2 = 96 cm2
∴ ਸਮਲੰਬ BEFC ਦਾ ਖੇਤਰਫਲ = ਖੰਡ GADH ਦਾ ਖੇਤਰਫਲ = 96 cm2
