PSEB 8th Class Maths Solutions Chapter 11 ਖੇਤਰਮਿਤੀ Ex 11.3

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 11 ਖੇਤਰਮਿਤੀ Ex 11.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 11 ਖੇਤਰਮਿਤੀ Exercise 11.3

ਪ੍ਰਸ਼ਨ 1.
ਦੋ ਘਣਾਵਕਾਰ ਡੱਬੇ ਹਨ ਜਿਸ ਤਰ੍ਹਾਂ ਕਿ ਨਾਲ ਦਿੱਤੇ ਚਿੱਤਰ ਵਿਚ ਦਰਸਾਇਆ ਗਿਆ ਹੈ । ਕਿਸ ਡੱਬੇ ਨੂੰ ਬਣਾਉਣ ਦੇ ਲਈ ਘੱਟ ਸਮੱਗਰੀ ਦੀ ਜ਼ਰੂਰਤ ਹੈ ?

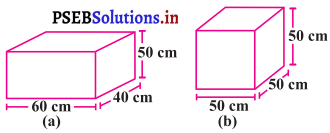
ਹੱਲ:
(a) ਦੀ ਸਥਿਤੀ ਵਿਚ :
ਘਣਾਵ ਦੀ ਲੰਬਾਈ (l) = 60 cm
ਘਣਾਵ ਦੀ ਚੌੜਾਈ (b) = 40 cm
ਘਣਾਵ ਦੀ ਉੱਚਾਈ (h)= 50 cm
∴ ਡੱਬੇ ਦਾ ਕੁੱਲ ਸਤ੍ਹਾ ਖੇਤਰਫਲ
= 2 (lb + bh + hl)
= 2 (60 × 40 + 40 × 50 + 50 × 60)
= 2 (2400 + 2000 + 3000)
= 2 × 7400 = 14800 cm²

(b) ਦੀ ਸਥਿਤੀ ਵਿਚ :
ਘਣਾਵ ਦੀ ਲੰਬਾਈ (l) = 50 cm
ਘਣਾਵ ਦੀ ਚੌੜਾਈ (b) = 50 cm
ਘਣਾਵ ਦੀ ਉੱਚਾਈ (h)= 50 cm
∴ ਡੱਬੇ ਦਾ ਕੁੱਲ ਸੜਾ ਦਾ ਖੇਤਰਫਲ
= 2 (lb + bh + hl)
= 2 (50 × 50 + 50 × 50 + 5 × 50)
= 2 (2500 + 2500 + 2500)
= 2 × 7500 = 15000 cm²
∴ ਡੱਬੇ (a) ਨੂੰ ਬਣਾਉਣ ਦੇ ਲਈ ਘੱਟ ਸਾਮਗਰੀ ਅਰਥਾਤ 14800 cm2 ਦੀ ਜ਼ਰੂਰਤ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
80 cm × 48 cm × 24 cm ਮਾਪ ਵਾਲੇ ਇਕ ਸੂਟਕੇਸ ਨੂੰ ਤਰਪਾਲ ਦੇ ਕੱਪੜੇ ਨਾਲ ਢੱਕਣਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਦੇ 100 ਸੂਟਕੇਸਾਂ ਨੂੰ ਢੱਕਣ ਦੇ ਲਈ 96 cm ਚੌੜਾਈ ਵਾਲੇ ਕਿੰਨੇ ਮੀਟਰ ਤਰਪਾਲ ਦੇ ਕੱਪੜੇ ਦੀ ਜ਼ਰੂਰਤ ਹੈ ?
ਹੱਲ:
ਸੂਟਕੇਸ ਦੀ ਲੰਬਾਈ (l) = 80 cm
ਸੂਟਕੇਸ ਦੀ ਚੌੜਾਈ (b) = 48 cm
ਸੂਟਕੇਸ ਦੀ ਉੱਚਾਈ (h) = 24 cm
∴ ਸੂਟਕੇਸ ਦਾ ਕੁੱਲ ਸੜਾ ਦਾ ਖੇਤਰਫਲ
= 2 (lb + bh + hl)
= 2 (80 × 48 +48 × 24 + 24 × 80)
= 2 (3840 + 1152 + 1920)
= 2 (6912)
= 13824 cm²
1 ਸੂਟਕੇਸ ਦਾ ਕੁੱਲ ਸੜਾ ਦਾ ਖੇਤਰਫਲ
= 13824 cm²
100 ਸੂਟਕੇਸਾਂ ਦਾ ਕੁੱਲ ਸੜਾ ਦਾ ਖੇਤਰਫਲ
= 100 × 13824
= 1382400 cm²
ਤਰਪਾਲ ਦੇ ਕੱਪੜੇ ਦੀ ਲੰਬਾਈ = x cm
ਤਰਪਾਲ ਦੇ ਕੱਪੜੇ ਦੀ ਚੌੜਾਈ = 96 cm
∴ ਤਰਪਾਲ ਦੇ ਕੱਪੜੇ ਦਾ ਖੇਤਰਫਲ = ਲੰਬਾਈ × ਚੌੜਾਈ
= x × 96
= 96x cm²
∴ 96x = 1382400
⇒ x = \(\frac{1382400}{96}\)
⇒ x = 14400 cm = 144 m.

ਪ੍ਰਸ਼ਨ 3.
ਇਕ ਇਸ ਤਰ੍ਹਾਂ ਦੇ ਘਣ ਦੀ ਭੁਜਾ ਪਤਾ ਕਰੋ ਜਿਸਦੀ ਕੁੱਲ ਸਤਾ ਦਾ ਖੇਤਰਫਲ 600 cm² ਹੈ ?
ਹੱਲ:
ਮੰਨ ਲਉ ਘਣ ਦੀ ਭੁਜਾ ਦੀ ਲੰਬਾਈ = x cm
ਘਣ ਦੀ ਕੁੱਲ ਸਤਾ ਦਾ ਖੇਤਰਫਲ = 600 cm²
⇒ 6x² = 600
⇒ x² = 100
⇒ x = 10 cm
∴ ਘਣ ਦੀ ਭੁਜਾ = 10 cm

ਪ੍ਰਸ਼ਨ 4.
ਰੁਖਸਾਰ ਨੇ 1 m × 2 m × 1.5 m ਮਾਪ ਵਾਲੀ ਇਕ ਪੇਟੀ ਨੂੰ ਬਾਹਰ ਤੋਂ ਪੇਂਟ ਕੀਤਾ । ਜੇ ਉਸਨੇ ਪੇਟੀ ਦੇ ਤਲ ਨੂੰ ਛੱਡ ਕੇ ਉਸਨੂੰ ਸਾਰੀ ਜਗਾ ਤੋਂ ਪੇਂਟ ਕੀਤਾ ਹੋਵੇ ਤਾਂ ਪਤਾ ਕਰੋ ਕਿ ਉਸਨੇ ਕਿੰਨੀ ਸਤ੍ਹਾ ਦੇ ਖੇਤਰਫਲ ਨੂੰ ਪੇਂਟ ਕੀਤਾ ।

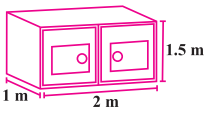
ਹੱਲ:
ਪੇਟੀ ਦੀ ਲੰਬਾਈ (l) = 1 m
ਪੇਟੀ ਦੀ ਚੌੜਾਈ (b) = 2 m
ਪੇਟੀ ਦੀ ਉੱਚਾਈ (h) = 1.5 m
∴ ਤਲ ਦੇ ਇਲਾਵਾ ਪੇਟੀ ਦਾ ਖੇਤਰਫਲ
= 2h (l + b) + l × b
= 2 (15) [1 + 2] + 1 × 2
= (3) (3) + 2
= 9 m² + 2 m²
= 11 m²

ਪ੍ਰਸ਼ਨ 5.
ਡੇਨੀਅਲ ਇਕ ਇਸ ਤਰ੍ਹਾਂ ਦੇ ਘਣਾਵਕਾਰ ਕਮਰੇ ਦੀਆਂ ਦੀਵਾਰਾਂ ਅਤੇ ਛੱਤ ਨੂੰ ਪੇਂਟ ਕਰ ਰਿਹਾ ਹੈ ਜਿਸਦੀ ਲੰਬਾਈ, ਚੌੜਾਈ ਅਤੇ ਉੱਚਾਈ ਕ੍ਰਮਵਾਰ 15 m, 10 m ਅਤੇ 7 m ਹੈ । ਪੇਟ ਦੇ ਹਰੇਕ ਡੱਬੇ ਨਾਲ 100 m² ਖੇਤਰਫਲ ਨੂੰ ਪੇਂਟ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ਤਾਂ ਉਸ ਕਮਰੇ ਦੇ ਲਈ ਉਸਨੂੰ ਪੇਂਟ ਦੇ ਕਿੰਨੇ ਡੱਬਿਆਂ ਦੀ ਜ਼ਰੂਰਤ ਹੈ ?
ਹੱਲ:
ਕਮਰੇ ਦੀ ਲੰਬਾਈ (l) = 15 m
ਕਮਰੇ ਦੀ ਚੌੜਾਈ (b) = 10 m
ਅਤੇ ਕਮਰੇ ਦੀ ਉੱਚਾਈ (h) = 7 m
∴ ਕਮਰੇ ਦੀਆਂ ਚਾਰਾਂ ਦੀਵਾਰਾਂ ਅਤੇ ਛੱਤਾਂ ਦਾ ਖੇਤਰਫਲ
= 2h (l + b) + l × b
= 2 × 7 (15 + 10) + 15 × 10
= 14 (25) + 150
= 350 + 150 = 500m²
1 ਕੈਨ ਪੇਂਟ ਕਰਦਾ ਹੈ = 100 m²
∴ ਜ਼ਰੂਰੀ ਕੈਨਾਂ ਦੀ ਸੰਖਿਆ = \(\frac{500}{100}\) = 5

ਪ੍ਰਸ਼ਨ 6.
ਵਰਣਨ ਕਰੋ ਕਿ ਹੇਠਾਂ ਦਿੱਤੇ ਗਏ ਚਿੱਤਰ ਕਿਸ ਤਰ੍ਹਾਂ ਇਕ ਸਮਾਨ ਹਨ ਅਤੇ ਕਿਸ ਤਰ੍ਹਾਂ ਇਕ-ਦੂਸਰੇ ਤੋਂ ਵੱਖਰੇ ਹਨ ? ਕਿਸ ਡੱਬੇ ਦਾ ਪਾਸਵੀਂ ਸਤਾ ਦਾ ਖੇਤਰਫਲ ਜ਼ਿਆਦਾ ਹੈ ?

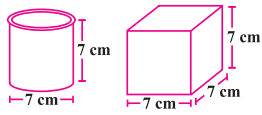
ਹੱਲ:
ਦਿੱਤੇ ਗਏ ਦੋ ਚਿੱਤਰਾਂ ਵਿਚੋਂ ਇਕ ਵੇਲਣ ਹੈ ਅਤੇ ਦੂਜਾ ਘਣ ਹੈ, ਇਕ ਸਮਾਨ ਉੱਚਾਈ ਅਤੇ ਵਿਆਸ ਅਰਥਾਤ 7 cm ਹੈ ਜਿਸਦੀ ਹਰੇਕ ਭੁਜਾ 7 cm ਦਾ ਵੇਲਣ ਹੈ ਅਤੇ ਦੂਸਰਾ ਘਣ ਹੈ ਜਿਸਦੀ ਹਰੇਕ ਭੁਜਾ 7 cm ਹੈ ।
ਵੇਲਣ ਦਾ ਵਿਆਸੇ = 7 cm
∴ ਵੇਲਣ ਦਾ ਅਧਵਿਆਸ = \(\frac{7}{2}\) cm
ਵੇਲਣ ਦੀ ਉੱਚਾਈ = 7 cm
∴ ਵੇਲਣ ਦੀ ਪਾਸਵੀਂ ਵਿਕਰ ਸਤਾ ਦਾ ਖੇਤਰਫਲ
= 2πrh
= 2 × \(\frac{22}{7}\) × \(\frac{7}{2}\) × 7
= 154 cm²
ਘਣ ਦੀ ਹਰੇਕ ਭੁਜਾ ਦੀ ਲੰਬਾਈ = 7 cm
∴ ਘਣ ਦੀ ਇਕ ਪਾਸੇ ਦੀ (ਕਰ) ਸੜਾ ਦਾ ਖੇਤਰਫਲ
= 4 (ਭੁਜਾ)²
= 4 (7)² = 4 × 49
= 196 cm²
∴ ਘਣ ਦੀ ਕੁੱਲ ਸਤਾ ਦਾ ਖੇਤਰਫਲ ਜ਼ਿਆਦਾ ਹੈ !

ਪ੍ਰਸ਼ਨ 7.
7 m ਅਰਧਵਿਆਸ ਅਤੇ 3 m ਉੱਚਾਈ ਵਾਲਾ | ਇਕ ਬੰਦ ਵੇਲਣਾਕਾਰ ਟੈਂਕ ਕਿਸੇ ਧਾਤੁ ਦੀ ਇਕ ਚਾਦਰ ਨਾਲ ਬਣਿਆ ਹੋਇਆ ਹੈ । ਉਸਨੂੰ ਬਣਾਉਣ ਦੇ ਲਈ ਲੋੜੀਂਦੀ ਧਾਤੂ ਦੀ ਚਾਦਰ ਦੀ ਮਾਤਰਾ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਵੇਲਣਾਕਾਰ ਟੈਂਕ ਦਾ ਅਰਧਵਿਆਸ = 7 m
ਵੇਲਣਾਕਾਰ ਟੈਂਕ ਦੀ ਉੱਚਾਈ = 3 m
ਟੈਂਕ ਦਾ ਕੁੱਲ ਸਤ੍ਹਾ ਦਾ ਖੇਤਰਫਲ = 2πr (h + r)
= 2 × \(\frac{22}{7}\) × 7(3 + 7)
= 2 × 22 × 10
= 440 m²
∴ ਲੋੜੀਂਦੀ ਧਾਤੂ ਦੀ ਚਾਦਰ ਦੀ ਮਾਤਰਾ = 440 m²

ਪ੍ਰਸ਼ਨ 8.
ਇਕ ਖੋਖਲੇ ਵੇਲਣ ਦੀ ਪਾਸਵੀਂ ਸੜ੍ਹਾ ਦਾ ਖੇਤਰਫਲ 4224 cm² ਹੈ । ਇਸਨੂੰ ਇਸਦੀ ਉੱਚਾਈ ਦੇ ਅਨੁਸਾਰ ਕੱਟ ਕੇ 33 cm ਚੌੜਾਈ ਦੀ ਇਕ ਆਇਤਾਕਾਰ ਚਾਦਰ ਬਣਾਈ ਜਾਂਦੀ ਹੈ । ਆਇਤਾਕਾਰ ਚਾਦਰ ਦਾ ਪਰਿਮਾਪ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਵੇਲਣ ਦੀ ਉੱਚਾਈ (h) = 33 cm
ਮੰਨ ਲਉ ਵੇਲਣ ਦਾ ਅਰਧਵਿਆਸ = r
ਵੇਲਣ ਦੀ ਵਕਰ ਸਤਾ ਦਾ ਖੇਤਰਫਲ = 4224 cm²
∴ 2πrh = 4224

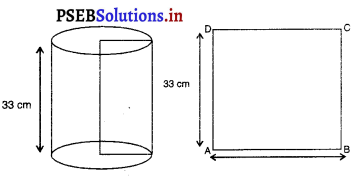
⇒ 2 × \(\frac{22}{7}\) × r × 33 = 4224
⇒ r = \(\frac{422×47}{2×22×33}\) = \(\frac{32×7}{11}\) cm
ਕਿਉਂਕਿ ਖੋਖਲੇ ਵੇਲਣ ਨੂੰ ਉਸਦੀ ਉੱਚਾਈ ਦੇ ਅਨੁਸਾਰ ਕੱਟਿਆ ਗਿਆ ਹੈ |
∴ ਆਧਾਰ ਦਾ ਪਰਿਮਾਪ ਆਇਤਾਕਾਰ ਚਾਦਰ ਦੀ ਉੱਚਾਈ ਬਣ ਜਾਂਦਾ ਹੈ ।
∴ ਗੋਲਾਕਾਰ ਆਧਾਰ ਦਾ ਪਰਿਮਾਪ = 2πr
= \(\frac{32×7}{11}\)
= 128 cm
∴ ਆਇਤਾਕਾਰ ਚਾਦਰ ਦੀ ਲੰਬਾਈ 128 cm
ਆਇਤਾਕਾਰ ਚਾਦਰ ਦੀ ਚੌੜਾਈ = 33 cm
∴ ਆਇਤਾਕਾਰ ਚਾਦਰ ਦਾ ਪਰਿਮਾਪ = 2 (l + b)
= 2(128 + 33).
= 2 × 16
= 322 cm

ਪ੍ਰਸ਼ਨ 9.
ਕਿਸੇ ਸੜਕ ਨੂੰ ਪੱਧਰਾ ਕਰਨ ਲਈ ਇੱਕ ਰੋਡਰੋਲਰ ਨੂੰ ਸੜਕ ਦੇ ਉੱਪਰ ਇਕ ਵਾਰ ਘੁੰਮਣ ਦੇ ਲਈ 750 ਚੱਕਰ ਲਗਾਉਣੇ ਪੈਂਦੇ ਹਨ । ਜੇ ਸੜਕ ਰੋਲਰ ਦਾ ਵਿਆਸ 84 cm ਅਤੇ 1 m ਲੰਬਾਈ ਹੈ, ਤਾਂ ਸੜਕ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।

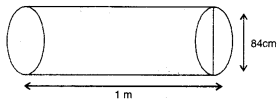
ਹੱਲ:
ਸੜਕ ਰੋਲਰ ਦੀ ਲੰਬਾਈ = 1 m
h = 100 cm
ਸੜਕ ਰੋਲਰ ਦਾ ਵਿਆਸ = 84 cm.
∴ ਸੜਕੂ ਰੋਲਰ ਦਾ ਅਰਵਿਆਸ (r) = \(\frac{84}{2}\) cm
= 42 cm.
ਸੜਕ ਰੋਲਰ ਦਾ ਵਕਰ ਸਤਾ ਦਾ ਖੇਤਰਫਲ
= 2πrh
= 2 × \(\frac{22}{7}\) × 42 × 100
= 26400 cm²
∴ 1 ਚੱਕਰ ਵਿਚ ਤੈਅ ਖੇਤਰਫਲ = 26400 cm²
= \(\frac{26400}{10,000}\) m²
= 2.64 m²
∴ ਸੜਕ ਦਾ ਖੇਤਰਫਲ : 750 ਚੱਕਰਾਂ ਵਿਚ ਤੈਅ ਖੇਤਰਫਲ
= 750 × 2.64
= 1980 m²

ਪ੍ਰਸ਼ਨ 10.
ਇਕ ਕੰਪਨੀ ਆਪਣੇ ਦੁੱਧ ਪਾਊਡਰ ਨੂੰ ਇਸ ਤਰ੍ਹਾਂ ਦੇ ਵੇਲਣਾਕਾਰ ਬਰਤਨਾਂ ਵਿਚ ਪੈਕ ਕਰਦੀ ਹੈ । ਜਿਹਨਾਂ ਦਾ ਵਿਆਸ 14 cm ਅਤੇ ਉੱਚਾਈ 20 cm ਹੈ। ਕੰਪਨੀ ਬਰਤਨ ਦੇ ਸਤਾ ਦੇ ਚਾਰੇ ਪਾਸੇ ਇਕ ਲੇਬਲ ਲਗਾਉਂਦੀ ਹੈ । (ਜਿਸ ਤਰ੍ਹਾਂ ਕਿ ਚਿੱਤਰ ਵਿਚ ਦਰਸਾਇਆ ਗਿਆ ਹੈ । ਜੇਕਰ ਇਹ ਲੇਬਲ ਬਰਤਨ ਦੇ ਤਲ ਅਤੇ ਸਿਖਰ ਦੋਨਾਂ ਤੋਂ 2 cm ਦੀ ਦੂਰੀ ਤੇ ਚਿਪਕਾਇਆ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਲੇਬਲ ਦਾ ਖੇਤਰਫਲ ਕੀ ਹੈ ?
ਹੱਲ:
ਬਰਤਨ ਦੇ ਆਧਾਰ ਦਾ ਵਿਆਸ = 14 cm
∴ ਬਰਤਨ ਦੇ ਅਧਾਰ ਦਾ ਅਰਧਵਿਆਸ (R) = \(\frac{14}{2}\) cm
= 7 cm
ਵੇਲਣਾਕਾਰ ਬਰਤਨ ਦੀ ਉੱਚਾਈ H = 20 cm

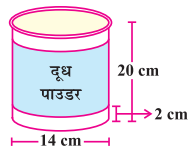
ਲੇਬਲ ਦੀ ਉੱਚਾਈ (h) = (20 – 2 – 2) cm
= (20 – 4)
h = 16 cm
∴ ਲੇਬਲ ਦਾ ਖੇਤਰਫਲ = 2πrh
= 2 × \(\frac{22}{7}\) × 7 × 16
= 704 cm²