PSEB 8th Class Maths Solutions Chapter 7 ਘਣ ਅਤੇ ਘਣਮੂਲ Ex 7.1

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 7 ਘਣ ਅਤੇ ਘਣਮੂਲ Ex 7.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 7 ਘਣ ਅਤੇ ਘਣਮੂਲ Exercise 7.1

1. ਹੇਠਾਂ ਲਿਖੀਆਂ ਵਿੱਚੋਂ ਕਿਹੜੀਆਂ ਸੰਖਿਆਵਾਂ ਪੂਰਨ ਘਣ ਨਹੀਂ ਹਨ ?

ਪ੍ਰਸ਼ਨ (i).
216
ਹੱਲ:
216

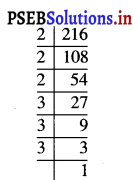
∴ 216 = \(\underline{2 \times 2 \times 2}\) × \(\underline{3 \times 3 \times 3}\)
ਇੱਥੇ, ਅਭਾਜ ਗੁਣਨਖੰਡ 2 ਅਤੇ 3 ਤਿੰਨ ਦੇ ਸਮੂਹ ਵਿਚ ਆਉਂਦੇ ਹਨ ।
ਇਸ ਲਈ, 216 ਇਕ ਪੂਰਨ ਘੁਣ ਹੈ ।

ਪ੍ਰਸ਼ਨ (ii).
128
ਹੱਲ:
128

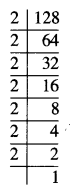
∴ 128 = \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) × 2
ਇੱਥੇ 128 ਦੇ ਅਭਾਜ ਗੁਣਨਖੰਡਾਂ ਤੋਂ ਅਸੀਂ ਪਾਉਂਦੇ ਹਾਂ ਕਿ ਜੇਕਰ ਅਸੀਂ ਸਮਾਨ ਗੁਣਨਖੰਡਾਂ ਨੂੰ ਤ੍ਰਿਗੁੱਟ ਵਿਚ ਸਮੂਹਿਤ ਕਰੀਏ ਤਾਂ ਇਕ ਗੁਣਨਖੰਡ 2 ਸਾਡੇ ਕੋਲ ਬਾਕੀ ਬਚਦਾ ਹੈ ।
∴ 128 ਇਕ ਪੂਰਨ ਘਣ ਨਹੀਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ (iii).
1000
ਹੱਲ:
1000
∴ 1000 = \(\underline{2 \times 2 \times 2}\) × \(\underline{5 \times 5 \times 5}\)

ਇੱਥੇ, 1000 ਦੇ ਅਭਾਜ ਗੁਣਨਖੰਡ ਤੋਂ ਅਸੀਂ ਪਾਉਂਦੇ ਹਾਂ ਕਿ ਜੇਕਰ ਅਸੀਂ ਸਮਾਨ ਗੁਣਨਖੰਡਾਂ ਤੋਂ ਤ੍ਰਿਗੁੱਟ ਵਿਚ ਸਮੂਹਿਕ ਕਰਨ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰਦੇ ਹਾਂ, ਤਾਂ ਕੋਈ ਗੁਣਨਖੰਡ ਬਾਕੀ ਨਹੀਂ ਬਚਦਾ ।
ਇਸ ਲਈ, 1000 ਇਕ ਪੂਰਨ ਘਣ ਹੈ ।

ਪ੍ਰਸ਼ਨ (iv).
100
ਹੱਲ:
100

∴ 100 = 2 × 2 × 5 × 5
ਇੱਥੇ, 100 ਦੇ ਅਭਾਜ ਗੁਣਨਖੰਡ ਤੋਂ ਅਸੀਂ ਪਾਉਂਦੇ ਹਾਂ ਕਿ ਗੁਣਨਖੰਡ 2 ਅਤੇ 5 ਦਾ ਕੋਈ ਤ੍ਰਿਗੁੱਟ ਨਹੀਂ ਬਣਦਾ ।
ਇਸ ਲਈ, 100 ਇਕ ਪੂਰਨ ਘਣ ਨਹੀਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ (v).
46656.
46656
∴ 46656 = \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) × \(\underline{3 \times 3 \times 3 \times 3 \times 3 \times 3}\)

ਇਥੇ, 46656 ਦੇ ਅਭਾਜ ਗੁਣਨਖੰਡਾਂ ਤੋਂ ਅਸੀਂ ਪਾਉਂਦੇ ਹਾਂ ਕਿ ਜੇਕਰ ਅਸੀਂ ਸਮਾਨ ਗੁਣਨਖੰਡਾਂ ਨੂੰ ਤ੍ਰਿਗੁੱਟ ਵਿਚ ਸ਼ਾਮਲ ਕਰਨ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰੀਏ ਤਾਂ 2 ਅਤੇ 3 ਦੇ ਤ੍ਰਿਗੁੱਟ ਬਣ ਜਾਂਦੇ ਹਨ ।
ਇਸ ਲਈ, 46656 ਇਕ ਪੂਰਨ ਘਣ ਹੈ ।

2. ਉਹ ਸਭ ਤੋਂ ਛੋਟੀ ਸੰਖਿਆ ਪਤਾ ਕਰੋ ਜਿਸ ਨਾਲ ਹੇਠਾਂ ਲਿਖੀਆਂ ਸੰਖਿਆਵਾਂ ਨੂੰ ਗੁਣਾ ਕਰਨ ‘ਤੇ ਪੂਰਨ ਘਣ ਪ੍ਰਾਪਤ ਹੋ ਜਾਂਵੇ :

ਪ੍ਰਸ਼ਨ (i).
243
ਹੱਲ:
ਅਸੀਂ ਦੇਖਦੇ ਹਾਂ ਕਿ 243 ਦੇ ਅਭਾਜ ਗੁਣਨਖੰਡਾਂ ਵਿਚ 3, ਤਿੰਨ ਦੇ ਸਮੂਹ ਵਿਚ ਹੈ । ਫਿਰ ਵੀ ਦੋ ਸਮੂਹ ਗੁਣਨਖੰਡ 3 ਅਤੇ 3 ਬਾਕੀ ਬਚਦੇ ਹਨ ।

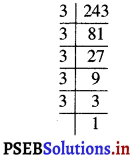
ਇਸ ਲਈ ਜੇਕਰ ਅਸੀਂ 3 × 3 ਨੂੰ 3 ਨਾਲ ਗੁਣਾ ਕਰੀਏ ਤਾਂ 3 ਦਾ ਇਕ ਹੋਰ ਤ੍ਰਿਗੁੱਟ ਬਣ ਜਾਏਗਾ ਅਤੇ ਗੁਣਨਫਲ ਇਕ ਪੂਰਨ ਘਣ ਹੋਵੇਗਾ |
ਅਰਥਾਤ
243 × 3 = \(\underline{3 \times 3 \times 3}\) x \(\underline{3 \times 3 \times 3}\) = 729
ਜੋ ਕਿ ਇਕ ਪੂਰਨ ਘਣ ਹੈ ।
ਇਸ ਲਈ ਸਭ ਤੋਂ ਛੋਟੀ ਸੰਖਿਆ ਜਿਸ ਨਾਲ 243 ਨੂੰ ਗੁਣਾ ਕੀਤਾ ਜਾਵੇ ਤਾਂਕਿ ਇਹ ਪੂਰਨ ਘਣ ਬਣ ਜਾਵੇ 3 ਹੈ ।

ਪ੍ਰਸ਼ਨ (ii).
256
ਹੱਲ:
256
256 = \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) × 2 × 2
ਅਸੀਂ ਦੇਖਦੇ ਹਾਂ ਕਿ 256 ਦੇ ਅਭਾਜ ਗੁਣਨਖੰਡਾਂ ਵਿਚ 2 ਦੇ ਦੋ ਤ੍ਰਿਗੁੱਟ ਬਣਦੇ ਹਨ । ਬਾਕੀ ਬਚੇ ਦੋ ਸਮਾਨ ਗੁਣਨਖੰਡ 2, 2 ਹੈ ।
ਇਸਨੂੰ ਪੂਰਨ ਘਣ ਬਣਾਉਣ ਲਈ ਸਾਨੂੰ ਇਕ 2 ਦੀ ਜ਼ਰੂਰਤ ਹੈ ।
ਇਸ ਸਥਿਤੀ ਵਿਚ :
256 × 2 = \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) = 512

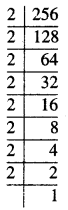
ਜੋ ਕਿ ਇਕ ਪੂਰਨ ਘਣ ਹੈ ।
ਇਸ ਲਈ, ਸਭ ਤੋਂ ਛੋਟੀ ਸੰਖਿਆ ਜਿਸ ਨਾਲ 256 ਨਾਲ ਗੁਣਾ ਕੀਤੀ ਜਾਵੇ ਤਾਂਕਿ ਉਹ ਪੂਰਨ ਘਣ ਬਣ ਜਾਏ 2 ਹੈ।

ਪ੍ਰਸ਼ਨ (iii).
72
ਹੱਲ:
72
72 = \(\underline{2 \times 2 \times 2}\) × 3 × 3
ਅਸੀਂ ਦੇਖਦੇ ਹਾਂ ਕਿ 72 ਦੇ ਅਭਾਜ ਗੁਣਨਖੰਡਾਂ ਵਿਚ ਤਿੰਨੁ ਦੇ ਸਮੂਹ ਵਿਚ ਆਉਂਦਾ ਹੈ । ਫਿਰ ਵੀ ਸਾਡੇ ਕੋਲ ਦੋ ਗੁਣਨਖੰਡ 3, 3 ਬਾਕੀ ਰਹਿ ਜਾਂਦਾ ਹੈ ।
ਇਸ ਨੂੰ ਪੂਰਨ ਘੰਣ ਬਣਾਉਣ ਲਈ ਸਾਨੂੰ ਇਕ 3 ਦੀ ਹੋਰ ਜ਼ਰੂਰਤ ਹੈ ।
ਇਸ ਸਥਿਤੀ ਵਿਚ ।

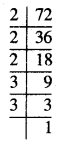
72 × 3 = \(\underline{2 \times 2 \times 2}\) × \(\underline{3 \times 3 \times 3}\) = 216
ਜੋ ਕਿ ਇਕ ਪੂਰਨ ਘਣ ਹੈ ।
ਇਸ ਲਈ, ਉਹ ਸਭ ਤੋਂ ਛੋਟੀ ਸੰਖਿਆ 3 ਹੈ, ਜਿਸਨੂੰ 72 ਨੂੰ ਪੂਰਨ ਘਣ ਬਣਾਉਣ ਲਈ 3 ਨਾਲ ਗੁਣਾ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ

ਪ੍ਰਸ਼ਨ (iv).
675
ਹੱਲ:
675
∴ 675 = \(\underline{3 \times 3 \times 3}\) × 5 × 5
ਅਸੀਂ ਦੇਖਦੇ ਹਾਂ ਕਿ 675 ਦੇ ਅਭਾਜ ਗੁਣਨਖੰਡਾਂ ਵਿਚ ਅਭਾਜ ਗੁਣਨਖੰਡ ਤਿੰਨ ਦੇ ਸਮੂਹ ਵਿਚ ਆਉਂਦਾ ਹੈ । ਫਿਰ ਵੀ ਸਾਡੇ ਕੋਲ 5 | ਦੇ ਦੋ ਗੁਣਨਖੰਡ ਬਾਕੀ ਬਚ ਜਾਂਦੇ ਹਨ ।

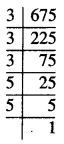
ਇਸਨੂੰ ਪੂਰਨ ਘਣ ਬਣਾਉਣ ਲਈ ਸਾਨੂੰ ਇਕ 5 ਦੀ ਜ਼ਰੂਰਤ ਹੈ !
ਇਸ ਸਥਿਤੀ ਵਿਚ,
675 × 5 = \(\underline{3 \times 3 \times 3}\) × \(\underline{5 \times 5 \times 5}\) = 3375
ਜੋ ਕਿ ਇਕ ਪੂਰਨ ਘਣ ਹੈ ।
ਇਸ ਲਈ, ਉਹ ਸਭ ਤੋਂ ਛੋਟੀ ਸੰਖਿਆ 5 ਹੈ ਜਿਸਨੂੰ 675 ਨੂੰ ਗੁਣਾ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ਕਿ ਇਹ ਪੁਰਨ ਘਣ ਬਣ ਜਾਵੇ ।

ਪ੍ਰਸ਼ਨ (v).
100.
ਹੱਲ:
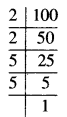
100
100 = 2 × 2 × 5 × 5
ਅਸੀਂ ਦੇਖਦੇ ਹਾਂ ਕਿ 100 ਦੇ ਅਭਾਜ ਗੁਣਨਖੰਡਾਂ ਵਿਚ 2 ਅਤੇ 5 ਤਿੰਨ-ਤਿੰਨ ਦੇ ਸਮੂਹਾਂ ਵਿਚ ਨਹੀਂ ਆ ਰਹੇ ਹਨ ।
∴ ਇਸਨੂੰ ਤਿੰਨ-ਤਿੰਨ ਦੇ ਸਮੂਹਾਂ ਵਿਚ ਬਣਾਉਣ ਲਈ ਸਾਨੂੰ ਇਕ 2 ਅਤੇ ਇਕ 5 ਹੋਰ ਚਾਹੀਦਾ ਹੈ ।

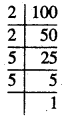
ਇਸ ਸਥਿਤੀ ਵਿਚ,
100 × 2 × 5 = \(\underline{2 \times 2 \times 2}\) × \(\underline{5 \times 5 \times 5}\) = 1000
ਜੋ ਕਿ ਇਕ ਪੂਰਨ ਘਣ ਹੈ ।
ਇਸ ਲਈ, ਉਹ ਸਭ ਤੋਂ ਛੋਟੀ ਸੰਖਿਆ 10 ਹੈ ਜਿਸਨੂੰ 100 ਨਾਲ ਗੁਣਾ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ਤਾਂਕਿ ਇਹ ਪੂਰਨ ਘਣ ਬਣ ਜਾਵੇ ।

3. ਉਹ ਸਭ ਤੋਂ ਛੋਟੀ ਸੰਖਿਆ ਪਤਾ ਕਰੋ ਜਿਸ ਨਾਲ ਹੇਠਾਂ ਲਿਖੀਆਂ ਸਿਖਿਆਵਾਂ ਨੂੰ ਵੰਡਣ ‘ਤੇ ਭਾਗਫਲ ਇਕ ਪੂਰਨ ਘਣ ਪ੍ਰਾਪਤ ਹੋ ਜਾਵੇ :

ਪ੍ਰਸ਼ਨ (i).
81
ਹੱਲ:
81

∴ 81 = \(\underline{3 \times 3 \times 3}\) × 3
ਅਭਾਜ ਗੁਣਨਖੰਡ 3 ਤਿੰਨ ਦੇ ਸਮੂਹ ਵਿਚ ਨਹੀਂ ਆਉਂਦਾ ਹੈ ।
∴ 81 ਇਕ ਪੂਰਨ ਘਣ ਨਹੀਂ ਹੈ ।
ਜੇਕਰ ਅਸੀਂ 81 ਨੂੰ 3 ਨਾਲ, ਤਾਂ ਭਾਗਫਲ ਦੇ ਅਭਾਜ ਗੁਣਨਖੰਡ ਬਣ ਜਾਂਦੇ ਹਨ :
81 ÷ 3 = \(\underline{3 \times 3 \times 3}\) = 27
ਜੋ ਕਿ ਇਕ ਪੂਰਨ ਘਣ ਹੈ ।
ਇਸ ਲਈ, ਉਹ ਸਭ ਤੋਂ ਛੋਟੀ ਸੰਖਿਆ 3 ਹੈ ਜਿਸ ਨਾਲ 81 ਨੂੰ ਵੰਡਣਾ ਚਾਹੀਦਾ ਹੈ ਤਾਂਕਿ ਇਹ ਪੂਰਨ ਘਣ ਬਣ ਜਾਵੇ ।

ਪ੍ਰਸ਼ਨ (ii).
128
ਹੱਲ:
128

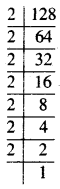
∴ 128 = \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) × 2
128 ਦੇ ਅਭਾਜ ਗੁਣਨਖੰਡਾਂ ਵਿਚ ਇਕ ਗੁਣਨਖੰਡ 2 ਸਮੂਹ ਵਿਚ ਨਹੀਂ ਆ ਰਿਹਾ ਹੈ ।
ਇਸ ਲਈ 128 ਪੂਰਨ ਘਣ ਨਹੀਂ ਹੈ ।
ਜੇਕਰ ਅਸੀਂ 128 ਨੂੰ 2 ਨਾਲ ਵੰਡਦੇ ਹਾਂ, ਤਾਂ ਭਾਗਫਲ ਦੇ ਗੁਣਨਖੰਡ ਬਣ ਜਾਂਦੇ ਹਨ :
128 ÷ 2 = \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) = 64
ਜੋ ਕਿ ਇਕ ਪੂਰਨ ਘਣ ਨਹੀਂ ਹੈ ।
ਇਸ ਲਈ ਉਹ ਸਭ ਤੋਂ ਛੋਟੀ ਸੰਖਿਆ 2 ਹੈ, ਜਿਸ ਨਾਲ 128 ਨੂੰ ਵੰਡਣਾ ਚਾਹੀਦਾ ਹੈ ਤਾਂਕਿ ਇਹ ਪੂਰਨ ਘਣ ਬਣ ਜਾਵੇ ।

ਪ੍ਰਸ਼ਨ (iii).
135
ਹੱਲ:
135

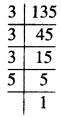
∴ 135 = \(\underline{3 \times 3 \times 3}\) × 5 × 5
675 ਦੇ ਅਭਾਜ ਗੁਣਨਖੰਡਾਂ ਵਿਚ ਗੁਣਨਖੰਡ 3 ਤਿੰਨ ਦੇ | ਸਮੂਹ ਵਿਚ ਨਹੀਂ ਆਉਂਦਾ ਹੈ ।
ਇਸ ਲਈ 675 ਇਕ ਪੂਰਨ ਘਣ ਨਹੀਂ ਹੈ ।
ਜੇਕਰ ਅਸੀਂ 675 ਨੂੰ 25 ਨਾਲ ਵੰਡਦੇ ਹਾਂ ਤਾਂ ਭਾਗਫਲ ਦੇ ਅਭਾਜ ਗੁਣਨਖੰਡ ਬਣ ਜਾਂਦੇ ਹਨ :
675 ÷ 25 = \(\underline{3 \times 3 \times 3}\) = 27
ਜੋ ਕਿ ਇਕ ਪੂਰਨ ਘਣ ਹੈ ।
ਇਸ ਲਈ, ਉਹ ਸਭ ਤੋਂ ਛੋਟੀ ਸੰਖਿਆ 25 ਹੈ ਜਿਸ ਨਾਲ 675 ਨੂੰ ਗੁਣਾ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ਤਾਂਕਿ ਇਹ ਪੂਰਨ ਘਣ ਬਣ ਜਾਵੇ ।

ਪ੍ਰਸ਼ਨ (iv).
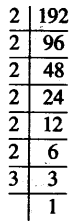
192
ਹੱਲ:
192
∴ 192 = \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) × 3
192 ਦੇ ਅਭਾਜ ਗੁਣਨਖੰਡਾਂ ਵਿਚ ਗੁਣਨਖੰਡ 3 ਤਿੰਨ ਦੇ ਸਮੂਹ ਵਿਚ ਨਹੀਂ ਆਉਂਦਾ ਹੈ ।
ਇਸ ਲਈ 192 ਪੁਰਨ ਘਣ ਨਹੀਂ ਹੈ ।
ਜੇਕਰ ਅਸੀਂ 192 ਨੂੰ 3 ਨਾਲ ਵੰਡਦੇ ਹਾਂ ਤਾਂ ਭਾਗਫਲ ਦੇ ਗੁਣਨਖੰਡ ਬਣ ਜਾਂਦੇ ਹਨ |
192 ÷ 3 = \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\)
ਜੋ ਕਿ ਇਕ ਪੂਰਨ ਘਣ ਹੈ ।
ਇਸ ਲਈ, ਉਹ ਸਭ ਤੋਂ ਛੋਟੀ ਸੰਖਿਆ 3 ਹੈ ਜਿਸ ਨਾਲ 392 ਨੂੰ ਵੰਡਣਾ ਚਾਹੀਦਾ ਹੈ ਤਾਂਕਿ ਇਹ ਪੂਰਨ ਘਣ ਬਣ ਜਾਵੇ ।

ਪ੍ਰਸ਼ਨ (v).
704.
ਹੱਲ:
704

∴ 704 = \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) × 11
704 ਦੇ ਅਭਾਜ ਗੁਣਨਖੰਡਾਂ ਵਿਚ ਇਕ ਗੁਣਨਖੰਡ 11 ਦੇ ਸਮੂਹ ਵਿਚ ਨਹੀਂ ਆਉਂਦਾ ਹੈ ।
ਇਸ ਲਈ, 704 ਇਕ ਪੂਰਨ ਘਣ ਨਹੀਂ ਹੈ ।
ਜੇਕਰ ਅਸੀਂ 704 ਨੂੰ 11 ਨਾਲ ਵੰਡਦੇ ਹਾਂ, ਤਾਂ ਭਾਗਫਲ ਗੁਣਨਖੰਡ ਬਣ ਜਾਂਦੇ ਹਨ ।
704 ÷ 11 = \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) = 64
ਜੋ ਕਿ ਇਕ ਪੂਰਨ ਘਣ ਹੈ ।
ਇਸ ਲਈ ਉਹ ਸਭ ਤੋਂ ਛੋਟੀ ਸੰਖਿਆ 11 ਹੈ ਜਿਸਨੂੰ 704 ਨਾਲ ਵੰਡਣਾ ਚਾਹੀਦਾ ਹੈ ਤਾਂਕਿ ਇਹ ਪੁਰਨ ਘਣ ਬਣ ਜਾਵੇ ।

ਪ੍ਰਸ਼ਨ 4.
ਪਰਿਕਸ਼ਤ ਪਲਾਸਟਿਕ ਦਾ ਇਕ ਘਣਾਵ ਬਣਾਉਂਦਾ ਹੈ, ਜਿਸ ਦੀਆਂ ਭੁਜਾਵਾਂ 5 cm, 2 cm ਅਤੇ 5 cm ਹਨ । ਇਕ | ਘਣ ਬਣਾਉਣ ਦੇ ਲਈ ਇਸ ਤਰ੍ਹਾਂ ਦੇ ਕਿੰਨੇ ਘਣਾਵਾਂ ਦੀ ਜ਼ਰੂਰਤ ਹੋਵੇਗੀ ?
ਹੱਲ:
ਇਕ ਘਣਾਵ ਦਾ ਆਇਤਨ = 5 cm × 2 cm × 5 cm = 50 cm³
∴ 50 = 2 × 5 × 5
50 ਨੂੰ ਪੂਰਨ ਘਣ ਬਣਾਉਣ ਲਈ ਅਸੀਂ ਇਸਨੂੰ 2 × 2 × 5 ਨਾਲ ਅਰਥਾਤ 20 ਨਾਲ ਗੁਣਾ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ।
ਇਸ ਲਈ ਇਕ ਘਣ ਬਣਾਉਣ ਦੇ ਲਈ ਸਾਨੂੰ ਇਸ ਤਰ੍ਹਾਂ ਦੇ 20 ਘਣਾਵਾਂ ਦੀ ਜ਼ਰੂਰਤ ਹੈ ।