Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 7 त्रिभुज MCQ Questions with Answers.
PSEB Solutions for Class 9 Maths Chapter 7 त्रिभुज MCQ Questions
बहुविकल्पीय प्रश्न :
नोट-नीचे प्रत्येक प्रश्न के चार-चार विकल्प दिए गए हैं। सही उत्तर का चयन कीजिए।
प्रश्न 1.
चतुर्भुज ABCD में AB = AD और AB, ∠A को समद्विभाजित करता है।
ΔABC ≅ ΔABD.BC और BD के बीच सम्बन्ध होगा –
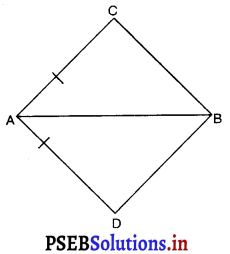
(A) BC > BD
(B) BC = BD
(C) BC < BD
(D) BC = \(\frac {1}{2}\)BD.
उत्तर –
(B) BC = BD
![]()
प्रश्न 2.
ABCD एक चतुर्भुज है, जिसमें AD = BC और ∠DAB = ∠CBA है, यदि ΔABD ≅ ΔBAC हो तो ∠ABD और ∠BAC में क्या सम्बन्ध है ?
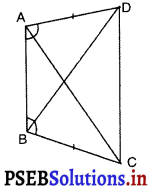
(A) ∠ABD = \(\frac {1}{2}\)∠BAC
(B) ∠ABD = ∠BAC
(C) ∠ABD > ∠BAC
(D) ∠ABD < ∠BAC.
उत्तर –
(A) ∠ABD = \(\frac {1}{2}\)∠BAC
प्रश्न 3.
एक रेखाखण्ड AB पर AD और BC दो बराबर लम्ब रेखाखण्ड हैं। यदि ΔBOC ≅ ΔAOD हो तो OC और OD में क्या सम्बन्ध है ?
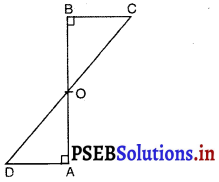
(A) OD = OC
(B) OD > OC
(C) OD < OC
(D) OD = \(\frac {1}{2}\)OC
उत्तर –
(A) OD = OC
प्रश्न 4.
यदि M, समकोण ΔARC के कर्ण AC का मध्य बिन्दु हो तो BM = \(\frac {1}{2}\)……………
(A) AC
(B) AB
(C) BC
(D) इनमें से कोई नहीं।
उत्तर –
(A) AC
![]()
प्रश्न 5.
दी गई आकृति में AB = AC और BF = CD तथा ΔACD ≅ ΔABE तो AD = ……..
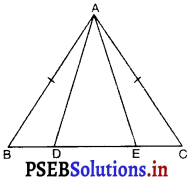
(A) AC
(B) AB
(C) AE
(D) इनमें से कोई नहीं।
उत्तर –
(A) AC
प्रश्न 6.
ΔARC एक समकोण त्रिभुज है, जिसमें ∠A = 90° और AB = AC है। ∠B और ∠C का मान होगा
(A) ∠B = ∠C = 60°
(B) ∠B = ∠C = 30°
(C) ∠B = ∠C = 50°
(D) ∠B = ∠C = 45°.
उत्तर –
(D) ∠B = ∠C = 45°.
प्रश्न 7.
समबाहु त्रिभुज के प्रत्येक कोण का माप होता
(A) 50°
(B) 40°
(C) 60°
(D) 65°.
उत्तर –
(C) 60°
प्रश्न 8.
यदि किसी समद्विबाहु त्रिभुज का शीर्ष कोण 40° हो तो अन्य दोनों कोणों का माप होगा
(A) 60°, 60°
(B) 70°, 70°
(C) 50°, 50°
(D) 75°, 75°.
उत्तर –
(B) 70°, 70°
![]()
प्रश्न 9.
ΔARC के कोण A, B और C परस्पर बराबर हों तो ये होगी
(A) समबाहु
(B) समद्विबाहु
(C) विषमबाहु
(D) इनमें से कोई नहीं।
उत्तर –
(A) समबाहु
प्रश्न 10.
यदि किसी त्रिभुज की दो भुजाएं असमान हों, तो लम्बी भुजा के सामने का सम्मुख कोण
(A) बड़ा होता है।
(B) 90° का होता है।
(C) छोटा होता है।
(D) इनमें से कोई नहीं।
उत्तर –
(A) बड़ा होता है।
प्रश्न 11.
किसी त्रिभुज में बड़े कोण के सम्मुख भुजा
(A) बड़ी होती है।
(B) छोटी होती है।
(C) बराबर होती है।
(D) इनमें से कोई नहीं।
उत्तर –
(A) बड़ी होती है।
प्रश्न 12.
किसी त्रिभुज की दो भुजाओं का योग उसकी तीसरी भुजा
(A) के बराबर होता है।
(B) से छोटा होता है।
(C) से बड़ा होता है।
(D) इनमें से कोई नहीं।
उत्तर –
(C) से बड़ा होता है।
![]()
प्रश्न 13.
किसी त्रिभुज की सबसे बड़ी भुजा का सम्मुख कोण –
(A) 60° से बड़ा होता है।
(B) 50° से बड़ा होता है।
(C) 90° से बड़ा होता है।
(D) इनमें से कोई नहीं।
उत्तर –
(A) 60° से बड़ा होता है।
प्रश्न 14.
आकृति में, ΔPQR की भुजा, QR पर T कोई बिन्दु है और s ऐसा बिन्दु है कि RT = ST तो PQ + PR …………… QS.
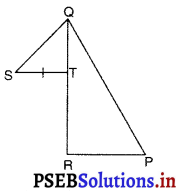
(A) PQ + PR > QS
(B) PQ + PR = QS
(C) PQ + PR < QS
(D) PQ + PR = \(\frac {1}{2}\)OS.
उत्तर –
(A) PQ + PR > QS
प्रश्न 15.
त्रिभुज के तीनों शीर्षलम्बों का योगफल त्रिभुज की तीनों भुजाओं के योगफल से ……….. होता है –
(A) कम
(B) अधिक
(C) बराबर
(D) इनमें से कोई नहीं।
उत्तर –
(A) कम
प्रश्न 16.
समकोण त्रिभुज में …………. सबसे लम्बी भुजा होती है
(A) लम्ब
(B) आधार
(C) कर्ण
(D) इनमें से कोई नहीं।
उत्तर –
(C) कर्ण
![]()
प्रश्न 17.
आकृति में ∠B < ∠A और ∠C < ∠D है तो AD और BC में सम्बन्ध है –
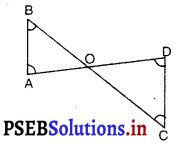
(A) AD > BC
(B) AD = BC
(C) AD < BC
(D) इनमें से कोई नहीं।
उत्तर –
(C) AD < BC
प्रश्न 18.
ΔABC में यदि ∠A = ∠B = 62\(\frac {1}{2}\)° हो तो सबसे बड़ी भुजा का नाम होगा –
(A) AB
(B) BC
(C) CA
(D) इनमें से कोई नहीं।
उत्तर –
(A) AB
प्रश्न 19.
ΔABC में AC > AB है। ∠A का समद्विभाजक BC को D पर मिलता है तो ∠ADB एक –
(A) न्यून कोण है
(B) अधिक कोण है
(C) सरल कोण है
(D) समकोण है।
उत्तर –
(A) न्यून कोण है
प्रश्न 20.
त्रिभुज की किन्हीं दो भुजाओं का अन्तर तीसरी भुजा से –
(A) बड़ा होता है
(B) छोटा होता है
(C) बराबर होता है
(D) आधा होता है।
उत्तर –
(B) छोटा होता है
![]()
प्रश्न 21.
यदि किसी त्रिभुज के दो कोण असमान हों, तो छोटे कोण के सामने की भुजा
(A) बड़ी होती है
(B) छोटी होती है
(C) 5 सेमी० होती है
(D) 10 सेमी० होती है।
उत्तर –
(B) छोटी होती है
प्रश्न 22.
ΔARC के अभ्यन्तर में …………….. बिन्दु इसके तीनों शीर्षों से समदूरस्थ होती है
(A) दो कोण समद्विभाजकों का प्रतिच्छेद
(B) दो भुजाओं के लम्ब समद्विभाजकों का प्रतिच्छेद
(C) a और b दोनों
(D) इनमें से कोई नहीं।
उत्तर –
(B) दो भुजाओं के लम्ब समद्विभाजकों का प्रतिच्छेद
प्रश्न 23.
ΔABC के अभ्यन्तर में ……………. बिन्दु इसकी तीनों भुजाओं से समदूरस्थ होता है
(A) दो भुजाओं के लम्ब समद्विभाजकों का प्रतिच्छेद
(B) दो कोण समद्विभाजकों का प्रतिच्छेद
(C) a और b दोनों
(D) इनमें से कोई नहीं।
उत्तर –
(B) दो कोण समद्विभाजकों का प्रतिच्छेद
प्रश्न 24.
नीचे षड्भुजीय आकार की रंगोली को 1 सेमी० भुजा वाले कितने समबाहु त्रिभुजों से भरा जा सकता है ?
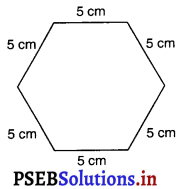
(A) 200
(B) 150
(C) 300
(D) 250.
उत्तर –
(B) 150
संकेत –
5 सेमी० भुजा वाली समबाहु त्रिभुज का क्षेत्रफल
= \(\frac{\sqrt{3}}{4}(5)^2=\frac{\sqrt{3}}{4} \times 25\)
षड्भुजीय रंगोली का क्षेत्रप = 6 × \(\frac{\sqrt{3}}{4}\) × 25
= 150 × \(\frac{\sqrt{3}}{4}\)सेमी०2
1 सेमी० भुजा वाली समबाहु त्रिभुज का क्षेत्रफल
= \(\frac{\sqrt{3}}{4}\) (1)2
= \(\frac{\sqrt{3}}{4}\) सेमी०2
षड्भुजीय रंगोली में 1 सेमी० भुजा वाले समबाहु त्रिभुजों की संख्या
= 150\(\frac{\sqrt{3}}{4}\) ÷ \(\frac{\sqrt{3}}{4}\) = 150
![]()
प्रश्न 25.
आकृति में तारे के आकार की रंगोली को 1 सेमी० भुजा वाले समबाहु त्रिभुज से पूरा कीजिए। त्रिभुजों की संख्या होगी
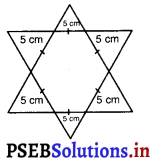
(A) 300
(B) 150
(C) 200
(D) 350.
उत्तर –
(A) 300
प्रश्न 26.
यदि किसी त्रिभुज के दो कोण सर्वांगसम हों तो इन कोणों की सम्मुख भुजाएँ
(A) समान होती हैं
(B) सर्वांगसम होती हैं
(C) सर्वांगसम हो सकती हैं
(D) सर्वांगसम नहीं होती।
उत्तर –
(B) सर्वांगसम होती हैं
प्रश्न 27.
सर्वांगसमता के लिए कौन-सा अभिगृहीत ठीक
(A) भु० क० भु०
(B) क० भु० भु०
(C) भु० भु० क०
(D) इनमें से कोई नहीं।
उत्तर –
(A) भु० क० भु०
प्रश्न 28.
ΔABC में यदि AB सबसे छोटी तथा BC सबसे लम्बी भुजा हो तो
(A) ∠A < ∠C
(B) ∠A > ∠B
(C) ∠A > ∠C
(D) ∠A < ∠C.
उत्तर –
(C) ∠A > ∠C
![]()
प्रश्न 29.
यदि शीर्ष कोण का समद्विभाजक आधार को समद्विभाजित करे तो त्रिभुज –
(A) समबाहु है
(B) समद्विबाहु है
(C) विषमबाहु है
(D) इनमें से कोई नहीं।
उत्तर –
(B) समद्विबाहु है
प्रश्न 30.
एक समकोण त्रिभुज में यदि एक न्यूनकोण दूसरे न्यूनकोण का दुगुना हो तो कर्ण –
(A) छोटी भुजा के समान होता है
(B) छोटी भुजा का तीन गुणा होता है
(C) छोटी भुजा का दुगुना होता है
(D) छोटी भुजा से छोटा होता है।
उत्तर –
(C) छोटी भुजा का दुगुना होता है
प्रश्न 31.
ΔABC में, यदि माध्यिका BE, माध्यिका CF के बराबर हो तो त्रिभुज
(A) समबाहु हैं
(B) समद्विबाहु हैं
(C) समकोणी हैं
(D) इनमें से कोई नहीं।
उत्तर –
(C) समकोणी हैं
प्रश्न 32.
एक समद्विबाहु त्रिभुज ABC में, D, E और F आधार BC और समान भुजाओं AB और AC के मध्य बिन्दु हैं तो
(A) DC = BC
(B) DF = BE
(C) DF = DE
(D) DC = DE
उत्तर –
(C) DF = DE
![]()
प्रश्न 33.
ΔABC में AB = AC और भुजा BA को D तक बढ़ाया गया है ताकि AB = AD तो ∠BCD बराबर है
(A) 80°
(B) 45°
(C) 60°
(D) इनमें से कोई नहीं।
उत्तर-
(D) इनमें से कोई नहीं।
प्रश्न 34.
एक त्रिभुज में अधिकतम एक……….. कोण हो सकता है
(A) न्यून
(B) अधिक
(C) सरल
(D) इनमें से कोई नहीं।
उत्तर-
(B) अधिक
प्रश्न 35.
नीचे दी गई त्रिभुजें सर्वांगसम हैं। बताइए ये किस अभिगृहीत से सर्वांगसम हैं ?
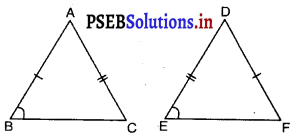
(A) भु०-भु०-भु०
(B) भु०-को०-भु०
(C) को०-को०-भु०
(D) को०-भु०-भु०।
उत्तर –
(B) भु०-को०-भु०
![]()
प्रश्न 36.
नीचे दी गई त्रिभुजें सर्वांगसम हैं। किस अभिगृहीत के कारण ये त्रिभुजें सर्वांगसम हैं ?
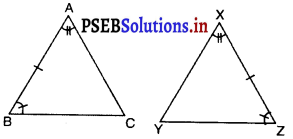
(A) भु०-को०-भु०
(B) को०-भु०-को०
(C) भु०-भु०-भु०
(D) इनमें से कोई नहीं।
उत्तर –
(B) को०-भु०-को०
प्रश्न 37.
l और m दो समान्तर रेखाएँ हैं जिन्हें समान्तर रेखाओं का एक अन्य युग्म प्रतिच्छेद करता है। ΔABC ≅ ΔCDA. ये सर्वांगसमता के किस अभिगृहीत के कारण सर्वांगसम हैं ?
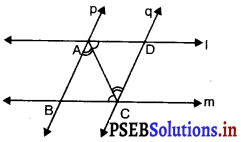
(A) भु०-भु०-भु०
(B) भु०-को०-भु०
(C) को०-को०-भु०
(D) इनमें से कोई नहीं।
उत्तर –
(C) को०-को०-भु०
संकेत –
l || m, AC एक तिर्यक रेखा है
∴ ∠DAC = ∠ACB
…..(एकांतर कोण)
p || q, AC एक तिर्यक रेखा है
∴ ∠BAC = ∠ACD
…..(एकांतर कोण)
ΔABC और ΔADC में
∠ACB = ∠DAC
∠BAC = ∠ACD ऊपर सिद्ध किया है (उभयनिष्ठ)
AC = AC
∠ABC ≅ ΔCDA (को-को-भुजा सर्वांगसमता)]
![]()
प्रश्न 38.
यदि एक त्रिभुज की ………. क्रमशः दूसरे त्रिभुज की तीन भुजाओं के बराबर हों तो त्रिभुज सर्वांगसम होते हैं
(A) एक भुजा
(B) दो भुजाएँ
(C) तीन भुजाएँ
(D) इनमें से कोई नहीं।
उत्तर –
(C) तीन भुजाएँ
प्रश्न 39.
यदि एक त्रिभुज की……………. और अन्तर्गत कोण क्रमश: दूसरे त्रिभुज की दो भुजाओं और अन्तर्गत कोण के बराबर हों, तो त्रिभुज सर्वांगमस होते हैं
(A) एक भुजा
(B) दो भुजाएँ
(C) तीन भुजाएँ
(D) इनमें से कोई नहीं।
उत्तर –
(B) दो भुजाएँ
प्रश्न 40.
ABC एक त्रिभुज है जिसमें AC और BC पर खींचे गए शीर्षलम्ब BF और CF बराबर हैं तथा ΔABF ≅ ΔACF. तब ΔABC.
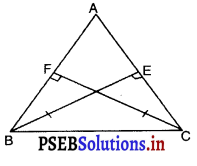
(A) समबाहु है
(B) विषमबाहु है
(C) समद्विबाहु है
(D) इनमें से कोई नहीं।
उत्तर-
(C) समद्विबाहु है
प्रश्न 41.
ABC और DBC समान आधार BC पर स्थित दो समद्विबाहु त्रिभुज हैं।
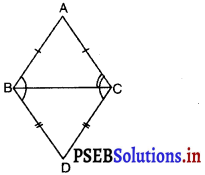
(A) ∠ABD = ∠ACD
(B) ∠ABD > ∠ACD
(C) ∠ACD > ∠ABD
(D) ∠ABD = \(\frac {1}{2}\)∠ACD
उत्तर –
(A) ∠ABD = ∠ACD
![]()
प्रश्न 42.
त्रिभुज का परिमाप उसके माध्यिकाओं के योग –
(A) के बराबर होता है
(B) से कम होता है
(C) से बड़ा होता है
(D) से आधा होता है।
उत्तर –
(C) से बड़ा होता है
प्रश्न 43.
निम्नलिखित में से कौन त्रिभुजों की सर्वांगसमता की एक कसौटी नहीं है?
(A) SAS
(B) ASA
(C) SSA
(D) SSS.
उत्तर :
(C) SSA
प्रश्न 44.
यदि AB = QR, BC = PR और CA = PQ है, तो
(A) ΔABC ≅ ΔPQR
(B) ΔCBA ≅ ΔPRQ
(C) ΔBAC ≅ ΔRPQ
(D) ΔPQR ≅ ΔBCA.
उत्तर :
(B) ΔCBA ≅ ΔPRQ
प्रश्न 45.
ΔABC में, AB = AC और ∠B = 50° है, तब ∠C बराबर है।
(A) 40°
(B) 50°
(C) 80°
(D) 130°
उत्तर :
(B) 50°
![]()
प्रश्न 46.
ΔABC में, BC = AB और ∠B = 80° है, तब ∠A बराबर है।
(A) 80°
(B) 40°
(C) 50°
(D) 100°
उत्तर :
(C) 50°
प्रश्न 47.
ΔPQR में, ∠R = ∠P तथा QR = 4 cm और PR = 5 cm है, तब PQ की लम्बाई है।
(A) 4 cm
(B) 5 cm
(C) 2 cm
(D) 2.5 cm.
उत्तर :
(A) 4 cm
प्रश्न 48.
D एक त्रिभुज ABC की भुजा BC पर एक बिंदु इस प्रकार स्थित है कि AD कोण BAC को समद्विभाजित करता है। तब,
(A) BD = CD
(B) BA > BD
(C) BD > BA
(D) CD >CA
उत्तर :
(B) BA > BD
प्रश्न 49.
यह दिया है कि ΔABC ≅ ΔFDE है तथा AB = 5cm, ∠B = 40° और ∠A = 80° है। तब निम्नलिखित में से कौन सत्य है ? (A) DF = 5 cm, ∠F = 60°
(B) DF = 5 cm, ∠E = 60°
(C) DE = 5 cm, ∠E = 60°
(D) DE = 5 cm, ∠D = 40°
उत्तर :
(B) DF = 5 cm, ∠E = 60°
प्रश्न 50.
एक त्रिभुज की दो भुजाओं की लम्बाइयां 5 cm और 1.5 cm हैं। इस त्रिभुज की तीसरी भुजा की लंबाई निम्नलिखित नहीं हो सकती।
(A) 3.6 cm
(B) 4.1 cm
(C) 3.8 cm
(D) 3.4 cm
उत्तर :
(D) 3.4 cm
प्रश्न 51.
ΔPQR में, यदि ∠R > ∠Q है, तो
(A) QR > PR
(B) PQ > PR
(C) PQ < PR
(D) QR < PR.
उत्तर :
(B) PQ > PR
![]()
प्रश्न 52.
त्रिभुजों ABC और PQR में, AB = AC, ∠C = ∠P और ∠B = ∠Q है। ये दोनों त्रिभुज हैं।
(A) समद्विबाहु परंतु सर्वांगसम नहीं
(B) समद्विबाहु और सर्वांगसम
(C) सर्वांगसम परंतु समद्विभाहु नहीं
(D) न तो सवांगसम और न ही समद्विबाहु ।
उत्तर :
(A) समद्विबाहु परंतु सर्वांगसम नहीं
प्रश्न 53.
त्रिभुजों ABC और DEF में, AB = FD तथा ∠A = ∠D है। दोनों त्रिभुज SAS अभिगृहीत से सर्वांगसम होंगे, यदि
(A) BC = EF
(B) AC = DE
(C) AC = EF
(D) BC = DE.
उत्तर :
(B) AC = DE
