Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 1 संख्या पद्धति Ex 1.1 Textbook Exercise Questions and Answers
PSEB Solutions for Class 9 Maths Chapter 1 संख्या पद्धति Ex 1.1
प्रश्न 1.
क्या शून्य एक परिमेय संख्या है ? क्या इसे आप के रूप में लिख सकते हैं, जहाँ p और q पूर्णांक हैं और q # 0 है ?
हल :
हाँ, शून्य एक परिमेय संख्या है और इसे \(\frac{p}{q}\) रूप में इस प्रकार से लिख सकते हैं,
0 = \(\frac{0}{1}\)
जहाँ p = 0 और q = 1
ध्यान दीजिए कि q कोई भी संख्या हो सकती है जो आप चाहते हैं।
[∵ 0 = \(\frac{0}{2}=\frac{0}{3}\) इत्यादि]
![]()
प्रश्न 2.
3 और 4 के बीच में छः परिमेय संख्याएँ ज्ञात कीजिए।
हल :
मान लीजिए a = 3, और b = 4
3 और 4 के बीच की परिमेय संख्या है।
\(\frac{a+b}{2}\) अर्थात् \(\frac{3+4}{2}=\frac{7}{2}\)
अब 3 और \(\frac{7}{2}\) के बीच परिमेय संख्या
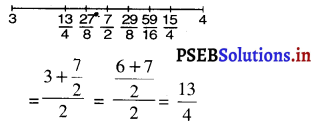
\(\frac{7}{2}\) और 4 के बीच परिमेय संख्या = \(\frac{\frac{7}{2}+4}{2}=\frac{\frac{7+8}{2}}{2}=\frac{15}{4}\)
\(\frac{13}{4}\) और \(\frac{7}{2}\) के बीच परिमेय संख्या
= \(\frac{\frac{13}{4}+\frac{7}{2}}{2}\)
= \(\frac{\frac{13+14}{4}}{2}=\frac{27}{8}\)
\(\frac{7}{2}\) और \(\frac{15}{4}\) के बीच परिमेय संख्या = \(\frac{\frac{7}{2}+\frac{15}{4}}{2}=\frac{\frac{14+15}{4}}{2}=\frac{29}{8}\)
\(\frac{29}{8}\) और \(\frac{15}{4}\) के बीच परिमेय संख्या = \(\frac{\frac{29}{8}+\frac{15}{4}}{2}\)
= \(\frac{\frac{29+30}{8}}{2}\)
= \(\frac{59}{16}\)
अतः छः परिमेय संख्याएँ हैं : \(\frac{13}{4}, \frac{27}{8}, \frac{7}{2}, \frac{29}{8}, \frac{59}{16}, \frac{15}{4}\)
![]()
वैकल्पिक विधि :
एक अन्य विकल्प है कि एक ही चरण में सभी छः परिमेय संख्याओं को ज्ञात कर लें। क्योंकि हम छ: संख्याएँ ज्ञात करना चाहते हैं इसलिए हम 6 + 1 अर्थात् 7 को हर लेकर 3 और 4 को परिमेय संख्याओं के रूप में लिखते हैं :
अर्थात् 3 = \(\frac{21}{6+1}=\frac{21}{7}\), 4 = \(\frac{28}{6+1}=\frac{28}{7}\), तब
3 और 4 के बीच छ: परिमेय संख्याएँ हैं :
\(\frac{22}{7}, \frac{23}{7}, \frac{24}{7}, \frac{25}{7}, \frac{26}{7}, \frac{27}{7}\)
प्रश्न 3.
\(\frac{3}{5}\) और \(\frac{4}{5}\) के बीच पाँच परिमेय संख्याएँ ज्ञात कीजिए।
हल :
मान लीजिए a = \(\frac{3}{5}\) और b = \(\frac{4}{5}\)
a और b के बीच की परिमेय संख्या है \(\frac{a+b}{2}\)
अर्थात् = \(\frac{\frac{3}{5}+\frac{4}{5}}{2}=\frac{\frac{3+4}{5}}{2}=\frac{7}{10}\)

= \(\frac{\frac{7}{10}+\frac{15}{20}}{2}=\frac{\frac{14+15}{20}}{2}=\frac{29}{40}\)
इस प्रकार \(\frac{3}{5}\) और \(\frac{4}{5}\) के बीच संख्याएँ हैं :
\(\frac{13}{20}, \frac{27}{40}, \frac{7}{10}, \frac{29}{40}, \frac{15}{20}\)
वैकल्पिक विधि :
हम एक ही चरण में सभी पाँच परिमेय संख्याएँ ज्ञात करना चाहते हैं। क्योंकि हम पाँच संख्याएं चाहते हैं इसलिए हम लिखते हैं :
\(\frac{3}{5}=\frac{18}{30}\) और \(\frac{4}{5}=\frac{24}{30}\)
अब हैं \(\frac{3}{5}\) और \(\frac{4}{5}\) की पाँच परिमेय संख्याएँ हैं :
\(\frac{19}{30}, \frac{20}{30}, \frac{21}{30}, \frac{22}{30}, \frac{23}{30}\)
![]()
प्रश्न 4.
नीचे दिए गए कथन सत्य हैं या असत्य ? कारण के साथ अपने उत्तर दीजिए।
(i) प्रत्येक प्राकृत संख्या एक पूर्ण संख्या होती है।
(ii) प्रत्येक पूर्णांक एक पूर्ण संख्या होती है।
(iii) प्रत्येक परिमेय संख्या एक पूर्ण संख्या होती
हल :
(i) सत्य है।
कारण : क्योंकि पूर्ण संख्याओं के संग्रह में सभी प्राकृत संख्याएँ होती हैं।

अतः प्रत्येक पूर्ण संख्या प्राकृत संख्या नहीं होती परंतु प्रत्येक प्राकृत संख्या एक पूर्ण संख्या होती है।
(ii) असत्य है
कारण : ऋणात्मक संख्याएँ – 3, – 2, – 1 पूर्ण संख्याएं नहीं हैं।

(iii) असत्य है।
परिमेय संख्याएँ हैं :
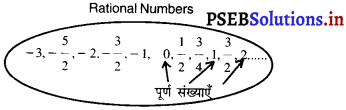
कारण :
पूर्ण संख्याएँ परिमेय संख्याओं का भाग है।
अतः प्रत्येक परिमेय संख्या पूर्ण संख्या नहीं है।
उदाहरण के लिए \(\frac{3}{4}\) एक परिमेय संख्या है, परंतु पूर्ण संख्या नहीं है।
