Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 10 Circles Ex 10.4 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 9 Maths Chapter 10 Circles Ex 10.4
Question 1.
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.
Answer:
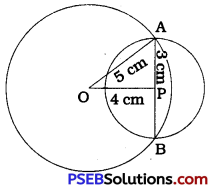
The circle with centre O and radius 5 cm intersects the circle with centre P and radius 3 cm at points A and B.
Hence, AB is their common chord.
Then, OP = 4 cm (Given),
OA = 5 cm and PA = 3 cm.
In ∆ OAP, OA2 = 52 = 25 and
OP2 + AP2 = 42 + 32 = 16 + 9 = 25
Thus, in ∆ OAP, OA2 = OP2 + AP2
∴ ∆ OAP is a right triangle in which ∠OPA is a right angle and OA is the hypotenuse.
Thus, in the circle with centre O, OP is perpendicular from centre O to chord AB.
∴ OP bisects AB.
AB = 2PA = 2 × 3 = 6 cm
Thus, the length of the common chord is 6 cm.
![]()
Question 2.
If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
Answer:
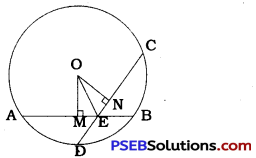
In the circle with centre O, equal chords AB and CD intersect at E.
Draw OM ⊥ AB and ON ⊥ CD.
∴ AM = BM = \(\frac{1}{2}\)AB and CN = DN = \(\frac{1}{2}\)CD.
But, AB = CD
∴AM = BM = CN = DN …………….. (1)
Chords AB and CD, being equal, are equidistant from the centre.
∴ OM = ON
In ∆ OME and ∆ ONE,
∠OME = ∠ONE (Right angles)
OE = OE (Common)
OM = ON
By RHS rule, ∆ OME ≅ ∆ ONE
∴ME = EN (CPCT) ……………… (2)
From (1) and (2),
AM + ME = CN + NE
∴ AE = CE
Similarly, BM – ME = DN – NE
∴ BE = DE
Thus, if two equal chords of a circle intersect within the circle, the segments of one chord are equal to corresponding segments of the other chord.
![]()
Question 3.
If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.
Answer:
As the data of example 2 and example 3 are same, we use the proof of example 2 up to the required stage and do not repeat it here.
In example 2, we proved that,
∆ OME ≅ ∆ ONE ,
∴ ∠ OEM = ∠ OEN
∴ ∠ OEA = ∠ OEC
Thus, the line joining the point of intersection of two equal chords of a circle to the centre makes equal angles with the chords.
Question 4.
If a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C and D, prove that AB = CD (see the given figure).
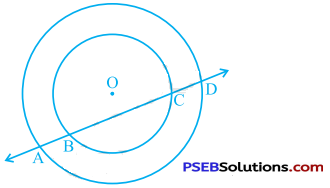
Answer:
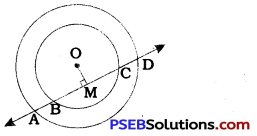
From centre O, draw perpendicular OM to line AD.
In the outer circle, OM is the perpendicular drawn from centre O to chord AD.
Hence, M is the midpoint of AD.
∴ MA = MD …………… (1)
In the inner circle, OM is the perpendicular drawn from centre O to chord BC.
Hence, M is the midpoint of BC.
∴ MB = MC ………….. (2)
Subtracting (2) from (1),
MA – MB = MD – MC
∴ AB = CD
![]()
Question 5.
Three girls Reshma, Salma and Mandip are playing a game by standing on a circle of radius 5 m drawn in a park. Reshma throws a ball to Salma, Salma to Mandip, Mandip to Reshma. If the distance between Reshma and Salma and between Salma and Mandip is 6 m each, what is the distance between Reshma and Mandip?
Answer:
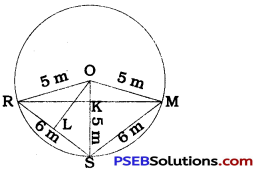
Here, OR = OM = OS = 5 m (Radius of the circle) and RS = SM = 6 m.
In quadrilateral ORSM, OR = OM = 5 m and RS = SM = 6 m.
∴ Quadrilateral ORSM is a kite.
∴ It diagonal OS bisects the diagonal RM at right angles.
∴ ∠RKO = 90° ………………. (1)
OK is perpendicular from centre O to chord RM.
Hence, K is the midpoint of RM.
∴ RM = 2RK ………………… (2)
From centre O, draw perpendicular OL to chord RS.
∴ RL = \(\frac{1}{2}\)RS = \(\frac{1}{2}\) × 6 = 3 m
In ∆ RLO, ∠ L = 90°
∴ RO2 = OL2 + RL2
∴ 52 = OL2 + 32
∴ 25 = OL2 + 9
∴ OL2 = 16
∴ OL = 4 m
Now, area of ∆ ROS = \(\frac{1}{2}\) × RS × OL
= \(\frac{1}{2}\) × OS × RK [by (1)]
∴RS × OL = OS × RK
∴ 6 × 4 = 5 × RK
∴ 24 = 5 × RK
∴ RK = \(\frac{24}{5}\) = 4.8 m
Then, RM = 2RK [by (2)]
∴ RM = 2 × 4.8
∴ RM = 9.6 m
Thus, the distance between Reshma and Mandip is 9.6 m.
![]()
Question 6.
A circular park of radius 20 m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk with each other. Find the length of the string of each phone.
Answer:
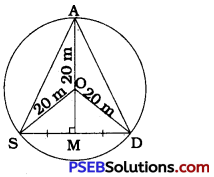
Here, the circle with centre O represents the park and the points A, S and D represent the positions of Ankur, Syed and David respectively. Since Ankur, Syed and David are sitting at equal distances from the others, ∆ ASD is an equilateral triangle.
Then, drawing the perpendicular bisector of SD from its midpoint M, it will pass through O as well as A.
Suppose, SM = x m
∴ SD = 2SM = 2xm
Area of equilateral ∆ ASD = \(\frac{\sqrt{3}}{4}\) (side)2
∴ Area of equilateral ∆ ASD = \(\frac{\sqrt{3}}{4}\) × (2x)2
∴ Area of equilateral ∆ ASD = √3x2 …………. (1)
In ∆ OMS, ∠M = 90°
∴ OM2 = OS2 – SM2 = (20)2 – (x)2 = 400 – x2
∴ OM = \(\sqrt{400-x^{2}}\)
Now, area of ∆ OSD = \(\frac{1}{2}\) × SD × OM
∴ Area of ∆ OSD = \(\frac{1}{2}\) × 2x × \(\sqrt{400-x^{2}}\)
∴ Area of ∆ OSD = x\(\sqrt{400-x^{2}}\) …………….. (2)
Here, ∆ OAS, ∆ OSD and ∆ ODA are congruent triangles.
Area of ∆ ASD = Area of ∆ OAS + Area of ∆ OSD + Area of ∆ ODA
∴ Area of ∆ ASD = 3 × Area of ∆ OSD
∴ √3 ∙ x<sup2 = 3 × x\(\sqrt{400-x^{2}}\)
∴x = √3 ∙ \(\sqrt{400-x^{2}}\)
∴ x2 = 3(400 – x22)
∴ x2= 1200 – 3x2
∴ 4x2 = 1200
∴x2 = 300
∴x= 10 √3
SD = 2x = 2 × 10 √3 = 20 √3 m
Thus, the length of the string of each phone is 20 √3m.
