Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 10 वृत्त Ex 10.5 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 9 Maths Chapter 10 वृत्त Ex 10.5
प्रश्न 1.
आकृति में, केंद्र O वाले एक वृत्त पर तीन बिंदु A, B, और C इस प्रकार है कि ∠BOC = 30° तथा ∠AOB = 60° हैं। यदि चाप ABC के अतिरिक्त वृत्त पर D एक बिंदु है, तो ∠ADC ज्ञात कीजिए।
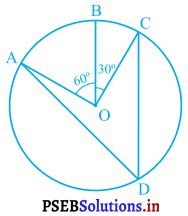
हल :
∠AOC = ∠AOB + ∠BOC
⇒ ∠AOC = 60° + 30°
⇒ ∠AOC = 90°
अब,
∠AOC = 2∠ADC
[∵ किसी चाप द्वारा केंद्र पर अंतरित कोण उसी चाप द्वारा वृत्त के शेष भाग पर अंतरित कोण का दुगुना होता है।
या ∠ADC = \(\frac{1}{2}\)∠AOC
⇒ ∠ADC = \(\frac{1}{2}\) × 90°
⇒ ∠ADC = 45°.
![]()
प्रश्न 2.
किसी वृत्त की एक जीवा वृत्त की त्रिज्या के बराबर है। जीवा दवारा लघु चाप के किसी बिंद पर अंतरित कोण ज्ञात कीजिए तथा दीर्घ चाप के किसी बिंदु पर भी अंतरित कोण ज्ञात कीजिए।
हल :
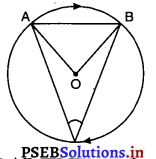
मान लीजिए AB एक लघु चाप है।
जीवा AB = त्रिज्या OA = त्रिज्या OB
∴ ΔAOB एक समबाहु त्रिभुज है।
∴ ∠AOB = 60°
[∵ समबाहु त्रिभुज का प्रत्येक कोण 60° है।]
अब m \(\widehat{\mathrm{AB}}\) + m\(\widehat{\mathrm{BA}}\) = 360°
⇒ ∠AOB + ∠BOA = 360°
⇒ 60° + ∠BOA = 360°
⇒ ∠BOA = 360° – 60°
⇒ ∠BOA = 300°
D लघु चाप पर एक बिंदु है।
∴ m\(\widehat{\mathrm{BA}}\) = 2∠BDA
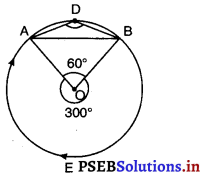
⇒ ∠BOA = 2∠BDA
[∵ किसी चाप द्वारा केंद्र पर अंतरित कोण उसी चाप द्वारा वृत्त के शेष भाग पर अंतरित कोण का दुगुना होता है।]
या ∠BDA = \(\frac{1}{2}\)∠BOA
∠BDA = \(\frac{1}{2}\) × 300°
⇒ ∠BDA = 150°
अतः, लघु चाप \(\widehat{\mathrm{BA}}\) द्वारा लघु चाप के किसी बिंदु D पर अंतरित कोण 150° है।
मान लीजिए दीर्घ चाप \(\widehat{\mathrm{BA}}\) पर एक बिंदु E है।
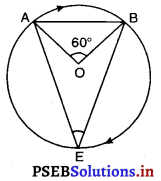
∴ m\(\widehat{\mathrm{AB}}\) = 2∠AEB
⇒ ∠AOB = 2∠AEB
[∵ किसी चाप द्वारा केंद्र पर अंतरित कोण उसी चाप द्वारा वृत्त के शेष भाग पर अंतरित कोण का दुगुना होता है।]
या ∠AEB = \(\frac{1}{2}\)∠AOB
⇒ ∠AEB = \(\frac{1}{2}\) × 60°
⇒ ∠AEB = 30°
अतः लघु चाप \(\widehat{\mathrm{AB}}\) द्वारा दीर्घ चाप के किसी बिंदु E पर अंतरित कोण 30° है।
प्रश्न 3.
आकृति में, ∠PQR = 100°है, जहाँ P, Q तथा R केंद्र O वाले एक वृत्त पर स्थित हैं। ∠OPR ज्ञात कीजिए।
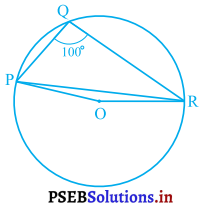
हल :
आकृति ; Q लघु चाप \(\widehat{\mathrm{PQR}}\) पर स्थित कोई बिंदु है।
∴ m\(\widehat{\mathrm{RP}}\) = 2∠PQR
⇒ ∠ROP = 2∠PQR
[∵ किसी चाप द्वारा केंद्र पर अंतरित कोण उसी चाप द्वारा वृत्त के शेष भाग पर अंतरित कोण का दुगुना होता है।]
∴ ∠ROP = 2 × 100°
⇒ ∠ROP = 200°
अब
m\(\widehat{\mathrm{PR}}\) + m\(\widehat{\mathrm{RP}}\) = 360°
⇒ ∠POR + ∠ROP = 360°
⇒ ∠POR + 200° = 360°
⇒ ∠POR = 360° – 200°
⇒ ∠POR = 160° ………(i)
अब, ΔOPR एक समद्विबाहु त्रिभुज है।
∴ OP = OR (वृत्त की त्रिज्याएँ)
∴ ∠OPR = ∠ORP
(बराबर भुजाओं के सम्मुख कोण) …….(ii)
अब समद्विबाहु त्रिभुज OPR में,
∠OPR + ∠ORP + ∠POR = 180°
⇒ ∠OPR + ∠OPR + 160° = 180°
[(i) और (ii) का प्रयोग करने पर]
⇒ 2∠OPR = 180° – 160°
⇒ 2∠OPR = 20°
⇒ ∠OPR = \(\frac{20^{\circ}}{2}\)
⇒ 2∠OPR = 10°
![]()
प्रश्न 4.
आकृति में, ∠ABC = 69° और ∠ACB = 31° हो, तो ∠BDC ज्ञात कीजिए।
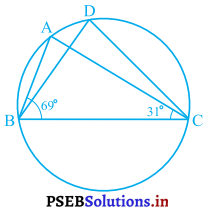
हल :
ΔABC में,
∠BAC + ∠ABC + ∠ACB = 180°
⇒ ∠BAC + 69° + 31° = 180°
⇒ ∠BAC = 180° – 69° – 31°
⇒ ∠BAC = 80° ……..(i)
बिंदु A और D वृत्त के एक ही वृत्तखंड में है।
इसलिए, ∠BDC = ∠BAC [∵ किसी चाप द्वारा केंद्र पर अंतरित कोण उसी चाप द्वारा वृत्त के शेष भाग पर अंतरित कोण का दुगुना होता है।]
⇒ ∠BDC = 80° [(i) का प्रयोग करने पर]
प्रश्न 5.
आकृति में, एक वृत्त पर A, B, C और D चार बिंदु हैं। AC और BD एक बिंदु E पर इस प्रकार प्रतिच्छेद करते हैं कि ∠BEC = 130° और ∠ECD = 20° हैं। ∠BAC ज्ञात कीजिए।
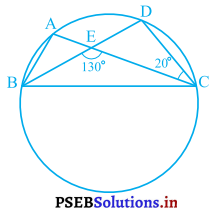
हल :
आकृति के अनुसार ∠CED + ∠BEC = 180° (रैखिक युग्म)
⇒ ∠CED + 130° = 180°
⇒ ∠CED = 180° – 130°
⇒ ∠CED = 50°… (i)
∠AEB = ∠CED (शीर्षाभिमुख कोण)
∠AEB = 50° [(i) का प्रयोग करने पर]
अब,
∠ABD = ∠ACD
[चाप AD द्वारा एक ही वृत्तखंड में अंतरित कोण बराबर होते हैं।]
⇒ ∠ABD = 20°
[∵ ∠ACD = 20° (दिया है)]
अब, ΔAEB में,
∠BAE + ∠ABE + ∠AEB = 180°
[त्रिभुज का कोण योग गुण]
⇒ ∠BAE + 20° + 50° = 180°
⇒ ∠BAE = 180° – 20° – 50°
⇒ ∠BAE = 110°
या ∠BAE = 110°
![]()
प्रश्न 6.
ABCD एक चक्रीय चतुर्भुज है जिसके विकर्ण एक बिंदु E पर प्रतिच्छेद करते हैं। यदि ∠DBC = 70° और ∠BAC = 30° हो, तो ∠BCD ज्ञात कीजिए। पुनः, यदि AB = BC हो, तो ∠ECD ज्ञात कीजिए।
हल :
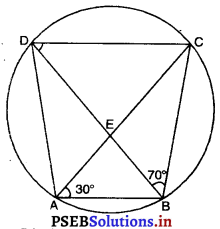
∠BDC = ∠BAC
[एक ही वृत्तखंड के कोण]
∠BDC = 30° (∵ ∠BAC = 30°)
ΔBCD में,
⇒ ∠BCD + ∠DBC + ∠BDC = 180°
⇒ ∠BCD + 70° + 30° = 180°
[∵ ∠DBC = 70°]
⇒ ∠BCD = 180° – 70° – 30°
⇒ ∠BCD = 80° ……(i)
यदि AB = BC
तो ΔABC में;
∠ACB = ∠BAC
(त्रिभुज की बराबर भुजाओं के सम्मुख कोण बराबर होते हैं।).
⇒ ∠ACB = 30° …….(ii)
अब
∠BCD = ∠ACB + ∠ACD
⇒ 80° = 30° + ∠ACD
[(i) और (ii) का प्रयोग करने पर]
⇒ 80° – 30° = ∠ACD
⇒ 50° = ∠ACD
या, ∠ACD = 50°
या, ∠ECD = 50°
प्रश्न 7.
यदि एक चक्रीय चतुर्भुज के विकर्ण उसके शीर्षों से जाने वाले वृत्त के व्यास हों, तो सिद्ध कीजिए कि वह एक आयत है।
हल :
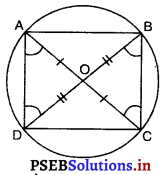
AC एक व्यास है।
∴ ∠B = ∠D = 90° ……(1)
(अर्धवृत्त में कोण समकोण होता है।)
इसी प्रकार BD व्यास है।
∴ ∠A = ∠C = 90° …(2)
अब, व्यास
AC = BD
⇒ \(\overparen{\mathrm{AC}}\) ≅ \(\overparen{\mathrm{BD}}\)
(बराबर जीवाओं की सम्मुख चापें)
\(\overparen{\mathrm{AC}}\) – \(\overparen{\mathrm{DC}}\) ≅ \(\overparen{\mathrm{BD}}\) – \(\overparen{\mathrm{DC}}\)
⇒ \(\overparen{\mathrm{AD}}\) ≅ \(\overparen{\mathrm{BC}}\)
⇒ AD = BC
(बराबर चापों को सम्मुख जीवाएँ ) ….. (3)
इसी प्रकार AB = DC ….. (4)
(1), (2), (3) और (4) में हम देखते हैं कि चतुर्भुज का प्रत्येक कोण 90° का है और सम्मुख भुजाएँ बराबर है।
अतः, ABCD एक आयत है।
![]()
प्रश्न 8.
यदि एक समलंब की असमांतर भुजाएँ बराबर हैं, तो सिद्ध कीजिए कि वह चक्रीय है।
हल :
दिया है : एक समलंब ABCD जिसमें AB || CD और AD = BC है।
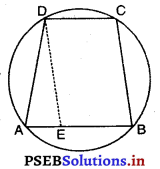
सिद्ध करना है : बिंदु A, B, C, D चक्रीय है। (अर्थात् ABCD चक्रीय समलंब है)
रचना : DE || CB खींचिए।
उपपत्ति : DE || CB और EB || DC.
∴ EBCD एक समांतर चतुर्भुज है।
∴ DE = CB और CDEB = LDCB.
∵ समांतर चतुर्भुज के सम्मुख कोण बराबर होते हैं।
अब, ∵ AD = BC और BC = DE
∴ DA = DE ⇒ ∠DAE = ∠DEA.
[∵ त्रिभुज की बराबर भुजाओं के सम्मुख कोण बराबर होते हैं]
परंतु ∠DEA + ∠DEB = 180° … ( रैखिक युग्म)
⇒ ∠DAE + ∠DCB = 180°
[∵ ∠DEA = ∠DAE और ∠DEB = ∠DCB] (ऊपर प्रमाणित)
⇒ ∠DAB + ∠DCB = 180° …….(1)
⇒ ∠A + ∠C = 180°
अतः, ABCD एक चक्रीय चतुर्भुज है।
[∵ चक्रीय चतुर्भुज के सम्मुख कोण संपूरक होते हैं जैसा कि परिणाम (1) है।]
प्रश्न 9.
दो वृत्त बिंदुओं B और C पर प्रतिच्छेद करते हैं। B से जाने वाले दो रेखाखंड ABD और PBQ वृत्तों को A, D और P, Q पर क्रमशः प्रतिच्छेद करते हुए खींचे गए हैं (देखिए आकृति)। सिद्ध कीजिए कि ∠ACP = ∠QCD है।
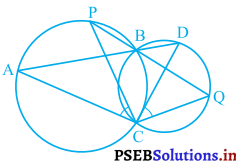
हल :
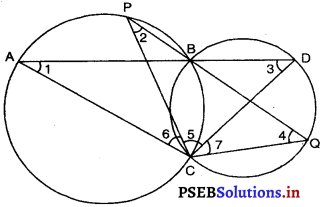
वृत्त I की चाप एक ही वृत्त खण्ड में ∠1 और ∠2 अंतरित करती है।
∴ ∠1 = ∠2
[एक ही वृत्त खण्ड के कोण बराबर होते हैं।]
चाप BC वृत्त II के एक ही वृत्तखण्ड में ∠3 और ∠4 अंतरित करती है।
∴ ∠3 = ∠4 [उपरोक्त कारण ही]
अब, ΔACD में,
∠A + ∠C + ∠D = 180° [त्रिभुज का कोण योग गुण]
∠1 + ∠5 + ∠6 + ∠3 = 180° … (i)
ΔPCQ में,
∠P + ∠C + ∠Q = 180°
[त्रिभुज का कोण योग गुण]
⇒ ∠2 + ∠5 + ∠7 + ∠4 = 180° ….. (ii)
(i) और (ii) से,
∠1 + ∠5 + ∠6 + ∠3 = ∠2 + ∠5 + ∠7 + ∠4 ……. (iii)
परंतु ∠1 = ∠2 और ∠3 = ∠4 (ऊपर प्रमाणित)
∴ (iii) से हमें प्राप्त होता है :
∠1 + ∠5 + ∠6 + ∠3 = ∠1 + ∠5 + ∠7 + ∠3
⇒ ∠6 = ∠7
या ∠ACP = ∠QCD इति सिद्धम
![]()
प्रश्न 10.
यदि किसी त्रिभुज की दो भुजाओं को व्यास मानकर वृत्त खींचे जाएं, तो सिद्ध कीजिए कि इन | वृत्तों का प्रतिच्छेद बिंदु तीसरी भुजा पर स्थित है।
हल :
दिया है : दो वृत्त एक दूसरे को बिंदुओं A और B प्रतिच्छेद करते हैं। AP और AQ उनके व्यास हैं।
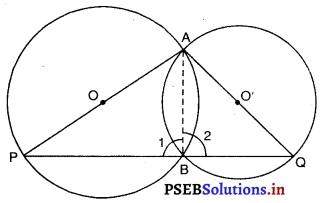
सिद्ध करना है : बिंदु B, तीसरी भुजा PQ पर स्थित है।
रचना : A और B को मिलाइए।
उपपत्ति : AP व्यास है।
∴ ∠1 = 90° (अर्धवृत्त का कोण)
साथ ही, AQ व्यास है।
∴ ∠2 = 90° (अर्धवृत्त का कोण)
∠1 + ∠2 = 90° + 90°
⇒ ∠PBQ = 180°
⇒ PBQ एक सरल रेखा है
अतः, B अर्थात् इन वृत्तों का प्रतिच्छेद बिंदु तीसरी भुजा अर्थात् PQ पर स्थित है।
प्रश्न 11.
उभयनिष्ठ कर्ण AC वाले दो समकोण त्रिभुज ABC और ADC है। सिद्ध कीजिए कि ∠CAD = ∠CBD है।
हल:
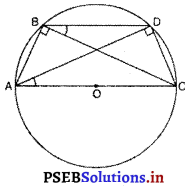
दिया है कि दो समकोण त्रिभुज ABC और ADC जिनमें B और D पर क्रमशः समकोण हैं।
∴ ∠ABC = ∠ADC (प्रत्येक 90°)
यदि हम AC (उभयनिष्ठ कर्ण) व्यास लेकर एक वृत्त खींचे तो यह निश्चित रूप से बिंदुओं B और D में से होकर जाएगा।
[क्योंकि B और D वे बिंदु है जो चाप AC के एकांतर खंडों में हैं।]
अब, \(\overparen{\mathrm{CD}}\) एक ही वृत्तखंड में ∠CBD और ∠CAD अंतरित करती है।
∴ ∠CAD = ∠CBD (इति सिद्धम)
![]()
प्रश्न 12.
सिद्ध कीजिए कि एक चक्रीय समांतर चतुर्भुज आयत होता है।
हल :
मान लीजिए ABCD एक चक्रीय समांतर चतुर्भुज है। यह सिद्ध करने के लिए कि यह एक आयत है इतना ही सिद्ध करना पर्याप्त है कि समांतर चतुर्भुज का एक कोण समकोण है।
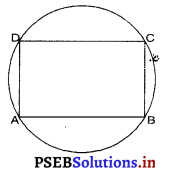
अब, ABCD एक समांतर चतुर्भुज है।
⇒ ∠B = ∠D …….(i)
[∵ समांतर चतुर्भुज के सम्मुख कोण बराबर होते हैं।]
साथ ही, ABCD एक चक्रीय चतुर्भुज है।
⇒ ∠B + ∠D = 180° …….(ii)
(i) और (ii) से हमें प्राप्त होता है :
∠B + ∠B = 180°
⇒ ∠2B = 180°
⇒ ∠B = 90°
इसलिए, ∠B = ∠D = 90°
अतः, ABCD एक आयत है।
