PSEB 9th Class Maths Solutions Chapter 10 वृत्त Ex 10.6

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 10 वृत्त Ex 10.6 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Maths Chapter 10 वृत्त Ex 10.6

प्रश्न 1.
सिद्ध कीजिए कि दो प्रतिच्छेदित करते हुए वृत्तों की केंद्रों की रेखा दोनों प्रतिच्छेद बिंदुओं पर समान कोण अंतरित करती है।
हल :
मान लीजिए दो वृत्त जिन के केंद्र क्रमश: A और B हैं, परस्पर C और D पर प्रतिच्छेद करते हैं। हमने सिद्ध करना है कि ∠ACB = ∠ADB

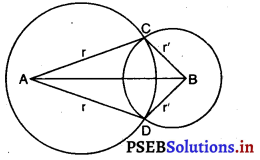
उपपति : ΔABC और ΔABD में,
AC = AD (प्रत्येक = r)
BC = BD (प्रत्येक = r)
AB = AB (उभयनिष्ठ)
∴ ΔABC ≅ ΔABD
(SSS सर्वांगसमता नियम)
⇒ ∠ACB = ∠ADB
(सर्वांगसम त्रिभुजों के संगत भाग)

प्रश्न 2.
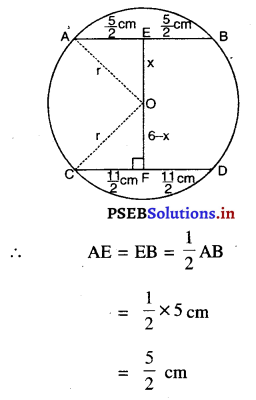
एक वृत्त की 5 cm तथा 11 cm लंबी दो जीवाएँ AB और CD समांतर हैं और केंद्र की विपरीत दिशा में स्थित हैं। यदि AB और CD के बीच की दूरी 6 cm हो, तो वृत्त की त्रिज्या ज्ञात कीजिए।
हल :
मान लीजिए O वृत्त का केंद्र है।
OA और OC को मिलाइए।
क्योंकि वृत्त के केंद्र से जीवा पर खींचा गया लंब जीवा को समद्विभाजित करता है।

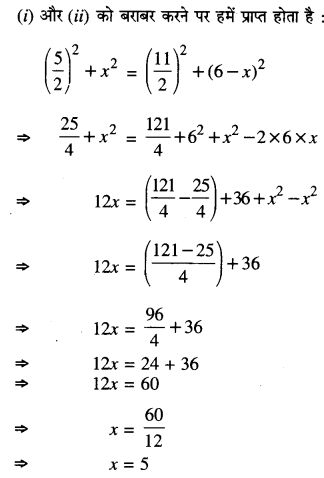
प्रश्न 3.
किसी वृत्त की दो समांतर जीवाओं की लंबाइयाँ 6 cm और 8 cm हैं। यदि छोटी जीवा केंद्र से 4 cm की दूरी पर हो, तो दूसरी जीवा केंद्र से कितनी दूर है ?
हल :
मान लीजिए AB = 6 cm और CD = 8 cm, O केंद्र वाले वृत्त की जीवाएँ हैं।

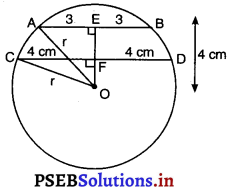
OA और C को मिलाइए।
क्योंकि वृत्त के केंद्र से जीवा पर खींचा गया लंब जीवा को समद्विभाजित करता है।
∴ AE = EB = \(\frac {1}{2}\)AB
= \(\frac {1}{2}\) × 6 = 3cm
और
CF = FD = \(\frac {1}{2}\)CD
= \(\frac {1}{2}\) × 8
= 4 cm
जीवा AB की केंद्र O से लंबात्मक दूरी OE है।
∴ OE = 4 cm
अब समकोण ΔAOE में,
OA² = AE² + OE² [पाइथागोरस का परिणाम प्रयोग करने पर]
⇒ r² = 3² + 4²
⇒ r² = 9 + 16
⇒ r² = 25
⇒ r² = \(\sqrt{25}\)
⇒ r² = 5cm
जीवा CD की केंद्र O से लंबात्मक दूरी OF है।
समकोण ΔOFC में,
OC² = CF² + OF²
[पाइथागोरस का परिणाम प्रयोग करने पर] |
⇒ r² = 4² + OF²
⇒ 5² = 4² + OF²
या OF² = 25 – 16
⇒ OF² = 9
⇒ OF = \(\sqrt{9}\)
⇒ OF = 3 cm
अतः, दूसरी जीवा की केंद्र से दूरी 3 cm है।

प्रश्न 4.
मान लीजिए कि कोण ABC का शीर्ष एक वृत्त के बाहर स्थित है और कोण की भुजाएँ वृत्त से बराबर जीवाएँ AD और CE काटती हैं। सिद्ध कीजिए कि ∠ABC जीवाओं AC तथा DE द्वारा केंद्र पर अंतरित कोणों के अंतर का आधा है।
हल :
∠ABC का शीर्ष B एक वृत्त (जिसका केंद्र O है) के बाहर स्थित है।

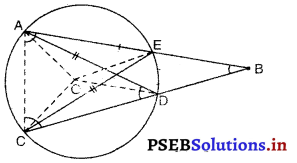
भुजा AB, जीवा CE को बिंदु E पर प्रतिच्छेद करती है और BC जीवा AD को बिंदु D पर प्रतिच्छेद करती है।
हमने सिद्ध करना है कि
∠ABC = \(\frac {1}{2}\)[∠AOC – ∠DOE]
OA, OC, OE और OD को मिलाइए।
अब, ∠AOC = 2∠AEC [चाप द्वारा केंद्र पर अंतरित कोण वृत्त के शेष भाग के किसी बिंदु पर अंतरित कोण का दुगुना होता है]
या \(\frac {1}{2}\)∠AOC = ∠AEC …………(i)
इसी प्रकार, \(\frac {1}{2}\) ∠DOE = ∠DCE …………..(ii)
[उपरोक्त कारण से]
(ii) को (i) में से घटाने पर हमें प्राप्त होता है,
\(\frac {1}{2}\)[∠AOC – ∠DOE] = ∠AEC – ∠DCE …………(iii)
अब, ∠AEC = ∠ADC …….(iv)
(एक ही वृत्तखंड के कोण)
साथ ही, ∠DCE = ∠DAE
(एक ही वृत्तखंड के कोण)
(iv) और (v) को (iii) में प्रयोग करने पर हमें प्राप्त होता है,
\(\frac {1}{2}\)[∠AOC – ∠DOE] = ∠ADC – ∠DAE …….(vi)
ΔADB में,
∠ADC = ∠DAE + ∠ABD …(vii) (त्रिभुज का बाह्य कोण अंत:अभिमुख कोणों के योग के बराबर होता है)
(vii) को (vi) में प्रयोग करने पर हमें प्राप्त होता है :
\(\frac {1}{2}\)[∠AOC – ∠DOE] = ∠DAE + ∠ABD – ∠DAE
⇒ \(\frac {1}{2}\)[∠AOC – ∠DOE] = ∠ABD
या \(\frac {1}{2}\)[∠AOC – ∠DOE] = ∠ABC
(इति सिद्धम)

प्रश्न 5.
सिद्ध कीजिए कि किसी चतुर्भुज की किसी भूजा को व्यास मानकर खींचा गया वृत्त उसके विकणों के प्रतिच्छेद बिंदु से होकर जाता है।
हल :
मान लीजिए कि ABCD एक समचतुर्भुज है जिसमें विकर्ण AC और BD परस्पर बिंदु पर प्रतिच्छेद करते हैं।

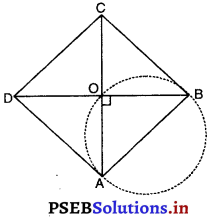
जैसा कि हमें ज्ञात है कि समचतुर्भुज के विकर्ण एकदूसरे के लंब समद्विभाजिक होते हैं।
∴ ∠AOB = 90°
यदि हम AB को व्यास मानकर वृत्त खींचे तो यह निश्चित रूप से ही बिंदु ०(विकर्णों का प्रतिच्छेद बिंदु) में से होकर जाएगा। क्योंकि तब ∠AOB = 90° इसके अर्धवृत्त में बना कोण होगा।

प्रश्न 6.
ABCD एक समांतर चतुर्भुज है। A, B और C से होकर जाने वाला वृत्त CD (यदि आवश्यक हो तो बढ़ाकर) को E पर प्रतिच्छेद करता है। सिद्ध कीजिए कि AE = AD है।
हल :

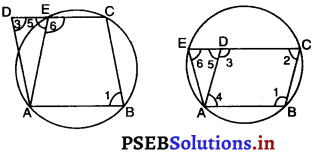
आकृति (a) में,
ABCD एक समांतर चतुर्भुज है।
⇒ ∠1 = ∠3 …………(i)
(समांतर चतुर्भुज के सम्मुख कोण)
ABCE एक चक्रीय चतुर्भुज है।
∠1 + ∠6 = 180° …… (ii)
∠5 + ∠6 = 180°…(रैखिक युग्म)… (iii)
(ii) और (iii) से
∠1 = ∠5 …. (iv)
अब, (i) और (iv) से
∠3 = ∠5
अब, ΔAED में,
∠3 = ∠5
⇒ AE = AD (∵ त्रिभुज के बराबर कोणों की सम्मुख भुजाएँ) आकृति (b) में,
ABCD एक समांतर चतुर्भुज है।
⇒ ∠1 = ∠3 (समांतर चतुर्भुज के सम्मुख कोण)
∠2 = ∠4
साथ ही AB || CD और BC इनको मिलती है।
∠1 + ∠2 = 180° ……. (1)
और AD || BC और EC इनको मिलती है।
∠5 = ∠2 (संगत कोण) …… (2)
ABCE एक चक्रीय चतुर्भुज है।
∴ ∠1 + ∠6 = 180°
(1) और (3) से हमें प्राप्त होता है :
∠1 + ∠2 = ∠1 + ∠6
⇒ ∠2 = ∠6
परंतु (2) से,
∠2 = ∠5
⇒ ∠5 = ∠6
अब, ΔAED में,
∠5 = ∠6
⇒ AE = AD
अतः, दोनों स्थितियों में,
AE = AD.

प्रश्न 7.
AC और BD एक वृत्त की जीवाएँ हैं जो परस्पर समद्विभाजित करती हैं। सिद्ध कीजिए :
(i) AC और BD व्यास हैं,
(ii) ABCD एक आयत है।
हल :

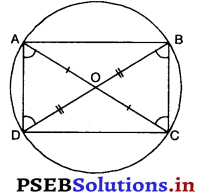
मान लीजिए वृत्त की जीवाएँ AC और BD परस्पर O पर समद्विभाजित करती हैं।
तो OA = OC और OB = OD.
हमने सिद्ध करना है कि (i) AC और BD व्यास हैं दूसरे शब्दों में, O वृत्त का केंद्र है।
ΔAOD और ΔBOC में,
AO = OC (दिया है।)
∠AOD = ∠BOC (शीर्षाभिमुख कोण)
OD = OB (दिया है)
∴ ΔAOD ≅ ΔCOB
(SAS सर्वांगसमता नियम)
⇒ AD = CB
(सर्वांगसम त्रिभुजों के संगत भाग)
इसी प्रकार, ΔAOB ≅ ΔCOD
⇒ AB = CD
⇒ \(\widehat{\mathrm{AB}}\) ≅ \(\widehat{\mathrm{CD}}\)
[बराबर जीवाओं की सम्मुख चा]
⇒ \(\widehat{\mathrm{AB}}\) + \(\widehat{\mathrm{BC}}\)
⇒ \(\widehat{\mathrm{CD}}\) + \(\widehat{\mathrm{BC}}\)
⇒ \(\widehat{\mathrm{ABC}}\) = \(\widehat{\mathrm{BCD}}\)
⇒ AC = BD
(बराबर चापों की सम्मुख जीवाएँ)
∴ AC और BD व्यास हैं। क्योंकि केवल व्यास ही, वृत्त की जीवाओं के रूप में परस्पर समदृविभाजित करते हैं।
(ii) के लिए (i) में जैसा कि सिद्ध हुआ ;
AC व्यास है।
∴ ∠B = ∠D = 90° ………(1)
[अन्त का कोण समकोण होता है]
इसी प्रकार BD व्यास है
∴ ∠A = ∠C = 90° …(2)
अब व्यास
AC = BD
⇒ \(\widehat{\mathrm{AC}}\) ≅ \(\widehat{\mathrm{BD}}\)
(बराबर जीवाओं की संगत चाप बराबर होती हैं)
⇒ \(\widehat{\mathrm{AC}}\) – \(\widehat{\mathrm{DC}}\) ≅ \(\widehat{\mathrm{BD}}\) – \(\widehat{\mathrm{DC}}\)
⇒ \(\widehat{\mathrm{AD}}\) ≅ \(\widehat{\mathrm{BC}}\)
⇒ AD = BC
(बराबर जीवाओं की संगत चाप बराबर होती हैं) ……..(3)
इसी प्रकार AB = DC ……..(4)
(1), (2), (3) और (4) से हम देखते हैं कि चतुर्भुज का प्रत्येक कोण 90° का है तथा सम्मुख भुजाएँ बराबर होती हैं।
अतः, ABCD एक आयत है।

प्रश्न 8.
एक त्रिभुज ABC के कोणों A, B और C के समद्विभाजक इसके परिवृत्त को क्रमश: D, E और F पर प्रतिच्छेद करते हैं। सिद्ध कीजिए कि त्रिभुज DEF के कोण 90° – \(\frac {1}{2}\)A, 90° – \(\frac {1}{2}\)B तथा 90° – \(\frac {1}{2}\)C हैं।
हल :
प्रश्न के अनुसार (नीचे दी गई आकृति को देखिए)।

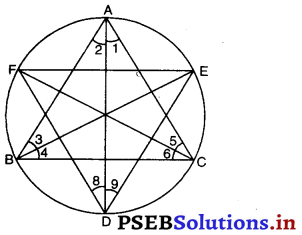
AD, ∠A का समद्विभाजक है
∴ ∠1 = ∠2 = \(\frac {A}{2}\)
BE, ∠B का समद्विभाजक है।
∴ ∠3 = ∠4 = \(\frac {B}{2}\)
CE, ∠C का समद्विभाजक है।
∴ ∠5 = ∠6 = \(\frac {C}{2}\)
जैसा कि हम जानते हैं कि एक ही वृत्तखंड के कोण बराबर होते हैं।
∴ ∠9 = ∠3
(\(\widehat{\mathrm{AE}}\) द्वारा अंतरित कोण)
∠8 =∠5
(\(\widehat{\mathrm{FA}}\) द्वारा अंतरित कोण)
∠9 + ∠8 = ∠3 + ∠5

प्रश्न 9.
दो सर्वांगसम वृत्त परस्पर बिंदुओं A और B पर प्रतिच्छेद करते हैं। A से होकर कोई रेखाखंड PAQ इस प्रकार खींचा गया है कि P और दोनों वृत्तों पर स्थित हैं। सिद्ध कीजिए कि BP = BQ है।
हल :

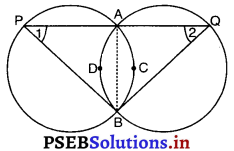
दिया है : दो सर्वांगसम वृत्त बिंदुओं A और B पर प्रतिच्छेद करते हैं।
A से खींची गई रेखा वृत्तों को P और Q पर मिलती
सिद्ध करना है : BP = BQ
रचना : A और B को मिलाइए
उपपत्ति : AB उभयनिष्ठ जीवा है और वृत्त बराबर हैं।
∴ उभयनिष्ठ जीवा के संगत चाप बराबर होते हैं।
अर्थात्
\(\widehat{\mathrm{ACB}}=\widehat{\mathrm{ADB}}\)
क्योंकि दो सर्वांगसम वृत्तों के सर्वांगसम चाप वृत्त के । शेष भाग पर बराबर कोण बनाते हैं
इसलिए, हमें प्राप्त है
∠1 = ∠2
APBQ में,
∠1 = ∠2 (सिद्ध किया है)
∴ त्रिभुज के बराबर कोणों की सम्मुख भुजाएँ बराबर होती हैं।
इसलिए :
BP = BQ.

प्रश्न 10.
किसी त्रिभुज ABC में, यदि ∠A का समद्विभाजक तथा BC का लंब समद्विभाजक प्रतिच्छेद करें, तो सिद्ध कीजिए कि वे ΔABC के परिवृत्त पर प्रतिच्छेद करेंगे।
हल :
दिया है कि ABC एक त्रिभुज है और इसके शीर्षों में से वृत्त गुजरता है।

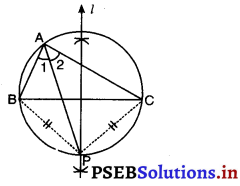
मान लीजिए कि कोण A का समद्विभाजक तथा सम्मुख भुजा BC का लंब समद्विभाजक (कह लीजिए) बिंदु P पर प्रतिच्छेद करते हैं।
हमें सिद्ध करना है कि त्रिभुज ABC का परिवृत्त भी बिंद P में से होकर जाएगा।
उपपत्ति : जैसा कि हमें ज्ञात है कि किसी भुजा के लंब समद्विभाजक पर कोई भी बिंदु इस संगत भुजा के अंत:बिंदुओं से समदूरस्थ होता है।
∴ BP = PC ………(i)
साथ ही प्राप्त है: ∠1 = ∠2 …… (ii) [ क्योंकि, AP, ∠A का समद्विभाजक है।
(दिया है)]
(i) और (ii) से हमें ज्ञात होता है कि बराबर रेखाखंड वृत्त के एक ही खंड (अर्थात् Δ ABC के परिवृत्त के बिंदु A पर) में बराबर कोण बनाते हैं।
इसलिए BP और PC, ΔABC के परिवृत्त की जीवाओं के रूप में हैं और उनकी संगत चापें ; \(\widehat{\mathrm{BP}}\) और \(\widehat{\mathrm{PC}}\) परिवृत्त के ही भाग हैं।
अतः बिंदु P परिवृत्त पर ही है।
दूसरे शब्दों में, बिंदु A, B, P और C एकवृत्तीय हैं।
(इति सिद्धम)