Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 11 रचनाएँ Ex 11.1 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 9 Maths Chapter 11 रचनाएँ Ex 11.1
प्रश्न 1.
एक दी हुई किरण के प्रारंभिक बिंदु पर 90° के कोण की रचना कीजिए और कारण सहित रचना की पुष्टि कीजिए।
हल :
रचना के चरण :
1. एक किरण OA खींचिए।
![]()
2. O को केंद्र मानकर और उपयुक्त त्रिज्या लेकर एक चाप LM खींचिए। OA को L पर काटे।

3. अब L को केंद्र मानकर और त्रिज्या OL, लेकर एक चाप खींचिए जो चाप LM को P पर काटे।

4. तब P को केंद्र मानकर और त्रिज्या OL, लेकर एक चाप खींचिए जो चाप PM को बिंदु Q पर काटे।
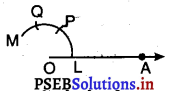
5. किरण OB खींचने के लिए OP को मिलाइए। साथ ही, किरण OC प्राप्त करने के लिए O और Q को मिलाइए। हम देखते हैं कि :
∠AOB = ∠BOC = 60°
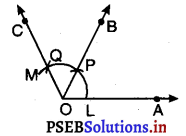
6. अब हमने ∠BOC को समद्विभाजित करना है। इसके लिए P को केंद्र मानकर और त्रिज्या \(\frac{1}{2}\)PQ से अधिक लेकर एक चाप खींचिए।
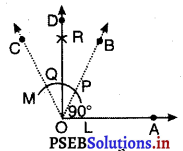
7. अब Q को केंद्र मानकर और चरण 6 वाली त्रिज्या लेकर एक अन्य चाप लगाइए जो चरण 6 वाली चाप को R पर काटे।
8. किरण OD खींचने के लिए और R को मिलाइए। तब ∠AOD ही अभीष्ट कोण 90° है।
सत्यापन : ∠AOD, को मापिए। आप देखेंगे कि ∠AOD = 90° है।
रचना की प्रमाणिकता :
PL, को मिलाइए, तब
OL = OP = PL (रचना से)
अतः, ΔOPL एक समबाहु त्रिभुज है और ∠POL जोकि ∠BOA के समान है जो 60° के बराबर है।
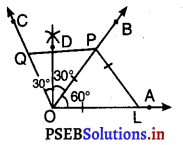
अब, QP को मिलाइए
OP = OQ = PQ (रचना से)
अतः, ΔOQP एक समबाहु त्रिभुज है।
∴ ∠POQ जोकि ∠BOC के बराबर है, 60° का है।
रचना से OD, ∠BOC का समद्विभाजक है।
∴ ∠DOC = ∠DOB = \(\frac{1}{2}\)∠BOC
= \(\frac{1}{2}\) × 60° = 30°
अब ∠DOA = ∠BOA + ∠DOB
⇒ ∠DOA = 60° + 30°
⇒ ∠DOA = 90°.
![]()
प्रश्न 2.
एक दी हुई किरण के प्रारंभिक बिंदु पर 45° के कोण की रचना कीजिए और कारण सहित रचना की पुष्टि कीजिए।
हल :
हम देखते हैं कि 45° = \(\frac{1}{2}\) × 90°
इसलिए हम अभीष्ट कोण प्राप्त करने के लिए दिए गए कोण को समद्विभाजित करने की प्रक्रिया का अनुसरण करते है।
अतः, 45° का कोण बनाने के लिए हम नीचे दिए अनुसार प्रक्रिया करते है :
रचना के चरण :
1. ∠AOD = 90° खींचिए। (टिप्पणी : उन्हीं चरणों का अनुसरण कीजिए जो कि 90° के कोण की रचना में किए हैं।)
2. L के केंद्र को केंद्र मानकर और त्रिज्या \(\frac{1}{2}\)LS, से बड़ी लेकर एक चाप खींचिए।
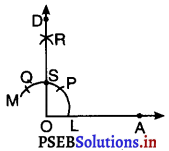
3. अब S को केंद्र मानकर और चरण 2 वाली ही त्रिज्या लेकर एक अन्य चाप खींचिए जो चरण 2 वाली चाप को T पर काटती है।
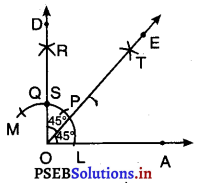
4. O और T को मिलाइए और किरण OE खींचिए।
अतः, OE, ∠AOD को समद्विभाजित करती है। इसलिए, ∠AOE = ∠DOE = 45° है।
सत्यापन : ∠AOE, को मापिए, आप देखोगे कि ∠AOE = 45° है।
रचना की प्रमाणिकता :
LS को मिलाइए तब ΔOLS समद्विबाहु त्रिभुज है जिसमें O पर समकोण है। .
∴ OL = OS
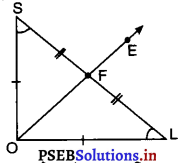
इसलिए O, SL के लंब समद्विभाजक पर स्थित है।
∴ SF = FL
और ∠OFS = ∠OFL (प्रत्येक 90°)
अब ΔOFS और ΔOFL में,
OF = OF (उभयनिष्ठा)
OS = OL (रचना से)
SF = FL (ऊपर प्रमाणित)
∴ ΔOFS ≅ ΔOFL (SSS नियम से)
⇒ ∠SOF = ∠LOF
(सर्वांगसम त्रिभुजों के संगत भाग।)
अब
∠SOF + ∠LOF = ∠SOL
⇒ ∠LOF + ∠LOF = 90°
⇒ 2∠LOF = 90°
⇒ ∠LOF = \(\frac{1}{2}\) × 90°
⇒ ∠LOF = 45°
या, ∠AOE = 45° (जोकि रचना के अनुसार सत्य है।)
![]()
प्रश्न 3.
निम्न मापों के कोणों की रचना कीजिए :
(i) 30°
(ii) \(22 \frac{1}{2}^{\circ}\)
(iii) 15°.
हल :
(i) 30° की रचना :
हम देखते हैं कि 30° = \(\frac{1}{2}\) × 60°
इसलिए हम अभीष्ट कोण प्राप्त करने के लिए दिए गए कोण को समदविभाजित करने की प्रक्रिया का अनुसरण करते हैं।
अतः 30° के कोण की रचना के लिए हम नीचे दिए अनुसार प्रक्रिया करते हैं :
रचना के चरण :
1. एक किरण OA खींचिए।
![]()
2. O को केंद्र मानकर और उपयुक्त त्रिज्या लेकर
चाप LM खींचिए जो OA को L पर काटती है।
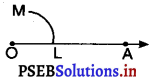
3. L को केंद्र मानकर और त्रिज्या OL लेकर एक चाप खींचिए जो LM को N पर काटती है।
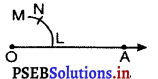
4. O और N को मिलाइए और रेखा OB खींचिए। तब ∠AOB = 60° है।
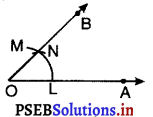
5. L को केंद्र मानकर और त्रिज्या \(\frac{1}{2}\)LN, से बड़ी लेकर एक चाप खींचिए।
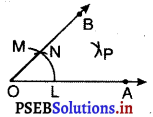
6. अब N को केंद्र मानकर और चरण 5 वाली त्रिज्या लेकर एक अन्य चाप खींचिए जो कि चरण 5 वाली चाप को P पर काटे।
7. O और P को मिलाइए और किरण OC खींचिए।
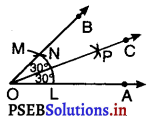
अतः, OC, ∠AOB को समद्विभाजित करती है और इसलिए
∠AOC = ∠BOC = 30°
सत्यापन : ∠AOC को मापिए, आप देखेंगे कि ∠AOC = 30° है।
(ii) \(22 \frac{1}{2}^{\circ}\) की रचना :
हम देखते हैं कि \(22 \frac{1}{2}^{\circ}\) = \(\frac{1}{2}\) × 45°
इसलिए हम अभीष्ट कोण प्राप्त करने के लिए दिए गए कोण को समद्विभाजित करने की प्रक्रिया का अनुसरण करते हैं।
\(22 \frac{1}{2}^{\circ}\) का कोण बनाने के लिए हम नीचे दिए अनुसार प्रक्रिया करते हैं :
रचना के चरण :
1. ∠AOD = 90° खींचिए।
(टिप्पणी : प्रश्न न० 1 में दिए गए चरणों का अनुसरण कीजिए जो कि 90° के कोण की रचना में लिए हैं।)
2. अब ∠AOD को किरण OE से इस प्रकार
समद्विभाजित ∠DOE = ∠AOE = 45° (टिप्पणी : उन्हीं चरणों का अनुसरण कीजिए जो प्रश्न न० 2 में 45° के कोण की रचना में लिए हैं।)
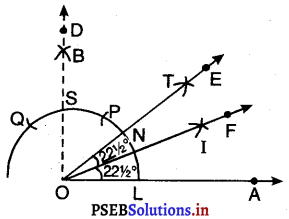
3. मान लीजिए किरण OE वृत्त की चाप को N पर प्रतिच्छेद करे।
4. अब L को केंद्र मानकर और त्रिज्या \(\frac{1}{2}\)LN से अधिक लेकर एक चाप खींचिए।
5. N को केंद्र मानकर और वही त्रिज्या जो चरण 4 में ली गई है। लेकर एक अन्य चाप खींचिए जो चरण 4 वाली चाप को I पर काटे।
6. O और I को मिलाइए और किरण OF खींचिए।
अतः, OF, ∠AOE को समद्विभाजित कीजिए।
∠AOF = ∠EOF = \(22 \frac{1}{2}^{\circ}\)
सत्यापन : ∠AOF को चाँदे की सहायता से मापिए। हम देखते हैं कि ∠AOF = \(22 \frac{1}{2}^{\circ}\)
(iii) 15° की रचना :
हम देखते हैं कि 15° = \(\frac{1}{2}\) × 30°
इसलिए अभीष्ट कोण प्राप्त करने के लिए हम दिए गए कोण को समद्विभाजित करने वाली विधि का अनुसरण करते हैं।
अतः, 15° के कोण की रचना के लिए हम निम्नलिखित चरणों का अनुसरण करते हैं।
रचना के चरण :
1. ∠AOB = 60° खींचिए।
2. अब ∠AOB को किरण OC से इस तरह समद्विभाजित कीजिए कि ∠BOC = ∠AOC = 30° [टिप्पणी : प्रश्न 3 (i) में 30° की रचना में लिए गए चरणों का अनुसरण कीजिए।]
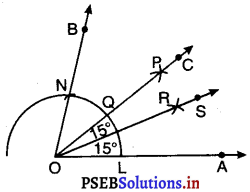
3. मान लीजिए किरण OC वृत्त की चाप को बिंदु Q पर प्रतिच्छेद करती है।
4. अब L को केंद्र मान कर और त्रिज्या \(\frac{1}{2}\)LQ से अधिक लेकर एक चाप खींचिए।
5. Q को केंद्र मानकर और चरण 4 वाली त्रिज्या लेकर एक अन्य चाप खींचिए जोकि चरण 4 वाली चाप को R पर प्रतिच्छेद करे।
6. O और R को मिलाइए और किरण OS खींचिए।
अत: OS, ∠AOC को समविभाजित करता है।
इसलिए, ∠COS = ∠AOS = 15° है।
सत्यापन : ∠AOS को चाँदे से मापिए हम देखते हैं कि ∠AOS = 15° है।
![]()
प्रश्न 4.
निम्न कोणों की रचना कीजिए और चाँदे द्वारा मापकर पुष्टि कीजिए :
(i) 75°
(ii) 105°
(ii) 135°
हल :
(i) 75° की रचना
रचना के चरण :
1. ∠ABE = 60° और ∠ABF = 90° खींचिए। (टिप्पणी : उदाहरण 1 और प्रश्न न० 1 में लिए गए चरणों का अनुसरण कीजिए।)
2. मान लीजिए किरण BF वृत्त की चाप को G पर काटती है।
3. अब M को केंद्र मानकर और त्रिज्या \(\frac{1}{2}\)MG से अधिक लेकर एक चाप खींचिए।
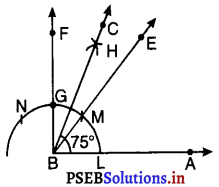
4. G को केंद्र मान कर और चरण 3 वाली त्रिज्या लेकर एक चाप खींचिए जो पहली चाप को H पर प्रतिच्छेद करे।
5. H में से एक किरण BC खींचिए जो ∠EBF को समद्विभाजित करती है।
अतः, ∠ABC = 75° अभीष्ट कोण है।
सत्यापन : ∠ABC को चाँदे द्वारा मापिए। हम देखते हैं कि ∠ABC = 75°
रचना की प्रमाणिकता :
∠EBF = ∠ABF – ∠ABE = 90° – 60° = 30°
∠EBC = ∠CBF
= \(\frac{1}{2}\)∠EBF = \(\frac{1}{2}\)(30°)
= 15°
[∵ BC ∠EBF को समद्विभाजित करता है]
∴ ∠ABC = ∠ABE + ∠EBC
= 60° + 150
⇒ ∠ABC = 750
(जोकि चाँद द्वारा मापे जाने पर सत्य है।)
(ii) 105° की रचना
रचना के चरण :
1. ∠ABE = 90° और ∠ABF = 120° खींचिए।
2. मान लीजिए किरण BE वृत्त की चाप को M पर तथा किरण BF वृत्त की चाप को N पर प्रतिच्छेद करती है।
3. M को केंद्र मानकर और त्रिज्या \(\frac{1}{2}\)MN से अधिक लेकर एक चाप खींचिए।
4. N को केंद्र मानकर और चरण 3 वाली त्रिज्या लेकर एक अन्य चाप खींचिए जो चरण 3 वाली चाप को P पर प्रतिच्छेद करे।
5. P में से किरण BC खींचिए जो ∠EBF को समद्विभाजित करती है।
अतः, ∠ABC = 105° अभीष्ट कोण है।
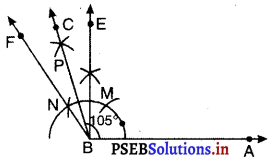
सत्यापन : ∠ABC को चाँद द्वारा मापिए। हम देखते हैं कि ∠ABC = 105° है।
रचना की प्रमाणिकता :
∠EBF = ∠ABF – ∠ABE
⇒ ∠EBF = 120° – 90° = 30°
∠EBC = ∠CBF = \(\frac{1}{2}\)∠EBF
= \(\frac{1}{2}\)(30°) = 15°
[∵ BC, ∠EBF का समद्विभाजक है।]
∴ ∠ABC = ∠ABE + ∠EBC
= 90° + 15°
⇒ ∠ABC = 105°
[जोकि चाँदे द्वारा मापे जाने पर सत्य है।]
(iii) 135° की रचना
रचना के चरण :
1. एक किरण OA खींचिए।
![]()
2. O को केंद्र मानकर और कोई सुविधाजनक त्रिज्या लेकर एक चाप LM (जिसकी लंबाई अर्धवृत्त से अधिक हो) खींचिए जो OA को L पर प्रतिच्छेद करे।

3. अब L को केंद्र मानकर और त्रिज्या = OL लेकर एक चाप खींचिए जो चाप LM को P पर प्रतिच्छेद करे।
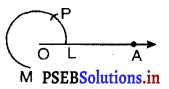
4. तब P को केंद्र और त्रिज्या OL लेकर एक चाप खींचिए जो चाप PM को Q पर प्रतिच्छेद करे।
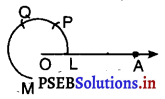
5. अब ∠POQ को किरण OB द्वारा समद्विभाजित करने पर हमें प्राप्त होता है ; ∠AOB = 90°
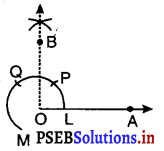
6. अब Q को केंद्र मानकर और त्रिज्या OL लेकर एक चाप खींचिए जो QM को N पर प्रतिच्छेद करे।
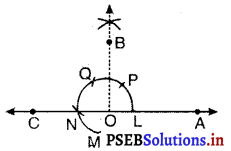
7. O और N को मिलाकर किरण OC खींचिए।
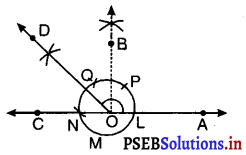
अतः, हम प्राप्त करते हैं ∠AOC = 180°
या ∠BOC = ∠AOB = 90°
8. अब ∠BOC को किरण OD द्वारा समद्विभाजित कीजिए।
तब ∠AOD ही अभीष्ट कोण 135° है।
[क्योंकि ∠AOD = ∠AOB+ ∠BOD
= 90° + 45°
= 135°]
सत्यापन : ∠AOD को चाँदे से मापिए। आप देखेंगे कि ∠AOD = 135°
![]()
प्रश्न 5.
एक समबाहु त्रिभुज की रचना कीजिए, जबकि इसकी भुजा दी हो, तथा कारण सहित रचना कीजिए।
हल :
दी गई भुजा (मान लीजिए यह ΔABC है जिसकी एक भुजा 6 cm. है।) की समबाहु त्रिभुज की रचना।
रचना के चरण :
1. 6 cm. की लंबाई का एक रेखाखंड BC खींचिए।
2. B पर ∠XBC = 60° खींचिए।
3. रेखाखंड BC का लंब समद्विभाजक PQ खींचिए।
4. मान लीजिए PQ किरण BX और BC को क्रमशः बिंदुओं A और D पर प्रतिच्छेद करती है।
5. AC को मिलाइए।
अतः, ABC ही अभीष्ट समबाहु त्रिभुज है।
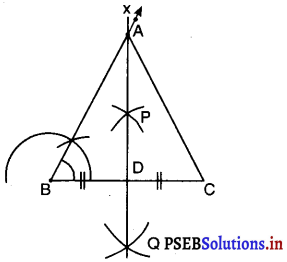
रचना की पुष्टि :
समकोण ΔADB और समकोण ΔADC में,
AD = AD (उभयनिष्ठ)
∠ADB = ∠ADC (प्रत्येक 90°)
(रचना से)
BD = CD. (रचना से)
∴ ΔADB ≅ ΔADC
(SAS सर्वांगसमता नियम से)
∴ ∠B = ∠C = 60°
(सर्वांगसम त्रिभुजों के संगत भाग)
इसलिए, ΔABC में तीसरा कोण,
∠A = 180° – (∠B + ∠C)
= 180° – (60° + 60°)
= 180° – 120°
= 60°
त्रिभुज का प्रत्येक कोण 60° का है। अतः, बनाई गई त्रिभुज समबाहु त्रिभुज है।
