Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 4 दो चरों वाले रैखिक समीकरण Ex 4.3 Textbook Exercise Questions and Answers
PSEB Solutions for Class 9 Maths Chapter 4 दो चरों वाले रैखिक समीकरण Ex 4.3
प्रश्न 1.
दो चरों वाले निम्नलिखित रैखिक समीकरणों में से प्रत्येक का आलेख खींचिएँ :
(i) x + y = 4
(ii) x – y = 2
(ii) y = 3x
(iv) 3 = 2x + y
हल :
(i) x + y = 4
⇒ y = 4 – x
x के मानों के संगत y के मानों को दर्शाती सारणी इस प्रकार है|
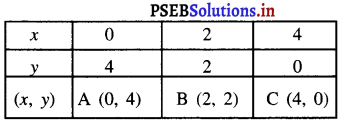
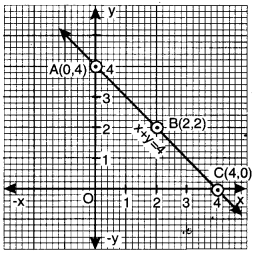
बिंदुओं A (0, 4), B (2, 2) और C (4, 0) को आलेख कागज़ पर आलेखित कीजिए। इन बिंदुओं को मिलाइए और रेखा प्राप्त कीजिए।
पैमाना (Scale chosen) :
X-अक्ष (X-axis) पर 5 भाग = 1 एकक
Y-अक्ष (Y-axis) पर 5 भाग = 1 एकक
![]()
(ii) x – y = 2
⇒ – y = 2 – x
या y = x – 2
x के मानों के संगत y के मानों को दर्शाती सारणी इस प्रकार है. :
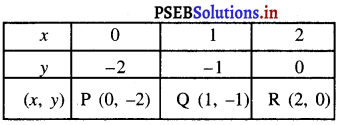
बिंदुओं P (0, – 2), Q (1, – 1) और R (2, 0) आलेख कागज़ पर आलेखित कीजिए। इन बिंदुओं को मिलाइए और रेखा प्राप्त कीजिए।
पैमाना (Scale chosen) :
X-अक्ष (X-axis) पर :
5 भाग = 1 एकक
Y-अक्ष (Y-axis) पर :
5 भाग = 1 एकक
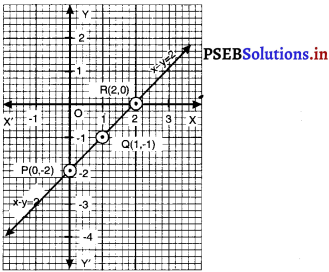
(iii) y = 3x
xके मानों के संगत । के मानों को दर्शाती सारणी इस प्रकार है
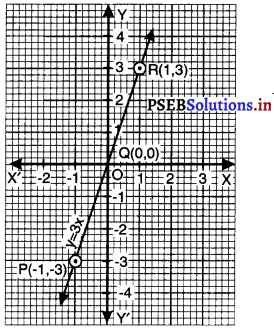
बिंदुओं P (- 1, – 3), Q (0, 0) और R (1, 3) को आलेख कागज़ पर आलेखित कीजिए।
इन बिंदुओं को मिलाइए और रेखा प्राप्त कीजिए।
पैमाना (Scale chosen) :
X-अक्ष (X-axis) पर :
5 भाग = 1 एकक
Y-अक्ष (Y-axis) पर :
5 भाग = 1 एकक
(iv) 3 = 2x + y
⇒ 3 – 2x = y
या y = 3 – 2x
x के मानों के संगत y के मानों को दर्शाती सारणी इस प्रकार है :

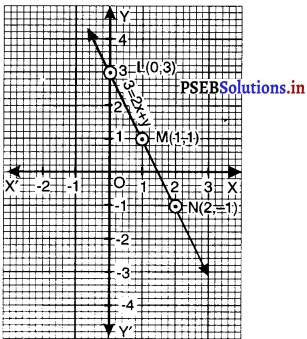
बिंदुओं L (0, 3), M (1, 1) और N (2, – 1) को आलेख कागज़ पर आलेखित कीजिए। इन बिंदुओं को मिलाइए और रेखा प्राप्त कीजिए।
पैमाना (Scale chosen) :
X-अक्ष (X-axis) पर :
5 भाग = 1 एकक
Y-अक्ष (Y-axis) पर :
5 भाग = 1 एकक
![]()
प्रश्न 2.
बिंदु (2, 14) से होकर जाने वाली दो रेखाओं के समीकरण लिखिए। इस प्रकार की और कितनी रेखाएं हो सकती हैं, और क्यों ?
हल :
हम जानते हैं कि एक बिंदु में से असीमित रूप से अनेक रेखाएँ खींची जा सकती हैं। इनमें से कोई दो रैखिक समीकरण जो बिंदु (2, 14) द्वारा संतुष्ट होते हैं। निम्न अनुसार हैं :
मान लीजिए x और y में रैखिक समीकरण में ax + by = c बिंदु (2, 14) द्वारा संतुष्ट होता हैं।
अतः, बिंदु (2, 14) इस पर स्थित हैं।
∴ 2a + 14b = c
समीकरण में c का मान भरने पर, हमें प्राप्त होता है
ax + by = 2a + 14b
⇒ a(x – 2) + b (y – 14) = D
⇒ b (y – 14) = – a (x – 2)
⇒ \(\frac{y-14}{x-2}=-\frac{a}{b}\)
a और b के विभिन्न मानों का प्रयोग करके हम अभीष्ट अनेक समीकरण प्राप्त कर सकते हैं।
यदि a = 2, b = 1
तो \(\frac{y-14}{x-2}=\frac{-2}{1}\)
⇒ y – 14 = – 2x + 4
⇒ 2x + y = 18
यदि a = 7, b = – 1
तो \(\frac{y-14}{x-2}=-\left(\frac{7}{-1}\right)\)
⇒ y – 14 = 7x – 14
⇒ 7x – y = 0
![]()
प्रश्न 3.
यदि बिंदु (3, 4) समीकरण 3y = ax + 7 के आलेख पर स्थित है, तो a का मान ज्ञात कीजिए।
हल :
यह दिया है कि बिंदु (3, 4) निम्नलिखित आलेख पर स्थित हैं :
3y = ax + 7
अतः, बिंदु (3, 4) इस समीकरण को संतुष्ट करता
∴ 3 × 4 = a × 3 + 7
⇒ 12 = 3a + 7
⇒ 12 – 7 = 3a
⇒ 5 = 3a
⇒ 3a = 5
⇒ a = \(\frac{3}{5}\)
अतः, a का अभीष्ट \(\frac{3}{5}\) है
स्पष्टीकरण :
दिए गए समीकरण में a = \(\frac{3}{5}\) प्रतिस्थापित करने पर हमें प्राप्त होता है :
⇒ 3y = \(\frac{3}{5}\) x + 7
9y = 5x + 21
⇒ y = \(\frac{5 x+21}{9}\)
x के मानों के संगत y के मानों को दर्शाती सारणी निम्न अनुसार है :

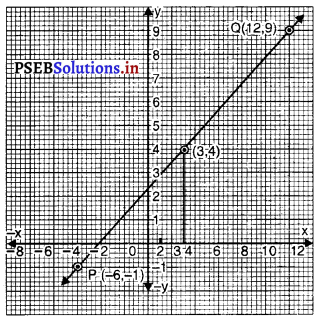
बिंदुओं P(- 6, – 1) और Q (12, 9) को आलेख पेपर पर आलेखित कीजिए। इन बिंदुओं को मिलाइए और एक रेखा प्राप्त कीजिए।
आलेख से हम देखते हैं कि बिंदु (3, 4) रेखा पर स्थित हैं।
अतः, यह समीकरण 3y = \(\frac{5}{3}\) x + 7 को संतुष्ट करता है।
अतः, a का प्राप्त किया गया मान सही है।
पैमाना x-अक्ष पर
5 भाग = 2 एकक
y-अक्ष पर
5 भाग = 1 एकक
![]()
प्रश्न 4.
एक नगर में टैक्सी का किराया निम्नलिखित पहले किलोमीटर का किराया 8 रु है और उसके बाद की दूरी के लिए प्रति किलोमीटर का किराया 5 रु है। यदि तय की गई दूरी x किलोमीटर हो, और कुल किरायाy रु हो, तो इसका एक रैखिक समीकरण लिखिए और उसका आलेख खींचिए।
हल :

तय की गई कुल दूरी x लेने पर पहले किलोमीटर का किराया = 8 रु
पहले किलोमीटर के बाद के प्रत्येक किमी का किराया = 5 रु
कुल किराया = y रु
∴ 8 रु + 5 (x – 1) रु = y रु
⇒ 8 + 5 (x – 1) = y
⇒ 8 + 5x – 5 = y
⇒ 5x + 3 = y
⇒ 5x – y + 3 = 0 …………..(1)
यह दी गई सूचना का एक रैखिक समीकरण है।
समीकरण (1) का आलेख खींचने के लिए x के मानों के संगत y के मानों की दर्शाती समीकरण निम्न अनुसार है :
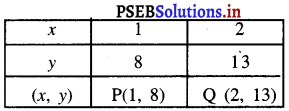
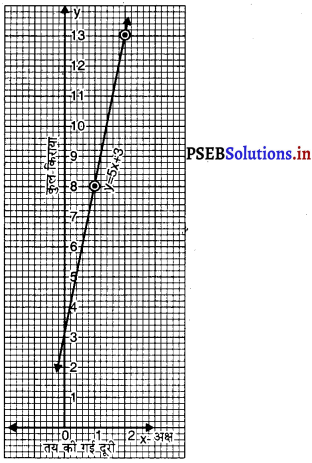
बिंदुओं P(1.8) और 0 (2, 13) को ग्राफ पेपर पर आलेखित कीजिए। इन बिंदुओं को मिलाइए और रेखा प्राप्त कीजिए।
पैमाना
x-अक्ष पर 5 भाग = 1 किमी
y-अक्ष पर 5 भाग = 1 रु
![]()
प्रश्न 5.
निम्नलिखित आलेखों में से प्रत्येक के लिए दिए गए विकल्पों से सही समीकरण का चयन कीजिए :
आकृति (क) के लिए आकृति (ख) के लिए
(i) y = x
(ii) x + y = 0
(iii) y = 2r
(iv) 2 + 3y = 7x
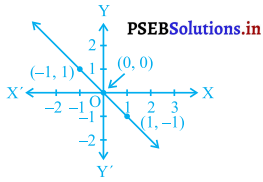
(i) y = x + 2
(ii) y = x -2
(ii) y = -x + 2
(iv) x + 2y = 6

हल :
आलेख (क) पर स्थित प्रत्येक बिंदु समीकरण (ii) x + y = 0 को संतुष्ट करता है।
अतः, आलेख (क) के लिए चारों समीकरणों में से सही समीकरण है :
x + y = 0
∵ x + y = 0
y = – x
x = 0 के लिए y = 0
x = 1 के लिए y = – 1.
x = – 1 के लिए y = 1 .
अब आलेख (ख) का प्रत्येक बिंदु समीकरण
(iii) y = – x + 2 में संतुष्ट है।
अतः, आलेख (ख) के लिए चारों समीकरणों में से सही समीकरण है :
y = – x + 2
∵ y = – x + 2 में
x = 2 के लिए y = – 2 + 2
⇒ y = 0
x = 0 के लिए y = – 0 = 2
⇒ y = 2
x = – 1 के लिए y = – (-1) + 2
⇒ y = 1 + 2
⇒ y = 3
![]()
प्रश्न 6.
एक अचर बल लगाने पर एक पिंड द्वारा किया गया कार्य पिंड द्वारा तय की गई दूरी के अनुक्रमानुपाती होता है। इस कथन को दो चरों वाले एक समीकरण के रूप में व्यक्त कीजिए और अचर बल 5 मात्रक लेकर इसका आलेख खींचिए। यदि पिंड द्वारा तय की गई दूरी
(i) 2 मात्रक
(ii) 0 मात्रक
हो, तो आलेख से किया हुआ कार्य ज्ञात कीजिए।
हल :
मान लीजिए स्थिर बल (माना k मात्रक) द्वारा किया गया कार्य y मात्रक है और पिंड द्वारा तय की गई दूरी x मात्रक है।
हम जानते हैं कि बल द्वारा किया गया कार्य पिंड द्वारा तय की गई दूरी के अनुक्रमानुपाती होता है।
अनुपात और समानुपात से, हम इस तथ्य को इस प्रकार व्यक्त कर सकते हैं :
y = kx
k = 5 मात्रक लेने पर
y = 5x …………(1)
जो कि दो चलों में रैखिक समीकरण है।
समीकरण (1) का आलेख खींचने के लिए ; x के मानों के संगत y के मानों को दर्शाती सारणी निम्न अनुसार है :
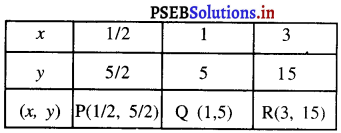
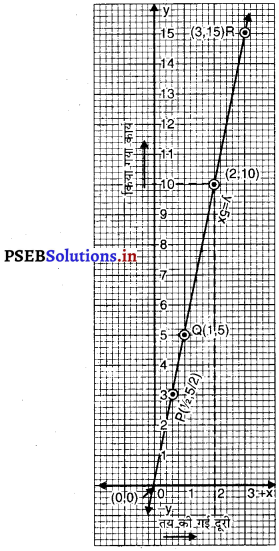
बिंदुओं P(1/2, 5/2) , Q (1, 5) और R(3, 15) को ग्राफ पेपर पर आलेखित कीजिए। इन बिंदुओं को मिलाइए और रेखा प्राप्त कीजिए।
पैमाना
x-अक्ष पर
5 भाग = 1 मात्रक तय की गई दूरी
y-अक्ष पर
5 भाग = 1 मात्रक किया गया कार्य।
आलेख से हम देखते हैं कि
(i) जब x = 2 मात्रक, तो y = 10 मात्रक
अतः जब पिंड द्वारा तय की गई दूरी 2 मात्रक हो, तो किया गया कार्य 10 मात्रक है।
(ii) जब x = 0 मात्रक
तब y = 0 मात्रक
अतः, जब कोई दूरी तय न की गई हो तब कोई कार्य नहीं होता।
![]()
प्रश्न 7.
एक विद्यालय की कक्षा IX की छात्राएँ यामिनी और फातिमा ने मिलकर भूकंप पीड़ित व्यक्तियों की सहायता के लिए प्रधानमंत्री राहत कोष में 100 रु अंशदान दिया। एक रैखिक समीकरण लिखिए जो इन आंकड़ों को संतुष्ट करती हो। (आप उनका अंशदान : रु और y रु मान सकते हैं)। इस समीकरण का आलेख खींचिए।
हल :
मान लीजिए दामिनी ने x रु और फातिमा ने y रु प्रधानमंत्री राहत कोष में अंशदान दिया
दोनों का कुल अंशदान = 100 रु
⇒ x + y = 100 …………(1)
जो कि दो चरों में एक रैखिक समीकरण है।
समीकरण (1) का आलेख खींचने के लिए हम x के मानों के संगत y के मानों को दर्शाती सारणी खींचते हैं।

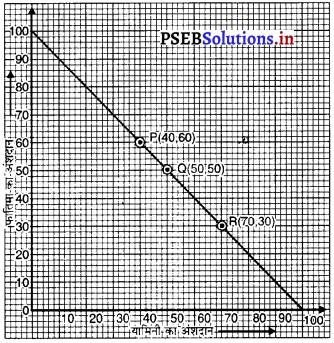
बिंदुओं P (40, 60), Q(50, 50) और P(70, 30) को ग्राफ पेपर पर आलेखित कीजिए। इन बिंदुओं को मिलाइए और रेखा प्राप्त कीजिए।
![]()
प्रश्न 8.
अमरीका और कनाडा जैसे देशों में तापमान फारेनहाइट में मापा जाता है, जबकि भारत जैसे देशों में तापमान सेल्सियस में मापा जाता है। यहाँ फारेनहाइट को सेल्सियस में रूपांतरित करने वाला एक रैखिक समीकरण दिया गया है :
F = (\(\frac{9}{5}\)) C + 32
(i) सेल्सियस को -अक्ष और फारेनहाइट को yअक्ष मानकर ऊपर दिए गए रैखिक समीकरण का आलेख खींचिए।।
(ii) यदि तापमान 30°C है, तो फारेनहाइट में तापमान क्या होगा?
(iii) यदि तापमान 95°F है, तो सेल्सियस में तापमान क्या होगा ?
(iv) यदि तापमान 0°C है, तो फारेनहाइट में तापमान क्या होगा और यदि तापमान 0°F है, तो सेल्सियस में तापमान क्या होगा ?
(v) क्या ऐसा भी कोई तापमान है जो फारेनहाइट और सेल्सियस दोनों के लिए संख्यात्मकतः समान है। यदि हाँ, तो उसे ज्ञात कीजिए।
हल :
दो चरों °F और °C में रैखिक समीकरण है :
F = (\(\frac{9}{5}\)) C + 32 ……………..(1)
समीकरण (1) का आलेख खींचने के लिए हम C के संगत F के मानों को दर्शाती सारणी खींचते हैं।
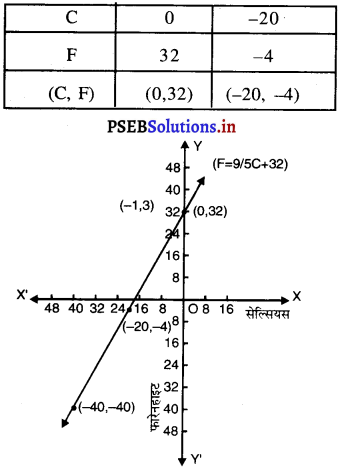
बिंदुओं (0, 32) और (- 20, – 4) को ग्राफ पेपर पर आलेखित कीजिए। इन बिंदुओं को मिलाइए और रेखा प्राप्त कीजिए।
(ii)आलेख से, यदि तापमान 30°C है तो फारेनहाइट में तापमान 86°F है।
(iii)आलेख से, यदि तापमान 95°F है, तो सेल्सियस में यह 35°C है।
(iv)आलेख से, यदि तापमान 0°C हो तो फारेनाहाइट में 32°F है।
यदि तापमान 0°F हो, तो सेल्सियस में यह तापमान – 17.8°C (लगभग) है।
(v) हाँ, ऐसा भी तापमान है जो फारेनहाइट और सेल्सियस दोनों के लिए संख्यात्मकतः समान है। आलेख से हम देखते हैं कि बिंदु (-40, – 40) रेखा पर स्थित
अतः, – 40 (दोनों F और C पर) संख्यात्मकतः समान तापमान है।
