PSEB 9th Class Science Solutions Chapter 8 ਗਤੀ

Punjab State Board PSEB 9th Class Science Book Solutions Chapter 8 ਗਤੀ Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Science Chapter 8 ਗਤੀ

PSEB 9th Class Science Guide ਗਤੀ Textbook Questions and Answers

ਅਭਿਆਸ ਦੇ ਪ੍ਰਸ਼ਨ

ਪ੍ਰਸ਼ਨ 1.
ਇੱਕ ਐਥਲੀਟ 200 m ਵਿਆਸ ਵਾਲੇ ਇੱਕ ਵਿਤੀ (ਚੱਕਰਾਕਾਰ) ਪੱਥ ਦਾ ਇੱਕ ਪੂਰਾ ਚੱਕਰ 40 s ਵਿੱਚ ਲਗਾਉਂਦਾ ਹੈ । 2 ਮਿੰਟ 20 s ਦੇ ਬਾਅਦ ਉਹ ਕਿੰਨੀ ਦੂਰੀ ਤੈਅ ਕਰੇਗਾ ਅਤੇ ਉਸ ਦਾ ਵਿਸਥਾਪਨ ਕਿੰਨਾ ਹੋਵੇਗਾ ?
ਹੱਲ :
ਦਿੱਤਾ ਹੈ, ਤੀ (ਚੱਕਰਾਕਾਰ ) ਪੱਥ ਦਾ ਵਿਆਸ (d) = 200 m
ਵਿਤੀ ਪੱਥ ਦਾ ਅਰਧ ਵਿਆਸ (r) = \(\frac{200}{2}\) =100 m
ਵਿਤੀ ਪੱਥ ਦੀ ਲੰਬਾਈ = 2πr
2 × \(\frac{22}{7}\) × 100
= \(\frac{4400}{7}\) m

1 ਚੱਕਰ ਪੂਰਾ ਕਰਨ ਲਈ ਲੱਗਾ ਸਮਾਂ (t) = 40 s
ਕੁੱਲ ਸਮਾਂ = 2 ਮਿੰਟ 20 ਸੈਕਿੰਡ
= (2 × 60 + 20) ਸੈਕਿੰਡ
= (120 + 20) ਸੈਕਿੰਡ
= 140 ਸੈਕਿੰਡ
40 s ਵਿੱਚ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ = \(\frac{4400}{7}\)m (= 1 ਚੱਕਰ)
1 s ਵਿੱਚ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ = \(\frac{4400}{7 \times 40}\)
∴ 140 s ਵਿੱਚ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ = [late]\frac{4400}{7 \times 40}[/latex] × 140
= 2200 m ( = [late]\frac{1}{2}[/latex] ਚੱਕਰ)

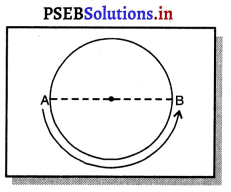
ਇਸ ਲਈ ਗਤੀ ਦੇ ਆਖੀਰ ਵਿੱਚ ਐਥਲੀਟ [late]\frac{1}{2}[/latex] ਚੱਕਰ ਲਗਾ ਕੇ ਵਿਆਸ ਦੇ ਸਾਹਮਣੇ ਸਿਰੇ B ‘ਤੇ ਪਹੁੰਚੇਗਾ ।
∴ ਵਿਸਥਾਪਨ ਮੂਲ ਬਿੰਦੂ ਅਤੇ ਅੰਤਿਮ ਬਿੰਦੂ ਵਿੱਚ ਦੂਰੀ) = ਵਿਤ ਦਾ ਵਿਆਸ = 100 m

ਪ੍ਰਸ਼ਨ 2.
300 m ਸਰਲ ਰੇਖੀ ਪੱਥ ‘ਤੇ ਜੋਸੇਫ ਜਾਗਿੰਗ ਕਰਦਿਆਂ ਹੋਇਆਂ 2 ਮਿੰਟ 30 ਸੈਕਿੰਡ ਵਿੱਚ ਇੱਕ ਸਿਰੇ A ਤੋਂ ਦੂਜੇ ਸਿਰੇ B ਤੱਕ ਪਹੁੰਚਦਾ ਹੈ ਅਤੇ ਘੁੰਮ ਕੇ 1 ਮਿੰਟ ਵਿੱਚ 100 m ਪਿੱਛੇ ਬਿੰਦੂ c ‘ਤੇ ਪਹੁੰਚਦਾ ਹੈ । ਜੋਸੇਫ ਦੀ ਔਸਤ ਬਾਲ ਅਤੇ ਔਸਤ ਵੇਗ ਕਿੰਨਾ ਹੋਵੇਗਾ ?
(a) ਸਿਰੇ A ਤੋਂ ਸਿਰੇ B ਤੱਕ ।
(b) ਸਿਰੇ A ਤੋਂ ਸਿਰੇ 0 ਤੱਕ ।
ਹੱਲ:
(a) A ਸਿਰੇ ਤੋਂ B ਸਿਰੇ ਤੱਕ ਲੰਬਾਈ = AB = 300 m
ਲੱਗਾ ਸਮਾਂ (t) = 2 ਮਿੰਟ 30 ਸੈਕਿੰਡ
= (2 × 60 + 30) s
= (120 + 30) s
= 150 s

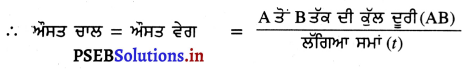
= \(\frac{300}{150}\)ms^-1
= 2ms^-1

(b) A. ਸਿਰੇ ਤੋਂ c ਸਿਰੇ ਤੱਕ ਤੈਅ ਕੀਤੀ ਕੁੱਲ ਲੰਬਾਈ = AC = AB + BC
= 300m + 100 m
= 400 m
ਕੁੱਲ ਸਮਾਂ = 2 ਮਿੰਟ 30 ਸੈਕਿੰਡ + 1 ਮਿੰਟ
= 3 mm 30 s.
= (3 × 60 + 30) s
= (180 + 30) s = 210 s
ਔਸਤ ਚਾਲ = \(\frac{400}{210}\)
= 1.91 ms^-1
ਔਸਤ ਵੇਗ = \(\frac{200}{210}\) 0.95 ms^-1

ਪ੍ਰਸ਼ਨ 3.
ਅਬਦੁਲ ਗੱਡੀ ਤੇ ਸਕੂਲ ਜਾਂਦਿਆਂ ਹੋਇਆਂ ਆਪਣੀ ਯਾਤਰਾ ਦੀ ਔਸਤ ਚਾਲ ਨੂੰ 20 km/h ਪੜ੍ਹਦਾ ਹੈ । ਵਾਪਸੀ ਵੇਲੇ ਘੱਟ ਭੀੜ ਹੋਣ ਕਾਰਣ ਉਸ ਦੀ ਔਸਤ ਚਾਲ 30 km/h ਹੈ | ਅਬਦੁਲ ਦੀ ਇਸ ਪੂਰੀ ਯਾਤਰਾ ਵਿੱਚ ਔਸਤ ਚਾਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਓ ਘਰ ਤੋਂ ਸਕੂਲ ਦੀ ਦੂਰੀ = L
ਘਰ ਤੋਂ ਸਕੂਲ ਅਤੇ ਵਾਪਸ ਸਕੂਲ ਤੋਂ ਘਰ ਤੱਕ ਤੈਅ ਕੀਤੀ ਦੂਰੀ = L + L
ਸਕੂਲ ਜਾਣ ਸਮੇਂ ਔਸਤ ਚਾਲ (v₁) = 20 kmh

ਪ੍ਰਸ਼ਨ 4.
ਇੱਕ ਮੋਟਰਬੋਟ ਇੱਕ ਝੀਲ ਵਿੱਚ ਵਿਰਾਮ ਅਵਸਥਾ ਤੋਂ ਸ਼ੁਰੂ ਹੋ ਕੇ ਇੱਕ ਸਿੱਧੀ ਰੇਖਾ ਵਿੱਚ ਗਤੀ ਕਰਦਿਆਂ ਹੋਇਆਂ 3 ms^-2 ਦੇ ਸਥਿਰ ਨਿਯਤ) ਵੇਗ ਨਾਲ 8 ਸੈਕਿੰਡ (s) ਤੱਕ ਚੱਲਦੀ ਹੈ । ਇਸ ਸਮੇਂ ਅੰਤਰਾਲ ਵਿੱਚ ਮੋਟਰਬੋਟ ਕਿੰਨੀ ਦੂਰੀ ਤੈਅ ਕਰਦੀ ਹੈ ?
ਹੱਲ:
ਇੱਥੇ ਮੁੱਢਲਾ ਵੇਗ (u) = 0 (ਵਿਰਾਮ ਅਵਸਥਾ).
ਪ੍ਰਵੇਗ (a) = 3 ms^-1
ਸਮਾਂ (t) = 8 s
ਦੂਰੀ (S) = ?
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ, S = ut + \(\frac{1}{2}\)at²
S = 0 × 8 + \(\frac{1}{2}\) × 3 × (8)²
S = 0 + \(\frac{1}{2}\) × 3 × 8 × 8
ਮੋਟਰਬੋਟ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ =. S = 96 m

ਪ੍ਰਸ਼ਨ 5.
ਕਿਸੇ ਕਾਰ ਦਾ ਚਾਲਕ 52 kmh^-1 ਦੀ ਗਤੀ ਨਾਲ ਚਲ ਰਹੀ ਕਾਰ ਵਿੱਚ ਬਰੇਕ ਲਗਾਉਂਦਾ ਹੈ ਅਤੇ ਉਹ ਉਲਟ ਦਿਸ਼ਾ ਵਿੱਚ ਇੱਕ ਸਮਾਨ ਗਤੀ ਦਰ ਨਾਲ ਗਿਤ ਹੁੰਦੀ ਹੈ ਅਤੇ ਕਾਰ 5 ਸੈਕਿੰਡ ਵਿੱਚ ਰੁੱਕ ਜਾਂਦੀ ਹੈ । ਦੂਜੀ ਕਾਰ ਦਾ ਚਾਲਕ 30 kmh^-1 ਦੀ ਗਤੀ ਨਾਲ ਚਲ ਰਹੀ ਕਾਰ ਤੇ ਹੌਲੀ ਬਰੇਕ ਲਗਾਂਦਾ ਹੈ ਅਤੇ 10 s ਵਿੱਚ ਕਾਰ ਰੁੱਕ ਜਾਂਦੀ ਹੈ । ਇੱਕ ਹੀ ਗਰਾਫ਼ ਵਿੱਚ ਦੋਨੋਂ ਕਾਰਾਂ ਦੇ ਲਈ ਚਾਲ-ਸਮਾਂ ਗਰਾਫ਼ ਬਣਾਓ । ਬਰੇਕ ਲਗਾਉਣ ਤੋਂ ਬਾਅਦ ਦੋਨਾਂ ਵਿੱਚੋਂ ਕਿਹੜੀ ਕਾਰ ਜ਼ਿਆਦਾ ਦੂਰ ਤੱਕ ਜਾਵੇਗੀ ।
ਹੱਲ:
ਚਿੱਤਰ ਵਿੱਚ ਦੋ ਕਾਰਾਂ ਦੇ ਚਾਲ-ਸਮਾਂ ਗਰਾਫ਼ AB ਅਤੇ CD ਦਰਸਾਏ ਗਏ ਹਨ ਜਿਨ੍ਹਾਂ ਦੀ ਕ੍ਰਮਵਾਰ ਚਾਲ 52 kmh^-1 ਅਤੇ 30 kmh^-1 ਹੈ ।
ਵਿਰਾਮ ਵਿੱਚ ਆਉਣ ਤੋਂ ਪਹਿਲਾਂ ਪਹਿਲੀ ਕਾਰ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਦੂਰੀ = ΔAOB ਦਾ ਖੇਤਰਫਲ
= \(\frac{1}{2}\) × AO × BO
= \(\frac{1}{2}\) ×(52 × \(\frac{5}{18}\))× 5
= 36.1 m
ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਆਉਣ ਤੋਂ ਪਹਿਲਾਂ ਦੂਜੀ ਕਾਰ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਦੂਰੀ = ΔCOD ਦਾ ਖੇਤਰਫਲ

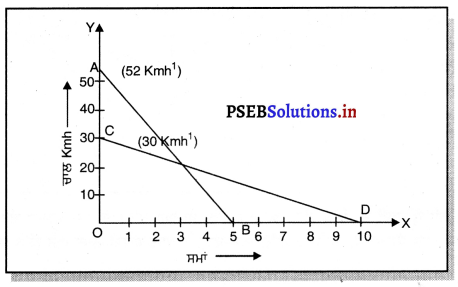
= \(\frac{1}{2}\) × CO × OD =
= \(\frac{1}{2}\) × (30 x \(\frac{5}{18}\)) × 10
= 47.2 m
ਇਸ ਤਰ੍ਹਾਂ ਬਰੇਕ ਲਗਾਉਣ ਤੋਂ ਬਾਅਦ ਦੂਜੀ ਕਾਰ ਨੇ ਪਹਿਲੀ ਕਾਰ ਦੀ ਤੁਲਨਾ ਵਿੱਚ ਜ਼ਿਆਦਾ ਦੂਰੀ ਤੈਅ ਕੀਤੀ ।

ਪ੍ਰਸ਼ਨ 6.
ਹੇਠ ਦਿੱਤੇ ਚਿੱਤਰ ਵਿੱਚ ਤਿੰਨ ਵਸਤੂਆਂ A,B ਅਤੇ C ਦੇ ਦੂਰੀ-ਸਮਾਂ ਗਰਾਫ਼ ਪ੍ਰਦਰਸ਼ਿਤ ਹੈ । ਗਰਾਫ਼ ਦਾ ਅਧਿਐਨ ਕਰਕੇ ਨਿਮਨ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਉੱਤਰ ਦਿਓ ।
(a) ਇਹਨਾਂ ਤਿੰਨਾਂ ਵਿੱਚੋਂ ਕਿਹੜਾ ਸਭ ਤੋਂ ਤੇਜ਼ ਚਲ ਰਿਹਾ ਹੈ ?
(b) ਕੀ ਇਹ ਤਿੰਨੋਂ ਕਿਸੇ ਸਮੇਂ ਸੜਕ ‘ਤੇ ਇੱਕ ਹੀ ਜਗਾ ਤੇ ਹੋਣਗੇ ?
(c) c ਕਿੰਨੀ ਦੂਰੀ ਤੈਅ ਕਰ ਚੁੱਕਿਆ ਹੋਵੇਗਾ, ਜਦੋਂ B, A ਤੋਂ ਗੁਜ਼ਰਦਾ ਹੈ ?
(d) ਜਿਸ ਸਮੇਂ B, C ਤੋਂ ਗੁਜ਼ਰਦਾ ਹੈ ਉਸ ਸਮੇਂ ਤੱਕ ਉਹ ਕਿੰਨੀ ਦੂਰੀ ਤੈਅ ਕਰ ਚੁੱਕਿਆ ਹੈ ?

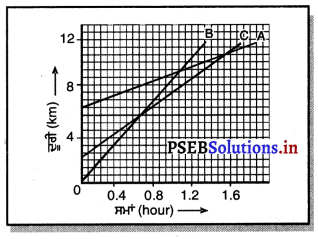
ਹੱਲ:
(a) A ਦੀ ਚਾਲ = PN ਦੀ ਢਾਲ (Slope) = \(\frac{10-6}{1.1-0}\)
\(\frac{40}{11}\) = 3.63kmh^-1
B ਦੀ ਚਾਲ = OM ਦੀ ਢਾਲ (Slope) = \(\frac{6-0}{0.7-0}=\frac{60}{7}\) 8.57kmh^-1
C ਦੀ ਚਾਲ = OM ਦੀ ਢਾਲ (Slope) = \(\frac{6-2}{0.7-0}=\frac{40}{7}\) 5.71kmh^-1

ਕਿਉਂਕਿ B ਵਸਤੂ ਦੀ ਢਾਲ (Slope) ਸਭ ਤੋਂ ਵੱਧ ਹੈ ਇਸ ਲਈ ਵਸਤੂ B ਸਭ ਤੋਂ ਤੇਜ਼ ਚਲ ਰਹੀ ਹੈ ।

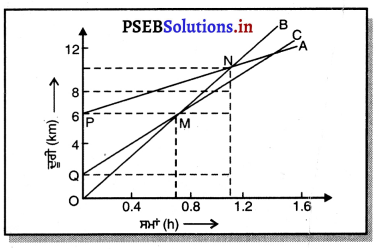
(b) ਕਿਉਂਕਿ ਤਿੰਨਾਂ ਦੇ ਗਰਾਫ਼ ਇੱਕ ਬਿੰਦੂ ‘ਤੇ ਨਹੀਂ ਕੱਟਦੇ ਹਨ, ਇਸ ਲਈ ਇਹ ਤਿੰਨੋਂ ਕਿਸੇ ਸਮੇਂ ਵੀ ਸੜਕ ‘ਤੇ ਇੱਕ ਬਿੰਦੂ ‘ਤੇ ਨਹੀਂ ਮਿਲਣਗੇ ।
(c) ਜਦੋਂ B, N ਬਿੰਦੂ ਤੇ ਨ ਨੂੰ ਮਿਲਦੀ ਹੈ । (1.1 ਘੰਟੇ ‘ਤੇ), ਉਸ ਸਮੇਂ C ਮੂਲ ਬਿੰਦੂ 0 ਤੋਂ ਲਗਪਗ 9 km ਦੀ ਦੂਰੀ ਤੇ ਹੁੰਦੀ ਹੈ ।
(d) B, M ਬਿੰਦੂ ‘ਤੇ C ਨੂੰ ਮਿਲਦੀ ਹੈ, ਉਸ ਸਮੇਂ ਦੌਰਾਨ B 9 km ਦੀ ਦੂਰੀ ਤੈਅ ਕਰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 7.
20 m ਦੀ ਉੱਚਾਈ ਤੋਂ ਇੱਕ ਗੇਂਦ ਆਰਾਮ ਨਾਲ ਸੁੱਟਿਆ ਜਾਂਦਾ ਹੈ । ਜੇ ਉਸਦਾ ਵੇਗ 10 ms^-2 ਦੇ ਇੱਕ ਸਮਾਨ ਵੇਗ ਦੀ ਦਰ ਨਾਲ ਵੱਧਦਾ ਹੈ, ਤਾਂ ਇਹ ਗੇਂਦ ਕਿਸ ਵੇਗ ਦੇ ਨਾਲ ਧਰਤੀ ਨਾਲ ਅਤੇ ਕਿੰਨੇ ਸਮੇਂ ਦੇ ਬਾਅਦ ਧਰਤੀ ਨਾਲ ਟਕਰਾਵੇਗਾ ?
ਹੱਲ:
ਇੱਥੇ,
u = 0,
S = 20 m
a = 10 ms^-2
v = ?
t = ?
v² – u² = 2 as ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ
v² – (0)² = 2 × 10 × 20
v² = 400
= 20 × 20
∴ v = \(\sqrt{20 \times 20}\)
= 20 ms-1
ਹੁਣ
v = u + at
20 = 0 + 10 × t
∴ t = \(\frac{20}{10}\) = 2 s

ਪ੍ਰਸ਼ਨ 8.
ਕਿਸੇ ਕਾਰ ਦਾ ਚਾਲ-ਸਮਾਂ ਗਰਾਫ਼ ਚਿੱਤਰ ਵਿੱਚ ਦਰਸਾਇਆ ਗਿਆ ਹੈ ?

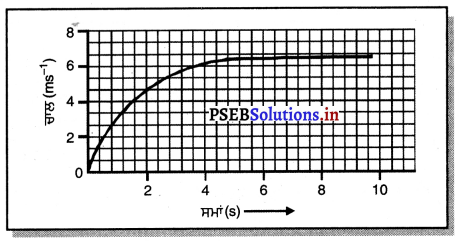
(ਕ) ਪਹਿਲੇ ਚਾਰ ਸੈਕਿੰਡਾਂ ਵਿੱਚ ਕਾਰ ਕਿੰਨੀ ਦੂਰੀ ਤੈਅ ਕਰਦੀ ਹੈ ? ਇਸ ਸਮੇਂ ਅੰਤਰਾਲ ਵਿੱਚ ਕਾਰ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ ਨੂੰ ਗਰਾਫ਼ ਵਿੱਚ ਕਾਲੇ (shaded) ਖੇਤਰ ਦੁਆਰਾ ਦਰਸਾਓ ।
(ਖ) ਗਰਾਫ਼ ਦਾ ਕਿਹੜਾ ਹਿੱਸਾ ਕਾਰ ਦੀ ਇੱਕ ਸਮਾਨ ਗਤੀ ਨੂੰ ਦਰਸਾਉਂਦਾ ਹੈ ?
ਹੱਲ:
(ਕ) X- ਅਕਸ਼ ਦੇ 5 ਛੋਟੇ ਨਿਸ਼ਾਨ = 2 s.
Y-ਅਕਸ਼ ਦੇ 3 ਛੋਟੇ ਨਿਸ਼ਾਨ = 2 ms^-1
15 ਛੋਟੇ ਵਰਗਾਂ ਦੀ ਲੰਬਾਈ = 2s × 2 ms^-1
= 4 m
∴ 1 ਛੋਟੇ ਵਰਗ ਦੀ ਲੰਬਾਈ = \(\frac{4}{15}\)m
0 ਤੋਂ 4 s ਹੇਠ ਚਾਲ-ਸਮਾਂ ਗਰਾਫ਼ ਦਾ ਕੁੱਲ ਖੇਤਰਫਲ
= 57 ਛੋਟੇ ਵਰਗ + \(\frac{1}{2}\) × 6 ਛੋਟੇ ਵਰਗ
= 60 ਛੋਟੇ ਵਰਗ
ਕਾਰ ਦੁਆਰਾ 4 ਸੈਕਿੰਡ ਵਿੱਚ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ = 60 ਛੋਟੇ ਵਰਗ
= 60 × \(\frac{4}{15}\)m
= 16 m

(ਖ) 6 s ਬਾਅਦ ਕਾਰ ਦੀ ਇਕ ਸਮਾਨ ਗਤੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 9.
ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚੋਂ ਕਿਹੜੀਆਂ ਅਵਸਥਾਵਾਂ ਸੰਭਵ ਹਨ ਅਤੇ ਹਰੇਕ ਦੇ ਲਈ ਵਿੱਚ ਉਦਾਹਰਣ ਦੇਵੋ-
(ਕ) ਕੋਈ ਵਸਤੂ ਜਿਸਦਾ ਵੇਗ ਸਥਿਰ (ਨਿਯਤ) ਹੋਵੇ ਪਰ ਵੇਗ ਸਿਫ਼ਰ ਹੋਵੇ ।
(ਖ) ਕੋਈ ਵਸਤੂ ਜਿਹੜੀ ਨਿਸਚਿਤ ਦਿਸ਼ਾ ਵਿੱਚ ਗਤੀ ਕਰ ਰਹੀ ਹੋਵੇ ਅਤੇ ਉਸਦਾ ਪਵੇਗ ਲੰਬਵਤ ਹੋਵੇ ।
ਉੱਤਰ-
(ਕ) ਹਾਂ, ਕਿਸੇ ਵਸਤੂ ਦਾ ਸਥਿਰ ਵੇਗ ਹੋ ਸਕਦਾ ਹੈ ਜਦੋਂ ਇਸ ਦਾ ਵੇਗ ਸਿਫ਼ਰ ਹੈ । ਉਦਾਹਰਣ ਲਈ ਜਦੋਂ ਕਿਸੇ ਵਸਤੂ ਨੂੰ ਉੱਪਰ ਵੱਲ ਲੰਬਵਤ ਸੁੱਟਿਆ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਸਭ ਤੋਂ ਵੱਧ ਉਚਾਈ ‘ਤੇ ਪਹੁੰਚ ਕੇ ਇਸ ਦਾ ਵੇਗ ਸਿਫ਼ਰ ਹੋ ਜਾਂਦਾ ਹੈ ਪਰੰਤੂ ਇਸ ਦਾ ਪ੍ਰਵੇਗ ਗੁਰੂਤਾ-ਪ੍ਰਵੇਗ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ ।

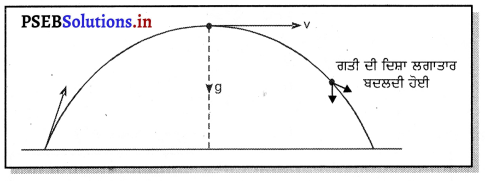
(ਖ) ਹਾਂ, ਖਿਤਿਜੀ ਦਿਸ਼ਾ ਵਿੱਚ ਚੱਲ ਰਹੇ ਜਹਾਜ਼ ਤੇ ਗੁਰੂਤੀ ਪ੍ਰਵੇਗ ਹੇਠਾਂ ਵੱਲ ਲੰਬਵਤ ਦਿਸ਼ਾ ਵਿੱਚ ਕਿਰਿਆ ਕਰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 10.
ਇੱਕ ਬਨਾਉਟੀ ਉਪਗ੍ਰਹਿ 42250 km ਅਰਧ-ਵਿਆਸ ਦੇ ਚੱਕਰਾਕਾਰ ਹਿ ਪੱਥ ਵਿੱਚ ਘੁੰਮ ਰਿਹਾ ਹੈ । ਜੇਕਰ ਉਹ 24 ਘੰਟਿਆਂ ਵਿੱਚ ਧਰਤੀ ਦੀ ਪਰਿਕਰਮਾ ਕਰਦਾ ਹੈ, ਤਾਂ ਉਸਦੀ ਚਾਲ ਪਤਾ ਕਰੋ ?
ਹੱਲ:
ਇੱਥੇ ਬਨਾਉਟੀ ਉਪਗ੍ਰਹਿ ਦੇ ਚੱਕਰਾਕਾਰ ਪੱਥ ਦਾ ਅਰਧ ਵਿਆਸ = (r) = 42250 km
ਧਰਤੀ ਦੇ ਕੇਂਦਰ ਤੇ ਬਣ ਰਿਹਾ ਕੋਣ (θ) = 2π ਰੇਡੀਅਨ
ਉਪਗ੍ਰਹਿ ਦੁਆਰਾ ਧਰਤੀ ਦੁਆਲੇ 1 ਚੱਕਰ ਲਗਾਉਣ ਲਈ ਲੱਗਿਆ ਸਮਾਂ
(t) = 24 ਘੰਟੇ
= 24 × 3600 ਸੈਕਿੰਡ
= 86400 ਸੈਕਿੰਡ
∴ ਕੋਣੀ ਵੇਗ (ω) = \(\frac{\theta}{t}\)
= \(\frac{2 \pi}{86400}\)rads^-1
ਉਪਗ੍ਰਹਿ ਦਾ ਰੇਖੀ ਵੇਗ (v) = r × ω
= 42250 × \(\frac{2 \pi}{86400}\) kms^-1
= \(\frac{42250 \times 2 \times 3.14}{86400}\) kms^-1
= 3.07 kms^-1

Science Guide for Class 9 PSEB ਗਤੀ InText Questions and Answers

ਪਾਠ-ਪੁਸਤਕ ਦੇ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਉੱਤਰ

ਪ੍ਰਸ਼ਨ 1.
ਇੱਕ ਵਸਤੂ ਦੁਆਰਾ ਕੁੱਝ ਦੂਰੀ ਤੈਅ ਕੀਤੀ ਗਈ । ਕੀ ਇਸਦਾ ਵਿਸਥਾਪਨ ਸਿਫ਼ਰ ਹੋ ਸਕਦਾ ਹੈ ? ਜੇਕਰ ਹਾਂ, ਤਾਂ ਆਪਣੇ ਉੱਤਰ ਨੂੰ ਉਦਾਹਰਣ ਨਾਲ ਸਮਝਾਓ ।
ਉੱਤਰ-ਗਤੀ ਦੌਰਾਨ ਵਿਸਥਾਪਨ ਦੀ ਮਾਤਰਾ ਸਿਫ਼ਰ (ਜ਼ੀਰੋ) ਹੋ ਸਕਦੀ ਹੈ ਜੇਕਰ ਉਹ ਵਸਤੂ ਗਤੀ ਕਰਦੇ ਹੋਏ ਆਪਣੀ ਪਹਿਲੀ ਸਥਿਤੀ ‘ਤੇ ਆ ਜਾਵੇ । ਇਸ ਅਵਸਥਾ ਵਿੱਚ ਅੰਤਿਮ ਸਥਿਤੀ, ਪਹਿਲੀ ਸਥਿਤੀ ਨਾਲ ਮਿਲ ਜਾਂਦੀ ਹੈ । ਉਦਾਹਰਣ ਵਜੋਂ ਮੰਨ ਲਓ ਇੱਕ ਵਸਤੂ ਮੂਲ ਬਿੰਦੂ 0 ਤੋਂ ਗਤੀ ਕਰਦੀ ਹੋਈ ਨ ਤੱਕ 60 km ਦੀ ਦੂਰੀ ਤੈਅ ਕਰਦੀ ਹੈ । ਜੇਕਰ ਉਹ ਵਸਤੂ ਗਤੀ ਕਰਦੀ ਹੋਈ ਵਾਪਿਸ 8 ਤੋਂ 0 ਤੱਕ ਆ ਜਾਵੇ ਤਾਂ ਉਸ ਅਵਸਥਾ ਵਿੱਚ ਉਸ

ਦਾ ਵਿਸਥਾਪਨ ਸਿਰ (ਜ਼ੀਰੋ) ਹੋਵੇਗਾ, ਪਰੰਤੂ ਤੈਅ ਕੀਤੀ ਗਈ ਕੁੱਲ ਦੂਰੀ
= OA + AO
60 km + 60 km = 120 km ਹੋਵੇਗੀ ।

ਪ੍ਰਸ਼ਨ 2.
ਇੱਕ ਕਿਸਾਨ 10 ਮੀਟਰ ਦੀ ਭੁਜਾ ਵਾਲੇ ਇੱਕ ਵਰਗਾਕਾਰ ਖੇਤ ਦੀ ਸੀਮਾ ਤੇ 40 s (ਸੈਕਿੰਡ) ਵਿੱਚ ਇੱਕ ਚੱਕਰ ਲਗਾਉਂਦਾ ਹੈ । 2 ਮਿੰਟ ਅਤੇ 20 s ਸੈਕਿੰਡ) ਦੇ ਬਾਅਦ ਕਿਸਾਨ ਦੇ ਵਿਸਥਾਪਨ ਦੀ ਮਾਤਰਾ ਕਿੰਨੀ ਸੰਖਿਆਤਮਕ ਮਾਨ) । ਹੋਵੇਗੀ ?
ਹੱਲ:

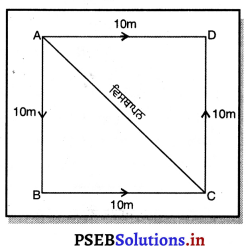
ਖੇਤ ਦੀ ਸੀਮਾ (1 ਚੱਕਰ) = AB + BC + CD + DA
= 10m + 10m + 10m + 10m = 40m
ਕੁੱਲ ਸਮਾਂ = 2 ਮਿੰਟ 20 ਸੈਕਿੰਡ
= (2 × 60 + 20) ਸੈਕਿੰਡ
= (120 + 20 ) ਸੈਕਿੰਡ
= 140 ਸੈਕਿੰਡ
ਖੇਤ ਦੀ ਸੀਮਾ ਦਾ 1 ਚੱਕਰ ਲਗਾਉਣ ਲਈ ਲੱਗਿਆ ਸਮਾਂ = 40 S
ਕਿਸਾਨ 3 ਚੱਕਰ ਲਗਾਉਣ ਲਈ ਸਮਾਂ ਲਵੇਗਾ
= 3 × 40 ਸੈਕਿੰਡ
= 120 ਸੈਕਿੰਡ
ਬਾਕੀ ਬਚਿਆ ਹੋਇਆ ਸਮਾਂ = 140 – 120 = 20 ਸੈਕਿੰਡ

∵ ਕਿਸਾਨ 40 s ਵਿੱਚ ਦੂਰੀ ਤੈਅ ਕਰਦਾ ਹੈ = 40 m
∴ 1s ਵਿੱਚ ਦੂਰੀ ਤੈਅ ਕਰੇਗਾ = 1 m
∴ 20 ਸੈਕਿੰਡ ਵਿੱਚ ਤੈਅ ਕੀਤੀ ਗਈ ਦੁਰੀ = 20 m
ਅਰਥਾਤ ਕਿਸਾਨ ਨੇ ਤੋਂ ਗਤੀ ਕਰਦਾ ਹੋਇਆ 3 ਚੱਕਰ ਪੂਰੇ ਕਰਨ ਤੋਂ ਬਾਅਦ c ‘ਤੇ ਪਹੁੰਚ ਜਾਏਗਾ ।
ਵਿਸਥਾਪਨ ਦੀ ਮਾਤਰਾ = \(\overrightarrow{\mathrm{AC}}\) (ਮੂਲ ਬਿੰਦੂ ਅਤੇ ਅੰਤਿਮ ਬਿੰਦੂ ਵਿਚਕਾਰ ਛੋਟੀ ਤੋਂ ਛੋਟੀ ਦੂਰੀ)
= \(\sqrt{\mathrm{AB}^{2}+\mathrm{BC}^{2}}\)
= \(\sqrt{(10)^{2}+(10)^{2}}\)
= \(\sqrt{100+100}\)
= \(\sqrt{200} \mathrm{~m}\)
= \(\sqrt{100 \times 2} \mathrm{~m}\)
= 10√2m
= 10 × 1.414 m
= 14.14m

ਪ੍ਰਸ਼ਨ 3.
ਵਿਸਥਾਪਨ ਲਈ ਹੇਠ ਲਿਖੇ ਵਿੱਚੋਂ ਕੀ ਸਹੀ ਹੈ ?
(a) ਇਹ ਸਿਫ਼ਰ ਨਹੀਂ ਹੋ ਸਕਦਾ ?
(b) ਇਸਦੀ ਮਾਤਰਾ ਵਸਤੂ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ ਤੋਂ ਜ਼ਿਆਦਾ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
(a) ਅਤੇ
(b) ਕਥਨਾਂ ਵਿੱਚੋਂ ਕੋਈ ਵੀ ਸਹੀ ਨਹੀਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ 4.
ਚਾਲ (Speed) ਅਤੇ ਵੇਗ (Velocity) ਵਿੱਚ ਅੰਤਰ ਦੱਸੋ ।
ਉੱਤਰ-
ਚਾਲ ਦਾ ਪੂਰੀ ਤਰ੍ਹਾਂ ਨਾਲ ਵਰਣਨ ਕਰਨ ਲਈ ਸਿਰਫ਼ ਮਾਤਰਾ ਦੀ ਲੋੜ ਪੈਂਦੀ ਹੈ ਜਦੋਂ ਕਿ ਵੇਗ ਦਾ ਪੂਰੀ ਤਰ੍ਹਾਂ ਨਾਲ ਵਰਣਨ ਕਰਨ ਲਈ ਮਾਤਰਾ ਪਰਿਮਾਣ ਅਤੇ ਦਿਸ਼ਾ ਦੋਨਾਂ ਦੀ ਜ਼ਰੂਰਤ ਹੁੰਦੀ ਹੈ । ਇਸ ਲਈ ਚਾਲ ਇੱਕ ਅਦਿਸ਼ ਰਾਸ਼ੀ ਹੈ, ਪਰੰਤੁ ਵੇਗ ਇੱਕ ਸਦਿਸ਼ ਰਾਸ਼ੀ ਹੈ । ਚਾਲ ਹਮੇਸ਼ਾ ਧਨਾਤਮਕ ਹੁੰਦੀ ਹੈ ਪਰੰਤੁ ਵੇਗ ਧਨਾਤਮਕ ਅਤੇ ਰਿਣਾਤਮਕ ਦੋਨੋਂ ਹੋ ਸਕਦੀ ਹੈ । ਚਾਲ ਕਿਸੇ ਵਸਤੂ ਦੀ ਇਕਾਈ ਸਮੇਂ ਵਿੱਚ ਤੈਅ ਕੀਤੀ ਗਈ ਦੁਰੀ ਹੁੰਦੀ ਹੈ । ਦੂਜੇ ਪਾਸੇ ਜੇਕਰ ਇਸਦੇ ਨਾਲ ਦਿਸ਼ਾ ਵੀ ਦੱਸੀ ਜਾਵੇ ਤਾਂ ਇਹ ਵੇਗ ਕਹਾਉਂਦੀ ਹੈ । ਅਰਥਾਤ ਇੱਕ ਨਿਸਚਿਤ ਦਿਸ਼ਾ ਵਿੱਚ ਚਾਲ ਨੂੰ ਵੇਗ ਕਹਿੰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 5.
ਕਿਹੜੀਆਂ ਅਵਸਥਾਵਾਂ ਵਿੱਚ ਔਸਤ ਵੇਗ ਦੀ ਮਾਤਰਾ ਔਸਤ ਚਾਲ ਦੇ ਬਰਾਬਰ ਹੁੰਦੀ ਹੈ ?
ਹੱਲ:

ਜਦੋਂ ਵਸਤੂ ਇੱਕ ਸਿੱਧੀ ਰੇਖਾ ਵਿੱਚ ਬਦਲਦੀ ਹੋਈ ਗਤੀ ਨਾਲ ਇੱਕ ਹੀ ਦਿਸ਼ਾ ਵਿੱਚ ਚਲਦੀ ਹੈ ਤਾਂ ਕੁੱਲ ਤੈਅ ਕੀਤੀ ਗਈ ਦੁਰੀ ਵਿਸਥਾਪਨ ਦੇ ਪਰਿਮਾਣ ਦੇ ਬਰਾਬਰ ਹੁੰਦੀ ਹੈ । ਇਸ ਲਈ ਔਸਤ ਚਾਲ ਅਤੇ ਔਸਤ ਵੇਗ ਬਰਾਬਰ ਹੁੰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 6.
ਸਵੈਚਾਲਿਤ ਵਾਹਨ ਦਾ ਉਡੋਮੀਟਰ ਕੀ ਮਾਪਦਾ ਹੈ ?
ਉੱਤਰ-
ਸਵੈਚਾਲਿਤ ਵਾਹਨ ਦਾ ਉਡੋਮੀਟਰ ਉਸ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ ਮਾਪਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 7.
ਜਦੋਂ ਵਸਤੂ ਇੱਕ ਸਮਾਨ ਗਤੀ ਵਿੱਚ ਹੁੰਦੀ ਹੈ ਤਾਂ ਉਸਦਾ ਮਾਰਗ ਕਿਹੋ ਜਿਹਾ ਦਿਖਾਈ ਦਿੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਜਦੋਂ ਵਸਤੁ ਇੱਕ ਸਮਾਨ ਗਤੀ ਵਿੱਚ ਹੁੰਦੀ ਹੈ ਤਾਂ ਉਸਦਾ ਮਾਰਗ ਇੱਕ ਸਿੱਧੀ ਸਰਲ ਰੇਖਾ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 8.
ਇੱਕ ਪ੍ਰਯੋਗ ਦੇ ਦੌਰਾਨ ਪੁਲਾੜਯਾਨ ਤੋਂ ਇੱਕ ਸਿਗਨਲ ਨੂੰ ਧਰਤੀ ਤੱਕ ਪੁੱਜਣ ਲਈ 5 ਮਿੰਟ ਦਾ ਸਮਾਂ ਲੱਗਦਾ ਹੈ । ਧਰਤੀ ‘ਤੇ ਸਥਿਤ ਸਟੇਸ਼ਨ ਤੋਂ ਉਸ ਪੁਲਾੜਯਾਨ ਦੀ ਦੂਰੀ ਕਿੰਨੀ ਹੈ ?
(ਸਿਗਨਲ ਦੀ ਚਾਲ = ਪ੍ਰਕਾਸ਼ ਦੀ ਚਾਲ = 3 × 10⁸ms^-1)
ਹੱਲ:
ਸਿਗਨਲ ਨੂੰ ਪੁਲਾੜਯਾਨ ਤੋਂ ਧਰਤੀ ਤੱਕ ਪਹੁੰਚਣ ਲਈ ਲੱਗਾ ਸਮਾਂ (t) = 5 ਮਿੰਟ
= 5 × 60 ਸੈਕਿੰਡ
= 300
ਸੈਕਿੰਡ ਸਿਗਨਲ ਦੀ ਚਾਲ (v) = 3 × 10⁸ ms^-1
ਪੁਲਾੜਯਾਨ ਦੀ ਧਰਤੀ ਤੋਂ ਦੂਰੀ (S) = ?
ਪੁਲਾੜਯਾਨ ਦੀ ਧਰਤੀ ਤੋਂ ਦੁਰੀ (S) = ਸਿਗਨਲ ਦੀ ਚਾਲ (v) × ਲੱਗਾ ਸਮਾਂ (t)
(ਸਿਗਨਲ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਗਈ ਦੁਰੀ)
= 3 × 10⁸ × 300
= 3 × 10⁸ × 3 × 100
= 9 × 10⁸ × 10²
= 9 × 10⁸⁺²
= 9 × 10¹⁰m
= 9 × 10⁷ km

ਪ੍ਰਸ਼ਨ 9.
ਤੁਸੀਂ ਕਿਸੇ ਵਸਤੂ ਬਾਰੇ ਕਦੋਂ ਕਹੋਗੇ ਕਿ .
(i) ਉਹ ਇੱਕ ਸਮਾਨ ਵੇਗ ਨਾਲ ਗਤੀ ਵਿੱਚ ਹੈ ?
(ii) ਉਹ ਅਸਮਾਨ ਵੇਗ ਨਾਲ ਗਤੀ ਵਿੱਚ ਹੈ ?
ਉੱਤਰ-
(i)ਜਦੋਂ ਕੋਈ ਵਸਤੁ ਸਰਲ ਰੇਖਾ ਵਿੱਚ ਚਲਦੀ ਹੈ ਅਤੇ ਇਸਦਾ ਵੇਗ ਬਰਾਬਰ ਸਮੇਂ ਅੰਤਰਾਲਾਂ ਵਿੱਚ ਬਰਾਬਰ ਮਾਤਰਾ ਵਿੱਚ ਘੱਟਦਾ ਜਾਂ ਵੱਧਦਾ ਹੈ ਤਾਂ ਵਸਤੂ ਦੇ ਵੇਗ ਨੂੰ ਇੱਕ ਸਮਾਨ ਵੇਗ ਨਾਲ ਗਤੀ ਕਰਦਾ ਹੋਇਆ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।

(ii) ਜਦੋਂ ਕਿਸੇ ਵਸਤੂ ਦਾ ਵੇਗ ਅਸਮਾਨ ਦਰ ਨਾਲ ਬਦਲਦਾ ਹੈ ਅਰਥਾਤ ਉਸ ਵਸਤੂ ਦਾ ਵੇਗ ਸਮਾਨ ਸਮੇਂ ਅੰਤਰਾਲਾਂ ਵਿੱਚ ਅਸਮਾਨ ਮਾਤਰਾ ਵਿੱਚ ਘੱਟਦਾ ਜਾਂ ਵੱਧਦਾ ਹੈ ਤਾਂ ਉਸ ਵੇਲੇ ਵਸਤੂ ਅਸਮਾਨ ਵੇਗ ਨਾਲ ਗਤੀ ਕਰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 10.
ਇੱਕ ਬੱਸ ਦੀ ਚਾਲ 80 kmh^-1 ਤੋਂ ਘੱਟ ਕੇ 60 kmh^-1 5 s ਵਿੱਚ ਹੋ ਜਾਂਦੀ ਹੈ । ਬੱਸ ਦਾ ਵੇਗ ਪਤਾ ਕਰੋ ?
ਹੱਲ:
ਬੱਸ ਦਾ ਮੁੱਢਲਾ ਵੇਗ (u) = 80 kmh^-1
= 80 × \(\frac{5}{18}\)ms^-1 (∵ 1 kmh^-1 = \(\frac{5}{18}\)ms^-1)
ਬੱਸ ਦਾ ਅੰਤਿਮ ਵੇਗ (v) = 60kmh^-1
= 60 × \(\frac{5}{18}\)ms^-1
ਲੱਗਾ ਸਮਾਂ (t) = 5 s
ਬੱਸ ਦਾ ਵੇਗ (a) = ?

ਪ੍ਰਸ਼ਨ 11.
ਇੱਕ ਰੇਲਗੱਡੀ ਰੇਲਵੇ ਸਟੇਸ਼ਨ ਤੋਂ ਚੱਲਣਾ ਸ਼ੁਰੂ ਕਰਦੀ ਹੈ ਅਤੇ ਇੱਕ ਸਮਾਨ ਵੇਗ ਨਾਲ ਚੱਲਦੇ ਹੋਏ 40 km/h ਦੀ ਚਾਲ 10 ਮਿੰਟਾਂ ਵਿੱਚ ਪ੍ਰਾਪਤ ਕਰ ਲੈਂਦੀ ਹੈ । ਉਸ ਦਾ ਵੇਗ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਰੇਲ ਗੱਡੀ ਦੀ ਮੁੱਢਲੀ ਚਾਲ (u) = 0
ਅੰਤਿਮ ਚਾਲ (v) = 40 kmh^-1
= 40 × \(\frac{5}{18}\)ms^-1
= \(\frac{100}{9}\)ms^-1
ਸਮਾਂ (t) = 10 ਮਿੰਟ
= 10 × 60 ਸੈਕਿੰਡ
= 600 ਸੈਕਿੰਡ
ਪ੍ਰਵੇਗ (a) = ?

= 0.018 ms^-2

ਪ੍ਰਸ਼ਨ 12.
ਕਿਸੇ ਵਸਤੂ ਦੇ ਇੱਕ ਸਮਾਨ ਅਤੇ ਅਸਮਾਨ ਗਤੀ ਦੇ ਲਈ ਦੂਰੀ ਸਮਾਂ (x – t) ਗਰਾਫ਼ ਦੀ ਦਿੱਖ ਕਿਹੋ ਜਿਹੀ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਜਦੋਂ ਕੋਈ ਵਸਤੂ ਬਰਾਬਰ ਸਮੇਂ ਵਿੱਚ ਸਮਾਨ ਦੂਰੀ ਤੈਅ ਕਰਦੀ ਹੈ ਤਦੋਂ ਉਹ ਇੱਕ ਸਮਾਨ ਗਤੀ ਨਾਲ ਚਲਦੀ ਹੈ । ਅਰਥਾਤ ਇਸ ਅਵਸਥਾ ਵਿੱਚ ਵਸਤੂ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ ਲੱਗੇ ਸਮੇਂ ਦੇ ਅਨੁਪਾਤੀ ਹੁੰਦੀ ਹੈ । ਇਸ ਲਈ ਇੱਕ ਸਮਾਨ ਗਤੀ ਵਾਲੀ ਵਸਤੂ ਲਈ ਦੁਰੀਸਮਾਂ ਗਰਾਫ਼ ਇੱਕ ਸਰਲ ਰੇਖੀ ਗਰਾਫ਼ ਹੁੰਦਾ ਹੈ ।

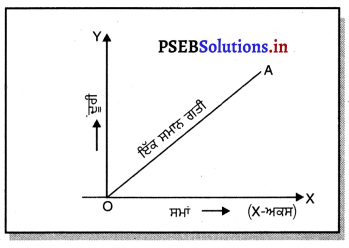
ਕਿਸੇ ਵਸਤੂ ਦੀ ਅਸਮਾਨ ਗਤੀ ਦੇ ਲਈ ਦੂਰੀ ਸਮਾਂ (x – t) ਗਰਾਫ਼ ਕਿਸੇ ਵੀ ਆਕਾਰ ਦਾ ਰੇਖੀ ਗਰਾਫ਼ ਹੋ ਸਕਦਾ ਹੈ ਕਿਉਂਕਿ ਜੋ ਇਹ ਵਸਤੂ ਬਰਾਬਰ ਸਮੇਂ ਅੰਤਰਾਲਾਂ ਵਿੱਚ ਅਸਮਾਨ ਦੂਰੀ ਤੈਅ ਕਰਦੀ ਹੈ ।

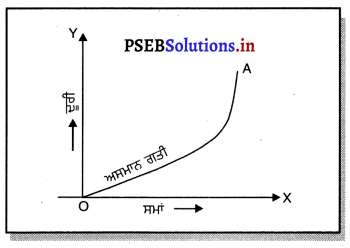
ਪ੍ਰਸ਼ਨ 13.
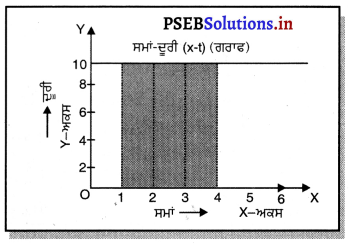
ਕਿਸੇ ਵਸਤੂ ਦੀ ਗਤੀ ਦੇ ਸੰਬੰਧ ਵਿੱਚ ਤੁਸੀਂ ਕੀ ਕਹਿ ਸਕਦੇ ਹੋ, ਜਿਸਦਾ ਚਾਲ ਸਮਾਂ (x – t) ਗਰਾਫ਼ ਸਮਾਂਅਕਸ ਦੇ ਸਮਾਨਾਂਤਰ ਇੱਕ ਸਰਲ ਰੇਖਾ ਹੋਵੇ ?
ਉੱਤਰ-
ਉਹ ਵਸਤੂ ਜਿਸ ਦਾ ਦੂਰੀ-ਸਮਾਂ (x – t) ਗਰਾਫ਼ ਸਮਾਂ-ਅਕਸ਼ (t-axis) ਦੇ ਸਮਾਨਾਂਤਰ ਇੱਕ ਸਰਲ ਰੇਖਾ ਹੈ, ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਹੋਵੇਗੀ ।

ਪ੍ਰਸ਼ਨ 14.
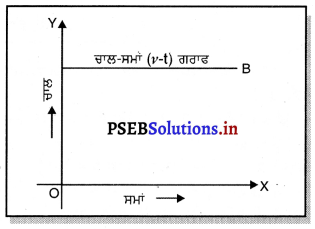
ਕਿਸੇ ਵਸਤੂ ਦੀ ਗਤੀ ਦੇ ਸੰਬੰਧ ਵਿੱਚ ਤੁਸੀਂ ਕੀ ਕਹਿ ਸਕਦੇ ਹੋ, ਜਿਸ ਦਾ ਚਾਲ-ਸਮਾਂ ਗਰਾਫ਼ (v – t), ਸਮਾਂ ਅਕਸ਼ ਦੇ ਸਮਾਨਾਂਤਰ ਇੱਕ ਸਰਲ ਰੇਖਾ ਹੋਵੇ ।
ਉੱਤਰ-
ਉਹ ਵਸਤੂ ਜਿਸਦਾ ਚਾਲ-ਸਮਾਂ ਗਰਾਫ਼ (v – t) ਸਮਾਂ-ਅਕਸ਼ ਦੇ ਸਮਾਨਾਂਤਰ ਇਕ ਸਰਲ ਰੇਖਾ ਹੈ, ਇੱਕ ਸਮਾਨ ਚਾਲ ਨਾਲ ਚੱਲ ਰਹੀ ਹੋਵੇਗੀ ।

ਪ੍ਰਸ਼ਨ 15.
ਵੇਗ-ਸਮੇਂ ਗਰਾਫ਼ (v -t) ਵਿੱਚ ਘੇਰੇ ਗਏ ਖੇਤਰਫਲ ਤੋਂ ਮਾਪੀ ਜਾਣ ਵਾਲੀ ਰਾਸ਼ੀ ਕਿਹੜੀ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਵੇ-ਸਮੇਂ ਗਰਾਫ਼ ਵਿੱਚ ਘੇਰੇ ਗਏ ਖੇਤਰਫਲ ਦੁਆਰਾ ਇੱਕ ਨਿਸ਼ਚਿਤ ਸਮੇਂ ਵਿੱਚ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ ਮਾਪਦਾ ਹੈ ।

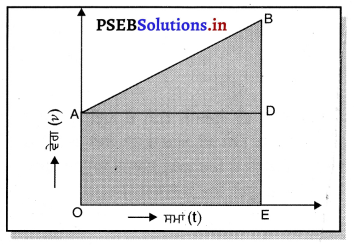
ਪ੍ਰਸ਼ਨ 16.
ਕੋਈ ਬੱਸ ਵਿਰਾਮ ਅਵਸਥਾ ਤੋਂ ਚਲਣਾ ਸ਼ੁਰੂ ਕਰਦੀ ਹੈ ਅਤੇ 2 ਮਿੰਟ ਤੱਕ 0.1 ms^-2 ਦੇ ਇੱਕ ਸਮਾਨ ਵੇਗ ਨਾਲ ਚੱਲਦੀ ਹੈ, ਪਤਾ ਕਰੋ-
(i) ਪ੍ਰਾਪਤ ਕੀਤੀ ਗਈ ਚਾਲ
(ii) ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ ।
ਹੱਲ:
(i) ਬੱਸ ਦਾ ਮੁੱਢਲਾ ਵੇਗ (u) = 0 (ਵਿਰਾਮ ਅਵਸਥਾ)
ਸਮਾਂ (t) = 2 ਮਿੰਟ
= 2 × 60 ਸੈਕਿੰਡ
= 120 ਸੈਕਿੰਡ ,
ਪਵੇਗ (a) = 0.1 ms^-2
ਬੱਸ ਦਾ ਅੰਤਿਮ ਵੇਗ (v) = ?
ਬੱਸ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ (S) = ?
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ, v = u + at
v = 0 + 0.1 × 120
v = 1 × 12
∴ v = 12 ms^-1

(ii) ਹੁਣ v² – u² = 2 aS ਦੀ ਵਰਤੋਂ ਕਰਕੇ
(12)² – (0)² = 2 × 0.1 × S
12 × 12 = 0.2 × S
∴ S = \(\frac{12 \times 12}{0.2}\)
= \(\frac{144 \times 10}{2}\)
= 720 m

ਪ੍ਰਸ਼ਨ 17.
ਕੋਈ ਰੇਲਗੱਡੀ 90 kmh^-1 ਦੀ ਚਾਲ ਨਾਲ ਚੱਲ ਰਹੀ ਹੈ । ਬਰੇਕ ਲਗਾਏ ਜਾਣ ਤੋਂ ਬਾਅਦ ਉਹ 0.5ms^-2 ਦਾ ਇੱਕ ਸਮਾਨ ਵੇਗ ਉਤਪੰਨ ਕਰਦੀ ਹੈ । ਰੇਲਗੱਡੀ ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਆਉਣ ਤੋਂ ਪਹਿਲਾਂ ਕਿੰਨੀ ਦੂਰੀ ਤੈਅ ਕਰੇਗੀ ?
ਹੱਲ:
ਰੇਲਗੱਡੀ ਦਾ ਮੁੱਢਲਾ ਵੇਗ (u) = 90 kmh^-1
= 90 × \(\frac{5}{18}\)ms^-1
= 5 × 5 ms^-1
= 25 ms^-1
ਪ੍ਰਵੇਗ (a) = -0.5 ms^-2
ਅੰਤਿਮ ਵੇਗ (v) = 0 (ਵਿਰਾਮ ਅਵਸਥਾ)
ਰੇਲਗੱਡੀ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ (S) = ?
v² – u² = 2 as ਦਾ ਪ੍ਰਯੋਗ ਕਰਕੇ
(0)² – (25)² = 2 × (-0.5) × S
– 25 × 25 = -1 × S
S = 25 × 25 m
= 625 m

ਪ੍ਰਸ਼ਨ 18.
ਇੱਕ ਟਰਾਲੀ ਇੱਕ ਢਾਲਵੇਂ ਤਲ ਤੇ 2 ms^-2 ਦੇ ਵੇਗ ਨਾਲ ਹੇਠਾਂ ਵੱਲ ਜਾ ਰਹੀ ਹੈ । ਗਤੀ ਸ਼ੁਰੂ ਕਰਨ ਦੇ 3 s ਦੇ ਬਾਅਦ ਉਸ ਦਾ ਵੇਗ ਕਿੰਨਾ ਹੋਵੇਗਾ ?
ਹੱਲ:
ਇੱਥੇ ਟਰਾਲੀ ਦਾ ਮੁੱਢਲਾ ਵੇਗ (u) = 0
ਪ੍ਰਵੇਗ (a) = 2 ms^-2
ਸਮਾਂ (t) = 3s
ਟਰਾਲੀ ਦਾ ਅੰਤਿਮ ਵੇਗ (v) = ?
v = u + at ਦੀ ਵਰਤੋਂ ਕਰਨ ਤੇ
v = 0 + 2 × 3
= 6 ms^-1

ਪ੍ਰਸ਼ਨ 19.
ਇੱਕ ਰੇਸਿੰਗ ਕਾਰ ਦਾ ਇੱਕ ਸਮਾਨ ਵੇਗ 4ms^-2 ਹੈ ਅਤੇ ਗਤੀ ਸ਼ੁਰੂ ਕਰਨ ਦੇ 3s ਬਾਅਦ ਉਸਦਾ ਕਿੰਨਾ ਵੇ ਹੋਵੇਗਾ ?
ਹੱਲ:
ਰੇਸਿੰਗ ਕਾਰ ਦਾ ਪ੍ਰਵੇਗ (a) = 4 ms^-2
ਕਾਰ ਦਾ ਮੁੱਢਲਾ ਵੇਗ (u) = 0
ਸਮਾਂ (t) = 3 s
ਰੇਨਿੰਗ ਕਾਰ ਦਾ ਅੰਤਿਮ ਵੇਗ (v) = ?
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ, v = u + at
v = 0 + 4 × 3
∴ ਰੇ ਸੰਗ ਕਾਰ ਦਾ 3 s ਤੋਂ ਬਾਅਦ ਵੇਗ, v = 12 ms^-1

ਪ੍ਰਸ਼ਨ 20.
ਕਿਸੇ ਪੱਥਰ ਨੂੰ ਖੜੀ ਲੰਬਵੱਤ ਦਿਸ਼ਾ ਵਿੱਚ ਉੱਪਰ ਵੱਲ ਨੂੰ 5 ms^-1 ਦੇ ਵੇਗ ਨਾਲ ਸੁੱਟਿਆ ਜਾਂਦਾ ਹੈ । ਜੇ ਗਤੀ ਦੌਰਾਨ ਪੱਥਰ ਦਾ ਹੇਠਾਂ ਵੱਲ ਨੂੰ ਵੇਗ 10ms-2 ਹੋਵੇ ਤਾਂ ਪੱਥਰ ਦੁਆਰਾ ਕਿੰਨੀ ਉੱਚਾਈ ਪ੍ਰਾਪਤ ਕੀਤੀ ਗਈ ਅਤੇ ਉਸਨੂੰ ਉੱਥੇ ਪਹੁੰਚਣ ਵਿੱਚ ਕਿੰਨਾ ਸਮਾਂ ਲੱਗੇਗਾ ?
ਹੱਲ :
ਇੱਥੇ ਮੁੱਢਲਾ ਵੇਗ (u) = 5 ms^-1
ਉੱਪਰ ਵੱਲ ਨੂੰ ਵੇਗ (g) = 10.0 ms^-2
ਅੰਤਿਮ ਵੇਗ (v) = 0
∵ ਅਧਿਕਤਮ ਉਚਾਈ ਤੇ ਪੁਹੰਚ ਕੇ ਪੱਥਰ ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਆ ਜਾਂਦਾ ਹੈ ।
ਲੱਗਾ ਸਮਾਂ (t) = ?
ਉੱਚਾਈ (S = h) = ?
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ, y = u + gt
0 = 5 +(-10) × t
0 = 5 – 10t
ਜਾਂ 10t = 5
t = \(\frac{5}{10}\)
= 0.5 s

ਹੁਣ v² – u² = 2gs ਦੀ ਵਰਤੋਂ ਕਰਨ ਤੇ
(0)² – (5)² = 2 × (-10) × h
– 5 × 5 = -20 h
∴ h = \(\frac{5 \times 5}{20}\)
= \(\frac{5}{4}\)m
∴ h = 1.25 m