PSEB 9th Class Science Solutions Chapter 9 बल तथा गति के नियम

Punjab State Board PSEB 9th Class Science Book Solutions Chapter 9 बल तथा गति के नियम Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Science Chapter 9 बल तथा गति के नियम

PSEB 9th Class Science Guide बल तथा गति के नियम Textbook Questions and Answers

प्रश्न 1.
कोई वस्तु शून्य बाह्य असंतुलित बल अनुभव करती है। क्या किसी भी वस्तु के लिए अशुन्य वेग से गति करना संभव है ? यदि हाँ, तो वस्तु के वेग के परिमाण एवं दिशा पर लगने वाली शर्तों का उल्लेख करें। यदि नहीं, तो कारण स्पष्ट करें।
उत्तर-
हाँ, किसी वस्तु के लिए कुछ वेग से गति करना संभव है, जबकि वह वस्तु बाह्य असंतुलित बल शून्य अनुभव कर रही हो। ऐसी अवस्था में वेग का परिमाण तथा दिशा समान रहेगी। उदाहरणार्थ, वर्षा के समय पानी की बूंद जब अचर वेग के साथ नीचे पृथ्वी की ओर गिरती है तो उस बूंद का भार तथा वायु का धकेल बल परस्पर एकदूसरे को संतुलित कर लेते हैं, अर्थात् पानी की बूंद पर परिणामी बल (नेट बल) शून्य होता है।

प्रश्न 2.
जब किसी छडी से एक दरी ( कार्पेट ) को पीटा जाता है, तो धूल के कण बाहर आ जाते हैं। स्पष्ट करें।
उत्तर-
जब हम दरी (कार्पेट) को छड़ी के साथ पीटते हैं तो दरी गति में आ जाती है जबकि धूल कण जड़त्व के कारण विराम अवस्था में बने रहते हैं। इस प्रकार धूल कण दरी (कार्पेट) से पृथक् होकर गिर जाते हैं।

प्रश्न 3.
बस की छत पर रखे सामान को रस्सी से क्यों बाँधा जाता है ?
उत्तर-
जब तीव्र गति से चल रही बस तीखे मोड़ पर गुड़ती है तो इसके छत पर रखा हुआ सामान एक ओर गिर (विस्थापित हो) जाता है। इसका कारण है कि सामान सरल रेखीय गति के साथ चलता रहना चाहता है जबकि बस की दिशा परिवर्तन के लिए ईंजन द्वारा असंतुलित बल लगाया जाता है तथा छत पर रखा सामान एक ओर खिसक जाता है।

प्रश्न 4.
किसी बल्लेबाज दवारा क्रिकेट की गेंद को मारने पर गेंद ज़मीन पर लुढ़कती है। कुछ दूरी चलने के पश्चात् गेंद रुक जाती है। गेंद रुकने के लिए धीमी होती है, क्योंकि
(a) बल्लेबाज ने गेंद को पर्याप्त प्रयास से हिट नहीं किया है।
(b) वेग गेंद पर लगाए गए बल के समानुपाती है।
(c) गेंद पर गति की दिशा के विपरीत एक बल कार्य कर रहा है।
(d) गेंद पर कोई असंतुलित बल कार्यरत नहीं है, अत: गेंद विरामावस्था में आने के लिए प्रयासरत है।
(सही विकल्प का चयन करें)
उत्तर-
(c) गेंद पर गति की दिशा के विपरीत एक बल कार्य कर रहा है।

प्रश्न 5.
एक टक विरामावस्था से किसी पहाड़ी से नीचे की ओर नियत त्वरण से लुढ़कना शुरू करता है। यह 20 s में 400 m की दूरी तय करता है। इसका त्वरण ज्ञात करें। अगर इसका द्रव्यमान 7 टन है तो इस पर लगने वाले बल की गणना करें। (1 टन = 1000 kg)।
हल-
यहां प्रारंभिक वेग (u) = 0
समय (t) = 20 s
दूरी (S) = 400 m
हम जानते हैं, S = ut + \(\frac {1}{2}\) at²
400 = 0 × 20 + \(\frac {1}{2}\) × a × (20)²
400 = 0 + \(\frac {1}{2}\) × a × 20 × 20
400 = 200a
या a = \(\frac{400}{200}\)
∴ a = 2 ms^-1
अब ट्रक का द्रव्यमान (m) = 7 टन
= 7 × 1000 kg
त्वरण (a) = 2 ms^-2
∴ बल, F = m × a
= 7000 kg × 2ms^-2
= 14000 kg m/s²
= 14000 N

प्रश्न 6.
1 kg द्रव्यमान के एक पत्थर को 20 ms^-1 के वेग से झील की जमी हुई सतह पर फेंका जाता है। पत्थर 50 m की दूरी तय करने के बाद रुक जाता है। पत्थर और बर्फ के बीच लगने वाले घर्षण बल की गणना करें।
हल-
यहाँ पत्थर का द्रव्यमान (m) = 1 kg
पत्थर का प्रारंभिक वेग (u) = 20 ms^-1
पत्थर द्वारा तय की गई दुरी (S) = 50 m
पत्थर का अंतिम वेग (v) = 0 (विराम अवस्था)
पत्थर तथा बर्फ में लगने वाला घर्षण बल (F) = ?
v² – u² = 2aS का प्रयोग करने पर
(0)² – (20)² = 2 × a × 50
-20 × 20 = 100 × a
या a = \(\frac{-20 \times 20}{100}\)
∴ a = -4 ms^-2
घर्षण बल, F = m × a
= 1 × (-4)
= -4 N

प्रश्न 7.
एक 8000 kg द्रव्यमान का रेल इंजन प्रति 2000 kg द्रव्यमान वाले पाँच डिब्बों को सीधी पटरी पर खींचता है। यदि इंजन 40000 N का बल आरोपित करता है तथा यदि पटरी 5000 N का घर्षण बल लगाती है, तो ज्ञात करें :
(a) नेट त्वरण बल,
(b) रेल का त्वरण तथा
(c) डिब्बे 1 द्वारा डिब्बे 2 पर लगाया गया बल।
हल-
इंजन का द्रव्यमान = 8000 kg 5
डिब्बों का द्रव्यमान = 5 × 2000 kg
= 10,000 kg
∴ इंजन तथा 5 डिब्बों का कुल द्रव्यमान = 8000 kg + 10,000 kg
= 18000 kg
इंजन द्वारा लगाया गया बल = 40000 N
पटरी द्वारा लगाया गया घर्षण बल = 5000 N

(a) नेट त्वरित बल = ईंजन का बल – पटरी का घर्षण बल
= 40000 N – 5000 N
= 35000 N

(b)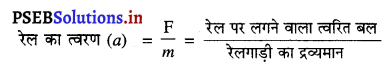
= \(\frac{35000}{18000}\)
= \(\frac{35}{18}\)
= 1.94 ms^-2

(c) पहले (1) डिब्बे द्वारा (2) दूसरे डिब्बे पर लगाया गया बल = नेट त्वरित बल – डिब्बे का द्रव्यमान × त्वरण

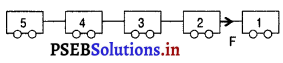
= 35000 – 2000 × \(\frac{35}{18}\)
= 35000 – 3888.8
= 31111.2N

प्रश्न 8.
एक गाड़ी का द्रव्यमान 1500 kg है। यदि गाड़ी को 1.7 ms^-2 के ऋणात्मक त्वरण (अवमंदन) के साथ विरामावस्था में लाना है, तो गाड़ी तथा सड़क के बीच लगने वाला बल कितना होगा ?
हल :
यहाँ गाड़ी का द्रव्यमान (m) = 1500 kg
त्वरण (a) = -1.7 ms^-2
घर्षण बल (F) = ?
हम जानते हैं, F = m × a
= 1500 × (-1.7)
= -2550 N
अर्थात् गाड़ी तथा सड़क के मध्य लगने वाला घर्षण बल 2550N है जिसकी दिशा गाड़ी की गति की दिशा के विपरीत है।

प्रश्न 9.
किसी m द्रव्यमान की वस्तु जिसका वेग । है का संवेग क्या होगा ?
(a) (mv)²
(b) mv²
(c) (1/2)mv²
(d) mv
(उपरोक्त में से सही विकल्प चुनें।)
उत्तर-
(d) mv.

प्रश्न 10.
हम एक लकड़ी के बक्से को 200 N बल लगाकर उसे नियत वेग से फ़र्श पर धकेलते हैं। बक्से पर लगने वाला घर्षण बल क्या होगा ?
उत्तर-
लकड़ी का बॉक्स उस अवस्था में स्थिर वेग से गति करेगा यदि नेट (परिणामी) बल शून्य होगा।
बॉक्स पर लगने वाला घर्षण बल = धकेल बल
= 200 N
परंतु इस घर्षण बल की दिशा बॉक्स की गति के विपरीत दिशा में होगा।

प्रश्न 11.
दो वस्तुएँ, प्रत्येक का द्रव्यमान 1.5 kg है, एक ही सीधी रेखा में एक-दूसरे के विपरीत दिशा में गति कर रही हैं। टकराने के पहले प्रत्येक का वेग 2.5 ms^-1 है। टकराने के बाद यदि दोनों एक-दूसरे से जुड़ जाती हैं, तब उनका सम्मिलित वेग क्या होगा ? ..
हल :
यहाँ, m₁ = m₂ = 1.5 kg
u₁ = 2.5 ms^-1, u₂ = -2.5 ms^-1
क्योंकि दोनों वस्तुएँ एक-दूसरे की विपरीत दिशा में जा रही हैं, इसलिए पहली वस्तु के वेग की दिशा धन तथा दूसरी वस्तु के वेग की दिशा को ऋण माना जाएगा।
मान लो टकराने के पश्चात् दोनों वस्तुओं के युग्म का वेग v है।
संवेग सरंक्षण नियमानुसार, टकराने से पहले दोनों वस्तुओं का कुल संवेग = टकराने के बाद कुल संवेग
m₁u₁ + m₂u₂ = m₁v + m₂v
m₁u₁ + m₂u₂ = (m₁ + m₂) × v
1.5 × 2.5 + 1.5 × (-2.5) = (1.5 + 1.5) × v
1.5 (2.5 – 2.5) = 3 × v
1.5 × 0 = 3 × v
0 = 3 × v
∴ v = 0 ms^-1

प्रश्न 12.
गति के तृतीय नियम के अनुसार जब हम किसी वस्तु को धक्का देते हैं, तो वस्तु उतने ही बल के साथ हमें भी विपरीत दिशा में धक्का देती है। यदि वह वस्तु एक ट्रक है जो सड़क के किनारे खड़ा है; संभवतः हमारे द्वारा बल आरोपित करने पर भी गतिशील नहीं हो पाएगा। एक विद्यार्थी इसे सही साबित करते हुए कहता है कि दोनों बल विपरीत एवं बराबर हैं जो एक-दूसरे को निरस्त कर देते हैं। इस तर्क पर अपने विचार दें और बताएँ कि ट्रक गतिशील क्यों नहीं हो पाता ?
उत्तर–
क्रिया तथा प्रतिक्रिया एक-दूसरे के समान तथा विपरीत होते हैं। ये एक-दूसरे को समाप्त (प्रभावहीन) नहीं करते हैं। जब हम एक भारी ट्रक को धक्का लगाते हैं,तो टायर तथा सड़क के मध्य घर्षण बल क्रिया करता है जो अत्यधिक मात्रा में होता है। इस कारण ट्रक गति नहीं करता है।

प्रश्न 13.
200 g द्रव्यमान की एक हॉकी की गेंद 10 ms^-1 की वेग से सीधी रेखा में चलती हुई 5 kg द्रव्यमान के लकड़ी के गुटके से संघट्ट करती है तथा उससे जुड़ जाती है। उसके बाद दोनों एक साथ उसी रेखा में गति करते हैं। संघट्ट के पहले और संघट्ट के बाद के कुल संवेगों की गणना करें। दोनों वस्तुओं की जुड़ी हुई अवस्था में वेग की गणना करें।
हल :
गेंद का द्रव्यमान (m) = 200g = 0.2 kg
गेंद का प्रारंभिक वेग (u) = 10 ms^-1
गेंद का अंतिम वेग (v) = -5 ms^-1 (∵ गेंद की दिशा पहली दिशा के विपरीत है।)
गेंद के संवेग में परिवर्तन = अंतिम संवेग – प्रारंभिक संवेग
= mv – mu
= m(v – u)
= 0.2 (-5 – 10)
= 0.2 × (-15)
= – 30 kg -ms^-1

प्रश्न 14.
10g. द्रव्यमान की एक गोली सीधी रेखा में 150 ms^-1 के वेग से चलकर एक लकड़ी के गुटके से टकराती है और 0.03 s के बाद रुक जाती है। गोली लकड़ी को कितनी दूरी तक भेदेगी ? लकड़ी के गुटके द्वारा गोली पर लगाए गए बल के परिमाण की गणना करें। हल :
यहाँ, गोली का द्रव्यमान (m) = 1g = 0.01 kg
गोली का प्रारंभिक वेग (u) = 150 ms^-1
गोली का अंतिम वेग (v) = 0
समय (t) = 0.03s
हम जानते हैं, गोली का प्रवेग (a) = \(\frac{v-u}{t}\)
= \(\frac{0-150}{0.03}\)
= -5000 ms^-1
लकड़ी के गुटके के भीतर घुसी गोली द्वारा तय की गई दूरी (S) = ?
सूत्र S = ut + \(\) at² का प्रयोग करके
S = 150 x 0.03 + \(\frac {1}{2}\) × (-5000) × (0.03)²
= 4.5 + (-2.25)
= 4.5 – 2.25
S = 2.25 m
प्रश्न 15.
एक वस्तु जिसका द्रव्यमान 1 kg है, 10 ms^-1 के वेग से एक सीधी रेखा में चलते हुए विरामावस्था में रखे 5 kg द्रव्यमान के एक लकड़ी के गुटके से टकराती है। उसके बाद दोनों साथ-साथ उसी सीधी रेखा में गति करते हैं। संघट्ट के पहले तथा बाद के कुल संवेगों की गणना करें। आपस में जुड़े हुए संयोजन के वेग की भी गणना करें।
हल :
वस्तु का द्रव्यमान (m₁) = 1 kg
वस्तु का प्रारंभिक वेग (u₁) = 10 ms^-1
लकड़ी के गुटके का द्रव्यमान (m₂) = 5 kg
लकड़ी के गुटके का प्रारंभिक वेग (u₂) = 0 (विराम अवस्था)
मान लो टकराने के पश्चात् वस्तु तथा गुटके के युग्म का अंतिम वेग है।
∴ टक्कर से पहले वस्तु तथा गुटके का कुल संवेग = m₁u₁ + m₂u₂
= 1 × 10 + 5 × 0
= 10 + 0
= 10 kg-ms^-1
टक्कर के पश्चात् युग्म (वस्तु तथा गुटके) का कुल संवेग = m₁v + m₂v
= (m₁ + m₂) × v
= (1 + 5) × v
= 6v kg-ms^-1
संवेग संरक्षण नियम अनुसार, टक्कर से पहले युग्म का कुल संवेग = टक्कर के पश्चात् युग्म का कुल संवेग
10 = 6v
∴ v = \(\frac{10}{6}[latex]
= [latex]\frac{5}{3}\) ms^-1 = 1.67 ms^-1
∴ टक्कर के पश्चात् युग्म का कुल संवेग = 6v
= 6 × \(\frac{5}{3}\)
= 10 kg – ms^-1

प्रश्न 16.
100 kg द्रव्यमान की एक वस्तु का वेग समान त्वरण से चलते हुए 6s में 5 ms^-1 से 8 ms^-1 हो जाता है। वस्तु के पहले और बाद के संवेगों की गणना करें। उस बल के परिमाण की गणना करें जो उस वस्तु पर आरोपित है।
हल :
यहाँ, वस्तु का द्रव्यमान (m) = 100 kg
वस्तु का प्रारंभिक वेग (u) = 5 ms^-1
वस्तु का अंतिम वेग (v) = 8 ms^-1
समय अंतराल (t) = 6s
वस्तु का प्रारंभिक संवेग (p) = m × u
= 100 × 5
= 500 kg-ms^-1
वस्तु का अंतिम संवेग (p₂) = m × v
= 100 × 8
= 800 kg-ms^-1
वस्तु पर लग रहा बल. F = \(\frac{p_{2}-p_{1}}{t}\)
= \(\frac{(800-500) \mathrm{kg}-\mathrm{ms}^{-1}}{6 \mathrm{~s}}\)
= 50 kg-ms^-2
= 50 N

प्रश्न 17.
अख्तर, किरण और राहुल किसी राजमार्ग पर बहुत तीव्र गति से चलती हुई कार में सवार हैं, अचानक उड़ता हुआ कोई कीड़ा, गाड़ी के सामने के शीशे से आ टकराया और वह शीशे से चिपक गया। अख़्तर और किरण इस स्थिति पर विवाद करते हैं। किरण का मानना है कि कीड़े के संवेग परिवर्तन का परिमाण कार के संवेग परिवर्तन के परिमाण की अपेक्षा बहुत अधिक है। (क्योंकि कीड़े के वेग में परिवर्तन का मान कार के वेग में परिवर्तन के मान से बहुत अधिक है।) अख़्तर ने कहा कि चूंकि कार का वेग बहुत अधिक था अतः कार ने कीड़े पर बहुत अधिक बल लगाया जिसके कारण कीड़े की मौत हो गई। राहुल ने एक नया तर्क देते हुए कहा कि कार तथा कीड़ा दोनों पर समान बल लगा और दोनों के संवेग में बराबर परिवर्तन हुआ। इन विचारों पर अपनी प्रतिक्रिया दें।
उत्तर-
राहुल का तर्क सही है। गति के तीसरे नियमानुसार क्रिया तथा प्रतिक्रिया समान तथा विपरीत होते हैं। इसलिए दोनों-कार तथा कीड़े पर समान मात्रा में बल लगेगा तथा दोनों में समान वेग परिवर्तन भी होगा। अब क्योंकि कीड़े का द्रव्यमान कार के द्रव्यमान की तुलना में अत्यधिक कम हैं, इसलिए कीड़े में हुआ संवेग परिवर्तन स्पष्ट दिखाई देता है। जड़त्व कम होने के कारण कीड़ा मर जाता है।

प्रश्न 18.
एक 10 kg द्रव्यमान की घंटी 80 cm की ऊँचाई से फ़र्श पर गिरी। इस अवस्था में घंटी द्वारा फ़र्श पर स्थानांतरित संवेग के मान की गणना करें। परिकलन में सरलता हेतु नीचे की ओर दिष्ट त्वरण का मान, 10 ms^-2 लें।
हल :
यहाँ, घंटी का द्रव्यमान (m) = 10 kg’
आरंभिक वेग (u) = 0 (विराम अवस्था)
तय की गई दूरी (S) = 80 cm
= 0.80 m
घंटी का त्वरण (a) = 10 ms^-2
मान लो पृथ्वी पर पहुँच कर घंटी का अंतिम वेग v है
∴ v² – u² = 2aS के प्रयोग से
v² – (0)² = 2 × 10 × 0.80
v² = 16
∴ घंटी का अंतिम वेग, v = \(\sqrt{16}\) = 4 ms^-1
घंटी द्वारा पृथ्वी को स्थानांतरित संवेग (p) = mv
= 10 × 4
= 40 kg – ms^-1

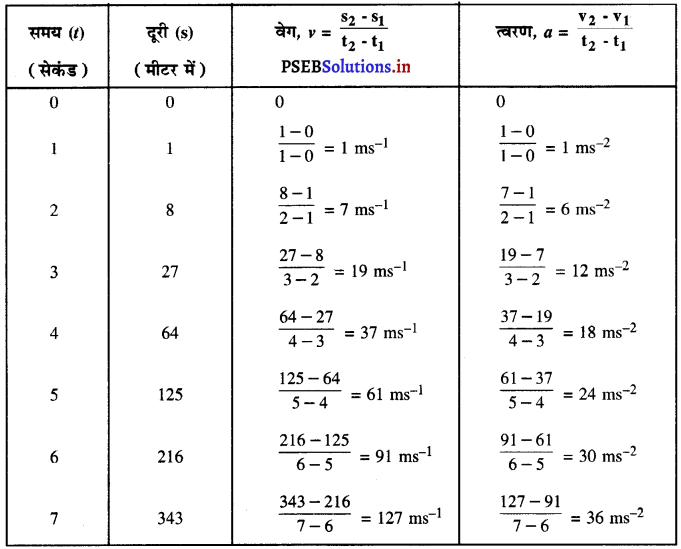
(a) ऊपर दी गई सारणी दर्शाती है कि गति त्वरित है तथा त्वरण समय के साथ-साथ एक समान रूप से बढ़ता है।
(b) क्योंकि त्वरण एक समान रूप से बढ़ रहा है, इसलिए वस्तु पर लग रहा बल भी समय के साथ समान रूप से बढ़ रहा है।

अतिरिक्त अभ्यास (Additional Exercises)

प्रश्न A1.
एक वस्तु की गति की अवस्था में दूरी समय सारणी निम्नवत् है:

समय (सेकंड)	दूरी (मीटर)
0	0
1	1
2	8
3	27
4	64
5	125
6	216
7	343

(a) त्वरण के बारे में आप क्या निष्कर्ष निकाल सकते हैं ? क्या यह नियत है ? बढ़ रहा है ? घट रहा है ? या शून्य है ?
(b) आप वस्तु पर लगने वाले बल के बारे में क्या निष्कर्ष निकाल सकते हैं ?
हल:

प्रश्न A2.
1200 kg द्रव्यमान की कार को एक समतल सड़क पर दो व्यक्ति समान वेग से धक्का देते हैं। उसी कार को तीन व्यक्तियों द्वारा धक्का देकर 0.2 ms-^-2का त्वरण उत्पन्न किया जाता है। कितने बल के साथ प्रत्येक व्यक्ति कार को धकेल पाते हैं। (मान लें कि सभी व्यक्ति समान पेशीय बल के साथ कार को धक्का देते हैं।)
हल :
यहाँ कार का द्रव्यमान (m) = 1200 kg
कार का त्वरण (a) = 0.2 ms^-2
पहले दो व्यक्तियों को धक्का देने से त्वरण = 0
स्पष्ट है कि जब तीसरा व्यक्ति कार को धक्का मारता है तो एक असंतुलित बल क्रिया करता है।
∴ तीसरे व्यक्ति द्वारा लगाया गया बल, F = m × a
= 1200 × 0.2
= 240 N
अब क्योंकि तीनों व्यक्ति पेशीय बल लगा कर कार को धकेलते हैं, इसलिए प्रत्येक व्यक्ति बल लगाता है = 240 N

प्रश्न A3.
500g द्रव्यमान के एक हथौड़े द्वारा 50 ms^-1 वेग से एक कील पर प्रहार किया जाता है। कील द्वारा हथौड़े को बहुत कम समय 0.01 s में ही रोक दिया जाता है। कील के द्वारा हथौड़े पर लगाए गए बल का परिकलन करें।
हल :
हथौड़े का द्रव्यमान (m) = 500g
= \(\frac{500}{1000}\) kg
= \(\frac{1}{2}\) kg
प्रारंभिक वेग (u) = 50 ms^-1
अंतिम वेग (v) = 0 ms^-1
समय (t) = 0.01s
बल (F) = ?
हम जानते हैं, v = u + at
0 = 50 + a × 0.01
-50 = a × \(\frac{1}{100}\)
∴ a = -50 × 100
= -5000 ms^-2
ऋणात्मक चिन्ह मंदन को दर्शाता है।
अब कील द्वारा हथौड़े पर लगाया गया बल (F) = m × a
= \(\frac{1}{2}\) × (-5000)
= -2500 N
∴ बल = 2500 N

प्रश्न A4.
एक 1200 kg द्रव्यमान की मोटरकार 90 km/h की वेग से एक सरल रेखा के अनुदिश चल रही है। उसका वेग बाहरी असंतुलित बल लगने के कारण 4s में घटकर 18 km/h हो जाता है। त्वरण और संवेग में परिवर्तन का परिकलन करें। लगने वाले बल के परिमाण का भी परिकलन करें।
हल :
यहाँ, कार का द्रव्यमान (m) = 1200 kg
समय (1) = 4s
कार का प्रारंभिक वेग (u) = 90 km/h
= \(\frac{90 \times 1000}{60 \times 60}\) m/s
= 25 ms^-1
कार का अंतिम वेग (v) = 18 km/h
= \(\frac{18 \times 1000 \mathrm{~m}}{60 \times 60 \mathrm{~s}}\)
= 5 ms^-1
कार का त्वरण (a) = ?
कार के संवेग में परिवर्तन = ?
कार पर लगने वाले बल का परिमाण (F) = ?
हम जानते हैं, v = u + at
5 = 25 + a x 4
-20 = 4a
∴ a = \(\frac{-20}{4}\)
= -5 ms^-2
कार के संवेग में परिवर्तन = अंतिम संवेग – प्रारंभिक संवेग
= mv – mu
= m (v – u)
= 1200 (5 – 25)
= 1200 × (-20)
= -24000 kg – ms^-1
= 24000 kg – ms^-1 की कमी उत्तर
परंतु F = m × a
= 1200 × 5
= 6000 N

Science Guide for Class 9 PSEB बल तथा गति के नियम InText Questions and Answers

पाठ्य-पुस्तक के प्रश्नों के उत्तर

प्रश्न 1.
निम्नलिखित में किस का जड़त्व अधिक है :
(a) एक रबर की गेंद एवं उसी आकार का पत्थर,
(b) एक साइकिल एवं एक रेलगाड़ी,
(c) पाँच रुपये का सिक्का एवं एक रुपये का सिक्का।
उत्तर-
हम जानते हैं कि किसी वस्तु का द्रव्यमान उसके जड़त्व का माप है, इसलिए जिस वस्तु का द्रव्यमान अधिक होगा उस वस्तु का जड़त्व भी अधिक होगा।
(a) गेंद के आकार वाले पत्थर का जड़त्व अधिक क्योंकि इसका द्रव्यमान गेंद के द्रव्यमान की अपेक्षा अधिक है।

(b) एक रेलगाड़ी का द्रव्यमान साइकिल के द्रव्यमान की तुलना से अधिक है इसलिए रेलगाड़ी का जड़त्व अधिक

(c) पाँच रुपये के सिक्के का जड़त्व एक रुपये के सिक्के से अधिक है क्योंकि पाँच रुपये के सिक्के का द्रव्यमान 1 रुपये के सिक्के की अपेक्षा अधिक है।

प्रश्न 2.
नीचे दिए गए उदाहरण में गेंद का वेग कितनी बार बदलता है, जानने का प्रयास करें :
“फुटबॉल का एक खिलाड़ी गेंद पर किक लगाकर गेंद को अपनी टीम के दूसरे खिलाड़ी के पास पहुँचाता है। दूसरा खिलाड़ी उस गेंद को किक लगाकर गोल की ओर पहुँचाने का प्रयास करता है। विपक्षी टीम का गोलकीपर गेंद को पकड़ता है और अपनी टीम के खिलाड़ी की ओर किक लगाता है।”
इसके साथ ही उस कारक की भी पहचान करें जो प्रत्येक अवस्था में बल प्रदान करता है।
उत्तर-
धक्का मारना, ठोकर लगानी, खींचना ये सभी क्रियाएँ वस्तु के वेग की मात्रा बदलने या गति की दिशा परिवर्तन के लिए बल के रूप में कार्य करती हैं। इसलिए ऊपर दी गई उदाहरण में गेंद का वेग तीन बार बदला है।

1. पहली बार प्रथम टीम के फुटबाल खिलाड़ी ने फुटबाल को किक (ठोकर) लगाकर गेंद के वेग में परिवर्तन किया।
2. द्वितीय बार उसी टीम के अन्य खिलाड़ी ने फुटबाल को किक (ठोकर) लगाकर गेंद में वेग परिवर्तन किया है।
3. तृतीय बार विरोधी टीम के गोलची ने फुटबाल को किक (ठोकर) लगाकर गेंद के वेग में परिवर्तन किया है।
   बल लगाने वाले कारक को मोटे अक्षरों में दिया गया है।

प्रश्न 3.
किसी पेड़ की शाखा को तीव्रता से हिलाने पर कुछ पत्तियाँ झड़ जाती हैं। क्यों ?
उत्तर-
टहनियों को हिलाने से पहले टहनियाँ तथा पत्ते दोनों विराम अवस्था में थे। हिलाने के फलस्वरूप टहिनयाँ गतिशील हो गईं जबकि पत्तियाँ विराम जड़त्व के कारण टहिनयों से अलग होकर नीचे गिर जाती हैं।

प्रश्न 4.
जब कोई गतिशील बस अचानक रुकती है तो आप आगे की ओर झुक जाते हैं और जब विरामावस्था से गतिशील होती है तो पीछे की ओर हो जाते हैं, क्यों ?
उत्तर-
जब गतिशील बस यकायक रुक जाती है तो हमारे शरीर का निचला भाग बस के संपर्क में होने से बस के साथ ही विराम अवस्था में आ जाता है, जबकि हमारे शरीर का ऊपर वाला भाग गतिशील रहने की प्रवृत्ति रखता है। इसलिए हम आगे की दिशा में गिर जाते हैं। जब बस अचानक त्वरित होती है तो हमारे शरीर का निचला भाग बस के संपर्क में होने से बस के साथ गतिशील हो जाता है, जबकि शरीर का ऊपरी भाग जड़त्व के कारण विराम अवस्था में रहने की प्रवृत्ति रखता है। इसलिए हम पीछे की ओर गिरते हैं।

प्रश्न 5.
यदि क्रिया सदैव प्रतिक्रिया के बराबर है तो स्पष्ट कीजिए कि घोड़ा गाड़ी को कैसे खींच पाता
है ?
उत्तर-
न्यूटन के गति के तीसरे नियम अनुसार, “क्रिया तथा प्रतिक्रिया सदैव समान तथा विपरीत दिशा में होते हैं।” घोड़ा-गाड़ी का बल (क्रिया) लगाकर आगे की ओर खींचता है। गाड़ी भी घोड़े को बल (प्रतिक्रिया) लगाकर (पीछे की) विपरीत दिशा में खींचती है। यह दोनों बल एक-दूसरे को संतुलित कर देते हैं। जब घोड़ा, गाड़ी को खींचता है तो वह अपने पैरों से पृथ्वी को पीछे की ओर धकेलता है। पृथ्वी की प्रतिक्रिया ऊपर की दिशा में कार्य करती है। इस प्रतिक्रिया बल को दो भागों में बाँटा जा सकता है। ऊपर की ओर लंबवत् दिशा में लगने वाला बल प्रतिक्रियात्मक बल घोड़े के भार को संतुलित करता है जबकि प्रतिक्रियात्मक बल का क्षितिज घटक गाड़ी को आगे की दिशा में गतिमान करता है। पृथ्वी तथा पहिए के मध्य घर्षण बल पीछे की दिशा में क्रिया करता है परंतु आगे की दिशा में लगने वाला बल घर्षण बल से अधिक होता है जिससे यह गाड़ी को गतिमान करने में सफल हो जाता है।

प्रश्न 6.
एक अग्निशमन कर्मचारी को तीव्र गति से बहुतायत मात्रा में पानी फेंकने वाली रबड़ की नली को पकड़ने में कठिनाई क्यों होती है ? स्पष्ट करें।
उत्तर-
रबड़ की नली में से पानी अत्यधिक बल (क्रिया) से बाहर निकलता है तथा उसी के समान बल (प्रतिक्रिया) को अग्निशमन कर्मचारी का हाथ अनुभव करता है। इसलिए उसे रबड़ की नली पकड़ने में असुविधा अनुभव होती है।

प्रश्न 7.
एक 50g द्रव्यमान की गोली 4kg द्रव्यमान, की रायफ़ल से 35 ms^-1 के प्रारंभिक वेग से छोड़ी जाती है। रायफल के प्रारंभिक प्रतिक्षेपित वेग की गणना कीजिए।
उत्तर-
गोली का द्रव्यमान (m₁) = 50 g = 0.05 kg
रायफल का द्रव्यमान (m₂) = 4 kg
गोली का प्रारंभिक वेग (u₁) = 0
रायफल का प्रारंभिक वेग (u₂) = 0
गोली का अंतिम वेग (v₁) = 35 ms^-1
रायफल का अंतिम वेग (v₂) = ?
संवेग संरक्षण के नियमानुसार, गोली तथा रायफ़ल का कुल प्रारंभिक संवेग = गोली तथा रायफल का कुल अंतिम संवेग
m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂
0.5 × 0 + 4 × 0 = 0.05 × 35 + 4 × v₂
0 + 0 = 1.75 + 4 × v₂
या -4 × v₂ = 1.75
v₂ = \(\frac{-1.75}{4}\)
= -0.437 ms^-1
= – 0.44 ms^-1
ऋणात्मक चिन्ह यह दर्शाता है कि रायफल के वेग की दिशा गोली के वेग की दिशा के विपरीत है।

प्रश्न 8.
100g और 200g द्रव्यमान की दो वस्तुएँ एक ही रेखा के अनुदिश एक ही दिशा में क्रमशः 2ms^-1 और 1ms^-1 के वेग से गति कर रही हैं। दोनों वस्तुएँ टकरा जाती हैं। टक्कर के पश्चात् प्रथम वस्तु का वेग 1.67 ^-1 हो जाता है, तो दूसरी वस्तु का वेग ज्ञात करें।
हल :
यहाँ, पहली वस्तु का द्रव्यमान (m₁) = 100g
= \(\frac{1}{10}\) kg
पहली वस्तु का प्रारंभिक वेग (u₁) = 2ms^-1
दूसरी वस्तु का द्रव्यमान (m₂) = 200g
= \(\frac{1}{5}\) kg
दूसरी वस्तु का प्रारंभिक वेग (u₂) = 1ms^-1
टकराने से पहले पहली वस्तु का प्रारंभिक संवेग = m₁ × u₁
= \(\frac{1}{10}\) × 2
= \(\frac{1}{5}\) kg – ms^-1
दूसरी वस्तु का प्रारंभिक संवेग = m₂ × u₂
= \(\frac{1}{5}\) × 1
= \(\frac{1}{5}\) kg -ms^-1
दोनों वस्तुओं का कुल प्रारंभिक संवेग = \(\frac{1}{5}+\frac{1}{5}\)
= \(\frac{2}{5}\)kg – ms^-1
टकराने के पश्चात् पहली वस्तु का अंतिम वेग (v₁) = 1.67 ms^-1
दूसरी वस्तु का अंतिम वेग (v₂) = ?
पहली वस्तु का अंतिम संवेग = m₁ × v₁
= \(\frac{1}{10}\) × 1.67
= 0.167 kg – ms^-1
दूसरी वस्तु का अंतिम वेग (v₂) = ?
दोनों वस्तुओं का कुल अंतिम संवेग = m₁ × v₁ + m₂ × v₂
= 0.167 + \(\frac{1}{5}\) × v₂
संवेग संरक्षण नियमानुसार
m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂
\(\frac{2}{5}\) = 0.167+ \(\frac{1}{5}\) × v₂
0.2 × v₂ = 0.4 – 0.167
0.2 × v₂ = 0.233
या v₂ = \(\frac{0.233}{0.2}\)
∴ v₂ = 0.116 ms^-1