PSEB 9th Class Science Solutions Chapter 9 ਬਲ ਅਤੇ ਗਤੀ ਦੇ ਨਿਯਮ

Punjab State Board PSEB 9th Class Science Book Solutions Chapter 9 ਬਲ ਅਤੇ ਗਤੀ ਦੇ ਨਿਯਮ Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Science Chapter 9 ਬਲ ਅਤੇ ਗਤੀ ਦੇ ਨਿਯਮ

PSEB 9th Class Science Guide ਬਲ ਅਤੇ ਗਤੀ ਦੇ ਨਿਯਮ Textbook Questions and Answers

ਅਭਿਆਸ ਦੇ ਪ੍ਰਸ਼ਨ

ਪ੍ਰਸ਼ਨ 1.
ਕੋਈ ਵਸਤੂ ਬਾਹਰੀ ਅਸੰਤੁਲਿਤ ਬਲ ਸਿਫ਼ਰ ਮਹਿਸੂਸ ਕਰਦੀ ਹੈ । ਕੀ ਕਿਸੇ ਵਸਤੂ ਦੇ ਲਈ ਸਿਫ਼ਰ ਵੇਗ ਨਾਲ ਗਤੀ ਕਰਨਾ ਸੰਭਵ ਹੈ ? ਜੇਕਰ ਹਾਂ, ਤਾਂ ਵਸਤੂ ਦੇ ਵੇਗ ਦੇ ਪਰਿਮਾਣ ਅਤੇ ਦਿਸ਼ਾ ਤੇ ਲੱਗਣ ਵਾਲੀਆਂ ਸ਼ਰਤਾਂ ਬਿਆਨ ਕਰੋ । ਜੇਕਰ ਨਹੀਂ ਤਾਂ ਕਾਰਨ ਸਪੱਸ਼ਟ ਕਰੋ ।
ਉੱਤਰ-
ਹਾਂ, ਕਿਸੇ ਵਸਤੂ ਲਈ ਕੁੱਝ ਵੇਗ ਨਾਲ ਗਤੀ ਕਰਨਾ ਸੰਭਵ ਹੈ ਜਦੋਂ ਕਿ ਉਹ ਵਸਤੂ ਬਾਹਰੀ ਅਸੰਤੁਲਿਤ ਬਲ ਸਿਫ਼ਰ ਮਹਿਸੂਸ ਕਰ ਰਹੀ ਹੋਵੇ । ਅਜਿਹੀ ਅਵਸਥਾ ਵਿੱਚ ਵੇਗ ਦਾ ਪਰਿਮਾਣ ਅਤੇ ਦਿਸ਼ਾ ਸਮਾਨ ਰਹੇਗੀ ।
ਉਦਾਹਰਨ ਲਈ, ਮੀਂਹ ਸਮੇਂ ਪਾਣੀ ਦੀ ਬੂੰਦ ਜਦੋਂ ਸਥਿਰ ਵੇਗ ਨਾਲ ਹੇਠਾਂ ਧਰਤੀ ਵੱਲ ਡਿੱਗਦੀ ਹੈ, ਤਾਂ ਉਸ ਬੂੰਦ ਦਾ ਭਾਰ ਅਤੇ ਹਵਾ ਦਾ ਧਕੇਲ ਬਲ ਇੱਕ-ਦੂਜੇ ਨੂੰ ਸੰਤੁਲਿਤ ਕਰ ਲੈਂਦੇ ਹਨ ਅਰਥਾਤ ਪਾਣੀ ਦੀ ਬੂੰਦ ’ਤੇ ਬਲ ਸਿਫ਼ਰ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਜਦੋਂ ਕਿਸੇ ਛੜੀ ਨਾਲ ਇੱਕ ਦਰੀ (ਗਲੀਚੇ) ਨੂੰ ਕੁੱਟਿਆ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਧੂੜ ਦੇ ਕਣ ਬਾਹਰ ਨਿਕਲ ਆਉਂਦੇ ਹਨ । ਸਪੱਸ਼ਟ ਕਰੋ ।
ਉੱਤਰ-
ਜਦੋਂ ਅਸੀਂ ਗਲੀਚੇ ਨੂੰ ਛੜੀ (ਸੋਟੀ) ਨਾਲ ਕੁੱਟਦੇ ਹਾਂ, ਤਾਂ ਗਲੀਚਾ ਗਤੀ ਵਿੱਚ ਆ ਜਾਂਦਾ ਹੈ ਜਦੋਂਕਿ ਧੂੜ ਕਣ ਜੜ੍ਹਤਾ ਕਾਰਨ ਵਿਰਾਮ ਵਿੱਚ ਬਣੇ ਰਹਿੰਦੇ ਹਨ । ਇਸ ਤਰ੍ਹਾਂ ਧੂੜ ਕਣ ਗਲੀਚੇ ਤੋਂ ਅਲੱਗ ਹੋ ਕੇ ਡਿੱਗ ਪੈਂਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 3.
ਬੱਸ ਦੀ ਛੱਤ ‘ਤੇ ਰੱਖੇ ਹੋਏ ਸਮਾਨ ਨੂੰ ਰੱਸੀ ਨਾਲ ਕਿਉਂ ਬੰਨਿਆ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਜਦੋਂ ਤੇਜ਼ ਗਤੀ ਨਾਲ ਚਲ ਰਹੀ ਬੱਸ ਕਿਸੇ ਤਿੱਖੇ ਮੋੜ ‘ਤੇ ਮੁੜਦੀ ਹੈ, ਤਾਂ ਇਸ ਦੀ ਛੱਤ ‘ਤੇ ਰੱਖਿਆ ਹੋਇਆ ਸਮਾਨ ਇੱਕ ਪਾਸੇ ਵੱਲ ਨੂੰ ਡਿੱਗ ਜਾਂਦਾ ਹੈ । ਇਸ ਦਾ ਕਾਰਨ ਇਹ ਹੈ ਕਿ ਸਮਾਨ ਸਰਲ ਰੇਖੀ ਗਤੀ ਵਿੱਚ ਹੀ ਚਲਦਾ ਰਹਿਣਾ ਚਾਹੁੰਦਾ ਹੈ । ਜਦੋਂ ਬੱਸ ਦੀ ਦਿਸ਼ਾ ਬਦਲਣ ਲਈ ਇੰਜਨ ਦੁਆਰਾ ਇੱਕ ਅਸੰਤੁਲਿਤ ਬਲ ਲਗਾਇਆ ਜਾਂਦਾ ਹੈ ਤਾਂ ਛੱਤ ‘ਤੇ ਰੱਖਿਆ ਸਮਾਨ ਇੱਕ ਪਾਸੇ ਨੂੰ ਖਿਸਕ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 4.
ਇੱਕ ਬੱਲੇਬਾਜ਼ (Batsman) ਦੁਆਰਾ ਕ੍ਰਿਕੇਟ ਦੀ ਗੇਂਦ ਨੂੰ ਜ਼ੋਰ ਦੀ ਮਾਰਣ ਨਾਲ ਉਹ ਜ਼ਮੀਨ ‘ਤੇ ਲੁੜਕਦੀ ਹੈ । ਕੁੱਝ ਦੂਰੀ ਚੱਲਣ ਦੇ ਬਾਅਦ ਗੇਂਦ ਰੁੱਕ ਜਾਂਦੀ ਹੈ । ਗੇਂਦ ਰੁੱਕਣ ਲਈ ਹੌਲੀ ਹੁੰਦੀ ਹੈ, ਕਿਉਂਕਿ
(a) ਬੱਲੇਬਾਜ਼ ਨੇ ਗੇਂਦ ਨੂੰ ਪੂਰੇ ਜ਼ੋਰ ਨਾਲ ਹਿੱਟ ਨਹੀਂ ਕੀਤਾ ਹੈ ।
(b) ਵੇਗ ਗੇਂਦ ਦੇ ਲਗਾਏ ਗਏ ਬਲ ਦੇ ਸਮਾਨੁਪਾਤੀ ਹੈ ।
(c) ਗੇਂਦ ਤੇ ਗਤੀ ਦੀ ਦਿਸ਼ਾ ਦੇ ਉਲਟ ਇੱਕ ਬਲ ਕਾਰਜ ਕਰ ਰਿਹਾ ਹੈ ।
(d) ਗੇਂਦ ‘ਤੇ ਕੋਈ ਅਸੰਤੁਲਿਤ ਬਲ ਨਹੀਂ ਕੰਮ ਕਰ ਰਿਹਾ । ਇਸ ਲਈ ਗੇਂਦ ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਆ ਜਾਵੇਗੀ ।
ਉੱਤਰ-
(c) ਗੇਂਦ ਤੇ ਗਤੀ ਦੀ ਦਿਸ਼ਾ ਦੇ ਉਲਟ ਇੱਕ ਬਲ ਕਾਰਜ ਕਰ ਰਿਹਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 5.
ਇੱਕ ਟਰੱਕ ਵਿਰਾਮ ਅਵਸਥਾ ਤੋਂ ਕਿਸੇ ਪਹਾੜੀ ਤੋਂ ਥੱਲੇ ਵੱਲ ਸਥਿਰ ਪ੍ਰਵੇਗ ਨਾਲ ਲੁੜਕਣਾ ਸ਼ੁਰੂ ਕਰਦਾ ਹੈ । ਇਹ 20s ਵਿੱਚ 400m ਦੀ ਦੂਰੀ ਤੈਅ ਕਰਦਾ ਹੈ । ਇਸ ਦਾ ਪ੍ਰਵੇਗ ਪਤਾ ਕਰੋ । ਜੇਕਰ ਇਸ ਦਾ ਪੁੰਜ 7 ਟਨ ਹੈ, ਤਾਂ ਇਸ ‘ਤੇ ਲੱਗਣ ਵਾਲੇ ਬਲ ਦਾ ਪਤਾ ਕਰੋ । (1 ਟਨ = 1000kg)
ਹੱਲ:
ਇੱਥੇ, ਮੁੱਢਲਾ ਵੇਗ (u) = 0
ਸਮਾਂ (t) = 20s
ਦੁਰੀ (S) = 400m
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ, s = ut + \(\frac{1}{2}\)at²
400 = 0 × 20 + \(\frac{1}{2}\)a × (20)²
400 = 0 + \(\frac{1}{2}\) × a × 20 × 20
400 = 200 a
∴ a = \(\frac{400}{200}\)
= 2ms^-2
ਹੁਣ ਟਰੱਕ ਦਾ ਪੁੰਜ (m) = 7 ਟਨ
= 7 × 1000 kg
= 7000 kg
ਪ੍ਰਵੇਗ (a) = 2 ms^-2
∴ ਲੱਗਣ ਵਾਲਾ ਬਲ, F = m × a
= 7000 × 2
= 14000 N (ਨਿਊਟਨ)

ਪ੍ਰਸ਼ਨ 6.
ਇੱਕ kg ਦੇ ਪੁੰਜ ਦੇ ਇੱਕ ਪੱਥਰ ਨੂੰ 20 ms^-1 ਦੇ ਵੇਗ ਨਾਲ ਜੰਮੀ ਹੋਈ ਝੀਲ ਦੀ ਸਤ੍ਹਾ ‘ਤੇ ਸੁੱਟਿਆ ਜਾਂਦਾ ਹੈ । ਪੱਥਰ 50m ਦੀ ਦੂਰੀ ਤੈਅ ਕਰਨ ਤੋਂ ਬਾਅਦ ਰੁਕ ਜਾਂਦਾ ਹੈ । ਪੱਥਰ ਅਤੇ ਬਰਫ਼ ਦੇ ਵਿੱਚ ਲੱਗਣ ਵਾਲੇ ਰਗੜ ਬਲ ਦਾ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਇੱਥੇ ਪੱਥਰ ਦਾ ਪੁੰਜ (m) = 1kg
ਪੱਥਰ ਦਾ ਮੁੱਢਲਾ ਵੇਗ (u) = 20 ms^-1
ਪੱਥਰ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ (S)= 50m
ਪੱਥਰ ਦਾ ਅੰਤਿਮ ਵੇਗ (υ) = 0 (ਰੁੱਕ ਜਾਂਦਾ ਹੈ)
ਪੱਥਰ ਅਤੇ ਬਰਫ਼ ਵਿੱਚ ਲੱਗਣ ਵਾਲਾ ਰਗੜ ਬਲ (F) = ?
υ² – u² = 2aS ਦੀ ਵਰਤੋਂ ਕਰਕੇ
(υ)² – (20)² = 2 × a × 50
(0)² – 20 × 20 = 100 × a
∴ a = \(\frac{-20 \times 20}{100}\)
a = – 4 ms^-2
ਰਗੜ ਬਲ, F = m × a
= 1 × (-4)
= – 4N

ਪ੍ਰਸ਼ਨ 7.
ਇੱਕ 8000 kg ਪੰਜ ਵਾਲਾ ਰੇਲ ਇੰਜਨ ਪ੍ਰਤੀ 2000 kg ਪੰਜ ਵਾਲੇ 5 ਡੱਬਿਆਂ ਨੂੰ ਸਿੱਧੀ ਪਟਰੀ ‘ਤੇ ਖਿੱਚਦਾ ਹੈ । ਇੱਕ ਇੰਜਨ 40000 N ਦਾ ਬਲ ਲਗਾਂਦਾ ਹੈ ਅਤੇ ਪਟਰੀ 5000 N ਬਲ ਲਗਾਉਂਦੀ ਹੈ,
ਪਤਾ ਕਰੋ –
(a) ਵੇਗਤ ਕਰਨ ਵਾਲਾ ਬਲ
(b) ਰੇਲ ਦਾ ਵੇਗ
(c) ਪਹਿਲੇ ਡੱਬੇ ਦੁਆਰਾ ਦੂਜੇ ਡੱਬੇ ‘ਤੇ ਲਗਾਇਆ ਗਿਆ ਬਲ
ਹੱਲ :
ਇੰਜਨ ਦਾ ਪੁੰਜ = 8000 kg …………… (i)
5 ਡੱਬਿਆਂ ਦਾ ਪੁੰਜ, = 5 × 2000 kg
= 10,000 kg ……………. (ii)
ਇੰਜਨ ਅਤੇ 5 ਡੱਬਿਆਂ ਦਾ ਕੁੱਲ ਪੰਜ = (i) + (ii)
= 8000 kg + 10,000 kg
= 18000 kg
ਇੰਜਨ ਦੁਆਰਾ ਲਗਾਇਆ ਗਿਆ ਬਲ = 40000 N
ਪਟਰੀ ਦੁਆਰਾ ਲਗਾਇਆ ਗਿਆ ਰਗੜ ਬਲ = 5000 N
= ਇੰਜਨ ਦਾ ਬਲ – ਪਟਰੀ ਦਾ ਰਗੜ ਬਲ
(a) ਨੈੱਟ ਪ੍ਰਵੇਗਿਤ ਬਲ = 40000 N – 5000 N
= 35000 N

(b)

= 1.94 ms^-2

(c) ਪਹਿਲੇ ਡੱਬੇ ਦੁਆਰਾ ਦੂਜੇ ਡੱਬੇ ‘ਤੇ ਲਗਾਇਆ ਬਲ = ਨੈੱਟ ਗਿਤ ਬਲ – ਡੱਬੇ ਦਾ ਪੁੰਜ × ਵੇਗ

= 35000 – 2000 × \(\frac{35}{18}\)
= 35000 – 3888.8
= 31111.2 N

ਪ੍ਰਸ਼ਨ 8.
ਇੱਕ ਗੱਡੀ ਦਾ ਪੁੰਜ 1500 kg ਹੈ । ਇਸ ਗੱਡੀ ਨੂੰ 1.7ms^-2 ਦੇ ਰਿਣਾਤਮਕ ਵੇਗ ਦੇ ਨਾਲ ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਲਿਆਂਦਾ ਹੈ । ਗੱਡੀ ਅਤੇ ਸੜਕ ਦੇ ਵਿੱਚ ਲੱਗਣ ਵਾਲਾ ਰਗੜ ਬਲ ਕਿੰਨਾ ਹੋਵੇਗਾ ?
ਹੱਲ:
ਇੱਥੇ, ਗੱਡੀ ਦਾ ਪੁੰਜ (m) = 1500 kg
ਪ੍ਰਵੇਗ (a) = – 1.7 ms^-2
ਰਗੜ ਬਲ (F) = ?
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ, F = m × a
= 1500 × -1.7
= – 2550 N
ਅਰਥਾਤ ਗੱਡੀ ਅਤੇ ਸੜਕ ਦੇ ਵਿੱਚ ਲੱਗਣ ਵਾਲਾ ਰਗੜ ਬਲ 2550 N ਹੈ ਜਿਸ ਦੀ ਦਿਸ਼ਾ ਗੱਡੀ ਦੀ ਦਿਸ਼ਾ ਦੇ ਉਲਟ ਹੈ ।

ਪ੍ਰਸ਼ਨ 9.
ਕਿਸੇ m ਪੁੰਜ ਵਾਲੀ ਵਸਤੂ ਜਿਸ ਦਾ ਵੇਗ υ ਹੈ, ਤਾਂ ਇਸ ਦਾ ਸੰਵੇਗ ਕਿੰਨਾ ਹੋਵੇਗਾ ?
(a) (mυ)²
(b) mυ²
(c) \(\frac{1}{2}\)mυ²
(d) mυ
ਇਹਨਾਂ ਵਿੱਚੋਂ ਸਹੀ ਦੀ ਚੋਣ ਕਰੋ ।
ਉੱਤਰ-
(d) mυ

ਪ੍ਰਸ਼ਨ 10.
ਅਸੀਂ ਇੱਕ ਲੱਕੜ ਦੇ ਬੱਸੇ ਨੂੰ 200 N ਦਾ ਬਲ ਲਗਾ ਕੇ ਉਸਨੂੰ ਸਥਿਰ ਵੇਗ ਨਾਲ ਫ਼ਰਸ਼ ‘ਤੇ ਧਕੇਲਦੇ ਹਾਂ । ਬਕਸੇ ‘ਤੇ ਲੱਗਣ ਵਾਲਾ ਰਗੜ ਬਲ ਕਿੰਨਾ ਹੋਵੇਗਾ ?
ਹੱਲ:
ਲੱਕੜ ਦਾ ਬਕਸਾ ਉਸ ਹਾਲਤ ਵਿੱਚ ਸਥਿਰ ਵੇਗ ਨਾਲ ਗਤੀ ਕਰੇਗਾ ਜੇਕਰ ਨੈੱਟ ਪਰਿਣਾਮੀ ਬਲ ਸਿਫ਼ਰ ਹੋਵੇਗਾ । ਇਸ ਲਈ ਬਕਸੇ ‘ਤੇ ਲੱਗਣ ਵਾਲਾ ਰਗੜ ਬਲ = ਧਕੇਲਣ ਬਲ = 200 N
ਪਰੰਤੂ ਇਸ ਰਗੜ ਬਲ ਦੀ ਦਿਸ਼ਾ ਬਕਸੇ ਦੀ ਗਤੀ ਦੇ ਉਲਟ ਦਿਸ਼ਾ ਵਿੱਚ ਹੋਵੇਗੀ ।

ਪ੍ਰਸ਼ਨ 11.
ਦੋ ਵਸਤੂਆਂ, ਹਰੇਕ ਦਾ ਪੁੰਜ 1.5 kg ਹੈ, ਇੱਕ ਹੀ ਸਿੱਧੀ ਰੇਖਾ ਵਿੱਚ ਇੱਕ-ਦੂਜੇ ਦੇ ਉਲਟ ਦਿਸ਼ਾ ਵਿੱਚ ਗਤੀ ਕਰ ਰਹੀਆਂ ਹਨ । ਟਕਰਾਉਣ ਤੋਂ ਪਹਿਲਾਂ ਹਰੇਕ ਦਾ ਵੇਗ 2.5 ms^-1 ਹੈ । ਟਕਰਾਉਣ ਤੋਂ ਬਾਅਦ ਇਹ ਦੋਨੋਂ ਇੱਕ-ਦੂਜੇ ਨਾਲ ਜੁੜ ਜਾਂਦੀਆਂ ਹਨ, ਤਾਂ ਇਹਨਾਂ ਵਸਤੂਆਂ ਦਾ ਟਕਰਾਉਣ ਤੋਂ ਬਾਅਦ ਜੁੜ ਜਾਣ ‘ਤੇ ਕਿੰਨਾ ਵੇਗ ਹੋਵੇਗਾ ?
ਹੱਲ:
ਇੱਥੇ m₁ = m₂ = 1.5 kg
u₁ = 2.5ms^-1, u₂ = -2.5 ms^-1

ਕਿਉਂਕਿ ਦੋਨੋਂ ਵਸਤੂਆਂ ਇੱਕ-ਦੂਜੇ ਤੋਂ ਉਲਟ ਦਿਸ਼ਾ ਵਿੱਚ ਜਾਂਦੀਆਂ ਹਨ, ਇਸ ਲਈ ਪਹਿਲੀ ਵਸਤੂ ਦੇ ਵੇਗ ਦੀ ਦਿਸ਼ਾ ਧਨ ਅਤੇ ਦੂਜੀ ਵਸਤੂ ਦੇ ਵੇਗ ਦੀ ਦਿਸ਼ਾ ਨੂੰ ਰਿਣ ਮੰਨਿਆ ਜਾਵੇਗਾ ।

ਮੰਨ ਲਉ ਟਕਰਾਉਣ ਤੋਂ ਬਾਅਦ ਦੋਨੋਂ ਵਸਤੂਆਂ ਦੇ ਜੋੜ ਦਾ ਵੇਗ υ ਹੈ ।
ਸੰਵੇਗ ਸੁਰੱਖਿਅਣ ਨਿਯਮ ਅਨੁਸਾਰ, ਟਕਰਾਉਣ ਤੋਂ ਪਹਿਲਾਂ ਦੋਨਾਂ ਵਸਤੂਆਂ ਦਾ ਕੁੱਲ ਸੰਵੇਗ = ਟਕਰਾਉਣ ਤੋਂ ਬਾਅਦ ਦੋਨਾਂ ਵਸਤੂਆਂ ਦਾ ਕੁੱਲ ਸੰਵੇਗ
m₁u₁ + m₂u₂ = (m₁ + m₂ ) × υ
1.5 × 2.5 + 1.5 × (-2.5) = (1.5 + 1.5) × υ
1.5 (2.5 – 2.5) = 3 × υ
1.5 × 0 = 3 × υ
0 = 3υ
υ = \(\frac{0}{3}\)
= 0 ms^-1

ਪ੍ਰਸ਼ਨ 12.
ਗਤੀ ਦੇ ਤੀਜੇ ਨਿਯਮ ਅਨੁਸਾਰ ਜਦੋਂ ਅਸੀਂ ਕਿਸੇ ਵਸਤੂ ਨੂੰ ਧੱਕਾ ਮਾਰਦੇ ਹਾਂ, ਤਾਂ ਵਸਤੂ ਵੀ ਸਾਨੂੰ ਉੱਨੇ ਹੀ ਬਲ ਨਾਲ ਉਲਟ ਦਿਸ਼ਾ ਵਿੱਚ ਧੱਕਾ ਦਿੰਦੀ ਹੈ । ਜੇ ਉਹ ਵਸਤੂ ਇੱਕ ਟਰੱਕ ਹੈ ਜੋ ਕਿ ਸੜਕ ਦੇ ਕਿਨਾਰੇ ਖੜ੍ਹਾ ਹੈ, ਸੰਭਵ ਹੈ ਕਿ ਸਾਡੇ ਦੁਆਰਾ ਬਲ ਲਗਾਉਣ ‘ਤੇ ਵੀ ਉਹ ਗਤੀ ਮਾਨ ਨਹੀਂ ਹੋ ਪਾਵੇਗਾ । ਇੱਕ ਵਿਦਿਆਰਥੀ ਇਸਨੂੰ ਸਹੀ ਸਿੱਧ ਕਰਦਿਆਂ ਹੋਇਆਂ ਕਹਿੰਦਾ ਹੈ ਕਿ ਦੋਨੋਂ ਬਲ ਉਲਟ ਅਤੇ ਬਰਾਬਰ ਹਨ ਅਤੇ ਇਸੇ ਕਰਕੇ ਦੋਨੋਂ ਇੱਕ-ਦੂਜੇ ਨੂੰ ਖ਼ਤਮ ਕਰ ਦਿੰਦੇ ਹਨ । ਇਸ ਤਰਕ ਤੇ ਆਪਣੇ ਵਿਚਾਰ ਦਿਉ ਅਤੇ ਵਿਆਖਿਆ ਕਰੋ ਕਿ ਟਰੱਕ ਕਿਉਂ ਨਹੀਂ ਗਤੀ ਕਰਦਾ ?
ਉੱਤਰ-
ਕਿਰਿਆ ਅਤੇ ਪ੍ਰਤੀਕਿਰਿਆ ਇਕ-ਦੂਜੇ ਦੇ ਬਰਾਬਰ ਅਤੇ ਉਲਟ ਹੁੰਦੇ ਹਨ ਅਤੇ ਵੱਖ-ਵੱਖ ਵਸਤੁਆਂ ‘ਤੇ ਲਗਦੇ ਹਨ । ਇਹ ਇੱਕ-ਦੂਜੇ ਨੂੰ ਨਹੀਂ ਕੱਟਦੇ (ਕੈਂਸਲ) ਹਨ । ਜਦੋਂ ਅਸੀਂ ਇਕ ਭਾਰੀ ਟਰੱਕ ਨੂੰ ਧੱਕਾ ਮਾਰਦੇ ਹਾਂ, ਤਾਂ ਟਾਇਰ ਅਤੇ ਸੜਕ ਦੇ ਵਿੱਚ ਰਗੜ ਬਲ ਕਿਰਿਆ ਕਰਦਾ ਹੈ ਜੋ ਬਹੁਤ ਮਾਤਰਾ ਵਿੱਚ ਹੁੰਦਾ ਹੈ, ਇਸ ਲਈ ਟਰੱਕ ਗਤੀ ਨਹੀਂ ਕਰਦਾ ।

ਪ੍ਰਸ਼ਨ 13.
ਇੱਕ ਹਾਕੀ ਦੀ ਗੇਂਦ ਜਿਸਦਾ ਪੁੰਜ 200g ਹੈ, 10 ms^-1 ਦੇ ਵੇਗ ਨਾਲ ਸਿੱਧੀ ਰੇਖਾ ਵਿੱਚ ਚਲਦਿਆਂ ਹੋਇਆਂ 5 kg ਪੁੰਜ ਵਾਲੀ ਲੱਕੜੀ ਦੀ ਹਾਕੀ ਦੀ ਛੜ ਨਾਲ ਟਕਰਾਉਂਦੀ ਹੈ ਅਤੇ 5 ms^-1 ਦੇ ਵੇਗ ਨਾਲ ਆਪਣੇ ਅਸਲੀ ਮਾਰਗ ‘ਤੇ ਵਾਪਸ ਆ ਜਾਂਦੀ ਹੈ । ਹਾਕੀ ਦੀ ਛੜ ਦੁਆਰਾ ਬਲ ਲਗਾਉਣ ਕਾਰਣ ਹਾਕੀ ਦੀ ਗੇਂਦ ਦੀ ਗਤੀ ਵਿੱਚ ਸੰਵੇਗ ਵਿੱਚ ਪਰਿਵਰਤਨ ਦਰ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਗੇਂਦ ਦਾ ਪੁੰਜ (m) = 200g = 0.2 kg
ਗੇਂਦ ਦਾ ਮੁੱਢਲਾ ਵੇਗ (u) = 10ms^-1
ਗੇਂਦ ਦਾ ਅੰਤਿਮ ਵੇਗ (υ) = -5ms^-1
(∵ ਹੁਣ ਗੇਂਦ ਦੀ ਦਿਸ਼ਾ ਪਹਿਲੀ ਦਿਸ਼ਾ ਦੇ ਉਲਟ ਹੈ ।)
ਗੇਂਦ ਦੇ ਸੰਵੇਗ ਵਿੱਚ ਪਰਿਵਰਤਨ = mυ – mu
= m (υ – u)
= 0.2 (-5 – 10)
= 0.2 × (15)
= – 3.0kg – ms^-1

ਪ੍ਰਸ਼ਨ 14.
10g ਪੁੰਜ ਵਾਲੀ ਇੱਕ ਬੰਦੂਕ ਦੀ ਗੋਲੀ ਜੋ ਕਿ 150 ms^-1 ਗਤੀ ਨਾਲ ਸਿੱਧੀ ਰੇਖਾ ਵਿੱਚ ਚਲਦੀ ਹੋਈ ਇੱਕ ਲੱਕੜੀ ਦੇ ਗੁਟਕੇ ਨਾਲ ਟਕਰਾਉਂਦੀ ਹੈ ਅਤੇ 0.03 s ਵਿੱਚ ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਆ ਜਾਂਦੀ ਹੈ । ਗੁਟਕੇ ਵਿੱਚ ਗੋਲੀ ਦੁਆਰਾ ਭੇਜੀ ਗਈ ਦੂਰੀ ਪਤਾ ਕਰੋ ਅਤੇ ਲੱਕੜੀ ਦੇ ਗੁਟਕੇ ਦੁਆਰਾ ਗੋਲੀ ‘ਤੇ ਲਗਾਏ ਗਏ ਬਲ ਦੀ ਮਾਤਰਾ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਇੱਥੇ, ਗੋਲੀ ਦਾ ਪੁੰਜ (m) = 10g = 0.01kg
ਗੋਲੀ ਦਾ ਮੁੱਢਲਾ ਵੇਗ (u = 150ms^-1
ਗੋਲੀ ਦਾ ਅੰਤਿਮ ਵੇਗ (υ) = 0
ਸਮਾਂ (t) = 0.03 s
ਗੋਲੀ ਦਾ ਵੇਗ (a) = \(\frac{v-u}{t}\)
= \(\frac{0-150}{0.03}\)
= -5000 ms^-2
ਲੱਕੜੀ ਦੇ ਗੁਟਕੇ ਵਿੱਚ ਖੁੱਭੀ ਹੋਈ ਗੋਲੀ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਦੂਰੀ (S) = ?
s = ut + \(\frac{1}{2}\) at² ਦੀ ਵਰਤੋਂ ਕਰਕੇ
= 150 × 0.03 + \(\frac{1}{2}\) × (-5000) × (0.03)²
= 4.5 – 2.25
S = 2.25m
ਲੱਕੜੀ ਦੇ ਗੁਟਕੇ ਦੁਆਰਾ ਗੋਲੀ ‘ਤੇ ਲੱਗੇ ਬਲ ਦਾ ਪਰਿਮਾਣ F = m × a
= 0.01 × 5000
= 50N

ਪ੍ਰਸ਼ਨ 15.
ਇੱਕ ਵਸਤੂ ਜਿਸਦਾ ਪੁੰਜ 1kg ਹੈ, 10ms^-1 ਦੇ ਵੇਗ ਨਾਲ ਇੱਕ ਸਿੱਧੀ ਰੇਖਾ ਨਾਲ ਚੱਲਦੇ ਹੋਏ ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਰੱਖੇ ਹੋਏ 5kg ਪੁੰਜ ਵਾਲੇ ਇੱਕ ਲੱਕੜੀ ਦੇ ਗੁਟਕੇ ਨਾਲ ਟਕਰਾਉਂਦੀ ਹੈ ਅਤੇ ਟਕਰਾਉਣ ਤੋਂ ਬਾਅਦ ਉਸ ਨਾਲ ਹੀ ਜੁੜ ਜਾਂਦੀ ਹੈ । ਉਸਦੇ ਬਾਅਦ ਦੋਨੋਂ ਇੱਕ ਸਿੱਧੀ ਰੇਖਾ ਵਿੱਚ ਗਤੀ ਕਰਦੇ ਹਨ । ਟੱਕਰ ਤੋਂ ਪਹਿਲਾਂ ਅਤੇ ਟੱਕਰ ਤੋਂ ਬਾਅਦ ਦਾ ਕੁੱਲ ਸੰਵੇਗ ਪਤਾ ਕਰੋ | ਆਪਸ ਵਿੱਚ ਜੁੜੀਆਂ ਹੋਈਆਂ ਦੋਨਾਂ ਵਸਤੂਆਂ ਦਾ ਵੇਗ ਵੀ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਵਸਤੂ ਦਾ ਪੁੰਜ (m₁) = 1kg .
ਵਸਤੁ ਦਾ ਮੁੱਢਲਾ ਵੇਗ (u₁) = 10ms^-1
ਲੱਕੜੀ ਦੇ ਗੁਟਕੇ ਦਾ ਪੁੰਜ (m₂) = 5kg
ਲੱਕੜੀ ਦੇ ਗੁਟਕੇ ਦਾ ਮੁੱਢਲਾ ਵੇਗ (u₂) = 0 (ਵਿਰਾਮ ਅਵਸਥਾ)
ਮੰਨ ਲਉ ਟਕਰਾਉਣ ਤੋਂ ਬਾਅਦ ਜੋੜ (ਵਸਤੂ ਅਤੇ ਗੁਟਕਾ) ਦਾ ਵੇਗ ) ਹੈ ।
ਟੱਕਰ ਤੋਂ ਪਹਿਲਾਂ ਵਸਤੂ ਅਤੇ ਗੁਟਕੇ ਦਾ ਕੁੱਲ ਸੰਵੇਗ = m₁ u₁ + m₂u₂
= 1 × 10 + 5 × 0
= 10 + 0
= 10kg ms^-1
ਟੱਕਰ ਤੋਂ ਬਾਅਦ ਜੋੜ (ਵਸਤੂ ਅਤੇ ਗੁਟਕੇ) ਦਾ ਕੁੱਲ ਸੰਵੇਗ = (m₁ + m₂) × υ
= (1 + 5) × υ
= 6υ kg ms^-1
ਸੰਵੇਗ ਸੁਰੱਖਿਅਣ ਨਿਯਮ ਅਨੁਸਾਰ,
ਟੱਕਰ ਤੋਂ ਪਹਿਲਾਂ ਜੋੜ ਦਾ ਕੁੱਲ ਸੰਵੇਗ = ਟੱਕਰ ਤੋਂ ਬਾਅਦ ਜੋੜ ਦਾ ਕੁੱਲ ਸੰਵੇਗ
10 = 6υ
∴ υ = \(\frac{10}{6}\)
\(\frac{5}{3}\) ms^-1 = 1.67ms^-1
∴ ਟੱਕਰ ਤੋਂ ਬਾਅਦ ਜੋੜ ਦਾ ਕੁੱਲ ਸੰਵੇਗ = 6υ
= 6 × \(\frac{5}{3}\)
= 10 kg – ms^-1

ਪ੍ਰਸ਼ਨ 16.
100kg ਪੰਜ ਵਾਲੀ ਇੱਕ ਵਸਤੂ 6 ਸੈਕਿੰਡਾਂ ਵਿੱਚ 5ms^-1 ਤੋਂ 8ms^-1 ਦੇ ਵੇਗ ਨਾਲ ਚਲਦੇ ਹੋਏ ਇੱਕ ਸਮਾਨ ਗਿਤ ਹੁੰਦੀ ਹੈ । ਵਸਤੂ ਦਾ ਪਹਿਲਾ ਅਤੇ ਅੰਤਿਮ ਸੰਵੇਗ ਪਤਾ ਕਰੋ | ਵਸਤੂ ਉੱਤੇ ਲੱਗੇ ਬਲ ਦਾ ਮਾਨ ਵੀ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਇੱਥੇ, ਵਸਤੂ ਦਾ ਪੁੰਜ (m) = 100 kg
ਵਸਤੂ ਦਾ ਮੁੱਢਲਾ ਵੇਗ (u) = 5 ms^-1
ਵਸਤੁ ਦਾ ਅੰਤਿਮ ਵੇਗ = (υ) 8 ms^-1
ਸਮਾਂ ਅੰਤਰਾਲ (t) = 6 ਸੈਕਿੰਡ
ਮੁੱਢਲਾ (ਜਾਂ ਪਹਿਲਾ) ਸੰਵੇਗ (P₁) = mu
= 100 × 5
= 500kg ms^-1
ਅੰਤਿਮ ਸੰਵੇਗ (p₂) = mυ
= 100 × 8
= 800kg ms^-1
ਵਸਤੁ ਤੇ ਲੱਗਦੇ ਬਲ ਦਾ ਮਾਨ, F = \(\frac{p_{2}-p_{1}}{t}\)
= \(\frac{800-500}{6}\)
= \(\frac{300}{6}\)
= 50N

ਪ੍ਰਸ਼ਨ 17.
ਅਖ਼ਤਰ, ਕਿਰਨ ਅਤੇ ਰਾਹੁਲ ਕਿਸੇ ਰਾਜ ਮਾਰਗ ਤੋਂ ਬਹੁਤ ਤੇਜ਼ ਗਤੀ ਨਾਲ ਚੱਲਦੀ ਹੋਈ ਕਾਰ ‘ਤੇ ਸਵਾਰ ਹਨ । ਅਚਾਨਕ ਇੱਕ ਕੀੜਾ ਉੱਡਦਾ ਹੋਇਆ ਕਾਰ ਦੇ ਸਾਹਮਣੇ ਵਾਲੇ ਸ਼ੀਸ਼ੇ ਵਿੱਚ ਆ ਟਕਰਾਇਆ ਅਤੇ ਸ਼ੀਸ਼ੇ ਨਾਲ ਚਿਪਕ ਗਿਆ । ਅਖ਼ਤਰ ਅਤੇ ਕਿਰਨ ਇਸ ਸਥਿਤੀ ‘ਤੇ ਵਿਚਾਰ ਕਰਦੇ ਹਨ । ਕਿਰਨ ਦਾ ਮੰਨਣਾ ਹੈ ਕਿ ਕਾਰ ਵਿੱਚ ਸੰਵੇਗ ਦੇ ਪਰਿਵਰਤਨ ਨਾਲੋਂ ਕੀੜੇ ਵਿੱਚ ਆਏ ਸੰਵੇਗ ਵਿੱਚ ਪਰਿਵਰਤਨ ਬਹੁਤ ਜ਼ਿਆਦਾ ਹੈ, ਕਿਉਂਕਿ ਕਾਰ ਨਾਲੋਂ ਕੀੜੇ ਵਿੱਚ ਆਇਆ ਵੇਗ ਵਿੱਚ ਪਰਿਵਰਤਨ ਬਹੁਤ ਜ਼ਿਆਦਾ ਹੈ । ਅਖ਼ਤਰ ਨੇ ਕਿਹਾ ਕਿਉਂਕਿ ਕਾਰ ਬਹੁਤ ਜ਼ਿਆਦਾ ਵੇਗ ਨਾਲ ਚਲ ਰਹੀ ਸੀ, ਇਸ ਕਰਕੇ ਇਸਨੇ ਕੀੜੇ ਉੱਪਰ ਬਹੁਤ ਜ਼ਿਆਦਾ ਬਲ ਲਗਾਇਆ ਅਤੇ ਇਸ ਕਾਰਣ ਕੀੜਾ ਮਰ ਗਿਆ । ਰਾਹੁਲ ਨੇ ਇੱਕ ਬਿਲਕੁਲ ਨਵਾਂ ਤਰਕ ਪੇਸ਼ ਕਰਦਿਆਂ ਹੋਇਆਂ ਕਿਹਾ ਕਿ ਦੋਨਾਂ ਨੇ ਮੋਟਰਕਾਰ ਅਤੇ ਕੀੜੇ ਦੇ ਬਰਾਬਰ ਬਲ ਮਹਿਸੂਸ ਕੀਤਾ ਅਤੇ ਦੋਨਾਂ ਵਿੱਚ ਸੰਵੇਗ ਦਾ ਪਰਿਵਰਤਨ ਵੀ ਬਰਾਬਰ ਹੋਇਆ । ਇਹਨਾਂ ਵਿਚਾਰਾਂ ‘ਤੇ ਆਪਣੀ ਪ੍ਰਤੀਕਿਰਿਆ ਦਿਓ ।
ਉੱਤਰ-
ਰਾਹੁਲ ਦਾ ਤਰਕ ਸਹੀ ਹੈ । ਗਤੀ ਦੇ ਤੀਸਰੇ ਨਿਯਮ ਅਨੁਸਾਰ ਕਿਰਿਆ ਅਤੇ ਪ੍ਰਤਿਕਿਰਿਆ ਬਰਾਬਰ ਹੁੰਦੇ ਹਨ । ਇਸ ਲਈ ਦੋਨਾਂ-ਕਾਰ ਅਤੇ ਕੀੜੇ ਤੇ ਸਮਾਨ ਬਲ ਲਗੇਗਾ ਅਤੇ ਦੋਨਾਂ ਵਿੱਚ ਸਮਾਨ ਸੰਵੇਗ ਪਰਿਵਰਤਨ ਹੋਵੇਗਾ । ਹੁਣ ਕੀੜੇ ਦਾ ਪੁੰਜ ਕਾਰ ਦੇ ਪੁੰਜ ਨਾਲੋਂ ਬਹੁਤ ਹੀ ਘੱਟ ਹੈ, ਇਸ ਲਈ ਕੀੜੇ ਵਿੱਚ ਹੋਇਆ ਸੰਵੇਗ ਪਰਿਵਰਤਨ ਸਾਫ਼ ਦਿਖਾਈ ਦਿੰਦਾ ਹੈ । ਜਤਾ ਘੱਟ ਹੋਣ ਕਾਰਨ ਕੀੜਾ ਮਰ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 18.
10 ਕਿਲੋਗ੍ਰਾਮ ਪੰਜ ਵਾਲੀ ਇੱਕ ਘੰਟੀ ਫ਼ਰਸ਼ ਨੂੰ ਕਿੰਨਾ ਸੰਵੇਗ ਸਥਾਨਾਂਤਰਿਤ ਕਰੇਗੀ ਜਦੋਂ ਇਹ 80cm ਦੀ ਉੱਚਾਈ ਤੋਂ ਥੱਲੇ ਵੱਲ ਨੂੰ ਡਿੱਗਦੀ ਹੈ । ਇਸਦਾ ਥੱਲੇ ਵੱਲ ਡਿੱਗਦਿਆਂ ਹੋਇਆਂ ਵੇਗ ਦਾ ਮਾਨ 10ms^-2 ਲੈ, ਲਓ ?
ਹੱਲ:
ਇੱਥੇ, ਘੰਟੀ ਦਾ ਪੁੰਜ (m) = 10kg
ਆਰੰਭਿਕ ਵੇਗ (u) = 0
ਤੈਅ ਕੀਤੀ ਗਈ ਦੁਰੀ (S) = 80cm = 0.80m
ਘੰਟੀ ਦਾ ਪ੍ਰਵੇਗ (a) = 10ms^-2
ਮੰਨ ਲਉ ਘੰਟੀ ਦਾ ਧਰਤੀ ‘ਤੇ ਪਹੁੰਚ ਕੇ ਵੇਗ υ ਹੈ
υ² – u² = 2aS ਦੀ ਵਰਤੋਂ ਮਗਰੋਂ
υ² – (0)² = 2 × 10 × 0.80
υ² = 16
∴ υ = \(\sqrt{16}\)
∴ ਘੰਟੀ ਦਾ ਅੰਤਿਮ ਵੇਗ, υ = 4ms^-1
ਘੰਟੀ ਦੁਆਰਾ ਧਰਤੀ ਨੂੰ ਸਥਾਨਾਂਤਰਿਤ ਕੀਤੇ ਗਏ ਸੰਵੇਗ ਦਾ ਮਾਨ
p = mυ
= 10 × 4
= 40kg ms^-1

ਅਤਿਰਿਕਤ ਅਭਿਆਸ (Additional Exercises)

ਪ੍ਰਸ਼ਨ A1.
ਇਕ ਵਸਤੂ ਦਾ ਗਤੀ ਦੀ ਅਵਸਥਾ ਵਿੱਚ ਦੂਰੀ-ਸਮਾਂ ਸਾਰਣੀ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਹੈ-

ਸਮਾਂ (ਸੈਕਿੰਡ)	ਦੂਰੀ (ਮੀਟਰ)
0	0
1	1
2	8
3	27
4	64
5	125
6	216

(a) ਪ੍ਰਵੇਗ ਦੇ ਬਾਰੇ ਤੁਸੀਂ ਕੀ ਸਿੱਟਾ ਕੱਢ ਸਕਦੇ ਹੋ ਕਿ ਇਹ ਸਥਿਰ ਹੈ, ਵੱਧ ਰਿਹਾ ਹੈ, ਘੱਟ ਰਿਹਾ ਹੈ ਜਾਂ ਸਿਫ਼ਰ ਹੈ ?
(b) ਤੁਸੀਂ ਵਸਤੂ ‘ਤੇ ਲੱਗਣ ਵਾਲੇ ਬਲ ਬਾਰੇ ਕੀ ਸਿੱਟਾ ਕੱਢ ਸਕਦੇ ਹੋ ?
ਹੱਲ:

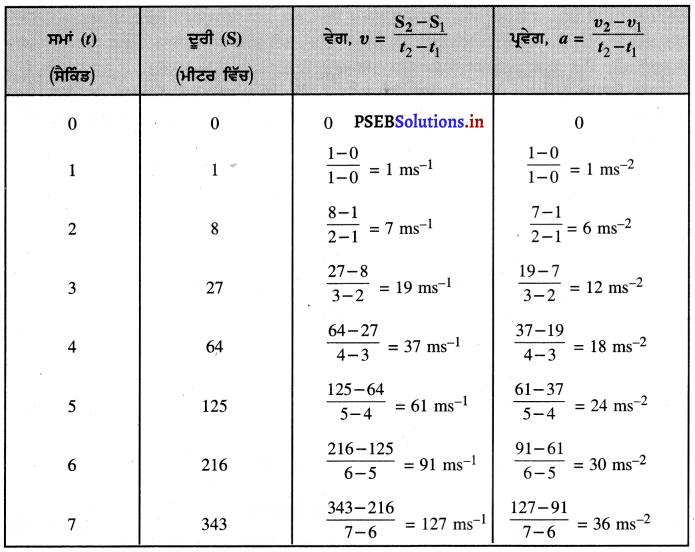
(a) ਉੱਪਰ ਦਿੱਤੀ ਗਈ ਸਾਰਣੀ ਦਰਸਾਉਂਦੀ ਹੈ ਕਿ ਗਤੀ ਪ੍ਰਵੇਗਿਤ ਹੈ ਅਤੇ ਵੇਗ ਸਮੇਂ ਨਾਲ ਸਮਾਨ ਰੂਪ ਨਾਲ ਵੱਧ ਜਾਂਦਾ ਹੈ ।
(b) ਕਿਉਂਕਿ ਵੇਗ ਇੱਕ ਸਮਾਨ ਵੱਧ ਰਿਹਾ ਹੈ, ਇਸ ਲਈ ਵਸਤੁ ’ਤੇ ਲੱਗ ਰਿਹਾ ਬਲ ਵੀ ਸਮੇਂ ਨਾਲ ਵੱਧ ਰਿਹਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ A2.
1200 kg ਪੁੰਜ ਵਾਲੀ ਕਾਰ ਨੂੰ ਇੱਕ ਸਮਤਲ ਸੜਕ ਤੇ ਦੋ ਵਿਅਕਤੀ ਸਮਾਨ ਵੇਗ ਨਾਲ ਧੱਕਾ ਦਿੰਦੇ ਹਨ । ਉਸੀ ਕਾਰ ਨੂੰ ਤਿੰਨ ਵਿਅਕਤੀਆਂ ਦੁਆਰਾ ਧੱਕਾ ਦੇ ਕੇ 0.2ms^-2 ਦਾ ਵੇਗ ਪੈਦਾ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਹਰੇਕ ਵਿਅਕਤੀ ਕਾਰ ਨੂੰ ਕਿੰਨੇ ਬਲ ਨਾਲ ਧੱਕਾ ਲਗਾਉਂਦਾ ਹੈ । (ਮੰਨ ਲਉ ਕਿ ਸਾਰੇ ਵਿਅਕਤੀ ਸਮਾਨ ਪੇਸ਼ੀ ਬਲ ਨਾਲ ਕਾਰ ਨੂੰ ਧੱਕਾ ਦਿੰਦੇ ਹਨ ।
ਹੱਲ :
ਇੱਥੇ ਕਾਰ ਦਾ ਪੁੰਜ (m) = 1200kg
| ਕਾਰ ਦਾ ਪ੍ਰਵੇਗ , (a) = 0.2ms^-2
ਪਹਿਲੇ ਦੋ ਵਿਅਕਤੀਆਂ ਦੇ ਧੱਕਾ ਦੇਣ ਕਾਰਣ ਵੇਗ = 0
ਸਪੱਸ਼ਟ ਹੈ ਕਿ ਜਦੋਂ ਤੀਜਾ ਵਿਅਕਤੀ ਕਾਰ ਨੂੰ ਧੱਕਾ ਲਗਾਉਂਦਾ ਹੈ, ਤਾਂ ਇਕ ਅਸੰਤੁਲਿਤ ਬਲ ਕਿਰਿਆ ਕਰਦਾ ਹੈ ।
∴ ਤੀਜੇ ਵਿਅਕਤੀ ਦੁਆਰਾ ਲਗਾਇਆ ਗਿਆ ਬਲ, F = m × a
= 1200 × 0.2
= 240N
ਹੁਣ ਕਿਉਂਕਿ ਤਿੰਨੋਂ ਵਿਅਕਤੀ ਕਾਰ ਨੂੰ ਪੱਠਿਆਂ ਦਾ ਬਲ ਲਗਾ ਕੇ ਕਾਰ ਨੂੰ ਧੱਕਦੇ ਹਨ, ਇਸ ਲਈ ਹਰੇਕ ਵਿਅਕਤੀ ਬਲ ਲਗਾਉਂਦਾ ਹੈ = 24ON

ਪ੍ਰਸ਼ਨ A3.
500 ਪੁੰਜ ਵਾਲਾ ਇੱਕ ਹਥੌੜਾ 50ms^-1, ਦੇ ਵੇਗ ਨਾਲ ਗਤੀਮਾਨ ਹੋ ਕੇ, ਇੱਕ ਕਿੱਲ ‘ਤੇ ਮਾਰਿਆ ਜਾਂਦਾ ਹੈ । ਕਿੱਲ, ਹਥੌੜੇ ਨੂੰ ਬਹੁਤ ਥੋੜ੍ਹੇ ਸਮੇਂ 0.015 s ਵਿੱਚ ਰੋਕ ਦਿੰਦਾ ਹੈ । ਕਿੱਲ ਦੁਆਰਾ ਹਥੌੜੇ ‘ਤੇ ਲਗਾਇਆ ਗਿਆ ਬਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਹਥੌੜੇ ਦਾ ਪੁੰਜ (m) = 500 g
= \(\frac{500}{1000}\) kg
= \(\frac{1}{2}\) kg
ਮੁੱਢਲਾ ਵੇਗ (u) = 50ms^-1
ਅੰਤਿਮ ਵੇਗ (υ) = 0 ms^-1
ਸਮਾਂ (t) = 0.01s
ਬਲ (F) = ?
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ, υ = u + at
0 = 50 + a × 0.01
-50 = a × \(\frac{1}{100}\)
a = -50 × 100
= -5000 ms^-2
(ਰਿਣਾਤਮਕ ਚਿੰਨ੍ਹ ਮੰਦਨ ਨੂੰ ਦਰਸਾਉਂਦਾ ਹੈ )
ਹੁਣ (F) = m × a
= \(\frac{1}{2}\) × -5000
= -2500N
∴ ਕਿੱਲ ਦੁਆਰਾ ਹਥੌੜੇ ‘ਤੇ ਲਗਾਇਆ ਬਲ = -2500N

ਪ੍ਰਸ਼ਨ A4.
ਇੱਕ 1200kg ਪੁੰਜ ਵਾਲੀ ਕਾਰ 90km/h ਦੇ ਵੇਗ ਨਾਲ ਇੱਕ ਸਰਲ ਰੇਖਾ ਵਿੱਚ ਚਲ ਰਹੀ ਹੈ । ਉਸਦਾ ਵੇਗ ਬਾਹਰੀ ਅਸੰਤੁਲਿਤ ਬਲ ਲੱਗਣ ਦੇ ਕਾਰਨ 4s ਵਿੱਚ ਘੱਟ ਕੇ 18km/h ਹੋ ਜਾਂਦਾ ਹੈ । ਵੇਗ ਅਤੇ ਸੰਵੇਗ ਵਿੱਚ ਪਰਿਵਰਤਨ ਪਤਾ ਕਰੋ । ਲੱਗਣ ਵਾਲੇ ਬਲ ਦੀ ਮਾਤਰਾ ਵੀ ਪਤਾ ਕਰੋ ।
ਹੱਲ : ਇੱਥੇ, ਕਾਰ ਦਾ ਪੁੰਜ (m) = 1200kg
ਸਮਾਂ (t) = 4s
ਕਾਰ ਦਾ ਮੁੱਢਲਾ ਵੇਗ (u) = 90km/h
= \(\frac{90 \times 1000}{60 \times 60}\) ms^-1
= 25 ms^-1
ਕਾਰ ਦਾ ਅੰਤਿਮ ਵੇਗ (υ) = 18km/h
= \(\frac{18 \times 1000}{60 \times 60}\)
= 5ms^-1
ਕਾਰ ਦਾ ਵੇਗ (a) = ?
ਕਾਰ ਦੇ ਸੰਵੇਗ ਵਿੱਚ ਪਰਿਵਰਤਨ = ?
ਕਾਰ ਤੇ ਲੱਗਣ ਵਾਲੇ ਬਲ ਦਾ ਪਰਿਮਾਣ (F) = ?
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ, υ = u + at
5 = 25 + a × 4
-20 = 4a
a = \(\frac{-20}{4}\)
= -5 ms^-2
ਕਾਰ ਦੇ ਸੰਵੇਗ ਵਿੱਚ ਪਰਿਵਰਤਨ = ਅੰਤਿਮ ਸੰਵੇਗ – ਮੁੱਢਲਾ ਸੰਵੇਗ
= mυ – mu
= m (υ – u)
= 1200 (5 – 25)
= 1200 × (-20)
= -2400 kg ms^-1
= 2400kg ms^-1 ਦੀ ਘਾਟ
F = m × a
= 1200 × 5
= 6000N

ਪ੍ਰਸ਼ਨ A5.
ਇੱਕ ਟਰੱਕ ਅਤੇ ਇੱਕ ਕਾਰ ਦਾ ਵੇਗ ਨਾਲ ਗਤੀਸ਼ੀਲ ਹਨ । ਦੋਨੋਂ ਇੱਕ-ਦੂਜੇ ਨਾਲ ਆਹਮਣੇ-ਸਾਹਮਣੇ ਟਕਰਾਉਂਦੇ ਹਨ ਅਤੇ ਕੁੱਝ ਸਮੇਂ ਬਾਅਦ ਦੋਨੋਂ ਰੁਕ ਜਾਂਦੇ ਹਨ | ਜੇਕਰ ਟਰੱਕ ਦਾ ਸਮਾਂ ਅੰਤਰਾਲ 1s ਹੈ, ਤਾਂ
(a) ਕਿਹੜੀ ਗੱਡੀ ‘ਤੇ ਬਲ ਦਾ ਪ੍ਰਭਾਵ ਸਭ ਤੋਂ ਜ਼ਿਆਦਾ ਪਵੇਗਾ ?
(b) ਕਿਹੜੀ ਗੱਡੀ ਦੇ ਸੰਵੇਗ ਵਿੱਚ ਪਰਿਵਰਤਨ ਸਭ ਤੋਂ ਜ਼ਿਆਦਾ ਹੋਵੇਗਾ ?
(c) ਕਿਸ ਗੱਡੀ ਦਾ ਵੇਗ ਸਭ ਤੋਂ ਜ਼ਿਆਦਾ ਹੋਵੇਗਾ ?
(d) ਟਰੱਕ ਦੀ ਬਜਾਏ ਕਾਰ ਨੂੰ ਜ਼ਿਆਦਾ ਨੁਕਸਾਨ ਕਿਉਂ ਹੋਵੇਗਾ ?
ਉੱਤਰ-
(a) ਦੋਨੋਂ ਗੱਡੀਆਂ ‘ਤੇ ਬਰਾਬਰ ਬਲ ਲੱਗੇਗਾ ਕਿਉਂਕਿ ਕਿਰਿਆ ਅਤੇ ਪ੍ਰਤੀਕਿਰਿਆ ਦੋਨੋਂ ਬਰਾਬਰ ਹੁੰਦੇ ਹਨ । ਹੁਣ ਕਿਉਂਕਿ ਕਾਰ ਦਾ ਪੁੰਜ ਘੱਟ ਹੈ ਇਸ ਲਈ ਕਾਰ ‘ਤੇ ਜ਼ਿਆਦਾ ਪ੍ਰਭਾਵ ਪਵੇਗਾ ।
(b) ਕਿਉਂਕਿ ਕਿਰਿਆ ਅਤੇ ਪ੍ਰਤੀਕਿਰਿਆ ਸਮਾਨ ਹੁੰਦੀ ਹੈ ਅਤੇ ਇਹ ਸੰਵੇਗ ਦਾ ਪਰਿਵਰਤਨ ਹੁੰਦਾ ਹੈ । ਇਸ ਲਈ ਕਾਰ ਅਤੇ ਟਰੱਕ ਦੋਨਾਂ ਦੇ ਸੰਵੇਗ ਵਿੱਚ ਪਰਿਵਰਤਨ ਬਰਾਬਰ ਹੋਵੇਗਾ ।
(c) ਕਾਰ ਦਾ ਪ੍ਰਵੇਗ ਜ਼ਿਆਦਾ ਹੋਵੇਗਾ ਕਿਉਂ ਜੋ ਇਸ ਦਾ ਪੁੰਜ ਟਰੱਕ ਨਾਲੋਂ ਘੱਟ ਹੈ ।
(d) ਕਾਰ ਦੀ ਘੱਟ ਜੜ੍ਹਤਾ ਕਾਰਨ ਇਸ ਨੂੰ ਜ਼ਿਆਦਾ ਨੁਕਸਾਨ ਹੋਵੇਗਾ ।

Science Guide for Class 9 PSEB ਬਲ ਅਤੇ ਗਤੀ ਦੇ ਨਿਯਮ InText Questions and Answers

ਪਾਠ-ਪੁਸਤਕ ਦੇ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਉੱਤਰ

ਪ੍ਰਸ਼ਨ 1.
ਨਿਮਨ ਵਿੱਚੋਂ ਕਿਸ ਦੀ ਜਤਾ ਜ਼ਿਆਦਾ ਹੈ ?
(a) ਇੱਕ ਰਬੜ ਦੀ ਗੇਂਦ ਅਤੇ ਉਸੀ ਆਕਾਰ ਦਾ ਪੱਥਰ ।
(b) ਇੱਕ ਸਾਈਕਲ ਅਤੇ ਇੱਕ ਰੇਲਗੱਡੀ ।
(c) ਪੰਜ ਰੁਪਏ ਦਾ ਇੱਕ ਸਿੱਕਾ ਅਤੇ ਇੱਕ ਰੁਪਏ ਦਾ ਸਿੱਕਾ ।
ਉੱਤਰ-
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ ਕਿ ਕਿਸੇ ਵਸਤੂ ਦਾ ਪੁੰਜ ਉਸ ਦੀ ਜੜ੍ਹਤਾ ਦਾ ਮਾਪ ਹੈ, ਇਸ ਲਈ ਜਿਸ ਵਸਤੁ ਦਾ ਪੁੰਜ ਜ਼ਿਆਦਾ ਹੋਵੇਗਾ ਉਸ ਵਸਤੂ ਦੀ ਜੜਤਾ ਵੱਧ ਹੋਵੇਗੀ ।
(a) ਗੇਂਦ ਦੇ ਆਕਾਰ ਦੇ ਪੱਥਰ ਦੀ ਜੜਤਾ ਵੱਧ ਹੈ ਕਿਉਂਕਿ ਇਸ ਦਾ ਪੁੰਜ ਗੇਂਦ ਦੇ ਪੁੰਜ ਨਾਲੋਂ ਜ਼ਿਆਦਾ ਹੈ ।
(b) ਇੱਕ ਰੇਲ ਗੱਡੀ ਦਾ ਪੁੰਜ ਸਾਈਕਲ ਦੇ ਪੁੰਜ ਨਾਲੋਂ ਜ਼ਿਆਦਾ ਹੈ ਜਿਸ ਕਰਕੇ ਰੇਲ ਗੱਡੀ ਦੀ ਜਤਾ ਵੱਧ ਹੈ ।
(c) ਪੰਜ ਰੁਪਏ ਦੇ ਸਿੱਕੇ ਦੀ ਜੜ੍ਹਤਾ ਇੱਕ ਰੁਪਏ ਦੇ ਸਿੱਕੇ ਨਾਲੋਂ ਵੱਧ ਹੈ ਕਿਉਂਕਿ ਪੰਜ ਰੁਪਏ ਦੇ ਸਿੱਕੇ ਦਾ ਪੁੰਜ ਇੱਕ ਰੁਪਏ ਦੇ ਸਿੱਕੇ ਨਾਲੋਂ ਜ਼ਿਆਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਥੱਲੇ ਦਿੱਤੇ ਗਏ ਉਦਾਹਰਨ ਵਿੱਚ ਗੇਂਦ ਦਾ ਵੇਗ ਕਿੰਨੀ ਵਾਰ ਬਦਲਦਾ ਹੈ ? ਜਾਣਨ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰੋ ।
“ਫੁਟਬਾਲ ਦਾ ਇੱਕ ਖਿਡਾਰੀ ਗੇਂਦ ਨੂੰ ਠੋਕਰ ਮਾਰ ਕੇ/ਕਿੱਕ ਲਗਾ ਕੇ ਗੇਂਦ ਨੂੰ ਆਪਣੀ ਟੀਮ ਦੇ ਦੂਜੇ ਖਿਡਾਰੀ ਦੇ ਕੋਲ ਪਹੁੰਚਾਉਂਦਾ ਹੈ । ਦੂਜਾ ਖਿਡਾਰੀ ਉਸ ਗੇਂਦ ਨੂੰ ਕਿੱਕ ਲਗਾ ਕੇ ਗੋਲ ਵੱਲ ਪਹੁੰਚਣ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰਦਾ ਹੈ । ਵਿਰੋਧੀ ਟੀਮ ਦਾ ਗੋਲਕੀਪਰ (ਗੋਲਚੀ ਗੇਂਦ ਨੂੰ ਪਕੜਦਾ ਹੈ ਅਤੇ ਆਪਣੀ ਟੀਮ ਦੇ ਖਿਡਾਰੀ ਵੱਲ ਕਿੱਕ ਠੋਕਰ ਲਗਾਉਂਦਾ ਹੈ।” ਇਸ ਦੇ ਨਾਲ ਹੀ ਉਸ ਕਾਰਣ ਦੀ ਪਹਿਚਾਣ ਕਰੋ ਜੋ ਹਰੇਕ ਅਵਸਥਾ ਵਿੱਚ ਬਲ ਪ੍ਰਦਾਨ ਕਰਦਾ ਹੈ ।
ਉੱਤਰ-
ਧੱਕਾ ਮਾਰਨਾ (ਠੋਕਰ ਮਾਰ), ਖਿੱਚਣਾ ਆਦਿ ਇਹ ਸਾਰੀਆਂ ਕਿਰਿਆਵਾਂ ਵਸਤੂ ਦੇ ਵੇਗ ਦੀ ਮਾਤਰਾ ਬਦਲਣ ਜਾਂ ਗਤੀ ਦੀ ਦਿਸ਼ਾ ਬਦਲਣ ਲਈ ਬਲ ਦੇ ਰੂਪ ਵਿੱਚ ਕੰਮ ਕਰਦੀਆਂ ਹਨ । ਇਸ ਲਈ ਉੱਪਰ ਦਿੱਤੀ ਉਦਾਹਰਨ ਵਿੱਚ ਗੇਂਦ ਦਾ ਵੇਗ ਤਿੰਨ ਵਾਰੀ ਬਦਲਿਆ ਹੈ-

1. ਪਹਿਲੀ ਵਾਰ ਪਹਿਲੀ ਟੀਮ ਦੇ ਫੁੱਟਬਾਲ ਖਿਡਾਰੀ ਨੇ ਗੇਂਦ ਨੂੰ ਕਿੱਕ ਮਾਰ ਕੇ ਗੇਂਦ ਦਾ ਵੇਗ ਬਦਲਿਆ ਹੈ ।
2. ਦੂਜੀ ਵਾਰ ਉਸੇ ਟੀਮ ਦੇ ਹੋਰ ਖਿਡਾਰੀ ਨੇ ਫੁੱਟਬਾਲ ਨੂੰ ਕਿੱਕ ਮਾਰ ਕੇ ਗੇਂਦ ਦਾ ਵੇਗ ਬਦਲਿਆ ਹੈ ।
3. ਤੀਸਰੀ ਵਾਰ ਵਿਰੋਧੀ ਟੀਮ ਦੇ ਗੋਲਚੀ ਨੇ ਫੁੱਟਬਾਲ ਨੂੰ ਕਿੱਕ ਲਗਾ ਕੇ ਗੇਂਦ ਦੇ ਵੇਗ ਵਿੱਚ ਪਰਿਵਰਤਨ ਕੀਤਾ ਹੈ । ਬਲ ਲਗਾਉਣ ਵਾਲੇ ਕਾਰਕ ਨੂੰ ਮੋਟਿਆਂ ਅੱਖਰਾਂ ਵਿੱਚ ਲਿਖਿਆ ਗਿਆ ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਕਿਸੇ ਰੁੱਖ ਦੀਆਂ ਟਾਹਣੀਆਂ ਨੂੰ ਤੇਜ਼ੀ ਨਾਲ ਹਿਲਾਉਣ ਨਾਲ ਕੁੱਝ ਪੱਤੀਆਂ ਝੜ ਜਾਂਦੀਆਂ ਹਨ । ਕਿਉਂ ?
ਉੱਤਰ-
ਟਾਹਣੀਆਂ ਨੂੰ ਹਿਲਾਉਣ ਤੋਂ ਪਹਿਲਾਂ ਟਹਿਣੀਆਂ ਅਤੇ ਪੱਤੇ ਦੋਨੋਂ ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਸਨ । ਹਿਲਾਉਣ ਨਾਲ ਟਾਹਣੀਆਂ ਗਤੀ ਵਿੱਚ ਆ ਗਈਆਂ ਜਦੋਂ ਕਿ ਪੱਤੀਆਂ ਵਿਰਾਮ ਜੜ੍ਹਤਾ ਕਾਰਨ ਟਾਹਣੀਆਂ ਤੋਂ ਵੱਖ ਹੋ ਕੇ ਹੇਠਾਂ ਡਿੱਗ ਜਾਂਦੀਆਂ ਹਨ ।

ਪ੍ਰਸ਼ਨ 4.
ਜਦੋਂ ਕੋਈ ਗਤੀਮਾਨ ਬੱਸ ਅਚਾਨਕ ਰੁੱਕ ਜਾਂਦੀ ਹੈ, ਤਾਂ ਤੁਸੀਂ ਅੱਗੇ ਵੱਲ ਨੂੰ ਡਿੱਗਦੇ ਹੋ ਅਤੇ ਜਦੋਂ ਵਿਰਾਮ ਅਵਸਥਾ ਤੋਂ ਪ੍ਰੇਰਿਤ ਹੁੰਦੀ ਹੈ, ਤਾਂ ਪਿੱਛੇ ਵੱਲ ਡਿੱਗਦੇ ਹੋ ? ਕਿਉਂ ?
ਉੱਤਰ-
ਜਦੋਂ ਗਤੀਮਾਨ ਬੱਸ ਅਚਾਨਕ ਰੁਕਦੀ ਹੈ, ਤਾਂ ਸਾਡੇ ਸਰੀਰ ਦਾ ਹੇਠਲਾ ਭਾਗ ਬੱਸ ਦੇ ਸੰਪਰਕ ਵਿੱਚ ਹੋਣ ਕਰਕੇ ਬੱਸ ਦੇ ਨਾਲ ਹੀ ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਆ ਜਾਂਦਾ ਹੈ ਜਦੋਂਕਿ ਸਾਡੇ ਸਰੀਰ ਦਾ ਉੱਪਰਲਾ ਭਾਗ ਗਤੀਮਾਨ ਰਹਿਣ ਦੀ ਪ੍ਰਵਿਰਤੀ ਰੱਖਦਾ ਹੈ । ਇਸ ਕਰਕੇ ਅਸੀਂ ਅੱਗੇ ਵੱਲ ਡਿੱਗਦੇ ਹਾਂ । ਜਦੋਂ ਬੱਸ ਅਚਾਨਕ ਵੇਗਤ ਹੁੰਦੀ ਹੈ, ਤਾਂ ਸਾਡੇ ਸਰੀਰ ਦਾ ਹੇਠਲਾ ਭਾਗ ਬੱਸ ਦੇ ਸੰਪਰਕ ਵਿੱਚ ਹੋਣ ਕਰਕੇ ਬੱਸ ਦੇ ਨਾਲ ਹੀ ਗਤੀਮਾਨ ਹੋ ਜਾਂਦਾ ਹੈ ਜਦਕਿ ਉੱਪਰਲਾ ਭਾਗ ਜੜ੍ਹਤਾ ਦੇ ਕਾਰਨ ਵਿਰਾਮ ਅਵਸਥਾ ਵਿੱਚ ਰਹਿਣ ਦੀ ਪ੍ਰਵਿਰਤੀ ਰੱਖਦਾ ਹੈ । ਇਸ ਲਈ ਅਸੀਂ ਪਿੱਛੇ ਵੱਲ ਡਿੱਗਦੇ ਹਾਂ ।

ਪ੍ਰਸ਼ਨ 5.
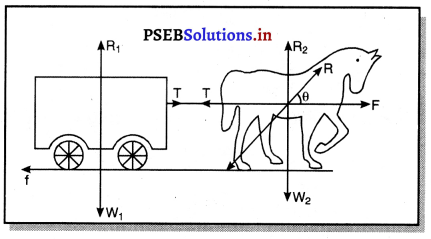
ਜੇਕਰ ਕਿਰਿਆ ਹਮੇਸ਼ਾਂ ਪ੍ਰਤੀਕਿਰਿਆ ਦੇ ਬਰਾਬਰ ਹੈ ਤਾਂ ਇਸ ਤੱਥ ਦੇ ਆਧਾਰ ‘ਤੇ ਵਿਆਖਿਆ ਕਰੋ ਕਿ ਘੋੜਾ, ਗੱਡੀ ਨੂੰ ਕਿਵੇਂ ਖਿੱਚ ਪਾਉਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਨਿਊਟਨ ਦੇ ਗਤੀ ਦੇ ਤੀਸਰੇ ਨਿਯਮ ਅਨੁਸਾਰ, ”ਕਿਰਿਆ ਅਤੇ ਪ੍ਰਤੀਕਿਰਿਆ ਹਮੇਸ਼ਾਂ ਬਰਾਬਰ ਅਤੇ ਵਿਪਰੀਤ ਦਿਸ਼ਾ ਵਿੱਚ ਹੁੰਦੇ ਹਨ | ਘੋੜਾ, ਗੱਡੀ ਨੂੰ ਬਲ (ਕਿਰਿਆ) ਲਗਾ ਕੇ ਅੱਗੇ ਵੱਲ ਖਿੱਚਦਾ ਹੈ । ਗੱਡੀ ਵੀ ਘੋੜੇ ਨੂੰ ਬਲ ਪ੍ਰਤੀਕਿਰਿਆ) ਲਗਾ ਕੇ ਪਿੱਛੇ ਵੱਲ ਖਿੱਚਦੀ ਹੈ । ਇਹ ਦੋਨੋਂ ਬਲ ਇੱਕ-ਦੂਜੇ ਨੂੰ ਸੰਤੁਲਿਤ ਕਰ ਦਿੰਦੇ ਹਨ । ਜਦੋਂ ਘੋੜਾ ਗੱਡੀ ਨੂੰ ਖਿੱਚਦਾ ਹੈ ਤਾਂ ਉਹ ਆਪਣੇ ਪੈਰਾਂ ਨਾਲ ਧਰਤੀ ਨੂੰ ਪਿਛਾਂਹ ਵੱਲ ਧੱਕਦਾ ਹੈ । ਧਰਤੀ ਦੀ ਪ੍ਰਤੀਕਿਰਿਆ ਉੱਪਰ ਵੱਲ ਕਾਰਜ ਕਰਦੀ । ਪ੍ਰਤੀਕਿਰਿਆ ਬਲ ਦੋ ਭਾਗਾਂ ਵਿੱਚ ਵੰਡਿਆ ਜਾਂਦਾ ਹੈ ।ਉੱਪਰ ਵੱਲ ਲੰਬਵਤ ਦਿਸ਼ਾ ਵਿੱਚ ਲੱਗਣ ਵਾਲਾ ਪ੍ਰਤੀਕਿਰਿਆਤਮਕ ਬਲ ਘੋੜੇ ਦੇ ਭਾਰ ਨੂੰ ਸੰਤੁਲਿਤ ਕਰਦਾ ਹੈ ਜਦ ਕਿ ਪ੍ਰਤੀਕਿਰਿਆਤਮਕ ਬਲ ਦਾ ਖਿਤਿਜੀ ਘਟਕ ਗੱਡੀ ਨੂੰ ਅੱਗੇ ਵੱਲ ਗਤੀਮਾਨ ਕਰ ਦਿੰਦਾ ਹੈ । ਧਰਤੀ ਅਤੇ ਪਹੀਆਂ ਵਿਚਕਾਰ ਰਗੜ ਬਲ ਪਿੱਛੇ ਵੱਲ ਲੱਗਦਾ ਹੈ ਪਰੰਤੂ ਅੱਗੇ ਵਾਲੀ ਦਿਸ਼ਾ ਵਿੱਚ ਲੱਗਣ ਵਾਲਾ ਬਲ ਰਗੜ ਬਲ ਨਾਲੋਂ ਜ਼ਿਆਦਾ ਹੁੰਦਾ ਹੈ ਜਿਸ ਕਰਕੇ ਉਹ ਗੱਡੀ ਨੂੰ ਗਤੀਸ਼ੀਲ ਕਰਨ ਵਿੱਚ ਕਾਮਯਾਬ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 6.
ਇੱਕ ਅੱਗ ਬੁਝਾਉਣ ਵਾਲੇ ਕਰਮਚਾਰੀ ਨੂੰ ਤੇਜ਼ ਗਤੀ ਨਾਲ ਬਹੁਤ ਜ਼ਿਆਦਾ ਮਾਤਰਾ ਵਿੱਚ ਪਾਣੀ ਸੁੱਟਣ ਵਾਲੀ ਰਬੜ ਦੀ ਨਲੀ ਨੂੰ ਪਕੜਨ ਵਿੱਚ ਮੁਸ਼ਕਿਲ ਕਿਉਂ ਆਉਂਦੀ ਹੈ ? ਸਪੱਸ਼ਟ ਕਰਦਿਆਂ ਸਮਝਾਉ ।
ਉੱਤਰ-
ਰਬੜ ਦੀ ਨਲੀ ਵਿੱਚੋਂ ਪਾਣੀ ਬਹੁਤ ਜ਼ਿਆਦਾ ਬਲ (ਕਿਰਿਆ) ਨਾਲ ਬਾਹਰ ਨਿਕਲਦਾ ਹੈ ਅਤੇ ਓਨੇ ਹੀ ਬਲ ਪ੍ਰਤੀਕਿਰਿਆ) ਨੂੰ ਅੱਗ ਬੁਝਾਉਣ ਵਾਲੇ ਕਰਮਚਾਰੀ ਦਾ ਹੱਥ ਅਨੁਭਵ ਕਰਦਾ ਹੈ । ਇਸ ਲਈ ਉਸ ਨੂੰ ਰਬੜ ਦੀ ਨਲੀ ਨੂੰ ਪਕੜਨ ਵਿੱਚ ਮੁਸ਼ਕਿਲ ਹੁੰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 7.
ਇੱਕ 50g ਪੁੰਜ ਦੀ ਗੋਲੀ 4kg ਪੁੰਜ ਦੀ ਬੰਦੂਕ (ਰਾਇਫ਼ਲ) ਤੋਂ 35 ms-1 ਦੇ ਮੁੱਢਲੇ ਵੇਗ ਨਾਲ ਛੱਡੀ ਜਾਂਦੀ ਹੈ । ਬੰਦੂਕ ਦੇ ਆਰੰਭਿਕ) ਮੁੱਢਲੇ ਪਿੱਛੇ ਵੱਲ ਨੂੰ ਲਗ ਰਹੇ ਵੇਗ ਦਾ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਗੋਲੀ ਦਾ ਪੁੰਜ (m₁ ) = 50g = 0.05kg
ਰਾਇਫ਼ਲ ਦਾ ਪੁੰਜ (m₂ ) = 4kg
ਗੋਲੀ ਦਾ ਮੁੱਢਲਾ ਵੇਗ (u₁ ) = 0
ਰਾਇਫ਼ਲ ਦਾ ਮੁੱਢਲਾ ਵੇਗ (u₂ ) = 0
ਗੋਲੀ ਦਾ ਅੰਤਿਮ ਵੇਗ (υ₁ ) = 35 ms^-1
ਰਾਇਫ਼ਲ ਦਾ ਅੰਤਿਮ ਵੇਗ (υ₂ ) = ?
ਸੰਵੇਗ ਦੇ ਸੁਰੱਖਿਅਣ ਨਿਯਮ ਅਨੁਸਾਰ,
ਗੋਲੀ ਅਤੇ ਰਾਇਫ਼ਲ ਦਾ ਕੁੱਲ ਮੁੱਢਲਾ ਸੰਵੇਗ = ਗੋਲੀ ਅਤੇ ਰਾਇਫ਼ਲ ਦਾ ਕੁੱਲ ਅੰਤਿਮ ਸੰਵੇਗ
m₁ u₁ + m₂ u₂ = m₁υ₁ + m₂υ₂
.05 × 0 + 4 × 0 = .05 × 35 + 4 × υ₂
0 + 0 = 1.75 +4 × υ₂
– 4 × υ₂ = 1.75
∴ υ₂ = –\(\frac{1.75}{4}\)
= – 0437 ms^-1
= – 0.44 ms^-1
ਰਿਣਾਤਮਕ ਚਿੰਨ੍ਹ ਇਹ ਦਰਸਾਉਂਦਾ ਹੈ ਕਿ ਰਾਇਫ਼ਲ ਦੇ ਵੇਗ ਦੀ ਦਿਸ਼ਾ ਗੋਲੀ ਦੇ ਵੇਗ ਦੀ ਦਿਸ਼ਾ ਦੇ ਵਿਪਰੀਤ ਹੈ ।

ਪ੍ਰਸ਼ਨ 8.
100g ਅਤੇ 200g ਪੁੰਜ ਦੀਆਂ ਦੋ ਵਸਤੂਆਂ ਇੱਕ ਹੀ ਰੇਖਾ ਵਿੱਚ ਅਤੇ ਇੱਕ ਹੀ ਦਿਸ਼ਾ ਵਿੱਚ ਕ੍ਰਮਵਾਰ 2ms^-1 ਅਤੇ 1 ms^-1 ਵੇਗ ਨਾਲ ਗਤੀ ਕਰ ਰਹੀਆਂ ਹਨ । ਦੋਨੋਂ ਵਸਤੂਆਂ ਟਕਰਾ ਜਾਂਦੀਆਂ ਹਨ ਟਕਰਾਉਣ ਤੋਂ ਬਾਅਦ ਪਹਿਲੀ ਵਸਤੂ ਦਾ ਵੇਗ 1.67 ms^-1 ਹੋ ਜਾਂਦਾ ਹੈ ਅਤੇ ਦੂਜੀ ਵਸਤੂ ਦਾ ਵੇਗ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਇੱਥੇ ਪਹਿਲੀ ਵਸਤੂ ਦਾ ਪੁੰਜ (m₁ ) = 100g = \(\frac{1}{10}\) kg
ਪਹਿਲੀ ਵਸਤੂ ਦਾ ਮੁੱਢਲਾ ਵੇਗ (u₁ ) = 2 ms^-1
ਦੂਜੀ ਵਸਤੂ ਦਾ ਪੁੰਜ (m₂ ) = 200g = \(\frac{1}{5}\) kg
ਦੂਜੀ ਵਸਤੂ ਦਾ ਮੁੱਢਲਾ ਵੇਗ (u₂ ) = 1 ms^-1

ਟਕਰਾਉਣ ਤੋਂ ਪਹਿਲਾਂ :
ਪਹਿਲੀ ਵਸਤੂ ਦਾ ਮੁੱਢਲਾ ਸੰਵੇਗ = : m₁ u₁
= \(\frac{1}{10}\) × 2
= \(\frac{1}{5}\) kg ms^-1
ਦੂਜੀ ਵਸਤੂ ਦਾ ਮੁੱਢਲਾ ਸੰਵੇਗ = m₂u₂ = \(\frac{1}{5}\) × 1
\(\frac{1}{5}\) kg ms^-1
ਦੋਨਾਂ ਵਸਤੂਆਂ ਦਾ ਕੁੱਲ ਮੁੱਢਲਾ ਸੰਵੇਗ (ਟਕਰਾਉਣ ਤੋਂ ਪਹਿ) = \(\frac{1}{5}\) + \(\frac{1}{5}\)
\(\frac{2}{5}\) kg ms^-1

ਟਕਰਾਉਣ ਤੋਂ ਬਾਅਦ
ਪਹਿਲੀ ਵਸਤੂ ਦਾ ਅੰਤਿਮ ਵੇਗ (υ₁ ) = 1.67 ms^-1
ਦੂਜੀ ਵਸਤੁ ਦਾ ਅੰਤਿਮ ਵੇਗ (υ₂ ) = ?
ਪਹਿਲੀ ਵਸਤੂ ਦਾ ਅੰਤਿਮ ਸੰਵੇਗ = m₁ υ₁
\(\frac{1}{10}\) × 1.67
= 0.167 kg ms^-1
ਦੂਜੀ ਵਸਤੂ ਦਾ ਅੰਤਿਮ ਸੰਵੇਗ = m₂ υ₂

ਸੰਵੇਗਾ ਸੁਰੱਖਿਅਣ ਨਿਯਮ ਅਨੁਸਾਰ, = \(\frac{1}{5}\)υ₂
ਦੋਨਾਂ ਵਸਤੂਆਂ ਦਾ ਟੱਕਰ ਤੋਂ ਪਹਿਲਾਂ ਕੁੱਲ ਸੰਵੇਗ = ਦੋਨਾਂ ਵਸਤੂਆਂ ਦਾ ਟੱਕਰ ਤੋਂ ਬਾਅਦ ਕੁੱਲ ਸੰਵੇਗ
\(\frac{2}{5}\) = 0.167 + \(\frac{1}{5}\) × υ₂
0.2 × υ₂ = 0.4 – 0.167 ms^-1
∴ υ₂ = 0.116 ms^-1