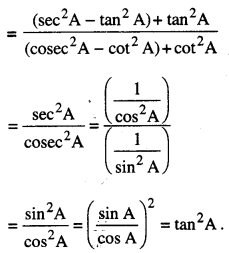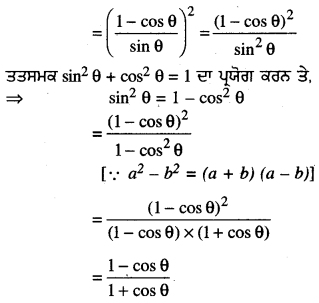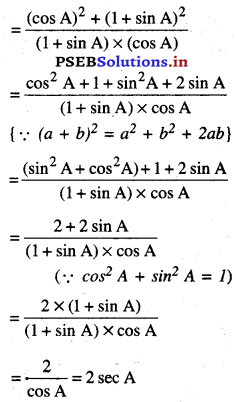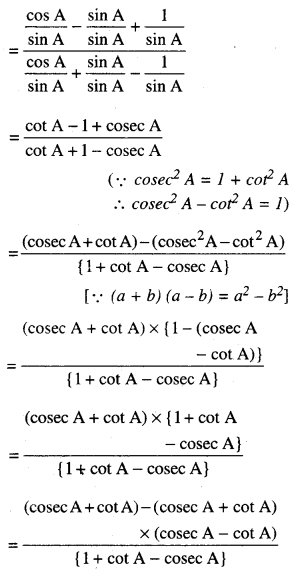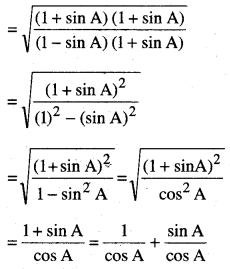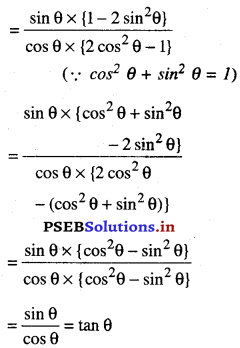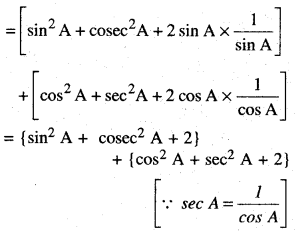Class 10

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 11 ਰਚਨਾਵਾਂ Ex 11.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 11 ਰਚਨਾਵਾਂ Exercise 11.1

ਹੇਠਾਂ ਦਿੱਤੇ ਵਿੱਚੋਂ ਹਰੇਕ ਦੇ ਲਈ ਰਚਨਾ ਦਾ ਸਪੱਸ਼ਟੀਕਰਣ ਵੀ ਦਿਓ :

ਪ੍ਰਸ਼ਨ 1.
7.6 cm ਲੰਬਾ ਇਕ ਰੇਖਾਖੰਡ ਖਿੱਚੋ ਅਤੇ ਇਸਨੂੰ 5 : 8 ਦੇ ਅਨੁਪਾਤ ਵਿਚ ਵੰਡੋ । ਦੋਨਾਂ ਭਾਗਾਂ ਨੂੰ ਮਾਪੋ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਇਕ 7.6 cm ਲੰਬਾ ਰੇਖਾਖੰਡ ਰਚਨਾ ਦੇ ਪਗ :
1. ਇਕ ਰੇਖਾਖੰਡ AB = 7.6 cm ਲਓ।
2. ਨਿਊਨ ਕੋਣ ∠BAX ਬਣਾਉਂਦੀ ਹੋਈ ਕੋਈ ਕਿਰਨ AX ਖਿੱਚੋ ।
3. ਕਿਰਨ AX ਉੱਤੇ 5 + 8 = 13 (ਦਿੱਤਾ ਗਿਆ | ਅਨੁਪਾਤ ਬਿੰਦੂ A₁, A₂, A₃, A₄, A₅……… A₁₁, A₁₂, A₁₃ ਇਸ ਤਰ੍ਹਾਂ ਅੰਕਿਤ ਕਰੋ ਕਿ A₁A₂ = A₂A₃ = A₃A₄ = ….. = A₁₂A₁₃ ਹੋਵੇ ।
4. BA₁₃ ਨੂੰ ਮਿਲਾਓ।
5. ਬਿੰਦੂ A₅, ਤੋਂ ਹੋ ਕੇ ਜਾਣ ਵਾਲੀ A₅C || A₁₃B (A₅ ਉੱਤੇ ∠AA₁₃B ਦੇ ਬਰਾਬਰ ਕੋਣ ਬਣਾਓ) AB ਨੂੰ ਇੱਕ ਬਿੰਦੂ “c’ ਤੇ ਕੱਟਦੀ ਹੋਈ ਰੇਖਾ ਖਿਚੋ ਤਾਂ AC : CB = 5 : 8

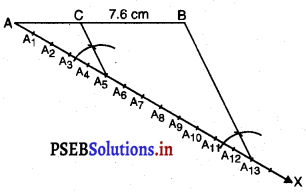
ਸਪੱਸ਼ਟੀਕਰਣ
ਆਓ ਅਸੀਂ ਦੇਖੀਏ ਕਿ ਇਹ ਵਿਧੀ ਕਿਵੇਂ ਸਾਨੂੰ ਲੋੜੀਂਦਾ ਵਿਭਾਜਨ ਦਿੰਦੀ ਹੈ।
△AA₁₃B ਵਿੱਚ
∴ A₅C || A₁₃B ਹੈ ।
∴ ਮੂਲ ਸਮਾਨ ਅਨੁਪਾਤਿਕਤਾ ਥਿਊਰਮ ਰਾਹੀਂ
\(\frac{\mathrm{AA}_{5}}{\mathrm{~A}_{5} \mathrm{~A}_{13}}\) = \(\frac{AC}{CB}\)
\(\frac{\mathrm{AA}_{5}}{\mathrm{~A}_{5} \mathrm{~A}_{13}}\) = \(\frac{5}{8}\)
∴ \(\frac{AC}{CB}\) = \(\frac{5}{8}\)
ਇਹ ਦਿਖਾਉਂਦਾ ਹੈ ਕਿ ‘C’, AB ਨੂੰ 5 : 8 ਦੇ ਅਨੁਪਾਤ ਵਿਚ ਵੰਡਦਾ ਹੈ ।
ਦੋਵੇਂ ਭਾਗ ਮਾਪਣ ਤੇ,
AC = 2.9 cm, CB = 47 cm
ਵੈਕਲਪਿਕ ਜਾਂ ਦੂਜੀ ਵਿਧੀ :
1. ਇਕ ਰੇਖਾਖੰਡ AB = 7.6 cm ਲਓ ।
2. ਇਕ ਨਿਊਨ ਕੋਣ ∠BAX ਖਿੱਚੋ ।
3. ∠ABY ਇਸ ਤਰ੍ਹਾਂ ਬਣਾਓ ਕਿ
∠ABY = ∠BAX.
4. ਬਿੰਦੂ A₁, A₂, A₃, A₄, A₅ ਕਿਰਨ AX ਉੱਤੇ ਇਸ ਤਰ੍ਹਾਂ ਅੰਕਿਤ ਕਰੋ ਤਾਂਕਿ A₁A₂ = A₂A₃ = A₃A₄
5. ਬਿੰਦੂ B₁, B₂, B₃, ………, B₈ ਰੇਖਾ BY ਤੇ ਇਸ ਤਰ੍ਹਾਂ ਅੰਕਿਤ ਕਰੋ ਕਿ B₁B₂ = B₂B₃ = …..B₇B₈
6. A₅B₈ ਨੂੰ ਮਿਲਾਓ ਮੰਨ ਲਓ ਇਹ AB ਨੂੰ ‘C’ ਤੇ ਕੱਟਦਾ ਹੈ ।
AC : CB = 5 : 8

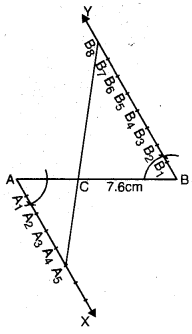
ਸਪੱਸ਼ਟੀਕਰਣ :
△ACA₅ ਅਤੇ △ BCB₈ ਵਿੱਚ
∠ACA₅ = ∠BCB₈ [ਸਿਖਰ ਸਨਮੁੱਖ ਕੋਣੀ ]
∠BAA₅ = ∠ABB₈ ([ਰਚਨਾ]
∴ △ACA₅ ~ △BCB₈ [AA ਸਮਰੂਪਤਾ]
∴ ਇਨ੍ਹਾਂ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਸਮਾਨ ਵਿੱਚ ਅਨੁਪਾਤ ਹੋਣਗੀਆਂ।

∴ AC : CB = 5 : 8.
∴ C, ਰੇਖਾਖੰਡ AB ਨੂੰ 5 : 8 ਦੇ ਅਨੁਪਾਤ ਵਿੱਚ | ਵੰਡਦਾ ਹੈ।

ਪ੍ਰਸ਼ਨ 2.
4 cm, 5 cm ਅਤੇ 6 cm ਭੁਜਾਵਾਂ ਵਾਲੇ ਇੱਕ | ਤਿਭੁਜ ਦੀ ਰਚਨਾ ਕਰੋ ਅਤੇ ਇਸ ਦੇ ਸਮਰੂਪ ਇੱਕ ਹੋਰ | ਤਿਭੁਜ ਦੀ ਰਚਨਾ ਕਰੋ ਜਿਸ ਦੀਆਂ ਭੁਜਾਵਾਂ ਦਿੱਤੇ ਹੋਏ ਤ੍ਰਿਭੁਜ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਦਾ \(\frac{2}{3}\) ਗੁਣਾ ਹੋਣ ।
ਹੱਲ:
ਰਚਨਾ ਦੇ ਪਗ :
1. ਦਿੱਤੀਆਂ ਹੋਈਆਂ ਸ਼ਰਤਾਂ ਅਤੇ ਮਾਪ ਅਨੁਸਾਰ ਤਿਭੁਜ ਦੀ ਰਚਨਾ ਕਰੋ । ਮੰਨ ਲਓ △ABC ਹੈ ਜਿਸ ਵਿੱਚ AB = 5 cm, AC = 4 cm ਅਤੇ BC = 6 cm ਹੈ ।
2. ਭੁਜਾ BC ਦੇ ਹੇਠਾਂ ਕੋਈ ਨਿਉਨ ਕੋਣ ∠CBX ਬਣਾਓ ।

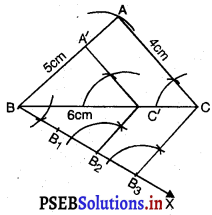
3. ਤਿੰਨ ਬਿੰਦੂ (\(\frac{2}{3}\) ਵਿੱਚ 2 ਅਤੇ 3 ਵਿੱਚੋਂ ਵੱਡੀ ਸੰਖਿਆ) B₁, B₂, B₃, BX ਉੱਤੇ ਇਸ ਤਰ੍ਹਾਂ ਅੰਕਿਤ ਕਰੋ ਕਿ BB₁ = B₁B₂ = B₂B₃ ਹੋਣ ।
4. B₃C ਨੂੰ ਮਿਲਾਓ।
5. B₂(\(\frac{2}{3}\) ਵਿੱਚ 2 ਅਤੇ 3 ਵਿੱਚੋਂ ਛੋਟੀ ਸੰਖਿਆ) ਵਿੱਚੋਂ ਇਕ ਰੇਖਾ B₃C ਦੇ ਸਮਾਂਤਰ ਖਿੱਚੋ ਜੋ BC ਨੂੰ C’ ਉੱਤੇ ਕੱਟੇ ।
6. C, ਤੋਂ ਹੋ ਕੇ ਜਾਣ ਵਾਲੀ CA ਦੇ ਸਮਾਂਤਰ ਇੱਕ ਰੇਖਾ ਖਿੱਚੋ ਜੋ BA ਨੂੰ A’ਤੇ ਮਿਲੇ ।
∴ △A’BC’ ਲੋੜੀਂਦੀ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸ ਦੀਆਂ ਭੁਜਾਵਾਂ △ABC ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਦੀ \(\frac{2}{3}\) ਗੁਣਾ ਹਨ !
ਰਚਨਾ ਦਾ ਸਪੱਸ਼ਟੀਕਰਣ :
ਪਹਿਲਾਂ ਅਸੀਂ ਇਹ ਦਿਖਾਵਾਂਗੇ ਕਿ ਪਹਿਲੀ ਤਿਭੁਜ ਅਤੇ ਰਚਨਾ ਕੀਤੀ ਗਈ ਤ੍ਰਿਭੁਜ ਸਮਰੂਪ ਹਨ }
ਭਾਵ △A’BC’ – △ABC
△ A’BC’ ਅਤੇ △ABC ਵਿਚ
∠B = ∠B [ਸਾਂਝਾ]
∠A’C’B= ∠ACB [ਚਨਾ]
△A’C’B ~ △ACB [AA ਸਮਰੂਪਤਾ]
∴ ਇਨ੍ਹਾਂ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਵੀ ਸਮਾਨ ਅਨੁਪਾਤ ਵਿਚ ਹੋਣਗੀਆਂ।

∴ △A’BC’ ਦੀਆਂ ਭੁਜਾਵਾਂ △ ABC ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਦਾ \(\frac{2}{3}\) ਗੁਣਾ ਹੈ।

ਪ੍ਰਸ਼ਨ 3.
5 cm, 6 cm ਅਤੇ 7 cm ਭੁਜਾਵਾਂ ਵਾਲੇ ਇੱਕ ਤ੍ਰਿਭੁਜ ਦੀ ਰਚਨਾ ਕਰੋ ਅਤੇ ਫਿਰ ਇੱਕ ਹੋਰ ਤ੍ਰਿਭੁਜ ਦੀ ਰਚਨਾ ਕਰੋ, ਜਿਸ ਦੀਆਂ ਭੁਜਾਵਾਂ ਦਿੱਤੇ ਗਏ ਤ੍ਰਿਭੁਜ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਦਾ \(\frac{7}{5}\) ਗੁਣਾ ਹੋਣ ।
ਹੱਲ:

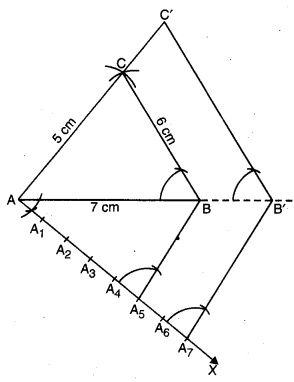
ਰਚਨਾ ਦੇ ਪਗ
1. △ABC ਦੀ ਰਚਨਾ ਕਰੋ ਜਿਸ ਵਿਚ AB = 7 cm, BC = 6 cm ਅਤੇ AC = 5 cm ਹੋਣ
2. ਆਧਾਰ AB ਦੇ ਹੇਠਾਂ ਨੂੰ ਕੋਈ ਨਿਊਨ ਕੋਣ ∠BAX ਬਣਾਉ ।
3. ਸੱਤ ਬਿੰਦੂ A₁, A₂, A₃, ……. A₇ ਰੇਖਾ AX ਇਸ ਤਰ੍ਹਾਂ ਅੰਕਿਤ ਕਰੋ ਕਿ
AA₁ = A₁A₂ = A₂A₃ = ………A₆A₇
4. BA₅ ਨੂੰ ਮਿਲਾਓ ।
5. A₇, ਤੋਂ A₅B ਦੇ ਸਮਾਂਤਰ ਇੱਕ ਰੇਖਾ ਖਿੱਚੋ । ਮੰਨ ਲਉ ਇਹ AB ਨੂੰ ਵਧਾਉਣ ਤੇ B’ ਤੇ ਇਸ ਤਰ੍ਹਾਂ ਮਿਲਦੀ ਹੈ ਕਿ AB’ = \(\frac{7}{5}\)AB.
6. B’ ਤੋਂ ਇੱਕ ਰੇਖਾ BC ਦੇ ਸਮਾਂਤਰ ਇੱਕ ਰੇਖਾ ਖਿੱਚੋ ਜੋ AC ਨੂੰ ਵਧਾਉਣ ਤੇ C’ ਤੇ ਮਿਲਦੀ ਹੈ । △AB’C ਲੋੜੀਂਦੀ ਹੈ ।
ਸਪੱਸ਼ਟੀਕਰਣ ,
△ABC ਅਤੇ △ AB’C’ ਵਿੱਚ,
∠A = ∠A [ਸਾਂਝਾ]
∠ABC = ∠AB’C’ [ਚਨਾ]
∴ ∠ABC ~ ∠ AB’C’ [AA ਸਮਰੂਪਤਾ]
∴ ਉਨ੍ਹਾਂ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਇੱਕ ਹੀ ਅਨੁਪਾਤ ਵਿਚ ਹੋਣਗੀਆਂ ।
\(\frac{\mathrm{AB}}{\mathrm{AB}^{\prime}}\) = \(\frac{\mathrm{BC}}{\mathrm{B}^{\prime} \mathrm{C}^{\prime}}\) = \(\frac{\mathrm{CA}}{\mathrm{C}^{\prime} \mathrm{A}}\) …(1)
ਪਰ △ AA₅B ਅਤੇ △AA₇ B’ ਵਿਚ
∠A = ∠A [ਸਾਂਝਾ]
∠AA₅B = ∠AA₇B’ [ਸੰਗਤ ਕੋਣ]
∴ △AA₅B – △AA₇B’ [AA ਸਮਰੂਪਤਾ]
∴ ਉਨ੍ਹਾਂ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਇੱਕ ਸਮਾਨ ਅਨੁਪਾਤ ਵਿਚ ਹੋਣਗੀਆਂ ।

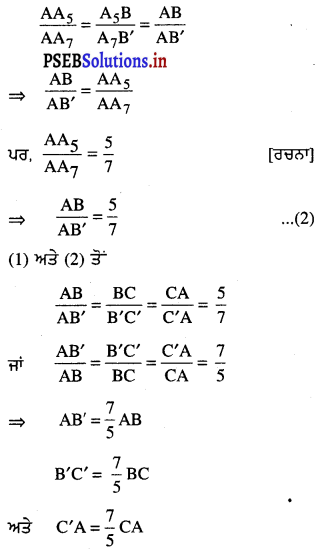
∴ △AB’C’ ਦੀਆਂ ਭੁਜਾਵਾਂ △ABC ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਦਾ \(\frac{7}{5}\) ਗੁਣਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 4.
ਆਧਾਰ 8 cm ਅਤੇ ਉੱਚਾਈ 4 cm ਦੇ ਇੱਕ ਸਮਦੋਭੁਜੀ ਤਿਭੁਜ ਦੀ ਰਚਨਾ ਕਰੋ ਅਤੇ ਫਿਰ ਇੱਕ ਹੋਰ ਤ੍ਰਿਭੁਜ ਦੀ ਰਚਨਾ ਕਰੋ, ਜਿਸ ਦੀਆਂ ਭੁਜਾਵਾਂ ਇਸ ਸਮਦੋਭੁਜੀ ਤ੍ਰਿਭੁਜ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਦਾ 1\(\frac{1}{2}\) ਗੁਣਾ ਹੋਣ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਸਮਦੋਭੁਜੀ ਤਿਭੁਜ ਦਾ ਆਧਾਰ = 8 cm ਅਤੇ ਉੱਚਾਈ = 4 cm
ਰਚਨਾ ਕਰਨਾ : ਇਕ ਤ੍ਰਿਭੁਜ ਜਿਸ ਦੀਆਂ ਭੁਜਾਵਾਂ ਸਮਦੋਭੁਜੀ ਤ੍ਰਿਭੁਜ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਦਾ 1\(\frac{1}{2}\) ਗੁਣਾ ਹੈ ।
ਰਚਨਾ ਦੇ ਪਗ :
1. ਆਧਾਰ AB = 8 cm ਲਉ |
2. AB ਦਾ ਲੰਬ ਸਮਦੁਭਾਜਕ ਖਿੱਚੋ ਜੋ AB ਨੂੰ ‘M’ | ਉੱਤੇ ਕੱਟੇ ।
3. M ਨੂੰ ਕੇਂਦਰ ਮੰਨ ਕੇ ਅਰਧ ਵਿਆਸ 4 cm ਲੈ ਕੇ ਇੱਕ ਚਾਪ ਲਗਾਓ ਜੋ ਲੰਬ ਸਮਦੁਭਾਜਕ ਨੂੰ C’ ਤੇ ਕੱਟਦੀ ਹੈ ।
4. CA ਅਤੇ CB ਨੂੰ ਮਿਲਾਓ ।
5. △ABC ਸਮਦੋਭੁਜੀ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸ ਵਿਚ CA = CB.
6. ਭੁਜਾ BC ਦੇ ਹੇਠਾਂ ਇਕ ਨਿਊਨ ਕੋਣ ∠BAX | ਬਣਾਓ ।
7. ਤਿੰਨ ਬਿੰਦੂ (1\(\frac{1}{2}\) ਜਾਂ \(\frac{3}{2}\) ਵਿੱਚ 2 ਜਾਂ 3 ਵਿੱਚੋਂ ਵੱਡੀ ਸੰਖਿਆ) A₁, A₂, A₃, …….. ‘AX’ ਉੱਤੇ ਇਸ ਤਰ੍ਹਾਂ | ਅੰਕਿਤ ਕਰੋ ਕਿ AA₁ = A₁A₂ = A₂A₃ ਹੋਵੇ ।

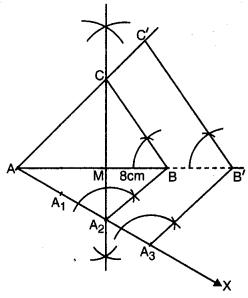
8. A₂ (\(\frac{1}{2}\) ਵਿੱਚ ‘2’ ਅਤੇ ‘3’ ਵਿੱਚੋਂ ਛੋਟੀ ਸੰਖਿਆ) | ਅਤੇ B ਨੂੰ ਮਿਲਾਓ ।
9. A₃ ਵਿਚੋਂ ਇਕ ਰੇਖਾ A₂B ਦੇ ਸਮਾਂਤਰ ਖਿੱਚੋ ਜੋ | AB ਨੂੰ ਵਧਾਉਣ ਤੇ B’ ਤੇ ਮਿਲੇ ।
10. B’ ਵਿੱਚੋਂ ਇਕ ਰੇਖਾ BC ਦੇ ਸਮਾਂਤਰ ਖਿੱਚੋ ਜੋ AC ਨੂੰ ਵਧਾਉਣ ਤੇ C’ ਤੇ ਮਿਲੇ । △AB’C’ ਲੋੜੀਂਦੀ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸ ਦੀਆਂ ਭੁਜਾਵਾਂ △ABC ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਦੀ 1\(\frac{1}{2}\) ਗੁਣੀ ਹੈ ।
ਸਪੱਸ਼ਟੀਕਰਣ :
ਸਭ ਤੋਂ ਪਹਿਲਾਂ ਅਸੀਂ ਇਹ ਸਿੱਧ ਕਰਾਂਗੇ ਕਿ △AB’C’ ਅਤੇ △ABC ਸਮਰੂਪ ਹੈ ।
△ ABC ਅਤੇ △ ABC ਵਿੱਚ,
∠A = ∠A [ਸਾਂਝਾ]
∠AB’C’ = ∠ABC [ਚਨਾ]
△AB’C’ ~ △ABC [AA ਸਮਰੂਪਤਾ]
∴ ਉਹਨਾਂ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਇੱਕ ਹੀ ਅਨੁਪਾਤ ਵਿਚ ਹੋਣ
\(\frac{\mathrm{AB}^{\prime}}{\mathrm{AB}}\) = \(\frac{\mathrm{B}^{\prime} \mathrm{C}^{\prime}}{\mathrm{BC}}\) = \(\frac{\mathrm{C}^{\prime} \mathrm{A}}{\mathrm{CA}}\) ………(1)
ਹੁਣ △ A3AB’ ਅਤੇ △AAB ਲਉ
∠A = ∠A [ਸਾਂਝਾ]
∠B’A₃A = ∠BA₂A [ਚਨਾ]
∴ △A₃AB’ ~ △A₂AB [AA ਸਮਰੂਪਤਾ]
∴ ਉਨ੍ਹਾਂ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਇਕ ਹੀ ਅਨੁਪਾਤ ਵਿਚ ਹੋਣ

ਅਤੇ C’A = 1\(\frac{1}{2}\) (CA)
∴ △ AB’C’ ਦੀਆਂ ਭੁਜਾਵਾਂ △ABC ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਦਾ 1\(\frac{1}{2}\) ਗੁਣਾ ਹੈ।

ਪ੍ਰਸ਼ਨ 5.
ਇੱਕ ਤਿਭੁਜ ABC ਬਣਾਓ ਜਿਸ ਵਿੱਚ BC = 6 cm, AB = 5 cm ਅਤੇ ∠ABC= 60° ਹੋਵੇ।ਫਿਰ ਇੱਕ ਤ੍ਰਿਭੁਜ ਦੀ ਰਚਨਾ ਕਰੋ ਜਿਸ ਦੀਆਂ ਭੁਜਾਵਾਂ △ABC ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਦਾ \(\frac{3}{4}\) ਗੁਣਾ ਹੋਣ ।
ਹੱਲ:
ਰਚਨਾ ਦੇ ਪਰਾ :
1. ਰੇਖਾਖੰਡ BC = 6 cm ਲਉ !
2. B ਉਤੇ 60° ਦਾ ਕੋਣ ਬਣਾਓ ਭਾਵ ∠BAX = 60° ਬਣਾਓ ।
3. B ਨੂੰ ਕੇਂਦਰ ਮੰਨ ਕੇ ਅਤੇ 5 cm ਅਰਧ ਵਿਆਸ ਲੈ ਕੇ ਇਕ ਚਾਪ ਖਿਚੋ ਜੋ BX ਨੂੰ ‘A’ ਤੇ ਕੱਟੇ ।

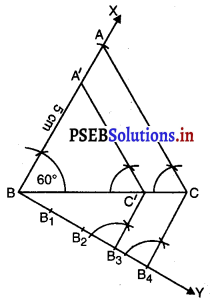
4. A ਅਤੇ C ਨੂੰ ਮਿਲਾਓ ।
5. BC ਦੇ ਥੱਲੇ B ਉੱਤੇ ਇਕ ਨਿਊਨ ਕੋਣ ਬਣਾਉ ॥
6. ਚਾਰ ਬਿੰਦੂ (\(\frac{3}{4}\) ਵਿਚ 3 ਅਤੇ 4 ਵਿੱਚੋਂ ਵੱਡੀ ਸੰਖਿਆ) B₁, B₂, B₃, B₄ ਰੇਖਾ BY ਇਸ ਤਰ੍ਹਾਂ ਅੰਕਿਤ ਕਰੇ ਕਿ BB₁ = B₁B₂ = ……..B₂B₃ = B₃B₄
7. B₄ ਅਤੇ C ਨੂੰ ਮਿਲਾਓ ।
8. B₃ ਤੋਂ (\(\frac{3}{4}\) ਵਿਚ 3 ਅਤੇ 4 ਵਿੱਚੋਂ ਛੋਟੀ ਸੰਖਿਆ) ਇੱਕ ਰੇਖਾ B₄C ਦੇ ਸਮਾਂਤਰ ਸੰਗਤ ਕੋਣ ਬਣਾਉਂਦੀ ਹੋਈ ਖਿੱਚੋ । ਮੰਨ ਲਓ B₃ ਵਿਚੋਂ ਖਿੱਚੀ ਰੇਖਾ BC ਨੂੰ C’ ਉੱਤੇ ਮਿਲਦੀ ਹੈ ।
9. C’ ਤੋਂ ਇਕ ਰੇਖਾ CA ਦੇ ਸਮਾਂਤਰ ਖਿਚੋ ਜੋ BA ਨੂੰ A’ ਉੱਤੇ ਕੱਟਦੀ ਹੈ ।
△A’BC ਲੋੜੀਂਦੀ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ △ABC ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਦੇ \(\frac{3}{4}\) ਗੁਣਾ ਹਨ।
ਸਪੱਸ਼ਟੀਕਰਣ :
△A’BC ਅਤੇ △ABC ਲਉ ॥
∠B = ∠B [ਸਾਂਝਾ]
∠A’C’B = ∠ACB [ਸੰਗਤ ਕੋਣ]
∴ △A’BC’ ~ △ABC [AA ਸਮਰੂਪਤਾ]
∴ ਉਹਨਾਂ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਇਕ ਹੀ ਅਨੁਪਾਤ ਵਿਚ ਹੋਣਗੀਆਂ ।
∴ \(\frac{A^{\prime} B}{A B}\) = \(\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}\) = \(\frac{\mathrm{C}^{\prime} \mathrm{A}^{\prime}}{\mathrm{CA}}\) …(1)
ਹੁਣ △BBC ਅਤੇ △BBC ਲਉ !
∠B = ∠B [ਸਾਂਝਾ]
∠C’ B₃B = ∠CB₄B [ਸੰਗਤ ਕੋਣ]
△B₃BC ~ △B₄BC [AA ਸਮਰੂਪਤਾ]
∴ ਉਹਨਾਂ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਇਕ ਹੀ ਅਨੁਪਾਤ ਵਿਚ ਹੋਣਗੀਆਂ

ਅਤੇ C’A’ = \(\frac{3}{4}\)CA.
ਭਾਵ △A’BC’ ਦੀਆਂ ਭੁਜਾਵਾਂ △ABC ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਦਾ \(\frac{3}{4}\) ਗੁਣਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 6.
ਇੱਕ ਤਿਭੁਜ ABC ਬਣਾਉ, ਜਿਸ ਵਿੱਚ BC = 7 ਤੋਂ cm, ∠B = 45°, ∠A = 105° ਹੋਵੇ । ਫਿਰ ਇੱਕ ਹੋਰ | ਤ੍ਰਿਭੁਜ ਦੀ ਰਚਨਾ ਕਰੋ ਜਿਸ ਦੀਆਂ ਭੁਜਾਵਾਂ △ABC ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਦਾ \(\frac{3}{4}\) ਗੁਣਾ ਹੋਣ ।
ਹੱਲ:
ਰਚਨਾ ਦੇ ਪਗ :
1. ਦਿੱਤੇ ਗਏ ਮਾਪਾਂ ਨਾਲ ਤ੍ਰਿਭੁਜ ABC ਦੀ ਰਚਨਾ ਕਰੋ ।
2. ਭੁਜਾ BC ਦੇ ਹੇਠਾਂ ਬਿੰਦੂ B ‘ਤੇ ਕੋਈ ਨਿਊਨ ਕੋਣ ∠CBX ਖਿੱਚੋ ।

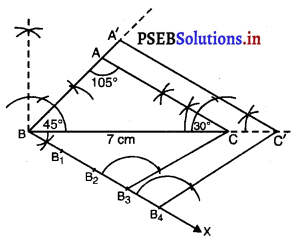
7 cm
ਤਿਭੁਜ ਦੇ ਕੋਣਾਂ ਦੇ ਜੋੜ ਗੁਣਧਰਮ ਦੁਆਰਾ
∠A + ∠B + ∠C = 180°
105° + 45° + ∠C = 180°
∠C = 180° – 150° = 30°
3. ਚਾਰ ਬਿੰਦੂ (\(\frac{4}{3}\) ਵਿੱਚ 3 ਅਤੇ 4 ਵਿਚੋਂ ਵੱਡੀ ਸੰਖਿਆ) B₁, B₂, B₃ …..B₄, ‘BX’ ਉੱਤੇ ਇਸ ਤਰ੍ਹਾਂ ਅੰਕਿਤ ਕਰੋ ਕਿ BB₁ = B₁B₂ = B₂B₃ = B₃B₄ ਹੋਵੇ ।
4. B₃C ਤੋਂ 3 ਅਤੇ 4 ਵਿੱਚੋਂ ਛੋਟੀ) ਨੂੰ ਮਿਲਾਓ ।
5. B₄ ਵਿਚੋਂ ਇਕ ਰੇਖਾ B₃C ਦੇ ਸਮਾਂਤਰ ਖਿੱਚੋ ਜੋ | BC ਨੂੰ ਵਧਾਉਣ ਤੇ C ‘ਤੇ ਕੱਟੇ ।
6. C’ ਤੋਂ ਇਕ ਹੋਰ ਰੇਖਾ CA ਦੇ ਸਮਾਂਤਰ ਖਿੱਚੋ | ਜੋ BA ਨੂੰ ਵਧਾਉਣ ਤੇ A’ ਉੱਤੇ ਕੱਟੇ ।
7. △A’BC’ ਲੋੜੀਂਦੀ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸ ਦੀਆਂ ਭੁਜਾਵਾਂ ਤ੍ਰਿਭੁਜ ABC ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਦੇ \(\frac{4}{3}\) ਗੁਣਾ ਹੈ।
ਸਪੱਸ਼ਟੀਕਰਣ :
△A’BC ਅਤੇ △ ABC ਲਓ ।
∠B = ∠B [ਸਾਂਝਾ]
∠A’C’B = ∠ACB [ਚਨਾ]
∴ △ A’BC ~ △ABC [AA ਸਮਰੂਪਤਾ]
∴ ਉਨ੍ਹਾਂ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਇਕ ਹੀ ਅਨੁਪਾਤ ਵਿਚ ਹੋਣਗੀਆਂ]
\(\frac{A^{\prime} B}{A B}\) = \(\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}\) = \(\frac{\mathrm{C}^{\prime} \mathrm{A}^{\prime}}{\mathrm{CA}}\) ….(1)
ਫਿਰ △B₄BC ਅਤੇ △B₃BC ਲਓ
∠B = ∠B [ਸਾਂਝਾ]
∠C’B₄B = ∠CB₃B [ਰਚਨਾ]
∴ △B₄BC’ ~ △B₃BC [AA-ਸਮਰੂਪਤਾ}
∴ ਉਨ੍ਹਾਂ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਇਕ ਹੀ ਅਨੁਪਾਤ ਵਿਚ ਹੋਣਗੀਆਂ ।

△A’BC’ ਦੀਆਂ ਭੁਜਾਵਾਂ △ABC ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਦਾ \(\frac{4}{3}\) ਗੁਣਾ ਹੈ।

ਪ੍ਰਸ਼ਨ 7.
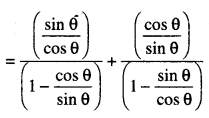
ਇੱਕ ਸਮਕੋਣ ਤਿਭੁਜ ਦੀ ਰਚਨਾ ਕਰੋ, ਜਿਸ ਦੀਆਂ ਭੁਜਾਵਾਂ (ਕਰਣ ਦੇ ਇਲਾਵਾ 4 cm ਅਤੇ 3 cm ਲੰਬਾਈ ਵਾਲੀਆਂ ਹੋਣ । ਫਿਰ ਇੱਕ ਹੋਰ ਤ੍ਰਿਭੁਜ ਦੀ ਰਚਨਾ ਕਰੋ, ਜਿਸ ਦੀਆਂ ਭੁਜਾਵਾਂ ਦਿੱਤੇ ਹੋਏ ਤ੍ਰਿਭੁਜ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਦਾ \(\frac{5}{3}\) ਗੁਣਾ ਹੋਣ ।
ਹੱਲ:
ਰਚਨਾ ਦੇ ਪਗ :
1. ਦਿੱਤੀਆਂ ਗਈਆਂ ਸ਼ਰਤਾਂ ਨਾਲ ਸਮਕੋਣ ਤਿਭੁਜ ਦੀ ਰਚਨਾ ਕਰੋ ਮੰਨ ਲਉ ਇਹ △ABC ਹੈ ।
BC = 4 cm; AB = 3 cm ਅਤੇ ∠B = 90°.
2. ਭੁਜਾ BC ਦੇ ਹੇਠਾਂ ਕੋਈ ਨਿਊਨ ਕੋਣ ∠CBX ਬਣਾਉ ।
3. ਪੰਜ ਬਿੰਦੂ (\(\frac{5}{3}\) ਵਿੱਚ 5 ਅਤੇ 3 ਵਿੱਚੋਂ ਵੱਡੀ ਸੰਖਿਆ) B₁, B₂, B₃, ……B₄, B₅, BX ਉੱਤੇ ਇਸ ਤਰ੍ਹਾਂ ਅੰਕਿਤ ਕਰੋ ਕਿ BB₁ = B₁B₂ = ….. = B₄B₅ ਹੋਵੇ ।
4. B₃ (\(\frac{5}{3}\) ਵਿੱਚ ‘5’ ਅਤੇ ‘3) ਵਿੱਚੋਂ ਛੋਟੀ ਸੰਖਿਆ) ਅਤੇ ‘C ਨੂੰ ਮਿਲਾਓ ।

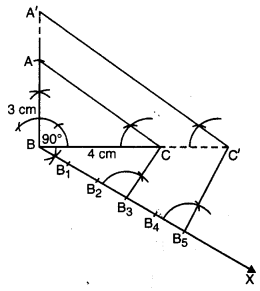
5. B₅ ਵਿਚੋਂ ਇਕ ਰੇਖਾ BC ਦੇ ਸਮਾਂਤਰ ਖਿੱਚੋ ਜੋ BC ਨੂੰ ਵਧਾਉਣ ਤੇ C’ ਤੇ ਕੱਟੇ ।
6. ਦੁਬਾਰਾ C ਵਿਚੋਂ ਇਕ ਰੇਖਾ CA ਦੇ ਸਮਾਂਤਰ ਤੇ ਖਿੱਚੋ ! ਜੋ BA ਨੂੰ ਵਧਾਉਣ ਤੇ A’ ਤੇ ਮਿਲੇ । △A’BC ਲੋੜੀਂਦੀ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸ ਦੀਆਂ ਭੁਜਾਵਾਂ △ABC ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਦਾ \(\frac{5}{3}\) ਗੁਣਾ ਹਨ।
ਸਪੱਸ਼ਟੀਕਰਣ
△A’BC ਅਤੇ △ABC ਲਉ
∠B = ∠B [ਸਾਂਝਾ]
∠A’C’B = ∠ACB [ਚਨਾ]
∴ △A’BC’ ~ △ABC [AA-ਸਮਰੂਪਤਾ]
∴ ਉਨ੍ਹਾਂ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਇਕ ਹੀ ਅਨੁਪਾਤ ਵਿਚ ਹੋਣਗੀਆਂ ।
ਭਾਵ \(\frac{A^{\prime} B}{A B}\) = \(\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}\) = \(\frac{\mathrm{C}^{\prime} \mathrm{A}^{\prime}}{\mathrm{CA}}\) …(1)
ਦੁਬਾਰਾ △B₅C’B ਅਤੇ △B₃CB ਵਿਚੋਂ
CB = CB [ਸਾਂਝਾ]
∠C’B₅B = ∠CB₃B [ਚਨਾ]
∴ △B₅C’B ~ △B₃CB [AA-ਸਮਰੂਪਤਾ]
∴ ਉਨ੍ਹਾਂ ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਇਕ ਸਮਾਨ ਅਨੁਪਾਤ ਵਿਚ ਹੋਣਗੀਆਂ ।

△A’BC’ ਦੀਆਂ ਭੁਜਾਵਾਂ △ABC ਦੀਆਂ ਸੰਗਤ ਭੁਜਾਵਾਂ ਦਾ \(\frac{5}{3}\) ਗੁਣਾ ਹੈ।

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 10 ਚੱਕਰ Ex 10.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 10 ਚੱਕਰ Exercise 10.2

ਪ੍ਰਸ਼ਨ ਨੰ : 1, 2, 3 ਵਿੱਚੋਂ ਸਹੀ ਵਿਕਲਪ ਚੁਣੋ ਅਤੇ ਉੱਚਿਤ ਕਾਰਣ ਦਿਓ।

ਪ੍ਰਸ਼ਨ 1.
ਇੱਕ ਬਿੰਦੂ Q ਤੋਂ ਇੱਕ ਚੱਕਰ ‘ਤੇ ਸਪਰਸ਼ ਰੇਖਾ ਦੀ ਲੰਬਾਈ 24 cm ਅਤੇ 9 ਦੀ ਕੇਂਦਰ ਤੋਂ ਦੂਰੀ 25 cm ਹੈ । ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ ਹੈ :
(A) 7 cm
(B) 12 cm
(C) 15 cm
(D) 24.5 cm
ਹੱਲ:
ਇੱਕ ਚੱਕਰ ਜਿਸਦਾ ਕੇਂਦਰ ਹੈ । ਬਾਹਰੀ ਬਿੰਦੂ Q ਤੋਂ ਸਪਸ਼ ਰੇਖਾ PQ ਦੀ ਲੰਬਾਈ 24 cm ਅਤੇ Q ਦੀ ਕੇਂਦਰ O ਤੋਂ ਦੂਰੀ 25 cm ਹੈ ।

∵ ∠QPO = 90°
ਹੁਣ, ਸਮਕੋਣ △OPQ ਵਿਚ
OQ² = PQ² + Op²
(25)² = (24)² + OP²
625 = 576 + OP²
OP² = 625 – 576
OP² = 49 = (7)²
OP = 7 cm
∴ ਵਿਕਲਪ (A) ਸਹੀ ਹੈ। ਉੱਤਰ

ਪ੍ਰਸ਼ਨ 2.
ਚਿੱਤਰ ਵਿਚ, ਜੇਕਰ TP, TQ ਕੇਂਦਰ O ਵਾਲੇ ਕਿਸੇ ਚੱਕਰ `ਤੇ ਦੋ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਇਸ ਤਰ੍ਹਾਂ ਹਨ ਕਿ ∠POQ = 110°, ਤਾਂ ∠PTQ ਬਰਾਬਰ ਹੈ : (A) 6o°
(B) 70°
(C) 80°
(D) 90°

ਹੱਲ:
ਚਿੱਤਰ ਵਿੱਚ OP ਅਰਧ ਵਿਆਸ ਹੈ ਅਤੇ PT ਚੱਕਰ ‘ਤੇ ਸਪਰਸ਼ ਰੇਖਾ ਹੈ
∴ ∠OPT = 90°
ਇਸੇ ਤਰ੍ਹਾਂ ∠OQT = 90°
ਅਤੇ ∠POQ = 110° ਦਿੱਤਾ ਹੈ
ਹੁਣ, POQT ਇੱਕ ਚਤੁਰਭੁਜ ਹੈ
∴ ∠POQ + ∠OQT + ∠QTP + ∠TPO = 360°
110° + 90° + ∠QTP + 90° = 360°
∠QTP + 290° = 360°
∠QTP = 360° – 290°
ਜਾਂ ∠QTP = 70°
∴ ਵਿਕਲਪ (B) ਸਹੀ ਹੈ।

ਪ੍ਰਸ਼ਨ 3.
ਜੇਕਰ ਇਕ ਬਿੰਦੂ P ਤੋਂ O ਕੇਂਦਰ ਵਾਲੇ ਕਿਸੇ ਚੱਕਰ ‘ਤੇ PA, PB ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਆਪਸ ਵਿੱਚ 80° ਦੇ ਕੋਣ ‘ਤੇ ਝੁਕੀਆਂ ਹੋਣ ਤਾਂ ∠POA ਬਰਾਬਰ ਹੈ :
(A) 50°
(B) 60°
(C) 70°
(D) 80°
ਹੱਲ:
ਦਿੱਤੇ ਹੋਏ ਚਿੱਤਰ ਵਿਚ OA ਅਰਧ ਵਿਆਸ ਹੈ ਅਤੇ AP ਚੱਕਰ ਦੀ ਸਪੱਰਸ਼ ਰੇਖਾ ਹੈ :
∴ ∠OAP = 90°

ਇਸੇ ਤਰ੍ਹਾਂ ∠OBP = 90°
ਹੁਣ, ਸਮਕੋਣ △PAO ਅਤੇ △PBO ਵਿੱਚ
∠PAO = ∠PBO = 90°
OP = OP (ਸਾਂਝੀ ਭੂਜਾ)
OA = OB (ਇੱਕ ਹੀ ਚੱਕਰ ਦੇ ਅਰਧ ਵਿਆਸ)
∴ ∠PAO ≅ △PBO
[RHS ਸਰਬੰਗਸਮਤਾ ਦੁਆਰਾ]
∴ ∠AOP = ∠BOP (CPCT)
ਜਾਂ ∠AOP = ∠BOP = \(\frac{1}{2}\)∠AOB …(1)
ਚਤੁਰਭੁਜ OAPB ਵਿਚ
∠OBP + ∠BPA + ∠PAO + ∠AOB = 360°
90° + 80° + 90° + ∠AOB = 360°
∠AOB = 360° – 260°
∠AOB = 100° …(2)
(1) ਅਤੇ (2) ਤੋਂ
∠AOP = ∠BOP = \(\frac{1}{2}\) × 100° = 50°
∴ ਵਿਕਲਪ (A) ਸਹੀ ਹੈ। ਉੱਤਰ

ਪ੍ਰਸ਼ਨ 4.
ਸਿੱਧ ਕਰੋ ਕਿ ਕਿਸੇ ਚੱਕਰ ਦੇ ਕਿਸੇ ਵਿਆਸ ਦੇ ਸਿਰਿਆਂ ‘ਤੇ ਖਿੱਚੀਆਂ ਗਈਆਂ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਸਮਾਂਤਰ ਹੁੰਦੀਆਂ ਹਨ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਇਕ ਚੱਕਰ ਜਿਸਦਾ ਕੇਂਦਰ ਹੈ O ਅਤੇ ਵਿਆਸ AB ਹੈ ਅਤੇ m ਬਿੰਦੂਆਂ A ਅਤੇ B ‘ਤੇ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਹਨ ।

ਸਿੱਧ ਕਰਨਾ : l || m
ਸਬੂਤ : ∴ OA ਇੱਕ ਅਰਧ ਵਿਆਸ ਹੈ ਅਤੇ l ਇੱਕ ਸਪਰਸ਼ ਰੇਖਾ ਹੈ ।
∴ ∠1 = 90°
∠2 = 90°
ਹੁਣ, ∠1 = ∠2 = 90°
ਪਰ ਇਹ ਦੋ ਰੇਖਾਵਾਂ ਦੇ ਇਕਾਂਤਰ ਕੋਣ ਹਨ । ਜਦੋਂ ਇੱਕ ਕਾਟਵੀਂ ਰੇਖਾ ਇਨ੍ਹਾਂ ਨੂੰ ਕੱਟਦੀ ਹੈ ।
∴ l || m
ਕਿਸੇ ਵਿਆਸ ਦੇ ਸਿਰਿਆਂ ਤੇ ਖਿੱਚੀਆਂ ਗਈ ਸਪੱਰਸ਼ ਰੇਖਾਵਾਂ ਪਰਸਪਰ ਸਮਾਂਤਰ ਹੁੰਦੀਆਂ ਹਨ।

ਪ੍ਰਸ਼ਨ 5.
ਸਿੱਧ ਕਰੋ ਕਿ ਸਪਰਸ਼ ਬਿੰਦੂ ਤੋਂ ਸਪੱਰਸ਼ ਰੇਖਾ ‘ਤੇ ਖਿੱਚਿਆ ਗਿਆ ਲੰਬ ਚੱਕਰ ਦੇ ਕੇਂਦਰ ਤੋਂ ਹੋ ਕੇ ਜਾਂਦਾ ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਇੱਕ ਚੱਕਰ ਜਿਸਦਾ ਕੇਂਦਰ O ਹੈ । AB ਇਸਦੀ ਇੱਕ ਸਪਰਸ਼ ਰੇਖਾ ਹੈਂ ਜੋ ਚੱਕਰ ਨੂੰ P ਉੱਤੇ ਮਿਲਦੀ ਹੈ ।
ਭਾਵ ਬਿੰਦੁ P ਚੱਕਰ ਦਾ ਸਪਰਸ਼ ਬਿੰਦੁ ਹੈ ।

ਸਿੱਧ ਕਰਨਾ : ਸਪਰਸ਼ ਬਿੰਦੂ ਤੋਂ ਸਪਰਸ਼ ਰੇਖਾ ‘ਤੇ ਖਿੱਚਿਆ ਗਿਆ ਲੰਬ ਚੱਕਰ ਦੇ ਕੇਂਦਰ ਤੋਂ ਹੋ ਕੇ ਜਾਂਦਾ ਹੈ ।
ਰਚਨਾ : OP ਨੂੰ ਮਿਲਾਓ ।
ਸਬੂਤ : ਕਿਉਂਕਿ OP ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ ਹੈ ਅਤੇ AB ਚੱਕਰ ਉੱਤੇ ਸਪਰਸ਼ ਰੇਖਾ ਹੈ ਜਿਸ ਵਿੱਚ ਬਿੰਦੁ P ਸਪਰਸ਼ ਬਿੰਦੂ ਹੈ।
∴ ∠OPA = ∠OPB = 90°
[∵ ਚੱਕਰ ਦੇ ਕਿਸੇ ਬਿੰਦੂ ‘ਤੇ ਸਪਰਸ਼ ਰੇਖਾ ਸਪਰਸ਼ ਬਿੰਦੂ ਤੋਂ ਜਾਣ ਵਾਲੇ ਅਰਧ ਵਿਆਸ ਉੱਤੇ ਲੰਬ ਹੁੰਦੀ ਹੈ ॥]
ਜਾਂ OP ⊥ AB
ਕਿਉਂਕਿ ਕਿਸੇ ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ ਹਮੇਸ਼ਾਂ ਚੱਕਰ ਦੇ ਕੇਂਦਰ ਵਿਚੋਂ ਲੰਘਦਾ ਹੈ ।
ਇਸ ਲਈ ਸਪਰਸ਼ ਬਿੰਦੂ ਤੋਂ ਸਪਸ਼ ਰੇਖਾ ਤੇ ਖਿੱਚਿਆ ਗਿਆ ਲੰਬ ਚੱਕਰ ਦੇ ਕੇਂਦਰ ਵਿਚੋਂ ਹੋ ਕੇ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 6.
ਇੱਕ ਬਿੰਦੂ A ਤੋਂ, ਜੋ ਇੱਕ ਚੱਕਰ ਦੇ ਕੇਂਦਰ ਤੋਂ 5 cm | ਦੀ ਦੂਰੀ ‘ਤੇ ਹੈ, ਚੱਕਰ ‘ ਤੇ ਸਪਰਸ਼ ਰੇਖਾ ਦੀ ਲੰਬਾਈ 4cm ਹੈ । ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਚੱਕਰ ਦਾ ਕੇਂਦਰ ‘O’ ਹੈ । ਚੱਕਰ ਦੇ ਬਾਹਰ 5 cm ਦੀ ਦੂਰੀ ‘ਤੇ ਇੱਕ ਬਿੰਦੂ A ਹੈ ।

ਸਪਰਸ਼ ਰੇਖਾ ਦੀ ਲੰਬਾਈ = PA = 4 cm
ਕਿਉਂਕਿ OP ਇੱਕ ਅਰਧ ਵਿਆਸ ਹੈ ਅਤੇ PA ਚੱਕਰ | ਦੀ ਸਪਰਸ਼ ਰੇਖਾ ਹੈ
∴ ∠OPA = 90°
ਸਮਕੋਣ △OPA ਵਿੱਚ ਪਾਈਥਾਗੋਰਸ ਥਿਊਰਮ ਤੋਂ
OA² = OP² + PA²
(5)² = OP² + (4)²
OP² = 25 – 16
OP² = 9 = (3)²
OP = 3 cm.
∴ ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ 3 cm ਹੈ ।

ਪ੍ਰਸ਼ਨ 7.
ਦੋ ਸਮਕੇਂਦਰੀ ਚੱਕਰਾਂ ਦੇ ਅਰਧ ਵਿਆਸ 5 cm ਤੇ 3 cm ਹਨ। ਵੱਡੇ ਚੱਕਰ ਦੀ ਉਸ ਜੀਵਾ ਦੀ ਲੰਬਾਈ ਪਤਾ ਕਰੋ ਜੋ ਛੋਟੇ ਚੱਕਰ ਨੂੰ ਸਪਰਸ਼ ਕਰਦੀ ਹੈ ।
ਹੱਲ:
ਦੋ ਸਮਕੇਂਦਰੀ ਚੱਕਰ ਜਿਨ੍ਹਾਂ ਦਾ ਕੇਂਦਰ O ਹੈ ਅਤੇ ਅਰਧ ਵਿਆਸ ਕ੍ਰਮਵਾਰ 5 cm ਅਤੇ 3 cm ਹਨ ।
ਮੰਨ ਲਉ PQ ਵੱਡੇ ਚੱਕਰ ਦੀ ਜੀਵਾ ਹੈ ਪਰ ਛੋਟੇ ਚੱਕਰ ਦੀ ਸਪਰਸ਼ ਰੇਖਾ ਹੈ ।

ਕਿਉਂਕਿ OM ਛੋਟੇ ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ ਹੈ ਅਤੇ PMQ ਸਪਰਸ਼ ਰੇਖਾ ਹੈ ।
∴ ∠OMP = ∠OMQ = 90°
ਸਮਕੋਣ ਤ੍ਰਿਭੁਜਾਂ OMP ਅਤੇ OMQ ਵਿੱਚ,
∠OMP = ∠OMQ = 90°
OP = OQ [ਇੱਕ ਹੀ ਚੱਕਰ ਦੇ ਅਰਧ ਵਿਆਸ ਸਾਂਝੀ ਭੁਜਾ]
OM = OM
∴ △OMP ≅ OMO [RHS ਸਰਬੰਸਮਤਾ ਦੁਆਰਾ]
∴ PM = MQ
PQ = 2 PM = 2 MQ
ਹੁਣ, ਸਮਕੋਣ △ OMQ ਵਿਚ ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਤੋਂ
OQ² = OM² + MQsup>2
(5)² = (3)² + (MQ)²
MQ² = 25 – 9
MQ² = 16 = (4)²
MQ = 4 cm
∴ ਜੀਵਾਂ ਦੀ ਲੰਬਾਈ PQ = 2 MQ
= 2 (4) cm
= 8 cm
ਲੋੜੀਂਦੀ ਜੀਵਾਂ ਦੀ ਲੰਬਾਈ 8 cm ਹੈ ।

ਪ੍ਰਸ਼ਨ 8.
ਇੱਕ ਚੱਕਰ ਨੂੰ ਬਾਹਰਲੇ ਪਾਸੇ ਤੋਂ ਛੂੰਹਦਾ ਚਤੁਰਭੁਜ ABCD ਖਿੱਚਿਆ ਗਿਆ ਹੈ (ਦੇਖੋ ਚਿੱਤਰ) । ਸਿੱਧ ਕਰੋ ਕਿ :
AB + CD = AD + BC.

ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਚੱਕਰ ਨੂੰ ਬਾਹਰਲੇ ਪਾਸੇ ਤੋਂ ਛੁੰਹਦਾ ਚਤੁਰਭੁਜ ABCD ਖਿੱਚਿਆ ਗਿਆ ਹੈ।
ਸਿੱਧ ਕਰਨਾ : AB + CD = AD + BC
ਸਬੂਤ : ਕਿਉਂਕਿ ਕਿਸੇ ਬਾਹਰੀ ਬਿੰਦੂ ਤੋਂ ਚੱਕਰ ਤੇ ਖਿੱਚੀਆਂ ਗਈਆਂ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਦੀ ਲੰਬਾਈ ਬਰਾਬਰ ਹੁੰਦੀ ਹੈ ।
ਹੁਣ, B ਚੱਕਰ ਦੇ ਬਾਹਰ ਸਥਿਤ ਕੋਈ ਬਿੰਦੂ ਹੈ ਅਤੇ | BP ; BQ ਚੱਕਰ ‘ਤੇ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਹਨ ।
∴ BP = BQ ….(1)
ਇਸੇ ਤਰ੍ਹਾਂ AP = AS …(2)
CR = CQ …(3)
DR = DS ….(4)
(1), (2), (3), (4) ਨੂੰ ਜੋੜਣ ‘ਤੇ
(BP + AP) +(CR + DR) = (BQ + CQ) + (AS + DS)
AB + CD = BC+ AD ਲੋੜੀਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 9.
ਚਿੱਤਰ ਵਿੱਚ, XY ਅਤੇ X’Y’, O ਕੇਂਦਰ ਵਾਲੇ ਕਿਸੇ ਚੱਕਰ ‘ਤੇ ਦੋ ਸਮਾਂਤਰ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਹਨ ਅਤੇ ਸਪਰਸ਼ ਬਿੰਦੂ C ’ਤੇ ਸਪਰਸ਼ ਰੇਖਾ AB, XY ਨੂੰ A ਅਤੇ X’Y’, ਨੂੰ B ’ਤੇ ਕੱਟਦੀ ਹੈ । ਸਿੱਧ ਕਰੋ ∠AOB = 90° ਹੈ ।

ਹੱਲ:
ਦਿੱਤਾ ਹੈ : XY ਅਤੇ X’Y’ ਕੇਂਦਰ O ਵਾਲੇ ਚੱਕਰ ਉੱਤੇ ਦੋ ਸਮਾਂਤਰ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਹਨ ਅਤੇ ਸਪਰਸ਼ ਬਿੰਦੁ cਉੱਤੇ ਇੱਕ ਹੋਰ ਸਪਰਸ਼ ਰੇਖਾ AB, XY ਨੂੰ A ਅਤੇ X’Y’ ਨੂੰ B ਉੱਤੇ ਕੱਟਦੀ ਹੈ ।
ਸਿੱਧ ਕਰਨਾ : ∠AOB = 90°
ਰਚਨਾ : OC, OA ਅਤੇ OB ਨੂੰ ਮਿਲਾਉ ।
ਸਬੂਤ : ਕਿਉਂਕਿ ਬਾਹਰੀ ਬਿੰਦੂ ਤੋਂ ਕਿਸੇ ਚੱਕਰ ਉੱਤੇ ਖਿੱਚੀਆਂ ਗਈਆਂ ਸਪੱਰਸ਼ ਰੇਖਾਵਾਂ ਦੀਆਂ ਲੰਬਾਈਆਂ ਬਰਾਬਰ ਹੁੰਦੀਆਂ ਹਨ ।
ਹੁਣ, A ਚੱਕਰ ਦੇ ਬਾਹਰ ਕੋਈ ਬਿੰਦੂ ਹੈ ਜਿਸ ਦੀਆਂ ਦੋ ਸਪੱਰਸ਼ ਰੇਖਾਵਾਂ PA ਅਤੇ PC ਹਨ ।
∴ PA = PC
ਨਾਲ ਹੀ, △POA ਅਤੇ △ AOC ਵਿਚ
PA = PC (ਸਿੱਧ ਕੀਤਾ)
OA = OA (ਸਾਂਝੀ ਭੁਜਾ)
OP = OC (ਇੱਕ ਹੀ ਚੱਕਰ ਦੇ ਅਰਧ ਵਿਆਸ)
∴ △POA ≅ △AOC [SSS]
∠PAO = ∠CAO [CPCT]
∠PAC = 2∠PAO = 2∠CAO …(1)
ਇਸੇ ਤਰ੍ਹਾਂ ∠QBC = 2∠OBC = 2∠OBQ …(2)
ਹੁਣ, ∠PAC + ∠QBC = 180° [∵ ਕਾਟਵੀਂ ਰੇਖਾ ਦੇ ਇੱਕੋ ਪਾਸੇ ਬਣੇ ਕੋਣਾਂ ਦਾ ਜੋੜ 180° ਹੁੰਦਾ ਹੈ |]
2∠CAO + 2∠OBC = 180° [(1) ਅਤੇ (2) ਤੋਂ।]
∠CAO + ∠OBC = \(\frac{180^{\circ}}{2}\) = 90° …(3)
ਹੁਣ, △OAB ਵਿਚ
∠CAO + ∠OBC + ∠AOB = 180°
90° + ∠AOB = 180° [(3) ਤੋਂ]
∠AOB = 180° – 90° = 90°
∴ ∠AOB = 90°

ਪ੍ਰਸ਼ਨ 10.
ਸਿੱਧ ਕਰੋ ਕਿ ਕਿਸੇ ਬਾਹਰੀ ਬਿੰਦੂ ਤੋਂ ਕਿਸੇ ਚੱਕਰ ਤੇ ਖਿੱਚੀਆਂ ਗਈਆਂ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਦਾ ਵਿਚਕਾਰਲਾ ਕੋਣ ਸਪਰਸ਼ ਬਿੰਦੂਆਂ ਨੂੰ ਮਿਲਾਉਣ ਵਾਲੇ ਰੇਖਾਖੰਡ ਦੁਆਰਾ ਕੇਂਦਰ ਤੇ ਬਣੇ ਕੋਣ ਦਾ ਸੰਪੂਰਕ ਹੁੰਦਾ ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਇੱਕ ਚੱਕਰ ਜਿਸਦਾ ਕੇਂਦਰ ) ਹੈ । ਦੇ ਚੱਕਰ ਦੇ ਬਾਹਰ ਸਥਿਤ ਕਿਸੇ ਬਿੰਦੂ P ਤੋਂ PQ ਅਤੇ PR ਦਿੱਤੇ ਗਏ ਚੱਕਰ ਦੀਆਂ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਹਨ ।

ਸਿੱਧ ਕਰਨਾ : ∠ROQ + ∠QPR = 180°
ਸਬੂਤ : OQ ਇਕ ਅਰਧ ਵਿਆਸ ਹੈ ਅਤੇ PQ ਬਿੰਦੂ P ਤੋਂ ਦਿੱਤੇ ਗਏ ਚੱਕਰ ਦੀ ਸਪਰਸ਼ ਰੇਖਾ ਹੈ ।
∴ ∠OQP = 90° …(1)
[∵ ਚੱਕਰ ਦੇ ਕਿਸੇ ਬਿੰਦੂ ‘ਤੇ ਸਪਰਸ਼ ਰੇਖਾ, ਸਪਰਸ਼ ਚੌਦੂ ਵਿਚੋਂ ਲੰਘਣ ਵਾਲੇ ਅਰਧ ਵਿਆਸ ‘ਤੇ ਲੰਬ ਹੁੰਦੀ ਹੈ ॥]
ਇਸੇ ਤਰ੍ਹਾਂ ∠ORP = 90° ….(2)
ਚਤੁਰਭੁਜ ROQP ਵਿੱਚ
∠ROQ + ∠PRO + ∠OQP + ∠QPR = 360°
∠ROQ + 90° + 90° + ∠QPR = 360° [(1) ਅਤੇ (2) ਤੋਂ।]
ROQ + ∠QPR + 180° = 360°
∠ROQ + ∠QPR = 360° -180°
∠ROQ + ∠QPR = 180°
ਕਿਸੇ ਬਾਹਰੀ ਬਿੰਦੂ ਤੋਂ ਕਿਸੇ ਚੱਕਰ ‘ਤੇ ਖਿੱਚੀਆਂ ਗਈਆਂ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਦਾ ਵਿਚਕਾਰਲਾ ਕੋਣ ਸਪਰਸ਼ ਬਿੰਦੂਆਂ ਨੂੰ ਮਿਲਾਉਣ ਵਾਲੇ ਰੇਖਾਖੰਡ ਦੁਆਰਾ ਕੇਂਦਰ ‘ਤੇ ਬਣੇ ਅੰਦਰਲੇ ਕੋਣ ਦਾ ਸੰਪੂਰਕ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 11.
ਸਿੱਧ ਕਰੋ ਕਿ ਕਿਸੇ ਚੱਕਰ ਦੇ ਬਾਹਰਲੇ ਪਾਸੇ ਛੂਹਦਾ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ, ਸਮਚਤੁਰਭੁਜ ਹੁੰਦਾ ਹੈ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਇੱਕ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ABCD ਕੇਂਦਰ O ਵਾਲੇ ਚੱਕਰ ਦੇ ਬਾਹਰ ਹੈ ।

ਸਿੱਧ ਕਰਨਾ : ABCD ਇਕ ਸਮਚਤੁਰਭੁਜ ਹੈ
ਸਬੂਤ : ਕਿਉਂਕਿ ਬਾਹਰੀ ਬਿੰਦੂ ਤੋਂ ਕਿਸੇ ਚੱਕਰ ਉੱਤੇ ਖਿੱਚੀਆਂ ਗਈਆਂ ਦੋਵੇਂ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਦੀਆਂ ਲੰਬਾਈਆਂ ਸਮਾਨ ਹੁੰਦੀਆਂ ਹਨ।
ਹੁਣ, ਚੱਕਰ ਦੇ ਬਾਹਰ ਸਥਿਤ ਕਿਸੇ ਬਿੰਦੂ B ਤੋਂ BE ਅਤੇ BF ਚੱਕਰ ਉੱਤੇ ਦੋ ਸਪੱਰਸ਼ ਰੇਖਾਵਾਂ ਹਨ ।
∴ BE = BF ….(1)
ਇਸੇ ਤਰ੍ਹਾਂ AE = AH …(2)
CG = CF ….(3)
DG = DH ….(4)
(1), (2), (3), (4) ਨੂੰ ਜੋੜਣ ‘ਤੇ
(BE + AE) + (CG + DG) = (BF + CF) + (AH + DH)
AB + CD = BC + AD …(5)
ਹੁਣ, ABCD ਇਕ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਹੈ ।
∴ AB = CD ਅਤੇ BC= AD …(6)
(5) ਅਤੇ (6) ਤੋਂ ਸਾਨੂੰ ਮਿਲਦਾ ਹੈ
AB + AB = BC + BC
2AB = 2BC
AB = BC
ਹੁਣ, AB = BC = CD = AD
∴ ABCD ਇੱਕ ਸਮਚਤੁਰਭੁਜ ਹੈ ।
∴ ਕਿਸੇ ਚੱਕਰ ਦੇ ਬਾਹਰਲੇ ਪਾਸੇ ਛੂੰਹਦਾ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਸਮਚਤੁਰਭੁਜ ਹੁੰਦਾ ਹੈ।

ਪ੍ਰਸ਼ਨ 12.
4 cm ਅਰਧ ਵਿਆਸ ਵਾਲੇ ਇੱਕ ਚੱਕਰ ਦੇ ਬਾਹਰਲੇ ਪਾਸੇ ਛੂਹਦਾ ਇੱਕ ਤ੍ਰਿਭੁਜ ABCਇਸ ਤਰ੍ਹਾਂ ਖਿੱਚਿਆ ਗਿਆ ਹੈ ਕਿ ਰੇਖਾਖੰਡ BD ਅਤੇDC (ਜਿਸ ਵਿੱਚ ਸਪਰਸ਼ ਬਿੰਦੂD ਦੁਆਰਾ BC ਵਿਭਾਜਿਤ ਹੈ ਦੀਆਂ ਲੰਬਾਈਆਂ ਕ੍ਰਮਵਾਰ 8 cm ਅਤੇ 6 cm ਹੈ (ਦੇਖੋ ਚਿੱਤਰ । ਭੁਜਾਵਾਂ AB ਅਤੇ AC ਪਤਾ ਕਰੋ ।

ਹੱਲ:
4 cm ਅਰਧ ਵਿਆਸ ਵਾਲੇ ਚੱਕਰ ਦੇ ਬਾਹਰਲੇ ਪਾਸੇ ਛੂੰਹਦਾ ਇੱਕ ਤਿਭੁਜ ABC ਖਿੱਚਿਆ ਗਿਆ ਹੈ ਤ੍ਰਿਭੁਜ ਦੀਆਂ ਭੁਜਾਵਾਂ BC, CA, AB ਚੱਕਰ ਨੂੰ ਕ੍ਰਮਵਾਰ ਬਿੰਦੂ D, E ਅਤੇ Fਉੱਤੇ ਸਪਰਸ਼ ਕਰਦੀਆਂ ਹਨ।
ਕਿਉਂਕਿ ਕਿਸੇ ਬਾਹਰੀ ਬਿੰਦੂ ਤੋਂ ਚੱਕਰ ‘ਤੇ ਖਿੱਚੀਆਂ ਗਈਆਂ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਦੀਆਂ ਲੰਬਾਈਆਂ ਬਰਾਬਰ ਹੁੰਦੀਆਂ ਹਨ।
∴ AE = AF = 1 cm (ਮੰਨ ਲਉ।)
CE = CD= 6 cm
BF = BD = 8 cm
ਕਿਉਂਕਿ ਚੱਕਰ ਦੀ ਸਪਰਸ਼ ਰੇਖਾ ਸਪੱਰਸ਼ ਬਿੰਦੂ ਤੋਂ ਜਾਣ ਵਾਲੇ ਅਰਧ ਵਿਆਸ ’ਤੇ ਲੰਬ ਹੁੰਦੀ ਹੈ ।

∴ OD ⊥ BC; OE ⊥ AC ਅਤੇ OF ⊥ AB.
ਨਾਲ ਹੀ, OE = OD = OF =4 cm.
△ ABC ਵਿਚ
a = AC = (x + 6) cm ;
b = CB = (6 + 8) cm = 14 cm
c = BA = (8 + x) cm

(△OBC) ਦਾ ਖੇਤਰਫਲ = \(\frac{1}{2}\) × ਅਧਾਰ × ਸਿਖਰਲੰਬ
= \(\frac{1}{2}\) × 14 × 4 = 28 cm2 …(2)
(△BOA) ਦਾ ਖੇਤਰਫਲ = \(\frac{1}{2}\) × ਅਧਾਰ × ਸਿਖਰਲੰਬ
= \(\frac{1}{2}\) × (8 + x) × 4
= (16 + 2x) cm2 …(3)
(△AOC) ਦਾ ਖੇਤਰਫਲ = \(\frac{1}{2}\) × ਅਧਾਰ × ਸਿਖਰਲੰਬ
= \(\frac{1}{2}\) × (6 + x) × 4
= (12 + 21) cm2 …(4)
ਚਿੱਤਰ ਤੋਂ ਖੇਤਰਫਲ ਜੋੜਣ ਤੇ ਸਾਨੂੰ ਮਿਲਦਾ ਹੈ
ar (△ABC) = ar (△OBC) + ar (△BOA) + ar (△AOC)
\(\sqrt{48 x^{2}+672 x}\) = 28 + 16 + 2x + 12 + 2x
\(\sqrt{48 x^{2}+672 x}\) = 4x + 56
\(\sqrt{48 x^{2}+672 x}\) = 4[x + 14]
ਦੋਵੇਂ ਪਾਸੇ ਵਰਗ ਕਰਨ ਤੇ
48x² + 672x = 16 (x + 14)²
48x(x + 14) = 16(x + 14)²
48x = 16(x + 14)
3x = x + 14
2x = 14
x = 7
x = \( \frac{14}{2}\) = 7
∴ AC = (x + 6) cm
= (7 + 6) cm = 13 cm
AB = (x + 8) cm
= (7 + 8) cm = 15 cm
AB = 15 cm ਅਤੇ AC = 13 cm

ਪ੍ਰਸ਼ਨ 13.
ਸਿੱਧ ਕਰੋ ਕਿ ਚੱਕਰ ਦੇ ਬਾਹਰਲੇ ਪਾਸੇ ਛੂੰਹਦੀ ਹੋਈ ਚਤੁਰਭੁਜ ਦੀਆਂ ਆਹਮਣੇ-ਸਾਹਮਣੇ ਦੀਆਂ ਭੁਜਾਵਾਂ ਕੇਂਦਰ ‘ਤੇ ਸੰਪੁਰਕ ਕੋਣ ਬਣਾਉਂਦੀਆਂ ਹਨ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : ਕੇਂਦਰ O ਵਾਲੇ ਚੱਕਰ ਦੇ ਬਾਹਰ ਬਣੀ ਚਤੁਰਭੁਜ PORS ਜਿਸ ਦੀਆਂ ਭੁਜਾਵਾਂ PQ, QR, RS ਅਤੇ SP ਚੱਕਰ ਨੂੰ ਕ੍ਰਮਵਾਰ L, M, N ਅਤੇ 1 ਤੇ ਸਪਰਸ਼ ਕਰਦੀਆਂ ਹਨ।

ਸਿੱਧ ਕਰਨਾ ਹੈ :
∠POQ + ∠SOR = 180°
ਅਤੇ ∠SOP + ∠ROQ = 180°
ਰਚਨਾ :
OP, OL, OQ, OM, OR, ON, OS ਅਤੇ OT ਨੂੰ ਮਿਲਾਉ ।
ਸਬੂਤ : ਕਿਉਂਕਿ ਬਾਹਰੀ ਬਿੰਦੂ ਤੋਂ ਕਿਸੇ ਚੱਕਰ ‘ਤੇ
ਖਿੱਚੀਆਂ ਗਈਆਂ ਦੋ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਕੇਂਦਰ ‘ਤੇ ਸਮਾਨ ਕੋਣ ਬਣਾਉਂਦੀਆਂ ਹਨ ।
∴ ∠2 = ∠3; ∠4 = ∠5 ; ∠6 = ∠7; ∠8 = ∠1 ….(1)
ਕਿਉਂਕਿ ਇਕ ਬਿੰਦੂ ਦੇ ਸਾਰੇ ਕੋਣਾਂ ਦਾ ਜੋੜ 360° ਹੁੰਦਾ ਹੈ ।
∴ ∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8 = 360°
∠1 + ∠2 + ∠2 + ∠5 + ∠5 + ∠6 + ∠6 + ∠1 = 360°
ਜਾਂ 2(∠1 + ∠2 + ∠5 + ∠6) = 360°
ਜਾਂ (∠1 + ∠2) + (∠5 + ∠6) = \(\frac{360^{\circ}}{2}\) = 180°
ਜਾਂ ∠POQ + ∠SOR = 180°
ਇਸੇ ਤਰ੍ਹਾਂ, ∠SOP + ∠ROQ = 180°
∴ ਚੱਕਰ ਦੇ ਬਾਹਰਲੇ ਪਾਸੇ ਛੂੰਹਦੀ ਹੋਈ ਚਤੁਰਭੁਜ ਦੀਆਂ ਆਹਮਣੇ-ਸਾਹਮਣੇ ਦੀਆਂ ਭੁਜਾਵਾਂ ਕੇਂਦਰ ’ਤੇ ਸੰਪੂਰਕ ਕੋਣ ਬਣਾਉਂਦੀਆਂ ਹਨ ।

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 10 ਚੱਕਰ Ex 10.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 10 ਚੱਕਰ Exercise 10.1

ਪ੍ਰਸ਼ਨ 1.
ਚੱਕਰ ਦੀਆਂ ਕਿੰਨੀਆਂ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਹੋ ਸਕਦੀਆਂ ਹਨ ।
ਹੱਲ:
ਕਿਉਂਕਿ ਚੱਕਰ ਦੇ ਕਿਸੇ ਬਿੰਦੂ ‘ਤੇ ਇੱਕ ਅਤੇ ਕੇਵਲ ਇੱਕ ਹੀ ਸਪਰਸ਼ ਰੇਖਾ ਹੁੰਦੀ ਹੈ । ਪਰ ਚੱਕਰ ਇਕ ਅਨੰਤ ਬਿੰਦੂਆਂ ਦਾ ਸਮੂਹ ਹੁੰਦਾ ਹੈ ਇਸ ਲਈ ਅਸੀਂ ਚੱਕਰ ਦੀਆਂ ਅਨੰਤ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਖਿੱਚ ਸਕਦੇ ਹਾਂ ।

ਪ੍ਰਸ਼ਨ 2.
ਖਾਲੀ ਸਥਾਨਾਂ ਨੂੰ ਭਰੋ :
(i) ਕਿਸੇ ਚੱਕਰ ਦੀ ਸਪਰਸ਼ ਰੇਖਾ ਉਸਨੂੰ ________________ ਬਿੰਦੂਆਂ ‘ਤੇ ਕੱਟਦੀ ਹੈ ।
(ii) ਚੱਕਰ ਨੂੰ ਦੋ ਬਿੰਦੂਆਂ ‘ਤੇ ਕੱਟਣ ਵਾਲੀ ਰੇਖਾ ਨੂੰ _________ ਕਹਿੰਦੇ ਹਨ ।
(iii) ਇੱਕ ਚੱਕਰ ਦੀਆਂ _________ ਸਮਾਂਤਰ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਹੋ ਸਕਦੀਆਂ ਹਨ।
(iv) ਚੱਕਰ ਅਤੇ ਉਸਦੀ ਸਪਰਸ਼ ਰੇਖਾ ਦੇ ਸਾਂਝੇ ਬਿੰਦੂ ਨੂੰ _________ ਕਹਿੰਦੇ ਹਨ ।
ਹੱਲ:
(i) ਕਿਸੇ ਚੱਕਰ ਦੀ ਸਪਰਸ਼ ਰੇਖਾ ਉਸਨੂੰ ਇਕ ਬਿੰਦੂ ‘ਤੇ ਕੱਟਦੀ ਹੈ ।
(ii) ਚੱਕਰ ਨੂੰ ਦੋ ਬਿੰਦੂਆਂ ‘ਤੇ ਕੱਟਣ ਵਾਲੀ ਰੇਖਾ ਨੂੰ ਛੇਦਕ ਰੇਖਾ ਕਹਿੰਦੇ ਹਨ ।
(iii) ਇੱਕ ਚੱਕਰ ਦੀਆਂ ਦੋ ਸਮਾਂਤਰ ਸਪਰਸ਼ ਰੇਖਾਵਾਂ ਹੋ ਸਕਦੀਆਂ ਹਨ ।
(iv) ਚੱਕਰ ਅਤੇ ਉਸਦੀ ਸਪਰਸ਼ ਰੇਖਾ ਦੇ ਸਾਂਝੇ ਬਿੰਦੂ ਨੂੰ ਸਪਰਸ਼ ਬਿੰਦੂ ਕਹਿੰਦੇ ਹਨ !

ਪ੍ਰਸ਼ਨ 3.
5cm ਅਰਧ ਵਿਆਸ ਵਾਲੇ ਇੱਕ ਚੱਕਰ ਦੇ ਬਿੰਦੂ ? ‘ਤੇ ਸਪਰਸ਼ ਰੇਖਾ PQ ਕੇਂਦਰ O ਤੋਂ ਜਾਣ ਵਾਲੀ ਇੱਕ ਰੇਖਾ ਨੂੰ ਬਿੰਦੂ Q’ ਤੇ ਇਸ ਤਰ੍ਹਾਂ ਮਿਲਦੀ ਹੈ ਕਿ OQ = 12 cm, PQ ਦੀ ਲੰਬਾਈ ਹੈ :
(A) 12 cm
(B) 13 cm
(C) 8.5 cm
(D) \(\sqrt {119}\) cm
ਹੱਲ:
ਦਿਤੀ ਗਈ ਸੂਚਨਾ ਅਨੁਸਾਰ ਅਸੀਂ ਚਿੱਤਰ ਬਣਾਉਂਦੇ ਹਾਂ :

OP = 5 cm ਅਤੇ OQ = 12 cm
∵ PQ ਇੱਕ ਸਪਰਸ਼ ਰੇਖਾ ਹੈ ਅਤੇ OP ਅਰਧ ਵਿਆਸ ਹੈ ,
∴ ∠OPQ = 90°
ਹੁਣ, ਸਮਕੋਣ △OPQ ਵਿਚ ਪਾਈਥਾਗੋਰਸ ਮੇਯ ਅਨੁਸਾਰ,
OQ² = OP² + QP²
(12)² = (5)² + OP²
QP² = (12)² – (5)²
= 144 – 25 = 119
QP = \(\sqrt {119}\) cm
∴ ਵਿਕਲਪ (D) ਸਹੀ ਹੈ।

ਪ੍ਰਸ਼ਨ 4.
ਇੱਕ ਚੱਕਰ ਖਿੱਚੋ ਅਤੇ ਇੱਕ ਦਿੱਤੀ ਗਈ ਰੇਖਾ ਦੇ । ਸਮਾਂਤਰ ਦੋ ਅਜਿਹੀਆਂ ਰੇਖਾਵਾਂ ਖਿੱਚੋ ਕਿ ਉਨ੍ਹਾਂ ਵਿੱਚੋਂ ਇੱਕ ਸਪਰਸ਼ ਰੇਖਾ ਹੋਵੇ ਅਤੇ ਦੂਸਰੀ ਚੱਕਰ ਦੀ ਛੇਦਕ ਰੇਖਾ ਹੋਵੇ ।
ਹੱਲ:
ਦਿੱਤੀ ਗਈ ਸੂਚਨਾ ਅਨੁਸਾਰ ਅਸੀਂ ਇੱਕ ਚਿੱਤਰ ਬਣਾਉਂਦੇ ਹਾਂ ਜਿਸਦਾ ਕੇਂਦਰ O ਅਤੇ l ਦਿੱਤੀ ਹੋਈ ਰੇਖਾ ਹੋਵੇ।

ਹੁਣ, ਅ ਅਤੇ n ਦੋ ਅਜਿਹੀਆਂ ਰੇਖਾਵਾਂ ਹਨ ਜੋ ਰੇਖਾ l ਦੇ ਇਸ ਤਰ੍ਹਾਂ ਸਮਾਂਤਰ ਹਨ ਕਿ m ਸਪੱਰਸ਼ ਰੇਖਾ ਵੀ ਹੈ ਅਤੇ l ਦੇ ਸਮਾਂਤਰ ਵੀ ਹੈ ਅਤੇ n ਚੱਕਰ ਦੀ ਛੇਦਰ ਰੇਖਾ ਵੀ ਹੈ ਅਤੇ l ਦੇ ਸਮਾਂਤਰ ਵੀ ਹੈ ।

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 8 ਤਿਕੋਣਮਿਤੀ ਬਾਰੇ ਜਾਣ ਪਛਾਣ Ex 8.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 8 ਤਿਕੋਣਮਿਤੀ ਬਾਰੇ ਜਾਣ ਪਛਾਣ Exercise 8.4

ਪ੍ਰਸ਼ਨ 1.
ਤਿਕੋਣਮਿਤਈ ਅਨੁਪਾਤਾਂ sin A, sec A ਅਤੇ tan A ਨੂੰ cot A ਦੇ ਪਦਾਂ ਵਿਚ ਦਰਸਾਉ।
ਹੱਲ:
ਤਤਸਮਕ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ,
cosec² A – cot² A = 1
⇒ cosec² A = 1 + cot² A
⇒ (cosec A)² = cot² A + 1
⇒ \(\left(\frac{1}{\sin A}\right)^{2}\) = cot² A + 1
⇒ (sin A)² = \(\frac{1}{\cot ^{2} \mathrm{~A}+1}\)
⇒ sin A = ±\(\frac{1}{\sqrt{\cot ^{2} A+1}}\)
ਅਸੀਂ ਨਿਉਨ ਕੋਣ A ਦੇ ਲਈ sin A ਦੇ ਰਿਣਾਤਮਕ ਮੁੱਲ ਛਡ ਦਿੰਦੇ ਹਨ ।
∴ sin A = \(\frac{1}{\sqrt{\cot ^{2} A+1}}\)
ਤਤਸਮਕ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ਤੇ,
sec² A – tan² A = 1
⇒ sec² A = 1 + tan² A

ਪ੍ਰਸ਼ਨ 2.
∠A ਦੇ ਬਾਕੀ ਸਾਰੇ ਤਿਕੋਣਮਿਤਈ ਅਨੁਪਾਤਾਂ ਨੂੰ sec A ਦੇ ਪਦਾਂ ਵਿੱਚ ਦਰਸਾਉ ।
ਹੱਲ:
sin² A + cos² A = 1
⇒ sin² A = 1 – cos² A

[ਨਿਊਨ ਕੋਣ A ਦੇ ਲਈ – ve ਚਿੰਨ੍ਹ ਨੂੰ ਛੱਡ ਦਿਓ]
⇒ sin A = \(\frac{\sqrt{\sec ^{2} A-1}}{\sec A}\)
cos A = \(\frac{1}{\sec A}\)
1 + tan² A = sec² A
tan² A = sec² A – 1
(tan A)² = sec² A – 1
⇒ tan A = ±\(\sqrt{\sec ^{2} A-1}\)
[ਨਿਊਨ ਕੋਣ A ਦੇ ਲਈ – ve ਚਿੰਨ੍ਹ ਨੂੰ ਛੱਡ ਦਿਓ]

3. ਮੁੱਲ ਪਤਾ ਕਰੇ :

ਪ੍ਰਸ਼ਨ (i).
\(\frac{\sin ^{2} 63^{\circ}+\sin ^{2} 27^{\circ}}{\cos ^{2} 17^{\circ}+\cos ^{2} 73^{\circ}}\)
ਉੱਤਰ:

∵ sin (90° – θ)= cos θ
ਅਤੇ cos (90° – θ) = sin θ.
= \(\frac{\cos ^{2} 27^{\circ}+\sin ^{2} 27^{\circ}}{\cos ^{2} 17^{\circ}+\sin ^{2} 17^{\circ}}\)
= \(\frac{1}{1}\) = 1

ਪ੍ਰਸ਼ਨ (ii).
sin 25° cos 65° + cos 25° sin 65°.
ਉੱਤਰ:
sin 25° cos 65° + cos 25° sin 65°
= sin 25° × cos (90° – 25°) + cos 25° × sin (90° – 25°)
∵ cos (90° – θ) = sin θ
sin (90° – θ) = cos θ
= sin 25° × sin 25° + cos 25° × cos 25°
= sin² 25° + cos² 25°
= 1.

4. ਸਹੀ ਉੱਤਰ ਚੁਣੋ ਅਤੇ ਆਪਣੇ ਵਿਕਲਪ ਦੀ ਪੁਸ਼ਟੀ ਕਰੇ:

ਪ੍ਰਸ਼ਨ (i).
9 sec² A – 9 tan²
(A) 1
(B) 9
(C) 8
(D) 0
ਉੱਤਰ:
9 sec² A – 9 tan² A
= 9 (sec² A – tan² A)
= 9 × 1 = 9.
∴ ਸਹੀ ਵਿਕਲਪ (B) ਹੈ

ਪ੍ਰਸ਼ਨ (ii).
(1 + tan θ + sec θ) (1 + cotθ – cosec θ) ਬਰਾਬਰ ਹੈ :
(A) 0
(B) 1
(C) 2
(D) -1.
ਉੱਤਰ:
(1 + tan θ + sec θ) (1 + cotθ – cosec θ)


∴ ਸਹੀ ਵਿਕਲਪ (C) ਹੈ

ਪ੍ਰਸ਼ਨ (iii).
(sec A + tan A) (1 – sin A) ਬਰਾਬਰ ਹੈ :
(A) sec A
(B) sin A
(C) cosec A
(D) cos A.
ਉੱਤਰ:
(sec A + tan A) (1 – sin A)

[∵ cos² A = 1 – sin² A]
= cos A.
∴ ਸਹੀ ਵਿਕਲਪ (D) ਹੈ

ਪ੍ਰਸ਼ਨ (iv).
\(\frac{1+\tan ^{2} A}{1+\cot ^{2} A}\)
(A) sec² A
(B) -1
(C) cot² A
(D) tan² A.
ਉੱਤਰ:
\(\frac{1+\tan ^{2} A}{1+\cot ^{2} A}\)

∴ ਸਹੀ ਵਿਕਲਪ (D) ਹੈ

5. ਹੇਠਾਂ ਦਿੱਤੀਆਂ ਸਰਬਸਮਤਾਵਾਂ (ਤਤਸਮਕਾਂ) ਸਿੱਧ ਕਰੋ, ਜਿੱਥੇ ਉਹ ਕੋਣ ਜਿਨ੍ਹਾਂ ਲਈ ਵਿਅੰਜਕਾਂ ਪਰਿਭਾਸ਼ਿਤ ਹਨ, ਨਿਊਨ ਕੋਣ ਹਨ :

ਪ੍ਰਸ਼ਨ (i).
(cosec θ – cot θ)² = \(\frac{1-\cos \theta}{1+\cos \theta}\)
ਉੱਤਰ:
L.H.S. = (cosec θ – cot θ)²
= \(\left\{\frac{1}{\sin \theta}-\frac{\cos \theta}{\sin \theta}\right\}^{2}\)

∴ L.H.S. = R.H.S.

ਪ੍ਰਸ਼ਨ (ii).
\(\frac{\cos A}{1+\sin A}\) + \(\frac{1+\sin A}{\cos A}\) = 2 sec A
ਉੱਤਰ:
L.H.S. = \(\frac{\cos A}{1+\sin A}\) + \(\frac{1+\sin A}{\cos A}\)

∴ L.H.S. = R.H.S.

ਪ੍ਰਸ਼ਨ (iii).
\(\frac{\tan \theta}{1-\cot \theta}\) + \(\frac{\cot \theta}{1-\tan \theta}\) = 1 + secθcosecθ
[ਸੰਕੇਤ : ਵਿਅੰਜਕ ਨੂੰ sin θ, ਅਤੇ cos θ ਦੇ ਪਦਾਂ ਵਿੱਚ ਲਿਖੋ1]
ਉੱਤਰ:
L.H.S. = \(\frac{\tan \theta}{1-\cot \theta}\) + \(\frac{\cot \theta}{1-\tan \theta}\)



= 1 + sec θ cosec θ
∴ L.H.S. = R.H.S.

ਪ੍ਰਸ਼ਨ (iv).
\(\frac{1+\sec A}{\sec A}\) = \(\frac{\sin ^{2} A}{1-\cos A}\)
[ਸੰਕੇਤ : ਖੱਬੇ ਪਾਸੇ ਅਤੇ ਸੱਜੇ ਪਾਸੇ ਨੂੰ ਅਲੱਗ-ਅਲੱਗ ਸਰਲ ਕਰੋ ]
ਉੱਤਰ:


= 1 + cos A.
∴ L.H.S. = R.H.S.

ਪ੍ਰਸ਼ਨ (v).
ਤਤਮਸਕ cosec² A = 1 + cot² A ਨੂੰ ਵਰਤਦੇ ਹੋਏ, ਸਿੱਧ ਕਰੋ :
\(\frac{\cos A-\sin A+1}{\cos A+\sin A-1}\) = cosec A + cot A,
ਉੱਤਰ:
\(\frac{\cos A-\sin A+1}{\cos A+\sin A-1}\)
(ਅੰਸ਼ ਅਤੇ ਹਰ ਨੂੰ sin A ਨਾਲ ਭਾਗ ਕਰਨ ਤੇ)

= cosec A + cot A
= R.H.S.

ਪ੍ਰਸ਼ਨ (vi).
\(\sqrt{\frac{1+\sin A}{1-\sin A}}\) = sec A + tan A
ਉੱਤਰ:
L.H.S. = \(\sqrt{\frac{1+\sin A}{1-\sin A}}\)

= sec A + tan A
∴ L.H.S. = R.H.S.

ਪ੍ਰਸ਼ਨ (vii).
\(\frac{\sin \theta-2 \sin ^{3} \theta}{2 \cos ^{3} \theta-\cos \theta}\) = tan θ
ਉੱਤਰ:
L.H.S. = \(\frac{\sin \theta-2 \sin ^{3} \theta}{2 \cos ^{3} \theta-\cos \theta}\)

∴ L.H.S. = R.H.S.

ਪ੍ਰਸ਼ਨ (viii).
(sin A + cosec A)² + (cos A + sec A)² = 7 + tan² A + cot² A
ਉੱਤਰ:
L.H.S. = (sin A + cosec A)² + (cos A + sec A)²
= {sin² A + cosec² A + 2 sin A × cosec A} + {cos² A + sec² A + 2 cos A × sec A}
[∵ cosec A = \(\frac{1}{\sin A}\)]

= 2 + 2 + (sin² A + cos² A) + sec² A + cosec² A
= 2 + 2 + 1 + 1 + tan² A + 1 + cot² A
(∵ sec² A = tan² A + 1,
(cosec² A = cot² A + 1)
= 7 + tan² A + cot² A
∴ L.H.S. = R.H.S.

ਪ੍ਰਸ਼ਨ (ix).
(cosec A – sin A) (sec A – cos A) = \(\frac{1}{\tan A+\cot A}\)
[ਸੰਕੇਤ : ਖੱਬੇ ਪਾਸੇ ਅਤੇ ਸੱਜੇ ਪਾਸੇ ਨੂੰ ਅਲੱਗ-ਅਲੱਗ ਸਰਲ ਕਰੋ]
ਉੱਤਰ:
L.H.S. = (cosec A – sin A) (sec A – cos A)

∴ L.H.S. = R.H.S.

ਪ੍ਰਸ਼ਨ (x).
\(\left(\frac{1+\tan ^{2} A}{1+\cot ^{2} A}\right)\) = \(\left(\frac{1-\tan A}{1-\cot A}\right)^{2}\) = tan² A
ਉੱਤਰ:

∴ L.H.S. = R.H.S.

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 9 ਤਿਕੋਣਮਿਤੀਦੇ ਕੁਝ ਉਪਯੋਗ Ex 9.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 9 ਤਿਕੋਣਮਿਤੀਦੇ ਕੁਝ ਉਪਯੋਗ Exercise 9.1

ਪ੍ਰਸ਼ਨ 1.
ਸਰਕਸ ਦਾ ਇੱਕ ਕਲਾਕਾਰ ਇੱਕ 20 m ਲੰਬੀ ਰੱਸੀ ‘ਤੇ ਚੜ੍ਹ ਰਿਹਾ ਹੈ ਜੋ ਪੂਰੀ ਤਰ੍ਹਾਂ ਨਾਲ ਤਣੀ (ਕਸੀ) ਹੋਈ ਹੈ ਅਤੇ ਧਰਤੀ ‘ਤੇ ਸਿੱਧੇ ਖੜੇ ਖੰਬੇ ਦੇ ਸਿਖਰ ਨਾਲ ਬੰਨੀ ਹੋਈ ਹੈ। ਜੇਕਰ ਰੱਸੀ ਧਰਤੀ ਦੇ ਤਲ ਨਾਲ 30° ਦਾ ਕੋਣ ਬਣਾਉਂਦੀ ਹੋਵੇ ਤਾਂ ਖੰਬੇ ਦੀ ਉੱਚਾਈ ਪਤਾ ਕਰੋ ।(ਦੇਖੋ ਚਿੱਤਰ)।

ਹੱਲ:
ਮੰਨ ਲਉ AB ਖੰਬੇ ਦੀ ਉੱਚਾਈ ਹੈ।
AC = 20 m ਰੱਸੀ ਦੀ ਲੰਬਾਈ

ਇਸ ਸਥਿਤੀ ਵਿਚ ਉਚਾਣ ਕੋਣ 30° ਹੈ ।
ਸਮਕੋਣ △ABC ਵਿੱਚ,
ਜਾਂ \(\frac{AB}{AC}\) = sin 30°
ਜਾਂ AB = \(\frac{1}{2}\) × 20 = 10
∴ ਖੰਬੇ ਦੀ ਉਚਾਈ 10 m ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਹਨੇਰੀ ਆਉਣ ਨਾਲ ਇੱਕ ਦਰੱਖਤ ਟੁੱਟ ਜਾਂਦਾ ਹੈ ਅਤੇ ਟੁੱਟਿਆ ਹੋਇਆ ਭਾਗ ਇਸ ਤਰ੍ਹਾਂ ਨਾਲ ਮੁੜ ਜਾਂਦਾ ਹੈ ਕਿ ਦਰੱਖਤ ਦਾ ਸਿਖ਼ਰ ਜਮੀਨ ਨੂੰ ਛੂਹਣ (touch) ਲੱਗਦਾ ਹੈ ਹੈ ਅਤੇ ਇਸ ਦੇ ਨਾਲ 30° ਦਾ ਕੋਣ ਬਣਾਉਂਦਾ ਹੈ । ਦਰੱਖ਼ਤ ਦੇ ਆਧਾਰ ਬਿੰਦੂ ਦੀ ਦੂਰੀ, ਜਿੱਥੇ ਦਰੱਖ਼ਤ ਦਾ ਸਿਖਰ ਜਮੀਨ ਨੂੰ ਛੂਹਦਾ ਹੈ, 8 m ਹੈ । ਦਰਖ਼ਤ ਦੀ ਉੱਚਾਈ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ ਹਨੇਰੀ ਤੋਂ ਪਹਿਲਾਂ ਦਰੱਖ਼ਤ ਦੀ ਉੱਚਾਈ BD ਹੈ । ਹਨੇਰੀ ਤੋਂ ਬਾਅਦ AD = AC = ਟੁੱਟੇ ਹੋਏ ਦਰੱਖ਼ਤ ਦੇ ਦੋ ਭਾਗਾਂ ਦੀ ਲੰਬਾਈ (ਚਿੱਤਰ ਵਿਚ ਦਿਖਾਏ ਤੋਂ ਅਨੁਸਾਰ

ਸਮਕੋਣ △ABC ਵਿੱਚ,
\(\frac{AB}{BC}\) = tan 30°

ਦਰੱਖਤ ਦੀ ਕੁੱਲ ਉੱਚਾਈ = h₁ + h₂
= \(\frac{8}{3}\)\(\sqrt {3}\) + \(\frac{16}{3}\)\(\sqrt {3}\) [(1) ਅਤੇ (2) ਤੋਂ।]
= [latex]\frac{8+16}{3}[/latex]\(\sqrt {3}\) = \(\frac{24}{3}\)\(\sqrt {3}\)
= 8\(\sqrt {3}\) m
∴ ਦਰੱਖ਼ਤ ਦੀ ਉੱਚਾਈ 83 m ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਇਕ ਠੇਕੇਦਾਰ ਬੱਚਿਆਂ ਦੇ ਖੇਡਣ ਵਾਲੇ ਇਕ ਪਾਰਕ ਵਿਚ ਦੋ ਤਿਲਕਣ ਪੱਟੀਆਂ (Slides) ਨੂੰ ਲਗਾਉਣਾ ਚਾਹੁੰਦਾ ਹੈ । 5 ਸਾਲ ਤੋਂ ਘੱਟ ਉਮਰ ਦੇ ਬੱਚਿਆਂ ਲਈ ਉਹ ਇਸ ਤਰਾਂ ਦੀ ਤਿਲਕਣ ਪੱਟੀ ਲਗਾਉਣਾ ਚਾਹੁੰਦਾ ਹੈ ਜਿਸ ਦਾ ਸਿਖਰ 1.5 m ਉੱਚਾਈ ‘ਤੇ ਹੋਵੇ ਅਤੇ ਉਹ ਜਮੀਨ ਨਾਲ 30° ਕੋਣ ‘ ਤੇ ਝੁਕੀ ਹੋਵੇ, ਜਦੋਂ ਕਿ ਇਸ ਤੋਂ ਵੱਧ ਉਮਰ ਦੇ ਬੱਚਿਆਂ ਲਈ ਉਹ 3m ਦੀ ਉੱਚਾਈ ‘ਤੇ ਇੱਕ ਵੱਧ ਢਾਲ ਦੀ ਤਿਲਕਣਪੱਟੀ ਲਗਾਉਣਾ ਚਾਹੁੰਦਾ ਹੈ ਜੋ ਜਮੀਨ ਨਾਲ 60° ਦਾ ਕੋਣ ਬਣਾਉਂਦੀ ਹੋਵੇ । ਹਰ ਇੱਕ ਸਥਿਤੀ ਵਿੱਚ ਤਿਲਕਣ ਪੱਟੀ ਦੀ ਲੰਬਾਈ ਕਿੰਨੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ।
ਹੱਲ:
ਸਥਿਤੀ 1. 5 ਸਾਲ ਤੋਂ ਛੋਟੇ ਬੱਚਿਆਂ ਲਈ
ਮੰਨ ਲਉ AC = l₁m ਤਿਲਕਣ ਪੱਟੀ ਦੀ ਲੰਬਾਈ ਹੈ ਅਤੇ BC = 1.5 m ਤਿਲਕਣ ਪੱਟੀ ਦੀ ਉੱਚਾਈ ਹੈ । ਇਸ ਸਥਿਤੀ ਵਿਚ ਜ਼ਮੀਨ ਨਾਲ ਬਣਿਆ ਕੋਣ 30° ਦਾ ਹੈ (ਦੇਖੋ ਚਿੱਤਰ)

ਸਮਕੋਣ △ABC ਵਿੱਚ,
\(\frac{BC}{AC}\) = sin 30°
ਜਾਂ \(\frac{1 \cdot 5}{l_{1}}\) = \(\frac{1}{2}\)
ਜਾਂ l₁ = 1.5 × 2 = 3m
ਸਥਿਤੀ II. 5 ਸਾਲ ਤੋਂ ਵੱਧ ਉਮਰ ਦੇ ਬੱਚਿਆਂ ਲਈ
ਮੰਨ ਲਉ AC = l₂m ਤਿਲਕਣ ਪੱਟੀ ਦੀ ਲੰਬਾਈ ਹੈ ਅਤੇ BC = 3 m ਤਿਲਕਣ ਪੱਟੀ ਦੀ ਉੱਚਾਈ ਹੈ ਅਤੇ ਜਮੀਨ ਨਾਲ ਬਣਿਆ ਕੋਣ 60° ਦਾ ਹੈ । (ਦੇਖੋ ਚਿੱਤਰ) ।

ਸਮਕੋਣ △ABC ਵਿੱਚ
\(\frac{BC}{AC}\) = sin 60°
ਜਾਂ \(\frac{3}{l_{2}}\) = \(\frac{\sqrt{3}}{2}\)
ਜਾਂ l₂ = \(\frac{3 \times 2}{\sqrt{3}}\) = \(\frac{6}{\sqrt{3}}\)
= \(\frac{6}{\sqrt{3}}\) × \(\frac{\sqrt{3}}{\sqrt{3}}\) = \(\frac{6 \sqrt{3}}{3}\) = 2\(\sqrt {3}\) m
∴ 5 ਸਾਲ ਤੋਂ ਛੋਟੇ ਬੱਚਿਆਂ ਲਈ ਅਤੇ ਉਸ ਤੋਂ ਵੱਧ ਉਮਰ ਦੇ ਬੱਚਿਆਂ ਲਈ ਤਿਲਕਣ ਪੱਟੀ ਦੀ ਲੰਬਾਈ ਕੁਮਵਾਰ
3 m ਅਤੇ 2\(\sqrt {3}\)m ਹੈ ।

ਪ੍ਰਸ਼ਨ 4.
ਜਮੀਨ ਦੇ ਇਕ ਬਿੰਦੂ ਤੋਂ ਜੋ ਮੀਨਾਰ ਦੇ ਆਧਾਰ ਬਿੰਦੂ ਤੋਂ 30 m ਦੀ ਦੂਰੀ ‘ਤੇ ਹੈ, ਮੀਨਾਰ ਦੇ ਸਿਖ਼ਰ ਦਾ ਉੱਚਾਣ ਕੋਣ 30° ਹੈ । ਮੀਨਾਰ ਦੀ ਉੱਚਾਈ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ BC = h m ਮੀਨਾਰ ਦੀ ਉੱਚਾਈ ਹੈ ਅਤੇ AB = 30 m ਆਧਾਰ ਤੋਂ ਬਿੰਦੂ ਦੀ ਦੂਰੀ (ਦੇਖੋ ਚਿੱਤਰ) ਹੈ।

ਸਮਕੋਣ △ABC ਵਿੱਚ,
\(\frac{BC}{AB}\) = tan 30°
ਜਾਂ \(\frac{h}{30}\) = \(\frac{1}{1}\)
ਜਾਂ h = \(\frac{30}{\sqrt{3}}\) × \(\frac{\sqrt{3}}{\sqrt{3}}\) = \(\frac{30 \sqrt{3}}{3}\)
= 10\(\sqrt {3}\) = 10 × 1.732
h = 17:32 m
ਮੀਨਾਰ ਦੀ ਉੱਚਾਈ ਲਗਭਗ 17.32 m. ਹੈ ।

ਪ੍ਰਸ਼ਨ 5.
ਜਮੀਨ ਤੋਂ 60 m ਉੱਚਾਈ ‘ਤੇ ਇੱਕ ਪਤੰਗ ਉੱਡ ਰਹੀ ਹੈ। ਪਤੰਗ ਨਾਲ ਲੱਗੇ ਧਾਗੇ ਨੂੰ ਅਸਥਾਈ ਰੂਪ ਵਿੱਚ ਜਮੀਨ ‘ਤੇ ਇੱਕ ਬਿੰਦੂ ਨਾਲ ਬੰਨ ਦਿੱਤਾ ਗਿਆ ਹੈ। ਜ਼ਮੀਨ ਨਾਲ ਧਾਗੇ ਦਾ ਝੁਕਾਵ 60° ਹੈ। ਇਹ ਮੰਨਕੇ ਕਿ ਧਾਗੇ ਵਿੱਚ ਕੋਈ ਢਿੱਲ ਨਹੀਂ ਹੈ , ਧਾਗੇ ਦੀ ਲੰਬਾਈ ਪਤਾ ਕਰੋ।
ਹੱਲ:
ਮੰਨ ਲਉ ਬਿੰਦੂ ਤੇ ਪਤੰਗ ਦੀ ਸਥਿਤੀ ਹੈ AC = l m ਪਤੰਗ ਦੇ ਨਾਲ ਲੱਗੇ ਧਾਗੇ ਦੀ ਲੰਬਾਈ ਸਿਖਰ ਕੋਣ 60° ਦਾ ਹੈ । (ਦੇਖੋ ਚਿੱਤਰ)

ਸਮਕੋਣ △ABC ਵਿੱਚ,
\(\frac{CB}{CA}\) = sin 60°
ਜਾਂ \(\frac{60}{l}\) = \(\frac{\sqrt{3}}{2}\)
ਜਾਂ l = \(\frac{60 \times 2}{\sqrt{3}}\) = \(\frac{120}{\sqrt{3}}\) × \(\frac{\sqrt{3}}{\sqrt{3}}\)
= \(\frac{120 \sqrt{3}}{3}\) = 40\(\sqrt {3}\) m
∴ ਧਾਗੇ ਦੀ ਲੰਬਾਈ 403 m ਹੈ ।

ਪ੍ਰਸ਼ਨ 6.
1.5 m ਲੰਬਾ ਲੜਕਾ 30 ਮੀਟਰ ਉੱਚੀ ਇੱਕ ਇਮਾਰਤ | ਤੋਂ ਕੁੱਝ ਦੂਰੀ ‘ਤੇ ਖੜ੍ਹਾ ਹੈ । ਜਦੋਂ ਉਹ ਇਮਾਰਤ ਵੱਲ ਜਾਂਦਾ ਹੈ (ਚਲਦਾ ਹੈ। ਤਾਂ ਉਸਦੀ ਅੱਖ ਨਾਲ ਇਮਾਰਤ ਦੇ ਸਿਖ਼ਰ ਦਾ | ਉੱਚਾਣ ਕੋਣ 30° ਤੋਂ 60° ਹੋ ਜਾਂਦਾ ਹੈ । ਦੱਸੋ ਕਿ ਉਹ | ਇਮਾਰਤ ਵੱਲ ਕਿੰਨੀ ਦੂਰੀ ਤੱਕ ਚਲ ਕੇ ਗਿਆ ?
ਹੱਲ:
ਮੰਨ ਲਉ ED = 30 m ਇਮਾਰਤ ਦੀ ਉੱਚਾਈ | ਹੈ ਅਤੇ EC = 1.5 m ਲੜਕੇ ਦੀ ਉੱਚਾਈ ਹੈ । ਭਿੰਨ-ਭਿੰਨ | ਸਥਿਤੀਆਂ ਵਿਚ ਸਿਖ਼ਰ ਦਾ ਉੱਚਾਣ ਕੋਣ 30° ਅਤੇ 60° ਹੈ । (ਦੇਖੋ ਚਿੱਤਰ)

ਸਮਕੋਣ △ACD ਵਿੱਚ,
\(\frac{DC}{AC}\) = tan 30°
ਜਾਂ \(\frac{28.5}{x+y}\) = \(\frac{1}{\sqrt{3}}\)
ਜਾਂ x + y = 28.5 × \(\sqrt {3}\) m …(1)
ਹੁਣ, ਸਮਕੋਣ △BCD ਵਿੱਚ,

∴ ਲੜਕੇ ਦੁਆਰਾ ਇਮਾਰਤ ਵੱਲ ਤੈਅ ਕੀਤੀ ਦੂਰੀ 19\(\sqrt {3}\) m ਹੈ ।

ਪ੍ਰਸ਼ਨ 7.
ਜਮੀਨ ਦੇ ਇੱਕ ਬਿੰਦੂ ਤੋਂ ਇੱਕ 20 m ਉੱਚੀ ਇਮਾਰਤ ਦੇ ਸਿਖ਼ਰ ‘ਤੇ ਲੱਗੇ ਸੰਚਾਰ ਮੀਨਾਰ (transmission tower) ਦੇ ਤਲ ਅਤੇ ਸਿਖ਼ਰ ਦਾ ਉੱਚਾਣ ਕੋਣ ਕੁਮਵਾਰ 45° ਅਤੇ 60° ਹੈ। ਸੰਚਾਰ ਮੀਨਾਰ ਦੀ ਉੱਚਾਈ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ BC = 20 m ਇਮਾਰਤ ਦੀ ਉੱਚਾਈ ਹੈ DC=h m ਸੰਚਾਰ ਮੀਨਾਰ ਦੀ ਉੱਚਾਈ ਹੈ । ਇਮਾਰਤ ਦੇ ਸਿਖਰ ਤੇ ਲੱਗੀ ਇਕ ਸੰਚਾਰ ਮੀਨਾਰ ਦੇ ਤਲ ਅਤੇ ਸਿਖਰ ਦੇ ਉੱਚਾਣ ਕੋਣ ਕੁਮਵਾਰ 45° ਅਤੇ 60° ਹੈ । (ਦੇਖੋ ਚਿੱਤਰ)

ਸਮਕੋਣ △ABC ਵਿੱਚ,
\(\frac{AB}{BC}\) = cot 45°
ਜਾਂ \(\frac{AB}{20}\) = 1
ਜਾਂ AB = 20 m ….(1)
ਨਾਲ ਹੀ, ਸਮਕੋਣ △ABD ਵਿੱਚ,
\(\frac{AB}{BD}\) = cot 60°
ਜਾਂ \(\frac{AB}{20+h}\) = \(\frac{1}{\sqrt{3}}\)
ਜਾਂ AB = \(\frac{20+h}{\sqrt{3}}\)
ਜਾਂ AB = \(\frac{(20+h)}{\sqrt{3}}\) ….(2)
(1) ਅਤੇ (2) ਤੋਂ ,
20 = \(\frac{(20+h)}{\sqrt{3}}\)
ਜਾਂ 20\(\sqrt {3}\) = 20 + h
ਜਾਂ h = 20\(\sqrt {3}\) – 20
ਜਾਂ h = 20(\(\sqrt {3}\) – 1)m
= 20 (1732 – 1) m
= 20 × 0.732 = 14∙64 m
∴ ਸੰਚਾਰ ਮੀਨਾਰ ਦੀ ਉੱਚਾਈ 1464 m ਹੈ ।

ਪ੍ਰਸ਼ਨ 8.
ਇੱਕ ਪੈਡਸਟਲ (Pedestal) ਦੇ ਸਿਖਰ ‘ਤੇ ਇੱਕ 1.6 m ਉੱਚੀ ਮੂਰਤੀ ਲੱਗੀ ਹੋਈ ਹੈ । ਜਮੀਨ ਦੇ ਇੱਕ ਬਿੰਦੂ ਤੋਂ ਮੂਰਤੀ ਦੇ ਸਿਖ਼ਰ ਦਾ ਉੱਚਾਣ ਕੋਣ 60° ਹੈ ਅਤੇ ਇਸ ਹੀ ਬਿੰਦੂ ਤੋਂ ਪੈਡਸਟਲ ਦੇ ਸਿਖ਼ਰ ਦਾ ਉੱਚਾਣ ਕੋਣ 45° ਹੈ । ਪੈਡਸਟਲ ਦੀ ਉੱਚਾਈ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ BC = hm ਪੈਡਸਟਲ ਦੀ ਉੱਚਾਈ ਹੈ CD = 1.6 m ਮੂਰਤੀ ਦੀ ਉੱਚਾਈ ਹੈ । ਜਮੀਨ ‘ਤੇ ਦਿੱਤੇ ਬਿੰਦੁ A ਤੋਂ ਮੁਰਤੀ ਦੇ ਸਿਖ਼ਰ ਅਤੇ ਪੈਡਸਟਲ ਦੇ ਸਿਖਰ ਦਾ ਉੱਚਾਂਣ ਕੋਣ 60° ਅਤੇ 45° ਹੈ । (ਦੇਖੋ ਚਿੱਤਰ)

ਸਮਕੋਣ △ABC ਵਿੱਚ,
\(\frac{AB}{BC}\) = cot 45°
ਜਾਂ \(\frac{AB}{h}\) = 1
ਜਾਂ AB = h m …(1)
ਸਮਕੋਣ △ABD ਵਿੱਚ,
\(\frac{AB}{BD}\) = cot 60°
ਜਾਂ \(\frac{AB}{h+1.6}\) = \(\frac{1}{\sqrt{3}}\)
ਜਾਂ AB = \(\frac{h+1.6}{\sqrt{3}}\) ….(2)
(1) ਅਤੇ (2), ਤੋਂ
h = \(\frac{h+1.6}{\sqrt{3}}\)
ਜਾਂ \(\sqrt {3}\)h = h + 1∙6
ਜਾਂ (\(\sqrt {3}\) – 1) h = 1∙6
ਜਾਂ (1∙732 – 1) h = 1∙6
ਜਾਂ (0∙732)h = 1∙6
ਜਾਂ h = \(\frac{1∙6}{0∙732}\) = 2·1857923
= 2·20 m (ਲਗਭਗ)
∴ ਪੈਡਸਟਲ ਦੀ ਉੱਚਾਈ 2:20 m ਹੈ ।

ਪ੍ਰਸ਼ਨ 9.
ਇੱਕ ਮੀਨਾਰ ਦੇ ਆਧਾਰ ਬਿੰਦੂ ਤੋਂ ਇੱਕ ਇਮਾਰਤ ਦੇ ਸਿਖ਼ਰ ਦਾ ਉੱਚਾਣ ਕੋਣ 30° ਹੈ ਅਤੇ ਇਮਾਰਤ ਦੇ ਆਧਾਰ ਬਿੰਦੂ ਤੋਂ ਮੀਨਾਰ ਦੇ ਸਿਖਰ ਦਾ ਉੱਚਾਣ ਕੋਣ 60° ਹੈ । ਜੇਕਰ ਮੀਨਾਰ 50 ਮੀਟਰ ਉੱਚੀ ਹੋਵੇ ਤਾਂ ਇਮਾਰਤ ਦੀ ਉੱਚਾਈ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ BC = 50 m ਮੀਨਾਰ ਦੀ ਉੱਚਾਈ ਹੈ AD = hm ਇਮਾਰਤ ਦੀ ਉੱਚਾਈ ਹੈ । ਮੀਨਾਰ ਦੇ ਆਧਾਰ ਬਿੰਦੂ ਤੋਂ ਇਮਾਰਤ ਦੇ ਸਿਖ਼ਰ ਤੱਕ ਅਤੇ ਇਮਾਰਤ ਦੇ ਆਧਾਰ ਬਿੰਦੂ ਤੋਂ ਮੀਨਾਰ ਦੇ ਸਿਖ਼ਰ ਦੇ ਉੱਚਾਣ ਕੋਣ ਕ੍ਰਮਵਾਰ 30° ਅਤੇ 60° ਹਨ । (ਦੇਖੋ ਚਿੱਤਰ)

ਸਮਕੋਣ △ABC ਵਿੱਚ,
\(\frac{AB}{BC}\) = cot 60°
ਜਾਂ \(\frac{AB}{50}\) = \(\frac{1}{\sqrt{3}}\)
ਜਾਂ AB = \(\frac{50}{\sqrt{3}}\) …(1)
ਸਮਕੋਣ △DAB ਵਿੱਚ,
\(\frac{AB}{DA}\) = cot 30°
ਜਾਂ \(\frac{AB}{h}\) = \(\sqrt {3}\)
ਜਾਂ AB = h\(\sqrt {3}\) …(2)
(1) ਅਤੇ (2), ਤੋਂ ,
\(\frac{50}{\sqrt{3}}\) = h \(\sqrt {3}\)
ਜਾਂ \(\frac{50}{\sqrt{3}}\) \(\frac{1}{\sqrt{3}}\) = h
ਜਾਂ h = \(\frac{50}{3}\) = 16∙6666
ਜਾਂ h = 16∙70 m (ਲਗਭਗ
∴ ਇਮਾਰਤ ਦੀ ਉੱਚਾਈ 16-70 m ਹੈ ।

ਪ੍ਰਸ਼ਨ 10.
ਇੱਕ 80 ਮੀਟਰ ਚੌੜੀ ਸੜਕ ਦੇ ਦੋਵਾਂ ਪਾਸਿਆਂ ‘ਤੇ ਆਹਮਣੇ-ਸਾਹਮਣੇ ਬਰਾਬਰ ਲੰਬਾਈ ਵਾਲੇ ਦੋ ਖੰਬੇ ਲੱਗੇ ਹੋਏ ਹਨ । ਇਹਨਾਂ ਦੋਹਾਂ ਖੰਬਿਆਂ ਦੇ ਵਿੱਚ ਸੜਕ ‘ਤੇ ਇੱਕ ਬਿੰਦੂ ਤੋਂ ਖੰਬਿਆਂ ਦੇ ਸਿਖ਼ਰਾਂ ਦੇ ਉੱਚਾਣ ਕੋਣ ਕੁਮਵਾਰ 60° ਅਤੇ 30° ਹੈ । ਖੰਬਿਆਂ ਦੀ ਉੱਚਾਈ ਅਤੇ ਖੰਬਿਆਂ ਤੋਂ ਬਿੰਦੁ ਦੀ ਦੂਰੀ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ BC = DE = hm ਦੋ ਬਰਾਬਰ ਲੰਬਾਈ ਵਾਲੇ ਖੰਬਿਆਂ ਦੀ ਉੱਚਾਈ ਹੈ ਅਤੇ ਬਿੰਦੂ A ਲੋੜੀਂਦਾ ਬਿੰਦੂ ਹੈ, ਜਿੱਥੇ ਦੋਹਾਂ ਖੰਬਿਆ ਦੇ ਉੱਚਾਣ ਕੋਣ ਕੁਮਵਾਰ 30° ਅਤੇ 60° ਹੈ । (ਦੇਖੋ ਚਿੱਤਰ)

ਸਮਕੋਣ △ADE ਵਿੱਚ,
\(\frac{ED}{DA}\) = tan 30°
ਜਾਂ \(\frac{h}{x}\) = \(\frac{1}{\sqrt{3}}\)
ਜਾਂ h = \(\frac{h}{\sqrt{3}}\) ….(1)
ਸਮਕੋਣ △ABC ਵਿੱਚ,
\(\frac{BC}{AB}\) = tan 60°
ਜਾਂ \(\frac{h}{80-x}\) = \(\sqrt {3}\)
ਜਾਂ h = (80 – x)\(\sqrt {3}\)
(1) ਅਤੇ (2) ਤੋਂ
\(\frac{x}{\sqrt{3}}\) = (80 – x)\(\sqrt {3}\)
ਜਾਂ x = (80 – x)\(\sqrt {3}\) × \(\sqrt {3}\)
ਜਾਂ x = (80 – x) 3
ਜਾਂ x = 240 – 3x
ਜਾਂ 4x = 240
ਜਾਂ x = \(\frac{240}{4}\) = 60
x ਦਾ ਮੁੱਲ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ
h = \(\frac{60}{\sqrt{3}}\) = \(\frac{60}{\sqrt{3}}\) × \(\frac{\sqrt{3}}{\sqrt{3}}\)
= \(\frac{60 \sqrt{3}}{3}\) = 20\(\sqrt {3}\)
= (20 × 1.732) m = 34.64 m
∴ DA = x = 60 m
ਅਤੇ AB = 80 – x = (80 – 60) m = 20m.
∴ ਹਰੇਕ ਖੰਬੇ ਦੀ ਉੱਚਾਈ 34:64 m ਅਤੇ ਖੰਬਿਆਂ ਤੋਂ ਬਿੰਦੁ ਦੀ ਦੂਰੀ 20 m ਅਤੇ 60 m ਹੈ ।

ਪ੍ਰਸ਼ਨ 11.
ਇੱਕ ਨਹਿਰ ਦੇ ਇੱਕ ਤੱਟ ‘ਤੇ ਇੱਕ ਟੀ. ਵੀ. ਟਾਵਰ ਸਿੱਧਾ ਖੜਾ ਹੈ । ਟਾਵਰ ਦੇ ਠੀਕ ਸਾਹਮਣੇ ਦੂਸਰੇ ਤੱਟ ‘ਤੇ ਇੱਕ ਹੋਰ ਬਿੰਦੂ ਤੋਂ ਟਾਵਰ ਦੇ ਸਿਖ਼ਰ ਦਾ ਉੱਚਾਣ ਕੋਣ 60° ਹੈ । ਇਸੇ ਤੱਟ ‘ਤੋਂ ਇਸ ਬਿੰਦੂ ਤੋਂ 20 m ਦੂਰ ਅਤੇ ਇਸ ਬਿੰਦੂ ਨੂੰ ਮੀਨਾਰ ਦੇ ਆਧਾਰ ਬਿੰਦੂ ਨਾਲ ਮਿਲਾਉਣ ਵਾਲੀ ਰੇਖਾ ‘ ਤੇ ਸਥਿਤ ਇੱਕ ਹੋਰ ਬਿੰਦੂ ਤੋਂ ਟਾਵਰ ਦੇ ਸਿੱਖ਼ਰ ਦਾ ਉੱਚਾਣ ਕੋਣ 30° ਹੈ (ਦੇਖੋ ਚਿੱਤਰ ਟਾਵਰ ਦੀ ਉੱਚਾਈ ਅਤੇ ਨਹਿਰ ਦੀ ਚੌੜਾਈ ਪਤਾ ਕਰੋ ।

ਹੱਲ:
ਮੰਨ ਲਉ BC = x m ਨਹਿਰ ਦੀ ਚੌੜਾਈ ਹੈ ਅਤੇ AB= hm ਟੀ.ਵੀ. ਟਾਵਰ ਦੀ ਉੱਚਾਈ ਹੈ | ਅਲੱਗਅਲੱਗ ਸਥਿਤੀਆਂ ਵਿਚ ਟਾਵਰ ਦੇ ਉੱਚਾਣ ਕੋਣ ਕ੍ਰਮਵਾਰ 30° ਅਤੇ 60° ਹਨ ।
(ਦੇਖੋ ਚਿੱਤਰ)

ਸਮਕੋਣ △ABC ਵਿੱਚ,
\(\frac{AB}{BC}\) = tan 60°
ਜਾਂ \(\frac{h}{x}\) = \(\sqrt {3}\)
ਜਾਂ h = \(\sqrt {3}\)x …(1)
ਨਾਲ ਹੀ, ਸਮਕੋਣ △ABD ਵਿੱਚ,
\(\frac{AB}{AD}\) = tan 30°
ਜਾਂ \(\frac{h}{20+x}\) = \(\frac{1}{\sqrt{3}}\)
ਜਾਂ h = \(\frac{20+x}{\sqrt{3}}\) …..(2)
(1) ਅਤੇ (2) ਤੋਂ
\(\sqrt {3}\)x = \(\frac{20+x}{\sqrt{3}}\)
ਜਾਂ \(\sqrt {3}\)(\(\sqrt {3}\)x) = 20 + x
ਜਾਂ 3x = 20 + x
ਜਾਂ 2x = 20
ਜਾਂ x = \(\frac{20}{2}\) = 10
x ਦਾ ਮੁੱਲ (1) ਵਿਚ ਭਰਨ ਤੇ
h= 10(\(\sqrt {3}\)).
= 10 × 1∙732
h= 17∙32 m
∴ ਟੀ.ਵੀ. ਟਾਵਰ ਦੀ ਉੱਚਾਈ 17:32 m ਹੈ ਅਤੇ ਨਹਿਰ ਦੀ ਚੌੜਾਈ 10 m. ਹੈ ।

ਪ੍ਰਸ਼ਨ 12.
7m ਉੱਚੀ ਇਮਾਰਤ ਦੇ ਸਿਖ਼ਰ ਤੋਂ ਇੱਕ ਕੇਬਲ ਟਾਵਰ ਦੇ ਸਿਖ਼ਰ ਦਾ ਉੱਚਾਣ ਕੋਣ 60° ਹੈ ਅਤੇ ਇਸਦੇ ਪੈਰ ਦਾ ਨੀਵਾਨ ਕੋਣ 45° ਹੈ। ਟਾਵਰ ਦੀ ਉੱਚਾਈ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ BD = hm ਕੇਵਲ ਟਾਵਰ ਦੀ ਉੱਚਾਈ ਹੈ ਅਤੇ AE = 7 m ਇਮਾਰਤ ਦੀ ਉੱਚਾਈ ਹੈ । ਕੇਵਲ ਟਾਵਰ ਦੇ ਸਿਖਰ ਦਾ ਉੱਚਾਣ ਕੋਣ ਅਤੇ ਪੈਰ ਦਾ ਨੀਵਾਨ ਕੋਣ ਕੁਮਵਾਰ 60° ਅਤੇ 45° ਹੈ ।
(ਦੇਖੋ ਚਿੱਤਰ)

ਸਮਕੋਣ △BAE ਵਿੱਚ
\(\frac{AB}{AE}\) = cot 45°
ਜਾਂ \(\frac{AB}{7}\) = 1
ਜਾਂ AB = 7 m …..(1)
ਸਮਕੋਣ △DCE ਵਿੱਚ
\(\frac{EC}{DC}\) = cot 60°
ਜਾਂ \(\frac{EC}{h-7}\) = \(\frac{1}{\sqrt{3}}\)
ਜਾਂ EC = \(\frac{h-7}{\sqrt{3}}\) …(2)
ਪਰ AB = EC …(ਦਿੱਤਾ ਹੈ।)
7 = \(\frac{h-7}{\sqrt{3}}\)
[(1) ਅਤੇ (2) ਤੋਂ।]
ਜਾਂ 7\(\sqrt {3}\) = h – 7
ਜਾਂ h = 7\(\sqrt {3}\) + 7 = 7 (\(\sqrt {x}\) + 1)
ਜਾਂ h = 7(1∙732 + 1) = 7(2∙732)
ਜਾਂ h = 19∙124
ਜਾਂ h = 19∙20 m (ਲਗਭਗ)
∴ ਕੇਬਲ ਟਾਵਰ ਦੀ ਉੱਚਾਈ 19.20 m ਹੈ ।

ਪ੍ਰਸ਼ਨ 13.
ਸਮੁੰਦਰ ਤਲ ਤੋਂ 75 m ਉੱਚੇ ਲਾਈਟ ਹਾਊਸ ਦੇ ਸਿਖ਼ਰ ਤੋਂ ਦੇਖਣ ਨਾਲ ਦੋ ਸਮੁੰਦਰੀ ਜਹਾਜ਼ਾਂ ਦੇ ਨੀਵਾਨ ਕੋਣ ਕੁਮਵਾਰ 30° ਅਤੇ 45° ਹਨ । ਜੇਕਰ ਲਾਈਟ ਹਾਊਸ ਦੇ ਇੱਕ ਹੀ ਪਾਸੇ ਤੋਂ ਇੱਕ ਜਹਾਜ਼ ਦੂਸਰੇ ਜਹਾਜ਼ ਦੇ ਬਿਲਕੁਲ ਪਿੱਛੇ ਹੋਵੇ ਤਾਂ ਦੋਵੇਂ ਜਹਾਜ਼ਾਂ ਦੀ ਵਿਚਕਾਰਲੀ ਦੂਰੀ ਪਤਾ ਕਰੋ ।
ਹੱਲ:

ਮੰਨ ਲਉ CD = 75 m ਲਾਈਟ ਹਾਊਸ ਦੀ ਉੱਚਾਈ | ਅਤੇ ਲਾਈਟ ਹਾਊਸ ਦੇ ਸਿਖ਼ਰ ਦੇ ਬਿੰਦੁ ਤੋਂ ਜਹਾਜਾਂ ਦੇ | ਨੀਵਾਨ ਕੋਣ ਕ੍ਰਮਵਾਰ 30° ਅਤੇ 45° ਹੈ ।
(ਦੇਖੋ ਚਿੱਤਰ)
ਸਮਕੋਣ △BCD ਵਿੱਚ,
\(\frac{BC}{CD}\) = cot 45°
ਜਾਂ \(\frac{y}{75}\) = 1
ਜਾਂ y = 75 m ….(1)
ਸਮਕੋਣ △ACD ਵਿੱਚ,
\(\frac{AC}{CD}\) = cot 30°
ਜਾਂ \(\frac{x+y}{75}\) = \(\sqrt {3}\)
ਜਾਂ x + y = 75\(\sqrt {3}\)
ਜਾਂ x + 75 = 75\(\sqrt {x}\)
[1) ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ਤੋਂ]
ਜਾਂ x = 75\(\sqrt {x}\) – 75
= 75 (\(\sqrt {x}\) – 1)
= 75 (1∙732 – 1)
= 75 (0∙732)
x = 54∙90
∴ ਦੋਵੇਂ ਜਹਾਜਾਂ ਵਿਚਕਾਰਲੀ ਦੂਰੀ 54∙90 m ਹੈ ।

ਪ੍ਰਸ਼ਨ 14.
1.2 m ਲੰਬੀ ਇੱਕ ਲੜਕੀ ਜਮੀਨ ਤੋਂ 88.2 m ਦੀ ਉੱਚਾਈ ‘ਤੇ ਇੱਕ ਖਿਤਿਜੇ ਰੇਖਾ ਵਿੱਚ ਉੱਡ ਰਹੇ ਗੁਬਾਰੇ ਨੂੰ ਦੇਖਦੀ ਹੈ । ਕਿਸੇ ਵੀ ਸਮੇਂ ਲੜਕੀ ਦੀ ਅੱਖ ਨਾਲ ਗੁਬਾਰੇ ਦਾ ਉੱਚਾਣ ਕੋਣ 60° ਹੈ । ਕੁੱਝ ਸਮੇਂ ਬਾਅਦ ਉੱਚਾਣ ਕੋਣ ਘੱਟ ਕੇ 30° ਹੋ ਜਾਂਦਾ ਹੈ ਦੇਖੋ ਚਿੱਤਰ) । ਇਸ ਅੰਤਰਾਲ ਦੌਰਾਨ ਗੁਬਾਰੇ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਦੂਰੀ ਪਤਾ ਕਰੋ ।

ਹੱਲ:
ਮੰਨ ਲਉ 1.2 m ਲੰਬੀ ਲੜਕੀ ਦੀ ਸਥਿਤੀ ‘A’ ਹੈ । ਇਸ ਬਿੰਦੂ ਤੋਂ ਗੁਬਾਰੇ ਦੇ ਉੱਚਾਣ ਕੋਣ ਕ੍ਰਮਵਾਰ 30° ਅਤੇ 60° ਹਨ । ਨਾਲ ਹੀ
BE = CD = 88.2 m ਗੁਬਾਰੇ ਦੀ ਉੱਚਾਈ ਹੈ।
(ਦੇਖੋ ਚਿੱਤਰ)

ਸਮਕੋਣ △ABE ਵਿੱਚ,
\(\frac{AB}{BE}\) = cot 60°
ਜਾਂ \(\frac{x}{88.2}\) = \(\frac{1}{\sqrt{3}}\)
ਜਾਂ x = \(\frac{88.2}{\sqrt{3}}\) m …(1)
ਸਮਕੋਣ △ACD ਵਿੱਚ
\(\frac{AC}{CD}\) = cot 30°
ਜਾਂ \(\frac{x+y}{88.2}\) = \(\sqrt {3}\)
ਜਾਂ x + y = 88.2\(\sqrt {3}\)
ਜਾਂ \(\frac{88.2}{\sqrt{3}}\) + y = 88.2\(\sqrt {3}\)
ਜਾਂ y = 88.2\(\sqrt {3}\) = \(\frac{88.2}{\sqrt{3}}\)
ਜਾਂ y = 88.2[\(\sqrt {3}\) – \(\frac{1}{\sqrt{3}}\)]
ਜਾਂ y = 88.2[latex]\frac{3-1}{\sqrt{3}}[/latex] × \(\frac{\sqrt{3}}{\sqrt{3}}\)
ਜਾਂ y = \(\frac{88.2 \times 2 \times \sqrt{3}}{3}\)
ਜਾਂ y = 58.8\(\sqrt {3}\) m
ਜਾਂ y = 58.8 (1.732) = 101.8416 m
ਜਾਂ y = 101.90 m
∴ ਗੁਬਾਰੇ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ 101.90 m. ਹੈ ।

ਪ੍ਰਸ਼ਨ 15.
ਇੱਕ ਸਿੱਧਾ ਰਾਜ ਮਾਰਗ ਇੱਕ ਮੀਨਾਰ ਦੇ ਆਧਾਰ ਤੱਕ ਜਾਂਦਾ ਹੈ । ਮੀਨਾਰ ਦੇ ਸਿਖ਼ਰ ‘ ਤੇ ਖੜਾ ਇੱਕ ਆਦਮੀ ਇੱਕ ਕਾਰ ਨੂੰ 30° ਨੀਵਾਨ ਕੋਣ ‘ਤੇ ਦੇਖਦਾ ਹੈ, ਜੋ ਮੀਨਾਰ ਦੇ ਆਧਾਰ ਵੱਲ ਇੱਕ ਸਮਾਨ ਚਾਲ ਨਾਲ ਆ ਰਹੀ ਹੈ । ਛੇ ਸੈਕਿੰਡ ਬਾਅਦ ਕਾਰ ਦਾ ਨੀਵਾਨ ਕੋਣ 60° ਹੋ ਗਿਆ । ਇਸ ਬਿੰਦੂ ਤੋਂ ਮੀਨਾਰ ਦੇ ਆਧਾਰ ਤੱਕ ਪਹੁੰਚਣ ਲਈ ਕਾਰ ਦੁਆਰਾ ਲਿਆ ਗਿਆ ਸਮਾਂ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ CD = hm ਮੀਨਾਰ ਦੀ ਉੱਚਾਈ ਹੈ । ਮੰਨ ਲਉ A’ ਕਾਰ ਦੀ ਪਹਿਲੀ ਸਥਿਤੀ ਹੈ ਅਤੇ ਛੇ ਸੈਕਿੰਡ ਦੇ ਬਾਅਦ ਕਾਰ B ਤੱਕ ਪਹੁੰਚ ਜਾਂਦੀ ਹੈ । A ਅਤੇ B ਉੱਤੇ ਕਾਰ ਦੇ ਨੀਵਾਨ ਕੋਣ 30° ਅਤੇ 60° ਹਨ ।
(ਦੇਖੇ ਚਿੱਤਰ)

ਮੰਨ ਲਉ ਕਾਰ ਦੀ ਚਾਲ v ਮੀਟਰ ਪ੍ਰਤੀ ਸੈਕਿੰਡ ਹੈ ਸੂਤਰ ਦੂਰੀ = ਚਾਲ × ਸਮਾਂ ਦਾ ਪ੍ਰਯੋਗ ਕਰਕੇ
AB = ਕਾਰਾਂ ਦੁਆਰਾ 6 ਸੈਕਿੰਡ ਵਿੱਚ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ
AB = 6v ਮੀਟਰ
ਕਾਰ ਦੁਆਰਾ ਮੀਨਾਰ ਤੱਕ ਪਹੁੰਚਣ ਵਿਚ ਲਿਆ ਗਿਆ ਸਮਾਂ ‘n’ ਸੈਕਿੰਡ ਹੈ ।
∴ BC = nv ਮੀਟਰ
ਸਮਕੋਣ △ACD ਵਿੱਚ
\(\frac{CD}{AC}\) = tan 30°
ਜਾਂ \(\frac{h}{6v+nv}\) = \(\frac{1}{\sqrt{3}}\)
ਜਾਂ h = \(\frac{6v+nv}{\sqrt{3}}\) …(1)
ਸਮਕੋਣ △BCD ਵਿੱਚ,
\(\frac{CD}{BC}\) = tan 60°
ਜਾਂ \(\frac{h}{nv}\) = \(\sqrt {3}\)
ਜਾਂ h = nv(\(\sqrt {3}\) ) ….(2)
(1) ਅਤੇ (2) ਤੋਂ ਸਾਨੂੰ ਮਿਲਦਾ ਹੈ।
ਜਾਂ \(\frac{6v+nv}{\sqrt{3}}\) = nv(\(\sqrt {3}\))
ਜਾਂ 6v + nv = nv(\(\sqrt {3}\) × \(\sqrt {3}\))
ਜਾਂ 6v + nv = 3nv ਜਾਂ 6v = 2nv
ਜਾਂ n = \(\frac{6v}{2v}\) = 3
ਮੀਨਾਰ ਦੇ ਆਧਾਰ ਤੱਕ ਪਹੁੰਚਣ ਲਈ ਕਾਰ ਦੁਆਰਾ ਲਿਆ ਗਿਆ ਸਮਾਂ 3 ਸੈਕਿੰਡ ਹੈ ।

ਪ੍ਰਸ਼ਨ 16.
ਮੀਨਾਰ ਦੇ ਆਧਾਰ ‘ਤੇ ਇੱਕ ਸਰਲ ਰੇਖਾ 4m ਅਤੇ 9 m ਦੀ ਦੂਰੀ ‘ਤੇ ਸਥਿਤ ਦੋ ਬਿੰਦੁਆਂ ਤੋਂ ਮੀਨਾਰ ਦੇ ਸਿਖ਼ਰ ਦੇ ਉੱਚਾਣ ਕੋਣ ਪੂਰਕ ਕੋਣ ਹਨ। ਸਿੱਧ ਕਰੋ ਕਿ ਮੀਨਾਰ ਦੀ ਉੱਚਾਈ 6 m ਹੈ ।
ਹੱਲ:
ਮੰਨ ਲਉ CD = h m ਮੀਨਾਰ ਦੀ ਉਚਾਈ ਹੈ। ਅਤੇ B; Aਲੋਂੜੀਂਦੇ ਬਿੰਦੂ ਹਨ ਜੋ ਮੀਨਾਰ ਤੋਂ ਕ੍ਰਮਵਾਰ 4 m ਅਤੇ 9 m ਦੀ ਦੂਰੀ ‘ਤੇ ਹਨ ।
(ਦੇਖੋ ਚਿੱਤਰ)

ਸਮਕੋਣ △BCD ਵਿੱਚ,
\(\frac{CD}{BC}\) = tan θ
ਜਾਂ \(\frac{h}{4}\) = tan θ …(1)
ਨਾਲ ਹੀ, ਸਮਕੋਣ △ACD ਵਿੱਚ,
\(\frac{CD}{AC}\) = tan (90 – θ)
\(\frac{h}{9}\) = cot θ …(2)
(1) ਅਤੇ (2) ਨੂੰ ਗੁਣਾ ਕਰਨ ‘ਤੇ
\(\frac{h}{4}\) × \(\frac{h}{9}\) = tan θ × cot θ
ਜਾਂ \(\frac{h^{2}}{36}\) = tan θ × \(\frac{1}{\tan \theta}\)
ਜਾਂ h² = 36 = (6)²
ਜਾਂ h= 6
∴ ਮੀਨਾਰ ਦੀ ਉੱਚਾਈ 6 m ਹੈ

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 8 ਤਿਕੋਣਮਿਤੀ ਬਾਰੇ ਜਾਣ ਪਛਾਣ Ex 8.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 8 ਤਿਕੋਣਮਿਤੀ ਬਾਰੇ ਜਾਣ ਪਛਾਣ Exercise 8.3

ਪ੍ਰਸ਼ਨ 1.
ਹੇਠ ਲਿਖਿਆਂ ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ :
(i) \(\frac{\sin 18^{\circ}}{\cos 72^{\circ}}\)
(ii) \(\frac{\tan 26^{\circ}}{\cot 64^{\circ}}\)
(iii) cos 48° – sin 42°
(iv) cosec 31° – sec 59o.
ਹੱਲ:
(i) \(\frac{\sin 18^{\circ}}{\cos 72^{\circ}}\) = \(\frac{\sin 18^{\circ}}{\cos \left(90^{\circ}-18^{\circ}\right)}\)
= \(\frac{\sin 18^{\circ}}{\sin 18^{\circ}}\) = 1.
[∵ cos (90° – θ) = sin θ]

(ii) \(\frac{\tan 26^{\circ}}{\cot 64^{\circ}}\) = \(\frac{\tan 26^{\circ}}{\cot \left(90^{\circ}-26^{\circ}\right)}\)
= \(\frac{\tan 26^{\circ}}{\tan 26^{\circ}}\) = 1.
[∵ cot (90° – θ) = tan θ]

(iii) cos 48° – sin 42° = cos (90° – 42°) – sin 42°
[∵ cos (90° – θ) = sin θ]
= sin 42° – sin 42° = 0.

(iv) cosec 31° – sec 59°
= cosec 31° – sec (90° – 31°)
= cosec 31° – cosec 31°
[∵ sec (90° – θ) = cosec θ]
= 0.

ਪ੍ਰਸ਼ਨ 2.
ਦਿਖਾਉ ਕਿ
(i) tan 48° tan 23° tan 42° tan 67° = 1
(ii) cos 38° cos 52° – sin 38° sin 52° = 0
ਹੱਲ:
(i) L.H.S.
= tan 48° tan 23° tan 42° tan 67°
= tan48° × tan 23° × tan(90° -48°) × tan (90°–23°)
= tan 48° × tan 23° × cot 48° × cot 23°
= tan 48° × tan 23° × \(\frac{1}{\tan 48^{\circ}}\) × \(\frac{1}{\tan 23^{\circ}}\) = 1.
∴ L.H.S. = R.H.S.

(ii) L.H.S.= cos 38° cos 52° – sin 38° sin 52°
= cos 38° × cos (90° – 38) – sin 38° × sin (90° – 380)
= cos 38° × sin 38° – sin 38° × cos 38°
= 0.
∴ L.H.S. = R.H.S.

ਪ੍ਰਸ਼ਨ 3.
ਜੇਕਰ tan 2A = cot (A – 18°), ਜਿੱਥੇ 2A ਇੱਕ ਨਿਊਨ ਕੋਣ ਹੈ, ਤਾਂ A ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : tan 2A = cot (A – 18°)
A ਦਾ ਮੁੱਲ ਪਤਾ ਕਰਨ ਲਈ ਸਾਨੂੰ ਦੋਵੇ ਪਾਸੇ ਜਾਂ ਤਾਂ cot θ ਚਾਹੀਦਾ ਹੈ ਜਾਂ tan θ ਚਾਹੀਦਾ ਹੈ ।
[∵ cot (90° – θ) = tan θ]
⇒ cot (90° – 2A) = cot (A – 18°)
⇒ 90° – 2A = A – 18°
⇒ 3A = 108°
A = 36°.

ਪ੍ਰਸ਼ਨ 4.
ਜੇਕਰ tan A = cot B, ਤਾਂ ਸਿੱਧ ਕਰੋ ਕਿ A + B = 90°.
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : tan A = cot B
A + B = 90° ਦਿਖਾਉਣ ਦੇ ਲਈ ਦੋਵੇ ਪਾਸੇ ਜਾਂ ਤਾਂ tan ਚਾਹੀਦਾ ਹੈ ਜਾਂ cotθ ਚਾਹੀਦਾ ਹੈ।
[∵ tan (90° – θ) = cot θ]
⇒ tan A = tan (90° – B)
⇒ A = 90° – B
⇒ A + B = 90°.

ਪ੍ਰਸ਼ਨ 5.
ਜੇਕਰ sec 4A = cosec (A – 20°), ਜਿੱਥੇ 4A ਇੱਕ ਨਿਊਨ ਕੋਣ ਹੈ ਤਾਂ A ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : sec 4A = cosec (A – 20°)
A, ਦਾ ਮੁੱਲ ਪਤਾ ਕਰਨ ਲਈ ਸਾਨੂੰ ਦੋਵੇਂ ਪਾਸੇ sec θ ਜਾਂ cosec θ ਚਾਹੀਦਾ ਹੈ
[∵ cosec (90° – θ) = sec θ]
⇒ cosec (90° – 4A) = cosec (A – 20°)
⇒ 90° – 4A = A – 20°
⇒ 90° + 20° = A + 4 A
110° = 5A
⇒ A = 22°.

ਪ੍ਰਸ਼ਨ 6.
ਜੇਕਰ A, B ਅਤੇ Cਤ੍ਰਿਭੁਜ ABC ਦੇ ਅੰਦਰੂਨੀ ਕੋਣ ਹਨ, ਤਾਂ ਦਿਖਾਓ ਕਿ
sin \(\left(\frac{B+C}{2}\right)\) = cos \(\left(\frac{,A}{2}\right)\)
ਹੱਲ:
ਕਿਉਂਕਿ A, B ਅਤੇ cਤ੍ਰਿਭੁਜ ਦੇ ਅੰਦਰੂਨੀ ਕੋਣ ਹਨ ।
∴ A + B + C = 180° [ਤਿਭੁਜ ਦੇ ਤਿੰਨੋਂ ਕੋਣਾਂ ਦਾ ਜੋੜ 180° ਹੁੰਦਾ ਹੈ।]
⇒ B + C = 180° – A
⇒ \(\frac{\mathrm{B}+\mathrm{C}}{2}\) = \(\frac{180^{\circ}-\mathrm{A}}{2}\)
⇒ \(\frac{\mathrm{B}+\mathrm{C}}{2}\) = (90° – \(\frac{\mathrm{A}}{2}\))
ਦੋਵੇਂ ਪਾਸੇ sin ਲੈਣ ਤੇ,
⇒ sin\(\left(\frac{B+C}{2}\right)\) = sin(90° – \(\frac{\mathrm{A}}{2}\))
= cos \(\frac{\mathrm{B}+\mathrm{C}}{2}\)
[∵ sin (90° – θ) = cos θ]

ਪ੍ਰਸ਼ਨ 7.
sin 67° + cos 75° ਨੂੰ 0° ਅਤੇ 45° ਦੇ ਵਿਚਕਾਰ ਦੇ ਕੋਣਾਂ ਦੇ ਤਿਕੋਣਮਿਤਈ ਅਨੁਪਾਤਾਂ ਦੇ ਪਦਾਂ ਵਿੱਚ ਦਰਸਾਉ।
ਹੱਲ:
sin 67° + cos 75°
= sin (90° – 23°) + cos (90° – 15°)
= cos 23° + sin 15°
{∵ sin (90° – θ) = cos θ
ਅਤੇ cos (90° – θ) = sin θ}

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 8 ਤਿਕੋਣਮਿਤੀ ਬਾਰੇ ਜਾਣ ਪਛਾਣ Ex 8.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 8 ਤਿਕੋਣਮਿਤੀ ਬਾਰੇ ਜਾਣ ਪਛਾਣ Exercise 8.2

ਪ੍ਰਸ਼ਨ 1.
ਹੇਠ ਲਿਖਿਆਂ ਦੇ ਮੁੱਲ ਪਤਾ ਕਰੋ :
(i) sin 60° cos 30° + sin 30° cos 60°
(ii) 2 tan² 45° + cos² 30° – sin² 60°
(iii) \(\frac{\cos 45^{\circ}}{\sec 30^{\circ}+{cosec} 30^{\circ}}\)
(iv) \(\frac{\sin 30^{\circ}+\tan 45^{\circ}-{cosec} 60^{\circ}}{\sec 30^{\circ}+\cos 60^{\circ}+\cot 45^{\circ}}\)
(v) \(\frac{5 \cos ^{2} 60^{\circ}+4 \sec ^{2} 30^{\circ}-\tan ^{2} 45^{\circ}}{\sin ^{2} 30^{\circ}+\cos ^{2} 30^{\circ}}\)
ਹੱਲ:
(i) ਦਿੱਤਾ ਹੈ :
sin 60° cos 30° + sin 30° cos 60°
= \(\left(\frac{\sqrt{3}}{2}\right)\)\(\left(\frac{\sqrt{3}}{2}\right)\) + \(\left(\frac{1}{2}\right)\)\(\left(\frac{1}{2}\right)\)
= \(\left(\frac{\sqrt{3}}{2}\right)^{2}\) + \(\left(\frac{1}{2}\right)^{2}\)
= \(\frac{3}{4}\) + \(\frac{1}{4}\) = 1.

(ii) ਦਿੱਤਾ ਹੈ :
2 tan² 45° + cos² 30° – sin² 60°
= 2 (tan 45°)² + (cos 30°)² – (sin 60°)²
= 2(1)² + \(\left(\frac{\sqrt{3}}{2}\right)^{2}\) – \(\left(\frac{\sqrt{3}}{2}\right)^{2}\) = 2.

(iii) ਦਿੱਤਾ ਹੈ : \(\frac{\cos 45^{\circ}}{\sec 30^{\circ}+{cosec} 30^{\circ}}\)

(iv) ਦਿੱਤਾ ਹੈ : \(\frac{\sin 30^{\circ}+\tan 45^{\circ}-{cosec} 60^{\circ}}{\sec 30^{\circ}+\cos 60^{\circ}+\cot 45^{\circ}}\)

(v) ਦਿੱਤਾ ਹੈ : \(\frac{5 \cos ^{2} 60^{\circ}+4 \sec ^{2} 30^{\circ}-\tan ^{2} 45^{\circ}}{\sin ^{2} 30^{\circ}+\cos ^{2} 30^{\circ}}\)

= \(\frac{5}{4}\) + \(\frac{16}{3}\) – 1 = \(\frac{15+64-12}{12}\)
= \(\frac{67}{12}\).

2. ਸਹੀ ਉੱਤਰ ਚੁਣੋ ਅਤੇ ਉਸਦਾ ਕਾਰਣ ਦੱਸੋ :

ਪ੍ਰਸ਼ਨ (i).
\(\frac{2 \tan 30^{\circ}}{1+\tan ^{2} 30^{\circ}}\)
(A) sin 60°
(B) cos 60°
(C) tan 60°
(D) sin 30°
ਉੱਤਰ:

∴ ਵਿਕਲਪ ‘A’ ਸਹੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ (ii).
\(\frac{1-\tan ^{2} 45^{\circ}}{1+\tan ^{2} 45^{\circ}}\)
(A) tan 90°
(B) 1
(C) sin45°
(D) 0.
ਉੱਤਰ:
\(\frac{1-\tan ^{2} 45^{\circ}}{1+\tan ^{2} 45^{\circ}}\) = \(\frac{1-(1)^{2}}{1+(1)^{2}}\) = 0.
∴ ਵਿਕਲਪ “D’ ਸਹੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ (iii).
sin2A = 2sin A ਉਦੋਂ ਸੱਚ ਹੁੰਦਾ ਹੈ, ਜਦੋਂ A ਬਰਾਬਰ ਹੈ :
(A) 0°
(B) 30°
(C) 450
(D) 60°
ਉੱਤਰ:
ਦਿੱਤਾ ਹੈ, sin 2A = 2 sin A
ਜਦੋਂ, A = 0° ਹੋਵੇ ਤਾਂ
sin 2(0) = 2 sin 0
sin 0 = 0
0 = 0; ਜੋ ਸੱਚ ਹੈ ।
∴ ਵਿਕਲਪ ‘A’ ਸਹੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ (iv).
\(\frac{2 \tan 30^{\circ}}{1-\tan ^{2} 30^{\circ}}\) ਬਰਾਬਰ ਹੈ :
(A) cos 60°
(B) sin 60°
(C) tan 60°
(D) sin 30°.
ਉੱਤਰ:

∴ ਵਿਕਲਪ ‘C’ ਸਹੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਜੇਕਰ tan (A + B) = \(\sqrt {3}\) ਅਤੇ tan (A – B) = \(\frac{1}{\sqrt{3}}\); 0° < A + B ≤ 90° ; A > B ਤਾਂ A ਅਤੇ B ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
tan (A + B) = \(\sqrt {3}\)
tan (A + B) = tan 60°
⇒ A + B = 60° …(1)
tan (A – B) = \(\frac{1}{\sqrt{3}}\)
ਜਾਂ tan (A – B) = tan 30°
⇒ A – B = 30° …(2)
(1) ਅਤੇ (2) ਜੋੜਨ ‘ਤੇ

A = 45°
(1) ਵਿਚ ਮੁੱਲ ਭਰਨ ‘ਤੇ
45° + B = 60°
B = 60° – 45°
B = 15°
∴ A = 45° ਅਤੇ B = 15°

ਪ੍ਰਸ਼ਨ 4.
ਦੱਸੋ ਹੇਠਾਂ ਦਿੱਤਿਆਂ ਵਿੱਚੋਂ ਕਿਹੜਾ ਸਹੀ ਹੈ ਅਤੇ ਕਿਹੜਾ ਗਲਤ। ਕਾਰਣ ਸਹਿਤ ਆਪਣੇ ਉੱਤਰ ਦੀ ਪੁਸ਼ਟੀ ਕਰੋ।
(i) sin (A + B) = sin A + sin B.
(ii) θ ਦੇ ਵੱਧਣ ਨਾਲ sin θ ਦਾ ਮੁੱਲ ਵੀ ਵਧਦਾ ਹੈ।
(iii) θ ਦੇ ਵੱਧਣ ਨਾਲ cos θ ਦਾ ਮੁੱਲ ਵੀ ਵਧਦਾ ਹੈ।
(iv) θ ਦੇ ਸਾਰੇ ਮੁੱਲਾਂ ਲਈ sin θ = cos θ.
(v) A = 0° ਤੇ cot A ਪਰਿਭਾਸ਼ਿਤ ਨਹੀਂ ਹੈ ।
ਹੱਲ:
(i) ਠੀਕ ਨਹੀਂ
ਜਦੋਂ A = 60°, B = 30°
L.H.S. = sin (A + B)
= sin (60° + 30°)
= sin 90° = 1
R.H.S. = sin A + sin B
= sin 60° + sin 30°
= \(\frac{\sqrt{3}}{2}\) + \(\frac{1}{2}\) ≠ 1
ਅਰਥ L.H.S. ≠ R.H.S.

(ii) ਠੀਕ ਹੈ sin 30° = \(\frac{1}{2}\) = 0.5,
ਕਿਉਂਕਿ, sin 45 = \(\frac{1}{\sqrt{2}}\) = 0.7 (ਲਗਭਗ )
sin 60° = \(\frac{\sqrt{3}}{2}\) = 0.87 (ਲਗਭਗ)
ਅਤੇ sin 90° = 1
ਅਰਥ, ਜਦੋਂ θ ਦਾ ਮੁੱਲ 0° ਤੋਂ 90° ਤਕ ਵਧਦਾ ਹੈ ਤਾਂ sin 6 ਦਾ ਮੁੱਲ ਵੀ ਵਧਦਾ ਹੈ ।

(iii) ਠੀਕ ਨਹੀਂ
ਕਿਉਂਕਿ cos 0° = 1,
cos 30° = \(\frac{\sqrt{3}}{2}\) = 0.87 (ਲਗਭਗ) ।
cos 45° = \(\frac{1}{\sqrt{2}}\) = 0.7 (ਲਗਭਗ)
cos 60°= \(\frac{1}{2}\) = 0.5
ਅਤੇ cos 90° = 0.
ਜਦੋਂ θ ਦਾ ਮੁੱਲ 0° ਤੋਂ 90° ਤੱਕ ਵਧਦਾ ਹੈ ਤਾਂ cos 9 ਦਾ ਮੁੱਲ ਘਟਦਾ ਹੈ ।

(iv) ਠੀਕ ਨਹੀਂ
ਕਿਉਂਕਿ sin 30° = \(\frac{1}{2}\)
ਅਤੇ cos 30° = \(\frac{\sqrt{3}}{2}\)
ਜਾਂ sin 30° ≠ cos 30°
ਸਾਨੂੰ ਮਿਲਦਾ ਹੈ :
sin 45° = cos 45°.
\(\frac{1}{\sqrt{2}}\) = \(\frac{1}{\sqrt{2}}\)

(v) ਠੀਕ ਹੈ
cot 0°= \(\frac{1}{\tan 0^{\circ}}\) = \(\frac{1}{0}\), ਜਾਂ ਪਰਿਭਾਸ਼ਿਤ ਨਹੀਂ ।

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 8 ਤਿਕੋਣਮਿਤੀ ਬਾਰੇ ਜਾਣ ਪਛਾਣ Ex 8.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 8 ਤਿਕੋਣਮਿਤੀ ਬਾਰੇ ਜਾਣ ਪਛਾਣ Exercise 8.1

ਪ੍ਰਸ਼ਨ 1.
△ABC ਵਿੱਚ, ਜਿਸਦਾ ਕੋਣ B ਸਮਕੋਣ ਹੈ, AB = 24 cm ਅਤੇ BC = 7 cm ਹੈ। ਹੇਠਾਂ ਦਿੱਤਿਆਂ ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ :
(i) sin A, cos A
(ii) sin C, cos C.
ਹੱਲ:
(i) ਅਸੀਂ ਪਤਾ ਕਰਨਾ ਹੈ sin A, cos A AB = 24 cm ; BC = 7 cm

ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਦਾ ਪ੍ਰਯੋਗ ਕਰਦੇ ਹੋਏ,
AC² = AB² + BC²
AC² = (24)² + (7)²
AC² = 576 + 49
AC² = 625.
AC = \(\sqrt {625}\)
AC = 25 cm.
sin A = \(\frac{BC}{AC}\)
sin A = \(\frac{7 cm}{25 cm}\) = \(\frac{7}{25}\)
cos A = \(\frac{AB}{AC}\) = \(\frac{24 cm}{25 cm}\)
cos A = \(\frac{24}{25}\)
sin A = \(\frac{7}{25}\) ਅਤੇ cos A = \(\frac{24}{25}\)

(ii) sin C = \(\frac{AB}{AC}\) = \(\frac{24 cm}{25 cm}\)

sin C = \(\frac{24}{25}\)
cos C = \(\frac{BC}{AC}\) = \(\frac{7 cm}{25 cm}\)
cos C = \(\frac{7}{25}\)
sin C = \(\frac{24}{25}\) ਅਤੇ cos C = \(\frac{7}{25}\)

ਪ੍ਰਸ਼ਨ 2.
ਚਿੱਤਰ ਵਿੱਚ, tan P – cot R ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ ।

ਹੱਲ:
ਕਰਣ PR = 13 cm, ਲੰਬ PQ = 12 cm

ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ,
PR² = PQ² + OR²
ਜਾਂ (13)² = (12)² + QR²
ਜਾਂ 169 = 144 + (OR)²
ਜਾਂ 169 – 144 = (QR)²
ਜਾਂ 25 = (QR)²
ਜਾਂ QR = ±\(\sqrt {25}\)
ਜਾਂ QR = 5, – 5.
ਪਰ QR = 5 cm.
[QR ≠ -5 ਕਿਉਂਕਿ ਭੁਜਾ ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੁੰਦੀ]
tan P = \(\frac{RQ}{QP}\) = \(\frac{5}{12}\)
cot R = \(\frac{RQ}{PQ}\) = \(\frac{5}{12}\)
∴ tan P – cot R = \(\frac{5}{12}\) – \(\frac{5}{12}\) = 0
ਇਸ ਲਈ tan P – cot R = 0.

ਪ੍ਰਸ਼ਨ 3.
ਜੇਕਰ sin A = \(\frac{3}{4}\), ਤਾਂ cos A ਅਤੇ tan A ਦਾ ਮਾਨ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ ABC ਕੋਈ ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸ ਵਿਚ ਕੋਣ B ਸਮਕੋਣ ਹੈ ।

sin A = \(\frac{3}{4}\)
ਪਰ sin A = \(\frac{BC}{AC}\) [ਚਿੱਤਰ ਵਿਚ]
∴ \(\frac{BC}{AC}\) = \(\frac{3}{4}\)
ਪਰ \(\frac{BC}{AC}\) = \(\frac{3}{4}\) = k
K, ਇਕ ਸਥਿਰ ਅੰਕ ਹੈ ।
⇒ BC = 3K,
AC = 4K
ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਦਾ ਪ੍ਰਯੋਗ ਕਰਕੇ,
AC² = AB² + BC²
ਜਾਂ (4K)² = (AB)² + (3K)²
ਜਾਂ 16K² = AB² + 9K²
ਜਾਂ 16K² – 9K² = AB²
ਜਾਂ 7K² = AB²
ਜਾਂ AB = ±\(\sqrt{7 \mathrm{~K}^{2}}\)
ਜਾਂ AB = ±\(\sqrt {7}\) K
[AB ≠ – 7K ਕਿਉਂਕਿ ਭੁਜਾ ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੋ ਸਕਦੀ ] AB= 17 K
⇒ AB = \(\sqrt {7}\) K
cos A = \(\frac{AB}{AC}\)
cos A = \(\frac{\sqrt{7} K}{4 K}\) = \(\frac{\sqrt{7}}{4}\)
tan A = \(\frac{\mathrm{BC}}{\mathrm{AB}}\) = \(\frac{3 K}{\sqrt{7} K}\) = \(\frac{3}{\sqrt{7}}\)
∴ cos A = \(\frac{\sqrt{7}}{4}\) ਅਤੇ tan A = \(\frac{3}{\sqrt{7}}\)

ਪ੍ਰਸ਼ਨ 4.
ਜੇਕਰ 15 cot A = 8 ਹੋਵੇ ਤਾਂ sin A ਅਤੇ sec A ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ ABC ਕੋਈ ਸਮਕੋਣ ਤਿਭੁਜ ਹੈ ਜਿਸ ਵਿਚ ∠A ਨਿਊਨ ਕੋਣ ਹੈ ਅਤੇ B ਸਮਕੋਣ ਹੈ ।

15 cot A = 8
cot A = \(\frac{8}{15}\)
ਪਰ cot A = \(\frac{AB}{BC}\) [ਚਿੱਤਰ ਵਿਚ]
⇒ \(\frac{AB}{BC}\) = \(\frac{8}{15}\) = K
K, ਸਥਿਰ ਅੰਕ ਹੈ ।
⇒ AB = 8 K, BC = 15 K
ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ
AC² = AB² + BC²
AC² = (8K)² + (15K)²
AC² = 64K² + 225 K²
AC² = 289 K²
AC = ±\(\sqrt{289 K^{2}}\)
AC = ±17K
⇒ AC = 17K
[AC = – 17 K, ਕਿਉਂਕਿ ਭੁਜਾ ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੋ ਸਕਦੀ ]

ਪ੍ਰਸ਼ਨ 5.
ਜੇਕਰ sec θ = \(\frac{13}{12}\) ਹੋਵੇ ਤਾਂ ਬਾਕੀ ਸਾਰੇ ਤਿਕੋਣਮਿਤਈ ਅਨੁਪਾਤ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ ABC ਕੋਈ ਸਮਕੋਣ ਤਿਭੁਜ ਹੈ ਜਿਸ ਵਿਚ ∠B ਸਮਕੋਣ ਹੈ ।
∠BAC = θ

sec θ = \(\frac{13}{12}\)
ਪਰ sec θ = \(\frac{AC}{AB}\) …[ਚਿੱਤਰ ਵਿਚ]
\(\frac{AC}{AB}\) = \(\frac{13}{12}\)
ਪਰ \(\frac{AC}{AB}\) = \(\frac{13}{12}\) = k
k ਸਥਿਰ ਅੰਕ ਹੈ ।
AC = 13k ਅਤੇ AB = 12k
ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਦੇ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ,
AC² = (AB)² + (BC)²
ਜਾਂ (13k)² = (12k)² + (BC)²
ਜਾਂ169k² = 144k² + BC²
ਜਾਂ 169k² – 144k² = BC²
ਜਾਂ (BC)² = 25k²
ਜਾਂ BC = ±\(\sqrt{25 k^{2}}\)
ਜਾਂ BC = ±5k
ਜਾਂ BC = 5k.
[BC ≠ – 5k ਕਿਉਂਕਿ ਭੁਜਾ ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੋ ਸਕਦੀ]

ਪ੍ਰਸ਼ਨ 6.
ਜੇਕਰ ∠A ਅਤੇ ∠B ਨਿਊਨ ਕੋਣ ਹੋਣ, ਜਿੱਥੇ cos A = cos B, ਤਾਂ ਦਿਖਾਉ ਕਿ ∠A = ∠B.
ਹੱਲ:
ਮੰਨ ਲਉ ABC ਕੋਈ ਤਿਭੁਜ ਹੈ ਜਿੱਥੇ ∠A ਅਤੇ ∠B ਨਿਊਨ ਕੋਣੇ ਹਨ | cos A ਅਤੇ cos B ਪਤਾ ਕਰੋ ।

CM ⊥ AB
∠AMC : ∠BMC = 90°
ਸਮਕੋਣ △AMC ਵਿਚ,
\(\frac{AM}{AC}\) = cos A …(1)
ਸਮਕੋਣ △BMC ਵਿਚ,
\(\frac{BM}{BC}\) = cos B …(2)
ਪਰ cos A = cos B [ਦਿੱਤਾ ਹੈ ] …(3)
(1), (2) ਅਤੇ (3) ਤੋਂ,
\(\frac{AM}{AC}\) = \(\frac{BM}{BC}\)
\(\frac{AM}{BM}\) = \(\frac{AC}{BC}\) = \(\frac{CM}{CM}\)
∴ △AMC ~ △BMC [SSS ਕਸੌਟੀ ]
⇒ ∠A = ∠B [∵ ਕਿਉਂਕਿ ਸਮਰੂਪ ਤ੍ਰਿਭੁਜਾਂ ਸੰਗਤ ਕੋਣ ਬਰਾਬਰ ਹੁੰਦੇ ਹਨ]

ਪ੍ਰਸ਼ਨ 7.
ਜੇਕਰ cot θ = \(\frac{7}{8}\), ਤਾਂ
(i) \(\frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}\)
(ii) cot²θ ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
(i) ∠ABC = θ
ਸਮਕੋਣ ਤਿਭੁਜ ABC ਵਿਚ C ਉੱਤੇ ਸਮਕੋਣ ਹੈ ।

ਦਿੱਤਾ ਹੈ : cot θ = \(\frac{7}{8}\)
ਪਰ cot θ = \(\frac{BC}{AC}\) [ਚਿੱਤਰ ਵਿਚ]
⇒ \(\frac{BC}{AC}\) = \(\frac{7}{8}\)
ਮੰਨ ਲਓ \(\frac{BC}{AC}\) = \(\frac{7}{8}\) = k
ਜਿੱਥੇ k ਸਥਿਰ ਅੰਕ ਹੈ ।
⇒ BC = 7k, AC = 8k
ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ,
AB² = (BC)² + (AC)²
ਜਾਂ (AB)² = (7k)² + (8k)²
ਜਾਂ (AB)² = 49k² + 64k²
ਜਾਂ(AB)² = 113k²
ਜਾਂ AB = ±\(\sqrt{113 k^{2}}\)
AB = \(\sqrt{113}\) k
[AB ≠ –\(\sqrt{113}\) k ਕਿਉਂਕਿ ਭੁਜਾ ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੋ ਸਕਦੀ]

[ਸੂਤਰ (a + b) (a – b) = a² – b² ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ]
= 1 – \(\frac{64}{113}\)
(1 + sin θ) (1 – sin θ)
= \(\frac{113-64}{113}\) = \(\frac{49}{113}\)
⇒ (1 + sin θ) (1 – sin θ) = \(\frac{49}{113}\) …(1)
(1 + cos θ) (1 – cos θ)

(ii) cot θ = \(\frac{BC}{AC}\) = \(\frac{7}{8}\)
cot² θ = (cot θ)²
cot² θ = \(\left(\frac{7}{8}\right)^{2}\)
⇒ cot² θ = \(\frac{49}{64}\).

ਪ੍ਰਸ਼ਨ 8.
ਜੇਕਰ 3 cot A = 4 ਤਾਂ ਪੜਤਾਲ ਕਰੋ ਕਿ \(\frac{1-\tan ^{2} A}{1+\tan ^{2} A}\) = cos²A – sin²A ਹੈ ਜਾਂ ਨਹੀਂ
ਹੱਲ:
ਮੰਨ ਲਉ ABC ਇਕ ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸ ‘ ਵਿਚ B ਸਮਕੋਣ ਹੈ ॥

ਇਹ ਦਿੱਤਾ ਹੈ ਕਿ 3 cot A = 4
cot A = \(\frac{4}{3}\)
ਪਰ cot A = \(\frac{AB}{BC}\) [ਚਿੱਤਰ ਵਿਚੀ]
\(\frac{AB}{BC}\) = \(\frac{4}{3}\)
ਪਰ \(\frac{AB}{BC}\) = \(\frac{4k}{3k}\)
⇒ AB = 4k, BC = 3k
ਪਾਈਥਾਗੋਰਸ, ਪ੍ਰਮੇਯ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ਤੇ,
AC² = AB² + BC²
AC² = 4k² + 3k²
AC² = 16k² + 9k²
AC² = 25²
AC = ± \(\sqrt{25 k^{2}}\)
AC = ± 5k
ਪਰ AC = 5k.
[AC ≠ – 5k, ਕਿਉਂਕਿ ਭੁਜਾ ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੁੰਦੀ ਹੈ।]

ਪ੍ਰਸ਼ਨ 9.
AABC ਵਿਚ, ਜਿਸਦਾ ਕੋਣ B ਸਮਕੋਣ ਹੈ, ਜੇਕਰ tan A = \(\frac{1}{\sqrt{3}}\), ਤਾਂ ਹੇਠਾਂ ਦਿੱਤੇ ਮੁੱਲ ਪਤਾ ਕਰੋ :
(i) sin A cos C + cos A sin C
(ii) cos A cos C – sin A sin C.
ਹੱਲ:
(i) ਦਿੱਤਾ ਹੈ : △ABC ਜਿਸਦਾ ਕੋਣ B ਸਮਕੋਣ ਹੈ ।

tan A = \(\frac{1}{\sqrt{3}}\) …(1)
ਪਰ tan A = \(\frac{BC}{AB}\) …(2)
(1) ਅਤੇ (2) ਤੋਂ, .
\(\frac{BC}{AB}\) = \(\frac{1}{\sqrt{3}}\)
ਮੰਨ ਲਉ \(\frac{BC}{AB}\) = \(\frac{1}{\sqrt{3}}\) = k
BC = k, AB = \(\sqrt {3}\) k
ਜਿੱਥੇ k ਸਥਿਰ ਅੰਕ ਹੈ ।
ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ ABC ਵਿਚ,
ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ‘ਤੇ,
AC² = AB² + Bc²
(AC)² = ( k)² + (k)²
AC² = 3k² + k²
AC² = 4k²
AC = ± \(\sqrt{4 k^{2}}\)
AC = ± 2k.
ਇੱਥੇ AC = 2k
[AC ≠ – 2k ∵ ਭੁਜਾ ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੋ ਸਕਦੀ]

sin A cos C = \(\left(\frac{1}{2}\right)\)\(\left(\frac{1}{2}\right)\) = \(\frac{1}{4}\)
cos A sin C = \(\left(\frac{\sqrt{3}}{2}\right)\)\(\left(\frac{\sqrt{3}}{2}\right)\) = \(\frac{3}{4}\)
sin A cos C + cos A sinC
= \(\frac{1}{4}\) + \(\frac{3}{4}\)
= \(\frac{1+3}{4}\) = \(\frac{4}{4}\) = 1
∴ sin A cos C + cos A sin C = 1.

(ii) cos A cos C = \(\left(\frac{\sqrt{3}}{2}\right)\)\(\left(\frac{1}{2}\right)\) = \(\frac{\sqrt{3}}{4}\) [(3) ਤੋਂ]
sin A sin C = \(\left(\frac{1}{2}\right)\)\(\left(\frac{\sqrt{3}}{2}\right)\) = \(\frac{\sqrt{3}}{4}\) [(3) ਤੋਂ।]
cos A cos C – sin A sin C
= \(\left(\frac{\sqrt{3}}{4}\right)\) – \(\left(\frac{\sqrt{3}}{4}\right)\) = 0

ਪ੍ਰਸ਼ਨ 10.
△POR ਵਿੱਚ, ਜਿਸਦਾ ਕੋਣ Q ਸਮਕੋਣ ਹੈ, PR + QR = 25 cm ਅਤੇ PQ = 5 cm ਹੈ । sin P, cos P ਅਤੇ tan P ਦੇ ਮੁੱਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ : △PQR, ਵਿੱਚ Q ਸਮਕੋਣ ਹੈ ।

PR + QR = 25 cm
PQ = 5 cm
ਸਮਕੋਣ ਭੁਜ PQR ਵਿਚ,
ਪਾਈਥਾਗੋਰਸ ਪ੍ਰਮੇਯ ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ਤੇ,
PR² = PQ² + RQ²
ਜਾਂ PR² = 5² + RQ²
[∵ PR + OR = 25
QR = 25 – PR]
PR² = 25 + [25 – PR]²
PR² = 25 + 25² + PR² – 2 × 25 × PR PR² = 25 + 625 + PR² – 50 PR
PR² – PR² + 50 PR = 650
PR = \(\frac{650}{50}\)
PR = 13
∴ QR = 25 – PR
⇒ 25 – 13
= 12 cm.
sin P = \(\frac{QR}{PR}\) = \(\frac{12}{13}\)
cos P = \(\frac{PQ}{PR}\) = \(\frac{5}{13}\)
tan P = \(\frac{QR}{PQ}\) = \(\frac{12}{5}\)

ਪ੍ਰਸ਼ਨ 11.
ਦੱਸੋ ਕਿ ਹੇਠਾਂ ਦਿੱਤੇ ਕਥਨ ਠੀਕ ਹਨ ਜਾਂ ਗਲਤ, ਕਾਰਣ ਸਹਿਤ ਆਪਣੇ ਉੱਤਰ ਦੀ ਪੁਸ਼ਟੀ ਕਰੋ।
(i) tan A ਦਾ ਮੁੱਲ ਹਮੇਸ਼ਾ 1 ਤੋਂ ਘੱਟ ਹੁੰਦਾ ਹੈ ।
(ii) ਕੋਣ A ਦੇ ਕਿਸੇ ਮੁੱਲ ਲਈ sec A = \(\frac{12}{5}\).
(iii) cos A, ਕੋਣ A ਦੇ cosecant ਦਾ ਸੰਖੇਪ ਰੂਪ ਹੈ ।
(iv) cot A, cot ਅਤੇ A ਦਾ ਗੁਣਨਫਲ ਹੁੰਦਾ ਹੈ !
(v) ਕਿਸੇ ਵੀ ਕੋਣ 8 ਦੇ ਲਈ sin θ = \(\frac{4}{3}\).
ਹੱਲ:
(i) ਠੀਕ ਨਹੀਂ ਹੈ
∵ tan 60° = \(\sqrt {3}\) = 1.732 > 1.
(ii) ਠੀਕ ਹੈ, sec A = \(\frac{12}{5}\) = 2:40 > 1
∵ Sec A ਹਮੇਸ਼ਾਂ A ਤੋਂ ਵੱਡਾ ਹੁੰਦਾ ਹੈ ।
(ii) ਠੀਕ ਨਹੀਂ
ਕਿਉਂਕਿ cos A, cosine A ਦੇ ਲਈ ਪ੍ਰਯੋਗ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।
(iv) ਠੀਕ ਨਹੀਂ
ਕਿਉਂਕਿ cot A, ਕੋਣ A ਦਾ cotangent ਹੈ ਨਾ ਕਿ cot ਅਤੇ A ਦਾ ਗੁਣਨਫਲ ।
(v) ਠੀਕ ਨਹੀਂ sin θ = \(\frac{4}{3}\) = 1 666 > 1
ਕਿਉਂਕਿ sin θ ਹਮੇਸ਼ਾਂ 1 ਤੋਂ ਘੱਟ ਹੁੰਦਾ ਹੈ ।

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 7 ਨਿਰਦੇਸ਼ ਅੰਕਜਿਮਾਇਤੀ Ex 7.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 7 ਨਿਰਦੇਸ਼ ਅੰਕਜਿਮਾਇਤੀ Exercise 7.4

ਪ੍ਰਸ਼ਨ 1.
ਬਿੰਦੂਆਂ A(2, – 2) ਅਤੇ B (3, 7) ਨੂੰ ਮਿਲਾਉਣ ਵਾਲੇ ਰੇਖਾਖੰਡ ਨੂੰ ਰੇਖਾ 2x + y – 4 = 0 ਕਿਸ ਅਨੁਪਾਤ ਵਿਚ ਵੰਡਦੀ ਹੈ, ਉਹ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ ਰੇਖਾ 2x + y – 4 = 0 ਬਿੰਦੂ A (2, – 2) ਅਤੇ B(3, 7) ਨੂੰ ਮਿਲਾਉਣ ਵਾਲੇ ਰੇਖਾਖੰਡ ਨੂੰ C(x, y) ਉੱਤੇ k : 1 ਅਨੁਪਾਤ ਵਿਚ ਵੰਡਦੀ ਹੈ ।

∴ C [\(\frac{3 k+2}{k+1}\), \(\frac{7 k-2}{k+1}\)] ਰੇਖਾ 2x + y – 4 = 0 ਉੱਤੇ ਹੋਵੇਗਾ ।
ਭਾਵ 2 \(\left(\frac{3 k+2}{k+1}\right)\) + \(\left(\frac{7 k-2}{k+1}\right)\) – 4 = 0
\(\frac{6 x+4+7 k-2-4 k-4}{k+1}\) = 0
9k – 2 = 0
9k = 2
k = \(\frac{2}{9}\)
∴ ਅਨੁਪਾਤ k : 1 = \(\frac{2}{9}\) : 1 = 2 : 9
∴ ਲੋੜੀਂਦਾ ਅਨੁਪਾਤ 2:9 ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
x ਅਤੇ y ਵਿਚਕਾਰ ਇਕ ਸੰਬੰਧ ਪਤਾ ਕਰੋ ਜੇਕਰ ਬਿੰਦੂ | (x, y) ; (1, 2) ਅਤੇ (7, 0) ਸਮਰੇਖੀ ਹਨ ।
ਹੱਲ:
ਦਿੱਤੇ ਗਏ ਬਿੰਦੂ A(x, y) ; B (1, 2) ਅਤੇ C (7, 0) ਹੈ ।
ਇੱਥੇ x₁ = 1, x₂ = 1, x₃ = 7
y₁ = y, y₂ = 2, y₃ = 0
∵ ਤਿੰਨ ਬਿੰਦੂ ਸਮਰੇਖੀ ਹਨ ਜੇਕਰ
= \(\frac{1}{2}\)[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)] = 0
\(\frac{1}{2}\)[x (2 – 0) + 1 (0 – y) + 7 (y – 2)] = 0
2x – y + 7y – 14 = 0
2x + 6y – 14 = 0
ਜਾਂ x + 3y – 7 = 0 ਲੋੜੀਂਦਾ ਸੰਬੰਧ ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਬਿੰਦੂਆਂ (6, – 6), (3, – 7) ਅਤੇ (3, 3) ਤੋਂ ਹੋ ਕੇ ਜਾਣ ਵਾਲੇ ਚੱਕਰ ਦਾ ਕੇਂਦਰ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਓ O (x, y) ਲੋੜੀਂਦਾ ਕੇਂਦਰ ਹੈ ਜੋ ਕਿ ਬਿੰਦੂ P(6, – 6) ; Q (3, – 7) ਅਤੇ R (3, 3) ਵਿਚੋਂ ਲੰਘਦਾ ਹੈ
∵ ਚੱਕਰ ਦੇ ਅਰਧ ਵਿਆਸ ਸਮਾਨ ਹੁੰਦੇ ਹਨ

∴ OP = OQ = OR
ਜਾਂ (OP)² = (OQ)² = (OR)²
(OP)² = (OQ)²
(x – 6)² + (y + 6)² = (x – 3)² + (y + 7)²
x² + 36 – 12 x + y² + 36 + 12y = x² +²9 – 6 + y² + 49 + 14y
-12x + 12y + 72 = -6x + 14y + 58
-6x – 2y + 14 = 0
3x + y -7 = 0 ….(1)
(OQ)² = (OR)²
(x – 3)² + (y + 7)² = (x – 3)² + (y – 3)²
(y + 7)² = (y – 3)²
y² + 49 + 14y = y² + 9 – 6y
20y = – 40
y = \(\frac{-40}{20}\) = -2
y ਦਾ ਮੁੱਲ (1) ਵਿਚ ਰੱਖਣ ਤੇ ਅਸੀਂ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ ।
3x – 2 – 7 = 0
3x – 9 = 0
3x = 9
x = 3
∴ ਲੋੜੀਂਦਾ ਕੇਂਦਰ ਹੈ (3, – 2)

ਪ੍ਰਸ਼ਨ 4.
ਜੇਕਰ ਇੱਕ ਵਰਗ ਦੇ ਦੋ ਸਾਹਮਣੇ (Opposite) ਦੇ ਸਿਖਰ (-1, 2) ਅਤੇ (3, 2) ਹਨ ਤਾਂ ਵਰਗ ਦੇ ਦੋਵੇਂ ਸਿਖਰ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ ਵਰਗ ABCD ਦੇ ਦੋ ਸਨਮੁੱਖ ਸਿਖਰ A (-1, 2) ਅਤੇ C (3, 2) ਅਤੇ B ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ (x, y) ਹਨ ।
∵ ਵਰਗ ਦੀ ਹਰੇਕ ਭੁਜਾ ਦੀ ਲੰਬਾਈ ਬਰਾਬਰ ਹੈ
∴ AB = BC
(AB)² = (BC)²
(x + 1)² + (y – 2)² = (x – 3)² + (y – 2)²

(x + 1)² = (x – 3)²
x² + 1 + 2x = x² + 9 – 6x
8x = 8
x = 1 …(1)
ਹੁਣ ਸਮਕੋਣ △ABC ਵਿਚ,
ਪਾਇਥਾਗੋਰਸ ਦਾ ਪਰਿਮੇਯ ਪ੍ਰਯੋਗ ਕਰਕੇ
(AB)² + (BC)² = (AC)²
(x + 1)² + (y – 2)² + (x – 3)² + (y – 2)²
= (3 + 1)² + (2 – 2)²
x² + 1 + 2x + y² + 4 – 4y + x² +9 – 6x + y² + 4 – 4y = 16
2x² + 2y² – 4x – 8y + 2 = 0
x² + y² – 2x – 4y + 1 = 0 …(2)
x = 1 ਦਾ ਮੁੱਲ (2) ਵਿਚ ਰੱਖਣ ਤੇ
(1)² + y² – 2 (1) – 4y + 1 = 0
y² – 4y = 0
y (y – 4) = 0
y = 0 ਜਾਂ y = 4
∴ ਲੋੜੀਂਦਾ ਬਿੰਦੁ (1, 0) ਅਤੇ (4, 0) ਹਨ ।

ਪ੍ਰਸ਼ਨ 5.
ਕ੍ਰਿਸ਼ਨਾ ਨਗਰ ਦੇ ਇਕ ਸੈਕੰਡਰੀ ਸਕੂਲ ਦੀ X ਜਮਾਤ ਦੇ ਵਿਦਿਆਰਥੀਆਂ ਨੂੰ ਬਾਗਬਾਨੀ ਕਿਰਿਆਵਾਂ ਕਰਨ ਲਈ ਇੱਕ ਆਇਤਾਕਾਰ ਜਮੀਨ ਦਾ ਟੁੱਕੜਾ ਦਿੱਤਾ ਗਿਆ ਹੈ । ਗੁਲਮੋਹਰ ਦੇ ਪੌਦੇ ਇਸ ਦੀ ਸੀਮਾਂ ‘ ਤੇ ਆਪਸ ਵਿਚ 1m ਦੀ ਦੂਰੀ ‘ਤੇ ਲਗਾਏ ਗਏ ਹਨ । ਜ਼ਮੀਨ ਦੇ ਇਸ ਟੁੱਕੜੇ ਦੇ ਅੰਦਰ ਇੱਕ ਤਿਭੁਜ ਅਕਾਰ ਦਾ ਘਾਹ ਲੱਗਿਆ ਹੋਇਆ ਲਾਅਨ (Law) ਹੈ ਜਿਸ ਤਰ੍ਹਾਂ ਕਿ ਚਿੱਤਰ ਵਿੱਚ ਦਿਖਾਇਆ ਗਿਆ ਹੈ । ਵਿਦਿਆਰਥੀਆਂ ਨੇ ਜ਼ਮੀਨ ਦੇ ਬਾਕੀ ਹਿੱਸੇ ਵਿਚ ਫੁੱਲਾਂ ਦੇ ਪੌਦਿਆਂ ਦੇ ਬੀਜ ਬੀਜਣੇ ਹਨ ।
(i) A ਨੂੰ ਮੂਲ ਬਿੰਦੂ ਮੰਨਦੇ ਹੋਏ, ਤਿਭੁਜ ਦੇ ਸਿਖਰਾਂ ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਪਤਾ ਕਰੋ ।
(ii) ਜੇਕਰ ਮੂਲ ਬਿੰਦੂ ਹੋਵੇ ਤਾਂ APR ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਕੀ ਹੋਣਗੇ ? ਨਾਲ ਹੀ, ਉਪਰੋਕਤ ਦੋਹਾਂ ਸਥਿਤੀਆਂ ਵਿੱਚ ਤਿਭੁਜਾਂ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ । ਤੁਸੀਂ ਕੀ ਦੇਖਦੇ ਹੋ ?

ਹੱਲ:
ਸਥਿਤੀ I ਜਦੋਂ A ਮੂਲ ਬਿੰਦੂ ਹੈ ਤਾਂ AD ; X-ਧੁਰੇ ਅਤੇ AB; Y-ਧੁਰਾ ਹੈ ।
∴ ਤਿਭੁਜਾਕਾਰ ਘਾਹ ਦੇ ਲਾਨ POR ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ P (4, 6); Q (3, 2) ਅਤੇ R( 6, 5) ਹੈ ।
ਇੱਥੇ x₁ = 4, x₂ = 3, x₃ = 6
y₁ = 6, y₂ = 2, y₃ = 5
ਹੁਣ, △PQR ਦਾ ਖੇਤਰਫਲ
= \(\frac{1}{2}\)[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]
= \(\frac{1}{2}\)[4 (2 – 5) + 3 (5 – 6) + 6 (6 – 2)]
= \(\frac{1}{2}\)[-12 – 3 + 24] = \(\frac{9}{2}\)
= 4.5 ਵ. ਇਕਾਈਆਂ
ਸਥਿਤੀ II. ਜਦੋਂ c ਮੂਲ ਬਿੰਦੂ ਹੈ ਤਾਂ CB ; X-ਧੁਰਾ । CD ; Y-ਧੁਰਾ ਹੈ
∴ ਤ੍ਰਿਭੁਜਾਕਾਰ ਘਾਹ ਦਾ ਲਾਨ PQR ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ : P (12, 2); Q (13, 6) ਅਤੇ R (10, 3) ਹੈ ।
ਇੱਥੇ x₁ = 12, x₂ = 13, x₃ = 10
y₁ = 2, y₂ = 6, y₃ = 3
ਹੁਣ △POR ਦਾ ਖੇਤਰਫਲ
= \(\frac{1}{2}\)[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]
= \(\frac{1}{2}\)[12 (6 – 3) + 13 (3 – 2) + 10 (2 – 6)]
= \(\frac{1}{2}\)[36 + 13 – 40] = \(\frac{9}{2}\)
= 4.5 ਵ. ਇਕਾਈਆਂ
ਇਸ ਤੋਂ ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਕਿ ਤਿਭੁਜਾਕਾਰ ਘਾਹ ਦੇ ਲਾਨ ਦਾ ਖੇਤਰਫਲ ਸਮਾਨ ਹੈ ।

ਪ੍ਰਸ਼ਨ 6.
ਇਕ ਤ੍ਰਿਭੁਜ ABC ਦੇ ਸਿਖਰ A(4, 6), B(1, 5) ਅਤੇ C(7, 2) ਹਨ । ਭੁਜਾਵਾਂ AB ਅਤੇ AC ਨੂੰ ਕ੍ਰਮਵਾਰ D ਅਤੇ E ਉੱਤੇ ਕੱਟਦੀ ਹੋਈ ਇਕ ਰੇਖਾ ਇਸ ਤਰ੍ਹਾਂ ਖਿੱਚੀ ਗਈ ਹੈ ਕਿ \(\frac{AD}{AB}\) = \(\frac{AE}{AC}\) = \(\frac{1}{4}\) ਹੈ । △ADE ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ਅਤੇ ਇਸਦੀ ਤੁਲਨਾ △ABC ਦੇ ਖੇਤਰਫਲ ਨਾਲ ਕਰੋ ਥਿਊਰਮ (ਮੇਯ 6.2 ਅਤੇ ਥਿਊਰਮ (ਮੇਯ) 6.6 ਨੂੰ ਯਾਦ ਕਰੋ ।
ਹੱਲ:
△ABC ਦੇ ਸਿਖਰ ਹਨ A (4, 6); B (1, 5) ਅਤੇ C (7, 2) ਹਨ ।

ਭੁਜਾ AB ਅਤੇ AC ਨੂੰ ਕ੍ਰਮਵਾਰ D (x, y) ਅਤੇ E (x₂, y₂) ਉੱਤੇ ਕੱਟਦੀ ਹੋਈ ਰੇਖਾ ਇਸ ਤਰ੍ਹਾਂ ਖਿੱਚੋ ਕਿ
\(\frac{AD}{AB}\) = \(\frac{AE}{AC}\) = \(\frac{1}{4}\)
∴ D ਅਤੇ E, AB ਅਤੇ AC ਨੂੰ ਅਨੁਪਾਤ 1 : 3 ਵਿੱਚ ਵੰਡਦੇ ਹਨ ।
∴ D ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਹਨ

△ADE ਵਿੱਚ,
= \(\frac{1}{2}\)[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]

△ABC ਵਿੱਚ,
x₁ =4, x₂ = 1, x₃ = 7
y₁ = 6, y₂ = 5, y₃ = 2
△ABC ਦਾ ਖੇਤਰਫਲ
= \(\frac{1}{2}\)[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]
= \(\frac{1}{2}\)[4 (5 – 2) + 1 (2 – 6) + 7 (6 – 5)]
= \(\frac{15}{2}\) ਵ. ਇਕਾਈਆਂ

ਪ੍ਰਸ਼ਨ 7.
ਮੰਨ ਲਉ A (4, 2), B (6, 5) ਅਤੇ C (1, 4) ਇਕ ਤ੍ਰਿਭੁਜ ABC ਦੇ ਸਿਖਰ ਹਨ ।
(i) A ਤੋਂ ਹੋ ਕੇ ਜਾਣ ਵਾਲੀ ਮੱਧਿਕਾ BC ਨੂੰ D’ਤੇ ਮਿਲਦੀ ਹੈ । ਬਿੰਦੁ D ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਪਤਾ ਕਰੋ ।
(ii) AD ‘ਤੇ ਸਥਿਤ ਅਜਿਹੇ ਬਿੰਦੂ P ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਪਤਾ ਕਰੋ ਕਿ AP : PD = 2 : 1 ਹੋਵੇ ।
(ii) ਮੱਧਿਕਾਵਾਂ BE ਅਤੇ CF ਉੱਤੇ ਅਜਿਹੇ ਬਿੰਦੂਆਂ Q ਅਤੇ R ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਪਤਾ ਕਰੋ ਕਿ BQ : QE = 2 : 1 ਹੋਵੇ ਅਤੇ CR : RF = 2 : 1 ਹੋਵੇ
(iv) ਤੁਸੀਂ ਕੀ ਦੇਖਦੇ ਹੋ ?
[ਨੋਟ : ਉਹ ਬਿੰਦੂ ਜੋ ਤਿੰਨਾਂ ਮੱਧਿਕਾਵਾਂ ਦਾ ਸਾਂਝਾ ਹੋਵੇ, ਉਸ 1 ਨੂੰ ਤ੍ਰਿਭੁਜ ਦਾ ਕੇਂਦਰਕ (Centroid) ਕਹਿੰਦੇ ਹਨ ਅਤੇ ਇਹ | ਹਰ ਇੱਕ ਮੱਧਿਕਾ ਨੂੰ 2:1 ਦੇ ਅਨੁਪਾਤ ਵਿੱਚ ਵੰਡਦਾ ਹੈ ।]
(v) ਜੇਕਰ A(x₁, y₁), B(x₂, y₂) ਅਤੇ C (x₃, y₃) ਤ੍ਰਿਭੁਜ ABC ਦੇ ਸਿਖਰ ਹੋਣ ਤਾਂ ਇਸ ਤ੍ਰਿਭੁਜ ਦੇ ਕੇਂਦਰਕ ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ ਕਿ △ABC ਦੇ ਸਿਖਰ A (4, 2); B (6, 5) ਅਤੇ C (1, 4) ਹੈ ।
(i) AD, ਸਿਖਰ A ਤੋਂ ਮੱਧਕਾ ਹੈ
∴ D, BC ਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ ।

∴ D ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਹਨ (\(\frac{7}{2}\), \(\frac{9}{2}\))

(ii) ਮੰਨ ਲਓ P (x, y), AD ਉੱਤੇ ਕੋਈ ਬਿੰਦੂ ਇਸ ਤਰ੍ਹਾਂ ਹੈ ਕਿ AP : PD = 2 : 1


∴ P ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ (\(\frac{11}{3}\), \(\frac{11}{3}\)) ਹਨ ।

(iii) ਮੰਨ ਲਉ BE ਅਤੇ CF, AABC ਦੀਆਂ ਕ੍ਰਮਵਾਰ AC ਅਤੇ AB ਉੱਤੇ ਮੱਧਿਕਾਵਾਂ ਹਨ
∴ E ਅਤੇ F, ਮਵਾਰ AC ਅਤੇ AB ਦੇ ਮੱਧ ਬਿੰਦੂ ਹਨ

E ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ
x₁ = \(\frac{4+1}{2}\) = \(\frac{5}{2}\)
ਅਤੇ y₁ = \(\frac{4+2}{2}\) = \(\frac{6}{2}\) = 3
∴ E ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਹਨ : (\(\frac{5}{2}\), 3)
F ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ
x₂ = \(\frac{4+6}{2}\) = \(\frac{10}{2}\) = 5
y₂ = \(\frac{5+2}{2}\) = \(\frac{7}{2}\)
∴ F ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਹਨ (5, \(\frac{7}{2}\))
ਹੁਣ, Q, BE ਨੂੰ ਇਸ ਤਰ੍ਹਾਂ ਕੱਟਦਾ ਹੈ ਕਿ BQ : QE = 2 : 1

ਨਾਲ ਹੀ R, CF ਨੂੰ ਇਸ ਤਰ੍ਹਾਂ ਵਿਭਾਜਤ ਕਰਦਾ ਹੈ ਕਿ CR : RF = 2 : 1

(iv) ਇਸ ਤੋਂ ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਕਿ P, Q ਅਤੇ R ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਇਕ ਸਮਾਨ ਹਨ ਅਤੇ ਇਕੋ ਬਿੰਦੂ ਉੱਤੇ ਕੱਟਦੇ ਹਨ ।ਇਹ ਬਿੰਦੁ ਤਿਭੁਜ ਦਾ ਕੇਂਦਰਿਕ ਕਹਿਲਾਉਂਦਾ ਹੈ । ਹਰੇਕ ਮੱਧਕਾ ਨੂੰ 2 : 1 ਵਿਚ ਵਿਭਾਜਤ ਕਰਦਾ ਹੈ ।

(v) ਦਿੱਤੀ ਹੋਈ △ABC ਦੇ ਸਿਖਰ A (x₁, y₁); B (x₂, y₂) ਅਤੇ C (x₃, y₃) ਹੈ ।

ਮੰਨ ਲਉ AD, △ABC ਦੀ ਮੱਧਕਾ ਹੈ :
∴ D, BC ਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ ਤਾਂ D ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ।
(\(\frac{x_{2}+x_{3}}{2}\), \(\frac{y_{2}+y_{3}}{2}\))
ਹੁਣ, G, △ABC ਦਾ ਕੇਂਦਰ ਹੈ ਜੋ ਮੱਧਿਕਾ AD ਨੂੰ 2 : 1 ਵਿਚ ਵਿਭਾਜਤ ਕਰਦਾ ਹੈ
∴ G ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਹਨ :

ਪ੍ਰਸ਼ਨ 8.
ਬਿੰਦੂਆਂ A (-1, -1), B (-1, 4), C (5, 4) ਅਤੇ D (5, -1) ਤੋਂ ਇਕ ਆਇਤ ABCD ਬਣਦਾ ਹੈ । P,Q,R ਅਤੇ 5 ਕੁਮਵਾਰ ਭੁਜਾਵਾਂ AB, BC, CD ਅਤੇ DA ਦੇ ਮੱਧ ਬਿੰਦੂ ਹਨ । ਕੀ ਚਤੁਰਭੁਜ PORS ਇੱਕ ਵਰਗ ਹੈ ? ਕੀ ਇਹ ਇੱਕ ਆਇਤ ਹੈ ? ਕੀ ਇਹ ਇਕ ਸਮਚਤੁਰਭੁਜ ਹੈ ? ਕਾਰਣ ਸਹਿਤ ਉੱਤਰ ਦਿਉ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ ABCD ਦੇ ਸਿਖਰ ਹਨ ।
A(-1, – 1); B (-1, 4); C (5, 4) ਅਤੇ D (5, – 1).

∵ P, AB ਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ
∴ P ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਹਨ ।
(\(\frac{-1-1}{2}\), \(\frac{-1+4}{2}\)) = (1, \(\frac{3}{2}\))
∵ Q, BC ਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ
∴ Q ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਹਨ
(\(\frac{-1+5}{2}\), \(\frac{4+4}{2}\)) = (2, 4)
∵ R, CD ਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ
∴ R ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਹਨ
(\(\frac{5+5}{2}\), \(\frac{4-1}{2}\)) = (5, \(\frac{3}{2}\))
∵ S, AD ਦਾ ਮੱਧ ਬਿੰਦੂ ਹੈ
∴ S ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਹਨ



ਹੁਣ ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਕਿ
PQ = Rs ਅਤੇ QR = SP
ਨਾਲ ਹੀ, PR ≠ QS
PQRS ਦੀਆਂ ਭੁਜਾਵਾਂ ਬਰਾਬਰ ਹਨ ਪਰ ਬਰਾਬਰ ਨਹੀਂ ਹਨ ।
∴ PQRS ਇਕ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ਹੈ ।

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 7 ਨਿਰਦੇਸ਼ ਅੰਕਜਿਮਾਇਤੀ Ex 7.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 7 ਨਿਰਦੇਸ਼ ਅੰਕਜਿਮਾਇਤੀ Exercise 7.3

ਪ੍ਰਸ਼ਨ 1.
ਉਸ ਤ੍ਰਿਭੁਜ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ਜਿਸਦੇ ਸਿਖਰ ਹਨ :
(i) (2, 3); (-1, 0); (2, – 4)
(ii) (-5, -1); (3, – 5); (5, 2)
ਹੱਲ:
(i) ਮੰਨ ਲਉ △ABC ਦੇ ਸਿਖਰ A (2, 3); B (-1, 0) ਅਤੇ C (2, – 4) ਹਨ ।
ਇੱਥੇ , x₁ = 2, x₂ = -1, x₃ = 2
y₁ =3, y₂ = 0, y₃ = – 4
∴ △ABC ਦਾ ਖੇਤਰਫਲ
= \(\frac{1}{2}\)[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂]
= \(\frac{1}{2}\)[2 × (0 + 4) – 1 × -4, -3) + 2 × (3 – 0)]
= \(\frac{1}{2}\)[18 + 7 + 6] = \(\frac{21}{2}\)
= 10.5 ਵਰਗ ਇਕਾਈਆਂ ।

(ii) ਮੰਨ ਲਉ BABC ਦੇ ਸਿਖਰ ਹਨ A (-5, -1) ; B (3, -5) ਅਤੇ C (5, 2) ਹਨ
ਇੱਥੇ , x₁ = -5, x₂ = 3, x₃ = 5
y₁ = -1, y₂ = -5, y₃ = 2
∴ △ABC ਦਾ ਖੇਤਰਫਲ
= \(\frac{1}{2}\)[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]
= \(\frac{1}{2}\)[(-5(-5 – 2) + 3 (2 + 1) + 5 (-1 + 5)]
= \(\frac{1}{2}\)[35 + 9 + 120] = \(\frac{1}{2}\) × 64
= 32 ਵ. ਇਕਾਈਆਂ

ਪ੍ਰਸ਼ਨ 2.
ਹੇਠਾਂ ਦਿੱਤੀਆਂ ਵਿੱਚੋਂ ਹਰੇਕ ਵਿਚ “k’ ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ ਤਾਂ ਕਿ ਤਿੰਨੇ ਬਿੰਦੂ ਸਮਰੇਖੀ ਹੋਣ :
(i) (7, -2); (5, 1); (3, k).
(ii) (8, 1); (k, -4); (2, – 5)
ਹੱਲ:
(i) ਮੰਨ ਲਉ ਦਿੱਤੇ ਗਏ ਬਿੰਦੂ A (7, – 2); B (5, 1) ਅਤੇ C (3, k) ਹਨ ।
ਇੱਥੇ x₁ = 7, x₂ = 5, x₃ = 3
y₁ = -2, y₂ = 1, y₃ = k
ਤਿੰਨ ਬਿੰਦੂ ਸਮਰੇਖੀ ਹੁੰਦੇ ਹਨ ਜੇਕਰ
= \(\frac{1}{2}\)[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]
= \(\frac{1}{2}\)[7 (1 – k) + 5 (k + 2) + 3 (-2 – 1)] = 0
7 – 7k + 5k + 10 – 9 = 0
-2k + 8 = 0
-2k = -8
k = 4

(ii) ਮੰਨ ਲਉ ਦਿੱਤੇ ਗਏ ਬਿੰਦੂ A(8, 1) B (k, -4) ਅਤੇ C (2, -5) ਹਨ ।
ਇੱਥੇ x₁ = 8, x₂ = k, x₃ = 2
y₁ = 1, y₂ = -4, y₃ = -5
ਤਿੰਨ ਬਿੰਦੁ ਸਮਰੇਖੀ ਹਨ ਜੇਕਰ
= \(\frac{1}{2}\)[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)] = 0
ਜਾਂ \(\frac{1}{2}\)[8(-4 + 5) + k (-5 – 1) + 2 (1 + 4)] = 0
8 – 6k + 10 = 0
-6k = – 18
k = 3

ਪ੍ਰਸ਼ਨ 3.
ਸਿਖਰਾਂ (0, -1), (2, 1) ਅਤੇ (0, 3) ਵਾਲੇ ਤ੍ਰਿਭੁਜ ਦੀਆਂ ਭੁਜਾਵਾਂ ਦੇ ਮੱਧ ਬਿੰਦੂਆਂ ਤੋਂ ਬਣਨ ਵਾਲੇ ਤ੍ਰਿਭੁਜ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।ਇਸ ਖੇਤਰਫਲ ਦਾ ਦਿੱਤੇ ਹੋਏ ਤ੍ਰਿਭੁਜ ਦੇ ਖੇਤਰਫਲ ਨਾਲ ਅਨੁਪਾਤ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ ਦਿੱਤੀ ਹੋਈ ਤ੍ਰਿਭੁਜ ABCਦੇ ਸਿਖਰ A(0, – 1); B (2, 1) ਅਤੇ C (0, 3) ਹਨ ।
D, E, F ਕੁਮਵਾਰ AB, BC, CA ਦੇ ਮੱਧ ਬਿੰਦੂ ਹਨ ।
∴ ਮੱਧ ਬਿੰਦੂ ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਕੇ

∴ △DEF ਦੇ ਸਿਖਰਾਂ ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ D (1, 0); E(1, 2); F (0, 1) ਹਨ ।
ਇੱਥੇ , x₁ = 1, x₂ = 1, x₃ = 0
y₁ = 0, y₂ = 2, y₃ = 1
∴ △DEF ਦਾ ਖੇਤਰਫਲ
= \(\frac{1}{2}\)[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]
= \(\frac{1}{2}\)[1(2 – 1) + 1(1 – 0) + 0(0 – 2)]
= \(\frac{1}{2}\)[1 + 1 + 0] = \(\frac{2}{2}\)
= 1 ਵ. ਇਕਾਈਆਂ
△ABC ਵਿਚ
x₁ = 0, x₂ = 2, x₃ = 0
y₁ = – 1, y₂ = 1, y₃ = 3
△ABC ਦਾ ਖੇਤਰਫਲ
= \(\frac{1}{2}\)[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]
= \(\frac{1}{2}\)[0 (1 – 3) + 2 (3 + 1) + 0 (-1 – 1)]
= \(\frac{1}{2}\)[0 + 8 + 0] = \(\frac{8}{2}\) = 4 ਵ. ਇਕਾਈਆਂ

= \(\frac{1}{4}\)

ਪ੍ਰਸ਼ਨ 4.
ਉਸ ਚਤੁਰਭੁਜ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ਜਿਸਦੇ | ਸਿਖਰ, ਇਸੇ ਕੂਮ ਵਿੱਚ (4, -2); (-3, -5); (3, – 2) ਵ ਅਤੇ (2, 3) ਹਨ ।
ਹੱਲ:
ਮੰਨ ਲਉ ਦਿੱਤੀ ਹੋਈ ਚਤੁਰਭੁਜ ABCD ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਹਨ A (-4, – 2); B (-3, – 5) ; c (3, -2) ਅਤੇ D (2, 3) ਹਨ ।
AC ਨੂੰ ਮਿਲਾਓ, ਚਤੁਰਭੁਜ ABCD, ਦੋ ਤ੍ਰਿਭੁਜਾਂ ਵਿਚ ਵਿਭਾਜਿਤ ਹੋ ਜਾਂਦੀ ਹੈ ।
ਭਾਵ △ABC ਅਤੇ △CDA ਵਿਚ

△ABC ਵਿਚ
x₁ = -4, x₂ = 3, x₃ = 3
y₁ = -2, y₂ = -5, y₃ = -2
△ABC ਦਾ ਖੇਤਰਫਲ
= \(\frac{1}{2}\)[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₃)]
= \(\frac{1}{2}\)[-4(-5 + 2) + (-3)(-2 + 2) + 3(-2 + 5)]
= \(\frac{1}{2}\)[12 + 0 + 9] = \(\frac{21}{2}\) ਵਰਗ ਇਕਾਈਆਂ
△CDA ਵਿਚ
x₁ = 3, x₂ = 2, x₃ = -4
y₁ = -2, y₂ = 3, y₃ = -2
△CDA ਦਾ ਖੇਤਰਫਲ
= \(\frac{1}{2}\)[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]
= \(\frac{1}{2}\)[3 (3 + 2) + 2 (2 + 2) + (-4) (-2 – 3)]
= \(\frac{1}{2}\)[20 + 15 + 0] = \(\frac{35}{2}\) ਵਰਗ ਇਕਾਈਆਂ
ਹੁਣ, ਚਤੁਰਭੁਜ ABCD ਦਾ ਖੇਤਰਫਲ
= (△ABC ਦਾ ਖੇਤਰਫਲ) + (△ACD ਦਾ ਖੇਤਰਫਲ)
= \(\frac{21}{2}\) + \(\frac{35}{2}\)
= \(\frac{56}{2}\) = 28 ਵਰਗ ਇਕਾਈਆਂ

ਪ੍ਰਸ਼ਨ 5.
ਜਮਾਤ IX ਵਿਚ ਤੁਸੀਂ ਪੜ੍ਹਿਆ ਹੈ (ਪਾਠ 9, ਉਦਾਹਰਣ 3) ਕਿ ਕਿਸੇ ਤ੍ਰਿਭੁਜ ਦੀ ਇੱਕ ਮੱਧਕਾ (Median) ਉਸਨੂੰ ਬਰਾਬਰ ਖੇਤਰਫਲਾਂ ਵਾਲੇ ਦੋ ਤ੍ਰਿਭੁਜਾਂ ਵਿਚ ਵੰਡਦੀ ਹੈ । ਇਸ ਨਤੀਜੇ ਦੀ ਪੜਤਾਲ ਉਸ ਤ੍ਰਿਭੁਜ ABC ਦੇ ਲਈ ਕਰੋ ਜਿਸਦੇ ਸਿਖਰ A(4, -6), B(3, -2) ਅਤੇ C(5, 2) ਹਨ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੈ △ABC ਦੇ ਸਿਖਰਾਂ ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ A(4, – 6) ; B (3, – 2) ਅਤੇ C (5, 2)
ਮੰਨ ਲਉ CD ਇਕ ਮੱਧਿਕਾ ਹੈ । ਅਰਥ D, AB ਦਾ ਮੱਧ ਬਿੰਦੁ ਹੈ ਜੋ △ABC ਨੂੰ ਦੋ ਭਾਗਾਂ ਵਿਚ ਵੰਡਦਾ ਹੈ।

(5, 2)
△ADC ਅਤੇ △CDB
D ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ = (\(\frac{4+3}{2}\), \(\frac{-6-2}{2}\))
= (\(\frac{7}{2}\), \(\frac{-8}{2}\))
= (3.5, 4)
△ADC ਵਿੱਚ,
x₁ = 4, x₂ = 3.5, x₃ = 5
y₁ = -6, y₂ = -4, y₃ = 2
△ADC ਦਾ ਖੇਤਰਫਲ
= \(\frac{1}{2}\)[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]
= \(\frac{1}{2}\)[4 (-4 – 2) + 3.5 (2 + 6) + 5 (-6 + 4)]
= \(\frac{1}{2}\)[-24 + 28 – 10]
= \(\frac{1}{2}\) × -6 = -3 = 3 ਵ. ਇਕਾਈਆਂ
(∵ ਖੇਤਰਫਲ ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੋ ਸਕਦਾ ਹੈ।)
△CDB ਵਿਚ,
x₁ = 5, x₂ = 3.5, x₃ = 3
y₁ = 2, y₂ = -4, y₃ = -2
△CDB ਦਾ ਖੇਤਰਫਲ = \(\frac{1}{2}\)[x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)]
= \(\frac{1}{2}\)[5 (-4 + 2) + 3.5 (-2 – 2) + 3 (2 + 4)]
= \(\frac{1}{2}\)[-10 – 14 + 18] = \(\frac{1}{2}\) × – 6 = -3
= 3 ਵ. ਇਕਾਈਆਂ
(∵ ਖੇਤਰਫਲ ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੋ ਸਕਦਾ)
ਇਸ ਲਈ ਇਹ ਸੱਪਸ਼ਟ ਹੈ ਕਿ △ADC ਦਾ ਖੇਤਰਫਲ = △CDB ਦਾ ਖੇਤਰਫਲ = 3 ਵ. ਇਕਾਈਆਂ
∴ ਤ੍ਰਿਭੁਜ ਦੀ ਮੱਧਿਕਾ ਇਸਨੂੰ ਬਰਾਬਰ ਖੇਤਰਫਲ ਵਾਲੇ ਦੋ ਤਿਭੁਜਾਂ ਵਿੱਚ ਵੰਡਦੀ ਹੈ ।