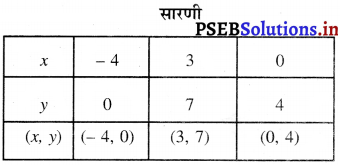
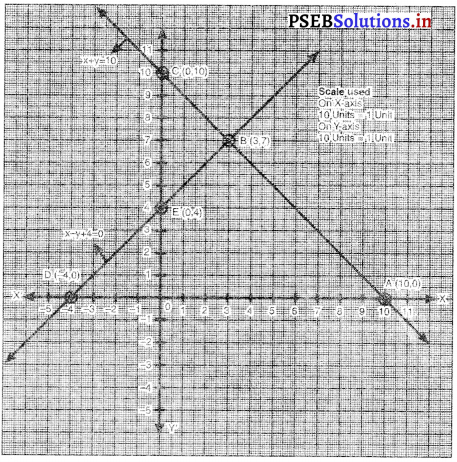
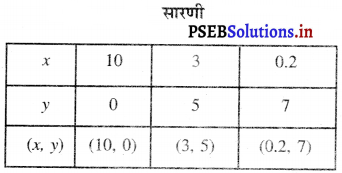
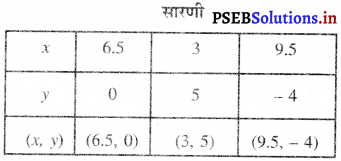
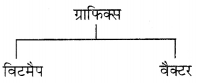
This PSEB 10th Class Computer Notes Chapter 7 माईक्रोसॉफ्ट पब्लिशर-I will help you in revision during exams.
PSEB 10th Class Computer Notes Chapter 7 माईक्रोसॉफ्ट पब्लिशर-I
जान पहचान
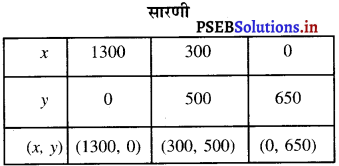
पब्लिशर में टैंपलेटस, विजार्डस और डिज़ाइन गैलरी का प्रयोग करके, प्रचार और मशहूरी करने वाले इश्तिहारों को बनाया जाता है। इन प्रकार और विज्ञापन करने वाले इश्तिहारों को पब्लिकेशन कहा जाता है।
पब्लिकेशन, पब्लिशर में एक फाईल होती है कि एक लेबल, बैनर, न्यूज़लैटर, पोस्टर, निमन्त्रण पत्र (इनवीटेशन), ग्रीटिंग कार्ड या एक लैटर-हैड (Letterhead) हो सकता है। पब्लिकेशन में बहुत सारे पेज़ हो सकते हैं और हर पेज़ में आब्जैकटस होते हैं, जैसे कि टैक्सट बाक्स और तस्वीरें ।
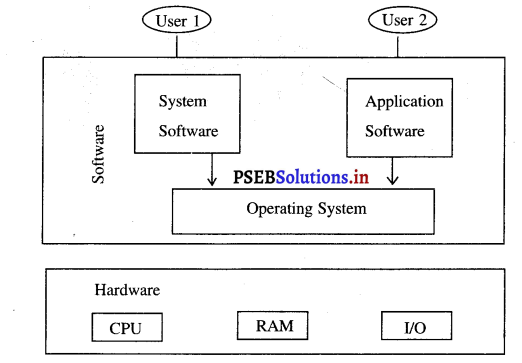
पब्लिशर एक ऐपलीकेशन है जो कि सुन्दर और बढ़िया प्रचार और विज्ञापन करने वाले इश्तिहारों को डिज़ाइन करने और बनाने के लिए प्रयोग किया जाता है, जैसे कि पैंफलैट, लैटर-हैड, न्यूज़लैटर, पोस्टर, कलैंडर, निमन्त्रण-पत्र आदि।
![]()
पब्लिशर विज़ार्ड और डिज़ाइन गैलरी का प्रयोग करके जल्दी से जल्दी पब्लिकेशन बनाने में मदद करता है। टैम्पलैट पब्लिकेशन का पहले से परिभाषित किया मॉडल होता है। आप पब्लिकेशन को जैसे मोनीटर पर देखते हो, प्रिंट होने के बाद वो बिल्कुल वैसे ही नज़र आता है। पब्लिशर आपकों रंगों का चुनाव करने में भी मदद करता है ताकि हाई-कुआलटी के रंगों की पब्लिकेशन प्राप्त हो सके। पब्लिशर की मदद से आप कम खर्चे में एक बढ़िया वैब-साईट भी बना सकते हो।
माईक्रोसॉफ्ट पब्लिशर 2010
पब्लिशर 2010 हमें प्रोफैशनल, जल्दी तथा आसानी से निम्न प्रकार के पब्लिकेशन तैयार करने में मदद करता है –

पब्लिशर कैसे शुरू करें ब्रोशर
पब्लिशर को खोलने के निम्नलिखित स्टैप हैं :
1. Start बटन पर क्लिक करें।
2. All Programs को हाइलाइट करें।
3. Microsoft Office हाइलाइट करें।
4. Microsoft Office Publisher 2010 पर क्लिक करें। पब्लिशर विंडो खुल जाएगी।
या
सर्च बार में Publisher या Pub टाइप करें तथा Enter कीअ दबाएं
पब्लिकेशन बनाना
तीन तरीके से पब्लिकेशन बनाई जा सकती है
- Blank Layout
- Installed Templates
- Online Templates
Blank layout से पब्लिकेशन बनाना
खाली पब्लिकेशन तैयार करने के स्टैप निम्नलिखित हैं :
- File Menu पर क्लिक करें।
- मौजूदा टैम्पलेट में Blank Publication Template पर क्लिक करें और बाद में Create में क्लिक करें।
- अब हम पब्लिकेशन में अपनी ज़रूरत के हिसाब से पब्लिकेशन बना सकते हैं। हम Blank Layout में टैक्सट, तस्वीरें, शब्द, कला और अधिक स्पेस जोड़ सकते हैं। Blank Layout विंडो नीचे दिखाई गई है।
4. पब्लिकेशन निर्माण के बाद File मीनू में Save विकल्प पर जा कर Save as dialogue बॉक्स दिखाई देगी। अपनी पब्लिकेशन का नाम टाइप करें और फोल्डर को चुनें जिसमें हम इसको सेव कर सकते हैं और फिर सेव बटन पर क्लिक करें। यह पब्लिकेशन एक्सटेंशन पर सेव हो जाएगा।
5. अब File मीनू में Close बटन पर क्लिक करके पब्लिकेशन को बंद करें। एक डॉयलाग बॉक्स दिखेगा। अगर हम सभी परिवर्तन सेव करना चाहते हैं तो Yes बटन क्लिक करें। अगर नहीं तो No पर क्लिक करें। पब्लिशर से बाहर भेजने से पहले सभी पब्लिकेशनों को बंद करना चाहिए। इसके बाद File मीनू में Exit पर क्लिक करें या फिर टाइटल बार पर क्रास (x) का बटन क्लिक करें।
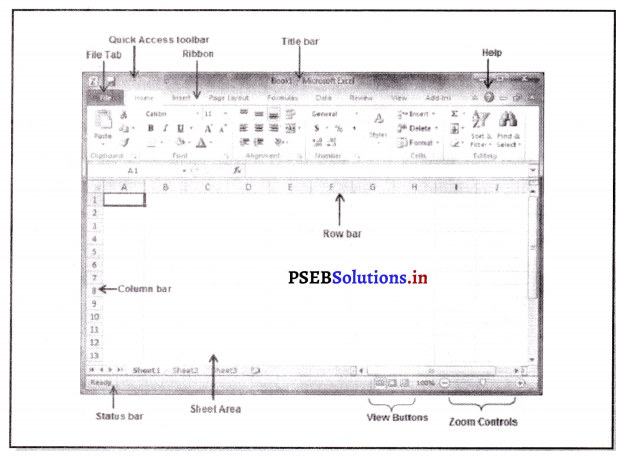
पब्लिशर बिंडो के कंपोनेंट पब्लिशर विंडो के नीचे लिखे भाग हैं :
पब्लिशर विंडो के भाग

1. क्विक ऐक्सैस टूलबार (Quick Access Toolbar)-क्विक एक्सैस टूलबार कस्टमाइज करने योग्य टूलबार होता है जिसमें वह कमांड होती है जिनको हम इस्तेमाल करना चाहते हैं। हम क्विक एक्सैस टूलबार को रिबन के ऊपर या नीचे रख सकते हैं। क्विक एक्सैस टूलबार की जगह परिवर्तन करने के लिए इसके अंत में बने तीर पर क्लिक करें और Show Below the Ribbon विकल्प पर क्लिक करें। रिबन (Ribbon)-दस्तावेजों के सबसे ऊपर वाले भाग के पैनल को रिबन कहा जाता है। इसके 6 टैब हैं। Home, Insert, Page, Design, Mailings, Review और View. हर टैब अलग-अलग समूहों में बांटा गया है।
टैब्ज (Tabs)-पब्लिशर में कुछ बहुत उपयोगी टैब्ज हैं जिसमें कई उपलब्ध होते हैं। हर टैब के फ़ीचर देखने के लिए उस टैब के नाम पर क्लिक करें। यहाँ प्रत्येक टैब के समूहों की सूची दी गई है।
- Home. Clipboard, Font, Paragraph, Styles, Objects, Arrange, Editing
- Insert. Pages, Tables, Illustrations, Buildings, Blocks, Text, Links, Headers & Footer.
- Page Design. Template, Page Setup, Layout, Pages, Schemes, Page Background.
- Mailing. Start, Write & Insert Fields, Preview Results, Finish.
- View. Views, Layout, Show, Zoom, Window.
3. फ़ाइल विंडो (File Window)-जब हम File Menu पर क्लिक करते हैं हमारे सामने Info Screen खुल जाती है। इस प्रकार लगता है कि हमारे दस्तावेज़ मिट गए हैं पर ऐसा नहीं होता। जैसे कि हम File Menu में Options पर क्लिक करते हैं Screen इस प्रकार बदल जाएगी।
- Save. फ़ाइल को 2010 फारमेट में सेव करने के लिए।
- Save As. हमें एक अलग File Type चुनने की आज्ञा देता है।
- Open. पब्लिशर फ़ाइल को ब्राउज़ करने के लिए।
- Close. फ़ाइल को बंद करने के लिए, परंतु पब्लिशर चलता रहेगा।
- Info. व्यापार सूचना को Edit करने के लिए, डिज़ाइन मेकर का उपयोग करने के लिए, या पेशेवर प्रिंट सूचना सैट करने के लिए।
- Recent. हमारे अभी प्रयोग की गई पब्लिशर फ़ाइलों की सूची।
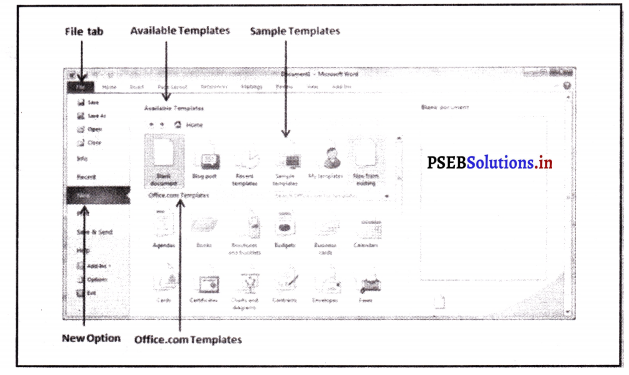
- New. नई पब्लिकेशन स्क्रीन।
- Print. प्रिंट करने के लिए विकल्प।
- Save & Send. फाइलों को Save और email करने का विकल्प।
- Help. माइक्रोसॉफ्ट मदद।
- Options. डिफाल्ट विकल्प सैट करने के लिए।
- Exit. पब्लिशर बंद करने के लिए।
पब्लिकेशन में कार्य करना
1. पब्लिकेशन में Text को Add करना।
- Home या Insert Tab में Draw Text Box चुनें।
- कर्सर को क्लिक करें और ड्रैग करके अपनी पसंद के नाम पर Text Box बनाएं। हम Text Box निर्माण के बाद भी इसका आकार बदल सकते हैं।
- कर्सर के पेज पर जहां हम Text Box बनाना चाहते हैं वहां क्लिक करें।
- जब हम माऊस को Left क्लिक करते हैं। हमारे सामने Format Tab, जिसमें Text Box से अधिक विकल्प होते हैं, वह खुल जाते हैं।
- अब Text Box पर Text टाइप करें।
2. Text को Edit करना :
- जिस Text को हम Edit करना चाहते हैं उसको हाइलाइट करें।
- जब हम Text Box Tool Format Tab पर नहीं हैं। इसको चुन लें।
3. Text Group का विकल्प :
- Text Fit यह बताता है कि Text Box में Text कैसे होगा। इसके विकल्प यह हैं: Best Fit, Shrink Text on Overflow, Grow Text Box to Fit, Do not Auto Fit.
- Text Direction. Text की दिशा Vertical और Horizontal करने के लिए।
- Hyphenation. Text की Hyphenation परिवर्तन करने के लिए।
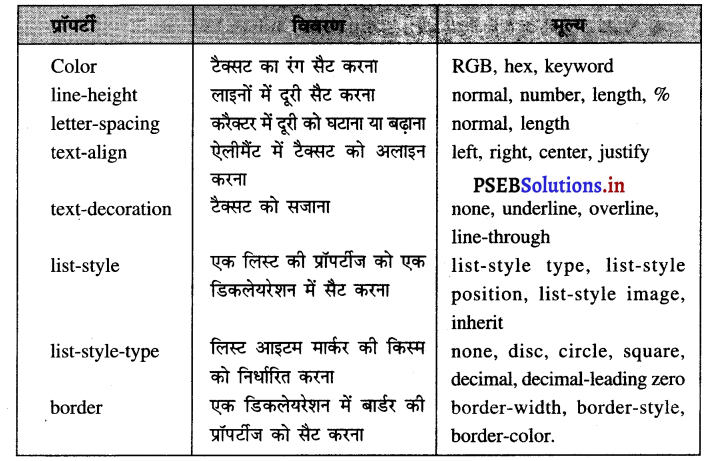
4. Font Group विकल्प: Style, Font Size, Bold, Italic, Underline, Text Spacing और Color.
5. Alignment Group Options: Text Box Alignment, Columns, Margins.
6. Effects Group विकल्प: Shadow, Outline, Engrave, Emboss.
![]()
3. Text Box का स्टाइल बदलना
- Text Box पर क्लिक करो।
- Fomat टैब पर Drawing tools पर क्लिक करो।
- Shape styles Group options में विकल्प चुनो।
- Arrange Group Options में विकल्प चुनो।
4. Clip Art इनसर्ट करना
- Insert → Clip Art पर क्लिक करो।
- Keyword type करो।
- Go पर क्लिक करो।
- अपनी जरूरत अनुसार Clip Art चुनो।
5. Picture SCRIE CARGA
- Insert → Picture पर क्लिक करो।
- अपनी Picture चुनो तथा Insert पर क्लिक करो।
6. Shape इनसर्ट करना
- Home या Insert Tab पर क्लिक करें।
- Shape पर क्लिक करें।
- Shape सिलैक्ट करें।
- पेज पर क्लिक करके Drag करें। Shape बन जाएगी।
7. Text Wrapping
- Object को चुने
- Formal → Arrang group → Wrap Text पर क्लिक करें।
- जरूरत अनुसार विकल्प चुने।
8. Objects का साइज़ बदलना
- Object का चुनाव करें
- Resize हैडर पर क्लिक कर आवश्यकता अनुसार Drag करें।
9. Object Move करना
- Object का चुनाव करें
- Solid line पर कर्सर ले जा Drag करके जहां जरूरत हो वहां ले जाए।
10. Object Delete करना
- Object का चुनाव करें।
- Del कीअ दबाएं।
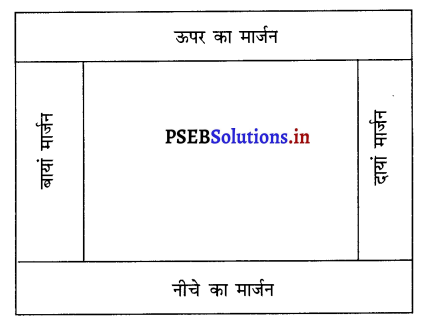
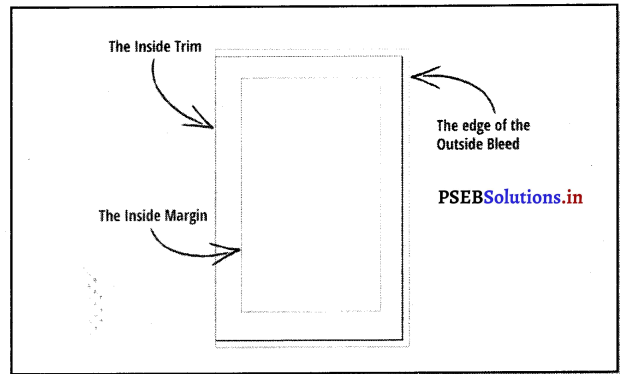
फ्रेम
पब्लिकेशन के हिस्से को फ्रेम कहते हैं। इसमें कई आब्जैक्ट हो सकते हैं।
फ्रेम के साथ काम करना फ्रेम पर जब क्लिक करते हैं तो उसके हैडल दिखाई देते हैं इनकी सहायता से हम कार्य कर सकते हैं।
हैडल : फ्रेम के चारों तरफ नजर आने वाले गोलों को हैडल कहते हैं। इन की सहायता से फ्रेम को मूव, रीसाइज आदि किया जाता है।
हैडल की सहायता से हम निम्न कार्य कर सकते हैं-
1. फ्रेम को मूव करना
- पिक्चर फ्रेम को मूव करना
- टैक्सट फ्रेम को मव करना
2. फरेम को रीसाइज़ करना
- पिक्चर फ्रेम को रीसाइज़ करना
- टैक्सट फ्रेम को रीसाइज़ करना।
3. फ्रेम को डीलीट करना फ्रेम पर क्लिक करें तथा Delete कीअ दबाएं।
4. टैक्सट फ्रेम इंसर्ट करना।
पब्लिकेशन में पेज देखना पब्लिकेशन में पेज देखने के तीन तरीके है।
- पेज के थंबनेल
- पेज टू पेज स्परैड वियू
- स्लाइडर जूम इन तथा जूम आऊट
![]()
टैंपलेट
टैंपलेट की मदद से आसानी से पब्लिकेशन तैयार की जा सकती है। टैंपलेट में पहले से ही तैयार किए हुए डिज़ाइन स्टाइल होते हैं। जिनको हम उसी तरह ही या उनमें फेरबदल करके अपनी ज़रूरत के अनुसार प्रयोग कर सकते हैं।
1. टैंपलेट कस्टमाइज़ करना- टैंपलेट कस्टमाइज़ करने का अर्थ है टैंपलेट का रंग, फोंट आदि अपनी आवश्यकता अनुसार बदलना। इसके लिए टेंपलेट का चुनाव कर दायीं ओर उपलब्ध आपशन से आवश्यकता अनुसार बदलाव करें। टैंपलेट का डिज़ाइन बदलना। टैम्पलेट का डिज़ाइन बदलने के लिए नीचे लिखे स्टैप हैं :
- Page Design टैब पर क्लिक करें।
- सभी टैम्पलेट को बदलने के लिए Change Template पर क्लिक करें। विंडो में टैम्पलेट का परिवर्तन चाहते हो तो भरी गई सूचना, नई टैम्पलेट मुताबिक दिखाई देगी।
3. रंग परिवर्तन के लिए समूह में Color Scheme के साथ ब्राऊज़ करें। कलर स्कीम को देखने के लिए माऊस को कलर स्कीम पर लेकर जाएं।
- किसी एक कलर स्कीम को चुनने के लिए उस पर क्लिक करें।
- कलर स्कीम चुनने के लिए उस पर क्लिक करें।
4. फोंट बदलने के लिए समूह में Font पर क्लिक करें।
- मौजूद फोंट स्कीम ब्राउज करें।
- फोंट स्कीम को देखने के लिए माऊस को फोंट स्कीम पर लेकर जाएं।
- फोंट स्कीम चुनने के लिए उस पर क्लिक करें।
- अगर हम अपनी नई फोंट स्कीम बनाना चाहते हैं, तो New Font Scheme पर क्लिक करें।
पब्लिकेशन सेव करना
पब्लिकेशन को सेव करने के निम्नलिखित स्टैप हैं :
- File मीनू पर क्लिक करें।
- Save पर क्लिक करें।
- फाइल का नाम लिखें।
- Save बटन पर क्लिक करें।
पब्लिकेशन प्रिंट करना
पब्लिकेशन को प्रिंट करने के दो तरीके हैं। पहले तरीके में अपनी टूलबार में Print आइकन पर क्लिक करें। इसके साथ हमारी पब्लिकेशन की डिफाल्ट प्रिंट विकल्प की एक कापी प्रिंट हो जाएगी। या
1. फाईल मीनू पर क्लिक करें।
2. जब Print में नंबर आए ज़रूरत से Number of Copies सिलेक्ट करें।
3. नीचे लिखे Print Setting में किसी को भी चुनें।
- All Pages, Selection, Current Page, or custom range.
- Manually पेज नंबर बताइए जो हम प्रिंट करना चाहते हैं। प्रत्येक पेपर शीट के कितने पेपर प्रिंट होते हैं।
Paper Size - 1-sided या 2-Sided Printing.
4. Print पर क्लिक करें।