Class 10

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 5 ਅੰਕਗਣਿਤਕ ਲੜੀਆਂ Ex 5.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 5 ਅੰਕਗਣਿਤਕ ਲੜੀਆਂ Exercise 5.2

ਪ੍ਰਸ਼ਨ 1.
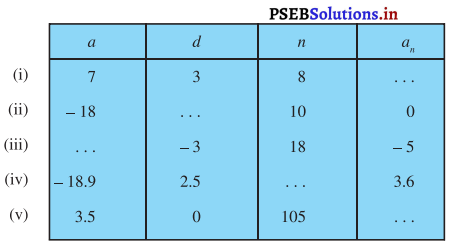
ਹੇਠਾਂ ਲਿਖੀ ਸਾਰਣੀ ਵਿਚ ਖ਼ਾਲੀ ਸਥਾਨਾਂ ਨੂੰ ਭਰੋ, ਜਿੱਥੇ A.P. ਦਾ ਪਹਿਲਾ ਪਦ ‘a’, ਸਾਂਝਾ ਅੰਤਰ ‘d’ ਅਤੇ n ਵਾਂ ਪਦ a_n ਹੈ ।

ਹੱਲ:
(i) a = 7, d = 3, n = 8
∵ a_n = a + (n – 1) d
∴ a₈ = 7 + ( 8 – 1) 3
= 7 + 21 = 28

(ii) a = – 18, n = 10, a_n = 0
∵ a_n = a + (n – 1) d
∴ a₁₀ = – 18 + (10 – 1)d
0 = – 18 + 9d
9d = 18
d = \(\frac{18}{9}\) = 2

(iii) d = -3, n= 18, a_n = -5
∵ a_n = a + (n – 1) d
∴ a₁₈ = a + (18 – 1) (-3)
-5 = a – 51
a = – 5 + 51 = 46

(iv) a = – 18.9, d = 2.5, a_n = 3.6
∵ a_n = a + (n – 1) d
∴ 3.6 = – 18. 9 + (n – 1) 2.5
3.6 + 18.9 = (n – 1) 2.5
(n – 1) 2.5 = 22.5
n – 1 = \(\frac{22.5}{2.5}\) = 9
n = 9 + 1 = 10

(v) a = 3.5, d = 0, n = 105
∵ a_n = + (n – 1) d
∴ a_n = 3.5 + (105 – 1) 0
a_n = 3.5 + 0 = 3.5

2. ਹੇਠ ਦਿੱਤਿਆਂ ਵਿਚੋਂ ਸਹੀ ਉੱਤਰ ਚੁਣੋ ਅਤੇ ਉਸਦਾ ਕਾਰਣ ਦੱਸੋ :

ਪ੍ਰਸ਼ਨ (i).
AP: 10, 7, 4……., ਦਾ 30 ਵਾਂ ਪਦ ਹੈ :
(A) 97
(B) 77
(C) -77
(D) -87
ਉੱਤਰ:
ਦਿੱਤੀ ਗਈ A.P. ਹੈ : 10, 7, 4, …..
T₁ = 10, T₂ = 7, T₃ = 4
T₂ – T₁ = 7 – 10 = – 3
T₃ – T₂ = 4 – 7 = -3
∵ T₂ – T₁ = T₃ – T₂ = – 3 = d
∴ T_n = a + (n – 1) d
T₃₀ = 10 + (30 – 1) (-3)
= 10 – 87 = -77
∴ ਸਹੀ ਉੱਤਰ (C) ਹੈ ।

ਪ੍ਰਸ਼ਨ (ii).
AP: -3, \(-\frac{1}{2}\), 2, …, ਦਾ 11 ਵਾਂ ਪਦ ਹੈ :
(A) 28
(B) 22
(C) -38
(D) -48\(\frac{1}{2}\)
ਉੱਤਰ:
ਦਿੱਤੀ ਗਈ A.P. ਹੈ : 3, \(-\frac{1}{2}\), 2, …
T₁ =-3, T₂ = \(-\frac{1}{2}\), T₃ = 2, …
T₂ – T₁ = \(-\frac{1}{2}\) + 3 = \(\frac{-1+6}{2}\) = \(\frac{5}{2}\)
T₃ – T₂ = 2 + \(\frac{1}{2}\) = \(\frac{4+1}{2}\) = \(\frac{5}{2}\)
∵ T₂ – T₁ = T₃ – T₂ = \(\frac{5}{2}\) = d (ਮੰਨ ਲਓ)
∴ T_n = a + (n – 1) d
T₁₁ = – 3 + (11 – 1)\(\frac{5}{2}\)
= -3 + 10 × \(\frac{5}{2}\) = – 3 + 25
= 22
∴ ਸਹੀ ਉੱਤਰ (B) ਤੇ ।

ਪ੍ਰਸ਼ਨ 3.
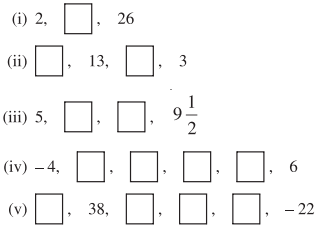
ਹੇਠ ਦਿੱਤੀਆਂ ਅੰਕ ਗਾਣਿਤਕ ਲੜੀਆਂ (A.P.) ਵਿੱਚ ਖ਼ਾਲੀ ਖ਼ਾਨਿਆਂ ਦੇ ਪਦਾਂ ਨੂੰ ਪਤਾ ਕਰੋ :

ਹੱਲ:
ਮੰਨ ਲਉ ਦਿੱਤੀ ਗਈ A.P. ਦਾ ਪਹਿਲਾ ਪਦ a ਅਤੇ ਸਾਂਝਾ ਅੰਤਰ d ਹੈ !
(i) ਇੱਥੇ , T₁ = a = 2
T₃ = a + 2d = 26
2 + 2d = 26
2d = 26 – 2 = 24
d = \(\frac{24}{2}\) = 12
∴ T₂ = a + d
= 2 + 12 = 14

(ii) ਇੱਥੇ T₂ = a + d = 13 …(1)
T₄ = a + 3d = 3 …(2)
(2) – (1) ਤੋਂ ਸਾਨੂੰ ਮਿਲਦਾ ਹੈ।

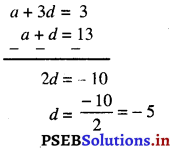
d ਦਾ ਇਹ ਮੁੱਲ (1), ਵਿਚ ਰੱਖਣ ‘ਤੇ
a – 5 = 13
a = 13 + 5 = 18
∴ T₁ = a = 18
T₂ = a + 2d = 18 + 2 (-5)
18 – 10 = 8

(iii) ਇੱਥੇ T₁ = a = 5
T₄ = a + 3d = 9\(\frac{1}{2}\)
a + 3d = \(\frac{19}{2}\),
5 + 3d = \(\frac{19}{2}\)
3d = \(\frac{19}{2}\) – 5
3d = \(\frac{19-10}{2}\) = \(\frac{9}{2}\)
d = \(\frac{9}{2}\) × \(\frac{1}{3}\) = \(\frac{3}{2}\)
T₂ = a + d = 5 + \(\frac{3}{2}\)
= \(\frac{10+3}{2}\) = \(\frac{13}{2}\)
T₃ = a + 2d = 5 + 2\(\left(\frac{3}{2}\right)\)
= 5 + 3 = 8

(iv) ਇੱਥੇ T₁ = a = -4
T₆ = a + 5d = 6
-4 + 5d = 6
5d = 6 + 4
5d = 10
d = \(\frac{10}{5}\) = 2
T₂ = a + d = -4 + 2 = -2
T₃ = a + 2d = -4 + 2(2)
= -4 + 4 = 0
T₄ = a + 3d = -4 + 3 (2)
= -4 + 6 = 2
T₅ = a + 4d = -4 + 4 (2)
= – 4 + 8 = 4

(v) ਇੱਥੇ T₂ = a + d = 38 …(1)
T₆ = a + 5d = – 22 …(2)
ਹੁਣ (2) – (1) ਤੋਂ ਮਿਲਦਾ ਹੈ।

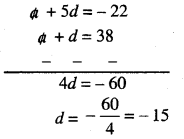
d ਦਾ ਮੁੱਲ (1), ਵਿਚ ਭਰਨ ‘ਤੇ
a + (-15) = 38
a = 38 + 15 = 53
∴ T₁ = a = 53
T₃ = a + 2d = 53 + 2 (-15)
= 53 – 30 = 23
T₄ = a + 3d = 53 + 3 (15)
= 53 – 45 = 8
T₅ = a + 4d = 53 + 4 (-15)
=53 – 60 = -7

ਪ੍ਰਸ਼ਨ 4.
A.P.: 3, 8, 13, 18,….ਦਾ ਕਿੰਨਵਾਂ ਪਦ 78 ਹੈ ?
ਹੱਲ:
ਦਿੱਤੀ ਹੋਈ A.P. ਹੈ: 3, 8, 13, 18, …..
T₁ = 3, T₂ = 8, T₃ = 13, T₄ = 18
T₂ – T₁ = 8 – 3 = 5
T₃ – T₂ = 13 – 8 = 5
∵ T₂ – T₁ = T₃ – T₂ = 5 = d
T_n = a + (n – 1)d ਦਾ ਪ੍ਰਯੋਗ ਕਰਕੇ
78 = 3 + (n – 1) 5
5(n -1) = 78 – 3
n – 1 = \(\frac{75}{5}\) = 15
n = 15 + 1 = 16
∴ ਦਿੱਤੀ ਗਈ A.P. ਦਾ 16ਵਾਂ ਪਦ 78 ਹੈ ।

5. ਹੇਠਾਂ ਦਿੱਤੀ ਅੰਕਗਣਿਤਕ ਲੜੀ ਵਿੱਚ ਹਰੇਕ ਵਿੱਚ ਕਿੰਨੇ ਪਦ ਹਨ ?

ਪ੍ਰਸ਼ਨ (i).
7, 13, 19,…, 205
ਉੱਤਰ:
ਦਿੱਤੀ ਹੋਈ A.P. ਹੈ : 7, 13, 19,…
T₁ = 7, T₂ = 13, T₃ = 19
T₂ – T₁ = 13 – 7 = 6
T₃ – T₂ = 19 – 13 = 6
∵ T₂ – T₁ = T₃ – T₂ = 6 = d.
ਸੂਤਰ T_n = a + (n – 1) d ਦਾ ਪ੍ਰਯੋਗ ਕਰਕੇ
205 = 7+ (n – 1)6
(n – 1)6 = 205 – 7
(n – 1) = \(\frac{196}{6}\)
n – 1 = 33
n = 33 + 1 = 34
∴ 34ਵਾਂ ਪਦ 205 ਹੈ ।

ਪ੍ਰਸ਼ਨ (ii).
18, 15\(\frac{1}{2}\), 13,…….., – 47
ਉੱਤਰ:
ਦਿੱਤੀ ਹੋਈ A.P. ਹੈ : 18, 15\(\frac{1}{2}\), 13,…
T₁ = 18, T₂ = 15\(\frac{1}{2}\) = \(\frac{31}{2}\), T₃ = 13
T₂ – T₁ = \(\frac{31}{2}\) – 18 = \(\frac{31-36}{2}\) = \(-\frac{5}{2}\)
T₃ – T₁ = 13 – \(\frac{31}{2}\) = \(\frac{26-31}{2}\) = \(-\frac{5}{2}\)
T₂ – T₁ = T₃ – T₂ = \(-\frac{5}{2}\) = d
ਸੂਤਰ T_n = a + (n – 1) d ਦਾ ਪ੍ਰਯੋਗ ਕਰਕੇ
-47 = 18 + (n – 1)\(\left(\frac{-5}{2}\right)\)
(n – 1)\(\left(\frac{-5}{2}\right)\) = -47 – 18
(n – 1)\(\left(\frac{-5}{2}\right)\) = -65
n – 1 = -65 × \(-\frac{2}{5}\)
n – 1 = 26
n = 26 + 1 = 27
∴ 27 ਵਾਂ ਪਦ -47 ਹੈ ।

ਪ੍ਰਸ਼ਨ 6.
ਕੀ A.P. 11, 8, 5, 2…. ਦਾ ਇੱਕ ਪਦ -150 ਹੈ ? ਕਿਉਂ ?
ਹੱਲ:
ਦਿੱਤੀ ਹੋਈ A.P. ਹੈ
11, 8, 5, 2…..
T₁ = 11, T₂ = 8, T₃ = 5, T₄ = 2
T₂ – T₁ = 8 – 11 = -3
T₃ – T₂ = 5 – 8 = – 3
T₄ – T₃ = 2 – 5 = -3
∵ T₂ – T₁ = T₃ – T₂
= T₄ – T₃ = -3 = d
ਮੰਨ ਲਉ -150 ਦਿੱਤੀ ਹੋਈ A.P. ਦਾ ਇਕ ਪਦ ਹੈ !
T_n = -150
a + (n – 1) d = -150
11 + (n – 1) (-3) = – 150
(n – 1) (-3) =- 150 – 11 = -161
n – 1 = \(\frac{161}{3}\)
n = \(\frac{161}{3}\) + 1 = \(\frac{161+3}{3}\)
n = \(\frac{164}{3}\) = 54\(\frac{2}{3}\)
ਜੋ ਪ੍ਰਾਕ੍ਰਿਤਕ ਸੰਖਿਆ ਨਹੀਂ ਹੈ ।
∴ -150 ਦਿੱਤੀ ਹੋਈ A.P. ਦਾ ਪਦ ਨਹੀਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ 7.
ਉਸ A.P. ਦਾ 31ਵਾਂ ਪਦ ਪਤਾ ਕਰੋ ਜਿਸਦਾ 11ਵਾਂ ਪਦ 38 ਹੈ ਅਤੇ 16ਵਾਂ ਪਦ 73 ਹੈ ।
ਹੱਲ:
ਮੰਨ ਲਉ ‘a’ ਅਤੇ ‘d’ ਦਿੱਤੀ ਹੋਈ A.P. ਦਾ ਪਹਿਲਾ ਪਦ ਅਤੇ ਸਾਂਝਾ ਅੰਤਰ ਹੈ ।
T₁₁ = 38
a + (11 – 1) d = 38
[∵ T_n = a + (n – 1) d]
a + 10 d = 38 …(1)
ਅਤੇ T₁₆ = 73
a + (16 – 1) d = 73
[∵ T_n = a + (n – 1) d]
a + 15 d = 73 …(2)
ਹੁਣ (2) – (1) ਤੋਂ

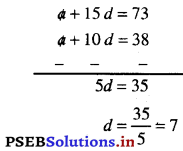
d ਦਾ ਮੁੱਲ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ .
a+ 10 (7) = 38
a + 70 = 38
a = 38 – 70 = -32
ਹੁਣ T₃₁ = a + (31 – 1) d = -32 + 30 (7)
= -32 + 210 = 178

ਪ੍ਰਸ਼ਨ 8.
ਇੱਕ A.P. ਵਿੱਚ 50 ਪਦ ਹਨ, ਜਿਸਦਾ ਤੀਸਰਾ ਪਦ 12 ਹੈ ਅਤੇ ਅੰਤਿਮ ਪਦ 106 ਹੈ । ਇਸ ਦਾ 29ਵਾਂ ਪਦ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ ‘a’ ਅਤੇ ‘d’ ਦਿੱਤੀ ਹੋਈ A.P. ਦਾ । ਪਹਿਲਾ ਪਦ ਅਤੇ ਸਾਂਝਾ ਅੰਤਰ ਹੈ ।
ਦਿੱਤਾ ਹੈ T₃ = 12
a + (3 – 1) d = 12
|∵ T_n = a + (n – 1)d
a + 2d = 12 …..(1)
∴ ਅੰਤਿਮ ਪਦ = T₅₀ = 106
a + (50 – 1) d = 106
|∵ T_n = a+ (n – 1) d
a + 49 d = 106 …(2)
ਹੁਣ (2) – (1) ਤੋਂ ਮਿਲਦਾ ਹੈ।

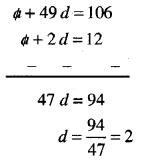
d ਦਾ ਮੁੱਲ (1) ਵਿਚ ਰੱਖਣ ‘ਤੇ
a + 2(2) = 12
a + 4 = 12
a + 12 – 4 = 8
ਹੁਣ T₂₉ = a + (29 – 1) d
= 8 + 28 (2)
= 8 + 56 = 64

ਪ੍ਰਸ਼ਨ 9.
ਜੇਕਰ ਕਿਸੇ A.P.ਦਾ ਤੀਸਰਾ ਅਤੇ 9ਵਾਂ ਪਦ ਕੁਮਵਾਰ 4 ਅਤੇ – 8 ਹੋਵੇ, ਤਾਂ ਇਸਦਾ ਕਿੰਨਵਾਂ ਪਦ ਸਿਫ਼ਰ ਹੋਵੇਗਾ ?
ਹਲ:
ਮੰਨ ਲਉ ‘a’ ਅਤੇ ‘d’ ਕੁਮਵਾਰ ਦਿੱਤੀ ਹੋਈ A.P. ਦਾ ਪਹਿਲਾ ਪਦ ਅਤੇ ਸਾਂਝਾ ਅੰਤਰ ਹੈ
ਦਿੱਤਾ ਹੈ T₃ = 4
a + (3 – 1) d = 4
|∵ T_n = a + (n – 1) d
a + 2d = 4
ਅਤੇ T₉ = – 8
a + (9 – 1) d = – 8
|∵ T_n = a + (n – 1) d
a + 8d = – 8 …(2)
ਹੁਣ (2) -(1) ਤੋਂ ਮਿਲਦਾ ਹੈ।

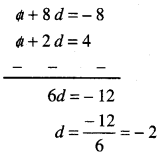
d ਦਾ ਇਹ ਮੁੱਲ (1) ਵਿਚ ਰੱਖਣ ‘ਤੇ
a + 2 (-2) = 4
a – 4 = 4
a = 4 + 4 = 8
ਹੁਣ T_n = 0
a + (n – 1) d = 0
8 + (n – 1) (-2) = 0
-2 (n – 1) = – 8
n – 1 = 4
n = 4 + 1 = 5
∴ A.P. ਦਾ ਪੰਜਵਾਂ ਪਦ ਸਿਫ਼ਰ ਹੈ ।

ਪ੍ਰਸ਼ਨ 10.
ਕਿਸੇ A.P. ਦਾ 17ਵਾਂ ਪਦ ਉਸਦੇ 10ਵੇਂ ਪਦ ਤੋਂ 7 ਤੋਂ ਵੱਧ ਹੈ । ਇਸਦਾ ਸਾਂਝਾ ਅੰਤਰ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ ‘a’ ਅਤੇ ‘d ਕੁਮਵਾਰ ਦਿੱਤੀ ਹੋਈ A.P. ਦਾ ਪਹਿਲਾ ਪਦ ਅਤੇ ਸਾਂਝਾ ਅੰਤਰ ਹੈ ।
ਹੁਣ T₁₇ = a (17 – 1)d
= a + 16d
T₁₀ = a + (10 – 1) d
= a + 9d
ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ
T₁₇ – T₁₀ = 7
(a + 16d) – (a + 9d) = 7
a + 16d – a – 9d = 7
7d = 7
d = \(\frac{7}{7}\) = 1
∴ ਸਾਂਝਾ ਅੰਤਰ 1 ਹੈ ।

ਪ੍ਰਸ਼ਨ 11.
A.P.:3, 15, 27, 39,.. ਦਾ ਕਿੰਨਵਾ ਪਦ ਉਸਦੇ 54ਵੇਂ ਪਦ ਤੋਂ 132 ਵੱਧ ਹੋਵੇਗਾ ?
ਹੱਲ:
ਮੰਨ ਲਉ ‘a’ ਅਤੇ ‘d’ ਕੁਮਵਾਰ ਦਿੱਤੀ ਹੋਈ A.P. ਦਾ ਪਹਿਲਾ ਪਦ ਅਤੇ ਸਾਂਝਾ ਅੰਤਰ ਹੈ ।
ਦਿੱਤੀ ਗਈ A.P. ਹੈ : 3, 15, 27, 39, …
T₁ = 3, T₂ = 15,
T₃ = 27, T₄ = 39
T₂ – T₂ = 15 – 3 = 12
T₃ – T₂ = 27 – 15 = 12
∴ d = T₂ – T₁ = T₃ – T₂ = 12
T₅₄ = a + (54 – 1) d
= 3 + 53 (12)
= 3 + 636 = 639
ਪ੍ਰਸ਼ਨ ਦੇ ਅਨੁਸਾਰ
T_n = T₅₄ + 132
a + (n – 1) d = 639 + 132
3 + (n – 1) (12) = 771
(n – 1) 12 = 771 – 3 = 768
n – 1 = \(\frac{768}{12}\) = 64
n = 64 + 1 = 65
∴ A.P. ਦਾ 65ਵਾਂ ਪਦ ਉਸਦੇ 54ਵੇਂ ਪਦ ਤੋਂ 132 ਜ਼ਿਆਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 12.
ਦੋ ਅੰਕ ਗਣਿਤਕ ਲੜੀਆਂ ਦਾ ਸਾਂਝਾ ਅੰਤਰ ਬਰਾਬਰ ਹੈ । ਜੇਕਰ ਇਹਨਾਂ ਦੇ 100ਵੇਂ ਪਦਾਂ ਦਾ ਅੰਤਰ 100 ਹੈ ਤਾਂ ਇਹਨਾਂ ਦੇ 1000ਵੇਂ ਪਦਾਂ ਦਾ ਅੰਤਰ ਕੀ ਹੋਵੇਗਾ ?
ਹੱਲ:
ਮੰਨ ਲਉ “a’ ਅਤੇ ‘d’ ਪਹਿਲੀ A.P. ਦਾ ਪਹਿਲਾ ਪਦ ਅਤੇ ਸਾਂਝਾ ਅੰਤਰ ਹੈ।
‘A’ ਅਤੇ ‘d’ ਦੂਸਰੀ A.P. ਦਾ ਪਹਿਲਾ ਪਦ ਅਤੇ ਸਾਂਝਾ ਅੰਤਰ ਹੈ ।
ਪ੍ਰਸ਼ਨ ਦੇ ਅਨੁਸਾਰ
[ਦੂਸਰੀ A.P. ਦਾ T₁₀₀] – ਪਹਿਲੀ A.P. ਦਾ T₁₀₀] = 100
[A+ (100 – 1)d] – [a + (100 – 1)d] = 100
A + 99 d – a – 99 d = 100
A – a = 100 …(1)
ਹੁਣ [ਦੂਸਰੀ A.P. ਦਾ T₁₀₀₀] – [ਪਹਿਲੀ A.P. ਦਾ T₁₀₀₀]
= [A + (1000 – 1) d] – a + (1000 – 1) d]
= A + 999d – a – 999 d
= A – a
= 100 [(1) ਦਾ ਪ੍ਰਯੋਗ ਕਰਕੇ]

ਪ੍ਰਸ਼ਨ 13.
ਤਿੰਨ ਅੰਕਾਂ ਵਾਲੀਆਂ ਕਿੰਨੀਆਂ ਸੰਖਿਆਵਾਂ 7 ਨਾਲ ਭਾਜਯੋਗ ਹਨ ।
ਹੱਲ:
7 ਨਾਲ ਵੰਡੀਆਂ ਜਾਣ ਵਾਲੀਆਂ ਤਿੰਨ ਅੰਕਾਂ , ਵਾਲੀਆਂ ਸੰਖਿਆਵਾਂ ਹਨ ।
105, 112, 119,…., 994 .
a = T₁ = 105,
T₂ = 112, T₃ = 119
T_n = 994
T₂ – T₁ = 112 – 105 = 7
T₃ – T₂ = 119 – 112 = 7
∴ d = T₂ – T₁
= T₃ – T₂ = 7
ਦਿੱਤਾ ਹੈ T_n = 994
a + (n – 1) d = 994
105 + (n – 1) 7 = 994
(n – 1) 7 = 994 – 105
(n – 1) 7 = 889
n – 1 = \(\frac{889}{7}\) = 123
n = 123 + 1 = 124.
∴ ਤਿੰਨ ਅੰਕਾਂ ਵਾਲੀ 124 ਸੰਖਿਆਵਾਂ 7 ਨਾਲ ਵੰਡੀਆਂ ਜਾਣ ਵਾਲੀਆਂ ਹਨ ।

ਪ੍ਰਸ਼ਨ 14.
10 ਅਤੇ 250 ਦੇ ਵਿਚਕਾਰ 4 ਦੇ ਕਿੰਨੇ ਗੁਣ ਹਨ ?
ਹੱਲ:
10 ਅਤੇ 250 ਦੇ ਵਿਚ 4 ਦੇ ਗੁਣਜ ਹਨ
12, 16, 20, 24, … 248
a = T₁ = 12,
T₂ = 16, T₃ = 20
T_n = 248
T₂ – T₁ = 16 – 12 =4
T₃ – T₂ = 20 – 16 = 4
∴ d = T₂ – T₁ = T₃ – T₂ = 4
ਦਿੱਤਾ ਹੈ T_n = 248
a + (n – 1)d = 248
12 + (n – 1) 4 = 248
4 (n – 1) = 248 – 12 = 236
n – 1 = \(\frac{236}{4}\) = 59
n = 59 + 1 = 60
∴ 10 ਅਤੇ 250 ਦੇ ਵਿਚ 4 ਦੇ ਗੁਣਜ 60 ਹਨ ।

ਪ੍ਰਸ਼ਨ 15.
n ਦੇ ਕਿਹੜੇ ਮੁੱਲ ਦੇ ਲਈ, ਦੋਵੇਂ ਅੰਕ ਗਣਿਤਕ ਲੜੀਆਂ 63, 65, 67… ਅਤੇ 3, 10, 17… ਦੇ ਵੇਂ ਪਦ ਬਰਾਬਰ ਹੋਣਗੇ ?
ਹੱਲ:
ਦਿੱਤੀ ਗਈ A.P. ਹੈ 63, 65, 67…….
ਇੱਥੇ a = T₁ = 63,
T₂ = 65, T₃ = 67
T₂ – T₁ = 65 – 63 = 2
T₃ – T₂ = 67 – 65 =2
∴ d = T₂ – T₁ = T₃ – T₂ = 2
ਦੁਸਰੀ A.P. ਹੈ 3, 10, 17, ….
ਇੱਥੇ a = T₁ = 3, T₂ = 10, T₃ = 17
T₂ – T₁ = 10 – 3 = 7
T₃ – T₂ = 17 – 10 = 7
ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ
[ਪਹਿਲੀ A.P ਦਾ ਵਾਂ ਪਦੀ] = [ਦੂਸਰੀ A.P. ਦਾ ਸਵਾਂ ਪ]
63 + (n – 1) 2 = 3 + (n – 1)7
63 + 2n – 2 = 3 + 7n -7
61 + 2n = 7n – 4
2n – 7n = -4 – 61
-5n = – 65
n = \(\frac{65}{5}\) = 13

ਪ੍ਰਸ਼ਨ 16.
ਉਹ A.P. ਪਤਾ ਕਰੋ ਜਿਸਦਾ ਤੀਜਾ ਪਦ 16 ਹੈ ਅਤੇ 7ਵਾਂ ਪਦ 5ਵੇਂ ਪਦ ਨਾਲੋਂ 12 ਵੱਧ ਹੈ ।
ਹੱਲ:
ਮੰਨ ਲਉ ‘a’ ਅਤੇ ‘d’ ਦਿੱਤੀ ਹੋਈ A.P. ਦਾ ਪਹਿਲਾਂ ਪਦ ਅਤੇ ਸਾਂਝਾ ਅੰਤਰ ਹੈ।
ਦਿੱਤਾ ਹੈ T₃ = 16
a + (3 – 1) d = 16
a + 2d = 16 …(1)
ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ T₇ – T₅ = 12.
a + (7 – 1) d – [a + (5 – 1) d] = 12
a + 6d – a – 4d = 12
2d = 12
d = \(\frac{12}{2}\) = 6
d ਦਾ ਇਹ ਮੁੱਲ (1), ਵਿੱਚ ਰੱਖਣ ‘ਤੇ
a + 2 (6) = 16
a = 16 – 12 =4
∴ ਦਿੱਤੀ ਹੋਈ A.P. ਹੈ 4, 10, 16, 22, 28,……

ਪ੍ਰਸ਼ਨ 17.
A.P. : 3, 8, 13…, 253 ਵਿੱਚ ਅੰਤਿਮ ਪਦ ਤੋਂ 20 ਵਾਂ ਪਦ ਪਤਾ ਕਰੋ ।
ਹਲ:
ਦਿੱਤੀ ਹੋਈ A.P. ਹੈ 3, 8, 13, …, 253
ਇੱਥੇ a = T₁ = 3, T₂ = 8, T₃ = 13
T_n = 253
T₂ – T₁ = 8 – 3 = 5
T₃ – T₂ = 13 – 8 = 5
∴ d = T₂ – T₁ = T₃ – T₂ = 5
ਹੁਣ T_n = 253
3 + (n – 1) 5 = 253
(n – 1) 5 = 250
n – 1 = \(\frac{250}{5}\) = 50 |∵ T_n = a + (n – 1)d
n – 1 = \(\frac{250}{5}\) = 50
(n – 1) = 50
n = 50 + 1 = 51
∴ AP ਦੇ ਅੰਤਿਮ ਪਦ ਤੋਂ 20ਵਾਂ ਪਦ
= (ਪਦਾਂ ਦੀ ਕੁੱਲ ਸੰਖਿਆ) – 20 +1
= 51 – 20 + 1 = 32ਵਾਂ ਪਦੇ
∴ AP ਦੇ ਅੰਤਿਮ ਪਦ ਤੋਂ 20ਵਾਂ ਪਦ
= ਸ਼ੁਰੂ ਤੋਂ 32ਵਾਂ ਪਦ
= 3 + (32 – 1) 5 |∵ T = a + (n – 1) d
= 3 + 31 × 5
= 3 + 155 = 158

ਪ੍ਰਸ਼ਨ 18.
ਕਿਸੇ A.P. ਦੇ ਚੌਥੇ ਅਤੇ 8ਵੇਂ ਪਦਾਂ ਦਾ ਜੋੜ 4 ਹੈ ਅਤੇ 6ਵੇਂ ਅਤੇ 10ਵੇਂ ਪਦਾਂ ਦਾ ਜੋੜ 4 ਹੈ । ਇਸ A.P. ਦੇ ਪਹਿਲੇ ਤਿੰਨ ਪਦ ਪਤਾ ਕਰੋ ।
ਹਲ:
ਮੰਨ ਲਉ ‘a’ ਅਤੇ ‘d` ਦਿੱਤੀ ਹੋਈ A.P. ਦੇ ਪਹਿਲਾ ਪਦ ਅਤੇ ਸਾਂਝਾ ਅੰਤਰ ਹੈ ।
ਪ੍ਰਸ਼ਨ ਦੀ ਪਹਿਲੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
T₄ + T₈ = 24
a + (4 – 1) d + a + (8 – 1) d = 24
|∵ T_n = a + (n – 1)d
2a + 3d + 7d = 24
2a + 10d = 24
a + 5d = 12 …..(1)
ਪ੍ਰਸ਼ਨ ਦੀ ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
T₆ + T₁₀ = 44
a + (6 – 1)d + a + (10 – 1)d = 44
|∵ T_n = a + (n – 1) d
2a + 5d + 9d = 44 ….(2)
2a + 14d = 4
a + 7d = 22
(2) – (1) ਤੋਂ ਮਿਲਦਾ ਹੈ

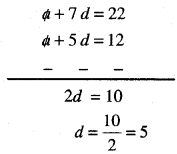
‘d’ ਦਾ ਇਹ ਮੁੱਲ (1) ਵਿਚ ਰੱਖਣ ‘ਤੇ ..
a + 5 (5) = 12
a + 25 = 12
a = 12 – 25 = – 13
T₁ = a = -13
T₂ = a + d
= – 13 + 5 = – 8
T₂ = a + 2d = – 13 + 2 (5)
= -13 + 10 = -3
∴ ਦਿੱਤੀ ਹੋਈ A.P. ਹੈ – 13, – 8, -3,…

ਪ੍ਰਸ਼ਨ 19.
ਸੁਬਾ ਰਾਓ ਨੇ 1995 ਵਿੱਚ ₹ 5000 ਪ੍ਰਤਿ ਮਹੀਨਾ ਤਨਖਾਹ ‘ਤੇ ਕੰਮ ਸ਼ੁਰੂ ਕੀਤਾ ਅਤੇ ਹਰੇਕ ਸਾਲ ₹ 200 ਦਾ ਸਾਲਾਨਾ ਵਾਧਾ ਪ੍ਰਾਪਤ ਕੀਤਾ । ਕਿਹੜੇ ਸਾਲ ਉਸਦੀ ਤਨਖਾਹ ₹ 7000 ਹੋ ਜਾਵੇਗੀ ?
ਹੱਲ:
ਸੂਬਾ ਰਾਓ ਦੀ ਅਰੰਭਿਕ ਤਨਖ਼ਾਹ = ₹ 5000
ਸਾਲਾਨਾ ਵਾਧਾ = ₹ 200 ਮੰਨ
ਲਉ ‘n’ ਸਾਲਾਂ ਦੀ ਸੰਖਿਆ ਦੱਸਦਾ ਹੈ
∴ ਪਹਿਲਾ ਪਦ = a = ₹ 5000
ਸਾਂਝਾ ਅੰਤਰ = d = ₹ 200
ਅਤੇ T_n = ₹ 7000
ਹੁਣ 5000 + (n – 1) 200 = 7000
|∵ T_n = a + (n – 1) d
(n – 1) 200 = 7000 – 5000
(n – 1) 200 = 2000
n – 1 = \(\frac{2000}{200}\) = 10
n – 1 = 10
n = 10+1
= 11
ਸਾਲਾਂ ਦੀ ਸਥਿਤੀ
1995, 1996, 1997, …
ਇੱਥੇ a = 1995, d= 1 n = 11
∴ T_n = 1995 + (11 – 1) 1
= 1995 + 10 = 2005
ਇਸ ਲਈ 2005 ਵਿਚ ਸੂਬਾ ਰਾਵ ਦੀ ਤਨਖ਼ਾਹ ₹ 7000 ਹੋ ਜਾਵੇਗੀ ।

ਪ੍ਰਸ਼ਨ 20.
ਰਾਮਕਲੀ ਨੇ ਕਿਸੇ ਸਾਲ ਦੇ ਪਹਿਲੇ ਹਫ਼ਤੇ ₹ 5 ਦੀ ਬੱਚਤ ਕੀਤੀ ਅਤੇ ਫਿਰ ਆਪਣੀ ਹਫਤਾਵਾਰੀ ਬੱਚਤ ₹ 1.75 ਵਧਾਉਂਦੀ ਗਈ । ਜੇਕਰ ਵੇਂ ਹਫਤੇ ਵਿਚ ਉਸ ਦੀ ਹਫਤਾਵਾਰੀ ਬੱਚਤ ₹ 20.75 ਹੋਵੇ ਤਾਂ ‘n’ ਪਤਾ ਕਰੋ ।
ਹਲ:
ਪਹਿਲੇ ਹਫ਼ਤੇ ਬੱਚਤ = ₹ 5
ਹਰੇਕ ਹਫ਼ਤੇ ਦੀ ਬਚਤ ਵਿਚ ਵਾਧਾ = ₹ 1.75
∴ ਇਹ A.P. ਹੈ ਜਿਸਦੇ ਪਦ ਹਨ
T₁ = 5, d = 1.75
∴ T₂ = 5 + 1.75 = 6.75
T₃ = 6.75 + 1.75 = 8.50
T_n = 20. 75 (ਦਿੱਤਾ ਹੈ)
5 + (n -1) 1.75 = 20.75
[∵ T_n = a + (n – 1) d]
(n – 1) 1.75 = 20.75 – 5
(n – 1) 1.75 = 15.75
(n – 1) = \(\frac{1575}{100}\) \(\frac{100}{175}\)
n – 1 = 9
n = 9 + 1 = 10
∴ 10ਵੇਂ ਹਫ਼ਤੇ ਰਾਮਕਲੀ ਦੀ ਬੱਚਤ 20.75 ਹੋ ਜਾਵੇਗੀ ।

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 5 ਅੰਕਗਣਿਤਕ ਲੜੀਆਂ Ex 5.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 5 ਅੰਕਗਣਿਤਕ ਲੜੀਆਂ Exercise 5.1

1. ਹੇਠਾਂ ਲਿਖੀਆਂ ਸਥਿਤੀਆਂ ਵਿਚੋਂ ਕਿਹੜੀਆਂ ਸਥਿਤੀਆਂ ਵਿਚ ਸੰਬੰਧਿਤ ਸੰਖਿਆਵਾਂ ਦੀ ਸੂਚੀ A.P. ਹੈ ਅਤੇ ਕਿਉਂ ?

ਪ੍ਰਸ਼ਨ (i).
ਹਰੇਕ ਕਿਲੋਮੀਟਰ ਦੇ ਬਾਅਦ ਟੈਕਸੀ ਦਾ ਕਿਰਾਇਆ, ਜਦੋਂ ਕਿ ਪਹਿਲੇ ਕਿਲੋਮੀਟਰ ਲਈ ਕਿਰਾਇਆ ₹ 15 ਹੈ ਅਤੇ ਹਰੇਕ ਵਾਧੂ ਕਿਲੋਮੀਟਰ ਦਾ ਕਿਰਾਇਆ
₹ 8 ਹੈ ।
ਉੱਤਰ:
ਮੰਨ ਲਓ ਟੈਕਸੀ ਦਾ ਵੇਂ ਕਿਲੋਮੀਟਰ ਦਾ ਕਿਰਾਇਆ T_n ਦੁਆਰਾ ਦਰਸਾਇਆ ਗਿਆ ਹੈ ।
ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ
T₁ = 15 ਕਿ.ਮੀ. ; T₂ = 15 + 8 = 23 ;
T₃ = 23 + 8 =31………
ਹੁਣ T₃ – T₂ = 31 – 23 = 8
T₂ – T₁ = 23 – 15 = 8
ਇੱਥੇ T₃ – T₂ = T₂ – T₁ = 8
∴ ਦਿੱਤੀ ਗਈ ਸਥਿਤੀ A.P. ਦਾ ਰੂਪ ਹੈ ।

ਪ੍ਰਸ਼ਨ (ii).
ਕਿਸੇ ਬੇਲਨ (cylinder) ਵਿਚ ਹਵਾ ਦੀ ਮਾਤਰਾ, ਜਦੋਂ ਕਿ ਹਵਾ ਕੱਢਣ ਵਾਲਾ ਪੰਪ ਹਰੇਕ ਵਾਰ ਬੇਲਨ ਵਿੱਚ ਬਾਕੀ ਹਵਾ ਦਾ \(\frac{1}{4}\) ਹਿੱਸਾ ਬਾਹਰ ਕੱਢ ਦਿੰਦਾ ਹੈ ।
ਉੱਤਰ:
ਮੰਨ ਲਓ ਬੇਲਨ ਵਿਚ ਭਰੀ ਹਵਾ ਨੂੰ T_n ਨਾਲ ਦਰਸਾਇਆ ਗਿਆ ਹੈ ।
ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ,

ਇੱਥੇ T₃ – T₂ ≠ T₂ – T₁
∴ ਦਿੱਤੀ ਗਈ ਸਥਿਤੀ A.P. ਦਾ ਰੂਪ ਨਹੀਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ (iii).
ਹਰੇਕ ਮੀਟਰ ਦੀ ਖੁਦਾਈ ਤੋਂ ਬਾਅਦ, ਇੱਕ ਖੂਹ | ਪੁਟੱਣ ਦੀ ਲਾਗਤ, ਜਦੋਂ ਕਿ ਪਹਿਲੇ ਮੀਟਰ ਖੁਦਾਈ ਦੀ ਲਾਗਤ ₹ 150 ਹੈ ਅਤੇ ਬਾਅਦ ਵਿੱਚ ਪ੍ਰਤਿ | ਮੀਟਰ ਖੁਦਾਈ ਦੀ ਲਾਗਤ ₹ 50 ਵੱਧ ਜਾਂਦੀ ਹੈ ।
ਉੱਤਰ:
ਮੰਨ ਲਉ ਖੂਹ ਪੁੱਟਣ ਦੇ ਵੇਂ ਮੀਟਰ ਦੀ ਲਾਗਤ ਨੂੰ T_n ਨਾਲ ਦਰਸਾਇਆ ਗਿਆ ਹੈ ।
ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ,
T₁ = ₹150
T₂ = ₹(150 + 50)
= ₹ 200
T₃ = ₹ (200 + 50)
= ₹ 250
ਹੁਣੌ T₃ – T₂ = ₹ (250 – 200) = ₹ 50
T₂ – T₁ = ₹ (200 – 150) = ₹ 50
ਇੱਥੇ T₃ – T₂ = T₂ – T₁ = 50
∴ ਦਿੱਤੀ ਗਈਸਥਿਥੀ A.P. ਦਾ ਰੂਪ ਹੈ ।

ਪ੍ਰਸ਼ਨ (iv).
ਖਾਤੇ ਵਿੱਚ ਹਰੇਕ ਸਾਲ ਦਾ ਮਿਸ਼ਰਧਨ, ਜਦੋਂ ਕਿ ₹ 10000 ਦੀ ਰਕਮ 8 ਸਾਲਾਨਾ ਦਰ ‘ਤੇ ਮਿਸ਼ਰਿਤ ਵਿਆਜ ‘ਤੇ ਜਮਾਂ ਕਰਵਾਈ ਜਾਂਦੀ ਹੈ।
ਉੱਤਰ:
ਮੰਨ ਲਉ ‘n’ਵੇਂ ਸਾਲ ਦਾ ਮਿਸ਼ਰਧਨ T_n ਹੈ :
ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ,
T₁ = ₹ 10,000
T₂ = ₹ \(\left[\frac{10,000 \times 8 \times 1}{100}\right]\)
= ₹ 10,000 + ₹ 800 = ਤ₹ 10,800
T₃ = ₹ \(\left[\frac{10,800 \times 8 \times 1}{100}\right]\)
= ₹ 10,800 + ₹ 864
= ₹11,640 ਇਸੇ ਤਰ੍ਹਾਂ ਅੱਗੇ ਵੀ
ਹੁਣ T₃ – T₂= ₹ (11,640 – 10,800)
= ₹ 840
T₂ – T₁= ₹ (10,800 – 10,000)
= ₹ 800 fent
ਇੱਥੇ T₃ – T₂ 6 T₂ – T₁
∴ ਦਿੱਤੀ ਹੋਈ ਸਥਿਤੀ A.P. ਦਾ ਰੂਪ ਨਹੀਂ ਹੈ ।

2. ਦਿੱਤੀ ਹੋਈ A.P. ਦੇ ਪਹਿਲੇ ਚਾਰ ਪਦ ਲਿਖੋ, ਜਦੋਂ | ਕਿ ਪਹਿਲਾ ਪਦ a ਅਤੇ ਸਾਂਝਾ ਅੰਤਰ dਹੇਠ ਅਨੁਸਾਰ ਹਨ :

ਪ੍ਰਸ਼ਨ (i).
a = 10, d= 10
ਉੱਤਰ:
ਦਿੱਤਾ ਹੋਇਆ ਪਹਿਲਾ ਪਦ a = 10
ਅਤੇ ਸਾਂਝਾ ਅੰਤਰ = d = 10
∴ T₁ = a = 10 ;
T₂ = a + d
= 10 + 10 = 20
T₃ = a + d = 10 + 2 × 10
= 10 + 20 == 30 ;
T₄ = a + 3d = 10 + 3 × 10
= 10 + 30 = 40
∴ A.P. ਦੇ ਪਹਿਲੇ ਚਾਰ ਪਦ ਹਨ
10, 20, 30, 40….

ਪ੍ਰਸ਼ਨ (ii).
a = -2, d = 0
ਉੱਤਰ:
ਦਿੱਤਾ ਹੋਇਆ ਪਹਿਲਾ ਪਦ = a = -2
ਸਾਂਝਾ ਅੰਤਰ = d = 0
∴ T₁ = a = -2 ;
T₂ = a + d = -2 + 0 = -2
T₃ = a + d = -2 + 2 × 0 = – 2
T₄ = a + 3d
– 2 + 3 × 0 = – 2
∴ A.P. ਦੇ ਪਹਿਲੇ ਚਾਰ ਪਦ ਹਨ – 2, – 2, — 2, – 2,…………

ਪ੍ਰਸ਼ਨ (iii).
a = 4, d = -3
ਉੱਤਰ:
ਦਿੱਤਾ ਹੋਇਆ ਪਹਿਲਾ ਪਦ = 4 =4
ਸਾਂਝਾ ਅੰਤਰ d = -3
∴ T₁ = a = 4 T₂ = a + d = 4 – 3 = 1
T₃ = a + 2d = 4 + 2(-3) = 4 – 6 = -2
T₄ = a + 3d = 4 + 3 (-3) = 4 – 9 = – 5
∴ A.P. ਦੇ ਪਹਿਲੇ ਚਾਰ ਪਦ ਹਨ
4, 1, – 2, – 5,……….

ਪ੍ਰਸ਼ਨ (iv).
a = -1, d = \(\frac{1}{2}\)
ਉੱਤਰ:
ਦਿੱਤਾ ਹੋਇਆ ਪਹਿਲਾ ਪਦ, = a = – 1
ਸਾਂਝਾ ਅੰਤਰ = d =\(\frac{1}{2}\)
T₁ = a = -1; T₂ = a + d
= -1 + \(\frac{1}{2}\) = \(\frac{-1}{2}\)
T₃ = a + 2d = -1 + 2\(\left(\frac{1}{2}\right)\)
= -1 + 1 = 0
T ₄= a + 3d = -1 + 3\(\left(\frac{1}{2}\right)\)
= \(\frac{-2+3}{2}\) = \(\frac{1}{2}\)
∴ A.P. ਦੇ ਪਹਿਲੇ ਚਾਰ ਪਦ ਹਨ
-1, \(\frac{-1}{2}\), 0, \(\frac{1}{2}\), ……

ਪ੍ਰਸ਼ਨ (v).
a = – 1.25, d = – 0.25
ਉੱਤਰ:
ਦਿੱਤਾ ਹੋਇਆ ਪਹਿਲਾ ਪਦ = a = – 1.25
ਸਾਂਝਾ ਅੰਤਰ d = – 0.25
∴ T₁ = a = – 1.25;
T₂ = a + d = – 1.25 – 0.25 – 1.50
T₃ = a + 2d = – 1.25 + 2(0.25)
=- 1.25 – 0.50
= – 1.75
T₄ = a + 3d = – 1.25 + 3 (0.25)
– 1.25 – 0.75 = – 2
∴ A.P. ਦੇ ਪਹਿਲੇ ਚਾਰ ਪਦ ਹਨ
– 1.25, – 1.50, – 1.75, -2, ……..

3. ਹੇਠਾਂ ਹਰੇਕ AP. ਦੇ ਲਈ ਪਹਿਲਾ ਪਦ ਅਤੇ ਸਾਂਝਾ ਅੰਤਰ ਪਤਾ ਕਰੋ :

ਪ੍ਰਸ਼ਨ (i).
3, 1, -1, -3, ……
ਉੱਤਰ:
ਦਿੱਤੀ ਹੋਈ A.P. ਹੈ, 3, 1, – 1, – 3, ….
ਇੱਥੇ T₁ = 3, T₂ = 1,
T₃ = -1, T₄ = -3
ਪਹਿਲਾ ਪਦ T₁ = 3
ਹੁਣ, T₂ – T₁ = 1 – 3 = -2
T₃ – T₂ = – 1 – 1 = -2
T₄ – T₃ = -3 + 1 = -2
∴ T₂ – T₁ = T₃ – T₂ = T₄ – T₃ = -2
∴ ਸਾਂਝਾ ਅੰਤਰ = – 2 ਅਤੇ ਪਹਿਲਾ ਪਦ = 3

ਪ੍ਰਸ਼ਨ (ii).
-5, -1, 3, 7, ……
ਉੱਤਰ:
ਦਿੱਤੀ ਹੋਈ A.P. ਹੈ
-5, – 1, 3, 7, …
ਇੱਥੇ T₁ = -5, T₂ = -1,
T₃ = 3, T₄ = 7
ਪਹਿਲਾ ਪਦ = T₁ = -5
T₂ – T₁ – 1 + 5 = 4
T₃ – T₂ = 3 + 1 = 4
T₄ – T₃ = 7 – 3 = 4
∴ T₂ – T₁ = T₃ – T₂ = T₄ – T₃ = 4
∴ ਸਾਂਝਾ ਅੰਤਰ = 4
ਪਹਿਲਾ ਪਦ = – 5

ਪ੍ਰਸ਼ਨ (iii).
\(\frac{1}{3}\), \(\frac{5}{3}\), \(\frac{9}{3}\), \(\frac{13}{3}\), ……
ਉੱਤਰ:
ਦਿੱਤੀ ਹੋਈ A.P. ਹੈ
\(\frac{1}{3}\), \(\frac{5}{3}\), \(\frac{9}{3}\), \(\frac{13}{3}\), ……
ਇੱਥੇ T₁ = \(\frac{1}{3}\), T₂ = \(\frac{5}{3}\)
T₃ = \(\frac{9}{3}\), T₄ = \(\frac{13}{3}\)
ਪਹਿਲਾ ਪਦ T₁ = \(\frac{1}{3}\)
ਹੁਣ, T₂ – T₁ = \(\frac{5}{3}\) – \(\frac{1}{3}\) = \(\frac{5-1}{3}\) = \(\frac{4}{3}\)
T₃ – T₂ = \(\frac{9}{3}\) – \(\frac{5}{3}\) = \(\frac{9-5}{3}\) = \(\frac{4}{3}\)
T₄ – T₃ = \(\frac{13}{3}\) – \(\frac{9}{3}\) = \(\frac{13-9}{3}\) = \(\frac{4}{3}\)
∴ T₂ – T₁ = T₃ – T₂ = T₄ – T₃ = \(\frac{4}{3}\)
∴ ਸਾਂਝਾ ਅੰਤਰ = \(\frac{4}{3}\)
ਪਹਿਲਾ ਪਦ = \(\frac{1}{3}\)

ਪ੍ਰਸ਼ਨ (iv).
0.6, 1.7, 28, 39, …..
ਉੱਤਰ:
ਦਿੱਤੀ ਹੋਈ A.P. ਹੈ
0.6, 1.7, 2.8, 3.9,…
ਇੱਥੇ T₁ = 0.6, T₂ = 1.7,
T₃ = 2.8, T₄ = 3.9
ਪਹਿਲਾ ਪਦ = T₁ = 0.6
ਹੁਣ T₂ – T₁ = 1.7 – 0.6 = 1.1
T₃ – T₂ = 2.8 – 1.7 = 1.1
T₄ – T₃ = 3.9 – 2.8 == 1.1
∴ T₂ = T₁ = T₃ = T₂ = T₄ = T₃ = 1.1
∴ ਸਾਂਝਾ ਅੰਤਰ = 1.1
ਪਹਿਲਾ ਪਦ = 0.6

4. ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚੋਂ ਕਿਹੜੇ-ਕਿਹੜੇ A.P. ਹਨ ? ਜੇਕਰ ਕੋਈ A.P ਹੈ ਤਾਂ ਉਸਦਾ ਸਾਂਝਾ ਅੰਤਰ ਪਤਾ ਕਰੋ ਅਤੇ ਉਸਦੇ ਤਿੰਨ ਪਦ ਲਿਖੋ :

ਪ੍ਰਸ਼ਨ (i).
2, 4, 8, 16…..
ਉੱਤਰ:
ਦਿੱਤੇ ਹੋਏ ਪਦ ਹਨ : 2, 4, 8, 16…
ਇੱਥੇ T₁ = 2, T₂ = 4, T₃ = 8, T₄ = 16
T₂ – T₁ = 4 – 2 = 2
T₃ – T₂ = 8 – 4 = 4
∵ T₂ – T₁ ≠ T₃ – T₂
∴ ਇਹ A.P. ਨਹੀਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ (ii).
2, \(\frac{5}{2}\), 3, \(\frac{7}{2}\), ………..
ਉੱਤਰ:
ਦਿੱਤੇ ਹੋਏ ਪਦ ਹਨ : 2, \(\frac{5}{2}\), 3, \(\frac{7}{2}\) …
ਇੱਥੇ T₁ = 2, T₂ = \(\frac{5}{2}\), T₃ = 3, T₄ = \(\frac{7}{2}\)
T₂ – T₁ = \(\frac{5}{2}\) – 2 = \(\frac{5-4}{2}\) = \(\frac{1}{2}\)
T₃ – T₂ = 3 – \(\frac{5}{2}\) = \(\frac{6-5}{2}=\frac{1}{2}\)
T₄ – T₃ = \(\frac{7}{2}-3=\frac{7-6}{2}=\frac{1}{2}\)
∵ T₂ – T₁ = T₃ – T₂ = T₄ – T₃ = \(\frac{1}{2}\)
∴ ਸਾਂਝਾ ਅੰਤਰ = d = \(\frac{1}{2}\)
ਹੁਣ, T₅ = a + 4d = 2 + 4\(\left(\frac{1}{2}\right)\) = 4
T₆ = a + 5d = 2 + 5\(\left(\frac{1}{2}\right)\) = \(\frac{4+5}{2}=\frac{9}{2}\)
T₇ = a + 6d = 2 + 6\(\left(\frac{1}{2}\right)\) = 2 + 3 = 5.

ਪ੍ਰਸ਼ਨ (iii).
– 1.2, – 3.2, – 5.2, -7.2 , …
ਉੱਤਰ:
ਦਿੱਤੇ ਹੋਏ ਪਦ ਹਨ।
– 1.2, – 3.2, – 5.2, – 7.2, …
ਇੱਥੇ T₁ = – 1.2, T₂ = – 3.2,
T₃ – 5.2, T₄ = – 7.2
T₂ – T₁ = -3.2 + 1.2 = -2
T₃ – T₂ = – 5.2 + 3.2 = – 2
T₄ – T₃ = -7.2 + 5.2 = – 2
∵ T₂ – T₁ = T₃ – T₂ = T₄ – T₃ = -2
∴ ਸਾਂਝਾ ਅੰਤਰ = d = -2
ਹੁਣ, T₅ = a + 4d
= – 1.2 + 4(-2)
= -1.2 – 8 = -9.2
T₆ = a + 5d = – 1.2 + 5 (-2)
= – 1.2 – 10 = – 11.2
T₇ = a + 6d = – 1.2 + 6 (-2)
= -1.2 – 12 = -13.2

ਪ੍ਰਸ਼ਨ (iv).
– 10, – 6, – 2, 2, ……
ਉੱਤਰ:
ਦਿੱਤੇ ਹੋਏ ਪਦ ਹਨ :
– 10, -6, -2, 2, ….
ਇੱਥੇ T₁ = – 10, T₂ = -6,
T₃ = -2, T₄ = 2
T₂ – T₁ = – 6 + 10 = 4
T₃ – T₂ = – 2 + 6 = 4
T₄ – T₃ = 2 + 2 = 4
∵ T₂ – T₁ = T₃ – T₂ = T₄ – T₃ = 4
∴ ਸਾਂਝਾ ਅੰਤਰ = d = 4
ਹੁਣ, T₅ = a + 4d = – 10 + 4 (4)
= – 10 + 16 = 6
T₆ = a + 5d = – 10 + 5 (4)
= -10 + 20 = 10
T₇ = a + 6d = – 10 + 6(4)
= -10 + 24 = 14

ਪ੍ਰਸ਼ਨ (v).
3, 3 + \(\sqrt {2}\), 3 + 2\(\sqrt {2}\), 3 + 3\(\sqrt {2}\) , …
ਉੱਤਰ:
ਦਿੱਤੇ ਹੋਏ ਪਦ ਹਨ
T₁ = 3, T₂ = 3 + \(\sqrt {2}\),
T₃ = 3 + 2\(\sqrt {2}\), T₄= 3 + 3\(\sqrt {2}\)
ਇੱਥੇ T₂ – T₁ = 3 + \(\sqrt {2}\) – 3 = \(\sqrt {2}\)
T₂ – T₃ = 3 + 2\(\sqrt {2}\) – (3 + \(\sqrt {2}\))
= 3 + 2\(\sqrt {2}\) – 3 – \(\sqrt {2}\) = \(\sqrt {2}\)
T₄ – T₃ = 3 + 3\(\sqrt {2}\) – (3 + 2\(\sqrt {2}\))
= 3 + 3\(\sqrt {2}\) – 3 – 2\(\sqrt {2}\) = \(\sqrt {2}\)
∵ T₂ -T₁ = T₃ – T₂ = T₄ – T₃ = \(\sqrt {2}\)
∴ ਸਾਂਝਾ ਅੰਤਰ = d = \(\sqrt {2}\)
ਹੁਣ, T₅ = a +4d = 3 + 4 (\(\sqrt {2}\) )
= 3 + 4\(\sqrt {2}\)
T₆ = a + 5d = 3 + 5\(\sqrt {2}\)
T₇ = a + 6d = 3 + 6\(\sqrt {2}\)

ਪ੍ਰਸ਼ਨ (vi).
0.2, 0.22, 0.222, 0.2222, …
ਉੱਤਰ:
ਦਿੱਤੇ ਹੋਏ ਪਦ ਹਨ :
0.2, 0.22, 0.222, 0.2222, …
T₁ = 0.2, T₂ = 0.22,
T₃ = 0.222,
T₄ = 0.2222.
T₂ – T₁ = 0.22 – 0.2 = 0.02
T₃ – T₂ = 0.222 – 0.22 = 0.002
T₂ – T₁ ≠ T₃ – T₂
∴ ਇਹ A.P. ਨਹੀਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ (vii).
0, -4, – 8, – 12, …
ਉੱਤਰ:
ਦਿੱਤੇ ਹੋਏ ਪਦ ਹਨ :
0, -4, – 8, — 12, ….
ਇੱਥੇ T₁, = 0, T₂ = -4,
T₃ =- 8, T₄ = – 12
T₂ -T₁ = -4 – 0 = -4
T₃ – T₂ = -8 + 4 = -4
T₄ – T₃ = – 12 + 8 = -4.
∵ T₂ – T₁ = T₃ – T₂ = T₄ – T₃
∴ ਸਾਂਝਾ ਅੰਤਰ = d = -4
ਹੁਣ, T₅ = a + 4d = 0 + 4 (-4) = -16
T₆ = a + 5d = 0 + 5(-4) = -20.
T₇ = a + 6d = 0 + 6(4) = – 24

ਪ੍ਰਸ਼ਨ (viii).
\(-\frac{1}{2}\), \(-\frac{1}{2}\), \(-\frac{1}{2}\), \(-\frac{1}{2}\), ……..
ਉੱਤਰ:
ਦਿੱਤੇ ਹੋਏ ਪਦ ਹਨ :
\(-\frac{1}{2}\), \(-\frac{1}{2}\), \(-\frac{1}{2}\), \(-\frac{1}{2}\), ……….
ਇੱਥੇ T₁ = \(-\frac{1}{2}\), T₂ = –\(\frac{1}{2}\)
T₃ = \(-\frac{1}{2}\), T₄ = \(-\frac{1}{2}\)
T₂ – T₁ = \(-\frac{1}{2}\) + \(\frac{1}{2}\) = 0
T₃ – T₂ = \(-\frac{1}{2}\) + \(\frac{1}{2}\) = 0
T₃ – T₂ = \(-\frac{1}{2}\) + \(\frac{1}{2}\) =0
∵ T₂ – T₁ = T₃ – T₂ = 0
∴ ਸਾਂਝਾ ਅੰਤਰ = 0 (∵ a = \(\frac{1}{2}\), d = 0)
ਹੁਣ T₅ = T₆ = T₇ = \(-\frac{1}{2}\)

ਪ੍ਰਸ਼ਨ (ix).
1, 3, 9, 27, …
ਉੱਤਰ:
ਦਿੱਤੇ ਹੋਏ ਪਦ ਹਨ : 1, 3, 9, 27
T₁ = 1, T₂ = 3, T₃ = 9, T₄ = 27
T₂ – T₁ = 3 – 1 = 2
T₃ – T₂ = 9 – 3 = 6
∵ T₂ – T₂ + T₃ – T₂
∴ ਇਹ A.P. ਨਹੀਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ (x).
a, 2a, 3a, 4a, …
ਉੱਤਰ:
ਦਿੱਤੇ ਹੋਏ ਪਦ ਹਨ : a, 2a, 3a, 4a, …
T₁ = a, T₂ = 2a, T₃ = 3a, T₁ = 4a
T₂ – T₁ = 2a – a = a
T₃ – T₂ = 3a – 2a = a
T₄ – T₃ = 4a – 3a = a
∵ T₂ – T₁ = T₃ – T₂ = T₄ – T₃ = a
∴ ਸਾਂਝਾ ਅੰਤਰ = d = a
ਇੱਥੇ T₅ = a + 4d = a + 4 (a) = a + 4a = 5a
T₆o = a + 5d = a + 5a = 6a
T₇ = a + 6d = a + 6d = 7a

ਪ੍ਰਸ਼ਨ (xi).
a, a², a³, a⁴, …
ਉੱਤਰ:
ਦਿੱਤੇ ਹੋਏ ਪਦ ਹਨ a, a², a³, a⁴, …
T₁ = a, T₂ = a, T₃ = a², T₄ = a³, T = a⁴
T₂ – T₁ = a² – a
T₃ – T₂ = a³ – a²
∵ T₂ – T₁ ≠ T₃ – T₂
∴ ਇਹ A.P. ਨਹੀਂ ਹੈ

ਪ੍ਰਸ਼ਨ (xii).
\(\sqrt {2}\), \(\sqrt {8}\), \(\sqrt {18}\), \(\sqrt {32}\), ………
ਉੱਤਰ:
ਦਿੱਤੇ ਹੋਏ ਪਦ ਹਨ \(\sqrt {2}\) , \(\sqrt {8}\) , \(\sqrt {18}\) , \(\sqrt {32}\) ,…
ਇੱਥੇ T₁ = \(\sqrt {2}\), T₂ = \(\sqrt {8}\) ,
T₃ = \(\sqrt {18}\) , T₄ = \(\sqrt {32}\)
ਜਾਂ T₁ = \(\sqrt {2}\), T₂ = 2\(\sqrt {2}\),
T₃ = 3\(\sqrt {2}\), T₄ = 4\(\sqrt {2}\)
T₂ – T₁ = 2\(\sqrt {2}\) – \(\sqrt {2}\) = \(\sqrt {2}\)
T₃ – T₂ = 3\(\sqrt {2}\) – 2\(\sqrt {2}\) = \(\sqrt {2}\)
T₄ – T₃ = 4\(\sqrt {2}\) – 3\(\sqrt {2}\) = \(\sqrt {2}\)
∵ T₂ – T₁ = T₃ – T₂ = T₄ – T₃ = \(\sqrt {2}\)
∴ ਸਾਂਝਾ ਅੰਤਰ = d = \(\sqrt {2}\)
ਇੱਥੇ T₅ = a + 4d = \(\sqrt {2}\) + 4\(\sqrt {2}\) = 5\(\sqrt {2}\)
T₆ = a + 5d = \(\sqrt {2}\) + 5\(\sqrt {2}\) = 6\(\sqrt {2}\)
T₇ = a + 6d = \(\sqrt {2}\) + 6\(\sqrt {2}\) = 7\(\sqrt {2}\)

ਪ੍ਰਸ਼ਨ (xiii).
\(\sqrt {3}\), \(\sqrt {6}\), \(\sqrt {9}\), \(\sqrt {12}\), …
ਉੱਤਰ:
ਦਿੱਤੇ ਹੋਏ ਪਦ ਹਨ
\(\sqrt {3}\), \(\sqrt {6}\), \(\sqrt {9}\), \(\sqrt {12}\),…
ਇੱਥੇ T₁ = \(\sqrt {3}\), T₂ = \(\sqrt {6}\),
T₃ = \(\sqrt {9}\), T₄ = \(\sqrt {12}\)
ਜਾਂ T₁ = \(\sqrt {3}\), T₂ = \(\sqrt {6}\),
T₃ = 3, T₄ = 2\(\sqrt {3}\)
T₂ – T₁ = \(\sqrt {6}\) – \(\sqrt {3}\)
ਹੁਣ, T₂₃ – T₂ = 3 – \(\sqrt {6}\)
∵ T₂ – T₁ ≠ T₃ – T₂
∴ ਇਹ A.P. ਨਹੀਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ (xiv).
1², 3², 5², 7², …
ਉੱਤਰ:
ਦਿੱਤੇ ਹੋਏ ਪਦ ਹਨ 1², 3², 5², 7²……
T₁ = 1², T₂ = 3², T₃ = 5², T₄ = 7²
ਜਾਂ T₁ = 1, T₂ = 9, T₃ = 25, T₄ = 49
T₂ – T₁ = 9 – 1= 8
T₃ – T₂ = 25 – 9 = 16
∵ T₂ – T₁ ≠ T₃ – T₂
∴ ਇਹ A.P. ਨਹੀਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ (xv).
1², 5², 7², 7³, …
ਉੱਤਰ:
ਦਿੱਤੇ ਹੋਏ ਪਦ ਹਨ 1², 5², 7², 73, ….
T₁ = 1², T₂ = 5², T₃ = 7², T₄ = 73
ਜਾਂ T₁ = 1, T₂ = 25, T₂₃ = 49, T₄ = 73
T₂ – T₁ = 25 – 1 = 24
T₃ – T₂ = 49 – 25 = 24
T₄ – T₃ = 73 – 49 = 24
∵ T₂ – T₁ = T₃ – T₂ = T₄ – T₃ = 24
∴ ਸਾਂਝਾ ਅੰਤਰ = d = 24
T₅ = a + 4d = 1 + 4 (24) = 1 + 96 = 97
T₆ = a + 5d = 1 + 5 (24) = 1 + 120 = 121
T₇ = a + 6d = 1 + 6 (24) = 1 + 144 = 145

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 4 ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ Ex 4.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 4 ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ Exercise 4.4

1. ਹੇਠਾਂ ਦਿੱਤੇ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣਾਂ ਦੇ ਮੂਲਾਂ ਦੀ ਪ੍ਰਕ੍ਰਿਤੀ ਪਤਾ ਲਗਾਉ । ਜੇਕਰ ਮੂਲ ਸੰਭਵ ਹੋਣ ਤਾਂ ਉਨ੍ਹਾਂ ਦਾ ਪਤਾ ਲਗਾਉ ।

ਪ੍ਰਸ਼ਨ (i).
2x² – 3x + 5 = 0
ਉੱਤਰ:
ਦਿੱਤੀ ਗਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਹੈ।
2x² – 3x + 5 = 0
ਇਸ ਦੀ ਤੁਲਨਾ ax² + bx + c = 0 ਨਾਲ ਕਰਨ ਤੇ
∴ a = 2, b = – 3, c = 5
D = b² – 4ac
= (-3)² – 4 × 2 × 5
= 9 – 40
= – 31 < 0
∴ ਦਿੱਤੀ ਹੋਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਦਾ ਕੋਈ ਵਾਸਤਵਿਕ ਮੂਲ ਨਹੀਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ (ii).
3x² – 4\(\sqrt {3}\) x + 4 = 0
ਉੱਤਰ:
ਦਿੱਤੀ ਗਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਹੈ
3x² – 4\(\sqrt {3}\)x + 4 = 0
ਇਸ ਦੀ ਤੁਲਨਾ ax² + bx + c = 0 ਨਾਲ ਕਰਨ ‘ਤੇ
∴ a = 3, b = -4\(\sqrt {3}\), c = 4
D = b² – 4ac
= (-4\(\sqrt {3}\)x)² -4 x 3 x 4
= 48 – 48 = 0
∴ ਦਿੱਤੀ ਹੋਈ ਸਮੀਕਰਣ ਦੇ ਵਾਸਤਵਿਕ ਅਤੇ ਬਰਾਬਰ ਮੂਲ ਹਨ ।

∴ ਦਿੱਤੀ ਹੋਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਦੇ ਮੂਲ ਹਨ \(\frac{2}{\sqrt{3}}\) ਅਤੇ \(\frac{2}{\sqrt{3}}\)

ਪ੍ਰਸ਼ਨ (iii).
2x² – 6x + 3 = 0
ਉੱਤਰ:
ਦਿੱਤੀ ਹੋਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਹੈ
2x² – 6x + 3 = 0
ਇਸ ਦੀ ਤੁਲਨਾ ax² + bx + c = 0 ਨਾਲ ਕਰਨ ‘ਤੇ
∴ a = 2, b = – 6, c = 3
D = b² – 4ac
= (-6)² – 4 × 2 × 3
= 36 – 24
= 12 > 0
∴ ਦਿੱਤੀ ਹੋਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਦੇ ਵਾਸਤਵਿਕ ਨੂੰ ਅਤੇ ਅਲਗ-ਅਲਗ ਮੂਲ ਹਨ :

∴ ਦਿੱਤੀ ਹੋਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਦੇ ਮੂਲ \(\frac{3+\sqrt{3}}{2}\) ਅਤੇ \(\frac{3-\sqrt{3}}{2}\) ਹਨ ।

2. ਹੇਠਾਂ ਦਿੱਤੇ ਹਰੇਕ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਵਿਚ k ਦਾ ਅਜਿਹਾ ਮੁੱਲ ਪਤਾ ਕਰੋ ਕਿ ਉਸ ਦੇ ਦੋ ਬਰਾਬਰ ਮੂਲ ਹੋਣ :

ਪ੍ਰਸ਼ਨ (i).
2x² + kx + 3 = 0
ਉੱਤਰ:
ਦਿੱਤੀ ਹੋਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਹੈ
2x² + kx + 3 = 0
ਇਸ ਦੀ ਤੁਲਨਾ ax² + bx + c = 0 ਨਾਲ ਕਰਨ ਤੇ
∴ a = 2, b = k, c = 3
∵ ਦਿੱਤੀ ਹੋਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਦੇ ਮੂਲ ਹਨ
∴ D = 0
b² – 4ac = 0
(k)² – 4 × 2 × 3 = 0
k² – 24 = 0 .
k² = 24
k² = ±\(\sqrt {24}\)
k = ±2\(\sqrt {6}\)

ਪ੍ਰਸ਼ਨ (ii).
kx (x – 2) + 6 = 0.
ਉੱਤਰ:
ਦਿੱਤੀ ਹੋਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਹੈ
kx(x – 2) + 6 = 0
kx² – 2kx + 6 = 0
ਇਸਦੀ ਤੁਲਨਾ ax² + bx + c = 0 ਨਾਲ ਕਰਨ ਤੇ
∴ a = k, b = -2k, c = 6
∵ ਦਿੱਤੀ ਹੋਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਦੇ ਮੂਲ ਬਰਾਬਰ | ਹਨ।
∴ D = 0
b² – 4ac = 0
(-2k)² – 4 × k × 6 = 0
4k² – 24k = 0
4k [k – 6] = 0
ਭਾਵ 4k = 0 ਜਾਂ k – 6 = 0
k = 0 ਜਾਂ . k = 6
∴ k = 0, 6

ਪ੍ਰਸ਼ਨ 3.
ਕੀ ਅਜਿਹਾ ਅੰਬਾਂ ਦਾ ਆਇਤਾਕਾਰ ਬਾਗ ਲਗਾਉਣਾ | ਸੰਭਵ ਹੈ ਜਿਸਦੀ ਲੰਬਾਈ, ਚੌੜਾਈ ਤੋਂ ਦੁੱਗਣੀ ਹੋਵੇ ਅਤੇ ਇਸਦਾ ਖੇਤਰਫਲ 800 m ਹੋਵੇ । ਜੇਕਰ ਸੰਭਵ ਹੈ ਤਾਂ ਇਸਦੀ ਲੰਬਾਈ ਅਤੇ ਚੌੜਾਈ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਓ ਆਇਤਾਕਾਰ ਬਾਗ ਦੀ ਲੰਬਾਈ = x m
ਅਤੇ ਆਇਤਾਕਾਰ ਬਾਗ ਦੀ ਚੌੜਾਈ = 2x m
ਆਇਤਾਕਾਰ ਬਾਗ ਦਾ ਖੇਤਰਫਲ = ਲੰਬਾਈ × ਚੌੜਾਈ
= [x × 2x] ਮੀ.²
= 2x² ਮੀ.²
ਪ੍ਰਸ਼ਨ ਦੇ ਅਨੁਸਾਰ,
2x² = 800
x² = \(\frac{800}{2}\) = 400
x = ±\(\sqrt {400}\)
x = ±20
∵ ਬਾਗ਼ ਦੀ ਲੰਬਾਈ ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੋ ਸਕਦੀ ।
∴ ਅਸੀਂ x = 20 ਨੂੰ ਛੱਡ ਦਿੰਦੇ ਹਾਂ ।
∴ x = 20
∴ ਬਾਗ਼ ਦੀ ਚੌੜਾਈ = 20 m
ਬਾਗ਼ ਦੀ ਲੰਬਾਈ
= (2 × 20) m = 40 m

ਪ੍ਰਸ਼ਨ 4.
ਕੀ ਹੇਠਾਂ ਦਿੱਤੀ ਸਥਿਤੀ ਸੰਭਵ ਹੈ । ਜੇਕਰ ਹਾਂ ਤਾਂ ਉਨ੍ਹਾਂ ਦੀ ਵਰਤਮਾਨ ਉਮਰਾਂ ਪਤਾ ਕਰੋ । ਦੋ ਮਿੱਤਰਾਂ ਦੀਆਂ ਉਮਰਾਂ ਦਾ ਜੋੜ 20 ਸਾਲ ਹੈ । ਚਾਰ ਸਾਲ ਪਹਿਲਾਂ ਉਨ੍ਹਾਂ ਦੀਆਂ ਉਮਰਾਂ ਸਾਲਾਂ ਵਿੱਚ) ਦਾ ਗੁਣਨਫਲ 48 ਸੀ ।
ਹੱਲ:
ਮੰਨ ਲਓ ਪਹਿਲੇ ਮਿੱਤਰ ਦੀ ਉਮਰ = x ਸਾਲ
ਦੂਸਰੇ ਮਿੱਤਰ ਦੀ ਉਮਰ = (20 – x) ਸਾਲ
ਚਾਰ ਸਾਲ ਪਹਿਲਾਂ :
ਪਹਿਲੇ ਮਿੱਤਰ ਦੀ ਉਮਰ = (x – 4) ਸਾਲ
ਦੂਸਰੇ ਮਿੱਤਰ ਦੀ ਉਮਰ = (20 – x – 4) ਸਾਲ
= (16 – x) ਸਾਲ
ਉਨ੍ਹਾਂ ਦਾ ਗੁਣਨਫਲ = (x – 4) (16 – x)
= 16x – x² – 64 + 4x
= -x² + 20x – 64
ਪ੍ਰਸ਼ਨੇ ਅਨੁਸਾਰ,
-x² + 20x – 64 = 48
-x² + 20x – 64 – 48 = 0
-x² + 20x – 112 = 0
x² – 20x + 12 = 0 …(1)
ਇਸ ਦੀ ਤੁਲਨਾ ax² + bx + c = 0 ਨਾਲ ਕਰਨ ਤੇ
a = 1, b = – 20, c = 112
D = b² – 4ac
= (-20)² – 4 × 1 × 112
= 400 – 448
= – 48 < 0
∵ ਮੂਲ ਵਾਸਤਵਿਕ ਨਹੀਂ ਹਨ
∴ ਦਾ ਕੋਈ ਮੁੱਲ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ (1) ਨੂੰ ਸੰਤੁਸ਼ਟ ਨਹੀਂ ਕਰਦਾ ਹੈ
∴ ਦਿੱਤੀ ਹੋਈ ਸਥਿਤੀ ਸੰਭਵ ਨਹੀਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ 5.
ਕੀ ਪਰਿਮਾਪ 80 m ਅਤੇ ਖੇਤਰਫਲ 400 m² ਦੇ ਇੱਕ ਪਾਰਕ ਨੂੰ ਬਣਾਉਣਾ ਸੰਭਵ ਹੈ ? ਜੇਕਰ ਹੈ ਤਾਂ ਉਸਦੀ ਲੰਬਾਈ, ਚੌੜਾਈ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਓ ਆਇਤਾਕਾਰ ਪਾਰਕ ਦੀ ਲੰਬਾਈ = x ਮੀ.
ਆਇਤਾਕਾਰ ਪਾਰਕ ਦੀ ਚੌੜਾਈ = y ਮੀ.
∴ ਆਇਤਾਕਾਰ ਪਾਰਕ ਦਾ ਪਰਿਮਾਪ =2 (x + y) ਮੀ.
∴ ਆਇਤਾਕਾਰ ਪਾਰਕ ਦਾ ਖੇਤਰਫਲ = xy ਮੀ.²
ਪਹਿਲੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
2 (x + y) = 80
x + y = \(\frac{80}{2}\) = 40
y = 40 – x …(1)
ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
xy = 400
x(40 – x) = 400 [(1) ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ਤੇ]
ਜਾਂ 40x – x² = 400
ਜਾਂ 40x – x² – 400 = 0
ਜਾਂ x² – 40x + 400 = 0
ਇਸ ਦੀ ਤੁਲਨਾ ax² + b + c = 0 ਨਾਲ ਕਰਨ ਤੇ
∴ a = 1, b = -40, c = 400
D = b² – 4ac
= (-40)² – 4 × 1 × 400
= 1600 – 1600 = 0

ਹੁਣ x = 20, ਤਾਂ (1) ਤੋਂ
y = 40 – 20 = 20
∴ ਆਇਤਾਕਾਰ ਪਾਰਕ ਦੀ ਲੰਬਾਈ ਅਤੇ ਚੌੜਾਈ ਦਾ | ਮਾਪ 20 m ਬਰਾਬਰ ਹੈ ।
∴ ਆਇਤਾਕਾਰ ਪਾਰਕ ਸੰਭਵ ਹੈ । ਇਹ ਵਰਗ ਹੈ ।

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 4 ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ Ex 4.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 4 ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ Exercise 4.3

1. ਜੇਕਰ ਹੇਠ ਲਿਖਿਆਂ ਸਮੀਕਰਣਾਂ ਦੇ ਮੂਲ ਸੰਭਵ ਹੋਣ ਤਾਂ ਪੂਰਨ ਵਰਗ ਬਣਾਉਣ ਦੀ ਵਿਧੀ ਰਾਹੀਂ ਪਤਾ ਕਰੋ ।

ਪ੍ਰਸ਼ਨ (i).
2x² – 7x + 3 = 0
ਉੱਤਰ:
ਦਿੱਤੀ ਗਈ ਸਮੀਕਰਣ ਹੈ
2x² – 7x + 3 = 0
ਜਾਂ 2x² – 7x = – 3


ਇਸ ਲਈ, ਦਿੱਤੀ ਗਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਦੇ ਮੂਲ 3, \(\frac{1}{2}\) ਹਨ

ਪ੍ਰਸ਼ਨ (ii).
2x² + x – 4 = 0
ਉੱਤਰ:
ਦਿੱਤੀ ਗਈ ਸਮੀਕਰਣ ਹੈ
2x² + x – 4 = 0
ਜਾਂ 2x² + x = 4


ਇਸ ਲਈ, ਦਿੱਤੀ ਗਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਦੇ ਮੂਲ ਹਨ: \(\frac{-1+\sqrt{33}}{4}\) ਅਤੇ \(\frac{-1-\sqrt{33}}{4}\)

ਪ੍ਰਸ਼ਨ (iii).
4x² + 4\(\sqrt {3}\) x + 3 = 0
ਉੱਤਰ:
ਦਿੱਤੀ ਗਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਹੈ
4x² + 4\(\sqrt {3}\)x + 3 = 0
ਜਾਂ 4x² + 4\(\sqrt {3}\)x = – 3

ਜਾਂ x + \(\frac{\sqrt{3}}{2}\) = 0
ਜਾਂ x = \(\frac{-\sqrt{3}}{2}\)
ਇਸ ਲਈ, ਦਿੱਤੀ ਗਈ ਸਮੀਕਰਣ ਦੇ ਮੂਲ ਹਨ :
\(\frac{-\sqrt{3}}{2}\) ਅਤੇ \(\frac{-\sqrt{3}}{2}\)

ਪ੍ਰਸ਼ਨ (iv).
2x² + x + 4 = 0
ਉੱਤਰ:
ਦਿੱਤੀ ਹੋਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਹੈ
2x² + x + 4 = 0
ਜਾਂ 2x² + x = -4

∵ ਕਿਸੇ ਸੰਖਿਆਂ ਦਾ ਵਰਗ ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੋ ਸਕਦਾ ।
∴ (x + \(\frac{1}{4}\))², x ਦੇ ਕਿਸੇ ਵੀ ਮੁੱਲ ਲਈ ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੋ ਸਕਦਾ ।
∴ ਇੱਥੇ x ਦਾ ਕੋਈ ਵਾਸਤਵਿਕ ਮੁਲ ਨਹੀਂ ਹੈ ਜੋ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਨੂੰ ਸੰਤੁਸ਼ਟ ਕਰਦਾ ਹੈ ।
∴ ਇਸਦੇ ਮੂਲ ਵਾਸਤਵਿਕ ਨਹੀਂ ਹਨ ।

ਪ੍ਰਸ਼ਨ 2.
ਉਪਰੋਕਤ ਪ੍ਰਸ਼ਨ (1) ਵਿੱਚ ਦਿੱਤੇ ਗਏ ਦੋ ਘਾਤੀ | ਸਮੀਕਰਣਾਂ ਦੇ ਮੂਲ ਦੋ ਘਾਤੀ ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਕੇ ਪਤਾ ਲਗਾਉ ॥
ਹੱਲ:
(i) ਦਿੱਤੀ ਗਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਹੈ
2x² – 7x + 3 = 0
ਇਸਦੀ ax² + bx + c = 0 ਨਾਲ ਤੁਲਨਾ ਕਰਨ ਤੇ ।
a = 2, b = – 7, c = 3
ਹੁਣ b² – 4ac = (-7) – 4 × 2 × 3
= 49 – 24
= 25 > 0

∴ 3 ਅਤੇ \(\frac{1}{2}\)ਦਿੱਤੀ ਗਈ ਸਮੀਕਰਣ ਦੇ ਮੂਲ ਹਨ ।

(ii) ਦਿੱਤੀ ਗਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਹੈ
2x² + x – 4 = 0
ਇਸ ਦੀ ਤੁਲਨਾ ax² + bx + c = 0 ਨਾਲ ਕਰਨ ਤੇ
∴ a = 1, b = 1, c = – 4
ਹੁਣ b² – 4ac = (1)² – 4 × 2 × (-4)
= 1 + 32
= 33 > 0

ਇਸ ਲਈ \(\frac{-1+\sqrt{33}}{4}\) ਅਤੇ \(\frac{-1-\sqrt{33}}{4}\) ਦਿੱਤੀ ਹੋਈ ਸਮੀਕਰਣ ਦੇ ਮੂਲ ਹਨ ।

(iii) ਦਿੱਤੀ ਗਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਹੈ
4x² + 4\(\sqrt {3}\) + 3 = 0
ਇਸ ਦੀ ਤੁਲਨਾ ax² + bx + = 0 ਨਾਲ ਕਰਨ ਤੇ :
∴ a = 4, b = 4\(\sqrt {3}\) , c = 3
ਹੁਣ b² – 4ac = (4\(\sqrt {3}\))² – 4 × 4 × 3
= 48 – 48 = 0

\(\frac{-\sqrt{3}}{2}\) ਅਤੇ \(\frac{-\sqrt{3}}{2}\) ਦਿੱਤੀ ਗਈ ਸਮੀਕਰਣ ਦੇ ਮੂਲ ਹਨ ।

(iv) ਦਿੱਤੀ ਗਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਹੈ
2x² + x + 4 = 0
ਇਸ ਦੀ ਤੁਲਨਾ ax² + bx + 0 = 0 ਨਾਲ ਕਰਨ ਤੇ
∴ a = 2, b = 1, c = 4
ਹੁਣ b² – 4ac = (1)² – 4 × 2 × 4
= 1 – 32 = – 31 < 0
∴ x = \(\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)
ਕਿਉਂਕਿ ਇਕ ਵਾਸਤਵਿਕ ਸੰਖਿਆ ਦਾ ਵਰਗ ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੋ ਸਕਦਾ ਹੈ । ਇਸ ਲਈ x ਦਾ ਕੋਈ ਵਾਸਤਵਿਕ ਮੂਲ ਹੀਂ ਹੈ !
∴ ਦਿੱਤੀ ਹੋਈ ਸਮੀਕਰਣ ਦੇ ਮੂਲ ਵਾਸਤਵਿਕ ਨਹੀਂ ਹਨ ।
ਉਪਰ ਦਿੱਤੇ ਦੋ ਪ੍ਰਸ਼ਨਾਂ ਵਿਚ ਅਸੀਂ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਦੇ ਮੁਲ ਪਤਾ ਕਰਨ ਲਈ ਦੋਵਾਂ ਵਿਧੀਆਂ ਦਾ ਪ੍ਰਯੋਗ ਕੀਤਾ ਹੈ । ਅਸੀਂ ਦੇਖਦੇ ਹਾਂ ਕਿ ਦੋ ਘਾਤੀ ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ, ਪੂਰਨ ਵਰਗ ਬਣਾਉਣ ਨਾਲੋਂ ਜ਼ਿਆਦਾ ਅਸਾਨ ਹੈ ।

3. ਹੇਠਾਂ ਲਿਖੀਆਂ ਸਮੀਕਰਣਾਂ ਦੇ ਮੂਲ ਪਤਾ ਕਰੋ :

ਪ੍ਰਸ਼ਨ (i).
x – \(\frac{1}{x}\) = 3, x ≠ 0
ਉੱਤਰ:
ਦਿੱਤੀ ਗਈ ਸਮੀਕਰਣ ਹੈ
x – \(\frac{1}{x}\) = 3
ਜਾਂ \(\frac{x^{2}-1}{x}\) = 3
ਜਾਂ x² – 1 = 3x
ਜਾਂ x² – 3x – 1 = 0
ਇਸ ਦੀ ਤੁਲਨਾ ax² + bx + c = 0 ਨਾਲ ਕਰਨ ਤੇ
∴ a = 1, b = – 3, c = – 1
ਹੁਣ b² – 4ac = (-3)² – 4. 1 (-1)
= 9 + 4 = 13 > 0

ਇਸ ਲਈ \(\frac{3+\sqrt{13}}{2}\) ਅਤੇ \(\frac{3-\sqrt{13}}{2}\) ਦਿੱਤੀ ਗਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਦੇ ਮੂਲ ਹਨ ।

ਪ੍ਰਸ਼ਨ (ii).
\(\frac{1}{x+4}\) – \(\frac{1}{x-7}\) = \(\frac{11}{30}\), x ≠ -4, 7
ਉੱਤਰ:
ਦਿੱਤੀ ਹੋਈ ਸਮੀਕਰਣ ਹੈ
\(\frac{1}{x+4}\) – \(\frac{1}{x-7}\) = \(\frac{11}{30}\)
ਜਾਂ \(\frac{(x-7)-(x+4)}{(x+4)(x-7)}\) = \(\frac{11}{30}\)

ਜਾਂ -11 × 30 = 11 (x² – 3x – 28)
ਜਾਂ x² – 3x – 28 + 30 = 0
ਜਾਂ x² – 3x + 2 = 0
ਇਸ ਦੀ ਤੁਲਨਾ ax² + bx + c = 0 ਨਾਲ ਕਰਨ ਤੇ
∴ a = 1, b = – 3, c = 2
ਹੁਣ, b² – 4ac = (-3)² – 4 × 1 × 2
= 9 – 8
= 1 > 0

∴ 2 ਅਤੇ 1 ਦਿੱਤੀ ਹੋਈ ਸਮੀਕਰਣ ਦੇ ਮੂਲ ਹਨ ।

ਪ੍ਰਸ਼ਨ 4.
3 ਸਾਲ ਪਹਿਲਾਂ ਰਹਿਮਾਨ ਦੀ ਉਮਰ (ਸਾਲਾਂ ਵਿੱਚ) ਅਤੇ ਹੁਣ ਤੋਂ ਪੰਜ ਸਾਲ ਬਾਅਦ ਦੀ ਉਮਰ ਦੇ ਉਲਟਮਾਂ ਦਾ ਜੋੜ \(\frac{1}{3}\) ਹੈ । ਉਸ ਦੀ ਵਰਤਮਾਨ ਉਮਰ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਓ ਰਹਿਮਾਨ ਦੀ ਵਰਤਮਾਨ ਉਮਰ = x ਸਾਲ
3 ਸਾਲ ਪਹਿਲਾਂ ਰਹਿਮਾਨ ਦੀ ਉਮਰ = (x – 3) ਸਾਲ
ਹੁਣ ਤੋਂ 5 ਸਾਲ ਬਾਅਦ ਰਹਿਮਾਨ ਦੀ ਉਮਰ = (x + 5) ਸਾਲ
ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ
\(\frac{1}{x-3}\) + \(\frac{1}{x+5}\) = \(\frac{1}{3}\)

ਜਾਂ 6x + 6 = x² + 2x – 15
ਜਾਂ x² + 2x – 15 – 6x – 6 = 0
ਜਾਂ x² – 4x – 21 = 0, ਜੋ ਕਿ 1 ਵਿਚ ਦੋ ਘਾਤ ਹੈ ਇਸ ਲਈ ਇਸ ਦੀ ਤੁਲਨਾ ax² + bx + c = 0 ਨਾਲ ਕਰਨ ਤੇ
∴ a = 1, b = – 4, c = – 21
ਹੁਣ b² – 4ac = (-4)² – 4 × 1 × (21)
= 16 + 84
= 100 > 0

= 7 ਅਤੇ – 2
∵ ਉਮਰ ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੋ ਸਕਦੀ ਹੈ
∴ x = – 3 ਨੂੰ ਛੱਡ ਦਿੰਦੇ ਹਾਂ
∴ x = 7
∴ ਰਹਿਮਾਨ ਦੀ ਵਰਤਮਾਨ ਉਮਰ x = 7 ਸਾਲ ।

ਪ੍ਰਸ਼ਨ 5.
ਇਕ ਸ਼੍ਰੇਣੀ ਟੈਸਟ ਵਿਚ ਸ਼ੈਫਾਲੀ ਦੇ ਗਣਿਤ ਅਤੇ ਅੰਗ੍ਰੇਜ਼ੀ ਵਿਚ ਪ੍ਰਾਪਤ ਕੀਤੇ ਅੰਕਾਂ ਦਾ ਜੋੜ 30 ਹੈ । ਜੇਕਰ ਉਸ ਨੂੰ ਗਣਿਤ ਵਿਚ 2 ਅੰਕ ਵੱਧ ਅਤੇ ਅੰਗ੍ਰੇਜ਼ੀ ਵਿਚ 3 ਅੰਕ ਘੱਟ ਮਿਲੇ ਹੁੰਦੇ ਤਾਂ ਉਸਦੇ ਅੰਕਾਂ ਦਾ ਗੁਣਨਫਲ 20 ਹੁੰਦਾ । ਉਸ ਦੁਆਰਾ ਦੋਵੇਂ ਵਿਸ਼ਿਆਂ ਵਿਚ ਪ੍ਰਾਪਤ ਅੰਕ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਓ ਸ਼ੈਫਾਲੀ ਨੇ ਗਣਿਤ ਵਿਚ ਪ੍ਰਾਪਤ ਕੀਤੇ ਅੰਕ = x
∴ ਸ਼ੈਫਾਲੀ ਦੇ ਅੰਗ੍ਰੇਜ਼ੀ ਵਿਚ ਪ੍ਰਾਪਤ ਅੰਕ = 30 – x
ਪ੍ਰਸ਼ਨ ਦੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
ਸ਼ੈਫਾਲੀ ਦੇ ਗਣਿਤ ਵਿਚ ਅੰਕ = x + 2
ਸ਼ੈਫਾਲੀ ਦੇ ਅੰਗੇਜ਼ੀ ਵਿੱਚ ਅੰਕ
= 30 – x – 3
= 27 – 1
∴ ਉਸਦੇ ਅੰਕਾਂ ਦਾ ਗੁਣਨਫਲ = (x + 27) (27 – x)
= 27x – x² + 54 – 2x
= -x² + 25x + 54
ਪ੍ਰਸ਼ਨ ਦੀ ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
-x² + 25x + 54 = 210
ਜਾਂ -x² + 25x + 54 – 210 = 0
ਜਾਂ -x² + 25x – 156 = 0
ਜਾਂ x² – 25x + 156 = 0
ਇਸ ਦੀ ਤੁਲਨਾ ax² + bx + c = 0 ਨਾਲ ਕਰਨ ਤੇ
a = 1, b = – 25, c = 156
ਹੁਣ b² – 4ac = (-25)² – 4 × 1 × 156
= 625 – 624
= 1 > 0

= 13 ਅਤੇ 12
ਸਥਿਤੀ I.
ਜਦੋਂ x = 13
∴ ਸ਼ੈਫਾਲੀ ਦੇ ਗਣਿਤ ਦੇ ਅੰਕ = 13
ਸ਼ੈਫਾਲੀ ਦੇ ਅੰਗ੍ਰੇਜ਼ੀ ਦੇ ਅੰਕ = 30 – 13 = 17
ਸਥਿਤੀ II.
ਜਦੋਂ = 12
ਸ਼ੈਫਾਲੀ ਦੇ ਗਣਿਤ ਦੇ ਅੰਕ = 12
ਅੰਗ੍ਰੇਜ਼ੀ ਦੇ ਅੰਕ = 30 – 12 = 18
∴ ਸ਼ੈਫਾਲੀ ਦੇ ਦੋ ਵਿਸ਼ਿਆਂ ਦੇ ਅੰਕ ਹਨ : 13 ਅਤੇ 17 ਜਾਂ 12 ਅਤੇ 18

ਪ੍ਰਸ਼ਨ 6.
ਇਕ ਆਇਤਾਕਾਰ ਖੇਤ ਦਾ ਵਿਕਰਣ ਉਸਦੀ ਛੋਟੀ ਭੁਜਾ ਤੋਂ 60 m ਲੰਬਾ ਹੈ । ਜੇਕਰ ਵੱਡੀ ਭੁਜਾ ਛੋਟੀ ਭੁਜਾ ਤੋਂ 30 m ਵੱਧ ਹੋਵੇ ਤਾਂ ਖੇਤ ਦੀਆਂ ਭੁਜਾਵਾਂ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਓ ਆਇਤਾਕਾਰ ਖੇਤ ਦੀ ਛੋਟੀ ਭੁਜਾ
= AD = x m

ਆਇਤਾਕਾਰ ਖੇਤ ਦੀ ਵੱਡੀ ਭੁ
= AB = (x + 30) m
ਆਇਤਾਕਾਰ ਖੇਤ ਦਾ ਵਿਕਰਣ
= DB = (x+ 60) m
ਇਕ ਆਇਤ ਵਿਚ ਲੰਬਾਈ ਅਤੇ ਚੌੜਾਈ ਦੇ ਵਿਚ ਦਾ } ਕੋਣ ਸਮਕੋਣ ਹੁੰਦਾ ਹੈ
∴ ∠AB = 90°
ਹੁਣ ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ DAB ਵਿਚ
ਪਾਇਥਾਗੋਰਸ ਦੇ ਸਿਧਾਂਤ ਅਨੁਸਾਰ
(DB)² = (AD)² + (AB)²
(x + 60)² = (x)² + (x + 30)²
ਜਾਂ x² + 3600 + 120x
= x² + x² + 900 + 60x
ਜਾਂ x² + 3600 + 120x – 2x² – 900 – 60x = 0
ਜਾਂ -x² + 6x + 2700 = 0
ਜਾਂ x² – 60x – 2700 = 0
ਇਸ ਦੀ ਤੁਲਣਾ ax² + bx + c = 0 ਨਾਲ ਕਰਨ ਤੇ
∴ a = 1, b = – 60, c = – 2700
ਅਤੇ b² – 4ac = (-60)² – 4 . 1. (-2700)
= 3600 + 10800
= 14400 > 0

= 90 ਅਤੇ -30
∵ ਕਿਸੇ ਖੇਤ ਦੀ ਭੁਜਾ ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੋ ਸਕਦੀ
∴ ਅਸੀਂ x = -30 ਨੂੰ ਛੱਡ ਦਿੰਦੇ ਹਾਂ
∴ x = 90
∴ ਆਇਤਾਕਾਰ ਖੇਤ ਦੀ ਸਭ ਤੋਂ ਛੋਟੀ ਭੁਜਾ
= 90 m
ਆਇਤਾਕਾਰ ਖੇਤ ਦੀ ਸਭ ਤੋਂ ਵੱਡੀ ਭੁਜਾ
= (9) + 30)
= 120 m

ਪ੍ਰਸ਼ਨ 7.
ਦੋ ਸੰਖਿਆਵਾਂ ਦੇ ਵਰਗਾਂ ਦਾ ਅੰਤਰ 180 ਹੈ । ਛੋਟੀ ਸੰਖਿਆ ਦਾ ਵਰਗ, ਵੱਡੀ ਸੰਖਿਆ ਦਾ ਅੱਠ ਗੁਣਾ ਹੈ । ਦੋਵੇਂ ਸੰਖਿਆਵਾਂ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਓ ਵੱਡੀ ਸੰਖਿਆ = 1
ਛੋਟੀ ਸੰਖਿਆ =y ਪ੍ਰਸ਼ਨ ਦੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
x² – y² = 180 ….(i)
ਪ੍ਰਸ਼ਨ ਦੀ ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
² = 8z …(ii)
(i) ਅਤੇ (ii) ਤੋਂ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
x² – 8x = 180
ਜਾਂ x² – 8x – 180 = 0
ਇਸਦੀ ਤੁਲਨਾ ax² + bx + c = 0 ਨਾਲ ਕਰਨ ਤੇ
a = 1, b = – 8, c = – 180
ਅਤੇ b² – 4ac = (-8)² – 4 × 1 × (-180)
= 64 + 720
= 784 > 0

= 18 ਅਤੇ – 10
ਜਦੋਂ x = – 10 ਤਾਂ, (ii) ਤੋਂ
y² = 8 (-10) = – 80, ਜੋ ਸੰਭਵ ਨਹੀਂ ਹੈ
∴ ਅਸੀਂ x = – 10 ਨੂੰ ਛੱਡ ਦਿੰਦੇ ਹਾਂ
ਜਦੋਂ x = 18, ਤਾਂ (2) ਤੋਂ,
y² = (18) 8 = 144
ਜਾਂ y = ±\(\sqrt {144}\)
ਜਾਂ y = ±12
∴ ਲੋੜੀਂਦੀਆਂ ਸੰਖਿਆਵਾਂ ਹਨ 18 ਅਤੇ 12 ਜਾਂ 18 ਅਤੇ – 12

ਪ੍ਰਸ਼ਨ 8.
ਇੱਕ ਰੇਲਗੱਡੀ ਇੱਕ ਸਮਾਨ ਚਾਲ ਨਾਲ 360 km ਦਾ ਸਫ਼ਰ ਤੈਅ ਕਰਦੀ ਹੈ । ਜੇਕਰ ਇਹ ਚਾਲ 5 km/h ਵੱਧ ਹੁੰਦੀ ਤਾਂ ਉਹ ਉਸੇ ਸਫ਼ਰ ਲਈ 1 ਘੰਟਾ ਘੱਟ ਸਮਾਂ ਲੈਂਦੀ । ਰੇਲਗੱਡੀ ਦੀ ਚਾਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਓ ਰੇਲਗੱਡੀ ਦੀ ਇਕ ਸਮਾਨ ਚਾਲ = x km/h
ਰੇਲਗੱਡੀ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਦੂਰੀ = 360 km

ਰੇਲਗੱਡੀ ਦੀ ਵੱਧੀ ਹੋਈ ਚਾਲ = (x + 5) km/h
∴ ਵੱਧੀ ਹੋਈ ਚਾਲ ਨਾਲ ਰੇਲਗੱਡੀ ਦੁਆਰਾ ਲੱਗਿਆ ਸਮਾਂ
= \(\frac{360}{x+5}\)
ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ
\(\frac{360}{x}\) – \(\frac{360}{x+5}\) = 1
\(\frac{360(x+5)-360 x}{x(x+5)}\) = 1
\(\frac{360 x+1800-360 x}{x^{2}+5 x}\) = 1
1800 = x² + 5x
x² + 5x – 1800 = 0
ਇਸ ਦੀ ਤੁਲਨਾ ax² + bx + c = 0 ਨਾਲ ਕਰਨ ਤੇ
a = 1, b = 5, c = – 1800
ਅਤੇ b² – 4ac = (5)² – 4 × 1 × (-1800)
= 25 + 7200
= 7225 > 0.

= 40 ਅਤੇ – 45
∴ ਕਿਸੇ ਰੇਲਗੱਡੀ ਦੀ ਚਾਲ ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੋ ਸਕਦੀ
∴ਅਸੀਂ x = – 45 ਨੂੰ ਛੱਡ ਦਿੰਦੇ ਹਾਂ
∴ x = 40
∴ ਰੇਲਗੱਡੀ ਦੀ ਚਾਲ = 40 km/h

ਪ੍ਰਸ਼ਨ 9.
ਦੋ ਟੁੱਟੀਆਂ ਮਿਲਕੇ ਇੱਕ ਹੌਜ ਨੂੰ 9\(\frac{3}{8}\) ਘੰਟਿਆਂ ਵਿੱਚ ਭਰ ਸਕਦੀਆਂ ਹਨ । ਵੱਡੇ ਵਿਆਸ ਵਾਲੀ ਟੁੱਟੀ, ਘੱਟ ਵਿਆਸ ਵਾਲੀ ਟੁੱਟੀ ਤੋਂ 10 ਘੰਟੇ ਘੱਟ ਸਮਾਂ ਲੈਂਦੀ ਹੈ । ਹਰੇਕ ਟੁੱਟੀ ਦੁਆਰਾ ਹੌਜ਼ ਨੂੰ ਭਰਨ ਲਈ ਲਿਆ ਗਿਆ ਸਮਾਂ | ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਓ ਵੱਡੇ ਵਿਆਸ ਵਾਲੀ ਟੁੱਟੀ ਹੌਜ਼ ਭਰਨ ਵਿਚ ਜਿਨ੍ਹਾਂ ਸਮਾਂ ਲੈਂਦੀ ਹੈ = x
ਘੰਟੇ ਛੋਟੇ ਵਿਆਸ ਵਾਲੀ ਲੈਂਦੀ ਜਿਨ੍ਹਾਂ ਸਮਾਂ ਲੈਂਦੀ ਹੈ = (x + 10)
ਘੰਟੇ ਇੱਕ ਘੰਟੇ ਦੀ ਸਥਿਤੀ
ਵੱਡੀ ਟੁੱਟੀ ਹੌਜ਼ ਭਰ ਸਕਦੀ ਹੈ = \(\frac{1}{x+10}\)
∴ ਵੱਡੀ ਅਤੇ ਛੋਟੀ ਟੁੱਟੀ ਹੌਜ਼ ਭਰ ਸਕਦੀਆਂ ਹਨ
= \(\frac{1}{x}\) = \(\frac{1}{x+10}\) ….(1)
ਪਰ ਦੋਵੇਂ ਟੁੱਟੀਆਂ ਹੌਜ਼ ਭਰਨ ਵਿਚ ਜਿਨ੍ਹਾਂ ਸਮਾਂ ਲੈਣਗੀਆਂ
= 9\(\frac{3}{8}\) ਘੰਟੇ = \(\frac{75}{8}\) ਘੰਟੇ
ਹੁਣ ਦੋਵੇਂ ਟੁੱਟੀਆਂ ਇਕ ਘੰਟੇ ਵਿਚ ਹੌਜ਼ ਭਰ ਸਕਦੀਆਂ ਹਨ
= \(\frac{8}{75}\) …(2)
(1) ਅਤੇ (2) ਤੋਂ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ

75 (2x + 10) = 8(x² + 10x)
150x + 750 = 8x² + 80x
ਜਾਂ 8x² + 80 – 150x – 750 = 0
8x² – 70x – 750 = 0
4x² – 35x – 375 = 0
ਇਸ ਦੀ ਤੁਲਨਾ ax² + bx + c = 0 ਨਾਲ ਕਰਨ ਤੇ ,
∴ a = 4, b = – 35, c = – 375
ਅਤੇ b² – 4ac = (-35)² –4 × 4 × (375)
= 1225 + 6000
= 7225 > 0

∵ ਸਮਾਂ ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੋ ਸਕਦਾ ਹੈ
ਇਸ ਲਈ, ਅਸੀਂ x = \(\frac{-25}{4}\)ਨੂੰ ਛੱਡ ਦਿੰਦੇ ਹਾਂ
∴ x = 15
ਇਸ ਲਈ ਵੱਡੀ ਟੁੱਟੀ ਹੌਜ਼ ਭਰਨ ਵਿਚ ਸਮਾਂ ਲੈਂਦੀ ਹੈ = 15 ਘੰਟੇ
ਅਤੇ ਛੋਟੀ ਟੁੱਟੀ ਹੌਜ਼ ਭਰਨ ਵਿੱਚ ਸਮਾਂ ਲੈਂਦੀ ਹੈ
= (15 + 10) ਘੰਟੇ
= 25 ਘੰਟੇ

ਪ੍ਰਸ਼ਨ 10.
ਮੈਸਰ ਅਤੇ ਬੰਗਲੌਰ ਦੇ ਵਿਚਕਾਰ 132 km ਦਾ ਸਫ਼ਰ ਕਰਨ ਲਈ ਇਕ ਐਕਸਪ੍ਰੈੱਸ ਰੇਲਗੱਡੀ, ਸਵਾਰੀ ਗੱਡੀ ਤੋਂ 1 ਘੰਟਾ ਘੱਟ ਸਮਾਂ ਲੈਂਦੀ ਹੈ । ਵਿਚਕਾਰਲੇ ਸਟੇਸ਼ਨਾਂ ਤੇ ਰੁਕਣ ਦਾ ਸਮਾਂ ਧਿਆਨ ਵਿੱਚ ਨਾ ਰੱਖਿਆ । ਜਾਵੇ) ਜੇਕਰ ਐਕਸਪ੍ਰੈਸ ਰੇਲਗੱਡੀ ਦੀ ਔਸਤ ਚਾਲ, ਸਵਾਰੀ ਗੱਡੀ ਦੀ ਔਸਤ ਚਾਲ ਤੋਂ 11 km/h ਜ਼ਿਆਦਾ ਹੋਵੇ ਤਾਂ ਦੋਵੇਂ ਰੇਲਗੱਡੀਆਂ ਦੀ ਔਸਤ ਚਾਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਓ ਸਵਾਰੀ ਗੱਡੀ ਦੀ ਔਸਤ ਚਾਲ
= x km/h
ਐਕਸਪ੍ਰੈੱਸ ਰੇਲਗੱਡੀ ਦੀ ਔਸਤ ਚਾਲ
= (x + 11) km/h
ਮੈਸੂਰ ਅਤੇ ਬੰਗਲੌਰ ਵਿਚ ਦੂਰੀ
= 132 ਕਿ.ਮੀ.
ਸਵਾਰੀ ਗੱਡੀ ਦੁਆਰਾ ਲਿਆ ਸਮਾਂ = \(\frac{132}{x}\) ਘੰਟੇ

1452 = x² + 11x
ਜਾਂ x² + 11x – 1452 = 0
ਇਸ ਦੀ ਤੁਲਨਾ ax² + bx + c = 0 ਨਾਲ ਕਰਨ ਤੇ
∴ a = 1, b = 11, c = – 1452
ਅਤੇ b² – 4ac = (11)² – 4 × 1 × (- 1452)
= 121 + 5808
= 5929 > 0

= \(\frac{66}{2}\) ਅਤੇ \(\frac{-88}{2}\)
= 33, – 44
∵ ਰੇਲਗੱਡੀ ਦੀ ਚਾਲ ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੋ ਸਕਦੀ
∴ x = 33
∴ ਸਵਾਰੀ ਗੱਡੀ ਦੀ ਔਸਤ ਚਾਲ
= 33 km/h.
ਅਤੇ ਐਕਸਪ੍ਰੈੱਸ ਰੇਲਗੱਡੀ ਦੀ ਔਸਤ ਚਾਲ
= (33 + 11) km/h
= 44 km/h

ਪ੍ਰਸ਼ਨ 11.
ਦੋ ਵਰਗਾਂ ਦੇ ਖੇਤਰਫਲਾਂ ਦਾ ਜੋੜ 48 m² ਹੈ । ਜੇਕਰ ਉਨ੍ਹਾਂ ਦੇ ਪਰਿਮਾਪਾਂ ਦਾ ਅੰਤਰ 24 m ਹੋਵੇ ਤਾਂ ਦੋਵੇਂ ਵਰਗਾਂ ਦੀਆਂ ਭੁਜਾਵਾਂ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਪਹਿਲਾਂ ਵੱਡੇ ਵਰਗ ਦੀ ਸਥਿਤੀ ਵਿਚ
ਮੰਨ ਲਓ ਵਰਗ ਦੀ ਹਰੇਕ ਭੁਜਾ ਦੀ ਲੰਬਾਈ = x m
ਵਰਗ ਦਾ ਖੇਤਰਫਲ = x² m²
ਵਰਗ ਦਾ ਪਰਿਮਾਪ = 4x m
ਛੋਟੇ ਵਰਗ ਦੀ ਸਥਿਤੀ ਵਿੱਚ
ਮੰਨ ਲਓ ਵਰਗ ਦੀ ਹਰੇਕ ਭੁਜਾ ਦੀ ਲੰਬਾਈ
= y m
ਵਰਗ ਦਾ ਖੇਤਰਫਲ = y²
ਵਰਗ ਦਾ ਪਰਿਮਾਪ = 4y m
ਪਹਿਲੀ ਸ਼ਰਤ ਅਨੁਸਾਰ,
x² + y² = 468 …(1)
ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ,
4x – 4y = 24
4(x – y) = 24
x – y = 6
ਜਾਂ x = 6 + y ….(2)
(1) ਅਤੇ (2) ਤੋਂ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ।
(6 + y)² + y² = 468
36 + y² + 12y + y² = 468
2y² + 12y + 36 – 468 = 0
2y² + 12y – 432 = 0
y² + 6y – 216 = 0
ਇਸ ਦੀ ਤੁਲਨਾ ay² + by + c = 0 ਨਾਲ ਕਰਨ ਤੇ
∴ a = 1, b = 6, c = – 216
ਅਤੇ b² – 4ac = (6)² – 4 × 1 × (216)
= 36 + 864
= 900 > 0

= 12 ਅਤੇ – 18
∵ ਵਰਗ ਦੀ ਭੁਜਾ ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੋ ਸਕਦੀ
∴ ਅਸੀਂ y = – 18 ਨੂੰ ਛੱਡ ਦਿੰਦੇ ਹਾਂ
∴ y = 12
(2) ਤੋਂ, x = 6 + 12 = 18
∴ ਦੋਵੇਂ ਵਰਗਾਂ ਦੀਆਂ ਭੁਜਾਵਾਂ
12 m ਅਤੇ 18 m ਹਨ ।

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 4 ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ Ex 4.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 4 ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ Exercise 4.2

1. ਗੁਣਨਖੰਡ ਵਿਧੀ ਰਾਹੀਂ ਹੇਠ ਲਿਖੇ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਦੇ ਮੁਲ ਪਤਾ ਕਰੋ :

ਪ੍ਰਸ਼ਨ (i).
x² – 3x – 10 = 0
ਉੱਤਰ:
ਦਿੱਤੀ ਗਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਹੈ
x² – 3x – 10 = 0 | S = – 3
x² – 5x + 2x – 10 = 0 | P = – 10
x(x – 5) + 2 (x – 5) = 0
(x – 5) (x + 2) = 0
ਭਾਵ x – 5 = 0 ਜਾਂ x + 2 = 0
x = 5 ਜਾਂ x = – 2
∴ 5 ਅਤੇ – 2 ਦਿੱਤੀ ਹੋਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਦੇ ਮੂਲ ਹਨ ।

ਪ੍ਰਸ਼ਨ (ii).
2x² + x – 6 = 0
ਉੱਤਰ:
ਦਿੱਤੀ ਹੋਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਹੈ :
2x² + x – 6 = 0 |S = 1
ਜਾਂ 2x² + 4x – 3x – 6 = 0 |P = – 6 × 2 = -12
2x (x + 2) – 3 (x + 2) = 0
(x + 2) (2x – 3) = 0
ਭਾਵ x + 2 = 0 ਜਾਂ 2x – 3 = 0
x = – 2 ਜਾਂ x = \(\frac{3}{2}\)
ਭਾਵ – 2 ਅਤੇ \(\frac{3}{2}\) ਦਿੱਤੀ ਹੋਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਦੇ ਮੂਲ ਹਨ ।

ਪ੍ਰਸ਼ਨ (iii).
\(\sqrt {2}\) x² + 7x + 5\(\sqrt {2}\) = 0
ਉੱਤਰ:
ਦਿੱਤੀ ਹੋਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਹੈ :
\(\sqrt {2}\)x² + 7x + 5\(\sqrt {2}\) = 0 |S = 7
|P = \(\sqrt {2}\) × \(\sqrt {5}\)
= 10
ਜਾਂ \(\sqrt {2}\)x² + 2x + 5x + 5\(\sqrt {2}\) = 0
ਜਾਂ \(\sqrt {2}\)x(x + \(\sqrt {2}\)) + 5(x +\(\sqrt {2}\)) = 0
ਜਾਂ (x + \(\sqrt {2}\)) (\(\sqrt {2}\)x + 5) = 0
ਭਾਵ x + \(\sqrt {2}\) = 0 ਜਾਂ \(\sqrt {2}\)x + 5 = 0
x = \(-\sqrt {2}\) x = \(\frac{-5}{\sqrt{2}}\)
ਇਸ ਲਈ, \(\sqrt {2}\) ਅਤੇ \(\frac{-5}{\sqrt{2}}\) ਦਿੱਤੀ ਹੋਈ ਸਮੀਕਰਣ ਦੇ ਹੱਲ ਹਨ ।

ਪ੍ਰਸ਼ਨ (iv).
2x² – x + \(\frac{1}{8}\) = 0
ਉੱਤਰ:
ਦਿੱਤੀ ਹੋਈ ਦੇ ਘਾਤੀ ਸਮੀਕਰਣ ਹੈ
2x² – x + \(\frac{1}{8}\) = 0
ਜਾਂ \(\frac{16 x^{2}-8 x+1}{8}\) = 0
S = – 8
|P = 16 × 1 = 16
16x² – 8x + 1= 0,
16x² – 4x – 4x + 1 = 0
4x(4x – 1) – 1 (4x – 1) = 0
ਜਾਂ (4x – 1) (4x – 1) = 0
ਭਾਵ 4x – 1 = 0
ਜਾਂ 4x – 1 = 0
4x = 1 4x = 1
x =\(\frac{1}{4}\) ਜਾਂ x = \(\frac{1}{4}\)
ਇਸ ਲਈ \(\frac{1}{4}\) ਅਤੇ \(\frac{1}{4}\) ਦਿੱਤੀ ਹੋਈ ਸਮੀਕਰਣ ਦੇ ਮੂਲ ਹਨ ।

ਪ੍ਰਸ਼ਨ (v).
100x² – 20x + 1 = 0
ਉੱਤਰ:
ਦਿੱਤੀ ਹੋਈ ਦੇ ਘਾਤੀ ਸਮੀਕਰਣ ਹੈ
100x² – 20x + 1 = 0
100x² – 10x – 10x + 1 = 0 | S = – 20
| P = 100 × 1
= 100
ਜਾਂ 10x (10x – 1) – (10x – 1) = 0
ਜਾਂ (10x – 1) (10x – 1) = 0
ਭਾਵ 10x – 1 = 0 ਜਾਂ 10x – 1 = 0
x = \(\frac{1}{10}\) ਜਾਂ x = \(\frac{1}{10}\)
ਇਸ ਲਈ \(\frac{1}{10}\) ਅਤੇ \(\frac{1}{10}\) ਦਿੱਤੀ ਹੋਈ ਸਮੀਕਰਣ ਦੇ ਮੂਲ ਹਨ ।

2. ਉਦਾਹਰਣ 1 ਵਿਚ ਦਿੱਤੀਆਂ ਸਮੱਸਿਆਵਾਂ ਨੂੰ ਹੱਲ ਕਰੋ । ਇਨ੍ਹਾਂ ਸਮੱਸਿਆਵਾਂ ਦੇ ਕਥਨ ਹੇਠ ਦਿੱਤੇ ਗਏ ਹਨ ।

ਪ੍ਰਸ਼ਨ (i).
ਜਾਂਨ ਅਤੇ ਰੇਖਾ ਦੋਹਾਂ ਕੋਲ ਕੁੱਲ 45 ਬੰਦੇ ਹਨ । ਦੋਵੇਂ ਪੰਜ-ਪੰਜ ਬੰਟੇ ਗੁਆ ਦਿੰਦੇ ਹਨ, ਹੁਣ ਉਹਨਾਂ ਕੋਲ ਬੰਟਿਆਂ ਦੀ ਗਿਣਤੀ ਦਾ ਗੁਣਨਫਲ 124 ਹੈ । ਅਸੀਂ ਜਾਨਣਾਂ ਚਾਹਾਂਗੇ ਕਿ | ਸ਼ੁਰੂ ਵਿੱਚ ਉਨ੍ਹਾਂ ਕੋਲ ਕਿੰਨੇ-ਕਿੰਨੇ ਬੰਟੇ ਸਨ ।
ਉੱਤਰ:
ਮੰਨ ਲਉ ਜਾਂਨ ਕੋਲ ਬੰਟਿਆਂ ਦੀ ਗਿਣਤੀ = x
ਰੇਖਾ ਕੋਲ ਬੰਟਿਆਂ ਦੀ ਗਿਣਤੀ = 45 – x
ਜਾਂਨ ਦੇ 5 ਬੰਟੇ ਗੁਆਉਣ ਪਿਛੋਂ ਗਿਣਤੀ = x – 5
ਰੇਖਾ ਦੇ 5 ਬੰਟੇ ਗੁਵਾਉਣ ਪਿਛੋਂ ਗਿਣਤੀ
= 45 – x – 5
= 40 – x
ਇਸ ਲਈ ਉਨ੍ਹਾਂ ਦਾ ਗੁਣਨਫਲ = (x – 5) (40 – x)
= 40x – x² – 200 + 5x
= – x² + 45x – 200
ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ,
-x² + 45x – 200 = 124
-x² + 45x – 324 = 0 |S = – 45,
ਜਾਂ x² – 45x + 324 = 0 | P = 324
x² – 36x – 9x + 324 = 0
ਜਾਂ x(x – 36) – 9 (x – 36) = 0
ਜਾਂ (x – 36) (x – 9) = 0
ਭਾਵ x – 36 = 10 ਜਾਂ x – 9 = 0
x = 36 ਜਾਂ x = 9
∴ x = 36, 9
ਇਸ ਲਈ, ਬੰਟਿਆਂ ਦੀ ਗਿਣਤੀ ਜੋ ਉਨ੍ਹਾਂ ਕੋਲ ਸੀ 36 ਅਤੇ 9 ਜਾਂ 9 ਅਤੇ 36 ਹੈ ।

ਪ੍ਰਸ਼ਨ (ii).
ਇਕ ਘਰੇਲੂ ਉਦਯੋਗ ਇੱਕ ਦਿਨ ਵਿਚ ਕੁਝ ਖਿਡੌਣੇ ਬਣਾਉਂਦਾ ਹੈ । ਹਰੇਕ ਖਿਡੌਣੇ ਦਾ ਮੁੱਲ (₹ ਵਿਚ) 55 ਵਿਚੋਂ | ਇੱਕ ਦਿਨ ਬਣਾਏ ਗਏ ਖਿਡੌਣਿਆਂ ਦੀ ਗਿਣਤੀ ਘਟਾਉਣ ਉਪਰੰਤ ਪ੍ਰਾਪਤ ਸੰਖਿਆ ਦੇ ਬਰਾਬਰ ਹੈ । ਕਿਸੇ ਇੱਕ ਦਿਨ ਖਿਡੌਣੇ ਬਣਾਉਣ ‘ਤੇ ਕੁੱਲ ਖਰਚ ਤੇ 750 ਸੀ । ਅਸੀਂ ਉਸ ਦਿਨ ਬਣਾਏ ਗਏ ਖਿਡੌਣਿਆਂ ਦੀ ਗਿਣਤੀ ਪਤਾ ਕਰਨਾ ਚਾਹਾਂਗੇ ।
ਉੱਤਰ:
ਮੰਨ ਲਓ ਉਸ ਦਿਨ ਨਿਰਮਾਣ ਕੀਤੇ ਖਿਡੌਣੇ = x
ਉਸ ਦਿਨ ਹਰੇਕ ਖਿਡੌਣੇ ਦੀ ਨਿਰਮਾਣ ਲਾਗਤ (₹ ਵਿੱਚ) = 55 – x
ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ
x (55 – x) = 750
ਜਾਂ 55x – x² = 750
ਜਾਂ -x² + 55x – 750 = 0 | S = – 33,
ਜਾਂ x² – 55x + 750 = 0 | P = 750
ਜਾਂ x² – 30x – 25x + 750 = 0
ਜਾਂ x (x – 30) – 25 (x – 30) = 0
ਜਾਂ (x – 30) (x – 25) = 0
ਭਾਵ x – 30 = 0 ਜਾਂ x – 25 = 0
x = 30 ਜਾਂ x = 25
∴ x = 30, 25
ਇਸ ਲਈ, ਉਸ ਦਿਨ ਬਣਾਏ ਗਏ ਖਿਡੌਣਿਆਂ ਦੀ ਗਿਣਤੀ 30 ਅਤੇ 25 ਜਾਂ 25 ਅਤੇ 30 ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਦੋ ਸੰਖਿਆਵਾਂ ਪਤਾ ਕਰ ਜਿਨ੍ਹਾਂ ਦਾ ਜੋੜ 27 ਅਤੇ ਗੁਣਨਫਲ 182 ਹੋਵੇ ।
ਹੱਲ:
ਮੰਨ ਲਓ ਪਹਿਲੀ ਸੰਖਿਆ = 1
ਦੂਸਰੀ ਸੰਖਿਆ = 27 – x
ਇਸ ਲਈ, ਉਨ੍ਹਾਂ ਦਾ ਗੁਣਨਫਲ = x (27 – x)
= 27x -x²
ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ,
27x – x² = 182
ਜਾਂ x² + 27x – 182 = 0 | S = – 27
ਜਾਂ x² – 27x + 182 = 0 | P = 182
ਜਾਂ x² – 13x – 14x + 182 = 0
ਜਾਂ x (x – 13) – 14 (x – 13) = 0
ਜਾਂ (x – 13) (x – 14) = 0
ਭਾਵ x – 13 = 0 ਜਾਂ x – 14 = 0
x = 13 ਜਾਂ x = 14
∴ x = 13, 14
ਇਸ ਲਈ, ਦੋ ਸੰਖਿਆਵਾਂ 13 ਅਤੇ 14 ਜਾਂ 14 ਅਤੇ 13 ਹਨ ।

ਪ੍ਰਸ਼ਨ 4.
ਦੋ ਲਗਾਤਾਰ ਧਨ ਸੰਪੂਰਨ ਸੰਖਿਆਵਾਂ ਪਤਾ ਕਰੋ ਜਿਨ੍ਹਾਂ ਦੇ ਵਰਗਾਂ ਦਾ ਜੋੜ 365 ਹੋਵੇ
ਹੱਲ:
ਮੰਨ ਲਓ ਪਹਿਲੀ ਧਨ ਸੰਪੂਰਨ ਸੰਖਿਆ = x
ਦੂਸਰੀ ਧਨ ਸੰਪੂਰਨ ਸੰਖਿਆ = x + 1
ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ,
(x)² + (x + 1)² = 365
ਜਾਂ , x² + x² + 1 + 2x = 365
ਜਾਂ 2x² + 2x + 1 – 365 = 0
ਜਾਂ 2x² + 2x – 364 = 0
ਜਾਂ x² + x – 182 = 0
ਜਾਂ x² + 14x – 13x – 182 = 0
ਜਾਂ x(x + 14) – 13 (x + 14) = 0
ਜਾਂ (x + 14) (x – 13) = 0
ਭਾਵ x + 14 = 0 , ਜਾਂ x – 13 = 0
x = – 14 ਜਾਂ x = 13
∵ ਸਾਨੂੰ ਧਨ ਸੰਪੂਰਨ ਸੰਖਿਆਵਾਂ ਚਾਹੀਦੀਆਂ ਹਨ ਇਸ ਲਈ x =- 14 ਨਹੀਂ ਹੈ ।
∴ x = 13
∴ ਪਹਿਲੀ ਧਨ ਸੰਪੂਰਨ ਸੰਖਿਆ = 13
ਦੂਸਰੀ ਧਨ ਸੰਪੂਰਨ ਸੰਖਿਆ = 13 + 1 = 14
ਇਸ ਲਈ ਦੋ ਧਨ ਸੰਪੂਰਨ ਸੰਖਿਆਵਾਂ 13 ਅਤੇ 14

ਪ੍ਰਸ਼ਨ 5.
ਇੱਕ ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ ਦੀ ਉੱਚਾਈ ਇਸ ਦੇ ਆਧਾਰ ਤੋਂ 7 cm ਘੱਟ ਹੈ । ਜੇਕਰ ਕਰਣ 13 cm ਹੈ ਤਾਂ ਬਾਕੀ ਦੋ । ਭੁਜਾਵਾਂ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਓ ਸਮਕੋਣ ਤਿਭੁਜ ਦਾ ਆਧਾਰ = x cm
ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ ਦੀ ਉੱਚਾਈ (ਲੰਬ) = x – 7 cm
ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ ਦਾ ਕਰਣ = 13 cm ……(ਦਿੱਤਾ ਹੈ।)
ਪਾਇਥਾਗੋਰਸ ਪਮੇਯ ਅਨੁਸਾਰ,
(ਅਧਾਰ)² + (ਲੰਬ)² = (ਕਰਣ)²
(x)² + (x – 7)² = (13)²
ਜਾਂ x² + x² + 49 – 14x = 169
ਜਾਂ 2x² – 14x + 49 – 169 = 0
2x² – 14x – 120 = 0
ਜਾਂ 2 [x² – 7x – 60] = 0
ਜਾਂ x² – 7x – 60 = 0 | S = 7
ਜਾਂ x² – 12x + 5x – 60 = 0 | P = – 60
ਜਾਂ x (x – 12) + 5 (x – 12) = 0
ਜਾਂ (x – 12) (x + 5) = 0
ਭਾਵ x – 12 = 0 ਜਾਂ x + 5 = 0
x = 12 ਜਾਂ x = – 5
ਇਸ ਲਈ, ਤ੍ਰਿਭੁਜ ਦੀ ਲੰਬਾਈ ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੋ ਸਕਦੀ
∴ x = -5 ਨੂੰ ਛੱਡ ਦਿੰਦੇ ਹਾਂ
∴ x = 12
∴ ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ ਦਾ ਆਧਾਰ = 12 cm
ਸਮਕੋਣ ਤ੍ਰਿਭੁਜ ਦੀ ਉੱਚਾਈ (ਲੰਬ) = (12 – 7) cm
= 5 cm

ਪ੍ਰਸ਼ਨ 6.
ਇਕ ਘਰੇਲੂ ਉਦਯੋਗ ਇੱਕ ਦਿਨ ਵਿਚ ਕੁਝ ਬਰਤਨ ਬਣਾਉਂਦਾ ਹੈ । ਇੱਕ ਦਿਨ ਇਹ ਵੇਖਿਆ ਗਿਆ ਕਿ ਹਰੇਕ | ਨਗ ਦੀ ਨਿਰਮਾਣ ਲਾਗਤ (ਰੁਪਇਆਂ ਵਿਚ) ਉਸ ਦਿਨ | ਬਣਾਏ ਗਏ ਬਰਤਨਾਂ ਦੀ ਸੰਖਿਆ ਦੇ ਦੁੱਗਣੇ ਤੋਂ 3 ਵੱਧ ਸੀ । ਜੇਕਰ ਉਸ ਦਿਨ ਦੀ ਕੁੱਲ ਨਿਰਮਾਣ ਲਾਗਤ ₹ 90 ਸੀ | ਤਾਂ ਉਸ ਦਿਨ ਬਣਾਏ ਗਏ ਬਰਤਨਾਂ ਦੀ ਸੰਖਿਆ ਅਤੇ ਹਰੇਕ ਨਗ ਨੂੰ ਬਣਾਉਣ ਦੀ ਲਾਗਤ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਓ ਇਕ ਦਿਨ ਵਿਚ ਬਣਾਏ ਗਏ ਬਰਤਨਾਂ ਦੀ ਸੰਖਿਆ = x
ਹਰੇਕ ਨਗ ਬਣਾਉਣ ਦੀ ਲਾਗਤ = ₹ (2x + 3)
∴ ਇਕ ਦਿਨ ਤੇ ਕੁਲ ਨਿਰਮਾਣ ਲਾਗਤ
= ₹ [x (2x + 3)]
= ₹ (2x² + 3x)
ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ,
2x² + 3x = 90
| S = 3,
P = 2 × -90
= – 180
2x² + 3x – 90 = 0
ਜਾਂ 2x² – 12x + 15x – 90 = 0
ਜਾਂ 2x (x – 6) + 15 (x – 6) = 0
ਜਾਂ (x – 6) (2x + 15) = 0
ਭਾਵ x – 6 = 0 ਜਾਂ 2x + 15 = 0
x = 6 ਜਾਂ x = \(\frac{-15}{2}\)
∵ ਨਗਾਂ ਦੀ ਸੰਖਿਆ ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੋ ਸਕਦੀ ।.
∴ ਅਸੀਂ x = \(\frac{-15}{2}\) ਨੂੰ ਛੱਡ ਦਿੰਦੇ ਹਾਂ ।
∴ x = 6
∴ ਵਿਸ਼ੇਸ਼ ਦਿਨ ਨਗਾਂ ਦੀ ਸੰਖਿਆ = 6
ਹਰੇਕ ਨਗ ਦੀ ਲਾਗਤ = ₹(2 × 6 + 3)
= ₹15

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 4 ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ Ex 4.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 4 ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ Exercise 4.1

1. ਜਾਂਚ ਕਰੋ ਕਿ ਦਿੱਤੀਆਂ ਸਮੀਕਰਣਾਂ ਦੇ ਘਾਤੀ ਹਨ ਜਾਂ ਨਹੀਂ :

ਪ੍ਰਸ਼ਨ (i).
(x + 1)² = 2 (x – 3)
ਉੱਤਰ:
ਦਿੱਤਾ ਹੈ ਕਿ
(x + 1)² = 2 (x – 3)
ਜਾਂ x² + 1 + 2x = 2x – 6
ਜਾਂ x² + 1 + 2x – 2x + 6 = 0
ਜਾਂ x² + 7 = 0
x² + 0x + 7 = 0
ਜੋ ਕਿ x² + bx + 0 = 0; (a ≠ 0) ਦੇ ਰੂਪ ਦਾ ਸਮੀਕਰਣ ਹੈ
∴ ਇਹ ਇੱਕ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਹੈ ।

ਪ੍ਰਸ਼ਨ (ii).
x² – 2x = (-2) (3 – x)
ਉੱਤਰ:
ਦਿੱਤਾ ਹੈ ਕਿ
x² – 2x = (-2) (3 – x)
x² – 2x = – 6 + 2x
ਜਾਂ x² – 2x + 6 – 2x = 0
ਜਾਂ x² – 4x + 6 = 0
ਜੋ ਕਿ ax² + bx + 0 = 0; a ≠ 0 ਦੇ ਰੂਪ ਦਾ ਹੈ |
∴ ਇਹ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਹੈ ।

ਪ੍ਰਸ਼ਨ (iii).
(x – 2) (x + 1) = (x – 1) (x + 3)
ਉੱਤਰ:
ਦਿੱਤਾ ਹੈ ਕਿ
(x – 2) (x + 1) = (x – 1) (x + 3)
ਜਾਂ x² + x – 2x – 2 = x² + 3x – x – 3
ਜਾਂ x² – x – 2 = x² + 2x – 3
ਜਾਂ x² – x – 2 – x² – 2x + 3 =0
– 3x + 1 = 0,
ਜਿਸ ਵਿਚ x² ਦਾ ਕੋਈ ਪਦ ਨਹੀਂ ਹੈ
∴ ਇਹ ਇੱਕ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਨਹੀਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ (iv).
(x – 3) (2x + 1) = x(x + 5)
ਉੱਤਰ:
ਦਿੱਤਾ ਹੈ ਕਿ
(x – 3) (2x + 1) = x (x + 5)
ਜਾਂ 2x² + x – 6x – 3 = x² + 5x
ਜਾਂ 2x² – 5x – 3 – x² – 5 = 0
ਜਾਂ x² – 10x – 3 = 0
ਜੋ ਕਿ ax² + bx + c = 0; (a ≠ 0) ਦੇ ਰੂਪ ਦਾ ਹੈ ।
∴ ਇਹ ਇੱਕ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਹੈ ।

ਪ੍ਰਸ਼ਨ (v).
(2x – 1) (x – 3) = (x + 5) (x – 1)
ਉੱਤਰ:
ਦਿੱਤਾ ਹੈ ਕਿ
(2x – 1) (x – 3) = (x + 5) (x – 1)
ਜਾਂ 2x² – 6x – x + 3 = x² – x + 5x – 5
ਜਾਂ 2x² – 7x + 3 = x² + 4x + 5 = 0
x² – 11x + 8 = 0
ਜੋ ਕਿ ax² + bx + x = 0, a ≠ 0 ਦੇ ਰੂਪ ਦਾ ਹੈ।
∴ ਇਹ ਇੱਕ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਹੈ ।

ਪ੍ਰਸ਼ਨ (vi).
x² + 3x + 1 = (x – 2)²
ਉੱਤਰ:
ਦਿੱਤਾ ਹੈ ਕਿ
x² + 3x + 1 = (x – 2)²
ਜਾਂ x² + 3x + 1 = x² + 4 – 4x
ਜਾਂ x² + 3x + 1 – x² – 4 + 4x = 0
ਜਾਂ 7x – 3 = 0
ਜਿਸ ਵਿੱਚ x² ਦਾ ਪਦ ਨਹੀਂ ਹੈ।
∴ ਇਹ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਨਹੀਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ (vii).
(x + 2)² = 2x(x² – 1)
ਉੱਤਰ:
ਦਿੱਤਾ ਹੈ ਕਿ (x + 2)³ = 2x (x² – 1)
ਜਾਂ x³ + (2)³ + 3(x)²2 + 3x (2)²
= 2x³ – 2x
ਜਾਂ x³ + 8 + 6x² + 12x = 23x³ – 2x
ਜਾਂ x³ + 8 + 6x² + 12x – 2x³ + 2x = 0
ਜਾਂ – x³ + 6x² + 14x – 8 = 0
ਇੱਥੇ x ਦੀ ਉੱਚਤਮ ਘਾਤ 3 ਹੈ ।
ਇਹ ਇੱਕ ਤ੍ਰਿਘਾਤੀ ਸਮੀਕਰਣ ਹੈ
∴ ਇਹ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਨਹੀਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ (viii).
x³ – 4x² – x + 1 = (x – 2)³
ਉੱਤਰ:
ਦਿੱਤਾ ਹੈ।
x³ – 4x² – x + 1 = (x – 2)³
ਜਾਂ x³ – 4x² – x + 1 = x³ – (2)³ + 3 (x)² (-2) + 3 (x) (- 2)²
ਜਾਂ x³ – 4x² – x + 1 = x³ – 8 – 6x² + 12x
ਜਾਂ x³ – 4x² – x + 1 – x³ + 8 + 6x² – 12x = 0
ਜਾਂ 2x² – 13x + 9 = 0.
ਜੋ ਕਿ ax² + bx + c = 0; (a ≠ 0) ਦੇ ਰੂਪ ਦਾ ਹੈ।
∴ ਇਹ ਇੱਕ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਹੈ ।

2. ਹੇਠਾਂ ਦਿੱਤੀਆਂ ਸਥਿਤੀਆਂ ਨੂੰ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਦੇ ਰੂਪ ਵਿਚ ਬਦਲੋ :

ਪ੍ਰਸ਼ਨ (i).
ਇੱਕ ਆਇਤਾਕਾਰ ਪਲਾਟ ਦਾ ਖੇਤਰਫਲ 528 m² ਹੈ । ਪਲਾਟ ਦੀ ਲੰਬਾਈ (ਮੀਟਰਾਂ ਵਿੱਚ) ਚੌੜਾਈ ਦੇ ਦੁੱਗਣੇ ਤੋਂ ਇੱਕ ਵੱਧ ਹੈ । ਅਸੀਂ ਪਲਾਟ ਦੀ ਲੰਬਾਈ ਅਤੇ ਚੌੜਾਈ ਪਤਾ ਕਰਨੀ ਹੈ ।
ਉੱਤਰ:
ਮੰਨ ਲਓ ਆਇਤਾਕਾਰ ਪਲਾਟ ਦੀ ਚੌੜਾਈ = x m
ਆਇਤਾਕਾਰ ਪਲਾਟ ਦੀ ਲੰਬਾਈ = (2x + 1) m
∴ ਆਇਤਾਕਾਰ ਪਲਾਟ ਦਾ ਖੇਤਰਫਲ
= [x (2 + 1)] m²
= (2x² + x) m²
ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ 2x² + x = 528
|S = 1
P = – 528 × 2
= – 1056
ਜਾਂ 2x² + x – 528 = 0
2x² – 32x + 33x – 528 = 0
2x (x – 16) + 33 (x – 16) = 0
(x – 16) (2x + 33) = 0
ਭਾਵ x – 16 = 0 ਜਾਂ 2x + 33 = 0
x = 16 ਜਾਂ x = \(\frac{-33}{2}\)
∴ ਕਿਸੇ ਆਇਤ ਦੀ ਚੌੜਾਈ ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੋ ਸਕਦੀ ਇਸ ਲਈ ਅਸੀਂ \(\frac{-33}{2}\) ਨੂੰ ਛੱਡ ਦਿੰਦੇ ਹਾਂ
∴ x = 16
ਪਲਾਟ ਦੀ ਚੌੜਾਈ = 16 m
ਲੰਬਾਈ = (2 × 16 + 1) = 33 m
ਦਿੱਤੀ ਹੋਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਦਾ ਰੂਪ ਹੈ।
2x² + x – 528 = 0

ਪ੍ਰਸ਼ਨ (ii).
ਦੋ ਲਗਾਤਾਰ ਧਨਾਤਮਕ ਸੰਪੂਰਨ ਸੰਖਿਆਵਾਂ ਦਾ ਗੁਣਨਫਲ 306 ਹੈ | ਅਸੀਂ ਸੰਪੂਰਨ ਸੰਖਿਆਵਾਂ ਪਤਾ ਕਰਨੀਆਂ ਹਨ ।
ਉੱਤਰ:
ਮੰਨ ਲਓ x ਅਤੇ x + 1 ਦੋ ਲਗਾਤਾਰ ਧਨਾਤਮਕ ਸੰਪੂਰਨ ਸੰਖਿਆਵਾਂ ਹਨ
ਸੰਪੁਰਨ ਸੰਖਿਆਵਾਂ ਦਾ ਗੁਣਨਫਲ = x (x + 1)
= x² + x
ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ
x² + x = 306
ਜਾਂ x² + x – 306 = 0
| S = 1,
| P = – 306
x² + 18 – 17x – 306 = 0
x(x + 18) – 17 (x + 18) = 0
(x + 18) (x – 17) = 0
x = – 18 ਜਾਂ x = 17
∵ ਅਸੀਂ ਧਨਾਤਮਕ ਸੰਪੂਰਨ ਸੰਖਿਆਵਾਂ ਪਤਾ ਕਰਨੀਆਂ ਹਨ ।
∴ ਅਸੀਂ x = -18 ਨੂੰ ਛੱਡ ਦਿੰਦੇ ਹਾਂ ।
∴ x = 17
ਦੋ ਲਗਾਤਾਰ ਧਨਾਤਮਕ ਸੰਪੂਰਨ ਸੰਖਿਆਵਾਂ ਹਨ
17, 17 + 1 = 18
ਦਿੱਤੀ ਹੋਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਦਾ ਰੂਪ ਹੈ
x² + x – 306 = 0

ਪ੍ਰਸ਼ਨ (iii).
ਰੋਹਨ ਦੀ ਮਾਂ ਉਸ ਨਾਲੋਂ 26 ਸਾਲ ਵੱਡੀ ਹੈਂ । ਹੁਣ ਤੋਂ ਤਿੰਨ ਸਾਲ ਬਾਅਦ ਉਨਾਂ ਦੀਆਂ ਉਮਰਾਂ ਦਾ ਗੁਣਨਫਲ 360 ਹੋ ਜਾਵੇਗਾ ਅਸੀਂ ਰੋਹਨ ਦੀ ਵਰਤਮਾਨ ਉਮਰ ਪਤਾ ਕਰਨੀ ਹੈ ।
ਉੱਤਰ:
ਮੰਨ ਲਓ ਰੋਹਨ ਦੀ ਵਰਤਮਾਨ ਉਮਰ = x ਸਾਲ
ਰੋਹਨ ਦੀ ਮਾਂ ਦੀ ਉਮਰ = (x + 26) ਸਾਲ
3 ਸਾਲ ਬਾਅਦ
ਰੋਹਨ ਦੀ ਉਮਰ = (x + 3) ਸਾਲ
ਰੋਹਨ ਦੀ ਮਾਂ ਦੀ ਉਮਰ = (x + 26 + 3) ਸਾਲ
= (x + 29) ਸਾਲ
∴ ਉਹਨਾਂ ਦੀਆਂ ਉਮਰਾਂ ਦਾ ਗੁਣਨਫਲ
= (x + 3) (x + 29)
= x² + 29x + 3x + 87
= x² + 32x + 87
ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ
x² + 32x + 87 = 360
x² + 32x + 87 – 360 = 0
x² + 32x – 273 = 0
|S = 32,
|P = – 273
x² + 39x – 7x – 273 = 0
x(x + 39) – 7(x + 39) = 0
(x + 39) (x – 7) = 0
ਭਾਵ x + 39 = 0 ਜਾਂ x – 7 = 0
x = – 39 ਜਾਂ x = 7
∵ ਕਿਸੇ ਆਦਮੀ ਦੀ ਉਮਰ ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੋ ਸਕਦੀ ਅਸੀਂ x = – 39 ਨੂੰ ਛੱਡ ਦਿੰਦੇ ਹਾਂ
∴ x = 7
ਰੋਹਨ ਦੀ ਵਰਤਮਾਨ ਉਮਰ = 7 ਸਾਲ
ਦਿੱਤੀ ਹੋਈ ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਦਾ ਰੂਪ ਹੈ :
x² + 32x – 273 = 0

ਪ੍ਰਸ਼ਨ (iv).
ਇਕ ਰੇਲਗੱਡੀ 480 km ਦੀ ਦੂਰੀ ਇੱਕ ਸਮਾਨ ਚਾਲ ਨਾਲ ਤੈਅ ਕਰਦੀ ਹੈ । ਜੇਕਰ ਇਸਦੀ ਚਾਲ 8 km/h ਘੱਟ ਹੁੰਦੀ ਤਾਂ ਉਹ ਉਸ ਦੂਰੀ ਨੂੰ ਤੈਅ ਕਰਨ ਲਈ 3 ਘੰਟੇ ਵੱਧ ਸਮਾਂ ਲੈਂਦੀ | ਅਸੀਂ ਰੇਲਗੱਡੀ ਦੀ ਚਾਲ ਪਤਾ ਕਰਨੀ ਹੈ ।
ਉੱਤਰ:
ਮੰਨ ਲਓ ਰੇਲਗੱਡੀ ਦੁਆਰਾ ਲਿਆ ਗਿਆ ਸਮਾਂ = x ਘੰਟੇ
ਰੇਲਗੱਡੀ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਦੂਰੀ = 480 km

ਰੇਲਗੱਡੀ ਦੁਆਰਾ ਲਿਆ ਗਿਆ ਨਵਾਂ ਸਮਾਂ = (x + 3) ਘੰਟੇ
ਦੁਰੀ = 480 km
ਸੂਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਕੇ

ਜਾਂ -8x² + 456x + 1440 – 480x = 0
-8x² – 24x + 1440 = 0
-8[x² + 3x – 180] = 0
x² + 3x – 180 = 0
x² + 15x – 12x – 180 = 0
x(x + 15) – 12(x + 15) = 0
(x + 15) (x – 12) = 0
ਭਾਵ x + 15 = 0 ਜਾਂ x – 12 = 0
x = – 15 ਜਾਂ x = 12
∵ ਸਮਾਂ ਰਿਣਾਤਮਕ ਨਹੀਂ ਹੋ ਸਕਦਾ ਹੈ।
ਅਸੀਂ x = – 15 ਨੂੰ ਛੱਡ ਦਿੰਦੇ ਹਾਂ
∴ x = 12
ਹੁਣ ਰੇਲਗੱਡੀ ਦੁਆਰਾ ਲਿਆ ਸਮਾਂ = 12 ਘੰਟੇ
ਰੇਲਗੱਡੀ ਦੁਆਰਾ ਤੈਅ ਦੂਰੀ = 480 km/h
ਰੇਲਗੱਡੀ ਦੀ ਚਾਲ = \(\left(\frac{480}{12}\right)\)km/h
= 40 km/h
∴ ਰੇਲਗੱਡੀ ਦੀ ਚਾਲ = 40 km/h
ਦੋ ਘਾਤੀ ਸਮੀਕਰਣ ਦਾ ਰੂਪ ਹੈ
x² + 3x – 180 = 0

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 3 ਦੋ ਚਲਾਂ ਵਿੱਚ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦੇ ਜੋੜੇ Ex 3.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 3 ਦੋ ਚਲਾਂ ਵਿੱਚ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦੇ ਜੋੜੇ Exercise 3.2

1. ਹੇਠਾਂ ਦਿੱਤੀਆਂ ਸਮੱਸਿਆਵਾਂ ਵਿੱਚ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦੇ ਜੋੜੇ ਬਣਾਉ ਅਤੇ ਉਹਨਾਂ ਦੇ ਗ੍ਰਾਫੀ (ਆਲੇਖੀ) ਵਿਧੀ ਨਾਲ ਹੱਲ ਪਤਾ ਕਰੋ ।

ਪ੍ਰਸ਼ਨ (i).
ਜਮਾਤ X ਦੇ 10 ਵਿਦਿਆਰਥੀਆਂ ਨੇ ਗਣਿਤ ਦੀ ਇੱਕ ਬੁਝਾਰਤ ਮੁਕਾਬਲੇ ਵਿਚ ਭਾਗ ਲਿਆ । ਜੇਕਰ ਲੜਕੀਆਂ ਦੀ ਗਿਣਤੀ, ਲੜਕਿਆਂ ਦੀ ਗਿਣਤੀ ਤੋਂ 4 ਵੱਧ ਹੋਵੇ ਤਾਂ ਮੁਕਾਬਲੇ ਵਿਚ ਭਾਗ ਲੈਣ ਵਾਲੇ ਲੜਕੇ ਅਤੇ ਲੜਕੀਆਂ ਦੀ ਗਿਣਤੀ ਪਤਾ ਕਰੋ ।
ਉੱਤਰ:
ਮੰਨ ਲਉ – ਮੁਕਾਬਲੇ ਵਿਚ ਲੜਕਿਆਂ ਦੀ ਗਿਣਤੀ = x
ਅਤੇ ਮੁਕਾਬਲੇ ਵਿਚ ਲੜਕੀਆਂ ਦੀ ਗਿਣਤੀ = y
ਮੁਕਾਬਲੇ ਵਿੱਚ ਭਾਗ ਲੈਣ ਵਾਲੇ ਕੁੱਲ ਵਿਦਿਆਰਥੀ = 10
∴ x + y = 10
ਜਾਂ x + y – 10 = 0
ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ
y = x + 4
ਜਾਂ x = y – 4
ਹੁਣ, ਰੇਖੀ ਸਮੀਕਰਣਾਂ ,
x + y = 10
ਅਤੇ x – y + 4 = 0 ਦਾ ਗ੍ਰਾਫ ਖਿੱਚੋ ।
x + y = 10
ਜਾਂ x = 10 – y …..(1)
y = 0 ਨੂੰ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
x = 10 – 0 = 10
y = 7 ਨੂੰ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
x = 10 – 7 = 3
y = 10 ਨੂੰ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
x = 10 – 10 = 0 .
ਸਾਰਣੀ

ਬਿੰਦੂਆਂ A (10, 0), B (3, 7), C (0, 10) ਨੂੰ ਆਖਿਤ ਕਰਨ ‘ਤੇ ਅਤੇ ਉਹਨਾਂ ਨੂੰ ਮਿਲਾਉਂਦੇ ਹੋਏ ਰੇਖਾ ਖਿੱਚਣ ‘ਤੇ ਸਾਨੂੰ ਸਮੀਕਰਣ x + y = 10 ਦਾ ਗ੍ਰਾਫ਼ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x – y + 4 = 0
ਜਾਂ x = y – 4 ….(2)
y = 0 ਨੂੰ (2) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
x = 0 – 4 = -4
y = 7 ਨੂੰ (2) ਵਿਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਮਿਲਦਾ ਹੈ ।
x = 7 – 4 = 3
y = 4 ਨੂੰ (2) ਵਿਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਮਿਲਦਾ ਹੈ ।
x = 4 – 4 = 0
ਸਾਰਣੀ

ਬਿੰਦੁਆਂ D (-4, 0), B (3, 7), E (0, 4) ਨੂੰ ਆਲੇਖਿਤ ਕਰਨ ਅਤੇ ਉਹਨਾਂ ਨੂੰ ਮਿਲਾਉਂਦੇ ਹੋਏ ਰੇਖਾ ਖਿੱਚਣ ‘ਤੇ ਸਾਨੂੰ ਸਮੀਕਰਣ x – y + 4 = 0 ਦਾ ਗ੍ਰਾਫ਼ ਆਲੇਖ) ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।

ਆਲੇਖ ਤੋਂ ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਕਿ ਦੋਵੇਂ ਰੇਖੀ ਸਮੀਕਰਣਾਂ | ਬਿੰਦੂ B (3, 7) ਉੱਤੇ ਮਿਲਦੀਆਂ ਹਨ ।
∴ ਬਿੰਦੂ B (3, 7) ਆਲੇਖੀ ਸਥਿਤੀ ਹੈ ।
ਮੁਕਾਬਲੇ ਵਿਚ ਲੜਕਿਆਂ ਦੀ ਗਿਣਤੀ = 3
ਮੁਕਾਬਲੇ ਵਿਚ ਲੜਕੀਆਂ ਦੀ ਗਿਣਤੀ = 7

ਪ੍ਰਸ਼ਨ (ii).
5 ਪੈਨਸਿਲਾਂ ਅਤੇ 7 ਕਲਮਾਂ ਦਾ ਮੁੱਲ ₹ 50 ਹੈ, ਜਦ ਕਿ 7 ਪੈਨਸਿਲਾਂ ਅਤੇ 5 ਕਲਮਾਂ ਦਾ ਮੁੱਲ ₹ 46 ਹੈ । ਇਕ ਪੈਨਸਿਲ ਅਤੇ ਇਕ ਕਲਮ ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ ।
ਉੱਤਰ:
ਮੰਨ ਲਉ 1 ਪੈਨਸਿਲ ਦਾ ਮੁੱਲ = ₹ 2
ਅਤੇ 1 ਕਲਮ ਦਾ ਮੁੱਲ = ₹ y
ਪਹਿਲੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
5x + 7y = 50
ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
7x + 5y = 46
∴ ਰੇਖੀ ਸਮੀਕਰਣ ਜੋੜਾ ਹੈ :
5x + 7y = 50
7x + 5y = 46
ਹੁਣ, ਇਨ੍ਹਾਂ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਆਲੇਖ ਖਿੱਚੋ !
5x + 7y = 50
ਜਾਂ 5x = 50 – 7y
ਜਾਂ x = \(\frac{50-7 y}{5}\) …(1)
y = 0 ਨੂੰ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :

ਬਿੰਦੁਆਂ A (10, 0), B (3, 5), C (0.2, 7) ਨੂੰ । ਆਲੇਖਿਤ ਕਰਨ ਅਤੇ ਉਨ੍ਹਾਂ ਨੂੰ ਮਿਲਾਉਣ ‘ਤੇ ਸਾਨੂੰ ਸਮੀਕਰਣ 5x + 7y =50 ਦਾ ਆਲੇਖ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
7x + 5y = 46
ਨੂੰ 7x = 46 – 5y

ਬਿੰਦੂਆਂ E (6.5, 0), B (3, 5), F (9.5, – 4) ਨੂੰ ਆਲੇਖਿਤ ਕਰਨ ਅਤੇ ਉਨ੍ਹਾਂ ਨੂੰ ਮਿਲਾਉਂਦੇ ਹੋਏ ਰੇਖਾ ਖਿੱਚਣ ‘ਤੇ ਸਾਨੂੰ ਸਮੀਕਰਣ 7x + 5y = 46 ਦਾ ਆਲੇਖ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
ਆਲੇਖ ਤੋਂ ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਕਿ ਦੋਵੇਂ ਰੇਖੀ ਸਮੀਕਰਣ ਬਿੰਦੂ B (3, 5) ਤੇ ਮਿਲਦੇ ਹਨ ।
∴ ਬਿੰਦੂ B (3, 5) ਆਲੇਖੀ ਸਥਿਤੀ ਹੈ ।
ਇਕ ਪੈਨਸਿਲ ਦਾ ਮੁੱਲ = ₹ 3
ਇਕ ਕਲਮ ਦਾ ਮੁੱਲ = ₹ 5

2. ਅਨੁਪਾਤਾਂ \(\frac{a_{1}}{a_{2}}\), \(\frac{b_{1}}{b_{2}}\) ਅਤੇ \(\frac{c_{1}}{c_{2}}\) ਦੀ ਤੁਲਨਾ ਕਰਕੇ ਪਤਾ ਕਰੋ ਕਿ ਹੇਠਾਂ ਦਿੱਤੇ ਸਮੀਕਰਣ ਜੋੜਿਆਂ ਦੁਆਰਾ ਦਰਸਾਉਂਦੀਆਂ ਰੇਖਾਵਾਂ, ਇੱਕ ਬਿੰਦੂ ’ਤੇ ਕੱਟਦੀਆਂ ਹਨ, ਸਮਾਂਤਰ ਹਨ ਜਾਂ ਸੰਪਾਤੀ ਹਨ :

ਪ੍ਰਸ਼ਨ (i).
5x – 4y + 8 = 0
7x + 6y – 9 = 4
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
5x – 4y + 8 = 0
ਅਤੇ 7x + 6y – 9 = 0
ਇੱਥੇ a₁ = 5, b₁ = – 4, c₁ = 8
a₂ = 7, b₂ = 6, c₂ = – 9

∴ \(\frac{a_{1}}{a_{2}}\) ≠ \(\frac{b_{1}}{b_{2}}\) ≠ \(\frac{c_{1}}{c_{2}}\)
ਇਸ ਲਈ ਦਿੱਤਾ ਗਿਆ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਇੱਕ ਬਿੰਦੂ ਉੱਤੇ ਕੱਟਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ (ii).
9x + 3y + 12 = 0
18x + 6y + 24 = 0
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
9x + 3y + 12 = 0
ਅਤੇ 18x + 6y + 24 = 0
ਇੱਥੇ a₁ = 9, b₁ = 3, c₁ = 12
a₂ = 18, b₂ = 6, c₂ = 24

ਇਸ ਲਈ ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਸੰਪਾਤੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ (iii).
6x – 3y + 10 = 0
2x – y + 9 = 0
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
6x – 3y + 10 = 0,
ਅਤੇ 2x – y + 9 = 0
ਇੱਥੇ a₁ = 6, b₁ = -3, c₁ = 10
a₂ = 2, b₂ = -1, c₂ = 9

ਇਸ ਲਈ ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ । ਇੱਕ-ਦੂਜੇ ਦੇ ਸਮਾਂਤਰ ਹੈ ।

3. ਅਨੁਪਾਤਾਂ \(\frac{a_{1}}{a_{2}}\), \(\frac{b_{1}}{b_{2}}\) ਅਤੇ \(\frac{c_{1}}{c_{2}}\) ਦੀ ਤੁਲਨਾ ਕਰਕੇ ਪਤਾ ਕਰੋ ਕਿ ਹੇਠਾਂ ਦਿੱਤੇ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦੇ ਜੋੜੇ ਸੰਗਤ ਹਨ ਜਾਂ ਅਸੰਗਤ :

ਪ੍ਰਸ਼ਨ (i).
3x + 2y = 5; 2x – 3y = 7
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
3x + 2y = 5
ਅਤੇ 2x – 3y = 7
ਜਾਂ 3x + 2y – 5 = 0
ਅਤੇ 2x – 3y – 7 = 0
ਇੱਥੇ a₁ = 3, b₁ = 2, c₁ = – 5
a₂ = 2, b₂ = – 3, c₂ = – 7

ਇਸ ਲਈ ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਸੰਗਤ ਹੈ ।

ਪ੍ਰਸ਼ਨ (ii).
2x – 3y = 8; 4x – 6y = 9
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
2x – 3y = 8
ਅਤੇ 4x – 6y = 9
ਜਾਂ 2x – 3y – 8 = 0
4x – 6y – 9 = 0
ਇੱਥੇ a₁ = 2, b₁ = – 3, c₁ = – 8
a₂ = 4, b₂ = – 6, c₂ = -9

ਇਸ ਲਈ ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਅਸੰਗਤ ਹੈ ।

ਪ੍ਰਸ਼ਨ (iii).
\(\frac{3}{2}\)x + \(\frac{5}{3}\)y = 7; 9x – 10y = 14
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
\(\frac{3}{2}\)x + \(\frac{5}{3}\)y = 7
ਅਤੇ 9x – 10y = 14
ਜਾਂ \(\frac{3}{2}\)x + \(\frac{5}{3}\)y – 7 = 0
ਅਤੇ 9x – 10y – 14 = 0
ਇੱਥੇ a₁ = \(\frac{3}{2}\), b₁ = \(\frac{5}{3}\), c₁ = -7
a₂ = 9, b₂ = – 10, c₂ = – 14

ਇਸ ਲਈ ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਸੰਗਤ ਹੈ ।

ਪ੍ਰਸ਼ਨ (iv).
5x – 3y = 11; -10x + 6y = – 22
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
5x – 3y = 11
ਅਤੇ -10x + 6y = – 22
ਜਾਂ 5x – 3y – 11 = 0
ਅਤੇ -10x + 6y + 22 = 0
ਇੱਥੇ a₁ = 5, b₁ = -3, c₁ = – 11
a₂ = – 10, b₂ = 6, c₂ = 22

ਇਸ ਲਈ ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਸੰਗਤ ਹੈ ।

ਪ੍ਰਸ਼ਨ (v).
\(\frac{4}{3}\)x + 2y = 8; 2x + 3y = 12
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
\(\frac{4}{3}\)x + 2y = 8 ਅਤੇ 2x + 3y = 12
ਅਤੇ \(\frac{4}{3}\)x + 2y – 8 = 0
ਜਾਂ 2x + 3y – 12 = 0
ਇੱਥੇ a₁ = \(\frac{4}{3}\), b₁ = 2, c₁ = -12 .
a₂ = 2, b₂ = 3, c₂ = – 12

ਇਸ ਲਈ ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਸੰਗਤ ਹੈ ।

4. ਹੇਠਾਂ ਦਿੱਤੇ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦੇ ਜੋੜਿਆਂ ਵਿੱਚ ਕਿਹੜਾ ਜੋੜਾ ਸੰਗਤ ਹੈ ਅਤੇ ਕਿਹੜਾ ਅਸੰਗਤ ਜੇਕਰ ਜੋੜਾ ਸੰਗਤ ਹੈ ਤਾਂ ਆਲੇਖੀ (ਫੀ) ਵਿਧੀ ਨਾਲ ਹੱਲ ਪਤਾ ਕਰੋ :

ਪ੍ਰਸ਼ਨ (i).
x + y = 5, 2x + 2y = 10
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
x + y = 5
ਅਤੇ 2x + 2y = 10
ਜਾਂ x + y – 5 = 0
2x + 2y – 10 = 0
ਇੱਥੇ a₁ = 1, b₁ = 1, c₁ = -5
a₂ = 2, b₂ = 2, c₂ = – 10

∴ ਦਿੱਤੀ ਹੋਈ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦੇ ਜੋੜੇ ਦਾ ਆਲੇਖ | ਖਿੱਚੋ
x + y = 5
x = 5 – y …..(1)
y = 0 ਨੂੰ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = 5 – 0 = 5
y = 3 ਨੂੰ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = 5 – 3 = 2
y = 5 ਨੂੰ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = 5 – 5 = 0
ਸਾਰਣੀ

ਬਿੰਦੂਆਂ A (5, 0), B (2, 3), C (0, 5) ਨੂੰ ਆਲੇਖਿਤ ਕਰਨ ਅਤੇ ਉਹਨਾਂ ਨੂੰ ਮਿਲਾਉਣ ਤੇ ਸਾਨੂੰ ਸਮੀਕਰਣ x + y = 5 ਦਾ ਆਲੇਖ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
2x + 2y = 10 ਜਾਂ 2 (x + y) = 10
ਜਾਂ x + y = 5
ਜਾਂ x = 5 – …(2)
y = 0 ਨੂੰ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = 5 – 0 = 5
y = 2 ਨੂੰ (2) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = 5 – 2 = 3

ਬਿੰਦੂਆਂ A (5, 0), D (3, 2), C (0, 5) ਨੂੰ ਆਲੇਖਿਤ ਕਰਨ ਅਤੇ ਉਹਨਾਂ ਨੂੰ ਮਿਲਾਉਣ ਤੇ ਸਾਨੂੰ ਸਮੀਕਰਣ 2x + 2y = 10 ਦਾ ਆਲੇਖ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
ਆਲੇਖ ਤੋਂ ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਕਿ ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਸੰਪਾਤੀ, ਅਤੇ ਇਨ੍ਹਾਂ ਦੇ ਅਨੇਕ ਹੱਲ ਹਨ !

ਪ੍ਰਸ਼ਨ (ii).
x – y = 8, 3x – 3y = 16
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
x – y = 8
ਅਤੇ 3x – 3y = 16
ਜਾਂ x – y – 8 = 0
ਅਤੇ 3x – 3y – 16 = 0
ਇੱਥੇ a₁ =1, b₁ = -1 , c₁ = – 8
a₂ = 3, b₂ = – 3, c₂ = – 16
y = 5 ਨੂੰ (2) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = 5 – 5 = 0
ਸਾਰਣੀ


ਇਸ ਲਈ ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਮੀਕਣਾਂ ਦਾ ਹੋ ਅਸੰਗਤ ਹੈ ।

ਪ੍ਰਸ਼ਨ (iii).
2x + y – 6 = 0, 4x – 2y – 4 = 0
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
2x + y – 6 = 0
ਅਤੇ 4x – 2y – 4 = 0
ਇੱਥੇ a₁ = 2, b₁ = 1, c₁ = 6
a₂ = 4, b₂ = -2, c₂ = -4

∴ ਦਿੱਤੇ ਗਏ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦੇ ਜੋੜੇ ਦਾ ਗ੍ਰਾਫ ਖਿੱਚੋ :
2x + y – 6 = 0
ਜਾਂ 2x = 6 – y
ਜਾਂ y = \(\frac{6-y}{2}\) ….(1)
y = 0 ਨੂੰ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = \(\frac{6-0}{2}\) = \(\frac{6}{2}\) = 3
y = 2 ਨੂੰ (1), ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = \(\frac{6-2}{2}\)
= \(\frac{4}{2}\) = 2
y = -2 ਨੂੰ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = \(\frac{6-(-2)}{2}\) = \(\frac{6+2}{2}\)
= \(\frac{8}{2}\) = 4
ਸਾਰਣੀ

ਬਿੰਦੂਆਂ A (3, 0), B (2, 2), C (4, – 2) ਨੂੰ ਆਖਿਤ ਕਰਨ ‘ਤੇ ਉਨ੍ਹਾਂ ਨੂੰ ਮਿਲਾਉਂਦੇ ਹੋਏ ਰੇਖਾ ਖਿਚਣ ‘ਤੇ ਸਮੀਕਰਣ 2x +y – 6 = 0 ਦਾ ਆਲੇਖ ਮਿਲਦਾ ਹੈ ।
4x – 2y – 4 = 0
ਜਾਂ 2[2x – y – 2] = 0
ਜਾਂ 2x – y – 2 = 0
ਜਾਂ 2x = y + 2
ਜਾਂ x = \(\frac{y+2}{2}\) …(2)
y = 0 ਨੂੰ (2) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = \(\frac{0+2}{2}\) = \(\frac{2}{2}\) = 1
y = 2 ਨੂੰ (2) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = \(\frac{2+2}{2}\) = \(\frac{4}{2}\) = 2
y = -2 ਨੂੰ (2) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸ਼ਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = \(\frac{-2+2}{2}\)
= \(\frac{0}{2}\) = 0
ਸਾਰਣੀ

ਬਿੰਦੂਆਂ D (1, 0), B (2, 2), E (0, -2) ਨੂੰ ਆਲੇਖਿਤ ਕਰਨ ‘ਤੇ ਉਨ੍ਹਾਂ ਨੂੰ ਮਿਲਾਉਂਦੇ ਹੋਏ ਰੇਖਾ ਖਿਚਣ ‘ਤੇ ਸਾਨੂੰ ਸਮੀਕਰਣ 4x – 2y -4 = 0 ਦਾ ਆਲੇਖ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
ਆਲੇਖ ਤੋਂ ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਬਿੰਦੂ B (2, 2) ਉੱਤੇ ਮਿਲਦਾ ਹੈ ।
∴ ਦਿੱਤੀ ਹੋਈ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਵਿਲੱਖਣ ਹੈ ।

ਪ੍ਰਸ਼ਨ (iv).
2x – 2y – 2 = 0, 4x – 4y – 5 = 0
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
2x – 2y – 2 = 0
ਅਤੇ 4x – 4y – 5 = 0
ਇੱਥੇ a₁ = 2, b₁ = – 2, c₁ = – 2
a₂ = 4, b₂ = – 4, c₂ = – 5

ਇਸ ਲਈ ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਅਸੰਗਤ ਹੈ ।

ਪ੍ਰਸ਼ਨ 5.
ਇੱਕ ਆਇਤਾਕਾਰ ਬਾਗ, ਜਿਸਦੀ ਲੰਬਾਈ, ਚੌੜਾਈ ਤੋਂ 4 ਮੀ. ਵੱਧ ਹੈ, ਦਾ ਅਰਧ ਪਰਿਮਾਪ 36 ਮੀ. ਹੈ । ਬਾਗ ਦੀ ਲੰਬਾਈ ਅਤੇ ਚੌੜਾਈ ਪਤਾ ਕਰੋ ।
ਹੱਲ :
ਮੰਨ ਲਓ ਬਾਗ ਦੀ ਲੰਬਾਈ = x ਮੀ.
ਬਾਗ ਦੀ ਚੌੜਾਈ = y ਮੀ.
ਬਾਗ ਦਾ ਪਰਿਮਾਪ = 2 [x + y] ਮੀ.
ਬਾਗ ਦਾ ਅਰਧ ਪਰਿਮਾਪ = (x + y) ਮੀ
ਪ੍ਰਸ਼ਨ ਦੀ ਪਹਿਲੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
x = y + 4
ਪ੍ਰਸ਼ਨ ਦੀ ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
x + y = 36
∴ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
x = y + 4
ਅਤੇ x + y = 36
x = y + 4 …(1)
y = 0 ਨੂੰ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = 0 + 4 = 4
y = -4 ਨੂੰ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = – 4 + 4 = 0
y = 16 ਨੂੰ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = 16 + 4 = 20
ਸਾਰਣੀ

ਬਿੰਦੁਆਂ A (4, 0), B (0, – 4), C (20, 16) ਨੂੰ ਆਲੇਖਿਤ ਕਰਨ ਤੇ ਅਤੇ ਉਹਨਾਂ ਨੂੰ ਮਿਲਾਉਂਦੇ ਹੋਏ ਰੇਖਾ ਖਿੱਚਣ ‘ਤੇ ਸਾਨੂੰ ਸਮੀਕਰਣ x = y + 4 ਦਾ ਆਲੇਖ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x + y = 36
x = 36 – y …..(2)
y = 12 ਨੂੰ (2) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = 36 – 12 = 24

ਆਲੇਖ ਤੋਂ ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਕਿ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਬਿੰਦੂ C (20, 16) ਤੇ ਮਿਲਦਾ ਹੈ ।
∴ C (20, 16) ਭਾਵ x = 20 ਅਤੇ y = 16 ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦੇ ਜੋੜੇ ਦਾ ਹੱਲ ਹੈ ।
∴ ਬਾਗ ਦੀ ਲੰਬਾਈ = 20 ਮੀ.
ਬਾਗ ਦੀ ਚੌੜਾਈ = 16 ਮੀ. ||
y = 24 ਨੂੰ (2) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = 36 – 24 = 12
y = 16 ਨੂੰ (2) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = 36 – 16 = 20
ਸਾਰਣੀ

ਬਿੰਦੂਆਂ D (24, 12), E ( 12, 24), C (20, 16) ਨੂੰ ਆਲੇਖਿਤ ਕਰਨ ‘ਤੇ ਉਹਨਾਂ ਨੂੰ ਮਿਲਾਉਂਦੇ ਹੋਏ ਰੇਖਾ ਖਿੱਚਣ ‘ਤੇ ਸਾਨੂੰ ਸਮੀਕਰਣ x + y = 36 ਦਾ ਆਲੇਖ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
ਇੱਕ ਹੋਰ ਵਿੱਧੀ
ਮੰਨ ਲਉ ਬਾਗ ਦੀ ਚੌੜਾਈ = x ਮੀ.
ਬਾਗ ਦੀ ਲੰਬਾਈ = (x + 4) ਮੀ.
ਬਾਗ ਦਾ ਪਰਿਮਾਪ = 2 ਲੰ: + ਚੌ:]
= 2 [x + x + 4] ਮੀ.
= 2 [2x + 4] ਮੀ.
∴ ਬਾਗ ਦਾ ਅਰਧ ਪਰਿਮਾਪੁ = (2x + 4)
ਪ੍ਰਸ਼ਨ ਅਨੁਸਾਰ
2x + 4 = 36
ਜਾਂ 2x = 36 – 4
ਜਾਂ 2x = 32
ਜਾਂ x = \(\frac{32}{2}\) = 16
∴ ਬਾਗ ਦੀ ਚੌੜਾਈ = 16 ਮੀ.
ਬਾਗ ਦੀ ਲੰਬਾਈ = (16 + 4) ਮੀ.
= 20 ਮੀ.

6. ਇਕ ਰੇਖੀ ਸਮੀਕਰਣ 2x + 3y – 8 = 9 ਦਿੱਤੀ ਗਈ । ਹੈ । ਦੋ ਚਲਾਂ ਵਿੱਚ ਇਕ ਇਸ ਤਰ੍ਹਾਂ ਦੀ ਰੇਖੀ ਸਮੀਕਰਣ ਲਿਖੋ ਤਾਂ ਕਿ ਪ੍ਰਾਪਤ ਜੋੜੇ ਦਾ ਜਿਮਾਇਤੀ ਰੂਪ

ਪ੍ਰਸ਼ਨ (i).
ਕੱਟਦੀਆਂ ਰੇਖਾਵਾਂ ਹੋਣ ।
ਉੱਤਰ:
ਸਥਿਤੀ (i) ਕੱਟਦੀਆਂ ਰੇਖਾਵਾਂ
ਦਿੱਤੀ ਹੋਈ ਰੇਖੀ ਸਮੀਕਰਣ ਹੈ :
2x + 3y – 8 = 0 ….(1)
ਇੱਥੇ ਕਾਟਵੀਂ ਰੇਖਾਵਾਂ ਦੀ ਸ਼ਰਤਾਂ ਨੂੰ ਪੂਰਾ ਕਰਨ ਲਈ ਅਨੇਕ ਮੁੱਲ ਹਨ ।
ਭਾਵ \(\frac{a_{1}}{a_{2}}\) ≠ \(\frac{b_{1}}{b_{2}}\) ≠ \(\frac{c_{1}}{c_{2}}\)
ਇਨ੍ਹਾਂ ਵਿੱਚੋਂ ਇੱਕ ਹੈ ।
3x – 2y – 6 = 0 ….(2)
ਰੇਖੀ ਸਮੀਕਰਣਾਂ ( 1 ) ਅਤੇ (2) ਦਾ ਆਲੇਖ ਖਿੱਚੋ ।
2x + 3y – 8 = 0
ਜਾਂ 2x = 8 – 3y
ਜਾਂ x = \(\frac{8-3y}{2}\) …… (3)
y = 0 ਨੂੰ (3) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = \(\frac{8-30}{2}\) = \(\frac{8}{2}\) = 4
y = – 2 ਨੂੰ (3) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = \(\frac{8-3(-2)}{2}\) = \(\frac{14}{2}\) = 7
y = 2 ਨੂੰ (3) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = \(\frac{8-3×2}{2}\) = \(\frac{8-6}{2}\) = \(\frac{2}{2}\) = 1
ਸਾਰਣੀ

ਬਿੰਦੁਆਂ A (4, 0), B (7, – 2), C (1, 2) ਨੂੰ ਆਲੇਖਿਤ ਕਰਨ ‘ਤੇ ਅਤੇ ਉਹਨਾਂ ਨੂੰ ਮਿਲਾਉਣ ‘ਤੇ ਸਾਨੂੰ ਰੇਖਾ ਸਮੀਕਰਣ 2x + 3y – 8 = 9 ਦਾ ਆਲੇਖ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
3x – 2y – 6 = 0
ਜਾਂ 3x = 6 + 2y
ਜਾਂ x = \(\frac{6+2y}{3}\) …(4)
y = 0 ਨੂੰ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = \(\frac{6+2×0}{3}\) = \(\frac{6}{3}\) = 2
y = – 3 ਨੂੰ (4) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = \(\frac{6+2(-3)}{3}\)
= \(\frac{6-6}{3}\) = 0
y = 3 ਨੂੰ (4) ਵਿਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = \(\frac{6+2×3}{3}\) = \(\frac{6+6}{3}\)
= \(\frac{12}{3}\) = 4

ਸਾਰਣੀ

ਬਿੰਦੂਆਂ D (2, 0), E (0, -3), F (4, 3) ਨੂੰ ਆ ਖਿਤ ਕਰਨ ‘ਤੇ ਅਤੇ ਉਹਨਾਂ ਨੂੰ ਮਿਲਾਉਂਦੇ ਹੋਏ ਰੇਖਾ ਖਿਚਣ ‘ਤੇ ਸਾਨੂੰ ਸਮੀਕਰਣ’ 3x – 2y – 6 = 0 ਦਾ ਆਲੇਖ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ !
ਆਲੇਖ ਤੋਂ ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਕਿ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਬਿੰਦੂ G ਉੱਤੇ ਕੱਟਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ (ii).
ਸਮਾਂਤਰ ਰੇਖਾਵਾਂ ਹੋਣ ।
ਉੱਤਰ:
ਸਥਿਤੀ (ii) ਸਮਾਂਤਰ ਰੇਖਾਵਾਂ ਦਿੱਤੀ ਹੋਈ ਰੇਖੀ ਸਮੀਕਰਣ ਹੈ :
2x + 3y – 8 = 9 …(1)
ਇੱਥੇ ਦੋ ਚਲਾਂ ਵਾਲੀਆਂ ਹੋਰ ਵੀ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਹੋ
ਸਕਦੀਆਂ ਹਨ ਜੋ ਸਮਾਂਤਰ ਰੇਖਾਵਾਂ ਦੀ ਸ਼ਰਤ ਨੂੰ ਪੂਰਾ ਕਰਦੀਆਂ ਹਨ ਭਾਵ
\(\frac{a_{1}}{a_{2}}\) = \(\frac{b_{1}}{b_{2}}\) ≠ \(\frac{c_{1}}{c_{2}}\)
ਉਨ੍ਹਾਂ ਵਿੱਚੋਂ ਇੱਕ ਹੈ ।
2x + 3y – 5 = 0 ….(2)
ਹੁਣ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ( 1 ) ਅਤੇ (2) ਦਾ ਆਲੇਖ ਖਿੱਚੋ । ਰੇਖੀ ਸਮੀਕਰਣ 2x + 3 – 8 = 0 ਲਈ ਆਲੇਖ ਹੈ :
ਸਾਰਣੀ

2x + 3y – 5 = 0
ਜਾਂ 2x = 5 – 3y
ਜਾਂ x = \(\frac{5-3y}{2}\) …(3)
y = 0 ਨੂੰ (3) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = \(\frac{5-3×0}{2}\) = \(\frac{5}{2}\) = 2.5

ਸਾਰਣੀ

ਬਿੰਦੂਆਂ G (2.5, 0), H (- 2, 3), I (7, – 3) ਨੂੰ ਆਲੇਖਿਤ ਕਰਨ ‘ਤੇ ਅਤੇ ਮਿਲਾਉਂਦੇ ਹੋਏ ਰੇਖਾ ਖਿੱਚਣ ‘ਤੇ ਸਾਨੂੰ ਸਮੀਕਰਣ 2x + 3y – 5 = 0 ਦਾ ਆਲੇਖ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
y = 3 ਨੂੰ (3) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
y = \(\frac{5-3×3}{2}\) = \(\frac{5-9}{2}\) = \(\frac{-4}{2}\) = -2
y = -3 ਨੂੰ (3) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = \(\frac{5-3(-3)}{2}\) = \(\frac{5+9}{2}\) = \(\frac{14}{2}\)
= 7

ਪ੍ਰਸ਼ਨ (iii).
ਸੰਪਾਤੀ ਰੇਖਾਵਾਂ ਹੋਣ ।
ਉੱਤਰ:
ਸਥਿਤੀ (iii) ਸੰਪਾਤੀ ਰੇਖਾਵਾਂ ਲਈ
ਦਿੱਤੀ ਹੋਈ ਸਮੀਕਰਣ
2x + 3y – 8 = 0 ….(1)
ਦੋ ਚਲਾਂ ਵਿੱਚ ਅਜਿਹੇ ਹੋਰ ਵੀ ਰੇਖੀ ਸਮੀਕਰਣ ਹੋ ਸਕਦੇ ਹਨ ਜੋ ਸੰਪਾਤੀ ਰੇਖਾਵਾਂ ਦੀਆਂ ਸ਼ਰਤਾਂ ਨੂੰ ਸੰਤੁਸ਼ਟ ਕਰਦੇ ਹੋਣ ।
ਭਾਵ \(\frac{a_{1}}{a_{2}}\) = \(\frac{b_{1}}{b_{2}}\) = \(\frac{c_{1}}{c_{2}}\)
ਉਨ੍ਹਾਂ ਵਿਚ ਇਸ ਪ੍ਰਕਾਰ ਹੈ ।
6x + 9y – 24 = 0 ….(2)

ਹੁਣ ਰੇਖੀ (1) ਅਤੇ (2) ਦਾ ਆਲੇਖ ਖਿਚਣ ‘ਤੇ
ਰੇਖੀ ਸਮੀਕਰਣ (2) ਲਉ ॥
6x + 9y – 24 = 0
ਜਾਂ 3 [2x + 3y – 8] = 0
ਜਾਂ 2 + 3y – 8 = 0
∴ ਦੋਵਾਂ ਵਿਚ ਬਿੰਦੂ ਇਕ ਸਮਾਨ ਹਨ ਇਸ ਲਈ ਦੋਵੇਂ ਸਮੀਕਰਣਾਂ ਇਕ ਹੀ ਰੇਖਾ ਹਨ ।

ਪ੍ਰਸ਼ਨ 7.
ਸਮੀਕਰਣਾਂ x – y + 1 = 0 ਅਤੇ 3x + 2y – 12 = 0 ਦਾ ਗ੍ਰਾਫ਼ ਖਿੱਚੋ । x-ਧੁਰੇ ਅਤੇ ਇਨ੍ਹਾਂ ਰੇਖਾਵਾਂ ਨਾਲ ਬਣ ਤ੍ਰਿਭੁਜ ਦੇ ਸਿਖ਼ਰਾਂ ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਪਤਾ ਕਰੋ ਅਤੇ ਤਿਭੁਜ ਆਕਾਰ ਨੂੰ ਛਾਇਆ-ਅੰਕਿਤ (Shade) ਕਰੋ ।
ਹੱਲ :
ਇੱਕ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ ।
x – y + 1 = 0
ਅਤੇ 3x + 2y – 12 = 0
x – y + 1 = 0
ਜਾਂ x = y – 1 ……(1)
y = 0 ਨੂੰ (1) ਵਿਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = 0 – 1 = – 1
y = 3 ਨੂੰ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = 3 – 1 = 2
y = 1 ਨੂੰ ( 3 ) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = 1 – 1 = 0
ਸਾਰਣੀ

ਬਿੰਦੁਆਂ A -1, 0), B (2, 3), C (0, 1) ਨੂੰ ਆਲੇਖਿਤ ਕਰਨ ‘ਤੇ ਉਹਨਾਂ ਨੂੰ ਮਿਲਾਉਂਦੇ ਹੋਏ ਰੇਖਾ ਖਿੱਚਣ ‘ਤੇ ਸਾਨੂੰ ਸਮੀਕਰਣ x – y + 1 = 0 ਦਾ ਆਲੇਖ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
ਜਾਂ 3x + 2y – 12 = 0
3x = 12 – 2y
x = \(\frac{12-2y}{3}\) …….(2)

y = 0 ਨੂੰ (2) ਵਿੱਚ ਰੱਖਣ ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = \(\frac{12-2×0}{3}\) = \(\frac{12}{3}\) = 4
y = 3 ਨੂੰ (2), ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = \(\frac{12-2×3}{3}\) = \(\frac{12-6}{3}\) = \(\frac{6}{3}\) = 2
y = 6 ਨੂੰ (2) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
x = \(\frac{12-2×6}{3}\) = \(\frac{12-12}{3}\) = 0
ਸਾਰਣੀ

ਬਿੰਦੂਆਂ D (4, 0), B (2, 3), E (0, 6) ਨੂੰ ਆਲੇਖਿਤ ਕਰਨ ‘ਤੇ ਉਨ੍ਹਾਂ ਨੂੰ ਮਿਲਾਉਂਦੇ ਹੋਏ ਰੇਖਾ ਖਿੱਚਣ ‘ਤੇ ਸਾਨੂੰ ਸਮੀਕਰਣ 3x +2y – 12 = 0 ਦਾ ਆਲੇਖ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦੇ ਜੋੜੇ x-ਧੁਰੇ ਦੁਆਰਾ ਬਣਾਏ ਗਏ ਤਿਭੁਜ ਦੇ ਸਿਖ਼ਰਾਂ ਦੇ ਆਲੇਖ ਨੂੰ ਦਿਖਾਇਆ ਗਿਆ ਹੈ ।
∴ △ABD ਇਸ ਪ੍ਰਕਾਰ ਬਣੀ ਤ੍ਰਿਭੁਜ ਹੈ ।
△ABD ਦੇ ਸਿਖ਼ਰ ਹਨ : A (-1, 0), B (2, 3) ਅਤੇ D (4, 0).
ਹੁਣ, ਅਧਾਰ AD ਦੀ ਲੰਬਾਈ = AO + OD
= 1+ 4 = 5 ਇਕਾਈਆਂ
ਲੰਬ BF ਦੀ ਲੰਬਾਈ = 3 ਇਕਾਈਆਂ
∴ △ABD ਦਾ ਖੇਤਰਫਲ = \(\frac{1}{2}\) × ਅਧਾਰ × ਲੰਬ
= \(\frac{1}{2}\) × AD × BF
= (\(\frac{1}{2}\) × 5 × 3)
ਵਰਗ ਇਕਾਈਆਂ |
= \(\frac{15}{2}\) = 7.5
ਵਰਗ ਇਕਾਈਆਂ

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 3 ਦੋ ਚਲਾਂ ਵਿੱਚ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦੇ ਜੋੜੇ Ex 3.7 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 3 ਦੋ ਚਲਾਂ ਵਿੱਚ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦੇ ਜੋੜੇ Exercise 3.7

ਪ੍ਰਸ਼ਨ 1.
ਦੋ ਦੋਸਤਾਂ ਹਨੀ ਅਤੇ ਸੰਨੀ ਦੀ ਉਮਰ ਵਿਚ 3 ਸਾਲ ਦਾ ਅੰਤਰ ਹੈ । ਹਨੀ ਦੇ ਪਿਤਾ ਹਰਮਿੰਦਰ ਦੀ ਉਮਰ ਹਨੀ ਦੀ ਉਮਰ ਤੋਂ ਦੁੱਗਣੀ ਹੈ ਅਤੇ ਸੰਨੀ ਦੀ ਉਮਰ ਆਪਣੀ ਭੈਣ ਨੂੰ ਤੋਂ ਦੁੱਗਣੀ ਹੈ । ਗੁਨੂੰ ਅਤੇ ਹਰਮਿੰਦਰ ਦੀ ਉਮਰ ਵਿੱਚ 30 ਸਾਲ ਦਾ ਅੰਤਰ ਹੈ । ਹਨੀ ਅਤੇ ਸੰਨੀ ਦੀ ਉਮਰ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ ਹਨੀ ਦੀ ਉਮਰ = x ਸਾਲ
ਅਤੇ ਸੰਨੀ ਦੀ ਉਮਰ = y ਸਾਲ
ਹਰਮਿੰਦਰ ਦੀ ਉਮਰ = 2x ਸਾਲ
ਗੁਨੂੰ ਦੀ ਉਮਰ = \(\frac{1}{2}\)y ਸਾਲ
ਪਹਿਲੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
ਹਨੀ ਦੀ ਉਮਰ – ਸੰਨੀ ਦੀ ਉਮਰ = 3 ਸਾਲ
x – y = 3 …(1)
ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
ਹਰਮਿੰਦਰ ਦੀ ਉਮਰ – ਗਨੂੰ ਦੀ ਉਮਰ = 30 ਸਾਲ
2x – \(\frac{y}{2}\) = 30
ਜਾਂ \(\frac{4x-y}{2}\) = 30
ਜਾਂ 4x – y = 60 ….(2)
ਹੁਣ, (2) – (1) ਤੋਂ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।

x ਦਾ ਮੁੱਲ (1) ਵਿੱਚ ਤਿਸਥਾਪਿਤ ਕਰਨ ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
19 – y = 3
ਜਾਂ -y = 3 – 19
ਜਾਂ -y = – 16
ਜਾਂ y = 16
ਹਨੀ ਦੀ ਉਮਰ = 19 ਸਾਲ
ਸੰਨੀ ਦੀ ਉਮਰ =16 ਸਾਲ

ਪ੍ਰਸ਼ਨ 2.
ਇਕ ਮਿੱਤਰ ਦੂਸਰੇ ਨੂੰ ਕਹਿੰਦਾ ਹੈ ਕਿ, “ਜੇਕਰ | ਤੁਸੀਂ ਮੈਨੂੰ ਇੱਕ ਸੌ ਰੁਪਏ ਦੇ ਦਿਉ ਤਾਂ ਮੇਰੇ ਕੋਲ ਤੁਹਾਡੇ ਨਾਲੋਂ ਦੋ ਗੁਣਾ ਪੈਸੇ ਹੋ ਜਾਣਗੇ | ਦੂਸਰਾ ਕਹਿੰਦਾ ਹੈ ਕਿ | ‘‘ਜੇਕਰ ਤੁਸੀਂ ਮੈਨੂੰ ₹ 10 ਦੇ ਦਿਉ ਤਾਂ ਮੈਂ ਤੁਹਾਡੇ ਤੋਂ ਛੇ ਗੁਣਾ ਅਮੀਰ ਹੋ ਜਾਵਾਂਗਾ ” ਪਤਾ ਕਰੋ ਉਹਨਾਂ ਕੋਲ ਕੁਮਵਾਰ ਕਿੰਨੇ ਪੈਸੇ ਹਨ ? (ਭਾਸ਼ਕਰ II ਦੇ ਬੀਜ ਗਣਿਤ ਤੋਂ)
[ਸੰਕੇਤ : x + 100 = 2(y – 100),
y + 10 = 6 (x – 10)].
ਹੱਲ:
ਮੰਨ ਲਉ ਇਕ ਮਿੱਤਰ ਕੋਲ ਪੈਸੇ = ₹ x
ਦੂਸਰੇ ਮਿੱਤਰ ਕੋਲ ਪੈਸੇ = ₹ y
ਪਹਿਲੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
x + 100 = 2 (y – 100)
ਜਾਂ x + 100 = 2y – 200
ਜਾਂ x – 2y = – 200 – 100
ਜਾਂ x – 2y = – 300 ….(1)
ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
y + 10 = 6 (x – 10)
ਜਾਂ y + 10 = 6x – 60
ਜਾਂ 6x – y = 10 + 60
ਜਾਂ 6x – y = 70 ….(2)
(1) ਨੂੰ 6 ਨਾਲ ਗੁਣਾ ਕਰਨ ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
6x – 12y = – 1800 …(3)
ਹੁਣ (3) – (2) ਤੋਂ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :

y ਨੂੰ (2) ਨਾਲ ਗੁਣਾ ਕਰਨ ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
6x – 170 = 70
ਜਾਂ 6x = 70 + 170
ਜਾਂ 6x = 240
ਜਾਂ x = \(\frac{240}{6}\) = 40
ਪਹਿਲੇ ਮਿੱਤਰ ਕੋਲ ਪੈਸੇ : ₹ 40
ਦੁਸਰੇ ਮਿੱਤਰ ਕੋਲ ਪੈਸੇ : ₹ 170 ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਇੱਕ ਰੇਲਗੱਡੀ ਕੁੱਝ ਦੂਰੀ ਇਕ ਸਮਾਨ ਚਾਲ ਨਾਲ ਤੈਅ ਕਰਦੀ ਹੈ । ਜੇਕਰ ਗੱਡੀ ਦੀ ਗਤੀ 10 km/h ਵਧਾ ਦਿੱਤੀ ਜਾਵੇ ਤਾਂ ਉਹ ਉੱਨੀ ਦੂਰੀ ਲਈ 2 ਘੰਟੇ ਘੱਟ ਸਮਾਂ ਲਵੇਗੀ ਅਤੇ ਜੇਕਰ ਰੇਲਗੱਡੀ ਦੀ ਗਤੀ 10 km/h ਘਟਾ ਦਿੱਤੀ ਜਾਵੇ ਤਾਂ ਉਹ ਉੱਨੀ ਦੂਰੀ ਲਈ 3 ਘੰਟੇ ਵੱਧ ਸਮਾਂ ਲਵੇਗੀ 1 ਰੇਲਗੱਡੀ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਦੂਰੀ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ ਰੇਲਗੱਡੀ ਦੀ ਚਾਲ = x ਕਿ.ਮੀ. /ਘੰਟਾ
ਰੇਲਗੱਡੀ ਦੁਆਰਾ ਲਿਆ ਗਿਆ ਸਮਾਂ = y ਘੰਟਾ
∴ ਰੇਲਗੱਡੀ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਦੂਰੀ
= ਚਾਲ × ਸਮਾਂ
= (xy) ਕਿਮੀ
ਪਹਿਲੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
(x + 10) (y – 2) = xy
ਜਾਂ y – 2x + 10y – 20 = xy
ਜਾਂ – 2x + 10y – 20 = 0
ਜਾਂ x – 5y + 10 = 0 ……(1)
ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
(x – 10) (y + 3) = xy
ਧੀ xy + 3x – 10y – 30 = xy
ਜਾਂ 3x – 10y – 30 = 0 …(2)
(1) ਨੂੰ 3 ਨਾਲ ਗੁਣਾ ਕਰਨ ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
3x – 15y + 30 = 0 ….(3)
ਹੁਣ, (3) – (2) ਤੋਂ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :

y ਦਾ ਇਹ ਮੁੱਲ (1) ਵਿੱਚ ਰੱਖਣ ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
x – 5 × 12 + 10 = 0
ਜਾਂ x – 60 + 10 = 0
ਜਾਂ x – 50 = 0
ਜਾਂ x = 50
∴ ਰੇਲਗੱਡੀ ਦੀ ਚਾਲ = 50 ਕਿ.ਮੀ. /ਘੰਟਾ
ਰੇਲਗੱਡੀ ਦੁਆਰਾ ਲਿਆ ਗਿਆ ਸਮਾਂ = 12 ਬੰਟੇ
ਰੇਲਗੱਡੀ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਦੂਰੀ
= (50 × 12) ਕਿ.ਮੀ.
= 600 ਕਿ.ਮੀ.

ਪ੍ਰਸ਼ਨ 4.
ਇਕ ਜਮਾਤ ਵਿੱਚ ਵਿਦਿਆਰਥੀਆਂ ਨੂੰ ਪੰਗਤੀਆਂ ਵਿਚ ਖੜਾ ਕਰਨਾ ਹੈ । ਜੇਕਰ ਪੰਗਤੀਆਂ ਵਿਚ 3 ਵਿਦਿਆਰਥੀ ਵੱਧ ਹੁੰਦੇ ਤਾਂ ਇੱਕ ਪੰਗਤੀ ਘੱਟ ਹੁੰਦੀ । ਜੇਕਰ ਪੰਗਤੀ ਵਿਚ 3 ਵਿਦਿਆਰਥੀ ਘੱਟ ਹੁੰਦੇ, ਤਾਂ 2 ਪੰਗਤੀਆਂ ਵੱਧ ਬਣਦੀਆਂ ਜਮਾਤ ਵਿੱਚ ਵਿਦਿਆਰਥੀਆਂ ਦੀ ਗਿਣਤੀ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਉ ਹਰ ਇੱਕ ਪੰਗਤੀ ਵਿਚ ਵਿਦਿਆਰਥੀਆਂ ਦੀ ਗਿਣਤੀ = x
ਅਤੇ ਪੰਗਤੀਆਂ ਦੀ ਗਿਣਤੀ = y
ਜਮਾਤ ਵਿਚ ਵਿਦਿਆਰਥੀਆਂ ਦੀ ਗਿਣਤੀ = xy
ਪਹਿਲੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
(x + 3) (y – 1) = xy
ਜਾਂ xy – x + 3y – 3 = xy
ਜਾਂ -x + 3y – 3 = 0
ਜਾਂ x – 3y + 3 = 0 …(1)
ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
(x – 3) (y + 2) = xy
ਜਾਂ xy + 2x – 3y – 6 = xy
ਜਾਂ 2x + 3y – 6 = 0 …(2)
ਹੁਣ, (2) – (1) ਤੋਂ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :

x ਦਾ ਮੁੱਲ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
9 – 3y + 3 = 0
ਜਾਂ -3y + 12 = 0
ਜਾਂ -3y = – 12
ਜਾਂ y = \(\frac{12}{3}\) = 4
∴ ਹਰ ਇੱਕ ਪੰਗਤੀ ਵਿਚ ਵਿਦਿਆਰਥੀਆਂ ਦੀ ਗਿਣਤੀ = 9
ਪੰਗਤੀਆਂ ਦੀ ਗਿਣਤੀ = 4
ਜਮਾਤ ਵਿਚ ਵਿਦਿਆਰਥੀਆਂ ਦੀ ਗਿਣਤੀ
= 9 × 4 = 36

ਪ੍ਰਸ਼ਨ 5.
ਇੱਕ △ABC ਵਿੱਚ ∠C = 3 ∠B = 2 (∠A + ∠B) ਹੈ ।ਤ੍ਰਿਭੁਜ ਦੇ ਤਿੰਨੋਂ ਕੋਣ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਇਕ △ABC ਵਿੱਚ
∠C = 3∠B = 2 (∠A + ∠B)
I II III
II ਅਤੇ III, ਤੋਂ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
3∠B = 2 (∠A + ∠B)
ਜਾਂ 3∠B = 2∠A + 2∠B
ਜਾਂ 3∠B – 2∠B = 2∠A
ਜਾਂ ∠B = 2∠A
I ਅਤੇ II, ਤੋਂ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
∠C = 3∠B
ਜਾਂ ∠C = 3(2∠A)
[(1) ਦਾ ਪ੍ਰਯੋਗ ਕਰਨ ਤੇ ]
ਜਾਂ ∠C = 6∠A …..(2)
ਤਿਭੁਜ ਦੇ ਤਿੰਨਾਂ ਕੋਣਾਂ ਦਾ ਜੋੜ 180° ਹੁੰਦਾ ਹੈ ।.
∠A + ∠B + ∠C = 180°
ਜਾਂ ∠A + 2∠A + 6∠A = 180°
ਜਾਂ 9∠A = 180°
ਜਾਂ ∠A = \(\frac{180^{\circ}}{9}\) = 20°
∠A = 20°; ∠B = 2 × 20° = 40°
∠C = 6 × 20° = 120°.

ਪ੍ਰਸ਼ਨ 6.
ਸਮੀਕਰਣਾਂ 5r – y = 5 ਅਤੇ 3x – y = 3 ਦੇ ਗ੍ਰਾਫ ਖਿੱਚੋ । ਇਹਨਾਂ ਰੇਖਾਵਾਂ ਅਤੇ y-ਧੁਰੇ ਨਾਲ ਬਣੇ ਤਿਭਜ ਦੇ ਸਿਖਰਾਂ ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਅਤੇ ਤਿਭੁਜ ਦ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਦਿੱਤਾ ਹੋਇਆ ਰੇਖੀ ਸਮੀਕਰਣ ਜੋੜਾ ਹੈ :
5x – y = 5 ਅਤੇ 3x – y = 3
5x – y = 5
ਜਾਂ 5x = 5 + y
ਜਾਂ x = \(\frac{5+y}{5}\) …(1)
y = 0 ਨੂੰ (1), ਵਿੱਚ ਰੱਖਣ ’ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
x = \(\frac{5+0}{5}\) = \(\frac{5}{5}\) = 1
y = -5 ਨੂੰ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
x = \(\frac{5-5}{5}\) = \(\frac{0}{5}\) = 0
y = 5 ਨੂੰ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
x = \(\frac{5+5}{5}\) = \(\frac{10}{5}\) = 2
ਸਾਰਣੀ

ਬਿੰਦੁਆਂ A (1, 0); B (0, – 5); C (2, 5) ਦੇ ਗਾਫ਼ ਨੂੰ ਆਲੇਖਿਤ ਕਰਨ ਤੇ ਸਾਨੂੰ ਸਮੀਕਰਣ 5x – y = 5 ਦੀ ਰੇਖਾ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ ।
ਅਤੇ 3x – y = 3
ਜਾਂ 3x = 3 + y
ਜਾਂ x = \(\frac{3+y}{3}\) ….(2)
y = 0 ਨੂੰ (2) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
x = \(\frac{3+0}{3}\) = \(\frac{3}{3}\) = 1
y = -3 ਨੂੰ (2) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
x = \(\frac{3-3}{3}\) = \(\frac{0}{3}\) = 0
y = 3 ਨੂੰ (2) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
x = \(\frac{3+3}{3}\) = \(\frac{6}{3}\) = 2

ਬਿੰਦੁਆਂ A (1, 0); D (0, – 3); E (2, 3) ਨੂੰ ਗ੍ਰਾਫ਼ ਪੇਪਰ ਤੇ ਆਲੇਖਿਤ ਕਰਨ ਤੇ ਸਾਨੂੰ ਸਮੀਕਰਣ 3x – y = 3 ਦੀ ਰੇਖਾ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ ।
ਗ੍ਰਾਫ਼ ਤੋਂ ਇਹ ਸਪੱਸ਼ਟ ਹੈ ਕਿ ਦਿੱਤੀਅ ਹੋਈ ਹਥਾਵਾਂ -A (1, 0) ਉੱਤੇ ਕੱਟਦੀਆਂ ਹਨ ।y- ਧੂਰੇ ਤੇ ਬਣੀ △ABD ਨੂੰ ਛਾਇਆ ਅੰਕਿਤ ਕੀਤਾ ਗਿਆ ਹੈ । △ABD ਦੇ ਸਿਖ਼ਰਾਂ ਦੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਹਨ : A (1, 0); B (0, – 5) ਅਤੇ D (0, – 3)
ਸਾਰਣੀ

7. ਹੇਠਾਂ ਦਿੱਤੇ ਰੇਖੀ ਸਮੀਕਰਣ ਜੋੜਿਆਂ ਨੂੰ ਹੱਲ ਕਰੋ :

ਪ੍ਰਸ਼ਨ (i).
px + qy = p – q
qx – py = p + q
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣ ਜੋੜਾ ਹੈ :
px + qy = p – q ..(1)
ਅਤੇ qx – py = p + q …(2)
(1) ਨੂੰ q ਨਾਲ ਅਤੇ (2) ਨੂੰ p ਨਾਲ ਗੁਣਾ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :

ਜਾਂ y = -1
y ਦਾ ਇਹ ਮੁੱਲ (1) ਵਿਚ ਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ | ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
px + q(-1) = p – qx
ਜਾਂ px – q = p – q
ਜਾਂ px = p – q + q
ਜਾਂ px = p
ਜਾਂ x = 1
∴ x = 1 ਅਤੇ y = – 1

ਪ੍ਰਸ਼ਨ (ii).
ax + by = c
bx + ay = 1 + c
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣ ਜੋੜਾ ਹੈ :
ax + by = c
ਅਤੇ bx + ay = 1 + c
ਜਾਂ ax + by – c = 0
ਅਤੇ bx + ay – (1 + c) = 0

I ਅਤੇ III ਤੋਂ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :

ਪ੍ਰਸ਼ਨ (iii).
\(\frac{x}{a}\) – \(\frac{y}{b}\) =0
ax + by = a² + b²
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣ ਜੋੜਾ ਹੈ :
\(\frac{x}{a}\) – \(\frac{y}{b}\) = 0
ਜਾਂ \(\frac{bx-ay}{ab}\) = 0
ਜਾਂ bx – ay = 0 ….(1)
ਅਤੇ ax + by = a² + b²
ਜਾਂ ax + by = (a² + b²) = 0 …..(2)
ਤਿਰਛੀ ਗੁਣਾ ਵਿਧੀ ਦੁਆਰਾ

I ਅਤੇ III ਤੋਂ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
\(\frac{x}{a}\) = \(\frac{1}{1}\) ⇒ x = a
II ਅਤੇ III ਤੋਂ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
\(\frac{y}{b}\) = \(\frac{1}{1}\) ⇒ y = b
x = a ਅਤੇ y = b

ਪ੍ਰਸ਼ਨ (iv).
(a – b)x + (a + b) y = a² – 2ab – b²
(a + b) (x + y) = a² + b²
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣ ਜੋੜਾ ਹੈ :
(a – b)x + (a + b) y = a² – 2ab – b²
ਜਾਂ ax – bx + ay + by = a² – 2ab – b² …(1)
ਅਤੇ (a + b) (x + y) = a² + b²
ਜਾਂ ax + bx + ay + by = a² + b² …(2)
ਹੁਣ (1) – (2) ਤੋਂ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :

x ਦਾ ਮੁੱਲ (1) ਵਿੱਚ ਰੱਖਣ ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
(a – b) (a + b) + (a + b) y = a² – 2ab – b²
ਜਾਂ a² – b² + (a + b) y = a² – 2ab – b²
ਜਾਂ (a + b) y = a² – 2ab – b² – a² + b²
ਜਾਂ (a + b) y = – 2ab
ਜਾਂ y = \(\frac{-2ab}{a+b}\)
x = a + b ਅਤੇ y = \(\frac{-2ab}{a+b}\)

ਪ੍ਰਸ਼ਨ (v).
152x – 378y = -74
– 378x + 152y =- 604
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣ ਜੋੜਾ ਹੈ :
152x – 378y = – 74
ਅਤੇ – 378x + 152y = – 604
ਜਾਂ 76x – 189y + 37 = 0
ਅਤੇ – 189x + 76y + 302 = 0
ਤਿਰਛੀ ਗੁਣਾ ਵਿਧੀ ਦੁਆਰਾ

⇒ y = 1
x = 2 ਅਤੇ y = 1

ਪ੍ਰਸ਼ਨ 8.
ABCD ਇੱਕ ਚੱਕਰੀ ਚਤੁਰਭੁਜ ਹੈ । ਇਸ ਚੱਕਰੀ ਚਤੁਰਭੁਜ ਦੇ ਕੋਣ ਪਤਾ ਕਰੋ । (ਦੇਖੋ ਚਿੱਤਰ)

ਹੱਲ:
ਚੱਕਰੀ ਚਤੁਰਭੁਜ ABCD ਵਿੱਚ
∠A = (4y + 20); ∠B = 3y – 5;
∠C = 4x ਅਤੇ ∠D = 7x + 5
∠C = 4x = 4 x 15 = 60°
∠D = 7x + 5 = 7 x 15 + 5 = 110°
∠A = 120°, ∠B = 70°; ∠C = 60°
ਅਤੇ ∠D = 110°
∴ ∠A + ∠C = 180°,
ਜਾਂ 4y + 20 + (4x) = 180°
ਜਾਂ 4x + 4y = 180° – 20°
ਜਾਂ 4x + 4y = 160
ਜਾਂ x + y = 40
ਜਾਂ y = 40 – x ….(1)
ਅਤੇ ∠B + ∠D = 180°
ਜਾਂ 3y – 5 + (7x + 5) = 180°
ਜਾਂ 3y – 5 + 7x + 5 = 180°
ਜਾਂ 7x + 3y = 180° …(2)
(1) ਤੋਂy ਦਾ ਮੁੱਲ (2) ਵਿਚ ਰੱਖਣ ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
7x + 3 (40 – x) = 180°
ਜਾਂ 7x + 120 – 3x = 180
ਜਾਂ 4x = 180 – 120
ਜਾਂ 4x = 60
ਜਾਂ x = \(\frac{60}{4}\) = 15
x ਦਾ ਇਹ ਮੁੱਲ (1) ਵਿੱਚ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ !
y = 40 – 15 = 25
∴ ∠A = 4y + 20 = 4 × 25 + 20
= 120°
∠B = 3y – 5 = 3 × 25 – 5 = 70°
∠C = 4x = 4 × 15 = 60°
∠D = 7x + 5 = 7 × 15 + 5 = 110°
∴ ∠A = 120°, ∠B = 70°; ∠C = 60°
ਅਤੇ ∠D = 110°

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 3 ਦੋ ਚਲਾਂ ਵਿੱਚ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦੇ ਜੋੜੇ Ex 3.6 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 3 ਦੋ ਚਲਾਂ ਵਿੱਚ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦੇ ਜੋੜੇ Exercise 3.6

1. ਹੇਠਾਂ ਦਿੱਤੇ ਸਮੀਕਰਣ ਜੋੜਿਆਂ ਨੂੰ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦੇ ਵਿੱਚ ਬਦਲ ਕੇ ਹੱਲ ਕਰੋ :

ਪ੍ਰਸ਼ਨ (i).
\(\frac{1}{2x}\) + \(\frac{1}{3y}\) = 2
\(\frac{1}{3x}\) + \(\frac{1}{2y}\) = \(\frac{13}{6}\)
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ
\(\frac{1}{2x}\) + \(\frac{1}{3y}\) = 2
ਮਤੇ \(\frac{1}{3x}\) + \(\frac{1}{2y}\) = \(\frac{13}{6}\)
\(\frac{1}{x}\) = u, \(\frac{1}{v}\) = v ਮਤੇ ਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ

(1) ਨੂੰ 2 ਨਾਲ ਅਤੇ (2) ਨੂੰ 3 ਨਾਲ ਗੁਣਾ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
6u + 4v = 24 …(3)
ਅਤੇ 6u + 9v = 39 …(4)
ਹੁਣ, (4) – (3) ਤੋਂ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।

v ਦੇ ਇਸ ਮੁੱਲ ਨੂੰ (1) ਵਿਚ ਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
3u + 2 (3) = 12
ਜਾਂ 3u + 6 = 12
ਜਾਂ 3u = 12 – 6 = 6
ਜਾਂ u = \(\frac{6}{3}\) = 2

x = \(\frac{1}{2}\) ਮਤੇ y = \(\frac{1}{3}\)

ਪ੍ਰਸ਼ਨ (ii).
\(\frac{2}{\sqrt{x}}\) + \(\frac{3}{\sqrt{y}}\) = 2
\(\frac{4}{\sqrt{x}}\) – \(\frac{9}{\sqrt{y}}\) = -1
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
\(\frac{2}{\sqrt{x}}\) + \(\frac{3}{\sqrt{y}}\) = 2 ਅਤੇ \(\frac{4}{\sqrt{x}}\) – \(\frac{9}{\sqrt{y}}\) = -1
\(\frac{1}{\sqrt{x}}\) = u ਅਤੇ \(\frac{1}{\sqrt{y}}\) = v ਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ
2u + 3v = 2 ….(1)
ਅਤੇ 4u – 9y = – 1 …(2)
(1) ਨੂੰ 2 ਨਾਲ ਗੁਣਾ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
4u + 6v = 4 …(3)
ਹੁਣ (2) – (3) ਤੋਂ ਸਾਨੂੰ ਮਿਲਦਾ ਹੈ ।

v ਦਾ ਇਹ ਮੁੱਲ (1) ਵਿਚ ਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
2u + 3\(\left(\frac{1}{3}\right)\) = 2
ਜਾਂ 2u + 1 = 2
ਜਾਂ 2u = 2 – 1 = 1
ਜਾਂ u = \(\frac{1}{2}\)

x = 4 ਅਤੇ y = 9

ਪ੍ਰਸ਼ਨ (iii).
\(\frac{4}{x}\) + 3y = 14
\(\frac{3}{x}\) – 4y = 23
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
\(\frac{4}{x}\) + 3y = 14 ਅਤੇ \(\frac{3}{x}\) – 4y = 23
\(\frac{1}{x}\) = v ਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ
4v + 3y = 14 …(1)
ਅਤੇ 3v – 4y = 23 …(2)
(1) ਨੂੰ 3 ਨਾਲ (2) ਨੂੰ 4 ਨਾਲ ਗੁਣਾ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
12v + 9y = 42 ….(3)
ਅਤੇ 12v – 16y = 92 …..(4)
ਹੁਣ, (4) – (3) ਤੋਂ

y ਦਾ ਮੁੱਲ (1) ਵਿੱਚ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
ਜਾਂ 4v + 3 (-2) = 14
ਜਾਂ 4v – 6 = 14
ਜਾਂ 4v = 14 + 6 = 20
ਪਰ \(\frac{1}{x}\) = v
ਜਾਂ x = \(\frac{1}{v}\) = \(\frac{1}{5}\)
x = \(\frac{1}{5}\) ਅਤੇ y = – 2

ਪ੍ਰਸ਼ਨ (iv).
\(\frac{5}{x-1}\) + \(\frac{1}{y-2}\) = 2
\(\frac{6}{x-1}\) – \(\frac{3}{y-2}\) = 1
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
\(\frac{5}{x-1}\) + \(\frac{1}{y-2}\) = 2 ਅਤੇ \(\frac{6}{x-1}\) – \(\frac{3}{y-1}\) = 1
\(\frac{1}{x-1}\) = u ਅਤੇ \(\frac{1}{y-2}\) = v ਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ
5u + v = 2 …(1)
ਅਤੇ 6u – 3v = 1 …(2)
(1) ਨੂੰ 3 ਤੇ ਗੁਣਾ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
15u + 3v = 6 …….3)
ਹੁਣ, (3) + (2) ਤੋਂ ਸਾਨੂੰ ਮਿਲਦਾ ਹੈ ।
15u + 3v = 6
6u – 3v = 1
21u = 7
u = \(\frac{7}{21}\) = \(\frac{1}{3}\)
u ਦੇ ਮੁੱਲ ਨੂੰ (1) ਵਿੱਚ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ | ਮਿਲਦਾ ਹੈ :
5 x \(\frac{1}{3}\) + v = 2
ਜਾਂ v = 2 – \(\frac{5}{3}\) = \(\frac{6-5}{3}\)
ਜਾਂ v = \(\frac{1}{3}\)

x = 4 ਅਤੇ y = 5

ਪ੍ਰਸ਼ਨ (v).
\(\frac{7x-2y}{xy}\) = 5
\(\frac{8x+7y}{xy}\) = 15
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :

\(\frac{1}{x}\) = u ਅਤੇ \(\frac{1}{y}\) = v, ਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ
– 2u + 7v = 5 …..(1)
ਅਤੇ 7u + 8 = 15 …(2)
(1) ਨੂੰ 7 ਨਾਲ ਅਤੇ (2) ਨੂੰ 2 ਨਾਲ ਗੁਣਾ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
-14v + 49u = 35 ……(3)
ਅਤੇ 14v + 16u = 30 ……..(4)
ਹੁਣ (3) + (4) ਤੋਂ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
-14v + 49u = 35
14v + 16u = 30
65u = 65
u = \(\frac{65}{65}\) = 1
u ਦੇ ਮੁੱਲ ਨੂੰ (1) ਵਿੱਚ ਰੱਖਣ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
-2 (1) + 7v = 5
ਜਾਂ 7v = 5 + 2
ਜਾਂ 7v = 7
ਜਾਂ v = \(\frac{7}{7}\) = 1

x = 1 ਅਤੇ y = 1

ਪ੍ਰਸ਼ਨ (vi).
6x + 3y = 6xy
2x + 4y = 5xy
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :

\(\frac{1}{x}\) = u ਅਤੇ \(\frac{1}{y}\) = v, ਵਿੱਚ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ
u + 2v = 2 …(1)
ਅਤੇ 4u + 2y = 5 ……(2)
ਹੁਣ (2) – (1) ਤੋਂ

u ਜਾ ਇਹ ਮੁੱਲ (1) ਵਿੱਚ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ
1 + 2v = 2
ਜਾਂ 2v = 2 – 1 = 1
ਜਾਂ v = \(\frac{1}{2}\)

ਹੁਣ x = 1 ਅਤੇ y = 2

ਪ੍ਰਸ਼ਨ (vii).
\(\frac{10}{x+y}\) + \(\frac{2}{x-y}\) = 4
\(\frac{15}{x+y}\) – \(\frac{5}{x-y}\) = -2
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
\(\frac{10}{x+y}\) + \(\frac{2}{x-y}\) = 4 ਅਤੇ \(\frac{15}{x+y}\) – \(\frac{5}{x-y}\) = -2
\(\frac{1}{x+y}\) = u ਅਤੇ \(\frac{1}{x-y}\) = v ਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
10u + 2v = 4 ਜਾਂ 5u + v = 2 …(1)
15u – 5v = -2 …(2)
(1) ਨੂੰ 5 ਨਾਲ ਗੁਣਾ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
25u + 5y = 10 …(3)
(3) + (2) ਤੋਂ

u ਨੂੰ (1) ਵਿੱਚ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
5\(\left(\frac{1}{5}\right)\) + v = 2
ਜਾਂ 1 + v = 2
ਜਾਂ v = 1

ਹੁਣ (4) + (5) ਤੋਂ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ

x ਦਾ ਇਹ ਮੁੱਲ (4) ਵਿੱਚ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
3 + y = 5
y = 5 – 3 = 2
x = 3 ਅਤੇ y = 2

ਪ੍ਰਸ਼ਨ (viii).
\(\frac{1}{3x+y}\) + \(\frac{1}{3x-y}\) = \(\frac{3}{4}\)
\(\frac{1}{2(3 x+y)}\) – \(\frac{1}{2(3 x-y)}\) = \(\frac{-1}{8}\)
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :

ਹੁਣ (1) + (2) ਤੋਂ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
4u + 4v = 3
4u – 4v = – 1
8u = 2
u = \(\frac{8}{2}\) = \(\frac{1}{4}\)
u ਦਾ ਮੁੱਲ (1) ਵਿੱਚ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
4\(\left(\frac{1}{4}\right)\) + 4v = 3
ਜਾਂ 4v = 2
ਜਾਂ v = \(\frac{2}{4}\) = \(\frac{1}{2}\)

ਹੁਣ (3) + (4) ਤੋਂ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ’ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
3x + y = 4
3x – y = 2
6x = 6
x = 1
x ਦਾ ਮੁੱਲ (3) ਵਿਚ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
3 (1) + y = 4
ਜਾਂ 3 + y = 4
y = 4 – 3 = 1
x = 1 ਅਤੇ y = 1

2. ਹੇਠਾਂ ਦਿੱਤੀਆਂ ਸਮੱਸਿਆਵਾਂ ਰੇਖੀ ਸਮੀਕਰਣ ਜੋੜੇ ਦੇ ਰੂਪ ਵਿੱਚ ਦਰਸਾਓ ਅਤੇ ਉਹਨਾਂ ਦਾ ਹੱਲ ਪਤਾ ਕਰੋ :

ਪ੍ਰਸ਼ਨ (i).
ਰਿਤੂ ਧਾਰਾ ਦੀ ਦਿਸ਼ਾ ਦੇ ਅਨੁਸਾਰ 2 ਘੰਟਿਆਂ ਵਿੱਚ 20 ਕਿ.ਮੀ. ਤੈਰ ਸਕਦੀ ਹੈ ਅਤੇ ਧਾਰਾਂ ਦੀ ਦਿਸ਼ਾ ਦੇ ਉਲਟ 2 ਘੰਟਿਆਂ ਵਿੱਚ 4 ਕਿ.ਮੀ. ਤੇਰ ਸਕਦੀ ਹੈ । ਉਸਦੀ ਖੜੇ ਪਾਣੀ ਵਿੱਚ ਤੈਰਨ ਦੀ ਚਾਲ · ਗਤੀ) ਅਤੇ ਧਾਰਾਂ ਦੀ ਚਾਲ ਗਤੀ) ਪਤਾ ਕਰੋ ।
ਉੱਤਰ:
ਮੰਨ ਲਉ ਸਥਿਰ ਪਾਣੀ ਵਿਚ ਰਿਤੂ
ਦੀ ਚਾਲ = x ਕਿ.ਮੀ./ਘੰਟਾ
ਅਤੇ ਧਾਰਾ ਦੀ ਚਾਲ = y ਕਿ.ਮੀ. /ਘੰਟਾ
∴ ਧਾਰਾ ਦੀ ਦਿਸ਼ਾ ਦੇ ਉਲਟ ਚਾਲ = (x – y) ਕਿ.ਮੀ.
ਧਾਰਾ ਦੇ ਦਿਸ਼ਾ ਵਿਚ ਚਾਲ = (x + y) ਕਿ.ਮੀ.
ਰਿਤੂ ਧਾਰਾ ਦੀ ਦਿਸ਼ਾ ਵਿਚ 2 ਘੰਟੇ ਵਿੱਚ ਜਿੰਨੀ ਦੂਰੀ ਤੈਅ ਕਰਦੀ ਹੈ ।
= ਚਾਲ × ਸਮਾਂ
= (x + y) × 2 ਕਿ.ਮੀ.
ਪਹਿਲੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
2 (x + y) = 20
x + y = 10 …..(1)
ਰਿਤੂ ਧਾਰਾ ਦੀ ਦਿਸ਼ਾ ਵਿਚ 2 ਘੰਟੇ ਵਿਚ ਜਿੰਨੀ ਦੂਰੀ ਤੈਅ ਕਰਦੀ ਹੈ = ਚਾਲ × ਸਮਾਂ
= 2 (x – y) ਕਿ.ਮੀ.
ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
2 (x – y) = 4
x – y = 2 …(2)
ਹੁਣ, (1) + (2) ਤੋਂ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
x + y = 10
x – y = 2
2x = 12
x = \(\frac{12}{2}\) = 6
x ਦਾ ਮੁੱਲ (1) ਵਿਚ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ
6 + y = 10
y = 10 – 6 = 4
ਰਿਤੂ ਦੀ ਸਥਿਰ ਪਾਣੀ ਵਿਚ ਚਾਲ = 6 ਕਿ.ਮੀ. /ਘੰਟਾ
ਪਾਣੀ ਦੀ ਚਾਲ = 4 ਕਿ.ਮੀ. /ਘੰਟਾ

ਪ੍ਰਸ਼ਨ (ii).
2 ਇਸਤਰੀਆਂ ਅਤੇ 5 ਆਦਮੀ ਇਕ ਕਸੀਦੇ ਦੇ ਕੰਮ ਨੂੰ ਇਕੱਠੇ 4 ਦਿਨ ਵਿਚ ਪੂਰਾ ਕਰ ਸਕਦੇ ਹਨ, ਜਦ ਕਿ 3 ਇਸਤਰੀਆਂ ਅਤੇ 6 ਆਦਮੀ ਇਸਨੂੰ 3 ਦਿਨ ਵਿੱਚ ਪੂਰਾ ਕਰ ਸਕਦੇ ਹਨ । ਪਤਾ ਕਰੋ ਕਿ ਇਸ ਕੰਮ ਨੂੰ ਇੱਕ ਇਕੱਲੀ ਇਸਤਰੀ ਕਿੰਨੇ ਸਮੇਂ ਵਿੱਚ ਪੂਰਾ ਕਰੇਗੀ ? ਇਸ ਕੰਮ ਨੂੰ ਇਕੱਲਾ ਇੱਕ ਆਦਮੀ ਕਿੰਨੇ ਸਮੇਂ ਵਿੱਚ ਪੂਰਾ ਕਰੇਗਾ ?
ਉੱਤਰ:
ਮੰਨ ਲਉ ਇੱਕ ਇਸਤਰੀ ਕੰਮ ਕਰਦੀ ਹੈ = x ਦਿਨ
ਆਦਮੀ ਕੰਮ ਖ਼ਤਮ ਕਰਦਾ ਹੈ = y ਦਿਨ
ਇਸਤਰੀ ਦਾ ਇਕ ਦਿਨ ਦਾ ਕੰਮ = \(\frac{1}{x}\)
ਆਦਮੀ ਦਾ ਇਕ ਦਿਨ ਦਾ ਕੰਮ = \(\frac{1}{y}\)
ਪਹਿਲੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
\(\frac{2}{x}\) + \(\frac{5}{y}\) = \(\frac{1}{4}\) …(1)
ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
\(\frac{3}{x}\) + \(\frac{6}{y}\) = \(\frac{1}{3}\) …..(2)
\(\frac{1}{x}\) = u ਅਤੇ \(\frac{1}{y}\) = v ਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ ਸਮੀਕਰਣ (1) ਅਤੇ (2) ਤੋਂ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :

(3) ਨੂੰ 9 ਨਾਲ ਅਤੇ (4) ਨੂੰ 8 ਨਾਲ ਗੁਣਾ ਕਰਨ ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
72u + 180v = 9 …(5)
ਅਤੇ 72u + 144v = 8 …(6)
ਹੁਣ, (5) – (6) ਤੋਂ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :

v ਦੇ ਇਸ ਮੁੱਲ (4) ਵਿੱਚ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
9u + 18\(\left(\frac{1}{36}\right)\) = 1
ਜਾਂ 9u + \(\frac{1}{2}\) = 1
ਜਾਂ 9u = 1 – \(\frac{1}{2}\) = \(\frac{2-1}{2}\)
ਜਾਂ 9u = \(\frac{1}{2}\)
ਜਾਂ u = \(\frac{1}{2×9}\) = \(\frac{1}{18}\)

ਇੱਕ ਇਸਤਰੀ ਅਤੇ ਇੱਕ ਆਦਮੀ ਇੱਕਲੇ-ਇੱਕਲੇ ਕੰਮ ਨੂੰ ਕ੍ਰਮਵਾਰ 18 ਦਿਨ ਅਤੇ 36 ਦਿਨ ਵਿੱਚ ਪੂਰਾ ਕਰ ਸਕਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ (iii).
ਦੀਪਿਕਾ 300 km ਦੂਰੀ ‘ਤੇ ਸਥਿਤ ਆਪਣੇ ਘਰ ਜਾਣ ਦੇ ਲਈ ਕੁੱਝ ਦੂਰੀ ਰੇਲਗੱਡੀ ਦੁਆਰਾ ਅਤੇ ਕੁੱਝ ਦੂਰੀ ਬੱਸ ਦੁਆਰਾ ਤੈਅ ਕਰਦੀ ਹੈ । ਜੇਕਰ ਉਹ 60 km ਰੇਲਗੱਡੀ ਦੁਆਰਾ ਅਤੇ ਬਾਕੀ ਬੱਸ ਦੁਆਰਾ ਤੈਅ ਕਰਦੀ ਹੈ ਤਾਂ ਉਸਨੂੰ 4 ਘੰਟੇ ਲੱਗਦੇ ਹਨ । ਜੇਕਰ ਉਹ 100 km ਦੁਬਾਰਾ ਰੇਲਗੱਡੀ ਰਾਹੀਂ ਅਤੇ ਬਾਕੀ ਯਾਤਰਾ ਬੱਸ ਦੁਆਰਾ ਕਰੇ ਤਾਂ ਉਸਨੂੰ 10 ਮਿੰਟ ਵੱਧ ਲੱਗਦੇ ਹਨ | ਰੇਲਗੱਡੀ ਅਤੇ ਬੱਸ ਦੀ ਕੁਮਵਾਰ ਚਾਲ ਪਤਾ ਕਰੋ ।
ਉੱਤਰ:
ਮੰਨ ਲਉ ਰੇਲ ਗੱਡੀ ਦੀ ਚਾਲ = x ਕਿ.ਮੀ. /ਘੰਟਾ
ਅਤੇ ਬੱਸ ਦੀ ਚਾਲ = y ਕਿ.ਮੀ. /ਘੰਟਾ
ਕੁੱਲ ਦੂਰੀ = 300 ਕਿ.ਮੀ.
ਸਥਿਤੀ I
60 ਕਿ.ਮੀ. ਦੂਰੀ ਤੈਅ ਕਰਨ ਲਈ ਲੱਗਾ ਸਮਾਂ

ਬੱਸ ਦੁਆਰਾ(= 300 – 60) 240 ਕਿ.ਮੀ. ਦੂਰੀ ਤੈਅ ਕਰਨ ਵਿਚ ਲੱਗਾ ਸਮਾਂ

ਸਥਿਤੀ II
ਰੇਲਗੱਡੀ ਦੁਆਰਾ 100 ਕਿ.ਮੀ. ਦੂਰੀ ਤੈਅ ਕਰਨ ਵਿਚ ਲੱਗਾ ਸਮਾਂ = \(\frac{100}{x}\)
ਬਸ ਦੁਆਰਾ 200 ਕਿ.ਮੀ. ਦੂਰੀ ਤੈਅ ਕਰਨ ਵਿਚ
ਲਗਾ ਸਮਾਂ = (300 – 100) = \(\frac{200}{y}\) ਘੰਟੇ
∴ ਕੁੱਲ ਸਮਾਂ = (\(\frac{100}{x}\) + \(\frac{200}{y}\))ਘੰਟੇ
ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ

\(\frac{1}{x}\) = u ਅਤੇ \(\frac{1}{y}\) = v ਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ ਅਸੀਂ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਨ :
(1) ਅਤੇ (2) ਤੋਂ
15u + 60v = 1
ਅਤੇ 24u + 48v = 1
ਜਾਂ 15u + 60v – 1 = 0
24u + 48v – 1 = 0
ਤਿਰਛੀ ਗੁਣਾ ਵਿਧੀ ਰਾਹੀਂ :

I ਅਤੇ III ਤੋਂ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :

ਰੇਲ ਗੱਡੀ ਦੀ ਚਾਲ ਅਤੇ ਬੱਸ ਦੀ ਚਾਲ ਕ੍ਰਮਵਾਰ 60 ਕਿ.ਮੀ. /ਘੰਟਾ ਅਤੇ 80 ਕਿ.ਮੀ. /ਘੰਟਾ ਹੈ ।

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 3 ਦੋ ਚਲਾਂ ਵਿੱਚ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦੇ ਜੋੜੇ Ex 3.5 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 3 ਦੋ ਚਲਾਂ ਵਿੱਚ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦੇ ਜੋੜੇ Exercise 3.5

1. ਹੇਠਾਂ ਦਿੱਤੇ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦੇ ਜੋੜੇ ਵਿੱਚੋਂ ਕਿਸ | ਦਾ ਇੱਕ ਵਿਲੱਖਣ ਹੱਲ ਹੈ, ਕਿਸ ਦਾ ਕੋਈ ਹੱਲ ਨਹੀਂ | ਜਾਂ ਕਿਸਦੇ ਅਸੀਮਿਤ ਰੂਪ ਵਿੱਚ ਅਨੇਕ ਹੱਲ ਹਨ । ਇੱਕ ਹੱਲ ਦੀ ਸਥਿਤੀ ਵਿੱਚ, ਉਸਨੂੰ ਤਿਰਛੀ ਗੁਣਾ ਦੀ ਵਿਧੀ ਨਾਲ ਪਤਾ ਕਰੋ ।

ਪ੍ਰਸ਼ਨ (i).
x – 3y – 3 = 0
3x – 9y – 2 = 0
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
x – 3y – 3 = 0
ਅਤੇ 3x – 9y – 2 = 0
ਇੱਥੇ a₁ = 1, b₁ = -3, c₁ = – 3
a₂ = 3, b₂ = – 9, c₂ = – 2

∴ ਦਿੱਤੇ ਹੋਏ ਸਮੀਕਰਣ ਜੋੜੇ ਦਾ ਕੋਈ ਹੱਲ ਨਹੀਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ (ii).
2x + y = 5
3x + 2y = 8
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
2x + y = 5
ਅਤੇ 3x + 2y = 8
ਜਾਂ 2x + y – 5 = 0
ਅਤੇ 3x + 2y – 8 = 0
ਇੱਥੇ a₁ = 2, b₁ = 1, c₁ = -5
a₂ = 3, b₂ = 2, c₂ = – 8

∴ ਇਸ ਲਈ ਦਿੱਤੇ ਗਏ ਸਮੀਕਰਣ ਜੋੜੇ ਦਾ ਇੱਕ ਵਿਲੱਖਣ ਹੱਲ ਹੈ

∴ x = 2 ਅਤੇ y = 1

ਪ੍ਰਸ਼ਨ (iii).
3x – 5y = 20
6r – 10y = 40
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
3x – y = 20
ਅਤੇ 6x – 10y = 40
ਜਾਂ 3x – 5y – 20 = 0
ਅਤੇ 6 – 10y – 40 = 0
ਇੱਥੇ a₁ = 3, b₁ = -5, c₁ = – 20
a₂ = 6, b₂ = – 10, c₂ = – 40


ਦਿੱਤੇ ਗਏ ਸਮੀਕਰਣ ਜੋੜੇ ਦੇ ਅਸੀਮਤ ਰੂਪ ਵਿਚ ਅਨੇਕ ਹਲ ਹਨ ।

ਪ੍ਰਸ਼ਨ (iv).
x – 3y – 7 = 0
3x – 3y – 15 = 0
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
x – 3y – 7 = 0
ਅਤੇ 3x – 3y – 15 = 0
ਇੱਥੇ a₁ = 1, b₁ = – 3, c₁ = -7
a₂ = 3, b₂ = – 3, c₂ = – 15

I ਅਤੇ III ਤੋਂ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
\(\frac{x}{24}\) = \(\frac{1}{6}\) ⇒ x = \(\frac{1}{6}\) × 24 = 4
II ਅਤੇ III ਤੋਂ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
\(\frac{y}{-6}\) = \(\frac{1}{6}\) ⇒ y = \(\frac{1}{6}\) × -6 = -1
ਇੱਥੇ x = 4, y = – 1

ਪ੍ਰਸ਼ਨ 2.
(i) a ਅਤੇ b ਦੇ ਕਿਹੜੇ ਮੁੱਲਾਂ ਦੇ ਲਈ, ਹੇਠਾਂ ਦਿੱਤੇ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦੇ ਜੋੜੇ ਦੇ ਅਪਰਿਮਿਤ ਰੂਪ ਵਿਚ ਅਨੇਕ ਹੱਲ ਹੋਣਗੇ ?
2x + 3y = 7
(a – b) x + (a + b) y = 3a + b – 2
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
2 + 3y = 7
ਅਤੇ (a – b) x + (a + b) y = 3a + b – 2
ਜਾਂ 2x + 3y – 7 = 9
ਜਾਂ (a – b)x + (a + b) y – (3a + b – 2) = 0
ਇੱਥੇ a₁ = 2, b₁ = 3, c₁ = -7.
a₂ = a – b, b₂ = a + b,
c₂ = – (3a + b – 2)
∴ ਦਿੱਤੇ ਗਏ ਸਮੀਕਰਣ ਜੋੜੇ ਦੇ ਅਸੀਮਿਤ ਰੂਪ ਵਿਚ ਅਨੇਕ ਹੱਲ ਹਨ ।

ਜਾਂ 6a + 2b – 4 = 7a – 7b
ਜਾਂ -a + 9b – 4 = 0
ਜਾਂ a = 9b – 4 ……(1)
II ਅਤੇ III ਤੋਂ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
\(\frac{3}{a+b}\) = \(\frac{7}{3a+b-2}\)
ਜਾਂ 9a + 3b – 6 = 7a + 7b
ਜਾਂ 2a – 4b – 6 = 0
ਜਾਂ a – 2b – 3 = 0 .
ਸਮੀਕਰਣ (1) ਤੋਂ a ਦਾ ਮੁੱਲ ਉਪਰੋਕਤ ਵਿਚ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
ਜਾਂ 9b – 4 – 2b – 3 = 0
ਜਾਂ 7b – 7 = 0
ਜਾਂ 7b = 7
ਜਾਂ b = 1
b ਦਾ ਇਹ ਮੁੱਲ (1) ਵਿੱਚ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
a = 9 × 1 – 4 = 9 – 4
a = 5
∴ a = 5 ਅਤੇ b = 1

ਪ੍ਰਸ਼ਨ (ii).
k ਦੇ ਕਿਹੜੇ ਮੁੱਲਾਂ ਲਈ, ਹੇਠਾਂ ਦਿੱਤੇ ਰੇਖੀ ਸਮੀਕਰਣ ਦੇ ਜੋੜੇ ਦਾ ਕੋਈ ਹੱਲ ਨਹੀਂ ਹੈ ?
3x + y = 1
(2k – 1) + (k – 1) y = 2 + 1
ਉੱਤਰ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
3x + y = 1
ਅਤੇ 2k – 1 x + (k -11) y = 2k + 1
ਜਾਂ 3x + y – 1 = 0
ਅਤੇ (2k – 1) x + (k – 1) y – (2k + 1) = 0
ਇੱਥੇ a₁ = 3, b₁ = 1, c₁ = -1
a₂ = (2k – 1), b₂ = k – 1, c₂ = – (2k + 1)
∴ ਦਿੱਤੇ ਗਏ ਸਮੀਕਰਣ ਜੋੜੇ ਦਾ ਕੋਈ ਹੱਲ ਨਹੀਂ ਹੈ ।

⇒ 4k ≠ – 4
⇒ k ≠ \(-\frac{4}{4}\)
⇒ k ≠ -1
I ਅਤੇ II ਤੋਂ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
\(\frac{3}{2k-1}\) = \(\frac{1}{k-1}\) ⇒ 3k – 3 = 2k – 1
⇒ k = 2
∴ k = 2 ਅਤੇ k ≠ -1

ਪ੍ਰਸ਼ਨ 3.
ਹੇਠਾਂ ਦਿੱਤੇ ਰੇਖੀ ਸਮੀਕਰਣ ਜੋੜੇ ਨੂੰ ਪ੍ਰਤਿਸਥਾਪਨ ਅਤੇ ਤਿਰਛੀ ਗੁਣਾ ਵਿੱਧੀ ਨਾਲ ਹੱਲ ਕਰੋ । ਤੁਸੀਂ ਕਿਹੜੀ ਵਿਧੀ ਨੂੰ ਵੱਧ ਢੁਕਵੀਂ ਮੰਨਦੇ ਹੋ ?
8x + 5y = 9
3x + 2y = 4
ਹੱਲ:
ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
8x + 5y = 9 ……(1)
3x + 2y = 4 …(2)
ਪ੍ਰਤਿਸਥਾਪਨ ਵਿਧੀ
(2) ਤੋਂ 2y = 4 – 3x
y = \(\frac{4-3x}{2}\) …(3)
y ਦਾ ਮੁੱਲ (1), ਵਿੱਚ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
8x + 5[latex]\frac{4-3x}{2}[/latex] = 9
ਜਾਂ \(\frac{16x+20-15x}{2}\) = 9
ਜਾਂ x + 20 = 18
ਜਾਂ x = 18 – 20 = – 2
x ਦਾ ਇਹ ਮੁੱਲ (3) ਵਿੱਚ ਪ੍ਰਤਿਸਥਾਪਿਤ ਕਰਨ ‘ਤੇ ਸਾਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ :
y = \(\frac{4-3(-2)}{2}\) = \(\frac{4+6}{2}\)
= \(\frac{10}{2}\) = 5
∴ x = – 2 ਅਤੇ y = 5
ਤਿਰਛੀ ਗੁਣਾ ਵਿਧੀ ਨਾਲ ਦਿੱਤਾ ਗਿਆ ਰੇਖੀ ਸਮੀਕਰਣਾਂ ਦਾ ਜੋੜਾ ਹੈ :
8x + 5y – 9 = 0
ਅਤੇ 3x + 2y – 4 = 0
ਇੱਥੇ a₁ = 8, b₁ = 5, c₁ = – 9
a₂ = 3, b₂ = 2, c₂ = -4
ਹੁਣ, \(\frac{a_{1}}{a_{2}}\) = \(\frac{8}{3}\); \(\frac{b_{1}}{b_{2}}\) = \(\frac{5}{2}\);

∴ x = – 2 ਅਤੇ y = 5

4. ਹੇਠਾਂ ਦਿੱਤੀਆਂ ਸਮੱਸਿਆਵਾਂ ਵਿੱਚ ਰੇਖੀ ਸਮੀਕਰਣ ਦੇ ਜੋੜੇ ਬਣਾਉ ਅਤੇ ਉਹਨਾਂ ਦੇ ਹੱਲ ਜੇਕਰ ਉਹਨਾਂ ਦੀ ਹੋਂਦ ਹੋਵੇ) ਕਿਸੇ ਵੀ ਬੀਜ ਗਣਿਤਿਕ ਵਿਧੀ ਨਾਲ ਪਤਾ ਕਰੋ :

ਪ੍ਰਸ਼ਨ (i).
ਇਕ ਹੋਸਟਲ (Hostel) ਦੇ ਮਹੀਨਾਵਾਰ ਖਰਚ ਦਾ ਇੱਕ ਭਾਗ ਨਿਸ਼ਚਿਤ ਹੈ ਅਤੇ ਬਾਕੀ ਇਸ ‘ਤੇ ਨਿਰਭਰ ਕਰਦਾ ਹੈ ਕਿ ਵਿਦਿਆਰਥੀ ਨੇ ਕਿੰਨੇ ਦਿਨ ਭੋਜਨ ਕੀਤਾ ਹੈ । ਇੱਕ ਵਿਦਿਆਰਥੀ A ਜਿਸਨੇ 20 ਦਿਨ ਭੋਜਨ ਕੀਤਾ ਹੈ, ₹ 1000 ਹੋਸਟਲ (Hostel) ਦੇ ਖਰਚ ਲਈ ਦਿੰਦਾ ਹੈ, ਜਦੋਂ ਕਿ ਦੂਸਰਾ ਵਿਦਿਆਰਥੀ B 26 ਦਿਨ ਭੋਜਨ ਕੀਤਾ ਹੈ ₹ 1180 ਖਰਚ ਦਿੰਦਾ ਹੈ । ਨਿਸ਼ਚਿਤ ਖਰਚ ਅਤੇ ਹਰ ਇੱਕ ਦਿਨ ਦੇ ਭੋਜਨ ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ ।
ਉੱਤਰ:
ਮੰਨ ਲਉ ਹੋਸਟਲ ਦਾ ਨਿਸ਼ਚਿਤ ਮਾਸਿਕ ਕਿਰਾਇਆ = ₹ x
ਪ੍ਰਤੀਦਿਨ ਭੋਜਨ ਦਾ ਮੁੱਲ = ₹ y
ਪਹਿਲੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
x + 20y = 1000
⇒ x + 26y – 1180 = 0 ………(1)
ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ. .
x + 26y = 1180
⇒ x + 26y – 1180 = 0 …..(2)
ਤਿਰਛੀ ਗੁਣਾ ਵਿਧੀ ਨਾਂਲ (1) ਅਤੇ (2) ਸਮੀਕਰਣਾਂ ਨੂੰ ਹੱਲ ਕਰਨ ਲਈ ਅਸੀਂ ਹੇਠਾਂ ਦਿੱਤਾ ਚਿੱਤਰ ਬਣਾਉਂਦੇ ਹਾਂ :

ਹੋਸਟਲ ਦਾ ਨਿਸ਼ਚਿਤ ਮਾਸਿਕ ਕਿਰਾਇਆ ਅਤੇ ਪ੍ਰਤੀ ਦਿਨ ਭੋਜਨ ਦਾ ਮੁੱਲ ਕੁਮਵਾਰ ₹ 400 ਅਤੇ ₹ 30 ਹੈ

ਪ੍ਰਸ਼ਨ (ii).
ਇੱਕ ਭਿੰਨ ਦੇ ਸਿਰਫ਼ ਅੰਸ਼ ਵਿੱਚੋਂ 1 ਘਟਾਉਣ ਨਾਲ ਉਹ \(\frac{1}{3}\) ਹੋ ਜਾਂਦੀ ਹੈ ਅਤੇ ਹਰ ਵਿੱਚ 8 ਜੋੜਨ ਨਾਲ ਉਹ \(\frac{1}{4}\) ਜਾਂਦੀ ਹੈ । ਭਿੰਨ ਪਤਾ ਕਰੋ ।
ਉੱਤਰ:
ਮੰਨ ਲਉ ਭਿੰਨ ਦਾ ਅੰਸ਼ = x
ਭਿੰਨ ਦਾ ਹਰ = y
∴ ਭਿੰਨ = \(\frac{x}{y}\)
ਪਹਿਲੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
\(\frac{x-1}{y}\) = \(\frac{1}{3}\)
ਜਾਂ 3x – 3 = y
ਜਾਂ 3x – y – 3 = 0 …..(1)
ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
\(\frac{x}{y+8}\) = \(\frac{1}{4}\)
ਜਾਂ 4x = y + 8
ਜਾਂ 4x – y – 8 = 0 …(2)
ਤਿਰਛੀ ਗੁਣਾ ਡਿੱਬੀ ਨਾਲ ਸਮੀਕਰਣਾਂ (1) ਅਤੇ (2) ਨੂੰ ਹੱਲ ਕਰਨ ਲਈ ਅਸੀਂ ਹੇਠਾਂ ਦਿੱਤਾ ਚਿੱਤਰ ਬਣਾਉਂਦੇ ਹਾਂ :

ਪ੍ਰਸ਼ਨ (iii).
ਯਸ਼ਪਾਲ ਨੇ ਇੱਕ ਟੈਸਟ ਵਿਚੋਂ 40 ਅੰਕ ਪ੍ਰਾਪਤ ਕੀਤੇ, ਜਦੋਂ ਉਸਨੂੰ ਸਹੀ ਉੱਤਰ ਦੇ 3 ਅੰਕ ਮਿਲੇ ਅਤੇ ਗ਼ਲਤ ਉੱਤਰ ਤੇ 1 ਅੰਕ ਦੀ ਕਟੌਤੀ ਕੀਤੀ ਗਈ । ਜੇਕਰ ਉਸ ਨੂੰ ਸਹੀ ਉੱਤਰ ਦੇ 4 ਅੰਕ ਮਿਲਣ ਅਤੇ ਗ਼ਲਤ ਉੱਤਰ ਦੇ 2 ਅੰਕ ਕਟੇ ਜਾਣ ਤਾਂ ਉਹ 50 ਅੰਕ ਪ੍ਰਾਪਤ ਕਰਦਾ ਹੈ । ਟੈਸਟ ਵਿਚ ਕਿੰਨੇ ਪ੍ਰਸ਼ਨ ਸਨ ?
ਉੱਤਰ:
ਮੰਨ ਲਉ ਯਸ਼ਪਾਲ ਦੁਆਰਾ ਕੀਤੇ ਸਹੀ ਪ੍ਰਸ਼ਨ = x
ਯਸ਼ਪਾਲ ਦੁਆਰਾ ਕੀਤੇ ਗ਼ਲਤ ਪ੍ਰਸ਼ਨ = y
ਪਹਿਲੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
3x – y = 40
ਜਾਂ 3x – y – 40 = 0 …….(1)
ਦੂਜੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
4x – 2y = 50
ਜਾਂ 4x – 2y – 50 = 0 …(2)
ਤਿਰਛੀ ਗੁਣਾ ਵਿਧੀ ਨਾਲ ਸਮੀਕਰਣਾਂ (1) ਅਤੇ (2) ਨੂੰ ਹੱਲ ਕਰਨ ਲਈ ਅਸੀਂ ਹੇਠਾਂ ਦਿੱਤਾ ਚਿੱਤਰ ਬਣਾਉਂਦੇ ਹਾਂ :


⇒ y = 5
∴ ਸਹੀ ਪ੍ਰਸ਼ਨਾਂ ਦੀ ਗਿਣਤੀ = 15
ਗ਼ਲਤ ਪ੍ਰਸ਼ਨਾਂ ਦੀ ਗਿਣਤੀ = 5
ਕੁਲ ਪ੍ਰਸ਼ਨ = ਸਹੀ ਪ੍ਰਸ਼ਨ + ਗ਼ਲਤ ਪ੍ਰਸ਼ਨ
=15 + 5 = 20

ਪ੍ਰਸ਼ਨ (iv).
ਇੱਕ ਰਾਜਮਾਰਗ ‘ਤੇ ਦੋ ਸਥਾਨ A ਅਤੇ B, 100 ਕਿ.ਮੀ. ਦੀ ਦੂਰੀ ‘ਤੇ ਹਨ । ਇਕ ਕਾਰ A ਤੋਂ ਅਤੇ ਦੂਸਰੀ ਕਾਰ B ਤੋਂ ਇੱਕੋ ਤੋਂ ਹੀ ਸਮੇਂ ‘ਤੇ ਚਲਣਾ ਸ਼ੁਰੂ ਕਰਦੀਆਂ ਹਨ । ਜੇਕਰ ਇਹ ਕਾਰਾਂ ਅਲੱਗ-ਅਲੱਗ ਚਾਲ ਗਤੀ ਨਾਲ ਇੱਕ ਹੀ ਦਿਸ਼ਾ ਵਿੱਚ ਚਲਦੀਆਂ ਹਨ, ਤਾਂ ਇਹ 5 ਘੰਟੇ ਬਾਅਦ ਮਿਲ ਜਾਣਗੀਆਂ | ਦੋਵਾਂ ਕਾਰਾਂ ਦੀ ਗਤੀ (ਚਾਲ) ਪਤਾ ਕਰੋ ।
ਉੱਤਰ:
ਮੰਨ ਲਉ ਸਥਾਨ A ਵਾਲੀ ਕਾਰ ਦੀ ਚਾਲ = 1 ਕਿ.ਮੀ. /ਘੰਟਾ
ਅਤੇ ਸਥਾਨ B ਵਾਲੀ ਕਾਰ ਦੀ ਚਾਲ = y ਕਿ.ਮੀ. /ਘੰਟਾ
A ਅਤੇ B ਵਿਚਕਾਰਲੀ ਦੂਰੀ = 100 ਕਿ.ਮੀ.
5 ਘੰਟੇ ਦੀ ਸਥਿਤੀ ਵਿਚ
ਕਾਰ A ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ = 5 ਕਿ.ਮੀ.
[∵ ਦੂਰੀ = ਚਾਲ × ਸਮਾਂ]
ਕਾਰ B ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ = 5y ਕਿ.ਮੀ.
ਪਹਿਲੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
5x – 5y = 100
ਜਾਂ x – y = 20
ਜਾਂ x – y – 20 = 0 …..(1)
ਇੱਕ ਘੰਟੇ ਦੀ ਸਥਿਤੀ ਵਿੱਚ
ਕਾਰ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ = 1 ਕਿ.ਮੀ.
[∵ ਦੂਰੀ = ਚਾਲ × ਸਮਾਂ]
ਕਾਰ B ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਦੂਰੀ = y ਕਿ.ਮੀ.
ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
x + y = 10 ,
ਜਾਂ x + y – 100 = 00 …..(2)
ਤਿਰਛੀ ਗੁਣਾ ਵਿੱਧੀ ਨਾਲ ਸਮੀਕਰਣ (1) ਅਤੇ (2) ਨੂੰ ਹੱਲ ਕਰਨ ਲਈ ਅਸੀਂ ਹੇਠਾਂ ਦਿੱਤਾ ਚਿੱਤਰ ਬਣਾਉਂਦੇ ਹਾਂ :

ਬਿੰਦੂ A ਅਤੇ B ਤੋਂ ਚੱਲਣ ਵਾਲੀ ਕਾਰਾਂ ਦੀ ਚਾਲ ਕ੍ਰਮਵਾਰ 60 ਕਿ.ਮੀ./ਘੰਟਾ ਅਤੇ 40 ਕਿ.ਮੀ. /ਘੰਟਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ (v).
ਜੇਕਰ ਇੱਕ ਆਇਤ ਦੀ ਲੰਬਾਈ ਨੂੰ 5 ਇਕਾਈਆਂ ਘਟਾ ਦੇਈਏ ਅਤੇ ਚੌੜਾਈ ਨੂੰ 3 ਇਕਾਈਆਂ ਵਧਾ ਦੇਈਏ ਤਾਂ ਆਇਤ ਦਾ ਖੇਤਰਫਲ 9 ਵਰਗ ਇਕਾਈਆਂ ਘੱਟ ਜਾਂਦਾ ਹੈ । ਜੇਕਰ ਅਸੀਂ ਲੰਬਾਈ । 6 ਇਕਾਈਆਂ ਅਤੇ ਚੌੜਾਈ ਨੂੰ 2 ਇਕਾਈਆਂ ਵਧਾ ਦੇਈਏ ਤਾਂ ਖੇਤਰਫਲ 67 ਵਰਗ ਇਕਾਈਆਂ ਵੱਧ ਜਾਂਦਾ ਹੈ । ਆਇਤ ਦੀ ਲੰਬਾਈ ਅਤੇ ਚੌੜਾਈ ਪਤਾ ਕਰੋ ।
ਉੱਤਰ:
ਮੰਨ ਲਉ ਆਇਤ ਦੀ ਲੰਬਾਈ = x ਇਕਾਈਆਂ
ਆਇਤ ਦੀ ਚੌੜਾਈ = y ਇਕਾਈਆਂ
∴ ਆਇਤ ਦਾ ਖੇਤਰਫਲ = xy ਵਰਗ ਇਕਾਈਆਂ
ਪਹਿਲੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
(x – 5) (y + 3) = xy – 9
ਜਾਂ xy + 3x – 5y – 15 = xy – 9
ਜਾਂ 3x – 5y – 6 = 0 ….(1)
ਦੂਸਰੀ ਸ਼ਰਤ ਅਨੁਸਾਰ
(x + 3) (y + 2) = xy + 67
ਜਾਂ xy + 2x + 3y + 6 = xy + 67
ਜਾਂ 2x + 35 – 61 = 0 …(2)
ਤਿਰਛੀ ਗੁਣਾ ਵਿਧੀ ਨਾਲ ਸਮੀਕਰਣਾਂ (1) ਅਤੇ (2) ਨੂੰ ਕੱਲ ਕਰਨ ਲਈ ਅਸੀਂ ਹੇਠਾਂ ਦਿੱਤਾ ਚਿੱਤਰ ਬਣਾਉਂਦੇ ਹਾਂ,

ਆਇਤ ਦੀ ਲੰਬਾਈ ਅਤੇ ਚੌੜਾਈ ਕ੍ਰਮਵਾਰ 17 ਇਕਾਈਆਂ ਅਤੇ 9 ਇਕਾਈਆਂ ਹੈ ।