Class 11

Punjab State Board PSEB 11th Class Sociology Book Solutions Chapter 10 ਸਮਾਜਿਕ ਸਤਰੀਕਰਨ Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Sociology Chapter 10 ਸਮਾਜਿਕ ਸਤਰੀਕਰਨ

Sociology Guide for Class 11 PSEB ਸਮਾਜਿਕ ਸਤਰੀਕਰਨ Textbook Questions and Answers

I. ਨਿਮਨਲਿਖਤ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਉੱਤਰ 1-15 ਸ਼ਬਦਾਂ ਵਿੱਚ ਦਿਓ ।

ਪ੍ਰਸ਼ਨ 1.
ਸਮਾਜਿਕ ਸਤਰੀਕਰਨ ਤੋਂ ਤੁਸੀਂ ਕੀ ਸਮਝਦੇ ਹੋ ?
ਉੱਤਰ-
ਸਮਾਜ ਨੂੰ ਅਲੱਗ-ਅਲੱਗ ਆਧਾਰਾਂ ਉੱਤੇ ਅਲੱਗ-ਅਲੱਗ ਸਤਰਾਂ ਵਿਚ ਵੰਡਣ ਦੀ ਪ੍ਰਕ੍ਰਿਆ ਨੂੰ ਸਮਾਜਿਕ ਸਤਰੀਕਰਨ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਸਮਾਜਿਕ ਸਤਰੀਕਰਨ ਦੀਆਂ ਕਿਸਮਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਸਮਾਜਿਕ ਸਤਰੀਕਰਨ ਦੇ ਚਾਰ ਰੂਪ ਹਨ ਅਤੇ ਉਹ ਹਨ-ਜਾਤੀ, ਵਰਗ, ਜਾਗੀਰਦਾਰੀ ਅਤੇ ਗੁਲਾਮੀ ।

ਪ੍ਰਸ਼ਨ 3.
ਸਮਾਜਿਕ ਸਤਰੀਕਰਨ ਦੇ ਤੱਤਾਂ ਦੇ ਨਾਮ ਲਿਖੋ ।
ਉੱਤਰ-
ਇਹ ਸਰਵਵਿਆਪਕ ਹੈ, ਇਹ ਸਮਾਜਿਕ ਹੈ, ਇਸ ਵਿਚ ਅਸਮਾਨਤਾ ਹੁੰਦੀ ਹੈ ਅਤੇ ਹਰੇਕ ਸਮਾਜ ਵਿਚ ਇਸ ਦਾ ਅਲੱਗ ਆਧਾਰ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 4.
ਜਾਗੀਰਦਾਰੀ ਵਿਵਸਥਾ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਮੱਧਕਾਲੀਨ ਯੂਰਪ ਦੀ ਉਹ ਵਿਵਸਥਾ ਜਿਸ ਵਿਚ ਇਕ ਵਿਅਕਤੀ ਨੂੰ ਬਹੁਤ ਸਾਰੀ ਜ਼ਮੀਨ ਦੇ ਕੇ ਜਾਗੀਰਦਾਰ ਬਣਾ ਕੇ ਉਸਨੂੰ ਉਸ ਜ਼ਮੀਨ ਤੋਂ ਲਗਾਨ ਇਕੱਠਾ ਕਰਨ ਦੀ ਆਗਿਆ ਦਿੱਤੀ ਜਾਂਦੀ ਸੀ ।

ਪ੍ਰਸ਼ਨ 5.
‘ਕਾਸਟ’ ਸ਼ਬਦ ਦੀ ਉਤਪੱਤੀ ਕਿੱਥੋਂ ਹੋਈ ਹੈ ?
ਉੱਤਰ-
ਸ਼ਬਦ Caste (ਜਾਤੀ) ਸਪੈਨਿਸ਼ ਅਤੇ ਪੁਰਤਗਾਲੀ ਸ਼ਬਦ Caste ਤੋਂ ਨਿਕਲਿਆ ਹੈ ਜਿਸ ਦਾ ਅਰਥ ਹੈ ਪ੍ਰਜਾਤੀ, ਵੰਸ਼ ਜਾਂ ਨਸਲ ।

ਪ੍ਰਸ਼ਨ 6.
ਵਰਨ ਵਿਵਸਥਾ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਪ੍ਰਾਚੀਨ ਭਾਰਤੀ ਸਮਾਜ ਦੀ ਉਹ ਵਿਵਸਥਾ ਜਿਸ ਵਿਚ ਸਮਾਜ ਨੂੰ ਪੇਸ਼ੇ ਦੇ ਆਧਾਰ ਉੱਤੇ ਚਾਰ ਭਾਗਾਂ ਵਿਚ ਵੰਡ ਦਿੱਤਾ ਜਾਂਦਾ ਸੀ ।

ਪ੍ਰਸ਼ਨ 7.
ਹਿੰਦੂ ਸਮਾਜ ਵਿਚ ਪੱਦਮਾਤਮਕ ਸਥਿਤੀ ਦੇ ਤਿੰਨ ਨਾਮ ਦੱਸੋ 1
ਉੱਤਰ-
ਪ੍ਰਾਚੀਨ ਸਮੇਂ ਦੇ ਹਿੰਦੂ ਸਮਾਜ ਵਿਚ ਚਾਰ ਵਰਣ ਸਨ-ਬ੍ਰਾਹਮਣ, ਕਸ਼ੱਤਰੀ, ਵੈਸ਼ ਅਤੇ ਨਿਮਨ ਵਰਣ ।

ਪ੍ਰਸ਼ਨ 8.
ਛੂਤਛਾਤ (Untouchability) ਤੋਂ ਤੁਸੀਂ ਕੀ ਸਮਝਦੇ ਹੋ ?
ਉੱਤਰ-
ਜਾਤੀ ਵਿਵਸਥਾ ਦੇ ਸਮੇਂ ਅਲੱਗ-ਅਲੱਗ ਜਾਤਾਂ ਨੂੰ ਇਕ-ਦੂਜੇ ਨੂੰ ਛੂਹਣ ਦੀ ਮਨਾਹੀ ਸੀ ਜਿਸ ਨੂੰ ਛੂਤਛਾਤ ਕਹਿੰਦੇ ਸਨ ।

ਪ੍ਰਸ਼ਨ 9.
ਕੁੱਝ ਸੁਧਾਰਕਾਂ ਦੇ ਨਾਮ ਲਿਖੋ, ਜਿਨ੍ਹਾਂ ਨੇ ਛੂਤਛਾਤ ਦੇ ਖਿਲਾਫ ਵਿਰੋਧ ਕੀਤਾ ਹੈ ।
ਉੱਤਰ-
ਰਾਜਾ ਰਾਮ ਮੋਹਨ ਰਾਏ, ਜਯੋਤੀਬਾ ਫੁਲੇ, ਮਹਾਤਮਾ ਗਾਂਧੀ, ਡਾ: ਬੀ. ਆਰ. ਅੰਬੇਦਕਰ ਆਦਿ ।

ਪ੍ਰਸ਼ਨ 10.
ਵਰਗ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਵਰਗ ਲੋਕਾਂ ਦਾ ਉਹ ਸਮੂਹ ਹੈ ਜਿਨ੍ਹਾਂ ਵਿਚ ਕਿਸੇ ਨਾ ਕਿਸੇ ਆਧਾਰ ਉੱਤੇ ਸਮਾਨਤਾ ਹੁੰਦੀ ਹੈ; ਜਿਵੇਂ ਕਿਪੈਸਾ, ਪੇਸ਼ਾ, ਸੰਪੱਤੀ ਆਦਿ ।

ਪ੍ਰਸ਼ਨ 11.
ਵਰਗ ਵਿਵਸਥਾ ਦੀਆਂ ਕਿਸਮਾਂ ਦੇ ਨਾਂ ਲਿਖੋ ।
ਉੱਤਰ-
ਮੁੱਖ ਤੌਰ ਉੱਤੇ ਤਿੰਨ ਪ੍ਰਕਾਰ ਦੇ ਵਰਗ ਪਾਏ ਜਾਂਦੇ ਹਨ-ਉੱਚ ਵਰਗ, ਮੱਧ ਵਰਗ ਅਤੇ ਨਿਮਨ ਵਰਗ ।

ਪ੍ਰਸ਼ਨ 12.
ਮਾਰਕਸ ਦੁਆਰਾ ਦਿੱਤੇ ਗਏ ਦੋ ਵਰਗਾਂ ਦੇ ਨਾਂ ਲਿਖੋ ।
ਉੱਤਰ-
ਪੂੰਜੀਪਤੀ ਵਰਗ ਅਤੇ ਮਜ਼ਦੂਰ ਵਰਗ ।

II. ਨਿਮਨਲਿਖਤ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਉੱਤਰ 30-35 ਸ਼ਬਦਾਂ ਵਿੱਚ ਦਿਓ ।

ਪ੍ਰਸ਼ਨ 1.
ਸਮਾਜਿਕ ਅਸਮਾਨਤਾ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਜਦੋਂ ਸਮਾਜ ਦੇ ਸਾਰੇ ਵਿਅਕਤੀਆਂ ਨੂੰ ਆਪਣੇ ਵਿਅਕਤਿੱਤਵ ਦੇ ਪੂਰੇ ਵਿਕਾਸ ਦੇ ਮੌਕੇ ਪ੍ਰਾਪਤ ਨਾ ਹੋਣ ਉਹਨਾਂ ਵਿਚ ਜਾਤ, ਜਨਮ, ਨਸਲ, ਰੰਗ, ਪੈਸਾ, ਪੇਸ਼ੇ ਦੇ ਆਧਾਰ ਉੱਤੇ ਅੰਤਰ ਹੋਵੇ ਅਤੇ ਵੱਖ-ਵੱਖ ਸਮੂਹਾਂ ਵਿਚ ਵੱਖ-ਵੱਖ ਆਧਾਰਾਂ ਉੱਤੇ ਅੰਤਰ ਪਾਇਆ ਜਾਂਦਾ ਹੋਵੇ ਤਾਂ ਇਸਨੂੰ ਅਸਮਾਨਤਾ ਦਾ ਨਾਮ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਸਮਾਜਿਕ ਸਤਰੀਕਰਨ ਦੀਆਂ ਦੋ ਕਿਸਮਾਂ ਲਿਖੋ ।
ਉੱਤਰ-

1. ਜਾਤੀ-ਜਾਤੀ ਸਤਰੀਕਰਨ ਦਾ ਇਕ ਰੂਪ ਹੈ ਜਿਸ ਵਿਚ ਅਲੱਗ-ਅਲੱਗ ਜਾਤਾਂ ਦੇ ਵਿਚਕਾਰ ਸਤਰੀਕਰਨ ਪਾਇਆ ਜਾਂਦਾ ਹੈ ।
2. ਵਰਗ-ਸਮਾਜ ਵਿਚ ਬਹੁਤ ਸਾਰੇ ਵਰਗ ਪਾਏ ਜਾਂਦੇ ਹਨ ਅਤੇ ਉਹਨਾਂ ਵਿਚ ਅਲੱਗ-ਅਲੱਗ ਆਧਾਰਾਂ ਉੱਤੇ ਅੰਤਰ ਪਾਇਆ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਜਾਤੀ ਵਿਵਸਥਾ ਦੀਆਂ ਦੋ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਦੱਸੋ
ਉੱਤਰ-

1. ਜਾਤੀ ਦੀ ਮੈਂਬਰਸ਼ਿਪ ਜਨਮ ਉੱਤੇ ਆਧਾਰਿਤ ਹੁੰਦੀ ਸੀ ਅਤੇ ਵਿਅਕਤੀ ਯੋਗਤਾ ਹੋਣ ਦੇ ਬਾਵਜੂਦ ਵੀ ਇਸ ਨੂੰ ਬਦਲ ਨਹੀਂ ਸਕਦਾ ।
2. ਜਾਤੀ ਇਕ ਅੰਤਰ-ਵਿਆਹੀ ਸਮੂਹ ਹੁੰਦਾ ਸੀ ਅਤੇ ਅਲੱਗ-ਅਲੱਗ ਜਾਤਾਂ ਵਿਚਕਾਰ ਵਿਆਹ ਕਰਵਾਉਣ ਦੀ ਮਨਾਹੀ ਹੁੰਦੀ ਸੀ ।

ਪ੍ਰਸ਼ਨ 4.
ਅੰਤਰ ਜਾਤੀ ਵਿਆਹ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਅੰਤਰ-ਵਿਆਹ ਕਰਵਾਉਣ ਦਾ ਹੀ ਇਕ ਪ੍ਰਕਾਰ ਹੈ ਜਿਸ ਅਨੁਸਾਰ ਵਿਅਕਤੀ ਨੂੰ ਆਪਣੇ ਸਮੂਹ ਅਰਥਾਤ ਜਾਤੀ ਜਾਂ ਉਪਜਾਤੀ ਵਿਚ ਹੀ ਵਿਆਹ ਕਰਵਾਉਣਾ ਪੈਂਦਾ ਸੀ । ਜੇਕਰ ਕੋਈ ਇਸ ਨਿਯਮ ਦੀ ਉਲੰਘਣਾ ਕਰਦਾ ਸੀ ਤਾਂ ਉਸ ਨੂੰ ਜਾਤੀ ਵਿਚੋਂ ਬਾਹਰ ਕੱਢ ਦਿੱਤਾ ਜਾਂਦਾ ਸੀ । ਇਸ ਕਰਕੇ ਸਾਰੇ ਆਪਣੇ ਸਮੂਹ ਵਿਚ ਹੀ ਵਿਆਹ ਕਰਵਾਉਂਦੇ ਸਨ ।

ਪ੍ਰਸ਼ਨ 5.
ਸ਼ੁੱਧਤਾ ਅਤੇ ਅਸ਼ੁੱਧਤਾ (Pollution and Purity) ਤੋਂ ਤੁਸੀਂ ਕੀ ਸਮਝਦੇ ਹੋ ?
ਉੱਤਰ-
ਜਾਤੀ ਵਿਵਸਥਾ ਦਾ ਕੂਮ ਪਵਿੱਤਰਤਾ ਅਤੇ ਅਪਵਿੱਤਰਤਾ ਦੇ ਸੰਕਲਪ ਨਾਲ ਜੁੜਿਆ ਹੋਇਆ ਸੀ । ਇਸਦਾ ਅਰਥ ਹੈ ਕਿ ਕੁੱਝ ਜਾਤਾਂ ਨੂੰ ਪਰੰਪਰਾਗਤ ਰੂਪ ਨਾਲ ਸ਼ੁੱਧ ਸਮਝਿਆ ਜਾਂਦਾ ਸੀ ਅਤੇ ਉਹਨਾਂ ਨੂੰ ਸਮਾਜ ਵਿਚ ਉੱਚਾ ਦਰਜਾ ਹਾਸਲ ਸੀ । ਕੁੱਝ ਜਾਤਾਂ ਨੂੰ ਅਸ਼ੁੱਧ ਸਮਝਿਆ ਜਾਂਦਾ ਸੀ ਅਤੇ ਉਹਨਾਂ ਨੂੰ ਸਮਾਜਿਕ ਵਿਵਸਥਾ ਵਿਚ ਨੀਵਾਂ ਦਰਜਾ ਦਿੱਤਾ ਗਿਆਂ ਸੀ ।

ਪ੍ਰਸ਼ਨ 6.
ਉਦਯੋਗੀਕਰਨ ਅਤੇ ਸ਼ਹਿਰੀਕਰਨ ਤੇ ਛੋਟਾ ਨੋਟ ਲਿਖੋ ।
ਉੱਤਰ-
ਉਦਯੋਗੀਕਰਨ ਦਾ ਅਰਥ ਹੈ ਦੇਸ਼ ਵਿਚ ਵੱਡੇ-ਵੱਡੇ ਉਦਯੋਗਾਂ ਦਾ ਵੱਧਣਾ । ਜਦੋਂ ਪਿੰਡਾਂ ਤੋਂ ਲੋਕ ਸ਼ਹਿਰਾਂ ਵੱਲ ਨੂੰ ਜਾਣ ਅਤੇ ਉੱਥੇ ਰਹਿਣ ਲਗ ਜਾਣ ਤਾਂ ਇਸ ਪ੍ਰਕ੍ਰਿਆ ਨੂੰ ਸ਼ਹਿਰੀਕਰਨ ਦਾ ਨਾਮ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ਉਦਯੋਗੀਕਰਨ ਅਤੇ ਸ਼ਹਿਰੀਕਰਨ ਦੀ ਪ੍ਰਕ੍ਰਿਆ ਨੇ ਜਾਤੀ ਵਿਵਸਥਾ ਨੂੰ ਖ਼ਤਮ ਕਰਨ ਵਿਚ ਬਹੁਤ ਮਹੱਤਵਪੂਰਨ ਭੂਮਿਕਾ ਨਿਭਾਈ ਹੈ ।

ਪ੍ਰਸ਼ਨ 7.
ਵਰਗ ਵਿਵਸਥਾ ਦੀਆਂ ਦੋ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਦੱਸੋ ।
ਉੱਤਰ-

1. ਹਰੇਕ ਵਰਗ ਵਿਚ ਇਸ ਗੱਲ ਦੀ ਚੇਤਨਤਾ ਹੁੰਦੀ ਹੈ ਕਿ ਉਸਦਾ ਪਦ ਜਾਂ ਸਨਮਾਨ ਦੂਜੀ ਸ਼੍ਰੇਣੀ ਦੀ ਤੁਲਨਾ ਵਿਚ ਵੱਧ ਹੈ ।
2. ਇਸ ਵਿਚ ਲੋਕ ਆਪਣੀ ਹੀ ਸ਼੍ਰੇਣੀ ਦੇ ਮੈਂਬਰਾਂ ਨਾਲ ਗੂੜੇ ਸੰਬੰਧ ਰੱਖਦੇ ਹਨ ਅਤੇ ਦੂਜੀ ਸ਼੍ਰੇਣੀ ਦੇ ਲੋਕਾਂ ਨਾਲ ਉਹਨਾਂ ਦੇ ਸੰਬੰਧ ਸੀਮਿਤ ਹੁੰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 8.
ਨਵੇਂ ਮੱਧ ਵਰਗ ਤੇ ਛੋਟਾ ਨੋਟ ਲਿਖੋ ।
ਉੱਤਰ-
ਪਿਛਲੇ ਕੁੱਝ ਸਮੇਂ ਤੋਂ ਸਮਾਜ ਵਿਚ ਇਕ ਨਵਾਂ ਮੱਧ ਵਰਗ ਸਾਹਮਣੇ ਆਇਆ ਹੈ । ਇਸ ਵਰਗ ਵਿਚ ਡਾਕਟਰ, ਇੰਜੀਨੀਅਰ, ਮੈਨੇਜਰ, ਟੀਚਰ, ਛੋਟੇ-ਮੋਟੇ ਵਪਾਰੀ, ਨੌਕਰੀ ਪੇਸ਼ਾ ਲੋਕ ਹੁੰਦੇ ਹਨ । ਉੱਚ ਵਰਗ ਇਸ ਮੱਧ ਵਰਗ ਦੀ ਮੱਦਦ ਨਾਲ ਹੇਠਲੇ ਵਰਗ ਦਾ ਸ਼ੋਸ਼ਣ ਕਰਦਾ ਹੈ ।

III. ਨਿਮਨਲਿਖਤ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਉੱਤਰ 75-85 ਸ਼ਬਦਾਂ ਵਿੱਚ ਦਿਓ ।

ਪ੍ਰਸ਼ਨ 1.
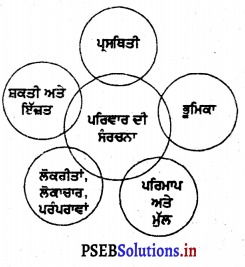
ਸਮਾਜਿਕ ਸਤਰੀਕਰਨ ਦੀਆਂ ਚਾਰ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਲਿਖੋ ।
ਉੱਤਰ-

1. ਸਤਰੀਕਰਨ ਇਕ ਸਰਵਵਿਆਪਕ ਪ੍ਰਕ੍ਰਿਆ ਹੈ । ਕੋਈ ਵੀ ਮਨੁੱਖੀ ਸਮਾਜ ਅਜਿਹਾ ਨਹੀਂ ਹੈ ਜਿੱਥੇ ਸਤਰੀਕਰਨ ਦੀ ਪ੍ਰਕ੍ਰਿਆ ਨਾ ਪਾਈ ਜਾਂਦੀ ਹੋਵੇ ।
2. ਸਤਰੀਕਰਨ ਵਿਚ ਸਮਾਜ ਦੇ ਹਰੇਕ ਮੈਂਬਰ ਦੀ ਸਥਿਤੀ ਸਮਾਨ ਨਹੀਂ ਹੁੰਦੀ । ਕਿਸੇ ਦੀ ਸਥਿਤੀ ਉੱਚੀ ਅਤੇ ਕਿਸੇ ਦੀ ਸਥਿਤੀ ਨੀਵੀਂ ਹੁੰਦੀ ਹੈ ।
3. ਸਤਰੀਕਰਨ ਵਿਚ ਸਮਾਜ ਦੀ ਵੰਡ ਵਿਭਿੰਨ ਸਤਰਾਂ ਵਿਚ ਹੁੰਦੀ ਹੈ ਜਿਹੜੀ ਵਿਅਕਤੀ ਦੀ ਸਥਿਤੀ ਨੂੰ ਨਿਰਧਾਰਿਤ ਕਰਦੀ ਹੈ । ਅਲੱਗ-ਅਲੱਗ ਵਰਗਾਂ ਵਿਚ ਉੱਚ-ਨੀਚ ਦੇ ਸੰਬੰਧ ਹੁੰਦੇ ਹਨ ।
4. ਚਾਹੇ ਇਸ ਵਿਚ ਅਲੱਗ-ਅਲੱਗ ਸਤਰਾਂ ਹੁੰਦੀਆਂ ਹਨ, ਪਰ ਉਹਨਾਂ ਸਤਰਾਂ ਵਿਚ ਆਪਸੀ ਨਿਰਭਰਤਾ ਵੀ ਪਾਈ ਜਾਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਕਿਸ ਪ੍ਰਕਾਰ ਵਰਗ ਸਮਾਜਿਕ ਸਤਰੀਕਰਨ ਨਾਲ ਸੰਬੰਧਿਤ ਹੈ ? ਸੰਖੇਪ ਵਿੱਚ ਨੋਟ ਲਿਖੋ ।
ਉੱਤਰ-
ਸਮਾਜਿਕ ਸਤਰੀਕਰਨ ਨਾਲ ਵਰਗ ਹਮੇਸ਼ਾਂ ਹੀ ਸੰਬੰਧਿਤ ਰਿਹਾ ਹੈ । ਅਸੀਂ ਦੇਖਦੇ ਹਾਂ ਕਿ ਅਲੱਗ-ਅਲੱਗ ਹਮੇਸ਼ਾਂ ਹੀ ਕਈ ਵਰਗ ਪਾਏ ਜਾਂਦੇ ਹਨ । ਚਾਹੇ ਪ੍ਰਾਚੀਨ ਸਮਾਜ ਹੋਣ ਜਾਂ ਆਧੁਨਿਕ ਸਮਾਜ, ਇਹਨਾਂ ਵਿਚ ਅਲੱਗ-ਅਲੱਗ ਆਧਾਰਾਂ ਉੱਤੇ ਵਰਗ ਪਾਏ ਜਾਂਦੇ ਹਨ । ਇਹ ਆਧਾਰ ਪੇਸ਼ਾ, ਪੈਸਾ, ਜਾਤ, ਧਰਮ, ਜਾਤੀ, ਜ਼ਮੀਨ ਆਦਿ ਹੁੰਦੇ ਹਨ । ਇਹਨਾਂ ਆਧਾਰਾਂ ਉੱਤੇ ਕਈ ਪ੍ਰਕਾਰ ਦੇ ਵਰਗ ਮਿਲਦੇ ਸਨ ।

ਪ੍ਰਸ਼ਨ 3.
ਜਾਤੀ ਅਤੇ ਵਰਗ ਵਿਵਸਥਾ ਵਿਚ ਅੰਤਰ ਦੱਸੋ ।
ਉੱਤਰ-

ਵਰਗ	ਜਾਤੀ
(i) ਵਰਗ ਦੇ ਮੈਂਬਰਾਂ ਦੀ ਵਿਅਕਤੀਗਤ ਯੋਗਤਾ ਨਾਲ ਵਿਅਕਤੀ ਦੀ ਸਮਾਜਿਕ ਸਥਿਤੀ ਬਣਦੀ ਹੈ ।	(i) ਜਾਤੀ ਵਿਚ ਵਿਅਕਤੀਗਤ ਯੋਗਤਾ ਦੀ ਕੋਈ ਥਾਂ ਨਹੀਂ ਹੁੰਦੀ ਸੀ ਅਤੇ ਸਮਾਜਿਕ ਸਥਿਤੀ ਜਨਮ ਉੱਤੇ ਆਧਾਰਿਤ ਹੁੰਦੀ ਸੀ ।
(ii) ਵਰਗ ਦੀ ਮੈਂਬਰਸ਼ਿਪ, ਹੈਸੀਅਤ, ਪੇਸ਼ੇ ਆਦਿ ਉੱਤੇ ਆਧਾਰਿਤ ਹੁੰਦੀ ਹੈ ।	(ii) ਜਾਤੀ ਦੀ ਮੈਂਬਰਸ਼ਿਪ ਜਨਮ ਉੱਤੇ ਆਧਾਰਿਤ ਹੁੰਦੀ ਹੈ ।
(iii) ਵਰਗ ਵਿਚ ਵਿਅਕਤੀ ਨੂੰ ਵਧੇਰੇ ਸੁਤੰਤਰਤਾ ਹੁੰਦੀ ਹੈ ।	(iii) ਜਾਤ ਵਿਚ ਵਿਅਕਤੀ ਉੱਪਰ ਖਾਣ-ਪੀਣ ਸੰਬੰਧੀ ਆਦਿ ਦੀਆਂ ਬਹੁਤ ਪਾਬੰਦੀਆ ਹੁੰਦੀਆਂ ਸਨ ।
(iv) ਵਰਗਾਂ ਵਿਚ ਆਪਸੀ ਦੂਰੀ ਕਾਫ਼ੀ ਘੱਟ ਹੁੰਦੀ ਹੈ ।	(iv) ਜਾਤਾਂ ਵਿਚ ਆਪਸੀ ਦੂਰੀ ਕਾਫ਼ੀ ਜ਼ਿਆਦਾ ਹੁੰਦੀ ਹੈ ।
(v) ਵਰਗ ਵਿਵਵਥਾ ਪ੍ਰਜਾਤੰਤਰ ਦੇ ਸਿਧਾਂਤ ਉੱਪਰ ਆਧਾਰਿਤ ਹੈ ।	(v) ਜਾਤ ਵਿਵਵਥਾ ਜਾਤੰਤਰ ਦੇ ਸਿਧਾਂਤ ਦੇ ਵਿਰੁੱਧ ਹੈ ।

ਪ੍ਰਸ਼ਨ 4.
ਜਾਤੀ ਵਿਵਸਥਾ ਵਿਚ ਪਰਿਵਰਤਨ ਦੇ ਚਾਰ ਕਾਰਕ ਲਿਖੋ ।
ਉੱਤਰ-

• ਭਾਰਤ ਵਿਚ 19ਵੀਂ ਸਦੀ ਅਤੇ 20ਵੀਂ ਸਦੀ ਵਿਚਕਾਰ ਸਮਾਜਿਕ, ਧਾਰਮਿਕ ਸੁਧਾਰ ਲਹਿਰਾਂ ਚਲੀਆਂ ਜਿਨ੍ਹਾਂ ਕਾਰਨ ਜਾਤੀ ਪ੍ਰਥਾ ਨੂੰ ਬਹੁਤ ਡੂੰਘੀ ਸੱਟ ਵੱਜੀ ।
• ਭਾਰਤ ਸਰਕਾਰ ਨੇ ਸੁਤੰਤਰਤਾ ਤੋਂ ਬਾਅਦ ਬਹੁਤ ਸਾਰੇ ਕਾਨੂੰਨ ਪਾਸ ਕੀਤੇ ਅਤੇ ਸੰਵਿਧਾਨ ਵਿਚ ਕਈ ਪ੍ਰਕਾਰ ਦੇ ਪ੍ਰਾਵਧਾਨ ਰੱਖੇ ਜਿਨ੍ਹਾਂ ਨਾਲ ਜਾਤੀ ਵਿਵਸਥਾ ਵਿਚ ਪਰਿਵਰਤਨ ਆ ਗਏ ।
• ਦੇਸ਼ ਵਿਚ ਉਦਯੋਗਾਂ ਦੇ ਵੱਧਣ ਨਾਲ ਅਲੱਗ-ਅਲੱਗ ਜਾਤਾਂ ਦੇ ਲੋਕ ਇਕੱਠੇ ਮਿਲ ਕੇ ਇਹਨਾਂ ਵਿਚ ਕੰਮ ਕਰਨ ਲੱਗ ਪਏ ਅਤੇ ਜਾਤੀ ਵਿਵਸਥਾ ਦੇ ਪ੍ਰਤਿਬੰਧਾਂ ਉੱਤੇ ਸੱਟ ਵੱਜੀ ।
• ਸ਼ਹਿਰਾਂ ਵਿਚ ਅਲੱਗ-ਅਲੱਗ ਜਾਤਾਂ ਦੇ ਲੋਕ ਇਕੱਠੇ ਮਿਲ ਕੇ ਰਹਿੰਦੇ ਹਨ ਜਿਸ ਕਾਰਨ ਜਾਤੀ ਪ੍ਰਥਾ ਦੇ ਮੇਲ-ਜੋਲ ਦੀ ਪਾਬੰਦੀ ਵਾਲਾ ਨਿਯਮ ਵੀ ਖ਼ਤਮ ਹੋ ਗਿਆ ।
• ਸਿੱਖਿਆ ਦੇ ਪ੍ਰਸਾਰ ਨੇ ਵੀ ਜਾਤੀ ਵਿਵਸਥਾ ਨੂੰ ਖ਼ਤਮ ਕਰਨ ਵਿਚ ਬਹੁਤ ਵੱਡਾ ਯੋਗਦਾਨ ਦਿੱਤਾ ।

ਪ੍ਰਸ਼ਨ 5.
ਸਮਾਜਿਕ ਸਤਰੀਕਰਨ ਦੇ ਦੋ ਪ੍ਰਮੁੱਖ ਰੂਪਾਂ ਦੇ ਰੂਪ ਵਿੱਚ ਜਾਤੀ ਅਤੇ ਵਰਗ ਦੇ ਵਿਚ ਅੰਤਰ ਦੱਸੋ ।
ਉੱਤਰ-

ਵਰਗ	ਜਾਤੀ
(i) ਵਰਗ ਦੇ ਮੈਂਬਰਾਂ ਦੀ ਵਿਅਕਤੀਗਤ ਯੋਗਤਾ ਨਾਲ ਵਿਅਕਤੀ ਦੀ ਸਮਾਜਿਕ ਸਥਿਤੀ ਬਣਦੀ ਹੈ ।	(i) ਜਾਤੀ ਵਿਚ ਵਿਅਕਤੀਗਤ ਯੋਗਤਾ ਦੀ ਕੋਈ ਥਾਂ ਨਹੀਂ ਹੁੰਦੀ ਸੀ ਅਤੇ ਸਮਾਜਿਕ ਸਥਿਤੀ ਜਨਮ ਉੱਤੇ ਆਧਾਰਿਤ ਹੁੰਦੀ ਸੀ ।
(ii) ਵਰਗ ਦੀ ਮੈਂਬਰਸ਼ਿਪ, ਹੈਸੀਅਤ, ਪੇਸ਼ੇ ਆਦਿ ਉੱਤੇ ਆਧਾਰਿਤ ਹੁੰਦੀ ਹੈ ।	(ii) ਜਾਤੀ ਦੀ ਮੈਂਬਰਸ਼ਿਪ ਜਨਮ ਉੱਤੇ ਆਧਾਰਿਤ ਹੁੰਦੀ ਹੈ ।
(iii) ਵਰਗ ਵਿਚ ਵਿਅਕਤੀ ਨੂੰ ਵਧੇਰੇ ਸੁਤੰਤਰਤਾ ਹੁੰਦੀ ਹੈ ।	(iii) ਜਾਤ ਵਿਚ ਵਿਅਕਤੀ ਉੱਪਰ ਖਾਣ-ਪੀਣ ਸੰਬੰਧੀ ਆਦਿ ਦੀਆਂ ਬਹੁਤ ਪਾਬੰਦੀਆ ਹੁੰਦੀਆਂ ਸਨ ।
(iv) ਵਰਗਾਂ ਵਿਚ ਆਪਸੀ ਦੂਰੀ ਕਾਫ਼ੀ ਘੱਟ ਹੁੰਦੀ ਹੈ ।	(iv) ਜਾਤਾਂ ਵਿਚ ਆਪਸੀ ਦੂਰੀ ਕਾਫ਼ੀ ਜ਼ਿਆਦਾ ਹੁੰਦੀ ਹੈ ।
(v) ਵਰਗ ਵਿਵਵਥਾ ਪ੍ਰਜਾਤੰਤਰ ਦੇ ਸਿਧਾਂਤ ਉੱਪਰ ਆਧਾਰਿਤ ਹੈ ।	(v) ਜਾਤ ਵਿਵਵਥਾ ਜਾਤੰਤਰ ਦੇ ਸਿਧਾਂਤ ਦੇ ਵਿਰੁੱਧ ਹੈ ।

IV. ਨਿਮਨਲਿਖਤ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਉੱਤਰ 25-300 ਸ਼ਬਦਾਂ ਵਿੱਚ ਦਿਓ ।

ਪ੍ਰਸ਼ਨ 1.
ਸਤਰੀਕਰਨ ਨੂੰ ਪਰਿਭਾਸ਼ਿਤ ਕਰੋ ? ਇਸ ਦੀਆਂ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਕੀ ਹਨ ?
ਉੱਤਰ-
ਜਿਹੜੀ ਪ੍ਰਕਿਰਿਆ ਦੇ ਦੁਆਰਾ ਅਸੀਂ ਵਿਅਕਤੀਆਂ ਦੇ ਸਮੂਹਾਂ ਨੂੰ ਸਥਿਤੀ ਪਦਮ ਅਨੁਸਾਰ ਸਤਰੀਕ੍ਰਿਤ ਕਰਦੇ ਹਾਂ, ਉਸ ਨੂੰ ..ਸਤਰੀਕਰਨ ਦਾ ਨਾਮ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ । ਸ਼ਬਦ ‘ਸਤਰੀਕਰਨ’ ਦਾ ਅੰਗਰੇਜ਼ੀ ਸ਼ਬਦ ‘Stratification’ ਵਿਚ Strata ਦਾ ਅਰਥ ਹੈ ਸਤਰਾਂ (layers) । ਇਸ ਸ਼ਬਦ ਦੀ ਉਤਪੱਤੀ ਲਾਤੀਨੀ ਭਾਸ਼ਾ ਦੇ ਸ਼ਬਦ ‘Stratum’ ਤੋਂ ਹੋਈ ਹੈ । ਇਸ ਵਿਵਸਥਾ ਦੇ ਦੁਆਰਾ ਸਮਾਜਿਕ ਜੀਵਨ ਨੂੰ ਤਰਤੀਬ ਵਿੱਚ ਕਰਨ ਲਈ ਸਮਾਜ ਨੂੰ ਵਿਭਿੰਨ ਸਤਰਾਂ ਵਿਚ ਵੰਡਿਆ ਹੋਇਆ ਹੈ । ਕੋਈ ਵੀ ਦੋ ਵਿਅਕਤੀ ਭਾਵੇਂ ਇਕੋ ਪਰਿਵਾਰ ਵਿਚ ਜਨਮੇ ਹੁੰਦੇ ਹਨ ਪਰੰਤੁ ਸੁਭਾਅ ਵਜੋਂ ਜਾਂ ਕਿਸੇ ਹੋਰ ਪੱਖੋਂ ਉਹ ਇਕ ਦੂਸਰੇ ਤੋਂ ਵੱਖ ਹੁੰਦੇ ਹਨ । ਇਸੇ ਵਖਰੇਵੇਂ ਕਰਕੇ ਉਨ੍ਹਾਂ ਵਿਚ ਕੰਮ ਕਰਨ ਦੀ ਸਮਰੱਥਾ ਜਾਂ ਯੋਗਤਾ ਦਾ ਗੁਣ ਵੀ ਵੱਖਰਾ ਹੁੰਦਾ ਹੈ । ਇਸੇ ਕਰਕੇ ਅਸਮਾਨ ਗੁਣਾਂ ਵਾਲੇ ਵਿਅਕਤੀਆਂ ਨੂੰ ਵਿਭਿੰਨ ਵਰਗਾਂ ਵਿਚ ਵੰਡਣ ਨਾਲ ਸਾਡਾ ਸਮਾਜ ਵਿਵਸਥਿਤ ਰੂਪ ਵਿਚ ਕੰਮ ਕਰਨ ਲੱਗ ਪੈਂਦਾ ਹੈ । ਵਿਅਕਤੀ ਨੂੰ ਵਿਭਿੰਨ ਸਤਰਾਂ ਵਿਚ ਵੰਡ ਕੇ ਉਨ੍ਹਾਂ ਵਿਚਲੇ ਉੱਚੇ ਤੇ ਨੀਵੇਂ ਸੰਬੰਧਾਂ ਦਾ ਵਰਣਨ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਭਾਵੇਂ ਉਨ੍ਹਾਂ ਵਿਚ ਸਥਿਤੀ ਦੇ ਆਧਾਰ ‘ਤੇ ਉੱਚੇ ਤੇ ਨੀਵੇਂ ਸੰਬੰਧ ਹੁੰਦੇ ਹਨ ਪਰੰਤੂ ਉਹ ਫਿਰ ਵੀ ਇਕ ਦੂਸਰੇ ਤੇ ਆਧਾਰਿਤ ਹੁੰਦੇ ਹਨ । ਅਰਸਤੂ (Aristotal) ਨੇ ਤਾਂ ਹੀ ਕਿਹਾ ਸੀ ਕਿ ਮਨੁੱਖ ਇਕ ਸਮਾਜਿਕ ਪਸ਼ੂ ਹੈ ।

ਵੱਖ-ਵੱਖ ਸਮਾਜਾਂ ਦੇ ਵਿਚ ਸਤਰੀਕਰਨ ਵੀ ਵੱਖੋ-ਵੱਖਰਾ ਪਾਇਆ ਜਾਂਦਾ ਹੈ । ਵਧੇਰੇ ਕਰਕੇ ਵਿਅਕਤੀਆਂ ਨੂੰ ਪੈਸੇ, ਸ਼ਕਤੀ, ਸੱਤਾ ਆਦਿ ਦੇ ਆਧਾਰ ‘ਤੇ ਵੱਖਰਾ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਸੰਖੇਪ ਵਿਚ ਅਸੀਂ ਇਹ ਕਹਿ ਸਕਦੇ ਹਾਂ ਕਿ ਸਮਾਜਿਕ ਸਤਰੀਕਰਨ ਦਾ ਭਾਵ ਵੱਖ-ਵੱਖ ਸਮਾਜਿਕ ਸਮੂਹਾਂ ਨੂੰ ਵਿਭਿੰਨ ਭਾਗਾਂ ਵਿੱਚ ਵੰਡਣ ਤੋਂ ਹੁੰਦਾ ਹੈ । ਸਮਾਜਿਕ ਸਤਰੀਕਰਨ ਦੀ ਪਰਿਭਾਸ਼ਾ ਵੱਖ-ਵੱਖ ਸਮਾਜ ਵਿਗਿਆਨੀਆਂ ਨੇ ਦਿੱਤੀ ਹੈ ਜਿਸ ਦਾ ਵਰਣਨ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਹੈ-

1. ਪੀ. ਏ. ਸੋਰੋਕਿਨ (P.A. Sorokin) ਦੇ ਅਨੁਸਾਰ, “ਸਮਾਜਿਕ ਸਤਰੀਕਰਨ ਤੋਂ ਭਾਵ ਸਮਾਜ ਦੀ ਜਨਸੰਖਿਆ ਦਾ ਉੱਚੇ ਤੇ ਨੀਵੇਂ ਪਦਮਾਤਮਕ ਤੌਰ ਤੇ ਉੱਪਰ ਆਰੋਪਿਤ ਵਰਗਾਂ ਵਿੱਚ ਵਿਭੇਦੀਕਰਣ ਤੋਂ ਹੈ । ਇਸ ਦਾ ਪ੍ਰਗਟਾਵਾ ਉੱਚਤਮ ਤੇ ਨਿਮਨਤਮ ਸਮਾਜਿਕ ਸਤਰਾਂ ਦੇ ਵਿਦਮਾਨ ਹੋਣ ਦੇ ਮਾਧਿਅਮ ਰਾਹੀਂ ਹੁੰਦਾ ਹੈ । ਇਸ ਸਮਾਜਿਕ ਸਤਰੀਕਰਨ ਦਾ ਸਾਰ ਅਤੇ ਆਧਾਰ ਸਮਾਜ ਵਿਸ਼ੇਸ਼ ਦੇ ਮੈਂਬਰਾਂ ਵਿਚ ਅਧਿਕਾਰ ਅਤੇ ਰਿਆਇਤਾਂ, ਕਰਤੱਵਾਂ ਅਤੇ ਜ਼ਿੰਮੇਵਾਰੀਆਂ, ਸਮਾਜਿਕ ਕੀਮਤਾਂ ਅਤੇ ਅਭਾਵਾਂ, ਸਮਾਜਿਕ ਸ਼ਕਤੀਆਂ ਅਤੇ ਪ੍ਰਭਾਵਾਂ ਦੀ ਅਸਮਾਨ ਵੰਡ ਤੋਂ ਹੁੰਦਾ ਹੈ । ”

2. ਕਿੰਗਸਲੇ ਡੇਵਿਸ (Kingsley Davis) ਦੇ ਅਨੁਸਾਰ, “ਸਮਾਜਿਕ ਅਸਮਾਨਤਾ ਅਚੇਤਨ ਰੂਪ ਨਾਲ ਅਪਣਾਇਆ ਇਕ ਇਹੋ ਜਿਹਾ ਢੰਗ ਹੈ ਜਿਸ ਦੇ ਦੁਆਰਾ ਵਿਭਿੰਨ ਸਮਾਜ ਇਹ ਵਿਸ਼ਵਾਸ ਦਿੰਦੇ ਹਨ ਕਿ ਸਭ ਤੋਂ ਵਧੇਰੇ ਅਹੁਦਿਆਂ ਤੇ ਚੇਤੰਨ ਰੂਪ ਨਾਲ ਸਭ ਤੋਂ ਵੱਧ ਯੋਗ ਵਿਅਕਤੀਆਂ ਨੂੰ ਰੱਖਿਆ ਗਿਆ ਹੈ । ਇਸ ਲਈ ਹਰ ਇਕ ਸਮਾਜ ਵਿਚ ਜ਼ਰੂਰੀ ਰੂਪ ਨਾਲ ਅਸਮਾਨਤਾ ਅਤੇ ਸਮਾਜਿਕ ਸਤਰੀਕਰਨ ਰਹਿਣਾ ਚਾਹੀਦਾ ਹੈ ।”

3. ਕਰਟ ਬੀ. ਮੇਅਰ (Kurt B. Mayer) ਦੇ ਅਨੁਸਾਰ, “ਸਮਾਜਿਕ ਸਤਰੀਕਰਨ ਵਿਭੇਦੀਕਰਣ ਦੀ ਵਿਵਸਥਾ ਹੁੰਦੀ ਹੈ ਜਿਸ ਵਿਚ ਸਮਾਜਿਕ ਪਦ ਦਾ ਪਦਮ ਹੁੰਦਾ ਹੈ ਅਤੇ ਜਿਨ੍ਹਾਂ ਪਦਾਂ ਨੂੰ ਧਾਰਣ ਕਰਨ ਵਾਲਿਆਂ ਨੂੰ ਸਮਾਜਿਕ ਤੌਰ ਤੇ ਮਹੱਤਵਪੂਰਨ ਪੱਖਾਂ ਤੋਂ ਇਕ ਦੂਸਰੇ ਦੇ ਟਾਕਰੇ ਤੇ ਉੱਤਮ, ਸਮਾਨ ਜਾਂ ਘਟੀਆ ਸਮਝਿਆ ਜਾਂਦਾ ਹੈ ।”

ਉਪਰੋਕਤ ਪਰਿਭਾਸ਼ਾਵਾਂ ਦੇ ਆਧਾਰ ਤੇ ਅਸੀਂ ਇਸ ਨਤੀਜੇ ਤੇ ਪਹੁੰਚਦੇ ਹਾਂ ਕਿ ਸਮਾਜਿਕ ਸਤਰੀਕਰਨ ਸਮਾਜ ਨੂੰ ਉੱਚੇ ਅਤੇ ਨੀਵੇਂ ਵੱਖ-ਵੱਖ ਸਮੂਹਾਂ ਅਤੇ ਵਿਅਕਤੀਆਂ ਦੀਆਂ ਭੂਮਿਕਾਵਾਂ ਅਤੇ ਪਦਾਂ ਨੂੰ ਨਿਰਧਾਰਿਤ ਕਰਦਾ ਹੈ । ਇਸ ਵਿਚ ਜਨਮ, ਜਾਤ, ਕਿੱਤਾ, ਲਿੰਗ, ਪੈਸਾ, ਸ਼ਕਤੀ ਆਦਿ ਦੇ ਆਧਾਰ ਉੱਤੇ ਵਿਅਕਤੀਆਂ ਵਿਚ ਪਾਏ ਜਾਣ ਵਾਲੇ ਪਦਰੂਮ ਨੂੰ ਦਰਸਾਇਆ ਜਾਂਦਾ ਹੈ । ਵਿਭਿੰਨ ਸਮੂਹਾਂ ਵਿਚ ਉੱਚਤਾ ਅਤੇ ਅਧੀਨਤਾ ਵਾਲੇ ਸੰਬੰਧ ਪਾਏ ਜਾਂਦੇ ਹਨ ਅਤੇ ਵਿਅਕਤੀ ਦੀ ਸਥਿਤੀ ਦਾ ਸਮਾਜ ਦੇ ਵਿਚ ਨਿਸ਼ਚਿਤ ਸਥਾਨ ਵੀ ਹੁੰਦਾ ਹੈ । ਇਸੀ ਦੇ ਆਧਾਰ ਉੱਤੇ ਵਿਅਕਤੀ ਨੂੰ ਸਮਾਜ ਵਿਚ ਆਦਰ ਸਨਮਾਨ ਵੀ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।

ਸਤਰੀਕਰਨ ਦੀਆਂ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਜਾਂ ਲੱਛਣ (Features or characteristics of Stratification)

1. ਸਤਰੀਕਰਨ ਸਮਾਜਿਕ ਹੁੰਦਾ ਹੈ (Stratification is Social) – ਅੱਡ-ਅੱਡ ਸਮਾਜਾਂ ਵਿਚ ਸਤਰੀਕਰਨ ਦੇ ਆਧਾਰਾਂ ਵਿਚ ਵੀ ਭਿੰਨਤਾ ਪਾਈ ਜਾਂਦੀ ਹੈ । ਜਦੋਂ ਵੀ ਅਸੀਂ ਸਮਾਜ ਵਿਚ ਪਾਈ ਜਾਣ ਵਾਲੀ ਕਿਸੇ ਚੀਜ਼ ਨੂੰ ਦੁਸਰੇ ਨਾਲੋਂ ਵੱਖਰਾ ਕਰਦੇ ਹਾਂ ਤਾਂ ਜਦੋਂ ਤਕ ਉਸ ਵੱਖਰੇਵੇਂ ਬਾਰੇ ਸਮਾਜ ਦੇ ਬਾਕੀ ਮੈਂਬਰ ਨਾ ਸਵੀਕਾਰ ਕਰ ਲੈਣ ਉਦੋਂ ਤੱਕ ਉਸ ਵਿਭਿੰਨਤਾ ਨੂੰ ਸਤਰੀਕਰਨ ਦਾ ਆਧਾਰ ਨਹੀਂ ਮੰਨਿਆ ਜਾਂਦਾ ।

2. ਸਤਰੀਕਰਨ ਸਰਬਵਿਆਪਕ ਪ੍ਰਕਿਰਿਆ ਹੈ (Stratification is a Universal Process) – ਸਮਾਜਿਕ ਸਤਰੀਕਰਨ ਦੀ ਪ੍ਰਕਿਰਿਆ ਹਰੇਕ ਸਮਾਜ ਵਿਚ ਪਾਈ ਜਾਂਦੀ ਹੈ । ਜੇਕਰ ਅਸੀਂ ਪ੍ਰਾਚੀਨ ਭਾਰਤੀ ਕਬਾਇਲੀ ਜਾਂ ਕਿਸੇ ਵੀ ਹੋਰ ਸਮਾਜ ਦੇ ਵਿਚ ਝਾਤ ਮਾਰੀਏ ਤਾਂ ਅਸੀਂ ਕੀ ਮਹਿਸੂਸ ਕਰਦੇ ਹਾਂ ਕਿ ਕੁਝ ਨਾ ਕੁਝ ਭਿੰਨਤਾ ਤਾਂ ਉਦੋਂ ਵੀ ਪਾਈ ਜਾਂਦੀ ਸੀ । ਲਿੰਗ ਦੀ ਭਿੰਨਤਾ ਤਾਂ ਪ੍ਰਕਿਰਤਕ ਦੇਣ ਹੈ ਜਿਸ ਦੇ ਆਧਾਰ ਤੇ ਵਿਅਕਤੀ ਵੰਡ ਕਰ ਸਕਦਾ ਹੈ । ਆਧੁਨਿਕ ਗੁੰਝਲਦਾਰ ਸਮਾਜ ਦੇ ਵਿਚ ਸਤਰੀਕਰਨ ਦੇ ਕਈ ਆਧਾਰ ਹਨ ।

3. ਵੱਖ-ਵੱਖ ਵਰਗਾਂ ਦੀ, ਅਸਮਾਨ ਸਥਿਤੀ (Inequality of Status of different Classe) – ਸਮਾਜਿਕ ਸਤਰੀਕਰਨ ਦੇ ਵਿਚ ਵਿਅਕਤੀਆਂ ਦੀ ਸਥਿਤੀ ਜਾਂ ਭੂਮਿਕਾ ਸਮਾਨ ਨਹੀਂ ਹੁੰਦੀ ਹੈ । ਕਿਸੇ ਦੀ ਸਭ ਤੋਂ ਉੱਚੀ, ਕਿਸੇ ਦੀ ਉਸ ਤੋਂ ਘੱਟ, ਕਿਸੀ ਦੀ ਬਹੁਤ ਨੀਵੀਂ ਆਦਿ । ਦੂਸਰਾ ਇਹ ਕਿ ਵਿਅਕਤੀ ਦੀ ਸਥਿਤੀ ਦਾ ਇਕ ਸਮਾਨ ਨਹੀਂ ਰਹਿੰਦੀ । ਉਸ ਵਿਚ ਬਦਲਾਅ ਆਉਂਦੇ ਰਹਿੰਦੇ ਹਨ । ਕਦੇ ਉਹ ਉੱਚੀ ਸਥਿਤੀ ਤੇ ਪਹੁੰਚ ਜਾਂਦਾ ਹੈ ਤੇ ਕਦੀ ਨੀਵੀਂ ਸਥਿਤੀ ਤੇ ।

4. ਊਚ ਤੇ ਨੀਚ ਦਾ ਸੰਬੰਧ (Relation of upper and lower class) – ਸਤਰੀਕਰਨ ਦੇ ਵਿਚ ਸਮਾਜ ਦੀ ਵੰਡ ਵਿਭਿੰਨ ਸਤਰਾਂ ਵਿਚ ਹੁੰਦੀ ਹੈ ਜਿਹੜੀ ਵਿਅਕਤੀ ਦੀ ਸਥਿਤੀ ਨੂੰ ਨਿਰਧਾਰਿਤ ਕਰਦੀ ਹੈ । ਮੁੱਖ ਤੌਰ ਤੇ ਸਮਾਜ ਨੂੰ ਦੋ ਹਿੱਸਿਆਂ ਵਿਚ ਵੰਡਿਆ ਜਾਂਦਾ ਹੈ । ਉੱਚਤਮ ਤੇ ਨਿਮਨਤਮ ਭਾਵ ਉੱਚਾ ਅਤੇ ਨੀਵਾਂ । ਸਮਾਜ ਦੇ ਵਿਚ ਇਕ ਪਾਸੇ ਉਹ ਲੋਕ ਹੁੰਦੇ ਹਨ ਜਿਨ੍ਹਾਂ ਦੀ ਸਥਿਤੀ ਉੱਚੀ ਹੁੰਦੀ ਹੈ ਤੇ ਇਕ ਪਾਸੇ ਉਹ ਲੋਕ ਹੁੰਦੇ ਹਨ ਜਿਨ੍ਹਾਂ ਦੀ ਸਥਿਤੀ ਨੀਵੀਂ ਹੁੰਦੀ ਹੈ ਇਸ ਦੇ ਵਿਚਕਾਰ ਵੀ ਕਈ ਵਰਗ ਸਥਾਪਿਤ ਹੁੰਦੇ ਹਨ । ਇਨ੍ਹਾਂ ਵਰਗਾਂ ਵਿਚ ਵੀ ਕਈ ਤਰ੍ਹਾਂ ਦੇ ਵਰਗ ਸਥਾਪਿਤ ਹੋ ਜਾਂਦੇ ਹਨ ਜਿਵੇਂ ਮੱਧ ਉੱਚ ਵਰਗ, ਮੱਧ ਨਿਮਨ ਵਰਗ । ਪਰ ਇਨ੍ਹਾਂ ਵਿੱਚ ਉੱਚ ਤੇ ਨੀਚ ਦਾ ਸੰਬੰਧ ਜ਼ਰੂਰ ਹੁੰਦਾ ਹੈ ।

5. ਸਤਰੀਕਰਨ ਅੰਤਰ ਕਿਰਿਆਵਾਂ ਨੂੰ ਸੀਮਿਤ ਕਰਦੀ ਹੈ (Stratification restricts interaction) – ਸਤਰੀਕਰਨ ਦੀ ਪ੍ਰਕਿਰਿਆ ਵਿਚ ਅੰਦਰਲੀਆਂ ਕਿਰਿਆਵਾਂ ਸਤਰ-ਵਿਸ਼ੇਸ਼ ਤੱਕ ਹੀ ਸੀਮਿਤ ਹੁੰਦੀਆਂ ਹਨ | ਆਮ ਤੌਰ ਤੇ ਅਸੀਂ ਵੇਖਦੇ ਹਾਂ ਕਿ ਹਰ ਇੱਕ ਵਿਅਕਤੀ ਆਪਣੇ ਸਤਰ ਦੇ ਮੈਂਬਰਾਂ ਨਾਲ ਹੀ ਸੰਬੰਧ ਸਥਾਪਿਤ ਕਰਦਾ ਹੈ । ਇਸ ਕਰਕੇ ਉਹ ਆਪਣੇ ਦਿਲ ਦੀਆਂ ਗੱਲਾਂ ਵੀ ਉਨ੍ਹਾਂ ਨਾਲ ਹੀ ਸਾਂਝੀਆਂ ਕਰਦਾ ਹੈ । ਵਿਅਕਤੀ ਦੀ ਦੋਸਤੀ ਵੀ ਉਸ ਦੀ ਆਪਣੀ ਹੀ ਸ਼੍ਰੇਣੀ ਦੇ ਮੈਂਬਰਾਂ ਨਾਲ ਹੁੰਦੀ ਹੈ । ਇਸ ਪ੍ਰਕਾਰ ਵਿਅਕਤੀ ਦੀ ਅੰਤਰ ਕਿਰਿਆ ਵੀ ਵਿਭਿੰਨ ਸਤਰਾਂ ਦੇ ਵਿਅਕਤੀਆਂ ਨਾਲ ਨਹੀਂ ਹੁੰਦੀ ਬਲਕਿ ਆਪਣੀ ਸਤਰ ਨਾਲ ਹੁੰਦੀ ਹੈ ।

6. ਸਤਰੀਕਰਨ ਪ੍ਰਤੀਯੋਗਤਾ ਦੀ ਭਾਵਨਾ ਨੂੰ ਵਿਕਸਿਤ ਕਰਦੀ ਹੈ (It develops the feeling of competition) – ਸਤਰੀਕਰਨ ਦੀ ਪ੍ਰਕਿਰਿਆ ਵਿਅਕਤੀ ਵਿਚ ਮਿਹਨਤ ਅਤੇ ਲਗਨ ਪੈਦਾ ਕਰਦੀ ਹੈ । ਇਸ ਵਿੱਚ ਹਰ ਇੱਕ ਵਿਅਕਤੀ ਆਪਣੀ ਸਮਾਜਿਕ ਸਥਿਤੀ ਬਾਰੇ ਚੇਤੰਨ ਹੁੰਦਾ ਹੈ । ਉਹ ਹਮੇਸ਼ਾ ਅੱਗੇ ਵਧਣ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰਨੀ ਸ਼ੁਰੂ ਕਰ ਦਿੰਦਾ ਹੈ ਕਿਉਂਕਿ ਉਸ ਨੂੰ ਆਪਣੇ ਤੋਂ ਉੱਚੀ ਸਥਿਤੀ ਵਾਲੇ ਵਿਅਕਤੀ ਨਜ਼ਰ ਆਉਂਦੇ ਹਨ । ਵਿਅਕਤੀ ਆਪਣੀ ਯੋਗਤਾ ਦਾ ਇਸਤੇਮਾਲ ਕਰਕੇ ਮੁਕਾਬਲੇ ਵਿੱਚੋਂ ਅੱਗੇ ਲੰਘਣਾ ਚਾਹੁੰਦਾ ਹੈ । ਇਸ ਪ੍ਰਕਾਰ ਵਿਅਕਤੀ ਦੀ ਉੱਚੇ ਪੱਧਰ ਲਈ ਪਾਈ ਗਈ ਚੇਤਨਤਾ ਵਿਅਕਤੀ ਵਿੱਚ ਪ੍ਰਤੀਯੋਗਤਾ ਦੀ ਭਾਵਨਾ ਪੈਦਾ ਕਰਦੀ ਹੈ । ਹਰੇਕ ਵਿਅਕਤੀ ਵਿੱਚ ਆਪਣੇ ਆਪ ਨੂੰ ਸਮਾਜ ਵਿੱਚ ਉੱਚਾ ਚੁੱਕਣ ਦੀ ਇੱਛਾ ਹੁੰਦੀ ਹੈ ਅਤੇ ਉਹ ਆਪਣੇ ਆਪ ਨੂੰ ਉੱਚਾ ਚੁੱਕ ਸਕਦਾ ਹੈ ਆਪਣੀ ਮਿਹਨਤ ਨਾਲ ਉਹ ਮਿਹਨਤ ਕਰਦਾ ਹੈ ਤੇ ਹੋਰ ਵਰਗਾਂ ਦੇ ਵਿਅਕਤੀਆਂ ਨਾਲ ਪ੍ਰਤੀਯੋਗਤਾ ਕਰਦਾ ਹੈ ਤੇ ਉਸ ਨੂੰ ਵੇਖ ਕੇ ਆਪਣੇ ਆਪ ਨੂੰ ਉੱਪਰ ਚੁੱਕਦਾ ਹੈ ।

7. ਪ੍ਰਤਿਸ਼ਠਾ ਦੀ ਨਾ ਬਰਾਬਰ ਵੰਡ (Unequal division of prestige) – ਸਮਾਜਿਕ ਸਤਰੀਕਰਨ ਦੀ ਵਿਵਸਥਾ ਵਿਚ ਹਰ ਇੱਕ ਵਿਅਕਤੀ ਦੀ ਸਥਿਤੀ ਨਾਲ ਪ੍ਰਤਿਸ਼ਠਾ ਸੰਬੰਧਿਤ ਹੁੰਦੀ ਹੈ । ਸਮਾਜ ਵਿਚ ਵਿਅਕਤੀ ਨੂੰ ਸਹੂਲਤਾਂ ਵੀ ਉਸ ਦੀ ਸਥਿਤੀ ਦੇ ਆਧਾਰ ਤੇ ਹੀ ਪ੍ਰਾਪਤ ਹੁੰਦੀਆਂ ਹਨ । ਉੱਚੇ ਵਰਗ ਵਾਲਿਆਂ ਕੋਲ ਐਸ਼ੋ ਆਰਾਮ ਦੀਆਂ ਵਧੇਰੇ ਸਹੂਲਤਾਂ ਹੁੰਦੀਆਂ ਹਨ ਜਦੋਂ ਕਿ ਨੀਵੀਂ ਸਥਿਤੀ ਵਾਲੇ ਵਿਅਕਤੀ ਕੋਲ ਖਾਣ ਲਈ ਦੋ ਸਮੇਂ ਦੀ ਰੋਟੀ ਵੀ ਨਹੀਂ । ਸਮਾਜ ਦੇ ਵਿੱਚ ਆਂਦਰ, ਸਨਮਾਨ ਵੀ ਉੱਚੀ ਸਥਿਤੀ ਵਾਲਿਆਂ ਨਾਲ ਹੀ ਜੁੜਿਆ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਸਤਰੀਕਰਨ ਦੀਆਂ ਕਿਸਮਾਂ ਤੇ ਵਿਸਤਾਰਪੂਰਵਕ ਨੋਟ ਲਿਖੋ ।
ਉੱਤਰ-
1. ਵਰਣ ਸਤਰੀਕਰਨ (Varna Stratification) – ਵਰਣ ਸਤਰੀਕਰਨ ਵਿੱਚ ਜਾਤੀਗਤ ਭਿੰਨਤਾ ਅਤੇ ਵਿਅਕਤੀ ਦੀ ਯੋਗਤਾ ਦੇ ਸੁਭਾਅ ਕਾਫ਼ੀ ਮਹੱਤਵਪੂਰਨ ਆਧਾਰ ਸੀ ! ਭਾਰਤ ਵਿੱਚ ਆਰੀਆ ਲੋਕਾਂ ਦੇ ਆਉਣ ਤੋਂ ਬਾਅਦ ਸਮਾਜ ਦੋ ਭਾਗਾਂ ਆਰੀਆ ਲੋਕਾਂ ਤੇ Original inhabitants ਵਿੱਚ ਵੰਡਿਆ ਗਿਆ । ਬਾਅਦ ਵਿੱਚ ਆਰੀਆ ਲੋਕ, ਜਿਨ੍ਹਾਂ ਨੂੰ ਵਿਜ ਵੀ ਕਿਹਾ ਜਾਂਦਾ ਸੀ, ਆਪਣੇ ਗੁਣਾਂ ਅਤੇ ਸੁਭਾਅ ਦੇ ਆਧਾਰ ਉੱਤੇ ਬਾਹਮਣ, ਖੱਤਰੀ, ਵੈਸ਼ ਅਤੇ ਚੌਥੇ ਵਰਣ ਵਿੱਚ ਵੰਡੇ ਗਏ । ਇਸ ਤਰਾਂ ਸਮਾਜ ਚਾਰ ਵਰਣਾਂ ਜਾਂ ਚਾਰ ਭਾਗਾਂ ਵਿੱਚ ਵੰਡਿਆਂ ਗਿਆ ਅਤੇ ਸਤਰੀਕਰਨ ਦਾ ਇਹ ਸਰੂਪ ਸਾਹਮਣੇ ਆਇਆ ਸੀ । ਇਸ ਪਦਮ ਵਿੱਚ ਬਾਹਮਣ ਦੀ ਸਥਿਤੀ ਸਭ ਤੋਂ ਉੱਚੀ ਹੁੰਦੀ ਸੀ ਤੇ ਫਿਰ ਖੱਤਰੀ, ਵੈਸ਼ ਅਤੇ ਅੰਤ ਵਿੱਚ ਚੌਥੇ ਵਰਣ ਦੇ ਲੋਕ ਆਉਂਦੇ ਸਨ । ਇਸ ਵਿਵਸਥਾ ਵਿੱਚ ਹਰੇਕ ਵਰਣ ਦਾ ਕੰਮ ਨਿਸ਼ਚਿਤ ਅਤੇ ਇੱਕ ਦੂਜੇ ਤੋਂ ਅੱਡ ਸੀ । ਵਰਣ ਵਿਵਸਥਾ ਦਾ ਸ਼ੁਰੂਆਤੀ ਰੂਪ ਜਨਮ ਉੱਤੇ ਆਧਾਰਿਤ ਨਹੀਂ ਸੀ ਬਲਕਿ ਵਿਅਕਤੀ ਦੇ ਗੁਣਾਂ ਉੱਤੇ ਆਧਾਰਿਤ ਸੀ ਜਿਸ ਵਿੱਚ ਵਿਅਕਤੀ ਆਪਣੇ ਗੁਣਾਂ ਤੇ ਆਦਤਾਂ ਨੂੰ ਬਦਲ ਕੇ ਵਰਣ ਬਦਲ ਸਕਦਾ ਸੀ । ਪਰ ਵਰਣ ਬਦਲਨਾ ਇੱਕ ਮੁਸ਼ਕਿਲ ਕੰਮ ਸੀ ਜਿਸ ਨੂੰ ਆਸਾਨੀ ਨਾਲ ਬਦਲਿਆ ਨਹੀਂ ਜਾ ਸਕਦਾ ਸੀ ।

2. ਦਾਸਤਾ ਜਾਂ ਗੁਲਾਮੀ ਦਾ ਸਤਰੀਕਰਨ (Slavery Stratification) – ਦਾਸ ਜਾਂ ਗੁਲਾਮ ਇੱਕ ਮਨੁੱਖ ਹੁੰਦਾ ਹੈ ਜਿਹੜਾ ਕਿਸੇ ਹੋਰ ਮਨੁੱਖ ਦੇ ਪੂਰੀ ਤਰ੍ਹਾਂ ਨਿਯੰਤਰਣ ਵਿੱਚ ਹੁੰਦਾ ਹੈ । ਉਹ ਆਪਣੇ ਮਾਲਕ ਦੀ ਦਇਆ ਉੱਤੇ ਜਿਉਂਦਾ ਹੈ ਜਿਸ ਨੂੰ ਕੋਈ ਵੀ ਅਧਿਕਾਰ ਨਹੀਂ ਹੁੰਦਾ ਹੈ । ਮਾਲਕ ਕੁਝ ਮਾਮਲਿਆਂ ਵਿੱਚ ਉਸਦੀ ਸੁਰੱਖਿਆ ਕਰਦਾ ਹੈ ਜਿਵੇਂ ਕਿ ਉਸ ਨੂੰ ਕਿਸੇ ਹੋਰ ਦਾ ਗੁਲਾਮ ਬਣਨ ਤੋਂ ਰੋਕਣਾ । ਪਰ ਉਹ ਬਿਨਾਂ ਅਧਿਕਾਰ ਵਾਲਾ ਵਿਅਕਤੀ ਹੁੰਦਾ ਹੈ । ਉਹ ਪੂਰੀ ਤਰ੍ਹਾਂ ਆਪਣੇ ਮਾਲਕ ਦੀ ਸੰਪਤੀ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਦਾਸ ਪ੍ਰਥਾ ਵਾਲੇ ਸਮਾਜਾਂ ਵਿੱਚ ਬਹੁਤ ਜ਼ਿਆਦਾ ਅਸਮਾਨਤਾ ਪਾਈ ਜਾਂਦੀ ਹੈ । ਅਮਰੀਕਾ, ਅਫਰੀਕਾ ਆਦਿ ਮਹਾਂਦੀਪਾਂ ਵਿੱਚ ਇਹ ਪ੍ਰਥਾ 19ਵੀਂ ਸਦੀ ਵਿੱਚ ਪਾਈ ਜਾਂਦੀ ਸੀ । ਇਸ ਵਿੱਚ ਦਾਸ ਆਪਣੇ ਮਾਲਕ ਦੇ ਅਧੀਨ ਹੁੰਦਾ ਸੀ ਅਤੇ ਮਾਲਕ ਉਸਨੂੰ ਵੇਚ ਵੀ ਸਕਦਾ ਸੀ । ਦਾਸ ਦੀ ਇਸ ਨੀਵੀਂ ਸਥਿਤੀ ਦੇ ਕਾਰਨ ਉਸਨੂੰ ਕੋਈ ਅਧਿਕਾਰ ਪ੍ਰਾਪਤ ਨਹੀਂ ਸਨ । ਉਸ ਦਾ ਮਾਲਕ ਉਸ ਤੋਂ ਸਖ਼ਤ ਮਿਹਨਤ ਕਰਵਾਉਂਦਾ ਸੀ ਤੇ ਉਹਨਾਂ ਨੂੰ ਖਰੀਦਿਆ ਅਤੇ ਵੇਚਿਆ ਵੀ ਜਾਂਦਾ ਸੀ । ਆਧੁਨਿਕ ਸਮਾਂ ਆਉਂਦੇ-ਆਉਂਦੇ ਦਾਸ ਪ੍ਰਥਾ ਦਾ ਵਿਰੋਧ ਹੋਣ ਲੱਗ ਗਿਆ ਜਿਸ ਨਾਲ ਇਹ ਪ੍ਰਥਾ ਹੌਲੀ-ਹੌਲੀ ਖ਼ਤਮ ਹੋ ਗਈ ਤੇ ਦਾਸਾਂ ਨੇ ਕਿਸਾਨਾਂ ਦਾ ਰੂਪ ਲੈ ਲਿਆ ਪਰ ਇਹਨਾਂ ਵਿੱਚ ਗੁਲਾਮ ਅਤੇ ਮਾਲਕ ਦੇ ਰੂਪ ਵਿੱਚ ਸਤਰੀਕਰਨ ਪਾਇਆ ਜਾਂਦਾ ਸੀ ।

3. ਸਾਮੰਤਵਾਦ (Feudalism) – ਦਾਸ ਪ੍ਰਥਾ ਦੇ ਨਾਲ-ਨਾਲ ਸਾਮੰਤਵਾਦ ਵੀ ਸਾਹਮਣੇ ਆਇਆ । ਸਾਮੰਤ ਲੋਕ ਬਹੁਤ ਵੱਡੇ ਜ਼ਮੀਨ ਦੇ ਟੁਕੜੇ ਦੇ ਮਾਲਕ ਹੁੰਦੇ ਸਨ ਅਤੇ ਉਹ ਆਪਣੀ ਜ਼ਮੀਨ ਖੇਤੀ ਕਰਨ ਦੇ ਲਈ ਹੋਰ ਲੋਕਾਂ ਨੂੰ ਤਾਂ ਕਿਰਾਏ ਉੱਤੇ ਦਿੰਦੇ ਸਨ ਜਾਂ ਪੈਦਾਵਾਰ ਨੂੰ ਵੰਡਦੇ ਸਨ । ਮੱਧ-ਕਾਲ ਵਿੱਚ ਤਾਂ ਸਾਮੰਤ ਪ੍ਰਥਾ ਨੂੰ ਯੂਰਪ ਵਿੱਚ ਕਾਨੂੰਨੀ ਮਾਨਤਾ ਪ੍ਰਾਪਤ ਸੀ ! ਹਰੇਕ ਸਾਮੰਤ ਜਾਂ ਜਗੀਰਦਾਰ ਦੀ ਇੱਕ ਵਿਸ਼ੇਸ਼ ਸਥਿਤੀ, ਵਿਸ਼ੇਸ਼ ਅਧਿਕਾਰ ਅਤੇ ਕਰਤੱਵ ਹੁੰਦੇ ਸਨ । ਉਸ ਸਮੇਂ ਜ਼ਮੀਨ ਉੱਤੇ ਖੇਤੀ ਕਰਨ ਵਾਲੇ ਲੋਕਾਂ ਦੇ ਅਧਿਕਾਰ ਕਾਫੀ ਘੱਟ ਹੁੰਦੇ ਸਨ । ਉਹ ਨਿਆਂ ਪ੍ਰਾਪਤ ਨਹੀਂ ਕਰ ਸਕਦੇ ਸਨ ਤੇ ਉਹਨਾਂ ਨੂੰ ਜਗੀਰਦਾਰਾਂ ਦੇ ਰਹਿਮ ਉੱਤੇ ਨਿਰਭਰ ਰਹਿਣਾ ਪੈਂਦਾ ਸੀ । ਉਸ ਸਮੇਂ ਕਿਰਤ ਵੰਡ ਵੀ ਹੁੰਦਾ ਸੀ । ਇਸ ਪ੍ਰਥਾ ਵਿੱਚ ਸ਼ਕਤੀ ਸਰਦਾਰਾਂ ਅਤੇ ਪੁਜਾਰੀਆਂ ਦੇ ਹੱਥਾਂ ਵਿੱਚ ਹੁੰਦੀ ਸੀ । ਭਾਰਤ ਵਿੱਚ ਜ਼ਮੀਂਦਾਰ ਤਾਂ ਸਨ ਪਰ ਸਾਮੰਤ ਪ੍ਰਥਾ ਦੇ ਲੱਛਣ ਜਾਤੀ ਪ੍ਰਥਾ ਦੇ ਕਾਰਨ ਨਹੀਂ ਸਨ । ਭਾਰਤ ਵਿੱਚ ਮਿਲਣ ਵਾਲੇ ਜਮੀਂਦਾਰ ਯੂਰਪ ਵਿੱਚ ਮਿਲਣ ਵਾਲੇ ਜਗੀਰਦਾਰਾਂ ਤੋਂ ਅੱਡ ਸਨ । ਭਾਰਤ ਵਿੱਚ ਜ਼ਿਮੀਂਦਾਰ ਰਾਜੇ ਲਈ ਪ੍ਰਜਾ ਤੋਂ ਟੈਕਸ ਇਕੱਠਾ ਕਰਨ ਦਾ ਕੰਮ ਕਰਦੇ ਸਨ ਅਤੇ ਜ਼ਰੂਰਤ ਪੈਣ ਉੱਤੇ ਰਾਜੇ ਨੂੰ ਆਪਣੀ ਸੈਨਾ ਵੀ ਦਿੰਦੇ ਸਨ । ਜਦੋਂ ਰਾਜੇ ਕਮਜ਼ੋਰ ਹੋ ਗਏ ਤਾਂ ਬਹੁਤ ਸਾਰੇ ਜ਼ਮੀਂਦਾਰ ਤੇ ਜਗੀਰਦਾਰਾਂ ਨੇ ਆਪਣੇ ਰਾਜ ਸਥਾਪਿਤ ਕਰ ਲਏ । ਇਸ ਤਰ੍ਹਾਂ ਜ਼ਮੀਂਦਾਰੀ ਪ੍ਰਥਾ ਜਾਂ ਸਾਮੰਤਵਾਦ ਦੇ ਸਮੇਂ ਵੀ ਸਮਾਜਿਕ ਸਤਰੀਕਰਨ ਸਮਾਜ ਵਿੱਚ ਮਿਲਦਾ ਸੀ ।

4. ਨਸਲੀ ਸਤਰੀਕਰਨ (Racial stratification) – ਅੱਡ-ਅੱਡ ਸਮਾਜਾਂ ਵਿੱਚ ਨਸਲ ਦੇ ਆਧਾਰ ਉੱਤੇ ਸਤਰੀਕਰਨ ਪਾਇਆ ਜਾਂਦਾ ਹੈ । ਨਸਲ ਦੇ ਆਧਾਰ ਉੱਤੇ ਸਮਾਜ ਨੂੰ ਅੱਡ-ਅੱਡ ਸਮੂਹਾਂ ਵਿੱਚ ਵੰਡਿਆ ਹੁੰਦਾ ਹੈ । ਮੁੱਖ ਤੌਰ ਉੱਤੇ ਮਨੁੱਖ ਜਾਤੀ ਦੀਆਂ ਤਿੰਨ ਨਸਲਾਂ ਪਾਈਆਂ ਜਾਂਦੀਆਂ ਹਨ – ਕਾਕੇਸ਼ੀਅਨ (ਸਫ਼ੇਦ ਮੰਗੋਲਾਈਡ (ਪੀਲੇ ਅਤੇ ਨੀਗਰੋਆਈਡ ਕਾਲੇ) ਲੋਕ । ਇਹਨਾਂ ਸਾਰੀਆਂ ਨਸਲਾਂ ਵਿੱਚ ਪਦਮ ਦੀ ਵਿਵਸਥਾ ਪਾਈ ਜਾਂਦੀ ਹੈ । ਸਫ਼ੇਦ ਨਸਲ ਨੂੰ ਸਮਾਜ ਵਿੱਚ ਉੱਚਾ ਸਥਾਨ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਸੀ । ਪੀਲੀ ਨਸਲ ਨੂੰ ਵਿਚਲਾ ਸਥਾਨ ਅਤੇ ਕਾਲੀ ਨਸਲ ਨੂੰ ਸਮਾਜ ਵਿੱਚ ਸਭ ਤੋਂ ਨੀਵਾਂ ਸਥਾਨ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਸੀ । ਅਮਰੀਕਾ ਵਿੱਚ ਅੱਜ ਵੀ ਨਸਲੀ ਆਧਾਰ ਉੱਤੇ ਭੇਦਭਾਵ ਪਾਇਆ ਜਾਂਦਾ ਹੈ । ਅੱਡ-ਅੱਡ ਨਸਲਾਂ ਦੇ ਲੋਕ ਆਪਸ ਵਿੱਚ ਵਿਆਹ ਵੀ ਨਹੀਂ ਕਰਦੇ । ਚਾਹੇ ਆਧੁਨਿਕ ਸਮਾਜ ਵਿੱਚ ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਸਰੂਪ ਵਿੱਚ ਕੁਝ ਪਰਿਵਰਤਨ ਆਇਆ ਹੈ। ਪਰ ਫਿਰ ਵੀ ਇਹ ਸਤਰੀਕਰਨ ਮਿਲਦਾ ਜ਼ਰੂਰ ਹੈ ।

5. ਜਾਤੀਗਤ ਸਤਰੀਕਰਨ (Caste Stratification) – ਜਿਹੜਾ ਸਤਰੀਕਰਨ ਜਨਮ ਦੇ ਆਧਾਰ ਉੱਤੇ ਹੁੰਦਾ ਹੈ ਉਸਨੂੰ ਜਾਤੀਗਤ ਸਤਰੀਕਰਨ ਕਹਿੰਦੇ ਹਨ ਕਿਉਂਕਿ ਬੱਚੇ ਦੀ ਸਥਿਤੀ ਉਸਦੇ ਜਨਮ ਦੇ ਅਨੁਸਾਰ ਹੀ ਨਿਸ਼ਚਿਤ ਹੋ ਜਾਂਦੀ ਸੀ । ਪ੍ਰਾਚੀਨ ਅਤੇ ਪਰੰਪਰਾਗਤ ਭਾਰਤੀ ਸਮਾਜ ਵਿੱਚ ਅਸੀਂ ਜਾਤੀਗਤ ਸਤਰੀਕਰਨ ਦੇ ਸਰੂਪ ਦੀ ਉਦਾਹਰਣ ਦੇਖ ਸਕਦੇ ਹਾਂ। ਇਸਦਾ ਭਾਰਤੀ ਸਮਾਜ ਵਿੱਚ ਜ਼ਿਆਦਾ ਪ੍ਰਭਾਵ ਸੀ ਕਿਉਂਕਿ ਭਾਰਤ ਵਿੱਚ ਵਿਦੇਸ਼ਾਂ ਤੋਂ ਆ ਕੇ ਲੋਕ ਰਹਿਣ ਲੱਗ ਪਏ ਅਤੇ ਇਹਨਾਂ ਲੋਕਾਂ ਵਿੱਚ ਵੀ ਜਾਤੀ ਉੱਤੇ ਆਧਾਰਿਤ ਸਤਰੀਕਰਨ ਸ਼ੁਰੂ ਹੋ ਗਿਆ ਸੀ । ਉਦਾਹਰਣ ਦੇ ਲਈ ਮੁਸਲਮਾਨਾਂ ਵਿੱਚ ਵੀ ਕਈ ਪ੍ਰਕਾਰ ਦੇ ਸਮੂਹ ਪਾਏ ਜਾਂਦੇ ਹਨ । ਜਾਤੀਗਤ ਸਤਰੀਕਰਨ ਵਿੱਚ ਮੁੱਖ ਤੌਰ ਉੱਤੇ ਚਾਰ ਜਾਤਾਂ ਪਾਈਆਂ ਜਾਂਦੀਆ ਸਨ ਪਰ ਇਨ੍ਹਾਂ ਚਾਰ ਜਾਤਾਂ ਅੱਗੇ ਬਹੁਤ ਸਾਰੀਆਂ ਉਪਜਾਤਾਂ ਵਿੱਚ ਵੰਡੀਆਂ ਹੁੰਦੀਆਂ ਸਨ । ਇਹਨਾਂ ਉਪਜਾਤਾਂ ਵਿੱਚ ਵੀ ਸਤਰੀਕਰਨ ਹੁੰਦਾ ਸੀ । ਸਤਰੀਕਰਨ ਦਾ ਇਹ ਸਰੂਪ ਹੋਰਾਂ ਸਰੂਪਾਂ ਨਾਲੋਂ ਸਥਿਰ ਸੀ ਕਿਉਂਕਿ ਵਿਅਕਤੀ ਆਪਣੀ ਜਾਤੀ ਨੂੰ ਬਦਲ ਨਹੀਂ ਸਕਦਾ ।

6. ਵਰਗ ਸਤਰੀਕਰਨ (Class Stratification) – ਇਸ ਨੂੰ ਸਰਵਵਿਆਪਕ ਸਤਰੀਕਰਨ ਵੀ ਕਹਿੰਦੇ ਹਨ । ਕਿਉਂਕਿ ਇਸ ਪ੍ਰਕਾਰ ਦਾ ਸਤਰੀਕਰਨ ਹਰੇਕ ਸਮਾਜ ਵਿੱਚ ਵੇਖਣ ਨੂੰ ਮਿਲ ਜਾਂਦਾ ਹੈ । ਇਸ ਨੂੰ ਖੁੱਲਾ ਸਤਰੀਕਰਨ ਵੀ ਕਹਿੰਦੇ ਹਨ । ਇਸ ਪ੍ਰਕਾਰ ਦਾ ਸਤਰੀਕਰਨ ਸਮਾਜਿਕ ਸੰਸਕ੍ਰਿਤਕ ਆਧਾਰਾਂ ਜਿਵੇਂ ਕਿ ਆਮਦਨੀ, ਪੇਸ਼ਾ, ਸੱਤਾ, ਸੰਪਤੀ, ਧਰਮ, ਸਿੱਖਿਆ, ਕੰਮ ਆਦਿ ਦੇ ਆਧਾਰ ਉੱਤੇ ਵੇਖਣ ਨੂੰ ਮਿਲਦਾ ਹੈ । ਇਸ ਵਿੱਚ ਵਿਅਕਤੀ ਨੂੰ ਇੱਕ ਨਿਸ਼ਚਿਤ ਸਥਾਨ ਪ੍ਰਾਪਤ ਹੋ ਜਾਂਦਾ ਹੈ ਅਤੇ ਸਮਾਨ ਸਥਿਤੀ ਵਾਲੇ ਵਿਅਕਤੀ ਇਕੱਠੇ ਹੋ ਕੇ ਇੱਕ ਵਰਗ ਦਾ ਨਿਰਮਾਣ ਕਰਦੇ ਹਨ । ਇਸ ਤਰ੍ਹਾਂ ਸਮਾਜ ਵਿੱਚ ਅੱਡ-ਅੱਡ ਵਰਗ ਬਣ ਜਾਂਦੇ ਹਨ ਅਤੇ ਉਹਨਾਂ ਵਿੱਚ ਉੱਚੇ ਨੀਵੇਂ ਸੰਬੰਧ ਸਥਾਪਿਤ ਹੋ ਜਾਂਦੇ ਹਨ । ਇਸੇ ਕਾਰਨ ਸਮਾਜ ਵਿੱਚ ਸਤਰੀਕਰਨ ਪਾਇਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਵਿੱਚ ਵਿਅਕਤੀ ਦੀ ਸਥਿਤੀ ਕਿਸੇ ਵੀ ਸਮੇਂ ਬਦਲ ਸਕਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਜਾਤੀ ਵਿਵਸਥਾ ਵਿੱਚ ਬਦਲਾਵ ਲਿਆ ਰਹੇ ਕਾਰਨਾਂ ਉੱਪਰ ਨੋਟ ਲਿਖੋ ।
ਉੱਤਰ-
1. ਸਮਾਜਿਕ ਧਾਰਮਿਕ ਸੁਧਾਰ ਲਹਿਰਾਂ (Socio-religious reform movement) – ਭਾਰਤ ਵਿਚ ਅੰਗਰੇਜ਼ੀ ਸਾਮਰਾਜ ਦੇ ਸਥਾਪਿਤ ਹੋਣ ਤੋਂ ਪਹਿਲਾਂ ਵੀ ਕੁਝ ਧਾਰਮਿਕ ਲਹਿਰਾਂ ਨੇ ਜਾਤੀ ਪ੍ਰਥਾ ਦੀ ਨਿਖੇਧੀ ਕੀਤੀ ਸੀ । ਬੁੱਧ ਮਤ ਅਤੇ ਜੈਨ ਮਤ ਤੋਂ ਲੈ ਕੇ ਇਸਲਾਮ ਅਤੇ ਸਿੱਖ ਧਰਮ ਨੇ ਵੀ ਜਾਤੀ ਪ੍ਰਥਾ ਦਾ ਖੰਡਨ ਕੀਤਾ । ਇਨ੍ਹਾਂ ਦੇ ਨਾਲ-ਨਾਲ ਇਸਲਾਮ ਅਤੇ ਸਿੱਖ ਧਰਮ ਨੇ ਤਾਂ ਜਾਤੀ ਪ੍ਰਥਾ ਦੀ ਜੰਮ ਕੇ ਨਿਖੇਧੀ ਕੀਤੀ । 19ਵੀਂ ਸਦੀ ਵਿਚ ਕੁਝ ਹੋਰ ਮਹੱਤਵਪੂਰਨ ਸਮਾਜ ਸੁਧਾਰਕ ਲਹਿਰਾਂ ਨੇ ਵੀ ਜਾਤੀ ਪ੍ਰਥਾ ਦੇ ਵਿਰੁੱਧ ਅੰਦੋਲਨ ਚਲਾਇਆ । ਰਾਜਾ ਰਾਮ ਮੋਹਨ ਰਾਇ ਵਲੋਂ ਚਲਾਏ ਮੋ ਸਮਾਜ, ਦਯਾਨੰਦ ਸਰਸਵਤੀ ਵਲੋਂ ਚਲਾਇਆ ਆਰੀਆ ਸਮਾਜ, ਰਾਮ ਕ੍ਰਿਸ਼ਨ ਮਿਸ਼ਨ ਆਦਿ ਇਨ੍ਹਾਂ ਵਿਚੋਂ ਕੁੱਝ ਮਹੱਤਵਪੂਰਨ ਸਮਾਜ ਸੁਧਾਰਕ ਲਹਿਰਾਂ ਸਨ ।

ਇਨ੍ਹਾਂ ਤੋਂ ਇਲਾਵਾ ਜਯੋਤੀ ਰਾਉ ਫੂਲੇ ਨੇ 1873 ਵਿਚ ਸਤਿਆ ਸ਼ੋਧਨ ਸਮਾਜ ਦੀ ਸਥਾਪਨਾ ਕੀਤੀ ਜਿਸ ਦਾ ਮੁੱਖ ਮੰਤਵੇਂ ਸਮਾਜ ਵਿਚ ਸਾਰਿਆਂ ਨੂੰ ਬਰਾਬਰੀ ਦਾ ਦਰਜਾ ਦਿਵਾਉਣਾ ਸੀ । ਜਾਤੀ ਪ੍ਰਥਾ ਦੀ ਵਿਰੋਧਤਾ ਮਹਾਤਮਾ ਗਾਂਧੀ ਅਤੇ ਡਾ: ਬੀ. ਆਰ. ਅੰਬੇਦਕਰ ਨੇ ਵੀ ਕੀਤੀ ਸੀ । ਮਹਾਤਮਾ ਗਾਂਧੀ ਨੇ ਹੇਠਲੀਆਂ ਜਾਤਾਂ ਨੂੰ ਹਰੀਜਨ ਦਾ ਨਾਮ ਦਿੱਤਾ ਅਤੇ ਉਨ੍ਹਾਂ ਨੂੰ ਹੋਰ ਜਾਤੀਆਂ ਦੇ ਵਾਂਗ ਸਮਾਨ ਅਧਿਕਾਰ ਦਿਵਾਉਣ ਦੀ ਕੋਸ਼ਿਸ਼ ਕੀਤੀ । ਆਰੀਆ ਸਮਾਜ ਨੇ ਮਨੁੱਖ ਦੇ ਜਨਮ ਦੀ ਥਾਂ ਉਸਦੇ ਗੁਣਾਂ ਨੂੰ ਜ਼ਿਆਦਾ ਮਹੱਤਵ ਦਿੱਤਾ । ਇਨ੍ਹਾਂ ਸਾਰੇ ਲੋਕਾਂ ਦੀਆਂ ਕੋਸ਼ਿਸ਼ਾਂ ਨਾਲ ਇਹ ਸਪੱਸ਼ਟ ਹੋ ਗਿਆ ਕਿ ਮਨੁੱਖ ਦੀ ਸਮਾਜ ਵਿਚ ਪਛਾਣ ਉਸਦੇ ਗੁਣਾਂ ਨਾਲ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ਨਾ ਕਿ ਉਸਦੇ ਜਨਮ ਨਾਲ ।

2. ਭਾਰਤ ਸਰਕਾਰ ਦੀਆਂ ਕੋਸ਼ਿਸ਼ਾਂ (Efforts of Indian Government) – ਅੰਗਰੇਜ਼ੀ ਰਾਜ ਸਮੇਂ ਅਤੇ ਭਾਰਤ ਦੀ ਆਜ਼ਾਦੀ ਪਿੱਛੋਂ ਕਈ ਮਹੱਤਵਪੂਰਨ ਕਾਨੂੰਨ ਪਾਸ ਕੀਤੇ ਗਏ ਜਿਨ੍ਹਾਂ ਨੇ ਜਾਤੀ ਪ੍ਰਥਾ ਨੂੰ ਕਮਜ਼ੋਰ ਕਰਨ ਵਿਚ ਡੂੰਘਾ ਅਸਰ ਪਾਇਆ । ਅੰਗਰੇਜ਼ੀ ਰਾਜ ਤੋਂ ਪਹਿਲਾਂ ਜਾਤੀ ਅਤੇ ਪੇਂਡੂ ਪੰਚਾਇਤਾਂ ਬਹੁਤ ਸ਼ਕਤੀਸ਼ਾਲੀ ਸਨ । ਇਹ ਪੰਚਾਇਤਾਂ ਅਪਰਾਧੀਆਂ ਨੂੰ ਸਜ਼ਾਵਾਂ ਵੀ ਦੇ ਸਕਦੀਆਂ ਸਨ ਅਤੇ ਜ਼ੁਰਮਾਨੇ ਵੀ ਕਰ ਸਕਦੀਆਂ ਸਨ | ਅੰਗਰੇਜ਼ੀ ਸ਼ਾਸਨ ਦੌਰਾਨ ਜਾਤ ਅਸਰਥਾਵਾਂ ਦੂਰ ਕਰਨ ਦਾ ਕਾਨੂੰਨ (Caste Disabilities Removal Act, 1850) ਪਾਸ ਕੀਤਾ ਗਿਆ ਜਿਸ ਨੇ ਜਾਤੀ ਪੰਚਾਇਤਾਂ ਨੂੰ ਕਾਫ਼ੀ ਕਮਜ਼ੋਰ ਕਰ ਦਿੱਤਾ । ਇਸੇ ਤਰ੍ਹਾਂ ਵਿਸ਼ੇਸ਼ ਵਿਆਹ ਕਾਨੂੰਨ (Special Marriage Act, 1872) ਨੇ ਵੱਖ-ਵੱਖ ਜਾਤਾਂ ਵਿਚ ਵਿਆਹ ਨੂੰ ਮਾਨਤਾ ਦਿੱਤੀ ਜਿਸ ਨਾਲ ਪਰੰਪਰਾਗਤ ਜਾਤੀ ਪ੍ਰਥਾ ਉੱਤੇ ਕਾਫ਼ੀ ਡੂੰਘਾ ਪ੍ਰਭਾਵ ਪਿਆ । ਭਾਰਤ ਦੀ ਆਜ਼ਾਦੀ ਤੋਂ ਬਾਅਦ Untouchability Offence Act, 1955 ਅਤੇ Hindu Marriage Act, 1955 ਨੇ ਵੀ ਜਾਤੀ ਪ੍ਰਥਾ ਉੱਪਰ ਕਾਫ਼ੀ ਸੱਟ ਮਾਰੀ | Hindu Marriage Validation Act, ਪਾਸ ਹੋਇਆ ਜਿਸ ਨਾਲ ਵੱਖ-ਵੱਖ ਧਰਮਾਂ, ਜਾਤਾਂ, ਉਪਜਾਤਾਂ ਆਦਿ ਦੇ ਵਿਅਕਤੀਆਂ ਵਿਚ ਹੋਣ ਵਾਲੇ ਵਿਆਹ ਨੂੰ ਕਾਨੂੰਨੀ ਘੋਸ਼ਿਤ ਕੀਤਾ ਗਿਆ ।

3. ਅੰਗਰੇਜ਼ਾਂ ਦਾ ਯੋਗਦਾਨ (Contribution of Britishers) – ਜਾਤੀ ਪ੍ਰਤਾ ਦੇ ਵਿਰੁੱਧ ਇੱਕ ਖੁੱਲ੍ਹਾ ਸੰਘਰਸ਼ ਬ੍ਰਿਟਿਸ਼ . ਕਾਲ ਵਿਚ ਸ਼ੁਰੂ ਹੋਇਆ | ਅੰਗਰੇਜ਼ਾਂ ਨੇ ਭਾਰਤ ਵਿਚ ਕਾਨੂੰਨ ਦੇ ਸਾਹਮਣੇ ਸਭ ਦੀ ਸਮਾਨਤਾ ਦਾ ਸਿਧਾਂਤ ਲਾਗੂ ਕੀਤਾ | ਜਾਤੀ ਆਧਾਰਿਤ ਪੰਚਾਇਤਾਂ ਤੋਂ ਉਨ੍ਹਾਂ ਦੇ ਨਿਆਂ ਕਰਨ ਦੇ ਅਧਿਕਾਰ ਵਾਪਿਸ ਲੈ ਲਏ ਗਏ । ਸਰਕਾਰੀ ਨੌਕਰੀਆਂ ਹਰੇਕ ਜਾਤੀ ਲਈ ਖੋਲ੍ਹ ਦਿੱਤੀਆਂ ਗਈਆਂ । ਅੰਗਰੇਜ਼ਾਂ ਦੀ ਸਿੱਖਿਆ ਪ੍ਰਣਾਲੀ ਧਰਮ ਨਿਰਪੱਖ ਸੀ । ਅੰਗਰੇਜ਼ਾਂ ਨੇ ਭਾਰਤ ਵਿਚ ਆਧੁਨਿਕ ਉਦਯੋਗਾਂ ਦੀ ਸਥਾਪਨਾ ਕਰਕੇ ਅਤੇ ਰੇਲਾਂ, ਬੱਸਾਂ ਆਦਿ ਦੀ ਸ਼ੁਰੂਆਤ ਕਰਕੇ ਜਾਤੀ ਪ੍ਰਥਾ ਨੂੰ ਕਰਾਰਾ ਝਟਕਾ ਦਿੱਤਾ । ਉਦਯੋਗਾਂ ਵਿਚ ਸਾਰੇ ਮਿਲ ਕੇ ਕੰਮ ਕਰਦੇ ਸਨ ਅਤੇ ਰੇਲਾਂ, ਬੱਸਾਂ ਦੇ ਸਫ਼ਰ ਨੇ ਵੱਖ-ਵੱਖ ਜਾਂਤਾ ਦੇ ਵਿਚ ਸੰਪਰਕ ਸਥਾਪਿਤ ਕੀਤਾ । ਅੰਗਰੇਜ਼ਾਂ ਵਲੋਂ ਜ਼ਮੀਨ ਦੀ ਖੁੱਲ੍ਹੀ ਖ਼ਰੀਦ-ਫਰੋਖਤ ਦੇ ਅਧਿਕਾਰ ਨੇ ਪਿੰਡਾਂ ਵਿਚ ਜਾਤੀ ਸੰਤੁਲਨ ਨੂੰ ਬਹੁਤ ਮੁਸ਼ਕਿਲ ਕਰ ਦਿੱਤਾ ।

4. ਉਦਯੋਗੀਕਰਨ (Industrialization) – ਉਦਯੋਗੀਕਰਨ ਨੇ ਅਜਿਹੇ ਹਾਲਾਤ ਪੈਦਾ ਕੀਤੇ ਜੋ ਜਾਤੀ ਵਿਵਸਥਾ ਦੇ ਵਿਰੁੱਧ ਸਨ । ਇਸ ਕਾਰਨ ਫ਼ੈਕਟਰੀਆਂ ਵਿਚ ਕਈ ਨਵੇਂ ਕੰਮ ਪੈਦਾ ਹੋ ਗਏ ਜਿਹੜੇ ਤਕਨੀਕੀ ਸਨ । ਇਨ੍ਹਾਂ ਨੂੰ ਕਰਨ ਲਈ ਵਿਸ਼ੇਸ਼ ਯੋਗਤਾ ਅਤੇ ਸਿਖਲਾਈ ਦੀ ਲੋੜ ਸੀ । ਅਜਿਹੇ ਕੰਮ ਯੋਗਤਾ ਦੇ ਆਧਾਰ ਉੱਤੇ ਮਿਲਦੇ ਸਨ । ਇਸ ਨਾਲ ਸਮਾਜਿਕ ਸੰਸਤਰਣ ਵਿਚ ਮੌਜੂਦ ਹੇਠਲੀਆਂ ਜਾਤਾਂ ਨੂੰ ਉੱਪਰ ਆਉਣ ਦਾ ਮੌਕਾ ਪ੍ਰਾਪਤ ਹੋਇਆ । ਉਦਯੋਗੀਕਰਨ ਨੇ ਭੌਤਿਕਤਾ ਵਿਚ ਵਾਧਾ ਕਰਕੇ ਪੈਸੇ ਦੇ ਮਹੱਤਵ ਨੂੰ ਵਧਾਇਆ । ਪੈਸੇ ਦੇ ਆਧਾਰ ਉੱਤੇ ਤਿੰਨ ਵਰਗ ਪੈਦਾ ਹੋਏ-ਧਨੀ ਵਰਗ, ਮੱਧ ਵਰਗ ਅਤੇ ਗ਼ਰੀਬ ਵਰਗ । ਹਰੇਕ ਵਰਗ ਵਿਚ ਵੱਖ-ਵੱਖ ਜਾਤਾਂ ਦੇ ਲੋਕ ਪਾਏ ਜਾਂਦੇ ਸਨ । ਉਦਯੋਗੀਕਰਨ ਨਾਲ ਵੱਖ-ਵੱਖ ਜਾਤਾਂ ਦੇ ਲੋਕ ਇਕੱਠੇ ਫੈਕਟਰੀਆਂ ਵਿਚ ਕੰਮ ਕਰਨ ਲੱਗੇ, ਇਕੱਠੇ ਸਫ਼ਰ ਕਰਨ ਲੱਗੇ ਤੇ ਇਕੱਠੇ ਹੀ ਰੋਟੀ ਖਾਣ ਲੱਗੇ ਜਿਸ ਨਾਲ

ਛੂਤਛਾਤ ਦੀ ਭਾਵਨਾ ਖ਼ਤਮ ਹੋਣੀ ਸ਼ੁਰੂ ਹੋ ਗਈ । ਆਵਾਜਾਈ ਦੇ ਸਾਧਨਾਂ ਦੇ ਵਿਕਾਸ ਦੇ ਕਾਰਨ ਵੱਖ-ਵੱਖ ਧਰਮਾਂ ਅਤੇ ਜਾਤਾਂ ਵਿਚਕਾਰ ਉਦਾਰ ਦ੍ਰਿਸ਼ਟੀਕੋਣ ਦਾ ਵਿਕਾਸ ਹੋਇਆ ਜੋ ਕਿ ਜਾਤੀ ਵਿਵਸਥਾ ਦੇ ਲਈ ਖ਼ਤਰਨਾਕ ਸੀ । ਉਦਯੋਗੀਕਰਨ ਨੇ ਦੂਤੀਆ ਸੰਬੰਧਾਂ ਨੂੰ ਵਧਾਇਆ ਅਤੇ ਵਿਅਕਤੀਵਾਦਿਤਾ ਨੂੰ ਜਨਮ ਦਿੱਤਾ ਜਿਸ ਨਾਲ ਸਮੁਦਾਇਕ ਨਿਯਮਾਂ ਦਾ ਪ੍ਰਭਾਵ ਬਿਲਕੁਲ ਹੀ ਖ਼ਤਮ ਹੋ ਗਿਆ | ਸਮਾਜਿਕ ਪ੍ਰਥਾਵਾਂ ਅਤੇ ਪਰੰਪਰਾਵਾਂ ਦਾ ਮਹੱਤਵ ਖ਼ਤਮ ਹੋ ਗਿਆ ! ਸੰਬੰਧ ਕਾਨੂੰਨ ਦੇ ਅਨੁਸਾਰ ਹੋਣ ਲੱਗ ਪਏ 1 ਹੁਣ ਸੰਬੰਧ ਆਰਥਿਕ ਸਥਿਤੀ ਦੇ ਆਧਾਰ ਉੱਤੇ ਹੁੰਦੇ ਸਨ । ਇਸ ਤਰ੍ਹਾਂ ਉਦਯੋਗੀਕਰਨ ਨੇ ਜਾਤੀ ਵਿਵਸਥਾ ਉੱਪਰ ਕਾਫ਼ੀ ਡੂੰਘੀ ਸੱਟ ਮਾਰੀ ।

5. ਸ਼ਹਿਰੀਕਰਨ (Urbanization) – ਸ਼ਹਿਰੀਕਰਨ ਦੇ ਕਾਰਨ ਵੀ ਜਾਤੀ ਪ੍ਰਥਾ ਵਿਚ ਕਾਫ਼ੀ ਬਦਲਾਵ ਆਏ । ਸੰਘਣੀ ਆਬਾਦੀ, ਨਿਜੀ ਭਾਵਨਾ, ਸਮਾਜਿਕ ਗਤੀਸ਼ੀਲਤਾ ਅਤੇ ਜ਼ਿਆਦਾ ਕੰਮ ਵਰਗੀਆਂ ਸ਼ਹਿਰੀ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਨੇ ਜਾਤੀ ਪ੍ਰਥਾ ਨੂੰ ਕਾਫ਼ੀ ਕਮਜ਼ੋਰ ਕੀਤਾ । ਵੱਡੇ-ਵੱਡੇ ਸ਼ਹਿਰਾਂ ਵਿਚ ਲੋਕਾਂ ਨੂੰ ਇੱਕ-ਦੂਜੇ ਦੇ ਨਾਲ ਮਿਲ ਕੇ ਰਹਿਣਾ ਪੈਂਦਾ ਹੈ । ਉਹ ਇਹ ਨਹੀਂ ਦੇਖਦੇ ਕਿ ਉਨ੍ਹਾਂ ਦਾ ਪੜੋਸੀ ਕਿਸ ਜਾਤੀ ਦਾ ਹੈ । ਇਸ ਨਾਲ ਉਚ-ਨੀਚ ਦੀ ਭਾਵਨਾ ਖ਼ਤਮ ਹੋ ਗਈ । ਸ਼ਹਿਰੀਕਰਨ ਦੇ ਕਾਰਨ ਜਦੋਂ ਲੋਕ ਇੱਕ-ਦੂਜੇ ਦੇ ਸੰਪਰਕ ਵਿਚ ਆਏ ਤਾਂ ਅੰਤਰ ਜਾਤੀ ਵਿਆਹ ਹੋਣ ਲੱਗ ਪਏ । ਇਸ ਤਰ੍ਹਾਂ ਸ਼ਹਿਰੀਕਰਨ ਨੇ ਛੂਤ-ਛਾਤ ਦੇ ਭੇਦਾਂ ਨੂੰ ਕਾਫ਼ੀ ਹੱਦ ਤੱਕ ਦੂਰ ਕਰ ਦਿੱਤਾ ।

6. ਸਿੱਖਿਆ ਦਾ ਪ੍ਰਸਾਰ (Spread of Education) – ਅੰਗਰੇਜ਼ਾਂ ਨੇ ਭਾਰਤ ਵਿਚ ਪੱਛਮੀ ਸਿੱਖਿਆ ਪ੍ਰਣਾਲੀ ਨੂੰ ਲਾਗੂ ਕੀਤਾ ਜਿਸ ਵਿਚ ਵਿਗਿਆਨ ਅਤੇ ਤਕਨੀਕ ਉੱਪਰ ਵਧੇਰੇ ਜ਼ੋਰ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ । ਸਿੱਖਿਆ ਦੇ ਪ੍ਰਸਾਰ ਨਾਲ ਲੋਕਾਂ ਵਿਚ ਜਾਗ੍ਰਿਤੀ ਆਈ ਅਤੇ ਇਸਦੇ ਨਾਲ ਪਰੰਪਰਾਗਤ ਕਦਰਾਂ ਕੀਮਤਾਂ ਵਿਚ ਮਹੱਤਵਪੂਰਨ ਪਰਿਵਰਤਨ ਵੀ ਆਏ । ਜਨਮ ਉੱਪਰ ਆਧਾਰਿਤ ਦਰਜੇ ਦੀ ਥਾਂ ਮੁਕਾਬਲੇ ਵਿਚ ਪ੍ਰਾਪਤ ਕੀਤੇ ਦਰਜ਼ੇ ਦਾ ਮਹੱਤਵ ਵੱਧ ਗਿਆ | ਸਕੂਲ, ਕਾਲਜ ਆਦਿ ਪੱਛਮੀ ਤਰੀਕੇ ਨਾਲ ਖੁੱਲ੍ਹ ਗਏ ਜਿੱਥੇ ਸਾਰੀਆਂ ਜਾਤਾਂ ਦੇ ਬੱਚੇ ਇਕੱਠੇ ਮਿਲ ਕੇ ਸਿੱਖਿਆ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਨ । ਇਸ ਨਾਲ ਵੀ ਜਾਤੀ ਵਿਵਸਥਾ ਨੂੰ ਕਾਫ਼ੀ ਸੱਟ ਵੱਜੀ ।

ਪ੍ਰਸ਼ਨ 4.
ਵਰਗ ਵਿਵਸਥਾ ਕੀ ਹੈ ? ਇਸ ਦੀਆਂ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਕੀ ਹਨ ?
ਉੱਤਰ-
ਹਰੇਕ ਸਮਾਜ ਕਈ ਵਰਗਾਂ ਵਿਚ ਵੰਡਿਆ ਹੁੰਦਾ ਹੈ ਅਤੇ ਹਰ-ਇਕ ਵਰਗ ਦੀ ਸਮਾਜ ਵਿਚ ਵੱਖੋ-ਵੱਖਰੀ ਸਥਿਤੀ ਹੁੰਦੀ ਹੈ । ਇਸ ਸਥਿਤੀ ਦੇ ਆਧਾਰ ‘ਤੇ ਹੀ ਵਿਅਕਤੀ ਨੂੰ ਉੱਚਾ ਨੀਵਾਂ ਜਾਣਿਆ ਜਾਂਦਾ ਹੈ । ਵਰਗ ਦੀ ਮੁੱਖ ਵਿਸ਼ੇਸ਼ਤਾ ਵਰਗ ਚੇਤੰਨਤਾ ਹੁੰਦੀ ਹੈ । ਇਸ ਪ੍ਰਕਾਰ ਸਮਾਜ ਵਿਚ ਜਦੋਂ ਵਿਭਿੰਨ ਵਿਅਕਤੀਆਂ ਨੂੰ ਵਿਸ਼ੇਸ਼ ਸਮਾਜਿਕ ਸਥਿਤੀ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ ਤਾਂ ਉਸ ਨੂੰ ਵਰਗ ਵਿਵਸਥਾ ਕਹਿੰਦੇ ਹਨ । ਹਰ ਇਕ ਵਰਗ ਆਰਥਿਕ ਪੱਖੋਂ ਇਕ ਦੂਸਰੇ ਨਾਲੋਂ ਵੱਖ ਹੁੰਦਾ ਹੈ । ਵਰਗ ਦੇ ਅਰਥ ਬਾਰੇ ਵੱਖ-ਵੱਖ ਸਮਾਜ ਵਿਗਿਆਨੀਆਂ ਨੇ ਆਪਣੇ ਵੱਖ-ਵੱਖ ਵਿਚਾਰ ਦਿੱਤੇ ਹਨ ਜੋ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਹਨ-

• ਮੈਕਾਈਵਰ (MacIver) ਨੇ ਵਰਗ ਨੂੰ ਸਮਾਜਿਕ ਆਧਾਰ ਉੱਪਰ ਬਿਆਨ ਕੀਤਾ ਹੈ । ਉਸ ਅਨੁਸਾਰ, “ਸਮਾਜਿਕ ਵਰਗ ਇਕੱਠ ਦਾ ਉਹ ਹਿੱਸਾ ਹੁੰਦਾ ਹੈ ਜਿਸਨੂੰ ਸਮਾਜਿਕ ਸਥਿਤੀ ਦੇ ਆਧਾਰ ‘ਤੇ ਬਚੇ ਹਿੱਸਿਆਂ ਨਾਲੋਂ ਵੱਖ ਕਰ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ।
• ਮੌਰਿਸ ਜਿਨਜ਼ਬਰਗ (Morris Ginsberg) ਦੇ ਅਨੁਸਾਰ, ਵਰਗ ਵਿਅਕਤੀਆਂ ਦਾ ਅਜਿਹਾ ਸਮੂਹ ਹੈ ਜਿਹੜੇ ਸਾਂਝੇ · ਸ਼ਕੂਮ, ਕਿੱਤਾ, ਸੰਪੱਤੀ ਅਤੇ ਸਿੱਖਿਆ ਦੇ ਦੁਆਰਾ ਇਕੋ ਜਿਹਾ ਜੀਵਨ ਢੰਗ, ਇੱਕੋ ਜਿਹੇ ਵਿਚਾਰਾਂ ਦਾ ਸਟਾਕ, ਭਾਵਨਾਵਾਂ, ਰਵੱਈਏ ਅਤੇ ਵਿਵਹਾਰ ਦੇ ਰੂਪ ਰੱਖਦੇ ਹੋਣ ਅਤੇ ਜੋ ਇਨ੍ਹਾਂ ਵਿਚੋਂ ਕੁੱਝ ਜਾਂ ਸਾਰੇ ਆਧਾਰ ਉੱਤੇ ਇੱਕ ਦੂਸਰੇ ਨਾਲ ਸਮਾਨ ਰੂਪ ਵਿਚ ਮਿਲਦੇ ਹੋਣ ਅਤੇ ਆਪਣੇ ਆਪ ਨੂੰ ਇੱਕ ਸਮੂਹ ਦਾ ਮੈਂਬਰ ਸਮਝਦੇ ਹੋਣ । ਭਾਵੇਂ ਇਸ ਸੰਬੰਧ ਵਿਚ ਚੇਤਨਾ ਉਨ੍ਹਾਂ ਵਿਚ ਭਿੰਨ-ਭਿੰਨ ਮਾਤਰਾ ਵਿਚ ਪਾਈ ਜਾਂਦੀ ਹੋਵੇ ।”
• ਗਿਲਬਰਟ (Gilbert) ਦੇ ਅਨੁਸਾਰ, “ਇਕ ਸਮਾਜਿਕ ਵਰਗ ਵਿਅਕਤੀਆਂ ਦਾ ਇਕੱਠ ਅਤੇ ਖ਼ਾਸ ਸ਼੍ਰੇਣੀ ਹੈ ਜਿਸ ਦੀ ਸਮਾਜ ਵਿਚ ਇਕ ਖ਼ਾਸ ਸਥਿਤੀ ਹੁੰਦੀ ਹੈ । ਇਹ ਖ਼ਾਸ ਸਥਿਤੀ ਹੀ ਦੂਸਰੇ ਸਮੂਹਾਂ ਤੋਂ ਉਨ੍ਹਾਂ ਦੇ ਸੰਬੰਧ ਨਿਰਧਾਰਿਤ ਕਰਦੀ ਹੈ ।’

ਉਪਰੋਕਤ ਵਿਵਰਣ ਦੇ ਆਧਾਰ ‘ਤੇ ਅਸੀਂ ਇਹ ਕਹਿ ਸਕਦੇ ਹਾਂ ਕਿ ਸਮਾਜਿਕ ਵਰਗ ਕਈ ਵਿਅਕਤੀਆਂ ਦਾ ਵਰਗ ਹੁੰਦਾ ਹੈ ਜਿਸਨੂੰ ਸਮਾਂ ਵਿਸ਼ੇਸ਼ ਵਿਚ ਇੱਕ ਵਿਸ਼ੇਸ਼ ਸਥਿਤੀ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ । ਇਸੇ ਕਰਕੇ ਉਨ੍ਹਾਂ ਨੂੰ ਕੁੱਝ ਵਿਸ਼ੇਸ਼ ਸ਼ਕਤੀ, ਅਧਿਕਾਰ ਅਤੇ ਜ਼ਿੰਮੇਵਾਰੀਆਂ ਵੀ ਮਿਲੀਆਂ ਹੁੰਦੀਆਂ ਹਨ । ਵਰਗ ਵਿਵਸਥਾ ਵਿਚ ਵਿਅਕਤੀ ਦੀ ਯੋਗਤਾ ਮਹੱਤਵਪੂਰਨ ਹੁੰਦੀ ਹੈ । ਇਸੇ ਕਰਕੇ ਹਰ ਵਿਅਕਤੀ ਮਿਹਨਤ ਕਰਕੇ ਸਮਾਜਿਕ ਵਰਗ ਵਿਚ ਆਪਣੀ ਸਥਿਤੀ ਨੂੰ ਉੱਚੀ ਕਰਨਾ ਚਾਹੁੰਦਾ ਹੈ । ਹਰ ਇਕ ਸਮਾਜ ਵਿਭਿੰਨ ਵਰਗਾਂ ਵਿਚ ਵੰਡਿਆ ਹੁੰਦਾ ਹੈ । ਵਰਗ ਵਿਵਸਥਾ ਵਿਚ ਵਿਅਕਤੀ ਦੀ ਸਥਿਤੀ ਨਿਸ਼ਚਿਤ ਨਹੀਂ ਹੁੰਦੀ । ਉਸ ਦੀ ਸਥਿਤੀ ਵਿਚ ਗਤੀਸ਼ੀਲਤਾ ਪਾਈ ਜਾਂਦੀ ਹੈ । ਇਸੇ ਕਰਕੇ ਇਹ ਖੁੱਲਾ ਸਤਰੀਕਰਨ ਵੀ ਕਹਾਇਆ ਜਾਂਦਾ ਹੈ । ਵਿਅਕਤੀ ਆਪਣੀ ਵਰਗ ਸਥਿਤੀ ਨੂੰ ਆਪ ਨਿਰਧਾਰਿਤ ਕਰਦਾ ਹੈ । ਇਹ ਜਨਮ ਉੱਪਰ ਆਧਾਰਿਤ ਨਹੀਂ ਹੁੰਦਾ ।

ਵਰਗ ਦੀਆਂ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ (Characteristics of Class)

1. ਸ਼ੇਸ਼ਟਤਾ ਤੇ ਹੀਣਤਾ ਦੀ ਭਾਵਨਾ (Feeling of superiority and inferiority) – ਵਰਗ ਵਿਵਸਥਾ ਦੇ ਵਿਚ ਵੀ ਉੱਚਤਾ ਅਤੇ ਨੀਚਤਾ ਦੇ ਸੰਬੰਧ ਪਾਏ ਜਾਂਦੇ ਹਨ । ਉਦਾਹਰਨ ਦੇ ਤੌਰ ਤੇ ਉੱਚੇ ਵਰਗ ਦੇ ਲੋਕ, ਨੀਵੇਂ ਵਰਗ ਦੇ ਲੋਕਾਂ ਤੋਂ ਆਪਣੇ ਆਪ ਨੂੰ ਅਲੱਗ ਅਤੇ ਉੱਚਾ ਮਹਿਸੂਸ ਕਰਦੇ ਹਨ । ਉੱਚੇ ਵਰਗ ਵਿਚ ਅਮੀਰ ਲੋਕ ਆ ਜਾਂਦੇ ਹਨ ਤੇ ਨੀਵੇਂ ਵਰਗ ਦੇ ਵਿਚ ਗਰੀਬ ਲੋਕ | ਅਮੀਰ ਲੋਕਾਂ ਦੀ ਸਮਾਜ ਵਿਚ ਉੱਚੀ ਸਥਿਤੀ ਹੁੰਦੀ ਹੈ ਤੇ ਗ਼ਰੀਬ ਲੋਕ ਵੱਖੋ-ਵੱਖਰੇ ਨਿਵਾਸ ਸਥਾਨ ਤੇ ਰਹਿੰਦੇ ਹਨ । ਉਨ੍ਹਾਂ ਨਿਵਾਸ ਸਥਾਨਾਂ ਨੂੰ ਵੇਖ ਕੇ ਹੀ ਪਤਾ ਲੱਗ ਜਾਂਦਾ ਹੈ ਕਿ ਉਹ ਅਮੀਰ ਵਰਗ ਨਾਲ ਸੰਬੰਧਿਤ ਹਨ ਜਾਂ ਗਰੀਬ ਵਰਗ ਦੇ ਨਾਲ ।

2. ਸਮਾਜਿਕ ਗਤੀਸ਼ੀਲਤਾ (Social mobility) – ਵਰਗ ਵਿਵਸਥਾ ਕਿਸੀ ਵੀ ਵਿਅਕਤੀ ਲਈ ਨਿਸ਼ਚਿਤ ਨਹੀਂ ਹੁੰਦੀ । ਉਹ ਬਦਲਦੀ ਰਹਿੰਦੀ ਹੈ । ਵਿਅਕਤੀ ਆਪਣੀ ਮਿਹਨਤ ਨਾਲ ਨੀਵੀਂ ਤੋਂ ਉੱਚੀ ਸਥਿਤੀ ਪ੍ਰਾਪਤ ਕਰ ਲੈਂਦਾ ਹੈ ਤੇ ਆਪਣੇ ਗਲਤ ਕੰਮਾਂ ਦੇ ਨਤੀਜੇ ਵਜੋਂ ਉੱਚੀ ਤੋਂ ਨੀਵੀਂ ਸਥਿਤੀ ਤੇ ਵੀ ਪਹੁੰਚ ਜਾਂਦਾ ਹੈ ।ਹਰ ਵਿਅਕਤੀ ਕਿਸੇ ਨਾ ਕਿਸੇ ਆਧਾਰ ਤੇ ਸਮਾਜ ਵਿਚ ਆਪਣੀ ਇੱਜ਼ਤ ਵਧਾਉਣੀ ਚਾਹੁੰਦਾ ਹੈ । ਇਸੀ ਕਰਕੇ ਵਰਗ ਵਿਵਸਥਾ ਵਿਅਕਤੀ ਨੂੰ ਕਿਰਿਆਸ਼ੀਲ ਵੀ ਰੱਖਦੀ ਹੈ ।

3. ਖੁੱਲਾਪਣ (Openness) – ਵਰਗ ਵਿਵਸਥਾ ਵਿਚ ਖੁੱਲ੍ਹਾਪਣ ਪਾਇਆ ਜਾਂਦਾ ਹੈ ਕਿਉਂਕਿ ਇਸ ਵਿਚ ਵਿਅਕਤੀ ਨੂੰ ਪੂਰੀ ਆਜ਼ਾਦੀ ਹੁੰਦੀ ਹੈ ਕਿ ਉਹ ਕੁੱਝ ਵੀ ਕਰ ਸਕੇ । ਉਹ ਆਪਣੀ ਇੱਛਾ ਦੇ ਅਨੁਸਾਰ ਕਿਸੇ ਵੀ ਕਿੱਤੇ ਨੂੰ ਅਪਣਾ ਸਕਦਾ ਹੈ । ਕਿਸੇ ਵੀ ਜਾਤ ਦਾ ਵਿਅਕਤੀ ਕਿਸੇ ਵੀ ਵਰਗ ਦਾ ਮੈਂਬਰ ਆਪਣੀ ਯੋਗਤਾ ਦੇ ਆਧਾਰ ਤੇ ਬਣ ਸਕਦਾ ਹੈ । ਨਿਮਨ ਵਰਗ ਦੇ ਲੋਕ ਮਿਹਨਤ ਕਰਕੇ ਉੱਚੇ ਵਰਗ ਵਿਚ ਆ ਸਕਦੇ ਹਨ । ਇਸ ਵਿਚ ਵਿਅਕਤੀ ਦੇ ਜਨਮ ਦੀ ਕੋਈ ਮਹੱਤਤਾ ਨਹੀਂ ਹੁੰਦੀ । ਵਿਅਕਤੀ ਦੀ ਸਥਿਤੀ ਉਸ ਦੀ ਯੋਗਤਾ ਤੇ ਨਿਰਭਰ ਕਰਦੀ ਹੈ ।

4. ਸੀਮਿਤ ਸਮਾਜਿਕ ਸੰਬੰਧ (Limited social relations) – ਵਰਗ ਵਿਵਸਥਾ ਵਿਚ ਵਿਅਕਤੀ ਦੇ ਸਮਾਜਿਕ ਸੰਬੰਧ ਸੀਮਿਤ ਹੁੰਦੇ ਹਨ | ਹਰ ਵਰਗ ਦੇ ਲੋਕ ਆਪਣੇ ਬਰਾਬਰ ਦੇ ਵਰਗ ਦੇ ਲੋਕਾਂ ਨਾਲ ਸੰਬੰਧ ਰੱਖਣਾ ਵਧੇਰੇ ਠੀਕ ਸਮਝਦੇ ਹਨ । ਹਰ ਵਰਗ ਆਪਣੇ ਹੀ ਵਰਗ ਦੇ ਲੋਕਾਂ ਨਾਲ ਸੰਬੰਧ ਸਥਾਪਿਤ ਕਰਨਾ ਚਾਹੁੰਦਾ ਹੈ । ਉਹ ਦੁਸਰੇ ਵਰਗਾਂ ਦੇ ਨਾਲ ਵਧੇਰੇ ਨਜ਼ਦੀਕਤਾ ਨਹੀਂ ਰੱਖਦੇ ।

5. ਉਪ ਵਰਗਾਂ ਦਾ ਵਿਕਾਸ (Development of sub-classes) – ਭਾਵੇਂ ਆਰਥਿਕ ਦ੍ਰਿਸ਼ਟੀਕੋਣ ਤੋਂ ਅਸੀਂ ਵਰਗ ਵਿਵਸਥਾ ਨੂੰ ਤਿੰਨ ਹਿੱਸਿਆਂ ਵਿਚ ਵੰਡਦੇ ਹਾਂ-

• ਉੱਚਾ ਵਰਗ (Upper Class)
• ਮੱਧ ਵਰਗ (Middle Class)
• ਨੀਵਾਂ ਵਰਗ (Lower Class) ।

ਪਰੰਤੂ ਅੱਗੋਂ ਹਰ ਵਰਗ ਕਈ ਹੋਰ ਉਪ-ਵਰਗਾਂ ਵਿਚ ਵੰਡਿਆ ਹੁੰਦਾ ਹੈ, ਜਿਵੇਂ ਇਕ ਅਮੀਰ ਵਰਗ ਦੇ ਵਿਚ ਵੀ ਭਿੰਨਤਾ ਨਜ਼ਰ ਆਉਂਦੀ ਹੈ, ਕੁੱਝ ਲੋਕ ਬਹੁਤ ਅਮੀਰ ਹਨ, ਕੁੱਝ ਉਸ ਤੋਂ ਘੱਟ ਤੇ ਕੁੱਝ ਸਭ ਤੋਂ ਘੱਟ । ਇਸੇ ਪ੍ਰਕਾਰ ਮੱਧ ਵਰਗ ਤੇ ਨੀਵੇਂ ਵਰਗ ਵਿਚ ਵੀ ਉਪ-ਵਰਗ ਪਾਏ ਜਾਂਦੇ ਹਨ । ਹਰ ਵਰਗ ਦੇ ਉਪ ਵਰਗਾਂ ਵਿਚ ਵੀ ਅੰਤਰ ਪਾਇਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਪ੍ਰਕਾਰ ਵਰਗ, ਉਪ-ਵਰਗਾਂ ਤੋਂ ਮਿਲ ਕੇ ਹੀ ਬਣਦਾ ਹੈ ।

6. ਵਿਭਿੰਨ ਆਧਾਰ (Different basis) – ਜਿਵੇਂ ਅਸੀਂ ਸ਼ੁਰੂ ਵਿਚ ਹੀ ਵਿਭਿੰਨ ਸਮਾਜ ਵਿਗਿਆਨੀਆਂ ਦੇ ਵਿਚਾਰਾਂ ਤੋਂ ਇਹ ਨਤੀਜਾ ਕੱਢ ਚੁੱਕੇ ਹਾਂ ਕਿ ਵਰਗ ਦੇ ਵੱਖੋ-ਵੱਖਰੇ ਆਧਾਰ ਹਨ | ਪ੍ਰਸਿੱਧ ਸਮਾਜ ਵਿਗਿਆਨੀ ਕਾਰਲ ਮਾਰਕਸ ਨੇ ਆਰਥਿਕ ਆਧਾਰ ਨੂੰ ਵਰਗ ਵਿਵਸਥਾ ਦਾ ਮੁੱਖ ਆਧਾਰ ਮੰਨਿਆ ਹੈ । ਉਸ ਦੇ ਅਨੁਸਾਰ ਸਮਾਜ ਵਿਚ ਕੇਵਲ ਦੋ ਹੀ ਵਰਗ ਪਾਏ ਗਏ ਹਨ । ਇਕ ਤਾਂ ਪੂੰਜੀਪਤੀ ਵਰਗ, ਦੂਸਰਾ ਕਿਰਤੀ ਵਰਗ । ਹਰਟਨ ਅਤੇ ਹੰਟ ਦੇ ਅਨੁਸਾਰ, “ਸਾਨੂੰ ਯਾਦ ਰੱਖਣਾ ਚਾਹੀਦਾ ਹੈ ਕਿ ਵਰਗ ਮੂਲ ਵਿਚ, ਵਿਸ਼ੇਸ਼ ਜੀਵਨ ਢੰਗ ਹੈ ।” ਔਗਬਰਨ ਅਤੇ ਨਿਮਕੌਫ਼, ਮੈਕਾਈਵਰ ਅਤੇ ਗਿਲਬਰਟ ਨੇ ਵਰਗ ਦੇ ਲਈ ਸਮਾਜਿਕ ਆਧਾਰ ਨੂੰ ਮੁੱਖ ਮੰਨਿਆ ਹੈ । ਜਿਨਜ਼ਬਰਗ, ਲੇਪਿਅਰ ਵਰਗੇ ਵਿਗਿਆਨੀਆਂ ਨੇ ਸੰਸਕ੍ਰਿਤਕ ਆਧਾਰ ਨੂੰ ਹੀ ਵਰਗ ਵਿਵਸਥਾ ਦਾ ਮੁੱਖ ਆਧਾਰ ਮੰਨਿਆ ਹੈ ।

7. ਵਰਗ ਪਹਿਚਾਣ (Identification of class) – ਵਰਗ ਵਿਵਸਥਾ ਵਿਚ ਬਾਹਰੀ ਦਿਸ਼ਟੀਕੋਣ ਵੀ ਮਹੱਤਵਪੂਰਨ ਹੁੰਦਾ ਹੈ । ਕਈ ਵਾਰੀ ਅਸੀਂ ਵੇਖ ਕੇ ਹੀ ਇਹ ਅਨੁਮਾਨ ਲਗਾ ਲੈਂਦੇ ਹਾਂ ਕਿ ਇਹ ਵਿਅਕਤੀ ਉੱਚੇ ਵਰਗ ਦਾ ਹੈ ਜਾਂ ਨੀਵੇਂ ਵਰਗ ਦਾ । ਸਾਡੇ ਆਧੁਨਿਕ ਸਮਾਜ ਦੇ ਵਿਚ ਕੋਠੀ, ਕਾਰ, ਸਕੂਟਰ, ਟੀ.ਵੀ., ਵੀ. ਸੀ.ਆਰ., ਫਰਿੱਜ਼ ਆਦਿ ਵਿਅਕਤੀ ਦੇ ਸਥਿਤੀ ਚਿੰਨ੍ਹ ਨੂੰ ਨਿਰਧਾਰਿਤ ਕਰਦੇ ਹਨ । ਇਸ ਪ੍ਰਕਾਰ ਬਾਹਰੀ ਸੰਕੇਤਾਂ ਤੋਂ ਸਾਨੂੰ ਵਰਗ ਭਿੰਨਤਾ ਦਾ ਪਤਾ ਲੱਗ ਜਾਂਦਾ
ਹੈ ।

8. ਵਰਗ ਚੇਤਨਤਾ (Class consciousness) – ਹਰ ਇਕ ਮੈਂਬਰ ਆਪਣੀ ਵਰਗ ਸਥਿਤੀ ਪ੍ਰਤੀ ਪੂਰਾ ਚੇਤੰਨ ਹੁੰਦਾ ਹੈ । ਇਸੀ ਕਰਕੇ ਵਰਗ ਚੇਤਨਾ, ਵਰਗ ਵਿਵਸਥਾ ਦੀ ਮੁੱਖ ਵਿਸ਼ੇਸ਼ਤਾ ਹੈ । ਵਰਗ ਚੇਤਨਾ ਵਿਅਕਤੀ ਨੂੰ ਅੱਗੇ ਵੱਧਣ ਦੇ ਮੌਕੇ ਪ੍ਰਦਾਨ ਕਰਦੀ ਹੈ ਕਿਉਂਕਿ ਚੇਤਨਾ ਦੇ ਆਧਾਰ ‘ਤੇ ਹੀ ਅਸੀਂ ਇਕ ਵਰਗ ਨੂੰ ਦੂਸਰੇ ਵਰਗ ਤੋਂ ਵੱਖਰਾ ਕਰਦੇ ਹਾਂ । ਵਿਅਕਤੀ ਦਾ ਵਿਵਹਾਰ ਵੀ ਇਸ ਦੇ ਦੁਆਰਾ ਹੀ ਨਿਸ਼ਚਿਤ ਹੁੰਦਾ ਹੈ ।

9. ਉਤਾਰ-ਚੜਾਅ ਦਾ ਕੂਮ (Hierarchical order) – ਹਰ ਇੱਕ ਸਮਾਜ ਵਿਚ ਵੱਖ-ਵੱਖ ਸਥਿਤੀ ਰੱਖਣ ਵਾਲੇ · ਵਰਗ ਪਾਏ ਜਾਂਦੇ ਹਨ । ਸਥਿਤੀ ਦਾ ਉਤਾਰ-ਚੜਾਅ ਚਲੱਦਾ ਰਹਿੰਦਾ ਹੈ ਤੇ ਵੱਖ-ਵੱਖ ਵਰਗਾਂ ਦਾ ਨਿਰਮਾਣ ਹੁੰਦਾ ਰਹਿੰਦਾ ਹੈ । ਆਮ ਤੌਰ ‘ਤੇ ਇਹ ਦੱਖਣ ਵਿਚ ਆਇਆ ਹੈ ਕਿ ਸਮਾਜ ਵਿਚ ਉੱਚ ਵਰਗ ਦੇ ਲੋਕਾਂ ਦੀ ਗਿਣਤੀ ਘੱਟ ਹੁੰਦੀ ਹੈ ਅਤੇ ਮੱਧ ਤੇ ਨੀਵੇਂ ਵਰਗਾਂ ਦੇ ਲੋਕਾਂ ਦੀ ਗਿਣਤੀ ਜ਼ਿਆਦਾ ਹੁੰਦੀ ਹੈ । ਹਰ ਵਰਗ ਦੇ ਲੋਕ ਆਪਣੀ ਮਿਹਨਤ ਤੇ ਯੋਗਤਾ ਨਾਲ ਆਪਣੇ ਤੋਂ ਉੱਚੇ ਵਰਗ ਵਿੱਚ ਜਾਣ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰਦੇ ਰਹਿੰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 5.
ਭਾਰਤ ਵਿਚ ਕਿਹੜੇ ਨਵੇਂ ਵਰਗ ਉਭਰੇ ਹਨ ?
ਉੱਤਰ-
ਪਿਛਲੇ ਕੁੱਝ ਸਮੇਂ ਤੋਂ ਦੇਸ਼ ਵਿਚ ਜਾਤੀ ਵਿਵਸਥਾ ਦੀ ਥਾਂ ਵਰਗ ਵਿਵਸਥਾ ਸਾਹਮਣੇ ਆ ਰਹੀ ਹੈ । ਸੁਤੰਤਰਤਾ ਤੋਂ ਬਾਅਦ ਸਾਰੇ ਕਾਨੂੰਨ ਪਾਸ ਹੋਏ, ਲੋਕਾਂ ਨੇ ਪੜ੍ਹਨਾ-ਲਿਖਣਾ ਸ਼ੁਰੂ ਕੀਤਾ ਜਿਸ ਕਾਰਨ ਜਾਤੀ ਵਿਵਸਥਾ ਹੌਲੀ-ਹੌਲੀ ਖ਼ਤਮ ਹੋ ਰਹੀ ਹੈ ਅਤੇ ਵਰਗ ਵਿਵਸਥਾ ਦਾ ਦਾਇਰਾ ਵੱਧ ਰਿਹਾ ਹੈ । ਹੁਣ ਵਰਗ ਵਿਵਸਥਾ ਕੋਈ ਸਾਧਾਰਨ ਸੰਕਲਪ ਨਹੀਂ ਰਿਹਾ । ਆਧੁਨਿਕ ਸਮੇਂ ਵਿਚ ਅਲੱਗ-ਅਲੱਗ ਆਧਾਰਾਂ ਉੱਤੇ ਬਹੁਤ ਸਾਰੇ ਵਰਗ ਸਾਹਮਣੇ ਆ ਰਹੇ ਹਨ ਅਤੇ ਆ ਵੀ ਰਹੇ ਹਨ । ਉਦਾਹਰਨ ਦੇ ਲਈ ਆਜ਼ਾਦੀ ਤੋਂ ਬਾਅਦ ਦੇਸ਼ ਵਿਚ ਬਹੁਤ ਸਾਰੇ ਭੂਮੀ ਸੁਧਾਰ ਆਏ ਜਿਸ ਨਾਲ ਪੇਂਡੂ ਅਰਥਵਿਵਸਥਾ ਵਿਚ ਬਹੁਤ ਵੱਡੇ ਪਰਿਵਰਤਨ ਆਏ । ਹਰੀ ਕ੍ਰਾਂਤੀ ਨੇ ਇਸ ਪ੍ਰਕ੍ਰਿਆ ਵਿਚ ਹੋਰ ਯੋਗਦਾਨ ਦਿੱਤਾ | ਪੁਰਾਣੇ ਕਿਸਾਨਾਂ, ਜਿਨ੍ਹਾਂ ਕੋਲ ਬਹੁਤ ਸਾਰੀ ਜ਼ਮੀਨ ਸੀ, ਦੇ ਨਾਲ ਇਕ ਅਜਿਹਾ ਨਵਾਂ ਕਿਸਾਨੀ ਵਰਗ ਸਾਹਮਣੇ ਆਇਆ ਜਿਸ ਕੋਲ ਖੇਤੀ ਕਰਨ ਦੀਆਂ ਤਕਨੀਕਾਂ ਦੀ ਕਲਾ ਅਤੇ ਤਜਰਬਾ ਹੈ । ਇਹ ਉਹ ਲੋਕ ਹਨ ਜਿਹੜੇ ਫ਼ੌਜ ਜਾਂ ਪ੍ਰਸ਼ਾਸਨਿਕ ਸੇਵਾਵਾਂ ਤੋਂ ਰਿਟਾਇਰ ਹੋ ਕੇ ਆਪਣਾ ਪੈਸਾ ਖੇਤੀ ਦੇ ਕੰਮ ਵਿਚ ਲਗਾ ਰਹੇ ਹਨ ਅਤੇ ਬਹੁਤ ਜ਼ਿਆਦਾ ਪੈਸਾ ਕਮਾ ਰਹੇ ਹਨ । ਇਹ ਪਰੰਪਰਾਗਤ ਕਿਸਾਨੀ ਦਾ ਉੱਚ ਵਰਗ ਨਹੀਂ ਹਨ ਪਰ ਇਹਨਾਂ ਨੂੰ ਜੈਂਟਲਮੈਨ ਕਿਸਾਨੇ (Gentlemen Famers) ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।

ਇਸ ਦੇ ਨਾਲ-ਨਾਲ ਇਕ ਹੋਰ ਕਿਸਾਨੀ ਵਰਗ ਸਾਹਮਣੇ ਆ ਰਿਹਾ ਹੈ ਜਿਸ ਨੂੰ ‘ਪੂੰਜੀਪਤੀ ਕਿਸਾਨ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਇਹ ਉਹ ਕਿਸਾਨ ਹਨ ਜਿਨ੍ਹਾਂ ਨੇ ਨਵੀਆਂ ਤਕਨੀਕਾਂ, ਵੱਧ ਫ਼ਸਲ ਦੇਣ ਵਾਲੇ ਬੀਜਾਂ, ਨਵੀਆਂ ਖੇਤੀ ਦੀਆਂ ਤਕਨੀਕਾਂ, ਚੰਗੀਆਂ ਸਿੰਚਾਈ ਸੁਵਿਧਾਵਾਂ, ਬੈਂਕਾਂ ਤੋਂ ਉਧਾਰ ਲੈ ਕੇ ਅਤੇ ਆਵਾਜਾਈ ਅਤੇ ਸੰਚਾਰ ਦੇ ਸਾਧਨਾਂ ਦਾ ਲਾਭ ਚੁੱਕ ਕੇ ਚੰਗਾ ਪੈਸਾ ਕਮਾ ਲਿਆ ਹੈ । ਪਰ ਛੋਟੇ ਕਿਸਾਨ ਇਹਨਾਂ ਸਭ ਦਾ ਫਾਇਦਾ ਨਹੀਂ ਚੁੱਕ ਸਕੇ ਹਨ ਅਤੇ ਗ਼ਰੀਬ ਹੀ ਰਹੇ ਹਨ । ਇਸ ਤਰ੍ਹਾਂ ਭੂਮੀ ਸੁਧਾਰਾਂ ਅਤੇ ਨਵੀਆਂ ਤਕਨੀਕਾਂ ਦਾ ਫਾਇਦਾ ਸਾਰੇ ਕਿਸਾਂਨ ਸਮਾਨ ਰੂਪ ਨਾਲ ਨਹੀਂ ਚੁੱਕ ਸਕੇ ਹਨ । ਇਹ ਤਾਂ ਮੱਧ ਵਰਗੀ ਕਿਸਾਨ ਹਨ ਜਿਨ੍ਹਾਂ ਨੇ ਸਰਕਾਰ ਵਲੋਂ ਖੇਤੀ ਨੂੰ ਉਤਸ਼ਾਹਿਤ ਕਰਨ ਵਾਲੀਆਂ ਸੁਵਿਧਾਵਾਂ ਦਾ ਲਾਭ ਚੁੱਕਿਆ ਹੈ । ਅਲੱਗ-ਅਲੱਗ ਰਾਜਾਂ ਵਿਚ ਅਲੱਗ-ਅਲੱਗ ਜਾਤਾਂ ਦੇ ਕਿਸਾਨਾਂ ਨੇ ਖੇਤੀ ਦੀਆਂ ਆਧੁਨਿਕ ਸੁਵਿਧਾਵਾਂ ਦਾ ਲਾਭ ਚੁੱਕਿਆ ਹੈ ।

ਇਸ ਤੋਂ ਬਾਅਦ ਮੱਧ ਵਰਗ ਵੀ ਸਾਡੇ ਸਾਹਮਣੇ ਆਇਆ ਜਿਸ ਨੂੰ ਉਪਭੋਗਤਾਵਾਦ ਦੀ ਸੰਸਕ੍ਰਿਤੀ ਨੇ ਜਨਮ ਦਿੱਤਾ ਹੈ । ਇਸ ਮੱਧ ਵਰਗ ਨੂੰ ਸੰਭਾਵੀ ਮਾਰਕੀਟ (Potential Market) ਦੇ ਰੂਪ ਵਿਚ ਦੇਖਿਆ ਗਿਆ ਜਿਸ ਨੇ ਬਹੁਤ ਸਾਰੀਆਂ ਬਹੁਰਾਸ਼ਟਰੀ ਕੰਪਨੀਆਂ (Multinational Companies) ਇਸ ਵਰਗ ਵੱਲ ਆਕਰਸ਼ਿਤ ਹੋਈਆਂ । ਅਲੱਗ-ਅਲੱਗ ਕੰਪਨੀਆਂ ਦੀਆਂ ਮਸ਼ਹੂਰੀਆਂ (Advertisements) ਵਿਚ ਉੱਚ ਮੱਧ ਵਰਗ ਨੂੰ ਇਕ ਮਹੱਤਵਪੂਰਨ ਉਪਭੋਗਤਾ ਵਜੋਂ ਦੇਖਿਆ ਜਾਂਦਾ ਹੈ । ਅੱਜ-ਕਲ ਇਹ ਅਜਿਹਾ ਮੱਧ ਵਰਗ ਸਾਹਮਣੇ ਆ ਰਿਹਾ ਹੈ ਜਿਹੜਾ ਆਪਣੇ ਸਵਾਦ ਅਤੇ ਉਪਭੋਗ ਨੂੰ ਸਭ ਤੋਂ ਵੱਧ ਮਹੱਤਵ ਦਿੰਦਾ ਹੈ ਅਤੇ ਇਹ ਇਕ ਸੰਸਕ੍ਰਿਤਕ ਆਦਰਸ਼ ਬਣ ਰਿਹਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਨਵੇਂ ਮੱਧ ਵਰਗ ਦੇ ਉਭਾਰ ਨੇ ਦੇਸ਼ ਵਿਚ ਆਰਥਿਕ ਉਦਾਰਵਾਦ ਦੇ ਸੰਕਲਪ ਨੂੰ ਸਾਹਮਣੇ ਲਿਆਂਦਾ ਹੈ ।

ਆਧੁਨਿਕ ਭਾਰਤ ਵਿਚ ਮੌਜੂਦ ਵਰਗ ਵਿਵਸਥਾ ਦੀ ਇਕ ਮਹੱਤਵਪੂਰਨ ਵਿਸ਼ੇਸ਼ਤਾ ਇਹ ਹੈ ਕਿ ਸਾਰੇ ਵਰਗਾਂ ਨੇ ਇਕ ਦੇਸ਼ ਦੇ ਵਿਚ ਇਕ ਰਾਸ਼ਟਰੀ ਆਰਥਿਕਤਾ, ਬਣਾਉਣ ਵਿਚ ਬਹੁਤ ਮੱਦਦ ਕੀਤੀ ਹੈ । ਹੁਣ ਮੱਧ ਵਰਗ ਵਿਚ ਦੂਰ ਦੁਰਾਡੇ ਖੇਤਰਾਂ ਦੇ ਪਿੰਡਾਂ ਦੇ ਲੋਕ ਵੀ ਸ਼ਾਮਲ ਚੌ ਰਹੇ ਹਨ। ਹੁਣ ਪਿੰਡਾਂ ਵਿਚ ਰਹਿਣ ਵਾਲੇ ਅਲੱਗ-ਅਲੱਗ ਕੰਮ ਕਰਨ ਵਾਲੇ ਲੋਕ ਅਲੱਗ (isolated) ਨਹੀਂ ਰਹਿ ਗਏ ਹੁਣ ਜਾਤੀ ਆਧਾਰਿਤ ਪ੍ਰਤੀਬੰਧਾਂ ਦਾ ਖ਼ਾਤਮਾ ਹੋ ਗਿਆ ਹੈ ਅਤੇ ਵਰਗ ਆਧਾਰਿਤ ਚੇਤਨਾ ਸਾਹਮਣੇ ਆ ਰਹੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 6.
ਭਾਰਤ ਵਿਚ ਵਰੰਗ ਵਿਵਸਥੋਂ ਦੀਆਂ ਮੁੱਖ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਕੀ ਹਨ ?
ਉੱਤਰ-

1. ਭਾਰਤ ਵਿਚ 19ਵੀਂ ਸਦੀ ਅਤੇ 20ਵੀਂ ਸਦੀ ਵਿਚਕਾਰ ਸਮਾਜਿਕ, ਧਾਰਮਿਕ ਸੁਧਾਰ ਲਹਿਰਾਂ ਚਲੀਆਂ ਜਿਨ੍ਹਾਂ ਕਾਰਨ ਜਾਤੀ ਪ੍ਰਥਾ ਨੂੰ ਬਹੁਤ ਡੂੰਘੀ ਸੱਟ ਵੱਜੀ ।
2. ਭਾਰਤ ਸਰਕਾਰ ਨੇ ਸੁਤੰਤਰਤਾ ਤੋਂ ਬਾਅਦ ਬਹੁਤ ਸਾਰੇ ਕਾਨੂੰਨ ਪਾਸ ਕੀਤੇ ਅਤੇ ਸੰਵਿਧਾਨ ਵਿਚ ਕਈ ਪ੍ਰਕਾਰ ਦੇ ਪ੍ਰਾਵਧਾਨ ਰੱਖੇ ਜਿਨ੍ਹਾਂ ਨਾਲ ਜਾਤੀ ਵਿਵਸਥਾ ਵਿਚ ਪਰਿਵਰਤਨ ਆ ਗਏ ।
3. ਦੇਸ਼ ਵਿਚ ਉਦਯੋਗਾਂ ਦੇ ਵੱਧਣ ਨਾਲ ਅਲੱਗ-ਅਲੱਗ ਜਾਤਾਂ ਦੇ ਲੋਕ ਇਕੱਠੇ ਮਿਲ ਕੇ ਇਹਨਾਂ ਵਿਚ ਕੰਮ ਕਰਨ ਲੱਗ ਪਏ ਅਤੇ ਜਾਤੀ ਵਿਵਸਥਾ ਦੇ ਪ੍ਰਤਿਬੰਧਾਂ ਉੱਤੇ ਸੱਟ ਵੱਜੀ ।
4. ਸ਼ਹਿਰਾਂ ਵਿਚ ਅਲੱਗ-ਅਲੱਗ ਜਾਤਾਂ ਦੇ ਲੋਕ ਇਕੱਠੇ ਮਿਲ ਕੇ ਰਹਿੰਦੇ ਹਨ ਜਿਸ ਕਾਰਨ ਜਾਤੀ ਪ੍ਰਥਾ ਦੇ ਮੇਲ-ਜੋਲ ਦੀ ਪਾਬੰਦੀ ਵਾਲਾ ਨਿਯਮ ਵੀ ਖ਼ਤਮ ਹੋ ਗਿਆ ।
5. ਸਿੱਖਿਆ ਦੇ ਪ੍ਰਸਾਰ ਨੇ ਵੀ ਜਾਤੀ ਵਿਵਸਥਾ ਨੂੰ ਖ਼ਤਮ ਕਰਨ ਵਿਚ ਬਹੁਤ ਵੱਡਾ ਯੋਗਦਾਨ ਦਿੱਤਾ ।

ਪ੍ਰਸ਼ਨ 7.
ਮਾਰਕਸ ਅਤੇ ਵੈਬਰ ਢੇ-ਵਰਗ ਦੇ ਸਿਧਾਂਤ ਬਾਰੇ ਲਿਖੋ ।
ਉੱਤਰ-
ਕਾਰਲ ਮਾਰਕਸ ਨੇ ਸਮਾਜਿਕ ਸਤਰੀਕਰਨ ਦਾ ਸੰਘਰਸ਼ਵਾਦੀ ਸਿਧਾਂਤ ਦਿੱਤਾ ਹੈ ਤੇ ਇਹ ਸਿਧਾਂਤ 19ਵੀਂ ਸਦੀ ਦੇ ਰਾਜਨੀਤਿਕ ਤੇ ਸਮਾਜਿਕ ਸੰਘਰਸ਼ਾਂ ਕਰਕੇ ਹੀ ਅੱਗੇ ਆਇਆ ਹੈ । ਮਾਰਕਸ ਨੇ ਸਿਰਫ ਆਰਥਿਕ ਕਾਰਨ ਨੂੰ ਹੀ ਸਮਾਜਿਕ ਸਤਰੀਕਰਨ ਤੇ ਵੱਖ-ਵੱਖ ਵਰਗਾਂ ਵਿਚ ਸ਼ੰਘਰਸ਼ ਦਾ ਆਧਾਰ ਮੰਨਿਆ ਹੈ ।

ਮਾਰਕਸ ਨੇ ਇਹ ਸਿਧਾਂਤ ਕਿਰਤ ਵੰਡੇ ਦੇ ਆਧਾਰ ਉੱਤੇ ਦਿੱਤਾ ਹੈ । ਉਸ ਦੇ ਅਨੁਸਾਰ ਕਿਰਤ ਦੋ ਪ੍ਰਕਾਰ ਦੀ ਹੁੰਦੀ ਹੈ-ਸਰੀਰਕ ਅਤੇ ਬੌਧਿਕ ਕਿਰਤ ਅਤੇ ਇਹੀ ਅੰਤਰ ਹੀ ਸਮਾਜਿਕ ਵਰਗਾਂ ਦੇ ਵਿਚ ਫਰਕ ਦਾ ਕਾਰਨ ਹੈ ।

ਮਾਰਕਸ ਦਾ ਕਹਿਣਾ ਹੈ ਕਿ ਸਮਾਜ ਵਿਚ ਦੋ ਵਰਗ ਹੁੰਦੇ ਹਨ । ਪਹਿਲਾ ਵਰਗ ਉਤਪਾਦਨ ਦੇ ਸਾਧਨਾਂ ਦਾ ਮਾਲਕ ਹੁੰਦਾ ਹੈ ਤੇ ਦੂਜਾ ਵਰਗ ਉਤਪਾਦਨ ਦੇ ਸਾਧਨਾਂ ਦਾ ਮਾਲਕ ਨਹੀਂ ਹੁੰਦਾ । ਇਸ ਮਾਲਕੀ ਦੇ ਆਧਾਰ ਉੱਤੇ ਹੀ ਮਾਲਕ ਵਰਗ ਦੀ ਸਥਿਤੀ ਉੱਚੀ ਤੇ ਗੈਰ ਮਾਲਕ ਵਰਗ ਦੀ ਸਥਿਤੀ ਨੀਵੀਂ ਹੁੰਦੀ ਹੈ । ਮਾਲਕ ਵਰਗ ਨੂੰ ਮਾਰਕਸ ਪੂੰਜੀਪਤੀ ਵਰਗ ਕਹਿੰਦਾ ਹੈ ਅਤੇ ਗੈਰ ਮਾਲਕ ਵਰਗ ਨੂੰ ਮਜ਼ਦੂਰ ਵਰਗ ਕਹਿੰਦਾ ਹੈ । ਪੂੰਜੀਪਤੀ ਵਰਗ ਮਜ਼ਦੂਰ ਵਰਗ ਦਾ ਆਰਥਿਕ ਰੂਪ ਨਾਲ । ਸ਼ੋਸ਼ਣ ਕਰਦਾ ਹੈ ਅਤੇ ਮਜ਼ਦੂਰ ਵਰਗ ਆਪਣੇ ਅਧਿਕਾਰ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ ਪੂੰਜੀਪਤੀ ਵਰਗ ਨਾਲ ਸੰਘਰਸ਼ ਕਰਦਾ ਹੈ । ਇਹ ਹੀ ਸਤਰੀਕਰਨ ਦਾ ਨਤੀਜਾ ਹੈ ।

ਮਾਰਕਸ ਦਾ ਕਹਿਣਾ ਹੈ ਕਿ ਸਤਰੀਕਰਨ ਦੇ ਆਉਣ ਦਾ ਕਾਰਨ ਹੀ ਸੰਪੱਤੀ ਦੀ ਨਾ ਬਰਾਬਰ ਵੰਡ ਹੈ । ਸਤਰੀਕਰਨ ਦੀ ਪ੍ਰਕ੍ਰਿਤੀ ਉਸ ਸਮਾਜ ਦੇ ਵਰਗਾਂ ਉੱਤੇ ਨਿਰਭਰ ਕਰਦੀ ਹੈ ਤੇ ਵਰਗਾਂ ਦੀ ਪ੍ਰਕ੍ਰਿਤੀ ਉਤਪਾਦਨ ਦੇ ਤਰੀਕਿਆਂ ਉੱਤੇ । ਉਤਪਾਦਨ ਦਾ ਤਰੀਕਾ ਤਕਨੀਕ ਉੱਤੇ ਨਿਰਭਰ ਕਰਦਾ ਹੈ । ਵਰਗ ਇਕ ਸਮੂਹ ਹੁੰਦਾ ਹੈ ਜਿਸ ਦੇ ਮੈਂਬਰਾਂ ਦੇ ਸੰਬੰਧ ਉਤਪਾਦਨ ਦੀਆਂ ਸ਼ਕਤੀਆਂ ਨਾਲ ਸਮਾਨ ਹੁੰਦੇ ਹਨ । ਇਸ ਤਰ੍ਹਾਂ ਉਹ ਸਾਰੇ ਵਿਅਕਤੀ ਜਿਹੜੇ ਉਤਪਾਦਨ ਦੀਆਂ ਸ਼ਕਤੀਆਂ ਉੱਤੇ ਨਿਯੰਤਰਣ ਰੱਖਦੇ ਹਨ ਉਹ ਪਹਿਲਾ ਵਰਗ ਭਾਵ ਕਿ ਪੂੰਜੀਪਤੀ ਵਰਗ ਹੁੰਦਾ ਹੈ । ਦੂਜਾ ਵਰਗ ਉਹ ਹੈ ਜਿਹੜਾ ਉਤਪਾਦਨ ਦੀਆਂ ਸ਼ਕਤੀਆਂ ਦਾ ਮਾਲਕ ਨਹੀਂ ਹੈ ਬਲਕਿ ਆਪਣੀ ਮਜ਼ਦੂਰੀ ਜਾਂ ਕਿਰਤ ਵੇਚ ਕੇ ਆਪਣਾ ਗੁਜ਼ਾਰਾ ਕਰਦਾ ਹੈ ਭਾਵ ਕਿ ਮਜ਼ਦੂਰ ਵਰਗ । ਵੱਖ-ਵੱਖ ਸਮਾਜਾਂ ਵਿਚ ਇਹਨਾਂ ਦੇ ਨਾਮ ਵੱਖ-ਵੱਖ ਸਨ ਜਿਵੇਂ ਜਗੀਰਦਾਰੀ ਸਮਾਜ ਵਿਚ ਜਗੀਰਦਾਰ ਅਤੇ ਖੇਤੀ ਮਜ਼ਦੂਰ ਅਤੇ ਪੂੰਜੀਪਤੀ ਸਮਾਜ ਵਿਚ ਪੂੰਜੀਪਤੀ ਤੇ ਮਜ਼ਦੂਰ । ਪੂੰਜੀਪਤੀ ਵਰਗ ਕੋਲ ਉਤਪਾਦਨ ਦੀਆਂ ਸ਼ਕਤੀਆਂ ਹੁੰਦੀਆਂ ਹਨ ਤੇ ਮਜ਼ਦੂਰ ਵਰਗ ਕੋਲ ਸਿਰਫ ਮਜ਼ਦੂਰੀ ਹੁੰਦੀ ਹੈ ਜਿਸ ਦੀ ਮੱਦਦ ਨਾਲ ਉਹ ਆਪਣਾ ਗੁਜ਼ਾਰਾ ਕਰਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਉਤਪਾਦਨ ਦੇ ਤਰੀਕਿਆਂ ਅਤੇ ਸੰਪੱਤੀ ਦੀ ਨਾ ਬਰਾਬਰ ਵੰਡ ਦੇ ਅਧਾਰ ਉੱਤੇ ਬਣੇ ਵਰਗ ਨੂੰ ਮਾਰਕਸ ਨੇ ਸਮਾਜਿਕ ਵਰਗ ਦਾ ਨਾਮ ਦਿੱਤਾ ਹੈ ।

ਮਾਰਕਸ ਦੇ ਅਨੁਸਾਰ ਅੱਜ ਜਾਂ ਸਮਾਜ ਚਾਰ ਯੁੱਗਾਂ ਵਿਚੋਂ ਲੰਘ ਕੇ ਸਾਡੇ ਸਾਹਮਣੇ ਆਇਆ ਹੈ ।
(a) ਪ੍ਰਾਚੀਨ ਸਾਮਵਾਦੀ ਯੁੱਗ (Primitive Ancient Society or Communism)
(b) ਪ੍ਰਾਚੀਨ ਸਮਾਜ (Ancient Society)
(c) ਸਾਮੰਤਵਾਦੀ ਯੁੱਗ (Feudal Society)
(d) ਪੂੰਜੀਵਾਦੀ ਯੁੱਗ (Capitalist Society) ।

ਮਾਰਕਸ ਅਨੁਸਾਰ ਪਹਿਲੇ ਪ੍ਰਕਾਰ ਦੇ ਸਮਾਜ ਵਿਚ ਵਰਗ ਹੋਂਦ ਵਿਚ ਨਹੀਂ ਆਏ ਸਨ ਪਰ ਉਸ ਤੋਂ ਬਾਅਦ ਦੇ ਸਮਾਜਾਂ ਵਿਚ ਦੋ ਪ੍ਰਮੁੱਖ ਵਰਗ ਸਾਡੇ ਸਾਹਮਣੇ ਆਏ । ਪ੍ਰਾਚੀਨ ਸਮਾਜ ਵਿਚ ਮਾਲਕ ਤੇ ਦਾਸ, ਸਾਮੰਤਵਾਦੀ ਸਮਾਜ ਵਿਚ ਜਗੀਰਦਾਰ ਤੇ ਖੇਤੀ ਮਜ਼ਦੂਰ ਅਤੇ ਪੂੰਜੀਵਾਦੀ ਸਮਾਜ ਵਿਚ ਪੂੰਜੀਪਤੀ ਤੇ ਮਜ਼ਦੂਰ ਵਰਗ । ਹਰ ਇਕ ਸਮਾਜ ਵਿਚ ਮਜ਼ਦੂਰੀ ਦੂਜੇ ਵਰਗ ਦੁਆਰਾ ਹੀ ਕੀਤੀ ਗਈ । ਮਜ਼ਦੂਰ ਵਰਗ ਬਹੁਸੰਖਿਅਕ ਹੁੰਦਾ ਹੈ ਤੇ ਪੂੰਜੀਪਤੀ ਵਰਗ ਘੱਟ ਗਿਣਤੀ ਵਾਲਾ ।

ਮਾਰਕਸ ਨੇ ਹਰ ਇਕ ਸਮਾਜ ਵਿਚ ਦੋ ਵਰਗਾਂ ਦਾ ਜ਼ਿਕਰ ਕੀਤਾ ਹੈ ਪਰ ਮਾਰਕਸ ਦੇ ਫਿਰ ਵੀ ਇਸ ਮਾਮਲੇ ਉੱਤੇ ਵਿਚਾਰ ਇਕਸਾਰ ਨਹੀਂ ਸਨ । ਮਾਰਕਸ ਕਹਿੰਦਾ ਹੈ ਕਿ ਪੂੰਜੀਵਾਦੀ ਸਮਾਜ ਵਿਚ ਤਿੰਨ ਵਰਗ ਹੁੰਦੇ ਹਨ ਮਜ਼ਦੂਰ, ਪੂੰਜੀਪਤੀ ਤੇ ਜ਼ਮੀਨ ਦੇ ਮਾਲਕ (Land owners) । ਮਾਰਕਸ ਨੇ ਇਹਨਾਂ ਤਿੰਨਾਂ ਵਿਚ ਅੰਤਰ ਆਮਦਨ ਦੇ ਸਾਧਨਾਂ, ਲਾਭ ਤੇ ਜ਼ਮੀਨ ਦੇ ਕਿਰਾਏ ਦੇ ਆਧਾਰ ਉੱਤੇ ਕੀਤਾ ਹੈ । ਮਾਰਕਸ ਦੇ ਇੰਗਲੈਂਡ ਵਿਚ ਇਹ ਤਿੰਨ ਵਰਗੀ ਵਿਵਸਥਾ ਕਦੇ ਵੀ ਸਾਹਮਣੇ ਨਹੀਂ ਆਈ ਹੈ ।

ਮਾਰਕਸ ਨੇ ਕਿਹਾ ਸੀ ਕਿ ਪੂੰਜੀਵਾਦ ਦੇ ਵਿਕਾਸ ਦੇ ਨਾਲ ਨਾਲ ਤਿੰਨ ਵਰਗੀ ਵਿਵਸਥਾ ਦੋ ਵਰਗੀ ਵਿਵਸਥਾ ਵਿਚ ਬਦਲ ਜਾਵੇਗੀ ਤੇ ਮੱਧ ਵਰਗ ਖ਼ਤਮ ਹੋ ਜਾਵੇਗਾ । ਇਸ ਬਾਰੇ ਉਸ ਨੇ ਕਮਿਉਨਿਸਟ ਘੋਸ਼ਣਾ-ਪੱਤਰ ਵਿਚ ਕਿਹਾ ਹੈ । ਮਾਰਕਸ ਨੇ ਵਿਸ਼ੇਸ਼ ਸਮਾਜ ਵਿਚ ਹੋਰ ਵਰਗਾਂ ਬਾਰੇ ਵੀ ਦੱਸਿਆ ਹੈ । ਜਿਵੇਂ ਬੁਰਜੂਆ ਜਾਂ ਪੂੰਜੀਪਤੀ ਵਰਗ ਨੂੰ ਉਸ ਨੇ ਦੋ ਉਪਵਰਗਾਂ-ਪ੍ਰਭਾਵੀ ਬੁਰਜੂਆ ਤੇ ਛੋਟੇ ਬੁਰਜੁਆ ਵਰਗਾਂ ਵਿਚ ਵੰਡਿਆ ਹੈ । ਪ੍ਰਭਾਵੀ ਬੁਰਜੂਆ ਉਹ ਹੁੰਦੇ ਹਨ ਜਿਹੜੇ ਵੱਡੇਵੱਡੇ ਪੂੰਜੀਪਤੀ ਤੇ ਉਦਯੋਗਪਤੀ ਹੁੰਦੇ ਹਨ ਤੇ ਜਿਹੜੇ ਹਜ਼ਾਰਾਂ ਦੀ ਗਿਣਤੀ ਵਿਚ ਮਜ਼ਦੂਰਾਂ ਨੂੰ ਕੰਮ ਦਿੰਦੇ ਹਨ । ਛੋਟੇ ਬੁਰਜੂਆ ਉਹ ਛੋਟੇ ਉਦਯੋਗਪਤੀ ਜਾਂ ਦੁਕਾਨਦਾਰ ਹੁੰਦੇ ਹਨ ਜਿਨ੍ਹਾਂ ਦੇ ਵਪਾਰ ਛੋਟੇ ਪੱਧਰ ਦੇ ਹੁੰਦੇ ਹਨ ਤੇ ਉਹ ਬਹੁਤ ਜ਼ਿਆਦਾ ਮਜ਼ਦੂਰਾਂ ਨੂੰ ਕੰਮ ਨਹੀਂ ਦਿੰਦੇ । ਉਹ ਕਾਫੀ ਹੱਦ ਤੱਕ ਆਪ ਹੀ ਕੰਮ ਕਰਦੇ ਹਨ । ਮਾਰਕਸ ਇੱਥੇ ਫਿਰ ਕਹਿੰਦਾ ਹੈ ਪੂੰਜੀਵਾਦ ਦੇ ਵਿਕਸਿਤ ਹੋਣ ਦੇ ਨਾਲ ਨਾਲ ਮੱਧਵਰਗੀ ਅਤੇ ਛੋਟੇ ਬੁਰਜੂਆਂ ਜਾਤਾਂ ਖ਼ਤਮ ਹੋ ਜਾਣਗੀਆਂ ਜਾਂ ਫਿਰ ਮਜ਼ਦੂਰ ਵਰਗ ਵਿਚ ਮਿਲ ਜਾਣਗੇ । ਇਸ ਤਰ੍ਹਾਂ ਸਮਾਜ ਵਿਚ ਪੂੰਜੀਪਤੀ ਤੇ ਮਜ਼ਦੂਰ ਵਰਗ ਰਹਿ ਜਾਣਗੇ ।

ਵਰਗਾਂ ਵਿਚਕਾਰ ਸੰਬੰਧ (Relations between Classes) – ਮਾਰਕਸ ਅਨੁਸਾਰ ਪੂੰਜੀਪਤੀ ਵਰਗ ਮਜ਼ਦੂਰ ਵਰਗ ਦਾ ਆਰਥਿਕ ਸ਼ੋਸ਼ਣ ਕਰਦਾ ਰਹਿੰਦਾ ਹੈ ਅਤੇ ਮਜ਼ਦੂਰ ਵਰਗ ਆਪਣੇ ਅਧਿਕਾਰਾਂ ਲਈ ਸੰਘਰਸ਼ ਕਰਦਾ ਰਹਿੰਦਾ ਹੈ । ਇਸ ਕਰਕੇ ਦੋਹਾਂ ਵਰਗਾਂ ਵਿਚਕਾਰ ਸੰਬੰਧ ਵਿਰੋਧ ਵਾਲੇ ਹੁੰਦੇ ਹਨ । ਚਾਹੇ ਕੁਝ ਸਮੇਂ ਲਈ ਆਪਣੇ ਆਪਣੇ ਹਿੱਤਾਂ ਕਰਕੇ ਦੋਹਾਂ ਵਰਗਾਂ ਵਿਚਕਾਰ ਵਿਰੋਧ ਛੱਪ ਜਾਂਦਾ ਹੈ ਪਰ ਇਹ ਵਿਰੋਧ ਚਲਦਾ ਰਹਿੰਦਾ ਹੈ । ਇਹ ਜ਼ਰੂਰੀ ਨਹੀਂ ਕਿ ਇਹ ਵਿਰੋਧ ਉੱਪਰੀ ਤੌਰ ਉੱਤੇ ਦਿਖਾਈ ਦੇਵੇ ਪਰ ਉਹਨਾਂ ਨੂੰ ਇਸ ਵੈਰ-ਵਿਰੋਧ ਦਾ ਅਹਿਸਾਸ ਜ਼ਰੂਰ ਹੁੰਦਾ ਹੈ ।

ਮਾਰਕਸ ਅਨੁਸਾਰ ਵਰਗਾਂ ਵਿਚ ਆਪਸੀ ਸੰਬੰਧ ਆਪਸੀ ਨਿਰਭਰਤਾ ਅਤੇ ਸੰਘਰਸ਼ ਉੱਤੇ ਆਧਾਰਿਤ ਹੁੰਦੇ ਹਨ । ਅਸੀਂ ਉਦਾਹਰਣ ਲੈ ਸਕਦੇ ਹਾਂ ਪੂੰਜੀਵਾਦੀ ਸਮਾਜ ਦੇ ਦੋ ਵਰਗਾਂ ਦੀ । ਇਕ ਵਰਗ ਪੂੰਜੀਪਤੀ ਦਾ ਹੁੰਦਾ ਹੈ ਅਤੇ ਦੂਜਾ ਵਰਗ ਕਿਰਤੀਆਂ ਦਾ ਹੁੰਦਾ ਹੈ । ਇਸ ਦੋਵੇਂ ਵਰਗ ਆਪਣੀ ਹੋਂਦ ਲਈ ਇਕ ਦੂਜੇ ਉੱਤੇ ਨਿਰਭਰ ਹੁੰਦੇ ਹਨ । ਕਿਰਤੀ ਵਰਗ ਕੋਲ ਉਤਪਾਦਨ ਦੀਆਂ ਤਾਕਤਾਂ ਉੱਤੇ ਮਲਕੀਅਤ ਨਹੀਂ ਹੈ । ਉਸ ਕੋਲ ਰੋਟੀ ਕਮਾਉਣ ਲਈ ਆਪਣੀ ਕਿਰਤ ਵੇਚਣ ਤੋਂ ਇਲਾਵਾ ਕੋਈ ਸਾਧਨ ਨਹੀਂ ਹੈ । ਉਹ ਰੋਟੀ ਕਮਾਉਣ ਲਈ ਪੂੰਜੀਪਤੀਆਂ ਦੇ ਹੱਥ ਆਪਣੀ ਮਜ਼ਦੂਰੀ ਵੇਚਦੇ ਹਨ ਤੇ ਉਹਨਾਂ ਉੱਤੇ ਨਿਰਭਰ ਹੁੰਦੇ ਹਨ । ਉਹ ਆਪਣੀ ਮਜ਼ਦੂਰੀ ਪੂੰਜੀਪਤੀ ਨੂੰ ਦਿੰਦੇ ਹਨ ਜਿਸ ਦੇ ਬਦਲੇ ਵਿਚ ਪੂੰਜੀਪਤੀ ਮਜ਼ਦੂਰਾਂ ਨੂੰ ਉਹਨਾਂ ਦੀ ਮਜ਼ਦੂਰੀ ਦਾ ਕਿਰਾਇਆ ਦਿੰਦਾ ਹੈ । ਇਸ ਕਿਰਾਏ ਨਾਲ ਮਜ਼ਦੂਰ ਆਪਣਾ ਪੇਟ ਪਾਲਦਾ ਹੈ । ਪੂੰਜੀਪਤੀ ਵੀ ਮਜ਼ਦੂਰਾਂ ਦੀ ਕਿਰਤ ਉੱਤੇ ਨਿਰਭਰ ਹੈ ਕਿਉਂਕਿ ਮਜ਼ਦੂਰਾਂ ਦੇ ਕੰਮ ਕੀਤੇ ਬਗੈਰ ਉਸ ਦਾ ਨਾ ਤਾਂ ਉਤਪਾਦਨ ਹੋ ਸਕਦਾ ਹੈ ਤੇ ਨਾ ਹੀ ਉਸ ਕੋਲ ਪੂੰਜੀ ਇਕੱਠੀ ਹੋ ਸਕਦੀ ਹੈ ।

ਇਸ ਤਰ੍ਹਾਂ ਦੋਵੇਂ ਵਰਗ ਇਕ ਦੂਜੇ ਉੱਤੇ ਨਿਰਭਰ ਹਨ ਪਰ ਇਸ ਨਿਰਭਰਤਾ ਦਾ ਅਰਥ ਇਹ ਨਹੀਂ ਹੈ ਕਿ ਉਹਨਾਂ ਵਿਚ ਸੰਬੰਧ ਬਰਾਬਰੀ ਦੇ ਹੁੰਦੇ ਹਨ । ਪੂੰਜੀਪਤੀ ਵਰਗ ਮਜ਼ਦੂਰ ਵਰਗ ਦਾ ਸ਼ੋਸ਼ਣ ਕਰਦਾ ਹੈ । ਉਹ ਚੀਜ਼ਾਂ ਦਾ ਉਤਪਾਦਨ ਘੱਟ ਪੈਸੇ ਦੇ ਕੇ ਕਰਵਾਉਣਾ ਚਾਹੁੰਦਾ ਹੈ ਤਾਂ ਕਿ ਉਸ ਦਾ ਲਾਭ ਵੱਧ ਸਕੇ । ਮਜ਼ਦੂਰ ਜ਼ਿਆਦਾ ਮਜ਼ਦੂਰੀ ਮੰਗਦਾ ਹੈ ਤਾਂ ਕਿ ਉਹ ਆਪਣੇ ਪਰਿਵਾਰ ਦਾ ਪੇਟ ਪਾਲ ਸਕੇ । ਪੂੰਜੀਪਤੀ ਘੱਟ ਮਜ਼ਦੂਰੀ ਦੇ ਕੇ ਚੀਜ਼ ਨੂੰ ਵੱਧ ਕੀਮਤ ਉੱਤੇ ਵੇਚਣ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰਦਾ ਹੈ ਤਾਂ ਕਿ ਵੱਧ ਲਾਭ ਹੋ ਸਕੇ । ਇਸ ਤਰ੍ਹਾਂ ਦੋਹਾਂ ਵਰਗਾਂ ਵਿਚਕਾਰ ਆਪਣੇ ਆਪਣੇ ਹਿੱਤਾਂ ਦਾ ਸੰਘਰਸ਼ (Conflict of interest) ਚਲਦਾ ਰਹਿੰਦਾ ਹੈ । ਇਹ ਸੰਘਰਸ਼ ਅੰਤ ਵਿਚ ਸਮਤਾਵਾਦੀ ਵਿਵਸਥਾ (Communism) ਨੂੰ ਜਨਮ ਦੇਵੇਗਾ ਜਿਸ ਵਿਚ ਨਾ ਤਾਂ ਵਿਰੋਧ ਹੋਣਗੇ ਨਾ ਕਿਸੇ ਦਾ ਸ਼ੋਸ਼ਣ ਹੋਵੇਗਾ, ਨਾ ਕਿਸੇ ਉੱਤੇ ਅੱਤਿਆਚਾਰ ਹੋਵੇਗਾ ਤੇ ਨਾ ਹੀ ਹਿੱਤਾਂ ਦਾ ਸੰਘਰਸ਼ ਹੋਵੇਗਾ । ਇਹ ਸਮਾਜ ਵਰਗ ਰਹਿਤ ਸਮਾਜ ਹੋਵੇਗਾ ।

ਮਨੁੱਖੀ ਇਤਿਹਾਸ-ਵਰਗ ਸੰਘਰਸ਼ ਦਾ ਇਤਿਹਾਸ (Human History-History of class struggleਮਾਰਕਸ ਦਾ ਕਹਿਣਾ ਹੈ ਕਿ ਮਨੁੱਖੀ ਇਤਿਹਾਸ ਵਰਗ ਸੰਘਰਸ਼ ਦਾ ਇਤਿਹਾਸ ਰਿਹਾ ਹੈ । ਅਸੀਂ ਕਿਸੇ ਵੀ ਸਮਾਜ ਦੀ ਉਦਾਹਰਣ ਲੈ ਸਕਦੇ ਹਾਂ ਹਰੇਕ ਸਮਾਜ ਵਿਚ ਵੱਖ-ਵੱਖ ਵਰਗਾਂ ਵਿਚ ਕਿਸੇ ਨਾ ਕਿਸੇ ਰੂਪ ਵਿਚ ਸੰਘਰਸ਼ ਤਾਂ ਚਲਦਾ ਹੀ ਰਿਹਾ ਹੈ ।

ਇਸ ਤਰ੍ਹਾਂ ਮਾਰਕਸ ਦਾ ਕਹਿਣਾ ਸੀ ਕਿ ਸਾਰੇ ਸਮਾਜਾਂ ਵਿਚ ਆਮ ਤੌਰ ਉੱਤੇ ਦੋ ਪ੍ਰਕਾਰ ਦੇ ਵਰਗ ਰਹੇ ਹਨ-ਮਜ਼ਦੂਰ ਤੇ ਪੂੰਜੀਪਤੀ 1 ਦੋਹਾਂ ਵਿਚ ਵਰਗ ਸੰਘਰਸ਼ ਚਲਦਾ ਹੀ ਰਹਿੰਦਾ ਹੈ । ਇਹਨਾਂ ਵਿਚ ਵਰਗ ਸੰਘਰਸ਼ ਦੇ ਕਈ ਕਾਰਨ ਹੁੰਦੇ ਹਨ, ਜਿਵੇਂ ਕਿ ਦੋਹਾਂ ਵਰਗਾਂ ਵਿਚ ਬਹੁਤ ਜ਼ਿਆਦਾ ਆਰਥਿਕ ਅੰਤਰ ਹੁੰਦਾ ਹੈ ਜਿਸ ਕਾਰਨ ਉਹ ਇਕ ਦੂਜੇ ਦੀ ਵਿਰੋਧਤਾ ਕਰਦੇ ਹਨ । ਪੂੰਜੀਪਤੀ ਵਰਗ ਬਿਨਾਂ ਮਿਹਨਤ ਕੀਤੇ ਹੀ ਅਮੀਰ ਬਣਦਾ ਚਲਾ ਜਾਂਦਾ ਹੈ ਤੇ ਮਜ਼ਦੂਰ ਵਰਗ ਸਾਰਾ ਦਿਨ ਮਿਹਨਤ ਕਰਨ ਤੋਂ ਬਾਅਦ ਵੀ ਗਰੀਬ ਹੀ ਬਣਿਆ ਰਹਿੰਦਾ ਹੈ । ਸਮੇਂ ਦੇ ਨਾਲ-ਨਾਲ ਮਜ਼ਦੂਰ ਵਰਗ ਆਪਣੇ ਹਿੱਤਾਂ ਦੀ ਰਾਖੀ ਲਈ ਸੰਗਠਨ ਬਣਾ ਲੈਂਦਾ ਹੈ ਤੇ ਇਹ ਸੰਗਠਨ ਪੂੰਜੀਪਤੀਆਂ ਤੋਂ ਆਪਣੇ ਅਧਿਕਾਰ ਲੈਣ ਲਈ ਸੰਘਰਸ਼ ਕਰਦੇ ਹਨ ।

ਇਸ ਸੰਘਰਸ਼ ਦਾ ਨਤੀਜਾ ਇਹ ਹੁੰਦਾ ਹੈ ਕਿ ਸਮਾਂ ਆਉਣ ਉੱਤੇ ਮਜ਼ਦੂਰ ਵਰਗ ਪੂੰਜੀਪਤੀ ਵਰਗ ਦੇ ਵਿਰੁੱਧ ਕ੍ਰਾਂਤੀ ਕਰ ਦਿੰਦਾ ਹੈ ਅਤੇ ਕ੍ਰਾਂਤੀ ਤੋਂ ਬਾਅਦ ਪੂੰਜੀਪਤੀਆਂ ਦਾ ਖਾਤਮਾ ਕਰਕੇ ਆਪਣੀ ਸੱਤਾ ਸਥਾਪਿਤ ਕਰ ਲੈਂਦਾ ਹੈ । ਪੂੰਜੀਪਤੀ ਆਪਣੇ ਪੈਸੇ ਦੀ ਮਦਦ ਨਾਲ ਪ੍ਰਤੀ ਕ੍ਰਾਂਤੀ ਕਰਨ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰਨਗੇ ਪਰ ਉਹਨਾਂ ਦੀ ਪ੍ਰਤੀ ਕ੍ਰਾਂਤੀ ਨੂੰ ਦਬਾ ਦਿੱਤਾ ਜਾਵੇਗਾ ਤੇ ਮਜ਼ਦੂਰਾਂ ਦੀ ਸੱਤਾ ਸਥਾਪਿਤ ਹੋ ਜਾਵੇਗੀ । ਪਹਿਲਾਂ ਸਾਮਵਾਦ ਤੇ ਫਿਰ ਸਮਾਜਵਾਦ ਦੀ ਸਥਿਤੀ ਆਵੇਗੀ ਜਿਸ ਵਿਚ ਹਰੇਕ ਵਿਅਕਤੀ ਨੂੰ ਉਸ ਦੀ ਜ਼ਰੂਰਤ ਮੁਤਾਬਿਕ ਤੇ ਉਸਦੀ ਯੋਗਤਾ ਮੁਤਾਬਿਕ ਮੇਹਨਤਾਨਾ ਮਿਲੇਗਾ । ਸਮਾਜ ਵਿਚ ਕੋਈ ਵਰਗ ਨਹੀਂ ਹੋਵੇਗਾ ਤੇ ਇਹ ਵਰਗਹੀਣ ਸਮਾਜ ਹੋਵੇਗਾ ਜਿਸ ਵਿਚ ਸਾਰਿਆਂ ਨੂੰ ਬਰਾਬਰ ਦਾ ਹਿੱਸਾ ਮਿਲੇਗਾ | ਕੋਈ ਉੱਚਾ ਨੀਵਾਂ ਨਹੀਂ ਹੋਵੇਗਾ ਤੇ ਮਜ਼ਦੂਰ ਵਰਗ ਦੀ ਸੱਤਾ ਸਥਾਪਿਤ ਰਹੇਗੀ । ਮਾਰਕਸ ਦਾ ਕਹਿਣਾ ਸੀ ਕਿ ਚਾਹੇ ਇਹ ਸਥਿਤੀ ਹਾਲੇ ਤੱਕ ਆਈ ਨਹੀਂ ਹੈ ਪਰ ਜਲਦੀ ਹੀ ਇਹ ਸਥਿਤੀ ਆ ਜਾਵੇਗੀ ਤੇ ਸਮਾਜ ਵਿਚ ਸਤਰੀਕਰਨ ਦਾ ਖਾਤਮਾ ਹੋ ਜਾਵੇਗਾ ।

ਮੈਕਸ ਵੈਬਰ ਦਾ ਵਰਗ ਦਾ ਸਿਧਾਂਤ (Max Weber’s Theory of Class)

ਮੈਕਸ ਵੈਬਰ ਨੇ ਸਤਰੀਕਰਨ ਦਾ ਸਿਧਾਂਤ ਦਿੱਤਾ ਸੀ ਜਿਸ ਵਿੱਚ ਉਸਨੇ ਵਰਗ, ਰੁਤਬਾ ਸਮੂਹ ਅਤੇ ਦਲ ਦੀ ਅੱਡ-ਅੱਡ ਵਿਆਖਿਆ ਕੀਤੀ ਸੀ । ਵੈਬਰ ਦਾ ਸਤਰੀਕਰਨ ਦਾ ਸਿਧਾਂਤ ਤਰਕਸੰਗਤ ਅਤੇ ਵਿਹਾਰਕ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ । ਇਸੇ ਕਰਕੇ ਇਸ ਸਿਧਾਂਤ ਨੂੰ ਅਮਰੀਕੀ ਸਮਾਜ ਸ਼ਾਸਤਰੀਆਂ ਨੇ ਕਾਫ਼ੀ ਮਹੱਤਵ ਪ੍ਰਦਾਨ ਕੀਤਾ । ਵੈਬਰ ਨੇ ਸਤਰੀਕਰਨ ਨੂੰ ਤਿੰਨ ਪੱਖਾਂ ਤੋਂ ਸਮਝਾਇਆ ਹੈ ਅਤੇ ਉਹ ਹਨ ਵਰਗ, ਸਥਿਤੀ ਅਤੇ ਦਲ ! ਇਹਨਾਂ ਤਿੰਨੋਂ ਹੀ ਸਮੂਹਾਂ ਨੂੰ ਇਕ ਤਰੀਕੇ ਨਾਲ ਹਿੱਤ ਸਹ ਕਿਹਾ ਜਾ ਸਕਦਾ ਹੈ ਜਿਹੜੇ ਨਾ ਕੇਵਲ ਆਪਣੇ ਅੰਦਰ ਲੜ ਸਕਦੇ ਹਨ ਬਲਕਿ ਇਹ ਇੱਕ ਦੂਜੇ ਦੇ ਵਿਰੁੱਧ ਵੀ ਲੜ ਸਕਦੇ ਹਨ । ਇਹ ਇੱਕ ਵਿਸ਼ੇਸ਼ ਸੱਤਾ ਬਾਰੇ ਦੱਸਦੇ ਹਨ ਅਤੇ ਆਪਸ ਵਿੱਚ ਇੱਕ-ਦੂਜੇ ਨਾਲ ਸੰਬੰਧਿਤ ਵੀ ਹੁੰਦੇ ਹਨ । ਹੁਣ ਅਸੀਂ ਤਿੰਨਾਂ ਦਾ ਵਰਣਨ ਅੱਡ-ਅੱਡ ਅਤੇ ਵਿਸਤਾਰ ਨਾਲ ਕਰਾਂਗੇ-

ਵਰਗ (Class) – ਕਾਰਲ ਮਾਰਕਸ ਨੇ ਵਰਗ ਦੀ ਪਰਿਭਾਸ਼ਾ ਆਰਥਿਕ ਆਧਾਰ ਉੱਤੇ ਦਿੱਤੀ ਸੀ ਅਤੇ ਉਸੇ ਤਰਾਂ ਵੈਬਰ ਨੇ ਵੀ ਵਰਗ ਦੀ ਧਾਰਨਾ ਆਰਥਿਕ ਆਧਾਰ ਉੱਤੇ ਦਿੱਤੀ ਹੈ । ਵੈਬਰ ਦੇ ਅਨੁਸਾਰ, “ਵਰਗ ਅਜਿਹੇ ਲੋਕਾਂ ਦਾ ਸਮੂਹ ਹੁੰਦਾ ਹੈ ਜਿਹੜੇ ਕਿਸੇ ਸਮਾਜ ਦੇ ਆਰਥਿਕ ਮੌਕਿਆਂ ਦੀ ਸੰਰਚਨਾ ਵਿੱਚ ਸਮਾਨ ਸਥਿਤੀ ਵਿੱਚ ਹੁੰਦੇ ਹਨ ਅਤੇ ਜਿਹੜੇ ਸਮਾਨ ਸਥਿਤੀਆਂ ਵਿੱਚ ਰਹਿੰਦੇ ਹਨ । ਇਹ ਸਥਿਤੀਆਂ ਉਹਨਾਂ ਦੀ ਆਰਥਿਕ ਸ਼ਕਤੀ ਦੇ ਰੂਪ ਅਤੇ ਮਾਤਰਾ ਉੱਤੇ ਨਿਰਭਰ ਕਰਦੀਆਂ ਹਨ । ਇਸ ਤਰ੍ਹਾਂ ਵੈਬਰ ਇੱਕ ਅਜਿਹੇ ਵਰਗ ਦੀ ਗੱਲ ਕਰਦਾ ਹੈ ਜਿਸ ਵਿੱਚ ਲੋਕਾਂ ਦੀ ਇੱਕ ਵਿਸ਼ੇਸ਼ ਸੰਖਿਆ ਦੇ ਲਈ ਜੀਵਨ ਦੇ ਮੌਕੇ ਇੱਕ ਸਮਾਨ ਹੁੰਦੇ ਹਨ । ਚਾਹੇ ਵੈਬਰ ਇਹ ਧਾਰਣਾ ਮਾਰਕਸ ਦੀ ਵਰਗ ਦੀ ਧਾਰਣਾ ਤੋਂ ਅੱਡ ਨਹੀਂ ਹੈ ਪਰ ਵੈਬਰ ਨੇ ਵਰਗ ਦੀ ਕਲਪਨਾ ਸਮਾਨ ਆਰਥਿਕ ਸਥਿਤੀਆਂ ਵਿੱਚ ਰਹਿਣ ਵਾਲੇ ਲੋਕਾਂ ਦੇ ਰੂਪ ਵਿੱਚ ਕੀਤੀ ਹੈ ਆਤਮ ਚੇਤੰਨਤਾ ਸਮੂਹ ਦੇ ਰੂਪ ਵਿੱਚ ਨਹੀਂ ਵੈਬਰ ਨੇ ਵਰਗ ਦੇ ਤਿੰਨ ਪ੍ਰਕਾਰ ਦੱਸੇ ਹਨ ਜਿਹੜੇ ਕਿ ਹੇਠਾਂ ਲਿਖੇ ਹਨ

1. ਸੰਪੱਤੀ ਵਰਗ (A property class)
2. ਅਧਿਗ੍ਰਹਿਣ ਵਰਗ (An Acquisition class)
3. ਸਮਾਜਿਕ ਵਰਗ (A Social class) ।

(1) ਸੰਪੱਤੀ ਵਰਗ (A Property class) – ਸੰਪੱਤੀ ਵਰਗ ਉਹ ਵਰਗ ਹੁੰਦਾ ਹੈ ਜਿਸ ਦੀ ਸਥਿਤੀ ਇਸ ਗੱਲ ਉੱਤੇ ਨਿਰਭਰ ਕਰਦੀ ਹੈ ਕਿ ਉਹਨਾਂ ਦੇ ਕੋਲ ਕਿੰਨੀ ਸੰਪੱਤੀ ਜਾਂ ਜਾਇਦਾਦ ਹੈ । ਇਹ ਵਰਗ ਅੱਗੇ ਦੋ ਭਾਗਾਂ ਵਿੱਚ ਵੰਡਿਆ ਗਿਆ ਹੈ-
(i) ਸਕਾਰਾਤਮਕ ਰੂਪ ਨਾਲ ਵਿਸ਼ੇਸ਼ ਅਧਿਕਾਰ ਪ੍ਰਾਪਤ ਸੰਪੱਤੀ ਵਰਗ (The Positively Privileged Property Class) – ਇਸ ਵਰਗ ਕੋਲ ਕਾਫ਼ੀ ਸੰਪੱਤੀ ਜਾਂ ਜਾਇਦਾਦ ਹੁੰਦੀ ਹੈ ਅਤੇ ਇਹ ਇਸ ਜਾਇਦਾਦ ਤੋਂ ਹੋਈ ਆਮਦਨੀ ਉੱਤੇ ਆਪਣਾ ਗੁਜ਼ਾਰਾ ਕਰਦਾ ਹੈ । ਇਹ ਵਰਗ ਉਪਭੋਗ ਕਰਨ ਵਾਲੀਆਂ ਚੀਜ਼ਾਂ ਦੇ ਖਰੀਦਣ ਜਾਂ ਵੇਚਣ, ਜਾਇਦਾਦ ਇਕੱਠੀ ਕਰਕੇ ਜਾਂ ਫਿਰ ਸਿੱਖਿਆ ਲੈਣ ਉੱਤੇ ਆਪਣਾ ਏਕਾਧਿਕਾਰ ਕਰ ਸਕਦਾ ਹੈ ।

(ii) ਨਕਾਰਾਤਮਕ ਰੂਪ ਨਾਲ ਵਿਸ਼ੇਸ਼ ਅਧਿਕਾਰ ਪ੍ਰਾਪਤ ਸੰਪੱਤੀ ਵਰਗ (The Negatively Privileged Property Class) – ਇਸ ਵਰਗ ਦੇ ਮੁੱਖ ਮੈਂਬਰ ਅਨਪੜ੍ਹ, ਗਰੀਬ, ਸੰਪੱਤੀਹੀਨ ਅਤੇ ਕਰਜ਼ੇ ਦੇ ਬੋਝ ਥੱਲੇ ਦੱਬੇ ਹੋਏ ਲੋਕ ਹੁੰਦੇ ਹਨ । ਇਹਨਾਂ ਦੋਹਾਂ ਸਮੂਹਾਂ ਦੇ ਨਾਲ ਇੱਕ ਵਿਸ਼ੇਸ਼ ਅਧਿਕਾਰ ਪ੍ਰਾਪਤ ਮੱਧ ਵਰਗ ਵੀ ਹੁੰਦਾ ਹੈ ਜਿਸ ਵਿੱਚ ਉੱਪਰਲੇ ਦੋਹਾਂ ਵਰਗਾਂ ਦੇ ਲੋਕ ਸ਼ਾਮਲ ਹੁੰਦੇ ਹਨ । ਵੈਬਰ ਦੇ ਅਨੁਸਾਰ ਪੂੰਜੀਪਤੀ ਆਪਣੀ ਵਿਸ਼ੇਸ਼ ਸਥਿਤੀ ਹੋਣ ਕਰਕੇ ਅਤੇ ਮਜ਼ਦੂਰ ਆਪਣੀ ਨਕਾਰਾਤਮਕ ਰੂਪ ਨਾਲ ਵਿਸ਼ੇਸ਼ ਸਥਿਤੀ ਹੋਣ ਕਰਕੇ ਇਸ ਸਮੂਹ ਵਿੱਚ ਸ਼ਾਮਲ ਹੁੰਦਾ ਹੈ ।

(2) ਅਧਿਨ੍ਹਣ ਵਰਗਾ (An Acquisition Class) – ਇਹ ਉਸ ਪ੍ਰਕਾਰ ਦਾ ਸਮੂਹ ਹੁੰਦਾ ਹੈ ਜਿਸ ਦੀ ਸਥਿਤੀ ਬਜ਼ਾਰ ਵਿੱਚ ਮੌਜੂਦ ਸੇਵਾਵਾਂ ਦਾ ਲਾਭ ਚੁੱਕਣ ਦੇ ਮੌਕਿਆਂ ਨਾਲ ਨਿਰਧਾਰਿਤ ਹੁੰਦੀ ਹੈ । ਇਹ ਸਮੂਹ ਅੱਗੇ ਤਿੰਨ ਪ੍ਰਕਾਰ ਦਾ ਹੁੰਦਾ ਹੈ-
(i) ਸਕਾਰਾਤਮਕ ਰੂਪ ਨਾਲ ਵਿਸ਼ੇਸ਼ ਅਧਿਕਾਰ ਪ੍ਰਾਪਤ ਅਧਿਨ੍ਹਣ ਵਰਗ (The Positively Privileged Acquisition Class) – ਇਸ ਵਰਗ ਦਾ ਉਤਪਾਦਕ ਫੈਕਟਰੀ ਵਾਲਿਆਂ ਦੇ ਪ੍ਰਬੰਧ ਉੱਤੇ ਏਕਾਧਿਕਾਰ ਹੁੰਦਾ ਹੈ । ਇਹ ਫੈਕਟਰੀਆਂ ਵਾਲੇ ਬੈਂਕਰ, ਉਦਯੋਗਪਤੀ, ਫਾਈਨੈਂਸਰ ਆਦਿ ਹੁੰਦੇ ਹਨ । ਇਹ ਲੋਕ ਪ੍ਰਬੰਧਕ ਵਿਵਸਥਾ ਨੂੰ ਨਿਯੰਤਰਣ ਵਿੱਚ ਰੱਖਣ ਦੇ ਨਾਲਨਾਲ ਸਰਕਾਰੀ ਆਰਥਿਕ ਨੀਤੀਆਂ ਉੱਤੇ ਵੀ ਪੂਰਾ ਪ੍ਰਭਾਵ ਪਾਉਂਦੇ ਹਨ ।

(ii) ਵਿਸ਼ੇਧਿਕਾਰ ਪ੍ਰਾਪਤ ਮੱਧ ਅਧਿਹਿਣ ਵਰਗ (The Middle Privileged Acquisition Class-ਇਹ ਵਰਗ ਮੱਧ ਵਰਗ ਦੇ ਲੋਕਾਂ ਦਾ ਵਰਗ ਹੁੰਦਾ ਹੈ ਜਿਸ ਵਿੱਚ ਛੋਟੇ ਪੇਸ਼ੇਵਰ ਲੋਕ, ਕਾਰੀਗਰ, ਆਜ਼ਾਦ ਕਿਸਾਨ ਆਦਿ ਸ਼ਾਮਲ ਹੁੰਦੇ ਹਨ।

(iii) ਨਕਾਰਾਤਮਕ ਰੂਪ ਨਾਲ ਵਿਸ਼ੇਸ਼ ਅਧਿਕਾਰ ਪ੍ਰਾਪਤ ਅਧਿਹਿਣ ਵਰਗ (The Negatively Privileged Acquisition Class-ਇਸ ਵਰਗ ਵਿੱਚ ਛੋਟੇ ਵਰਗਾਂ ਦੇ ਲੋਕ ਖਾਸ ਕਰ ਕੁਸ਼ਲ, ਅਰਧ ਕੁਸ਼ਲ ਅਤੇ ਅਕੁਸ਼ਲ ਮਜ਼ਦੂਰ ਸ਼ਾਮਲ ਹੁੰਦੇ ਹਨ ।

(3) ਸਮਾਜਿਕ ਵਰਗ (Social Class) – ਇਸ ਵਰਗ ਦੀ ਸੰਖਿਆ ਕਾਫੀ ਜ਼ਿਆਦਾ ਹੁੰਦੀ ਹੈ । ਇਸ ਵਿੱਚ ਅੱਡ-ਅੱਡ ਪੀੜੀਆਂ ਦੀ ਤਰੱਕੀ ਦੇ ਕਾਰਨ ਨਿਸ਼ਚਿਤ ਰੂਪ ਨਾਲ ਪਰਿਵਰਤਨ ਦਿਖਾਈ ਦਿੰਦਾ ਹੈ । ਪਰ ਵੈਬਰ ਸਮਾਜਿਕ ਵਰਗ ਦੀ ਵਿਆਖਿਆ ਵਿਸ਼ੇਸ਼ ਅਧਿਕਾਰਾਂ ਦੇ ਅਨੁਸਾਰ ਨਹੀਂ ਕਰਦਾ । ਉਸ ਦੇ ਅਨੁਸਾਰ ਮਜ਼ਦੂਰ ਵਰਗ, ਨੀਵਾਂ ਮੱਧ ਵਰਗ, ਬੁੱਧੀਜੀਵੀ ਵਰਗ, ਸੰਪੱਤੀ ਵਾਲੇ ਲੋਕ ਆਦਿ ਇਸ ਵਿੱਚ ਆਉਂਦੇ ਹਨ ।

ਵੈਬਰ ਦੇ ਅਨੁਸਾਰ ਕਿਸੇ ਵਿਸ਼ੇਸ਼ ਹਾਲਾਤਾਂ ਵਿੱਚ ਵਰਗ ਦੇ ਲੋਕ ਮਿਲ-ਜੁਲ ਕੇ ਕੰਮ ਕਰਦੇ ਹਨ ਤੇ ਇਸ ਕੰਮ ਕਰਨ ਦੀ ਪ੍ਰਕ੍ਰਿਆ ਨੂੰ ਵੈਬਰ ਨੇ ਵਰਗ ਕਿਰਿਆ ਦਾ ਨਾਮ ਦਿੱਤਾ ਹੈ । ਵੈਬਰ ਦੇ ਅਨੁਸਾਰ ਆਪਣੀ ਸੰਬੰਧਿਤ ਹੋਣ ਦੀ ਭਾਵਨਾ ਨਾਲ ਵਰਗ ਕਿਆ ਪੈਦਾ ਹੁੰਦੀ ਹੈ । ਵੈਬਰ ਨੇ ਇਸ ਗੱਲ ਉੱਤੇ ਵਿਸ਼ਵਾਸ ਨਹੀਂ ਕੀਤਾ ਕਿ ਵਰਗ ਕਿਆ ਵਰਗੀ ਗੱਲ ਅਕਸਰ ਹੋ ਸਕਦੀ ਹੈ । ਵੈਬਰ ਦਾ ਕਹਿਣਾ ਸੀ ਕਿ ਵਰਗ ਵਿੱਚ ਆਤਮ ਚੇਤੰਨਤਾ ਨਹੀਂ ਹੁੰਦੀ ਬਲਕਿ ਉਹਨਾਂ ਦੀ ਪ੍ਰਕਿਰਤੀ ਪੂਰੀ ਤਰ੍ਹਾਂ ਆਰਥਿਕ ਹੁੰਦੀ ਹੈ । ਉਹਨਾਂ ਵਿੱਚ ਇਸ ਗੱਲ ਦੀ ਵੀ ਸੰਭਾਵਨਾ ਨਹੀਂ ਹੁੰਦੀ ਕਿ ਉਹ ਆਪਣੇ ਹਿੱਤਾਂ ਨੂੰ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ ਇਕੱਠੇ ਹੋ ਕੇ ਸੰਘਰਸ਼ ਕਰਨਗੇ । ਇੱਕ ਵਰਗ ਲੋਕਾਂ ਦਾ ਸਿਰਫ਼ ਇੱਕ ਸਮੂਹ ਹੁੰਦਾ ਹੈ ਜਿਨ੍ਹਾਂ ਦੀ ਆਰਥਿਕ ਸਥਿਤੀ ਬਾਜ਼ਾਰ ਵਿੱਚ ਇੱਕੋ ਜਿਹੀ ਹੁੰਦੀ ਹੈ ।ਉਹ ਉਹਨਾਂ ਚੀਜ਼ਾਂ ਨੂੰ ਇਕੱਠੇ ਕਰਨ ਵਿੱਚ ਜੀਵਨ ਦੇ ਇੱਕੋ ਜਿਹੇ ਪਰਿਵਰਤਨਾਂ ਨੂੰ ਮਹਿਸੂਸ ਕਰਦੇ ਹਨ, ਜਿਨ੍ਹਾਂ ਦੀ ਸਮਾਜ ਵਿੱਚ ਕੋਈ ਇੱਜ਼ਤ ਹੁੰਦੀ ਹੈ ਅਤੇ ਉਹਨਾਂ ਵਿੱਚ ਕਿਸੇ ਵਿਸ਼ੇਸ਼ ਸਥਿਤੀ ਵਿੱਚ ਵਰਗ ਚੇਤਨਾ ਵਿਕਸਿਤ ਹੋਣ ਦੀ ਅਤੇ ਇਕੱਠੇ ਹੋ ਕੇ ਕਿਰਿਆ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ ਹੁੰਦੀ ਹੈ । ਵੈਬਰ ਦਾ ਕਹਿਣਾ ਸੀ ਕਿ ਜੇਕਰ ਇਸ ਤਰ੍ਹਾਂ ਹੁੰਦਾ ਹੈ ਤਾਂ ਵਰਗ ਇੱਕ ਸਮੁਦਾਇ ਦਾ ਰੂਪ ਲੈ ਲੈਂਦਾ ਹੈ ।

ਰੁਤਬਾ ਸਮੂਹ (Status Group) – ਰੁਤਬਾ ਸਮੂਹ ਨੂੰ ਆਮ ਤੌਰ ਉੱਤੇ ਆਰਥਿਕ ਵਰਗ ਸਤਰੀਕਰਨ ਦੇ ਵਿਪਰੀਤ ਸਮਝਿਆਂ ਜਾਂਦਾ ਹੈ । ਵਰਗ ਸਿਰਫ਼ ਆਰਥਿਕ ਮਾਨਤਾਵਾਂ ਉੱਤੇ ਆਧਾਰਿਤ ਹੁੰਦਾ ਹੈ ਜੋ ਕਿ ਸਮਾਨ ਬਜ਼ਾਰੀ ਸਥਿਤੀਆਂ ਦੇ ਕਾਰਨ ਸਮਾਨ ਹਿੱਤਾਂ ਵਾਲਾ ਸਮੂਹ ਹੈ । ਪਰ ਦੂਜੇ ਪਾਸੇ ਰੁਤਬਾ ਸਮੁਹ ਸੰਸਕ੍ਰਿਤਕ ਖੇਤਰ ਵਿੱਚ ਪਾਇਆ ਜਾਂਦਾ ਹੈ । ਇਹ ਸਿਰਫ ਸੰਖਿਅਕ ਸ਼੍ਰੇਣੀਆਂ ਦੇ ਨਹੀਂ ਹੁੰਦੇ ਬਲਕਿ ਇਹ ਅਸਲ ਵਿੱਚ ਉਹ ਸਮੁਹ ਹੁੰਦੇ ਹਨ ਜਿਨ੍ਹਾਂ ਦੀ ਸਮਾਨ ਜੀਵਨ ਸ਼ੈਲੀ ਹੁੰਦੀ ਹੈ, ਸੰਸਾਰ ਪ੍ਰਤੀ ਸਮਾਨ ਦ੍ਰਿਸ਼ਟੀਕੋਣ ਹੁੰਦਾ ਹੈ ਅਤੇ ਇਹ ਲੋਕ ਆਪਸ ਵਿੱਚ ਏਕਤਾ ਵੀ ਰੱਖਦੇ ਹਨ ।

ਵੈਬਰ ਦੇ ਅਨੁਸਾਰ ਵਰਗ ਅਤੇ ਰੁਤਬਾ ਸਮੂਹ ਵਿੱਚ ਅੰਤਰ ਹੁੰਦਾ ਹੈ । ਹਰੇਕ ਦਾ ਆਪਣਾ ਢੰਗ ਹੁੰਦਾ ਹੈ ਅਤੇ ਇਹਨਾਂ ਵਿੱਚ ਲੋਕ ਅਸਮਾਨ ਹੋ ਸਕਦੇ ਹਨ । ਉਦਾਹਰਨ ਦੇ ਲਈ ਕਿਸੇ ਸਕੂਲ ਦਾ ਅਧਿਆਪਕ । ਚਾਹੇ ਉਸਦੀ ਆਮਦਨੀ 8-10 ਹਜ਼ਾਰ ਰੁਪਏ ਮਹੀਨਾ ਹੋਵੇਗੀ ਜੋ ਕਿ ਅੱਜ ਦੇ ਸਮੇਂ ਵਿੱਚ ਘੱਟ ਹੈ ਪਰ ਉਸਦਾ ਰੁਤਬਾ ਉੱਚਾ ਹੈ ਕਿਉਂਕਿ ਉਸਦਾ ਪੇਸ਼ਾ ਇੱਕ ਪਵਿੱਤਰ ਪੇਸ਼ਾ ਹੈ । ਪਰ ਇੱਕ ਸਮੱਗਲਰ ਜਾਂ ਵੇਸ਼ਯਾ ਚਾਹੇ ਮਹੀਨੇ ਦਾ ਲੱਖਾਂ ਰੁਪਏ ਕਮਾ ਲਵੇ ਪਰ ਉਸਦਾ ਰੁਤਬਾ ਸਮਰ ਨੀਵਾਂ ਹੀ ਰਹੇਗਾ ਕਿਉਂਕਿ ਉਸਦੇ ਪੇਸ਼ੇ ਨੂੰ ਸਮਾਜ ਮਾਨਤਾ ਨਹੀਂ ਦਿੰਦਾ। ਇਸ ਤਰ੍ਹਾਂ ਦੋਹਾਂ ਦੇ ਸਮੂਹਾਂ ਵਿੱਚ ਅੰਤਰ ਹੁੰਦਾ ਹੈ । ਕਿਸੇ ਪੇਸ਼ੇ ਸਮੂਹ ਨੂੰ ਵੀ ਸਥਿਤੀ ਸਮੂਹ ਦਾ ਨਾਮ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ਕਿਉਂਕਿ ਹਰੇਕ ਪ੍ਰਕਾਰ ਦੇ ਪੇਸ਼ੇ ਵਿੱਚ ਉਸ ਪੇਸ਼ੇ ਨਾਲ ਸੰਬੰਧਿਤ ਲੋਕਾਂ ਲਈ ਕਮਾਈ ਕਰਨ ਦੇ ਸਮਾਨ ਮੌਕੇ ਹੁੰਦੇ ਹਨ । ਇਹੀ ਸਮੂਹ ਉਹਨਾਂ ਦੀ ਜੀਵਨ ਸ਼ੈਲੀ ਨੂੰ ਸਮਾਨ ਵੀ ਬਣਾਉਂਦਾ ਹੈ । ਇੱਕ ਪੇਸ਼ਾ ਸਮੂਹ ਦੇ ਮੈਂਬਰ ਇੱਕ-ਦੂਜੇ ਦੇ ਨੇੜੇ ਰਹਿੰਦੇ ਹਨ, ਇੱਕ ਹੀ ਪ੍ਰਕਾਰ ਦੇ ਕੱਪੜੇ ਪਾਉਂਦੇ ਹਨ ਅਤੇ ਉਹਨਾਂ ਦੀਆਂ ਕਦਰਾਂ-ਕੀਮਤਾਂ ਵੀ ਇੱਕੋ ਜਿਹੀਆਂ ਹੁੰਦੀਆਂ ਹਨ । ਇਸੇ ਕਾਰਨ ਇਸਦੇ ਮੈਂਬਰਾਂ ਦਾ ਦਾਇਰਾ ਵਿਸ਼ਾਲ ਹੋ ਜਾਂਦਾ ਹੈ ।

ਦਲ (Party) – ਵੈਬਰ ਅਨੁਸਾਰ ਦਲ ਵਰਗ ਸਥਿਤੀ ਜਾਂ ਰੁਤਬਾ ਸਥਿਤੀ ਦੇ ਨਾਲ ਨਿਰਧਾਰਿਤ ਹਿੱਤਾਂ ਦਾ ਪ੍ਰਤੀਨਿਧੀਤਵ ਕਰਦਾ ਹੈ । ਇਹ ਦਲ ਕਿਸੇ ਨਾ ਕਿਸੇ ਸਥਿਤੀ ਵਿੱਚ ਉਹਨਾਂ ਮੈਂਬਰਾਂ ਦੀ ਭਰਤੀ ਕਰਦਾ ਹੈ ਜਿਨ੍ਹਾਂ ਦੀ ਵਿਚਾਰਧਾਰਾ ਦਲ ਦੀ ਵਿਚਾਰਧਾਰਾ ਨਾਲ ਮਿਲਦੀ ਹੈ । ਪਰ ਇਹ ਜ਼ਰੂਰੀ ਨਹੀਂ ਹੈ ਕਿ ਉਹਨਾਂ ਲਈ ਦਲ ਰੁਤਬਾ ਦਲ ਹੀ ਬਣੇ । ਵੈਬਰ ਦਾ ਕਹਿਣਾ ਹੈ ਕਿ ਦਲ ਹਮੇਸ਼ਾਂ ਇਸ ਤਾਕ ਵਿੱਚ ਰਹਿੰਦੇ ਹਨ ਕਿ ਸੱਤਾ ਉਹਨਾਂ ਦੇ ਹੱਥ ਵਿੱਚ ਆਵੇ ਅਰਥਾਤ ਰਾਜ ਜਾਂ ਸਰਕਾਰ ਦੀ ਸ਼ਕਤੀ ਉਹਨਾਂ ਦੇ ਹੱਥਾਂ ਵਿੱਚ ਹੋਵੇ । ਵੈਬਰ ਦਾ ਕਹਿਣਾ ਹੈ ਕਿ ਚਾਹੇ ਦਲ ਰਾਜਨੀਤਿਕ ਸੱਤਾ ਦਾ ਇੱਕ ਹਿੱਸਾ ਹੁੰਦੇ ਹਨ ਪਰ ਫਿਰ ਵੀ ਸੱਤਾ ਕਈ ਤਰੀਕਿਆਂ ਨਾਲ ਪ੍ਰਾਪਤ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ ਜਿਵੇਂ ਕਿ ਪੈਸਾ, ਅਧਿਕਾਰ, ਪ੍ਰਭਾਵ, ਦਬਾਓ ਆਦਿ ।

ਦਲ ਰਾਜ ਦੀ ਸੱਤਾ ਪ੍ਰਾਪਤ ਕਰਨਾ ਚਾਹੁੰਦੇ ਹਨ ਅਤੇ ਰਾਜ ਇੱਕ ਸੰਗਠਨ ਹੁੰਦਾ ਹੈ । ਦਲ ਦੀ ਹਰੇਕ ਪ੍ਰਕਾਰ ਦੀ ਕਿਰਿਆ ਇਸ ਗੱਲ ਵੱਲ ਧਿਆਨ ਦਿੰਦੀ ਹੈ ਕਿ ਸੱਤਾ ਕਿਸ ਤਰ੍ਹਾਂ ਪ੍ਰਾਪਤ ਕੀਤੀ ਜਾਵੇ । ਵੈਬਰ ਨੇ ਰਾਜ ਦਾ ਵਿਸ਼ਲੇਸ਼ਣ ਕੀਤਾ ਅਤੇ ਇੱਥੋਂ ਹੀ ਉਸਨੇ ਨੌਕਰਸ਼ਾਹੀ ਦਾ ਸਿਧਾਂਤ ਪੇਸ਼ ਕੀਤਾ । ਵੈਬਰ ਅਨੁਸਾਰ ਦਲ ਦੋ ਤਰ੍ਹਾਂ ਦੇ ਹੁੰਦੇ ਹਨ । ਪਹਿਲਾ ਹੈ ਸਰਪ੍ਰਸਤੀ ਦਾ ਦਲ (Patronage Party) ਜਿਨ੍ਹਾਂ ਦੇ ਕੋਈ ਸਪੱਸ਼ਟ ਨਿਯਮ, ਸੰਕਲਪ ਆਦਿ ਨਹੀਂ ਹੁੰਦੇ । ਇਹ ਕਿਸੇ ਮੌਕੇ ਲਈ ਬਣਾਏ ਜਾਂਦੇ ਹਨ ਤੇ ਹਿੱਤਾਂ ਦੀ ਪੂਰਤੀ ਤੋਂ ਬਾਅਦ ਇਹਨਾਂ ਨੂੰ ਛੱਡ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ । ਦੂਜੀ ਪ੍ਰਕਾਰ ਦਾ ਦਲ ਹੈ ਸਿਧਾਂਤਾਂ ਦਾ ਦਲ (Party of Principles) ਜਿਸ ਦੇ ਸਪੱਸ਼ਟ ਤੇ ਮਜ਼ਬੂਤ ਸਿਧਾਂਤ ਜਾਂ ਨਿਯਮ ਹੁੰਦੇ ਹਨ । ਇਹ ਦਲ ਕਿਸੇ ਵਿਸ਼ੇਸ਼ ਅਵਸਰ ਲਈ ਨਹੀਂ ਬਣਾਏ ਜਾਂਦੇ ਹਨ । ਵੈਬਰ ਅਨੁਸਾਰ ਚਾਹੇ ਇਹਨਾਂ ਤਿੰਨਾਂ ਵਰਗ, ਰੁਤਬਾ ਸਮੂਹ ਅਤੇ ਦਲ ਵਿੱਚ ਕਾਫੀ ਅੰਤਰ ਹੁੰਦਾ ਹੈ ਪਰ ਫਿਰ ਵੀ ਇਹਨਾਂ ਵਿੱਚ ਆਪਸੀ ਸੰਬੰਧ ਵੀ ਮੌਜੂਦ ਹੁੰਦਾ ਹੈ ।

Punjab State Board PSEB 11th Class Maths Book Solutions Chapter 6 Linear Inequalities Ex 6.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Maths Chapter 6 Linear Inequalities Ex 6.3

Question 1.
Solve the following system of inequalities graphically:
x ≥ 3,
y ≥ 2
Answer.
x ≥ 3 ……………(i)
y ≥ 2 ………….(ii)
The graph of the lines, x = 3 and y = 2, are drawn in the figure below.
Inequality (i) represents the region on the right hand side of the line, x = 3 (including the line x = 3) , and inequality (ii) represents the region above the line, y = 2 (including the line y = 2).
Hence, the solution of the given system of linear inequalities is represented by the common shaded region including the points on the respective lines as follows.

Question 2.
Solve the following system of inequalities graphically:
3x + 2y ≤ 12, x ≥ 1, y ≥ 2
Answer.
3x + 2y ≤ 12 …………..(i)
x > 1 ………….(ii)
y > 2 …………..(iii)
The graphs of the lines, 3x + 2y = 12, x = 1, and y = 2, are drawn in the figure below.

Inequality (i) represents the region below the line, 3x + 2y = 12 (including the line 3x + 2y = 12).
Inequality (ii) represents the region on the right side of the line, x = 1 (including the line x = 1).
Inequality (iii) represents the region above the line, y = 2 (including the line y = 2).
Hence, the solution of the given system of linear inequalities is represented by the common shaded region including the points on the respective lines as given figure.

Question 3.
Solve the following system of inequalities graphically :
2x + y ≥ 6, 3x + 4y ≤ 12
Answer.
2x + y ≥ 6 …………..(i)
3x + 4y ≤ 12 ……………..(ii)
The graph of the lines, 2x + y = 6 and 3x + 4y = 12, are drawn in the figure below.
Inequality (i) represents the region above the line, 2x + y = 6 (including the line 2x + y = 6), and inequality (ii) represents the region below the line, 3x + 4y = 12 (including the line 3x + 4y = 12).
Hence, the solution of the given system of linear inequalities is represented by the common shaded region including the points on the respective lines as follows.

Question 4.
Solve the following system of inequalities graphically :
x + y ≥ 4, 2x – y > 0
Answer.
x + y ≥ 4 …………….(i)
2x – y > 0 …………….. (ii)
The graph of the lines, x + y = 4 and 2x – y = 0, are drawn in the figure below.

Inequality (i) represents the region above the line, x + y = 4 (including the line x + y = 4).

Inequality (i) represents the region above the line, x + y = 4 (including the line x + y = 4).
It is observed that (1, 0) satisfies the inequality, 2x – y > 0. [2(1) – 0 = 2 > 0]
Therefore, inequality (ii) represents the half plane corresponding to the line, 2x – y = 0, containing the point (1, 0) [excluding the line 2x – y > 0].
Hence, the solution of the given system of linear inequalities is represented by the common shaded region including the points on line x + y = 4 and excluding the points on line 2x – y = 0 as given figure.

Question 5.
Solve the following system of inequalities graphically:
2x – y > 1, x – 2y < – 1 Answer. 2x – y> 1 ………….(i)
x – 2y < – 1 …………….(ii)
The graph of the lines, 2x – y= 1 and x – 2y = – 1, are drawn in the figure below.
Inequality (i) represents the region below the line, 2x – y = 1 (excluding the line 2x – y = 1), and inequality (ii) represents the region above the line, x – 2y = – 1 (excluding the line x – 2y = – 1).

Hence, the solution of the given system of linear inequalities is represented by the common shaded region excluding the points on the respective lines as follows.

Question 6.
Solve the following system of inequalities graphically : x + y ≤ 6, x + y > 4
Answer.
x + y ≤ 6 ……………..(i)
x + y ≥ 4 …………..(ii)
The graph of the lines, x + y = 6 and x + y = 4, are drawn in the figure below.

Inequality (i) represents the region below the line, x + y = 6 (including the line x + y = 6), and inequality (ii) represents the region above the line, x + y = 4 (including the line x + y = 4).
Hence, the solution of the given system of linear inequalities is represented by the common shaded region including the points on the respective lines as given in figure.

Question 7.
Solve the following system of inequalities graphically:
2x + y ≥ 8, x + 2y ≥ 10
Answer.
2x + y ≥ 8 …………..(i)
x + 2y ≥ 10 ……………(ii)
The graph of the lines, 2x + y = 8 and x + 2y = 10, are drawn in the figure below.

Inequality (i) represents the region above the line, 2x + y = 8, and inequality (ii) represents the region above the line, x + 2y = 10.
Hence, the solution of the given system of linear inequalities is represented by the common shaded region including the points on the respective lines as given in figure.

Question 8.
Solve the following system of inequalities graphically: x + y ≤ 9, y > x, x ≥ 0.
Answer.
x+y ≤ 9 ………..(i)
y > x …………..(ii)
x ≥ 0 ……………(iii)
The graph of the lines, x + y = 9 and y = x, are drawn in the figure below.
Inequality (i) represents the region below the line, x + y = 9 (including the line x + y = 9).
It is observed that (0, 1) satisfies the inequality, y > x. [1 > 0].
Therefore, inequality (ii) represents the half plane corresponding to the line, y = x, containing the point (0, 1) [excluding the line y = x].
Inequality (iii) represents the region on the right hand side of the line, x = 0 or y – axis (including y – axis).

Hence, the solution of the given system of linear inequalities is represented by the common shaded region including the points on the lines, x + y = 9 and x = 0, and excluding the points on line y = x as follows.

Question 9.
Solve the following system of inequalities graphically:
5x + 4y ≤ 20, x ≥ 1, y ≥ 2
Answer.
5x + 4y ≤ 20 …………..(i)
x ≥ 1 ………………(ii)
y ≥ 2 ……………(iii)
The graph of the lines, 5x + 4y = 20, x = 1, and y = 2, are drawn in the figure below.
Inequality (i) represents the region below the line, 5x + 4y = 20 (including the line 5x + 4y = 20).
Inequality (ii) represents the region on the right hand side of the line, x = 1 (including the line x = 1).
Inequality (iii) represents the region above the line, y = 2 (including the line y = 2).
Hence, the solution of the given system of linear inequalities is represented by the common shaded region including the points on the respective lines as follows.

Question 10.
Solve the following system of inequalities graphically:
3x + 4y ≤ 60, x + 3y ≤ 30, x ≥ 0, y ≥ 0
Answer.
3x + 4y ≤ 60 …………. (i)
x + 3y ≤ 30 ………….(ii)
The graph of the lines, 3x + 4y = 60 and x + 3y = 30, are drawn in the figure below.

Inequality (i) represents the region below the line, 3x + 4y = 60
(including the line 3x + 4y = 60), and inequality (ii) represents the region below the line, x + 3y = 30 (including the line x + 3y = 30).

Since x > 0 and y > 0, every point in the common shaded region in the first quadrant including the points on the respective line and the axes represents the solution of the given system of linear inequalities.

Question 11.
Solve the following system of inequalities graphically :
2x + y ≥ 4, x + y ≤ 3, 2x – 3y ≤ 6
Answer.
2x + y ≥ 4 ………….(i)
x + y ≤ 3 …………..(ii)
2x – 3y ≤ 6 …………….(iii)
The graph of the lines, 2x + y = 4, x + y = 3, and 2x – 3y = 6, are drawn in the figure below.
Inequality (i) represents the region above the line, 2x + y = 4 (including the line 2x + y = 4).
Inequality (ii) represents the region below the line, x + y = 3 (including the line x + y = 3).
Inequality (iii) represents the region above the line, 2x – 3y = 6 (including the line 2x – 3y = 6).

Hence, the solution of the given system of linear inequalities is represented by the common shaded region including the points on the respective lines as follows.

Question 12.
Solve the following system of inequalities graphically:
x – 2y ≤ 3, 3x + 4y ≥ 12, x ≥ 0, y ≥ 1
Answer.
We have
x – 2y ≤ 3 …………(i)
3x + 4y ≥ 12 …………….(ii)
x ≥ 0 …………….(iii)
and y ≥ 1 ……………….(iv)
Take inequality (i), x – 2y ≤ 3
Corresponding equation of the line is,
x – 2y = 3
Table of values satisfying the equation
x – 2y = 3

Join the points (0, – 1.5) and (3, 0) by a dark line.
On putting (0, 0) in the given inequality (i),we get 0 ≤ 3, which is true.
so, half plane of x – 2y ≤ 3 contains the origin.

Take inequality (ii), 3x + 4y ≥ 12
Corresponding equation of the line is 3x + 4y =12.
Table of values satisfying the equation 3x + 4y = 12.

Join the points (0, 3) and (4, 0) by a dark line.
On putting (0, 0) in the inequality (ii), we get 0 ≥ 12, wrhich is false.
So, half plane 3x + 4y > 12 does not contain the origin.

Take inequality (iii) x ≥ 0, this implies, area shaded in I quadrant.
Take inequality (iv), y ≥ 1 Corresponding equation of the line is y =1.
On putting (0,0) in the given inequality (iv), we get 0 ≥ 1, which is false.
So, half plane of y ≥ 1 is does not contain the origin.

Hence, shade the common region which gives required solution set.

Question 13.
Solve the following system of inequalities graphically:
4x + 3y ≤ 60, y ≥ 2x, x ≥ 3, x, y ≥ 0
Answer.
4x + 3y ≤ 60 ………….(i)
y ≥ 2x ………….(ii)
x ≥ 3 …………(iii)
The graph of the lines, 4x + 3y = 60, y = 2x, and x = 3, are drawn in the figure below.

Inequality (i) represents the region below the line, 4x + 3y = 60 (including the line 4x + 3y = 60).
Inequality (ii) represents the region above the line, y = 2x (including the line y = 2x).
Inequality (iii) represents the region on the right hand side of the line, x = 3 (including the line x = 3).

Hence, the solution of the given system of linear inequalities is represented by the common shaded region including the points on the respective lines as follows.

Question 14.
Solve the following system of inequalities graphically:
3x + 2y ≤ 150, x + 4y ≤ 80, x ≤ 15, y ≥ 0, x ≥ 0
Answer.
3x + 2y ≤ 150 ……………….(i)
x + 4y ≤ 80 ………………(ii)
x ≤ 15 ……………….(iii)
The graph of the lines, 3x + 2y = 150, x + 4y = 80, and x = 15, are drawn in the figure below.
Inequality (i) represents the region below the line, 3x + 2y = 150 (including the line 3x + 2y = 150).
Inequality (ii) represents the region below the line, x+4y=80 (including the line x + 4y = 80).
Inequality (iii) represents the region on the left hand side of the line, x = 15 (including the line x = 15).

Since x ≥ 0 and y ≥ 0, every point in the common shaded region in the first quadrant including the points on the respective lines and the axes represents the solution of the given system of linear inequalities.

Question 15.
Solve the following system of inequalities graphically :
x + 2y ≤ 10, x + y > 1, x – y < 0, x > 0, y > 0
Answer.
x + 2y ≤ 10 …………(i)
x + y ≥ 1 ………….(ii)
x – y ≤ 0 ……………(iii)
The graph of the lines, x + 2y = 10, x + y = 1, and x – y = 0, are drawn in the figure below.

Inequality (i) represents the region below the line, x + 2y = 10 (including the line x + 2y = 10).
Inequality (ii) represents the region above the line, x + y = 1 (including the line x + y = 1).
Inequality (iii) represents the region above the line, x – y = 0 (including the line x – y = 0).

Since x > 0 and y > 0, every point in the common shaded region in the first quadrant including the points on the respective lines and the axes represents the solution of the given system of linear inequalities.

This PSEB 11th Class Sociology Notes Chapter 11 ਸਮਾਜਿਕ ਪਰਿਵਰਤਨ will help you in revision during exams.

PSEB 11th Class Sociology Notes Chapter 11 ਸਮਾਜਿਕ ਪਰਿਵਰਤਨ

→ ਪਰਿਵਰਤਨ ਪ੍ਰਕਿਰਤੀ ਦਾ ਨਿਯਮ ਹੈ । ਇਸ ਸੰਸਾਰ ਵਿੱਚ ਕੋਈ ਅਜਿਹੀ ਚੀਜ਼ ਨਹੀਂ ਹੈ ਜਿਸ ਵਿੱਚ ਪਰਿਵਰਤਨ ਨਾ ਆਇਆ ਹੋਵੇ । ਕਿਰਤੀ ਵੀ ਆਪਣੇ ਵਿੱਚ ਸਮੇਂ-ਸਮੇਂ ਉੱਤੇ ਬਦਲਾਵ ਲਿਆਉਂਦੀ ਰਹਿੰਦੀ ਹੈ ।

→ ਜਦੋਂ ਸਮਾਜ ਦੇ ਵੱਖ-ਵੱਖ ਭਾਗਾਂ ਵਿੱਚ ਪਰਿਵਰਤਨ ਆਵੇ ਅਤੇ ਉਹ ਪਰਿਵਰਤਨ ਜੇਕਰ ਸਾਰੇ ਨਹੀਂ ਤਾਂ ਸਮਾਜ ਦੇ ਜ਼ਿਆਦਾਤਰ ਲੋਕਾਂ ਦੇ ਜੀਵਨ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰੇ ਤਾਂ ਉਸ ਨੂੰ ਸਮਾਜਿਕ ਪਰਿਵਰਤਨ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਇਸ ਦਾ ਅਰਥ ਹੈ ਕਿ ਸਮਾਜ ਦੇ ਲੋਕਾਂ ਦੇ ਜੀਵਨ ਜੀਣ ਦੇ ਤਰੀਕਿਆਂ ਵਿੱਚ ਸੰਰਚਨਾਤਮਕ ਪਰਿਵਰਤਨ ਆ ਜਾਂਦਾ ਹੈ ।

→ ਸਮਾਜਿਕ ਪਰਿਵਰਤਨ ਦੀਆਂ ਬਹੁਤ ਸਾਰੀਆਂ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਹੁੰਦੀਆਂ ਹਨ ਜਿਵੇਂ ਕਿ ਇਹ ਸਰਵਵਿਆਪਕ ਪ੍ਰਕਿਰਿਆ ਹੈ, ਵੱਖ-ਵੱਖ ਸਮਾਜਾਂ ਵਿੱਚ ਪਰਿਵਰਤਨ ਦੀ ਗਤੀ ਵੱਖ ਹੁੰਦੀ ਹੈ ਇਹ ਸਮੁਦਾਇਕ ਪਰਿਵਰਤਨ ਹੈ, ਇਸ ਬਾਰੇ ਨਿਸ਼ਚਿਤ ਭਵਿੱਖਬਾਣੀ ਨਹੀਂ ਕੀਤੀ ਜਾ ਸਕਦੀ, ਇਹ ਬਹੁਤ ਸਾਰੀਆਂ ਅੰਤਰਕਿਰਿਆਵਾਂ ਦਾ ਨਤੀਜਾ ਹੁੰਦਾ ਹੈ, ਇਹ ਨਿਯੋਜਿਤ ਵੀ ਹੋ ਸਕਦਾ ਹੈ ਅਤੇ ਅਨਿਯੋਜਿਤ ਵੀ ਆਦਿ ।

→ ਸਮਾਜਿਕ ਪਰਿਵਰਤਨ ਦੇ ਬਹੁਤ ਸਾਰੇ ਪ੍ਰਕਾਰ ਹੁੰਦੇ ਹਨ , ਜਿਵੇਂ ਕਿ ਉਦਵਿਕਾਸ, ਵਿਕਾਸ, ਪ੍ਰਗਤੀ ਅਤੇ ਸ਼ਾਂਤੀ । ਬਹੁਤ ਵਾਰੀ ਇਹਨਾਂ ਸ਼ਬਦਾਂ ਨੂੰ ਇੱਕ-ਦੂਜੇ ਦੇ ਲਈ ਪ੍ਰਯੋਗ ਕਰ ਲਿਆ ਜਾਂਦਾ ਹੈ | ਪਰ ਸਮਾਜ ਵਿਗਿਆਨ ਵਿੱਚ ਇਹ ਸਾਰੇ ਇੱਕ-ਦੂਜੇ ਤੋਂ ਬਹੁਤ ਹੀ ਵੱਖ ਹੁੰਦੇ ਹਨ ।

→ ਉਦਵਿਕਾਸ (Evolution) ਦਾ ਅਰਥ ਹੈ ਅੰਦੂਰਨੀ ਤੌਰ ਉੱਤੇ ਕ੍ਰਮਵਾਰ ਪਰਿਵਰਤਨ । ਇਸ ਪ੍ਰਕਾਰ ਦਾ ਪਰਿਵਰਤਨ ਬਹੁਤ ਹੌਲੀ ਹੁੰਦਾ ਹੈ ਜਿਸ ਨਾਲ ਸਮਾਜਿਕ ਸੰਸਥਾਵਾਂ ਸਾਧਾਰਨ ਤੋਂ ਜਟਿਲ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ।

→ ਵਿਕਾਸ ਵੀ ਸਮਾਜਿਕ ਪਰਿਵਰਤਨ ਦਾ ਇੱਕ ਪੱਖ ਹੈ । ਜਦੋਂ ਕਿਸੇ ਚੀਜ਼ ਵਿੱਚ ਪਰਿਵਰਤਨ ਆਵੇ ਅਤੇ ਉਹ ਪਰਿਵਰਤਨ ਇੱਛੁਕ ਦਿਸ਼ਾ ਵਿੱਚ ਆਵੇ ਤਾਂ ਇਸ ਨੂੰ ਵਿਕਾਸ ਕਹਿੰਦੇ ਹਨ । ਵੱਖ-ਵੱਖ ਸਮਾਜ ਵਿਗਿਆਨੀਆਂ ਨੇ ਵਿਕਾਸ ਦੇ ਵੱਖ-ਵੱਖ ਆਧਾਰ ਦਿੱਤੇ ਹਨ ।

→ ਪ੍ਰਤੀ ਸਮਾਜਿਕ ਪਰਿਵਰਤਨ ਦਾ ਇੱਕ ਹੋਰ ਪ੍ਰਕਾਰ ਹੈ । ਇਸ ਦਾ ਅਰਥ ਹੈ ਆਪਣੇ ਉਦੇਸ਼ ਦੀ ਪ੍ਰਾਪਤੀ ਵੱਲ ਵੱਧਣਾ ਪ੍ਰਤੀ ਆਪਣੇ ਉਦੇਸ਼ਾਂ ਦੀ ਪ੍ਰਾਪਤੀ ਲਈ ਕਰਨ ਵਾਲੇ ਯਤਨਾਂ ਨੂੰ ਕਹਿੰਦੇ ਹਨ ਜੋ ਨਿਸ਼ਚਿਤ ਹੈ ਅਤੇ ਜਿਸ ਨੂੰ ਸਮਾਜਿਕ ਕੀਮਤਾਂ ਵਲੋਂ ਵੀ ਸਹਿਯੋਗ ਮਿਲਦਾ ਹੈ ।

→ ਕ੍ਰਾਂਤੀ ਸਮਾਜਿਕ ਪਰਿਵਰਤਨ ਦਾ ਸਭ ਤੋਂ ਮਹੱਤਵਪੂਰਨ ਪ੍ਰਕਾਰ ਹੈ । ਸ਼ਾਂਤੀ ਨਾਲ ਸਮਾਜ ਵਿੱਚ ਅਚਾਨਕ ਅਤੇ ਤੇਜ਼ ਗਤੀ ਨਾਲ ਪਰਿਵਰਤਨ ਆਉਂਦੇ ਹਨ ਜਿਸ ਨਾਲ ਸਮਾਜ ਦਾ ਪੁਰਾਤਨ ਢਾਂਚਾ ਖ਼ਤਮ ਹੋ ਜਾਂਦਾ ਹੈ ਅਤੇ ਨਵਾਂ ਢਾਂਚਾ ਸਾਹਮਣੇ ਆ ਜਾਂਦਾ ਹੈ । ਕਈ ਵਾਰੀ ਲੋਕਾਂ ਵਿੱਚ ਮੌਜੂਦਾ ਵਿਵਸਥਾ ਦੇ ਵਿਰੁੱਧ ਅਸੰਤੋਸ਼ ਇੰਨਾ ਵੱਧ ਜਾਂਦਾ ਹੈ ਕਿ ਉਹ ਵਿਵਸਥਾ ਦੇ ਵਿਰੁੱਧ ਇਕਦਮ ਖੜੇ ਹੋ ਜਾਂਦੇ ਹਨ । ਇਸ ਨੂੰ ਸ਼ਾਂਤੀ ਕਹਿੰਦੇ ਹਨ । 1789 ਈ: ਵਿੱਚ ਫਰਾਂਸ ਵਿੱਚ ਵੀ ਅਜਿਹਾ ਪਰਿਵਰਤਨ ਆਇਆ ਸੀ ।

→ ਸਮਾਜਿਕ ਪਰਿਵਰਤਨ ਦੀ ਦਿਸ਼ਾ ਅਤੇ ਗਤੀ ਨੂੰ ਬਹੁਤ ਸਾਰੇ ਕਾਰਕ ਪ੍ਰਭਾਵਿਤ ਕਰਦੇ ਹਨ, ਜਿਵੇਂ ਕਿ-ਪ੍ਰਾਕ੍ਰਿਤਕ ਕਾਰਕ, ਵਿਸ਼ਵਾਸ ਅਤੇ ਮੁੱਲ, ਸਮਾਜ ਸੁਧਾਰਕ, ਜਨਸੰਖਿਆਤਮਿਕ ਕਾਰਕ, ਤਕਨੀਕੀ ਕਾਰਕ, ਸਿੱਖਿਆਤਮਕ ਕਾਰਕ ਆਦਿ ।

This PSEB 11th Class Sociology Notes Chapter 10 ਸਮਾਜਿਕ ਸਤਰੀਕਰਨ will help you in revision during exams.

PSEB 11th Class Sociology Notes Chapter 10 ਸਮਾਜਿਕ ਸਤਰੀਕਰਨ

→ ਸਾਡੇ ਸਮਾਜ ਵਿਚ ਹਰੇਕ ਪਾਸੇ ਅਸਮਾਨਤਾ ਵਿਆਪਤ ਹੈ । ਕੋਈ ਕਾਲਾ ਹੈ, ਕੋਈ ਗੋਰਾ ਹੈ, ਕੋਈ ਅਮੀਰ ਹੈ, ਕੋਈ ਗ਼ਰੀਬ ਹੈ, ਕੋਈ ਪਤਲਾ ਹੈ, ਕੋਈ ਮੋਟਾ ਹੈ, ਕੋਈ ਘੱਟ ਪੜਿਆ ਲਿਖਿਆ ਹੈ ਅਤੇ ਕੋਈ ਵੱਧ । ਅਜਿਹੇ ਕਿੰਨੇ ਹੀ ਆਧਾਰ ਹਨ, ਜਿਨ੍ਹਾਂ ਕਾਰਨ ਸਮਾਜ ਵਿਚ ਪ੍ਰਾਚੀਨ ਸਮੇਂ ਤੋਂ ਅਸਮਾਨਤਾ ਚਲੀ ਆ ਰਹੀ ਹੈ ਅਤੇ ਚਲਦੀ ਰਹੇਗੀ ।

→ ਸਮਾਜ ਨੂੰ ਅਲੱਗ-ਅਲੱਗ ਆਧਾਰਾਂ ਉੱਤੇ ਅਲੱਗ-ਅਲੱਗ ਸਤਰਾਂ ਵਿਚ ਵੰਡੇ ਜਾਣ ਦੀ ਪ੍ਰਕ੍ਰਿਆ ਨੂੰ ਸਮਾਜਿਕ ਸਤਰੀਕਰਨ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਅਜਿਹਾ ਕੋਈ ਵੀ ਸਮਾਜ ਨਹੀਂ ਹੈ ਜਿੱਥੇ ਸਤਰੀਕਰਨ ਮੌਜੂਦ ਨਾ ਹੋਵੇ । ਚਾਹੇ ਪ੍ਰਾਚੀਨ ਸਮਾਜਾਂ ਵਰਗੇ ਸਰਲ ਅਤੇ ਸਾਦੇ ਸਮਾਜ ਹੋਣ ਜਾਂ ਆਧੁਨਿਕ ਸਮਾਜਾਂ ਵਰਗੇ ਜਟਿਲ ਸਮਾਜ, ਸਤਰੀਕਰਨ ਹਰੇਕ ਸਮਾਜ ਵਿਚ ਮੌਜੂਦ ਹੁੰਦਾ ਹੈ ।

→ ਸਮਾਜੀਕਰਨ ਦੀਆਂ ਕਈ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਹੁੰਦੀਆਂ ਹਨ ਜਿਵੇਂ ਕਿ ਇਹ ਇਕ ਸਰਵਵਿਆਪਕ ਪ੍ਰਕ੍ਰਿਆ ਹੈ, ਇਸ ਦੀ ਪਵਿਤੀ ਸਮਾਜਿਕ ਹੁੰਦੀ ਹੈ, ਹਰੇਕ ਸਮਾਜ ਵਿਚ ਇਸ ਦੀ ਪ੍ਰਕਾਰ ਅਲੱਗ ਹੁੰਦੀ ਹੈ, ਇਸ ਵਿਚ ਉੱਚ-ਨੀਚ ਦੇ ਸੰਬੰਧ ਹੁੰਦੇ ਹਨ ਆਦਿ ।

→ ਸਾਰੇ ਸਮਾਜਾਂ ਵਿਚ ਮੁੱਖ ਰੂਪ ਨਾਲ ਚਾਰ ਤਰ੍ਹਾਂ ਦੇ ਸਤਰੀਕਰਨ ਰੂਪ ਹਨ ਅਤੇ ਉਹ ਹਨ ਜਾਤੀ, ਵਰਗ, ਜਾਗੀਰਦਾਰੀ ਅਤੇ ਗੁਲਾਮੀ । ਭਾਰਤੀ ਸਮਾਜ ਨੂੰ ਜਿੰਨਾ ਜਾਤੀ ਵਿਵਸਥਾ ਨੇ ਪ੍ਰਭਾਵਿਤ ਕੀਤਾ ਹੈ ਸ਼ਾਇਦ ਕਿਸੇ ਹੋਰ ਸਮਾਜਿਕ ਸੰਸਥਾ ਨੇ ਨਹੀਂ ਕੀਤਾ ਹੈ ।

→ ਜਾਤੀ ਇਕ ਅੰਤਰਵਿਆਹਕ ਸਮੂਹ ਹੈ ਜਿਸ ਵਿਚ ਵਿਅਕਤੀਆਂ ਉੱਪਰ ਹੋਰ ਜਾਤੀਆਂ ਨਾਲ ਮੇਲ-ਜੋਲ ਦੇ ਕਈ ਪ੍ਰਕਾਰ ਦੇ ਪ੍ਰਤੀਬੰਧ ਹੁੰਦੇ ਸਨ ਅਤੇ ਵਿਅਕਤੀ ਦੇ ਜਨਮ ਅਨੁਸਾਰ ਉਸਦੀ ਜਾਤੀ ਅਤੇ ਸਥਿਤੀ ਨਿਸ਼ਚਿਤ ਹੁੰਦੀ ਸੀ ।

→ ਆਧੁਨਿਕ ਸਮਾਜਾਂ ਵਿਚ ਸਤਰੀਕਰਨ ਦਾ ਇਕ ਨਵਾਂ ਰੂਪ ਸਾਹਮਣੇ ਆਇਆ ਹੈ ਅਤੇ ਉਹ ਹੈ ਵਰਗ ਵਿਵਸਥਾ ॥ ਵਰਗ ਲੋਕਾਂ ਦਾ ਇਕ ਸਮੂਹ ਹੁੰਦਾ ਹੈ ਜਿਨ੍ਹਾਂ ਵਿਚ ਕਿਸੇ ਨਾ ਕਿਸੇ ਆਧਾਰ ਉੱਤੇ ਸਮਾਨਤਾ ਹੁੰਦੀ ਹੈ । ਉਦਾਹਰਨ ਦੇ ਲਈ ਉੱਚ ਵਰਗ, ਮੱਧ ਵਰਗ, ਹੇਠਲਾ ਵਰਗ, ਮਜ਼ਦੂਰ ਵਰਗ, ਉਦਯੋਗਪਤੀ ਵਰਗ ਅਤੇ ਡਾਕਟਰ ਵਰਗ ।

→ ਜਗੀਰਦਾਰੀ ਵਿਵਸਥਾ ਮੱਧਕਾਲੀਨ ਯੂਰਪ ਦਾ ਇਕ ਮਹੱਤਵਪੂਰਨ ਹਿੱਸਾ ਰਹੀ ਹੈ । ਇਕ ਵਿਅਕਤੀ ਨੂੰ ਰਾਜੇ ਵੱਲੋਂ ਬਹੁਤ ਸਾਰੀ ਜ਼ਮੀਨ ਦੇ ਦਿੱਤੀ ਜਾਂਦੀ ਸੀ ਅਤੇ ਉਹ ਵਿਅਕਤੀ ਬਹੁਤ ਅਮੀਰ ਹੋ ਜਾਂਦਾ ਸੀ । ਉਸਦੇ ਬੱਚਿਆਂ ਕੋਲ | ਇਹ ਜ਼ਮੀਨ ਪੈਤਿਕ ਰੂਪ ਨਾਲ ਚਲੀ ਜਾਂਦੀ ਸੀ ।

→ ਗੁਲਾਮੀ ਵੀ 19ਵੀਂ ਅਤੇ 20ਵੀਂ ਸਦੀ ਵਿਚ ਸੰਸਾਰ ਦੇ ਅਲੱਗ-ਅਲੱਗ ਦੇਸ਼ਾਂ ਵਿਚ ਮੌਜੂਦ ਸੀ ਜਿਸ ਵਿਚ ਗੁਲਾਮ ਨੂੰ ਉਸਦਾ ਮਾਲਕ ਖਰੀਦ ਲੈਂਦਾ ਸੀ ਅਤੇ ਉਹ ਉਸ ਉੱਪਰ ਅਸੀਮਿਤ ਅਧਿਕਾਰ ਰੱਖਦਾ ਸੀ ।

→ ਜੀ. ਐੱਸ. ਘੁਰੀਏ (G.S. Ghurye) ਇਕ ਭਾਰਤੀ ਸਮਾਜ ਸ਼ਾਸਤਰੀ ਸੀ ਜਿਸਨੇ ਜਾਤੀ ਵਿਵਸਥਾ ਉੱਪਰ ਆਪਣੇ ਵਿਚਾਰ ਦਿੱਤੇ । ਉਸਦੇ ਅਨੁਸਾਰ ਜਾਤੀ ਵਿਵਸਥਾ ਇੰਨੀ ਜਟਿਲ ਹੈ ਕਿ ਇਸ ਦੀ ਪਰਿਭਾਸ਼ਾ ਦੇਣੀ ਮੁਮਕਿਨ ਨਹੀਂ ਹੈ । ਇਸ ਲਈ ਉਸਨੇ ਜਾਤੀ ਵਿਵਸਥਾ ਦੇ ਛੇ (6) ਲੱਛਣ ਦਿੱਤੇ ਸਨ ।

→ ਭਾਰਤ ਦੀ ਸੁਤੰਤਰਤਾ ਤੋਂ ਬਾਅਦ ਜਾਤੀ ਵਿਵਸਥਾ ਵਿਚ ਬਹੁਤ ਸਾਰੇ ਕਾਰਨਾਂ ਕਰਕੇ ਪਰਿਵਰਤਨ ਆਏ ਅਤੇ ਆ ਰਹੇ ਹਨ । ਹੁਣ ਹੌਲੀ-ਹੌਲੀ ਜਾਤੀ ਵਿਵਸਥਾ ਖ਼ਤਮ ਹੋ ਰਹੀ ਹੈ । ਹੁਣ ਜਾਤੀ ਨਾਲ ਆਧਾਰਿਤ ਪ੍ਰਤੀਬੰਧ ਖ਼ਤਮ ਹੋ ਰਹੇ ਹਨ, ਜਾਤੀ ਦੇ ਵਿਸ਼ੇਸ਼ਾਧਿਕਾਰ ਖ਼ਤਮ ਹੋ ਰਹੇ ਹਨ, ਸੰਵਿਧਾਨਿਕ ਪਾਵਧਾਨਾਂ ਨੇ ਸਾਰਿਆਂ ਨੂੰ ਸਮਾਨਤਾ ਪ੍ਰਦਾਨ ਕੀਤੀ ਹੈ ਅਤੇ ਜਾਤੀ ਪ੍ਰਥਾ ਨੂੰ ਖ਼ਤਮ ਕਰਨ ਵਿਚ ਮਹੱਤਵਪੂਰਨ ਭੂਮਿਕਾ ਨਿਭਾਈ ਹੈ ।

→ ਬਹੁਤ ਸਾਰੇ ਕਾਰਨਾਂ ਨੇ ਜਾਤੀ ਪ੍ਰਥਾ ਵਿਚ ਪਰਿਵਰਤਨ ਲਿਆਉਣ ਵਿਚ ਯੋਗਦਾਨ ਦਿੱਤਾ ਜਿਵੇਂ ਕਿ ਸਮਾਜ ਸੁਧਾਰਕ ਲਹਿਰਾਂ, ਆਧੁਨਿਕ ਸਿੱਖਿਆ, ਨਗਰੀਕਰਨ, ਆਧੁਨਿਕੀਕਰਨ, ਆਧੁਨਿਕ ਸਿੱਖਿਆ, ਆਵਾਜਾਈ ਅਤੇ | ਸੰਚਾਰ ਦੇ ਸਾਧਨਾਂ ਦਾ ਵਿਕਾਸ, ਸੰਵਿਧਾਨਿਕ ਪਾਵਧਾਨ ਆਦਿ ।

→ ਸਾਡੇ ਸਮਾਜਾਂ ਵਿੱਚ ਮੁੱਖ ਰੂਪ ਨਾਲ ਤਿੰਨ ਪ੍ਰਕਾਰ ਦੇ ਵਰਗ ਮਿਲਦੇ ਹਨ-ਉੱਚ ਵਰਗ, ਮੱਧ ਵਰਗ ਅਤੇ ਹੇਠਲਾ ਵਰਗ । ਇਹਨਾਂ ਵਰਗਾਂ ਵਿੱਚ ਮੁੱਖ ਰੂਪ ਨਾਲ ਪੈਸੇ ਦੇ ਆਧਾਰ ਉੱਤੇ ਅੰਤਰ ਪਾਇਆ ਜਾਂਦਾ ਹੈ ।

→ ਜਾਤੀ ਇਕ ਪ੍ਰਕਾਰ ਦਾ ਬੰਦ ਵਰਗ ਜਿਸ ਨੂੰ ਬਦਲਣਾ ਕਿਸੇ ਲਈ ਵੀ ਸੰਭਵ ਨਹੀਂ ਹੈ ਪਰ ਵਰਗ ਇਕ ਅਜਿਹਾ ਖੁੱਲਾ ਵਰਗ ਹੈ ਜਿਸ ਨੂੰ ਵਿਅਕਤੀ ਆਪਣੀ ਮਿਹਨਤ ਅਤੇ ਯੋਗਤਾ ਨਾਲ ਕਿਸੇ ਵੀ ਸਮੇਂ ਬਦਲ ਸਕਦਾ ਹੈ ।

→ ਕਾਰਲ ਮਾਰਕਸ ਦੇ ਅਨੁਸਾਰ ਸਮਾਜ ਵਿਚ ਅਲੱਗ-ਅਲੱਗ ਸਮਿਆਂ ਵਿਚ ਦੋ ਪ੍ਰਕਾਰ ਦੇ ਵਰਗ ਰਹੇ ਹਨ । ਪਹਿਲਾ ਹੈ ਪੂੰਜੀਪਤੀ ਵਰਗ ਅਤੇ ਦੂਜਾ ਹੈ ਮਜ਼ਦੂਰ ਵਰਗ । ਦੋਹਾਂ ਵਿਚ ਵੱਧ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ ਹਮੇਸ਼ਾਂ ਤੋਂ ਸੰਘਰਸ਼ ਚਲਿਆ ਆ ਰਿਹਾ ਹੈ ਅਤੇ ਦੋਹਾਂ ਵਿਚਕਾਰ ਸੰਘਰਸ਼ ਨੂੰ ਹੀ ਵਰਗ ਸੰਘਰਸ਼ ਕਹਿੰਦੇ ਹਨ ।

→ ਵਰਗ ਵਿਵਸਥਾ ਵਿਚ ਨਵੇਂ ਰੁਝਾਨ ਆ ਰਹੇ ਹਨ । ਪਿਛਲੇ ਕਾਫ਼ੀ ਸਮੇਂ ਤੋਂ ਇਕ ਨਵਾਂ ਵਰਗ ਉਭਰ ਕੇ ਸਾਹਮਣੇ ਆਇਆ ਹੈ ਜਿਸ ਨੂੰ ਅਸੀਂ ਮੱਧ ਵਰਗ ਦਾ ਨਾਮ ਦਿੰਦੇ ਹਾਂ । ਉੱਚ ਵਰਗ ਮੱਧ ਵਰਗ ਦੀ ਮੱਦਦ ਨਾਲ ਹੇਠਲੇ ਵਰਗ ਦਾ ਸ਼ੋਸ਼ਣ ਕਰਦਾ ਹੈ ।

This PSEB 11th Class Sociology Notes Chapter 9 ਸਮਾਜਿਕ ਸੰਰਚਨਾ will help you in revision during exams.

PSEB 11th Class Sociology Notes Chapter 9 ਸਮਾਜਿਕ ਸੰਰਚਨਾ

→ ਸਮਾਜ ਵਿਗਿਆਨ ਦੇ ਬਹੁਤ ਸਾਰੇ ਮੂਲ ਸੰਕਲਪ ਹਨ ਅਤੇ ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਉਹਨਾਂ ਵਿੱਚੋਂ ਇੱਕ ਹੈ । ਸਭ ਤੋਂ ਪਹਿਲਾਂ ਇਸ ਸ਼ਬਦ ਦਾ ਪ੍ਰਯੋਗ ਪ੍ਰਸਿੱਧ ਸਮਾਜ ਸ਼ਾਸਤਰੀ ‘ਹਰਬਰਟ ਸਪੈਂਸਰ ਨੇ ਕੀਤਾ ਸੀ । ਉਸ ਤੋਂ ਬਾਅਦ ਬਹੁਤ ਸਾਰੇ ਸਮਾਜ ਵਿਗਿਆਨੀਆਂ ਜਿਵੇਂ ਕਿ ਟਾਲਕਟ ਪਾਰਸੰਜ਼, ਰੈਡਕਲਿਫ਼ ਬਰਾਉਨ, ਮੈਕਾਈਵਰ ਆਦਿ ਨੇ ਇਸ ਬਾਰੇ ਬਹੁਤ ਕੁੱਝ ਲਿਖਿਆ ।

→ ਸਾਡੇ ਸਮਾਜ ਦੇ ਬਹੁਤ ਸਾਰੇ ਭਾਗ ਹੁੰਦੇ ਹਨ ਜਿਹੜੇ ਇੱਕ-ਦੂਜੇ ਨਾਲ ਕਿਸੇ ਨਾ ਕਿਸੇ ਰੂਪ ਵਿੱਚ ਜੁੜੇ ਹੁੰਦੇ ਹਨ । ਇਹ ਸਾਰੇ ਭਾਗ ਅੰਤਰ ਸੰਬੰਧਿਤ ਹੁੰਦੇ ਹਨ । ਇਹਨਾਂ ਸਾਰੇ ਭਾਗਾਂ ਦੇ ਵਿਵਸਥਿਤ ਰੂਪ ਨੂੰ ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਦਾ ਨਾਮ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ । ਇਹ ਚਾਹੇ ਅਮੂਰਤ ਹੁੰਦੇ ਹਨ ਪਰ ਸਾਡੇ ਜੀਵਨ ਨੂੰ ਨਿਰਦੇਸ਼ਿਤ ਕਰਦੇ ਰਹਿੰਦੇ ਹਨ ।

→ ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਦੀਆਂ ਬਹੁਤ ਸਾਰੀਆਂ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਹੁੰਦੀਆਂ ਹਨ ਜਿਵੇਂ ਕਿ ਇਹ ਅਮੂਰਤ ਹੁੰਦੀ ਹੈ, ਇਸ ਦੇ ਬਹੁਤ ਸਾਰੇ ਅੰਤਰ-ਸੰਬੰਧਿਤ ਭਾਗ ਹੁੰਦੇ ਹਨ, ਇਹਨਾਂ ਸਾਰੇ ਭਾਗਾਂ ਵਿੱਚ ਇੱਕ ਵਿਵਸਥਾ ਪਾਈ ਜਾਂਦੀ ਹੈ, ਇਹ ਸਾਡੇ ਵਿਵਹਾਰ ਨੂੰ ਨਿਰਦੇਸ਼ਿਤ ਕਰਦੇ ਹਨ, ਇਹ ਸਰਵਵਿਆਪਕ ਹੁੰਦੇ ਹਨ, ਇਹ ਸਮਾਜ ਦੇ ਬਾਹਰੀ ਰੂਪ ਨੂੰ ਵਿਖਾਉਂਦੇ ਹਨ ਆਦਿ ।

→ ਹਰਬਰਟ ਸਪੈਂਸਰ ਨੇ ਇੱਕ ਕਿਤਾਬ ਲਿਖੀ The Principal of Sociology’ ਜਿਸ ਵਿੱਚ ਉਸਨੇ ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਸ਼ਬਦ ਦਾ ਜ਼ਿਕਰ ਕੀਤਾ ਅਤੇ ਇਸਦੀ ਤੁਲਨਾ ਜੀਵਿਤ ਸਰੀਰ ਨਾਲ ਕੀਤੀ । ਉਸਨੇ ਕਿਹਾ ਜਿਵੇਂਸਰੀਰ ਦੇ ਅੱਡ-ਅੱਡ ਹਿੱਸੇ ਸਰੀਰ ਨੂੰ ਠੀਕ ਢੰਗ ਨਾਲ ਚਲਾਉਣ ਲਈ ਜ਼ਰੂਰੀ ਹੁੰਦੇ ਹਨ, ਉਸੇ ਤਰੀਕੇ ਨਾਲ ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਦੇ ਅੱਡ-ਅੱਡ ਹਿੱਸੇ ਇਸ ਸੰਰਚਨਾ ਨੂੰ ਚਲਾਉਣ ਵਿੱਚ ਮਹੱਤਵਪੂਰਨ ਭੂਮਿਕਾ ਅਦਾ ਕਰਦੇ ਹਨ ।

→ ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਦੇ ਬਹੁਤ ਸਾਰੇ ਤੱਤ ਹੁੰਦੇ ਹਨ ਜਿਨ੍ਹਾਂ ਵਿੱਚ ਪ੍ਰਸਥਿਤੀ ਅਤੇ ਭੂਮਿਕਾ ਕਾਫ਼ੀ ਮਹੱਤਵਪੂਰਨ ਹਨ । ਪ੍ਰਸਥਿਤੀ ਦਾ ਅਰਥ ਉਹ ਰੁਤਬਾ ਜਾਂ ਸਥਿਤੀ ਹੈ ਜਿਹੜੀ ਵਿਅਕਤੀ ਨੂੰ ਸਮਾਜ ਵਿੱਚ ਰਹਿੰਦੇ ਹੋਏ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ । ਇੱਕ ਵਿਅਕਤੀ ਦੀਆਂ ਬਹੁਤ ਸਾਰੀਆਂ ਪ੍ਰਸਥਿਤੀਆਂ ਹੁੰਦੀਆਂ ਹਨ ਜਿਵੇਂ ਕਿ ਅਫ਼ਸਰ, ਪਿਤਾ, ਪੁੱਤਰ, ਕਲੱਬ ਦਾ ਪ੍ਰਧਾਨ ਆਦਿ ।

→ ਪ੍ਰਸਥਿਤੀ ਦੋ ਪ੍ਰਕਾਰ ਦੀ ਹੁੰਦੀ ਹੈ-ਪ੍ਰਦਤ ਅਤੇ ਅਰਜਿਤ । ਪ੍ਰਦਤ ਪ੍ਰਸਥਿਤੀ ਉਹ ਹੁੰਦੀ ਹੈ ਜੋ ਵਿਅਕਤੀ ਨੂੰ ਬਿਨਾਂ ਕਿਸੇ ਮਿਹਨਤ ਦੇ ਆਪਣੇ ਆਪ ਹੀ ਪ੍ਰਾਪਤ ਹੋ ਜਾਂਦੀ ਹੈ । ਅਰਜਿਤ ਪ੍ਰਸ਼ਥਿਤੀ ਵਿਅਕਤੀ ਨੂੰ ਆਪਣੇ ਆਪ ਪ੍ਰਾਪਤ ਨਹੀਂ ਹੁੰਦੀ ਬਲਕਿ ਉਹ ਆਪਣੀ ਮਿਹਨਤ ਨਾਲ ਇਹਨਾਂ ਨੂੰ ਪ੍ਰਾਪਤ ਕਰਦਾ ਹੈ ।

→ ਭੂਮਿਕਾ ਉਮੀਦਾਂ ਦਾ ਉਹ ਗੁੱਛਾ ਹੈ ਜਿਸਦੀ ਵਿਅਕਤੀ ਤੋਂ ਪੂਰਾ ਕਰਨ ਦੀ ਉਮੀਦ ਕੀਤੀ ਜਾਂਦੀ ਹੈ । ਹਰੇਕ ਪ੍ਰਸਥਿਤੀ ਨਾਲ ਕੁੱਝ ਭੁਮਿਕਾਵਾਂ ਵੀ ਲਗਾ ਦਿੱਤੀਆਂ ਜਾਂਦੀਆਂ ਹਨ । ਭੁਮਿਕਾ ਨਾਲ ਹੀ ਪਤਾ ਚਲਦਾ ਹੈ ਕਿ ਅਸੀਂ ਕਿਸ ਤਰ੍ਹਾਂ ਇੱਕ ਪ੍ਰਸਥਿਤੀ ਉੱਤੇ ਰਹਿੰਦੇ ਹੋਏ ਕਿਸੇ ਵਿਸ਼ੇਸ਼ ਸਮੇਂ ਵਿਵਹਾਰ ਕਰਾਂਗੇ ।

→ ਭੂਮਿਕਾ ਦੀਆਂ ਕਈ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਹੁੰਦੀਆਂ ਹਨ ਜਿਵੇਂ ਕਿ ਭੂਮਿਕਾ ਸਿੱਖੀ ਜਾਂਦੀ ਹੈ, ਭੂਮਿਕਾ ਪ੍ਰਸਥਿਤੀ ਦਾ ਕਾਰਜਾਤਮਕ ਪੱਖ ਹੈ, ਭੂਮਿਕਾ ਦੇ ਮਨੋਵਿਗਿਆਨਿਕ ਆਧਾਰ ਹਨ ਆਦਿ ।

→ ਪ੍ਰਸਥਿਤੀ ਅਤੇ ਭੂਮਿਕਾ ਵਿਚਕਾਰ ਬਹੁਤ ਡੂੰਘਾ ਸੰਬੰਧ ਹੈ ਕਿਉਂਕਿ ਇਹ ਦੋਵੇਂ ਇੱਕ ਸਿੱਕੇ ਦੇ ਦੋ ਪਹਿਲੂ ਹਨ । ਜੇਕਰ ਕਿਸੇ ਵਿਅਕਤੀ ਨੂੰ ਕੋਈ ਪਸਥਿਤੀ ਪ੍ਰਾਪਤ ਹੋਵੇਗੀ ਤਾਂ ਉਸ ਨਾਲ ਸੰਬੰਧਿਤ ਭੂਮਿਕਾ ਵੀ ਆਪਣੇ ਆਪ ਹੀ ਮਿਲ ਜਾਵੇਗੀ । ਬਿਨਾਂ ਭੂਮਿਕਾ ਦੇ ਪ੍ਰਸਥਿਤੀ ਦਾ ਕੋਈ ਲਾਭ ਨਹੀਂ ਅਤੇ ਬਿਨਾਂ ਪ੍ਰਸਥਿਤੀ ਦੇ ਭੂਮਿਕਾ ਨਹੀਂ ਨਿਭਾਈ ਜਾ ਸਕਦੀ ।

Punjab State Board PSEB 11th Class Sociology Book Solutions Chapter 9 ਸਮਾਜਿਕ ਸੰਰਚਨਾ Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Sociology Chapter 9 ਸਮਾਜਿਕ ਸੰਰਚਨਾ

Sociology Guide for Class 11 PSEB ਸਮਾਜਿਕ ਸੰਰਚਨਾ Textbook Questions and Answers

I. ਨਿਮਨਲਿਖਤ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਉੱਤਰ 1-15 ਸ਼ਬਦਾਂ ਵਿੱਚ ਦਿਓ ।

ਪ੍ਰਸ਼ਨ 1.
ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਸ਼ਬਦ ਦਾ ਅਰਥ ਦੱਸੋ ।
ਉੱਤਰ-
ਸਮਾਜ ਦੇ ਅੱਡ-ਅੱਡ ਅੰਤਰ ਸੰਬੰਧਿਤ ਭਾਗਾਂ ਦੇ ਵਿਵਸਥਿਤ ਰੂਪ ਨੂੰ ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਸਟਰਕਚਰ ਸ਼ਬਦ ਕਿਸੇ ਭਾਸ਼ਾ ਤੋਂ ਲਿਆ ਗਿਆ ਹੈ ?
ਉੱਤਰ-
ਸੰਰਚਨਾ (Structure) ਸ਼ਬਦ ਲਾਤਿਨੀ ਭਾਸ਼ਾ ਦੇ ਸ਼ਬਦ ‘Staruere’ ਤੋਂ ਨਿਕਲਿਆ ਹੈ, ਜਿਸਦਾ ਅਰਥ ਹੈ ‘ਇਮਾਰਤ’ ।

ਪ੍ਰਸ਼ਨ 3.
ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਸ਼ਬਦ ਵਰਤਣ ਵਾਲਾ ਪਹਿਲਾ ਸਮਾਜ ਸ਼ਾਸਤਰੀ ਕੌਣ ਸੀ ?
ਉੱਤਰ-
ਹਰਬਰਟ ਸਪੈਂਸਰ (Herbert Spencer) ਨੇ ਸਭ ਤੋਂ ਪਹਿਲਾਂ ਸ਼ਬਦ ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਦਾ ਪ੍ਰਯੋਗ ਕੀਤਾ ।

ਪ੍ਰਸ਼ਨ 4.
ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਦੇ ਤੱਤਾਂ ਦੇ ਨਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਪ੍ਰਸਥਿਤੀ ਅਤੇ ਭੂਮਿਕਾ ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਦੇ ਮਹੱਤਵਪੂਰਨ ਤੱਤ ਹਨ ।

ਪ੍ਰਸ਼ਨ 5.
‘ਪ੍ਰਿੰਸੀਪਲ ਆਫ਼ ਸੋਸ਼ੋਲੋਜੀ’ ਕਿਤਾਬ ਕਿਸ ਨੇ ਲਿਖੀ ਹੈ ?
ਉੱਤਰ-
ਕਿਤਾਬ ‘The Principal of Sociology’ ਹਰਬਰਟ ਸਪੈਂਸਰ ਨੇ ਲਿਖੀ ਸੀ ।

ਪ੍ਰਸ਼ਨ 6.
ਰੁਤਬਾ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਰੁਤਬਾ ਵਿਅਕਤੀ ਨੂੰ ਮਿਲੀ ਪ੍ਰਸਥਿਤੀ ਹੈ ਜਿਹੜਾ ਉਸਨੂੰ ਸਮਾਜ ਵਿੱਚ ਰਹਿੰਦੇ ਹੋਏ ਮਿਲਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 7.
ਦੋ ਤਰ੍ਹਾਂ ਦੇ ਰੁਤਬਿਆਂ ਦੇ ਨਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਦੱਤ ਰੁਤਬਾ ਅਤੇ ਅਰਜਿਤ ਰੁਤਬਾ ਦੋ ਪ੍ਰਕਾਰ ਦੇ ਸਮਾਜਿਕ ਰੁਤਬੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 8.
ਅਰਜਿਤ ਰੁਤਬੇ ਤੇ ਦੱਤ ਰੁਤਬੇ ਦਾ ਸੰਕਲਪ ਕਿਸ ਨੇ ਦਿੱਤਾ ਹੈ ?
ਉੱਤਰ-
ਇਹ ਧਾਰਨਾਵਾਂ ਰਾਲਫ ਲਿੰਟਨ (Ralph Linton) ਨੇ ਦਿੱਤੀਆਂ ਸਨ ।

ਪ੍ਰਸ਼ਨ 9.
ਅਰਜਿਤ ਰੁਤਬੇ ਦੀਆਂ ਦੋ ਉਦਾਹਰਨਾਂ ਦਿਉ ।
ਉੱਤਰ-
ਡਿਪਟੀ ਕਮਿਸ਼ਨਰ ਦੀ ਪ੍ਰਸਥਿਤੀ ਅਤੇ ਪ੍ਰਧਾਨ ਮੰਤਰੀ ਦੀ ਪ੍ਰਸਥਿਤੀ ਅਰਜਿਤ ਪ੍ਰਸਥਿਤੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 10.
ਦੱਤ ਰੁਤਬੇ ਦੀਆਂ ਦੋ ਉਦਾਹਰਨਾਂ ਦਿਉ।
ਉੱਤਰ-
ਪਿਤਾ ਦੀ ਪ੍ਰਸਥਿਤੀ ਅਤੇ ਪਤੀ ਦੀ ਪ੍ਰਸਥਿਤੀ ਪ੍ਰਦਤ ਪ੍ਰਸਥਿਤੀ ਦੀਆਂ ਦੋ ਉਦਾਹਰਨਾਂ ਹਨ ।

ਪ੍ਰਸ਼ਨ 11.
ਭੂਮਿਕਾ ਨੂੰ ਪਰਿਭਾਸ਼ਿਤ ਕਰੋ ।
ਉੱਤਰ-
ਲੰਡਬਰਗ ਦੇ ਅਨੁਸਾਰ, ‘‘ਭੂਮਿਕਾ ਵਿਅਕਤੀ ਦਾ ਕਿਸੇ ਸਮੂਹ ਜਾਂ ਅਵਸਥਾ ਵਿੱਚ ਉਮੀਦ ਕੀਤਾ ਹੋਇਆ ਵਿਵਹਾਰਿਕ ਤਰੀਕਾ ਹੁੰਦਾ ਹੈ ।’’

ਪ੍ਰਸ਼ਨ 12.
ਭੂਮਿਕਾ ਦੀਆਂ ਕੋਈ ਦੋ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਦੱਸੋ ।
ਉੱਤਰ-

1. ਭੁਮਿਕਾ, ਪ੍ਰਸਥਿਤੀ ਜਾਂ ਪਦ ਦਾ ਕਾਰਜਾਤਮਕ ਪੱਖ ਹੁੰਦੀ ਹੈ ।
2. ਭੂਮਿਕਾ ਨੂੰ ਸਮਾਜਿਕ ਮਾਨਤਾ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ ।

II. ਨਿਮਨਲਿਖਤ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਉੱਤਰ 30-35 ਸ਼ਬਦਾਂ ਵਿੱਚ ਦਿਓ ।

ਪ੍ਰਸ਼ਨ 1.
ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਨੂੰ ਪਰਿਭਾਸ਼ਿਤ ਕਰੋ ।
ਉੱਤਰ-
ਦਾਲਕਟ ਪਾਰਜ਼ (Talcot Parsons) ਦੇ ਅਨੁਸਾਰ, “ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਸ਼ਬਦ ਨੂੰ ਪਰਸਪਰ ਸੰਬੰਧਿਤ ਸੰਸਥਾਵਾਂ, ਏਜੰਸੀਆਂ ਅਤੇ ਸਮਾਜਿਕ ਪ੍ਰਤੀਮਾਨਾਂ ਅਤੇ ਨਾਲ ਹੀ ਸਮੂਹ ਵਿੱਚ ਹਰੇਕ ਮੈਂਬਰ ਵਲੋਂ ਗ੍ਰਹਿਣ ਕੀਤੇ ਜਾਂਦੇ ਪਦਾਂ ਅਤੇ ਰੋਲਾਂ ਦੀ ਵਿਸ਼ੇਸ਼ ਤਰਤੀਬ ਜਾਂ ਕੁਮਬੱਧਤਾ ਲਈ ਵਰਤਿਆ ਜਾਂਦਾ ਹੈ ।”

ਪ੍ਰਸ਼ਨ 2.
ਰੁਤਬੇ ਅਤੇ ਭੂਮਿਕਾ ਵਿੱਚ ਦੋ ਸਮਾਨਤਾਵਾਂ ਦੱਸੋ ।
ਉੱਤਰ-

1. ਰੁਤਬਾ ਅਤੇ ਭੁਮਿਕਾ ਇੱਕ ਹੀ ਸਿੱਕੇ ਦੇ ਦੋ ਪਹਿਲੂ ਹਨ ।
2. ਰੁਤਬਾ ਸਮਾਜ ਵਿੱਚ ਵਿਅਕਤੀ ਦੀ ਸਥਿਤੀ ਹੁੰਦੀ ਹੈ ਅਤੇ ਭੂਮਿਕਾ ਪ੍ਰਸਥਿਤੀ ਦਾ ਵਿਵਹਾਰਿਕ ਪੱਖ ਹੈ ।
3. ਰੁਤਬਾ ਅਤੇ ਭੂਮਿਕਾ ਪਰਿਵਰਤਨਸ਼ੀਲ ਹਨ ਅਤੇ ਬਦਲਦੀਆਂ ਰਹਿੰਦੀਆਂ ਹਨ ।

ਪ੍ਰਸ਼ਨ 3.
ਪਰਿਵਾਰ ਦੀ ਸੰਰਚਨਾ ਦੀ ਤਸਵੀਰ ਬਣਾ ਕੇ ਵਰਣਨ ਕਰੋ ।
ਉੱਤਰ-

ਪ੍ਰਸ਼ਨ 4.
ਅਰਜਿਤ ਅਤੇ ਪ੍ਰਦੱਤ ਰੁਤਬੇ ਵਿੱਚ ਫ਼ਰਕ ਦੱਸੋ ।
ਉੱਤਰ-

1. ਤੇ ਪ੍ਰਸਥਿਤੀ ਵਿਅਕਤੀ ਨੂੰ ਜਨਮ ਦੇ ਅਨੁਸਾਰ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੋ ਜਦਕਿ ਅਰਜਿਤ ਪ੍ਰਸਥਿਤੀ ਹਮੇਸ਼ਾਂ ਵਿਅਕਤੀ ਆਪਣੀ ਮਿਹਨਤ ਨਾਲ ਪ੍ਰਾਪਤ ਕਰਦਾ ਹੈ ।
2. ਪ੍ਰਤ ਪ੍ਰਸਥਿਤੀ ਦੇ ਕਈ ਆਧਾਰ ਹੁੰਦੇ ਹਨ ਜਦਕਿ ਅਰਜਿਤ ਪ੍ਰਸਥਿਤੀ ਦਾ ਆਧਾਰ ਸਿਰਫ਼ ਵਿਅਕਤੀ ਦੀ ਮਿਹਨਤ ਹੁੰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 5.
ਭੂਮਿਕਾ ਇੱਕ ਸਿੱਖਿਅਤ ਵਿਵਹਾਰ ਹੈ । ਕਿਵੇਂ ?
ਉੱਤਰ-
ਇਹ ਸੱਚ ਹੈ ਕਿ ਭੂਮਿਕਾਵਾਂ ਸਿੱਖਿਆ ਵਿਵਹਾਰ ਹਨ ਕਿਉਂਕਿ ਭੂਮਿਕਾਵਾਂ ਵਿਵਹਾਰਾਂ ਦਾ ਉਹ ਗੁੱਡਾ ਹਨ ਜਿਨ੍ਹਾਂ ਨੂੰ ਜਾਂ ਤਾਂ ਸਮਾਜੀਕਰਣ ਨਾਲ ਜਾਂ ਫਿਰ ਨਿਰੀਖਣ ਨਾਲ ਸਿੱਖਿਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਦੇ ਨਾਲ ਵਿਅਕਤੀ ਸਿੱਖ ਕੇ ਵਿਵਹਾਰ ਨੂੰ ਜੋ ਅਰਥ ਦਿੰਦਾ ਹੈ, ਉਹ ਹੀ ਸਮਾਜਿਕ ਭੂਮਿਕਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 6.
ਭੂਮਿਕਾ ਅਤੇ ਰੁਤਬੇ ‘ ਤੇ ਨੋਟ ਲਿਖੋ ।
ਉੱਤਰ-
ਰੁਤਬਾ ਵਿਅਕਤੀ ਨੂੰ ਮਿਲੀ ਪ੍ਰਸਥਿਤੀ ਹੈ ਜਿਹੜਾ ਉਸਨੂੰ ਸਮਾਜ ਵਿੱਚ ਰਹਿੰਦੇ ਹੋਏ ਮਿਲਦਾ ਹੈ ।
ਲੰਡਬਰਗ ਦੇ ਅਨੁਸਾਰ, ‘‘ਭੂਮਿਕਾ ਵਿਅਕਤੀ ਦਾ ਕਿਸੇ ਸਮੂਹ ਜਾਂ ਅਵਸਥਾ ਵਿੱਚ ਉਮੀਦ ਕੀਤਾ ਹੋਇਆ ਵਿਵਹਾਰਿਕ ਤਰੀਕਾ ਹੁੰਦਾ ਹੈ ।’’

ਪ੍ਰਸ਼ਨ 7.
ਰੁਤਬਾ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਵਿਅਕਤੀ ਦੀ ਸਮੂਹ ਵਿਚ ਪਾਈ ਗਈ ਸਥਿਤੀ ਨੂੰ ਸਮਾਜਿਕ ਪ੍ਰਸਥਿਤੀ ਜਾਂ ਰੁਤਬੇ ਦਾ ਨਾਮ ਦਿੱਤਾ ਗਿਆ ਹੈ । ਇਹ ਸਥਿਤੀ ਉਹ ਹੈ ਜਿਸ ਨੂੰ ਵਿਅਕਤੀ ਆਪਣੇ ਲਿੰਗ, ਭੇਦ, ਉਮਰ, ਜਨਮ, ਕੰਮ ਆਦਿ ਦੀ ਪਹਿਚਾਣ ਵਿਸ਼ੇਸ਼ ਅਧਿਕਾਰਾਂ ਦੇ ਸੰਕੇਤਾਂ ਅਤੇ ਕੰਮਾਂ ਦੇ ਪਤੀਮਾਨ (Patterms) ਦੁਆਰਾ ਹੁੰਦੀ ਹੈ । ਜਿਵੇਂ ਕੋਈ ਵੱਡਾ ਅਫ਼ਸਰ ਆਉਂਦਾ ਹੈ, ਸਭ ਖੜੇ ਹੁੰਦੇ ਹਨ, ਇਹ ਸਤਿਕਾਰ ਉਸ ਨੂੰ ਸੰਬੰਧਿਤ ਪਦ ਕਾਰਨ ਹੀ ਪ੍ਰਾਪਤ ਹੋਇਆ ਹੈ । ਉਸਦੇ ਕੰਮਾਂ ਦੇ ਨਾਲ ਸੰਬੰਧਿਤ ਵਿਸ਼ੇਸ਼ ਤੀਮਾਨ ਨੂੰ ਹੀ ਸਮਾਜਿਕ ਪ੍ਰਸਥਿਤੀ (Social Status) ਦਾ ਨਾਮ ਦਿੱਤਾ ਗਿਆ ਹੈ ।

ਪ੍ਰਸ਼ਨ 8.
ਭੂਮਿਕਾ ਸੈੱਟ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਭੁਮਿਕਾ ਸੈੱਟ ਦਾ ਪ੍ਰਯੋਗ ਪਹਿਲੀ ਵਾਰ ਰਾਬਰਟ ਮਾਰਟਨ ਨੇ ਕੀਤਾ ਸੀ ਤੇ ਉਸ ਦੇ ਅਨੁਸਾਰ ਹਰੇਕ ਰੁਤਬਾ ਦੂਜੇ ਰੁਤਬਿਆਂ ਨਾਲ ਜੁੜਿਆ ਹੁੰਦਾ ਹੈ । ਇਸ ਨੂੰ ਹੀ ਭੁਮਿਕਾ ਸੈਂਟ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਉਦਾਹਰਨ ਲਈ ਡਾਕਟਰ ਮਰੀਜ਼, ਵਿਦਿਆਰਥੀ ਅਧਿਆਪਕ ।

ਪ੍ਰਸ਼ਨ 9.
ਭੂਮਿਕਾ ਸੰਘਰਸ਼ ਕੀ ਹੈ ? ਉਦਾਹਰਨ ਦਿਓ ।
ਉੱਤਰ-
ਹਰੇਕ ਵਿਅਕਤੀ ਕੋਲ ਬਹੁਤ ਸਾਰੇ ਪਦ ਹੁੰਦੇ ਹਨ ਅਤੇ ਹਰੇਕ ਪਦ ਨਾਲ ਅੱਡ-ਅੱਡ ਭੁਮਿਕਾ ਜੁੜੀ ਹੁੰਦੀ ਹੈ । ਵਿਅਕਤੀ ਨੂੰ ਇਹਨਾਂ ਭੂਮਿਕਾਵਾਂ ਨੂੰ ਨਿਭਾਉਂਣਾ ਪੈਂਦਾ ਹੈ । ਜਦੋਂ ਇਹਨਾਂ ਸਾਰੀਆਂ ਭੂਮਿਕਾਵਾਂ ਵਿੱਚ ਤਾਲਮੇਲ ਨਹੀਂ ਬੈਠ ਪਾਉਂਦਾ ਅਤੇ ਵਿਅਕਤੀ ਇਹਨਾਂ ਸਾਰੀਆਂ ਭੂਮਿਕਾਵਾਂ ਨੂੰ ਠੀਕ ਤਰੀਕੇ ਨਾਲ ਨਹੀਂ ਨਿਭਾ ਸਕਦਾ ਤਾਂ ਇਸ ਨੂੰ ਭੂਮਿਕਾ ਸੰਘਰਸ਼ ਕਹਿੰਦੇ ਹਨ ।

III. ਨਿਮਨਲਿਖਤ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਉੱਤਰ 75-85 ਸ਼ਬਦਾਂ ਵਿੱਚ ਦਿਓ ।

ਪ੍ਰਸ਼ਨ 1.
ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਦੀਆਂ ਤਿੰਨ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਦੱਸੋ ।
ਉੱਤਰ-

• ਹਰ ਇਕ ਸਮਾਜ ਦੀ ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਵੱਖੋ-ਵੱਖਰੀ ਹੁੰਦੀ ਹੈ ਕਿਉਂਕਿ ਸਮਾਜ ਵਿਚ ਪਾਏ ਜਾਣ ਵਾਲੇ ਅੰਗਾਂ ਦਾ ਸਮਾਜਿਕ ਜੀਵਨ ਵਿਚ ਵੱਖੋ-ਵੱਖਰਾ ਢੰਗ ਹੁੰਦਾ ਹੈ । ਪਰ ਇਕ ਸਮਾਜ ਦੇ ਸੰਸਥਾਗਤ ਨਿਯਮ ਵੱਖੋ-ਵੱਖਰੇ ਹੁੰਦੇ ਹਨ । ਇਸੇ ਕਰਕੇ ਕਿਸੇ ਵੀ ਦੋ ਸਮਾਜਾਂ ਦੀਆਂ ਸੰਰਚਨਾਵਾਂ ਇੱਕੋ ਜਿਹੀਆਂ ਨਹੀਂ ਹੁੰਦੀਆਂ ।
• ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਅਮੂਰਤ ਹੁੰਦੀ ਹੈ ਕਿਉਂਕਿ ਇਸਦਾ ਨਿਰਮਾਣ ਜਿਨ੍ਹਾਂ ਇਕਾਈਆਂ ਨਾਲ ਹੁੰਦਾ ਹੈ ਜਿਵੇਂ ਸੰਸਥਾ, ਸਭਾ, ਪਰਿਮਾਪ ਆਦਿ, ਸਭ ਅਮੂਰਤ ਹੁੰਦੀਆਂ ਹਨ । ਇਨ੍ਹਾਂ ਦਾ ਕੋਈ ਠੋਸ ਰੂਪ ਨਹੀਂ ਹੁੰਦਾ, ਅਸੀਂ ਕੇਵਲ ਇਨ੍ਹਾਂ ਨੂੰ ਮਹਿਸੂਸ ਕਰ ਸਕਦੇ ਹਾਂ । ਇਸ ਕਰਕੇ ਇਹ ਅਮੂਰਤ ਹੁੰਦੀ ਹੈ ।
• ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਦੇ ਵਿਚ ਸੰਸਥਾਵਾਂ, ਸਭਾਵਾਂ, ਪਰਿਮਾਪਾਂ ਆਦਿ ਨੂੰ ਇਕ ਵਿਸ਼ੇਸ਼ ਤਰੀਕੇ ਨਾਲ ਦੱਸਣ ਲਈ ਕੋਈ ਯੋਜਨਾ ਨਹੀਂ ਘੜੀ ਜਾਂਦੀ ਬਲਕਿ ਇਸ ਦਾ ਵਿਕਾਸ ਸਮਾਜਿਕ ਅੰਤਰ ਕ੍ਰਿਆਵਾਂ ਦੇ ਨਤੀਜੇ ਵਜੋਂ ਹੋ ਜਾਂਦਾ ਹੈ । ਇਸੀ ਕਰਕੇ ਇਸ ਸੰਬੰਧ ਵਿਚ ਚੇਤਨ ਰੂਪ ਵਿਚ ਕੋਸ਼ਿਸ਼ ਕਰਨ ਦੀ ਜ਼ਰੂਰਤ ਨਹੀਂ ਹੁੰਦੀ ।

ਪ੍ਰਸ਼ਨ 2.
ਦੰਤ ਰੁਤਬਾ ਕੀ ਹੈ ? ਉਦਾਹਰਨ ਦਿਓ ।.
ਉੱਤਰ-
ਇਹ ਉਹ ਪਦ ਹੁੰਦਾ ਹੈ ਜਿਸ ਨੂੰ ਵਿਅਕਤੀ ਬਿਨਾਂ ਮਿਹਨਤ ਕੀਤਿਆਂ ਹੀ ਪ੍ਰਾਪਤ ਕਰ ਲੈਂਦਾ ਹੈ । ਜਿਵੇਂ ਪ੍ਰਾਚੀਨ ਹਿੰਦੂ ਸਮਾਜ ਵਿਚ ਜਾਤੀ ਪ੍ਰਥਾ ਦੇ ਵਿਚ ਬ੍ਰਾਹਮਣਾਂ ਨੂੰ ਉੱਚਾ ਸਥਾਨ ਪ੍ਰਾਪਤ ਸੀ । ਜਿਹੜਾ ਵਿਅਕਤੀ ਇਸ ਜਾਤ ਵਿਚ ਪੈਦਾ ਹੁੰਦਾ ਸੀ ਉਸ ਦਾ ਸਥਾਨ ਸਮਾਜ ਵਿਚ ਉੱਚਾ ਸੀ । ਲਿੰਗ, ਜਾਤ, ਜਨਮ, ਉਮਰ, ਨਾਤੇਦਾਰੀ, ਆਦਿ (Sex, caste, birth, age, kinship etc.) ਸਭ ਤ ਪਦੇ ਹਨ ਜੋ ਬਿਨਾਂ ਯਤਨ ਕੀਤੇ ਪ੍ਰਾਪਤ ਕੀਤੇ ਜਾਂਦੇ ਹਨ । ਇਸ ਪ੍ਰਕਾਰ ਦਾ ਪਦ ਬਿਨਾਂ ਮਿਹਨਤ ਦੇ ਪ੍ਰਾਪਤ ਹੋ ਜਾਂਦਾ ਹੈ ਅਤੇ ਕੋਈ ਵੀ ਇਸ ਪਦ ਜਾਂ ਪ੍ਰਸਥਿਤੀ ਨੂੰ ਖੋਹ ਨਹੀਂ ਸਕਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਸੰਖੇਪ ਵਿੱਚ ਭੂਮਿਕਾ ਤੇ ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਦੇ ਤੱਤ ਉੱਪਰ ਨੋਟ ਲਿਖੋ ।
ਉੱਤਰ-
ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਦੀਆਂ ਇਕਾਈਆਂ ਦੇ ਉਪ ਸਮੂਹ ਹੁੰਦੇ ਹਨ ਅਤੇ ਇਹਨਾਂ ਸਮੂਹਾਂ ਵਿੱਚ ਮੈਂਬਰਾਂ ਨੂੰ ਨਿਸ਼ਚਿਤ ਨਿਯਮਾਂ ਅਨੁਸਾਰ ਭੂਮਿਕਾਵਾਂ ਦਿੱਤੀਆਂ ਜਾਂਦੀਆਂ ਹਨ । ਵਿਅਕਤੀਆਂ ਵਿਚਕਾਰ ਅੰਤਰਕ੍ਰਿਆਵਾਂ ਹੁੰਦੀਆਂ ਹਨ ਅਤੇ ਅੰਤਰਕ੍ਰਿਆਵਾਂ ਨੂੰ ਸਪੱਸ਼ਟ ਕਰਨ ਲਈ ਵਿਅਕਤੀਆਂ ਨੂੰ ਭੁਮਿਕਾਵਾਂ ਦਿੱਤੀਆਂ ਜਾਂਦੀਆਂ ਹਨ । ਭੁਮਿਕਾ ਵਿਅਕਤੀ ਦਾ ਵਿਸ਼ੇਸ਼ ਸਥਿਤੀ ਵਿੱਚ ਵਿਵਹਾਰ ਹੁੰਦਾ ਹੈ ਜੋ ਉਸ ਦੇ ਪਦ ਨਾਲ ਸੰਬੰਧਿਤ ਹੁੰਦੀ ਹੈ । ਜੇਕਰ ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਵਿੱਚ ਕੋਈ ਪਰਿਵਤਰਨ ਆਉਂਦਾ ਹੈ ਤਾਂ ਵਿਅਕਤੀਆਂ ਦੇ ਪਦਾਂ ਅਤੇ ਭੂਮਿਕਾਵਾਂ ਵਿੱਚ ਵੀ ਪਰਿਵਰਤਨ ਆ ਜਾਂਦਾ ਹੈ । ਇਹਨਾਂ ਭੂਮਿਕਾਵਾਂ ਦੇ ਕਾਰਨ ਹੀ ਲੋਕਾਂ ਵਿੱਚ ਸੰਬੰਧ ਸਥਾਪਿਤ ਰਹਿੰਦੇ ਹਨ ਅਤੇ ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਕਾਇਮ ਰਹਿੰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 4.
ਰੁਤਬੇ ਉੱਤੇ ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਦੇ ਤੱਤ ਵੱਜੋਂ ਨੋਟ ਲਿਖੋ ।’
ਉੱਤਰ-
ਇਸ ਵਿੱਚ ਕੋਈ ਸ਼ੱਕ ਨਹੀਂ ਹੈ ਕਿ ਸਥਿਤੀ ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਦਾ ਇੱਕ ਤੱਤ ਹੈ । ਉਪ ਸਮੂਹ ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਦੀਆਂ ਇਕਾਈਆਂ ਹੁੰਦੇ ਹਨ ਅਤੇ ਇਹਨਾਂ ਸਮੂਹਾਂ ਵਿੱਚ ਹਰੇਕ ਵਿਅਕਤੀ ਨੂੰ ਕਈ ਸਥਿਤੀਆਂ ਪ੍ਰਾਪਤ ਹੁੰਦੀਆਂ ਹਨ । ਲੋਕਾਂ ਵਿਚਕਾਰ ਅੰਤਰਆਵਾਂ ਹੁੰਦੀਆਂ ਰਹਿੰਦੀਆਂ ਹਨ ਅਤੇ ਇਹਨਾਂ ਅੰਤਰਕ੍ਰਿਆਵਾਂ ਨੂੰ ਸਪੱਸ਼ਟ ਕਰਨ ਲਈ ਵਿਅਕਤੀਆਂ ਨੂੰ ਕਈ ਸਥਿਤੀਆਂ ਦੇ ਦਿੱਤੀਆਂ ਜਾਂਦੀਆਂ ਹਨ । ਜਦੋਂ ਵਿਅਕਤੀ ਨੂੰ ਸਥਿਤੀ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ ਤਾਂ ਉਸ ਨੂੰ ਅਲੱਗ-ਅਲੱਗ ਸਥਿਤੀਆਂ ਦੇ ਅਨੁਸਾਰ ਵਿਵਹਾਰ ਕਰਨਾ ਪੈਂਦਾ ਹੈ । ਜੇਕਰ ਸਮਾਜਿਕ ਸੰਰਚਨਾਂ ਵਿੱਚ ਕੋਈ ਪਰਿਵਰਤਨ ਆਉਂਦਾ ਹੈ ਤਾਂ ਨਿਸ਼ਚਿਤ ਤੌਰ ਉੱਤੇ ਲੋਕਾਂ ਦੀਆਂ ਸਥਿਤੀਆਂ ਵਿਚ ਵੀ ਪਰਿਵਤਨ ਆ ਜਾਂਦਾ ਹੈ । ਇਹਨਾਂ ਸਥਿਤੀਆਂ ਕਾਰਨ ਹੀ ਲੋਕਾਂ ਵਿੱਚ ਸੰਬੰਧ ਸਥਾਪਿਤ ਹੁੰਦੇ ਹਨ ਅਤੇ ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਕਾਇਮ ਰਹਿੰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 5.
ਰੁਤਬੇ ਅਤੇ ਭੂਮਿਕਾਵਾਂ ਕਿਵੇਂ ਅੰਤਰ ਸੰਬੰਧਿਤ ਹਨ ? ਚਰਚਾ ਕਰੋ ।
ਉੱਤਰ-
ਇਹ ਸੱਚ ਹੈ ਕਿ ਪਦ ਅਤੇ ਭੂਮਿਕਾ ਅੰਤਰ ਸੰਬੰਧਿਤ ਹਨ । ਅਸਲ ਵਿੱਚ ਇਹ ਦੋਵੇਂ ਇੱਕ ਹੀ ਸਿੱਕੇ ਦੇ ਦੋ ਪਹਿਲੂ ਹਨ । ਜੇਕਰ ਦੋਹਾਂ ਵਿੱਚੋਂ ਇੱਕ ਚੀਜ਼ ਦਿੱਤੀ ਜਾਵੇਗੀ ਅਤੇ ਦੂਜੀ ਨਹੀਂ ਤਾਂ ਇਹਨਾਂ ਦੋਹਾਂ ਦਾ ਕੋਈ ਮੁੱਲ ਨਹੀਂ ਰਹਿ ਜਾਵੇਗਾ । ਇਸ ਦਾ ਤੇ ਉਹ ਅਰਥ ਹੋ ਗਿਆ ਕਿ ਅਧਿਕਾਰ ਦੇ ਦਿੱਤੇ ਪਰ ਜ਼ਿੰਮੇਵਾਰੀ ਨਹੀਂ ਜਾਂ ਜ਼ਿੰਮੇਵਾਰੀ ਦੇ ਦਿੱਤੀ ਪਰ ਅਧਿਕਾਰ ਨਹੀਂ । ਇੱਕ ਦੇ ਨਾਂ ਹੋਣ ਦੀ ਸੂਰਤ ਵਿੱਚ ਦੂਜਾ ਠੀਕ ਢੰਗ ਨਾਲ ਕੰਮ ਨਹੀਂ ਕਰ ਸਕਦਾ । ਜੇਕਰ ਕਿਸੇ ਕੋਲ ਅਧਿਕਾਰੀ ਦਾ ਪਦ ਹੈ ਪਰ ਉਸਨੂੰ ਉਸ ਪਦ ਨਾਲ ਸੰਬੰਧਿਤ ਕੋਈ ਜ਼ਿੰਮੇਵਾਰੀ ਨਹੀਂ ਦਿੱਤੀ ਗਈ ਤਾਂ ਉਸ ਅਧਿਕਾਰੀ ਦਾ ਸਮਾਜ ਲਈ ਕੋਈ ਫ਼ਾਇਦਾ ਨਹੀਂ ਹੈ । ਇਸੇ ਤਰ੍ਹਾਂ ਜੇਕਰ ਕਿਸੇ ਨੂੰ ਕੋਈ ਭੂਮਿਕਾ ਜਾਂ ਜਿੰਮੇਵਾਰੀ ਦੇ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ ਪਰ ਕੋਈ ਅਧਿਕਾਰ ਜਾਂ ਪਦ ਨਹੀਂ ਦਿੱਤਾ ਜਾਂਦਾ ਤਾਂ ਵੀ ਉਹ ਭੂਮਿਕਾ ਠੀਕ ਤਰ੍ਹਾਂ ਨਹੀਂ ਨਿਭਾ ਸਕੇਗਾ। ਇਸ ਤਰ੍ਹਾਂ ਇਹ ਦੋਵੇਂ ਡੂੰਘੇ ਰੂਪ ਨਾਲ ਸੰਬੰਧਿਤ ਹਨ ।

IV. ਨਿਮਨਲਿਖਤ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਉੱਤਰ 250-300 ਸ਼ਬਦਾਂ ਵਿੱਚ ਦਿਓ ।

ਪ੍ਰਸ਼ਨ 1.
ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਨੂੰ ਪਰਿਭਾਸ਼ਿਤ ਕਰੋ ਅਤੇ ਇਸਦੀਆਂ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਸਮਾਜ ਕੋਈ ਅਖੰਡ ਵਿਵਸਥਾ ਨਹੀਂ ਹੈ ਜੋ ਟੁੱਟ ਨਾ ਸਕੇ । ਸਮਾਜ ਕਈ ਹਿੱਸਿਆਂ ਨੂੰ ਮਿਲਾ ਕੇ ਬਣਦਾ ਹੈ । ਸਮਾਜ ਨੂੰ ਬਣਾਉਣ ਵਾਲੇ ਵੱਖ-ਵੱਖ ਭਾਗ ਜਾਂ ਇਕਾਈਆਂ ਆਪਣੇ ਨਿਰਧਾਰਿਤ ਕੰਮ ਕਰਦੇ ਹੋਏ ਆਪਸ ਵਿਚ ਅੰਤਰ ਸੰਬੰਧਿਤ ਰਹਿੰਦੀਆਂ ਹਨ ਅਤੇ ਇਕ ਪ੍ਰਕਾਰ ਦੇ ਸੰਤੁਲਨ ਨੂੰ ਪੈਦਾ ਕਰਦੀਆਂ ਹਨ । ਸਮਾਜ ਵਿਗਿਆਨ ਦੀ ਭਾਸ਼ਾ ਵਿਚ ਇਸ ਸੰਤੁਲਨ ਨੂੰ ਸਮਾਜਿਕ ਵਿਵਸਥਾ ਕਹਿੰਦੇ ਹਨ । ਇਸ ਦੇ ਉਲਟ ਜਦੋਂ ਸਮਾਜ ਦੇ ਇਹ ਵੱਖ-ਵੱਖ ਅੰਤਰ ਸੰਬੰਧਿਤ ਅੰਗ ਇਕਦੂਜੇ ਨਾਲ ਮਿਲ ਕੇ ਇਕ ਢਾਂਚੇ ਦਾ ਨਿਰਮਾਣ ਕਰਦੇ ਹਨ ਤਾਂ ਇਸ ਢਾਂਚੇ ਨੂੰ ਸਮਾਜਿਕ ਸੰਚਰਨਾ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਸੰਖੇਪ ਵਿਚ ਸੰਰਚਨਾ ਦਾ ਅਰਥ ਉਹਨਾਂ ਇਕਾਈਆਂ ਦੇ ਇਕੱਠ ਤੋਂ ਹੈ ਜੋ ਆਪਸ ਵਿਚ ਸੰਬੰਧਿਤ ਹਨ ।

• ਮੈਕਾਈਵਰ (Maclver) ਦੇ ਵਿਚਾਰ ਅਨੁਸਾਰ, “ਮੈਕਾਈਵਰ ਅਤੇ ਪੇਜ (Maclver and Page) ਦੇ ਅਨੁਸਾਰ, “ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਆਪਣੇ ਆਪ ਵਿਚ ਅਸਥਿਰ ਅਤੇ ਪਰਿਵਰਤਨਸ਼ੀਲ ਹੈ । ਇਸ ਦਾ ਹਰੇਕ ਅਵਸਥਾ ਵਿਚ ਨਿਸ਼ਚਿਤ ਸਥਾਨ ਹੁੰਦਾ ਹੈ ਅਤੇ ਇਸ ਦੇ ਕਈ ਮੁੱਖ ਤੱਤ ਇਹੋ ਜਿਹੇ ਵੀ ਹੁੰਦੇ ਹਨ ਜਿਨ੍ਹਾਂ ਵਿੱਚ ਵਧੇਰੇ ਪਰਿਵਰਤਨ ਪਾਇਆ ਜਾਂਦਾ ਹੈ ।
• ਹੈਰੀ ਐੱਮ. ਜਾਨਸਨ (Harry M. Johnson) ਦੇ ਵਿਚਾਰ ਅਨੁਸਾਰ, “ਜਾਨਸਨ ਨੇ ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਦੀ ਪਰਿਭਾਸ਼ਾ ਦਿੱਤੀ ਹੈ । ਉਸ ਦੇ ਅਨੁਸਾਰ, “ਕਿਸੇ ਵੀ ਵਸਤੂ ਦੀ ਸੰਰਚਨਾ ਉਸਦੇ ਅੰਗਾਂ ਵਿਚ ਪਾਏ ਜਾਣ ਵਾਲੇ ਸਾਪੇਖ ਤੌਰ’ ਤੇ ਸਥਾਈ ਅੰਤਰ ਸੰਬੰਧਾਂ ਨੂੰ ਕਹਿੰਦੇ ਹਨ । ਨਾਲ ਹੀ ਅੰਗ ਸ਼ਬਦ ਵਿਚ ਖ਼ੁਦ ਹੀ ਕੁੱਝ ਨਾ ਕੁੱਝ ਸਥਿਰਤਾ ਦੀ ਮਾਤਰਾ ਲੁਪਤ ਹੁੰਦੀ ਹੈ ਕਿਉਂਕਿ ਸਮਾਜਿਕ ਵਿਵਸਥਾ ਲੋਕਾਂ ਦੀ ਸੰਰਚਨਾ ਨੂੰ ਉਹਨਾਂ ਕਿਰਿਆਵਾਂ ਵਿਚ ਪਾਈ ਜਾਣ ਵਾਲੀ ਨਿਯਮਿਤਤਾ ਦੀ ਮਾਤਰਾ ਜਾਂ ਮੁੜ ਵਾਪਰਨ ਜਾਂ ਆਵਰਤਨ ਵਿਚ ਲੱਭਿਆ ਜਾਣਾ ਚਾਹੀਦਾ ਹੈ ।”
• ਜਿਨਸਬਰਗ (Ginsberg) ਦੇ ਅਨੁਸਾਰ, “ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਦੇ ਅਧਿਐਨ ਦਾ ਸੰਬੰਧ ਸਮਾਜਿਕ ਇਕੱਠ ਦੇ ਪ੍ਰਮੁੱਖ ਸਰੂਪਾਂ ਜਿਵੇਂ ਸਮੂਹਾਂ, ਸਮਿਤੀਆਂ ਅਤੇ ਸੰਸਥਾਵਾਂ ਦੇ ਪ੍ਰਕਾਰਾਂ ਅਤੇ ਇਹਨਾਂ ਦੇ ਸਰੂਪਾਂ ਜਿਹੜੇ ਸਮਾਜ ਦਾ ਨਿਰਮਾਣ ਕਰਦੇ ਹਨ, ਨਾਲ ਹੀ ……. ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਦੇ ਵਿਸ਼ਾਲ ਵਰਨਣ ਵਿਚ ਤੁਲਨਾਤਮਕ ਸੰਸਥਾਵਾਂ ਦੇ ਸਾਰੇ ਖੇਤਰਾਂ ਦਾ ਅਧਿਐਨ ਸ਼ਾਮਲ ਹੁੰਦਾ ਹੈ ।”

ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਦੀਆਂ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ (Characteristics of Social Structure)

1. ਵੱਖ-ਵੱਖ ਸਮਾਜਾਂ ਦੀ ਵੱਖ-ਵੱਖ ਸੰਰਚਨਾ ਹੁੰਦੀ ਹੈ (Different societies have different Social Structures) – ਹਰੇਕ ਸਮਾਜ ਦੀ ਸੰਰਚਨਾ ਵੱਖ-ਵੱਖ ਹੁੰਦੀ ਹੈ । ਹਰੇਕ ਸਮਾਜ ਦੇ ਆਪਣੇ ਹੀ ਨਿਯਮ ਅਤੇ ਪਰੰਪਰਾਵਾਂ ਹੁੰਦੀਆਂ ਹਨ ਕਿਉਂਕਿ ਉਸ ਦੀਆਂ ਵੱਖ-ਵੱਖ ਇਕਾਈਆਂ ਵਿਚ ਮਿਲਣ ਵਾਲੇ ਸੰਬੰਧਾਂ ਦੀ ਸਮਾਜਿਕ ਜੀਵਨ ਵਿਚ ਵੱਖ ਹੀ ਥਾਂ ਹੁੰਦੀ ਹੈ । ਇਸ ਦੇ ਨਾਲ ਹੀ ਵੱਖ-ਵੱਖ ਸਮਿਆਂ ਵਿਚ ਇਕ ਹੀ ਸਮਾਜ ਦੀ ਸੰਰਚਨਾ ਵੀ ਵੱਖ-ਵੱਖ ਹੁੰਦੀ ਹੈ । ਇਸ ਦਾ ਕਾਰਨ ਇਹ ਹੈ ਕਿ ਹਰੇਕ ਸਮਾਜ ਦੀਆਂ ਇਕਾਈਆਂ ਵਿਚ ਮਿਲਣ ਵਾਲੇ ਵਿਵਸਥਿਤ ਕੂਮ ਜਾਂ ਸੰਬੰਧੀ ਵੱਖ-ਵੱਖ ਸਮਾਜਾਂ ਵਿਚ ਵੱਖ-ਵੱਖ ਹੁੰਦੇ ਹਨ । ਇਹਨਾਂ ਦਾ ਸੰਬੰਧ ਵਿਸ਼ੇਸ਼ ਸਮਾਜ ਨਾਲ ਹੁੰਦਾ ਹੈ ।

2. ਸੰਰਚਨਾ ਸਮਾਜ ਦੇ ਬਾਹਰੀ ਰੂਪ ਨੂੰ ਦਰਸਾਉਂਦੀ ਹੈ (It refers to the external aspect of society) – ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਸਮਾਜ ਦੀ ਅੰਦਰੂਨੀ ਅਵਸਥਾ ਨਾਲ ਸੰਬੰਧਿਤ ਨਹੀਂ ਹੁੰਦੀ ਬਲਕਿ ਇਸ ਦਾ ਸੰਬੰਧ ਸਮਾਜ ਦੇ ਬਾਹਰੀ ਰੂਪ ਨਾਲ ਹੈ ਜਿਵੇਂ ਸਰੀਰ ਦੇ ਵੱਖ-ਵੱਖ ਹਿੱਸੇ ਇਕੱਠੇ ਮਿਲ ਕੇ ਸਰੀਰ ਦੇ ਬਾਹਰੀ ਢਾਂਚੇ ਨੂੰ ਬਣਾਉਂਦੇ ਹਨ । ਉਸੇ ਤਰ੍ਹਾਂ ਸਮਾਜ ਦੀਆਂ ਵੱਖ-ਵੱਖ ਇਕਾਈਆਂ ਸਮਾਜ ਦੀ ਬਾਹਰੀ ਸੰਰਚਨਾ ਦਾ ਨਿਰਮਾਣ ਕਰਦੀਆਂ ਹਨ । ਇਹ ਇਹਨਾਂ ਇਕਾਈਆਂ ਦੇ ਵੱਖ-ਵੱਖ ਕੰਮਾਂ ਬਾਰੇ ਨਹੀਂ ਦੱਸਦੇ ਸਿਰਫ਼ ਸਰੀਰਕ ਸੰਰਚਨਾ ਦੇ ਬਾਹਰਲੇ ਹਿੱਸੇ ਨੂੰ ਦਰਸਾਉਂਦੇ ਹਨ ।

3. ਇਕ ਸੰਰਚਨਾ ਵਿਚ ਕਈ ਉਪ-ਸੰਰਚਨਾਵਾਂ ਹੁੰਦੀਆਂ ਹਨ (Many Sub-Structures are there in one structure) – ਇਕ ਸੰਰਚਨਾ ਵਿਚ ਇਕ ਜਾਂ ਦੋ ਉਪ-ਸੰਰਚਨਾਵਾਂ ਨਹੀਂ ਬਲਕਿ ਕਈ ਉਪ-ਸੰਰਚਨਾਵਾਂ ਹੁੰਦੀਆਂ ਹਨ । ਉਦਾਹਰਨ ਦੇ ਤੌਰ ਉੱਤੇ ਸਕੂਲ ਦੀ ਇਕ ਸੰਰਚਨਾ ਹੁੰਦੀ ਹੈ ਪਰ ਉਸ ਦੀਆਂ ਕਈ ਉਪ-ਸੰਰਚਨਾਵਾਂ ਹੁੰਦੀਆਂ ਹਨ, ਜਿਵੇਂ ਕਿ ਵੱਖ-ਵੱਖ ਕਲਾਸਾਂ, ਟੀਚਰ, ਚਪੜਾਸੀ, ਕਲਰਕ, ਸਕੂਲ ਦਾ ਸਮਾਨ ਆਦਿ । ਇਹ ਸਾਰੇ ਮਿਲ ਕੇ ਸਕੂਲ ਦਾ ਨਿਰਮਾਣ ਕਰਦੇ ਹਨ । ਵੱਖ-ਵੱਖ ਇਹਨਾਂ ਦੀ ਆਪਣੀ ਕੋਈ ਹੋਂਦ ਨਹੀਂ ਹੈ ।

4. ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਅਮੂਰਤ ਹੁੰਦੀ ਹੈ (Social Structure is abstract) – ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਦਾ ਨਿਰਮਾਣ ਵੱਖ-ਵੱਖ ਇਕਾਈਆਂ ਦੇ ਸੰਬੰਧਾਂ ਦੀ ਭੂਮਬੱਧਤਾ ਦੇ ਕਾਰਨ ਹੁੰਦਾ ਹੈ । ਸੰਸਥਾਵਾਂ, ਸਮੂਹ, ਸ਼ੇਣੀਆਂ ਆਦਿ ਸੰਰਚਨਾ ਦੀਆਂ ਇਕਾਈਆਂ ਹਨ । ਸੰਰਚਨਾ ਵਿਚ ਇਕਾਈਆਂ ਕੂਮਬੱਧਤਾ ਨਾਲ ਕੰਮ ਕਰਦੀਆਂ ਹਨ । ਇਸ ਕੁਮਬੱਧਤਾ ਦਾ ਨਾ ਤਾਂ ਕੋਈ ਆਕਾਰ ਹੁੰਦਾ ਹੈ ਤੇ ਨਾ ਹੀ ਅਸੀਂ ਇਹਨਾਂ ਨੂੰ ਛੂਹ ਸਕਦੇ ਹਾਂ । ਇਹਨਾਂ ਇਕਾਈਆਂ ਦੇ ਸੰਬੰਧ ਵੀ ਅਮੂਰਤ ਹੁੰਦੇ ਹਨ ਜਿਸ ਕਾਰਨ ਇਹਨਾਂ ਨੂੰ ਅਸੀਂ ਛੂਹ ਨਹੀਂ ਸਕਦੇ ਸਿਰਫ਼ ਮਹਿਸੂਸ ਕਰ ਸਕਦੇ ਹਾਂ ।

5. ਸੰਰਚਨਾ ਵਿਚ ਹਰੇਕ ਇਕਾਈ ਦਾ ਨਿਸ਼ਚਿਤ ਸਥਾਨ ਹੁੰਦਾ ਹੈ (Every unit of Structure has a definite place) – ਸੰਰਚਨਾਂ ਵੱਖ-ਵੱਖ ਇਕਾਈਆਂ ਦੇ ਜੋੜ ਤੋਂ ਬਣਦੀ ਹੈ । ਇਹਨਾਂ ਇਕਾਈਆਂ ਵਿਚ ਇਕ ਕੁਮਬੱਧਤਾ ਅਤੇ ਨਿਸ਼ਚਿਤ ਸੰਬੰਧ ਹੁੰਦਾ ਹੈ । ਸੰਰਚਨਾ ਵਿਚ ਹਰੇਕ ਇਕਾਈ ਦਾ ਨਿਸ਼ਚਿਤ ਸਥਾਨ ਅਤੇ ਸਥਿਤੀ ਹੁੰਦੀ ਹੈ । ਕਦੇ ਵੀ ਇਕ ਇਕਾਈ ਦਾ ਸਥਾਨ ਦੂਜੀ ਇਕਾਈ ਨਹੀਂ ਲੈ ਸਕਦੀ ਅਤੇ ਨਾ ਹੀ ਕੋਈ ਇਕਾਈ ਆਪਣੀ ਸੀਮਾ ਜਾਂ ਮਰਿਆਦਾ ਤੋਂ ਬਾਹਰ · ਜਾਂਦੀ ਹੈ ।

6. ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਪਰਿਵਰਤਨਸ਼ੀਲ ਹੁੰਦੀ ਹੈ (Social Structure is changeable) – ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਕਦੇ ਵੀ ਸਥਿਰ ਨਹੀਂ ਹੁੰਦੀ ਬਲਕਿ ਪਰਿਵਰਤਨਸ਼ੀਲ ਹੁੰਦੀ ਹੈ । ਜਿਸ ਤਰੀਕੇ ਨਾਲ ਮਨੁੱਖ ਦੀ ਸਰੀਰਕ ਸੰਰਚਨਾ ਵਿਚ ਬਦਲਾਵ ਆਉਂਦੇ ਹਨ ਉਸੇ ਤਰੀਕੇ ਨਾਲ ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਵਿਚ ਵੀ ਪਰਿਵਰਤਨ ਆਉਂਦੇ ਹਨ । ਇਸ ਦਾ ਕਾਰਨ ਇਹ ਹੈ ਕਿ ਸੰਰਚਨਾ ਇਕਾਈਆਂ ਨੂੰ ਮਿਲਾ ਕੇ ਬਣਦੀ ਹੈ ਅਤੇ ਇਕਾਈਆਂ ਵਿਚ ਪਰਿਵਰਤਨ ਆਉਂਦੇ ਰਹਿੰਦੇ ਹਨ ।

7. ਸੰਰਚਨਾ ਦੇ ਕੁੱਝ ਤੱਤ ਸਰਵਵਿਆਪਕ ਹੁੰਦੇ ਹਨ (Some elements of Social Structure are universal) – ਚਾਹੇ ਸਾਰੇ ਸਮਾਜਾਂ ਦੀ ਸੰਰਚਨਾ ਵੱਖ-ਵੱਖ ਹੁੰਦੀ ਹੈ ਪਰ ਹਰੇਕ ਸਮਾਜ ਦੀ ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਵਿਚ ਕੁੱਝ ਅਜਿਹੇ ਤੱਤ ਹੁੰਦੇ ਹਨ ਜਿਹੜੇ ਸਾਰੇ ਸਮਾਜਾਂ ਵਿਚ ਇਕ ਸਮਾਨ ਜਾਂ ਸਰਵਵਿਆਪਕ ਹੁੰਦੇ ਹਨ । ਇਸ ਦਾ ਅਰਥ ਹੈ ਕਿ ਸਮਾਜ ਸੰਰਚਨਾ ਦੇ ਕੁੱਝ ਤੱਤ ਹਰੇਕ ਸਮਾਜ ਵਿਚ ਮੌਜੂਦ ਹੁੰਦੇ ਹਨ ਪਰ ਕੁੱਝ ਤੱਤ ਵੱਖ-ਵੱਖ ਸਮਾਜਾਂ ਵਿਚ ਵੱਖ-ਵੱਖ ਹੁੰਦੇ ਹਨ । ਇਹੀ ਕਾਰਨ ਹੈ ਕਿ ਇਕ ਸਮਾਜ ਦੀ ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਦੂਜੇ ਸਮਾਜ ਦੀ ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਤੋਂ ਵੱਖ ਹੁੰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਸਮਾਜਿਕ ਸੰਰਚਨਾਵਾਂ ਨੂੰ ਕਾਇਮ ਰੱਖਣ ਲਈ ਕਿਹੜੀ ਪ੍ਰਣਾਲੀ ਸਹਾਈ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਵਿੱਚ ਲਗਭਗ ਸਾਰੇ ਮਨੁੱਖਾਂ ਨੇ ਆਪਣੇ ਆਪ ਨੂੰ ਵੱਖ-ਵੱਖ ਸਭਾਵਾਂ ਨਾਲ ਸੰਗਠਿਤ ਕੀਤਾ ਹੁੰਦਾ ਹੈ ਤਾਂ ਕਿ ਕੁੱਝ ਸਮਾਨ ਉਦੇਸ਼ਾਂ ਦੀ ਪ੍ਰਾਪਤੀ ਲਈ ਕੋਸ਼ਿਸ਼ ਕੀਤੀ ਜਾ ਸਕੇ । ਪਰੰਤੁ ਇਨ੍ਹਾਂ ਉਦੇਸ਼ਾਂ ਦੀ ਪੂਰਤੀ ਤਾਂ ਹੀ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ ਜੇਕਰ ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਕੁੱਝ ਪ੍ਰਚਾਲਨ ਵਿਵਸਥਾਵਾਂ (Operational Systems) ਉੱਤੇ ਨਿਰਭਰ ਹੋਵੇ ਅਤੇ ਜੋ ਇਸਨੂੰ ਬਣਾਏ ਰੱਖਣ ਵਿੱਚ ਮੱਦਦ ਕਰ ਸਕੇ । ਇਸ ਦਾ ਅਰਥ ਹੈ ਕਿ ਕੁੱਝ ਪ੍ਰਚਾਲਨ ਵਿਵਸਥਾਵਾਂ ਅਜਿਹੀਆਂ ਹੋਣੀਆਂ ਚਾਹੀਦੀਆਂ ਹਨ ਜਿਨਾਂ ਦੀ ਮੱਦਦ ਨਾਲ ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਨੂੰ ਬਣਾ ਕੇ ਰੱਖਿਆ ਜਾ ਸਕੇ । ਕੁੱਝ-ਕੁ ਵਿਵਸਥਾਵਾਂ ਦਾ ਵਰਣਨ ਇਸ ਪ੍ਰਕਾਰ ਹੈ-

1. ਮਾਨਕ ਪ੍ਰਣਾਲੀ (Normative Systems) – ਮਾਨਕ ਪ੍ਰਣਾਲੀਆਂ ਸਮਾਜ ਦੇ ਮੈਂਬਰਾਂ ਦੇ ਸਾਹਮਣੇ ਕੁੱਝ ਆਦਰਸ਼ ਅਤੇ ਕੀਮਤਾਂ ਰੱਖਦੀਆਂ ਹਨ । ਸਮਾਜ ਦੇ ਮੈਂਬਰ ਸਮਾਜਿਕ ਕੀਮਤਾਂ ਅਤੇ ਆਦਰਸ਼ਾਂ ਦੇ ਨਾਲ ਭਾਵਾਤਮਕ ਮਹੱਤਵ (emotional importance) ਜੋੜ ਦਿੰਦੇ ਹਨ । ਵੱਖ-ਵੱਖ ਸਮੂਹ, ਸਭਾਵਾਂ, ਸੰਸਥਾਵਾਂ, ਸਮੁਦਾਇ ਆਦਿ ਇਹਨਾਂ ਨਿਯਮਾਂ, ਪਰਿਮਾਪਾਂ ਦੇ ਅਨੁਸਾਰ ਇੱਕ-ਦੂਜੇ ਨਾਲ ਅੰਤਰ ਸੰਬੰਧਿਤ ਹੁੰਦੇ ਹਨ । ਸਮਾਜ ਦੇ ਵੱਖ-ਵੱਖ ਮੈਂਬਰ ਇਹਨਾਂ ਨਿਯਮਾਂ ਪਰਿਮਾਪਾਂ ਦੇ ਅਨੁਸਾਰ ਆਪਣੀਆਂ ਭੂਮਿਕਾਵਾਂ ਨਿਭਾਉਂਦੇ ਰਹਿੰਦੇ ਹਨ ।

2. ਸਥਿਤੀ ਪ੍ਰਣਾਲੀਆ (Position System) – ਸਥਿਤੀ ਪ੍ਰਣਾਲੀ ਦਾ ਅਰਥ ਉਹਨਾਂ ਪ੍ਰਸਥਿਤੀਆਂ ਅਤੇ ਭੂਮਿਕਾਵਾਂ ਤੋਂ ਹੈ ਜੋ ਵੱਖ-ਵੱਖ ਵਿਅਕਤੀਆਂ ਨੂੰ ਦਿੱਤੇ ਜਾਂਦੇ ਹਨ | ਹਰੇਕ ਵਿਅਕਤੀ ਦੀਆਂ ਇੱਛਾਵਾਂ ਅਤੇ ਉਮੀਦਾਂ ਵੱਖ-ਵੱਖ ਅਤੇ ਅਸੀਮਿਤ ਹੁੰਦੀਆਂ ਹਨ । ਹਰੇਕ ਸਮਾਜ ਵਿੱਚ ਹਰੇਕ ਵਿਅਕਤੀ ਕੋਲ ਵੱਖ-ਵੱਖ ਅਤੇ ਬਹੁਤ ਸਾਰੀਆਂ ਸਥਿਤੀਆਂ ਜਾਂ ਪਦ ਹੁੰਦੇ ਹਨ । ਉਦਾਹਰਨ ਦੇ ਲਈ ਇੱਕ ਪਰਿਵਾਰ ਵਿੱਚ ਹੀ ਵਿਅਕਤੀ ਇੱਕ ਸਮੇਂ ਉੱਤੇ ਪੁੱਤਰ, ਪਿਤਾ, ਭਰਾ, ਜੇਠ, ਦਿਉਰ, ਜੀਜਾ, ਬਾਲਾ ਸਭ ਕੁੱਝ ਹੈ । ਜਦੋਂ ਉਹ ਆਪਣੀ ਪਤਨੀ ਨਾਲ ਗੱਲ ਕਰ ਰਿਹਾ ਹੁੰਦਾ ਹੈ ਤਾਂ ਉਸ ਸਮੇਂ ਉਹ ਪਤੀ ਦੀ ਭੂਮਿਕਾ ਨਿਭਾ ਰਿਹਾ ਹੁੰਦਾ ਹੈ । ਇਸ ਸਮੇਂ ਉਹ ਪਿਤਾ ਜਾਂ ਪੁੱਤਰ ਦੀ ਭੂਮਿਕਾ ਬਾਰੇ ਨਹੀਂ ਸੋਚ ਰਿਹਾ ਹੁੰਦਾ ਹੈ । ਦੂਜੇ ਸ਼ਬਦਾਂ ਵਿੱਚ ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਦੇ ਠੀਕ ਤਰੀਕੇ ਨਾਲ ਕੰਮ ਕਰਨ ਲਈ ਇਹ ਜ਼ਰੂਰੀ ਹੈ ਕਿ ਸਥਿਤੀਆਂ ਅਤੇ ਭੂਮਿਕਾਵਾਂ ਦੀ ਵੰਡ ਠੀਕ ਤਰੀਕੇ ਨਾਲ ਕੀਤੀ ਜਾਵੇ ।

3. ਪ੍ਰਵਾਨਗੀ ਵਿਵਸਥਾ (Sanction System) – ਨਿਯਮਾਂ ਨੂੰ ਠੀਕ ਤਰੀਕੇ ਨਾਲ ਲਾਗੂ ਕਰਨ ਲਈ ਸਮਾਜ ਇੱਕ ਪ੍ਰਵਾਨਗੀ ਵਿਵਸਥਾ ਪ੍ਰਦਾਨ ਕਰਦਾ ਹੈ । ਵੱਖ-ਵੱਖ ਭਾਗਾਂ ਦੇ ਵਿਚਕਾਰ ਤਾਲਮੇਲ ਬਠਾਉਣ ਲਈ ਇਹ ਜ਼ਰੂਰੀ ਹੈ ਕਿ ਨਿਯਮਾਂ, ਪਰਿਮਾਪਾਂ ਨੂੰ ਠੀਕ ਤਰੀਕੇ ਨਾਲ ਲਾਗੂ ਕੀਤਾ ਜਾਵੇ । ਪ੍ਰਵਾਨਗੀ ਸਕਾਰਾਤਮਕ ਵੀ ਹੋ ਸਕਦੀ ਹੈ ਅਤੇ ਨਕਾਰਾਤਮਕ ਵੀ । ਜਿਹੜੇ ਲੋਕ ਸਮਾਜਿਕ ਨਿਯਮਾਂ, ਪਰਿਮਾਪਾਂ ਨੂੰ ਮੰਨਦੇ ਹਨ ਉਹਨਾਂ ਨੂੰ ਸਮਾਜ ਵੱਲੋਂ ਇਨਾਮ ਮਿਲਦਾ ਹੈ । ਜਿਹੜੇ ਲੋਕ ਸਮਾਜ ਦੇ ਨਿਯਮਾਂ ਨੂੰ ਨਹੀਂ ਮੰਨਦੇ ਹਨ ਉਹਨਾਂ ਨੂੰ ਸਮਾਜ ਵਲੋਂ ਸਜ਼ਾ ਮਿਲਦੀ ਹੈ । ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਦੀ ਸਥਿਰਤਾ ਪ੍ਰਵਾਨਗੀ ਵਿਵਸਥਾ ਦੀ ਪ੍ਰਭਾਵਸ਼ੀਲਤਾ ਉੱਤੇ ਨਿਰਭਰ ਕਰਦੀ ਹੈ ।

4. ਪੂਰਵ ਅਨੁਮਾਨਿਤ ਕ੍ਰਿਆਵਾਂ ਦੀ ਵਿਵਸਥਾ (System of Anticipated Responses) – ਪੂਰਵ ਅਨੁਮਾਨਿਕ ਪ੍ਰਕ੍ਰਿਆਵਾਂ ਦੀ ਵਿਵਸਥਾ ਵਿਅਕਤੀਆਂ ਤੋਂ ਉਮੀਦ ਕਰਦੀ ਹੈ ਕਿ ਉਹ ਸਮਾਜਿਕ ਵਿਵਸਥਾ ਵਿੱਚ ਭਾਗ ਲੈਣ | ਸਮਾਜ ਦੇ ਮੈਂਬਰਾਂ ਦੇ ਭਾਗ ਲੈਣ ਨਾਲ ਹੀ ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਚਲਦੀ ਰਹਿੰਦੀ ਹੈ | ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਦੇ ਸਫਲਤਾਪੂਰਵਕ ਕੰਮ ਕਰਨ ਲਈ ਇਹ ਜ਼ਰੂਰੀ ਹੈ ਕਿ ਵਿਅਕਤੀਆਂ ਨੂੰ ਆਪਣੀਆਂ ਜ਼ਿੰਮੇਵਾਰੀਆਂ ਦਾ ਪਤਾ ਹੋਵੇ । ਸਮਾਜ ਦੇ ਮੈਂਬਰ ਪ੍ਰਵਾਨਿਤ ਵਿਵਹਾਰ ਨੂੰ ਸਮਾਜੀਕਰਣ ਦੀ ਪ੍ਰਕ੍ਰਿਆ ਦੀ ਮੱਦਦ ਨਾਲ ਤ੍ਰਿਣ ਕਰਦੇ ਹਨ ਜਿਸ ਨਾਲ ਉਹ ਹੋਰ ਵਿਅਕਤੀਆਂ ਦੇ ਵਿਵਹਾਰ ਦਾ ਪੁਰਵ ਅਨੁਮਾਨ ਲਗਾ ਲੈਂਦੇ ਹਨ ਅਤੇ ਉਸੇ ਤਰ੍ਹਾਂ ਵਿਵਹਾਰ ਕਰਦੇ ਹਨ । ਇਸ ਤਰ੍ਹਾਂ ਪੂਰਵ ਅਨੁਮਾਨਿਤ ਕ੍ਰਿਆਵਾਂ ਦੀ ਵਿਵਸਥਾ ਵੀ ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਦੀ ਸਥਿਰਤਾ ਦਾ ਕਾਰਨ ਬਣਦੀ ਹੈ ।

5. ਕਾਰਜਾਤਮਕ ਵਿਵਸਥਾ (Action System) – ਦਾਲਕਟ ਪਾਰਸੰਜ਼ ਨੇ ਸਮਾਜਿਕ ਕਾਰਜ (Social Action) ਦੇ ਸੰਕਲਪ ਉੱਤੇ ਕਾਫ਼ੀ ਜ਼ੋਰ ਦਿੱਤਾ ਹੈ । ਉਸਦੇ ਅਨੁਸਾਰ ਸਮਾਜਿਕ ਸੰਬੰਧਾਂ ਦਾ ਜਾਲ (ਸਮਾਜ ਵਿਅਕਤੀਆਂ ਦੇ ਵਿਚਕਾਰ ਹੋਣ ਵਾਲੀਆਂ ਕ੍ਰਿਆਵਾਂ ਅਤੇ ਅੰਤਰਕ੍ਰਿਆਵਾਂ ਵਿੱਚੋਂ ਨਿਕਲਿਆ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਕਾਰਜ ਵਿਵਸਥਾ ਇੱਕ ਪ੍ਰਮੁੱਖ ਤੱਤ ਬਣ ਦਾ ਹੈ ਜਿਸ ਨਾਲ ਸਮਾਜ ਕ੍ਰਿਆਤਮਕ (active) ਰਹਿੰਦਾ ਹੈ ਅਤੇ ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਚਲਦੀ ਰਹਿੰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਕੀ ਹੈ ? ਇਸ ਦੇ ਤੱਤ ਕਿਹੜੇ ਹਨ ?
ਉੱਤਰ-
ਮੈਕਾਈਵਰ ਦਾ ਕਹਿਣਾ ਸੀ ਕਿ ਸਮਾਜ ਸਮਾਜਿਕ ਸੰਬੰਧਾਂ ਦਾ ਜਾਲ ਹੈ । ਇਸ ਦੇ ਵੱਖ-ਵੱਖ ਹਿੱਸੇ ਹੁੰਦੇ ਹਨ ਜਿਹੜੇ ਨਾ ਕੇਵਲ ਇਕ-ਦੂਜੇ ਨਾਲ ਜੁੜੇ ਹੁੰਦੇ ਹਨ ਬਲਕਿ ਇਕ-ਦੂਜੇ ਨਾਲ ਸੰਬੰਧਿਤ ਵੀ ਹੁੰਦੇ ਹਨ : ਇਕ ਦੀ ਮੱਦਦ ਤੋਂ ਬਿਨਾਂ ਦੂਜਾ ਹਿੱਸਾ ਕਿਸੇ ਕੰਮ ਨੂੰ ਪੂਰਾ ਨਹੀਂ ਕਰ ਸਕਦਾ ਹੈ । ਇਸ ਦਾ ਅਰਥ ਹੈ ਕਿ ਇਹਨਾਂ ਹਿੱਸਿਆਂ ਵਿਚ ਮਿਲਵਰਤਨ ਹੁੰਦਾ ਹੈ । ਸਮੂਹ, ਸੰਗਠਨ, ਸੰਸਥਾਵਾਂ, ਸਭਾਵਾਂ ਆਦਿ ਇਸ ਦੀਆਂ ਇਕਾਈਆਂ ਹਨ । ਇਹਨਾਂ ਇਕਾਈਆਂ ਦੀ ਇਕੱਲੇ ਅਤੇ ਆਪਣੇ ਆਪ ਵਿਚ ਕੋਈ ਹੋਂਦ ਨਹੀਂ ਹੈ । ਜਦੋਂ ਇਹੋ ਵੱਖ-ਵੱਖ ਇਕਾਈਆਂ ਇਕ-ਦੂਜੇ ਨਾਲ ਸੰਬੰਧ ਸਥਾਪਿਤ ਕਰ ਲੈਂਦੀਆਂ ਹਨ ਤਾਂ ਇਕ ਢਾਂਚੇ ਦਾ ਰੂਪ ਧਾਰਨ ਕਰ ਲੈਂਦੀਆਂ ਹਨ । ਇਹਨਾਂ ਵਿਚ ਸੰਬੰਧ ਸਥਾਪਿਤ ਹੋ ਕੇ ਇਕ ਕੂਮ ਬਣ ਜਾਂਦਾ ਹੈ ਤਾਂ ਕਿ ਸਾਡਾ ਸਮਾਜ ਸੁਚਾਰੂ ਰੂਪ ਨਾਲ ਕੰਮ ਕਰ ਸਕੇ ।

ਉਦਾਹਰਨ ਦੇ ਤੌਰ ਉੱਤੇ ਇਕ ਸਕੂਲ ਵਿਚ ਬਹੁਤ ਸਾਰੇ ਵਿਦਿਆਰਥੀ, ਟੀਚਰ, ਚਪੜਾਸੀ, ਟੇਬਲ, ਬੈਂਚ, ਬਲੈਕ ਬੋਰਡ ਆਦਿ ਹੁੰਦੇ ਹਨ । ਪਰ ਜਦੋਂ ਤੱਕ ਇਹ ਸਹੀ ਤਰੀਕੇ ਕਿਸੇ ਕ੍ਰਮ ਅਤੇ ਵਿਵਸਥਾ ਵਿਚ ਕੰਮ ਨਹੀਂ ਕਰਦੇ, ਉਦੋਂ ਤੱਕ ਇਸ ਨੂੰ ਸਕੂਲ ਨਹੀਂ ਕਿਹਾ ਜਾ ਸਕਦਾ । ਇਸੇ ਤਰ੍ਹਾਂ ਜਦੋਂ ਸਮਾਜ ਦੀਆਂ ਵੱਖ-ਵੱਖ ਇਕਾਈਆਂ ਆਪਣੀ-ਆਪਣੀ ਥਾਂ ਉੱਤੇ ਅਤੇ ਇਕ-ਦੂਜੇ ਨਾਲ ਅੰਤਰ ਸੰਬੰਧਿਤ ਹੁੰਦੇ ਹੋਏ ਕੰਮ ਕਰਦੀਆਂ ਹਨ ਤਾਂ ਇਸ ਨੂੰ ਸੰਰਚਨਾ ਦਾ ਨਾਂ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ।

ਸਾਡੇ ਸਮਾਜ ਦੀ ਸੰਰਚਨਾ ਹਮੇਸ਼ਾਂ ਬਦਲਦੀ ਰਹਿੰਦੀ ਹੈ ਕਿਉਂਕਿ ਸਾਡਾ ਸਮਾਜ ਪਰਿਵਰਤਨਸ਼ੀਲ ਹੈ ਅਤੇ ਇਸ ਵਿਚ ਪ੍ਰਾਕ੍ਰਿਤਕ ਸ਼ਕਤੀਆਂ ‘ਤੇ ਮਨੁੱਖਾਂ ਦੀਆਂ ਖੋਜਾਂ ਕਰਕੇ ਪਰਿਵਰਤਨ ਆਉਂਦੇ ਰਹਿੰਦੇ ਹਨ । ਸਮਾਜ ਦੀਆਂ ਵੱਖ-ਵੱਖ ਇਕਾਈਆਂ ਅਮੂਰਤ ਹੁੰਦੀਆਂ ਹਨ ਜਿਸ ਕਾਰਨ ਨਾ ਤਾਂ ਅਸੀਂ ਇਹਨਾਂ ਨੂੰ ਪਕੜ ਸਕਦੇ ਹਾਂ ਤੇ ਨਾ ਹੀ ਇਹਨਾਂ ਨੂੰ ਛੂਹ ਸਕਦੇ ਹਾਂ । ਹਰੇਕ ਸਮਾਜ ਦੀਆਂ ਸੰਸਥਾਵਾਂ ਇੱਕੋ ਜਿਹੀਆਂ ਹੁੰਦੀਆਂ ਹਨ , ਜਿਵੇਂ ਕਿ-ਵਿਆਹ, ਪਰਿਵਾਰ, ਸਮੂਹ, ਸੰਸਥਾਵਾਂ, ਆਰਥਿਕ ਸੰਸਥਾਵਾਂ ਆਦਿ ਪਰ ਉਹਨਾਂ ਦੇ ਪ੍ਰਕਾਰਾਂ ਵਿਚ ਅੰਤਰ ਹੁੰਦਾ ਹੈ । ਇਸੇ ਕਾਰਨ ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਇਕ ਵਿਵਸਥਿਤ ਪ੍ਰਬੰਧ ਹੈ ਜਿਸ ਨਾਲ ਸਮਾਜਿਕ ਸੰਬੰਧਾਂ ਨੂੰ ਇਕ-ਦੂਜੇ ਨਾਲ ਜੋੜਿਆ ਜਾਂਦਾ ਹੈ ।

ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਦੇ ਤੱਤ (Elements of Social Structure) – ਮਸ਼ਹੂਰ ਸਮਾਜ ਸ਼ਾਸਤਰੀਆਂ ਦਾਲਕਟ ਪਾਰਸੰਜ਼ ਅਤੇ ਹੈਰੀ ਐੱਮ. ਜਾਨਸਨ ਨੇ ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਦੇ ਚਾਰ ਮੁੱਖ ਤੱਤ ਦੱਸੇ ਹਨ, ਜਿਨ੍ਹਾਂ ਦਾ ਵਰਣਨ ਇਸ ਪ੍ਰਕਾਰ ਹੈ-

1. ਉਪ-ਸਮੂਹ (Sub-groups) – ਦਾਲਕਟ ਪਾਰਜ਼ ਦੇ ਅਨੁਸਾਰ ਇਕਾਈਆਂ ਦਾ ਉਪ-ਸਮੂਹਾਂ ਤੋਂ ਹੀ ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਦਾ ਨਿਰਮਾਣ ਹੁੰਦਾ ਹੈ । ਕਈ ਉਪ-ਸਮੂਹਾਂ ਤੋਂ ਇਕ ਵੱਡਾ ਸਮੂਹ ਬਣਦਾ ਹੈ । ਉਦਾਹਰਨ ਦੇ ਤੌਰ ਉੱਤੇ ਕਿਸੇ ਯੂਨੀਵਰਸਿਟੀ ਅਰਥਾਤ ਵੱਡੇ ਸਮੂਹ ਵਿਚ ਬਹੁਤ ਸਾਰੇ ਵਿਭਾਗ ਅਰਥਾਤ ਉਪ-ਸਮੂਹ ਹੁੰਦੇ ਹਨ । ਇਹ ਸਾਰੇ ਉਪ-ਸਮੂਹ ਕਿਸੇ ਨਾ ਕਿਸੇ ਤਰੀਕੇ ਨਾਲ ਇਕ-ਦੂਜੇ ਨਾਲ ਜੁੜੇ ਹੁੰਦੇ ਹਨ । ਇਹਨਾਂ ਉਪ-ਸਮੂਹਾਂ ਵਿਚ ਵਿਅਕਤੀਆਂ ਨੂੰ ਪਦ ਅਤੇ ਭੂਮਿਕਾਵਾਂ ਮਿਲੀਆਂ ਹੁੰਦੀਆਂ ਹਨ ; ਹਰੇਕ ਵਿਅਕਤੀ ਦਾ ਪਦ ਅਤੇ ਭੂਮਿਕਾ ਨਿਸ਼ਚਿਤ ਹੁੰਦੀ ਹੈ । ਉਹ ਵਿਅਕਤੀ ਰਿਟਾਇਰ ਹੋਣ ਤੋਂ ਬਾਅਦ ਜਾਂ ਮੌਤ ਤੋਂ ਬਾਅਦ ਉਹ ਸਥਾਨ ਛੱਡ ਕੇ ਚਲੇ ਜਾਂਦੇ ਹਨ ਪਰ ਪਦ ਅਤੇ ਭੂਮਿਕਾ ਉੱਥੇ ਹੀ ਨਿਸ਼ਚਿਤ ਰਹਿੰਦੇ ਹਨ । ਇਸ ਦੀ ਉਦਾਹਰਨ ਅਸੀਂ ਲੈ ਸਕਦੇ ਹਾਂ ਕਿਸੇ ਕਾਲਜ ਦੇ ਪ੍ਰਿੰਸੀਪਲ ਦੀ । ਪ੍ਰਿੰਸੀਪਲ ਬਦਲੀ ਹੋਣ ਤੋਂ ਬਾਅਦ ਜਾਂ ਮੌਤ ਤੋਂ ਬਾਅਦ ਜਾਂ ਨੌਕਰੀ ਛੱਡਣ ਤੋਂ ਬਾਅਦ ਆਪਣਾ ਸਥਾਨ ਛੱਡ ਕੇ ਚਲਾ ਜਾਂਦਾ ਹੈ ਪਰ ਉਸ ਦਾ ਪਦ ਅਤੇ ਭੂਮਿਕਾ ਉੱਥੇ ਹੀ ਨਿਸ਼ਚਿਤ ਰਹਿੰਦੇ ਹਨ । ਇਸ ਦਾ ਅਰਥ ਇਹ ਹੈ ਕਿ ਉਪ-ਸਮੂਹ ਸਥਾਈ ਹੁੰਦੇ ਹਨ, ਜਿਹੜੇ ਕਦੇ ਵੀ ਖ਼ਤਮ ਨਹੀਂ ਹੁੰਦੇ । ਚਾਹੇ ਇਹਨਾਂ ਸਮੂਹਾਂ ਦੇ ਮੈਂਬਰ ਬਦਲ ਜਾਂਦੇ ਹਨ ਪਰ ਇਹ ਸਮੁਹ ਨਹੀਂ ਬਦਲਦੇ : ਇਸ ਤਰ੍ਹਾਂ ਇਹ ਉਪ-ਸਮੂਹ ਸੰਰਚਨਾ ਦੇ ਮੁੱਖ ਤੱਤਾਂ ਵਿਚੋਂ ਇਕ ਹਨ । ਚਾਹੇ ਇਸਦੇ ਮੈਂਬਰ ਬਦਲਦੇ ਰਹਿੰਦੇ ਹਨ ਪਰ ਉਪ-ਸਮੂਹ ਸਥਿਰ ਹੀ ਰਹਿੰਦੇ ਹਨ ।

2. ਭੂਮਿਕਾ (Role) – ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਦੀਆਂ ਇਕਾਈਆਂ ਦੇ ਉਪ-ਸਮੂਹ ਹੁੰਦੇ ਹਨ ਤੇ ਇਹਨਾਂ ਸਮੂਹਾਂ ਵਿਚ ਮੈਂਬਰਾਂ ਨੂੰ ਨਿਸ਼ਚਿਤ ਨਿਯਮਾਂ ਦੇ ਅਨੁਸਾਰ ਭੂਮਿਕਾਵਾਂ ਦਿੱਤੀਆਂ ਜਾਂਦੀਆਂ ਹਨ । ਸਮਾਜ ਸਮਾਜਿਕ ਸੰਬੰਧਾਂ ਕਰਕੇ ਹੀ ਬਣਦਾ ਹੈ ਤੇ ਸੰਬੰਧ ਬਣਾਉਣ ਲਈ ਵਿਅਕਤੀਆਂ ਤੇ ਸਮੂਹਾਂ ਦੇ ਵਿਚ ਅੰਤਰ-ਕਿਰਿਆਵਾਂ ਹੋਣੀਆਂ ਜ਼ਰੂਰੀ ਹਨ । ਇਹਨਾਂ ਅੰਤਰ-ਕਿਰਿਆਵਾਂ ਨੂੰ ਸਪੱਸ਼ਟ ਕਰਨ ਦੇ ਲਈ ਵਿਅਕਤੀਆਂ ਨੂੰ ਭੂਮਿਕਾਵਾਂ ਦਿੱਤੀਆਂ ਜਾਂਦੀਆਂ ਹਨ । ਭੂਮਿਕਾ ਕਿਸੇ ਵਿਸ਼ੇਸ਼ ਸਥਿਤੀ ਵਿਚ ਵਿਅਕਤੀ ਦੁਆਰਾ ਕੀਤਾ ਗਿਆ ਵਿਵਹਾਰ ਹੁੰਦਾ ਹੈ ਜਿਹੜੇ ਕਿ ਉਸ ਵਿਅਕਤੀ ਨੂੰ ਪ੍ਰਾਪਤ ਵਿਸ਼ੇਸ਼ ਪਦ ਨਾਲ ਸੰਬੰਧਿਤ ਹੁੰਦਾ ਹੈ ਤੇ ਉਹਨਾਂ ਨੂੰ ਸਮਾਜਿਕ ਪ੍ਰਵਾਨਗੀ ਦੁਆਰਾ ਨਿਰਧਾਰਿਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਜੇਕਰ ਸਮਾਜਿਕ ਸੰਰਚਨਾਂ ਵਿਚ ਕਿਸੇ ਪ੍ਰਕਾਰ ਦਾ ਪਰਿਵਰਤਨ ਆਉਂਦਾ ਹੈ ਤਾਂ ਸਮਾਜ ਦੇ ਮੈਂਬਰਾਂ ਦੇ ਪਦਾਂ ਅਤੇ ਭੂਮਿਕਾਵਾਂ ਵਿਚ ਵੀ ਪਰਿਵਰਤਨ ਆ ਜਾਂਦਾ ਹੈ । ਇਹਨਾਂ ਭੂਮਿਕਾਵਾਂ ਦੇ ਕਾਰਨ ਹੀ ਲੋਕਾਂ ਵਿਚ ਸੰਬੰਧ ਸਥਾਪਿਤ ਰਹਿੰਦੇ ਹਨ ਅਤੇ ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਕਾਇਮ ਰਹਿੰਦੀ ਹੈ ।

3. ਸਮਾਜਿਕ ਪਰਿਮਾਪ (Social Norms) – ਸਮਾਜਿਕ ਪਰਿਮਾਪਾਂ ਦੇ ਰਾਹੀਂ ਵਿਅਕਤੀਆਂ ਦੇ ਕੰਮ ਨਿਸ਼ਚਿਤ ਕੀਤੇ ਜਾਂਦੇ ਹਨ । ਉਪ-ਸਮੂਹ ਅਤੇ ਭੂਮਿਕਾਵਾਂ ਸਮਾਜਿਕ ਪਰਿਮਾਪਾਂ ਨਾਲ ਸੰਬੰਧਿਤ ਹੁੰਦੇ ਹਨ ਤੇ ਇਸੇ ਕਰਕੇ ਹੀ ਉਪ-ਸਮੂਹ ਤੇ ਭੂਮਿਕਾਵਾਂ ਸਥਿਰ ਰਹਿੰਦੇ ਹਨ । ਸਮਾਜਿਕ ਪਰਿਮਾਪ ਵਿਅਕਤੀਗਤ ਵਿਵਹਾਰ ਦੇ ਉਹ ਸਮਾਜ ਵਲੋਂ ਪ੍ਰਵਾਨ ਕੀਤੇ ਤਰੀਕੇ ਹੁੰਦੇ ਹਨ ਜਿਨ੍ਹਾਂ ਨਾਲ ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਦਾ ਨਿਰਮਾਣ ਹੁੰਦਾ ਹੈ । ਸਮਾਜਿਕ ਪਰਿਮਾਪਾਂ ਵਿਚ ਬਹੁਤ ਸਾਰੇ ਨਿਯਮ ਤੇ ਉਪਨਿਯਮ ਹੁੰਦੇ ਹਨ । ਸਮਾਜਿਕ ਆਦਰਸ਼ ਵੀ ਸਮਾਜਿਕ ਪਰਿਮਾਪਾਂ ਨਾਲ ਸੰਬੰਧਿਤ ਹੁੰਦੇ ਹਨ । ਸਮਾਜਿਕ ਪਰਿਮਾਪਾਂ ਦੀ ਅਣਹੋਂਦ ਵਿਚ ਨਾ ਤਾਂ ਵਿਅਕਤੀਆਂ ਨੂੰ ਆਪਣੀਆਂ ਜ਼ਿੰਮੇਦਾਰੀਆਂ ਦਾ ਪਤਾ ਚਲੇਗਾ ਅਤੇ ਨਾ ਹੀ ਸਾਡੀ ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਸਥਿਰ ਰਹੇਗੀ । ਉਦਾਹਰਨ ਦੇ ਤੌਰ ਉੱਤੇ ਜੇਕਰ ਸਕੂਲ ਦਾ ਸਟਾਫ਼ ਨਿਯਮਾਂ ਜਾਂ ਪਰਿਮਾਪਾਂ ਦੇ ਅਨੁਸਾਰ ਨਾ ਚਲੇ ਤਾਂ ਸਕੂਲ ਦਾ ਢਾਂਚਾ ਹਿੱਲ ਜਾਵੇਗਾ । ਪਰਿਮਾਪਾਂ ਨਾਲ ਹੀ ਵਿਅਕਤੀ ਦੇ ਵਿਵਹਾਰ ਨੂੰ ਵਿਸ਼ੇਸ਼ ਹਾਲਾਤਾਂ ਵਿਚ ਨਿਰਦੇਸ਼ਿਤ ਅਤੇ ਸੰਚਾਲਿਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਇਸ ਨਾਲ ਹੀ ਸਮਾਜਿਕ ਭੂਮਿਕਾਵਾਂ ਤੇ ਉਪ-ਸਮੂਹ ਸਥਿਰ ਰਹਿੰਦੇ ਹਨ । ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਵਿਚ ਸਮਾਜਿਕ ਪਰਿਮਾਪਾਂ ਦੀ ਬਹੁਤ ਮਹੱਤਤਾ ਹੈ ।

4. ਸਮਾਜਿਕ ਕੀਮਤਾਂ (Social Values) – ਕੀਮਤਾਂ ਉਹ ਮਾਪਦੰਡ ਹੁੰਦੀਆਂ ਹਨ, ਜਿਨ੍ਹਾਂ ਦੇ ਨਾਲ ਸਮਾਜਿਕ ਪਰਿਮਾਪਾਂ ਦਾ ਮੁਲਾਂਕਣ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਇਹ ਸਮਾਜ ਦੇ ਮੈਂਬਰਾਂ ਦੀਆਂ ਭਾਵਨਾਵਾਂ ਦੇ ਅਨੁਸਾਰ ਹੀ ਹੁੰਦੀਆਂ ਹਨ । ਮਨੁੱਖ ਜਦੋਂ ਵੀ ਕੋਈ ਫ਼ੈਸਲਾ ਲੈਂਦਾ ਹੈ ਜਾਂ ਕਿਸੇ ਚੀਜ਼ ਬਾਰੇ ਗੱਲ ਕਰਦਾ ਹੈ ਤਾਂ ਉਹ ਸਮਾਜਿਕ ਕੀਮਤਾਂ ਦੇ ਅਨੁਸਾਰ ਹੀ ਫ਼ੈਸਲਾ ਲੈਂਦਾ ਹੈ ਜਾਂ ਗੱਲ ਕਰਦਾ ਹੈ । ਕੀਮਤਾਂ ਸਾਧਾਰਨ ਮਾਪਦੰਡ ਹੁੰਦੀਆਂ ਹਨ । ਕੀਮਤਾਂ ਨੂੰ ਉੱਚੇ ਪੱਧਰ ਤੇ ਪਰਿਮਾਪ ਵੀ ਕਿਹਾ ਜਾ ਸਕਦਾ ਹੈ । ਸਮਾਜਿਕ ਵਿਵਸਥਾ ਨੂੰ ਕਾਇਮ ਰੱਖਣ ਲਈ ਅਤੇ ਸਮਾਜਿਕ ਵਿਘਟਨ ਨੂੰ ਰੋਕਣ ਲਈ ਸਮਾਜਿਕ ਕੀਮਤਾਂ ਦਾ ਆਪਣਾ ਹੀ ਵਿਸ਼ੇਸ਼ ਮਹੱਤਵ ਹੁੰਦਾ ਹੈ । ਕਿਸੇ ਵੀ ਸਮੂਹ ਦੀਆਂ ਭਾਵਨਾਵਾਂ ਦਾ ਸੰਬੰਧ ਸਮਾਜਿਕ ਕੀਮਤਾਂ ਨਾਲ ਹੁੰਦਾ ਹੈ । ਸਮਾਜਿਕ ਕੀਮਤਾਂ ਦੇ ਵਿਚ ਇਕ ਪ੍ਰਕਾਰ ਦਾ ਕਾਰਜਾਤਮਕ ਸੰਬੰਧ ਹੁੰਦਾ ਹੈ । ਜਿਸ ਨਾਲ ਸਮਾਜਿਕ ਕੀਮਤਾਂ ਦੇ ਵਿਚ ਇਕ ਪ੍ਰਕਾਰ ਦਾ ਕਾਰਜਾਤਮਕ ਸੰਬੰਧ ਹੁੰਦਾ ਹੈ ਜਿਸ ਨਾਲ ਸਮਾਜਿਕ ਸੰਬੰਧ ਟੁੱਟਦੇ ਨਹੀਂ ਅਤੇ ਸਮਾਜਿਕ ਵਿਵਸਥਾ ਕਾਇਮ ਰਹਿੰਦੀ ਹੈ । ਵਿਅਕਤੀ ਅਤੇ ਸਮੂਹ ਵਿਚ ਭਾਵਨਾਵਾਂ ਦਾ ਤਾਲਮੇਲ ਸਥਾਪਿਤ ਹੋ ਜਾਂਦਾ ਹੈ ਜਿਸ ਨਾਲ ਵਿਵਹਾਰਾਂ ਦੇ ਮੁਲਾਂਕਣ ਕਰਨ ਲਈ ਕੀਮਤਾਂ ਨੂੰ ਮਾਪਦੰਡਾਂ ਦੇ ਰੂਪ ਵਿਚ ਪ੍ਰਯੋਗ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਸਮਾਜਿਕ ਕੀਮਤਾਂ ਦੇ ਨਾਲ ਵਿਅਕਤੀਆਂ ਜਾਂ ਸਮੂਹਾਂ ਦੀਆਂ ਕਿਰਿਆਵਾਂ ਦੀ ਜਾਂਚ ਕਰਕੇ ਉਹਨਾਂ ਨੂੰ ਚੰਗੇ ਜਾਂ ਮਾੜੇ ਦੀ ਸ਼੍ਰੇਣੀ ਵਿਚ ਰੱਖ ਸਕਦੇ ਹਾਂ ।

ਪ੍ਰਸ਼ਨ 4
ਰੁਤਬਾ ਕੀ ਹੈ ? ਇਸ ਦੀਆਂ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ‘ਤੇ ਵਿਸਤਰਿਤ ਨੋਟ ਲਿਖੋ ।
ਉੱਤਰ-
ਰੁਤਬੇ ਦਾ ਅਰਥ (Meaning of Status) – ਕਿਸੇ ਵੀ ਸਮਾਜ ਵਿੱਚ ਵਿਅਕਤੀ ਵਿਸ਼ੇਸ਼ ਦੀ ਸਮਾਜਿਕ ਸਥਿਤੀ ਸਮਾਜਿਕ ਕੀਮਤਾਂ ਦੇ ਅਨੁਸਾਰ ਹੁੰਦੀ ਹੈ । ਉਦਾਹਰਨ ਦੇ ਲਈ ਭਾਰਤੀ ਸਮਾਜਾਂ ਦੇ ਵਿੱਚ ਵਿਅਕਤੀ ਨੂੰ ਸਮਾਜਿਕ ਸਥਿਤੀ ਲਿੰਗ ਦੇ ਅਨੁਸਾਰ ਹੀ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਸੀ । ਕਿਸੇ ਸਮੂਹ ਵਿੱਚ ਵਿਅਕਤੀ ਨੂੰ ਜੋ ਸਥਾਨ ਮਿਲਦਾ ਹੈ ਉਸਨੂੰ ਉਸਦੀ ਸਥਿਤੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਇਹ ਸਥਿਤੀ ਵਿਅਕਤੀ ਨੂੰ ਆਪਣੇ ਕਾਰਜਾਂ ਅਤੇ ਵਿਸ਼ੇਸ਼ ਕਿਸਮਾਂ ਦੁਆਰਾ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ ਤੇ ਇਨ੍ਹਾਂ ਨੂੰ ਸਮਾਜ ਦੁਆਰਾ ਸਵੀਕਾਰ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਵਿਅਕਤੀ ਨੂੰ ਸਮਾਜ ਵਿਚ ਰਹਿ ਕੇ ਅਨੇਕਾਂ ਪ੍ਰਕਾਰ ਦੀਆਂ ਭੂਮਿਕਾਵਾਂ ਅਦਾ ਕਰਨੀਆਂ ਪੈਂਦੀਆਂ, ਹਨ । ਵਿਅਕਤੀ ਜਿਸ ਸਮੂਹ ਵਿੱਚ ਜਾਂਦਾ ਹੈ ਜਾਂ ਭਾਗ ਲੈਂਦਾ ਹੈ ਉਸਦੇ ਅਨੁਸਾਰ ਹੀ ਉਸਦਾ ਉਸ ਵਿੱਚ ਪਦ ਨਿਰਧਾਰਿਤ ਹੋ ਜਾਂਦਾ ਹੈ । ਕਿਸੇ ਸਮੂਹ ਜਾਂ ਸੰਸਥਾ ਵਿੱਚ ਵਿਅਕਤੀ ਦਾ ਪਦ ਜਿੰਨਾ ਉੱਚਾ ਜਾਂ ਨੀਵਾਂ ਹੁੰਦਾ ਹੈ ਉਤਨੀ ਹੀ ਉਸਦੀ ਸਮਾਜ ਵਿਚ ਸਮਾਜਿਕ ਸਥਿਤੀ ਵੀ ਉਸਦੇ ਅਨੁਸਾਰ ਹੀ ਨਿਰਧਾਰਿਤ ਹੋ ਜਾਂਦੀ ਹੈ । ਕਿਸੇ ਵੀ ਵਿਅਕਤੀ ਦਾ ਪਦ ਮਾਲਕ, ਨੌਕਰ, ਪਤੀ, ਪੁੱਤਰ, ਪਿਤਾ ਦੇ ਰੂਪ ਵਿਚ ਵੀ ਹੋ ਸਕਦਾ ਹੈ ।

ਪਦ ਵਿਅਕਤੀ ਦੀ ਉਹ ਸਮਾਜਿਕ ਸਥਿਤੀ ਹੁੰਦੀ ਹੈ ਜਿਸ ਨੂੰ ਉਹ ਸਮਾਜ ਵਿਚ ਰਹਿ ਕੇ ਹੀ ਪ੍ਰਾਪਤ ਕਰ ਸਕਦਾ ਹੈ । ਇਹ ਸਮਾਜਿਕ ਸਥਿਤੀ ਸਮਾਜ ਦੇ ਮੈਂਬਰਾਂ ਦੁਆਰਾ ਉਸ ਨੂੰ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ । ਸਮਾਜ ਵਿਚ ਜਨਮ ਲੈਣ ਨਾਲ ਹੀ ਵਿਅਕਤੀ ਨੂੰ ਕੋਈ ਨਾ ਕੋਈ ਪਦ ਜ਼ਰੂਰ ਮਿਲ ਜਾਂਦਾ ਹੈ ! ਪਦ ਦੀ ਪ੍ਰਾਪਤੀ ਹੀ ਵਿਅਕਤੀ ਨੂੰ ਪੂਰਨ ਸਮਾਜਿਕ ਸਥਿਤੀ ਪ੍ਰਦਾਨ ਕਰਦੀ ਹੈ ਜਿਸ ਨਾਲ ਸਮਾਜਿਕ ਪ੍ਰਾਣੀਆਂ ਵਿੱਚ ਸਮਾਜਿਕ ਵਿਵਸਥਾ ਕਾਇਮ ਰਹਿੰਦੀ ਹੈ । ਵਿਅਕਤੀ ਕਿਸ ਪਦ ਤੇ ਬਿਰਾਜਮਾਨ ਹੈ ਉਸਦਾ ਪ੍ਰਗਟਾਵਾ ਇਸ ਪਦ ਨਾਲ ਜੁੜੇ ਹੋਏ ਕੰਮਾਂ ਨੂੰ ਕਰਕੇ ਹੀ ਕਰਦਾ ਹੈ ਜਿਸ ਨਾਲ ਉਸਦੇ ਪਦ ਦੀ ਤੁਲਨਾ ਦੂਸਰੇ ਵਿਅਕਤੀ ਦੇ ਪਦ ਨਾਲ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ । ਇਹ ਪਦ ਵਿਅਕਤੀ ਦੀ ਪਛਾਣ ਬਣ ਜਾਂਦਾ ਹੈ ।

ਪਦ ਦੀਆਂ ਪਰਿਭਾਸ਼ਾਵਾਂ (Definitions of Status)

• ਮੈਕਾਈਵਰ ਅਤੇ ਪੇਜ (MacIver and Page) ਦੇ ਅਨੁਸਾਰ, “ਪਦ ਉਹ ਸਮਾਜਿਕ ਸਥਾਨ ਹੈ ਜੋ ਉਸ ਨੂੰ ਗ੍ਰਹਿਣ ਕਰਨ ਵਾਲੇ ਦੇ ਲਈ ਉਸਦੇ ਵਿਅਕਤੀਗਤ ਗੁਣਾਂ ਅਤੇ ਸਮਾਜਿਕ ਸੇਵਾਵਾਂ ਦੇ ਇਲਾਵਾ, ਆਦਰ, ਪ੍ਰਤਿਸ਼ਠਾ ਅਤੇ ਪ੍ਰਭਾਵ ਦੀ ਮਾਤਰਾ ਨਿਸ਼ਚਿਤ ਕਰਦਾ ਹੈ ।”
• ਲਿੰਟਨ (Linton) ਦੇ ਅਨੁਸਾਰ, “ਕਿਸੇ ਵਿਵਸਥਾ ਵਿਸ਼ੇਸ਼ ਵਿੱਚ ਕਿਸੇ ਸਮੇਂ ਵਿਸ਼ੇਸ਼ ਵਿੱਚ ਇੱਕ ਵਿਅਕਤੀ ਨੂੰ ਜੋ ਸਥਾਨ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ਉਹ ਹੀ ਉਸਦੀ ਵਿਵਸਥਾ ਦੇ ਵਿੱਚ ਉਸ ਵਿਅਕਤੀ ਦਾ ਪਦ ਜਾਂ ਸਥਿਤੀ ਹੁੰਦੀ ਹੈ । ਆਪਣੀ ਸਥਿਤੀ ਨੂੰ ਵੈਧ ਸਿੱਧ ਕਰਨ ਲਈ ਵਿਅਕਤੀ ਨੂੰ ਜੋ ਕੁਝ ਕਰਨਾ ਪੈਂਦਾ ਹੈ, ਉਸ ਨੂੰ ਪਦ ਕਹਿੰਦੇ ਹਨ ।”
• ਕਿੰਗਸਲੇ ਡੇਵਿਸ (Kingsley Davis) ਦੇ ਅਨੁਸਾਰ, “ਪਦ ਆਮ ਸਮਾਜਿਕ ਵਿਵਸਥਾ ਵਿੱਚ ਸਾਰੇ ਸਮਾਜ ਦੁਆਰਾ ਮਾਨਤਾ ਪ੍ਰਾਪਤ ਅਤੇ ਪ੍ਰਦਾਨ ਕੀਤੇ ਗਏ ਅਹੁਦੇ ਹਨ ਜੋ ਵਿਚਾਰ ਪੂਰਵ ਨਿਯਮਿਤ ਨਾ ਹੋ ਕੇ ਆਪਣੇ ਆਪ ਵਿਕਸਤ ਹੁੰਦੇ ਹਨ ਅਤੇ ਲੋਕਾਂ ਦੇ ਵਿਚਾਰਾਂ ਅਤੇ ਲੋਕ ਰੀਤੀਆਂ ਉੱਤੇ ਆਧਾਰਿਤ ਹੁੰਦਾ ਹੈ ।”

ਇਸ ਤਰ੍ਹਾਂ ਇਹਨਾਂ ਪਰਿਭਾਸ਼ਾਵਾਂ ਦੇ ਆਧਾਰ ਉੱਤੇ ਅਸੀਂ ਕਹਿ ਸਕਦੇ ਹਾਂ ਕਿ ਸਮੂਹ ਦੇ ਵਿਚ ਇੱਕ ਨਿਸ਼ਚਿਤ ਸਮੇਂ ਵਿਚ ਵਿਅਕਤੀ ਨੂੰ ਜਿਹੜਾ ਦਰਜਾ ਜਾਂ ਸਥਾਨ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ਉਹ ਉਸਦਾ ਸਮਾਜਿਕ ਪਦ ਹੁੰਦਾ ਹੈ । ਪਦ ਸਮੂਹ ਵਿਚ ਹੁੰਦਾ ਹੈ ਇਸ ਲਈ ਉਹ ਜਿੰਨੇ ਸਮੂਹਾਂ ਦਾ ਮੈਂਬਰ ਹੁੰਦਾ ਹੈ ਉਸ ਨੂੰ ਉਹਨੇ ਹੀ ਪਦ ਪ੍ਰਾਪਤ ਹੁੰਦੇ ਹਨ । ਸਮਾਜ ਦੁਆਰਾ ਨਿਸ਼ਚਿਤ ਕੀਤੀ ਗਈ ਵਿਅਕਤੀ ਦੀ ਉਹ ਸਥਿਤੀ ਜਿਸਨੂੰ ਉਹ ਆਪਣੇ ਜਨਮ, ਲਿੰਗਕ ਭਿੰਨਤਾਵਾਂ, ਵਿਆਹ, ਯੋਗਤਾਵਾਂ, ਕਰਤੱਵਾਂ ਆਦਿ ਨਾਲ ਪ੍ਰਾਪਤ ਕਰਦਾ ਹੈ ਉਹ ਇਸਦਾ ਪਦ ਅਖਵਾਉਂਦੀ ਹੈ ਅਤੇ ਇਸ ਪਦ ਨਾਲ ਜੁੜੇ ਹੋਏ ਸਾਰੇ ਕੰਮ ਉਸਨੂੰ ਕਰਨੇ ਪੈਂਦੇ ਹਨ ।

ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ (Characteristics)

(1) ਹਰੇਕ ਪਦ ਦਾ ਸਮਾਜਿਕ ਸਮੂਹਕਤਾ ਵਿੱਚ ਇੱਕ ਸਥਾਨ ਹੁੰਦਾ ਹੈ (Every Status has a place in society) – ਹਰੇਕ ਸਮਾਜ ਦੀ ਪਛਾਣ ਉਸਦੇ ਵਿਸ਼ੇਸ਼ ਅਧਿਕਾਰਾਂ, ਆਦਰ ਅਤੇ ਕੰਮਾਂ ਦੇ ਪਰਿਮਾਪਾਂ ਦੁਆਰਾ ਕੀਤੀ ਜਾਂਦੀ ਹੈ । ਉਦਾਹਰਣ ਦੇ ਲਈ ਹਸਪਤਾਲ ਵਿਚ ਡਾਕਟਰ ਅਤੇ ਨਰਸ ਦਾ ਪਦ ਅਲੱਗ-ਅਲੱਗ ਹੁੰਦਾ ਹੈ । ਪਰ ਦੋਵਾਂ ਨੂੰ ਸਮੂਹਿਕਤਾ ਦੇ ਆਧਾਰ ਤੇ ਪਛਾਣਿਆ ਜਾਂਦਾ ਹੈ ।

(2) ਪਦ ਦੇ ਆਧਾਰ ਤੇ ਸਮਾਜ ਵਿਚ ਸੱਤਰੀਕਰਣ ਹੋ ਜਾਂਦਾ ਹੈ (Stratification in society based on status) – ਪਦ ਦੁਆਰਾ ਹੀ ਵਿਅਕਤੀ ਵੱਖ-ਵੱਖ ਸ਼੍ਰੇਣੀਆਂ ਵਿਚ ਸਥਾਨ ਪ੍ਰਾਪਤ ਕਰਦਾ ਹੈ । ਉਹ ਜ਼ਿਆਦਾ ਮਿਹਨਤ ਕਰਕੇ ਉੱਚੇ ਪਦ ਨੂੰ ਪ੍ਰਾਪਤ ਕਰ ਸਕਦਾ ਹੈ ਅਤੇ ਨਾ ਕੰਮ ਕਰਨ ਤੇ ਆਪਣੇ ਪਦ ਤੋਂ ਵੰਚਿਤ ਵੀ ਹੋ ਸਕਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਸਮਾਜ ਵਿੱਚ ਨਿਰੰਤਰ ਗਤੀਸ਼ੀਲਤਾ ਹੁੰਦੀ ਰਹਿੰਦੀ ਹੈ ।

(3) ਵਿਅਕਤੀ ਦਾ ਪਦ ਸਮਾਜ ਦੀ ਸੰਸਕ੍ਰਿਤੀ ਦੁਆਰਾ ਹੁੰਦਾ ਹੈ (Status of man determined by culture of the society) – ਵਿਅਕਤੀ ਦਾ ਪਦ ਸਮਾਜ ਦੀਆਂ ਸੰਸਕ੍ਰਿਤਕ ਕੀਮਤਾਂ ਦੁਆਰਾ ਨਿਰਧਾਰਿਤ ਹੁੰਦਾ ਹੈ । ਕਿਹੜਾ ਵਿਅਕਤੀ ਕਿਸ ਪਦ ਉੱਤੇ ਬੈਠੇਗਾ, ਇਸ ਪਦ ਨਾਲ ਜੁੜੇ ਹੋਏ ਕਿਹੜੇ ਅਧਿਕਾਰ ਅਤੇ ਕਰਤੱਵ ਹਨ ਇਸਦਾ ਫ਼ੈਸਲਾ ਸਮਾਜ ਦੇ ਬਣਾਏ ਹੋਏ ਨਿਯਮ ਕਰਨਗੇ ਨਾ ਕਿ ਵਿਅਕਤੀ । ਸਮਾਜ ਵਿੱਚ ਵਿਅਕਤੀ ਨੂੰ ਜੋ ਪਦ ਜਾਂ ਸਥਿਤੀ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ । ਉਸਨੂੰ ਉਸ ਨਾਲ ਸੰਬੰਧਿਤ ਕੰਮ ਵੀ ਕਰਨੇ ਪੈਂਦੇ ਹਨ ।

(4) ਪਦ ਦੇ ਦੁਆਰਾ ਵਿਅਕਤੀ ਦੀ ਭੂਮਿਕਾ ਵੀ ਨਿਸ਼ਚਿਤ ਹੁੰਦੀ ਹੈ (Role of individual determine by status) – ਕਿਸੇ ਵੀ ਪਦ ਦੀ ਪ੍ਰਾਪਤੀ ਤੋਂ ਬਾਅਦ ਵਿਅਕਤੀ ਨੂੰ ਉਸ ਪਦ ਵਿਸ਼ੇਸ਼ ਨਾਲ ਜੁੜੀਆਂ ਹੋਈਆਂ ਭੂਮਿਕਾਵਾਂ ਵੀ ਨਿਭਾਉਣੀਆਂ ਪੈਂਦੀਆਂ ਹਨ । ਇਹ ਭੂਮਿਕਾਵਾਂ ਸਮਾਜ ਦੇ ਮਹੱਤਵਪੂਰਨ ਕਾਰਜਾਂ ਨਾਲ ਸੰਬੰਧਿਤ ਹੁੰਦੀਆਂ ਹਨ । ਇਹਨਾਂ ਦਾ ਸਮਾਜ ਵਿੱਚ ਵਿਸ਼ੇਸ਼ ਸਥਾਨ ਹੋਣ ਕਰਕੇ ਇਹਨਾਂ ਨੂੰ ਸਮਾਜ ਲਈ ਖ਼ਾਸ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ ।

(5) ਸਮਾਜ ਵਿਚ ਵਿਅਕਤੀ ਦੇ ਪਦ ਨੂੰ ਸਮਝਣ ਦੇ ਲਈ ਦੂਜੇ ਵਿਅਕਤੀਆਂ ਦੇ ਪਦਾਂ ਦੀ ਤੁਲਨਾ ਨਾਲ ਸੰਬੰਧਿਤ ਕਰਕੇ ਹੀ ਜਾਣਿਆ ਜਾਂਦਾ ਹੈ। (We can understand the status of individual only in comparisorrwith the status of other individuals) – ਜਿਵੇਂਮਰੀਜ਼ ਤੋਂ ਬਿਨਾਂ ਡਾਕਟਰ ਦੀ ਸਥਿਤੀ ਅਸੰਭਵ ਹੁੰਦੀ ਹੈ, ਅਧਿਆਪਕ ਤੋਂ ਬਿਨਾਂ ਵਿਦਿਆਰਥੀਆਂ ਦੀ, ਪਤੀ-ਪਤਨੀ, ਭਰਾ-ਭੈਣ ਆਦਿ ਦੇ ਬਿਨਾਂ ਵਿਅਕਤੀਆਂ ਦੇ ਪਦ ਨੂੰ ਜਾਣਨਾ ਮੁਸ਼ਕਲ ਹੁੰਦਾ ਹੈ ਉਸੇ ਤਰ੍ਹਾਂ ਪਦ ਤੁਲਨਾਤਮਕ ਸ਼ਬਦ ਹੈ ਜਿਸਨੂੰ ਕਿ ਦੂਜੇ ਵਿਅਕਤੀਆਂ ਦੇ ਸੰਦਰਭ ਵਿੱਚ ਪਛਾਣਿਆ ਜਾ ਸਕਦਾ ਹੈ ।

(6) ਇੱਕ ਵਿਅਕਤੀ ਕਈ ਪਦਾਂ ਉੱਤੇ ਹੋ ਸਕਦਾ ਹੈ (One person can be on many status) – ਵਿਅਕਤੀ ਸਮਾਜ ਵਿੱਚ ਇੱਕ ਹੀ ਪਦ ਉੱਤੇ ਬਿਰਾਜਮਾਨ ਨਹੀਂ ਹੁੰਦਾ ਬਲਕਿ ਉਹ ਅਲੱਗ-ਅਲੱਗ ਸਮਾਜਿਕ ਹਾਲਤਾਂ ਵਿਚ ਅਲੱਗ-ਅਲੱਗ ਪਦਾਂ ਨੂੰ ਪ੍ਰਾਪਤ ਕਰਦਾ ਹੈ । ਇੱਕ ਵਿਅਕਤੀ ਕਲੱਬ ਦਾ ਪ੍ਰਧਾਨ, ਦਫ਼ਤਰ ਵਿਚ ਕਰਮਚਾਰੀ, ਪਰਿਵਾਰ ਵਿੱਚ ਪੁੱਤਰ, ਪਿਤਾ, ਚਾਚਾ, ਮਾਮਾ ਆਦਿ ਦੇ ਪਦਾਂ ਦੀ ਭੂਮਿਕਾ ਨਿਭਾ ਰਿਹਾ ਹੁੰਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਵਿਅਕਤੀ ਆਪਣੀ ਸਿੱਖਿਆ, ਯੋਗਤਾ, ਸਮਰੱਥਾ ਦੇ ਅਨੁਸਾਰ ਸਾਰੇ ਪਦਾਂ ਵਿਚ ਸੰਬੰਧ ਅਤੇ ਸੰਤੁਲਨ ਬਣਾਈ ਰੱਖਦਾ ਹੈ ਜਾਂ ਰੱਖਣ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰਦਾ ਹੈ ।

(7) ਸਮਾਜਿਕ ਪਦਾਂ ਦੇ ਦੁਆਰਾ ਸਮਾਜ ਵਿਚ ਵੀ ਸਥਿਰਤਾ ਬਣੀ ਰਹਿੰਦੀ ਹੈ (Stability in Society comes with social status) – ਸਮਾਜ ਵਿਚ ਹਰੇਕ ਵਿਅਕਤੀ ਨੂੰ ਆਪਣੇ ਪਦ ਨਾਲ ਸੰਬੰਧਿਤ ਕੰਮ ਕਰਨੇ ਪੈਂਦੇ ਹਨ ਜਿਸ ਨਾਲ ਕਿ ਕੰਮਾਂ ਦਾ ਵਰਗੀਕਰਣ ਹੋ ਜਾਂਦਾ ਹੈ ਅਤੇ ਸਮਾਜ ਵਿਚ ਸਥਿਰਤਾ ਬਣੀ ਰਹਿੰਦੀ ਹੈ । ਵਿਅਕਤੀ ਨੂੰ ਪਦ ਪ੍ਰਦਾਨ ਕੀਤੇ ਬਿਨਾਂ ਸਮਾਜਿਕ ਨਿਯੰਤਰਣ ਬਣਾਏ ਰੱਖਣਾ ਅਸੰਭਵ ਹੈ ! ਕਿਰਤ ਵੰਡ ਦਾ ਸਿਧਾਂਤ ਪ੍ਰਾਚੀਨ ਸਮੇਂ ਤੋਂ ਹੀ ਚੱਲਿਆ ਆ ਰਿਹਾ ਹੈ | ਪਹਿਲਾਂ ਕੰਮਾਂ ਦੀ ਵੰਡ ਜਾਤ ਦੇ ਆਧਾਰ ਤੇ ਹੁੰਦੀ ਸੀ । ਪਰ ਆਧੁਨਿਕ ਸਮੇਂ ਵਿਚ ਵੰਡ ਯੋਗਤਾ ਦੇ ਆਧਾਰ ਉੱਤੇ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ਜਿਸ ਨਾਲ ਸਮਾਜ ਵਧੇਰੇ ਤਰੱਕੀ ਕਰ ਰਿਹਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 5.
ਭੁਮਿਕਾ ਕੀ ਹੈ ? ਇਸ ਦੀਆਂ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਤੇ ਵਿਸਤਾਰਪੂਰਵਕ ਨੋਟ ਲਿਖੋ ।
ਉੱਤਰ-
ਹਰ ਇੱਕ ਸਥਿਤੀ ਨਾਲ ਕੁੱਝ ਮੰਗਾਂ (demands) ਜੁੜੀਆਂ ਹੁੰਦੀਆਂ ਹਨ ਜਿਹੜੀਆਂ ਇਹ ਦੱਸਦੀਆਂ ਹਨ ਕਿਸ ਸਮੇਂ ਵਿਅਕਤੀ ਤੋਂ ਕਿਸ ਪ੍ਰਕਾਰ ਦੇ ਵਿਵਹਾਰ ਦੀ ਉਮੀਦ ਕੀਤੀ ਜਾਂਦੀ ਹੈ । ਇਹ ਭੂਮਿਕਾ ਦਾ ਕ੍ਰਿਆਤਮਕ ਪੱਧਰ ਹੈ । ਇਸ ਵਿੱਚ ਵਿਅਕਤੀ ਆਪਣੀ ਯੋਗਤਾ, ਲਿੰਗ, ਪੇਸ਼ੇ, ਪੈਸੇ ਆਦਿ ਦੇ ਆਧਾਰ ਉੱਤੇ ਕੋਈ ਪਦ ਪ੍ਰਾਪਤ ਕਰਦਾ ਹੈ ਅਤੇ ਉਸਨੂੰ ਉਸ ਪਦ ਦੇ ਸੰਦਰਭ ਵਿੱਚ ਪਰੰਪਰਾ, ਕਾਨੂੰਨ ਜਾਂ ਨਿਯਮਾਂ ਦੇ ਅਨੁਸਾਰ ਜਿਹੜੀ ਵੀ ਭੂਮਿਕਾ ਨਿਭਾਉਂਣੀ ਪੈਂਦੀ ਹੈ ਉਹ ਉਸਦਾ ਕੰਮ ਹੈ । ਇਸ ਤਰਾਂ ਇਹ ਸਪੱਸ਼ਟ ਹੁੰਦਾ ਹੈ ਕਿ ਕੰਮ ਦੀ ਧਾਰਨਾ ਵਿੱਚ ਦੋ ਤੱਤ ਹਨ ਇਕ ਉਮੀਦ ਅਤੇ ਦੂਜੀ ਕ੍ਰਿਆਵਾਂ ।ਉਮੀਦ ਦਾ ਅਰਥ ਹੈ ਕਿ ਉਹ ਕਿਸੇ ਖਾਸ ਸਮੇਂ ਖ਼ਾਸ ਤਰ੍ਹਾਂ ਦਾ ਵਿਵਹਾਰ ਕਰੇ ਅਤੇ ਕ੍ਰਿਆਵਾਂ ਜਾਂ ਭੂਮਿਕਾ ਉਸ ਵਿਸ਼ੇਸ਼ ਸਥਿਤੀ ਦਾ ਕੰਮ ਹੋਵੇਗਾ । ਇਸ ਤਰ੍ਹਾਂ ਉਸਦੀ ਭੂਮਿਕਾ ਲੰਮੀ ਜਾਂਦੀ ਹੈ ।

ਕਿਸੇ ਵੀ ਸਮਾਜ ਦੀ ਸਮਾਜਿਕ ਵਿਵਸਥਾ ਨੂੰ ਉਦੋਂ ਹੀ ਕਾਇਮ ਰੱਖਿਆ ਜਾ ਸਕਦਾ ਹੈ ਜਦੋਂ ਵਿਅਕਤੀ ਨੂੰ ਸਮਾਜਿਕ ਪਦਾਂ ਦੇ ਨਾਲ ਜੁੜੀਆਂ ਭੂਮਿਕਾਵਾਂ ਵੀ ਉਸਨੂੰ ਪ੍ਰਦਾਨ ਕੀਤੀਆਂ ਜਾਣ ਕਿਉਂਕਿ ਭੂਮਿਕਾ ਤੋਂ ਬਿਨਾਂ ਪਦ ਦਾ ਕੋਈ ਮਹੱਤਵ ਨਹੀਂ ਰਹਿ ਜਾਂਦਾ । ਇਸ ਲਈ ਪਦ ਅਤੇ ਭੂਮਿਕਾ ਨੂੰ ਇਕ ਸਿੱਕੇ ਦੇ ਦੋ ਪਹਿਲੂ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ਜੋ ਇਕੱਠੇ ਹੀ ਚੱਲਦੇ ਹਨ । ਸਮਾਜਿਕ ਵਿਅਕਤੀਆਂ ਨੂੰ ਉਹਨਾਂ ਦੇ ਕਿੱਤਿਆਂ ਦੇ ਆਧਾਰ ਉੱਤੇ ਹੀ ਇੱਕ ਦੂਜੇ ਤੋਂ ਵੱਖਰਾ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।

ਪਰਿਭਾਸ਼ਾਵਾਂ (Definitions)

• ਆਗਬਰਨ ਅਤੇ ਨਿਮਕਾਫ (Ogburn and Nimkoff) ਦੇ ਅਨੁਸਾਰ, “ਭੂਮਿਕਾ ਸਮਾਜਿਕ ਤੌਰ ਤੇ ਆਸ਼ਾ ਕੀਤੇ ਹੋਏ ਤੇ ਪ੍ਰਵਾਨ ਕੀਤੇ ਹੋਏ ਵਿਵਹਾਰ ਦੇ ਉਹ ਤਰੀਕੇ ਹੁੰਦੇ ਹਨ, ਜਿਨ੍ਹਾਂ ਨਾਲ ਵਿਅਕਤੀ ਜ਼ਿੰਮੇਵਾਰੀਆਂ ਅਤੇ ਅਧਿਕਾਰ ਸਮੂਹ ਵਿੱਚ ਪਾਏ ਗਏ ਵਿਸ਼ੇਸ਼ ਸਥਾਨ ਨਾਲ ਬੰਨ੍ਹੇ ਹੁੰਦੇ ਹਨ।”
• ਝੰਡਬਰਗ (Lundberg) ਦੇ ਅਨੁਸਾਰ, “ਭੂਮਿਕਾ ਵਿਅਕਤੀ ਦਾ ਕਿਸੇ ਸਮੂਹ ਜਾਂ ਅਵਸਥਾ ਵਿੱਚ ਉਮੀਦ ਕੀਤਾ ਹੋਇਆ ਵਿਵਹਾਰਿਕ ਤਰੀਕਾ ਹੁੰਦਾ ਹੈ ।”
• ਲਿੰਟਨ (Linton) ਦੇ ਅਨੁਸਾਰ, “ਰੋਲ ਦਾ ਅਰਥ ਸੰਸਕ੍ਰਿਤਕ ਪ੍ਰਤਿਮਾਨਾਂ ਦੇ ਉਸ ਯੋਗ ਤੋਂ ਹੈ ਜੋ ਕਿਸੇ ਵਿਸ਼ੇਸ਼ ਪਦ ਨਾਲ ਸੰਬੰਧਿਤ ਹੁੰਦਾ ਹੈ । ਇਸ ਪ੍ਰਕਾਰ ਇਸ ਵਿੱਚ ਉਹ ਸਭ ਰਵੱਈਏ, ਕੀਮਤਾਂ ਅਤੇ ਵਿਵਹਾਰ ਸੰਮਿਲਤ ਹਨ ਜੋ ਸਮਾਜ ਕਿਸੇ ਪਦ ਨੂੰ ਗ੍ਰਹਿਣ ਕਰਨ ਵਾਲੇ ਵਿਅਕਤੀ ਜਾਂ ਵਿਅਕਤੀਆਂ ਨੂੰ ਪ੍ਰਦਾਨ ਕਰਦਾ ਹੈ ।”

ਇਸ ਵਿਆਖਿਆ ਤੋਂ ਇਹ ਪਤਾ ਚੱਲਦਾ ਹੈ ਕਿ ਭੂਮਿਕਾ ਉਹ ਪ੍ਰਵਾਨਿਤ ਤਰੀਕਾ ਹੈ ਜਿਸ ਦੇ ਵਿਚ ਵਿਅਕਤੀ ਸਮਾਜ ਦੁਆਰਾ ਪ੍ਰਦਾਨ ਕੀਤੀ ਗਈ ਸਥਿਤੀ ਨਾਲ ਜੁੜੇ ਫਰਜ਼ਾਂ ਨੂੰ ਪੂਰਾ ਕਰਦਾ ਹੈ ਅਤੇ ਇਸ ਸਥਿਤੀ ਨਾਲ ਪ੍ਰਾਪਤ ਹੋਏ ਵਿਸ਼ੇਸ਼ ਅਧਿਕਾਰਾਂ ਦਾ ਪ੍ਰਯੋਗ ਕਰਦਾ ਹੈ । ਹਰੇਕ ਸਥਿਤੀ ਨਾਲ ਹੀ ਸੰਬੰਧਿਤ ਸਾਰੀਆਂ ਭੂਮਿਕਾਵਾਂ ਸਮਾਜਿਕ ਨਿਯਮਾਂ ਦੁਆਰਾ ਨਿਯਮਿਤ ਹੁੰਦੀਆਂ ਹਨ । ਸਮਾਜਿਕ ਨਿਯਮਾਂ ਵਿੱਚ ਕਿਸੇ ਵੀ ਪ੍ਰਕਾਰ ਦਾ ਪਰਿਵਰਤਨ ਹੋਣ ਨਾਲ ਭੂਮਿਕਾਵਾਂ ਵੀ ਬਦਲ ਜਾਂਦੀਆਂ ਹਨ । ਸੰਖੇਪ ਵਿੱਚ ਅਸੀਂ ਕਹਿ ਸਕਦੇ ਹਾਂ ਕਿ ਭੁਮਿਕਾ ਉਹ ਵਿਵਹਾਰ ਹੁੰਦਾ ਹੈ ਜੋ ਅਸਲੀਅਤ ਦੇ ਵਿੱਚ ਕਿਸੇ ਵੀ ਸਥਿਤੀ ਤੇ ਜਦੋਂ ਵਿਅਕਤੀ ਬੈਠਾ ਹੁੰਦਾ ਹੈ ਤਾਂ ਕਰਦਾ ਹੈ ।

ਭੂਮਿਕਾ ਦੀਆਂ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ (Characteristics of Social Role)

(1) ਭੂਮਿਕਾ ਕਾਰਜਾਤਮਕ ਹੁੰਦੀ ਹੈ (Role is Functional) – ਭੂਮਿਕਾ ਦੀ ਪਹਿਲੀ ਵਿਸ਼ੇਸ਼ਤਾ ਇਸਦਾ ਕਾਰਜਾਤਮਕ ਰੂਪ ਹੈ । ਇਹਨਾਂ ਨੂੰ ਸਮਝਣ ਦੇ ਲਈ ਇਸਦੀ ਤੁਲਨਾ ਦੂਜੇ ਲੋਕਾਂ ਦੀ ਭੂਮਿਕਾ ਨਾਲ ਕੀਤੀ ਜਾਂਦੀ ਹੈ । ਸਮਾਜ ਵਿਅਕਤੀ ਨੂੰ ਜੋ ਪਦ ਪ੍ਰਦਾਨ ਕਰਦਾ ਹੈ ਉਸ ਪਦ ਨਾਲ ਸੰਬੰਧਿਤ ਭੂਮਿਕਾਵਾਂ ਵੀ ਉਸਨੂੰ ਨਿਭਾਉਣੀਆਂ ਪੈਂਦੀਆਂ ਹਨ । ਇਸ ਤਰ੍ਹਾਂ ਅਸੀਂ ਕਹਿ ਸਕਦੇ ਹਾਂ ਕਿ ਭੂਮਿਕਾਵਾਂ ਕਾਰਜਾਤਮਕ ਹੁੰਦੀਆਂ ਹਨ ।

(2) ਭੂਮਿਕਾ ਨੂੰ ਸਮਾਜਿਕ ਪ੍ਰਵਾਨਗੀ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ (Role is determined by social sanctions) – ਵਿਅਕਤੀ ਸਮਾਜ ਵਿੱਚ ਰਹਿ ਕੇ ਹੀ ਆਪਣੀ ਯੋਗਤਾ ਅਨੁਸਾਰ ਪਦ ਦੀ ਪ੍ਰਾਪਤੀ ਕਰਦਾ ਹੈ । ਜੇਕਰ ਵਿਅਕਤੀ ਨੂੰ ਬਿਨਾਂ ਯੋਗਤਾ ਦੇ ਪਦ ਦੀ ਪ੍ਰਾਪਤੀ ਹੋ ਜਾਵੇ ਤਾਂ ਉਹ ਅਜਿਹੇ ਕੰਮ ਕਰਨਗੇ ਜੋ ਸਮਾਜਿਕ ਕੀਮਤਾਂ ਦੇ ਵਿਰੁੱਧ ਹੋਣਗੇ । ਇਸੇ ਕਰਕੇ ਸਮਾਜ ਕੇਵਲ ਉਹਨਾਂ ਹੀ ਭੁਮਿਕਾਵਾਂ ਨੂੰ ਸਵੀਕ੍ਰਿਤੀ ਦਿੰਦਾ ਹੈ ਜੋ ਸਮਾਜ ਦੁਆਰਾ ਪ੍ਰਮਾਣਿਤ ਅਤੇ ਸਮਾਜ ਦੁਆਰਾ ਵਿਅਕਤੀ ਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦੀਆਂ ਹਨ ! ਹਰੇਕ ਵਿਅਕਤੀ ਦੂਜੇ ਵਿਅਕਤੀ ਤੋਂ ਭਿੰਨ ਹੁੰਦਾ ਹੈ । ਕੋਈ ਇੱਕ ਵਿਅਕਤੀ ਸਮਾਜ ਵਿੱਚ ਸਾਰੀਆਂ ਭੂਮਿਕਾਵਾਂ ਜਿਵੇਂ ਡਾਕਟਰ, ਪ੍ਰੋਫੈਸਰ, ਇੰਜੀਨੀਅਰ ਆਦਿ ਨਹੀਂ ਨਿਭਾ ਸਕਦਾ । ਇਸੇ ਕਰਕੇ ਸਮਾਜਿਕ ਸੰਸਕ੍ਰਿਤੀ ਹੀ ਇਹ ਨਿਰਧਾਰਿਤ ਕਰਦੀ ਹੈ ਕਿ ਕਿਹੜੀਆਂ ਭੂਮਿਕਾਵਾਂ ਕਿਸ ਵਿਅਕਤੀ ਤੋਂ ਅਤੇ ਕਿਸੇ ਸਮੇਂ, ਕਿਵੇਂ ਕੀਤੀਆਂ ਜਾਣੀਆਂ ਚਾਹੀਦੀਆਂ ਹਨ ।

(3) ਸੰਸਕ੍ਰਿਤੀ ਦੁਆਰਾ ਨਿਯਮਿਤ (Culture determines role) – ਵਿਅਕਤੀ ਨੂੰ ਜੋ ਵਿਸ਼ੇਸ਼ ਸਥਿਤੀ ਸਮਾਜ ਵਿੱਚ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ ਉਸ ਨਾਲ ਜੁੜੀਆਂ ਭੂਮਿਕਾਵਾਂ ਨੂੰ ਨਿਭਾਉਣ ਲਈ ਸਮਾਜਿਕ ਪ੍ਰਵਾਨਗੀ ਦੀ ਜ਼ਰੂਰਤ ਹੁੰਦੀ ਹੈ ਅਤੇ ਇਹ ਪ੍ਰਵਾਨਗੀ ਮੁੱਖ ਤੌਰ ਉੱਤੇ ਸੰਸਕ੍ਰਿਤੀ ਵੱਲੋਂ ਹੀ ਮਿਲਦੀ ਹੈ । ਸਮਾਜਿਕ ਭੂਮਿਕਾ ਨੂੰ ਸੰਸਕ੍ਰਿਤੀ ਦੁਆਰਾ ਨਿਯਮਿਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ਅਤੇ ਪ੍ਰਵਾਨਗੀ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ ।

(4) ਵਿਅਕਤੀ ਦੀ ਯੋਗਤਾ ਦਾ ਮਹੱਤਵ (Importance of Individual’s ability) – ਵਿਅਕਤੀ ਆਪਣੀ ਯੋਗਤਾ ਅਤੇ ਸਮਰੱਥਾ ਦੇ ਅਨੁਸਾਰ ਕਈ ਤਰ੍ਹਾਂ ਦੀਆਂ ਭੂਮਿਕਾਵਾਂ ਨਿਭਾ ਸਕਦਾ ਹੈ । ਪਰ ਇਹ ਜ਼ਰੂਰੀ ਨਹੀਂ ਕਿ ਉਹ ਸਾਰੀਆਂ ਭੂਮਿਕਾਵਾਂ ਨੂੰ ਨਿਭਾਉਣ ਵਿੱਚ ਸਫਲਤਾ ਪ੍ਰਾਪਤ ਕਰੇ ।ਉਹ ਸਿਰਫ ਉਹਨਾਂ ਭੂਮਿਕਾਵਾਂ ਨੂੰ ਹੀ ਕਰਨ ਵਿੱਚ ਸਫਲ ਹੁੰਦਾ ਹੈ ਜਿਸ ਵਿੱਚ ਉਸਨੂੰ ਵਿਸ਼ੇਸ਼ ਯੋਗਤਾ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ । ਵਿਅਕਤੀ ਦੀ ਯੋਗਤਾ ਕਾਰਨ ਹੀ ਉਹ ਆਪਣੀ ਸਥਿਤੀ ਨਾਲ ਜੁੜੀਆਂ ਭੂਮਿਕਾਵਾਂ ਨੂੰ ਚੰਗਾ ਵਧੇਰੇ ਚੰਗਾ ਜਾਂ ਮਾੜੇ ਢੰਗ ਨਾਲ ਨਿਭਾ ਕੇ ਇੱਕ ਪਦ ਤੋਂ ਦੂਜੇ ਪਦ ਵਿੱਚ ਸਥਿਤੀ ਪ੍ਰਾਪਤ ਕਰਦਾ ਹੈ ਭਾਵ ਚੰਗੀਆਂ ਭੂਮਿਕਾਵਾਂ ਨਿਭਾ ਕੇ ਉੱਚੀ ਅਤੇ ਮਾੜੀਆਂ ਭੂਮਿਕਾਵਾਂ ਨਿਭਾ ਕੇ ਨੀਵੀਂ ਸਥਿਤੀ ਸਮਾਜ ਵਿੱਚ ਪ੍ਰਾਪਤ ਕਰਦਾ ਹੈ ।

(5) ਭੂਮਿਕਾ ਪਰਿਵਰਤਨਸ਼ੀਲ ਹੁੰਦੀ ਹੈ (Roles are changeable) – ਭੂਮਿਕਾਵਾਂ ਪਰਿਵਰਤਨਸ਼ੀਲ ਹੁੰਦੀਆਂ ਹਨ ਕਿਉਂਕਿ ਪਰਿਵਰਤਨ ਕੁਦਰਤ ਦਾ ਨਿਯਮ ਹੈ । ਸਮਾਜ ਸਮਾਜਿਕ ਸੰਬੰਧਾਂ ਦਾ ਤਾਣਾ-ਬਾਣਾ ਹੈ ਤੇ ਇਹਨਾਂ ਦੇ ਕਿਸੇ ਇੱਕ ਭਾਰਾ ਵਿੱਚ ਪਰਿਵਰਤਨ ਦੇ ਨਾਲ-ਨਾਲ ਪੁਰੀ ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਵਿਚ ਪਰਿਵਰਤਨ ਹੁੰਦਾ ਰਹਿੰਦਾ ਹੈ ਜਿਸ ਕਾਰਨ ਭੂਮਿਕਾਵਾਂ ਦੇ ਖੇਤਰ ਵਿੱਚ ਵੀ ਪਰਿਵਰਤਨ ਪਾਏ ਜਾਂਦੇ ਹਨ । ਇਸਦੇ ਨਾਲ ਸਮਾਜਿਕ ਕੀਮਤਾਂ ਅਤੇ ਸਮਾਜਿਕ ਪਰਿਮਾ ਵਿਚ ਵੀ ਬਦਲਾ ਆ ਜਾਂਦਾ ਹੈ । ਪੁਰਾਣੇ ਪਰਿਮਾਪਾਂ ਦੀ ਥਾਂ ਨਵੇਂ ਪਰਿਮਾਪ ਸਾਹਮਣੇ ਆ ਜਾਂਦੇ ਹਨ ਜਿਸ ਕਾਰਨ ਭੂਮਿਕਾਵਾਂ ਵਿੱਚ ਵੀ ਪਰਿਵਰਤਨ ਹੋ ਜਾਂਦਾ ਹੈ ।ਉਦਾਹਰਣ ਦੇ ਤੌਰ ਉੱਤੇ ਪੁਰਾਣੇ ਸਮਿਆਂ ਵਿਚ ਵਿਅਕਤੀ ਜਿਸ ਜਾਤ ਨਾਲ ਸੰਬੰਧ ਰੱਖਦਾ ਸੀ ਉਸੀ ਜਾਤ ਨਾਲ ਸੰਬੰਧਿਤ ਕਿੱਤਾ ਵੀ ਅਪਣਾਉਂਦਾ ਸੀ ਪਰ ਅੱਜ ਕੱਲ ਦੇ ਆਧੁਨਿਕ ਸਮੇਂ ਵਿੱਚ ਉਹਨਾਂ ਦੀਆਂ ਭੂਮਿਕਾਵਾਂ ਵਿੱਚ ਬਿਲਕੁਲ ਹੀ ਤਬਦੀਲੀ ਆ ਗਈ ਹੈ । ਅੱਜ ਵਿਅਕਤੀ ਆਪਣੀ ਭੂਮਿਕਾ ਨੂੰ ਜਾਤ ਨਾਲ ਸੰਬੰਧਿਤ ਕਿੱਤੇ ਵਿੱਚ ਨਾ ਨਿਭਾ ਕੇ ਆਪਣੀ ਯੋਗਤਾ ਅਨੁਸਾਰ ਕਿਸੇ ਵੀ ਪਦ ਦੀ ਪ੍ਰਾਪਤੀ ਕਰਕੇ ਉਸ ਨਾਲ ਜੁੜੀਆਂ ਹੋਈਆਂ ਭੂਮਿਕਾਵਾਂ ਨਿਭਾਉਂਦਾ ਹੈ ।

(6) ਵਿਅਕਤੀ ਸਮਾਜ ਵਿਚ ਕਈ ਤਰ੍ਹਾਂ ਦੀਆਂ ਭੂਮਿਕਾਵਾਂ ਨਾਲ ਸੰਬੰਧਿਤ ਹੁੰਦਾ ਹੈ (Man is related with differe in society) – ਵਿਅਕਤੀ ਅਨੇਕਾਂ ਤਰ੍ਹਾਂ ਦੇ ਕੰਮ ਕਰਨ ਦੇ ਯੋਗ ਹੁੰਦਾ ਹੈ ਜਿਸ ਕਾਰਨ ਸਮਾਜ ਵਿੱਚ ਉਹ ਕਈ ਭੂਮਿਕਾਵਾਂ ਅਵਾ ਕਰਦਾ ਹੈ । ਜਿਵੇਂ ਇੱਕ ਵਿਅਕਤੀ ਘਰ ਵਿੱਚ ਪੁੱਤਰ, ਪਿਉ, ਭਾਈ, ਪਤੀ ਦੀ ਭੂਮਿਕਾ ਨਿਭਾ ਰਿਹਾ ਹੁੰਦਾ ਹੈ ਤੇ ਉਹੀ ਵਿਅਕਤੀ ਜਦੋਂ ਘਰ ਤੋਂ ਬਾਹਰ ਕਿਸੇ ਸੰਸਥਾ ਵਿਚ ਜਾਂਦਾ ਹੈ ਤਾਂ ਉੱਥੇ ਦਾ ਮੈਂਬਰ, ਦਫਤਰ ਵਿੱਚ ਜਾ ਕੇ ਕਰਮਚਾਰੀ, ਧਾਰਮਿਕ ਸਥਾਨ ਵਿੱਚ ਜਾ ਕੇ ਉੱਥੇ ਦਾ ਨੇਤਾ ਆਦਿ ਅਲੱਗ-ਅਲੱਗ ਭੂਮਿਕਾਵਾਂ ਨਿਭਾਉਂਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਵਿਅਕਤੀ ਸਮਾਜ ਵਿੱਚ ਰਹਿੰਦਾ ਹੋਇਆ ਹਰ ਸਮੇਂ ਅਲੱਗ-ਅਲੱਗ ਭੂਮਿਕਾਵਾਂ ਨਿਭਾਉਂਦਾ ਹੈ ਅਤੇ ਇਹਨਾਂ ਨੂੰ ਨਿਭਾਉਣ ਦੇ ਯੋਗ ਬਣਦਾ ਹੈ ।

(7) ਸਮਾਜਿਕ ਭੂਮਿਕਾਵਾਂ ਦਾ ਸੀਮਤ ਖੇਤਰ (Roles have limited scope) – ਸਾਰੀਆਂ ਸਮਾਜਿਕ ਭੂਮਿਕਾਵਾਂ ਜੋ ਸਮਾਜ ਵਿਚ ਰਹਿ ਕੇ ਨਿਭਾਈਆਂ ਜਾਂਦੀਆਂ ਹਨ ਉਹਨਾਂ ਦਾ ਸੀਮਤ ਖੇਤਰ ਹੁੰਦਾ ਹੈ । ਵਿਅਕਤੀ ਜਿਸ ਸਥਿਤੀ ਵਿਚ ਪ੍ਰਵੇਸ਼ ਕਰਦਾ ਹੈ ਉਹ ਉਸੀ ਸਥਿਤੀ ਅਨੁਸਾਰ ਹੀ ਭੁਮਿਕਾਵਾਂ ਨਿਭਾਉਂਦਾ ਹੈ ਹੈ ਅਤੇ ਉਸ ਸਥਿਤੀ ਤੋਂ ਬਾਹਰ ਆਉਂਦੇ ਸਾਰ ਹੀ ਉਸ ਦੀਆਂ ਭੂਮਿਕਾਵਾਂ ਵੀ ਬਦਲ ਜਾਂਦੀਆਂ ਹਨ ।

This PSEB 11th Class Sociology Notes Chapter 8 ਰਾਜਨੀਤਿਕ, ਧਾਰਮਿਕ, ਆਰਥਿਕ ਅਤੇ ਸਿੱਖਿਆ ਸੰਸਥਾਵਾਂ will help you in revision during exams.

PSEB 11th Class Sociology Notes Chapter 8 ਰਾਜਨੀਤਿਕ, ਧਾਰਮਿਕ, ਆਰਥਿਕ ਅਤੇ ਸਿੱਖਿਆ ਸੰਸਥਾਵਾਂ

→ ਸਾਡੇ ਸਮਾਜ ਵਿੱਚ ਬਹੁਤ ਸਾਰੀਆਂ ਸੰਸਥਾਵਾਂ ਹੁੰਦੀਆਂ ਹਨ । ਸਮਾਜਿਕ ਸੰਸਥਾਵਾਂ ਵਿੱਚ ਅਸੀਂ ਵਿਆਹ, ਪਰਿਵਾਰ ਅਤੇ ਨਾਤੇਦਾਰੀ ਨੂੰ ਸ਼ਾਮਲ ਕਰਦੇ ਹਾਂ । ਸਮਾਜਿਕ ਸੰਸਥਾਵਾਂ ਤੋਂ ਇਲਾਵਾ ਹੋਰ ਬਹੁਤ ਸਾਰੀਆਂ ਸੰਸਥਾਵਾਂ ਹੁੰਦੀਆਂ ਹਨ , ਜਿਵੇਂ ਕਿ-ਰਾਜਨੀਤਿਕ, ਧਾਰਮਿਕ, ਆਰਥਿਕ, ਸਿੱਖਿਅਕ ਆਦਿ ।

→ ਰਾਜਨੀਤਿਕ ਵਿਵਸਥਾ ਸਮਾਜ ਦੀ ਹੀ ਇੱਕ ਉਪ-ਵਿਵਸਥਾ ਹੈ । ਇਹ ਮਨੁੱਖਾਂ ਦੀਆਂ ਉਨ੍ਹਾਂ ਭੂਮਿਕਾਵਾਂ ਨੂੰ ਨਿਰਧਾਰਿਤ ਕਰਦੀ ਹੈ ਜਿਹੜੀ ਕਾਨੂੰਨ ਅਤੇ ਵਿਵਸਥਾ ਨੂੰ ਬਣਾਈ ਰੱਖਣ ਲਈ ਜ਼ਰੂਰੀ ਹੁੰਦੀਆਂ ਹਨ । ਰਾਜਨੀਤੀ ਅਤੇ ਸਮਾਜ ਵਿਚਕਾਰ ਬਹੁਤ ਡੂੰਘਾ ਸੰਬੰਧ ਹੈ ।

→ ਸਮਾਜ ਸ਼ਾਸਤਰ ਵਿੱਚ ਰਾਜਨੀਤਿਕ ਸੰਸਥਾਵਾਂ ਦੀ ਮੱਦਦ ਲਈ ਜਾਂਦੀ ਹੈ ਅਤੇ ਕਈ ਸੰਕਲਪਾਂ ਨੂੰ ਸਮਝਿਆ ਜਾਂਦਾ ਹੈ ; ਜਿਵੇਂ ਕਿ-ਸ਼ਕਤੀ, ਨੇਤਾਗਿਰੀ, ਸੱਤਾ ਆਦਿ । ਇਹ ਰਾਜਨੀਤਿਕ ਸੰਸਥਾਵਾਂ ਸਮਾਜ ਵਿਚ ਸ਼ਾਂਤੀ ਅਤੇ ਵਿਵਸਥਾ ਰੱਖਣ ਵਿੱਚ ਮੱਦਦ ਕਰਦੀਆਂ ਹਨ ।

→ ਸ਼ਕਤੀ ਸਮੂਹ ਜਾਂ ਵਿਅਕਤੀਆਂ ਦੀ ਉਹ ਸਮਰੱਥਾ ਹੁੰਦੀ ਹੈ, ਜਿਸ ਨਾਲ ਉਹ ਉਸ ਸਮੇਂ ਆਪਣੀ ਗੱਲ ਮੰਨਵਾਉਂਦੇ ਹਨ ਜਦੋਂ ਉਹਨਾਂ ਦਾ ਵਿਰੋਧ ਹੋ ਰਿਹਾ ਹੁੰਦਾ ਹੈ । ਸਮਾਜ ਵਿੱਚ ਸ਼ਕਤੀ ਇੱਕ ਨਿਸ਼ਚਿਤ ਮਾਤਰਾ ਵਿੱਚ ਮੌਜੂਦ ਹੈ । ਕੁੱਝ ਸਮੂਹਾਂ ਕੋਲ ਵੱਧ ਸ਼ਕਤੀ ਹੁੰਦੀ ਹੈ ਅਤੇ ਉਹ ਘੱਟ ਸ਼ਕਤੀ ਵਾਲੇ ਵਿਅਕਤੀਆਂ ਜਾਂ ਸਮੂਹਾਂ ਉੱਤੇ ਆਪਣੀ ਗੱਲ ਥੋਪਦੇ ਹਨ ।

→ ਸ਼ਕਤੀ ਨੂੰ ਸੱਤਾ ਦੀ ਮੱਦਦ ਨਾਲ ਲਾਗੂ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਸੱਤਾ ਸ਼ਕਤੀ ਦਾ ਉਹ ਰੂਪ ਹੈ ਜਿਸ ਨੂੰ ਸਹੀ ਅਤੇ ਵੈਧ ਸਮਝਿਆ ਜਾਂਦਾ ਹੈ । ਜਿਨ੍ਹਾਂ ਕੋਲ ਸੱਤਾ ਹੁੰਦੀ ਹੈ, ਉਹ ਸ਼ਕਤੀ ਦਾ ਪ੍ਰਯੋਗ ਕਰਦੇ ਹਨ ਕਿਉਂਕਿ ਇਸ ਨੂੰ ਨਿਆਂਕਾਰੀ ਸਮਝਿਆ ਜਾਂਦਾ ਹੈ ।

→ ਮੈਕਸ ਵੈਬਰ ਨੇ ਸੱਤਾ ਦੇ ਤਿੰਨ ਪ੍ਰਕਾਰ ਦਿੱਤੇ ਹਨ-ਪਰੰਪਰਾਗਤ ਸੱਤਾ, ਕਾਨੂੰਨੀ ਸੱਤਾ ਅਤੇ ਕਰਿਸ਼ਮਈ ਸੱਤਾ । ਪਿਤਾ ਦੀ ਸੱਤਾ ਪਰੰਪਰਾਗਤ ਹੁੰਦੀ ਹੈ, ਸਰਕਾਰ ਦੀ ਸ਼ਕਤੀ ਕਾਨੂੰਨੀ ਸੱਤਾ ਹੁੰਦੀ ਹੈ ਅਤੇ ਕਿਸੇ ਗੁਰੂ ਦੀ ਗੱਲ ਮੰਨਣਾ ਕਰਿਸ਼ਮਈ ਸੱਤਾ ਹੁੰਦੀ ਹੈ ।

→ ਅਲੱਗ-ਅਲੱਗ ਪ੍ਰਕਾਰ ਦੇ ਸਮਾਜਾਂ ਵਿਚ ਅਲੱਗ-ਅਲੱਗ ਰਾਜ ਹੁੰਦੇ ਹਨ | ਕਈ ਸਮਾਜਾਂ ਵਿੱਚ ਰਾਜ ਨਾਮ ਦਾ ਕੋਈ ਸੰਕਲਪ ਨਹੀਂ ਹੁੰਦਾ ਜਿਸ ਕਰਕੇ ਇਹਨਾਂ ਨੂੰ ਰਾਜ ਰਹਿਤ ਸਮਾਜ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ਅਤੇ ਇਹ ਪੁਰਾਤਨ ਸਮਾਜਾਂ ਵਿੱਚ ਮਿਲਦੇ ਸਨ । ਆਧੁਨਿਕ ਸਮਾਜਾਂ ਵਿੱਚ ਸੱਤਾ ਨੂੰ ਰਾਜ ਨਾਮਕ ਸੰਸਥਾ ਦੇ ਵਿੱਚ ਸ਼ਾਮਲ ਕੀਤਾ ਹੈ ਅਤੇ ਇਹ ਸੱਤਾ ਜਨਤਾ ਤੋਂ ਹੀ ਪ੍ਰਾਪਤ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ।

→ ਰਾਜ ਰਾਜਨੀਤਿਕ ਵਿਵਸਥਾ ਦੀ ਇੱਕ ਮੂਲ ਸੰਸਥਾ ਹੈ । ਇਸ ਦੇ ਚਾਰ ਜ਼ਰੂਰੀ ਤੱਤ ਹੁੰਦੇ ਹਨ ਅਤੇ ਉਹ ਹਨ ਜਨਸੰਖਿਆ, ਭੂਗੋਲਿਕ ਖੇਤਰ, ਸੁਤੰਤਰਤਾ ਅਤੇ ਸਰਕਾਰ ॥

→ ਸਰਕਾਰ ਦੇ ਤਿੰਨ ਅੰਗ ਹੁੰਦੇ ਹਨ ਅਤੇ ਉਹ ਹਨ-ਵਿਧਾਨਪਾਲਿਕਾ, ਕਾਰਜਪਾਲਿਕਾ ਅਤੇ ਨਿਆਂਪਾਲਿਕਾ ਰਾਜ ਅਤੇ ਸਰਕਾਰ ਨੂੰ ਬਣਾਈ ਰੱਖਣ ਲਈ ਇਹਨਾਂ ਤਿੰਨਾਂ ਵਿਚਕਾਰ ਤਾਲਮੇਲ ਦਾ ਹੋਣਾ ਬਹੁਤ ਜ਼ਰੂਰੀ ਹੈ ।

→ ਅੱਜ-ਕਲ੍ਹ ਦੀ ਰਾਜਨੀਤਿਕ ਵਿਵਸਥਾ ਲੋਕਤੰਤਰ ਦੇ ਨਾਲ ਚਲਦੀ ਹੈ । ਲੋਕਤੰਤਰ ਦੋ ਪ੍ਰਕਾਰ ਦਾ ਹੁੰਦਾ ਹੈ । ਪ੍ਰਤੱਖ ਲੋਕਤੰਤਰ ਵਿੱਚ ਜਨਤਾ ਆਪਣੇ ਫ਼ੈਸਲੇ ਆਪ ਲੈਂਦੀ ਹੈ ਅਤੇ ਅਪ੍ਰਤੱਖ ਲੋਕਤੰਤਰ ਵਿੱਚ ਜਨਤਾ ਦੇ ਚੁਣੇ ਹੋਏ ਪ੍ਰਤੀਨਿਧੀ ਸਾਰੇ ਫੈਸਲੇ ਲੈਂਦੇ ਹਨ ।

→ ਸਾਡੇ ਦੇਸ਼ ਵਿਚ ਸਰਕਾਰ ਨੇ ਵਿਕੇਂਦਰੀਕਰਣ ਦੀ ਵਿਵਸਥਾ ਨੂੰ ਅਪਣਾਇਆ ਹੈ ਅਤੇ ਸਥਾਨਕ ਪੱਧਰ ਤੱਕ ਸਰਕਾਰ ਬਣਾਈ ਜਾਂਦੀ ਹੈ । ਪੇਂਡੂ ਖੇਤਰਾਂ ਵਿੱਚ ਪਿੰਡ ਦੇ ਪੱਧਰ ਉੱਤੇ ਪੰਚਾਇਤ, ਬਲਾਕ ਪੱਧਰ ਉੱਤੇ ਬਲਾਕ ਸਮਿਤੀ ਅਤੇ ਜ਼ਿਲ੍ਹਾ ਪੱਧਰ ਉੱਤੇ ਜ਼ਿਲ੍ਹਾ ਪਰਿਸ਼ਦ ਹੁੰਦੇ ਹਨ ਜਿਹੜੇ ਆਪਣੇ ਇਲਾਕਿਆਂ ਵਿੱਚ ਵਿਕਾਸ ਕਰਵਾਉਂਦੇ ਹਨ ।

→ ਲੋਕਤੰਤਰ ਵਿੱਚ ਰਾਜਨੀਤਿਕ ਦਲ ਮਹੱਤਵਪੂਰਨ ਸਥਾਨ ਰੱਖਦੇ ਹਨ । ਇੱਕ ਰਾਜਨੀਤਿਕ ਦਲ ਉਨ੍ਹਾਂ ਲੋਕਾਂ ਦਾ ਸਮੂਹ ਹੁੰਦਾ ਹੈ ਜਿਨ੍ਹਾਂ ਦਾ ਮੁੱਖ ਮੰਤਵ ਚੋਣਾਂ ਲੜ ਕੇ ਸੱਤਾ ਪ੍ਰਾਪਤ ਕਰਨਾ ਹੁੰਦਾ ਹੈ । ਕੁੱਝ ਦਲ ਰਾਸ਼ਟਰੀ ਦਲ ਹੁੰਦੇ ਹਨ ਅਤੇ ਕੁੱਝ ਦਲ ਪ੍ਰਦੇਸ਼ਿਕ ਦਲ ਹੁੰਦੇ ਹਨ ।

→ ਲੋਕਤੰਤਰ ਵਿੱਚ ਹਿੱਤ ਸਮੂਹਾਂ ਦਾ ਮਹੱਤਵਪੂਰਨ ਸਥਾਨ ਹੁੰਦਾ ਹੈ । ਇਹ ਹਿੱਤ ਸਮੁਹ ਕਿਸੇ ਵਿਸ਼ੇਸ਼ ਸਮੁਹ ਨਾਲ | ਜੁੜੇ ਹੁੰਦੇ ਹਨ ਅਤੇ ਉਹ ਆਪਣੇ ਸਮੂਹ ਦੇ ਹਿੱਤਾਂ ਦੀ ਪ੍ਰਾਪਤੀ ਲਈ ਕੰਮ ਕਰਦੇ ਰਹਿੰਦੇ ਹਨ ।

→ ਜਦੋਂ ਤੋਂ ਮਨੁੱਖੀ ਸਮਾਜ ਸ਼ੁਰੂ ਹੋਏ ਹਨ, ਧਰਮ ਉਸ ਸਮੇਂ ਤੋਂ ਹੀ ਮੌਜੂਦ ਹਨ । ਧਰਮ ਹੋਰ ਕੁੱਝ ਨਹੀਂ ਬਲਕਿ ਉਸ ਅਲੌਕਿਕ ਸ਼ਕਤੀ ਵਿੱਚ ਵਿਸ਼ਵਾਸ ਹੈ ਜੋ ਸਾਡੇ ਅਸਤਿੱਤਵ ਅਤੇ ਪਹੁੰਚ ਤੋਂ ਬਹੁਤ ਦੂਰ ਹੈ ।

→ ਸਾਡੇ ਦੇਸ਼ ਭਾਰਤ ਵਿੱਚ ਬਹੁਤ ਸਾਰੇ ਧਰਮ ਮੌਜੂਦ ਹਨ ; ਜਿਵੇਂ ਕਿ-ਹਿੰਦੂ, ਇਸਲਾਮ, ਸਿੱਖ, ਇਸਾਈ, ਬੋਧ ਧਰਮ, ਜੈਨ ਧਰਮ, ਪਾਰਸੀ ਧਰਮ ਆਦਿ । ਭਾਰਤ ਇੱਕ ਬਹੁ-ਧਰਮੀ ਦੇਸ਼ ਹੈ ਜਿੱਥੇ ਬਹੁਤ ਸਾਰੇ ਧਰਮਾਂ ਦੇ ਲੋਕ ਇਕੱਠੇ ਮਿਲ ਕੇ ਰਹਿੰਦੇ ਹਨ ।

→ ਹਰੇਕ ਵਿਅਕਤੀ ਨੂੰ ਭੋਜਨ, ਕੱਪੜਾ, ਮਕਾਨ, ਸਿਹਤ ਸੁਵਿਧਾਵਾਂ ਨੂੰ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ ਪੈਸੇ ਦੀ ਜ਼ਰੂਰਤ ਪੈਂਦੀ ਹੈ ਅਤੇ ਇਹ ਸਭ ਸਾਡੀ ਆਰਥਿਕਤਾ ਦਾ ਮਹੱਤਵਪੂਰਨ ਭਾਗ ਹੁੰਦੇ ਹਨ | ਆਰਥਿਕਤਾ ਸਾਡੇ ਪੈਸੇ ਅਤੇ ਖ਼ਰਚ ਦਾ ਧਿਆਨ ਰੱਖਦੀ ਹੈ ।

→ ਵੱਖ-ਵੱਖ ਸਮਾਜਾਂ ਵਿੱਚ ਵੱਖ-ਵੱਖ ਆਰਥਿਕਤਾ ਮੌਜੂਦ ਹੁੰਦੀ ਹੈ | ਕਈ ਸਮਾਜ ਚੀਜ਼ਾਂ ਇਕੱਠਾ ਕਰਨ ਵਾਲੇ ਹੁੰਦੇ ਹਨ, ਕਈ ਸਮਾਜ ਚਰਾਗਾਹ ਆਰਥਿਕਤਾ ਵਾਲੇ ਹੁੰਦੇ ਹਨ, ਕਈ ਸਮਾਜ ਪੇਂਡੂ ਆਰਥਿਕਤਾ ਵਾਲੇ ਹੁੰਦੇ ਹਨ, ਕਈ ਸਮਾਜ ਉਦਯੋਗਿਕ ਆਰਥਿਕਤਾ ਅਤੇ ਕਈ ਸਮਾਜ ਪੂੰਜੀਵਾਦ ਵਾਲੇ ਵੀ ਹੁੰਦੇ ਹਨ । ਕਾਰਲ ਮਾਰਕਸ ਨੇ | ਸਮਾਜਵਾਦੀ ਆਰਥਿਕਤਾ ਬਾਰੇ ਦੱਸਿਆ ਹੈ ।

→ ਕਿਰਤ ਵੰਡ ਦਾ ਸੰਕਲਪ ਸਾਡੇ ਸਮਾਜ ਲਈ ਨਵਾਂ ਨਹੀਂ ਹੈ । ਜਦੋਂ ਲੋਕ ਕਿਸੇ ਵਿਸ਼ੇਸ਼ ਕੰਮ ਨੂੰ ਕਰਨ ਲੱਗ ਜਾਣ ਅਤੇ ਉਹ ਸਾਰੇ ਕੰਮਾਂ ਨੂੰ ਨਾ ਕਰ ਸਕਣ ਤਾਂ ਇਸ ਨੂੰ ਵਿਸ਼ੇਸ਼ੀਕਰਣ ਅਤੇ ਕਿਰਤ ਵੰਡ ਦਾ ਨਾਮ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ । ਭਾਰਤੀ ਸਮਾਜ ਵਿੱਚ ਜਾਤੀ ਵਿਵਸਥਾ ਅਤੇ ਜਜਮਾਨੀ ਵਿਵਸਥਾ ਕਿਰਤ ਵੰਡ ਦਾ ਹੀ ਇੱਕ ਪ੍ਰਕਾਰ ਹੈ ।

→ ਜੇਕਰ ਅਸੀਂ ਆਪਣੇ ਸਮਾਜ ਵੱਲ ਦੇਖੀਏ ਤਾਂ ਅਸੀਂ ਕਹਿ ਸਕਦੇ ਹਾਂ ਕਿ ਸਿੱਖਿਆ ਬਿਨਾਂ ਸਮਾਜ ਵਿੱਚ ਕੁੱਝ ਨਹੀਂ ਹੁੰਦਾ । ਸਿੱਖਿਆ ਵਿਅਕਤੀ ਨੂੰ ਜਾਨਵਰ ਤੋਂ ਸਭਿਅ ਮਨੁੱਖ ਦੇ ਰੂਪ ਵਿੱਚ ਪਰਿਵਰਤਿਤ ਕਰ ਦਿੰਦੀ ਹੈ ।

→ ਸਿੱਖਿਆ ਦੋ ਪ੍ਰਕਾਰ ਦੀ ਹੁੰਦੀ ਹੈ ਅਤੇ ਉਹ ਹਨ-ਰਸਮੀ ਸਿੱਖਿਆ ਅਤੇ ਗੈਰ-ਰਸਮੀ ਸਿੱਖਿਆ । ਰਸਮੀ ਸਿੱਖਿਆ | ਉਹ ਹੁੰਦੀ ਹੈ ਜਿਹੜੀ ਅਸੀਂ ਸਕੂਲ, ਕਾਲਜ ਆਦਿ ਤੋਂ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ ਅਤੇ ਗੈਰ ਰਸਮੀ ਸਿੱਖਿਆ ਉਹ ਹੁੰਦੀ ਹੈ ਜਿਹੜੀ ਅਸੀਂ ਆਪਣੇ ਰੋਜ਼ਾਨਾ ਦੇ ਅਨੁਭਵਾਂ, ਬਜ਼ੁਰਗਾਂ ਤੋਂ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ ।

This PSEB 11th Class Sociology Notes Chapter 7 ਵਿਆਹ, ਪਰਿਵਾਰ ਅਤੇ ਨਾਤੇਦਾਰੀ will help you in revision during exams.

PSEB 11th Class Sociology Notes Chapter 7 ਵਿਆਹ, ਪਰਿਵਾਰ ਅਤੇ ਨਾਤੇਦਾਰੀ

→ ਹਰੇਕ ਸਮਾਜ ਨੇ ਆਪਣੇ ਮੈਂਬਰਾਂ ਦੀਆਂ ਜ਼ਰੂਰਤਾਂ ਪੂਰੀਆਂ ਕਰਨ ਲਈ ਕੁੱਝ ਸੰਸਥਾਵਾਂ ਬਣਾਈਆਂ ਹੁੰਦੀਆਂ ਹਨ । ਸੰਸਥਾ ਸਮਾਜਿਕ ਵਿਵਸਥਾ ਦਾ ਇੱਕ ਢਾਂਚਾ ਹੈ ਜਿਹੜੀ ਇੱਕ ਸਮੁਦਾਇ ਦੇ ਮੈਂਬਰਾਂ ਦੇ ਵਿਵਹਾਰ ਨੂੰ ਨਿਰਦੇਸ਼ਿਤ ਕਰਦੀ ਹੈ । ਇਹ ਵਿਸ਼ੇਸ਼ ਪ੍ਰਕਾਰ ਦੀ ਜ਼ਰੂਰਤ ਨੂੰ ਪੂਰਾ ਕਰਦੀ ਹੈ ਜੋ ਕਿ ਸਮਾਜ ਦੀ ਹੋਂਦ ਲਈ ਜ਼ਰੂਰੀ ਹੈ ।

→ ਸੰਸਥਾਵਾਂ ਦੀਆਂ ਕੁਝ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਹੁੰਦੀਆਂ ਹਨ ਜਿਵੇਂ ਕਿ ਇਹ ਵਿਸ਼ੇਸ਼ ਜ਼ਰੂਰਤਾਂ ਪੂਰੀਆਂ ਕਰਦੀਆਂ ਹਨ, ਇਹ ਨਿਯਮਾਂ ਦਾ ਇੱਕ ਗੁੱਛਾ ਹੈ, ਇਹ ਅਮੂਰਤ ਹੁੰਦੀਆਂ ਹਨ, ਇਹ ਸਰਵਵਿਆਪਕ ਹੁੰਦੀਆਂ ਹਨ, ਇਹ ਸਥਾਈ ਹੁੰਦੀਆਂ ਹਨ ਜਿਨ੍ਹਾਂ ਵਿੱਚ ਪਰਿਵਰਤਨ ਆਸਾਨੀ ਨਾਲ ਨਹੀਂ ਆਉਂਦੇ, ਇਹਨਾਂ ਦੀ ਪ੍ਰਕ੍ਰਿਤੀ ਸਮਾਜਿਕ ਹੁੰਦੀ ਹੈ ਆਦਿ ।

→ ਵਿਆਹ ਇੱਕ ਅਜਿਹੀ ਸਮਾਜਿਕ ਸੰਸਥਾ ਹੈ ਜਿਹੜੀ ਹਰੇਕ ਸਮਾਜ ਵਿੱਚ ਪਾਈ ਜਾਂਦੀ ਹੈ । ਇਹ ਸਮਾਜ ਦੀ ਇੱਕ ਮੌਲਿਕ ਸੰਸਥਾ ਹੈ । ਵਿਆਹ ਨਾਲ ਦੋ ਵਿਰੋਧੀ ਲਿੰਗਾਂ ਦੇ ਵਿਅਕਤੀਆਂ ਨੂੰ ਪਤੀ-ਪਤਨੀ ਦੇ ਰੂਪ ਵਿੱਚ ਇਕੱਠੇ ਰਹਿਣ ਦੀ ਮਾਨਤਾ ਮਿਲ ਜਾਂਦੀ ਹੈ । ਇਹ ਲੈਂਗਿਕ ਸੰਬੰਧ ਸਥਾਪਿਤ ਕਰਦੇ ਹਨ, ਬੱਚੇ ਪੈਦਾ ਕਰਦੇ ਹਨ ਅਤੇ ਸਮਾਜ ਦੇ ਅੱਗੇ ਵੱਧਣ ਵਿੱਚ ਯੋਗਦਾਨ ਦਿੰਦੇ ਹਨ ।

→ ਵੈਸੇ ਤਾਂ ਸਮਾਜ ਵਿੱਚ ਵਿਆਹ ਦੇ ਕਈ ਪ੍ਰਕਾਰ ਮਿਲਦੇ ਹਨ ਪਰ ਇੱਕ ਵਿਆਹ ਅਤੇ ਬਹੁ-ਵਿਆਹ ਹੀ ਪ੍ਰਮੁੱਖ ਹਨ । ਬਹੁ-ਵਿਆਹ ਅੱਗੇ ਫਿਰ ਦੋ ਭਾਗਾਂ ਵਿੱਚ ਵੰਡਿਆ ਜਾਂਦਾ ਹੈ-ਬਹੁ-ਪਤੀ ਵਿਆਹ ਅਤੇ ਬਹੁ-ਪਤਨੀ ਵਿਆਹ ! ਬਹੁ-ਪਤੀ ਵਿਆਹ ਕਈ ਕਬਾਇਲੀ ਸਮਾਜਾਂ ਵਿੱਚ ਪ੍ਰਚਲਿਤ ਹੈ ਅਤੇ ਬਹੁ-ਪਤਨੀ ਵਿਆਹ ਸਾਡੇ ਸਮਾਜਾਂ ਵਿੱਚ ਪਹਿਲਾਂ ਪ੍ਰਚਲਿਤ ਸੀ ।

→ ਸਾਡੇ ਸਮਾਜ ਵਿੱਚ ਜੀਵਨ ਸਾਥੀ ਦੇ ਚੁਨਾਵ ਦੇ ਕਈ ਤਰੀਕੇ ਪ੍ਰਚਲਿਤ ਹਨ ਜਿਨ੍ਹਾਂ ਵਿੱਚੋਂ ਅੰਤਰ ਵਿਆਹ (Endogamy) ਅਤੇ ਬਾਹਰ ਵਿਆਹ (Exogamy) ਪ੍ਰਮੁੱਖ ਹਨ । ਅੰਤਰ ਵਿਆਹ ਵਿੱਚ ਵਿਅਕਤੀ ਨੂੰ ਇੱਕ ਨਿਸ਼ਚਿਤ ਸਮੂਹ ਦੇ ਵਿੱਚ ਹੀ ਵਿਆਹ ਕਰਵਾਉਣਾ ਪੈਂਦਾ ਹੈ ਅਤੇ ਬਾਹਰ ਵਿਆਹ ਵਿੱਚ ਵਿਅਕਤੀ ਨੂੰ ਇਕ ਨਿਸ਼ਚਿਤ ਸਮੂਹ ਤੋਂ ਬਾਹਰ ਵਿਆਹ ਕਰਵਾਉਣਾ ਪੈਂਦਾ ਹੈ ।

→ ਵਿਆਹ ਨਾਮਕ ਸੰਸਥਾ ਵਿੱਚ ਪਿਛਲੇ ਕੁੱਝ ਸਮੇਂ ਵਿੱਚ ਕਈ ਪ੍ਰਕਾਰ ਦੇ ਪਰਿਵਰਤਨ ਆਏ ਹਨ । ਇਹਨਾਂ ਪਰਿਵਰਤਨਾਂ ਦੇ ਕਈ ਮੁੱਖ ਕਾਰਨ ਹਨ ਜਿਵੇਂ ਕਿ ਉਦਯੋਗੀਕਰਨ, ਸ਼ਹਿਰੀਕਰਨ, ਆਧੁਨਿਕ ਸਿੱਖਿਆ, ਨਵੇਂ ਕਾਨੂੰਨਾਂ ਦਾ ਬਣਨਾ, ਔਰਤਾਂ ਦੀ ਸੁਤੰਤਰਤਾ, ਪੱਛਮੀ ਸਮਾਜਾਂ ਦਾ ਪ੍ਰਭਾਵ ਆਦਿ ।’

→ ਪਰਿਵਾਰ ਇੱਕ ਅਜਿਹੀ ਸਰਵਵਿਆਪਕ ਸਮਾਜਿਕ ਸੰਸਥਾ ਹੈ ਜਿਹੜੀ ਹਰੇਕ ਸਮਾਜ ਵਿੱਚ ਕਿਸੇ ਨਾ ਕਿਸੇ ਰੂਪ ਵਿੱਚ ਮੌਜੂਦ ਹੈ । ਵਿਅਕਤੀ ਦੇ ਜੀਵਨ ਵਿੱਚ ਪਰਿਵਾਰ ਨਾਮਕ ਸੰਸਥਾ ਦਾ ਬਹੁਤ ਡੂੰਘਾ ਪ੍ਰਭਾਵ ਹੁੰਦਾ ਹੈ ਅਤੇ ਇਸਦੇ ਬਿਨਾਂ ਵਿਅਕਤੀ ਜਿਊਂਦਾ ਨਹੀਂ ਰਹਿ ਸਕਦਾ ।

→ ਪਰਿਵਾਰ ਦੀਆਂ ਕਈ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਹੁੰਦੀਆਂ ਹਨ ਜਿਵੇਂ ਕਿ ਇਹ ਸਰਵਵਿਆਪਕ ਸੰਸਥਾ ਹੈ, ਇਸਦਾ ਭਾਵਨਾਤਮਕ ਆਧਾਰ ਹੁੰਦਾ ਹੈ, ਇਸਦਾ ਆਕਾਰ ਛੋਟਾ ਹੁੰਦਾ ਹੈ, ਇਹ ਸਥਾਈ ਅਤੇ ਅਸਥਾਈ ਦੋਵੇਂ ਪ੍ਰਕਾਰ ਦਾ ਹੁੰਦਾ ਹੈ, ਇਹ ਵਿਅਕਤੀ ਦੇ ਵਿਵਹਾਰ ਨੂੰ ਨਿਯੰਤਰਿਤ ਕਰਦਾ ਹੈ ।

→ ਪਰਿਵਾਰ ਦੇ ਕਈ ਪ੍ਰਕਾਰ ਹੁੰਦੇ ਹਨ ਅਤੇ ਇਹਨਾਂ ਨੂੰ ਰਹਿਣ ਦੇ ਸਥਾਨ, ਸੁੱਤਾ, ਮੈਂਬਰਾਂ ਆਦਿ ਦੇ ਆਧਾਰ ਉੱਤੇ ਕਈ ਭਾਗਾਂ ਵਿੱਚ ਵੰਡਿਆ ਜਾ ਸਕਦਾ ਹੈ ।

→ ਪਿਛਲੇ ਕੁੱਝ ਸਮੇਂ ਵਿੱਚ ਪਰਿਵਾਰ ਨਾਮਕ ਸੰਸਥਾ ਵਿੱਚ ਕਈ ਪ੍ਰਕਾਰ ਦੇ ਪਰਿਵਰਤਨ ਆ ਰਹੇ ਹਨ ਅਤੇ ਉਹ ਹਨ, ਆਕਾਰ ਦਾ ਛੋਟਾ ਹੋਣਾ, ਪਰਿਵਾਰਾਂ ਦਾ ਟੁੱਟਣਾ, ਔਰਤਾਂ ਦੀ ਸਥਿਤੀ ਵਿੱਚ ਪਰਿਵਰਤਨ, ਰਿਸ਼ਤੇਦਾਰੀ ਦੇ ਸੰਬੰਧਾਂ ਦਾ ਕਮਜ਼ੋਰ ਪੈਣਾ, ਕੰਮਾਂ ਵਿੱਚ ਪਰਿਵਰਤਨ ਆਦਿ ।

→ ਨਾਤੇਦਾਰੀ ਵਿਅਕਤੀ ਦੇ ਰਿਸ਼ਤਿਆਂ ਦੀ ਵਿਵਸਥਾ ਹੈ । ਇਸ ਵਿੱਚ ਕਈ ਪ੍ਰਕਾਰ ਦੇ ਰਿਸ਼ਤੇ ਆਉਂਦੇ ਹਨ । ਰਿਸ਼ਤੇਦਾਰੀ ਨੂੰ ਦੋ ਆਧਾਰਾਂ ਉੱਤੇ ਵੰਡਿਆ ਜਾ ਸਕਦਾ ਹੈ ਅਤੇ ਉਹ ਦੋ ਆਧਾਰ ਹਨ-ਰਕਤ ਸੰਬੰਧ ਅਤੇ ਵਿਆਹ । ਨੇੜਤਾ ਅਤੇ ਦੂਰੀ ਦੇ ਆਧਾਰ ਉੱਤੇ ਤਿੰਨ ਪ੍ਰਕਾਰ ਦੇ ਰਿਸ਼ਤੇਦਾਰ ਪਾਏ ਹਨ-ਪਹਿਲੇ, ਦੂਤੀਆ ਅਤੇ ਤੀਜੇ ਪ੍ਰਕਾਰ ਦੇ ਰਿਸ਼ਤੇਦਾਰ । ਪ੍ਰਾਥਮਿਕ ਰਿਸ਼ਤੇਦਾਰ ਮਾਤਾ-ਪਿਤਾ, ਭੈਣ-ਭਰਾ ਹੁੰਦੇ ਹਨ । ਦੂਤੀਆ ਪ੍ਰਕਾਰ ਦੇ ਰਿਸ਼ਤੇਦਾਰ ਸਾਡੇ ਪ੍ਰਾਥਮਿਕ ਰਿਸ਼ਤੇਦਾਰ ਦੇ ਪ੍ਰਾਥਮਿਕ ਰਿਸ਼ਤੇਦਾਰ ਹੁੰਦੇ ਹਨ ਜਿਵੇਂ ਪਿਤਾ ਦਾ ਪਿਤਾ-ਦਾਦਾ । ਤੀਜੇ ਪ੍ਰਕਾਰ ਦੇ ਰਿਸ਼ਤੇਦਾਰ ਦੂਤੀਆ ਰਿਸ਼ਤੇਦਾਰਾਂ ਦੇ ਪਹਿਲੇ ਰਿਸ਼ਤੇਦਾਰ ਹੁੰਦੇ ਹਨ ਜਿਵੇਂ ਕਿ ਚਾਚੇ ਦਾ ਪੁੱਤਰ-ਕਜ਼ਨ ।

This PSEB 11th Class Sociology Notes Chapter 6 ਸਮਾਜੀਕਰਨ will help you in revision during exams.

PSEB 11th Class Sociology Notes Chapter 6 ਸਮਾਜੀਕਰਨ

→ ਜਦੋਂ ਇੱਕ ਬੱਚਾ ਪੈਦਾ ਹੁੰਦਾ ਹੈ ਤਾਂ ਉਸਨੂੰ ਕੁੱਝ ਵੀ ਨਹੀਂ ਪਤਾ ਹੁੰਦਾ । ਹੌਲੀ-ਹੌਲੀ ਉਹ ਵੱਡਾ ਹੁੰਦਾ ਹੈ ਅਤੇ | ਸਮਾਜ ਵਿੱਚ ਰਹਿਣ ਦੇ ਤੌਰ-ਤਰੀਕੇ ਸਿੱਖਦਾ ਜਾਂਦਾ ਹੈ । ਸਮਾਜ ਦੇ ਵਿੱਚ ਰਹਿਣ ਦੇ ਤੌਰ-ਤਰੀਕੇ ਸਿੱਖਣ ਦੀ ਪ੍ਰਕਿਰਿਆ ਨੂੰ ਹੀ ਸਮਾਜੀਕਰਨ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।

→ ਸਮਾਜੀਕਰਨ ਦੀ ਪ੍ਰਕਿਰਿਆ ਬੱਚੇ ਦੇ ਜਨਮ ਤੋਂ ਬਾਅਦ ਹੀ ਸ਼ੁਰੂ ਹੋ ਜਾਂਦੀ ਹੈ ਅਤੇ ਸਾਰੀ ਉਮਰ ਚਲਦੀ ਰਹਿੰਦੀ ਹੈ । ਵਿਅਕਤੀ ਖ਼ਤਮ ਹੋ ਜਾਂਦਾ ਹੈ ਪਰ ਇਹ ਪ੍ਰਕਿਰਿਆ ਕਦੇ ਵੀ ਖ਼ਤਮ ਨਹੀਂ ਹੁੰਦੀ । ਜੇਕਰ ਸਮਾਜੀਕਰਨ ਦੀ ਪ੍ਰਕਿਰਿਆ ਨਹੀਂ ਹੋਵੇਗੀ ਤਾਂ ਮਨੁੱਖ ਜਾਨਵਰਾਂ ਵਾਂਗ ਵਿਵਹਾਰ ਕਰਨਗੇ ਅਤੇ ਸਮਾਜ ਨਾਮ ਦੀ ਕੋਈ ਚੀਜ਼ ਨਹੀਂ ਹੋਵੇਗੀ ।

→ ਸਮਾਜੀਕਰਨ ਦੀ ਪ੍ਰਕਿਰਿਆ ਸਾਰੀ ਉਮਰ ਚੱਲਣ ਵਾਲੀ ਪ੍ਰਕਿਰਿਆ ਹੈ । ਜਿਵੇਂ-ਜਿਵੇਂ ਬੱਚਾ ਵੱਡਾ ਹੁੰਦਾ ਜਾਂਦਾ ਹੈ, ਸੁਤੰਤਰ ਹੁੰਦਾ ਜਾਂਦਾ ਹੈ ਅਤੇ ਸਮਾਜੀਕਰਨ ਦੀ ਪ੍ਰਕਿਰਿਆ ਜ਼ਰੂਰੀ ਹੋ ਜਾਂਦੀ ਹੈ । ਇਸ ਉਮਰ ਵਿੱਚ ਆ ਕੇ | ਉਸ ਨੂੰ ਨਿਯੰਤਰਣ ਵਿੱਚ ਰੱਖਣਾ ਪੈਂਦਾ ਹੈ ਤਾਂਕਿ ਉਹ ਗਲਤ ਰਸਤੇ ਉੱਤੇ ਨਾ ਜਾਵੇ । ਇੱਥੇ ਆ ਕੇ ਸਮਾਜੀਕਰਨ ਦੀ ਪ੍ਰਕਿਰਿਆ ਦਾ ਅਸਲੀ ਫਾਇਦਾ ਨਜ਼ਰ ਆਉਂਦਾ ਹੈ |

→ ਸਮਾਜੀਕਰਨ ਦੀ ਪ੍ਰਕਿਰਿਆ ਦੇ ਪੰਜ ਪੱਧਰ ਹੁੰਦੇ ਹਨ-ਬਾਲ ਅਵਸਥਾ (Infant Stage), ਬਚਪਨ ਅਵਸਥਾ (Childhood Stage), ਕਿਸ਼ੋਰ ਅਵਸਥਾ (Adolescent Stage), ਜਵਾਨੀ ਦੀ ਅਵਸਥਾ (Adulthood Stage) ਅਤੇ ਬੁਢਾਪਾ ਅਵਸਥਾ (Old Age) ।

→ ਬਾਲ ਅਵਸਥਾ ਪੈਦਾ ਹੋਣ ਤੋਂ ਸ਼ੁਰੂ ਹੋ ਕੇ ਇੱਕ ਸਾਲ ਚਲਦੀ ਹੈ । ਬਚਪਨ ਅਵਸਥਾ 13-14 ਸਾਲ ਦੀ ਉਮਰ ਤੱਕ ਚਲਦੀ ਰਹਿੰਦੀ ਹੈ । ਕਿਸ਼ੋਰ ਅਵਸਥਾ 17-18 ਸਾਲ ਤੱਕ ਚਲਦੀ ਰਹਿੰਦੀ ਹੈ । ਜਵਾਨੀ ਦੀ ਅਵਸਥਾ 18 – 50 ਸਾਲ ਤੱਕ ਚਲਦੀ ਹੈ ਅਤੇ ਇਸ ਤੋਂ ਬਾਅਦ ਬੁਢਾਪਾ ਸ਼ੁਰੂ ਹੋ ਜਾਂਦਾ ਹੈ ।

→ ਸਮਾਜੀਕਰਨ ਦੀ ਪ੍ਰਕਿਰਿਆ ਨੂੰ ਪੂਰਾ ਕਰਨ ਦੇ ਕਈ ਸਾਧਨ ਹੁੰਦੇ ਹਨ । ਇਹਨਾਂ ਸਾਧਨਾਂ ਨੂੰ ਅਸੀਂ ਦੋ ਭਾਰਾ ਵਿੱਚ ਵੰਡਦੇ ਹਾਂ-ਰਸਮੀ ਅਤੇ ਗ਼ੈਰ-ਰਸਮੀ। ਸਮਾਜੀਕਰਨ ਦੇ ਗ਼ੈਰ-ਰਸਮੀ ਸਾਧਨਾਂ ਵਿੱਚ ਅਸੀਂ ਪਰਿਵਾਰ, ਖੇਡ ਸਮੂਹ, ਧਰਮ ਆਦਿ ਨੂੰ ਲੈ ਸਕਦੇ ਹਾਂ ਅਤੇ ਰਸਮੀ ਸਾਧਨਾਂ ਵਿੱਚ ਕਾਨੂੰਨ, ਕਾਨੂੰਨੀ ਵਿਵਸਥਾ, ਰਾਜਨੀਤਕ ਵਿਵਸਥਾ ਆਦਿ ਆਉਂਦੇ ਹਨ ।

Punjab State Board PSEB 11th Class Maths Book Solutions Chapter 6 Linear Inequalities Ex 6.2 Textbook  Exercise Questions and Answers.

PSEB Solutions for Class 11 Maths Chapter 6 Linear Inequalities Ex 6.2

Question 1.
Solve the given inequality graphically in two-dimensional plane: x + y < 5.
Answer.
The graphical representation of x + y = 5 is given as dotted line in the figure below.
This line divides the xy-plane in two half planes, I and II.
Select a point (not on the line), which lies in one of the half planes, to determine whether the point satisfies the given inequality or not.
We select the point as (0, 0).
It is observed that, 0 + 0 < 5 or, 0 < 5, which is true. Therefore, half plane II is not the solution region of the given inequality. Also, it is evident that any point on the line does not satisfy the given strict inequality. Thus, the solution region of the given inequality is the shaded half plane I excluding the points on the line. This can be represented as follows.

Question 2.
Solve the given inequality graphically in two-dimensional plane : 2x + y > 6.
Answer.
The graphical representation of 2x + y = 6 is given in the figure below.
This line divides the xy-plane in two half planes, I and II.
Select a point (not on the line), which lies in one of the half planes, to determine whether the point satisfies the given inequality or not.
We select the point as (0, 0).
It is observed that,
2(0) + 0 ≥ 6 or 0 ≥ 6, which is false.
Therefore, half plane I is not the solution region of the given inequality.
Also, it is evident that any point on the line satisfies the given inequality.
Thus, the solution region of the given inequality is the shaded half plane II including the points on the line.
This can be represented as follows.

Question 3.
Solve the given inequality graphically in two-dimensional plane : 3x + 4y ≤ 12
Answer.
3x + 4y ≤ 12
The graphical representation of 3x + 4y = 12 is given in the figure below.
This line divides the xy-plane in two half planes, I and II.
Select a point (not on the line), which lies in one of the half planes, to determine whether the point satisfies the given inequality or not.
We select the point as (0, 0).
It is observed that,
3(0) + 4(0) ≤ 12 or 0 ≤ 12, which is true.
Therefore, half plane II is not the solution region of the given inequality.
Also, it is evident that any point on the line satisfies the given inequality.
Thus, the solution region of the given inequality is the shaded half plane I including the points on the line.
This can be represented as follows.

Question 4.
Solve the given inequality graphically in two-dimensional plane : y + 8 > 2x.
Answer.
The graphical representation of y + 8 = 2x is given in the figure below.
This line divides the xy-plane in two half planes.
Select a point (not on the line), which lies in one of the half planes, to determine whether the point satisfies the given inequality or not.
We select the point as (0, 0).
It is observed that,
0 + 8 ≥ 2(0) or 8 ≥ 0, which is true.
Therefore, lower half plane is not the solution region of the given inequality.
Also, it is evident that any point on the line satisfies the given inequality.
Thus, the solution region of the given inequality is the half plane containing the point (0, 0) including the line.
The solution region is represented by the shaded region as follows.

Question 5.
Solve the given inequality graphically in two-dimensional plane: x – y < 2
Answer.
The graphical representation of x – y = 2 is given in the figure below.
This line divides the xy-plane in two half planes.
Select a point (not on the line), which lies in one of the half planes, to determine whether the point satisfies the given inequality or not.
We select the point as (0, 0).
It is observed that, 0 – 0 < 2 or 0 < 2, which is true. Therefore, the lower half plane is not the solution region of the given inequality. Also, it is clear that any point on the line satisfies the given inequality. Thus, the solution region of the given inequality is the half plane containing the point (0, 0) including the line. The solution region is represented by the shaded region as follows.

Question 6.
Solve the given inequality graphically in two-dimensional plane: 2x – 3y > 6.
Answer.
The graphical representation of 2x – 3y = 6 is given as dotted line in the figure below.
This line divides the xy-plane in two half planes.
Select a point (not on the line), which lies in one of the half planes, to determine whether the point satisfies the given inequality or not.
We select the point as (0, 0).
It is observed that,
2(0) – 3(0) > 6 or 0 > 6, which is false.
Therefore, the upper half plane is not the solutibn region of the given inequality.
Also, it is clear that any point on the line does not satisfy the given inequality.
Thus, the solution region of the given inequality is the half plane that does not contain the point (0, 0) excluding the line.
The solution region is represented by the shaded region as follows.

Question 7.
Solve the given inequality graphically in two-dimensional plane: – 3x + 2y > – 6.
Ans.
The graphical representation of – 3x + 2y = – 6 is given in the figure below.
This line divides the xy-plane in two half planes.
Select a point (not on the line), which lies in one of the half planes, to determine whether the point satisfies the given inequality or not.
We select the point as (0, 0).
It is observed that,
– 3(0) + 2(0) >- 6 or 0 > – 6, which is true.
Therefore, the lower half plane is not the solution region of the given inequality.
Also, it is evident that any point on the line satisfies the given inequality.
Thus, the solution region of the given inequality is the half plane containing the point (0, 0) including the line.
The solution region is represented by the shaded region as follows.

Question 8.
Solve the given inequality graphically in two-dimensional plane: 3y 5x < 30.
Answer.
The given inequality is 3y – 5x < 30.
Corresponding equation of line is 3y – 5x = 30.
On putting x = 0, we get
3y – 5(0) = 30
⇒ 3y = 30
⇒ y = 10
Thus, line intersect the Y-axis at (0, 0).
On putting y = 0, we get
3(0) – 5x = 30
⇒ x = – 6
Thus, line intersect the X-axis at (- 6,0).

Join the points (0, 10) and (- 6,0) by a dotted line, since given inequality has sign <.
On putting (0, 0) in given inequality, we get

Question 9.
Solve the given inequality graphically in two-dimensional plane: y < – 2.
Ans.
The graphical representation of y = – 2 is given as dotted line in the figure below.
This line divides the xy-plane in two half planes.
Select a point (not on the line), which lies in one of the half planes, to determine whether the point satisfies the given inequality or not.
We select the point as (0, 0).
It is observed that,
0 < – 2, which is false. Also, it is evident that any point on the line does not satisfy the given inequality. Hence, every point below the line, y = – 2 (excluding all the points on the line), determines the solution of the given inequality. The solution region is represented by the shaded region as follows.

Question 10.
Solve the given inequality graphically in two-dimensional plane: x > -3
Answer.
The graphical representation of x = – 3 is given as dotted line in the figure below.
This line divides the xy-plane in two half planes.
Select a point (not on the line), which lies in one of the half planes, to determine whether the point satisfies the given inequality or not.
We select the point as (0, 0).
It is observed that,
0 > – 3, which is true.
Also, it is evident that any point on the line does not satisfy the given inequality.
Hence, every point on the right side of the line, x = – 3 (excluding all the points on the line), determines the solution of the given inequality.
The solution region is represented by the shaded region as follows.