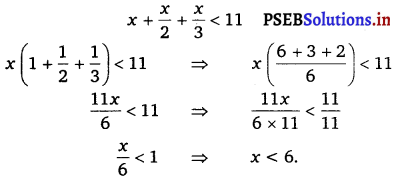Punjab State Board PSEB 11th Class Sociology Book Solutions Chapter 7 ਵਿਆਹ, ਪਰਿਵਾਰ ਅਤੇ ਨਾਤੇਦਾਰੀ Textbook Exercise Questions and Answers.
PSEB Solutions for Class 11 Sociology Chapter 7 ਵਿਆਹ, ਪਰਿਵਾਰ ਅਤੇ ਨਾਤੇਦਾਰੀ
Sociology Guide for Class 11 PSEB ਵਿਆਹ, ਪਰਿਵਾਰ ਅਤੇ ਨਾਤੇਦਾਰੀ Textbook Questions and Answers
I. ਨਿਮਨਲਿਖਤ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਉੱਤਰ 1-15 ਸ਼ਬਦਾਂ ਵਿੱਚ ਦਿਓ ।
ਪ੍ਰਸ਼ਨ 1.
ਅੰਤਰ-ਵਿਆਹ ਤੋਂ ਤੁਸੀਂ ਕੀ ਸਮਝਦੇ ਹੋ ?
ਉੱਤਰ-
ਉਹ ਵਿਆਹ ਜਿਹੜਾ ਕਿ ਵਿਅਕਤੀ ਇੱਕ ਨਿਸ਼ਚਿਤ ਸਮੂਹ, ਜਾਤੀ ਜਾਂ ਉਪਜਾਤੀ ਦੇ ਅੰਦਰ ਹੀ ਕਰਵਾਉਂਦਾ ਹੈ, ਅੰਤਰ-ਵਿਆਹ ਹੁੰਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 2.
ਵਿਆਹ ਸੰਸਥਾ ਦੀ ਉੱਤਪੱਤੀ ਦੇ ਕੋਈ ਦੋ ਮਹੱਤਵਪੂਰਣ ਅਧਾਰ ਦੱਸੋ ।
ਉੱਤਰ-
ਸਰੀਰਕ ਜ਼ਰੂਰਤ, ਭਾਵਨਾਤਮਕ ਜ਼ਰੂਰਤ, ਸਮਾਜ ਨੂੰ ਅੱਗੇ ਵਧਾਉਣਾ ਅਤੇ ਬੱਚਿਆਂ ਦੇ ਪਾਲਣ-ਪੋਸ਼ਣ ਕਰਕੇ ਵਿਆਹ ਦੀ ਸੰਸਥਾ ਸਾਹਮਣੇ ਆਈ ।

ਪ੍ਰਸ਼ਨ 3.
ਇੱਕ ਵਿਆਹ ਕਿਸਨੂੰ ਕਹਿੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਜਦੋਂ ਇੱਕ ਆਦਮੀ ਦਾ ਇੱਕ ਸਮੇਂ ਇੱਕ ਔਰਤ ਨਾਲ ਵਿਆਹ ਹੁੰਦਾ ਹੈ ਤਾਂ ਇਸ ਨੂੰ ਇੱਕ ਵਿਆਹ ਦਾ ਨਾਮ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 4.
ਸਾਲੀ ਵਿਆਹ ਕਿਸਨੂੰ ਕਹਿੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਜਦੋਂ ਇੱਕ ਵਿਅਕਤੀ ਆਪਣੀ ਪਤਨੀ ਦੀ ਮੌਤ ਤੋਂ ਬਾਅਦ ਉਸਦੀ ਭੈਣ ਨਾਲ ਵਿਆਹ ਕਰ ਲੈਂਦਾ ਹੈ ਤਾਂ ਉਸਨੂੰ ਸਾਲੀ ਵਿਆਹ ਕਹਿੰਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 5.
ਬਹੁ-ਪਤੀ ਵਿਆਹ ਦੀਆਂ ਕਿਸਮਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਇਹ ਦੋ ਪ੍ਰਕਾਰ ਦਾ ਹੁੰਦਾ ਹੈ-ਭਰਾਤਰੀ ਬਹੁ-ਪਤੀ ਵਿਆਹ ਜਿਸ ਵਿੱਚ ਇੱਕ ਔਰਤ ਦੇ ਸਾਰੇ ਪਤੀ ਭਰਾ ਹੁੰਦੇ ਹਨ ਅਤੇ ਗੈਰ ਭਰਾਤਰੀ ਬਹੁ-ਪਤੀ ਵਿਆਹ ਜਿਸ ਵਿੱਚ ਔਰਤ ਦੇ ਸਾਰੇ ਪਤੀ ਭਰਾ ਨਹੀਂ ਹੁੰਦੇ ।
ਪ੍ਰਸ਼ਨ 6.
ਬਹੁ-ਪਤਨੀ ਵਿਆਹ ਦੀਆਂ ਕਿਸਮਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਇਹ ਦੋ ਪ੍ਰਕਾਰ ਦਾ ਹੁੰਦਾ ਹੈ-ਦੋ ਪਤਨੀ ਵਿਆਹ ਜਿਸ ਵਿੱਚ ਵਿਅਕਤੀ ਦੀਆਂ ਦੋ ਪਤਨੀਆਂ ਹੁੰਦੀਆਂ ਹਨ ਅਤੇ ਬਹੁ-ਪਤਨੀ ਵਿਆਹ ਜਿਸ ਵਿੱਚ ਵਿਅਕਤੀ ਦੀਆਂ ਕਈ ਪਤਨੀਆਂ ਹੁੰਦੀਆਂ ਹਨ ।
ਪ੍ਰਸ਼ਨ 7.
ਅੰਤਰਵਿਆਹ ਦੀਆਂ ਕੁੱਝ ਉਦਾਹਰਨਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਮੁਸਲਮਾਨਾਂ ਵਿੱਚ ਸ਼ਿਆ ਅਤੇ ਸੁੰਨੀ ਅੰਤਰ-ਵਿਆਹੀ ਸਮੂਹ ਹਨ । ਇਸਾਈਆਂ ਵਿੱਚ ਵੀ ਰੋਮਨ-ਕੈਥੋਲਿਕ ਅਤੇ ਪ੍ਰੋਟੈਸਟੈਂਟ ਅੰਤਰ-ਵਿਆਹੀ ਸਮੂਹ ਹਨ ।
ਪ੍ਰਸ਼ਨ 8.
ਵਿਆਹ ਦੀ ਪਰਿਭਾਸ਼ਾ ਦਿਉ ।
ਉੱਤਰ-
ਲੰਡਬਰਗ ਦੇ ਅਨੁਸਾਰ, “ਵਿਆਹ ਦੇ ਨਿਯਮ ਅਤੇ ਤੌਰ-ਤਰੀਕੇ ਹੁੰਦੇ ਹਨ ਜੋ ਪਤੀ-ਪਤਨੀ ਦੇ ਇੱਕ-ਦੂਜੇ ਪ੍ਰਤੀ ਅਧਿਕਾਰਾਂ, ਕਰਤੱਵਾਂ ਅਤੇ ਵਿਸ਼ੇਸ਼ ਅਧਿਕਾਰਾਂ ਦਾ ਵਰਣਨ ਕਰਦੇ ਹਨ ।”

ਪ੍ਰਸ਼ਨ 9.
ਪਰਿਵਾਰ ਦੇ ਕੋਈ ਦੋ ਕੰਮ ਦੱਸੋ ।
ਉੱਤਰ-
- ਪਰਿਵਾਰ ਬੱਚੇ ਦਾ ਸਮਾਜੀਕਰਣ ਕਰਦਾ ਹੈ ।
- ਪਰਿਵਾਰ ਬੱਚੇ ਨੂੰ ਸੰਪੱਤੀ ਪ੍ਰਦਾਨ ਕਰਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 10.
ਅਕਾਰ ਦੇ ਆਧਾਰ ਉੱਤੇ ਪਰਿਵਾਰ ਦੇ ਸਰੂਪਾਂ ਦੇ ਨਾਂ ਲਿਖੋ ।
ਉੱਤਰ-
ਆਕਾਰ ਦੇ ਆਧਾਰ ਉੱਤੇ ਪਰਿਵਾਰ ਤਿੰਨ ਪ੍ਰਕਾਰ ਦੇ ਹੁੰਦੇ ਹਨ-ਕੇਂਦਰੀ ਪਰਿਵਾਰ, ਸੰਯੁਕਤ ਪਰਿਵਾਰ ਅਤੇ ਵਿਸਤ੍ਰਿਤ ਪਰਿਵਾਰ ।
ਪ੍ਰਸ਼ਨ 11.
ਸੱਤਾ ਦੇ ਆਧਾਰ ਉੱਤੇ ਪਰਿਵਾਰ ਦੇ ਸਰੂਪਾਂ ਦੇ ਨਾਂ ਲਿਖੋ ।
ਉੱਤਰ-
ਸੱਤਾ ਦੇ ਆਧਾਰ ਉੱਤੇ ਪਰਿਵਾਰ ਦੇ ਦੋ ਪ੍ਰਕਾਰ ਹੁੰਦੇ ਹਨ-ਪਿੱਤਰ ਸੱਤਾਤਮਕ ਅਤੇ ਮਾਤਰ ਸੱਤਾਤਮਕ ।
ਪ੍ਰਸ਼ਨ 12.
ਵਿਆਹ ਸੰਬੰਧ ਕਿਸਨੂੰ ਕਹਿੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਉਹ ਰਿਸ਼ਤੇਦਾਰੀ ਜੋ ਵਿਆਹ ਤੋਂ ਬਾਅਦ ਬਣਦੀ ਹੈ, ਉਸ ਨੂੰ ਵਿਆਹਕ ਸੰਬੰਧ ਕਹਿੰਦੇ ਹਨ । ਉਦਾਹਰਨ ਦੇ ਲਈ ਸੱਸ, ਸਹੁਰਾ, ਸਾਲਾ, ਸਾਲੀ, ਜਵਾਈ ਅਤੇ ਨੂੰਹ ਆਦਿ ।
ਪ੍ਰਸ਼ਨ 13.
ਸੰਯੁਕਤ ਪਰਿਵਾਰ ਤੋਂ ਤੁਸੀਂ ਕੀ ਸਮਝਦੇ ਹੋ ?
ਉੱਤਰ-
ਉਹ ਪਰਿਵਾਰ ਜਿਸ ਵਿੱਚ ਦੋ ਤੋਂ ਵੱਧ ਪੀੜ੍ਹੀਆਂ ਦੇ ਲੋਕ ਰਹਿੰਦੇ ਹਨ ਅਤੇ ਇੱਕ ਰਸੋਈ ਵਿੱਚ ਹੀ ਰੋਟੀ ਖਾਂਦੇ ਹਨ, ਸੰਯੁਕਤ ਪਰਿਵਾਰ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 14.
ਨਾਤੇਦਾਰੀ ਤੋਂ ਤੁਸੀਂ ਕੀ ਸਮਝਦੇ ਹੋ ?
ਉੱਤਰ-
ਨਾਤੇਦਾਰੀ ਵਿੱਚ ਉਹ ਸੰਬੰਧ ਸ਼ਾਮਿਲ ਹੁੰਦੇ ਹਨ ਜੋ ਕਲਪਿਤ ਜਾਂ ਅਸਲੀ ਵੰਸ਼ ਪਰੰਪਰਾਗਤ ਬੰਧਨਾਂ ਉੱਤੇ ਆਧਾਰਿਤ ਅਤੇ ਸਮਾਜ ਦੁਆਰਾ ਪ੍ਰਭਾਵਿਤ ਹੁੰਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 15.
ਨਾਤੇਦਾਰੀ ਦੀਆਂ ਕਿਸਮਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਨਾਤੇਦਾਰੀ ਦੀਆਂ ਤਿੰਨ ਸ਼੍ਰੇਣੀਆਂ ਹੁੰਦੀਆਂ ਹਨ-ਪ੍ਰਾਥਮਿਕ ਰਿਸ਼ਤੇਦਾਰੀ, ਗੌਣ ਸੰਬੰਧੀ ਅਤੇ ਤੀਜੇ ਦਰਜੇ ਦੇ ਸੰਬੰਧੀ ।
II. ਨਿਮਨਲਿਖਤ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਉੱਤਰ 30-35 ਸ਼ਬਦਾਂ ਵਿੱਚ ਦਿਓ ।
ਪ੍ਰਸ਼ਨ 1.
ਸੰਸਥਾ ਸ਼ਬਦ ਤੋਂ ਤੁਸੀਂ ਕੀ ਸਮਝਦੇ ਹੋ ?
ਉੱਤਰ-
ਸੰਸਥਾ ਨਾ ਤਾਂ ਲੋਕਾਂ ਦਾ ਸਮੂਹ ਹੈ ਅਤੇ ਨਾ ਹੀ ਸੰਗਠਨ ਹੈ । ਸੰਸਥਾ ਤਾਂ ਕਿਸੇ ਕੰਮ ਜਾਂ ਉਦੇਸ਼ ਨੂੰ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ ਪਰਿਮਾਪਾਂ ਦੀ ਵਿਵਸਥਾ ਹੈ । ਸੰਸਥਾ ਤਾਂ ਕਿਸੇ ਵਿਸ਼ੇਸ਼ ਮਹੱਤਵਪੂਰਨ ਮਨੁੱਖੀ ਕਿਰਿਆ ਦੁਆਲੇ ਕੇਂਦਰਿਤ ਰੂੜੀਆਂ ਅਤੇ ਲੋਕ-ਰੀਤਾਂ ਦਾ ਗੁੱਛਾ ਹੈ । ਸੰਸਥਾਵਾਂ ਤਾਂ ਸੰਚਾਰਿਤ ਕਿਰਿਆਵਾਂ ਹਨ ਜਿਨ੍ਹਾਂ ਰਾਹੀਂ ਵਿਅਕਤੀ ਆਪਣੇ ਕਾਰਜ ਕਰਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 2.
ਨਿਰਧਾਰਨਾਤਮਕ ਨਿਯਮ ਕਿਸ ਨੂੰ ਕਹਿੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਹਰੇਕ ਸੰਸਥਾ ਦੇ ਕੁੱਝ ਨਿਰਧਾਰਨਾਤਮਕ ਨਿਯਮ ਹੁੰਦੇ ਹਨ ਜਿਨ੍ਹਾਂ ਨੂੰ ਸਭ ਨੂੰ ਮੰਨਣਾ ਪੈਂਦਾ ਹੈ । ਉਦਾਹਰਣ ਦੇ ਲਈ ਵਿਆਹ ਇੱਕ ਅਜਿਹੀ ਸੰਸਥਾ ਹੈ ਜਿਹੜੀ ਪਤੀ-ਪਤਨੀ ਵਿਚਕਾਰ ਸੰਬੰਧਾਂ ਨੂੰ ਨਿਯਮਿਤ ਕਰਦਾ ਹੈ । ਇਸੇ ਤਰ੍ਹਾਂ ਸਿੱਖਿਅਕ ਸੰਸਥਾਵਾਂ ਦੇ ਰੂਪ ਵਿੱਚ ਸਕੂਲ ਅਤੇ ਕਾਲਜ ਦੇ ਆਪਣੇ-ਆਪਣੇ ਨਿਯਮਾ ਅਤੇ ਕੰਮ ਕਰਨ ਦੇ ਤੌਰ-ਤਰੀਕੇ ਹੁੰਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 3.
ਅਨੁਲੋਮ ਅਤੇ ਪਤੀਲੋਮ ਕੀ ਹੈ ?
ਉੱਤਰ-
- ਅਨੁਲੋਮ-ਇਹ ਇੱਕ ਪ੍ਰਕਾਰ ਦਾ ਸਮਾਜਿਕ ਨਿਯਮ ਹੈ ਜਿਸ ਅਨੁਸਾਰ ਉੱਚੀ ਜਾਤੀ ਦਾ ਮੁੰਡਾ ਹੇਠਲੀ ਜਾਤੀ ਦੀ ਲੜਕੀ ਨਾਲ ਵਿਆਹ ਕਰਦਾ ਹੈ ।
- ਪਤੀਲੋਮ-ਇਹ ਇੱਕ ਪ੍ਰਕਾਰ ਦਾ ਵਿਆਹ ਹੈ ਜਿਸ ਵਿੱਚ ਹੇਠਲੀ ਜਾਤੀ ਦਾ ਮੁੰਡਾ ਉੱਚੀ ਜਾਤੀ ਦੀ ਲੜਕੀ ਨਾਲ ਵਿਆਹ ਕਰਦਾ ਹੈ । ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਵਿਆਹ ਨੂੰ ਹਿੰਦੂ ਧਾਰਮਿਕ ਗ੍ਰੰਥਾਂ ਵਿੱਚ ਮਾਨਤਾ ਨਹੀਂ ਦਿੱਤੀ ਗਈ ਸੀ ।
ਪ੍ਰਸ਼ਨ 4.
ਬਹੁ-ਵਿਆਹ ਦੇ ਦੋ ਪ੍ਰਕਾਰਾਂ ਉੱਤੇ ਸੰਖੇਪ ਟਿੱਪਣੀ ਕਰੋ !
ਉੱਤਰ-
- ਬਹੁ-ਪਤੀ ਵਿਆਹ-ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਵਿਆਹ ਵਿੱਚ ਇੱਕ ਔਰਤ ਦੇ ਕਈ ਪਤੀ ਹੁੰਦੇ ਹਨ ਅਤੇ ਅੱਗੇ ਇਸ ਦੇ ਦੋ ਪ੍ਰਕਾਰ ਹਨ । ਭਰਾਤਰੀ ਬਹੁ-ਪਤੀ ਵਿਆਹ ਵਿੱਚ ਸਾਰੇ ਪਤੀ ਭਰਾ ਹੁੰਦੇ ਹਨ ਅਤੇ ਗੈਰ-ਭਰਾਤਰੀ ਬਹੁ-ਪਤੀ ਵਿਆਹ ਵਿੱਚ ਸਾਰੇ ਪਤੀ ਆਪਸ ਵਿੱਚ ਭਰਾ ਨਹੀਂ ਹੁੰਦੇ ।
- ਬਹੁ-ਪਤਨੀ ਵਿਆਹ-ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਵਿਆਹ ਵਿੱਚ ਇੱਕ ਪਤੀ ਦੀਆਂ ਇੱਕੋ ਸਮੇਂ ਵਿੱਚ ਕਈ ਪਤਨੀਆਂ ਹੁੰਦੀਆਂ ਸਨ ।
ਪ੍ਰਸ਼ਨ 5.
ਭਰਾਤਰੀ ਬਹੁਪਤੀ ਵਿਆਹ ਕਿਸ ਨੂੰ ਕਹਿੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਵਿਆਹ ਵਿੱਚ ਇੱਕ ਪਤਨੀ ਦੇ ਕਈ ਪਤੀ ਹੁੰਦੇ ਹਨ ਅਤੇ ਉਹ ਸਾਰੇ ਆਪਸ ਵਿੱਚ ਭਰਾ ਹੁੰਦੇ ਹਨ | ਬੱਚਿਆਂ ਦਾ ਪਿਤਾ ਵੱਡੇ ਭਰਾ ਨੂੰ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ ਅਤੇ ਪਤਨੀ ਨਾਲ ਸੰਬੰਧ ਬਣਾਉਣ ਤੋਂ ਪਹਿਲਾਂ ਵੱਡੇ ਭਰਾ ਦੀ ਇਜ਼ਾਜ਼ਤ ਲੈਣੀ ਪੈਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 6.
ਵਰਜਿਤ ਮਨਾਹੀ (Incest Taboo) ਦੀ ਚਰਚਾ ਕਰੋ ।
ਉੱਤਰ-
ਵਰਜਿਤ ਮਨਾਹੀ ਦਾ ਅਰਥ ਹੈ ਸਰੀਰਕ ਜਾਂ ਵਿਆਹਕ ਸੰਬੰਧ ਉਹਨਾਂ ਦੋ ਵਿਅਕਤੀਆਂ ਵਿਚਕਾਰ ਜਿਹੜੇ ਇੱਕਦੂਜੇ ਨਾਲ ਖੂਨ ਸੰਬੰਧਾਂ ਨਾਲ ਸੰਬੰਧਿਤ ਹਨ ਜਾਂ ਇੱਕ ਪਰਿਵਾਰ ਨਾਲ ਸੰਬੰਧ ਰੱਖਦੇ ਹਨ । ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਸੰਬੰਧ ਸਾਰੇ ਮਨੁੱਖੀ ਸਮਾਜਾਂ ਵਿੱਚ ਵਰਜਿਤ ਹਨ । ਕਿਸੇ ਵੀ ਸੰਸਕ੍ਰਿਤੀ ਵਿੱਚ ਖੂਨ ਸੰਬੰਧੀਆਂ ਵਿਚਕਾਰ ਕਿਸੇ ਪ੍ਰਕਾਰ ਦੇ ਲੈਂਗਿਕ ਸੰਬੰਧਾਂ ਦੀ ਮਨਾਹੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 7.
ਗੋਤਰ ਕਿਸਨੂੰ ਕਹਿੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਗੋਤਰ ਰਿਸ਼ਤੇਦਾਰਾਂ ਦਾ ਸਮੂਹ ਹੁੰਦਾ ਹੈ ਜਿਹੜੇ ਕਿਸੇ ਸਾਂਝੇ ਪੂਰਵਜਾਂ ਦੀ ਇੱਕ-ਰੇਖਕੀ ਸੰਤਾਨ ਹੁੰਦੇ ਹਨ । ਪੂਰਵਜ ਆਮ ਤੌਰ ਉੱਤੇ ਕਲਪਿਤ ਹੀ ਹੁੰਦੇ ਹਨ ਕਿਉਂਕਿ ਉਹਨਾਂ ਬਾਰੇ ਕਿਸੇ ਨੂੰ ਕੁੱਝ ਪਤਾ ਨਹੀਂ ਹੁੰਦਾ । ਇਹ ਬਾਹਰ ਵਿਆਹੀ ਸਮੂਹ ਹੁੰਦੇ ਹਨ । ਇਹ ਵੰਸ਼ ਸਮੂਹ ਦਾ ਹੀ ਵਿਸਤ੍ਰਿਤ ਰੂਪ ਹੈ ਜੋ ਕਿ ਮਾਤਾ ਜਾਂ ਪਿਤਾ ਦੇ ਕਿਸੇ ਵਿੱਚੋਂ ਇੱਕ ਤੋਂ ਅਨੁਰੇਖਿਤ ਖੂਨ ਸੰਬੰਧੀਆਂ ਤੋਂ ਮਿਲ ਕੇ ਬਣਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 8.
ਸਮਾਂਨਾਤਰ ਅਤੇ ਵਿਪਰੀਤ ਚਚੇਰੇ/ਮਮੇਰੇ ਵਿਆਹ ਦੇ ਵਿਚਕਾਰ ਅੰਤਰ ਦੱਸੋ ।
ਉੱਤਰ-
- ਸਮਾਨਾਂਤਰ ਚਚੇਰੇ/ਮਮੇਰੇ ਵਿਆਹ ਇੱਕ ਪ੍ਰਕਾਰ ਦਾ ਵਿਆਹ ਹੈ ਜਿਸ ਵਿੱਚ ਦੋ ਭਰਾਵਾਂ ਜਾਂ ਦੋ ਭੈਣਾਂ ਦੇ ਬੱਚਿਆਂ ਦਾ ਵਿਆਹ ਕਰ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ । ਮੁਸਲਮਾਨਾਂ ਵਿੱਚ ਇਹ ਪ੍ਰਚਲਿਤ ਹੈ ।
- ਵਿਪਰੀਤ ਚਚੇਰੇ/ਮਮੇਰੇ ਵਿਆਹ ਵਿੱਚ ਵਿਅਕਤੀ ਦਾ ਮਾਮੇ ਦੀ ਕੁੜੀ ਨਾਲ ਜਾਂ ਭੂਆ ਦੀ ਕੁੜੀ ਨਾਲ ਵਿਆਹ ਹੋ ਜਾਂਦਾ ਹੈ । ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਵਿਆਹ ਗੋਂਡ, ਉਰਾਉਂ ਅਤੇ ਖਰੀਆਂ ਕਬੀਲਿਆਂ ਵਿੱਚ ਪ੍ਰਚਲਿਤ ਹੈ ।
ਪ੍ਰਸ਼ਨ 9.
ਨੇੜੇ ਅਤੇ ਦੂਰੀ ਦੇ ਆਧਾਰ ਉੱਤੇ ਰਿਸ਼ਤੇਦਾਰੀ ਨੂੰ ਪਰਿਭਾਸ਼ਿਤ ਕਰੋ ।
ਉੱਤਰ-
ਨੇੜੇ ਅਤੇ ਦੁਰੀ ਦੇ ਆਧਾਰ ਉੱਤੇ ਤਿੰਨ ਪ੍ਰਕਾਰ ਦੀ ਰਿਸ਼ਤੇਦਾਰੀ ਹੁੰਦੀ ਹੈ-
- ਪ੍ਰਾਥਮਿਕ ਰਿਸ਼ਤੇਦਾਰੀ – ਉਹ ਰਿਸ਼ਤੇਦਾਰ ਜਿਨ੍ਹਾਂ ਨਾਲ ਸਾਡਾ ਸਿੱਧਾ ਅਤੇ ਨੇੜੇ ਦਾ ਖੂਨ ਦਾ ਸੰਬੰਧ ਹੁੰਦਾ ਹੈ ਜਿਵੇਂ ਕਿ ਮਾਤਾ-ਪਿਤਾ, ਭੈਣ-ਭਰਾ ਆਦਿ ।
- ਦੂਜੇ ਦਰਜੇ ਦੇ ਰਿਸ਼ਤੇਦਾਰ – ਇਹ ਸਾਡੇ ਪ੍ਰਾਥਮਿਕ ਰਿਸ਼ਤੇਦਾਰਾਂ ਦੇ ਪ੍ਰਾਥਮਿਕ ਰਿਸ਼ਤੇਦਾਰ ਹੁੰਦੇ ਹਨ ਜਿਵੇਂ ਕਿ ਪਿਤਾ , ਦੇ ਪਿਤਾ-ਦਾਦਾ ਜਾਂ ਮਾਤਾ ਦੇ ਪਿਤਾ-ਨਾਨਾ ਆਦਿ ।
- ਤੀਜੇ ਦਰਜੇ ਦੇ ਰਿਸ਼ਤੇਦਾਰ-ਉਹ ਰਿਸ਼ਤੇਦਾਰ ਜਿਹੜੇ ਸਾਡੇ ਦੁਤੀਆਂ ਸੰਬੰਧੀਆਂ ਦੇ ਪ੍ਰਾਥਮਿਕ ਰਿਸ਼ਤੇਦਾਰ ਹੁੰਦੇ ਹਨ ਜਿਵੇਂ ਕਿ ਚਾਚੇ ਦੀ ਪਤਨੀ ਚਾਚੀ ਜਾਂ ਭੂਆ ਦਾ ਪਤੀ ਫੁਫੜ ।
III. ਨਿਮਨਲਿਖਤ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਉੱਤਰ 75-85 ਸ਼ਬਦਾਂ ਵਿੱਚ ਦਿਓ ।
ਪ੍ਰਸ਼ਨ 1.
ਮਹੱਤਵਪੂਰਨ ਸਮਾਜਿਕ ਸੰਸਥਾਵਾਂ ‘ਤੇ ਸੰਖੇਪ ਵਿੱਚ ਚਰਚਾ ਕਰੋ ।
ਉੱਤਰ-
- ਵਿਆਹ – ਵਿਆਹ ਸਭ ਤੋਂ ਮਹੱਤਵਪੂਰਨ ਸਮਾਜਿਕ ਸੰਸਥਾ ਹੈ ਜਿਸਦੀ ਮੱਦਦ ਨਾਲ ਵਿਅਕਤੀ ਨੂੰ ਆਪਣੀ ਪਤਨੀ ਨਾਲ ਲੈਂਗਿਕ ਸੰਬੰਧ ਬਣਾਉਣ, ਬੱਚੇ ਪੈਦਾ ਕਰਨ ਦੀ ਆਗਿਆ ਹੁੰਦੀ ਹੈ । ਵਿਆਹ ਤੋਂ ਬਾਅਦ ਹੀ ਪਰਿਵਾਰ ਦਾ ਨਿਰਮਾਣ ਹੁੰਦਾ ਹੈ ।
- ਪਰਿਵਾਰ – ਜਦੋਂ ਵਿਅਕਤੀ ਵਿਆਹ ਕਰਦਾ ਹੈ ਅਤੇ ਬੱਚੇ ਪੈਦਾ ਕਰਦਾ ਹੈ ਤਾਂ ਪਰਿਵਾਰ ਦਾ ਨਿਰਮਾਣ ਹੁੰਦਾ ਹੈ । ਪਰਿਵਾਰ ਹੀ ਵਿਅਕਤੀ ਨੂੰ ਜੀਵਨ ਜੀਊਣ ਦੇ ਤਰੀਕੇ ਸਿਖਾਉਂਦਾ ਹੈ ਅਤੇ ਉਸਨੂੰ ਸਮਾਜ ਵਿੱਚ ਰਹਿਣ ਦੇ ਤਰੀਕੇ ਸਿਖਾਉਂਦਾ ਹੈ।
- ਨਾਤੇਦਾਰੀ – ਨਾਤੇਦਾਰੀ ਰਿਸ਼ਤੇਦਾਰਾਂ ਦੀ ਵਿਵਸਥਾ ਹੈ ਜਿਸ ਵਿੱਚ ਖੂਨ ਸੰਬੰਧੀ ਅਤੇ ਵਿਆਹ ਸੰਬੰਧੀ ਰਿਸ਼ਤੇਦਾਰ ਸ਼ਾਮਿਲ ਹੁੰਦੇ ਹਨ । ਰਿਸ਼ਤੇਦਾਰੀ ਤੋਂ ਬਿਨਾਂ ਵਿਅਕਤੀ ਜੀਵਨ ਨਹੀਂ ਜਾ ਸਕਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 2.
ਵਿਆਹ ਦੀਆਂ ਮਹੱਤਵਪੂਰਨ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਕਿਹੜੀਆਂ ਹਨ ?
ਉੱਤਰ-
- ਵਿਆਹ ਇੱਕ ਸਰਵਵਿਆਪਕ ਸੰਸਥਾ ਹੈ ਜਿਹੜੀ ਹਰੇਕ ਸਮਾਜ ਵਿੱਚ ਪਾਈ ਜਾਂਦੀ ਹੈ ।
- ਵਿਆਹ ਲੈਂਗਿਕ ਸੰਬੰਧਾਂ ਨੂੰ ਸੀਮਿਤ ਅਤੇ ਨਿਯੰਤਰਿਤ ਕਰਦਾ ਹੈ ।
- ਵਿਆਹ ਨਾਲ ਵਿਅਕਤੀ ਦੇ ਲੈਂਗਿਕ ਸੰਬੰਧਾਂ ਨੂੰ ਸਮਾਜਿਕ ਮਾਨਤਾ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ ।
- ਵਿਆਹ ਨਾਲ ਆਦਮੀ ਅਤੇ ਔਰਤ ਨੂੰ ਸਮਾਜਿਕ ਸਥਿਤੀ ਪ੍ਰਾਪਤ ਹੋ ਜਾਂਦੀ ਹੈ ।
- ਵੱਖ-ਵੱਖ ਸਮਾਜਾਂ ਵਿੱਚ ਵੱਖ-ਵੱਖ ਪ੍ਰਕਾਰ ਦੇ ਵਿਆਹ ਹੁੰਦੇ ਹਨ।
- ਵਿਆਹ ਦੀ ਸੰਸਥਾ ਦੀ ਮੱਦਦ ਨਾਲ ਧਾਰਮਿਕ ਰੀਤੀ-ਰਿਵਾਜਾਂ ਨੂੰ ਸੁਰੱਖਿਅਤ ਰੱਖਿਆ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਵਿਆਹ ਦੀਆਂ ਕਿਸਮਾਂ ਦੇ ਰੂਪ ਵਿੱਚ ਇੱਕ-ਵਿਆਹ ਅਤੇ ਬਹੁ-ਵਿਆਹ ਦੇ ਵਿੱਚਕਾਰ ਅੰਤਰ ਦੱਸੋ ।
ਉੱਤਰ-
- ਇੱਕ ਵਿਆਹ – ਅੱਜ-ਕਲ ਦੇ ਸਮੇਂ ਵਿੱਚ ਇੱਕ ਵਿਆਹ ਦਾ ਪ੍ਰਚਲਨ ਸਭ ਤੋਂ ਵੱਧ ਹੈ । ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਵਿਆਹ ਵਿੱਚ ਇੱਕ ਆਦਮੀ ਇੱਕ ਹੀ ਸਮੇਂ ਵਿੱਚ ਇੱਕ ਹੀ ਔਰਤ ਨਾਲ ਵਿਆਹ ਕਰਵਾ ਸਕਦਾ ਹੈ । ਇਸ ਵਿੱਚ ਇੱਕ ਪਤੀ ਜਾਂ ਪਤਨੀ ਦੇ ਰਹਿੰਦੇ ਹੋਏ ਦੂਜਾ ਵਿਆਹ ਕਰਨਾ ਗੈਰ-ਕਾਨੂੰਨੀ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ । ਪਤੀ-ਪਤਨੀ ਦੇ ਸੰਬੰਧ ਡੂੰਘੇ, ਸਥਾਈ ਅਤੇ ਪਿਆਰ ਨਾਲ ਭਰਪੂਰ ਹੁੰਦੇ ਹਨ ।
- ਬਹੁ-ਵਿਆਹ – ਬਹੁ-ਵਿਆਹ ਦਾ ਅਰਥ ਇੱਕ ਤੋਂ ਵੱਧ ਵਿਆਹ ਕਰਵਾਉਣਾ ਹੈ । ਜੇਕਰ ਇੱਕ ਔਰਤ ਜਾਂ ਆਦਮੀ ਇੱਕ ਤੋਂ ਵੱਧ ਵਿਆਹ ਕਰਵਾਏ ਤਾਂ ਇਸਨੂੰ ਬਹੁ-ਵਿਆਹ ਕਹਿੰਦੇ ਹਨ । ਇਹ ਦੋ ਪ੍ਰਕਾਰ ਦਾ ਹੁੰਦਾ ਹੈ-ਬਹੁ-ਪਤਨੀ ਵਿਆਹ ਅਤੇ ਬਹੁ-ਪਤੀ ਵਿਆਹ । ਬਹੁ-ਪਤੀ ਵਿਆਹ ਵੀ ਦੋ ਪ੍ਰਕਾਰ ਦਾ ਹੁੰਦਾ ਹੈ-ਭਰਾਤਰੀ ਬਹੁਪਤੀ ਵਿਆਹ ਅਤੇ ਗੈਰ ਭਰਾਤਰੀ ਬਹੁਪਤੀ ਵਿਆਹ ।
ਪ੍ਰਸ਼ਨ 4.
ਪਰਿਵਾਰ ਦੇ ਕੰਮਾਂ ਬਾਰੇ ਸਮਝਾਉ ।
ਉੱਤਰ-
- ਪਰਿਵਾਰ ਵਿੱਚ ਬੱਚੇ ਦਾ ਸਮਾਜੀਕਰਨ ਹੁੰਦਾ ਹੈ । ਪਰਿਵਾਰ ਵਿੱਚ ਵਿਅਕਤੀ ਸਮਾਜ ਵਿੱਚ ਰਹਿਣ ਦੇ ਤੌਰਤਰੀਕੇ ਸਿੱਖਦਾ ਹੈ ਅਤੇ ਚੰਗਾ ਨਾਗਰਿਕ ਬਣਦਾ ਹੈ ।
- ਪਰਿਵਾਰ ਸਾਡੀ ਸੰਸਕ੍ਰਿਤੀ ਸਾਂਭਦਾ ਹੈ । ਹਰੇਕ ਪਰਿਵਾਰ ਆਪਣੇ ਬੱਚਿਆਂ ਨੂੰ ਸੰਸਕ੍ਰਿਤੀ ਦਿੰਦਾ ਹੈ ਜਿਸ ਨਾਲ ਸੰਸਕ੍ਰਿਤੀ ਦਾ ਪੀੜ੍ਹੀ ਦਰ ਪੀੜ੍ਹੀ ਸੰਚਾਰ ਹੁੰਦਾ ਰਹਿੰਦਾ ਹੈ ।
- ਪਰਿਵਾਰ ਵਿੱਚ ਵਿਅਕਤੀ ਦੀ ਸੰਪੱਤੀ ਇੱਕ ਪੀੜ੍ਹੀ ਤੋਂ ਦੂਜੀ ਪੀੜ੍ਹੀ ਤੱਕ ਪਹੁੰਚ ਜਾਂਦੀ ਹੈ ਅਤੇ ਇਸ ਨਾਲ ਵਿਅਕਤੀ ਦੀ ਸਾਰੇ ਜੀਵਨ ਦੀ ਕਮਾਈ ਸੁਰੱਖਿਅਤ ਰਹਿ ਜਾਂਦੀ ਹੈ ।
- ਪੈਸੇ ਦੀ ਜ਼ਰੂਰਤ ਪਰਿਵਾਰ ਦੇ ਮੈਂਬਰਾਂ ਦੀਆਂ ਜ਼ਰੂਰਤਾਂ ਪੂਰੀਆਂ ਕਰਨ ਦੇ ਲਈ ਹੁੰਦੀ ਹੈ ਅਤੇ ਇਸ ਕਾਰਨ ਹੀ ਪਰਿਵਾਰ ਪੈਸੇ ਦਾ ਪ੍ਰਬੰਧ ਕਰਦਾ ਹੈ ।
- ਪਰਿਵਾਰ ਵਿਅਕਤੀ ਉੱਤੇ ਨਿਯੰਤਰਣ ਰੱਖਦਾ ਹੈ ਤਾਂਕਿ ਉਹ ਗ਼ਲਤ ਰਸਤੇ ਉੱਤੇ ਨਾ ਜਾਵੇ ।
ਪ੍ਰਸ਼ਨ 5.
(ਉ) ਅਨੁਲੋਮ
(ਅ) ਲੋਮ
(ੲ) ਦੇਵਰ ਵਿਆਹ
(ਸ) ਸਾਲੀ ਵਿਆਹ, ਅਜਿਹੀਆਂ ਧਾਰਨਾਵਾਂ ਦੀ ਵਿਆਖਿਆ ਕਰੋ ।
ਉੱਤਰ-
(ਉ) ਅਨੁਲੋਮ ਵਿਆਹ – ਦੇਖੋ ਅਭਿਆਸ ਦੇ ਪ੍ਰਸ਼ਨ II (3).
(ਅ ਪ੍ਰਤੀਲੋਮ ਵਿਆਹ – ਦੇਖੋ ਅਭਿਆਸ ਦੇ ਪ੍ਰਸ਼ਨ II (3).
(ੲ) ਦੇਵਰ ਵਿਆਹ – ਵਿਆਹ ਦੀ ਇਸ ਪ੍ਰਥਾ ਵਿੱਚ ਪਤੀ ਦੀ ਮੌਤ ਹੋ ਜਾਣ ਤੋਂ ਬਾਅਦ ਪਤਨੀ ਪਤੀ ਦੇ ਛੋਟੇ ਭਰਾ ਨਾਲ ਵਿਆਹ ਕਰਵਾ ਲੈਂਦੀ ਹੈ । ਇਸ ਨਾਲ ਪਰਿਵਾਰ ਦੀ ਜਾਇਦਾਦ ਸੁਰੱਖਿਅਤ ਰਹਿ ਜਾਂਦੀ ਹੈ । ਪਰਿਵਾਰ ਟੁੱਟਣ ਤੋਂ ਬੱਚ ਜਾਂਦਾ ਹੈ, ਬੱਚਿਆਂ ਦਾ ਪਾਲਣ-ਪੋਸ਼ਣ ਠੀਕ ਤਰੀਕੇ ਨਾਲੇ ਹੋ ਜਾਂਦਾ ਹੈ ।
(ਸ ਸਾਲੀ ਵਿਆਹ – ਇਸ ਵਿਆਹ ਵਿੱਚ ਆਦਮੀ ਆਪਣੀ ਪਤਨੀ ਦੀ ਮੌਤ ਤੋਂ ਬਾਅਦ ਆਪਣੀ ਸਾਲੀ ਨਾਲ ਵਿਆਹ ਕਰਵਾ ਲੈਂਦਾ ਹੈ । ਇਹ ਦੋ ਪ੍ਰਕਾਰ ਦਾ ਹੁੰਦਾ ਹੈ-ਸੀਮਿਤ ਸਾਲੀ ਵਿਆਹ ਅਤੇ ਸਮਕਾਲੀ ਸਾਲੀ ਵਿਆਹ ।
IV. ਨਿਮਨਲਿਖਤ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਉੱਤਰ 250-300 ਸ਼ਬਦਾਂ ਵਿੱਚ ਦਿਓ ।
ਪ੍ਰਸ਼ਨ 1.
ਸੰਸਥਾ ਤੋਂ ਤੁਸੀਂ ਕੀ ਸਮਝਦੇ ਹੋ ? ਇਸ ਦੀਆਂ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਸੰਸਥਾ ਦਾ ਅਰਥ (Meaning of Institution) – ਅਸੀਂ ਆਪਣੇ ਜੀਵਨ ਵਿੱਚ ਸੈਂਕੜੇ ਵਾਰ ਇਸ ਸੰਸਥਾ ਸ਼ਬਦ ਦਾ ਪ੍ਰਯੋਗ ਕਰਦੇ ਹਾਂ । ਆਮ ਆਦਮੀ ਇਸ ਸ਼ਬਦ ਦੇ ਅਰਥ ਕਿਸੇ ਇਮਾਰਤ (Building) ਤੋਂ ਲੈਂਦਾ ਹੈ ਪਰ ਸਮਾਜ ਵਿਗਿਆਨ ਵਿੱਚ ਇਸ ਦੇ ਮਤਲਬ ਕਿਸੇ ਇਮਾਰਤ ਜਾਂ ਲੋਕਾਂ ਦੇ ਸਮੂਹ ਤੋਂ ਨਹੀਂ ਲਏ ਜਾਂਦੇ | ਸਮਾਜ ਵਿਗਿਆਨੀ ਤਾਂ ਸੰਸਥਾ ਸ਼ਬਦ ਦੇ ਅਰਥ ਵਿਸਤ੍ਰਿਤ ਸ਼ਬਦਾਂ ਅਤੇ ਸਮਾਜ ਦੇ ਅਨੁਸਾਰ ਕਰਦੇ ਹਨ । ਇਹਨਾਂ ਦੇ ਅਨੁਸਾਰ ਸੰਸਥਾ ਤਾਂ ਇੱਕ ਅਜਿਹੀ ਨਿਯਮਾਂ ਜਾਂ ਪਰਿਮਾਪਾਂ ਦੀ ਵਿਵਸਥਾ ਜਿਹੜੀ ਲੋਕਾਂ ਦੀਆਂ ਜ਼ਰੂਰਤਾਂ ਪੂਰੀਆਂ ਕਰਨ ਵਿੱਚ ਮੱਦਦ ਕਰਦੀ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਸੰਸਥਾ ਤਾਂ ਵਿਅਕਤੀਆਂ ਦੀਆਂ ਕਿਰਿਆਵਾਂ ਜਾਂ ਜ਼ਰੂਰਤਾਂ ਨੂੰ ਪੂਰਾ ਕਰਨ ਲਈ ਰੂੜੀਆਂ ਅਤੇ ਲੋਕ ਗੀਤਾਂ ਦਾ ਇਕੱਠ ਹੈ । ਇਹ ਤਾਂ ਉਹ ਪ੍ਰਕ੍ਰਿਆਵਾਂ ਹਨ ਜਿਨ੍ਹਾਂ ਦੀ ਮਦਦ ਨਾਲ ਵਿਅਕਤੀ ਆਪਣੇ ਕਾਰਜ ਕਰਦਾ ਹੈ । ਸੰਸਥਾ ਤਾਂ ਸੰਬੰਧਾਂ ਦੀ ਉਹ ਸੰਗਠਿਤ ਵਿਵਸਥਾ ਹੈ ਜਿਸ ਵਿੱਚ ਸਮਾਜ ਦੀਆਂ ਕੀਮਤਾਂ ਸ਼ਾਮਲ ਹੁੰਦੀਆਂ ਹਨ ਅਤੇ ਜੋ ਸਮਾਜ ਦੀਆਂ ਜ਼ਰੂਰਤਾਂ ਪੂਰੀਆਂ ਕਰਦੀਆਂ ਹਨ । ਇਹਨਾਂ ਦਾ ਕੰਮ ਵਿਅਕਤੀ ਦੀਆਂ ਜ਼ਰੂਰਤਾਂ ਪੂਰੀਆਂ ਕਰਨਾ ਹੁੰਦਾ ਹੈ ਅਤੇ ਵਿਅਕਤੀ ਦੇ ਕਾਰਜਾਂ ਅਤੇ ਵਿਵਹਾਰਾਂ ਨੂੰ ਪੂਰਾ ਕਰਨਾ ਹੁੰਦਾ ਹੈ । ਇਸ ਵਿੱਚ ਪਦਾਂ ਅਤੇ ਭੂਮਿਕਾਵਾਂ ਦਾ ਵੀ ਜਾਲ ਹੁੰਦਾ ਹੈ ਅਤੇ ਇਹਨਾਂ ਦੀ ਵੀ ਵੰਡ ਹੋਈ ਹੁੰਦੀ ਹੈ ।
ਇਸ ਤਰ੍ਹਾਂ ਅਸੀਂ ਕਹਿ ਸਕਦੇ ਹਾਂ ਕਿ ਸੰਸਥਾ ਮਨੁੱਖਾਂ ਦੀਆਂ ਜ਼ਰੂਰਤਾਂ ਪੂਰੀਆਂ ਕਰਨ ਲਈ ਕਾਰਜਵਿਧੀਆਂ, ਪ੍ਰਣਾਲੀਆਂ ਅਤੇ ਨਿਯਮਾਂ ਦੇ ਸੰਗਠਨ ਹੈ । ਮਨੁੱਖ ਨੂੰ ਆਪਣੀਆਂ ਜ਼ਰੂਰਤਾਂ ਪੂਰੀਆਂ ਕਰਨ ਲਈ ਅਨੇਕਾਂ ਸਮੂਹਾਂ ਦਾ ਮੈਂਬਰ ਬਣਨਾ ਪੈਂਦਾ ਹੈ । ਹਰੇਕ ਸਮੂਹ ਵਿੱਚ ਆਪਣੇ ਮੈਂਬਰਾਂ ਦੀਆਂ ਜ਼ਰੂਰਤਾਂ ਪੂਰੀਆਂ ਕਰਨ ਲਈ ਬਹੁਤ ਸਾਰੀਆਂ ਕੋਸ਼ਿਸ਼ਾਂ ਹੁੰਦੀਆਂ ਰਹਿੰਦੀਆਂ
ਹਨ । ਬਹੁਤ ਸਾਰੀਆਂ ਸਫ਼ਲ ਅਸਫਲ ਕੋਸ਼ਿਸ਼ਾਂ ਤੋਂ ਬਾਅਦ ਸਮੂਹ ਆਪਣੇ ਮੈਂਬਰਾਂ ਦੀਆਂ ਜ਼ਰੂਰਤਾਂ ਪੂਰੀਆਂ ਕਰਨ ਦੇ ਤਰੀਕੇ ਲੱਭ ਲੈਂਦਾ ਹੈ ਅਤੇ ਸਮੂਹ ਦੇ ਸਾਰੇ ਮੈਂਬਰ ਇਹਨਾਂ ਤਰੀਕਿਆਂ ਨੂੰ ਪ੍ਰਵਾਨ ਕਰ ਲੈਂਦੇ ਹਨ । ਇਸ ਤਰ੍ਹਾਂ ਸਮੂਹ ਦੇ ਸਾਰੇ ਨਹੀਂ ਤਾਂ ਬਹੁਤ ਸਾਰੇ ਮੈਂਬਰ ਇਹਨਾਂ ਦਾ ਪਾਲਣ ਕਰਨ ਲੱਗ ਜਾਂਦੇ ਹਨ । ਇਸ ਤਰ੍ਹਾਂ ਸਮਾਜ ਵਿੱਚ ਖਾਸ ਹਾਲਾਤਾਂ ਲਈ ਖਾਸ ਪ੍ਰਕਾਰ ਦੇ ਤਰੀਕੇ ਨਿਰਧਾਰਿਤ ਹੋ ਜਾਂਦੇ ਹਨ ਅਤੇ ਇਹਨਾਂ ਤਰੀਕਿਆਂ ਦੇ ਵਿਰੁੱਧ ਕੰਮ ਕਰਨਾ ਗ਼ਲਤ ਸਮਝਿਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਵਿਅਕਤੀਆਂ ਦੀ ਵਿਸ਼ੇਸ਼ ਜ਼ਰੂਰਤ ਨੂੰ ਪੂਰਾ ਕਰਨ ਅਤੇ ਸਾਰਿਆਂ ਦੁਆਰਾ ਮਾਨਤਾ ਪ੍ਰਾਪਤ ਕਾਰਜ ਵਿਧੀਆਂ ਨੂੰ ਸੰਸਥਾ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।
ਪਰਿਭਾਸ਼ਾਵਾਂ (Definitions)-
- ਮੈਰਿਲ ਅਤੇ ਏਲਡਰਿਜ (Meril and Eldridge) ਦੇ ਅਨੁਸਾਰ, “ਸਮਾਜਿਕ ਸੰਸਥਾਵਾਂ ਸਮਾਜਿਕ ਪ੍ਰਤੀਮਾਨ ਹਨ ਜੋ ਮਾਨਵ ਪਾਣੀਆਂ ਦੇ ਆਪਣੇ ਮੌਲਿਕ ਕਾਰਜਾਂ ਦੇ ਕਰਨ ਵਿਚ ਵਿਵਸਥਿਤ ਵਿਵਹਾਰ ਨੂੰ ਸਥਾਪਿਤ ਕਰਦੇ ਹਨ ।”
- ਏਲਡ (Elwood) ਦੇ ਅਨੁਸਾਰ, “ਸੰਸਥਾਵਾਂ ਇਕੱਠੇ ਮਿਲ ਕੇ ਰਹਿਣ ਦੇ ਰਿਵਾਜੀ ਢੰਗ ਹਨ ਜੋ ਸਮੁਦਾਵਾਂ ਦੀ ਸੱਤਾ ਦੁਆਰਾ ਸਵੀਕ੍ਰਿਤ, ਵਿਵਸਥਿਤ ਅਤੇ ਸਥਾਪਤ ਕੀਤੇ ਗਏ ਹੋਣ ।”
- ਸੁਦਰਲੈਂਡ (Sutherland) ਦੇ ਅਨੁਸਾਰ, “ਸਮਾਜ-ਸ਼ਾਸਤਰੀ ਭਾਸ਼ਾ ਵਿੱਚ ਸੰਸਥਾ ਉਹਨਾਂ ਲੋਕ ਗੀਤਾਂ ਅਤੇ ਰੁੜੀਆਂ ਦਾ ਸਮੂਹ ਹੈ ਜੋ ਮਨੁੱਖੀ ਉਦੇਸ਼ਾਂ ਜਾਂ ਲਕਸ਼ਾਂ ਦੀ ਪ੍ਰਾਪਤੀ ਵਿੱਚ ਕੇਂਦਰਤ ਹੋ ਜਾਂਦਾ ਹੈ ।”
ਇਸ ਤਰ੍ਹਾਂ ਇਹਨਾਂ ਪਰਿਭਾਸ਼ਾਵਾਂ ਤੋਂ ਇਹ ਸਪੱਸ਼ਟ ਹੋ ਜਾਂਦਾ ਹੈ ਕਿ ਸੰਸਥਾ ਦਾ ਵਿਕਾਸ ਕਿਸੇ ਵਿਸ਼ੇਸ਼ ਉਦੇਸ਼ ਦੀ ਪ੍ਰਾਪਤੀ ਲਈ ਹੀ ਹੋਇਆ ਹੈ । ਇਸ ਕਰਕੇ ਇਹ ਰੀਤੀ-ਰਿਵਾਜਾਂ, ਪਰਿਮਾਪਾਂ, ਨਿਯਮਾਂ, ਕੀਮਤਾਂ ਆਦਿ ਦਾ ਵੀ ਸਮੂਹ ਹੈ । ਸੰਸਥਾ ਵਿਅਕਤੀ ਨੂੰ ਵਿਅਕਤੀਗਤ ਵਿਵਹਾਰ ਦੇ ਢੰਗ ਜਾਂ ਤਰੀਕੇ ਪੇਸ਼ ਕਰਦੀ ਹੈ । ਸੰਖੇਪ ਦੇ ਵਿੱਚ ਅਸੀਂ ਇਹ ਕਹਿ ਸਕਦੇ ਹਾਂ ਕਿ ਸੰਸਥਾ ਕਿਰਿਆਵਾਂ ਦਾ ਉਹ ਸੰਗਠਨ ਹੁੰਦਾ ਹੈ, ਜਿਸ ਨੂੰ ਸਮਾਜ ਮਨੋਰਥਾਂ ਜਾਂ ਉਦੇਸ਼ਾਂ ਦੀ ਪੂਰਤੀ ਲਈ ਸਵੀਕਾਰ ਕਰ ਲੈਂਦਾ ਹੈ ।
ਸੰਸਥਾ ਦੀਆਂ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ (Characteristics of Institution)
1. ਇਹ ਸੰਸਕ੍ਰਿਤਕ ਤੱਤਾਂ ਤੋਂ ਬਣਦੀ ਹੈ (It is made up of cultural things) – ਸਮਾਜ ਵਿੱਚ ਸੰਸਕ੍ਰਿਤੀ ਦੇ ਕਈ ਤੱਤ ਮੌਜੂਦ ਹੁੰਦੇ ਹਨ, ਜਿਵੇਂ ਰੂੜੀਆਂ, ਲੋਕ ਰੀਤਾਂ, ਪਰਿਮਾਪ, ਤੀਮਾਨ ਅਤੇ ਇਹਨਾਂ ਦੇ ਸੰਗਠਨ ਨੂੰ ਸੰਸਥਾ ਕਹਿੰਦੇ ਹਨ। ਇਕ ਸਮਾਜ ਵਿਗਿਆਨੀ ਨੇ ਤਾਂ ਇਸ ਨੂੰ ਪ੍ਰਥਾਵਾਂ ਦਾ ਗੁੱਛਾ ਕਿਹਾ ਹੈ । ਜਦੋਂ ਸਮਾਜ ਵਿੱਚ ਮਿਲਣ ਵਾਲੀਆਂ ਥਾਵਾਂ, ਰੀਤੀਰਿਵਾਜ, ਲੋਕ-ਰੀਤਾਂ, ਰੂੜੀਆਂ ਸੰਗਠਿਤ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ਅਤੇ ਇੱਕ ਵਿਵਸਥਾ ਦਾ ਰੂਪ ਧਾਰਨ ਕਰ ਲੈਂਦੀਆਂ ਹਨ ਤਾਂ ਇਹ ਸੰਸਥਾ ਹੁੰਦੀ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਇਹ ਵਿਵਸਥਾ ਸੰਸਕ੍ਰਿਤੀ ਵਿੱਚ ਮਿਲਦੇ ਤੱਤਾਂ ਤੋਂ ਬਣਦੀ ਹੈ ਅਤੇ ਇਹ ਫਿਰ ਮਨੁੱਖਾਂ ਦੀਆਂ ਵੱਖਵੱਖ ਜ਼ਰੂਰਤਾਂ ਪੂਰੀਆਂ ਕਰਦੀਆਂ ਹਨ ।
2. ਇਹ ਸਥਾਈ ਹੁੰਦੀਆਂ ਹਨ (These are Permanent) – ਇੱਕ ਸੰਸਥਾ ਉਸ ਸਮੇਂ ਤਕ ਉਪਯੋਗੀ ਨਹੀਂ ਹੋ ਸਕਦੀ ਜਦੋਂ ਤਕ ਉਹ ਲੰਮੇ ਸਮੇਂ ਤਕ ਲੋਕਾਂ ਦੀਆਂ ਜ਼ਰੂਰਤਾਂ ਪੂਰੀਆਂ ਨਾ ਕਰੇ । ਜੇਕਰ ਉਹ ਥੋੜ੍ਹੇ ਸਮੇਂ ਲਈ ਲੋਕਾਂ ਦੀਆਂ ਜ਼ਰੂਰਤਾਂ ਪੂਰੀਆਂ ਕਰਦੀ ਹੈ ਤਾਂ ਉਹ ਸੰਸਥਾ ਨਹੀਂ ਬਲਕਿ ਸਭਾ ਕਹਾਵੇਗੀ । ਇਸ ਤਰ੍ਹਾਂ ਸੰਸਥਾ ਲੰਮੇ ਸਮੇਂ ਲਈ ਲੋਕਾਂ ਦੀਆਂ ਜ਼ਰੂਰਤਾਂ ਪੂਰੀਆਂ ਕਰਦੀ ਹੈ । ਇਸ ਤੋਂ ਇਹ ਅਰਥ ਨਹੀਂ ਕੱਢਿਆ ਜਾਣਾ ਚਾਹੀਦਾ ਕਿ ਸੰਸਥਾ ਕਦੇ ਵੀ ਖਤਮ ਨਹੀਂ ਹੁੰਦੀ। ਕਿਸੇ ਵੀ ਸੰਸਥਾ ਦੀ ਮੰਗ ਸਮੇਂ ਦੇ ਅਨੁਸਾਰ ਹੁੰਦੀ ਹੈ । ਕਿਸੇ ਖਾਸ ਸਮੇਂ ਤੇ ਕਿਸੇ ਸੰਸਥਾ ਦੀ ਮੰਗ ਘੱਟ ਵੀ ਹੋ ਸਕਦੀ ਹੈ ਅਤੇ ਵੱਧ ਵੀ। ਜੇਕਰ ਕਿਸੇ ਸਮੇਂ ਵਿੱਚ ਕਿਸੇ ਸੰਸਥਾ ਦੀ ਲੋੜ ਨਹੀਂ ਹੁੰਦੀ ਜਾਂ ਕੋਈ ਸੰਸਥਾ ਜੇਕਰ ਲੋਕਾਂ ਦੀਆਂ ਜ਼ਰੂਰਤਾਂ ਪੂਰੀਆਂ ਨਹੀਂ ਕਰ ਸਕਦੀ ਤਾਂ ਉਹ ਹੌਲੀ-ਹੌਲੀ ਖਤਮ ਹੋ ਜਾਂਦੀ ਹੈ ।
3. ਇਸਦੇ ਕੁੱਝ ਖਾਸ ਮੰਤਵ ਹੁੰਦੇ ਹਨ (It has some special motives or objectives) – ਜੇਕਰ ਕਿਸੇ ਵੀ ਸੰਸਥਾ ਦਾ ਨਿਰਮਾਣ ਹੁੰਦਾ ਹੈ ਤਾਂ ਉਸ ਦਾ ਕੋਈ ਖਾਸ ਉਦੇਸ਼ ਹੁੰਦਾ ਹੈ । ਇਹ ਉਸ ਸੰਸਥਾ ਨੂੰ ਪਤਾ ਹੁੰਦਾ ਹੈ ਕਿ ਜੇਕਰ ਉਹ ਬਣ ਰਹੀ ਹੈ ਤਾਂ ਉਸਦਾ ਕੀ ਕੰਮ ਹੈ । ਇਸਦਾ ਕੀ ਕੰਮ ਹੁੰਦਾ ਹੈ ਵਿਅਕਤੀਆਂ ਦੀਆਂ ਕਿਸੇ ਖਾਸ ਪ੍ਰਕਾਰ ਦੀਆਂ ਜ਼ਰੂਰਤਾਂ ਨੂੰ ਪੂਰੀਆਂ ਕਰਨਾ । ਇਸ ਤਰ੍ਹਾਂ ਲੋਕਾਂ ਦੀਆਂ ਜ਼ਰੂਰਤਾਂ ਪੂਰੀਆਂ ਕਰਨਾ ਹੀ ਇਹਨਾਂ ਦਾ ਖਾਸ ਮੰਤਵ ਹੁੰਦਾ ਹੈ ਪਰ ਇਹ ਵੀ ਹੋ ਸਕਦਾ ਹੈ ਕਿ ਸਮਾਂ ਬਦਲਣ ਦੇ ਨਾਲ-ਨਾਲ ਉਹ ਸੰਸਥਾ ਲੋਕਾਂ ਦੀਆਂ ਜ਼ਰੂਰਤਾਂ ਪੂਰੀਆਂ ਨਾ ਕਰ ਸਕੇ ਤਾਂ ਫਿਰ ਉਸ ਹਾਲਾਤ ਵਿੱਚ ਉਸ ਦੀ ਥਾਂ ਕੋਈ ਹੋਰ ਸੰਸਥਾ ਹੋਂਦ ਵਿੱਚ ਆ ਜਾਂਦੀ ਹੈ ।
4. ਸੰਸਕ੍ਰਿਤਕ ਸਾਜ਼ੋ-ਸਾਮਾਨ (Cultural Equipments) – ਸੰਸਥਾ ਦੇ ਉਦੇਸ਼ਾਂ ਦੀ ਪੂਰਤੀ ਲਈ ਸੰਸਕ੍ਰਿਤੀ ਦੇ ਭੌਤਿਕ ਪੱਖ ਦਾ ਸਹਾਰਾ ਲਿਆ ਜਾਂਦਾ ਹੈ , ਜਿਵੇਂ ਫਰਨੀਚਰ, ਇਮਾਰਤ ਆਦਿ । ਇਹਨਾਂ ਦਾ ਰੂਪ ਅਤੇ ਵਿਵਹਾਰ ਦੋਵੇਂ ਹੀ ਨਿਸਚਿਤ ਕੀਤੇ ਜਾਂਦੇ ਹਨ । ਇਸ ਤਰ੍ਹਾਂ ਜੇਕਰ ਸੰਸਥਾ ਨੂੰ ਆਪਣੇ ਮੰਤਵ ਪੂਰੇ ਕਰਨੇ ਹਨ ਤਾਂ ਉਸਨੂੰ ਭੌਤਿਕ ਸੰਸਕ੍ਰਿਤੀ ਤੋਂ ਕਾਫੀ ਕੁੱਝ ਲੈਣਾ ਪੈਂਦਾ ਹੈ । ਅਭੌਤਿਕ ਸੰਸਕ੍ਰਿਤੀ ; ਜਿਵੇਂ ਵਿਚਾਰ, ਲੋਕ-ਰੀਤਾਂ, ਰੂੜੀਆਂ ਆਦਿ ਤਾਂ ਪਹਿਲਾਂ ਹੀ ਸੰਸਥਾ ਵਿੱਚ ਵਾਸ ਕਰਦੇ ਹਨ ।
5. ਅਮੂਰਤਤਾ (Abstractness) – ਸੰਸਥਾ ਦਾ ਵਿਕਾਸ ਲੋਕ-ਰੀਤਾਂ, ਰੂੜੀਆਂ, ਰਿਵਾਜਾਂ ਦੇ ਨਾਲ ਹੁੰਦਾ ਹੈ । ਇਹ ਸਾਰੇ ਅਭੌਤਿਕ ਸੰਸਕ੍ਰਿਤੀ ਦਾ ਹਿੱਸਾ ਹਨ ਅਤੇ ਅਭੌਤਿਕ ਸੰਸਕ੍ਰਿਤੀ ਦੇ ਇਹਨਾਂ ਪੱਖਾਂ ਨੂੰ ਅਸੀਂ ਵੇਖ ਨਹੀਂ ਸਕਦੇ ਸਿਰਫ਼ ਮਹਿਸੂਸ ਕਰ ਸਕਦੇ ਹਾਂ । ਇਸ ਤਰ੍ਹਾਂ ਸੰਸਥਾ ਵਿੱਚ ਅਮੂਰਤਤਾ ਦਾ ਪੱਖ ਸ਼ਾਮਲ ਹੁੰਦਾ ਹੈ । ਇਸ ਨੂੰ ਛੂਹਿਆ ਨਹੀਂ ਸਿਰਫ ਮਹਿਸੂਸ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ । ਸੰਸਥਾ ਕਿਸੇ ਛੂਹਣ ਵਾਲੀਆਂ ਚੀਜ਼ਾਂ ਦਾ ਸੰਗਠਨ ਨਹੀਂ ਬਲਕਿ ਨਿਯਮਾਂ, ਕਾਰਜ ਪ੍ਰਣਾਲੀਆਂ ਲੋਕ-ਰੀਤਾਂ ਦਾ ਸੰਗਠਨ ਹੈ ਜੋ ਕਿਸੇ ਮਨੁੱਖੀ ਜ਼ਰੂਰਤ ਨੂੰ ਪੂਰਾ ਕਰਨ ਲਈ ਵਿਕਸਿਤ ਹੁੰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਇੱਕ ਸਮਾਜਿਕ ਸੰਸਥਾ ਦੇ ਰੂਪ ਵਿੱਚ ਵਿਆਹ ਉੱਤੇ ਚਰਚਾ ਕਰੋ ।
ਉੱਤਰ-
ਵਿਆਹ ਦਾ ਅਰਥ (Meaning of Marriage) – ਹਰ ਸਮਾਜ ਵਿੱਚ ਪਰਿਵਾਰ ਦੀ ਸਥਾਪਨਾ ਦੇ ਲਈ ਔਰਤ ਅਤੇ ਮਰਦ ਦੇ ਲੈਂਗਿਕ ਸੰਬੰਧਾਂ ਨੂੰ ਸਥਾਪਿਤ ਕਰਨ ਦੀ ਮਾਨਤਾ ਵਿਆਹ ਦੁਆਰਾ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਲਿੰਗ ਸੰਬੰਧਾਂ ਨੂੰ ਨਿਸ਼ਚਿਤ ਕਰਨ ਅਤੇ ਸੰਚਾਲਿਤ ਕਰਨ ਲਈ, ਬੱਚਿਆਂ ਦੇ ਪਾਲਣ-ਪੋਸ਼ਣ ਦੀ ਜ਼ਿੰਮੇਵਾਰੀ ਨੂੰ ਨਿਰਧਾਰਿਤ ਕਰਨ ਅਤੇ ਪਰਿਵਾਰ ਨੂੰ ਸਥਾਈ ਰੂਪ ਦੇਣ ਲਈ ਬਣਾਏ ਗਏ ਨਿਯਮਾਂ ਨੂੰ ਵਿਆਹ ਕਹਿੰਦੇ ਹਨ । ਪਰਿਵਾਰ ਵਸਾਉਣ ਦੇ ਲਈ ਦੋ ਜਾਂ ਦੋ ਤੋਂ ਜ਼ਿਆਦਾ ਔਰਤਾਂ ਅਤੇ ਆਦਮੀਆਂ ਵਿਚਕਾਰ ਜ਼ਰੂਰੀ ਸੰਬੰਧ ਸਥਾਪਿਤ ਕਰਨ ਅਤੇ ਉਨ੍ਹਾਂ ਨੂੰ ਸਥਿਰ ਰੱਖਣ ਦੇ ਲਈ ਕੋਈ ਨਾ ਕੋਈ ਸੰਸਥਾਤਮਕ ਵਿਵਸਥਾ ਸਮਾਜ ਵਿੱਚ ਪਾਈ ਜਾਂਦੀ ਹੈ ਜਿਸ ਨੂੰ ਵਿਆਹ ਕਹਿੰਦੇ ਹਨ । ਸਪੱਸ਼ਟ ਹੈ ਕਿ ਵਿਆਹ ਦਾ ਅਰਥ ਸਿਰਫ਼ ਲਿੰਗ ਸੰਬੰਧੀ ਇੱਛਾਵਾਂ ਦੀ ਪੂਰਤੀ ਨਹੀਂ ਹੈ । ਇਹ ਪੂਰਤੀ ਤਾਂ ਜੈਵਿਕ ਜ਼ਰੂਰਤ ਹੈ । ਵਿਆਹ ਲਿੰਗ ਸੰਬੰਧੀ ਜ਼ਰੂਰਤ ਦੀ ਪੂਰਤੀ ਦਾ ਸਾਧਨ ਹੈ, ਟੀਚਾ ਨਹੀਂ । ਵਿਆਹ ਦੇ ਮਾਧਿਅਮ ਨਾਲ ਵਿਅਕਤੀ ਲਿੰਗਕ ਸੰਬੰਧਾਂ ਵਿੱਚ ਪ੍ਰਵੇਸ਼ ਕਰਕੇ ਘਰ ਵਸਾਉਂਦਾ ਹੈ, ਸੰਤਾਨ ਪੈਦਾ ਕਰਦਾ ਹੈ ਅਤੇ ਉਨ੍ਹਾਂ ਦੇ ਪਾਲਣ-ਪੋਸ਼ਣ ਦੇ ਲਈ ਸਥਾਈ ਆਧਾਰ ਪ੍ਰਦਾਨ ਕਰਦਾ ਹੈ ।
- ਵੈਸਟਰ ਮਾਰਕ (Wester Marck) ਦੇ ਅਨੁਸਾਰ, “ਵਿਆਹ ਇੱਕ ਜਾਂ ਅਧਿਕ ਇਸਤਰੀ ਪੁਰਸ਼ ਵਿੱਚ ਹੋਣ ਵਾਲਾ ਕਾਨੂੰਨ ਜਾਂ ਪ੍ਰਥਾ ਦੁਆਰਾ ਸਵੀਕ੍ਰਿਤੀ ਪ੍ਰਾਪਤ ਸੰਬੰਧ ਹੈ ਜੋ ਇਨ੍ਹਾਂ ਨੂੰ ਸਥਾਪਤ ਕਰਨ ਵਾਲਿਆਂ ਅਤੇ ਇਨ੍ਹਾਂ ਤੋਂ ਉਤਪੰਨ ਸੰਤਾਨਾਂ ਦੇ ਲਈ ਕਰਤੱਵਾਂ ਅਤੇ ਅਧਿਕਾਰਾਂ ਨੂੰ ਨਿਰਧਾਰਿਤ ਕਰਦਾ ਹੈ ।’’
- ਲੰਡਬਰਗ (Lundberg) ਦੇ ਅਨੁਸਾਰ, “ਵਿਆਹ ਦੇ ਨਿਯਮ ਅਤੇ ਤੌਰ ਤਰੀਕੇ ਹੁੰਦੇ ਹਨ ਜੋ ਪਤੀ-ਪਤਨੀ ਦੇ ਇੱਕ ਦੂਜੇ ਪ੍ਰਤੀ ਅਧਿਕਾਰਾਂ, ਕਰਤੱਵਾਂ ਅਤੇ ਵਿਸ਼ੇਸ਼ ਅਧਿਕਾਰਾਂ ਦਾ ਵਰਣਨ ਕਰਦੇ ਹਨ ।”
- ਹਰਟਨ ਅਤੇ ਹੰਟ (Harton and Hunt) ਦੇ ਅਨੁਸਾਰ, “ਵਿਆਹ ਸਮਾਜ ਦੇ ਦੁਆਰਾ ਸਵੀਕਾਰੀ ਹੋਈ ਉਹ ਸੰਸਥਾ ਹੈ ਜਿਸ ਵਿੱਚ ਦੋ ਜਾਂ ਵੱਧ ਵਿਅਕਤੀਆਂ ਨੂੰ ਪਰਿਵਾਰ ਦਾ ਨਿਰਮਾਣ ਕਰਨ ਲਈ ਸਵੀਕਾਰਿਆ ਜਾਂਦਾ ਹੈ ।”
ਇਸ ਤਰ੍ਹਾਂ ਇਨ੍ਹਾਂ ਪਰਿਭਾਸ਼ਾਵਾਂ ਦੇ ਆਧਾਰ ਉੱਤੇ ਅਸੀਂ ਕਹਿ ਸਕਦੇ ਹਾਂ ਕਿ ਵਿਆਹ ਦੀ ਸੰਸਥਾ ਉੱਤੇ ਸਾਡੇ ਸਮਾਜ ਅਤੇ ਸਮਾਜ ਦੀ ਸੰਰਚਨਾ ਨਿਰਭਰ ਕਰਦੀ ਹੈ । ਵਿਆਹ ਦੀ ਸੰਸਥਾ ਆਦਮੀ ਅਤੇ ਔਰਤ ਦੇ ਲੈਂਗਿਕ ਸੰਬੰਧਾਂ ਨੂੰ ਨਿਯਮਿਤ ਕਰਦੀ ਹੈ ਅਤੇ ਇਸ ਨਾਲ ਬੱਚਿਆਂ ਦਾ ਪਾਲਨ ਪੋਸ਼ਣ ਵੀ ਸਹੀ ਢੰਗ ਨਾਲ ਹੋ ਜਾਂਦਾ ਹੈ । ਵਿਆਹ ਦੀ ਸੰਸਥਾ ਨੂੰ ਸਮਾਜਿਕ ਮਾਨਤਾ ਵੀ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ । ਜੇਕਰ ਕੋਈ ਆਦਮੀ ਜਾਂ ਔਰਤ ਬਿਨਾਂ ਵਿਆਹ ਕੀਤੇ ਲੈਂਗਿਕ ਸੰਬੰਧ ਸਥਾਪਿਤ ਕਰ ਲੈਣ ਤਾਂ ਉਨ੍ਹਾਂ ਦੇ ਸੰਬੰਧਾਂ ਨੂੰ ਸਮਾਜ ਵਿਚ ਗੈਰ-ਕਾਨੂੰਨੀ ਕਰਾਰ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਦੇ ਗੈਰ ਕਾਨੂੰਨੀ ਸੰਬੰਧਾਂ ਤੋਂ ਪੈਦਾ ਹੋਏ ਬੱਚੇ ਨੂੰ ਵੀ ਗੈਰ-ਕਾਨੂੰਨੀ ਜਾਂ ਨਜਾਇਜ ਦਾ ਨਾਮ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਦੀ ਸੰਸਥਾ ਦੀ ਮੱਦਦ ਨਾਲ ਆਦਮੀ ਅਤੇ ਔਰਤ ਨਾ ਸਿਰਫ ਆਪਣੀਆਂ ਲੈਂਗਿਕ ਇੱਛਾਵਾਂ ਦੀ ਪੂਰਤੀ ਕਰਦੇ ਹਨ ਬਲਕਿ ਇਸ ਨਾਲ ਕਈ ਪ੍ਰਕਾਰ ਦੀਆਂ ਸੰਸਥਾਵਾਂ ਦੇ ਮੈਂਬਰ ਵੀ ਬਣਦੇ ਹਨ । ਇਸ ਨਾਲ ਵਿਅਕਤੀ ਸਮਾਜ ਦਾ ਵਿਕਾਸ ਕਰਨ ਦੇ ਵੀ ਸਮਰਥ ਹੋ ਜਾਂਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 3.
ਵਿਆਹ ਦੇ ਭਿੰਨ-ਭਿੰਨ ਪ੍ਰਕਾਰਾਂ ਅਤੇ ਸਰੂਪਾਂ ਨੂੰ ਵਿਸਤਾਰ ਨਾਲ ਸਮਝਾਉ ।
ਉੱਤਰ-
ਹਰ ਸਮਾਜ ਆਪਣੇ ਆਪ ਵਿੱਚ ਦੂਜੇ ਸਮਾਜ ਤੋਂ ਵੱਖਰਾ ਹੈ । ਹਰੇਕ ਸਮਾਜ ਦੇ ਆਪਣੇ-ਆਪਣੇ ਨਿਯਮ, ਪਰੰਪਰਾਵਾਂ ਅਤੇ ਸੰਸਥਾਵਾਂ ਹੁੰਦੀਆਂ ਹਨ ਅਤੇ ਹਰੇਕ ਸਮਾਜ ਵਿੱਚ ਵੱਖ-ਵੱਖ ਸੰਸਥਾਵਾਂ ਦੇ ਭਿੰਨ-ਭਿੰਨ ਪ੍ਰਕਾਰ ਹੁੰਦੇ ਹਨ । ਇਹ ਭਿੰਨ-ਭਿੰਨ ਇਸ ਕਰਕੇ ਹੁੰਦੇ ਹਨ ਕਿਉਂਕਿ ਹਰੇਕ ਸਮਾਜ ਨੇ ਇਹਨਾਂ ਪ੍ਰਕਾਰਾਂ ਨੂੰ ਆਪਣੀਆਂ ਸਹੂਲਤਾਂ ਅਤੇ ਆਪਣੀਆਂ ਜ਼ਰੂਰਤਾਂ ਦੇ ਮੁਤਾਬਿਕ ਢਾਲਿਆ ਹੁੰਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਵਿਆਹ ਨਾਮਕ ਸੰਸਥਾ ਦੀਆਂ ਵੱਖ-ਵੱਖ ਸਮਾਜਾਂ ਵਿੱਚ ਉਹਨਾਂ ਦੀਆਂ ਜ਼ਰੂਰਤਾਂ ਦੇ ਮੁਤਾਬਿਕ ਵੱਖ-ਵੱਖ ਕਿਸਮਾਂ ਜਾਂ ਰੂਪ ਹਨ । ਇਹਨਾਂ ਸਾਰੇ ਰੂਪਾਂ ਦਾ ਵਰਣਨ ਅੱਗੇ ਲਿਖਿਆ ਹੈ-
1. ਇੱਕ ਵਿਆਹ (Monogamy) – ਅੱਜ-ਕਲ ਦੇ ਆਧੁਨਿਕ ਯੁੱਗ ਵਿੱਚ ਇੱਕ ਵਿਆਹ ਦਾ ਪ੍ਰਚਲਨ ਕਾਫੀ ਜ਼ਿਆਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਦੇ ਵਿਆਹ ਵਿੱਚ ਇੱਕ ਆਦਮੀ ਜਾਂ ਔਰਤ ਇੱਕ ਸਮੇਂ ਵਿੱਚ ਇੱਕ ਹੀ ਔਰਤ ਜਾਂ ਆਦਮੀ ਨਾਲ ਵਿਆਹ ਕਰਵਾ ਸਕਦਾ ਹੈ । ਇੱਕ ਪਤਨੀ ਜਾਂ ਪਤੀ ਰਹਿੰਦੇ ਹੋਏ ਦੂਜਾ ਵਿਆਹ ਗੈਰ-ਕਾਨੂੰਨੀ ਹੈ । ਇਸ ਵਿੱਚ ਪਤੀ-ਪਤਨੀ ਦੇ ਸੰਬੰਧ ਜ਼ਿਆਦਾ ਸਥਾਈ, ਡੂੰਘੇ, ਪਿਆਰ ਅਤੇ ਹਮਦਰਦੀ ਵਾਲੇ ਹੁੰਦੇ ਹਨ । ਇਸ ਵਿੱਚ ਬੱਚਿਆਂ ਦਾ ਪਾਲਣ-ਪੋਸ਼ਣ ਸਹੀ ਢੰਗ ਨਾਲ ਹੋ ਸਕਦਾ ਹੈ ਅਤੇ ਉਹਨਾਂ ਨੂੰ ਮਾਤਾ-ਪਿਤਾ ਦਾ ਪੂਰਾ ਪਿਆਰ ਮਿਲਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਦੇ ਵਿਆਹ ਵਿੱਚ ਪਤੀ-ਪਤਨੀ ਵਿੱਚ ਪੂਰਾ ਤਾਲਮੇਲ ਹੁੰਦਾ ਹੈ ਜਿਸ ਕਰਕੇ ਪਰਿਵਾਰ ਵਿੱਚ ਝਗੜੇ ਹੋਣ ਦੀ ਸੰਭਾਵਨਾ ਕਾਫ਼ੀ ਘੱਟ ਹੁੰਦੀ ਹੈ । ਪਰ ਇਸ ਤਰ੍ਹਾਂ ਦੇ ਵਿਆਹ ਵਿੱਚ ਕਈ ਸਮੱਸਿਆਵਾਂ ਵੀ ਹਨ । ਪਤਨੀ ਦੇ ਬਿਮਾਰ ਪੈਣ ‘ਤੇ ਸਾਰੇ ਕੰਮ ਰੁਕ ਜਾਂਦੇ ਹਨ ਅਤੇ ਬੱਚਿਆਂ ਵੱਲ ਪੂਰਾ ਧਿਆਨ ਨਹੀਂ ਦਿੱਤਾ ਜਾ ਸਕਦਾ ।
2. ਭਰਾਤਰੀ ਬਹੁਪਤੀ ਵਿਆਹ (Fraternal Polyandry) – ਇਸ ਵਿਆਹ ਦੀ ਕਿਸਮ ਅਨੁਸਾਰ ਇਸਤਰੀ ਦੇ ਸਾਰੇ ਪਤੀ ਭਰਾ ਹੁੰਦੇ ਹਨ ਪਰ ਕਦੀ-ਕਦੀ ਇਹ ਸਕੇ ਭਰਾ ਨਾ ਹੋ ਕੇ ਇੱਕ ਹੀ ਗੋਤ ਦੇ ਵਿਅਕਤੀ ਵੀ ਹੁੰਦੇ ਹਨ । ਇਸ ਵਿਆਹ ਦੀ ਪ੍ਰਥਾ ਵਿੱਚ ਸਭ ਤੋਂ ਵੱਡਾ ਭਰਾ ਇੱਕ ਇਸਤਰੀ ਨਾਲ ਵਿਆਹ ਕਰਦਾ ਹੈ ਅਤੇ ਉਸ ਦੇ ਸਭ ਭਰਾਵਾਂ ਦਾ ਉਸ ਉੱਤੇ ਪਤਨੀ ਦੇ ਰੂਪ ਵਿੱਚ ਅਧਿਕਾਰ ਹੁੰਦਾ ਹੈ ਅਤੇ ਸਾਰੇ ਉਸ ਨਾਲ ਲਿੰਗ ਸੰਬੰਧ ਰੱਖਦੇ ਹਨ | ਜੇਕਰ ਕੋਈ ਛੋਟਾ ਭਰਾ ਵਿਆਹ ਕਰਦਾ ਹੈ ਤਾਂ ਉਸਦੀ ਪਤਨੀ ਵੀ ਸਭ ਭਰਾਵਾਂ ਦੀ ਪਤਨੀ ਹੁੰਦੀ ਹੈ । ਜਿੰਨੇ ਬੱਚੇ ਹੁੰਦੇ ਹਨ ਉਹ ਸਭ ਵੱਡੇ ਭਰਾ ਦੇ ਮੰਨੇ ਜਾਂਦੇ ਹਨ ਅਤੇ ਸੰਪੱਤੀ ਉੱਤੇ ਅਧਿਕਾਰ ਵੀ ਸਭ ਤੋਂ ਜ਼ਿਆਦਾ ਵੱਡੇ ਭਰਾ ਜਾਂ ਸਭ ਤੋਂ ਪਹਿਲੇ ਪਤੀ ਦਾ ਹੁੰਦਾ ਹੈ । ਭਾਰਤ ਵਿੱਚ ਇਹ ਪ੍ਰਥਾ ਮਾਲਾਬਾਰ, ਪੰਜਾਬ, ਨੀਲਗੀਰੀ, ਲੱਦਾਖ, ਸਿੱਕਮ ਅਤੇ ਆਸਾਮ ਵਿੱਚ ਪਾਈ ਜਾਂਦੀ ਹੈ ।
3. ਗੈਰ-ਭਰਾਤਰੀ ਬਹੁਪਤੀ ਵਿਆਹ (Non-Fraternal Polyandry) – ਬਹੁ-ਪਤੀ ਵਿਆਹ ਦੀ ਇਸ ਕਿਸਮ ਵਿੱਚ ਇੱਕ ਔਰਤ ਦੇ ਪਤੀ ਆਪਸ ਵਿੱਚ ਭਰਾ ਨਹੀਂ ਹੁੰਦੇ ਹਨ । ਇਹ ਸਭ ਪਤੀ ਅਲੱਗ-ਅਲੱਗ ਜਗਾ ‘ਤੇ ਰਹਿੰਦੇ ਹਨ । ਅਜਿਹੀ ਹਾਲਾਤ ਵਿੱਚ ਔਰਤ ਨਿਸ਼ਚਿਤ ਸਮੇਂ ਲਈ ਇੱਕ ਪਤੀ ਕੋਲ ਰਹਿੰਦੀ ਹੈ ਅਤੇ ਫਿਰ ਦੂਸਰੇ ਕੋਲ ਫਿਰ ਤੀਸਰੇ ਕੋਲ । ਇਸ ਤਰ੍ਹਾਂ ਸਾਰਾ ਸਾਲ ਉਹ ਅੱਡ-ਅੱਡ ਪਤੀਆਂ ਕੋਲ ਆਪਣਾ ਜੀਵਨ ਬਤੀਤ ਕਰਦੀ ਹੈ । ਜਿਸ ਸਮੇਂ ਵਿੱਚ ਇੱਕ ਇਸਤਰੀ ਇੱਕ ਪਤੀ ਕੋਲ ਰਹਿੰਦੀ ਹੈ ਉਸ ਸਮੇਂ ਦੌਰਾਨ ਹੋਰ ਪਤੀਆਂ ਨੂੰ ਉਸ ਨਾਲ ਸੰਬੰਧ ਬਣਾਉਣ ਦਾ ਅਧਿਕਾਰ ਨਹੀਂ ਹੁੰਦਾ । ਬੱਚਾ ਹੋਣ ਸਮੇਂ ਕੋਈ ਇੱਕ ਪਤੀ ਇੱਕ ਵਿਸ਼ੇਸ਼ ਸੰਸਕਾਰ ਨਾਲ ਉਸ ਦਾ ਪਿਤਾ ਬਣ ਜਾਂਦਾ ਹੈ । ਉਹ ਗਰਭ ਅਵਸਥਾ ਵਿੱਚ ਔਰਤ ਨੂੰ ਤੀਰ ਕਮਾਨ ਭੇਂਟ ਕਰਦਾ ਹੈ ਅਤੇ ਉਸ ਨੂੰ ਬੱਚੇ ਦਾ ਬਾਪ ਮੰਨ ਲਿਆ ਜਾਂਦਾ ਹੈ । ਵਾਰੀ-ਵਾਰੀ ਸਾਰੇ ਪਤੀਆਂ ਨੂੰ ਅਜਿਹਾ ਕਰਨ ਦਾ ਮੌਕਾ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ।
4. ਬਹੁ-ਪਤਨੀ ਵਿਆਹ (Polygyny) – ਬਹੁ-ਪਤਨੀ ਵਿਆਹ ਦੀ ਪ੍ਰਥਾ ਭਾਰਤ ਵਿੱਚ ਪੁਰਾਣੇ ਸਮਿਆਂ ਵਿੱਚ ਪ੍ਰਚੱਲਿਤ ਸੀ । ਰਾਜੇ ਅਤੇ ਰਾਜ ਦੇ ਵੱਡੇ-ਵੱਡੇ ਸਰਦਾਰ ਬਹੁਤ ਸਾਰੀਆਂ ਪਤਨੀਆਂ ਰੱਖਦੇ ਸਨ । ਰਾਜੇ ਦੇ ਰੁਤਬੇ ਦਾ ਅੰਦਾਜ਼ਾ ਉਸ ਦੁਆਰਾ ਰੱਖੀਆਂ ਗਈਆਂ ਪਤਨੀਆਂ ਤੋਂ ਲਗਾਇਆ ਜਾਂਦਾ ਸੀ । ਮੱਧਕਾਲ ਵਿੱਚ ਮੁਸਲਮਾਨਾਂ ਵਿੱਚ ਵੀ ਇਹ ਪ੍ਰਥਾ ਪ੍ਰਚੱਲਿਤ ਸੀ ਅਤੇ ਹੁਣ ਵੀ ਮੁਸਲਮਾਨਾਂ ਨੂੰ ਚਾਰ ਪਤਨੀਆਂ ਰੱਖਣ ਦੀ ਇਜਾਜ਼ਤ ਹੈ ਪੁਰਸ਼ਾਂ ਦੀ ਲਿੰਗਕ ਇੱਛਾ ਨੂੰ ਪੂਰਾ ਕਰਨ ਅਤੇ ਵੱਡੇ ਪਰਿਵਾਰ ਦੀ ਇੱਛਾ ਕਾਰਨ ਵਿਆਹ ਦੀ ਇਸ ਪ੍ਰਥਾ ਨੂੰ ਅਪਣਾਇਆ ਗਿਆ । ਇਸ ਪ੍ਰਥਾ ਕਾਰਨ ਕਈ ਮਨੋਵਿਗਿਆਨਿਕ ਸਮੱਸਿਆਵਾਂ ਪੈਦਾ ਹੋ ਜਾਂਦੀਆਂ ਹਨ । ਇਸ ਕਾਰਨ ਸਮਾਜ ਵਿੱਚ ਇਸਤਰੀਆਂ ਨੂੰ ਨੀਵਾਂ ਦਰਜਾ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
5. ਸਾਲੀ ਵਿਆਹ (Sorogate Marriage) – ਇਸ ਵਿਆਹ ਵਿੱਚ ਪੁਰਸ਼ ਆਪਣੀ ਪਤਨੀ ਦੀ ਭੈਣ ਨਾਲ ਵਿਆਹ ਕਰਦਾ ਹੈ । ਸਾਲੀ ਵਿਆਹ ਦੀਆਂ ਦੋ ਕਿਸਮਾਂ ਹਨ । ਸੀਮਿਤ ਸਾਲੀ ਵਿਆਹ ਵਿੱਚ ਪੁਰਸ਼ ਆਪਣੀ ਪਤਨੀ ਦੀ ਮੌਤ ਤੋਂ ਬਾਅਦ ਉਸ ਦੀ ਭੈਣ ਨਾਲ ਵਿਆਹ ਕਰਵਾਉਂਦਾ ਹੈ । ਸਮਕਾਲੀ ਵਿਆਹ ਵਿੱਚ ਪੁਰਸ਼ ਆਪਣੀ ਪਤਨੀ ਦੀਆਂ ਸਾਰੀਆਂ ਛੋਟੀਆਂ ਭੈਣਾਂ ਨੂੰ ਆਪਣੀਆਂ ਪਤਨੀਆਂ ਸਮਝ ਲੈਂਦਾ ਹੈ । ਵਿਆਹ ਦੀ ਪਹਿਲੀ ਕਿਸਮ ਦਾ ਪ੍ਰਚਲਨ ਦੂਜੀ ਕਿਸਮ ਦੀ ਤੁਲਨਾ ਵਿੱਚ ਜ਼ਿਆਦਾ ਹੈ । ਇਸ ਕਾਰਨ ਪਰਿਵਾਰ ਟੁੱਟਣ ਦੀ ਸਮੱਸਿਆ ਨਹੀਂ ਆਉਂਦੀ ਸੀ ਅਤੇ ਬੱਚਿਆਂ ਦਾ ਪਾਲਣ-ਪੋਸ਼ਣ ਚੰਗੀ ਤਰ੍ਹਾਂ ਹੋ ਜਾਂਦਾ ਹੈ ।
6. ਦਿਉਰ ਵਿਆਹ (Levirate) – ਵਿਆਹ ਦੀ ਇਸ ਪ੍ਰਥਾ ਦੇ ਅਨੁਸਾਰ ਪਤੀ ਦੀ ਮੌਤ ਹੋ ਜਾਣ ਮਗਰੋਂ ਪਤਨੀ ਪਤੀ ਦੇ ਛੋਟੇ ਭਰਾ ਨਾਲ ਵਿਆਹ ਕਰਵਾ ਲੈਂਦੀ ਹੈ । ਇਸ ਪ੍ਰਥਾ ਕਾਰਨ ਇੱਕ ਤਾਂ ਪਰਿਵਾਰ ਦੀ ਜਾਇਦਾਦ ਸੁਰੱਖਿਅਤ ਰਹਿੰਦੀ ਸੀ । ਦੂਜਾ ਪਰਿਵਾਰ ਟੁੱਟਣ ਤੋਂ ਬਚ ਜਾਂਦਾ ਸੀ, ਤੀਜਾ ਬੱਚਿਆਂ ਦਾ ਪਾਲਣ-ਪੋਸ਼ਣ ਠੀਕ ਢੰਗ ਨਾਲ ਹੋ ਜਾਂਦਾ ਸੀ ਅਤੇ ਇਸ ਕਾਰਨ ਲੜਕੇ ਦੇ ਮਾਤਾ-ਪਿਤਾ ਨੂੰ ਲੜਕੀ ਵਾਲਿਆਂ ਨੂੰ ਲੜਕੀ ਦਾ ਮੁੱਲ ਵਾਪਸ ਨਹੀਂ ਕਰਨਾ ਪੈਂਦਾ ਸੀ ।
7. ਪ੍ਰੇਮ ਵਿਆਹ (Love Marriage) – ਆਧੁਨਿਕ ਸਮਾਜ ਵਿੱਚ ਪ੍ਰੇਮ ਵਿਆਹ ਦਾ ਪ੍ਰਚਲਨ ਵੀ ਵੱਧਦਾ ਜਾ ਰਿਹਾ ਹੈ । ਲੜਕਾ ਅਤੇ ਲੜਕੀ ਵਿੱਚ ਕਾਲਜ ਵਿੱਚ ਪੜ੍ਹਦੇ ਸਮੇਂ ਜਾਂ ਨੌਕਰੀ ਕਰਦੇ ਸਮੇਂ ਇੱਕ ਦੂਜੇ ਨਾਲ ਪਹਿਲੀ ਨਜ਼ਰ ਵਿੱਚ ਹੀ ਪਿਆਰ ਹੋ ਜਾਂਦਾ ਹੈ । ਉਹਨਾਂ ਵਿੱਚ ਆਪਸੀ ਮੁਲਾਕਾਤਾਂ ਦਾ ਸਿਲਸਿਲਾ ਸ਼ੁਰੂ ਹੋ ਜਾਂਦਾ ਹੈ । ਉਹ ਹੋਟਲ, ਸਿਨੇਮਾ, ਪਾਰਕ ਆਦਿ ਵਿੱਚ ਮਿਲਦੇ ਰਹਿੰਦੇ ਹਨ । ਉਹ ਸੱਚੇ ਪਿਆਰ ਅਤੇ ਇਕੱਠੇ ਜੀਉਣ ਮਰਨ ਦੀਆਂ ਕਸਮਾਂ ਖਾ ਲੈਂਦੇ ਹਨ । ਸਮਾਜ ਉਹਨਾਂ ਨੂੰ ਵਿਆਹ ਕਰਨ ਤੋਂ ਰੋਕਦਾ ਹੈ ਅਤੇ ਉਹਨਾਂ ਦੇ ਰਸਤੇ ਵਿੱਚ ਕਈ ਮੁਸ਼ਕਿਲਾਂ ਖੜੀਆਂ ਕਰਦਾ ਹੈ ਪਰ ਉਹ ਆਪਣੇ ਫੈਸਲੇ ਉੱਤੇ ਅਟੱਲ ਰਹਿੰਦੇ ਹਨ । ਜੇ ਮਾਂ ਬਾਪ ਅਜਿਹੇ ਵਿਆਹ ਦੀ ਸਹਿਮਤੀ ਨਹੀਂ ਦਿੰਦੇ ਹਨ ਤਾਂ ਉਹ ਅਦਾਲਤ ਵਿੱਚ ਜਾ ਕੇ ਵਿਆਹ ਕਰਵਾ ਲੈਂਦੇ ਹਨ । ਇਸ ਤਰ੍ਹਾਂ ਉਹਨਾਂ ਦਾ ਪ੍ਰੇਮ ਵਿਆਹ ਹੋ ਜਾਂਦਾ ਹੈ ।
8. ਅੰਤਰ ਵਿਆਹ (Endogamy) – ਅੰਤਰ ਵਿਆਹ ਵਿੱਚ ਵਿਅਕਤੀ ਨੂੰ ਆਪਣੀ ਹੀ ਜਾਤ ਵਿੱਚ ਵਿਆਹ ਕਰਵਾਉਣਾ ਪੈਂਦਾ ਸੀ । ਅੰਤਰ ਵਿਆਹ ਦੇ ਗੁਣਾਂ ਦਾ ਵਰਣਨ ਇਸ ਤਰ੍ਹਾਂ ਹੈ । ਇਸ ਨਾਲ ਖੂਨ ਦੀ ਸ਼ੁੱਧਤਾ ਨੂੰ ਬਣਾਈ ਰੱਖਿਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਨਾਲ ਸਮੁਹ ਵਿੱਚ ਏਕਤਾ ਕਾਇਮ ਰੱਖੀ ਜਾ ਸਕਦੀ ਹੈ । ਇਸ ਕਾਰਨ ਸਮੂਹ ਦੀ ਸੰਪੱਤੀ ਸੁਰੱਖਿਅਤ ਰਹਿੰਦੀ ਹੈ । ਇਸ ਕਾਰਨ ਇਸਤਰੀਆਂ ਵਧੇਰੇ ਖੁਸ਼ ਰਹਿੰਦੀਆਂ ਹਨ ਕਿਉਂਕਿ ਆਪਣੀ ਹੀ ਸੰਸਕ੍ਰਿਤੀ ਵਿੱਚ ਉਹਨਾਂ ਦਾ ਤਾਲਮੇਲ ਆਸਾਨੀ ਨਾਲ ਹੋ ਜਾਂਦਾ ਹੈ । ਪਰ ਦੂਜੇ ਪਾਸੇ ਇਸ ਕਾਰਨ ਰਾਸ਼ਟਰੀ ਏਕਤਾ ਦੇ ਮਾਰਗ ਵਿੱਚ ਰੁਕਾਵਟ ਪੈਦਾ ਹੁੰਦੀ ਹੈ । ਇਸ ਨਾਲ ਜਾਤੀਵਾਦ ਦੀ ਭਾਵਨਾ ਨੂੰ ਉਤਸ਼ਾਹ ਮਿਲਦਾ ਹੈ । ਇਹ ਸਮਾਜਿਕ ਪ੍ਰਤੀ ਦੀ ਰਾਹ ਵਿੱਚ ਇੱਕ ਰੁਕਾਵਟ ਹੈ ।
9. ਬਾਹਰ ਵਿਆਹ (Exogamy) – ਬਾਹਰ ਵਿਆਹ ਦਾ ਅਰਥ ਆਪਣੀ ਗੋਤ, ਪਿੰਡ ਅਤੇ ਟੋਟਮ ਤੋਂ ਬਾਹਰ ਵਿਆਹ ਸੰਬੰਧ ਕਾਇਮ ਕਰਨਾ ਹੈ । ਇੱਕ ਹੀ ਗੋਤ, ਪਿੰਡ ਅਤੇ ਟੋਟਮ ਦੇ ਆਦਮੀ, ਔਰਤ ਆਪਸ ਵਿੱਚ ਭੈਣ ਭਰਾ ਮੰਨੇ ਜਾਂਦੇ ਹਨ । ਵੈਸਟਮਾਰਕ ਅਨੁਸਾਰ ਇਸ ਵਿਆਹ ਦਾ ਉਦੇਸ਼ ਨੇੜੇ ਦੇ ਸੰਬੰਧੀਆਂ ਵਿੱਚ ਯੌਨ ਸੰਬੰਧ ਨਾ ਹੋਣ ਦੇਣਾ ਹੈ । ਇਹ ਵਿਆਹ ਪ੍ਰਗਤੀਵਾਦ ਦਾ ਸੂਚਕ ਹੈ । ਇਸ ਵਿੱਚ ਵੱਖ-ਵੱਖ ਸਮੂਹਾਂ ਵਿਚਕਾਰ ਸੰਪਰਕ ਵੱਧਦਾ ਹੈ । ਜੈਵਿਕ ਨਜ਼ਰੀਏ ਤੋਂ ਇਹ ਵਿਆਹ ਠੀਕ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਵਿਆਹ ਦਾ ਸਭ ਤੋਂ ਵੱਡਾ ਔਗੁਣ ਇਹ ਹੈ ਕਿ ਵਰ ਕੰਨਿਆ ਨੂੰ ਇੱਕ ਦੂਜੇ ਦੇ ਵਿਚਾਰਾਂ ਨੂੰ ਜਾਨਣ ਵਿੱਚ ਅਨੇਕਾਂ ਮੁਸ਼ਕਿਲਾਂ ਦਾ ਸਾਹਮਣਾ ਕਰਨਾ ਪੈਂਦਾ ਹੈ । ਬਾਹਰ ਵਿਆਹ ਕਾਰਨ ਵਿਭਿੰਨ ਸਮੂਹਾਂ ਵਿੱਚ ਆਪਸੀ ਪਿਆਰ ਵੱਧਦਾ ਹੈ । ਇਸ ਕਾਰਨ ਰਾਸ਼ਟਰੀ ਏਕਤਾ ਦੀ ਭਾਵਨਾ ਨੂੰ ਬਲ ਮਿਲਦਾ ਹੈ ।
10. ਅਨੁਲੋਮ ਵਿਆਹ (Anulom Marriage) – ਅਨੁਲੋਮ ਹਿੰਦੂ ਵਿਆਹ ਦਾ ਇੱਕ ਨਿਯਮ ਹੈ ਜਿਸ ਅਨੁਸਾਰ ਉੱਚੀ ਜਾਤ ਦਾ ਪੁਰਸ਼ ਆਪਣੇ ਤੋਂ ਹੇਠਲੀ ਜਾਤ ਦੀਆਂ ਲੜਕੀਆਂ ਨਾਲ ਵਿਆਹ ਕਰ ਸਕਦੇ ਹਨ ।ਉਦਾਹਰਨ ਦੇ ਤੌਰ ‘ਤੇ ਇੱਕ ਬਾਹਮਣ ਕਸ਼ੱਤਰੀ, ਵੈਸ਼ ਅਤੇ ਨਿਮਨ ਜਾਤੀ ਦੀ ਲੜਕੀ ਨਾਲ ਵਿਆਹ ਕਰਵਾ ਸਕਦਾ ਸੀ । ਇਸ ਦਾ ਮੁੱਖ ਕਾਰਨ ਹੇਠਲੀਆਂ ਜਾਤਾਂ ਦੇ ਲੋਕਾਂ ਵਲੋਂ ਉੱਚੀਆਂ ਜਾਤਾਂ ਵਿੱਚ ਵਿਆਹ ਕਰਨਾ ਇੱਜ਼ਤ ਦਾ ਕੰਮ ਸਮਝਦੇ ਸਨ ਕਿਉਂਕਿ ਇਸ ਨਾਲ ਉਹਨਾਂ ਨੂੰ ਸਮਾਜ ਵਿੱਚ ਉੱਚ ਸਥਾਨ ਹਾਸਿਲ ਹੋ ਜਾਂਦਾ ਸੀ ।
11. ਪ੍ਰਤੀਲੋਮ ਵਿਆਹ (Pratilom Marriage) – ਇਸ ਵਿੱਚ ਹੇਠਲੀਆਂ ਜਾਤਾਂ ਦੇ ਮਰਦ ਉੱਚੀਆਂ ਜਾਤਾਂ ਦੀਆਂ ਔਰਤਾਂ ਨਾਲ ਵਿਆਹ ਕਰਦੇ ਸਨ | ਮਨੂੰ ਨੇ ਇਸ ਕਿਸਮ ਦੇ ਵਿਆਹ ਦਾ ਸਖ਼ਤ ਵਿਰੋਧ ਕੀਤਾ ਸੀ । ਉਸਨੇ ਇਸ ਕਿਸਮ ਦੇ ਵਿਆਹ ਤੋਂ ਪੈਦਾ ਹੋਈ ਸੰਤਾਨ ਨੂੰ ਚੰਡਾਲ ਮੰਨਿਆ ਸੀ । ਉਸਨੇ ਉੱਪਰਲੀ ਜਾਤੀ ਦੀ ਔਰਤ ਅਤੇ ਹੇਠਲੀ ਜਾਤੀ ਦੇ ਮਰਦ ਤੋਂ ਪੈਦਾ ਹੋਈ ਸੰਤਾਨ ਨੂੰ ਚੰਡਾਲ ਕਿਹਾ ਸੀ । ਇਸ ਲਈ ਇਸ ਕਿਸਮ ਦੇ ਵਿਆਹ ਨੂੰ ਹਮੇਸ਼ਾ ਨੀਵੀਆਂ ਨਜ਼ਰਾਂ ਨਾਲ ਵੇਖਿਆ ਜਾਂਦਾ ਸੀ । ਅਜਿਹੇ ਵਿਆਹ ਤੋਂ ਪੈਦਾ ਹੋਈ ਸੰਤਾਨ ਮਾਤਾ ਜਾਂ ਪਿਤਾ ਕਿਸੇ ਦੇ ਵੰਸ਼ ਦਾ ਨਾਂ ਧਾਰਨ ਨਹੀਂ ਕਰ ਸਕਦੀ ਸੀ ।

ਪ੍ਰਸ਼ਨ 4.
ਵਿਆਹ ਨੂੰ ਪਰਿਭਾਸ਼ਿਤ ਕਰੋ । ਜੀਵਨ ਸਾਥੀ ਚੁਣਨ ਦੇ ਨਿਯਮਾਂ ਨੂੰ ਵਿਸਤਾਰ ਨਾਲ ਲਿਖੋ ।
ਉੱਤਰ-
ਵਿਆਹ ਦੀ ਪਰਿਭਾਸ਼ਾ-ਦੇਖੋ ਅਭਿਆਸ ਦੇ ਪ੍ਰਸ਼ਨ IV (2).
ਸਾਥੀ ਚੁਣਨ ਦੇ ਨਿਯਮ (Rules of Mate Selection) :
ਵੈਸੇ ਤਾਂ ਹਰੇਕ ਸਮਾਜ ਨੇ ਜੀਵਨ ਸਾਥੀ ਦੀ ਚੋਣ ਕਰਨ ਦੇ ਲਈ ਵੱਖ-ਵੱਖ ਨਿਯਮਾਂ ਦਾ ਨਿਰਮਾਣ ਕੀਤਾ ਹੋਇਆ ਹੈ ਪਰ ਆਮ ਤੌਰ ਉੱਤੇ ਸਾਡੇ ਸਮਾਜ ਵਿਚ ਹੇਠ ਲਿਖੇ ਨਿਯਮ ਮੰਨੇ ਜਾਂਦੇ ਹਨ । ਇਹ ਨਿਯਮ ਹਨ-
I. ਅੰਤਰ ਵਿਆਹ (Endogamy)
II. ਬਾਹਰ ਵਿਆਹ (Exogamy)
III. ਅਨੁਲੋਮ ਵਿਆਹ (Hypergamy)
IV. ਪਤੀਲੋਮ ਵਿਆਹ (Hypogamy) ।
ਹੁਣ ਅਸੀਂ ਇਨ੍ਹਾਂ ਦਾ ਵਰਣਨ ਵਿਸਤਾਰ ਨਾਲ ਕਰਾਂਗੇ ।
I. ਅੰਤਰ ਵਿਆਹ (Endogamy) – ਹਿੰਦੂ ਸਮਾਜ ਵਿਚ ਅੰਤਰ ਵਿਆਹ ਦਾ ਨਿਯਮ ਪਾਇਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਨਿਯਮ ਦੇ ਅਨੁਸਾਰ ਵਿਅਕਤੀ ਨੂੰ ਆਪਣੀ ਹੀ ਜਾਤ ਵਿਚ ਵਿਆਹ ਕਰਵਾਉਣਾ ਪੈਂਦਾ ਸੀ । ਸਾਡੇ ਦੇਸ਼ ਵਿਚ ਕਈ ਜਾਤਾਂ ਪਾਈਆਂ ਜਾਂਦੀਆਂ ਸਨ ਅਤੇ ਹਰੇਕ ਜਾਤ ਕਈ ਉਪਜਾਤਾਂ ਵਿਚ ਵੰਡੀ ਹੁੰਦੀ ਸੀ । ਇਸ ਤਰ੍ਹਾਂ ਵਿਅਕਤੀ ਨੂੰ ਨਾ ਸਿਰਫ ਆਪਣੀ ਹੀ ਜਾਤ ਬਲਕਿ ਉਪਜਾਤ ਵਿਚ ਵਿਆਹ ਕਰਵਾਉਣਾ ਪੈਂਦਾ ਸੀ । ਜੇਕਰ ਕੋਈ ਵੀ ਜਾਤ ਦੇ ਇਸ ਨਿਯਮ ਦੇ ਵਿਰੁੱਧ ਜਾਂਦਾ ਸੀ ਜਾਂ ਇਸ ਨਿਯਮ ਨੂੰ ਤੋੜਦਾ ਸੀ ਤਾਂ ਉਸਨੂੰ ਆਮ ਤੌਰ ਉੱਤੇ ਜਾਤ ਤੋਂ ਬਾਹਰ ਕੱਢ ਦਿੱਤਾ ਜਾਂਦਾ ਸੀ ਤੇ ਉਸਦੇ ਨਾਲ ਸਮਾਜਿਕ ਸੰਬੰਧ ਤੋੜ ਲਏ ਜਾਂਦੇ ਸਨ ।
ਭਾਰਤੀ ਸਮਾਜ ਚਾਰ ਜਾਤਾਂ ਵਿਚ ਵੰਡਿਆ ਹੋਇਆ ਸੀ । ਇਹ ਚਾਰ ਜਾਤਾਂ ਅੱਗੇ ਕਈ ਹਜ਼ਾਰਾਂ ਉਪਜਾਤਾਂ ਵਿਚ ਵੰਡੀਆਂ ਹੋਈਆਂ ਸਨ । ਵਿਅਕਤੀ ਨੂੰ ਆਪਣੀ ਹੀ ਜਾਤ ਵਿਚ ਵਿਆਹ ਕਰਵਾਉਣਾ ਪੈਂਦਾ ਸੀ । ਇਸਨੂੰ ਹੀ ਅੰਤਰ ਵਿਆਹ ਦਾ ਨਾਮ ਦਿੱਤਾ ਜਾਂਦਾ ਸੀ ।
ਸਾਡੇ ਦੇਸ਼ ਵਿਚ ਅੰਤਰ ਵਿਆਹ ਦੇ ਕਈ ਰੂਪ ਪਾਏ ਜਾਂਦੇ ਹਨ, ਜਿਵੇਂ ਕਿ-
- ਕਬਾਇਲੀ ਅੰਤਰ ਵਿਆਹ (Tribal Endogamy) – ਕਬਾਇਲੀ ਅੰਤਰ ਵਿਆਹ ਦੇ ਵਿਚ ਵਿਅਕਤੀ ਨੂੰ ਆਪਣੇ ਕਬੀਲੇ ਵਿਚ ਹੀ ਵਿਆਹ ਕਰਵਾਉਣਾ ਪੈਂਦਾ ਹੈ । ਭਾਰਤ ਵਿਚ ਬਹੁਤ ਸਾਰੇ ਕਬੀਲੇ ਪਾਏ ਜਾਂਦੇ ਹਨ ਅਤੇ ਆਮ ਤੌਰ ਉੱਤੇ ਸਾਰੇ ਕਬੀਲਿਆਂ ਵਿਚ ਇਹ ਨਿਯਮ ਪ੍ਰਚਲਿਤ ਹੈ । ਇਸ ਨਿਯਮ ਨੂੰ ਨਾ ਮੰਨਣ ਵਾਲਿਆਂ ਨੂੰ ਕਬੀਲੇ ਤੋਂ ਬਾਹਰ ਕੱਢ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ।
- ਜਾਤ ਅੰਤਰ ਵਿਆਹ (Caste Endogamy) – ਅੰਤਰ ਵਿਆਹ ਦਾ ਇਹ ਰੂਪ ਪੂਰੇ ਭਾਰਤ ਵਿਚ ਪ੍ਰਚਲਿਤ ਸੀ । ਜਾਤ ਅੰਤਰ ਵਿਆਹ ਦੇ ਨਿਯਮ ਦੇ ਅਨੁਸਾਰ ਵਿਅਕਤੀ ਨੂੰ ਆਪਣੀ ਹੀ ਜਾਤ ਅਤੇ ਉਪਜਾਤ ਦੇ ਅੰਦਰ ਵਿਆਹ ਕਰਵਾਉਣਾ ਪੈਂਦਾ ਸੀ ਨਹੀਂ ਤਾਂ ਉਸ ਨੂੰ ਜਾਤ ਤੋਂ ਬਾਹਰ ਕੱਢ ਦਿੱਤਾ ਜਾਂਦਾ ਸੀ ।
- ਉਪਜਾਤ ਅੰਤਰਵਿਆਹ (Sub Caste Endogamy) – ਸਾਡੇ ਦੇਸ਼ ਵਿਚ ਚਾਰ ਮੁੱਖ ਜਾਤਾਂ ਪਾਈਆਂ ਜਾਂਦੀਆਂ ਸਨ ਅਤੇ ਇਹ ਚਾਰ ਜਾਤਾਂ ਅੱਗੇ ਕਈ ਉਪਜਾਤਾਂ ਵਿਚ ਵੰਡੀਆਂ ਹੋਈਆਂ ਸਨ । ਵਿਅਕਤੀ ਨੂੰ ਆਪਣੀ ਹੀ ਉਪਜਾਤ ਵਿਚ ਵਿਆਹ ਕਰਵਾਉਣਾ ਪੈਂਦਾ ਸੀ ਨਹੀਂ ਤਾਂ ਉਸ ਨਾਲ ਸੰਬੰਧ ਹੀ ਤੋੜ ਲਏ ਜਾਂਦੇ ਸਨ ।
- ਵਰਗੀ ਅੰਤਰਵਿਆਹ (Class Endogamy) – ਅੱਜ-ਕਲ੍ਹ ਦੇ ਸਮਾਜ ਵਿਚ ਜਾਤ ਦੀ ਥਾਂ ਬਹੁਤ ਸਾਰੇ ਵਰਗ ਪਾਏ ਜਾਂਦੇ ਹਨ । ਆਮ ਤੌਰ ਉੱਤੇ ਵਿਅਕਤੀ ਆਪਣੇ ਵਰਗ ਨੂੰ ਛੱਡ ਕੇ ਕਿਸੇ ਹੋਰ ਵਰਗ ਵਿਚ ਵਿਆਹ ਕਰਵਾਉਣਾ ਪਸੰਦ ਨਹੀਂ ਕਰਦਾ ।
5. ਨਸਲੀ ਅੰਤਰਵਿਆਹ (Racial Endogamy) – ਦੁਨੀਆਂ ਵਿਚ ਤਿੰਨ ਨਸਲਾਂ ਪਾਈਆਂ ਜਾਂਦੀਆਂ ਹਨ ਗੋਰੀ, ਪੀਲੀ ਅਤੇ ਕਾਲੀ । ਆਮ ਤੌਰ ਉੱਤੇ ਲੋਕ ਆਪਣੀ ਹੀ ਨਸਲ ਵਿਚ ਵਿਆਹ ਕਰਵਾਉਣਾ ਪਸੰਦ ਕਰਦੇ ਹਨ । ਇਸ ਨੂੰ ਨਸਲੀ ਅੰਤਰਵਿਆਹ ਕਹਿੰਦੇ ਹਨ ।
ਇਸ ਤਰ੍ਹਾਂ ਅਸੀਂ ਕਹਿ ਸਕਦੇ ਹਾਂ ਕਿ ਚਾਹੇ ਅੰਤਰ ਵਿਆਹ ਦੇ ਇਸ ਨਿਯਮ ਦੇ ਕਈ ਗੁਣ ਹਨ ਪਰ ਬਹੁਤ ਸਾਰੀਆਂ ਹਾਨੀਆਂ ਵੀ ਹਨ। ਇਸ ਨਿਯਮ ਨਾਲ ਵਿਅਕਤੀ ਦੇ ਲਈ ਜੀਵਨ ਸਾਥੀ ਦੀ ਚੋਣ ਕਰਨਾ ਦਾ ਘੇਰਾ ਸੀਮਿਤ ਹੋ ਜਾਂਦਾ ਹੈ । ਅੱਜ-ਕੱਲ੍ਹ ਦੇ ਆਧੁਨਿਕ ਸਮੇਂ ਵਿਚ ਲੋਕ ਪੜ-ਲਿਖ ਰਹੇ ਹਨ ਅਤੇ ਇਸ ਨਿਯਮ ਨੂੰ ਭੁੱਲਦੇ ਜਾ ਰਹੇ ਹਨ । ਅੰਤਰਜਾਤੀ ਵਿਆਹ ਵੱਧ ਰਹੇ ਹਨ । ਅਖਬਾਰਾਂ ਦੇ Matrimonials ਵਿਚ Caste No Bar ਅਸੀਂ ਆਮ ਲਿਖਿਆ ਹੋਇਆ ਦੇਖ ਸਕਦੇ ਹਾਂ ।
II. ਬਾਹਰ ਵਿਆਹ ਜਾਂ ਵਿਜਾਤੀ ਵਿਆਹ (Exogamy) – ਸਾਡੇ ਸਮਾਜ ਵਿਚ ਵਿਆਹ ਕਰਵਾਉਣ ਦੇ ਬਹੁਤ ਸਾਰੇ ਨਿਯਮ ਪਾਏ ਜਾਂਦੇ ਹਨ । ਕਿਸੇ ਵੀ ਸਮਾਜ ਵਿਚ ਬਿਨਾਂ ਵਿਆਹ ਕੀਤੇ ਆਦਮੀ ਅਤੇ ਔਰਤ ਦੇ ਸੰਬੰਧਾਂ ਨੂੰ ਮਾਨਤਾ ਨਹੀਂ ਦਿੱਤੀ ਜਾਂਦੀ ਬਲਕਿ ਉਨ੍ਹਾਂ ਨੂੰ ਨਜਾਇਜ਼ ਸਮਝਿਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਲਈ ਵਿਅਕਤੀ ਨੂੰ ਜੀਵਨ ਜੀਣ ਦੇ ਲਈ ਵਿਆਹ ਕਰਵਾਉਣਾ ਬਹੁਤ ਜ਼ਰੂਰੀ ਹੁੰਦਾ ਹੈ । ਵਿਆਹ ਦੇ ਲਈ ਜੀਵਨ ਸਾਥੀ ਦੀ ਜ਼ਰੂਰਤ ਹੁੰਦੀ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਜੀਵਨ ਸਾਥੀ ਦੀ ਚੋਣ ਕਰਨ ਦੇ ਲਈ ਬਾਹਰ ਵਿਆਹ ਵੀ ਇਕ ਨਿਯਮ ਹੈ ।
ਸਾਡੇ ਸਮਾਜ ਵਿਚ ਸਾਡੇ ਕੁਝ ਸੰਬੰਧ ਅਜਿਹੇ ਹੁੰਦੇ ਹਨ ਜਿਨ੍ਹਾਂ ਦੇ ਨਾਲ ਵਿਆਹਕ ਸੰਬੰਧ ਜਾਂ ਲੈਂਗਿਕ ਸੰਬੰਧ ਸਥਾਪਿਤ ਕਰਨ ਦੀ ਆਗਿਆ ਸਮਾਜ ਨਹੀਂ ਦਿੰਦਾ | ਖੂਨ ਦੇ ਸੰਬੰਧੀ ਅਜਿਹੇ ਹੀ ਸੰਬੰਧਾਂ ਵਿਚ ਆਉਂਦੇ ਹਨ । ਇਸ ਦਾ ਅਰਥ ਇਹ ਹੈ ਕਿ ਵਿਅਕਤੀ ਆਪਣੇ ਰਕਤ ਸੰਬੰਧੀਆਂ ਨਾਲ ਵਿਆਹ ਨਹੀਂ ਕਰਵਾ ਸਕਦਾ ਹੈ । ਬਾਹਰ ਵਿਆਹ ਦਾ ਨਿਯਮ ਵੀ ਇਸੇ ਉੱਤੇ ਹੀ ਆਧਾਰਿਤ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਬਾਹਰ ਵਿਆਹ ਦੇ ਨਿਯਮ ਦੇ ਅਨੁਸਾਰ ਵਿਅਕਤੀ ਆਪਣੇ ਰਕਤ ਸੰਬੰਧੀਆਂ ਜਾਂ ਕਿਸੇ ਹੋਰ ਅਜਿਹੇ ਹੀ ਸੰਬੰਧੀਆਂ ਨਾਲ ਵਿਆਹਕ ਸੰਬੰਧ ਸਥਾਪਿਤ ਨਹੀਂ ਕਰ ਸਕਦਾ ਅਰਥਾਤ ਵਿਅਕਤੀ ਆਪਣੇ ਹੀ ਸਮੂਹ ਵਿਚ ਵਿਆਹ ਨਹੀਂ ਕਰਵਾ ਸਕਦਾ । ਇਹ ਉਸਦੇ ਲਈ ਪ੍ਰਤੀਬੰਧਿਤ ਹੈ । ਇਸ ਕਾਰਨ ਹੀ ਕਦੇ ਵੀ ਇਕ ਹੀ ਮਾਤਾ ਪਿਤਾ ਦੇ ਬੱਚੇ ਆਪਸ ਵਿਚ ਵਿਆਹ ਨਹੀਂ ਕਰਵਾ ਸਕਦੇ ।
ਚਾਹੇ ਕਈ ਸਮੁਦਾਵਾਂ ਵਿਚ ਥੋੜੀ ਦੂਰ ਦੇ ਰਿਸ਼ਤੇਦਾਰਾਂ ਵਿਚ ਵਿਆਹ ਕਰਵਾਉਣ ਦੀ ਆਗਿਆ ਹੁੰਦੀ ਹੈ । ਉਦਾਹਰਨ ਦੇ ਤੌਰ ਉੱਤੇ ਮਾਤਾ-ਪਿਤਾ ਦੇ ਰਿਸ਼ਤੇਦਾਰਾਂ ਨਾਲ ਵਿਆਹ ਕਰਵਾਉਣ ਦੀ ਆਗਿਆ ਹੁੰਦੀ ਹੈ । ਇੱਥੋਂ ਤਕ ਕਿ ਆਸਟਰੇਲੀਆ ਦੇ ਕਬੀਲਿਆਂ ਵਿਚ ਵਿਅਕਤੀ ਆਪਣੀ ਸੌਤੇਲੀ ਮਾਂ ਨਾਲ ਵਿਆਹ ਕਰਵਾ ਸਕਦਾ ਹੈ | ਪਰ ਆਮ ਤੌਰ ਉੱਤੇ ਅਜਿਹਾ ਨਹੀਂ ਹੁੰਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਬਾਹਰ ਵਿਆਹ ਦੇ ਨਿਯਮ ਦੇ ਅਨੁਸਾਰ ਵਿਅਕਤੀ ਆਪਣੇ ਸਵਰ, ਪਿੰਡ, ਪਿੰਡ ਰਕਤ ਸੰਬੰਧੀਆਂ ਵਿਚ ਵਿਆਹ ਨਹੀਂ ਕਰਵਾ ਸਕਦਾ | ਜੇਕਰ ਕੋਈ ਅਜਿਹਾ ਕਰਦਾ ਹੈ ਤਾਂ ਉਸਨੂੰ ਸਮਾਜ ਵੱਲੋਂ ਮਾਨਤਾ ਨਹੀਂ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ ।
ਬਾਹਰ ਵਿਆਹ ਦੇ ਸਾਡੇ ਸਮਾਜ ਵਿਚ ਕਈ ਪ੍ਰਕਾਰ ਪਾਏ ਜਾਂਦੇ ਹਨ ਜੋ ਕਿ ਹੇਠਾਂ ਲਿਖੇ ਹਨ-
(i) ਗੋਤਰ ਬਾਹਰ ਵਿਆਹ (Gotra exogamy) – ਗੋਤਰ ਬਾਹਰ ਵਿਆਹ ਦੇ ਨਿਯਮ ਦੇ ਅਨੁਸਾਰ ਵਿਅਕਤੀ ਨੂੰ ਆਪਣੇ ਗੋਤਰ ਵਿਚ ਵਿਆਹ ਕਰਵਾਉਣ ਦੀ ਆਗਿਆ ਨਹੀਂ ਹੁੰਦੀ । ਕਪਾੜੀਆ (Kapadia) ਦੇ ਅਨੁਸਾਰ, “ਗੋਤਰ ਬਾਹਰ ਵਿਆਹ ਦੇ ਨਿਯਮ ਨੂੰ ਮੰਨਿਆ ਜਾ ਸਕਦਾ ਹੈ ਕਿ ਗੋਤਰ ਬਾਹਰ ਵਿਆਹ ਦਾ ਪਹਿਲਾ ਪ੍ਰਗਟਾਵਾ ਬਾਹਮਣਾਂ ਦੇ ਸਮੇਂ ਵਿਚ ਹੋਇਆ ਸੀ । ਗਾਵਾਂ ਨੂੰ ਪਾਲਣ ਵਾਲੇ ਸਮੂਹ ਨੂੰ ਗੋਤਰ ਕਹਿੰਦੇ ਹਨ | ਮੈਕਸ ਮੂਲਰ ਦਾ ਕਹਿਣਾ ਹੈ ਜਿਹੜੇ ਲੋਕ ਇਕ ਹੀ ਥਾਂ ਉੱਤੇ ਆਪਣੀਆਂ ਗਾਵਾਂ ਨੂੰ ਬੰਨਦੇ ਸਨ ਉਹ ਇਕ ਦੂਜੇ ਦੇ ਨਾਲ ਨੈਤਿਕ ਰੂਪ ਵਿਚ ਸੰਬੰਧਿਤ ਹੋ ਜਾਂਦੇ ਹਨ । ਇਸ ਕਾਰਨ ਉਹ ਇਕ-ਦੂਜੇ ਨਾਲ ਵਿਆਹ ਨਹੀਂ ਕਰਵਾ ਸਕਦੇ । ਇਸ ਲਈ ਗੋਤਰ ਵਿਚ ਉਹ ਵਿਅਕਤੀ ਸ਼ਾਮਲ ਹੁੰਦੇ ਹਨ ਜਿਨ੍ਹਾਂ ਵਿਚ ਰਕਤ ਸੰਬੰਧ ਹੋਣ ਜਾਂ ਨੈਤਿਕ ਸੰਬੰਧ ਹੋਣ । ਇਸ ਲਈ ਇਕ ਹੀ ਗੋਤਰ ਦੇ ਵਿਅਕਤੀ ਨੂੰ ਆਪਣੇ ਹੀ ਗੋਤਰ ਵਿਚ ਵਿਆਹ ਕਰਨ ਦੀ ਆਗਿਆ ਨਹੀਂ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ ।
(ii) ਸਵਰ ਬਾਹਰੀ ਵਿਆਹ (Sparvar Exogamy) – ਇਹ ਵੀ ਬਾਹਰ ਵਿਆਹ ਦਾ ਹੀ ਇਕ ਨਿਯਮ ਹੈ ਜਿਸਦੇ ਅਨੁਸਾਰ ਹੀ ਇੱਕੋ ਪ੍ਰਵਰ ਦੇ ਮੁੰਡੇ ਤੇ ਕੁੜੀਆਂ ਆਪਸ ਵਿਚ ਵਿਆਹ ਨਹੀਂ ਕਰਵਾ ਸਕਦੇ । ਪ੍ਰਭੂ (Prabu) ਦੇ ਅਨੁਸਾਰ, ‘‘ਪ੍ਰਵਰ ਦਾ ਅਰਥ ਹੈ ਕਿ ਵੈਦਿਕ ਸਮੇਂ ਵਿਚ ਹਵਨ ਕਰਦੇ ਸਮੇਂ ਪੂਰੋਹਿਤ ਆਪਣੇ ਪੂਰਵਜ ਦਾ ਨਾਮ ਲੈਂਦੇ ਸਨ । ਇਸ ਤਰ੍ਹਾਂ ਪ੍ਰਵਰ ਵਿਅਕਤੀਆਂ ਦੇ ਅਜਿਹੇ ਪੁਰਵਜਾਂ ਦਾ ਚਿੰਨ੍ਹ ਹੁੰਦਾ ਹੈ ਜਿਨ੍ਹਾਂ ਨੇ ਪਹਿਲਾਂ ਵੀ ਹਵਨ ਕੀਤਾ ਸੀ ।” ਇਸ ਤਰ੍ਹਾਂ ਇਹ ਕਿਹਾ ਜਾ ਸਕਦਾ ਹੈ ਕਿ ਪ੍ਰਵਰ ਵਿਚ ਉਹ ਵਿਅਕਤੀ ਸ਼ਾਮਲ ਹੁੰਦੇ ਹਨ ਜਿਨ੍ਹਾਂ ਦੇ ਰਿਸ਼ੀ ਪੁਰਵਜ ਆਦਿ ਸਾਂਝੇ ਹੋਣ । ਜਿਨ੍ਹਾਂ ਲੋਕਾਂ ਵਿਚ ਰਿਸ਼ੀ ਜਾਂ ਪੁਰਵਜ ਸਾਂਝੇ ਹਨ ਜਾਂ ਇਕ ਹੀ ਹਨ ਉਹ ਆਪਸ ਵਿਚ ਵਿਆਹ ਨਹੀਂ ਕਰਵਾ ਸਕਦੇ । ਇਕ ਹੀ ਪ੍ਰਵਰ ਦੇ ਆਦਮੀ ਨੂੰ ਉਸੀ ਦੇ ਪ੍ਰਵਾਰ ਦੀ ਔਰਤ ਨਾਲ ਵਿਆਹ ਕਰਨ ਦੀ ਆਗਿਆ ਨਹੀਂ ਹੈ ।
(iii) ਸਪਿੰਡਾ ਬਾਹਰ ਵਿਆਹ (Spinda Exogamy) – ਇਹ ਵੀ ਬਾਹਰ ਵਿਆਹ ਦਾ ਹੀ ਇਕ ਰੂਪ ਹੈ ਕਿ ਇਕ ਹੀ ਪਿੰਡ ਦੇ ਮਰਦ ਅਤੇ ਔਰਤ ਆਪਸ ਵਿਚ ਵਿਆਹ ਨਹੀਂ ਕਰਵਾ ਸਕਦੇ : ਸਪਿੰਡ ਵਿਚ ਉਹ ਸਾਰੇ ਵਿਅਕਤੀ ਸ਼ਾਮਲ ਹੁੰਦੇ ਹਨ ਜਿਨ੍ਹਾਂ ਦੇ ਦਾਦਾ-ਦਾਦੀ, ਮਾਤਾ-ਪਿਤਾ ਜਾਂ ਨਾਨਾ-ਨਾਨੀ ਇਕ ਹੀ ਹੋਣ । ਇਸ ਦਾ ਅਰਥ ਇਹ ਹੈ ਕਿ ਪੁੱਤਰ ਦੇ ਸਰੀਰ ਵਿਚ ਮਾਤਾ-ਪਿਤਾ ਦੋਹਾਂ ਦੇ ਖੂਨ ਦੇ ਕਣ ਸ਼ਾਮਲ ਹੁੰਦੇ ਹਨ । ਵਿਗਿਆਨਿਕਾਂ ਦੇ ਅਨੁਸਾਰ ਪਿੰਡ ਵਿਚ ਪਿਤਾ ਦੇ ਵੱਲੋਂ ਸੱਤ ਪੀੜੀਆਂ ਦੇ ਵਿਅਕਤੀ ਅਤੇ ਮਾਤਾ ਦੇ ਵੱਲੋਂ ਪੰਜ ਪੀੜੀਆਂ ਦੇ ਵਿਅਕਤੀ ਸ਼ਾਮਿਲ ਕੀਤੇ ਜਾਂਦੇ ਹਨ । ਇਸ ਲਈ ਵਿਅਕਤੀ ਆਪਣੇ ਪਿਤਾ ਦੀਆਂ ਸੱਤ ਪੀੜੀਆਂ ਅਤੇ ਮਾਤਾ ਦੇ ਪਾਸੇ ਪੰਜ ਪੀੜ੍ਹੀਆਂ ਦੇ ਵਿਅਕਤੀਆਂ ਦੇ ਨਾਲ ਵਿਆਹਕ ਸੰਬੰਧ ਸਥਾਪਿਤ ਨਹੀਂ ਕਰ ਸਕਦਾ ।
(iv) ਪਿੰਡ ਬਾਹਰ ਵਿਆਹ (Village Exogamy) – ਸਾਡੇ ਪਿੰਡਾਂ ਵਿਚ ਇਕ ਗੱਲ ਪ੍ਰਚਲਿਤ ਹੈ ਕਿ ਪਿੰਡ ਵਿਚ ਰਹਿਣ ਵਾਲੇ ਕਿਸੇ ਵੀ ਵਿਅਕਤੀ ਦੀ ਧੀ-ਭੈਣ ਸਾਰਿਆਂ ਦੀ ਸਾਂਝੀ ਧੀ-ਬੈਣ ਹੁੰਦੀ ਹੈ । ਇਸ ਲਈ ਕੋਈ ਇਕ ਹੀ ਪਿੰਡ ਵਿਚ ਕਿਸੇ ਵੀ ਲੜਕੀ ਦੇ ਨਾਲ ਵਿਆਹਕ ਸੰਬੰਧ ਸਥਾਪਿਤ ਨਹੀਂ ਕਰ ਸਕਦਾ । ਇਸ ਤਰ੍ਹਾਂ ਪਿੰਡ ਬਾਹਰੀ ਵਿਆਹ ਦੇ ਅਨੁਸਾਰ ਪਿੰਡ ਵਿਚ ਰਹਿਣ ਵਾਲੇ ਸਾਰੇ ਵਿਅਕਤੀਆਂ ਨੂੰ ਕਿਸੇ ਦੂਜੇ ਪਿੰਡ ਵਿਚ ਵਿਆਹ ਕਰਵਾਉਣਾ ਪੈਂਦਾ ਹੈ । ਉਹ ਆਪਣੇ ਹੀ ਪਿੰਡ ਵਿਚ ਵਿਆਹ ਨਹੀਂ ਕਰਵਾ ਸਕਦਾ । ਪਿੰਡ ਦੇ ਲੋਕਾਂ ਨੂੰ ਤਾਂ ਆਪਣੇ ਰਿਸ਼ਤੇਦਾਰਾਂ, ਸੰਬੰਧੀਆਂ ਤੋਂ ਵੱਧ ਸਮਝਿਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਲਈ ਇਕ ਹੀ ਪਿੰਡ ਵਿਚ ਵਿਆਹ ਕਰਨਾ ਪ੍ਰਤੀਬੰਧਿਤ ਹੈ ।
(v) ਟੋਟਮ ਬਾਹਰ ਵਿਆਹ (Totem Exogamy) – ਇਸ ਤਰ੍ਹਾਂ ਦਾ ਵਿਆਹ ਸਾਡੇ ਸਮਾਜਾਂ ਵਿਚ ਨਹੀਂ ਬਲਕਿ ਕਬਾਇਲੀ ਸਮਾਜਾਂ ਵਿਚ ਪ੍ਰਚਲਿਤ ਹੈ । ਟੋਟਮ ਇਕ ਚਿੰਨ, ਪੱਥਰ, ਪੇੜ, ਜਾਨਵਰ ਆਦਿ ਹੁੰਦਾ ਹੈ ਜਿਸਨੂੰ ਲੋਕ ਆਪਣਾ ਦੇਵਤਾ ਮੰਨਦੇ ਹਨ ਤੇ ਉਸਦੀ ਪੂਜਾ ਕਰਦੇ ਹਨ । ਇਸ ਲਈ ਜੋ ਲੋਕ ਇੱਕ ਟੋਟਮ ਦੀ ਪੂਜਾ ਕਰਦੇ ਹਨ ਉਹ ਆਪਸ ਵਿਚ ਵਿਆਹ ਨਹੀਂ ਕਰਵਾ ਸਕਦੇ । ਇਸ ਤਰ੍ਹਾਂ ਟੋਟਮ ਬਾਹਰ ਵਿਆਹ ਦੇ ਅਨੁਸਾਰ ਵਿਅਕਤੀ ਨੂੰ ਆਪਣੇ ਟੋਟਮ ਤੋਂ ਬਾਹਰ ਵਿਆਹ ਕਰਵਾਉਣਾ ਪੈਂਦਾ ਹੈ ।
III. ਅਨੁਲੋਮ ਵਿਆਹ (Hypergamy) – ਇਸ ਤਰ੍ਹਾਂ ਦਾ ਵਿਆਹ ਪ੍ਰਾਚੀਨ ਸਮੇਂ ਵਿਚ ਪ੍ਰਚਲਿਤ ਸੀ । ਹਰੇਕ ਵਿਅਕਤੀ ਚਾਹੁੰਦਾ ਹੈ ਕਿ ਉਸਦੀ ਕੁੜੀ ਦਾ ਵਿਆਹ ਬਰਾਬਰ ਜਾਂ ਉੱਚੀ ਜਾਤ ਵਿਚ ਹੋਵੇ । ਇਹ ਵੀ ਅਨੁਲੋਮ ਵਿਆਹ ਦਾ ਨਿਯਮ ਹੈ । ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਵਿਆਹ ਵਿਚ ਕੁੜੀ ਦਾ ਵਿਆਹ ਬਰਾਬਰ ਜਾਤ ਜਾਂ ਆਪਣੇ ਤੋਂ ਉੱਚੀ ਜਾਤ ਵਿਚ ਕਰ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਜਦੋਂ ਹੇਠਲੀ ਜਾਤ ਦੀ ਕੁੜੀ ਦਾ ਵਿਆਹ ਉੱਚੀ ਜਾਤ ਦੇ ਮੁੰਡੇ ਨਾਲ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ਤਾਂ ਇਸ ਨੂੰ ਅਨੁਲੋਮ ਵਿਆਹ ਕਹਿੰਦੇ ਹਨ । ਇਸ ਤਰ੍ਹਾਂ ਅਨੁਲੋਮ ਵਿਆਹ ਵਿਚ ਬਾਹਮਣ ਮੁੰਡੇ ਦਾ ਵਿਆਹ ਸਿਰਫ ਬ੍ਰਾਹਮਣ ਲੜਕੀ ਨਾਲ ਹੁੰਦਾ ਹੈ । ਕਸ਼ੱਤਰੀ ਲੜਕੀ ਦਾ ਵਿਆਹ ਸਿਰਫ਼ ਕਸ਼ੱਤਰੀ ਲੜਕੇ ਜਾਂ ਬ੍ਰਾਹਮਣ ਮੁੰਡੇ ਨਾਲ ਹੋ ਸਕਦਾ ਹੈ । ਇਸੇ ਤਰ੍ਹਾਂ ਵੈਸ਼ ਲੜਕੀ ਦਾ ਵਿਆਹ ਵੈਸ਼, ਕਸ਼ੱਤਰੀ ਅਤੇ ਬ੍ਰਾਹਮਣ ਲੜਕੇ ਦੇ ਨਾਲ ਵੀ ਹੋ ਸਕਦਾ ਹੈ ।
ਇਸ ਤਰ੍ਹਾਂ ਬ੍ਰਾਹਮਣ ਲੜਕਾ ਕਿਸੇ ਵੀ ਜਾਤ ਦੀ ਲੜਕੀ ਨਾਲ ਵਿਆਹ ਕਰਵਾ ਸਕਦਾ ਹੈ । ਕਸ਼ੱਤਰੀ ਲੜਕਾ ਬ੍ਰਾਹਮਣ ਲੜਕੀ ਤੋਂ ਇਲਾਵਾ ਕਿਸੇ ਵੀ ਲੜਕੀ ਨਾਲ ਵਿਆਹ ਕਰਵਾ ਸਕਦਾ ਹੈ । ਵੈਸ਼ ਲੜਕਾ ਬਾਹਮਣ ਅਤੇ ਕਸ਼ੱਤਰੀ ਲੜਕੀ ਨੂੰ ਛੱਡ ਕੇ ਕਿਸੇ ਵੀ ਲੜਕੀ ਨਾਲ ਵਿਆਹ ਕਰਵਾ ਸਕਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਦਾ ਵਿਆਹ ਪ੍ਰਾਚੀਨ ਸਮੇਂ ਵਿਚ ਸਾਹਮਣੇ ਆਇਆ ਸੀ ਕਿਉਂਕਿ ਆਰੀਆ ਲੋਕ ਜਦੋਂ ਭਾਰਤ ਵਿਚ ਆਏ ਸਨ ਤਾਂ ਉਹ ਆਪਣੇ ਪਰਿਵਾਰ ਆਪਣੇ ਨਾਲ ਨਹੀਂ ਲਿਆਏ ਸਨ । ਉਨ੍ਹਾਂ ਵਿਚ ਔਰਤਾਂ ਦੀ ਕਮੀ ਸੀ ਜਿਸ ਕਾਰਨ ਉਨ੍ਹਾਂ ਨੇ ਭਾਰਤ ਦੇ ਮੂਲ ਨਿਵਾਸੀਆਂ ਦੀਆਂ ਕੁੜੀਆਂ ਨਾਲ ਵਿਆਹ ਕਰਨਾ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤਾ । ਜਦੋਂ ਉਨ੍ਹਾਂ ਵਿਚ ਔਰਤਾਂ ਦੀ ਕਮੀ ਪੂਰੀ ਹੋ ਗਈ ਤਾਂ ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਵਿਆਹ ਵੀ ਖ਼ਤਮ ਹੋ ਗਏ 1 ਕੁਲੀਨ ਵਿਆਹ ਵੀ ਅਨੁਲੋਮ ਵਿਆਹ ਦੀ ਹੀ ਤਰ੍ਹਾਂ ਹੈ ਜਿਸ ਵਿਚ ਕਿਸੇ ਵੀ ਜਾਤ ਦਾ ਵਿਅਕਤੀ ਉਸੇ ਜਾਂ ਨੀਵੀਂ ਜਾਤ ਦੀ ਕੁੜੀ ਨਾਲ ਵਿਆਹ ਕਰਵਾ ਸਕਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਦੇ ਵਿਆਹ ਨਾਲ ਬਹੁਤ ਸਾਰੀਆਂ ਸਮਾਜਿਕ ਬੁਰਾਈਆਂ ਸਾਹਮਣੇ ਆ ਗਈਆਂ ਜਿਸ ਕਾਰਨ ਸਰਕਾਰ ਨੇ ਕਾਨੂੰਨ ਬਣਾਕੇ ਇਸ ਨੂੰ ਖ਼ਤਮ ਕਰ ਦਿੱਤਾ ।
IV. ਲੋਮ ਵਿਆਹ (Hypogamy) – ਪ੍ਰਤੀਲੋਮ ਵਿਆਹ ਅੰਤਰਜਾਤੀ ਵਿਆਹ ਦਾ ਦੂਜਾ ਰੂਪ ਹੈ ਜਦਕਿ ਅਨੁਲੋਮ ਵਿਆਹ ਅੰਤਰਜਾਤੀ ਵਿਆਹ ਦਾ ਪਹਿਲਾ ਰੂਪ ਸੀ । ਵਿਆਹ ਦਾ ਇਹ ਨਿਯਮ ਅਨੁਲੋਮ ਵਿਆਹ ਦੇ ਬਿਲਕੁਲ ਉਲਟ ਹੈ । ਅਨੁਲੋਮ ਵਿਆਹ ਵਿਚ ਨੀਵੀਂ ਜਾਤ ਦੀ ਲੜਕੀ ਉੱਚੀ ਜਾਤ ਦੇ ਲੜਕੇ ਨਾਲ ਵਿਆਹ ਕਰਵਾ ਸਕਦੀ ਹੈ ਪਰ ਪ੍ਰਤੀਲੋਮ ਵਿਆਹ ਵਿਚ ਨਿਮਨਜਾਤੀ ਦਾ ਮੁੰਡਾ ਉੱਚੀ ਜਾਤ ਦੀ ਕੁੜੀ ਨਾਲ ਵਿਆਹ ਕਰਦਾ ਹੈ । ਉਦਾਹਰਣ ਦੇ ਤੌਰ ਉੱਤੇ ਨਿਮਨਜਾਤੀ ਦਾ ਮੁੰਡਾ ਵੈਸ਼, ਕਸ਼ੱਤਰੀ ਜਾਂ ਬ੍ਰਾਹਮਣ ਜਾਤ ਦੀ ਕੁੜੀ ਨਾਲ ਵਿਆਹ ਕਰਵਾਏ ਤਾਂ ਉਸਨੂੰ ਪ੍ਰਤੀਲੋਮ ਵਿਆਹ ਕਹਿੰਦੇ ਹਨ । ਇਸ ਤਰ੍ਹਾਂ ਦੇ ਵਿਆਹ ਨੂੰ ਧਾਰਮਿਕ ਵੇਦਾਂ ਅਤੇ ਗ੍ਰੰਥਾਂ ਵਿਚ ਮਾਨਤਾ ਪ੍ਰਾਪਤ ਨਹੀਂ ਹੈ ਤੇ ਮਨੂੰ ਨੇ ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਵਿਆਹ ਤੋਂ ਪੈਦਾ ਹੋਈ ਸੰਤਾਨ ਨੂੰ ਚੰਡਾਲ ਕਿਹਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 5.
ਪਰਿਵਾਰ ਕਿਸਨੂੰ ਕਹਿੰਦੇ ਹਨ ? ਪਰਿਵਾਰ ਦੀਆਂ ਮੁੱਢਲੀਆਂ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਦਾ ਵਰਣਨ ਕਰੋ ।
ਉੱਤਰ-
ਪਰਿਵਾਰ ਦਾ ਅਰਥ (Meaning of Family) – ਸ਼ਬਦ ਪਰਿਵਾਰ ਅੰਗਰੇਜ਼ੀ ਦੇ ਸ਼ਬਦ Family ਦਾ ਪੰਜਾਬੀ ਰੂਪਾਂਤਰ ਹੈ | Family ਸ਼ਬਦ ਰੋਮਨ ਸ਼ਬਦ Famulous ਤੋਂ ਲਿਆ ਗਿਆ ਹੈ ਜਿਸਦਾ ਮਤਲਬ ਹੈ ਨੌਕਰ ਜਾਂ ਦਾਸ । ਰੋਮਨ ਕਾਨੂੰਨ ਵਿੱਚ ਪਰਿਵਾਰ ਤੋਂ ਮਤਲਬ ਅਜਿਹੇ ਸਮੂਹ ਤੋਂ ਹੈ ਜਿਸ ਵਿੱਚ ਨੌਕਰ ਜਾਂ ਦਾਸ, ਮਾਲਿਕ ਜਾਂ ਮੈਂਬਰ ਸ਼ਾਮਲ ਹਨ ਜੋ ਕਿ ਰਕਤ ਸੰਬੰਧਾਂ ਜਾਂ ਵਿਆਹ ਸੰਬੰਧਾਂ ਨਾਲ ਪਰਸਪਰ ਸੰਬੰਧਤ ਹੋਏ । ਇਸ ਸ਼ਬਦਿਕ ਅਰਥ ਤੋਂ ਸਪੱਸ਼ਟ ਹੈ ਕਿ ਪਰਿਵਾਰ ਕੁੱਝ ਲੋਕਾਂ ਦਾ ਸਿਰਫ ਇਕੱਠ ਨਹੀਂ ਹੈ ਬਲਕਿ ਉਨ੍ਹਾਂ ਵਿੱਚ ਸੰਬੰਧਾਂ ਦੀ ਵਿਵਸਥਾ ਹੈ । ਇਹ ਇੱਕ ਅਜਿਹੀ ਸੰਸਥਾ ਹੈ ਜਿਸਦੇ ਅੰਤਰਗਤ ਔਰਤ ਅਤੇ ਆਦਮੀ ਦਾ ਸਮਾਜ ਤੋਂ ਮਾਨਤਾ ਪ੍ਰਾਪਤ ਲਿੰਗ ਸੰਬੰਧ (Sex relation) ਸਥਾਪਿਤ ਰਹਿੰਦਾ ਹੈ । ਸੰਖੇਪ ਵਿੱਚ ਪਰਿਵਾਰ ਵਿਅਕਤੀਆਂ ਦਾ ਉਹ ਸਮੁਹ ਹੈ ਜੋ ਇੱਕ ਵਿਸ਼ੇਸ਼ ਨਾਮ ਨਾਲ ਪਛਾਣਿਆ ਜਾਂਦਾ ਹੈ । ਜਿਸ ਵਿੱਚ ਔਰਤ ਅਤੇ ਆਦਮੀ ਵਿੱਚ, ਪਤੀ ਪਤਨੀ ਵਿੱਚ ਸਥਾਈ ਲਿੰਗ ਸੰਬੰਧ ਹੋਣ, ਜਿਸ ਵਿੱਚ ਮੈਂਬਰਾਂ ਦੇ ਪਾਲਣ-ਪੋਸ਼ਣ ਦੀ ਪੂਰੀ ਵਿਵਸਥਾ ਹੋਵੇ, ਜਿਸਦੇ ਮੈਂਬਰਾਂ ਵਿੱਚ ਖ਼ੂਨ ਦੇ ਸੰਬੰਧ ਹੋਣ ਅਤੇ ਜੋ ਇੱਕ ਖ਼ਾਸ ਨਿਵਾਸ ਅਸਥਾਨ ਉੱਪਰ ਰਹਿੰਦੇ ਹੋਣ ।
ਜੇਕਰ ਸਮਾਜਿਕ ਦਿਸ਼ਟੀਕੋਣ ਤੋਂ ਦੇਖਿਆ ਜਾਵੇ ਤਾਂ ਸਮਾਜ ਦਾ ਪਹਿਲਾ ਅਤੇ ਸਭ ਤੋਂ ਮਹੱਤਵਪੂਰਨ ਸਮੂਹ ਹੀ ਪਰਿਵਾਰ ਹੈ ਜਿਸ ਵਿਚ ਮਾਤਾ-ਪਿਤਾ ਅਤੇ ਉਨ੍ਹਾਂ ਦੇ ਬੱਚੇ ਸ਼ਾਮਿਲ ਹੁੰਦੇ ਹਨ । ਹਰੇਕ ਸਮਾਜ ਅਤੇ ਹਰੇਕ ਕਾਲ ਵਿਚ ਇਹ ਸਮੂਹ ਪਾਇਆ ਜਾਂਦਾ ਰਿਹਾ ਹੈ ਜਿਸ ਕਾਰਨ ਇਸ ਨੂੰ ਇਕ ਸਰਵਵਿਆਪਕ ਸਮੂਹ ਹੀ ਕਿਹਾ ਜਾ ਸਕਦਾ ਹੈ । ਇਸ ਲਈ ਹੀ ਪ੍ਰਸਿੱਧ ਸਮਾਜਸ਼ਾਸਤਰੀ ਮੈਕਾਈਵਰ (MacIver) ਦਾ ਕਹਿਣਾ ਹੈ ਕਿ, “ਪਰਿਵਾਰ ਬੱਚਿਆਂ ਦੀ ਉੱਤਪਤੀ ਅਤੇ ਪਾਲਣ ਪੋਸ਼ਣ ਦੀ
ਵਿਵਸਥਾ ਕਰਨ ਦੇ ਲਈ ਕਾਫੀ ਰੂਪ ਵਿਚ ਨਿਸ਼ਚਿਤ ਅਤੇ ਸਥਾਈ ਯੌਨ ਸੰਬੰਧਾਂ ਨਾਲ ਪਰਿਭਾਸ਼ਿਤ ਇਕ ਸਮੂਹ ਹੈ ।” ਪਰਿਵਾਰ ਵਿਚ ਹੀ ਬੱਚਾ ਵੱਡਾ ਹੁੰਦਾ ਹੈ, ਉਸਦਾ ਸਮਾਜੀਕਰਣ ਹੁੰਦਾ ਹੈ ਅਤੇ ਉਹ ਸਮਾਜ ਦਾ ਇਕ ਜ਼ਿੰਮੇਵਾਰ ਨਾਗਰਿਕ ਬਣਦਾ ਹੈ । ਜਿਸ ਤਰ੍ਹਾਂ ਦਾ ਚਰਿੱਤਰ ਪਰਿਵਾਰ ਦਾ ਹੁੰਦਾ ਹੈ, ਉਸੇ ਪ੍ਰਕਾਰ ਦਾ ਚਰਿੱਤਰ ਬੱਚੇ ਦਾ ਵੀ ਬਣਦਾ ਹੈ । ਇਸ ਕਾਰਨ ਹੀ ਪਰਿਵਾਰ ਨੂੰ ਬਹੁਤ ਮਹੱਤਵਪੂਰਨ ਸਮੂਹ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।
ਪਰਿਭਾਸ਼ਾਵਾਂ (Definitions)
- ਆਗਬਰਨ ਅਤੇ ਨਿਮਕਾਫ (Ogburn and Nimkoff) ਦੇ ਅਨੁਸਾਰ, “ਪਰਿਵਾਰ ਬੱਚਿਆਂ ਸਹਿਤ ਜਾਂ ਬੱਚਿਆਂ ਰਹਿਤ ਪਤੀ ਪਤਨੀ ਜਾਂ ਇਕੱਲਾ ਇੱਕ ਆਦਮੀ ਜਾਂ ਔਰਤ ਅਤੇ ਬੱਚਿਆਂ ਦੀ ਲਗਪਗ ਇੱਕ ਸਥਾਈ ਸਭਾ ਹੈ ।” .
- ਮੈਕਾਈਵਰ ਅਤੇ ਪੇਜ (MacIver and Page) ਦੇ ਅਨੁਸਾਰ, “ਪਰਿਵਾਰ ਇੱਕ ਅਜਿਹਾ ਸਮੂਹ ਹੈ ਜੋ ਨਿਸ਼ਚਿਤ ਅਤੇ ਸਥਾਈ ਲਿੰਗ ਸੰਬੰਧਾਂ ਦੁਆਰਾ ਪਰਿਭਾਸ਼ਿਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ, ਜੋ ਬੱਚਿਆਂ ਨੂੰ ਪੈਦਾ ਕਰਨ ਅਤੇ ਪਾਲਣ-ਪੋਸ਼ਣ ਦੇ ਅਵਸਰ ਪ੍ਰਦਾਨ ਕਰਦਾ ਹੈ ”
- ਮਰਡੋਕ (Murdock) ਦੇ ਅਨੁਸਾਰ, ”ਪਰਿਵਾਰ ਇੱਕ ਅਜਿਹਾ ਸਮੂਹ ਹੈ ਜਿਸ ਦੀਆਂ ਵਿਸ਼ੇਸ਼ਤਾਈਆਂ ਸਾਡੀ ਰਿਹਾਇਸ਼, ਆਰਥਿਕ ਸਹਿਯੋਗ ਅਤੇ ਸੰਤਾਨ ਦੀ ਉਤਪੱਤੀ ਜਾਂ ਪ੍ਰਜਣਨ ਹਨ । ਇਸ ਵਿੱਚ ਦੋਵਾਂ ਲਿੰਗਾਂ ਦੇ ਬਾਲਗ ਸ਼ਾਮਲ ਹੁੰਦੇ ਹਨ, ਜਿਨ੍ਹਾਂ ਵਿੱਚ ਘੱਟ ਤੋਂ ਘੱਟ ਦੋ ਵਿੱਚ ਸਮਾਜਿਕ ਵਿਸ਼ਟੀ ਤੋਂ ਸਵੀਕ੍ਰਿਤ ਲਿੰਗ ਸੰਬੰਧ ਹੁੰਦਾ ਹੈ ਅਤੇ ਲਿੰਗ ਸੰਬੰਧਾਂ ਵਿੱਚ ਬਣੇ ਇਨ੍ਹਾਂ ਬਾਲਗਾਂ ਦੇ ਆਪਣੇ ਜਾਂ ਗੋਦ ਲਏ ਹੋਏ ਇੱਕ ਜਾਂ ਜ਼ਿਆਦਾ ਬੱਚੇ ਹੁੰਦੇ ਹਨ ।”
ਇਸ ਤਰ੍ਹਾਂ ਉੱਪਰ ਅਸੀਂ ਵੱਖ-ਵੱਖ ਸਮਾਜਸ਼ਾਸਤਰੀਆਂ ਦੁਆਰਾ ਦਿੱਤੀਆਂ ਪਰਿਵਾਰ ਦੀਆਂ ਪਰਿਭਾਸ਼ਾਵਾਂ ਵੇਖੀਆਂ ਹਨ ਅਤੇ ਇਨ੍ਹਾਂ ਨੂੰ ਵੇਖ ਕੇ ਅਸੀਂ ਇਸ ਨਤੀਜੇ ਉੱਤੇ ਪਹੁੰਚੇ ਹਾਂ ਕਿ ਪਰਿਵਾਰ ਉਹ ਸਮੂਹ ਹੈ ਜਿਸ ਵਿੱਚ ਆਦਮੀ ਅਤੇ ਔਰਤ ਦੇ ਲਿੰਗਕ ਸੰਬੰਧਾਂ ਨੂੰ ਸਮਾਜ ਵਲੋਂ ਮਾਨਤਾ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ । ਇਹ ਇੱਕ ਜੈਵਿਕ ਇਕਾਈ ਹੈ ਜਿਸ ਵਿੱਚ ਲਿੰਗਕ ਸੰਬੰਧਾਂ ਦੀ ਪੂਰਤੀ ਅਤੇ ਸੰਤੁਸ਼ਟੀ ਹੁੰਦੀ ਹੈ, ਬੱਚੇ ਪੈਦਾ ਕੀਤੇ ਜਾਂਦੇ ਹਨ, ਬੱਚਿਆਂ ਦਾ ਪਾਲਣ-ਪੋਸ਼ਣ ਅਤੇ ਉਨ੍ਹਾਂ ਨੂੰ ਵੱਡਾ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਇੱਥੇ ਲਿੰਗ ਸੰਬੰਧਾਂ ਨੂੰ ਵਿਧੀਪੂਰਵਕ ਸਵੀਕਾਰ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ਅਤੇ ਇਹ ਆਰਥਿਕ ਸਹਿਯੋਗ ਉੱਤੇ ਵੀ ਟਿਕਿਆ ਹੁੰਦਾ ਹੈ, ਇਸ ਵਿੱਚ ਬੱਚਿਆਂ ਦੀ ਜ਼ਿੰਮੇਵਾਰੀ ਵੀ ਸ਼ਾਮਲ ਹੁੰਦੀ ਹੈ ।
ਪਰਿਵਾਰ ਦੀਆਂ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਜਾਂ ਲੱਛਣ (Characteristics of Features or Family)
1. ਪਰਿਵਾਰ ਇਕ ਸਰਵਵਿਆਪਕ ਸਮੂਹ ਹੈ (Family is a universal group) – ਪਰਿਵਾਰ ਨੂੰ ਇਕ ਸਰਵਵਿਆਪਕ ਸਮੂਹ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ ਕਿਉਂਕਿ ਇਹ ਹਰੇਕ ਸਮਾਜ ਤੇ ਹਰੇਕ ਕਾਲ ਵਿਚ ਪਾਇਆ ਜਾਂਦਾ ਰਿਹਾ ਹੈ । ਜੇਕਰ ਅਸੀਂ ਮਨੁੱਖਾਂ ਦੇ ਇਤਿਹਾਸ ਦੇ ਪਹਿਲੇ ਸਮੂਹ ਦੇ ਰੂਪ ਵਿਚ ਇਸ ਨੂੰ ਮੰਨੀਏ ਤਾਂ ਗ਼ਲਤ ਨਹੀਂ ਹੋਵੇਗਾ । ਵਿਅਕਤੀ ਕਿਸੇ ਨਾ ਕਿਸੇ ਪਰਿਵਾਰ ਵਿਚ ਹੀ ਜਨਮ ਲੈਂਦਾ ਹੈ ਅਤੇ ਉਹ ਸਾਡਾ ਉਮਰ ਉਸ ਪਰਿਵਾਰ ਦਾ ਮੈਂਬਰ ਬਣ ਕੇ ਹੀ ਰਹਿੰਦਾ ਹੈ ।
2. ਪਰਿਵਾਰ ਛੋਟੇ ਆਕਾਰ ਦਾ ਹੁੰਦਾ ਹੈ (Family is of small size) – ਹਰੇਕ ਪਰਿਵਾਰ ਛੋਟੇ ਅਤੇ ਸੀਮਿਤ ਆਕਾਰ ਦਾ ਹੁੰਦਾ ਹੈ । ਇਸਦਾ ਕਾਰਨ ਇਹ ਹੈ ਕਿ ਵਿਅਕਤੀ ਦਾ ਜਿਸ ਸਮੂਹ ਜਾਂ ਪਰਿਵਾਰ ਵਿਚ ਜਨਮ ਹੁੰਦਾ ਹੈ ਉਸ ਵਿਚ ਜਾਂ ਤਾਂ ਰਕਤ ਸੰਬੰਧੀ ਜਾਂ ਵਿਆਹਕ ਸੰਬੰਧੀ ਹੀ ਸ਼ਾਮਿਲ ਕੀਤੇ ਜਾਂਦੇ ਹਨ । ਪ੍ਰਾਚੀਨ ਸਮੇਂ ਵਿਚ ਤਾਂ ਸੰਯੁਕਤ ਪਰਿਵਾਰ ਹੁੰਦੇ ਸਨ ਜਿਨ੍ਹਾਂ ਵਿਚ ਬਹੁਤ ਸਾਰੇ ਰਿਸ਼ਤੇਦਾਰ ਜਿਵੇਂ ਕਿ ਦਾਦਾ-ਦਾਦੀ, ਤਾਇਆ-ਤਾਈ, ਚਾਚਾ-ਚਾਈ, ਉਨ੍ਹਾਂ ਦੇ ਬੱਚੇ ਆਦਿ ਸ਼ਾਮਲ ਹੁੰਦੇ ਸਨ । ਪਰ ਸਮੇਂ ਦੇ ਨਾਲ-ਨਾਲ ਬਹੁਤ ਸਾਰੇ ਕਾਰਨਾਂ ਦੇ ਕਾਰਨ ਸਮਾਜ ਵਿਚ ਪਰਿਵਰਤਨ ਆਏ ਅਤੇ ਸੰਯੁਕਤ ਪਰਿਵਾਰਾਂ ਦੀ ਥਾਂ ਕੇਂਦਰੀ ਪਰਿਵਾਰ ਸਾਹਮਣੇ ਆਏ ਜਿਨ੍ਹਾਂ ਵਿਚ ਸਿਰਫ ਮਾਤਾ-ਪਿਤਾ ਅਤੇ ਉਨ੍ਹਾਂ ਦੇ ਬਿਨਾਂ ਵਿਆਹੇ ਬੱਚੇ ਰਹਿੰਦੇ ਹਨ ।
3. ਪਰਿਵਾਰ ਦਾ ਭਾਵਾਤਮਕ ਆਧਾਰ ਹੁੰਦਾ ਹੈ (Family has emotional base) – ਹਰੇਕ ਪਰਿਵਾਰ ਦਾ ਭਾਵਾਤਮਕ ਆਧਾਰ ਹੁੰਦਾ ਹੈ ਕਿਉਂਕਿ ਪਰਿਵਾਰ ਵਿਚ ਰਹਿ ਕੇ ਹੀ ਵਿਅਕਤੀ ਵਿਚ ਬਹੁਤ ਸਾਰੀਆਂ ਭਾਵਨਾਵਾਂ ਦਾ ਵਿਕਾਸ ਹੁੰਦਾ ਹੈ । ਪਰਿਵਾਰ ਨੂੰ ਸਮਾਜ ਦਾ ਆਧਾਰ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ ਅਤੇ ਵਿਅਕਤੀ ਦੀ ਮੂਲ ਪ੍ਰਵਿਰਤੀਆਂ ਪਰਿਵਾਰ ਉੱਤੇ ਹੀ ਨਿਰਭਰ ਹੁੰਦੀਆਂ ਹਨ ।
4. ਪਰਿਵਾਰ ਦਾ ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਵਿਚ ਕੇਂਦਰੀ ਸਥਾਨ ਹੁੰਦਾ ਹੈ (Family has a central position in Social Structure) – ਪਰਿਵਾਰ ਇਕ ਸਰਵਵਿਆਪਕ ਸਮੂਹ ਹੈ ਅਤੇ ਇਹ ਹਰੇਕ ਸਮਾਜ ਵਿਚ ਪਾਇਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਨੂੰ ਸਮਾਜ ਦਾ ਪਹਿਲਾ ਸਮੂਹ ਵੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ਜਿਸ ਕਾਰਨ ਸਮਾਜ ਦਾ ਪੂਰਾ ਢਾਂਚਾ ਹੀ ਪਰਿਵਾਰ ਉੱਤੇ ਨਿਰਭਰ ਕਰਦਾ ਹੈ । ਸਮਾਜ ਵਿਚ ਵੱਖ-ਵੱਖ ਸਭਾਵਾਂ ਵੀ ਪਰਿਵਾਰ ਦੇ ਕਾਰਨ ਹੀ ਬਣਦੀਆਂ ਹਨ ਅਤੇ ਇਸ ਕਾਰਨ ਹੀ ਪਰਿਵਾਰ ਨੂੰ ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਵਿਚ ਕੇਂਦਰੀ ਸਥਾਨ ਪ੍ਰਾਪਤ ਹੈ । ਪ੍ਰਾਚੀਨ ਸਮੇਂ ਵਿਚ ਤਾਂ ਪਰਿਵਾਰ ਦੇ ਉੱਤੇ ਹੀ ਸਮਾਜਿਕ ਸੰਗਠਨ ਨਿਰਭਰ ਕਰਦਾ ਸੀ । ਵਿਅਕਤੀ ਦੇ ਲਗਭਗ ਸਾਰੇ ਹੀ ਕੰਮ ਪਰਿਵਾਰ ਵਿਚ ਹੀ ਪੂਰੇ ਹੋ ਜਾਂਦੇ ਸਨ । ਚਾਹੇ ਆਧੁਨਿਕ ਸਮਾਜ ਵਿਚ ਬਹੁਤ ਸਾਰੀਆਂ ਹੋਰ ਸੰਸਥਾਵਾਂ ਸਾਹਮਣੇ ਆ ਗਈਆਂ ਹਨ ਅਤੇ ਪਰਿਵਾਰ ਦੇ ਕੰਮ ਹੋਰ ਸੰਸਥਾਵਾਂ ਵੱਲੋਂ ਲੈ ਲਏ ਗਏ ਹਨ ਪਰ ਫਿਰ ਵੀ ਵਿਅਕਤੀ ਨਾਲ ਸੰਬੰਧਿਤ ਬਹੁਤ ਸਾਰੇ ਅਜਿਹੇ ਕੰਮ ਹਨ ਜੋ ਸਿਰਫ ਪਰਿਵਾਰ ਹੀ ਕਰ ਸਕਦਾ ਹੈ ਅਤੇ ਹੋਰ ਕੋਈ ਸੰਸਥਾ ਨਹੀਂ ਕਰ ਸਕਦੀ ਹੈ ।
5. ਪਰਿਵਾਰ ਦਾ ਰਚਨਾਤਮਕ ਪ੍ਰਭਾਵ ਹੁੰਦਾ ਹੈ (Family has a formative influence) – ਪਰਿਵਾਰ ਨਾਮ ਦੀ ਸੰਸਥਾ ਅਜਿਹੀ ਸੰਸਥਾ ਹੈ ਜਿਸ ਨਾਲ ਵਿਅਕਤੀ ਦੇ ਵਿਅਕਤਿੱਤਵ ਦੇ ਵਿਕਾਸ ਉੱਤੇ ਇਕ ਰਚਨਾਤਮਕ ਪ੍ਰਭਾਵ ਪੈਂਦਾ ਹੈ ਅਤੇ ਇਸ ਕਾਰਨ ਹੀ ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਵਿਚ ਪਰਿਵਾਰ ਨੂੰ ਸਭ ਤੋਂ ਮਹੱਤਵਪੂਰਨ ਸਥਾਨ ਪ੍ਰਾਪਤ ਹੈ । ਜੇਕਰ ਬੱਚੇ ਦਾ ਸਰਵਪੱਖੀ ਵਿਕਾਸ ਕਰਨਾ ਹੈ ਤਾਂ ਉਹ ਸਿਰਫ ਪਰਿਵਾਰ ਵਿਚ ਰਹਿ ਕੇ ਹੀ ਹੋ ਸਕਦਾ ਹੈ | ਪਰਿਵਾਰ ਵਿਚ ਹੀ ਬੱਚੇ ਨੂੰ ਸਮਾਜ ਵਿਚ ਰਹਿਣ-ਸਹਿਣ, ਵਿਵਹਾਰ ਕਰਨ ਦੇ ਢੰਗਾਂ ਦਾ ਪਤਾ ਚਲ ਜਾਂਦਾ ਹੈ ।
6. ਲੈਗਿਕ ਸੰਬੰਧਾਂ ਨੂੰ ਮਾਨਤਾ (Sanction to sexual relations) – ਵਿਅਕਤੀ ਜਦੋਂ ਵਿਆਹ ਕਰਦਾ ਹੈ ਤੇ ਪਰਿਵਾਰ ਦਾ ਨਿਰਮਾਣ ਕਰਦਾ ਹੈ ਤਾਂ ਹੀ ਉਸਦੇ ਅਤੇ ਉਸਦੀ ਪਤਨੀ ਦੇ ਲੈਂਗਿਕ ਜਾਂ ਯੌਨ ਸੰਬੰਧਾਂ ਨੂੰ ਸਮਾਜ ਵਲੋਂ ਮਾਨਤਾ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ । ਪਰਿਵਾਰ ਦੇ ਨਾਲ ਹੀ ਆਦਮੀ ਅਤੇ ਔਰਤ ਇਕ ਦੂਜੇ ਨਾਲ ਯੌਨ ਸੰਬੰਧ ਸਥਾਪਿਤ ਕਰਦੇ ਹਨ । ਪ੍ਰਾਚੀਨ ਸਮਾਜਾਂ ਵਿਚ ਯੌਨ ਸੰਬੰਧ ਸਥਾਪਿਤ ਕਰਨ ਦੇ ਕੋਈ ਨਿਯਮ ਨਹੀਂ ਸਨ ਅਤੇ ਕੋਈ ਵੀ ਆਦਮੀ ਕਿਸੇ ਵੀ ਔਰਤ ਨਾਲ ਯੌਨ ਸੰਬੰਧ ਸਥਾਪਿਤ ਕਰ ਸਕਦਾ ਸੀ । ਇਸ ਕਾਰਨ ਹੀ ਪਰਿਵਾਰ ਦਾ ਕੋਈ ਰੂਪ ਸਾਡੇ ਸਾਹਮਣੇ ਨਹੀਂ ਆਇਆ ਸੀ ਅਤੇ ਸਮਾਜ ਆਮ ਤੌਰ ਉੱਤੇ ਵਿਘਟਿਤ ਰਹਿੰਦੇ ਸਨ । ਇਸ ਤਰ੍ਹਾਂ ਪਰਿਵਾਰ ਦੇ ਕਾਰਨ ਹੀ ਆਦਮੀ ਅਤੇ ਔਰਤ ਦੇ ਸੰਬੰਧਾਂ ਨੂੰ ਮਾਨਤਾ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 6.
ਪਰਿਵਾਰ ਦੇ ਭਿੰਨ-ਭਿੰਨ ਪ੍ਰਕਾਰਾਂ ਨੂੰ ਵਿਸਥਾਰ ਨਾਲ ਸਮਝਾਉ ।
ਉੱਤਰ-
ਇਹ ਸੰਸਾਰ ਬਹੁਤ ਵੱਡਾ ਹੈ । ਇਸ ਵਿੱਚ ਕਈ ਪ੍ਰਕਾਰ ਦੇ ਸਮਾਜ ਪਾਏ ਜਾਂਦੇ ਹਨ । ਹਰ ਸਮਾਜ ਦੀਆਂ ਵੱਖਵੱਖ ਭੂਗੋਲਿਕ, ਸਮਾਜਿਕ ਅਤੇ ਸੰਸਕ੍ਰਿਤਕ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਹੁੰਦੀਆਂ ਹਨ ਅਤੇ ਇਹ ਹਰ ਸਮਾਜ ਦੀਆਂ ਵੱਖ-ਵੱਖ ਹੁੰਦੀਆਂ ਹਨ ਅਤੇ ਇਸੇ ਕਰਕੇ ਹੀ ਹਰ ਸਮਾਜ ਵਿੱਚ ਵੱਖ-ਵੱਖ ਪ੍ਰਕਾਰ ਦੇ ਪਰਿਵਾਰ ਪਾਏ ਜਾਂਦੇ ਹਨ । ਇਹ ਇਸ ਕਰਕੇ ਹੁੰਦਾ ਹੈ। ਕਿਉਂਕਿ ਹਰ ਸਮਾਜ ਦੇ ਵੱਖ-ਵੱਖ ਆਦਰਸ਼, ਵਿਸ਼ਵਾਸ, ਸੰਸਕ੍ਰਿਤੀ ਆਦਿ ਹੁੰਦੇ ਹਨ । ਇੱਕ ਹੀ ਦੇਸ਼ ਵਿੱਚ ਜਿਵੇਂ ਭਾਰਤ ਵਿੱਚ ਹੀ ਕਈ ਪ੍ਰਕਾਰ ਦੇ ਸਮਾਜ ਪਾਏ ਜਾਂਦੇ ਹਨ । ਉਦਾਹਰਨ ਦੇ ਤੌਰ ਉੱਤੇ ਪਿੱਤਰ ਸੱਤਾਤਮਕ, ਮਾਤਰ ਸੱਤਾਤਮਕ ਸਮਾਜ । ਇਸੇ ਤਰ੍ਹਾਂ ਪਰਿਵਾਰ ਦੇ ਵੀ ਅਨੇਕ ਰੂਪ ਹੁੰਦੇ ਹਨ । ਇਨ੍ਹਾਂ ਰੂਪਾਂ ਨੂੰ ਗਿਣਤੀ ਦੇ ਆਧਾਰ ਤੇ, ਵਿਆਹ ਦੇ ਆਧਾਰ ਤੇ, ਸੱਤਾ ਦੇ ਆਧਾਰ ਤੇ, ਵੰਸ਼ ਦੇ ਆਧਾਰ ਤੇ, ਰਹਿਣ ਦੀ ਥਾਂ ਦੇ ਆਧਾਰ ਉੱਤੇ ਆਦਿ ਕਈ ਪ੍ਰਕਾਰ ਦੇ ਵਿੱਚ ਵੰਡਿਆ ਜਾ ਸਕਦਾ ਹੈ । ਹੁਣ ਅਸੀਂ ਇਨ੍ਹਾਂ ਨੂੰ ਵੱਖ-ਵੱਖ ਕਰਕੇ ਵੇਖਾਂਗੇ ।
1. ਵਿਆਹ ਦੇ ਆਧਾਰ ‘ਤੇ ਪਰਿਵਾਰ ਦੀਆਂ ਕਿਸਮਾਂ (On the basis of Marriage) – ਇਹ ਦੋ ਪ੍ਰਕਾਰ ਦੇ ਹੁੰਦੇ ਹਨ ।
(i) ਇੱਕ ਵਿਆਹੀ ਪਰਿਵਾਰ (Monogamous family) – ਇਸ ਤਰ੍ਹਾਂ ਦੇ ਪਰਿਵਾਰ ਵਿੱਚ ਇੱਕ ਆਦਮੀ ਇੱਕ ਹੀ ਔਰਤ ਨਾਲ ਵਿਆਹ ਕਰਵਾਉਂਦਾ ਹੈ ਤਾਂ ਅਜਿਹੇ ਵਿਆਹ ਦੇ ਆਧਾਰ ਵਾਲੇ ਪਰਿਵਾਰ ਨੂੰ ਇੱਕ ਵਿਆਹ ਪਰਿਵਾਰ ਕਹਿੰਦੇ ਹਨ । ਅੱਜ-ਕਲ੍ਹ ਦੇ ਸਮੇਂ ਵਿੱਚ ਇਸ ਤਰ੍ਹਾਂ ਦੇ ਪਰਿਵਾਰ ਨੂੰ ਇੱਕ ਸਹੀ ਪਰਿਵਾਰ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ ।
(ii) ਬਹੁ-ਵਿਆਹੀ ਪਰਿਵਾਰ (Polygamous family) – ਇਸ ਤਰ੍ਹਾਂ ਦੇ ਪਰਿਵਾਰ ਵਿੱਚ ਜਦੋਂ ਇੱਕ ਆਦਮੀ ਇੱਕ ਤੋਂ ਜ਼ਿਆਦਾ ਇਸਤਰੀਆਂ ਨਾਲ ਜਾਂ ਇੱਕ ਇਸਤਰੀ ਦਾ ਇੱਕ ਤੋਂ ਜ਼ਿਆਦਾ ਆਦਮੀਆਂ ਨਾਲ ਵਿਆਹ ਹੁੰਦਾ ਹੈ ਤਾਂ ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਪਰਿਵਾਰ ਨੂੰ ਬਹੁ-ਵਿਆਹੀ (ਪਰਿਵਾਰ) ਕਹਿੰਦੇ ਹਨ । ਇਹ ਵੀ ਅੱਗੇ ਦੋ ਕਿਸਮ ਦਾ ਹੁੰਦਾ ਹੈ।
(a) ਬਹੁ-ਪਤੀ ਵਿਆਹ (Polyandrous family) – ਜਦੋਂ ਇੱਕ ਔਰਤ ਇੱਕ ਤੋਂ ਜ਼ਿਆਦਾ ਆਦਮੀਆਂ ਨਾਲ ਵਿਆਹ ਕਰਵਾਉਂਦੀ ਹੈ ਤਾਂ ਉਹ ਬਹੁ-ਪਤੀ ਵਿਆਹ ਹੁੰਦਾ ਹੈ । ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਪਰਿਵਾਰ ਦੀ ਮੁੱਖ ਵਿਸ਼ੇਸ਼ਤਾ ਇੱਕ ਔਰਤ ਦੇ ਕਈ ਪਤੀ ਹੋਣਾ ਹੈ । ਇੱਥੇ ਇਹ ਵੀ ਦੋ ਪ੍ਰਕਾਰ ਦੇ ਹੁੰਦੇ ਹਨ । ਪਹਿਲੀ ਪ੍ਰਕਾਰ ਵਿੱਚ ਉਸ ਔਰਤ ਦੇ ਸਾਰੇ ਪਤੀ ਸਕੇ ਭਰਾ ਹੁੰਦੇ ਹਨ ਅਤੇ ਦੂਜੀ ਪ੍ਰਕਾਰ ਦੇ ਬਹੁ-ਪਤੀ ਵਿਆਹ ਵਿੱਚ ਉਸ ਔਰਤ ਦੇ ਪਤੀ ਸਕੇ ਭਰਾ ਜ਼ਰੂਰੀ ਨਹੀਂ ਹੁੰਦੇ ।
(b) ਬਹੁ-ਪਤਨੀ ਵਿਆਹ (Polygamous Family) – ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਵਿਆਹ ਵਿੱਚ ਇੱਕ ਆਦਮੀ ਇੱਕ ਤੋਂ ਜ਼ਿਆਦਾ ਔਰਤਾਂ ਨਾਲ ਵਿਆਹ ਕਰਵਾਉਂਦਾ ਹੈ । ਇਸ ਕਿਸਮ ਦੇ ਪਰਿਵਾਰ ਵਿੱਚ ਇੱਕ ਆਦਮੀ ਦੀਆਂ ਕਈ ਪਤਨੀਆਂ ਹੁੰਦੀਆਂ ਹਨ । ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਪਰਿਵਾਰ ਮੁਸਲਮਾਨਾਂ ਵਿੱਚ ਆਮ ਪਾਏ ਜਾਂਦੇ ਹਨ । ਮੁਸਲਮਾਨਾਂ ਵਿੱਚ ਇੱਕ ਆਦਮੀ ਨੂੰ ਚਾਰ ਪਤਨੀਆਂ ਰੱਖਣ ਦੀ ਇਜਾਜ਼ਤ ਹੁੰਦੀ ਹੈ । ਪੁਰਾਣੇ ਸਮਿਆਂ ਵਿੱਚ ਚਾਹੇ ਹਿੰਦੂ ਰਾਜੇ ਕਈ ਪਤਨੀਆਂ ਰੱਖਦੇ ਸਨ ਪਰ 1955 ਦੇ ਹਿੰਦੂ ਵਿਆਹ ਕਾਨੂੰਨ ਅਨੁਸਾਰ ਹਿੰਦੂਆਂ ਨੂੰ ਇੱਕ ਪਤਨੀ ਤੋਂ ਜ਼ਿਆਦਾ ਰੱਖਣ ਦੀ ਮਨਾਹੀ ਹੈ । ਭਾਰਤ ਵਿੱਚ ਕੁੱਝ ਅਜਿਹੇ ਕਬੀਲੇ ਹਨ ਜਿਵੇਂ ਨਾਗਾ, ਗੌਡ ਆਦਿ ਜਿਨ੍ਹਾਂ ਵਿੱਚ ਇਸ ਤਰ੍ਹਾਂ ਦੇ ਪਰਿਵਾਰ ਪਾਏ ਜਾਂਦੇ ਹਨ ।
2. ਮੈਂਬਰਾਂ ਦੀ ਗਿਣਤੀ ਦੇ ਆਧਾਰ ਤੇ ਪਰਿਵਾਰ ਦੀਆਂ ਕਿਸਮਾਂ (Family on the basis of Numbers) – ਮੈਂਬਰਾਂ ਦੀ ਗਿਣਤੀ ਦੇ ਆਧਾਰ ਉੱਤੇ ਪਰਿਵਾਰ ਦੀਆਂ ਤਿੰਨ ਕਿਸਮਾਂ ਹਨ-
- ਕੇਂਦਰੀ ਪਰਿਵਾਰ (Nuclear Family) – ਇਹ ਪਰਿਵਾਰ ਛੋਟਾ ਪਰਿਵਾਰ ਹੁੰਦਾ ਹੈ ਜਿਸ ਵਿੱਚ ਪਤੀ-ਪਤਨੀ ਅਤੇ ਉਨ੍ਹਾਂ ਦੇ ਬਗੈਰ ਵਿਆਹੇ ਬੱਚੇ ਹੁੰਦੇ ਹਨ । ਇਸ ਵਿੱਚ ਹੋਰ ਰਿਸ਼ਤੇਦਾਰ ਸ਼ਾਮਲ ਨਹੀਂ ਹੁੰਦੇ । ਅੱਜ-ਕਲ੍ਹ ਆਮ ਤੌਰ ਤੇ ਅਜਿਹੇ ਪਰਿਵਾਰ ਪਾਏ ਜਾਂਦੇ ਹਨ ਕਿਉਂਕਿ ਲੋਕ ਸ਼ਹਿਰਾਂ ਵਿੱਚ ਨੌਕਰੀਆਂ ਕਰਦੇ ਹਨ । ਬੱਚੇ ਵਿਆਹ ਤੋਂ ਬਾਅਦ ਆਪਣਾ ਹੋਰ ਕੇਂਦਰੀ ਪਰਿਵਾਰ ਬਣਾ ਲੈਂਦੇ ਹਨ ।
- ਸੰਯੁਕਤ ਪਰਿਵਾਰ (Joint Family) – ਇਸ ਤਰ੍ਹਾਂ ਦੇ ਪਰਿਵਾਰ ਵਿੱਚ ਬਹੁਤ ਸਾਰੇ ਮੈਂਬਰ ਹੁੰਦੇ ਹਨ । ਦਾਦਾਦਾਦੀ, ਚਾਚਾ-ਚਾਚੀ, ਤਾਇਆ-ਤਾਈ, ਉਨ੍ਹਾਂ ਦੇ ਬੱਚੇ, ਮਾਤਾ-ਪਿਤਾ, ਭੈਣ-ਭਾਈ ਆਦਿ ਸਾਰੇ ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਪਰਿਵਾਰ ਵਿੱਚ ਸ਼ਾਮਲ ਹੁੰਦੇ ਹਨ । ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਪਰਿਵਾਰ ਆਮ ਤੌਰ ਉੱਤੇ ਪਿੰਡਾਂ ਵਿੱਚ ਪਾਏ ਜਾਂਦੇ ਹਨ ।
- ਵਿਸਤ੍ਰਿਤ ਪਰਿਵਾਰ (Extended Family) – ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਪਰਿਵਾਰ ਸੰਯੁਕਤ ਪਰਿਵਾਰ ਤੋਂ ਹੀ ਬਣਦੇ ਹਨ । ਜਦੋਂ ਸੰਯੁਕਤ ਪਰਿਵਾਰ ਅੱਗੇ ਵੱਧ ਜਾਂਦੇ ਹਨ ਤਾਂ ਉਹ ਵਿਸਤ੍ਰਿਤ ਪਰਿਵਾਰ ਕਹਾਉਂਦੇ ਹਨ । ਇਸ ਵਿੱਚ ਸਾਰੇ ਭਰਾ, ਉਨ੍ਹਾਂ ਦੇ ਬੱਚੇ ਵਿਆਹ ਕਰ ਕੇ ਰਹਿੰਦੇ ਹਨ ਅਤੇ ਉਨ੍ਹਾਂ ਦੇ ਵੀ ਅੱਗੇ ਬੱਚੇ ਹੋ ਜਾਂਦੇ ਹਨ | ਅੱਜ-ਕਲ੍ਹ ਦੇ ਸਮਾਜਾਂ ਵਿੱਚ ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਪਰਿਵਾਰ ਮੁਮਕਿਨ ਨਹੀਂ ਹਨ । ਪੁਰਾਣੇ ਸਮਿਆਂ ਵਿੱਚ ਜਦੋਂ ਸਾਰਿਆਂ ਦਾ ਇਕੱਠਾ ਕੰਮ ਹੁੰਦਾ ਸੀ ਤਾਂ ਉਹ ਇਕੱਠੇ ਰਹਿੰਦੇ ਸਨ ਪਰ ਅੱਜ-ਕਲ੍ਹ ਇਹ ਮੁਮਕਿਨ ਨਹੀਂ ਹੈ ।
3. ਵੰਸ਼ ਨਾਮ ਦੇ ਆਧਾਰ ਤੇ ਪਰਿਵਾਰ ਦੀਆਂ ਕਿਸਮਾਂ (On the basis of Nomenclature) – ਇਸ ਆਧਾਰ ਤੇ ਚਾਰ ਪ੍ਰਕਾਰ ਦੀਆਂ ਕਿਸਮਾਂ ਮਿਲਦੀਆਂ ਹਨ-
- ਪਿਤਰ ਵੰਸ਼ੀ ਪਰਿਵਾਰ (Patrilineal Family) – ਇਸ ਤਰ੍ਹਾਂ ਦਾ ਪਰਿਵਾਰ ਪਿਤਾ ਦੇ ਨਾਮ ਤੇ ਚਲਦਾ ਹੈ ਜਿਸ ਦਾ ਮਤਲਬ ਹੈ ਕਿ ਪਿਤਾ ਦੇ ਵੰਸ਼ ਦਾ ਨਾਮ ਪੁੱਤਰ ਨੂੰ ਮਿਲਦਾ ਹੈ ਅਤੇ ਪਿਤਾ ਦੇ ਵੰਸ਼ ਦਾ ਮਹੱਤਵ ਹੁੰਦਾ ਹੈ । ਅੱਜ-ਕਲ੍ਹ ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਪਰਿਵਾਰ ਮਿਲਦੇ ਹਨ ।
- ਮਾਤਰ ਵੰਸ਼ੀ ਪਰਿਵਾਰ (Matrilineal Family) – ਇਸ ਤਰ੍ਹਾਂ ਦਾ ਪਰਿਵਾਰ ਮਾਂ ਦੇ ਨਾਮ ਤੇ ਚਲਦਾ ਹੈ ਜਿਸਦਾ ਮਤਲਬ ਹੈ ਕਿ ਬੱਚੇ ਦੇ ਨਾਮ ਦੇ ਨਾਲ ਮਾਤਾ ਦੇ ਵੰਸ਼ ਦਾ ਨਾਮ ਲਗਦਾ ਹੈ | ਮਾਤਾ ਦੇ ਵੰਸ਼ ਦਾ ਨਾਮ ਬੱਚਿਆਂ ਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ । ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਪਰਿਵਾਰ ਭਾਰਤ ਦੇ ਕੁੱਝ ਕਬੀਲਿਆਂ ਵਿੱਚ ਮਿਲ ਜਾਂਦੇ ਹਨ ।
- ਦੋ ਵੰਸ਼ ਨਾਮੀ ਪਰਿਵਾਰ (Bilinear Family) – ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਪਰਿਵਾਰਾਂ ਵਿੱਚ ਮਾਂ ਅਤੇ ਬਾਪ ਦੋਵਾਂ ਦੇ ਵੰਸ਼ ਦਾ ਨਾਮ ਬੱਚੇ ਨੂੰ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ਅਤੇ ਦੋਵੇਂ ਵੰਸ਼ਾਂ ਦੇ ਨਾਮ ਨਾਲ-ਨਾਲ ਚਲਦੇ ਹਨ ।
- ਅਰੇਖਕੀ ਪਰਿਵਾਰ (Non-Unilinear Family) – ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਪਰਿਵਾਰਾਂ ਵਿੱਚ ਵੰਸ਼ ਦੇ ਨਾਂ ਦਾ ਨਿਰਧਾਰਨ ਸਭ ਨੇੜੇ ਦੇ ਰਿਸ਼ਤੇਦਾਰਾਂ ਦੇ ਆਧਾਰ ਤੇ ਹੁੰਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਇਨ੍ਹਾਂ ਨੂੰ ਅਰੇਖਕੀ ਪਰਿਵਾਰ ਕਹਿੰਦੇ ਹਨ ।
4. ਰਿਸ਼ਤੇਦਾਰਾਂ ਦੀ ਕਿਸਮ ਦੇ ਆਧਾਰ ਤੇ ਪਰਿਵਾਰ ਦੀਆਂ ਕਿਸਮਾਂ (On the basis of types of Relatives) ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਪਰਿਵਾਰ ਵੀ ਦੋ ਪ੍ਰਕਾਰ ਦੇ ਹੁੰਦੇ ਹਨ-
- ਰਕਤ ਸੰਬੰਧੀ ਪਰਿਵਾਰ (Consanguine Family) – ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਪਰਿਵਾਰਾਂ ਵਿੱਚ ਰਕਤ ਸੰਬੰਧ ਦਾ ਸਥਾਨ ਸਰਵਉੱਚ ਹੁੰਦਾ ਹੈ ਅਤੇ ਇਨ੍ਹਾਂ ਵਿੱਚ ਕਿਸੇ ਪ੍ਰਕਾਰ ਦੇ ਲਿੰਗ ਸੰਬੰਧ ਨਹੀਂ ਹੁੰਦੇ । ਇਸ ਪਰਿਵਾਰ ਵਿੱਚ ਪਤੀ-ਪਤਨੀ ਵੀ ਹੁੰਦੇ ਹਨ ਪਰ ਉਹ ਇਸ ਪਰਿਵਾਰ ਦੇ ਆਧਾਰ ਨਹੀਂ ਹੁੰਦੇ । ਇਸ ਪਰਿਵਾਰ ਵਿੱਚ ਮੈਂਬਰਸ਼ਿਪ ਜਨਮ ਦੇ ਆਧਾਰ ਉੱਤੇ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ । ਤਲਾਕ ਵੀ ਇਨ੍ਹਾਂ ਪਰਿਵਾਰਾਂ ਨੂੰ ਖ਼ਤਮ ਨਹੀਂ ਕਰ ਸਕਦਾ ਅਤੇ ਇਹ ਸਥਾਈ ਹੁੰਦੇ ਹਨ ।
- ਵਿਆਹ ਸੰਬੰਧੀਆਂ ਦਾ ਪਰਿਵਾਰ (Conjugal Family) – ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਪਰਿਵਾਰ ਵਿੱਚ ਪਤੀ-ਪਤਨੀ ਅਤੇ ਉਨ੍ਹਾਂ ਦੇ ਅਣਵਿਆਹੇ ਬੱਚੇ ਹੁੰਦੇ ਹਨ । ਇਸ ਵਿੱਚ ਪਤੀ-ਪਤਨੀ ਅਤੇ ਉਨ੍ਹਾਂ ਦੇ ਰਿਸ਼ਤੇਦਾਰ ਸ਼ਾਮਲ ਹੁੰਦੇ ਹਨ । ਇਹ ਪਤੀ ਜਾਂ ਪਤਨੀ ਦੀ ਮੌਤ ਤੋਂ ਬਾਅਦ ਜਾਂ ਤਲਾਕ ਤੋਂ ਬਾਅਦ ਭੰਗ ਵੀ ਹੋ ਸਕਦਾ ਹੈ ।
5. ਰਹਿਣ ਦੀ ਥਾਂ ਦੇ ਆਧਾਰ ਉੱਤੇ ਪਰਿਵਾਰ (Family on the basis of Residence) – ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਪਰਿਵਾਰ ਤਿੰਨ ਤਰ੍ਹਾਂ ਦੇ ਹੁੰਦੇ ਹਨ
- ਪਿਤਰ ਸਥਾਨੀ ਪਰਿਵਾਰ (Patrilocal Family) – ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਪਰਿਵਾਰ ਵਿੱਚ ਲੜਕੀ ਵਿਆਹ ਪਿੱਛੋਂ ਆਪਣੇ ਪਿਤਾ ਦਾ ਘਰ ਛੱਡ ਕੇ ਆਪਣੇ ਪਤੀ ਦੇ ਘਰ ਜਾ ਕੇ ਰਹਿਣ ਲੱਗ ਜਾਂਦੀ ਹੈ ਅਤੇ ਪਰਿਵਾਰ ਵਸਾਉਂਦੀ ਹੈ । ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਪਰਿਵਾਰ ਆਮ ਤੌਰ ਤੇ ਮਿਲ ਜਾਂਦੇ ਹਨ ।
- ਮਾਤਰ ਸਥਾਨੀ ਪਰਿਵਾਰ (Matrilocal Family) – ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਪਰਿਵਾਰ ਪਿੱਤਰ ਸਥਾਨੀ ਪਰਿਵਾਰ ਤੋਂ ਉਲਟ ਹਨ । ਇਸ ਵਿੱਚ ਲੜਕੀ ਵਿਆਹ ਪਿੱਛੋਂ ਆਪਣੇ ਪਿਤਾ ਦਾ ਘਰ ਛੱਡ ਕੇ ਨਹੀਂ ਜਾਂਦੀ ਬਲਕਿ ਉੱਥੇ ਹੀ ਰਹਿੰਦੀ ਹੈ । ਇਸ ਵਿੱਚ ਪਤੀ ਆਪਣੇ ਪਿਤਾ ਦਾ ਘਰ ਛੱਡ ਕੇ ਪਤਨੀ ਦੇ ਘਰ ਆ ਕੇ ਰਹਿਣ ਲੱਗ ਜਾਂਦਾ ਹੈ । ਇਸ ਨੂੰ ਮਾਤਰ ਸਥਾਨੀ ਪਰਿਵਾਰ ਕਹਿੰਦੇ ਹਨ । ਗਾਰੋ, ਖਾਸੀ ਕਬੀਲਿਆਂ ਵਿੱਚ ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਪਰਿਵਾਰ ਪਾਏ ਜਾਂਦੇ ਹਨ ।
- ਨਵ-ਸਥਾਨੀ ਪਰਿਵਾਰ (Neo-Local Family) – ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਪਰਿਵਾਰ ਪਹਿਲੀਆਂ ਦੋਹਾਂ ਕਿਸਮਾਂ ਤੋਂ ਵੱਖ ਹਨ । ਇਸ ਵਿੱਚ ਪਤੀ-ਪਤਨੀ ਕੋਈ ਵੀ ਇੱਕ ਦੂਜੇ ਦੇ ਪਿਤਾ ਦੇ ਘਰ ਜਾ ਕੇ ਨਹੀਂ ਰਹਿੰਦਾ ਬਲਕਿ ਉਹ ਕਿਸੇ ਹੋਰ ਥਾਂ ਉੱਤੇ ਜਾ ਕੇ ਨਵਾਂ ਘਰ ਵਸਾਉਂਦੇ ਹਨ ਤਾਂ ਇਸ ਲਈ ਇਸ ਨੂੰ ਨਵ-ਸਥਾਨੀ ਪਰਿਵਾਰ ਕਹਿੰਦੇ ਹਨ । ਅੱਜ-ਕਲ੍ਹ ਦੇ ਉਦਯੋਗਿਕ ਸਮਾਜਾਂ ਵਿੱਚ ਇਸ ਤਰ੍ਹਾਂ ਦੇ ਪਰਿਵਾਰ ਆਮ ਪਾਏ ਜਾਂਦੇ ਹਨ ।
6. ਸੱਤਾ ਦੇ ਆਧਾਰ ਤੇ ਪਰਿਵਾਰ ਦੀਆਂ ਕਿਸਮਾਂ (On the basis of Authority) – ਇਸ ਤਰ੍ਹਾਂ ਦੇ ਪਰਿਵਾਰ ਦੋ ਕਿਸਮ ਦੇ ਹੁੰਦੇ ਹਨ
- ਪਿੱਤਰ ਸੱਤਾਤਮਕ ਪਰਿਵਾਰ (Patriarchal Family) – ਜਿਵੇਂ ਨਾਮ ਤੋਂ ਹੀ ਪਤਾ ਚਲਦਾ ਹੈ ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਪਰਿਵਾਰ ਵਿੱਚ ਪਰਿਵਾਰ ਦੀ ਸੱਤਾ ਜਾਂ ਸ਼ਕਤੀ ਪੂਰੀ ਤਰ੍ਹਾਂ ਪਿਤਾ ਦੇ ਹੱਥ ਵਿੱਚ ਹੁੰਦੀ ਹੈ । ਪਰਿਵਾਰ ਦੇ ਸਾਰੇ ਕੰਮ ਪਿਤਾ ਦੇ ਹੱਥ ਵਿੱਚ ਹੁੰਦੇ ਹਨ । ਉਹ ਹੀ ਕਰਤਾ ਹੁੰਦਾ ਹੈ । ਪਰਿਵਾਰ ਦੇ ਸਾਰੇ ਛੋਟੇ-ਵੱਡੇ ਫੈਸਲਿਆਂ ਵਿੱਚ ਵੀ ਪਿਤਾ ਦਾ ਕਿਹਾ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ । ਪਰਿਵਾਰ ਦੇ ਸਾਰੇ ਮੈਂਬਰਾਂ ਉੱਤੇ ਨਿਯੰਤਰਣ ਵੀ ਪਿਤਾ ਦਾ ਹੀ ਹੁੰਦਾ ਹੈ । ਅੱਜ-ਕਲ੍ਹ ਭਾਰਤ ਵਿੱਚ ਇਸੇ ਪ੍ਰਕਾਰ ਦੇ ਪਰਿਵਾਰ ਹੀ ਪਾਏ ਜਾਂਦੇ ਹਨ ।
- ਮਾਤਰ ਸੱਤਾਤਮਕ ਪਰਿਵਾਰ (Matriarchal Family) – ਜਿਵੇਂ ਕਿ ਨਾਮ ਤੋਂ ਹੀ ਸਪੱਸ਼ਟ ਹੈ ਕਿ ਪਰਿਵਾਰ ਵਿੱਚ ਸੱਤਾ ਜਾਂ ਸ਼ਕਤੀ ਮਾਤਾ ਦੇ ਹੱਥ ਵਿੱਚ ਹੁੰਦੀ ਹੈ । ਬੱਚਿਆਂ ਉੱਤੇ ਮਾਤਾ ਦੇ ਰਿਸ਼ਤੇਦਾਰਾਂ ਦਾ ਅਧਿਕਾਰ ਜ਼ਿਆਦਾ ਹੁੰਦਾ ਹੈ ਨਾ ਕਿ ਪਿਤਾ ਦੇ ਰਿਸ਼ਤੇਦਾਰਾਂ ਦਾ । ਇਸਤਰੀ ਹੀ ਮੁਲ ਪੁਰਵ ਮੰਨੀ ਜਾਂਦੀ ਹੈ । ਸੰਪੱਤੀ ਦਾ ਵਾਰਸ ਪੁੱਤਰ ਨਹੀਂ ਬਲਕਿ ਮਾਂ ਦਾ ਭਰਾ ਜਾਂ ਭਾਣਜਾ ਹੁੰਦਾ ਹੈ । ਕਈ ਪ੍ਰਕਾਰ ਦੇ ਕਬੀਲਿਆਂ ਜਿਵੇਂ ਗਾਰੋ, ਖਾਸੀ ਆਦਿ ਵਿੱਚ ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਪਰਿਵਾਰ ਪਾਏ ਜਾਂਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 7.
ਸਮਕਾਲੀਨ ਸਮੇਂ ਵਿੱਚ ਪਰਿਵਾਰ ਸੰਸਥਾ ਵਿੱਚ ਹੋਣ ਵਾਲੇ ਪਰਿਵਰਤਨਾਂ ਉੱਤੇ ਚਾਨਣਾ ਪਾਓ ।
ਉੱਤਰ-
1. ਕੇਂਦਰੀ ਪਰਿਵਾਰਾਂ ਦਾ ਵੱਧਣਾ (Increasing Nuclear families) – ਭਾਰਤੀ ਸਮਾਜ ਵਿਚ ਪਰੰਪਰਾਗਤ ਪੇਂਡੂ ਸਮਾਜ ਹੈ ਜਿੱਥੇ ਪ੍ਰਾਚੀਨ ਸਮੇਂ ਵਿਚ ਸੰਯੁਕਤ ਪਰਿਵਾਰ ਮਿਲਦੇ ਸਨ | ਮੁੱਖ ਪੇਸ਼ਾ ਖੇਤੀ ਹੋਣ ਦੇ ਕਾਰਨ ਪਰਿਵਾਰ ਵਿਚ ਵੱਧ ਮੈਂਬਰਾਂ ਦੀ ਜ਼ਰੂਰਤ ਪੈਂਦੀ ਸੀ । ਇਸ ਲਈ ਸੰਯੁਕਤ ਪਰਿਵਾਰ ਸਾਡੇ ਸਮਾਜ ਵਿਚ ਪਾਏ ਜਾਂਦੇ ਸਨ । ਪਰ ਸਮੇਂ ਦੇ ਨਾਲ-ਨਾਲ ਸਿੱਖਿਆ ਦੇ ਵੱਧਣ ਨਾਲ ਅਤੇ ਸਮਾਜਿਕ ਗਤੀਸ਼ੀਲਤਾ ਦੇ ਵੱਧਣ ਦੇ ਨਾਲ ਲੋਕ ਸ਼ਹਿਰਾਂ ਦੇ ਵੱਲ ਜਾਣ ਲੱਗੇ । ਲੋਕ ਸੰਯੁਕਤ ਪਰਿਵਾਰਾਂ ਨੂੰ ਛੱਡ ਕੇ ਸ਼ਹਿਰਾਂ ਵਿਚ ਜਾ ਕੇ ਕੇਂਦਰੀ ਪਰਿਵਾਰ ਵਸਾਉਣ ਲੱਗ ਪਏ । ਇਸ ਤਰ੍ਹਾਂ ਪਰਿਵਾਰ ਦੇ ਢਾਂਚੇ ਪੱਖ ਵਿਚ ਪਰਿਵਰਤਨ ਆਉਣ ਲੱਗ ਗਏ ਅਤੇ ਸੰਯੁਕਤ ਪਰਿਵਾਰਾਂ ਦੀ ਥਾਂ ਕੇਂਦਰੀ ਪਰਿਵਾਰ ਸਾਹਮਣੇ ਆਉਣ ਲੱਗ ਗਏ ।
2. ਆਰਥਿਕ ਕੰਮਾਂ ਵਿਚ ਪਰਿਵਰਤਨ (Changes in economic functions) – ਪਰਿਵਾਰ ਦੇ ਆਰਥਿਕ ਕੰਮਾਂ ਵਿਚ ਵੀ ਬਹੁਤ ਸਾਰੇ ਪਰਿਵਰਤਨ ਆਏ ਹਨ । ਪ੍ਰਾਚੀਨ ਸਮੇਂ ਵਿਚ ਤਾਂ ਵਿਅਕਤੀ ਦੀਆਂ ਆਰਥਿਕ ਕ੍ਰਿਆਵਾਂ ਪਰਿਵਾਰ ਦੇ ਆਲੇ ਦੁਆਲੇ ਹੀ ਸਿਮਟਦੇ ਰਹਿੰਦੀਆਂ ਸਨ । ਪੈਸਾ ਕਮਾਉਣ ਦਾ ਪੂਰਾ ਕੰਮ ਪਰਿਵਾਰ ਵਿਚ ਹੀ ਹੁੰਦਾ ਸੀ ਜਿਵੇਂ ਕਿ ਕਣਕ ਉਗਾਉਣ ਦਾ ਕੰਮ ਜਾਂ ਅੱਟਾ ਪੀਸਣ ਦਾ ਕੰਮ । ਪਰਿਵਾਰ ਵਿਚ ਹੀ ਜੀਵਨ ਜੀਣ ਦੇ ਸਾਰੇ ਸਾਧਨ ਮੌਜੂਦ ਸਨ । ਪਰ ਸਮੇਂ ਦੇ ਨਾਲ-ਨਾਲ ਸਮਾਜ ਵਿਚ ਪਰਿਵਰਤਨ ਆਏ ਅਤੇ ਸਾਡੇ ਸਮਾਜਾਂ ਵਿਚ ਉਦਯੋਗਿਕੀਕਰਣ ਸ਼ੁਰੂ ਹੋਇਆ । ਪਰਿਵਾਰ ਦੇ ਆਰਥਿਕ ਕੰਮਾਂ ਉਦਯੋਗਾਂ ਦੇ ਕੋਲ ਚਲੇ ਗਏ ਜਿਵੇਂ ਕਿ ਅੱਟਾ ਹੁਣ ਚੱਕੀਆਂ ਉੱਤੇ ਪਿਸਦਾ ਹੈ ਜਾਂ ਕਪੜਾ ਵੱਡੀਆਂ-ਵੱਡੀਆਂ ਮਿੱਲਾਂ ਵਿਚ ਬਣਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਪਰਿਵਾਰ ਦੇ ਆਰਥਿਕ ਉਤਪਾਦਨ ਦੇ ਕੰਮ ਹੌਲੀ-ਹੌਲੀ ਖ਼ਤਮ ਹੋ ਗਏ ਅਤੇ ਪਰਿਵਾਰ ਦੇ ਆਰਥਿਕ ਕੰਮ ਹੋਰ ਸੰਸਥਾਵਾਂ ਦੇ ਕੋਲ ਚਲੇ ਗਏ ।
3. ਸਿੱਖਿਅਕ ਕੰਮਾਂ ਦਾ ਪਰਿਵਰਤਿਤ ਹੋਣਾ (Changed in Educational functions) – ਪ੍ਰਾਚੀਨ ਸਮੇਂ ਵਿਚ ਬੱਚਿਆਂ ਨੂੰ ਸਿੱਖਿਆ ਦੇਣ ਦਾ ਕੰਮ ਜਾਂ ਤਾਂ ਗੁਰੂਕੁੱਲ ਵਿਚ ਹੁੰਦਾ ਸੀ ਜਾਂ ਫਿਰ ਘਰ ਵਿਚ । ਬੱਚਾ ਜੇਕਰ ਗੁਰੂ ਦੇ ਕੋਲ ਸਿੱਖਿਆ ਲੈਣ ਜਾਂਦਾ ਵੀ ਸੀ ਤਾਂ ਉਸਨੂੰ ਸਿਰਫ਼ ਵੇਦਾਂ, ਪੁਰਾਣਾਂ ਆਦਿ ਦੀ ਸਿੱਖਿਆ ਹੀ ਦਿੱਤੀ ਜਾਂਦੀ ਸੀ । ਉਸ ਨੂੰ ਪੇਸ਼ੇ ਜਾਂ ਕੰਮ ਨਾਲ ਸੰਬੰਧਿਤ ਕੋਈ ਸਿੱਖਿਆ ਨਹੀਂ ਦਿੱਤੀ ਜਾਂਦੀ ਸੀ ਅਤੇ ਇਹ ਕੰਮ ਪਰਿਵਾਰ ਵਲੋਂ ਹੀ ਕੀਤਾ ਜਾਂਦਾ ਸੀ । ਹਰੇਕ ਜਾਤ ਜਾਂ ਪਰਿਵਾਰ ਦਾ ਇਕ ਪਰੰਪਰਾਗਤ ਪੇਸ਼ਾ ਹੁੰਦਾ ਸੀ ਅਤੇ ਉਸ ਪੇਸ਼ੇ ਨਾਲ ਸੰਬੰਧਿਤ ਗੁਣ ਵੀ ਉਸ ਪਰਿਵਾਰ ਨੂੰ ਪਤਾ ਹੁੰਦੇ ਸਨ । ਉਹ ਪਰਿਵਾਰ ਆਪਣੇ ਬੱਚਿਆਂ ਨੂੰ ਹੌਲੀ-ਹੌਲੀ ਪੇਸ਼ੇ ਨਾਲ ਸੰਬੰਧਿਤ ਸਿੱਖਿਆ ਦਿੰਦਾ ਜਾਂਦਾ ਸੀ ਅਤੇ ਬੱਚਿਆਂ ਦੀ ਸਿੱਖਿਆ ਪੂਰੀ ਹੋ ਜਾਂਦੀ ਸੀ । ਪਰ ਸਮੇਂ ਦੇ ਨਾਲ-ਨਾਲ ਪਰਿਵਾਰ ਦੇ ਇਸ ਕੰਮ ਵਿਚ ਪਰਿਵਰਤਨ ਆਇਆ ਹੈ । ਹੁਣ ਪੇਸ਼ਿਆਂ ਨਾਲ ਸੰਬੰਧਿਤ ਸਿੱਖਿਆ ਦੇਣ ਦਾ ਕੰਮ ਪਰਿਵਾਰ ਦੁਆਰਾ ਨਹੀਂ ਬਲਕਿ ਸਰਕਾਰ ਵਲੋਂ ਖੋਲੇ ਗਏ Professional Colleges, Medical Colleges, Engineering Colleges, I.I.M’s, I.I.T’s, I.T.I.’s wife ਕਰਦੇ ਹਨ । ਬੱਚਾਂ ਇਨ੍ਹਾਂ ਵਿਚ ਪੇਸ਼ੇ ਨਾਲ ਸੰਬੰਧਿਤ ਸਿੱਖਿਆ ਗ੍ਰਹਿਣ ਕਰਕੇ ਆਪਣਾ ਪੇਸ਼ਾ ਹੀ ਅਪਨਾਉਂਦਾ ਹੈ ਅਤੇ ਪਰਿਵਾਰ ਦਾ ਪਰੰਪਰਾਗਤ ਪੇਸ਼ਾ ਛੱਡ ਦਿੰਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਪਰਿਵਾਰ ਦਾ ਸਿੱਖਿਆ ਦੇਣ ਦੀ ਪਰੰਪਰਾਗਤ ਕੰਮ ਹੋਰ ਸੰਸਥਾਵਾਂ ਦੇ ਕੋਲ ਚਲਾ ਗਿਆ ਹੈ ।
4. ਪਰਿਵਾਰਿਕ ਏਕਤਾ ਦਾ ਘੱਟ ਹੋਣਾ (Decreasing unity of family) – ਪ੍ਰਾਚੀਨ ਸਮੇਂ ਵਿਚ ਸੰਯੁਕਤ ਪਰਿਵਾਰ ਹੁੰਦੇ ਸਨ ਅਤੇ ਪਰਿਵਾਰ ਦੇ ਸਾਰੇ ਮੈਂਬਰ ਪਰਿਵਾਰ ਦੇ ਹਿੱਤਾਂ ਦੇ ਲਈ ਕੰਮ ਕਰਦੇ ਸਨ । ਉਹ ਆਪਣੇ ਹਿੱਤਾਂ ਨੂੰ ਪਰਿਵਾਰ ਦੇ ਹਿੱਤਾਂ ਦੇ ਲਈ ਕੁਰਬਾਨ ਕਰ ਦਿੰਦੇ ਸਨ । ਪਰਿਵਾਰ ਦੇ ਮੈਂਬਰਾਂ ਵਿਚ ਪੂਰੀ ਏਕਤਾ ਹੁੰਦੀ ਸੀ । ਸਾਰੇ ਮੈਂਬਰ ਪਰਿਵਾਰ ਦੇ ਬਜ਼ੁਰਗ ਦੀ ਗੱਲ ਮੰਨਿਆ ਕਰਦੇ ਸਨ ਅਤੇ ਆਪਣੇ ਫ਼ਰਜ਼ ਚੰਗੇ ਤਰੀਕੇ ਨਾਲ ਪੂਰਾ ਕਰਿਆ ਕਰਦੇ ਸਨ । ਪਰ ਸਮੇਂ ਦੇ ਨਾਲ-ਨਾਲ ਪਰਿਵਾਰਿਕ ਏਕਤਾ ਵਿਚ ਕਮੀ ਆਈ । ਸੰਯੁਕਤ ਪਰਿਵਾਰ ਖ਼ਤਮ ਹੋਣੇ ਸ਼ੁਰੂ ਹੋ ਗਏ ਅਤੇ ਕੇਂਦਰੀ ਪਰਿਵਾਰ ਸਾਹਮਣੇ ਆਉਣ ਲੱਗ ਪਏ ਪਰਿਵਾਰ ਦੇ ਸਾਰੇ ਮੈਂਬਰਾਂ ਦੇ ਆਪਣੇ-ਆਪਣੇ ਹਿੱਤ ਹੁੰਦੇ ਹਨ ਅਤੇ ਕੋਈ ਵੀ ਪਰਿਵਾਰ ਦੇ ਹਿੱਤਾਂ ਦੇ ਲਈ ਆਪਣੇ ਹਿੱਤਾਂ ਦਾ ਤਿਆਗ ਨਹੀਂ ਕਰਦਾ ਹੈ । ਸਾਰਿਆਂ ਦੇ ਆਪਣੇ-ਆਪਣੇ ਆਦਰਸ਼ ਹੁੰਦੇ ਹਨ ਜਿਸ ਕਾਰਨ ਕਈ ਵਾਰ ਤਾਂ ਉਹ ਘਰ ਵੀ ਛੱਡ ਦਿੰਦੇ ਹਨ । ਇਸ ਤਰ੍ਹਾਂ ਸਮੇਂ ਦੇ ਨਾਲ-ਨਾਲ ਪਰਿਵਾਰਿਕ ਏਕਤਾ ਵਿਚ ਕਮੀ ਆਈ ਹੈ ।
5. ਸਮਾਜਿਕ ਕੰਮਾਂ ਵਿਚ ਪਰਿਵਰਤਨ (Change in Social functions) – ਪਰਿਵਾਰ ਦੇ ਸਮਾਜਿਕ ਕੰਮ ਵੀ ਕਾਫੀ ਬਦਲ ਗਏ ਹਨ | ਪ੍ਰਾਚੀਨ ਸਮੇਂ ਵਿਚ ਪਰਿਵਾਰ ਸਮਾਜਿਕ ਨਿਯੰਤਰਣ ਦੇ ਸਾਧਨ ਦੇ ਰੂਪ ਵਿਚ ਕਾਫ਼ੀ ਮਹੱਤਵਪੂਰਨ ਕੰਮ ਕਰਦਾ ਸੀ । ਪਰਿਵਾਰ ਆਪਣੇ ਮੈਂਬਰਾਂ ਉੱਤੇ ਪੂਰਾ ਨਿਯੰਤਰਣ ਰੱਖਦਾ ਸੀ । ਉਸਦੀਆਂ ਚੰਗੀਆਂ ਮਾੜੀਆਂ ਆਦਤਾਂ ਉੱਤੇ ਨਜ਼ਰ ਰੱਖਦਾ ਸੀ ਅਤੇ ਉਸ ਨੂੰ ਸਮੇਂ-ਸਮੇਂ ਉੱਤੇ ਗ਼ਲਤ ਕੰਮ ਨਾ ਕਰਨ ਦੀ ਚੇਤਾਵਨੀ ਦਿੰਦਾ ਸੀ । ਮੈਂਬਰ ਵੀ ਪਰਿਵਾਰ ਦੇ ਬਜ਼ੁਰਗਾਂ ਤੋਂ ਡਰਦੇ ਸਨ ਜਿਸ ਕਾਰਨ ਉਹ ਨਿਯੰਤਰਣ ਵਿਚ ਰਹਿੰਦੇ ਸਨ | ਪਰ ਸਮੇਂ ਦੇ ਨਾਲ-ਨਾਲ ਵਿਅਕਤੀ ਉੱਤੇ ਪਰਿਵਾਰ ਦਾ ਨਿਯੰਤਰਣ ਘੱਟ ਹੋਣ ਲੱਗ ਗਿਆ ਅਤੇ ਨਿਯੰਤਰਣ ਦੇ ਰਸਮੀ ਸਾਧਨ ਸਾਹਮਣੇ ਆਏ ਜਿਵੇਂ ਕਿ ਪੁਲਿਸ, ਫੌਜ, ਅਦਾਲਤ, ਜੇਲ ਆਦਿ ।
ਇਸਦੇ ਨਾਲ ਪਾਚੀਨ ਸਮੇਂ ਵਿਚ ਔਰਤ ਆਪਣੇ ਪਤੀ ਨੂੰ ਪਰਮੇਸ਼ਵਰ ਹੀ ਸਮਝਦੀ ਸੀ ਅਤੇ ਉਸਨੂੰ ਭਗਵਾਨ ਦਾ ਦਰਜਾ ਦਿੰਦੀ ਸੀ । ਪਤੀ ਦੀ ਇੱਛਾ ਦੇ ਸਾਹਮਣੇ ਉਹ ਆਪਣੀ ਇੱਛਾ ਦਾ ਤਿਆਗ ਕਰ ਦਿੰਦੀ ਸੀ ਪਰ ਹੁਣ ਇਹ ਧਾਰਣਾ ਬਦਲ ਗਈ ਹੈ । ਹੁਣ ਪਤਨੀ ਪਤੀ ਨੂੰ ਪਰਮੇਸ਼ਵਰ ਨਹੀਂ ਬਲਕਿ ਆਪਣੇ ਸਾਥੀ ਜਾਂ ਦੋਸਤ ਸਮਝਦੀ ਹੈ ਜਿਸ ਨਾਲ ਕਿ ਉਹ ਆਪਣੀਆਂ ਸਮੱਸਿਆਵਾਂ ਸਾਂਝੀਆਂ ਕਰ ਸਕੇ ।
6. ਧਾਰਮਿਕ ਕੰਮਾਂ ਵਿਚ ਪਰਿਵਰਤਨ (Change in religious functions) – ਪ੍ਰਾਚੀਨ ਸਮੇਂ ਵਿਚ ਚਾਹੇ ਬੱਚਿਆਂ ਨੂੰ ਗੁਰੂ ਦੇ ਆਸ਼ਰਮ ਵਿਚ ਧਾਰਮਿਕ ਸਿੱਖਿਆ ਦਿੱਤੀ ਜਾਂਦੀ ਸੀ ਅਤੇ ਉਸ ਨੂੰ ਉੱਥੇ ਹੀ ਵੇਦਾਂ, ਧਾਰਮਿਕ ਗ੍ਰੰਥਾਂ ਆਦਿ ਦੀ ਸਿੱਖਿਆ ਦਿੱਤੀ ਜਾਂਦੀ ਸੀ ਪਰ ਫਿਰ ਵੀ ਪਰਿਵਾਰ ਉਸ ਨੂੰ ਧਾਰਮਿਕ ਸਿੱਖਿਆ ਵੀ ਦਿੰਦਾ ਸੀ । ਉਸਨੂੰ ਧਰਮ ਅਤੇ ਨੈਤਿਕਤਾ ਦਾ ਪਾਠ ਪੜਾਇਆ ਜਾਂਦਾ ਸੀ । ਸਮੇਂ-ਸਮੇਂ ਉੱਤੇ ਪਰਿਵਾਰ ਵਿਚ ਧਾਰਮਿਕ ਸੰਸਕਾਰ, ਯੱਗ ਆਦਿ ਹੁੰਦੇ ਰਹਿੰਦੇ ਸਨ ਜਿਸ ਨਾਲ ਬੱਚਿਆਂ ਨੂੰ ਧਰਮ ਦੇ ਬਾਰੇ ਵਿਚ ਕੁੱਝ ਪਤਾ ਚਲਦਾ ਰਹਿੰਦਾ ਸੀ । ਇਸ ਤਰ੍ਹਾਂ ਪਰਿਵਾਰ ਵਿਚ ਹੀ ਬੱਚਿਆਂ ਨੂੰ ਧਾਰਮਿਕ ਸਿੱਖਿਆ ਮਿਲ ਜਾਂਦੀ ਸੀ । ਪਰ ਸਮੇਂ ਦੇ ਨਾਲ ਬਹੁਤ ਸਾਰੀਆਂ ਖੋਜਾਂ ਹੋਈਆਂ, ਵਿਗਿਆਨ ਨੇ ਪ੍ਰਗਤੀ ਕੀਤੀ ਅਤੇ ਵਿਗਿਆਨ ਹਰੇਕ ਗੱਲ ਵਿਚ ਤਰਕ ਵੇਖਦਾ ਹੈ ।
ਲੋਕ ਵਿਗਿਆਨ ਦੀ ਸਿੱਖਿਆ ਲੈ ਕੇ ਧਰਮ ਨੂੰ ਭੁੱਲਣ ਲੱਗ ਗਏ ! ਹੁਣ ਲੋਕ ਹਰੇਕ ਧਾਰਮਿਕ ਸੰਸਕਾਰ ਨੂੰ ਤਰਕ ਦੀ ਕਸੌਟੀ ਉੱਤੇ ਤੋਲਣ ਲੱਗ ਗਏ ਹਨ ਕਿ ਇਹ ਕਿਉਂ ਅਤੇ ਕਿਵੇਂ ਹੈ । ਹੁਣ ਲੋਕਾਂ ਦੇ ਕੋਲ ਧਾਰਮਿਕ ਯੱਗਾਂ ਦੇ ਲਈ ਸਮਾਂ ਨਹੀਂ ਹੈ । ਹੁਣ ਲੋਕ ਧਾਰਮਿਕ ਕੰਮਾਂ ਦੇ ਲਈ ਥੋੜ੍ਹਾ ਜਿਹਾ ਸਮਾਂ ਹੀ ਕੱਢ ਸਕਦੇ ਹਨ ਅਤੇ ਉਹ ਵੀ ਆਪਣੇ ਸਮੇਂ ਦੇ ਅਨੁਸਾਰ । ਹੁਣ ਲੋਕ ਵਿਆਹ ਵਰਗੇ ਧਾਰਮਿਕ ਸੰਸਕਾਰ ਨੂੰ ਸਮਾਜਿਕ ਉਤਸਵ ਦੇ ਰੂਪ ਵਿਚ ਮਨਾਉਂਦੇ ਹਨ ਤਾਕਿ ਵੱਧ ਤੋਂ ਵੱਧ ਲੋਕਾਂ ਨੂੰ ਸੱਦਿਆ ਜਾ ਸਕੇ । ਲੋਕ ਇਨ੍ਹਾਂ ਵਿਚ ਵੱਧ ਤੋਂ ਵੱਧ ਪੈਸਾ ਖ਼ਰਚ ਕਰਦੇ ਹਨ ਜਿਸ ਕਾਰਨ ਧਾਰਮਿਕ ਕ੍ਰਿਆਵਾਂ ਦਾ ਮਹੱਤਵ ਘੱਟ ਹੋ ਗਿਆ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਪਰਿਵਾਰ ਦੇ ਧਾਰਮਿਕ ਕੰਮ ਘੱਟ ਹੋ ਗਏ ਹਨ ।

ਪ੍ਰਸ਼ਨ 8.
ਰਿਸ਼ਤੇਦਾਰੀ ਨੂੰ ਪਰਿਭਾਸ਼ਿਤ ਕਰੋ ਅਤੇ ਇਸ ਦੇ ਪ੍ਰਕਾਰਾਂ ਨੂੰ ਵਿਸਤਾਰ ਨਾਲ ਲਿਖੋ ।
ਉੱਤਰ-
ਸਾਕਾਦਾਰੀ ਜਾਂ ਰਿਸ਼ਤੇਦਾਰੀ ਦਾ ਅਰਥ (Meaning of Kinship) – Kin ਸ਼ਬਦ ਅੰਗਰੇਜ਼ੀ ਭਾਸ਼ਾ ਦਾ ਸ਼ਬਦ ਹੈ, ਜੋ ਕਿ ਸ਼ਬਦ Cynn ਤੋਂ ਨਿਕਲਿਆ ਹੈ ਜਿਸ ਦਾ ਮਤਲਬ ਸਿਰਫ਼ ‘ਰਿਸ਼ਤੇਦਾਰ’ ਹੁੰਦਾ ਹੈ ਅਤੇ ਸਮਾਜ ਵਿਗਿਆਨਿਆਂ ਅਤੇ ਮਾਨਵ ਵਿਗਿਆਨੀਆਂ ਨੇ ਆਪਣੇ ਅਧਿਐਨ ਵੇਲੇ ਇਸ ‘ਰਿਸ਼ਤੇਦਾਰ’ ਸ਼ਬਦ ਨੂੰ ਮੁੱਖ ਰੱਖਿਆ ਹੈ । ਸਾਕਾਦਾਰੀ ਸ਼ਬਦ ਵਿੱਚ ਰਿਸ਼ਤੇਦਾਰ ਹੁੰਦੇ ਹਨ , ਜਿਵੇਂ ਰਕਤ ਸੰਬੰਧੀ, ਸਕੇ ਅਤੇ ਰਿਸ਼ਤੇਦਾਰ ਆਦਿ ।
ਆਮ ਸ਼ਬਦਾਂ ਵਿੱਚ ਸਮਾਜ ਵਿਗਿਆਨ ਅਤੇ ਮਾਨਵ ਵਿਗਿਆਨ ਵਿੱਚ ਸਾਕਾਦਾਰੀ ਵਿਵਸਥਾ ਤੋਂ ਮਤਲਬ ਉਹਨਾਂ ਨਿਯਮਾਂ ਦੇ ਸੰਕੁਲ ਤੋਂ ਹੈ ਜੋ ਵੰਸ਼ ਰੂਮ, ਉੱਤਰਾਧਿਕਾਰ, ਵਿਰਾਸਤ, ਵਿਆਹ, ਵਿਆਹ ਤੋਂ ਬਾਹਰ ਲਿੰਗੀ ਸੰਬੰਧਾਂ, ਨਿਵਾਸ ਆਦਿ ਦਾ ਨਿਯਮਨ ਕਰਦੇ ਹੋਏ ਸਮਾਜ ਵਿਸ਼ੇਸ਼ ਵਿੱਚ ਮਨੁੱਖ ਜਾਂ ਉਸਦੇ ਸਮੂਹ ਦੀ ਸਥਿਤੀ ਉਸ ਦੇ ਖੂਨ ਦੇ ਸੰਬੰਧਾਂ ਜਾਂ ਵਿਆਹਕ ਸੰਬੰਧਾਂ ਦੇ ਪੱਖ ਤੋਂ ਨਿਰਧਾਰਿਤ ਕਰਦੇ ਹੋਈਏ । ਇਸ ਦਾ ਅਰਥ ਹੈ ਕਿ ਅਸਲੀ ਜਾਂ ਖੂਨ ਅਤੇ ਵਿਆਹ ਦੁਆਰਾ ਬਣਾਏ ਅਤੇ ਵਿਕਸਿਤ ਸਮਾਜਿਕ ਸੰਬੰਧਾਂ ਦੀ ਵਿਵਸਥਾ ਸਾਕਾਦਾਰੀ ਵਿਵਸਥਾ ਕਹਾਉਂਦੀ ਹੈ । ਇਸ ਦਾ ਸਾਫ਼ ਅਤੇ ਸਪੱਸ਼ਟ ਮਤਲਬ ਇਹ ਹੋਇਆ ਕਿ ਉਹ ਸੰਬੰਧ ਜਿਹੜੇ ਖ਼ੂਨ ਦੁਆਰਾ ਬਣੇ ਹੁੰਦੇ ਹਨ ਅਤੇ ਵਿਆਹ ਦੁਆਰਾ ਬਣ ਜਾਂਦੇ ਹਨ ਉਹ ਸਾਰੇ ਸਾਕਾਦਾਰੀ ਵਿਵਸਥਾ ਦਾ ਹਿੱਸਾ ਹੁੰਦੇ ਹਨ । ਇਸ ਵਿੱਚ ਉਹ ਸਾਰੇ ਰਿਸ਼ਤੇਦਾਰ ਸ਼ਾਮਲ ਹੁੰਦੇ ਹਨ ਜੋ ਕਿ ਖੂਨ ਅਤੇ ਵਿਆਹ , ਦੁਆਰਾ ਬਣਦੇ ਹਨ । ਉਦਾਹਰਨ ਦੇ ਤੌਰ ਉੱਤੇ ਮਾਤਾ-ਪਿਤਾ, ਦਾਦਾ-ਦਾਦੀ, ਚਾਚਾ-ਚਾਚੀ, ਮਾਮਾ-ਮਾਮੀ, ਤਾਇਆ-ਤਾਈ, ਭੈਣ-ਭਾਈ, ਸੱਸ-ਸਹੁਰਾ, ਸਾਲਾ-ਸਾਲੀ ਆਦਿ । ਇਸ ਸਭ ਸਾਡੇ ਰਿਸ਼ਤੇਦਾਰ ਹੁੰਦੇ ਹਨ ਅਤੇ ਸਾਕਾਦਾਰੀ ਵਿਵਸਥਾ ਦਾ ਹਿੱਸਾ ਹੁੰਦੇ ਹਨ ।
ਪਰਿਭਾਸ਼ਾਵਾਂ (Definitions)
- ਲੈਵੀ ਸਟਰਾਸ (Levi Strauss) ਦੇ ਅਨੁਸਾਰ, “ਸਾਕਾਦਾਰੀ ਵਿਵਸਥਾ ਇੱਕ ਨਿਰੰਕੁਸ਼ ਵਿਵਸਥਾ ਹੈ ।”
- ਚਾਰਲਸ ਵਿਕ (Charles Winick) ਦੇ ਅਨੁਸਾਰ, “ਸਾਕਾਦਾਰੀ ਵਿਵਸਥਾ ਵਿੱਚ ਉਹ ਸੰਬੰਧ ਸ਼ਾਮਲ ਕੀਤੇ ਜਾਂਦੇ ਹਨ ਜੋ ਕਲਪਿਤ ਜਾਂ ਵਾਸਤਵਿਕ ਵੰਸ਼ ਪਰੰਪਰਾਗਤ ਬੰਧਨਾਂ ਉੱਤੇ ਆਧਾਰਿਤ ਅਤੇ ਸਮਾਜ ਦੁਆਰਾ ਪ੍ਰਭਾਵਿਤ ਹੁੰਦੇ ਹਨ ।”
- ਰੈਡਕਲਿਫ ਬਰਾਉਨ (Redcliff Brown) ਦੇ ਅਨੁਸਾਰ, “ਪਰਿਵਾਰ ਅਤੇ ਵਿਆਹ ਦੀ ਹੋਂਦ ਤੋਂ ਪੈਦਾ ਹੋਏ ਜਾਂ ਇਸ ਦੇ ਸਿੱਟੇ ਵਜੋਂ ਪੈਦਾ ਹੋਏ ਸਾਰੇ ਸੰਬੰਧ ਸਾਕਾਦਾਰੀ ਵਿਵਸਥਾ ਵਿੱਚ ਹੁੰਦੇ ਹਨ ।”
- ਲੂਸੀ ਮੇਯਰ (Lucy Mayor) ਦੇ ਅਨੁਸਾਰ, “ਬੰਧੂਤਵ ਜਾਂ ਸਾਕਾਦਾਰੀ ਵਿੱਚ ਸਮਾਜਿਕ ਸੰਬੰਧਾਂ ਨੂੰ ਜੈਵਿਕ ਸ਼ਬਦਾਂ ਵਿੱਚ ਵਿਅਕਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।”
ਇਹਨਾਂ ਪਰਿਭਾਸ਼ਾਵਾਂ ਦੇ ਆਧਾਰ ਉੱਤੇ ਅਸੀਂ ਕਹਿ ਸਕਦੇ ਹਾਂ ਕਿ ਦੋ ਵਿਅਕਤੀ ਰਿਸ਼ਤੇਦਾਰ ਹੁੰਦੇ ਹਨ । ਜੇਕਰ ਉਹਨਾਂ ਦੇ ਪੁਰਵਜ ਇੱਕ ਹੀ ਹੋਣ ਤਾਂ ਉਹ ਇੱਕ ਵਿਅਕਤੀ ਦੀ ਔਲਾਦ ਹੁੰਦੇ ਹਨ | ਸਾਕਾਦਾਰੀ ਵਿਵਸਥਾ ਰਿਸ਼ਤੇਦਾਰਾਂ ਦੀ ਵਿਵਸਥਾ ਹੈ ਜੋ ਕਿ ਰਕਤ ਸੰਬੰਧਾਂ ਜਾਂ ਵਿਆਹ ਸੰਬੰਧਾਂ ਉੱਤੇ ਆਧਾਰਿਤ ਹੁੰਦੀ ਹੈ । ਸਾਕਾਦਾਰੀ ਵਿਵਸਥਾ ਸੰਸਕ੍ਰਿਤਕ ਹੈ ਅਤੇ ਇਸ ਦੀ ਬਣਤਰ ਸਾਰੇ ਸੰਸਾਰ ਵਿੱਚ ਵੱਖ-ਵੱਖ ਹੈ । ਸਾਕਾਦਾਰੀ ਵਿਵਸਥਾ ਵਿੱਚ ਉਨ੍ਹਾਂ ਸਾਰੇ ਅਸਲੀ ਜਾਂ ਨਕਲੀ ਰਕਤ ਸੰਬੰਧਾਂ ਨੂੰ ਸ਼ਾਮਲ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ਜਿਹੜੇ ਸਮਾਜ ਦੁਆਰਾ ਮਾਨਤਾ ਪ੍ਰਾਪਤ ਹੁੰਦੇ ਹਨ । ਇੱਕ ਨਜਾਇਜ਼ ਬੱਚੇ ਨੂੰ ਸਾਕਾਦਾਰੀ ਵਿੱਚ ਉੱਚਾ ਸਥਾਨ ਪ੍ਰਾਪਤ ਨਹੀਂ ਹੋ ਸਕਦਾ ਪਰ ਇੱਕ ਗੋਦ ਲਏ ਬੱਚੇ ਨੂੰ ਸਾਕਾਦਾਰੀ ਵਿਵਸਥਾ ਵਿੱਚ ਉੱਚਾ ਸਥਾਨ ਪ੍ਰਾਪਤ ਹੋ । ਜਾਂਦਾ ਹੈ । ਇਹ ਇੱਕ ਵਿਸ਼ੇਸ਼ ਸਾਕਾਦਾਰੀ ਸਮੂਹ ਦੀ ਵਿਵਸਥਾ ਹੈ ਜਿਸ ਵਿੱਚ ਸਾਰੇ ਰਿਸ਼ਤੇਦਾਰ ਸ਼ਾਮਲ ਹੁੰਦੇ ਹਨ ਅਤੇ ਜਿਹੜੇ ਇੱਕ ਦੂਜੇ ਪ੍ਰਤੀ ਆਪਣੀਆਂ ਜ਼ਿੰਮੇਵਾਰੀਆਂ ਸਮਝਦੇ ਹਨ । ਇਸ ਤਰ੍ਹਾਂ ਸਮਾਜ ਦੁਆਰਾ ਮਾਨਤਾ ਪ੍ਰਾਪਤ ਅਸਲੀ ਜਾਂ ਨਕਲੀ ਰਕਤ ਅਤੇ ਵਿਆਹ ਦੁਆਰਾ ਸਥਾਪਿਤ ਅਤੇ ਗੂੜ੍ਹੇ ਸਮਾਜਿਕ ਸੰਬੰਧਾਂ ਦੀ ਵਿਵਸਥਾ ਨੂੰ ਸਾਕਾਦਾਰੀ ਵਿਵਸਥਾ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।
ਨਾਤੇਦਾਰੀ ਦੀਆਂ ਸ਼੍ਰੇਣੀਆਂ Categories of Kinship
ਵਿਅਕਤੀ ਦੀ ਨੇੜਤਾ ਤੇ ਦੂਰੀ ਦੇ ਆਧਾਰ ਉੱਤੇ ਨਾਤੇਦਾਰੀ ਨੂੰ ਵੱਖ-ਵੱਖ ਸ਼੍ਰੇਣੀਆਂ ਵਿੱਚ ਵੰਡਿਆ ਗਿਆ ਹੈ | ਸਾਕੇਦਾਰੀ ਵਿੱਚ ਸਾਰੇ ਰਿਸ਼ਤੇਦਾਰਾਂ ਵਿੱਚ ਇੱਕੋ ਜਿਹੇ ਸੰਬੰਧ ਨਹੀਂ ਪਾਏ ਜਾਂਦੇ ਹਨ । ਜਿਹੜੇ ਸੰਬੰਧ ਸਾਡੇ ਆਪਣੇ ਮਾਤਾ-ਪਿਤਾ, ਪਤੀਪਤਨੀ, ਬੱਚਿਆਂ ਨਾਲ ਹੋਣਗੇ ਉਹ ਸਾਡੇ ਆਪਣੇ ਚਾਚੇ, ਭਤੀਜੇ ਮਾਮੇ, ਮਾਸੀ ਨਾਲ ਨਹੀਂ ਹੋ ਸਕਦੇ ਕਿਉਂਕਿ ਸਾਡਾ ਆਪਣੇ ਮਾਤਾ-ਪਿਤਾ, ਪਤੀ-ਪਤਨੀ ਨਾਲ ਜੋ ਸੰਬੰਧ ਹੈ ਉਹ ਚਾਚੇ, ਭਤੀਜੇ, ਮਾਮੇ ਆਦਿ ਨਾਲ ਨਹੀਂ ਹੋ ਸਕਦਾ । ਉਹਨਾਂ ਵਿਚ ਬਹੁਤ ਜ਼ਿਆਦਾ ਗੁੜੇ ਸੰਬੰਧ ਨਹੀਂ ਪਾਏ ਜਾਂਦੇ । ਇਸ ਨੇੜਤਾ ਅਤੇ ਦੁਰੀ ਦੇ ਆਧਾਰ ਉੱਤੇ ਨਾਤੇਦਾਰੀ ਨੂੰ ਤਿੰਨ ਸ਼੍ਰੇਣੀਆਂ ਵਿੱਚ ਵੰਡਿਆ ਗਿਆ ਹੈ ਜਿਨ੍ਹਾਂ ਦਾ ਵਰਣਨ ਇਸ ਪ੍ਰਕਾਰ ਹੈ ।
(1) ਪ੍ਰਾਥਮਿਕ ਰਿਸ਼ਤੇਦਾਰ (Primary Relations) – ਪਹਿਲੀ ਸ਼੍ਰੇਣੀ ਦੀ ਸਾਕੇਦਾਰੀ ਵਿੱਚ ਪ੍ਰਾਥਮਿਕ ਰਿਸ਼ਤੇਦਾਰ ਜਿਵੇਂ ਪਤੀ-ਪਤਨੀ, ਪਿਤਾ-ਪੁੱਤਰ, ਮਾਤਾ-ਪੁੱਤਰ, ਮਾਤਾ-ਪੁੱਤਰੀ, ਪਿਤਾ-ਪੁੱਤਰੀ, ਭੈਣ ਭੈਣ, ਭਰਾ-ਭੈਣ, ਭੈਣ-ਭਰਾ, ਭਰਾ ਭਰਾ ਆਦਿ ਆਉਂਦੇ ਹਨ | ਮਰਡੋਕ ਦੇ ਅਨੁਸਾਰ ਇਹ ਅੱਠ ਪ੍ਰਕਾਰ ਦੇ ਹੁੰਦੇ ਹਨ । ਇਹ ਪਾਥਮਿਕ ਇਸ ਲਈ ਹੁੰਦੇ ਹਨ ਕਿਉਂਕਿ ਇਹਨਾਂ ਵਿੱਚ ਸੰਬੰਧ ਪ੍ਰਤੱਖ ਅਤੇ ਗੁੜੇ ਹੁੰਦੇ ਹਨ ।
(2) ਗੌਣ ਸੰਬੰਧੀ (Secondary Relations) – ਸਾਡੇ ਕੁੱਝ ਰਿਸ਼ਤੇਦਾਰ ਪ੍ਰਾਥਮਿਕ ਹੁੰਦੇ ਹਨ ਜਿਵੇਂ ਮਾਤਾ-ਪਿਤਾ, ਭੈਣ ਭਰਾ ਆਦਿ । ਇਹਨਾਂ ਨਾਲ ਸਾਡਾ ਪ੍ਰਤੱਖ ਰਿਸ਼ਤਾ ਹੁੰਦਾ ਹੈ । ਪਰ ਕੁੱਝ ਰਿਸ਼ਤੇਦਾਰ ਅਜਿਹੇ ਹੁੰਦੇ ਹਨ । ਜਿਨ੍ਹਾਂ ਨਾਲ ਸਾਡਾ ਪ੍ਰਤੱਖ ਰਿਸ਼ਤਾ ਨਹੀਂ ਹੁੰਦਾ ਬਲਕਿ ਅਸੀਂ ਉਹਨਾਂ ਨਾਲ ਪ੍ਰਾਥਮਿਕ ਰਿਸ਼ਤੇਦਾਰਾਂ ਦੇ ਮਾਧਿਅਮ ਨਾਲ ਜੁੜੇ ਹੁੰਦੇ ਹਾਂ ਜਿਵੇਂ ਮਾਤਾ ਦਾ ਭਰਾ, ਪਿਤਾ ਦਾ ਭਰਾ, ਮਾਤਾ ਦੀ ਭੈਣ, ਪਿਤਾ ਦੀ ਭੈਣ, ਭੈਣ ਦਾ ਪਤੀ, ਭਰਾ ਦੀ ਪਤਨੀ ਆਦਿ । ਇਹਨਾਂ ਸਾਰਿਆਂ ਨਾਲ ਸਾਡਾ ਨਿੱਘਾ ਰਿਸ਼ਤਾ ਨਹੀਂ ਹੁੰਦਾ ਬਲਕਿ ਇਹ ਗੌਣ ਸੰਬੰਧੀ ਹੁੰਦੇ ਹਨ । ਮਰਡੋਕ ਦੇ ਅਨੁਸਾਰ ਇਹ ਸੰਬੰਧ 33 ਪ੍ਰਕਾਰ ਦੇ ਹੁੰਦੇ ਹਨ ।
(3) ਤੀਜੇ ਦਰਜੇ ਦੇ ਸੰਬੰਧੀ (Tertiary Kins) – ਸਭ ਤੋਂ ਪਹਿਲੇ ਰਿਸ਼ਤੇਦਾਰ ਪ੍ਰਾਥਮਿਕ ਹੁੰਦੇ ਹਨ ਤੇ ਫਿਰ ਕੌਣ ਸੰਬੰਧੀ ਯਾਨਿ ਕਿ ਪਾਥਮਿਕ ਸੰਬੰਧੀਆਂ ਦੀ ਮਦਦ ਨਾਲ ਰਿਸ਼ਤੇ ਬਣਦੇ ਹਨ | ਤੀਜੀ ਪ੍ਰਕਾਰ ਦੇ ਸੰਬੰਧੀ ਉਹ ਹੁੰਦੇ ਹਨ ਜਿਹੜੇ ਗੌਣ ਸੰਬੰਧੀਆਂ ਦੇ ਪਾਥਮਿਕ ਰਿਸ਼ਤੇਦਾਰ ਹਨ । ਜਿਵੇਂ ਪਿਤਾ ਦੇ ਭਰਾ ਦਾ ਪੱਤਰ, ਮਾਤਾ ਦੇ ਭਰਾ ਦੀ ਪਤਨੀ-ਮਾਮੀ, ਪਤਨੀ ਦੇ ਭਰਾ ਦੀ ਪਤਨੀ ਅਰਥਾਤ ਸਾਲੇ ਦੀ ਪਤਨੀ, ਮਾਤਾ ਦੀ ਭੈਣ ਦਾ ਪਤੀ-ਮਾਸੜ ਆਦਿ | ਮਰਡੈਕ ਨੇ ਇਹਨਾਂ ਦੀ 151 ਦੀ ਗਿਣਤੀ ਦਿੱਤੀ ਹੈ ।
ਇਸ ਤਰ੍ਹਾਂ ਇਹ ਤਿੰਨ ਸ਼੍ਰੇਣੀਆਂ ਦੀ ਸਾਕੇਦਾਰੀ ਹੁੰਦੀ ਹੈ ਪਰ ਜੇਕਰ ਅਸੀਂ ਚਾਹੀਏ ਤਾਂ ਅਸੀਂ ਚੌਥੀ ਅਤੇ ਪੰਜਵੀਂ ਸ਼੍ਰੇਣੀ ਬਾਰੇ ਵੀ ਜਾਣ ਸਕਦੇ ਹਾਂ ।
ਪ੍ਰਸ਼ਨ 9.
ਸਮਾਜਿਕ ਜੀਵਨ ਵਿੱਚ ਨਾਤੇਦਾਰੀ ਦੇ ਮਹੱਤਵ ਨੂੰ ਸਮਝਾਉ ।
ਉੱਤਰ-
ਸਾਕਾਦਾਰੀ ਵਿਵਸਥਾ ਦਾ ਸਮਾਜਿਕ ਸੰਰਚਨਾ ਵਿੱਚ ਇੱਕ ਵਿਸ਼ੇਸ਼ ਸਥਾਨ ਹੈ । ਇਸ ਦੇ ਨਾਲ ਹੀ ਸਮਾਜ ਦੀ ਬਣਤਰ ਬਣਦੀ ਹੈ । ਜੇਕਰ ਨਾਤੇਦਾਰੀ ਜਾਂ ਸਾਕਾਦਾਰੀ ਵਿਵਸਥਾ ਹੀ ਨਾ ਹੋਵੇ ਤਾਂ ਸਮਾਜ ਇੱਕ ਸੰਗਠਨ ਦੀ ਤਰ੍ਹਾਂ ਨਹੀਂ ਬਣ ਸਕੇਗਾ ਅਤੇ ਸਹੀ ਤਰੀਕੇ ਕੰਮ ਨਹੀਂ ਕਰ ਸਕੇਗਾ । ਇਸ ਲਈ ਇਸ ਦਾ ਮਹੱਤਵ ਕਾਫ਼ੀ ਵੱਧ ਗਿਆ ਹੈ ਜਿਸ ਦਾ ਵਰਣਨ ਹੇਠਾਂ ਲਿਖਿਆ ਹੈ-
(1) ਨਾਤੇਦਾਰੀ ਸੰਬੰਧਾਂ ਦੇ ਮਾਧਿਅਮ ਤੋਂ ਹੀ ਕਬਾਇਲੀ ਅਤੇ ਖੇਤੀ ਵਾਲੇ ਸਮਾਜਾਂ ਦੇ ਵਿੱਚ ਅਧਿਕਾਰ ਅਤੇ ਪਰਿਵਾਰ ਤੇ ਵਿਆਹ, ਉਤਪਾਦਨ ਅਤੇ ਉਪਭੋਗ ਦੀ ਪੱਧਤੀ ਅਤੇ ਰਾਜਨੀਤਿਕ ਸੱਤਾ ਦੇ ਅਧਿਕਾਰਾਂ ਦਾ ਨਿਰਧਾਰਨ ਹੁੰਦਾ ਹੈ । ਸ਼ਹਿਰੀ ਸਮਾਜਾਂ ਵਿੱਚ ਵੀ ਵਿਆਹ ਅਤੇ ਪਰਿਵਾਰਿਕ ਉਤਸਵਾਂ ਦੇ ਸਮੇਂ ਨਾਤੇਦਾਰੀ ਸੰਬੰਧਾਂ ਦਾ ਮਹੱਤਵ ਵੇਖਣ ਨੂੰ ਮਿਲਦਾ ਹੈ ।
(2) ਨਾਤੇਦਾਰੀ, ਪਰਿਵਾਰ ਅਤੇ ਵਿਆਹ ਵਿੱਚ ਡੂੰਘਾ ਸੰਬੰਧ ਹੈ । ਨਾਤੇਦਾਰੀ ਦੇ ਮਾਧਿਅਮ ਤੋਂ ਹੀ ਇਸ ਗੱਲ ਦਾ ਨਿਰਧਾਰਨ ਹੁੰਦਾ ਹੈ ਕਿ ਕੌਣ ਕਿਸ ਦੇ ਨਾਲ ਵਿਆਹ ਕਰ ਸਕਦਾ ਹੈ ਅਤੇ ਕਿਹੜੇ-ਕਿਹੜੇ ਸੰਬੰਧਾਂ ਦੀ ਕੀ ਸ਼ਬਦਾਵਲੀ ਹੈ । ਨਾਤੇਦਾਰੀ ਤੋਂ ਹੀ ਵੰਸ਼ ਸੰਬੰਧ, ਗੋਤਰ ਅਤੇ ਖ਼ਾਨਦਾਨ ਦਾ ਨਿਰਧਾਰਨ ਹੁੰਦਾ ਹੈ ਅਤੇ ਵੰਸ਼, ਗੋਤਰ ਅਤੇ ਖ਼ਾਨਦਾਨ ਵਿੱਚ ਬਾਹਰ ਵਿਆਹ ਦਾ ਸਿਧਾਂਤ ਪਾਇਆ ਜਾਂਦਾ ਹੈ ।
(3) ਪਰਿਵਾਰਿਕ ਜੀਵਨ, ਵੰਸ਼ ਸੰਬੰਧ, ਗੋਤਰ ਅਤੇ ਖ਼ਾਨਦਾਨ ਦੇ ਮੈਂਬਰਾਂ ਦੇ ਵਿੱਚ ਨਾਤੇਦਾਰੀ ਦੇ ਆਧਾਰ ਉੱਤੇ ਹੀ ਜਨਮ ਤੋਂ ਲੈ ਕੇ ਮੌਤ ਤਕ ਦੇ ਸੰਸਕਾਰਾਂ ਅਤੇ ਕਰਮ-ਕਾਂਡਾਂ ਵਿੱਚ ਕਿਸਦਾ ਕੀ ਅਧਿਕਾਰ ਅਤੇ ਜ਼ਿੰਮੇਵਾਰੀ ਹੈ, ਇਸ ਦਾ ਨਿਰਧਾਰਨ ਹੁੰਦਾ ਹੈ, ਜਿਵੇਂ ਵਿਆਹ ਦੇ ਸੰਸਕਾਰ ਅਤੇ ਇਸ ਨਾਲ ਜੁੜੇ ਕਰਮ ਕਾਂਡਾਂ ਵਿੱਚ ਵੱਡੇ ਭਾਈ, ਮਾਂ ਅਤੇ ਭੂਆ ਦਾ ਵਿਸ਼ੇਸ਼ ਮਹੱਤਵ ਹੈ । ਮੌਤ ਤੋਂ ਬਾਅਦ ਅੱਗ ਕੌਣ ਦੇਵੇਗਾ, ਇਸ ਦਾ ਸੰਬੰਧ ਵੀ ਸਾਕੇਦਾਰੀ ਉੱਤੇ ਨਿਰਭਰ ਕਰਦਾ ਹੈ । ਜਿਹੜੇ ਲੋਕਾਂ ਨੂੰ ਅੱਗ ਦੇਣ ਦਾ ਅਧਿਕਾਰ ਹੁੰਦਾ ਹੈ, ਸਾਕੇਦਾਰੀ ਉਹਨਾਂ ਦੇ ਉੱਤਰਾਧਿਕਾਰ ਨੂੰ ਨਿਸ਼ਚਿਤ ਕਰਦੀ ਹੈ । ਸਮਾਜਿਕ ਸੰਗਠਨ (ਜਨਮ, ਵਿਆਹ, ਮੌਤ) ਅਤੇ ਸਮੂਹਿਕ ਉਤਸਵਾਂ ਦੇ ਮੌਕਿਆਂ ਉੱਤੇ ਸਾਕੇਦਾਰੀ ਜਾਂ ਰਿਸ਼ਤੇਦਾਰਾਂ ਨੂੰ ਸੱਦਿਆ ਜਾਣਾ ਜ਼ਰੂਰੀ ਹੁੰਦਾ ਹੈ, ਅਜਿਹਾ ਕਰਨ ਨਾਲ ਸੰਬੰਧਾਂ ਵਿੱਚ ਹੋਰ ਮਜ਼ਬੂਤੀ ਵੱਧਦੀ ਹੈ ।
(4) ਨਾਤੇਦਾਰੀ ਵਿਵਸਥਾ ਨਾਲ ਸਮਾਜ ਨੂੰ ਮਜ਼ਬੂਤੀ ਮਿਲਦੀ ਹੈ | ਸਾਕਾਦਾਰੀ ਵਿਵਸਥਾ ਸਮਾਜਿਕ ਸੰਗਠਨ ਨੂੰ ਬਣਾਉਣ ਵਿੱਚ ਮਹੱਤਵਪੂਰਨ ਭੂਮਿਕਾ ਨਿਭਾਉਂਦੀ ਹੈ । ਜੇਕਰ ਸਾਕਾਦਾਰੀ ਵਿਵਸਥਾ ਹੀ ਨਾ ਹੋਵੇ ਤਾਂ ਸਮਾਜਿਕ ਸੰਗਠਨ ਟੁੱਟ ਜਾਵੇਗਾ ਅਤੇ ਸਮਾਜ ਵਿੱਚ ਅਵਿਵਸਥਾ ਫੈਲ ਜਾਵੇਗੀ ।
(5) ਨਾਤੇਦਾਰੀ ਵਿਵਸਥਾ ਲਿੰਗ ਸੰਬੰਧਾਂ ਨੂੰ ਨਿਸ਼ਚਿਤ ਕਰਦੀ ਹੈ । ਸਾਕਾਦਾਰੀ ਵਿਵਸਥਾ ਵਿੱਚ ਲਿੰਗ ਸੰਬੰਧ ਬਣਾਉਣੇ, ਸਾਡੇ ਸਮਾਜਾਂ ਵਿੱਚ ਵਰਜਿਤ ਹੈ । ਜੇਕਰ ਸਾਕਾਦਾਰੀ ਵਿਵਸਥਾ ਨਾ ਹੋਵੇ ਤਾਂ ਸਮਾਜ ਵਿੱਚ ਅਵਿਵਸਥਾ ਫੈਲ ਜਾਵੇਗੀ ਅਤੇ ਨਜਾਇਜ਼ ਲਿੰਗ ਸੰਬੰਧ ਅਤੇ ਅਵੈਧ ਬੱਚਿਆਂ ਦੀ ਭਰਮਾਰ ਹੋਵੇਗੀ ਜਿਸ ਨਾਲ ਸਮਾਜ ਭਿੰਨ-ਭਿੰਨ ਹੋ ਜਾਵੇਗਾ ।
(6) ਨਾਤੇਦਾਰੀ ਵਿਵਸਥਾ ਵਿਆਹ ਨਿਰਧਾਰਨ ਵਿੱਚ ਮਹੱਤਵਪੂਰਨ ਭੂਮਿਕਾ ਨਿਭਾਉਂਦੀ ਹੈ । ਆਪਣੇ ਗੋਤਰ ਵਿੱਚ ਵਿਆਹ ਨਹੀਂ ਕਰਵਾਉਣਾ, ਮਾਤਾ ਦੇ ਪਾਸਿਉਂ ਕਿੰਨੇ ਰਿਸ਼ਤੇਦਾਰ ਛੱਡਣੇ ਹਨ, ਪਿਤਾ ਦੇ ਪਾਸਿਉਂ ਕਿੰਨੇ ਰਿਸ਼ਤੇਦਾਰ ਛੱਡਣੇ ਹਨ, ਇਹ ਸਭ ਕੁੱਝ ਸਾਕਾਦਾਰੀ ਵਿਵਸਥਾ ਉੱਤੇ ਹੀ ਨਿਰਭਰ ਕਰਦਾ ਹੈ । ਜੇਕਰ ਇਹ ਵਿਵਸਥਾ ਨਾ ਹੋਵੇ ਤਾਂ ਵਿਆਹ ਕਰਾਉਣ ਵਿੱਚ ਕਿਸੇ ਵੀ ਨਿਯਮ ਦੀ ਪਾਲਣਾ ਨਹੀਂ ਹੋਵੇਗੀ ਜਿਸ ਕਾਰਨ ਸਮਾਜ ਵਿੱਚ ਅਵਿਵਸਥਾ ਫੈਲ ਜਾਵੇਗੀ ।
(7) ਨਾਤੇਦਾਰੀ ਵਿਵਸਥਾ ਮਨੁੱਖ ਨੂੰ ਮਾਨਸਿਕ ਸ਼ਾਂਤੀ ਪ੍ਰਦਾਨ ਕਰਦੀ ਹੈ । ਅੱਜ-ਕਲ੍ਹ ਦੇ ਉਦਯੋਗਿਕ ਸਮਾਜ ਵਿੱਚ ਚਾਹੇ ਸਾਡੇ ਵਿਚਾਰ Practical ਹੋ ਚੁੱਕੇ ਹਨ ਪਰ ਫਿਰ ਵੀ ਮਨੁੱਖ ਸਾਕੇਦਾਰੀ ਦੇ ਬੰਧਨਾਂ ਤੋਂ ਮੁਕਤ ਨਹੀਂ ਹੋ ਸਕਿਆ ਹੈ । ਉਹ ਆਪਣੇ ਬਜ਼ੁਰਗਾਂ ਦੀਆਂ ਤਸਵੀਰਾਂ ਘਰ ਵਿੱਚ ਟੰਗ ਕੇ ਰੱਖਦਾ ਹੈ, ਉਹਨਾਂ ਦੀਆਂ ਤਸਵੀਰਾਂ ਦਾ ਸੰਗ੍ਰਹਿ ਕਰਦਾ ਹੈ, ਮਰਨ ਤੋਂ ਬਾਅਦ ਉਹਨਾਂ ਦਾ ਸ਼ਰਾਧ ਕਰਦਾ ਹੈ । ਮਨੁੱਖੀ ਜਾਤੀ ਸਾਕੇਦਾਰੀ ਤੇ ਆਧਾਰਿਤ ਸਮੂਹਾਂ ਵਿੱਚ ਰਹੀ ਹੈ । ਸਾਕੇਦਾਰੀ ਤੋਂ ਬਿਨਾਂ ਵਿਅਕਤੀ ਇੱਕ ਮਰੇ ਹੋਏ ਵਿਅਕਤੀ ਦੇ ਸਮਾਨ ਹੈ । ਸਾਡੇ ਰਿਸ਼ਤੇਦਾਰ ਸਾਨੂੰ ਸਭ ਤੋਂ ਜ਼ਿਆਦਾ ਜਾਣਦੇ ਹਨ, ਪਛਾਣਦੇ ਹਨ । ਉਹ ਆਪਣੇ ਆਪ ਨੂੰ ਆਪਣੇ ਪਰਿਵਾਰ ਦਾ ਹਿੱਸਾ ਸਮਝਦੇ ਹਨ । ਜੇਕਰ ਅਸੀਂ ਕਿਸੇ ਪਰੇਸ਼ਾਨੀ ਵਿੱਚ ਹੁੰਦੇ ਹਾਂ ਤਾਂ ਸਾਡੇ ਰਿਸ਼ਤੇਦਾਰ ਹੀ ਸਾਨੂੰ ਮਾਨਸਿਕ ਤੌਰ ਤੇ ਸ਼ਾਂਤ ਕਰਦੇ ਹਨ | ਅਸੀਂ ਆਪਣੇ ਰਿਸ਼ਤੇਦਾਰਾਂ ਵਿੱਚ ਹੀ ਰਹਿ ਕੇ ਸਭ ਤੋਂ ਜ਼ਿਆਦਾ ਪ੍ਰਸੰਨਤਾ ਤੇ ਆਨੰਦ ਮਹਿਸੂਸ ਕਰਦੇ ਹਾਂ ।
(8) ਸਾਡੀ ਨਾਤੇਦਾਰੀ ਹੀ ਸਾਡੇ ਵਿਆਹ ਅਤੇ ਪਰਿਵਾਰ ਦਾ ਨਿਰਧਾਰਨ ਕਰਦੀ ਹੈ । ਕਿਸ ਨਾਲ ਵਿਆਹ ਕਰਨਾ ਹੈ, ਕਿਸ ਨਾਲ ਨਹੀਂ ਕਰਨਾ ਹੈ, ਸਗੋਡਰ, ਅੰਤਰਜਾਤੀ ਵਿਆਹ ਸਭ ਕੁੱਝ ਹੀ ਸਾਕੇਦਾਰੀ ਉੱਤੇ ਹੀ ਨਿਰਭਰ ਕਰਦਾ ਹੈ । ਪਰਿਵਾਰ ਵਿੱਚ ਹੀ ਖੂਨ ਤੇ ਵਿਆਹ ਦੇ ਸੰਬੰਧ ਪਾਏ ਜਾਂਦੇ ਹਨ | ਸਾਕੇਦਾਰੀ ਕਰਕੇ ਹੀ ਵਿਆਹ ਤੇ ਸਾਕੇਦਾਰੀ ਵਿਚਕਾਰ ਵਿਵਸਥਾ ਪੈਦਾ ਹੁੰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 10.
ਵਿਆਹ ਅਤੇ ਖੂਨ ਸੰਬੰਧਾਂ ਵਿੱਚ ਅੰਤਰ ਦੱਸੋ ।
ਉੱਤਰ-
ਸਗੋਤਰ ਸਾਕਾਦਾਰੀ ਜਾਂ ਖੂਨ ਸੰਬੰਧੀ-ਮੁੱਢਲੇ ਪਰਿਵਾਰ ਦੇ ਆਧਾਰ ਉੱਤੇ ਅਤੇ ਇਸ ਵਿੱਚ ਪੈਦਾ ਹੋਏ ਅਸਲੀ ਜਾਂ ਨਕਲੀ ਖ਼ੂਨ ਦੇ ਵੰਸ਼ ਪਰੰਪਰਾਗਤ ਸੰਬੰਧਾਂ ਨੂੰ ਗੋਤਰ ਸਾਕਾਦਾਰੀ ਕਹਿੰਦੇ ਹਨ । ਆਮ ਸ਼ਬਦਾਂ ਵਿੱਚ ਉਹ ਸਭ ਰਿਸ਼ਦੇਤਾਰ ਜਾਂ ਵਿਅਕਤੀ ਜਿਹੜੇ ਖ਼ੂਨ ਦੇ ਬੰਧਨਾਂ ਵਿਚ ਬੰਨ੍ਹੇ ਹੁੰਦੇ ਹਨ ਉਹਨਾਂ ਨੂੰ ਸਗੋਤਰ ਸਾਕਾਦਾਰੀ ਕਹਿੰਦੇ ਹਨ । ਖੂਨ ਦਾ ਸੰਬੰਧ ਚਾਹੇ ਅਸਲੀ ਹੋਵੇ ਜਾਂ ਨਕਲੀ ਇਸ ਨੂੰ ਸਾਕਾਦਾਰੀ ਵਿਵਸਥਾ ਵਿਚ ਤਾਂ ਹੀ ਉੱਚਾ ਸਥਾਨ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ । ਜੇਕਰ ਇਸ ਸੰਬੰਧ ਨੂੰ ਸਮਾਜ ਦੀ ਮਾਨਤਾ ਪ੍ਰਾਪਤ ਹੈ । ਉਦਾਹਰਨ ਤੇ ਤੌਰ ਤੇ ਨਜਾਇਜ਼ ਬੱਚੇ ਨੂੰ, ਚਾਹੇ ਉਸ ਨਾਲ ਵੀ ਰਕਤ ਸੰਬੰਧ ਹੁੰਦਾ ਹੈ, ਸਮਾਜ ਵਿੱਚ ਮਾਨਤਾ ਪ੍ਰਾਪਤ ਨਹੀਂ ਹੁੰਦੀ ਕਿਉਂਕਿ ਉਸ ਨੂੰ ਸਮਾਜ ਦੀ ਮਾਨਤਾ ਪ੍ਰਾਪਤ ਨਹੀਂ ਹੁੰਦੀ ਅਤੇ ਗੋਦ ਲਏ ਬੱਚੇ ਨੂੰ, ਚਾਹੇ ਉਸ ਨਾਲ ਰਕਤ ਸੰਬੰਧ ਨਹੀਂ ਹੁੰਦਾ, ਸਮਾਜ ਵਿੱਚ ਮਾਨਤਾ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ ਅਤੇ ਉਹ ਸਗੋਤਰ ਪ੍ਰਣਾਲੀ ਦਾ ਹਿੱਸਾ ਹੁੰਦੇ ਹਨ । ਰਕਤ ਸੰਬੰਧਾਂ ਨੂੰ ਹਰ ਪ੍ਰਕਾਰ ਦੇ ਸਮਾਜਾਂ ਵਿੱਚ ਮਾਨਤਾ ਪ੍ਰਾਪਤ ਹੈ ।
ਇਸ ਤਰ੍ਹਾਂ ਇਸ ਚਰਚਾ ਤੋਂ ਸਪੱਸ਼ਟ ਹੈ ਕਿ ਸ਼ੁਰੂਆਤੀ ਪਰਿਵਾਰ ਦੇ ਆਧਾਰ ਤੇ ਰਕਤ-ਵੰਸ਼ ਪਰੰਪਰਾਗਤ ਸੰਬੰਧਾਂ ਤੋਂ ਪੈਦਾ ਹੋਏ ਸਾਰੇ ਰਿਸ਼ਤੇਦਾਰ ਇਸ ਗੋਤਰ ਸਾਕਾਦਾਰੀ ਪ੍ਰਣਾਲੀ ਵਿੱਚ ਸ਼ਾਮਲ ਹਨ । ਅਸੀਂ ਉਦਾਹਰਨ ਲੈ ਸਕਦੇ ਹਾਂ ਭੈਣ-ਭਰਾ, ਮਾਮਾ, ਚਾਚਾ, ਤਾਇਆ, ਨਾਨਾ, ਨਾਨੀ, ਦਾਦਾ-ਦਾਦੀ, ਆਦਿ । ਇੱਥੇ ਇਹ ਦੱਸਣ ਯੋਗ ਹੈ ਕਿ ਰਕਤ ਸੰਬੰਧ ਸਿਰਫ਼ ਪਿਤਾ ਵਾਲੇ ਪਾਸੇ ਹੀ ਨਹੀਂ ਹੁੰਦਾ ਬਲਕਿ ਮਾਤਾ ਵਾਲੇ ਪਾਸੇ ਵੀ ਹੁੰਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਪਿਤਾ ਵਾਲੇ ਪਾਸੇ ਦੇ ਰਕਤ ਸੰਬੰਧੀਆਂ ਨੂੰ ਪਿਤਰ ਪੱਖੀ ਰਿਸ਼ਤੇਦਾਰ ਕਹਿੰਦੇ ਹਨ ਅਤੇ ਮਾਤਾ ਵਾਲੇ ਪਾਸੇ ਦੇ ਰਕਤ ਸੰਬੰਧੀਆਂ ਨੂੰ ਮਾਤਰ ਪੱਖੀ ਰਿਸ਼ਤੇਦਾਰ ।
ਵਰਗੀਕਰਨ – ਖੂਨ ਦੇ ਆਧਾਰ ਉੱਤੇ ਆਧਾਰਿਤ ਰਿਸ਼ਤੇਦਾਰਾਂ ਨੂੰ ਵੱਖ-ਵੱਖ ਨਾਂਵਾਂ ਨਾਲ ਜਾਣਿਆ ਜਾਂਦਾ ਹੈ । ਇੱਕੋ ਹੀ ਮਾਂ-ਬਾਪ ਦੇ ਬੱਚਿਆਂ, ਜੋ ਆਪਸ ਵਿੱਚ ਸਕੇ ਭੈਣ ਭਰਾ ਹੁੰਦੇ ਹਨ, ਨੂੰ ਸਿਬਲਿੰਗ (Sibling) ਕਹਿੰਦੇ ਹਨ ਅਤੇ ਮਤਰੇਏ ਭੈਣਭਰਾ ਨੂੰ ਹਾਫ਼ ਸਿਬਲਿੰਗ (Half Sibling) ਕਹਿੰਦੇ ਹਨ । ਪਿਤਾ ਵਾਲੇ ਪਾਸੇ ਸਿਰਫ਼ ਆਦਮੀਆਂ ਦੇ ਖੂਨ ਸੰਬੰਧੀਆਂ ਜੋ ਸਿਰਫ਼ ਆਦਮੀ ਹੁੰਦੇ ਹਨ ਉਹਨਾਂ ਨੂੰ ਸਕਾ-ਸੰਬੰਧੀ (agnates) ਕਹਿੰਦੇ ਹਨ ਅਤੇ ਇਸੇ ਤਰ੍ਹਾਂ ਮਾਤਾ ਵਾਲੇ ਪਾਸੇ ਸਿਰਫ਼ ਔਰਤਾਂ ਦੇ ਖੂਨ ਸੰਬੰਧੀਆਂ ਜੋ ਸਿਰਫ਼ ਔਰਤਾਂ ਹੁੰਦੀਆਂ ਹਨ, ਉਹਨਾਂ ਨੂੰ (Utrine) ਕਹਿੰਦੇ ਹਨ । ਇਸੇ ਤਰ੍ਹਾਂ ਉਹ ਲੋਕ ਜੋ ਖੂਨ ਦੇ ਸੰਬੰਧਾਂ ਕਾਰਨ ਸੰਬੰਧਿਤ ਹੋਣ, ਉਹਨਾਂ ਨੂੰ ਰਕਤ ਸੰਬੰਧੀ ਰਿਸ਼ਤੇਦਾਰ (consanguined kin) ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਇਹਨਾਂ ਰਕਤ ਸੰਬੰਧੀਆਂ ਨੂੰ ਦੋ ਹਿੱਸਿਆਂ ਵਿੱਚ ਵੰਡਿਆ ਜਾਂਦਾ ਹੈ ।
- ਇਕ ਰੇਖਕੀ ਰਿਸ਼ਤੇਦਾਰ (Unilineal Kin) – ਇਸ ਪ੍ਰਕਾਰ ਦੀ ਰਿਸ਼ਤੇਦਾਰੀ ਵਿੱਚ ਉਹ ਵਿਅਕਤੀ ਆਉਂਦੇ ਹਨ ਜੋ ਵੰਸ਼ ਭੂਮ ਦੀ ਸਿੱਧੀ ਰੇਖਾ ਦੁਆਰਾ ਸੰਬੰਧਿਤ ਹੋਣ ਜਿਵੇਂ ਪਿਤਾ, ਪਿਤਾ ਦਾ ਪਿਤਾ, ਪੁੱਤਰ ਅਤੇ ਪੁੱਤਰ ਦਾ ਪੁੱਤਰ ।
- ਕੁਲੇਟਰਲ ਜਾਂ ਸਮਾਨਾਂਤਰ ਰਿਸ਼ਤੇਦਾਰ (Collateral Kin) – ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਰਿਸ਼ਤੇਦਾਰ ਉਹ ਵਿਅਕਤੀ ਹੁੰਦੇ ਹਨ, ਜੋ ਹੋਰ ਰਿਸ਼ਤੇਦਾਰਾਂ ਦੇ ਦੁਆਰਾ ਅਸਿੱਧੇ ਤੌਰ ਉੱਤੇ ਸੰਬੰਧਿਤ ਹੋਣ ਜਿਵੇਂ ਪਿਤਾ ਦਾ ਭਰਾ ਚਾਚਾ, ਮਾਂ ਦੀ ਭੈਣ ਮਾਸੀ, ਮਾਂ ਦਾ ਭਰਾ ਮਾਮਾ ਆਦਿ ।
ਵਿਆਹ ਸੰਬੰਧ – ਇਸ ਨੂੰ ਸਮਾਜਿਕ ਸਾਕੇਦਾਰੀ ਦਾ ਨਾਮ ਵੀ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ । ਇਸ ਪ੍ਰਕਾਰ ਦੀ ਸਾਕੇਦਰੀ ਵਿੱਚ ਉਸ ਤਰ੍ਹਾਂ ਦੇ ਰਿਸ਼ਤੇਦਾਰ ਸ਼ਾਮਲ ਹੁੰਦੇ ਹਨ ਜਿਹੜੇ ਕਿਸੇ ਆਦਮੀ ਜਾਂ ਔਰਤ ਦੇ ਵਿਆਹ ਕਰਨ ਦੇ ਨਾਲ ਪੈਦਾ ਹੁੰਦੇ ਹਨ । ਜਦੋਂ ਕਿਸੇ ਮੁੰਡੇ ਦਾ ਕੁੜੀ ਨਾਲ ਵਿਆਹ ਹੁੰਦਾ ਹੈ ਤਾਂ ਉਸ ਦਾ ਸਿਰਫ਼ ਕੁੜੀ ਨਾਲ ਹੀ ਸੰਬੰਧ ਸਥਾਪਿਤ ਨਹੀਂ ਹੁੰਦਾ ਬਲਕਿ ਕੁੜੀ ਦੇ ਮਾਧਿਅਮ ਨਾਲ ਉਸ ਦੇ ਪਰਿਵਾਰ ਦੇ ਬਹੁਤ ਸਾਰੇ ਮੈਂਬਰਾਂ ਨਾਲ ਸੰਬੰਧ ਸਥਾਪਿਤ ਹੋ ਜਾਂਦਾ ਹੈ । ਇਸੇ ਤਰ੍ਹਾਂ ਜਦੋਂ ਕੁੜੀ ਦਾ ਮੁੰਡੇ ਨਾਲ ਵਿਆਹ ਹੁੰਦਾ ਹੈ ਤਾਂ ਕੁੜੀ ਦਾ ਵੀ ਮੁੰਡੇ ਦੇ ਪਰਿਵਾਰ ਦੇ ਸਾਰੇ ਮੈਂਬਰਾਂ ਨਾਲ ਸੰਬੰਧ ਸਥਾਪਿਤ ਹੋ ਜਾਂਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਸਿਰਫ ਵਿਆਹ ਕਰਵਾਉਣ ਨਾਲ ਹੀ ਮੁੰਡੇ ਕੁੜੀ ਦੇ ਕਈ ਪ੍ਰਕਾਰ ਦੇ ਨਵੇਂ ਰਿਸ਼ਤੇ ਹੋਂਦ ਵਿਚ ਆ ਜਾਂਦੇ ਹਨ । ਇਸ ਤਰ੍ਹਾਂ ਵਿਆਹ ਉੱਤੇ ਆਧਾਰਿਤ ਸਾਕੇਦਾਰੀ ਨੂੰ ਵਿਆਹਕ ਸਾਕੇਦਾਰੀ ਦਾ ਨਾਮ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ।
ਉਦਾਹਰਨ ਦੇ ਤੌਰ ਤੇ ਜੀਜਾ ਸਾਲਾ, ਸਾਂਢੂ, ਜਵਾਈ, ਸਹੁਰਾ, ਨਨਾਣ, ਭਰਜਾਈ, ਨੂੰਹ, ਸੱਸ ਭਾਈ ਆਦਿ । ਇਸ ਸਾਕੇਦਾਰੀ ਦੀ ਸਾਕੇਦਾਰੀ ਦੀ ਪਾਣੀਸ਼ਾਸਤਰੀ ਮਹੱਤਤਾਂ ਦੇ ਨਾਲ-ਨਾਲ ਸਮਾਜਿਕ ਮਹੱਤਤਾ ਵੀ ਹੁੰਦੀ ਹੈ । ਪਾਣੀਸ਼ਾਸਤਰੀ ਮਹੱਤਤਾ ਤਾਂ ਪਤੀ-ਪਤਨੀ ਲਈ ਹੈ ਪਰ ਸੱਸ, ਸਹੁਰਾ, ਦਿਉਰ, ਨਨਾਣ, ਭਰਜਾਈ, ਸਾਂਢ, ਸਾਲੀ, ਸਾਲਾ, ਜਵਾਈ ਆਦਿ ਰਿਸ਼ਤੇ ਸਮਾਜਿਕ ਹੁੰਦੇ ਹਨ । ਮਾਰਗਨ ਨੇ ਦੁਨੀਆ ਦੇ ਕਈ ਭਾਗਾਂ ਵਿੱਚ ਪ੍ਰਚਲਿਤ ਸਾਕੇਦਾਰੀਆਂ ਦਾ ਅਧਿਐਨ ਕੀਤਾ ਤੇ ਇਹਨਾਂ ਨੂੰ ਵਰਣਨਾਤਮਕ ਤੇ ਵਿਅਕਤੀਨਿਸ਼ਠ ਨਾਮਕਰਨ ਦੇ ਨਾਲ ਦੋ ਮੁੱਖ ਸ਼੍ਰੇਣੀਆਂ ਵਿੱਚ ਵੰਡਿਆ ਹੈ । ਵਰਣਨਾਤਮਕ ਪ੍ਰਣਾਲੀ ਵਿੱਚ ਆਮ ਤੌਰ ਤੇ ਵਿਆਹਕ ਸੰਬੰਧੀਆਂ ਲਈ ਇੱਕੋ ਹੀ ਨਾਮ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ । ਅਜਿਹੇ ਨਾਮ ਸਾਕੇਦਾਰੀ ਦੀ ਤੁਲਨਾ ਵਿੱਚ ਸੰਬੰਧ ਬਾਰੇ ਜ਼ਿਆਦਾ ਦੱਸਦੇ ਹਨ । ਵਿਅਕਤੀਨਿਸ਼ਠ ਸ਼ਬਦ ਅਸਲੀ ਸੰਬੰਧਾਂ ਬਾਰੇ ਦੱਸਦੇ ਹਨ । ਜਿਵੇਂ ਅੰਕਲ ਨੂੰ ਅਸੀਂ ਮਾਮੇ, ਚਾਚੇ, ਫੁੱਫੜ ਤੇ ਮਾਸੜ ਲਈ ਪ੍ਰਯੋਗ ਕਰਦੇ ਹਾਂ ।
ਇਹ ਪਹਿਲੇ ਪ੍ਰਕਾਰ ਦੀ ਉਦਾਹਰਣ ਹੈ । ਪ੍ਰੰਤੂ ਫਾਦਰ ਜਾਂ ਪਿਤਾ ਲਈ ਕੋਈ ਸ਼ਬਦ ਪ੍ਰਯੋਗ ਨਹੀਂ ਹੋ ਸਕਦੇ । ਇਸੇ ਤਰ੍ਹਾਂ Nephew ਨੂੰ ਭਤੀਜੇ ਅਤੇ ਭਾਣਜੇ ਲਈ Cousin ਨੂੰ ਮਾਮੇ, ਚਾਚੇ, ਤਾਏ, ਮਾਸੀ, ਭੂਆ ਦੇ ਬੱਚਿਆਂ ਲਈ ਪ੍ਰਯੋਗ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਇਸੇ ਤਰ੍ਹਾਂ Sister in Law ਨੂੰ ਸਾਲੀ ਤੇ ਨਨਾਣ ਅਤੇ Brother in Law ਨੂੰ ਦਿਓਰ ਤੇ ਸਾਲੇ ਲਈ ਪ੍ਰਯੋਗ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਆਧੁਨਿਕ ਸਮਾਜ ਵਿੱਚ ਨਵੇਂ-ਨਵੇਂ ਸ਼ਬਦਾਂ ਦਾ ਪ੍ਰਯੋਗ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਅਸਲ ਵਿਚ ਇਹ ਸਾਰੇ ਸ਼ਬਦ ਸਾਕੇਦਾਰੀ ਦੇ ਸੂਚਕ ਹਨ ਤੇ ਵਿਆਹਕ ਸਾਕੇਦਾਰੀ ਉੱਤੇ ਆਧਾਰਿਤ ਹੁੰਦੇ ਹਨ । ਜਿਵੇਂ ਵਿਅਕਤੀ ਨੂੰ ਜਵਾਈ ਦਾ ਦਰਜਾ, ਪਤੀ ਦਾ ਦਰਜਾ, ਔਰਤ ਨੂੰ ਨੂੰਹ ਤੇ ਪਤਨੀ ਦਾ ਦਰਜਾ ਵਿਆਹ ਕਰਕੇ ਹੀ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਅਸੀਂ ਬਹੁਤ ਸਾਰੀਆਂ ਵਿਆਹਕ ਰਿਸ਼ਤੇਦਾਰੀਆਂ ਨੂੰ ਗਿਣ ਸਕਦੇ ਹਾਂ ।
![]()
![]()