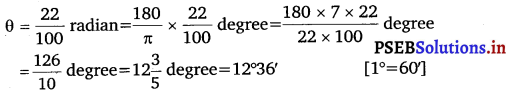Class 11

Punjab State Board PSEB 11th Class Maths Book Solutions Chapter 3 Trigonometric Functions Ex 3.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Maths Chapter 3 Trigonometric Functions Ex 3.2

Question 1.
Find the values of other five trigonometric functions if cos x = – \(\frac{1}{2}\) x lies in third quadrant.
Answer.

Question 2.
Find the values of other five trigonometric functions if sin x = \(\frac{3}{5}\), x lies in second quadrant.
Answer.
sin x = \(\frac{3}{5}\)

cosec x = \(\frac{1}{\sin x}=\frac{1}{\left(\frac{3}{5}\right)}=\frac{5}{3}\)
sin² x + cos² x = 1
⇒ cos² x = 1 – sin² x
⇒ cos² x = 1 – (\(\frac{3}{5}\))²

⇒ cos² x = 1 – \(\frac{9}{25}\)

⇒ cos² x = \(\frac{16}{25}\)

⇒ cos x = ± \(\frac{4}{5}\)
Since x lies in the 2nd quadrant, the value of cos x will be negative

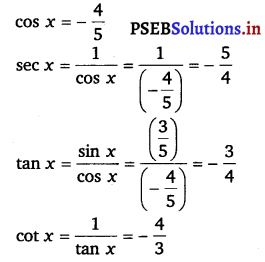
Question 3.
Find the values of other five trigonometric functions if cot x = \(\frac{3}{4}\), x lies in third quadrant.
Answer.

⇒ \(\frac{4}{3}=\frac{\sin x}{\frac{-3}{5}}\)

⇒ sin x = \(\left(\frac{4}{3}\right) \times\left(\frac{-3}{5}\right)=-\frac{4}{5}\)

⇒ cosec x = \(\frac{1}{\sin x}=-\frac{5}{4}\).

Question 4.
Find the values of other five trigonometric functions if sec x = \(\frac{13}{5}\), x lies in fourth quadrant.
Answer.

Question 5.
Find the values of other five trigonometric functions if tan x = \(\frac{5}{12}\), x lies in second quadrant.
Answer.
tan x = – \(\frac{5}{12}\)

cot x = \(\frac{1}{\tan x}=\frac{1}{\left(-\frac{5}{12}\right)}=-\frac{12}{5}\)

1 + tan² x = sec² x

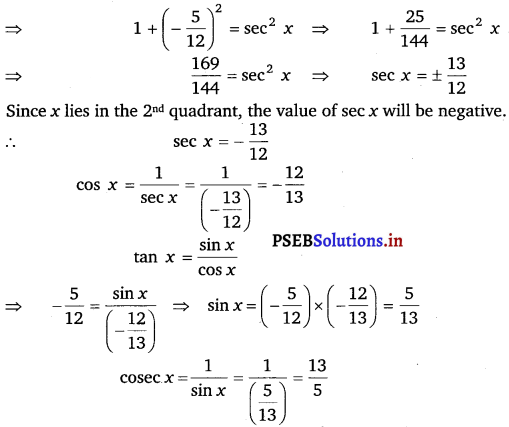
Question 6.
Find the value of the trigonometric function sin 765°.
Ans.
It is known that the values of sin x repeat after an interval of 2π or 360°.
∴ sin 765° = sin (2 × 360° + 45°)
= sin 45° = 1

Question 7.
Find the value of the trigonometric function cosec (- 1410°).
Answer.
It is known that the values of cosec x repeat after an interval of 2π or 360°.
∴ cosec (- 1410°) = cosec (- 1410° + 4 x 360°)
= cosec (- 1410° + 1440°)
= cosec 30° = 2.

Question 8.
Find the value of the trigonometric function tan \(\frac{19 \pi}{3}\).
Answer.
It is known that the values of tan x repeat after an interval of π or 180°.
∴ \(\tan \frac{19 \pi}{3}=\tan 6 \frac{1}{3} \pi\)

= \(\tan \left(6 \pi+\frac{\pi}{3}\right)=\tan \frac{\pi}{3}\)

= tan 60° = √3.

Question 9.
Find the value of the trigonometric function sin \(\left(-\frac{11 \pi}{3}\right)\).
Answer.
It is known that the values of cot x repeat after an interval of π or 180°.

∴ \(\sin \left(\frac{11 \pi}{3}\right)=\sin \left(-\frac{11 \pi}{3}+2 \times 2 \pi\right)\)

= \(\sin \left(\frac{\pi}{3}\right)=\sin 60^{\circ}=\frac{\sqrt{3}}{2}\)

Question 10.
Find the value of the trigonometric function cot \(\left(-\frac{15 \pi}{4}\right)\).
Answer.
It is known that the values of cot x repeat after an interval of ir or 1800.
∴ \(\cot \left(-\frac{15 \pi}{4}\right)=\cot \left(-\frac{15 \pi}{4}+4 \pi\right)=\cot \frac{\pi}{4}\) = 1.

Punjab State Board PSEB 11th Class Environmental Education Book Solutions Chapter 3 ਮਨੁੱਖੀ ਗਤੀਵਿਧੀਆਂ ਦਾ ਵਾਤਾਵਰਣ ਉੱਪਰ ਪ੍ਰਭਾਵ Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Environmental Education Chapter 3 ਮਨੁੱਖੀ ਗਤੀਵਿਧੀਆਂ ਦਾ ਵਾਤਾਵਰਣ ਉੱਪਰ ਪ੍ਰਭਾਵ

Environmental Education Guide for Class 11 PSEB ਮਨੁੱਖੀ ਗਤੀਵਿਧੀਆਂ ਦਾ ਵਾਤਾਵਰਣ ਉੱਪਰ ਪ੍ਰਭਾਵ Textbook Questions and Answers

(ਉ) ਬਹੁਤ ਛੋਟੇ ਪੁੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ

ਪ੍ਰਸ਼ਨ 1.
ਸ਼ਹਿਰੀਕਰਨ (Urbanisation) ਕੀ ਹੈ ?
ਉੱਤਰ-
ਸ਼ਹਿਰੀਕਰਨ ਉਹ ਕ੍ਰਿਆ ਹੈ ਜਿਸਦੇ ਰਾਹੀਂ ਜ਼ਿਆਦਾ ਸੰਖਿਆ ਵਿਚ ਲੋਕ ਪੂਰਨ ਰੂਪ ਵਿਚ ਸ਼ਹਿਰਾਂ ਵਿਚ ਵਸ ਜਾਂਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 2.
ਗੰਦੀਆਂ ਬਸਤੀਆਂ (Slums) ਕੀ ਹਨ ?
ਉੱਤਰ-
ਗਰੀਬ ਲੋਕਾਂ ਦੁਆਰਾ ਸ਼ਹਿਰਾਂ ਅਤੇ ਪਿੰਡਾਂ ਦੇ ਚਾਰੇ ਪਾਸੇ ਖ਼ਾਲੀ ਸਥਾਨਾਂ ‘ਤੇ ਝੌਪੜੀਆਂ ਅਤੇ ਝੁੱਗੀਆਂ ਦੇ ਨਿਰਮਾਣ ਦੇ ਦੁਆਰਾ ਵਸਾਈਆਂ ਗਈਆਂ ਬਸਤੀਆਂ ਨੂੰ ਗੰਦੀਆਂ ਬਸਤੀਆਂ ਕਹਿੰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 3.
ਭੂਮੀਗਤ ਪਾਣੀ (Underground water) ਦੀ ਪਰਿਭਾਸ਼ਾ ਲਿਖੋ ।
ਉੱਤਰ-
ਜ਼ਮੀਨ ਦੇ ਹੇਠਾਂ ਤਰੇੜਾਂ ਵਿਚ ਜਮਾਂ ਪਾਣੀ ਨੂੰ ਭੂਮੀਗਤ ਪਾਣੀ ਕਹਿੰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 4.
ਫਸਲ ਚੱਕਰ (Rotation of Crops) ਤੋਂ ਕੀ ਭਾਵ ਹੈ ?
ਉੱਤਰ-
ਇੱਕ ਖੇਤ ਵਿਚ ਫਸਲਾਂ ਨੂੰ ਲਗਾਤਾਰ ਬਦਲ-ਬਦਲ ਕੇ ਲਗਾਉਣ ਦੀ ਪ੍ਰਕਿਰਿਆ ਨੂੰ ਫਸਲ ਚੱਕਰ ਕਹਿੰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 5.
ਧੁਆਂਖੀ-ਧੁੰਦ ਜਾਂ ਧੁੰਦ-ਧੂੰਆਂ ਜਾਂ ਸਮੋਗ (Smog) ਕੀ ਹੈ ?
ਉੱਤਰ-
ਆਵਾਜਾਈ ਦੇ ਸਾਧਨਾਂ ਦੇ ਚੱਲਣ ਨਾਲ ਨਾਈਟਰੋਜਨ ਆਕਸਾਈਡ ਨਿਕਲਦੀ ਹੈ । ਸੂਰਜ ਦੇ ਪ੍ਰਕਾਸ਼ ਦੀ ਉਪਸਥਿਤੀ ਵਿਚ ਹਵਾ ਦੇ ਕਣਾਂ ਵਿਚ ਇਸ ਦੇ ਮਿਲਣ ਨਾਲ ਜੋ ਧੂੰਆਂ ਪੈਦਾ ਹੁੰਦਾ ਹੈ ਉਸ ਨੂੰ ਧੁਆਂਖੀ-ਧੁੰਦ/ਧੁੰਦ-ਧੂੰਆਂ ਕਹਿੰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 6.
ਗਰੀਨ ਹਾਊਸ ਪ੍ਰਭਾਵ (Green House Effect) ਕਿਵੇਂ ਪੈਦਾ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਵਾਤਾਵਰਣ ਵਿਚ ਕਾਰਬਨ ਡਾਈਆਕਸਾਈਡ ਦੀ ਮਾਤਰਾ ਵਧ ਹੋਣ ਨਾਲ ਗਰੀਨ ਹਾਊਸ ਪ੍ਰਭਾਵ ਪੈਦਾ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 7.
ਸਮੁੰਦਰ ਤੋਂ ਪ੍ਰਾਪਤ ਹੋਣ ਵਾਲੇ ਖਣਿਜਾਂ ਦੇ ਨਾਮ ਲਿਖੋ ।
ਉੱਤਰ-
ਸਮੁੰਦਰ ਵਿਚੋਂ ਆਇਓਡੀਨ ਅਤੇ ਪੈਟਰੋਲੀਅਮ ਆਦਿ ਖਣਿਜ ਪ੍ਰਾਪਤ ਹੁੰਦੇ ਹਨ |

(ਅ) ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ (Type I)

ਪ੍ਰਸ਼ਨ 1.
ਪ੍ਰਵਾਸ (Migration) ਵਾਤਾਵਰਣ ਨੂੰ ਕਿਵੇਂ ਪ੍ਰਭਾਵਿਤ ਕਰਦਾ ਹੈ ?
ਉੱਤਰ-
ਆਬਾਦੀ ਦੇ ਇਕ ਸਥਾਨ ਤੋਂ ਦੂਸਰੇ ਸਥਾਨ ਤੇ ਸਥਾਨਾਂਤਰਨ ਨੂੰ ਪ੍ਰਵਾਸ ਕਹਿੰਦੇ ਹਨ । ਜ਼ਿਆਦਾਤਰ ਸ਼ਹਿਰੀ ਇਲਾਕਿਆਂ ਵਿਚ ਜ਼ਿਆਦਾ ਲੋਕਾਂ ਦਾ ਮੂਲ ਸਥਾਨ ਸ਼ਹਿਰ ਨਹੀਂ ਹੈ । ਪੇਂਡੂ ਇਲਾਕਿਆਂ ਤੋਂ ਲੋਕ ਸ਼ਹਿਰਾਂ ਵਿਚ ਰੁਜ਼ਗਾਰ, ਵਪਾਰ, ਸਿੱਖਿਆ ਆਦਿ ਪ੍ਰਾਪਤ ਕਰਨ ਜਾਂਦੇ ਹਨ | ਪ੍ਰਵਾਸ ਦੇ ਕਾਰਨ ਸ਼ਹਿਰੀ ਵਾਤਾਵਰਣ ਨੂੰ ਕਈ ਸਮੱਸਿਆਵਾਂ ਦਾ ਸਾਹਮਣਾ ਕਰਨਾ ਪੈਂਦਾ ਹੈ । ਇਨ੍ਹਾਂ ਵਿਚੋਂ ਪ੍ਰਮੁੱਖ ਹਨ –

• ਰਹਿਣ ਦੀ ਸਮੱਸਿਆ ।
• ਪ੍ਰਦੂਸ਼ਣ ਦੀ ਸਮੱਸਿਆ
• ਵਸੋਂ ਵਿਚ ਵਾਧਾ
• ਖੇਤੀ ਯੋਗ ਭੂਮੀ ਤੇ ਦਬਾਉ
• ਕੂੜੇ-ਕਰਕਟ ਵਿਚ ਵਾਧਾ
• ਗੰਦੀਆਂ ਬਸਤੀਆਂ ਦਾ ਵਿਕਾਸ ॥

ਪ੍ਰਸ਼ਨ 2.
ਚਲਦੀ-ਫਿਰਦੀ ਵਸੋਂ (Floating Population) ਕਿਸ ਨੂੰ ਆਖਦੇ ਹਨ ?
ਉੱਤਰ-
ਚਲਦੀ-ਫਿਰਦੀ ਵਸੋਂ ਵਿਚ ਉਹ ਲੋਕ ਆਉਂਦੇ ਹਨ ਜਿਹੜੇ ਹਰ ਰੋਜ਼ ਰੋਜ਼ੀ-ਰੋਟੀ ਕਮਾਉਣ ਲਈ ਇਕ ਸਥਾਨ ਤੋਂ ਦੂਜੇ ਸਥਾਨ ਤੇ ਜਾਂਦੇ ਹਨ । ਅਜਿਹੇ ਲੋਕ ਜਿੱਥੇ ਕੰਮ ਕਰਦੇ ਹਨ ਉੱਥੇ ਨਹੀਂ ਰਹਿੰਦੇ ਬਲਕਿ ਹਰ ਰੋਜ਼ ਆਪਣੇ ਘਰੇਲੂ ਸਥਾਨ ਤੋਂ ਕੰਮ ਕਰਨ ਵਾਲੇ ਸਥਾਨ ‘ਤੇ ਜਾਂਦੇ ਹਨ | ਚਲਦੀ-ਫਿਰਦੀ ਵਸੋਂ ਵਿਚ ਜ਼ਿਆਦਾਤਰ ਮੱਧ-ਵਰਗ ਦੇ ਲੋਕ ਆਉਂਦੇ ਹਨ । ਇਹ ਲੋਕ ਆਪਣੇ ਕੰਮ ਕਰਨ ਵਾਲੇ ਸਥਾਨ ‘ਤੇ ਜਾਣ ਲਈ ਬੱਸ ਅਤੇ ਰੇਲ ਗੱਡੀ ਰਾਹੀਂ ਯਾਤਰਾ ਕਰਦੇ ਹਨ।

ਪ੍ਰਸ਼ਨ 3.
ਲੋਕ ਸ਼ਹਿਰਾਂ ਵੱਲ ਕਿਉਂ ਜਾ ਰਹੇ ਹਨ ? ਕਾਰਨ ਦੱਸੋ ।
ਉੱਤਰ-
ਲੋਕ ਹੇਠ ਲਿਖੇ ਕਾਰਨਾਂ ਕਰਕੇ ਸ਼ਹਿਰਾਂ ਵੱਲ ਜਾ ਰਹੇ ਹਨ

1. ਰੋਜ਼ੀ-ਰੋਟੀ ਕਮਾਉਣ ਲਈ ।
2. ਚੰਗੀਆਂ ਸੁੱਖ ਸੁਵਿਧਾਵਾਂ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ ।
3. ਸਮਾਜਿਕ ਸੁਰੱਖਿਆ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ ।
4. ਸਿੱਖਿਆ ਦੇ ਚੰਗੇ ਅਵਸਰਾਂ ਲਈ ।
5. ਚੰਗੀਆਂ ਡਾਕਟਰੀ ਸਹੂਲਤਾਂ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ ।

ਪ੍ਰਸ਼ਨ 4.
ਦੋ ਮਨੁੱਖੀ ਗਤੀਵਿਧੀਆਂ ਦੱਸੋ, ਜਿਨ੍ਹਾਂ ਨਾਲ ਭੂਮੀ-ਖੋਰ (Soil-erosion) ਹੁੰਦਾ ਹੈ।
ਉੱਤਰ-

• ਕੀਟਨਾਸ਼ਕ ਅਤੇ ਰਸਾਇਣਿਕ ਦਵਾਈਆਂ ਦਾ ਜ਼ਿਆਦਾ ਉਪਯੋਗ ਕਰਨਾ ।
• ਇੱਕੋ ਹੀ ਖੇਤ ਵਿੱਚ ਇਕ ਹੀ ਪ੍ਰਕਾਰ ਦੀ ਫਸਲ ਨੂੰ ਬਾਰ-ਬਾਰ ਉਗਾਉਣਾ ।

ਪ੍ਰਸ਼ਨ 5.
ਵਾਹਨਾਂ ਦੇ ਧੂੰਏਂ ਦੇ ਅਸਰ ਉੱਪਰ ਇੱਕ ਨੋਟ ਲਿਖੋ।
ਉੱਤਰ-
ਆਧੁਨਿਕ ਯੁੱਗ ਵਿਚ ਆਵਾਜਾਈ ਦੇ ਸਾਧਨਾਂ ਦੀ ਸੰਖਿਆ ਦਿਨੋ-ਦਿਨ ਵਧ ਰਹੀ ਹੈ । ਇਹ ਸਾਰੇ ਸਾਧਨ ਪੈਟਰੋਲ, ਡੀਜ਼ਲ, ਕੋਲਾ, ਕੁਦਰਤੀ ਗੈਸ ਆਦਿ ਨਾਲ ਚੱਲਦੇ ਹਨ । ਪੈਟਰੋਲੀਅਮ ਬਾਲਣਾਂ ਦੇ ਬਲਣ ਦੇ ਕਾਰਨ ਵਾਹਨਾਂ ਵਿਚ ਕਾਰਬਨ, ਨਾਈਟਰੋਜਨ, ਸਲਫਰ ਦੇ ਆਕਸਾਈਡ ਆਦਿ ਗੈਸਾਂ ਪੈਦਾ ਹੁੰਦੀਆਂ ਹਨ |
ਇਹ ਗੈਸਾਂ ਹਵਾ ਪ੍ਰਦੂਸ਼ਣ ਦਾ ਮੁੱਖ ਕਾਰਨ ਹਨ | ਹਵਾ ਪ੍ਰਦੂਸ਼ਣ ਦੇ ਨਾਲ ਮਨੁੱਖਾਂ ਅਤੇ ਪਸ਼ੂਆਂ ਦੀ ਸਿਹਤ ਤੇ ਉਲਟ ਪ੍ਰਭਾਵ ਪੈਂਦਾ ਹੈ । ਇਸਦੇ ਨਾਲ ਸਾਹ ਸੰਬੰਧੀ ਰੋਗ ਵਧਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 6.
ਮਨੁੱਖੀ ਗਤੀਵਿਧੀਆਂ ਕਰਕੇ ਜੰਗਲਾਂ ਦੀ ਖੀਣਤਾ ਕਿਉਂ ਹੋਈ ਹੈ ?
ਉੱਤਰ-
ਜੰਗਲਾਂ ਨੂੰ ਨਸ਼ਟ ਕਰਨ ਦੇ ਮਨੁੱਖੀ ਕਾਰਨ ਹੇਠ ਲਿਖੇ ਹਨ –

1. ਖੇਤੀ ਲਈ ਭੂਮੀ ਦਾ ਵਿਸਥਾਰ
2. ਬਦਲਵੀਂ ਖੇਤੀ
3. ਪਸ਼ੂਆਂ ਦਾ ਜ਼ਿਆਦਾ ਚਰਾਉਣਾ
4. ਬੰਨ੍ਹ ਪਰਿਯੋਜਨਾਵਾਂ
5. ਬਾਲਣ ਲਈ ਲੱਕੜੀ ਕੱਟਣਾ।
6. ਸੜਕਾਂ ਅਤੇ ਰੇਲ ਮਾਰਗਾਂ ਦਾ ਵਿਕਾਸ
7. ਵਪਾਰਿਕ ਉਦੇਸ਼ਾਂ ਦੇ ਲਈ
8. ਖੁਦਾਈ ॥

(ੲ) ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ (Type II)

ਪ੍ਰਸ਼ਨ 1.
ਸੋਤਾਂ ਦੀ ਅਸਾਵੀਂ ਵੰਡ ਦੇ ਵਿਕਾਸ ਉੱਪਰ ਕੀ ਪ੍ਰਭਾਵ ਹਨ ?
ਉੱਤਰ-
ਪ੍ਰਾਕ੍ਰਿਤਿਕ ਸੰਪੱਤੀ ਜਾਂ ਸ੍ਰੋਤਾਂ ਦੀ ਅਸਾਵੀਂ ਵੰਡ ਦੇ ਕਾਰਨ, ਉਹਨਾਂ ਦੀ ਵਰਤੋਂ ਸੰਬੰਧੀ ਕਈ ਸਮੱਸਿਆਵਾਂ ਪੈਦਾ ਹੁੰਦੀਆਂ ਹਨ । ਜਿਸ ਖੇਤਰ ਵਿੱਚ, ਇਕ ਵਿਸ਼ੇਸ਼ ਪ੍ਰਕਾਰ ਦੇ ਸਾਧਨ ਜ਼ਿਆਦਾ ਹੋਣ ਉਸ ਖੇਤਰ ਵਿਚ ਉਸ ਸਾਧਨ ਦੀ ਜ਼ਿਆਦਾ ਵਰਤੋਂ ਹੁੰਦੀ ਹੈ ਜਿਸਦੇ ਕਾਰਨ ਉਸ ਖੇਤਰ ਵਿਚ ਸਾਧਨ ਦੇ ਭੰਡਾਰ ਖ਼ਤਮ ਹੋ ਜਾਂਦੇ ਹਨ । ਉਦਾਹਰਨ ਦੇ ਤੌਰ ‘ਤੇ ਅਮਰੀਕਾ ਵਿਚ ਮੇਸਾਵੀ ਰੱਜ ਲੋਹੇ ਦੀਆਂ ਚੱਟਾਨਾਂ ਦੇ ਭੰਡਾਰਾਂ ਨਾਲ ਭਰਿਆ ਹੋਇਆ ਹੈ ਅਤੇ ਇਸਦੇ ਜ਼ਿਆਦਾ ਪ੍ਰਯੋਗ ਕਾਰਨ ਇਸਦੇ ਭੰਡਾਰ ਦੀਆਂ ਖਾਣਾਂ ਸਮਾਪਤ ਹੋ ਰਹੀਆਂ ਹਨ । ਦੂਜੀ ਤਰਫ ਰੂਸ ਦੇ ਪੂਰਬੀ ਭਾਗ ਵਿਚ ਟਿਨ ਅਤੇ ਸੋਨੇ ਦੀਆਂ ਖਾਣਾਂ ਹਨ ਪਰ ਉਹ ਖਾਣਾਂ ਉੱਥੇ ਦੀ ਜਲਵਾਯੂ ਅਤੇ ਪਰਿਸਥਿਤੀਆਂ ਕਾਰਨ ਵਰਤੋਂ ਵਿਚ ਨਹੀਂ ਲਿਆਂਦੀਆਂ ਗਈਆਂ । ਪ੍ਰਾਕ੍ਰਿਤਿਕ ਭੰਡਾਰ ਦੀ ਅਸਾਂਵੀ ਵੰਡ ਕਾਰਨ ਉਤਪਾਦਨ ਦੀ ਲਾਗਤ ਵਧ ਜਾਂਦੀ ਹੈ । ਉਦਯੋਗਾਂ ਲਈ ਕੱਚਾ ਮਾਲ ਚਾਹੀਦਾ ਹੁੰਦਾ ਹੈ ਜੋ ਹਰ ਜਗਾ ਉਪਲੱਬਧ ਨਹੀਂ ਹੁੰਦਾ ਹੈ | ਕੱਚੇ ਮਾਲ ਦਾ ਅਯਾਤ ਉਸ ਖੇਤਰ ਵਿਚੋਂ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ਜਿੱਥੇ ਇਨ੍ਹਾਂ ਦਾ ਭੰਡਾਰ ਹੋਣ 1 ਕੱਚੇ ਮਾਲ ਨੂੰ ਲੰਬੀ ਦੂਰੀ ਤੋਂ ਮੰਗਵਾਉਣ ਵਿਚ ਬਹੁਤ ਸਾਰਾ ਧਨ ਅਤੇ ਸਮਾਂ ਖ਼ਰਚ ਹੁੰਦਾ ਹੈ । ਜਿਸ ਨਾਲ ਉਤਪਾਦਨ ਅਤੇ ਲਾਗਤ ਉੱਤੇ ਮਾੜਾ ਪ੍ਰਭਾਵ ਪੈਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2. ਸ਼ਹਿਰੀ ਲੋਕਾਂ ਦੁਆਰਾ ਜ਼ਮੀਨ ਅਤੇ ਪਾਣੀ ਨੂੰ ਕਿਵੇਂ ਪ੍ਰਦੂਸ਼ਿਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਸ਼ਹਿਰਾਂ ਵਿਚ ਜ਼ਮੀਨ ਅਤੇ ਪਾਣੀ ਦੀ ਵੱਧ ਵਰਤੋਂ ਦੇ ਕਾਰਨ ਗੰਭੀਰ ਵਾਤਾਵਰਣੀ ਸਮੱਸਿਆਵਾਂ ਦੇਖੀਆਂ ਜਾ ਸਕਦੀਆਂ ਹਨ । ਜ਼ਿਆਦਾ ਸ਼ਹਿਰੀਕਰਨ ਅਤੇ ਉਦਯੋਗੀਕਰਨ ਦੇ ਕਾਰਨ ਪਾਕਿਤਿਕ ਸਾਧਨਾਂ ਨੂੰ ਖ਼ਪਤ ਕਰਨ ਦੀ ਦਰ ਵੀ ਵੱਧ ਜਾਂਦੀ ਹੈ । ਇਸ ਲਈ ਸ਼ਹਿਰਾਂ ਅਤੇ ਜ਼ਿਆਦਾ ਉਦਯੋਗਿਕ ਖੇਤਰਾਂ ਵਿਚ ਕੁਦਰਤੀ ਸਾਧਨਾਂ ਦਾ ਜ਼ਿਆਦਾ ਵਿਘਟਨ ਹੋ ਰਿਹਾ ਹੈ । ਸ਼ਹਿਰਾਂ ਵਿਚ ਵਿਕਾਸ ਗਤੀਵਿਧੀਆਂ, ਜਿਵੇਂ ਭਵਨ ਨਿਰਮਾਣ, ਰੇਲ ਅਤੇ ਸੜਕਾਂ ਦੇ ਨਿਰਮਾਣ, ਪੁਲਾਂ ‘ਤੇ ਬੰਨ੍ਹ ਬਣਾਉਣ ਦੀ ਪ੍ਰਕਿਰਿਆ ਆਦਿ ਭੂਮੀ ਉੱਤੇ ਪ੍ਰਤੀਕੂਲ ਪ੍ਰਭਾਵ ਪਾਉਂਦੀਆਂ ਹਨ | ਉਦਯੋਗਿਕ ਵਸਤੂਆਂ; ਜਿਵੇਂ ਪਲਾਸਟਿਕ, ਰੰਗ, ਰਸਾਇਣ, ਸੀਮੇਂਟ, ਚਮੜਾ ਆਦਿ ਭੂਮੀ ਪ੍ਰਦੂਸ਼ਣ ਲਈ ਜ਼ਿੰਮੇਵਾਰ ਹਨ । ਖੇਤੀ ਪ੍ਰਕਿਰਿਆ ਵਿਚ ਕੀਟਨਾਸ਼ਕ ਦਵਾਈਆਂ ਦੀ ਜ਼ਿਆਦਾ ਵਰਤੋਂ ਵੀ ਵਾਤਾਵਰਣ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਦੀ ਹੈ ।

ਜ਼ਿਆਦਾਤਰ ਸ਼ਹਿਰਾਂ ਵਿਚ ਕਾਰਬਨੀ ਅਤੇ ਅਕਾਰਬਨੀ ਪਦਾਰਥ ਰਹਿੰਦ-ਖੂੰਹਦ ਦੇ ਰੂਪ ਵਿਚ ਖੁੱਲ੍ਹੇ ਵਿਚ ਪਏ ਹੁੰਦੇ ਹਨ । ਇਹੋ ਜਿਹੇ ਪਦਾਰਥਾਂ ਨੂੰ ਅਲੱਗ ਕਰਨ ਦੀ ਕੋਈ ਘਰੇਲੁ ਪ੍ਰਣਾਲੀ ਉਪਲੱਬਧ ਨਹੀਂ ਹੈ । ਇਸਦੇ ਕਾਰਨ ਵੀ ਭੂਮੀ ਦਾ ਪ੍ਰਦੂਸ਼ਣ (Land Pollution or Soil Pollution) ਹੋ ਜਾਂਦਾ ਹੈ । ਸ਼ਹਿਰਾਂ ਵਿਚ ਵਸੋਂ ਦੇ ਵਾਧੇ ਦੇ ਕਾਰਨ ਕੁੜਾ-ਕਰਕਟ ਵੀ ਭਾਰੀ ਮਾਤਰਾ ਵਿਚ ਪਾਇਆ ਜਾਂਦਾ ਹੈ | ਪਾਣੀ ਸਰੋਤਾਂ ਦੇ ਕੋਲ ਪਾਏ ਜਾਣ ਵਾਲੇ ਕੁੜੇ ਦੇ ਢੇਰਾਂ ਅਤੇ ਗੰਦਗੀ ਇਨ੍ਹਾਂ ਸੈਤਾਂ ਤਕ ਪਹੁੰਚ ਕੇ ਪਾਣੀ ਨੂੰ ਪ੍ਰਦੂਸ਼ਿਤ ਕਰਦੀ ਹੈ ।

ਉਦਯੋਗਾਂ ਦੇ ਕਾਰਨ ਪਾਣੀ ਵਿਚ ਵੀ ਕਈ ਪ੍ਰਕਾਰ ਦੇ ਪ੍ਰਦੂਸ਼ਤ ਪਾਏ ਜਾਂਦੇ ਹਨ, ਜਿਵੇਂ ਪਾਰਾ, ਲੈਂਡ, ਤਾਂਬਾ, ਅਮਲ (Acid), ਫਰਨਾਈਲ ਆਦਿ ਜ਼ਿਆਦਾ ਉਤਪਾਦਨ ਕੇਂਦਰ, ਤੇਲ ਸੋਧਕ ਕਾਰਖ਼ਾਨੇ ਆਦਿ ਦੇ ਗਰਮ ਵਹਾਵ ਪਾਣੀ ਸਰੋਤਾਂ ਜਿਵੇਂ ਝੀਲ, ਸਮੁੰਦਰ, ਨਦੀਆਂ, ਆਦਿ ਵਿਚ ਛੱਡੇ ਜਾਣ ਨਾਲ ਤਾਪਮਾਨ ਵਿਚ ਵਾਧਾ ਹੋ ਜਾਂਦਾ ਹੈ ਅਤੇ ਜਿਸਦੇ ਕਾਰਨ ਜੀਵ-ਜੰਤੂ ਮਰ ਜਾਂਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 3.
ਜ਼ਮੀਨ ਨੂੰ ਵਰਤਣ ਦੇ ਢੰਗ ਉੱਪਰ ਇੱਕ ਨੋਟ ਲਿਖੋ ।…
ਉੱਤਰ-
ਭੂਮੀ ਇਕ ਅਧਾਰਭੂਤ ਪਾਤਿਕ ਸੰਪੱਤੀ ਹੈ । ਇਹ ਸਭ ਨੂੰ ਆਧਾਰ ਪ੍ਰਦਾਨ ਕਰਦੀ ਹੈ । ਭੂਮੀ ਪੌਦਿਆਂ ਨੂੰ ਪਾਣੀ ਅਤੇ ਪੋਸ਼ਟਿਕ ਤੱਤ ਪ੍ਰਦਾਨ ਕਰਦੀ ਹੈ । ਸਾਰੇ ਜੀਵ-ਜੰਤੂ ਮਨੁੱਖੀ ਗਤੀਵਿਧੀਆਂ ਦਾ ਵਾਤਾਵਰਣ ਉੱਪਰ ਪ੍ਰਭਾਵ ਅਤੇ ਮਨੁੱਖ ਪ੍ਰਤੱਖ ਜਾਂ ਅਪ੍ਰਤੱਖ ਰੂਪ ਵਿਚ ਆਪਣਾ ਭੋਜਨ ਭੂਮੀ ਤੋਂ ਹੀ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਨ ।
ਖੇਤੀ ਦੇ ਲਈ ਜ਼ਿਆਦਾ ਭੂਮੀ ਉਪਲੱਬਧ ਕਰਵਾਉਣ ਦੇ ਲਈ ਵਣਾਂ ਨੂੰ ਕੱਟਿਆ ਜਾਂਦਾ ਹੈ । ਜਿਸਦੇ ਕਾਰਨ ਹੜ੍ਹ, ਭੂਮੀ ਖੋਰ, ਸੋਕਾ ਅਤੇ ਰੇਗਿਸਤਾਨੀਕਰਨ ਆਦਿ ਦਾ ਖਤਰਾ ਵਧ ਗਿਆ ਹੈ ।

ਵਸੋਂ ਵਾਧੇ ਨਾਲ ਉਤਪੰਨ ਹੋਈ ਖਾਧ ਪਦਾਰਥਾਂ ਦੀ ਸਮੱਸਿਆ ਨਾਲ ਨਿਪਟਣ ਲਈ ਖੇਤਾਂ ਨੂੰ ਖਾਲੀ ਨਹੀਂ ਛੱਡਿਆ ਜਾਂਦਾ ਹੈ । ਭੂਮੀ ਉੱਪਰ ਜ਼ਿਆਦਾ ਫਸਲ ਉਗਾਉਣ ਦੇ ਕਾਰਨ ਭੂਮੀ ਦੀ ਉਪਜਾਊ ਸ਼ਕਤੀ ਘੱਟ ਜਾਂਦੀ ਹੈ । ਇਸ ਲਈ ਪੌਸ਼ਟਿਕ ਤੱਤਾਂ ਨੂੰ ਪੂਰਾ ਕਰਨ ਲਈ ਰਸਾਇਣਕ ਪਦਾਰਥਾਂ ਦੀ ਵਰਤੋਂ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ਪਰ ਇਹਨਾਂ ਦੀ ਜ਼ਿਆਦਾ ਵਰਤੋਂ ਕਾਰਨ, ਭੂਮੀ ਦੀ ਸ਼ਕਤੀਹੀਣਤਾ, ਰੇਗਿਸਤਾਨੀਕਰਨ, ਭੂਮੀ ਖੋਰ ਜਿਹੀਆਂ ਸਮੱਸਿਆਵਾਂ ਪੈਦਾ ਹੋ ਜਾਂਦੀਆਂ ਹਨ । ਇਸੇ ਤਰ੍ਹਾਂ ਭੂਮੀ ਤੇ ਇਕ ਹੀ ਪ੍ਰਕਾਰ ਦੀ ਫ਼ਸਲ ਉਗਾਉਣ ਨਾਲ ਭੂਮੀ ਦੀ ਉਪਜਾਊ ਸ਼ਕਤੀ ਪ੍ਰਭਾਵਿਤ ਹੁੰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 4.
ਸ਼ਹਿਰੀ ਖੇਤਰਾਂ ਦੀਆਂ ਮੁੱਖ ਸਮੱਸਿਆਵਾਂ ਦੀ ਚਰਚਾ ਕਰੋ ।
ਉੱਤਰ-
ਸ਼ਹਿਰੀ ਖੇਤਰਾਂ ਦੀਆਂ ਮੁੱਖ ਸਮੱਸਿਆਵਾਂ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਹੈ –

1. ਪ੍ਰਦੂਸ਼ਣ ਵਿਚ ਵਾਧਾ (Increase in Pollution)-ਸ਼ਹਿਰੀ ਖੇਤਰਾਂ ਵਿਚ ਵਸੋਂ ਦੇ ਵਾਧੇ ਦੇ ਕਾਰਨ ਵਾਹਨਾਂ ਦੀ ਸੰਖਿਆ ਵਧ ਗਈ ਹੈ | ਆਵਾਜਾਈ ਦੇ ਸਾਧਨਾਂ ਦੇ ਵਾਧੇ ਦੇ ਫਲਸਰੂਪ ਹਵਾ ਅਤੇ ਧੁਨੀ ਪ੍ਰਦੂਸ਼ਣ ਦੀ ਦਰ ਵਿਚ ਵਾਧਾ ਹੋ ਗਿਆ ਹੈ । ਵਾਹਨਾਂ ਵਿਚ ਜਲਨ ਵਾਲੇ ਬਾਲਣ ਦੇ ਕਾਰਨ ਜ਼ਹਿਰੀਲੀ ਗੈਸ ਪੈਦਾ ਹੁੰਦੀ ਹੈ ਜਿਸਦੇ ਕਾਰਨ ਸਾਹ ਦੀਆਂ ਸਮੱਸਿਆਵਾਂ ਪੈਦਾ ਹੋ ਰਹੀਆਂ ਹਨ । ਧੁਨੀ ਪ੍ਰਦੂਸ਼ਣ ਮਾਨਸਿਕ ਸਮੱਸਿਆਵਾਂ ਪੈਦਾ ਕਰਦਾ ਹੈ ।
2. ਗੰਦੀਆਂ ਬਸਤੀਆਂ ਦਾ ਵਿਕਾਸ (Development of Slums)-ਗੰਦੀਆਂ ਬਸਤੀਆਂ ਅਨਿਯਮਿਤ ਜਾਂ ਸੰਘਣੀ ਵਸੋਂ ਵਾਲੇ ਇਸ ਤਰ੍ਹਾਂ ਦੇ ਖੇਤਰ ਹਨ ਜਿਨ੍ਹਾਂ ਦਾ ਜੀਵਨ ਪੱਧਰ ਬਹੁਤ ਨੀਵਾਂ ਹੁੰਦਾ ਹੈ । ਪੇਂਡੂ ਲੋਕ ਸ਼ਹਿਰਾਂ ਵਲ ਆ ਰਹੇ ਹਨ ਅਤੇ ਸ਼ਹਿਰੀ ਇਲਾਕਿਆਂ ਦੇ ਬਾਹਰੀ ਖੇਤਰਾਂ ਵਿਚ ਆਪਣਾ ਘਰ ਬਣਾ ਕੇ ਰਹਿੰਦੇ ਹਨ । ਹੌਲੀ-ਹੌਲੀ ਇਹ ਖੇਤਰ ਦੀ ਬਸਤੀ ਦਾ ਰੂਪ ਧਾਰ ਲੈਂਦੇ ਹਨ । ਇਨ੍ਹਾਂ ਬਸਤੀਆਂ ਵਿਚ ਗੰਦਗੀ ਦੇ ਢੇਰ ਵਾਤਾਵਰਣ ਨੂੰ ਪ੍ਰਦੂਸ਼ਿਤ ਕਰਦੇ ਹਨ ।
3. ਠੋਸ ਪਦਾਰਥਾਂ ਵਿਚ ਵਾਧਾ ਜਾਂ ਕੂੜੇ-ਕਰਕਟ ਵਿਚ ਵਾਧਾ (Increase in Waste Materials/Garbage)-ਸ਼ਹਿਰਾਂ ਵਿਚ ਕੂੜੇ-ਕਰਕਟ ਵਿਚ ਵਾਧਾ ਵੀ ਇਕ ਗੰਭੀਰ ਸਮੱਸਿਆ ਹੈ । ਕੂੜੇ ਦੇ ਢੇਰ ਬੀਮਾਰੀਆਂ ਫਲਾਉਣ ਵਾਲੇ ਕਾਰਕਾਂ ਜਿਵੇਂ ਮੱਖੀਆਂ ਤੇ ਮੱਛਰਾਂ ਦੇ ਘਰ ਬਣ ਗਏ ਹਨ ।

(ਸ) ਵੱਡੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ

ਪ੍ਰਸ਼ਨ 1.
ਜੀਵਨ ਪੱਧਰ ਉੱਚਾ ਚੁੱਕਣ ਲਈ ਬੁਨਿਆਦੀ ਸਹੂਲਤਾਂ ਜ਼ਰੂਰੀ ਕਿਉਂ ਹਨ ? ਵਸੋਂ ਵਿਸਫੋਟ (Population Explosion) ਦਾ ਇਹਨਾਂ ਬੁਨਿਆਦੀ ਸਹੂਲਤਾਂ ਉੱਪਰ ਕੀ ਪ੍ਰਭਾਵ ਹੈ ?
ਉੱਤਰ-
ਸ਼ਹਿਰੀਕਰਨ ਦੇ ਬਾਅਦ ਸ਼ਹਿਰਾਂ ਵਿਚ ਬੁਨਿਆਦੀ ਸਹੂਲਤਾਂ ਦਾ ਵਿਕਾਸ ਹੋਣ ਦੇ ਕਾਰਨ ਜ਼ਿਆਦਾ ਲੋਕਾਂ ਨੇ ਸ਼ਹਿਰਾਂ ਦੇ ਵਲ ਆਉਣਾ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤਾ |
ਸ਼ਹਿਰਾਂ ਵਿਚ ਚੰਗੀਆਂ ਨੌਕਰੀਆਂ ਦੀਆਂ ਸੰਭਾਵਨਾਵਾਂ, ਚੰਗੀਆਂ ਡਾਕਟਰੀ ਸੇਵਾਵਾਂ, ਸਿੱਖਿਆ ਸਹੂਲਤਾਂ ਅਤੇ ਆਧੁਨਿਕ ਸੁੱਖ-ਸੁਵਿਧਾਵਾਂ ਮਨੁੱਖ ਨੂੰ ਆਪਣੇ ਵੱਲ ਆਕਰਸ਼ਿਤ ਕਰਦੀਆਂ ਹਨ । ਬੁਨਿਆਦੀ ਸਹੂਲਤਾਂ ਜੀਵਨ ਵਿਚ ਉੱਨਤੀ ਦੇ ਲਈ ਅਤਿ ਜ਼ਰੂਰੀ ਹਨ । ਵਰਤਮਾਨ ਯੁੱਗ ਤਕਨੀਕੀ ਅਤੇ ਵਿਗਿਆਨਿਕ ਯੁੱਗ ਹੈ | ਮਨੁੱਖ ਦੀ ਜ਼ਿੰਦਗੀ ਤੇਜ਼ੀ ਨਾਲ ਚਲ ਰਹੀ ਹੈ । ਇਹ ਤੇਜ਼ ਰਫ਼ਤਾਰ ਜ਼ਿੰਦਗੀ ਦੇ ਠੀਕ ਢੰਗ ਨਾਲ ਚਲਣ ਦੇ ਲਈ ਆਧੁਨਿਕ ਸੁੱਖ-ਸਹੂਲਤਾਂ ਦੀ ਜ਼ਰੂਰਤ ਹੈ । ਸ਼ਹਿਰਾਂ ਵਿਚ ਹਰ ਚੀਜ਼ ਆਸਾਨੀ ਨਾਲ ਉਪਲੱਬਧ ਹੈ | ਆਵਾਜਾਈ ਅਤੇ ਸੰਚਾਰ ਦੇ ਆਧੁਨਿਕ ਸਾਧਨਾਂ ਨੇ ਜੀਵਨ ਨੂੰ ਸੁਖੀ ਬਣਾ ਦਿੱਤਾ ਹੈ । ਆਧੁਨਿਕ ਸਾਧਨਾਂ ਅਤੇ ਯੰਤਰਾਂ ਦੇ ਪ੍ਰਯੋਗ ਨੇ ਹਰ ਕੰਮ ਨੂੰ ਅਸਾਨ ਕਰ ਦਿੱਤਾ ਹੈ । ਸ਼ਹਿਰਾਂ ਵਿਚ ਉਪਲੱਬਧ ਆਧੁਨਿਕ ਸਿਹਤ ਸਹੂਲਤਾਂ ਨੇ ਮੌਤ ਦਰ ‘ਤੇ ਵੀ ਕਾਬੂ ਪਾ ਲਿਆ ਹੈ ।

ਸ਼ਹਿਰਾਂ ਦੀ ਸੁੱਖ ਭਰੀ ਜ਼ਿੰਦਗੀ ਹੀ ਪੇਂਡੂ ਲੋਕਾਂ ਨੂੰ ਸ਼ਹਿਰਾਂ ਵਲ ਆਉਣ ਲਈ ਆਕਰਸ਼ਿਤ ਕਰਦੀ ਹੈ । ਇਸ ਗੱਲ ਵਿਚ ਕੋਈ ਵੀ ਸੰਦੇਹ ਨਹੀਂ ਹੈ ਕਿ ਸ਼ਹਿਰਾਂ ਵਿਚ ਵਿਗਿਆਨ ਦੇ ਸਭ ਖੇਤਰਾਂ ਵਿਚ ਪ੍ਰਗਤੀ ਹੋਈ ਹੈ । ਜਿਸ ਵਿਚ ਮਨੁੱਖ ਨੂੰ ਕਈ ਸਹੂਲਤਾਂ ਪ੍ਰਾਪਤ ਹਨ ਪਰ ਇਸ ਉੱਨਤੀ ਨੇ ਆਸ-ਪਾਸ ਦੇ ਵਾਤਾਵਰਣ ਨੂੰ ਬਹੁਤ ਹਾਨੀ ਪਹੁੰਚਾਈ ਹੈ । | ਵਾਤਾਵਰਣ ਵਿਚ ਪ੍ਰਦੂਸ਼ਣ ਦਾ ਇਕ ਮਹੱਤਵਪੂਰਨ ਕਾਰਨ ਸ਼ਹਿਰਾਂ ਵਿਚ ਵਧ ਰਹੀ ਵਸੋਂ ਹੈ । ਵਾਤਾਵਰਣ ‘ਤੇ ਸ਼ਹਿਰੀ ਸੁੱਖ-ਸਹੂਲਤਾਂ ਤੇ ਵਸੋਂ ਵਿਸਫੋਟ ਨੇ ਪ੍ਰਤਿਕੂਲ ਪ੍ਰਭਾਵ ਪਾਏ ਹਨ ।

ਇਹਨਾਂ ਪ੍ਰਭਾਵਾਂ ਦਾ ਵਰਣਨ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ –
ਪਾਣੀ ਦੀ ਸਪਲਾਈ (Water Supply-ਆਬਾਦੀ ਵਾਧੇ ਦੇ ਕਾਰਨ ਮਨੁੱਖੀ ਸਮਾਜ ਦੁਆਰਾ ਪਾਣੀ ਦਾ ਘਰੇਲੂ ਉਪਯੋਗ, ਸਿੰਜਾਈ ਅਤੇ ਉਦਯੋਗਿਕ ਇਕਾਈਆਂ ਦੇ ਲਈ ਪਾਣੀ ਦੀ ਜ਼ਰੂਰਤ ਵਧਦੀ ਜਾ ਰਹੀ ਹੈ । ਇਸ ਵਧਦੀ ਹੋਈ ਜ਼ਰੂਰਤ ਦੀ ਪੂਰਤੀ ਦੇ ਲਈ ਭੂਮੀਗਤ ਪਾਣੀ ਦਾ ਵੱਧ ਮਾਤਰਾ ਵਿਚ ਘਾਟਾ ਹੋ ਰਿਹਾ ਹੈ, ਜਿਸ ਨਾਲ ਪਾਣੀ ਦਾ ਪੱਧਰ ਡਿਗ ਰਿਹਾ ਹੈ । ਵੱਡੇ ਸ਼ਹਿਰਾਂ ਵਿਚ ਗਰਮੀਆਂ ਵਿਚ ਪਾਣੀ ਸੰਬੰਧੀ ਸਮੱਸਿਆ ਭਿਅੰਕਰ ਰੂਪ ਧਾਰਨ ਕਰ ਲੈਂਦੀ ਹੈ ।

ਬਿਜਲੀ ਅਪੂਰਤੀ (Power Supply-ਆਬਾਦੀ ਵਿਸਫੋਟ ਅਤੇ ਤੇਜ਼ ਉਦਯੋਗੀਕਰਨ ਨੇ ਬਿਜਲੀ ਦੀ ਖਪਤ ਵਿਚ ਵਾਧਾ ਕਰ ਦਿੱਤਾ ਹੈ । ਜ਼ਿਆਦਾਤਰ ਉਦਯੋਗਾਂ ਵਿਚ ਬਿਜਲੀ ਦਾ ਜ਼ਿਆਦਾ ਉਪਯੋਗ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ਅਤੇ ਇਸ ਨਾਲ ਘਰੇਲੂ ਪੱਧਰ ‘ਤੇ ਬਿਜਲੀ ਸੰਕਟ ਪੈਦਾ ਹੋ ਜਾਂਦਾ ਹੈ । ਗਰਮੀਆਂ ਦੇ ਮੌਸਮ ਵਿਚ ਬਿਜਲੀ ਦੀ ਮੰਗ, ਪੂਰਤੀ ਨਾਲੋਂ ਜ਼ਿਆਦਾ ਹੁੰਦੀ ਹੈ । ਇਸ ਲਈ ਸ਼ਹਿਰਾਂ ਵਿਚ ਬਿਜਲੀ ਦੀ ਅਪੂਰਤੀ ਇਕ ਗੰਭੀਰ ਸਮੱਸਿਆ ਬਣ ਜਾਂਦੀ ਹੈ ।

ਆਵਾਜਾਈ ਸਹੂਲਤਾਂ ‘ਤੇ ਦਬਾਅ (Pressure on Transportation System)- ਵਧਦੀ ਵਸੋਂ ਦੇ ਕਾਰਨ ਆਵਾਜਾਈ ਸਹੂਲਤਾਂ ਉੱਤੇ ਵੀ ਦਬਾਅ ਵਧਦਾ ਜਾ ਰਿਹਾ ਹੈ | ਸੜਕਾਂ ਉੱਤੇ ਵਾਹਨਾਂ ਦੀ ਭੀੜ ਵਧਣ ਨਾਲ ਦੁਰਘਟਨਾਵਾਂ ਦੀ ਸੰਭਾਵਨਾ ਵੀ ਵਧ ਗਈ ਹੈ । ਇਸ ਭੀੜ ਦੇ ਕਾਰਨ ਯਾਤਰਾ ਵਿਚ ਵਧ ਸਮਾਂ ਲਗਦਾ ਹੈ ਜਿਸ ਨਾਲ ਸਮੇਂ ਦੀ ਬਰਬਾਦੀ ਹੁੰਦੀ ਹੈ । ਹਵਾ ਪ੍ਰਦੂਸ਼ਣ ਅਤੇ ਧੁਨੀ ਪ੍ਰਦੂਸ਼ਣ ਵਿਚ ਵਾਧੇ ਦੇ ਕਾਰਨ ਸਿਹਤ ‘ਤੇ ਵੀ ਪ੍ਰਤੀਕੂਲ ਪ੍ਰਭਾਵ ਪੈਂਦਾ ਹੈ । ਵੱਡੇ ਸ਼ਹਿਰਾਂ ਵਿਚ ਵਧ ਵਾਹਨਾਂ ਦੇ ਕਾਰਨ ਆਵਾਜਾਈ ਖੜੀ ਹੋ ਜਾਂਦੀ ਹੈ ਜਾਂ ਜਾਮ ਲਗਦੇ ਹਨ |

ਰਹਿੰਦ-ਖੂੰਹਦ ਦਾ ਨਿਪਟਾਰਾ (Disposal of Water Materials/Garbage)- ਆਬਾਦੀ ਵਾਧੇ ਦੇ ਕਾਰਨ ਸਾਰੇ ਪ੍ਰਕਾਰ ਦੇ ਠੋਸ ਰਹਿੰਦ-ਖੂੰਹਦ ਦਾ ਉਤਪਾਦਨ ਵੀ ਤੇਜ਼ੀ ਨਾਲ ਮਨੁੱਖੀ ਗਤੀਵਿਧੀਆਂ ਦਾ ਵਾਤਾਵਰਣ ਉੱਪਰ ਪ੍ਰਭਾਵ ਵਧ ਰਿਹਾ ਹੈ । ਇਸਦੇ ਕਾਰਨ ਥਾਂ-ਥਾਂ ਗੰਦਗੀ ਦੇ ਢੇਰ ਵਧ ਰਹੇ ਹਨ । ਉਹਨਾਂ ਨੂੰ ਕਿਸੇ ਟਿਕਾਣੇ ਲਗਾਉਣ ਦੀ ਸਮੱਸਿਆ ਉਤਪੰਨ ਹੋ ਗਈ ਹੈ । ਰਹਿੰਦ-ਖੂੰਹਦ ਦਾ ਠੀਕ ਪ੍ਰਕਾਰ ਨਾਲ ਨਿਪਟਾਰਾ ਨਾ ਹੋਣ ਕਾਰਨ ਹਵਾ ਅਤੇ ਪਾਣੀ ਪ੍ਰਦੂਸ਼ਣ ਵਧ ਰਿਹਾ ਹੈ ਅਤੇ ਵਾਤਾਵਰਣ ਦਾ ਪ੍ਰਦੁਸ਼ਣ ਹੋ ਰਿਹਾ ਹੈ । ਜ਼ਿਆਦਾਤਰ ਸ਼ਹਿਰਾਂ ਵਿਚ ਘਰੇਲ, ਅਤੇ ਉਦਯੋਗਿਕ ਰਹਿੰਦ-ਖੂੰਹਦ ਨੂੰ ਬਿਨਾਂ ਕਿਸੇ ਉਪਚਾਰ ਤੋਂ ਨਦੀਆਂ ਵਿਚ ਛੱਡਿਆ ਜਾਂਦਾ ਹੈ । ਜਿਸ ਨਾਲ ਪਾਣੀ ਦੂਸ਼ਿਤ ਹੁੰਦਾ ਹੈ । ਇਸ ਦੂਸ਼ਿਤ ਪਾਣੀ ਵਿਚ ਰਹਿਣ ਵਾਲੇ ਜੀਵ-ਜੰਤੁ ਮਰ ਜਾਂਦੇ ਹਨ ਅਤੇ ਇਹ ਪਾਣੀ ਪੀਣ ਨਾਲ ਮਨੁੱਖ ਨੂੰ ਕਈ ਬੀਮਾਰੀਆਂ ਦਾ ਸਾਹਮਣਾ ਕਰਨਾ ਪੈਂਦਾ ਹੈ ।

ਸਿਹਤ ਸਹੂਲਤਾਂ : (Health Services)-ਆਬਾਦੀ ਵਿਸਫੋਟ ਦੇ ਕਾਰਨ ਕਈ ਵਾਤਾਵਰਣ ਸਮੱਸਿਆਵਾਂ ਪੈਦਾ ਹੋਈਆਂ ਹਨ ।
ਜਿਸ ਨਾਲ ਸਿਹਤ ‘ਤੇ ਵੀ ਪ੍ਰਤੀਕੂਲ ਅਸਰ ਪਿਆ ਹੈ । ਇਸ ਨਾਲ ਹਸਪਤਾਲਾਂ ਅਤੇ ਸਿਹਤ ਕੇਂਦਰਾਂ ਉੱਤੇ ਦਬਾਅ ਪੈਂਦਾ ਹੈ ਅਤੇ ਸਿਹਤ ਸੁਵਿਧਾਵਾਂ ਦੀ ਘਾਟ ਪੈਦਾ ਹੋ ਜਾਂਦੀ ਹੈ । ਹਸਪਤਾਲਾਂ ਵਿਚ ਦਵਾਈਆਂ, ਡਾਕਟਰਾਂ ਅਤੇ ਬਿਸਤਰਿਆਂ ਦੀ ਕਮੀ ਕਾਰਨ ਲੋਕ ਬਿਨਾਂ ਇਲਾਜ ਦੇ ਗੰਭੀਰ ਹਾਲਾਤਾਂ ਵਿਚੋਂ ਗੁਜ਼ਰ ਰਹੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 2.
ਪੇਂਡੂ ਖੇਤਰਾਂ ਦੀਆਂ ਵਾਤਾਵਰਣੀ ਸਮੱਸਿਆਵਾਂ (Environmental Problems of Rural Areas) ਦੀ ਚਰਚਾ ਕਰੋ ।
ਉੱਤਰ-
ਭਾਰਤ ਵਿਚ ਜ਼ਿਆਦਾ ਲੋਕ ਪਿੰਡਾਂ ਵਿਚ ਰਹਿੰਦੇ ਹਨ । ਪੇਂਡੂ ਖੇਤਰਾਂ ਦੀਆਂ ਸਮੱਸਿਆਵਾਂ ਸ਼ਹਿਰੀ ਖੇਤਰਾਂ ਤੋਂ ਵੱਖਰੀਆਂ ਹਨ ।
ਇਹਨਾਂ ਖੇਤਰਾਂ ਦੀਆਂ ਪ੍ਰਮੁੱਖ ਵਾਤਾਵਰਣ ਸਮੱਸਿਆਵਾਂ ਹੇਠ ਲਿਖੀਆਂ ਹਨ-

1. ਪੇਂਡੂ ਖੇਤਰਾਂ ਵਿਚ ਸਿੱਖਿਆ ਦੀ ਘਾਟ ਦੇ ਕਾਰਨ ਲੋਕ ਖੇਤੀ ਦੇ ਨਜਾਇਜ਼ ਤਰੀਕੇ ਅਪਣਾਉਂਦੇ ਹਨ ਜਿਸਦੇ ਕਾਰਨ ਭੁਮੀ ਸਾਧਨਾਂ ਨੂੰ ਹਾਨੀ ਪਹੁੰਚਦੀ ਹੈ ।
2. ਖਾਣ ਵਾਲੇ ਪਦਾਰਥਾਂ ਦੀ ਅਪੂਰਤੀ ਦੇ ਲਈ ਖੇਤੀ ਯੋਗ ਭੂਮੀ ਉੱਪਰ ਕੀਟਨਾਸ਼ਕਾਂ ਅਤੇ ਰਸਾਇਣਿਕ ਖਾਦਾਂ ਦਾ ਉਪਯੋਗ ਕੀਤਾ ਜਾ ਰਿਹਾ ਹੈ ਪਰ ਇਸਦੇ ਕਾਰਨ ਕਈ ਵਾਤਾਵਰਣ ਸਮੱਸਿਆਵਾਂ ਪੈਦਾ ਹੋ ਰਹੀਆਂ ਹੈ । ਕੀਟਨਾਸ਼ਕਾਂ ਦੇ ਕਾਰਨ ਪਾਣੀ ਸੋਤ ਪ੍ਰਦੂਸ਼ਿਤ ਹੋ ਰਹੇ ਹਨ ਅਤੇ ਇਸ ਪ੍ਰਦੂਸ਼ਿਤ ਪਾਣੀ ਦੇ ਉਪਯੋਗ ਦੇ ਕਰਕੇ ਮਨੁੱਖ ਨੂੰ ਕਈ ਸਿਹਤ ਸੰਬੰਧੀ ਸਮੱਸਿਆਵਾਂ ਦਾ ਸਾਹਮਣਾ ਕਰਨਾ ਪੈ ਰਿਹਾ ਹੈ । ਇਸਦੇ ਇਲਾਵਾ ਭੂਮੀ ਦੀ ਉਪਜਾਊ ਸ਼ਕਤੀ ਦੀ ਹਾਨੀ ਹੋਣ ਦੇ ਨਾਲ-ਨਾਲ ਭੂਮੀ ਦਾ ਲਘੂਕਰਨ, ਰੇਗਿਸਤਾਨੀਕਰਨ, ਭੂਮੀ-ਖੋਰਨ ਆਦਿ ਵੀ ਹੋ ਰਿਹਾ ਹੈ ।
3. ਫ਼ਸਲਾਂ ਦੀਆਂ ਵੱਧ ਉਤਪਾਦਨ ਦੇਣ ਵਾਲੀਆਂ ਕਿਸਮਾਂ ਨੂੰ ਲਗਾਤਾਰ ਉਗਾਉਣ ਕਰਕੇ ਭੂਮੀਗਤ ਪਾਣੀ ਦਾ ਸਤਰ ਹੇਠਾਂ ਚਲਾ ਗਿਆ ਹੈ । ਪੇਂਡੂ ਲੋਕ ਆਪਣੀਆਂ ਪਾਣੀ ਸੰਬੰਧੀ ਜ਼ਰੂਰਤਾਂ ਦੇ ਲਈ ਟਿਉਬਵੈੱਲ, ਤਾਲਾਬਾਂ ਅਤੇ ਖੁਹਾਂ ਉੱਪਰ ਨਿਰਭਰ ਕਰਦੇ ਹਨ ਪਰ ਪਾਣੀ ਸਤਰ ਡਿਗਣ ਦੇ ਕਾਰਨ ਪਾਣੀ ਦੀ ਗੰਭੀਰ ਸਮੱਸਿਆ ਉਤਪੰਨ ਹੋ ਗਈ ਹੈ ।
4. ਖੁੱਲ੍ਹੇ ਸਥਾਨਾਂ ਉੱਤੇ ਇਕੱਠਾ ਹੋਇਆ ਪਾਣੀ ਮੱਛਰਾਂ ਦਾ ਪ੍ਰਜਨਣ ਸਥਾਨ ਬਣ ਜਾਂਦਾ ਹੈ ਅਤੇ ਕਈ ਬੀਮਾਰੀਆਂ ਪੈਦਾ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ।
5. ਬਾਲਣ ਦੇ ਰੂਪ ਵਿਚ ਲੱਕੜੀ ਅਤੇ ਗੋਹੇ ਦੀਆਂ ਪਾਥੀਆਂ ਦੀ ਵਰਤੋਂ ਨਾਲ ਧੂੰਆਂ ਉਤਪੰਨ ਹੁੰਦਾ ਹੈ । ਜਿਸਦੇ ਕਾਰਨ ਪੇਂਡੂ ਔਰਤਾਂ ਦੀਆਂ ਸਿਹਤਾਂ ਉੱਤੇ ਬੁਰਾ ਪ੍ਰਭਾਵ ਪੈਂਦਾ ਹੈ ।
6. ਖੁੱਲ੍ਹੀ ਟੱਟੀ-ਪਿਸ਼ਾਬ ਪ੍ਰਣਾਲੀ ਦੇ ਕਾਰਨ ਵਾਤਾਵਰਣ ਦੂਸ਼ਿਤ ਹੁੰਦਾ ਹੈ । ਇਸਦੇ ਨਾਲਨਾਲ ਅਨੁਚਿਤ ਨਿਕਾਸ ਪ੍ਰਣਾਲੀ ਵੀ ਵਾਤਾਵਰਣ ਸਮੱਸਿਆਵਾਂ ਨੂੰ ਵਧਾਉਂਦੀ ਹੈ ।

Punjab State Board PSEB 11th Class Maths Book Solutions Chapter 3 Trigonometric Functions Ex 3.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Maths Chapter 3 Trigonometric Functions Ex 3.1

Question 1.
Find the radian measures corresponding to the following degree measures:
(i) 25°
(ii) – 47° 30′
(iii) 240°
(iv) 520°
Answer.
(i) 25°
We know that: 180° = π radian
∴ 25° = \(\frac{\pi}{180}\) x 25 radian
= \(\frac{5 \pi}{36}\) radian

(ii) – 47° 30′
-47° 30′ = 47 \(\frac{1}{2}\) degree
= \(-\frac{95}{2}\) degree
Since 180° = π radian
\(-\frac{95}{2}\) degree = \(\frac{\pi}{180}\) × \(-\frac{95}{2}\)

= \(\left(\frac{-19}{36 \times 2}\right)\) π degree

= \(-\frac{19}{72}\) π radian

∴ – 47° 30′ = \(-\frac{19}{72}\) π radian.

(iii) 240°
We know that: 180° = π radian
∴ 240° = \(\frac{\pi}{180}\) × 240
= \(\frac{4}{3}\) π radian.

(iv) 520°
We know that: 180° = π radian
∴ 520° = \(\frac{\pi}{180}\) × 520 radian
= \(26 \frac{\pi}{9}\) radian

Question 2.
Find the degree measures corresponding to the following radian measures. (Use π = \(\frac{22}{7}\))
(i) \(\frac{11}{16}\)

(ii) – 4

(iii) \(\frac{5 \pi}{3}\)

(iv) \(\frac{7 \pi}{3}\)
Answer.
(i) \(\frac{11}{16}\)
We know that: π radian = 180°
∴ \(\frac{11}{16}\) radain = \(\frac{180}{\pi} \times \frac{11}{16}\) × degree

= \(\frac{45 \times 11}{\pi \times 4}\) degree

= \(\frac{45 \times 11 \times 7}{22 \times 4}\) degree

= \(\frac{315}{8}\) degree

= 39 \(\frac{3}{8}\) degree

= 39° + \(\frac{3 \times 60}{8}\) minutes [1° = 60′]

= 39° + 22′ + \(\frac{1}{2}\) minutes

= 39°22’30” [1′ = 60°].

(ii) – 4

(iii) \(\frac{5 \pi}{3}\)
We know that : π radian = 180°
∴ \(\frac{5 \pi}{3}\) radian = \(\frac{180}{\pi} \times \frac{5 \pi}{3}\) degree = 300°

(iv) \(\frac{7 \pi}{6}\)
We know that : π radian = 180°
∴ \(\frac{7 \pi}{6}\) = \(\frac{180}{\pi} \times \frac{7 \pi}{6}\) = 210°.

Question 3.
A wheel makes 360 revolutions in one minute. Through how many radians does it turn in one second?
Answer.
Number of revolutions made by the wheel in 1 minute = 360
∴ Number of revolutions made by the wheel in 1 second = \(\frac{360}{6}\) = 6
In one complete revolution, the wheel turns an angle of 2π radian.
Hence, in 6 complete revolutions, it will turn an angle of 6 × 2π radian, i.e., 12π radian
Thus, in one second, the wheel turns an angle of 12π radian.

Question 4.
Find the degree measure of the angle subtended at the centre of a circle of radius 100 cm y an arc of length 22 cm (Use π = \(\frac{22}{7}\)).
Answer.
We know that in a circle of radius r unit, if an arc of length l unit subtends an angle θ radian at the centre, then θ = \(\frac{l}{r}\)
Therefore, for r = 100 cm, l = 22 cm,
we have

Thus, the required angle is 12°36′.

Question 5.
In a circle of diameter 40 cm, the length of a chord is 20 cm. Find the length of minor arc of the chord.
Answer.

Given, diameter = 40 cm
∴ radius (r) = \(\frac{40}{2}\) = 20 cm
and length of chord, AB = 20 cm
Thus, ∆OAB is an equilateral triangle.
We know that,
θ = \(\frac{\text { Arc } A B}{\text { radius }}\)
⇒ Arc AB = θ × r
= \(\frac{\pi}{3}\) × 20 .
= \(\frac{20}{3}\) π cm.

Question 6.
If in two circles, arcs of the same length subtend angles 60° and 75° at the centre, find the ratio of their radii.
Answer.
Let the radii of the two circles be r₁ and r₂.
Let an arc of length l subtend an angle of 60° at the centre of the circle of radius r₁, while let an arc of length l subtend an angle of 75° at the centre of the circle of radius r₂.
Now, 6o° = \(\frac{\pi}{3}\) radian and
75° = \(\frac{5 \pi}{12}\) radian
We know that in a circle of radius r unit, if an arc of length l unit subtends an angle θ radian at the centre, then θ = \(\frac{l}{r}\) or l = rθ
∴ l = \(\frac{r_{1} \pi}{3}\) and

l = \(\frac{r_{2} 5 \pi}{12}\)

⇒ \(\frac{r_{1} \pi}{3}=\frac{r_{2} 5 \pi}{12}\)

⇒ r = \(\frac{r_{2} 5}{4}\)

\(\frac{r_{1}}{r_{2}}=\frac{5}{4}\)
Thus, the ratio of the radii is 5 : 4.

Question 7.
Find the angle in radian through which a pendulum swings if its length is 75 cm and the tip describes an arc of length
(i) 10 cm
(ii) 15 cm
(iii) 21 cm.
Answer.
We know that in a circle of radius r unit, if an arc of length l unit subtends an angle θ radian at the centre, then
θ = \(\frac{l}{r}\).
It is given that r = 75 cm

(i) Here, l = 10 cm
θ = \(\frac{10}{75}\) radian
= \(\frac{2}{15}\) radian

(ii) Here, l = 15 cm
θ = \(\frac{15}{75}\) radian
θ = \(\frac{1}{5}\) radian

(iii) Here, l = 21 cm
θ = \(\frac{21}{75}\) radian
= \(\frac{7}{75}\) radian.

Punjab State Board PSEB 11th Class Environmental Education Book Solutions Chapter 2 ਵਸੋਂ ਅਤੇ ਵਾਤਾਵਰਣ Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Environmental Education Chapter 2 ਵਸੋਂ ਅਤੇ ਵਾਤਾਵਰਣ

Environmental Education Guide for Class 11 PSEB ਵਸੋਂ ਅਤੇ ਵਾਤਾਵਰਣ Textbook Questions and Answers

(ਉ) ਬਹੁਤ ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ

ਪ੍ਰਸ਼ਨ 1.
ਜਨ-ਅੰਕਣ (Demography) ਕੀ ਹੈ ?
ਉੱਤਰ-
ਵਸੋਂ ਦੇ ਅਲੱਗ-ਅਲੱਗ ਪਹਿਲੂ ਜਿਵੇਂ ਵਸੋਂ ਵਿਚ ਵਾਧਾ, ਵੰਡ, ਵਸੋਂ ਵਾਧੇ ਦੇ ਕਾਰਕ ਆਦਿ ਬਾਰੇ ਅੰਕੜੇ ਇਕੱਠੇ ਕਰਨ ਨੂੰ ਜਨ-ਅੰਕਣ ਕਿਹਾ ਜਾਂਦਾ ਹੈ।

ਪ੍ਰਸ਼ਨ 2.
ਜਨਮ ਦਰ (Birth Rate) ਦੀ ਪਰਿਭਾਸ਼ਾ ਦਿਓ।
ਉੱਤਰ-
ਕਿਸੇ ਖੇਤਰ ਵਿਚ ਪ੍ਰਤੀ ਹਜ਼ਾਰ ਵਿਅਕਤੀਆਂ ਉੱਪਰ ਜਨਮ ਲੈਣ ਵਾਲੇ ਬੱਚਿਆਂ ਦੀ ਗਿਣਤੀ ਦੀ ਔਸਤ ਨੂੰ ਜਨਮ ਦਰ ਕਹਿੰਦੇ ਹਾਂ ।

ਪ੍ਰਸ਼ਨ 3.
ਲਿੰਗ ਅਨੁਪਾਤ (Sex Ratio) ਕਿਸ ਨੂੰ ਆਖਦੇ ਹਨ ?
ਉੱਤਰ-
ਪ੍ਰਤੀ ਹਜ਼ਾਰ ਆਦਮੀਆਂ (ਮਰਦਾਂ) ਦੀ ਵਸੋਂ ਪਿੱਛੇ ਔਰਤਾਂ ਦੀ ਪ੍ਰਤੀਸ਼ਤ/ਵਸੋਂ ਨੂੰ ਲਿੰਗ ਅਨੁਪਾਤ ਆਖਦੇ ਹਾਂ ।

ਪ੍ਰਸ਼ਨ 4.
ਮੌਤ ਦਰ (Death Rate) ਦੀ ਪਰਿਭਾਸ਼ਾ ਦਿਓ ।
ਉੱਤਰ-
ਕਿਸੇ ਦੇਸ਼ ਜਾਂ ਦੇਸ਼ ਵਿਚ ਇਕ ਸਾਲ ਵਿਚ ਵਸੋਂ ਦੇ ਪ੍ਰਤੀ ਹਜ਼ਾਰ ਆਦਮੀਆਂ ਉੱਪਰ ਮਰਨ ਵਾਲੇ ਆਦਮੀਆਂ ਦੀ ਸੰਖਿਆ ਨੂੰ ਮੌਤ ਦਰ ਕਹਿੰਦੇ ਹਨ|

ਪ੍ਰਸ਼ਨ 5.
ਵਸੋਂ ਦੇ ਵਾਧੇ, ਪਰਵਾਸ ਜਾਂ ਆਵਾਸ ਲਈ ਕਿਹੜਾ ਕਾਰਕ ਜ਼ਿੰਮੇਵਾਰ ਹੈ ?
ਉੱਤਰ-
ਵਸੋਂ ਦੇ ਵਾਧੇ, ਪਰਵਾਸ ਜਾਂ ਆਵਾਸ ਲਈ ਰੋਜ਼ੀ-ਰੋਟੀ ਕਮਾਉਣਾ ਅਤੇ ਆਪਣੇ ਪਰਿਵਾਰ ਦਾ ਪਾਲਨ-ਪੋਸ਼ਣ ਕਰਨਾ ਆਦਿ ਕਾਰਨ ਜਾਂ ਕਾਰਕ ਜੁੰਮੇਵਾਰ ਹਨ।

ਪ੍ਰਸ਼ਨ 6.
ਗਰੀਬੀ (Poverty) ਕੀ ਹੈ ?
ਉੱਤਰ-
ਆਪਣੀਆਂ ਆਰਥਿਕ ਅਤੇ ਮਾਲੀ ਜ਼ਰੂਰਤਾਂ ਨੂੰ ਪੂਰਾ ਕਰਨ ਵਿਚ ਅਸਮਰਥ ਹੋਣ ਨੂੰ ਗ਼ਰੀਬੀ ਕਹਿੰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 7.
ਸਾਖਰਤਾ (Literacy) ਦੀ ਪਰਿਭਾਸ਼ਾ ਦਿਓ ।
ਉੱਤਰ-
ਪੜ੍ਹਨ ਅਤੇ ਲਿਖਣ ਦੀ ਯੋਗਤਾ ਨੂੰ ਸਾਖਰਤਾ ਕਹਿੰਦੇ ਹਨ।

(ਅ) ਛੋਟ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ (Type I)

ਪ੍ਰਸ਼ਨ 1.
ਪਾਲਣ-ਸੰਭਾਲਣ ਸਮਰੱਥਾ (Carrying Capacity) ਦੀ ਵਿਆਖਿਆ ਕਰੋ ।
ਉੱਤਰ-
ਵਸੋਂ ਦੀ ਵਾਧੂ ਗਿਣਤੀ ਵਾਤਾਵਰਣ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਦੀ ਹੈ, ਕਿਸੇ ਵੀ ਖੇਤਰ ਦੀ ਵਾਤਾਵਰਣ ਸਥਿਤੀ ਦੇ ਅਨੁਸਾਰ ਉਸ ਖੇਤਰ ਦੀ ਵਸੋਂ ਦੇ ਵਾਧੂਪਣ ਨੂੰ ਪਾਲਣ-ਸੰਭਾਲਣ ਦੀ ਸਮਰੱਥਾ ਤੋਂ ਪਤਾ ਲਗਾਇਆ ਜਾ ਸਕਦਾ ਹੈ। ਇਸ ਦੇ ਅਨੁਸਾਰ ਵਸੋਂ ਦੇ ਵਾਧੂਪਣ ਦੇ ਆਧਾਰ ਤੇ ਵਾਤਾਵਰਣ ਦੇ ਦੋ ਮਹੱਤਵਪੂਰਨ ਘਟਕ ਹਨ ।

• ਜੀਵਨ ਰੱਖਿਅਕ ਘਟਕ (Life Supportive Components)-ਉਹ ਘਟਕ ਜੋ ਹਵਾ, ਭੋਜਨ, ਜਲ ਅਤੇ ਗਰਮੀ ਦਿੰਦੇ ਹਨ।
• ਰਹਿੰਦ-ਖੂੰਹਦ ਪਾਚਣਸ਼ੀਲ ਘਟਕ (Waste Assimilative Components) ਵਾਤਾਵਰਣ ਦੇ ਇਸ ਹਿੱਸੇ ਵਿਚ ਮਨੁੱਖੀ ਕਿਰਿਆ ਦੁਆਰਾ ਉਤਪੰਨ ਵਿਅਰਥ ਪਦਾਰਥਾਂ ਦਾ ਪਾਚਨ ਸ਼ਾਮਿਲ ਹੈ।

ਪ੍ਰਸ਼ਨ 2.
ਵਾਧੇ ਦੀ ਦਰ ਨੇ ਭੋਜਨ ਦੇ ਉਤਪਾਦਨ ਨੂੰ ਕਿਵੇਂ ਪ੍ਰਭਾਵਿਤ ਕੀਤਾ ਹੈ ?
ਉੱਤਰ-
ਵਧਦੀ ਹੋਈ ਵਸੋਂ ਦੇ ਕਾਰਨ ਖਾਣ ਵਾਲੀਆਂ ਚੀਜ਼ਾਂ ਦੀ ਮੰਗ ਵੀ ਵਧਦੀ ਹੈ। ਇਸਦੇ ਨਤੀਜੇ ਵਜੋਂ, ਖੇਤੀ ਕਰਨ ਵਾਸਤੇ ਧਰਤੀ ਨੂੰ ਪ੍ਰਕਾਸ਼, ਜਲ, ਖਾਦਾਂ ਅਤੇ ਕੀਟਨਾਸ਼ਕ ਦਵਾਈਆਂ ਦੀ ਸਹਾਇਤਾ ਅਤੇ ਆਧੁਨਿਕ ਤਰੀਕਿਆਂ ਨਾਲ ਜ਼ਿਆਦਾ ਵਰਤੋਂ ਵਿਚ ਲਿਆਂਦਾ ਗਿਆ ਹੈ। ਇਸ ਨਾਲ ਸੰਸਾਰ ਵਿਚ ਖਾਣ ਵਾਲੀਆਂ ਚੀਜ਼ਾਂ ਦਾ ਉਤਪਾਦਨ 50 ਪ੍ਰਤੀਸ਼ਤ ਤੋਂ ਜ਼ਿਆਦਾ ਵਧ ਗਿਆ ਹੈ। ਪਰੰਤੁ ਮਨੁੱਖ ਦੀਆਂ ਮਾੜੀਆਂ ਗਤੀਵਿਧੀਆਂ ਨਾਲ ਜਿਵੇਂ ਪਸ਼ੂਆਂ ਦਾ ਜ਼ਿਆਦਾ ਚਾਰਨਾ , ਰਸਾਇਣਿਕ ਖਾਦਾਂ ਦੀ ਜ਼ਿਆਦਾ ਵਰਤੋਂ ਅਤੇ ਭੂਮੀਗਤ ਜਲ ਦਾ ਗ਼ਲਤ ਉਪਯੋਗ ਆਦਿ ਦੇ ਕਾਰਨ ਕਈ ਮੁਸ਼ਕਿਲਾਂ ਪੈਦਾ ਹੋ ਗਈਆਂ ਹਨ । ਧਰਤੀ ਦਾ ਖਾਰਾਪਨ, ਰੇਗਿਸਤਾਨੀ ਕਰਨ, ਭੂਮੀ ਦਾ ਕਟਾਵ ਹੋਣਾ, ਭੂਮੀ ਦਾ ਵਿਤੀਕਰਨ ਆਦਿ ਇਸ ਦੇ ਨਤੀਜੇ ਹਨ। ਇਸ ਤੋਂ ਇਲਾਵਾ ਵਸੋਂ ਦੇ ਵਾਧੁਪਨ ਦੇ ਕਾਰਨ ਬਹੁਤ ਸਾਰੇ ਲੋਕੀ ਕੁਪੋਸ਼ਣ ਦਾ ਸ਼ਿਕਾਰ ਹੋਏ ਹਨ। ਭਾਰਤ ਵਿਚ ਲਗਪਗ 70 ਤੋਂ 80 ਪ੍ਰਤੀਸ਼ਤ ਬੱਚੇ ਕੁਪੋਸ਼ਣ ਦਾ ਸ਼ਿਕਾਰ ਹਨ । ਇਸ ਕਾਰਨ ਵਸੋਂ ਵਿਸਫੋਟ ਦੇ ਕਾਰਨ ਵਧਦੀ ਹੋਈ ਆਬਾਦੀ ਦੇ ਕਾਰਨ ਖਾਣ ਵਾਲੇ ਪਦਾਰਥਾਂ ਦੀ ਮੰਗ ਨੂੰ ਪੂਰਾ ਕਰਨਾ ਮੁਸ਼ਕਿਲ ਹੈ।

ਪ੍ਰਸ਼ਨ 3.
ਚਾਰ ਸੈਟੇਲਾਇਟ ਸ਼ਹਿਰਾਂ ਦੇ ਨਾਂ ਲਿਖੋ ।
ਉੱਤਰ-
ਨੋਇਡਾ, ਫਰੀਦਾਬਾਦ, ਗਾਜ਼ੀਆਬਾਦ, ਗੁੜਗਾਂਵ, ਮੁਹਾਲੀ ਅਤੇ ਪੰਚਕੂਲਾ ।

ਪ੍ਰਸ਼ਨ 4.
ਵਸੋਂ ਦੇ ਵਾਧੇ ਦਾ ਊਰਜਾ ਉੱਪਰ ਕੀ ਪ੍ਰਭਾਵ ਹੈ ?
ਉੱਤਰ-
ਸੰਸਾਰ ਦੇ ਜ਼ਿਆਦਾ ਵਿਕਸਿਤ ਅਤੇ ਵਿਕਾਸਸ਼ੀਲ ਦੇਸ਼ਾਂ ਵਿਚ ਵਧਦੀ ਹੋਈ ਵਸੋਂ ਵਾਸਤੇ ਰੋਜ਼ਗਾਰ ਵਧਾਉਣ ਅਤੇ ਉਹਨਾਂ ਦੀਆਂ ਮੰਗਾਂ ਨੂੰ ਪੂਰਾ ਕਰਨ ਵਾਸਤੇ ਉਤਪਾਦਨ ਨੂੰ ਵਧਾਉਣ ਵਾਸਤੇ ਕਾਰਖਾਨਿਆਂ ਦੀ ਜ਼ਰੂਰਤ ਪੈ ਰਹੀ ਹੈ। ਊਰਜਾ ਦੇ ਬਗੈਰ ਕਾਰਖਾਨੇ ਚਲਾਉਣੇ ਬੜੇ ਮੁਸ਼ਕਿਲ ਹਨ । ਵਧਦੀ ਵਸੋਂ ਦੇ ਕਾਰਨ ਊਰਜਾ ਦੇ ਸੋਮੇ ਪਹਿਲਾਂ ਤੋਂ ਬੜੇ ਘੱਟ ਹਨ, ਜਿਵੇਂ ਲੱਕੜੀ, ਪਥਰਾਟ ਬਾਲਣ ਅਤੇ ਬਿਜਲੀ ਦੀ ਜ਼ਰੂਰਤ ਵੱਧ ਰਹੀ ਹੈ। ਪਥਰਾਟ ਬਾਲਣ ਸੀਮਿਤ ਮਾਤਰਾ ਵਿਚ ਹੀ ਮਿਲ ਰਿਹਾ ਹੈ, ਅਤੇ ਇਹ ਹੌਲੀ-ਹੌਲੀ ਖ਼ਤਮ ਹੋ ਰਹੇ ਹਨ। ਇਹਨਾਂ ਕਾਰਨਾਂ ਕਰਕੇ ਹੀ ਊਰਜਾ ਉੱਪਰ ਵਧਦੀ ਵਸੋਂ ਦਾ ਦਬਾਅ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਊਰਜਾ ਦੀ ਜ਼ਿਆਦਾ ਵਰਤੋਂ ਨਾਲ ਊਰਜਾ ਸੰਕਟ ਪੈਦਾ ਹੋ ਰਿਹਾ ਹੈ।

(ੲ) ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ (Type II)

ਪ੍ਰਸ਼ਨ 1.
ਵਸੋਂ ਨਾਲ ਸੰਬੰਧਿਤ ਮਾਲਬੇਸ ਦਾ ਸਿਧਾਂਤ ਕੀ ਹੈ ?
ਉੱਤਰ-
18ਵੀਂ ਸ਼ਤਾਬਦੀ ਦੇ ਅੰਤ ਤੇ ਇਕ ਅੰਗਰੇਜ਼ੀ ਆਰਥਿਕ ਵਿਗਿਆਨੀ ਅਤੇ ਵਸੋਂ ਵਿਵਰਨ ਸ਼ਾਸਤਰੀ ਥਾਮਸ ਰਾਬਰਟ ਮਾਲਥਸ (1798) ਨੇ ਆਪਣੇ ਵਲੋਂ ਸਿਧਾਂਤ ਦਾ ਵਰਣਨ ਕੀਤਾ ਹੈ। ਇਸ ਸਿਧਾਂਤ ਦੇ ਅਨੁਸਾਰ ਵਸੋਂ ਹਮੇਸ਼ਾ ਰੇਖਾ ਗਣਿਤ ਵਾਧਾ (2, 4, 8, 16, 32) ਵਿਚ ਵਧਦੀ ਹੈ। ਜਦੋਂ ਕਿ ਭੋਜਨ ਅਤੇ ਜੀਵਤ ਰਹਿਣ ਦੇ ਸਾਧਨ ਸਮਾਂਤਰੀ ਸ਼੍ਰੇਣੀ (2, 4, 6, 8, 10) ਵਿਚ ਵਧਦੀ ਹੈ। ਇਸ ਲਈ ਵਸੋਂ, ਭੋਜਨ ਅਤੇ ਥਾਂ ਦੇ ਵਿਚ ਅਸੰਤੁਲਨ ਬਣਿਆ ਰਹਿੰਦਾ ਹੈ। ਮਾਲਥਸ ਨੇ ਇਹ ਨਤੀਜਾ ਕੱਢਿਆ ਕਿ ਜੇਕਰ ਵਸੋਂ ਦਾ ਵਾਧੂਪਣ ਨਹੀਂ ਰੁਕਦਾ ਤੇ ਕੁਦਰਤ ਆਪਣੇ ਤਰੀਕੇ ਨਾਲ; ਜਿਵੇਂ-ਜੰਗ, ਭੁੱਖਮਰੀ, ਹੜ੍ਹ, ਸੁਨਾਮੀ, ਬੀਮਾਰੀਆਂ ਆਦਿ ਨਾਲ ਵਸੋਂ ਵਿਚ ਕਮੀ ਕਰਦੀ ਹੈ।

ਪ੍ਰਸ਼ਨ 2.
ਸ਼ਹਿਰੀਕਰਨ (Urbanisation) ਵਾਤਾਵਰਣ ਨੂੰ ਕਿਵੇਂ ਪ੍ਰਭਾਵਿਤ ਕਰਦਾ ਹੈ ?
ਉੱਤਰ-
ਵਸੋਂ ਵਿਚ ਵਾਧਾ ਹੋਣ ਕਰਕੇ ਕਈ ਲੋਕੀਂ ਪਿੰਡਾਂ ਤੋਂ ਸ਼ਹਿਰਾਂ ਵੱਲ ਨੂੰ ਜਾਣਾ ਸ਼ੁਰੂ ਹੋ ਗਏ ਹਨ ਤੇ ਸ਼ਹਿਰਾਂ ਦਾ ਖੇਤਰ ਤੇਜ਼ੀ ਨਾਲ ਵਧ ਰਿਹਾ ਹੈ। ਇਸਨੂੰ ਸ਼ਹਿਰੀਕਰਨ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਜਿਸ ਕਾਰਨ ਖੇਤੀ ਕਰਨ ਯੋਗ ਧਰਤੀ ਘਟ ਰਹੀ ਹੈ। ਇਸ ਤਰ੍ਹਾਂ ਸ਼ਹਿਰੀਕਰਨ ਦਾ ਵਾਤਾਵਰਣ ਉੱਪਰ ਕਾਫ਼ੀ ਮਾੜਾ ਅਸਰ ਹੋਇਆ ਹੈ। ਸ਼ਹਿਰੀਕਰਨ ਦੇ ਵਾਤਾਵਰਣ ਉੱਪਰ ਹੋਣ ਵਾਲੇ ਕੁੱਝ ਮਾੜੇ ਪ੍ਰਭਾਵ ਹੇਠ ਲਿਖੇ ਹਨ-

1. ਸ਼ਹਿਰਾਂ ਦੀ ਵਧਦੀ ਵਸੋਂ ਦੇ ਕਾਰਨ ਠੋਸ ਫਾਲਤੂ ਪਦਾਰਥ ਜਿਵੇਂ ਘਰੇਲੂ ਕਚਰਾ, ਕਾਰਖਾਨਿਆਂ ਦਾ ਰਿਸਾਵ ਆਦਿ ਦਾ ਉਤਪਾਦਨ ਬੜੀ ਤੇਜ਼ੀ ਨਾਲ ਵੱਧ ਰਿਹਾ ਹੈ। ਜਿਸ ਕਰਕੇ ਵਾਤਾਵਰਣ ਦੂਸ਼ਿਤ ਹੋ ਰਿਹਾ ਹੈ ਤੇ ਬੀਮਾਰੀਆਂ ਵਧ ਰਹੀਆਂ ਹਨ ।
2. ਜ਼ਿਆਦਾ ਸ਼ਹਿਰੀਕਰਨ ਅਤੇ ਕਾਰਖਾਨਿਆਂ ਤੋਂ ਕੁਦਰਤੀ ਸੰਸਾਧਨਾਂ ਦੀ ਖਪਤ ਦਰ ਵਧ ਗਈ ਹੈ, ਇਸ ਨਾਲ ਵਾਤਾਵਰਣ ਵਿਚ ਅਸੰਤੁਲਨ ਪੈਦਾ ਹੋਇਆ ਹੈ ।
3. ਸ਼ਹਿਰੀਕਰਨ ਦੇ ਨਾਲ ਸ਼ਹਿਰੀ ਖੇਤਰਾਂ ਦੇ ਚਾਰੋਂ ਪਾਸੇ ਗੰਦੀਆਂ ਬਸਤੀਆਂ ਪੈ ਗਈਆਂ ਹਨ । ਇਹਨਾਂ ਬਸਤੀਆਂ ਦੇ ਨਾਲ ਸ਼ਹਿਰਾਂ ਦਾ ਵਾਤਾਵਰਣ ਖ਼ਰਾਬ ਹੋਇਆ ਹੈ।
4. ਸ਼ਹਿਰਾਂ ਵਿਚ ਹਵਾ ਪ੍ਰਦੂਸ਼ਣ, ਧੁਨੀ ਪ੍ਰਦੂਸ਼ਣ, ਜਲ ਪ੍ਰਦੂਸ਼ਣ ਆਦਿ ਵਾਤਾਵਰਣ ਨੂੰ ਖ਼ਰਾਬ ਕਰਦੇ ਹਨ।

(ਸ) ਵੱਡੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ –

ਪ੍ਰਸ਼ਨ 1.
ਵਸੋਂ ਵਾਧੇ ਦੇ ਵਾਤਾਵਰਣ ਦੀ ਪਾਲਣ-ਸੰਭਾਲਣ ਸਮਰੱਥਾ ਦੇ ਵੱਖ-ਵੱਖ ਅੰਗਾਂ ਉੱਪਰ ਪੈਣ ਵਾਲੇ ਪ੍ਰਭਾਵਾਂ ਦੀ ਚਰਚਾ ਕਰੋ।
ਉੱਤਰ-
ਵਸੋਂ ਵਾਧਾ ਵਾਤਾਵਰਣ ਦੀ ਪਾਲਣ-ਸੰਭਾਲਣ ਸਮਰੱਥਾ ਦੇ ਵੱਖ-ਵੱਖ ਅੰਗਾਂ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਦਾ ਹੈ। ਵਾਤਾਵਰਣ ਅਤੇ ਵਸੋਂ ਆਪਸ ਵਿਚ ਬਹੁਤ ਡੂੰਘਾਈ ਤੋਂ ਜੁੜੇ ਹਨ। ਸਾਡਾ ਜੀਵਨ ਕੁਦਰਤੀ ਸਾਧਨਾਂ ਦੇ ਸੰਤੁਲਿਤ ਉਪਯੋਗ ‘ਤੇ ਨਿਰਭਰ ਕਰਦਾ ਹੈ। ਇਹ ਸੰਤੁਲਿਤ ਪ੍ਰਯੋਗ ਤਾਂ ਹੀ ਸੰਭਵ ਹਨ ਜਦੋਂ ਵਸੋਂ ਘੱਟ ਹੋਵੇ । ਜੇ ਵਸੋਂ ਵਿਚ ਵਾਧਾ ਹੁੰਦਾ ਰਹਿੰਦਾ ਹੈ ਤਾਂ ਕੁਦਰਤ ਦੇ ਵਾਧੂ ਦੋਹਣ ਦੀ ਲੋੜ ਪਏਗੀ । ਇਸ ਵਾਧੂ ਦੋਹਣ ਤੋਂ ਵਾਤਾਵਰਣ ਦੀ ਸਮੱਸਿਆ ਦਾ ਜਨਮ ਹੁੰਦਾ ਹੈ। ਵਸੋਂ ਵਿਸਫੋਟ ਦੇ ਕਾਰਨ ਵਾਤਾਵਰਣ ਸੁਰੱਖਿਆ ਦਾ ਸੰਕਟ ਪੈਦਾ ਹੋ ਗਿਆ ਹੈ। ਵਾਤਾਵਰਣ ‘ਤੇ ਉਸ ਦੀ ਪਾਲਣ ਸੰਭਾਲਣ ਸਮਰੱਥਾ ਤੋਂ ਜ਼ਿਆਦਾ ਭਾਰ ਪੈ ਰਿਹਾ ਹੈ। ਜਿਸ ਨਾਲ ਜੀਵਨਦਾਇਕ ਕਾਰਕ ਪ੍ਰਭਾਵਿਤ ਹੁੰਦੇ ਹਨ। ਵਾਤਾਵਰਣ ਦੀ ਪਾਲਣ-ਸੰਭਾਲਣ ਸਮਰੱਥਾ ਦੇ ਆਧਾਰ ‘ਤੇ ਉਸ ਦੇ ਦੋ ਪ੍ਰਕਾਰ ਦੇ ਘਟਕ ਹੁੰਦੇ ਹਨ|

ਜੀਵਨ ਰੱਖਿਅਕ ਸੰਘਟਕ (Life Supportive Components)-ਵਾਤਾਵਰਣ ਦਾ ਉਹ ਭਾਗ ਹੈ ਜੋ ਉਰਜਾ, ਭੋਜਨ, ਹਵਾ ਅਤੇ ਪਾਣੀ ਦਿੰਦਾ ਹੈ।
ਰਹਿੰਦ-ਖੂੰਹਦ ਪਾਚਣਸ਼ੀਲ ਘਟਕ (Waste Assimilative Components)ਵਾਤਾਵਰਣ ਦੇ ਇਸ ਭਾਗ ਵਿਚ ਮਨੁੱਖੀ ਕਿਰਿਆਂ ਵਲੋਂ ਪੈਦਾ ਫਾਲਤੂ ਪਦਾਰਥਾਂ ਦਾ ਪਾਚਣ ਜਾਂ ਨਿਪਟਾਰਾ ਸ਼ਾਮਿਲ ਹੈ। ਧਰਤੀ ਦੀ ਪਾਲਣ ਸੰਭਾਲਣ ਦੀ ਸਮਰੱਥਾ ਸੀਮਿਤ ਹੈ, ਇਸ ਲਈ ਵਸੋਂ ਵਾਧੇ ਦੇ ਕਾਰਨ ਵਾਤਾਵਰਣ ਦੀ ਪਾਲਣ ਸੰਭਾਲਣ ਦੀ ਸਮਰੱਥਾ ਦੇ ਹਿੱਸਿਆਂ ‘ਤੇ ਬੁਰਾ ਪ੍ਰਭਾਵ ਪੈਂਦਾ ਹੈ।

ਇਹਨਾਂ ਦਾ ਵਿਵਰਣ ਹੇਠਾਂ ਲਿਖਿਆ ਹੈ –
ਖਾਣ ਵਾਲੇ ਪਦਾਰਥਾਂ ‘ ਤੇ ਅਸਰ (Impact on Food Stuffs)ਵੱਧਦੀ ਹੋਈ ਵਸੋਂ ਦੇ ਕਾਰਨ ਖਾਣ ਵਾਲੇ ਪਦਾਰਥਾਂ ਦੀ ਮੰਗ ਵਧਦੀ ਹੈ। ਇਸ ਲਈ ਖੇਤੀ ਯੋਗ ਜ਼ਮੀਨ ਨੂੰ ਉਰਜਾ, ਪਾਣੀ, ਖਾਦਾਂ ਅਤੇ ਕੀਟਾਣੂ ਨਾਸ਼ਕ ਦਵਾਈਆਂ ਦੀ ਮਦਦ ਨਾਲ ਤੇ ਆਧੁਨਿਕ ਤਰੀਕਿਆਂ ਦੀ ਵਰਤੋਂ ਦੁਆਰਾ ਜ਼ਿਆਦਾ ਵਰਤਿਆ ਜਾ ਰਿਹਾ ਹੈ। ਇਸ ਨਾਲ ਸੰਸਾਰ ਵਿਚ ਖਾਣ ਵਾਲੇ ਪਦਾਰਥਾਂ ਦੀ ਉਤਪਾਦਕਤਾ 50 ਪ੍ਰਤੀਸ਼ਤ ਤੋਂ ਵੀ ਜ਼ਿਆਦਾ ਵੱਧ ਗਈ ਹੈ, ਪਰ ਮਾਨਵ ਦੀਆਂ ਅਨਿਆਂਸੰਗਤ ਗਤੀਵਿਧੀਆਂ ਦੇ ਵੱਧ ਚਾਰਨ, ਰਸਾਇਣਿਕ ਖਾਦਾਂ ਦੀ ਜ਼ਿਆਦਾ ਵਰਤੋਂ ਅਤੇ ਭੂਮੀਗਤ ਪਾਣੀ ਦੇ ਦੁਰਉਪਯੋਗ ਦੇ ਕਾਰਨ ਨਵੀਆਂ-ਨਵੀਆਂ ਵਾਤਾਵਰਣ ਦੀਆਂ ਸਮੱਸਿਆਵਾਂ ਪੈਦਾ ਹੋ ਰਹੀਆਂ ਹਨ । ਭੂਮੀ ਦਾ ਲੂਣੀਕਰਣ, ਮਾਰੂਸਥਲੀਕਰਣ, ਭੂ-ਖੋਰਣ, ਭੂਮੀ ਵਿਕਤੀਕਰਣ ਆਦਿ ਇਸਦੇ ਨਤੀਜੇ ਹਨ। ਇਸਦੇ ਨਾਲ-ਨਾਲ ਖਾਣ ਦੇ ਪਦਾਰਥਾਂ ਦੀ ਕਮੀ ਦੇ ਕਾਰਨ ਜ਼ਿਆਦਾਤਰ ਲੋਕ, ਅਲਪ-ਪੋਸ਼ਿਤ ਹਨ । ਭਾਰਤ ਵਿਚ ਲਗਪਗ 70 ਤੋਂ 80 ਪ੍ਰਤੀਸ਼ਤ ਬੱਚੇ ਕੁਪੋਸ਼ਣ ਦੇ ਸ਼ਿਕਾਰ ਹਨ ।

ਊਰਜਾ ’ਤੇ ਪ੍ਰਭਾਵ (Impact on Energy) -ਵਿਸ਼ਵ ਦੇ ਜ਼ਿਆਦਾਤਰ ਵਿਕਸਿਤ ਅਤੇ ਵਿਕਾਸਸ਼ੀਲ ਦੇਸ਼ ਵੱਧਦੀ ਹੋਈ ਆਬਾਦੀ ਦੇ ਲਈ ਰੋਜ਼ਗਾਰ ਵਧਾਉਣ ਅਤੇ ਉਹਨਾਂ ਦੀਆਂ ਮੰਗਾਂ ਨੂੰ ਪੂਰਾ ਕਰਨ ਲਈ, ਉਤਪਾਦਨ ਵਧਾਉਣ ਲਈ ਉਦਯੋਗੀਕਰਨ ਦੇ ਵੱਲ ਵੱਧ ਰਹੇ ਹਨ ਅਤੇ ਊਰਜਾ ਦੇ ਬਗੈਰ ਉਦਯੋਗ ਨਹੀਂ ਚਲ ਸਕਦੇ । ਇਸ ਤਰ੍ਹਾਂ ਵਸੋਂ ਵਾਧਾ, ਤੇਜ਼ ਉਦਯੋਗੀਕਰਨ ਅਤੇ ਸ਼ਹਿਰੀਕਰਨ ਦੇ ਨਤੀਜੇ ਵਜੋਂ ਪਹਿਲਾਂ ਤੋਂ ਹੀ ਘੱਟ ਮਾਤਰਾ ਵਿਚ ਹਾਸਿਲ ਊਰਜਾ ਸਰੋਤ ਜਿਵੇਂ, ਲੱਕੜੀ, ਪਥਰਾਟ ਬਾਲਣ ਅਤੇ ਬਿਜਲੀ ਦੀ ਮੰਗ ਵੱਧ ਰਹੀ ਹੈ। ਪਥਰਾਟ ਬਾਲਣ ਸੀਮਿਤ ਮਾਤਰਾ ਵਿਚ ਹਾਸਲ ਹੋਣ ਦੇ ਕਾਰਨ ਹੌਲੀ-ਹੌਲੀ ਖ਼ਤਮ ਹੋ ਰਹੇ ਹਨ। ਇਸ ਤਰ੍ਹਾਂ ਵਸੋਂ ਦੇ ਵਾਧੇ ਦੇ ਕਾਰਨ ਕੁਦਰਤੀ ਸੋਮਿਆਂ ਵਿਚ ਨਾ-ਬਰਾਬਰਤਾ ਦੀ ਸਥਿਤੀ ਪੈਦਾ ਹੋਣ ‘ਤੇ ਵਾਤਾਵਰਣ ਵਿਕੂਤ ਹੋਣ ਦੀ ਸਥਿਤੀ ਪੈਦਾ ਹੋ ਗਈ ਹੈ।

ਗਰੀਬੀ ‘ ਤੇ ਪ੍ਰਭਾਵ (Impact on Poverty)-ਵਸੋਂ ਅਤੇ ਗਰੀਬੀ ਦਾ ਇਕ ਦੁਸਰੇ ਨਾਲ ਬਹੁਤ ਗਹਿਰਾ ਸੰਬੰਧ ਹੈ। ਵਿਸ਼ਵ ਦੀ ਤਿੰਨ-ਚੌਥਾਈ ਵਸੋਂ ਕਾਸਸ਼ੀਲ ਦੇਸ਼ਾਂ ਵਿਚ ਰਹਿੰਦੀ ਹੈ। ਇਹਨਾਂ ਦੇਸ਼ਾਂ ਵਿਚ ਬੇਰੋਜ਼ਗਾਰੀ ਇਕ ਵੱਡੀ ਸਮੱਸਿਆ ਹੈ ਜੋ ਗਰੀਬੀ ਨੂੰ ਵਜੋਂ ਅਤੇ ਵਾਤਾਵਰਣ ਜਨਮ ਦਿੰਦੀ ਹੈ। ਗਰੀਬੀ ਦੇ ਕਾਰਨ ਲੋਕਾਂ ਨੂੰ ਪੌਸ਼ਟਿਕ ਆਹਾਰ, ਘਰਾਂ ਅਤੇ ਕੱਪੜਿਆਂ ਦੀ ਕਮੀ ਰਹਿੰਦੀ ਹੈ। ਨਾਲ ਹੀ ਸਿੱਖਿਆ ਅਤੇ ਸਫ਼ਾਈ ਦੀ ਵੀ ਕਮੀ ਰਹਿੰਦੀ ਹੈ। ਇਹਨਾਂ ਸਭ ਕਾਰਨਾਂ ਨਾਲ ਉਤਪਾਦਕਤਾ ਘੱਟ ਹੋ ਜਾਂਦੀ ਹੈ। ਉਤਪਾਦਕਤਾ ਦੀ ਕਮੀ ਨਾਲ ਮੁੜ ਗਰੀਬੀ ਵਿਚ ਵਾਧਾ ਹੋ ਜਾਂਦਾ ਹੈ। ਆਰਥਿਕ ਸੰਸਾਧਨਾਂ ਦੀ ਇੱਕੋ ਜਿਹੀ ਵੰਡ ਨਾ ਹੋਣ ਅਤੇ ਆਬਾਦੀ ਵਧਣ ਨਾਲ ਸਮੱਸਿਆ ਹੋਰ ਵੀ ਭਿਆਨਕ ਹੋ ਜਾਂਦੀ ਹੈ ਕਿਉਂਕਿ ਵਸੋਂ ਵਾਧਾ ਮੁੱਢਲੀਆਂ ਲੋੜਾਂ ਜਿਵੇਂ ਘਰ, ਰੁਜ਼ਗਾਰ, ਚਿਕਿਤਸਾ ਸੁਵਿਧਾਵਾਂ ਆਦਿ ‘ਤੇ ਦਬਾਓ ਪਾਉਂਦੀ ਹੈ। ਇਸ ਨਾਲ ਗਰੀਬੀ ਵਿਚ ਵਾਧਾ ਹੁੰਦਾ ਹੈ।

ਕੱਚੇ ਮਾਲ ‘ਤੇ ਪ੍ਰਭਾਵ (Impact on Raw Materials)-ਆਬਾਦੀ ਵਿਚ ਵਾਧੇ ਦਾ ਸਿੱਧਾ ਅਸਰ ਲੋਕਾਂ ਦੀਆਂ ਮੰਗਾਂ ਨੂੰ ਪੂਰਾ ਕਰਨ ਲਈ ਉਦਯੋਗਾਂ ‘ਤੇ ਵੱਧ ਤੋਂ ਵੱਧ ਮਾਲ ਬਨਾਉਣ ਦਾ ਦਬਾਓ ਪਾਉਣ ਤੋਂ ਹੈ। ਉਦਯੋਗਾਂ ਵਿਚ ਉਤਪਾਦਨ ਲਈ ਕੱਚੇ ਮਾਲ ਦੀ ਲੋੜ ਹੁੰਦੀ ਹੈ।

ਕੱਚੇ ਮਾਲ ਦੇ ਦੋ ਮੁੱਖ ਸੋਮੇ (Two Major Sources of Raw Materials) -ਕੱਚੇ ਮਾਲ ਦੇ ਦੋ ਮੁੱਖ ਸੋਮੇ ਜੰਗਲ ਅਤੇ ਖਾਣਾਂ ਹਨ । ਖਾਣਾਂ ਤੋਂ ਸਾਨੂੰ ਕੋਲਾ, ਲੋਹਾ ਅਤੇ ਹੋਰ ਧਾਤੂ ਮਿਲਦੇ ਹਨ। ਪਰ ਆਬਾਦੀ ਵਧਣ ਨਾਲ ਜ਼ਿਆਦਾ ਉਤਪਾਦਨ ਲਈ ਖਾਣਾਂ ਖੋਦਣ ਕਿਰਿਆਵਾਂ ਖਣਨ) ਵਿਚ ਵਾਧਾ ਹੁੰਦਾ ਹੈ। ਜਿਸਦੇ ਨਤੀਜੇ ਵਜੋਂ ਕਿੰਨੀਆਂ ਖਾਣਾਂ ਖ਼ਤਮ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ।

ਜੰਗਲਾਂ ਤੋਂ ਸਾਨੂੰ ਬਹੁਤ ਸਾਰੇ ਉਪਯੋਗੀ ਪਦਾਰਥ ਜਿਵੇਂ ਇਮਾਰਤੀ ਲੱਕੜੀ, ਰਬੜ, ਦਵਾਈਆਂ ਆਦਿ ਮਿਲਦੇ ਹਨ ਪਰ ਇਹਨਾਂ ਦੀ ਪੂਰਤੀ ਲਈ ਜੰਗਲਾਂ ਦੀ ਅੰਨ੍ਹੇਵਾਹ ਦੋਹਣ ਕੀਤਾ ਜਾਂਦਾ ਹੈ। | ਜੰਗਲਾਂ ਦੇ ਵਿਨਾਸ਼ ਦੇ ਬਹੁਤ ਸਾਰੇ ਬੁਰੇ ਨਤੀਜੇ ਹਨ। ਜੰਗਲਾਂ ਦੇ ਨਸ਼ਟ ਹੋਣ ਨਾਲ ਗਰੀਨ ਹਾਊਸ ਪ੍ਰਭਾਵ ਵੱਧ ਰਿਹਾ ਹੈ। ਜਿਸ ਨਾਲ ਵਿਸ਼ਵ-ਵਿਆਪੀ ਤਾਪਮਾਨ ਵਿਚ ਵਾਧਾ ਹੋਣ ਦੀ ਸਮੱਸਿਆ ਪੈਦਾ ਹੋ ਰਹੀ ਹੈ।

ਵਿਸ਼ਵ-ਵਿਆਪੀ ਤਾਪਮਾਨ ਵਿਚ ਵਾਧਾ (Global Warming) ਹੋਣ ਕਾਰਨ ਧਰੁਵਾਂ ‘ਤੇ ਜੰਮੀ ਬਰਫ਼ ਪਿਘਲ ਰਹੀ ਹੈ ਅਤੇ ਸਮੁੰਦਰ ਦੇ ਪਾਣੀ ਦਾ ਪੱਧਰ ਉੱਪਰ ਉੱਠ ਰਿਹਾ ਹੈ। | ਜਿਸ ਦੇ ਨਤੀਜੇ ਵਜੋਂ ਕਈ ਦੀਪਾਂ ਅਤੇ ਸਮੁੰਦਰ ਦੇ ਕੰਡੇ ਦੇ ਖੇਤਰਾਂ ਦੇ ਪਾਣੀ ਵਿਚ ਡੁੱਬਣ ਦੀ ਸੰਭਾਵਨਾ ਬਣੀ ਹੋਈ ਹੈ।

Punjab State Board PSEB 11th Class Environmental Education Book Solutions Chapter 1 ਵਾਤਾਵਰਣ (Environment) Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Environmental Education Chapter 1 ਵਾਤਾਵਰਣ

Environmental Education Guide for Class 11 PSEB ਵਾਤਾਵਰਣ Textbook Questions and Answers

(ਉ) ਬਹੁਤ ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ

ਪ੍ਰਸ਼ਨ 1.
ਕੁਦਰਤੀ ਵਾਤਾਵਰਣ ਕਿਸ ਨੂੰ ਆਖਦੇ ਹਨ ?
ਉੱਤਰ-
ਕੁਦਰਤੀ ਵਾਤਾਵਰਣ ਤੋਂ ਭਾਵ ਹੈ ਸਾਡਾ ਆਲਾ-ਦੁਆਲਾ ਜਿਸ ਵਿਚ ਸਜੀਵ ਅਤੇ ਨਿਰਜੀਵ ਦੋਵੇਂ ਅੰਸ਼ ਆਪਸ ਵਿਚ ਕਿਰਿਆ ਕਰਦੇ ਹਨ । ਕੁਦਰਤੀ ਵਾਤਾਵਰਣ ਬਣਾਉਣ ਵਿੱਚ ਸਾਡਾ ਕੋਈ ਰੋਲ ਨਹੀਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਵਾਤਾਵਰਣ ਦੇ ਅੰਗਾਂ ਦੇ ਨਾਂ ਲਿਖੋ ।
ਉੱਤਰ-
ਸਜੀਵ/ਜੈਵ ਅੰਗ (Biotic Components) ਅਤੇ ਨਿਰਜੀਵਅਜੈਵ ਅੰਗ (Abiotic Components) ।

ਪ੍ਰਸ਼ਨ 3.
ਵਾਤਾਵਰਣ ਦੇ ਤਿੰਨ ਪਸਾਰ ਦੱਸੋ ।
ਉੱਤਰ-
ਭੌਤਿਕ ਵਾਤਾਵਰਣ, ਜੈਵਿਕ ਵਾਤਾਵਰਣ ਅਤੇ ਸਮਾਜਿਕ ਵਾਤਾਵਰਣ ।

ਪ੍ਰਸ਼ਨ 4.
ਸਵੈ ਪੋਸ਼ੀ/ਸਵੈ-ਆਹਾਰੀ (Autotrophs) ਦੀ ਪਰਿਭਾਸ਼ਾ ਦਿਓ ।
ਉੱਤਰ-
ਉਹ ਜੀਵ ਜਿਹੜੇ ਪ੍ਰਕਾਸ਼ ਸੰਸ਼ਲੇਸ਼ਣ ਦੀ ਕਿਰਿਆ ਦੁਆਰਾ ਕਾਰਬਨ ਡਾਈਆਕਸਾਈਡ, ਪਾਣੀ ਤੋਂ ਸੂਰਜ ਦੀ ਰੌਸ਼ਨੀ ਅਤੇ ਕਲੋਰੋਫਿਲ ਦੀ ਮੱਦਦ ਨਾਲ ਆਪਣਾ ਭੋਜਨ ਆਪ ਤਿਆਰ ਕਰਦੇ ਹਨ, ਉਹ ਸਵੈਪੋਸ਼ੀ/ਸਵੈ-ਆਹਾਰੀ ਜੀਵ ਕਹਾਉਂਦੇ ਹਨ, ਜਿਵੇਂ ਸਾਰੇ ਹਰੇ ਪੌਦੇ ਆਦਿ । ਦੂਸਰੇ ਸ਼ਬਦਾਂ ਵਿੱਚ ਉਹ ਜੀਵ, ਜੋ ਆਪਣੇ ਆਪ ਨੂੰ ਜੀਵਤ ਰੱਖਣ ਲਈ ਲੋੜੀਂਦਾ ਭੋਜਨ ਤਿਆਰ ਕਰ ਸਕਦੇ ਹਨ, ਸਵੈਪੋਸ਼ੀ ਅਖਵਾਉਂਦੇ ਹਨ । ਉਦਾਹਰਨਾਂ ਵਿੱਚ ਸਾਰੇ ਹਰੇ ਪੌਦੇ ਅਤੇ ਕੁੱਝ ਬੈਕਟੀਰੀਆ ਸ਼ਾਮਲ ਹਨ ।

ਪ੍ਰਸ਼ਨ 5.
ਪਰ-ਆਹਾਰੀ (Heterotrophs) ਕਿਸ ਨੂੰ ਆਖਦੇ ਹਨ ?
ਉੱਤਰ-
ਉਹ ਜੀਵ ਜੋ ਆਪਣਾ ਭੋਜਨ ਆਪ ਤਿਆਰ ਨਹੀਂ ਕਰ ਸਕਦੇ ਅਤੇ ਸਵੈਆਹਾਰੀਆਂ ਜਾਂ ਦੂਸਰੇ ਜੀਵਾਂ ਉੱਪਰ ਆਪਣੀਆਂ ਭੋਜਨ ਸੰਬੰਧੀ ਲੋੜਾਂ ਦੀ ਪੂਰਤੀ ਲਈ ਨਿਰਭਰ ਕਰਦੇ ਹੋਣ, ਉਹਨਾਂ ਨੂੰ ਪਰ-ਆਹਾਰੀ (Heterotrophs) ਆਖਦੇ ਹਨ , ਜਿਵੇਂਉੱਲੀ, ਸ਼ੇਰ, ਪੰਛੀ ਆਦਿ। ਇਨ੍ਹਾਂ ਨੂੰ ਖਪਤਕਾਰ (Consumers) ਵੀ ਕਹਿੰਦੇ ਹਨ । ਉਦਾਹਰਨਾਂ ਵਿੱਚ ਸਾਰੇ ਜੀਵ-ਜੰਤੂ ਅਤੇ ਪੌਦੇ ਜੋ ਕਿ ਹਰੇ ਨਹੀਂ ਹਨ) ਸ਼ਾਮਲ ਹਨ ।

ਪ੍ਰਸ਼ਨ 6.
ਸਮਾਜਿਕ ਵਾਤਾਵਰਣ ਦੇ ਅੰਗਾਂ ਦਾ ਨਾਂ ਦੱਸੋ।
ਉੱਤਰ-
ਮਨੁੱਖ।

ਪ੍ਰਸ਼ਨ 7.
ਜੀਵ-ਮੰਡਲ (Biosphere) ਸੁਰੱਖਿਆ ਖੇਤਰ ਜਾਂ ਰਿਜ਼ਰਵ ਕੀ ਹੁੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਉਹ ਸੁਰੱਖਿਅੰਤ ਖੇਤਰ ਜਿਸ ਵਿਚ ਮਨੁੱਖ ਦੇ ਦਖ਼ਲ ਉੱਪਰ ਪਾਬੰਦੀ ਨਹੀਂ ਹੁੰਦੀ ਹੈ।

ਪ੍ਰਸ਼ਨ 8.
ਸਾਡੇ ਵਾਤਾਵਰਣ ਦੇ ਪੰਜ ਤੱਤ ਕਿਹੜੇ ਹਨ ?
ਉੱਤਰ-
ਧਰਤੀ, ਜਲ, ਹਵਾ, ਊਰਜਾ ਅਤੇ ਪੁਲਾੜ

(ਅ) ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ (Type I)

ਪ੍ਰਸ਼ਨ 1.
ਜੈਵਿਕ ਅਤੇ ਅਜੈਵਿਕ ਵਾਤਾਵਰਣੀ ਅੰਗਾਂ ਵਿੱਚ ਅੰਤਰ ਸਪੱਸ਼ਟ ਕਰੋ।
ਉੱਤਰ –
ਜੈਵ ਅੰਗ (Biotics) |’ ਅਜੈਵ ਅੰਗ (Abiotic) 1. ਵਾਤਾਵਰਣ ਦੇ ਸਜੀਵ ਅੰਗਾਂ ਨੂੰ ਜੈਵਿਕ | 1. ਵਾਤਾਵਰਣ ਦੇ ਨਿਰਜੀਵ ਅੰਗਾਂ ਨੂੰ, | • ਅੰਸ਼ ਕਿਹਾ ਜਾਂਦਾ ਹੈ।
ਅਜੈਵਿਕ ਅੰਸ਼ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । 2. ਜਿਵੇਂ-ਉਤਪਾਦਕ ਪੌਦੇ), ਖ਼ਪਤਕਾਰ 2. ਜਿਵੇਂ-ਜਲਵਾਯੂ, ਊਰਜਾ, ਵਰਖਾ, (ਮਨੁੱਖ, ਜਾਨਵਰ) , ਅਤੇ ਨਿਖੇੜਕ ਸੌਰ ਵਿਕਿਰਨਾਂ, ਤਾਪਮਾਨ, ਹਵਾ, ਸੂਖ਼ਮ ਜੀਵ) ਆਦਿ।
ਮਿੱਟੀ, ਰੌਸ਼ਨੀ ਆਦਿ ।

ਪ੍ਰਸ਼ਨ 2.
ਵਾਤਾਵਰਣ ਦੀ ਸੁਰੱਖਿਆ ਲਈ ਸਮਾਜਵਾਦੀ ਸਮਾਜ (Socialistic Society)ਚੰਗਾ ਕਿਉਂ ਹੁੰਦਾ ਹੈ ? |
ਉੱਤਰ-
ਵਾਤਾਵਰਣ ਦੀ ਸੁਰੱਖਿਆ ਲਈ ਸਮਾਜਵਾਦੀ ਸਮਾਜ (Socialistic Society) ਇਸ ਲਈ ਚੰਗਾ ਹੈ ਕਿਉਂਕਿ ਸਮਾਜਵਾਦੀ ਸਮੂਹ ਨੇ ਕੁਦਰਤੀ ਸਰੋਤਾਂ ਦੇ
ਮਹੱਤਵ ਨੂੰ ਧਿਆਨ ਵਿਚ ਰੱਖਦੇ ਹੋਏ ਇਹਨਾਂ ਦੇ ਲੋੜ ਤੋਂ ਵੱਧ ਸ਼ੋਸ਼ਣ ਨੂੰ ਰੋਕਣ ਲਈ ਨਿਯਮ ਨਿਰਧਾਰਿਤ ਕੀਤੇ ਹਨ ਅਤੇ ਇਹਨਾਂ ਨਿਯਮਾਂ ਦੀ ਪਾਲਣਾ ਦੁਆਰਾ ਮਨੁੱਖ ਅਤੇ ਕੁਦਰਤ ਵਿਚਾਲੇ ਸੰਤੁਲਨ ਪੈਦਾ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ। ਸਮਾਜਵਾਦੀ ਢਾਂਚੇ ਦੇ ਲੋਕਾਂ ਨੂੰ ਕੁਦਰਤੀ ਸਾਧਨਾਂ ਦੇ ਲਾਭ ਅਤੇ ਹਾਨੀਆਂ ਦਾ ਅੰਦਾਜ਼ਾ ਹੁੰਦਾ ਹੈ ਅਤੇ ਉਹ ਇਹਨਾਂ ਦੀ ਵਰਤੋਂ ਅਤੇ ਕੁਵਰਤੋਂ ਪ੍ਰਤੀ ਵੱਧ ਸੁਚੇਤ ਹੁੰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 3.
ਥਲ-ਮੰਡਲ (Hydrosphere) ਅਤੇ ਜਲ-ਮੰਡਲ (Lithosphere) ਵਿੱਚ ਕੀ ਅੰਤਰ ਹੈ ?
ਉੱਤਰ-
ਥਲ-ਮੰਡਲ (Lithosphere) ਤੋਂ ਭਾਵ ਧਰਤੀ ਦੀ ਸਤਾ ਦਾ ਉਪਰਲਾ ਹਿੱਸਾ ਹੈ ਜੋ ਜੀਵਾਂ, ਪੌਦਿਆਂ, ਸੂਖ਼ਮ ਜੀਵਾਂ ਆਦਿ ਦੇ ਵਿਕਾਸ ਲਈ ਖਣਿਜੀ ਤੱਤ ਅਤੇ ਮਿੱਟੀ ਪ੍ਰਦਾਨ ਕਰਦਾ ਹੈ।

ਜਲ-ਮੰਡਲ (Hydrosphere) ਵਿਚ ਧਰਤੀ ਦੀ ਸਤ੍ਹਾ ‘ਤੇ ਪਾਏ ਜਾਣ ਵਾਲੇ ਸਮੁੰਦਰ, ਝੀਲਾਂ, ਨਦੀਆਂ ਅਤੇ ਹੋਰ ਜਲ-ਸਰੋਤ ਸ਼ਾਮਿਲ ਹਨ। ਇਹਨਾਂ ਵਿਚ ਜਲੀ-ਜੀਵ ਅਤੇ ਜਲੀਪੌਦੇ ਵੀ ਸ਼ਾਮਿਲ ਹਨ।

ਪ੍ਰਸ਼ਨ 4.
ਸਿੱਧ ਕਰੋ ਕਿ , ਜੈਵਿਕ ਵਾਤਾਵਰਣ (Biological atmosphere) ਵਿੱਚ ਉਤਪਾਦਕ (Producers) ਸਭ ਤੋਂ ਮਹੱਤਵਪੂਰਨ ਹਨ।
ਉੱਤਰ-
ਉਤਪਾਦਕਾਂ ਵਿਚ ਹਰੇ ਪੌਦੇ, ਘਾਹ, ਝਾੜੀਆਂ, ਹਰੀ-ਕਾਈ, ਫਾਈਟੋ ਪਲੈਂਕਟਾਨ ਅਤੇ ਗੰਧਕ ਜੀਵਾਣੂ ਆਦਿ ਸ਼ਾਮਿਲ ਹਨ। ਉਤਪਾਦਕ ਪ੍ਰਕਾਸ਼ ਸੰਸ਼ਲੇਸ਼ਣ ਦੀ
ਕਿਰਿਆ ਰਾਹੀਂ ਕਾਰਬਨ ਡਾਈਆਕਸਾਈਡ ਪਾਣੀ ਤੋਂ ਸੂਰਜ ਦੀ ਰੌਸ਼ਨੀ ਅਤੇ ਕਲੋਰੋਫਿਲ (Chlorophyll ਦੀ ਮੱਦਦ ਨਾਲ ਕਾਰਬਨੀ ਪਦਾਰਥਾਂ ਦਾ
ਨਿਰਮਾਣ ਕਰਦੇ ਹਨ। ਗੰਧਕ (Sulphur) ਜੀਵਾਣੁ ਆਪਣੇ ਕਾਰਬਨੀ ਭੋਜਨ ਦਾ ਨਿਰਮਾਣ ਰਸਾਇਣਿਕ ਕਿਰਿਆ ਦੁਆਰਾ ਕਰਦੇ ਹਨ। ਉਤਪਾਦਕ ਪੁਰੇ ਜੈਵਿਕ ਵਾਤਾਵਰਣ ਨੂੰ ਭੋਜਨ, ਆਸਰਾ ਅਤੇ ਆਕਸੀਜਨ ਦਿੰਦੇ ਹਨ। ਇਸ ਲਈ ਇਨ੍ਹਾਂ ਨੂੰ ਜੀਵਨ ਦੀ ਮੁੱਢਲੀ ਜ਼ਰੂਰਤ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ।

(ੲ) ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ

ਪ੍ਰਸ਼ਨ 1.
ਵਾਤਾਵਰਣ ਨੂੰ ਬਚਾਉਣ ਲਈ ਆਮ ਜਨਤਾ ਦੀ ਭੂਮਿਕਾ ਉੱਪਰ ਟਿੱਪਣੀ ਕਰੋ।
ਉੱਤਰ-
ਆਮ ਜਨਤਾ ਦੀ ਵਾਤਾਵਰਣ ਨੂੰ ਬਚਾਉਣ ਲਈ ਭੂਮਿਕਾ ਨੂੰ ਸਮਝਣ ਲਈ ਸਾਨੂੰ ਇਸ ਗੱਲ ਨੂੰ ਚੰਗੀ ਤਰਾਂ ਸਮਝ ਲੈਣਾ ਚਾਹੀਦਾ ਹੈ ਕਿ ਵਾਤਾਵਰਣ ਤੋਂ ਬਗੈਰ ਮਨੁੱਖ ਦੀ ਇਸ ਧਰਤੀ ਤੋਂ ਹੋਂਦ ਹੀ ਮੁੱਕ ਜਾਵੇਗੀ। ਜਿਸ ਕਰਕੇ ਲੋਕਾਂ ਵਿਚ ਵਾਤਾਵਰਣ ਦੀਆਂ ਸਮੱਸਿਆਵਾਂ ਲਈ ਜਾਗਰੂਕਤਾ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ। ਸੰਚਾਰ ਦੇ ਵੱਖ-ਵੱਖ ਸਾਧਨਾਂ ਅਤੇ ਅਵਲੋਚਨਾ ਦੁਆਰਾ ਵਾਤਾਵਰਣ ਦੀਆਂ ਸਮੱਸਿਆਵਾਂ ਵੱਲ ਲੋਕਾਂ ਦਾ ਧਿਆਨ ਖਿੱਚਿਆ ਜਾਣਾ ਚਾਹੀਦਾ ਹੈ। ਇਸ ਲਈ ਕੁਦਰਤੀ ਸੰਸਾਧਨਾਂ ਦੇ ਵਧ ਰਹੇ ਸ਼ੋਸ਼ਣ ਦੇ ਹਾਨੀਕਾਰਕ ਪ੍ਰਭਾਵਾਂ ਤੋਂ ਹੋਣ ਵਾਲੇ ਵਿਨਾਸ਼ ਤੋਂ ਬਚਣ ਲਈ ਪੋਸਟਰਾਂ, ਰੈਲੀਆਂ, ਨਾਟਕਾਂ, ਫਿਲਮਾਂ ਆਦਿ ਰਾਹੀਂ ਲੋਕਾਂ ਵਿਚ ਜਾਗਰੂਕਤਾ ਪੈਦਾ ਕਰਨ ਦੀ ਕੋਸ਼ਿਸ਼ ਕੀਤੀ ਜਾਣੀ ਚਾਹੀਦੀ ਹੈ। ਸਮਝਦਾਰ ਅਤੇ ਅਸਰ ਰਸੂਖ ਵਾਲੇ ਲੋਕ ਵਾਤਾਵਰਣ ਸੁਧਾਰਣ ਲਈ ਗੰਭੀਰ ਰੂਚੀ ਦਿਖਾ ਕੇ ਵਾਤਾਵਰਣ ਨੂੰ ਬਚਾਉਣ ਲਈ ਆਪਣਾ ਯੋਗਦਾਨ ਪਾਉਣ। ਇਸ ਨਾਲ ਲੋਕਾਂ ਨੂੰ ਵਾਤਾਵਰਣ ਦੇ ਅਪਘਟਨ ਦੇ ਕਾਰਨ ਸਮਝ ਵਿਚ ਆ ਜਾਣਗੇ ਅਤੇ ਲੋਕ ਇਹ ਵੀ ਸਮਝ ਜਾਣਗੇ ਕਿ ਤਕਨੀਕੀ ਵਿਕਾਸ ਵਾਤਾਵਰਣ ਦੇ ਸੁਧਾਰ ਦਾ ਸਹੀ ਵਿਕਲਪ ਨਹੀਂ ਹੈ। ਇਸ ਦੇ ਨਾਲ-ਨਾਲ ਵਾਤਾਵਰਣੀ ਸਮੱਸਿਆਵਾਂ ਦੇ ਸੁਧਾਰ ਲਈ ਵਰਤੇ ਜਾ ਸਕਣ ਵਾਲੇ ਤਰੀਕਿਆਂ ਦੀ ਚੋਣ ਕੀਤੀ ਜਾਣੀ ਚਾਹੀਦੀ ਹੈ।

ਪ੍ਰਸ਼ਨ 2.
ਭੌਤਿਕ ਵਾਤਾਵਰਣ (Physical Environment ਦਾ ਵਿਸਤ੍ਰਿਤ ਵੇਰਵਾ ਦਿਓ। ‘ ‘
ਉੱਤਰ-
ਥਲ ਮੰਡਲ, ਵਾਯੂ ਮੰਡਲ ਅਤੇ ਜਲ ਮੰਡਲ ਭੌਤਿਕ ਵਾਤਾਵਰਣ (Physical Environment) ਦੇ ਤਿੰਨ ਅੰਸ਼ ਹਨ-
ਵਾਯੂਮੰਡਲ (Atmosphere)-ਇਹ ਜੀਵਨ ਰੱਖਿਅਕ ਗੈਸਾਂ ਦਾ ਇਕ ਗਿਲਾਫ਼ ਹੁੰਦਾ ਹੈ ਜੋ ਧਰਤੀ ਨੂੰ ਚਾਰੇ ਪਾਸੇ ਤੋਂ ਢੱਕੀ ਰੱਖਦਾ ਹੈ। ਇਸ ਵਿਚ O₂, (ਆਕਸੀਜਨ ਗੈਸ ਹੁੰਦੀ ਹੈ ਜਿਸ ਤੋਂ ਬਿਨਾਂ ਜੀਵਾਂ ਦਾ ਸਾਹ ਲੈਣਾ ਵੀ ਮੁਸ਼ਕਿਲ ਹੈ। ਇਸਦਾ ਉਪਯੋਗ ਜੀਵਨ ਕਿਰਿਆਵਾਂ ਨੂੰ ਕਰਨ ਲਈ ਜ਼ਰੂਰੀ ਹੈ। ਇਸ ਵਿਚ CO₂, ਵੀ ਪਾਈ ਜਾਂਦੀ ਹੈ ਜੋ ਪੌਦਿਆਂ ਲਈ ਪ੍ਰਕਾਸ਼ ਸੰਸ਼ਲੇਸ਼ਣ ਕਿਰਿਆ ਵਾਸਤੇ ਬਹੁਤ ਜ਼ਰੂਰੀ ਹੈ। ਵਾਤਾਵਰਨ ਨੂੰ ਸ਼੍ਰੀਨ ਹਾਉਸ ਵੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ਕਿਉਂਕਿ ਇਹ ਵਾਤਾਵਰਣ ਦੇ ਤਾਪਮਾਨ ਨੂੰ ਸੰਤੁਲਿਤ ਰੱਖ ਕੇ ਠੰਡਾ ਅਤੇ ਗਰਮ ਹੋਣ ਤੋਂ ਬਚਾਉਂਦਾ ਹੈ। ਇਸ ਵਿਚ O₂, CO, ਤੋਂ ਇਲਾਵਾ ਜਲ ਵਾਸ਼ਪ, N₂ਰ ਆਦਿ ਵੀ ਹੁੰਦੇ ਹਨ। |

ਜਲ-ਮੰਡਲ (Hydrosphere)-ਇਸ ਵਿਚ ਧਰਤੀ ਦੇ ਸਾਰੇ ਜਲ ਸਰੋਤ; ਜਿਵੇਂ ਸਮੁੰਦਰ, ਝੀਲਾਂ, ਨਦੀਆਂ ਆਦਿ ਸ਼ਾਮਿਲ ਹਨ। ਜਲ-ਮੰਡਲ ਸਾਰੇ ਜੀਵਾਂ ਦੀਆਂ ਸਰੀਰਕ, ਕਿਰਿਆਵਾਂ ਲਈ ਜਲ ਪ੍ਰਦਾਨ ਕਰਦਾ ਹੈ। ਇਸ ਦੇ ਕਾਰਨ ਹੀ ਵਾਤਾਵਰਣ ਦੀਆਂ ਤਾਪਮਾਨ ਸਥਿਤੀਆਂ ਵੀ ਔਸਤ ਪੱਧਰ ਤੇ ਹੀ ਰਹਿੰਦੀਆਂ ਹਨ।

ਥਲ-ਮੰਡਲ (Lithosphere)-ਇਸ ਦਾ ਅਰਥ ਹੈ ਧਰਤੀ ਦੀ ਸੜਾ। ਥਲ-ਮੰਡਲ ਵਿਚ ਪੌਦਿਆਂ, ਜੀਵ-ਜੰਤੂਆਂ ਅਤੇ ਸੂਖ਼ਮ ਜੀਵਾਂ ਦੇ ਵਿਕਾਸ ਲਈ ਖਣਿਜ ਤੱਤ ਅਤੇ ਮਿੱਟੀ ਮੌਜੂਦ ਹੁੰਦੀ ਹੈ। ਧਰਤੀ ਦੀਆਂ ਅਲੱਗ-ਅਲੱਗ ਥਾਂਵਾਂ ਅਤੇ ਹਾਲਤਾਂ, ਜੀਵਾਂ ਦੀ ਹੋਂਦ ਅਤੇ ਵਿਕਾਸ ਲਈ ਅਨੁਕੂਲ ਵਾਤਾਵਰਣ ਉਪਲੱਬਧ ਕਰਾਉਂਦੀਆਂ ਹਨ। |

ਪ੍ਰਸ਼ਨ 3.
ਤੁਸੀਂ ਇਸ ਗੱਲ ਦੀ ਕਿਵੇਂ ਵਿਆਖਿਆ ਕਰੋਗੇ ਕਿ ਵਾਤਾਵਰਣੀ ਸਰਗਰਮੀਆਂ ਵਿਚ ਮਨੁੱਖ ਇਕ ਵਿਚਾਰਸ਼ੀਲ ਅਤੇ ਸਮਾਜਿਕ ਭਾਈਵਾਲ ਹੈ।
ਉੱਤਰ-
ਮਨੁੱਖ, ਸਮਾਜ ਅਤੇ ਵਾਤਾਵਰਣ ਇਕ-ਦੂਸਰੇ ਨਾਲ ਸੰਬੰਧਿਤ ਹਨ। ਸਭਿਆਚਾਰਕ . ਦੇ ਅੰਸ਼, ਕੁਦਰਤੀ ਅੰਸ਼ਾਂ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਦੇ ਹਨ। ਸਾਡਾ ਵਾਤਾਵਰਣ, ਸਾਡੀਆਂ ਸਮਾਜਿਕ ਲੋੜਾਂ ਅਤੇ ਸਮਾਜਿਕ ਕਿਰਿਆਵਾਂ ਤੇ ਨਿਰਭਰ ਕਰਦਾ ਹੈ; ਜਿਵੇਂ-ਖੇਤੀਬਾੜੀ ਇਕ ਸਮਾਜਿਕ ਕਿਰਿਆ ਹੈ ਪਰ ਇਸ ਕਿਰਿਆ ਵਿਚ ਕੁਦਰਤ ਦੇ ਬਹੁਤ ਸਾਰੇ ਅੰਸ਼ ਲੋੜੀਂਦੇ ਹਨ ਅਤੇ ਪ੍ਰਭਾਵਿਤ ਹੁੰਦੇ ਹਨ, ਜਿਵੇਂ- ਸਾਨੂੰ ਖੇਤੀ ਕਰਨ ਲਈ ਪਾਣੀ ਦੀ ਲੋੜ ਹੁੰਦੀ ਹੈ ਜਿਸਨੂੰ ਪੂਰਾ ਕਰਨ ਲਈ ਨਹਿਰਾਂ ਦਾ ਨਿਰਮਾਣ ਕਰਨਾ ਪੈਂਦਾ ਹੈ। ਜਲ ਸੰਸਾਧਨਾਂ ਦੀ ਲੋੜ ਤੋਂ ਵੱਧ ਵਰਤੋਂ ਕਰਨ ਨਾਲ ਧਰਤੀ ਹੇਠਲੇ ਪਾਣੀ ਦਾ ਪੱਧਰ ਹੇਠਾਂ ਡਿਗਦਾ ਜਾ ਰਿਹਾ ਹੈ। ਇਸ ਤਰ੍ਹਾਂ ਬਹੁਤ ਸਾਰੀਆਂ ਖਾਦਾਂ ਅਤੇ ਕੀਟਨਾਸ਼ਕਾਂ ਦੀ ਵਰਤੋਂ ਨਾਲ ਮਿੱਟੀ ਦੀ ਬਣਤਰ ਬਦਲਦੀ ਰਹਿੰਦੀ ਹੈ। ਉਦਯੋਗਾਂ ਕਾਰਨ ਵੀ ਵਾਤਾਵਰਣ ਦੇ ਵੱਖ-ਵੱਖ ਅੰਸ਼ ਜਿਵੇਂ ਜਲ, ਮਿੱਟੀ ਅਤੇ ਹਵਾ ਪ੍ਰਭਾਵਿਤ ਹੋ ਰਹੇ ਹਨ।

ਇਸ ਤਰ੍ਹਾਂ ਸਮਾਜਿਕ ਕਿਰਿਆਵਾਂ ਨਾਲ ਵਾਤਾਵਰਣ ਉੱਪਰ ਬੜਾ ਪ੍ਰਭਾਵ ਪੈਂਦਾ ਹੈ। ਸਮਾਜ ਤੇ ਮਨੁੱਖ ਆਪਣੀ ਹੋਂਦ ਨੂੰ ਬਣਾਈ ਰੱਖਣ ਲਈ ਬਹੁਤ ਸਾਰੀਆਂ ਗਤੀਵਿਧੀਆਂ ਵਿਚ ਹਿੱਸਾ ਪਾ ਰਹੇ ਹਨ, ਪਰ ਇਹਨਾਂ ਕਾਰਨ ਵਾਤਾਵਰਣ ਬਹੁਤ ਬੁਰੀ ਤਰ੍ਹਾਂ ਪ੍ਰਭਾਵਿਤ ਹੋ ਰਿਹਾ ਹੈ। ਸਮਾਜਿਕ ਗਤੀਵਿਧੀਆਂ, ਭੌਤਿਕ ਅਤੇ ਜੈਵਿਕ ਵਾਤਾਵਰਣ ਨੂੰ ਵੀ ਪ੍ਰਭਾਵਿਤ ਕਰ ਰਹੀਆਂ ਹਨ। ਜਿਸ ਨਾਲ ਵਾਤਾਵਰਣ ਪ੍ਰਦੂਸ਼ਣ ਵੱਧ ਰਿਹਾ ਹੈ। ਇਸ ਕਰਕੇ ਵਾਤਾਵਰਣ ਨੂੰ ਬਚਾਉਣ ਲਈ ਸਮਾਜ ਦੇ ਹਰੇਕ ਪ੍ਰਾਣੀ ਦਾ ਇਹ ਫਰਜ਼ ਬਣਦਾ ਹੈ ਕਿ ਆਉਣ ਵਾਲੀਆਂ ਪੀੜ੍ਹੀਆਂ ਲਈ ਵਾਤਾਵਰਣ ਨੂੰ ਸੁਰੱਖਿਅਤ ਕਰੇ। ਆਮ ਜਨਤਾ ਦੇ ਸਹਿਯੋਗ ਨਾਲ ਹੀ ਵਾਤਾਵਰਣ ਸੁਰੱਖਿਅਣ ਪ੍ਰੋਗਰਾਮਾਂ ਨੂੰ ਸਫਲ ਬਣਾਇਆ ਜਾ ਸਕਦਾ ਹੈ। ਇਸ ਤਰ੍ਹਾਂ ਇਹ ਗੱਲ ਸਾਫ਼ ਹੋ ਜਾਂਦੀ ਹੈ ਕਿ ਜੇਕਰ ਮਨੁੱਖ ਵਾਤਾਵਰਣੀ ਸਰਗਰਮੀਆਂ ਵਿੱਚ ਇਕ ਵਿਚਾਰਸ਼ੀਲ ਅਤੇ ਸਮਾਜਿਕ ਭਾਈਵਾਲ ਦੀ ਭੂਮਿਕਾ ਅਦਾ ਕਰੇ ਤਾਂ ਹੀ ਵਾਤਾਵਰਣ ਨੂੰ ਆਉਣ ਵਾਲੀਆਂ ਪੀੜੀਆਂ ਲਈ ਸੁਰੱਖਿਅਤ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ।

ਪ੍ਰਸ਼ਨ 4.
ਜੈਵਿਕ ਵਾਤਾਵਰਣ (Biological Atmosphere) ’ਤੇ ਸੰਖੇਪ ਨੋਟ ਲਿਖੋ।
ਉੱਤਰ-
ਇਸ ਵਾਤਾਵਰਣ ਵਿਚ ਹਰ ਤਰ੍ਹਾਂ ਦੇ ਜੀਵ ਸ਼ਾਮਿਲ ਹਨ। ਇਹਨਾਂ ਨੂੰ ਖੁਰਾਕੀ ਸੰਬੰਧਾਂ ਦੇ ਆਧਾਰ ‘ਤੇ ਉਤਪਾਦਕ, ਖ਼ਪਤਕਾਰ ਅਤੇ ਨਿਖੇੜਕਾਂ ਵਿਚ ਵੰਡ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ।

ਉਤਪਾਦਕ (Producers)-ਉਤਪਾਦਕਾਂ ਵਿਚ ਹਰੇ ਪੌਦੇ, ਘਾਹ, ਝਾੜੀਆਂ, ਹਰੀਕਾਈ, ਫਾਈਟੋ ਪਲੈਂਕਟਾਨ ਅਤੇ ਗੰਧਕ ਜੀਵਾਣੁ ਆਦਿ ਸ਼ਾਮਿਲ ਹਨ। ਉਤਪਾਦਕ ਪ੍ਰਕਾਸ਼ ਸੰਸ਼ਲੇਸ਼ਣ ਦੀ ਕਿਰਿਆ ਰਾਹੀਂ CO₂, ਅਤੇ ਪਾਣੀ ਤੋਂ ਸੂਰਜ ਦੀ ਰੌਸ਼ਨੀ ਅਤੇ ਕਲੋਰੋਫਿਲ ਦੀ ਮੱਦਦ ਨਾਲ ਕਾਰਬਨੀ ਪਦਾਰਥਾਂ ਦਾ ਨਿਰਮਾਣ ਕਰਦੇ ਹਨ। ਗੰਧਕ ਜੀਵਾਣੂ ਆਪਣੇ ਕਾਰਬਨੀ ਭੋਜਨ ਦਾ ਨਿਰਮਾਣ ਰਸਾਇਣਿਕ ਊਰਜਾ ਦੁਆਰਾ ਕਰਦੇ ਹਨ। ਉਤਪਾਦਕ ਪੂਰੇ ਜੈਵਿਕ ਵਾਤਾਵਰਣ ਨੂੰ ਭੋਜਨ, ਆਸਰਾ ਅਤੇ ਆਕਸੀਜਨ ਦਿੰਦੇ ਹਨ। ਇਸ ਲਈ ਉਤਪਾਦਕਾਂ ਨੂੰ ਜੀਵਨ ਦੀ ਮੁੱਢਲੀ ਜ਼ਰੂਰਤ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ।

ਖ਼ਪਤਕਾਰ (Consumers)-ਮਨੁੱਖ ਸਹਿਤ ਸਾਰੇ ਜੀਵ ਖਪਤਕਾਰ ਵਰਗ ਵਿਚੋਂ ਹਨ, ਕਿਉਂਕਿ ਉਹ ਆਪਣਾ ਭੋਜਨ ਖ਼ੁਦ ਸੰਸ਼ਲੇਸ਼ਿਤ ਨਹੀਂ ਕਰ ਸਕਦੇ। ਭੋਜਨ ਦੇ ਆਧਾਰ ਤੇ ਖਪਤਕਾਰਾਂ ਨੂੰ ਹੇਠ ਲਿਖੀਆਂ ਕਿਸਮਾਂ ਵਿਚ ਵੰਡਿਆ ਜਾ ਸਕਦਾ ਹੈ ,

• ਪਹਿਲੇ ਦਰਜੇ ਦੇ ਖ਼ਪਤਕਾਰ (Primary Consumer)
• ਦੂਸਰੇ ਦਰਜੇ ਦੇ ਖ਼ਪਤਕਾਰ (Secondary Consumer)
• ਤੀਸਰੇ ਦਰਜੇ ਦੇ ਖ਼ਪਤਕਾਰ (Tertiary Consumer)
• ਚੌਥੇ ਦਰਜੇ ਦੇ ਖ਼ਪਤਕਾਰ (Quatenary Consumer |

ਨਿਖੇੜਕ (Decomposers)-ਉਹ ਸੂਖ਼ਮ ਜੀਵ, ਜਿਹੜੇ ਮਰੇ ਹੋਏ ਜਾਨਵਰਾਂ ਅਤੇ ਪੌਦਿਆਂ ਆਦਿ ਦੇ ਅਵਸ਼ੇਸ਼ਾਂ ਨੂੰ ਐਂਜਾਇਮਾਂ ਦਾ ਰਿਸਾਅ ਕਰਕੇ ਅਪਘਟਿਤ ਕਰਦੇ ਹਨ ਅਤੇ ਅਪਘਟਨ ਦੌਰਾਨ ਬਹੁਤ ਸਾਰੇ ਕਾਰਬਨੀ ਤੱਤ, ਗੈਸਾਂ ਅਤੇ ਅਕਾਰਬਨੀ ਤੱਤ ਪੈਦਾ ਕਰਦੇ ਹਨ, ਨੂੰ ਨਿਖੇੜਕ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।

(ਸ) ਵੱਡੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ

ਪ੍ਰਸ਼ਨ 1.
ਡਾਊਨ (Down) ਦੇ ‘ਸਮੱਸਿਆ ਧਿਆਨ ਚੱਕਰ ਦੇ ਪੰਜ ਪੜਾਵਾਂ ਬਾਰੇ ਚਰਚਾ ਕਰੋ ।
ਉੱਤਰ-
ਡਾਊਨ ਦੇ ‘ਸਮੱਸਿਆ ਧਿਆਨ ਚੱਕਰ’ (Issue Attention Cycle) ਅਨੁਸਾਰ, ਜਨਤਾ ਦੀ ਰੁਚੀ ਨੂੰ ਬਦਲਣ ਲਈ ਪੰਜ ਪੜਾਵਾਂ ਵਾਲਾ ਚੱਕਰ ਪੂਰਾ ਕਰਨਾ ਪੈਂਦਾ ਹੈ।
ਇਸ ਚੱਕਰ, ਦੇ ਪੰਜ ਪੜਾਅ ਅੱਗੇ ਲਿਖੇ ਹਨ –

1. ਪਹਿਲਾ ਪੜਾਅ (First State)-ਇਹ ਉਹ ਪੜਾਅ ਹੈ ਜਿਸ ਵਿਚ ਲੋਕਾਂ ਵਿਚ ਵਾਤਾਵਰਣ ਦੀਆਂ ਸਮੱਸਿਆਵਾਂ ਲਈ ਜਾਗਰੂਕਤਾ ਨਹੀਂ ਹੁੰਦੀ ਹੈ।
2. ਦੂਸਰਾ ਪੜਾਅ (Second Stage-ਇਸ ਪੜਾਅ ਵਿਚ ਸੰਚਾਰ ਦੇ ਵੱਖ-ਵੱਖ ਸਾਧਨਾਂ ਅਤੇ ਅਵਲੋਕਨਾਂ ਦੁਆਰਾ ਵਾਤਾਵਰਣ ਦੀਆਂ ਸਮੱਸਿਆਵਾਂ ਵੱਲ ਲੋਕਾਂ ਦਾ ਧਿਆਨ ਖਿੱਚਿਆ ਜਾਂਦਾ ਹੈ। ਇਸ ਵਿਚ ਕੁਦਰਤੀ ਸੰਸਾਧਨਾਂ ਦੇ ਵਧ ਰਹੇ ਸ਼ੋਸ਼ਣ ਦੇ ਹਾਨੀਕਾਰਕ ਪ੍ਰਭਾਵਾਂ ਤੋਂ ਹੋਣ ਵਾਲੇ ਪਤਨ ਤੋਂ ਬਚਣ ਲਈ ਪੋਸਟਰਾਂ, ਰੈਲੀਆਂ, ਨਾਟਕਾਂ, ਫਿਲਮਾਂ ਆਦਿ ਰਾਹੀਂ ਲੋਕਾਂ ਵਿਚ ਜਾਗਰੂਕਤਾ ਪੈਦਾ ਕਰਨ ਦੀ ਕੋਸ਼ਿਸ਼ ਕੀਤੀ ਜਾਂਦੀ ਹੈ।
3. ਤੀਸਰਾ ਪੜਾਅ (Third Stageਇਸ ਪੜਾਅ ਵਿਚ ਲੋਕ ਵਾਤਾਵਰਣ ਸੁਧਾਰਨ ਲਈ ਗੰਭੀਰ ਰੂਚੀ ਦਿਖਾਉਂਦੇ ਹਨ ਅਤੇ ਆਪਣਾ ਯੋਗਦਾਨ ਵੀ ਦਿੰਦੇ ਹਨ। ਇਸ ਵਿਚ ਲੋਕਾਂ ਨੂੰ ਵਾਤਾਵਰਣ ਦੇ ਅਪਘਟਨ ਦੇ ਕਾਰਨ ਸਮਝ ਵਿਚ ਆ ਜਾਂਦੇ ਹਨ ਅਤੇ ਲੋਕ ਇਹ ਵੀ ਸਮਝ ਜਾਂਦੇ ਹਨ ਕਿ ਤਕਨੀਕੀਵਿਕਾਸ ਵਾਤਾਵਰਣ ਦੇ ਸੁਧਾਰ ਦਾ ਸਹੀ ਵਿਕਲਪ ਨਹੀਂ ਹੈ। ਇਸ ਵਿਚ ਵਾਤਾਵਰਣੀ ਸਮੱਸਿਆਵਾਂ ਦੇ ਸੁਧਾਰ ਲਈ ਵਰਤੇ ਜਾ ਸਕਣ ਵਾਲੇ ਤਰੀਕਿਆਂ ਦੀ ਚੋਣ ਕੀਤੀ ਜਾਂਦੀ ਹੈ।

4. ਚੌਥਾ ਪੜਾਅ (Fourth Stage-ਇਸ ਪੜਾਅ ਵਿਚ ਲੋਕਾਂ ਦੀ ਵਾਤਾਵਰਣ ਸੁਧਾਰ ਸੰਬੰਧੀ ਰੁਚੀ ਵਿਚ ਕੰਮੀ ਆਉਣ ਲਗਦੀ ਹੈ। ਇਸ ਕਮੀ ਦੇ ਦੋ ਕਾਰਨ ਹਨ –

• ਵਾਤਾਵਰਣ ਦੀਆਂ ਸਮੱਸਿਆਵਾਂ ਦੇ ਸੁਧਾਰ ਲਈ ਕੰਮ ਕਰਨ ਵਾਲੀਆਂ ਸੰਸਥਾਵਾਂ ਦਾ ਉਦਾਸੀਨ (Neutral) ਰਵੱਈਆ ਅਤੇ ਸਹਿਯੋਗ ਨਾ ਦੇਣ ਕਾਰਨ, ਲੋਕਾਂ ਨੂੰ ਵਾਤਾਵਰਣ ਸੁਧਾਰ ਪ੍ਰੋਗਰਾਮ ਲਾਗੂ ਕਰਨ ਵਿਚ ਔਖ ਹੁੰਦੀ ਹੈ।
• ਵਾਤਾਵਰਣ ਸੁਧਾਰ ਵਿਚ ਆਉਣ ਵਾਲੀ ਵਾਧੂ ਲਾਗਤ ਵੀ ਉਹਨਾਂ ਦੀ ਰੁਚੀ ਨੂੰ ਘਟਾਉਂਦੀ ਹੈ।

5. ਪੰਜਵਾਂ ਪੜਾਅ (Fifth Stage-ਇਹ ਅੰਤਿਮ ਪੜਾਅ ਹੈ ਜਿਸ ਵਿਚ ਜਨਤਾ ਦੀ ਰੁਚੀ ਸਮੇਂ-ਸਮੇਂ ਤੇ ਬਦਲਦੀ ਹੈ। ਕਦੀ ਇਹ ਘੱਟ ਹੁੰਦੀ ਹੈ ਤੇ ਕਦੀ ਇਹ ਫਿਰ ਵੱਧ ਜਾਂਦੀ ਹੈ। ਅੱਜ ਦੇ ‘ਸਮੱਸਿਆ ਧਿਆਨ ਚੱਕਰ (Issue Attention Cycle) ਦੀ ਸਥਿਤੀ ਡਾਉਨ ਦੇ ਅਨੁਸਾਰ ਵਿਚਕਾਰਲੀ ਹੈ।

ਪ੍ਰਸ਼ਨ 2.
ਭਾਰਤ ਦੇ ਅਤੀਤ ਤੇ ਅਜੋਕੇ ਰੀਤੀ-ਰਿਵਾਜਾਂ ਅਤੇ ਸਭਿਆਚਾਰ ਦਾ ਸੰਖੇਪ ਵੇਰਵਾ ਦਿਓ। ਤੁਹਾਡੀ ਸੋਚ ਅਨੁਸਾਰ ਕਿਹੜਾ ਜ਼ਿਆਦਾ ਚੰਗਾ ਹੈ ?
ਉੱਤਰ-
ਭਾਰਤੀ ਸਮਾਜ ਵਿਚ ਕੁਦਰਤ ਅਤੇ ਵਾਤਾਵਰਣ ਲਈ ਗੰਭੀਰ ਚੇਤਨਾ ਅਤੇ ਸ਼ਰਧਾ ਦੇਖਣ ਨੂੰ ਮਿਲਦੀ ਹੈ। ਮਨੁੱਖੀ ਸੰਸਕ੍ਰਿਤੀ ਅਤੇ ਵਾਤਾਵਰਣ ਇੱਕ ਸੰਤੁਲਿਤ ਕਿਰਿਆ ਦੁਆਰਾ ਆਪਸ ਵਿਚ ਜੁੜੇ ਹੋਏ ਹਨ। ਭਾਰਤ ਦੇ ਪੁਰਾਤਨ ਅਤੇ ਅਜੋਕੇ ਸਭਿਆਚਾਰ ਅਤੇ ਸੱਭਿਅਤਾ ਦਾ ਵਾਤਾਵਰਣ ਨਾਲ ਸੰਬੰਧ ਨੂੰ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਸਮਝਿਆ ਜਾ ਸਕਦਾ ਹੈ –
1. ਅਤੀਤ ਦੇ ਰੀਤੀ-ਰਿਵਾਜ ਅਤੇ ਸਭਿਆਚਾਰ (Past Customs and Cultuersਭਾਰਤ ਦੇ ਪੁਰਾਤਨ ਸਭਿਆਚਾਰ ਵਿਚ ਵਾਤਾਵਰਣ ਦੇ ਪ੍ਰਤੀ ਆਦਰ ਸਾਡੀਆਂ ਪਰੰਪਰਾਵਾਂ ਅਤੇ ਰੀਤੀ-ਰਿਵਾਜਾਂ ਵਿਚ ਝਲਕਦਾ ਹੈ। ਪੁਰਾਤਨ ਭਾਰਤੀ ਸਭਿਆਚਾਰ ਕੁਦਰਤ ਤੇ ਆਧਾਰਿਤ ਸੀ। ਪੁਰਾਤਨ ਗਿਆਨੀ ਅਤੇ ਵੇਦ ਸ਼ਾਸਤਰੀਆਂ ਨੇ ਵੀ ਕੁਦਰਤ ਨੂੰ ਬਹੁਤ ਮਹੱਤਵਪੂਰਨ ਅਤੇ ਪਵਿੱਤਰ ਮੰਨਿਆ ਹੈ। ਰਿਗਵੇਦ ਵਿਚ ਵੀ ਕੁਦਰਤ ਦੇ ਪੰਜ ਤੱਤਾਂ (ਧਰਤੀ, ਜਲ, ਵਾਯੂ, ਉਰਜਾ ਅਤੇ ਪੁਲਾੜ ਨੂੰ ਉਦਾਹਰਣਾਂ ਸਹਿਤ ਸਪੱਸ਼ਟ ਕੀਤਾ ਗਿਆ ਹੈ। ਅਤੀਤ ਦੀਆਂ । ਪਰੰਪਰਾਵਾਂ ਵਿਚ ਮਨੁੱਖ ਦੀ ਸੰਪੰਨਤਾ ਦੇ ਲਈ ਇਹਨਾਂ ਤੱਤਾਂ ਦਾ ਸੁਰੱਖਿਅਣ ਅਤੇ ਉਪਯੋਗ ਦੀ ਵਿਵਸਥਾ ਕੀਤੀ ਗਈ ਸੀ। ਸਾਡੇ ਦੇਸ਼ ਵਿਚ ਦਰੱਖ਼ਤਾਂ ਨੂੰ ਕੱਟਣਾ ਮਨ੍ਹਾਂ ਸੀ ਕਿਉਂਕਿ ਲੋਕ ਇਹਨਾਂ ਦੀ ਪੂਜਾ ਕਰਦੇ ਸਨ।

ਭਾਰਤੀ ਦਾਰਸ਼ਨਿਕਾਂ ਦੇ ਵਿਚਾਰਾਂ ਅਨੁਸਾਰ ਮਨੁੱਖ ਅਤੇ ਬਾਕੀ ਸਾਰੇ ਜੀਵ ਵੀ ਇਕ ਹੀ ਪਰਮਾਤਮਾ ਨੇ ਬਣਾਏ ਹਨ ਅਤੇ ਸਾਰੇ ਇਕ ਤਰ੍ਹਾਂ ਦੇ ਤੱਤਾਂ ਤੋਂ ਬਣੇ ਹਨ। ਇਸ ਲਈ ਸਭ ਵਿਚ ਇਕ ਆਦਰ ਅਤੇ ਦਇਆ ਦਾ ਸੰਬੰਧ ਹੈ। ਭਾਰਤੀਆਂ ਦੇ ਵਿਚਾਰ ਅਨੁਸਾਰ ਕੋਈ ਵੀ ਵਸਤੂ ਨਿਰਜੀਵ ਨਹੀਂ ਹੈ । ਇਹ ਜੀਵਨ ਪ੍ਰਣਾਲੀ ਹੈ ਜਿਸ ਵਿਚ ਮਨੁੱਖ ਦੁਸਰੀਆਂ ਜਾਤੀਆਂ ਵਾਂਗ ਇਕ ਅੰਗ ਹੈ।

ਸਾਡੇ ਪੁਰਾਣੇ ਵੇਦ, ਉਪਨਿਸ਼ਦ ਅਤੇ ਪੁਰਾਨ ਆਦਿ ਮਨੁੱਖ ਨੂੰ ਪਰਿਸਥਿਕੀ ਅਤੇ ਵਾਤਾਵਰਣ ਸੰਹਿਤਾ ਦਾ ਉਪਦੇਸ਼ ਦਿੰਦੇ ਹਨ। ਸ਼ਾਸਤਰਾਂ ਵਿਚ ਅੱਗ, ਪਾਣੀ ਅਤੇ ਹਵਾ ਨੂੰ ਦੇਵਤਾ ਅਤੇ ਧਰਤੀ ਨੂੰ ਦੇਵੀ ਮਾਂ ਦਾ ਦਰਜਾ ਦਿੱਤਾ ਗਿਆ ਹੈ। ਅਸਮਾਨ ਨੂੰ ਪਿਤਾ ਦਾ ਦਰਜਾ ਦਿੱਤਾ ਗਿਆ ਹੈ। ਪੁਰਾਤਨ ਸਭਿਆਚਾਰ ਵਿਚ ਮਨੁੱਖ ਦੀ ਸੰਪੰਨਤਾ ਅਤੇ ਵਾਤਾਵਰਣ ਦੀ ਸੁਰੱਖਿਆ ਸੰਬੰਧੀ ਪ੍ਰਬੰਧ ਵੀ ਕੀਤੇ ਗਏ। ਉਪਨਿਸ਼ਦਾਂ ਰਾਹੀਂ ਕੁਦਰਤੀ ਸਾਧਨਾਂ ਦੀ ਵਰਤੋਂ ਤੇ ਰੋਕ ਲਗਾਉਣ ਦੇ ਵਿਸ਼ੇ ਨੂੰ ਵੀ ਸਮਝਾਇਆ ਗਿਆ ਹੈ। ਈਸ਼ਾ ਉਪਨਿਸ਼ਦ (Isha Upnished) ਅਨੁਸਾਰ ““ਇਹ ਸਾਰਾ ਸੰਸਾਰ ਤੇ ਇਸ ਦੀਆਂ ਪ੍ਰਜਾਤੀਆਂ ਸਾਰੇ ਇਕ ਹੀ ਪ੍ਰਮਾਤਮਾ ਨਾਲ ਜੁੜੀਆਂ ਹੋਈਆਂ ਹਨ। ਇਸ ਲਈ ਕੋਈ ਪ੍ਰਜਾਤੀ ਦੂਸਰੀ ਪ੍ਰਜਾਤੀ ਦਾ ਦਮਨ ਨਾ ਕਰੇ।”

2. ਅਜੋਕੇ ਰੀਤੀ-ਰਿਵਾਜ ਅਤੇ ਸਭਿਆਚਾਰ (Present Customs and Culturesਅਜੋਕੇ ਸਭਿਆਚਾਰ ਅਤੇ ਅਜੋਕੀ ਸੱਭਿਅਤਾ ਦਾ ਵੀ ਵਾਤਾਵਰਣ ਦੇ ਨਾਲ ਅਟੁੱਟ ਸੰਬੰਧ ਹੈ। ਅੱਜ ਵੀ ਵੱਖ-ਵੱਖ ਖੇਤਰਾਂ ਵਿਚ ਰਹਿਣ ਵਾਲੇ ਲੋਕਾਂ ਦਾ ਖਾਣ-ਪੀਣ, ਰਹਿਣ-ਸਹਿਣ, ਬੋਲਚਾਲ ਆਦਿ ਵਾਤਾਵਰਣ ਦੀਆਂ ਹਾਲਤਾਂ ਤੇ ਨਿਰਭਰ ਕਰਦਾ ਹੈ।

ਜੰਮੂ-ਕਸ਼ਮੀਰ ਦੇ ਲੋਕ ਠੰਡ ਤੋਂ ਬਚਣ ਲਈ ਕਾਹਵਾ ਪੀਂਦੇ ਹਨ, ਫਿਰਨ ਪਹਿਨਦੇ ਹਨ ਅਤੇ ਕਾਂਗੜੀ ਦਾ ਉਪਯੋਗ ਕਰਦੇ ਹਨ। ਦੂਸਰੇ ਪਾਸੇ ਰਾਜਸਥਾਨ ਦੇ ਲੋਕ ਮਨੁੱਖ) ਗਰਮੀ ਤੋਂ ਬਚਣ ਲਈ ਲੰਬੀ ਪਗੜੀ, ਵੱਡੀਆਂ-ਵੱਡੀਆਂ ਮੁੱਛਾਂ ਅਤੇ ਔਰਤਾਂ ਲੰਬੇ ਘੁੰਡ ਕੱਢ ਕੇ ਰੱਖਦੇ ਹਨ। ਨਾਲ ਹੀ ਦੱਖਣ ਭਾਰਤ ਦੋ ਲੋਕ ਗਰਮੀ ਅਤੇ ਹੁੰਮਸ ਭਰੇ ਵਾਤਾਵਰਣ ਵਿਚ ਰਹਿਣ ਲਈ ਸੂਤੀ ਕੱਪੜਿਆਂ ਦੀ ਵਰਤੋਂ ਕਰਦੇ ਹਨ ਅਤੇ ਨਾਲ ਇਕ ਅੰਗਵਸਤਰ ਆਪਣੇ ਮੋਢੇ ਤੇ ਰੱਖਦੇ ਹਨ।
ਹਰ ਵਿਅਕਤੀ ਦੀ ਭਾਸ਼ਾ, ਖਾਣ-ਪੀਣ ਦੀਆਂ ਆਦਤਾਂ ਵਿਚ ਸੱਭਿਅਤਾ ਦਾ ਪ੍ਰਭਾਵ ਦਿਖਾਈ ਦਿੰਦਾ ਹੈ। ਦੋਨਾਂ ਸੱਭਿਅਤਾਵਾਂ ਦੇ ਅਧਿਐਨ ਤੋਂ ਪਤਾ ਲਗਦਾ ਹੈ ਕਿ ਵਾਤਾਵਰਣ ਸੁਰੱਖਿਅਣ ਲਈ ਅਤੀਤ ਦੇ ਰੀਤੀ-ਰਿਵਾਜ ਅਤੇ ਸਭਿਆਚਾਰ ਹੀ ਸਹੀ ਸਨ ਕਿਉਂਕਿ ਪੁਰਾਤਨ ਲੋਕ ਕੁਦਰਤੀ ਸੰਸਾਧਨਾਂ ਦੀ ਘੱਟ ਤੋਂ ਘੱਟ ਵਰਤੋਂ ਕਰਦੇ ਸਨ ਅਤੇ ਉਸਦੇ ਸੁਰੱਖਿਅਣ ਅਤੇ ਸੰਭਾਲ ਤੇ ਜ਼ੋਰ ਦਿੰਦੇ ਸਨ।

ਪਰ ਅਜੋਕੇ ਭਾਰਤ ਵਿਚ ਵੱਧਦੀ ਹੋਈ ਆਬਾਦੀ ਅਤੇ ਉਦਯੋਗਿਕ ਵਿਕਾਸ ਨੇ ਕੁਦਰਤੀ ਸੰਸਾਧਨਾਂ ਦੀ ਬੇਲੋੜੀ ਵਰਤੋਂ ਨੂੰ ਵਧਾ ਦਿੱਤਾ ਹੈ । ਜਿੱਥੇ ਲੋਕ ਪੁਰਾਣੇ ਸਮੇਂ ਵਿਚ ਦਰੱਖ਼ਤਾਂ ਨੂੰ ਪੂਜਦੇ ਸਨ, ਅਜੋਕੇ ਯੁੱਗ ਵਿਚ ਲੋੜਾਂ ਦੀ ਪੂਰਤੀ ਲਈ · ਅੰਨੇਵਾਹ ਦਰੱਖ਼ਤਾਂ ਨੂੰ ਕੱਟਿਆ ਜਾ ਰਿਹਾ ਹੈ। ਅੱਜ ਸਾਨੂੰ ਲੋੜ ਹੈ ਵਾਤਾਵਰਣ ਨੂੰ ਸੁਰੱਖਿਅਤ ਰੱਖਣ ਲਈ ਵਾਤਾਵਰਣ ਸੰਬੰਧੀ ਨਵੀਆਂ ਨੀਤੀਆਂ ਅਤੇ ਨਿਯਮ ਲਾਗੂ ਕਰਨ ਦੀ, ਤਾਂ ਜੋ ਵਾਤਾਵਰਣ ਨੂੰ ਬਚਾਇਆ ਜਾ ਸਕੇ।

Punjab State Board PSEB 11th Class Maths Book Solutions Chapter 1 Sets Miscellaneous Exercise Questions and Answers.

PSEB Solutions for Class 11 Maths Chapter 1 Sets Miscellaneous Exercise

Question 1.
Decide, among the following sets, which sets are subsets of one and another:
A = {x : x ∈ R and x satisfy x² – 8x + 12 = 0},
B = {2, 4, 6}, C = {2, 4, 6, 8…}, D = {6}.
Answer.
A={x : x ∈ R and x satisfies x² – 8x + 12 = 0}
2 and 6 are the only solutions of x² – 8x + 12 = 0.
∴ A = {2, 6}
B = {2, 4, 6}, C = {2, 4, 6, 8 …}, D = {6}
∴ D ⊂ A ⊂ B ⊂ C
Hence, A ⊂ B, A ⊂ C, B ⊂ C, D ⊂ A, D ⊂ B, D ⊂ C.

Question 2.
In each of the following, determine whether the statement is true or false. If it is true, prove it. If it is false, give an example.
(i) If x ∈ A and A ∈ B, then x ∈ B
(ii) If A⊂ B and B ∈ C, then A ∈ C
(iii) If A ⊂B and B ⊂ C, then A ⊂ C
(iv) If A ⊄ B and B ⊄ C, then A ⊄ C
(v) If x ∈ A and A ⊄ B, then x ∈ B
(vi) If A ⊂ B and x ∉ B, then x ∉ A
Answer.
(i) False
Let A = {1, 2} and B={1, {1, 2}, {3}}
2 ∈ {1, 2} and {1, 2} ∈ {{3}, 1, {1, 2}}
Now, A ∈ B
∴ However, 2 ∉ {{3}, 1, {1, 2}}

(ii) False
Let A = {2}, B = {0, 2}, and C = {1, {0, 2}, 3}
As A ⊂ B
B ∈ C
However, A ∉ C

(iii) True
Let A ⊂ B and B ⊂ C.
Let x ∈ A
x ∈ B [∵ A ⊂ B]
x ∈ C [∵ B ⊂ C]
∴ A ⊂ C

(iv) False
A = {1, 2}, B = {0, 6, 8}, and C = {0, 1, 2, 6, 9}
Accordingly, A ⊄ B and B ⊄ C.
However, A ⊂ C

(v) False
A = {3, 5, 7} and B = {3, 4, 6}
5 ∈ A and A ⊄ B
However, 5 ∉ B

(vi) True
Let A ⊂ B and x ∉ B.
To show x ∉ A
If possile, suppose x ∉ A
Then, x ∉ B, which is a conadicon as x ∉ B
∴ x ∉ A.

Question 3.
Let A, B and C be the sets such that A ∪ B = A ∪ C andA ∪ B = A ∪ C. Show that B = C.
Answer:
A ∪ B = A ∪ C
⇒ (A ∪ B) ∩ C = (A ∪ C) ∩ C
⇒ (A ∩ C) ∪ (B ∩ C) = C
⇒ (A ∩ B) ∪ (B ∩ C) = C …………….(i)
Again, A ∪ B = A ∪ C
⇒ (A ∪ B) ∩ B = (A ∪ C) ∩ B
⇒ B = (A ∩ B) ∪ (C ∩ B)
⇒ B = (A ∩ B) ∪ (B ∩ C)
From eqs. (i) and (ii), we get
B = C.

Question 4.
Show that the following four conditions are equivalent:
(i) A ⊂ B
(ii) A – B = Φ
(iii) A ∪ B = B
(iv) A ∩ B = A
Answer.
(i) ⟺
(ii) A ⊂ B ⟺ All elements of A are in B ⟺ A – B = Φ
(ii) ⟺
(iii) A – B = Φ ⟺ All elements of A are in B ⟺ A ∪ B = B.
(iii) ⟺ (iv)
A ∪ B = B ⟺ All the elements of A are in B.
⟺ All the elements of A are common in A and B ⟺ A ∩ B = A.
Thus, all the four given conditions are equivalent.

Question 5.
Show that if A ⊂ B, then C – B ⊂ C – A.
Answer.
Let A ⊂ B
To show: C – B ⊂ C – A
Let x ∈ C – B
⇒ x ∈ C and x ∉ B
⇒ x ∈ C and x ∉ A [A ⊂ B]
⇒ x ∈ C – A
C – B ⊂ C – A

Question 6.
Assume that P(A) = P(B). Show that A = B.
Answer.
Let P(A) =P (B)
To show: A = B
Let x ∈ A
A ∈ P(A) = P(B)
∴ x ∈ C,
for some C ∈ P(B)
C ⊂ B
∴ x ∈B
∴ A ⊂ B
Similarly, B ⊂ A
∴ A = B.

Question 7.
Is it true that for any sets A and B, P (A) ∪ P (B) = P (A ∪ B)? Justify your answer.
Answer.
Let A = {a}, B = {b} and A ∪ B = {a, b}
∴ P(A) = {Φ, {a}}, P(B) = {Φ, {b}}
P(A ∪ B) = {Φ, {a}, {b}, {a, b}} …………….(i)
and P(A) ∪ P(B) = {Φ, {a}, {b}} …………..(ii)
From eqs. (i) and (ii), we have
P(A ∪ B) ≠ P(A) ∪ P(B).

Question 8.
Show that for any sets A and B, A = (A ∩ B) ∪ (A – B) and A ∪ (B – A) = A ∪ B.
Answer.
(A ∩ B) ∪ (A – B) = (A ∩ B) ∪ (A ∩ B) [∵ A – B = A ∩ B]
= A ∩ (B ∪ B’) [Distributive law]
= A ∩ X, where X is universal set.
= A
A ∪ (B – A) = A ∪ (B ∩ A) [∵ B – A = B ∩ A’]
= (A ∪ B) ∩ (A ∪ A) [Distributive law]
= (A ∪ B) ∩ X
where X = A ∩ A’ is universal set
= A ∪ B [∵ A∪ B ⊂ X].

Question 9.
Using properties of sets, show that
(i) A ∪ (A ∩ B) = A
(ii) A ∩ (A ∪ B) = A.
Answer.
(i) A ∪ (A ∩B) = (A ∪ A) ∩ (A ∪ B) [Distributive law]
= A ∩ (A ∪ B) [∵ A ∪ A = A]
= A [∵ A ⊆ A ∪ B]

(ii) A ∩ (A ∪ B) = (A ∩ A) ∪ (A ∩ B)
= A ∪ (A ∩ B)
= A [∵ A ∩ B ⊂ A]

Question 10.
Show that A ∩ B=A ∩ C need not imply B = C.
Answer.
With the help of an example, we may try to establish it.
Let A = {1, 2}, B = {1, 3} and C = {1, 4}
Now A ∩ B = {1, 2} ∩{1, 3} = {1}
and A ∩ C = {1, 2} ∩{1, 4} = {1}
A ∩ B = A ∩ C
still B ≠ C.

Question 11.
Let A and B be sets. If A ∩ X = B ∩ X = Φ and A ∪ X = B ∪ X for some set X, show that A = B.
Answer. We have, A ∩ X = B ∩ X for some set X
⇒ A ∩ (A ∪ X) = A ∩(B ∪ X)
⇒ A = (A ∩ B) ∪ (A ∩ X) [∵ A ∩ (A ∪ X) = A]
⇒ A = (A ∩ B) ∪ Φ) [∵ A ∩ X = Φ (given)]
⇒ A = A ∩ B
⇒ A ⊂ B ………..(i)
Again, A ∪ X = B ∪ X
⇒ B ∩ (A ∪ X) = B ∩ (B ∪ X)
⇒ (B ∩ A) ∪ (B ∩ X) = B
⇒ (B ∩ A) ∪ Φ = B
⇒ B ∩ A = B
⇒ A ∩ B = B
⇒ B ⊂ A ……………(ii)
From eqs. (i) and (ii), we get A = B.

Question 12.
Find sets A, B and C such that A n B, B n C and A n C are non-empty sets and AnBnC=<(>.
Answer.
Let A = {1, 2}, B = {2, 3} and C = {1, 3}.
Clearly A ∩ B = {2}, B ∩ C = {3}and A ∩ C = {1}
i.e., A ∩ B, B ∩ C and A ∩ C are non-empty sets.
∴ (A ∩ B) ∩ C = {2} ∩ {1, 3}
⇒ A ∩ B ∩ C = Φ.

Question 13.
In a survey of 600 students in a school, 150 students were found to he taking tea and 225 taking coffee, 1Q0 were taking both tea and coffee. Find how many students were taking neither tea nor coffee?
Answer.

Here, n(T) = 150, n(C) = 225,
n(T ∩ C) = 100
Also we know that
n(T ∪ C) = n(T) + n(C) – n(T ∩ C)
= 150 + 225 – 100 = 275
Total mimber of students = 600
∴ Number of students who neither take tea nor coffee.
= 600 – n(T ∪ C)
= 600 – 275 = 325.

Question 14.
In a group pf students, 100 students know Hindi, 50 know English and 25 know bote. Each of the students knows either Hindi or English. How many students are there in tee group?
Answer.

Here, n(H) = 100, n(E) = 50 and n(H ∩ E) = 25
We know that
n(H ∪ E) = n(H) + n(E) – n(H ∩ E)
= 100 + 50 – 25 = 125.
Hence there are 125 students in the group.

Question 15.
In a survey of 60 people, it was found that 25 people read newspaper H, 26 read newspaper T, 26 read newspaper 1,9 read bote H and 1,11 read both H and T, 8 read both T and 1, 3 read all three newspapers. Find:
(i) the number of people who read at least one of the newspapers.
(ii) the number of people who read exactly one newspaper.
Answer.
Let A be the set of people who read newspaper H.
Let B be the set of people who read newspaper T.
Let C be the set of people who read newspaper I.
Accordingly, n (A) = 25, n(B) = 26, and n(C) = 26
n(A ∩ C) = 9, n(A ∩ B) = 11, and n(B ∩ C) = 8 n(A ∩ B ∩ C) = 3
Let U be the set of people who took part in the survey.
(i) Accordingly,
n(A ∪ B ∪ C) = n(A) + n(B) + n(C) – n(A ∩ B) – n(B ∩ C) – n(C ∩ A)
+n(A ∩ B ∩ C)
= 25 + 26 + 26 – 11 – 8 – 9 + 3 = 52
Hence, 52 people read at least one of the newspapers.

(ii)

Let a be the number of people who read newspapers H and T only.
Let b denote the number of people who read newspapers I and H only.
Let c denote the number of people who read newspapers T and I only.
Let d denote the number of people who read all three newspapers.
Accordingly, d = n(A ∩ B ∩ C) = 3
Now, n(A ∩ B) = a + d,
n(B ∩ C) = c + d,
n(C ∩ A) = b + d
∴ a + d + c + d + b + d = 11 + 8 + 9 = 28
a + b + c + d = 28 – 2d
= 28 – 6 = 22
Hence, (52 – 22) = 30
people read exactly one newspaper.

 

Question 16.
In a survey it was found that 21 people liked product A, 26 liked product B and 29 liked product C. If 14 people liked products A and B, 12 people liked products C and A, 14 people liked products B and C and 8 liked all the three products. Find how many liked product C only?
Answer.
Let A, B, and C be the set of people who like product A, product B, and product C respectively.
Accordingly, n(A) = 21, n(B) = 26,
n(C) = 29, n(A ∩ B) = 14,
n(C ∩ A) = 12, n(B ∩ C) = 14,
n(A ∩ B ∩ C) = 8
The Venn diagram for the given problem can be drawn as

It can be seen that number of people who like product C only is
{29 – (4 + 8 + 6)} = 11.

Punjab State Board PSEB 11th Class Maths Book Solutions Chapter 2 Relations and Functions Miscellaneous Exercise Questions and Answers.

PSEB Solutions for Class 11 Maths Chapter 2 Relations and Functions Miscellaneous Exercise

Question 1.
The relation f is defined by f (x) =

The relation g isdefined by g(x) =
Show that f is a function and g is not a function.
Answer.
The relation f is defined as f (x) =
It is observed that for
0 ≤ x < 3, f(x) = x²
3 ≤ x ≤ 10, f(x) = 3x
Also, at x = 3, f(x) = 3² = 9 or f(x) = 3 × 3 = 9
i.e., at x = 3, f(x) = 9
Therefore, for 0 ≤ x ≤ 10, the images of f(x) are unique.
Thus, the given relation is a function.
The relation g is defined as g (x) =
It can be observed that for x = 2, g(x) = 2² = 4 and g(x) = 3 × 2 = 6
Hence, element 2 of the domain of the relation g corresponds to two different images te., 4 and 6. Hence, this relation is not a function.

Question 2.
If f(x) = x², find \(\frac{f(1.1)-f(1)}{(1.1-1)}\).
Ans.
f(x) = x²
∴ \(\frac{f(1.1)-f(1)}{(1.1-1)}\) = \(\frac{(1.1)^{2}-(1)^{2}}{(1.1-1)}=\frac{1.21-1}{0.1}=\frac{0.21}{0.1}\)= 2.1

Question 3.
Find the domain of the function f(x) = \(\frac{x^{2}+2 x+1}{x^{2}-8 x+12}\).
Answer.
The given function is f(x) = \(\frac{x^{2}+2 x+1}{x^{2}-8 x+12}\)

f(x) = \(\frac{x^{2}+2 x+1}{x^{2}-8 x+12}=\frac{x^{2}+2 x+1}{(x-6)(x-2)}\)

It can be seen that function f is defined for all real numbers except at x = 6 and x = 2.
Hence, the domain off is R – {2, 6}.

Question 4.
Find the domain and the renie of the real function f defined by f(x) = \(\sqrt{(x-1)}\).
Answer.
The given real function is f (x) = \(\sqrt{(x-1)}\).
It can be seen that \(\sqrt{(x-1)}\) is defined for (x – 1) ≥ 0.
i.e., f(x) = \(\sqrt{(x-1)}\) is defined for x ≥ 1.
Therefore, the domain off is the set of all real numbers greater than or equal to 1 i.e., the domain of f = [1, ∞).
As x ≥ 1
⇒ (x – 1) ≥ 0
⇒ \(\sqrt{(x-1)}\) ≥ 0
Therefore, the range off is the set of all real numbers greater than or equal to 0 i.e., the range of f = [0, ∞).

Question 5.
Find the domnin and the range of the real function f defined by f(x) = |x – 1|.
Answer.
The given real function isf (x) = |x – 1|.
It is clear that |x – 1| is defined for all real numbers.
∴ Domain of f = R
Also, for x ∈ R, |x – 1| assumes all real numbers.
Hence, the range of f is the set of all non-negative real numbers.

Question 6.
Let f = {(x, \(\frac{x^{2}}{1+x^{2}}\))} : x ∈ R be a function from R into R. Determine the range of f.
Answer.
f = {(x, \(\frac{x^{2}}{1+x^{2}}\))} : x ∈ R

= {(0, 0), (±0.5, \(\frac{1}{5}\)), (±1, \(\frac{1}{2}\)), (±1.5, \(\frac{9}{13}\)), (±2, \(\frac{4}{5}\)), (3, \(\frac{9}{10}\)), (4, \(\frac{16}{17}\))}

The range of f is the set of all second elements. It can be observed that all these elements are greater than or equal to 0 but less than 1, [∵ Denominator is greater than numerator]
Thus, range of f = [0,1).

Question 7.
Let f, g : R → R be defined, respectively by f(x) = x + 1, g(x) = 2x – 3. Find f + g, f – g and \(\frac{f}{g}\).
Answer.
f, g : R → R is defined as f(x) = x + 1, g(x) = 2x – 3
(i) (f + g) (x) = f(x) + g(x)
= (x + 1) + (2x – 3) = 3x – 2
∴ (f + g) (x) = 3x – 2

(ii) (f – g) (x) = f(x) – g(x)
= (x + 1) – (2x – 3)
= x + 1 – 2x + 3 = – x + 4
∴ (f – g) (x) = – x + 4

(iii) \(\frac{f}{g}\) (x) = \(\frac{f(x)}{g(x)}\), g(x) ≠ 0, x ∈ R.

∴ \(\left(\frac{f}{g}\right)(x)=\frac{x+1}{2 x-3}\), 2x – 3 ≠ 0 or 2x ≠ 3

∴ \(\left(\frac{f}{g}\right)(x)=\frac{x+1}{2 x-3}\), x ≠ \(\frac{3}{2}\).

Question 8.
Let f ={(1, 1), (2, 3), (0, – 1), (- 1, – 3)} be a function from Z to Z defined by f(x) = ax + b, for some integers a, b. Determine a, b.
Solution.
f = {(1, 1), (2, 3), (0, – 1), (- 1, – 3)}
f(x) = ax + b
(1, 1) ∈ f
⇒ f (1) = 1
⇒ a × 1 + b = 1
⇒ a + b = 1
(0, – 1) ∈ f
⇒ f (0) = – 1
⇒ a × 0 + b = – 1
⇒ b = – 1
On substituting b= – 1 in a + b = 1, we obtain a + (- 1) = 1
⇒ a = 1 + 1 = 2.
Thus, the respective values of a and b are 2 and – 1.

Question 9.
Let R be a relation from N to N defined by R = {(a, b) : a, b ∈ N and a = b²}. Are the following true?
(i) (a, a) ∈ R, for all a ∈ N
(ii) (a, b) ∈ R, implies (b, a) ∈ R
(iii) (a, b) ∈ R, (b, c) ∈ R implies (a, c) ∈ R.
Justify your answer in each case.
Answer.
R = {(a, b) : a, b ∈ N and a = b²}
(i) It can be seen that 2 ∈ N; however, 2 ≠ 2² = 4.
Therefore, the statement “(a, a) ∈ R, for all a ∈ N” is not true.

(ii) It can be seen that (9, 3) ∈ N because 9, 3 ∈ N and 9 = 3².
Now, 3 ≠ 9² = 81; therefore, (3, 9) ∈ N
Therefore, the statement “(a, b) ∈ R, implies (b, a) ∈ R is not true.

(iii) It can be seen that (16, 4) ∈ R, (4, 2) ∈ R because 16, 4, 2 e∈ N and 16 = 4² and 4 = 2².
Now, 16 ≠ 2² = 4; therefore, (16, 2) ∈ N
Therefore, the statement “(a, b) ∈ R, (b, c) ∈ R implies (a, c) ∈ R” is not true.

Question 10.
Let A = {1, 2, 3, 4}, B = {1, 5, 9, 11, 15, 16} and f = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}. Are the following true?
(i) f is a relation from A to B
(ii) fis a function from A to B.
Justify your answer in each case.
Answer.
A = {1, 2, 3, 4} and B = {1, 5, 9,11, 15, 16}
∴ A × B = {(1, 1), (1, 5), (1, 9), (1, 11), (1, 15), (1, 16), (2, 1), (2, 5), (2, 9), (2, 11), (2, 15), (2,16), (3, 1), (3, 5), (3, 9),(3, 11),
(3, 15), (3, 16), (4, 1), (4, 5), (4, 9), (4, 11), (4, 15), (4, 16)}
It is given that f = {( 1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}.

(i) A relation from a non-empty set A to a non-empty set B is a subset of the Cartesian product A × B.
It is observed that f is a subset of A × B.
Thus, f is a relation from A to B.
(ii) Since the same first element i.e., 2 corresponds to two different images
i.e., 9 and 11, relation f is not a function.

Question 11.
Let f be the subset of Z × Z defined by f = {(ab, a + b) : a,b ∈ Z}. Is f a function from Z to Z ? Justify your answer.
Answer.
The relation f is defined as f = {(ab, a + b) : a, b ∈ Z}
We know that a relation f from a set A to a set B is said to be a function if every element of set A has unique images in set B.
Since 2, 6, – 2, – 6 ∈ Z, (2 × 6, 2 + 6), (- 2 × – 6, – 2 + (- 6)) ∈ f.
i.e., (12, 8), (12, – 8)
It can be seen that the same first element i.e., 12 corresponds to two different images i.e., 8 and – 8.
Thus, relation f is not a function.

Question 12.
Let A = {9, 10, 11, 12, 13} and let f: A→ N be defined by f(n) = the highest prime factor of n. Find the range of f.
Answer.
A = {9, 10,11, 12, 13}
f : A → N is defined as f(n) = The highest prime factor of n
Prime factor of 9 = 3;
Prime factors of 10 = 2, 5;
Prime factor of 11 = 11;
Prime factors of 12 = 2, 3;
Prime factor of 13 = 13
f(9) = The highest prime factor of 9 = 3
f(10) = The highest prime factor of 10 = 5 .
f(11) = The highest prime factor of 11 = 11
f(12) = The highest prime factor of 12 = 3
f(13) = The highest prime factor of 13 = 13
The range of f is the set of all f(n), where n ∈ A.
∴ Range of f = {3, 5, 11, 13}.

Punjab State Board PSEB 11th Class Maths Book Solutions Chapter 2 Relations and Functions Ex 2.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Maths Chapter 2 Relations and Functions Ex 2.3

Question 1.
Which of the following relations are functions? Give reasons. If it is a function, determine its domain and range.
(i) {(2, 1), (5, 1), (8, 1), (11, 1), (14, 1), (17, 1)}
(ii) {(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}
(iii) (1, 3), (1, 5), (2, 5)}
Answer.
(i) {(2, 1), (5,1), (8, 1), (11, 1), (14, 1), (17,1)}
Since 2, 5, 8, 11, 14, and 17 are the elements of the domain of the given relation having their unique images, this relation is a function.
Here, domain={2, 5, 8, 11, 14, 17} and range={l}

(ii) {(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}
Since 2, 4, 6, 8, 10, 12, and 14 are the elements of the domain of the given relation having their unique images, this relation is a function.
Here, domain = {2, 4, 6, 8, 10, 12, 14} and range = {1, 2, 3, 4, 5, 6, 7}

(iii) {(1, 3), (1, 5), (2, 5)}
Since the same first element i.e., 1 corresponds to two different images i.e.,3 and 5, this relation is not a function.

Question 2.
Find the domain and range of the following real functions:
(i) f(x) = – |x|
(ii) f(x) = \(\sqrt{9-x^{2}}\)
Answer.
(i) f(x) = – |x|, f(x) ≤ 0, ∀ x ∈ R
Domain of f = R
Range of f = {y ∈ R, y < 0}

(ii) f(x) = \(\sqrt{9-x^{2}}\)
All, f is not defined for 9 – x² ≤ 0 or x² ≤ 9 or when x ≥ 3 or x ≤ – 3.
Also, for each real number x lying between – 3 and 3 or for x = – 3, 3 f(x) is unique.
∴ Domain (f) = {x : x ∈ R and – 3 < x < 3}
Further, y = \(\sqrt{9-x^{2}}\) or y² = 9 – x²
or x = \(\sqrt{9-x^{2}}\)
Again, x is not defined for
9 – y² < 0 or y² > 9 or y > 3 or y < – 3.
But y cannot be – ve
∴ Range (f) = {y : y ∈ R and 0 < y < 3}

Question 3.
A function fis defined by f(x) = 2x – 5. Write down the values of
(i) f(0)
(ii) f(7)
(iii) f(- 3)
Answer.
The given function is f(x) = 2x – 5. Therefore,
(i) f(0) = 2 × 0 – 5 = 0 – 5 = – 5
(ii) f(7) = 2 × 7 – 5 = 14 – 5 = 9
(iii) f(- 3) = 2 × (- 3) – 5 = – 6 – 5 = -11.

Question 4.
The function ‘t’ which maps temperature in degree Celsius into temperature in degree Fahrenheit is defined by t(C) = \(\frac{9 C}{5}\) + 32. Find
(i) f(0)
(ii) t(28)
(iii) t(- 10)
(iv) The value of C, when t(C) = 212.
Answer.
The given function is t (C) = \(\frac{9 C}{5}\) + 32. Therefore,
(i) t(0) = \(\frac{9 \times 0}{5}\) + 32 = 0 + 32 = 32

(ii) t(28) = \(\frac{9 \times 28}{5}\) + 32 = \(\frac{252+160}{5}=\frac{412}{5}\)

(iii) t (- 10) = \(\frac{9 \times(-10)}{5}\) + 32 = 9 × ( – 2) + 32

(iv) It is given that t(C) = 212
∴ 212 = \(\frac{9 C}{5}\) + 32 \(\frac{9 C}{5}\)
= 212 – 32 \(\frac{9 C}{5}\) = 180
9C = 180 × 5 C = \(\frac{180 \times 5}{9}\) = 100.
Thus, the value of t, when t(C) = 212, is 100.

Question 5.
Find the range of each of the following functions :
(i) f(x) = 2 – 3x, x ∈ R, x > 0.
(ii) f(x) = x² + 2, x is a real number.
(iii) f(x) = x, x is a real number.
Answer.
(i) Let f(x) = y = 2 – 3x is x = \(\frac{2-y}{3}\)
Now x > 0 is 2 – y > 0 or y < 2
Range (f) = {y : y ∈ R and y < 2}

(ii) Let f(x) = y = x² + 2 is x² = y – 2 or x = \(\sqrt{y-2}\) ⇒ y > 2
Range (f) = {y : y ∈ R and y > 2}

(iii) f(x) = x, x is a real number
x = f(x) = y = a real number
Range (f) = {y : y ∈ R}

Punjab State Board PSEB 11th Class Maths Book Solutions Chapter 2 Relations and Functions Ex 2.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Maths Chapter 2 Relations and Functions Ex 2.2

Question 1.
Let A = {1, 2, 3, …………. , 14}. Define a relation R from A to A by R = {(x, y) : 3x – y = 0, where x, y ∈ A}. Write down its domain, codomain and range.
Answer.
The relation R from A to A is given as
R = (x, y) : 3x – y = 0, where x, y ∈ A} i.e., R = { y} : 3x = y, where x, y ∈ A}
R = {(1, 3), (2, 6), (3, 9), (4, 12)}
The domain of R is the set of all first elements of the ordered pairs in the relation.
Domain of R = {1, 2, 3, 4}
The whole set A is the codomain of the relation R.
Codomain of R = A = {1, 2, 3, …………., 14}
The range of R is the set of all second elements of the ordered pairs in the relation.
Range of R = {3, 6, 9, 12}.

Question 2.
Define a relation R on the set N of natural numbers by R= {(x, y): y = x + 5, x is a natural number less than 4 : x, y ∈ N}. Depict this relationship using roster form. Write down the domain and the range.
Answer.
R = { (x, y) : y = x+ 5, x is a natural number less than 4 ,x} y ∈ N}
The natural numbers less than 4 are 1, 2, and 3.
∴ R = {(1, 6), (2, 7), (3, 8)}
The domain of R is the set of all first elements of the ordered pairs in the relation.
∴ Domain of R = {1, 2, 3}
The range of R is the set of all second elements of the ordered pairs in the relation.
∴ Range of R = {6, 7, 8}

Question 3.
A = {1, 2, 3, 5} and B = {4, 6, 9}. Define a relation R from A to B by R = {(x, y): the difference between x and y is odd; x ∈ A, y ∈ B}. Write R in roster form.
Answer.
A = {1, 2, 3, 5} and B = {4, 6, 9}
R = { (x, y) the difference between x and y is odd; x ∈ A, y ∈ B}
R = {(1, 4), (1, 6), (2, 9), (3, 4), (3, 6), (5, 4), (5, 6)}.

Question 4.
The given figure shows a relationship between the sets P and Question Write this relation
(i) in set-builder form
(ii) in roster form. What is its domain and range?

Answer.
According to the given figure, P = {5, 6, 7}, Q = {3, 4, 5}
(i) R = {(x, y) : y = x – 2 x ∈ P} or R = {(x, y) : y = x – 2 for x = 5, 6, 7}
(ii) R = {(5, 3), (6, 4), (7, 5)}
Domain of R = {5, 6, 7}
Range of R = {3, 4, 5}

Question 5.
Let A = {1, 2, 3, 4, 6}. Let R be the relation on A defined by {(a, 6) : a, b ∈ A, 6 is exactly divisible by a}.
(i) Write R in roster form
(ii) Find the domain of R
(iii) Find the range of R.
Answer.
A = {1, 2, 3, 4, 6}, R = {(a, b): a, b ∈ A, b is exactly divisible by a}
(i) R = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 6), (2, 2), (2, 4), (2, 6), (3, 3), (3, 6), (4, 4), (6, 6)}
(ii) Domain of R = {1, 2, 3, 4, 6}
(iii) Range of R = {1, 2, 3, 4, 6}.

Question 6.
Determine the domain and range of the relation R defined by R = {x, x + 5) : x ∈ {0, 1, 2, 3, 4, 5}}.
Answer.
R = {(x, x + 5) : x ∈ {0, 1, 2, 3, 4, 5}
R = {(0, 5), (1, 6), (2, 7), (3, 8), (4, 9), (5, 10)}
Domain of R = {0, 1, 2, 3, 4, 5}
Range of R = {5, 6, 7, 8, 9, 10}

Question 7.
Write the relation R = {(x, x³) : x is a prime number less than 10} in roster form.
Answer.
R = {(x, x³) : x is a prime number less than 10}
The prime numbers less than 10 are 2, 3, 5, and 7.
R = {(2, 8), (3, 27), (5, 125), (7, 343)}

Question 8.
Let A = {x, y, z} and B = {1, 2}. Find the number of relations from A to B.
Answer.
It is given that A = {x, y, z} and B = {1, 2}.
∴ A × B = {(x, 1), (x, 2), (y, 1), (y, 2), (z, 1), (z, 2)}
Since h(A × B) = 6, the number of subsets of A × B is 26.
Therefore, the number of relations from A to B is 26.

Question 9.
Let R be the relation on Z defined by R = {(a, b) : a, b ∈ Z, a b is an integer}. Find the domain and range of R.
Answer.
R = {(a, b) : a, b ∈ Z, a – b is an integer}
It is known that the difference between any two integers is always an integer.
∴ Domain of R = Z
Range of R = Z.

Punjab State Board PSEB 11th Class Maths Book Solutions Chapter 2 Relations and Functions Ex 2.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Maths Chapter 2 Relations and Functions Ex 2.1

Question 1.
If (\(\frac{x}{3}\) + 1, y – \(\frac{2}{3}\)) = (\(\frac{5}{3}\), \(\frac{1}{3}\))
find the values of x and y.
Answer.
It is given that (\(\frac{x}{3}\) + 1, y – \(\frac{2}{3}\)) = (\(\frac{5}{3}\), \(\frac{1}{3}\))
Since the ordered pairs are equal, the corresponding elements will also be equal.
Therefore, \(\frac{x}{3}\) + 1 = \(\frac{5}{3}\) and y – \(\frac{2}{3}\)) = (\(\frac{1}{3}\)

⇒ \(\frac{x}{3}\) = \(\frac{5}{3}\) – 1 and y = \(\frac{1}{3}\) + \(\frac{2}{3}\)

⇒ \(\frac{x}{3}\) = \(\frac{5}{3}\) and y = \(\frac{3}{3}\)
⇒ x = 2 and y= 1
∴ x = 2 and y = 1.

Question 2.
If the set A has 3 elements and the set B = {3, 4, 5}, then find the number of elements in (A × B).
Answer.
It is given that set A has 3 elements and the elements of set B are 3, 4, and 5.
⇒ Number of elements in set B = 3
Number of elements in (A × B) = (Number of elements in A) × (Number of elements in B)
= 3 × 3 = 9
Thus, the number of elements in (A × B) is 9.

Question 3.
If G = {7, 8} and H = {5, 4, 2}, find G × H and H × G.
Answer.
G = {7, 8} and H = {5, 4, 2}
We know that the Cartesian product P × Q of two non-empty sets P and Q is defined as
P × Q = {(p, q) : p ∈ P, q ∈ Q}
∴ G × H = {(7, 5), (7, 4), (7, 2), (8, 5), (8, 4), (8, 2)}
H × G = {(5, 7), (5, 8), (4, 7), (4, 8), (2, 7), (2, 8)}.

Question 4.
State whether each of the following statements are true or false. If the statement is false, rewrite the given statement correctly,
(i) If P = {m, n} and Q = {n, m}, then P × Q = {(m, n), (n, m)}.
(ii) If A and B are non-empty sets, then A × B is a non-empty set of ordered pairs (x, y) such that x ∈ A and y ∈ B.
(iii) If A = {1, 2}, B = {3, 4}, then A × (B ∩ Φ) = Φ.
Answer.
(i) False
If P = {m, n} and Q = {n, m}, then P × Q = {(m, m), (m, n), {n, m), (n, n)}
(ii) True
(iii) True.

Question 5.
If A = {- 1, 1}, find A × A × A.
Answer.
It is known that for any non-empty set A, A × A × A is defined as
A × A × A = {(a, b, c) : a, b, c ∈ A}
It is given that A = {- 1, 1}
∴ A × A × A = {(- 1, – 1, – 1), (- 1, – 1, 1), (- 1, 1, – 1), (- 1, 1, 1), (1, – 1, – 1), (1, – 1, 1), (1, 1, – 1), (1, 1, 1)}

Question 6.
If A × B = {(o, x), (a, y), (b, x), (b, y)}. Find A and B.
Answer.
It is given that A × B = {(a, x), (a, y), (b, x), (b, y)}
We know that the Cartesian product of two non-empty sets P and Q is defined as P × Q = {(p, q): p ∈ P, q ∈ Q}
A is the set of all first elements and B is the set of all second elements.
Thus, A = {a, b} and B = {x, y}.

Question 7.
Let A = {1, 2}, B = {1, 2, 3, 4}, C = {5, 6} and D = {5, 6, 7, 8}. Verify that
(i) A × (B ∩ C) = (A × B) ∩ (A × C)
(ii) A × C is a subset of B × D
Answer.
(i) To verify: A × (B ∩ C) = (A × B) ∩ (A × C)
We have B ∩ C = {1, 2, 3, 4} ∩ {5, 6} = Φ
L.H.S. = A × (B ∩ C) = A × Φ = Φ
A × B = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4)}
A × C = {(1, 5), (1,6), (2, 5), (2,6)}
R.H.S. = (A × B) ∩ (A × C) = Φ
L.H.S. = R.H.S
Hence, A × (B ∩ C) = (A × B) ∩ (A × C)

(ii) To verify: A × C is a subset of B × D
A × C = {(1, 5), (1, 6), (2, 5), (2, 6)}
B × D = {(1, 5), (1, 6), (1, 7), (1, 8), (2, 5), (2, 6), (2, 7), (2, 8), (3, 5), (3, 6), (3, 7), (3, 8), (4, 5), (4, 6), (4, 7), (4, 8)}
We can observe that all the elements of set A × C are the elements of set B × D.
Therefore, A × C is a subset of B × D.

Question 8.
Let A = {1, 2} and B = {3, 4}. Write A × B. How many subsets will A x B have? List them.
Answer.
A = {1, 2} and B = {3, 4}
A × B = {(1, 3), (1, 4), (2, 3), (2, 4)}
⇒ n(A × B) = 4
We know that if C is a set with n(C) = m, then n[P(C)] = 2m.
Therefore, the set A × B has 2⁴ = 16 subsets.
These are {Φ, (1, 3)}, {(1, 4)}, {(2, 3)}, {(2, 4)}, {(1, 3), (1, 4)}, {(1, 3), (2, 3)}, {(1, 3), (2, 4)}, {(1, 4), (2, 3)}, {(1, 4), (2, 4)}, {(2, 3), (2, 4)}, {(1, 3), (1, 4), (2, 3)}, {(1, 3), (1, 4), (2, 4)}, {(1, 3), (2, 3), (2,4)}, {(1, 4), (2, 3), (2, 4)}, {(1, 3), (1, 4), (2, 3), (2, 4)}

Question 9.
Let A and B be two sets such that n(A) = 3 and n(B) = 2. If (x, 1), (y, 2), (z, 1) are in A × B, find A and B, where x, y andz are distinct elements.
Answer.
It is given that n(A) = 3 and n(B) = 2; and (x, 1), (y, 2), (z, 1) are in A × B.
We know that A=Set of first elements of the ordered pair elements of A × B
B = Set of second elements of the ordered pair elements of A × B.
∴ x, y, and z are the elements of A; and 1 and 2 are the elements of B.
Since n(A) = 3 and n(B) = 2, it is clear that A = {x, y, z} and B = {1, 2}.

Question 10.
The Cartesian product A × A has 9 elements among which are found (-1, 0) and (0, 1). Find the set A and the remaining elements of A × A.
Answer.
We know that if n(A) =p and n(B) =q, then n(A × B) = pq.
∴ n(A × A) = n(A) × n(A)
It is given that n(A × A) = 9
n(A) × n(A) = 9
=> n (A) = 3
The ordered pairs (- 1, 0) and (0, 1) are two of the nine elements of A × A.
We know that A x A={(a, a) : a ∈ A}.
Therefore, – 1, 0, and 1 are elements of A.
Since n(A} = 3, it is clear that A = {- 1, 0, 1}.
The remaining elements of set A × A are (- 1, – 1), (- 1, 1), (0, – 1), (0, 0), (1, – 1), (1, 0), and (1, 1).