Class 11

Punjab State Board PSEB 11th Class Sociology Important Questions Chapter 3 Society, Community and Association Important Questions and Answers.

PSEB 11th Class Sociology Important Questions Chapter 3 Society, Community and Association

Multiple Choice Questions

Question 1.
Who said this: “Man is a social animal.”?
(a) Maclver
(b) Weber
(c) Aristotle
(d) Plato
Answer:
(c) Aristotle.

Question 2.
What is the need of similarities and differences for the formation of society?
(а) To make relations
(b) For social progress
(c) To take forward society from demographic point of view
(d) All of these.
Answer:
(d) All of these.

Question 3.
According to Marx, which was the first historical society?
(a) Early communism
(b) Feudal
(c) Slave
(d) Capitalist.
Answer:
(a) Early Communism.

Question 4.
Why an individual makes relations with others?
(a) To fulfil his needs
(b) To achieve his objectives
(c) To save himself from other’s selfish interests
(d) All of these.
Answer:
(d) All of these.

Question 5.
Man and society are considered ………… to each other?
(a) against
(b) complementary
(c) equal
(d) none of these.
Answer:
(b) complementary.

Question 6.
Which of these is available in society?
(a) Equality
(b) Cooperation
(c) Conflict
(d) Cooperation and Conflict.
Answer:
(d) Cooperation and Conflict.

Question 7.
An organisation of individuals formed to achieve common objectives ………..
is known as
(a) a society
(b) a class
(c) a group
(d) an organisation.
Answer:
(a) a society.

Question 8.
Which of these is not a community?
(a) People of Kerala in Delhi
(b) People born in USA
(c) Trade union movement
(d) None of these.
Answer:
(d) None of these.

Question 9.
Society is the web of …………
(a) Social norms
(b) Mutual relations
(c) Individual relations
(d) None of these.
Answer:
(b) Mutual relations.

Question 10.
What is the relation between an individual and society?
(a) Man is social by nature and he cannot live alone
(b) Man lives in society to fulfil his needs
(c) Society makes personality of an individual
(d) All of these.
Answer:
(d) All of these.

Fill in the Blanks :

1. Society is made up of ………….
2. Community develops automatically with the ………….. of people.
3. …………… is established deliberately to achieve certain goals.
4. Membership of …………… depends upon one’s wish.
5. Society is …………… in nature.
6. Totem is of great importance in …………. society.
7. Membership of is …………… formal.

Answer:

1. social relations
2. interactions
3. An association
4. association,
5. abstract
6. tribal
7. association.

True/False:

Question 1.
Membership of society depends upon one’s wish.
Answer:
False

Question 2.
Society is made up of social relationships.
Answer:
True

Question 3.
Community develops automatically.
Answer:
True

Question 4.
Association is ‘deliberately formed.
Answer:
True

Question 5.
Membership of association is informal.
Answer:
False

Question 6.
Language is of great importance in human society.
Answer:
True

Question 7.
An institution is a system of norms to achieve certain objectives.
Answer:
True.

One Word/Line Question Answers:

Question 1.
Who says that the group of persons, is society ?
Answer:
A common man says that the group of persons is society.

Question 2.
If co-operation between the members of society comes to an end, what will happen ? , .
Answer:
If co-operation between the members of society comes to an end, society will also come to an end.

Question 3.
On what factor is society based ?
Answer:
Society is based on social relations.

Question 4.
Who said, “Society cannot move without similarities and differences.” ?
Answer:
These words are of Westermarck.

Question 5.
In which society, totem is of great importance ?
Answer:
Totem is of great importance in tribal society.

Question 6.
Why is society abstract in nature ?
Anseer:
Society is a web of social relationships and relations are abstract which we can’t see. That’s why society is abstract in nature.

Question 7.
What is society ?
Answer:
In Sociology, society is the web of social relationships.

Question 8.
Give one characteristic of society.
Answer:
Society is based on relations. It is also based on similarities and differences.

Question 9.
What is the base of society ?
Answer:
Relations between individuals are the base of society.

Question 10.
What is Community ?
Answer:
Community is a group of people in a geographical area where they spend whole of their lives.

Question 11.
Do all the human groups are Communities ?
Answer:
No, they could be institutions or any other groups.

Question 12.
Give literal meaning of Community.
Answer:
The word community is derived from the Latin word ‘Communities’ which means things held in common or shared.

Question 13.
How does community develop ?
Answer:
Community develops automatically due to human interactions.

Question 14.
Is there any community feeling in community ?
Answer:
Yes, community feeling does exist among the community members

Very Short Answer Type Questions

Question 15.
What is Association ?
Answer:
When few individuals come together to form an association to achieve their objectives, it is known as association.

Question 1.
Society.
Answer:
The meaning of society is not by the aggregate of people but is by the web of relationships which exist among the people and with which people are connected with each other. When relations are formed by the people, society is formed.

Question 2.
Definition of Society.
Answer:
According to Morris Ginsberg, “Society is a collection of individuals united by certain relations or mode of behaviour which mark them off from others who do not enter into these relations or who differ from them in behaviour.”

Question 3.
Two features of Society.
Answer:
(i) Society is based on relations. Society cannot be formed without the relations among the people.
(ii) Society also depends upon similarities and differences. Society cannot exist in their absence.

Question 4.
Abstractness.
Answer:
Society is abstract because it is a web of social relationships which we cannot see or touch. We can only feel them. Because we cannot touch them, that’s why society is abstract in nature.

Question 5.
Importance of language in society.
Answer:
Language is of great importance in the society because it is the best method to express our views and ideals. In the absence of language, we cannot establish relations with any one and then society cannot be established.

Question 6.
Community.
Answer:
When few individuals live in a group, in a particular geographical area, in an organised manner and spend whole of their lives without any particular motive, it is known as Community. We-feeling always exists in society.

Question 7.
Literal meaning of Community.
Answer:
Community is an English word. It is made up of two Latin words ‘Com’ whose meaning is to live collectively and ‘Munus’ which means making. So its meaning is to make collective living.

Question 8.
Meaning of Association.
Answer:
Association is based on particular motive and co-operation. When few individuals, for a particular objective, co-operate with each other and form an organisation, this, organised organisation is known as association.

Question 9.
Definition of Association.
Answer:
According to Gillin and Gillin, “An association is a group of individuals united for a specific purpose and held together by recognized or sanctioned modes or procedure and behaviour.”

Short Answer Type Questions 

Question 1.
Two definitions of Society.
Answer:
(i) According to Maclver, “Society is the system of usages and procedure of authority and mutual aid, of many groupings and divisions of controls of human behaviour and of liberties. This everchanging complex system is called society. It is the web of social relationships.”
(ii) According to Giddings, “Society is the union itself, the organization is the sum of formal relations in which individuals are bound together.”

Question 2.
Characteristics of Society.
Answer:

1. Society is based on relationships.
2. Society depends on likeness and differences.
3. Humans of a Society are interdependent.
4. Society is abstract because it is the web of social relationships.
5. Most important feature of society is that it has the population.
6. Cooperation and struggle are must for society.

Question 3.
Relationship between Individual and Society.
Answer:
Greak philosopher Aristotle once said that man is a social animal. It means that the man lives in society and he is nothing without society. Until or unless he does not spend his life with other people, he remains at the lowest level of civilisation. Man needs to live a long life and for this, he is required to depend upon each other to fulfill his needs.

He needs to depend upon others for almost all of his needs ; like protection, food, education, other services etc. He alone cannot do any thing. With this, his existence is nothing without the society. They both are complimentary to each other and they are nothing without each other.

Question 4.
What is Community ?
Answer:
In simple words when some people are living jointly for a particular purpose then that is called a community. It is a concrete concept. Community is not established with conscious efforts. It also not takes birth but it develops and it develops automatically. When people are living in an area and are doing social processes then community develops automatically.

Community has its own geographical area where members are fulfilling their needs themselves. Members of a community fulfil their every type of need because members have mutual exchange. When people cooperate with each other to fulfil their needs then we-feeling comes in them.

Question 5.
Characteristics of Community
Answer:

1. Every community has we-feeling.
2. Members of the community have role feeling among them.
3. Members of the community depend upon each other to fulfil their needs.
4. Community is permanent and its members are not temporary but are permanent.
5. Members of the community spend their life in community.
6. Every community has its own geographical area in which it lives.
7. Community doesn’t have any specific motive. It comes out spontaneously.

Question 6.
Association.
Answer:
Association is based on cooperation. When some people are cooperating with each other for a specific purpose and make an organization then this organization is known as Association. Association has a definite purpose and anyone can leave it after the attainment of his objective.

Question 7.
Characteristics of Association.
Answer:

1. Association is a group of people.
2. Association is formed for the fulfilment of a specific aim and is established with a lot of thpughts.
3. Association takes birth and destroys.
4. Membership of an association is based on the wish of the person.
5. Membership of an association is formal.
6. Every association selects some of its office bearers. .
7. Every association has some definite rules.

Long Answer Type Questions

Question 1.
Define Society. Give its characteristics.
Answer:
Definitions of society given by different sociologists .are given below :

1. According to Maclver, “Society is the system of usages and procedures, of authority and mutual aid, of many groupings and divisions of controls of human behaviour and of liberties. This ever-changing complex system we call society. It is the web of social relationships.”

2. According to Giddings, “Society is the union itself, the organization is the sum of formal’ relations in which individuals are bound together.”

3. According to Talcot Parsons, “Society may be defined as total complex of human relationships in so far as they grow out of action in terms of means and relationship intrinsic or symbolic.”

4. According to Cooley, “Scfciety is the complex of forms or processes each of which
is living and growing by interaction with the others, the whole being so unified that what takes place in one part affects all the rest.”

5. According to Green, “A society is a larger group to which any individual belongs.”

6. According to Reuter, “An abstract term that connotes the complex of interrelations that exist between and among the people.”

After looking at these given definitions we can say that these definitions are of two types.
The first type is of functional definitions and the second type is of structural definitions. From functional aspect we can define society as a web of groups in which people have complimentary relations, which help the people to do their functions of life and will help the people to fulfil their wishes by living with them. From structural aspect society is a social culture of customs, habits, institutions, wishes etc.

In this way society has been defined from functional and structural aspect that it has been made by mutual relationships of humans and with that it is a system or web, not only the collection of people.

1. Society is based on relationships. According to Maclver and Page, “Society is the web of social relationships.” It means that society is based on social relationships. Why the word Web’ is used here ? Because thousands of relationships exist in society. Just in one family more than 15 types of relations exist. From this we can imagine that how many types of relations are there in society.

Society is not just a collection of humans. For the formation of society some type of relations should be there. But here one” thing should be kept in mind that these relations should be complimentary. If these relations are not complimentary then society cannot be made. Social relations exist in every type of society and among all humans because the relations of humans Are based on mutual consciousness.

2. Society depends upon likeness and differences. Society depends both upon likeness and differences. Without them society cannot exist. Yet they both are opposite to each other but they cannot live without each other. Sometimes uniformity comes in society and sometimes differences come in -society and that’s why they are complimentary to each other.

Social relations can be established if there will be some type of uniformity in them because without this they cannot attract each other and society cannot be formed. Except this differences are also necessary.

3. Interdependence. For the,existence of society interdependence is a necessary element. It is necessary for humans to keep relations with other persons to fulfil their needs because it is not possible for every person to do all of his works. He has to depend upon others. The way in which man grows his dependence upon others also increases and his needs also start to increase. In this way interdependence is a necessary element of. society.

4. Society is abstract. Society is abstract because it is the web of relationships. We neither can see these relations and nor can touch them. We can only feel them. Because 4ve cannot touch them and that’s why they don’t have any concrete form. That’s ,why they are abstract. Because relations are abstract, that’s why the society made by relations is also abstract.

5. Population. The most important element of the society is humans. Without humans society cannot be made. If humans will not be there then who will establish relations and how society will be formed. Without the existence of humans, the existence of society is impossible. That’s why population is a necessary factor.

For population many things are required like availability of enough food, protection of population from every type of problem and the continuation of population and society because if the population will not continue then one day will come when everyone will come to an end. In this way without population, the existence of society is impossible.

6. Cooperation and conflict are a must for society. The way in which likes and differences are necessary for the existence of society, in that same way cooperation and conflict are also necessary for the existence of society. Cooperation is a necessary element for the formation of society. Humans live in society and they depend upon each other.

This interdependence is there only if there will be some cooperation among them. For the upbringing of a child many hands play an important role and it depends upon cooperation. Family runs if husband and wife cooperate with each other. In this way in every part of society cooperation is required. In the same way conflict is also necessary. To live man has to struggle with many forces and has to struggle in life.

Question 2.
What do you mean by association ? Explain it with definitions and characteristics.
Answer:
Man is a social animal and as a social animal he has some basic needs. Man does a lots of efforts to fulfil his basic needs. He does three types of efforts.

1. First effort is that he should fulfil his needs alone and without any one’s help. But in today’s modem age it is impossible to live alone and to fulfil all the needs alone.

2. Second way is that he should fulfil his needs by snatching things from others. But it is not possible to fulfil Ms needs by snatching things from the others because this way is non-social and while living in human society he cannot adopt this type of method.

3. The third and the best method is that man should fulfil his needs while living in the society by cooperating with others because this is the base of life. Association is also based on this co-operation. When some people cooperate with each other for a specific purpose and make an organization then this organized organization is known as association.

Association has a definite purpose and any one can leave it after the attainment of his objective. Natural and the social needs of man force him to five in society. Like animals, humans do not have just physical needs but they have other important social needs also which must be fulfilled. In this way when different persons of a society cooperate with each other to fulfil their needs then an association is formed.

Here one thing should be kept in mind that man can leave tMs association after the attainment of his objectives.

Definitions:
1. According to Bogardus, “An Association is usually a working together of people to achieve some purpose.”

2. According to Ginsberg, “An association is a group of social beings related to one another by the fact that they possess or have instituted in common an organization with a view of securing a specific end or specific ends.”

3. According to Gillin and Gillin, “An association is a group of individuals united for a specific purpose and held together by recognised or sanctioned modes or procedure and behaviour.”

From the given definitions it is clear that Association has three main bases:

1. Association is a group of people.
2. This organization is based on cooperation.
3. It fulfil? some of-our needs.

In this way association cannot fulfil all of our needs. In short when people cooperate with each other in an organized and thoughtful way for the attainment of any particular aim then an association is formed.

Characteristics of Association:
1. Association is a group of people. Association is established bysome persons because of which it is known as a group. In this way association is concrete because humans are concrete.

2. Thoughtful establishment. Association does not take place spontaneously like community. It is formed for the fulfilment of any specific aim and is established with a lot of thoughts.

3. Definite aim. Association has a definite aim. Association does not fulfil all the needs of our social life but it fulfils some of our needs and it protects the interests of its members.

4. Association takes birth and comes to an end. Nature of association is temporary because it is established for the attainment of some of our specific aims and after the attainment of those aims, need of association also comes to an end. That’s why it takes .birth and comes to an end.

5. Membership is based on wish. Association is a willful organization. Any one can become member of any association according to his wish and he can leave it at anytime. It is so because when man feels that association is useful for him then he takes its membership and when he feels that his hims are attained then he leaves

6. Formal membership. The membership of an association is formal. Whenever any person wants then he can take its membership and whenever he wants he can leave it but for this he has to resign from its membership. He has to give membership fee also.

7. Selection of office bearers. Every association selects some of its officers like a chairman, deputy chairman, secretary, cashier etc. for conducting and performing its functions. All these are selected for a specific period.

8. Every association has some definite rules. Every association makes some rules for doing its functions and every member has to work according to these rules.

Punjab State Board PSEB 11th Class Sociology Important Questions Chapter 2 Relationship of Sociology with Other Social Sciences Important Questions and Answers.

PSEB 11th Class Sociology Important Questions Chapter 2 Relationship of Sociology with Other Social Sciences

Multiple Choice Questions

Question 1.
Who wrote the book ‘Das Capital’?
Answer:
(c) Marx.

Question 2.
Which of these is not directly related with Economics?
(a) Consumption
(b) Religious activities
(c) Production
(d) Distribution.
Answer:
(b) Religious activities.

Question 3.
What is the contribution of Sociology to History?
(a) History uses the material of Sociology
(b) History has included many Sociological concepts in its subject matter
(c) Social History studies sequal development and changes of any institution
(d) All of these.
Answer:
(d) All of these.

Question 4.
Whose words are these, “Society is the detailed form of society”?
(a) Maclver
(b) Aristotle
(c) Weber
(d) Durkheim.
Answer:
(b) Aristotle.

Question 5.
Which of these is the biological feature of human society?
(a) Ability to stand
(b) Developed brain
(c) Ability to speak
(d) All of these.
Answer:
(d) All of these.

Question 6.
What is the difference between Sociology and Economics ?
(a) Subject matter of Sociology is whole of society but study of Economics is confined to economic activities
(b) Outlook of .Sociology is social and of Economics it is economic
(c) Sociology studies the group but economics studies an individual
(d) All of these.
Answer:
(d) All of these.

Question 7.
What name Comte gave to his philosophy ?
(a) Idealism
(b) Positivism
(c) Experimentation
(d) None of these.
Answer:
(b) Positivism.

Question 8.
Which of these branches of Psychology is related with Sociology ?
(a) Social Psychology
(b) Economic Psychology
(c) Structural Psychology
(d) Cultural Science.
Answer:
(a) Social Psychology.

Question 9.
Sociology takes the help of to study historical facts.
(a) Economics
(b) History
(c) Political Science
(d) Anthropology.
Answer:
(b) History.

Question 10.
Which of these methods is used in Psychology ?
(a) Historical Method
(b) Comparative Method
(c) Experimental Method
(d) Structural Method.
Answer:
(c) Experimental Method.

Fill in the Blanks:

Question 1.
………….. called Sociology and Anthropology as twin sisters.
Answer:
Krober

Question 2.
There are areas of the study of Anthropology.
Answer:
two

Question 3.
………….. is related with the development of man.
Answer:
Anthropology

Question 4.
…………… stresses on the study of human events.
Answer:
History

Question 5.
Society is made up of …………..
Answer:
humans

Question 6.
…………. is related with production, consumption and distribution.
Answer:
Economics

Question 7.
studies the functions of state and government.
Answer:

True/False:

Question 1.
Astronomy is a natural science.
Answer:
True

Question 2.
Economics takes the help of sociology to understand social problems.
Answer:
True

Question 3.
Aristotle is known as the father of Political Science.
Answer:
True

Question 4.
Sciences can be divided into four parts.
Answer:
False

Question 5.
Outlook of Political Science is social.
Answer:
False

Question 6.
Inductive and deductive methods are used in Economics.
Answer:
True

Question 7.
Economics is related with production, consumption and distribution.
Answer:
True

One Word/Line Question Answers:

Question 1.
With what does Anthropology relate ?
Answer:
Anthropology is related with evolution and development of individuals.

Question 2.
Which branch of Anthropology is related with Sociology ?
Answer:
Social and Cultural Anthropology is a branch of Anthropology which is related with Sociology. >

Question 3.
On whose study History gives stress ? .
Answer:
History stresses on the study of human experiences of the past.

Question 4.
What is society made up of ?
Answer:
Society is made up of humans.

Question 5.
Give examples of natural science.
Answer:
Chemistry, Astronomy, Physics, Biology etc.

Question 6.
Why Sociology depends upon History ?
Answer:
Sociology depends upon History to understand modern society.

Question 7.
What type of Science is History ?
Answer:
History is a concrete science.

Question 8.
With what Economics is related ?
Answer:
Economics is related with production, consumption and distribution.

Question 9.
Why does Economics take help of Sociology ?
Answer:
To understand social problems, Economics takes help of Sociology.

Question 10.
Which method is used by History ?
Answer:
History uses descriptive method.

Question 11.
Who is considered as the father of Political Science ?
Answer:
Aristotle is considered as the father of Political Science.

Question 12.
Who wrote the book ‘Arthashastra’ ?
Answer:
Arthashastra was written by Kautilya or Chanakya.

Question 13.
In how many parts can we divide Science ?
Answer:
Science can be divided into two parts-Natural sciences and Social sciences.

Question 14.
Name the branch of Sociology associated with History.
Answer:
Historical Sociology is a branch of Sociology associated with History.

Very Short Answer Type Questions

Question 1.
Division of Science.
Answer:
In Science, we try to find new concepts and methods. That’s why we can divide science into two parts and these are :
(i) Natural Sciences
(ii) Social Sciences.

Question 2.
Natural Sciences.
Answer:
Natrual Sciences are the sciences which are related with nature and biological phenomenon about which they try to find new facts, concepts, theories etc., for example, Physics, Chemistry, Biology, Astronomy etc.

Question 3.
Social Sciences.
Answer:
Social Sciences are the sciences which try to find concepts, facts and theories related with human society. In these scientific study of social life is done; for exmple, Economics, Political Science, Sociology, Anthropology etc.

Question 4.
History.
Answer:
History studies the past time of human society. It tries to understand and explain social life on the basis of past time events. It is mainly concerned with life and events of different kings, important years of their lives etc.

Question 5.
Economic Institutions.
Answer:
Economic institutions study economic aspects of humans. They study how the money can be produced, distributed and consumed. In simple words, all the economic activities of human society are studied by “economic institutions.

Question 6.
Political Science.
Answer:
Political Science is related with the political aspect of human s’oeiety. It studies origin of state, its development and features, organisation, system of government, other political institutions, associations, their functions etc.

Question 7.
Literal meaning of Sociology.
Answer:
Word ‘Sociology’ is made up of two words ‘Socio’ and ‘Logos’. Socio is a Latin word which means society and Logos is a Greek word which means science. So, the literal meaning of Sociology is science of society.

Question 8.
Methods used in Sociology and Economics.
Answer:
Economics uses Inductive method and Deductive method but Sociology uses a number of methods such as Observation, Interview, Schedule, Questionnaire, Case study, Sociometry method etc.

Short Answer Type Questions 

Question 1.
Division of Science.
Answer:
In Science we research for theories and methods and on the basis of this we can divide Sciences in two parts :
(а) Natural Sciences
(b) Social Sciences.

Question 2.
Meaning of Natural Sciences.
Answer:
Natural Science is that branch of science which is related with nature and biological phenomenon with which it tries to find the related facts and theories; for example, Physics, Chemistry, Biology, Astronomy etc.

Question 3.
Meaning of Social Sciences.
Answer:
Social Sciences are those Sciences which find facts and theories related with human society. Scientific study of Social Life is also being studied in this; for example, Economics, Political Science, Anthropology, Sociology etc.

Question 4.
Relation of Sociology with other Social Sciences.
Answer:
All Social Sciences are not only different from each other from the point of view of their subject matter but they are also different from their outlook and point of view. But all the Social Sciences are studying the human society because of which we cannot differentiate one Social Science from another.

For example, Economics is related with economic problems but these economic problems are the one part of Society. That’s why we have to take help of other Sciences to find its solution.

Question 5.
How is Sociology the mixture of Social Sciences ?
Answer:
Sociology is known as the mixture of the other Social Sciences. It depends upon other Sciences for many things and sometimes it depends upon others to solve its problems. Every problem, which exists in Society, cannot be solved by just Sociology. That’s why* we can not differentiate Sociology from other Social Sciences. Sociology alone is unable to find solution of any problem. That’s why taking help of others is known as mixture of Social Sciences.

Question 6.
What is History?
Answer:
History studies the past time of human history. It also studies phenomenon occurred in past and tries to understand ideology of Social Life on the basis of that phenomenon. In this way it analyzes both the situations ‘what was’ ? And ‘How it happened’ ? In this way we can come to know about Social organization, customs, traditions etc. of human history.

Question 7.
Give difference between Sociology and History.
Answer:
These both Social Sciences study same subject matter from different point of views. History studies some specific phenomenon but Sociology finds rules of general phenomenon and explains their inter-relationships. Sociology uses comparative method but History uses descriptive method.

Sociology studies human groups but History gives emphasis on the study of human action. History is related with phenomenon of past but Sociology is related with the Society of present.

Question 8.
Sociology depends upon History. How ?
Answer:
Sociology takes helps of History to understand modern Society because we can get Social facts of ancient Society from History. To use historical method we need the matter of History because of which Sociology depends upon History. Different Social institutions change because they affect each other and to understand this change historical material helps us. Historical Sociology is a branch of Sociology with which we can understand social circumstances.

Question 9.
What is Anthropology ?
Answer:
Anthropology is made up of two Greek words ‘Anthropos’ and ‘Logy’. ‘Anthropos’ means human and the meaning of Logy is Science which means Science of Man. Subject matter of this Science is quite wide. That’s why it has been divided in three parts.

(i) Physical Anthropology. In this human physical features are being studied from which we can come to know about the origin, development and races of man.

(ii) Pre-historic Archaeology. In this branch the early part of human history is being studied about which we don’t have any written proof like by digging of ancient buildings.

(iii) Social and Cultural Anthropology. In this complete human society is being studied. In this every thing of one Society like economic system, political, religion, art etc. is being studied. Social Anthropology studies primitive society.

Question 10.
What is Psychology ?
Answer:
Psychology studies the individual behaviour and it uses Neuro glandular system to understand mental behaviour and processes of humans. In this the related factors of memory, intelligence, attitude, sympathy etc. are studied. Main centre of its study is human. That’s why it studies the behaviour of man.

Question 11.
Give relation between Sociology and Psychology.
Answer:
Actually the social phenomena are related with individual phenomenon and Society cannot be made with humans. We cannot differentiate man and society. Social relations, which exist in society, have been made by humans. Without society man is just like an animal. In this way they both are related with each other.

Long Answer Type Questions

Question 1.
Discuss the relation of Sociology and Anthropology.
Or
How can you say that inspite of different from each other, Sociology and Anthropology are complementary to each other ?
Answer:
The source of origin of Sociology is History but the source of origin of Anthropology is Biology. If we look at the methods, subject matter of these two, then they are different from each other but their relation is very deep. They cannot be separated from each other. They take each other’s help for their existence. To understand both of these, let us study their subject matter so that we can understand their relation.

Sociology is the study of modern society. Sociology studies social relationships, social institutions, social groups and their inter-relations. With that Sociology also studies different parts of culture and many types of institutions of society.

The word Anthropology has been made by two Greek words ‘Anthropos’ whose meaning is human and ‘Logia’ whose meaning is science. So its literal meaning is science of humans. Anthropology is the science of man’.

Anthropology studies the origin and development of man from physical, cultural and social point of view. Scope of Anthropology is very wide.

That’s why it has been divided in three parts :
1. Physical Anthropology:
This part of Anthropology studies the physical features of man with which humans came into being and developed.

2. Pre-Historical Archaeology:
This part of Anthropology finds that part of history about which no written evidence is available. Digging up of old buildings, skeletons, ancient things come under this. With these physical proofs a light is thrown on the origin, development and the culture of man. In this way it tries to find human culture during ancient times.

3. Social and Cultural Anthropology:
It studies completely the human society. It studies everything of a society like economic, political, family system, religion, art, beliefs etc. It analytically does comparative study of contemporary structures, institutions and behaviour. Kroeber called these both as Twin Sisters. According to Malbet, “Sociology and Social Anthropology in their broadest sense are one and the same.”

According to Kluckhon, ’’The sociological attitude has tended towards the practical and present, the Anthropology towards pure understanding and the past.” According to Redfield, “Viewing the whole united states, one sees that the social relations between Sociology and Anthropology are closer than those between Anthropology and Political Science.”

The branch Of Anthropology, the Social Anthropology is very closely related with Sociology. Sociology studies social relationships, their forms, institutions, groups and processes and Anthropology studies ancient society, ancient human’s origin, development and culture.

From this given description it is clear that Anthropolgy studies the ancient societies. The meaning of ancient society is those groups which live in smaller geogrpahical area, less in numbers and who have less contacts with outer world and which use simple technique.

Contribution of Anthropology to Sociology. Sociology takes a lot of help from the study of Anthropology. Physical Anthropology, which studies groups and races, is used by sociologists to understand various institutions and systems. Exept this Sociologists have tried to understand social stratification on racial basis.

Except this Anthropology also tells us that institutions, system and organization of ancient society were very simple which helps Sociology to understand modern society. Anthropology has given material of origin of relation to Sociology.

In this \yay Sociology shows very keen interest in ancient society which is the subject matter of Anthropology. Sociology has borrowed some concepts of cultural area, cultural trait, cultural complexity, cultural lag etc.

from Anthropology and they are very useful for sociological study. That’s why a new branch Cultural Sociology has been developed. According to Samuel Koening,“Our present forms of social life, our customs, or ways of living have their roots in the past that one can best explain them by tracing them back to their sources.”

Contribution of Sociology to Anthropology. It’s not that only Sociology takes help from Anthropology, but Anthropology also takes help from Sociology. It is necessary for Anthropology to understand social interactions and relationships for the origin and development of culture which come in the area of Sociology. No society is without any culture and its origin depends upon interactions and relations.

One more contribution of Sociology to Anthropology is that the Anthropology has made many hypotheses on the basis of knowledge of modern societies to understand ancient societies which have given a lot of help to Anthropology to understand its subject matter. Anthropology has included some of the concepts and methods of Sociology in its own subject matter. Anthropology has studied the cultural and social facts which produce social solidarity.

Difference between Sociology and Anthropology :
1. There is a difference of subject matter between Sociology and Anthropology. Sociology studies social relations, organizations, social system etc. but Anthropology studies the entire society. It means that it studies every aspect of society like religious, political, economic, cultural etc. That’s why it is also known as science of social heritage because it takes care of culture.

2. Anthropology studies those cultures which are small, and static. But Sociology studies those cultures which are large in size and changeable in nature. On this base we can see that Anthropology grows very fast and is known as better than Sociology.

3. Anthropology and Sociology are different sciences. Anthropology studies man and his culture of ancient times. But Sociology studies same subject matter in modern system. In this way Sociology goes even in future but Anthropology keeps itself upto the limits of past.

4. The methods used by Sociology and Anthropology are also different. Anthropology uses participant observation and inductive method and Sociology uses survey, schedule, questionnaire, statistics methods.

5. Sociology is related with social relationship and Anthropology is related with the whole society. In this way there is a difference of scope between both of these.

Question 2.
Explain the relation between Sociology and Economics.
Or
Explain the relation between Sociology and Economics with their differences.
Answer:
Sociology and Economics are both interrelated and as well as different from each other. That’s why to know their relation and difference first of all it is necessary for us to understand the meanings of Sociology and Economics. In simple words, whatever economic activities are being done by a person, are being studied by economics.

Economics tells us that how a person can fulfil his unending demands or wishes with limited resources. Economic demands of a person are fulfilled by money.

That’s why the study of human behaviour related to production, distribution and consumption of money is being done by Economics. In this explanation, much emphasis is given to money but modern economists give more importance to humans instead of money. According to Dr. Marshall, “Economics is the study of activities of simple business of human life.”

In this way Economics studies money on one side and on the other side it also studies humans which are more important. Economics tries to find that how a person earns the money and how he spends that money. At another place Dr. Marshall has written that, “ Economics on one side is a study of wealth and on the other and more important side a part of the study of man.”

Sociology studies human institutions, relations, groups, traditions, folkways, values, mutual relations, system of relations, ideology and results and changes which come in them. Sociology studies the society which is the web of social relationships. Every economic activity of the the person is the result of interactions of humans.

With this, social relations and social system are also affected by economic activities. That is why to know about Social system, we should know about economic institutions and to know about economic activities we should know about social interactions. After looking at the meanings of Sociology and Economics we come to conclusion that both the sciences are related with society and its humans.

Sociology studies the social aspect of society and Economics studies the economic aspect of society. Person is related with both social and economic activities while living in society. Economist is related with economic conditions of a person and Sociologist is related with social conditions of that same person. According to Karl Marx, “Economic factors are responsible for change in society.”

Contribution of Sociology to Economics. Now we will see that how economists need the help of sociologists. Economics tells a person how to fulfill his unending wishes with limited means. Economist can help a person, if he knows about the social conditions of a person and to know about this he needs the help of a Sociologist.

For example, the problem of poverty. This problem is an economic problem. But the reasons behind the occurrence of this problem are social. Until or unless an economist is able to understand the social conditions, he cannot help us in solving that problem.

It means that our society is surrounded by many ideals which forced the person not to do any work like when caste system was prevailing in Indian society then every person used to adopt his hereditary occupation.

If he vas going against this rule, he was generally thrown out of the caste. In this way, we can see that the ties of caste system have been loosened but still persons of higher castes are feeling shy of doing any work. Another is that even today women are not allowed to come out of the house to work in interiors of India.

So after looking at the problem if any economist thinks that by giving money to poor people, this problem can be solved then it will be incorrect. We have to bring change in social conditions to eradicate poverty. We have to make new social ideals by eradicating old social ideals. So, from this given description it is clear that Economist cannot do anything without the help of Sociologists.

It means that they neither can bring social progress nor they can solve their problems. In this way we can say that economists depend upon sociologists for the study of their subject matter. So, we can say that every economic activity of a person is the result of social interactions. That’s why every economic activity can be understood by keeping it in social context. So, if we want to do economic progress of society or we want to make economic planning then we need to take care of social aspect of that society.

That’s why Economics depends upon Sociology. Contribution of Economics to Sociology. Sociology also takes a lot of help from economics. All the aspects of the society are affected by economic activities in modern society. Many famous sociologists like Max Weber, Karl Marx, Durkheim and Sorokin had studied the social sector after studying the economic sector.

Whenever any change came in society due to economic factors then our society was also affected by this. Whenever sociologist wants to study this why social relations of our society are breaking or why humans are adopting individualistic approach then he always studies the economic activities of that society.

After that he feels that the way in which the need of money in society is increasing, in that same way people are trying to get things which give them more facilities. With this the outlook of society also becomes capitalistic. Every person has to work hard to live in society.

That’s why joint families are disintegrating and person becomes individualistic. Except this Sociology also has to take help of Economics to study many social problems; for example, the problem of Drug addiction. . Because of this problem our young generation is weakening day by day.

The main reason of this problem is economic because the way in which people are earning more money with illegal means (smuggling), in that same way they are misusing that money. So, the problem of drug addiction is weakening our society. We have to check those illegal means of earning, to solve this problem so that the other related problems of dowry, drug abuse, gambling etc. can be eradicated. So, Sociology depends upon economics to solve these problems.

In modern times many new economic classes are coming forward like labourer class, capitalist class, consumer class, producer class etc. That’s why to understand the relation of these classes it is necessary for Sociology to understand the economic relations of these classes. To understand their economic relations Sociology needs the help of Economics.

Difference between Sociology and Economics. Sociology and Economics are very much related with each other and they both use each other’s rules and results. But still they are different from each other in many ways.

Their differences are given below :
1. Difference of Scope:
The Scope of Sociology-and Economics is different from each other. Sociology gives a clear picture of different sectors of society. That’s why the scope of Sociology is wide. But Economics is confined only to the study of economic sector of society. That’s why its scope is limited.

2. General and Specific:
Sociology is a general science because it studies every type of social phenomenon which are not related with one aspect of society but are related with the whole society. But Economics is a special science because it is confined only to the economic activities of society.

3. Different point of view:
Sociology is .related to understanding the social activities which exist in society and it studies the social problems. That’s why its point of view is social. On the other side, Economics is related with materialistic happiness of a person like how to earn more money, its distribution and consumption. That’s why its point of view is economic.

4. Difference in unit of study:
Unit of Sociology is group. It studies the behaviour of a person living in group. But on the other side Economics is related with study of economic aspect of a person. That’s why its unit is one person or human being.

5. Difference in methods:
Sociology and Economics both use different methods:
to study their subject matter because the subject matter of both is different. Sociology uses historical method, comparative method, sociometry method. Economics uses inductive method and deductive method.

Question 3.
Discuss the relations of Sociology and Psychology.
Or
What is the relation of Sociology and Psychology ? Explain it with differences.
Answer:
Sociology and Psychology both are deeply inter-related. They both study the behaviour of man. According to Cretch and Cretchfield, “Social Psychology is the science of behaviour of the man in the society.” In short, Sociology studies the social relations and Psychology studies mental relationships. Now we will see literal meaning of Social Psychology.

Social Psychology studies individual behaviour. It means that whatever effect of society is exerted on mental part, Psychology studies that effect. To understand individual behaviour it is not necessary to see its social circumstances but it is necessary to see Neuro Glandular system. Mind, Reflection, Learning, Love, Hatred, Emotions and these are mental processes which are actually studied by Social Psychology. Sociology studies, scientifically, these social processes.

Both these sciences are very much inter-related. According to Maclver, “Sociology in special gives aid tp Psychology just as Psychology gives special aid to Sociology.” According to Allport, “Social Psychology is the study of the behaviour of the individuals in their reactions with other individuals and the behaviour through which individuals stimulate one another in such situations.”

From this given description we can say that the base of scientific study of social phenomenon is Psychology and we can observe it directly. So, in this way they both are inter-related and that’s why a new branch of Psychology called ‘Social Psychology’ came into being. Contribution of Psychology to Sociology. In Sociology we study social relationships.

To understand social relationships, we need to understand human behaviour because the mental and physical needs of a man affect its relations with other human. Psychology studies these mental processes, thoughts, ideas of mind minutely.

To understand behaviour of man and society, Sociology needs the help of Psychology, For this a branch of Psychology, Social Psychology is very helpful which studies experiences, behaviour and personality of humans in the social context.

Sociologists are also of the view that psychological bases are very important to understand the changes of society. In this way we can say that to understand society we need to understand behaviour of man which is the work of Psychology.

Contribution of Sociology to Psychology. Psychology also depends on Sociology to understand human behaviour because behaviour of man is influenced by culture of society and Sociology gives knowledge of that culture.

Man is a social animal. Humans are more dependent upon parents and society than animal. While living in society and with the process of socialization, a number of qualities develop within individuals.

There are certain laws to live in society. Humans can learn these laws by living in society and these laws change with the passage of time and generations. Every culture develops a personality and this personality is the result of cultural experiences of childhood age.

To understand Political Science studies the origin and development of state, organization of state, administrative system of government and functions related with institution. It studies the groups and institutions related with political life of a person. Political Science studies the political life of a person and the related institutions.

It also studies the origin and development of state, characteristics, organization of state, government and its administrative system and the institutions related to state. In this way Political Science studies only political relations. On the other hand Sociology studies social relations, different forms of relations, groups, customs, norms, structures, institutions and their inter relations, mores, traditions, etc.

Political Science studies the politics means state and government and on the other side Sociology studies the main agencies of social control i.e. political institutions. These both sciences study the whole society. Sociology looks at the state as political institution and Political Science looks it in the form of law and organization of state.

On the basis of given description we can say that Political Science is related with study of the institutions which exist in state, government and its organization but Sociology is related with study of institutions of state. But the scope of Political Science is a part of whole society which is being studied by the Sociology. In this way both these are interdependent.

The Contribution of Sociology to Political Science. Political Science considers a person as a political person but it never tells us that how and when he becomes political. For this Political Science takes help of Sociology.

If Political Science takes help of the rules of Sociology then it can make studies related to a person very easy and correct. When Political Science is making its policies then it has to keep in mind the social values, and social ideals.

While making laws, political science has to keep in mind the social conditions of society. Our social customs, traditions, values, culture etc. are made to control the members of society and to run the society in an organized way. But when these are accepted by government then they become laws; for example, we can see that different countries have different customs. Status of women was very low in India. People tried to change this custom.

When some leaders tried to uplift the status of women with some movements, many laws were made to uplift the status of women. It was so because social sanctions were there behind these movements. Actually we cannot overlook the social traditions and customs while making laws for society. Sometimes public movements come into being due to laws made by government.

When government tries to overlook the customs made by society then the society moves toward the situation of social disorganization which can create obstacles in the way of social progress. Political Science depends upon Sociology to know about social conditions or customs. We can solve many problems of society with the help of laws.

So from the given description it is clear that Political Science needs a lot of help from Sociology to study its subject matter. It helps in social progress, development and maintenance of organization. But it doesn’t mean that only Sociology gives help to Political Science. Infact Political Science also gives help to Sociology.

Contribution of Political Science to Sociology. If Sociology gives something to Political Science then it also takes a lot from Political Science. Sociology also depends upon Political Science and it takes its help. We cannot imagine any society without controls, which come from Political Science in the form of law. Sociology has one branch known as Political Sociology.

If we look carefully then we will come to know that Sociology gets real social life from Political Science. Progress of society, organization, institutions, processes, traditions, culture, social relations depends upon this element. If we discuss the ancient society, when Political Science was not started in its complete form, then the life of a person was very simple and the simple life was controlled by informal means of control.

Slowly and slowly with the development of society, it started to feel the need of laws to control the people. For example when caste system was in its full swing in India then many castes were in very good conditions and they were running the society in their own way. But people of lower castes were living in the hell like circumstances. They were tired of these rules. The main reason of origin of caste system was to maintain social balance.

When Political Science strengthened its roots then it started to control the people with the help of laws. Customs of social evils, which were a type of burden on people, were removed or eradicated with the help of laws. Because every one was equal in front of law that’s why people started to respect those laws. Except this it was not possible for society to eradicate those social evils. In that case Political Science came forward for its help.

On the basis of given description we can say that problem is whether social or political, we need help of both the sciences. Sociology and Political Science both study society from different point of views but still their problems are related with society and that’s why they both are inter-dependent.

Difference between Sociology and Political Science:
1. General and Special:
Sociology is a general science and Political Science is a special science. Sociology is related to the study of every aspect of every person of the society. All the social processes, customs, social control etc. come in this. It means that Sociology studies all those phenomenon which are related with every type of human activities.

It studies the whole society and that’s why it is a general science. But on the other hand Political Science studies the political aspect of human life. It means that it studies all those activities which get legality and security from humans, government or state. That’s why it is a special science.

2. Positive and Idealistic:
Sociology is a positive science and Political Science is an idealistic science because it is related with the form of state. Socially sanctioned rules are accepted in this. But Sociology with complete independence means it studies with objectivity.

3. Difference of Scope:
Sociology and Political Science both are quite different from each other from the point of view of their subject matter. Sociology studies the mutual relations of social, religious, historical, psychological, economic institutions and tells us about individual life. But Political Science tells us about the individual life by studying only state and its different parts.

It is related only with state and state’s government but Sociology is related with the relations which exist in every type of social institutions. That’s why its subject matter is wide. Sociology is related with unconscious processes but Political Science is related with the conscious activities of a person. That’s why it is related only with organized communities.

Punjab State Board PSEB 11th Class Sociology Book Solutions Chapter 8 Polity, Religion, Economy and Education Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Sociology Chapter 8 Polity, Religion, Economy and Education

Sociology Guide for Class 11 PSEB Polity, Religion, Economy and Education Textbook Questions and Answers

Answer the following very short answer questions in 1-15 words each:

Question 1.
What do you mean by power?
Answer:
Power is the ability of individuals or groups to carry out their will even when opposed by others.

Question 2.
Name the three types of authority given by Max Weber.
Answer:
Traditional authority, Legal authority and Charismatic authority.

Question 3.
What do you mean by economy ?
Answer:
According to Sociologists, “Economy is human activities which are associated with food or property.”

Question 4.
Mention any two elements of state.
Answer:
Population, geographical area, sovereignty and government.

Question 5.
Who gave the theory of animism ?
Answer:
The theory of animism was given by E.B. Tylor.

Question 6.
Who made a ‘distinction between sacred and profane things ?
Answer:
Emile Durkheim made a distinction between sacred and profane things.

Question 7.
Who discussed the idea of naturism ?
Answer:
The idea of naturism was given by Max Muller.

Question 8.
Who calls religion ‘a belief in supernatural being’ ?
Answer:
E.B. Tylor called religion ‘a belief in supernatural being’.

Question 9.
Give the names of two Semitic religions.
Answer:
Islam and Christianity are the two Semitic religions in India.

Question 10.
What do you understand by sect ?
Answer:
Sect is a religious group which is having some specific rituals.

Question 11.
Give the meaning of cult.
Answer:
Cult is a religious organisation originated from the views and ideology of an individual leader.

Question 12.
Name the two major classes in the capitalist society as given by Karl Marx.
Answer:
Capitalist class and Labour class.

Question 13.
What is formal education ?
Answer:
The education which we get in school, college, university is known as formal education.

Question 14.
Define informal education.
Answer:
The education we get from our family, our daily experiences, our friends etc. is known as informal education.

Answer the following short answer questions in 30-35 words each:

Question 1.
What is stateless society ?
Answer:
The societies where there is no institution called state are known as stateless societies. These are simple and ancient societies. These have very less population and people have direct relations. That’s why, to control individual behaviour, there is no need of a formal organisation called state. Council of elders is enough to do so.

Question 2.
Discuss charismatic authority.
Answer:
When a person is influenced by the other in a way that he can do any thing for him, the authority enjoyed by the other is charismatic authority. Many a time people are influenced by the personality of an individual. Religious leaders, political leaders enjoy such authority.

Question 3.
What is legal-rational authority ?
Answer:
The authority given according to some rules and regulations is known as legal rational authority. Government enjoys legal authority. The President, Prime Minister, different officers have such authority which they enjoy according to the rules given in the constitution.

Question 4.
Write down two merits of Panchayati Raj System.
Answer:
(i) Panchayati Raj System is implemented at local level and common people get a chance to participate in the govt.
(ii) In this system, local problems are solved at local level and the work is done very quickly.

Question 5.
What do you mean by animism and naturism ?
Answer:
(i) Animism : This theory was given by Tylor and according to him, religion originated from the idea of spirit. It means that people believe in spirits and consequently religion originated.

(ii) Naturism : According to this theory, humans in ancient times were afraid of natural phenomona such as thunder, rain, fire etc. That’s why they started worshipping nature and thus religion originated.

Question 6.
What is an interest group ?
Answer:
An interest group is a group formed by people of a particular group who work only for the interests of their people. They never care about the interests of other people while achieving their interests. For example, trade union, labour union, FICCI etc. .

Question 7.
Write a short note on sacred and profane.
Answer:
Durkheim gave a description of sacred and profane things associated with religion. He says that sacred things are those which are considered above all and seen with great respect. These are not general and are away .from our daily functions. But there are few things which we confront and use on daily basis. These are known as profane.

Question 8.
WTrite a short note on totemism.
Answer:
In totemism, any tribe starts to associate itself with any object especially any animal, tree, plant, stone or anything. They give respect to it and worship it. They consider their origin from that thing. That thing is known as totem.

Question 9.
What is a ‘pastoral economy ?
Answer:
It is a type of economy in which people depend upon domestic animals to earn their livelihood. They are known as pastorals. They rear sheep, goat, cow, camel and horse. Such societies live in the plains with lot of grass or in mountains. They change their habitat with the change in climate.

Question 10.
How does agrarian economy differ from industrial economy ?
Answer:
In agrarian economy, main occupation of the people is agriculture and they live on this. These societies have less population and informal relations. In industrial economy, people are engaged in industries to earn their livelihood. These societies have more population and formal relations among
them.

Question 11.
What is Jajmani system ?
Answer:
This is a system of exchange in which lower castes provide their service to upper castes and they get renumeration for their service. One who gets service is known as Jajman and one who gives is known as Kameen.

Question 12.
Discuss capitalist society.
Answer:
Western societies are known as capitalist societies where money is earned by investing in industries. Means of production are in the hands of factory owners and they employ labourers to produce things. Major elements of Capitalism are – labourers, means of production, industries, relations between mechanics and owners etc.

Question 13.
What is socialist society ?
Answer:
This concept was given by Karl Marx which says that whole of the economy is in the hands of labourers. Labourers will start revolution against capitalist and will throw away his authority. Then they will establish classless society. Every one will be equal in front of law and they will get according to their needs.

Question 14.
Give example of privatisation of education.
Answer:
In present age, thousands of private schools have opened up in every town, city and metropoliton eity. Private colleges and universities have also opened up. These are the examples of privatisation of education.

Answer the following short answer questions in 75-85 words each:

Question 1.
Discuss the views of Emile Durkheim on religion.
Answer:
According to Durkheim, “ A religion is a unified system of beliefs and practices relative to sacred things, that is to say, things set apart and forbidden beliefs and practices which unite into one single moral comnjunity, called a church, also those who adhere to them.” It means that religion is a collective or social phenomenon which is found as a result of beliefs and practices. On this basis, the people of a group get organised. He divided religious things into sacred and profane.

Question 2.
In what way does religion play an important role in society ?
Answer:
Religion plays an important role in giving stability to society and maintaining social organisation. One religion has millions of followers with common beliefs. Such common beliefs, values and ways of behaviour form a sense of unity atleast in that religion and consequently they unite with each other. This unity helps in strengthening social organization. Each religion tells its followers to give alms, to show sympathy and cooperate with others. It also strengthens society. In this way religion plays a very important role in society.

Question 3.
What is an educational institution ? Write down the educational policies adopted by the government.
Answer:
An educational institution gives necessary knowledge to an individual and makes him a responsible citizen. The educational policies adopted by the government are as follows :

1. According to article 45 of the constitution, free and compulsory education will be given to the children upto the age of 14 years.
2. In 1960, the Kothari Commission laid emphasis on universal enrolment and retention.
3. In 1986, a national education policy was adopted with emphasis on vocational education and equal educational opportunities for deprived groups.
4. Sarva Shiksha Abhiyan 1986 and 1992 laid emphasis on providing useful and relevant educational for all children in the age group of 6 to 14 years.
5. Right of children to Free and Compulsory Education (RTE) Act (2010) states that every child in the age group of 6-14 years will be provided 8 years of elementary education in age appropriate classroom, in the vicinity of the child’s neighbourhood.

Question 4.
Write the functions of education in brief.
Answer:

1. Education helps in the intellectual development of an individual.
2. Education connects an individual with the society.
3. It helps in maintaining balance in society.
4. Education helps in transmitting culture from one generation to another.
5. It helps in developing individual ability.
6. It develops moral values among children.
7. It also helps in doing socialisation of an individual.

Question 5.
Write a short note on types of authority by Max Weber.
Answer:
Max Weber gave three types of authority – traditional, legal and charismatic. Traditional authority is that which is traditionally going on and no one raises question mark against it. Father’s authority is of this type of authority in the house. Legal authority is that which one gets according to certain rules and laws. Government is having such authority. Charismatic authority is that which one gets due to his charismatic personality and his followers accept his orders without any cry. Religious leaders, Political leaders enjoy such authority.

Question 6.
Differentiate a state society from a stateless society.
Answer:
1. Stateless society:
The society which lacks the institution of state is known as stateless society. These are simple and ancient societies. They have less population and people have direct relation among them. That’s why, to control individual behaviour, there is no need of state or government. It is controlled by council of elders.

2. State society:
Modern societies are state societies where authority is in the hands of state which is obtained from the people. Max Weber says that state is a community of people which uses authority in a geographical area with the help of physical force.

Answer the following short answer questions in 250-300 words each:

Question 1.
What is meant by political institutions ? Discuss in detail.
Answer:
Our society is quite large and the political system is one of its parts. Political system defines those human roles which help in regulating society. Polity and society are closely related. To control social humans, political institutions are required and these are-power, authority, state, government, Legislature, Executive, Judiciary etc.

These political institutions keep formal control on society and the means to keep this control are government, police, army, courts at etc. So, political institutions are the means which help in maintaining social order. Political institutions are mainly associated with the distribution of power. Among all the political institutions, few are quite important and these are :

1. Power:
Power is the ability of an individual or a group to force their will on others even when they are opposed. It means that those who have power, they enjoy it at the cost of others. The quantity of power is limited in society. Those who have more power, they use it on those who have less or no power and influence them. Elders of the family, General Manager of a company, Government, Ministers etc. enjoy such power.

2. Authority:
Power is used with the help of authority. It is a form of power which is just and legal. It is institutional and based on legitimacy. Those who have authority, force their will on others as it is considered legitimate. It is implemented not only on humans but on groups and institutions as well. For example, in dictatorship, authority is in the hands of one person, group or party but in democracy, it is in the hands of elected representatives of the people.

3. State:
State is the most important political institution. It is a group of people having a definite geographical area, have population, government and sovereignty. State is a part of society. It affects all the aspects of life but it cannot take the place of society. State is an agency which controls social associations. State influences all the aspects of society and plays a very important role in maintaining balance between them.

4. Government:
Government is an agency of state which has the authority to control the people. It helps in maintaining peace in society. Government has legal sanction because it is elected under certain rules and .has the majority in legislature. Government is an agency to achieve the aims of state. There are three organs of government – Legislature, Executive and Judiciary.
(i) Legislature : It is a part of government whose function is to make laws for the country. Parliament of the country is known as Legislature.

(ii) Executive : It is another organ of government which implements the laws made by legislature. The President, Prime Minister and other ministers are the part of executive.

(iii) Judiciary : It is the third organ of government which uses the laws made by legislature and implemented by the executive. Our Courts, Judges are the part of Judiciary.

So, different political institutions contribute in running our country in a smooth way. These institutions do their work without interfering in each other’s matters.

Question 2.
Write a note on Panchayati Raj.
Answer:
There are two ways of development of the local areas in our country. Local governments are there for the development of urban areas and panchayati raj institutions are there for the development of rural areas. Institutions of local government are based upon the concept of division of labour because functions here are divided in government and local groups. 70% of the population in our country lives in rural areas. The institution of local government which administers the rural areas is known as Panchayat.

Panchayati Raj expresses only the institutional structure of rural area. When the British Empire was established in our country, the entire country was under the control of landlords and Zamindars. In 1935, Indian government passed a law which has given the complete sovereignty to states and the panchayati laws were given a new form. In Punjab, one Panchayat Act was passed in 1939 whose aim was to give some powers to the democratically elected institutions with which they could be able to work at a unit of local administration.

On 2nd October, 1961 the three tier structure of Panchayati Raj was applied in the whole country. 73rd constitutional amendment was made in 1992 in which powers were decentralized upto the local level. With this the panchayati raj institutions were given many financial and other types of powers.

Many changes have taken place in Indian rural community during last 65 years. Most of the powers of Indian panchayats were taken away by Britishers. They wanted to run these panchayats according to their own way because of which they applied a new and common legal system in all the villages. Today’s panchayats are the results of the laws made after the independence.

Organization of Village Panchayats. There are two types of panchayats in the village. First type of panchayats which are elected according to the laws made by government and are formal in nature. 2nd type of panchayats are informal and they are known as caste panchayats. They don’t have any legal status but they plays a very important role in keeping social control.

Three types of organization of panchayats exists in our country and these are :

(1) Gram Sabha
(2) Gram Panchayat
(3) Nyaya Panchayat.

1. Gram Sabha.r All the adult persons of total population, of the village, are the members pf Gram Sabha and it is the complete unit of the whole population of the village. This is the basic unit on which the whole structure of our democracy rests. Gram Sabha can be made in that village whose population is more then 250.

If the population of one village is less than 250 then two villages can jointly make the Gram Sabha. Every adult of the village is the member of Gram Sabha, who has the right to vote. There is one chairman and some members of every Gram Sabha. It is elected for 5 years. ,

Functions of Gram Sabha. Gram Sabha approves the annual budget and the functions to be done for the development of the village and helps in applying these function. It also helps in doing the functions of social welfare, programmes of adult education and of family welfare. It also plays an important role in keeping unity in the village.

Village Panchayat or Gram Panchayat. Every Gram Sabha elects one Gram Panchayat from its area. In this way the Gram Sabha is an executive institution which elects members for the Gram Panchayat. It has one Sarpanch and 5-13 panches. There are certain places in Panchayats which are reserved for backward classes and females. It is generally elected for 5 years but state government can dissolve them even before 5 years if it will try to misuse its powers.

If any Gram Sabha is dissolved before completion of its term then all of its position will also comes to an end. Village is generally divided in different parts to elect Panchs and Gram Panchayats. Then the Panches and Sarpanch are elected by the members of Gram Sabha.

One third of the total seats in Gram Panchayat are reserved for women and the seats are also reserved for backward classes according to the ratio of their population in that area. Any governmental official and mentally ill person cannot be elected for panchayat. Gram Panchayat works for the sanitation, recreation, development of industries and means of communication. It also solves the problems of the village. Functions of Panchayats.

Gram Panchayat performs many functions for the village which are given below :
(1) The first important function of Gram Panchayat is to raise the economic and social standard of life of the people. There are many social evils in villages. Panchayat motivates the people to remove those evils and tries to change their traditional point of view.

(2) For the allround development of any area, it is necessary that illiteracy should be eradicated from that area and it is the main reason of backwardness of Indian Society. Indian villages are also backward due to this reason. Panchayat tries to open schools in village and motivates the people to send their children in the school. It also arranges the adult education centre to teach the adults of the village.

(3) Panchayat of the village also works for the welfare of the women and children of the village. It also arranges for giving education to females. The function of arrangement of good food and recreational facilities is also of Panchayat.

(4) There are no means of recreation in rural areas. That’s why Panchayat also arranges to provide recreational means in the village. Panchayat arranges for films, organizing fairs and to’opening up of library in the village.

(5) Increase in production is necessary in the agriculture based country. Panchayat tells the people about new techniques of agriculture, arranges for the new seeds and developed fertilizers for them so that their agricultural production could.be increased.

(6) It is very much necessary to establish small scale industries in villages for its allround development. That’s why Panchayat tries to establish small scale industries in villages with the help of governmental help. It helps in economic progress of the village and people get employment in their villages.

(7) Means of irrigation are of great importance in good production of agriculture. Gram Panchayat arranges the wells and tubewells in Gram Panchayat. It also arranges for river water so that the people could be able to irrigate their fields.

(8) Generally people are fighting in villages. Panchayat tries to solve their problems in village. Panchayat Samiti. Panchayats coming in one block are the members of the Panchayat Samiti and Sarpanchs of these Panchayats are the members of Panchayat Samiti.

Members of Panchayat Samiti are also elected. Panchayat Samiti takes care of the functions of the Panchayats which are coming in its area. It checks the developmental functions of the village and directs the Panchayat for the welfare of the village. It is the second level of Panchayati Raj.

Zila Parishad. The highest level of Panchayati Raj is Zila Parishad which takes care of the functions of the Panchayats which are coming in the district. It is an executive institution. Chairman’s of Panchayat Samiti, elected members, members of Lok Sabha, Rajya Sabha and Legislative Assemblies are the members of Zila Parishad.

All these take care of the developmental functions done in the villages of the district. Zila Parishad does many functions such as the improvement of agriculture, improvement of land, irrigation, rural electrification, arrangement of seeds and fertilizers, education, industries etc.

Question 3.
In what way do interest groups act as pressure groups ?
Answer:
During the last few decades, a new concept of division of labour has come forward. In this concept, different people are employed in different professions and as a result, many professional groups have emerged. All these professional groups have their personal interests and they continually work to achieve them. So, the groups which care about the interests of their people and continualy work to achieve their aims are known as interest groups.

In present democratic societies, they always try to change political decisions according to their interests. If need arises, they pledge their support to the political parties and through them, try to influence official decisions. Almost all the interest groups have an objective to achieve higher status in the national politics.

That’s why they pressurise the govt to make policies in their favour. When they start to pressurise the govt, they take the form of pressure group. Pressure groups are organised or unorganised groups who influence govt, policies and promote their interests.

The ways in which they try to influence politices are given below :

1. These pressure groups start a movement on a particular issue to gain public support. They take the help of mass media to draw attention of the people.
2. They generally opt. for strikes, processions and create hurdles in government functioning. They declare strikes to raise their voice. Most of the labour unions opt. for this method to get “their demands met.
3. Most of the trade groups create a loby, with few common motives, to pressurise the govt to change its policies.
4. Each pressure .group or interest group is associated with some political party.
   They support these parties during elections to get their demands met after winning elections and forming the government.

Question 4.
Define Religion. Describe its features.
Answer:
The most difficult function for sociologists is to give that definition which should be accepted by every one and all sections of the society. It’s reason is that the nature of religion is very complex and different Sociologists have different views about it.

It is so because different sociologists are related with different countries and different cultures. There are many religions in the world and because of this diversity, they all are unable to reach on any consensus about the definition of religion. But still different Sociologists have given different definitions of religion which are as follows –

• According to Frazer, “Religion is belief in powers superior to man which are believed to direct and control the course of nature and of human life.”
• According to Maclver, “Religion as we understand the term implies a relationship not merely between man and man but also between man and some higher power.”
• According to Durkheim, “Religion is a unified system of beliefs and practices related to sacred things is to say things set apart and forbidden.”
• According to Malinowski, “Religion is a mode of action as well as system of belief and an ecological, phenomenons as well as personal experience.”

Therefore, from these definitions it is clear that the base of religion is the belief in super- natural power and this power is believed as superior and powerful to man.

It keeps control over all the elements of life which are important for man. Its one base is emotional. There are many methods and rituals to keep this power happy. It is clear that the acceptance of religion is beyond social because religion is explained by supernatural forces. Religion is used very widely in society. According to sociologists, religion represents the habits and emotional experiences of man. Religion came into being because of the feelings of fear and the respect of humans towards many things.

According to Tylor, religion was developed because of belief of ancient humans in the spirits of ancestors. According to this belief, spirit lives at any place, in any thing or animal after the death. It can affect human life. To keep these spirits happy, man started to worship these spirits and from here the origin of religion starts.

Features of Religion:
1. Belief in Supernatural Power. Religion is the complexity of thoughts, feelings and methods which express its belief in super regulates powers. This power is universal and all powerful. It is believed that this power regulates human action. In this way the first characteristics of religion is the belief in supernatural power.

The basis of this super-natural power are different but this power definitely exists in all religions. If any one doesn’t have faith in this power than he doesn’t have faith in religion and because of, this, existence of that person comes to an end. This power is powerful and better than human power. This power is believed to be beyond the range of human brain about which man says that he is afraid of this power.

2. Rituals. Religious rituals are the actions determined by religion. They are sacred in themselves and are the symbols of sacredness. For example according to Hindu religion, there are many fasts and pilgrimages which are religious rituals. Religious rituals bind together the followers of one religion and differentiate them from the followers of another religion.

3. Religious Acts. Another important feature*of religion is that it has different religious acts and actions. With the help of these religious acts man always tries to keep happy to supernatural powers and he expresses his belief in these supernatural powers by doing those acts. These acts are of two kinds. First one are those actions for which special religious knowledge is necessary.

This function has been done by religious priests in every religion. Second are simple religious acts like prayer and going for pilgrimage which even a layman can do very easily. But in every religion one belief prevails that man can keep natural powers happy by completing religious functions.

4. Religious Symbols. In every religion certain symbols are used to see these super natural powers. Like in Hindu religion portraits and sculptures are worshipped. In every religion some stories are there related to this supernatural powers. People believe that by believing these supernatural stories they can keep happy that almighty.

5. Religious Hierarchy. All the followers of any religion don’t have equal status in religious group. In every religion, a system of hierarchy exists. People who sit at high posts, are generally those who are experts in doing religious acts like priests. At second place those persons come who have full faith in religious representatives and concepts. At the end those persons come who cannot be called as sacred and who do those impure functions given by religion. They are restricted in almost all the religions.

6. Religious books. Every religion has one important feature and that is the religious books related to those religions. In every religion, some religious persons are there who write religious books and every religion has some religious stories whose description is generally given in those books. Like in Hindu religion Mahabharta, Ramayana, Bhagwat Gita, Four Vedas, Manu Smriti etc. are there. In the same way ‘Quran’ of Islam, ‘Guru Granth Sahib’ of Sikhs and ‘Bible’ of Christianity are the religious books.

Question 5.
In what way is religion useful and harmful for the society ?
Answer:
1. To give stability to social organization. Religion plays an important role in providing stability to the society and maintaining social organization. Millions of people are there in one religion who have common beliefs. These common beliefs, values and ways of behaviour forms a sense of unity atleast in that religion with which unity comes in that group.

In this way this unity helps in strengthening social organization. Every religion tells its people to give alms, to show sympathy and to cooperate with others because of which stability comes in society. In this way religion saves its people from instability and gives stability to society.

2. Religion gives, definite form to Social Life. Religion is the collection of customs and mores. These customs and mores are parts of the culture also. In this way balance is maintained between social atmosphere and culture. Because of this balance social life gets definite form. Because of religion people respect customs, mores etc. and others also maintain this balance. In this way because of this balance social life moves in a proper way and all this is because of religion.

3. To organise Family Life. Marriage in different religions is done according to different religious traditions. Because of religious traditions religion becomes permanent and its life and organization strengthens. Every religion defines the duties and rights of different members. It tells the parents ahd children that what are their duties towards each other.

Every one, while living in family, obeys and fulfils the duties towards each other and cooperates with each other to run the family. It helps in maintaining balance between members of the family. All the functions of the family are determined by religion. ‘

4. To remove mutual differences. There are many religions in this world. They do not ask their followers to fight with the followers of another religion. Instead they ask to live with each other with love and peace and they ask their followers to remove their mutual differences. Removal of differences will increase unity in the society. That’s why all the religions and the leaders have tried to uplift the lower castes. Gandhiji had tried all his life to uplift scheduled castes and untouchables.

5. To keep Social Control. Religion is one of the important means of social control. Religion has the sanction of the society behind it. Religion affects the people forcefully even without their wish and the person feels that religion is putting a great effect on him.

Religion controls and directs its followers in such a way that the person has to obey the teachings of religion. Religion is the belief in the supernatural power and people never try to work against the wishes of that supernatural power because they are afraid of it. In this way the behaviour and ways of action are controlled by religion.

6. Social Welfare. Every religion encourages its members to do works of social welfare. In all the religions of the world giving alms is known as sacred. People are giving help to orphanages, hospitals, schools etc. and helping them by giving them money. People of every religion distribute food, clothes, medicine, money to poor people. They are doing this because their religion asks them to do so. In this way religion encourages the works of social welfare.

Dysfunctions or Demerits of Religion:
1. Religion is an Obstacle in Social Progress. Religion is fundamentalist by nature and change is the law of nature. Changes are often coming in society because of which society can develop from materialistic point of view but not from spiritual point of view. Religion is basically against any change.

Religion is not in the favour of any change. In fact it believes in keeping the situation as it is. Changed circumstances are not according to the religion because of which religion opposes the change. By opposing the change it becomes an obstacle.

2. Man becomes Fatalist. Religion says that whatever is written in man’s fate he will definitely get that. He will neither get more than that nor get less than that. After thinking this thing man stops working and says that if he will get according to fate then what is the advantage of doing work ? Whatever is written in his fate he will get that. In this way man leaves everything to fate. But he forgets that a person makes and change his own fate. If he will not work then what he will make and change. In this way man leaves everything to fate and becomes fatalist.

3. Opposite to National Unity. We can call the religion as opposite to National Unity. Generally every religion asks its followers to, go according to its rules and generally these rules are against other religion. While loving their religion, sometimes people start opposing other religions. This opposition results in religious narrowness and intolerance. This religious intolerance is dangerous for the unity of the country and even sometimes communal violence starts in different religions. In this way sometimes religion works against National Unity.

4. Religion Increases the Social Problems. There are certain custo’ms and rituals in every religion and according to priests and religious persons these customs and rituals are necessary for every person. Religious persons call their followers to go against other religion. Because of religion many problems in our country like child marriage, Sati system, Dowry system, no widow marriage, untouchability, poverty etc. came. Religion is responsible directly or indirectly for these problems. The government has made many laws to solve these problems but still religion is an obstacle in the way of their solution.

5. Religion is ah Obstacle in the Way of Change. Religion is always against change and is an obstacle in the way of change. Different types of inventions and discoveries are coming in the world. Because religion is always fundamentalist and that’s why it is against change. Any change of the society is opposed by religion. For example when a law was made against Sati system then it was opposed by religious persons. In this way religion is always against materialistic changes of the world.

Question 6.
Briefly discuss the characteristics of primitive, pastoral, agrarian and industrial economies.
Answer:
(i) Primitive Economy. Many tribes live in far off places in forests and mountains. Yet most of the tribes have joined the main stream due to means of transport and have also adopted the occupation of agriculture but still many tribes are there who still spend their life as hunters and food gatherers. They collect roots, fruits, honey etc. and even are hunting smaller animals. Some tribes also exchange many things. In this way they fulfil their needs in the absence of agriculture.

Those tribes are known as ancient tribes which fulfil their needs in this way. These people not only kill animals but also collect fruits, roots and honey from the jungles. In this way they fulfil their needs even without the presence of agriculture. We can come to know about their culture after looking at their way of hunting.

These societies lack tools and means because of which they are the shadow of ancient tribes. There is no concept of surplus production in their societies. It is so because they can neither produce any thing surplus nor they can keep the surplus production. They live like wanderers. Tribes of Chenchu, Katkari, Kames, Baija, Khariya, Kuch, Paliyan etc. live this type of life.

(ii) Pastoral Economy. Pastoral economy is one of the important parts of tribal economy. Tribal people rear animals for different purposes like to take milk, meat and wool and to carry weight. Pastoral tribes of India live a static and permanent life and none according to the season. Tribes of mountainous region move towards plains in the winter season and come back to their areas in summer season. The main pastoral tribe of India is the Gujjar tribe of Himachal Pradesh which rears buffaloes, cows and sheep for business purposes.

This custom also prevails in the Toda tribe of Tamilnadu. This tribe rears animals and gets milk from them. Milk is used either to exchange things or it is used to fulfil their own needs. Indian tribes generally live a permanent life. They live at one place, rear animals and get many things from them such as milk, wool, meat etc. They also trade in animals such as sheep, goat etc.

(iii) Agricultural economy. The main occupation of rural society is either agriculture or any of the related work because they are very much closely related with nature. Because they are closely related to nature, that’s why their views towards life are very much different.

Yet many other occupations like carpenter, blacksmith etc. are there in villages but they also make tools related to agriculture. Land is considered as a very important thing in tribal society and people like to live here because their life depends upon the land. Even the economic, system and development of people and villages depend upon agriculture.

(iv) Industrial economy. Urban economy can also be called industrial economy because urban economy depends upon industries. Very large industries are there in cities where thousands of people work with each other. Production is also on large scale due to large scale industries. Owners of these larger industries are different individuals.

Production is done for the market. They produce not only for internal markets of the country but for foreign markets as well. Even in some cases, production is being done only for foreign markets. Owners of these big industries produce things only for their profit and they exploit the labourers as well.

We can find a number of occupations and occupational diversity in urban societies. Family, in earlier times, was the unit of productions. All the functions were being done only in the family. But due to advent of urban areas, thousands of occupations and industries were developed. For example we confine many types of functions in a factory and we need specialised person to do any specific type to work.

Only the skilled person can do that specific work. In this way functions in cities are divided among different people because of which division of labour prevails in urban society. People are specialised in their work and that’s why specialisation is of great importance. In this way division of labour and specialisation are two important aspects of urban economy.

Question 7.
Write a note on division of labour.
Answer:
In 1893 Durkheim published his first book in French language called ‘De La Division du Trovail Social’. Yet it was his first writing but it was a strong base of his popularity. On this book only he got doctorate from Paris University in 1893. In this great book he has fully explained the social division of labour. Durkheim’s this book has been divided in three parts. In every part he has analysed the different aspects of labour.

In the first part of his book ‘Functions of Division of Labour’ he has tried to prove that division of labour is the base of social solidarity. With that from the point of view of scientific study he has explained different forms of Law, Types of solidarity, different forms of human relations, crime, punishment, social evolution and some problems of society. In second part of this book he has given detailed explanation of reasons and results of division of labour. In 3rd part of this book he has given some abnormal forms of division of labour.

1. Functions of Division of Labour. Durkheim accepts every , social fact as moral fact. Any social behaviour lives on the base of moral base. As a functionalist first of all Durkheim has given function of division of labour. According to him, division of labour is a social fact, that’s why he started his book from its functional analysis. First of all fourkheim has given the meaning of function.

He has given two meanings of function :
(а) Meaning of function is from system of movement which means from action.
(b) Second meaning of function is from this action or movement and from interrelation according to its needs which means The need to be fulfilled by action. Here Durkheim is using meaning of function from second point of view. In this way by function of division of labour his meaning is that by which basic of social existence is fulfilled by the process of division of labour. Function is that in the absence o’f which, the basic needs of its units cannot be fulfilled.

Generally it is been said that the function of division of labour is the development of society because it is a truth that with the development of division of labour and specialization, civilization in the societies increases. Because of division of labour the production force increases, material and intellectual aspect develops, leisure increases in general life and knowledge increases. That’s why generally division of labour is known as the source of civilization.

But Durkheim was against that. He said that the development of civilization is not the function of division of labour. According to him, the meaning of source is not the function. Increase in leisure, development of material and mental level comes due to result of division of labour. That’s why it is the result of this process, not the function. Meaning of function is not the result.

In the development of the society three kinds of development are included. Three types are :
(a) Industrial or economic aspect
(b) Intellectual aspect
(c) Scientific aspect.

Durkheim was of the view that all these three aspects of development are without moral facts. So with the development of industrial, intellectual and scientific aspect, crime, suicide and other immoral phenomena also increases in societies. So according to him the function of division of labour is not the development of civilization.

But what is the function of division of labour ? According to him to make new groups and their solidarity or unity are the functions of division of labour. He has tried to find any moral need related with the existence of society as the function of division of labour. According to him with the increase in members of society and their inter-relations, slowly and slowly the process of division of labour also develops.

In this process so many new business and social groups have been made. For the existence of society the unity or solidarity of these groups is must. Without the solidarity of these groups we cannot imagine the balance in social system. So solidarity is the moral need of different groups.

According to him this need of society is fulfilled by division of labour. On one side division of labour makes new social groups and with that it also helps in maintaining unity and collectivity of these groups. So the function of division of labour is to establish unity in society. Division of labour is related with the differences of functions of humans and these differences are the bases of social solidarity.

He has given factual base for this social reality. He was of the view that the important function is not that it increases the production with the divided work but it organises and unites them. So division of labour makes new social groups and produces unity among them.

(A) Law and Solidarity. Durkheim had the view .that the function of division of labour is to produce solidarity in society. Social solidarity is a moral fact. To clarify the social solidarity which came from division of labour classifies the laws. According to the classification of laws he has decided the types of social solidarity. To classify laws he has taken sanctions, related to that law, as base.

He has given two types of laws:
(i) Repressive law. Repressive laws can be called as Public laws.
These ar’e of two types.
(a) Penal law. These are related with giving suffering, causing loss, to kill and to obstract independence. We can call them organised Repressive laws.
(b) Diffused law. Some repressive laws are there which are spread in the whole society or group on the basis of morality. That’s why Durkheim is calling them diffused law. According to Durkheim, Repressive laws are related with criminal functions.

These laws explain the crime and its punishment. These laws also show the basic conditions of collective life of society. Every society has its basic circumstances. So in different societies repressive laws are also different. The power of these repressive laws is based in collective mind and collective mind gets power from equalities.

(ii) Restitutive law. Another type of law is the Restitutive law system. These laws provide balance to the imbalance produced in the human relations. In this group civil laws, business laws, constitutional laws, administrative laws are included. These laws are not related with , the whole society but are related with human. These laws are regulating the balance and imbalance produced in the personal relations of members of society. Restitutive laws are joining individuals and society with some middle institutions.

On the basis of these two types of laws according to Durkheim two types of solidarities can be made. These two types of solidarities are the result of two different types of lifestyles. Repressive laws are related with general nature of man and with equalities. But Restitutive laws are related with differences or with division of labour.

The type of solidarity which comes due to Repressive laws, according to Durkheim, is Mechanical Solidarity and the solidarity which comes due to Restitutive laws is called Organic Solidarity whose base is division of labour.

In this way according to Durkheim there are two types of social solidarities :
1. Mechanical Solidarity. According to Durkheim, Mechanical solidarity can be seen in the repressive laws of society. The bases of this solidarity are the equalities available in the members of the society. The society in which the life of members is full of equalities, where general norms of thoughts, beliefs, functions, lifestyle and ideal are there and the society which thinks, works as a collective unit on the basis of these equalities shows mechanical solidarity.

Its members are united like a machine. In old primitive societies mechanical solidarity was there. He was of the view that even crime helps in binding the people in solidarity. In this way there is existence of one social solidarity which comes out of definite conditions of consciousness which are normal for the members of any society. These can be shown by Repressive laws. These are based on the power of collective consciousness.

2. Organic Solidarity. According to Durkheim, the second type of solidarity is organic solidarity. The power of Repressive laws is in collective consciousness. Collective consciousness gets power from equalities. In primitive societies repressive laws were there because the base of social life were equalities. According to Durkheim, modern societies are influenced by division of labour and specialization in which instead of equalities, inequalities are the base. This difference of group or collective life gives importance to individual consciousness.

In modern societies man is not directly united with group. In these societies there is a lot of importance of mutual relations of humans. That’s why he was of the view that in modern societies instead of Repressive laws, Restitutive laws are important. In the societies which are based on differences humans are dependent upon each other. Every human can specialize in one field and for other works he is dependent upon others.

This inter-dependence of members of group or society and their personal inequalities force them to come closer to each other with the help of which solidarity in society would be established. To this type of solidarity Durkheim gives the name of organic solidarity. This can be seen in restitutive social system.

3. Contractual Solidarity. After analysing the mechanical and organic solidarity Durkheim has also written about one more solidarity which is known as Contractual Solidarity. According to Durkheim, the process of division of labour gives birth to contractual relations. People of a group are getting the services of each other on the basis of mutual contracts and mutually they are cooperating with each other.

It is right that in modern societies people are establishing cooperation and solidarity on the basis of contracts. But the function of division of labour is not to give birth to contractual solidarity. According to him, contractual solidarity is individual fact, but it is regulated by society.

2. Causes and Conditions. The second part of book ‘Division of Labour in Society’ is related with causes, conditions and results and these are given ahead :
Causes of Division of Labour. Durkheim has explained division of labour on Sociological basis. He has found the causes of division of labour in the conditions of social life and in the social needs produced from them. From this point of view, he has

divided the causes of division of labour in two parts :
(a) Primary Causes
(b) Secondary Causes.

(а) Increase in the size and density of Population. According to Durkheim, the increase in size and density of population is the central and primary reason of division of labour. He says that the increase of population has two aspects-increase in size of population and increase in density of population.

These both aspects give birth to division of labour. With the increase in population old primitive societies are disintegrating and new mixed societies are coming into being. Population started to concentrate in few centres. The density of population he has divided in two parts :

(i) Material Density:
From physical point of view concentration of people at one place is material density.

(ii) Moral Density:
Because of Material density relations of the people are increasing with which actions and reactions are increasing. The complexity which came out of increased rq,utual relations and inter-relations, Durkheim is calling dynamic or Moral Density.

(b) Unclarity of Collective Consciousness. In secondary reasons of division of labour he has given first place to unclarity of collective consciousness. In equality based societies, collective consciousness is quite strong because of which members of societies cannot be motivated by individual or personal point of view. Collective feelings are showing them the way.

Durkheim was of the view that division of labour and individual specialization is possible in that condition when instead of collective point of view, individual point of view will develop and when individual consciousness suppresses collective consciousness. So according to him, the development of division of labour will be slow and difficult if collective consciousness is strong and definite. If this collective consciousness will be loose enough then the division of labour vyill move with quite a good speed.

(c) Ancestral reason and division of labour. The second cause of the division of labour according to Durkheim is the decreasing influence of ancestral influence. How much more influence these ancestral qualities can exert on man that much less chances will be there for change. In other words for the development of division of labour it is must that we should not give importance to ancestral qualities. The development of the division of labour is possible only if there will be differences in the nature and behaviour of the people.

The result of classifying people on the base of their ancestral qualities and with binding them with their ancestors is that man has not been able to develop his special qualities and does not change. In this way it is an obstacle in the distribution of division of labour. He was of view that with the passage of time and change these ancestral bindings yvill become so weak that their ancestral qualities will also become weak. So slowly and slowly different qualities of people will develop and then division of labour will also develop.

Question 8.
Define economic institution. Write down the changes taking place in economic system.
Answer:
Every person has some of his basic needs like food, cloth and shelter. Man always does efforts to fulfil his basic needs. Because of these efforts, economic institutions come in front of us. But here one question arises that if economic activities of humans are being studied by Economics then what they are doing in Sociology ? Then its answer is that economic activities affect other aspects and institutions of human life like religion, family, marriage, kinship etc.

These institutions are of great importance in the human life. That’s why, because the economic institutions affect all the other institutions, interest of sociology has also increased to study these economic institutions. If any change comes in economic institutions then change also comes in all the other institutions. That’s why the importance of economic institutions has been increased. Now we will see that what are economic institutions.

Economic institutions are those institutions which arrange for the things for production, distribution and consumption for the people. Economic institutions are of great importance in society. That’s why different forms of society have been divided on the basis of economy or economic institutions like hunting society, agricultural society and industrial society. All the other institutions of society like family, marriage, religion etc. are affected by these economic institutions.

Economic institutions tell a person and to his coming generations that every society has some of its limited means. These institutions tell every person that he has to use those limited means, their production, distribution and consumption and how he has to use these means for every one. In this way it is a system with which people satisfy their needs and find the solutions of their economic problems. In this way the functions of economic institutions are the production, distribution, consumption and selection of exchange.

According to Jones, “The economic selection of Exchange, complex of techniques, ideas and customs relating to the exploitation of the environment for the satisfaction of subsistence needs.” According to Davis, “The basic ideas, norms,»and statuses which govern the allocation of scarce goods in any society whether the primitive or civilized, we call it economic institutions.” .

According to Ogburn and Nimkoff, “The activities of man in relation to fo,od and property constitute the economic institutions.”
In this way after looking at these given definitions we can say that the definite and organised forms of actions done by man to fulfil his basic needs are known as economic institutions.

Changes Coming in the Economic Institutions :
Right since the beginning of the 20th Century, many changes have started to come in the economic institutions

which are given below :

• Now production is done on a large scale and for this pupose, a new technique of‘Assembly Line’ has emerged. In this, humans and machines both help in producing a new thing.
• Large machines are used in the production so that it can be done on a large scale.
• Due to the process of globalisation, all the countries have opened up their economic barriers. Almost all the countries have reduced custom duties. That’s why goods made in a particular country are easily available everywhere.
• The process of Liberalisation has also brought many changes in the functioning of economic institutions. After 1991, Indian Government adopted the liberalisation policy which expanded the Indian economy. Many multi-national companies opened up their factories in India which reduced unemployment over here.
• Many computer based industries have opened up in India. B.P.O. Industry, Call centres, Software services etc. have played a very important role in earning foreign exchange for the country. It has connected Indian economy with the other economies. The use of machines in all the industries has been increased to a great extent.

Question 9.
Define education. Differentiate between formal and informal education with examples.
Answer:
Education is the most important mean of socialisation. It is the best method to transmit cultural values to the next generation. Education is of great help in maintaining balance with industrialisation, urbanisation and other processes. Education is not limited only to the bookish knowledge. It gives every type of knowledge to an individual regarding ways of living life.

It also develops many traits among individuals such as love, friendship, discipline etc. According to Durkheim, “Education is the influence exercised by the adult generation upon those who are not yet ready for adult life.”
According to Philips, “Education is the institution whose central point is collection of knowledge.” ‘

So we can say that education is a process which is a mixture of empirical knowledge and conceptual and practical ideas whose major aim is to establish balance between. an individual’s social and natural environment. It plays a very important role in social control.
Mainly education is of two types:
(i) Formal Education
(ii) Informal Education.

(i) Formal Education :
Formal education is the education which we get formally in school, college, university etc. Such education has definite curriculum and teachers teach according to this curriculum. Such education has a clear motive and that is allround development of an individual and to make him a better citizen of society. Such education is given according to a particular objective. It is having three levels- primary, college and university. Each level has a definite organisation which includes teachers, students and other staff.

(ii) Informal Education :
Informal education is the education which one never gets in school, college or university but he gets it from his daily experiences, views of other persons, family, neighbourhood, friends etc. It means that an individual always learns something from his daily life. It does not have a fixed time, fixed curriculum or a definite place. One can get it at any place and from any one. No degree is given for this but one becomes mature with informal education.

Question 10.
Discuss the views of functionalist sociologists on the role of education in society.
Answer:
If we observe the modern society, we come to know that no other factor has greatly contributed in changing society as education has contributed. Education has played a very important role in bringing change in society. With the increase in education, the first changes came in the European society, and later on in the second half of twentieth century, changes came in the Asian society. These changes completely revolutionized whole of society. Modernization in India came due to education. People in the Indian society, started taking education which brought allround development over here.

Change in the status of women, change in the status of lower castes, all this has happened due to education. That’s why for sociologists, education is a very important subject to study so that they could find its impact on society. As a factor of social change, sociologists show great interest in the study of education.

According to them, education changes a human from an animal to a cultural and civilized person. According to the French Sociologist Emile Durkheim, “Education is the influence exercised by the adult generation upon those who are not yet ready for adult life.”

It means that education exerts its impact on the coming generation with which it can prepare itself to live in society. Durkheim says that society can survive when homogeneity exists among members, which is reinforced by education. Only through education, a child learns the basic rules, norms, values, and ways to live in society.

Kingsley Davis and Wilbert Moore also highlighted the functional aspect of education. According to them, social stratification is a process by which able persons are given suitable status in society. This aim is achieved only through education and it ensures that suitable person should get a suitable place.

Punjab State Board PSEB 11th Class Sociology Book Solutions Chapter 7 Marriage, Family and Kinship Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Sociology Chapter 7 Marriage, Family and Kinship

Sociology Guide for Class 11 PSEB Marriage, Family and Kinship Textbook Questions and Answers

Answer the following very short answer questions in 1-15 words each:

Question 1.
What do you mean by endogamy?
Answer:
Endogamy is a type of marriage in which one needs to marry within a particular group, caste, or sub-caste.

Question 2.
Name the important bases for the emergence of the institution of marriage.
Answer:
Physical need, emotional need, the perpetuation of society, to upbring the children, etc.

Question 3.
What is Monogamy ?
Answer:
Monogamy is a type of marriage in which one male marries with one female.

Question 4.
What is sororate marriage ?
Answer:
In this type of marriage, man, after the death of his wife, marries her sister.

Question 5.
Mention the types of polyandry.
Answer:
It is of two types : fraternal polyandry in which all the husbands are the brothers and non-fraternal polyandry in which all the husbands are not brothers.

Question 6.
State the types of polygyny.
Answer:
It is of two types : Bigamy in which a male has two wives and polygamy in which a male has many wives.

Question 7.
Give few examples of endogamy.
Answer:
Among Muslims, Shias and Sunnis are endogamous groups and among Christians, Roman Catholics and Protestants are also endogamous groups.

Question 8.
Define Marriage.
Answer:
According to Lundberg, “Marriage consists of the rules and regulations, which define the rights, duties and privileges of husband and wife with respect to each other.”

Question 9.
Mention two functions of family.
Answer:
(i) Family socialises its children.
(ii) Family gives property to its children.

Question 10.
Write the name of the forms of family on the basis of composition.
Answer:
On the basis of composition, family is of three types-Nuclear family, Joint family and Extended family.

Question 11.
Write the name of the forms of family on the basis of authority.
Answer:
On the basis of authority, there are two types of family-Patriarchal and Matriarchal family.

Question 12.
What is affinal relationship ?
Answer:
Affinal relationship is the relationship which is made after marriage. For example, father-in-law, mother-in-law, son-in-law, daughter-in-law etc.

Question 13.
What do you mean by Joint family ?
Answer:
Joint family is the family in which members of two or more generations live under one roof and eat in a common kitchen.

Question 14.
What do you mean by kinship ?
Answer:
In Kinship, all the relations are included which are based on real or imaginative ties and are influenced by society.

Question 15.
Name the degrees of kinship.
Answer:
There are three degrees of kinship-primary, secondary and tertiary.

Answer the following short answer questions in 30-35 words each:

Question 1.
What do you understand by the term institution ?
Answer:
An institution is not a group of people or an organisation. It is a system of norms to achieve few objectives. It is a collection of folkways centred around specific human activities. Institutions are transmitted process with which humans complete their functions.

Answer the following short answer questions in 250-300 words each:

Question 1.
What do you mean by institution ? Discuss its characteristics.
Answer:
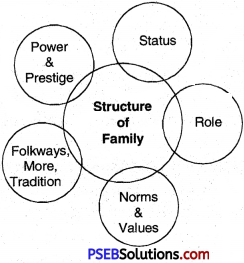
Meaning of Institution. We use the word ‘institution’ thousands of time in our life. According to a layman, the meaning of an institution is any building. But in sociology the meaning of an institution is not any building or collection of people. Sociologists use the meaning of institution in detail and according to society. According to them, an institution is a system of rules or norms which help people to fulfil their needs. In this way institution is the collection of folkways and mores to fulfil the needs or actions of society.

These are those processes with the help of which man does his work. Institution is that organized system of relations in which values of society are included and which fulfil the needs of society. Their function is to fulfil the needs of human and to fulfil functions and behaviour of an individual. In this web of status and roles, their an distribution is also there.

In this way we can say that an institution is an organisation of methods and rules for fulfilling the needs of individuals. Man has to take membership of many groups to fulfil his needs. In every group lots of efforts have been done to fulfil the needs of its members. After many successful and unsuccessful efforts members of the groups finds the ways of fulfilling their needs and all the members of the society accept these ways. In this Way most of the members of society start to obey those rules.

In this way for the specific conditions, specific ways will be decided and it will be wrong to go against those ways or rules. In this way socially accepted methods to fulfil specific needs of persons are known as an institution.

Definitions :
1. According to Merill and Eldridge, “Social institutions are the social patterns that establish the organized behaviour of human beings in the performance of basic social functions.”

2. According to El wood, “Institutions are habitual ways of living together which have been sanctioned, systematized and established by the authority of the communities.”

3. According to Sutherland, “In sociological parlance, an institution is a set of folkways and mores that centre in the achievement of some human end or purpose.” So from these given definitions it is clear that an institution is developed for the achievement of any specific aim. That’s why this is a group of customs, norms, rules, values etc. Sumner included social structure in institution in his book ‘Folk Ways’. An Institution expresses the ways of individual behaviour to man.

In short, we can say that an institution is the organization of actions which are accepted by society to fulfil its specific heeds. In society many types of different associations are there and every association has its own institution with which it fulfills its needs or achieve its aims.

Features or Characteristics of Institution :
1. It is made up of cultural elements. The organization of all the elements of culture of any society like folkways, mores, norms, values etc is called an institution. According to one sociologist it is the bunch of customs. When the customs, traditions, folkways, mores etc of a society integrate and take the form of a system then it is known as an institution. In this way it is the system of elements of the culture and it fulfills the different needs of humans.

2. They are Permanent. Any institution cannot be useful if it does not fulfil the needs of persons for a very long time. If it doesn’t fulfil the needs of people then it cannot be called as institution but can be called as the association. In this way institution fulfills the needs of the people for a long time.

But it doesn’t mean that an institution never comes to an end. Demand of any institution depends upon the time. Demand of any institution can be increased or decreased and it depends upon age. If any institution is of no use or any institution is unable to fulfil the needs of the persons then slowly and slowly it comes to an end.

3. It has some special motives or objectives. If any institution is formed then it is because it has some kind of specific motive. That institution knows that if it is formed then what is its function. Its function is to fulfil the specific needs of the people. In this way their main, aim is to fulfil the needs of the people but it is also possible that with the passage of time it will stop fulfiling the needs of the people. Then in that case that “institution can be replaced by any other institution.

4. Cultural Equipments. For the fulfilment of the aims of an institution material aspect of culture is used like furniture, building etc. Their form and behaviour is also fixed. In this way if an institution wants to achieve its objectives then it has to take help of material culture. Many aspects of non-material culture like folkways, mores etc already exist in an institution.

5. It is Abstract. An institution is developed with folkways, mores, customs etc. All these are the parts of non-material culture a©d we cannot see these aspects of non-material culture. We can just feel them.

In this,.the aspect of abstractness is included. It cannot be touched and can be felt only. Institution is not an organization of concrete things but is an organization of rules, methods, folkways etc. \yhich is being developed to fulfil human needs.

6. Tradition based. When an institution is formed then it is formed because of rules. Before the formation of an institution, rules are defined and then aims of that institution are clearly defined. The behaviour of the people who take part in this are also defined. If every thing will be defined earlier then no problem comes later on. If these are not defined then every one will try to change them in their own way which is dangerous for the existence of the institution.

Question 2.
Write a note on marriage as a social institution.
Answer:
Marriage is a socially approved relation of male and female which forms a new family. Marriage not only gives sanction to the relationship of male and female but it also gives approval to many other relations. Meaning of marriage is not sex alone. Marriage is the base of family. With the help of marriage, man enters into sexual relations, makes a house, produces children and upbrings them.

Institution of marriage is a universal social institution. It exists in every type of society whether it is modern or ancient. If we want to maintain human society then institution of marriage is necessary. Fulfilment of sexual needs is a biological need and if this need would be fulfilled outside the institution of marriage then the formation of family is almost impossible. Family is necessary to maintain social structure.

Marriage is an institution which gives permission to male and female to live a family life and legally accept the children produced by the relations of male and female. In this way it regulates the sexual relations of male and female.

Morgan has studied ancient societies and comes to know that life of people in ancient society was like of animals. No one was taking responsibility of upbringing of the children. Because of this problem need was aroused of the institution of marriage. That’s why for the maintenance of stability of modern society institution of marriage was accepted.

Definitions of Marriage:
(1) According to Wester Mark, “Marriage is a relation of one or more men to one or more women which is recognised by the institution of law, and involves certain rights and duties both in the case of parties entering the cyiion and in the case of children born out of it.”

(2) According to Majumdar, “Marriage is socially approved union of male and female, or as a secondary institution by society to sanction the union and mating of male and female, for purpose of (a) establishing a household (b) entering into sex relations (c) procreating and providing care for the offspring.”

(3) According to Lundberg, “Marriage consists of the rules and regulations, which define the rights, duties and privileges of husband and wife with respect to each other.”

(4) According to Anderson and Parker, “Marriage is the sanction by society of a double bond between one or more males and one,, or more females established to permit sexual intercourse for the implied purpose of’parenthood.”

On the basis of given definitions we can say that the institution of marriage is a type of institution on which the social structure of society depends. Only after the regulations of sexual relations between male and female, we can take care of upbringing of our children.

If these sexual relations will be without the approval of the society then they would be known as illegal or extra marital relations and the child produced by this relation would be known as illegal child. That’s why marriage not only fulfills the sexual needs but also does many functions for humans, as are necessary for the development of society.

Question 3.
Discuss in detail the different types or forms of marriage.
Answer:
Every society is different from another society in itself and is different from many aspects. Every society has some of its different rules, traditions, institutions etc. and every society has its different institutions for different purposes. These are different because every society has moulded them according to its facilities and needs. In this way the institution of marriage has different types according to the different needs of different societies.

All these types of marriage are given below :

1. Monogamy:
This type of marriage prevails and is very much popular in today’s modern age. In this type of marriage, one male can marry with one female at one time. Relations, in this type of marriage, are more stable, more loveable, deep and are full of sympathy. The upbringing of children can be done? in a proper way in this type of marriage and children get complete love from their parents.

Husband and wife have complete understanding in monogamy because of which there are very less chances of quarrels or creation of problems in them. But this type of marriage has some of its demerits. If wife or husband will fall ill then every work would be halted and they would not be able to give proper attention to their children.

2. Polyandry:
The custom of polyandry prevails in many societies of the world. The meaning of polyandry is the custom of that marriage in which one female marries to many males at a time and that’s why it is known as polyandry.

In this way when one female has more than one husband then it is known as Polyandry. It is of two types :
(i) Fraternal Polyandry
(ii) Non-Fraternal Polyandry.

(i) Fraternal Polyandry. In the custom of fraternal polyandry, all the husbands of a female are brothers among them. This type of marriage prevails in the Khas Tribe in India. Eldest brother is known as the father of the child and rest of the younger brothers are known as her husbands. They establish sexual relations with their wife without the permission of their elder brother. Elder brother is the head of the family and it is his duty to upbring the children in a proper way.

If even after the marriage, any brother of the husbands will be born then he will also become the husband of that wife. If except elder brother, any other younger brother will marry any where else then other brothers are also permitted to make relations with his wife. If that brother will not permit then he can be thrown out of his property right.

(ii) Non-Fraternal Polyandry. In this type of polyandry, all the husbands of a female are not the brothers. In fact, they live at different places. Time is determined for the female that for how much time she will live with any husband. After the expiry of time period she goes to the other husband and this process goes on. If in this type, female will die then all the males are forced to live the life of the widower.

If at the time of pregnancy any husband will gift her the arrow and the bow then he will be considered as the father of the child. All husbands get a chance for that and it is their right. In this way according to this custom, the rule is that if in a definite period, wife is living with any husband then other husbands are not permitted to establish sexual relations with her. .

3. Polygamy:
The custom of polygamy was prevailing in ancient times in India. Kings were keeping many wives and the status of any king was understandable by looking at the number of his wives. So the system of polygamy is that a person can keep many wives. Number of wives depends upon his ability to keep and economic capacity.

In middle ages this system was prevailing in Muslims and even today Muslims are permitted to keep four wives. The sexual need of males and the wish to have big family has encouraged this type of marriage. Many types of psychological problems are arising due to this system. Females are getting lower social status in society due to this type of marriage.

4. Sororate Marriage:
In this type of marriage male is marrying with the sister of his wife. Sororate marriage is of two types—Restricted Sororate marriage and Simultaneous Sororate marriage. In Restricted Sororate marriage man marries his sister-in-law after the death of his wife. In Simultaneous Sororate marriage man accepts or considers all the younger sisters of his wife as his wives. First type of this marriage is more prevailing as compared to second type. With this the problem of breaking up of families never arises and upbringing of children will be possible in an efficient way.

5. Levirate Marriage:
In this type of marriage, wife marries the younger brother of her husband after the death of her husband. With this type of marriage, property of the family can be secured and family is prevented from breaking. Upbringing of children can be done in an efficient way. Another reason of this type of marriage is that after marriage there is no need to give back the value of the bride.

6. Love Marriage:
We can see a number of love marriages in our day to day life and this type of marriage prevails in modern societies. Boy and girl both are studying in college or are working in any office and at first sight they start to love each other. They start to meet each other very frequently. They meet each other in cinema, parks etc.

They promise each other to live and die with each other and try to show their true love. Society tries to prevent them to be married and tries to obstruct their way but they remain fixed to their decision. Even if their parents are not permitting them to get married then they go to court and become married. In this way love marriage takes place.

7. Endogamy:
According to the rules of Endogamy, a man has to marry in his own caste. Castes are divided into sub-castes and he has to marry in his sub-caste. In the times of caste system this rule was strictly applied. If any one was trying to break this rule then he was thrown out of the caste. So every person had to marry in his sub-caste in endogamy.

It is so because it maintains the purity of blood, it protects the occupation of caste, it fosters the sense of unity within the group, it preserves the property of the caste, it keeps the women happier also because it is easy for them to maintain balance in their own culture. But on the other side it encourages casteism, it limits the sphere of mate selection, it is a danger to national unity and it hinders the social progress also.

8. Exogamy:
The meaning of exogamy is to establish marital relations out of its clan, village and totem. All the persons of one clan, village and totem are considered as the sisters and brothers of each other. According to Wester mark, the main reason behind this type of marriage was to prevent close relatives to establish sexual relations with each other. This marriage is a symbol of progressiveness. It increases the contacts between different groups. This type of marriage is considered as right from biological point of view.

One of the biggest disadvantages of this type of marriage is that the husband and wife have to face many problems in understanding each other’s view because they belong to different groups. Mutual love and co-operation also increase in different groups due to this marriage. It also helps in strengthening national unity.

9. Anulom Marriage:
Anulom marriage is a type of Hindu marriage according to which the males of higher castes can marry the girls of lower castes. For example, one Brahmin boy can marry with the girl of Kshatriya, Vaishya, and Shudra castes. The main reason behind this type of marriage is that the people of lower castes consider it respectful to marry their daughter in the higher castes. It is so because it gives higher position to them in society.

10. Pratilom Marriage:
In this type of marriage males of lower castes marry the females of higher castes. Manu was strictly opposed to this type of marriage. According to Manu, the children produced from this type of marriage should be considered as untouchables or ‘chandals’. Manu says that the children produced by Brahmin girl and Shudra boy are chandals. That’s why this type of marriage is seen with the hatredness. Children from this type of marriage cannot adopt the name of any family.

Question 4.
Define marriage. Write the rules of mate selection in detail.
Answer:
Definitions of Marriage:
(1) According to Wester Mark, “Marriage is a relation of one or more men to one or more women which is recognised by the institution of law, and involves certain rights and duties both in the case of parties entering the cyiion and in the case of children born out of it.”

(2) According to Majumdar, “Marriage is socially approved union of male and female, or as a secondary institution by society to sanction the union and mating of male and female, for purpose of (a) establishing a household (b) entering into sex relations (c) procreating and providing care for the offspring.”

(3) According to Lundberg, “Marriage consists of the rules and regulations, which define the rights, duties and privileges of husband and wife with respect to each other.”

(4) According to Anderson and Parker, “Marriage is the sanction by society of a double bond between one or more males and one,, or more females established to permit sexual intercourse for the implied purpose of’parenthood.”

On the basis of given definitions we can say that the institution of marriage is a type of institution on which the social structure of society depends. Only after the regulations of sexual relations between male and female, we can take care of upbringing of our children.

If these sexual relations will be without the approval of the society then they would be known as illegal or extra marital relations and the child produced by this relation would be known as illegal child. That’s why marriage not only fulfills the sexual needs but also does many functions for humans, as are necessary for the development of society.

Rules of Mate Selection:
In every society rules of selection of mate are there which tell the persons that with which boy or girl he/she can marry and with whom he/she cannot marry. These rules are given ahead :

1. Endogamy
2. Exogamy
3. Hypergamy
4. Hypogamy

1. Endogamy:
According to the rules of Endogamy man has to marry within his own caste. Caste was again divided into sub-castes. In this way man had to marry in sub-caste. In the times of caste system this rule was strictly applied. If any one was trying to break or was breaking this rule then the caste was throwing him out of caste and they were breaking or severing all types of relations with it.

According to religious books society was divided into four castes. These castes were again divided into sub-castes. Every person has to marry in his own sub-caste. In this form of marriage many changes have come due to the passage of time.

There are different forms of endogamy available in India and these are :

1. Tribal Endogamy
2. Caste Endogamy
3. Class Endogamy
4. Sub-caste Endogamy
5. Racial Endogamy.

According to the rule of tribal endogamy the man has the permission to marry only in his tribe. In the same way man should marry in his caste, class, sub-class, race etc.

2. Exogamy. Institution of marriage is one of the important social institutions. Any society cannot give permission to any couple to live as husband and wife-without marriage. That’s why every society has made some rules to establish marriage system in society. The most important function is the selection of the mate. Exogamy is also one of the rules of mate selection.

In many societies the marital relations are forbidden between the persons who are related with each other by blood. According to Sumner, “Endogamy is conservative while exogamy is progressive.” In this way in exogamy marriage is prohibited within the group. Children of same parents are also forbidden to marry.

Among Muslims, marriage between the relatives of parents is permitted. In the Roman Catholic Church of England marriage with the sister-in-law, after the death of the wife, or Sororate marriage was not allowed. In Australia, boy can marry with the wife of his father if she is not his mother.

According to the rule of Exogamy, man is not permitted to marry within his caste, clan, Spraver, Spinda etc. Some of its types are given below :

1. Gotra Exogamy.
2. Spraver Exogamy.
3. Spinda Exogamy.
4. Village Exogamy.
5. Totem Exogamy.

3. Hypergamy and Hypogamy. In ancient Indian Society two forms of inter caste marriages existed (1) Hypergamy and (2) Hypogamy. Hypergamy marriage is that law in which girl can marry either in the same or equal caste or with the boy of higher caste. In other words when a boy of higher caste marries a girl of lower caste then it is known as Hypergamy. In this type of marriage Brahmin girl, can only marry Brahmin boy. Kshatriya girl can marry either to Kshatriya boy or Brahmin boy.

Vaishya girl can marry with Vaishya boy or Kshatriya boy or Brahmin boy. Except this Brahmin boy can marry with the girl of any caste. Kshatriya boy can marry the girl of any caste except Brahmin girl. Vaishya boy can marry with the girl of any caste except Brahmin and Kshatriya girl. When t

he problems were started with the rule of endogamy then this rule of marriage of hypergamy was encouraged. According to Risley, “Aryan women were less in number. That’s why to remove this problem they were accepting the girls of Indian origin and when this problem was removed then this type of marriages came to an end.”

Second type of marriage in this category is Hypogamy. This rule is totally opposite to the rule of Hypergamy. According to this rule boy of a lower caste marries to the girl of higher caste. Like girl of the Brahmin caste would marry with the boy of Kshatriya caste or boy of Kshatriya caste marries the girl of Brahmin caste. According to Radha Krishnan, “In the rule of hypogamy boy of lower caste used to marry with the girl of higher caste. The children produced by this type of marriage were not kept in any caste and they were known as chandal.”

So this type of marriage was restricted in caste system. Only on some special condition this type of marriage was allowed. In the end we can say that now both types of inter-caste marriages are developing in Indian society. In today’s society people are free to do inter-caste marriage. Now people feel that the clutches of caste system have been finished but still we are living in the caste system.

Question 5.
What is family ? What are the basic features of family ?
Answer:
If we study human society we observe that the first group in human society was family. In ancient times division of labour was based on the family. We will not find any society in which the institution of family does not exist. This institution exists from ancient societies till modern societies and it will remain forever yet many other institutions came into being and came to an end. But the institution of family is standing there as it is.

Yet in present developed societies, the importance of family has been reduced because most of the functions have been taken by many other institutions but still even today most of the human actions are centred around family. Psychologists have proved that character of a child will be made in the way in which he gets the family and he functions according to that in his future life. The main reason behind the social disorganization and many other problems is the disintegration of the family.

Family is an important group for social structure. The word family has been taken from the word ‘Famulous’ which is a Roman word that means servant. According to Roman Law, the meaning of this word is by that group in which all those servants, slaves or owners are included which are based on blood relations or marital relations. It is that type of group in which the satisfaction of sexual needs of males and females

are sanctioned by the society. After the upbringing of the child, one becomes the citizen of the society. In simple words the meaning of family is the group of husband, wife and their children. But from sociological point of view its meaning is not only a collection of people but is by the system of their mutual relationship and its main objectives are to produce children, their up-bringing, their socialization and satisfaction of sexual instincts.

Different sociologists have given different views about the family and some of these definitions are given below –
(1) According to Maclver, “Family is a group defined by sex relationship sufficiently precise and enduring to provide for the procreation and upbringing of children.”

(2) According to G.P. Murdock, “The family is a social group characterized by common residence, economic cooperation and reproduction. It includes adults of both sexes, at least two of whom maintain a socially approved sexual relationship and one or more children, own or adopted, of the sexually co-habitating adults.”

(3) According to H.M. Johnson, “Family is a group of two or more individuals related by blood, marriage or adoption and residing together, all such persons are considered as members of one family.”

(4) According to Elliot and Merrill, “Family is the biological social unit which consists of husband, wife and children.” Many differences are there in the definitions given by different sociologists but on one thing their views are same that the family is a group in which the sexual relationships of male and female are accepted by society and it is a universal group.

About its meaning in the end we can say that family is a biological unit which is related as an institution for sexual relationships. Its members are personally related with each other with the process of reproduction. In short, we can say that mother, father and their children are included in the family and if is developed in every society.

Characteristics of Family:
1. Family is a universal group. Family is a social group. It is also known as the first institution in human history because it exists in every society and in all times. Every member of society is definitely a member of any family. It is so because wherever we take birth, we are related with those members of the group. Except this, man can fulfil his basic needs by living only in society.

2. Emotional base. Family is the base of the human society which is based on basic instincts of human like to produce children, relations of husband and wife, maintenance of descent, protection of property and emotions are also included in this. Feelings of cooperation, love, sympathy also are developed in this which is necessary for progress and development of the society.

3. Formative Influence. Family is an important unit in social structure. Family exerts a formative influence on the development of the personality of the child. Family is an institution in which child gets knowledge about social behaviour. All round development of the man is possible only in family. Whatever child observes in family, tries to learn and imitate that thing as quickly as possible.

4. Small in size. Size of family is limited because only those persons are included in family who either have taken birth in family or who have a marital relation. In ancient times when society was based on agriculture then joint families were there in which father-mother, grandfather-grandmother, uncle, aunt etc.

lived collectively. With the development of society, females started to move out of family for the job. Then nuclear family came into being in which only parents and their unmarried children are included. The meaning of small size is that membership of the person in the family is based on birth and blood relatives are also included in this.

5. Central position in the social structure. Our society is based on family and different associations are formed only from family. That’s why it has central position in society. In earlier societies social organization was based upon family. Social progress was also based upon this. Yet most of the functions of family have been taken by other institutions but still a number of functions are there which only family can do for society. No other institution can do that work. ’

6. Sexual relations. In family, male establishes sexual relations with female because society gives sanction to the formation of family only after marriage. In earlier societies there was no rule regarding sexual relation and there was no real form of family and society was moving towards disintegration.

Question 6.
Discuss in detail the different types of family.
Answer:
This world is too big and many types of societies exist in this world. Every society has some of‘its distinct geographical, social and cultural features. These features are different in different societies and that’s .why different types of families exist in different types of societies. It is so because every society has its different ideals, beliefs, culture etc.

For example in India we can see many types of societies like Patriarchal or Matriarchal. In this way family also has many forms. All these forms can be divided on the basis of numbers, on the basis of marriage, on the basis of authority, on the basis of nomenclature, on the basis of place of residence etc. Now we’ll see them one by one.

1. Types of Family on the basis of Marriage. It is of two types :
(i) Monogamous Family. In this type of family, one male marries one female and the family on this type of base is known as Monogamous family. In modern age, this type of family is known as correct type of family.
(ii) Polygamous Family. When one male marries more than one female or one female marries more than one male then this type of family is known as polygamous family.

It is further of two types:
(а) Polyandrous Family. When one female marries with more than one male then it is known as polyandrous marriage. The main feature of this type of family is that one female has many husbands. It is again of two types. First type is Fraternal polyandrous family in which all the husbands are brothers. Second type is non- fraternal polyandrous family in which all the husbands are not the brothers.

(b) Polygamous Family. When a male marries more than one female then it is known as polygamous family. In this type of family, one male has many wives. For example, a Muslim is permitted to keep four wives. Hindu kings, in ancient times, kept many wives. But according to Hindu Marriage Act of 1955, Hindus are not permitted to keep more than one wife. Many tribes in India are still there who have this type of family like Nagas, Gonds etc.

2. Family on the basis of Numbers. Family on the basis of numbers is of three types :
(i) Nuclear Family. Nuclear family is a very small family in which husband, wife and their unmarried children are living. Other relations are not included in nuclear family. This type of family exists in today’s modem societies because people are doing jobs in cities. Children make their own nuclear family after their marriage.

(ii) Joint Family. There are many members in this type of family. Grandfather- grandmother, elder uncle-aunt, younger uncle-aunt, brothers, sisters are included in this type of family. Generally this type of family exists in villages.

(iii) Extended Family. This type of family is generally made only after and with the help of joint family. The advanced stage of joint family is known as extended family. In this all the brothers, their married children and even their grand children are also living. This type of family is not possible in modem societies. This type of family was possible in earlier time when the whole family was engaged in same occupation but today it is not possible.

3. Family on the basis of Nomenclature.

It is further of four types :
(i) Patrilineal Family. In Patrilineal family descent is of the father which generally exists in today’s life. It means that the son gets nomenclature of the father and the nomenclature of the father is of great importance.

(ii) Matrilineal Family. This type of family runs on the name of the mother. It
means that the child gets nomenclature of the mother. This type of family exists in many tribes of India. «

(iii) Bilinear Family. In this type of family descents of both mother and father
are going side by side. It means that the child gets the nomenclature of both the mother and the father. . ”

(iv) Non-Unilinear Family. In this type of family, nomenclature is determined on the basis of nearest relative. It is known as non-unilinear family.

4. Family on the basis of types of relatives. This type of family is of two types :
(i) Consanguine Family. In this type of family, blood relations are at highest place and there are no sexual relations in it. Husband and wife are also there in this type of family but they are not the base of this family. Membership of this type of family can be attained only on the basis of birth. This type of family never comes to an end even after divorce and it is permanent.

(ii) Conjugal Family. Husband-wife and their unmarried children are here in this type of family. In this husband-wife and their relatives are included. This type of family can be broken after the death of either husband or wife or both.

5. Family on the basis of Residence. This type of family is of three types :
(i) Patrilocal Family. In this type of family, bride leaves her father’s house and
goes to the house of her husband to live and establish the family. We can see this type of family very often. – ”

(ii) Matrilocal Family. This type of family is definitely opposite to Patrilocal family in which girl never leaves her father’s house after marriage but lives there only. In this, her husband leaves his father’s house and goes to the house of his wife to live. It is known as Matrilocal family. We can find this type of family in Garo and Khasi tribes.

(iii) Neolocal Family. This type of family is different from other two types. Husband and wife are not living at their father’s house but are making a new house after their marriage and that is why it is known as Neolocal family. We can find this type of family in today’s modern age.

6. Family on the basis of Authority. This type of family is of two types :
(i) Patriarchal Family. In this type of family whole power is in the hands of males. Head of the family is male. Descent also depends upon the father. After marriage wife goes to the husband’s house and property is distributed among the boys of the family. Eldest son of the family gets most respect. His respect in the home is equal to the respect of the father.

In every type of necessary family matters, male’s interference is necessary. It we look at the ancient Hindu society then according to the Vedic descriptions male was just like a God for the female. Eldest son gets all the rights of the family after the death of his father.

(ii) Matriarchal Family. In this type of family, female is dominant in the family, whole ownership of the property of family is in the hands of the female. Females of the family have the right over the property. After marriage husband goes to the house of wife to live. Function of the Brahmin was being done by females. Property was divided among the females of the family. Descent was also moved from females.

Question 7.
Highlight the changes that have taken place in the institution of family in contemporary period.
Answer:
1. Changes brought by the Government. When marriage got sanction of society in the form of an institution then many changes were brought in it. Many laws were passed related to marriage out of which Hindu Marriage Act, 1955 was the most important. According to this law, Polygamy was now restricted and Monogamy was accepted by the society and was ’accepted as an ideal marriage. Problem of child marriage also came to an end and it was written that if any one will try to break the law then he will be punished severely.

A law related to divorce was also passed so that the life of male and female should last without any problems. In earlier times if the wife was manhandled by the husband even then she had to live with her husband because she was dependent on him. But now male and female both are free to use their legal right to get divorce so that they can live a happy life.

2. Marriage is related to social contract. According to ancient ideology of marriage, it was related and limited to religion and couple had to live with each other even if they didn’t like each other. But according to modem ideology if the relations between husband and wife are not good then this contract can be severed. In some cases when the marriage is done forcefully then they both can decide to break this marriage. Now it is equated with a contract that marriage is a social contract and it ean be broken at will.

According to T.B. Bothomore,” Marriage is no longer an economic partnership, and is no longer sustained by wider kinship groups. Finally, the desire for a Hemerous progeny is replaced by the aim of deliberate aim of limiting size. Thus the marriage bond is reduced to simple relations of mutual attraction.” In modern times marriage is related with personal happiness so that the family could take care of their children properly.

3. Change in the status of women. The way in which females started to take part in other sectors of society, in that same way the form of marriage was changed.

Marriage, Family And Kinship:
In earlier societies females were economically dependent upon others. That’s why they loved to suffer a lot of hardships. But slowly and slowly, with the education of females, she became economially independent. She started to take her decisions herself. She got a lot of help from the law. Now she can take divorce from her husband and can live a happy life.

In this way when a female has made her place in the society then the institution of the marriage also changed. Divorce rate is increased. Now females have a better status as compared to earlier times. Now she is economically viable. She can take her decision. She takes part in the economic activities of the family and stand jointly with the husband to face the problems of life.

4. Changes because of development in education. In earlier times, no one was bothering about importance of education. That’s why the institution of marriage was developed to fulfil religious situation. But after the spread of education, compulsion of marriage comes to an end. Child marriage comes to an end. Now educated children marry according to their wish.

5. Changes because of development in industries. In ancient societies rules related to marriage were so strict that one had to marry in his own caste. If he was breaking this rule then he was punished by caste. But with the increased importance of money, marital relations are also changed. Now purity of earliest times does not exist.

Relations of male and female are generally related to money because of which sometimes they hardly believe each other and start to live separately. Except this, many problems have emerged from both sides because of which the importance of marriage is reduced.

6. Changes in the outlook regarding arranged marriages. In ancient societies the institution of marriage was dependent upon elders because a child had to do what his elders wanted. But in modern times the importance of arranged marriage has been reduced because both boy and girl want to marry according to their ideas, ideals and views.

They do not accept the preferences regarding marriage given by their parents because the point of view of new generation has been changed regarding marriage. Sometimes even their decisions are proved wrong but still they want to give importance to their independent thoughts.

7. Change due to scientific outlook. People have changed their views regarding the institution of marriage because of the new inventions which came in the society. Now point of view of the people regarding religious sacrament has been changed. Now people are doing court marriage. The religious feelings of humans are now related to the scientific outlook.

In ancient times husband was like a god for wife and some religious rules were there even for males for marriage. But now all these things have changed and because of which the stability of the family has been decreased. Families have started to disintegrate.

Question 8.
Define Kinship and discuss its types in detail.
Answer:
Meaning of Kinship. ‘Kin’ word is an English word which has been taken from the word ‘Cynn’ meaning relative. Sociologists and Anthropologists have kept this word ‘relatives’ while studying Kinship. In word Kinship all the relatives are included like blood relatives, relatives made by marriage etc.

In simple words, according to Sociology and Anthropology. Kinship System is that collection of rules which regulates the nomenclature, heirness, heritage, marriage, extra marital relations, place of living etc. and determines the status of person in any specific Society or in group from the point of view of blood relation and marital relations.

It means that the system of social relations developed and made by blood relations or affinal relations is known as Kinship system. Its clear meaning is that all those relations which have been made by blood or by marriage are the part of Kinship system. In this all those relations are included which have been made by blood or by marriage. For example, mother-father, uncle-aunt, maternal uncle-aunt, brother-sister, father-in-law-mother-in-law, brother-in-law, sister-in-law etc. All these are relatives and are the part of Kinship System.

1. According to Levi Strauss, “Kinship is an arbitrary system of ideas.”
2. According to Charles Winick, “Kinship system may include socially recognized relationship based on supposed as well as actual geneolocal ties.”
3. According to Redcliffe Brown, “All those relations which came as a result or made because of family and marriage are the part of Kinship System.”

Brown further says that it is that web of relationship which forms due to marriage and family and these relations are the part of our social structure. Relatives keep duties and rights towards each other and obey the social customs in Social meetings because with their help Kinship can be explained.

4. According to Dr. Majumdar, “An individual is tied with many types of relations of group in all societies. The most basic and usual relation among these relations is that which is based upon reproduction which is the internal human motivation. It is ‘ known as Kinship.”

On the basis of given definitions we can say that two persons are relatives. If their ancestor is one then they are the offsprings of one person. Kinship system is the system of relatives which is based on blood relations or affipal relations. Kinship system is cultural and its structure is different in the whole world. In Kinship system all those real or imaginative blood relations are included which are sanctioned by the society.

One illegal child can never get high place in society but one adopted child can get highest place in Kinship system. It is a system of specific relation group in which all the relatives are included which understand the responsibilities towards each other. In this way system of social relations established by socially sanctioned real or imaginative blood and affinal relatives is known as Kinship system.

On the basis of the closeness and distance from a person, Kinship has been divided in different categories. In Kinship we don’t have the same type of relations with all the relatives. The type of relations which we have with our parents, husband-wife and children, we cannot have that type of relations with our uncle, aunt, nephew etc. We don’t have very close relations with them. On the basis of this closeness and distance, Kinship has been divided in three categories

which are given below :
1. Primary Relatives. In the first category of Kinship primary relatives like husband-wife, father-son, mother-son, mother-daughter, father-daughter, sister-sister, brother-sister, brother-brother are coming. According to Murdock, they are of 8 types. They are primary because relations among them are direct and very close.

2. Secondary Relatives. Some of our relatives are primary like mother-father, brother-sister etc. and have direct relations with them. But some relatives are there who are not directly related with us. In fact we are connected with them through the medium of our primary relatives like brother of mother, brother of father, sister of mother, sister of father, husband of sister, wife of brother etc. We don’t have very close relation with them. In fact they are our secondary relatives. According to Murdock, these are of 33 types.

3. Tertiary Kins. First relatives are primary. Then comes secondary relatives which are related with us with the medium of primary relatives. Third type are of those relatives which are primary relatives of secondary relatives. Like son of brother of father, wife of brother of mother, wife of brother of mother etc. According to Murdock these are of 151 types. So in this way there are three types of categories of Kinship but if we want then we can make fourth and fifth categories of Kinship also.

Question 9.
Discuss the importance of Kinship in social life.
Answer:
Kinship system has an important place in the social structure. With this structure, the society .can be formed. If the Kinship system would not be there, society cannot be made like an organization and would not be able to function in a proper way. That’s why it’s importance has been increased

1. With the help of Kinship system rights, marriage, family, production and method of consumption, rights of political power are fixed in tribal and agricultural societies. Even in urban societies we can see the importance of Kinship relations at the time of marriage and family festivals.

2. Kinship, family and marriage are deeply related to each other. With the help of
Kinship system we can determine that who willmarry whom and which name would be given to which relation.’ From Kinship only we can come to know about the nomenclature, clan, and the family of the person and of the concept of exogamy exists in family or linage or clan. , „

3. Family life, relations of family, nomenclature, clan and rituals related to birth and death are fixed by the Kinship and who will perform all the rituals is also fixed by Kinship.

For example, in the rituals related to marriage big brother, mother and sister of the father are of great importance. Who will give fire to the dead body is also related with Kinship. Who will be the heir of the person is also determined by the Kinship. At the time of Social functions, festivals, relatives are of great importance because at these moments it is necessary to call them. It will strengthen the relationship.

4. Kinship system gives strength to the society. Kinship system plays an important role in making social organization. If Kinship system would not be there then the social system will break down and there will be chaos all over the society. ,,

5. Kinship system determines the sexual relations. Sexual relations in;3E^jship system are restricted in our society. If Kinship system would not be there then there will be a lot of illegal relations and children in the society and social disorders will prevail.

6. Kinship System plays an important role in the determination of marriage. You are not supposed to marry in your clan, how many relatives would be left from mother’s side and father’s side all depend upon Kinship system. If this system would not be there then no one will obey the rules related to marriage and social disorder will prevail in society.

7. Kinship system gives mental peace to an individual. Yet in modern industrial Society our views have been changed from emotional to practical but still man is tied with the Kinship ties. He hangs the pictures of his ancestors in his house, he collects their pictures, he even does ‘Shradha’ after their death. Humans are based on the group and Kinship.

Without Kinship man is just like a dead man. Our relatives know us very well. They accept themselves as the part of the family. If we are in any tension then our relatives give us mental peace. Only by lining with our relatives we become happy and feel pleasure in their company.

In this way we can say that Kinship is of great importance in our Society. Nothing will be left in our society if we will take out Kinship system from it. So that’s why Kinship system is very important for our society.

Question 10.
Differentiate between affinal and consanguinal relations.
Answer:
Consanguinity. Consanguinity are the relations based on basic family and the relations based on real or imaginative traditional blood relations. In simple words, all those relatives or persons which are tied with blood relations are known as Consanguinity. Blood relations whether real or imaginary keep a higher place in the Kinship system if these relations are sanctioned by the society.

For example, an illegal child never gets sanction from the society even if he is related by blood. But the adopted child is sanctioned by the Society even if he is not blood relative and is a part of consanguinity system. Blood relations have the Social Sanctions in every type of Society.

In this way it is clear that all those relatives which come out of traditional relatives of blood relations of early family are included in consanguinity system, for example, brother, sister, uncle, grand parents etc. Here one thing should be kept in mind that blood relations are not only from father’s side but are also from the mother’s side. In this way blood relatives of father’s side are known as Patrilineal relatives and blood relatives from mother’s side are know as matrilineal relatives.’

Classification. On the basis of blood relations, relatives can be called by different names. Children of the same parents, which are real brothers and sisters are known as siblings. Step brothers and sisters are known as half siblings. From the side of father blood relatives of only males, which are also only males, are known as agnates.

In the same way from the side of mother blood relatives of only females, which are also only females, are known as utrive. In the same way those persons who are blood relatives are known as consanguined kin.

These blood relatives can be divided in two parts :
1. Unilineal Kin. In this type of Kinship those persons are coming which are related to the single line or unilineal of a descent. For example Father, Father’s father, Son and son’s son.

2. Collateral Kin. These types of relatives are those relatives which are indirectly related through every relative. For example’ Brother of father uncle, Sister of Mother – aunt, Brother of mother – uncle etc. Affinity. It is also known as Social Kinship. In this type of Kinship all those persons are included which are produced because of the marriage of a male and female.

When a boy marries a girl then he not only establishes relation with the girl but with the medium of girl he establishes relations with many members with the family of the girl.

In the same way, when a girl marries a boy then girl also establishes relations with all the members of the family of the boy. In this way just with marriage many new relationships come into being. So in this way the Kinship based on marriage is known as Affinal Kinship.

For example, brother-in-law, son-in-law, father-in-law, mother-in-law, sister- in-law etc. from both sides. This type of Kinship is not only important from biological point of view but it also has social importance. Biological importance is only for husband and wife but mother-in-law, father-in-law, brother- in-law, sister-in-law, son-in-law, daughter-in-law etc. are the social relationships.

Morgan studied Kinship of many parts of the world and gave them the names of descriptive and objective categories. In descriptive system generally one name is given to marital relatives. These names tell more about a relationship as compared to Kinship. Objective words tell more about real relationship. For example, ‘uncle’ word is used for Mama, Chacha, Fuffa, Mausa etc.

This is example of first type.
But no word can be used for father. In the same way ‘Nephew’ word is used for (Bhatija and Bhanja,) ‘Cousin’ word is used for the children of Mama, Chacha, Taya, Maasi, Bua etc. In the same way the word sister-in-law is used for Sali and Ninaan and brother-in-law is used for Deor and Sala. In this way new words are used in modern society.

Actually all these words are the symbols of kinship and are based on affinal kinship or Affinity. Like the status of son-in-law and husband to man and the status of daughter-in-law and wife to female can be given only after marriage. In this way we can count a number of affinal relationships.

Punjab State Board PSEB 11th Class Sociology Book Solutions Chapter 6 Socialization Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Sociology Chapter 6 Socialization

Sociology Guide for Class 11 PSEB Socialization Textbook Questions and Answers

Answer the following very short answer questions in 1-15 words each:

Question 1.
What do you mean by socialisation?
Answer:
The process with which an individual learns the ways to live in society.

Question 2.
Name the stages of socialisation.
Answer:
Infant stage, childhood stage, adolescent stage, adulthood stage, and old age.

Question 3.
What is the adolescent stage?
Answer:
The stage starts at the age of 12-13 years and goes till 18-19 years. In this stage, physical changes come in an individual.

Question 4.
What is the infancy stage?
Answer:
This is the stage which starts with the birth and goes till one and half years and child depends upon others to fulfill his basic needs.

Question 5.
Which are the primary agencies of socialisation?
Answer:
Family, school, and play groups are the primary agencies of socialisation.

Question 6.
Give two examples of formal agencies of socialisation.
Answer:
Government, Laws, Courts, Political System etc.

Question 7.
Mention two informal agencies of socialisation.
Answer:
Family, institutions, religion, play group etc.

Answer the following short answer questions in 30-35 words each:

Question 1.
Define socialisation.
Answer:
According to Bogardus, “Socialisation is the -process of working together of developing group responsibility of being guided by the welfare needs of others.”

Question 2.
Write down the stages of socialisation.
Answer:

1. Infant stage
2. Childhood stage
3. Adolescent stage
4. Adulthood’ stage
5. Old age.

Question 3.
Discuss the role of family in the process of socialisation.
Answer:
Family plays a very important role in an individual’s socialisation. Child’s unconscious mind is greatly affected by family. In family, child learns many feelings such as love, sympathy etc. Family tells him about values, cutoms, ways of living etc. which helps in his socialisation.

Question 4.
Describe three formal agencies of socialisation.
Answer:
Police, laws and political system are three formal agencies of socialisation.
If any one commits a crime, he is caught by the police. With the help of laws, he is punished. Our political system prepares strict laws which helps in the reduction of crimes. An individual is having fear of all these and it helps in his socialisation.

Question 5.
Write a short note on primary socialisation.
Answer:
Family and play group are the means of primary socialisation. While living . in family, child learns ways of living in society and becomes a good citizen. In play group, he comes to know that other children also have same aspirations like him and he cares about them. It helps in his socialisation.

Question 6.
Discuss mass media as an agency of socialisation.
Answer:
In present age, the importance of mass media has greatly increased. Different news channels telecast their news all around and inform us about the whole world. We come to know about the events happening everywhere which helps in our socialisation.

Answer the following short answer questions in 75-85 words each:

Question 1.
Discuss the characteristics of socialisation.
Answer:

1. The process of socialisation is universal which exists in all the societies.
2. This process is a iearning process and an individual learns a lot during whole of his life.
3. There are different stages of socialisation and process of learning in different stages is different.
4. The intensity of learning in adulthood stages reduces but it is continued till death.
5. There are many means of socialisation but family is the most important agency which plays the most important role in this process.

Question 2.
What is the importance of peer groups in socialisation ?
Answer:
After family and neighbourhood, the agency which socialises an individual is peer group or play group. Child starts to play with his friends and forms a peer group. His social education starts in the peer group. Here he learns all the things which he cannot learn in family.

He is required to sacrifice his wish in peer group and he comes to know that others also have the same aspirations like him. In peer group, relations are based on equality. That’s why when he takes part in its activities, he learns discipline and co-operation. All these greatly affect his future. While playing children often fight with each other and learn to .protect their rights. So peer group keeps a very important place in one’s socialisation. .

Question 3.
Describe in brief the process of socialisation in youth and old age.
Answer:
(i) Adulthood stage or young age :
This stage keeps a very important place in the process of socialisation. In this stage, one learns to accomodate with others. The major question in this stage is to find employment. While doing so, many a time he gets rejected but he never loses his heart and continues with his efforts. It makes him learn a lot. After marriage and having kids, his role changes which helps him to learn a lot.

(ii) Old age :
In this stage, an individual learns many new things. He starts to realise that he is now dependent upon his family, he gets afflicted with many diseases and needs to learn new ways of accommodation. He is required to work according to his children which further creates many problems. He tries to maintain balance with all these situations.

Answer the following short answer questions in 250-300 words each:

Question 1.
Discuss the development of an individual through the process of socialisation.
Answer:
How man becomes able to live in society ? It is because of his contact with people and materialistic things. When anyone is a child then he doesn’t have the ability to do any of the social work and he is unaware of the things belonging to his surroundings.

But slowly and slowly he starts to see all of them. Child becomes social man because of those persons who surround him all the times because these people tell him the ways of living in society. He adjusts with others and compares his and other’s work.

Slowly and slowly he learns from his experience that other persons are also like him and he expresses his feelings to others. He does this at that time when he thinks that others have also feelings like him. He wanders here and there and he tries to know about every thing which comes in front of him. In this way parents try to explain him with the help of symbols that what is right and what is wrong for him.

Slowly and slowly he is told about going to temple, school, education etc. He is sent to school where he learns to adapt according to the other situations and learns every type of the way of life which is necessary to live a happy life. In this way slowly and slowly he grows up and learns the rules of society.

First relation of child is with his family. After birth his first need is of physical need that is of hunger and thirst. He is more interested in mother because she fulfills his basic needs. After mother other members of the family like father, uncle, aunt, grandfather, grandmother, brother, sister etc. come. All these members tell him about the world in which he has to spend his whole life. In family he experiences things like love, power, force, rights etc. because all these things he gets in the family.

In the beginning child wants everything whatever he likes because he thinks that he has a right over them. If he is unable to get that then he starts crying. When he becomes 2-3 years of age he starts to understand that he cannot get everything what he wants. He feels sad if he is unable to get that thing but slowly and slowly he starts to control himself.

Child is dependent ugon his family for his needs and for this it is necessary for him to get cooperation of the family. He gets their cooperation with self control and he learns norms, values of society which are necessary for him to live and behave in society.

When a person develops then he learns ways of talking, sitting, walking and mannerism. With this his self also develops. When man beqomes conscious about his functions then this consciousness is known as self. In the beginning he cannot differentiate between others and members of the family because he doesn’t know about the relationship of the world. But slowly and slowly he interacts with members of the family and with this he comes to know about socialization also.

After his family members, he goes to his friends. These are his friends who grew in different circumstances. His friends have different ideals which a child learns very slowly and he learns to adjust with difficult circumstances. In play ground he learns to govern and to be governed and learns to make balance with others which is a part of process of socialization.

Another very big change comes in the life of a child and that is when he enters the school. In school he comes under the influence of other students and by the character of teacher. In this way in college he learns a lot of things from his teachers and other students like ways of sitting, walking, talking, behaving etc. which is necessary for his future’s life. After college, business or job, marriage also helps in his socialization.

Personality of husband and wife puts a great effect on each other and on their future. After marriage he has to fulfil a number of duties like of husband, father etc. With these new duties he learns a lot. In this way the process of socialization starts with the birth and ends at the death. Man can finish but this process cannot finish.

Question 2.
Write down about the various stages of socialisation.
Answer:
The process of socialisation is quite wide and starts with the birth of a child. When a child is ban then he is not more than an animal because he does’t know about the ways of living in society and there is lack of social life in him. But with the passage of time when child grows then the process of socialization also goes on with his age and he moulds himself according to the social life. He learns the ideals, values, norms, rules, beliefs, motivations etc. When a child takes birth then he has natural instincts but when he comes in contact with society, his natural instincts change into social habits.

All this happens at different times whose description is given below –

1. Infant Stage
2. Childhood Stage
3. Adolescent Stage
4. Adulthood Stage
5. Old Age.

1. Infant Stage. While explaining the first stage Johnson wrote that this stage starts at the birth of the child and goes up to the age of one and a half years. In this stage child neither can speak nor he can walk. Except this he cannot fulfil his basic needs. He has to depend upon his mother. This is a type of stage in which he is unable to differentiate in things. For the fulfilment of his basic needs like hunger, thrust etc, he depends upon the members of the family.

He tries to take that thing which he likes. According to Talcot Parsons, “Child is a mean of recreation for others in this stage. Generally he can recognise his mother and becomes happy when he comes in contact with his mother. According to him there is no difference in imaginative and real situations.”

After the birth of the child this is the first stage when child doesn’t know’to walk or talk. He has some basic needs and he depends upon his mother for the fulfilment of his basic needs. He cannot differentiate in real and artificial elements. He thinks that others are also like him. Child wants that thing which he likes. This stage goes up to the age of one and half years. In this he tries to establish uniformity with his mother because of which he learns to control his hunger, thirst etc.

2. Childhood Stage. This stage starts at one and half years and goes up to 12 years and in this stage child learns to talk and walk properly. Child starts to fulfil most of his needs himself. Till the age of 2 years he comes to know that except him, other children also have same rights and he cannot get all the things which he needs. He feels sad when all of his demands are not fulfilled but gradually he learns to control himself.

During this time family members try to impart good habits in him by giving reward or punishment. During this time he gets love from others and starts to love others. He starts to learn values of the family and to imitate family members. marriage he has to fulfil a number of duties like of husband, father etc. With these new duties he learns a lot. In this way the process of socialization starts with the birth and ends at the death. Man can finish but this process cannot finish.

Question 2.
Write down about the various stages of socialisation.
Answer:
The process of socialisation is quite wide and starts with the birth of a child. When a child is ban then he is not more than an animal because he does’t know about the ways of living in society and there is lack of social life in him. But with the passage of time when child grows then the process of socialization also goes on with his age and he moulds himself according to the social life. He learns the ideals, values, norms, rules, beliefs, motivations etc. When a child takes birth then he has natural instincts but when he comes in contact with society, his natural instincts change into social habits.

All this happens at different times whose description is given below-

1. Infant Stage
2. Childhood Stage
3. Adolescent Stage
4. Adulthood Stage
5. Old Age.

1. Infant Stage:
While explaining the first stage Johnson wrote that this stage starts at the birth of the child and goes up to the age of one and a half years. In this stage child neither can speak nor he can walk. Except this he cannot fulfil his basic needs. He has to depend upon his mother.

This is a type of stage in which he is unable to differentiate in things. For the fulfilment of his basic needs like hunger, thrust etc, he depends upon the members of the family.

He tries to take that thing which he likes. According to Talcot Parsons, “Child is a mean of recreation for others in this stage. Generally he can recognise his mother and becomes happy when he comes in contact with his mother. According to him there is no difference in imaginative and real situations.”

After the birth of the child this is the first stage when child doesn’t know’to walk or talk. He has some basic needs and he depends upon his mother for the fulfilment of his basic needs. He cannot differentiate in real and artificial elements. He thinks that others are also like him.

Child wants that thing which he likes. This stage goes up to the age of one and half years. In this he tries to establish uniformity with his mother because of which he learns to control his hunger, thirst etc.

2. Childhood Stage. This stage starts at one and half years and goes up to 12 years and in this stage child learns to talk and walk properly. Child starts to fulfil most of his needs himself. Till the age of 2 years he comes to know that except him, other children also have same rights and he cannot get all the things which he needs.

He feels sad when all of his demands are not fulfilled but gradually he learns to control himself. During this time family members try to impart good habits in him by giving-reward or punishment. During this time he gets love from others and starts to love others. He starts to learn values of the family and to imitate family members.

Sometimes he starts crying for that. During this stage he starts talking and walking properly. He also starts to control his wishes. During this age he is motivated to grasp good habits with the help of reward and punishment. For example if he obeys his parents, they love him or give him something to eat or play and if he disobeys them then they either shout on him or slap him. In this stage he starts to grasp the nature of society. He is also influenced by the members of the family. Some things he learns automatically.

Some things he learns by imitation and imitation is a means of entertainment for him. For example he reads newspaper like his father or acts as his grandfather or grandmother. In this stage he starts to adopt that behaviour which he observes in the family. During this stage the internal qualities of a child start to develop. In this way, in this stage, he starts to reeongnise about good or bad works.

In this stage child becomes a member of the group and starts to know about status of others. Even mental consciousness starts up to certain extent. He is hardly conscious about the sexual instincts. Gradually he starts to control his anger and natural instincts. He learns to differentiate between himself and other children. He starts to be influenced by members of the society. This stage gives mental security to him and he stays away from mental tensions.

3. Adolescent Stage. This stage starts at the age of 14-15 years and goes up to 20-21 years. In this age it is not possible for parents to control their children because children think that they are mature enough and need more freedom. That’s why they demand for more freedom! Now his different parts start to develop and with their development new feelings come in him and he starts .to learn new ways of behaviour. It is necessary for girls to stay away from boys. They need readjustments towards other sex or gender.

During this stage many rules related to sex, business, values, beliefs are kept in front of them. They want freedom from these bondages because they thinks that their parents are binding him. Because of this a sense of rebelliousness comes in them. Fast mental conflict starts in them and they learn self-control by tussling with conflict.

4. Adulthood Stage. At this stage, the social circle of an individual becomes quite wide as compared to the third stage. He gets employment and becomes a member of a political group, political party, club, trade union etc. He gets married in this stage and makes new relations in his life, in-laws and new friends.

He is required to maintain balance with his wife and in-laws family. Now he is not dependent upon others instead he becomes a responsible person. He needs to perform many roles such as husband-wife, mother-father, head of family, citizen of country etc. It is expected from him to perform certain roles and continue with the process of socialisation.

5. Old Age. Life of an old age person is greatly influenced by his surroundings, occupations, friends and membership of many groups. He internalises many new values and needs to learn to maintain balance with the new situations. Maintaining balance is quite important in this stage as he faces many adverse circumstances. He gets new roles in this stage such as father-in-law, grandfather, retired person etc. So even in this stage his process of socialisation continues although pace of this process is quite slow.

Question 3.
Write a note on the agencies of socialisation.
Answer:
1. Family:
Family plays the most important role in the socialization of man. According to some prominent Sociologists, the mind of a child is in unconscious state and the effect which family can put on that unconscious mind no one else can put. In childhood we can mould the mind of child in any desired direction. On his unconscious mind every thing puts its effect.

If the behaviour of parents towards child is rude then the child will try to go out of their control when he grows up and if the child will get lots of love and affection then there is no possibility for a child to go to a wrong way. If the child will not be able to get the love of his parents then imbalance can come in his personality. The base of basic education of a child is family. In family many feelings like love and affection always influence the mind of the child from which he learns many qualities.

Family tells the child about the traditions, customs, norms, ways of behaviour of the family and society. Child gets education about ways of behaviour, rules only in the family. In family child learns to obey and respect the elders. If the child is under the control of the parents then it means that child is under the control of society because at the time of the socialization of the child, parents are the representatives of the society. In family child learns many types of qualities and with which he becomes a responsible citizen of society or country. In the family only child gets the chance to express his views and development of his personality.

In its early age whatever a child observes, he starts imitating it. That’s why he depends upon the family so that the family could take him in right direction. According to some psychologists the family puts a great effect not only on the unconscious mind of the child but also affects his future. For example if parents are fighting in the family then the child will definitely live without the love of the parents and this will affect his personality. –

2. Play group:
Play group comes after family as an important means of socialization. Child comes out of the scope of the family, plays with his friends and forms a play group. In play group child starts to get social training. Child can learn a lot of things in play group which he cannot learn in the fatnily.

He has to sacrifice many of his washes while living in play group and he comes to know that others also have wishes like him. Except this relationships in play group are based on equality. That’s why when child plays in play group then he learns discipline, cooperation etc.

which affects his future life. Except this leadership qualities also come in him only by living in play group. While playing children fight with each other and learn to protect the rights of others. Here child comes to know about his role, capabilities, non-capabilities. In play group child grasps many feelings and capabilities. In short, play group plays an important role in shaping the future of the child. If play group is good then child becomes a good human being and if not then he can grasp many bad habits which can affect his future.

3. Neighbourhood:
Neighbourhood of the person is also an important means of socialization. When child comes out of the family and goes in the hands of neighbours then he comes to know that how he has to behave with others. It is so because if the child’s behaviour is not good then the family can ignore it but if his behaviour out of the family is wrong then they can feel.

He has to adapt continuously with his neighbours because neighbours will not tolerate his wrong behaviour and this adjustment will help him for his whole life that how he has to adjust in different circumstances. When he interacts with his neighbours then he comes to know that how he has to behave according to the rules of the society.

4. School:
After all these the next turn is of school whose function is to change an uncivilised child into a civilised child or you can say that school gives shape to raw material into a finished product. In school lots of qualities are developed. In school child studies with other students and many teachers are there in school who exert a great influence on him. Teacher’s ways of talking, walking, sitting, behaving, teaching puts a great influence on the mind of the child.

Here one thing should be kept in mind that different students are influenced by different teachers and they make their teachers as their ideals. They always try to imitate the behaviour of the teachers which puts a great impact on the personality of the child. Except teachers, other students also play an important role in socialization.

While living with them, he gets many roles and status which helps him in future life. Ways of sitting and playing with other children also helps in the development of the personality.In school the scope of play group and interaction of a child becomes so wide because he meets many children in the school. In school child learns many rules, discipline, traditions, subjects etc. which are very helpful in the future life of a child.

5. Social Institutions:
In the process of socialization, not only family or school, but many types of institutions play an important role. In society many types of institutions are there like religious, political, economic, marriage etc. and they play an important role in his socialization. Political institutions tell him the ways of behaving with state or country. Economic institutions tell him about the ways of business. Religious institutions create many types of qualities in him like cooperation, love, sympathy etc.

Every person accepts ways of behaviour given in religion, ways and rules of living, beliefs, with unconscious mind. In this way every society.or caste also tells him about the rules of living in society. Except these many types of recreational activities and behaviour also motivate the mian to become an active member of the society. Social institutions like religious, economic, political also influence the personality of man. For example, man spends most of his time under the influence of economic institutions because he has to earn to live ami earning depends upon his occupation.

A person gets an occupation according to his ability. He has to obey certain rules while accepting any occupation. It means that he changes himself according to the situation. In the area of occupation, he makes relations with many types of individuals. He comes in contact with many persons. That’s why his character and personality is also influenced by all these things.

Except this if we see then we can see that there is no area or part of society which is not under the influence of political institutions. Every type of group like business, language, art, music, education, family etc. are under the control of law. Man has to take the help of law to improve or to do progress in life. That’s why he changes himself according to them.

6. Needs. Man has many types of social and physical needs because of which he has to coordinate with other members of society. Man uses accepted ways of society to fulfil his needs so that he should not be condemned. In this way man does his work which is according to the norms of society with which a sense of accommodation comes in him.

7. Language. Just language can develop every aspect of a child. If child doesn’t know any language then how will he express his views, ideas and feelings towards others. With the help of language, child comes in contact with others because of which he gets many chances to express his ideas. The way in which he learns language, in the same way he gets more chances to express his views. With help of language he makes his social point of view.

With language only he expresses his needs and problems. With language he exchanges his ideas and relations with other people and he learns those rules which can run his life. With this, morality also develops in him. Language prepares him for different types of roles.

With language he comes to know about ideas of others and he also comes to know that what is his position in society. In this way language helps a lot in the process of socialization. Language also helps in the development of the personality. With the help of language, child comes in contact with others and learns social rules, ideals, norms, relations etc.

Question 4.
Discuss the relationship between the various stages of the individual’s development and the agents of socialisation.
Answer:
various stages of socialisation:
The process of socialisation is quite wide and starts with the birth of a child. When a child is ban then he is not more than an animal because he does’t know about the ways of living in society and there is lack of social life in him. But with the passage of time when child grows then the process of socialization also goes on with his age and he moulds himself according to the social life. He learns the ideals, values, norms, rules, beliefs, motivations etc. When a child takes birth then he has natural instincts but when he comes in contact with society, his natural instincts change into social habits.

All this happens at different times whose description is given below:

1. Infant Stage
2. Childhood Stage
3. Adolescent Stage
4. Adulthood Stage
5. Old Age.

1. Infant Stage:
While explaining the first stage Johnson wrote that this stage starts at the birth of the child and goes up to the age of one and a half years. In this stage child neither can speak nor he can walk. Except this he cannot fulfil his basic needs. He has to depend upon his mother. This is a type of stage in which he is unable to differentiate in things. For the fulfilment of his basic needs like hunger, thrust etc, he depends upon the members of the family.

He tries to take that thing which he likes. According to Talcot Parsons, “Child is a mean of recreation for others in this stage. Generally he can recognise his mother and becomes happy when he comes in contact with his mother. According to him there is no difference in imaginative and real situations.”

After the birth of the child this is the first stage when child doesn’t know’to walk or talk. He has some basic needs and he depends upon his mother for the fulfilment of his basic needs. He cannot differentiate in real and artificial elements. He thinks that others are also like him. Child wants that thing which he likes. This stage goes up to the age of one and half years. In this he tries to establish uniformity with his mother because of which he learns to control his hunger, thirst etc.

2. Childhood Stage. This stage starts at one and half years and goes up to 12 years and in this stage child learns to talk and walk properly. Child starts to fulfil most of his needs himself. Till the age of 2 years he comes to know that except him, other children also have same rights and he cannot get all the things which he needs.

He feels sad when all of his demands are not fulfilled but gradually he learns to control himself. During this time family members try to impart good habits in him by giving-reward or punishment. During this time he gets love from others and starts to love others. He starts to learn values of the family and to imitate family members.

Sometimes he starts crying for that. During this stage he starts talking and walking properly. He also starts to control his wishes. During this age he is motivated to grasp good habits with the help of reward and punishment. For example if he obeys his parents, they love him or give him something to eat or play and if he disobeys them then they either shout on him or slap him. In this stage he starts to grasp the nature of society. He is also influenced by the members of the family. Some things he learns automatically.

Some things he learns by imitation and imitation is a means of entertainment for him. For example he reads newspaper like his father or acts as his grandfather or grandmother. In this stage he starts to adopt that behaviour which he observes in the family. During this stage the internal qualities of a child start to develop. In this way, in this stage, he starts to reeongnise about good or bad works.

In this stage child becomes a member of the group and starts to know about status of others. Even mental consciousness starts up to certain extent. He is hardly conscious about the sexual instincts. Gradually he starts to control his anger and natural instincts. He learns to differentiate between himself and other children. He starts to be influenced by members of the society. This stage gives mental security to him and he stays away from mental tensions.

3. Adolescent Stage. This stage starts at the age of 14-15 years and goes up to 20-21 years. In this age it is not possible for parents to control their children because children think that they are mature enough and need more freedom. That’s why they demand for more freedom! Now his different parts start to develop and with their development new feelings come in him and he starts .to learn new ways of behaviour. It is necessary for girls to stay away from boys. They need readjustments towards other sex or gender.

During this stage many rules related to sex, business, values, beliefs are kept in front of them. They want freedom from these bondages because they thinks that their parents are binding him. Because of this a sense of rebelliousness comes in them. Fast mental conflict starts in them and they learn self-control by tussling with conflict.

4. Adulthood Stage. At this stage, the social circle of an individual becomes quite wide as compared to the third stage. He gets employment and becomes a member of a political group, political party, club, trade union etc. He gets married in this stage and makes new relations in his life, in-laws and new friends.

He is required to maintain balance with his wife and in-laws family. Now he is not dependent upon others instead he becomes a responsible person. He needs to perform many roles such as husband-wife, mother-father, head of family, citizen of country etc. It is expected from him to perform certain roles and continue with the process of socialisation.

5. Old Age. Life of an old age person is greatly influenced by his surroundings, occupations, friends and membership of many groups. He internalises many new values and needs to learn to maintain balance with the new situations. Maintaining balance is quite important in this stage as he faces many adverse circumstances. He gets new roles in this stage such as father-in-law, grandfather, retired person etc. So even in this stage his process of socialisation continues although pace of this process is quite slow.

agencies of socialisation:
1. Family:
Family plays the most important role in the socialization of man. According to some prominent Sociologists, the mind of a child is in unconscious state and the effect which family can put on that unconscious mind no one else can put. In childhood we can mould the mind of child in any desired direction. On his unconscious mind every thing puts its effect.

If the behaviour of parents towards child is rude then the child will try to go out of their control when he grows up and if the child will get lots of love and affection then there is no possibility for a child to go to a wrong way. If the child will not be able to get the love of his parents then imbalance can come in his personality. The base of basic education of a child is family. In family many feelings like love and affection always influence the mind of the child from which he learns many qualities.

Family tells the child about the traditions, customs, norms, ways of behaviour of the family and society. Child gets education about ways of behaviour, rules only in the family. In family child learns to obey and respect the elders. If the child is under the control of the parents then it means that child is under the control of society because at the time of the socialization of the child, parents are the representatives of the society. In family child learns many types of qualities and with which he becomes a responsible citizen of society or country. In the family only child gets the chance to express his views and development of his personality.

In its early age whatever a child observes, he starts imitating it. That’s why he depends upon the family so that the family could take him in right direction. According to some psychologists the family puts a great effect not only on the unconscious mind of the child but also affects his future. For example if parents are fighting in the family then the child will definitely live without the love of the parents and this will affect his personality. –

2. Play group:
Play group comes after family as an important means of socialization. Child comes out of the scope of the family, plays with his friends and forms a play group. In play group child starts to get social training. Child can learn a lot of things in play group which he cannot learn in the fatnily. He has to sacrifice many of his washes while living in play group and he comes to know that others also have wishes like him. Except this relationships in play group are based on equality. That’s why when child plays in play group then he learns discipline, cooperation etc.

which affects his future life. Except this leadership qualities also come in him only by living in play group. While playing children fight with each other and learn to protect the rights of others. Here child comes to know about his role, capabilities, non-capabilities. In play group child grasps many feelings and capabilities. In short, play group plays an important role in shaping the future of the child. If play group is good then child becomes a good human being and if not then he can grasp many bad habits which can affect his future.

3. Neighbourhood:
Neighbourhood of the person is also an important means of socialization. When child comes out of the family and goes in the hands of neighbours then he comes to know that how he has to behave with others. It is so because if the child’s behaviour is not good then the family can ignore it but if his behaviour out of the family is wrong then they can feel.

He has to adapt continuously with his neighbours because neighbours will not tolerate his wrong behaviour and this adjustment will help him for his whole life that how he has to adjust in different circumstances. When he interacts with his neighbours then he comes to know that how he has to behave according to the rules of the society.

4. School:
After all these the next turn is of school whose function is to change an uncivilised child into a civilised child or you can say that school gives shape to raw material into a finished product. In school lots of qualities are developed. In school child studies with other students and many teachers are there in school who exert a great influence on him. Teacher’s ways of talking, walking, sitting, behaving, teaching puts a great influence on the mind of the child.

Here one thing should be kept in mind that different students are influenced by different teachers and they make their teachers as their ideals. They always try to imitate the behaviour of the teachers which puts a great impact on the personality of the child. Except teachers, other students also play an important role in socialization.

While living with them, he gets many roles and status which helps him in future life. Ways of sitting and playing with other children also helps in the development of the personality.In school the scope of play group and interaction of a child becomes so wide because he meets many children in the school. In school child learns many rules, discipline, traditions, subjects etc. which are very helpful in the future life of a child.

5. Social Institutions:
In the process of socialization, not only family or school, but many types of institutions play an important role. In society many types of institutions are there like religious, political, economic, marriage etc. and they play an important role in his socialization. Political institutions tell him the ways of behaving with state or country. Economic institutions tell him about the ways of business. Religious institutions create many types of qualities in him like cooperation, love, sympathy etc.

Every person accepts ways of behaviour given in religion, ways and rules of living, beliefs, with unconscious mind. In this way every society.or caste also tells him about the rules of living in society. Except these many types of recreational activities and behaviour also motivate the nian to become an active member of the society.

Social institutions like religious, economic, political also influence the personality of man. For example, a man spends most of his time under the influence of economic institutions because he has to earn to live ami earning depends upon his occupation.

A person gets an occupation according to his ability. He has to obey certain rules while accepting any occupation. It means that he changes himself according to the situation. In the area of occupation, he makes relations with many types of individuals. He comes in contact with many persons. That’s why his character and personality is also influenced by all these things.

Except this, if we see then we can see that there is no area or part of society that is not under the influence of political institutions. Every type of group like business, language, art, music, education, family, etc. is under the control of law. Man has to take the help of the law to improve or to do progress in life. That’s why he changes himself according to them.

6. Needs. Man has many types of social and physical needs because of which he has to coordinate with other members of society. Man uses accepted ways of society to fulfill his needs so that he should not be condemned. In this way, man does his work which is according to the norms of society with which a sense of accommodation comes in him.

7. Language. Just language can develop every aspect of a child. If a child doesn’t know any language then how will he express his views, ideas, and feelings towards others. With the help of language, the child comes in contact with others because of which he gets many chances to express his ideas. The way in which he learns language, in the same way, he gets more chances to express his views. With help of language, he makes his social point of view.

With language only, he expresses his needs and problems. With language, he exchanges his ideas and relations with other people and he learns those rules which can run his life. With this, morality also develops in him. Language prepares him for different types of roles.

With language, he comes to know about the ideas of others and he also comes to know that what is his position in society. In this way, language helps a lot in the process of socialization. Language also helps in the development of personality. With the help of language, the child comes in contact with others and learns social rules, ideals, norms, relations, etc.

Punjab State Board PSEB 11th Class Sociology Book Solutions Chapter 10 Social Stratification Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Sociology Chapter 10 Social Stratification

Sociology Guide for Class 11 PSEB Social Stratification Textbook Questions and Answers

Answer the following very short answer questions in 1-15 words each:

Question 1.
What do you mean by social stratification ?
Answer:
The process of dividing society in different layers and on different basis is known as stratification.

Question 2.
Name the forms of social stratification,
Answer:
There are four forms of social stratification caste, class feudalism and slavery.

Question 3.
Name the elements of social stratification.
Answer:
It is universal and social, inequality exists in it and it has different base in different societies.

Question 4.
What is estate system ?
Answer:
This system prevailed in the medieval European society in which an individual was made feudal lord by giving a large piece of land.

Question 5.
From where has the word ‘Caste’ been derived ?
Answer:
The word ‘Caste’ has been derived from a Spanish and Portuguese word ‘Casta’ which means race, lineage or breed.

Question 6.
What is Varna System?
Answer:
The system of ancient India in which society was divided into four parts on the basis of occupation.

Question 7.
Name the hierarchical positions of the different Varnas in Hindu society.
Answer:
Ancient Hindu society had four Varnas : Brahmins, Kshatriyas Vaishyas and Shudras.

Question 8.
What do you mean by untouchability?
Answer:
During the times of caste system, different castes were not allowed to touch each other which is known as untouchability.

Question 9.
Name some reformers who protested against untouchability.
Answer:
Raja Ram Mohan Roy, Jyatiba Phuley, Mahatma Gandhi, B.R. Ambedkar etc.

Question 10.
What is Class?
Answer:
Class is a group of people having similarity on any basis such as money, occupation, property etc.

Question 11.
Name the types of Classes.
Answer:
Mainly three classes exist in society-upper class, middle class and lower class.

Question 12.
What are the two classes mentioned by Marx?
Answer:
Capitalist Class and Labour Class.

Answer the following short answer questions in 30-35 words each:

Question 1.
What is social inequality ?
Answer:
When all the members of the society do not get enough chances to develop their personality, differences prevail among them on the basis of caste, birth, race, colour, wealth, occupation etc. then this is known as inequality.

Question 2.
Name two forms of social stratification.
Answer:

1. Caste : Caste is a form of stratification in which stratification prevails among different castes.
2. Class : Many classes prevail in society and difference exists among them on different basis.

Question 3.
Write two features of caste system.
Answer:

1. Membership of caste is based upon birth and one cannot change his caste even if he has the ability to do so.
2. Caste is an endogamous group and marriage among different castes is not allowed.

Question 4.
What is endogamy ?
Answer:
Endogamy is a type of marriage in which one needs to marry within his group i.e. caste or sub-caste. If any one tried to break this rule, he was severely punished and thrown out of the group. That’s why every one preferred to marry in his group;

Question 5.
What do you mean by pollution and purity ?
Answer:
The hierarchy of caste was attached was the concept of pollution and purity. It means that traditionally few castes were considered pure and they had higher status in society. Few castes were considered impure or polluted and they had low status in society.

Question 6.
Write a short note on industrialisation and urbanisation.
Answer:
The meaning of industralisation is advent of large scale industries in the country. When people migrate from rural areas to urban areas it is known as urbanisation. Both these processes played a very important role in the decline of caste system. ,

Question 7.
Write two features of class system.
Answer:

1. Each class is conscious about the fact that its status is higher or lower than the others.
2. Members of one class prefer to keep relations within their own class and have very limited relations with other classes.

Question 8.
Write a short note on new middle class.
Answer:
During last few decades, a new middle class has emerged in our society. Doctors, engineers, managers, small traders, job-oriented people etc. come in this class. Upper class exploits lower class with the help of middle class.

Answer the following short answer questions in 75-85 words each:

Question 1.
Write down four characteristics of social stratification.
Answer:

1. Stratification is a universal process. There is no society where this process doesn’t exist.
2. In stratification, all the members of society have an unequal status. Someone has higher status and someone has lower status.
3. In stratification, society is divided into different layers which determines an individual’s status. All the classes have mutual relations based on superiority or inferiority.
4. Yet many layers are there in this but these layers have mutual interdependence.

Question 2.
How is class related to social stratification? Discuss it briefly.
Answer:
Social stratification is always related with class. We can see that there exist many classes in society. Classes in different societies, ancient or modern, depend upon different basis and these bases can be caste, occupation, money, wealth, race, religion etc. All the classes depend upon each other for their own existence.

Question 3.
Differentiate between caste and class.
Answer:
Class:

• One gets social status according to one’s personal ability.
• Membership of class is based upon wealth, money, occupation etc.
• An individual gets more freedom in class system.
• Mutual difference is quite less in different classes.
• Class system is based upon the concept of democracy.

Caste:

• There was no place of personal ability in this and social status was based upon birth.
• Membership of caste is based upon birth.
• Many restrictions are imposed on an individual such as keeping relations, exchange of eatables, marriage etc.
• Different castes are quite far away from each other.
• It is completely against the system of democracy.

Question 4.
Write the four factors of change in caste system.
Answer:

• During 19th and 20th centuries, many socio-reform movements started which greatly affected the caste system.
• After independence, Indian government passed many laws and many provisions were kept in the constitution which brought many changes in caste system.
• With the advent of industrialisation, members of different castes started working with each other which reduced the caste based restrictions.
• In urban areas, people belonging to different castes live with each other which has reduced the caste’s rule of keeping relations with the same caste.
• Spread of education has also contributed a lot in reducing the impacj of caste system.

Question 5.
Distinguish between caste and class as two major forms of social stratification.
Answer:
Class:

• One gets social status according to one’s personal ability.
• Membership of class is based upon wealth, money, occupation etc.
• An individual gets more freedom in class system.
• Mutual difference is quite less in different classes.
• Class system is based upon the concept of democracy.

Caste:

• There was no place of personal ability in this and social status was based upon birth.
• Membership of caste is based upon birth.
• Many restrictions are imposed on an individual such as keeping relations, exchange of eatables, marriage etc.
• Different castes are quite far away from each other.
• It is completely against the system of democracy.

Answer the following short answer questions in 250-300 words each:

Question 1.
Define stratification. What are the features of social stratification ?
Answer:
Eight from the ancient times, humans have tried to make a society based on equality and where there will be no class in it. In other words society based on equality is that society in which there is no class, social and economic status of all the members is equal, every one gets equal number of facilities. But till today none of the society of this type has come into being. Different types of classes exist in all the societies and all the societies are stratified.

All the societies, from ancient times till today are divided in different classes. In earlier times, society was divided on the basis of age, sex, head of the societies etc. but due to increased complexity, modern societies are divided in higher or lower classes on different basis. If we observe our society carefully then we will come to know that there are many inequalities existing in our society.

For example, some persons are rich and some are poor. Our society has been divided on the basis of political, social, religious, economic basis etc. Because of this division, relations of different individuals in our society are based on higher and lower positions. In this way the division of society in different parts is known as stratification.

(1) According to Sorokin, “Social Stratification means the differention of a given population into hierarchically superposed classes. It is manifested in the existence of upper and lower social layers. Its basis and very essence consist of unequal distribution of rights and privileges, duties and responsibilities, social values and privation, social power and influences among the members of a society.”

(2) According to Kurt B. Mayer, “Social Stratification is a System of social position whose occupants are treated as superior, equal or inferior relative to one another in social important respects.”

(3) According to Kingsley Davis, “Social inequality is thus an unconsciously evolved device by which societies ensure that the most important positions are consciously filled by the most qualified persons. Hence every society, no matter how simple or complex must differentiate persons in terms of both prestige and esteem.”

(4) According to Raymond W. Moorey, “Stratification is a horizontal division of society into higher and lower units.” On the basis of these definitions, we can conclude that the social stratification determines the higher and the lower social groups and status and roles of different humans.

It shows hierarchy among persons on the basis of birth, caste, occupation, gender, money, power etc. Relations of inferiority and superiority exist among different groups and every person has a definite position m society. That is why man gets status and respect in society.

Features or Characteristics of Stratification:
1. Stratification is social:
Differences exist on the basis of stratification in different societies. Whenever we differentiate anything, which exists in society, from other thing and until that difference is not accepted by all the members of society, we cannot accept that difference as the base of stratification.

It means that until members of a group will not determine the stratification, this stratification cannot exist in society. Stratification is possible only then when all the members of society will accept these differences. In this way, it is social because it is accepted by all the members of society.

2. Stratification is a universal process:
Process of stratification exists in every society. We can check every type of society, whether it is ancient, tribal, rural or modern complex society. Then we can see that definitely there were and there are some differences among people. Difference of Gender is natural on the basis of which we can divide the humans. There are many bases of stratification in modern complex society.

It means that yet the bases of stratification are different in different societies but stratification exists in every type of society. Each country and society is divided in different layers on different basis yet inequalities may be different. So we can say that it is a universal process.

3. Inequality of status of different classes:
Status and role of humans is not the same in social stratification. Any one has higher status and any one has low status. Position of persons never remains the same all the times. Changes keep on coming in this. It can go higher at anytime and can go to a low level. It means that inequality exists in position of humans.

If any one has higher position on the basis of money then other might have lower position. Anyone is officer and other one is clerk. Position of both is unequal. Yet the base might be different like gender, age, money, status, job etc. but the position of different classes is unequal.

4. Relation of upper and lower classes:
Society has been divided into different layers in stratification which determine the position of a person. Generally society can be divided in two parts higher and lower. Some people in society have higher position and some people in society have low status. Some people exist between them. In this way in higher and lower classes, there exists one middle class. All of them have some relations of higher and lower positions.

5. Stratification restricts interaction:
The interactions in the process of stratification are only restricted to a specific layer. Generally we can see that every person establishes relations with the members of his layer or class. That is why he shares his feelings with them. Person has friends in his class only. Sometimes man is unable to adjust by keeping contacts with the members of other strata.

Like in modern age interaction between a rich person and a poor person is not possible. Stratification restricts the interaction between different classes. Every class has class consciousness because of which they interact .with other classes in a limited way. In this way stratification restricts the interaction.

6. It develops the sense of competition:
The process of stratification produces the sense of hard work in person. In this every person is conscious about his social status. He always tries to move forward because he thinks that people around him are of higher strata. He tries to move forward by using his capabilities in competition with them.

In this way this consciousness produces the sense of competition, Every person wishes to take himself up in society and he can do this by hard work. He does this hard work and competes with members of other classes and takes himself up in stratification.

Question 2.
Discuss in detail the forms of stratification.
Answer:
(i) Varna Stratification:
After the advent of the Aryans in India, society was divided among the Aryans and the original inhabitants of India. Later on Aryan people, on the basis of their traits and behaviour, were divided among Brahmins, Kshatriyas, Vaishyas and Shudras. In this way, society was divided among four Varnas and this form of stratification came in front.

In this hierarchy, Brahmins had the highest place, Kshatriyas came second, Vaishyas at third and at the end, people of fourth varna were there. In this system, occupation of each varna was fixed and separate from each other. Initial form of Varna system was not based on birth but was based on individual traits and one was free to change his varna. But it was quite a difficult process to change one’s varna.

(ii) Slavery Stratification:
Slave is a human who is completely controlled by the other individual. He lives on the mercy of his owner. He has no rights. In certain cases he is protected by his owner such as to protect him from becoming other’s slave. But still he is an individual without rights. He is considered as the property of his owner.

So, there existed a lot of inequality in slave societies. This custom prevailed, during 19th century, in America, Africa etc. Owner was free to sell his slave. He had to work very hard for his owner. With time, this custom was strongly opposed and gradually came to an end. Slave became farmers but still some sort of this stratification existed among farmers and labourers.

(iii) Feudalism:
Along with slavery, the institution of feudalism came into being. Feudal lords were the owners of large piece of land and they rented out their land to others on project sharing basis. During the medieval period, feudalism had legal sanction in Europe and feudal lords had special status, special privileges and duties.

Farmers, during those days, had very few rights. They had to depend upon the mercy of feudal lords for justice. Major power was in the hands of feudal lords and clergy. Zamindars existing in India were very much different from the feudalism existing in Europe. So stratification based on feudalism existed in society.

(iv) Racial Stratification:
Stratification on the basis of race also exists in different societies. Whole of the world is divided on the bases of race. Mainly three racial groups are there : Caucasion (white), Mongoloid (yellow or brown) and Negroid (black). A system of hierarchy exists among these races. White race is considered superior among all.

Yellow race is considered at middle leval and black race is at lower level. Racial discrimination in U.S. A. also exists on this base. People of different races never marry eaph other. Yet few changes are coming in modern society but still this system prevails in the world.

(v) Caste Stratification:
The stratification on the basis of birth is known as caste stratification because status of a child was determined according to his birth. In ancient and traditional Indian society this type of statification prevailed. It was having great impact on the Indian society. Mainly four castes existed-Brahmins, Kshatriyas, Vaishyas and the Shudras. This form of stratification was more stable because one was not allowed to change his caste. ,

(vi) Class Stratification:
It is also known as universal stratification because such stratification exists in every society. It is an open stratification and bases of this stratification are income, power, property, religion, education, occupation etc. One gets a definite position in this and people with equal status form a class. With this, different classes are formed and relations are established among them. One can change his status or class with his efforts.

Question 3.
What factors are causing change in caste system?
Answer:
1. Socio-Religious Reforms Movements:
Even before the advent of British empire many religious movements had criticised the caste system. Buddhism, Jainism, Islam and Sikhism had criticised caste system. Gautam Buddha had criticised caste system 2500 years back. Except this Islam and later on Sikhism had also criticised caste system.

In 19th century many social reformers had started movements against this. Some of these movements Brahmo Samaj by Raja Ram Mohan Roy, Arya Samaj by Dayanand Saraswati, Rama Krishna Mission etc. were important. Except these Jyoti Ba Phule established Satya Shodhan Samaj in 1873 whose main aim was to provide equality to every person. Mahatma Gandhi and B.R. Ambedkar also criticised the caste system.

2. Efforts of Indian Government:
During British empire and after independence many important laws were passed by government which contributed towards weakening of caste system. Caste and rural panchayats were very powerful before British rule. These panchayats had the rights to give punishment to criminals.

During British empire One Law i.e. ‘Caste Disabilities Removal Act, 1850’ was passed which weakened the caste Panchayats. In this way ‘Special Marriage Act, 1872’ gave approval to the marriage of different castes. After independence a number of laws like Untouchability Offences Act, 1955 and Hindu Marriage Act, 1955 also weakened the caste system. In 1949 Hindu Marriage Validation Act was passed in which legal sanction was given to inter-caste marriage.

3. Contribution of the Britishers:
A comprehensive opposition against the caste system began during the British reign. The British had applied the rule of equality in front of law. Rights from caste based Panchayats were taken back. Educational system of the British was secular. Government jobs were open to everyone.

The British started modern industries, rails, buses etc. which was a strong slap on the face of caste system. All the people jointly worked in the industries and travelled in rails and buses with each other which resulted in the establishment of contacts between different castes.

4. Industrialization:
Industrialization played an important role in bringing change in caste system. It increased the importance of ability of the person. Importance of materialism has also been increased. People came out of their houses to go to job. Everyone started to work in industries. In industries no one asks for anyone’s caste but they look to each other’s abilities. Lower castes have also got higher status with their hard work.

5. Modern Education:
Modern education has also put a great effect on the caste system. In ancient Hindu Society, education was confined only to higher castes and education was also based upon religion. But with the advent of Britishers, a rule of equality was started by Britishers. Then educational institutions were opened for everyone.

Western Education was started instead of religious education. Boys and girls both started to get education. In this way modern educational system started to give importance to individual’s abilities instead of any one’s caste. With this intercaste relations started to establish. After independence Indian Constitution also started to implement democratic values which was a great setback to caste system.

6. Urbanization:
Urbanization was also developed with industrialization because people came out of their houses for work. Urban features like more density of population, individual’s feelings, social mobility, more occupations etc. have weakened the caste system. People live with each other in big cities. Feeling of assimilation of higher and lower caste was increased. The individual abilities started to control the society. Man has to achieve status in society.

Difference on the basis of gender in cities was decreased. Males and females started to work together. In this way females came out of the four walls of house and started to work in offices. They became economically independent. Urbanization has increased the mutual contacts between different castes which resulted in exogamy instead of endogamy.

7. Importance of Money:
Caste System started to weaken due to increase in materialistic approach of the people. People get status due to money in society. Every one gives respect to rich persons irrespective of his caste. In Modern Society a person works only for the sake of his profit. Every one tries to earn more and more money. It increses the importance of individuals’ abilities. Inthisthe importance of moneyhas been increased and the importance of caste system has been reduced.

Question 4.
Define class system. Write down its characteristics.
Answer:
The base of social stratification is class. Status of a person in class depends upon his role in class. Position of all the persons is not same in all the societies. Some type of inequality is always there in class and because of this inequality of classes came into being. Especially because of westernization, industrialization, educational system, modernization etc. classes came into being in India. Stratification in Western Societies is also Based upon class system. Many classes also came into being in India like Teacher class, Business class, Doctor class etc. ‘

Meaning and Definitions of Class:
Every society has been divided into classes and every class has a different status in the society. On the basis of status person’s status is high or low. In this way when different persons achieve special social status in society, then it is known as class system. Every class is economically different from the other.

Different Sociologists have given different views about class system which are given below :
(1) According to Maclver, “A social class is any position of Community marked off from the rest by Social Status.”

(2) According to Morris Ginsberg, “A class is group of individuals who through common descent, similarity of occupation, wealth and education have come to have a similar mode of life, n similar stock of those ideas, feelings, attitudes and forms of behaviours and who on any or all of these grounds meet one another on equal terms and regard themselves, with varying degrees of explicitness as belonging to one group.”

(3) According to Gilbert, “A social class is a category of group of persons having a definite status in a society which permanently determines their relationships to other groups.”

(4) According to Ogburn and Nimkoff, “The fundamental attribute of social class is thus its local position of relative superiority or inferiority to other social classes.”

On the basis of given definitions we can say that social class is a class of many persons which has one specific status in a specific time. That is why they have some special power, rights and duties. Ability of an individual is important in class system. That is why every person wants to achieve higher status in society with hard work.

Every society is divided in many classes. Status of a person is not definite in class system. There is some sort of mobility existing in his status. That is why it is known as open stratification. Person determines his class status himself. It is not based on birth.

Characteristics of Class:
1. Feelings of Superiority and Inferiority: Relationships of inferior and superior exist in class system. For example, people of higher class think themselves as different and superior from lower class. Rich persons are coming in higher class and poor people are coming in lower class. Rich people have higher status in society and poor people live at different places. By looking at the residence of the person we can imagine about the class of the person.

2. Social Mobility:
Class system is not definite for person. It keeps on changing. Man can achieve higher status with hard work and can go to lower status with wrong deeds. Every person wants to increase his prestige in society. That is why class system makes the person active. So in this way social mobility is there in class system.

For example if a person, who is working as a clerk in any office, does a lot of hard work and passes the I.A.S. exam then his status and position will be completely changed. It means that class system has social mobility in which person can make from one place to another with his hard work and ability.

3. Openness:
Openness exists in the class system because in this every person is free to do anything. He is free to adopt any occupation. Any one can become the member of any class on the basis of his ability. Person from lower class can go to higher class with his hard work. In this there is no value of birth of the person.

Status of person depends upon his ability. A boy from rich family can become rich only if he has the property. If this property will finish then he can become poor. This class system gives opportunity to every one to move forward. In this way openness exists in class system.

4. Limited Social Relations:
Social relations of a person are limited in class system. Persons of every class love to establish relations with the people of their own class. Every class wants to establish contacts with persons of their own class. They don’t like to keep contacts with the people of other castes.

5. Development of Sub-classes:
We can divide class system into three parts from economic point of view and these are :

1. Upper Class
2. Middle Class
3. Lower Class.

These classes are again divided into sub-classes. For example, we can see difference between rich people. Some one is Billionaire and some one is Millionaire. In the same way we can see sub-classes in middle class and lower class. In every class we can see sub-classes. In this way class is made up of sub-classes.

6. Different Basis :
Classes are made on different basis. According to Karl Marx, the main base of class system is economic. According to him, there are two classes in society. First one is capitalist class and second is labour class. According to Ogburn and Nimkoff, Maclver and Gilberg, social base is important for class. Ginsberg and Lapire has accepted cultural base as the main base of class system.
In this way we can say that there is not a single base of class system but there are many bases of class system.

7. Identification of Class:
External outlook is important in class system. Sometimes just by external outlook we can imagine about the class of the person. In modern society big house, car, scooter, T.V., V.C.R., Fridge etc. symbolise towards the position of the person. In this way external symbols tell us about class differences. Life Style of one class is almost same and their necessities are generally same.

Question 5.
What new classes have emerged in India ?
Answer:
Durings the last few decades, the caste system has been replaced by the class system.After independence, many new laws were passed, people started taking education which resulted in the decline of the caste system and the advent of class system. Now class system is not a simple concept. In modern times, many new classes have emerged on different basis and the process is going on.

For example, after the Indian Independence, many land reforms were introduced which brought many changes in the rural economy. Green revolution greatly contributed in it. Along with old farmers, who had large pieces of land, a new farmer class emerged which had experience of new methods of agriculture.

These were the people who were retired from army or administrative services. They started investing their money in agriculture and earning lot of money. This is not the class of traditional farmers but are known as Gentlemen Farmers. Along with this, a new class of farmers, Capitalist farmers, is also emerging.

These are the farmers who earn a lot of money by using new techniques, HYV seeds, new techniques of agriculture, modern irrigation facilities, taking loans and by using modern means of transport and communication. But small farmers were unable to take advantage of this and are still poor.

They are unable to take advantage of the land reforms introduced by the government. After this, a middle class has also emerged which gave birth to the culture of consumerism. This middle class was seen as a potential market and many multinational companies get attracted towards this group. In the advertisements of different companies, upper middle class is seen as the most important consumer.

These days, a new middle class is emerging which gives more importance to its taste and consumption and it has become a cultural idea. In this way with the emergence of middle class, the concept of economic liberalism is also emerging. One of the important features of existing class system in modern India is that all these classes have helped in creating a national economy.

Now people from the far off villages are becoming a part of middle classes. People living in villages and engaged in different occupations have not remained isolated. Now caste based restrictions have come to an end and class based consciousness is coming forward.

Question 6.
Bring out the main features of class system in India.
Answer:
The base of social stratification is class. Status of a person in class depends upon his role in class. Position of all the persons is not same in all the societies. Some type of inequality is always there in class and because of this inequality of classes came into being. Especially because of westernization, industrialization, educational system, modernization etc. classes came into being in India. Stratification in Western Societies is also Based upon class system. Many classes also came into being in India like Teacher class, Business class, Doctor class etc. ‘

Meaning and Definitions of Class:
Every society has been divided into classes and every class has a different status in the society. On the basis of status person’s status is high or low. In this way when different persons achieve special social status in society, then it is known as class system. Every class is economically different from the other.

Different Sociologists have given different views about class system which are given below :
(1) According to Maclver, “A social class is any position of Community marked off from the rest by Social Status.”

(2) According to Morris Ginsberg, “A class is group of individuals who through common descent, similarity of occupation, wealth and education have come to have a similar mode of life, n similar stock of those ideas, feelings, attitudes and forms of behaviours and who on any or all of these grounds meet one another on equal terms and regard themselves, with varying degrees of explicitness as belonging to one group.”

(3) According to Gilbert, “A social class is a category of group of persons having a definite status in a society which permanently determines their relationships to other groups.”

(4) According to Ogburn and Nimkoff, “The fundamental attribute of social class is thus its local position of relative superiority or inferiority to other social classes.”

On the basis of given definitions we can say that social class is a class of many persons which has one specific status in a specific time. That is why they have some special power, rights and duties. Ability of an individual is important in class system. That is why every person wants to achieve higher status in society with hard work.

Every society is divided in many classes. Status of a person is not definite in class system. There is some sort of mobility existing in his status. That is why it is known as open stratification. Person determines his class status himself. It is not based on birth.

Characteristics of Class:
1. Feelings of Superiority and Inferiority: Relationships of inferior and superior exist in class system. For example, people of higher class think themselves as different and superior from lower class. Rich persons are coming in higher class and poor people are coming in lower class. Rich people have higher status in society and poor people live at different places. By looking at the residence of the person we can imagine about the class of the person.

2. Social Mobility:
Class system is not definite for person. It keeps on changing. Man can achieve higher status with hard work and can go to lower status with wrong deeds. Every person wants to increase his prestige in society. That is why class system makes the person active. So in this way social mobility is there in class system.

For example if a person, who is working as a clerk in any office, does a lot of hard work and passes the I.A.S. exam then his status and position will be completely changed. It means that class system has social mobility in which person can make from one place to another with his hard work and ability.

3. Openness:
Openness exists in the class system because in this every person is free to do anything. He is free to adopt any occupation. Any one can become the member of any class on the basis of his ability. Person from lower class can go to higher class with his hard work. In this there is no value of birth of the person.

Status of person depends upon his ability. A boy from rich family can become rich only if he has the property. If this property will finish then he can become poor. This class system gives opportunity to every one to move forward. In this way openness exists in class system.

4. Limited Social Relations:
Social relations of a person are limited in class system. Persons of every class love to establish relations with the people of their own class. Every class wants to establish contacts with persons of their own class. They don’t like to keep contacts with the people of other castes.

5. Development of Sub-classes:
We can divide class system into three parts from economic point of view and these are :

1. Upper Class
2. Middle Class
3. Lower Class.

These classes are again divided into sub-classes. For example, we can see difference between rich people. Some one is Billionaire and some one is Millionaire. In the same way we can see sub-classes in middle class and lower class. In every class we can see sub-classes. In this way class is made up of sub-classes.

6. Different Basis :
Classes are made on different basis. According to Karl Marx, the main base of class system is economic. According to him, there are two classes in society. First one is capitalist class and second is labour class. According to Ogburn and Nimkoff, Maclver and Gilberg, social base is important for class. Ginsberg and Lapire has accepted cultural base as the main base of class system.
In this way we can say that there is not a single base of class system but there are many bases of class system.

7. Identification of Class:
External outlook is important in class system. Sometimes just by external outlook we can imagine about the class of the person. In modern society big house, car, scooter, T.V., V.C.R., Fridge etc. symbolise towards the position of the person. In this way external symbols tell us about class differences. Life Style of one class is almost same and their necessities are generally same.

Question 7.
What are the Marxian and Weberian perspectives on class?
Answer:
Marxian Conflict Theory of Stratification. Karl Marx has given conflict theory of social stratification and this theory comes out because of political and social conflicts of 19th century. According to Marx, economic factor is the alone factor of social stratification and struggle in different classes. Marx has given this theory on the base of division of labour.

According to him, labour is of two types, physical and mental and this difference is the main reason of difference in social classes. Marx was of the view that there are only two classes in society. First class is the owner of the means of production and second class is not the owner of means of production.

On the basis of this ownership the position of owner class is higher and position of non-owner class is lower. According to Marx, owner class is capitalist class and non-owner class is labourer class. Capitalist class economically exploits the labourer class and labourer class fights with capitalist class to get their rights. This is the result of stratification.

Marx was of the view that the main reason of stratification is the unequal distribution of property. The nature of stratification depends upon the classes of that society and the nature of the classes depends upon the means of production. Ways of production depend upon technique. Class is a group in which relations of its members with forces of production are equal.

In this way all those persons, who control the forces of production, come in first class i.e. capitalist class. Second class is that class which is not the owner of forces of production but it earns its livelihood by selling its labour and that is labourer class. Their name in different societies is different. For example, Feudal Lords and agricultural labourers in Feudal societies and capitalist and labourer in capitalist societies.

Capitalist class has all the forces of production and labourer class has only its labour to sell with which it earns its livelihood. In this way the classes made on the basis of ways of production and unequal distribution of property are, according to Marx, social classes.

According to Marx, society today comes out of four stages or societies and these are :
(a) Primitive ancient society or communism
(b) Ancient society.
(c) Feudal society
(d) Capitalist society

According to Marx, classes did not come into being in first type of society but in later societies two main classes came into being. In ancient society owner and servant, Feudal Lords and agricultural labourer in Feudal society and Capitalist and Labourer class in Capitalist society came into being. In every society labour was being done by second class. Labour class is more in number and capitalist class is less in number.

Marx has given two classes in every type of society but on this point his views were not the same. Marx was of the view that there are three classes in capitalist society and these are labour class, capitalist class and land owners. Marx has given difference in these three classes on the basis of means of income, profit and rent of land. But Marx’s this three classes system never came into being in England.

Marx has written that with the development of capitalism three classes system will change into two classes system and middle class will come to an end. About this he has written in Cfommunist Manifesto. Marx also wrote about other classes in specific society. He has divided the capitalist class into two sub groups and these are effective capitalists and smaller capitalists.

Effective capitalists are those capitalists which are bigger capitalists and industrialists which give work to thousands of labourers in their industries. Small capitalists are those small industrialists or shopkeepers whose business is at low level and they are not giving work to many labourers. They are doing most of their work themselves.

Here Marx again says that with the development of capitalism middle class and small capitalists will* come to an end and will join hands with labourer class. In this way, there will be two classes in society and that is capitalist class and labourer class. Relations between Classes. According to Marx, the capitalist class always exploits the labourer class and labourer class always fights for its rights.

That is why the relations between both the groups are of opposition. Yet this opposition between these groups will hide due to their mutual interests but this opposition is always there. It is not necessary that we can see this opposition directly or opposition never comes in front of us but they know about each other’s opposition.

According to Marx, the relations between the classes depend upon the mutual interdependence and conflict. We can take example of capitalist society in which two classes are there. First class is of capitalist class and second class is of labour class. These both classes depend upon each other for their existence. Labour class doesn’t have the ownership of forces of production.

It doesn’t have any other mean to earn its livelihood except selling its labour. Labourers sell their labour to the capitalist class and are dependent upon them. They give their labour to capitalist and for that capitalist gives money to labourers for their labour. With this money or rent of labour, labourer takes care of the needs of the family. Capitalist also depends upon the labour of labourer because without their work, production in his factory is not possible and accumulation of capital is also not possible.

In this way both these classes depend upon each other. But this dependency doesn’t mean that they have relations of equality. Capitalist class always exploits the labour class. They want to make things in their factory by giving less money so that they can earn more profit. Labourer wants more money so that he can take care of the needs of his family. Capitalist tries to sell his product with more value by paying less money so that he can earn more profit.

In this way conflict of interests is always there between both the classes. This conflict will give birth to communism later on in which there would be no opposition, there would be no exploitation and there would be no conflict of interests. This society will be classless society. Karl Marx has explained the conflict theory of stratification on historical basis.

Important things in the conflict theory of stratification of Marx are given below :
1. Two classes in Society. Marx was of the view that generally two types of classes exist in every type of society. First one is that which has all the means of production in its hands and this class is known as capitalist class.

Second class is that which doesn’t have any means of production and which earns money only by selling its labour. This class is known as labour class. First class exploits the other class. It means that capitalist exploits and labourer is being exploited by capitalist.

2. Right over means of production:
While explaining stratification on histrical basis Marx says that the stratification in society is based on the right over means of production. There exist two types of classes in every society on this base. First class is that which has the right over all the means of production. Second class is that which doesn’t have any right over means of production and which earns money by selling its labour.

3. Modes of production:
The nature of social stratification depends upon the modes of production. Position of that class is higher than other classes which has all the means of production. According to Marx, this class’ is known as capitalist or Bourgoisie. Second class is that which doesn’t have m^ans of production, which is not satisfied by its position and which wants to change its position. Marx has given it the name of labour class or proletariat class.

4. Human History-History of class struggle:
Marx was of the view that human history is the history of class struggle. We can take example of any society. Struggle in classs is going on, in every society, in one form or the other. In this way Marx was of the vew that two types of classes exist in all the societies- capitalist and labour class. Class struggle always goes on in both the classes.

There are many reasons of class struggle in both the classes for example too much economic differences between both the classes because of which class struggle is going on. Capitalist becomes rich even without doing any hard work and labourer becomes poor even after doing a lot of hard work.

With the passage of time, labour class makes its organization to meet its demands and this organisation does struggle with capitalist class to meet its demands. Result of this struggle between both the classes comes in the form of revolution which labour class does against the capitalist class.

After revolution, labourer class will eliminate the capitalist class and establishes its authority. Capitalist class tries to start anti-revolution movement against labourers but this movement will be suppressed and authority of the labourer class will be established. First of all communism and then the state of socialism will come in which every one will get according to his needs and ability.

There will be no class in society and this will be a classless society in which every one will get equal share. No one will be of higher or lower status and the authority of labour class will remain there. Marx was of the view that this state has not yet come but it will come very shortly and stratification in society will come to an end.

Max Weber gave the theory of stratification in which he explained class, status group and party differently. Weber’s theory of stratification is considered as practical and rational. That’s why his theory is given enough importance by American Sociologists.

Weber has explained stratification from three aspects and these are class, status and party. All these groups could be called as interest groups which not only can fight within themselves but they can fight even against each other. They tell us about a specific authority and are interrelated as well.

Now we will explain them one by one :
CLASS. Karl Marx has defined class on economic basis and in the same way Weber has also defined class on economic basis. According to Weber, “Class is a group of those people which are at equal status in structure of social economic opportunities and which live in same condition. These conditions depend upon their form and quantity of economic power.”

In this way Weber talks about a type of group in which a specific number of people have equal chances in life. Yet this concept of Weber is not very much different from Marx’s concept of class but Weber has imagined class as the group of people living in same economic conditions q,ot as a group of self-consciousness.

Weber has given three types of classes which are given below :

1. A Property Class
2. An Acquisition Class
3. A Social Class.

1. A Property Class:
A property class is the group whose position depends upon the fact that how much property it has?

This class is again further divided into two parts :
(i) The Positively Privileged Property Class. This class owns a lot of property and it lives on the income generated from its property. This class can keep monopoly over selling or buying of consumer goods, by collecting property or on taking education.

(ii) The Negatively Privileged Property Class:
Illiterate, poor, property less and people under debt are major members of this group. But there is one another group between these two groups and that is Privileged Middle class in which members of both the given classes are included. According to Weber, Capitalist is member of this group due to his privileged position and Labourer is its member due to his negatively4 privileged position.

2. An Acquisition Class:
It is that type of group whose position is determined by taking advantage from opportunities of services available in the market.

This group is of three types :
(i) The Positively Privileged Acquisition Class. This class keeps monopoly over administration of producer manufacturers. These factory owners are bankers, industrialists, financiers etc. These people not only keep control over administrative system but they exert influence on government’s economic policies as well.

(ii) The Middle Privileged Acquisition Class. This class belongs to middle class people in which small professional people, artisans, independent farmers etc. are included.

(iii) The Negatively Privileged Acquisition Class. People of lower classes are part of this group which include trained, semi trained and untrained labourers.

3. Social Class:
Most numbers of people are included in this group. This class observes definite changes due to progress made by different generations. But Weber does not explain social class according to privileges. According to him, people of labour class, lower middle class, intellectual class, property owner class are included in it.

According to Weber, members of class work with each other under specific circumstances and to this protest of doing work is being given the name of class action by Weber. According to Weber, feeling of mutually related gives birth to class action. Weber has not believed that the thing like class action could take place all the times.

Weber, was of the view that there is no class consciousness in class but its nature is completely economic. There is no possibility among them that they would struggle collectively to achieve their common objectives. A class is only a group of people whose economic condition is same in the market.

They can feel changes in their lives while collecting those things which have some respect in society and there is a possibility that they would collectively perform s,ome action. Weber was of the view that if it does so then class can take the form of community.

Status Group:
Status group is generally considered as opposite to economic class stratification. Class is only based on economic assumption which is a group of same interests due to market conditions. These are not statistical classes but these are actually those groups whose life-style is common, outlook towards the society is common and which keep unity among them.

According to Weber, there is some difference between status group and class. Each has its own style and people can be unequal among them. For example, teacher of a school. Yet his income might be 8-10,000 per month which is quite less in today’s age but his status is quite high due to his sacred profession.

But on the other hand any smuggler or a prostitute could earn lakhs in a month but their status group will remain low because their profession is not sanctioned by society. In this way difference is there between both the groups. Any occupational group can be called as a status group because in each type of profession, people get equal opportunities to earn money.

This group also leads to same life-style of people. Members of one occupational group remain near to each other, wear same type of clothes and even have same type of values. That’s why its members have quite a wide circle.

Party:
According to Weber, Party represents the determined interests associated with class status or a status group. This party enrolls those members, in any condition, whose ideology matches with the ideology of party. But it is not necessary that the party could become status party for them. Weber was of the view that Parties always want to keep control over power.

It means power should remain in their hands. Weber was of the view that yet parties are a part of political authority but even then power could be gained through various means like wealth, influence, pressure, rights etc.

Parties want to obtain power of State and State is an organisation. Each activitiy of the party is concentrated on the fact that how the power could be obtained ? Weber analysed the state and from here he gave the theory of Bureaucracy. According to Weber, parties are of two types.

First one is Patronage party in which there are no class rules, concepts, ideology etc. These are made for special purposes and could be left after the completion of objective. Second type of party is party of Principles which has clear and strong rules. These parties are not made for specific purposes.

Weber was of the view that there is quite much difference between these three i.e. class, status group, and party but the mutual relationship is always there among them.

Punjab State Board PSEB 11th Class Sociology Book Solutions Chapter 9 Social Structure Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Sociology Chapter 9 Social Structure

Sociology Guide for Class 11 PSEB Social Structure Textbook Questions and Answers

Answer the following very short answer questions in 1-15 words each:

Question 1.
Give the meaning of the term social structure.
Answer:
Systematic form of interrelated parts of society is known as social structure.

Question 2.
From which word the word ‘structure’ is derived ?
Answer:
The word ‘structure’ is derived from the Latin word ‘Staruere’ whose meaning is ‘building’.

Question 3.
Who was the first sociologist to use the term social structure ?
Answer:
Herbert Spencer was the first sociologist to use the term social structure,

Question 4.
Name the elements of social structure.
Answer:
Status and role are the elements of social structure.

Question 5.
Who wrote the book ‘The Principles of Sociology’?
Answer:
This book was written by Herbert Spencer.

Question 6.
What is Status ?
Answer:
Status is a position given to a person while living in society.

Question 7.
Name two types of social statuses.
Answer:
Ascribed status and Achieved status are the two types of social statuses.

Question 8.
Who gave the terms ascribed and achieved status?
Answer:
These terms are given by Ralph Linton.

Question 9.
Give two examples of ascribed status.
Answer:
Status of father and brahmin are the examples of ascribed status.

Question 10.
Give two example of achieved status.
Answer:
The status of Prime Minister and Deputy Commissioner are the examples of achieved status.

Question 11.
Define Role.
Answer:
According to Ogburn and Nimkoff, “Role is a set of socially expected and approved behaviour patterns consisting of both duties and privileges, associated with a particular position in a group.

Question 12.
Mention any two characteristics of Role.
Answer:
(i) Role is the functional aspect of status.
(iii) Role is always having social sanction.

Answer the following short answer questions in 30-35 words each:

Question 1.
Define social structure.
Answer:
According to Talcott Parsons, “ The term social structure applies to the particular arrangement of the interrelated institutions, agencies, social patterns, as well as the statuses and roles which each person assumes in the group.”

Question 2.
Give two points of similarities between status and role.
Answer:

• Status and role are the two sides of same coin.
• Status is the position of an individual in society and role is the functional aspect of status.
• Both status and role change with time and circumstances.

Question 3.
Give the diagrammatic representation of structure of family.
Answer:

Question 4.
Distinguish between ascribed and achieved status.
Answer:

• One gets ascribed status according to his birth but one gets achieved status according to his ability.
• There are many bases of ascribed status but the only base of achieved status is one’s hard work.

Question 5.
In what ways are roles learned behaviour ?
Answer:
It is true that roles are learned behaviour as they are the collection of rules which are learned either through socialization or observation. After learning, whatever meaning man gives to it is a social role.

Question 6.
Write a short note on status and role.
Answer:
status:
Status is a position given to a person while living in society.

Role:
According to Ogburn and Nimkoff, “Role is a set of socially expected and approved behaviour patterns consisting of both duties and privileges, associated with a particular position in a group.

Question 7.
What is Status ?
Answer:
The position in a group, given to an individual, is known as social status. It is the position which one gets through his gender, age, birth, occupation, activities, patterns of work etc. For example an officer is respected by every one due to his post. Specific patterns related with his activities are known as status.

Question 8.
What is role set?
Answer:
While living in society, an individual gets many statuses. The collection of roles related with all such statuses is known as role set. For example students of 11th class of any school need to meet many persons in their daily routine and have to behave differently with them. Collection of roles related with all is known as role set.

Question 9.
What do you mean by role conflict ? Give its example.
Answer:
Every individual has many a status and a particular role is attached with each status. One has to fulfill all the roles attached with him. When he is unable to maintain balance with all of them and is not in a position to do justice with all of them, it is known as role conflict.

Answer the following short answer questions in 75-85 words each:

Question 1.
State the three characteristics of social structure.
Answer:
(i) Different social structures of different societies : Social structure of each society is different because the social life of different parts of a society is different. Every society has its different institutionalised rules. That’s why structures of all the societies are different.

(ii) Social structure is abstract : Social structure is abstract because the units with which this structure is formed like institution, association, norms etc. all are abstract. They don’t have any concrete form, we can only feel them. That’s why they are abstract.

(iii) Formed due to interactions : No proper planning is made to keep all the social units in a system. It is developed due to human interactions. That’s why no conscious efforts are required for its formation etc.

Question 2.
What is ascribed status ? Give its example.
Answer:
Ascribed status is the status which a person gets without doing any effort or hard work. Like, Brahmans have the higher status in caste system of Hindu society. Person gets social status according to his caste in which he was born. Sex, caste, birth, age, kinship all are ascribed status which a person gets without any effort.

Question 3.
Role is an element of social structure. Discuss in brief.
Answer:
Sub groups are the units of social structure and in these groups, members are given roles according to definite rules. Interactions take place among humans and to clarify them, roles are given to individual. Role is the behaviour of an individual in a particular situation which is associated with his status. If any change comes in social structure, change often comes in the status and role of an individual. Due to these roles, people establish contacts with each other and consequently social structure is maintained.

Question 4.
Status is an element of social structure. Discuss.
Answer:
There is no denying the fact that status is an element of social structure. Sub-groups are the units of social structure and every one gets many a status in these groups. People mutually interact and to clarify them, many status and roles are given to the people. When one gets any status, he needs to behave differently in different circumstances. If any change comes in social structure, change also comes in the status of people. Due to these statuses, people establish mutual relations and social structure is maintained.

Question 5.
Discuss how status and role are interrelated ?
Answer:
It is true that status and role are intererelated. Actually they are two sides of the same coin. If out of these two only one is given, other is of no importance. It means rights are given but not responsibility or vice versa. In the absence of one, other cannot work properly. If any one is given the status of an officer but he is not given any responsibility, the officer is of no advantage for people. If any one is given responsibility but no status is given, he will not be able to fulfill his role. So, they both are deeply related.

Answer the following short answer questions in 250-300 words each:

Question 1.
Define social structure and discuss its characteristics.
Answer:
Society is not an unbreakable system. Society is made up of many parts. These parts of society are interrelated with each other by doing their respective functions and they produce one type of balance. In the words of Sociology this balance is known as social system. On contrary to that when these different interrelated parts join each other and make a structure then this structure is known as social structure. In short the meaning of structure is the collection of those units or parts of society which are interrelated with each other.

(i) According to Maclver, “Social structure is abstract and many groups like family, class, caste and community come in this.–MacIver has accepted the stability and changing nature of social structure. According-to Maclver, “For a while the social structure itself is unstable and changeful, it has a definite character at every stage and many of its major elements have shown greater persistence of type through change.”

(ii) According to Morris Ginsberg, “Ginsberg has not differentiated between social structure and organization. He used the word social structure for systematic relations. According to him humans combine themselves with groups, institutions, associations etc. to achieve any purpose with which social structure is formulated.

According to Ginsberg, “The study of social structure is concerned with the principal forms of social organization i.e. types of groups, associations and institutions and the complex of these which constitute societies…full account of social structure would involve a review of the whole field of comparative institutions.”

(iii) According to Harry M. Johnson, “The structure of anything consists of relatively stable inter-relationship among its parts, moreover the part itself implies a certaip degree of stability since a social system is composed of the inter-related acts of people, its structure must be sought in some degree of regularity or recurrence in these acts.”

1. Different societies have different social structure. Every society has its own different rules because the relations which exist in different units of society have different place in social life. Except this social structure in different times is different. This difference is so because the relations which exist in units of society are different in different societies. It is related with specific society. That’s why social structure is related with specific society. Its different units like family institution, group, caste etc. have different forms.

2. It refers to the external aspect of society. Social structure is not related to internal system of society but is related with external aspect of soceity. For example the way in which different parts of human body make the full body and make the external structure of body, in that same way different parts of society combine and form the external structure of society. Hands, legs, head, nose etc. only show the external parts of body.

3. Social structure is abstract. Social structure is the sequence of interrelations of different units of society. Groups, castes, institutions, categories etc. are these units. This sequence of social structure doesn’t have any concrete form. That’s why it cannot be touched and seen. It can be felt only. Different relations which exist in different units are without any form and that’s why structure is abstract.

4. Social structure is changeable. Brown was of the view that mobility and continuity exist in social structure. It is not static. The way in which physical body changes in the same way change comes in structure of society but it doesn’t mean that the basic elements of structure also change.

5. Hierarchy of sub-structure in a structure. Our physical body is made up of many small structures, like backbone, neck, hands, feet etc.All these small structures form a big structure. In the same way we can take structure of educational institution. Staff, Principal office etc. are sub-structures which form the complete structure of educational institutions. In the same way in society, different categories and layers are there which jointly make a social structure.

6. Every unit of social structure has a definite position. Our social structure is made up of various units. Their position is definite and limited. No unit can take place of the other and cannot go beyond its limits. For example religion, school, family, caste etc. are different units of social structure. All of these have different place in social structure.

Religion never does function of school, school never does function of family etc. because every unit works in its limited area. If any unit comes out of its limits and works in the area of other unit then it will not be accepted by society. Every unit has different and definite place in society in different times. That’s why social structure is maintained.

7. Social structure is the product of social interactions. Development of social structure in every society is the product of social interactions. Different units of social structure are interrelated with each other. That’s why single unit is of no importance. Social interactions are very helpful in giving sequence to family, group, institution, association etc.

Question 2.
Which system helps in the maintenance of social structure ?
Answer:
In social structure, all the human beings have organised themselves into different associations to pursue some common goals. Such goals can be achieved if the social structure is based upon operational systems which help in its maintenance. Few of such systems are given below :

1. Normative System : Normative system presents some ideals and values in front of members of society. Members of society attach emotional importance to these values and ideas. Different groups, associations, institutions, communities etc. are interrelated according to norms and values. Different members of society perform their roles according to these norms. .

2. Position System : Position system refers to status and roles given to different individuals. Every one has unlimited and multiple aspirations and expectations. Different individuals in different societies have different status. For example, an individual in a family is a father, son, brother, uncle, husband etc. When he is in conversation with his wife, he acts as her husband and he forgets about other status. In the same way, while interacting with his son, he acts like a father. In other words, for the smooth functioning of social structure it is a must to properly allocate status and roles in society.

3. Sanction System: For the proper implementation of rules, society also provides a sanction system. To maintain balance between different parts, it is necessary to properly implement norms and values. Sanction can be negative as well as positive. Those who follow norms and values are rewarded by society and those who do not follow them are punished. Stability of social structure depends upon the effectiveness of sanction system. ‘

4. System of Anticipated Responses : A system of anticipated responses expects the individuals to participate in the social system. With their participation, social structure sets in metiori. The successful working of social structure depends upon the realisation of duties by the individuals. Members of society internalise the sanctioned behaviour with the help of socialisation with which they anticipate the experted behaviour of others in different situations. So the system of anticipated responses becomes one of the reason of stability-of a social structure.

5. Action System : Talcott Parsons gave special-stress on the concept of social action. He was of the view that society (web of social relationships) has emerged out of the action and interactions of the individual. Thus, the action system becemes one of the important elements that makes society active and sets the social structure in motion.

Question 3.
What is social structure ? What are the elements of social structure ?
Answer:
Our society is the web of social relationships. It has different units which are related with each other. They cannot do anything without each other’s help. It means they have the sense of cooperation These units are groups, institutions, associations, organizations etc. These units don’t have any independent existence, in fact when they relate with each other then they take the form of one structure. One sequence is there in their relations. With this sequence our society works properly.

We clarify the words sequence and arrangement pattern in an easy way with another example. If desk, bench, black-board, teacher, principal, peon, student and building can be kept at one place then it cannot be called as school. It can be called as school at that time when these different units will work in proper sequence with a proper arrangement pattern and on their definite place. Then only it can be called a school. We can take another example that we buy cloth for the shirt then it cannot be called as shirt until it doesn’t have any shape.

In this way every society has different social structure because there is always some difference in the units of the structure which makes the social structure. Our society is changeable. Time to time change comes in this due to natural forces or due to inventions by humans. That’s why social structure also changes. Its units are not concrete because we cannot touch them.

Yet these units of social structure like family, religion, institution, association, economy etc. are like each other but their types are different. Like any society is Patriarchal and any society is Matriarchal. It means that except some similarity its types are different. In short we can say that social structure it that systematic arragngement through which social relations can be tied in one thread.

Elements of Social Structure:
According to Harry M. Johnson and Talcot Parsons, there are four main elements of social structure which are given below :
1. Sub-Groups. According to Johnson and Parsons, every social structure is made up of units or sub-groups. Bigger group is made up of some sub-groups.

For example under educational group, school, college, university, family, religion etc. all these sub-groups are included which are related with educational group in one way or the other. Humans are getting roles and status through these groups and sub-groups. Place of every status and role is definite in the society.

Humans get birth and dying in society but these roles and status are definite. Humans get them after birth and after their death, other humans get their place. For example if principal of any school dies then other person takes his responsibilities by taking his status and role by becoming principal of that school. It means that sub-groups are short and permanent. They never come to an end. Their members are changing due to birth and death. Family, school, college etc. remain at their same place as they were 50 years ago but the members working in it are changing with time.

2. Roles. In sub-groups of social structure, humans are related to their roles through definite patterns. Society is the web of social relationships. Interactions take place between humans and groups to develop these relations. To clarify the activeness of these interactions, status and roles are defined.

Role is related with that behaviour of person which humans perform in specific condition and whichever function person has to perform related with specific status, are determined by social sanctions. Roles and status of members of society are changed when changes come in social structure. Social structure is maintained with these roles and definite social relations.

3. Social Norms. Roles and sub-groups are related with social norms because functions of humans are determined by these norms. That’s why roles and sub-groups become static. Social norms have many rules and sub-rules. These are those sanctioned ways of individual behaviour with which social structure is being formulated. Social ideals are related with these norms.

Humans would not be able to know about their responsiblities in the absence of these norms and our social structure cannot be maintained in its absence. For example, humans which are getting roles of father- son, mother-daughter, brother-sister, teacher-student etc.

are told about their responsibilities through these social norms. That’s why these are very important for social structure. Behaviour of humans is being regulated and directed by social norms in specific conditions with which roles and sub-groups are maintained. It is the third important element of social structure.

4. Social Values. According to Harry M. Johnson, “Value may be defined as a conception or standard cultural or merely personal, by which things are compared and approved or disapproved relative to one another held to be relatively desirable or undeiable, more meritorious or less, more or less correct. All kinds of things may be evaluated, feelings, ideas, actions, qualities, objects, persons, groups, goals and means.”

According to Johnson, values are measured because through them social norms are being evaluated. They appeal to the feelings of the members of society. Whenever person decides about any thing then he is definitely under the effect of his feelings. According to Johnson, everything is evaluated through values.”

The word ‘norm’ is used for specific behaviour pattern but values are simple measurements. These can be called as the norms of higher level. Social values are very important for social system and to stop social disorganization. Feelings of group are also related with these values. They also have functional relation between them because of which web of social relationship never breaks up.

With this our social structure and social system are maintained. With them balance is generally established between the feelings of human and group with which values are used as measures for the selection of behaviour. Human functions are divided in good or bad, high or low classes through these social values.

Question 4.
Define Status. Write its characteristics in detail.
Answer:
Society is the web of social relationships. The system of society is maintained through relations. No society can live without system. So to maintain this social system, every person in society is given one specific position. It is necessary for the maintenence of social system and organization that different persons should work according to their status in an efficient way and society expects from them that they should perform their duties in a proper way.

In this way every person has a position or status in society. Some persons are at higher posts and some persons are at lower posts. Status is the social position of a person which a person gets while living in society. Every person is related with some status.

All these statuses are the part of social position of a person because of which all these are the basis of social system. We can come to know about importance of status by comparing it with other status. Society has been divided into different parts due to status and as a result identity of person establishes in society.

In simple words, word ‘status’ is taken as social prestige. Higher status leads to more prestige. Social position of a person depends upon the evolution done by society. In sociology, meaning of status is taken by the position of person in society. There are many statuses in society and person gets some of them. Number of status, which a person gets, depends upon his membership of different groups.

In this way we can say that status is the position of a person which is given to him by organisation of group. Person gets status due to his age, gender, equality, birth, duty and his relations with other members. Every person has got some status like status of father, son, uncle, peon, officer etc. Person has to do some work according to his status. In this way we come to know about status by its functions. Person gets different status in different situations.

Definitions of Status:

•  According to Secard and Berkman, “Status is the worth of a person as estimated by a group or a class of persons.”
• According to Kingsley Davis, “Status is a position in the general institutional system recognized and adopted by the entire society, spontaneously evolved rather than deliberately created, rooted in the folk ways and customs.”
• According to Linton, “The place in a particular system which a certain individual occupies at a particular time will be referred to as his status with respect to that system The role is what the individual has to do in order to validate his occupation of the status.”
• According to Maclver and Page, “Status is the social position that determines for its possessor apart from his personal attribute or social service, a degree of respect, prestige and influence.”

In this way on the basis of these definitions we can say that whichever position a person gets in specific group is his status. Because status is in group, that’s why number of status depends upon the number of groups of which a person is the member. In this way status is the social position of a person which a person gets due to his abilities, birth, gender, age, qualities etc. Person has to do a number of works related with his status. Person has to obey the orders of person of higher status than him. It maintains the social system and social discipline. Social prestige is also related with every status.

Characteristics of Social Status:
1. Every status has a place in society : Every status is known by the related rights, duties, norms and prestige of the group because a person has to do functions related to that. Like status of high ranked officer and low ranked officer is different in an office and this status can be known on the basis of group.

2. Status is determined by the culture of the society : Status is determined by the specific cultural values of a specific society that which status should be given to which person and what would be the related rights and duties. Person has to do functions according to social status. Like an elder member of the house father gets status and related roles automatically. All in all we can say that the status of every person is determined by the culture of that society.

3. Status is always comparable : Status is always comparable because we can come to know about our status by comparing it with the status of another person. If there would be no comparison of two status then how can we come to know that which status is higher or lower. For example, the status of owner of a factory is definitely higher than the status of a manager and we can come to know about this only by comparing it.

4. Every status has psychological base : Person always does hard work to get higher status because of which feelings also come in person. Respect and disrespect are also related with every status and these are related with psychological sector of person. When person achieves that social status with hard work then he gets mental satisfaction. In this way status has a psychological base.

5. Sthtus is of two types : Two types of status are there for every person. First one is Ascribed Status which a person gets without any effort and hard work. For example son, elder brother, elder sister etc. Second type of status is Achieved Status and this type of status person achieves with his hard work while living in society like officer, clerk etc.

6. Role is determined by status : Any role is definitely related to every status and this role is determined on the basis of social values. Person performs his role according to his status. Some statuses in society are very important and the roles of these statuses are also very important which the relative person has to perform. For example D.C. or S.S.P.

7. Similarity of status but not of functions : Many times it happens that many statuses in society are equal but their functions are different, for example, professors of any college. Status of all of them is same but their function, means subject of teaching is different. They teach different subjects or do different functions but their status is same. There are many engineers in a factory but their functions may be different.

Question 5.
Define role. Write its characteristics in detail.
Answer:
Every person has definitely any status in the society and some demands and responsibilities are also related to that status. These demands tell us that what a person has to do. Person achieves many status on the basis of ability, age, caste, sex etc. and person has to do a number of functions on the basis of tradition of that status. In this way it is expected from the person that what specific function he has to do in specific condition and this function is his role.

Importance of social role is at that time when person performs relative role. In this way status and role are the two sides of the same coin. Humans are differentiated on the basis of their functions. For example doctor, teacher, engineer etc.

It means functions of person are divided on the basis of different sectors. In this way person is given any function in social status on the basis of rules, laws or traditions. This function is role. Role is related with every status.

In this way we can say that every status has a set of relative functions. This set of functions is known as role. Person is always there on any status and some responsibilities are also there related with those status. The collection of those responsibilities is known as role.

Role of every one is different. In this way roles tell the person about that behaviour which is expected from the person who has that status. Role and status cannot be differentiated. Role is related with status. To know the more clear meaning of status now we will see the definitions of role.

Definitions:
1. According to Ogburn and Nimkoff, “A role is a set of socially expected and approved behaviour patterns, consisting of both duties and privileges, associated with a particular position in a group.”

2. According to Ginsberg, “Status is a position and a role is the manner in which that position is supposed to be filled.” .

3. According to Fitcher, “When a number of interrelated behaviour patterns are clustered around a social function we call this combination a social role.”

4. According to Kingsley Davis, “Role is the manner in which a person actually carries out the requirements of the position.”
In this way on the basis of these definitions we can say that the meaning of role is related with the specific behaviour of a person which he does in specific conditions.

Role is the way with which person fulfils his responsibilities or functions related with his status. For the maintenance of our social system it is necessary because society cannot run without doing work. In this way role is the accepted way in which a person performs his duties related with his status and uses rights of his status.

Characteristics of Role:
1. One person has many roles. A person gets many statuses while living in society and automatically gets many roles related with those status because he is able to perform those responsibilities or roles. For example, role of father and husband in family, role of clerk or officer in office, role of chairman in club etc. In this way one person performs many roles.

2. Role is determined by our culture. Because a person has many statuses, that’s why he needs to perform roles related with status according to the relative rules, laws, values and traditions. These laws, rules, traditions and values are the part of our culture. That’s why role is regulated by our culture.

3. Role is functional. Role always has one functional aspect. The meaning of functional aspect is that to do work related with that status. Person has to do work related to the status which he has and this is the functional aspect of role.

4. Role is determined by the social sanctions. The nature of humans is not same. If the members of the society will be allowed to work according to their wish then no work would be done in an efficient way. It is so because some will not be able to do that work and some will work against the values of society. That’s why only those roles are accepted by society which have social sanctions. These are determined by our culture that which role would be performgd by which person.

5. Different importance of different roles. S.ome roles in society are very important because they are related with any specific aspect and for them, person needs special training. That’s why they have more importance. In the same way some roles are of less importance because their status is of less importance and there is no need of special training for them. For example, there is a great difference between the role of the I.A.S. officer and a clerk.

6. Importance of ability in Role. Individual’s ability is of great importance in performing any role. It is so because it is not necessary that he can perform his role in proper way. One person performs one role successfully and in another he fails. It means that person can perform his role in right or wrong way according to his ability.

Punjab State Board PSEB 11th Class Sociology Book Solutions Chapter 5 Culture Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Sociology  Chapter 5 Culture

Sociology Guide for Class 11 PSEB Culture Textbook Questions and Answers

Answer the following very short answer questions in 1-15 words each:

Question 1.
State the basic elements of culture.
Answer:
Traditions, social norms and values are the basic elements of culture.

Question 2.
Who called culture a ‘total way of life of the people?
Answer:
These words are of Clyde Kluckhohn.

Question 3.
In what way is culture transmitted in non-literate societies?
Answer:
Because culture is a learned behaviour, that’s why in non-literate societies culture is transmitted through learning.

Question 4.
Give a broad classification of culture.
Answer:
Culture is of two types-material culture and non-material culture.

Question 5.
Name few examples of non-material culture.
Answer:
Views, norms, values, habits, ideals, traditions etc.

Question 6.
Who gave the theory of cultural lag?
AnsweR:
The theory of cultural lag was given by William F. Ogburn.

Answer the following short answer questions in 30-35 words each:

Question 1.
What is culture ?
Answer:
Our ways of living, philosophy, feelings, views, machines; tools etc. all material and non-material things and this is culture. All these things are produced and used by group. So, culture is that on which we work upon, think on it and keep it.

Question 2.
What is cultural lag ?
Answer:
Culture consists of two parts-material and non-material. Due to new inventions, change comes very quickly in material culture but our views, traditions etc. i.e. non-material culture does not change very quickly. As a result, gap is created between the two which is known as cultural lag.

Question 3.
What are social norms ?
Answer:
Each society makes certain rules for the behaviour of its members and these are known as norms. So, norms are few directions for behaviour. Norms regulate and direct the behaviour of individuals. They are very important aspects of culture.

Question 4.
What are the central values of modern India ?
Answer:
Democratic system, equality, justice, freedom, secularism etc. are the central values of modern India. Each society has its own central values. Small communities stress on any specific value but large societies stress on universal values.

Question 5.
Mention some values of traditional Indian society.
Answer:
Each society is having different values. One society streses on one value and other society stresses on the other. Important values of traditional Indian society are detachment, materialism and religion, attainment of four purusharthas, dharma, artha, kama and moksha.

Question 6.
How is the cognitive component of culture expressed ?
Answer:
The cognitive components of culture are expressed with the help of imagination, literature, art, religion and scientific theories. Views are expressed in literature and in this way the cognitive aspect of culture is preserved.

Answer the following short answer questions in 75-85 words each:

Question 1.
How is culture a total way of life of the people ?
Answer:
There is no denying fact that culture is a total way of life of the people. Whatever we have is our culture. Our views, ideals, habits, clothes, money, property etc. and whatever humans have achieved till today is our culture. If we separate all these from human life, nothing will be left in it and then human life will reach the level of early man. Yet each society has its different culture but they have certain elements which are common everywhere. So, we can say that culture is a total way of human life.

Question 2.
Write a note on material and non-material culture.
Answer:
The meaning of material culture is by that culture in which all the man made things are included. This culture is concrete because we can see or touch it such as scooter, T.V. table, chair, pen, bus, car etc. All these things are concrete and thus a part of material culture.

In non-material culture, all the things are included which are abstract in nature. We can neither see non touch them. We can just feel them such as traditions, customs, values, skills, norms etc. All such things are abstract so non-material culture is abstract in nature.

Question 3.
Discuss in brief the basic elements of culture.
Answer:

1. Customs and traditions are the types of organised social behaviour which are used again and again. They are permanent ways of.behaviour. Each society has its own customs and traditions.
2. Norms are also very essential elements of culture. It is expected from each person to behave in a specified way. Norms are the established ways of behaviour shared by the members of a group.
3. Values are also its inseparable part. Each society has its own values and it is expected from every one to accept them.

Question 4.
‘Culture is learned behaviour’. Explain the statement with suitable examples.
Answer:
There is no denying the fact that humans learn their culture. It is not a biological trait which one gets from his parents in the form of genes. An individual learns culture gradually through the process of learning. No one is having views and ideas when he takes birth but all these he learns while living in society after interacting with others. Every type of action or activity is learned only while living in society. So, it is clear that culture is learned behaviour.

Answer the following short answer questions in 250-300 words each:

Question 1.
How does the understanding of culture in social analysis differ from the everyday use of the word ‘culture’ ?
Answer:
The meaning of everyday use of the word ‘culture’ is very much different from the meaning given by sociologists. In every usage, culture is limited only to art or life style of different countries. But the meaning given by sociology is very much different. Sociology says that whatever man has achieved from his early life till today is his culture. Traditions, ideas, norms, values, mores, chair, table, car, pen, books, written knowledge etc. Whatever man has achieved only while living in society is his culture, So, the meaning of culture given in both the senses is different from each other.

Question 2.
What do you mean by culture ? Highlight the characteristics of culture.
Answer:
The most important thing which differentiates humans from animals is the culture which humans have but animals don’t. The most important thing which human has is his culture. If the culture would be taken away from them then nothing would be left with them. In all the organisms of the world, only humans have the capability to make and preserve their culture.

Culture comes out of the interactions of humans. Culture not only comes out of human interaction but it shows the way to future’s human interactions. Culture helps in the formation of personality of a man and helps him to live in society. Culture makes that type of atmosphere in which man becomes capable of doing functions of society. In this way man and culture are connected very deeply with each other because culture differentiates man from animals.

Culture, is the mest important feature of human society. According to Aristotle, “Man is a social animal.” If we will describe the differences between man and animal then this culture will be the decisive factor of difference between them. Man himself creates his culture and has the capacity to preserve it for its future generation. Actually it is the product of human interactions #nd on the basis of this culture we can differentiate one society from the other.

We cannot understand human society without understanding the culture because culture exerts a lot of effect on the social life. Cultural factor is also an important factor of social change. In this way we can say that man is not only a biological man but is a cultural man as well. In common language culture is equated with education means literate person is a cultured man and illiterate person is a non-cultured man. But this meaning of culture is not correct. Sociology takes its meaning in very wide sense. According to sociologists any thing which man has made to fulfil his needs is culture.

Definitions:
1. According to Maclver and Page, “It is the expression of our nature in our modes of living and thinking, in our everyday course, in art, in literature, in religion, in recreation and enjoyment.”

2. According to Bierstedt, “Culture is the complex whole that consists of everything we think and do and have as members of society.”

3. According to Ogburn and Nimkoff, “It is that part of man’s total environment into which he alone is born. It consists buildings, tools, wearing apparel, art, science, religion and all the ways of doing things which man learns.”

4. According to Majumdar, “Culture is the sum total of human achievement, material as well as non-material capable of transmission, sociologically
i.e. tradition and communication critically as well as horizontally.”

5. According to Lundberg, “Culture refers to the social mechanism of behaviour and to the physical and symbolic product of these behaviours.”
From the given definitions it is clear that all those things are included in culture which a man learns while living in society like art, law, feelings, customs, ways of wearing, eating, literature, knowledge, belief etc.

All these things are the part of culture and they do not work separately but they work with each other and form an organization. This organization is known as culture. In short, the things which a man has learnt and whatever he has got from his ancestors as heritage is known as culture. In heritage tools, ways of behaviour, ways of science, ways of doing work are included.

Functions or Characteristics of Culture:
1. Culture is transmitted from generation to generation. Culture is transmitted from one generation to another because a child learns many things from the behaviour of his parents. Man learns a lot from the achievements of his ancestors. No one wants to start any thing from the beginning and that’s why he takes care of that work which his ancestors have done.

This transmission is going on from the ages and that’s why every one gets separate personality. No one brings any thing with his birth. He needs to learn every thing by living in society with his parents, grandparents etc. In’this way culture is transmitted from one generation to another.

2. Culture is social. Culture cannot become the personal property of an individual. It is social because neither one man can make the whole culture and nor it is property of anyone. When any one invents any thing then that invention is not his personal thing but becomes property of society because that thing will be used by the whole society.

In this way different things of our culture are used by society. Any thing can be called a part of the culture at that time when that thing will be accepted by most of the people of society. In this way universality of that thing-is an essential element of culture. So culture is not individual but is social.

3. Culture can be learned. Culture is learned by humans. It is not a biological quality which a person gets from his parents by birth. Man learns culture by socialization. No one brings thoughts and ideas by birth but he learns them by interacting with other persons of society. Every type of work is learned by society. From this it is clear that culture is a learned behaviour.

4. Culture fulfills needs of society. If any thing is invented then that thing is invented because man needs that thing. In this way every thing of culture comes out so that the needs of man could be fulfilled. Why man learnt to grow wheat, because he needs wheat for his hunger. In this way man learnt to grow food and this learned behaviour is transmitted from generation to generation.

Needs are not only biological but are sociocultural also. With hunger, man needs love and sympathy which a man learns while living in society. In this way different parts of culture fulfil different needs of society. Whichever part of culture is unable to fulfil the needs of society, gradually it comes to an end.

5. Changes often come in culture. Culture never stops at one place but often changes because nothing is unchangeable in the world. Change is law of nature and if change is necessary then culture is also changeable. Culture fulfills all the needs of society which generally change with the passage of time because situations are not the same all the times.

With the change in situations, needs also change which means, the methods of fulfilling those needs also change. For example during earlier times agriculture was done with old means like plough but with the increase of population, needs were also increased and that’s why now agriculture is being done with tractors and combines to fulfil the increased needs. So with the change in situation, culture is also bound to change.

6. One culture consists of many cultures. In every culture we can see some common norms, traditions, feelings, rituals, behaviour etc. but with that we can see many types of ways of eating, wearing, ways of living, behaviour, etc. From this it is clear that one culture consists of many cultures. For example we can see many subcultures in Indian culture because every one has its own ways of living, behaving, eating etc. from which it is clear that one culture has many cultures.

Question 3.
Explain the two types of culture in detail.
Answer:
Culture is an important factor for social change. With the change in culture, society also changes because it is the social heritage of society. Famous sociologists Ogburn and Nimkoff,’in their book ‘Hand Book of Sociology’, have given two types of culture and these are :
(1) Material Culture
(2) Non-material Culture.

1. Material Culture:
Material culture is artificial culture. Its main feature is that all the things made by man are included in this. Material culture is related to concrete things. We can touch and see all the things of material culture. For example machines, tools, means of transport, books, phone, etc. Material culture is related with inventions of man.

New technological knowledge is also included in material culture. Everything is included in this type of culture which is made, changed and transmitted till today. These material aspects of culture help its members to define their behaviour. For example the people engaged in agriculture have occupation but they use different implements and tools. All these are the‘‘parts of material culture.

2. Non-material Culture:
Important feature of non-material culture is that it is abstract. Abstract means those things which we cannot touch, and see. We can only feel them. For example religion, traditions, rituals, customs, art, literature, music, values, ideas etc. are included in non-material culture. According to Ogburn and Nimkoff, culture is divided in two parts for the easiness of subject or just for analytical purposes.

Question 4.
Write a detailed note on cultural lag.
Answer:
First of all the concept of cultural lag was used by Ogburn to understand the problems of society and conditions of conflict. Ogburn was the first sociologist who has given the detailed meaning of the concept of Cultural Lag. Yet other sociologists like Spencer, Sumner, Muller etc. have also used the concept of cultural lag in their writings but Ogburn has used this concept in his book ‘Social Change’ to understand social disorganization problems and conflict. In sociology, this concept was accepted widely.

Meaning of Cultural Lag. According to Ogburn and Nimkoff, change in different parts of culture never comes with the same speed. The speed of change of one part is more as compared to the other. But culture is a system. It is made up of many parts. Its different parts are inter-connected and inter-related. This system of culture can be maintained if the change in all arts of culture will come at the same speed. Actually what happens is that if one part of culture changes due to any invention then another part of the culture, which depends upon that part, also changes. But the change in the second part comes very late.

How much time will this second part take, depends upon the nature of the second part. This lateness goes on for many years because of which problem comes in the system. This lag in different parts of culture is known as Cultural Lag. According to Ogburn, “The thesis is that the various parts of modern culture are not changing at the same rate, some parts are changing much more rapidly than others, and that since there is co-relation and inter-dependence of parts, a rapid change in one part of our culture requires re-adjustments through other changes in the various co-related parts of culture. where one part of culture changes first, through some discovery or invention and occasional changes in some part of culture-dependent upon it, there frequently is a delay in the changes occasioned in the dependent part of the culture.”

The meaning of lag is to stay behind. Ogburn has given example to explain the meaning of ‘Lag’. According to him, anything is made of two parts. If change comes in one part of that thing then this change will definitely affect the other parts. This part, which is affected by that change, slowly and slowly changes automatically. These changes come slowly and slowly take some time. This difference of time is known as lag or to stay behind. Ogburn has explained the concept of cultural lag in this way.

According to him, culture has two parts that are interrelated. If ally change comes in one part then the second part is bound to be affected by that change. This second part slowly and slowly adapts itself to change and makes itself according to that change. But this adaptation takes some time. This difference of time, which is there between ‘change and adaptation, is known as cultural lag. When any part of culture moves forward with some development or invention and the second part lags behind then we can say that cultural lag exists.

According to Ogburn, culture has two parts (1) Material Culture (2) Non-material Culture. In material culture, all those things are included which we can touch and see like a machine, table, chair, book, T.V. scooter, etc., and in non-material culture all those things are included which we cannot see and touch, only we can feel them. For example, habits, thought, behaviour, feelings, customs, etc. Both parts are closely interrelated. If change comes in any part then the second part is bound to change.

This law is also applicable to material and non-material cultures. Changes often come in material culture and these changes come very fast because of new inventions. Material culture changes very fast but the speed of changes in non-material is very slow. That’s why because of rapid changes material culture moves forward but non-material culture, whose speed is very slow, lags behind. In this way, the lagging behind of the non-material culture from the material culture is known as cultural lag.

According to Ogburn, change comes in material culture with great speed because people want to use material things in a proper way. To use material things we need money and there is no need to move away from traditions and thoughts. For example, we are ready to buy Fridge, T.V., Scooter, Car, etc. but are not willing to change our customs and traditions. With one more example everything will be clear.

Punjab State Board PSEB 11th Class Sociology Book Solutions Chapter 1 Emergence of Sociology Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Sociology  Chapter 1 Emergence of Sociology

Sociology Guide for Class 11 PSEB Emergence of Sociology Textbook Questions and Answers

Answer the following very short answer questions in 1-15 words each:

Question 1.
Who is regarded as the ‘Father of Sociology’?
Answer:
Auguste Comte is regarded as the ‘Father of SocioloH’

Question 2.
Name the two vital factors for the establishment of Sociology as a separate social science.
Answer:
French revolution, progress of natural sciences, industrial revolution and the process of urbanisation are the vital factors for the establishment of Sociology as a separate social science.

Question 3.
From which two words the word ‘Sociology’ came and in which year the subject Sociology emerged ?
Answer:
The word ‘Sociology’ came from the Latin word ‘Soeio’ means society and the Greek word ‘Logos’ which means study. The subject of Sociology
emerged in the year 1839.

Question 4.
Name the two schools regarding the scope of Sociology.
Answer:
There exist two schools regarding the scope of Sociology and these are Formalistic school and Synthetic school.

Question 5.
What is industrialisation ?
Answer:
Industrialisation is that age of social and economic change which converted human society from rural to industrial.

Question 6.
Name two scholars who contributed in the development of Sociology in India.
Answer:
G.S. Ghurye, Radha Kama! Mukherjee, M.N. Srinivas, A.R. Desai etc.

Answer the following short Answer Questions in 30-35 words each

Question 1.
What is the meaning of Sociology ?
Answer:
Science of society is known as Sociology. Groups, institutions, associations, organisations, interactions of individuals are studied scientifically in Sociology. In simple words, ‘Sociology’ is the scientific study of Society.

Question 2.
State two important changes brought about by the Industrial Revolution.
Answer:
(i) Due to the industrial revolution, the production of goods moved to large industries from homes where goods were produced on a large scale.
(ii) Urbanisation also increased and many problems originated in cities such as more population, pollution, traffic, crimes etc. ‘

Question 3.
What is Positivism ?
Answer:
The concept of positivism was given by Auguste Comte. According’ to him, positivism is a scientific method in which there is no place of imagination while understanding and defining any subject matter. In this, every thing about any subject is understood with experiment, classification, comparison and historical method.

Question 4.
What is Scientific method ?
Answer;
Scientific method is a method to attain knowledge with the help of which study is conducted in a scientific way. It is a collective effort which collects different phenomenon with which science is formed.

Question 5.
Define objectivity.
Answer:
When any social scientist studies without any partiality, it is known as objectivity. It is very important for a social scientist to remain objective because in its absence, his study can become biased and will become useless.

Question 6.
Discuss the issue of the hope and subject matter of Sociology.
Answer:
There prevail two schools about the scope of sociology. First school is the Formalistic school which says that sociology studies the forms of social relations and that’s why it is a special science. Second school is Synthetic school which says that sociology is the mixture of other social sciences. So it is a general science.

Question 7.
What are scientific methods employed by sociologists to study its subject matter ?
Answer:
Sociologists use many scientific methods to study their subject matter and these methods are Sampling method, Observation method, Interview method, Schedule method, Questionnaire method, Case study method etc.

Answer the following long Answer Questions in 75-85 words each:

Question 1.
In what way is the Formalistic School of thought different from Synthetic School ?
Answer:
(i) Formalistic School : According to the thinkers of Formalistic school, Sociology is a special science which studies the forms of social relations. No other social science studies such forms of social relationships. That’s why it is not a general science but a special science. Major exponents of this school are Max Weber, George Simmel, Vierkandt, Von Wiese, Richard etc.

(ii) Synthetic School : According to the thinkers of this school, Sociology is not a special science but a genernal science. It borrows and studies the subject matter of other social sciences. That’s why it is a general science. Major exponents of this school are Emile Darkheim, Hobhouse, Sorokin etc.

Question 2.
Discuss briefly the importance of Sociology.
Answer:

1. Sociology helps in conducting a scientific study of society.
2. Sociology helps in making plans of social welfare as after studing society in a scientific manner, iff gives us a clear picture of society.
3. Sociology explains the importance of different social institutions in our lives that how they contribute in the formation of an individual’s personality.
4. After studying social problems, sociology tells us the ways to eradicate such problems.
5. Sociology also helps in understanding different cultures.

Question 3.
In what way did the French Revolution have a great impact on society?
Answer:
French Revolution started in 1789 A.D. and it brought great changes in French society. Political system changed and it brought changes in social structure. Even before the revolution many philosophers gave their views on change. In this way the seeds of Sociology were sowed and need was felt to study society in a scientific way. Views of different scholars laid its foundation and the work of bringing Sociology in front was completed by Auguste Comte who himself was a French citizen.

Question 4.
In what way did the Industrial Revolution have a great impact on society?
Answer:
Industrial revolution brought forward many good and bad changes in society and social system. Many new issues such as cities, industries, urban problems came forward during those days and these issues laid the foundation of sociology. This was the time when earlier Sociologists like Auguste Comte, Emile Durkheim, Karl Marx, Max Weber etc. come into being and Sociology depends upon the ideas and theories given by them. The impacts of industrial revolution are hidden behind the ideas given by earlier Sociologists. In this way industrial revolution brought many changes in society and consequently played a great role in the emergence of Sociology.

Question 5.
Sociology makes use of scientific methods in its subject matter. Explain.
Answer:
Sociology uses many scientific methods for the study of social facts. It uses many scientific methods Like Comparative method, Historical method, Case Study method, Verstehen method, Observation, Interview, Schedule, Questionnaire etc. and solves the social problems. All these methods are scientific in nature. Knowledge of Sociology is systematic which is obtained by using scientific method.

Answer the following long answer Questions in 250-300 words each :

Question 1.
What do you mean by Sociology ? Highlight the scope of Sociology.
Answer:
In simple words Sociology is the scientific study of society in which mutual relations of humans are studied. Sociology studies mutual actions of human behaviour. It also tries to understand how different groups came into being, how they developed, how they came to an,end and then again came into being. In Sociology different methods, customs, groups, traditions and institutions are being studied.

Auguste Comte, a French philosopher is known as the father of Sociology. His famous book ‘Positive Philosophy’ was published during 1830-1842 in 6 different volumes. In this book he gave the name of Sociology to that science which studies the relations of society. This subject was started in 1839.

If we will see the literal meaning of Sociology then we can say that it has been made by two words ‘Socio’ and ‘Logos’. Meaning of ‘Socio’ is society and the meaning of ‘Logos’ is science. ‘Socio’ word is taken from Latin language and ‘Logos’ word is taken from Greek language. In this way literal meaning of Sociology is science of society. The science which studies the relations of society is known as Sociology.

Definitions:
(1) According to Giddings, “Sociology is the systematic description and explanation of society viewed as a whole.”
(2) According to Maclver and Page, “Sociology is about social relationship, the network of relationship we call society.”
(3) According to Durkheim, “Sociology is the science of social institutions, their genesis and development.”
(4) According to Ginsberg, “Sociology is the study of human interactions and consequences.”
(5) According to Max Weber, “Sociology is the science which attempts the interpretative understanding of social action.”

After studying these given definitions we can say that Sociology studies society scientifically. It also studies human social relations and their functions. Sociology also tells us that all the customs of humans, which connect them with each other, are studied by Sociology. .

Scope of Sociology:
Sociology studies society and society is the web of social relationships. Society is an unbreakable system. In its structure many classes, groups, associations, schools, institution etc. are included. When we say that Sociology studies the society, it means that a sociologist studies all the groups, institutions, associations etc. After analysing their origin and development, Sociology tells that how it will affect social organization and disorganization. The existence of society is based on the fact that how different parts of society change themselves according to others. About this we can come to know by the study of interactions of groups.

While studying society, sociologist also studies non-societai issues like the effect of physical environment on society. In this way it also studies the relation of social and non-social issues. This list is very long that which thing does it study. If we will study the literature of Sociology then we will come to know that different sociologists have different views about scope of its subject matter. To express the subject matter of Sociology two different views are there. According to the exponents of first view, Sociology is a special science but according to exponents of other view, Sociology is a simple or general science. It means that two opposite schools are there which gave the subject matter of Sociology in their own way.

These are given below:
1. Formalistic School-Sociology is a special science.
2. Synthetic School-Sociology is a general science.

1. Formalistic School:
Sociology is a special kind of science. Supports of Formalistic School are George Simmel, Tonnies, Richard, Von Wiese, Vier Kandt, Max Weber. According to these sociologists, Sociology is also a special science like other social sciences. Supporters of this school are limiting the study of Sociology to the forms of social relationships and they call it as a science. According to them, no other social science studies the forms of social relationships, just sociology is a science which studies the form of social relationships. That’s why it is a special science.

According to the supporters of this school, Sociology is a special science because it only studies forms of social relationships and forms and content are different things. To keep its special existence, Sociology studies the forms of social relationship, not the content. In this way Sociology is the scientific study of forms of human relationships. Because the supporters of this school give stress on form, that’s why it is known as formalistic school.

(i) Views of Simmel. According to Simmel, Sociology is a special science because Sociology studies the forms of social relationship but other social sciences study the content of these relationships. According to Simmel, the difference between Sociology and other social sciences is because of their different points of view. Any collective social phenomenon can be studied by any of the social sciences. In this way to become a special science, Sociology studies those parts which other social sciences do not study. According to Simmel, there are two forms of interactions :

(a) Abstract form
(b) Concrete form.

Social relationships like competition, conflict, domination, subordination, division ofTabour etc. are abstract forms of interaction. According to Simmel, Sociology studies scientifically these abstract forms. No other social science studies them. Except this Sociology is related with other social sciences in the same way in which Geometry is related with natural sciences. It means that Geometry studies the local forms of physical objects and natural sciences study the content of those physical objects. In this way when Sociology studies the social relationships then other social sciences study their content like natural sciences. In this way the abstract form of human behaviour is studied by Sociology and that’s why it is known as special science.

In this way according to Simmel, Sociology studies forms and the abstract forms of social relationships which differentiate it from other social sciences. That’s why it is a special science.

(ii) Views of Vierkandt. Vierkandt has also related Sociology with a special branch of knowledge in which he has taken forms of mental relationships and humans of a society. According to him, man cannot produce and establish relations with others without his imagination, wishes, dreams and community instincts. For example we can take the feeling of competition.

Different players have feeling of competition with each other and teachers also have feeling of competition with each other and students also have the same type of feeling. Here we can say that mental relationship in competition is same, yet feelings are not same. According to Vierkandt, Sociology studies social relationship by differentiating it from1 forms of mental relations. So because of*this he called sociology as a special science.

(iii) Views of Von Weise. In all of his writings Von Weise stressed on the fact that Sociology is a special science. He was of the view that forms of social relationships can be studied by differentiating it from its content. According to him, “Sociology is the study of social or inter-human processes.” From this point of view Sociology has limited scope on the basis of which we can differentiate it from other social sciences.

Sociology does not collect the results or conclusions of other social sciences as it is but it collects the whole information of social life and takes it into its subject matter. He gave two types of social relationships and classified their forms. It will be very easy to understand this thinking with his classification. In this way Von Weise gave stress on the fact that Sociology is a special science.

(iv) Views of Max Weber. Max Weber was also of the view that according to formalistic school, the scope of Sociology is very limited. According to Weber, Sociology is the science which attempts the interpretative understanding of social action. According to him we cannot call all the actions of society as social action. Only that action is social with which the behaviour of other persons is affected.

For example if two or more than two persons collide with each other then this is a natural phenomenon but their those efforts with which they differentiate from each other is their social behaviour. According to Weber, Sociology is related with the analysis and classification of types of social relationships. In this way according to Weber the aim of Sociology is to understand and explain social behaviour. That’s why it is a special science.

2. Synthetic School:
According to the thinkers of Synthetic school, Sociology is a general science. According to them the scope of study of Sociology is very wide. That’s why different aspects of social life like political, cultural, psychological, economical are studied by different social sciences like Political Science, Anthropology, Psychology, Economics.

But except these special sciences which study a special aspect, we need a general social science which can tell us about the general conditions of social life on the basis of results given by a special types of science. This school is totally different from Formalistic school because thinkers of this school stress on the concrete form of social relationships. According to this school we cannot understand social relationship without the help of other social sciences. Main supporters of this school are Sorokin, Durkheim and Hobhouse.

1. Views of Sorokin. Sorokin criticised the views of the formalistic school and accepted Sociology as a general science. According to him, Sociology studies the relationship of different parts of social phenomenon. Secondly, it also studies the social and unsocial-relationships and it also studies the general features of social phenomenon. In this way according to him, “Sociology is a general science of socio-cultural phenomenon views in their generic forms, types and many folded inter connection.” In this way Sociology studies common socio-cultural phenomenon from generalizing point of view.

2. Views of Hobhouse. Hobhouse also accepted the views of Sorokin about the functions of Sociology. According to him, Sociology is the mixture of many social sciences but it studies the whole of»social life. Yet Sociology studies differently the different parts of society but it cannot separate any part from society and it cannot attain complete knowledge without the help of other social sciences.

Actually every social science is related with other in one Way or the other. History is related with Psychology, Psychology with Political Science, Political Science with Sociology etc. In this way Sociology is known as general science of all of these because it studies completely the human social life, and because of which it is related with other sciences.

3. Views of Durkheim. According to Durkheim, all social institutions are related with each other and we cannot study them by separating them from each other. Sociology is dependent upon other social sciences for the study of society. According to him, we can divide Sociology in three parts :

• Social Morphology
• Social Physiology
• General Sociology.

The first part is related with humans such as size of population and division. Second part is very complex and further is divided in many parts like sociology of religion, sociology of economics, sociology of law, political sociology. All these sciences study different parts of social life but their point of view is always social. In third part social laws are formulated. In this way according to these views of Durkheim, Sociology is a general science because it is related with the study of every type of institution and social processes.

Question 2.
What do you understand by Sociology ? Discuss the nature of Sociology.
Answer:
Meaning of Sociology:

1. According to Giddings, “Sociology is the systematic description and explanation of society viewed as a whole.”
2. According to Maciver and Page, “Sociology is about social relationship. the network of relationship we call society.”
3. According to Durkheim, “Sociology is the science of social institutions, their genesis and development.”
4. According to Ginsberg, “Sociology is the study of human interactions and consequences.”
5. According to Max Weber, “Sociology is the science which attempts the interpretative understanding of social action.”

After studying these given definitions we can say that Sociology studies society scientifically. It. àlso studies human social relations and their functions. Sociology also tells us that all the customs of humans, which connect them with each other, are studied by Sociology.

Nature of Sociology :
Sociology is a science but after the following discussion it will become clear that features of science exist in the nature of Sociology.

1. Sociology uses scientific methods. Sociology uses scientific methods for the study of social facts. These methods are historical method, comparative method, case study method, experimental method, ideal type, verstehen etc. These methods of Sociology are made on the basis of scientific method. Sociology uses all the steps of scientific method to find facts like all the natural sciences are using. The base of all those methods is scientific and all these methods are used in Sociology. In present age except these methods, some other methods are also used in Sociology. So in this way if we can use scientific method in the study of Sociology then we can call it as a science.

2. Sociology explains the causal-effect relations. Sociology not only collects the facts but also tries to know their causal-effect relationships. It just not tries to know that ‘why it is’ but it also tries to know about ‘Why’ and ‘How’. It means it tries to know about reasons and results of different facts. For example if any sociologist is studying the problem of unemployment or low status of women then he is just not limiting himself to the collection of data related with that problem but he also tries to know about why this problem came into being and what are its results. It means that why and how this problem came into being. So on the basis of giving explanation of causal-effect relations we can call it a science.

3. Sociology only explains ‘what is’. It does not explain about what should be. Sociology expresses different social facts and phenomena in their original form, the form in which it has seen them. It observes social facts with objectivity and does not accept any fact without reason. It explains subject in its real form and explains ‘what is’ When sociologist studies social phenomena then he does not accept social fact without any reason.

He restricts himself only with the explanation of truth, the way in which Physical Sciences do while studying physical processes. In this way when sociologist studies social processes then he studies and explains without any other effect. In this way Sociology is also known as Positive Science because in this we study any social phenomenon on the basis of facts. So that’s why we can call it as a science.

4. Sociology studies anything with objectivity. In Sociology all facts are observed without any bias. Sociologist tries to study facts and phenomena with objectivity and on the basis of any reason. According to his nature, man can be biased. His interests, habits, feelings can come in study but sociologist studies everything with objectivity and does not bring his likings and dislikings in his study.

The study of any society by Sociology is always based on objectivity because sociologist tries to study on the basis of social facts. For example, if he studies the problem of caste system he keeps his beliefs, thoughts and feelings away from his study. If he will not then it will be difficult to find solution of that problem. Sociologist tries to observe any problem with objectivity and on the basis of this we can call it a Science.

5. Sociology uses Laws and Coincepts. Sociologist also uses scientific methods. The laws and concepts of Sociology are universal but because of changes in Sociology these also changed with the passage of time. But some concepts are there which are same everywhere in every time. If there will be no change in Sociology then these laws can be applicable in all ages. Except this by using scientific methods we can also study any topic many times with which we can come to know about social reality. That’s why we can call it a science.

6. Sociology can predict. We can predict with the help of Sociology. If any problem arises in Society then Sociology not only collects subject matter related with that problem but it gives the result of that problem after its analysis. It also tells us that how it will affect that society and which type of problem will be faced by that society.

7. Laws of Sociology are verifiable. Laws of Sociology are not applicable for a long time. That’s why their truth is verified in different conditions. Sociologists use some of the scientific methods in its study. It is not necessary that the results given by one sociologist will be approved by other. He can verify those results again by using scientific methods.

8. Sociology also signals towards ‘what it will be’ on the basis of ‘what is’ Sociology also signals towards ‘what it will be’ on the basis of ‘what is’. Sociology has the capacity to think about future on the basis of past and present phenomena. It can predict that what would be the effect of any fact in future. For example after analysing the reasons of crime sociologist can tell that what would happen if these reasons could not be removed. In short it has the capacity to predict about any social condition.

Question 3.
What were the factors responsible for the emergence of Sociology ?
Answer:
During the 18th century, many factors emerged which clearly transformed our society. Out of all such factors, three important factors are given ahead :
(i) French Revolution and the Enlightenment Movement’
(ii) The Growth of Natural Science.
(iii) Industrial Revolution and Urbanisation

Their description is given below :
(i) French Revolution and the Enlightenment Movement. In 1789, a revolution took place in France i.e. the French Revolution. This revolution in itself was first of its kind. It had a great impact on the French society because it transformed old society into the new one and feudal system into the capitalistic system. Along with the French Revolution, Enlightenment period also started and many scholars contributed in it. These scholars wrote many books and motivated the people to change the old regimes of monarchy. They challenged the authority of Church which in itself was a major religious institution of that time. They urged the people not to follow the church’s teachings and decisions blindly and start thinking on their own. It encouraged the people and they started solving their problems-in a much logical manner.

In this way, Enlightenment age thinking emerged as an important factor. It was considered an important source of critical thinking. It stressed on the democratic and independent ideas of the modern society. It greatly reduced the differences prevailing in the feudal society. It took away the authority from church and gave it to the democratic elected people. In short, Industrial Revolution of England and democratic revolution of America and France removed the existing organisational authority and paved way to the emergence of new authority.

(ii) Growth of Natural Science. During the 18th century, natural science made a great progress. Natural science attained great success. Many social thinkers got inspired and they also followed the same way. A belief emerged that if by using the methods of natural science, physical and natural phenomenon could be understtood the same process can be used while understanding social phenomenon. Many Sociologists, such as Auguste Comte, Herbert Spencer, Emile Durkheim, Max Weber etc. also advocated the usage of scientific methods while studying society. Consequently it began the usage of scientific methods in social sciences which paved way for the emergence of Sociology.

(iii) Industrial Revolution and Urbanisation. Industrial revolution also affected the emergence of Sociology. Industrial revolution started, after 1760’s, in Europe especially in England. This revolution completely transformed whole of the Europe. Initially production was done at home which after the beginning of industrial revolution, moved into’ the factories and on a large scale. Normal rural life and household industries declined and stratified urban life along with factory based production came into being. It completely changed the beliefs and views of medieval age and old society cpnvered into the modern society.

Along with this, industrialisation gave birth to urbanisation. Size of the urban centres expanded and new cities came into being. Many unending problems emerged in cities such as great rush, pollution, traffic, noise etc. Due to urbanisation, people started migrating toward cities.

Consequently they moved away from their rural atmosphere and started living in slums. Many new classes emerged in urban areas. Rich became more rich and poor became poorer. Cities also witnessed the rise in number of crime. Many scholars such as Auguste Comte, Herbert Spencer, Max Weber, Durkheim, Simmel etc. felt the need of scientific study of society to remove newly emerged social problems. This led to the emergence and development of Sociology.

Question 4.
Why is the study of the origin and the growth of Sociology important ?
Answer:
(i) Sociology is only a new science which is still in its early stages. If we compare Sociology with other social sciences, we realise that all the other social sciences are quite old and Sociology originated only in 1839 A.D. This was the time when not only Europe but whole of the world was going through a process of transformation. Due to this process of transformation, many social problems were coming forward. It was very much necessary to get knowledge about such changes and problems. Only then the social welfare was possible. That’s why the study of the origin and growth of Sociology is important.

(ii) Many problems exist in the present day European society. If we carefully observe these problems, we realise that they originated in Europe only after the industrial revolution. Later on, other countries also started facing these problems. So, if we want to remove these problems, we need to know about the origins of Sociology which came into being during this, period.

(iii) If we want to get knowledge about any subject, first of all it is necessary to know about its origin. So, before studying Sociology, we need to know about its origin.

Question 5.
Write a note on the Enlightenment period of Sociology.
Answer:
Enlightenment period. The enlightenment period refers to the period of European intellectual history that had its beginnings in the early years of the eighteenth century and was largly over the end of the same century. Many of the most important thinkers, movements and projects associated with the Enlightenment were based in France. However Enlightenment thinkers were also active in most of the Major European states of the day, including importantly, Scotland.

The Enlightenment is widely credited with creating a new framework of ideas about human beings and their societies. During the period of the Enlightenment, there was an intense new preoccupation with the social world, which began to be seen as a specific and important realm of human activity.

This focus on the social world generated new questions about human history, political and economic activity and social interaction. These questions were asked within a recognisable paradigm. Paradigm is a set of interconnected ideas, values, principles and facts within which coherent theories are developed. Key aspects of the Enlightenment paradigm included reason, empiricism, science, universalism, progress, individualism, toleration, freedom, secularism etc.

There had been speculation about human beings and their social, political and historical circumstances. For example, in the seventeenth century, the philosopher Hobbes (1588-1679) and Locke (1632-1704) had both written extensively about social and political issues from a secular and a historical perspective.

That is, they had conceived of human affairs strictly in their own terms. They saw them as produced by human beings and as having definite historical conditions and as such they were thought to be susceptible to positive change. In other words, reflections on how and why circumstances were as they were, could lead tp change in order to improve those circumstances.

It was during the eighteenth century that people began to think more clearly about how social, economic and historical processes might be a complex phenomena with their own laws. Social, cultural and political arrangements began to be thought of as the product of complex processes that were not immediately obvious from a casual observation of the social world. In this sense, the study of societies and their development became more closely related to the scientific study of the natural world and began to draw on similar methodologies.

Two thinkers in particular were highly important in the development of these ideas : Vico (1668-1774) and Montesquieu (1689-1755). Their ‘New Science’ (1725) and ‘Spirit of the Laws’ (1748) respectively were attempts to explain how different social conditions were subject to specific cultural and material determination. In other words, complex historical (and even environmental) factors were taken into account when describing specific societies and their operation.

Rousseau was another thinker who was also quite important in the development of these ideas. He wrote a book, ‘The Social Contract’ in which he wrote that people of any country must have the right to choose their ruler. He also wrote that if people want to develop themselves then it can be done only under a government of their choosing.

Enlightenment writers rejected the idea that society and estates are the basic units of social analysis. Instead they gave the idea that individual is the basis of social analysis. According to them, individuals have the abilities, qualities and rights inherent among them and society was developed due to social contact between these individuals.

Enlightenment thinkers viewed human reason as dominant in contrast to the system thought where the questioning was discouraged and the sacred had dominated, They supported the idea that every subject of study should be allowed, no unaskable questions should be there and all aspects of human life are subject to examination and study.

Here they combined the philosophical tradition of abstract rational thought with the tradition of experimentation. The result of this combination comes in a new way. New system of human inquiry attacked the old system, it stressed on faith in science, scientific method and education, raised question over existence of existing institutions and demanded that reasonable institutions must be changed which are contrary to human nature.

All social obstacles must be eliminated which are obstacles in the way of human perfectability. The new approach was not only empirical and scientific but was philosophical as well. Enlightenment thinkers thought that the world was an object of study and people must understand and control it with reason and empirical research. Now social laws must be discovered and society must be improved with the rational and empirical inquiry. This type of thought can be called as reformist which must challenge the old order. These thinkers were very much optimistic about improving the social world with the help of new world order.

Hence a new social thought emerged due to views of Enlightenment thinkers and early sociology also emerged out of this. Auguste Comte a French philosopher, was the first one to coin the word sociology. Firstly he called it social physics which is the science to study society.

Sometime later sociologists also adopted the same idea that sociology is the science of society. The new ideas propounded by the Enlightenment thinkers paved way for the emergence and development of sociology in many ways. Many people believe that sociology emerged due to the Enlightenment ideas and the reaction of conservatives who wanted to restore the old social order.

Comte was also a part of the conservative reaction who also thought of a return to the old social order. Few early sociologists took few ideas of the Enlightenment and gave the idea that with the help of a few social reforms, old social order could be preserved. As a result, a conservative sociological school was created. Comte was the one who represented the old social order. Then it was Karl Marx who completely worked out the implications of the Enlightenment views. Karl Marx grew up in Germany where Enlightenment was of little importance as it had in Britain, France, or North America. If we observe Marxian views then we can see that these views can be seen as resulting partly from Enlightenment ideas.

Punjab State Board PSEB 11th Class Sociology Important Questions Chapter 1 Emergence of Sociology Important Questions and Answers.

PSEB 11th Class Sociology Important Questions Chapter 1 Emergence of Sociology

Multiple Choice Questions

Question 1.
Who said that Sociology is the queen of other sciences?
(a) Comte
(b) Durkheim
(c) Weber
(d) Spencer
Answer:
(a) Comte.

Question 2.
Whose words are these : “Sociology is the illegitimate child of two languages.”?
(a) Maclver
(b) Jinsberg
(c) Bierstdt
(d) Durkheim.
Answer:
(c) Bierstdt.

Question 3.
Which of these is not the follower of synthetic school of Sociology?
(a) Durkheim
(b) Weber
(c) Hobhouse
(d) Sorokin.
Answer:
(b) Weber.

Question 4.
Which of these is the feature of nature of Sociology?
(a) It is not a practical science but a pure science.
(b) It is not a concrete science but an abstract science.
(c) It is not a neutral science but an idealistic science.
(d) All of these.
Answer:
(d) All of these.

Question 5.
Why is the subject matter of Sociology not fixed?
(a) Because it is an old science
(b) Because it is a new science
(c) Because background of every society is different
(d) Because social relations are not fixed.
Answer:
(d) Because social relations are not fixed.

Question 6.
Who wrote the book, “Social Order”?
(a) Maclver
(b) Simmel
(c) Robert Bierstdt
(d) Max Weber.
Answer:
(c) Robert Bierstdt

Question 7.
Who divided Sociology in Social Morphology, Social Physiology and General Sociology?
(a) Spencer
(b) Durkheim
(c) Comte
(d) Weber.
Answer:
(b) Durkheim.

Question 8.
Which of these according to Weber is correct?
(a) There is Sociology of general things
(b) Nature of Sociology is general
(c) Sociology is not a special science
(d) None of these.
Answer:
(c) Sociology is not a special science.

Question 9.
…………… In which country the study of Sociology was started?
(a) France
(b) Germany
(c) USA
(d) India.
Answer:
(c) USA.

Question 10.
Who said that the name of Sociology should be kept as ‘Ethology’?
(a) Weber
(b) Spencer
(c) J.S. Mill
(d) Comte.
Answer:
(c) J.S. Mill.

Fill in the Blanks:
1. …………… gave Sociology its name.
Answer:
Auguste Comte

2. The first printed book in Sociology was ………….
Answer:
Principles of Sociology

3. There are …………… schools of thought associated with the scope of Sociology.
Answer:
two

4. Weber belongs to ………….. school of Sociology.
Answer:
Formalistic

5. Durkheim belongs to ………….. school of Sociology.
Answer:
Synthetic

6. The Web of ………….. is known as Society.
Answer:
social relations

7. …………… called sociology as pure sociology.
Answer:
Comte.

True/False:

Question 1.
Max Weber is considered as the father of Sociology.
Answer:
False

Question 2.
The word Sociology was used ffrst time in 1839.
Answer:
True

Question 3.
The book Society was written by Maclver and Page.
Answer:
True

Question 4.
Simmel belongs to Formalistic school of thought.
Answer:
True

Question 5.
There is no contribution of the French Revolution in the Emergence of Sociology.
Answer:
False

Question 6.
Enlightenment period had a great impact on the emergence of Sociology.
Answer:
True

One Word/Line Question Answers:

Question 1.
When and who coined the term Sociology ?
Answer:
Auguste Comte coined the term Sociology in 1839 A.D.

Question 2.
Who said that ‘Sociology is the queen of all the Social Sciences’?
Answer:
Auguste Comte was of the view that ‘Sociology is the queen of all the social sciences’.

Question 3.
Who wrote the book ‘Sociology’ ?
Answer:
The book ‘Sociology’ was written by Harry M. Johnson.

Question 4.
Who wrote the book ‘Society’ ?
Answer:
Maelver has written the book “Society”.

Question 5.
According to Comte, which are the major parts of Sociology ?
Answer:
According to Comte, Sociology is divided into two parts-Social statics and Social dynamics.

Question 6.
Name the two schools regarding the scope of Sociology.
Answer:
There are two schools about the scope of Sociology-Formalistic school and Synthetic school.

Question 7.
Name the major exponents of the formalistic school.
Answer:
Simmel, Vierkandt, Weber etc. are the major exponents of this school.

Question 8.
Name the major exponents of the synthetic school of Sociology.
Answer:
Durkheim, Sorokin, Hobhouse etc. are the major exponents of this school.

Question 9.
What does Sociology study?
Answer:
Sociology studies social relations and social phenomenon.

Question 10.
Who is considered as the father of Sociology?
AnsweR:
Auguste Comte is considered as the father of Sociology.

Question 11.
What is Sociology?
AnsweR:
Science which studies social relations in a systematic way is known as Sociology.

Question 12.
What is Society?
Answer:
According to Maclver and Page, “Society is the web of social relationships.”

Question 13.
Who gave the form of science to Sociology?
Answer:
French Sociologist Emile Durkheim gave the form of science to Sociology.

Question 14.
With which two words Sociology is made up?
Answer:
Sociology is made up of two words i.e. Latin word ‘Socio’ and Greek word ‘logos’.

Vary Short Answer Type Questions

Question 1.
Meaning of Sociology.
Answer:
Science of Sociology is known as Sociology. In Sociology, groups, institutions, organisations, associations, mutual relations of individuals are studied. Most importantly it studies all these in a scientific way.

Question 2.
Name the Founding fathers of Sociology.
Answer:
Auguste Comte : He started Sociology.
Emile Durkheim : He converted Sociology into a science.
Karl Marx : He gave conflict theory to Sociology.
Max Weber : He gave action theory and many other concepts to Sociology.

Question 3.
Subject matter of Sociology.
Answer:
In the subject matter of Sociology many concepts are included and these are social order, social institutions, social process, social codes, cultures, civilization, social organisation, socialisation, status, role, social control,’ social problems etc.

Question 4.
Meaning of Society
Answer:
According to Maclver, ” Society is the web of social relationships.” It means that society is the organisation of specific type of social relations which exist among the people who live in a particular period for a long time.

Question 5.
Formalistic School.
Answer:
According to the thinkers of this school, Sociology only studies the forms of social relationships, that’s why it is a special Science. No other science studies the forms of social relationship, only Sociology does such study.

Question 6.
Synthetic School.
Answer:
According to the exponents of Synthetic school, Sociology is a general science because its subject matter is quite wide. Sociology studies whole of society and the concrete form of social relationships.

Question 7.
Importance of Sociology.
AnsweR:

• Sociology studies whole of society, by considering it as a single unit.
• Sociology helps us in understanding and solving the social problems.
• Sociology clearly helps us in understanding different cultures.

Question 8.
Sociology is a Science.-How ?
Answer:
Yes, Sociology is a science because it studies its subject matter with objectivity while studying social relations. That’s why we can call it a science.

Question 1.
Meaning of Sociology.
Answer:
French philosopher, Auguste Comte is known as the Father of Sociology. Sociology has been made by two words-Socio and Logos. Meaning of Socio is society and meaning of Logos is Science. So, literal meaning of Sociology is Science of society. In simple words, Sociology scientifically studies groups, institutions, communities, associations and inter-relations of humans. It also studies the customs, traditions, mores which exist in social relations. Except these, it also studies the culture.

Question 2.
Literal Meaning of Sociology.
AnsweR:
The word Sociology is an English word. The word Sociology has been taken from two words ‘Socio’ and ‘Logus’. Socio is a Latin word whose meaning is Society and Logus is a Latin word whose meaning is Science. In this way the meaning of Sociology is Science of Society which studies the human society.

Question 3.
Who is the father of Sociology and in which year name Sociology was given by him ?
Answer:
French philosopher Auguste Comte is known as the Father of Sociology. His book ‘Positive Philosophy’ was published in six volumes between 1830 to 1842. In this book he imagined a science which should study society. To this Science he gave the name of Sociology in 1839.

Question 4.
What is Scientific Method ?
Answer:
Scientific method is the method which helps a Scientist to study any phenomena systematically and in proper sequence. In Scientific method we should select that problem which is able to be studied with this method. We should find out literature related with that problem and that should be checked.

Formulation of Hypothesis is necessary with this so that we can make our thesis on the basis of this. Except that in Scientific method we have to collect data with a proper planning so that it can be analysed and processed. Observation is the main base of Scientific method. That’s why any technique can be used and later on after recording data should be analysed and studied.

Question 5.
Is Sociology a Science ?
Answer:
Yes, Sociology is a Science because Sociology uses scientific methods to collect facts. It not only collects facts of the problem about ‘what is’ but it also studies why and ‘how’. It also tries to know about reality of Sociology. Predictions done by Sociology are proved correct. In this way from this it is clear that Sociology uses scientific method to study anything. That’s why it can be called as a Science.

Question 6.
Lack of Experimental method in Sociology.
Answer:
Subject matter of Sociology is society and it studies the human behaviour and relationships. Human behaviour is quite different from each other. If we will take relations of brother-sister, mother-father or mother-son then we will not find same behaviour of two brothers or sisters.

This type of difference does not exist in natural sciences but they have universality of nature of any element. That’s why Experimental method can be used in natural sciences because result of mixing two chemicals will be the same in the whole world. But this type of stability is very less in Sociology. That’s why we cannot use experimental method in Sociology.

Question 7.
Sociology is an independent Science. How ?
Answer:
Different Sociologists have different views about this. According to them Sociology is an independent science because it studies the whole society and it is based on sociological theories to understand its subject matter. It has its own point of view. The supporters of this view are Lesterward, Giddings, Barner etc.

Question 8.
Sociological concepts are not Universal. How ?
Answer:
Sociological concepts cannot be proved correct everywhere. It is so because one society is quite different from other society and change comes in every society at different speed. We cannot generalize the relations of sociology by studying it. That’s why in the absence of rules or concept it cannot be called as a science and if it is not a science then its concepts are not universal.

Question 9.
Scope of Sociology.
Answer:
Society is a web of social relationships and sociology studies it scientifically. In its study sociology, studies all the social classes, institutions, associations etc. About the scope and subject matter of sociology there are two types of views.
1. Formalistic School : According to this it is a special science which studies the forms of social relations. Main supporters of this school are Simmel, Weber, Small, Vierkandt, Von Wiese and Ward.

2. Synthetic School : According to this school it is a general science which studies society as a whole. Main supporters of this school are Durkheim, Hobhouse and Sorokin.

Question 10.
Lack of objectivity in Sociology.
Answer:
Sociology lacks objectivity because the Sociologist who is studying anything, is a member of any group or society and he is definitely affected by the values of that group or society. It is almost impossible for him to remove that effect and’bias can come in his study. That’s why there is lack of objectivity in Sociology.

Question 11.
Sociology cannot predict. Comment.
Answer:
Sociology cannot predict like Natural Sciences. It studies the social relations and proceses. These relations and processes are different in each society and they keep changing all the times. Because of this changing nature of subject matter of Sociology it is unable to predict. It cannot predict in that way the way in which Natural Sciences are predicting. It is so because Sociology is related with behaviours or forms of social relations which are unstable. They keep changing. So by looking at the nature of social relations we can say that we cannot bring reality in the study of social relations.

Question 12.
Who was Auguste Comte ?
Answer:
Auguste Comte is also known as the Father of Sociology. In 1839, Auguste Comte told that the way in which natural phenomenon are studied by different social sciences, in the same way there is a science which studies society and he gave it the name of Social Physics. Later on he changed the name of Social Physics to Sociology. Comte gave many concepts to Sociology like the Theory of Social Evolution, Hierarchy of Sciences, Positivism etc.

Question 13.
Write about development of Sociology in Europe.
Answer:
In the beginning of 19th Century, great French philosopher Auguste Comte gave the name of Social Physics to science of society. In 1839 he changed its name – to Sociology. J.S. Mill started sociology in England in 1843. Herbert Spencer, in his book Principles of Sociology, studied society in a scientific way.

First of all, Sociology started as an independent subject at Yale University, USA in 1876. Durkheim, through his books, developed Sociology as an independent subject. In the same way Karl Marx and Max Weber gave many theoriec to Sociology and developed it as an independent subject.

Question 14.
Enlightenment period and Sociology.
Answer:
The Enlightenment period played a very important role in the emergence of Sociology. This period started in the beginning of 18th century and remained there during the whole century. Many thinkers of this era like Vico, Montesquieu, Rousseou etc, gave many views and these views keep a very important place in the birth of sociology.

They all were of the view that the phenomenon must be studied in a scientific way and believed that everything should have a reason. They also believed that society should be developed on the basis of empirical investigation. In this way these vieWs brought forward a new social idea and earlier Sociologists came out of this idea.

Long Answer Type Questions

Question 1.
Describe the different stages of the origin of Sociology.
Answer:
An individual is a thoughtful person. Right from his early childhood, there is an urge in him to know about his surroundings. Humans collectively tried to face the problems which came in front. Due to interactions between different individuals, social relations came into being and consequently new groups came into being. Human behaviour is controlled by different customs, traditions, norms and values. In this way humans have tried to understand different aspects of society in one way or the other.

Stages of Origin and Development of Sociology:
The origin and development of Sociology can be broadly divided into four stages :

1. First Stage:
The development of Sociology can be better understood by dividing it into two parts.

(i) Vedic and Epic Era. In general sense, the origin of Sociology is widely considered to be in Europe but its history itself tells us that different saints toured India, studied the problems of people and did lot of brainstorm about this. They, as a result, developed the Varna system in Indian society. This thing is explained in the oldest religious book of the world i.e. Rigveda.

Vedas, Upnishdas, Puranas, Ramayana, Mahabharata, Geeta etc. are the scriptures through which Sociology started in India. Except Varna System, Ashrama System, Four Purusharthas, the concept of debt (Rina), joint family etc. are the institutions developed in India. Except these religious scriptures, lot of sociological explanation, about the prevailing Indian problems, is given in the Arthashastra written by Kautilya.

(ii) Studies of Greek Scholars. After Socrates, Plato (427-347 B.C.), Aristotle (384-322 B.C.) were the Greek scholars. Plato wrote ‘Republic’ and Aristole wrote ‘Ethics and Politics’ in which they described in detail about family life, customs, traditions, status of women etc. Plato studied around 50 and Aristotle studied around 150 large and small states and gave their views about political, social, religious and economic conditions prevailing during those days.

2. Second Stage:
The age from 6th century to 14th century is considered the second stage of development of Sociology. During the beginning of this stage, help of religion and philosophy was taken to understand social problems. But during 13th century, efforts were made to understand social problems on logical basis. Thomas Acquires and Dante clarified the causal-effect relationship to understand social events. In this way, the rough sketch of Sociology was made during this age.

3. Third Stage:
Third stage of the development of Sociology started in 15th century. During this age, a number of great philosophers used scientific method to study social events. Hobbes, Locke and Rousseau gave Social Contract Theory. Thomas Moore in his book ‘Utopia’, Montesque in his book ‘The Spirit of Laws’ and Malthus though his ‘Theory of Population’ studied social events and gave their contribution in the development of Sociology.

4. Fourth Stage:
Great French scholar Auguste Comte, in the beginning of 19th century, gave the name of ‘Social Physics’ to Sociology. In 1838 A.D., he changed this name to Sociology. He is also known as the ‘Father of Sociology’.

J.S. Mill in 1843, started Sociology in England. Herbert Spencer in his book ‘Principles of Sociology’ and ‘Theory of Organism’ studied society through scientific method. First of all at Tale University’ in U.S.A., the study of Sociology started as an independent subject.

Emile Durkheim gave gregt contribution in the development of Sociology as an independent subject. Max Weber, Karl Marx and other sociologists gave many sociological theories. Presently in almost all the countries of World, it is trying to collect new knowledge as an independent subject.

Development of Sociology in India:
The process of development of Sociology in India can be divided into many parts :
1. Development of Sociology in Ancient India. The origin of Sociology in India came about during the ancient times. Maharishi Ved Vyas compiled four Vedas and created the epic of Mahabharta. Ramayana was also written. Except these, Upnishads, Puranas and Smritis throw a great light on ancient Indian Philosophy.

From all these scriptures, it is quite clear that the ideology and philosophy during the ancient India was of topmost quality. From these scriptures, it is also clear that the Indian social problems, needs, events, values, facts, ideals, beliefs etc. were deeply studied. Many social institutions which exist in present age, were actually originated during the ancient age.

Varna, Ashrama, Purusharthas, Religion, Samskaras, Joint family etc. are few of them. Arthashastra of Chanakya, Manu Smriti and ‘Niti Shastra’ of Shukracharya throw a great light on the customs, values, ideals etc. of ancient times.

In this way it is clear that Sociology in itself, in India, originated during the ancient age. During the Medieval age, India was ruled by the Muslims and Mughals. We can get a great deal of knowledge, through the writings of the era, about the prevailing ideology, institutions, values, customs etc.

2. Formal Establishment Era of Sociology:
The age between 1914 A.D. to 1947 A.D. is considered as the formal establishment era of Sociology in India. First of all the work of teaching Sociology at Graduate level started in 1914 A.D. in Bombay University. From 1919 A.D. onwards, the work of teaching Sociology at post-graduate level was started by ‘Patric Geddes’.

Famous Sociologist ‘G.S. Ghurye’ was one of his students. Due to the efforts of Prof. Vrijendranath Sheel, the work of teaching Sociology started in Calcutta University in 1917 A.D. Famous Sociologists Dr. Radha Kamal Mukharjee and Dr. D.N. Majumdar were his students. Yet this development till 1947 was quite slow but even then, the work of teaching Sociology was already on in almost all the universities.

3. Expansion Era of Sociology:
After the Independence in 1947, most of the Indian Universities gave their sanction to teach Sociology as an independent subject. Presently, this subject is taught in almost all the colleges and universities all across India. Except at University level, many Sociological research works are going on in different institutions.

Tata Institute of Social Sciences Mumbai, Institute of Social Sciences Agra, Institute of Sociology and Social Work Lucknow, I.I.T Kanpur and I.I.T Delhi are fevy of the major institutions in the country where Sociological researches are going on. With these, the Sociological methods and knowledge are continually increasing.

Question 2.
Briefly describe about French Revolution and Emergence of Sociology.
Answer:
Social thought is as old as society itself, yet the. origin of Sociology is traced back to 19th century Western Europe. Sometimes Sociology is called the child of the ‘age of revolution’. The revolutionary changes in the preceding three centuries had decisively changed the way people lived thereby paving the way for the emergence of Sociology as we have today.

Sociology took birth in such a climate of social upheavel. The roots of the ideas developed by the early sociologists lie in the then social conditions that prevailed in Europe.

The modern era in Europe and the conditions of modernity were brought about by three major processes-The Enlightenment, The French Revolution and the Industrial Revolution. Sociology was originated due to the changes brought about by these three processes. The French Revolution and the Emergence of Sociology

The French Revolution erupted in 1789 A.D. and it marked a turning point in the history of human struggle for freedom and equality. It changed the political structure of European society. It put an end to the age of feudalism and brought forward a new order of society. It replaced the age of feudalism by announcing the arrival of democracy.

Before the French Revolution, French society was divided into three classes. First class or order was clergy. Second order was of nobles or nobility and third order was of common people. Total population of first two orders was around 2% of total but they enjoyed unlimited rights. They never paid any taxes to government. But no rights were given to third order and they had to face whole burden of all the taxes.

Description of all these three orders is given ahead :
1. The First Order-Clergy. In Europe’s social life, Roman Catholic Church was the most powerful and influential institution. Lot of land in different countries was in Church’s possession.

Except this, church used to get ten per cent (tithe) of the total produce of land. Church was cared by the Priest or Clergy which was the first order of society. Clergy was divided into two parts i.e. Upper clergy and Lower clergy. Priests of upper clergy were related with families of nobles and they had actual rights over church’s property.

Most of the part of tithe was also going in their pockets. They were given special rights and they never paid any taxes to government. They were quite rich and used to live a luxurious life. Priests of Lower clergy belonged to families of general classes. They used to perform their duties with complete devotion and honesty. They used to give religious education to people. They used to perform rituals related to birth, marriage, baptism, death etc. They used to check schools of church as well.

2. Second Order-Nobility. Second order of French society belonged to Nobles. They were only 4 lakhs out of 2.5 crore population of France. It means they were less than 2% of the total population. Right from their early times they used to use sword and used to fight for the protection of general masses. That’s why they were known as Nobles of Sword. NobleS were also divided into two parts i.e. Old nobles and New nobles. Old nobles were owners of l/5th of total land of country.

The status of Nobles was hereditary because of which they were known as real and pure Nobles. All of these were feudal loyds. For quite some time, they performed the functions of administration, Judge and military leader. They lived a luxurious life.

They were also given a number of privileges, New Nobles were those nobles who were given this status by Emperor by taking money from them. This class played a great role in the beginning of French Revolution of 1789. After some time, their status also became hereditary.

3. Third Order-Commoners. Only 2% of population belonged to the first and second order but rest of the 98% population belonged to this third order. This was rightless class which included rich industrialists and poor beggars as well. Farmers, middle class, labourers, artisans and other poor people were also included in this class.

These people were not given any type of right. Farmers wanted to eliminate the special privileges of Nobility. That’s why they greatly participated in French Revolution of 1789. Industrialists, businessmen, money-lenders, doctors, lawyers, scholars, teachers, journalists etc. were included in the middle class.

Middle class patronised the French Revolution. Condition of labourers was also not good. They were not only given less wages but they also had to do Begar (forced labour). These people participated in riots due to poverty. They joined the crowd during French Revolution.

Outbreak of Revolution. Louis XVI became the French King and there was a financial crisis in France. As a result, he required money to run the daily affairs of the country. He wanted to levy new taxes on the people. That’s way he was compelled to call a meeting of the Estate General which was the old feudal assembly.

Its meeting was not called during last 150 years. On 5th May, 1789, the Estate Generalmet arid the representatives of third estate wanted that whole of the estate must meet and vote as one assembly. On 20th June 1789, they found that their meeting hall was occupied by the royal guards. But third estate was determined to meet. So it moved to the tennis court to frame a new constitution. This was the beginning of the French Revolution.

One of the most important events of the French Revolution took place on 14th July, 1789 when a mob of Paris including few middle class leaders, broke open the Bastill prison. They set all of its prisoners free. In France, this day is celebrated as an Independence day. Now Louis XVI was the French king only by name.

The national assembly was organised to form a new French constitution. It started to enact laws. Then it adopted the famous declaration of the rights of man and citizen. This declaration declared certain necessary points including equality of all men before law, freedom of speech and freedom of press and eligibility of all the citizens for all public offices.

In 1791, the king tried to run away from France but was captured and was brought back. He was thrown in jail and on 21 January, 1793 he was beheaded in public after he was tried in court and was proved guilty of treason. Then France was declared as Republic. King was guillotined. But after this, a Reign of Terror started in France when a number of nobles, priests and few revolutionaries were beheaded who tried to oppose the government. This reign of terror lasted for three years.

Then in 1795, Directorate was established in France. This Directorate lasted for four years. Then in 1799, Directorate was overthrown by Napoleon. He then declared himself as director and later on the king. He provided a stable government to France and French people. In this way French Revolution came to an end when Directorate was overthrown by Napoleon.

Effects of French«Revolution: French Revolution exerted lasting effects on France and rest of the world which are given below :
1. Major effect of French Revolution was the destruction of old economic system i.e.
Feudalism and the advent of new economic system. This new economic system was capitalism. .

2. All the privileges of the upper class i.e. clergy and nobles were abolished and were taken back by the government. Whole of property of church was confiscated. All the ancient laws were removed and new laws were made by National Assembly.

3. All the men and citizens were given rights of equality and freedom. The term ‘nation’ was given its modern meaning that France was not only the territories but the ‘French people’. From here on the idea of sovereignty come into being. It means the nation’s law and authority is above its own.

4. French Revolution also had great impacts on the world. It inspired the revolutionaries of other countries to work against the existing autocratic monarchs. It also paved way for removal of ancient systems and establishment of new system of democracy. It also gave the slogan of ‘liberty, equality and fraternity’. As a result of French Revolution, many revolutions occurred in Europe and south central America. Finally monarchy was replaced by democracy.

The French Revolution played a great role in the history of human civilization. It completely changed the Europe’s political scenario and European society. The earlier order was replaced by the new order and as a result new economic order also come into being. Many revolutionary changes took place in France as a number of nobles were either killed or were beheaded. As a result, their role in French society came to an end.

A number of laws were made during tenure of National Assembly and the Directorate which brought many fundamental changes in the society. Church was made subordinate to the state and was restricted to take part in the affairs of politics and administration.

Each individual was given certain rights and even laws were made to divide family property among all the sons of family. The French Revolution also exerted a great impact on other countries of the world. A number of political revolutions broke out in different countries during 19th century. Political scenario of those countries was completely changed.

It was the most important factor in the advent of sociology. Many societies were positively affected by these revolutions and it was a main concern of early sociologists. Many early sociologists, who always thought that revolutions only have negative consequences, changed their opinion about revolution.

These sociologists including Comte and Durkheim gave their views about the positive consequences of it especially the establishment of theme of – liberty, fraternity and equality. In this way French Revolution played great role in the emergence of sociology.

Question 3.
Briefly describe about Industrial Revolution and the Emergence of Sociology.
Answer:
The foundation of modern industry was laid by the industrial Revolution, which began in England in the late 18th and early 19th centuries. It brought about great changes in the social and economic life of the people first in England, then in other countries of Europe and later in other continents. It had two important aspects.

1. Systematic application of science and technology to industrial production, particularly invention of new machines and harnessing of new sources of powers. These encouraged the production process and gave rise to the factory system and mass manufacture of goods.

2. New ways of organizing labour and markets on a scale larger than anything in the past were evolved. The goods were produced on a gigantic scale for distant markets across the world. The raw materials used in their production were also obtained from all over the world. Industrialization threw all societies into turmoil that have been relatively stable for centuries.

New industries and technologies changed the face of social and physical environment. Peasants left rural areas and flocked to the towns, where they worked under appalling conditions. Cities grew at a very fast rate. Social problems became common in the teeming cities. The direction of change was unclear and the stability of social order was under great threat.

The first Industrial Revolution was started in the later part of 18th century. But it was merged into the second Industrial Revolution around 1850 A.D. At that time technological and economic progress took some speed with the invention of steam powered ships and engines railways and later on with the invention of electrical power generation.

Time frame of this merger is still debated among historians as they have different opinions about it. Historians believe that the .industrial revolution was one of the most important events in the human history.

Industrial Revolution exerted a great impact on the society. Rural people started to move towards cities where they had to live in unhygienic conditions. Growing population, increasing demand, increasing output led to demand of other markets. It led to the race between big powers to win over colonies from Asia and Africa. Whole of the world order changed. There prevailed a chaos and disorder in the world. During 1800-1850, different classes started agitating for their rights.

The Significant themes of this Revolution which concerned the early sociologists were the condition of labour, transformation of property, industrial city means urbanism and technology and the factory system. Against such background, some thinkers of that time were concerned about building their society anew.

Those who dealt with these problems are considered as the founding fathers of sociology because they were seriously concerned with these problems in a systematic way. Most notable among the thinkers have been Auguste Comte, Herbert Spencer, Emile Durkheim, Karl Marx and Max Weber. All these pioneers came from different disciplines.

Auguste Comte (1798-1857), who is known as the Father of Sociology, argued that the method used in physics should be used for the study of society. Such a study would reveal the laws of evolution and the laws of the functioning of society. Once this knowledge was available, we would be able to build society.

Auguste Comte, who gave sociology its name, identified three stages of human society i.e. Theological (various phenomena were explained in religious terms), Metaphysical (explanations were philosophical) and Positivism (phenomena were explained in terms of the scientific approach to the social world).

The idea of evolution was carried forward in the works of the British sociologist Herbert Spencer (1820-1903). He argued for the universality of the principle of evolution. His view of the evolution of societies is known as Social Darwinism. The credit for developing sociology as an independent discipline and science goes to Emile Durkheim (1858-1917), a French Sociologist.

Durkheim said that sociologists study social facts which are objective and exist in the” consciousness of the collectivity. Thus social fact is exterior to human mind but it puts constraints on human behaviour. Hence social facts do not have their origin in the individual. Further, they should be explained by other social facts, rather than in terms of biological, psychological, environmental or geographical facts.

Among the Germans, the most influential work was of Max Weber (1864-1920). In comparison to Durkheim, Weber said that the sociologist studies ‘social action’ which is an act an individual performs and assigns meaning and the task of sociologist is to understand the subjective meaning of an act. German social thinker Karl Marx’s (1818-1883) ideas were influential in sociology.

He argued that every society was divided into two classes i.e. Haves and Have-nots. He believed that conflict was initiator of change in history. He, therefore, gave central importance to class and class conflict. Thus the development of sociology in France (Comte, Durkheim), Germany (Marx, Weber) and England (Spencer) paved way to development of sociology everywhere in the world.

Sociology thus flowered in precisely those societies that had experienced the most pronounced or greatest social changes. France, Germany and England underwent a truly revolutionary social transformation, and in all these countries the study of Sociology had emerged by the end of 19th century.