Class 12

Punjab State Board PSEB 12th Class Physical Education Book Solutions ਹਾਕੀ (Hockey) Game Rules.

ਹਾਕੀ (Hockey) Game Rules – PSEB 12th Class Physical Education

ਇਤਿਹਾਸ
(History)

ਇਤਿਹਾਸਕ ਰਿਕਾਰਡ ਦੱਸਦੇ ਹਨ ਕਿ ਇਸ ਖੇਲ ਦੀ ਸ਼ੁਰੂਆਤ | ਯੂਰਪ ਵਿਚ ਹੋਈ ਸੀ । ਇਹ ਸਪਸ਼ਟ ਹੈ ਕਿ ਉਸ ਸਮੇਂ ਦੇ ਦੌਰਾਨ | ਇਸ ਖੇਲ ਨੂੰ ਸਟਿਕ ਅਤੇ ਗੇਂਦ ਨਾਲ ਖੇਡਿਆ ਜਾਂਦਾ ਸੀ । ਪਰ | ਆਧੁਨਿਕ ਖੇਤਰੀ (Field) ਹਾਕੀ ਦੀ ਸ਼ੁਰੂਆਤ ਇੰਗਲੈਂਡ ਵਿਚ 18ਵੀਂ ਸਦੀ ਵਿਚ ਹੋਈ 1876 ਵਿਚ ਪਹਿਲੀ ਹਾਕੀ ਸੰਸਥਾ ਨੇ | ਪਹਿਲੇ ਨਿਯਮ ਸਮੂਹ ਨੂੰ ਪੇਸ਼ ਕੀਤਾ | ਸਾਲ 1908 ਵਿਚ, ਲੰਡਨ ਉਲੰਪਿਕ ਖੇਡਾਂ ਵਿਚ ਇਸ ਖੇਲ ਨੂੰ ਸ਼ਾਮਿਲ ਕਰ ਲਿਆ ਗਿਆ |

19ਵੀਂ ਸਦੀ ਦੇ ਅੰਤ ਵਿਚ, ਅੰਗਰੇਜ਼ੀ ਰਾਜ ਦੁਆਰਾ ਭਾਰਤ ਵਿਚ ਇਸ ਖੇਲ ਨੂੰ ਬਹੁਤ ਜ਼ਿਆਦਾ ਲੋਕਪ੍ਰਿਯ ਬਣਾਇਆ ਗਿਆ । ਭਾਰਤ ਵਿਚ ਪਹਿਲੇ ਹਾਕੀ ਕਲੱਬ ਦਾ ਗਠਨ ਸਾਲ 1885 ਵਿਚ ਕੋਲਕਾਤਾ ਕਲਕੱਤਾ) ਵਿਚ ਹੋਇਆ ਸੀ ।

ਸਾਲ 1925 ਵਿਚ ਭਾਰਤੀ ਹਾਕੀ ਸੰਘ (Indian Hockey Federation) ਦੀ ਸਥਾਪਨਾ ਹੋਈ ਸੀ 1924 ਵਿਚ, | ਅੰਤਰਰਾਸ਼ਟਰੀ ਹਾਕੀ ਸੰਘ (International Hockey Federation) ਦੀ ਸਥਾਪਨਾ ਕੀਤੀ । ਭਾਰਤ 1928 ਵਿਚ ਏਮਸਟਡਮ ਉਲੰਪਿਕ ਖੇਡਾਂ ਵਿਚ ਭਾਗ ਲੈ ਸਕਿਆ ।

ਯਾਦ ਰੱਖਣ ਯੋਗ ਗੱਲਾਂ
(Tips to Remember)

1. 1. ਹਾਕੀ ਮੈਦਾਨ ਦੀ ਲੰਬਾਈ : 91.40 ਮੀ.
   2. ਹਾਕੀ ਮੈਦਾਨ ਦੀ ਚੌੜਾਈ : 55.0 ਮੀ.
   3. ਟੀਮ ਮੈਂਬਰ : 18 ਖਿਡਾਰੀ 2 ਗੋਲਕੀਪਰਾਂ ਸਮੇਤ)
   4. ਖੇਲ ਦਾ ਸਮਾਂ : 15-2-15 (10) 15-2-15
   5. ਗੋਲ ਪੋਸਟ (Goal Post) ਦਾ ਨਾਮ : • ਉਚਾਈ = 2.14 ਮੀ. (7 ਫੁੱਟ).
      • ਚੌੜਾਈ = 3.66 ਮੀ. (12 ਫੁੱਟ)
      • ਡੂੰਘਾਈ = 120 ਮੀ. 4 ਫੁੱਟ
      • ਬੈਕਬੋਰਡ (Backboard) ਦੀ ਉਚਾਈ = 460 ਮਿ.ਮੀ.
   6. ਗੇਂਦ ਦਾ ਭਾਰ : 156 ਗ੍ਰਾਮ ਤੋਂ 163 ਗ੍ਰਾਮ
   7. ਹਾਕੀ ਸਟਿਕ (Stick) ਦਾ ਭਾਰ : 737 ਗਾਮ ਜ਼ਿਆਦਾ
   8. ਬਾਲ ਦਾ ਘੇਰਾ : 224 ਤੋਂ 235 ਮਿ.ਮੀ.
   9. ਕਾਰਡ : ਹਰਾ – 2 ਮਿੰਟ ਦਾ ਨਿਲੰਬਨ, ਪੀਲਾ -5-10 ਮਿੰਟ ਦਾ ਨਿਲੰਬਨ, ਲਾਲ-ਸਥਾਈ ਰੂਪ ਤੋਂ ਨਿਲੰਬਨ
   10. ਸ਼ੂਟਿੰਗ ਘੇਰੇ ‘ਡੀ’ (Shooting Circle ‘D’) ਦਾ ਘੇਰਾ : 14.63 ਮੀ. (16 ਗਜ਼)
   11. ਅਧਿਕਾਰੀਆਂ ਦੀ ਸੰਖਿਆ : 04 (ਦੋ ਫੀਲਡ ਅੰਪਾਇਰ, ਇਕ ਰਿਕਾਰਡ ਕੀਪਰ, ਇਕ ਟਾਈਮ ਕੀਪਰ
   12. ਪਿਨੈਲਟੀ ਸਥਲ ਦੀ ਦੂਰੀ (ਗੋਲ ਪੋਸਟ ਤੋਂ) : 640 ਮੀ.

ਖੇਲ ਦੇ ਮੈਦਾਨ ਦਾ ਨਾਪ ਅਤੇ ਉਪਕਰਨ
(Dimensions of Playfield and Equipment)

1. ਖੇਲ ਦਾ ਮੈਦਾਨ (Playfield) – ਆਯਤਾਕਾਰ ਅਕਾਰ ਵਿਚ (Rectangular in Shape), ਅਜਕਲ ਹਾਕੀ ਮੈਦਾਨ ਨੂੰ ਏਸਟੋ ਟਰਫ਼ (Astro Turf) ਦੀ ਖੇਲ ਸਤਹ ਤੇ ਚਿੰਨਿਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ, ਜਿਸਦੀ ਲੰਬਾਈ 299 ਫੁੱਟ, 10 ਇੰਚ (91.4 ਮੀ.) ਅਤੇ ਚੌੜਾਈ 180 ਫੁੱਟ 5 ਇੰਚ ਅਰਥਾਤ 55.0 ਮੀ. ਹੁੰਦੀ ਹੈ ।
   
   25 ਗਜ (22.9 ਮੀ.) ਦੀ ਲਾਈਨ ਮੈਦਾਨ ਦੇ ਆਰ-ਪਾਰ ਚਿੰਨਿਤ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ਜਿਸਦੇ ਦੋਨੋਂ ਪਾਸੇ, ਗੋਲ ਪੋਸਟ ਦੀ ਬੈਕ ਲਾਈਨ (Back line) ਦੇ ਵਲ ਸਮਾਨਾਂਤਰ ਹੁੰਦੇ ਹਨ ।
2. ਗੋਲ ਪੋਸਟ (Goal Post) – ਹਾਕੀ ਦੇ ਮੈਦਾਨ ਵਿਚ ਗੋਲ ਪੋਸਟ ਦੀ ਉਚਾਈ 2.14 ਮੀ. (7 ਫੁੱਟ) ਅਤੇ ਚੌੜਾਈ 3.66 ਮੀ. (12 ਫੁੱਟ) ਹੁੰਦੀ ਹੈ | ਭਾਰਤੀ ਹਾਕੀ ਸੰਘ (FIH) ਦੇ ਨਿਯਮਾਂ ਅਨੁਸਾਰ ਗੋਲ ਪੋਸਟ ਦੀ ਡੂੰਘਾਈ 120 ਮੀ. (4 ਫੁੱਟ) ਹੁੰਦੀ ਹੈ ।
3. ਸਟਰਾਈਕਿੰਗ ਘੇਰਾ ‘ਡੀ (Striking Circle ‘D’) – ਮੈਦਾਨ ਦੇ ਅੰਦਰ ਸਟਰਾਈਕਿੰਗ ਘੇਰੇ ਦੋ ਚੌਥਾਈ | ਭਾਗ) ਨੂੰ ‘ਡੀ’ ਨਾਲ 3.66 ਮੀ. ਤੇ ਚਿੰਨਿਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ, ਜਿਸਦਾ 16.63 ਮੀ. ਦਾ ਅਰਧ ਵਿਆਸ ਹੁੰਦਾ ਹੈ । ਇਹ ਚੌਥਾਈ ਭਾਗ ਸਿੱਧੀ ਰੇਖਾ ਨਾਲ ਜੁੜੇ ਹੁੰਦੇ ਹਨ ।
4. ਪਿਨੈਲਟੀ ਸਥਲ (Penalty Spot) – ਮੂਲ ਰੇਖਾ (Base line) ਤੋਂ 6.475 ਮੀ. ਦੀ ਦੂਰੀ ਤੇ ਇਹ ਬਿੰਦੂ ਚਿੰਨਿਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।
5. ਹਾਕੀ ਸਟਿਕ (Hockey Stick) – ਇਹ ਸਟਿਕ ਲਕੜੀ, ਕਾਰਬਨ, ਫਾਈਬਰ, ਫਾਈਬਰ ਗਿਲਾਸ ਜਾਂ ਇਨ੍ਹਾਂ ਫਾਈਬਰਾਂ ਦੇ ਮਿਸ਼ਨਰ ਤੋਂ ਬਣਾਈ ਜਾਂਦੀ ਹੈ । ਇਸ ਸਟਿਕ ਦਾ ਭਾਗ 737 ਗ੍ਰਾਮ ਤੋਂ ਜ਼ਿਆਦਾ ਨਹੀਂ ਹੋਣਾ ਚਾਹੀਦਾ ।
6. ਗੇਂਦ (Ball) – ਇਹ ਖੇਲ ਚਿੱਟੇ ਰੰਗ ਦੀ ਪਲਾਸਟਿਕ ਦੀ ਗੇਂਦ ਨਾਲ ਖੇਲਿਆ ਜਾਂਦਾ ਹੈ । ਗੇਂਦ ਦਾ ਭਾਰ 5.5 ਤੋਂ 5.7 ਐੱਸ ਜਾਂ 156-163 ਗਾ. ਤੋਂ ਜ਼ਿਆਦਾ ਨਹੀਂ ਹੋਣਾ ਚਾਹੀਦਾ |ਗੋਂਦ ਦਾ ਘੇਰਾ 224 ਤੋਂ 235 ਮਿ.ਮੀ. ਤਕ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ।
7. ਗੋਲ ਕੀਪਿੰਗ ਕਿਟ (Goal Keeping Kit) – ਇਕ ਗੋਲ ਕੀਪਰ ਇਕ ਅਲੱਗ ਰੰਗ ਦੀ ਕਮੀਜ਼ ਅਤੇ ਪੂਰਨ ਰਕਸ਼ਾਤਮਕ ਉਪਕਰਨ ਪਾਉਣਾ ਹੈ, ਜਿਸ ਵਿਚ ਹੈੱਡ ਗਿਰ (Head Gear), ਲੈਂਗ ਗਾਰਡਸ (Leg Guards) ਅਤੇ ਕਿਕਰਸ (Kickers) ਆਦਿ ਸ਼ਾਮਿਲ ਹੁੰਦੇ ਹਨ ।

ਨਿਯਮ ਅਤੇ ਅਧਿਨਿਯਮ ।
(Rules and Regulations)

1. ਖਿਡਾਰੀ ਸਟਿਕ ਦੇ ਸਾਹਮਣੇ ਵਾਲੇ ਭਾਗ ਤੋਂ ਗੇਂਦ ਨੂੰ ਮਾਰਨਗੇ ਜਾਂ ਸਟਿਕ ਦੇ ਚਪਟੇ ਪਾਸਿਓ ।
2. ਗੇਂਦ ਦੀ ਗਤੀ ਦੇ ਸਮੇਂ ਗੋਲ ਕੀਪਰ ਦੇ ਅਲਾਵਾ ਕੋਈ ਹੋਰ ਖਿਡਾਰੀ ਗੇਂਦ ਨੂੰ ਪੈਰ, ਹੱਥ ਜਾਂ ਸਰੀਰ ਦੇ ਕਿਸੇ ਹੋਰ ਹਿੱਸੇ ਨਾਲ ਸਪਰਸ਼ ਨਹੀਂ ਕਰੇਗਾ। ਕਿਸੇ ਵੀ ਹਾਲਤ ਵਿਚ, ਜਾਨਬੁੱਝ ਕੇ ਗੇਂਦ ਤੇ ਲੇਟ ਜਾਣ ਦੀ ਇਜ਼ਾਜ਼ਤ ਨਹੀਂ ਹੁੰਦੀ ।
3. ਵਿਰੋਧੀ ਟੀਮ ਦੇ ਸਿਰਫ਼ ਦੋ ਖਿਡਾਰੀ ਹੀ ਗੇਂਦ ਲਈ ਜੂਝ ਸਕਦੇ ਹਨ, ਤੀਜੇ ਦਲ ਜਾਂ ਖਿਡਾਰੀ ਨੂੰ ਰੁਕਾਵਟ ਪਾਉਣ ਦੀ ਇਜਾਜ਼ਤ ਨਹੀਂ ਹੁੰਦੀ ।
4. ਜਦੋਂ ਗੇਂਦ ਕਿਨਾਰੇ ਦੀਆਂ ਰੇਖਾਵਾਂ (Side lines) ਨੂੰ ਪਾਰ ਕਰ ਜਾਂਦੀ ਹੈ ਤਾਂ ਵਿਰੋਧੀ ਟੀਮ ਦੇ ਖਿਡਾਰੀ ਨੂੰ ਸਾਈਡਲਾਈਨ (Sideline) ਹਿੱਟ ਦਿੱਤੀ ਜਾਵੇਗੀ ।
   
5. ਵੀ ਹਿੱਟ ਲੈਂਦੇ ਸਮੇਂ, ਸਾਰੇ ਖਿਡਾਰੀਆਂ ਨੂੰ ਗੇਂਦ ਤੋਂ 5 ਮੀਟਰ ਦੂਰ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ।
   
6. ਜਿਸ ਖਿਡਾਰੀ ਦੇ ਕਬਜ਼ੇ ਵਿਚ ਗੇਂਦ ਹੁੰਦੀ ਹੈ, ਉਸਨੂੰ ਇਸ ਗੱਲ ਦੀ ਇਜਾਜ਼ਤ ਨਹੀਂ ਹੁੰਦੀ ਕਿ ਉਹ ਬਚਾਓ : ਕਰਨ ਵਾਲੇ ਖਿਡਾਰੀ ਨੂੰ ਆਪਣੇ ਰਸਤੇ ਤੋਂ ਹਟਾਉਣ ਲਈ ਜਾਨ-ਬੁੱਝ ਕੇ ਆਪਣੇ ਸਰੀਰ ਦਾ ਪ੍ਰਯੋਗ ਕਰਕੇ ਉਸਨੂੰ ਧੱਕਾ ਦੇਵੇ ।
7. ਗੋਡਿਆਂ ਦੇ ਪੱਧਰ ਤੋਂ ਉੱਤੇ ਗੇਂਦ ਨੂੰ ਮਾਰਨ ਦੀ ਇਜਾਜ਼ਤ ਨਹੀਂ ਹੁੰਦੀ । ਪਰੰਤੂ ਸਕੂਪ (Scoop) ਅਤੇ ਫਲਿਕ (Flick) ਵਰਗੇ ਕੁਝ ਕੌਸ਼ਲਾਂ ਵਿਚ, ਇਸ ਤੇ ਵਿਚਾਰ ਕੀਤਾ ਜਾਂਦਾ ਹੈ, ਜਿਥੇ ਇਹ ਦੂਜੇ ਖਿਡਾਰੀਆਂ ਲਈ ਖ਼ਤਰਨਾਕ ਨਹੀਂ ਹੁੰਦਾ । ਜਦਕਿ ਨਿਯਮਾਂ ਵਿਚ ਕਿਤੇ ਵੀ ਗੇਂਦ ਦੀ ਗਤੀ ਨੂੰ ਪਰਿਭਾਸ਼ਿਤ ਨਹੀਂ ਕੀਤਾ ਗਿਆ ਹੈ ।

ਮਹੱਤਵਪੂਰਨ ਪਰਿਭਾਸ਼ਿਕ ਸ਼ਬਦਾਵਲੀ
(Important Terminologies)

1. ਵੀ ਹਿੱਟ (Free Hit) – ਇਹ ਉਦੋਂ ਕੀਤਾ ਜਾਂਦਾ ਹੈ, ਜਦੋਂ ਸਕੋਰਿੰਗ ਚੱਕਰ (Scoring Circle) ਦੇ ਬਾਹਰ ਨਿਯਮਾਂ ਦਾ ਉਲੰਘਨ (Foul) ਹੁੰਦਾ ਹੈ । ਇਸ ਦਸ਼ਾ ਵਿਚ, ਰਕਸ਼ਕ ਨੂੰ ਖਿਡਾਰੀ ਤੋਂ 5 ਮੀ. ਦੂਰ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ।
2. ਪਿਨੈਲਟੀ ਕਾਰਨਰ (Penalty Corner) – ਹਮਲਾ ਕਰਨ ਵਾਲੀ ਟੀਮ ਨੂੰ ਪਨੈਲਟੀ ਕਾਰਨਰ ਉਦੋਂ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ਜਦੋਂ ਰਕਸ਼ਾਤਮਕ ਖਿਡਾਰੀ ਸਟਰਾਈਕਿੰਗਾਂ ਚੱਕਰ ਦੇ ਅੰਦਰ ਜਾਂ ਗੋਲ ਖੇਤ ਦੇ 25 ਗਜ਼ ਦੇ ਅੰਦਰ ਤੋਂ ਨਿਯਮਾਂ ਦਾ ਉਲੰਘਨ (Foul) ਕਰੇ ।
3. ਪਿਨੈਲਟੀ ਸਟਰੋਕ (Penalty Stroke) – ਜਦੋਂ ਰਕਸ਼ਾਤਮਕ ਖਿਡਾਰੀ ਜੰਗਲ ਨੂੰ ਬਚਾਉਣ ਦੇ ਲਈ ਚੱਕਰ ਦੇ ਅੰਦਰ ਨਿਯਮ ਦਾ ਉਲੰਘਨ ਕਰਦਾ ਹੈ ਜਾਂ ਜੇਕਰ ਇਕ ਖਿਡਾਰੀ ਪਿਛਲੀ ਰੇਖਾ (Backline) ਤੋਂ ਪਿਨੈਲਟੀ ਕਾਰਨਰ ਦੇ ਦੌਰਾਨ ਜਲਦੀ ਦੌੜ ਪੈਂਦਾ ਹੈ, ਤਾਂ ਵਿਰੋਧੀ ਟੀਮ ਨੂੰ ਪਿਨੈਲਟੀ ਸਟਰੋਕ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ।
4. ਫਲਿਕ (Flick) – ਇਹ ਮਿੱਥੀ ਹੋਈ ਉੱਚਾਈ ਤੋਂ ਉਪਰ ਦੇ ਪ੍ਰਕਾਰ ਦਾ ਇਕ ਸ਼ਾਟ ਹੁੰਦਾ ਹੈ ਪਰੰਤੂ ਇਹ ਵਿਰੋਧੀ ਦਲ ਦੇ ਲਈ ਚੋਟ ਪਹੁੰਚਾਉਣ ਤਕ ਖਤਰਨਾਕ ਨਹੀਂ ਹੁੰਦਾ ਅਰਥਾਤ ਗੋਲੇ ਤੇ ਸ਼ਾਟ ਦਾ ਦੌਰਾਨ ਡਰੈਗ ਫਲਿਕ ।
5. ਸਡਨ ਡੈਥ (Sudden Death) – ਜੇਕਰ ਜ਼ਿਆਦਾ ਸਮੇਂ ਦੇ ਪੂਰਾ ਹੋਣ ਤੋਂ ਬਾਅਦ ਵੀ ਖੇਲ ਬਰਾਬਰੀ (Tie) ਤੇ ਰਹਿੰਦਾ ਹੈ, ਤਾਂ ਇਹ ਬਰਾਬਰੀ (Tie) ਉਦੋਂ ਹੀ ਖ਼ਤਮ ਹੋ ਜਾਏਗੀ, ਜੇਕਰ ਇਕ ਟੀਮ ਪਿਨੈਲਟੀ ਸਟੋਕ ਦੇ ਦੌਰਾਨ ਗੋਲ ਕਰ ਦਿੰਦੀ ਹੈ । ਇਸਨੂੰ ਸਡਨ ਡੈਥ ਕਹਿੰਦੇ ਹਨ ।
6. ਸਕੂਪ (Scoop) – ਇਸ ਤਕਨੀਕ ਦਾ ਪ੍ਰਯੋਗ ਮੈਦਾਨ ਤੇ ਰਕਸ਼ਕਾਂ ਨੂੰ ਹਰਾਉਣ ਲਈ ਐਵਰਹੈੱਡ ਪਾਸ (Overhead pass) ਦੇ ਰੂਪ ਵਿਚ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।
7. ਹਮਲਾਵਰ ਅਟੈਕਰਸ (Attackers-ਜਿਨ੍ਹਾਂ ਖਿਡਾਰੀਆਂ ਦੇ ਅਧਿਕਾਰ ਵਿਚ ਗੇਂਦ ਹੁੰਦੀ ਹੈ, ਉਨ੍ਹਾਂ ਨੂੰ ਅਟੈਕਰਸ (Attackers) ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।
8. ਰਕਸ਼ਕ (Defenders) – ਜਿਨ੍ਹਾਂ ਖਿਡਾਰੀਆਂ ਦੇ ਕੋਲ ਗੇਂਦ ਨਹੀਂ ਹੁੰਦੀ, ਉਨ੍ਹਾਂ ਨੂੰ ਰਕਸ਼ਕ (Defenders) ਕਹਿੰਦੇ ਹਨ ।

ਵਿਕਲਪ (Substitution) – ਖਿਡਾਰੀਆਂ ਦੇ ਲਈ ਅਸੀਮਿਤ ਵਾਰ ਵਿਕਲਪਾਂ ਦਾ ਪ੍ਰਯੋਗ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਪਿਨੈਲਟੀ ਕਾਰਨਰ ਦੇਣ ਅਤੇ ਉਸਦੇ ਅੰਤ ਤਕ ਦੀਆਂ ਦੋ ਸਥਿਤੀਆਂ ਦੇ ਇਲਾਵਾ ਇਸਨੂੰ ਰੋਲਿੰਗ ਵਿਕਲਪ (Rolling Substitution) ਕਹਿੰਦੇ ਹਨ ।

ਬੁਨਿਆਦੀ ਕੋਸ਼ਲ
(Basic Skills)

1. ਹਿਟਿੰਗ (Hitting) – ਗੇਂਦ ਨੂੰ ਹਿੱਟ ਕਰਨ ਦੇ ਲਈ ਖਿਡਾਰੀ ਸਟਿਕ ਨੂੰ ਦੋਨਾਂ ਹੱਥਾਂ ਨਾਲ ਫੜਦਾ ਹੈ ਅਤੇ ਸਟਿਕ ਦੀ ਚਪਟੀ ਸਤਿਹ ਤੋਂ ਗੇਂਦ ਨੂੰ ਮਾਰਨ ਲਈ ਇਕ ਮਿੱਥੇ ਹੋਏ ਪੱਧਰ ਤੇ ਪਿੱਛੇ ਵੱਲ ਉੱਠਦਾ ਹੈ ।

2. ਡਰਿਬਲਿੰਗ (Dribbling) – ਵਿਰੋਧੀ ਟੀਮ ਦੇ ਖੇਤਰ ਵਿਚ ਹਮਲਾ ਕਰਨ ਲਈ ਅੱਗੇ ਵੱਧਣ ਦਾ ਇਹ ਸਭ ਤੋਂ ਵਧੀਆ ਤਰੀਕਾ ਹੈ । ਇਸਦਾ ਪ੍ਰਯੋਗ ਰਕਸ਼ਕਾਂ ਨੂੰ ਹਰਾਉਣ ਲਈ ਅਤੇ ਨਾਲ ਹੀ ਦੂਸਰੀ ਟੀਮ ਦੇ ਸਾਥੀਆਂ ਨੂੰ ਗੇਂਦ ਪਾਸ ਕਰਨ ਲਈ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਇਸਦੇ ਲਈ ਉਪਰੀ ਹੱਥ ਦੀ ਪਕੜ ਦਾ ਪ੍ਰਯੋਗ ਕਰਕੇ ਹਾਕੀ ਸਟਿਕ ਨੂੰ ਘੁਮਾਉਣ ਲਈ ਗੇਂਦ ਤੇ ਬਹੁਤ ਜ਼ਿਆਦਾ ਕੰਟਰੋਲ ਦੀ ਜ਼ਰੂਰਤ ਹੁੰਦੀ ਹੈ ।

3. ਡੋਜ਼ਿੰਗ (Dodging) – ਇਸ ਕੌਸ਼ਲ ਦਾ ਪ੍ਰਯੋਗ ਰਕਸ਼ਕ ਨੂੰ ਗੇਂਦ ਤੋਂ ਇਕ ਪਾਸੇ ਰੱਖਣ ਲਈ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਹਮਲਾਵਰ ਦੁਆਰਾ ਇਸ ਚਾਲ ਦੀ ਬਹੁਤ ਘੱਟ ਆਸ਼ਾ ਹੁੰਦੀ ਹੈ ਕਿ ਉਹ ਰਕਸ਼ਕ ਨੂੰ ਗੇਂਦ ਨਾਲ ਬਹੁਤ ਪਿੱਛੇ ਛੱਡ ਦੇਵੇ ।

4. ਸਟਾਪਿੰਗ ਬਾਲ (Stopping ball) – ਇਸ ਵਿਚ ਖਿਡਾਰੀ ਸਟਿਕ ਦੇ ਸਾਹਮਣੇ ਵਾਲੇ ਭਾਗ ਜਾਂ ਬਲੇਡ ਦੀ ਸਹਾਇਤਾ ਨਾਲ ਗੇਂਦ ਤੇ ਕੰਟਰੋਲ ਰੱਖਦਾ ਹੈ । ਪਿਨੈਲਟੀ ਕਾਰਨਰ ਦੇ ਦੌਰਾਨ, ਗੇਂਦ ਨੂੰ ਰੋਕਣ ਲਈ ਕੁਸ਼ਲਤਾਪੂਰਵਕ ਯੁਕਤੀਆਂ ਦੀ ਜ਼ਰੂਰਤ ਹੁੰਦੀ ਹੈ, ਜਿਸ ਵਿਚ ਖਿਡਾਰੀਆਂ ਨੂੰ ਕਦੇ-ਕਦੇ ਗੇਂਦ ਨੂੰ ਪੂਰਨਰੂਪ ਵਿਚ ਰੋਕਣ ਦੇ ਲਈ ਸਟਿਕ ਨੂੰ ਧਰਤੀ ਤੇ ਸਮਤਲ ਰੱਖਣ ਦੀ ਜ਼ਰੂਰਤ ਹੁੰਦੀ ਹੈ ।

5. ਗੋਲ ਕੀਪਿੰਗ (Goal Keeping) – ਇਕ ਗੋਲਕੀਪਰ ਨੂੰ ਚੱਕਰ ਦੇ ਅੰਦਰ ਸਟਿਕ, ਪੈਰ, ਲੈਂਗ ਗਾਰਡ ਜਾਂ ਸਰੀਰ ਦੇ ਕਿਸੇ ਦੂਜੇ ਭਾਗ ਦੇ ਪ੍ਰਯੋਗ ਦੁਆਰਾ ਗੇਂਦ ਨੂੰ ਰੋਕਣ ਜਾਂ ਮੋੜਣ ਦੀ ਇਜ਼ਾਜ਼ਤ ਹੁੰਦੀ ਹੈ । ਇਹ ਦੂਸਰੇ ਖਿਡਾਰੀਆਂ ਦੇ ਲਈ ਖਤਰਨਾਕ ਢੰਗ ਨਾਲ ਨਹੀਂ ਹੋਣਾ ਚਾਹੀਦਾ ਜਦਕਿ ਕਿਸੀ ਵੀ ਦਸ਼ਾ ਵਿਚ ਗੇਂਦ ਤੇ ਲੇਟਣ ਦੀ ਇਜ਼ਾਜ਼ਤ ਨਹੀਂ ਹੁੰਦੀ ।

6. ਉਲਟਾ ਸ਼ਾਟ (Reverse Shot) – ਉਲਟੇ ਫਲਿਟ ਦੇ ਲਈ ਸਟਿਕ ਨੂੰ ਦੋਨਾਂ ਹੱਥਾਂ ਨਾਲ ਉੱਪਰ ਵਲ ਫੜੋ । ਸਟਿਕ ਦੀ ਹੁਕ ਨੂੰ ਘੜੀ ਦੀ ਸੂਈ ਦੀ ਦਿਸ਼ਾ ਵਿਚ, ਚਪਟੇ ਪਾਸੇ ਵਲ ਉੱਪਰ ਰੱਖ ਕੇ ਘੁਮਾਣਾ ਚਾਹੀਦਾ ਹੈ ।

7. ਵਿੰਗ ਦੀ ਬਾਲ (Pushing the Ball) – ਹਾਕੀ ਵਿਚ ਪੁਸ਼ ਪਾਸ ਜਾਂ ਬਾਲ ਨੂੰ ਅੱਗੇ ਧਕੇਲਣਾ ਇਕ ਬੁਨਿਆਦੀ ਕੌਸ਼ਲ ਹੈ । ਇਸ ਪਾਸ ਦਾ ਪ੍ਰਯੋਗ ਪ੍ਰਮੁੱਖ ਰੂਪ ਤੇ ਘੱਟ ਦੂਰੀ ਦੇ ਲਈ ਗੇਂਦ ਨੂੰ ਪਾਸ ਕਰਨ ਲਈ ਹੁੰਦਾ ਹੈ । ਗੇਂਦ ਨੂੰ ਹਿੱਟ ਕਰਦੇ ਸਮੇਂ ਇਸ ਵਿਚ ਕੋਈ ਆਵਾਜ਼ ਨਹੀਂ ਆਉਂਦੀ । ਪੁਸ਼ ਪਾਸ ਦੇ ਦੌਰਾਨ ਇਕ ਹੱਥ ਦੀ ਪਕੜ ਸਟਿਕ ਦੇ ਵਿਚ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ।

ਮਹੱਤਵਪੂਰਨ ਟੂਰਨਾਮੈਂਟ
(Important Tournaments)

ਅੰਤਰਰਾਸ਼ਟਰੀ ਪੱਧਰ (International Level)
1. ਐੱਫ.ਆਈ.ਐੱਚ. (FIH) (ਅੰਤਰਰਾਸ਼ਟਰੀ ਹਾਕੀ ਸੰਘ ਓਲੰਪਿਕ ਖੇਲ, ਵਿਸ਼ਵ ਕਪ, ਵਿਸ਼ਵ ਲੀਗ, ਚੈਂਪੀਅਨ ਫੀ, ਜੂਨੀਅਰ ਵਿਸ਼ਵ ਕਪ, ਏਸ਼ੀਆ ਕਪ ਦਾ ਆਯੋਜਨ ਕਰਨ ਲਈ ਜ਼ਿੰਮੇਵਾਰ ਹੈ ।

ਰਾਸ਼ਟਰੀ ਪੱਧਰ (National Level)
2. ਫੈਡਰੇਸ਼ਨ ਰੂਪ, ਇੰਦਰਾ ਗਾਂਧੀ ਗੋਲਡ ਕਪ, ਜੂਨੀਅਰ ਨਹਿਰੂ ਹਾਕੀ ਫ਼ੀ, ਅਬਦੁੱਲ ਗੋਲਡ ਕਪ, ਆਭਾ ਖਾਨ ਕਪ, ਬੰਬੇ ਗੋਲਡ ਕਪ ।

ਸਪਰੋਟਸ ਅਵਾਰਡ
(Sports Award)

ਅਰਜੁਨ ਪੁਰਸਕਾਰ ਜੇਤੂਆਂ ਦੀ ਸੂਚੀ (List of Arjuna Award Winners) – ਪ੍ਰਿਥੀਪਾਲ ਸਿੰਘ, ਐੱਨ. ਲਮਸਡਨ (1961), ਚਰਨਜੀਤ ਸਿੰਘ (1963), ਐੱਸ ਲਕਸ਼ਮਨ (1964), ਊਧਮ ਸਿੰਘ, ਕੁਮਾਰੀ ਏਲਵੀਰਾ ਬਰੀਟੋ (1965), ਵੀ. ਜੇ. ਪੀਟਰ, ਕੁਮਾਰੀ ਸੁਨੀਤਾ ਪੁਰੀ, ਗੁਰਬਖਸ਼ ਸਿੰਘ (1966), ਹਰਬਿੰਦਰ ਸਿੰਘ (1967), ਮੋਹਿੰਦਰ ਲਾਲ (1967), ਕੈਡੇਟ ਬਲਬੀਰ ਸਿੰਘ (1968), ਅਜੀਤ ਪਾਲ ਸਿੰਘ (1970), ਪੀ. ਕ੍ਰਿਸ਼ਨਾਮੂਰਤੀ (1971), ਮਾਈਕਲ ਕਿੰਡੋ (1972), ਐੱਮ.ਪੀ. ਗਣੇਸ਼, ਡਾ: ਕੁਮਾਰੀ ਮੱਸਰੀਨਾਜ਼ (1973), ਅਸ਼ੋਕ ਕੁਮਾਰ, ਅਜਿੰਦਰ ਕੌਰ (1974), ਬੀ.ਪੀ. ਗੋਵਿੰਦਾ, ਰੂਪਾ ਸੈਨੀ (1975), ਕੈਪਟਨ ਹਰਚਰਨ ਸਿੰਘ, ਐੱਲ. ਐਲ. ਫਰਨਾਂਡੀਜ਼ (1977-78), ਵਾਸੂਦੇਵ ਭਾਸਕਰਨ, ਆਰ.ਬੀ. ਮੁੰਡਨ (1979-80), ਮੁਹੰਮਦ ਸ਼ਾਹਿਦ, ਮਤੀ ਏਲਿਜ਼ਾ ਨੈਲਸਨ (1980-81), ਵਰਸ਼ਾ ਸੋਨੀ (1980), ਜ਼ਫ਼ਰ ਇਕਬਾਲ (1983), ਰਾਜਬੀਰ ਕੌਰ (1984), ਐੱਸ.· ਮੈਸੀ, ਪ੍ਰੇਮ ਮਾਇਆ ਸੋਨਅਰ (1985), ਪਾਂਡਾ ਮੁਥਾਨਾ (1986), ਜੇ.ਐੱਮ. ਕਾਰਵੇਹੋ (1986), ਐੱਮ.ਪੀ. ਸਿੰਘ (1989), ਪ੍ਰਗਟ ਸਿੰਘ (1989), ਜਗਬੀਰ ਸਿੰਘ (1990), ਸ੍ਰੀ ਜਗਬੀਰੂ ਸਿੰਘ (1990), ਮਰਵਿਨ ਫਰਨਾਡੀਜ਼ (1992), ਜੂਡ ਫਿਲਿਕਸ ਸਬਾਸਤਿਅਨ (1994), ਧਨਰਾਜ ਪਿੱਲੇ (1995), ਮੁਕੇਸ਼ ਕੁਮਾਰ (1995), ਏ.ਬੀ. ਸੁਬੈਇਆ, ਆਸ਼ੀਸ਼ ਕੁਮਾਰ ਬੱਲਾਲ (1996), ਪ੍ਰੀਤਮ ਰਾਣੀ, ਓਮਾਨਾ, ਸੁਰਜੀਤ ਸਿੰਘ, ਬੀ.ਐੱਸ. ਢਿੱਲੋਂ, ਮੁਹੰਮਦ ਰਿਆਜ਼, ਬਲਦੇਵ ਸਿੰਘ, ਐੱਮ.ਕੇ. ਕੌਸ਼ਿਕ (1999), ਰਮਨਦੀਪ ਸਿੰਘ, ਬਲਬੀਰ ਸਿੰਘ ਕੁੱਲਰ, ਵੀ.ਜੇ. ਫਿਲਿਪਸ, ਹਰੀਪਾਲ ਕੌਸ਼ਲ, ਗਰੁੱਪ ਕੈਪਟਨ ਆਰ. ਐੱਸ. ਭੋਲਾ (ਰਿਟਾਇਰਡ), ਬਾਲ ਕਿਸ਼ਨ ਸਿੰਘ, ਜਲਾਲੂਦੀਨ ਰਜਵੀ, ਮਧੂ ਯਾਦਵ (2000), ਦਲੀਪ ਟਰਕੀ, ਸੀਤਾ ਗੋਸਾਈਂ (2002), ਗਗਨ ਜੀਤ ਸਿੰਘ, ਮਮਤਾ ਖਰਵ (2003), ਦੇਵੇਸ਼ ਚੌਹਾਨ, ਸੂਰਜ ਲਤਾ ਦੇਵੀ (2004), ਦੀਪਕ ਠਾਕੁਰ, ਹੈਲਨ ਮੈਰੀ (2005), ਵੀਰਨ ਰਸਕੁਈਨਾ (2006), ਇਗਨੀਜ ਟਿਰਕੀ (2009), ਸੁਰਿੰਦਰ ਕੌਰ (2009), ਸੰਦੀਪ ਸਿੰਘ, ਜਸਮੀਤ ਕੌਰ (2010) ।

ਪਦਮ ਸ਼੍ਰੀ ਅਵਾਰਡ-ਪ੍ਰਗਟ ਸਿੰਘ, ਚਰਨਜੀਤ ਸਿੰਘ, ਸ਼ੰਕਰ ਲਕਸ਼ਮਣ, ਅਜੀਤ ਪਾਲ ਸਿੰਘ, ਪ੍ਰਿਥੀਪਾਲ ਸਿੰਘ, ਦਲੀਪ ਟਿਰਕੀ (2004) ।
ਦਰੋਣਾਚਾਰੀਆ ਅਵਾਰਡ-ਜ਼ਫ਼ਰ ਇਕਬਾਲ, ਰਾਜੇਂਦਰ ਸਿੰਘ (2005), ਬਲਦੇਵ ਸਿੰਘ (2009) ।

PSEB 12th Class Physical Education Practical ਹਾਕੀ (Hockey)

ਪ੍ਰਸ਼ਨ 1.
ਹਾਕੀ ਦੇ ਖੇਡ ਦੇ ਮੈਦਾਨ ਦੀ ਲੰਬਾਈ ਕਿੰਨੀ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਹਾਕੀ ਦੇ ਖੇਡ ਦੇ ਮੈਦਾਨ ਦੀ ਲੰਬਾਈ 91.40 ਮੀ. (100 ਗਜ਼) ਹੁੰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਗੇਂਦ ਦਾ ਘੇਰਾ ਕਿੰਨਾ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਗੇਂਦ ਦਾ ਘੇਰਾ 224-235 ਮਿ.ਮੀ. ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਹਾਕੀ ਮੈਚ ਦੀ ਅਵਧੀ ਕਿੰਨੀ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
15 ਮਿੰਟ ਦੇ ਚਾਰ ਭਾਗ ਹੁੰਦੇ ਹਨ, ਜਿੰਨ੍ਹਾਂ ਵਿਚ 10 ਮਿੰਟ ਦੇ ਇੰਟਰਵਲ ਹੁੰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 4.
ਹਾਕੀ ਮੈਚ ਲਈ ਕਿੰਨੇ ਅਧਿਕਾਰੀਆਂ ਦੀ ਜ਼ਰੂਰਤ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਹਾਕੀ ਮੈਚ ਦੇ ਲਈ ਚਾਰ ਅਧਿਕਾਰੀਆਂ ਦੀ ਜ਼ਰੂਰਤ ਹੁੰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 5.
ਹਾਕੀ ਮੈਚ ਵਿਚ ਕਿੰਨੇ ਖਿਡਾਰੀਆਂ ਦੀ ਜ਼ਰੂਰਤ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਇਕ ਟੀਮ ਵਿਚ ਦੋ ਗੋਲਕੀਪਰਾਂ ਸਮੇਤ ਕੁੱਲ 18 ਖਿਡਾਰੀ ਹੁੰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 6.
ਗੋਲ ਪੋਸਟ ਦੀ ਚੌੜਾਈ ਕਿੰਨੀ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਗੋਲ ਪੋਸਟ ਦੀ ਚੌੜਾਈ 3.66 ਮੀ. ਹੁੰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 7.
ਹਾਕੀ ਵਿਚ ਡਾਢੰਗ (Dodging) ਕੀ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਇਸ ਕੌਸ਼ਲ ਦਾ ਪ੍ਰਯੋਗ ਰੱਖਿਅਕ ਨੂੰ ਗੇਂਦ ਤੋਂ ਇਕ ਪਾਸੇ ਰੱਖਣ ਲਈ ਕੀਤਾ ਜਾਂਦਾ ਹੈ | ਹਮਲਾਵਰ ਦੁਆਰਾ ਇਸ ਚਾਲ ਦੀ ਬਹੁਤ ਆਸ਼ਾ ਜਾਂ ਉਮੀਦ ਹੁੰਦੀ ਹੈ ਕਿ ਉਹ ਰੱਖਿਅਕ ਨੂੰ ਗੇਂਦ ਤੋਂ ਬਹੁਤ ਪਿੱਛੇ ਛੱਡ ਦੇਵੇ ।

ਪ੍ਰਸ਼ਨ 8.
ਹਾਕੀ ਸਟਿਕ ਦਾ ਅਧਿਕਤਮ ਭਾਰ ਕਿੰਨਾ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ?
ਉੱਤਰ-
737 ਗ੍ਰਾ ਤੋਂ ਜ਼ਿਆਦਾ ਨਹੀਂ ਹੋਣਾ ਚਾਹੀਦਾ ।

ਪ੍ਰਸ਼ਨ 9.
ਹਾਕੀ ਗੇਂਦ ਦਾ ਭਾਰ ਕਿੰਨਾ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
156-163 ਗ੍ਰਾ.

ਪ੍ਰਸ਼ਨ 10.
ਹਾਕੀ ਦੇ ਸਕੂਪ (Scoop) ਕੀ ਹੁੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਇਸ ਤਕਨੀਕ ਦਾ ਪ੍ਰਯੋਗ ਮੈਦਾਨ ਤੇ ਰੱਖਿਅਕ ਨੂੰ ਹਰਾਉਣ ਲਈ ਐਵਰਹੈਡ ਪਾਸ (Overhead Pass) ਦੇ ਰੂਪ ਵਿਚ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 11.
ਗੋਲ ਪੋਸਟ ਵਿਚ ਬੈਕਬੋਰਡ (Backboard) ਦੀ ਉੱਚਾਈ ਕਿੰਨੀ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਗੋਲ ਪੋਸਟ ਵਿਚ ਬੈਕਬੋਰਡ ਦੀ ਉੱਚਾਈ 460 ਮਿ.ਮੀ. ਹੁੰਦੀ ਹੈ ।

Punjab State Board PSEB 12th Class Physical Education Book Solutions ਖੋ-ਖੋ (Kho-Kho) Game Rules.

ਖੋ-ਖੋ (Kho-Kho) Game Rules – PSEB 12th Class Physical Education

ਖੋ-ਖੋ ਦਾ ਇਤਿਹਾਸ
(History of Kho-Kho)

ਖੋ-ਖੋ ਇੱਕ ਭਾਰਤੀ ਖੇਡ ਹੈ । ਭਾਰਤ ਵਿੱਚ ਇਹ ਲੜਕੇ ਤੇ ਲੜਕੀਆਂ ਦੁਆਰਾ ਖੇਡੀ ਜਾਂਦੀ ਹੈ । ਇਹ ਖੇਡ ਮਹਾਂਰਾਸ਼ਟਰਾਂ ਵਿੱਚ ਪ੍ਰਫੁੱਲਿਤ ਹੋਈ । ਇਸ ਖੇਡ ਦਾ ਸੰਬੰਧ ਮਹਾਂਰਾਸ਼ਟਰ ਦੇ ਪਹਾੜਾਂ ਦੇ ਕਸਰਤਕਰਾਂ ਨਾਲ ਰਿਹਾ ਹੈ । ਇਸ ਖੇਡ ਦਾ ਜਨਮ ਮਹਾਂਰਾਸ਼ਟਰ ਦੇ ਸ਼ਹਿਰ ‘ਪੂਨਾ’ ਵਿੱਚ ਹੋਇਆ । ਇਸ ਤੋਂ ਮਗਰੋਂ ਹਨੂੰਮਾਨ ਵਿਯਯਾਮ ਪ੍ਰਚਾਰਕ ਮੰਡਲ ਦੁਆਰਾ ਖੋ-ਖੋ ਖੇਡ ਦਾ ਆਧੁਨਿਕ ਰੂਪ ਦਿੱਤਾ ਗਿਆ । ਸੰਨ 1928 ਵਿੱਚ ਅਖਿਲ ਮਹਾਂਰਾਸ਼ਟਰ ਸਰੀਰਕ ਸਿੱਖਿਅਕ ਮੰਡਲ ਦੀ ਸਥਾਪਨਾ ਹੋਈ । ਉਸਦੇ ਨਾਲ-ਨਾਲ ਖੋ-ਖੋ ਦੇ ਨਵੇਂ ਨਿਯਮ ਬਣਾਏ ਗਏ । ਸੰਨ 1960 ਵਿੱਚ ਭਾਰਤੀ ਖੋ-ਖੋ ਫੈਡਰੇਸ਼ਨ ਦੀ ਸਥਾਪਨਾ ਹੋਈ ਅਤੇ ਇਸ ਸਾਲ ਹੀ ਪਹਿਲੀ ਰਾਸ਼ਟਰੀ ਚੈਂਪੀਅਨਸ਼ਿਪ ਦੇ ਮੁਕਾਬਲੇ ਕਰਵਾਏ ਗਏ । ਅਗਲੇ ਸਾਲ 1961 ਵਿੱਚ ਮਹਿਲਾਵਾਂ ਦਾ ਰਾਸ਼ਟਰੀ ਪੱਧਰ ਦਾ ਟੂਰਨਾਮੈਂਟ ਕਰਵਾਇਆ ਗਿਆ ।

ਸੰਨ 1982 ਵਿੱਚ ਏਸ਼ੀਅਨ ਖੇਡਾਂ ਵੀ ਦਿੱਲੀ ਵਿਖੇ ਹੋਈਆਂ । ਉਸ ਵਿੱਚ ਖੋ-ਖੋ ਦਾ ਪ੍ਰਦਰਸ਼ਨੀ ਮੈਚ ਕਰਵਾਇਆ ਗਿਆ | ਪਰ ਹੁਣ ਤੱਕ ਏਸ਼ੀਅਨ ਖੇਡਾਂ ਵਿੱਚ ਖੋ-ਖੋ ਸ਼ਾਮਿਲ ਨਹੀਂ ਕੀਤੀ ਗਈ । 1963-64 ਵਿੱਚ ਇੰਦੋਰ ਵਿਖੇ ਇਹ ਫ਼ੈਸਲਾ ਕੀਤਾ ਗਿਆ ਕਿ ਜਿਹੜੇ ਚੰਗੇ ਖੋ-ਖੋ ਦੇ ਖਿਡਾਰੀ ਹਨ । ਉਨ੍ਹਾਂ ਨੂੰ ਇਨਾਮ ਦਿੱਤਾ ਜਾਵੇ । ਇਸ ਫ਼ੈਸਲੇ ਅਨੁਸਾਰ ਪੁਰਖਾਂ ਦੇ ਵਰਗ ਵਿੱਚ ‘ਇੱਕਲਵੱਯ’ ਇਨਾਮ ਅਤੇ ਮਹਿਲਾ ਵਰਗ ਵਿੱਚ ‘ਝਾਂਸੀ ਦੀ ਰਾਣੀ’ ਨਾਂ ਰੱਖਿਆ ਗਿਆ । 1963 ਵਿੱਚ ਬੰਬਈ ਗੋਲਡ ਟਰਾਫ਼ੀ ਟੂਰਨਾਮੈਂਟ ਸ਼ੁਰੂ ਹੋਇਆ । ਸੰਨ 1970-72 ਵਿੱਚ ਹੈਦਰਾਬਾਦ ਵਿਖੇ 16 ਸਾਲ ਦੀ ਉਮਰ ਦੇ ਖਿਡਾਰੀਆਂ ਲਈ ਅਲੱਗ ਖੋ-ਖੋ ਮੁਕਾਬਲੇ ਕਰਵਾਏ ਜਾਣ ਲੱਗੇ । ਜਿਸ ਵਿੱਚ ਵੀਰ ਅਭਿਮੰਨਯੂ ਇਨਾਮ ਦੇਣ ਦਾ ਫ਼ੈਸਲਾ ਕੀਤਾ ਗਿਆ ।1976-78 ਵਿੱਚ ਬੰਗਲੌਰ ਵਿਖੇ ਖੋ-ਖੋ ਦੀ ਤਕਨੀਕੀ ਸਿੱਖਿਆ NIS ਰਾਹੀਂ ਇਸ ਖੇਡ ਨੂੰ ਸ਼ੁਰੂ ਕੀਤਾ ਗਿਆ । ਭਾਰਤ ਵਿੱਚ ਇਸ ਖੇਡ ਨੂੰ ਖੋ-ਖੋ ਫੈਡਰੇਸ਼ਨ ਆਫ਼ ਇੰਡੀਆ ਕੰਟਰੋਲ ਕਰ ਰਹੀ ਹੈ ।

ਯਾਦ ਰੱਖਣ ਯੋਗ ਗੱਲਾਂ
(Tips to Remember)

1. ਖੋ-ਖੋ ਮੈਦਾਨ ਦੀ ਲੰਬਾਈ ਅਤੇ ਚੌੜਾਈ ਪੁਰਸ਼ਾਂ ਲਈ = 29 ਮੀਟਰ × 16 ਮੀਟਰ
2. ਕੇਂਦਰੀ ਲੇਨ ਵਿਚ ਵਰਗਾਂ ਦੀ ਸੰਖਿਆ = 8
3. ਮੈਦਾਨ ਦੇ ਅੰਤ ਵਿਚ ਆਇਤਕਾਰ ਦਾ ਮਾਪ = 16 ਮੀਟਰ ਪੁਰਸ਼ਾਂ ਲਈ 2.75 ਮੀ.
4. ਇਕ ਵਰਗ ਤੋਂ ਦੂਸਰੇ ਵਰਗ ਦੀ ਦੂਰੀ = 2.50 ਮੀਟਰ
5. ਕੇਂਦਰੀ ਗਲੀ ਦੀ ਚੌੜਾਈ, ਲੰਬਾਈ = 30 ਸੈਂ.ਮੀ. ਲੰਬਾਈ, 23.50 ਮੀ. ਚੌੜਾਈ
6. ਵਰਗ ਦਾ ਆਕਾਰ = 30 ਸੈਂ.ਮੀ. ਪੁਰਸ਼ਾਂ ਲਈ 30 ਸੈਂ.ਮੀ
7. ਖੋ-ਖੋ ਦੇ ਖਿਡਾਰੀਆਂ ਦੀ ਸੰਖਿਆ = 9.
8. ਬਦਲਵੇਂ ਖਿਡਾਰੀ = 3
9. ਮੈਚ ਦਾ ਸਮਾਂ = 9-5-9 (7) 9-5-9
10. ਖੋ-ਖੋ ਮੈਚ ਵਿਚ ਇਨਿੰਗ = 2
11. ਫਰੀ ਜੋਨ ਦਾ ਮਾਪ = 2.75 × 16 ਮੀ.
12. ਲਾਬੀ = 1.50 ਮੀਟਰ
13. ਵਰਗਾਂ ਵਿਚ ਬੈਠੇ ਖਿਡਾਰੀ = ਚੇਜ਼ਰ
14. ਵਰਗਾਂ ਦੇ ਵਿਰੋਧੀ ਖਿਡਾਰੀ = ਰਨਰ
15. ਔਰਤਾਂ ਲਈ ਸਮਾਂ = 7-5-7-5) 7.5-7
16. ਅਧਿਕਾਰੀਆਂ ਦੀ ਗਿਣਤੀ = 1 ਰੈਫ਼ਰੀ, 2 ਅੰਪਾਇਰ, ਇਕ ਟਾਈਮ ਕੀਪਰ, ਇਕ ਸਕੋਰਰ ।
17. ਪੋਲ ਦੀ ਜ਼ਮੀਨ ਤੋਂ ਉਚਾਈ = 1.20 ਮੀਟਰ ,

ਖੋ-ਖੋ ਦੇ ਨਵੇਂ ਸਧਾਰਨ ਨਿਯਮ
(Latest General Rules of Kho-Kho)

1. ਖੋ-ਖੋ ਦਾ ਮੈਦਾਨ ਆਇਤ ਆਕਾਰ ਦਾ ਹੁੰਦਾ ਹੈ । ਇਹ 29 ਮੀ. ਲੰਬਾ ਅਤੇ 16 ਮੀ. ਚੌੜਾ ਹੁੰਦਾ ਹੈ ।
2. ਖੋ-ਖੋ ਦੀ ਖੇਡ ਦੀ ਟੀਮ ਵਿੱਚ 12 ਖਿਡਾਰੀ ਹੁੰਦੇ ਹਨ । ਜਿਸ ਵਿਚੋਂ 9 ਖਿਡਾਰੀ ਖੇਡਦੇ ਹਨ ਅਤੇ 3 ਖਿਡਾਰੀ ਬਦਲਵੇਂ ਹੁੰਦੇ ਹਨ ।
3. ਖੇਡ ਟਾਸ ਰਾਹੀਂ ਸ਼ੁਰੂ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਟਾਸ ਜਿੱਤਣ ਵਾਲੀ ਟੀਮ ਦਾ ਕਪਤਾਨ ਚੇਜ਼ਰ ਜਾਂ ਰਨਰ ਬਣਾਉਣ ਦਾ ਫ਼ੈਸਲਾ ਕਰਦਾ ਹੈ ।
4. ਇੱਕ ਚੇਜ਼ਰ ਨੂੰ ਛੱਡ ਕੇ ਸਾਰੇ ਚੇਜ਼ਰ ਇਸ ਤਰ੍ਹਾਂ ਬੈਠਣਗੇ ਕਿ ਚੇਜ਼ਰ ਦਾ ਮੂੰਹ ਇਕ ਦਿਸ਼ਾ ਵਿੱਚ ਨਾ ਹੋਵੇ ।
5. ਖੋ-ਖੋ ਵਿੱਚ ਬੈਠੇ ਹੋਏ ਚੇਜ਼ਰ ਦੇ ਪਿੱਛੋਂ ਦੀ ਖੋ ਦੇਣੀ ਹੁੰਦੀ ਹੈ । ਬਿਨਾਂ ਖੋ ਹਾਸਲ ਕੀਤੇ ਚੇਜ਼ਰ ਉੱਠ ਨਹੀਂ ਸਕਦਾ |
6. ਖੋ-ਖੋ ਮੈਚ ਦੀਆਂ ਦੋ ਇਨਿੰਗ ਹੁੰਦੀਆਂ ਹਨ । ਦੋਨੋਂ ਇਨਿੰਗ ਵਿੱਚ ਜ਼ਿਆਦਾ ਪੁਆਇੰਟ ਜਿੱਤਣ ਵਾਲੀ ਟੀਮ ਜਿੱਤ ਜਾਂਦੀ ਹੈ ।
7. ਖੇਡ ਦੇ ਸਮੇਂ ਜੇਕਰ ਕਿਸੇ ਖਿਡਾਰੀ ਨੂੰ ਸੱਟ ਲੱਗ ਜਾਵੇ ਤਾਂ ਰੈਫ਼ਰੀ ਦੀ ਆਗਿਆ ਅਨੁਸਾਰ ਉਸਦੀ ਥਾਂ ਤੇ ਦੂਜਾ ਖਿਡਾਰੀ ਖੇਡ ਸਕਦਾ ਹੈ ।
8. ਕੋਈ ਵੀ ਚੇਜ਼ਰ ਆਪਣੇ ਅੰਗ ਨਾਲ ਕੇਂਦਰੀ ਪੱਟੀ ਨੂੰ ਛੁਹ ਨਹੀਂ ਸਕਦਾ ।
9. ਜੇਕਰ ਕੋਈ ਟੀਮ ਬਰਾਬਰ ਰਹਿ ਜਾਂਦੀ ਹੈ ਤਾਂ ਇੱਕ ਇਨਿੰਗ ਹੋਰ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ । ਜੇਕਰ ਫੇਰ ਵੀ ਬਰਾਬਰ ਰਹਿ ਜਾਵੇ ਤਾਂ ਫਿਰ ਇਨਿੰਗ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ ।
10. ਜੇਕਰ ਕਿਸੇ ਖਿਡਾਰੀ ਦੇ ਸੱਟ ਲੱਗ ਜਾਵੇ ਤਾਂ ਉਸਦੀ ਥਾਂ ਬਦਲਵਾਂ ਖਿਡਾਰੀ ਖੇਡ ਸਕਦਾ ਹੈ । 11. ਖੇਡ ਦਾ ਸਮਾਂ 9-5-9, 10, 9-5-9 ਦਾ ਹੁੰਦਾ ਹੈ ।
11. ਜੇਕਰ ਸਮੇਂ ਤੋਂ ਪਹਿਲਾਂ ਸਾਰੇ ਖਿਡਾਰੀ ਆਊਟ ਹੋ ਜਾਂਦੇ ਹਨ ਤਾਂ ਉਸਦੀ ਜਗ੍ਹਾ ਪਹਿਲੇ ਕ੍ਰਮ ਅਨੁਸਾਰ ਦੂਜੇ ਰਨਰ ਦੁਆਰਾ ਜਾਣਗੇ ।
12. ਖੋ-ਖੋ ਦੇਣ ਤੋਂ ਪਿੱਛੋਂ ਚੇਜ਼ਰ ਨੂੰ ਉਸਦੇ ਖ਼ਾਲੀ ਸਥਾਨ ‘ਤੇ ਬੈਠਣਾ ਹੁੰਦਾ ਹੈ ।
13. ਇਕ ਰੱਖਿਅਕ ਖਿਡਾਰੀ ਆਊਟ ਮੰਨਿਆ ਜਾਵੇਗਾ, ਜੇਕਰ ਕਿਸੇ ਐਸਟਿਵ ਚੇਜ਼ਰ ਹੱਥ ਨਾਲ ਉਸਨੂੰ ਛੂੰਹਦਾ ਹੈ ।

ਖੋ-ਖੋ ਦਾ ਮੈਦਾਨ, ਖੇਡ ਦਾ ਆਰੰਭ, ਪਰਿਭਾਸ਼ਿਕ ਸ਼ਬਦ, ਖੇਡ ਦੇ ਨਿਯਮ, ਮੈਚ ਦੇ
ਨਿਯਮ ਅਤੇ ਖੇਡ ਦੇ ਅਧਿਕਾਰੀ
ਖੇਡ ਦਾ ਮੈਦਾਨ
(Play Ground)

ਖੋ-ਖੋ ਦਾ ਖੇਡ ਦਾ ਮੈਦਾਨ ਆਇਤਾਕਾਰ ਹੁੰਦਾ ਹੈ । ਇਹ 27 ਮੀਟਰ ਲੰਬਾ ਤੇ 15 ਮੀਟਰ ਚੌੜਾ ਹੁੰਦਾ ਹੈ । ਮੈਦਾਨ ਦੇ ਅੰਤ ਵਿਚ ਦੋ ਆਇਤਾਕਾਰ ਹੁੰਦੇ ਹਨ | ਆਇਤਾਕਾਰ ਦੀ ਇਕ ਭੁਜਾ 15 ਮੀਟਰ ਅਤੇ ਦੂਸਰੀ ਭੁਜਾ 2.70 ਮੀਟਰ ਹੁੰਦੀ ਹੈ । ਇਨ੍ਹਾਂ ਦੋਹਾਂ ਆਇਤਾਕਾਰਾਂ ਦੇ ਵਿਚਕਾਰ ਦੋ ਲੱਕੜੀ ਦੇ ਖੰਭੇ ਹੁੰਦੇ ਹਨ । ਮੈਦਾਨ ਦੇ ਵਿਚਕਾਰ 2.10 ਮੀਟਰ ਲੰਬੀ ਅਤੇ 30 ਸੈਂਟੀਮੀਟਰ ਚੌੜੀ ਪੱਟੀ ਹੁੰਦੀ ਹੈ । ਇਸ ਵਿਚ 30 ਸਮ x 30 ਸਮ ਦੇ ਅੱਠ ਵਰਗ ਹੋਣਗੇ । ਪੋਲ ਜ਼ਮੀਨ ਤੋਂ 1.20 ਸੈਂਟੀਮੀਟਰ ਉੱਚਾ ਹੁੰਦਾ ਹੈ । ਹਰ ਪੋਲ ਤੋਂ ਚੌੜਾਈ ਵੱਲ ਇਕ ਰੇਖਾ ਖਿੱਚੀ ਜਾਂਦੀ ਹੈ । ਇਸ ਰੇਖਾ ਦੇ ਸਮਾਨਾਂਤਰ 8 ਪੱਟੀਆਂ ਬਣਾਈਆਂ ਜਾਂਦੀਆਂ ਹਨ । ਹਰ ਪੱਟੀ ਦੀ ਲੰਬਾਈ 15 ਮੀਟਰ ਅਤੇ ਚੌੜਾਈ 30 ਸੈਂਟੀਮੀਟਰ ਹੁੰਦੀ ਹੈ । ਕੇਂਦਰੀ ਗਲੀ ਦੁਆਰਾ ਇਹ ਗਲੀ 7.10 ਮੀਟਰ ਦੇ ਦੋ ਬਰਾਬਰ ਹਿੱਸਿਆਂ ਵਿਚ ਵੰਡੀ ਹੁੰਦੀ ਹੈ । ਹਰ ਇਕ ਲਾਈਨ ਦੀ ਮੋਟਾਈ 2 ਸੈਂਟੀਮੀਟਰ ਹੁੰਦੀ ਹੈ । ਪਰ ਪੱਟੀ 2.10 ਮੀਟਰ ਹੁੰਦੀ ਹੈ, ਹਰ ਇਕ ਬਾਹਰਲੀ ਪੱਟੀ ਅਤੇ ਪੋਲ ਰੇਖਾ ਇਕ-ਦੂਜੇ ਤੋਂ 2.25 ਮੀਟਰ ਹੁੰਦੀ ਹੈ, ਹਰ ਪੋਲ ਰੇਖਾ ਬਾਹਰਲੀ ਸੀਮਾਂ ਤੋਂ 2.70 ਮੀਟਰ ਦੂਰ ਹੁੰਦੀ ਹੈ । ਖੇਡ ਦੇ ਮੈਦਾਨ ਦੇ ਚਾਰੇ ਪਾਸੇ 3 ਮੀਟਰ ਚੌੜੀ ਲਾਬੀ ਹੁੰਦੀ ਹੈ ।

ਪਰਿਭਾਸ਼ਿਕ ਸ਼ਬਦ (Definitions)-

 

 

1. ਖੰਭਾ ਜਾਂ ਸਤੰਭ (Posts) – ਮੱਧ ਰੇਖਾ I ਅੰਤ ਵਿਚ ਦੋ ਖੰਭੇ ਗੱਡੇ ਜਾਂਦੇ ਹਨ ਜੋ ਜ਼ਮੀਨ ਤੋਂ 120 ਸੈਂਟੀਮੀਟਰ ਉੱਚੇ ਹੁੰਦੇ ਹਨ । ਇਹਨਾਂ ਦੀ ਪਰਿਧੀ 30 ਸੈਂਟੀਮੀਟਰ ਤੋਂ ਘੱਟ ਜਾਂ 40 ਸੈਂਟੀਮੀਟਰ ਤੋਂ ਜ਼ਿਆਦਾ ਨਹੀਂ ਹੋ ਸਕਦੀ ।
2. ਕੇਂਦਰੀ ਗਲੀ ਜਾਂ ਲੇਨ (Central lane) – ਦੋਹਾਂ ਖੰਭਿਆਂ ਦੇ ਵਿਚਕਾਰ ਇਕ ਕੇਂਦਰੀ ਗਲੀ ਹੁੰਦੀ ਹੈ । ਇਹ 21.60 ਮੀਟਰ ਲੰਬੀ ਅਤੇ 30 ਸਮ ਚੌੜੀ ਹੁੰਦੀ ਹੈ ।
3. ਕਰਾਸ ਲੇਨ (Cross lane) – ਹਰੇਕ ਆਇਤਾਕਾਰ 15 ਮੀਟਰ ਲੰਬਾ ਅਤੇ 30 ਸੈਂਟੀਮੀਟਰ ਚੌੜਾ ਹੁੰਦਾ ਹੈ । ਇਹ ਕੇਂਦਰੀ ਰੇਖਾ ਨੂੰ ਸਮਕੋਣ (909) ’ਤੇ ਕੱਟਦਾ ਹੈ । ਇਹ ਆਪ ਵੀ ਦੋ ਅਰਧਕਾਂ ਵਿਚ ਵੰਡਿਆ ਹੁੰਦਾ ਹੈ । ਇਸ ਨੂੰ ਕਰਾਸ ਲੇਨ ਕਹਿੰਦੇ ਹਨ ।
4. ਵਰਗ (Square) – ਕੇਂਦਰੀ ਰੇਖਾ ਅਤੇ ਕਰਾਸ ਲੇਨ ਦੇ ਆਪਸ ਵਿਚ ਕੱਟਣ ਨਾਲ ਬਣਿਆ 30 ਸਮ x 30 ਸਮ ਦਾ ਖੇਤਰ ਵਰਗ ਅਖਵਾਉਂਦਾ ਹੈ ।
5. ਸਤੰਭ ਰੇਖਾ (The kine of the post) – ਕੇਂਦਰ ਤੋਂ ਲੰਘਦੀ ਹੋਈ ਕਰਾਸਲੇਨ ਅਤੇ ਕੇਂਦਰੀ ਰੇਖਾ ਦੇ ਸਮਾਨ ਅੰਤਰ ਰੇਖਾ ਨੂੰ ਸਤੰਭ ਰੇਖਾ ਕਹਿੰਦੇ ਹਨ ।
6. ਆਇਤਾਕਾਰ (Rectangle) – ਸਤੰਭ ਰੇਖਾ ਦਾ ਬਾਹਰੀ ਖੇਤਰ ਆਇਤਾਕਾਰ ਅਖਵਾਉਂਦਾ ਹੈ ।
7. ਪਰਿਧੀਆਂ (Limits) – ਕੇਂਦਰੀ ਰੇਖਾ ਤੋਂ ਬਾਹਰੀ ਸੀਮਾ ਨਿਸਚਿਤ ਕਰਨ ਵਾਲੇ ਦੋਵੇਂ ਆਇਤਾਕਾਰਾਂ ਦੀਆਂ ਰੇਖਾਵਾਂ ਤੋਂ 7.30 ਮੀਟਰ ਦੂਰ ਦੋਵੇਂ ਛੂੰਹਦੀਆਂ ਰੇਖਾਵਾਂ ਨੂੰ ਪਰਿਧੀਆਂ ਕਹਿੰਦੇ ਹਨ ।
8. ਚੇਜ਼ਰ (Chasers) – ਵਰਗਾਂ ਵਿਚ ਬੈਠੇ ਖਿਡਾਰੀ ਜ਼ਰ ਅਖਵਾਉਂਦੇ ਹਨ । ਵਿਰੋਧੀ ਖਿਡਾਰੀਆਂ ਨੂੰ ਫੜਨ ਜਾਂ ਨੱਠਣ ਵਾਲਾ ਚੇਜ਼ਰ ਸਰਗਰਮ ਚੇਜ਼ਰ ਅਖਵਾਉਂਦਾ ਹੈ ।
9. ਧਾਵਕ (Runners )- ਚੇਜ਼ਰਾਂ ਜਾਂ ਅਨੁਧਾਵਕਾਂ ਦੇ ਵਿਰੋਧੀ ਖਿਡਾਰੀ ਧਾਕ ਜਾਂ ਰਨਰ ਕਹਾਉਂਦੇ ਹਨ ।
10. ਖੋ-ਦੇਣਾ (To give Kho) – ਚੰਗੀ ਖੋ ਦੇਣ ਲਈ ਸਰਗਰਮ ਚੇਜ਼ਰ ਨੂੰ ਬੈਠੇ ਹੋਏ ਚੇਜ਼ਰ ਦੇ ਪਿੱਛੋਂ ਦੀ ਹੱਥ ਨਾਲ ਛੁਹ ਕੇ ਖੋ ਸ਼ਬਦ ਉੱਚੀ ਅਤੇ ਸਪੱਸ਼ਟ ਆਵਾਜ਼ ਵਿਚ ਕਹਿਣਾ ਚਾਹੀਦਾ ਹੈ । ਛੂਹਣ ਅਤੇ ਖੋ ਦੇਣ ਦਾ ਕੰਮ ਇਕੱਠਾ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ।
11. ਫਾਉਲ (Foul) – ਜੇਕਰ ਬੈਠਿਆ ਹੋਇਆ ਜਾਂ ਸਰਗਰਮ ਚੇਜ਼ਰ ਕਿਸੇ ਨਿਯਮ ਦਾ ਉਲੰਘਣ ਕਰੇ ਤਾਂ ਉਹ ਫਾਊਲ ਹੁੰਦਾ ਹੈ ।
12. ਦਿਸ਼ਾ ਹਿਣ ਕਰਨਾ (To take a direction) – ਇਕ ਖੰਭੇ ਤੋਂ ਦੂਸਰੇ ਖੰਭੇ ਵੱਲ ਜਾਣਾ ਦਿਸ਼ਾ ਹਿਣ ਕਰਨਾ ਕਹਾਉਂਦਾ ਹੈ ।
13. ਮੂੰਹ ਮੋੜਨਾ (To turn the face) – ਜਦੋਂ ਸਰਗਰਮ ਚੇਜ਼ਰ ਇਕ ਖਾਸ ਦਿਸ਼ਾ ਵੱਲ ਜਾਂਦੇ ਸਮੇਂ ਆਪਣੇ ਮੋਢੇ ਦੀ ਰੇਖਾ (90°) ਦੇ ਕੋਣ ਤੋਂ ਵੱਧ ਦਿਸ਼ਾ ਵੱਲ ਮੋੜ ਲੈਂਦਾ ਹੈ, ਤਾਂ ਉਸ ਨੂੰ ਮੂੰਹ ਮੋੜਨਾ ਕਹਿੰਦੇ ਹਨ । ਇਹ ਫਾਊਲ ਹੁੰਦਾ ਹੈ ।
14. ਪਲਟਨਾ (Returning) – ਕਿਸੇ ਵਿਸ਼ੇਸ਼ ਦਿਸ਼ਾ ਵੱਲ ਜਾਂਦਾ ਹੋਇਆ ਸਰਗਰਮ ਚੇਜ਼ਰ ਜਦੋਂ ਉਲਟ ਦਿਸ਼ਾ ਵੱਲ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਇਸ ਨੂੰ ਪਲਟਨਾ ਕਹਿੰਦੇ ਹਨ ।
15. ਸਤੰਭ ਰੇਖਾ ਤੋਂ ਹਟਣਾ (To Leave the past line) – ਜਦੋਂ ਕੋਈ ਸਰਗਰਮ ਚੇਜ਼ਰ ਖੰਭੇ ਦਾ ਅਧਿਕਾਰ ਛੱਡ ਦੇਵੇ ਜਾਂ ਆਇਤਾਕਾਰ ਤੋਂ ਪਰ੍ਹਾਂ ਚਲਾ ਜਾਵੇ, ਤਾਂ ਇਸ ਨੂੰ ਸਤੰਭ ਰੇਖਾ ਤੋਂ ਹਟਣਾ ਕਹਿੰਦੇ ਹਨ ।
16. ਪੈਰ ਬਾਹਰ (Footout) – ਜਦੋਂ ਰਨਰ ਦੇ ਦੋਵੇਂ ਪੈਰ ਸੀਮਾਵਾਂ ਤੋਂ ਬਾਹਰ ਭੂਮੀ ਨੂੰ ਛੂਹ ਲੈਣ, ਤਾਂ ਉਸ ਨੂੰ ਪੈਰ ਬਾਹਰ ਮੰਨਦੇ ਹਨ । ਉਸ ਨੂੰ ਆਉਟ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ ।
17. ਲੋਨਾ (Lona) – ਜਦੋਂ ਸਾਰੇ ਰਨਰ 7 ਮਿੰਟਾਂ ਦੇ ਅੰਦਰ-ਅੰਦਰ ਆਊਟ ਹੋ ਜਾਣ, ਤਾਂ ਚੇਜ਼ਰ ਦੁਆਰਾ ਰਨਰਾਂ ਦੇ ਵਿਰੁੱਧ ‘ਲੋਨਾ’ ਅੰਕਿਤ ਕੀਤਾ ਜਾਵੇਗਾ | ਪਰ ਲੋਨੇ ਦਾ ਅੰਕ ਨਹੀਂ ਮਿਲਦਾ ।

ਖੇਡ ਆਰੰਭ ਕਰਨਾ (To begin the Play) – ਖੇਡ ਟਾਸ ਦੁਆਰਾ ਆਰੰਭ ਕੀਤੀ ਜਾਂਦੀ ਹੈ । ਟਾਸ ਜਿੱਤਣ ਵਾਲੀ ਟੀਮ ਦਾ ਕਪਤਾਨ ਛੂਹਣ ਜਾਂ ਛੂਹੇ ਜਾਣ ਦਾ ਫੈਸਲਾ ਕਰੇਗਾ ਅਤੇ ਆਪਣੇ ਫੈਸਲੇ ਦੀ ਰੈਫਰੀ ਨੂੰ ਸੂਚਨਾ ਦੇਵੇਗਾ । ਇਸ ਵਿਚ ਬੈਠੇ ਖਿਡਾਰੀ ਚੇਜ਼ਰ ਹੁੰਦੇ ਹਨ । ਚੇਜ਼ਰ ਦੇ ਵਿਰੋਧੀ ਪੱਖ ਦੇ ਖਿਡਾਰੀ ਰਨਰਜ਼ ਅਖਵਾਉਂਦੇ ਹਨ । ਇਸ ਚੇਜ਼ਰ ਨੂੰ ਛੱਡ ਕੇ ਸਾਰੇ ਚੇਜ਼ਰ ਵਰਗ ਇਸ ਪ੍ਰਕਾਰ ਬੈਠ ਜਾਂਦੇ ਹਨ ਕਿ ਕਿਸੇ ਕੋਲ-ਕੋਲ ਬੈਠੇ ਦੋ ਚੇਜ਼ਰਾਂ ਦਾ ਮੂੰਹ ਇਕ ਦਿਸ਼ਾ ਵਿਚ ਨਹੀਂ ਹੁੰਦਾ | ਖੇਡ ਆਰੰਭ ਕਰਦੇ ਸਮੇਂ ਨੌਵਾਂ ਚੇਜ਼ਰ ਕਿਸੇ ਇਕ ਪੋਲ ਦੇ ਕੋਲ ਖੜਾ ਹੁੰਦਾ ਹੈ । ਫਿਰ ਰੈਫਰੀ ਰਾਹੀਂ ਸੀਟੀ ਮਾਰ ਕੇ ਆਗਿਆ ਦੇਣ ਨਾਲ ਛੂਹਣ ਦਾ ਕੰਮ ਸ਼ੁਰੂ ਹੋ ਜਾਂਦਾ ਹੈ ।

ਖੇਡ ਦੇ ਨਿਯਮ (Rules of the Play)-

1. ਕਾਰਜਸ਼ੀਲ ਚੇਜ਼ਰ (Active chaser) ਦੇ ਸਰੀਰ ਦਾ ਕੋਈ ਹਿੱਸਾ ਕੇਂਦਰੀ ਪੱਟੀ ਦੀ ਜ਼ਮੀਨ ਨੂੰ ਨਹੀਂ ਛੂਹਣਾ ਚਾਹੀਦਾ । ਇਸ ਤੋਂ ਇਲਾਵਾ ਇਹ ਕੇਂਦਰੀ ਪੱਟੀ ਨੂੰ ਪੋਸਟਾਂ ਦੇ ਅੰਦਰ ਤੋਂ ਕੁੱਦ ਕੇ ਪਾਰ ਕਰ ਸਕਦਾ ।
2. ਖੇਡ ਦੇ ਮੈਦਾਨ ਨੂੰ ਆਕਾਰ ਵਿਚ ਵਰਣਨ ਕੀਤੇ ਅਨੁਸਾਰ ਚਿੰਨ੍ਹ ਲਗਾਏ ਜਾਣਗੇ ।
3. ਦੌੜਨ ਜਾਂ ਚੇਜ਼ਰ ਬਣਨ ਦਾ ਫੈਸਲਾ ਟਾਸ ਦੁਆਰਾ ਕੀਤਾ ਜਾਵੇਗਾ ।
4. ਜੇਕਰ ਖੋ ਦੇਣੀ ਹੋਵੇ ਤਾਂ ਇਹ ਦੂਰ ਬੈਠੇ ਹੋਏ ਚੇਜ਼ਰ ਨੂੰ ਪਿੱਛੋਂ ਤੋਂ ਦੇਣੀ ਹੋਵੇਗੀ । ਖੋ ਪ੍ਰਾਪਤ ਕੀਤੇ ਬਿਨਾਂ ਬੈਠਾ ਹੋਇਆ ਚੇਜ਼ਰ ਨਹੀਂ ਉੱਠ ਸਕਦਾ | ਕਾਰਜਸ਼ੀਲ ਚੇਜ਼ਰ ਬੈਠੇ ਹੋਏ ਚੇਜ਼ਰ ਦੀ ਫੈਲਾਈ ਹੋਈ ਬਾਂਹ ਜਾਂ ਟੰਗ ਨੂੰ ਛੂ ਕੇ ਖੋ ਨਹੀਂ ਦੇਵੇਗਾ । ਜੇਕਰ ਚੇਜ਼ਰ ਨੰ: 1 ਅਤੇ 2 ਦੀ ਉਲੰਘਣਾ ਕਰੇਗਾ ਤਾਂ ਰੈਫਰੀ ਫਾਊਲ ਦੇ ਦੇਵੇਗਾ ।
5. ਖੇਡਣ ਤੋਂ ਬਾਅਦ ਕਾਰਜਸ਼ੀਲ ਚੇਜ਼ਰ ਬੈਠੇ ਹੋਏ ਚੇਜ਼ਰ ਜਿਸ ਨੂੰ ਕਿ ਉਸ ਨੇ ਖੋ ਦਿੱਤੀ ਹੋਵੇ, ਉਸ ਦੀ ਥਾਂ ਸੰਭਾਲ ਲਵੇਗਾ ।
6. ਖੋ ਮਿਲਣ ਦੇ ਬਾਅਦ ਭੱਜਣ ਵਾਲਾ ਚੇਜ਼ਰ ਉਸ ਦਿਸ਼ਾ ਵਿਚ ਜਾਵੇਗਾ, ਜੋ ਦਿਸ਼ਾ ਆਪਣੇ ਵਰਗ ਤੋਂ ਉੱਠ ਕੇ ਕੇਂਦਰੀ ਪੱਟੀ ਨੂੰ ਪਾਰ ਕਰਕੇ ਅਪਣਾਈ ਹੋਵੇ ।
7. ਜਦ ਤਕ ਉਹ ਕਿਸੇ ਹੋਰ ਬੈਠੇ ਹੋਏ ਚੇਜ਼ਰ ਨੂੰ ਨਾ ਕਹਿ ਦੇਵੇ, ਤਾਂ ਉਹ ਕੇਂਦਰੀ ਪੱਟੀ ਦੇ ਦੂਸਰੇ ਪਾਸੇ ਪੋਲ ਦੇ ਉੱਪਰ ਤੋਂ ਹੋ ਕੇ ਹੀ ਆ ਸਕਦਾ ਹੈ ।
8. ਭੱਜਣ ਵਾਲੇ ਦਾ ਮੁੰਹ ਉਸ ਦੇ ਭੱਜਣ ਦੀ ਦਿਸ਼ਾ ਵਿਚ ਹੀ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ।
9. ਚੇਜ਼ਰ ਇਸ ਪ੍ਰਕਾਰ ਬੈਠੇ ਕਿ ਉਸ ਨਾਲ ਭੱਜਣ ਵਾਲਿਆਂ ਨੂੰ ਰੋਕ ਨਾ ਪਵੇ । ਜੇਕਰ ਕੋਈ ਭੱਜਣ ਵਾਲਾ ਇਸ ਪ੍ਰਕਾਰ ਦੀ ਰੋਕ ਨਾਲ ਆਉਟ ਹੋ ਜਾਵੇ, ਤਾਂ ਉਸ ਨੂੰ ਆਉਟ ਐਲਾਨ ਕੀਤਾ ਜਾਵੇਗਾ ।
10. ਕਾਰਜਸ਼ੀਲ ਚੇਜ਼ਰ (Active chaser) ਸੀਮਾ ਤੋਂ ਬਾਹਰ ਨਿਕਲ ਸਕਦਾ ਹੈ । ਪਰੰਤੂ ਉਸ ਨੂੰ ਦਿਸ਼ਾ ਹਿਣ ਕਰਨ ਅਤੇ ਮੂੰਹ ਘੁਮਾਉਣ ਆਦਿ ਦੇ ਸਾਰੇ ਨਿਯਮਾਂ ਦਾ ਪਾਲਣ ਕਰਨਾ ਪਵੇਗਾ ।
11. ਡਾਇਰੈਕਸ਼ਨ ਲੈਣ ਤੋਂ ਬਾਅਦ ਐਕਟਿਵ ਚੇਜ਼ਰ ਦੁਬਾਰਾ ਕਰਾਸ ਲਾਈਨ ਵਿਚ ਅਟੈਕ ਕਰ ਸਕਦਾ ਹੈ ਅਤੇ ਇਸ ਨੂੰ ਫਾਊਲ ਨਹੀਂ ਮੰਨਿਆ ਜਾਵੇਗਾ ।
12. ਭੱਜਣ ਵਾਲਾ ਬੈਠੇ ਚੇਜ਼ਰ ਨੂੰ ਨਹੀਂ ਛੂਹੇਗਾ । ਜੇਕਰ ਉਹ ਅਜਿਹਾ ਕਰ ਲਵੇ, ਤਾਂ ਉਸ ਨੂੰ ਇਕ ਵਾਰ ਚੇਤਾਵਨੀ ਦਿੱਤੀ ਜਾਵੇਗੀ । ਜੇਕਰੇ ਚੇਤਾਵਨੀ ਦੇ ਬਾਅਦ ਵੀ ਅਜਿਹਾ ਕਰੇ ਤਾਂ ਉਸ ਨੂੰ ਆਉਟ ਐਲਾਨ ਕਰ ਦਿੱਤਾ ਜਾਵੇਗਾ ।
13. ਭੱਜਣ ਵਾਲਾ ਆਊਟ ਸਮਝਿਆ ਜਾਵੇਗਾ, ਜੇਕਰ ਕੋਰਟ ਤੋਂ ਬਾਹਰ ਚਲਾ ਜਾਵੇ ।
14. ਭੱਜਣ ਵਾਲਾ ਜੇਕਰ ਚੇਜ਼ਰ ਦੁਆਰਾ ਹੱਥ ਨਾਲ ਛੁਹ ਦਿੱਤਾ ਜਾਵੇ, ਤਾਂ ਵੀ ਉਹ ਆਉਟ ਸਮਝਿਆ ਜਾਵੇਗਾ ।
15. ਦਿਸ਼ਾ ਹਿਣ ਕਰਨ ਵਾਲੇ ਅਤੇ ਦਿਸ਼ਾ ਮੋੜਨ ਵਾਲੇ ਨਿਯਮ ਆਇਤਾਕਾਰ ਖੇਤਰ ਵਿਚ ਲਾਗੂ ਨਹੀਂ ਹੋਣਗੇ ।
16. ਜੇਕਰ ਇਕ ਐਕਟਿਵ ਚੇਜ਼ਰ ਲਗਾਤਾਰ ਤਿੰਨ ਰਨਰਜ਼ ਨੂੰ ਆਊਟ ਕਰ ਦੇਵੇ, ਤਾਂ ਉਹ ਚੌਥੇ ਰਨਰ ਨੂੰ ਛੂਹ ਨਹੀਂ ਸਕਦਾ । ਉਹ ਬੈਠੇ ਹੋਏ ਚੇਜ਼ਰ ਨੂੰ ਖੋ ਦੇਵੇਗਾ ।

ਮੈਚ ਦੇ ਨਿਯਮ (Rules about the Match)-
1. ਹਰੇਕ ਟੀਮ ਵਿਚ ਖਿਡਾਰੀਆਂ ਦੀ ਗਿਣਤੀ 9 ਹੋਵੇਗੀ ਅਤੇ ਤਿੰਨ ਖਿਡਾਰੀ ਵਾਧੂ ਹੁੰਦੇ ਹਨ ।

2. ਹਰੇਕ ਪਾਰੀ ਵਿਚ 7-7 ਮਿੰਟ ਛੂਹਣ ਅਤੇ ਦੌੜਨ ਦਾ ਕੰਮ ਵਾਰੀ-ਵਾਰੀ ਹੋਵੇਗਾ । ਹਰੇਕ ਮੈਚ ਵਿਚ ਚਾਰ ਇਨਿੰਗਜ਼ ਹੁੰਦੀਆਂ ਹਨ । ਦੋ ਪਾਰੀਆਂ ਛੂਹਣ ਅਤੇ ਦੋ ਪਾਰੀਆਂ ਦੌੜਨ ਦੀਆਂ ਹੁੰਦੀਆਂ ਹਨ ।

3. ਮੈਚ ਸ਼ੁਰੂ ਕਰਨ ਤੋਂ ਪਹਿਲਾਂ ਦੋਵੇਂ ਟੀਮਾਂ ਦੇ ਕਪਤਾਨ ਟਾਸ ਕਰਕੇ ਚੇਜ਼ਰ ਜਾਂ ਰਨਰ ਦੀ ਵਾਰੀ ਦਾ ਫੈਸਲਾ ਕਰਦੇ ਹਨ ।

4. ਰਨਰ ਖੇਡਣ ਦੇ ਕ੍ਰਮ ਦੇ ਅਨੁਸਾਰ ਸਕੋਰਰ ਦੇ ਕੋਲ ਆਪਣੇ ਨਾਂ ਦਰਜ ਕਰਾਉਣਗੇ । ਵਾਰੀ ਦੇ ਆਰੰਭ ਵਿਚ ਪਹਿਲੇ ਤਿੰਨ ਖਿਡਾਰੀ ਸੀਮਾ ਦੇ ਅੰਦਰ ਹੋਣਗੇ । ਇਨ੍ਹਾਂ ਤਿੰਨਾਂ ਦੇ ਆਊਟ ਹੋਣ ਦੇ ਬਾਅਦ ਤਿੰਨ ਹੋਰ ਖਿਡਾਰੀ ਖੋ ਦੇਣ ਤੋਂ ਪਹਿਲਾਂ ਅੰਦਰ ਆ ਜਾਣਗੇ । ਜਿਹੜੇ ਇਸ ਮਿਆਦ ਵਿਚ ਅੰਦਰ ਦਾਖਲ ਨਾ ਹੋ ਸਕਣਗੇ, ਉਨ੍ਹਾਂ ਨੂੰ ਆਊਟ ਕਰਾਰ ਦਿੱਤਾ ਜਾਵੇਗਾ ।
ਆਪਣੀ ਵਾਰੀ ਦੇ ਬਿਨਾਂ ਦਾਖਲ ਹੋਣ ਵਾਲਾ ਖਿਡਾਰੀ ਵੀ ਆਊਟ ਕਰਾਰ ਦਿੱਤਾ ਜਾਵੇਗਾ । ਇਹ ਖੇਡ ਵਾਰੀ ਦੇ ਅੰਤ ਤਕ ਜਾਰੀ ਰਹੇਗੀ । ਤੀਜੇ ਰਨਰ ਨੂੰ ਕੱਢਣ ਵਾਲਾ ਸਰਗਰਮ ਚੇਜ਼ਰ ਨਵੇਂ ਦਾਖਲ ਹੋਣ ਵਾਲੇ ਰਨਰ ਦਾ ਪਿੱਛਾ ਨਹੀਂ ਕਰੇਗਾ । ਉਹ ਖੋ ਦੇਵੇਗਾ | ਹਰੇਕ ਟੀਮ ਖੇਡ ਦੇ ਮੈਦਾਨ ਦੇ ਸਿਰਫ ਇਕ ਪਾਸਿਓਂ ਹੀ ਆਪਣੇ ਰਨਰ ਅੰਦਰ ਭੇਜੇਗੀ ।

5. ਚੇਜ਼ਰ ਜਾਂ ਰਨਰ ਆਪਣੀ ਟਰਨ ਨੂੰ ਨਿਰਧਾਰਿਤ ਸਮੇਂ ਤੋਂ ਪਹਿਲਾਂ ਵੀ ਸਮਾਪਤ ਕਰ ਸਕਦੇ ਹਨ । ਰਨਰ ਜਾਂ ਚੇਜ਼ਰ ਟੀਮ ਦਾ ਕਪਤਾਨ ਆਪਣੇ ਫੈਸਲੇ ਦੀ ਸੂਚਨਾ ਰੈਫਰੀ ਨੂੰ ਦੇ ਦੇਵੇਗਾ ਅਤੇ ਉਸ ਨੂੰ ਵਾਰੀ ਦੇ ਬੰਦ ਕਰਨ ਦੀ ਪ੍ਰਾਰਥਨਾ ਕਰੇਗਾ । ਇਸ ਪ੍ਰਕਾਰ ਦੀ ਪ੍ਰਾਰਥਨਾ ਤੇ ਰੈਫਰੀ ਖੇਡ ਰੋਕ ਕੇ ਵਾਰੀ ਬੰਦ ਕਰ ਦੇਵੇਗਾ ਇਸ ਵਾਰੀ ਦੇ ਬਾਅਦ ਦੋ ਮਿੰਟ ਅਤੇ ਦੋ ਪਾਰੀਆਂ ਦੇ ਵਿਚਕਾਰ ਪੰਜ ਮਿੰਟ ਦਾ ਆਰਾਮ ਹੋਵੇਗਾ ।

6. ਚੇਜ਼ਰ ਟੀਮ ਨੂੰ ਹਰੇਕ ਰਨਰ ਦੇ ਆਉਟ ਹੋਣ ਉੱਤੇ ਇਕ ਨੰਬਰ ਮਿਲੇਗਾ | ਸਾਰੇ ਰਨਰਾਂ ਦੇ ਸਮੇਂ ਤੋਂ ਪਹਿਲਾਂ ਹੀ ਆਊਟ ਹੋ ਜਾਣ ਉੱਤੇ ਉਨ੍ਹਾਂ ਦੇ ਵਿਰੁੱਧ ਇਕ “ਲੋਨਾ” ਦੇ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ । ਇਸ ਦੇ ਬਾਅਦ ਉਹ ਟੀਮ ਉਸੇ ਕੁਮ ਨਾਲ ਆਪਣੇ ਰਨਰ ਭੇਜੇਗੀ । ਲੋਨਾ’ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ ਕੋਈ ਵਾਧੂ ਨੰਬਰ ਨਹੀਂ ਦਿੱਤਾ ਜਾਂਦਾ | ਪਾਰੀ ਖ਼ਤਮ ਹੋਣ ਤਕ ਇਸੇ ਢੰਗ ਨਾਲ ਖੇਡ ਜਾਰੀ ਰਹੇਗੀ । ਪਾਰੀ ਦੇ ਦੌਰਾਨ ਰਨਰਾਂ ਦੇ ਕੂਮ ਵਿਚ ਤਬਦੀਲੀ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ ।

7. ਨਾਕ ਆਊਟ (Knock out) ਪ੍ਰਣਾਲੀ ਵਿਚ ਮੈਚ ਦੇ ਅੰਤ ਵਿਚ ਵਧੇਰੇ ਅੰਕ ਪ੍ਰਾਪਤ ਕਰਨ ਵਾਲੀ ਟੀਮ ਨੂੰ ਜੇਤੂ ਘੋਸ਼ਿਤ ਕੀਤਾ ਜਾਵੇਗਾ । ਜੇਕਰ ਅੰਕ ਬਰਾਬਰ ਹੋਣ, ਤਾਂ ਇਕ ਹੋਰ ਵਾਰੀ ਦੇ ਲਈ ਚੇਜ਼ਰ ਅਤੇ ਰਨਰ ਦੀ ਖੇਡ ਹੋਵੇਗੀ । ਜੇ ਫਿਰ ਵੀ ਅੰਕ ਬਰਾਬਰ ਰਹਿਣ ਤਾਂ ਬੇਕਰ ਰੁਲ ਨਿਯਮ 29 ਦੀ ਵਰਤੋਂ ਕੀਤੀ ਜਾਂਦੀ ਹੈ । ਇਸ ਸਥਿਤੀ ਵਿਚ ਇਹ ਜ਼ਰੂਰੀ ਨਹੀਂ ਕਿ ਟੀਮਾਂ ਵਿਚ ਉਹ ਖਿਡਾਰੀ ਹੋਣ । ਲੀਗ ਪ੍ਰਣਾਲੀ ਵਿਚ ਜੇਤੂ ਟੀਮ ਨੂੰ ਦੋ ਅੰਕ ਪ੍ਰਾਪਤ ਹੋਣਗੇ । ਹਾਰੀ ਟੀਮ ਨੂੰ ਜ਼ੀਰੋ ਅੰਕ ਅਤੇ ਬਰਾਬਰ ਰਹਿਣ ਦੀ ਹਾਲਤ ਵਿਚ ਹਰੇਕ ਟੀਮ ਨੂੰ ਇਕ-ਇਕ ਅੰਕ ਦਿੱਤਾ ਜਾਵੇਗਾ । ਜੇਕਰ ਲੀਗ ਪ੍ਰਣਾਲੀ ਉੱਪਰ ਲੀਗ ਅੰਕ ਬਰਾਬਰ ਹੋਣ ਤਾਂ ਟੀਮ ਜਾਂ ਟੀਮਾਂ ਪਰਚੀਆਂ ਰਾਹੀਂ ਦੁਬਾਰਾ ਮੈਚ ਖੇਡਣਗੀਆਂ | ਅਜਿਹੇ ਮੈਚ ਨਾਕ ਆਉਟ ਪ੍ਰਣਾਲੀ ਦੇ ਆਧਾਰ ਉੱਤੇ ਖੇਡੇ ਜਾਣਗੇ ।

8. ਜੇਕਰ ਕਿਸੇ ਕਾਰਨ ਮੈਚ ਪੂਰਾ ਨਹੀਂ ਹੁੰਦਾ, ਤਾਂ ਇਹ ਕਿਸੇ ਹੋਰ ਸਮੇਂ ਖੇਡਿਆ ਜਾਵੇਗਾ ਅਤੇ ਪਿਛਲੇ ਅੰਕ ਨਹੀਂ ਗਿਣੇ ਜਾਣਗੇ । ਮੈਚ ਸ਼ੁਰੂ ਤੋਂ ਹੀ ਖੇਡਿਆ ਜਾਵੇਗਾ |

9. ਜੇਕਰ ਕਿਸੇ ਇਕ ਟੀਮ ਦੇ ਅੰਕ ਦੁਸਰੀ ਟੀਮ ਤੋਂ 12 ਜਾਂ ਇਸ ਤੋਂ ਵੱਧ ਜ਼ਿਆਦਾ ਹੋ ਜਾਣ ਤਾਂ ਪਹਿਲੀ ਟੀਮ ਦੂਸਰੀ ਟੀਮ ਨੂੰ ਚੇਜ਼ਰ ਦੇ ਰੂਪ ਵਿਚ ਪਿੱਛਾ ਕਰਨ ਲਈ ਕਹਿ ਸਕਦੀ ਹੈ । ਜੇ ਦੂਜੀ ਟੀਮ ਇਸ ਵਾਰੀ ਵਧੇਰੇ ਅੰਕ ਲੈ . ਲੈਂਦੀ ਹੈ ਤਾਂ ਵੀ ਉਸ ਦਾ ਚੇਜ਼ਰ ਬਣਨ ਦਾ ਹੱਕ ਬਣਿਆ ਰਹਿੰਦਾ ਹੈ ।

10. ਖੇਡ ਦੇ ਦੌਰਾਨ ਕਿਸੇ ਖਿਡਾਰੀ ਨੂੰ ਚੋਟ ਲੱਗ ਜਾਵੇ, ਤਾਂ ਰੈਫਰੀ ਦੀ ਆਗਿਆ ਮਿਲਣ ‘ਤੇ ਕੋਈ ਹੋਰ ਖਿਡਾਰੀ ਉਸ ਦੀ ਥਾਂ ਤੇ ਖੇਡ ਸਕਦਾ ਹੈ ।

ਮੈਚ ਲਈ ਅਧਿਕਾਰੀ (Officials) – ਮੈਚ ਦਾ ਪ੍ਰਬੰਧ ਕਰਨ ਲਈ ਹੇਠ ਲਿਖੇ ਅਧਿਕਾਰੀ ਨਿਯੁਕਤ ਕੀਤੇ ਜਾਂਦੇ ਹਨ

1. ਦੋ ਅੰਪਾਇਰ (Two umpires)
2. ਇਕ ਰੈਫਰੀ (One Referee)
3. ਇਕ ਟਾਈਮ ਕੀਪਰ (One time keeper)
4. ਇਕ ਸਕੋਰਰ (One Scorer) ।

1. ਅੰਪਾਇਰ (Umpire) – ਅੰਪਾਇਰ ਲੌਬੀ ਮੈਦਾਨ ਤੋਂ ਬਾਹਰ ਖੜ੍ਹਾ ਹੋਵੇਗਾ ਅਤੇ ਕੇਂਦਰੀ ਗਲੀ ਰਾਹੀਂ ਵੰਡੀ ਹੋਈ ਆਪਣੀ ਥਾਂ ਤੋਂ ਖੇਡ ਦੀ ਦੇਖ-ਰੇਖ ਕਰੇਗਾ । ਉਹ ਆਪਣੇ ਅੱਧ ਵਿਚ ਸਾਰੇ ਫੈਸਲੇ ਦੇਵੇਗਾ ਅਤੇ ਦੂਜੇ ਅੱਧ ਦੇ ਅੰਪਾਇਰ ਨੂੰ ਫ਼ੈਸਲੇ ਦੇਣ ਵਿਚ ਸਹਾਇਤਾ ਕਰੇਗਾ |

2. ਰੈਫਰੀ (Referee) – ਖੋ-ਖੋ ਖੇਡ ਵਿਚ ਇਕ ਰੈਫਰੀ ਹੁੰਦਾ ਹੈ । ਉਸ ਦੇ ਹੇਠ ਲਿਖੇ ਕਰਤੱਵ ਇਸ ਤਰ੍ਹਾਂ ਹਨ-

1. ਉਹ ਅੰਪਾਇਰਾਂ ਦੀ ਉਨ੍ਹਾਂ ਦੇ ਹਰੇਕ ਕਰਤੱਵ ਪਾਲਣ ਵਿਚ ਸਹਾਇਤਾ ਕਰੇਗਾ ਅਤੇ ਉਨ੍ਹਾਂ ਵਿਚ ਮਤ-ਭੇਦ ਹੋਣ ਦੀ ਦਸ਼ਾ ਵਿਚ ਆਪਣਾ ਫੈਸਲਾ ਦੇਵੇਗਾ ।
2. ਜੇਕਰ ਖਿਡਾਰੀ ਜਾਣ-ਬੁਝ ਕੇ ਖੇਡ ਵਿਚ ਰੁਕਾਵਟ ਪੈਦਾ ਕਰਦਾ ਹੈ ਜਾਂ ਬੁਰੇ ਢੰਗ ਨਾਲ ਵਿਵਹਾਰ ਕਰਦਾ ਹੈ, ਤਾਂ ਉਸ ਨੂੰ ਰੈਫ਼ਰੀ ਸਜ਼ਾ ਦਿੰਦਾ ਹੈ ।
3. ਇਨਿੰਗਜ਼ ਦੇ ਅੰਤ ਵਿਚ ਉਹ ਸਕੋਰ ਦੱਸਦਾ ਹੈ ਅਤੇ ਨਤੀਜੇ ਦਾ ਐਲਾਨ ਕਰਦਾ ਹੈ ।
4. ਉਹ ਖੇਡ ਅਤੇ ਮੈਚ ਨੂੰ ਠੀਕ ਢੰਗ ਨਾਲ ਚਲਾਉਣ ਦਾ ਜਵਾਬਦੇਹ ਹੁੰਦਾ ਹੈ ।

3. ਟਾਈਮ ਕੀਪਰ (Time Keeper) – ਟਾਈਮ ਕੀਪਰ ਦਾ ਕੰਮ ਸਮੇਂ ਦਾ ਰਿਕਾਰਡ ਰੱਖਣਾ ਹੈ । ਉਹ ਵਿਸਲ ਦੇ ਕੇ ਵਾਰੀ ਦੇ ਆਰੰਭ ਜਾਂ ਸਮਾਪਤੀ ਦਾ ਸੰਕੇਤ ਦਿੰਦਾ ਹੈ ।

4. ਸਕੋਰਰ (Scorer) – ਸਕੌਰਰ ਇਸ ਗੱਲ ਦਾ ਧਿਆਨ ਰੱਖਦਾ ਹੈ ਕਿ ਖਿਡਾਰੀ ਨਿਸਚਿਤ ਕੂਮ ਨਾਲ ਮੈਦਾਨ ਵਿਚ ਉੱਤਰਨ । ਉਹ ਆਊਟ ਹੋਏ ਰਨਰਾਂ ਦਾ ਰਿਕਾਰਡ ਰੱਖਦਾ ਹੈ । ਹਰੇਕ ਵਾਰੀ ਦੇ ਅੰਤ ਵਿਚ ਉਹ ਸਕੋਰ ਸ਼ੀਟ ਉੱਤੇ ਅੰਕ ਦਰਜ ਕਰਦਾ ਹੈ ਅਤੇ ਚੇਜ਼ਰਾਂ ਦੇ ਸਕੋਰ ਤਿਆਰ ਕਰਦਾ ਹੈ । ਮੈਚ ਦੇ ਅੰਤ ਵਿਚ ਉਹ ਨਤੀਜੇ ਤਿਆਰ ਕਰਦਾ ਹੈ ਅਤੇ ਰੈਫਰੀ ਨੂੰ ਸੁਣਾਉਣ ਲਈ ਦਿੰਦਾ ਹੈ ।

ਸਪਰੋਟਸ ਅਵਾਰਡ
(Sports Award)

ਅਰਜੁਨ ਅਵਾਰਡ ਜੇਤੂਆਂ ਦੀ ਸੂਚੀ (List of Arjuna Award Winners) – ਸੁਧੀਰ ਭਾਸਕਰ ਰਾਵ ਪਰਬ (1970), ਅਚਲਾ ਦੇਵਰੇ (1971), ਭਾਵਨਾ ਹੁੰਮੁਖਲਾਲ ਪਾਰਿਖ (1973), ਨੀਲਿਆ ਚੰਦਰਕਾਂਤ ਸਰੋਲਕਰ (1974), ਰੰਗਜਨਾਰਦਨ ਇਨਾਮਦਾਰ, ਊਸ਼ਾ ਵਸੰਤ ਨਾਗਰਕਰ (1975), ਐੱਸ. ਧਾਰਵਾੜਕ (1976), ਹੇਮੰਤ ਮੋਹਨ ਕਾਲਕਰ, ਸੁਸ਼ਮਾ ਸੋਲਕਰ (1981), ਵੀਨਾ ਨਰਾਇਣ ਪਰਬ (1983), ਐੱਸ ਪ੍ਰਕਾਸ਼ (1984), ਐੱਸ ਭਗਵਾਨ ਕੁਲਕਰਨੀ, ਸੁਰੇਖਾ (1985), ਸ਼ੋਭਾ ਨਰਾਇਣਾ (1999) ।
ਦਰੋਣਾਚਾਰੀਆ ਅਵਾਰਡ ਜੇਤੂ-ਫਾਦਕੇ ਗੋਪਾਲ ਪੁਰਸ਼ੋਤਮ (2000) ।

PSEB 12th Class Physical Education Practical ਖੋ-ਖੋ (Kho-Kho)

ਪ੍ਰਸ਼ਨ 1.
ਖੋ-ਖੋ ਦੀ ਖੇਡ ਵਿਚ ਕਿੰਨੇ ਖਿਡਾਰੀ ਖੇਡਦੇ ਹਨ ?
ਉੱਤਰ-9.

ਪ੍ਰਸ਼ਨ 2.
ਮੈਦਾਨ ਦੀ ਲੰਬਾਈ ਅਤੇ ਚੌੜਾਈ ਦੱਸੋ ।
ਉੱਤਰ-
ਖੋ-ਖੋ ਮੈਦਾਨ ਦੀ ਲੰਬਾਈ ਅਤੇ ਚੌੜਾਈ = 29 ਮੀਟਰ × 16 ਮੀਟਰ ।

ਪ੍ਰਸ਼ਨ 3.
ਖੋ-ਖੋ ਦੀ ਖੇਡ ਵਿਚ ਚੇਜ਼ਰ ਤੇ ਰਨਰ ਕਿਸੇ ਨੂੰ ਆਖਦੇ ਹਨ ?
ਉੱਤਰ-
ਚੇਜ਼ਰ ਜੋ ਪੀਰੇ ਕਰਦਾ ਹੈ ਅਤੇ ਰਨਰ ਜੋ ਭੱਜਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 4.
ਮੈਚ ਵਿਚ ਕਿੰਨੀਆਂ ਇਨਿੰਗਜ਼ ਹੁੰਦੀਆਂ ਹਨ ?
ਉੱਤਰ-
2.

ਪਸ਼ਨ 5.
ਖੋ-ਖੋ ਦਾ ਮੈਚ ਕਿਵੇਂ ਸ਼ੁਰੂ ਹੁੰਦਾ ਹੈ ਅਤੇ ਇਸ ਦਾ ਸਮਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਮੈਚ ਟਾਸ ਨਾਲ ਸ਼ੁਰੂ ਹੁੰਦਾ ਹੈ ਅਤੇ ਇਹ 95-9 ਦੀਆਂ ਦੋ ਇੰਨਿੰਗ ਵਿਚ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 6.
ਰਨਰ ਦੇ ਆਊਟ ਹੋਣ ਤੇ ਕਿੰਨੇ ਨੰਬਰ ਮਿਲਦੇ ਹਨ ?
ਉੱਤਰ-
1 ਨੰਬਰ ।

ਪ੍ਰਸ਼ਨ 7.
ਖੋ-ਖੋ ਦੀ ਖੇਡ ਵਿਚ ਕਿੰਨੀਆਂ ਪੱਟੀਆਂ ਹੁੰਦੀਆਂ ਹਨ ?
ਉਤਰ-
8.

ਪ੍ਰਸ਼ਨ 8.
ਇਨ੍ਹਾਂ ਦਾ ਆਕਾਰ ਕਿੰਨਾਂ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
30 × 30 ਇੰਚ ।

ਪ੍ਰਸ਼ਨ 9.
ਖੋ-ਖੋ ਦੇ ਪੋਲ ਦੀ ਲੰਬਾਈ ਕਿੰਨੀ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਲੰਬਾਈ, 23.50 ਮੀ. ।

ਪ੍ਰਸ਼ਨ 10.
ਖੋ-ਖੋ ਦੇ ਪੋਲ ਦੀ ਲੰਬਾਈ ਅਤੇ ਘੇਰਾ ਦੱਸੋ ! ਉੱਤਰ-
1.20 ਮੀਟਰ !

ਪ੍ਰਸ਼ਨ 11.
ਖੋ-ਖੋ ਦੇ ਖਿਡਾਉਣ ਵਾਲੇ ਅਧਿਕਾਰੀਆਂ ਦੀ ਕੁੱਲ ਗਿਣਤੀ ਦੱਸੋ ।
ਉੱਤਰ-

1. ਰੈਫ਼ਰੀ,
2. ਅੰਪਾਇਰ, ਇਕ ਟਾਈਮ ਕੀਪਰ, ਇਕ ਸਕੋਰਰ । ,

Punjab State Board PSEB 12th Class Physical Education Book Solutions ਕ੍ਰਿਕੇਟ (Cricket) Game Rules.

ਕ੍ਰਿਕੇਟ (Cricket) Game Rules – PSEB 12th Class Physical Education

ਕ੍ਰਿਕੇਟ ਦਾ ਇਤਿਹਾਸ
(History of Cricket)

ਕ੍ਰਿਕੇਟ ਖੇਡ ਦੀ ਸ਼ੁਰੁਆਤ ਇੰਗਲੈਂਡ ਵਿਚ ਹੋਈ ਸੀ, ਪਰ ਕੁਝ ਇਤਿਹਾਸਕਾਰਾਂ ਦੇ ਅਨੁਸਾਰ ਇਸ ਖੇਡ ਦਾ ਜਨਮ ਫਰਾਂਸ ਵਿੱਚ ਹੋਇਆ ਸੀ । ਜ਼ਿਆਦਾਤਰ ਲੋਕ ਇਸ ਦਾ ਜਨਮ ਇੰਗਲੈਂਡ ਵਿੱਚ ਮੰਨਦੇ ਹਨ । ‘ਵਿਜਡਨ’ ਜਿਸਨੂੰ ਕ੍ਰਿਕੇਟ ਦਾ ਬਾਈਬਲ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਕ੍ਰਿਕੇਟ ਦਾ ਪਹਿਲਾ ਉਲੇਖ 1300 ਵਿੱਚ ਹੋਇਆ ਸੀ। ਕ੍ਰਿਕੇਟ ਦੀ ਜਾਣਕਾਰੀ ਕਿੰਗ ਐਡਵਰਲਡ ਦੀ ਅਲਮਾਰੀ ਤੋਂ ਮਿਲੇ, ਬੱਲੇ ਤੇ ਗੇਂਦ ਤੋਂ ਹੁੰਦੀ ਹੈ । ਕੁੱਝ ਮਨੁੱਖਾਂ ਅਨੁਸਾਰ 13ਵੀਂ ਸਦੀ ਵਿੱਚ ਇਹ ਖੇਡ ਇੰਗਲੈਂਡ ਦੇ ਗਵਾਲੋਂ ਅਤੇ ਚਰਵਾਹੋਂ ਦੁਆਰਾ ਖੇਡਿਆ ਜਾਂਦਾ ਸੀ । ਸੰਨ 1706 ਵਿੱਚ ਵਿਲੀਅਮ ਗੋਲਡ ਨੇ ਆਪਣੀ ਕਵਿਤਾ ਵਿੱਚ ਵਿਕੇਟ ਦਾ ਵਰਣਨ ਕੀਤਾ ਸੀ । ਸੰਨ 1709 ਵਿੱਚ ਲੰਡਨ ਅਤੇ ਕੈਟ ਦੀਆਂ ਟੀਮਾਂ ਵਿੱਚ ਪਹਿਲਾਂ ਮੈਚ ਖੇਡਿਆ ਗਿਆ । ਫੇਰ 1770 ਵਿੱਚ ਕੈਮਬਰਿਜ ਵਿਸ਼ਵਵਿਦਿਆਲਾ ਫੇਰ 1729 ਵਿੱਚ ਐਕਸਪੋਰਟ ਵਿਸ਼ਵਵਿਦਿਆਲਿਆ ਵਿੱਚ ਇਹ ਖੇਡ ਖੇਡਿਆ ਜਾਂਦਾ ਸੀ ।

ਅਸਲ ਵਿੱਚ ਕ੍ਰਿਕੇਟ ਦਾ ਸੁਨਹਿਰਾ ਅਧਿਆਇ 1760 ਵਿੱਚ ਸ਼ੁਰੂ ਹੋਇਆ । 1760 ਵਿੱਚ ਇੰਗਲੈਂਡ ਵਿੱਚ ਪਹਿਲੀ ਕ੍ਰਿਕੇਟ ਕਲੱਬ ਦੀ ਸਥਾਪਨਾ ਕੀਤੀ ਗਈ । ਇਸ ਕਲੱਬ ਦਾ ਨਾਂ ਹੈਬਲਡਨ ਰੱਖਿਆ ਸੀ । ਤਕਰੀਬਨ 30 ਸਾਲ ਤੱਕ ਇਹ ਕਲੱਬ ਕ੍ਰਿਕੇਟ ਦੇ ਇਤਿਹਾਸ ਵਿੱਚ ਛਾ ਗਿਆ । ‘ਜਾਨ ਨਾਇਰਣ’ ਨਾਮਕ ਖਿਡਾਰੀ ਇਸ ਕਲੱਬ ਦੀ ਦੇਣ ਸੀ । ਕ੍ਰਿਕੇਟ ਦਾ ਦੂਜਾ ਇਤਿਹਾਸ ਦਾ ਸੁਨਹਿਰਾ ਅਧਿਆਇ ਐੱਨ. ਸੀ. ਸੀ. ਕਲੱਬ ਦੀ ਸਥਾਪਨਾ ਨਾਲ ਹੋਇਆ । ਇਸ ਕਲੱਬ ਦੀ ਸਥਾਪਨਾ ਸੰਨ 1787 ਵਿੱਚ ਇੰਗਲੈਂਡ ਵਿੱਚ ਹੋਈ । ਲਾਈਟ ਦੇ ਪ੍ਰਸਿੱਧ ਮੈਦਾਨ ਵਿੱਚ ਪਹਿਲਾਂ ਮੈਚ ਜੂਨ 1788 ਵਿੱਚ ਹੋਇਆ ।

ਸੰਨ 1887 ਵਿੱਚ ਆਸਟ੍ਰੇਲੀਆ ਤੇ ਇੰਗਲੈਂਡ ਵਿੱਚ ਪਹਿਲਾਂ ਮੰਜੂਰਸ਼ੁਦਾ ਟੈਸਟ ਮੈਚ ਖੇਡਿਆ ਗਿਆ । ਇਸ ਮੈਚ ਵਿੱਚ ਜਿੱਤ ਆਸਟ੍ਰੇਲੀਆ ਦੀ ਹੋਈ, ਜਿਸ ਦੇ ਵਿਰੋਧ ਵਿਚ ਅੰਗਰੇਜ਼ ਔਰਤਾਂ ਨੇ ਵੇਦ ਨੂੰ ਜਲਾ ਕੇ ਕ੍ਰਿਕੇਟ ਦਾ ਦਾਹ ਸੰਸਕਾਰ ਕੀਤਾ । ਵੇਦ ਦੀ ਰਾਖ ਨੂੰ ਆਸਟ੍ਰੇਲੀਆ ਦੀ ਟੀਮ ਨੂੰ ਅਰਪਣ ਕੀਤਾ ਗਿਆ |
ਉਸ ਸਮੇਂ ਤੋਂ ਹੀ ਇੰਗਲੈਂਡ ਤੇ ਆਸਟ੍ਰੇਲੀਆ ਦੀਆਂ ਕ੍ਰਿਕੇਟ ਟੀਮਾਂ ਇੱਕ ਦੂਜੇ ਦੇ ਵਿਰੁੱਧ ਐਸ ਲਈ ਮੈਚ ਖੇਡਦੇ ਹਨ । ਇਸ ਤੋਂ ਬਾਅਦ 1909 ਵਿੱਚ ਇੰਗਲੈਂਡ ਵਿੱਚ ਇਨਟਰੀਅਰ ਕ੍ਰਿਕੇਟ ਦੀ ਸਥਾਪਨਾ ਹੋਈ । ਜਿਸ ਦੇ ਨਾਲ ਅੰਤਰ-ਰਾਸ਼ਟਰੀ ਕ੍ਰਿਕੇਟ ਨੂੰ ਮਾਨਤਾ ਮਿਲ ਗਈ ।

ਇੰਗਲੈਂਡ ਤੋਂ ਇਲਾਵਾ ਆਸਟੇਲੀਆ ਤੇ ਦੱਖਣੀ ਅਫ਼ਰੀਕਾ ਵਿੱਚ ਵੀ ਮੈਂਬਰ ਬਣ ਗਏ । ਸੰਨ 1971 ਵਿੱਚ ਰੰਗ ਭੇਦ ਦੀ ਨੀਤੀ ਕਾਰਨ ਦੱਖਣੀ ਅਫ਼ਰੀਕਾ ਦੀ ਮੈਂਬਰਸ਼ਿਪ ਖ਼ਤਮ ਕਰ ਦਿੱਤੀ ਗਈ ਸੀ । ਸੰਨ 1956 ਵਿੱਚ ਇਸ ਕਾਂਗਰਸ ਦਾ ਨਾਂ ਬਦਲ ਕੇ ਇੰਟਰਨੈਸ਼ਨਲ ਕ੍ਰਿਕੇਟ ਕਾਂਗਰਸ ਰੱਖ ਦਿੱਤਾ ਗਿਆ । ਕੁੱਝ ਸਮੇਂ ਬਾਅਦ ਦੂਜੇ ਦੇਸ਼ਾਂ ਨੇ ਇਸਦੀ ਮੈਂਬਰਸ਼ਿਪ ਲੈ ਲਈ । ਹੁਣ ਇੰਗਲੈਂਡ, ਆਸਟ੍ਰੇਲੀਆ, ਭਾਰਤ, ਸ੍ਰੀਲੰਕਾ, ਵੈਸਟ ਇੰਡੀਜ਼, ਨਿਊਜ਼ੀਲੈਂਡ, ਪਾਕਿਸਤਾਨ, ਅਰਜਨਟੀਨਾ, ਕੇਨੈਡਾ, ਡੈਨਮਾਰਕ, ਕੀਨੀਆ, ਜਿੰਬਾਵੇ, ਬੰਗਲਾਦੇਸ਼, ਹਾਲੈਂਡ, ਬਰਹੁੱਡਾ, ਫਿਜੀ, ਸਿੰਗਾਪੁਰ, ਹਾਂਗਕਾਂਗ, ਇਸਰਾਈਲ ਤੇ ਮਲੇਸ਼ੀਆ ਆਦਿ ਦੇਸ਼ ਇਸ ਦੇ ਮੈਂਬਰ ਹਨ ।

5 ਜਨਵਰੀ, 1971 ਵਿੱਚ ਕ੍ਰਿਕੇਟ ਦੇ ਇਤਿਹਾਸ ਦਾ ਪਹਿਲਾ ਇਕ ਦਿਨਾਂ ਅੰਤਰਰਾਸ਼ਟਰੀ ਮੈਚ ਇੰਗਲੈਂਡ ਤੇ ਆਸਟ੍ਰੇਲੀਆ ਵਿੱਚ ਖੇਡਿਆ ਗਿਆ । ਇਸ ਵਿੱਚ 40 ਓਵਰ ਹਰੇਕ ਪਾਰੀ ਵਿੱਚ ਰੱਖੇ ਗਏ । ਇਕ ਦਿਨਾਂ ਅੰਤਰਰਾਸ਼ਟਰੀ ਕ੍ਰਿਕੇਟ ਮੈਚਾਂ ਦੇ ਆਯੋਜਨ ਦੇ ਵਿਕਾਸ ਦਾ ਸਿਹਰਾ ਵੀ ਇੰਗਲੈਂਡ ਨੂੰ ਜਾਂਦਾ ਹੈ । ਇੰਗਲੈਂਡ ਦੇ ਮਿਹਨਤ ਦੇ ਫਲਸਰੂਪ ਇੰਗਲੈਂਡ ਵਿੱਚ ਪਹਿਲਾ ਵਿਸ਼ਵ ਕੱਪ ਦੇ ਮੁਕਾਬਲੇ ਕਰਵਾਏ ਗਏ ।ਇਸ ਵਿਸ਼ਵ ਕੱਪ ਕ੍ਰਿਕੇਟ ਵਿੱਚ 8 ਦੇਸ਼ਾਂ ਦੀਆਂ ਟੀਮਾਂ ਨੇ ਭਾਗ ਲਿਆ। ਇਸ ਵਿਸ਼ਵ ਕੱਪ ਦੇ ਫਾਈਨਲ ਵਿੱਚ ਵੈਸਟ ਇੰਡੀਜ਼ ਨੇ ਆਸਟ੍ਰੇਲੀਆ ਨੂੰ ਸਾਰਿਆਂ ਨਾਲ ਮਿਲਾਇਆ ਸੀ । | ਭਾਰਤ ਵਿੱਚ ਕ੍ਰਿਕੇਟ ਦੀ ਸ਼ੁਰੂਆਤ ਅੰਗਰੇਜ਼ਾਂ ਦੇ ਭਾਰਤ ਆਉਣ ਨਾਲ ਹੋਈ ।

ਭਾਰਤ ਦੇ ਕ੍ਰਿਕੇਟ ਦਾ ਇਤਿਹਾਸ ਸੰਨ 1721 ਤੋਂ ਸ਼ੁਰੂ ਹੁੰਦਾ ਹੈ । ਸੰਨ 1792 ਵਿੱਚ ਕਲਕੱਤਾ ਵਿੱਚ ਕ੍ਰਿਕੇਟ ਕਲੱਬ ਦੀ ਸਥਾਪਨਾ ਹੋਈ । ਪਹਿਲਾਂ-ਪਹਿਲਾ ਕ੍ਰਿਕੇਟ ਰਾਜਘਰਾਨਿਆਂ ਤੱਕ ਹੀ ਸੀਮਿਤ ਰਿਹਾ । ਪਰ ਹੁਣ ਇਹ ਖੇਡ ਸਭ ਤੋਂ ਜ਼ਿਆਦਾ ਮਸ਼ਹੂਰ ਹੋ ਚੁੱਕਿਆ ਹੈ । ਭਾਰਤ ਦੀ ਪਹਿਲੀ ਕ੍ਰਿਕੇਟ ਟੀਮ ਨੇ ਸੰਨ 1874 ਵਿੱਚ ਇੰਗਲੈਂਡ ਦਾ ਦੌਰਾ ਕੀਤਾ ਸੀ ।

ਇਸ ਵਿੱਚ ਭਾਰਤ ਦੇ ਖਿਡਾਰੀਆਂ ਨੇ ਵਿਦੇਸ਼ੀ ਟੀਮਾਂ ਨਾਲ ਮੈਚ ਖੇਡ ਕੇ ਆਪਣੀ ਤਾਕਤ ਯਾਦ ਕਰਵਾਈ । ਸਭ ਤੋਂ ਪਹਿਲਾਂ ਮਹਾਰਾਜਾ ਰਣਜੀਤ ਸਿੰਘ ਨੇ ਇੰਗਲੈਂਡ ਦੀ ਟੀਮ ਵਿੱਚ ਭਾਗ ਲੈ ਕੇ ਵਿਸ਼ਵ ਕੱਪ ਟੀਮ ਵਿੱਚ ਪਹਿਲਾ ਸੈਂਕੜਾ ਬਣਾਇਆ ਸੀ । ਸੰਨ 1952 ਵਿੱਚ ਲਾਈਟ ਦੇ ਮੈਦਾਨ ਵਿੱਚ ਭਾਰਤ ਨੇ ਪਹਿਲਾਂ ਕ੍ਰਿਕੇਟ ਮੈਚ ਇੰਗਲੈਂਡ ਦੇ ਵਿਰੁੱਧ ਖੇਡਿਆ ।

ਸੰਨ 1934 ਵਿੱਚ ਰੰਜ਼ੀ ਵਾਫ਼ੀ ਸ਼ੁਰੂ ਹੋਈ । ਸੰਨ 1928 ਵਿੱਚ ਆਰ.ਈ.’ ਗਾਂਟ ਦੀ ਪ੍ਰਧਾਨਗੀ ਹੇਠ ਭਾਰਤੀ ਕ੍ਰਿਕੇਟ ਕੰਟਰੋਲ ਬੋਰਡ ਦੀ ਸਥਾਪਨਾ ਹੋਈ । ਪਹਿਲਾਂ ਆਈ.ਸੀ.ਸੀ. ਟਵੰਟੀ ਵਰਲੱਡ ਕੱਪ ਕ੍ਰਿਕੇਟ ਸੰਨ 2007 ਵਿੱਚ ਖੇਡਿਆ ਗਿਆ ।

ਯਾਦ ਰੱਖਣ ਯੋਗ ਗੱਲਾਂ
(Tips to Remember)

1. ਕ੍ਰਿਕੇਟ ਟੀਮ ਵਿਚ ਖਿਡਾਰੀਆਂ ਦੀ ਗਿਣਤੀ = 16 (11+5)
2. ਵਿਕਟਾਂ ਦੇ ਵਿਚਾਲੇ ਦੀ ਦੁਰੀ = 22 ਗਜ਼ (20.12 ਸੈਂ.ਮੀ.).
3. ਪਿੱਚ ਦੀ ਚੌੜਾਈ . = 4’4” (3.05 ਮੀ.)
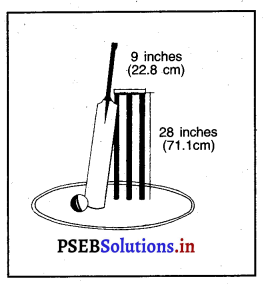
4. ਵਿਕਟਾਂ ਦੀ ਚੌੜਾਈ = 9 ਇੰਚ (22.9 ਸੈਂ.ਮੀ.).
5. ਕ੍ਰਿਕੇਟ ਗੇਂਦ ਦਾ ਘੇਰਾ = 8.1 ਤੋਂ 9 ਇੰਚ (22.4 ਸੈਂ.ਮੀ.-22.9 ਸੈਂ.ਮੀ.)
6. ਕ੍ਰਿਕੇਟ ਗੇਂਦ ਦਾ ਭਾਰ = (155.9 ਗਰਾਮ-163 ਗਰਾਮ)
7. ਬੈਟ ਦੀ ਚੌੜਾਈ = 425” ਇੰਚ (10.8 ਸੈਂ.ਮੀ.)
8. ਬੈਟ ਦੀ ਲੰਬਾਈ = 38 ਇੰਚ (96.52 ਸੈਂ.ਮੀ.).
9. ਗੇਂਦ ਦਾ ਰੰਗ = ਦਿਨ ਦੇ ਮੈਚ ਲਈ ਲਾਲ ਅਤੇ ਰਾਤ ਦੇ ਮੈਚ ਲਈ ਸਫ਼ੈਦ
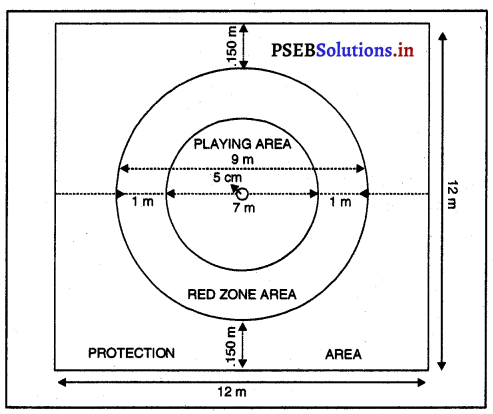
10. ਕੇਂਦਰ ਤੋਂ ਵੱਡੇ ਚੱਕਰ ਦੀ ਦੂਰੀ = 75 ਗਜ਼ ਤੋਂ 85 ਗਜ਼ (137 ਮੀ.-150 ਮੀ.)
11. ਵਿਕਟਾਂ ਦੀ ਜ਼ਮੀਨ ਤੋਂ ਉਚਾਈ = 28 ਇੰਚ (71 ਸੈਂ.ਮੀ.)
12. ਮੈਚ ਦੀਆਂ ਕਿਸਮਾਂ = 20-20, ਇਕ ਦਿਨ ਦਾ ਮੈਚ, ਪੰਜ ਦਿਨ ਦਾ ਟੈਸਟ ਮੈਚ
13. ਮੈਚ ਦੇ ਅੰਪਾਇਰਾਂ ਦੀ ਗਿਣਤੀ : 2
14. ਤੀਜਾ ਅੰਪਾਇਰ = ਇਕ ਮੈਚ ਰੈਫ਼ਰੀ
15. ਛੋਟੇ ਸਰਕਲ ਦਾ ਰੇਡੀਅਸ = 27.4 ਮੀ.
16. ਬਾਊਲਿੰਗ ਕੀਜ਼ ਦੀ ਲੰਬਾਈ = 8′.8 (2.64 ਮੀ.)
17. ਪੀਚਿੰਗ ਕੁੰਜ . = 4′ (1.22 ਮੀ.)

ਕ੍ਰਿਕੇਟ ਦੇ ਸਧਾਰਨ ਨਿਯਮ
(Latest General Rules of Cricket)

1. ਕ੍ਰਿਕੇਟ ਦਾ ਮੈਚ ਦੋ ਟੀਮਾਂ ਦੇ ਵਿੱਚ ਹੀ ਹੁੰਦਾ ਹੈ ਅਤੇ ਇਸ ਵਿੱਚ ਹਰੇਕ ਟੀਮ ਦੇ 11 ਖਿਡਾਰੀ ਭਾਗ ਲੈਂਦੇ ਹਨ । ਹਰੇਕ ਟੀਮ ਦਾ ਇੱਕ ਖਿਡਾਰੀ ਕੈਪਟਨ ਹੁੰਦਾ ਹੈ । ਜੇਕਰ ਕੈਪਟਨ ਗੈਰ ਹਾਜਰ ਹੋਵੇ ਤਾਂ ਵਾਈਸ-ਕੈਪਟਨ ਹੀ ਕੈਪਟਨ ਦੀ ਭੂਮਿਕਾ ਅਦਾ ਕਰਦਾ ਹੈ ।
2. ਖੇਡਣ ਦੇ ਲਈ ਟਾਸ ਤੋਂ ਪਹਿਲੇ ਕੈਪਟਨ ਰਾਹੀਂ ਖਿਡਾਰੀਆਂ ਦਾ ਨਾਮਾਂਕਨ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।
3. ਮੈਚ ਦੇ ਦੌਰਾਨ ਕਿਸੇ ਖਿਡਾਰੀ ਦੇ ਬੀਮਾਰ ਹੋਣ ਦੀ ਦਿਸ਼ਾ ਵਿੱਚ ਜਾਂ ਜ਼ਖ਼ਮੀ ਹੋਣ ਤੇ ਉਸਦੇ ਸਥਾਨ ਤੇ ਜ਼ਿਆਦਾ ਖਿਡਾਰੀ (Subsititutes) ਨੂੰ ਅਵਸਰ ਦਿੱਤਾ ਜਾਵੇਗਾ ।
4. ਜ਼ਿਆਦਾਤਰ ਖਿਡਾਰੀ ਨੂੰ ਕੇਵਲ ਫੀਲਡਿੰਗ (Fielding) ਦੇ ਲਈ ਬਦਲਿਆ ਜਾਵੇਗਾ, ਬੈਟਿੰਗ ਜਾਂ ਬਾਲਿੰਗ ਦੇ ਲਈ ਨਹੀਂ ।
5. ਮੈਚ ਦੇ ਦੌਰਾਨ ਇੱਕ ਜ਼ਖ਼ਮੀ ਜਾਂ ਬੀਮਾਰ ਬੈਟਸਮੈਨ ਦੇ ਲਈ ਇਕ ਰਨਰ ਦਿੱਤਾ ਜਾ ਸਕਦਾ ਹੈ । ਇਹ ਖਿਡਾਰੀ . ਜੋ ਰਨਰ ਦੇ ਰੂਪ ਵਿੱਚ ਖੇਡਦਾ ਹੈ, ਉਹ ਬੈਟਿੰਗ ਟੀਮ ਦਾ ਮੈਂਬਰ ਹੋਵੇਗਾ ।
6. ਹਾਲਾਂਕਿ ਵਿਕੇਟ ਨਾਲ ਬਾਊਂਰੀਜ਼ ਦੀ ਦੂਰੀ ਨਿਸ਼ਚਿਤ ਨਹੀਂ ਹੁੰਦੀ, ਪਰ ਇਹ 75 ਤੋਂ 85 ਗਜ ਹੋ ਸਕਦੀ ਹੈ । ਇਸ ਲਈ ਹਰੇਕ ਜਗ੍ਹਾ ਦੇ ਖੇਡ ਮੈਦਾਨ ਅਲੱਗ-ਅਲੱਗ ਆਕਾਰ (Size) ਦਾ ਹੁੰਦਾ ਹੈ ।
7. ਉਹ ਟੀਮ, ਜੋ ਪਹਿਲੇ ਬੈਟਿੰਗ ਕਰਦੀ ਹੈ ਅਤੇ ਪੰਜ ਦਿਨਾਂ ਮੈਚ ਵਿੱਚ 200 ਰਨ ਦੀ ਲੀਡ, ਤਿੰਨ ਦਿਨਾਂ ਮੈਚ ਵਿੱਚ 150 ਰਣ ਦੀ ਫੀਲਡ ਤੇ ਦੋ ਦਿਨਾਂ ਮੈਚ ਵਿਚ 100 ਰਨ ਦੀ ਲੀਡ ਲੈ ਲੈਂਦੀ ਹੈ, ਤਾਂ ਉਹ ਵਿਰੋਧੀ ਟੀਮ ਨੂੰ ਆਪਣੀ ਇਨਿੰਗ ਨੂੰ ਫਾਲੋਆਨ ਦੇ ਲਈ ਕਹਿ ਸਕਦੀ ਹੈ ।
8. ਬਾਲਿੰਗ ਹਰੇਕ ਵਿਕੇਟ ਤੋਂ ਵਾਰ-ਵਾਰ ਨਾਲ ਕਰਨੀ ਚਾਹੀਦੀ । ਇਕ ਓਵਰ ਵਿੱਚ 6 ਤੋਂ 8 ਬਾਲ ਹੋ ਸਕਦੇ ਹਨ।
9. ਕ੍ਰਿਕਟ ਦੇ ਖਿਡਾਰੀਆਲ ਓਵਰ ਵਿੱਚ ਨਹੀਂ ਗਿਣੀ ਚਾਹੀਦੀ । ਇਕ ਓਵਰ ਵਿੱਚ
9. ਕ੍ਰਿਕਟ ਦੇ ਖਿਡਾਰੀ ਲਈ ਕਿੱਟ ਪਹਿਨਣਾ ਜ਼ਰੂਰੀ ਹੈ । ਕਿੱਟ ਤੋਂ ਭਾਵ ਸਫ਼ੈਦ ਪੈਂਟ, ਕਮੀਜ਼, ਬੂਟ, ਜੁਰਾਬਾਂ, ਪੈਡ, ਅਬਡਾਮਨਲ ਗਾਰਡ, ਗਲਵਜ ਅਤੇ ਬੈਟ ਹਨ ।
10. ਬਾਉਲਿੰਗ ਕ੍ਰੀਜ਼ ਸਟੰਪਾਂ ਦੇ ਨਾਲ 8 ਫੁੱਟ 8 ਇੰਚ (2.64 gm) ਲੰਮੀ ਖਿੱਚੀ ਜਾਵੇਗੀ । ਸਟੰਪਾਂ ਵਿਚਕਾਰ ਹੋਣਗੀਆਂ | ਪਾਪਿੰਗ ਝੀਜ਼ ਬਾਉਲਿੰਗ ਕੀਜ਼ ਦੇ ਸਮਾਨਾਂਤਰ 3 ਫੁੱਟ (90 cm) ਤੇ ਖਿੱਚੀ ਜਾਵੇਗੀ ਅਤੇ ਇਹ ਸਟੰਪਾਂ ਦੇ ਦੋਵੇਂ ਪਾਸੇ 6 ਫੁੱਟ (1.80 m) ਵਧਾਈ ਜਾਵੇਗੀ । ਰਿਟਰਨ ਭੀਜ਼ ਬਾਊਲਿੰਗ ਕੀਜ਼ ਦੇ ਦੋਨਾਂ ਸਿਰਿਆਂ ਤੇ ਸਮਕੋਣ ‘ਤੇ ਖਿੱਚੀ ਜਾਵੇਗੀ ਅਤੇ ਇਸ ਨੂੰ ਪਾਪਿੰਗ ਝੀਜ਼ ਦੇ ਮਿਲਣ ਲਈ ਵਧਾਇਆ ਜਾਵੇਗਾ | ਪਾਪਿੰਗ ਝੀਜ਼ ਤੇ ਰਿਟਰਨ ਭੀਜ਼ ਦੋਨੋਂ ਹੀ ਲੰਬਾਈ ਵਿਚ ਅਸੀਮਿਤ ਮੰਨੀਆਂ ਜਾਂਦੀਆਂ ਹਨ । .

11. ਹਰੇਕ ਟੀਮ ਨੂੰ ਵਾਰੀ-ਵਾਰੀ ਨਾਲ ਦੋ ਵਾਰ ਖੇਡਣਾ ਪੈਂਦਾ ਹੈ । ਇਸ ਦਾ ਫੈਸਲਾ ਟਾਸ ਦੁਆਰਾ ਕੀਤਾ ਜਾਵੇਗਾ ਕਿ ਕਿਹੜੀ ਟੀਮ ਪਹਿਲਾਂ ਖੇਡੇ ।
ਜੋ ਵੀ ਟੀਮ ਪਹਿਲੇ ਖੇਡੇਗੀ, ਜੇਕਰ ਉਸ ਨੇ ਵਿਰੋਧੀ ਟੀਮ ਤੇ ਪੰਜ ਦਿਨ ਜਾਂ ਵਧੇਰੇ ਦੇ ਮੈਚ ਵਿਚ 200 ਦੌੜਾਂ, ਤਿੰਨ ਦਿਨ ਦੇ ਮੈਚ ਵਿਚ 150, ਦੋ ਦਿਨ ਦੇ ਮੈਚ ਵਿਚ 100 ਅਤੇ ਇਕ ਦਿਨ ਦੇ ਮੈਚ ਵਿਚ 25 ਦੌੜਾਂ ਵਧੇਰੇ · ਬਣਾ ਲਈਆਂ ਹਨ, ਤਾਂ ਉਹ ਦੁਸਰੀ ਟੀਮ ਨੂੰ ਦੁਬਾਰਾ ਖੇਡਣ ਲਈ ਕਹਿ ਸਕਦੀ ਹੈ ਅਰਥਾਤ Follow on ਕਰਵਾ ਸਕਦੀ ਹੈ । ਬੈਟ ਕਰਨ ਵਾਲੀ ਟੀਮ ਦਾ ਕਪਤਾਨ ਸਮੇਂ ਤੋਂ ਪਹਿਲਾਂ ਵੀ ਪਾਰੀ ਦੀ ਸਮਾਪਤੀ ਦੀ ਘੋਸ਼ਣਾ (Declare) ਕਰ ਸਕਦਾ ਹੈ ।

12. ਹਰੇਕ ਪਾਰੀ ਦੇ ਆਰੰਭ ਤੇ ਪ੍ਰਤੀ ਦਿਨ ਖੇਡ ਆਰੰਭ ਕਰਨ ਤੋਂ ਪਹਿਲਾਂ ਕੈਪਟਨ ਕਹਿੰਦਾ ਹੈ “ਖੇਡੋ’ ਅਤੇ ਜੇਕਰ ਟੀਮ ਖੇਡਣ ਤੋਂ ਇਨਕਾਰ ਕਰੇ, ਤਾਂ ਉਹ ਮੈਚ ਹਾਰ ਜਾਵੇਗੀ । ਹਰੇਕ ਪਾਰੀ ਵਿਚ 10 ਮਿੰਟ ਅਤੇ ਹਰੇਕ ਨਵੇਂ ਬੈਟਸਮੈਨ ਦੇ ਆਉਣ ਵਿਚ ਵੱਧ ਤੋਂ ਵੱਧ ਦੋ ਮਿੰਟ ਦਿੱਤੇ ਜਾਣਗੇ । ਭੋਜਨ ਲਈ ਇੰਟਰਵਲ ਅਕਸਰ 45 ਮਿੰਟ ਤੋਂ ਵੱਧ ਨਹੀਂ ਹੋਵੇਗਾ । ਚਾਹ ਲਈ ਇੰਟਰਵਲ 20 ਮਿੰਟ ਤੋਂ ਜ਼ਿਆਦਾ ਨਹੀਂ ਹੋਵੇਗਾ । ਜੇਕਰ ਚਾਹ ਦੇ ਨਿਰਧਾਰਿਤ ਸਮੇਂ ਤੇ 9 ਖਿਡਾਰੀ ਆਊਟ ਹੋਏ ਹਨ, ਤਾਂ ਖੇਡ ਨੂੰ 30 ਮਿੰਟ ਤਕ ਜਾਂ ਪਾਰੀ ਦੀ ਸਮਾਪਤੀ ਤਕ ਜਾਰੀ ਰੱਖਿਆ ਜਾਂਦਾ ਹੈ ।

ਵੱਖ-ਵੱਖ ਪ੍ਰਕਾਰ ਦੇ ਮੈਚ
(Various Types of Matches)

1. ਟੈਸਟ ਮੈਚ (Test Match-ਟੈਸਟ ਮੈਚ ਵਿਚ ਦੋਨਾਂ ਟੀਮਾਂ ਨੂੰ ਦੋ-ਦੋ ਇਨਿੰਗ ਖੇਡਣ ਦਾ ਮੌਕਾ ਮਿਲਦਾ ਹੈ । ਇਹ ਮੈਚ ਪੰਜ ਦਿਨਾਂ ਦਾ ਹੁੰਦਾ ਹੈ ।
2. ਇਕ ਦਿਨ ਦਾ ਮੈਚ (One day Match)-ਇਕ ਦਿਨ ਦੇ ਮੈਚ ਵਿਚ ਦੋਨੋ ਟੀਮਾਂ 50 ਓਵਰ ਦੇ ਲਈ ਬੈਟ , ਕਰਨਗੀਆਂ । ਇਹ ਮੈਚ ਦਿਨ ਜਾਂ ਰਾਤ ਨੂੰ ਖੋਲ੍ਹਿਆ ਜਾ ਸਕਦਾ ਹੈ ।
3. 20-20 ਮੈਚ (20-20 Match-ਇਹ ਇਕ ਦਿਨ ਦੇ ਮੈਚ ਦੀ ਤਰ੍ਹਾਂ ਹੈ ਇਸ ਨੂੰ 20-20 ਓਵਰ ਹੀ ਬੰਡਦਿਆਂ ਹਨ । ਇਸ ਵਿਚ ਨਵੇਂ ਨਿਯਮ ਜੋ ਇਸ ਤਰ੍ਹਾਂ ਹਨ’-

• ਜਦੋਂ ਬਾਲਰ ਬਾਉਲਿੰਗ ਕਰੀਜ਼ ਪਾਰ ਕਰਕੇ ਬਾਲ ਸੁੱਟਦਾ ਹੈ ਤਾਂ ਉਸ ਨੂੰ ਨੋ ਬਾਲ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ਜਿਸ ਨਾਲ ਬੈਟਸਮੈਨ ਨੂੰ ਫ਼ਰੀ ਹਿੱਟ ਮਿਲਦੀ ਹੈ । ਇਸ ਫ਼ਰੀ ਹਿਟ ਵਿਚ ਬੈਟਸਮੈਨ ਆਊਟ ਨਹੀਂ ਹੋ ਸਕਦਾ ਸਿਰਫ਼ ਰਨ ਆਊਟ ਹੋ ਸਕਦਾ ਹੈ ।
• ਜਦੋਂ ਮੈਚ ਬਰਾਬਰ ਹੋ ਜਾਵੇ ਤਾਂ ਬਾਲ ਆਉਟ ਦੇ ਨਾਲ ਜਿੱਤ ਹਾਰ ਦਾ ਫੈਸਲਾ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਇਸ ਵਿਚ । ਦੋਨਾਂ ਟੀਮਾਂ ਦੇ ਪੰਜ-ਪੰਜ ਖਿਡਾਰੀਆਂ ਨੂੰ ਬਾਲ ਦਰਜ ਦਾ ਮੌਕਾ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ਇਸ ਗੇਂਦ ਨੂੰ ਬੈਟਸਮੈਨ ਨਹੀਂ ਖੇਡਦਾ . ਜਿਹੜੀ ਟੀਮ ਜ਼ਿਆਦਾ ਵਿਕਟ ਲੈਂਦੀ ਹੈ ਜੇਤੂ ਹੁੰਦੀ ਹੈ ।
• ਕ੍ਰਿਕੇਟ ਵਿਚ ਨਵੇਂ ਨਿਯਮ ਲਾਗੂ ਹਨ ਜੋ ਇਸ ਤਰ੍ਹਾਂ ਹਨ, 50 ਓਵਰ ਦੇ ਮੈਚ ਵਿਚ ਤਿੰਨ ਪਾਵਰ ਪਲੇ 10 ਓਵਰ, 5 ਓਵਰ ਅਤੇ 5 ਓਵਰ ਦੇ ਹੁੰਦੇ ਹਨ, ਪਹਿਲੇ 10 ਪਾਵਰ ਪਲੇ ਖੇਡ ਦੇ ਸ਼ੁਰੂ ਵਿਚ ਲੈਣੇ ਹੁੰਦੇ ਹਨ । ਬਾਕੀ 5, 5 ਓਵਰ ਬੈਟਿੰਗ ਅਤੇ ਫੀਲਡਿੰਗ ਟੀਮ ਜਦੋਂ ਚਾਹੇ ਲੈ ਸਕਦੀ ਹੈ ।

4. ਪਹਿਲਾਂ ਬੈਟਸਮੈਨ ਗੇਂਦ ਨੂੰ ਚੋਟ ਲਗਾਉਣ ਦੇ ਬਾਅਦ ਗੇਂਦ ਮੈਦਾਨ ਵਿਚ ਰਹਿਣ ਦੇ ਸਮੇਂ ਵਿਚ ਇਕ ਸਾਈਡ ਤੋਂ ਦੂਸਰੀ ਸਾਈਡ ਤਕ ਦੌੜਦਾ ਹੈ । ਉਹ ਜਿੰਨੀ ਵਾਰ ਅਜਿਹਾ ਕਰੇਗਾ, ਉਤਨੇ ਰਨ ਹੋ ਜਾਂਦੇ ਹਨ | ਸਕੋਰ ਲਈ ਦੌੜਾਂ ਦੀ ਗਿਣਤੀ ਕੀਤੀ ਜਾਂਦੀ ਹੈ । ਜਦੋਂ ਬੈਟਸਮੈਨ ਗੇਂਦ ਨੂੰ ਹਿੱਟ ਕਰਨ ਮਗਰੋਂ ਇਕ ਸਿਰੇ ਤੋਂ ਦੂਸਰੇ ਸਿਰੇ ‘ਤੇ ਪਹੁੰਚ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਇਕ ਦੌੜ ਪੂਰੀ ਸਮਝੀ ਜਾਂਦੀ ਹੈ । ਜੇਕਰ ਕੋਈ ਬੈਟਸਮੈਨ ਦੂਜੇ ਪਾਸੇ ਪਹੁੰਚੇ ਬਿਨਾਂ ਰਾਹ ਤੋਂ ਵਾਪਸ ਪਰਤ ਜਾਂਦਾ ਹੈ, ਉਹ ਦੌੜ ਨਹੀਂ ਗਿਣੀ ਜਾਂਦੀ । ਇਸ ਨੂੰ ਸ਼ਾਰਟ ਰਨ (Short Run) ਕਹਿੰਦੇ ਹਨ । ਜੇਕਰ ਰਨ ਬਣਾਉਂਦੇ ਸਮੇਂ ਬਾਲ ਹਵਾ ਵਿਚ ਹੋਵੇ, ਉਹ ਲਪਕ ਲਿਆ ਜਾਵੇ, ਤਾਂ ਉਹ ਰਨ (ਦੌੜ) ਗਿਣੀ ਨਹੀਂ ਜਾਵੇਗੀ । ਇਸੇ ਤਰ੍ਹਾਂ ਜੇਕਰ ਬੈਟਸਮੈਨ ਦੌੜ ਬਣਾਉਂਦੇ ਸਮੇਂ ਰਨ ਆਉਟ (Run Out) ਹੋ ਜਾਵੇ, ਤਾਂ ਉਹ ਦੌੜ ਨਹੀਂ ਗਿਣੀ ਜਾਵੇਗੀ । , 17 ਜੇਕਰ ਬੈਟਸਮੈਨ ਦੇ ਹਿਟ ਕਰਨ ਤੇ ਗੇਂਦ ਮੈਦਾਨ ਨੂੰ ਛੂੰਹਦੀ ਹੋਈ ਸੀਮਾ ਰੇਖਾ ਦੇ ਪਾਰ ਚਲੀ ਜਾਂਦੀ ਹੈ, ਤਾਂ ਉਸ ਨੂੰ ਬਾਊਂਡਰੀ ਕਹਿੰਦੇ ਹਨ । ਬਾਊਂਡਰੀ ਦਾ ਚਾਰ ਸਕੋਰ ਹੁੰਦਾ ਹੈ । ਜੇਕਰ ਗੇਂਦ ਜ਼ਮੀਨ ਨੂੰ ਲੱਗੇ ਬਿਨਾਂ ਬਾਊਂਡਰੀ ਤੋਂ ਬਾਹਰ ਜਾ ਕੇ ਡਿੱਗੇ ਤਾਂ 6 ਦੌੜਾਂ ਹੋ ਜਾਂਦੀਆਂ ਹਨ | ਬਾਊਂਡਰੀ ਜੇਕਰ ਓਵਰ ਥਰੋ ਤੇ ਹੋਈ ਹੈ ਜਾਂ ਖੇਤਰ ਰੱਖਿਅਕ ਨੇ ਜਾਣ ਬੁੱਝ ਕੇ ਕੀਤੀ ਹੈ ਤਾਂ ਬਣੇ ਹੋਏ ਰਨ ਅਤੇ ਬਾਊਂਡਰੀ ਦਾ ਸਕੋਰ ਫਲਅੰਕਣ ਵਿਚ ਜੋੜੇ ਜਾਣਗੇ ।

5. ਜੇਕਰ ਗੇਂਦ ਗੁੰਮ ਹੋ ਜਾਵੇ ਤਾਂ ਕੋਈ ਵੀ ਖੇਤਰ ਰੱਖਿਅਕ ਗੁੰਮ ਹੋ ਜਾਣ ਦਾ ਐਲਾਨ ਕਰ ਦਿੰਦਾ ਹੈ | ਅਜਿਹੀ ਹਾਲਤ ਵਿਚ ਅੰਪਾਇਰ ਗੁੰਮ ਹੋਈ ਗੇਂਦ ਨਾਲ ਮਿਲਦੀ-ਜੁਲਦੀ ਹਾਲਤ ਵਾਲੀ ਗੇਂਦ ਨਾਲ ਖੇਡ ਮੁੜ ਸ਼ੁਰੂ ਕਰਵਾ ਦਿੰਦਾ ਹੈ ।

6. ਜੋ ਵੀ ਟੀਮ ਦੋ ਪਾਰੀਆਂ (ਇਨਿੰਗਜ਼) ਵਿਚ ਜ਼ਿਆਦਾ ਦੌੜਾਂ ਬਣਾ ਲੈਂਦੀ ਹੈ ਉਸ ਨੂੰ ਜੇਤੂ ਮੰਨਿਆ ਜਾਵੇਗਾ । | ਪਰ ਜੇਕਰ ਮੈਚ ਪੂਰਾ ਨਾ ਹੋ ਸਕੇ, ਤਾਂ ਇਹ ਬਰਾਬਰ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ ।

ਟਵੰਟੀ-20 ਮੈਚ ਨਾਲ ਸੰਬੰਧਿਤ ਨਿਯਮ .
(Rules Related to Twenty-20 Match)

1. ਹਰੇਕ ਟੀਮ 20 ਓਵਰ ਦੇ ਲਈ ਬੱਲੇਬਾਜ਼ੀ ਕਰੇਗੀ ।

2. ਇਕ ਮੈਚ ਦੀ ਅਵਧੀ 3 ਘੰਟੇ ਹੋਵੇਗੀ | ਪਾਰੀਆਂ ਦੇ ਮੱਧ 20 ਮਿੰਟ ਦਾ ਮੱਧ-ਅੰਤਰ ਹੋਵੇਗਾ ।

3. ਇਕ ਮੈਚ ਪੂਰਾ ਹੋਣ ਦੇ ਲਈ ਘੱਟ ਤੋਂ ਘੱਟ 5 ਓਵਰ ਹਰੇਕ ਟੀਮ ਰਾਹੀਂ ਪੂਰੇ ਕੀਤੇ ਜਾਣੇ ਜ਼ਰੂਰੀ ਹਨ ।

4. ਆਉਣ ਵਾਲੇ ਬੱਲੇਬਾਜ਼ ਨੂੰ 90 ਸੈਕਿੰਡ ਦੇ ਅੰਦਰ ਅਗਲੀ ਬਾਲ ਦਾ ਸਾਹਮਣਾ ਕਰਨਾ ਹੋਵੇਗਾ । ਇਸ ਲਈ ਮੈਚ ਦੇ ਦੌਰਾਨ ਟੀਮ ਨੂੰ ਪੈਵੇਲੀਅਨ ਦੇ ਸਥਾਨ ਤੇ ਸੀਮਾ-ਰੇਖਾ ਦੇ ਨਜ਼ਦੀਕ ਬੈਠਣਾ ਹੋਵੇਗਾ ।

5. ਦੋਵੇਂ ਟੀਮਾਂ ਨੂੰ ਆਪਣੀ-ਆਪਣੀ ਪਾਰੀ 75 ਮਿੰਟ ਵਿੱਚ ਖ਼ਤਮ ਕਰਨੀ ਹੋਵੇਗੀ । ਜੇਕਰ ਖੇਤਰਕਸ਼ਨ’ (Field) ਕਰਨ ਵਾਲੀ ਟੀਮ ਇਸ ਤਰ੍ਹਾਂ ਕਰਨ ਵਿੱਚ ਅਸਫਲ ਹੁੰਦੀ ਹੈ ਤਾਂ ਬੱਲੇਬਾਜ਼ੀ ਕਰਨ ਵਾਲੀ ਟੀਮ ਨੂੰ ਬੋਨਸ ਦੇ ਤੌਰ ਤੇ ਪ੍ਰਤੀ ਓਵਰ 6 ਰਨ ਪ੍ਰਦਾਨ ਕੀਤੇ ਜਾਣਗੇ ।

6. ਇਕ ਬੱਲੇਬਾਜ਼ ਨੂੰ ਮੈਦਾਨ ਵਿੱਚ ਪਹੁੰਚਣ ਦੇ ਲਈ 90 ਸੈਕਿੰਡ ਮਿਲਦੇ ਹਨ । ਜੇਕਰ ਉਹ ਇਸ ਤਰ੍ਹਾਂ ਨਹੀਂ ਕਰਦਾ, ਤਾਂ ਉਸਨੂੰ ਟਾਈਮ ਆਊਟ ਮੰਨਿਆ ਜਾਵੇਗਾ ।

7.ਪਹਿਲੇ 6 ਓਵਰ ਵਿੱਚ ਕੇਵਲ ਦੋ ਖੇਤਰ ਰੱਖਿਅਕ 30 ਗਜ਼ ਦੇ ਦਾਇਰੇ ਦੇ ਬਾਹਰ ਰਹਿ ਸਕਦੇ ਹਨ । ਬਾਕੀ 14 ਓਵਰ ਵਿੱਚ 5 ਤੋਂ ਜ਼ਿਆਦਾ ਖੇਤਰ ਰੱਖਿਅਕ 30 ਗਜ਼ ਦੇ ਦਾਇਰੇ ਤੋਂ ਬਾਹਰ ਨਹੀਂ ਰਹਿ ਸਕਦੇ ।

8. ਇਕ ਗੇਂਦਬਾਜ਼ ਅਧਿਕਤਮ 4 ਓਵਰ ਕਰ ਸਕਦਾ ਹੈ |

9. ਇਕ ਨੋ ਬਾਲ ਸੁੱਟੇ ਜਾਣ ਦੇ ਬਾਅਦ ਖੇਡਣ ਵਾਲੇ ਬੱਲੇਬਾਜ਼ ਨੂੰ ਇਕ ਫਰੀ ਹਿੱਟ ਦਿੱਤੀ ਜਾਵੇਗੀ । ਉਹ ਰਨ ਆਊਟ ਹੋਣ ਦੇ ਇਲਾਵਾ ਕਿਸੇ ਵੀ ਸਥਿਤੀ ਵਿੱਚ ਆਊਟ ਨਹੀਂ ਮੰਨਿਆ ਜਾਵੇਗਾ ।

10. ਜੇਕਰ ਮੈਚ ਟਾਈ ਹੋ ਜਾਂਦਾ ਹੈ ਤਾਂ ਪੈਨਲਟੀ ਸ਼ੂਟ ਆਊਟ ਲਾਗੂ ਕੀਤਾ ਜਾਵੇਗਾ | ਹਰੇਕ ਟੀਮ ਪੰਜ ਗੇਂਦਬਾਜ਼ਾਂ ਨੂੰ ਚੁਣੇਗੀ ਜਾਂ ਦੂਸਰੇ ਦੇ ਵਿਕੇਟ ਨੂੰ ਹਿੱਟ ਕਰਨਗੇ । ਪਰ ਕੋਈ ਬੱਲੇਬਾਜ਼ ਇਸਦਾ ਸਾਹਮਣਾ ਨਹੀਂ ਕਰੇਗਾ । ਜ਼ਿਆਦਾਤਰ ਪ੍ਰਹਾਰ ਕਰਨ ਵਾਲੀ ਟੀਮ ਵਿਜੇਤਾ ਘੋਸ਼ਿਤ ਕੀਤੀ ਜਾਵੇਗੀ । ਇਸਨੂੰ ਬਾਲ ਆਊਟ ਰੂਲ ਵੀ ਕਹਿੰਦੇ ਹਨ ।

ਖੇਡ ਦੀ ਸ਼ਬਦਾਵਲੀ
(Important Terminology of the Game)

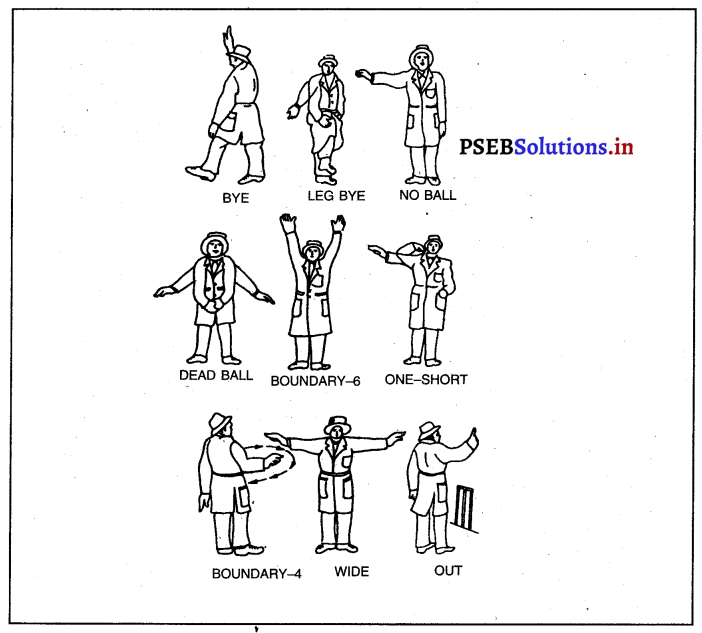
1. ਓਵਰ (Overy-ਇਕ ਓਵਰ ਵਿਚ 6 ਵਾਰ ਗੇਂਦ ਸੁੱਟੀ ਜਾਂਦੀ ਹੈ । ਇਹ ਓਵਰ ਵਿਕਟ ਦੇ ਸਿਰੇ ਤੇ ਵਾਰੀ-ਵਾਰੀ ਦਿੱਤੇ ਜਾਂਦੇ ਹਨ | ਜੇਕਰ ਪਹਿਲਾਂ ਨਿਸਚਿਤ ਕਰ ਲਿਆ ਜਾਵੇ, ਤਾਂ ਇਕ ਵਾਰ ਓਵਰ ਵਿਚ ਅੱਠ ਗੇਂਦਾਂ ਖੇਡੀਆਂ ਜਾ ਸਕਦੀਆਂ ਹਨ । “ਨੋ ਬਾਲ’ ਅਤੇ ‘ਵਾਈਡ ਬਾਲ’ ਓਵਰ ਵਿਚ ਨਹੀਂ ਗਿਣੇ ਜਾਣਗੇ । ਜਿੰਨੇ ਨੋ ਬਾਲ ਉਸ ਓਵਰ ਵਿਚ ਹੋਣਗੇ, ਉੱਨੀਆਂ ਹੀ ਹੋਰ ਗੇਂਦਾਂ ਸੁੱਟੀਆਂ ਜਾਣਗੀਆਂ । ਇਕ ਇਨਿੰਗਜ਼ ਵਿਚ ਕੋਈ ਵੀ ਬਾਊਲਰ ਲਗਾਤਾਰ ਦੋ ਓਵਰ ਬਾਉਲ ਨਹੀਂ ਕਰ ਸਕਦਾ । ਜੇਕਰ ਅੰਪਾਇਰ ਤੋਂ ਓਵਰ ਦੀਆਂ ਬਾਲਾਂ ਦੀ ਗਿਣਤੀ ਵਿਚ ਭੁੱਲ ਹੋ ਜਾਂਦੀ ਹੈ, ਤਾਂ ਅੰਪਾਇਰ ਦੁਆਰਾ ਗਿਣਿਆ ਗਿਆ ਓਵਰ ਨਹੀਂ ਮੰਨਿਆ ਜਾਵੇਗਾ ।

2. ਵਿਕਟਾਂ ਦਾ ਡਿੱਗਣਾ all of wicketsਗੇਂਦ ਬੈਟਸਮੈਨ ਖੁਦ ਜਾਂ ਉਸ ਦਾ ਬੈਟ ਜਾਂ ਗੇਂਦ ਸਟੈਪਜ਼ ਦੇ ਉੱਪਰ ਦੀਆਂ ਦੋਨੋਂ ਗਿੱਲੀਆਂ ਡੇਗ ਦੇਣ ਜਾਂ ਜ਼ੋਰ ਨਾਲ ਸਟੰਪ ਧਰਤੀ ਤੋਂ ਉੱਖੜ ਜਾਵੇ ਤਾਂ ਵਿਕਟ ਡਿੱਗਣਾ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।

3. ਨੋ ਬਾਲ (No Ball-ਗੇਂਦ ਕਰਨ ਦੇ ਸਮੇਂ ਜੇਕਰ ਗੇਂਦਬਾਜ਼ ਦਾ ਅਗਲਾ ਪੁਰਾ ਪੈਰ ਬੈਟਿੰਗ ਕੀਜ਼ ਤੋਂ ਅੱਗੇ ਟੱਪ ਜਾਂਦਾ ਹੈ ਜਾਂ (Returning Crease) ਨੂੰ ਕੱਟਦਾ ਹੈ ਤਾਂ ਅੰਪਾਇਰ ਨੋ ਬਾਲ ਘੋਸ਼ਿਤ ਕਰ ਦਿੰਦਾ ਹੈ । ਬੈਟਸਮੈਨ ਨੋ ਬਾਲ ’ਤੇ ਹਿੱਟ ਲਗਾ ਕੇ ਜਿੰਨੀਆਂ ਵੀ ਦੌੜਾਂ ਸੰਭਵ ਹੋਣ, ਬਣਾ ਸਕਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਬਣੀਆਂ ਦੌੜਾਂ ਨੂੰ ਕੁੱਲ ਸਕੋਰ ਵਿਚ ਜੋੜ ਲਿਆ ਜਾਵੇਗਾ । ਜੇਕਰ ਕੋਈ ਦੌੜ ਨਾ ਬਣੀ ਹੋਵੇ ਤਾਂ ਕੇਵਲ ਇਕ ਦੌੜ ਹੀ ਸਕੋਰ ਵਿਚ ਜੋੜੀ ਜਾਵੇਗੀ । ਅੰਪਾਇਰ ਆਪਣੀ ਇਕ ਭੁਜਾ ਫੈਲਾ ਕੇ ਨੋ ਬਾਲ ਦਾ ਇਸ਼ਾਰਾ ਦਿੰਦਾ ਹੈ ।

4. ਵਾਈਡ ਬਾਲ (wide Ball-ਜੇਕਰ ਬਾਉਲਰ ਬਾਲ ਨੂੰ ਵਿਕਟ ਤੋਂ ਇੰਨੀ ਉਚਾਈ ‘ਤੇ ਜਾਂ ਚੌੜਾਈ ‘ਤੇ ਸੁੱਟਦਾ ਹੈ ਕਿ ਅੰਪਾਇਰ ਦੇ ਵਿਚਾਰ ਵਿਚ ਇਹ ਬੈਟਸਮੈਨ ਦੀ ਪਹੁੰਚ ਤੋਂ ਬਾਹਰ ਹੈ, ਤਾਂ ਉਹ ਵਾਈਡ ਬਾਲ ਦੀ ਘੋਸ਼ਣਾ ਕਰ ਦਿੰਦਾ ਹੈ । ਜੋ ਦੌੜਾਂ ਵਾਈਡ ਬਾਲ ਦੇ ਸਮੇਂ ਬਣਨ ਉਨ੍ਹਾਂ ਨੂੰ ਵਾਈਡ ਬਾਲ ਵਿਚ ਗਿਣਿਆ ਜਾਂਦਾ ਹੈ । ਜੇਕਰ ਕੋਈ ਵੀ ਦੌੜ ਨਾ ਬਣੇ, ਤਾਂ ਇਕ ਦੌੜ ਸਮਝੀ ਜਾਂਦੀ ਹੈ । ਵਾਈਡ ਬਾਲ ਦਾ ਇਸ਼ਾਰਾ ਅੰਪਾਇਰ ਆਪਣੀਆਂ ਦੋਵੇਂ ਭੁਜਾਵਾਂ ਸਿੱਧੀਆਂ ਫੈਲਾ ਕੇ ਕਰਦਾ ਹੈ ।

5. ਬਾਈ ਅਤੇ ਲੈਗ ਬਾਈ (Bye and Leg-byਜੇਕਰ ਕੋਈ ਚੰਗੀ ਤਰ੍ਹਾਂ ਨਾਲ ਸੱਟੀ ਗੇਂਦ ਜਾਂ ਬੈਟਸਮੈਨ ਸਟਰਾਈਕਰ ਦੇ ਬੈਟ ਜਾਂ ਸਰੀਰ ਨੂੰ ਬਿਨਾਂ ਛੂਹੇ ਕੋਲੋਂ ਲੰਘ ਜਾਵੇ ਅਤੇ ਦੌੜ ਬਣ ਜਾਵੇ ਤਾਂ ਅੰਪਾਇਰ ਬਾਈ ਘੋਸ਼ਿਤ ਕਰੇਗਾ । ਪਰ ਨੋ ਬਾਲ ਜਾਂ ਵਾਈਡ ਬਾਲ ਨਹੀਂ ਹੋਣਾ ਚਾਹੀਦਾ | ਪਰ ਜੇਕਰ ਗੇਂਦ ਬੈਟਸਮੈਨ ਦੇ ਬੈਟ ਵਾਲੇ ਹੱਥ ਨੂੰ ਛੱਡ ਕੇ ਸਰੀਰ ਦੇ ਕਿਸੇ ਭਾਗ ਨੂੰ ਛੂਹ ਕੇ ਕੋਲੋਂ ਲੰਘ ਜਾਵੇ ਅਤੇ ਦੌੜ ਬਣ ਜਾਵੇ ਤਾਂ ਅੰਪਾਇਰ ਲੈਗ ਬਾਈ ਘੋਸ਼ਿਤ ਕਰੇਗਾ ।

6. ਆਪਣੇ ਖੇਤਰ ਤੋਂ ਬਾਹਰ (Out of his Area-ਬੈਟਸਮੈਨ ਆਪਣੇ ਖੇਤਰ ਤੋਂ ਬਾਹਰ ਮੰਨਿਆ ਜਾਵੇਗਾ, ਜਦੋਂ ਤਕ ਉਸ ਦੇ ਹੱਥ ਦੇ ਬੈਟ ਦਾ ਕੁੱਝ ਭਾਗ ਜਾਂ ਉਸ ਦਾ ਸਰੀਰ ਕਲਪਿਤ ਮੰਜ ਰੇਖਾ ਦੇ ਪਿੱਛੇ ਜ਼ਮੀਨ ਤੇ ਨਾ ਹੋਵੇ |

7. ਬੈਟਸਮੈਨ ਦਾ ਰਿਟਾਇਰ ਹੋਣਾ (Getting Retired of a batsmen)-ਬੈਟਸਮੈਨ ਕਿਸੇ ਵੀ ਸਮੇਂ ਜ਼ਖ਼ਮੀ ਜਾਂ ਬੀਮਾਰੀ ਦੀ ਹਾਲਤ ਵਿਚ ਰਿਟਾਇਰ ਹੋ ਸਕਦਾ ਹੈ । ਉਹ ਬੱਲੇਬਾਜ਼ੀ ਤਾਂ ਕਰ ਸਕਦਾ ਹੈ ਪਰ ਉਸ ਨੂੰ ਵਿਰੋਧੀ ਕਪਤਾਨ ਤੋਂ ਆਗਿਆ ਲੈਣੀ ਹੋਵੇਗੀ ਕਿ ਕਿੰਨਵੇਂ ਨੰਬਰ ਤੇ ਬੱਲੇਬਾਜ਼ੀ ਕਰੇ ।

8. ਬਾਊਲਡ (Bowled–ਜੇਕਰ ਵਿਕਟ ਗੇਂਦ ਕਰ ਕੇ ਡੇਗ ਦਿੱਤੀ ਜਾਵੇ, ਤਾਂ ਗੇਂਦ ਖੇਡਣ ਵਾਲਾ ਬਾਊਲਡ (Bowled Out) ਅਖਵਾਉਂਦਾ ਹੈ, ਭਾਵੇਂ ਗੇਂਦ ਪਹਿਲੇ ਉਸ ਦੇ ਪੈਰ ਜਾਂ ਸਰੀਰ ਨੂੰ ਛੂਹ ਚੁੱਕੀ ਹੋਵੇ ।

9. ਕੈਚ (Catchਜੇਕਰ ਗੇਂਦ ਬੈਟ ਦੇ ਵਾਰ ਨਾਲ, ਜਾਂ ਬੈਟ ਨਾਲੋਂ ਹੱਥ ਨਾਲ ਕਲਾਈ ਨਾਲ ਨਹੀਂ ਲਗ ਕੇ ਧਰਤੀ ਛੂਹਣ ਤੋਂ ਪਹਿਲਾਂ ਕਿਸੇ ਫੀਲਡਰ ਦੁਆਰਾ ਬੋਚ ਲਈ (ਲਪਕ) ਲਈ ਜਾਵੇ ਤਾਂ ਬੈਟਸਮੈਨ ਕੈਚ ਆਊਟ ਹੋਵੇਗਾ । ਕੈਚ ਦੇ ਸਮੇਂ ਰੱਖਿਅਕ ਦੇ ਦੋਵੇਂ ਪੈਰ ਪੂਰੀ ਤਰ੍ਹਾਂ ਮੈਦਾਨ ਵਿਚ ਹੋਣ । ਜੇਕਰ ਖੇਤਰ ਰੱਖਿਅਕ ਸੀਮਾ ਰੇਖਾ ਤੋਂ ਬਾਹਰ ਕੈਚ ਫੜਦਾ ਹੈ ਤਾਂ ਬੈਟਸਮੈਨ ਆਉਟ ਨਹੀਂ ਮੰਨਿਆ ਜਾਂਦਾ, ਸਗੋਂ ਉਸ ਨੂੰ 6 ਰਨ ਮਿਲਦੇ ਹਨ । ਜੇਕਰ ਗੇਂਦ ਵਿਕਟ ਕੀਪਰ ਦੇ ਪੈਰਾਂ ਵਿਚ ਜਾ ਵਸੇ ਤਾਂ ਵੀ ਬੈਟਸਮੈਨ ਆਉਟ ਮੰਨਿਆ ਜਾਵੇਗਾ |

10. ਗੇਂਦ ਨੂੰ ਹੱਥ ਲਾਉਣਾ (Handle the Ballਜੇਕਰ ਹੱਥਾਂ ਨਾਲ ਖੇਡਦੇ ਸਮੇਂ ਕੋਈ ਬੈਟਸਮੈਨ ਗੇਂਦ ਨੂੰ ਛੂਹ ਲੈਂਦਾ ਹੈ ਤਾਂ ਉਸ ਨੂੰ ਗੇਂਦ ਦੇ ਨਾਲ ਹੱਥ ਲਗਾਇਆ ਆਉਟ ਮੰਨਿਆ ਜਾਵੇਗਾ ।

11. ਗੇਂਦ ‘ਤੇ “ਦੋ ਵਾਰ (Hit the Ball twice-ਬੈਟਸਮੈਨ ਗੇਂਦ ਤੇ ਦੋ ਵਾਰ ਕਰਨ ਨਾਲ ਆਊਟ ਹੋਵੇਗਾ । ਜੇਕਰ ਗੇਂਦ ਉਸਦੇ ਸਰੀਰ ਦੇ ਕਿਸੇ ਭਾਗ ਨੂੰ ਲਗ ਕੇ ਰੁਕ ਜਾਂਦੀ ਹੈ ਜਾਂ ਉਹ ਉਸ ਤੇ ਦੁਬਾਰਾ ਜਾਣ ਬੁੱਝ ਕੇ ਵਾਰ ਕਰਦਾ ਹੈ । ਕੇਵਲ ਆਪਣੀ ਵਿਕਟ ਦੇ ਬਚਾਅ ਲਈ ਵੀ ਵਾਰ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ । ਪਰੰਤੂ ਇਹ ਸ਼ਰਤ ਹੈ ਕਿ ਅਜਿਹਾ ਵਿਕਟ ਦੇ ਬਚਾਅ ਲਈ ਕੀਤਾ ਗਿਆ ਹੋਵੇ ਇਸ ਪ੍ਰਕਾਰ ਜੇ ਕੋਈ ਰਨ ਬਣ ਵੀ ਜਾਵੇ ਤਾਂ ਉਹ ਗਿਣਿਆ ਨਹੀਂ ਜਾਂਦਾ ।

12. ਵਿਕਟ ‘ਤੇ ਵਾਰ (wicket is down or Hit wicketਜੇਕਰ ਗੇਂਦ ਖੇਡਦੇ ਸਮੇਂ ਬੈਟਸਮੈਨ ਆਪਣੇ ਬੈਟ ਜਾਂ ਸਰੀਰ ਦੇ ਕਿਸੇ ਭਾਗ ਨਾਲ ਵਿਕਟਾਂ ਡੇਗਦਾ ਹੈ, ਤਾਂ ਉਸ ਨੂੰ ‘ਵਿਕਟ ਤੇ ਵਾਰ’ ਆਊਟ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ । ਜੇਕਰ ਉਸ ਦੀ ਵਿਕਟ ਟੋਪੀ ਜਾਂ ਹੈਟ ਡਿੱਗਣ ਜਾਂ ਬੈਟ ਦੇ ਟੁੱਟੇ ਹੋਏ ਕਿਸੇ ਭਾਗ ਦੇ ਵੱਜਣ ਨਾਲ ਡਿਗ ਜਾਂਦੀ ਹੈ, ਤਾਂ ਉਸਨੂੰ ਵੀ ‘ਵਿਕਟ ਤੇ ਵਾਰ` ਮੰਨਿਆ ਜਾਵੇਗਾ ।

13. ਐੱਲ. ਬੀ.ਡਬਲਿਉ. ‘ (ਲੈਂਗ ਬਿਫੋਰ ਵਿਕੇਟ (Leg Before wicked-ਬੈਟਸਮੈਨ ਉਸ ਸਮੇਂ ਐੱਲ. ਬੀ. ਡਬਲਿਊ. ਆਉਟ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ, ਜਦੋਂ ਉਹ ਗੇਂਦ ਨੂੰ ਬੱਲੇ ਨਾਲ ਛੁਹਣ ਤੋਂ ਪਹਿਲਾਂ ਸਰੀਰ ਦੇ ਕਿਸੇ ਭਾਗ ਨਾਲ ਰੋਕਣ ਦਾ ਯਤਨ ਕਰਦਾ ਹੈ ਅਤੇ ਅੰਪਾਇਰ ਅਨੁਸਾਰ ਗੇਂਦ ‘ਤੇ ਵਿਕਟ ਸਿੱਧੀ ਰੇਖਾ ਵਿਚ ਹੈ । ਜੇਕਰ ਬੈਟਸਮੈਨ ਇਸ ਨੂੰ ਆਪਣੇ ਸਰੀਰ ਦੇ ਕਿਸੇ ਭਾਗ ਨਾਲ ਨਾ ਰੋਕਦਾ ਤਾਂ ਗੇਂਦ ਵਿਕਟ ‘ਤੇ ਹੀ ਲਗਦੀ ।

14. ਖੇਤਰ ਵਿਚ ਰੋਕ (Intervene in Area)-ਕੋਈ ਵੀ ਬੈਟਸਮੈਨ ਖੇਤਰ ਵਿਚ ਰੋਕ ਆਉਟ ਹੋ ਸਕਦਾ ਹੈ, ਜੇਕਰ ਉਹ ਜਾਣ-ਬੁੱਝ ਕੇ ਕਿਸੇ ਫੀਲਡਰ ਨੂੰ ਗੇਂਦ ਫੜਨ ਤੋਂ ਰੋਕਦਾ ਹੈ ।

15. ਸਟੰਪਡ (Stumped-ਬੈਟਸਮੈਨ ਦੇ ਹੱਥ ਦਾ ਬੈਟ ਜਾਂ ਉਸ ਦਾ ਪੈਰ ਮੰਨੀ ਗਈ ਮੰਜ ਰੇਖਾ ਦੇ ਪਿੱਛੇ ਧਰਤੀ ‘ਤੇ ਨਾ ਹੋਵੇ, ਤਾਂ ਉਹ ਖੇਤਰ ਤੋਂ ਬਾਹਰ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ । ਬੈਟਸਮੈਨ ਉਸ ਸਮੇਂ ਸਟੰਪ ਆਉਟ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ, ਜਦੋਂ ਗੇਂਦ ਨੋ ਬਾਲ ਨਾ ਹੋਵੇ ਅਤੇ ਬਾਉਲਰ ਦੁਆਰਾ ਸੁੱਟੀ ਗਈ ਹੋਵੇ ਅਤੇ ਉਹ ਦੌੜ ਬਣਾਉਣ ਦੀ ਕੋਸ਼ਿਸ਼ ਦੀ ਸਥਿਤੀ ਤੋਂ ਇਲਾਵਾ ਉਹ ਖੇਤਰ ਤੋਂ ਬਾਹਰ ਚਲਿਆ ਜਾਵੇ ਅਤੇ ਵਿਕਟ ਕੀਪਰ ਵਿਕਟ ਉਖਾੜ ਸੁੱਟੇ ।ਉਖਾੜ ਸੁੱਟੇ ਜਾਂ ਵਿਕਟਾਂ ਦੇ ਉੱਪਰ ਰੱਖੀਆਂ ਗੁੱਲੀਆਂ ਉਤਾਰ ਦੇਵੇ ।

16. ਰਨ ਆਊਟ (Run Out-ਜਿਸ ਸਮੇਂ ਗੇਂਦ ਮੈਦਾਨ ਵਿਚ ਹੋਵੇ ਤਾਂ ਬੈਟਸਮੈਨ ਭੱਜਦੇ ਹੋਏ ਖੇਤਰ ਤੋਂ ਬਾਹਰ ਚਲਿਆ ਜਾਏ ਅਤੇ ਵਿਰੋਧੀ ਟੀਮ ਦਾ ਖਿਡਾਰੀ ਉਸ ਦੀ ਵਿਕਟ ਡੇਗ ਦੇਵੇ, ਤਾਂ ਬੈਟਸਮੈਨ ਰਨ ਆਉਟ ਹੋ ਜਾਂਦਾ ਹੈ । ਜੇਕਰ ਬੈਟਸਮੈਨ ਇਕ ਦੂਜੇ ਨੂੰ ਪਾਰ ਕਰ ਜਾਣ, ਤਾਂ ਉਸ ਬੈਟਸਮੈਨ ਨੂੰ ਆਉਟ ਮੰਨਿਆ ਜਾਵੇਗਾ, ਜੋ ਡਿੱਗੀ ਹੋਈ ਵਿਕਟ ਵਲ ਦੌੜ ਰਿਹਾ ਹੋਵੇ ।

17. ਵਿਕਟ ਰੱਖਿਅਕ (wicket Keeper)-ਵਿਕਟ ਕੀਪਰ ਸਦਾ ਵਿਕਟਾਂ ਦੇ ਪਿੱਛੇ ਰਹੇਗਾ ਜਦੋਂ ਤਕ ਕਿ ਬਾਉਲਰ ਦੁਆਰਾ ਟੁੱਟੀ ਹੋਈ ਗੇਂਦ ਨੂੰ ਬੈਟਸਮੈਨ ਦੇ ਬੈਟ ਜਾਂ ਸਰੀਰ ਦੇ ਕਿਸੇ ਹਿੱਸੇ ਨਾਲ ਛੋਹ ਨਹੀਂ ਜਾਂਦੀ ਜਾਂ ਵਿਕਟ ਦੇ ਪਾਰ ਨਹੀਂ ਜਾਂਦੀ ਜਾਂ ਬੈਟਸਮੈਨ ਆਊਟ ਨਹੀਂ ਹੋ ਜਾਂਦਾ, ਵਿਕਟ ਰੱਖਿਅਕ ਗੇਂਦ ਨੂੰ ਨਹੀਂ ਪਕੜ ਸਕਦਾ ।

18. ਖੇਤਰ ਰੱਖਿਅਕ (Fielders)-ਖੇਤਰ ਰੱਖਿਅਕ ਆਪਣੇ ਸਰੀਰ ਦੇ ਕਿਸੇ ਵੀ ਹਿੱਸੇ ਨਾਲ ਗੇਂਦ ਨੂੰ ਰੋਕ ਸਕਦਾ ਹੈ । ਉਸ ਨੂੰ ਆਪਣੀ ਟੋਪੀ ਨਾਲ ਗੱਦ ਰੋਕਣ ਦੀ ਆਗਿਆ ਨਹੀਂ । ਜੇਕਰ ਉਹ ਇਸ ਤਰ੍ਹਾਂ ਕਰਦਾ ਹੈ, ਤਾਂ ਇਸ ਦੀ ਸਜ਼ਾ ਚਾਰ ਦੌੜਾਂ ਹੋਣਗੀਆਂ । ਜੇਕਰ ਉਸ ਦੀ ਕੋਈ ਦੌੜ ਨਾ ਬਣੀ ਹੋਵੇ, ਤਾਂ ਚਾਰ ਦੌੜਾਂ ਜੋੜ ਦਿੱਤੀਆਂ ਜਾਣਗੀਆਂ।

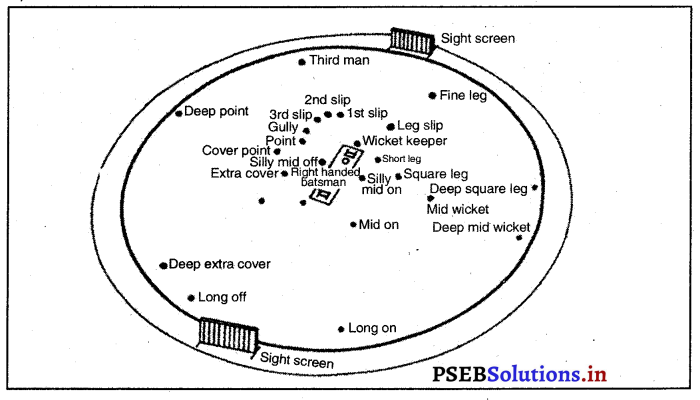
ਕ੍ਰਿਕੇਟ ਖੇਡ ਵਿਚ ਫੀਲਡ ਸੈਟਿੰਗ

19. ਮੈਡੇਟਰੀ ਓਵਰ (Mandatory Over-ਮੈਚ ਦੇ ਆਖ਼ਰੀ ਦਿਨ ਮੈਚ ਸਮਾਪਤ ਹੋਣ ਤੋਂ ਇਕ ਘੰਟਾ ਪਹਿਲਾਂ ਅੰਪਾਇਰ ਮੈਂਡੇਟਰੀ ਓਵਰ ਦਾ ਸੰਕੇਤ ਦਿੰਦਾ ਹੈ । ਉਸ ਤੋਂ ਬਾਅਦ 20 ਓਵਰਾਂ ਦੀ ਇਕ ਹੋਰ ਖੇਡ ਖੇਡੀ ਜਾਂਦੀ ਹੈ । ਹਰ ਇਕ ਓਵਰ ਵਿਚ 6 ਬਾਲ ਖੇਡੇ ਜਾਂਦੇ ਹਨ । ਜੇਕਰ ਮੈਚ ਬਰਾਬਰ ਹੁੰਦਾ ਪ੍ਰਤੀਤ ਹੋਵੇ, ਤਾਂ ਇਨ੍ਹਾਂ ਓਵਰਾਂ ਤੋਂ ਪਹਿਲਾਂ ਵੀ ਖੇਡ ਸ਼ਮਾਪਤ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ ।

20. ਡੈੱਡ ਬਾਲ (Dead Ballਬਾਲ ਉਨ੍ਹਾਂ ਹਾਲਤਾਂ ਵਿਚ ਹੀ ਰੈੱਡ ਮੰਨੀ ਜਾਂਦੀ ਹੈ, ਜਦ ਕਿ ਉਹ ਠੀਕ ਤਰ੍ਹਾਂ ਬਾਉਲਰ ਜਾਂ ਵਿਕਟ ਕੀਪਰ ਦੇ ਕਾਬੂ ਹੋ ਜਾਏ ਜਾਂ ਸੀਮਾ ਤੇ ਪਹੁੰਚ ਜਾਵੇ, ਅੰਪਾਇਰ ਜਾਂ ਬੈਟਸਮੈਨ ਦੇ ਕੱਪੜਿਆਂ ਵਿਚ , ਉਲਝ ਜਾਵੇ ਜਾਂ ਅੰਪਾਇਰ ਦੁਆਰਾ ਸਮੇਂ ਜਾਂ ਓਵਰ ਦੀ ਘੋਸ਼ਣਾ ਕਰ ਦਿੱਤੀ ਜਾਵੇ ; ਇਨ੍ਹਾਂ ਤੋਂ ਇਲਾਵਾ ਜਦ ਖਿਡਾਰੀ ਆਊਟ ਹੋ ਜਾਂਦਾ ਹੈ ਜਾਂ ਉਸ ਨੂੰ ਗੰਭੀਰ ਸੱਟ ਲੱਗ ਜਾਂਦੀ ਹੈ ।

21. ਮੈਦਾਨ ਦੀ ਅੜਚਨ (Obstructing the Field)-ਜੇਕਰ ਕੋਈ ਬੱਲੇ-ਬਾਜ਼ ਜਾਣ ਬੁੱਝ ਕੇ ਦੂਸਰੀ ਟੀਮ ਦੀ . ਖੇਡ ਵਿਚ ਅੜਚਨ ਪਾਉਂਦਾ ਹੈ, ਜਿਸ ਕਾਰਨ ਵਿਰੋਧੀ ਟੀਮ ਨੂੰ ਬਾਲ ਫੜਨ ਵਿਚ ਰੁਕਾਵਟ ਆਉਂਦੀ ਹੈ ਤਾਂ ਰੋਕਣ ਵਾਲੇ , ਬੈਟਸਮੈਨ ਨੂੰ ਆਊਟ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ | ਅਜਿਹਾ ਕਰਨੇ ਨੂੰ ਮੈਦਾਨ ਦੀ ਅੜਚਨ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।

22. ਇਕ ਦਿਨ ਦਾ ਮੈਚ (One Day Match-ਰਾਸ਼ਟਰੀ ਅਤੇ ਅੰਤਰ ਰਾਸ਼ਟਰੀ ਇਕ ਦਿਨ ਦਾ ਮੈਚ ਹੁੰਦਾ ਹੈ । ਜਿਸ ਵਿਚ ਦੋਵੇਂ ਟੀਮਾਂ 40-40 ਜਾਂ 50-50 ਓਵਰ ਦੇ ਮੈਚ ਖੇਡਦੀਆਂ ਹਨ, ਜੋ ਟੀਮ ਵੱਧ ਰਨ ਬਣਾ ਜਾਵੇ, ਉਹ ਜਿੱਤ ਜਾਂਦੀ ਹੈ ।

ਕ੍ਰਿਕਟ ਖੇਡ ਦੀਆਂ ਕੁੱਝ ਮਹੱਤਵਪੂਰਨ ਤਕਨੀਕਾਂ (Important techniques of Cricket Game):
ਕ੍ਰਿਕਟ ਵਿਚ ਬੈਟਿੰਗ ਮੁਹਾਰਿਤ ਅਤੇ ਤਕਨੀਕਾਂ ਕਿਸੇ ਵੀ ਹਿਟ ਨੂੰ ਸਫਲਤਾ ਪੂਰਵਕ ਖੇਡਣ ਲਈ ਬੈਟਸਮੈਨਾਂ ਨੂੰ ਤਿੰਨ ਗੱਲਾਂ ਦਾ ਧਿਆਨ ਰੱਖਣਾ ਚਾਹੀਦਾ ਹੈ ; ਉਸ ਨੂੰ ਜ਼ਰੂਰ ਹੀ ਪਹਿਲਾਂ ਬਾਲ ਨੂੰ ਲੱਭਣਾ ਚਾਹੀਦਾ ਹੈ ਅਤੇ ਫਿਰ ਬਾਲ ਵੱਲ ਧਿਆਨ ਰੱਖਣਾ । ਉਸ ਨੇ ਇਹ ਫੈਸਲਾ ਕਰਨਾ ਹੁੰਦਾ ਹੈ ਕਿ ਕਿਹੜੀ ਹਿੱਟ ਠੀਕ ਹੈ ।ਉਸ ਹਿੱਟ ਨੂੰ ਠੀਕ ਤਰ੍ਹਾਂ ਖੇਡਣ ਲਈ ਆਪਣੇ ਬਦਨ ਨੂੰ ਮੋੜਨਾ ਚਾਹੀਦਾ ਹੈ ।

ਕਹਿਣ ਨੂੰ ਤਾਂ ਕਾਫੀ ਆਸਾਨ ਹੈ, ਪਰ ਅਸਲ ਵਿਚ ਏਨਾ ਆਸਾਨ ਨਹੀਂ ਹੈ । ਇਹ ਗੱਲ ਸੋਚਣ ਲਈ ਤਾਂ ਆਸਾਨ ਹੈ ਕਿ ਤੁਸੀਂ ਬਾਲ ਵੱਲ ਵੇਖ ਰਹੇ ਹੋ । ਸੱਚਮੁੱਚ ਕਿਸੇ ਆ ਰਹੇ ਬਾਲ ਨੂੰ ਤੱਕਣਾ ਆਸਾਨ ਹੈ, ਬਸ਼ਰਤੇ ਕਿ ਤੁਸੀਂ ਆਪਣਾ ਮਨ ਬਣਾਇਆ ਹੋਇਆ ਹੋਵੇ | ਪਰ ਪੂਰੀ ਪਾਰੀ ਵਿਚ ਹਰੇਕ ਬਾਲ ਦੀ ਜਾਂਚ ਕਰਨ ਦੀ ਆਦਤ ਬਣਾਉਣੀ, ਸਹੀ ਅਰਥਾਂ ਵਿਚ ਜਾਂਚ ਕਰਨ ਦੀ, ਇਕ ਬੜਾ ਔਖਾ ਕੰਮ ਹੈ, ਤੁਸੀਂ ਅਜਿਹਾ ਸਿਰਫ ਆਪਣੇ ਹੱਥਾਂ ਵਿਚਲੇ ਕੰਮ ਉੱਤੇ ਧਿਆਨ ਕੇਂਦਰਿਤ ਕਰਨਾ ਸਿੱਖ ਕੇ ਹੀ ਕਰ ਸਕਦੇ ਹੋ । ਇਹ ਸੱਚਮੁੱਚ ਬੜਾ ਔਖਾ ਹੈ, ਪਰ ਜੇ ਤੁਸੀਂ ਇਸ ਤਰ੍ਹਾਂ ਕਰਨਾ ਸਿੱਖ | ਲੈਂਦੇ ਹੋ, ਤਾਂ ਉਹ ਤੁਹਾਨੂੰ ਕ੍ਰਿਕਟ ਵਿਚ ਹੀ ਸਹਾਈ ਸਿੱਧ ਨਹੀਂ ਹੋਵੇਗਾ, ਸਗੋਂ ਜ਼ਿੰਦਗੀ ਵਿਚ ਵੀ । ਠੀਕ ਇਸ ਤਰ੍ਹਾਂ ਇਹ ਫੈਸਲਾ ਕਰਨਾ ਕਿ ਕਿਸੇ ਵਿਸ਼ੇਸ਼ ਬਾਲ ਨੂੰ ਕਿਸ ਤਰ੍ਹਾਂ ਹਿੱਟ ਕਰਨਾ ਹੈ, ਇਹ ਇਕ ਤਰ੍ਹਾਂ ਨਾਲ ਅੰਤਰ-ਪ੍ਰੇਰਨਾ ਦਾ ਮਾਮਲਾ ਹੈ, ਜਾਂ ਜਿਸ ਨੂੰ ਅਕਸਰ ਕ੍ਰਿਕਟ ਵਿਚ ‘ਬਾਲ ਸੂਝ’ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਪਰ ਇਹ ਮੁੱਖ ਤੌਰ ਤੇ ਤਜਰਬੇ ਦਾ ਕੰਮ ਹੈ ।

ਖਿਡਾਰੀ ਦੀ ਸਥਿਤੀ ‘
ਇਕ ਖਿਡਾਰੀ ਦੀ ਆਰਾਮਦਾਇਕ, ਤਣਾਅ-ਰਹਿਤ ਅਤੇ ਸੰਤਲਿਤ ਸਥਿਤੀ ਬੜੀ ਜ਼ਰੂਰੀ ਹੈ, ਬਾਲ ਦੀ ਸਹੀ ਪਰਖ ਕਰਨੀ ਅਤੇ ਹਰੇਕ ਸਟਰੋਕ ਲਈ ਪੈਰਾਂ ਦੀ ਹਿਲਜੁਲ ਇਸ ਉੱਤੇ ਹੀ ਨਿਰਭਰ ਕਰਦੀ ਹੈ ।
ਪੈਰ ਸਾਧਾਰਨ ਤੌਰ ‘ਤੇ ਕਰੀਜ਼ ਦੇ ਪਾਸਿਆਂ ਵੱਲ ਸਮਾਨਾਂਤਰ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ। ਅਤੇ ਉਨ੍ਹਾਂ ਦੇ ਪੰਜੇ ਨਿਸ਼ਾਨੇ ਵੱਲ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ ।

ਬੈਕ ਲਿਫਟ
ਇਕ ਸਹੀ ‘ਬੈਕ ਲਿਫਟ ਦੀ ਬਹੁਤ ਮਹੱਤਤਾ ਹੈ । ਖੱਬੀ ਬਾਂਹ ਅਤੇ ਗੁੱਟ ਨੂੰ ਹੀ ਸਾਰਾ ਕੰਮ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ਅਤੇ ਬੈਟ ਦਾ ਸਾਹਮਣਾ ਪਾਸਾ ਨਿਸ਼ਾਨੇ ਵੱਲ, ਜਿਵੇਂ ਕਿ ਬੈਟ ਉਭਰਦਾ ਹੈ । ਸਿਰ ਅਤੇ ਬਦਨ ਬਿਲਕੁਲ ਸਥਿਰ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ | ਉਭਾਰ ਕੇ ਅਖੀਰ ਤੇ ਸੱਜੀ ਕੂਹਣੀ ਬਦਨ ਤੋਂ ਥੋੜ੍ਹੀ ਜਿਹੀ ਹਟੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ਅਤੇ ਖੱਬਾ ਹੱਥ ਪੈਂਟ ਦੀ ਸੱਜੀ ਜੇਬ ਦੇ ਬਿਲਕੁਲ ਸਾਹਮਣੇ ਉੱਪਰ ਵੱਲ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ।

ਸਿੱਧੇ ਬਾਲ ਲਈ ਸਾਹਮਣੀ ਸੁਰੱਖਿਆ ਹਿੱਟ
ਸਾਹਮਣੀ ਹਿੱਟ ਸੁਰੱਖਿਆ ਵਿਚ ਨਾ ਸਿਰਫ ਬਹੁ-ਕੀਮਤੀ ਹੈ, ਸਗੋਂ ਸਾਰੀਆਂ ਹਿੱਟਾਂ ਦਾ | ਆਧਾਰ ਵੀ ਹੈ, ਇਸ ਨੂੰ ਠੀਕ ਢੰਗ ਨਾਲ ਖੇਡਣਾ ਲਗਪਗ ਅੱਧਾ ਬੈਟਸਮੈਨ ਬਣਨ ਦੇ ਤੁਲ ਹੈ । ਉਦੇਸ਼ ਬਾਲ ਨੂੰ ਜਿੰਨਾ ਪੁਆਇੰਟ ਦੇ ਨੇੜੇ ਸੰਭਵ ਹੋ ਸਕੇ ਖੇਡਣਾ ਹੈ । ਸਿਰ ਅੱਗੇ ਵੱਲ ਵਧਾਉਂਦਿਆਂ, ਖੱਬਾ ਕੂਲਾ : ਤੇ ਮੋਢਾ ਬਾਲ ਦੀ ਰੇਖਾ ਤੋਂ ਬਾਹਰ ਰੱਖ ਕੇ ਬਾਲ ਨੂੰ ਬੈਟ ਤੇ ਖੱਬੇ ਪੈਰ ਦੇ ਕੁੱਝ ਇੰਚ ਸਾਹਮਣੇ ਲੈਣਾ ਹੁੰਦਾ ਹੈ ਅਤੇ ਪੈਰ ਮਿਡ-ਆਫ ਅਤੇ ਐਕਸਟਰਾ ਕਵਰ ਦੇ ਵਿਚਕਾਰ ਦੀ ਸੇਧ ਵਿਚ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ।

ਬਦਨ ਦਾ ਭਾਰ ਮੁੜੇ ਹੋਏ ਖੱਬੇ ਗੋਡੇ ਨਾਲ ਬਿਲਕੁਲ ਸਾਹਮਣੇ ਵੱਲ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ । ਬਾਲ ਦੀ ਸਾਰਾ ਰਸਤਾ ਪਰਖ ਕਰੋ । ਇਸ ਤਰ੍ਹਾਂ ਕਰਨ ਲਈ ਤੁਹਾਨੂੰ ਆਪਣਾ ਸਿਰ ਜਿੱਥੇ ਤਕ ਹੋ ਸਕੇ ਸੰਤੁਲਨ ਵਿਚ ਰੱਖਣਾ ਚਾਹੀਦਾ ਹੈ । ਸਿਰ ਉੱਪਰ ਚੁੱਕਣ ਲਈ ਲਾਲਚ ਨੂੰ ਘੱਟ ਕਰੋ ।

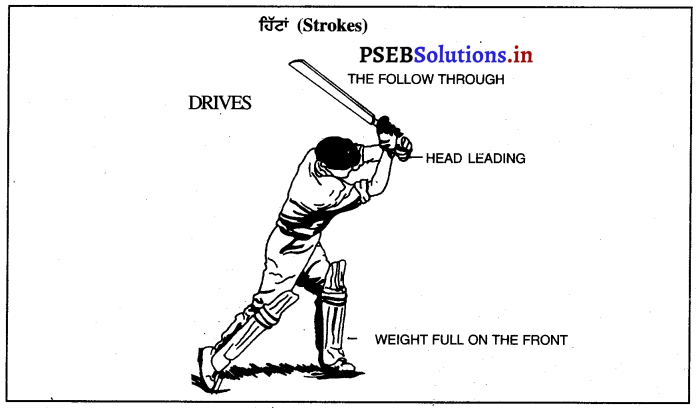
ਹਿੱਟਾਂ ਵਿਚ ਕੰਟਰੋਲ ਲਾਜ਼ਮੀ ਹੈ-ਜੇ ਤੁਸੀਂ ਮਜ਼ਬੂਤ ਹਿੱਟ ਮਾਰਨੀ ਚਾਹੁੰਦੇ ਹੋ, ਤਾਂ ਤੁਹਾਡੀ ਹਿੱਟ ਘੁੰਮਣ ਦੀ ਬਜਾਏ ਵਧੇਰੇ ਲੰਬੀ ਹੋ ਸਕਦੀ ਹੈ । | ਬਾਲ ਨੂੰ ਸਾਫ-ਸਾਫ ਤੇ ਸੌਖੀ ਤਰ੍ਹਾਂ ਹਿਟ ਕਰਨ ਲਈ, ਉਸ ਨੂੰ ਸੀਮਾ (ਬਾਊਂਡਰੀ) ਵਲ ਸੁੱਟਣ ਨਾਲੋਂ ਮੈਦਾਨ ਵਿਚ ਸੁੱਟਣਾ ਚਾਹੀਦਾ ਹੈ । ਜੇ ਬਾਲ ਕਾਫੀ ਦੂਰ ਉੱਪਰ ਹੈ ਤਾਂ ਹਿੱਟ ਇੱਕੋ ਲੰਬੇ ਕਦਮ ਨਾਲ ਮਾਰੀ ਜਾ ਸਕਦੀ ਹੈ, ਪਰ ਤੁਹਾਨੂੰ ਪਿੱਚ ਉੱਤੇ ਘੱਟ ਰਫਤਾਰ, ਤੇਜ਼ ਅਤੇ ਅਧੂਰੇ (Shorter) ਬਾਲ ਨੂੰ ਖੇਡਣ ਲਈ ਪੈਰਾਂ ਦੀ ਵਰਤੋਂ ਕਰਨੀ ਵੀ ਸਿੱਖਣੀ ਜ਼ਰੂਰੀ ਹੈ ।

ਸੁਰੱਖਿਆ ਲਈ ਬੈਕ ਸਟਰੋਕ
ਜਦੋਂ ਤਕ ਇਕ ਬੈਟਸਮੈਨ ਬਾਲ ਦੀ ਪਿੱਚ ਦੀ ਚੰਗੀ ਤਰ੍ਹਾਂ ਪਰਖ ਨਹੀਂ ਕਰ ਲੈਂਦਾ ਤਾਂ ਉਸ ਨੂੰ ਬੈਕ ਸਟਰੋਕ ਨਾਲ ਹੀ ਖੇਡਣਾ ਚਾਹੀਦਾ ਹੈ ਅਤੇ ਇਸ ਤਰ੍ਹਾਂ ਉਸ ਨੂੰ ਬਾਲ ਦੀ ਪਿੱਚ ਤੋਂ ਬਾਅਦ ਜਾਂਚ ਕਰਨ ਦਾ ਸਮਾਂ ਵੀ ਮਿਲੇਗਾ | ਹੌਲੀ ਬਾਲ ਅਤੇ ਵਧੇਰੇ ਮੁਸ਼ਕਿਲ ਵਿਕਟ ਵਿਚ ਉਸ ਨੂੰ ਜ਼ਰੂਰ ਹੀ ਬੈਕ ਸਟਰੋਕ ਉੱਤੇ ਨਿਰਭਰ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ।

ਸੱਜਾ ਪੈਰ ਕਰੀਜ਼ ਵੱਲ ਪੰਜਾ ਸਮਾਨਅੰਤਰ ਰਹਿੰਦਿਆਂ ਬਾਲ ਦੀ ਰੇਖਾ ਦੇ ਅੰਦਰ ਅਤੇ ਪਿੱਛੇ ਵੱਲ ਚੰਗੀ ਤਰ੍ਹਾਂ ਹਿਲਜੁਲ ਕਰ ਸਕਦਾ ਹੈ | ਬਦਨ ਦਾ ਭਾਰ ਇਸ ਪੈਰ ਉੱਤੇ ਬਦਲੀ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ, ਪਰ ਸਿਰ ਅੱਗੇ ਵੱਲ ਥੋੜਾ ਝੁਕਿਆ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ । ਖੱਬਾ ਪੈਰ ਪੰਜੇ ਪਰਨੇ ਹੁੰਦਿਆਂ ਹੋਇਆਂ ਇਕ ਸੰਤੁਲਨਕਾਰ ਵਜੋਂ ਕੰਮ ਕਰਦਾ ਹੈ ।

ਬਾਲ ਨਜ਼ਰਾਂ ਤੋਂ ਥੋੜ੍ਹਾ ਜਿਹਾ ਹੇਠਾਂ ਮਿਲਣਾ ਚਾਹੀਦਾ ਹੈ, ਜਿਹੜਾ ਕਿ ਜਿੰਨਾ ਸੰਭਵ ਪੱਧਰ ਹੋ ਸਕੇ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ, ਕਿਉਂਕਿ ਉਹ ਬਾਲ ਨੂੰ ਹੇਠਾਂ ਪਿੱਚ ਵੱਲ ਤੱਕਦੀਆਂ ਹਨ । ਹਿੱਟ ਉੱਤੇ ਕੰਟਰੋਲ ਖੱਬੇ ਹੱਥ ਤੇ ਬਾਂਹ ਵਲੋਂ ਕੂਹਣੀ ਉੱਪਰ ਚੁੱਕ ਕੇ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਸੱਜਾ ਹੱਥ ਅੰਗੂਠੇ ਤੇ ਉਂਗਲਾਂ ਦੀ ਪਕੜ ਵਿਚ ਅਰਾਮਦਾਇਕ ਹੁੰਦਾ ਹੈ । ਬਦਨ ਨੂੰ ਜਿੰਨਾ ਸੰਭਵ ਹੋ ਸਕੇ ਪਾਸਿਆਂ ਵੱਲ ਰੱਖਣਾ ਚਾਹੀਦਾ ਹੈ ।

ਸਮਤਲ ਬੈਕ ਸਟਰੋਕ
ਇਕ ਲੜਕਾ ਜਦ ਤਕ ਸਿੱਧੀ ਹਿੱਟ ਮਾਰਨੀ, ਨਹੀਂ ਸਿੱਖਦਾ, ਤਦ ਤਕ ਬੈਟਸਮੈਨ ਨਹੀਂ ਬਣਦਾ, ਪਰ ਉਸ ਨੂੰ ਮਾੜੇ ਭਾਵ ਗਲਤ ਬਾਲ ਨਾਲ ਖੇਡਣ ਦੀ ਜਾਂਚ ਵੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ਅਤੇ ਉਹ ਗੱਲ ਕਰਾਸ-ਬੈਟ ਹਿੱਟਾਂ ਰਾਹੀਂ ਅਕਸਰ ਵਧੇਰੇ ਅਸਰਦਾਰ ਹੋ ਸਕਦੀ ਹੈ । ਇਹ ਗੱਲ ਵਿਸ਼ੇਸ਼ ਕਰਕੇ ਲੰਬੇ ਟੱਪਿਆਂ ਅਤੇ ਪੂਰਨ ਉਛਾਲ ਵਿਚ ਸੱਚੀ ਲੱਗਦੀ ਹੈ ਅਤੇ | ਖ਼ਾਸ ਕਰਕੇ ਜੂਨੀਅਰ ਵਿਕਟ ਵਿਚ ਚੌਕੇ ਮਾਰਨ ਦੇ ਉੱਤਮ ਮੌਕੇ ਪ੍ਰਦਾਨ ਕਰਦੀ ਹੈ । ਇਹ ਹਿੱਟਾਂ ਵਧੇਰੇ ਆਸਾਨ ਹੁੰਦੀਆਂ ਹਨ, ਕਿਉਂਕਿ ਇਹ ਸਿੱਧੀਆਂ ਬੈਟ ਹਿੱਟਾਂ ਨਾਲੋਂ ਵਧੇਰੇ ਕੁਦਰਤੀ ਹੁੰਦੀਆਂ ਹਨ, ਪਰ ਇਨ੍ਹਾਂ ਨੂੰ ਦ੍ਰਿੜ੍ਹਤਾ ਨਾਲ ਖੇਡਣ ਵਾਸਤੇ ਤੁਹਾਨੂੰ ਦਰੁਸਤੀ ਨਾਲ ਖੇਡਣ ਦੀ ਜਾਂਚ ਸਿੱਖਣੀ ਚਾਹੀਦੀ ਹੈ ।

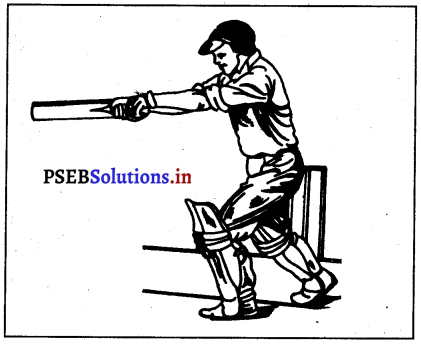
ਪਿਛਲੇ ਪੈਰ ਦਾ ਸੁਏਰ ਕੱਟ
ਬਾਲ ਰੇਖਾ ਅਤੇ ਪੁਆਇੰਟ ਉੱਤੇ ਸਾਹਮਣੇ ਤੋਂ ਜਾਂ ਪਿੱਛੇ ਮਿਲਦੇ ਬਾਲ ਨਾਲ ਨਿਪਟਣ ਲਈ ਸੱਜਾ ਪੈਰ ਕੂਲ਼ੇ ਦੀ ਰੇਖਾ ਦੇ ਆਰ-ਪਾਰ ਘੁੰਮਦਾ ਹੈ । ਫਿਰ ਗੁਟ ਅਤੇ ਹੱਥਾਂ ਨੂੰ ਇਕ ਉੱਚੇ ਬੈਟ ਲਿਫ਼ਟ ਤੋਂ ਹੇਠਾਂ ਮੋੜਿਆ ਜਾਂਦਾ ਹੈ ਅਤੇ ਸਿਰ ਦੇ ਬਦਨ, ਝੁਕੇ ਹੋਏ ਸੱਜੇ ਗੋਡੇ ਤੇ ਸਟਰੋਕ ਦੀ ਰੇਖਾ ਵਿਚ ਘੁੰਮਦਾ ਹੈ ।

ਲੇਟ ਕੱਟ
ਇਹ ਹਿੱਟ ਵੀ ਉੱਪਰ ਵਾਲੀ ਹਿੱਟ ਵਰਗੀ ਹੀ ਹੈ, ਸਿਵਾਏ ਇਸ ਦੇ ਕਿ ਇਹ ਖੱਬੇ ਮੋਢੇ ਦੇ ਵਧੇਰੇ ਮੋੜ ਨਾਲ ਸ਼ੁਰੂ ਹੁੰਦੀ ਹੈ ਅਤੇ ਸੱਜਾ ਪੈਰ ਥਰਡ ਸਲਿਪ ਵੱਲ ਪੰਜੇ ਦੇ ਰੁਖ ਨਾਲ ਧਰਤੀ ਉੱਤੇ ਹੁੰਦਾ ਹੈ | ਬਾਲ ਵਿਕਟਾਂ ਦੀ ਸਤਹ ਦੇ ਬਰਾਬਰ ਮਿਲਦਾ ਹੈ ਅਤੇ ਗੁੱਟ ਅੱਗੇ ਵਧਾਉਂਦਿਆਂ ਬੈਟਸਮੈਨ ਇਸ ਨੂੰ ਗਲੀ ਜਾਂ ਸੈਕਿੰਡ ਸਲਿਪ ਦੀ ਦਿਸ਼ਾ ਵਿਚ ਹਿੱਟ ਕਰਦਾ ਹੈ । ਇਨ੍ਹਾਂ ਦੋਹਾਂ ਕੱਟਾਂ ਵਿਚ ਖੱਬਾ ਪੈਰ ਪੰਜੇ ਉੱਤੇ ਆਰਾਮ ਦੀ ਹਾਲਤ ਵਿਚ ਰਹਿੰਦਾ ਹੈ ਅਤੇ ਭਾਰ ਝੁਕੇ ਹੋਏ ਸੱਜੇ ਗੋਡੇ , ਉੱਤੇ ਪੂਰੀ ਤਰ੍ਹਾਂ ਰਹਿੰਦਾ ਹੈ ।

ਸਪਰੋਟਸ ਅਵਾਰਡ (Sports Award)

ਅਰਜੁਨ ਪੁਰਸਕਾਰ ਜੇਤੂਆਂ ਦੀ ਸੂਚੀ (List of Arjuna Award Winners)-ਸਲੀਮ ਦੁਰਾਨੀ (1961), ਮਨਸੂਰ ਅਲੀ ਖ਼ਾਨ ਪਟੌਦੀ (1964), ਵਿਜੈ ਮਾਂਜਰੇਕਰ (1965), ਚੰਦਰਕਾਂਤ ਜੀ, ਬੋਰਡੇ(1966), ਅਜੀਤ ਵਾਡੇਕਰ (1967), ਈ.ਏ.ਐਸ. ਨਾ (1968), ਬਿਸ਼ਨ ਸਿੰਘ ਬੇਦੀ (1969), ਡੀ. ਐੱਨ. ਸਰਦੇਸਾਈ (1970), ਐੱਸ. ਵੈੱਕਟਰਾਘਵਨ (1971), ਏਕਨਾਥ ਸੈਲਕਰ (1972), ਬੀ.ਐੱਸ. ਚੰਦਰਸ਼ੇਖਰ (1973), ਅੰਜਨ ਭੱਟਾਚਾਰਜੀ ਡੀਫ ਐਂਡ ਡੈਮ) (1974), ਸੁਨੀਲ ਗਵਾਸਕਰ (1975), ਸ਼ਾਂਤਾ ਰੰਗਸੁਆਮੀ (1976), ਜੀ.ਆਰ. ਵਿਸ਼ਵਨਾਥ (1977-78), ਕਪਿਲ ਦੇਵ ਨਿਖੰਜ (1979-80), ਸੀ.ਪੀ.ਐੱਸ. ਚੌਹਾਨ (1980-81), ਸੈਯਦ ਐੱਮ.ਐੱਚ. ਕਿਰਮਾਨੀ (1980-81), ਦਲੀਪ ਵੈਂਗਸਰਕਰ (1981), ਮੋਹਿੰਦਰ ਅਮਰਨਾਥ (1982), ਡਾਇਨਾ ਇਡੁਲਜੀ (1983), ਰਵੀ ਸ਼ਾਸਤਰੀ (1984), ਐੱਸ. ਡੀ. ਕੁਲਕਰਨੀ (1985), ਮੁਹੰਮਦ ਅਜ਼ਹਰੂਦੀਨ, ਸੰਧਿਆ ਅਗਰਵਾਲ (1986), ਮਦਨ ਲਾਲ (1989), ਮਨੋਜ ਪ੍ਰਭਾਕਰ (1993), ਕਿਰਨ ਮੋਰੇ (1993), ਸਚਿਨ ਤੇਂਦੁਲਕਰ (1994), ਅਨਿਲ ਕੁੰਬਲੇ (1995), ਜਵਾਗਲ ਨਾਥ (1996),ਰਾਹੂਲ ਵਿਡ,ਨਯਨ ਮੋਗਿਆ (1999), ਵੈਂਕਟੇਸ਼ ਪ੍ਰਸ਼ਾਦ (2000), ਵੀ.ਵੀ.ਐੱਸ. ਲਕਸ਼ਮਣ (2002), ਵਰਿੰਦਰ ਸਹਿਵਾਗ (2003), ਹਰਭਜਨ ਸਿੰਘ (2004), ਅੰਜੂ ਜੈਨ (2006), ਗੌਤਮ ਗੰਭੀਰ(2009), ਹਰਭਜਨ ਸਿੰਘ ਅਤੇ ਜ਼ਹੀਰ ਖ਼ਾਨ (2010) । ਦਰੋਣਾਚਾਰੀਆ ਅਵਾਰਡ-ਡੀ.ਪੀ. ਆਜ਼ਾਦ, ਗੁਰਚਰਨ ਸਿੰਘ, ਆਰ. ਆਚਰੇਕਰ, ਸੁਨੀਤਾ ਸ਼ਰਮਾ (2005), ਸਚਿਨ ਤੇਂਦੁਲਕਰ ।

PSEB 12th Class Physical Education Practical ਕ੍ਰਿਕੇਟ (Cricket)

ਪ੍ਰਸ਼ਨ 1.
ਕ੍ਰਿਕਟ ਖੇਡ ਵਿਚ ਕੁੱਲ ਕਿੰਨੇ ਖਿਡਾਰੀ ਹੁੰਦੇ ਹਨ ?
ਉੱਤਰ:
11.

ਪ੍ਰਸ਼ਨ 2.
ਵਿਕਟ ਦੀ ਚੌੜਾਈ ਕਿੰਨੀ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ:
9 (22.9 ਸੈਂਟੀ ਮੀਟਰ)

ਪ੍ਰਸ਼ਨ 3.
ਕ੍ਰਿਕਟ ਗੇਂਦ ਦਾ ਵਜ਼ਨ ਕਿੰਨਾ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ:
155.9 ਗਰਾਮ ਤੋਂ 163 ਗਰਾਮ ਤੱਕ ।

ਪ੍ਰਸ਼ਨ 4.
ਪਹਿਲੇ ਕ੍ਰਿਕਟ ਕਲੱਬ ਦਾ ਕੀ ਨਾਮ ਸੀ ?
ਉੱਤਰ:
ਹੈਬਲਡਨ ।

ਪ੍ਰਸ਼ਨ 5.
ਭਾਰਤ ਵਿਚ ਪਹਿਲਾ ਵਨ-ਡੇ ਮੈਚ ਕਦੋਂ ਖੇਡਿਆ ਗਿਆ ?
ਉੱਤਰ:
5 ਜਨਵਰੀ, 1971.

ਪ੍ਰਸ਼ਨ 6.
ਐੱਲ. ਬੀ. ਡਬਲਯੂ. (LBW) ਦਾ ਪੂਰਾ ਨਾਂ ਕੀ ਹੈ ?
ਉੱਤਰ:
ਲੈਗ ਬੀਫੇਅਰ ਵਿਕਟ (Leg before wicket)

ਪ੍ਰਸ਼ਨ 7.
ਕਿਸੇ ਚਾਰ ਕ੍ਰਿਕਟ ਸਟਰੋਕ ਦੇ ਨਾਮ ਦੱਸੋ ।
ਉੱਤਰ:

1. ਆਨ ਡਾਈਵ
2. ਬੈਕ ਸਟਰੋਕ
3. ਸਮਤਲ ਬੈਕ ਸਟਰੋਕ
4. ਲੇਟ ਕੱਟ ।

ਪ੍ਰਸ਼ਨ 8.
ਕ੍ਰਿਕਟ ਵਿਚ ਕਿੰਨੇ ਅੰਪਾਇਰ ਹੁੰਦੇ ਹਨ ?
ਉੱਤਰ:
3.

ਪ੍ਰਸ਼ਨ 9.
ਕ੍ਰਿਕਟ ਪਿੱਚ ਅਤੇ ਵਿਕਟ ਵਿਚਕਾਰ ਕਿੰਨੀ ਲੰਬਾਈ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ:
22 ਗਜ਼ (20.12 ਮੀਟਰ)

ਪ੍ਰਸ਼ਨ 10.
ਪਹਿਲਾ ਟੈਸਟ ਮੈਚ ਕਦੋਂ ਖੇਡਿਆ ਗਿਆ ?
ਉੱਤਰ:
1877 ਵਿਚ ਅਸਟ੍ਰੇਲੀਆ ਅਤੇ ਇੰਗਲੈਂਡ ਵਿਚਕਾਰ)

ਪ੍ਰਸ਼ਨ 11.
ਕਿਸ ਦੀ ਕਪਤਾਨੀ ਵਿਚ ਭਾਰਤ ਨੂੰ ਪਹਿਲਾ ਵਰਲਡ ਕੱਪ ਮਿਲਿਆ ਸੀ ?
ਉੱਤਰ:
ਕਪਿਲ ਦੇਵ (1983 ਵਿਚ)

ਪ੍ਰਸ਼ਨ 12.
ਕ੍ਰਿਕਟ ਵਿਚ ਕਿੰਨੇ ਪ੍ਰਕਾਰ ਦੇ ਮੈਚ ਹੁੰਦੇ ਹਨ ?
ਉੱਤਰ:
ਇਕ ਦਿਨ ਦਾ ਮੈਚ, ਟੈਸਟ ਮੈਚ, 20-20 ਕੱਪ |

ਪ੍ਰਸ਼ਨ 13.
ਬਾਊਲਿੰਗ ਕੀਜ਼ ਦੀ ਲੰਬਾਈ ਕਿੰਨੀ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ:
8′ 8″ (2.64 ਮੀਟਰ)

ਪ੍ਰਸ਼ਨ 14.
ਛੋਟੇ ਸਰਕਲ ਦਾ ਖੇਤਰ ਕਿੰਨਾ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ:
22.4 ਮੀਟਰ ।

ਪ੍ਰਸ਼ਨ 15.
ਮੈਦਾਨ ਤੋਂ ਵਿਕਟ ਦੀ ਉਚਾਈ ਕਿੰਨੀ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ:
28’’ (71 ਸੈਂ.ਮੀ.)।

Punjab State Board PSEB 12th Class Physical Education Book Solutions ਕੁਸ਼ਤੀਆਂ-ਫਰੀ ਸਟਾਈਲ ਅਤੇ ਗਰੀਕੋ ਰੋਮਨ (Wrestling Free Style and Greeco Roman) Game Rules.

ਕੁਸ਼ਤੀਆਂ-ਫਰੀ ਸਟਾਈਲ ਅਤੇ ਗਰੀਕੋ ਰੋਮਨ (Wrestling Free Style and Greeco Roman) Game Rules – PSEB 12th Class Physical Education

ਕੁਸ਼ਤੀਆਂ ਦਾ ਇਤਿਹਾਸ
(History of Wrestling)

ਇਹ ਦੋ ਹੱਥਾਂ ਨਾਲ ਖੇਡੀ ਜਾਣ ਵਾਲੀ ਖੇਡ ਹੈ । ਜਿਸ ਵਿੱਚ ਦੋ ਵਿਰੋਧੀ ਆਪਣੇ ਵਿਰੋਧੀ ਨੂੰ ਥੱਲੇ ਸੁੱਟਣ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰਦੇ ਹਨ ਅਤੇ ਉਸਦੇ ਦੋਵੇਂ ਕੰਧੇ ਜ਼ਮੀਨ ਤੇ ਲਾਉਣ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰਦੇ ਹਨ । ਇਸ ਵਿੱਚ ਪਕੜ ਅਤੇ ਕਈ ਪ੍ਰਕਾਰ ਦੀ ਤਕਨੀਕ ਵਰਤੀ ਜਾਂਦੀ ਹੈ । ਕੁਸ਼ਤੀਆਂ ਸਭ ਤੋਂ ਪੁਰਾਣੀ ਖੇਡ ਹੈ । (ਯੁਨਾਨ ਵਿੱਚ ਇਹ ਮਿਲਟਰੀ ਟਰੇਨਿੰਗ ਦਾ ਇਕ ਭਾਗ ਹੁੰਦਾ ਸੀ । 776 ਬੀ.ਸੀ. ਵਿੱਚ ਉਲੰਪਿਕ ਦੀ ਇਕ ਮਹੱਤਵਪੂਰਨ ਖੇਡ ਸੀ | 15ਵੀਂ ਸਦੀ ਵਿੱਚ ਇਹ ਇੰਗਲੈਂਡ, ਜਾਪਾਨ ਅਤੇ ਫਰਾਂਸ ਵਿੱਚ ਪ੍ਰਚਲਿਤ ਹੋਈ । 1896 ਐਂਥਨ ਦੀ ਉਲੰਪਿਕ ਖੇਡਾਂ ਵਿੱਚ ਇਹ ਖੇਡ ਸ਼ਾਮਲ ਕੀਤੀ ਗਈ । ਇਸ ਦੇ ਦੋ ਭਾਗ ਹਨ-

1. ਫਰੀ ਸਟਾਈਲ
2. ਗਰੀਕੋ ਰੋਮਨ ।

ਇੰਟਰਨੈਸ਼ਨਲ ਐਸੋਸ਼ੀਏਸ਼ਨ ਫੈਡਰੇਸ਼ਨ (I.F.W.) 1912 ਵਿੱਚ ਹੋਂਦ ਵਿੱਚ ਆਈ । ਮਹਿਲਾਵਾਂ ਦੀ ਖੇਡ 1987 ਵਿੱਚ ਸ਼ੁਰੂ ਹੋਈ । ਰੂਸ ਦੇ ਰੈਸਲਰ ਇਸ ਖੇਡ ਵਿੱਚ ਬਹੁਤ ਮਾਹਰ ਹਨ ਅਤੇ ਭਾਰਤਵਾਸੀ ਵੀ ਰੈਸਲਿੰਗ ਵਿੱਚ ਚੰਗੇ ਹਨ | ਭਾਰਤਵਾਸੀ ਮਿਸਟਰ ਯਾਦਵ ਨੇ 1952 ਵਿੱਚ ਉਲੰਪਿਕ ਵਿੱਚ ਤੀਜਾ ਸਥਾਨ ਪ੍ਰਾਪਤ ਕੀਤਾ। ਰੂਸ ਦੇ ਪਹਿਲਵਾਨ ਆਪਣੀ ਤਕਨੀਕ ਵਿੱਚ ਮਸ਼ਹੂਰ ਹਨ । ਭਾਰਤ ਨੇ ਬਹੁਤ ਚੰਗੇ ਰੈਸਲਰ ਪੈਦਾ ਕੀਤੇ ਹਨ, ਜਿਸ ਵਿੱਚ ਦਾਰਾ ਸਿੰਘ, ਕਰਤਾਰ ਸਿੰਘ ਅਤੇ ਪੱਪੂ ਯਾਦਵ ਹਨ ।

ਯਾਦ ਰੱਖਣ ਯੋਗ ਗੱਲਾਂ
(Tips of Remember)

1.  ਕੁਸ਼ਤੀ ਦੇ ਮੈਟ ਦਾ ਆਕਾਰ = ਗੋਲ
2. ਮੈਟ ਦਾ ਸਾਈਜ਼ = 4.50 ਮੀਟਰ ਅਰਧ-ਵਿਆਸ
3. ਘੇਰੇ ਦਾ ਰੰਗ = ਲਾਲ
4. ਪਲੇਟਫਾਰਮ ਤੋਂ ਮੈਟ ਦੀ ਉਚਾਈ = 1.10 ਮੀਟਰ
5. ਕਾਰਨਰ ਦੇ ਰੰਗ = ਲਾਲ ਅਤੇ ਨੀਲਾ
6. ਕੁਸ਼ਤੀ ਦੀ ਮਿਆਦ = 6 ਮਿੰਟ ਤਿੰਨ-ਤਿੰਨ ਮਿੰਟ ਦੇ ਦੋ ਹਾਫ
7. ਪੁਰਸ਼ਾਂ ਦੇ ਕੁੱਲ ਭਾਰ = 9
8. ਇਸਤਰੀਆਂ = 7
9. ਯੂਨੀਅਰ = 10
10. ਅਧਿਕਾਰੀ = ਮੈਟ ਚੇਅਰ-ਮੈਨ, 2 ਰੈਫ਼ਰੀ 3 ਜੱਜ
11. ਮੈਟ ਦੇ ਆਲੇ-ਦੁਆਲੇ ਦਾ ਖ਼ਾਲੀ ਸਥਾਨ = 1.50 ਮੀਟਰ
12. ਰਾਉਂਡ ਪਿੱਛੋਂ ਆਰਾਮ ਦਾ ਸਮਾਂ = 30 ਸੈਕਿੰਡ

ਕੁਸ਼ਤੀ ਦੇ ਆਧੁਨਿਕ ਸਧਾਰਨ ਨਿਯਮ
(Latest Rules of Wrestling)\

1. ਕੁਸ਼ਤੀ ਦਾ ਸਮਾਂ 5 ਮਿੰਟ ਦਾ ਹੁੰਦਾ ਹੈ ।
2. ਕੁਸ਼ਤੀ ਦੋ ਖਿਡਾਰੀਆਂ ਦੇ ਭਾਰ ਦੇ ਅਨੁਸਾਰ ਖੇਡੀ ਜਾਂਦੀ ਹੈ ।
3. ਕੁਸ਼ਤੀ ਦੇ ਮੱਧ ਵਿੱਚ ਕਿਸੇ ਅਧਿਕਾਰੀ ਨੂੰ ਨਹੀਂ ਬਦਲਿਆ ਜਾ ਸਕਦਾ ਹੈ ।
4. ਜੇਕਰ ਰੈਫ਼ਰੀ ਨੇ ਕਿਸੇ ਖਿਡਾਰੀ ਨੂੰ ਤਿੰਨ ਵਾਰ ਚੇਤਾਵਨੀ ਦਿੱਤੀ ਹੈ ਤਾਂ ਉਸ ਨੂੰ ਹਾਰਿਆ ਮੰਨਿਆ ਜਾਵੇਗਾ ।
5. ਜਦੋਂ ਦੋ ਵਿਰੋਧੀ ਖਿਡਾਰੀਆਂ ਦੇ ਸਕੋਰ ਦਾ ਅੰਤਰ ਇਕ ਅੰਕ ਤੋਂ ਘੱਟ ਹੋਵੇ ਤਾਂ ਕੁਸ਼ਤੀ ਨੂੰ ਬਰਾਬਰ ਘੋਸ਼ਿਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।
6. ਕੁਸ਼ਤੀ ਵਿੱਚ ਜਦੋਂ ਇਕ ਵਾਰ ਜਾਂ ਇਕ ਤੋਂ ਜ਼ਿਆਦਾ ਦਾ ਅੰਤਰ ਹੋਵੇ ਤਾਂ ਜ਼ਿਆਦਾ ਅੰਕ ਪ੍ਰਾਪਤ ਕਰਨ ਵਾਲੇ ਨੂੰ ਜੇਤੂ ਘੋਸ਼ਿਤ ਕੀਤਾ ਜਾਵੇਗਾ ।
7. ਕੁਸ਼ਤੀ ਵਿੱਚ ਕਿਸੇ ਨੂੰ ਵੀ ਕੜਾ, ਅੰਗੂਠੀ ਪਾਉਣਾ ਜਾਂ ਦਾੜੀ ਰੱਖਣਾ ਮਨ੍ਹਾਂ ਹੈ ।
   (1) ਭਾਰ ਤੋਲਣਾ (Weighting)-ਪ੍ਰਤੀਯੋਗੀ ਨਿਰਵਸਤਰ ਹੋ ਕੇ ਭਾਰ ਕਰਵਾਉਣਗੇ । ਤੋਲ ਤੋਂ ਪਹਿਲਾਂ ਉਸਦੀ ਡਾਕਟਰੀ ਜਾਂਚ ਕਰਾਈ ਜਾਵੇਗੀ ।
   (2) ਕੁਸ਼ਤੀ ਦਾ ਸ਼ੁਰੂ ਅਤੇ ਸਮਾਂ (Start and Duration of wrestling Bout)-ਹਰੇਕ ਕੁਸ਼ਤੀ ਦਾ ਕੁੱਲ ਸਮਾਂ 5 ਮਿੰਟ ਹੁੰਦਾ ਹੈ । ਇਹ 1-1-2 ਮਿੰਟ ਦੇ ਦੋ Half ਵਿੱਚ ਹੁੰਦਾ ਹੈ, ਜਿਸ ਵਿੱਚ ਇਕ ਮਿੰਟ ਦਾ ਆਰਾਮ ਹੁੰਦਾ ਹੈ । ਕੁਸ਼ਤੀ ਉਸ ਸਮੇਂ ਤੱਕ ਜਾਰੀ ਰਹੇਗੀ ਜਦੋਂ ਤੱਕ ਇਕ ਖਿਡਾਰੀ ਡਿੱਗ ਨਹੀਂ ਜਾਂਦਾ ਜਾਂ ਫਿਰ ਉਹ 5 ਮਿੰਟ ਦੇ ਸਮੇਂ ਤੱਕ ਜਾਰੀ ਰਹੇਗੀ ।
   (3) ਕੁਸ਼ਤੀ ਦੀ ਸਮਾਪਤੀ (End of Bout-ਘੰਟੀ ਵੱਜਣ ਤੇ ਕੁਸ਼ਤੀ ਸਮਾਪਤ ਹੋ ਜਾਵੇਗੀ । ਮੈਚ ਦਾ ਮੁਖੀਆ ਜੇਤੂ ਕਲਰ ਦਿਖਾ ਕੇ ਵਿਜੇਤਾ ਨੂੰ ਸੂਚਨਾ ਦਿੰਦਾ ਹੈ ।
   (4) ਸਕੋਰ (Score(1) ਇੱਕ ਅੰਕ-ਉਸ ਖਿਡਾਰੀ ਨੂੰ ਇਕ ਅੰਕ ਮਿਲਦਾ ਹੈ, ਜੋ ਵਿਰੋਧੀ ਨੂੰ ਮੈਟ ਤੇ ਸੁੱਟ ਕੇ ਉਸ ‘ਤੇ ਨਿਯੰਤਰਣ ਪ੍ਰਾਪਤ ਕਰ ਲੈਂਦਾ ਹੈ ।

• ਦੋ ਅੰਕ-ਜਦੋਂ ਇਕ ਪਹਿਲਵਾਨ ਦੂਸਰੇ ਪਹਿਲਵਾਨ ਦੇ ਇਕ ਕੰਧੇ ਨੂੰ ਮੈਟ ‘ਤੇ ਲਗਾ ਦਿੰਦਾ ਹੈ ਤਾਂ ਦੋ ਅੰਕ ਪ੍ਰਾਪਤ ਹੁੰਦੇ ਹਨ ।
• ਤਿੰਨ ਅੰਕ-ਜਦੋਂ ਇਕ ਪਹਿਲਵਾਨ ਆਪਣੇ ਵਿਰੋਧੀ ਨੂੰ ਸਾਹਮਣੇ ਅਤੇ ਸਿੱਧਾ ਡੇਂਜਰ ਪੋਜ਼ੀਸ਼ਨ ਵਿੱਚ ਸੁੱਟ ਦਿੰਦਾ ਹੈ, ਤਾਂ ਤਿੰਨ ਅੰਕ ਪ੍ਰਾਪਤ ਹੁੰਦੇ ਹਨ ।
• ਪੰਜ ਅੰਕ-ਜਦੋਂ ਇਕ ਪਹਿਲਵਾਨ ਆਪਣੇ ਵਿਰੋਧੀ ਨੂੰ ਸਾਹਮਣੇ ਤੋਂ 90° ਦੀ ਆਰਕ ਪੋਜ਼ੀਸ਼ਨ ਤੋਂ ਸਿੱਧਾ ਜਰ ਪੋਜ਼ੀਸ਼ਨ ਵਿੱਚ ਸੁੱਟਦਾ ਹੈ ਤਾਂ ਉਸਨੂੰ ਪੰਜ ਅੰਕ ਪ੍ਰਾਪਤ ਹੁੰਦੇ ਹਨ ।

ਮੁਕਾਬਲੇ (Competitions) – ਸਕੂਲ ਪੱਧਰ ਤੇ ਹੇਠ ਲਿਖੇ ਭਾਗਾਂ ਦੇ ਆਧਾਰ ਤੇ ਮੁਕਾਬਲੇ ਕਰਵਾਏ ਜਾਂਦੇ ਹਨ –



ਹਰੇਕ ਪ੍ਰਤਿਯੋਗੀ ਮੁਕਾਬਲੇ ਵਿਚ ਆਪਣੇ ਸਰੀਰ ਦੇ ਭਾਰ ਅਨੁਸਾਰ ਆਪਣੇ ਵਰਗ ਵਿਚ ਭਾਗ ਲੈ ਸਕਦਾ ਹੈ ।
MEN = Total Categories Nine
WOMEN = Total Categories Seven.
JUNIOR = Total Categories Ten.

ਫਰੀ ਸਟਾਈਲ ਕੁਸ਼ਤੀਆਂ (Free Style Wrestling) – ਫਰੀ ਸਟਾਈਲ ਕੁਸ਼ਤੀਆਂ ਵਿਚ ਸਰੀਰ ਦੇ ਕਿਸੇ ਹਿੱਸੇ ਤੋਂ ਫੜਿਆ ਜਾ ਸਕਦਾ ਹੈ । ਲੱਤਾਂ, ਬਾਂਹਾਂ ਨਾਲ ਕੋਈ ਵੀ ਤਕਨੀਕ ਲਗਾਈ ਜਾ ਸਕਦੀ ਹੈ ਪਰ ਵਾਲ, ਕੰਨ ਅਤੇ ਲੰਗੋਟ ਨਹੀਂ ਫੜ ਸਕਦੇ ।

ਗਰੀਕੋ ਰੋਮਨ ਕੁਸ਼ਤੀਆਂ (Greeco Roman Wrestling) – ਗਰੀਕੋ ਰੋਮਨ ਕੁਸ਼ਤੀਆਂ ਵਿਚ ਲੱਤਾਂ ਦਾ ਇਸਤੇਮਾਲ ਨਹੀਂ ਕੀਤਾ ਜਾ ਸਕਦਾ | ਲੱਕ ਤੋਂ ਉੱਪਰੀ ਭਾਗ ਨਾਲ ਕਿਸੇ ਵੀ ਤਕਨੀਕ ਦਾ ਇਸਤੇਮਾਲ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ । ਇਨ੍ਹਾਂ ਕੁਸ਼ਤੀਆਂ ਵਿਚ ਵੀ ਕੰਨ, ਵਾਲ, ਲੰਗੋਟਾ ਨਹੀਂ ਫੜ ਸਕਦੇ | ਬਾਕੀ ਸਾਰੇ ਨਿਯਮ ਫਰੀ ਸਟਾਈਲ ਕੁਸ਼ਤੀਆਂ ਵਾਲੇ ਹਨ । ਹਰੇਕ ਪ੍ਰਤੀਯੋਗੀ ਕਿਸੇ ਮੁਕਾਬਲੇ ਵਿਚ ਆਪਣੇ ਸਰੀਰਕ ਭਾਰ ਦੇ ਅਨੁਸਾਰ ਵਾਲੇ ਵਰਗ ਵਿਚ ਹਿੱਸਾ ਲੈ ਸਕਦਾ ਹੈ ।

ਕੁਸ਼ਤੀ ਪ੍ਰਤੀਯੋਗਤਾ ਵਿਚ ਹਿੱਸਾ ਲੈਣ ਵਾਲਿਆਂ ਲਈ ਭਾਰ ਤੋਲਣ ਸੰਬੰਧੀ ਨਿਯਮਾਂ
ਅਤੇ ਉਹਨਾਂ ਦੇ ਜੋੜੇ ਬਣਾਉਣ ਦੀ ਵਿਧੀ

ਕੁਸ਼ਤੀ ਮੁਕਾਬਲਿਆਂ ਵਿਚ ਭਾਗ ਲੈਣ ਵਾਲਿਆਂ ਲਈ ਭਾਰ ਤੋਲਣ ਸੰਬੰਧੀ ਨਿਯਮ (Rules for the Competitions in wrestling competitions regarding their weighting).

1. ਭਾਰ ਤੋਲਣ ਦਾ ਕੰਮ ਕੁਸ਼ਤੀਆਂ ਦੇ ਮੁਕਾਬਲੇ (wrestling competition) ਦੇ ਆਰੰਭ ਹੋਣ ਤੋਂ ਜੋ ਚਾਰ ਘੰਟੇ ਪਹਿਲਾਂ ਸ਼ੁਰੂ ਕੀਤਾ ਜਾਵੇਗਾ ।
2. ਪ੍ਰਤੀਯੋਗੀ ਕੱਪੜੇ-ਰਹਿਤ ਹੋ ਕੇ ਭਾਰ ਤੋਲੇ ਜਾਣਗੇ । ਤੋਲ ਤੋਂ ਪਹਿਲਾਂ ਉਨ੍ਹਾਂ ਦਾ ਡਾਕਟਰੀ ਨਿਰੀਖਣ ਕੀਤਾ ਜਾਵੇਗਾ । ਕਿਸੇ ਛੂਤ ਦੇ ਰੋਗ ਤੋਂ ਪੀੜਤ ਪ੍ਰਤੀਯੋਗੀ ਨੂੰ ਡਾਕਟਰ ਹਿੱਸਾ ਲੈਣ ਤੇ ਰੋਕ ਦੇਵੇਗਾ ।
3. ਹਰੇਕ ਪ੍ਰਤੀਯੋਗੀ (Competitor) ਆਪਣੇ ਬਰਾਬਰ ਭਾਰ ਵਾਲੇ ਨਾਲ ਕੁਸ਼ਤੀ ਲੜ ਸਕਦਾ ਹੈ ।
   
4. ਖਿਡਾਰੀਆਂ ਦੀ ਸਰੀਰਕ ਹਾਲਤ ਸੰਤੋਖਜਨਕ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ । ਉਨ੍ਹਾਂ ਦੇ ਨਹੁੰ ਖੂਬ ਚੰਗੀ ਤਰ੍ਹਾਂ ਕੱਟੇ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ । ਇਹ ਭਾਰ ਤੋਲਣ ਦੇ ਸਮੇਂ ਚੈਕ ਕੀਤੇ ਜਾਣਗੇ ।
5. ਅਗਲੇ ਦਿਨਾਂ ਵਿਚ ਭਾਰ ਤੋਲਣ ਦਾ ਕੰਮ ਘੱਟੋ-ਘੱਟ ਦੋ ਘੰਟਿਆਂ ਤੋਂ ਪਹਿਲਾਂ ਸ਼ੁਰੂ ਹੋਵੇਗਾ ਅਤੇ ਪਹਿਲੀ ਕੁਸ਼ਤੀ ਤੇ ਇਕ ਘੰਟਾ ਪਹਿਲਾਂ ਖ਼ਤਮ ਹੋ ਜਾਵੇਗਾ ।
6. ਭਾਰ ਤੋਲਣ ਦੇ ਕੰਮ ਦੀ ਸਮਾਪਤੀ ਤੋਂ ਪਹਿਲਾਂ ਪ੍ਰਤੀਯੋਗੀ ਜਿੰਨੀ ਵਾਰ ਚਾਹੁਣ, ਭਾਰ ਤੋਲਣ ਦੀ ਮਸ਼ੀਨ ਤੇ ਖੜੇ ਹੋ ਸਕਦੇ ਹਨ, ਪਰ ਆਪਣੀ ਵਾਰੀ ਨਾਲ ਹੀ ।

ਪਰਚੀਆਂ ਦੁਆਰਾ ਜੋੜੇ ਬਣਾਉਣਾ (Drawing lots-pairing off) – ਹਰੇਕ ਰਾਊਂਡ ਲਈ ਸਾਰੇ ਖਿਡਾਰੀਆਂ ਨੂੰ ਪਰਚੀ ਦੁਆਰਾ ਸ਼ਾਮਲ ਕੀਤਾ ਜਾਵੇਗਾ । ਉਹ ਪ੍ਰਤੀਯੋਗੀ ਜਿਨ੍ਹਾਂ ਦੀ ਪਰਚੀ ਇਕ ਦੂਸਰੇ ਦੇ ਬਾਅਦ ਨਿਕਲ ਆਵੇ, ਉਹ ਆਪੋ ਵਿਚ ਪਹਿਲੇ ਰਾਊਂਡ ਵਿਚ ਕੁਸ਼ਤੀ ਲੜਨਗੇ । ਜੇਕਰ ਕੁਸ਼ਤੀ ਲੜਨ ਵਾਲੇ ਬਿਖਮ ਗਿਣਤੀ (Odd Number) ਵਿਚ ਹੋਣ ਤਾਂ ਸਭ ਤੋਂ ਵਧੇਰੇ ਨੰਬਰ ਲੈਣ ਵਾਲਾ ਬਿਨਾਂ ਪੈਨਲਟੀ ਮਾਰਕ ਕੀਤੇ ਅਗਲੇ ਰਾਊਂਡ ਦੀ ਬਾਈ (Bye) ਵਿਚ ਜਾਵੇਗਾ । ਲੰਬਾਈ ਦਾ ਅਧਿਕਾਰ ਕੇਵਲ ਪਰਚੀ ਦੁਆਰਾ ਪ੍ਰਾਪਤ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ । ਦੂਸਰੇ ਰਾਉਂਡ ਦੇ ਜੋੜੇ ਬਣਾਉਂਦੇ ਸਮੇਂ ਸੂਚੀ ਦੇ ਪਹਿਲੇ ਨਾਂ ਨੂੰ ਲੈ ਕੇ ਦੂਜੇ ਉਸ ਦੇ ਨੇੜੇ ਦੇ ਵਿਰੋਧੀ ਨੂੰ ਜੋੜੇ ਵਿਚ ਰੱਖਿਆ ਜਾਂਦਾ ਹੈ, ਪਰੰਤੂ ਅਜਿਹਾ ਤਦੇ ਹੁੰਦਾ ਹੈ, ਜੇ ਉਹ ਪਹਿਲਾਂ ਆਪਸ ਵਿਚ ਕੁਸ਼ਤੀ ਨਾ ਲੜੇ ਹੋਣ ! ਜੇ ਜੋੜੇ ਬਣਾਉਂਦੇ ਸਮੇਂ ਇਕ ਹੀ ਥਾਂ ਦੇ ਦੋ ਖਿਡਾਰੀ ਜੋੜੇ ਵਿਚ ਆ ਜਾਣ ਤਾਂ ਉਹ ਦੋਵੇਂ ਆਪਸ ਵਿਚ ਪਹਿਲੇ ਰਾਊਂਡ ਵਿਚ ਇਕ ਦੂਜੇ ਦੇ ਵਿਰੁੱਧ ਕੁਸ਼ਤੀ ਲੜਨਗੇ ।

ਕੁਸ਼ਤੀ ਲੜਨ ਵਾਲਿਆਂ ਦੀ ਪੁਸ਼ਾਕ, ਮੈਟ, ਕੁਸ਼ਤੀ ਦਾ ਆਰੰਭ ਅਤੇ ਮਿਆਦ, ਕੁਸ਼ਤੀ ਨੂੰ ਬੰਦ ਕਰਨਾ,
ਕੁਸ਼ਤੀ ਦੀ ਸਮਾਪਤੀ ਬਾਰੇ ਜਾਣਕਾਰੀ

ਪੁਸ਼ਾਕ (Dress) – ਪ੍ਰਤੀਯੋਗੀ ਅਖਾੜੇ ਵਿਚ ਇਕ ਟੁਕੜੇ ਵਾਲੇ ਬੁਨਿਆਣ-ਕੱਛਾ ਜਾਂ ਜਰਸੀ ਲਾਲ ਜਾਂ ਨੀਲੀ) ਵਿਚ ਉਤਰਨ ਅਤੇ ਉਸ ਦੇ ਹੇਠਾਂ ਇਕ ਲੰਗੋਟੀ ਜਾਂ ਪੇਟੀ ਪਹਿਣਨਗੇ 1 ਕਟਿਉਮ ਸਰੀਰ ਨਾਲ ਚਿਪਕਿਆ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ । ਖਿਡਾਰੀ ਸਪੋਰਟਸ ਜੁੱਤੇ ਪਹਿਨਣਗੇ ਜੋ ਗਿੱਟਿਆਂ ਨਾਲ ਚੰਗੀ ਤਰ੍ਹਾਂ ਬੰਨ੍ਹੇ ਹੋਣਗੇ । ਉਹ ਅੱਡੀ ਵਾਲੇ ਜਾਂ ਕਿੱਲਾਂ ਵਾਲੇ ਤਲੇ ਵਾਲੇ ਬੂਟਾਂ ਦੀ ਵਰਤੋਂ ਨਹੀਂ ਕਰ ਸਕਦੇ । ਗੋਡਿਆਂ ਦੇ ਹਲਕੇ ਕਵਰਜ਼ (Light Knee guards) ਦੀ ਵਰਤੋਂ ਮਨ੍ਹਾਂ ਨਹੀਂ ਹੈ । ਪ੍ਰਤੀਯੋਗੀਆਂ ਦੀ ਦਾੜ੍ਹੀ ਤਾਜ਼ੀ ਮੁੰਨੀ ਹੋਈ ਜਾਂ ਕਈ ਮਹੀਨਿਆਂ ਦੀ ਵਧੀ ਹੋਈ ਹੋਵੇ । ਪ੍ਰਤੀਯੋਗੀ ਆਪਣੇ ਸਰੀਰ ‘ਤੇ ਚਿਕਨੇ ਪਦਾਰਥਾਂ ਜਿਵੇਂ ਤੇਲ ਆਦਿ ਦੀ ਵਰਤੋਂ ਨਹੀਂ ਕਰ ਸਕਦੇ ਅਤੇ ਨਾ ਹੀ ਉਹਨਾਂ ਦਾ ਬਦਨ ਪਸੀਨੇ ਨਾਲ ਤਰ ਹੋਵੇ । ਅੰਗੂਠੀਆਂ (Rings), ਕੜੇ, ਬਟਣ ਵਾਲੇ ਬੂਟਾਂ ਅਤੇ ਹੋਰ ਕਿਸੇ ਅਜਿਹੀ ਚੀਜ਼ ਦਾ ਪਹਿਣਨਾ ਮਨ੍ਹਾਂ ਹੈ, ਜਿਸ ਨਾਲ ਵਿਰੋਧੀ ਖਿਡਾਰੀ ਨੂੰ ਚੋਟ ਪਹੁੰਚਣ ਦੀ ਸੰਭਾਵਨਾ ਹੋਵੇ । ਹਰ ਇਕ ਪ੍ਰਤੀਯੋਗੀ ਕੋਲ ਉਸ ਦਾ ਆਪਣਾ ਰੁਮਾਲ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ।

ਮੈਟ (Mat) – ਸਾਰੇ ਅੰਤਰ-ਰਾਸ਼ਟਰੀ ਮੈਚਾਂ ਵਿਚ ਮੈਟ ਦਾ 4.50 ਮੀਟਰ ਅਰਧ ਵਿਆਸ ਦਾ ਗੋਲ ਘੇਰਾ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ਅਤੇ ਇਸ ਦੇ ਬਾਹਰਲੇ ਘੇਰੇ ਤੋਂ ਅੰਦਰਲੇ 50 ਸੈਂਟੀਮੀਟਰ ਦਾ ਘੇਰਾ ਲਿਆ ਜਾਂਦਾ ਹੈ । ਇਹ ਥਾਂ ਲਾਲ ਰੰਗ ਨਾਲ ਅੰਕਿਤ ਕੀਤੀ ਜਾਂਦੀ ਹੈ । ਇਹ ਮੈਟ ਵੱਧ ਤੋਂ ਵੱਧ 1.10 ਮੀਟਰ ਉੱਚੇ ਪਲੇਟਫਾਰਮ (Platform) ਤੇ ਫਿਟ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ । ਮੈਟ ਦੇ ਆਹਮਣੇ-ਸਾਹਮਣੇ ਦੇ ਕੋਨਿਆਂ ਤੇ ਲਾਲ ਅਤੇ ਨੀਲਾ ਕਾਰਨਰ ਲੱਗਿਆ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ਅਤੇ ਇਸ ਮੈਟ ਦੇ ਵਿਚਕਾਰ ਇਕ ਮੀਟਰ ਦਾ ਲੰਬਾ ਚੱਕਰ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ।

ਕੁਸ਼ਤੀ ਦਾ ਆਰੰਭ ਅਤੇ ਮਿਆਦ (Start of Wrestling Bout and Its Duration)-

1. ਹਰੇਕ ਕੁਸ਼ਤੀ ਦਾ ਕੁੱਲ ਸਮਾਂ 5 ਮਿੰਟ ਹੁੰਦਾ ਹੈ ।
2. ਕੁਸ਼ਤੀ ਉਸ ਸਮੇਂ ਤਕ ਜਾਰੀ ਰਹੇਗੀ, ਜਦੋਂ ਤਕ ਕੋਈ ਇਕ ਖਿਡਾਰੀ ਡਿਗ ਨਹੀਂ ਜਾਂਦਾ ਜਾਂ ਫਿਰ ਇਹ 6 ਮਿੰਟ ਤਕ ਜਾਰੀ ਰਹੇਗੀ ।
3. ਜੇ ਕੋਈ ਖਿਡਾਰੀ ਆਪਣਾ ਨਾਂ ਸੱਦੇ ਜਾਣ ਦੇ ਪਿੱਛੋਂ 5 ਮਿੰਟਾਂ ਦੇ ਅੰਦਰ-ਅੰਦਰ ਮੈਟ ‘ਤੇ ਨਹੀਂ ਪਹੁੰਚਦਾ, ਤਾਂ ਉਸ , ਨੂੰ ਡਿੱਗਿਆ ਹੋਇਆ ਮੰਨਿਆ ਜਾਵੇਗਾ ਅਤੇ ਮੁਕਾਬਲੇ ਤੋਂ ਬਾਹਰ ਕੱਢਿਆਂ ਹੋਇਆ ਮੰਨਿਆ ਜਾਵੇਗਾ ।
4. ਰੈਫਰੀ ਦੇ ਸੀਟੀ ਵਜਾਉਣ ਤੇ ਕੁਸ਼ਤੀ ਆਰੰਭ ਹੋਵੇਗੀ ਜਾਂ ਰੋਕੀ ਜਾਵੇਗੀ ਜਾਂ ਸਮਾਪਤ ਕੀਤੀ ਜਾਵੇਗੀ ।

ਕੁਸ਼ਤੀ ਦੀ ਸਮਾਪਤੀ (End of the Bout) – ਟਾਈਮ ਕੀਪਰ (Time Keeper) ਘੰਟੀ ਵਜਾ ਕੇ ਕੁਸ਼ਤੀ ਦੇ ਸਮਾਪਤ ਹੋਣ ਦਾ ਇਸ਼ਾਰਾ ਕਰਦਾ ਹੈ । ਇਸ ਦੇ ਨਾਲ ਹੀ ਰੈਫਰੀ ਆਪਣੀ ਸੀਟੀ ਵਜਾ ਕੇ ਕੁਸ਼ਤੀ ਦੀ ਸਮਾਪਤੀ ਦਾ ਇਸ਼ਾਰਾ ਕਰਦਾ ਹੈ । ਜੇਕਰ ਰੈਫਰੀ ਨੇ ਘੰਟੀ ਨਾ ਸੁਣੀ ਹੋਵੇ ਤਾਂ ਮੈਟ ਦਾ ਮੁਖੀ (Mat Chairman) ਤੁਰੰਤ ਦਖ਼ਲ-ਅੰਦਾਜ਼ੀ ਕਰਦਾ ਹੈ ਅਤੇ ਕੁਸ਼ਤੀ ਦੀ ਸਮਾਪਤੀ ਕਰ ਦਿੰਦਾ ਹੈ । ਘੰਟੀ ਵੱਜਣ ਅਤੇ ਸੀਟੀ ਵੱਜਣ ਦੇ ਦੌਰਾਨ ਕੀਤਾ ਗਿਆ ਕੋਈ ਵੀ ਕੰਮ ਜਾਇਜ਼ (Valid) ਨਹੀਂ ਹੁੰਦਾ । ਕੁਸ਼ਤੀ ਦੀ ਸਮਾਪਤੀ ਤੇ ਦੋਨੋਂ ਖਿਡਾਰੀ ਹੱਥ ਮਿਲਾ ਕੇ ਵਿਚਕਾਰ ਰੈਫਰੀ ਕੋਲ ਖੜ੍ਹੇ ਹੋ ਜਾਂਦੇ ਹਨ, ਤਾਂ ਜੋ ਉਹ ਫ਼ੈਸਲਾ ਪ੍ਰਾਪਤ ਕਰ ਸਕਣ । ਮੈਟ ਦੇ ਮੁਖੀ (Winner colour) ਨੂੰ ਉੱਚਾ ਚੁੱਕ ਕੇ ਜੇਤੂ ਦਾ ਐਲਾਨ ਕਰਦਾ ਹੈ । ਇਸ ਦੇ ਬਾਅਦ ਵਿਚ ਰੈਫਰੀ ਜੇਤੂ ਦੀ ਬਾਂਹ ਉੱਪਰ ਚੁੱਕਦਾ ਹੈ । ਜੇਕਰ ਕੁਸ਼ਤੀ ਬਰਾਬਰ ਹੋਵੇ,

ਤਾਂ ਦੋਵੇਂ ਕੁਸ਼ਤੀ ਕਰਨ ਵਾਲਿਆਂ ਦੀਆਂ ਬਾਂਹਾਂ ਉੱਪਰ ਕਰ ਦਿੱਤੀਆਂ ਜਾਂਦੀਆਂ ਹਨ । ਫ਼ੈਸਲੇ ਦੇ ਐਲਾਨ ਤੋਂ ਪਹਿਲਾਂ ਕੋਈ ਵੀ ਆਪਣੀ ਪੁਸ਼ਾਕ ਦੇ ਫੀਤੇ ਢਿੱਲੇ ਨਹੀਂ ਕਰੇਗਾ ।
ਕੁਸ਼ਤੀ ਵਿਚ ਫਾਊਲ ਪਕੜਨਾ :
ਫਾਊਲ ਪਕੜਨਾ (Foul Holds) – ਹੇਠ ਲਿਖੇ ਫਾਊਲ ਮੰਨੇ ਜਾਂਦੇ ਹਨ-

1. ਵਾਲਾਂ ਜਾਂ ਮਾਸ, ਕੰਨਾਂ ਅਤੇ ਗੁਪਤ ਅੰਗਾਂ ਨੂੰ ਖਿੱਚਣਾ ।
2. ਉਂਗਲੀਆਂ ਮਰੋੜਨਾ, ਗੱਲ ਦੱਬਣਾ ਅਤੇ ਜੀਵਨ ਲਈ ਘਾਤਕ ਦੁਸਰੀਆਂ ਤਰ੍ਹਾਂ ਦੀਆਂ ਪਕੜਾਂ ।
3. ਇਸੇ ਤਰ੍ਹਾਂ ਪਕੜ ਕਰਨੀ ਕੀ ਉਹ ਵਿਰੋਧੀ ਪੱਖ ਦੀ ਜਾਨ ਦਾ ਖੌਫ਼ ਬਣ ਜਾਵੇ, ਜਾਂ ਇਹ ਖੌਫ ਹੋਵੇ ਕਿ ਵਿਰੋਧੀ ਖਿਡਾਰੀ ਦੇ ਅੰਗਾਂ ‘ਤੇ ਸੱਟ ਲੱਗ ਜਾਵੇਗੀ ਜਾਂ ਉਸ ਨੂੰ ਕਸ਼ਟ ਦੇਵੇ, ਦਰਦ ਕਰੇ ਤਾਂ ਕਿ ਦੂਜੇ ਖਿਡਾਰੀ ਮਜਬੂਰ ਹੋ ਕੇ ਖੇਡ ਛੱਡ ਜਾਣ ।
4. ਵਿਰੋਧੀ ਖਿਡਾਰੀ ਦੇ ਪੈਰਾਂ ਤੇ ਆਪਣਾ ਪੈਰ ਰੱਖਣਾ ।
5. ਵਿਰੋਧੀ ਪੱਖ ਦੇ ਚਿਹਰੇ ਅੱਖਾਂ ਦੇ ਭਰਵੱਟਿਆਂ ਤੋਂ ਲੈ ਕੇ ਠੋਡੀ ਤਕ) ਨੂੰ ਛੂਹਣਾ ।
6. ਗਲੋਂ ਫੜਨਾ ।
7. ਵਿਰੋਧੀ ਨੂੰ ਉਠਾਉਣਾ, ਜਦੋਂ ਕਿ ਉਹ ਬ੍ਰਿਜ ਪੁਜ਼ੀਸ਼ਨ ਵਿਚ ਹੋਵੇ ਤਾਂ ਉਸ ਨੂੰ ਮੈਟ ਤੇ ਡੇਗਣਾ ।
8. ਸਿਰ ਵਲੋਂ ਧੱਕਾ ਦੇ ਕੇ ਬ੍ਰਿਜ ਤੋੜਨਾ ।
9. ਵਿਰੋਧੀ ਖਿਡਾਰੀਆਂ ਦੀਆਂ ਬਾਂਹਾਂ ਨੂੰ 90° ਦੇ ਕੋਣ ਤੋਂ ਜ਼ਿਆਦਾ ਮੋੜਨਾ ।
10. ਦੋਹਾਂ ਹੱਥਾਂ ਨਾਲ ਸਿਰ ਨੂੰ ਫੜਨਾ ।
11. ਕੂਹਣੀ ਜਾਂ ਗੋਡਿਆਂ ਨੂੰ ਵਿਰੋਧੀ ਖਿਡਾਰੀ ਦੇ ਪੇਟ ਵਿਚ ਮਾਰਨਾ ।
12. ਵਿਰੋਧੀ ਦੀਆਂ ਬਾਹਾਂ ਨੂੰ ਪਿਛਾਂਹ ਨੂੰ ਮੋੜਨਾ ਅਤੇ ਦਬਾਉਣਾ ।
13. ਕਿਸੇ ਤਰ੍ਹਾਂ ਨਾਲ ਸਿਰ ਨੂੰ ਕਾਬੂ ਕਰਨਾ
14. ਸਰੀਰ ਨੂੰ ਜਾਂ ਸਿਰ ਨੂੰ ਲੱਤਾਂ ਰਾਹੀਂ ਕੈਂਚੀ ਮਾਰਨਾ
15. ਮੈਟ ਨੂੰ ਫੜੀ ਰੱਖਣਾ ।
16. ਇਕ ਦੂਜੇ ਨਾਲ ਗੱਲਾਂ ਕਰਨੀਆਂ ਅਤੇ ਖ਼ਤਰਨਾਕ ਹਮਲਾ ਕਰਨਾ ਜਾਂ ਡੇਗਣਾ ।

ਸਾਵਧਾਨੀਆਂ (Precautions) – ਹੇਠ ਲਿਖੀਆਂ ਹਾਲਤਾਂ ਵਿਚ ਸਾਵਧਾਨੀਆਂ ਦਿੱਤੀਆਂ ਜਾ ਸਕਦੀਆਂ ਹਨ-
(ੳ) ਸਥਿਰ ਰੁਕਾਵਟਾਂ,
(ਅ) ਫਾਊਲ ਪਕੜਾਂ,
(ਈ) ਕੁਸ਼ਤੀ ਸਮੇਂ ਅਨੁਸ਼ਾਸ਼ਨਹੀਨਤਾ,
(ਸ) ਨੇਮਾਂ ਦੀ ਉਲੰਘਣਾ ਕਰਨਾ ।

• ਇਹ ਸਾਵਧਾਨੀਆਂ ਖੇਡ ਦੇ ਸਮੇਂ ਕੀਤੇ ਗਏ ਦੂਜੇ ਫਾਉਲਾਂ ਨਾਲ ਗਿਣੀਆਂ ਜਾਣਗੀਆਂ |
• ਤਿੰਨ ਸਾਵਧਾਨੀਆਂ ਜਾਂ ਚੇਤਾਵਨੀਆਂ ਪਿੱਛੋਂ ਬਿਨਾਂ ਕਾਰਨ ਦੱਸੇ ਖਿਡਾਰੀ ਨੂੰ ਹਾਰਿਆ ਹੋਇਆ ਐਲਾਨਿਆ ਜਾ ਸਕਦਾ ਹੈ ।
• ਕਿਸੇ ਵੱਡੀ ਉਲੰਘਣਾ ਕਰਨ ਦੇ ਦੋਸ਼ ਵਿਚ ਕਿਸੇ ਖਿਡਾਰੀ ਨੂੰ ਖੇਡ ਵਿਚੋਂ ਕੱਢਿਆ ਜਾ ਸਕਦਾ ਹੈ ।

ਸਥਿਰ ਰੋਕਾਂ (Obstacles) –

• ਪੇਟ ਦੇ ਭਾਰ ਲੇਟੇ ਰਹਿਣਾ
• ਜਾਣ-ਬੁੱਝ ਕੇ ਮੈਟ ਤੋਂ ਬਾਹਰ ਜਾਣਾ
• ਵਿਰੋਧੀ ਦੇ ਦੋਵੇਂ ਹੱਥ ਫੜੇ ਰੱਖਣਾ ਤਾਂਕਿ ਉਹ ਖੇਡ ਨਾ ਸਕੇ ।
• ਮੈਟ ਤੋਂ ਬਾਹਰ ਜਾਣ ਦੀ ਹਾਲਤ ਵਿਚ ਖਿਡਾਰੀ ਨੂੰ ਚੇਤਾਵਨੀ ਦਿੱਤੀ ਜਾ ਸਕਦੀ ਹੈ ।

ਕੁਸ਼ਤੀਆਂ ਵਿਚ ਰੋਕਾਂ (Stoppages of Bout) – ਨੱਕ ਤੋਂ ਖੂਨ ਵਗਣਾ, ਸਿਰ ਦੇ ਭਾਰ ਡਿਗਣਾ ਜਾਂ ਕਿਸੇ ਦੂਜੇ ਕਾਰਨ ਜ਼ਿਆਦਾ ਤੋਂ ਜ਼ਿਆਦਾ ਪੰਜ ਮਿੰਟਾਂ ਲਈ ਖੇਡ ਨੂੰ ਰੋਕਿਆ ਜਾ ਸਕਦਾ ਹੈ । ਖੇਡ ਦੀ ਇਹ ਰੋਕ ਇਕ ਜਾਂ ਦੋ ਜ਼ਿਆਦਾ ਪੰਜ ਮਿੰਟਾਂ ਲਈ ਹਰੇਕ ਖੇਡ ਨੂੰ ਹੋ ਸਕਦੀ ਹੈ ।

ਕੁਸ਼ਤੀ ਵਿਚ ਸਕੋਰਾਂ ਦੀ ਗਿਣਤੀ-
ਸਕੋਰ (Score) – (ੳ) ਇਕ ਪੁਆਇੰਟ –

• ਇਸ ਖਿਡਾਰੀ ਨੂੰ ਜੋ ਵਿਰੋਧੀ ਖਿਡਾਰੀ ਨੂੰ ਮੈਟ ‘ਤੇ ਡੇਗਦਾ ਹੈ ਅਤੇ ਉਸ ਤੇ ਕੰਟਰੋਲ ਕਾਇਮ ਕਰ ਲੈਂਦਾ ਹੈ ।
• ਉਸ ਖਿਡਾਰੀ ਨੂੰ ਜੋ ਕਿ ਹੇਠੋਂ ਨਿਕਲ ਕੇ ਉੱਪਰ ਆ ਜਾਂਦਾ ਹੈ ਅਤੇ ਵਿਰੋਧੀ ਖਿਡਾਰੀ ‘ਤੇ ਕੰਟਰੋਲ ਕਾਇਮ ਕਰਦਾ ਹੈ ।
• ਜੋ ਖਿਡਾਰੀ ਠੀਕ ਪਕੜ ਲਗਾਉਂਦਾ ਹੈ ਅਤੇ ਵਿਰੋਧੀ ਖਿਡਾਰੀ ਦੇ ਸਿਰ ਅਤੇ ਮੋਢਿਆਂ ਨੂੰ ਮੈਟ ‘ਤੇ ਨਹੀਂ ਲੱਗਣ ਦਿੰਦਾ |
• ਇਕ ਸਾਵਧਾਨੀ ਦਾ ਵਿਰੋਧੀ ਲਈ ਇਕ ਪੁਆਇੰਟ ਹੋਵੇਗਾ ।

(ਅ) ਦੋ ਪੁਆਇੰਟ –
(i) ਉਸ ਖਿਡਾਰੀ ਨੂੰ ਠੀਕ ਪਕੜ ਕਰਦਾ ਹੈ ਅਤੇ ਵਿਰੋਧੀ ਖਿਡਾਰੀ ਨੂੰ ਕੁਝ ਸਮੇਂ ਲਈ ਆਪਣੇ ਅਧੀਨ ਰੱਖਦਾ ਹੈ । (5 ਸੈਕਿੰਡ ਤੋਂ ਘੱਟ ਸਮੇਂ ਲਈ) ਉਸ ਖਿਡਾਰੀ ਨੂੰ ਜਿਸ ਦਾ ਵਿਰੋਧੀ ਛੇਤੀ ਹੀ ਡਿਗ ਜਾਂਦਾ ਹੈ ਜਾਂ ਲੁੜਕਦਾ ਹੋਇਆ ਡਿਗ ਜਾਂਦਾ ਹੈ ।

(ਈ) ਤਿੰਨ ਪੁਆਇੰਟ-

• ਜੋ ਖਿਡਾਰੀ ਆਪਣੇ ਵਿਰੋਧੀ ਨੂੰ ਖ਼ਤਰੇ ਵਿਚ ਰੱਖਦਾ ਹੈ । (ਘੱਟ ਤੋਂ ਘੱਟ ਪੰਜ ਸੈਕਿੰਡ ਤਕ 90° ਤੋਂ ਘੱਟ ਕੌਣ ਬਣਾਉਂਦੇ ਹੋਏ )
• ਕਈ ਵਾਰ ਲੁਕਦੇ ਹੋਏ ਡਿੱਗ ਜਾਣ ਦੀ ਸਥਿਤੀ ਜਾਂ 5 ਸੈਕਿੰਡ ਲਗਾਤਾਰ ਤਿੰਨ ਦੀ ਗਿਣਤੀ ਤਕ ਬ੍ਰਿਜ ਦੀ ਸਥਿਤੀ ।

ਫੈਸਲਾ (Decision) – ਜਦੋਂ ਵਿਰੋਧੀ ਖਿਡਾਰੀਆਂ ਦਾ ਅੰਤਰ ਇਕ ਪੁਆਇੰਟ ਤੋਂ ਘੱਟ ਹੋਵੇ ਤਾਂ ਮੈਚ ਬਰਾਬਰ ਰਹਿੰਦਾ ਹੈ । ਜੇ ਕੋਈ ਵੀ ਅੰਕ ਨਾ ਬਣਿਆ ਹੋਇਆ ਹੋਵੇ ਜਾਂ ਅੰਕ ਬਰਾਬਰ ਹੋਣ ਤਾਂ ਵੀ ਕੁਸ਼ਤੀ ਬਰਾਬਰ ਸਮਝੀ ਜਾਵੇਗੀ । ਜੇ ਇਕ ਤੋਂ ਜ਼ਿਆਦਾ ਅੰਕਾਂ ਦਾ ਫਰਕ ਹੋਵੇ ਤਾਂ ਜ਼ਿਆਦਾ ਅੰਕਾਂ ਵਾਲਾ ਖਿਡਾਰੀ ਜੇਤੁ ਹੋਵੇਗਾ |

ਡਿਗਣਾ (Fall) – (ਉ) ਪੂਰੀ ਤਰ੍ਹਾਂ ਡਿਗ ਜਾਣ ਲਈ ਮੋਢੇ ਅਤੇ ਮੈਟ ਦਾ ਸੰਬੰਧ ਇਕ ਹੀ ਸੰਖਿਆ ਤਕ ਜ਼ਰੂਰੀ ਹੈ । (ਅ) ਮੈਟ ਦੇ ਕਿਨਾਰੇ ‘ਤੇ ਲੀਕ ਡਿਗ ਜਾਣ ਲਈ ਇੰਨਾ ਹੀ ਕਾਫੀ ਹੈ ਕਿ ਡਿਗਦੇ ਸਮੇਂ ਸਿਰ ਅਤੇ ਮੋਢੇ ਮੈਟ ਨੂੰ ਛੂਹ ਜਾਣ ।

(ਬ) ਜੇ ਜੱਜ ਕੋਈ ਇਤਰਾਜ਼ ਨਾ ਕਰੇ ਤਾਂ ਡਿਗ ਜਾਣਾ ਠੀਕ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ ।
ਪੁਆਇੰਟਾਂ ‘ਤੇ ਜਿੱੜਣਾ (Winning by Points) – ਜੇ 6 ਮਿੰਟਾਂ ਵਿਚ ਫਾਊਲ ਨਾ ਹੋਵੇ, ਤਾਂ ਫੈਸਲਾ ਪੁਆਇੰਟਾਂ ਵਿਚ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।
ਜ਼ਿਆਦਾ ਅੰਕ ਪ੍ਰਾਪਤ ਕਰਨ ਵਾਲਾ ਖਿਡਾਰੀ ਜੇਤੂ ਹੋਵੇਗਾ ।

ਫਾਈਨਲ ਲਈ ਨਿਯਮ (Rules for Final) –
(ਉ) ਫਾਈਨਲ ਮੈਚ ਤਿੰਨਾਂ ਖਿਡਾਰੀਆਂ ਵਿਚ ਹੋਵੇਗਾ ।
(ਅ) ਜਿਨ੍ਹਾਂ ਖਿਡਾਰੀਆਂ ਨੇ 6 ਪੈਨਲਟੀ ਅੰਕ ਪ੍ਰਾਪਤ ਕੀਤੇ ਹੋਣ ਉਹ ਫਾਈਨਲ ਵਿਚ ਹਿੱਸਾ ਨਹੀਂ ਲੈ ਸਕਦੇ ।
(ਬ) ਜਦੋਂ ਤਿੰਨ ਖਿਡਾਰੀ 6 ਪੈਨਲਟੀ ਅੰਕਾਂ ਤੋਂ ਘੱਟ ਫਾਈਨਲਾਂ ਵਿਚ ਪਹੁੰਚ ਜਾਣ ਤਾਂ ਪ੍ਰਾਪਤ ਕੀਤੇ ਅੰਕ ਖ਼ਤਮ ਹੋ ਜਾਂਦੇ ਹਨ ।
(ਸ) ਜੇ ਉਹਨਾਂ ਖਿਡਾਰੀਆਂ ਦਾ ਪਹਿਲਾਂ ਹੀ ਮੁਕਾਬਲਾ ਹੋ ਚੁੱਕਿਆ ਹੋਵੇ ਤਾਂ ਪਹਿਲਾਂ ਪ੍ਰਾਪਤ ਕੀਤੇ ਹੋਏ ਪੈਨਲਟੀ ਅੰਕ ਫਾਈਨਲ ਵਿਚ ਹੀ ਗਿਣੇ ਜਾਂਦੇ ਹਨ ।
(ਹ) ਫਾਈਨਲ ਵਿਚ ਖੇਡਣ ਵਾਲੇ ਤਿੰਨ ਖਿਡਾਰੀਆਂ ਦੇ ਪੈਨਲਟੀ ਅੰਕਾਂ ਦੀ ਗਣਨਾ ਜ਼ਰੂਰ ਧਿਆਨ ਵਿਚ ਰੱਖੀ . ਜਾਵੇ ।
(ਕ) ਜੇ ਤਿੰਨਾਂ ਵਿਚੋਂ ਹਰੇਕ ਖਿਡਾਰੀ ਨੇ ਪਹਿਲੇ ਹੀ 6 ਪੈਨਲਟੀ ਅੰਕ ਪ੍ਰਾਪਤ ਕਰ ਲਏ ਹੋਣ ਤਾਂ ਉਹ ਉੱਪਰ ਲਿਖੇ ਅਨੁਸਾਰ ਅੰਕ ਖੋ ਦੇਣਗੇ ।
(ਖ) ਜੇ ਫਾਈਨਲ ਵਿਚ ਪਹੁੰਚੇ ਤਿੰਨਾਂ ਖਿਡਾਰੀਆਂ ਨੇ ਪਹਿਲਾਂ ਹੀ 6 ਅੰਕ ਲਏ ਹੋਣ ਤਾਂ ਉਸ ਨੂੰ ਤੀਜਾ ਸਥਾਨ ਪ੍ਰਾਪਤ ਹੋਵੇਗਾ ਅਤੇ ਬਾਕੀ ਦੋ ਪਹਿਲੀ ਹਾਲਤ ਲਈ ਕੁਸ਼ਤੀ ਕਰਨਗੇ ।
(ਗ) ਜੇਤੂ ਉਹੀ ਹੋਵੇਗਾ ਜੋ ਅੰਤਮ ਤਿੰਨਾਂ ਕੁਸ਼ਤੀਆਂ ਦੇ ਸਮੇਂ ਘੱਟੋ-ਘੱਟ ਪੈਨਲਟੀ ਅੰਕ ਪ੍ਰਾਪਤ ਕਰੇਗਾ ।
(ਘ) ਜੇ ਫਾਈਨਲ ਦੇ ਖਿਡਾਰੀਆਂ ਦੇ ਪੈਨਲਟੀ ਅੰਕ ਬਰਾਬਰ ਹੋਣ ਤਾਂ ਉਹਨਾਂ ਦੀ ਸਥਿਤੀ ਇਸ ਤਰ੍ਹਾਂ ਹੋਵੇਗੀ ।

• (i) ਫਾਊਲ ਦੀ ਗਿਣਤੀ ।
• (ii) ਅੰਕਾਂ ਤੇ ਪ੍ਰਾਪਤ ਕੀਤੀ ਹੋਈ ਜਿੱਤ ।
• (iii) ਬਰਾਬਰ ਰਹਿਣ ਦੀ ਗਿਣਤੀ ।
• (iv) ਜੇ ਟਾਈ ਦੀ ਹਾਲਤ ਅਜੇ ਰਹਿੰਦੀ ਹੋਵੇ ਤਾਂ ਜਿਸ ਖਿਡਾਰੀ ਨੇ ਘੱਟੋ-ਘੱਟ ਚੇਤਾਵਨੀਆਂ ਲਈਆਂ ਹੋਣ ਤਾਂ ਉਹ ਜੇਤੂ ਹੁੰਦਾ ਹੈ ।
• (v) ਜੇ ਫਿਰ ਵੀ ਟਾਈ ਰਹਿੰਦੀ ਹੋਵੇ ਤਾਂ ਦੋਵੇਂ ਖਿਡਾਰੀ ਬਰਾਬਰ ਮੰਨੇ ਜਾਂਦੇ ਹਨ ।

ਅਧਿਕਾਰੀ (Officials) – ਕੁਸ਼ਤੀ ਵਿਚ ਜਿੰਨੀਆਂ ਵੀ ਪ੍ਰਤਿਯੋਗਤਾਵਾਂ ਹੋਣ, ਉਹਨਾਂ ਵਿਚ ਤਿੰਨ ਅਧਿਕਾਰੀ ਹੁੰਦੇ ਹਨ

1. ਮੈਟ ਚੇਅਰਮੈਨ (Met Chairman)
2. ਰੈਫਰੀ (Referee)
3. ਜੱਜ (Judge)
   ਕੁਸ਼ਤੀ ਦੇ ਦੌਰਾਨ ਕੋਈ ਵੀ ਅਧਿਕਾਰੀ ਬਦਲਿਆ ਨਹੀਂ ਜਾ ਸਕਦਾ ।

ਸਪਰੋਟਸ ਅਵਾਰਡਨ
(Sports Award)

ਅਰਜੁਨ ਅਵਾਰਡ ਜੇਤੂਆਂ ਦੀ ਸੂਚੀ (List of Arjuna Award Winners) – ਉਦੈ ਚੰਦ (1961), ਮਲਵਾ (1962), ਜੀ.ਅੰਦਾਲਕਰ (1963), ਬਿਸ਼ੰਬਰ ਸਿੰਘ (1964), ਭੀਮ ਸਿੰਘ (1966), ਮੁਖਤਿਆਰ ਸਿੰਘ (1967), ਚੰਦਗੀ ਰਾਮ (1969), ਸੁਦੇਸ਼ ਕੁਮਾਰ (1970), ਪ੍ਰੇਮ ਨਾਥ (1972), ਜਗਰੂਪ ਸਿੰਘ (1973), ਸਤਪਾਲ (1974), ਰਾਜਿੰਦਰ ਸਿੰਘ (1978-79), ਜਗਮਿੰਦਰ ਸਿੰਘ (1980-81), ਕਰਤਾਰ ਸਿੰਘ (1982), ਮਹਾਬੀਰ ਸਿੰਘ (1985), ਸੁਭਾਸ਼ (1987), ਰਾਜੇਸ਼ ਕੁਮਾਰ (1988), ਸਤਿਆਵਾਨ (1989), ਉਮਬੀਰ ਸਿੰਘ (1990), ਪੱਪੂ ਯਾਦਵ (1992), ਅਸ਼ੋਕ ਕੁਮਾਰ (1993), ਕਾਕਾ ਪਵਾਰ, ਰੋਹਤਾਸ ਸਿੰਘ ਦਾਹੀਆਂ (1999), ਰਣਧੀਰ ਸਿੰਘ, ਕ੍ਰਿਪਾ ਸ਼ੰਕਰ, ਸੁਰਗਵਾਸੀ ਕੇ.ਡੀ. ਯਾਦਵ (ਮੌਤ ਤੋਂ ਬਾਅਦ, ਨਰੇਸ਼ ਕੁਮਾਰ (2000), ਪਲਵਿੰਦਰ ਚੀਮਾਂ (2002), ਸੋਕੇਂਦਰ ਤੋਮਰ (2004), ਰਵਿੰਦਰ ਸਿੰਘ (2011) ।
ਦਰੋਣਾਚਾਰੀਆ ਅਵਾਰਡ (ਕੋਚਾਂ ਲਈ)-ਗੁਰੂ ਹਨੂਮਾਨ ਸਿੰਘ, ਬਾਲਾ ਚੰਦਰ ਭਾਸਕਰ, ਭਾਗਵਤ, ਸੁਖਚੈਨ ਚੀਮਾ ।. ਧਿਆਨ ਚੰਦ ਅਵਾਰਡ-ਰਾਜ ਕੁਮਾਰ (2011) ।

PSEB 12th Class Physical Education Practical ਕੁਸ਼ਤੀਆਂ-ਫਰੀ ਸਟਾਈਲ ਅਤੇ ਗਰੀਕੋ ਰੋਮਨ (Wrestling Free Style and Greeco Roman)

ਪ੍ਰਸ਼ਨ 1.
ਕੁਸ਼ਤੀਆਂ ਦੇ ਭਾਗ ਦਾ ਵਰਣਨ ਕਰੋ ।
ਉੱਤਰ-

1. ਫਰੀ ਸਟਾਈਲ
2. ਗਰੀਕੋ ਰੋਮਨ ।

ਪ੍ਰਸ਼ਨ 2.
ਕੁਸ਼ਤੀਆਂ ਦਾ ਸਮਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
6 ਮਿੰਟ, ਤਿੰਨ-ਤਿੰਨ ਮਿੰਟ ਦੇ ਦੋ ਹਾਫ਼ ।

ਪ੍ਰਸ਼ਨ 3.
ਕੁਸ਼ਤੀਆਂ ਦੇ ਮੈਟ ਦਾ ਅਰਧ ਵਿਆਸ ਦੱਸੋ ।
ਉੱਤਰ-
4.50 ਮੀਟਰ ਅਰਧ-ਵਿਆਸ ।

ਪ੍ਰਸ਼ਨ 4.
ਰੈਫਰੀ ਖਿਡਾਰੀ ਨੂੰ ਕਿੰਨੀ ਵਾਰ ਚੇਤਾਵਨੀ ਦੇ ਸਕਦਾ ਹੈ ?
ਉੱਤਰ-
ਤਿੰਨ ਵਾਰ ।

ਪ੍ਰਸ਼ਨ 5.
ਕੁਸ਼ਤੀ ਲੜਨ ਵਾਲੇ ਖਿਡਾਰੀ ਲਈ ਕਿਸ ਤਰ੍ਹਾਂ ਦਾ ਪਹਿਰਾਵਾ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ?
ਉੱਤਰ-
ਬਨਿਆਨ, ਕੱਛਾ ਜਾਂ ਜਰਸੀ ।

ਪ੍ਰਸ਼ਨ 6.
ਕੁਸ਼ਤੀਆਂ ਦੀ ਹਾਰ ਜਿੱਤ ਦਾ ਫੈਸਲਾ ਕਿਵੇਂ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਜਿਸ ਦੇ ਅੰਕ ਜ਼ਿਆਦਾ ਹੋਣ, ਉਹ ਜੇਤੂ ਅਤੇ ਜਿਸਦੇ ਅੰਕ ਘੱਟ ਹੋਣ, ਉਹ ਹਾਰਿਆ ਹੋਇਆ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 7.
ਕੁਸ਼ਤੀਆਂ ਦੇ ਅਧਿਕਾਰੀਆਂ ਬਾਰੇ ਦੱਸੋ ।
ਉੱਤਰ-
ਕੁਸ਼ਤੀ ਵਿਚ ਛੇ ਅਧਿਕਾਰੀ ਹੁੰਦੇ ਹਨ । ਮੈਟ ਚੇਅਰਮੈਨ 1, ਰੈਫਰੀ 2 ਅਤੇ ਜੱਜ ਤੇ ਹੁੰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 8.
ਕੁਸ਼ਤੀਆਂ ਵਿਚ ਫਾਊਲ ਪਕੜਾਂ ਕਿਹੜੀਆਂ ਹੁੰਦੀਆਂ ਹਨ ?
ਉੱਤਰ-

1. ਵਾਲਾਂ ਜਾਂ ਮਾਸ, ਕੰਨਾਂ ਅਤੇ ਗੁਪਤ ਅੰਗਾਂ ਨੂੰ ਖਿੱਚਣਾ ।
2. ਉਂਗਲੀਆਂ ਮਰੋੜਨਾ, ਗਲ ਦੱਬਣਾ ਅਤੇ ਜੀਵਨ ਲਈ ਘਾਤਕ ਦੂਸਰੀਆਂ ਤਰ੍ਹਾਂ ਦੀਆਂ ਪੰਕੜਾਂ ।
3. ਇਸੇ ਤਰ੍ਹਾਂ ਪਕੜ ਕਰਨੀ ਕੀ ਉਹ ਵਿਰੋਧੀ ਪੱਖ ਦੀ ਜਾਨ ਦਾ ਖੌਫ਼ ਬਣ ਜਾਵੇ, ਜਾਂ ਇਹ ਖੌਫ ਹੋਵੇ ਕਿ ਵਿਰੋਧੀ ਖਿਡਾਰੀ ਦੇ ਅੰਗਾਂ ‘ਤੇ ਸੱਟ ਲੱਗ ਜਾਵੇਗੀ ਜਾਂ ਉਸ ਨੂੰ ਕਸ਼ਟ ਦੇਵੇ, ਦਰਦ ਕਰੇ ਤਾਂ ਕਿ ਦੂਜੇ ਖਿਡਾਰੀ ਮਜਬੂਰ ਹੋ ਕੇ ਖੇਡ ਛੱਡ ਜਾਣ ।
4. ਵਿਰੋਧੀ ਖਿਡਾਰੀ ਦੇ ਪੈਰਾਂ ਤੇ ਆਪਣਾ ਪੈਰ ਰੱਖਣਾ ।.

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 1 Relations and Functions Miscellaneous Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 1 Relations and Functions Miscellaneous Exercise

Question 1.
Let f: R → R be defined as f(x) = 10x + 7. Find the function g: R → R such that gof = fog = I_R.
Solution.
It is given that f: R → R is defined as f(x) = 10x + 7.
One – one :
Let f(x) = f(y), where x, y ∈ R.
⇒ 10x + 7 = 10y + 7
⇒ x = y
∴ f is a one-one function.

Onto :
For y ∈ R, let y = 10x + 7.
⇒ x = \(\frac{y-7}{10}\) ∈ R
Therefore, for any y ∈ R, there exists x = \(\frac{y-7}{10}\) ∈ R such that
f(x) = f(\(\frac{y-7}{10}\))
= 10(\(\frac{y-7}{10}\)) + 7
= y – 7 + 7 = y
∴ f is onto.
Therefore f is one-one and onto.
Thus f is an invertible function.
Let us define g : R → R as g(y) = \(\frac{y-7}{10}\)
Now, we have
gof(x) = g(f(x)) = g(10x + 7)
= \(\frac{(10 x+7)-7}{10}=\frac{10 x}{10}\) = x
And, fog(y) = f(g(y))
= f(\(\frac{y-7}{10}\))
= 10(\(\frac{y-7}{10}\)) + 7
= y – 7 + 7 = y
∴ gof = I_R and fog = I_R
Hence, the required functiong:R → R is defined as g(y) = \(\frac{y-7}{10}\)

Question 2.
Let f: W → W be defined as f(n) = n – 1, if n is odd and f(n) = n + 1, if n is even. Show that f is invertible. Find the inverse of f. Here, W is the set of all whole numbers.
Solution.
It is given that
f: W → W is defined as f(n) =

One-one :
Let f(n) = f(m)
It can be observed that if n is odd and m is even, then we will have
n – 1 = m + 1
⇒ n – m = 2
However, this is impossible.
Similarly, the possibility of n being even and m being odd can also ignored under a similar argument.
∴ Both n and m must be either odd or even.
Now, if both n and m are odd, then we have
f(n) = f(m) ⇒ n – 1 = m – 1 ⇒ n = m
Again, if both n and m are even , then we have
f(n) = f(m) ⇒ n + 1 = m+1 ⇒ n = m
∴ f is one – one.

Onto :
It is clear that any odd number 2r + 1 in co-domain W is the image of 2r in domain W and any even number 2r in co-domain W is the image of 2r + 1 in domain W.
∴ f is onto.
Hence, f is an invertible function.
Let us define g : W → W as

g(m) =

Now, when n is odd
gof(n) = g(f(n)) = g(n – 1) = n – 1 + 1 = n
and, when n is even
gof(n) = g(f(n)) = g(n + 1) = n + 1 – 1 = n
Similarly, when m is odd
fog(m) = f(g(m)) = f(m – 1) = m – 1 + 1 = m
and when m is even
fog(m) = f(g(m)) = f(m + 1) = m + 1 – 1 = m
∴ gof = I_W and fog = I_W
Thus, f is invertible and the inverse of f is given by f^-1 = g, which is the same as f.
Hence, the inverse of f is itself.

Question 3.
If f: R → R is defined by f(x) = x² – 3x + 2, find f(f(x)).
Solution.
It is given that f: R → R is defined as f(x) = x² – 3x + 2.
f(f(x)) = f(x² – 3x + 2)
= (x² – 3x + 2)² – 3(x² -3x + 2) + 2
= x⁴ + 9x² + 4 – 6x³ – 12x + 4x² – 3x² + 9x – 6 + 2
= x⁴ – 6x³ + 10x² – 3x.

Question 4.
Show that the function f: R → {x ∈ R: – 1 < x < 1} defined by f(x) = \(\frac{x}{1+|x|}\) ∈ R is one-one and onto function.
Solution.
It is given that f: R → {x ∈ R: – 1 < x < 1} is defined as f(x) = \(\frac{x}{1+|x|}\), x ∈ R.
Suppose f(x) = f(y), where x,y ∈ R ⇒ \(\frac{x}{1+|x|}=\frac{y}{1+|y|}\)
It can be observed that if x is positive and y is negative, then we have \(\frac{x}{1+x}=\frac{y}{1-y}\)
⇒ 2xy = x – y
Since x is positive and y is negative, then x > y ⇒ x – y > 0
But, 2xy is negative.
Then, 2xy ≠ x – y.
Thus, the case of x being positive and y being negative can be ruled out.
Under a similar argument, x being negative and y being positive can also be ruled out.
∴ x and y have to be either positive or negative.
When x and y are both positive, we have x y
f(x) = f(y)
⇒ \(\frac{x}{1+x}=\frac{y}{1+y}\)
⇒ x + xy = y + xy
⇒ x = y
When x and y are both negative, we have
f(x) = f(y)
⇒ \(\frac{x}{1-x}=\frac{y}{1-y}\)
⇒ x – xy = y – yx
⇒ x = y
∴ f is one-one.
Now, let y ∈ R such that – 1 < y < 1.
If y is negative, then there exists x = \(\frac{y}{1+y}\) ∈ R such that
f(x) = f(\(\frac{y}{1+y}\))
= \(\frac{\left(\frac{y}{1+y}\right)}{1+\left|\frac{y}{1+y}\right|}=\frac{\frac{y}{1+y}}{1+\left(\frac{-y}{1+y}\right)}=\frac{y}{1+y-y}\) = y
If y is positive, then there exists x = \(\frac{y}{1-y}\) ∈ R such that
f(x) = \(f\left(\frac{y}{1-y}\right)=\frac{\left(\frac{y}{1-y}\right)}{1+\left(\frac{y}{1-y}\right)}\)

= \(\frac{\frac{y}{1-y}}{1+\left(\frac{y}{1-y}\right)}=\frac{y}{1-y+y}\) = y
∴ f is onto.
Hence, f is one-one and onto.

Question 5.
Show that the function f: R → R given by f(x) = x³ in injective.
Solution.
f: R → R is given as f(x) = x³.
Suppose f(x) = f(y), where x, y ∈ R.
⇒ x³ = y³ …………(i)
Now, we need to show that x = y
Suppose x * y, their cubes will also not be equal.
⇒ x³ ≠ y³
However, this will be a contradiction to Eq. (i).
∴ x = y
Hence, f is injective.

c

Question 6.
Give examples of two functions f: N → Z and g: Z → Z such that gof is injective but g is not injective.
[Hint: consider f(x) x and g(x) = |x|].
Solution.
Define f: N → Z as f(x) – x and g: Z → Z as g(x) =|x|
We first show that g is not injective.
It can be observed that
g(- 1) = |- 1|= 1; g(1) = |1|= 1
∴ g(- 1) = g(1), but – 1 ≠ 1.
∴ g is not injective.
Now, gof: N → Z is defined as gof(x) = g(f(x)) = g(x) =|x|.
Let x, y ∈ N such that gof(x) – gof(y).
⇒ |x| = |y|
Since x and y ∈ N, both are positive.
∴ |x |= |y |=> x = y
Hence, gof is injective.

Question 7.
Give examples of two functions f: N → N and g: N → N such that gof is onto but f is not onto.
[Hint: consider f(x) = x + 1 and g(x) = i]
Solution.
Define f: N → N by f(x) = x +1
and, g: N → N by g(x) =
We first show that f is not onto.
For this, consider element 1 in co-domain N. It is clear that this element is not an image of any of the elements in domain N.
∴ f is not onto.
Now, gof: N → N is defined by,
gof(x) = g(f(x)) = g(x + 1) = (x + 1) – 1 = x [∵ x ∈ N ⇒ (x + 1) > 1]
Then, it is clear that for y ∈ N, there exists x = y ∈ N such that gof(x) = y.
Hence, gof is onto.

Question 8.
Given a non-empty set X, consider P(X) which is the set of all subsets of X.
Define the relation R in P(X) as follows:
For subsets A, B in P(X), ARB if and only if A c B. Is R an equivalence relation on P(X)? Justify your answer.
Solution.
Since every set is a subset of itself, ARA for all A ∈ P(X).
∴ R is reflexive.
Let ARB ⇒ A ⊂ B.
This cannot be implied to B ⊂ A.
For instance, if A = {1, 2} and B = {1, 2,3}, then it cannot be implied that B is related to A.
∴ R is not symmetric.
Further, if ARB and BRC, then A c B and B c C.
⇒ A ⊂ C
⇒ ARC
R is transitive.
Hence, R is not an equivalence relation since it is not symmetric.

Question 9.
Given a non-empty set X, consider the binary operation *: P(X) × P(X) P(X) given by A * B = A ∩ B ∀ A, B in P(X) where P(X) is the power set of X. Show that X is the identity element for this operation and X is the only invertible element in P(X) with respect to the operation*.
Solution.
It is given that * : P(X) × P(X) → P(X) is defined as A * B = A ∩ B ∀ A, B ∈ P(X).
We know that A * X = A ∩ X = A = X ∩ A ∀ A ∈ P(X).
⇒ A * X = A = X * A ∀ A ∈ P (X)
Thus, X is the identity element for the given binary operation*.
Now, an element A ∈ P(X) is invertible if there exists B ∈ P(x) such that
A * B = X = B * A. (As X is the identity element)
i.e., A ∩ B = X = B ∩ A
This case in possible only when A = X = B.
Thus, X is the only invertible element in P(X) with respect to the given operation*.
Hence, the given result is proved.

Question 10.
Find the number of all onto functions from the set {1, 2, 3, n} to itself.
Solution.
Onto functions from the set {1, 2, 3, …, n} to itself is simply a permutation on n symbols 1, 2, …, n.
Thus, the total number of onto maps from {1, 2, 3,…, n} to itself is the same as the total number of permutations on symbols 1, 2,…, n, which is n!.

Question 11.
Let S = {a, b, c} and T = {1,2, 3}. Find F^-1 of the following functions F from S to T, if it exists.
(i) F = {(o, 3), (6, 2), (c, 1)}
(ii) F = {(a, 2), (6, 1), (c, 1)}
Solution.
Given, S = {a, b, c}, and T = {1, 2, 3}
F: S → T is defined as :
F = {(a, 3), (b, 2), (c, 1)}
⇒ f(a) = 3, F(b) = 2, F(c) = 1
Therefore, F^-1 : T → S is given by
F^-1 = {(3, a), (2, b), (1, c)}

(ii) F: S → T is defined as
F = {(a, 2), (b, 1), (c, 1)}
Since F (b) = F (c) = 1, F is not one-one.
Hence, F is not invertible i. e., F^-1 does not exist.

Question 12.
Consider the binary operations * : R × R → R and o: R × R → R defined as a * b = | a – b| and a o b = a, ∀ a, b ∈ R. Show that * is commutative hut not associative, o is associative but not commutative. Further, show that ∀ a, b, c ∈ R, a* (b o c) = (a * b) o (a * c). [If it is so, we say that the operation * distributes over the operation o]. Does o distribute over *? Justify your answer.
Solution.
It is given that *: R × R R and o: R × R → R is defined as a * b = |a – b| and a o b = a ∀ a, b ∈ R.
For a, b ∈ R, we have
a * b = |a – b|
b * a = |b – a| = |- (a – b)|= |a – b|
∴ a * b = b * a
Therefore, the operation * is commutative..
It can be observed that
(1 * 2) * 3 = (|1 – 2|) * 3 = 1 * 3 = |1 – 3|= 2
1 * (2 * 3) = 1 * (|2 – 3|) = 1 * 1 =|1 – 1 |= 0
∴ (1 * 2) * 3 ≠ 1 * (2 * 3) (where 1, 2, 3 ∈ R)
Therefore, the operation * is not associative.
Now, consider the operation o
It can be observed that 1 o 2 = 1 and 2 o 1 = 2.
∴ 1 o 2 ≠ 2 o 1 where 1, 2 ∈ R
Therefore, the operation o is not commutative.
Let a, b, c ∈ R. Then, we have
(a o b) o c = a o c = a
a o (b o c) = a o b = a
⇒ (a o b) o c = a o (b o c)
Therefore, the operation o is associative.
Now, let a, b, c ∈ R, then we have
a * (b o c) = a * b = |a – b|
(a * b) o (a * c) = (|a – b|) o (|a – c|) = |a – b|
Hence a * (b o c) = (a * b) o (a * c)
Now, 1 o(2 * 3) = 1 o (|2 – 3|) = 1 o 1 = 1
(1 o 2) * (1 o 3) = 1 * 1 = |1 – 1|= 0
1 o (2 * 3) ≠ (1 o 2) * (1 o 3)
where 1, 2, 3 ∈ R Therefore, the operation o does not distribute over *.

Question 13.
Given a non-empty set X, let *: P(X) × P(X) → P(X) be defined as A * B – (A – B) ∪ (B – A), ∀ A, B ∈ P(X). Show that the empty set Φ is the identity for the operation * and all the elements A of P(X) are invertible with A^-1 = A.
[Hint: (A – Φ) ∪ (Φ – A) = A and (A – A) ∪ (A – A) = A * A = Φ]
Solution.
It is given that *: P(X) × P(X) → P(X) is defined as
A * B = (A – B) ∪ (B – A) ∀ A, B, ∈ P(X).
Let A ∈ P(X). Then, we have
A * (Φ) = (A – Φ) ∪ (Φ – A) = A ∪ Φ = A
Φ * A = (Φ – A) ∪ (A – Φ) = Φ ∪ A = A
A * Φ = A = Φ * A ∀ A ∈ P(X)
Thus, Φ is the identity element for the given operation *.
Now, an element A s P(X) will be invertible if there exists B ∈ P(X) such that
A * B = Φ = B * A. (As Φ is the identity element)
Now, we observed that
A * A = (A – A) ∪ (A – A) = Φ ∪ Φ = Φ ∀ A ∈ P(X).
Hence, all the elements A of P(X) are invertible with A^-1 = A.

Question 14.
Define a binary operation * on the set {0, 1, 2, 3, 4, 5) as
a * b =
Show that zero is the identity for this operation and each element a ≠ 0 of the set is invertible with 6 – a being the inverse of a.
Solution.
(i) e is the identity element if a * e = e * a = a
a * 0 = a + 0, 0 * a = 0 + a = a
⇒ a * 0 = 0 * a = a
∴ 0 is the identity of the operation.

(ii) b is the inverse of a if a * b = b * a = e
Now a * (6 – a) = a + (6 – a) – 6 = 0
(6 – a) * a = (6 – a) + a – 6 = 0
Hence, each element of a of the set is invertible with inverse.

Question 15.
Let A = {-1, 0, 1, 2}, B = {-4,-2, 0,2} and f, g: A → B be functions defined by f(x) = x² – x, x ∈ A and g(x) = 2|x – \(\frac{1}{2}\)| – 1, x ∈ A. Are f and g equal? Justify your answer.
[Hint: One may not be that two functions f: A → B and g: A → B
such that f(a) = g(a) ∀ a ∈ A, are called equal functions.]
Solution.
It is given that A = {- 1,0,1, 2}, B = {- 4, – 2, 0, 2).
Also, it is given that f, g: A → B are defined by f(x) = x² – x, x ∈ A and
g(x) = 2 |x – \(\frac{1}{2}\)| – 1, x ∈ A
It is observed that
f(- 1) = (- 1)² – (- 1) = 1 + 1 = 2
and g(- 1) = 2|(- 1) – \(\frac{1}{2}\)| – 1
= 2(\(\frac{3}{2}\)) – 1 = 3 – 1 = 2
⇒ f(- 1) = g(- 1)

⇒ f(0) = (0)² – 0 = 0
and g(0) = 2|0 – \(\frac{1}{2}\)|
= 2(\(\frac{3}{2}\)) – 1 = 1 – 1 = 0

⇒ f(0) = g(0)
f(1) = (1)² – 1 = 1 – 1 = 0
and g(1)= 2|1 – \(\frac{1}{2}\)|
= 2(\(\frac{1}{2}\)) – 1 = 1 – 1 = o

⇒ f(1) = g(1)
f(2) = (2)² – 2 = 4 – 2 = 2
and g(2) = 2 |2 – \(\frac{1}{2}\)|
= 2(\(\frac{3}{2}\)) – 1 = 3 – 1 = 2
⇒ f(2) = g(2)
∴ f(a) = g(a) ∀ a ∈ A
Hence, the functions f and g are equal.

Question 16.
Let A = {1, 2, 3}. Then, number of relations containing (1, 2) and (1, 3) which are reflexive and symmetric but not transitive, is
(A) 1
(B) 2
(C) 3
(D) 4
Solution.
This is because relation R is reflexive as (1, 1), (2, 2), (3, 3) ∈ R.
Relation R is symmetric since (1, 2), (2 ,1) ∈ R and (1, 3), (3, 1) ∈ R.
But relationR is not transitive as (3, 1), (1, 2) ∈ R but (3, 2) ∈ R.
Now, if we add any one of the two pairs (3, 2) and (2, 3) (or both) to relation R, then relation R will become transitive.
Hence, the total number of desired relation is one.
Thus, the correct option is (A).

Question 17.
Let A = {1, 2, 3}. Then, number of equivalence relations containing (1, 2) is
(A) 1
(B) 2
(C)3
(D) 4
Solution.
It is given that A = {1, 2, 3}
The smallest equivalence relation containing (1, 2) is given by,
R₁ = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 1)}
Now, we are left with only four pairs i. e., (2, 3), (3, 2), (1, 3), and (3, 1).
If we add any one pair [say (2, 3)] to R₁ then for symmetry we must add (3, 2). Also, for transitivity, we are required to add (1, 3) and (3,1). Hence, the only equivalence relation (bigger than R₁) is the universal relation.
This shows that the total number of equivalence relations containing (1, 2) is two. The correct option is (B).

Question 18.
Let f: R → R be the signum function defined as
f(x) =
and g: R → R be the greatest integer function given by g(x) = [x], where [x] is greatest integer less than or equal to x. Then, does fog and gof coincide in (0, 1]?
Solution.
It is given that
f: R → R is defined as f(x) =
Also, g: R → R is defined as g(x) = [x], where [x] is the greatest integer less than or equal to x .
Now, let x ∈ (0, 1]
Then, we have
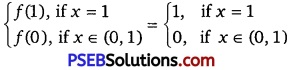[x] = 1, if x = 1 and [x] = 0 if 0 < x < 1. ∴ fog(x) = f (g(x)) = f([x]) = gof(x) = g(f(x))= g(1) [∵ x > 0]
= [1] = 1 .
Thus, when x ∈ (0, 1), we have fog(x) = 0 and gof(x) = 1.
But fog (1) ≠ gof (1)
Hence, fog and gof do not coincide in (0,1].

Question 19.
Number of binary operations on the set {a, b} are (A) 10 (B) 16 (C) 20 (D) 8
Solution.
A binary operation * on {a, b} is a function from {a, b} × {a, b} → {a, b} i. e.,* is a function from {(a, a), (a, b), (b, a), (b, b)} → {a, b}.
Hence, the total number of binary operations on the set {a, b} is 2⁴ i.e. 16.
Thus, the correct option is (B).

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 2 Inverse Trigonometric Functions Ex 2.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 2 Inverse Trigonometric Functions Ex 2.2

Direction (1 – 4): Prove the following.

Question 1.
3 sin^-1 x = sin^-1 (3x – 4x³), x ∈ [- \(\frac{1}{2}\), \(\frac{1}{2}\)]
Solution.
Let x = sin θ. Then, sin^-1 x = θ.
We have,
R.H.S. = sin^-1 (3x – 4x³) = sin^-1(3 sin θ – 4 sin³ θ)
= sin^-1 (sin 3θ) = 3θ = 3 sin^-1 x
= L.H.S.
Hence proved.

Question 2.
3 cos^-1 x = cos^-1 (4x³ – 3x), x ∈ [\(\frac{1}{2}\), 1]
Solution.
Let x = cos θ. Then, cos^-1 x = θ.
We have, R.H.S. = cos^-1 (4x³ – 3x)
= cos^-1 (4cos 3θ – 3 cos θ)
= cos^-1 (cos 3θ) = 3θ = 3 cos^-1 x
= L.H.S.
Hence proved.

Question 3.
tan^-1 \(\frac{2}{11}\) + tan^-1 \(\frac{7}{24}\) = tan^-1 \(\frac{1}{2}\).
Solution.
Given, tan^-1 \(\frac{2}{11}\) + tan^-1 \(\frac{7}{24}\) = tan^-1 \(\frac{1}{2}\)

Question 4.
2 tan^-1 \(\frac{1}{2}\) + tan^-1 \(\frac{1}{7}\) = tan^-1 \(\frac{31}{17}\)
Solution.
Given, 2 tan^-1 \(\frac{1}{2}\) + tan^-1 \(\frac{1}{7}\) = tan^-1 \(\frac{31}{17}\)
L.H.S. = 2 tan^-1 \(\frac{1}{2}\) + tan^-1 \(\frac{1}{7}\)
= \(\tan ^{-1}\left[\frac{2 \cdot \frac{1}{2}}{1-\left(\frac{1}{2}\right)^{2}}\right]+\tan ^{-1}\left(\frac{1}{7}\right)\) [∵ 2 tan^-1 x = tan^-1 (\(\frac{2 x}{1-x^{2}}\))]

Direction (5 – 10):- Write the following functions in the simplest form:

Question 5.
tan^-1 \(\frac{\sqrt{1+x^{2}}-1}{x}\), x ≠ 0.
Solution.
We have, tan^-1 \(\frac{\sqrt{1+x^{2}}-1}{x}\)
put x = tan θ
⇒ θ = tan^-1 x

Question 6.
tan^-1 \(\frac{1}{\sqrt{x^{2}-1}}\), |x| > 1
Solution.
Let x = sec θ, then θ = sec^-1 x
∴ tan^-1 \(\frac{1}{\sqrt{x^{2}-1}}\) = tan^-1 \(\left(\frac{1}{\sqrt{\sec ^{2} \theta-1}}\right)\)
= tan^-1 \(\left(\frac{1}{\sqrt{\tan ^{2} \theta}}\right)\) [∵ sec² θ – 1 = tan² θ]
= tan^-1 \(\left(\frac{1}{\tan \theta}\right)\)
= tan^-1 (cot θ)
= tan^-1 [tan (\(\frac{\pi}{2}\) – θ)] [∵ tan (\(\frac{\pi}{2}\) – θ) = cot θ]
= \(\frac{\pi}{2}\) – θ
= \(\frac{\pi}{2}\) – sec^-1 x

Question 7.
tan^-1 \(\left(\sqrt{\frac{1-\cos x}{1+\cos x}}\right)\), x < π.
Solution.
We have, tan^-1 \(\left(\sqrt{\frac{1-\cos x}{1+\cos x}}\right)\)
= tan^-1 \(\left(\sqrt{\frac{2 \sin ^{2} \frac{x}{2}}{2 \cos ^{2} \frac{x}{2}}}\right)\)
= tan^-1 (tan \(\left(\frac{\sin \frac{x}{2}}{\cos \frac{x}{2}}\right)\))
= tan^-1 (tan \(\frac{x}{2}\))
= \(\frac{x}{2}\).

Question 8.
tan^-1 (\(\frac{\cos x-\sin x}{\cos x+\sin x}\)), 0 < x < π.
Solution.

Question 9.
tan^-1 \(\frac{x}{\sqrt{a^{2}-x^{2}}}\), |x| < a.
Solution.
We have, tan^-1 \(\frac{x}{\sqrt{a^{2}-x^{2}}}\)
Let x = a sin θ
⇒ \(\frac{x}{a}\) = sin θ
⇒ θ = sin^-1 (\(\frac{x}{a}\))
∴ tan^-1 \(\frac{x}{\sqrt{a^{2}-x^{2}}}\) = tan^-1 \(\left(\frac{a \sin \theta}{\sqrt{a^{2}-a^{2} \sin ^{2} \theta}}\right)\)
= tan^-1 \(\left(\frac{a \sin \theta}{a \sqrt{1-\sin ^{2} \theta}}\right)\)
= tan^-1 \(\left(\frac{a \sin \theta}{a \cos \theta}\right)\)
= tan^-1 (tan θ)
= θ = sin^-1 \(\frac{x}{a}\).

Question 10.
tan^-1 \(\left(\frac{3 a^{2} x-x^{3}}{a^{3}-3 a x^{2}}\right)\), a > 0; \(\frac{-a}{\sqrt{3}} \leq x \leq \frac{a}{\sqrt{3}}\).
Solution.
We have, tan^-1 \(\left(\frac{3 a^{2} x-x^{3}}{a^{3}-3 a x^{2}}\right)\), a > 0; \(\frac{-a}{\sqrt{3}} \leq x \leq \frac{a}{\sqrt{3}}\)
Let x = a tan θ
⇒ \(\frac{x}{a}\) = tan θ
⇒ θ = tan^-1 \(\frac{x}{a}\)

∴ tan^-1 \(\left(\frac{3 a^{2} x-x^{3}}{a^{3}-3 a x^{2}}\right)\), a > 0; \(\frac{-a}{\sqrt{3}} \leq x \leq \frac{a}{\sqrt{3}}\) = tan^-1 \(\left(\frac{3 a^{2} \cdot(a \tan \theta)-a^{3} \tan ^{3} \theta}{a^{3}-3 a \cdot\left(a^{2} \tan ^{2} \theta\right)}\right)\)

= tan ^-1 \(\left(\frac{3 a^{3} \tan \theta-a^{3} \tan ^{3} \theta}{a^{3}-3 a^{3} \tan ^{2} \theta}\right)\)

= tan^-1 \(\left(\frac{3 \tan \theta-\tan ^{3} \theta}{1-3 \tan ^{2} \theta}\right)\)

= tan^-1 (tan 3θ) [∵ tan 3θ = \(\frac{3 \tan \theta-\tan ^{3} \theta}{1-3 \tan ^{2} \theta}\)]

= 3θ = 3 tan^-1 \(\frac{x}{a}\).

Direction (11 – 15) : Find the value of each of the following.

Question 11.
tan^-1 [2 cos(2 sin^-1 \(\frac{1}{2}\))].
Solution.
Let sin^-1 \(\frac{1}{2}\) = x
Then, sin x = \(\frac{1}{2}\) = sin (\(\frac{\pi}{6}\)))
Now, tan^-1 [2 cos(2 sin^-1 \(\frac{1}{2}\))] = tan^-1 [2 cos(2 × \(\frac{\pi}{6}\))]
= tan^-1 [2 cos \(\frac{\pi}{3}\)]
= tan^-1 [2 × \(\frac{1}{2}\)] [∵ cos (\(\frac{\pi}{3}\)) = \(\frac{1}{2}\))
= tan^-1 1 = \(\frac{\pi}{4}\).

Question 12.
cot(tan^-1 a + cot^-1 a).
Solution.
We have, cot(tan^-1 a + cot^-1 a)
= cot (\(\frac{\pi}{2}\))
= 0 [∵ tan^-1 x + cot^-1 x = \(\frac{\pi}{2}\)]

Question 13.
tan \(\frac{1}{2}\) [sin^-1 \(\frac{2 x}{1+x^{2}}\) + cos^-1 \(\frac{1-y^{2}}{1+y^{2}}\)], |x| < 1, y > 0 and xy < 1.
Solution.
Let x = tan θ.
Then, θ = tan^-1 x.
∴ sin^-1 \(\frac{2 x}{1+x^{2}}\) = sin^-1 \(\left(\frac{2 \tan \theta}{1+\tan ^{2} \theta}\right)\)
= sin^-1 (sin 2θ) = 2θ = 2 tan^-1 x
Again, let y = tan φ.
Then, φ = tan^-1 y
∴ cos^-1 \(\frac{1-y^{2}}{1+y^{2}}\) = cos^-1 \(\left(\frac{1-\tan ^{2} \varphi}{1+\tan ^{2} \varphi}\right)\)
= cos^-1 (cos 2φ) = 2φ = 2 tan^-1 y
Now, tan \(\frac{1}{2}\) [sin^-1 \(\frac{2 x}{1+x^{2}}\) + cos^-1 \(\frac{1-y^{2}}{1+y^{2}}\)]
= tan \(\frac{1}{2}\) [2 tan^-1 x + tan^-1 y]
= tan [tan^-1 x + tan^-1 y]
= tan[tan^-1 \(\left(\frac{x+y}{1-x y}\right)\)]
[∵ tan^-1 x + tan^-1 y = tan^-1 \(\left(\frac{x+y}{1-x y}\right)\)]
= \(\frac{x+y}{1-x y}\)

Question 14.
If sin(sin^-1 \(\frac{1}{5}\) + cos^-1 x) = 1, then find the value of x.
Solution.
Given, sin(sin^-1 \(\frac{1}{5}\) + cos^-1 x) = 1
⇒ sin^-1 \(\frac{1}{5}\) + cos^-1 x = sin^-1 (1)
[∵ sin θ = x ⇒ θ = sin^-1 x]
⇒ sin^-1 \(\frac{1}{5}\) + cos^-1 x = sin^-1 (sin \(\frac{\pi}{2}\))
[∵ sin (\(\frac{\pi}{2}\)) = 1]
⇒ sin^-1 \(\frac{1}{5}\) + cos^-1 x = \(\frac{\pi}{2}\)
⇒ sin^-1 \(\frac{1}{5}\) = \(\frac{\pi}{2}\) – cos^-1 x
sin^-1 \(\frac{1}{5}\) = sin^-1 x
[∵ sin^-1 x + cos^-1 x = \(\frac{\pi}{2}\)]
⇒ \(\frac{1}{5}\) = x
Hence, the value of x is \(\frac{1}{5}\).

Question 15.
If tan^-1 \(\frac{x-1}{x-2}\) + tan^-1 \(\frac{x+1}{x+2}=\frac{\pi}{4}\), then find the value of x.
Solution.
We have, tan^-1 \(\frac{x-1}{x-2}\) + tan^-1 \(\frac{x+1}{x+2}=\frac{\pi}{4}\)

⇒

Direction (16 – 18): Find the value of each expression.

Question 16.
sin^-1 (sin \(\frac{2 \pi}{3}\))
Solution.
We have, sin^-1 (sin \(\frac{2 \pi}{3}\))
We know that sin^-1(sin x) = x , if x ∈ (- \(\frac{\pi}{2}\), \(\frac{\pi}{2}\)) which is the principal value branch of sin^-1 x.
Here, \(\frac{2 \pi}{3}\) ∉ (- \(\frac{\pi}{2}\), \(\frac{\pi}{2}\)
Now, sin^-1 (sin \(\frac{2 \pi}{3}\)) can be written as
sin^-1 (sin \(\frac{2 \pi}{3}\)) = \(\sin ^{-1}\left[\sin \left(\pi-\frac{\pi}{3}\right)\right]=\sin ^{-1}\left(\sin \frac{\pi}{3}\right)\) where \(\frac{\pi}{3}\) ∈ (- \(\frac{\pi}{2}\), \(\frac{\pi}{2}\))
∴ sin^-1 (sin \(\frac{2 \pi}{3}\)) = sin^-1 (sin \(\frac{\pi}{3}\)) = \(\frac{\pi}{3}\)

Question 17.
tan^-1 (tan \(\frac{3 \pi}{4}\))
Solution.
We have, tan^-1 (tan \(\frac{3 \pi}{4}\))
We know that tan^-1 (tan x) = x, if x ∈ (- \(\frac{\pi}{2}\), \(\frac{\pi}{2}\)), which is the principal value branch of tan^-1 x.
Here, \(\frac{3 \pi}{4}\) ∉ (- \(\frac{\pi}{2}\), \(\frac{\pi}{2}\))
Now, tan^-1 (tan \(\frac{3 \pi}{4}\)) can be written as
tan^-1 (tan \(\frac{3 \pi}{4}\)) = tan^-1 [tan(π – \(\frac{\pi}{4}\))]
= tan^-1 [- tan \(\frac{\pi}{4}\)]
= tan^-1 [tan (- \(\frac{\pi}{4}\))]
where – \(\frac{\pi}{4}\) ∈ (- \(\frac{\pi}{2}\), \(\frac{\pi}{2}\))
[∵ – tan θ = tan(- θ)]
∴ tan^-1 (tan \(\frac{3 \pi}{4}\)) = tan^-1 [tan (- \(\frac{\pi}{4}\))]
= – \(\frac{\pi}{4}\).

Question 18.
tan (sin^-1 \(\frac{3}{5}\) + cot^-1 \(\frac{3}{2}\))
Solution.
Let sin^-1 \(\frac{3}{5}\) = x.
Then, sin x = \(\frac{3}{5}\)
⇒ cos x = \(\sqrt{1-\sin ^{2} x}\) = \(\frac{4}{5}\)
⇒ sec x = \(\frac{5}{4}\)
∴ tan x = \(\sqrt{\sec ^{2} x-1}=\sqrt{\frac{25}{16}-1}=\frac{3}{4}\)
∴ x = tan^-1 \(\frac{3}{4}\)
∴ sin^-1 \(\frac{3}{5}\) = tan^-1 \(\frac{3}{4}\) ………..(i)
Now, cot^-1 \(\frac{3}{2}\) = tan^-1 \(\frac{2}{3}\)
[∵ tan^-1 \(\frac{1}{x}\) = cot^-1 x] ……………(ii)
Hence, tan (sin^-1 \(\frac{3}{5}\) + cot^-1 \(\frac{3}{2}\))
= tan (tan^-1 \(\frac{3}{4}\) + tan^-1 \(\frac{2}{3}\))
= \(\tan \left(\tan ^{-1} \frac{\frac{3}{4}+\frac{2}{3}}{1-\frac{3}{4} \cdot \frac{2}{3}}\right)\)
[∵ tan^-1 x + tan^-1 y = tan^-1 \(\left(\frac{x+y}{1-x y}\right)\)]
= tan (tan^-1 \(\frac{9+8}{12-6}\))
= tan (tan^-1 \(\frac{17}{6}\))
= \(\frac{17}{6}\).

Question 19.
cos^-1 (cos \(\frac{7 \pi}{6}\)) is equal to
(A) \(\frac{7 \pi}{6}\)

(B) \(\frac{5 \pi}{6}\)

(C) \(\frac{\pi}{3}\)

(D) \(\frac{\pi}{6}\)

Solution.
We know that cos^-1 (cos x) = x if x ∈ [0, x], which is the principal value branch of cos^-1 x.
Here, \(\frac{7 \pi}{6}\) ∉ x ∈ [0, π]
Now, cos^-1 (cos \(\frac{7 \pi}{6}\)) can be written as
cos^-1 (cos \(\frac{7 \pi}{6}\)) = cos^-1 [cos(2π – \(\frac{5 \pi}{6}\))]

= cos^-1 [cos \(\frac{5 \pi}{6}\)], where \(\frac{5 \pi}{6}\) ∈ [0, π]
[∵ cos(2π – x) = cos x]
∴ cos^-1 (cos \(\frac{7 \pi}{6}\)) = cos^-1 (cos \(\frac{5 \pi}{6}\))
= \(\frac{5 \pi}{6}\)
The correct option is (B).

Question 20.
sin[\(\frac{\pi}{3}\) – sin^-1 (- \(\frac{1}{2}\))] is equal to
(A) \(\frac{1}{2}\)

(B) \(\frac{1}{3}\)

(C) \(\frac{1}{4}\)

(D) 1
Solution.
Let sin^-1 (- \(\frac{1}{2}\)) = x.
Then, sin x = – \(\frac{1}{2}\) = – sin \(\frac{\pi}{6}\) = sin(-\(\frac{\pi}{6}\))
We know that the range of the principal value of sin^-1 x is (- \(\frac{\pi}{2}\), –\(\frac{\pi}{2}\))
∴ sin^-1 (- \(\frac{1}{2}\)) = – \(\frac{\pi}{6}\)
Now, sin[\(\frac{\pi}{6}\) – sin^-1 (- \(\frac{1}{2}\))] = sin \(\left[\frac{\pi}{3}-\left(-\frac{\pi}{6}\right)\right]\)
= sin \(\left(\frac{\pi}{3}+\frac{\pi}{6}\right)\)
= sin (\(\frac{3 \pi}{6}\))
= sin (\(\frac{\pi}{2}\)) = 1
The correct option is (D).

Question 21.
tan^-1 (- √3) – cot^-1 (- √3) is equal to
(A) π
(B) – \(\frac{\pi}{2}\)
(C) 0
(D) 2√3
Solution.
Let tan^-1 √3 = x
⇒ tan x = √3 = tan \(\frac{\pi}{3}\)
∴ tan^-1 √3 = \(\frac{\pi}{3}\)
Again, let cos^-1(- √3) = x
⇒ cot x = – √3 = – cot \(\frac{\pi}{6}\)
= cot (π – \(\frac{\pi}{6}\))
= cot \(\frac{5 \pi}{6}\)
∴ cot^-1 (- √3) = \(\frac{5 \pi}{6}\)
Now, tan^-1 (- √3) – cot^-1 (- √3) = \(\frac{\pi}{3}\) – \(\frac{5 \pi}{6}\)
= \(\frac{2 \pi-5 \pi}{6}=\frac{-3 \pi}{6}=-\frac{\pi}{2}\)
Hence, correct option is (B).

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 2 Inverse Trigonometric Functions Ex 2.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 2 Inverse Trigonometric Functions Ex 2.1

Direction (1-10):
Find the principal values of the folLowing.
Question 1.
sin^-1 (- \(\frac{1}{2}\))
Solution.
Let sin^-1 (- \(\frac{1}{2}\)) = y
Then, sin y = – \(\frac{1}{2}\)
= – sin (\(\left(\frac{\pi}{6}\right)\))
= sin (- \(\left(\frac{\pi}{6}\right)\))
We know that the range of the principal value of sin^-1 y is
[latex]-\frac{\pi}{2}, \frac{\pi}{2}[/latex] and sin[- \(\left(\frac{\pi}{6}\right)\)] = – \(\frac{1}{2}\)
Therefore, the principal value of sin^-1 (- \(\frac{1}{2}\)) is – \(\left(\frac{\pi}{6}\right)\).

Question 2.
cos^-1 (\(\frac{\sqrt{3}}{2}\))
Solution.
Let cos^-1 (\(\frac{\sqrt{3}}{2}\)) = y.
Then, cos y = \(\frac{\sqrt{3}}{2}\) = cos (\(\left(\frac{\pi}{6}\right)\))
We know that the range of the principal value of cos^-1 y is [0, π] and cos (\(\left(\frac{\pi}{6}\right)\)) = \(\frac{\sqrt{3}}{2}\).
Therefore, the principal value of cos^-1 (\(\frac{\sqrt{3}}{2}\)) is \(\left(\frac{\pi}{6}\right)\).

Question 3.
cosec^-1 (2)
Solution.
Let cosec^-1 (2) = y. Then, cosec y = 2 = cosec(\(\left(\frac{\pi}{6}\right)\))
We know that the range of the principal value of cosec^-1 y is [latex]\left[-\frac{\pi}{2}, \frac{\pi}{2}\right][/latex] – {0} and cosec (\(\left(\frac{\pi}{6}\right)\)) = 2.
Therefore, the principal value of cosec^-1 (2) is \(\left(\frac{\pi}{6}\right)\).

Question 4.
tan^-1 (- √3)
Solution.
Let tan^-1 (- √3) = y.
Then, tan y = – √3 = – tan \(\left(\frac{\pi}{3}\right)\) = tan (- \(\left(\frac{\pi}{3}\right)\))
We know that the range of the principal value of tan^-1 y is [latex]\left[-\frac{\pi}{2}, \frac{\pi}{2}\right][/latex] and tan(- \(\left(\frac{\pi}{2}\right)\)) is – √3
Therefore, the principal value of tan^-1 (- √3) is – \(\frac{\pi}{3}\).

Question 5.
cos^-1 (- \(\frac{1}{2}\))
Solution.
Let cos^-1 (- \(\frac{1}{2}\)) = y. Then,
cos y = – \(\frac{1}{2}\) = – cos (\(\left(\frac{\pi}{3}\right)\))
= cos (π – \(\frac{\pi}{3}\)) = cos \(\left(\frac{2 \pi}{3}\right)\)
We know that the range of the principal value of cos^-1 y is [0, π] and cos \(\left(\frac{2 \pi}{3}\right)\) = – \(\frac{1}{2}\).
Therefore, the principal value of cos^-1 (- \(\frac{1}{2}\)) is \(\left(\frac{2 \pi}{3}\right)\).

Question 6.
tan^-1 (- 1)
Solution.
Let tan^-1 (- 1) = y.
Then, tan y = – 1 = – tan (\(\frac{\pi}{4}\)) = tan (- \(\frac{\pi}{4}\))
We know that the range of the principal value of tan^-1 y is (\(-\frac{\pi}{2}, \frac{\pi}{2}\)) and tan (- \(\frac{\pi}{4}\)) = – 1.
Therefore, the principal value of tan^-1 (- 1) is (- \(\frac{\pi}{4}\))

Question 7.
sec^-1 (\(\frac{2}{\sqrt{3}}\))
Solution.
Let sec^-1 (\(\frac{2}{\sqrt{3}}\)) = y.
Then, sec y = \(\frac{2}{\sqrt{3}}\) = sec (\(\frac{\pi}{6}\))
We know that the range of the principal value of sec^-1 y is [0, π] – {\(\frac{\pi}{2}\)} and sec (\(\frac{\pi}{6}\)) = \(\frac{2}{\sqrt{3}}\).
Therefore, the principal value of sec^-1 (\(\frac{2}{\sqrt{3}}\)) is \(\frac{\pi}{6}\).

Question 8.
cot^-1 (√3)
Solution.
Let cot^-1 (√3) = y. Then, cot y = √3 = cot (\(\frac{\pi}{6}\))
We know that the range of the principal value of cot^-1 y is (0, π) and cot (\(\frac{\pi}{6}\)) = √3
Therefore, the principal value of cot^-1 (√3) is \(\frac{\pi}{6}\).

Question 9.
cos^-1 (- \(\frac{1}{\sqrt{2}}\))
Solution.
Let cos^-1 (- \(\frac{1}{\sqrt{2}}\)) = y. Then,
cos y = – \(\frac{1}{\sqrt{2}}\) = – cos (\(\frac{\pi}{4}\))
= cos(\(\pi-\frac{\pi}{4}\)) = cos(\(\frac{3 \pi}{4}\))
We know that the range of the principal value of cos^-1 y is [0, π] and cos (\(\frac{3 \pi}{4}\)) = – \(\frac{1}{\sqrt{2}}\)
Therefore, the principal value of cos^-1 (- \(\frac{1}{\sqrt{2}}\)) is \(\frac{3 \pi}{4}\)

Question 10.
cosec^-1 (√2)
Solution.
Let cosec^-1 (√2) = y.
Then, cosec y = – √2 = – cosec (\(\frac{\pi}{4}\)) = cosec (- \(\frac{\pi}{4}\))
We know that the range of the principal value of cosec^-1 y is
[latex]-\frac{\pi}{2}, \frac{\pi}{2}[/latex] – {0} and cosec (- \(\frac{\pi}{4}\)) = – √2.
Therefore, the principal value of cosec^-1 (- √2) is – \(\frac{\pi}{4}\).

DirectIon (11 – 14): Find the value of the following.

Question 11.
tan^-1 (1) + cos^-1 (- \(\frac{1}{2}\)) + sin^-1 (- \(\frac{1}{2}\))
Solution.
Let tan^-1 (1) = x. Then, tan x = 1 = tan \(\frac{\pi}{4}\)
∴ tan^-1 (1) = \(\frac{\pi}{4}\)
Let cos^-1 (- \(\frac{1}{2}\)) = y.
Then, cos y = – \(\frac{1}{2}\)
= – cos (\(\frac{\pi}{3}\))
= cos (π – \(\frac{\pi}{3}\))
= cos \(\frac{2 \pi}{3}\)
∴ cos^-1 (- \(\frac{1}{2}\)) = \(\frac{2 \pi}{3}\)
Let sin^-1 (- \(\frac{1}{2}\)) = z.
Then, sin z = – \(\frac{1}{2}\)
= – sin (\(\frac{\pi}{6}\))
= sin (- \(\frac{\pi}{6}\))
∴ sin^-1 (- \(\frac{1}{2}\)) = – \(\frac{\pi}{6}\)
∴ tan^-1 (1) + cos^-1 (- \(\frac{1}{2}\)) + sin^-1 (- \(\frac{1}{2}\)) = \(\frac{\pi}{4}+\frac{2 \pi}{3}-\frac{\pi}{6}\)
= \(\frac{3 \pi+8 \pi-2 \pi}{12}=\frac{9 \pi}{12}=\frac{3 \pi}{4}\).

Question 12.
cos^-1 (\(\frac{1}{2}\)) + 2 sin^-1 \(\frac{1}{2}\)
Solution.
Let cos^-1 (\(\frac{1}{2}\)) = x.
Then, cos x = \(\frac{1}{2}\) = cos (\(\frac{\pi}{3}\)).
∴ cos^-1 (\(\frac{1}{2}\)) = \(\frac{\pi}{3}\)
Let sin^-1 (\(\frac{1}{2}\)) = y.
Then, sin y = \(\frac{1}{2}\) = sin (\(\frac{\pi}{6}\))
∴ sin^-1 (\(\frac{1}{2}\)) = \(\frac{\pi}{6}\)
∴ cos^-1 (\(\frac{1}{2}\)) + 2 sin^-1 (\(\frac{1}{2}\)) = \(\frac{\pi}{3}+\frac{2 \pi}{6}=\frac{\pi}{3}+\frac{\pi}{3}=\frac{2 \pi}{3}\)

Question 13.
If sin^-1 x = y, then
(A) 0 ≤ y ≤ K
(B) \(-\frac{\pi}{2} \leq y \leq \frac{\pi}{2}\)
(C) 0 < y < π
(D) \(-\frac{\pi}{2}<y<\frac{\pi}{2}\)
Solution.
It is given that sin^-1 x = y.
We know that the range of the principal value branch of sin^-1 is [latex]-\frac{\pi}{2}, \frac{\pi}{2}[/latex]
Therefore, \(-\frac{\pi}{2} \leq y \leq \frac{\pi}{2}\).
Hence, the correct option is (B).

Question 14.
tan^-1 √3 – sec^-1 (- 2) is equal to
(A) π
(B) – \(\frac{\pi}{3}\)
(C) \(\frac{\pi}{3}\)
(D) \(\frac{2 \pi}{6}\)
Solution.
Let tan^-1 √3 = x.
Then, tan x = √3 = tan \(\frac{\pi}{3}\)
We know that the range of the principal value of tan^-1 x is (\(-\frac{\pi}{2}, \frac{\pi}{2}\))
∴ tan^-1 √3 = \(\frac{\pi}{3}\)
Let sec^-1 (- 2) = y.
Then, sec y = – 2 = – sec (\(\frac{\pi}{3}\))
= sec (π – \(\frac{\pi}{3}\)) = sec(\(\frac{2 \pi}{3}\))
Now, tan^-1 (√3) – sec^-1 (- 2) = \(\frac{\pi}{3}\) – \(\frac{2 \pi}{3}\)
= – \(\frac{\pi}{3}\)
Hence, correct option is (B).

Punjab State Board PSEB 12th Class Chemistry Book Solutions Chapter 6 General Principles and Processes of Isolation of Elements Textbook Exercise Questions and Answers.

PSEB 12th Class Chemistry Important Questions Chapter 6 General Principles and Processes of Isolation of Elements

Very Short Answer Type Questions

Question 1.
Zinc acts as a reducing agent in the extraction of silver. Comment.
Answer:
Zinc acts as a reducing agent in the extraction of silver. It reduces Ag⁺ to Ag and itself get oxidised to Zn²⁺.
2Na[Ag(CN)₂] + Zn → Na₂[Zn(CN)₄] + 2Ag↓

Question 2.
Winch reducing agent is employed to get copper from the leached low grade copper ore?
Answer:
Scrap iron, Cu²⁺(aq) + Fe(s) → Cu(s) + Fe²⁺(aq)
or H₂ gas, Cu²⁺(aq) + H₂(g) → Cu(s) + 2H⁺(aq)

Question 3.
Name the method used for refining of zirconium.
Answer:
Van Arkel method

Question 4.
Name the method that is used for refining of nickel.
Answer:
Mond process (Vapour phase refining)

Question 5.
Name the method used for refining of copper metal.
Answer:
Electrolytic refining

Question 6.
Although carbon and hydrogen are better reducing agents but they are not used to reduce metallic oxides at high temperatures. Why?
Answer:
At high temperature carbon and hydrogen react with metals to form carbides and hydrides respectively.

Question 7.
What is the function of collectors in the froth floatation process for the concentration of ores?
Answer:
Collectors (e.g., pine oil, xanthates etc.) enhance non-wettability of the ore particles.

Question 8.
Why is it that only sulphide ores are concentrated by froth floatation process?
Answer:
This is because the sulphide ore particles are preferentially wetted by oil and gangue particles are preferentially wetted by water.

Question 9.
At temperatures above 1073 K, coke can be used to reduce FeO to Fe. How can you justify this reduction with Ellingham diagram?
Answer:
Using Ellingham diagram, we observe that at temperature greater than 1073 K; △G(C, CO) < △G (Fe, FeO).
Hence, coke can reduce FeO to Fe.

Question 10.
The mixture of compounds A and B is passed through a column of Al₂O₃ by using alcohol as eluant. Compound A is eluted in preference to compound B. Which of the compounds A or B, is more readily adsorbed on the column?
Answer:
Since, compound ‘A’ comes out before compound ‘B’ the compound ‘B’ is more readily adsorbed on the column.

Short Answer Type Questions

Question 1.
Write the role of:
(i) I₂ in the van Arkel method of refining.
(ii) Dilute NaCN in the extraction of silver.
Answer:
(i) Impure titanium is heated with iodine to form volatile TiI₄, which decomposes on tungsten filament at high temperature to give pure titanium.

(ii) Dilute NaCN forms a soluble complex with Ag or Ag₂S while the impurities remain unaffected which are filtered off.
4Ag + 8NaCN + O₂ + 2H₂O → 4Na[Ag(CN)₂] + 4NaOH
or

Question 2.
Describe the role of
(i) Iodine in the refining of zirconium.
(ii) NaCN in the extraction of gold from gold ore.
Write chemical equations for the involved reactions.
Answer:
(i) Impure zirconium is heated with iodine to form volatile compound ZrI₄ which on further heating over tungsten filament decomposes to give pure zirconium.

(ii) Gold ore is leached with dilute solution of NaCN in the presence of air from which the metal is obtained later by replacement.
4Au + 8NaCN + O₂ + 2H₂O → 4Na[Au(CN)₂] + 4NaOH

Question 3.
Explain the role of each of the following in the extraction of metals from their ores:
(i) CO in the extraction of nickel.
(ii) Zinc in the extraction of silver.
Answer:
(i) CO in the extraction of nickel: Impure nickel is heated in a stream of carbon monoxide when volatile nickel tetracarbonyl is formed and the impurities are left behind in the solid state. The vapour of nickel tetracarbonyl is taken to a decomposer chamber maintained at 450-470 K where it decomposes to give pure nickel metal and carbon monoxide.

(ii) Zinc in the extraction of silver : Silver present in the ore is leached with dilute solution of NaCN in the presence of air or oxygen to form a soluble complex.

Silver is then recovered from the complex by displacement method using more electropositive zinc metal.
2[Ag(CN)₂]^– (aq) + Zn(s) → 2Ag(s) + [Zn(CN)₂]^2- (aq)

Question 4.
Wrought iron is the purest form of iron. Write a reaction used for the preparation of wrought iron from cast iron. How can the impurities of sulphur, silicon and phosphorus be removed from cast iron?
Answer:

This reaction takes place in reverberatory furnace lined with haematite.

(b) Limestone is added as flux. Impurities of S, Si and P oxidise and pass into slag. The metal is removed and freed from slag by passing through rollers.

Question 5.
Write the chemical reactions involved in the extraction of gold by cyanide process. Also give the role of zinc in the reaction.
Answer:
(i) 4Au(s) + 8CN^– (aq) + 2H₂O(aq) + O₂(g) → 4[Au(CN)₂]^– (aq) + 4OH^–(aq)
(ii) 2[Au(CN)₂]^– (aq) + Zn(s) → 2Au(s) + [Zn(CN)₄]^2- (aq)
Zinc acts as a reducing agent in this reaction.

Question 6.
Describe the role of
(i) NaCN in the extraction of gold from its ore.
(ii) Cryolite in the extraction of aluminium from pure alumina.
(iii) CO in the purification of nickel.
Answer:
(i) Gold is leached with a dilute solution of NaCN in the presence of air.
(ii) Cryolite lowers the high melting point of alumina and makes it a good conductor of electricity.
(iii) CO forms a volatile complex with metal nickel which is further decomposed to give pure Ni metal.

Long Answer Type Questions

Question 1.
(a) Explain how an element can be extracted using an oxidation reaction?
(b) What do you mean by refining? Mention some of the methods used for refining of metals.
Answer:
(a) Some of the extractions, particularly of non-metals are based upon oxidation.
A very common example of extraction based on oxidation is the extraction of chlorine from brine (Chlorine is abundant in sea water as common salt).
2Cl^–(aq) + 2H₂O(l) → 2OH^–(aq) + H₂(g) + Cl₂(g)
The △G⁰ for this reaction is + 422 kJ. When it is converted to E⁰ (using △G⁰ = -nE⁰F), we get E⁰ = -2.2 V. Naturally, it will require an external e.m.f. that is greater than 2.2 V. But the electrolysis requires an excess potential to overcome some other hindering reactions. Thus, Cl₂ is obtained by electrolysis giving out H₂ and aqueous NaOH as by products. Electrolysis of molten NaCl is also carried out. But in that case, Na metal is produced and not NaOH.

The extraction of gold and silver involves leaching the metal with CN^–. This is also an oxidation reaction (Ag → Ag⁺ or Au → Au⁺). The metal is later recovered by displacement method.
4Au(s) + 8CN^–(aq) + 2H₂O(aq) + O₂(g) → 4[Au(CN₂)]^–(aq) + 4OH(aq)
2[Au(CN)₂]^–(aq) + Zn(s) → 2Au(s) + [Zn(CN)₄]^2- (aq)
In this reaction zinc acts as a reducing agent.

(b) A metal extracted by any method is usually contaiminated with some impurity. For obtaining metals of high purity, several techniques are used depending upon the difference in properties of the metal and the impurity. The process is called refining. Some of them are listed below :

1. Distillation,
2. Liquation,
3. Electrolysis,
4. Zone-refining,
5. Vapour phase refining,
6. Chromatographic methods.

Question 2.
How is the concept of coupling reactions useful in explaining the occurrence of non-spontaneous thermochemical reactions? Explain giving an example?
Answer:
Coupled reactions : Many reactions which are non-spontaneous (△G^⊖ is positive) can be made to occur spontaneously if these are coupled with reactions having larger negative free energy. By coupling means carrying out simultaneously both non- spontaneous and spontaneous reactions. For example, decomposition of Fe₂O₃into iron is a non-spontaneous reaction (△G^⊖ = +1487 kJ mol^-1). However, this decomposition can take place spontaneously if carbon monoxide is simultaneously burnt in oxygen (△G^⊖ = – 514.4 kJ mol^-1).
2Fe₂O₃(s) → 4Fe(s) + 3O₂(g); …(i);
△G^⊖ = + 1487.0 kJmol^-1
2CO(g) + O₂(g) → 2CO₂(g); … (ii);
△G^⊖ = -514.4 kJmol^-1
Multiplying equation (ii) by 3 and then adding to equation (i), we get
6CO(g) + 3O₂(g) → 6CO₂(g) △G^⊖ = -1543.2 kJ mol^-1
2Fe₂O₃ (s) → 4Fe(s) + 3O₂(s) △G^⊖ = +1487.0 kJ mol^-1
2Fe₂O₃(s) + 6CO(g) → 4Fe(s) + 6CO₂(g) △G^⊖ = – 56.2 kJ mol^-1
Since, △G^⊖ in the reduction of Fe₂O₃ with CO is negative, therefore, the reaction is feasible and spontaneous.

Punjab State Board PSEB 12th Class Chemistry Book Solutions Chapter 6 General Principles and Processes of Isolation of Elements Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Chemistry Chapter 6 General Principles and Processes of Isolation of Elements

PSEB 12th Class Chemistry Guide General Principles and Processes of Isolation of Elements InText Questions and Answers

Question 1.
Copper can be extracted by hydrometallurgy but not zinc% Explain.
Answer:
The E^⊖ value of zinc (Zn²⁺/Zn = – 0.76 V) is lower than that of copper (Cu2+/Cu = 0.34 V). This means that .zinc is a stronger reducing agent and can displace copper from solution of Cu²⁺ ions.
Zn(s) + Cu²⁺ (aq) → Zn²⁺(aq) + Cu(s)
In order to extract zinc by hydrometallurgy, we need stronger reducing agent like

etc. However, all these metals reduce water to hydrogen gas. Therefore, these metals cannot be used to displace Zn from solution of Zn²⁺ ions. Thus, copper can be extracted by hydrometallurgy but not zinc.

Question 2.
What is the role of depressant in froth floatation process?
Answer:
In the froth floatation process, the role of the depressants is to separate two sulphide ores by selectively preventing one ore from forming froth. For example, to separate two sulphide ores (ZnS and PbS), NaCN is used as a depressant which selectively allows PbS to come with froth, but prevents ZnS from coming to froth. This happens because NaCN reacts with ZnS to form Na₂[Zn(CN)₄].
4NaCN + ZnS → Na₂[Zn(CN)₄] + Na₂S

Question 3.
Why is the extraction of copper from pyrites more difficult than that from its oxide ore through reduction?
Answer:
The Gibbs free energy of formation (△_fG) of Cu₂S is less than that of H₂S and CS₂. Therefore, H₂ and C cannot reduce Cu₂S to Cu.

On the other hand, the Gibbs free energy of formation of Cu₂O is greater than that of CO. Hence, C can reduce Cu₂O to Cu.
C(s) + Cu₂O(s) → 2Cu(s) + CO(g)
Hence, the extraction of copper from its pyrite ore is difficult than from its oxide ore through reduction.

Question 4.
Explain:
(i) Zone refining
(ii) Column chromatography.
Answer:
(i) Zone refining : This method is based on the principle that impurities are more soluble in the molten state of metal (the melt) than in the solid state. In the process of zone refining, a circular mobile heater is fixed at one end of a rod of impure metal. As the heater moves, the molten zone of the rod also moves with it. As a result, pure metal crystallizes out of the melt and the impurities pass onto the adjacent molten zone. This process is repeated several times, which leads to the segregation of impurities at one end of the rod. Then, the end with the impurities is cut off. Silicon, boron, gallium, indium etc. can be purified by this process.

(ii) Column chromatography : Column chromatography is a technique used to separate different components of a mixture. It is a very useful technique used for the purification of elements available in minute quantities. It is also used to remove the impurities that are not very different in chemical properties from the element to be purified. Chromatography is based on the principle that different components of a mixture are differently adsorbed on an adsorbent. In chromatography, there are two phases: mobile phase and stationary phase. The stationary phase is immobile and immiscible. Al₂O₃ column is usually used as the stationary phase in column chromatography. The mobile phase may be a gas, liquid, or supercritical fluid in which the sample extract is dissolved. Then, the mobile phase is forced to move through the stationary phase. The component that is more strongly adsorbed on the column takes a longer time to travel through it than the component that is weakly adsorbed. The adsorbed components are then removed (eluted) using a suitable solvent (eluant).

Question 5.
Out of C and CO, which is a better reducing agent at 673 K?
Answer:
At 673 K, the value of △G_(CO,CO2) is less than that of △G_(C,CO).
Therefore, CO can be oxidised more easily to CO₂ than C to CO. Hence, CO is a better reducing agent than C at 673 K.

Question 6.
Name the common elements present in the anode mud in electrolytic refining of copper. Why are they so present ?
Answer:
In electrolytic refining of copper, the common elements present in anode mud are selenium, tellurium, silver, gold, platinum, and antimony.

These elements are very less reactive and are not affected during the purification process. Hence, they settle down below the anode as anode mud.

Question 7.
Write down the reactions taking place in different zones in the blast furnace during the extraction of iron.
Answer:
Reactions in blast furnace are as follows :
(a) Reactions at lower temperature range (500 to 800 K)
3Fe₂O₃ + CO → 2Fe₃O₄ + CO₂
Fe₃O₄ + 4CO → 3Fe + 4CO₂
Fe₂O₃ + C0 → 2FeO + CO₂

(b) Reactions at higher temperature range (900-1500 K)
C + CO₂ → 2CO
FeO + CO → Fe + CO₂

Question 8.
Write chemical reactions taking place in the extraction of zinc from zinc blende. .
Answer:
The different steps involved in the extraction of zinc from zinc blende (ZnS) are given below:
(i) Concentration of ore : First, the gangue from zinc blende is removed by the froth floatation method.
(ii) Conversion to oxide (Roasting) : Sulphide ore is converted into oxide by the process of roasting. In this process, ZnS is heated in a regular supply of air in a furnace at a temperature, which is below the melting point of Zn.
2ZnS + 3O₂2 → 2ZnO + 2SO₂

(iii) Extraction of zinc from zinc oxide (Reduction) : Zinc is extracted from zinc oxide by the process of reduction. The reduction of zinc oxide is carried out by mixing it with powdered coke and then, heating it at 1673 K.

(iv) Electrolytic refining: Zinc can be refined by the process of electrolytic refining. In this process, impure zinc is made the anode while a pure copper strip is made the cathode. The electrolyte used is an acidified solution of zinc sulphate (ZnSO₄). Electrolysis results in the transfer of zinc in pure form from the anode to the cathode.
Anode : Zn → Zn²⁺ + 2e^–
Cathode : Zn²⁺ + 2e^– → Zn

Question 9.
State the role of silica in the metallurgy of copper.
Answer:
During the roasting of pyrite ore, a mixture of FeO and Cu₂O is obtained.

The role of silica in the metallurgy of copper is to remove the iron oxide obtained during the process of rosting as ‘slag’. If the sulphide ore of copper contains iron, then silica (SiO₂) is added as flux before roasting. Then, FeO combines with silica to form iron silicate, FeSiO₃ (slag).

Question 10.
What is meant by the term “chromatography”?
Answer:
Chromatography is a collective term used for a family of laboratory techniques for the separation of mixtures. The term is derived from Greek words ‘chroma’ meaning ‘colour’ and ‘graphy5 meaning ‘writing’. Chromatographic techniques are based on the principle that different components are absorbed differently on an absorbent. There are several chromatographic techniques such as paper chromatography, column chromatography, gas chromatography, etc.

Question 11.
What criterion is followed for the selection of the stationary phase in chromatography?
Answer:
The stationary phase is selected in such a way that the components of the sample have different solubility’s in the phase. Hence, different components have different rates of movement through the stationary phase and as a result, can be separated from each other.

Question 12.
Describe a method for refining nickel.
Answer:
Nickel is refined by Mond’s process. In this process, nickel is heated in the presence of carbon monoxide to form nickel tetracarbonyl, which is a volatile complex.

Then, the obtained nickel tetracarbonyl is decomposed by subjecting it to a higher temperature (450-470 K) to obtain pure nickel metal.

Question 13.
How can you separate alumina from silica in a bauxite ore associated with silica? Give equations, if any.
Answer:
(i) To separate alumina from silica in a bauxite ore associated with silica, first the powdered ore is digested with a concentrated NaOH solution at 473-523 K and 35-36 bar pressure. This results in the leaching out of alumina (Al₂O₃) as sodium aluminate and silica (SiO₂) as sodium silicate leaving the impurities behind.

(ii) Then, CO₂gas is passed through the resulting solution to neutralise the aluminate in the solution, which results in the precipitation of hydrated alumina. To induce precipitation, the solution is seeded with freshly prepared samples of hydrated alumina.

(iii) During this process, sodium silicate remains in the solution. The obtained hydrated alumina is filtered, dried, and heated to get back pure alumina.

Question 14.
Giving examples, differentiate between ‘roasting’ and ‘calcination’.
Answer:

Roasting	Calcination
1.  Sulphur dioxide is produced along with metal oxide.	Carbon dioxide is produced along with metal oxide.
2.  Ore is heated in the presence of excess of air or oxygen.	Ore is heated in the absence or limited supply of air or O2.
3. Volatile impurities are removed as oxides, such as SO2, As2O3, etc.	Water and organic impurities are removed.

Question 15.
How is ‘cast iron’ different from ‘pig iron”?
Answer:
The iron obtained from blast furnaces is known as pig iron. It contains around 4% carbon and many impurities such as S, P, Si, Mn in smaller amounts.

Cast iron is obtained by melting pig iron and coke using a hot air blast. It contains a lower amount of carbon (3%) than pig iron. Unlike pig iron, cast iron is extremely hard and brittle.

Question 16.
Differentiate between “minerals” and “ores”.
Answer:

Mineral	Ore
Naturally occurring substances of metals present in the earth’s crust are called minerals.	Minerals which can be used to obtain the metal profitably are cahed ores.
All minerals are not ores.	All ores are essentially minerals too.
e.g,, bauxite (Al2O3-xH2O) and clay (A12O3 -2SiO2 -2H2O)	e.g., bauxite (A12O3 ∙xH2O)

Question 17.
Why copper matte is put in silica lined converter?
Answer:
Copper matte contains Cu₂S and FeS. Copper matte is put in a silica-lined converter to remove the remaining FeO and FeS present in the matte as slag (FeSiO₃). Also, some silica is added to the silica-lined converter. Then, a hot air blast is blown. As a result, the remaining FeS and FeO are converted to iron silicate (FeSiO₃) and Cu₂S is converted into metallic copper.
2FeS + 3O₂ → 2FeO + 2SO₂
FeO + SiO₂ → FeSiO₂
2Cu₂S + 3O₂ → 2Cu₂O + 2SO₂
2Cu₂O + Cu₂S → 6Cu + SO₂

Question 18.
What is the role of cryolite in the metallurgy of aluminium?
Answer:
Cryolite (Na₃AlF₆) has two roles in the metallurgy of aluminium :

1. To decrease the melting point of the mixture from 2323 K to 1140 K.
2. To increase the electrical conductivity of Al₂O₃.

Question 19.
How is leaching carried out in case of low grade copper ores?
Answer:
In case of low grade copper ores, leaching is carried out using acid or bacteria in the presence of air. In this process, copper goes into the solution as Cu²⁺ ions.
Cu(s) + 2H⁺(aq) + \(\frac{1}{2}\)O₂(g) → Cu²⁺(aq) + 2H₂O(l)
The resulting solution is treated with scrap iron or H₂ to get metallic copper.
Cu²⁺(aq) + H₂(g) → Cu(s) + 2H⁺(aq)

Question 20.
Why is zinc not extracted from zinc oxide through reduction using CO?
Answer:
The standard free energy of formation (△_fG^⊖) of CO₂ from CO is
higher than that of the formation of ZnO from Zn. Therefore, CO cannot be used to reduce ZnO to Zn.

Question 21.
The value of △_fG^⊖ for formation of Cr₂O₃ is – 540 kJmol^-1 and that of A₂O₃ is – 827 kJ mol^-1. Is the reduction of Cr₂O₃ possible with Al?
Answer:
The two thermochemial equations may be written as
(i) 2Al + \(\frac{1}{2}\)O₂ → Al₂O₃ △_fG^⊖ = -827kJmol^-1
(ii) 2Cr + \(\frac{1}{2}\)O₂ → Cr₂O₃ △_fG^⊖ = -540kJmol^-1
Subtracting equation (ii) from (i), we have
2Al + Cr₂O₃ → Al₂O₃ + 2Cr
△_fG^⊖ = -827-(-540)
= -287kJmol^-1
As △_fG^⊖ for the reduction reaction of Cr₂O₃ by Al is negative, this reaction is possible.

Question 22.
Out of C and CO, which is a better reducing agent for ZnO?
Answer:
The free energy of formation (△_fG^⊖) of CO from C becomes lower at temperatures above 1120 K whereas that of CO₂ from C becomes lower above 1323 K than △_fG^⊖ of ZnO. However, △_fG^⊖ of CO₂ from CO is always higher than that of ZnO. Therefore, C and reduce ZnO to Zn but not CO. Therefore, out of C can CO, C is a better reducing agent than CO for ZnO.

Question 23.
The choice of a reducing agent in a particular case depends on thermodynamic factor. How far do you agree with this statement? Support your opinion with two examples.
Answer:
For any spontaneous reaction, the Gibbs free energy change (△G) must be negative. △G = △H – T△S where △H is the enthalpy change during the reaction, T is the absolute temperature and △S is the change in entropy.

Consider the Ellingham diagram (given below) for some metal oxides. From the diagram, it is evident that metals for which the free energy of formation of their oxides is more negative can reduce those metal oxides for which the free energy of formation of their respective oxides is less negative. In other words, any metal will reduce the oxide of other metals which lie above it in the Ellingham diagram because the free energy will become more negative by an amount equal to the difference in the two graphs at that particular temperature. Thus, Al reduces FeO, Cr₂O₃ and NiO in Thermite reaction, but Al will not reduce MgO at a temperature below 1773 K.

It can be followed that:
(i) 2Al + Cr₂O₃→ Al₂O₃ + 2Cr
(Aluminothermic process)
(ii) 2Al + Fe₂O₃ → Al₂O₃ + 2Fe are spontaneous.
But Al can’t be used to reduce MgO below 1500°C. From the above it is clear that thermodynamic considerations help us in choosing a suitable reducing agent in metallurgy.

Question 24.
Name the processes from which chlorine is obtained as a by-product. What will happen if an aqueous solution of NaCl is subjected to electrolysis?
Answer:
(i) Down’s process for the manufacture of Na metal: When molten NaCl is subjected to electrolysis, chlorine is obtained as a by product at anode because in molten state only Na⁺ and Cl^– ions are present.
NaCl (melt) → Na⁺ (melt) + Cl^– (melt)
At cathode : Na⁺ (melt) + e^– → Na(s)
At anode : Cl^–(melt) → Cl(g) + e^–

(ii) Manufacture of NaOH : If an aqueous solution of NaCl is electrolysed, Cl₂ will be obtained at the anode but at the cathode, H₂ will be obtained instead of Na. This is because the standard reduction potential of Na (E^⊖ = – 2.71 V) is more negative than that of H₂O (E^⊖ = – 0.83 V). Hence, H₂O will get preference to get reduced at the cathode and as a result, H₂ is evolved.
NaCl(aq) → Na⁺(aq) + Cl^– (aq)
H₂O ⇌ H⁺(aq) + OH^–(aq)
At cathode : 2H₂O(l) + 2e^– → H₂(g) + 2OH^– (aq)
At anode : Cl^– (melt) → Cl(g) + e^–
2Cl (g) → Cl₂(g)
H₂ gas is obtained at cathode; chlorine gas at anode and NaOH is formed in the solution.
Na⁺(aq) + OH^–(aq) → NaOH (aq)

Question 25.
What is the role of graphite rod in the electrometallurgy of aluminium?
Answer:
In the electrometallurgy of aluminium, a fused mixture of purified alumina (Al₂O₃), cryolite (Na₃AlF₆) and fluorspar (CaF₂) is electrolysed. In this electrolysis, graphite is used as the anode and graphite-lined iron is used as the cathode. During the electrolysis, A1 is liberated at the cathode, while CO and CO₂ are liberated at the anode, according to the following equation :
At cathode: Al³⁺(melt) + 3e^– → Al(l)
At anode: C(s) + O^2- (melt) → CO(g) + 2e^–
C(s) + 2O^2- (melt) → CO₂(g) + 4e^–
If a metal is used instead of graphite as the anode, then 02will be liberated. This will not only oxidise the metal of the electrode, but also convert some of the A1 liberated at the cathode back into Al₂O₃. Hence, graphite is used for preventing the formation of O₂ at the anode.

Question 26.
Outline the principles of refining of metals by the following methods:
(i) Zone refining
(ii) Electrolytic refining
(iii) Vapour phase refining
Answer:
(i) Zone refining : This method is based on the principle that impurities are more soluble in the molten state of metal (the melt) than in the solid state. In the process of zone refining, a circular mobile heater is fixed at one end of a rod of impure metal. As the heater moves, the molten zone of the rod also moves with it. As a result, pure metal crystallizes out of the melt and the impurities pass onto the adjacent molten zone. This process is repeated several times, which leads to the segregation of impurities at one end of the rod. Then, the end with the impurities is cut off. Silicon, boron, gallium, indium etc. can be purified by this process.

(ii) Electrolytic refining : Electrolytic refining is the process of refining impure metals by using electricity. In this process, impure metal is made the anode and a strip of pure metal is made the cathode. A solution of a soluble salt of the same metal is taken as the electrolyte. When an electric current is passed, metal ions from the electrolyte are deposited at the cathode as pure metal and the impure metal from the anode dissolves into the electrolyte in the form of ions. The impurities present in the impure metal gets collected below the anode. This is known as anode mud.
At anode: M → Mⁿ⁺ + ne^–
At cathode: Mⁿ⁺ + ne^– → M

(iii) Vapour phase refining : Vapour phase refining is the process of refining metal by converting it into its volatile compound and then, decomposing it to obtain a pure metal. To carry out this process,

•  the metal should form a volatile compound with an available reagent, and
• the volatile compound should be easily decomposable so that the metal can be easily recovered.
  Nickel, zirconium, and titanium are refined using this method.

Question 27.
Predict conditions under which Al might be expected to reduce MgO. (Hint: See Intext Question 4)
Answer:
The equations for the formation of two oxides are :
\(\frac{4}{3}\)Al(s) + O₂(g) → \(\frac{2}{3}\)Al₂O₃(s)
2Mg(s) + O₂(g) → 2MgO(s)
If we observe the plots for the formation of the two oxides on the Ellingham diagram, we find the two curves intersect each other at a certain point. The corresponding value of △_fG^⊖ becomes zero for the reduction of MgO by aluminium metal.
2MgO(s) + \(\frac{4}{3}\)Al(s) ⇌ 2Mg(s) + \(\frac{2}{3}\)Al₂O₃(s)
This means that the reduction of MgO by A1 metal cannot occur below this temperature (1665 K). Instead, Mg can reduce Al₂O₃ to Al below 1665 K.
Aluminium metal (Al) can reduce MgO to Mg above 1665 K
because △_fG^⊖ for Al₂O₃ is less as compared to that of MgO.

Chemistry Guide for Class 12 PSEB General Principles and Processes of Isolation of Elements Textbook Questions and Answers

Question 1.
Which of the ores mentioned in Table 6.1 can be concentrated by magnetic separation method?
Answer:
If the ore or the gangue can be attracted by the magnetic field, then the ore can be concentrated by the process of magnetic separation. The ores of iron such as haematite (Fe₂O₃), magnetite (Fe₃O₄), siderite (FeCO₃) and iron pyrites (FeS₂) can be separated by the process of magnetic separation.

Question 2.
What is the significance of leaching in the extraction of aluminium?
Answer:
In the extraction of aluminium, the significance of leaching is to concentrate pure alumina (Al₂O₃) from bauxite ore. Bauxite usually contains silica, iron oxide, and titanium oxide as impurities. In the process of leaching, alumina is concentrated by digesting the powdered ore with a concentrated solution of NaOH at 473-523 K and 35-36 bar. Under these conditions, alumina (Al₂O₃) dissolves as sodium meta-aluminate and silica (SiO₂) dissolves as sodium silicate leaving the impurities behind.

The impurities are then filtered and the solution is neutralised by passing CO₂ gas. In this process, hydrated Al₂O₃ gets precipitated and sodium silicate remains in the solution. Precipitation is induced by seeding the solution with freshly prepared samples of hydrated Al₂O₃.
2Na[Al(OH)₄](aq) + CO₂(g) → Al₂O₃∙xH₂O(S) + 2NaHCO₃(aq)
Hydrated alumina
Hydrated alumina Al₂O₃∙xH₂O is filtered, dried, and heated to give back pure alumina (Al₂O₃).

Question 3.
The reaction,
Cr₂O₃ + 2Al > Al₂O₃ + 2Cr (△_fG^⊖ = -421kJ) is thermodynamically feasible as is apparent from the Gibbs energy value.
Why does it not take place at room temperature?
Answer:
The change in Gibbs energy is related to the equilibrium constant, K as
△G = – RT in K
At room temperature, all reactants and products of the given reaction are in the solid state. As a result, equilibrium does not exist between the reactants and th e prod ac ts lienee, the reaction does not take place at room temperature.
However, at a higher temperature, chromium melts and the reaction takes place.
We also know that according to the equation
△G = △H – T△S,
Increasing the temperature increases die value of T△S, making the value of △G more and more negative. Therefore, the reaction becomes more and more feasible as the temperature is increased.

Question 4.
Is it true that under certain conditions. Mg can reduce Al₂O₃ and Al can reduce MgO? What are those conditions?
Answer:
If we look at the Ellingbam diagram wo observe that the plots for Al and Mg cross each other at 1350°C (1623k) Below this temperature Mg can reduce Al₂O₃ and above this temperature., Al can reduce MgO.

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 1 Relations and Functions Ex 1.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 1 Relations and Functions Ex 1.4

Question 1.
Determine whether or not each of the definition of * given below gives a binary operation. In the event that * is not a binary operation, give justification for this.
(i) On Z⁺, define * by a * b = a – b
(ii) On Z⁺, define * by a * b = ab
(iii) On R, define * by a * b = ab²
(iv) On Z⁺, define * by a * b = |a – b|
(v) On Z⁺, define * by a * b = a
Sol.
(i) On Z⁺, * is defined by a * b = a – b.
It is not a binary operation as the image of (1, 2) under * is
1 * 2 = 1 – 2 = – 1 ∉ Z⁺.

(ii) On Z⁺, * is defined by a * b = ab.
It is seen that for each a, b ∈ Z⁺, there is a unique element ab in Z⁺.
This means that * carries each pair (a, b) to a unique element a * b = ab in Z⁺. Therefore, * is a binary operation.

(iii) On R, * is defined by a * b = ab².
It is seen that for each a, b ∈ R, there is a unique element ab² in R.
This means that * carries each pair (a, b) to a unique element a * b = ab² in R. Therefore, * is a binary operation.

(iv) On Z⁺, * is defined by a * b =|a – b|.
It is seen that for each a, b ∈ Z⁺, there is a unique element | a – b | in Z⁺. This means that * carries each pair (a, b) to a unique element a * b = |a – b|in Z⁺. Therefore, * is a binary operation.

(v) On Z⁺, * is defined by a * b = a.
It is seen that for each a, b ∈ Z⁺, there is a unique element a ∈ Z⁺. This means that * carries each pair (a, b) to a unique element a * b = a in Z⁺. Therefore, * is a binary operation.

Question 2.
For each operation * defined below, determine whether * is binary commutative or associative.
(i) On Z, define a* b = a – b
(ii) On Q, define a * b = ab + 1
(iii) On Q, define a* b = \(\frac{a b}{2}\)
(iv) On Z⁺, define a * b = 2^ab
(v) On Z⁺, define a * b = a^b
(vi) On R – {- 1},define a * b = \(\frac{a}{b+1}\)
Solution.
(i) On Z, operation * is defined as
(a) a * b = a – b
⇒ b * a = b – a
But a – b ≠ b – a
⇒ a * b ≠ b * a
∴ Defined operation is not commutative.

(b) a – (b – c) ≠ (a – b) – c
∴ Binary operation * as defined is not associative.

(ii) On Q, operation * is defined as a * b = ab +1
(a) ab + 1 = ba + 1, a * b = b * a
∴ Defined binary operation is commutative.

(b) a * (b * c) = a * (bc + 1) = a (bc + 1) + 1 = abc + a + 1
and (a * b)* c = (ab + 1) * c = (ab + 1)c + 1
= abc + c + 1
a * (b * c) ≠ (a * b) * c
∴ Binary operation defined is not associative.

(iii) (a) On Q, operation * is defined as a * b = \(\frac{ab}{2}\)
∴ a * b = b * a
∴ Operation binary defined is commutative.

(b) a * b = a * \(\frac{b c}{2}=\frac{a b c}{4}\)
and (a * b) * c = \(\frac{b c}{2}\) * c = \(\frac{a b c}{4}\)
⇒ Defined binary operation is associative.

(iv) On Z⁺, operation * is defined as a * b = 2^ab
(a) a * b = 2^ab, b * a = 2^ba = 2^ab
a * b = b * a
Binary operation defined is commutative.

(b) a * (b * c) = a * 2^ba = 2^{a . bc}
(a * b) * c = 2^ab * c = 2^2ab
Thus, (a * b) * c ≠ a * (b * c)
∴ Binary operation * as defined is not associative.

(v) On Z⁺, a * b = a^b
(a) b * a = b^a
∴ a^b = b^a
⇒ a * b ≠ b * a
* is not commutative.

(b) (a * b) * c = a^b * c
= (a^b)^c = a^bc
a * (b * c) = a * bc = a^bc.
This (a * b) * c ≠ (a * b * c)
∴ Operation * is not associative.

(vi) On Z⁺ operation * is defined as
a * b = \(\frac{a}{b+1}\), b ≠ – 1
∴ b * a = \(\frac{b}{a+1}\)
(a) a * b ≠ b * a
Binary operation defined is not commutative.

(b) (a * b) * c = \(a^{*}\left(\frac{b}{c+1}\right)=\frac{a}{\frac{b}{c+1}+1}=\frac{a(c+1)}{b+c+1}\)

(a * b) * c = \(\frac{a}{b+1} * c=\frac{\frac{a}{b+1}}{c+1}=\frac{a}{(b+1)(c+1)}\)

∴ a * (b * c) ≠ (a * b) * c
⇒ Binary operation defined above is not associative.

Question 3.
Consider the binary operation ^ on the set (1, 2, 3, 4, 5} defined by a ^ b = min {a, b}. Write the multiplication table of the operation ^.
Solution.
The binary operation ^ on the set {1, 2, 3, 4, 5} is defined as
a ^ b = min{a, b} for a, b ∈ {1, 2, 3, 4, 5}.
Thus, the operation table for the given operation ^ can be given as

Question 4.
Consider a binary operation * on the set {1, 2, 3, 4, 5} given by the following multiplication table.
(i) Compute (2 * 3) * 4 and 2 * (3 * 4)
(ii) Is * commutative?
(iii) Compute (2* 3) * (4* 5).
(Hint: use the following table) (i)

Solution.
(i) We have (2 * 3) *4 = 1 * 4 = 1
and 2 * (3 * 4) = 2 * 1 = 1

(ii) For every a, b ∈ (1, 2, 3, 4, 5}, we have a * b = b * a. Therefore, the operation * is commutative.
(iii) We have (2 * 3) = 1 and (4 * 5) = 1 .
∴ (2 * 3) * (4 * 5) = 1 * 1 = 1.

Question 5.
Let *’ be the binary operation on the set {1, 2, 3, 4, 5} is defined by a *’ b = H.C.F. of a and b. Is the operation *’ same as the operation * defined in Q. 4 above? Justify your answer.
Solution.
The binary operation *’ on the set {1, 2, 3, 4, 5} is defined as
a*’ b = HCF of a and b.
The operation table for the operation * can be given as :

We observe that the operation table for the operations * and *’ are the same.
Thus, the operation *’ is same as the operation *.

Question 6.
Let * be the binary operation on N given by a * b = L.C.M. of a and b.
(i) Find 5 * 7, 20 * 16
(ii) Is * commutative?
(iii) Is * associative?
(iv) Find the identity of * in N.
(v) Which elements of N are invertible for the operation *?
Solution.
The binary operation * defined as a * b = L.C.M. of a and b
(i) 5 * 7 = L.C.M. of 5 and 7 = 35
and 20 * 16 = L.C.M. of 20 and 16 = 80

(ii) a * b = L.C.M. of a and b
b * a = L.C.M. of b and a
⇒ a * b = b * a L.C.M. of a, b and b, a are equal
∴ Binary operation * is commutative.

(iii) a * (b * c) = L.C.M. of a, b, c
and (a * b)* c = L.C.M. of a, b, c
⇒ a * (b * c) = (a * b) * c
⇒ Binary operation * is associative.

(iv) Identity of * in N is 1
1 * a = a * 1 = a = L.C.M. of 1 and a.

(v) Let * : N × N → N defined as a * b = L.C.M. of (a, b)
For a = 1, b = 1, a * b = 1 = b * a. Otherwise a * b ≠ 1
∴ Binary operation * is not invertible.
⇒ 1 is invertible for operaiton *.

Question 7.
Is * defined on the set {1, 2, 3, 4, 5} by a * 6 = L.C.M. of a and 6 a binary operation? Justify your answer.
Solution.
The operation * on the set A = {1, 2, 3, 4, 5} is defined as a * b = L.C.M. of a and b.
Now, 2 * 3 = L.C.M. of 2 and 3 = 6.
But 6 does not belong to the given set.
Hence, the given operation * is not a binary operation.

Question 8.
Let * be the binary operation on N defined by a * 6 = H.C.F. of a and b. Is * commutative? Is * associative? Does there exist identity for this binary operation on N?
Solution.
The binary operation * on N is defined as a * b = H.C.F. of a and b It is known that
H.C.F. of a and b = H.C.F. of b and a V a, b ∈ N.
∴ a * b = b * a
Thus, the operation * is commutative.
For a, b, c ∈ N, we have
(a * b) * c = (H.C.F. of a and b) * c = H.C.F. of a, b and c
a * (b * c) = a * (H.C.F. of b and c) = H.C.F. of a, b, and c
∴ (a * b) * c = a* (b * c)
Thus, the operation * is associative.
Now, an element e ∈ N will be the identity for the operation * if a * e = a = e * a for ∀ a ∈ N.
But this relation is not true for any a ∈ N.
Thus, the operation * does not have any identity in N.

Question 9.
Let * be a binary operation on the set Q of rational numbers as
(i) a * b = a – b
(ii) a * b = a² + b²
(iii) a * b = a + ab
(iv) a * b = (a – b)²
(v) a * b = \(\frac{ab}{4}\)
(vi) a * b = ab²
Find which of the binary operations are commutative and which are associative.
Solution.
Operation is on the set Q.
(i) defined as a * b = a – b
(a) Now b * a = b – a But a – b *b – a
∴ a * b * b * a
∴ Operation * is not commutative.

(b) a* (b * c) = a * (b – c) = a – (b – c) = a – b + c
(a * b) * c = (a – b) * c = a – b – c
Thus, a * (b * c) ^ (a * b) * c
∴ The operation * as defined is not associative.

(ii) (a) a * b = a² + b²
b * a = b² + a² = a² + b²
∴ a * b = b * a
∴ This binary operation is commutative.

(b) a * (b * c) = a * (b² + c²)
= a² + (b² + c²)²
(a * b) * c = (a² + b²) * c = (a² + b²)² + c²
⇒ a * (b * c) * (a * b) * c
∴ The operation * given is not associative.

(iii) Operation * is defined as
a * b = a + ab
(a) b* a = b + ba
∴ a * b ≠ b * a
∴ This operation is not commutative.

(b) a * (b * c) = a * (b + bc)
= a + a(b + bc)
= a + ab + abc
(a* b) * c = (a + ab) *c = a + ab + (a + ab) . c
= a + ab + ac + abc
⇒ a* (b* c)& (a* b)* c
⇒ The binary operation is not associative.

(iv) The binary operation is defined as a * b = (a – b)²
(a) b * a = (b – a)² = (a – b)²
⇒ a * b = b * a
∴ This binary operation * is commutative.

(b) a * (b * c) = a * (b – c)²
= [a – (b – c)²]²
(a * b) * c = (a – b)² * c = [(a – b)² – c]²
⇒ (a * b) * c ≠ a * (b * c)
Thus, the operation given is associative.

(v) Binary operation is * defined as
a * b = \(\frac{ab}{4}\)

(a) b * a = \(\frac{ba}{4}\) = \(\frac{ab}{4}\)
a* b^b* a
∴ The operation is not commutative.

(b) a * (b * c) = a * \(\frac{bc}{4}\)
= \(\frac{a}{4}\left(\frac{b c}{4}\right)=\frac{a b c}{16}\)
(a * b) * c = \(\frac{ab}{4}\) * c
= \(\frac{a b}{4} \cdot \frac{c}{4}=\frac{a b c}{16}\)
⇒ a * (b* c) = (a * b) * c
Thus, the operation given is associative.

(vi) Binary operation is defined as
a * b = ab²
(a) b * a = ba² ≠ ab²
∴ a * b ≠ b * a
∴ The operation is not commutative.

(b) a * (b * c) = a * bc²
= a(bc²)²
= ab²c⁴
(a * b)* c = ab² * c
= (ab²)c²
= ab²c²
∴ a * (b * c) ≠ (a * b) * c
∴ Binary operation * given is not associative.

Question 10.
Find which of the operations given above has identity.
Solution.
An element e ∈ Q will be the identity element for the operation * if
a * e = a = e * a, ∀ a ∈ Q
(i) a * b = a – b
lf a * e = a, a ≠ 0
⇒ a – e = a, a ≠ 0 ⇒ e = 0
Also, e * a = a
⇒ e – a = a ⇒ e = 2 a
e = 0 = 2a, a ≠ 0
But the identity is unique. Hence this operation has no identity.

(ii) a * b = a² + b²
If a * e = a, then a² + e² = a
For a = – 2, (- 2)² + e² = 4 + e² ≠ – 2
Hence, there is no identity element.

(iii) a * b = a + ab
If a * e = a
⇒ a + ae a
⇒ ae = 0
⇒ e = 0, a ≠ 0
Also a * e = a
⇒ e + ae = a
⇒ e = \(\frac{a}{a+1}\), a ≠ 1
∴ e = 0 = \(\frac{a}{a+1}\), a ≠ 0
But the identity in unique. Hence this operation has no identify.

(iv) a * b = (a – b)²
If a* e = a, then (a – e)² = a.
A square is always positive, so for a = – 2, (- 2 – e)² ≠ – 2.
Hence, there is no identity element.

(v) a * b – ab/ 4
If a * e = a, then ae / 4 = a.
Hence, e = 4 is the identity element.
∴ a * 4 = 4 * a = 4a/4 = a.

(vi) a * b = ab²
If a * e = a
⇒ ae² = a
⇒ e² = 1
⇒ e = ±1
But identity is unique. Hence this operation has no identity.
Therefore only part (v) has an identity element.

Question 11.
Let A = N × N and * be the binary operation on A defined by (a, b) * (c, d) = (a + c, b + d). Show that * is commutative and associative. Find the identity element for * on A, if any.
Solution.
Given that A = N × N and * is a binary operation on A and is defined by (a, b) * (c, d) = (a + c,b + d.)
Let (a, b), (c, d) ∈ A
Then, a, b, c, d ∈ N
We have (a, b) * (c, d) = (a + c, b + d)
and (c, d) * (a, b) = (c + a, d + b) = (a + c, b + d)
[Addition is commutative in the set of natural numbers]
∴ (a, b) * (c, d) = (c, d) * (a, b)
Therefore, the operation * is commutative.
Now, let (a, b), (c, d), (e, f) ∈ A
Then, a, b, c, d, e, f ∈ N
We have {(a, b) * (c, d)} * (e, f) = (a + c,b + d) * (e, f)
= (a+ c + e, b + d + f)
(a, b) * ((c, d) * (e, f)) = (a, b) * (c + e, d + f) = (a + c + e, b + d + f)
((a, b) * (c, d)) * (e, f) = (a, b) * ((c, d) * (e, f))
Therefore, the operation * is associative.
An element e = (e₁, e₂) ∈ A will be an identity element for the operation * if
a * e = a = e * a ∀ a = (a₁, a₂) ∈ A, i.e., (a₁ + e₁, a₂ + e₂)
= (a₁, a₂) = (e₁ + a₁; e₂ + a₂)
which is not true for any element in A.
Therefore, the operation * does not have any identity element.

Question 12.
State whether the following statements are true or false. Justify.
(i) For an arbitrary binaiy operation * on a set N, a * a = a ∀ a ∈ N.
(ii) If * is a commutative binary operation on N, then a* (b* c) = (c * b) * a
Solution.
(i) Define an operation * on IV as a * b – a + b ∀ a, b ∈ N
Then, in particular, for b = a = 3, we have 3 * 3 = 3 + 3 = 6 ≠ 3
Therefore, statement (i) is false.

(ii) R.H.S. = (c * b) * a
= (b * c) * a [* is commutative]
= a * (b * c) [Again, as * is commutative]
= L.H.S.
∴ a * (b * c) = (c * b) * a
Therefore, statement (ii) is true.

Question 13.
Consider a binary operation * on N defined as a * b = a3 +b3. Choose the correct answer.
(A) Is * both associative and commutative?
(B) Is * commutative but not associative?
(C) Is * associative but not commutative?
(D) Is * neither commutative nor associative?
Solution.
On N, the operation * is defined as a * b = a³ + b³.
For, a, b ∈ N, we have
a * b = a³ + b³
= b³ + a³ = b * a [Addition is commutative in N]
Therefore, the operation * is commutative.
It can be observed that
(1 * 2) * 3 = (1³ + 2³) * 3 = 9 * 3
= 9³ + 3³
= 729 + 27 = 756

1 * (2 * 3) = 1 * (2³ +3³)
= 1 * (8 + 27) = 1 * 35
= 1³ + 35³
= 1 + (35)³
= 1 + 42875 = 42876
∴ (1 * 2) * 3 ≠ 1 * (2 * 3) where 1, 2, 3 ∈ N
Therefore, the operation * is not associative.
Hence, the operation * is commutative, but not associative.
Thus, the correct answer is (B).