Class 12

Punjab State Board PSEB 12th Class Physics Book Solutions Chapter 8 Electromagnetic Waves Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Physics Chapter 8 Electromagnetic Waves

PSEB 12th Class Physics Guide Electromagnetic Waves Textbook Questions and Answers

Question 1.
Figure 8.6 shows a capacitor made of two circular plates each of radius 12 cm, and separated by 5.0 cm. The capacitor is being charged by an external source (not shown in the figure). The charging current is constant and equal to 0.15 A.

(a) Calculate the capacitance and the rate of charge of potential difference between the plates.
(b) Obtain the displacement current across the plates.
(c) Is Kirchhoffs first rule (junction rule) valid at each plate of the capacitor? Explain.
Answer:
(a) Capacitance of capacitor is given by the relation
C = \(\frac{\varepsilon_{0} A}{d}\) = \(\frac{8.854 \times 10^{-12} \times \pi \times(0.12)^{2}}{5 \times 10^{-2}}\)
= 8.01F
Also \(\frac{d Q}{d t}\) = \(\frac{d V}{d t}\)
∴ \(\frac{d V}{d t}\) = \(\frac{0.15}{8.01 \times 10^{-12}}\)
= 1.87 × 10¹⁰V /s

(b) Displacement current I_d = ε₀ × \(\frac{d}{d t}\) (Φ_E)
Again Φ_E – EA across Hence,(negative end constant).
Hence, I_d = ε₀ A\(\frac{d E}{d t}\)
Again, E = \(\frac{Q}{\varepsilon_{0} A}\)
So, \(\frac{d E}{d t}=\frac{i}{\varepsilon_{0} A}\)
which corresponds i_d = i = 1.5A

(c) Yes, Kirchhoffs law is valid provided by current, we mean the sum of condition and displacement current.

Question 2.
A parallel plate capacitor (Fig. 8.7) made of circular plates each of radius R = 6.0 cm has a capacitance C = 100 pF. The capacitor is connected to a 230 V ac supply with a (angular) frequency of 300 rad s^-1.

(a) What is the rms value of the conduction current?
(b) Is the conduction current equal to the displacement current?
(c) Determine the amplitude of B at a point 3.0 cm from the axis between the plates.
Answer:
(a) I_rms = V_rms × Cω
= 230 × 100 × 10¹² × 300
= 6.9 × 10^-6 A = 6.9 μ A

(b) Yes, we know that the deviation is correct even if I is steady DC or AC (oscillating in time) can be proved as
I_d = ε₀\(\frac{d}{d t}\) (σ) = ε₀\(\frac{d}{d t}\) (EA) (> σ = EA)
ε₀A \(\frac{d E}{d t}\) = ε₀A \(\frac{d}{d t}\) (\(\frac{\sigma}{\varepsilon_{0}}\))
ε₀A \(\frac{d}{d t}\) (\(\frac{\sigma}{\varepsilon_{0} A}\)) (> σ = \(\frac{q}{A}\))
ε₀A × \(\frac{1}{\varepsilon_{0} A} \cdot \frac{d q}{d t}\) = I
which is the required proof.

(c) The region formula for magnetic field
B = \(\frac{\mu_{0} r}{2 \pi R^{2}}\)i_d
even if I_d is oscillating (and so magnetic field B): The formula is valid. I_D oscillates in phase as i₀ = i (peak value of current). Now, we have
B₀ = \(\frac{\mu_{0} r}{2 \pi R^{2}}\)i₀
where B₀ and i₀ are the amplitude of magnetic field and current respectively.
So, i₀ = √2I_rms = 6.96 × 1.414 μA = 9.76μA
Given, r = 3 cm, R = 6cm
B₀ = \(\frac{\mu_{0} r i_{0}}{2 \pi R^{2}}\)
= \(\frac{10^{-7} \times 2 \times 3 \times 10^{-2} \times 9.76 \times 10^{-6}}{(6)^{2} \times\left(10^{-2}\right)^{2}}\)
= 1.633 × 10^-11 T

Question 3.
What physical quantity is the same for X-rays of wavelength 10^-10 m, red light of wavelength 6800 Å and radiowaves of wavelength 500 m?
Answer:
X-rays, red light and radiowaves all are the electromagnetic waves. They have different wavelengths and frequencies. But the physical quantity which is same for all of these is the velocity of light in vacuum which is denoted by c and is equal to 3 × 10⁸ ms^-1 W

Question 4.
A plane electromagnetic wave travels in vacuum along z-direction. What can you say about the directions of its electric and magnetic field vectors? If the frequency of the wave is 30 MHz, what is its wavelength?
Answer:
In an electromagnetic wave’s propagation vector \(\vec{K}\), electric field vector \(\vec{E}\) and magnetic field vector \(\vec{K}\) form a right handed system. As the propagation vector is along Z-direction, electric field vector will be along X-direction and magnetic field vector will be along Y-direction.
Frequency v = 30 MHz = 30 × 10⁶Hz
Speed of light c = 3 × 10⁸ ms^-1
Wavelength, λ = \(\frac{c}{v}\) = \(\frac{3 \times 10^{8}}{30 \times 10^{6}}\) = 10 m

Question 5.
A radio can tune in to any station in the 7.5 MHz to 12 MHz hand. What is the corresponding wavelength band?
Answer:
Speed of wave c = 3 × 10⁸ ms^-1
When frequency, V₁ = 7.5MHz = 7.5 × 10⁶ Hz
Wavelength, λ₁ = \(\frac{c}{v_{1}}\) = \(\frac{3 \times 10^{8}}{7.5 \times 10^{6}}\) = 40m
When frequency, V₂ 12 MHZ = 12 × 10⁶HZ
Wavelength, λ₂ = \(\frac{c}{v_{2}}\) = \(\frac{3 \times 10^{8}}{12 \times 10^{6}}\) = 25m
Wavelength band is from 25 m to 40 m.

Question 6.
A charged particle oscillates about its mean equilibrium position with a frequency of 10⁹ Hz. What is the frequency of the electromagnetic waves produced by the oscillator?
Answer:
According to Maxwell’s theory, an oscillating charged particle with a frequency v radiates electromagnetic waves of frequency v.
So, the frequency of electromagnetic waves produced by the oscillator is v = 10⁹ Hz.

Question 7.
The amplitude of the magnetic field part of a harmonic electromagnetic wave in vacuum is B₀ =510 nT. What is the amplitude of the electric field part of the wave?
The relation between magnitudes of magnetic and electric field vectors in vacuum is
\(\frac{E_{0}}{B_{0}}\) = c
⇒ E₀ = B₀C
Here, B₀ = 510 × 10^-9T, c = 3 × 10⁸ ms^-1
E₀ = 510 × 10^-9 × 3 × 10⁸ = 153N/C

Question 8.
Suppose that the electric field amplitude of an electromagnetic wave is E₀ = 120 N/C and that its frequency is v = 50.0 MHz. (a) Determine, B₀, ω, k and λ. (b) Find expressions for E and B.
Answer:
Electric field amplitude, E₀ = 120 N/C
Frequency of source, v = 50.0 MHz = 50 × 10⁶ Hz
Speed of light, c = 3 × 10⁸ m/s

(a) Magnitude of magnetic field strength is given as
B₀ \(\frac{E_{0}}{\mathcal{C}}\) = \(\frac{120}{3 \times 10^{8}}\)
40 × 10^-8T
= 400 × 10^-9 T
= 400 nT
Angular frequency of source is given as
ω = 2πv = 2π × 50 × 10⁶
= 3.14 × 10⁸ rad/s
Propagation constant is given as
k = \(\frac{\omega}{c}\) = \(\frac{3.14 \times 10^{8}}{3 \times 10^{8}}\) = 1.05 rad /m
Wavelength of wave is given us
λ = \(\frac{c}{v}\) = \(\frac{3 \times 10^{8}}{50 \times 10^{6}}\) = 6.0m

(b) Suppose the wave is propagating in the positive x direction. Then, the electric field vector will be in the positive y direction and the magnetic field vector will be in the positive z direction. This is because all three vectors are mutually perpendicular.
Equation of electric field vector is given as
\(\vec{E}\) = E₀sin (kx – ωt) ĵ
= 120 sin [1.05 x – 3.14 × 10⁸t] ĵ
And, magnetic field vector is given as
\(\vec{B}\) = B₀ sin (kx – ωt)k̂
\(\vec{B}\) = (4 × 10^-7)sin[1.05 x – 3.14 × 10⁸t]k̂

Question 9.
The terminology of different parts of the electromagnetic spectrum is given in the text. Use the formula E – hv (for energy of a quantum of radiation : photon) and obtain the photon energy in units of eV for different parts of the electromagnetic spectrum. In what way are the different scales of photon energies that you obtain related to the sources of electromagnetic radiation?
Answer:
Energy of a photon is given as
E = hv = \(\frac{h c}{\lambda}\)
where,
h = Planck’s constant = 6.6 × 10^-34 Js
c = Speed of light = 3 × 10⁸ m/s
λ = Wavelength of radiation
∴ E = \(\frac{6.6 \times 10^{-34} \times 3 \times 10^{8}}{\lambda}\) = \(\frac{19.8 \times 10^{-26}}{\lambda}\) = J
= \(\frac{19.8 \times 10^{-26}}{\lambda \times 1.6 \times 10^{-19}}\) = \(\frac{12.375 \times 10^{-7}}{\lambda}\) = eV
The given table lists the photon energies for different parts of an electromagnetic spectrum for different λ.

The photon energies for the different parts of the spectrum of a source indicate the spacing of the relevant energy levels of the source.

Question 10.
In a plane electromagnetic wave, the electric field oscillates sinusoidally at a frequency of 2.0 × 10¹⁰Hz and amplitude 48 Vm^-1.
(a) What is the wavelength of the wave?
(b) What is the amplitude of the oscillating magnetic field?
(c) Show that the average energy density of the E field equals the average energy density of the B field, [c = 3 × 10⁸ ms^-1]
Answer:
Frequency of the electromagnetic wave, v = 2.0 × 10¹⁰ Hz
Electric field amplitude, E₀ = 48 V m^-1
Speed of light, c = 3 × 10⁸ m/s

(a) Wavelength of the wave is given as
λ = \(\frac{\mathcal{C}}{\mathrm{v}}\) = \(\frac{3 \times 10^{8}}{2 \times 10^{10}}\) 0.015 m

(b) Magnetic field strength is given as
B₀ = \(\frac{E_{0}}{c}\)
= \(\frac{48}{3 \times 10^{8}}\) = 1.6 × 10^-7 T

(c) Let U_E and U_B be the energy density of \(\) field and \(\) field respectively. Energy density of the electric field is given as
U_E = \(\frac{1}{2}\) ε₀E²
And, energy density of the magnetic field is given as
U_B = \(\frac{1}{2 \mu_{0}}\)²
We have the relation connecting E and B as
E = cB ………….. (1)
where,
c = \(\frac{1}{\sqrt{\varepsilon_{0} \mu_{0}}}\) ……………. (2)
Putting equation (2) in equation (1), we get
E = \(\frac{1}{\sqrt{\varepsilon_{0} \mu_{0}}}\)B
Squaring both sides, we get
E² = \(\frac{1}{\varepsilon_{0} \mu_{0}}\) B²
ε₀E² = \(\frac{B^{2}}{\mu_{0}}\)
\(\frac{1}{2}\)ε₀E² = \(\frac{1}{2} \frac{B^{2}}{\mu_{0}}\)
⇒ U_E = E_B

Question 11.
Suppose that the electric field part of an electromagnetic wave in vacuum is
E = {(3.1 N/C) cos [(1.8 rad/m) y + (5.4 × 10⁶ rad/s) t]}î
(a) What is the direction of propagation?
(b) What is the wavelength λ ?
(c) What is the frequency v?
(d) What is the amplitude of the magnetic field part of the wave?
(e) Write an expression for the magnetic field part of the wave.
Answer:
(a) Wave is propagating along negative y-axis.

(b) Standard equation of wave is \(\vec{E}\) = E₀ cos(ky + cot)î
Comparing the given equation with standard equation, we have
E₀ = 3.1 N/C, k = 1.8 rad/m, ω = 5.4 × 10⁶ rad/s
Propagation constant k = \(\frac{2 \pi}{\lambda}\)
∴ λ = \(\frac{2 \pi}{k}\) = \(\frac{2 \times 3.14}{1.8}\) m = 3.49 m

(c) We have ω = 5.4 × 10⁶ rad/s
Frequency, v = \(\frac{\omega}{2 \pi}\) = \(\frac{5.4 \times 10^{6}}{2 \times 3.14}\) Hz
= 8.6 × 10⁵ Hz

(d) Amplitude of magnetic field,
B₀ = \(\frac{E_{0}}{c}\) = \(\frac{3.1}{3 \times 10^{8}}\) = 1.03 × 10^-8 T

(e) The magnetic field is vibrating along Z-axis because \(\vec{K}\),\(\vec{E}\),\(\vec{B}\) form a right handed system -ĵ × î = k̂
> Expression for magnetic field is
\(\vec{B}\) = B₀ cos(ky+ ωt)k̂
= [1.03 × 10^-8Tcos{(1.8rad / m) y +(5.4 × ⁶ rad/s)t}]k̂

Question 12.
About 5% of the power of a 100 W light bulb is converted to visible radiation. What is the average intensity of visible radiation
(a) at a distance of 1 m from the bulb?
(b) at a distance of 10 m?
Assume that the radiation is emitted isotropically and neglect reflection.
Answer:
Power in visible radiation, P = \(\frac{5}{100}\) × 100 = 5W
For a point source, intensity I = \(\frac{P}{4 \pi r^{2}}\), where r is distance from the source.

(a) When distance r = 1 m,
I = \(\frac{5}{4 \pi(1)^{2}}=\frac{5}{4 \times 3.14}\) = 0.4 W/m²

(b) When distance r = 10 m,
I = \(\frac{5}{4 \pi(10)^{2}}=\frac{5}{4 \times 3.14 \times 100}\)
= 0.004 W/m²

Question 13.
Use the formula λ_m T = 0.29 cm K to obtain the characteristic temperature ranges for different parts of the electromagnetic spectrum. What do the numbers that you obtain tell you?
Answer:
A body at a particular temperature produces a continuous spectrum of wavelengths. In case of a black body, the wavelength corresponding to maximum intensity of radiation is given according to Planck’s law. It can be given by the relation,
λ_m = \(\frac{0.29}{T}\) cm K
where, λ_m = maximum wavelength
T = temperature
Thus, the temperature for different wavelengths can be obtained as
For λ_m = 10^-4 cm; T = \(\frac{0.29}{10^{-4}}\) = 2900°K
For λ_m = 5 × 10^-5 cm; T = \(\frac{0.29}{5 \times 10^{-5}}\) = 5800°K
For λ_m = 10^-6 cm; T = \(\frac{0.29}{10^{-6}}\) = 290000 °K and so on.

The numbers obtained tell us that temperature ranges are required for obtaining radiations in different parts of an electromagnetic spectrum. As the wavelength decreases, the corresponding temperature increases.

Question 14.
Given below are some famous numbers associated with electromagnetic radiations in different contexts in physics. State the part of the electromagnetic spectrum to which each belongs.
(a) 21 cm (wavelength emitted by atomic hydrogen in interstellar space).

(b) 1057 MHz (frequency of radiation arising from two close energy levels in hydrogen; known as Lamb shift).

(c) 2.7 K (temperature associated with the isotropic radiation filling all space-thought to be a relic of the ‘big-bang’ origin of the universe).

(d) 5890 Å – 5896 Å (double lines of sodium).

(e) 14.4 keV [energy of a particular transition in ⁵⁷ Fe nucleus associated with a famous high resolution spectroscopic method (Mossbauer spectroscopy)].
Answer:
(a) 21 cm belongs to short wavelength end of radiowaves (or Hertizan waves).

(b) Wavelength, λ = \(\frac{c}{v}\) = \(\frac{3 \times 10^{8}}{1057 \times 10^{6}}\) = 0.28 m = 28 cm.
This also belongs to short wavelength end of radiowaves.

(c) From relation λ_mT = 0.29 × 10^-2 K,
λ_m = \(\frac{0.29 \times 10^{-2} \mathrm{~K}}{T}=\frac{0.29 \times 10^{2}}{2.7}\)
= 0.107 × 10^-2m= 0.107 cm.
This corresponds to microwaves.

(d) Wavelength doublet 5890Å – 5896Å belongs to the visible region. These are emitted by sodium vapour lamp.

(e) From relation, E = \(\frac{h c}{\lambda}\)
we have λ = \(\frac{h c}{E}\)
λ = \(\frac{6.63 \times 10^{-34} \times 3 \times 10^{8}}{14.4 \times 10^{3} \times 1.6 \times 10^{-19}} \mathrm{~m}\)
= 0.86 × 10^-10 m = 0.86 Å
It belongs to the X-ray region of electromagnetic spectrum.

Question 15.
Answer the following questions :
(a) Long distance radio broadcasts use short-wave bands. Why?

(b) It is necessary to use satellites for long distance TV transmission. Why?

(c) Optical and radiotelescopes are built on the ground but X-ray astronomy is possible only from satellites orbiting the earth Why?

(d) The small ozone layer on top of the stratosphere is crucial for human survival. Why?

(e) If the earth did not have an atmosphere, would its average surface temperature be higher or lower than what it is now?

(f) Some scientists have predicted that a global nuclear war on the earth would be followed by a severe ‘nuclear winter’ with a devastating effect on life on earth. What might be the basis of this prediction?
Answer:
(a) Long distance radio broadcasts use short-wave bands because only these bands can be refracted by the ionosphere.

(b) Yes, it is necessary to use satellites for long distance TV transmissions because television signals are of high frequencies and high energies. Thus, these signals are not reflected by the ionosphere. Hence, satellites are helpful in reflecting TV signals. Also, they help in long distance TV transmissions.

(c) With reference to X-ray astronomy, X-rays are absorbed by the atmosphere. However, visible and radiowaves can penetrate it. Hence, optical and radiotelescopes are built on the ground, while X-ray astronomy is possible only with the help of satellites orbiting the Earth.

(d) The small ozone layer on the top of the stratosphere is crucial for human survival because it absorbs harmful ultraviolet radiations present in sunlight and prevents it from reaching the Earth’s surface.

(e) In the absence of an atmosphere, there would be no greenhouse effect on the surface of the Earth. As a result, the temperature of the Earth would decrease rapidly, making it chilly and difficult for human survival.

(f) A global nuclear war on the surface of the Earth would have disastrous consequences. Post nuclear war, the Earth will experience severe winter as the war will produce clouds of smoke -that would cover maximum parts of the sky, thereby preventing solar light form reaching the atmosphere. Also, it will lead to the depletion of the ozone layer.

Punjab State Board PSEB 12th Class Physical Education Book Solutions Chapter 1 ਸਰੀਰਕ ਯੋਗਤਾ Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Physical Education Chapter 1 ਸਰੀਰਕ ਯੋਗਤਾ

Physical Education Guide for Class 12 PSEB ਸਰੀਰਕ ਯੋਗਤਾ Textbook Questions and Answers

ਇੱਕ ਅੰਕ ਵਾਲੇ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ (One Mark Question Answers)

ਪ੍ਰਸ਼ਨ 1.
ਤਾਕਤ ਕਿੰਨੇ ਪ੍ਰਕਾਰ ਦੀ ਹੁੰਦੀ ਹੈ ? ਉੱਤਰ-ਤਾਕਤ ਦੋ ਪ੍ਰਕਾਰ ਦੀ ਹੁੰਦੀ ਹੈ-

1. ਸਥਿਰ ਤਾਕਤ,
2. ਗਤੀਸ਼ੀਲ ਤਾਕਤ !

ਪ੍ਰਸ਼ਨ 2.
ਸਰੀਰਕ ਯੋਗਤਾ ਦੇ ਕਿੰਨੇ ਅੰਗ ਹੁੰਦੇ ਹਨ ?
ਉੱਤਰ:
ਤਾਕਤ, ਸਹਿਣਸ਼ੀਲਤਾ, ਰਫਤਾਰ, ਲੱਚਕ, ਫੁਰਤੀ ਅਤੇ ਤਾਲਮੇਲ ਯੋਗਤਾ ।

ਪ੍ਰਸ਼ਨ 3.
ਛੋਟੀ ਦੂਰੀ ਦੀਆਂ ਦੌੜਾਂ ਦੱਸੋ ।
ਉੱਤਰ:
100 ਮੀ., 200 ਮੀ., 400 ਮੀ., 100 ਹਰਡਲ ਅਤੇ 110 ਮੀ. ਹਰਡਲ, 4 × 100 ਰਿਲੇਅ ਅਤੇ 4 × 200 ਰਿਲੇਅ ।

ਪ੍ਰਸ਼ਨ 4.
ਸੁਸਤ ਲਚਕ ਵੱਧ ਹੁੰਦੀ ਹੈ ਜਾਂ ਚੁਸਤ ਲਚਕ ?
ਉੱਤਰ:
ਸੁਸਤ ਲਚਕ ।

ਦੋ ਅੰਕਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ (Two Marks Question Answers)

ਪ੍ਰਸ਼ਨ 5.
ਮੱਧ ਸਮੇਂ ਦੀ ਸਹਿਨਸ਼ੀਲਤਾ ਕੀ ਹੈ ?
ਉੱਤਰ:
ਮੱਧ ਸਮੇਂ ਦੀ ਸਹਿਣਸ਼ੀਲਤਾ (Middle Term Endurance)-ਇਸ ਦੀ ਜ਼ਰੂਰਤ ਉਹਨਾਂ ਮੁਕਾਬਲਿਆਂ ਵਿਚ ਪੈਂਦੀ ਹੈ ਜੋ ਕਿ 2 ਤੋਂ 10 ਮਿੰਟ ਵਿਚ ਖ਼ਤਮ ਹੋ ਜਾਂਦੇ ਹਨ , ਜਿਵੇਂ ਕਿ ਮੱਧ ਦੂਰੀ ਦੀਆਂ ਦੌੜਾਂ ਇਸ ਦੀਆਂ ਉਦਾਹਰਣਾਂ ਹਨ ।

ਪ੍ਰਸ਼ਨ 6.
ਲੰਮੇ ਸਮੇਂ ਦੀ ਸਹਿਣਸ਼ੀਲਤਾ ਬਾਰੇ ਤੁਸੀਂ ਕੀ ਜਾਣਦੇ ਹੋ ?
ਉੱਤਰ:
ਲੰਬੇ ਸਮੇਂ ਦੀ ਸਹਿਣਸ਼ੀਲਤਾ (Long Term Endurance) – ਇਸ ਕਿਸਮ ਦੀ ਸਹਿਣਸ਼ੀਲਤਾ ਐਰੋਬਿਕ ਊਰਜਾ ਪ੍ਰਣਾਲੀ ‘ਤੇ ਨਿਰਭਰ ਕਰਦੀ ਹੈ । ਲੰਬੇ ਸਮੇਂ ਦੀ ਸਹਿਣਸ਼ੀਲਤਾ ਦਾ ਵਿਕਾਸ ਉਹਨਾਂ ਮੁਕਾਬਲਿਆਂ ਲਈ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ਜੋ ਕਿ 10 ਮਿੰਟ ਜਾਂ ਇਸ ਤੋਂ ਵੀ ਵੱਧ ਸਮੇਂ ਲਈ ਖੇਡੇ ਜਾਂਦੇ ਹਨ । ਜਿਵੇਂ ਕਿ ਮੈਰਾਥਨ, 5000 ਮੀਟਰ ਅਤੇ ‘ 10,000 ਮੀਟਰ ਦੀਆਂ ਦੌੜਾਂ ਇਸ ਦੀਆਂ ਉਦਾਹਰਨਾਂ ਹਨ ।

ਪ੍ਰਸ਼ਨ 7.
ਸੁਸਤ ਲਚਕ ਬਾਰੇ ਤੁਸੀਂ ਕੀ ਜਾਣਦੇ ਹੋ ?
ਉੱਤਰ:
ਸੁਸਤ ਲਚਕ (Passive Flexibility) – ਇਹ ਬਿਨਾਂ ਕਿਸੇ ਬਾਹਰੀ ਮੱਦਦ ਜਾਂ ਸਹਾਰੇ ਦੇ ਵੱਡੀ ਦਰ ਤੇ ਕ੍ਰਿਆਵਾਂ ਕਰਨ ਦੀ ਯੋਗਤਾ ਹੁੰਦੀ ਹੈ । ਉਦਾਹਰਨ ਦੇ ਤੌਰ ਤੇ ਕਿਸੇ ਸਾਥੀ ਖਿਡਾਰੀ ਦੀ ਮਦਦ ਨਾਲ ਸਚਿੰਗ (Stretching) ਕਸਰਤਾਂ ਕਰਨਾ । ਇਹ ਚੁਸਤ ਲਚਕ ਤੋਂ ਵੱਧ ਹੁੰਦੀ ਹੈ ।

ਤਿੰਨ ਅੰਕਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ (Three Marks Question Answers)

ਪ੍ਰਸ਼ਨ 8.
ਸਹਿਣਸ਼ੀਲਤਾ ਨੂੰ ਕਿੰਨੇ ਭਾਗਾਂ ਵਿੱਚ ਵੰਡਿਆ ਗਿਆ ਹੈ ? ਇਹਨਾਂ ਬਾਰੇ ਵਿਸਥਾਰਪੂਰਵਕ ਜਾਣਕਾਰੀ ਦਿਉ ।
ਉੱਤਰ:
ਸਹਿਣਸ਼ੀਲਤਾ ਦੇ ਪ੍ਰਕਾਰ (Types of Endurance) – ਲੋੜਾਂ ਮੁਤਾਬਿਕ ਸਹਿਣਸ਼ੀਲਤਾ ਨੂੰ ਹੇਠ ਲਿਖੇ ਭਾਗਾਂ ਵਿਚ ਵੰਡਿਆ ਜਾ ਸਕਦਾ ਹੈ-
1. ਕਿਆ ਦੇ ਸੁਭਾਅ ਅਨੁਸਾਰ (As per Nature of the Activity)
(ਉ) ਬੁਨਿਆਦੀ ਸਹਿਣਸ਼ੀਲਤਾ (Basic Endurance) – ਬੁਨਿਆਦੀ ਸਹਿਣਸ਼ੀਲਤਾ ਮੁੱਖ ਤੌਰ ਤੇ ਐਰੋਬਿਕ ਸਹਿਣਸ਼ੀਲਤਾ ਤੇ ਨਿਰਭਰ ਕਰਦੀ ਹੈ । ਐਰੋਬਿਕ ਤੋਂ ਭਾਵ ਹੈ ਕਿ ਜਿਸ ਵਿਚ ਆਕਸੀਜਨ ਦੀ ਪੂਰਤੀ ਕਸਰਤਾਂ ਅਤੇ ਅਭਿਆਸ ਨਾਲ ਮਿਲਦੀ ਰਹੇ । ਇਹ ਹੌਲੀ-ਹੌਲੀ ਕੀਤੀਆਂ ਜਾਂਦੀਆਂ ਹਨ ਜਿਸ ਵਿਚ ਸਰੀਰ ਦੇ ਸਾਰੇ ਮਸਲ ਗਰੁੱਪ ਭਾਗ ਲੈਂਦੇ ਹਨ ਜਾਂ ਸ਼ਾਮਲ ਹੁੰਦੇ ਹਨ । ਦੌੜਨਾ, ਜੋਗਿੰਗ, ਚੱਲਣਾ ਅਤੇ ਤੈਰਾਕੀ ਬੁਨਿਆਦੀ ਸਹਿਣਸ਼ੀਲਤਾ ਦੇ ਉਦਾਹਰਨ ਹਨ ।

(ਅ) ਆਮ ਸਹਿਣਸ਼ੀਲਤਾ (General Endurance – ਇਹ ਐਰੋਬਿਕਸ ਅਤੇ ਐਨਰੋਬਿਕਸ ਦੋਵੇਂ ਕ੍ਰਿਆਵਾਂ ‘ਤੇ ਨਿਰਭਰ ਕਰਦੀ ਹੈ । ਇਹ ਹੌਲੀ ਅਤੇ ਤੇਜ਼ ਗਤੀ ਦੋਵਾਂ ਪ੍ਰਕਾਰਾਂ ਨਾਲ ਕੀਤੀ ਜਾਂਦੀ ਹੈ । ਇਹ ਸਹਿਣਸ਼ੀਲਤਾ ਖਿਡਾਰੀ ਨੂੰ ਬਿਨਾਂ ਥਕਾਵਟ ਦੇ ਲੰਬੇ ਸਮੇਂ ਦੇ ਕੰਮ ਕਰਨ ਦੇ ਯੋਗ ਬਣਾਉਂਦੀ ਹੈ ।

(ਬ) ਵਿਸ਼ੇਸ਼ ਸਹਿਣਸ਼ੀਲਤਾ (Specific Endurance) – ਵਿਸ਼ੇਸ਼ ਸਹਿਣਸ਼ੀਲਤਾ ਹਰ ਖੇਡ ਲਈ ਅਲੱਗ-ਅਲੱਗ ਹੁੰਦੀ ਹੈ । ਹਰ ਖੇਡ ਦੀ ਆਪਣੀ ਗਤੀ ਹੁੰਦੀ ਹੈ , ਜਿਵੇਂ ਕਿ ਮੈਰਾਥਨ ਦੌੜਾਕਾਂ ਨੂੰ ਲੰਬੇ ਸਮੇਂ ਤੱਕ ਕਿਰਿਆ ਵੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ:ਜਿਵੇਂ ਕਿ ਛੋਟੀਆਂ ਦੌੜਾਂ ; ਜਿਵੇਂ (ਸਪਰਿੰਟ) ਤੇ ਮੱਧ ਦੂਰੀ ਦੀਆਂ ਦੌੜਾਂ ਆਦਿ ਇਸ ਦੇ ਉਦਾਹਰਨ ਹਨ ।

(ਅ) ਮੱਧ ਸਮੇਂ ਦੀ ਸਹਿਣਸ਼ੀਲਤਾ (Middle Term Endurance) – ਇਸ ਦੀ ਜ਼ਰੂਰਤ ਉਹਨਾਂ ਮੁਕਾਬਲਿਆਂ ਵਿਚ ਪੈਂਦੀ ਹੈ ਜੋ ਕਿ 2 ਤੋਂ 10 ਮਿੰਟ ਵਿਚ ਖ਼ਤਮ ਹੋ ਜਾਂਦੇ ਹਨ , ਜਿਵੇਂ ਕਿ ਮੱਧ ਦੁਰੀ ਦੀਆਂ ਦੌੜਾਂ ਇਸ ਦੀਆਂ ਉਦਾਹਰਨਾਂ ਹਨ । ਇਸ ਸਹਿਣਸ਼ੀਲਤਾ ਨੂੰ ਐਨਰੋਬਿਕ ਸਹਿਣਸ਼ੀਲਤਾ ਵੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।

(ਇ) ਲੰਬੇ ਸਮੇਂ ਦੀ ਸਹਿਣਸ਼ੀਲਤਾ (Long Term Endurance) – ਇਸ ਕਿਸਮ ਦੀ ਸਹਿਣਸ਼ੀਲਤਾ ਐਰੋਬਿਕ ਊਰਜਾ ਪ੍ਰਣਾਲੀ ‘ਤੇ ਨਿਰਭਰ ਕਰਦੀ ਹੈ । ਲੰਬੇ ਸਮੇਂ ਦੀ ਸਹਿਣਸ਼ੀਲਤਾ ਦਾ ਵਿਕਾਸ ਉਹਨਾਂ ਮੁਕਾਬਲਿਆਂ ਲਈ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ਜੋ ਕਿ 10 ਮਿੰਟ ਜਾਂ ਇਸ ਤੋਂ ਵੀ ਵੱਧ ਸਮੇਂ ਲਈ ਖੇਡੇ ਜਾਂਦੇ ਹਨ , ਜਿਵੇਂ ਕਿ ਮੈਰਾਥਨ, 5000 ਮੀਟਰ ਅਤੇ 10,000 ਮੀਟਰ ਦੀਆਂ ਦੌੜਾਂ ਇਸ ਦੀਆਂ ਉਦਾਹਰਨਾਂ ਹਨ ।

ਪ੍ਰਸ਼ਨ 9.
ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚੋਂ ਕਿਸੇ ਇੱਕ ‘ਤੇ ਨੋਟ ਲਿਖੋ । (ਉ) ਗਤੀ (ਅ) ਲਚਕ (ਬ) ਤਾਲਮੇਲ ਯੋਗਤਾ ।
ਉੱਤਰ:
(ੳ) ਗਤੀ (ਰਫਤਾਰ) (Speed)-ਗਤੀ ਇਕ ਅਧਿਕਤਮ ਦਰ ਹੁੰਦੀ ਹੈ, ਜਿਸ ਵਿਚ ਇਕ ਵਿਅਕਤੀ ਇਕ ਵਿਸ਼ੇਸ਼ ਦੂਰੀ ਨੂੰ ਤੈਅ ਕਰਨ ਲਈ ਆਪਣੇ ਸਰੀਰ ਵਿਚ ਗਤੀ ਲੈ ਕੇ ਆਉਂਦਾ ਹੈ । ਅਸੀਂ ਕਹਿ ਸਕਦੇ ਹਾਂ ਕਿ ਰਫਤਾਰ ਘੱਟ ਤੋਂ ਘੱਟ ਮੁਸ਼ਕਿਲ ਸਮੇਂ ਵਿਚ ਇਕ ਥਾਂ ਤੋਂ ਦੂਜੀ ਥਾਂ ਤੇ ਪਹੁੰਚਣ ਦੀ ਯੋਗਤਾ ਹੁੰਦੀ ਹੈ । ਇਹ ਯੋਗਤਾ ਜ਼ਿਆਦਾਤਰ ਜਨਮ-ਜਾਤ ਵਿਤੀ ‘ਤੇ ਨਿਰਭਰ ਕਰਦੀ ਹੈ । ਇਸ ਲਈ ਅਸੀਂ ਜਟਿਲ ਅਭਿਆਸ ਤੋਂ ਬਾਅਦ ਵੀ ਸਿਰਫ 20% ਗਤੀ ਹੀ ਵਿਕਸਿਤ ਕਰ ਸਕਦੇ ਹਾਂ | ਤਦ ਹੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ਕਿ ਤੇਜ਼ ਦੌੜਾਕ ਜਨਮ ਲੈਂਦੇ ਹਨ, ਬਣਾਏ ਨਹੀਂ ਜਾਂਦੇ ।

ਰਫਤਾਰ ਦੇ ਪ੍ਰਕਾਰ (Types of Speed)
1. ਪ੍ਰਤੀਕ੍ਰਿਆ ਰਫਤਾਰ (Reaction Speed) – ਇਹ ਸਿਗਨਲ ਮਿਲਣ ਤੇ ਤੁਰੰਤ ਪ੍ਰਤੀਕ੍ਰਿਆ ਕਰਨ ਦੀ ਯੋਗਤਾ ਹੁੰਦੀ ਹੈ । ਇਸ ਵਿਚ ਖਿਡਾਰੀ ਪ੍ਰਸਥਿਤੀ ਦੇ ਵਿਰੁੱਧ ਪ੍ਰਤੀਕ੍ਰਿਆ ਕਰਦਾ ਹੈ , ਜਿਵੇਂ ਕਿ ਕੋਚ (Coach) ਦੀ ਸੀਟੀ ਵੱਜਣ ਤੇ ਅੱਗੇ ਵੱਲ, ਪਿੱਛੇ ਵੱਲ, ਖੱਬੇ ਅਤੇ ਸੱਜੇ ਪਾਸੇ ਤੇਜ਼ ਗਤੀ ਨਾਲ ਜਾਣਾ ਆਦਿ ।

2. ਗਤੀ ਦੀ ਯੋਗਤਾ (Acceleration Ability) – ਇਹ ਸਥਿਰ (Stationary) ਅਵਸਥਾ ਤੋਂ ਵੱਧ ਤੋਂ ਵੱਧ (Maximum) ਰਫਤਾਰ ਵਿਚ ਇਕਦਮ ਜਾਣ ਦੀ ਯੋਗਤਾ ਹੈ : ਜਿਵੇਂ ਕਿ ਅਸੀਂ ਇਹਨਾਂ ਨੂੰ ਸਪਰਿੰਟ (Sprint) ਛੋਟੀ ਦੂਰੀ ਦੀਆਂ ਦੌੜਾਂ ਵਿਚ ਦੇਖ ਸਕਦੇ ਹਾਂ ਜਿੱਥੇ ਇਕ ਵਿਸਫੋਟਕ ਤਾਕਤ, ਤਕਨੀਕ ਅਤੇ ਲਚਕ ਦੀ ਜ਼ਰੂਰਤ ਪੈਂਦੀ ਹੈ ।

3. ਲੋਕੋਮੋਟਰ ਜਾਂ ਗਮਨ ਦੀ ਯੋਗਤਾ ਜਾਂ ਇੰਜਣ ਯੋਗਤਾ (Locomotor Ability) – ਇਹ ਇਕਦਮ ਰਫਤਾਰ ਬਣਾ ਕੇ ਉਸਨੂੰ ਉਸੇ ਸਥਿਤੀ ਵਿਚ ਬਣਾਏ ਰੱਖਣ ਦੀ ਯੋਗਤਾ ਹੈ । ਜਿਵੇਂ ਕਿ ਛੋਟੀ ਦੁਰੀ ਦੀਆਂ ਦੌੜਾਂ 100 ਮੀ: 200 ਮੀ: ਅਤੇ 400 ਮੀ: ਆਦਿ ਇਸ ਦੀਆਂ ਉਦਾਹਰਣਾਂ ਹਨ ।

4. ਸੰਚਲਨ ਵੇਗ (Movement Speed) – ਇਹ ਉਹ ਯੋਗਤਾ ਜਿਸ ਵਿਚ ਘੱਟ ਤੋਂ ਘੱਟ ਸਮੇਂ ਵਿਚ ਵੱਧ ਤੋਂ ਵੱਧ | ਕ੍ਰਿਆ ਨੂੰ ਪੂਰਾ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।

5. ਰਫ਼ਤਾਰ ਸਹਿਣਸ਼ੀਲਤਾ (Speed Endurance) – ਇਹ ਉਹ ਯੋਗਤਾ ਹੁੰਦੀ ਹੈ ਜਿਸ ਵਿਚ ਖਿਡਾਰੀ ਆਪਣੀ ਰਫ਼ਤਾਰ ਨੂੰ ਖੇਡ ਦੇ ਆਖਰੀ ਪੜਾਅ ਤਕ ਬਣਾ ਕੇ ਰੱਖਦਾ ਹੈ ।

(ਅ) ਲਚਕ (Flexibility) – ਲਚਕ ਗਤੀਸ਼ੀਲਤਾ ਦੀ ਉਹ ਦਰ ਜੋ ਕਿ ਜੋੜਾਂ ਤੇ ਸੰਭਵ ਹੁੰਦੀ ਹੈ | ਅਸੀਂ ਆਮ ਸ਼ਬਦਾਂ ਵਿਚ ਇਹ ਕਹਿ ਸਕਦੇ ਹਾਂ ਕਿ ਲਚਕ ਨੂੰ ਸੁਸਤ (Passive) ਕ੍ਰਿਆਵਾਂ ਦੇ ਦੌਰਾਨ, ਜੋੜਾਂ ਅਤੇ ਉਹਨਾਂ ਦੇ ਆਸਪਾਸ ਦੀਆਂ ਮਾਸਪੇਸ਼ੀਆਂ (Muscles) ਦੀ ਗਤੀ ਦੀ ਦਰ ਦੇ ਰੂਪ ਵਿਚ ਪਰਿਭਾਸ਼ਿਤ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ । ‘ ਲਚਕ ਹੋਰਨਾਂ ਸਰੀਰਕ ਗੁਣਾਂ ਵਾਂਗ ਇਕ ਬਹੁਮੁੱਲਾ ਗੁਣ ਹੈ ਅਤੇ ਸਰੀਰਕ ਸਿੱਖਿਆ ਅਤੇ ਖਿਡਾਰੀਆਂ ਵਿਚ ਇਸਦੀ ਆਪਣੀ ਮਹੱਤਤਾ ਹੈ ਕਿਉਂਕਿ ਲਚਕਦਾਰ ਖਿਡਾਰੀ ਮੈਦਾਨ ਵਿਚ ਕਈ ਤਰ੍ਹਾਂ ਦੀਆਂ ਸੱਟਾਂ ਤੋਂ ਬਚਿਆ ਰਹਿੰਦਾ ਹੈ । ਲਚਕ ਦੇ ਕਈ ਪ੍ਰਕਾਰ ਹੁੰਦੇ ਹਨ ਅਤੇ ਇਹਨਾਂ ਦਾ ਵਰਗੀਕਰਨ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਹੈ-
ਸਥਿਰ ਲਚਕ (Static Flexibility) – ਇਹ ਸਥਿਰ ਲਚਕ ਸਰੀਰਕ ਜੋੜਾਂ ਨੂੰ ਸਥਿਰ ਸਥਿਤੀ ਵਿਚ ਰੱਖਣ ਦੀ ਯੋਗਤਾ ਹੈ ।

(i) ਸੁਸਤ ਲਚਕ (Passive Flexibility) – ਇਹ ਬਿਨਾਂ ਕਿਸੇ ਬਾਹਰੀ ਮੱਦਦ ਜਾਂ ਸਹਾਰੇ ਦੇ ਵੱਡੀ ਦਰ ਤੇ ਕ੍ਰਿਆਵਾਂ ਕਰਨ ਦੀ ਯੋਗਤਾ ਹੁੰਦੀ ਹੈ । ਉਦਾਹਰਨ ਦੇ ਤੌਰ ਤੇ ਕਿਸੇ ਸਾਥੀ ਖਿਡਾਰੀ ਦੀ ਮਦਦ ਨਾਲ ਸਚਿੰਗ (Stretching) ਕਸਰਤਾਂ ਕਰਨਾ । ਇਹ ਚੁਸਤ ਲਚਕ ਤੋਂ ਵੱਧ ਹੁੰਦੀ ਹੈ ।
(ii) ਚੁਸਤ ਲਚਕ (Active Flexibility – ਇਹ ਬਿਨਾਂ ਕਿਸੇ ਬਾਹਰੀ ਮੱਦਦ ਜਾਂ ਸਹਾਰੇ ਤੋਂ ਕ੍ਰਿਆਵਾਂ ਕਰਨ ਦੀ ਦਰ ਦੀ ਯੋਗਤਾ ਹੈ । ਉਦਾਹਰਨ ਦੇ ਤੌਰ ਤੇ ਲੱਤਾਂ ਨੂੰ ਝੂਲਾਉਣਾ ਆਦਿ ।
(iii) ਗਤੀਸ਼ੀਲ ਲਚਕ (Dynamic Flexibility) – ਇਹ ਉਹ ਲਚਕ ਹੁੰਦੀ ਹੈ ਜਦ ਸਰੀਰ ਗਤੀ ਵਿਚ ਹੁੰਦਾ ਹੈ ਅਤੇ ਕ੍ਰਿਆਵਾਂ ਪ੍ਰਦਰਸ਼ਨ ਕਰਦਾ ਹੈ । ਜਿਵੇਂ ਕਿ ਦੌੜਨਾ, ਤੈਰਨਾ ਜਾਂ ਸਮਰਸੱਲਟ (Samersault) ਆਦਿ ।

(ਇ) ਤਾਲਮੇਲ ਯੋਗਤਾ (Coordination Ability) – ਤਾਲਮੇਲ ਦੀ ਯੋਗਤਾ ਉਹ ਯੋਗਤਾ ਹੁੰਦੀ ਹੈ ਜਿਸ ਵਿਚ ਮੋਟਰ ਟਾਸਕ (Motor task) ਸਹਜ ਅਤੇ ਸਹੀ ਢੰਗ ਨਾਲ ਕੀਤੇ ਜਾਂਦੇ ਹਨ ਅਤੇ ਜਿਸ ਵਿਚ ਇੰਦਰੀਆਂ ਅਤੇ ਮਾਸਪੇਸ਼ੀਆਂ ਦੀ ਸੁੰਗੜਨ ਦਾ ਪਰਸਪਰ ਸੰਬੰਧ ਹੁੰਦਾ ਹੈ ਅਤੇ ਜੋ ਕਿ ਜੋੜਾਂ ਦੀ ਗਤੀ ਅਤੇ ਉਸਦੇ ਆਸ-ਪਾਸ ਦੇ ਅੰਗਾਂ ਅਤੇ ਸਰੀਰ ਦੀ ਸਥਿਤੀ ‘ਤੇ ਨਿਰਭਰ ਕਰਦੀ ਹੈ । ਤਾਲਮੇਲ ਸਨਾਯੁਤੰਤਰ ਤੇ ਵੀ ਨਿਰਭਰ ਕਰਦਾ ਹੈ । ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਵਿਚ ਤਾਲਮੇਲ ਦਾ ਅਹਿਮ ਰੋਲ ਹੈ ਜਿਸ ਤੋਂ ਬਿਨਾਂ ਕੋਈ ਵੀ ਖੇਡ ਜਾਂ ਕ੍ਰਿਆ ਸੰਭਵ ਹੀ ਨਹੀਂ ਹੈ ।

ਤਾਲਮੇਲ ਦੇ ਪ੍ਰਕਾਰ (Types of co-ordination) – ਖੇਡਾਂ ਦੀ ਦੁਨੀਆਂ ਵਿਚ ਮੁੱਖ ਤੌਰ ਤੇ ਸੱਤ (7) ਪ੍ਰਕਾਰ ਦੀ ਤਾਲਮੇਲ ਯੋਗਤਾ ਪਾਈ ਜਾਂਦੀ ਹੈ

1. ਹਿਣ ਯੋਗਤਾ (Orientation Ability) – ਇਹ ਵਿਅਕਤੀ ਦੀ ਉਹ ਯੋਗਤਾ ਹੈ ਜਿਸ ਵਿਚ ਉਹ ਜ਼ਰੂਰਤ ਅਨੁਸਾਰ ਸਥਾਨ ਅਤੇ ਸਮੇਂ ਤੇ ਆਪਣੇ ਸਰੀਰ ਦਾ ਵਿਸ਼ਲੇਸ਼ਣ ਕਰਕੇ ਪਰਿਵਰਤਨ ਕਰ ਲੈਂਦਾ ਹੈ । ਉਦਾਹਰਨ ਦੇ ਤੌਰ ਤੇ ਜਿਮਨਾਸਟਿਕ ਵਿਚ ਖੇਡ ਪ੍ਰਦਰਸ਼ਨ ਮੁਤਾਬਿਕ ਸਰੀਰ ਦੀ ਸਥਿਤੀ ਨੂੰ ਬਦਲਣਾ, ਬਾਸਕਟਬਾਲ ਵਿਚ ਅਫੈਨਸ ਤੇ ਡੀਫੈਨਸ (Offense and defense) ਵਿਚ ਆਪਣੇ ਸਰੀਰ ਦੀ ਸਥਿਤੀ ਵਿਚ ਬਦਲਾਵ ਕਰ ਲੈਂਦਾ ਹੈ ।

2. ਸੰਯੋਜਨ ਦੀ ਯੋਗਤਾ (Coupling Ability) – ਇਹ ਵਿਅਕਤੀ ਦੀ ਉਹ ਯੋਗਤਾ ਹੈ ਜਿਸ ਵਿਚ ਉਹ ਸਰੀਰ ਦੇ ਅੰਗਾਂ ਨੂੰ ਗਤੀ ਵਿਚ ਅਰਥਪੂਰਨ ਢੰਗ ਨਾਲ ਸੰਯੋਜਨ ਕਰਕੇ ਕੀਤਾ ਜਾਂਦਾ ਹੈ , ਜਿਵੇਂ ਵਾਲੀਬਾਲ ਵਿਚ ਸਪਾਈਕਿੰਗ ਦੇ ਦੌਰਾਨ ਖਿਡਾਰੀ ਤੇਜ਼ ਗਤੀ ਨਾਲ ਜੰਪ ਕਰਦਾ ਹੈ | ਬਾਲ ਨੂੰ ਹਿੱਟ ਕਰਦਾ ਹੈ । ਇਸ ਸਮੇਂ
ਉਸ ਦੇ ਸਰੀਰ ਦੇ ਸਾਰੇ ਅੰਗਾਂ ਵਿਚ ਇਕਸਾਰਤਾ ਦਾ ਤਾਲਮੇਲ ਹੁੰਦਾ ਹੈ ।

3. ਅੰਤਰ ਯੋਗਤਾ (Differentiation Ability – ਇਹ ਵਿਅਕਤੀ ਦੀ ਉਹ ਯੋਗਤਾ ਹੁੰਦੀ ਹੈ ਜਿਸ ਖਿਡਾਰੀ ਮੋਟਰ ਐਕਸ਼ਨ (Motor action) ਦੇ ਦੌਰਾਨ ਸਰੀਰ ਦੇ ਅਲੱਗ-ਅਲੱਗ ਅੰਗਾਂ ਤੋਂ ਕਿਆ ਕਰਵਾਉਣ ਦੀ ਸਮਰੱਥਾ ਦਾ ਪ੍ਰਦਰਸ਼ਨ ਕਰਦਾ ਹੈ , ਜਿਵੇਂ ਕਿ ਵਾਲੀਬਾਲ ਵਿਚ ਸਪਾਈਕਿੰਗ ਜੰਪ ਦੇ ਦੌਰਾਨ ਸਥਿਤੀ ਦੇ
ਅਨੁਸਾਰ ਬਾਲ ਨੂੰ ਸੁੱਟਣਾ (Drop) ।

4. ਪ੍ਰਤੀਕ੍ਰਿਆ ਕਰਨ ਦੀ ਯੋਗਤਾ (Reaction Ability) – ਇਹ ਵਿਅਕਤੀ ਦੀ ਉਹ ਯੋਗਤਾ ਹੈ ਜਿਸ ਵਿਚ ਸਿੰਗਨਲ ਮਿਲਣ ਤੇ ਖਿਡਾਰੀ ਪ੍ਰਤੀਕ੍ਰਿਆ ਕਰਦਾ ਹੈ , ਜਿਵੇਂ 100 ਮੀ: ਦੌੜ ਵਿਚ ਸਿੰਗਨਲ ਹੁੰਦੇ ਹੀ ਇਕ ਵੇ ਤੇ ਦਿਸ਼ਾ ਵੱਲ ਤੇਜ਼ ਗਤੀ ਨਾਲ ਦੌੜਨਾ ।

5. ਸੰਤੁਲਨ ਯੋਗਤਾ (Balance Ability) – ਇਹ ਵਿਅਕਤੀ ਦੀ ਉਹ ਯੋਗਤਾ ਹੈ ਜਿਸ ਵਿਚ ਉਹ ਗਤੀ ਵਿਚ ਸਰੀਰ ਦੀ ਸਥਿਤੀ ਬਣਾਈ ਰੱਖਦਾ ਹੈ ਜਿਵੇਂ ਕਿ 400 ਮੀ: ਵਿਚ ਆਪਣੀ ਲਾਈਨ ਵਿਚ ਰਹਿ ਕੇ ਦੌੜਨਾ ਆਦਿ ।

6. ਲੈਅ ਦੀ ਯੋਗਤਾ (Rhythm Ability) – ਇਹ ਵਿਅਕਤੀ ਦੀ ਉਹ ਯੋਗਤਾ ਹੈ ਜਿਸ ਵਿਚ ਉਹ ਲੈਅ ਨੂੰ ਸਮਝਦੇ ਹੋਏ ਲੈਅ ਵਿਚ ਗਤੀ ਬਣਾ ਕੇ ਰੱਖਦਾ ਹੈ । ਉਦਾਹਰਨ ਦੇ ਤੌਰ ਤੇ ਬਾਸਕਟ ਬਾਲ ਵਿਚ ਲੈ-ਅੱਪ (Lay-up) ਸਾਂਟ ਲਗਾਉਣਾ ।

7. ਹਿਣ ਯੋਗਤਾ (Adaptation Ability) – ਇਹ ਵਿਅਕਤੀ ਦੀ ਉਹ ਯੋਗਤਾ ਹੈ ਜਿਸ ਵਿਚ ਉਹ ਪ੍ਰਸਥਿਤੀ ਨੂੰ ਸਮਝ ਕੇ ਉਸ ਵਿੱਚ ਪ੍ਰਭਾਵੀ ਪਰਿਵਰਤਨ ਲੈ ਕੇ ਆਵੇ । ਉਦਾਹਰਨ ਦੇ ਤੌਰ ਤੇ ਬਾਸਕਟ ਬਾਲ ਵਿਚ ਜੰਪ ਸਾਂਟ ਕਿਆ ਦੇ ਅਨੁਕੂਲ ਬਣਾਉਣਾ ਆਦਿ ।

ਪੰਜ ਅੰਕਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ (Five Marks Question Answers)

ਪ੍ਰਸ਼ਨ 10.
ਸਰੀਰਕ ਯੋਗਤਾ ਦੀ ਮਹੱਤਤਾ ਬਾਰੇ ਤੁਸੀਂ ਕੀ ਜਾਣਦੇ ਹੋ ? ਵਿਸਥਾਰਪੂਰਵਕ ਲਿਖੋ ।
ਉੱਤਰ:
ਉਹ ਵਿਅਕਤੀ ਜੋ ਸਰੀਰਕ ਤੌਰ ਤੇ ਤੰਦਰੁਸਤ ਹਨ ਉਹ ਆਪਣੇ ਜੀਵਨ ਦਾ ਆਨੰਦ ਪੂਰੀ ਤਰ੍ਹਾਂ ਨਾਲ ਉਠਾਉਣ ਦੇ ਯੋਗ ਹਨ | ਅੱਜ ਦੇ ਤਕਨੀਕੀ ਵਿਕਾਸ ਦੇ ਯੁੱਗ ਵਿਚ ਲੋਕਾਂ ਕੋਲੋਂ ਮੁਸ਼ਕਿਲ ਨਾਲ ਹੀ ਆਪਣੀ ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਲਈ ਸਮਾਂ ਹੁੰਦਾ ਹੈ । ਹੁਣ ਪ੍ਰਸ਼ਨ ਇਹ ਉੱਠਦਾ ਹੈ ਕਿ ਸਰੀਰਕ ਤੰਦਰੁਸਤ ਹੋਣਾ ਇੰਨਾ ਮਹੱਤਵਪੂਰਨ ਕਿਉਂ ਹੈ ? ਇਹਨਾਂ ਸਵਾਲਾਂ ਦਾ ਜਵਾਬ ਹੇਠ ਦਿੱਤੇ ਅਨੁਸਾਰ ਹੈ-
1. ਸੰਪੂਰਨ ਸਿਹਤ ਦਾ ਸੁਧਾਰ (Improves Overall Health) – ਸਰੀਰਕ ਤੌਰ ਤੇ ਤੰਦਰੁਸਤ ਵਿਅਕਤੀ ਕਈ ਤਰ੍ਹਾਂ ਦੇ ਸਰੀਰਕ ਫਾਇਦਿਆਂ ਨੂੰ ਮਾਣਦਾ ਹੈ , ਜਿਵੇਂ ਕਿ ਸਾਹ ਪ੍ਰਕ੍ਰਿਆ, ਲਹੂ ਸੰਚਾਰ ਪ੍ਰਣਾਲੀ ਅਤੇ ਸਰੀਰ ਦੀਆਂ ਸਮੁੱਚੀ ਪ੍ਰਣਾਲੀਆਂ ਦਾ ਠੀਕ ਢੰਗ ਨਾਲ ਕੰਮ ਕਰਨਾ ਅਤੇ ਸਰੀਰ ਦਾ ਕ੍ਰਿਆਤਮਕ ਰੂਪ ਵਿਚ ਤਿਆਰ ਰਹਿਣਾ ।ਉਹ ਕਈ ਤਰ੍ਹਾਂ ਦੀਆਂ ਬਿਮਾਰੀਆਂ ਜਿਵੇਂ ਡਾਈਬੀਟੀਜ਼ ਟਾਇਪ-2, ਦਿਲ ਦੀਆਂ ਬਿਮਾਰੀਆਂ, ਕੈਂਸਰ ਤੋਂ ਬਚਾਅ, ਆਦਿ ਤੋਂ ਬਚਿਆ ਰਹਿੰਦਾ ਹੈ ।

2. ਭਾਰ ਪ੍ਰਬੰਧਨ (Weight Management) – ਜਿਵੇਂ ਕਿ ਅਸੀਂ ਸਾਰੇ ਜਾਣਦੇ ਹਾਂ ਕਿ ਵਾਧੂ ਵਜ਼ਨ ਕਈ ਤਰ੍ਹਾਂ ਦੀਆਂ ਸਿਹਤ ਸੰਬੰਧੀ ਸਮੱਸਿਆਵਾਂ : ਜਿਵੇਂ ਕਿ ਉੱਚਾ ਖੁਨ ਚਾਪ (High Blood Pressure), ਕੈਸਟਰੋਲ ਪੱਧਰ, ਡਾਇਬਟੀਜ਼ ਆਦਿ ਦੀ ਜੜ੍ਹ ਹੈ । ਇਸ ਲਈ ਉਹ ਵਿਅਕਤੀ ਜੋ ਸਰਗਰਮ ਅਤੇ ਸਰੀਰਕ ਤੌਰ ਤੇ ਤੰਦਰੁਸਤ ਹੁੰਦੇ ਹਨ, ਉਹਨਾਂ ਵਿੱਚ ਉਪਰੋਕਤ ਬਿਮਾਰੀਆਂ ਦੀ ਸੰਭਾਵਨਾ ਘੱਟ ਹੁੰਦੀ ਹੈ ।

3. ਤਨਾਵ ਪ੍ਰਬੰਧ ਵਿਚ ਮਹੱਤਵਪੂਰਨ (Importance as a stress Management) – ਇਕ ਵਿਅਕਤੀ ਤੰਦਰੁਸਤੀ ਅਤੇ ਤੰਦਰੁਸਤੀ ਪ੍ਰੋਗਰਾਮ ਦੇ ਜਰੀਏ ਤਣਾਅ ਨੂੰ ਬਰਦਾਸ਼ਤ ਕਰਨਾ, ਉਸ ਤੋਂ ਬਾਹਰ ਨਿਕਲਣਾ ਅਤੇ ਰੋਜ਼ਮਰਾ ਦੇ ਵਿਚਿਲਤ ਕਰਨ ਵਾਲੇ ਤਣਾਅ ਤੇ ਕਾਬੂ ਪਾਉਣਾ ਸਿੱਖ ਲੈਂਦਾ ਹੈ । ਇਸ ਲਈ ਇਹ ਜੀਵਨ ਵਿੱਚ ਸੰਤੁਲਨ ਅਤੇ ਸ਼ਾਤੀ ਬਣਾਏ ਰੱਖਣ ਵਿਚ ਮਦਦ ਕਰਦਾ ਹੈ । ਇਸ ਲਈ ਜ਼ਰੂਰੀ ਹੈ ਕਿ ਜੀਵਨ ਵਿਚ ਸ਼ਾਂਤੀ ਬਣਾਈ ਰੱਖਣ ਲਈ ਵਿਅਕਤੀ ਦਾ ਤੰਦਰੁਸਤ ਹੋਣਾ ਜ਼ਰੂਰੀ ਹੈ ।

4. ਸੱਟਾਂ ਦੀ ਸੰਭਾਵਨਾ ਨੂੰ ਘਟਾਉਣਾ (Reduce risk of Injuries) – ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਜੀਵਨ ਦੇ ਅਗਲੇ ਪੜਾਅ ਵਿਚ ਸੱਟਾਂ ਦੇ ਜ਼ੋਖ਼ਿਮ ਨੂੰ ਘਟਾਉਂਦੀ ਹੈ । ਇਸ ਦਾ ਕਾਰਨ ਮਾਸਪੇਸ਼ੀਆਂ ਦੀ ਤਾਕਤ, ਹੱਡੀਆਂ ਵਿਚਲੀ ਘਣਤਾ, ਲਚਕਤਾ ਅਤੇ ਸਥਿਰਤਾ ਹੁੰਦੀ ਹੈ ਜੋ ਕਿ ਸੱਟਾਂ ਦੀ ਸੰਭਾਵਨਾ ਨੂੰ ਘਟਾਉਂਦੀ ਹੈ ।

5. ਜੀਵਨ ਦੀ ਸੰਭਾਵਨਾ ਵਿਚ ਵਾਧਾ (Increases life Expectancy) – ਨਿਯਮਿਤ ਕਸਰਤਾਂ ਅਤੇ ਤੰਦਰੁਸਤੀ ਸੰਬੰਧਿਤ ਪ੍ਰੋਗਰਾਮ ਸਿਹਤ ਸੰਬੰਧਿਤ ਬਿਮਾਰੀਆਂ ਨੂੰ ਘਟਾਉਣ ਵਿਚ ਲਾਭਦਾਇਕ ਹੁੰਦੇ ਹਨ, ਜੋ ਕਿ ਉਮਰ ਦਰ ਦੀਆਂ ਸੰਭਾਵਨਾਵਾਂ ਨੂੰ ਵਧਾਉਂਦੀਆਂ ਹਨ ਅਤੇ ਸਮੇਂ ਤੋਂ ਪਹਿਲਾਂ ਹੋਣ ਵਾਲੀ ਮੌਤ ਦਰ ਨੂੰ ਘਟਾਉਂਦੀ ਹੈ । ਇਹ ਦੇਖਿਆ ਗਿਆ ਹੈ ਕਿ ਜੋ ਵਿਅਕਤੀ ਸਰੀਰਕ ਤੌਰ ਤੇ ਸਰਗਰਮ ਰਹਿੰਦੇ ਹਨ, ਉਹ ਸਵਸਥ ਅਤੇ ਲੰਬਾ ਜੀਵਨ ਗੁਜ਼ਾਰਦੇ ਹਨ ।

6. ਸਹੀ ਵਾਧਾ ਅਤੇ ਵਿਕਾਸ (Proper growth and Development) – ਤੰਦਰੁਸਤੀ ਅਤੇ ਤੰਦਰੁਸਤੀ ਪ੍ਰੋਗਰਾਮਾਂ ਦੀ ਸਹਾਇਤਾ ਨਾਲ ਬੱਚਿਆਂ ਵਿਚ ਵਧੀਆ ਵਿਕਾਸ ਹੁੰਦਾ ਹੈ । ਉਹਨਾਂ ਦੀ ਸਿਹਤ, ਉਚਾਈ, ਸਰੀਰਕ ਸੰਰਚਨਾ ਅਤੇ ਭਾਰ ਸਹੀ ਅਨੁਪਾਤ ਅਤੇ ਕੂਮ ਵਿਚ ਵੱਧਦੇ ਹਨ ।

7. ਕੰਮ ਕਰਨ ਦੀ ਸਮਰੱਥਾ ਵਿਚ ਵਾਧਾ (Improves work Efficiency) – ਸਰੀਰਕ ਤੌਰ ਤੇ ਤੰਦਰੁਸਤ ਵਿਅਕਤੀ ਜੀਵਨ ਦੇ ਹਰ ਪਹਿਲੂ ਜਿਵੇਂ ਕੰਮ ਕਰਨ ਦੀ ਥਾਂ, ਪਰਿਵਾਰ ਅਤੇ ਦੋਸਤਾਂ ਵਿਚ ਸੰਤਲੁਨ ਬਣਾ ਕੇ ਰੱਖਦਾ ਹੈ । ਉਸ ਦੀ ਸਰਗਰਮ ਜੀਵਨ ਸ਼ੈਲੀ ਅਤੇ ਤੰਦਰੁਸਤੀ ਕਾਰਨ ਉਹ ਕੰਮ ਨੂੰ ਸਫਲਤਾ ਨਾਲ ਕਰਦਾ ਹੈ। ਅਤੇ ਆਪਣੇ ਸਮਾਜਿਕ ਸਮੂਹ ਦਾ ਵੀ ਉਤਸ਼ਾਹ ਨਾਲ ਆਨੰਦ ਮਾਣਦਾ ਹੈ । ਇਸ ਲਈ ਅਸੀਂ ਉਪਰੋਕਤ ਤੱਥਾਂ ਤੋਂ ਇਹ ਅਨੁਮਾਨ ਲਗਾ ਸਕਦੇ ਹਾਂ ਕਿ ਇਕ ਤੰਦਰੁਸਤ ਸਰੀਰ ਵਿਚ ਤੰਦਰੁਸਤ ਮਨ ਦਾ ਵਾਸ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 11.
ਸਰੀਰਿਕ ਯੋਗਤਾ ਦਾ ਅਰਥ ਅਤੇ ਇਸ ਦੀ ਪਰਿਭਾਸ਼ਾ ਲਿਖੋ ।
ਉੱਤਰ:
ਅੱਜ ਦੇ ਬਦਲਦੇ ਤਕਨੀਕੀ ਯੁੱਗ ਵਿਚ ਲੋਕਾਂ ਕੋਲ ਸਰੀਰਿਕ ਤੰਦਰੁਸਤੀ ਅਤੇ ਸਰੀਰਿਕ ਸਿਹਤ ਦੇ ਲਈ ਲੋੜੀਂਦੀਆਂ ਕਿਰਿਆਵਾਂ ਕਰਨ ਦਾ ਸਮਾਂ ਨਹੀਂ ਹੈ | ਸਰੀਰਿਕ ਤੰਦਰੁਸਤੀ ਸ਼ਬਦ ਲੋਕਾਂ ਵਾਸਤੇ ਅਲੱਗ-ਅਲੱਗ ਭਾਗਾਂ ਵਿਚ ਅਲੱਗ-ਅਲੱਗ ਮਹੱਤਤਾ ਰੱਖਦਾ ਹੈ । ਇਕ ਆਮ ਇਨਸਾਨ ਲਈ ਸਰੀਰਿਕ ਤੰਦਰੁਸਤੀ ਤੋਂ ਭਾਵ ਹੈ ਬਿਮਾਰੀ ਰਹਿਤ ਸਰੀਰ ਤੋਂ ਹੈ । ਡਾਕਟਰਾਂ ਦੇ ਅਨੁਸਾਰ ਜਿਸ ਵਿਅਕਤੀ ਨੂੰ ਕੋਈ ਬਿਮਾਰੀ ਨਹੀਂ ਹੈ ਉਹ ਸਰੀਰਿਕ ਤੌਰ ਤੇ ਤੰਦਰੁਸਤ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ | ਸਰੀਰਿਕ ਸਿੱਖਿਆ ਦੇ ਖੇਤਰ ਵਿਚ ਬਿਨਾਂ ਥੱਕੇ, ਤਨਾਓ ਮੁਕਤ ਕਿਰਿਆਵਾਂ ਨੂੰ ਕਰਨਾ ਸਰੀਰਿਕ ਤੰਦਰੁਸਤੀ ਹੈ ।

ਅਸੀਂ ਕਹਿ ਸਕਦੇ ਹਾਂ ਕਿ ਸਰੀਰਿਕ ਤੰਦਰੁਸਤੀ ਇਕ ਵਿਆਪਕ ਖੇਤਰ ਹੈ | ਸਰੀਰਿਕ ਤੰਦਰੁਸਤੀ ਤੋਂ ਭਾਵ ਇਕ ਵਿਅਕਤੀ ਜੋ ਆਪਣੇ ਰੋਜ਼ਮੱਰਾ ਦੇ ਕੰਮ-ਕਾਜ ਬਿਨਾ ਥੱਕੇ ਕਰਦਾ ਹੈ ਅਤੇ ਉਸ ਤੋਂ ਬਾਅਦ ਵੀ ਉਸ ਵਿਚ ਵਿਆਪਕ ਸਰੀਰਿਕ ਊਰਜਾ ਹੋਰ ਮਨੋਰੰਜਕ ਕਿਰਿਆਵਾਂ ਨੂੰ ਕਰਨ ਲਈ ਰਹਿੰਦੀ ਹੈ ਜਾਂ ਬਚੀ ਰਹਿੰਦੀ ਹੈ, ਉਸਨੂੰ ਸਰੀਰਿਕ ਤੰਦਰੁਸਤੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਅਸੀਂ ਥੋੜੇ ਸ਼ਬਦਾਂ ਵਿਚ ਕਹਿ ਸਕਦੇ ਹਾਂ ਕਿ ਜੋ ਵਿਅਕਤੀ ਬਿਨਾਂ ਥੱਕੇ ਆਪਣੇ ਕੰਮ ਕਰਦਾ ਹੈ ਉਹ ਸਰੀਰਿਕ ਤੌਰ ਤੇ ਤੰਦਰੁਸਤ ਵਿਅਕਤੀ ਹੈ ।

ਸਰੀਰਕ ਯੋਗਤਾ ਦਾ ਅਰਥ ਅਤੇ ਧਾਰਣਾ-ਸਰੀਰਕ ਯੋਗਤਾ ਜੀਵਨ ਦੀਆਂ ਬੁਨਿਆਦੀ ਜ਼ਰੂਰਤਾਂ ਵਿਚੋਂ ਇਕ ਹੈ । ਇਹ ਬਿਨਾਂ ਥੱਕੇ ਹਰ ਰੋਜ਼ ਕੰਮ ਕਰਨ ਦੀ ਯੋਗਤਾ ਹੁੰਦੀ ਹੈ । ਇਸ ਨੂੰ ਮਨੋਵਿਗਿਆਨ, ਸਰੀਰਕ ਕ੍ਰਿਆ ਵਿਗਿਆਨ ਅਤੇ ਸਰੀਰਕ ਸੰਰਚਨਾ ਦੇ ਰੂਪ ਵਿਚ ਦੇਖਿਆ ਜਾਂਦਾ ਹੈ ।

ਕਲਾਰਕ ਦੇ ਅਨੁਸਾਰ, ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਰੋਜ਼ਮੱਰਾ ਦੇ ਕੰਮ ਨੂੰ ਅਤਿਅੰਤ ਥਕਾਵਟ ਅਤੇ ਬਹੁਤ ਜ਼ਰੂਰਤ ਊਰਜਾ ਤੋਂ ਉਤਸ਼ਾਹ ਅਤੇ ਚੌਕਸੀ ਨਾਲ ਲੈ ਜਾਣ ਦੀ ਸਮਰੱਥਾ ਹੈ ਤਾਂ ਕਿ ਬਿਨਾਂ ਥੱਕੇ ਪੂਰੀ ਊਰਜਾ ਦੇ ਨਾਲ ਮਨੋਰੰਜਨ ਦੀਆਂ ਗਤੀਵਿਧੀਆਂ ਦਾ ਆਨੰਦ ਲੈਣ ਅਤੇ ਅਚਾਨਕ ਸੰਕਟਕਾਲੀਨ ਹਾਲਾਤਾਂ ਨੂੰ ਪੂਰਾ ਕਰਨ ਦੀ ਸਮਰੱਥਾ ਹੈ ।”

ਬੂਚਰ ਅਤੇ ਪ੍ਰੇਹਟਿਸ ਦੇ ਅਨੁਸਾਰ, ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਇਕ ਜੈਵਿਕ ਵਿਕਾਸ, ਮਾਸਪੇਸ਼ੀਆਂ ਦੀ ਤਾਕਤ ਅਤੇ ਸਟੈਮਿਨਾ ਹੁੰਦੀ ਹੈ । ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਤੋਂ ਭਾਵ ਅਭਿਆਸ ਵਿਚ ਕੁਸ਼ਲਤਾਪੂਰਵਕ ਪ੍ਰਦਰਸ਼ਨ ਤੋਂ ਹੈ ।’’

ਥਾਮਸ ਦੇ ਅਨੁਸਾਰ, “ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਵਿਅਕਤੀ ਨੂੰ ਦਿੱਤੀ ਗਈ ਕੁੱਲ ਬੁਨਿਆਦੀ ਸਮਰੱਥਾ ਹੈ ।”
ਮੈਥਿਊਜ਼ ਦੇ ਅਨੁਸਾਰ, “ਮਾਸਪੇਸ਼ੀਆਂ ਦੇ ਅਭਿਆਸ ਲਈ ਦਿੱਤੇ ਗਏ ਭੌਤਿਕ ਕੰਮਾਂ ਨੂੰ ਕਰਨ ਲਈ ਵਿਅਕਤੀ ਦੀ ਸਮਰੱਥਾ ਨੂੰ ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਕਹਿੰਦੇ ਹਨ ।
ਵਿਲਿਅਮ ਦੇ ਅਨੁਸਾਰ, “ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਸਰੀਰਕ ਕੰਮ ਕਰਨ ਲਈ ਵਿਅਕਤੀ ਦੀ ਸਮਰੱਥਾ ਹੈ ।”
ਵਿਲਗੂਜ਼ ਦੇ ਅਨੁਸਾਰ, ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਇਕ ਗਤੀਵਿਧੀ ਦੀ ਸਮਰੱਥਾ ਹੈ ਜੋ ਕਿ ਦਿੱਤੇ ਗਏ ਕੰਮ ਨੂੰ ਕਰਨ ਲਈ ਕਾਫ਼ੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ।”
ਹਾਰਬਰਟ ਦੇ ਅਨੁਸਾਰ, “ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਸਰੀਰ ਦੀ ਯੋਗਤਾ ਨਾਲ ਸਾਰੇ ਕਿਸਮ ਦੇ ਦਬਾਅ ਨੂੰ ਬਰਦਾਸ਼ਤ ਕਰਨ ਅਤੇ ਪ੍ਰਗਟਾਵੇ ਨੂੰ ਬਰਕਰਾਰ ਰੱਖਣ ਦਾ ਸੰਕੇਤ ਹੈ।”

ਡੇਵਿਡ ਆਰ. ਲੈਂਬ ਦੇ ਅਨੁਸਾਰ, ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਜੀਵਨ ਦੇ ਮੌਜੂਦਾ ਅਤੇ ਸੰਭਾਵੀ ਭੌਤਿਕ ਚੁਣੌਤੀਆਂ ਨੂੰ ਸਫਲਤਾਪੂਰਵਕ ਕਰਨ ਦੀ ਸਮਰੱਥਾ ਹੈ ।”
ਵੇਬਸਟਰ ਵਿਸ਼ਵ ਕੋਸ਼ ਅਨੁਸਾਰ, “ਇਹ ਇਕ ਮਨੁੱਖ ਦੇ ਬਿਨਾਂ ਥੱਕੇ ਹੋਏ ਹਰ ਰੋਜ਼ ਦੈਨਿਕ ਕੰਮ ਕਰਨ ਦੀ ਯੋਗਤਾ ਹੈ । ਇਸ ਵਿਚ ਖੇਡ-ਕੁੱਦ ਵਿਚ ਭਾਗ ਲੈਣਾ ਅਤੇ ਫਿਰ ਵੀ ਅਚਾਨਕ ਘਟਨਾਵਾਂ ਦਾ ਸਾਹਮਣਾ ਕਰਨ ਲਈ ਊਰਜਾ ਬਚਾ ਕੇ ਰੱਖਣਾ ਹੈ ।”
ਡਾ: ਕਰੋਲਸ ਦੇ ਅਨੁਸਾਰ, “ਕਿਸੇ ਦੇ ਜਿਉਣ ਦੇ ਢੰਗ ਦੇ ਦਬਾਓ ਦਾ ਸਫਲ ਅਨੁਕੂਲਣ ਹੈ ।”
ਐਡਵਰਡ ਬੋਰਟਜ ਦੇ ਅਨੁਸਾਰ, ‘ਸਰੀਰਕ ਯੋਗਤਾ ਇਹ ਯਕੀਨੀ ਬਣਾਉਂਦੀ ਹੈ ਕਿ ਸਰੀਰਕ ਪ੍ਰਣਾਲੀਆਂ ਦੀਆਂ ਆਪਣੀਆਂ ਕਿਰਿਆਵਾਂ ਨੂੰ ਸਤੋਖਜਨਕ ਢੰਗ ਨਾਲ ਕਰਨ ਦੀ ਵਿਧੀ ਹੈ ।” ਤੋਂ ਬਰੂਸੇ ਬਾਲੇ ਦੇ ਅਨੁਸਾਰ, ”‘ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਗਤੀਸ਼ੀਲ ਸੰਭਾਵਨਾ ‘ਤੇ ਨਿਰਭਰ ਕਰਦੀ ਹੈ ਜੋ ਕਿ ਕ੍ਰਿਆਤਮਕ ਅਤੇ ਅੰਦਰੂਨੀ ਰਸਾਇਣਿਕ ਪਰਿਵਰਤਨ ਦੀਆਂ ਸੰਭਾਵਨਾਵਾਂ ਰਾਹੀਂ ਬਣਦੀ ਹੈ।” ,

ਇਕ ਆਮ ਐਥਲੈਟਿਕ ਸ਼ਬਦ ਵਿਚ ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਦੀ ਧਾਰਣਾ ਤੋਂ ਭਾਵ ਹੈ ਕਿ ਵਿਅਕਤੀ ਦੀ ਉਹ ਯੋਗਤਾ ਜਿਸ ਵਿਚ ਉਹ ਥਕਾਵਟ ਭਰੀ ਅਵਸਥਾ ਨੂੰ ਘੱਟ ਕੀਤੇ ਬਿਨਾਂ, ਖੇਡ ਦੀਆਂ ਗਤੀਵਿਧੀਆਂ ਦੁਆਰਾ ਸਰੀਰਕ ਅਤੇ ਮਾਨਸਿਕ ਅਵਸਥਾ ਦੀਆਂ ਮੰਗਾਂ ਦੀ ਪੂਰਤੀ ਕਰੇ । ਥਕਾਵਟ ਦੀ ਅਵਸਥਾ ਤਦ ਹੁੰਦੀ ਹੈ ਜਦ ਵਿਅਕਤੀ ਗਤੀਵਿਧੀਆਂ ਨੂੰ ਸਹੀ ਢੰਗ ਅਤੇ ਸਫਲਤਾਪੂਰਵਕ ਨਾਲ ਨਾ ਨਿਭਾ ਸਕੇ ।

ਹਰ ਵਿਅਕਤੀ ਲਈ ਬਹੁਤ ਜ਼ਰੂਰੀ ਹੈ ਕਿ ਉਹ ਆਪਣੇ ਰੋਜ਼ਮਰਾ ਦੇ ਕੰਮਾਂ ਨੂੰ ਆਸਾਨੀ ਨਾਲ ਕਰਨ ਅਤੇ ਵੱਖ-ਵੱਖ ਗਤੀਵਿਧੀਆਂ ਨੂੰ ਆਸਾਨੀ ਨਾਲ ਨਿਭਾਉਣ ਲਈ ਤੰਦਰੁਸਤ ਹੋਵੇ । ਹਰ ਇਕ ਵਿਅਕਤੀ ਨੂੰ ਸਰੀਰਕ ਗਤੀਵਿਧੀਆਂ ਵਿਚ ਭਾਗ ਲੈਣ ਲਈ ਪੁਸ਼ਟ ਹੋਣਾ ਜ਼ਰੂਰੀ ਹੈ ਤਾਂ ਕਿ ਸਰੀਰਕ ਯੋਗਤਾ ਦੇ ਵਿਭਿੰਨ-ਵਿਭਿੰਨ ਅੰਗਾਂ ਦਾ ਵਿਕਾਸ ਹੋ ਸਕੇ ।

ਪ੍ਰਸ਼ਨ 12.
ਸਰੀਰਿਕ ਯੋਗਤਾ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਨ ਵਾਲੇ ਤੱਤਾਂ ਦਾ ਵਿਸਥਾਰਪੂਰਵਕ ਵਰਣਨ ਕਰੋ ।
ਉੱਤਰ:
ਅਨੇਕਾਂ ਅਜਿਹੇ ਕਈ ਕਾਰਨ ਹੁੰਦੇ ਹਨ ਜੋ ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਦੇ ਹਨ । ਨਿਸ਼ਕ੍ਰਿਆ ਦੇ ਕਾਰਨ ਛੋਟੇ ਅਤੇ ਲੰਬੇ ਸਮੇਂ ਦੇ ਅਭਿਆਸ ਕਾਲ ਤੇ ਕਈ ਤਰੀਕਿਆਂ ਨਾਲ ਪ੍ਰਭਾਵ ਪੈਂਦਾ ਹੈ । ਇਹ ਕਾਰਕ ਜੋ ਕਿ ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਤੇ ਪ੍ਰਭਾਵ ਪਾਉਂਦੇ ਹਨ, ਹੇਠ ਲਿਖੇ ਪ੍ਰਕਾਰ ਹਨ-
1. ਸਰੀਰਕ ਢਾਂਚਾ (Anatomical Structure) – ਸਰੀਰਕ ਢਾਂਚਾ ਅਲੱਗ-ਅਲੱਗ ਅਕਾਰ ਅਤੇ ਰੂਪ ਵਿਚ ਹੁੰਦਾ ਹੈ | ਕਈ ਵਾਰ ਅਨੁਚਿਤ ਆਕਾਰ ਅਤੇ ਰੂਪ ਸਰੀਰਕ ਕ੍ਰਿਆਵਾਂ ਵਿਚ ਉਲਝਣਾਂ ਪੈਦਾ ਕਰਦਾ ਹੈ ਅਤੇ ਕਈ ਵਾਰ, ਕਮਜ਼ੋਰ ਅੰਗ ਵਿਅਕਤੀ ਦੇ ਕੰਮਾਂ ਜਾਂ ਕ੍ਰਿਆਵਾਂ ਨੂੰ ਘਟਾ ਦਿੰਦੇ ਹਨ ।

2. ਸਰੀਰਕ ਕਿਰਿਆ ਬਣਤਰ (Physiological Structures) – ਸਾਡੇ ਸਰੀਰ ਦੀਆਂ ਪ੍ਰਣਾਲੀਆਂ ਜਿਵੇਂ ਸਾਹ ਪ੍ਰਣਾਲੀ, ਲਹੂ ਸੰਚਾਰ ਪ੍ਰਣਾਲੀ, ਮਾਸਪੇਸ਼ੀ ਪ੍ਰਣਾਲੀ ਅਤੇ ਅਨੇਕਾਂ ਹੋਰ ਪ੍ਰਣਾਲੀਆਂ ਨੇ ਕੁਸ਼ਲਤਾਪੂਰਵਕ ਕੰਮ ਕਰਨਾ ਹੁੰਦਾ ਹੈ । ਸਰੀਰਕ ਪ੍ਰਣਾਲੀ ਵਿਚ ਖ਼ਰਾਬੀ ਸਰੀਰਕ ਕੰਮਾਂ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਦੀ ਹੈ ਜਿਵੇਂ ਕਿ ਸਾਹ ਲੈਣ ਵਿਚ ਔਖ ਹੋਣਾ ਜਾਂ ਫਿਰ ਦਿਲ ਦੀ ਬਿਮਾਰੀ ਆਦਿ । ਇਸ ਲਈ ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਵਿਚ ਵਿਅਕਤੀ ਦਾ ਫਿਟ ਹੋਣਾ ਬੜਾ ਜ਼ਰੂਰੀ ਹੈ ।

3. ਮਨੋਵਿਗਿਆਨਿਕ ਕਾਰਨ (Psychological Factor) – ਕਈ ਤਰ੍ਹਾਂ ਦੇ ਮਾਨਸਿਕ ਵਿਗਾੜ ਜੋ ਕਿ ਸਰੀਰਕ ਕੰਮਾਂ ਵਿਚ ਉਲਝਣਾਂ ਪੈਦਾ ਕਰਦੇ ਹਨ , ਜਿਵੇਂ ਕਿ ਦਬਾਅ, ਤਨਾਵ, ਚਿੰਤਾਵਾਂ ਆਦਿ । ਇਹ ਸਰੀਰਕ ਕ੍ਰਿਆਵਾਂ ਵਿਚ ਰੁਕਾਵਟ ਦਾ ਕਾਰਨ ਬਣਦੀਆਂ ਹਨ | ਮਾਨਸਿਕ ਰੂਪ ਨਾਲ ਮਜ਼ਬੂਤ ਅਤੇ ਤਨਾਅ-ਮੁਕਤ ਵਿਅਕਤੀ ਖੇਡਾਂ ਲਈ ਯੋਗ ਹੁੰਦਾ ਹੈ । ਦਬਾਅ ਅਤੇ ਤਨਾਅ ਹਮੇਸ਼ਾ ਹੀ ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਨੂੰ ਘਟਾ ਦਿੰਦਾ ਹੈ ।

4. ਜੱਦ ਅਤੇ ਵਾਤਾਵਰਣ (Heredity and Environment) – ਜੱਦ ਅਤੇ ਵਾਤਾਵਰਣ ਦੋਵੇਂ ਹੀ ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਦੇ ਹਨ । ਜਿਵੇਂ ਕਿ ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ ਕਿ ਮਨੁੱਖੀ ਸੈੱਲ 23 (ਜੋੜੇ) ਕੋਮੋਸੋਮਜ ਤੋਂ ਬਣਿਆ ਹੁੰਦਾ ਹੈ । ਜਿਸ ਵਿਚ 75% ਮਾਤਾ ਅਤੇ ਪਿਤਾ ਅਤੇ 25% ਬਾਕੀ ਖਾਨਦਾਨੀ ਜੀਨਸ ਦਾ ਸੰਚਾਰਣ ਹੁੰਦਾ ਹੈ । ਇਸ ਲਈ ਅਸੀਂ ਕਹਿ ਸਕਦੇ ਹਾਂ ਕਿ ਜੱਦੀ ਗੁਣ ਜਿਵੇਂ ਕਿ ਕਈ ਤਰ੍ਹਾਂ ਦੇ ਔਗੁਣ, ਚਮੜੀ ਅਤੇ ਅੱਖਾਂ ਦਾ ਰੰਗ, ਸਰੀਰਕ ਬਣਾਵਟ ਆਦਿ ਮਨੁੱਖ ਨੂੰ ਜੱਦ ਵਿਚ ਮਿਲਦੀ ਹੈ ਅਤੇ ਇਹ ਜੱਦ ਅਤੇ ਵਾਤਾਵਰਣ ਦੇ ਗੁਣ ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ‘ਤੇ ਵੀ ਪ੍ਰਭਾਵ ਪਾਉਂਦੇ ਹਨ ।

5. ਚੰਗਾ ਸਰੀਰਕ ਆਸਣ (Good Posture) – ਸਰੀਰਕ ਤਰੁੱਟੀਆਂ, ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਵਿਚ ਹਮੇਸ਼ਾ ਹੀ ਮੁਸ਼ਕਿਲ ਪੈਦਾ ਕਰਦੀਆਂ ਹਨ , ਜਿਵੇਂ ਕਿ ਅਸੰਤੁਲਨ ਮਾਸਪੇਸ਼ੀਆਂ, ਕੁਪੋਸ਼ਣ, ਦਰਦ, ਲੋਰਡੋਸਿਸ (Lordosis), ਸਕੋਲਿਸਿਸ (Scoliosis), ਗੋਲ ਮੋਢੇ, ਗੋਡਿਆਂ ਦਾ ਟਕਰਾਉਣਾ ਆਦਿ ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਨੂੰ ਪ੍ਰਭਾਵਿਤ
ਕਰਦੇ ਹਨ । ਸ .

6. ਅਹਾਰ (Diet) – ਸਰੀਰਕ ਪ੍ਰਦਰਸ਼ਨ ਵਿਚ ਅਹਾਰ ਪ੍ਰਮੁੱਖ ਭੂਮਿਕਾ ਨਿਭਾਉਂਦਾ ਹੈ ਅਤੇ ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਦੇ ਸਤਰ ਨੂੰ ਬਣਾਏ ਰੱਖਣ ਵਿਚ ਬਹੁਤ ਸਹਾਇਕ ਹੁੰਦਾ ਹੈ । ਆਹਾਰ ਵਿਚ ਕੈਲਰੀ ਦੀ ਉਪਯੁਕਤ ਮਾਤਰਾ ਖਿਡਾਰੀਆਂ ਨੂੰ ਸਰਵ-ਉੱਚ ਪ੍ਰਦਰਸ਼ਨ ਕਰਨ ਵਿਚ ਮਦਦਗਾਰ ਸਾਬਿਤ ਹੁੰਦੀ ਹੈ । ਕਾਰਬੋਹਾਈਡਰੇਟਸ ਅਤੇ ਤਰਲ ਪਦਾਰਥਾਂ ਦੀ ਕਮੀ ਕਾਰਨ ਇਕ ਖਿਡਾਰੀ ਜਲਦੀ ਹੀ ਥਕਾਵਟ ਮਹਿਸੂਸ ਕਰਨ ਲੱਗ ਪੈਂਦਾ ਹੈ । ਮਾਸ਼ਪੇਸ਼ੀਆਂ ਦੇ ਪੁਨਰ-ਨਿਰਮਾਣ ਵਾਸਤੇ ਪ੍ਰੋਟੀਨ ਦੀ ਜ਼ਰੂਰਤ ਹੁੰਦੀ ਹੈ । ਕਾਰਬੋਹਾਈਡਰੇਟ, ਪ੍ਰੋਟੀਨ ਅਤੇ ਵਿਟਾਮਿਨ ਤੋਂ ਬਿਨਾਂ ਖਿਡਾਰੀ ਬੇਹਤਰ ਪ੍ਰਦਰਸ਼ਨ ਨਹੀਂ ਕਰ ਸਕਦਾ ਅਤੇ ਉਸਦੀ ਸਰੀਰਕ ਯੋਗਤਾ ਵੀ ਘੱਟ ਜਾਂਦੀ ਹੈ ।

7. ਜੀਵਨ ਸ਼ੈਲੀ (Life Style) – ਉਹ ਖਿਡਾਰੀ ਜੋ ਚੰਗੀ ਜੀਵਨ ਸ਼ੈਲੀ ਨੂੰ ਅਪਨਾਉਂਦੇ ਹਨ, ਉਹ ਹਮੇਸ਼ਾ ਬੇਹਤਰ ਪ੍ਰਦਰਸ਼ਨ ਕਰਦੇ ਹਨ । ਜੀਵਨ ਸ਼ੈਲੀ ਤੋਂ ਭਾਵ ਸ਼ਾਨੋ-ਸ਼ੌਕਤ ਵਾਲਾ ਜੀਵਨ ਤੋਂ ਨਹੀਂ ਹੈ ਬਲਕਿ ਇਸ ਤੋਂ ਭਾਵ ਹੈ ਕਿ ਚੰਗੀਆਂ ਆਦਤਾਂ ਵਾਲਾ ਜੀਵਨ ਜਿਉਣਾ । ਇਕ ਵਿਅਕਤੀ ਜੋ ਸਿਗਰੇਟ, ਸ਼ਰਾਬ ਜਾਂ ਨਸ਼ੇ ਆਦਿ ਦਾ ਆਦੀ ਹੁੰਦਾ ਹੈ ਉਹੀ ਚੰਗਾ ਪ੍ਰਦਰਸ਼ਨ ਨਹੀਂ ਕਰ ਸਕਦਾ । ਇਹ ਉਸਦੀ ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਦਾ ਹੈ ।

8. ਜਲਵਾਯੂ (Climate) – ਅਲੱਗ-ਅਲੱਗ ਤਰ੍ਹਾਂ ਦੀ ਜਲਵਾਯੂ ਸਰੀਰਕ ਯੋਗਤਾ ‘ਤੇ ਪ੍ਰਭਾਵ ਪਾਉਂਦੀ ਹੈ । ਸਰਦੀ, ਗਰਮੀ ਅਤੇ ਨਮੀ ਵਰਗੇ ਭਿੰਨ-ਭਿੰਨ ਜਲਵਾਯੂ ਸਰੀਰਕ ਯੋਗਤਾ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਦੇ ਹਨ । ਵਧੀਆ ਪ੍ਰਦਰਸ਼ਨ ਵਾਸਤੇ ਇਕ ਖਿਡਾਰੀ ਨੂੰ ਅਲੱਗ-ਅਲੱਗ ਜਲਵਾਯੂ ਪ੍ਰਸਿਥਤੀਆਂ ਵਿਚ ਰਹਿ ਕੇ ਅਭਿਆਸ ਕਰਨਾ ਬਹੁਤ ਜ਼ਰੂਰੀ ਹੁੰਦਾ ਹੈ । ਉਦਾਹਰਨ ਦੇ ਤੌਰ ਤੇ ਜੇਕਰ ਖਿਡਾਰੀ ਗਰਮ ਜਾਂ ਮੈਦਾਨੀ ਇਲਾਕਿਆਂ ਦਾ ਰਹਿਣ ਵਾਲਾ ਹੈ ਤਾਂ ਉਸਨੂੰ ਠੰਡੇ ਇਲਾਕੇ ਵਿਚ ਜ਼ਰੂਰ ਅਭਿਆਸ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ਤਾਂ ਜੋ ਉਸਦਾ ਪ੍ਰਦਰਸ਼ਨ ਵਧੀਆ ਹੋ ਸਕੇ । ਇਹਨਾਂ ਜਲਵਾਯੂ ਰੁਕਾਵਟਾਂ ਨੂੰ ਦੂਰ ਕਰਨ ਦਾ ਤਰੀਕਾ ਇਹ ਹੀ ਹੈ ਕਿ ਅਲੱਗ-ਅਲੱਗ ਜਲਵਾਯੂ ਵਾਤਾਵਰਣ ਵਿਚ ਅਭਿਆਸ ਕੀਤਾ ਜਾਵੇ ।

9. ਨਿਸ਼ਕ੍ਰਿਆ (Inactivity) – ਸਰੀਰਕ ਕ੍ਰਿਆਵਾਂ ਦੀ ਘਾਟ ਨਾਲ ਵਿਅਕਤੀ ਗਤੀਹੀਨ ਜੀਵਨ ਸ਼ੈਲੀ ਵੱਲ ਚਲਿਆ ਜਾਂਦਾ ਹੈ ਜਿਸ ਨਾਲ ਸਰੀਰਕ ਪ੍ਰਣਾਲੀਆਂ ਵਿਚ ਖ਼ਰਾਬੀ ਪੈਦਾ ਹੁੰਦੀ ਹੈ | ਸਰੀਰਕ ਗਤੀਵਿਧੀ ਸ਼ਬਦ ਰੋਜ਼ਮੱਰਾ ਦੇ ਕੰਮ ਨਾਲ ਖ਼ਰਚ ਹੋਣ ਵਾਲੀ ਊਰਜਾ ਦੇ ਰੂਪ ਵਿਚ ਲਿਆ ਜਾਂਦਾ ਹੈ । ਇਹ ਰੋਜ਼ਮੱਰਾ ਦੇ ਕੰਮ ਜਿਵੇਂ ਕਿ ਚੱਲਣਾ, ਦੌੜਨਾ, ਸਾਈਕਲ ਚਲਾਉਣਾ, ਤੈਰਨਾ, ਝਾੜੂ ਮਾਰਨਾ ਆਦਿ ਘਰੇਲੂ ਕੰਮ ਹੁੰਦੇ ਹਨ । ਨਿਸ਼ਕ੍ਰਿਆ ਦੇ ਕਾਰਨ ਸਰੀਰਕ ਪ੍ਰਣਾਲੀ ਕਮਜ਼ੋਰ ਹੋ ਜਾਂਦੇ ਹਨ ਅਤੇ ਕਈ ਸਿਹਤ ਨੂੰ ਲੈ ਕੇ ਮਸਲੇ ਖੜ੍ਹੇ ਹੋ
ਜਾਂਦੇ ਹਨ ਜੋ ਕਿ ਸਰੀਰਕ ਯੋਗਤਾ ‘ਤੇ ਪ੍ਰਭਾਵ ਪਾਉਂਦੇ ਹਨ ।

10. ਸੱਟਾਂ (Injuries) – ਸੱਟਾਂ ਲੱਗਣਾ ਖੇਡਾਂ ਦਾ ਹਿੱਸਾ ਹਨ । ਸੱਟਾਂ ਦੀ ਦੇਖਭਾਲ ਦੀ ਕਮੀ ਦੇ ਕਾਰਨ ਖੇਡ ਪ੍ਰਦਰਸ਼ਨ ਵਿਚ ਕਮੀ ਆ ਜਾਂਦੀ ਹੈ ਅਤੇ ਨਾਲ ਹੀ ਖਿਡਾਰੀ ਦੇ ਮਾਨਸਿਕ ਸੰਤੁਲਨ ‘ਤੇ ਵੀ ਪ੍ਰਭਾਵ ਪੈਂਦਾ ਹੈ ।

11. ਉਮਰ (Age) – ਉਮਰ ਵਿਚ ਅੰਤਰ ਹਮੇਸ਼ਾ ਹੀ ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਦਾ ਹੈ । ਜਦ ਅਸੀਂ
ਛੋਟੇ ਬੱਚੇ ਹੁੰਦੇ ਹਾਂ ਤਾਂ ਅਸੀਂ ਵੱਡੀ ਉਮਰ ਦੇ ਵਿਅਕਤੀ ਦੀ ਸਰੀਰਕ ਯੋਗਤਾ ਦੀ ਤੁਲਨਾ ਵਿਚ ਨਹੀਂ ਖੇਡ ਸਕਦੇ। ਇਸ ਤਰ੍ਹਾਂ ਜਦ ਅਸੀਂ ਬੁਢਾਪੇ ਵੱਲ ਵੱਧਦੇ ਹਾਂ ਤਾਂ ਸਾਡੀਆਂ ਮਾਸਪੇਸ਼ੀਆਂ ਕਮਜ਼ੋਰ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ਅਤੇ ਸਰੀਰ ਉੱਤੇ ਚਰਬੀ ਵੱਧ ਜਾਂਦੀ ਹੈ ਜੋ ਕਿ ਸਰੀਰਕ ਯੋਗਤਾ ‘ਤੇ ਪ੍ਰਭਾਵ ਪਾਉਂਦੀ ਹੈ ।

12. ਲਿੰਗ (Gender) – ਲਿੰਗ ਸਰੀਰਕ ਯੋਗਤਾ ਵਿਚ ਹਮੇਸ਼ਾਂ ਹੀ ਵਿਸ਼ੇਸ਼ ਭੂਮਿਕਾ ਨਿਭਾਉਂਦਾ ਹੈ । ਔਰਤ ਅਤੇ ਆਦਮੀ ਦੋਨਾਂ ਦੇ ਸਰੀਰ ਵਿਚ ਕਈ ਵਿਲੱਖਣਤਾਵਾਂ ਪਾਈਆਂ ਜਾਂਦੀਆਂ ਹਨ । ਉਦਾਹਰਨ ਦੇ ਤੌਰ ਤੇ ਔਰਤਾਂ ਦੇ ਸਰੀਰ ਦੀਆਂ ਮਾਸਪੇਸ਼ੀਆਂ, ਆਦਮੀ ਨਾਲੋਂ ਘੱਟ ਮਜ਼ਬੂਤ ਹੁੰਦੀਆਂ ਹਨ, ਪਰ ਔਰਤਾਂ ਦੇ ਜੋੜਾਂ ਵਿਚ ਲਚਕਤਾ ਆਦਮੀ ਦੇ ਮੁਕਾਬਲੇ ਜ਼ਿਆਦਾ ਹੁੰਦੀ ਹੈ ਜਿਸ ਕਰਕੇ ਉਹਨਾਂ ਨੂੰ ਜਿਮਨਾਸਟਿਕ ਵਰਗੀਆਂ ਖੇਡਾਂ ਵਿਚ ਬਹੁਤ ਲਾਭ ਮਿਲਦਾ ਹੈ । ਉੱਥੇ ਹੀ ਆਦਮੀਆਂ ਦੀਆਂ ਮਾਸਪੇਸ਼ੀਆਂ ਮਜ਼ਬੂਤ ਹੁੰਦੀਆਂ ਹਨ ਅਤੇ ਦਿਲ ਦਾ ਆਕਾਰ ਵੱਡਾ ਹੁੰਦਾ ਹੈ ਜਿਸ ਕਰਕੇ ਉਹਨਾਂ ਨੂੰ ਖੇਡਾਂ ਵਿਚ ਸ਼ਕਤੀ, ਤਾਕਤ ਅਤੇ ਗਤੀ ਮਿਲਦੀ ਹੈ ।

13. ਸਿਹਤਮੰਦ ਵਾਤਾਵਰਣ (Healthy Envrionment) – ਸਕੂਲ, ਘਰ ਅਤੇ ਖੇਡਾਂ ਦਾ ਮੈਦਾਨ ਬੇਹਤਰ ਸਿੱਖਿਆ ਪ੍ਰਦਾਨ ਕਰਨ ਵਿਚ ਮੱਦਦਗਾਰ ਸਾਬਿਤ ਹੁੰਦਾ ਹੈ । ਇਸ ਨਾਲ ਖਿਡਾਰੀ ਨੂੰ ਚੰਗਾ ਪ੍ਰਦਰਸ਼ਨ ਕਰਨ ਲਈ ਉਤਸ਼ਾਹ ਮਿਲਦਾ ਹੈ । ਇਕ ਚੰਗਾ ਵਾਤਾਵਰਣ ਅਤੇ ਚੰਗੀ ਭਾਗਦਾਰੀ ਵਧੀਆ ਵਿਕਾਸ ਅਤੇ ਵਾਧੇ ਲਈ ਜ਼ਰੂਰੀ ਹੈ ਜੋ ਕਿ ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਵਿਚ ਅਹਿਮ ਭੂਮਿਕਾ ਨਿਭਾਉਂਦੀ ਹੈ ।

PSEB 12th Class Physical Education Guide ਸਰੀਰਕ ਯੋਗਤਾ Important Questions and Answers

ਇੱਕ ਅੰਕ ਵਾਲੇ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ (One Mark Question Answers)

ਪ੍ਰਸ਼ਨ 1.
ਰਫ਼ਤਾਰ ਦੇ ਦੋ ਪ੍ਰਕਾਰਾਂ ਦੀ ਸੂਚੀ ਲਿਖੋ ।
ਉੱਤਰ:

1. ਪ੍ਰਤੀਕ੍ਰਿਆ ਰਫ਼ਤਾਰ
2. ਤੇਜ਼ ਰਫ਼ਤਾਰ ਦੀ ਯੋਗਤਾ/ਗਤੀ ਯੋਗਤਾ ।

ਪ੍ਰਸ਼ਨ 2.
ਸਹਿਣਸ਼ੀਲਤਾ ਨੂੰ ਕਿੰਨੇ ਭਾਗਾਂ ਵਿਚ ਵੰਡਿਆ ਜਾ ਸਕਦਾ ਹੈ ?
ਉੱਤਰ-
ਦੋ ਪ੍ਰਕਾਰ ।

ਪ੍ਰਸ਼ਨ 3.
ਤਾਕਤ ਕਿੰਨੀ ਪ੍ਰਕਾਰ ਦੀ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਤਾਕਤ ਦੋ ਪ੍ਰਕਾਰ ਦੀ ਹੁੰਦੀ ਹੈ

1. ਗਤੀਸ਼ੀਲ ਤਾਕਤ
2. ਸਥਿਰ ਤਾਕਤ ।

ਪ੍ਰਸ਼ਨ 4.
ਕਿਸ ਉਮਰ ਵਿਚ ਭਾਰ ਸਿਖਲਾਈ ਸ਼ੁਰੂ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ ?
ਉੱਤਰ-
18 ਸਾਲ ਤੋਂ ।

ਪ੍ਰਸ਼ਨ 5.
ਸਰੀਰਕ ਯੋਗਤਾ ਦੇ ਕੋਈ ਦੋ ਮਹੱਤਵ ਲਿਖੋ ।
ਤਾਂ ,
ਉੱਤਰ-

1. ਸੰਪੂਰਨ ਤੰਦਰੁਸਤੀ
2. ਭਾਰ ਪ੍ਰਬੰਧਨ ।

ਪ੍ਰਸ਼ਨ 6.
ਸਰੀਰਕ ਯੋਗਤਾ ਦੇ ਅੰਗ ਲਿਖੋ ।
ਉੱਤਰ-
ਤਾਕਤ, ਸਹਿਣਸ਼ੀਲਤਾ, ਫੁਰਤੀ, ਸੰਤੁਲਨ, ਲਚਕ ਅਤੇ ਤਾਲਮੇਲ ਯੋਗਤਾ |

ਪ੍ਰਸ਼ਨ 7.
ਗਤੀਸ਼ੀਲ ਤਾਕਤ ਦਾ ਦੂਜਾ ਨਾਮ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਆਈਸੋਟੋਨਿਕ ।

ਪ੍ਰਸ਼ਨ 8.
ਸਥਿਰ ਤਾਕਤ ਨੂੰ ਹੋਰ ਕਿਸ ਨਾਮ ਨਾਲ ਜਾਣਿਆ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਆਈਸੋਮੀਟਰਿਕ ।

ਪ੍ਰਸ਼ਨ 9.
ਸੰਤੁਲਨ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ?
ਉੱਤਰ-
ਸਰੀਰ ਦੀ ਉਹ ਸਥਿਤੀ ਚਾਹੇ ਉਹ ਸਥਿਰ ਹੋਵੇ ਜਾਂ ਗਤੀ ਵਿਚ ‘ਤੇ ਕੰਟਰੋਲ ਰੱਖਣਾ ।

ਪ੍ਰਸ਼ਨ 10.
ਲਚਕ ਕਿੰਨੇ ਪ੍ਰਕਾਰ ਦੀ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਸਥਿਰ ਲਚਕ ਅਤੇ ਗਤੀਸ਼ੀਲ ਲਚਕ ।

ਪ੍ਰਸ਼ਨ 11.
ਤਾਲਮੇਲ ਯੋਗਤਾ ਦੇ ਕੋਈ ਦੋ ਨਾਮ ਦੱਸੋ ।
ਉੱਤਰ-
ਸਥਿਤੀ ਨਿਰਧਾਰਣ, ਸੰਯੋਜਨ ਦੀ ਯੋਗਤਾ ।

ਪ੍ਰਸ਼ਨ 12.
ਫੁਰਤੀ ਨੂੰ ਵਧਾਉਣ ਦੇ ਤਰੀਕੇ ਦੱਸੋ ।
ਉੱਤਰ-
ਫੁਰਤੀ ਨੂੰ ਸੈਟਲ ਰਨ, ਪੌੜੀ ਨੁਮਾ ਜੰਪ ਨਾਲ ਵਧਾਇਆ ਜਾ ਸਕਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 13.
ਵਿਲਿਅਮ ਸਰੀਰਕ ਯੋਗਤਾ ਪ੍ਰਤੀ ਆਪਣੇ ਵਿਚਾਰਾਂ ਨੂੰ ਕਿਵੇਂ ਪ੍ਰਗਟਾਉਂਦੇ ਹਨ ?
ਉੱਤਰ-
ਵਿਲਿਅਮ ਦੇ ਅਨੁਸਾਰ, “ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਸਰੀਰਕ ਕੰਮ ਕਰਨ ਲਈ ਵਿਅਕਤੀ ਦੀ ਸਮਰੱਥਾ ਹੈ ।”

ਪ੍ਰਸ਼ਨ 14.
ਤਾਕਤ ਕੀ ਹੈ ? ਉੱਤਰ-ਜਿੱਥੇ ਮਾਸਪੇਸ਼ੀ ਪ੍ਰਤੀਰੋਧ ਦੇ ਖਿਲਾਫ਼ ਬਲ ਪੈਦਾ ਕਰਦੀ ਹੈ ਉਸਨੂੰ ਤਾਕਤ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 15.
ਮੁਲਰ ਦੇ ਸ਼ਬਦਾਂ ਵਿਚ ਤਾਕਤ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ?
ਉੱਤਰ-
ਮੂਲਰ (Muller) ਦੇ ਅਨੁਸਾਰ, “ਤਾਕਤ ਨੂੰ ਇਸ ਪ੍ਰਕਾਰ ਪਰਿਭਾਸ਼ਿਤ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ, ਉਹ ਬਲ ਜੋ ਕਿ ਮਾਸਪੇਸ਼ੀ ਜ਼ਿਆਦਾ ਤੋਂ ਜ਼ਿਆਦਾ ਵਿਰੋਧ ਦੇ ਵਿਰੁੱਧ ਲਗਾਉਦੀ ਹੈ । ਇਸ ਨੂੰ ਪਾਊਂਡ ਅਤੇ ਕਿਲੋਗ੍ਰਾਮ ਦੀ ਇਕਾਈ ਵਿਚ ਮਾਪਿਆ ਜਾਂਦਾ ਹੈ ।”

ਪ੍ਰਸ਼ਨ 16.
ਮੈਥਿਊਜ਼ ਤਾਕਤ ਨੂੰ ਕਿਵੇਂ ਪਰਿਭਾਸ਼ਿਤ ਕਰਦਾ ਹੈ ?
ਉੱਤਰ-
ਮੈਥਿਊਜ਼ (Mathews) ਦੇ ਅਨੁਸਾਰ, “ਮਾਸਪੇਸ਼ੀਆਂ ਦੀ ਤਾਕਤ ਉਹ ਸ਼ਕਤੀ ਹੁੰਦੀ ਹੈ ਜੋ ਕਿ ਇਕ | ਮਾਸਪੇਸ਼ੀ ਅਤੇ ਮਾਸਪੇਸ਼ੀਆਂ ਦੇ ਸਮੂਹ ਦੁਆਰਾ ਵੱਧ ਤੋਂ ਵੱਧ ਜਨਤਾ ਨਾਲ ਵਿਰੋਧ ਦੇ ਵਿਰੁੱਧ ਲਗਾਉਂਦਾ ਹੈ ।”

ਪ੍ਰਸ਼ਨ 17.
ਸਥਿਰ ਤਾਕਤ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਇਹ ਵਿਰੋਧ ਦੇ ਵਿਰੁੱਧ ਕ੍ਰਿਆਵਾਂ ਕਰਨ ਲਈ ਮਾਸਪੇਸ਼ੀ ਯੋਗਤਾ ਹੁੰਦੀ ਹੈ । ਇਸ ਵਿਚ ਮਾਸਪੇਸ਼ੀ ਆਪਣੀ ਲੰਬਾਈ ਬਦਲੇ ਬਿਨਾਂ ਹੀ ਤਨਾਵ ਦਾ ਵਿਕਾਸ ਕਰਦੀ ਹੈ , ਜਿਵੇਂ ਕੰਧ ਨੂੰ ਧੱਕਾ ਮਾਰਨਾ ਆਦਿ ।

ਪ੍ਰਸ਼ਨ 18.
ਵਿਸਫੋਟਕ ਤਾਕਤ ਬਾਰੇ ਦੱਸੋ ।
ਉੱਤਰ-
ਇਹ ਗਤੀ ਅਤੇ ਤਾਕਤ ਦਾ ਮਿਸ਼ਰਣ ਹੈ । ਇਹ ਗਤੀ ਦੇ ਵਿਰੋਧ ਤੇ ਕਾਬੂ ਪਾਉਣ ਦੀ ਕਾਬਲੀਅਤ ਹੁੰਦੀ ਹੈ । ਵਿਸਫੋਟਕ ਉੱਚ ਤਾਕਤ ਤੇਜ਼ ਗਤੀ ਦੀਆਂ ਦੌੜਾਂ, ਭਾਰ ਚੁੱਕਣਾ, ਹੈਮਰ ਥਰੋ, ਲੰਬੀ ਕੁੱਦ ਅਤੇ ਉੱਚੀ ਕੁੱਦ ਵਿਚ ਦੇਖੀ ਜਾ ਸਕਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 19.
ਤਾਕਤ ਸਹਿਣਸ਼ੀਲਤਾ ਨੂੰ ਬਿਆਨ ਕਰੋ ।
ਉੱਤਰ-
ਇਹ ਤਾਕਤ ਅਤੇ ਸਹਿਣਸ਼ੀਲਤਾ ਦਾ ਮਿਸ਼ਰਣ ਹੁੰਦੀ ਹੈ । ਇਹ ਵਿਰੋਧ ਤੇ ਕਾਬੂ ਪਾਉਣ ਦੀ ਯੋਗਤਾ ਹੁੰਦੀ ਹੈ । ਲੰਬੀ ਦੂਰੀ ਦੀਆਂ ਦੌੜਾਂ, ਤੈਰਾਕੀ ਅਤੇ ਸਾਈਕਲਿੰਗ ਆਦਿ ਇਸ ਦੀਆਂ ਉਦਾਹਰਨਾਂ ਹਨ ।

ਪ੍ਰਸ਼ਨ 20.
ਕੀ ਸਥਿਰ ਤਾਕਤ ਵਿਚ ਮਾਸਪੇਸ਼ੀ ਆਪਣੀ ਲੰਬਾਈ ਬਦਲਦੀ ਹੈ ?
ਉੱਤਰ-
ਨਹੀਂ ।

ਪ੍ਰਸ਼ਨ 21.
ਬੁਨਿਆਦੀ ਸਹਿਣਸ਼ੀਲਤਾ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਬੁਨਿਆਦੀ ਸਹਿਣਸ਼ੀਲਤਾ ਮੁੱਖ ਤੌਰ ਤੇ ਐਰੋਬਿਕ ਸਹਿਣਸ਼ੀਲਤਾ ‘ਤੇ ਨਿਰਭਰ ਕਰਦੀ ਹੈ । ਐਰੋਬਿਕ ਤੋਂ ਭਾਵ ਹੈ ਕਿ ਜਿਸ ਵਿਚ ਆਕਸੀਜਨ ਦੀ ਪੂਰਤੀ ਕਸਰਤਾਂ ਅਤੇ ਅਭਿਆਸ ਨਾਲ ਮਿਲਦੀ ਰਹੇ ।

ਪ੍ਰਸ਼ਨ 22.
ਆਮ ਸਹਿਣਸ਼ੀਲਤਾ ਕੀ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਇਹ ਐਰੋਬਿਕਸ ਅਤੇ ਐਨਰੋਬਿਕਸ ਦੋਵੇਂ ਕ੍ਰਿਆਵਾਂ ਤੇ ਨਿਰਭਰ ਕਰਦੀ ਹੈ । ਇਹ ਹੌਲੀ ਅਤੇ ਤੇਜ਼ ਗਤੀ ਦੋਵਾਂ ਪ੍ਰਕਾਰਾਂ ਨਾਲ ਕੀਤੀ ਜਾਂਦੀ ਹੈ । ਇਹ ਸਹਿਣਸ਼ੀਲਤਾ ਖਿਡਾਰੀ ਨੂੰ ਬਿਨਾਂ ਥਕਾਵਟ ਦੇ ਲੰਬੇ ਸਮੇਂ ਦੇ ਕੰਮ ਕਰਨ ਦੇ ਯੋਗ ਬਣਾਉਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 23.
ਆਮ ਸ਼ਹਿਣਸ਼ੀਲਤਾ, ਕਿਸ ਸਹਿਣਸ਼ੀਲਤਾ ਦਾ ਹਿੱਸਾ ਹੈ ?
ਉੱਤਰ-
ਕਿਰਿਆ ਦੇ ਸੁਭਾਅ ਅਨੁਸਾਰ ਦਾ ।

ਪ੍ਰਸ਼ਨ 24.
ਜੇਕਰ ਕਿਸੇ ਮੁੱਕੇਬਾਜ਼ ਨੂੰ ਤਿੰਨ ਮਿੰਟ ਵਿਚ ਆਪਣੀ ਬਾਊਟ ਖ਼ਤਮ ਕਰਨੀ ਹੈ ਤਾਂ ਉਸਨੂੰ ਕਿਸ ਪ੍ਰਕਾਰ ਦੀ ਸਹਿਣਸ਼ੀਲਤਾ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ?
ਉੱਤਰ-
ਵਿਸ਼ੇਸ਼ ਸਹਿਣਸ਼ੀਲਤਾ ਦੀ ।

ਪ੍ਰਸ਼ਨ 25.
ਐਰੋਬਿਕ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ?
ਉੱਤਰ-
ਐਰੋਬਿਕ ਤੋਂ ਭਾਵ ਹੈ ਕਿ ਜਿਸ ਵਿਚ ਆਕਸੀਜਨ ਦੀ ਪੂਰਤੀ ਕਸਰਤਾਂ ਅਤੇ ਅਭਿਆਸ ਦੌਰਾਨ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਰਹੇ ।

ਪ੍ਰਸ਼ਨ 26.
ਮੱਧ ਸਮੇਂ ਦੀ ਸਹਿਣਸ਼ੀਲਤਾ ਨੂੰ ਆਪਣੇ ਸ਼ਬਦਾਂ ਵਿਚ ਬਿਆਨ ਕਰੋ ।
ਉੱਤਰ-
ਇਸ ਦੀ ਜ਼ਰੂਰਤ ਉਹਨਾਂ ਮੁਕਾਬਲਿਆਂ ਵਿਚ ਪੈਂਦੀ ਹੈ ਜੋ ਕਿ 2 ਤੋਂ 10 ਮਿੰਟ ਵਿਚ ਖ਼ਤਮ ਹੋ ਜਾਂਦੇ ਹਨ : ਜਿਵੇਂ ਕਿ ਮੱਧ ਦੂਰੀ ਦੀਆਂ ਦੌੜਾਂ ਇਸ ਦੀਆਂ ਉਦਾਹਰਨਾਂ ਹਨ ।

ਪ੍ਰਸ਼ਨ 27,
ਘੱਟ ਸਮੇਂ ਦੀ ਸਹਿਣਸ਼ੀਲਤਾ ਕਿਹੜੀਆਂ ਦੌੜਾਂ ਵਿਚ ਇਸਤੇਮਾਲ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਛੋਟੀ ਦੁਰੀ ਦੀਆਂ ਦੌੜਾਂ ਵਿਚ ਜਿਵੇਂ ਕਿ 100 ਮੀ., 200 ਮੀ. ਅਤੇ 400 ਮੀ. ਆਦਿ ।

ਪ੍ਰਸ਼ਨ 28.
ਉਹ ਮੁਕਾਬਲੇ ਜੋ 2 ਮਿੰਟ ਤੋਂ 10 ਮਿੰਟ ਵਿਚ ਖ਼ਤਮ ਹੋ ਜਾਂਦੇ ਹਨ, ਉਹ ਕਿਹੜੀ ਸਹਿਣਸ਼ੀਲਤਾ ਦਾ ਪ੍ਰਤੀਕ ਹਨ ?
ਉੱਤਰ-
ਮੱਧ ਸਮੇਂ ਦੀ ਸਹਿਣਸ਼ੀਲਤਾ ਦੇ ।

ਪ੍ਰਸ਼ਨ 29.
5000 ਮੀਟਰ ਤੇ 10000 ਮੀਟਰ ਦੇ ਦੌੜਾਕਾਂ ਵਿਚ ਕਿਹੜੀ ਸਹਿਣਸ਼ੀਲਤਾ ਜ਼ਿਆਦਾ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ?
ਉੱਤਰ-
ਲੰਬੇ ਸਮੇਂ ਦੀ ਸਹਿਣਸ਼ੀਲਤਾ ।

ਪ੍ਰਸ਼ਨ 30.
ਮੱਧ ਸਮੇਂ ਦੀ ਸਹਿਣਸ਼ੀਲਤਾ ਕਿਸ ਸਹਿਣਸ਼ੀਲਤਾ ਦਾ ਹਿੱਸਾ ਹੈ ?
ਉੱਤਰ-
ਕਿਆ ਦੇ ਸਮੇਂ ਅਨੁਸਾਰ ਸਹਿਣਸ਼ੀਲਤਾ |

ਪ੍ਰਸ਼ਨ 31.
ਜਟਿਲ ਅਭਿਆਸ ਤੋਂ ਬਾਅਦ ਕਿੰਨੇ ਪ੍ਰਤੀਸ਼ਤ ਰਫ਼ਤਾਰ ਵਿਕਸਿਤ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ ?
ਉੱਤਰ-
20% ਤੱਕ ।

ਪ੍ਰਸ਼ਨ 32.
ਇੰਜਣ ਯੋਗਤਾ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਇਹ ਇਕਦਮ ਰਫਤਾਰ ਬਣਾ ਕੇ ਉਸਨੂੰ ਉਸੇ ਸਥਿਤੀ ਵਿਚ ਬਣਾਏ ਰੱਖਣ ਦੀ ਯੋਗਤਾ ਹੈ । ਜਿਵੇਂ ਕਿ ਛੋਟੀ ਦੂਰੀ ਦੀਆਂ ਦੌੜਾਂ 100 ਮੀ: 200 ਮੀ: ਅਤੇ 400 ਮੀ: ਆਦਿ ਇਸ ਦੀਆਂ ਉਦਾਹਰਨਾਂ ਹਨ।

ਪ੍ਰਸ਼ਨ 33.
ਰਫ਼ਤਾਰ ਸਹਿਣਸ਼ੀਲਤਾ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਇਹ ਉਹ ਯੋਗਤਾ ਹੁੰਦੀ ਹੈ ਜਿਸ ਵਿਚ ਖਿਡਾਰੀ ਆਪਣੀ ਰਫ਼ਤਾਰ ਨੂੰ ਖੇਡ ਦੇ ਆਖਰੀ ਪੜਾਅ ਤਕ ਬਣਾ ਕੇ ਰੱਖਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 34.
ਸ਼ੱਟਲ ਰਨ, ਪੋਮੀਟਿਕ ਜੰਪ ਅਤੇ ਟੈਕ ਜੰਪ ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਦੇ ਕਿਹੜੇ ਅੰਗ ਦੇ ਸੁਧਾਰ ਲਈ ਕਰਵਾਏ ਜਾਂਦੇ ਹਨ ?
ਉੱਤਰ-
ਫੁਰਤੀ ਲਈ ।

ਪ੍ਰਸ਼ਨ 35.
ਗ੍ਰਹਿਣ ਯੋਗਤਾ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਇਹ ਵਿਅਕਤੀ ਦੀ ਉਹ ਯੋਗਤਾ ਹੈ ਜਿਸ ਵਿਚ ਉਹ ਪ੍ਰਸਥਿਤੀ ਨੂੰ ਸਮਝ ਕੇ ਉਸ ਵਿਚ ਪ੍ਰਭਾਵੀ ਪਰਿਵਰਤਨ ਲੈ ਕੇ ਆਵੇ । ਉਦਾਹਰਨ ਦੇ ਤੌਰ ਤੇ ਬਾਸਕਟ ਬਾਲ ਵਿਚ ਜੰਪ ਸਾਂਟ ਕਿਆ ਦੇ ਅਨੁਕੂਲ ਬਣਾਉਣਾ ਆਦਿ ।

ਦੋ ਅੰਕਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ (Two Marks Question Answers)

ਪ੍ਰਸ਼ਨ 1.
ਸਰੀਰਕ ਯੋਗਤਾ ਕੀ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਬੂਚਰ ਅਤੇ ਪ੍ਰੇਹਟਿਸ ਦੇ ਅਨੁਸਾਰ, “ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਇਕ ਜੈਵਿਕ ਵਿਕਾਸ, ਮਾਸਪੇਸ਼ੀਆਂ ਦੀ ਤਾਕਤ ਅਤੇ ਸਟੈਮਿਨਾ ਹੁੰਦੀ ਹੈ | ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਤੋਂ ਭਾਵ ਅਭਿਆਸ ਵਿਚ ਕੁਸ਼ਲਤਾਪੂਰਵਕ ਪ੍ਰਦਰਸ਼ਨ ਤੋਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਸਰੀਰਕ ਯੋਗਤਾ ਦੇ ਕੋਈ ਦੋ ਮਹੱਤਵ ਲਿਖੋ ।
ਉੱਤਰ-
1. ਸੰਪੂਰਨ ਸਿਹਤ ਦਾ ਸੁਧਾਰ-ਸਰੀਰਕ ਤੌਰ ‘ਤੇ ਤੰਦਰੁਸਤ ਵਿਅਕਤੀ ਕਈ ਤਰ੍ਹਾਂ ਦੇ ਸਰੀਰਕ ਫਾਇਦਿਆਂ ਨੂੰ ਮਾਣਦਾ ਹੈ , ਜਿਵੇਂ ਕਿ ਸਾਹ ਕਿਰਿਆ, ਲਹੂ ਸੰਚਾਰ ਪ੍ਰਣਾਲੀ ਅਤੇ ਸਰੀਰ ਦੀਆਂ ਸਮੁੱਚੀ ਪ੍ਰਣਾਲੀਆਂ ਦਾ ਠੀਕ ਢੰਗ ਨਾਲ ਕੰਮ ਕਰਨਾ ਅਤੇ ਸਰੀਰ ਦਾ ਕ੍ਰਿਆਤਮਕ ਰੂਪ ਵਿਚ ਤਿਆਰ ਰਹਿਣਾ । ਉਹ ਕਈ ਤਰ੍ਹਾਂ ਦੀਆਂ ਬਿਮਾਰਿਆਂ ਜਿਵੇਂ ਕਿ ਸ਼ੂਗਰ, ਦਿਲ ਦੀਆਂ ਬਿਮਾਰੀਆਂ ਅਤੇ ਕੈਂਸਰ ਆਦਿ ਤੋਂ ਬਚਿਆ ਰਹਿੰਦਾ ਹੈ ।

2. ਭਾਰ ਪ੍ਰਬੰਧਨ-ਵਾਧੂ ਵਜ਼ਨ ਕਈ ਤਰ੍ਹਾਂ ਦੀਆਂ ਸਿਹਤ ਸੰਬੰਧੀ ਸਮੱਸਿਆਵਾਂ ਜਿਵੇਂ ਕਿ ਖੁਨ ਚਾਪ, ਕੈਸਟਰੋਲ ਪੱਧਰ, ਸ਼ੂਗਰ ਆਦਿ ਦੀ ਜੜ੍ਹ ਹੈ । ਜੋ ਵਿਅਕਤੀ ਸਰਗਰਮ ਅਤੇ ਸਰੀਰਕ ਤੌਰ ‘ਤੇ ਚੁਸਤ ਰਹਿੰਦੇ ਹਨ, ਉਹਨਾਂ ਨੂੰ ਉਪਰੋਕਤ ਬਿਮਾਰੀਆਂ ਦੀ ਸੰਭਾਵਨਾ ਘੱਟ ਹੁੰਦੀ ਹੈ ,

ਪ੍ਰਸ਼ਨ 3.
ਸਹਿਣਸ਼ੀਲਤਾ ਨੂੰ ਪਰਿਭਾਸ਼ਿਤ ਕਰੋ ।
ਉੱਤਰ-
ਬੈਰੋ ਅਤੇ ਮੈਕੇਜੀ (Barrow and McGee) ਦੇ ਅਨੁਸਾਰ ਸਹਿਣਸ਼ੀਲਤਾ, ਇਕ ਸਮੇਂ ਮਿਆਦ ਵਿਚ \ ਵਿਅਕਤੀ ਦੀ ਗਤੀ ਨੂੰ ਬਣਾਏ ਰੱਖਣ ਦੀ ਸਰੀਰਕ ਸਥਿਤੀ ਦੀ ਯੋਗਤਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 4.
ਵਿਸਫੋਟਕ ਤਾਕਤ ਤੋਂ ਤੁਸੀਂ ਕੀ ਸਮਝਦੇ ਹੋ ?
ਉੱਤਰ-
ਇਹ ਗਤੀ ਅਤੇ ਤਾਕਤ ਦਾ ਮਿਸ਼ਰਣ ਹੈ । ਇਹ ਗਤੀ ਦੇ ਵਿਰੋਧ ਤੇ ਕਾਬੂ ਪਾਉਣ ਦੀ ਕਾਬਲੀਅਤ ਹੁੰਦੀ ਹੈ । ਵਿਸਫੋਟਕ ਉੱਚ ਤਾਕਤ ਤੇਜ਼ ਗਤੀ ਦੀਆਂ ਦੌੜਾਂ, ਭਾਰ ਚੁੱਕਣਾ, ਹੈਮਰ ਥਰੋ, ਲੰਬੀ ਕੁੱਦ ਅਤੇ ਉੱਚੀ ਕੁੱਦ ਵਿਚ ਦੇਖੀ ਜਾ ਸਕਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 5.
ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਨ ਵਾਲੇ ਕਾਰਕਾਂ ਬਾਰੇ ਲਿਖੋ ।
ਉੱਤਰ-

1. ਸਰੀਰਕ ਢਾਂਚਾ
2. ਜੱਦ ਅਤੇ ਵਾਤਾਵਰਣ
3. ਮਨੋਵਿਗਿਆਨਿਕ ਕਾਰਜ
4. ਸਰੀਰਕ ਕਿਰਿਆ ਵਿਗਿਆਨ ।

ਪ੍ਰਸ਼ਨ 6.
ਰਫ਼ਤਾਰ ਨੂੰ ਪਰਿਭਾਸ਼ਿਤ ਕਰੋ ।
ਉੱਤਰ-
ਜਾਨਸਨ ਅਤੇ ਨੇਲਸਨ (Johnson and Nelson) ਦੇ ਅਨੁਸਾਰ ਰਫਤਾਰ ਉਹ ਦਰ ਹੁੰਦੀ ਹੈ ਜਿਸ ਵਿਚ ਵਿਅਕਤੀ ਮੈਦਾਨ ਵਿਚ ਆਪਣੇ ਸਰੀਰ ਅਤੇ ਸਰੀਰ ਦੇ ਅੰਗਾਂ ਨੂੰ ਅੱਗੇ ਵਧਾਉਣ ਲਈ ਉਤਸ਼ਾਹਿਤ ਕਰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 7.
ਤਾਕਤ ਸਹਿਣਸ਼ੀਲਤਾ ਤੋਂ ਤੁਸੀਂ ਕੀ ਸਮਝਦੇ ਹੋ ?
ਉੱਤਰ-
ਇਹ ਤਾਕਤ ਅਤੇ ਸਹਿਣਸ਼ੀਲਤਾ ਦਾ ਮਿਸ਼ਰਣ ਹੁੰਦੀ ਹੈ । ਇਹ ਵਿਰੋਧ ‘ਤੇ ਕਾਬੂ ਪਾਉਣ ਦੀ ਯੋਗਤਾ ਹੁੰਦੀ ਹੈ । ਲੰਬੀ ਦੂਰੀ ਦੀਆਂ ਦੌੜਾਂ, ਤੈਰਾਕੀ ਅਤੇ ਸਾਈਕਲਿੰਗ ਆਦਿ ਇਸ ਦੀਆਂ ਉਦਾਹਰਨਾਂ ਹਨ ।

ਪ੍ਰਸ਼ਨ 8.
ਸਰੀਰਕ ਯੋਗਤਾ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਨ ਵਾਲੇ ਕੋਈ ਦੋ ਕਾਰਕ ਲਿਖੋ ।
ਉੱਤਰ-

1. ਮਨੋਵਿਗਿਆਨਕ ਕਾਰਕ
2. ਖੁਰਾਕ ।

ਪ੍ਰਸ਼ਨ 9.
ਸਰੀਰਕ ਯੋਗਤਾ ਦਾ ਪ੍ਰੋਗਰਾਮ ਬਣਾਉਂਦੇ ਸਮੇਂ ਕਿਹੜੀਆਂ ਗੱਲਾਂ ਦਾ ਧਿਆਨ ਰੱਖਣਾ ਚਾਹੀਦਾ ਹੈ ?
ਉੱਤਰ-
ਸਰੀਰਕ ਯੋਗਤਾ ਪ੍ਰੋਗਰਾਮ ਬਣਾਉਂਦੇ ਸਮੇਂ ਹੇਠ ਲਿਖੀਆਂ ਗੱਲਾਂ ਦਾ ਧਿਆਨ ਰੱਖਣਾ ਚਾਹੀਦਾ ਹੈ ।

1. ਉਮਰ
2. ਲਿੰਗ |

ਪ੍ਰਸ਼ਨ 10.
ਤਾਕਤ ਸਹਿਣਸ਼ੀਲਤਾ ਤੋਂ ਤੁਸੀਂ ਕੀ ਸਮਝਦੇ ਹੋ ?
ਉੱਤਰ-
ਇਹ ਤਾਕਤ ਅਤੇ ਸਹਿਣਸ਼ੀਲਤਾ ਦਾ ਮਿਸ਼ਰਣ ਹੁੰਦੀ ਹੈ । ਇਹ ਵਿਰੋਧ ਤੇ ਕਾਬੂ ਪਾਉਣ ਦੀ ਯੋਗਤਾ ਹੁੰਦੀ ਹੈ । ਲੰਬੀ ਦੂਰੀ ਦੀਆਂ ਦੌੜਾਂ, ਤੈਰਾਕੀ ਅਤੇ ਸਾਈਕਲਿੰਗ ਆਦਿ ਇਸ ਦੀਆਂ ਉਦਾਹਰਨਾਂ ਹਨ ।

ਪ੍ਰਸ਼ਨ 11.
ਗਤੀ ਅਤੇ ਤਾਕਤ ਬਾਰੇ ਲਿਖੋ ।
ਉੱਤਰ-ਗਤੀ (Speed)-ਗਤੀ ਤੋਂ ਭਾਵ ਸਰੀਰ ਦੇ ਅੰਗਾਂ ਵਿਚ ਤੇਜ਼ੀ ਲਿਆਉਣ ਤੋਂ ਹੈ । ਇਹ ਗਤੀ ਭਾਵੇਂ , ਦੌੜਾਕ ਦੀਆਂ ਲੱਤਾਂ ਵਿਚ ਹੋਵੇ ਜਾਂ ਫਿਰ ਸ਼ਾਟ ਪੁੱਟ ਲਗਾਉਣ ਵਾਲੇ ਦੀਆਂ ਬਾਂਹਾਂ ਦੀ ਹੋਵੇ ।
ਤਾਕਤ (Strength)-ਜਿੱਥੇ ਮਾਸਪੇਸ਼ੀ ਪ੍ਰਤੀਰੋਧ ਦੇ ਵਿਰੁੱਧ ਬਲ ਪੈਦਾ ਕਰਦੀ ਹੈ ਉਸਨੂੰ ਤਾਕਤ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 12.
ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਨ ਵਾਲੇ ਕਾਰਕ ਕਿਹੜੇ ਹਨ ? .
ਉੱਤਰ-

1. ਸਰੀਰਕ ਕ੍ਰਿਆ ਦੀ ਬਣਤਰ
2. ਮਨੋਵਿਗਿਆਨਕ ਕਾਰਕ ।

ਪ੍ਰਸ਼ਨ 13.
ਪ੍ਰਤੀਕ੍ਰਿਆ ਰਫ਼ਤਾਰ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਇਹ ਸਿਗਨਲ ਮਿਲਣ ਤੇ ਤੁਰੰਤ ਪ੍ਰਤੀਕ੍ਰਿਆ ਕਰਨ ਦੀ ਯੋਗਤਾ ਹੁੰਦੀ ਹੈ । ਇਸ ਵਿਚ ਖਿਡਾਰੀ ਪਰਿਸਥਿਤੀ ਦੇ ਵਿਰੁੱਧ ਪ੍ਰਤੀਕ੍ਰਿਆ ਕਰਦਾ ਹੈ ਜਿਵੇਂ ਕਿ ਕੱਚ ਦੀ ਸੀਟੀ ਵੱਜਣ ਤੇ ਅੱਗੇ ਵੱਲ, ਪਿੱਛੇ ਵੱਲ, ਖੱਬੇ ਅਤੇ ਸੱਜੇ ਪਾਸੇ ਤੇਜ਼ ਗਤੀ ਨਾਲ ਜਾਣਾ ਆਦਿ ।

ਪ੍ਰਸ਼ਨ 14.
ਫੁਰਤੀ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ?
ਉੱਤਰ-
ਫੁਰਤੀ ਨਿਯੰਤਰਣ (Control) ਵਿਚ ਰਹਿ ਕੇ, ਤੇਜ਼ੀ ਅਤੇ ਪ੍ਰਭਾਵੀ ਢੰਗ ਨਾਲ ਸਰੀਰ ਦੀ ਦਿਸ਼ਾ ਵਿਚ ਪਰਿਵਰਤਨ ਲਿਆਉਣ ਦੀ ਯੋਗਤਾ ਹੁੰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 15.
ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਦੀ ਕੋਈ ਇੱਕ ਪਰਿਭਾਸ਼ਾ ਲਿਖੋ ।
ਉੱਤਰ-
ਡੇਵਿਡ ਆਰ. ਲੈਂਬ ਦੇ ਅਨੁਸਾਰ, “ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਜੀਵਨ ਦੇ ਮੌਜੂਦਾ ਅਤੇ ਸੰਭਾਵੀ ਭੌਤਿਕ ਚੁਣੌਤੀਆਂ ਨੂੰ ਸਫਲਤਾਪੂਰਵਕ ਕਰਨ ਦੀ ਸਮਰੱਥਾ ਹੈ ।”

ਪ੍ਰਸ਼ਨ 16.
ਸਰੀਰਕ ਯੋਗਤਾ ਦੇ ਕੋਈ ਦੋ ਅੰਗਾਂ ਦੇ ਨਾਮ ਲਿਖੋ ।
ਉੱਤਰ-

1. ਤਾਕਤ
2. ਫੁਰਤੀ ।

ਪ੍ਰਸ਼ਨ 17.
ਸਰੀਰਕ ਢਾਂਚੇ ਸ਼ਬਦ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ?
ਉੱਤਰ-
ਸਰੀਰਕ ਢਾਂਚਾ (Anatomical Structure) – ਸਰੀਰਕ ਢਾਂਚਾ ਅਲੱਗ-ਅਲੱਗ ਅਕਾਰ ਅਤੇ ਰੂਪ ਵਿਚ ਹੁੰਦਾ ਹੈ । ਕਈ ਵਾਰ ਅਨੁਚਿਤ ਆਕਾਰ ਅਤੇ ਰੂਪ ਸਰੀਰਕ ਕ੍ਰਿਆਵਾਂ ਵਿਚ ਉਲਝਣਾਂ ਪੈਦਾ ਕਰਦਾ ਹੈ ਅਤੇ ਕਈ ਵਾਰ ਕਮਜ਼ੋਰ ਅੰਗ ਵਿਅਕਤੀ ਦੇ ਕੰਮਾਂ ਜਾਂ ਕ੍ਰਿਆਵਾਂ ਨੂੰ ਘਟਾ ਦਿੰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 18.
ਕੀ ਸੱਟਾਂ ਸਰੀਰਕ ਯੋਗਤਾ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਦੀਆਂ ਹਨ ਅਤੇ ਕਿਉਂ ?
ਉੱਤਰ-
ਹਾਂ, ਕਿਉਂਕਿ ਸੱਟਾਂ ਦੀ ਦੇਖਭਾਲ ਦੀ ਕਮੀ ਦੇ ਕਾਰਨ ਖੇਡ ਪ੍ਰਦਰਸ਼ਨ ਵਿਚ ਕਮੀ ਆ ਜਾਂਦੀ ਹੈ ਅਤੇ ਨਾਲ ਹੀ ਖਿਡਾਰੀ ਦੇ ਮਾਨਸਿਕ ਸੰਤੁਲਨ ‘ਤੇ ਵੀ ਪ੍ਰਭਾਵ ਪੈਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 19.
ਸਿਹਤਮੰਦ ਵਾਤਾਵਰਣ ਦਾ ਸਰੀਰਕ ਯੋਗਤਾ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਨ ਦਾ ਕੀ ਕਾਰਨ ਹੈ ?
ਉੱਤਰ-
ਸਕੂਲ, ਘਰ ਅਤੇ ਖੇਡਾਂ ਦਾ ਮੈਦਾਨ ਬੇਹਤਰ ਸਿੱਖਿਆ ਪ੍ਰਦਾਨ ਕਰਨ ਵਿਚ ਮੱਦਦਗਾਰ ਸਾਬਿਤ ਹੁੰਦਾ ਹੈ । ਇਸ ਨਾਲ ਖਿਡਾਰੀ ਨੂੰ ਚੰਗਾ ਪ੍ਰਦਰਸ਼ਨ ਕਰਨ ਲਈ ਉਤਸ਼ਾਹ ਮਿਲਦਾ ਹੈ । ਇਕ ਚੰਗਾ ਵਾਤਾਵਰਣ ਅਤੇ ਚੰਗੀ ਭਾਗਦਾਰੀ ਵਧੀਆ ਵਿਕਾਸ ਅਤੇ ਵਾਧੇ ਲਈ ਜ਼ਰੂਰੀ ਹੈ ਜੋ ਕਿ ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਵਿਚ ਅਹਿਮ ਭੂਮਿਕਾ ਨਿਭਾਉਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 20.
ਆਮ ਸਹਿਣਸ਼ੀਲਤਾ ਅਤੇ ਮੱਧ ਸਮੇਂ ਦੀ ਸਹਿਣਸ਼ੀਲਤਾ ਨੂੰ ਬਿਆਨ ਕਰੋ ।
ਉੱਤਰ-
(ੳ) ਆਮ ਸਹਿਣਸ਼ੀਲਤਾ (General Endurance)-ਇਹ ਐਰੋਬਿਕਸ, ਅਤੇ ਐਨਰੋਬਿਕਸ ਦੋਵੇਂ ਕ੍ਰਿਆਵਾਂ ਤੇ ਨਿਰਭਰ ਕਰਦੀ ਹੈ । ਇਹ ਹੌਲੀ ਅਤੇ ਤੇਜ਼ ਗਤੀ ਦੋਵਾਂ ਪ੍ਰਕਾਰਾਂ ਨਾਲ ਕੀਤੀ ਜਾਂਦੀ ਹੈ । ਇਹ ਸਹਿਣਸ਼ੀਲਤਾ ਖਿਡਾਰੀ ਨੂੰ ਬਿਨਾਂ ਥਕਾਵਟ ਦੇ ਲੰਬੇ ਸਮੇਂ ਦੇ ਕੰਮ ਕਰਨ ਦੇ ਯੋਗ ਬਣਾਉਂਦੀ ਹੈ ।

(ਅ) ਮੱਧ ਸਮੇਂ ਦੀ ਸਹਿਣਸ਼ੀਲਤਾ (Middle Term Endurance-ਇਸ ਦੀ ਜ਼ਰੂਰਤ ਉਹਨਾਂ ਮੁਕਾਬਲਿਆਂ ਵਿਚ ਪੈਂਦੀ ਹੈ ਜੋ ਕਿ 2 ਤੋਂ 10 ਮਿੰਟ ਵਿਚ ਖ਼ਤਮ ਹੋ ਜਾਂਦੇ ਹਨ , ਜਿਵੇਂ ਕਿ ਮੱਧ ਦੁਰੀ ਦੀਆਂ ਦੌੜਾਂ ਇਸ ਦੀਆਂ ਉਦਾਹਰਨਾਂ ਹਨ ।

ਪ੍ਰਸ਼ਨ 21.
ਪ੍ਰਤੀਕ੍ਰਿਆ ਰਫ਼ਤਾਰ ਅਤੇ ਗਤੀ ਯੋਗਤਾ ਵਿਚ ਕੀ ਫ਼ਰਕ ਹੈ ?
ਉੱਤਰ-
(ੳ) ਪ੍ਰਤੀਕ੍ਰਿਆ ਰਫਤਾਰ (Reaction Speed)-ਇਹ ਸਿਗਨਲ ਮਿਲਣ ਤੇ ਤੁਰੰਤ ਪ੍ਰਤੀਕ੍ਰਿਆਂ ਕਰਨ ਦੀ ਯੋਗਤਾ ਹੁੰਦੀ ਹੈ । ਇਸ ਵਿਚ ਖਿਡਾਰੀ ਸਥਿਤੀ ਦੇ ਵਿਰੁੱਧ ਪ੍ਰਤੀਕ੍ਰਿਆ ਕਰਦਾ ਹੈ , ਜਿਵੇਂ ਕਿ ਕੋਚ (Coach) ਦੀ ਸੀਟੀ ਵੱਜਣ ਤੇ ਅੱਗੇ ਵੱਲ, ਪਿੱਛੇ ਵੱਲ, ਖੱਬੇ ਅਤੇ ਸੱਜੇ ਪਾਸੇ ਤੇਜ਼ ਗਤੀ ਨਾਲ ਜਾਣਾ ਆਦਿ ।

(ਅ) ਗਤੀ ਯੋਗਤਾ (Acceleration Ability)-ਇਹ ਸਥਿਰ (Stationary) ਅਵਸਥਾ ਤੋਂ ਵੱਧ ਤੋਂ ਵੱਧ (Maximum) ਰਫਤਾਰ ਵਿਚ ਇਕਦਮ ਜਾਣ ਦੀ ਯੋਗਤਾ ਹੈ ; ਜਿਵੇਂ ਕਿ ਅਸੀਂ ਇਹਨਾਂ ਨੂੰ ਸਪਰਿੰਟ (Sprint) ਛੋਟੀ ਦੁਰੀ ਦੀਆਂ ਦੌੜਾਂ ਵਿਚ ਦੇਖ ਸਕਦੇ ਹਾਂ ਜਿੱਥੇ ਇਕ ਵਿਸਫੋਟਕ ਤਾਕਤ, ਤਕਨੀਕ ਅਤੇ ਲਚਕ ਦੀ ਜ਼ਰੂਰਤ ਪੈਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 22.
ਇੰਜਨ ਯੋਗਤਾ ਅਤੇ ਸੰਚਲਨ ਵੇਗ ਨੂੰ ਆਪਣੇ ਸ਼ਬਦਾਂ ਵਿਚ ਲਿਖੋ ।
ਉੱਤਰ-
(ਉ) ਲੋਕੋਮੋਟਰ ਜਾਂ ਮਨ ਦੀ ਯੋਗਤਾ ਜਾਂ ਇੰਜਣ ਯੋਗਤਾ (Locomotor Ability)-ਇਹ ਇਕਦਮ ਰਫਤਾਰ ਬਣਾ ਕੇ ਉਸਨੂੰ ਉਸੇ ਸਥਿਤੀ ਵਿਚ ਬਣਾਏ ਰੱਖਣ ਦੀ ਯੋਗਤਾ ਹੈ । ਜਿਵੇਂ ਕਿ ਛੋਟੀ ਦੂਰੀ ਦੀਆਂ ਦੌੜਾਂ 100 ਮੀ: 200 ਮੀ: ਅਤੇ 400 ਮੀ: ਆਦਿ ਇਸ ਦੀਆਂ ਉਦਾਹਰਨਾਂ ਹਨ ।

( ਅ) ਸੰਚਲਨ ਵੇਗ (Movement Speed)-ਇਹ ਉਹ ਯੋਗਤਾ ਜਿਸ ਵਿਚ ਘੱਟ ਤੋਂ ਘੱਟ ਸਮੇਂ ਵਿਚ ਵੱਧ ਤੋਂ ਵੱਧ ਕ੍ਰਿਆ ਨੂੰ ਪੂਰਾ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।

ਤਿੰਨ ਅੰਕਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ (Three Marks Question Answers)

ਪ੍ਰਸ਼ਨ 1.
ਆਈਸੋਟੋਨਿਕ ਅਤੇ ਆਈਸੋਮੀਟਰਿਕ ਵਿਚ ਕੀ ਅੰਤਰ ਹੈ ?
ਉੱਤਰ-
1. ਗਤੀਸ਼ੀਲ ਤਾਕਤ ਜਾਂ ਆਈਸੋਟੋਨਿਕ ਤਾਕਤ (Dynamic or Isotonic Strength)- ਜਦ ਸੁੰਗੜਨ ਨਾਲ ਮਾਸਪੇਸ਼ੀ ਦੀ ਲੰਬਾਈ ਵਿਚ ਪਰਿਵਰਤਨ ਹੁੰਦਾ ਹੈ ਤਾਂ ਉਸਨੂੰ ਗਤੀਸ਼ੀਲ ਤਾਕਤ ਕਹਿੰਦੇ ਹਨ । ਉਦਾਹਰਨ ਲਈ ਜਦ ਇਕ ਤੋਂ ਵੱਧ ਜੋੜਾਂ ਵਿਚ ਗਤੀ ਹੋਵੇ ਜਿਵੇਂ ਕਿ ਪੁਸ਼-ਅਪ, ਪੁਲ-ਅਪ, ਬਾਰਬੈਲ ਪੇਸ਼, ਸਕੈਊਟ ਜੰਪ (Squat Jump), ਡੈਡ ਲਿਫਟਜ (Dead lifts) ਆਦਿ । ਗਤੀਸ਼ੀਲ ਤਾਕਤ ਨੂੰ ਤਿੰਨ ਭਾਗਾਂ ਵਿਚ ਵਿਭਾਜਿਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।

2. ਸਥਿਰ ਤਾਕਤ ਜਾਂ ਆਈਸੋਮੀਟਰਿਕ (Static or Isometric Strength)-ਇਹ ਵਿਰੋਧ ਦੇ ਵਿਰੁੱਧ ਕ੍ਰਿਆਵਾਂ ਕਰਨ ਲਈ ਮਾਸਪੇਸ਼ੀ ਯੋਗਤਾ ਹੁੰਦੀ ਹੈ । ਇਸ ਵਿਚ ਮਾਸਪੇਸ਼ੀ ਆਪਣੀ ਲੰਬਾਈ ਬਦਲੇ ਬਿਨਾਂ ਹੀ ਤਨਾਵ ਦਾ ਵਿਕਾਸ ਕਰਦੀ ਹੈ , ਜਿਵੇਂ ਕੰਧ ਨੂੰ ਧੱਕਾ ਮਾਰਨਾ ਆਦਿ। |

ਪ੍ਰਸ਼ਨ 2.
ਸਹਿਣਸ਼ੀਲਤਾ ਨੂੰ ਕ੍ਰਿਆ ਦੇ ਸੁਭਾਅ ਅਨੁਸਾਰ ਕਿਵੇਂ ਪਰਿਭਾਸ਼ਿਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
(ੳ) ਬੁਨਿਆਦੀ ਸਹਿਣਸ਼ੀਲਤਾ (Basic Endurance) – ਬੁਨਿਆਦੀ ਸਹਿਣਸ਼ੀਲਤਾ ਮੁੱਖ ਤੌਰ ਤੇ ਐਰੋਬਿਕ ਸਹਿਣਸ਼ੀਲਤਾ ਤੇ ਨਿਰਭਰ ਕਰਦੀ ਹੈ । ਐਰੋਬਿਕ ਤੋਂ ਭਾਵ ਹੈ ਕਿ ਜਿਸ ਵਿਚ ਆਕਸੀਜਨ ਦੀ ਪੂਰਤੀ ਕਸਰਤਾਂ ਅਤੇ ਅਭਿਆਸ ਨਾਲ ਮਿਲਦੀ ਰਹੇ ।
ਇਹ ਹੌਲੀ-ਹੌਲੀ ਕੀਤੀਆਂ ਜਾਂਦੀਆਂ ਹਨ ਜਿਸ ਵਿਚ ਸਰੀਰ ਦੇ ਸਾਰੇ ਮਸਲ ਗਰੁੱਪ ਭਾਗ ਲੈਂਦੇ ਹਨ ਜਾਂ ਸ਼ਾਮਲ ਹੁੰਦੇ ਹਨ । ਦੌੜਨਾ, ਜੋਗ, ਚੱਲਣਾ ਅਤੇ ਤੈਰਾਕੀ ਬੁਨਿਆਦੀ ਸਹਿਣਸ਼ੀਲਤਾ ਦੇ ਉਦਾਹਰਨ ਹਨ ।

(ਅ) ਆਮ ਸਹਿਣਸ਼ੀਲਤਾ (General Endurance) – ਇਹ ਐਰੋਬਿਕਸ ਅਤੇ ਐਰੋਬਿਕਸ ਦੋਵੇਂ ਕ੍ਰਿਆਵਾਂ ਤੇ ਨਿਰਭਰ ਕਰਦੀ ਹੈ । ਇਹ ਹੌਲੀ ਅਤੇ ਤੇਜ਼ ਗਤੀ ਦੋਵਾਂ ਪ੍ਰਕਾਰਾਂ ਨਾਲ ਕੀਤੀ ਜਾਂਦੀ ਹੈ । ਇਹ ਸਹਿਣਸ਼ੀਲਤਾ ਖਿਡਾਰੀ ਨੂੰ ਬਿਨਾਂ ਥਕਾਵਟ ਦੇ ਲੰਬੇ ਸਮੇਂ ਦੇ ਕੰਮ ਕਰਨ ਦੇ ਯੋਗ ਬਣਾਉਂਦੀ ਹੈ ।
(ਈ ਵਿਸ਼ੇਸ਼ ਸਹਿਣਸ਼ੀਲੜਾ (Specific Endurance)–ਵਿਸ਼ੇਸ਼ ਸਹਿਣਸ਼ੀਲਤਾ ਹਰ ਖੇਡ ਲਈ ਅਲੱਗਅਲੱਗ ਹੁੰਦੀ ਹੈ । ਹਰ ਖੇਡ ਦੀ ਆਪਣੀ ਗਤੀ ਹੁੰਦੀ ਹੈ , ਜਿਵੇਂ ਕਿ ਮੈਰਾਥਨ ਦੌੜਾਕਾਂ ਨੂੰ ਲੰਬੇ ਸਮੇਂ ਤੱਕ ਦੌੜਨਾ ਪੈਂਦਾ ਹੈ ਤੇ ਉਹੀ ਮੁੱਕੇਬਾਜ਼ (Boxer) ਨੂੰ ਆਪਣੀ ਬਾਊਟ (Bout) ਨੂੰ 3 ਮਿੰਟ ਵਿਚ ਖ਼ਤਮ ਕਰਨੀ ਹੁੰਦੀ ਹੈ । ਇਸ ਲਈ ਹਰ ਖੇਡ ਵਿਚ ਖਿਡਾਰੀ ਨੂੰ ਉੱਪਰ ਦਿੱਤੀਆਂ ਸਹਿਣਸ਼ੀਲਤਾ ਦੇ ਪ੍ਰਕਾਰ ਤੋਂ ਇਲਾਵਾ ਵਿਸ਼ੇਸ਼ ਪ੍ਰਕਾਰ ਦੀ ਸਹਿਣਸ਼ੀਲਤਾ ਦੀ ਤਿਆਰੀ ਵੀ ਕਰਨੀ ਪੈਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਘੱਟ ਸਮੇਂ ਦੀ ਸਹਿਣਸ਼ੀਲਤਾ ਅਤੇ ਮੱਧ ਸਮੇਂ ਦੀ ਸਹਿਣਸ਼ੀਲਤਾ ਨੂੰ ਪਰਿਭਾਸ਼ਿਤ ਕਰੋ ।
ਉੱਤਰ-
(ੳ) ਘੱਟ ਸਮੇਂ ਦੀ ਸਹਿਣਸ਼ੀਲਤਾ (Short Term Endurance) – ਖੇਡ ਕ੍ਰਿਆਵਾਂ ਦੀ ਥਕਾਨ ਤੇ ਕਾਬੂ ਪਾਉਣ ਦੇ ਲਈ ਘੱਟ ਸਮੇਂ ਦੀ ਸਹਿਣਸ਼ੀਲਤਾ ਦੀ ਲੋੜ ਹੁੰਦੀ ਹੈ : ਜਿਵੇਂ ਕਿ ਛੋਟੀਆਂ ਦੌੜਾਂ ਜਿਵੇਂ (ਸਪਰਿੰਟ) ਤੇ ਮੱਧ ਦੁਰੀ ਦੀਆਂ ਦੌੜਾਂ ਆਦਿ ਇਸ ਦੇ ਉਦਾਹਰਨ ਹਨ । ਇਸਨੂੰ ਐਨੋਰੋਬਿਕ ਕਿਰਿਆ ਵੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।

(ਅ) ਮੱਧ ਸਮੇਂ ਦੀ ਸਹਿਣਸ਼ੀਲਤਾ (Middle Term Endurance – ਇਸ ਦੀ ਜ਼ਰੂਰਤ ਉਹਨਾਂ ਮੁਕਾਬਲਿਆਂ ਵਿਚ ਪੈਂਦੀ ਹੈ ਜੋ ਕਿ 2 ਤੋਂ 10 ਮਿੰਟ ਵਿਚ ਖ਼ਤਮ ਹੋ ਜਾਂਦੇ ਹਨ ਜਿਵੇਂ ਕਿ ਮੱਧ ਦੂਰੀ ਦੀਆਂ ਦੌੜਾਂ ਇਸ ਦੀਆਂ ਉਦਾਹਰਨਾਂ ਹਨ ।

ਪਸ਼ਨ 4.
ਤਾਲਮੇਲ ਯੋਗਤਾ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ?
ਉੱਤਰ-
ਤਾਲਮੇਲ ਦੀ ਯੋਗਤਾ ਉਹ ਯੋਗਤਾ ਹੁੰਦੀ ਹੈ ਜਿਸ ਵਿਚ ਮੋਟਰ ਟਾਸਕ (Motor task) ਸਹਜ ਅਤੇ ਸਹੀ ਢੰਗ ਨਾਲ ਕੀਤੇ ਜਾਂਦੇ ਹਨ ਅਤੇ ਜਿਸ ਵਿਚ ਇੰਦਰੀਆਂ ਅਤੇ ਮਾਸਪੇਸ਼ੀਆਂ ਦੀ ਸੁੰਗੜਨ ਦਾ ਪਰਸਪਰ ਸੰਬੰਧ ਹੁੰਦਾ ਹੈ ਅਤੇ ਜੋ ਕਿ ਜੋੜਾਂ ਦੀ ਗਤੀ ਅਤੇ ਉਸਦੇ ਆਸ-ਪਾਸ ਦੇ ਅੰਗਾਂ ਅਤੇ ਸਰੀਰ ਦੀ ਸਥਿਤੀ ਤੇ ਨਿਰਭਰ ਕਰਦੀ ਹੈ । ਤਾਲਮੇਲ ਸਨਾਯੁਤੰਤਰ ਤੇ ਵੀ ਨਿਰਭਰ ਕਰਦਾ ਹੈ | ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਵਿਚ ਤਾਲਮੇਲ ਦਾ ਅਹਿਮ ਰੋਲ ਹੈ ਜਿਸ ਤੋਂ ਬਿਨਾਂ ਕੋਈ ਵੀ ਖੇਡ ਜਾਂ ਕ੍ਰਿਆ ਸੰਭਵ ਹੀ ਨਹੀਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ 5.
ਫੁਰਤੀ ਅਤੇ ਰਫ਼ਤਾਰ ਵਿਚ ਕੀ ਅੰਤਰ ਹੈ ?
ਉੱਤਰ-
ਗਤੀ (Speed) – ਗਤੀ ਤੋਂ ਭਾਵ ਸਰੀਰ ਦੇ ਅੰਗਾਂ ਵਿਚ ਤੇਜ਼ੀ ਲਿਆਉਣ ਤੋਂ ਹੈ । ਇਹ ਗਤੀ ਭਾਵੇਂ ਦੌੜਾਕ ਦੀਆਂ ਲੱਤਾਂ ਵਿਚ ਹੋਵੇ ਜਾਂ ਫਿਰ ਸ਼ਾਟ ਪੁੱਟ ਲਗਾਉਣ ਵਾਲੇ ਦੀਆਂ ਬਾਹਾਂ ਦੀ ਹੋਵੇ ।

ਫੁਰਤੀ (Agility) – ਉਲਟੀ ਦਿਸ਼ਾਵਾਂ ਵਿਚ ਅੱਗੇ ਵੱਧਣਾ ਅਤੇ ਵਿਸਫੋਟਕ ਊਰਜਾ ਨਾਲ ਗਤੀਵਿਧੀਆਂ ਦਾ ਪ੍ਰਦਰਸ਼ਨ ਕਰਨਾ, ਜਿਵੇਂ ਕਿ, ਜੀ-ਜੈਗ ਦੌੜ ਆਦਿ ।

ਪ੍ਰਸ਼ਨ 6.
ਤਾਕਤ ਕਿੰਨੇ ਪ੍ਰਕਾਰ ਦੀ ਹੁੰਦੀ ਹੈ ? ਵਿਸਥਾਰ ਸਹਿਤ ਲਿਖੋ ।
ਉੱਤਰ-
ਤਾਕਤ ਨੂੰ ਇਕ ਮਾਸਪੇਸ਼ੀ ਦੇ ਜ਼ਿਆਦਾ ਤੋਂ ਜ਼ਿਆਦਾ ਸੁੰਗੜਨ ਤੋਂ, ਮਾਸਪੇਸ਼ੀਆਂ ਦੇ ਸਮੂਹ ਦੁਆਰਾ ਇਕੱਠੇ ਲਗਾਏ ਬਲ ਦੇ ਰੂਪ ਵਿਚ ਪਰਿਭਾਸ਼ਿਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਤਾਕਤ ਨੂੰ ਸਹੀ ਮਾਤਰਾ ਵਿਚ ਕੀਤੇ ਅਭਿਆਸ ਨਾਲ ਵਧਾਇਆ ਜਾ ਸਕਦਾ ਹੈ ।
ਤਾਕਤ ਦੇ ਪ੍ਰਕਾਰ (Types of Strength-ਖੇਡਾਂ ਦੀਆਂ ਲੋੜਾਂ ਮੁਤਾਬਿਕ ਤਾਕਤ ਨੂੰ ਹੇਠਾਂ ਲਿਖੇ ਭਾਗਾਂ ਵਿਚ ਵੰਡਿਆ ਜਾਂਦਾ ਹੈ-

1. ਗਤੀਸ਼ੀਲ ਤਾਕਤ ਜਾਂ ਆਈਸੋਟੋਨਿਕ ਤਾਕਤ (Dynamic or Isotonic Strength)
2. ਸਥਿਰ ਤਾਕਤ ਜਾਂ ਆਈਸੋਮੀਟਰਿਕ (Static or Isometic Strength) ।

1. ਗਤੀਸ਼ੀਲ ਤਾਕਤ ਜਾਂ ਆਈਸੋਟੋਨਿਕ ਤਾਕਤ (Dynamic or sotonic Strength – ਜਦ ਸੁੰਗੜਨ ਨਾਲ ਮਾਸਪੇਸ਼ੀ ਦੀ ਲੰਬਾਈ ਵਿਚ ਪਰਿਵਰਤਨ ਹੁੰਦਾ ਹੈ ਤਾਂ ਉਸਨੂੰ ਗਤੀਸ਼ੀਲ ਤਾਕਤ ਕਹਿੰਦੇ ਹਨ । ਉਦਾਹਰਨ ਲਈ | ਜਦ ਇਕ ਤੋਂ ਵੱਧ ਜੋੜਾਂ ਵਿਚ ਗਤੀ ਹੋਵੇ ; ਜਿਵੇਂ ਕਿ ਪੁਸ਼-ਅਪ, ਪੁਲ-ਅਪ, ਬਾਰਬੈਲ ਪੇਸ਼, ਸਕੈਊਟ ਜੰਪ (Squat Jump), ਡੈਡ ਲਿਫਟਜ (Dead lifts) ਆਦਿ । ਗਤੀਸ਼ੀਲ ਤਾਕਤ ਨੂੰ ਤਿੰਨ ਭਾਗਾਂ ਵਿਚ ਵਿਭਾਜਿਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।

2. ਸਥਿਰ ਤਾਕਤ ਜਾਂ ਆਈਸੋਮੀਟਰਿਕ ਤਾਕਤ (Static or Isometric strength – ਇਹ ਵਿਰੋਧ ਦੇ ਵਿਰੁੱਧ ‘ ਕ੍ਰਿਆਵਾਂ ਕਰਨ ਲਈ ਮਾਸਪੇਸ਼ੀ ਯੋਗਤਾ ਹੁੰਦੀ ਹੈ । ਇਸ ਵਿਚ ਮਾਸਪੇਸ਼ੀ ਆਪਣੀ ਲੰਬਾਈ ਬਦਲੇ ਬਿਨਾਂ ਹੀ ਤਨਾਵ ਦਾ ਵਿਕਾਸ ਕਰਦੀ ਹੈ ,:ਜਿਵੇਂ ਕੰਧ ਨੂੰ ਧੱਕਾ ਮਾਰਨਾ ਆਦਿ।

ਪ੍ਰਸ਼ਨ 7.
ਲਚਕ ਤੋਂ ਤੁਸੀਂ ਕੀ ਸਮਝਦੇ ਹੋ, ਲਚਕ ਕਿੰਨੇ ਪ੍ਰਕਾਰ ਦੀ ਹੈ ? ਵਿਆਖਿਆ ਕਰੋ ।
ਉੱਤਰ-
ਲਚਕ ਗਤੀਸ਼ੀਲਤਾ ਦੀ ਉਹ ਦਰ ਹੈ ਜੋ ਕਿ ਜੋੜਾਂ ਤੋਂ ਸੰਭਵ ਹੁੰਦੀ ਹੈ । ਲਚਕ ਦੇ ਹੇਠ ਲਿਖੇ ਪ੍ਰਕਾਰ ਹਨ-

1. ਸੁਸਤ ਲਚਕ (Pasive Flexibility)-ਇਹ ਬਿਨਾਂ ਕਿਸੇ ਬਾਹਰੀ ਮੱਦਦ ਜਾਂ ਸਹਾਰੇ ਦੇ ਵੱਡੀ ਦਰ ਤੇ ਕ੍ਰਿਆਵਾਂ ਕਰਨ ਦੀ ਯੋਗਤਾ ਹੁੰਦੀ ਹੈ । ਉਦਾਹਰਨ ਦੇ ਤੌਰ ਤੇ ਕਿਸੇ ਸਾਥੀ ਖਿਡਾਰੀ ਦੀ ਮਦਦ ਨਾਲ ਸਟ੍ਰੇਚਿੰਗ (Stretching) ਕਸਰਤਾਂ ਕਰਨਾ |
2. ਚੁਸਤ ਲਚਕ (Active Flexibility-ਇਹ ਬਿਨਾਂ ਕਿਸੇ ਬਾਹਰੀ ਮੱਦਦ ਜਾਂ ਸਹਾਰੇ ਤੋਂ ਕ੍ਰਿਆਵਾਂ ਕਰਨ ਦੀ | ਦਰ ਦੀ ਯੋਗਤਾ ਹੈ । ਉਦਾਹਰਨ ਦੇ ਤੌਰ ਤੇ ਲੱਤਾਂ ਨੂੰ ਬੁਲਾਉਣਾ ਆਦਿ ।
3. ਡਾਇਨਾਮਿਕ ਲਚਕ (Dynamic Flexibility-ਇਹ ਉਹ ਲਚਕ ਹੁੰਦੀ ਹੈ ਜਦ ਸਰੀਰ ਗਤੀ ਵਿਚ ਹੁੰਦਾ
   ਹੈ ਅਤੇ ਕ੍ਰਿਆਵਾਂ ਪ੍ਰਦਰਸ਼ਨ ਕਰਦਾ ਹੈ । ਜਿਵੇਂ ਕਿ ਦੌੜਨਾ, ਤੈਰਨਾ ਜਾਂ ਸਮਰਸੱਲਟ (Samersault) ਆਦਿ ।

ਪ੍ਰਸ਼ਨ 8.
ਰਫ਼ਤਾਰ ਕਿੰਨੇ ਪ੍ਰਕਾਰ ਦੀ ਹੈ ? ਵਿਸਥਾਰ ਸਹਿਤ ਲਿਖੋ ।
ਉੱਤਰ-ਰਫ਼ਤਾਰ ਪੰਜ ਪ੍ਰਕਾਰ ਦੀ ਹੁੰਦੀ ਹੈ ਜੋ ਕਿ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਹੈ-
1. ਪ੍ਰਤੀਕ੍ਰਿਆ ਰਫਤਾਰ (Reaction Speed – ਇਹ ਸਿਗਨਲ ਮਿਲਣ ਤੇ ਤੁਰੰਤ ਪ੍ਰਤੀਕ੍ਰਿਆ ਕਰਨ ਦੀ ਯੋਗਤਾ ਹੁੰਦੀ ਹੈ । ਇਸ ਵਿਚ ਖਿਡਾਰੀ ਪਰਿਸਥਿਤੀ ਦੇ ਵਿਰੁੱਧ ਪ੍ਰਤੀਕ੍ਰਿਆ ਕਰਦਾ ਹੈ ਜਿਵੇਂ ਕਿ ਕੱਚ ਦੀ ਸੀਟੀ ਵੱਜਣ ਤੇ ਅੱਗੇ ਵੱਲ, ਪਿੱਛੇ ਵੱਲ, ਖੱਬੇ ਅਤੇ ਸੱਜੇ ਪਾਸੇ ਤੇਜ਼ ਗਤੀ ਨਾਲ ਜਾਣਾ ਆਦਿ ।

2. ਤੇਜ਼ ਰਫਤਾਰ ਦੀ ਯੋਗਤਾ (Acceleration Ability) – ਇਹ ਸਥਿਰ (Stationary) ਅਵਸਥਾ ਤੋਂ ਵੱਧ ਤੋਂ . ਵੱਧ (Maximum) ਰਫਤਾਰ ਵਿਚ ਇਕਦਮ ਜਾਣ ਦੀ ਯੋਗਤਾ ਹੈ ; ਜਿਵੇਂ ਕਿ ਅਸੀਂ ਇਹਨਾਂ ਨੂੰ ਸਪਰਿੰਟ (Sprint) ਛੋਟੀ ਦੁਰੀ ਦੀਆਂ ਦੌੜਾਂ ਵਿਚ ਦੇਖ ਸਕਦੇ ਹਾਂ ਜਿੱਥੇ ਇਕ ਵਿਸਫੋਟਕ ਤਾਕਤ, ਤਕਨੀਕ ਅਤੇ ਲਚਕ ਦੀ ਜ਼ਰੂਰਤ ਪੈਂਦੀ ਹੈ ।

3. ਲੋਕੋਮੋਟਰ ਜਾਂ ਗਮਨ ਦੀ ਯੋਗਤਾ (Locomotor Ability) – ਇਹ ਇਕਦਮ ਰਫਤਾਰ ਬਣਾ ਕੇ ਉਸਨੂੰ ਉਸੇ ਸਥਿਤੀ ਵਿਚ ਬਣਾਏ ਰੱਖਣ ਦੀ ਯੋਗਤਾ ਹੈ । ਜਿਵੇਂ ਕਿ 100 ਮੀ: 200 ਮੀ: ਅਤੇ 400 ਮੀ: ਆਦਿ ਇਸ ਦੀਆਂ ਉਦਾਹਰਨਾਂ ਹਨ ।

4. ਗਤੀ ਮੀਲ ਰਫ਼ਤਾਰ (Movement Ability) – ਘੱਟ ਤੋਂ ਘੱਟ ਸਮੇਂ ਵਿਚ ਜ਼ਿਆਦਾ ਤੋਂ ਜ਼ਿਆਦਾ ਗਤੀ ਕਰਨ ਦੀ ਯੋਗਤਾ ਹੈ ; ਜਿਵੇਂ ਕਿ ਟੀਮ ਖੇਡਾਂ, ਲੜਾਕੂ ਖੇਡਾਂ, ਰੈਕਟ ਖੇਡਾਂ, ਸੁੱਟਣਾ ਅਤੇ ਜਿਮਨਾਸਟਿਕ ਆਦਿ ਵਿਚ ਦੇਖਿਆ ਜਾ ਸਕਦਾ ਹੈ ।

5. ਸਹਿਣਸ਼ੀਲਤਾ ਰਫ਼ਤਾਰ (Speed Endurance – ਇਹ ਉਹ ਯੋਗਤਾ ਹੁੰਦੀ ਹੈ ਜਿਸ ਵਿਚ ਖਿਡਾਰੀ ਆਪਣੀ ਰਫ਼ਤਾਰ ਨੂੰ ਖੇਡ ਦੇ ਆਖਰੀ ਪੜਾਅ ਤੱਕ ਬਣਾ ਕੇ ਰੱਖਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 9.
ਪ੍ਰਤੀਕ੍ਰਿਆ ਰਫ਼ਤਾਰ ਅਤੇ ਗਮਨ ਰਫ਼ਤਾਰ ਬਾਰੇ ਲਿਖੋ ।
ਉੱਤਰ-

1. ਇੰਜਨ ਜਾਂ ਗਮਨ ਦੀ ਯੋਗਤਾ (Locomotor Ability) – ਇਹ ਇਕਦਮ ਰਫਤਾਰ ਬਣਾ ਕੇ ਉਸਨੂੰ ਉਸੇ ਸਥਿਤੀ ਵਿਚ ਬਣਾਏ ਰੱਖਣ ਦੀ ਯੋਗਤਾ ਹੈ । ਜਿਵੇਂ ਕਿ 100 ਮੀ:, 200 ਮੀ: ਅਤੇ 400 ਮੀ: ਆਦਿ ਇਸ ਦੀਆਂ ਉਦਾਹਰਨਾਂ ਹਨ ।
2. ਗਤੀਸ਼ੀਲ ਰਫ਼ਤਾਰ (Movement Ability) – ਘੱਟ ਤੋਂ ਘੱਟ ਸਮੇਂ ਵਿਚ ਜ਼ਿਆਦਾ ਤੋਂ ਜ਼ਿਆਦਾ ਗਤੀ ਕਰਨ ਦੀ ਯੋਗਤਾ ਹੈ ; ਜਿਵੇਂ ਕਿ ਟੀਮ ਖੇਡਾਂ, ਲੜਾਕੂ ਖੇਡਾਂ, ਰੈਕਟ ਖੇਡਾਂ, ਸੁੱਟਣਾ ਅਤੇ ਜਿਮਨਾਸਟਿਕ ਆਦਿ ਵਿਚ ਦੇਖਿਆ ਜਾ ਸਕਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 10.
ਹੇਠ ਲਿਖਿਆਂ ਦੇ ਅਰਥ ਸਮਝਾਉ ।
1. ਚੰਗਾ ਸਰੀਰਕ ਆਸਣ
2. ਖ਼ੁਰਾਕ
3. ਜੀਵਨ ਸ਼ੈਲੀ ।
ਉੱਤਰ-
ਅਨੇਕਾਂ ਅਜਿਹੇ ਕਈ ਕਾਰਨ ਹੁੰਦੇ ਹਨ ਜੋ ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਦੇ ਹਨ । ਨਿਸ਼ਕ੍ਰਿਆਂ ਦੇ ਕਾਰਨ ਛੋਟੇ ਅਤੇ ਲੰਬੇ ਸਮੇਂ ਦੇ ਅਭਿਆਸ ਕਾਲ ਤੇ ਕਈ ਤਰੀਕਿਆਂ ਨਾਲ ਪ੍ਰਭਾਵ ਪੈਂਦਾ ਹੈ । ਇਹ ਕਾਰਕ ਜੋ ਕਿ ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ‘ਤੇ ਪ੍ਰਭਾਵ ਪਾਉਂਦੇ ਹਨ, ਹੇਠ ਲਿਖੇ ਪ੍ਰਕਾਰ ਹਨ-
1. ਚੰਗਾ ਸਰੀਰਕ ਆਸਣ (Good Posture) – ਸਰੀਰਕ ਤਰੁੱਟੀਆਂ, ਸਰੀਰਕ ਯੋਗਤਾ ਵਿਚ ਹਮੇਸ਼ਾ ਹੀ ਮੁਸ਼ਕਿਲ ਪੈਦਾ ਕਰਦੀਆਂ ਹਨ , ਜਿਵੇਂ ਕਿ ਅਸੰਤੁਲਨ ਮਾਸਪੇਸ਼ੀਆਂ, ਕੁਪੋਸ਼ਣ, ਦਰਦ, ਲੋਰਡੋਸਿਸ (Lordosis) ਸਕੋਲਿਸਿਸ (Scoliosis), ਗੋਲ ਮੋਢੇ, ਗੋਡਿਆਂ ਦਾ ਟਕਰਾਉਣਾ ਆਦਿ ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਦੇ ਹਨ ।

2. ਅਹਾਰ (Diet) – ਸਰੀਰਕ ਪ੍ਰਦਰਸ਼ਨ ਵਿਚ ਅਹਾਰ ਪ੍ਰਮੁੱਖ ਭੂਮਿਕਾ ਨਿਭਾਉਂਦਾ ਹੈ ਅਤੇ ਸਰੀਰਕ ਯੋਗਤਾ ਦੇ ਸਤਰ ਨੂੰ ਬਣਾਏ ਰੱਖਣ ਵਿਚ ਬਹੁਤ ਸਹਾਇਕ ਹੁੰਦਾ ਹੈ , ਆਹਾਰ ਵਿਚ ਕੈਲਰੀ ਦੀ ਉਪਯੁਕਤ ਮਾਤਰਾ ਖਿਡਾਰੀਆਂ ਨੂੰ ਸਰਵ-ਉੱਚ ਪ੍ਰਦਰਸ਼ਨ ਕਰਨ ਵਿਚ ਮਦਦਗਾਰ ਸਾਬਿਤ ਹੁੰਦੀ ਹੈ । ਕਾਰਬੋਹਾਈਡਰੇਟਸ ਅਤੇ ਤਰਲ ਪਦਾਰਥਾਂ ਦੀ ਕਮੀ ਕਾਰਨ ਇਕ ਖਿਡਾਰੀ ਜਲਦੀ ਹੀ ਥਕਾਵਟ ਮਹਿਸੂਸ ਕਰਨ ਲੱਗ ਪੈਂਦਾ ਹੈ । ਮਾਸ਼ਪੇਸ਼ੀਆਂ ਦੇ ਪੁਨਰ-ਨਿਰਮਾਣ ਵਾਸਤੇ ਪ੍ਰੋਟੀਨ ਦੀ ਜ਼ਰੂਰਤ ਹੁੰਦੀ ਹੈ । ਕਾਰਬੋਹਾਈਡਰੇਟਸ, ਪ੍ਰੋਟੀਨ ਅਤੇ ਵਿਟਾਮਿਨਸ ਤੋਂ ਬਿਨਾਂ ਖਿਡਾਰੀ ਬੇਹਤਰ ਪ੍ਰਦਰਸ਼ਨ ਨਹੀਂ ਕਰ ਸਕਦਾ ਅਤੇ ਉਸਦੀ ਸਰੀਰਕ ਯੋਗਤਾ ਵੀ ਘੱਟ ਜਾਂਦੀ ਹੈ ।

3. ਜੀਵਨ ਸ਼ੈਲੀ (Life Style) – ਉਹ ਖਿਡਾਰੀ ਜੋ ਚੰਗੀ ਜੀਵਨ ਸ਼ੈਲੀ ਨੂੰ ਅਪਨਾਉਂਦੇ ਹਨ, ਉਹ ਹਮੇਸ਼ਾ ਬੇਹਤਰ ਪ੍ਰਦਰਸ਼ਨ ਕਰਦੇ ਹਨ । ਜੀਵਨ ਸ਼ੈਲੀ ਤੋਂ ਭਾਵ ਸ਼ਾਨੋ-ਸ਼ੌਕਤ ਵਾਲਾ ਜੀਵਨ ਤੋਂ ਨਹੀਂ ਹੈ ਬਲਕਿ ਇਸ ਤੋਂ ਭਾਵ ਹੈ ਕਿ ਚੰਗੀਆਂ ਆਦਤਾਂ ਵਾਲਾ ਜੀਵਨ ਜਿਉਣਾ | ਇਕ ਵਿਅਕਤੀ ਜੋ ਸਿਗਰੇਟ, ਸ਼ਰਾਬ ਜਾਂ ਨਸ਼ੇ ਆਦਿ ਦਾ ਆਦੀ ਹੁੰਦਾ ਹੈ ਉਹੀ ਚੰਗਾ ਪ੍ਰਦਰਸ਼ਨ ਨਹੀਂ ਕਰ ਸਕਦਾ । ਇਹ ਉਸਦੀ ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 11.
ਸੰਤੁਲਨ ਪ੍ਰਤਿਕ੍ਰਿਆ ਅਤੇ ਯੋਗਤਾ ਕਰਨ ਦੀ ਯੋਗਤਾ ਕੀ ਹੈ ?
ਉੱਤਰ-

1. ਪ੍ਰਤੀਕ੍ਰਿਆ ਕਰਨ ਦੀ ਯੋਗਤਾ Reaction Ability) – ਇਹ ਵਿਅਕਤੀ ਦੀ ਉਹ ਯੋਗਤਾ ਹੈ ਜਿਸ ਵਿਚ ਸਿੰਗਨਲ ਮਿਲਣ ਤੇ ਖਿਡਾਰੀ ਪ੍ਰਤੀਕ੍ਰਿਆ ਕਰਦਾ ਹੈ , ਜਿਵੇਂ 100 ਮੀ: ਦੌੜ ਵਿਚ ਸਿੰਗਨਲ ਹੁੰਦੇ ਹੀ ਇਕ ਵੇਗ ਤੇ ਦਿਸ਼ਾ ਵੱਲ ਤੇਜ਼ ਗਤੀ ਨਾਲ ਦੌੜਨਾ ।
2. ਸੰਤੁਲਨ ਯੋਗਤਾ (Balance Ability) – ਇਹ ਵਿਅਕਤੀ ਦੀ ਉਹ ਯੋਗਤਾ ਹੈ ਜਿਸ ਵਿਚ ਉਹ ਗਤੀ ਵਿਚ ਸਰੀਰ ਦੀ ਸਥਿਤੀ ਬਣਾਈ ਰੱਖਦਾ ਹੈ ; ਜਿਵੇਂ ਕਿ ਸਕੂਟ ਸਟਾਂਪ (Scoot stop) ਅਤੇ 400 ਮੀ: ਵਿਚ ਆਪਣੀ ਲਾਈਨ ਵਿਚ ਰਹਿ ਕੇ ਦੌੜਨਾ ਆਦਿ ।

ਪੰਜ ਅੰਕਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ ਤੋਂ (Five Marks Question Answers)

ਪ੍ਰਸ਼ਨ 1.
ਸਰੀਰਕ ਯੋਗਤਾ ਦੇ ਅੰਗ ਤਾਕਤ, ਰਫ਼ਤਾਰ ਬਾਰੇ ਲਿਖੋ ।
ਉੱਤਰ-
1. ਤਾਕਤ (Strength) – ਤਾਕਤ ਨੂੰ ਇਕ ਮਾਸਪੇਸ਼ੀ ਦੇ ਜ਼ਿਆਦਾ ਤੋਂ ਜ਼ਿਆਦਾ ਸੁੰਗੜਨ ਤੋਂ, ਮਾਸਪੇਸ਼ੀਆਂ ਦੇ ਸਮੂਹ ਦੁਆਰਾ ਇਕੱਠੇ ਲਗਾਏ ਬਲ ਦੇ ਰੂਪ ਵਿਚ ਪਰਿਭਾਸ਼ਿਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਤਾਕਤ ਨੂੰ ਸਹੀ ਮਾਤਰਾ ਵਿਚ ਕੀਤੇ ਅਭਿਆਸ ਨਾਲ ਵਧਾਇਆ ਜਾ ਸਕਦਾ ਹੈ ।

ਤਾਕਤ ਦੇ ਪ੍ਰਕਾਰ (Types of Strength) – ਖੇਡਾਂ ਦੀਆਂ ਲੋੜਾਂ ਮੁਤਾਬਿਕ ਤਾਕਤ ਨੂੰ ਹੇਠ ਲਿਖੇ ਭਾਗਾਂ ਵਿਚ ਵੰਡਿਆ ਜਾਂਦਾ ਹੈ-
(ਉ) ਗਤੀਸ਼ੀਲ ਤਾਕਤ ਜਾਂ ਆਈਸੋਟੋਨਿਕ ਤਾਕਤ (Dynamic or isotonic strength)
(ਅ) ਸਥਿਰ ਤਾਕਤ ਜਾਂ ਆਈਸੋਮੀਟਰਿਕ (Static or isometic strength) ।

(ਉ) ਗਤੀਸ਼ੀਲ ਤਾਕਤ ਜਾਂ ਆਈਸੋਟੋਨਿਕ ਤਾਕਤ (Dynamic or Isotonic Strength) – ਜਦ ਸੁੰਗੜਨ ਨਾਲ ਮਾਸਪੇਸ਼ੀ ਦੀ ਲੰਬਾਈ ਵਿਚ ਪਰਿਵਰਤਨ ਹੁੰਦਾ ਹੈ ਤਾਂ ਉਸਨੂੰ ਗਤੀਸ਼ੀਲ ਤਾਕਤ ਕਹਿੰਦੇ ਹਨ । ਉਦਾਹਰਨ ਲਈ ਜਦ ਇਕ ਤੋਂ ਵੱਧ ਜੋੜਾਂ ਵਿਚ ਗਤੀ ਹੋਵੇ ; ਜਿਵੇਂ ਕਿ ਪੁਸ਼-ਅਪ, ਪੁਲ-ਅਪ, ਬਾਰਬੈਲ ਪੇਸ਼, ਸਕੈਊਟ ਜੰਪ (Squat Jump), ਡੈਡ ਲਿਫਟਜ (Dead lifts) ਆਦਿ । ਗਤੀਸ਼ੀਲ ਤਾਕਤ ਨੂੰ ਤਿੰਨ ਭਾਗਾਂ ਵਿਚ ਵਿਭਾਜਿਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।
(i) ਵੱਧ ਤੋਂ ਵੱਧ ਤਾਕਤ (Maximum Strength)-ਇਹ ਸਭ ਤੋਂ ਵੱਡੀ ਤਾਕਤ ਹੁੰਦੀ ਹੈ ਜੋ ਕਿ ਵਿਰੋਧ ਦੇ ਵਿਰੁੱਧ ਸਵੈ-ਇੱਛਾ ਨਾਲ ਪ੍ਰਾਪਤ ਕੀਤੀ ਜਾਂਦੀ ਹੈ । ਵੱਧ ਤਾਕਤ ਨੂੰ ਅਸੀਂ ਮਸਕੂਲੋਸਕੇਟਲ (Musculosketal) ਬਲ ਦੀ ਮਾਤਰਾ ਦੇ ਰੂਪ ਵਿਚ ਪਰਿਭਾਸ਼ਿਤ ਕਰ ਸਕਦੇ ਹਾਂ ਜੋ ਕਿ ਵਿਅਕਤੀ ਬਾਹਰੀ ਯਤਨਾਂ ਨਾਲ ਪੈਦਾ ਕਰਦਾ ਹੈ । ਉਦਾਹਰਨ ਦੇ ਤੌਰ ਤੇ ਦੋ ਮਿੰਟ ਵਿਚ ਵਿਅਕਤੀ ਕਿੰਨੀਆਂ ਡੰਡ ਪੇਲ ਸਕਦਾ ਹੈ, ਕਿੰਨੀਆਂ ਬੈਠਕਾਂ ਮਾਰ ਸਕਦਾ ਹੈ ।

(ii) ਵਿਸਫੋਟਕ ਤਾਕਤ (Explosive Strength) – ਇਹ ਗਤੀ ਅਤੇ ਤਾਕਤ ਦਾ ਮਿਸ਼ਰਣ ਹੈ । ਇਹ ਗਤੀ ਦੇ ਵਿਰੋਧ ਤੇ ਕਾਬੂ ਪਾਉਣ ਦੀ ਕਾਬਲੀਅਤ ਹੁੰਦੀ ਹੈ । ਵਿਸਫੋਟਕ ਉੱਚ ਤਾਕਤ ਤੇਜ਼ ਗਤੀ ਦੀਆਂ ਦੌੜਾਂ, ਭਾਰ ਚੁੱਕਣਾ, ਹੈਮਰ ਥਰੋ, ਲੰਬੀ ਕੁੱਦ ਅਤੇ ਉੱਚੀ ਕੁੱਦ ਵਿਚ ਦੇਖੀ ਜਾ ਸਕਦੀ ਹੈ ।

(iii) ਤਾਕਤ ਦੀ ਸਹਿਣਸ਼ੀਲਤਾ (Strength Endurance) – ਇਹ ਤਾਕਤ ਅਤੇ ਸਹਿਣਸ਼ੀਲਤਾ ਦਾ ਮਿਸ਼ਰਣ ਹੁੰਦੀ ਹੈ । ਇਹ ਵਿਰੋਧ ’ਤੇ ਕਾਬੂ ਪਾਉਣ ਦੀ ਯੋਗਤਾ ਹੁੰਦੀ ਹੈ । ਲੰਬੀ ਦੂਰੀ ਦੀਆਂ ਦੌੜਾਂ, ਤੈਰਾਕੀ ਅਤੇ ਸਾਈਕਲਿੰਗ ਆਦਿ ਇਸ ਦੀਆਂ ਉਦਾਹਰਨਾਂ ਹਨ । ਆ ਸਥਿਰ ਤਾਕਤ ਜਾਂ ਆਈਸੋਮੀਟਰਿਕ (Static or Isometic Strength)-ਇਹ ਵਿਰੋਧ ਦੇ ਵਿਰੁੱਧ ਕਿਆਵਾਂ ਕਰਨ ਲਈ ਮਾਸਪੇਸ਼ੀ ਯੋਗਤਾ ਹੁੰਦੀ ਹੈ । ਇਸ ਵਿਚ ਮਾਸਪੇਸ਼ੀ ਆਪਣੀ ਲੰਬਾਈ ਬਦਲੇ ਬਿਨਾਂ ਹੀ ਤਨਾਵ ਦਾ ਵਿਕਾਸ ਕਰਦੀ ਹੈ : ਜਿਵੇਂ ਕੰਧ ਨੂੰ ਧੱਕਾ ਮਾਰਨਾ ਆਦਿ ।

2. ਗਤੀ (ਰਫਤਾਰ) (Speed – ਗਤੀ ਇਕ ਅਧਿਕਤਮ ਦਰ ਹੁੰਦੀ ਹੈ, ਜਿਸ ਵਿਚ ਇਕ ਵਿਅਕਤੀ ਇਕ ਵਿਸ਼ੇਸ਼ ਦੂਰੀ ਨੂੰ ਤੈਅ ਕਰਨ ਲਈ ਆਪਣੇ ਸਰੀਰ ਵਿਚ ਗਤੀ ਲੈ ਕੇ ਆਉਂਦਾ ਹੈ । ਅਸੀਂ ਕਹਿ ਸਕਦੇ ਹਾਂ ਕਿ ਰਫਤਾਰ ਘੱਟ ਤੋਂ ਘੱਟ ਮੁਸ਼ਕਿਲ ਸਮੇਂ ਵਿਚ ਇਕ ਥਾਂ ਤੋਂ ਦੂਜੀ ਥਾਂ ਤੇ ਪਹੁੰਚਣ ਦੀ ਯੋਗਤਾ ਹੁੰਦੀ ਹੈ । | ਰਫਤਾਰ, ਇਕਦਮ ਕ੍ਰਿਆ (Quick response), ਤੇਜ਼ੀ (acceleration), ਇਕਦਮ ਗਤੀ (maximum speed), ‘ ਰਫਤਾਰ ਸਹਿਣਸ਼ੀਲਤਾ ( speed cladira:ce ਤੋਂ ਮਿਲ ਕੇ ਬਣਦੀ ਹੈ ।

ਸਰੀਰਕ ਸਿੱਖਿਆ ਵਿਚ ਰਫਤਾਰ ਦਾ ਆਪਣਾ ਮਹੱਤਵ ਹੈ । ਇਸ ਨੂੰ ਅਸੀਂ ਇਹ ਵੀ ਕਹਿ ਸਕਦੇ ਹਾਂ ਕਿ Speed is the rate of motion” ਭਾਵ ਕੋਈ ਵਿਅਕਤੀ ਕਿੰਨੇ ਸਮੇਂ ਵਿਚ ਤੇਜ਼ ਰਫਤਾਰ ਬਣਾ ਕੇ ਆਪਣੇ ਸਥਾਨ ਤੇ ਪਹੁੰਚ ਸਕਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਸਰੀਰਕ ਯੋਗਤਾ ਦੀ ਮਹੱਤਤਾ ਬਾਰੇ ਲਿਖੋ ।
ਉੱਤਰ-
ਉਹ ਵਿਅਕਤੀ ਜੋ ਸਰੀਰਕ ਤੌਰ ਤੇ ਤੰਦਰੁਸਤ ਹਨ ਉਹ ਆਪਣੇ ਜੀਵਨ ਦਾ ਆਨੰਦ ਪੂਰੀ ਤਰ੍ਹਾਂ ਨਾਲ ਉਠਾਉਣ ਦੇ ਯੋਗ ਹਨ । ਅੱਜ ਦੇ ਤਕਨੀਕੀ ਵਿਕਾਸ ਦੇ ਯੁੱਗ ਵਿਚ ਲੋਕਾਂ ਕੋਲ ਮੁਸ਼ਕਿਲ ਨਾਲ ਹੀ ਆਪਣੀ ਸਰੀਰਕ ਯੋਗਤਾ ਲਈ ਸਮਾਂ ਹੁੰਦਾ ਹੈ । ਹੁਣ ਪ੍ਰਸ਼ਨ ਇਹ ਉੱਠਦਾ ਹੈ ਕਿ ਸਰੀਰਕ ਯੋਗਤਾ ਹੋਣਾ ਇੰਨਾ ਮਹੱਤਵਪੂਰਨ ਕਿਉਂ ਹੈ ? ਇਹਨਾਂ ਸਵਾਲਾਂ ਦਾ ਜਵਾਬ ਹੇਠ ਦਿੱਤੇ ਅਨੁਸਾਰ ਹੈ-
1. ਸੰਪੂਰਨ ਸਿਹਤ ਦਾ ਸੁਧਾਰ (Improves Overall Health – ਸਰੀਰਕ ਯੋਗਤਾ ਨਾਲ ਵਿਅਕਤੀ ਕਈ ਤਰ੍ਹਾਂ ਦੇ ਸਰੀਰਕ ਫਾਇਦਿਆਂ ਨੂੰ ਮਾਣਦਾ ਹੈ ; ਜਿਵੇਂ ਕਿ ਸਾਹ ਪ੍ਰਕ੍ਰਿਆ, ਲਹੂ ਸੰਚਾਰ ਪ੍ਰਣਾਲੀ ਅਤੇ ਸਰੀਰ ਦੀਆਂ ਸਮੁੱਚੀ ਪ੍ਰਣਾਲੀਆਂ ਦਾ ਠੀਕ ਢੰਗ ਨਾਲ ਕੰਮ ਕਰਨਾ ਅਤੇ ਸਰੀਰ ਦਾ ਕ੍ਰਿਆਤਮਕ ਰੂਪ ਵਿਚ ਤਿਆਰ ਰਹਿਣਾ । ਉਹ ਕਈ ਤਰ੍ਹਾਂ ਦੀਆਂ ਬਿਮਾਰੀਆਂ ਜਿਵੇਂ ਡਾਈਬੀਟੀਜ਼ ਟਾਇਪ-2, ਦਿਲ ਦੀਆਂ ਬਿਮਾਰੀਆਂ, ਕੈਂਸਰ ਤੋਂ ਬਚਾਅ, ਆਦਿ ਤੋਂ ਬਚਿਆ ਰਹਿੰਦਾ ਹੈ ।

2. ਭਾਰ ਪ੍ਰਬੰਧਨ (Weight Management – ਜਿਵੇਂ ਕਿ ਅਸੀਂ ਸਾਰੇ ਜਾਣਦੇ ਹਾਂ ਕਿ ਵਾਧੂ ਵਜ਼ਨ ਕਈ ਤਰ੍ਹਾਂ ਦੀਆਂ ਸਿਹਤ ਸੰਬੰਧੀ ਸਮੱਸਿਆਵਾਂ ; ਜਿਵੇਂ ਕਿ ਉੱਚਾ ਖੁਨ ਚਾਪ (High Blood Pressure), ਕੈਸਟਰੋਲ ਪੱਧਰ, ਡਾਇਬਟੀਜ਼ ਆਦਿ ਦੀ ਜੜ੍ਹ ਹੈ । ਇਸ ਲਈ ਉਹ ਵਿਅਕਤੀ ਜੋ ਸਰਗਰਮ ਅਤੇ ਸਰੀਰਕ ਤੌਰ ਤੇ ਤੰਦਰੁਸਤ ਹੁੰਦੇ ਹਨ, ਉਹਨਾਂ ਵਿੱਚ ਉਪਰੋਕਤ ਬਿਮਾਰੀਆਂ ਦੀ ਸੰਭਾਵਨਾ ਘੱਟ ਹੁੰਦੀ ਹੈ ।

3. ਤਨਾਵ ਪ੍ਰਬੰਧ ਵਿਚ ਮਹੱਤਵਪੂਰਨ (Importance as a stress Management) – ਇਕ ਵਿਅਕਤੀ ਸਰੀਰਕ ਯੋਗਤਾ ਅਤੇ ਸਰੀਰਕ ਯੋਗਤਾ ਦੇ ਪ੍ਰੋਗਰਾਮ ਦੇ ਜਰੀਏ ਤਣਾਅ ਨੂੰ ਬਰਦਾਸ਼ਤ ਕਰਨਾ, ਉਸ ਤੋਂ ਬਾਹਰ ਨਿਕਲਣਾ ਅਤੇ ਰੋਜ਼ਮਰਾ ਦੇ ਵਿਚਿਲਤ ਕਰਨ ਵਾਲੇ ਤਣਾਅ ਤੇ ਕਾਬੂ ਪਾਉਣਾ ਸਿੱਖ ਲੈਂਦਾ ਹੈ । ਇਸ ਲਈ ਇਹ ਜੀਵਨ ਵਿਚ ਸੰਤੁਲਨ ਅਤੇ ਸ਼ਾਤੀ ਬਣਾਏ ਰੱਖਣ ਵਿਚ ਮਦਦ ਕਰਦਾ ਹੈ । ਇਸ ਲਈ ਜ਼ਰੂਰੀ ਹੈ ਕਿ ਜੀਵਨ ਵਿਚ ਸ਼ਾਂਤੀ ਬਣਾਈ ਰੱਖਣ ਲਈ ਵਿਅਕਤੀ ਦਾ ਤੰਦਰੁਸਤ ਹੋਣਾ ਜ਼ਰੂਰੀ ਹੈ ।

4. ਸੱਟਾਂ ਦੀ ਸੰਭਾਵਨਾ ਨੂੰ ਘਟਾਉਣਾ (Reduce risk of Injuries) – ਸਰੀਰਕ ਯੋਗਤਾ ਜੀਵਨ ਦੇ ਅਗਲੇ ਪੜਾਅ ਵਿਚ ਸੱਟਾਂ ਦੇ ਜ਼ੋਖ਼ਿਮ ਨੂੰ ਘਟਾਉਂਦੀ ਹੈ । ਇਸ ਦਾ ਕਾਰਨ ਮਾਸਪੇਸ਼ੀਆਂ ਦੀ ਤਾਕਤ, ਹੱਡੀਆਂ ਵਿਚਲੀ ਘਣਤਾ, ਲਚਕਤਾ ਅਤੇ ਸਥਿਰਤਾ ਹੁੰਦੀ ਹੈ ਜੋ ਕਿ ਸੱਟਾਂ ਦੀ ਸੰਭਾਵਨਾ ਨੂੰ ਘਟਾਉਂਦੀ ਹੈ ।

5. ਜੀਵਨ ਦੀ ਸੰਭਾਵਨਾ ਵਿਚ ਵਾਧਾ (Increases life Expectancy – ਨਿਯਮਿਤ ਕਸਰਤਾਂ ਅਤੇ ਯੋਗਤਾ ਸੰਬੰਧਿਤ ਪ੍ਰੋਗਰਾਮ ਸਿਹਤ ਸੰਬੰਧਿਤ ਬਿਮਾਰੀਆਂ ਨੂੰ ਘਟਾਉਣ ਵਿਚ ਲਾਭਦਾਇਕ ਹੁੰਦੇ ਹਨ ਜੋ ਕਿ ਉਮਰ ਦਰ ਦੀਆਂ ਸੰਭਾਵਨਾਵਾਂ ਨੂੰ ਵਧਾਉਂਦੀਆਂ ਹਨ ਅਤੇ ਸਮੇਂ ਤੋਂ ਪਹਿਲਾਂ ਹੋਣ ਵਾਲੀ ਮੌਤ ਦਰ ਨੂੰ ਘਟਾਉਂਦੀ ਹੈ । ਇਹ ਦੇਖਿਆ ਗਿਆ ਹੈ ਕਿ ਜੋ ਵਿਅਕਤੀ ਸਰੀਰਕ ਤੌਰ ਤੇ ਸਰਗਰਮ ਰਹਿੰਦੇ ਹਨ, ਉਹ ਸਵਸਥ ਅਤੇ ਲੰਬਾ ਜੀਵਨ ਗੁਜ਼ਾਰਦੇ ਹਨ ।

6. ਸਹੀ ਵਾਧਾ ਅਤੇ ਵਿਕਾਸ (Proper growth and Development) – ਸਰੀਰਕ ਯੋਗਤਾ ਅਤੇ ਸਰੀਰਕ ਯੋਗਤਾ ਦੇ ਪ੍ਰੋਗਰਾਮਾਂ ਦੀ ਸਹਾਇਤਾ ਨਾਲ ਬੱਚਿਆਂ ਵਿਚ ਵਧੀਆ ਵਿਕਾਸ ਹੁੰਦਾ ਹੈ । ਉਹਨਾਂ ਦੀ ਸਿਹਤ, ਉਚਾਈ, ਸਰੀਰਕ ਸੰਰਚਨਾ ਅਤੇ ਭਾਰ ਸਹੀ ਅਨੁਪਾਤ ਅਤੇ ਕੂਮ ਵਿਚ ਵੱਧਦੇ ਹਨ ।

7. ਕੰਮ ਕਰਨ ਦੀ ਸਮਰੱਥਾ ਵਿਚ ਵਾਧਾ Improves work Efficiency) – ਸਰੀਰਕ ਤੌਰ ਤੇ ਯੋਗ ਵਿਅਕਤੀ ਜੀਵਨ ਦੇ ਹਰ ਪਹਿਲੂ ਜਿਵੇਂ ਕੰਮ ਕਰਨ ਦੀ ਥਾਂ, ਪਰਿਵਾਰ ਅਤੇ ਦੋਸਤਾਂ ਵਿਚ ਸੰਤਲੁਨ ਬਣਾ ਕੇ ਰੱਖਦਾ ਹੈ । ਉਸ ‘ ਦੀ ਸਰਗਰਮ ਜੀਵਨ ਸ਼ੈਲੀ ਅਤੇ ਤੰਦਰੁਸਤੀ ਕਾਰਨ ਉਹ ਕੰਮ ਨੂੰ ਸਫਲਤਾ ਨਾਲ ਕਰਦਾ ਹੈ ਅਤੇ ਆਪਣੇ ਸਮਾਜਿਕ ਸਮੂਹ ਦਾ ਵੀ ਉਤਸ਼ਾਹ ਨਾਲ ਆਨੰਦ ਮਾਣਦਾ ਹੈ । ਇਸ ਲਈ ਅਸੀਂ ਉਪਰੋਕਤ ਤੱਥਾਂ ਤੋਂ ਇਹ ਅਨੁਮਾਨ ਲਗਾ ਸਕਦੇ ਹਾਂ ਕਿ ਇਕ ਤੰਦਰੁਸਤ ਸਰੀਰ ਵਿਚ ਤੰਦਰੁਸਤ ਮਨ ਦਾ ਵਾਸ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਸਰੀਰਕ ਯੋਗਤਾ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਨ ਵਾਲੇ ਕਾਰਕਾਂ ਬਾਰੇ ਵਿਸਥਾਰ ਨਾਲ ਚਰਚਾ ਕਰੋ ।
ਉੱਡਰ-
ਅਨੇਕਾਂ ਅਜਿਹੇ ਕਈ ਕਾਰਨ ਹੁੰਦੇ ਹਨ ਜੋ ਸਰੀਰਕ ਯੋਗਤਾ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਦੇ ਹਨ । ਨਿਸ਼ਕ੍ਰਿਆਂ ਦੇ ਕਾਰਨ ਛੋਟੇ ਅਤੇ ਲੰਬੇ ਸਮੇਂ ਦੇ ਅਭਿਆਸ ਕਾਲ ਤੇ ਕਈ ਤਰੀਕਿਆਂ ਨਾਲ ਪ੍ਰਭਾਵ ਪੈਂਦਾ ਹੈ । ਇਹ ਕਾਰਕ ਜੋ ਕਿ ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਤੇ ਪ੍ਰਭਾਵ ਪਾਉਂਦੇ ਹਨ, ਹੇਠ ਲਿਖੇ ਪ੍ਰਕਾਰ ਹਨ-
1. ਸਰੀਰਕ ਢਾਂਚਾ (Anatomical Structure-ਸਰੀਰਕ ਢਾਂਚਾ ਅਲੱਗ-ਅਲੱਗ ਅਕਾਰ ਅਤੇ ਰੂਪ ਵਿਚ ਹੁੰਦਾ ਹੈ । ਕਈ ਵਾਰ ਅਨੁਚਿਤ ਆਕਾਰ ਅਤੇ ਰੂਪ ਸਰੀਰਕ ਕ੍ਰਿਆਵਾਂ ਵਿਚ ਉਲਝਣਾਂ ਪੈਦਾ ਕਰਦਾ ਹੈ ਅਤੇ ਕਈ ਵਾਰ ਕਮਜ਼ੋਰ ਅੰਗ ਵਿਅਕਤੀ ਦੇ ਕੰਮਾਂ ਜਾਂ ਕ੍ਰਿਆਵਾਂ ਨੂੰ ਘਟਾ ਦਿੰਦੇ ਹਨ ।

2. ਸਰੀਰਕ ਕਿਰਿਆ ਦੀ ਬਣਤਰ (Physiological Structures) – ਸਾਡੇ ਸਰੀਰ ਦੀਆਂ ਪ੍ਰਣਾਲੀਆਂ ਜਿਵੇਂ ਸਾਹ ਪ੍ਰਣਾਲੀ, ਲਹੂ ਸੰਚਾਰ ਪ੍ਰਣਾਲੀ, ਮਾਸਪੇਸ਼ੀ ਪ੍ਰਣਾਲੀ ਅਤੇ ਅਨੇਕਾਂ ਹੋਰ ਪ੍ਰਣਾਲੀਆਂ ਨੇ ਕੁਸ਼ਲਤਾਪੂਰਵਕ ਕੰਮ ਕਰਨਾ ਹੁੰਦਾ ਹੈ । ਸਰੀਰਕ ਪ੍ਰਣਾਲੀ ਵਿਚ ਖ਼ਰਾਬੀ, ਸਰੀਰਕ ਕੰਮਾਂ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਦੀ ਹੈ ਜਿਵੇਂ ਕਿ ਸਾਹ ਲੈਣ ਵਿਚ ਔਖ ਹੋਣਾ ਜਾਂ ਫਿਰ ਦਿਲ ਦੀ ਬਿਮਾਰੀ ਆਦਿ । ਇਸ ਲਈ ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਵਿਚ ਵਿਅਕਤੀ ਦਾ ਫਿਟ ਹੋਣਾ ਬੜਾ ਜ਼ਰੂਰੀ ਹੈ ।

3. ਮਨੋਵਿਗਿਆਨਿਕ ਕਾਰਨ (Psychological Factor) – ਕਈ ਤਰ੍ਹਾਂ ਦੇ ਮਾਨਸਿਕ ਵਿਗਾੜ ਜੋ ਕਿ ਸਰੀਰਕ | ਕੰਮਾਂ ਵਿਚ ਉਲਝਣਾਂ ਪੈਦਾ ਕਰਦੇ ਹਨ , ਜਿਵੇਂ ਕਿ ਦਬਾਅ, ਤਨਾਵ, ਚਿੰਤਾਵਾਂ ਆਦਿ । ਇਹ ਸਰੀਰਕ ਕ੍ਰਿਆਵਾਂ ਵਿਚ ਰੁਕਾਵਟ ਦਾ ਕਾਰਨ ਬਣਦੀਆਂ ਹਨ । ਮਾਨਸਿਕ ਰੂਪ ਨਾਲ ਮਜ਼ਬੂਤ ਅਤੇ ਤਨਾਅ-ਮੁਕਤ ਵਿਅਕਤੀ ਖੇਡਾਂ
ਲਈ ਯੋਗ ਹੁੰਦਾ ਹੈ । ਦਬਾਅ ਅਤੇ ਤਨਾਅ ਹਮੇਸ਼ਾ ਹੀ ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਨੂੰ ਘਟਾ ਦਿੰਦਾ ਹੈ ।

4. ਜੱਦ ਅਤੇ ਵਾਤਾਵਰਣ (Heedity and Environment) – ਜੱਦ ਅਤੇ ਵਾਤਾਵਰਣ ਦੋਵੇਂ ਹੀ ਸਰੀਰਕ ਯੋਗਤਾ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਦੇ ਹਨ । ਜਿਵੇਂ ਕਿ ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ ਕਿ ਮਨੁੱਖੀ ਸੈੱਲ 23 (ਜੋੜੇ) ਕੋਰਮੋਸੋਮਜ ਤੋਂ ਬਣਿਆ ਹੁੰਦਾ ਹੈ । ਜਿਸ ਵਿਚ 75% ਮਾਤਾ ਅਤੇ ਪਿਤਾ ਅਤੇ 25% ਬਾਕੀ ਖਾਨਦਾਨੀ ਜੀਨਸ ਦਾ ਸੰਚਾਰਣ ਹੁੰਦਾ ਹੈ । ਇਸ ਲਈ ਅਸੀਂ ਕਹਿ ਸਕਦੇ ਹਾਂ ਕਿ ਜੱਦੀ ਗੁਣ ਜਿਵੇਂ ਕਿ ਕਈ ਤਰ੍ਹਾਂ ਦੇ ਔਗੁਣ, ਚਮੜੀ ਅਤੇ ਅੱਖਾਂ ਦਾ ਰੰਗ, ਸਰੀਰਕ ਬਣਾਵਟ ਆਦਿ ਮਨੁੱਖ ਨੂੰ ਜੱਦ ਵਿਚ ਮਿਲਦੀ ਹੈ ਅਤੇ ਇਹ ਜੱਦ ਅਤੇ ਵਾਤਾਵਰਣ ਦੇ ਗੁਣ ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ‘ਤੇ ਵੀ ਪ੍ਰਭਾਵ ਪਾਉਂਦੇ ਹਨ ।

5. ਚੰਗਾ ਸਰੀਰਕ ਆਸਣ (Good Posur) – ਸਰੀਰਕ ਤਰੁੱਟੀਆਂ, ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਵਿਚ ਹਮੇਸ਼ਾ ਹੀ ਮੁਸ਼ਕਿਲ ਪੈਦਾ ਕਰਦੀਆਂ ਹਨ , ਜਿਵੇਂ ਕਿ ਅਸੰਤੁਲਨ ਮਾਸਪੇਸ਼ੀਆਂ, ਕੁਪੋਸ਼ਣ, ਦਰਦ, ਲੋਰਡੋਸਿਸ (Lordosis) ਸਕੋਲਿਸਿਸ (Scoliosis), ਗੋਲ ਮੋਢੇ, ਗੋਡਿਆਂ ਦਾ ਟਕਰਾਉਣਾ ਆਦਿ ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ‘ ਕਰਦੇ ਹਨ ।

6. ਅਹਾਰ (Diet) – ਸਰੀਰਕ ਪ੍ਰਦਰਸ਼ਨ ਵਿਚ ਅਹਾਰ ਪ੍ਰਮੁੱਖ ਭੂਮਿਕਾ ਨਿਭਾਉਂਦਾ ਹੈ ਅਤੇ ਸਰੀਰਕ ਯੋਗਤਾ ਦੇ ਸਤਰ ਨੂੰ ਬਣਾਏ ਰੱਖਣ ਵਿਚ ਬਹੁਤ ਸਹਾਇਕ ਹੁੰਦਾ ਹੈ । ਆਹਾਰ ਵਿਚ ਕੈਲਰੀ ਦੀ ਉਪਯੁਕਤ ਮਾਤਰਾ ਖਿਡਾਰੀਆਂ ਨੂੰ ਸਰਵ-ਉੱਚ ਪ੍ਰਦਰਸ਼ਨ ਕਰਨ ਵਿਚ ਮਦਦਗਾਰ ਸਾਬਿਤ ਹੁੰਦੀ ਹੈ । ਕਾਰਬੋਹਾਈਡਰੇਟਸ ਅਤੇ ਤਰਲ ਪਦਾਰਥਾਂ ਦੀ ਕਮੀ ਕਾਰਨ ਇਕ ਖਿਡਾਰੀ ਜਲਦੀ ਹੀ ਥਕਾਵਟ ਮਹਿਸੂਸ ਕਰਨ ਲੱਗ ਪੈਂਦਾ ਹੈ | ਮਾਸ਼ਪੇਸ਼ੀਆਂ ਦੇ ਪੁਨਰ-ਨਿਰਮਾਣ ਵਾਸਤੇ ਪ੍ਰੋਟੀਨ ਦੀ ਜ਼ਰੂਰਤ ਹੁੰਦੀ ਹੈ । ਕਾਰਬੋਹਾਈਡਰੇਟਸ, ਪ੍ਰੋਟੀਨ ਅਤੇ ਵਿਟਾਮਿਨਸ ਤੋਂ ਬਿਨਾਂ ਖਿਡਾਰੀ ਬੇਹਤਰ ਪ੍ਰਦਰਸ਼ਨ ਨਹੀਂ ਕਰ ਸਕਦਾ ਅਤੇ ਉਸਦੀ ਸਰੀਰਕ ਯੋਗਤਾ ਵੀ ਘੱਟ ਜਾਂਦੀ ਹੈ ।

7. ਜੀਵਨ ਸ਼ੈਲੀ (Life Style)ਉਹ ਖਿਡਾਰੀ ਜੋ ਚੰਗੀ ਜੀਵਨ ਸ਼ੈਲੀ ਨੂੰ ਅਪਨਾਉਂਦੇ ਹਨ, ਉਹ ਹਮੇਸ਼ਾ ਬੇਹਤਰ ਪ੍ਰਦਰਸ਼ਨ ਕਰਦੇ ਹਨ । ਜੀਵਨ ਸ਼ੈਲੀ ਤੋਂ ਭਾਵ ਸ਼ਾਨੋ-ਸ਼ੌਕਤ ਵਾਲਾ ਜੀਵਨ ਤੋਂ ਨਹੀਂ ਹੈ ਬਲਕਿ ਇਸ ਤੋਂ ਭਾਵ ਹੈ ਕਿ ਚੰਗੀਆਂ ਆਦਤਾਂ ਵਾਲਾ ਜੀਵਨ ਜਿਉਣਾ । ਇਕ ਵਿਅਕਤੀ ਜੋ ਸਿਗਰੇਟ, ਸ਼ਰਾਬ ਜਾਂ ਨਸ਼ੇ ਆਦਿ ਦਾ ਆਦੀ ਹੁੰਦਾ ਹੈ ਉਹੀ ਚੰਗਾ ਪ੍ਰਦਰਸ਼ਨ ਨਹੀਂ ਕਰ ਸਕਦਾ । ਇਹ ਉਸਦੀ ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਦਾ ਹੈ ।

8. ਜਲਵਾਯੂ (Climate) – ਅਲੱਗ-ਅਲੱਗ ਤਰ੍ਹਾਂ ਦੀ ਜਲਵਾਯੂ ਸਰੀਰਕ ਯੋਗਤਾ ‘ਤੇ ਪ੍ਰਭਾਵ ਪਾਉਂਦੀ ਹੈ ! ਸਰਦੀ, ਗਰਮੀ ਅਤੇ ਨਮੀ ਵਰਗੇ ਭਿੰਨ-ਭਿੰਨ ਜਲਵਾਯੂ ਸਰੀਰਕ ਯੋਗਤਾ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਦੇ ਹਨ । ਵਧੀਆ ਪ੍ਰਦਰਸ਼ਨ ਵਾਸਤੇ ਇਕ ਖਿਡਾਰੀ ਨੂੰ ਅਲੱਗ-ਅਲੱਗ ਜਲਵਾਯੂ ਪ੍ਰਸਿਥਤੀਆਂ ਵਿਚ ਰਹਿ ਕੇ ਅਭਿਆਸ ਕਰਨਾ ਬਹੁਤ ਜ਼ਰੂਰੀ ਹੁੰਦਾ ਹੈ । ਉਦਾਹਰਨ ਦੇ ਤੌਰ ਤੇ ਜੇਕਰ ਖਿਡਾਰੀ ਗਰਮ ਜਾਂ ਮੈਦਾਨੀ ਇਲਾਕਿਆਂ ਦਾ ਰਹਿਣ ਵਾਲਾ ਹੈ ਤਾਂ ਉਸਨੂੰ ਠੰਡੇ ਇਲਾਕੇ ਵਿਚ ਜ਼ਰੂਰ ਅਭਿਆਸ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ਤਾਂ ਜੋ ਉਸਦਾ ਪ੍ਰਦਰਸ਼ਨ ਵਧੀਆ ਹੋ ਸਕੇ । ਇਹਨਾਂ ਜਲਵਾਯੂ ਰੁਕਾਵਟਾਂ ਨੂੰ ਦੂਰ ਕਰਨ ਦਾ ਤਰੀਕਾ ਇਹ ਹੀ ਹੈ ਕਿ ਅਲੱਗ-ਅਲੱਗ ਜਲਵਾਯੂ ਵਾਤਾਵਰਣ ਵਿਚ ਅਭਿਆਸ ਕੀਤਾ ਜਾਵੇ ।

9. ਨਿਸ਼ਕ੍ਰਿਆ (Inactivity) – ਸਰੀਰਕ ਕ੍ਰਿਆਵਾਂ ਦੀ ਘਾਟ ਨਾਲ ਵਿਅਕਤੀ ਗਤੀਹੀਨ , ਜੀਵਨ ਸ਼ੈਲੀ ਵੱਲ ਚਲਿਆ ਜਾਂਦਾ ਹੈ ਜਿਸ ਨਾਲ ਸਰੀਰਕ ਪ੍ਰਣਾਲੀਆਂ ਵਿਚ ਖ਼ਰਾਬੀ ਪੈਦਾ ਹੁੰਦੀ ਹੈ | ਸਰੀਰਕ ਗਤੀਵਿਧੀ ਸ਼ਬਦ ਰੋਜ਼ਮੱਰਾ ਦੇ ਕੰਮ ਨਾਲ ਖ਼ਰਚ ਹੋਣ ਵਾਲੀ ਉਰਜਾ ਦੇ ਰੂਪ ਵਿਚ ਲਿਆ ਜਾਂਦਾ ਹੈ । ਇਹ ਰੋਜ਼ਮੱਰਾ ਦੇ ਕੰਮ ਜਿਵੇਂ ਕਿ ਚੱਲਣਾ, ਦੌੜਨਾ, ਸਾਈਕਲ ਚਲਾਉਣਾ, ਤੈਰਨਾ, ਝਾੜੂ ਮਾਰਨਾ ਆਦਿ ਘਰੇਲੂ ਕੰਮ ਹੁੰਦੇ ਹਨ । ਨਿਸ਼ਕ੍ਰਿਆ ਦੇ ਕਾਰਨ ਸਰੀਰਕ ਪ੍ਰਣਾਲੀ ਕਮਜ਼ੋਰ ਹੋ ਜਾਂਦੇ ਹਨ ਅਤੇ ਕਈ ਸਿਹਤ ਨੂੰ ਲੈ ਕੇ ਮਸਲੇ ਖੜ੍ਹੇ ਹੋ ਜਾਂਦੇ ਹਨ ਜੋ ਕਿ ਸਰੀਰਕ ਯੋਗਤਾ ‘ਤੇ ਪ੍ਰਭਾਵ ਪਾਉਂਦੇ ਹਨ ।

10. ਸੱਟਾਂ (Injuries) – ਸੱਟਾਂ ਲੱਗਣਾ ਖੇਡਾਂ ਦਾ ਹਿੱਸਾ ਹਨ । ਸੱਟਾਂ ਦੀ ਦੇਖਭਾਲ ਦੀ ਕਮੀ ਦੇ ਕਾਰਨ ਖੇਡ ਪ੍ਰਦਰਸ਼ਨ ਵਿਚ ਕਮੀ ਆ ਜਾਂਦੀ ਹੈ ਅਤੇ ਨਾਲ ਹੀ ਖਿਡਾਰੀ ਦੇ ਮਾਨਸਿਕ ਸੰਤੁਲਨ ‘ਤੇ ਵੀ ਪ੍ਰਭਾਵ ਪੈਂਦਾ ਹੈ ।

11. ਉਮਰ (Age) – ਉਮਰ ਵਿਚ ਅੰਤਰ ਹਮੇਸ਼ਾ ਹੀ ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਦਾ ਹੈ । ਜਦ ਅਸੀਂ ਛੋਟੇ | ਬੱਚੇ ਹੁੰਦੇ ਹਾਂ ਤਾਂ ਅਸੀਂ ਵੱਡੀ ਉਮਰ ਦੇ ਵਿਅਕਤੀ ਦੀ ਸਰੀਰਕ ਯੋਗਤਾ ਦੀ ਤੁਲਨਾ ਵਿਚ ਨਹੀਂ ਖੇਡ ਸਕਦੇ । ਇਸ ਤਰ੍ਹਾਂ ਜਦ ਅਸੀਂ ਬੁਢਾਪੇ ਵੱਲ ਵੱਧਦੇ ਹਾਂ ਤਾਂ ਸਾਡੀਆਂ ਮਾਸਪੇਸ਼ੀਆਂ ਕਮਜ਼ੋਰ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ਅਤੇ ਸਰੀਰ
ਉੱਤੇ ਚਰਬੀ ਵੱਧ ਜਾਂਦੀ ਹੈ ਜੋ ਕਿ ਸਰੀਰਕ ਯੋਗਤਾ ‘ਤੇ ਪ੍ਰਭਾਵ ਪਾਉਂਦੀ ਹੈ ।

12. ਲਿੰਗ (Gender) – ਲਿੰਗ ਸਰੀਰਕ ਯੋਗਤਾ ਵਿਚ ਹਮੇਸ਼ਾਂ ਹੀ ਵਿਸ਼ੇਸ਼ ਭੂਮਿਕਾ ਨਿਭਾਉਂਦਾ ਹੈ । ਔਰਤ ਅਤੇ ਆਦਮੀ ਦੋਨਾਂ ਦੇ ਸਰੀਰ ਵਿਚ ਕਈ ਵਿਲੱਖਣਤਾਵਾਂ ਪਾਈਆਂ ਜਾਂਦੀਆਂ ਹਨ । ਉਦਾਹਰਨ ਦੇ ਤੌਰ ਤੇ ਔਰਤਾਂ ਦੇ ਸਰੀਰ ਦੀਆਂ ਮਾਸਪੇਸ਼ੀਆਂ, ਆਦਮੀ ਨਾਲੋਂ ਘੱਟ ਮਜ਼ਬੂਤ ਹੁੰਦੀਆਂ ਹਨ ਪਰ ਔਰਤਾਂ ਦੇ ਜੋੜਾਂ ਵਿਚ ਲਚਕਤਾ ਆਦਮੀ ਦੇ ਮੁਕਾਬਲੇ ਜ਼ਿਆਦਾ ਹੁੰਦੀ ਹੈ ਜਿਸ ਕਰਕੇ ਉਹਨਾਂ ਨੂੰ ਜਿਮਨਾਸਟਿਕ ਵਰਗੀਆਂ ਖੇਡਾਂ ਵਿਚ ਬਹੁਤ ਲਾਭ ਮਿਲਦਾ ਹੈ । ਉੱਥੇ ਹੀ ਆਦਮੀਆਂ ਦੀਆਂ ਮਾਸਪੇਸ਼ੀਆਂ ਮਜ਼ਬੂਤ ਹੁੰਦੀਆਂ ਹਨ ਅਤੇ ਦਿਲ ਦਾ ਆਕਾਰ ਵੱਡਾ ਹੁੰਦਾ ਹੈ ਜਿਸ ਕਰਕੇ ਉਹਨਾਂ ਨੂੰ ਖੇਡਾਂ ਵਿਚ ਸ਼ਕਤੀ, ਤਾਕਤ ਅਤੇ ਗਤੀ ਮਿਲਦੀ ਹੈ ।

13. ਸਿਹਤਮੰਦ ਵਾਤਾਵਰਣ (Healthy Envrionment) – ਸਕੂਲ, ਘਰ ਅਤੇ ਖੇਡਾਂ ਦਾ ਮੈਦਾਨ ਬੇਹਤਰ ਸਿੱਖਿਆ ਪ੍ਰਦਾਨ ਕਰਨ ਵਿਚ ਮੱਦਦਗਾਰ ਸਾਬਿਤ ਹੁੰਦਾ ਹੈ । ਇਸ ਨਾਲ ਖਿਡਾਰੀ ਨੂੰ ਚੰਗਾ ਪ੍ਰਦਰਸ਼ਨ ਕਰਨ ਲਈ ਉਤਸ਼ਾਹ ਮਿਲਦਾ ਹੈ । ਇਕ ਚੰਗਾ ਵਾਤਾਵਰਣ ਅਤੇ ਚੰਗੀ ਭਾਗਦਾਰੀ ਵਧੀਆ ਵਿਕਾਸ ਅਤੇ ਵਾਧੇ ਲਈ ਜ਼ਰੂਰੀ
ਹੈ ਜੋ ਕਿ ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਵਿਚ ਅਹਿਮ ਭੂਮਿਕਾ ਨਿਭਾਉਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 4.
ਲਚਕ ਨੂੰ ਬਿਆਨ ਕਰੋ ਅਤੇ ਇਸਦੇ ਅਲੱਗ-ਅਲੱਗ ਪ੍ਰਕਾਰਾਂ ਬਾਰੇ ਲਿਖੋ ।
ਉੱਤਰ-
ਲਚਕ ਗਤੀਸ਼ੀਲਤਾ ਦੀ ਉਹ ਦਰ ਜੋ ਕਿ ਜੋੜਾਂ ਤੇ ਸੰਭਵ ਹੁੰਦੀ ਹੈ | ਅਸੀਂ ਆਮ ਸ਼ਬਦਾਂ ਵਿਚ ਇਹ ਕਹਿ ਸਕਦੇ ਹਾਂ ਕਿ ਲਚਕ ਨੂੰ ਸੁਸਤ (Possive) ਕ੍ਰਿਆਵਾਂ ਦੇ ਦੌਰਾਨ, ਜੋੜਾਂ ਅਤੇ ਉਹਨਾਂ ਦੇ ਆਸ-ਪਾਸ ਦੀਆਂ ਮਾਸਪੇਸ਼ੀਆਂ (Muscles) ਦੀ ਗਤੀ ਦੀ ਦਰ ਦੇ ਰੂਪ ਵਿਚ ਪਰਿਭਾਸ਼ਿਤ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ।

ਲਚਕ ਹੋਰਨਾਂ ਸਰੀਰਕ ਗੁਣਾਂ ਵਾਂਗ ਇਕ ਬਹੁਮੁੱਲਾ ਗੁਣ ਹੈ ਅਤੇ ਸਰੀਰਕ ਸਿੱਖਿਆ ਅਤੇ ਖਿਡਾਰੀਆਂ ਵਿਚ ਇਸਦੀ ਆਪਣੀ ਮਹੱਤਤਾ ਹੈ ਕਿਉਂਕਿ ਲਚਕਦਾਰ ਖਿਡਾਰੀ ਮੈਦਾਨ ਵਿਚ ਕਈ ਤਰ੍ਹਾਂ ਦੀਆਂ ਸੱਟਾਂ ਤੋਂ ਬਚਿਆ ਰਹਿੰਦਾ ਹੈ । ਲਚਕ ਦੇ ਕਈ ਪ੍ਰਕਾਰ ਹੁੰਦੇ ਹਨ ਅਤੇ ਇਹਨਾਂ ਦਾ ਵਰਗੀਕਰਨ ਅੱਗੇ ਲਿਖੇ ਅਨੁਸਾਰ ਹੈ-
ਲਚਕ ਦੇ ਪ੍ਰਕਾਰ (Types of Flexibility) –

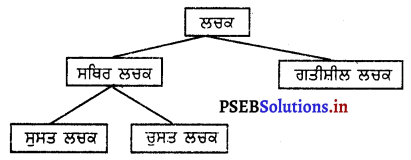
1. ਸੁਸਤ ਲਚਕ (Pasive Flexibility) – ਇਹ ਬਿਨਾਂ ਕਿਸੇ ਬਾਹਰੀ ਮੱਦਦ ਜਾਂ ਸਹਾਰੇ ਦੇ ਵੱਡੀ ਦਰ ਤੇ ਕ੍ਰਿਆਵਾਂ ਕਰਨ ਦੀ ਯੋਗਤਾ ਹੁੰਦੀ ਹੈ । ਉਦਾਹਰਨ ਦੇ ਤੌਰ ਤੇ ਕਿਸੇ ਸਾਥੀ ਖਿਡਾਰੀ ਦੀ ਮਦਦ ਨਾਲ ਸਚਿੰਗ (Stretching) ਕਸਰਤਾਂ ਕਰਨਾ ।

2. ਚੁਸਤ ਲਚਕ (Active Flexibility) – ਇਹ ਬਿਨਾਂ ਕਿਸੇ ਬਾਹਰੀ ਮੱਦਦ ਜਾਂ ਸਹਾਰੇ ਤੋਂ ਕ੍ਰਿਆਵਾਂ ਕਰਨ ਦੀ ਦਰ ਦੀ ਯੋਗਤਾ ਹੈ । ਉਦਾਹਰਨ ਦੇ ਤੌਰ ਤੇ ਲੱਤਾਂ ਨੂੰ ਝੂਲਾਉਣਾ ਆਦਿ ।

3. ਗਤੀਸ਼ੀਲ ਲਚਕ (Dynamic Flexibility) – ਇਹ ਉਹ ਲਚਕ ਹੁੰਦੀ ਹੈ ਜਦ ਸਰੀਰ ਗੜੀ ਵਿਚ ਹੁੰਦਾ ਹੈ ਅਤੇ ਕ੍ਰਿਆਵਾਂ ਪ੍ਰਦਰਸ਼ਨ ਕਰਦਾ ਹੈ । ਜਿਵੇਂ ਕਿ ਦੌੜਨਾ, ਤੈਰਨਾ ਜਾਂ ਸਮਰਸੱਲਟ (Samersault) ਆਦਿ ।

ਪ੍ਰਸ਼ਨ 5.
ਤੁਸੀਂ ਤਾਲਮੇਲ ਯੋਗਤਾ ਤੋਂ ਕੀ ਸਮਝਦੇ ਹੋ ? ਤਾਲਮੇਲ ਦੇ ਅਲੱਗ-ਅਲੱਗ ਅੰਗਾਂ ਨੂੰ ਬਿਆਨ ਕਰੋ ।
ਉੱਤਰ-
ਤਾਲਮੇਲ ਦੀ ਯੋਗਤਾ ਉਹ ਯੋਗਤਾ ਹੁੰਦੀ ਹੈ ਜਿਸ ਵਿਚ ਮੋਟਰ ਟਾਸਕ ( Motor task) ਸਹਜ ਅਤੇ ਸਹੀ ਢੰਗ ਨਾਲ ਕੀਤੇ ਜਾਂਦੇ ਹਨ ਅਤੇ ਜਿਸ ਵਿਚ ਇੰਦਰੀਆਂ ਅਤੇ ਮਾਸਪੇਸ਼ੀਆਂ ਦੀ ਸੁੰਗੜਨ ਦੀ ਪਰਸਪਰ ਸੰਬੰਧ ਹੁੰਦਾ ਹੈ। ਅਤੇ ਜੋ ਕਿ ਜੋੜਾਂ ਦੀ ਗਤੀ ਅਤੇ ਉਸਦੇ ਆਸ-ਪਾਸ ਦੇ ਅੰਗਾਂ ਅਤੇ ਸਰੀਰ ਦੀ ਸਥਿਤੀ ਤੇ ਨਿਰਭਰ ਕਰਦੀ ਹੈ । ਤਾਲਮੇਲ ਸਨਾਯੁਤੰਤਰ ਤੇ ਵੀ ਨਿਰਭਰ ਕਰਦਾ ਹੈ । ਸਰੀਰਕ ਤੰਦਰੁਸਤੀ ਵਿਚ ਤਾਲਮੇਲ ਦਾ ਅਹਿਮ ਰੋਲ ਹੈ ਜਿਸ ਤੋਂ ਬਿਨਾਂ ਕੋਈ ਵੀ ਖੇਡ ਜਾਂ ਕਿਆ ਸੰਭਵ ਹੀ ਨਹੀਂ ਹੈ ।
ਤਾਲਮੇਲ ਦੇ ਪ੍ਰਕਾਰ (Types of co-ordination-ਖੇਡਾਂ ਦੀ ਦੁਨੀਆਂ ਵਿਚ ਮੁੱਖ ਤੌਰ ਤੇ ਸੱਤ (7) ਪ੍ਰਕਾਰ ਦੀ ਤਾਲਮੇਲ ਯੋਗਤਾ ਪਾਈ ਜਾਂਦੀ ਹੈ ।

1. ਸਥਿਤੀ ਨਿਰਧਾਰਣ ਯੋਗਤਾ (Orientation) – ਯੋਗਤਾ-ਇਹ ਵਿਅਕਤੀ ਉਹ ਯੋਗਤਾ ਹੈ ਜਿਸ ਵਿਚ ਉਹ ਜ਼ਰੂਰਤ ਅਨੁਸਾਰ ਸਥਾਨ ਅਤੇ ਸਮੇਂ ਤੇ ਆਪਣੇ ਸਰੀਰ ਦਾ ਵਿਸ਼ਲੇਸ਼ਣ ਕਰਕੇ ਪਰਿਵਰਤਨ ਕਰ ਲੈਂਦਾ ਹੈ । ਉਦਾਹਰਨ ਦੇ ਤੌਰ ਤੇ ਜਿਮਨਾਸਟਿਕ ਵਿਚ ਖੇਡ ਪ੍ਰਦਰਸ਼ਨ ਮੁਤਾਬਿਕ ਸਰੀਰ ਦੀ ਸਥਿਤੀ ਨੂੰ ਬਦਲਣਾ, ਬਾਸਕਟਬਾਲ ਵਿਚ ਅਫੈਨਸ ਤੇ ਡੀਫੈਨਸ (Offense and defense) ਵਿਚ ਆਪਣੇ ਸਰੀਰ ਦੀ ਸਥਿਤੀ ਵਿਚ ਬਦਲਾਵ ਕਰ ਲੈਂਦਾ ਹੈ ।

2. ਸੰਯੋਜਨ ਦੀ ਯੋਗਤਾ (Coupling Ability) – ਇਹ ਵਿਅਕਤੀ ਦੀ ਉਹ ਯੋਗਤਾ ਹੈ ਜਿਸ ਵਿਚ ਉਹ ਸਰੀਰ ਦੇ ਅੰਗਾਂ ਨੂੰ ਗਤੀ ਵਿਚ ਅਰਥਪੂਰਨ ਢੰਗ ਨਾਲ ਸੰਯੋਜਨ ਕਰਕੇ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ; ਜਿਵੇਂ ਵਾਲੀਬਾਲ ਵਿਚ ਸਪਾਈਕਿੰਗ ਦੇ ਦੌਰਾਨ ਖਿਡਾਰੀ ਤੇਜ਼ ਗਤੀ ਨਾਲ ਜੰਪ ਕਰਦਾ ਹੈ | ਬਾਲ ਨੂੰ ਹਿੱਟ ਕਰਦਾ ਹੈ । ਇਸ ਸਮੇਂ ਉਸ ਦੇ ਸਰੀਰ ਦੇ ਸਾਰੇ ਅੰਗਾਂ ਵਿਚ ਇਕਸਾਰਤਾ ਦਾ ਤਾਲਮੇਲ ਹੁੰਦਾ ਹੈ ।

3. ਡਿਫਰੇਂਸੀਏਸ਼ਨ (Differentiation Ability) – ਇਹ ਵਿਅਕਤੀ ਦੀ ਉਹ ਯੋਗਤਾ ਹੁੰਦੀ ਹੈ ਜਿਸ ਖਿਡਾਰੀ ਮੋਟਰ ਐਕਸ਼ਨ (Motor action) ਦੇ ਦੌਰਾਨ ਸਰੀਰ ਦੇ ਅਲੱਗ-ਅਲੱਗ ਅੰਗਾਂ ਤੋਂ ਕ੍ਰਿਆ ਕਰਵਾਉਣ ਦੀ ਸਮਰੱਥਾ ਦਾ ਪ੍ਰਦਰਸ਼ਨ ਕਰਦਾ ਹੈ , ਜਿਵੇਂ ਕਿ ਵਾਲੀਬਾਲ ਵਿਚ ਸਪਾਈਕਿੰਗ ਜੰਪ ਦੇ ਦੌਰਾਨ ਸਥਿਤੀ ਦੇ ਅਨੁਸਾਰ ਬਾਲ ਨੂੰ ਸੁੱਟਣਾ (Drop) ਕਰਨਾ ।

4. ਪ੍ਰਤੀਕ੍ਰਿਆ ਕਰਨ ਦੀ ਯੋਗਤਾ (Reaction Ability) – ਇਹ ਵਿਅਕਤੀ ਦੀ ਉਹ ਯੋਗਤਾ ਹੈ ਜਿਸ ਵਿਚ ਸਿੰਗਨਲ ਮਿਲਣ ਤੇ ਖਿਡਾਰੀ ਪ੍ਰਤੀਕ੍ਰਿਆ ਕਰਦਾ ਹੈ , ਜਿਵੇਂ 100 ਮੀ: ਦੌੜ ਵਿਚ ਸਿੰਗਨਲ ਹੁੰਦੇ ਹੀ ਇਕ ਵੇ ਤੇ ਦਿਸ਼ਾ ਵੱਲ ਤੇਜ਼ ਗਤੀ ਨਾਲ ਦੌੜਨਾ ।

5. ਸੰਤੁਲਨ ਯੋਡਾ (Balance Ability) – ਇਹ ਵਿਅਕਤੀ ਦੀ ਉਹ ਯੋਗਤਾ ਹੈ ਜਿਸ ਵਿਚ ਉਹ ਗਤੀ ਵਿਚ ਸਰੀਰ ਦੀ ਸਥਿਤੀ ਬਣਾਈ ਰੱਖਦਾ ਹੈ ; ਜਿਵੇਂ ਕਿ ਸਕੂਟ ਸਟਾਂਪ (Scoot stop) ਅਤੇ 400 ਮੀ: ਵਿਚ ਆਪਣੀ ਲਾਈਨ ਵਿਚ ਰਹਿ ਕੇ ਦੌੜਨਾ ਆਦਿ ।

6. ਲੈਅ ਦੀ ਯੋਗਤਾ (Rhythm Abhity) – ਇਹ ਵਿਅਕਤੀ ਦੀ ਉਹ ਯੋਗਤਾ ਹੈ ਜਿਸ ਵਿਚ ਉਹ ਲੈਅ ਨੂੰ ਸਮਝਦੇ ਹੋਏ ਲੈਅ ਵਿਚ ਗਤੀ ਬਣਾ ਕੇ ਰੱਖਦਾ ਹੈ । ਉਦਾਹਰਨ ਦੇ ਤੌਰ ਤੇ ਬਾਸਕਟ ਬਾਲ ਵਿਚ ਲੈ-ਅਪ (Lay up) ਸਾਂਟ ਲਗਾਉਣਾ ।

7. ਹਿਣ ਯੋਸਤਾ (Alkation Ability) – ਇਹ ਵਿਅਕਤੀ ਦੀ ਉਹ ਯੋਗਤਾ ਹੈ ਜਿਸ ਵਿਚ ਉਹ ਪ੍ਰਸਥਿਤੀ ਨੂੰ ਸਮਝ ਕੇ ਉਸ ਵਿਚ ਪ੍ਰਭਾਂਵੀ ਪਰਿਵਰਤਨ ਲੈ ਕੇ ਆਵੇ । ਉਦਾਹਰਨ ਦੇ ਤੌਰ ਤੇ ਬਾਸਕਟ ਬਾਲ ਵਿਚ ਜੰਪ ਸੱਟ ਕਿਆ ਦੇ ਅਨੁਕੂਲ ਬਣਾਉਣਾ ਆਇ ॥

Punjab State Board PSEB 12th Class Physics Book Solutions Chapter 5 Magnetism and Matter Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Physics Chapter 5 Magnetism and Matter

PSEB 12th Class Physics Guide Magnetism and Matter Textbook Questions and Answers

Question 1.
Answer the following questions regarding earth’s magnetism:
(a) A vector needs three quantities for its specification. Name the three independent quantities conventionally used to specify the earth’s magnetic field.

(b) The angle of dip at a location in southern India is about 18°
Would you expect a greater or smaller dip angle in Britain?

(c) If you made a map of magnetic field lines at Melbourne in Australia, would the lines seem to go into the ground or come out of the ground?

(d) In which direction would a compass free to move in the vertical plane point to, if located right on the geomagnetic north or south pole?

(e) The earth’s field, it is claimed, roughly approximates the field due to a dipole of magnetic moment 8 × 10²² JT^-1 located at its centre. Check the order of magnitude of this number in some way.

(f) Geologists claim that besides the main magnetic N-S poles, there are several local poles on the earth’s surface oriented in different directions. How is such a thing possible at all?
Answer:
(a) The three independent quantities conventionally used for specifying earth’s magnetic field are magnetic declination, angle of dip and horizontal component of earth’s magnetic field.

(b) The angle of dip at a point depends on how far the point is located with respect to the North Pole or the South Pole. The angle of dip would be greater in Britain (it is about 70°) than in southern India because the location of Britain on the globe is closer to the magnetic North Pole.

(c) It is hypothetically considered that a huge bar magnet is dipped inside earth with its North Pole near the geographic South Pole and its South Pole near the geographic North Pole.

Magnetic field lines emanate from a magnetic North Pole and terminate at a magnetic South Pole. Hence, in a map depicting earth’s magnetic field lines, the field lines at Melbourne, Australia would seem to come out of the ground.

(d) If a compass is located on the geomagnetic North Pole or South Pole, then the compass will be free to move in the horizontal plane while earth’s field is exactly vertical to the magnetic poles. In such a case, the compass can point in any direction.

(e) Magnetic moment, M = 8 × 10²² JT^-1
Radius of earth, r = 6.4 × 10⁶ m
Magnetic field strength, B = \(\frac{\mu_{0} M}{4 \pi r^{3}}\)
∴ B = \(\frac{4 \pi \times 10^{-7} \times 8 \times 10^{22}}{4 \pi \times\left(6.4 \times 10^{6}\right)^{3}}\) = 0.3G
This quantity is of the order of magnitude of the observed field on earth.

(f) Yes, there are several local poles on earth’s surface oriented in different directions. A magnetised mineral deposit is an example of a local N-S pole.

Question 2.
Answer the following questions :
(a) The earth’s magnetic field varies from point to point in space. Does it also change with time? If so, on what time scale does it change appreciably?

(b) The earth’s core is known to contain iron. Yet geologists do not regard this as a source of the earth’s magnetism. Why?

(c) The charged currents in the outer conducting regions of the earth’s core are thought to be responsible for earth’s magnetism. What might be the ’battery’ (i.e., the source of energy) to sustain these currents?

(d) The earth may have even reversed the direction of its field several times during its history of 4 to 5 billion years. How can geologists know about the earth’s field in such distant past?

(e) The earth’s field departs from its dipole shape substantially at large distances (greater than about 30,000 km). What agencies may be responsible for this distortion?

(f) Interstellar space has an extremely weak magnetic field of the order of 10^-12 T. Can such a weak field he of any significant consequence? Explain.
[Note: Exercise 5.2 is meant mainly to arouse your curiosity. Answers to some questions above are tentative or unknown. Brief answers wherever possible are given at the end. For details, you should consult a good text on geomagnetism.]
Answer:
(a) Earth’s magnetic field changes with time. It takes a few hundred years to change by an appreciable amount. The variation in earth’s magnetic field with the time cannot be neglected.

(b) Earth’s core contains molten iron. This form of iron is not ferromagnetic. Hence, this is not considered as a source of earth’s magnetism.

(c) The radioactivity in earth’s interior is the source of energy that sustains the currents in the outer conducting regions of earth’s core. These charged currents are considered to be responsible for earth’s magnetism.

(d) Earth reversed the direction of its field several times during its history of 4 to 5 billion years. These magnetic fields got weakly recorded in rocks during their solidification. One can get clues about the geomagnetic history from the analysis of this rock magnetism.

(e) Earth’s field departs from its dipole shape substantially at large distances (greater than about 30,000 km) because of the presence of the ionosphere. In this region, earth’s field gets modified because of the field of single ions. While in motion, these ions produce the magnetic field associated with them.

(f) An extremely weak magnetic field can bend charged particles moving in a circle. This may not be noticeable for a large radius path. With reference to the gigantic interstellar space, the deflection can affect the passage of charged particles.

Question 3.
A short bar magnet placed with its axis at 30° with a uniform external magnetic field of 0.25 T experiences a torque of magnitude equal to 4.5 × 10^-2 J. What is the magnitude of magnetic moment of the magnet?
Answer:
Magnetic field strength, B = 0.25 T
Torque on the bar magnet, τ = 4.5 × 10^-2J
Angle between the bar magnet and the external magnetic field, θ = 30°
Torque is related to magnetic moment (M) as
τ = MB sinθ
∴ M = \(\frac{\tau}{B \sin \theta}\)
= \(\frac{4.5 \times 10^{-2}}{0.25 \times \sin 30^{\circ}}\)
\(\frac{4.5 \times 10^{-2} \times 2}{0.25 \times 1}\)
(∵ sin30° = \(\frac{1}{2}\))
= 0.36 JT^-1
Hence, the magnetic moment of the magnet is 0.36 JT^-1.

Question 4.
A short bar magnet of magnetic moment m = 0.32 JT^-1 is placed in a uniform magnetic field of 0.15 T. If the bar is free to rotate in the plane of the field, which orientation would correspond to its (a) stable, and (b) unstable equilibrium? What is the potential energy of the magnet in each case?
Answer:
Given, M = 0.32 JT^-1, B = 0.15T,U = ?
(a) Stable Equilibrium: The magnetic moment should be parallel to the magnetic field. In this position, the potential energy is
U = -MB cos θ =0.32 × 0.15 × 1
= -0.048 J or-4.8 × 10^-2 J\

(b) Unstable Equilibrium: The magnetic moment should be antiparallel to the magnetic field. In this position, the potential energy is
U = -MBcosθ = 0.32 × 0.15 × (-1)
= +0.048 J or + 4.8 × 10^-2 J

Question 5.
A closely wound solenoid of 800 turns and area of cross-section 2.5 × 10^-4 m² carries a current of 3.0 A. Explain the sense in which the solenoid acts like a bar magnet. What is its associated magnetic moment?
Answer:
Solenoid acts as a bar magnet, its magnetic moment is along the axis of the solenoid, the direction determined by the sense of flow of current. The magnetic moment of a current carrying loop having N turns
= NIA = 800 × 3 × 2.5 × 10^-4
= 6 × 10^-1
= 0.60 A-m²
= 0.60 JT^-1

Question 6.
If the solenoid in Exercise 5.5 is free to turn about the vertical direction and a uniform horizontal magnetic field of 0.25 T is applied, what is the magnitude of torque on the solenoid when its axis makes an angle of 30° with the direction of applied field?
Answer:
Magnetic field strength, B = 0.25 T
Magnetic moment, M = 0.6 JT^-1
The angle θ, between the axis of the solenoid and the direction of the applied field is 30°.
Therefore, the torque acting on the solenoid is given as
τ = MB sinθ
= 0.6 × 0.25 × sin30°
= 0.6 × 0.25 × \(\frac{1}{2}\)
= 0.075 N-m

Question 7.
A bar magnet of magnetic moment 1.5 J T^-1 lies aligned with the direction of a uniform magnetic field of 0.22 T.
(a) What is the amount of work required by an external torque to turn the magnet so as to align its magnetic moment:
(i) normal to the field direction,
(ii) opposite to the field direction?

(b) What is the torque on the magnet in cases (i) and (ii)?
Answer:
Given, M = 1.5 JT^-1,B = 0.22 T,θ₁ =0°

(a) To align the dipole normal to the field direction θ₂ = 90°. Therefore,
W = MB(cosθ₁ – cosθ₂)
W = 1.5 × 0.22(cos0° – cos90°) = 0.33 J
Also, τ = MB sinθ₂
or τ = 1.5 × 0.22sin90° = 0.33 Nm

(b) To align the dipole opposite to the field direction θ₂ = 180°. Therefore,
W =MB(cosθ₁ – cosθ₂)
W = 1.5 × 0.22(cos0° – cos180°) = 0.66 J
Also, τ = MB sinθ₂
or τ = 1.5 × 0.22sinl80° = 0 Nm

Question 8.
A closely wound solenoid of2000 turns and area of cross-section 1.6 × 10^-4 m², carrying a current of 4.0 A, is suspended through its centre allowing it to turn in a horizontal plane.
(a) What is the magnetic moment associated with the solenoid?
(b) What is the force and torque on the solenoid if a uniform horizontal magnetic field of 7.5 × 10^-2 T is set up at an angle of 30° with the axis of the solenoid?
Answer:
Number of turns on the solenoid, N = 2000
Area of cross-section of the solenoid, A = 1.6 × 10^-4 m^{2</sup
Current in the solenoid, I = 4 A}

(a) Let M = magnetic moment of the solenoid.
∴ Using the relation M = NIA, we get
M = 2000 × 4.0 × 1.6 × 10^{-4</sup
= 1.28 JT-1</sup}

The direction of \(\vec{M}\) is along the axis of the solenoid in the direction related to the sense of current according to right-handed screw rule.

(b) Here θ = 30°
\(\vec{B}\) = 7.5 × 10^-2 T
Let F = force on the solenoid = ?
τ = torque on the solenoid = ?
The solenoid behaves as a bar magnet placed in a uniform magnetic field, so the force is
F = m \(\vec{B}\) + (-m \(\vec{B}\)) = 0
where m = pole strength of the magnet.

Using the relation, τ = MB sinθ, we get
τ = 1.28 × 7.5 × 10^-2 × sin30°
= 1.28 × 7.5 × 10^-2 × \(\frac{1}{2}\) = 0.048 J
The direction of the torque is such that it tends to align the axis of the solenoid (i. e., magnetic moment vector \(\vec{M}\)) along \(\vec{B}\).

Question 9.
A circular coil of 16 turns and radius 10 cm carrying a current of 0.75 A rests with its plane normal to an external field of magnitude 5.0 × 10^-2 T. The coil is free to turn about an axis in its plane perpendicular to the field direction. When the coil is turned slightly and released, it oscillates about its stable equilibrium with a frequency of 2.0 s^-1. What is the moment of inertia of the coil about its axis of rotation?
Answer:
Number of turns in the circular coil, N = 16
Radius of the coil, r = 10cm = 0.1m
Cross-section of the coil, A = πr² = π × (0.1)² m²
Current in the coil, I = 0.75 A
Magnetic field strength, B = 5.0 × 10^-2 T
Frequency of oscillations of the coil, v = 2.0 s^-1
∴ Magnetic moment, M = NIA = 16 × 0.75 × π × (0.1)² = 0.377 JT^-1
Frequency is given by the relation
v = \(\frac{1}{2 \pi} \sqrt{\frac{M B}{I}}\)
where, I = Moment of inertia of the coil
I = \(\frac{M B}{4 \pi^{2} v^{2}}\) = \(\frac{0.377 \times 5 \times 10^{-2}}{4 \pi^{2} \times(2)^{2}}\)
= 1.19 × 10^-4 kg m²
Hence, the moment of inertia of the coil about its axis of rotation is 1.19 × 10^-4 kg m².

Question 10.
A magnetic needle free to rotate in a vertical plane parallel to the magnetic meridian has its north tip pointing down at 22° with the horizontal. The horizontal component of the earth’s magnetic field at the place is known to be 0.35 G. Determine the magnitude of the earth’s magnetic field at the place.
Answer:
Horizontal component of earth’s magnetic field, B_H = 0.35 G
Angle made by the needle with the horizontal plane
= Angle of dip = δ = 22°
Earth’s magnetic field strength = B
We can relate B and B_H as
B_H = B cosδ
∴ B = \(\frac{B_{H}}{\cos \delta}=\frac{0.35}{\cos 22^{\circ}}=\frac{0.35}{0.9272}\) = 0.377 G
Hence, the strength of earth’s magnetic field at the given location is 0.377 G.

Question 11.
At a certain location in Africa, a compass points 12° west of the geographic north. The north tip of the magnetic needle of a dip circle placed in the plane of magnetic meridian points 60° above the horizontal. The horizontal component of the earth’s field is measured to he 0.16 G. Specify the direction and magnitude of the earth’s field at the location.
Answer:
Angle of declination, θ = 12°
Angle of dip, δ = 60°
Horizontal component of earth’s magnetic field, B_H = 0.16 G
Earth’s magnetic field at the given location = B
We can relate B and B_H as
B_H = B cosδ
B= \(\frac{B_{H}}{\cos \delta}\) = \(=\frac{0.16}{\cos 60^{\circ}}\) = \(\frac{0.16}{\left(\frac{1}{2}\right)}\) = 0.16 × 2 = 0.32 G
Earth’s magnetic field lies in the vertical plane, 12° west of the geographic meridian, making an angle of 60° (Upward) with the horizontal direction. Its magnitude is 0.32 G.

Question 12.
A short bar magnet has a magnetic moment of 0.48 JT^-1. Give the direction and magnitude of the magnetic field produced by the magnet at a distance of 10 cm from the centre of the magnet on (a) the axis, (b) the equatorial lines (normal bisector) of the magnet.
Answer:
Magnetic moment of the bar magnet, M = 0.48 JT^-1
Distance, d = 10cm = 0.1m

(a) The magnetic field at distance d, from the centre of the magnet on the axis is given by the relation,
B = \(\frac{\mu_{0}}{4 \pi} \frac{2 M}{d^{3}}\)
∴ B = \(\frac{4 \pi \times 10^{-7} \times 2 \times 0.48}{4 \pi \times(0.1)^{3}}\)
= 0.96 × 10^-4 T = 0.96 G
The magnetic field is along the S-N direction.

(b) The magnetic field at a distance of 10 cm (i.e., d = 0.1 m) on the equatorial line of the magnet is given as,
B = \(\frac{\mu_{0} \times M}{4 \pi \times d^{3}}\)
∴ B = \(\frac{4 \pi \times 10^{-7} \times 0.48}{4 \pi \times(0.1)^{3}}\) = 0.48G
The magnetic field is along the N-S direction.

Question 13.
A short bar magnet placed in a horizontal plane has its axis aligned along the magnetic north-south direction. Null points are found on the axis of the magnet at 14 cm from the centre of the magnet. The earth’s magnetic field at the place is 0.36 G and the angle of dip is zero. What is the total magnetic field on the normal bisector of the magnet at the same distance as the null-point (i. e., 14 cm) from the centre of the magnet? (At null points, field due to a magnet is equal and opposite to the horizontal component of earth’s magnetic field.)
Answer:
Distance of the null point from the centre of magnet
d = 14 cm = 0.14 m
The earth’s magnetic field where the angle of dip is zero, is the horizontal component of earth’s magnetic field. i.e., H = 0.36 G
Initially, the null points are on the axis of the magnet. We use the formula of magnetic field on axial line (consider that the magnet is short in length).
B₁ = \(\frac{\mu_{0}}{4 \pi} \cdot \frac{2 m}{d^{3}}\)
This magnetic field is equal to the horizontal component of earth’s magnetic field.
i.e., B₁ = \(\frac{\mu_{0}}{4 \pi} \cdot \frac{2 m}{d^{3}}\) = H ……….(1)
On the equitorial line of magnet at same distance (d) magnetic field due to the magnet
B₂ = \(\frac{\mu_{0}}{4 \pi} \cdot \frac{m}{d^{3}}=\frac{B_{1}}{2}=\frac{H}{2}\) …………….. (2)
The total magnetic field on equitorial line at this point (as given in question)
B = B₂ + H = \(\frac{H}{2}\) + H = \(\frac{3}{2}\)H = \(\frac{3}{2}\) × 0.36 = 0.54G
The direction of magnetic field is in the direction of earth’s field.

Question 14.
If the bar magnet in exercise 5.13 is turned around by 180°, where will the new null points be located?
Answer:
When the bar magnet is turned by 180°, then the null points are obtained on the equitorial line.
So, magnetic field on the equitorial line at distance d’ is
B’ = \(\frac{\mu_{0}}{4 \pi} \cdot \frac{m}{d^{3}}\)
This magnetic field is equal to the horizontal component of earth’s magnetic field
B’ = \(\frac{\mu_{0}}{4 \pi} \cdot \frac{m}{d^{3}}\) = H ………… (1)
From Q.No. 13 MISS
Magnetic field B₁ = \(\frac{\mu_{0}}{4 \pi} \cdot \frac{2 m}{d^{3}}\) = H ………….. (2)
From eqs. (1) and (2), we get

Thus, the null points are located on the equitorial line at a distance of 11.1 cm.

Question 15.
A short bar magnet of magnetic moment 5.25 × 10^-2 JT^-1 is placed with its axis perpendicular to the earth’s field direction. At what distance from the centre of the magnet, the resultant field is inclined at 45° with earth’s field on (a) its normal bisector and (b) its axis. Magnitude of the earth’s field at the place is given to be 0.42 G. Ignore the length of the magnet in comparison to the distances involved.
Answer:
Given, magnetic moment m = 5.25 × 10^-2 J/T
Let the resultant magnetic field is B_net. It makes an angle of 45° with B_e.
∴ B_e = 0.42G =0.42 × 10^-4 T
(a) At normal bisector
Let r is the distance between axial line and point P.
The magnetic field at point P, due to a short magnet
B = \(\frac{\mu_{0}}{4 \pi} \cdot \frac{m}{r^{3}}\) …………. (1)

The direction of B is along PB, i.e., along N pole to S pole.
According to the vector analysis,

r = 0.05 m
r = 5 cm

(b) When point lies on axial line
Let the resultant magnetic field B_net makes an angle 45° from B_e. The magnetic field on the axial line of the magnet at a distance of r from the centre of magnet
B’ = \(\frac{\mu_{0}}{4 \pi} \cdot \frac{2 m}{r^{3}}\) (S to N)

Direction of magnetic field is from S to N.
According to the vector analysis,

Question 16.
Answer the following questions :
(a) Why does a paramagnetic sample display greater magnetisation (for the same magnetising field) when cooled?

(b) Why is diamagnetism, in contrast, almost independent of temperature?

(c) If a toroid uses bismuth for its core, will the field in the core be (slightly) greater or (slightly) less than when the core is empty?

(d) Is the permeability of a ferromagnetic material independent of the magnetic field? If not, is it more for lower or higher fields?

(e) Magnetic field lines are always nearly normal to the surface of a ferromagnet at every point. (This fact is analogous to the static electric field lines being normal to the surface of a conductor at every point). Why?

(f) Would the maximum possible magnetisation of a paramagnetic sample be of the same order of magnitude as the magnetisation of a ferromagnet?
Answer:
(a) Owing to the random thermal motion of molecules, the alignments of dipoles get disrupted at high temperatures. On cooling, this disruption is reduced.’Hence, a paramagnetic sample displays greater magnetisation when cooled.

(b) The induced dipole moment in a diamagnetic substance is always opposite to the magnetising field. Hence, the internal motion of the atoms (which is related to the temperature) does not affect the diamagnetism of a material.

(c) Bismuth is a diamagnetic substance. Hence, a toroid with a bismuth core has a magnetic field slightly greater than a toroid whose core is empty.

(d) The permeability of ferromagnetic materials is not independent of the applied magnetic field. It is greater for a lower field and vice versa.

(e) The permeability of ferromagnetic materials is not less than one. It is always greater than one. Hence, magnetic field lines are always nearly normal to the surface of such materials at every point.

(f) The maximum possible magnetisation of a paramagnetic sample can be of the same order of magnitude as the magnetisation of a ferromagnet. This requires high magnetising fields for saturation.

Question 17.
Answer the following questions:
(a) Explain qualitatively on the basis of domain picture the irreversibility in the magnetisation curve of a ferromagnet.

(b) The hysteresis loop of a soft iron piece has a much smaller area than that of a carbon steel piece. If the material is to go through repeated cycles of magnetisation, which piece will dissipate greater heat energy?

(c) ‘A system displaying a hysteresis loop such as a ferromagnet, is a device for storing memory?’ Explain the meaning of this statement.

(d) What kind of ferromagnetic material is used for coating magnetic tapes in a cassette player,’ or for building ‘memory stores’ in a modern computer?

(e) A certain region of space is to be shielded from magnetic fields. Suggest a method.
Answer:
(a) The hysteresis curve (B-H curve) of a ferromagnetic material is shown in the following figure

It can be observed from the given curve that magnetisation persists even when the external field is removed. This reflects the irreversibility of a ferromagnet.

(b) The dissipated heat energy is directly proportional to the area of a hysteresis loop. A carbon steel piede has a greater hysteresis curve area. Hence, it dissipates greater heat energy.

(c) The value of magnetisation is memory or record of hysteresis loop cycles of magnetisation. These bits of information correspond to the cycle of magnetisation. Hysteresis loops can be used for storing information.

(d) Ceramic is used for coating magnetic tapes in cassette players and for building memory stores in modern computers.

(e) A certain region of space can be shielded from magnetic fields if it is – surrounded by soft iron rings. In such arrangements, the magnetic lines are drawn out of the region.

Question 18.
A long straight horizontal cable carries a current of 2.5 A in the direction 10° south of west to 10° north of east. The magnetic meridian of the place happens to be 10° west of the geographic meridian. The earth’s magnetic field at the location is 0.33 G, and the angle of dip is zero. Locate the line of neutral points (ignore the thickness of the cable). (At neutral points, magnetic field due to a current-carrying cable is equal and opposite to the horizontal component of earth’s magnetic field.)
Answer:
Given, current in the cable
I = 2.5 A

Magnetic meridian M_NM_S is 10° west of geographical meridian G_NG_S earth’s magnetic field R = 0.33 G
= 0.33 × 10^-4 T ……….. (1)
Angle of dip δ = _S0°
The neutral point is the point where the magnetic field due to the current carrying cable is equal to the horizontal component of earth’s magnetic field.
Horizontal component of earth’s magnetic field
H = Rcosθ = 0.33 × 10-4 cos0°
= 0.33 × 10^-4 T
Using the formula of magnetic field at distance r due to an infinite long current carrying conductor
B = \(\frac{\mu_{0}}{4 \pi} \cdot \frac{2 I}{r}\)
At neutral points,
H = B
0.33 × 10^-4 = \(\frac{\mu_{0}}{4 \pi} \cdot \frac{2 I}{r}\)
0.33 × 10^-4 = \(\frac{10^{-7} \times 2 \times 2.5}{r}\)
or r = \(\frac{5 \times 10^{-7}}{0.33 \times 10^{-4}}\)
or r = 1.5 × 10^-2 m = 1.5cm
Thus, the line of neutral points is at a distance of 1.5 cm from the cable.

Question 19.
A telephone cable at a place has four long straight horizontal wires carrying a current of 1.0 A in the same direction east to west. The earth’s magnetic field at the place is 0.39 G, and the angle of dip is 35°. The magnetic declination is nearly zero. What are the resultant magnetic fields at points 4.0 cm above and below the cable?
Answer:
Number of horizontal wires in the telephone cable, n = 4
Current in each wire, I = 1.0 A
Earth’s magnetic field at the location, H = 0.39 G = 0.39 × 10^-4 T
Angle of dip at the location, δ = 35°
Angle of declination, θ = 0°
For a point 4 cm below the cable
Distance, r = 4 cm = 0.04 m
The horizontal component of earth’s magnetic field can be written as
H_h, = Hcosδ – B
where,
B = Magnetic field at 4 cm due to current I in the four wires
= 4 × \(\frac{\mu_{0} I}{2 \pi r}\)
μ₀ = 4π × 10^-7 TmA^-1
∴ B = 4 × \(\frac{4 \pi \times 10^{-7} \times 1}{2 \pi \times 0.04}\)
= 0.2 × 10^-4 T = 0.2G
∴ H_h = 0.39 cos35°- 0.2
= 0.39 × 0.819 – 0.2 ≈ 0.12 G

The vertical component of earth’s magnetic field is given as
H_v = H sinδ
= 0.39 sin35°= 0.22 G
The angle made by the field with its horizontal component is given as
θ = tan^-1 \(\frac{H_{v}}{H_{b}}\)
= tan^-1 \(\frac{0.22}{0.12}\) = 61.39°
The resultant field at the point is given as
H₁ = \(\sqrt{\left(H_{v}\right)^{2}+\left(H_{h}\right)^{2}}\)
= \(\sqrt{(0.22)^{2}+(0.12)^{2}}\) = 0.25 G

For a point 4 cm above the cable
Horizontal component of earth’s magnetic field
H_h = Hcosδ +B = 0.39 cos35° + 0.2 = 0.52 G
Vertical component of earth’s magnetic field
H_v = H sinδ
= 0.39 sin35° = 0.22 G
Angle, θ = tan^-1 \(\frac{H_{v}}{H_{h}}\) = tan^-1\(\frac{0.22}{0.52}\) = 22.90
And resultant field
H₂ = \(\sqrt{\left(H_{v}\right)^{2}+\left(H_{h}\right)^{2}}\)
= \(\sqrt{(0.22)^{2}+(0.52)^{2}}\) = 0.56 G

Question 20.
A compass needle free to turn in a horizontal plane is placed at the centre of circular coil of 30 turns and radius 12 cm. The coil is in a vertical plane making an angle of 45° with the magnetic meridian. When the current in the coil is 0.35 A, the needle points west to east.
(a) Determine the horizontal component of the earth’s magnetic field at the location.
(b) The current in the coil is reversed, and the coil is rotated about its vertical axis by an angle of 90° in the anticlockwise sense looking from above. Predict the direction of the needle. Take the magnetic declination at the places to be zero.
Answer:
Number of turns in the circular coil, N = 30
Radius of the circular coil, r = 12cm = 0.12m
Current in the coil, I = 0.35 A
Angle of dip, δ = 45°

(a) The magnetic field due to current I, at a distance r, is given as
B = \(\frac{\mu_{0} 2 \pi N I}{4 \pi r}\)
∴ B = \(\frac{4 \pi \times 10^{-7} \times 2 \pi \times 30 \times 0.35}{4 \pi \times 0.12}\)
= 5.49 × 10^-5 T
The compass needle points from west to east. Hence, the horizontal component of earth’s magnetic field is given as
B_H = B sinδ
= 5.49 × 10^-5 sin 45°
= 3.88 × 10^-5 T = 0.388G

(b) When the current in the coil is reversed and the coil is rotated about its vertical axis by an angle of 90°, the needle will reverse its original direction. In this case, the needle will point from east to west.

Question 21.
A magnetic dipole is under the influence of two magnetic fields. The angle between the field directions is 60°, and one of the fields has a magnitude of 1.2 × 10^-2 T. If the dipole comes to stable equilibrium at an angle of 15° with this field, what is the magnitude of the other field?
Answer:
The two fields \(\vec{B}\)₁ and \(\vec{B}\)₂ are shown in the figure

here in which a magnet is placed s.t.
∠NOB = 15°
∠B₁OB₂ = 60°
∴ ∠NOB₂ = 60 – 15 = 45°
B₁ = 1.2 × 10^-2 T
B₂ = ?
Let θ₁ and θ₂ he the inclination of the dipole
with \(\vec{B}\)₁ and \(\vec{B}\)₂ respectively.
∴ θ₁ = 15°,θ₂ = 45°
If τ₁ and τ₂ be the torques on the dipole due to \(\vec{B}\)₁ and \(\vec{B}\)₂ respectively, then
Using the relation,
τ = MB sin θ, we get
τ₁ = MB₁ sinθ₁
and τ₂ = MB₂ sinθ₂
As the dipole is in equilibrium, the torques on the dipole due to \(\vec{B}\)₁ and \(\vec{B}\)₂ are equal and opposite, i. e.,

Question 22.
A monoenergetic (18 keV) electron beam initially in the horizontal direction is subjected to a horizontal magnetic field of 0.40 G normal to the initial direction. Estimate the up or down deflection of the beam over a distance of 30 cm (me = 9.11 × 10^-31 kg). [Note : Data in this exercise are so chosen that the answer will give you an idea of the effect of earth’s magnetic field on the motion of the electron beam from the electron gun to the screen in a TV set.]
Answer:
Here, energy = E = 18 KeV = 18 × 1.6 × 10^-16 J
(∵ 1 KeV=10³eV = 10³ × 1.6 × 10^-19 J)
B = horizontal magnetic field = 0.40 G = 0.40 × 10^-4 J
m = 9.11 × 10^-31 kg, e = 1.6 × 10^-19 C
x = 30 cm = 0.30 m
As the magnetic field is normal to the velocity, the charged particle follows circular path in magnetic field. The centrepetal force \(\frac{m v^{2}}{r}\) required for this purpose is provided by force on electron due to magnetic field i. e., BeV

Question 23.
A sample of paramagnetic salt contains 2.0 × 10²⁴ atomic dipoles each of dipole moment 1.5 × 10^-23 JT^-1. The sample is placed under a homogeneous magnetic field of 0.64 T, and cooled to a temperature of 4.2 K. The degree of magnetic saturation achieved is equal to 15%. What is the total dipole moment of the sample for a magnetic field of 0.98 T and a temperature of 2.8 K? (Assume Curie’s law)
Answer:
Number of atomic dipoles, n = 2.0 × 10²⁴
Dipole moment of each atomic dipole, M = 1.5 × 10^-23 JT^-1
When the magnetic field, B₁ = 0.64 T
The sample is cooled to a temperature, T₁ = 4.2 K
Total dipole moment of the atomic dipole, M_tot = n × M
= 2 × 10²⁴ × 1.5 × 10^-23 = 30 JT^-1
Magnetic saturation is achieved at 15%.
Hence, effective dipole moment, M₁ = \(\frac{15}{100}\) × 30 = 4.5 JT^-1
When the magnetic field, B₂ = 0.98 T
Temperature, T₂ = 2.8 K
Its total dipole moment = M₂
According to Curie’s law, we have the ratio of two magnetic dipoles as
\(\frac{M_{2}}{M_{1}}=\frac{B_{2}}{B_{1}} \times \frac{T_{1}}{T_{2}}\)
∴ M₂ = \(\frac{B_{2} T_{1} M_{1}}{B_{1} T_{2}}\) = \(\frac{0.98 \times 4.2 \times 4.5}{2.8 \times 0.64}\) = 10 336 JT^-1
Therefore, 10.336 J T^-1 is the total dipole moment of the sample for a magnetic field of 0.98 T and a temperature of 2.8 K.

Question 24.
A Rowland ring of mean radius 15 cm has 3500 turns of wire wound on a ferromagnetic core of relative permeability 800. What is the magnetic field B in the core for a magnetising current of 1.2 A?
Answer:
Mean radius of the Rowland ring, r = 15 cm = 0.15 m
Number of turns on the ferromagnetic core, N = 3500
Relative permeability of the core material, μ_r = 800
Magnetising current, I = 1.2 A
The magnetic field is given by the relation
B = \(\frac{\mu_{r} \mu_{0} I N}{2 \pi r}\)
B = \(\frac{800 \times 4 \pi \times 10^{-7} \times 1.2 \times 3500}{2 \pi \times 0.15}\) = 4.48T
Therefore, the magnetic field in the core is 4.48 T.

Question 25.
The magnetic moment vectors μ_s and μ_l associated with the intrinsic spin angular momentum S and orbital angular momentum l, respectively, of an electron are predicted by quantum theory (and verified experimentally to a high accuracy) to be given by
μ_g = -(e/m)S, μ_l = -(e/2m)l
Which of these relations is in accordance with the result expected classically? Outline the derivation of the classical result.
Answer:
Out of these two relations, \(\overrightarrow{\mu_{l}}=-\frac{e}{2 m} \vec{l}\) is in accordance with classical physics and can be derived as follows

We know that electrons revolving around the nucleus of an atom in circular orbits behave as tiny current loops having angular momentum \(\vec{\imath}\) given in magnitude as
\(\vec{\imath}\) = mvr …………. (1)
where m = mass of an electron
v = its orbital velocity
r = radius of the circular orbit.
or v_r = \(\frac{l}{m}\) …………… (2)

\(\vec{\imath}\) acts along the normal to the plane of the orbit in upward direction. The orbital motion of electron is taken as equivalent to the flow of conventional current I given by

where – ve sign shows that the electron is negatively
charged. The eqn. (3) shows that μ_e and \(\vec{\imath}\) are opposite to each other i. e., antiparallel and both being normal to the plane of the orbit as shown in the figure

∴ \(\overrightarrow{\mu_{l}}=-\frac{e}{2 m} \cdot \vec{l}\)
\(\frac{\mu_{s}}{S}\) in contrast to \(\frac{\mu_{l}}{\vec{l}}\) is \(\frac{e}{m}\) i.e., twice the classically
expected value. This latter result is an outstanding consequence of modern quantum theory and cannot be obtained classically.

Punjab State Board PSEB 12th Class Physics Book Solutions Chapter 11 Dual Nature of Radiation and Matter Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Physics Chapter 11 Dual Nature of Radiation and Matter

PSEB 12th Class Physics Guide Dual Nature of Radiation and Matter Textbook Questions and Answers

Question 1.
Find the
(a) maximum frequency, and
(b) minimum wavelength of X-rays produced by 30 kV electrons.
Answer:
Potentialoftheelectrons, V=30 kV= 3O x 10³ V=3 x 10⁴ V
Hence, energy of the electrons, E = 3 x 10⁴ eV
where, e = Charge on an electron = 1.6 x 10^-19C
(a) Maximum frequency produced by the X-rays = v
The energy of the electrons is given by the relation
E=eV=hv
where, h = Planck’s constant = 6.63 x 10^-34 Js
∴ v = \(\frac{e V}{h} \) (∵ E = eV)
= \(\frac{1.6 \times 10^{-19} \times 3 \times 10^{4}}{6.63 \times 10^{-34}}\) = 7.24 x 10¹⁸ Hz
Hence, the maximum frequency of X-rays produced is 7.24 x 10¹⁸ Hz

(b) The minimum wavelength produced by the X-rays is given as
λ = \(\frac{c}{v}\)
= \(\frac{3 \times 10^{8}}{7.24 \times 10^{18}}\)
= 0.414 x 10^-10
= 0.0414 x 10^-9 m
= 0.0414 nm
Hence, the minimum wavelength of X-rays produced is 0.0414 nm.

Question 2.
The work function of caesium metal is 2.14 eV. When light of frequency 6 x 10¹⁴ Hz is incident on the metal surface, photoemission of electrons occurs.
What is the
(a) maximum kinetic energy of the emitted electrons,
(b) stopping potential, and
(c) maximum speed of the emitted photoelectrons?
Answer:
Work function of caesium metal, Φ₀ = 2.14 eV
Frequency of light, v = 6.0 x 10¹⁴ Hz
The maximum kinetic energy is given by the photoelectric effect as
K = hv- Φ₀
where, h = Planck’s constant = 6.63 x 10^-34 Js .
∴ k = \(\frac{6.63 \times 10^{-34} \times 6 \times 10^{14}}{1.6 \times 10^{-19}}-2.14 \)
( ∵ e=1.6 x 10^-19)
= 2.485-2.140 =0.345eV
Hence, the maximum kinetic energy of the emitted electrons is 0.345 eV.

(b) For stopping potential V₀, we can write the equation for kinetic energy
as K=eV₀
∴ V₀ = \(\frac{K}{e}\) (∵ e=1.6×10¹⁹)
= \(\frac{0.345 \times 1.6 \times 10^{-19}}{1.6 \times 10^{-19}}\) =0.345V
Hence, the stopping potential of the material is 0.345 V.

(c) Maximum speed of the emitted photoelectrons = y
Hence, the relation for kinetic energy can be written as
K = \(\frac{1}{2}\) mv²
where, m = mass of an electron = 9.1 x 10^-31 kg
(∴ e=1.6 x 10^-19)
= \(\frac{2 \times 0.345 \times 1.6 \times 10^{-19}}{9.1 \times 10^{-31}}\) = 0.1104 x 10¹²
∴ v = 3.323 x 10⁵ m/s = 332.3 km/s
Hence, the maximum speed of the emitted photoelectrons is 332.3 km/s.

Question 3.
The photoelectric cut off voltage n a certain experiment is 1.5 V. What is the maximum kinetic energy of photoelectrons emitted?
Answer:
Cut-off voltage, V₀ = 1.5 V
Maximum kinetic energy of photoelectrons
E_K =eV₀ =1.5eV=1.5 x 1.6 x 10^-19J
=2.4 x 10^-19J.

Question 4.
Monochromatic light of wavelength 632.8 mn is produced by a helium-neon laser. The power emitted is 9.42 mW.
(a) Find the energy and momentum of each photon in the light beam,
(b) How many photons per second, on the average, arrive at a target irradiated by this beam? (Assume the beam to have uniform cross-section which is less than the target area), and
(c) How fast does a hydrogen atom have to travel in order to have the same momentum as that of the photon?
Answer:
Wavelength of the monochromatic light, 632.8 nm = 632.8 x 10^-9 m
Power emitted by the laser, P = 9.42 mW = 9.42 x 10^-3 W
Planck’s constant, h = 6.63 x 10^-34Js
Speed of light, c=3 x 10⁸ m/s
Mass of a hydrogen atom, m =1.66 x 10^-27 kg
(a) The energy of each photon is given as
E = \(\frac{h c}{\lambda}\)
= \(\frac{6.63 \times 10^{-34} \times 3 \times 10^{8}}{632.8 \times 10^{-9}}\)
= 3.141 x 10^-19

The momentum of each photon is given as
p = \(\frac{h}{\lambda}\)
= \(\frac{6.63 \times 10^{-34}}{632.8 \times 10^{-9}}=1.047 \times 10^{-27} \mathrm{~kg} \mathrm{~ms}^{-1} \)

(b) Number of photons arriving per second, at a target irradiated by the beam = n.
Assume that the beam has a uniform cross-section that is less than the
target area.
Hence, the equation for power can be written as
P=nE
∴ n= \(\frac{P}{E}\)
= \(\frac{9.42 \times 10^{-3}}{3.141 \times 10^{-19}}\) = 3 x 10¹⁶

(c) Momentum of the hydrogen atom is the same as the momentum of the photon, .
p=1.047 x 10²⁷ kgms^-1
Momentum is given as
p = mv
where, v = speed of the hydrogen atom
v = \(\frac{p}{m}\)
= \(=\frac{1.047 \times 10^{-27}}{1.66 \times 10^{-27}}\) = 0.630m/s

Question 5.
The enery flux of sunlight reaching the surface of the earth is 1.388 x 10³ W/m².
How many photons (nearly) per square metre are incident on the Earth per second? Assume that the photons in the sunlight have an average wavelength of 550 rims.
Answer:
Energy flux of sunlight reaching the surface of earth,
Φ = 1.388 x 10³ W/m²
Hence, power of sunlight per square metre, P = 1.388 x 10³W
Speed of light, c = 3 x 10⁸ m/s
Planck’s constant, h = 6.63 x 10^-34 Js
Average wavelength of photons present in sunlight, λ = 550 nm.
=550 x 10^-9m
Number of photons per square metre incident on earth per second = n

Hence, the equation for power can be written as
P = nE
∴ n = \(\frac{P}{E}=\frac{P \lambda}{h c}=\frac{1.388 \times 10^{3} \times 550 \times 10^{-9}}{6.63 \times 10^{-34} \times 3 \times 10^{8}}\)
= 3.84 x 10²¹ photons/m²/s
Therefore, every second, 3.84×1021 photons are incident per square metre on earth.

Question 6.
In an experiment on photoelectric effect, the slope of the cut-off voltage versus frequency of incident light is found to be 4.12 x 10^-15 Vs. Calculate the value of Planck’s constant.
Answer:
The slope of the cut-off voltage (V) versus frequency (v) of an incident light is given as
\(\frac{V}{v}\) = 4.12 x 10^-15 Vs
V is related to frequency by the equation
hv = eV

where, e = charge on an electron = 1.6 x 10^-19
h = Planck’s constant
∴ h = e x \(\frac{V}{v}\)
= 1.6 x 10^-19 x 4.12 x 10^-15
= 6.592 x 10^-34 Js
Therefore, the value of Planck’s constant is 6.592 x 10^-34 Js.

Question 7.
A 100 W sodium lamp radiates energy uniformly in all directions. The lamp is located at the centre of a large sphere that absorbs all the sodium light which is incident on it. The wavelength of the sodium light is 589 nm.
(a) What is the energy per photon associated with the sodium light?
(b) At what rate are the photons delivered to the sphere?
Answer:
Power of the sodium lamp,. P = 100 W
Wavelength of the emitted sodium light, λ = 589 nm = 589 x 10⁹ m
Planck’s constant, h = 6.63 x 10^-34 Js
Speed of light, c = 3 x 10⁸ m/s
The energy per photon associated with the sodium light is given as
E= \(\frac{h c}{\lambda}\)

(b) Number of photons delivered to the sphere = n
The equation for power can be written as
P=nE
∴ n = \(\frac{P}{E}=\frac{100}{3.37 \times 10^{-19}}\) = 2.96 x 10²⁰ photons/s
Therefore, every second, 2.96 x 10²⁰ photons are delivered to the sphere.

Question 8.
The threshold frequency for a certain metal is 3.3 x 10¹⁴ Hz. If light of frequency 8.2 x 10¹⁴ Hz is incident on the metal, predict the cut-off voltage for the photoelectric emission.
Answer:
Threshold frequency of the metal, v₀ = 3.3 x 10¹⁴ Hz
Frequency of light incident on the metal, v = 82 x 10¹⁴ Hz
Charge on’an electron, e = 1.6 x 10^-19 C .
Planck’s constant, h = 6.63 x 10^-34 Js
Cut-off voltage for the photoelectric emission from the metal = V₀
The equation for the cut-off energy is given as
eV₀ = h(v-v₀)
V_o = \(\frac{h\left(v-v_{0}\right)}{e}\)
= \(\frac{6.63 \times 10^{-14} \times\left(8.2 \times 10^{14}-3.3 \times 10^{14}\right)}{1.6 \times 10^{-19}}\)
= 2.0292 V
Therefore, the cut-off voltage for the photoelectric emission is 2.0292 V.

Question 9.
The work function for a certain metal Is 4.2 eV. Will this metal give photoelectric emission for incident radiation of
wavelength 330 nm?
Answer:
The energy of incident radiations
E = \(\frac{h c}{\lambda}\) = \(\frac{6.63 \times 10^{-34} \times 3 \times 10^{8}}{330 \times 10^{-9}}\) J
= 6.03 x 10^-19 J
= \(\frac{6.03 \times 10^{-19}}{1.6 \times 10^{-19}}\)eV = 3.77 eV
The work function of photometal, Φ₀ = 4.2 eV
As energy of incident photon is less than work function, photoemission is not possible.

Question 10.
Light of frequency 7.21 x 10¹⁴ Hz is incident on a metal surface. Electrons with a maximum speed of 6.0 x10s m/s are ejected from the surface. What is the threshold frequency for photoemission of electrons?
Answer:
Frequency of light incident on the metal surface, v = 7.21 x 10¹⁴ Hz
Maximum speed of the electrons, v = 6.0 x 10⁵ m/s
Planck’s constant, h = 6.63 x 10^-34 Js
Mass of an electron, m = 9.1 x 10^-31 kg
For threshold frequency v₀, the relation for kinetic energy is written asFor threshold frequency y0, the relation for kinetic energy is written as
\(\frac{1}{2} m v^{2}\) = h(v-v₀)
v₀ = v – \(\frac{m v^{2}}{2 h}\)

Therefore, the threshold frequency for the photoemission of electrons is 4.738 x 10¹⁴ Hz.

Question 11.
Light of wavelength 488 mn is produced by an argon laser which is used in the photoelectric effect. When light from this spectral line is incident on the emitter, the stopping (cut-off) potential of photoelectrons is 0.38 V. Find the work function of the material from which the emitter is made.
Answer:
Wavelength of light produced by the argon laser,
λ = 488 nm = 488 x 10^-9 m
Stopping potential of the photoelectrons, V₀ = 0.38 V
1 eV=l.6 x 10^-19 J
∴ V₀= \(\frac{0.38}{1.6 \times 10^{-19}}\) eV
Planck’s constant, h = 6.63 x 10^-34 Js
Charge on an electron, e = 1.6 x 10^-19 C
Speed of light, c =3 x 10 m/s
From Einstein’s photoelectric effect, we have the relation involving the work function Φ₀ of the material of the emitter as

Therefore, the material with which the emitter is made has the work function of 2.16 eV.

Question 12.
Calculate the
(a) momentum, and
(b) de Broglie wavelength of the electrons accelerated through a potential difference of 56 V.
Answer:
Potential difference, V = 56 V
Planck’s constant, h = 6.63 x 10^-34 Js
Mass of an electron, m = 9.1 x 10^-31 kg
Charge on an electron, e = 1.6 x 10^-19 C
(a) At equilibrium, the kinetic energy of each electron is equal to the accelerating potential, i.e., we can write the relation for velocity (v) of each electron as

The momentum of each accelerated electron is given as
P = mv
= 9.1 x 10^-31 x 4.44 x 10⁶
= 4.04 x 10^-24 kg m s^-1
Therefore, the momentum of each electron is 4.04 x 10^-24 kg m s^-1.

(b) de Broglie wavelength of an electron accelerating through a potential V is given by the relation

Therefore, the de Broglie wavelength of each electron is 0.1639 nm.

Question 13.
What is the
(a) momentum,
(b) speed, and
(c) de Broglie wavelength of an electron with kinetic energy of 120 eV.
Answer:
Kinetic energy of the electron, E_k = 120 eV
Planck’s constant, h = 6.63 x 10^-34 Js
Mass of an electron, m = 9.1 x 10^-31
Charge on an electron, e = 1.6 x 10^-19 C

(a) For the electron, we can write the relation for kinetic energy as
Ek = \(\frac{1}{2}\) mv²
where, v = speed of the electron
∴ v² = \(\sqrt{\frac{2 e E_{k}}{m}}=\sqrt{\frac{2 \times 1.6 \times 10^{-19} \times 120}{9.1 \times 10^{-31}}}\)
= \(\sqrt{42.198 \times 10^{12}}\) = 6.496 x 10⁶ m/s
Momentum of the electron, p = mv = 9.1 x 10^-31 x 6.496 x 10⁶
=5.91 x 10²⁴ kg ms^-1
Therefore, the momentum of the electron is 5.91 x 10²⁴ kg ms^-1.

Question 14.
The wavelength of light from the spectral emission line of sodium is 589 nm. Find the kinetic energy at which an electron, and a neutron, would have the same de Broglie wavelength.
Answer:
Wavelength of light of sodium line, λ = 589 nm = 589 x 10^-9 m
Mass of an electron, m_e = 9.1 x 10^-31 kg
Mass of a neutron, m_n = 1.66 x 10^-27 kg
Planck’s constant, h = 6.63 x 10^-34 Js

(a) For the kinetic energy K, of an electron accelerating with a velocity v, we have the relation
K = \(\frac{1}{2}\) m_ev² ………………………… (1)
We have the relation for de Broglie wavelength as
λ = \(\frac{h}{m_{e} v}\)
∴ v² = \(\frac{h^{2}}{\lambda^{2} m_{e}^{2}}\) ………………………… (2)
Substituting equation (2) in equation (1), we get the relation
K = \(\frac{1}{2} \frac{m_{e} h^{2}}{\lambda^{2} m_{e}^{2}}=\frac{h^{2}}{2 \lambda^{2} m_{e}}\) ………….. (3)

Hence, the kinetic energy of the electron is 6.9 x 10^-25 J or 4.31 µeV.

(b) Using equation (3), we can write the relation for the kinetic energy of the neutron as = \(\frac{h^{2}}{2 \lambda^{2} m_{n}}\)
= \(\frac{\left(6.63 \times 10^{-34}\right)^{2}}{2 \times\left(589 \times 10^{-9}\right)^{2} \times 1.66 \times 10^{-27}}\)
= 3.78 x 10^-28
= \(\frac{3.78 \times 10^{-28}}{1.6 \times 10^{-19}} \) = 2.36 x 10^-9 eV
= 2.36 neV
Hence, the kinetic energy of the neutron is 3.78 x 10^-28 J or 2.36 neV.

Question 15.
What is the de Broglie wavelength of
(a) a bullet of mass 0.040 kg travelling at the speed of 1.0 km/s,
(b) a ball of mass 0.060 kg moving at a speed of 1.0 m/s, and
(c) a dust particle of mass 1.0 x 10^-9 kg drifting with a speed of 2.2 m/s?
Answer:
(a) Mass of the bullet, m = 0.040 kg
Speed of the bullet, v = 1.0 km/s = 1000 m/s
Planck’s constant, h = 6.63 x 10^-34 Js
de Broglie wavelength of the bullet is given by the relation
λ = \(\frac{h}{m v}\)
= \(\frac{6.63 \times 10^{-34}}{0.040 \times 1000} \) = 1.65 x 10^-35 m

(b) Mass of the ball, m = 0.060 kg
Speed of the ball, v =1.0 m/s
de Brogue wavelength of the ball is given by the relation
λ = \(\frac{h}{m v}\)
= \(\frac{6.63 \times 10^{-34}}{0.060 \times 1}\) = 1.1 x 10^-32 m

(c) Mass of the dust particle, m = 1 x 10^-9 kg
Speed of the dust particle, v = 2.2 m/s
de Brogue wavelength of the dust particle is given by the relation
λ = \(\frac{h}{m v}\)
= \(\frac{6.63 \times 10^{-34}}{2.2 \times 1 \times 10^{-9}}\) = 3.0 x 10^-25 m.

Question 16.
An electron and a photon each have a wavelength of 1.00 run. Find
(a) their momenta,
(b) the energy of the photon, and
(c) the kinetic energy of electrons.
Answer:
Wavelength of an electron (λe) and a photon (λp),λe = λp = λ = 1 nm
= 1 x 10^-9 m
Planck’s constant, h = 6.63 x 10^-34 Js

(a) The momentum of an elementary particle is given by de Broglie relation
λ = \(\frac{h}{p}\)
p = \(\frac{h}{\lambda}\)
It is clear that momentum depends only on the wavelength of the particle. Since the wavelengths of an electron and a photon are equal, both have an equal momentum.
∴ p= \(\frac{6.63 \times 10^{-34}}{1 \times 10^{-9}} \) =6.63 x 10^-25 kgms^-1

(b) The energy of a photon is given by the relation
E= \(\frac{h c}{\lambda}\)
where, speed of light, c =3 x 10⁸ m/s
∴ E = \(\frac{6.63 \times 10^{-34} \times 3 \times 10^{8}}{1 \times 10^{-9} \times 1.6 \times 10^{-19}}\)
= 1243.1 eV = 1.243 keV
Therefore, the energy of the photon is 1.243 keV.

(c) The kinetic energy (K) of an electron having momentum p, is given by the relation
K = \(\frac{1}{2} \frac{p^{2}}{m}\)
where, m = mass of the electron = 9.1 x 10^-31 kg;
p = 6.63 x 10^-25 kgm s^-1

∴ K = \(\frac{1}{2} \times \frac{\left(6.63 \times 10^{-25}\right)^{2}}{9.1 \times 10^{-31}}\) = 2.415 x 10^-19 J
= \(\frac{2.415 \times 10^{-19}}{1.6 \times 10^{-19}}\) = 1.51 eV
Hence, the kinetic energy of the electron is 1.51 eV.

Question 17.
(a) For what kinetic energy of a neutron will the associated de Broglie wavelength be 1.40x 10^-10 m?
(b) Also, find the de Brogue wavelength of a neutron, in thermal equilibrium with matter, having an average kinetic energy of (3/2) kT at 300 K.
Answer:
(a) de Brogue wavelength of the neutron, λ =1.40 x 10^-10 m
Mass of a neutron,m_n =1. 66 x 10^-27 kg
Planck’s constant, h = 6.63 x 10^-34 Js
Kinetic energy (K) and velocity ( v) are related as
K = \( \frac{1}{2} m_{n} v^{2}\) ……………………………… (1)
de Brogue wavelength (λ) and velocity (v) are related as
λ= \(\frac{h}{m_{n} v}\) ……………………………….. (2)
Using equation (2) in equation (1), we get


Hence, the kinetic energy of the neutron is 6.75 x 10^-21 J or 4.219 x 10^-2 eV.

(b) Temperature of the neutron, T = 300 K
Boltzmann’s constant, k =1.38 x 10^-23 kg m² s^-2 K^-1
Average kinetic energy of the neutron,
K’ = \(\frac{3}{2} \) kT.
= \(\frac{3}{2} \) x 1.38 x 10^-23 x 300 = 6.21 x 10^-21 J
The relation for the de Broglie wavelength is given as
λ ‘ = \(\frac{h}{\sqrt{2 K^{\prime} m_{n}}}\)

where, m_n = 1.66 x 10^-27 kg
h = 6.63 x 10^-34 Js
K’ = 6.21 x 10^-21 J
∴ λ’ = \(\frac{6.63 \times 10^{-34}}{\sqrt{2 \times 6.21 \times 10^{-21} \times 1.66 \times 10^{-27}}}\)
=1.46 x 10^-10
m = 0.146 nm
Therefore, the de Broglie wavelength of the neutron is 0.146 nm.

Question 18.
Show that the wavelength cf electromagnetic radiation is equal to the de Broglie wavelength of its quantum (photon).
Answer:
The momentum of a photon having energy (hv) is given as ’
p = \(\frac{h v}{c}=\frac{h}{\lambda}\)
λ = \(\frac{h}{p}\) ………………………….. (1)
where, λ = wavelength of the electromagnetic radiation
c = speed of light
h = Planck’s constant
de Broglie wavelength of the photon is given as
λ = \(\frac{h}{m v}\)
But p = mv
∴ λ =\(\frac{h}{p}\) ………………………………….. (2)
where, m = mass of the photon
v = velocity of the photon
Hence, it can be inferred from equations (1) and (2) that the wavelength of the electromagnetic radiation is equal to the de Broglie wavelength of the photon.

Question 19.
What is the de Broglie wavelength of a nitrogen molecule in air at 300 K?
Assume that the molecule is moving with the root mean square speed of molecules at this temperature. (Atomic mass of nitrogen = 140076 u)
Answer:
Temperature of the nitrogen molecule, T = 300 K
Atomic mass of nitrogen = 14.0076 u
Hence, mass of the nitrogen molecule, m = 2 x 14.0076 = 28.0152 u
But 1 u = 1.66 x 10^-27 kg
∴ m=28.0152 x 1.66 x 10^-27 kg
Planck’s constant, h = 6.63 x 10^-34 Js
Boltzmann’s constant, k = 1.38 x 10^-23 K^-1
We have the expression that relates mean kinetic energy \(\left(\frac{3}{2} k T\right)\) of the nitrogen molecuLe with the root mean square speed (v_rms) as

Hence, the de Broglie wavelength of the nitrogen molecule is given as
λ = \(\frac{h}{m v_{\text {rms }}}=\frac{h}{\sqrt{3 m k T}}\)
= \(\frac{6.63 \times 10^{-34}}{\sqrt{3 \times 28.0152 \times 1.66 \times 10^{-27} \times 1.38 \times 10^{-23} \times 300}}\)
= 0.028 x 10^-9 m
= 0.028 nm
Therefore, the de Broglie wavelength of the nitrogen molecule is 0.028 nm.

[Additional Exercises]

Question 20.
(a) Estimate the speed with which electrons emitted from a heated emitter of an evacuated tube impinge on the collector maintained at a potential difference of 500 V with respect to the emitter.
Ignore the small initial speeds of the electrons. The specific charge of the electron, i.e., its elm, is given to be 1.76 x 10¹¹ Ckg^-1.
(b) Use the same formula you employ in (a) to obtain electron speed for an collector potential of 10 MV. Do you see what is wrong? In what way is the formula to be modified?
Answer:
(a) Potential difference across the evacuated tube, V = 500 V
Specific charge of the electron, e/m = 1.76 x 10¹¹ C kg^-1
The speed of each emitted electron is given by the relation for kinetic energy as

KE = \(\frac{1}{2}\) mv²
Therefore, the speed of each emitted electron is
KE =\(\frac{1}{2}\) mv² = eV
∴ v = \(\left(\frac{2 e V}{m}\right)^{1 / 2}=\left(2 V \times \frac{e}{m}\right)^{1 / 2} \)
= (2x 500 xl.76 x 10¹¹)^1/2
= 1.327 x 10⁷ m/s

(b) Potential of the anode, V = 10 MV = 10 x 10⁶ = 10⁷ V
The speed of each electron is given as
v = \(\left(2 V \frac{e}{m}\right)^{1 / 2}\)
= (2 x 10⁷x 1.76 x 10¹¹)^1/2
= 1.88 x 10⁹ m/s .
This result is wrong because nothing can move faster than light. In the above formula, the expression (mv² / 2) for energy can only be used in the non-relativistic limit, i. e., for v < < c.
For very high speed problems, relativistic equations must be considered for solving them. In the relativistic limit, the total energy is given as E = mc²
where, m = relativistic mass
m₀ = \(\left(1-\frac{v^{2}}{c^{2}}\right)^{1 / 2}\) = mass of the particle at rest
Kinetic energy is given as
K = mc² – m₀c²

Question 21.
(a) A monoenergetic electron beam with electron speed of 5.20x 10⁶ ms^-1 is subject to a magnetic field of 1.30 x 10 ⁴T normal to the beam velocity. What is the radius of the circle traced by the beam, given elm for electron equals 1.76x 10¹¹ C kg^-1
(b) Is the formula you employ in (a) valid for calculating radius of the path of a 20 MeV electron beam? If not, in what way is it modified? [Note: Exercises 11.20 (b) and 11.21 (b) take you to relativistic mechanics which is beyond the scope of this book. They have been inserted here simply to emphasise the point that the formulas you use in part (a) of the exercises are not valid at very high speeds or energies. See answers at the end to know what ‘very high speed or energy’ means.]
Answer:
(a) Speed of the electron, v = 5.20 x 10⁶ m/s
Magnetic field experienced by the electron, B = 1.30 x 10^-4 T
Specific charge of the electron, e/m = 1.76 x 10¹¹ C kg’
where, e = charge on the electron = 1.6 x 10^-19 C
m = mass of the electron = 9.1 x 10^-31 kg
The force exerted on the electron is given as
F = e\(|\vec{v} \times \vec{B}|\)
= evBsinθ
θ = angle between the magnetic field and the beam velocity.

The magnetic field is normal to the direction of beam.
∴ θ = 90°
F = evB ……………………………. (1)
The beam traces a circular path of radius, r. It is the magnetic field, due to its bending nature, that provides the centripetal force \(\left(F=\frac{m v^{2}}{r}\right)\) for the
beam.
Hence, equation (1) reduces to
evB = \(\frac{m v^{2}}{r}\)
∴ r = \(\frac{m v}{e B}=\frac{v}{\left(\frac{e}{m}\right) B}=\frac{5.20 \times 10^{6}}{\left(1.76 \times 10^{11}\right) \times 1.30 \times 10^{-4}}\)
= 0.227 m
= 0.227 x 100 cm = 22.7 cm
Therefore, the radius of the circular path is 22.7 cm.

(b) Energy of the electron beam, E = 20 MeV = 20 x 10⁶ x 1.6 x 10^-19 J
The energy of the electron is given as
E = \(\frac{1}{2} \) mv²
∴ v = \(\left(\frac{2 E}{m}\right)^{1 / 2}\)
= \(\sqrt{\frac{2 \times 20 \times 10^{6} \times 1.6 \times 10^{-19}}{9.1 \times 10^{-31}}}\) = 2.652 x 10⁹ m/s

This result is incorrect because nothing can move faster than light. In the above formula, the expression (mv² / 2) for energy can only be used in the non-relativistic limit, i. e., for v« c.

When very high speeds are concerned, the relativistic domain comes into consideration. In the relativistic domain, mass is given as
m = m₀ \(\left[1-\frac{v^{2}}{c^{2}}\right]^{1 / 2}\)
where, m₀ = mass of the particle at rest

Hence, the radius of the circular path is given as
r = mv/eB = \(\frac{m_{0} v}{e B \sqrt{\frac{c^{2}-v^{2}}{c^{2}}}}\).

Question 22.
An electron gun with its collector at a potential of 100 V fires out electrons in a spherical hulh containing hydrogen gas at low pressure (~ 10^-2 nun of Hg). A magnetic field of 2.83 x 10^-4 T curves the path of the electrons in a circular orbit of radius 12.0 cm. (The path can be viewed because the gas ions in the path focus the beam by attracting electrons, and emitting light by electron capture; this method is known as the ‘fine beam tube’ method). Determine elm from the data.
Answer:
Potential of the anode, V = 100 V
Magnetic field experienced by the electrons, B = 2.83 x 10,sup>-4 T
Radius of the circular orbit r = 12.0 cm = 12.0 x 10^-2 m
Mass of each electron = m
Charge on each electron = e ‘
Velocity of each electron = v

The energy of each electron is equal to its kinetic energy, i. e.,
\(\frac{1}{2}\) mv² = eV
v² = \(\frac{2 e V}{m}\)
It is the magnetic field, due to its bending nature, that provides the \(\left(F=\frac{m v^{2}}{r}\right) \) for the beam.
Hence, we can write Centripetal force = Magnetic force mv²
\(\frac{m v^{2}}{r}\) = evB
eB = \(\frac{m v}{r}\)
v = \(\frac{e B r}{m}\) ………………………………. (2)
Putting the value of y in equation (1), we get

Therefore, the specific charge ratio (e/ m) is 1.73 x 10¹¹ C kg^-1.

Question 23.
(a) An X-ray tube produces a continuous spectrum of radiation with its short wavelength end at 0.45 A. What is the maximum energy of a photon in the radiation?
(b) From your answer to (a), guess what order of accelerating voltage (for electrons) is required in such a tube?
Answer:
(a) Wavelength produced by the X-ray tube, λ= 0.45Å= 0.45 x 10^-10 m
Planck’s constant, h = 6.63 x 10^-34 Js
Speed of light, c = 3 x 10⁸ m/s
The maximum energy of a photon is given as
E = \(=\frac{h c}{\lambda}\frac{6.63 \times 10^{-34} \times 3 \times 10^{8}}{0.45 \times 10^{-10} \times 1.6 \times 10^{19}} \) = 27.6 x 10³ eV = 27.6 keV
Therefore, the maximum energy of the X-ray photon is 27.6 keV.

(b) Accelerating voltage provides energy to the electrons for producing X-rays.
To get an X-ray of 27.6 keV, the incident electrons must possess at least 27.6 keV of kinetic electric energy. Hence, an accelerating voltage of the order of 30 keV is required for producing X-rays.

Question 24.
In an accelerator experiment on high-energy collisions of electrons with positrons, a certain event is interpreted as an annihilation of an electron-positron pair of total energy 10.2 BeV into two y-rays of equal energy. What is the wavelength associated with each γ-ray? (1 BeV = 10⁹ eV)
Answer:
Total energy of two γ-rays
E = 10.2 BeV
= 10.2 x 10⁹ eV
= 10.2 x 10⁹ x 1.6 x 10^-19 J
= 10.2 x 1.6 x 10^-10

Hence, the energy of each γ-ray
E’ = \(\frac{E}{2}\)
= \(\frac{10.2 \times 1.6 \times 10^{-10}}{2}\)
= 8.16 x 10^-10 J
Planck’s constant, h = 6.63 x 10^-34 Js
Speed of light, c = 3 x 10⁸ m/s
Energy is related to wavelength as
E ‘ = \(\frac{h c}{\lambda}\)
∴ λ = \(\frac{h c}{E^{\prime}}=\frac{6.63 \times 10^{-34} \times 3 \times 10^{8}}{8.16 \times 10^{-10}}\)
= 2.436 x 10^-16 m
Therefore, the wavelength associated with each γ-ray is 2.436 x 10^-16 m.

Question 25.
Estimating the following two numbers should be interesting. The first number will tell you why radio engineers do not need to worry much about photons. The second number tells you why our eye can never ‘count photons’, even in barely detectable light.
(a) The number of photons emitted per second by a Mediumwave transmitter of 10 kW power, emitting radio waves of wavelength 500 m.
(b) The number of photons entering the pupil of our eye per second corresponding to the minimum intensity of white light that we humans can perceive (~ 10^-10 W m^-2). Take the area of the pupil to be about 0.4 cm², and the average frequency of white light to be about 6 x 10¹⁴ Hz.
Answer:
(a) Power of the medium wave transmitter,
P = 10kW = 10⁴ W = 10⁴ J/s
Hence, the energy emitted by the transmitter per second, E = 10⁴
The wavelength of the radio wave, λ = 500 m
The energy of the wave is given as E₁ = \(\frac{h c}{\lambda}\)
where, h = Planck’s constant = 6.63 x 10^-34 Js
c = speed of light = 3 x 10⁸ m/s
∴ E₁ = \(\frac{6.63 \times 10^{-34} \times 3 \times 10^{8}}{500}\) = 3.96 x 10^-28

Let n be the number of photons emitted by the transmitter.
∴ nE₁ = E
n = \(\frac{E}{E_{1}}\) =\(\frac{10^{4}}{3.96 \times 10^{-28}}\) = 2.525 x 10³¹
≈ 3 x 10³¹
The energy (E₁) of a radio photon is very less, but the number of photons (n) emitted per second in a radio wave is very large. The existence of a minimum quantum of energy can be ignored and the total energy of a radio wave can be treated as being continuous.

(b) Intensity of light perceived by the human eye, I = 10^-10 W m^-2
Area of the pupil, A = 0.4 cm² = 0.4 x 10^-4 m²
Frequency of white light, v = 6 x 10¹⁴ Hz
The energy emitted by a photon is given as
E = hv
where, h = Planck’s constant = 6.63 x 10^-34 Js
∴ E = 6.63 x 10^-34 x 6 x 10¹⁴
= 3.96 x 10^-19 J
Let n be the total number of photons falling per second, per unit area of the pupil. The total energy per unit for n falling photons is given as
E = n x 3.96 x 10^-19 Js^-1 m^-2
The energy per unit area per second is the intensity of light.
∴ E = I
n x 3.96 x 10^-19 = 10^-10
n = \(\frac{10^{-10}}{3.96 \times 10^{-19}}\)
= 2.52 x 10⁸ m² s^-1

The total number of photons entering the pupil per second is given as
n_A =n x A
= 2.52 x 10⁸ x 0.4 x 10^-4
= 1.008 x 10⁴ s^-1
This number is not as large as the one found in problem (a), but it is large enough for the human eye to never see the individual photons.

Question 26.
Ultraviolet light of wavelength 2271 Å from a 100 W mercury source irradiates a photo-cell made of molybdenum metal. If the stopping potential is -1.3 V, estimate the work function of the metal. How would the photo-cell respond to a high intensity (~10⁵ Wm^-2) red light of wavelength 6328 Å produced by a He-Ne laser?
Answer:
Wavelength of ultraviolet light, λ = 2271 Å = 2271 x 10^-10 m
Stopping potential of the metal, V₀ = 1.3 V
Planck’s constant, h = 6.63 x 10^-34 Js
Charge on an electron, e = 1.6 x 10^-19 C
Work function of the metal = Φ₀
Frequency of light = v
We have the photo-energy relation from the photoelectric effect as
Φ₀ =hv₀
v₀ = \(\frac{\phi_{0}}{h}\)
= \(\frac{6.64 \times 10^{-19}}{6.63 \times 10^{-34}} \)
= 1.006 x 10¹⁵ Hz = 4.15 eV
Let v₀ be the threshold frequency of the metal.
∴ Φ₀ = hv₀
v₀ = \(\frac{\phi_{0}}{h}\)
= \(\frac{6.64 \times 10^{-19}}{6.63 \times 10^{-34}}\)
= 1.006 x 10¹⁵ Hz

Wavelength of red light, λ_r = 6328 Å = 6328 x 10^-10
∴ Frequency of red light, v_r = \(\frac{c}{\lambda_{r}}=\frac{3 \times 10^{8}}{6328 \times 10^{-10}} \)
= 4.74 x 10¹⁴ Hz
Since v₀ > v_r, the photocell will not respond to the red light produced by the laser.

Question 27.
Monochromatic radiation of wavelength 640.2 nm (1 nm = 10^-9 m) from a neon lamp irradiates photosensitive material made of caesium on tungsten. The stopping voltage is measured to be 0.54 V. The source is replaced by an iron source and its 427.2 nm line irradiates the same photo-cell. Predict the new stopping voltage.
Answer:
Wavelength of the monochromatic radiation, λ = 640.2 nm = 640.2 x 10^-9 m
Stopping potential of the neon lamp, V₀ = 0.54 V
Charge on an electron, e = 1.6 x 10^-19 C
Planck’s constant, h = 6.63 x 10^-34 Js
Let Φ₀ the work function and v be the frequency of emitted light. We have the photo-energy relation from the photoelectric effect as

Wavelength of the radiation emitted from an iron source, λ’ = 427.2 nm = 427.2 x 10^-9 m
Let V’₀ be the new stopping potential. Hence, photo-energy is given as
eV’₀ = \(\frac{h c}{\lambda^{\prime}}-\phi_{0}\)

Hence, the new stopping potential is 1.50 eV.

Question 28.
A mercury lamp is a convenient source for studying frequency dependence of photoelectric emission, since it gives a number of spectral lines ranging from the UV to the red end of the visible spectrum. In our experiment with rubidium photo-cell, the following lines from a mercury source were used :
λ₁ =3650 Å,
λ₂ = 4047 Å,
λ₃ =4358 Å,
λ₄ =5461 Å,
λ₅ =6907 Å,
The stopping voltages, respectively, were measured to be :
V₀₁ = 1.28 V,
V₀₂ = 0.95 V,
V₀₃ = 0.74 V,
V₀₄ = 0.16 V,
V₀₅ = 0 V.
Determine the value of Planck’s constant h, the threshold frequency and work function for the material.
[Note: You will notice that to get h from the data, you will need to know e (which you can take to be 1.6 x 10^-19 C). Experiments of this kind on Na, Li, K, etc. were performed by Millikan, who, using his own value of e (from the oil-drop experiment) confirmed Einstein’s photoelectric equation and at the same time gave an independent estimate of the value of h.]
Answer:
Given, the following wavelength from a mercury source were used
λ₁ =3650 Å, = 3650 x 10^-10 m
λ₂ = 4047 Å, = 4047 x 10^-10m
λ₃ =4358 Å, = 4358 x 10^-10 m
λ₄ =5461 Å, = 5461 x 10^-10 m
λ₅ =6907 Å, = 6907 x 10^-10m
The stopping voltages are as follows
V01 =1.28 V,
V02 = 0.95V,
V03 =0.74V,
V04 =0.16 V,
V5 =0

Frequencies corresponding to wavelengths

As we know that
eV₀ = hv-Φ₀
v₀ = \(\frac{h v}{e}-\frac{\phi_{0}}{e}\)

As the graph between V₀ and frequency v is a straight line.
The slope of this graph gives the values of \(\frac{h}{e} \)

(b) Work function, Φ₀ = hv₀
= 6.574 x 10^-34 x 5 x 10¹⁴
= 32.870 x 10^-20J
= 2.05eV.

Question 29.
The work function for the following metals is given: Na: 2.75 eV; K: 2.30 eV; Mo: 4.17 eV; Ni: 5.15 eV.
Which of these metals will not give photoelectric emission for a radiation of wavelength 3300 Å from a He-Cd laser placed 1 m away from the photo-cell? What happens if the laser is brought nearer and placed 50 cm away?
Answer:
Mo and Ni will not show photoelectric emission in both cases.
Wavelength for the radiation, λ – 3300 Å = 3300 x 10^-10 m
Speed of light, c = 3 x 10⁸ m/s
Planck’s constant, h = 6.63 x 10^-34 Js
The energy of incident radiation is given as
E = \(\frac{h c}{\lambda}\)

= 3.758eV
It can be observed that the energy of the incident radiation is greater than the work function of Na and K only. It is less for Mo and Ni. Hence, Mo and Ni will not show photoelectric emission. If the source of light is brought near the photocells and placed 50 cm away from them, then the intensity of radiation will increase. This does not affect the energy of the radiation. Hence, the result will be the same as before. However, the photoelectrons emitted from Na and K will increase in proportion to intensity.

Question 30.
Light of intensity 10^-5 W m^-2 falls on a sodium photo-cell of surface area 2 cm². Assuming that the top 5 layers of sodium absorb the incident energy, estimate time required for photoelectric emission in the wave-picture of radiation. The work function for the metal is given to be about 2 eV. What is the implication of your answer?
Answer:
Given, intensity of light = 10^-5 W/m²
Area = 2 cm² = 2 x 10^-4 m²
Work function for the metal Φ₀ = 2 eV
Let t be the time.
The effective atomic area of Na = 10^-20 m² and it contains one conduction electron per atom.
Number of conduction electrons in five layers
= \(\frac{5 \times \text { Area of one layer }}{\text { Effective atomic area }}=\frac{5 \times 2 \times 10^{-4}}{10^{-20}}\)
= 10⁷
We know that sodium has one free electron (or conduction electron) per atom.
Incident power on the surface area of photocell
= Incident intensity x Area on the surface area of photocell
= 10^-5 x 2 x 10^-4
= 2 x 10^-9W
The electron present in all the 5 layers of sodium will share the incident energy equally.
Energy absorbed per second per electron,
E = \(\frac{\text { Incident power }}{\text { Number of electrons in five layers }} \)
= \(\frac{2 \times 10^{-9}}{10^{17}}\) = 2 x 10^-26W
Time required for emission by each electron, t = \(\frac{\text { Energy required per electron }}{\text { Energy absorbed per second }} \) = \(\frac{2 \times 1.6 \times 10^{-19}}{2 \times 10^{-26}} \) = 1.6 x 10⁷s
which is about 0.5 yr.
The answer obtained implies that the time of emission of electrons is very large and is not agreement with the observed time of emission. There is no time lag between the incidence of light and the emission of photoelectrons. Thus, it is implied that the wave theory cannot be applied in this experiment.

Question 31.
Crystal diffraction experiments can be performed using X-rays, or electrons accelerated through appropriate voltage. Which probe has greater energy? (For quantitative comparison, take the wavelength of the probe equal to 1 Å, which is of the order of interatomic spacing in the lattice) (m_e = 9.11 x 10^-31 kg).
Answer:
An X-ray probe has a greater energy than an electron probe for the same wavelength.
Wavelength of light emitted from the probe, λ = 1 Å = 10^-10 m
Mass of an electron, me = 9.11 x 10^-31 kg
Planck’s constant, h = 6.63 x 10^-34 Js
Charge on an electron, e = 1.6 x 10^-19 C
The kinetic energy of the electron is given as
K = \(\frac{1}{2} m_{n} v^{2}\)
m_nv = \(\sqrt{2 K m_{n}}\)
where, v = velocity of the electron
m_nv = momentum (p) of the electron

According to the de Brogue principle, the de Brogue wavelength is given as

The energy of a photon,

Hence, a photon has a greater energy than an electron for the same wavelength.

Question 32.
(a) Obtain the de Broglie wavelength of a neutron of kinetic energy 150 eV. As you have seen in Exercise 11.31, an electron beam of this energy is suitable for crystal diffraction experiments. Would a neutron beam of the same energy be equally suitable? Explain. (m = 1.675x 10^-27 kg)
(b) Obtain the de Brogue wavelength associated with thermal neutrons at room temperature (27C). Hence, explain why a fast neutron beam needs to be thermalised with the environment before it can be used for neutron diffraction experiments.
Answer:
(a) de Brogue wavelength= 2.327 x 10^-12 m; neutron is not suitable for
the diffraction experiment Kinetic energy of the neutron, K = 150 eV
= 150 x 1.6 X 10^-19
=2.4 x 10^-17 J
Mass of a neutron, m_n = l.675 x 10^-27 kg
The kinetic energy of the neutron is given by the relation
K = \(\frac{1}{2} m_{n} v^{2}\)
m_nv = \(\sqrt{2 K m_{n}}\)
where, y = velocity of the neutron
m_nv = momentum of the neutron

deBroglie wavelength of the neutron is given as
λ = \(\frac{h}{m_{n} v}=\frac{h}{\sqrt{2 K m_{n}}}\)
It is clear that wavelength is inversely proportional to the square root of mass.
Hence, wavelength decreases with increase in mass and vice versa.
∴ λ = \(\frac{6.63 \times 10^{-34}}{\sqrt{2 \times 2.4 \times 10^{-17} \times 1.675 \times 10^{-27}}}\)
= 2.327 x 10^-12 m
It is given in the previous problem that the interatomic spacing of a crystal is about 1 Å, i.e., 10^-10 m.
Hence, the interatomic spacing is about a hundred times greater. Hence, a neutron beam of energy 150 eV is not
suitable for diffraction experiments.

(b) de Brogue wavelength =1.447 x 10^-10 m
Room temperature, T = 27°C = 27+ 273 = 300 K
The average kinetic energy of the neutron is given as
E=\(\frac{3}{2}\) kT
where, k = Boltzmann’s constant = 1.38 x10^-23 J mol^-1K^-1
The wavelength of the neutron is given as
λ = \(\frac{h}{\sqrt{2 m_{n} E}}=\frac{h}{\sqrt{3 m_{n} k T}}\)
= \(\frac{6.63 \times 10^{-34}}{\sqrt{3 \times 1.675 \times 10^{-27} \times 1.38 \times 10^{-23} \times 300}}\)
=1.447 x 10^-10 m
This wavelength is comparable to the interatomic spacing of a crystal. Hence, the high energy neutron beam should first be thermalised, before using it for diffraction.

Question 33.
An electron microscope uses electrons accelerated by a voltage of 50 kV. Determine the de Brogue wavelength associated with the electrons, if other factors (such as numerical aperture, etc.) are taken to be roughly the same, how does the resolving power of an electron microscope compare with that of an optical microscope which uses yellow light?
Answer:
Electrons are accelerated by a voltage, V = 50 kV = 50 x 10³ V
Charge on an electron, e 1.6 x 10^-19 C
Mass of an electron, me = 9.11 x 10^-31 kg
Wavelength of yellow light = 5.9 x 10^-7 m

The kinetic energy of the electron is given as
E=eV
=l.6 x 10^-19x 50x 10³
= 8 x 10^-15 J
de Brogue wavelength is given by the relation
λ = \(\frac{h}{\sqrt{2 m_{e} E}}\)
= \(\frac{6.63 \times 10^{-34}}{\sqrt{2 \times 9.11 \times 10^{-31} \times 8 \times 10^{-15}}}\)
= 5.467 x 10^-12 m
This wavelength is nearly 10⁵ times less than the wavelength of yellow light. The resolving power of a microscope is inversely proportional to the wavelength of light used. Thus, the resolving power of an electron microscope is nearly 10⁵ times that of an optical microscope.

Question 34.
The wavelength of a probe is roughly a measure of the size of a structure that it can probe in some detail. The quark structure of protons and neutrons appears at the minute length scale of 10^-15 m or less. This structure was first, probed in early 1970s using high energy electron beams produced by a linear accelerator at Stanford, USA. Guess what might have been the order of energy of these electron beams. (Rest mass energy of electron = 0.511 MeV.)
Answer:
Wavelength of a proton or a neutron, λ ≈ 10^-15 m
Rest mass energy of an electron,
m₀c² =0.511 MeV
= 0.511 x 10⁶ x 1.6 x 10^-19
= 0.8176 x 10^-13 J
Planck’s constant, h = 6.63 x 10^-34 Js
Speed of light, c = 3 x 10⁸ m/s ,

The momentum of a proton or a neutron is given as
p = \(\frac{h}{\lambda}\)
= \(\frac{6.63 \times 10^{-34}}{10^{-15}}\) = 6.6 x 10^-19 kg m/s
The relativistic relation for energy (E) is given as
E² = p²c² +m₀²c⁴
= (6.6x 10^-19 x 3 x 10⁸)² + (0.8176 x 10^-13)²
= 392.04 x 10^-22 +0.6685 x 10^-26
≈ 392.04 x 10^-22
∴ E = 1.98x 10^-10 J
Thus, the electron energy emitted from the accelerator at Stanford, USA might be of the order of 1.24 BeV.

Question 35.
Find the typical de Broglie wavelength associated with a He atom in helium gas at room temperature (27°C) and 1 atm pressure, and compare it with the mean separation between two atoms under these conditions.
Answer:
de Broglie wavelength associated with He atom = 0.7268 x 10^-10 m .
Room temperature, T = 27°C =27 + 273 = 300 K
Atmospheric pressure, P = 1 atm = 1.01 x 10⁵ Pa
Atomic weight of a He atom = 4
Avogadro’s number, N_A = 6.023 x 10²³
Boltzmann’s constant, k = 1.38 x 10^-23 J mol^-1 K^-1

Average energy of a gas at temperature T, is given as
E = \(\frac{3}{2}\) kT
de Broglie wavelength is given by the relation
λ = \(\frac{h}{\sqrt{2 m E}}\)
where, m = mass of a He atom

We have the ideal gas formula
PV = RT
PV = kNT
∵ \(\frac{V}{N}=\frac{k T}{P}\)
where V = volume of the gas
N = number of moles of the gas
Mean separation between two atoms of the gas is given by the relation
r = \(\left(\frac{V}{N}\right)^{1 / 3}=\left(\frac{k T}{P}\right)^{1 / 3}=\left[\frac{1.38 \times 10^{-23} \times 300}{1.01 \times 10^{5}}\right]^{1 / 3}\)
= 3.35 x 10^-9 m
Hence, the mean separation between the atoms is much greater than the de Broglie wavelength.

Question 36.
Compute the typical de Broglie wavelength of an electron in a metal at 2 7° C and compare it with the mean separation between two electrons in a metal which is given to be about 2 x 10¹⁰ m. [Note: Exercises 11.35 and 11.36 reveal that while the wave-packets associated with gaseous molecules under ordinary conditions are non-overlapping, the electron wave- packets in a metal strongly overlap with one another. This suggests that whereas molecules in an ordinary gas can be distinguished apart, electrons in a metal cannot be distinguished apart from one another. This indistinguishability has many fundamental implications which you will explore in more advanced Physics courses.]
Answer:
Temperature, T = 27°C = 27 +273 = 300 K
Mean separation between two electrons, r = 2 x 10^-10 m
de Broglie wavelength of an electron is given as
λ = \(\frac{h}{\sqrt{3 m k T}}\)
where,
h = Planck’s constant = 6.63 x 10^-34 Js
m = Mass of an electron = 9.11 x 10 ^-31 kg
k = Boltzmann’s constant = 1.38 x 10^-23 J mol^-1 K^-1
∴ λ = \(\frac{6.63 \times 10^{-34}}{\sqrt{3 \times 9.11 \times 10^{-31} \times 1.38 \times 10^{-23} \times 300}}\)
= 6.2 x 10⁹ m
Hence, the de Broglie wavelength is much greater than the given inter-electron separation.

Question 37.
Answer the following questions :
(a) Quarks inside protons and neutrons are thought to carry fractional charges [(+2/3)e ; (-1/3)e]. Why do they not show up in Millikan’s oil-drop experiment?
(b) What is so special about the combination e/m? Why do we not simply talk of e and m separately?
(c) Why should gases be insulators at ordinary pressures and start conducting at very low pressures?
(d) Every metal has a definite work function. Why do all photoelectrons not come out with the same energy if incident radiation is monochromatic? Why is there an energy distribution of photoelectrons?
(e) The energy and momentum of an electron are related to the frequency and wavelength of the associated matter wave by the relations :
E = hv, p = \(\frac{\boldsymbol{h}}{\lambda}\)
But while the value of λ is physically significant, the value of v (and therefore, the value of the phase speed vλ) has no physical significance. Why?
Answer:
(a) Quarks inside protons and neutrons carry fractional charges. This is because nuclear force increases extremely if they are pulled apart. Therefore, fractional charges may exist in nature; observable charges are siti the integral multiple of an electrical charge.

(b) Thè basic relations for electric field and magnetic field are \(\left(e V=\frac{1}{2} m v^{2}\right)\) and \(\left(e B v=\frac{m v^{2}}{r}\right) \) respectively.

These relations include e (electric charge), y (velocity), m (mass), V (potential), r (radius), and B (magnetic field)._These relations give the value of velocity of an electron as \(\left(v=\sqrt{2 v\left(\frac{e}{m}\right)}\right) \text { and }\left(v=B r\left(\frac{e}{m}\right)\right)\) respectively. It can be observed from these relations that the dynamics of an electron is determined not by e and m separately, but by the ratio e / m.

(c) At atmospheric pressure, the ions of gases have no chance of reaching their respective electrons because of collision and recombination with other gas molecules. Hence, gases are insulators at atmospheric pressure. At low pressure, ions have a chance of reaching their respective electrodes and constitute a current. Hence, they conduct electricity at these pressures.

(d) The work function of a metal is the minimum energy required for a conduction electron to get out of the metal surface. All the electrons in an atom do not have the same energy level. When a ray having some photon energy is incident on a metal surface, the electrons come out from different levels with different energies. Hence, these emitted electrons show different energy distributions.

(e) The absolute value of energy of a particle is arbitrary within the additive constant. Hence, wavelength (λ) is significant, but the frequency (v) associated with an electron has no direct physical significance. Therefore, the product vλ (phase speed) has no physical significance. Group speed is given as

This Quantity has a physical meaning.

Punjab State Board PSEB 12th Class Physics Book Solutions Chapter 12 Atoms Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Physics Chapter 12 Atoms

PSEB 12th Class Physics Guide Atoms Textbook Questions and Answers

Question 1.
Choose the correct alternative from the clues given at the end of the each statement:
(a) The size of the atom in Thomson’s model is ………………….. the atomic size in Rutherford’s model, (much greater than/no different from/much less than.)
(b) In the ground state of ………………………………… electrons are in stable equilibrium, while in …………………….. electrons always experience a net force. (Thomson’s model/Rutherford’s model.)
(c) A classical atom based on ……………………………. is doomed to collapse. (Thomson’s model/Rutherford’s model.)
(d) An atom has a nearly continuous mass distribution in a ………………………… but has a highly non-uniform mass distribution in …………………….. (Thomson’s model/Rutherford’s model.)
(e) The positively charged part of the atom possesses most of ………………………. the mass in ………………….. (Rutherford’s model/both the models.)
Answer:
(a) The size of the atom in Thomson’s model is no different from the atomic size in Rutherford’s model.
(b) In the ground state of Thomson’s model, electrons are in stable equilibrium while, in Rutherford’s model, electrons always experience a net force.
(c) A classical atom based on Rutherford’s model is doomed to collapse.
(d) An atom has a nearly continuous mass distribution in Thomson’s model but has a highly non-uniform mass distribution in Rutherford’s model.
(e) The positively charged part of the atom possesses most of the mass in both the models.

Question 2.
Suppose you are given a chance to repeat the alpha-particle scattering experiment using a thin sheet of solid hydrogen in place of the gold foil. (Hydrogen is a solid at temperatures below 14 K.) What results do you expect?
Answer:
The basic purpose of scattering experiment is not completed because solid hydrogen will be a much lighter target as compared to the alpha particle acting as a projectile. By using the conditions of elastic collisions, the hydrogen will move much faster as compared to alpha after the collision. We cannot determine the size of hydrogen nucleus.

Question 3.
What is the shortest wavelength present in the Paschen series of spectral lines?
Answer:
Rydberg’s formula is given as
\(\frac{h c}{\lambda}\) = \(21.76 \times 10^{-19}\left[\frac{1}{n_{1}^{2}}-\frac{1}{n_{2}^{2}}\right]\)
where, h = Planck’s constant = 6.63 x 10^-34 Js
c=Speed oflight=3 x 10⁸ m/s (n₁ and n₂ are integers)
The shortest wavelength present in the Paschen series of the spectral lines
is given for values n₁ = 3 and n₂ = ∞

= 822.65 nm

Question 4.
A difference of 2.3 eV separates two energy levels in an atom. What is the frequency of radiation emitted when the atom makes a transition from the upper level to the lower level?
Answer:
According to Bohr’s postulate
E₂ – E₁ = hv
∴ Frequency of emitted radiation

Question 5.
The ground state energy of hydrogen atom is -13.6 eV. What are the kinetic and potential energies of the electron in this state?
Answer:
Given, the ground state energy of hydrogen atom
E=-13.6eV
We know that,
Kinetic Energy, E_K = -E = 13.6 eV
Potential Energy E_p = -2KE =-2 x 13.6 = -27.2eV

Question 6.
A hydrogen atom initially In the ground level absorbs a photon, which excites it to the n = 4 level. Determine the wavelength and frequency of photons.
Answer:
The energy levels of H-atom are given by
E_n = \(-\frac{R h c}{n^{2}}\)
For given transition n₁ =1, n₂ = 4
∴ E₁ = \(-\frac{R h c}{1^{2}}\) ,E₂= \(-\frac{R h c}{4^{2}}\)
∴ Energy of absorbed photon
ΔE=E₂ -E₁ =Rhc \(\left(\frac{1}{1^{2}}-\frac{1}{4^{2}}\right)\)
or
ΔE = \(\frac{15}{16}\) Rhc ………………………….. (1)
∴ The wavelength of absorbed photon λ is given by

Question 7.
(a) Using the Bohr’s model, calculate the speed of the electron in a hydrogen atom in the n =1, 2, and 3 levels.
(b) Calculate the orbital period in each of these levels.
Answer:
(a) Let y1 be the orbital speed of the electron in a hydrogen atom in the ground state level, n₁ =1.
For charge (e) of an electron, v₁ is given by the relation,
v₁ = \(\frac{e^{2}}{n_{1} 4 \pi \varepsilon_{0}\left(\frac{h}{2 \pi}\right)}=\frac{e^{2}}{2 \varepsilon_{0} h} \)
where, e=1.6 x 10^-19 C
\(\varepsilon_{0}\) = Permittivity of free space = 8.85 x 10^-12 N^-1 C²m²
h = Planck’s constant = 6.63 x 10^-34 Js
∴ v₁ = \(\frac{\left(1.6 \times 10^{-19}\right)^{2}}{2 \times 8.85 \times 10^{-12} \times 6.63 \times 10^{-34}}\)
= 0.0218 x 10⁸ =2.18 x 10⁶ m/s

For level n₂ =2, we can write the relation for the corresponding orbital speed as
v₂ = \(\frac{e^{2}}{n_{2} 2 \varepsilon_{0} h}\) = \(\frac{\left(1.6 \times 10^{-19}\right)^{2}}{2 \times 2 \times 8.85 \times 10^{-12} \times 6.63 \times 10^{-34}}\) = 1.09 x 10⁶ m/s
And, for n₃ =3, we can write the relation for the corresponding orbital speed as


Hence, the speed of the electron in a hydrogen atom in n = 1, n = 2 and n = 3 is 2.18 x 10⁶ m/s,
1.09 x 10⁶ m/s, 7.27 x 10⁵ m/s respectively.

(b) Orbital period of electron is given by
T = \(\frac{2 \pi r}{v}\)
Radius of nth orbit
r_n = \(\frac{n^{2} h^{2}}{4 \pi^{2} K m e^{2}}\)
∴ r₁ = \(\frac{(1)^{2} \times\left(6.63 \times 10^{-34}\right)^{2}}{4 \times 9.87 \times\left(9 \times 10^{9}\right) \times 9 \times 10^{-31} \times\left(1.6 \times 10^{-19}\right)}\)
= 0.53 x 10^-10 m
For n=1, T₁ = \(\frac{2 \pi r_{1}}{v_{1}}\)
= \(\frac{2 \times 3.14 \times 0.53 \times 10^{-10}}{2.19 \times 10^{6}}\) = 1.52 x 10^-16s

For n = 2, radius r_n = n²r₁
∴ r₂ =’2².r₁ =4 x0.53 x 10^-10
and velocity v_n, = \(\frac{v_{1}}{n}\)
∴ v₂ = \(\frac{v_{1}}{2}=\frac{2.19 \times 10^{6}}{2}\)
Time period T₂ = \(\frac{2 \times 3.14 \times 4 \times 0.53 \times 10^{-10} \times 2}{2.19 \times 10^{6}}\)
=1216 x 10^-15 s
For n=3,radius r³ =3²,r₁ =9r₁ =9 x 0.53 x 10^-10m and velocity v₃ = \(\frac{v_{1}}{3}=\frac{2.19 \times 10^{6}}{3}\) m/s
Time period T₃ = \(\frac{2 \pi r_{3}}{v_{3}}=\frac{2 \times 3.14 \times 9 \times 0.53 \times 10^{-10} \times 3}{2.19 \times 10^{6}}\) = 4.1 x 10^-15 s

Question 8.
The radius of the innermost electron orbit of a hydrogen atom is 5.3 x 10^-11 m. What are the radii of the n = 2 and n = 3 orbits?
Answer:
The radius of the innermost electron orbit of a hydrogen atom, r₁ = 5.3 x 10^-11 m.
Let r₂ be the radius of the orbit at n = 2.
It is related to the radius of the innermost orbit as r₂ = (n)²r₁ = (2)² x 5.3 x 10^-11
= 4 x 5.3 x 10^-11 = 2.12 x 10^-10m
For n = 3, we can write the corresponding electron radius as
r³ =(n)²r₁ = (3)² x 5.3 x 10^-11
n = 9 x 5.3 x 10^-11 = 4.77 x 10^-10m
Hence, the radii of an electron for n = 2 and n = 3 orbits are 2.12 x 10^-10 m and 4.77 x 10^-10 m respectively.

Question 9.
A 12.5 eV electron beam is used to bombard gaseous hydrogen at room temperature. What series of wavelengths will be emitted?
Answer:
It is given that the energy of the electron beam used to bombard gaseous hydrogen at room temperature is 12.5 eV. Also, the energy of the gaseous hydrogen in its ground state at room temperature is -13.6 eV. When gaseous hydrogen is bombarded with an electron beam, the energy of the gaseous hydrogen becomes -13.6 + 12.5 eV i. e., -1.1 eV.

Orbital energy is related to orbit level (n) as
E = \(\frac{-13.6}{(n)^{2}}\)eV
For n=3, E = \(\frac{-13.6}{(3)^{2}}=\frac{-13.6}{9}\) = -1.5 eV
This energy is approximately equal to the energy of gaseous hydrogen. it can be concluded that the electron has jumped from n I to n = 3 level.

During its de-excitation, the electrons can jump from n = 3 to n = 1 directly, which forms a line of the Lyman series of the hydrogen spectrum.
We have the relation for wave number for Lyman series as
\(\frac{1}{\lambda}=R_{y}\left(\frac{1}{1^{2}}-\frac{1}{n^{2}}\right)\)
where, R_y =Rydberg constant = 1.097 x 10⁷ m^-1,
λ = Wavelength of radiation emitted by the transition of the electron for
n =3,
We can obtain λ as
\(\frac{1}{\lambda}\) = 1.097 x 10⁷\(\left(\frac{1}{1^{2}}-\frac{1}{3^{2}}\right)\)
= 1.097 x 10⁷ \(\left(1-\frac{1}{9}\right)\) = 1.097 x 10⁷x \(\frac{8}{9}\)

λ = \(\frac{9}{8 \times 1.097 \times 10^{7}}\) = 102.55nm
If the electron jumps from n = 2 to n = 1, then the wavelength of the radiation is given as
\(\frac{1}{\lambda}\) = 1.097 x 10⁷ \(\left(\frac{1}{1^{2}}-\frac{1}{2^{2}}\right)\)
= 1.097 x 10⁷\(\left(1-\frac{1}{4}\right)\) = 1.097 x 10⁷x \(\frac{3}{4}\)
λ = \(\frac{4}{1.097 \times 10^{7} \times 3}\) = 121.54 nm

If the transition takes place from n = 3 to n = 2, then the wavelength of the radiation is given as

This radiation corresponds to the Balmer series of the hydrogen spectrum. Hence, in Lyman series, two wavelengths i. e., 102.54 nm, and 121.55 nm are emitted. And in the Balmer series, one wavelength i. e., 656.33 nm is emitted.

Question 10.
In accordance with the Bohr’s model, find the quantum number that characterizes the earth’s revolution around the sun in an orbit of radius 1.5 x 10¹¹ m with orbital speed 3 x 10⁴ m/s. (Mass of earth = 6.0 x 10²⁴ kg.)
Answer:
Radius of the orbit of the Earth around the Sun, r = 1.5 x 10¹¹ m
Orbital speed of the Earth, v = 3 x 10⁴ m/s
Mass of the Earth, m = 6.0 x 10²⁴ kg
According to Bohr’s model, angular momentum is quantized and given as
mvr = \(\frac{n h}{2 \pi}\)

where, h = Planck’s constant = 6.63 x 10^-34 Js
n = Quantum number
∴ n = \(\frac{m v r 2 \pi}{h}\)
= \(\frac{2 \pi \times 6 \times 10^{24} \times 3 \times 10^{4} \times 1.5 \times 10^{11}}{6.63 \times 10^{-34}} \) = 25.61 x 10⁷³ = 2.6 x 10⁷⁴
Hence, the quanta number that characterizes the Earth’s revolution is 2.6 x 10⁷⁴.

Additional Exercises

Question 11.
Answer the following questions, which help you to understand the difference between Thomson’s model and Rutherford’s model better.
(a) Is the average angle of deflection of α-particles by a thin gold foil predicted by Thomson’s model much less, about the same, or much greater than that predicted by Rutherford’s model?

(b) Is the probability of backward scattering (i. e., scattering of α-particles at angles greater than 90°) predicted by Thomson’s model much less, about the same, or much greater than that predicted by Rutherford’s model?

(c) Keeping other factors fixed, it is found experimentally that for small thickness t, the number of α-particles scattered at moderate angles is proportional to t. What clue does this linear dependence on t provide?

(d) In which model is it completely wrong to ignore multiple scattering for the calculation of average angle of scattering of α-particles by. a thin foil?
Answer:
(a) The average angle of deflection of α-particles by a thin gold foil predicted by Thomson’s model is about the same size as predicted by Rutherford’s model. This is because the average angle was taken in both models.

(b) The probability of scattering of α-particles at angles greater than 90° predicted by Thomson’s model is much less than that predicted by Rutherford’s model. This is because there is no such massive central core called the nucleus in Rutherford’s model.

(c) Scattering is mainly due to single collisions. The chances of a single collision increase linearly with the number of target atoms. Since the number of target atoms increases with an increase in thickness, the collision probability depends linearly on the thickness of the target.

(d) It is wrong to ignore multiple scattering in Thomson’s model for the calculation of average angle of scattering of α-particles by a thin foil. This is because a single collision causes very little deflection in this model. Hence, the observed average scattering angle can be explained only by considering multiple scattering.

Question 12.
The gravitational attraction between electron and proton in a hydrogen atom is weaker than the Coulomb attraction by a factor of about 10^-40. An alternative way of looking at this fact is to estimate the radius of the first Bohr orbit of a hydrogen atom if the electron and proton were bound by gravitational attraction. You will find the answer interesting.
Answer:
Radius of the first Bohr orbit is given by the relation,
r₁ = \(\frac{4 \pi \varepsilon_{0}\left(\frac{h}{2 \pi}\right)^{2}}{m_{e} e^{2}}\) ……………….. (i)
where, ε₀ = Permittivity of free space
h = Planck’s constant = 6.63 x 10^-34 Js
m_e = Mass of an electron = 9.1 x 10^-31 kg
e = Charge of an electron = 1.9x 10^-19C
m_p = Mass of a proton = 1.67 x 10^-27 kg
r = Distance between the electron and the proton Coulomb attraction between an electron and a proton is given as
F_C = \(\frac{e^{2}}{4 \pi \varepsilon_{0} r^{2}} \) ………………………….. (2)

Gravitational force of attraction between an electron and a proton is
F_G = \(\frac{G m_{p} m_{e}}{r^{2}}\) ……………………………………. (3)
where, G = Gravitational constant = 6.67 x 10^-11 N m²/kg²
If the electrostatic (Coulomb) force and the gravitational force between an electron and a proton are equal, then we can write
∴ F_G = F_C
\(\frac{G m_{p} m_{e}}{r^{2}}\) = \(\frac{e^{2}}{4 \pi \varepsilon_{0} r^{2}}\)
\(\frac{e^{2}}{4 \pi \varepsilon_{0} r^{2}}\) = Gm_pm_e …………………………. (4)
Putting the value of equation (4) in equation (1), we get

Question 13.
Obtain an expression for the frequency of radiation emitted when a hydrogen atom de-excites from level n to level (n -1). For large n, show that this frequency equals the classical frequency of revolution of the electron in the orbit.
Answer:
It is given that a hydrogen atom de-excites from an upper level (n) to a lower level (n —1). We have the relation for energy (E₁) of radiation at level n as
E₁ = hv₁ = \(\frac{h m e^{4}}{(4 \pi)^{3} \varepsilon_{0}^{2}\left(\frac{h}{2 \pi}\right)^{3}} \times\left(\frac{1}{n^{2}}\right)\)
where, v₁ = Frequency of radiation at level n
h = Planck’s constant
m = Mass of hydrogen atom
e = Charge on an electron
ε_o = Permittivity of free space

Now, the relation for energy (E₂) of radiation at level (n -1) is given as
E₂ = hv₂ = \(\frac{h m e^{4}}{(4 \pi)^{3} \varepsilon_{0}^{2}\left(\frac{h}{2 \pi}\right)^{3}} \times \frac{1}{(n-1)^{2}}\) ………………………… (2)
where, v₂ = Frequency of radiation at level (n -1)
Energy (E) released as a result of de-excitation
E = E₂ – E₁ hv= E₂ – E ₁ ………………….. (3)
where, v = Frequency of radiation emitted
Putting values from equations (1) and (2) in equation (3), we get

For large n, we can write (2 n -1) ≈ 2 n and (n-1) ≈ n.
V = \(\frac{m e^{4}}{32 \pi^{3} \varepsilon_{0}^{2}\left(\frac{h}{2 \pi}\right)^{3} n^{3}} \)
∵ v = \(\frac{m e^{4}}{32 \pi^{3} \varepsilon_{0}^{2}\left(\frac{h}{2 \pi}\right)^{3} n^{3}}\) ………………….. (4)
Classical relation of frequency of revolution of an electron is given as
V_c = \(\frac{v}{2 \pi r}\) ……………………………….. (5)
where, velocity of the electron in the n^th orbit is given as
v = \(\frac{e^{2}}{4 \pi \varepsilon_{0}\left(\frac{h}{2 \pi}\right) n}\) ……………………………… (5)
And, radius of the n^th orbit is given as
v = \(\frac{e^{2}}{4 \pi \varepsilon_{0}\left(\frac{h}{2 \pi}\right) n}\) ………………………………(6)
Putting the values of equations (6) and (7) in equation (5), we get
V_c = \( \frac{m e^{4}}{32 \pi^{3} \varepsilon_{0}^{2}\left(\frac{h}{2 \pi}\right)^{3} n^{3}}\)
Hence, the frequency of radiation emitted by the hydrogen atom is equal to its classical orbital frequency.

Question 14.
Classically, an electron can be in any orbit around the nucleus of an atom. Then what determines the typical atomic size? Why is an atom not, say, a thousand times bigger than its typical size? The question had greatly puzzled Bohr before he arrived at his famous model of the atom that you have learnt in the text.

To simulate what he might well have done before his discovery, let us play as follows with the basic constants of nature and see if we can get a quantity with the dimensions of length that is roughly equal to the known size of an atom (~10^-10 m).

(a) Construct a quantity with the dimensions of length from the fundamental constants e, me and c. Determine its numerical value.

(b) You will find that the length obtained in (a) is many orders of magnitude smaller than the atomic dimensions. Further, it involves c. But energies of atoms are mostly in non-relativistic domain where c is not expected to play any role. This is what may have suggested Bohr to discard c and look for ‘something else’ to get the right atomic size. Now, the Planck’s constant h had already made its appearance elsewhere. Bohr’s great insight lay in recognizing that h, me, and e will yield the right atomic size.

Construct a quantity with the dimension of length from h, me, and e and confirm that its numerical value has indeed the correct order of magnitude.
Answer:
(a) Charge on an electron, e = 1.6 x 10^-19 C
Mass of an electron, m_e = 9.1 x 10^-31 kg
Speed of light, c = 3 x 10⁸ m/s
Let us take a quantity involving the given quantities as \(\left(\frac{e^{2}}{4 \pi \varepsilon_{0} m_{e} c^{2}}\right)\)
where, ε₀ = Permittivity of free space and, \(\frac{1}{4 \pi \varepsilon_{0}}\) = 9 x 10⁹ Nm²C^-2 .
The numerical value of the taken quantity will be

Hence, the numerical value of the taken quantity is much smaller than the typical size of an atom.

(b) Charge on an electron, e = 1.6 x 10^-19 C
Mass of an electron, me = 9.1 x 10^-31 kg
Planck’s constant, h = 6.63 x 10^-34 Js
Let us take a quantity involving the given quantities as \(\frac{4 \pi \varepsilon_{0}\left(\frac{h}{2 \pi}\right)^{2}}{m_{e} e^{2}}\)
where, ε₀ = Permittivity of free space
and, \(\frac{1}{4 \pi \varepsilon_{0}}\) = 9 x 10⁹Nm²C^-2

The numerical value of the taken quantity will be
\(\frac{1}{4 \pi \varepsilon_{0}} \times \frac{\left(\frac{h}{2 \pi}\right)^{2}}{m_{e} e^{2}}=9 \times 10^{9} \times \frac{\left(\frac{6.63 \times 10^{-34}}{2 \times 3.14}\right)^{2}}{9.1 \times 10^{-31} \times\left(1.6 \times 10^{-19}\right)^{2}} \)
= 0.53 x 10^-10 m
Hence, the value of the quantity taken is of the order of the atomic size.

Question 15.
The total energy of an electron in the first excited state of the hydrogen atom is about -3.4 eV.
(a) What is the kinetic energy of the electron in this state?
(b) What is the potential energy of the electron in this state?
(c) Which of the answers above would change if the choice of the zero of potential energy is changed?
Answer:
(a) Total energy of the electron, E = -3.4 eV ’
Kinetic energy of the electron is equal to the negative of the total energy.
⇒ K = -E
= -(-3.4) = + 3.4 eV
Hence, the kinetic energy of the electron in the given state is + 3.4 eV.

(b) Potential energy (JJ) of the electron is equal to the negative of twice of its kinetic energy.
⇒ U = -2 K
= -2 x 3.4 = -6.8 eV
Hence, the potential energy of the electron in the given state is -6.8 eV.

(c) The potential energy of a system depends on the reference point taken. Here, the potential energy of the reference point is taken as zero. If the reference point is changed, then the value of the potential energy of the system also changes. Since total energy is the sum of kinetic and potential energies, total energy of the system will also change.

Question 16.
If Bohr’s quantization postulate (angular momentum = nh/2π) is a basic law of nature, it should be equally valid for the case of planetary motion also. Why then do we never speak of quantization of orbits of planets around the sun?
Answer:
We never speak of quantization of orbits of planets around the Sun because the angular momentum associated with planetary motion is largely relative to the value of Planck’s constant (h).
The angular momentum of the Earth in its orbit is of the order of 10⁷⁰h. This leads to a very high value of quantum levels n of the order of 10⁷⁰.
For large values of n, successive energies and angular momenta are relatively very small. Hence, the quantum levels for planetary motion are considered continuous.

Question 17.
Obtain the first Bohr’s radius and the ground state energy of a muonic hydrogen atom an atom in which a negatively
charged muon (μ^– ) of mass about 207 m_e orbits around a proton.
Answer:
Muonic hydrogen is the atom in which a negatively charged muon of mass about 207 m_e revolves around a proton.
In Bohr’s atom model, r ∝ \(\frac{1}{m}\)
∵ \(\frac{r_{\text {muon }}}{r_{\text {electron }}}=\frac{m_{e}}{m_{\mu}}=\frac{m_{e}}{207 m_{e}}=\frac{1}{207}\) [ ∵m_μ = 207 m_e]
Here, r_e is radius of orbit of electron in hydrogen atom is 0.53 Å.

Punjab State Board PSEB 12th Class Physics Book Solutions Chapter 2 Electrostatic Potential and Capacitance Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance

PSEB 12th Class Physics Guide Electrostatic Potential and Capacitance Textbook Questions and Answers

Question 1.
Two charges 5 × 10^-8 C and -3 × 10^-8 C are located 16 cm apart. At what point(s) on the line joining the two charges is the electric potential zero? Take the potential at infinity to be zero.
Answer:
There are two charges,
q ₁ = 5 × 10^-8 C
q₂ = -3 × 10^-8 C
Distance between the two charges, d =16 cm = 0.16 m
Consider a point P on the line joining the two charges, as shown in the given figure

r = Distance of point P from charge q₁
Let the electric potential (V) at point P be zero. r.
Potential at point P is the sum of potentials caused by charges q₁ and q₂ respectively.

∴ r = 0.1m = 10 cm
Therefore, the potential is zero at a distance of 10 cm from the positive charge between the charges.

Suppose point P is outside the system of two charges at a distance s from the negative charge, where potential is zero, as shown in the following figure:

For this arrangement, potential is given by,

∴ s = 0.4 m = 40 cm
Therefore, the potential is zero at a distance of 40 cm from the positive charge outside the system of charges.

Question 2.
A regular hexagon of side 10 cm has a charge 5 μC at each of its vertices. Calculate the potential at the centre of the hexagon.
Answer:
The given figure shows six equal amount of charges q, at the vertices of a regular hexagon.

where, charge, q = 5μC = 5 × 10^-6C
Side of the hexagon,
l = AB = BC = CD = DE = EF = FA = 10 cm
Distance of each vertex from centre, O, d = 10 cm = 0.1 m
Electric potential at point O,
V = \(\frac{6 \times q}{4 \pi \varepsilon_{0} d}\)
∴ \(\frac{1}{4 \pi \varepsilon_{0}}\) = 9 × 10⁹NC^-2m^-2
∴ V = \(\frac{6 \times 9 \times 10^{9} \times 5 \times 10^{-6}}{0.1}\) = 2.7 × 10⁶ V
Therefore, the potential at the centre of the hexagon is 2.7 × 10⁶ V.

Question 3.
Two charges 2 μC and -2μC are placed at points A and B 6 cm apart.
(a) Identify an equipotential surface of the system.
(b) What is the direction of the electric field at every point on this surface?
Answer:
(a) Here, two charges 2 μC and -2μC are situated at points A and B.
∴ AB = 6 cm = 0.06 m

For the given system of two charges, the equipotential surface is a plane normal to the line joining points A and B. The plane passes through the mid point C of the line AB. The potential at C is

Thus potential at all points lying on this plane is equal and is zero, so it is an equipotential surface.

(b) We know that the electric field always acts from +ve to -ve charge, thus here the electric field acts from point A (having +ve charge) to point B (having -ve charge) and is normal to the equipotential surface.

Question 4.
A spherical conductor of radius 12 cm has a charge of 1.6 x 10^-7 C distributed uniformly on its surface. What is the electric field
(a) inside the sphere
(b) just outside the sphere
(c) at a point 18 cm from the centre of the sphere?
Answer:
Radius of the spherical conductor, r = 12cm = 0.12m
Charge is uniformly distributed over the conductor, q = 1.6 x 10^-7C
(a) Electric field inside a spherical conductor is zero. This is because if there is field inside the conductor, then charges will move to neutralize it.

(b) Electric field E just outside the conductor is given by the relation,
E = \(\frac{q}{4 \pi \varepsilon_{0} r^{2}}\)
\(=\frac{1.6 \times 10^{-7} \times 9 \times 10^{5}}{(0.12)^{2}}[latex] = 10⁵ NC ^-1
(0.12) 2
Therefore, the electric field just outside the sphere is 10⁵ NC^-1

(c) Electric field at a point 18 m from the centre of the sphere = E₁
Distance of the point from the centre, d=18cm = 0.18m
E₁ = [latex]\frac{q}{4 \pi \varepsilon_{0} d^{2}}\)
= \(\frac{9 \times 10^{9} \times 1.6 \times 10^{-7}}{\left(18 \times 10^{-2}\right)^{2}}\)
= 4.4 × 10⁴ N/C
Therefore, the electric field at a point 18 cm from the centre of the sphere is 4.4 × 10⁴N/C.

Question 5.
A parallel plate capacitor with air between the plates has a capacitance of 8 pF (1 pF = 10^-2 F). What will be the capacitance if the distance between the plates is reduced by half, and the space between them is filled with a substance of dielectric constant 6?
Answer:
Capacitance between the parallel plates of the capacitor, C = 8 pF
Initially, distance between the parallel plates was d and it was filled with air. Dielectric constant of air, k = 1
Capacitance, C is given by the formula,
C = \(\frac{k \varepsilon_{0} A}{d}[latex]
= [latex]\frac{\varepsilon_{0} A}{d}\) …………… (1)

If distance between the plates is reduced to half, then new distance,
d’ = \(\frac{d}{2}\)
Dielectric constant of the substance filled in between the plates, k’ Hence, capacitance of the capacitor becomes
C’ = \(\frac{k^{\prime} \varepsilon_{0} A}{d^{\prime}}=\frac{6 \varepsilon_{0}^{*} A}{\frac{d}{2}}\) …………….. (2)
Taking ratios of equations (1) and (2), we obtain
C’ = 2 × 6C
= 12C
= 12 × 8 = 96 pF
Therefore, the capacitance between the plates is 96 pF.

Question 6.
Three capacitors each of capacitance 9 pF are connected in series.
(a) What is the total capacitance of the combination?
(b) What is the potential difference across each capacitor if the combination is connected to a 120 V supply?
Answer:
(a) Given C₁ = C₂ = C₃ = 9 pF
When capacitors are connected in series, the equivalent capacitance Cs is given by
\(\frac{1}{C_{S}}=\frac{1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}}=\frac{1}{9}+\frac{1}{9}+\frac{1}{9}=\frac{3}{9}=\frac{1}{3}\)
C_S 3PF

(b) In series charge on each capacitor remains the same, so charge on each capacitor.
q = C_SV = (3 × 10^-12 F) × (120 V)
= 3.6 × 10^-10 coulomb
Potential difference across each capacitor, q 3.6 × 10^-10
V = \(\frac{q}{C_{1}}=\frac{3.6 \times 10^{-10}}{9 \times 10^{-12}}\) = 40V

Question 7.
Three capacitors of capacitances 2 pF, 3 pF and 4pF are connected in parallel
(a) What is the total capacitance of the combination?
(b) Determine the charge on each capacitor if the combination is connected to a 100 V supply.
Answer:
C₁ = 2 pF, C₂ = 3 pF, C₃ = 4 pF
(a) Total capacitance when connected in parallel,
C_p = C₁ + C₂ + C₃ = 2 + 3 + 4 = 9 pF,

(b) In parallel, the potential difference across each capacitor remains the same, i.e.,
V = 100 V.
Charge on C₁ = 2 pF,
q₁ = C₁V = 2 × 10^-12 × 100
= 2 × 10 ^-10C

Charge on C₂ = 3pF,
q₂ = C₂V = 3 × 10^-10 × 100
= 3 × 10^-10 C

Charge on C₃ = 4 pF,
q₃ = C₃V = 4 × 10^-12 × 100
= 4 × 10^-10C

Question 8.
In a parallel plate capacitor with air between the plates, each plate has an area of 6 × 10^-3 m² and the distance between the plates is 3 mm. Calculate the capacitance of the capacitor. If this capacitor is connected to a 100 V supply, what is the charge on each plate of the capacitor?
Answer:
Area of each plate of the parallel plate capacitor, A = 6 10^-3m²
Distance between the plates, d = 3 mm = 3 × 10^-3 m
Supply voltage, V = 100 V
Capacitance C of a parallel plate capacitor is given by,
C = \(\frac{\varepsilon_{0} A}{d}\)
where, ε₀ = 8.854 × 10^-12 N^-1m^-2C^-2
C = \(\frac{8.854 \times 10^{-12} \times 6 \times 10^{-3}}{3 \times 10^{-3}}\)
= 17.71 × 10^-12F
= 17.71 pF or 18 pF

Potential V is related with the charge q and capacitance C as
V = \(\frac{q}{C}\)
∴ q = VC = 100 × 17.71 × 10^-12
= 1.771 × 10⁹C
Therefore, capacitance of the capacitor is 17.71 pF and charge on each plate is 1.771 × 10^-9 C.

Question 9.
Explain what would happen if in the capacitor given in Exercise 2.8, a 3 mm thick mica sheet (of dielectric constant = 6) were inserted between the plates,
(a) while the voltage supply remained connected.
(b) after the supply was disconnected.
Answer:
(a) Here C₀ = Capacitance of the capacitor with air as medium = 18 pF
d = distance between the plates = 3 × 10^-3 m
t = thickness of mica sheet = 3 × 10^-3 m = d
K = dielectric constant of the mica sheet = 6

As the mica sheet completely fills the space between the plates, thus the capacitance of the capacitor (C) is given by
C =KC₀ = 6 × 18 × 10^-12 F
= 108 × 10^-12 F = 108 pF
Thus the capacitance of the capacitor increases by K times on inserting the mica sheet.
Potential difference across this capacitor, V = 100 V
∴ Charge q’ on the capacitor with mica sheet as medium is given by
q’ = CV= 108 × 10^-12 × 100
= 108 × 10^-8 C
Now clearly q’ = KC₀V = Kq = 6 × 1.8 × 10^-9
= 1.08 × 10^-8C

Clearly charge becomes K times the charge on the plates with air as medium, i.e., charge on the plates increases when supply remains connected and mica sheet is inserted.

(b) Here, capacitance of capacitor with mica as medium C = KC₀ 108 × 10^-12F
When supply is disconnected, i. e., mV = 0,
The potential difference across on the plates of the reduces by K times.
i.e., V’ = \(\frac{100}{6}\) 16.67V
C-becomes 6 times.
Thus if qi be the charge on its plates after disconnecting the supply,
Then q₁ = CV’ = KC₀ × \(\frac{100}{6}\)
= 6 × 18 × 10^-12 × \(\frac{100}{6}\)
= 18 × 10^-10C
q₀ = 1.8 × 10^-9C =1.8 nC
i.e., the charge on the capacitor with mica as medium remains same as with air medium.

Question 10.
A 12 pF capacitor is connected to a 50 V battery. How much electrostatic energy is stored in the capacitor?
Answer:
Given, C = 12 pF = 12 × 10^-12 F and V = 50 V, U = ?
Using the relation U = \(\frac{1}{2}\) CV², we have
U = \(\frac{1}{2}\)CV² = \(\frac{1}{2}\) × 12 × 10^-12(50)²
= 1.5 × 10⁸ J

Question 11.
A 600 pF capacitor is charged by a 200 V supply. It is then disconnected from the supply and is connected to another uncharged 600 pF capacitor. How much electrostatic energy is lost in the process?
Answer:
Given, C₁ = C₂ = 600 pF = 600 × 10_-12F, V = 200 V, ∆U = ?
Using the relation ∆U = \(\frac{C_{1} C_{2}\left(V_{1}-V_{2}\right)^{2}}{2\left(C_{1}+C_{2}\right)}\) , we get
∆U = \(\frac{600 \times 600 \times 10^{-24}(200-0)^{2}}{2(600+600) \times 10^{-12}}[latex] = 6 × 10^-6 j

Question 12.
A charge of 8 mC is located at the origin. Calculate the work done in taking a small charge of -2 × 10^-9 C from a point P(0, 0, 3 cm) to a point Q (0, 4 cm, 0), viaa point R (0,6 cm, 9 cm). Answer:
Charge located at the origin, q = 8 mC = 8 × 10^-3 C
Magnitude of a small charge, which is taken from a point P to point R to point Q, = -2 × 10^-9 C
All the points are represented in the given figure

Point P is at a distance, d₁ = 3 cm, from the origin along z-axis.
Point Q is at a distance, d₂ = 4 cm, from the origin along y-axis.

Therefore, work done during the process is 1.27 J.

Question 13.
A cube of side b has a charge q at each of its vertices. Determine the potential and electric field due to this charge array at the centre of the cube.
Answer:
Length of the side of a cube = b
Charge at each of its vertices = q
A cube of side b is shown in the following figure:

is the distance between the centre of the cube and one of the eight vertices.

The electric potential (V) at the centre of the cube is due to the presence of eight charges at the vertices.
V = [latex]\frac{8 q}{4 \pi \varepsilon_{0} r}\)
= \(\frac{8 q}{4 \pi \varepsilon_{0}\left(b \frac{\sqrt{3}}{2}\right)}\)
= \(\frac{4 q}{\sqrt{3} \pi \varepsilon_{0} b}\)
Therefore, the potential at the centre of the cube is \(\frac{4 q}{\sqrt{3} \pi \varepsilon_{0} b}\)
The electric field at the centre of the cube, due to the eight charges, gets cancelled. This is because the charges are distributed symmetrically with respect to the centre of the cube. Hence, the electric field is zero at the centre.

Question 14.
Two tiny spheres carrying charges 1.5 μC and 2.5 μC are located 30 cm apart. Find the potential and electric field :
(a) at the mid-point of the line joining the two charges, and
(b) at a point 10 cm from this midpoint in a plane normal to the line and passing through the mid-point.
Answer:
Two charges placed at points A and B are represented in the given figure. O is the mid-point of the line joining the two charges.

Magnitude of charge located at A, q₁ = 1.5 μC
Magnitude of charge located at B, q₂ = 2.5 μC
Distance between the two charges, d = 30 cm = 0.3 m

(a) Let V₁ and E₁ are the electric potential and electric field respectively at O.
V₁ = Potential due to charge at A + Potential due to charge at B


Therefore, the potential at mid-point is 2.4 x 10⁵ V and the electric field at mid-point is 4 x 10⁵Vm^-1. The field is directed from the larger charge to the smaller charge.

(b) Consider a point Z such that normal distance OZ =10 cm = 0.1 m, as shown in the following figure:

V₂ and E₂ are the electric potential and electric field respectively at Z. It can be observed from the figure that distance,

θ = cos^-1 (0.5556) = 56.25
∴ 2θ = 112.5°
cos 2θ = -0.38

E = 6.6 × 10⁵ Vm^-1
Therefore, the potential at a point 10 cm (perpendicular to the mid point) is 2.0 × 10⁵ V and electric field is 6.6 × 10⁵ Vm^-1.

Question 15.
A spherical conducting shell of inner radius and r₁outer radius r₂ has a charge Q.
(a) A charge q is placed at the centre of the shell. What is the surface charge density on the inner and outer surfaces of the shell?
(b) Is the electric field inside a cavity (with no charge) zero, even if the shell is not spherical, but has any irregular shape? Explain.
Answer:
(a) Charge placed at the centre of a shell is+q. Hence, a charge of magnitude -q will be induced to the inner surface of the shell. Therefore, total charge on the inner surface of the shell is -q.
Surface charge density at the inner surface of the shell is given by the relation,
σ₁ = \(\frac{\text { Total charge }}{\text { Inner surface area }}=\frac{-q}{4 \pi r_{1}^{2}}\) ……………… (1)

A charge of + q is induced on the outer surface of the shell. A charge of magnitude Q is placed on the outer surface of the shell. Therefore, total charge on the outer surface of the shell is Q + q. Surface charge density at the outer surface of the shell,
σ₂ = \(=\frac{\text { Total charge }}{\text { Outer surface area }}=\frac{Q+q}{4 \pi r^{2}}\) …………… (2)

(b) Yes.
The electric field intensity inside a cavity is zero, even if the shell is not spherical and has any irregular shape. Take a closed loop such that a part of it is inside the cavity along a field line while the rest is inside the conductor. Net work done by the field in carrying a test charge over a closed loop is zero because the field inside the conductor is zero.
Hence, electric field is zero, whatever is the shape.

Question 16.
(a) Show that the normal component of electrostatic field has a discontinuity from one side of a charged surface to another given by
(E₂ – E₁)n̂ = \(\frac{\sigma}{\varepsilon_{0}}\)
where n is a unit vector normal to the surface at a point ando is the surface charge density at that point. (The direction of n is from side 1 to side 2.) Hence show that just outside a conductor, the electric field is σ = n̂ ε₀.

(b) Show that the tangential component of electrostatic field is continuous from one side of a charged surface to another.
[Hint : For (a), use Gauss’s law. For, (b) use the fact that work done by electrostatic field on a closed loop is zero.]
Answer:
(a) Let AB be a charged surface having two sides as marked in the figure.
A cylinder enclosing a small area element ∆ S of the charged surface is the , Gaussian surface.

Let σ = surface charge density
∴ q = charge enclosed by the Gaussian cylinder = σ . ∆ S.
∴ According to Gauss’s Theorem,

where \(\overrightarrow{E_{1}}+\overrightarrow{E_{2}}\) are the electric fields through circular cross-sections of cylinder at II and III respectively.

It is clear from the figure that \(\overrightarrow{E_{1}}\) lies inside the conductor. Also we know that the electric field inside the conductor is zero.
∴ \(\overrightarrow{E_{1}}\) = 0
Thus from eq. (1)
\(\overrightarrow{E_{2}} \cdot \hat{n}=\frac{\sigma}{\varepsilon_{0}}[latex]
or [latex]\left(\overrightarrow{E_{2}} \cdot \hat{n}\right) \cdot \hat{n}=\frac{\sigma}{\varepsilon_{0}} \hat{n}\)
or \(\overrightarrow{E_{2}}=\frac{\sigma}{\varepsilon_{0}} \hat{n}\)
or electric field just outside the conductor = \(\frac{\sigma}{\varepsilon_{0}} \hat{n}\) Hence proved

(b) Let AaBbA be a charged surface in the field of a point charge q lying at origin.
Let \(\overrightarrow{r_{A}}\) and \(\overrightarrow{r_{B}}\) be its position vectors at points A and B respectively.

Let \(\vec{E}\) be the electric field at point P, thus E cosG is the tangential component of electric field \(\vec{E}\).

Question 17.
A long charged cylinder of linear charged density λ is surrounded by a hollow co-axial conducting cylinder. What is tihe electric field in the space between the two cylinders?
Answer:
Charge density of the long charged cylinder of length L and radius r is λ. Another cylinder of same length surrounds the previous cylinder. The radius of this cylinder is R.
Let £ be the electric field produced in the space between the two cylinders.
Electric flux through the Gaussian surface is given by Gauss’s theorem as,
Φ = E (2πd)L
where d = Distance of a point from the common axis of the cylinders Let q be the total charge on the cylinder.
It can be written as
Φ = E (2πdL) = \(\frac{q}{\varepsilon_{0}}\)
where, q = Charge on the inner sphere of the outer cylinder, ε₀ = Permittivity of free space
E (2πdL) = \(\frac{\lambda L}{\varepsilon_{0}}\)
E = \(\frac{\lambda}{2 \pi \varepsilon_{0} d}\)
Therefore, the electric field in the space between the two cylinders is \(\frac{\lambda}{2 \pi \varepsilon_{0} d}\)

Question 18.
In a hydrogen atom, the electron and proton are bound at a distance of about 0.53 Å.
(a) Estimate the potential energy of the system in eV, taking the zero of the potential energy at infinite separation of the electron from proton.
(b) What is the minimum work required to free the electron, given that its kinetic energy in the orbit is half the magnitude of potential energy obtained in (a)?
(c) What are the answers to (a) and (b) above if the zero of potential energy is taken as 1.06 A separation?
Answer:
The distance between electron-proton of a hydrogen atom, d = 0.53 Å
Charge on an electron,q₁ = -1.6 × 10^-19 C
Charge on a proton, q₂ = +1.6 × 10^-19 C
(a) Potential energy at infinity is zero.
Potential energy of the system,
P.E. = P.E. at ∞ – P.E. at d
= 0 – \(\frac{q_{1} q_{2}}{4 \pi \varepsilon_{0} d}\)
∴ P.E 0 = – \(\frac{9 \times 10^{9} \times\left(1.6 \times 10^{-19}\right)^{2}}{0.53 \times 10^{-10}}\)
= -43.47 × 10^-19J
Since 1.6 × 10^-19 J = 1eV
∴ P.E. = -43.47 × 10^-19

= \(\frac{-43.47 \times 10^{-19}}{1.6 \times 10^{-19}}\) = -27.2 eV
Therefore, the potential energy of the system is -27.2 eV.

(b) Kinetic energy is half of the magnitude of potential energy
Kinetic energy = \(\frac{1}{2}\) × (-27.2) = 13.6 eV
[v K.E. of the system is always +ve]
Total energy = 13.6 – 27.2 = 13.6 eV
Therefore, the minimum work required to free the electron is 13.6 eV.

(c) When zero of potential energy is taken, d₁ = 1.06 A
Potential energy of the system = P.E. at – P.E. at d₁ – P.E. at d
= \(\frac{q_{1} q_{2}}{4 \pi \varepsilon_{0} d_{1}}\) -27.2 eV
= \(\frac{9 \times 10^{9} \times\left(1.6 \times 10^{-19}\right)^{2}}{1.06 \times 10^{-10}}\) -27.2 eV
= 21.73 × 10^-19 J -27.2 eV
= 13.58 eV- 27.2 eV .
= -13.6 eV

Question 19.
If one of the two electrons of aH₂ molecule is removed, we get a hydrogen molecular ion H₂⁺. In the ground state of an H₂⁺ the two protons are separated by roughly 1.5 Å, and the electron is roughly 1 Å from each proton. Determine the potential energy of the system. Specify your choice of the zero of potential energy.
Answer:
The system of two protons and one electron is represented in the given figure

Charge on proton 1, q₁ = 1.6 × 10^-19 C
Charge on proton 2, q₂ = 1.6 × 10^-19 C
Charge on electron, q₃ = -1.6 × 10^-19 C
Distance between protons 1 and 2, dj = 1.5 × 10^-10 m
Distance between proton 1 and electron, d₂ = 1 × 10^-10 m
Distance between proton 2 and electron, d₃ = 1 × 10^-10 m The potential energy at infinity is zero.
Potential energy of the system,
V = \(\frac{q_{1} q_{2}}{4 \pi \varepsilon_{0} d_{1}}\) + \(\frac{q_{2} q_{3}}{4 \pi \varepsilon_{0} d_{3}}\) + \(\frac{q_{3} q_{1}}{4 \pi \varepsilon_{0} d_{2}}\)
Substituting \(\frac{1}{4 \pi \varepsilon_{0}}\) = 9 × 10⁹ Nm²C^-2, we obtain

= -30.7 × 10^-19 J
= -19.2 eV
Therefore, the potential energy of the system is -19.2 eV.

Question 20.
Two charged conducting spheres of radii a and b are connected to each other by a wire. What is the ratio of electric fields at the surfaces of the two spheres? Use the result obtained to explain why charge density on the sharp and pointed ends of a conductor is higher than on its flatter portions.
Answer:
Let a be the radius of a sphere A, Q_A be the charge on the sphere, and C_A be the capacitance of the sphere. Let b be the radius of a sphere B, Q_B be the charge on the sphere, and CB be the capacitance of the sphere. Since the two spheres are connected with a wire, their potential (V) will become equal.
Let E_A be the electric field of sphere A and E_B be the electric field of sphere B. Therefore, their ratio,

Putting the value of eqn. (2) in eqn. (1), we obtain
\(\frac{E_{A}}{E_{B}}=\frac{a b^{2}}{b a^{2}}=\frac{b}{a}\)
Therefore, the ratio of electric fields at the surface is b/a.
A flat portion may be taken as a spherical surface of large radius and a pointed portion may be taken as a spherical surface of small radius.
As ε ∝ \(\frac{l}{\text { radius }}\),
thus pointed portion has larger fields than the flat one. Also we know that
E = \(\frac{\sigma}{\varepsilon_{0}}\)
i.e., E ∝ σ,
thus clearly the surface charge density on the sharp and pointed ends will be large.

Question 21.
Two charges -q and +q are located at points (0, 0, – a) and (0, 0, a), respectively.
(a) What is the electrostatic potential at the points (0, 0, z) and (x, y, 0)?
(b) Obtain the dependence of potential on the distance r of a point from the origin when r/ a >> 1.
(c) How much work is done in moving a small test charge from the point (5, 0, 0) to (-7, 0, 0) along the x-axis? Does the answer change if the path of the test charge between the same points is not along the x-axis?
Answer:
(a) Here -q and + q are situated at points A (0, 0, -a) and B (0, 0, a) respectively.

∴ Dipole length = 2a
If p be the dipole moment of the dipole, then
p = 2aq
Let P₁ (0, 0, z) be the point at which V is to be calculated. It lies on the axial line of the dipole.

Now point P₂ (x, y, O’) lies in XY plane which is normal to the axis of the dipole, i. e., lies on the line parallel to the equitorial line on which potential due to the dipole is zero as given below:

(b) Let r = distance of the point P from the centre (O) of the dipole at which
V is to be calculated. Let ∠POB = θ, i.e., OP makes an angle θ with \(\).
Also let r₁ and r₂ be the distances of the point P from -q and +q respectively. To find r₁ and r₂, draw AC and BD ⊥ arc to OP.

∴ In Δ ACO, OC = a cos θ
and in Δ BDO, OD = a cos θ
Thus, if V₁ and V₂ be the potentials at P due to – q and + q respectively, then total potential V at P is given by
V = V₁ + V₂

Thus,V = \(=\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{p \cos \theta}{r^{2}}\) ………….. (2)
Thus, we see that the dependence of V on r is of \(\frac{1}{r^{2}}\) type, i.e.,V ∝ \(\frac{1}{r^{2}}\).

(c) Let W₁ and W₂ be the work done in moving a test charge q₀ from E(5,0,0) to F(-7, 0,0) in the fields of + q(0, 0, a) and -q(0, 0,-a) respectively.


No, because work done in moving a test charge in an electric field between two points is independent of the path connecting the two point.

Question 22.
Figure 2.34 shows a charge array known as an electric quadrupole. For a point on the axis of the quadrupole, obtain the dependence of potential on r for r/a >> 1, and contrast your results with that due to an electric dipole, and an electric monopole (i. e., a single charge).

Answer:
Four charges of same magnitude are placed at points X, Y, Y and Z respectively, as shown in the following figure:

A point is located at P, which is r distance away from point Y.
The system of charges forms an electric quadrupole.
It can be considered that the system of the electric quadrupole has three charges.
Charge + q placed at point X
Charge -2q placed at point Y
Charge + q placed at point Z
XY = YZ = a
YP = r
PX = r + a
PZ = r – a
Electrostatic potential caused by the system of three charges at point P is given by,

It can be inferred that potential, V ∝ \(\frac{1}{r^{3}}\).
However, it is known that for a dipole, V ∝ \(\frac{1}{r^{2}}\). and, for monopole V ∝ \(\frac{1}{r}\)

Question 23.
An electrical technician requires a capacitance of 2 μF in a circuit across a potential difference of 1 kV. A large number of 1 μF capacitors are available to him each of which can withstand a potential difference of not more than 400 V. Suggest a possible arrangement that requires the minimum number of capacitors.
Answer:
Total required capacitance, C = 2 μF
Potential difference, V = 1 kV = 1000 V
Capacitance of each capacitor, C = 1 μF
Each capacitor can withstand a potential difference, V₁ = 400 V
Suppose a number of capacitors are connected in series and these series circuits are connected in parallel (row) to each other. The potential difference across each row must be 1000 V and potential difference across each capacitor must be 400 V. Hence, number of capacitors in each row is given as
\(\frac{1000}{400}\) = 25 .
Hence, there are three capacitors in each row.
Capacitance of each row = \(\frac{1}{1+1+1}=\frac{1}{3}\) μF
Let there are n rows, each having three capacitors, which are connected in parallel.
Hence, equivalent capacitance of the circuit is given as
\(\frac{1}{3}+\frac{1}{3}+\frac{1}{3}\) + ….. + n terms = \(\frac{n}{3}\)
However, capacitance of the circuit is given as 2 μF.
∴ \(\frac{n}{3}\) = 2
n = 6
Hence, 6 rows of three capacitors are present in the circuit. A minimum of 6 × 3, i.e., 18 capacitors are required for the given arrangement.

Question 24.
What is the area of the plates of a 2 F parallel plate capacitor, given that the separation between the plates is 0.5 cm? [You will realize from your answer why ordinary capacitors are in the range of μF or less. However, electrolytic capacitors do have a much larger capacitance (0.1 F) because of very minute separation between the conductors.]
Answer:
Capacitance of a parallel capacitor, C = 2 F
Distance between the two plates, d = 0.5 cm = 0.5 × 10^-2 m
Capacitance of a parallel plate capacitor is given by the relation,
C = \(\frac{\varepsilon_{0} A}{d}\)
A = \(\frac{C d}{\varepsilon_{0}}\)
Where ε₀ = 8.85 × 10^-12C²N^-1m^-2
∴ A = \(\frac{2 \times 0.5 \times 10^{-2}}{8.85 \times 10^{-12}}\) = 1130 km²
Hence, the area of the plates is too large. To avoid this situation, the capacitance is taken in the range of μF.

Question 25.
Obtain the equivalent capacitance of the network in Fig. 2.35. For a 300 V supply, determine the charge and voltage across each capacitor.

Answer:

Question 26.
he plates of a parallel plate capacitor have an area of 90 cm² each and are separated by 2.5 nun. The capacitor is charged by connecting it to a 400 V supply.
(a) How much electrostatic energy is stored by the capacitor?
(b) View this energy as stored in the electrostatic field between the plates, and obtain the energy per unit volume u. Hence arrive at a relation between u and the magnitude of electric field E between the plates.
Answer:
Area of the plates of a parallel plate capacitor,
A = 90 cm² = 90 × 10^-4 m²
Distance between the plates, d = 2.5mm 2.5 × 10^-3 m
Potential difference across the plates, V = 4OO V
Capacitance of the capacitor is given by the relation,
C = \(\)
(a) Electrostatic energy stored in the capacitor is given by the relation,

Hence, the electrostatic energy stored by the capacitor is 2.55 × 10^-6 J

(b) Volume of the given capacitor,
V’= A × d
= 90 × 10^-4 × 2.5 × 10^-3
= 2.25 × 10^-5 m³
Energy stored in the capacitor per unit volume is given by,

Question 27.
A 4 μF capacitor is charged by a 200 V supply. It is then disconnected from the supply, and is connected to another uncharged 2 μF capacitor. How much electrostatic energy of the first capacitor is lost in the form of heat and electromagnetic radiation?
Answer:

Question 28.
Show that the force on each plate of a parallel plate capacitor has a magnitude equal to (\(\frac{1}{2}\)) QE, where Q is the charge on the capacitor, and E is the magnitude of electric field between the plates. Explain the origin of the factor \(\frac{1}{2}\).
Answer:
Let F be the force applied to separate the plates of a parallel plate capacitor by a distance of Δx. Hence, work done by the force to do so = FΔx
As a result, the potential energy of the capacitor increases by an amount given as uA Δx.
where, u = Energy density
A = Area of each plate
The work done will be equal to the increase in the potential energy, i. e.,
FΔx = uA Δx

The physical origin of the factor, 1/2 in the force formula lies in the fact that just outside the conductor, field is E and inside it is zero. Hence, it is the averge value, E/2 of the field that contributes to the force.

Question 29.
A spherical capacitor consists of two concentric spherical conductors, held in position by suitable insulating supports (Fig. 2.36). Show that the capacitance of a spherical capacitor is given by
C = \(\frac{4 \pi \varepsilon_{0} r_{1} r_{2}}{r_{1}-r_{2}}\)
where r ₁and r₂ are the radii of outer and inner spheres, respectively.

Answer:
Radius of the outer shell = r₁
Radius of the inner shell = r₂
The inner surface of the outer shell has charge +Q
The outer surface of the inner shell has induced charge -Q.
Potential difference between the two shells is given by,

Question 30.
A spherical capacitor has an inner sphere of radius 12 cm and an outer sphere of radius 13 cm. The outer sphere is earthed and the inner sphere is given a charge of 2.5 µC. The space between the concentric spheres is filled with a liquid of dielectric constant 32.
(a) Determine the capacitance of the capacitor.
(b) What is the potential of the inner sphere?
(c) Compare the capacitance of this capacitor with that of an isolated sphere of radius 12 cm. Explain why the latter is much smaller.
Answer:
Radius of the inner sphere, r₂ = 12 cm = 0.12m
Radius of the outer sphere, r₁ = 13 cm = 0.13m
Charge on the inner sphere, q = 2.5 µC = 2.5 × 10^-6 C
Dielectric constant of the liquid, ε_r = 32
Capacitance of the capacitor is given by the relation,
C = \(\frac{4 \pi \varepsilon_{0} \varepsilon_{r} r_{1} r_{2}}{r_{1}-r_{2}}\)
C = \(\frac{32 \times 0.12 \times 0.13}{9 \times 10^{9} \times(0.13-0.12)}\)
≈ 5.5 × 10^-9 F
Hence, the capacitance of the capacitor is approximately 5.5 × 10^-9 F.

(b) Potential of the inner sphere is given by,
V = \(\frac{q}{C}=\frac{2.5 \times 10^{-6}}{5.5 \times 10^{-9}}\) = 4.5 × 10²V
Hence, the potential of the inner sphere is 4.5 × 10² V

(c) Radius of an isolated sphere, r = 12cm = 12 × 10^-2m
Capacitance of the sphere is given by the relation,
C’ = 4πε₀r
= 4π × 8.85 × 10^-12 × 12 × 10^-12
= 1.33 × 10^-11F
The capacitance of the isolated sphere is less in comparison to the concentric spheres. This is because the outer sphere of the concentric spheres is earthed. Hence, the potential difference is less and the capacitance is more than the isolated sphere.

Question 31.
Answer carefully:
(a) Two large conducting spheres carrying charges Q₁ and Q₂ are brought close to each other. Is the magnitude of electrostatic force between them exactly given by Q₁Q₂ / πε₀ r², where r is the distance between their centres?
(b) If Coulomb’s law involved 1/r³ dependence (instead of 1/r²), would Gauss’s law be still true?
(c) A small test charge is released at rest at a point in an electrostatic field configuration. Will it travel along the field line passing through that point?
(d) What is the work done by the field of a nucleus in a complete circular orbit of the electron? What if the orbit is elliptical?
(e) We know that electric field is discontinuous across the surface of a charged conductor. Is electric potential also discontinuous there?
(f) What meaning would you give to the capacitance of a single conductor?
(g) Guess a possible reason why water has a much greater dielectric constant (= 80) than say, mica (= 6).
Answer:
(a) The force between two conducting spheres is not exactly given by the expression,Q₁Q₂ / πε₀ r², because there is a non-uniform charge distribution on the spheres.

(b) Gauss’s law will not be true, if Coulomb’s law involved 1/r³ dependence, instead of 1/r², on r.

(c) Yes, If a small test charge is released at rest at a point in an electrostatic field configuration, then it will travel along the field lines passing through the point, only if the field lines are straight. This is because the field lines give the direction of acceleration and not of velocity.

(d) Whenever the electron completes an orbit, either circular or elliptical, the work done by the field of a nucleus is zero.

(e) No, electric field is discontinuous across the surface of a charged conductor. However, electric potential is continuous.

(f) The capacitance of a single conductor is considered as a parallel plate capacitor with one of its two plates at infinity.

(g) Water has an unsymmetrical space as compared to mica. Since it has a permanent dipole moment, it has a greater dielectric constant than mica.

Question 32.
A cylindrical capacitor has two co-axial cylinders of length 15 cm and radii 1.5 cm and 1.4 cm. The outer cylinder is earthed and the inner cylinder is given a charge of 3.5 μC. Determine the capacitance of the system and the potential of the inner cylinder. Neglect end effects (i. e., bending of field lines at the ends).
Answer:
Length of a co-axial cylinder, l = 15 cm = 0.15 m
Radius of outer cylinder, r₁ = 1.5 cm = 0.015 m
Radius of inner cylinder, r₂ = 1.4 cm = 0.014 m
Charge on the inner cylinder, q = 3.5 μC = 3.5 × 10^-6 C

Capacitance of a co-axial cylinder of radii r₁ and r₂ is given by the relation,

Question 33.
A parallel plate capacitor is to be designed with a voltage rating 1 kV, using a material of dielectric constant 3 and dielectric strength about 10⁷ Vm^-1. (Dielectric strength is the maximum electric field a material can tolerate without breakdown, i. e., without starting to conduct electricity through partial ionisation.) For safety, we should like the field never to exceed, say 10% of the dielectric strength. What minimum area of the plates is required to have a capacitance of 50 pF?
Answer:
Potential rating of the parallel plate capacitor, V = 1 kV = 1000 V
Dielectric constant of the material, ε_r = 3
Dielectric strength = 10⁷ V/m
For safety, the field intensity never exceeds 10% of the dielectric strength.
Hence, electric field intensity, E = 10% of 10⁷ =10⁶V/m
Capacitance of the parallel plate capacitor C = 50 pF = 50 × 10^-12F
Distance between the plates is given by,
d = \(\frac{V}{E}=\frac{1000}{10^{6}}\) = 10^-3 m
Capacitance is given by the relation,
C = \(\frac{\varepsilon_{0} \varepsilon_{r} A}{d}\)
∴ A = \(\frac{C d}{\varepsilon_{0} \varepsilon_{r}}\) = \(\frac{50 \times 10^{-12} \times 10^{-3}}{8.85 \times 10^{-12} \times 3}\) ≈ 19cm ²
Hence, the area of each plate is about 19 cm² .

Question 34.
Describe schematically the equipotential surfaces corresponding to
(a) a constant electric field in the z-direction,
(b) a field that uniformly increases in magnitude but remains in a constant (say, z) direction,
(c) a single positive charge at the origin, and
(d) a uniform grid consisting of long equally spaced parallel charged wires in a plane.
Answer:
Equipotential surface is a surface having the same potential at each of its points. In the given cases the equipotential surface are

(a) The planes are parallel to XY plane. For same potential difference, the planes are equidistant.

(b) The planes are parallel to XY plane, but for the same potential difference, the separation between the planes decreases.

(c) Concentric spheres centred at the origin.

(d) A periodically varying shape near the grid which gradually attains the shape of planes parallel to grid at far distances.

Question 35.
In a Van de Graff type generator a spherical metal shell is to be a 15 × 10⁶ V electrode. The dielectric strength of the gas surrounding the electrode is 5 × 10⁷ Vm^-1. What is the minimum radius of the spherical shell required? (You will learn from this exercise why one cannot build an electrostatic generator using a very small shell which requires a small charge to acquire a high potential.)
Answer:

Question 36.
A small sphere of radius r₁and charge q₁ is enclosed by a spherical shell of radius r₂ and charge q₂. Show that if q₁ is positive, charge will necessarily flow from the sphere to the shell (when the two are connected by a wire) no matter what the charge q₂ on the shell is.
Answer:
Here r₁, r₂ are the radii of small sphere and the spherical shell respectively. The shell surrounds the sphere +q₁ is the charge on the sphere +q₂ is the charge on the shell. We know that the electric field
inside a conductor is zero, i.e.,\(\vec{E}\) = 0. Thus according to Gauss’s Theorem

Hence q₂ must reside on the outer surface of the spherical shell.
Now the sphere having +q₁ charge is enclosed inside the spherical shell. So – q₁ charge will be induced on the inside side and +q₁ charge will be induced on the outer surface the spherical shell.

∴ Total charge on the outer surface of the shell = q₂ + q₁.
As the charge always resides on the outer surface, thus charge q₁ from the outer surface of sphere will flow to the other surface of spherical shell when connected with a wire.

Question 37.
Answer the following:
(a) The top of the atmosphere is at about 400 kV with respect to the surface of the earth, corresponding to an electric field that decreases with altitude. Near the surface of the earth, the field is about 100 Vm^-1. Why then do we not get an electric shock as we step out of our house into the open? (Assume the house to be a steel cage so there is no field inside.)

(b) A man fixes outside his house one evening a two metre high insulating slab carrying on its top a large aluminium sheet of area 1 m². Will he get an electric shock if he touches the metal sheet next morning?

(c) The discharging current in the atmosphere due to the small conductivity of air is known to be 1800 A on an average over the globe. Why then does the atmosphere not discharge itself completely in due course and become electrically neutral? In other words, what keeps the atmosphere charged?

(d) What are the forms of energy into which the electrical energy of the atmosphere is dissipated during a lightning? (Hint : The earth has an electric field of about 100 Vm-1 at its surface in the downward direction, corresponding to a surface charge density = -10^-9 Cm^-2. Due to the slight conductivity of the atmosphere up to about 50 km (beyond which it is good conductor), about +1800 C is pumped every second into the earth as a whole. The earth, however, does not get discharged since thunderstorms and lightning occurring continually all over the globe pump an equal amount of negative charge on the earth.)
Answer:
(a) We do not get an electric shock as we step out of our house because the original equipotential surfaces of open air changes, keeping our body and the ground at the same potential.

(b) Yes, the man will get an electric shock if he touches the metal slab next morning. The steady discharging current in the atmosphere charges up the aluminium sheet. As a result, its voltage rises gradually. The raise in the voltage depends on the capacitance of the capacitor formed by the aluminium slab and the ground.

(c) The occurrence of thunderstorms and lightning charges the atmosphere continuously. Hence, even with the presence of discharging current of 1800 A, the atmosphere is not discharged completely. The two opposing currents are in equilibrium and the atmosphere remains electrically neutral.

(d) During lightning and thunderstorm, light energy, heat energy and sound energy are dissipated in the atmosphere.

Punjab State Board PSEB 12th Class Physics Book Solutions Chapter 3 Current Electricity Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Physics Chapter 3 Current Electricity

PSEB 12th Class Physics Guide Current Electricity Textbook Questions and Answers

Question 1.
The storage battery of a car has an emf of 12 V. If the internal resistance of the battery is 0.4 Ω, what is the maximum current that can be drawn from the battery?
Answer:
Emf of the battery, E = 12 V
Internal resistance of the battery, r = 0.4 Ω
Maximum current drawn from the battery = I
According to Ohm’s law,
E = Ir
I = \(\frac{12}{0.4}\) = 30
The maximum current drawn from the given battery is 30 A.

Question 2.
A battery of emf 10 V and internal resistance 3 Ω is connected to a resistor. If the current in the circuit is 0.5 A, what is the resistance of the resistor? What is the terminal voltage of the battery when the circuit is closed?
Answer:
Emf of the battery, E = 10 V
Internal resistance of the battery, r = 3 Ω
Current in the circuit, I = 0.5 A
Resistance of the resistor = R
The relation for current using Ohm’s law is,
I = \(\frac{E}{R+r}\)
R + r = \(\frac{E}{I}\)
= \(\frac{10}{0.5}\) = 20Ω
∴ R = 20 – 3 = 17Ω
Terminal voltage of the battery = V
According to Ohm’s law,
V = IR
= 0.5 × 17 = 8.5 V
Therefore, the resistance of the resistor is 17 Ω and the terminal voltage of the battery is 8.5 V.

Question 3.
(a) Three resistors 1Ω, 2 Ω and 3 Ω are combined in series. What is the total resistance of the combination?
(b) If the combination is connected to a battery of emf 12 V and negligible internal resistance, obtain the potential drop across each resistor.
Answer:
(a) r₁ = 1Ω, r₂ = 2Ω, r₃ = 3Ω
R_S = ?
R_S = r₁ + r₂ + r₃ = 6Ω

(b) ∵ V = 12 V
R_S = 6Ω
I = ?
∵ V = IR_S
⇒ I = \(\) = 2A
Let V₁,V₂, V₃ be the potential drops across r₁ r₂, r₃. Then,
> V = V₁ + V₂ + V₃
V₁ = =Ir₁ = 2 × 1 = 2V
V₂ =Ir₂ = 2 × 2 = 4 V
V₃ = Ir₃ = 2 × 3 = 6V

Question 4.
(a) Three resistors 2 Ω, 4 Ω and 5 Ω are combined in parallel. What is the total resistance of the combination?
(b) If the combination is connected to a battery of emf 20 V and negligible internal resistance, determine the current through each resistor and the total current drawn from the battery.
Answer:
(a) r₁ = 2Ω,r₂ = 4Ω,r₃ = 5Ω

Question 5.
At room temperature (27.0°C) the resistance of a heating element is 100 Ω. What is the temperature of the element if the resistance is found to be 117 Ω, given that the temperature coefficient of the material of the resistor is 1.70 × 10^-4 C^-1.
Answer:
Room temperature, T = 27°C
Resistance of the heating element at T, R = 100 Ω
Let Ti is the increased temperature of the element.
Resistance of the heating element at T₁,R₁ = 117 Ω
Temperature co-efficient of the material of the element,
α = 1.70 × 10^-4°C^-1
α is given by the relation,
α = \(\frac{R_{1}-R}{R\left(T_{1}-T\right)}\)
T₁ – T = \(\frac{R_{1}-R}{R \alpha}\)
T₁ – 27 = \(\frac{117-100}{100\left(1.7 \times 10^{-4}\right)}\)
T₁ – 27 = 1000
T₁ = 1000 + 27
T₁ = 1027°C
Therefore, at 1027°C the resistance of the element is 117 Ω.

Question 6.
A negligibly small current is passed through a wire of length 15 m and uniform cross-section 6.0 × 10^-7 m², and its resistance is measured to be 5.0 Ω. What is the resistivity of the material at the temperature of the experiment?
Answer:
Length of the wire, l = 15 m
Area of cross-section of the wire, A = 6.0 × 10^-7 m²
Resistance of the material of the wire, R = 5.0 Ω
Resistivity of the material of the wire = ρ
Resistance is related with the resistivity as
R = ρ\(\frac{l}{A}\)
ρ = \(\frac{R A}{l}\)
= \(\frac{5 \times 6 \times 10^{-7}}{15}\) = 2 × 10^-7Ωm
Therefore, the resistivity of the material is 2 × 10^-7 Ωm.

Question 7.
A silver wire has a resistance of 2.1 Ω at 27.5°C, and a resistance of 2.7Ω at 100°C. Determine the temperature coefficient of resistivity of silver.
Answer:
Temperature, T₁ = 27.5°C
Resistance of the silver wire at T₁, R₁ = 2.1 Ω
Temperature, T₂ = 100 °C
Resistance of the silver wire at T₂, R₂ = 2.7 Ω
Temperature coefficient of resistivity of silver = a It is related with temperature and resistance as
α = \(\frac{R_{2}-R_{1}}{R_{1}\left(T_{2}-T_{1}\right)}\)
= \(\frac{2.7-2.1}{2.1(100-27.5)}\) = 0.0039°C^-1
Therefore, the temperature coefficient of resistivity of silver is 0.0039 °C^-1.

Question 8.
A heating element using nichrome connected to a 230 V supply draws an initial current of 3.2 A which settles after a few seconds to a steady value of 2.8 A. What is the steady temperature of the heating element if the room temperature is 27.0°C? Temperature coefficient of resistance of nichrome averaged over the temperature range involved is 1.70 x 10^-4°C^-1.
Answer:
Supply voltage, V = 230 V
Initial current drawn, I₁ = 3.2 A
Initial resistance = R₁, which is given by the relation,
R₁ = \(\frac{V}{I_{1}}=\frac{230}{3.2}\) = 71.87 Ω
Steady state value of the current, I₂ = 2.8 A
Resistance at the steady state = R₂, which is given as
R₂ = \(\frac{230}{2.8}\) = 82.14 Ω
Temperature coefficient of resistance of nichrome, α = 1.70 × 10^-4°C^-1
Initial temperature of nichrome, T₁ = 27.0 °C
Steady state temperature reached by nichrome = T₂
T₂ can be obtained by the relation for α,
α = \(\frac{R_{2}-R_{1}}{R_{1}\left(T_{2}-T_{1}\right)}\)
T₂ – 27°C = \(\frac{82.14-71.87}{71.87 \times 1.7 \times 10^{-4}}\) = 840.5
T₂ = 840.5 + 27 = 867.5°C
Therefore, the steady temperature of the heating element is 867.5°C.

Question 9.
Determine the current in each branch of the network shown in ‘ Fig. 3.30.

Let I be the total current in the circuit.
I₁ = Current flowing through AB.
∴ I – I₁ = Current flowing through AD.
I₂ = Current flowing through BD.
∴ I₁ – I₂ = Current flowing through BC.
and I₁ – I₁ + I₂ = Current flowing through DC.
Applying loop law to ABDA, we get

10I₁ + 5I₂ – 5(I – I₁) = 10
or 3I₁ + I₂ – I = 0 …………….. (1)
Again applying loop law to BCDB, we get
5(I₁ – I₂) – 10(I – I₁ + I₂) -5I₂ = 0 or 15I₁ – 20I₂ – 10I = 0
or 3I₁ – 4I₂ – 2I = 0 …………….. (2)
Applying loop law to ABCEFA, we get
10I + 10I₁ + 5(I₁ – I₂) = 10
or 3F₁ – I₂ + 2I = 2 ………….. (3)
Eqn. (2) + (3) gives, 6I₁ – 5I₂ = 2 …………… (4)
Multiplying eqn. (1) by 2 and then adding to eqn. (4), we get
9I₁ + I₂ = 2 …………… (5)
Eqn. (4) + 5 x eqn. (5) gives,
6I₁ – 5I₂ + 45I₁ +5I₂ = 2 + 10
or 51I₁ = 12
or I₁ = \(\frac{4}{17}\) A …………….. (6)
∴ Current in branch AB,I₁ = \(\frac{4}{17}\)A
∴ From eqns. (5) and (6), we get
I₂ = 2 – 9 x \(\frac{4}{17}\) = –\(\frac{2}{17}\)A
-ve sign shows that 12 is actually from D to B. Now from eqn. (1), we get

Question 10.
(a) In a metre bridge [Fig. 3.27], the balance point is found to be at 39.5 cm from the end A, when the resistor Y is of 12.5 Ω. Determine the resistance of X. Why are the connections between resistors in a Wheatstone or meter bridge made of thick copper strips?
(b) Determine the balance point of the bridge above if X and Y are interchanged.
(c) What happens if the galvanometer and cell are interchanged at the balance point of the bridge? Would the galvanometer show any current?
Answer:
(a) A metre bridge with resistors X and Y is represented in the given figure.

Balance point from end A,l₁ = 39.5 cm
Resistance of the resistor Y = 12.5 Ω
Condition for the balance is given as,

Therefore, the resistance of resistor X is 8.2 Ω.
The connection between resistors in a Wheatstone or metre bridge is made of thick copper strips to minimize the resistance, which is not taken into consideration in the bridge formula.

(b) If X and Y are interchanged, then l₁ and 100 – l₁ get interchanged.
The balance point of the bridge will be 100 – l₁ from A.
100 – l₁ =100 – 39.5 = 60.5 cm
Therefore, the balance point is 60.5 cm from A.

(c) When the galvanometer and cell are interchanged at the balance point of the bridge, the galvanometer will show no deflection. Hence, no current would flow through the galvanometer.

Question 11.
A storage battery of emf 8.0 V and internal resistance 0.5 Ω is being charged by a 120 V dc supply using a series resistor of 15.5 Ω. What is the terminal voltage of the battery during charging? What is the purpose of having a series resistor in the charging circuit?
Answer:
Emf of the storage battery, E = 8.0 V
Internal resistance of the battery, r = 0.5 Ω
DC supply voltage, V = 120 V
Resistance of the resistor, R = 15.5 Ω
Effective voltage in the circuit = V’
R is connected to the storage battery in series. Hence, it can be written as
V’ = V – E
V’= 120 – 8 = 112 V
Current flowing in the circuit = I, which is given by the relation,
I = \(\frac{V^{\prime}}{R^{\prime}+r}\)
= \(\frac{112}{15.5+0.5}=\frac{112}{16}\) = 7A
15.5 + 0.5 16
Voltage across resistor R given by the product, IR = 7 × 15.5 = 108.5 V
∵ DC supply voltage = Terminal voltage of battery+Voltage drop across R
∴ Terminal voltage of battery = 120 -108.5 = 11.5 V
A series resistor in a charging circuit limits the current drawn from the external source. The current will be extremely high in its absence. This is very dangerous.

Question 12.
In a potentiometer arrangement, a cell of emf 1.25 V gives a balance point at 35.0 cm length of the wire. If the cell is replaced by another cell and the balance point shifts to 63.0 cm, what is the emf of the second cell?
Answer:
Emf of the cell, E₁ = 1.25 V
Balance point of the potentiometer,l₁ = 35 cm
The cell is replaced by another cell of emf E₂.
New balance point of the potentiometer, l₂ = 63 cm
The balance condition is given by the relation,
\(\frac{E_{1}}{E_{2}}=\frac{l_{1}}{l_{2}}\)
E₂ = E₁ × \(\frac{l_{2}}{l_{1}}\) = 1.25 × \(\frac{63}{35}\) = 2.25V
Therefore, emf of the second cell is 2.25 V.

Question 13.
The number density of free electrons in a copper conductor estimated in Example 3.1 is 8.5 × 10²⁸ m^-3. How long does an electron take to drift from one end of a wire 3.0 m long to its other end? The area of cross-section of the wire is 2.0 × 10^-6 m² and it is carrying a current of 3.0 A.
Answer:
Here, n = number density of free electrons = 8.5 × 10²⁸ m^-3
l = length of wire = 3m
A = Area of cross-section of wire = 2.0 × 10^-6 m²
I = current in the wire = 3.0 A
e = 1.6 × 10^-19C
Let t = time taken by electron to drift from one end to another of the wire = ?
Using the relation, I – neA v_d, we get
v_d = I/neA
= \(\frac{3}{8.5 \times 10^{28} \times 1.6 \times 10^{-19} \times 2.0 \times 10^{-6}}\) ms^-1
= 1.103 × 10^-4 ms^-1
∴ t = \(\frac{l}{v_{d}}\) = \(\frac{3}{1.103 \times 10^{-4}}\) = 2.72 × 10⁴ s = 7 h 33 min.

Question 14.
The earth’s surface has a negative surface charge density of 10^-9 Cm^-2. The potential difference of 400 kV between the top of the atmosphere and the surface results (due to the low conductivity of the lower atmosphere) in a current of only 1800 A over the entire globe. If there were no mechanism of sustaining atmospheric electric field, how much time (roughly) would be required to neutralise the earth’s surface? (This never happens in practice because there is a mechanism to replenish electric charges, namely the continual thunderstorms and lightning in different parts of the globe.) (Radius of earth = 6.37 × 10⁶m.)
Answer:
Surface charge density of the earth, σ = 10^-9 Cm ^-2
Current over the entire globe, I = 1800 A .
Radius of the earth, r = 6.37 × 10⁶ m
Surface area of the earth,
A = 4πr²
= 4π × (6.37 × 10⁶)²
= 5.09 × 10¹⁴ m²
Charge on the earth surface,
q = σ × A
= 10^-9 × 5.09 × 10¹⁴
= 5.09 × 10⁵ C
Time taken to neutralise the earth’s surface = t
Current, I = \(\frac{q}{t}\)
t = \(\frac{q}{I}\)
= \(\frac{5.09 \times 10^{5}}{1800}\) = 282.77 s
Therefore, the time taken to neutralize the earth’s surface is 282.77 s.

Question 15.
(a) Six lead-acid type of secondary cells each of emf 2.0 V and internal resistance 0.015 Ω are joined in series to provide a supply to a resistance of 8.5 Ω. What are the current drawn from the supply and its terminal voltage?
(b) A secondary cell after long use has an emf of 1.9 V and a large internal resistance of 380 Ω. What maximum current can be drawn from the cell? Could the cell drive the starting motor of a car?
Answer:
(a) Number of secondary cells, n = 6
Emf of each secondary cell, E = 2.0 V
Internal resistance of each cell, r = 0.015 Ω
Series resistor is connected to the combination of cells.
Resistance of the resistor, R – 8.5 Ω
Current drawn from the supply = I, which is given by the relation,
I = \(\frac{n E}{R+n r}\)
= \(\frac{6 \times 2}{8.5+6 \times 0.015}\)
= \(\frac{12}{8.59}\) = 1.39 A
Terminal voltage, V = IR = 1.39 × 8.5 =11.87 A
Therefore, the current drawn from the supply is 1.39 A and terminal voltage is 11.87 A.

(b) After a long use, emf of the secondary cell, E = 1.9 V
Internal resistance of the cell, r = 380 Ω
Hence, maximum current, I_max = \(\frac{E}{r}=\frac{1.9}{380}\) = 0.005 A

Therefore, the maximum current drawn from the cell is 0.005 A. Since a large current is required to start the motor of a car, the cell cannot be used to start a motor.

Question 16.
Two wires of equal length, one of aluminium and the other of copper have the same resistance. Which of the two wires is lighter? Hence explain why aluminium wires are preferred for overhead power cables. (ρAl = 2.63 × 10^-8 Ω m, ρCu = 1.72 × 10^-8 Ω m, Relative density of A1 = 2.7, of Cu = 8.9.)
Answer:
Resistivity of aluminium, ρAl = 2.63 × 10^-8 Ωm
Relative density of aluminium, d₁ = 2.7
Let l₁be the length of aluminium wire and ₁ be its mass.
Resistance of the aluminium wire = R₁
Area of cross-section of the aluminium wire = A₁
Resistivity of copper, ρCu = 1.72 × 10^-8 Ωm
Relative density of copper, d₂ = 8.9
Let l₂ be the length of copper wire and m₂ be its mass.
Resistance of the copper wire = R₂
Area of cross-section of the copper wire = A₂
R₁ = ρ₁\(\frac{l_{1}}{A_{1}}\) …………… (1)
R₂ = ρ₂\(\frac{l_{2}}{A_{2}}\) …………… (2)
It is given that,

It can be inferred from this ratio that m₁ is less than m₂. Hence, aluminium is lighter than copper.
Since aluminium is lighter, it is preferred for overhead power cables over copper.

Question 17.
What conclusion can you draw from the following observations on a resistor made of alloy manganin?

Answer:
It can be inferred from the given table that the ratio of voltage with current is a Constant, which is equal to 19.7. Hence, manganin is an ohmic conductor i. e., the alloy obeys Ohm’s law. According to Ohm’s law, the ratio of voltage with current is the resistance of the conductor. Hence, the resistance of manganin is 19.7 Ω.

Question 18.
Answer the following questions :
(a) A steady current flows in a metallic conductor of non-uniform cross-section. Which of these quantities is constant along the conductor : current, current density, electric field, drift speed?
(b) Is Ohm’s law universally applicable for all conducting elements?
If not, give examples of elements which do not obey Ohm’s law.
(c) A low voltage supply from which one needs high currents must have very low internal resistance. Why?
(d) A high tension (HT) supply of, say 6 kV must have a very large internal resistance. Why?
Answer:
(a) When a steady current flows in a metallic conductor of non-uniform cross-section, the current flowing through the conductor is constant. Current density, electric field, and drift speed are inversely proportional to the area of cross-section. Therefore, they are not constant.

(b) No, Ohm’s law is not universally applicable for all conducting elements. Vacuum diode semi-conductor is a non-ohmic conductor. Ohm’s law is not valid for it.

(c) According to Ohm’s law, the relation for the potential is V = IR
Voltage (V) is directly proportional to current (I).
R is the internal resistance of the source.
I = \(\frac{V}{R}\)
If V is low, then R must be very low, so that high current can be drawn from the source.

(d) In order to prohibit the current from exceeding the safety limit, a high tension supply must have a very large internal resistance. If the internal resistance is not large, then the current drawn can exceed the safety limits in case of a short circuit.

Question 19.
Choose the correct alternative:
(a) Alloys of metals usually have (greater/less) resistivity than that of their constituent metals.
(b) Alloys usually have much (lower/higher) temperature coefficients of resistance than pure metals.
(c) The resistivity of the alloy manganin is nearly independent of/increases rapidly with increase of temperature.
(d) The resistivity of a typical insulator (e. g., amber) is greater than that of a metal by a factor of the order of (10²² /10³).
Answer:
(a) Alloys of metals usually have greater resistivity than that of their constituent metals.
(b) Alloys usually have much lower temperature coefficients of resistance than pure metals.
(c) The resistivity of the alloy, manganin, is nearly independent of increase of temperature.
(d) The resistivity of a typical insulator is greater than that of a metal by a factor of the order of 10²².

Question 20.
(a) Given n resistors each of resistance R, how will you combine them to get the (i) maximum (ii) minimum effective resistance? What is the ratio of the maximum to minimum resistance?
(b) Given the resistances of 1 Ω, 2 Ω, 3 Ω, how will be combine them to get an equivalent resistance of (i) (11/3) Ω (ii) (11/5) Ω, (iii) 6 Ω, (iv) (6/11) Ω?
(c) Determine the equivalent resistance of networks shown in Fig. 3.31.

Answer:
(a) For maximum resistance, we shall connect all the resistors in series. Maximum resistance
R_max = nR
For minimum resistance, we shall connect all the resistors in parallel. Minimum resistance,
R_min = \(\frac{R}{n}[latex]
Ratio, [latex]\frac{R_{\max }}{R_{\min }}=\frac{n R}{R / n}\) = n²

(b) The combinations are shown in figure.

(c) (a) It can be observed from the given circuit that in the first small loop, two resistors of resistance 1 Ω each are connected in series.
Hence, their equivalent resistance = (1 + 1) = 2Ω
It can also be observed that two resistors of resistance 2Ω each,are
connected in series.
Hence, their equivalent resistance = (2 + 2) = 4Ω.
Therefore, the circuit can be redrawn as:

It can be observed that 2 Ω and 4 Ω resistors are connected in parallel in all the four loops. Hence, equivalent resistance (R’) of each loop is given by,
R’ = \(\frac{2 \times 4}{2+4}=\frac{8}{6}=\frac{4}{3}\)Ω
The circuit reduces to,

All the four resistors are connected in series.
Hence, equivalent resistance of the given circuit is \(\frac{4}{3}\) × 4 = \(\frac{16}{3}\) Ω

(b) It can be observed from the given circuit that five resistors of resistance R each are connected in series.
Hence, equivalent resistance of the circuit = R + R + R + R + R
= 5 R

Question 21.
Determine the current drawn from a 12 V supply with internal resistance 0.5 Ω by the infinite network shown in Fig. 3.32. Each resistor has 1Ω resistance.

Answer:
Let X be the equivalent resistance of the network. Since network is infinite adding one more set of three resistances each of value R = 1 Ω across the terminals will not affect the total resistance i.e., it should still remain equal to X. Thus this network can be represented as :

Let R_eq be the equivalent resistance of this network, then
R_eq = R + equivalent resistance of parallel combination of X and R + R
= R + \(\frac{X R}{X+R}\) + R
= 2 R + \(\frac{X R}{X+R}\)
Addition of 3 resistances to resistance X of infinite network should not alter the total resistance of the infinite network. Thus
R_eq =X
or 2R + \(\frac{X R}{X+R}\) = X
or 2 × 1 + \(\frac{X \times 1}{X+1}\) = 1 (∵ R = 1Ω)
or 2(X + 1) + X = X(X + 1)
or X² – 2X – 2 = 0

Question 22.
Figure 3.33 shows a potentiometer with a cell of 2.0 V and internal resistance 0.40 Ω maintaining a potential drop across the resistor wire AB. A standard cell which maintains a constant emf of 1.02 V (for very moderate currents upto a few mA) gives a balance point at 67.3 cm length of the wire. To ensure very low currents drawn from the standard cell, a very high resistance, of 600 kΩ is put in series with it, which is shorted close to the balance point. The standard cell is then replaced by a cell of unknown emf e and the balance point found similarly, turns out to be at 82.3 cm length of the wire.

(a) What is the value of e ?
(b) What purpose does the high resistance of 600 kΩ have?
(c) Is the balance point affected by this high resistance?
(d) Is the balance point affected by the internal resistance of the driver cell?
(e) Would the method work in the above situation if the driver cell of the potentiometer had an emf of 1.0 V instead of 2.0 V?
(f) Would the circuit work well for determining an extremely small emf, say of the order of a few mV (such as the typical emf of thermo-couple)? If not, how will you modify the circuit?
Answer:
Constant emf of the given standard cell, E₁ = 1.02 V
Balance point on the wire, l₁ = 67.3 cm
A cell of unknown emf, ε, replaced the standard cell. Therefore, new balance point on the wire, l = 82.3 cm.
(a) The relation between connecting emf and balance point is,
\(\frac{E_{1}}{l_{1}}=\frac{\varepsilon}{l}\)
ε = \(\frac{l}{l_{1}}\) × E₁
= \(\frac{82.3}{67.3}[latex] × 1.02 = 1.247 V
The value of unknown emf is 1.247 V.

(b) The purpose of using the high resistance of 600 kΩ is to reduce the current through the galvanometer when the movable contact is far from the balance point.

(c) The balance point is not affected by the presence of high resistance.

(d) The balance point is not affected by the internal resistance of the driver cell.

(e) The method would not work if the driver cell of the potentiometer had an emf of 1.0 V instead of 2.0 V. This is because if the emf of the driver cell of the potentiometer is less than the’ emf of the other cell, then there would be no balance point on the wire.

(f) The circuit would not work well for determining an extremely small emf. As the circuit would be unstable, the balance point would be close to end A. Hence, there would be a large percentage of error.
The given circuit can be modified if a series resistance is connected with the wire AB. The potential drop across AB is slightly greater than the emf measured. The percentage error would be small.

Question 23.
Figure 3.34 shows a potentiometer circuit for comparison of two resistances. The balance point with a standard resistor R = 10.0 Ω is found to be 58.3 cm, while that with the unknown resistance X is 68.5 cm. Determine the value of X. What might you do if you failed to find a balance point with the given cell of emf ε?

Answer:
Resistance of the standard resistor, R = 10.0 Ω
Balance point for this resistance, l₁ = 58.3 cm
Current in the potentiometer wire = i
Hence, potential drop across R,E₁ = iR
Resistance of the unknown resistor = X
Balance point for this resistor, l₂ = 68.5 cm
Hence, potential drop across X, E₂ = iX
The relation between connecting emf and balance point is,
[latex]\frac{E_{1}}{E_{2}}=\frac{l_{1}}{l_{2}}\)
\(\frac{i R}{i X}=\frac{l_{1}}{l_{2}}\)
X = \(\frac{l_{2}}{l_{1}}\) x R = \(\frac{68.5}{58.3}\) x 10 = 11.749 Ω
Therefore, the value of the unknown resistance, X is 11.75 Ω.
If we fail to find a balance point with the given cell of emf, ε, then the potential drop across R and X must be reduced by putting a resistance in series with it. Only if the potential drop across R or X is smaller than the potential drop across the potentiometer wire AB, a balance point is
obtained.

Question 24.
Figure 3.35 shows a 2.0 V potentiometer used for the determination of internal resistance of a 1.5 V cell. The balance point of the cell in open circuit is 76.3 cm. When a resistor of 9.5 Ω is used in the external circuit of the cell, the balance point shifts to 64.8 cm length of the potentiometer wire. Determine the internal resistance of the cell.

Internal resistance of the cell = r
Balance point of the cell in open circuit, l₁ = 76.3 cm
An external resistance (JR) is connected to the circuit with R = 9.5 Ω.
New balance point of the circuit, l₂ = 64.8 cm
Current flowing through the circuit = I
The relation connecting resistance and emf is,
r = (\(\frac{l_{1}-l_{2}}{l_{2}}\))R
= \(\frac{76.3-64.8}{64.8}\) x 9.5 = 1.68 Ω.
Therefore, the internal resistance of the cell is 1.68 Q.

Punjab State Board PSEB 12th Class Physics Book Solutions Chapter 10 Wave Optics Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Physics Chapter 10 Wave Optics

PSEB 12th Class Physics Guide Wave Optics Textbook Questions and Answers

Question 1.
Monochromatic light of wavelength 589 nm is incident from air on a water surface. What are the wavelength, frequency and speed of (a) reflected, and (b) refracted light? The Refractive index of water is 1.33.
Answer:
Wavelength of incident monochromatic light, λ = 589 nm = 589 x 10^-9 m
Speed of light in air, c = 3 x 10⁸ m/s
Refractive index of water, µ = 1.33

(a) The ray will reflect back in the same medium as that of the incident ray. Hence, the wavelength, speed and frequency of the reflected ray will be the same as that of the incident ray.
Frequency of light is given by the relation,
v = \(\frac{c}{\lambda}=\frac{3 \times 10^{8}}{589 \times 10^{-9}}\)
= 5.09 x 10¹⁴ Hz
Hence, the speed, frequency, and wavelength of the reflected light are 3 x 10⁸ m/s, 5.09 x 10¹⁴ Hz, and 589 nm respectively.

(b) Frequency of light does not depend on the property of the medium in which it is travelling. Hence, the frequency of the refracted ray in water will be equal to the frequency of the incident or reflected light in air.
Refracted frequency, v = 5.09 x 10¹⁴ Hz
Speed of light in water is related to the refractive index of water as
v_w = \(\frac{c}{\mu}\)
v_w = \(\frac{3 \times 10^{8}}{1.33} \) = 2.26 x 10⁸ m/s
Wavelength of light in water is given by the relation,
λ = \(\frac{v_{w}}{v}=\frac{2.26 \times 10^{8}}{5.09 \times 10^{14}}\)
= 444.007 x 10^-9 m
= 444.01 nm
Hence, the speed, frequency and wavelength of refracted light are 2.26 x 10⁸ m/s, 5.09 x 10¹⁴ Hz
and 444.01 nm respectively.

Question 2.
What is the shape of the wavefront in each of the following cases:
(a) Light diverging from a point source. ;
(b) Light emerging out of a convex lens when a point source is placed at its focus.
(c) The portion of the wavefront of light from a distant star intercepted hy the Earth.
Answer:
(a) The shape of the wavefront in case of a light diverging from a point source is spherical. The wavefront emanating from a point source is shown in the given figure

(b) The shape of the wavefront in case of a light emerging out of a convex lens when a point source is placed at its focus is a plane or a parallel grid. This is shown in the given figure

(c) The portion of the wavefront of light from a distant star intercepted by the Earth is a plane.

Question 3.
(a) The refractive index of glass is 1.5. What is the speed of light in glass? (Speed of light in vacuum is 3.0x 10⁸ ms^-1). Is the speed of light in glass independent of the colour of light? If not, which of the two colours red and violet travels slower in a glass prism?
Answer:
(a) Refractive index of glass, µ = 1.5
Speed of light, c = 3 x 10⁸ m/s
Speed of light in glass is given by the relation,
v = \(\frac{c}{\mu}=\frac{3 \times 10^{8}}{1.5} \) = 2 x 10⁸ m/s
Hence, the speed of light in glass is 2 x 10⁸ m/s.

(b) The speed of light in glass is not independent of the colour of light.
The refractive index of a violet component of white light is greater than the refractive index of a red component. Hence, the speed of violet light is less than the speed of red light in glass. Hence, violet light travels slower than red light in a glass prism.

Question 4.
In a Young’s double-slit experiment, the slits are separated by 0.28 mm and the screen is placed 1.4 m away. The distance between the central bright fringe and the fourth bright fringe is measured to be 1.2 cm. Determine the wavelength of light used in the experiment.
Answer:
Distance between the slits, d = 0.28 mm = 0.28 x 10^-3 m
Distance between the slits and the screen, D = 1.4m
Distance between the central fringe and the fourth (n = 4) fringe, u = 1.2 cm = 1.2 x 10^-2 m
In case of a constructive interference, we have the ‘relation for the distance between the two fringes as
u = \(n \lambda \frac{D}{d}\)

where, n = order of fringes = 4 = 4λ= wavelength of light used
∴ λ = \(\frac{u d}{n D}\)
= \(\frac{1.2 \times 10^{-2} \times 0.28 \times 10^{-3}}{4 \times 1.4}\)
= 6 x 10^-7 = 600 nm
Hence, the wavelength of the light is 600 nm.

Question 5.
In Young’s double-slit experiment using monochromatic light of wavelength λ, the intensity of light at a point on the screen where path difference is λ is K units. What is the intensity of light at a point where path difference is λ / 3?
Answer:
Here, I =K when path difference = λ
I’ = ? when path difference = \(\frac{\lambda}{3}\)
We know that the intensity I is given by
I = 2I₀(1 + cosΦ) ………………………….. (1)
When Φ = phase difference

When path difference is λ, let Φ be the phase difference.
∴ From relation,
Φ’ = \(\frac{2 \pi}{\lambda}\) x, we get
Φ’ = \(\frac{2 \pi}{\lambda} \cdot \lambda\) = 2π
∴From eqn.(1),
K = 2I₀ (1+ cos 2π) (∵ cos 2π =1)
= 2I₀(1+1)
or K = 4I₀
or I₀ = \(\frac{K}{4}\) ……………………………… (2)
Let Φ, be the phase difference for a path difference \(\frac{\lambda}{3}\)
∴ Φ₁ = \(\frac{2 \pi}{\lambda} \times \frac{\lambda}{3}\)
= \(\frac{2 \pi}{3}\)
∴ I’ = 2I₀(1+cosΦ₁)

Question 6.
A beam of light consisting of two wavelengths, 650 mn and 520 nm, is used to obtain interference fringes in a Young’s double-slit experiment.
(a) Find the distance of the third bright fringe on the screen from the central maximum for wavelength 650 nm.
(b) What is the least distance from the central maximum where the bright fringes due to both the wavelengths coincide?
Answer:
First wavelength of the light beam, λ₁ = 650 nm
Second wavelength of the light beam, λ₂ = 520 nm
Distance of the slits from the screen = D
Distance between the two slits = d
(a) Distance of the n^th bright fringe on the screen from the central maximum is given by the relation,
x = nλ₁\(\left(\frac{D}{d}\right)\)
For third bright fringe, n = 3
∴ x = 3x 650\(\left(\frac{D}{d}\right)\) = 1950\(\left(\frac{D}{d}\right)\) nm

(b) Let the n^th bright fringe due to wavelength λ₂ and (n – 1)^th bright fringe due to wavelength λ₁ coincide on the screen. We can equate the conditions for bright fringes as nλ₂ = (n-1)λ
520 n = 650 n -650
650 = 130 n
∴ n = 5
Hence, the least distance from the central maximum can be obtained by the relation
x = nλ₂\(\left(\frac{D}{d}\right)\) = 5 x 520\(\left(\frac{D}{d}\right)\) = 2600\(\left(\frac{D}{d}\right)\) nm
Note : The value of d and D are not given in the question.

Question 7.
In a double-slit experiment, the angular width of a fringe is found to be 0.2° on a screen placed 1 m away. The wavelength of light used is 600 nm. What will be the angular width of the fringe if the entire experimental apparatus is immersed in water? Take refractive index of water to be 4/ 3.
Answer:
Distance of the screen from the slits, D = 1 m
The wavelength of light used, λ₁ = 600 nm
Angular width of the fringe in air, θ₁=0.2°
Angular width of the fringe in water = θ₂
Refractive index of water, µ = \(\frac{4}{3}\)
Refractive index is related to angular width as

Therefore, the angular width of the fringe in water will reduce to 0.15°.

Question 8.
What is the Brewster angle for air to glass transition? (Refractive index of glass = 1.5)
Answer:
Refractive index of glass, µ = 1.5
Brewster angle = θ
Brewster angle is related to refractive index as
tanθ = µ
θ= tan^-1 (1.5)=56.31°
Therefore, the Brewster angle for air to glass transition is 56.3 1°.

Question 9.
Light of wavelength 5000 A falls on a plane reflecting surface. What are the wavelength and frequency of the reflected light? For what angle of incidence is the reflected ray normal to the incident ray?
Answer:
Wavelength of incident light, λ = 5000 Å = 5000 x 10^-10 m
Speed of light, c =3 x 10⁸ m
Frequency of incident light is given by the relation,
v = \(\frac{c}{\lambda}=\frac{3 \times 10^{8}}{5000 \times 10^{-10}}\) = 6 x 10¹⁰ Hz

The wavelength and frequency of incident light is the same as that of reflected ray. Hence, the wavelength of reflected light is 5000 Å and its frequency is 6 x 10¹⁴ Hz. When reflected ray is normal to incident ray, the sum of the angle of incidence, ∠i and angle of reflection, ∠r is 90°.

According to the law of reflection, the angle of incidence is always equal to the angle of reflection. Hence, we can write the sum as
∠i + ∠r =90
∠i + ∠i=90
∠i = \( \frac{90}{2}\) = 45°
Therefore, the angle of incidence for the given condition is 45°.

Question 10.
Estimate the distance for which ray optics is a good approximation for an aperture of 4 mm and wavelength 400 nm.
Answer:
Fresnel’s distance (Z_F) is the distance for which the ray optics is a good approximation. It is given by the relation,
Z_F = \(\frac{a^{2}}{\lambda}\)
where,
aperture width, a = 4 mm = 4 x 10^-3m
wavelength of light, λ = 400 nm = 400 x 10^-9 m
Z_F = \(\frac{\left(4 \times 10^{-3}\right)^{2}}{400 \times 10^{-9}}\) = 40 m
Therefore, the distance for which the ray optics is a good approximation is 40 m.

Additional Exercises

Question 11.
The 6563 Å H_α line emitted by hydrogen in a star is found to be red-shifted by 15 Å. Estimate the speed with which the star is receding from the Earth.
Answer:
Wavelength of H_α line emitted by hydrogen, λ = 6563 Å
= 6563 x 10^-10 m.
Star’s red-shift, (λ’ – λ) = 15 Å = 15 x 10^-10 m
Speed of light, c = 3 x 10⁸ m/s
Let the velocity of the star receding away from the Earth be v.
The redshift is related with velocity as

Therefore, the speed with which the star is receding away from the Earth is 6.87 x10⁵ m/s.

Question 12.
Explain how corpuscular theory predicts the speed of light in a medium, say, water, to be greater than the speed of light in vacuum. Is the prediction confirmed by experimental determination of the speed of light in water? If not, which alternative picture of light is consistent with experiment?
Answer:
According to Newton’s corpuscular theory of light, when light corpuscles strike the interface of two media from a rarer (air) to a denser (water) medium, the particles experience forces of attraction normal to the surface. Hence, the normal component of velocity increases while the component along the surface remains unchanged.
Hence, we can write the expression
c sin i = v sin r …………………………… (1)
where i = Angle of incidence
r = Angle of reflection
c = Velocity of light in air
v = Velocity of light in water

We have the relation for a relative refractive index of water with respect to air as
μ = \(\frac{v}{c}\)
Hence, equation (1) reduces to
\(\frac{v}{c}=\frac{\sin i}{\sin r}\) = μ
But, μ > 1
Hence, it can.be inferred from equation (2) that v > c. This is not possible since this prediction is opposite to the experimental results of c > v. The wave picture of light is consistent with the experimental results.

Question 13.
You have learnt in the text how Huygen’s principle leads to the laws of reflection and refraction. Use the same principle to deduce directly that a point object placed in front of a plane mirror produces a virtual image whose distance from the mirror is equal to the object’s distance from the mirror.
Answer:
Let an object at 0 be placed in front of a plane mirror MO’ at a distance r (as shown in the given figure).

A circle is drawn from the centre (0) such that it just touches the plane mirror at point 0′. According to Huygen’s principle, XY is the wavefront of incident light. If the mirror is absent, then a similar wavefront X’ Y’ (as XT) would form behind 0′ at distance r (as shown in the given figure).

X’ Y’ can be considered as a virtual reflected ray for the plane mirror. Hence, a point object placed in front of the plane mirror produces a virtual image whose distance from the mirror is equal to the object distance (r).

Question 14.
Let us list some of the factors, which could possibly influence the speed of wave propagation :
(i) nature of the source.
(ii) direction of propagation.
(iii) motion of the source and/or observer.
(iv) wavelength.
(v) intensity of the wave.
On which of these factors, if any, does
(a) the speed of light in vacuum,
(b) the speed of light in a medium (say, glass Or water), depend?
Answer:
(a) The speed of light in a vacuum i. e., 3 x 10⁸ m/s (approximately) is a universal constant. It is not affected by the motion of the source, the observer, or both. Hence, the given factor does not affect, the speed of light in a vacuum.
(b) Out of the listed factors, the speed of light in a medium depends on the wavelength of light in that medium.

Question 15.
For sound waves, the Doppler formula for frequency shift differs slightly between the two situations : (i) source at rest; observer moving, and (ii) source moving; observer at rest. The exact Doppler formulas for the case of light waves in a vacuum are, however, strictly identical for these situations. Explain why this should be so. Would you expect the formulas to be strictly identical for the two situations in the case of light travelling in a medium?
Answer:
No, sound waves can propagate only through a medium. The two given situations are not scientifically identical because the motion of an observer relative to a medium is different in the two situations. Hence, the Doppler formulas for the two situations cannot be the same.

In the case of light waves, sound can travel in a vacuum. In a vacuum, the above two cases are identical because the speed of light is independent of the motion of the observer and the motion of the source. When light travels in a medium, the above two cases are not identical because the speed of light depends on the wavelength of the medium.

Question 16.
In a double-slit experiment using light of wavelength 600 nm, the angular width of a fringe formed on a distant screen is 0.1°. What is the spacing between the two slits?
Answer:
Wavelength of light used, λ = 600 nm = 600 x 10^-9 m
Angular width of fringe, θ = 0.1° = 0.1 x \(\frac{\pi}{180}=\frac{3.14}{1800}\)rad
Angular width of a fringe is related to slit spacing (d) as
θ = \(\frac{\lambda}{d}\)

Therefore, the spacing between the two slits is 3.44 x 10^-4 m.

Question 17.
Answer the following questions:
(a) In a single slit diffraction experiment, the width of the slit is made double the original width. How does this affect the size and intensity of the central diffraction band?
(b) In what way is diffraction from each slit related to the interference pattern in a double-slit experiment?
(c) When a tiny circular obstacle is placed in the path of light from a distant source, a bright spot is seen at the centre of the shadow of the obstacle. Explain why?
(d) Two students are separated by a 7 m partition wall in a room 10 m high. If both light and sound waves can bend around obstacles, how is it that the? students are unable to see each other even though they can converse easily.
(e) Ray optics is based on the assumption that light travels in a straight line. Diffraction effects (observed when light propagates through small apertures/slits or around small obstacles) disprove this assumption. Yet the ray optics assumption is so commonly used in an understanding of location and several other properties of images in optic instruments. What is the justification?
Answer:
(a) In a single slit diffraction experiment, if the width of the slit is made double the original width, then the size of the central diffraction band reduces to half and the intensity of the central diffraction band increase up to four times.

(b) The interference pattern in a double-slit experiment is modulated by diffraction from each slit. The pattern is the result of the interference of the diffracted wave from each slit.

(c) When a tiny circular obstacle is placed in the path of light from a distant source, a bright spot is seen at the centre of the shadow of the obstacle. This is because light waves are diffracted from the edge of the circular obstacle, which interferes constructively at the centre of the shadow. This constructive interference produces a bright spot.

(d) Bending of waves by obstacles by a large angle is possible when the size of the obstacle is comparable to the wavelength of the waves. On the one hand, the wavelength of the light waves is too small in comparison to the size of the obstacle. Thus, the diffraction angle will be very small. Hence, the students are unable to see each other. On the other hand, the size of the wall is comparable to the wavelength of the sound waves. Thus, the bending of the waves takes place at a large angle. Hence, the students are able to hear each other.

(e) The justification is that in ordinary optical instruments, the size of the aperture involved is much larger than the wavelength of the light used.

Question 18.
Two towers on top of two hills are 40 km apart. The line joining them passes 50 m above a hill halfway between the towers. What is the longest wavelength of radio waves, which can be sent between the towers without appreciable diffraction effects?
Answer:
Distance between the towers, d = 40 km
Height of the line joining the hills, d = 50 m
Thus, the radial spread of the radio waves should not exceed 50 km.
Since the hill is located halfway between the towers, Fresnel’s distance can be obtained as
Z_P = 20 km = 20 x 10³m
Aperture can be taken as
a = d= 50 m

Fresnel’s distance is given by the relation,
Z_p = \(\frac{a^{2}}{\lambda}\)
where, λ = wavelength of radio waves
∴ λ = \(\frac{a^{2}}{Z_{P}}\)
= \(\frac{(50)^{2}}{20 \times 10^{3}}\) = 1250 x 10^-4 = 0.1250 m
= 12.5 cm
Therefore, the wavelength of the radio waves is 12.5 cm.

Question 19.
A parallel beam of light of wavelength 500 nm falls on a narrow slit and the resulting diffraction pattern is observed on a screen 1 m away. It is observed that the first minimum is at a distance of 2.5 mm from the centre of the screen. Find the width of the slit.
Answer:
Wavelength of light beam, λ = 500 nm = 500 x 10^-9 m
Distance of the screen from the slit, D=1m
For first minima, n = 1
Distance between the slits = d
Distance of the first minimum from the centre of the screen can be obtained as
x = 2.5mm = 2.5 x 10^-3 m
It is related to the order of minima as

Therefore, the width of the slits is 0.2 mm.

Question 20.
Answer the following questions :
(a) When a low flying aircraft passes overhead, we sometimes notice a slight shaking of the picture on our TV screen. Suggest a possible explanation.
(b) As you have learnt in the text, the principle of linear superposition of wave displacement is basic to understanding intensity distributions in diffraction and interference patterns. What is the justification of this principle?
Answer:
(a) Weak radar signals sent by a low flying aircraft can interfere with the TV signals received by the antenna. As a result, the TV signals may get distorted. Hence, when a low flying aircraft passes overhead, we sometimes notice a slight shaking of the picture on our TV screen.

(b) The principle of linear superposition of wave displacement is essential to our understanding of intensity distributions and interference patterns. This is because superposition follows from the linear character of a differential equation that governs wave motion. If y₁ and y₂ are the solutions of the second-order wave equation, then any linear combination of y± and y2 will also be the solution of the wave equation.

Question 21.
In deriving the single slit diffraction pattern, it was stated that the intensity is zero at angles of n λ/a. Justify this by suitably dividing the slit to bring out the cancellation.
Answer:
Consider that a single slit of width d is divided into n smaller slits.
∴ Width of each slit, d’ = \(\frac{d}{n}\)
Angle of diffraction is given by the relation,
θ = \(\frac{\frac{d}{d^{\prime}} \lambda}{d}=\frac{\lambda}{d^{\prime}} \)
Now, each of these infinitesimally small slit sends zero intensity in direction θ. Hence, the combination of these slits will give zero intensity.

Punjab State Board PSEB 12th Class Physics Book Solutions Chapter 4 Moving Charges and Magnetism Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism

PSEB 12th Class Physics Guide Moving Charges and Magnetism Textbook Questions and Answers

Question 1.
A circular coil of wire consisting of 100 turns, each of radius
8.0 cm carries a current of 0.40 A. What is the magnitude of the magnetic field B at the centre of the coil?
Answer:
Number of turns on the circular coil, n = 100
Radius of each turn, r = 8.0 cm = 0.08 m
Current flowing in the coil, I = 0.4 A
Magnitude of the magnetic field at the centre of the coil is given by the relation,
\(|B|=\frac{\mu_{0}}{4 \pi} \frac{2 \pi n I}{r}\)
where, μ₀ = 4π × 10^-7 TmA^-1
\(|B|\) = \(\frac{4 \pi \times 10^{-7}}{4 \pi}\) × \(\frac{2 \pi \times 100 \times 0.4}{0.08}\)
= 3.14 × 10^-4T
Hence, the magnitude of the magnetic field is 3.14 × 10^-4 T

Question 2.
A long straight wire carries a current of 35 A. What is the magnitude of the field B at a point 20 cm from the wire?
Answer:
Current in the wire, I = 35 A
Distance of the point from the wire, r = 20 cm = 0.2 m
Magnitude of the magnetic field at this point is given as
B = \(\frac{\mu_{0}}{4 \pi} \frac{2 I}{r}\)
B = \(\frac{4 \pi \times 10^{-7} \times 2 \times 35}{4 \pi \times 0.2}\)
= 3.5 × 10^-5T
Hence, the magnitude of the magnetic field at a point 20 cm from the wire is 3.5 × 10^-5 T.

Question 3.
A long straight wire in the horizontal plane carries a current of 50 A in north to south direction. Give the magnitude and direction of B at a point 2.5 m east of the wire.
Answer:
Current in the wire, I = 50 A
A point is 2.5 m away from the east of the wire.
∴ Magnitude of the distance of the point from the wire, r = 2.5 m
Moving Charges and Magnetism ini
Magnitude of the magnetic field at that point is given by the relation,
B = \(\frac{\mu_{0} 2 I}{4 \pi r}\)
= \(\frac{4 \pi \times 10^{-7} \times 2 \times 50}{4 \pi \times 2.5}\)
= 4 × 10^-6 T
The point is located normal to the wire length at a distance of 2.5 m. The direction of the current in the wire is vertically downward. Hence, according to the Maxwell’s right hand thumb rule, the direction of the magnetic field at the given point is vertically upward.

Question 4.
A horizontal overhead power line carries a current of 90 A in east to west direction. What is the magnitude and direction of the magnetic field due to the current 1.5 m below the line?
Answer:
Current in the power line, I = 90 A
Point is located below the power line at distance, r = 1.5 m
Hence, magnetic field at that point is given by the relation,
B = \(\frac{\mu_{0} 2 I}{4 \pi r}\)
= \(\frac{4 \pi \times 10^{-7} \times 2 \times 90}{4 \pi \times 1.5}\) = 1.2 × 10^-5T
The current is flowing from east to west. The point is below the power line. Hence, according to Maxwell’s right hand thumb rule, the direction of the magnetic field is towards the south.

Question 5.
What is the magnitude of magnetic force per unit length on a wire carrying a current of 8 A and making an angle of 30° with the direction of a uniform magnetic field of 0.15 T?
Answer:
Current in the wire, I = 8 A
Magnitude of the uniform magnetic field, B = 0.15 T
Angle between the wire and magnetic field, θ = 30°.
Magnetic force per unit length on the wire is given as,
F = BI sinθ
= 0.15 × 8 × sin30°
= 0.15 × 8 × \(\frac{1}{2}\)
= 0.15 × 4 = 0.6 Nm^-1
Hence, the magnetic force per unit length on the wire is 0.6 Nm^-1.

Question 6.
A 3.0 cm wire carrying a current of 10 A is placed inside a solenoid perpendicular to its axis. The magnetic field inside the solenoid is given to be 0.27 T. What is the magnetic force on the wire?
Answer:
Length of the wire, l = 3 cm = 0.03 m
Current flowing in the wire, I = 10 A
Magnetic field, B = 0.27 T
Angle between the current and magnetic field, θ = 90°
Magnetic force exerted on the wire is given as,
F = BIl sinθ
= 0.27 × 10 × 0.03 × sin 90°
= 8.1 × 10^-2N
Hence, the magnetic force on the wire is 8.1 × 10^-2 N.

Question 7.
Two long and parallel straight wires A and B carrying currents of
8.0 A and 5.0 A in the same direction are separated by a distance of 4.0 cm. Estimate the force on a 10 cm section of wire A.
Answer:
Here, let I₁ and I₂ be the currents flowing in the straight long and parallel wires A and B respectively.
∴ I₁ = 8.0 A, I₂ = 5.0 A flowing in the same direction
r = distance between A and B = 4.0 cm = 4 × 10^-2 m
If F’ be the force per unit length on wire A, then using
F’ = \(\frac{\mu_{0}}{4 \pi} \cdot \frac{2 I_{1} I_{2}}{r}\), we get
F’ = 10^-7 × \(\frac{2 \times 8 \times 5}{4 \times 10^{-2}}\) Nm^-1
= 20 × 10^-5 Nm^-1

If F be the force on a section of length 10 cm of wire A, then
F = F’ × l (Here,l = 10 × 10^-2m)
= 20 × 10^-5 × 10 × 10^-2N
= 2 × 10^-5N

Question 8.
A closely wound solenoid 80 cm long has 5 layers of windings of 400 turns each. The diameter of the solenoid is 1.8 cm. If the current carried is 8.0 A, estimate the magnitude of B inside the solenoid near its centre.
Answer:
Length of the solenoid, l = 80 cm = 0.8 m
Number of turns in each layer = 400
Number of layers in the solenoid = 5
∴ Total number of turns on the solenoid, N = 5 × 400 = 2000
Diameter of the solenoid, D = 1.8 cm = 0.018 m
Current carried by the solenoid, I = 8.0 A
Magnitude of the magnetic field inside the solenoid near its centre is given by the relation,
g.hoM
B = \(=\frac{\mu_{0} N I}{l}\)
B = \(\frac{4 \pi \times 10^{-7} \times 2000 \times 8}{0.8}\)
= 8 π × 10^-3 = 2.512 × 10^-2 T
Hence, the magnitude of the magnetic field inside the solenoid near its centre is 2.512 × 10^-2 T.

Question 9.
A square coil of side 10 cm consists of 20 turns and carries a current of 12 A. The coil is suspended vertically and the normal to the plane of the coil makes an angle of 30° with the direction of a uniform horizontal magnetic field of magnitude 0.80 T. What is the magnitude of torque experienced by the coil?
Answer:
Length of a side of the square coil, l = 10 cm = 0.1 m
Current flowing in the coil, I = 12 A
Number of turns on the coil, N = 20
Angle made by the plane of the coil with magnetic field, θ = 30°
Strength of magnetic field, B = 0.80 T
Magnitude of the torque experienced by the coil in the magnetic field is given by the relation,
τ = NBIAsinθ
where, A = Area of the square coil
⇒ l × l = 0.1 × 0.1 = 0.01 m²
∴ τ = 20 × 0.80 × 12 × 0.01 × sin30°
= 20 × 0.80 × 12 × 0.01 × \(\frac{1}{2}\)
= 0.96 N m
Hence, the magnitude of the torque experienced by the coil is 0.96 N m.

Question 10.
Two moving coil meters, M₁ and M₂ have the following particulars:
R₁ = 10 Ω, N₁ = 30,
A₁ = 3.6 × 10^-3 m², B₁ = 0.25T
R₂ = 14Ω, N₂ = 42,
A₂ = 1.8 × 10^-3 m², B₂ = 0.50 T
(The spring constants are identical for the two meters). Determine the ratio of (a) current sensitivity and (b) voltage sensitivity of M₂ and M₁.
Answer:
Here,R₁ = 10 n, N₁ = 30, A₁ = 3.6 x 10^-3 m²,B₁ = 0.25T for coil M₁
R₂ = 14 Q, N₂ = 42, A₂ = 1.8 x 10^-3 m²,B₂ = 0.50T for coil M₂.
We know that current sensitivity and voltage sensitivity are given by the formulae
Current sensitivity = \(\frac{N B A}{k}\)
and Voltage sensitivity = \(\frac{N B A}{k R}\)
Here, k₁ = k₂ for the two coils = k (say)
∴ Current sensitivity for M₁ is given by = N₁B₁A₁/ k and for M₂ = N₂B₂A₂ / k

(a) Current sensitivity ratio for M₂ and M₁ is given by
= \(\frac{\frac{N_{2} B_{2} A_{2}}{k}}{\frac{N_{1} B_{1} A_{1}}{k}}\)

Question 11.
In a chamber, a uniform magnetic field of 6.5 G (1 G = 10^-4 T) is maintained. An electron is shot into the field with a speed of 4.8 × 10⁶ ms^-1 normal to the field. Explain why the path of the electron is a circle. Determine the radius of the circuit orbit.
e,= 1.6 × 10^-19 (m_e = 9.1 × 10 ^-31 kg
Answer:
Magnetic field strength, B = 6.5 G = 6.5 × 10^-4 T
Speed of the electron, y = 4.8 × 10⁶ m/s
Charge on the electron, e,= 1.6 × 10^-19 C
Mass of the electron, me 9.1 × 10^-31 kg
Angle between the electron and magnetic field, θ = 90°
Magnetic force exerted on the electron in the magnetic field is given as :
F = evBsinθ
This force provides centripetal force to the moving electron. Hence, the electron starts moving in a circular path of radius r.
Hence, centripetal force exerted on the electron,
F_e = \(\frac{m v^{2}}{r}\)
In equilibrium, the centripetal force exerted on the electron is equal to the magnetic force t.e.,
F_e = F
\(\frac{m v^{2}}{r}\) = evBsinθ
r = \(\frac{m v}{B e \sin \theta}\)
= \(\frac{9.1 \times 10^{-31} \times 4.8 \times 10^{6}}{6.5 \times 10^{-4} \times 1.6 \times 10^{-19} \times \sin 90^{\circ}}\)
= 4.2 × 10^-2 m = 4.2 cm
Hence, the radius of the circular orbit of the electron is 4.2 cm.

Question 12.
In Exercise 4.11 obtain the frequency of revolution of the electron in its circular orbit. Does the answer depend on the speed of the electron? Explain.
Answer:
Magnetic field strength, B = 6.5 × 10^-4 T
Charge on the electron, e = 1.6 × 10^-19 C
Mass of the electron, m_e = 9.1 × 10^-31 kg
Velocity of the electron, v = 4.8 × 10⁶ m/s
Radius of the orbit, r = 4.2 cm = 0.042 m
Frequency of revolution of the electron = v
Angular frequency of the electron = ω = 2πv
Velocity of the electron is related to the angular frequency as :
v = rω
In the circular orbit, the magnetic force on the electron is balanced by the centripetal force. Hence, we can write :
evB = \(\frac{m v^{2}}{r}\)
eB = \(\frac{m}{r}\) (rω) = \(\frac{m}{r}\) (r2πv)
v = \(\frac{B e}{2 \pi m}\)

This expression for frequency is independent of the speed of the electron. On substituting the known values in this expression, we get the frequency as:
V = \(=\frac{6.5 \times 10^{-4} \times 1.6 \times 10^{-19}}{2 \times 3.14 \times 9.1 \times 10^{-31}}\)
= 18.2 × 10⁶ Hz ≈ 18 MHz
Hence, the frequency of the electron is around 18 MHz and is independent of the speed of the electron.

Question 13.
(a) A circular coil of 30 turns and radius 8.0 cm carrying a current of 6.0 A is suspended vertically in a uniform horizontal magnetic field of magnitude 1.0 T. The field lines make an angle of 60° with the normal of the coil. Calculate the magnitude of the counter torque that must be applied to prevent the coil from turning.

(b) Would your answer change, if the circular coil in (a) were replaced by a planar coil of some irregular shape that encloses, the same area? (All other particulars are also unaltered.)
Answer:
(a) Number of turns on the circular coil, N = 30
Radius of the coil, r = 8.0 cm = 0.08 m
Area of the coil = πr² = π(0.08)² = 0.0201 m²
Current flowing in the coil, I = 6.0 A
Magnetic field strength, B = 1.0 T
Angle between the field lines and normal with the coil surface,
θ = 60°
The coil experiences a torque in the magnetic field. Hence, it turns. The. counter torque applied to prevent the coil from turning is given by the relation,
τ = N IBAsinθ …………… (1)
= 30 × 6 × 1 × 0.0201 × sin60°
= 180 × 0.0201 × \(\frac{\sqrt{3}}{2}\)
= 3.133 Nm

(b) It can be inferred from relation (1) that the magnitude of the applied torque is not dependent on the shape of the coil. It depends on the area of the coil. Hence, the answer would not change if the circular coil in the above case is replaced by a planar coil of some irregular shape that encloses the same area.

Question 14.
Two concentric circular coils X and Y of radii 16 cm and 10 cm, respectively, lie in the same vertical plane containing the north to south direction. Coil X has 20 turns and carries a current of 16 A; coil Y has 25 turns and carries a current of 18 A. The sense of the current in X is anticlockwise, and clockwise in Y, for an observer looking at the coils facing west. Give the magnitude and direction of the net magnetic field due to the coils at their centre.
Answer:
Radius of coil X, r₁ = 16 cm = 0.16 m
Radius of coil Y, r₂ = 10 cm = 0.10 m
Number of turns on coil X, n₁ = 20
Number of turns on coil Y, n₂ = 25
Current in coil X,I₁ =16 A
Current in coil Y, I₂ = 18 A
Magnetic field due to coil X at their centre is given by the relation,
B₁ = \(\frac{\mu_{0} n_{1} I_{1}}{2 r_{1}}\)
∴ B₁ = \(\frac{4 \pi \times 10^{-7} \times 20 \times 16}{2 \times 0.16}\)
= 4π × 10^-4 T (towards East)
Magnetic field due to coil Y at their centre is given by the relation,
B₂ = \(\frac{\mu_{0} n_{2} I_{2}}{2 r_{2}}\)
\(\frac{4 \pi \times 10^{-7} \times 25 \times 18}{2 \times 0.10}\)
= 9π × 10^-4 T (towards West)

Hence, net magnetic field can be obtained as:
B = B₂ – B₁
= 9π × 10^-4 – 4π × 10^-4
= 5π × 10 T
= 1.57 × 10^-3 T (towards West)

Question 15.
A magnetic field of 100 G (1 G = 10^-4 T) is required which is uniform in a region of linear dimension about 10 cm and area of cross-section about 10^-3 m². The maximum current-carrying capacity of a given coil of wire is 15 A and the number of turns per unit length that can be wound round a core is at most 1000 turns m^-1 . Suggest some appropriate design particulars of a solenoid for the required purpose. Assume the core is not ferromagnetic.
Answer:
Here, B = magnetic field = 100 G = 100 × 10^-4 = 10^-2 T,
I_max = maximum current carried by the coil = 15 A
n = number of turns per unit length = 1000 turns m^-1 = 10 tums/cm
l = length of linear region = 10 cm
A = area of cross-section = 10^-3 m².

To produce a magnetic field in the above mentioned region, a solenoid can be made so that well within the solenoid, the magnetic field is uniform. To do so, we may take the length L of the solenoid 5 times the length of the region and area of the solenoid 5 times the area of region.

∴ L = 5l = 5 × 10 = 50 cm = 0.5m
and A = 5 × 10^-3 m²
∴ If r be the radius of the solenoid, then
πr² = A = 5 × 10^-3
or r = \(\sqrt{\frac{5 \times 10^{-3}}{3.14}}\) = 0.04 m = 4 cm
Also let us wind 500 turns on the coil so that the number of turns per m is
n = \(\frac{500}{0.5}\) = 1000 turns m^-1
∴ Using formula, μ₀nI = B, we get
I = \(\frac{B}{\mu_{0} n}\) = \(\frac{10^{-2}}{4 \pi \times 10^{-7} \times 1000}\) = 7.96 A ≈ 8A

So, a current of 8 A can be passed through it to produce a uniform magnetic field of 100 G in the region. But this is not a unique way. If we wind 300 turns on the solenoid, then number of turns is
n = \(\frac{300}{0.5}\) = 600 per m.
∴ I= \(\frac{B}{\mu_{0} n}\) = \(\frac{10^{-2}}{4 \pi \times 10^{-7} \times 600}\) = 13.3 A
i. e., a current of 13.3 A can be passed through it to produce the magnetic field of loo G.
Similarly, if no. of turns = 400,
then, n = \(\frac{400}{0.5}\) = 800 per m.
∴ I = \(\frac{B}{\mu_{0} n}\) = \(\frac{10^{-2}}{4 \pi \times 10^{-7} \times 800}\) = 9.95 A
i. e., a current of 10 A can be passed ≈ 10 A
Through it to produce B = 100 G
Thus we may achieve the result in a number of ways.

Question 16.
For a circular coil of radius R and N turns carrying current J, the magnitude of the magnetic field at a point on its axis at a distance x from its centre is given by,
B = \(\frac{\mu_{0} I R^{2} N}{2\left(x^{2}+R^{2}\right)^{3 / 2}}\)
(a) Show that this reduces to the familiar result for field at the centre of the coil.
(b) Consider two parallel co-axial circular coils of equal radius R, and number of turns N, carrying equal currents in the same direction, and separated by a distance R. Show that the field on the axis around the mid-point between the coils is uniform over a distance that is small as compared to JR, and is given by,
B = 0.72 \(\frac{\mu_{0} \boldsymbol{N I}}{\boldsymbol{R}}\), approximately.
[Such an arrangement to produce a nearly uniform magnetic field over a small region is known as Helmholtz coils.]
Answer:
Radius of circular coil = R
Number of turns on the coil = N
Current in the coil = I
Magnetic field at a point on its axis at distance x from its centre is given by the relation,
B = \(\frac{\mu_{0} I R^{2} N}{2\left(x^{2}+R^{2}\right)^{3 / 2}}\)

(a) If the magnetic field at the centre of the coil is considered, then x = 0
∴ B = \(\frac{\mu_{0} I R^{2} N}{2 R^{3}}=\frac{\mu_{0} I N}{2 R}\)
This is the familiar result for magnetic field at the centre of the coil,

(b) Radii of two parallel co-axial circular coils = R
Number of turns on each coil = N
Current in both coils = I
Distance between both the coils = R
Let us consider point Q at distance d from the centre.
Then, one coil is at a distance of \(\frac{R}{2}\) + d from point Q.


Hence, it is proved that the field on the axis around the mid-point between the coils is uniform.

Question 17.
A toroid has a core (non-ferromagnetic) of inner radius 25 cm and outer radius 26 cm, around which 3500 turns of a wire are wound. If the current in the wire is 11 A, what is the magnetic field (a) outside the toroid, (b) inside the core of the toroid, and (c) in the empty space surrounded by the toroid.
Answer:
Here, I = 11 A,
Total number of turns = 3500
Mean radius of toroid, r = \(\frac{25+26}{2}\)
r = 25.5cm = 25.5 × 10^-2 m
Total length of the toroid = 2πr = 2π × 25.5 × 10^-2
= 51π × 10^-2m
Therefore, number of turns per unit length,
n = \(\frac{3500}{51 \pi \times 10^{-2}}\)

(a) The field is non-zero only inside the core surrounded by the windings of the toroid. Therefore, the field outside the toroid is zero.

(b) The field inside the core of the toroid
B = μ₀nI
B = 4π × 10^-7 × \(\frac{3500}{51 \pi \times 10^{-2}}\) × 11
B = 3.02 × 10^-2 T

(c) For the reason given in (a), the field in the empty space surrounded by toroid is also zero.

Question 18.
Answer the following questions:
(a) A magnetic field that varies in magnitude from point to point but has a constant direction (east to west) is set up in a chamber. A charged particle enters the chamber and travels undeflected along a straight path with constant speed. What can you say about the initial velocity of the particle?

(b) A charged particle enters an environment of a strong and non-uniform magnetic field varying from point to point both in magnitude and direction and comes out of it following a complicated trajectory. Would its final speed equal the initial speed if it suffered no collisions with the environment?

(c) An electron travelling west to east enters a chamber having a uniform electrostatic field in north to south direction. Specify the direction in which a uniform magnetic field should be set up to prevent the electron from deflecting from its straight line path.
Answer:
(a) The initial velocity of the particle is either parallel or anti-parallel to the magnetic field. Hence, it travels along a straight path without suffering any deflection in the field.

(b) Yes, the final speed’ of the charged particle will be equal to its initial speed. This is because magnetic force can change the direction of velocity, but not its magnitude.

(c) An electron travelling from west to east enters a chamber having a uniform electrostatic field in the north-south direction. This moving electron can remain undeflected if the electric force acting on it is equal and opposite of magnetic field. Magnetic force is directed towards the south. According to Fleming’s left hand rule, magnetic field should be applied in a vertically downward direction.

Question 19.
An electron emitted by a heated cathode and accelerated through a potential difference of 2.0 kV, enters a region with uniform magnetic field of 0.15 T. Determine the trajectory of the electron if the field (a) is transverse to its initial velocity, (b) makes an angle of 30° with the initial velocity.
Answer:
Magnetic field strength, B = 0.15 T
Charge on the electron, e = 1.6 × 10^-19C
Mass of the electron, m = 9.1 × 10^-31 kg
Potential difference, V = 2.0 kV = 2 × 10³ V
Thus, kinetic energy of the electron = eV
⇒ eV = \(\frac{1}{2}\)mv²
v = \(\sqrt{\frac{2 e V}{m}}\) ……………. (1)
where, v = Velocity of the electron
Magnetic force on the electron provides the required centripetal force of the electron. Hence, the electron traces a circular path of radius r.

(a) When the magnetic field is transverse to the initial velocity. The force on the electron due to transverse magnetic field = Bev

= 100.55 × 10^-5
= 1.01 × 10^-3 m = 1 mm
Hence, the electron has a circular trajectory of radius 1.0 mm normal to the magnetic field.

(b) When the magnetic field makes an angle θ of 30° with initial velocity, the initial velocity will be,
v₁ = vsinθ
From equation (2), we can write the expression for new radius as :
r₁ = \(\frac{m v_{1}}{B e}\)
= \(\frac{m v \sin \theta}{B e}\)

= 0.5 × 10^-3 m = 0.5mm
Hence, the electron has a helical trajectory of radius 0.5 mm along the magnetic field direction.

Question 20.
A magnetic field set up using Helmholtz coils (described in Exercise 4.16) is uniform in a small region and has a magnitude of 0.75 T. In the same region, a uniform electrostatic field is maintained in a direction normal to the common axis of the coils. A narrow beam of (single species) charged particles all accelerated through 15 kV enters this region in a direction perpendicular to both the axis of the coils and the electrostatic Held. If the beam remains undeflected when the electrostatic field is 9.0 × 10^-5 V m^-1, make a simple guess as to what the beam contains. Why is the answer not unique?
Answer:
Magnetic field, B = 0.75 T
Accelerating voltage, V = 15 kV = 15 × 10³ V
Electrostatic field, E = 9 × 10^-5 Vm^-1
Mass of the electron = m
Charge on the electron = e
Velocity of the electron = v
Kinetic energy of the electron = eV
⇒ \(\frac{1}{2}\)mv² = eV
∴ \(\frac{e}{m}=\frac{v^{2}}{2 V}\) ……………. (1)
Since the particle remains undeflected by electric and magnetic fields, we can infer that the electric field is balancing the magnetic field.
∴ eE = evB
v = \(\frac{E}{B}\) …………. (2)
Putting equation (2) in equation (1), we get

= 4.8 × 10⁷ C/kg
Also, we know that \(\frac{e}{m}\) for proton is 9.6 × 10^-7 C kg^-1 . It follows that the charged particle under reference has the value of \(\frac{e}{m}\) half of that for the
proton, so its mass is clearly double the mass of proton. Thus the beam may be of deutrons.
The answer is not unique as the ratio of charge to mass i. e.,
4.8 × 10⁷ C kg^-1 may be satisfied by many other charged particles, surch as
He⁺⁺(\(\frac{2 e}{2 m}\)) and Li³⁺ (\(\frac{3 e}{3 m}\))
which have the same value of \(\frac{e}{m}\).

Question 21.
A straight horizontal conducting rod of length 0.45 m and mass 60 g is suspended by two vertical wires at its ends. A current of 5.0 A is set up in the rod through the wires.
(a) What magnetic field should be set up normal to the conductor in order that the tension in the wires is zero?
(b) What will be the total tension in the wires if the direction of current is reversed keeping the magnetic field same as before? (Ignore the mass of the wires.) g = 9.8 ms^-2.
Answer:
Length of the rod, l = 0.45 m
Mass of the rod, m = 60 g = 60 × 10^-3 kg
Acceleration due to gravity, g = 9.8 m/s²
Current in the rod flowing through the wire, I = 5 A

(a) Magnetic field (B) is equal and opposite to the weight of the rod i.e.,
BIl = mg
∴ B = \(\frac{m g}{I l}\) = \(\frac{60 \times 10^{-3} \times 9.8}{5 \times 0.45}\) = 0.26T
A horizontal magnetic field of 0.26 T normal to the length of the conductor should be set up in order to get zero tension in the wire. The magnetic field should be such that Fleming’s left hand rule gives an upward magnetic force.

(b) If the direction of the current is reversed, then the force due to magnetic field and the weight of the rod acts in a vertically downward direction.
∴ Total tension in the wire = BIl + mg
= 0.26 × 5 × 0.45 + (60 × 10^-3) × 9.8
= 1.176 N

Question 22.
The wires which connect the battery of an automobile to its starting motor carry a current of 300 A (for a short time). What is the force per unit length between the wires if they are 70 cm long and 1.5 cm apart? Is the force attractive or repulsive?
Answer:
Current in both wires, I = 300 A
Distance between the wires, r = 1.5 cm = 0.015 m
Length of the both wires, l = 70 cm = 0.7 m
Force between the two wires is given by the relation,
F = \(\frac{\mu_{0} I^{2}}{2 \pi r}\)
∴ F = \(\frac{4 \pi \times 10^{-7} \times(300)^{2}}{2 \pi \times 0.015}\) = 1.2 N/M
Since the direction of the current in the wires is opposite, a repulsive force exists between them.

Question 23.
A uniform magnetic field of 1.5 T exists in a cylindrical region of radius 10.0 cm, its direction parallel to the axis along east to west. A wire carrying current of 7.0 A in the north to south direction passes through this region. What is the magnitude and direction of the force on the wire if,
(a) the wire intersects the axis,
(b) the wire is turned from N-S to northeast-northwest direction,
(c) the wire in the N-S direction is lowered from the axis by a distance of 6.0 cm?
Answer:
Magnetic field strength, B = 1.5 T
Radius of the cylindrical region, r = 10cm = 0.1m
Current in the wire passing through the cylindrical region, I = 7 A

(a) If the wire intersects the axis, then the length of the wire is the diameter of the cylindrical region.
Thus, l = 2r = 2 × 0.1 = 0.2 m
Angle between magnetic field and current, θ = 90°
Magnetic force acting on the wire is given by the relation,
F = BIl sinθ
= 1.5 × 7 × 0.2 × sin90° = 2.1N
Hence, a force of 2.1 N acts on the wire in a vertically downward direction.

(b) New length of the wire after turning it to the northeast-northwest direction can be given as:
l₁ = \(\frac{l}{\sin \theta}\)
Angle between magnetic field and current, θ = 45°
Force on the wire,
F₁ = BIl₁ sinθ
\(\frac{B I l}{\sin \theta}\) = sinθ
= BIl = 1.5 × 7 × 0.2 = 2.1 N
Hence, a force of 2.1 N acts vertically downward on the wire. This is independent of angle because Z sinG is fixed.

(c) The wire is lowered from the axis by distance, d = 6.0 cm
Let l₂ be the new length of the wire.
∴ (\(\frac{l_{2}}{2}\))² = 4(d + r)
= 4 (10 + 6) = 4(16)
∴ l₂ = 8 × 2 = 16 cm = 0.16 m
Magnetic force exerted on the wire,
F₂ = BIl₂
= 1.5 × 7 × 0.16 = 1.68 N
Hence, a force of 1.68 N acts in a vertically downward direction on the wire.

Question 24.
A uniform magnetic field of 3000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop in the different cases shown in Fig. 4.28? What is the force on each case? Which case corresponds to stable equilibrium?

Answer:
Here,
B = uniform magnetic field
= 3000 gauss along z-axis
= 3000 × 10^-4T = 0.3 T
l = length of rectangular loop
= 10 cm = 0.1 m
b = breath of rectangular loop
= 5 cm = 0.05 m
∴ A = area of rectangular loop
= l × b = 10 × 5 = 50cm² = 50 × 10^-4 m²
Torque on the loop is given by
\(\vec{\tau}\) = (I\(\vec{A}\)) × \(\vec{B}\)
IA = 50 × 10^-4 × 12 = 0.06 Am⁺²

(a) Here, I\(\vec{A}\) = 0.06î Am², \(\vec{B}\) = 0.3k̂T
∴ \(\vec{\tau}\) = 0.06î × 0.3k̂= -1.8 × 10^-2 Nm ĵ
i.e., τ = 1.8 × 10^-2 Nm and acts along negative y-axis.



Net force on a planar loop in a magnetic field is always zero, so force is
zero in each case.
Case (e) corresponds to stable equilibrium as 7 A is aligned with B while (f) corresponds to unstable equilibrium as 7 A is antiparallel to B.

Question 25.
A circular coil of 20 turns and radius 10 cm is placed in a uniform magnetic field of 0.10 T normal to the plane of the coil. If the current in the coil is 5.0 A, what is the
(a) total torque on the coil,
(b) total force on the coil,
(c) average force on each electron in the coil due’ to the magnetic field?
(The coil is made of copper wire of cross-sectional area 10^-5 m², and the free electron density in copper is given to be about 10²⁹ m^-3.)
Answer:
Number of turns on the circular coil, n = 20
Radius of the coil, r = 10cm = 0.1m
Magnetic field strength, B = 0.10 T
Current in the coil, I = 5.0 A
(a) The total torque on the coil is zero because the field is uniform.
(b) The total force on the coil is zero because the field is uniform.
(c) Cross-sectional area of copper coil, A = 10^-5 m²
Number of free electrons per cubic meter in copper, N = 10²⁹ / m³
Charge on the electron, e = 1.6 × 10^-19C
Magnetic force, F = Bev_d
Where, v_d = \(\frac{I}{N e A}\)
∴ F = \(\frac{B e I}{N e A}=\frac{B I}{N A}\) = \(\frac{0.10 \times 5.0}{10^{29} \times 10^{-5}}\) 5 × 10^-25N
Hence, the average force on each electron is 5 × 10^-25 N.

Question 26.
A solenoid 60 cm long and of radius 4.0 cm has 3 layers of windings of 300 turns each. A 2.0 cm long wire of mass 2.5 g lies inside the solenoid (near its centre) normal to its axis; both the wire and the axis of the solenoid are in the horizontal plane. The wire is connected through two leads parallel to the axis of the solenoid to an external battery which supplies a current of 6.0 A in the wire. What value of current (with appropriate sense of circulation) in the windings of the solenoid can support the weight of the wire? g = 9.8 ms^-2.
Length of the solenoid, L = 60 cm = 0.6 m
Radius of the solenoid, r = 4.0 cm = 0.04 m
It is given that there are 3 layers of windings of 300 turns each.
∴ Total number of turns, n = 3 × 300 = 900
Length of the wire, l = 2 cm = 0.02 m
Mass of the wire, m = 2.5 g = 2.5 × 10 ^-3 kg
Current flowing through the wire, i = 6 A
Acceleration due to gravity, g=9.8m/s²
Magnetic field produced inside the solenoid, B = \(\frac{\mu_{0} n I}{L}\)
where, μ₀ = 4π × 10^-7 TmA^-1
I = Current flowing through the windings of the solenoid Magnetic force is given by the relation,
F = Bil = \(\frac{\mu_{0} n i I}{L}\)l
Also, the force on the wire is equal to the weight of the wire.
∴ mg = \(\frac{\mu_{0} n \text { Iil }}{L}\)
I = \(\frac{m g L}{\mu_{0} \text { nil }}\)
= \(\frac{2.5 \times 10^{-3} \times 9.8 \times 0.6}{4 \pi \times 10^{-7} \times 900 \times 0.02 \times 6}\) = 108A
Hence, the current flowing through the solenoid is 108 A.

Question 27.
A galvanometer coil has a resistance of 12 Ω and the metre shows full scale deflection for a current of 3 mA. How will you convert the metre into a voltmeter of range 0 to 18 V?
Answer:
Resistance of the galvanometer coil, G = 12 Ω
Current for which there is full scale deflection, I_g = 3 mA = 3 × 10^-3 A
Range of the voltmeter is 0, which needs to be converted to 18 V.
∴ V = 18 V
Let a resistor of resistance R be connected in series with the galvanometer to convert it into a voltmeter. This resistance is given as
R = \(\frac{V}{I_{g}}\) – G
= \(\frac{18}{3 \times 10^{-3}}\) – 12 = 6000 – 12 = 5988 Ω
Hence, a resistor of resistance 5988 Ω is to be connected in series with the galvanometer.

Question 28.
A galvanometer coil has a resistance of 15 Ω and the metre shows full scale deflection for a current of 4 mA. How will you convert the metre into an ammeter of range 0 to 6 A?
Answer:
Resistance of the galvanometer coil, G = 15 Ω
Current for which the galvanometer shows full scale deflection,
I_g = 4 mA = 4 × 10^-3A
Range of the ammeter is 0, which needs to be converted to 6 A.
∴ Current, I = 6 A
A shunt resistor of resistance S is to be connected in parallel with the galvanometer to convert it into an ammeter. The value of S is given as :
S = \(\frac{I_{g} G}{I-I_{g}}\) = \(\frac{4 \times 10^{-3} \times 15}{6-4 \times 10^{-3}}\)
S = \(\frac{6 \times 10^{-2}}{6-0.004}=\frac{0.06}{5.996}\) ≈ 0.01Ω = 10mΩ
Hence, a 10 mΩ shunt resistor is to be connected in parallel with the galvanometer.