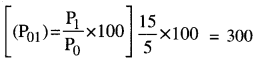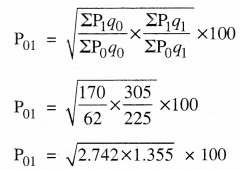Punjab State Board PSEB 12th Class Economics Book Solutions Chapter 31 सूचकांक Textbook Exercise Questions, and Answers.
PSEB Solutions for Class 12 Economics Chapter 31 सूचकांक
PSEB 12th Class Economics सूचकांक Textbook Questions and Answers
I. वस्तुनिष्ठ प्रश्न (Objective Type Questions)
प्रश्न 1.
सूचकांक किसे कहते हैं? उत्तर-सूचकांक वह अंक है जो किसी पूर्व निश्चित तिथि की चुनी हुई वस्तुओं या वस्तु समूह की कीमतों का प्रतिनिधित्व करता है।
प्रश्न 2.
सूचकांकों का एक लाभ लिखिए।
उत्तर-
सूचकांकों का सबसे महत्त्वपूर्ण लाभ यह है कि इनके द्वारा समय-समय पर कीमत-स्तर में होने वाले परिवर्तन या मुद्रा के मूल्य की क्रय-शक्ति में होने वाले परिवर्तन को मापा जा सकता है।
प्रश्न 3.
सूचकांकों की एक सीमा लिखिए। .
उत्तर-
सूचकांक पूर्णतया सत्य नहीं होते। उदाहरण के लिए, कीमत सूचकांकों की सहायता से मुद्रा के मूल्य में होने वाले परिवर्तन का केवल अनुमान ही लगाया जा सकता है।
प्रश्न 4.
सूचकांकों का व्यापारियों के लिए क्या लाभ है?
उत्तर-
उत्पादक तथा व्यापारी वर्ग सूचकांकों की सहायता से कीमत-स्तर में परिवर्तन तथा सामान्य आर्थिक स्थिति का अनुमान लगाता है।
प्रश्न 5.
सूचकांकों का सरकार के लिए क्या लाभ है?
उत्तर-
सरकार सूचकांकों की सहायता से ही अपनी मौद्रिक अथवा कर-नीति का निर्धारण करती है और देश के आर्थिक विकास के लिए ठोस कदम उठाती है।

प्रश्न 6.
वह माप जिस द्वारा समय, मात्रा, स्थान अथवा किसी अन्य आधार पर चरों में होने वाले परिवर्तन ………………….. कहते हैं।
उत्तर-
सूचकांक।
प्रश्न 7.
सूचकांक का निर्माण करने की लास्पीयर तथा पाश्चे की विधियों में क्या अन्तर है ?
उत्तर-
लास्पीयर मदों के भार के रूप में आधार वर्ष की मात्राओं का प्रयोग करते हैं जबकि पाश्चे चालू वर्ष की मात्राओं का प्रयोग करते हैं।
प्रश्न 8.
सूचकांक का यह सूत्र किस द्वारा दिया गया है ?
Po1 = \(\frac{\Sigma \mathrm{P}_{1} q_{0}}{\Sigma \mathrm{P}_{0} q_{0}} \times 100\)
(a) लास्पीयर
(b) पाश्चे
(c) फिशर
(d) मार्शल।
उत्तर-
(a) लास्पीयर।
प्रश्न 9.
निम्नलिखित सूत्र किसने दिया है ?
P01 = \(\sqrt{\frac{\Sigma \mathrm{P}_{1} \mathrm{q}_{0}}{\Sigma \mathrm{P}_{0} \mathrm{q}_{0}} \times \frac{\Sigma \mathrm{P}_{1} \mathrm{q}_{1}}{\Sigma \mathrm{P}_{0} \mathrm{q}_{1}}} \times 100\)
(a) लास्पीयर
(b) पाश्चे
(c) फिशर
(d) उपरोक्त में से कोई नहीं।
उत्तर-
(c) फिशर।
प्रश्न 10.
जिस सूचकांक द्वारा थोक बाज़ार में बेची जाने वाली वस्तुओं की थोक कीमतों में होने वाले सापेक्ष परिवर्तनों को मापते हैं उसको …………… कहते हैं।
उत्तर-
थोक कीमत सूचकांक।
प्रश्न 11.
वह सूचकांक जो औद्योगिक उत्पादन की मात्रा में होने वाले परिवर्तन को मापते हैं उनको ………….. कहते हैं।
उत्तर-
औद्योगिक सूचकांक।

प्रश्न 12.
मुद्रा स्फीति को थोक कीमत सूचकांक में परिवर्तन के रूप में मापते हैं जो कि थोक कीमतों के ……………… समय पर आधारित होते हैं।
उत्तर-
साप्ताहिक।
प्रश्न 13.
फिशर का सूचकांक समय उल्टाऊ परीक्षण तथा तत्त्व (Factor) उल्टाऊ परीक्षण पर ठीक उत्तर देता है इसलिए फिशर के सूचकांक को आदर्श सूत्र माना जाता है।
उत्तर-
सही।
प्रश्न 14.
सबसे अच्छा सूचकांक किस सांख्यिकी शास्त्री का माना जाता है ?
उत्तर-
फिशर का।
प्रश्न 15.
सरल सूचकांक की रचना चार प्रकार की होती है।
उत्तर-
ग़लत।
प्रश्न 16.
भारित सूचकांक के परिणाम अधिक उपयुक्त होते हैं।
उत्तर-
सही।
प्रश्न 17.
समूहीकरण व्यय विधि अनुसार उपभोक्ता कीमत सूचकांक का सूत्र लिखें।
उत्तर-
उपभोक्ता कीमत सूचकांक = \(\frac{\Sigma p_{1} q_{0}}{\Sigma p_{0} q_{0}} \times 100\)
प्रश्न 18.
परिवारिक बजट विधि अनुसार उपभोक्ता सूचकांक बनाने का सूत्र लिखो।
उत्तर-
उपभोक्ता कीमत सूचकांक = \(\frac{\Sigma \mathrm{RW}}{\Sigma \mathrm{W}}\)
प्रश्न 19.
उपभोक्ता कीमत सूचकांक को जीवन निर्वाह लागत सूचकांक भी कहा जाता है।
उत्तर-
सही।
प्रश्न 20.
मुद्रा स्फीति की दर के माप का सूत्र लिखो।
उत्तर-
मुद्रा स्फीति की दर = \(\frac{\mathrm{A}_{2}-\mathrm{A}_{1}}{\mathrm{~A}_{1}} \times 100\)
प्रश्न 21.
औद्योगिक उत्पादन के सूचकांक के माप का सूत्र लिखो।
उत्तर-
औद्योगिक उत्पादन का सूचकांक = \(\frac{\Sigma\left(\frac{p_{1}}{q_{0}}\right) W}{\Sigma W} \times 100\)

II. अति लघु उत्तरीय प्रश्न । (Very Short Answer Type Questions)
प्रश्न 1.
कीमत सूचकांक से क्या अभिप्राय है ?
उत्तर-
कीमत सूचकांक से अभिप्राय किसी देश में कीमत में हुए परिवर्तन को प्रकट करना होता है। जब किसी देश में कीमत सूचकांक में वृद्धि होती है तो इसका अर्थ देश की कीमत स्तर में वृद्धि हो रही है तथा मुद्रा स्फीति की स्थिति उत्पन्न हो रही है। जब कीमत सूचकांक में कमी होती है तो इससे अभिप्राय है कि देश में मुद्रा अस्फीति की स्थिति है। मुद्रा स्फीति तथा अस्फीति के अर्थव्यवस्था पर महत्त्वपूर्ण प्रभाव पड़ते हैं।
प्रश्न 2.
सूचकांक बनाने की विधि की कोई दो समस्याएँ बताएं।
उत्तर-
1. सूचकांक का उद्देश्य (Purpose of Index Numbers)-सूचकांक तैयार करने के लिए आंकड़े एकत्रित करने से पहले सूचकांक का उद्देश्य स्पष्ट होना चाहिए। यदि बिना उद्देश्य से आंकड़ें एकत्रित किए जाते हैं तो इससे आर्थिक स्थिति का पूरा ज्ञान प्राप्त नहीं होता।
2. वस्तुओं का चयन (Selection of Commodities)-सूचकांक का निर्माण करते समय वस्तुओं का चयन भी महत्त्वपूर्ण होता है। सभी वस्तुओं को शामिल करके सूचकांकों का निर्माण नहीं किया जाता, बल्कि यह फैसला करना पड़ता है कि –
- कितनी वस्तुओं को लेकर सूचकांकों का निर्माण किया जाए ?
- कौन-सी वस्तुओं का चयन किया जाए ?
- वस्तुओं की कौन-सी किस्म को शामिल किया जाए ? वस्तुओं का चयन करते समय यह ध्यान रखना चाहिए कि सूचकांक में शामिल की वस्तुएं साधारण लोगों के उपभोग अनुसार होनी चाहिए तथा चुनी हुई वस्तुएं उच्च गुण वाली होनी चाहिए।
प्रश्न 3.
सूचकांक तथा मुद्रा स्फीति के सम्बन्ध को स्पष्ट करें।
उत्तर-
हमारी रोज़ाना की ज़िन्दगी में वस्तुओं तथा सेवाओं की कीमतों की वृद्धि का अनुभव किया जाता है। जब वस्तुओं तथा सेवाओं की कीमतों के स्तर में वृद्धि तीव्रता से तथा निरन्तर होती है तो इस स्थिति को मुद्रा-स्फीति कहा जाता है। मुद्रा-स्फीति के परिणामस्वरूप मुद्रा की खरीद शक्ति कम हो जाती है। मुद्रा-स्फीति का सम्बन्ध थोक की कीमतों (Wholesale Prices) से है। भारत में थोक की कीमतें प्रत्येक सप्ताह मापी जाती है। इस उद्देश्य के लिए सूचकांकों का प्रयोग किया जाता है।
प्रश्न 4.
भारित सूचकांक से क्या अभिप्राय है ?
उत्तर-
भारित सूचकांक (Weighted Index Numbers)-सूचकांक की भारित सूचकांक विधि अधिक प्रचलित है तथा विधि का साधारण तौर पर प्रयोग किया जाता है। इस विधि में भिन्न-भिन्न वस्तुओं के भार दिए होते हैं। जब वस्तुओं के भार अथवा महत्त्व को ध्यान में रखकर सूचकांक तैयार किया जाता है तो इसको भारित सूचक कहते
प्रश्न 5.
फिशर की सूचकांक माप विधि का सूत्र बताएँ।
उत्तर-
फिशर की विधि (Fisher’s Method)-प्रो० इरविंग फिशर के फार्मले में आधार वर्ष तथा वर्तमान वर्ष की मात्राओं को आधार माना जाता है। प्रो० फिशर ने सूचकांक की गणना करने के लिए लास्पेयर तथा पास्चे के सूचकांकों की रेखागणितीय औसत का प्रयोग किया है। इस सूत्र को सूचकांक की रचना का आदर्श सूत्र कहा जाता है-
P01(F) = \(\sqrt{\frac{\Sigma \mathrm{P}_{1} q_{0}}{\Sigma \mathrm{P}_{0} q_{0}} \times \frac{\Sigma \mathrm{P}_{1} q_{1}}{\Sigma \mathrm{P}_{0} q_{1}}} \times 100\)
प्रश्न 6.
उपभोक्ता सूचकांक से क्या अभिप्राय है ?
उत्तर-
उपभोक्ता सूचकांक वह सूचकांक है जो उपभोक्ता द्वारा खरीदी जाने वाली वस्तुओं तथा सेवाओं की कीमतों में परिवर्तन का माप करने के लिए प्रयोग किया जाता है। भिन्न-भिन्न वर्ग के लोग भिन्न-भिन्न वस्तुओं का प्रयोग करते हैं। पिछले वर्ष की तुलना में वर्तमान वर्ष में इन वस्तुओं तथा सेवाओं की लागत में आए परिवर्तन का माप किया जाता है। इसीलिए उपभोक्ता सूचकांक को जीवन निर्वाह लागत (Cost of Living Index Number) भी कहा जाता है। यह सूचकांक परचून कीमतों (Retail Price) के आधार पर बनाया जाता है।

प्रश्न 7.
औद्योगिक उत्पादन सूचकांक का अर्थ बताएँ।
उत्तर-
औद्योगिक उत्पादन सूचकांक वह सूचकांक होता है जो हमें आधार वर्ष की तुलना में किसी देश में औद्योगिक उत्पादन की वृद्धि अथवा कमी को प्रकट करता है। इस सूचकांक की सहायता से किसी देश में औद्योगिक विकास का ज्ञान प्राप्त होता है। भारत में 1993-94 को आधार वर्ष मान कर औद्योगिक उत्पादन सूचकांक की गणना की जाती है।
III. लघु उत्तरीय प्रश्न (Short Answer Type Questions)
प्रश्न 1.
कीमत सूचकांक से क्या अभिप्राय है ? इसका क्या उद्देश्य होता है ?
उत्तर-
कीमत सूचकांक से अभिप्राय किसी देश में कीमत में हुए परिवर्तन को प्रकट करना होता है। जब किसी देश में कीमत सूचकांक में वृद्धि होती है तो इसका अर्थ देश की कीमत स्तर में वृद्धि हो रही है तथा मुद्रा स्फीति की स्थिति उत्पन्न हो रही है। जब कीमत सूचकांक में कमी होती है तो इससे अभिप्राय है कि देश में मुद्रा अस्फीति की स्थिति है। मुद्रा स्फीति तथा अस्फीति के अर्थव्यवस्था पर महत्त्वपूर्ण प्रभाव पड़ते हैं।
कीमत सूचकांक के उद्देश्य-
- देश में कीमत स्तर का ज्ञान प्राप्त करना।
- आर्थिक प्रगति का सूचक।
- आर्थिक प्रगति में कीमत स्तर पर तथा वास्तविक वृद्धि का ज्ञान।
प्रश्न 2.
मात्रा सूचकांक से क्या अभिप्राय है? मात्रा सूचकांक का क्या उद्देश्य होता है ?
उत्तर-
मात्रा सूचकांक वस्तुओं की मात्रा में हुई तबदीली का सूचक होता है। मात्रा सूचकांक इस बात का प्रकटावा करता है कि विभिन्न वस्तुओं के उत्पादन में प्रतिशत परिवर्तन कितना हुआ है। इस द्वारा अर्थव्यवस्था के विभिन्न क्षेत्रों में हुई पैदावार का ज्ञान होता है। जब मात्रा सूचकांक बढ़ता है तो इससे अभिप्राय है कि अर्थव्यवस्था में आर्थिक क्रिया बढ़ रही है-मात्रा सूचकांक घटता है तो देश में आर्थिक क्रिया में घाटे का प्रतीक है।
प्रश्न 3.
आधार वर्ष से क्या अभिप्राय है ? आधार वर्ष की विशेषताएँ बताओ।
उत्तर-
आधार वर्ष वह वर्ष होता है, जिसको आधार मान कर तुलना की जाती है। आधार वर्ष को 100 मानकर वर्तमान वर्ष से तुलना करते है। इसकी विशेषताएँ यह हैं-
- यह वर्ष परिवर्तनों रहित साधारण होना चाहिए।
- इस वर्ष सम्बन्धी विश्वसनीय तथा उचित आंकड़े उपलब्ध होने चाहिए।
- आधार वर्ष तुलना के वर्ष से बहुत दूर नहीं होना चाहिए।
- आधार वर्ष की अवधि उचित होनी चाहिए।
कम-से-कम एक माह तथा अधिक-से-अधिक एक वर्ष।
प्रश्न 4.
सूचकांकों की विशेषताएँ लिखो।
उत्तर-
सूचकांकों की मुख्य विशेषताएँ इस प्रकार हैं –
- परिवर्तनों का सापेक्ष माप-सूचकांकों द्वारा विशेष चर अथवा चरों में सापेक्ष अथवा प्रतिशत परिवर्तनों का माप किया जाता है। जैसे कि कीमत सूचकांक आधार वर्ष की तुलना में वर्तमान वर्ष में कीमत में प्रतिशत वृद्धि अथवा घाटे को स्पष्ट करते हैं।
- संख्यात्मक व्याख्या- सूचकांक संख्याओं के रूप में परिवर्तनों को स्पष्ट करते हैं, जैसे कि 2000 की तुलना में 2006 में सूचकांक 115 हो गया है तो इससे अभिप्राय है कीमतों में 15% वृद्धि हो गई है।
- औसतों का माप-सूचकांक औसतों का माप करते हैं। इनको विभिन्न इकाइयों टन, क्विटल, मीटर में व्यक्त नहीं किया जाता, बल्कि इकाई के रूप में माप किया जाता है।
प्रश्न 5.
सूचकांकों का साधारण लोगों को क्या लाभ है ?
उत्तर-
सूचकांकों द्वारा साधारण लोगों को कई प्रकार की सूचना प्राप्त होती है।
- देश में कीमत स्तर में हुई वृद्धि का ज्ञान प्राप्त होता है।
- बैंक अधिकारी मुद्रा की मांग तथा पूर्ति अनुसार ब्याज की दर निश्चित करते हैं।
- रेल का किराया निश्चित करने में सहायक होते हैं।
- श्रम संघ मज़दूरों की मजदूरी में वृद्धि कीमत स्तर की वृद्धि अनुसार बढ़ाने का यत्न करते हैं।
- समाज सुधारकों, राजनीतिज्ञों तथा सट्टेबाजों को निर्णय लेने में सहायक होते हैं।
प्रश्न 6.
सूचकांकों की सीमाएं बताओ।
उत्तर-
सूचकांकों की सीमाएं इस प्रकार हैं-
- सूचकांक पूर्ण सच्चाई प्रकट नहीं करते। यह अनुमानित परिवर्तन का ज्ञान देते हैं।
- सूचकांक विशेष उद्देश्यों अनुसार तैयार किए जाते हैं। इन को दूसरे उद्देश्यों पर लागू नहीं किया जा सकता।
- सूचकांक थोक कीमतों (Wholesale Price) अनुसार बनाए जाते हैं। इनको परचून कीमतों पर लागू नहीं किया जा सकता।
- सूचकांक को वज़न (Weight) देने की कोई विधि नहीं है।
- सूचकांकों द्वारा अन्तर्राष्ट्रीय तुलना नहीं की जा सकती।

प्रश्न 7.
सूचकांक निर्माण करने की सरल सामूहिक विधि क्या है ?
उत्तर-
सरल सामूहिक विधि द्वारा सूचकांक का निर्माण करने के लिए वर्तमान वर्ष के मूल्यों के जोड़ को आधार वर्ष के मूल्यों से जोड़ने तथा विभाजित करने से 100 गुणा किया जाता है। इस उद्देश्य के लिए निम्नलिखित सूत्र का प्रयोग किया जाता है-
P01 = \(\frac{\Sigma P_{1}}{\Sigma P_{0}} \times 100\)
इसमें P01= कीमत सूचकांक,
ΣP = वर्तमान वर्ष में वस्तुओं की कीमतों का जोड़,
ΣP = आधार वर्ष में वस्तुओं की कीमतों का जोड़।
प्रश्न 8.
सूचकांक निर्माण करने के लिए सरल कीमत अनुपात विधि को स्पष्ट करो।
उत्तर-
सूचकांक निर्माण में सभी वस्तुओं को शामिल नहीं किया जाता है बल्कि सैंपल के आधार पर वस्तुओं को शामिल किया जाता है। प्रत्येक वस्तु का अलग-अलग कीमत अनुपात मापा जाता है।
कीमत अनुपात P01 = \(\left(\frac{P_{1}}{P_{0}} \times 100\right)\)
विभिन्न वस्तुओं की कीमत अनुपात का माप करने के उपरान्त उनको जोड़ कर वस्तुओं की संख्या पर विभाजित किया जाता है, जिससे सरल कीमत अनुपात सूचकांक प्राप्त हो जाता है।
P01 = \(\frac{\sum\left(\frac{P_{1}}{P_{0}} \times 100\right)}{N}\)
ΣN इसमें P01 = कीमत सूचकांक, P1 = वर्तमान वर्ष में कीमत, P0 = आधार वर्ष की कीमत,
N = वस्तुओं की संख्या।
प्रश्न 9.
थोक कीमत सूचकांकों से क्या अभिप्राय है ? थोक कीमत सूचकांक में परिवर्तन किस बात का सूचक है ?
उत्तर-
थोक कीमत सूचकांक से अभिप्राय उस सूचकांक से है, जिसके निर्माण में थोक कीमतों का प्रयोग किया जाता है। थोक कीमत सूचकांक को साप्ताहिक आधार पर प्रकाशित किया जाता है। इसका मुख्य उद्देश्य देश में कीमतों में परिवर्तन का माप करना होता है।
प्रश्न 10.
उपभोक्ता कीमत सूचकांक से क्या अभिप्राय है ? इसका माप कैसे किया जाता है ?
उत्तर-
उपभोक्ता कीमत सूचकांक (C.P.I.) को निर्वाह लागत सूचकांक (Cost of living Index Number) भी कहा जाता है। यह सूचकांक विभिन्न वर्ग के उपभोक्ताओं के लिए तैयार किया जाता है। इसमें एक वर्ग के लोगों द्वारा वर्तमान वर्ष में आधार वर्ष की तुलना परचून कीमतों (Retail Prices) के आधार पर की जाती है। इसकी दो माप विधियां हैं-
- सामूहिक व्यय विधि-इस उद्देश्य के लिए लास्पेयर्स के सूत्र का प्रयोग किया जाता है-
उपभोक्ता कीमत सूचकांक अथवा निर्वाह लागत सूचकांक = \(\frac{\Sigma p_{1} q_{0}}{\Sigma p_{0} q_{0}} \times 100\)
- पारिवारिक बजट विधि- इसमें आनुपातिक कीमत विधि का प्रयोग किया जाता है उपभोक्ता कीमत सूचकांक अथवा निर्वाह लागत सूचकांक = \(\frac{\Sigma \mathrm{RW}}{\Sigma \mathrm{W}}\)
यहां R = \(\left(\frac{P_{1}}{P_{0}} \times 100\right)\) तथा W = P0q0
सामूहिक व्यय विधि तथा पारिवारिक बजट विधि का परिणाम समान होता है।
प्रश्न 11.
औद्योगिक उत्पादन सूचकांक से क्या अभिप्राय है ? इसका माप क्या स्पष्ट करता है ?
उत्तर-
औद्योगिक उत्पादन सूचकांक वह सूचकांक होता है जो कि आधार वर्ष की तुलना में औद्योगिक उत्पादन की वृद्धि अथवा घाटे को व्यक्त करता है। औद्योगिक उत्पादन सूचकांक का माप इस सूत्र द्वारा किया जाता है-
औद्योगिक उत्पादन सूचकांक = \(\frac{\Sigma\left(\frac{q_{1}}{q_{0}}\right) w}{\Sigma w} \times 100\)
इस सूत्र में q1 = वर्तमान वर्ष का औद्योगिक उत्पादन, q0 = आधार वर्ष का औद्योगिक उत्पादन, w = वज़न अथवा भार।
प्रश्न 12.
सूचकांक मुद्रा स्फीति का सूचक कैसे होते हैं ?
अथवा
मुद्रा-स्फीति तथा सूचकांकों के सम्बन्ध को स्पष्ट करो।
उत्तर-
हमारी रोज़ाना की ज़िन्दगी में वस्तुओं तथा सेवाओं की कीमतों की वृद्धि का अनुभव किया जाता है। जब वस्तुओं तथा सेवाओं की कीमतों के स्तर में वृद्धि तीव्रता से तथा निरन्तर होती है तो इस स्थिति को मुद्रा-स्फीति कहा जाता है। मुद्रा-स्फीति के परिणामस्वरूप मुद्रा की खरीद शक्ति कम हो जाती है। मुद्रा-स्फीति का सम्बन्ध थोक की कीमतों (Wholesale Prices) से है। भारत में थोक की कीमतें प्रत्येक सप्ताह मापी जाती है। इस उद्देश्य के लिए सूचकांकों का प्रयोग किया जाता है।
IV. दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)
प्रश्न 1.
सूचकांक से क्या अभिप्राय है ? सूचकांक की विशेषताएं बताओ। (What is the meaning of Index Numbers ? Explain its characteristics.)
उत्तर-
सूचकांक का अर्थ (Meaning of Index Numbers)-सूचकांक एक विशेष प्रकार की औसत होती है जोकि समय, मात्रा अथवा स्थान इत्यादि के आधार पर कीमत, उपभोग, उत्पादन, राष्ट्रीय आय इत्यादि में परिवर्तन को प्रतिशत के रूप में प्रकट करती है। सूचकांक का प्रयोग सबसे पहले जी० आर० चारली ने किया है। वह इटली के रहने वाले थे। सन् 1500 से लेकर 1750 तक कीमत स्तर में हुए परिवर्तन का अध्ययन करना उनका मुख्य उद्देश्य था।
इस प्रकार सूचकांक का प्रयोग केवल कीमत स्तर में परिवर्तनों को मापने के लिए की जाने लगी। सांख्यिकी के विकास से सूचकांक का क्षेत्र भी विशाल हो गया। सामाजिक, राजनीतिक तथा आर्थिक क्षेत्र के प्रत्येक पहल में परिवर्तन का अध्ययन करने के लिए सूचकांकों का प्रयोग किया जाता है। इसलिए सूचकांक एक ऐसा यन्त्र है जिस द्वारा एक चर अथवा चरों के समूहों में भिन्न-भिन्न समय में होने वाले परिवर्तनों का माप किया जाता है।

परिभाषाएं-
- प्रो० क्राक्सटन तथा काउडन के अनुसार, “सूचकांक वह यन्त्र है जिनके द्वारा सम्बन्धित तथ्यों के मूल्यों के आकार में होने वाले परिवर्तनों का माप किया जाता है।” (“Index Numbers are devices for measuring difference in the magnitude of a group of related variables.” -Croxton and Cowden)
- प्रो० एस० आर० सपीगल के शब्दों में, “सूचकांक एक सांख्यिकी माप है, जिस द्वारा एक चर अथवा चरों के समूह में समय, स्थान अथवा अन्य विशेषताओं के आधार पर होने वाले परिवर्तनों को दर्शित करना है।” (“As Index number is a statistical measure designed to show changes in variables or a group of related variabels with respect to time, geographical location or other characteristics.” -M.R. Spiegal)
इन परिभाषाओं से स्पष्ट होता है कि सूचकांक विशेष प्रकार की औसत होती है, जिस द्वारा समय अथवा स्थान अनुसार होने वाले परिवर्तनों का माप किया जाता है।
सूचकांक की विशेषताएं (Features of Index Number)- सूचकांक की विशेषताएं निम्नलिखित अनुसार-
1. विशेष प्रकार की औसत (Special Average)-सूचकांक विशेष प्रकार के औसत होते हैं। केन्द्रीय प्रवृत्तियों के माप में भिन्न-भिन्न मदों की इकाइयां एक जैसी होती हैं, जहां भिन्न-भिन्न मदों की इकाइयां एक समान न हों, उस स्थिति में सूचकांक का प्रयोग किया जा सकता है। जब यह कहा जाता है कि सूचकांक में वृद्धि 10% हो गई है। इसका अर्थ यह नहीं कि सभी वस्तुओं की कीमतों में वृद्धि हुई है। कुछ वस्तुओं की कीमत कम भी हो सकती है अथवा समान रहती है। परन्तु औसत वृद्धि को व्यक्त सूचकांक द्वारा किया जाता है।
2. परिवर्तन का माप (Measurement of Change)- सूचकांक द्वारा समय, स्थान अथवा दूसरे किसी आधार पर तथ्यों में होने वाले परिवर्तन का माप किया जाता है। यह माप कीमत, उत्पादन, उपभोग इत्यादि में परिवर्तन का हो सकता है।
3. तुलना में प्रयोग (Used for Comparison).- सूचकांक की एक विशेषता यह है कि इसका प्रयोग तुलना के लिए किया जाता है। समय, स्थान अथवा किसी अन्य आधार पर एक चर अथवा एक से अधिक चरों में तुलना की जा सकती है। यदि 1980 से 1990 तक कीमत स्तर में तुलनात्मक अध्ययन किया जाता है तो 1980 को आधार वर्ष कहते हैं।
4. प्रतिशत में प्रदर्शन (Presented in Percentages)-सूचकांक को प्रतिशत के रूप में व्यक्त किया जाता है। आधार वर्ष के मूल्य को 100 के समान मानकर वर्तमान वर्ष के मूल्य का अध्ययन किया जाता है। यदि सूचकांक 112 हो गया है तो कीमत स्तर में वृद्धि 12% हुई है। यदि कीमत सूचकांक 96 है तो कीमत स्तर में कमी 4% हो गई है। इस प्रकार सूचकांक को प्रतिशत रूप में व्यक्त किया जाता है।
5. सर्व-व्यापक प्रयोग (Universal Application)-सूचकांक का प्रयोग प्रत्येक क्षेत्र तथा प्रत्येक देश में किया जाता है। प्रत्येक देश में कीमत स्तर, उत्पादन, उपभोग, बचत, राष्ट्रीय आय में परिवर्तन का माप करने के लिए सूचकांक एक सर्व-व्यापक विधि है।
प्रश्न 2.
सूचकांक बनाने की विधि तथा इसकी समस्याओं का वर्णन करो। (Explain the method for the construction and problems of Index Numbers.)
अथवा
सूचकांक बनाते समय कौन-सी मुश्किलें आती हैं ? (What are the difficulties in the construction of Index Numbers ?)
अथवा
सूचकांक बनाने सम्बन्धी समस्याओं, फ़ैसलों अथवा निर्देशों की व्याख्या करो। (Explain the problems in the construction of Index Numbers, Decisions and Directions.)
उत्तर-
सूचकांक बनाते समय बहुत-सी समस्याएं आती हैं। अब हम उन समस्याओं से सम्बन्धित फ़ैसलों तथा निर्देशों का अध्ययन करते हैं-
- सूचकांक का उद्देश्य (Purpose of Index Numbers)-सूचकांक तैयार करने के लिए आंकड़े एकत्रित करने से पहले सूचकांक का उद्देश्य स्पष्ट होना चाहिए। यदि बिना उद्देश्य से आंकड़े एकत्रित किए जाते हैं तो इससे आर्थिक स्थिति का पूरा ज्ञान प्राप्त नहीं होता।
- वस्तुओं का चयन (Selection of Commodities)-सूचकांक का निर्माण करते समय वस्तुओं का चयन भी महत्त्वपूर्ण होता है।
सभी वस्तुओं को शामिल करके सूचकांकों का निर्माण नहीं किया जाता, बल्कि यह फैसला करना पड़ता है कि-
- कितनी वस्तुओं को लेकर सूचकाकों का निर्माण किया जाए ?
- कौन-सी वस्तुओं का चयन किया जाए ?
- वस्तुओं की कौन-सी किस्म को शामिल किया जाए ?
वस्तुओं का चयन करते समय यह ध्यान रखना चाहिए कि सूचकांक में शामिल की वस्तुएं साधारण लोगों के उपभोग अनुसार होनी चाहिए तथा चुनी हुई वस्तुएं उच्च गुण वाली होनी चाहिए।
3. कीमतों का चयन (Selection of Prices)-वस्तुओं का चयन करने के पश्चात् वस्तुओं की कीमतें एकत्रित करने की समस्याओं का सामना करना पड़ता है अर्थात् थोक की कीमतें ली जाएं अथवा परचून कीमतें लेकर सूचकांक तैयार किया जाए। इसलिए वस्तुओं की कीमतें थोक बाज़ार में से प्राप्त की जाएं अथवा परचून बाज़ार में से प्राप्त की जाएं। कीमतों में करों को शामिल किया जाए अथवा न किया जाए। यह फ़ैसले करते समय सूचकांक के उद्देश्य को ध्यान में रखना चाहिए । यदि सूचकांक का उद्देश्य लोगों के जीवन निर्वाह व्यय में परिवर्तन सम्बन्धी अध्ययन करना है तो सूचकांक का निर्माण करते समय परचून कीमतों का प्रयोग करना चाहिए।
4. आधार वर्ष का चयन (Selection of Base Year)-सूचकांक का निर्माण करते समय आधार वर्ष चुनना पड़ता है। जिस वर्ष से चालू वर्ष की कीमतों की तुलना की जाती है, उसको आधार वर्ष कहा जाता है। इस वर्ष के सूचकांक को 100 अंक लिया जाता है। आधार वर्ष का चयन करते समय यह ध्यान रखना चाहिए कि –
- यह वर्ष साधारण हो अर्थात् इस वर्ष कोई असाधारण घटना न घटी हो जैसे कि युद्ध, जंग अथवा बाढ़ इत्यादि न आए हों।
- यह वर्ष बहुत पुराना नहीं होना चाहिए। इन बातों को ध्यान में रखना चाहिए। भारत में 1980-81 का वर्ष सूचकांक का आधार वर्ष माना जाता है।
5. औसत चयन (Selection of Average)-सूचकांक बनाते समय यह निर्णय भी करना पड़ता है कि कौन-सी औसत समान्तर औसत अथवा रेखा गणिती औसत का प्रयोग किया जाए। चाहे रेखा गणिती औसत से अधिक विश्वसनीय परिणाम प्राप्त होते हैं परन्तु व्यावहारिक तौर पर समान्तर औसत का प्रयोग किया जाता है।
6. सूचकांक की गणना (Calculation of Index Numbers)-सूचकांक की गणना करते समय आधार वर्ष की कीमतों (P1) को 100 मान लिया जाता है इसके पश्चात् वर्तमान वर्ष की कीमतों (P0) में परिवर्तन की प्रतिशत का माप किया जाता है। इस प्रकार सूचकांक (P01) अर्थात् आधार वर्ष की कीमतों की तुलना में वर्तमान वर्ष (1) की कीमतों में कितने प्रतिशत परिवर्तन हुआ है, उसको सूचकांक कहते हैं।
उदाहरणस्वरूप आधार वर्ष में दूध की कीमत 5 रु० प्रति लिटर थी। वर्तमान वर्ष की दूध की कीमत 15 रु० प्रति लिटर है तो सूचकांक |
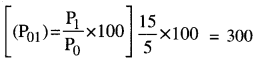
होगा अर्थात् आधार वर्ष के सूचकांक 100 से वर्तमान वर्ष का सूचकांक 300 है तो दूध की कीमत में तीन गुणा अथवा 300% वृद्धि हो गई है। इस प्रकार सूचकांक की गणना की जाती है।
7. भार का निर्धारण (Determination of Weights)-सूचकांक में शामिल की वस्तुओं को एक समान महत्त्व नहीं दिया जाता। जैसे कि गेहूँ, दूध, सब्जियां, अधिक महत्त्वपूर्ण हैं तथा स्कूटर, कार कम महत्त्वपूर्ण वस्तुएं हैं। इसलिए गेहूं, दूध, सब्जियों को अधिक भार देना चाहिए। स्कूटर का महत्त्व गांवों से अधिक शहरों में है। इसलिए भार का निर्धारण करते समय समस्या का सामना करना पड़ता है। किसी स्थान पर लोगों की आर्थिक, सामाजिक, धार्मिक इत्यादि स्थिति को ध्यान में रखकर वस्तुओं को भार देने चाहिए।
8. सूत्र का चयन (Selection of Formula)-सूचकांक बनाने के बहुत से सूत्र हैं। इनमें से किस सूत्र का प्रयोग किया जाए। इस सम्बन्धी फ़ैसला करने के लिए आंकड़ों की प्रकृति तथा सूचकांक के उद्देश्य को ध्यान में रखना चाहिए। सूचकांक बनाने की मुख्य दो विधियां हैं –
A. साधारण सूचकांक (Simple Index Numbers)-साधारण सूचकांक निर्माण के दो ढंग हैं-
- सरल समूहीकरण विधि
- सरल कीमत अनुपात औसत विधि।
B. भारित सूचकांक (Weighted Index Numbers)
(i) भारित समूहीकरण विधि –
(a) लास्पेयर्स की विधि
(b) पास्चे की विधि
(c) डारब्शि तथा बाऊले की विधि
(d) फिशर की विधि।
(ii) भारित कीमत अनुपात औसत विधि-इन विधियों में से चयन की समस्या होती है। इसका निर्णय सूचकांक के उद्देश्य को ध्यान में रखकर करना चाहिए।

प्रश्न 3.
सूचकांक बनाने की मुख्य विधियां बताओ। (Explain the methods of Constructing Index Numbers.)
अथवा
सूचकांक की मुख्य किस्में लिखो। (Explain the main types of Index Numbers.)
उत्तर-
सूचकांक बनाने की मुख्य विधियां (Main methods of Constructing Index Numbers)सूचकांक बनाने की विधियों को सूचकांक की किस्में भी कहा जा सकता है। सूचकांक की मुख्य विधियां निम्नलिखित अनुसार हैं –
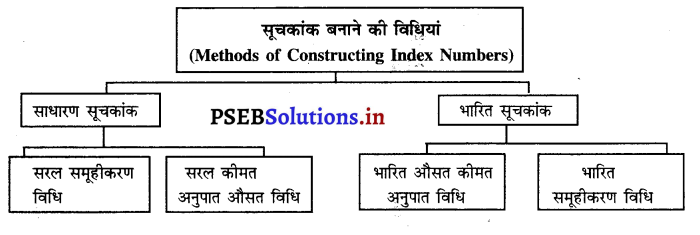
पीछे दिए चार्ट अनुसार सूचकांक मुख्य तौर पर दो प्रकार के होते हैं –
A. साधारण सूचकांक
B. भारित सूचकांक।
A. साधारण सूचकांक (Simple Index Numbers)-साधारण सूचकांक निर्माण की दो विधियां हैं-
1. सरल समूहीकरण विधि (Simple Index Numbers)-सूचकांक बनाने की सरल समूहीकरण विधि में वर्तमान वर्ष में भिन्न-भिन्न वस्तुओं की दी हुई कीमतों का जोड़ (ΣP1 ) किया जाता है। आधार वर्ष में भिन्न-भिन्न वस्तुओं की कीमतों का जोड़ (ΣP0) किया जाता है। वर्तमान वर्ष की कीमतों के जोड़ को आधार वर्ष की कीमतों के जोड़ से विभाजित करके 100 गुणा कर दिया जाता है। इससे सूचकांक प्राप्त हो जाता है।
इस विधि द्वारा सूचकांक की गणना का सूत्र निम्नलिखित अनुसार है-
कीमत सूचकांक (P01) = \(\frac{\Sigma P_{1}}{\Sigma P_{0}} \times 100\)
इस सूत्र में P01 = कीमत सूचकांक, 0 = आधार वर्ष, 1 = वर्तमान वर्ष ।
ΣP1 = वर्तमान वर्ष में भिन्न-भिन्न वस्तुओं की कीमतों का जोड़।
ΣP0 = आधार वर्ष में भिन्न-भिन्न वस्तुओं की कीमतों का जोड़।
2. सरल कीमत अनुपात औसत विधि (Simple Average of Price Relative Method) – सरल कीमत अनुपात औसत विधि में पहले प्रत्येक वस्तु की कीमत अनुपात पता किया जाता है। किसी वस्तु की कीमत अनुपात वर्तमान वर्ष की कीमत (P1) तथा आधार वर्ष की कीमत (P0) का प्रतिशत अनुपात होता है। यदि दो वस्तुओं की कीमत अनुपात का प्रतिशत निकालकर वस्तुओं की संख्या से विभाजित किया जाए तो हमारे पास कीमत अनुपात सूचकांक प्राप्त हो जाता है।
कीमत अनुपात सूचकांक (P01) = \(\frac{\Sigma\left(\frac{P_{1}}{P_{0}} \times 100\right)}{\mathrm{N}}=\frac{\Sigma \mathrm{R}}{\mathrm{N}}\)
B. भारित सूचकांक (Weighted Index Numbers)-सूचकांक की भारित सूचकांक विधि अधिक प्रचलित है तथा विधि का साधारण तौर पर प्रयोग किया जाता है। इस विधि में भिन्न-भिन्न वस्तुओं के भार दिए होते हैं। जब वस्तुओं के भार अथवा महत्त्व को ध्यान में रखकर सूचकांक तैयार किया जाता है तो इसको भारित सूचक कहते हैं।
भारित सूचकांक निर्माण की दो विधियां हैं –
1. भारित औसत कीमत अनुपात विधि (Weighted Average of Price Relative Method)-इस विधि में भिन्न-भिन्न वस्तुओं की कीमत अनुपातों को वस्तुओं के भार से गुणा करके गुणनफल का पता किया जाता है। जो गुणनफल प्राप्त होता है, उसको भार के जोड़ से विभाजित किया जाता है। इस प्रकार भारित औसत कीमत अनुपात विधि का सूत्र निम्नलिखित अनुसार होता है-
P01 = \(\frac{\Sigma R W}{\Sigma W}\)
P01 = कीमत सूचकांक
R = कीमत अनुपात \(\left(\frac{\mathrm{P}_{1}}{\mathrm{P}_{0}} \times 100\right)\)
w = भार (Weight)
2. भारित समूहीकरण विधि (Weighted Aggregative Method)-इस विधि में विभिन्न वस्तुओं की कीमतों को उन वस्तुओं की खरीदी गई मात्रा अनुसार भार दिया जाता है। इस विधि का निर्माण बहुत से सांख्यिकी शास्त्रियों द्वारा किया गया है। इन सांख्यिकी शास्त्रियों द्वारा दी गई विधियों में मुख्य अन्तर भार देने की विधि में है। कुछ विद्वान् आधारवर्ष की मात्रा को आधार बना कर भार देते हैं जबकि कुछ वर्तमान वर्ष की वस्तुओं की खरीदी गई मात्रा को आधार बनाकर भार देते हैं। कुछ अन्य दोनों समयों को मात्राओं का आधार बनाकर भार देते हैं।
भारित समूहीकरण की भिन्न-भिन्न विधियाँ निम्नलिखित अनुसार हैं –
- लास्पेयर की विधि (Laspeyer’s Method)-इस विधि में प्रो० लास्पेयर ने आधार वर्ष की मात्रा (q0) को आधार बनाकर वस्तुओं को भार दिए हैं। लास्पेयर ने सूचकांक की गणना का सूत्र निम्नलिखित अनुसार दिया
P01 (La) = \(\frac{\Sigma \mathrm{P}_{1} \mathrm{q}_{0}}{\Sigma \mathrm{P}_{0} \mathrm{q}_{0}} \times 100\)
- पास्चे की विधि (Pasche’s Method)-प्रो० पास्चे ने वर्तमान वर्ष की मात्रा (q1) को आधार बनाकर वस्तुओं को भार दिए हैं। पास्चे ने सूचकांक की रचना का सूत्र इस प्रकार दिया P01 (Pa) = \(\frac{\Sigma \mathrm{P}_{1} q_{1}}{\Sigma \mathrm{P}_{0} q_{1}} \times 100\)
- फिशर की विधि (Fisher’s Method)-प्रो० इरविंग फिशर के फार्मले में आधार वर्ष तथा वर्तमान वर्ष की मात्राओं को आधार माना जाता है। प्रो० फिशर ने सूचकांक की गणना करने के लिए लास्पेयर तथा पास्चे के सूचकांकों की रेखा गणिती औसत का प्रयोग किया है।
इस सूत्र को सूचकांक की रचना का आदर्श सूत्र कहा जाता है-
P01 (F) = \(\sqrt{\frac{\Sigma P_{1} q_{0}}{\Sigma P_{0} q_{0}} \times \frac{\Sigma P_{1} q_{1}}{\Sigma P_{0} q_{1}}} \times 100\)
इस सूत्र को निम्नलिखित कारणों से आदर्श सूत्र कहा जाता है –
- यह सूत्र पक्षपात से मुक्त है।
- इस सूत्र में रेखा गणिती औसत द्वारा गणना की जाती है। इसलिए विश्वसनीय परिणाम प्राप्त होते हैं।
- इस सूत्र में आधार वर्ष तथा वर्तमान वर्ष की मात्राओं दोनों को ही भार माना जाता है।
- यह सूत्र परख की कसौटी पर ठीक उतरता है। फिशर ने परख की कसौटियों दो दी हैं।
1. समय उत्क्रामता (Time Reversal Test)-जब हम आधार वर्ष शून्य (0) जगह पर 1 तथा 1 की जगह पर शून्य (0) लिख देते हैं तथा फार्मूले को इस परिवर्तन अनुसार गुणा करते हैं तो जवाब 1 के समान होता
\(\frac{\mathrm{P}_{01} \times \mathrm{P}_{10}}{100}=\sqrt{\frac{\Sigma \mathrm{P}_{1} q_{0}}{\Sigma P_{0} q_{0}} \times \frac{\Sigma \mathrm{P}_{1} q_{1}}{\Sigma \mathrm{P}_{0} \mathrm{q}_{1}} \times \frac{\Sigma P_{0} q_{1}}{\Sigma P_{1} q_{1}} \times \frac{\Sigma P_{0} q_{0}}{\Sigma P_{1} q_{0}}}=1\)
2. साधन उत्क्रामता (Factor Reversal Test)-जब फार्मूले में P की जगह पर q तथा की जगह पर के समान P लिखते हैं तो जवाबः\(\frac{\Sigma \mathrm{P}_{1} q_{1}}{\Sigma \mathrm{P}_{0} q_{0}}\) के समान होता है।

यह परख केवल फिशर के फार्मूले में ठीक लागू होती है। लास्पेयर तथा पास्चे की विधि पर ठीक लागू नहीं होती। इसलिए फिशर के सूत्र को आदर्श सूत्र कहा जाता है।
साधारण कीमत सूचकांक की रचना (Construction of Simple Index Numbers)
साधारण कीमत सूचकांक की रचना दो विधियों द्वारा की जाती है –
(i) सरल समूहीकरण विधि (Simple Aggregative Method) माप विधि (Measurement Method)-
- इस विधि द्वारा सूचकांक ज्ञात करने के लिए भिन्न-भिन्न वस्तुओं के आधार वर्ष की कीमतों का जोड़ (ΣP0) पता करो।
- भिन्न-भिन्न वस्तुओं के वर्तमान वर्ष की कीमतों का जोड़ (ΣP) किया जाता है।
- वर्तमान वर्ष की कीमतों के जोड़ को आधार वर्ष की कीमतों के जोड़ से विभाजित करो तथा 100 से गुणा करो।
अर्थात् निम्नलिखित सूत्र का प्रयोग करें-
P01 = \(\frac{\Sigma P_{1}}{\Sigma P_{0}} \times 100\)

प्रश्न 4.
निम्नलिखित आंकड़ों से सरल समूहीकरण विधि द्वारा 1981 को आधार वर्ष मान कर कीमत सूचकांक का पता करो।
| वस्तुएं |
A |
B |
C |
D |
E |
| 1999 की कीमतें (रु०) प्रति किलोग्राम |
20 |
15 |
35 |
26 |
5 |
| 2006 की कीमतें (रु०) प्रति किलोग्राम |
30 |
18 |
34 |
30 |
12 |
हल (Solution) :
साधारण कीमत सूचकांक की रचना (सरल समूहीकरण विधि)-
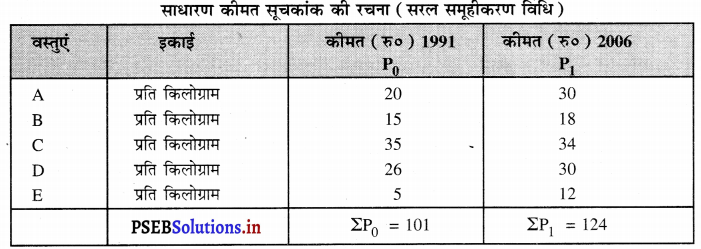
कीमत सूचकांक (P01)= \(\frac{\Sigma P_{1}}{\Sigma P_{0}} \times 100\) = \(\frac{124}{101} \times100 \)
= 122.77
P01 = 122.77 उत्तर
आधार वर्ष के सूचकांक 100 की तुलना में 2006 की वर्तमान कीमतों का सूचकांक 122.77 हो गया है। इन वस्तुओं की कीमतों में औसतन 122.77 % वृद्धि हो गई है। इस विधि में सभी वस्तुओं का मूल्य एक माप किलोग्राम, मीटर इत्यादि में दिया होता है।
(ii) सरल कीमत अनुपात औसत विधि (Simple Average of Price Relative Method)-
माप विधि
- इस विधि में प्रत्येक वस्तु के कीमत अनुपात P01= \(\left(\frac{P_{1}}{P_{0}} \times 100\right)\) का पता किया जाता है।
- कीमत अनुपातों का जोड़ \(\Sigma\left(\frac{P_{1}}{P_{0}} \times 100\right)\) का पता किया जाता है।
- वस्तुओं की संख्या (N) से कीमत अनुपातों के जोड़ को विभाजित करो। इससे सूचकांक प्राप्त हो जाता है। इसका सूत्र निम्नलिखित अनुसार है
P01 = \(\frac{\Sigma\left(\frac{P_{1}}{P_{0}} \times 100\right)}{\mathrm{N}} \text { or } \frac{\Sigma \mathrm{R}}{\mathrm{N}}\)
- इस विधि का माप उस समय किया जाता है जब भिन्न-भिन्न वस्तुओं की कीमत भिन्न-भिन्न माप (किलोग्राम, मीटर, लिटर) में दी हो।
प्रश्न 5.
कीमत अनुपात विधि द्वारा निम्नलिखित आंकड़ों का सूचकांक ज्ञात करो।
हल (Solution) :
सरल कीमत अनुपात विधि द्वारा सूचकांक की गणना
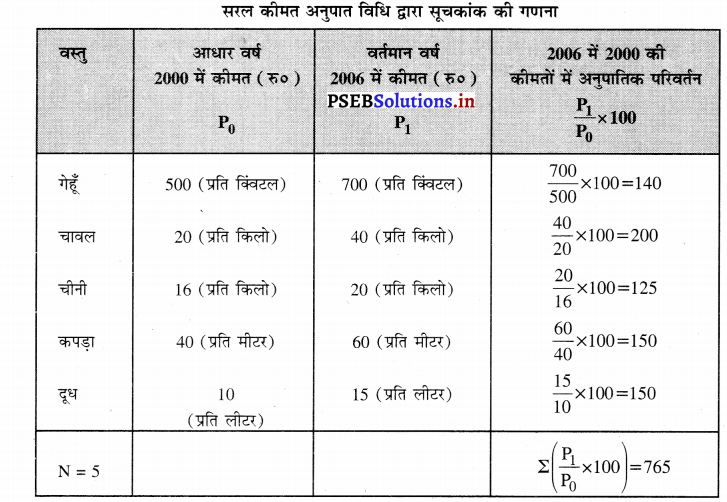
सरल कीमत अनुपात सूचकांक (P01) = \(\frac{\Sigma\left(\frac{\mathrm{P}_{1}}{\mathrm{P}_{0}} \times 100\right)}{\mathrm{N}}\) = \(\frac{765}{5}\) = 153
इसका अभिप्राय यह है कि ऊपर दी वस्तुओं की कीमतों में सरल कीमत अनुपात विधि अनुसार 53 प्रतिशत वृद्धि हो गई है।
भारित सूचकांकों की रचना
भारित सूचकांक अधिक प्रचलित हैं। वस्तुओं के महत्त्व अनुसार उनको भार दिया जाता है, जैसे कि गेहूँ तथा चावल का महत्त्व फलों से अधिक है। इसलिए गेहूँ तथा चावल को अधिक महत्त्व अथवा भार दिया जाएगा तथा फलों को कम भार दिया जाएगा। भार अनुसार सूचकांक की रचना को भारित सूचकांक कहा जाता है। इसकी गणना की दो विधियां हैं –
(iii) भारित औसत कीमत अनुपात विधि माप विधि-
- भारित सूचकांक का माप करने के लिए भिन्न-भिन्न वस्तुओं के कीमत अनुपात R = \(\left(\frac{\mathrm{P}_{1}}{\mathrm{P}_{0}} \times 100\right)\) पत्ता|
- कीमत अनुपात (R) को भार (W) से गुणा करके गुणनफल (RW) निकालो।
- कीमत अनुपात तथा भाग के गुणनफलों का जोड़ = (ΣRW) करो।
- गुणनफल के जोड़ को भागों के जोड़ (ΣW) से विभाजित करो। भारित सूचकांक ज्ञात करने के लिए निम्नलिखित सूत्र का प्रयोग करो-
Po1 = \(\frac{\Sigma R W}{\Sigma W}\)
- सभी वस्तुओं को सूचकांक बनाने में शामिल नहीं किया जाता बल्कि वस्तुओं का सैंपल के तौर पर चयन करके सूचकांक का निर्माण किया जाता है, जोकि सभी वस्तुओं की कीमतों में परिवर्तनों को समझने के लिए सहायक होता है।
प्रश्न 6.
कीमत अनुपात विधि द्वारा निम्नलिखित आंकड़ों की सहायता से 1991 को आधार वर्ष मानकर 2005 का भारित सूचकांक ज्ञात करो।

हल (Solution) :
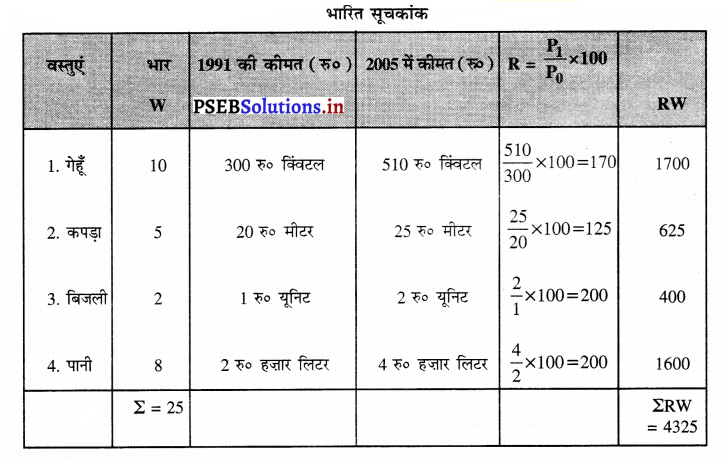
भारित सूचकांक
Po1 = \(\frac{\Sigma \mathrm{RW}}{\Sigma \mathrm{W}}\)
= \(\frac{4325}{25}\) = 173 उत्तर
इससे अभिप्राय यह है कि अध्ययन अधीन वस्तुओं की औसतन भारित कीमतों में परिवर्तन 73 प्रतिशत हो गया है। इसलिए भारित सूचकांक 100 से 173 हो गया है।

(iv) भारित समूहीकरण विधि (Weighted Aggregative Method)
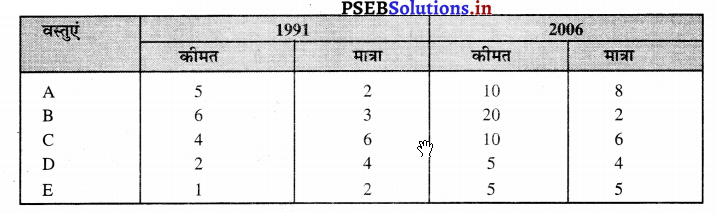
प्रश्न 7.
निम्नलिखित आंकड़ों की सहायता से
(i) लास्पेयर
(ii) पास्चे
(iii) फिशर की विधि द्वारा सूचकांक पता करो।
हल (Solution) :
भारित सूचकांक की गणना
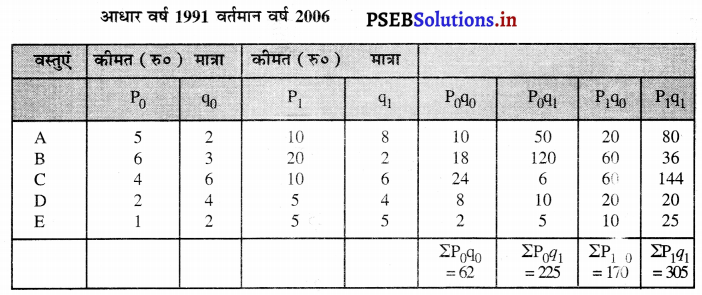
1. लास्पेयर विधि अनुसार सूचकांक
P01 = \(\frac{\Sigma \mathrm{P}_{1} q_{0}}{\Sigma \mathrm{P}_{0} q_{0}} \times 100\)
P01 = \(\frac{170}{62} \times 100\) = 274.19 उत्तर
2. पास्चे विधि अनुसार सूचकांक
P01 = \(\frac{\Sigma \mathrm{P}_{1} q_{1}}{\Sigma \mathrm{P}_{0} q_{1}} \times 100\)
P01 = \(\frac{305}{225} \times 100\) = 135.55 उत्तर
3. फिशर विधि अनुसार सूचकांक
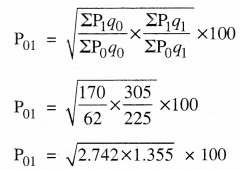
P01 = 192.75 उत्तर
लास्पेयर विधि अनुसार सूचकांक 274.19 है जो यह बताता है कि कीमतों में परिवर्तन लगभग पौने तीन गुणा है। पास्चे की विधि अनुसार कीमतों में परिवर्तन 33.55 प्रतिशत है परन्तु फिशर अनुसार कीमतों में परिवर्तन लगभग दो गुणा हो गया है जोकि 192.75% वृद्धि को प्रकट करता है। फिशर की विधि का परिणाम उचित है।
सूचकांकों की किस्में (Types of Index Numbers)
ऊपर हम सूचकांकों का अर्थ तथा माप विधि का अध्ययन कर चुके हैं। भारत में कई किस्म के सूचकांक तैयार किए जाते हैं। इनमें से तीन महत्त्वपूर्ण सूचकांक निम्नलिखित अनुसार हैं, जिनके बारे अध्ययन किया जाएगा।
A. थोक कीमत सूचकांक (Wholesale Price Index)
B. उपभोक्ता कीमत सूचकांक (Consumer’s Price Index)
C. औद्योगिक उत्पादन सूचकांक (Industrial Production Index).
A. थोक कीमत सूचकांक [Wholesale Price Index (W. P. I.)]
प्रश्न 8.
थोक कीमत सूचकांक से क्या अभिप्राय है ? थोक कीमत सूचकांक की निर्माण विधि को स्पष्ट करो। इसका महत्त्व बताओ।
(What is meant by Wholesale Price Index ? Explain the method for the construction of Wholesale Price Index. Give its importance.)
उत्तर-
थोक कीमत सूचकांक का अर्थ-थोक कीमत सूचकांक वह सूचकांक है जिसके निर्माण में थोक कीमतों का प्रयोग किया जाता है। साधारण तौर पर किसी देश में कीमतों के परिवर्तन के लिए इस सूचकांक का प्रयोग किया जाता है। भारत में प्रत्येक सप्ताह के अन्त में थोक कीमत सूचकांक तैयार किया जाता है। इस समय 1993-94 की कीमतों को आधार वर्ष मान कर सूचकांक तैयार किया जाता है। इसमें वस्तुओं को तीन कॉलमों में विभाजित किया गया है |
- प्राथमिक वस्तुएं-इनमें चावल, दालें, कपास इत्यादि 98 वस्तुओं को शामिल किया गया है।
- बिजली गैस तेल-इनमें 19 वस्तुएं शामिल हैं।
- निर्माण वस्तुएं-इनमें कपड़ा, चीनी, मशीनें इत्यादि 318 वस्तुएं शामिल हैं। इन वस्तुओं को महत्त्वानुसार वज़न (weights) दिए जाते हैं।
थोक कीमत सूचकांकों का महत्त्व (Importance of W.P.I.) –
1. वास्तविक मूल्य का अनुमान-थोक कीमत सूचकांकों द्वारा राष्ट्रीय आय, बचत, राष्ट्रीय निवेश इत्यादि के वास्तविक मूल्यों का निर्धारण करने के लिए किया जाता है। जब हम राष्ट्रीय आय का माप करते हैं तो इसको प्रचलित कीमतों अनुसार मापते हैं। राष्ट्रीय आय में परिवर्तन को स्थिर कीमतें (Constant Prices) तथा माप के पता किया जाता है। प्रचलित कीमतों पर राष्ट्रीय आय को स्थिर कीमतों में परिवर्तन करने के लिए निम्नलिखित सूत्र का प्रयोग किया जाता है-

थोक कीमत सूचकांक इस प्रकार वास्तविक मूल्य वृद्धि अथवा कमी का पता लग जाता है।
2. मांग तथा पूर्ति का अनुमान-थोक कीमत सूचकांक द्वारा किसी देश में मांग तथा पूर्ति का अनुमान लगाया जा सकता है। यदि थोक कीमत सूचकांक बढ़ रहा है तो इससे अभिप्राय है कि देश में मांग अधिक है। यदि थोक कीमत सूचकांक घट रहा है तो इसका अर्थ है कि वस्तुओं की पूर्ति अधिक है।
3. मुद्रा स्फीति दर का सूचक-थोक कीमत सूचकांक का प्रयोग मुद्रा-स्फीति दर ज्ञात करने के लिए भी किया जाता है। इससे पता चलता है कि समय के साथ कीमत में कितना परिवर्तन हुआ है। इसको उदाहरण से स्पष्ट करते हैं। मान लो प्रथम सप्ताह में थोक सूचकांक P1 है, द्वितीय सप्ताह में थोक कीमत सूचकांक P2 हो जाता है तो थोक कीमत सूचकांक का माप इस प्रकार किया जाएगा।
\(\frac{\mathrm{P}_{2}-\mathrm{P}_{1}}{\mathrm{P}_{1}} \times 100\)
उदाहरणस्वरूप प्रथम सप्ताह थोक सूचकांक 100 है। द्वितीय सप्ताह सूचकांक 105 हो जाता है तो इस समय में थोक कीमत सूचकांक में परिवर्तन का माप इस प्रकार किया जाता है-

मुद्रा स्फीति दर = \(\frac{P_{2}-P_{1}}{P_{1}} \times 100=\frac{105-100}{100} \times 100\) = 5 %
इसी तरह वार्षिक मुद्रा स्फीति की दर का माप किया जा सकता है।

प्रश्न 9.
1993-94 की कीमतों को आधार वर्ष मानकर 2005-06 के लिए थोक कीमत सूचकांक (W.P.I.) 215 है। वर्ष 2005-06 की राष्ट्रीय आय प्रचलित कीमतों पर 47527 करोड़ रु० है। आधार वर्ष की कीमतों पर राष्ट्रीय आय का मूल्य ज्ञात करो।
हल (Solution)-
2005-06 का थोक कीमत सूचकांक = 215
2005-06 की प्रचलित कीमतों पर राष्ट्रीय आय = 47527 करोड़ रु०
प्रचलित कीमतों पर राष्ट्रीय आय 1993-94 की कीमतों अनुसार वास्तविक राष्ट्रीय आय = img
\(\frac{47527}{215} \times 100\) = 22105.58 करोड़ रु० उत्तर
B. उपभोक्ता कीमत सूचकांक [Consumer Price Index (C.P.I.)]
प्रश्न 10.
उपभोक्ता सूचकांक से क्या अभिप्राय है ? उपभोक्ता सूचकांक का निर्माण कैसे किया जाता है ? इसका महत्त्व तथा मुश्किलें बताओ।
(What is meant by Consumer Price Index ? What is the method for the construction of Consumer Price Index. Explain its importance & Problems.)
उत्तर-
उपभोक्ता सूचकांक वह सूचकांक है जो उपभोक्ता द्वारा खरीदी जाने वाली वस्तुओं तथा सेवाओं की कीमतों में परिवर्तन का माप करने के लिए प्रयोग किया जाता है। भिन्न-भिन्न वर्ग के लोग भिन्न-भिन्न वस्तुओं का प्रयोग करते हैं। पिछले वर्ष की तुलना में वर्तमान वर्ष में इन वस्तुओं तथा सेवाओं की लागत में आए परिवर्तन का माप किया जाता है। इसीलिए उपभोक्ता सूचकांक को जीवन निर्वाह लागत (Cost of Living Index Number) भी कहा जाता है।
यह सूचकांक परचून कीमतों (Retail price) के आधार पर बनाया जाता है। भारत में तीन प्रकार के उपभोगी समूहों के लिए उपभोक्ता कीमत सूचकांक तैयार किए जाते हैं-
- औद्योगिक मज़दूरों के लिए उपभोक्ता कीमत सूचकांक।
- कृषि मजदूरों के लिए उपभोक्ता कीमत सूचकांक।
- शहरी दिमागी कार्य करने वाले मजदूरों के लिए उपभोक्ता कीमत सूचकांक।
उपभोक्ता कीमत सूचकांक की निर्माण विधि-उपभोक्ता कीमत सूचकांक बनाने के लिए मज़दूर वर्ग का चयन किया जाता है। उन द्वारा प्रयोग की जाने वाली वस्तुओं तथा उन वस्तुओं की खरीदी जाने वाली मात्रा का पता लगाया जाता है। इन वस्तुओं पर किए जाने वाले व्यय का पता लगाकर निम्नलिखित दो सूत्रों का प्रयोग किया जाता है-
1. कुल व्यय विधि (Aggregate Expenditure Method)—यह विधि लास्पेयर की विधि है। इसमें निम्नलिखित सूत्र का प्रयोग किया जाता है
उपभोक्ता कीमत सूचकांक (C.P.I.) = \(\frac{\Sigma \mathrm{P}_{1} q_{0}}{\Sigma \mathrm{P}_{0} q_{0}} \times 100\) इसमें P1 का अर्थ वर्तमान वर्ष की कीमतें, P0 का अर्थ आधार वर्ष की कीमतें तथा Q0 का अर्थ आधार वर्ष में खरीदी वस्तुओं की मात्रा।
2. पारिवारिक बजट विधि (Family Budget Method)-इस विधि में उपभोक्ता कीमत सूचकांक के लिए निम्नलिखित सूत्र का प्रयोग किया जाता है
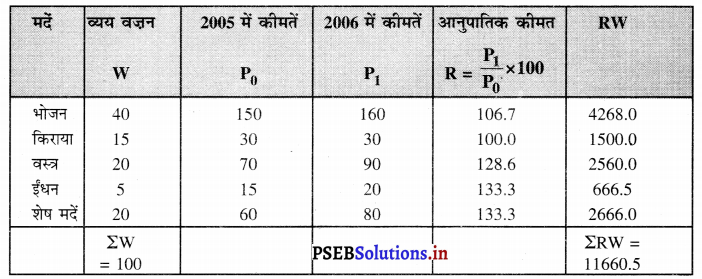
उपभोक्ता कीमत सूचकांक (C.P.I.) = [/latex]\frac{\Sigma \mathrm{RW}}{\Sigma \mathrm{W}}[/latex]
इस सूत्र में कीमत अनुपात (R) = \(\frac{\mathrm{P}_{1}}{\mathrm{P}_{0}} \times 100\)
सभी वस्तुओं पर व्यय = वज़न (W) = P0q
कुल व्यय विधि तथा पारिवारिक बजट विधि का परिणाम एक समान होता है।
महत्त्व (Importance)-
- इनकी सहायता से कीमत नीति का निर्माण किया जाता है।
- लागत में वृद्धि होने के कारण मजदूरी में वृद्धि की जाती है।
- रु० के वास्तविक मूल्य का पता लगता है।
- बाज़ार में मांग तथा पूर्ति का ज्ञान प्राप्त होता है।
- राष्ट्रीय आय में शुद्ध वृद्धि अथवा कमी का ज्ञान प्राप्त होता है।
मुश्किलें (Difficulties)
- भिन्न-भिन्न उपभोगी वर्गों के लिए एक उपभोगी कीमत सूचकांक नहीं बनाया जा सकता।
- परचून कीमतों अनुसार इसका निर्माण होता है जोकि भिन्न-भिन्न स्थानों पर भिन्न-भिन्न होती हैं।
- भिन्न-भिन्न वर्ग के लोग भिन्न-भिन्न मदों पर एक अनुपात में व्यय नहीं करते।
प्रश्न 11.
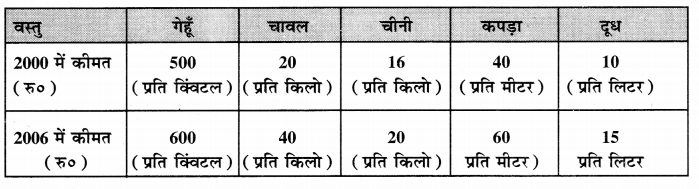
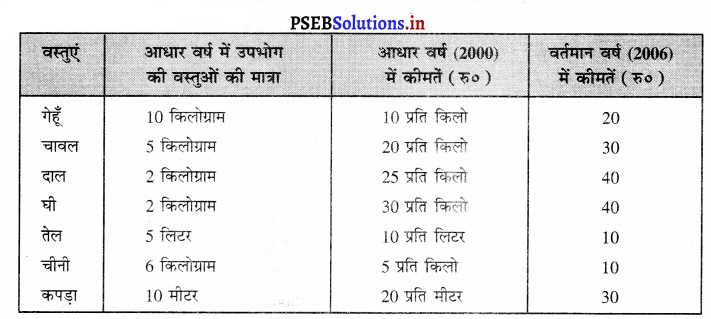
निम्नलिखित आंकड़ों के आधार पर
(i) कुल व्यय विधि
(ii) पारिवारिक बजट विधि द्वारा उपभोक्ता कीमत सूचकांक की गणना करो।
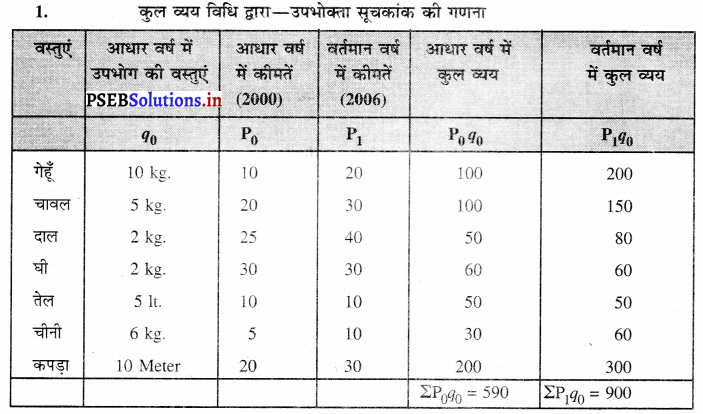
उपभोक्ता सूचकांक (C.P.I.) = \(\frac{\sum \mathrm{P}_{1} q_{0}}{\sum \mathrm{P}_{0} q_{0}} \times 100[/ltex]
= [latex]\frac{900}{590} \times 100\)
= 152.54 वर्तमान वर्ष में आधार वर्ष 2000 की परचून कीमतों की तुलना में 52.54 % वृद्धि हुई है।
2. पारिवारिक बजट विधि–उपभोक्ता कीमत सूचकांक की गणना-
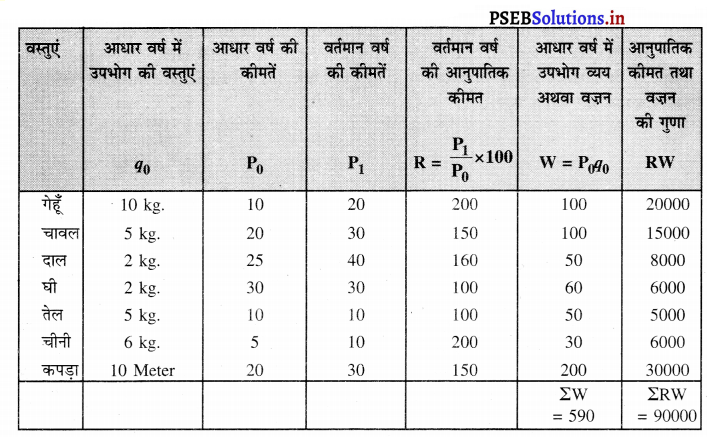
उपभोक्ता कीमत सूचकांक (C.P.I.) = \(\frac{\Sigma \mathrm{RW}}{\Sigma \mathrm{W}}\)
= \(\frac{9000}{590}\) = 152.54
दोनों विधियों द्वारा एक समान परिणाम प्राप्त होता है।
प्रश्न 12.
भारत के एक मध्य वर्ग परिवार के सम्बन्ध में निम्नलिखित सूचना के आधार पर उपभोक्ता कीमत सूचकांक ज्ञात करो।
अथवा
निम्नलिखित सूचना के आधार पर 2005 को आधार वर्ष मानकर 2006 के जीवन निर्वाह लागत सूचकांक की गणना करो।
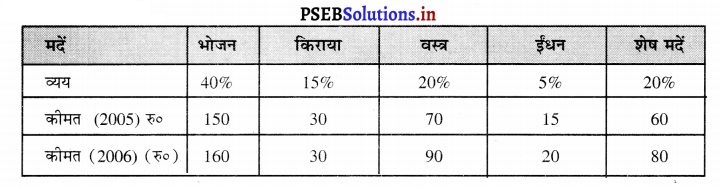
हल (Solution) :
उपभोक्ता कीमत सूचकांक अथवा जीवन निर्वाह लागत सूचकांक की गणना वज़न (weights) दिए गए हैं। इसी लिए परिवार बजट विधि का प्रयोग किया जाएगा।
औद्योगिक उत्पादन सूचकांक | (Industrial Production Index Number)
प्रश्न 13.
औद्योगिक उत्पादन सूचकांक से क्या अभिप्राय है? औद्योगिक उत्पादन सूचकांक का निर्माण कैसे किया जाता है ? इसके महत्त्व को स्पष्ट करो।
उत्तर-
औद्योगिक उत्पादन सूचकांक वह सूचकांक होता है जो हमें आधार वर्ष की तुलना में किसी देश में औद्योगिक उत्पादन की वृद्धि अथवा कमी को प्रकट करता है। इस सूचकांक की सहायता से किसी देश में औद्योगिक विकास का ज्ञान प्राप्त होता है। भारत में 1993-94 को आधार वर्ष मान कर औद्योगिक उत्पादन सूचकांक की गणना की जाती है।
औद्योगिक उत्पादन सूचकांक का निर्माण- औद्योगिक उत्पादन सूचकांक का निर्माण करते समय उद्योगों का वर्गीकरण
- खाने तथा खनन
- निर्माण उद्योग
- बिजली उत्पादन इत्यादि में किया जाता है।
इन क्षेत्रों सम्बन्धी प्रत्येक माह, तिमाही अथवा वार्षिक आंकड़े एकत्रित किए जाते हैं। इनके महत्त्व अनुसार भिन्न-भिन्न क्षेत्रों को वज़न दिए जाते हैं। इसके पश्चात् निम्नलिखित सूत्र का प्रयोग किया जाता है-
औद्योगिक उत्पादन सूचकांक = \(\frac{\sum\left(\frac{\mathrm{P}_{1}}{q_{0}}\right) \mathrm{W}}{\sum \mathrm{W}}\)
इसमें q1 = वर्तमान वर्ष का उत्पादन स्तर, q0 = आधार वर्ष का उत्पादन स्तर, W = वज़न।

प्रश्न 14.
निम्नलिखित आंकड़ों के आधार पर औद्योगिक उत्पादन का सूचकांक ज्ञात करो।
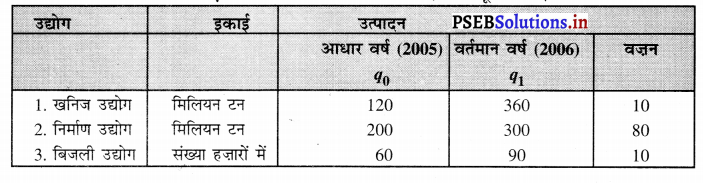
हल (Solution) :
औद्योगिक उत्पादन सूचकांक की गणना
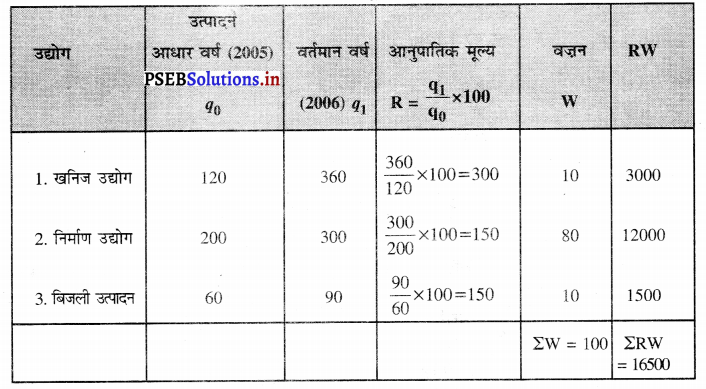
औद्योगिक उत्पादन सूचकांक = \(\frac{\Sigma R W}{\Sigma W}=\frac{16500}{100}\) = 165
इसका अर्थ है कि 2005 की तुलना में 2006 में औद्योगिक उत्पादन में वृद्धि 65% हुई है।
प्रश्न 15.
मुद्रा स्फीति और सूचकांक में क्या सम्बन्ध है ? मुद्रा स्फीति की दर और कीमत स्तर में सम्बन्ध स्पष्ट करें।
उत्तर-
मुद्रा स्फीति का माप थोक कीमत सूचकांक में होने वाले परिवर्तन के रूप में किया जाता है। जो कि बाज़ार में थोक कीमतों की साप्ताहिक तबदीली को प्रकट करती है। मुद्रा स्फीति वह स्थिति होती है जिसमें कीमत स्तर में वृद्धि लम्बे समय के दौरान दिखाई जाती है। आजकल प्रत्येक व्यक्ति मुद्रा स्फीति की दर का ध्यान रखता है। जैसा कि हम जानते हैं कि, “सूचकांक वह यंत्र है जिसके द्वारा सम्बन्धित तथ्यों के मूल्यों के आकार में होने वाले परिवर्तनों का माप किया जाता है।” सूचकांक की गणना करते समय किसी साधारण वर्ष को आधार साल मान कर उसको 100 मान लेते हैं।
जैसा कि भारत में 2001 साल को आधार साल मान लिया गया है तथा आधार साल की तुलना में 2008 में यदि सूचकांक 200 हो गया है तो हम कह सकते हैं कि भारत में 2001 से 2008 तक मुद्रा स्फीति के कारण मुद्रा के मूल्य में गिरावट आ गई है अथवा मुद्रा की खरीद शक्ति निरन्तर कम हो रही है। परन्तु यह भी देखना चाहिए कि लोगों की आय में कोई तबदीली हुई है या नहीं। यदि लोगों की आय भी इस समय में दो गुणा बढ़ गई है तो इससे मुद्रा स्फीति का लोगों पर बुरा प्रभाव नहीं पड़ता । मुद्रा स्फीति के मापने के लिए प्रति सप्ताह में थोक कीमत में परिवर्तन इस प्रकार मापते हैं :
मुद्रा स्फीति की दर = \(\frac{A_{2}-A_{1}}{A_{1}} \times 100\)
इसमें
A1 = पहले सप्ताह के थोक कीमत सूचकांक
A2 = दूसरे सप्ताह के थोक कीमत सूचकांक
इस प्रकार प्रति सप्ताह सूचकांक का माप सरकार द्वारा किया जाता है। थोक कीमत सूचकांक में एक लम्बे समय के दौरान होने वाली वृद्धि स्फीति को दर्शाती है। इस प्रकार मुद्रा स्फीति को थोक कीमतों के सूचकांक के परिवर्तन द्वारा मापा जाता है जिससे हमें थोक कीमतों में परिवर्तन का ज्ञान होता है।
मुद्रा स्फीति और कीमत स्तर का सम्बन्ध (Relationship between Inflation and Price Level)
जब मुद्रा स्फीति की दर में परिवर्तन होता है तो इसका अर्थ यह नहीं कि बाजार में कीमत स्तर भी उसी अनुपात में परिवर्तित हो रहा है। बाजार में यदि मुद्रा स्फीति की दर में वृद्धि होती है तो हो सकता है कि कुछ वस्तुओं की कीमत पहले जैसी स्थिर हो जबकि थोड़ी सी वस्तुओं की कीमत में वृद्धि हो सकती है। जब देश में मुद्रा स्फीति में बढ़ोत्तरी हो जाती है तो लोग अधिक वेतन की मांग करते हैं। इससे स्पष्ट है कि मुद्रा स्फीति की दर में गिरावट कीमत स्तर में होने वाली कमी को नहीं दर्शाती।
![]()
![]()
![]()
![]()