Punjab State Board PSEB 12th Class History Book Solutions Chapter 3 16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦੀ ਰਾਜਨੀਤਿਕ, ਸਮਾਜਿਕ ਅਤੇ ਆਰਥਿਕ ਦਸ਼ਾ Textbook Exercise Questions and Answers.
PSEB Solutions for Class 12 History Chapter 3 16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦੀ ਰਾਜਨੀਤਿਕ, ਸਮਾਜਿਕ ਅਤੇ ਆਰਥਿਕ ਦਸ਼ਾ
Long Answer Type Questions
ਪ੍ਰਸ਼ਨ 1.
16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦੀ ਰਾਜਨੀਤਿਕ ਦਸ਼ਾ ਕਿਹੋ ਜਿਹੀ ਸੀ ? (What was the political condition of Punjab in the beginning of the 16th century ?)
ਜਾਂ
16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦੀ ਰਾਜਨੀਤਿਕ ਦਸ਼ਾ ਦਾ ਵਰਣਨ ਕਰੋ । (Explain the political condition of Punjab in the beginning of 16th century.)
ਉੱਤਰ-
16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦੀ ਰਾਜਨੀਤਿਕ ਦਸ਼ਾ ਬੜੀ ਡਾਵਾਂਡੋਲ ਸੀ । ਲੋਧੀ ਸੁਲਤਾਨਾਂ ਦੀਆਂ ਗਲਤ ਨੀਤੀਆਂ ਵਜੋਂ ਹਰ ਪਾਸੇ ਬਦਅਮਨੀ ਫੈਲੀ ਹੋਈ ਸੀ । ਸ਼ਾਸਕ ਵਰਗ ਭੋਗ ਵਿਲਾਸ ਵਿੱਚ ਡੁੱਬਿਆ ਰਹਿੰਦਾ ਸੀ । ਦਰਬਾਰਾਂ ਵਿੱਚ ਰੋਜ਼ਾਨਾ ਜਸ਼ਨ ਮਨਾਏ ਜਾਂਦੇ ਸਨ । ਇਨ੍ਹਾਂ ਜਸ਼ਨਾਂ ਵਿੱਚ ਨਾਚੀਆਂ ਵੱਡੀ ਗਿਣਤੀ ਵਿੱਚ ਹਿੱਸਾ ਲੈਂਦੀਆਂ ਸਨ ਅਤੇ ਸ਼ਰਾਬ ਦੇ ਦੌਰ ਚਲਦੇ ਸਨ । ਸਿੱਟੇ ਵਜੋਂ ਪਰਜਾ ਵੱਲ ਧਿਆਨ ਦੇਣ ਲਈ ਕਿਸੇ ਕੋਲ ਸਮਾਂ ਨਹੀਂ ਸੀ । ਸਰਕਾਰੀ ਕਰਮਚਾਰੀ ਭਿਸ਼ਟ ਹੋ ਚੁੱਕੇ ਸਨ ।ਹਰ ਪਾਸੇ ਰਿਸ਼ਵਤ ਦਾ ਬੋਲਬਾਲਾ ਸੀ । ਇੱਥੋਂ ਤਕ ਕਿ ਕਾਜ਼ੀ ਅਤੇ ਉਲਮਾ ਵੀ ਰਿਸ਼ਵਤ ਲੈ ਕੇ ਨਿਆਂ ਕਰਦੇ ਸਨ । ਮੁਸਲਮਾਨ ਹਿੰਦੂਆਂ ‘ਤੇ ਬਹੁਤ ਅੱਤਿਆਚਾਰ ਕਰਦੇ ਸਨ । ਉਨ੍ਹਾਂ ਨੂੰ ਤਲਵਾਰ ਦੇ ਜ਼ੋਰ ‘ਤੇ ਜ਼ਬਰਦਸਤੀ ਇਸਲਾਮ ਧਰਮ ਵਿੱਚ ਸ਼ਾਮਲ ਕੀਤਾ ਜਾਂਦਾ ਸੀ ।
ਰਾਜ ਦੀ ਸ਼ਾਸਨ ਵਿਵਸਥਾ ਖੇਰੂੰ-ਖੇਰੂੰ ਹੋ ਕੇ ਰਹਿ ਗਈ ਸੀ । ਅਜਿਹੀ ਸਥਿਤੀ ਦਾ ਫਾਇਦਾ ਉਠਾ ਕੇ ਪੰਜਾਬ ਦੇ ਗਵਰਨਰ ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਨੇ ਸੁਤੰਤਰ ਹੋਣ ਦਾ ਯਤਨ ਕੀਤਾ । ਇਸ ਸੰਬੰਧ ਵਿੱਚ ਉਸ ਨੇ ਬਾਬਰ ਨੂੰ ਭਾਰਤ ਉੱਤੇ ਹਮਲਾ ਕਰਨ ਦਾ ਸੱਦਾ ਦਿੱਤਾ । ਬਾਬਰ ਨੇ ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਨੂੰ ਹਰਾ ਕੇ 1525 ਈ. ਦੇ ਅਖੀਰ ਵਿੱਚ ਪੰਜਾਬ ‘ਤੇ ਕਬਜ਼ਾ ਕਰ ਲਿਆ ਸੀ । ਉਸ ਨੇ 21 ਅਪਰੈਲ, 1526 ਈ. ਨੂੰ ਪਾਨੀਪਤ ਦੀ ਪਹਿਲੀ ਲੜਾਈ ਵਿੱਚ ਸੁਲਤਾਨ ਇਬਰਾਹੀਮ ਲੋਧੀ ਨੂੰ ਹਰਾ ਕੇ ਭਾਰਤ ਵਿੱਚ ਮੁਗ਼ਲ ਵੰਸ਼ ਦੀ ਸਥਾਪਨਾ ਕੀਤੀ ।
![]()
ਪ੍ਰਸ਼ਨ 2.
“16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਤਿਕੋਣੇ ਸੰਘਰਸ਼ ਦਾ ਅਖਾੜਾ ਸੀ ” ਵਿਆਖਿਆ ਕਰੋ । (“In the beginning of the 16th century, the Punjab was a cockpit of triangular struggle.” Explain.)
ਜਾਂ
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਵਿੱਚ ਤਿਕੋਣੇ ਸੰਘਰਸ਼ ਦਾ ਵਰਣਨ ਕਰੋ । (Explain the Triangular Struggle of the Punjab in the beginning of the 16th century.)
ਉੱਤਰ-
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਤਿਕੋਣੇ ਸੰਘਰਸ਼ ਦਾ ਅਖਾੜਾ (Cockpit of triangular struggle) ਸੀ । ਇਹ ਤਿਕੋਣਾ ਸੰਘਰਸ਼ ਰਾਜ ਸੱਤਾ ਦੀ ਪ੍ਰਾਪਤੀ ਲਈ ਕਾਬਲ ਦੇ ਸ਼ਾਸਕ ਬਾਬਰ, ਦਿੱਲੀ ਦੇ ਸ਼ਾਸਕ ਇਬਰਾਹੀਮ ਲੋਧੀ ਅਤੇ ਪੰਜਾਬ ਦੇ ਸੂਬੇਦਾਰ ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਵਿਚਾਲੇ ਚਲ ਰਿਹਾ ਸੀ । ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਪੰਜਾਬ ਦਾ ਸੁਤੰਤਰ ਸ਼ਾਸਕ ਬਣਨ ਦੇ ਸੁਪਨੇ ਵੇਖ ਰਿਹਾ ਸੀ । ਇਸ ਸੰਬੰਧੀ ਜਦੋਂ ਇਬਰਾਹੀਮ ਲੋਧੀ ਨੂੰ ਪਤਾ ਚੱਲਿਆ ਤਾਂ ਉਸ ਨੇ ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਨੂੰ ਸਥਿਤੀ ਨੂੰ ਸਪੱਸ਼ਟ ਕਰਨ ਲਈ ਸ਼ਾਹੀ ਦਰਬਾਰ ਵਿੱਚ ਹਾਜ਼ਰ ਹੋਣ ਲਈ ਕਿਹਾ । ਦੌਲਤ ਖਾਂ ਨੇ ਸੁਲਤਾਨ ਦੇ ਗੁੱਸੇ ਤੋਂ ਬਚਣ ਲਈ ਆਪਣੇ ਛੋਟੇ ਪੁੱਤਰ ਦਿਲਾਵਰ ਖਾਂ ਨੂੰ ਦਿੱਲੀ ਭੇਜਿਆ ।ਦਿੱਲੀ ਪੁੱਜਣ ‘ਤੇ ਇਬਰਾਹੀਮ ਲੋਧੀ ਨੇ ਉਸ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰਕੇ ਕੈਦਖ਼ਾਨੇ ਵਿੱਚ ਸੁੱਟ ਦਿੱਤਾ । ਦਿਲਾਵਰ ਖਾਂ ਕਿਸੇ ਤਰ੍ਹਾਂ ਕੈਦਖ਼ਾਨੇ ਵਿੱਚੋਂ ਭੱਜ ਨਿਕਲਣ ਵਿੱਚ ਕਾਮਯਾਬ ਹੋ ਗਿਆ । ਪੰਜਾਬ ਪਹੁੰਚ ਕੇ ਉਸ ਨੇ ਆਪਣੇ ਪਿਤਾ ਦੌਲਤ ਖਾਂ ਨੂੰ ਉਸ ਨਾਲ ਦਿੱਲੀ ਵਿੱਚ ਕੀਤੇ ਗਏ ਮਾੜੇ ਵਿਵਹਾਰ ਬਾਰੇ ਦੱਸਿਆ ।ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਨੇ ਇਸ ਅਪਮਾਨ ਦਾ ਬਦਲਾ ਲੈਣ ਲਈ ਬਾਬਰ ਨੂੰ ਭਾਰਤ ਉੱਤੇ ਹਮਲਾ ਕਰਨ ਦਾ ਸੱਦਾ ਦਿੱਤਾ | ਬਾਬਰ ਵੀ ਇਸੇ ਸੁਨਹਿਰੀ ਮੌਕੇ ਦੀ ਤਲਾਸ਼ ਵਿੱਚ ਸੀ । ਇਸ ਤਿਕੋਣੇ ਸੰਘਰਸ਼ ਦੇ ਅੰਤ ਵਿੱਚ ਬਾਬਰ ਜੇਤੂ ਰਿਹਾ। ਉਸ ਨੇ 1525-26 ਈ. ਵਿੱਚ ਨਾ ਕੇਵਲ ਪੰਜਾਬ ਸਗੋਂ ਦਿੱਲੀ ‘ਤੇ ਵੀ ਕਬਜ਼ਾ ਕਰ ਲਿਆ । ਇਸ ਤਰ੍ਹਾਂ ਭਾਰਤ ਵਿੱਚ ਮੁਗ਼ਲ ਵੰਸ਼ ਦੀ ਸਥਾਪਨਾ ਹੋਈ ।
ਪ੍ਰਸ਼ਨ 3.
ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਕੌਣ ਸੀ ? ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਅਤੇ ਇਬਰਾਹੀਮ ਲੋਧੀ ਵਿੱਚੱਲੇ ਸੰਘਰਸ਼ ਦੇ ਕੀ ਕਾਰਨ ਸਨ ? (Who was Daulat Khan Lodhi ? What were the causes of struggle between Daulat Khan Lodhi and Ibrahim Lodhi ?)
ਜਾਂ
ਦੌਲਤ ਖਾਂ ਲੋਧੀ ‘ਤੇ ਇੱਕ ਸੰਖੇਪ ਨੋਟ ਲਿਖੋ । (Write a short note on Daulat Khan Lodhi.)
ਉੱਤਰ-
ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਪੰਜਾਬ ਦਾ ਸੂਬੇਦਾਰ (ਗਵਰਨਰ) ਸੀ । ਉਹ ਇਸ ਅਹੁਦੇ ‘ਤੇ 1500 ਈ. ਵਿੱਚ ਨਿਯੁਕਤ ਹੋਇਆ ਸੀ । ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਅਤੇ ਸੁਲਤਾਨ ਇਬਰਾਹੀਮ ਲੋਧੀ ਵਿਚਾਲੇ ਸੰਘਰਸ਼ ਦਾ ਮੁੱਖ ਕਾਰਨ ਇਹ ਸੀ ਕਿ ਦੌਲਤ ਮਾਂ ਪੰਜਾਬ ਵਿੱਚ ਸੁਤੰਤਰ ਸ਼ਾਸਨ ਸਥਾਪਿਤ ਕਰਨ ਦੇ ਯਤਨ ਕਰ ਰਿਹਾ ਸੀ । ਇਸ ਸੰਬੰਧੀ ਉਸ ਨੇ ਆਲਮ ਖਾਂ ਲੋਧੀ ਜੋ ਕਿ ਇਬਰਾਹੀਮ ਲੋਧੀ ਦਾ ਮਤਰੇਆ ਭਰਾ ਸੀ ਅਤੇ ਜੋ ਦਿੱਲੀ ਦਾ ਤਖ਼ਤ ਹਾਸਲ ਕਰਨਾ ਚਾਹੁੰਦਾ ਸੀ, ਦੇ ਨਾਲ ਮਿਲ ਕੇ ਸਾਜ਼ਸ਼ਾਂ ਕਰਨੀਆਂ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤੀਆਂ ਸਨ । ਜਦੋਂ ਇਨ੍ਹਾਂ ਸਾਜ਼ਸ਼ਾਂ ਸੰਬੰਧੀ ਇਬਰਾਹੀਮ ਲੋਧੀ ਨੂੰ ਪਤਾ ਚੱਲਿਆ ਤਾਂ ਉਸ ਨੇ ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਨੂੰ ਸ਼ਾਹੀ ਦਰਬਾਰ ਵਿੱਚ ਹਾਜ਼ਰ ਹੋਣ ਦਾ ਹੁਕਮ ਭੇਜਿਆ । ਦੌਲਤ ਖਾਂ ਨੇ ਸੁਲਤਾਨ ਦੇ ਗੁੱਸੇ ਤੋਂ ਬਚਣ ਲਈ ਆਪਣੇ ਛੋਟੇ ਪੁੱਤਰ ਦਿਲਾਵਰ ਖਾਂ ਨੂੰ ਦਿੱਲੀ ਭੇਜ ਦਿੱਤਾ । ਜਦੋਂ ਦਿਲਾਵਰ ਖਾਂ ਦਿੱਲੀ ਪਹੁੰਚਿਆ ਤਾਂ ਸੁਲਤਾਨ ਨੇ ਉਸ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰ ਲਿਆ । ਜੇਲ੍ਹ ਵਿੱਚ ਉਸ ਨਾਲ ਮਾੜਾ ਵਿਹਾਰ ਕੀਤਾ ਗਿਆ । ਛੇਤੀ ਹੀ ਉਹ ਕਿਸੇ ਤਰ੍ਹਾਂ ਜੇਲ੍ਹ ਵਿੱਚੋਂ ਭੱਜਣ ਅਤੇ ਵਾਪਸ ਪੰਜਾਬ ਪਹੁੰਚਣ ਵਿੱਚ ਕਾਮਯਾਬ ਹੋ ਗਿਆ । ਇੱਥੇ ਪਹੁੰਚ ਕੇ ਉਸ ਨੇ ਆਪਣੇ ਪਿਤਾ ਦੌਲਤ ਖਾਂ ਨੂੰ ਦਿੱਲੀ ਵਿੱਚ ਉਸ ਨਾਲ ਕੀਤੇ ਗਏ ਮਾੜੇ ਸਲੂਕ ਬਾਰੇ ਦੱਸਿਆ ।ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਨੇ ਇਸ ਅਪਮਾਨ ਦਾ ਬਦਲਾ ਲੈਣ ਲਈ ਬਾਬਰ ਨੂੰ ਭਾਰਤ ਉੱਤੇ ਹਮਲਾ ਕਰਨ ਦਾ ਸੱਦਾ ਦਿੱਤਾ । ਬਾਅਦ ਵਿੱਚ ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਬਾਬਰ ਦੇ ਵਿਰੁੱਧ ਹੋ ਗਿਆ ਸੀ । ਬਾਬਰ ਨੇ ਉਸ ਨੂੰ 1525 ਈ. ਵਿੱਚ ਹਰਾ ਕੇ ਪੰਜਾਬ ‘ਤੇ ਕਬਜ਼ਾ ਕਰ ਲਿਆ ਸੀ ।
ਪ੍ਰਸ਼ਨ 4.
ਬਾਬਰ ਕੌਣ ਸੀ ? ਉਸ ਨੇ ਪੰਜਾਬ ‘ਤੇ ਕਿਸ ਸਮੇਂ ਦੇ ਦੌਰਾਨ ਅਤੇ ਕਿੰਨੇ ਹਮਲੇ ਕੀਤੇ ? ਇਨਾਂ ਹਮਲਿਆਂ ਦੀ ਸੰਖੇਪ ਜਾਣਕਾਰੀ ਦਿਓ ।
(Who was Babar ? When and how many times did he invade Punjab ? Write briefly about these invasions.)
ਜਾਂ
ਪੰਜਾਬ ਉੱਤੇ ਬਾਬਰ ਦੁਆਰਾ ਕੀਤੇ ਗਏ ਹਮਲਿਆਂ ਦਾ ਸੰਖੇਪ ਵਰਣਨ ਕਰੋ । (Give a brief account of Babar’s invasions over Punjab.)
ਉੱਤਰ-
ਬਾਬਰ ਕਾਬਲ ਦਾ ਸ਼ਾਸਕ ਸੀ । ਉਸ ਨੇ 1519 ਈ. ਤੋਂ 1526 ਈ. ਦੇ ਸਮੇਂ ਦੇ ਦੌਰਾਨ ਪੰਜਾਬ ‘ਤੇ ਪੰਜ ਹਮਲੇ ਕੀਤੇ । ਬਾਬਰ ਨੇ ਪੰਜਾਬ ‘ਤੇ ਪਹਿਲਾ ਹਮਲਾ 1519 ਈ. ਵਿੱਚ ਕੀਤਾ । ਇਸ ਹਮਲੇ ਦੇ ਦੌਰਾਨ ਬਾਬਰ ਨੇ ਭੇਰਾ ਅਤੇ ਬਾਕੌਰ ਨਾਂ ਦੇ ਖੇਤਰਾਂ ‘ਤੇ ਕਬਜ਼ਾ ਕੀਤਾ । ਬਾਬਰ ਦੇ ਵਾਪਸ ਜਾਂਦਿਆਂ ਹੀ ਉੱਥੋਂ ਦੇ ਲੋਕਾਂ ਨੇ ਮੁੜ ਇਨ੍ਹਾਂ ਇਲਾਕਿਆਂ ‘ਤੇ ਕਬਜ਼ਾ ਕਰ ਲਿਆ । ਇਸੇ ਵਰ੍ਹੇ ਬਾਬਰ ਨੇ ਪੰਜਾਬ ‘ਤੇ ਦੂਸਰੀ ਵਾਰ ਹਮਲਾ ਕੀਤਾ । ਇਸ ਵਾਰੀ ਬਾਬਰ ਨੇ ਪਿਸ਼ਾਵਰ ਨੂੰ ਆਪਣੇ ਅਧੀਨ ਕੀਤਾ | 1520 ਈ. ਵਿੱਚ ਬਾਬਰ ਨੇ ਪੰਜਾਬ ‘ਤੇ ਆਪਣੇ ਤੀਸਰੇ ਹਮਲੇ ਦੇ ਦੌਰਾਨ ਬਾਜੌਰ, ਭਰਾ ਅਤੇ ਸਿਆਲਕੋਟ ਦੇ ਦੇਸ਼ਾਂ ਨੂੰ ਆਪਣੇ ਅਧੀਨ ਕੀਤਾ । ਇਸ ਤੋਂ ਬਾਅਦ ਬਾਬਰ ਨੇ ਸੈਦਪੁਰ ‘ਤੇ ਹਮਲਾ ਕੀਤਾ । ਇਸ ਹਮਲੇ ਦੇ ਦੌਰਾਨ ਬਾਬਰ ਨੇ ਸੈਦਪੁਰ ਵਿੱਚ ਭਾਰੀ ਲੁੱਟਮਾਰ ਕੀਤੀ ।
ਮੁਗ਼ਲ ਫ਼ੌਜਾਂ ਨੇ ਹੋਰ ਲੋਕਾਂ ਦੇ ਨਾਲ-ਨਾਲ ਗੁਰੂ ਨਾਨਕ ਸਾਹਿਬ ਨੂੰ ਵੀ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰ ਲਿਆ । ਬਾਅਦ ਵਿੱਚ ਬਾਬਰ ਦੇ ਕਹਿਣ ‘ਤੇ ਉਨ੍ਹਾਂ ਨੂੰ ਰਿਹਾਅ ਕਰ ਦਿੱਤਾ ਗਿਆ । 1524 ਈ. ਵਿੱਚ ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਦੇ ਸੱਦੇ ‘ਤੇ ਬਾਬਰ ਨੇ ਪੰਜਾਬ ’ਤੇ ਚੌਥੀ ਵਾਰ ਹਮਲਾ ਕੀਤਾ । ਬਾਬਰ ਨੇ ਬਿਨਾਂ ਕਿਸੇ ਔਕੜ ਦੇ ਪੰਜਾਬ ‘ਤੇ ਕਬਜ਼ਾ ਕਰ ਲਿਆ | ਬਾਅਦ ਵਿੱਚ ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਬਾਬਰ ਦੇ ਵਿਰੁੱਧ ਹੋ ਗਿਆ । ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਨੂੰ ਸਬਕ ਸਿਖਾਉਣ ਦੇ ਲਈ ਬਾਬਰ ਨੇ ਪੰਜਾਬ ‘ਤੇ ਪੰਜਵੀਂ ਵਾਰ ਨਵੰਬਰ, 1525 ਈ. ਵਿੱਚ ਹਮਲਾ ਕੀਤਾ । ਬਾਬਰ ਨੇ ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਨੂੰ ਹਰਾ ਕੇ ਪੰਜਾਬ ‘ਤੇ ਕਬਜ਼ਾ ਕਰ ਲਿਆ । ਇਸ ਤੋਂ ਬਾਅਦ ਬਾਬਰ ਨੇ 21 ਅਪਰੈਲ, 1526 ਈ. ਨੂੰ ਪਾਨੀਪਤ ਦੀ ਪਹਿਲੀ ਲੜਾਈ ਵਿੱਚ ਸੁਲਤਾਨ ਇਬਰਾਹੀਮ ਲੋਧੀ ਨੂੰ ਹਰਾ ਕੇ ਭਾਰਤ ਵਿੱਚ ਮੁਗਲ ਵੰਸ਼ ਦੀ ਸਥਾਪਨਾ ਕੀਤੀ ।
ਪਸ਼ਨ 5.
ਬਾਬਰ ਨੇ ਸੈਦਪੁਰ ’ਤੇ ਕਦੋਂ ਹਮਲਾ ਕੀਤਾ ? ਸਿੱਖ ਇਤਿਹਾਸ ਵਿੱਚ ਇਸ ਹਮਲੇ ਦਾ ਕੀ ਮਹੱਤਵ ਹੈ ? (When did Babar invade Saidpur ? What is its importance in Sikh History ?)
ਉੱਤਰ-
ਬਾਬਰ ਨੇ ਸੈਦਪੁਰ ’ਤੇ 1520 ਈ. ਵਿੱਚ ਹਮਲਾ ਕੀਤਾ । ਇੱਥੋਂ ਦੇ ਲੋਕਾਂ ਨੇ ਬਾਬਰ ਦਾ ਮੁਕਾਬਲਾ ਕੀਤਾ । ਸਿੱਟੇ ਵਜੋਂ ਬਾਬਰ ਨੇ ਗੁੱਸੇ ਵਿੱਚ ਆ ਕੇ ਵੱਡੀ ਗਿਣਤੀ ਵਿੱਚ ਲੋਕਾਂ ਨੂੰ ਕਤਲ ਕਰ ਦਿੱਤਾ ਅਤੇ ਲੁੱਟਮਾਰ ਕਰਨ ਮਗਰੋਂ ਉਨ੍ਹਾਂ ਦੇ ਮਕਾਨਾਂ ਅਤੇ ਮਹੱਲਾਂ ਨੂੰ ਅੱਗ ਲਗਾ ਦਿੱਤੀ । ਹਜ਼ਾਰਾਂ ਇਸਤਰੀਆਂ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰ ਲਿਆ ਗਿਆ ਅਤੇ ਉਨ੍ਹਾਂ ਨਾਲ ਬਦਸਲੂਕੀ ਕੀਤੀ ਗਈ । ਗੁਰੂ ਨਾਨਕ ਦੇਵ ਜੀ ਜੋ ਇਸ ਸਮੇਂ ਸੈਦਪੁਰ ਵਿੱਚ ਹੀ ਸਨ, ਨੇ ਬਾਬਰ ਦੀਆਂ ਫ਼ੌਜਾਂ ਵੱਲੋਂ ਲੋਕਾਂ ‘ਤੇ ਕੀਤੇ ਗਏ ਅੱਤਿਆਚਾਰਾਂ ਦਾ ਵਰਣਨ ‘ਬਾਬਰ ਬਾਣੀ’ ਵਿੱਚ ਕੀਤਾ ਹੈ । ਬਾਬਰ ਦੀਆਂ ਫ਼ੌਜਾਂ ਨੇ ਗੁਰੂ ਨਾਨਕ ਸਾਹਿਬ ਜੀ ਨੂੰ ਵੀ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰ ਲਿਆ ਸੀ । ਬਾਅਦ ਵਿੱਚ ਜਦੋਂ ਬਾਬਰ ਨੂੰ ਇਸ ਬਾਰੇ ਪਤਾ ਲੱਗਿਆ ਕਿ ਉਸ ਦੀਆਂ ਫ਼ੌਜਾਂ ਨੇ ਕਿਸੇ ਸੰਤ-ਮਹਾਪੁਰਸ਼ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕੀਤਾ ਹੈ ਤਾਂ ਉਸ ਨੇ ਫੌਰਨ ਉਨ੍ਹਾਂ ਦੀ ਰਿਹਾਈ ਦਾ ਹੁਕਮ ਦਿੱਤਾ | ਬਾਬਰ ਨੇ ਆਪਣੀ ਆਤਮ-ਕਥਾ ‘ਤਜ਼ਕ-ਏ-ਬਾਬਰੀ’ ਵਿੱਚ ਲਿਖਿਆ ਹੈ ਕਿ ਜੇ ਉਸ ਨੂੰ ਪਤਾ ਹੁੰਦਾ ਕਿ ਇਸ ਸ਼ਹਿਰ ਵਿੱਚ ਅਜਿਹਾ ਮਹਾਤਮਾ ਰਹਿੰਦਾ ਹੈ ਤਾਂ ਉਹ ਕਦੇ ਵੀ ਇਸ ਸ਼ਹਿਰ ‘ਤੇ ਹਮਲਾ ਨਾ ਕਰਦਾ । ਗੁਰੂ ਨਾਨਕ ਸਾਹਿਬ ਦੇ ਕਹਿਣ ‘ਤੇ ਬਾਬਰ ਨੇ ਬਹੁਤ ਸਾਰੇ ਹੋਰ ਨਿਰਦੋਸ਼ ਲੋਕਾਂ ਨੂੰ ਵੀ ਰਿਹਾਅ ਕਰ ਦਿੱਤਾ ।
ਪ੍ਰਸ਼ਨ 6.
ਬਾਬਰ ਅਤੇ ਇਬਰਾਹੀਮ ਲੋਧੀ ਵਿਚਕਾਰ ਯੁੱਧ ਕਿੱਥੇ ਤੇ ਕਿਉਂ ਹੋਇਆ ? (Why and where did the battle take place between Babar and Ibrahim Lodhi ?)
ਜਾਂ
ਪਾਨੀਪਤ ਦੀ ਪਹਿਲੀ ਲੜਾਈ ‘ਤੇ ਨੋਟ ਲਿਖੋ । (Give a brief account of the First Battle of Panipat.)
ਜਾਂ
ਪਾਨੀਪਤ ਦੀ ਪਹਿਲੀ ਲੜਾਈ ਅਤੇ ਉਸ ਦੇ ਮਹੱਤਵ ਦਾ ਸੰਖੇਪ ਵਰਣਨ ਕਰੋ । (Explain the First Battle of Panipat and its significance.)
ਉੱਤਰ-
ਬਾਬਰ ਨੇ ਪੰਜਾਬ ਦੇ ਗਵਰਨਰ ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਨੂੰ ਸਬਕ ਸਿਖਾਉਣ ਦੇ ਉਦੇਸ਼ ਨਾਲ ਨਵੰਬਰ, 1525 ਈ. ਵਿੱਚ ਪੰਜਾਬ ‘ਤੇ ਪੰਜਵੀਂ ਵਾਰ ਹਮਲਾ ਕੀਤਾ । ਦੌਲਤ ਖਾਂ ਨੇ ਕੁਝ ਚਿਰ ਮੁਕਾਬਲਾ ਕਰਨ ਮਗਰੋਂ ਆਪਣੇ ਹਥਿਆਰ ਸੁੱਟ ਦਿੱਤੇ । ਬਾਬਰ ਨੇ ਉਸ ਨੂੰ ਮੁਆਫ਼ ਕਰ ਦਿੱਤਾ । ਇਸ ਤਰ੍ਹਾਂ ਬਾਬਰ ਨੇ ਇੱਕ ਵਾਰ ਫਿਰ ਪੂਰੇ ਪੰਜਾਬ ਨੂੰ ਆਪਣੇ ਅਧੀਨ ਕਰ ਲਿਆ । ਪੰਜਾਬ ਦੀ ਜਿੱਤ ਤੋਂ ਉਤਸ਼ਾਹਿਤ ਹੋ ਕੇ ਬਾਬਰ ਨੇ ਇਬਰਾਹੀਮ ਲੋਧੀ ਨਾਲ ਦੋ-ਦੋ ਹੱਥ ਕਰਨ ਦਾ ਫ਼ੈਸਲਾ ਕੀਤਾ । ਇਸ ਉਦੇਸ਼ ਨਾਲ ਉਸ ਨੇ ਆਪਣੀਆਂ ਫ਼ੌਜਾਂ ਨੂੰ ਦਿੱਲੀ ਵੱਲ ਵਧਣ ਦਾ ਹੁਕਮ ਦਿੱਤਾ । ਜਦੋਂ ਇਬਰਾਹੀਮ ਲੋਧੀ ਨੂੰ ਇਸ ਬਾਰੇ ਖ਼ਬਰ ਮਿਲੀ ਤਾਂ ਉਹ ਆਪਣੇ ਨਾਲ 1 ਲੱਖ ਸੈਨਿਕਾਂ ਨੂੰ ਲੈ ਕੇ ਬਾਬਰ ਦਾ ਮੁਕਾਬਲਾ ਕਰਨ ਲਈ ਪੰਜਾਬ ਵੱਲ ਤੁਰ ਪਿਆ । ਬਾਬਰ ਅਧੀਨ ਉਸ ਸਮੇਂ ਲਗਭਗ 20 ਹਜ਼ਾਰ ਸੈਨਿਕ ਸਨ ।21 ਅਪਰੈਲ, 1526 ਈ. ਨੂੰ ਦੋਹਾਂ ਫ਼ੌਜਾਂ ਵਿਚਾਲੇ ਪਾਨੀਪਤ ਦੀ ਪਹਿਲੀ ਲੜਾਈ ਹੋਈ । ਇਸ ਲੜਾਈ ਵਿੱਚ ਇਬਰਾਹੀਮ ਲੋਧੀ ਦੀ ਹਾਰ ਹੋਈ ਅਤੇ ਉਹ ਲੜਾਈ ਦੇ ਮੈਦਾਨ ਵਿੱਚ ਮਾਰਿਆ ਗਿਆ । ਪਾਨੀਪਤ ਦੀ ਇਸ ਨਿਰਣਾਇਕ ਜਿੱਤ ਕਾਰਨ ਪੰਜਾਬ ਵਿੱਚੋਂ ਲੋਧੀ ਵੰਸ਼ ਦੇ ਸ਼ਾਸਨ ਦਾ ਹਮੇਸ਼ਾਂ ਲਈ ਖ਼ਾਤਮਾ ਹੋ ਗਿਆ ਅਤੇ ਹੁਣ ਇਹ ਮੁਗ਼ਲ ਵੰਸ਼ ਦੇ ਅਧੀਨ ਹੋ ਗਿਆ ।
![]()
ਪ੍ਰਸ਼ਨ 7.
ਪਾਨੀਪਤ ਦੀ ਪਹਿਲੀ ਲੜਾਈ ਵਿੱਚ ਬਾਬਰ ਕਿਉਂ ਜੇਤੂ ਰਿਹਾ ? (What led to the victory of Babar in the First Battle of Panipat ?)
ਜਾਂ
ਭਾਰਤ ਵਿੱਚ ਬਾਬਰ ਦੀ ਜਿੱਤ ਅਤੇ ਅਫ਼ਗਾਨਾਂ ਦੀ ਹਾਰ ਦੇ ਕਾਰਨਾਂ ਦਾ ਸੰਖੇਪ ਵਰਣਨ ਕਰੋ । (Give a brief account of the causes of victory of Babar and defeat of the Afghans in India.)
ਉੱਤਰ-
ਪਾਨੀਪਤ ਦੀ ਪਹਿਲੀ ਲੜਾਈ ਵਿੱਚ ਬਾਬਰ ਦੀ ਜਿੱਤ ਲਈ ਕਈ ਕਾਰਨ ਜ਼ਿੰਮੇਵਾਰ ਸਨ । ਦਿੱਲੀ ਦਾ ਸੁਲਤਾਨ ਇਬਰਾਹੀਮ ਲੋਧੀ ਆਪਣੇ ਬੁਰੇ ਵਤੀਰੇ ਅਤੇ ਅੱਤਿਆਚਾਰਾਂ ਕਾਰਨ ਆਪਣੇ ਸਰਦਾਰਾਂ ਅਤੇ ਪਰਜਾ ਵਿੱਚ ਬੜਾ ਬਦਨਾਮ ਸੀ ।ਉਹ ਅਜਿਹੇ ਸ਼ਾਸਕ ਤੋਂ ਛੁਟਕਾਰਾ ਪਾਉਣਾ ਚਾਹੁੰਦੇ ਸਨ । ਇਬਰਾਹੀਮ ਲੋਧੀ ਦੀ ਫ਼ੌਜ ਵੀ ਬੜੀ ਨਿਰਬਲ ਸੀ । ਉਸ ਦੇ ਵਧੇਰੇ ਸੈਨਿਕ ਲੁੱਟ-ਮਾਰ ਦੇ ਉਦੇਸ਼ ਨਾਲ ਇਕੱਠੇ ਹੋਏ ਸਨ । ਉਨ੍ਹਾਂ ਦੇ ਲੜਨ ਦੇ ਢੰਗ ਪੁਰਾਣੇ ਸਨ ਅਤੇ ਉਨ੍ਹਾਂ ਵਿੱਚ ਯੋਜਨਾ ਦੀ ਵੀ ਘਾਟ ਸੀ । ਇਬਰਾਹੀਮ ਲੋਧੀ ਨੇ ਪਾਨੀਪਤ ਵਿੱਚ 8 ਦਿਨਾਂ ਤਕ ਬਾਬਰ ਦੀ ਫ਼ੌਜ ਉੱਤੇ ਹਮਲਾ ਨਾ ਕਰਕੇ ਭਾਰੀ ਰਾਜਨੀਤਿਕ ਭੁੱਲ ਕੀਤੀ । ਜੇ ਉਹ ਬਾਬਰ ਨੂੰ ਸੁਰੱਖਿਆ ਪ੍ਰਬੰਧ ਮਜ਼ਬੂਤ ਨਾ ਕਰਨ ਦਿੰਦਾ ਤਾਂ ਸ਼ਾਇਦ ਲੜਾਈ ਦਾ ਸਿੱਟਾ ਕੁਝ ਹੋਰ ਹੀ ਹੋਣਾ ਸੀ | ਬਾਬਰ ਇੱਕ ਯੋਗ ਸੈਨਾਪਤੀ ਸੀ । ਉਸ ਨੂੰ ਲੜਾਈਆਂ ਦਾ ਕਾਫ਼ੀ ਤਜਰਬਾ ਸੀ । ਬਾਬਰ ਦੁਆਰਾ ਤੋਪਖ਼ਾਨੇ ਦੀ ਵਰਤੋਂ ਨੇ ਭਾਰੀ ਤਬਾਹੀ ਮਚਾਈ । ਇਬਰਾਹੀਮ ਦੇ ਸੈਨਿਕ ਆਪਣੇ ਤੀਰ ਕਮਾਨਾਂ ਅਤੇ ਤਲਵਾਰਾਂ ਨਾਲ ਇਨ੍ਹਾਂ ਦਾ ਮੁਕਾਬਲਾ ਨਾ ਕਰ ਸਕੇ । ਇਨ੍ਹਾਂ ਕਾਰਨਾਂ ਕਰਕੇ ਅਫ਼ਗਾਨਾਂ ਦੀ ਹਾਰ ਹੋਈ ਅਤੇ ਬਾਬਰ ਜੇਤੂ ਰਿਹਾ ।
ਪ੍ਰਸ਼ਨ 8.
16ਵੀਂ ਸਦੀ ਦੇ ਮੁੱਢਲੇ ਸਮੇਂ ਪੰਜਾਬ ਦੀ ਸਮਾਜਿਕ ਦਸ਼ਾ ਦਾ ਸੰਖੇਪ ਵਰਣਨ ਕਰੋ । (Model Test Paper, July 2019) (Explain the social condition of Punjab in the beginning of the 16th century.)
ਜਾਂ
ਗੁਰੂ ਨਾਨਕ ਦੇਵ ਜੀ ਦੇ ਜਨਮ ਸਮੇਂ ਪੰਜਾਬ ਦੀ ਸਮਾਜਿਕ ਦਸ਼ਾ ਦੇ ਬਾਰੇ ਤੁਸੀਂ ਕੀ ਜਾਣਦੇ ਹੋ ? (What do you know about the social condition of Punjab at the time of birth of Guru Nanak Dev Ji ?)
ਉੱਤਰ-
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦਾ ਸਮਾਜ ਦੋ ਮੁੱਖ ਵਰਗਾਂ-ਮੁਸਲਮਾਨਾਂ ਅਤੇ ਹਿੰਦੂਆਂ ਵਿੱਚ ਵੰਡਿਆ ਹੋਇਆ ਸੀ । ਸ਼ਾਸਕ ਵਰਗ ਨਾਲ ਸੰਬੰਧਿਤ ਹੋਣ ਕਾਰਨ ਮੁਸਲਮਾਨਾਂ ਨੂੰ ਸਮਾਜ ਵਿੱਚ ਕੁਝ ਵਿਸ਼ੇਸ਼ ਅਧਿਕਾਰ ਪ੍ਰਾਪਤ ਸਨ । ਉਹ ਰਾਜ ਦੇ ਉੱਚ ਅਹੁਦਿਆਂ ‘ਤੇ ਨਿਯੁਕਤ ਸਨ । ਦੂਜੇ ਪਾਸੇ ਹਿੰਦੂਆਂ ਨੂੰ ਲਗਭਗ ਸਾਰੇ ਅਧਿਕਾਰਾਂ ਤੋਂ ਵਾਂਝਿਆਂ ਰੱਖਿਆ ਗਿਆ ਸੀ । ਮੁਸਲਮਾਨ ਉਨ੍ਹਾਂ ਨੂੰ ਕਾਫ਼ਰ ਕਹਿੰਦੇ ਸਨ । ਮੁਸਲਮਾਨ ਹਿੰਦੁਆਂ ’ਤੇ ਇੰਨੇ ਅੱਤਿਆਚਾਰ ਕਰਦੇ ਸਨ ਕਿ ਬਹੁਤ ਸਾਰੇ ਹਿੰਦੂ ਮੁਸਲਮਾਨ ਬਣਨ ਲਈ ਮਜਬੂਰ ਹੋ ਗਏ । ਉਸ ਸਮੇਂ ਸਮਾਜ ਵਿੱਚ ਇਸਤਰੀਆਂ ਦੀ ਹਾਲਤ ਬਹੁਤ ਤਰਸਯੋਗ ਸੀ । ਉੱਚ ਸ਼੍ਰੇਣੀ ਦੇ ਮੁਸਲਮਾਨਾਂ ਦੀਆਂ ਪੁਸ਼ਾਕਾਂ ਬਹੁਤ ਕੀਮਤੀ ਹੁੰਦੀਆਂ ਸਨ । ਇਹ ਰੇਸ਼ਮ ਅਤੇ ਮਖਮਲ ਦੀਆਂ ਬਣੀਆਂ ਹੁੰਦੀਆਂ ਸਨ । ਨੀਵੀਂ ਸ਼੍ਰੇਣੀ ਦੇ ਲੋਕਾਂ ਅਤੇ ਹਿੰਦੂਆਂ ਦਾ ਪਹਿਰਾਵਾ ਬਿਲਕੁਲ ਸਾਦਾ ਹੁੰਦਾ ਸੀ । ਸ਼ਿਕਾਰ, ਘੋੜ-ਦੌੜ, ਸ਼ਤਰੰਜ, ਨਾਚ-ਗਾਣੇ, ਸੰਗੀਤ, ਜਾਨਵਰਾਂ ਦੀਆਂ ਲੜਾਈਆਂ ਅਤੇ ਤਾਸ਼ ਉਸ ਸਮੇਂ ਦੇ ਲੋਕਾਂ ਦੇ ਮਨੋਰੰਜਨ ਦੇ ਮੁੱਖ ਸਾਧਨ ਸਨ ।
ਪ੍ਰਸ਼ਨ 9.
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦੀਆਂ ਇਸਤਰੀਆਂ ਦੀ ਸਥਿਤੀ ਕਿਹੋ ਜਿਹੀ ਸੀ ? (What was the social condition of women in Punjab in the beginning of the 16th century ?)
ਉੱਤਰ-
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦੀਆਂ ਇਸਤਰੀਆਂ ਦੀ ਸਮਾਜਿਕ ਦਸ਼ਾ ਬਹੁਤ ਮਾੜੀ ਸੀ । ਹਿੰਦੂ ਸਮਾਜ ਵਿੱਚ ਇਸਤਰੀਆਂ ਦਾ ਦਰਜਾ ਪੁਰਸ਼ਾਂ ਦੇ ਬਰਾਬਰ ਨਹੀਂ ਸੀ ।ਉਨ੍ਹਾਂ ਨੂੰ ਘਰ ਦੀ ਚਾਰਦੀਵਾਰੀ ਅੰਦਰ ਬੰਦ ਰੱਖਿਆ ਜਾਂਦਾ ਸੀ । ਉਸ ਸਮੇਂ ਬਹੁਤ ਸਾਰੀਆਂ ਲੜਕੀਆਂ ਨੂੰ ਜੰਮਦੇ ਸਾਰ ਹੀ ਮਾਰ ਦਿੱਤਾ ਜਾਂਦਾ ਸੀ । ਉਸ ਸਮੇਂ ਕੁੜੀਆਂ ਦਾ ਵਿਆਹ ਛੋਟੀ ਉਮਰ ਵਿੱਚ ਹੀ ਕਰ ਦਿੱਤਾ ਜਾਂਦਾ ਸੀ । ਬਾਲ ਵਿਆਹ ਕਾਰਨ ਉਨ੍ਹਾਂ ਦੀ ਸਿੱਖਿਆ ਵੱਲ ਕੋਈ ਧਿਆਨ ਨਹੀਂ ਦਿੱਤਾ ਜਾਂਦਾ ਸੀ । ਉਸ ਸਮੇਂ ਸਤੀ ਪ੍ਰਥਾ ਵੀ ਪੂਰੇ ਜ਼ੋਰਾਂ ‘ਤੇ ਸੀ ।ਵਿਧਵਾ ਨੂੰ ਦੁਬਾਰਾ ਵਿਆਹ ਕਰਨ ਦੀ ਇਜਾਜ਼ਤ ਨਹੀਂ ਸੀ । ਮੁਸਲਿਮ ਸਮਾਜ ਵਿੱਚ ਵੀ ਇਸਤਰੀਆਂ ਦੀ ਹਾਲਤ ਚੰਗੀ ਨਹੀਂ ਸੀ । ਸਮਾਜ ਵੱਲੋਂ ਉਨ੍ਹਾਂ ‘ਤੇ ਕਈ ਤਰ੍ਹਾਂ ਦੀਆਂ ਪਾਬੰਦੀਆਂ ਲਗਾਈਆਂ ਗਈਆਂ ਸਨ । ਵੇਸਵਾ ਪ੍ਰਥਾ, ਤਲਾਕ ਪ੍ਰਥਾ ਅਤੇ ਪਰਦਾ ਪ੍ਰਥਾ ਕਾਰਨ ਉਨ੍ਹਾਂ ਦੀ ਹਾਲਤ ਤਰਸਯੋਗ ਹੋ ਗਈ ਸੀ । ਮੁਸਲਿਮ ਸਮਾਜ ਵਿੱਚ ਉੱਚ ਵਰਗ ਦੀਆਂ ਇਸਤਰੀਆਂ ਨੂੰ ਕੁਝ ਵਿਸ਼ੇਸ਼ ਸਹੂਲਤਾਂ ਪ੍ਰਾਪਤ ਸਨ ਪਰ ਇਨ੍ਹਾਂ ਦੀ ਗਿਣਤੀ ਬਹੁਤ ਥੋੜ੍ਹੀ ਸੀ ।
ਪ੍ਰਸ਼ਨ 10.
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਮੁਸਲਿਮ ਸਮਾਜ ਕਿਹੜੀਆਂ ਸ਼੍ਰੇਣੀਆਂ ਵਿੱਚ ਵੰਡਿਆ ਹੋਇਆ ਸੀ ਅਤੇ ਉਹ ਕਿਹੋ ਜਿਹਾ ਜੀਵਨ ਬਤੀਤ ਕਰਦੀਆਂ ਸਨ ? (Into which classes were the Muslim society of the Punjab divided and what type of life did they lead in the beginning of the 16th century ?)
ਜਾਂ
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਸਮਾਜ ਵਿੱਚ ਮੁਸਲਮਾਨਾਂ ਦੀਆਂ ਸ਼੍ਰੇਣੀਆਂ ਦਾ ਵਰਣਨ ਕਰੋ । (Give an account of the Muslim classes of Punjab in the beginning of the 16th century.)
ਉੱਤਰ-
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਮੁਸਲਿਮ ਸਮਾਜ ਇਨ੍ਹਾਂ ਤਿੰਨ ਸ਼੍ਰੇਣੀਆਂ ਵਿੱਚ ਵੰਡਿਆ ਹੋਇਆ ਸੀ-
- ਉੱਚ ਸ਼੍ਰੇਣੀ – ਉੱਚ ਸ਼੍ਰੇਣੀ ਵਿੱਚ ਅਮੀਰ, ਖ਼ਾਨ, ਸ਼ੇਖ਼, ਕਾਜ਼ੀ ਅਤੇ ਉਲਮਾ ਸ਼ਾਮਲ ਸਨ । ਇਸ ਸ਼੍ਰੇਣੀ ਦੇ ਲੋਕ ਬੜੇ ਐਸ਼ੋ-ਆਰਾਮ ਦਾ ਜੀਵਨ ਬਤੀਤ ਕਰਦੇ ਸਨ । ਉਹ ਵੱਡੇ-ਵੱਡੇ ਮਹੱਲਾਂ ਵਿੱਚ ਰਹਿੰਦੇ ਸਨ । ਉਹ ਆਪਣਾ ਜ਼ਿਆਦਾਤਰ ਸਮਾਂ ਜਸ਼ਨ ਮਨਾਉਣ ਵਿੱਚ ਬਤੀਤ ਕਰਦੇ ਸਨ । ਉਲਮਾ ਅਤੇ ਕਾਜ਼ੀ ਮੁਸਲਮਾਨਾਂ ਦੇ ਧਾਰਮਿਕ ਨੇਤਾ ਸਨ ।ਉਨ੍ਹਾਂ ਦਾ ਮੁੱਖ ਕੰਮ ਇਸਲਾਮੀ ਕਾਨੂੰਨਾਂ ਦੀ ਵਿਆਖਿਆ ਕਰਨਾ ਅਤੇ ਲੋਕਾਂ ਨੂੰ ਨਿਆਂ ਦੇਣਾ ਸੀ ।
- ਮੱਧ ਸ਼੍ਰੇਣੀ – ਮੱਧ ਸ਼੍ਰੇਣੀ ਵਿੱਚ ਵਪਾਰੀ, ਸੈਨਿਕ, ਕਿਸਾਨ ਅਤੇ ਰਾਜ ਦੇ ਛੋਟੇ ਕਰਮਚਾਰੀ ਸ਼ਾਮਲ ਸਨ । ਉਨ੍ਹਾਂ ਦੇ ਜੀਵਨ ਅਤੇ ਉੱਚ ਸ਼੍ਰੇਣੀ ਦੇ ਲੋਕਾਂ ਦੇ ਜੀਵਨ ਵਿੱਚ ਕਾਫ਼ੀ ਅੰਤਰ ਸੀ । ਪਰ ਉਨ੍ਹਾਂ ਦਾ ਜੀਵਨ ਪੱਧਰ ਹਿੰਦੁਆਂ ਦੀ ਉੱਚ ਸ਼੍ਰੇਣੀ ਦੇ ਮੁਕਾਬਲੇ ਕਾਫ਼ੀ ਚੰਗਾ ਸੀ ।
- ਨੀਵੀਂ ਸ਼੍ਰੇਣੀ – ਇਸ ਸ਼੍ਰੇਣੀ ਵਿੱਚ ਜ਼ਿਆਦਾਤਰ ਦਾਸ, ਕਾਮੇ ਅਤੇ ਮਜ਼ਦੂਰ ਸ਼ਾਮਲ ਸਨ । ਇਨ੍ਹਾਂ ਦਾ ਜੀਵਨ ਚੰਗਾ ਨਹੀਂ ਸੀ । ਉਨ੍ਹਾਂ ਨੂੰ ਆਪਣੇ ਜੀਵਨ ਨਿਰਬਾਹ ਲਈ ਸਖ਼ਤ ਮਿਹਨਤ ਕਰਨੀ ਪੈਂਦੀ ਸੀ । ਉਨ੍ਹਾਂ ਨੂੰ ਆਪਣੇ ਸੁਆਮੀ ਦੇ ਅੱਤਿਆਚਾਰਾਂ ਨੂੰ ਸਹਿਣ ਕਰਨਾ ਪੈਂਦਾ ਸੀ ।
![]()
ਪ੍ਰਸ਼ਨ 11.
16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਸਮਾਜ ਵਿੱਚ ਮੁਸਲਮਾਨਾਂ ਦੀ ਸਮਾਜਿਕ ਹਾਲਤ ਕਿਹੋ ਜਿਹੀ ਸੀ ? What was the condition of Muslims in the society of punjab in the beginning of the 16th century ?)
ਉੱਤਰ-
16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਮੁਸਲਿਮ ਸਮਾਜ ਦੀਆਂ ਮੁੱਖ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਹੇਠ ਲਿਖੀਆਂ ਹਨ-
1. ਸਮਾਜ ਤਿੰਨ ਸ਼੍ਰੇਣੀਆਂ ਵਿੱਚ ਵੰਡਿਆ ਹੋਇਆ ਸੀ – 16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦਾ ਮੁਸਲਿਮ ਸਮਾਜ ਉੱਚ ਸ਼੍ਰੇਣੀ, ਮੱਧ ਸ਼੍ਰੇਣੀ ਅਤੇ ਨੀਵੀਂ ਸ਼੍ਰੇਣੀ ਵਿੱਚ ਵੰਡਿਆ ਹੋਇਆ ਸੀ ।
(ਉ) ਉੱਚ ਸ਼੍ਰੇਣੀ – ਇਸ ਸ਼੍ਰੇਣੀ ਵਿੱਚ ਅਮੀਰ, ਖ਼ਾਨ, ਸ਼ੇਖ਼, ਮਲਿਕ, ਇਕਤਾਦਾਰ, ਉਲਮਾ ਅਤੇ ਕਾਜ਼ੀ ਆਦਿ ਸ਼ਾਮਲ ਸਨ । ਇਸ ਸ਼੍ਰੇਣੀ ਦੇ ਲੋਕ ਬੜਾ ਐਸ਼ੋ-ਆਰਾਮ ਦਾ ਜੀਵਨ ਬਤੀਤ ਕਰਦੇ ਸਨ । ਉਹ ਬੜੇ ਸ਼ਾਨਦਾਰ ਮਹੱਲਾਂ ਵਿੱਚ ਰਹਿੰਦੇ ਸਨ । ਉਨ੍ਹਾਂ ਦੀ ਸੇਵਾ ਲਈ ਵੱਡੀ ਗਿਣਤੀ ਵਿੱਚ ਨੌਕਰ ਹੁੰਦੇ ਸਨ ।
(ਅ) ਮੱਧ ਸ਼੍ਰੇਣੀ-ਇਸ ਸ਼੍ਰੇਣੀ ਵਿੱਚ ਸੈਨਿਕ, ਵਪਾਰੀ, ਕਿਸਾਨ ਅਤੇ ਰਾਜ ਦੇ ਛੋਟੇ ਕਰਮਚਾਰੀ ਸ਼ਾਮਲ ਸਨ । ਉਨ੍ਹਾਂ ਦੇ ਜੀਵਨ ਅਤੇ ਉੱਚ ਸ਼੍ਰੇਣੀ ਦੇ ਲੋਕਾਂ ਦੇ ਜੀਵਨ ਪੱਧਰ ਵਿੱਚ ਬੜਾ ਅੰਤਰ ਸੀ । ਉਹ ਹਿੰਦੂਆਂ ਦੇ ਮੁਕਾਬਲੇ ਬਹੁਤ ਚੰਗਾ ਜੀਵਨ ਬਤੀਤ ਕਰਦੇ ਸਨ ।
(ੲ) ਨੀਵੀਂ ਸ਼੍ਰੇਣੀ-ਇਸ ਸ਼੍ਰੇਣੀ ਵਿੱਚ ਦਾਸ-ਦਾਸੀਆਂ, ਨੌਕਰ ਅਤੇ ਕਾਮੇ ਸ਼ਾਮਲ ਸਨ । ਇਨ੍ਹਾਂ ਦੀ ਗਿਣਤੀ ਬਹੁਤ ਜ਼ਿਆਦਾ ਸੀ । ਉਨ੍ਹਾਂ ਦਾ ਜੀਵਨ ਚੰਗਾ ਨਹੀਂ ਸੀ । ਉਨ੍ਹਾਂ ਦੇ ਸੁਆਮੀ ਉਨ੍ਹਾਂ ‘ਤੇ ਬੜੇ ਅੱਤਿਆਚਾਰ ਕਰਦੇ ਸਨ ।
2. ਇਸਤਰੀਆਂ ਦੀ ਸਥਿਤੀ – ਮੁਸਲਿਮ ਸਮਾਜ ਵਿੱਚ ਇਸਤਰੀਆਂ ਦੀ ਸਥਿਤੀ ਚੰਗੀ ਨਹੀਂ ਸੀ । ਉਹ ਬਹੁਤ ਘੱਟ ਪੜੀਆਂ-ਲਿਖੀਆਂ ਹੁੰਦੀਆਂ ਸਨ । ਬਹੁ-ਵਿਆਹ ਅਤੇ ਤਲਾਕ-ਪ੍ਰਥਾ ਨੇ ਉਨ੍ਹਾਂ ਦੀ ਹਾਲਤ ਹੋਰ ਤਰਸਯੋਗ ਬਣਾ ਦਿੱਤੀ ਸੀ ।
3. ਖਾਣ-ਪੀਣ – ਉੱਚ ਸ਼੍ਰੇਣੀ ਦੇ ਮੁਸਲਮਾਨ ਕਈ ਤਰ੍ਹਾਂ ਦੇ ਸੁਆਦਲੇ ਖਾਣੇ ਖਾਂਦੇ ਸਨ । ਉਹ ਆਪਣੇ ਜਸ਼ਨਾਂ ਵਿੱਚ ਮੀਟ, ਹਲਵਾ, ਪੂੜੀ ਅਤੇ ਮੱਖਣ ਆਦਿ ਦੀ ਬਹੁਤ ਵਰਤੋਂ ਕਰਦੇ ਸਨ । ਨੀਵੀਂ ਸ਼੍ਰੇਣੀ ਨਾਲ ਸੰਬੰਧਿਤ ਲੋਕਾਂ ਦਾ ਖਾਣਾ ਸਾਧਾਰਨ ਹੁੰਦਾ ਸੀ ।
4. ਪਹਿਰਾਵਾ – ਉੱਚ ਸ਼੍ਰੇਣੀ ਦੇ ਮੁਸਲਮਾਨਾਂ ਦੀਆਂ ਪੁਸ਼ਾਕਾਂ ਬਹੁਤ ਕੀਮਤੀ ਹੁੰਦੀਆਂ ਸਨ । ਇਹ ਪੁਸ਼ਾਕਾਂ ਰੇਸ਼ਮ ਅਤੇ ਮਖਮਲ ਦੀਆਂ ਬਣੀਆਂ ਹੁੰਦੀਆਂ ਸਨ । ਨੀਵੀਂ ਸ਼੍ਰੇਣੀ ਦੇ ਲੋਕ ਸੂਤੀ ਕੱਪੜੇ ਪਹਿਨਦੇ ਸਨ । ਪੁਰਸ਼ਾਂ ਵਿੱਚ ਕੁੜਤਾ ਅਤੇ ਪਜਾਮਾ ਪਾਉਣ ਦਾ ਰਿਵਾਜ ਸੀ, ਜਦ ਕਿ ਇਸਤਰੀਆਂ ਲੰਬਾ ਬੁਰਕਾ ਪਾਉਂਦੀਆਂ ਸਨ ।
5. ਸਿੱਖਿਆ – 16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਮੁਸਲਮਾਨਾਂ ਨੂੰ ਸਿੱਖਿਆ ਦੇਣ ਦਾ ਕੰਮ ਉਲਮਾ, ਮੁੱਲਾਂ ਤੇ ਮੌਲਵੀ ਕਰਦੇ ਸਨ । ਉਹ ਮਸਜਿਦਾਂ, ਮਕਤਬਿਆਂ ਅਤੇ ਮਦਰੱਸਿਆਂ ਵਿੱਚ ਸਿੱਖਿਆ ਦਿੰਦੇ ਸਨ । ਮਸਜਿਦਾਂ ਅਤੇ ਮਕਤਬਿਆਂ ਵਿੱਚ ਮੁੱਢਲੀ ਸਿੱਖਿਆ ਦਿੱਤੀ ਜਾਂਦੀ ਸੀ ਜਦਕਿ ਮਦਰੱਸਿਆਂ ਵਿੱਚ ਉਚੇਰੀ । ਉਸ ਸਮੇਂ ਮੁਸਲਮਾਨਾਂ ਦੇ ਪੰਜਾਬ ਵਿੱਚ ਸਭ ਤੋਂ ਪ੍ਰਸਿੱਧ ਸਿੱਖਿਆ ਕੇਂਦਰ ਲਾਹੌਰ ਅਤੇ ਮੁਲਤਾਨ ਵਿੱਚ ਸਨ ।
6. ਮਨੋਰੰਜਨ ਦੇ ਸਾਧਨ – 16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਮੁਸਲਮਾਨ ਆਪਣਾ ਮਨੋਰੰਜਨ ਕਈ ਢੰਗਾਂ ਨਾਲ ਕਰਦੇ ਸਨ । ਉਨ੍ਹਾਂ ਦੇ ਮਨੋਰੰਜਨ ਦੇ ਮੁੱਖ ਸਾਧਨ ਸ਼ਿਕਾਰ, ਜਾਨਵਰਾਂ ਦੀਆਂ ਲੜਾਈਆਂ ਵੇਖਣਾ, ਜਸ਼ਨਾਂ ਵਿੱਚ ਹਿੱਸਾ ਲੈਣਾ ਅਤੇ ਸ਼ਤਰੰਜ ਆਦਿ ਸਨ । ਉਹ ਆਪਣੇ ਤਿਉਹਾਰਾਂ ਨੂੰ ਵੀ ਬੜੇ ਜੋਸ਼ ਨਾਲ ਮਨਾਉਂਦੇ ਸਨ ।
ਪ੍ਰਸ਼ਨ 12.
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਵਿੱਚ ਹਿੰਦੂਆਂ ਦੀ ਸਮਾਜਿਕ ਸਥਿਤੀ ਕਿਹੋ ਜਿਹੀ ਸੀ ? (What was the social condition of the Hindus of Punjab in the beginning of the 16th century ?)
ਉੱਤਰ-
16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਹਿੰਦੂ ਸਮਾਜ ਦੀਆਂ ਮੁੱਖ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਹੇਠ ਲਿਖੀਆਂ ਸਨ-
- ਜਾਤੀ ਪ੍ਰਥਾ – ਹਿੰਦੂ ਸਮਾਜ ਕਈ ਜਾਤਾਂ ਅਤੇ ਉਪ-ਜਾਤਾਂ ਵਿੱਚ ਵੰਡਿਆ ਹੋਇਆ ਸੀ । ਸਮਾਜ ਵਿੱਚ ਸਭ ਤੋਂ ਉੱਚਾ ਸਥਾਨ ਬਾਹਮਣਾਂ ਨੂੰ ਪ੍ਰਾਪਤ ਸੀ । ਮੁਸਲਿਮ ਸ਼ਾਸਨ ਦੀ ਸਥਾਪਨਾ ਦੇ ਕਾਰਨ ਕਸ਼ੱਤਰੀਆਂ ਨੇ ਨਵੇਂ ਕਿੱਤੇ ਜਿਵੇਂ ਦੁਕਾਨਦਾਰੀ, ਖੇਤੀ-ਬਾੜੀ ਆਦਿ ਅਪਣਾ ਲਏ ਸਨ । ਵੈਸ਼ ਵਪਾਰ ਅਤੇ ਖੇਤੀਬਾੜੀ ਦਾ ਹੀ ਧੰਦਾ ਕਰਦੇ ਰਹੇ । ਸ਼ੂਦਰਾਂ ਨਾਲ ਇਸ ਕਾਲ ਵਿੱਚ ਵੀ ਮਾੜਾ ਸਲੂਕ ਕੀਤਾ ਜਾਂਦਾ ਰਿਹਾ ।
- ਇਸਤਰੀਆਂ ਦੀ ਸਥਿਤੀ – ਹਿੰਦੂ ਸਮਾਜ ਵਿੱਚ ਇਸਤਰੀਆਂ ਦੀ ਦਸ਼ਾ ਚੰਗੀ ਨਹੀਂ ਸੀ । ਸਮਾਜ ਵਿੱਚ ਉਨ੍ਹਾਂ ਦਾ ਦਰਜਾ ਪੁਰਸ਼ਾਂ ਦੇ ਬਰਾਬਰ ਨਹੀਂ ਸੀ । ਉਸ ਸਮੇਂ ਲੜਕੀਆਂ ਦੀ ਸਿੱਖਿਆ ਵੱਲ ਕੋਈ ਧਿਆਨ ਨਹੀਂ ਦਿੱਤਾ ਜਾਂਦਾ ਸੀ । ਉਨ੍ਹਾਂ ਦਾ ਵਿਆਹ ਛੋਟੀ ਉਮਰ ਵਿੱਚ ਹੀ ਕਰ ਦਿੱਤਾ ਜਾਂਦਾ ਸੀ । ਇਸ ਕਾਲ ਵਿੱਚ ਸਤੀ ਪ੍ਰਥਾ ਬੜੀ ਜ਼ੋਰਾਂ ‘ਤੇ ਸੀ । ਵਿਧਵਾ ਨੂੰ ਦੁਬਾਰਾ ਵਿਆਹ ਕਰਨ ਦੀ ਇਜਾਜ਼ਤ ਨਹੀਂ ਸੀ ।
- ਖਾਣ-ਪੀਣ – ਹਿੰਦੂਆਂ ਦਾ ਭੋਜਨ ਸਾਦਾ ਹੁੰਦਾ ਸੀ । ਜ਼ਿਆਦਾਤਰ ਹਿੰਦੂ ਸ਼ਾਕਾਹਾਰੀ ਹੁੰਦੇ ਸਨ । ਉਨ੍ਹਾਂ ਦਾ ਭੋਜਨ ਕਣਕ, ਚੌਲ, ਸਬਜ਼ੀਆਂ, ਘਿਉ ਅਤੇ ਦੁੱਧ ਆਦਿ ਤੋਂ ਤਿਆਰ ਕੀਤਾ ਜਾਂਦਾ ਸੀ । ਉਹ ਮਾਸ, ਲਸਣ ਅਤੇ ਪਿਆਜ਼ ਦੀ ਵਰਤੋਂ ਨਹੀਂ ਕਰਦੇ ਸਨ । ਗ਼ਰੀਬ ਲੋਕ ਸਾਧਾਰਨ ਰੋਟੀ ਨਾਲ ਲੱਸੀ ਪੀ ਕੇ ਆਪਣਾ ਗੁਜ਼ਾਰਾ ਕਰਦੇ ਸਨ ।
- ਪਹਿਰਾਵਾ – ਹਿੰਦੂਆਂ ਦਾ ਪਹਿਰਾਵਾ ਬੜਾ ਸਾਦਾ ਹੁੰਦਾ ਸੀ । ਉਹ ਆਮ ਤੌਰ ‘ਤੇ ਸੂਤੀ ਕੱਪੜੇ ਪਾਉਂਦੇ ਸਨ । ਪੁਰਸ਼ ਧੋਤੀ ਅਤੇ ਕੁੜਤਾ ਪਾਉਂਦੇ ਸਨ । ਉਹ ਸਿਰ ‘ਤੇ ਪਗੜੀ ਵੀ ਬੰਦੇ ਸਨ । ਇਸਤਰੀਆਂ ਸਾੜ੍ਹੀ, ਚੋਲੀ ਅਤੇ ਲਹਿੰਗਾ ਪਾਉਂਦੀਆਂ ਸਨ । ਗਰੀਬ ਲੋਕ ਚਾਦਰ ਨਾਲ ਹੀ ਆਪਣਾ ਸਰੀਰ ਢੱਕ ਲੈਂਦੇ ਸਨ ।
- ਮਨੋਰੰਜਨ ਦੇ ਸਾਧਨ – ਹਿੰਦੂ ਨਾਚ, ਗਾਣੇ ਅਤੇ ਸੰਗੀਤ ਦੇ ਬਹੁਤ ਸ਼ੌਕੀਨ ਸਨ । ਉਹ ਤਾਸ਼ ਅਤੇ ਸ਼ਤਰੰਜ ਵੀ ਖੇਡਦੇ ਸਨ । ਪਿੰਡਾਂ ਦੇ ਲੋਕ ਜਾਨਵਰਾਂ ਦੀਆਂ ਲੜਾਈਆਂ ਵੇਖ ਕੇ ਅਤੇ ਘੋਲ ਵੇਖ ਕੇ ਆਪਣਾ ਮਨੋਰੰਜਨ ਕਰਦੇ ਸਨ । ਇਨ੍ਹਾਂ ਤੋਂ ਇਲਾਵਾ ਹਿੰਦੂ ਆਪਣੇ ਤਿਉਹਾਰਾਂ ਦੁਸਹਿਰਾ, ਦੀਵਾਲੀ, ਹੋਲੀ ਆਦਿ ਵਿੱਚ ਵੀ ਹਿੱਸਾ ਲੈਂਦੇ ਸਨ ।
- ਸਿੱਖਿਆ – 16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਹਿੰਦੂ ਆਪਣੀ ਮੁੱਢਲੀ ਸਿੱਖਿਆ ਬ੍ਰਾਹਮਣਾਂ ਤੋਂ ਮੰਦਰਾਂ ਅਤੇ ਪਾਠਸ਼ਲਾਵਾਂ ਵਿੱਚ ਪ੍ਰਾਪਤ ਕਰਦੇ ਸਨ । ਪੰਜਾਬ ਵਿੱਚ ਉਚੇਰੀ ਸਿੱਖਿਆ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ ਹਿੰਦੁਆਂ ਦਾ ਆਪਣਾ ਕੋਈ ਕੇਂਦਰ ਨਹੀਂ ਸੀ । ਉੱਚ ਵਰਗ ਦੇ ਹਿੰਦੂ ਮਦਰੱਸਿਆਂ ਵਿੱਚ ਆਪਣੀ ਉਚੇਰੀ ਸਿੱਖਿਆ ਪ੍ਰਾਪਤ ਕਰਦੇ ਸਨ ।
ਪ੍ਰਸ਼ਨ 13.
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਵਿੱਚ ਪ੍ਰਚਲਿਤ ਸਿੱਖਿਆ ਪ੍ਰਣਾਲੀ ਦੇ ਬਾਰੇ ਸੰਖੇਪ ਜਾਣਕਾਰੀ ਦਿਓ । (Give a brief account of the prevalent education in the Punjab in the beginning of the 16th century.)
ਉੱਤਰ-
16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਸਿੱਖਿਆ ਦੇ ਖੇਤਰ ਵਿੱਚ ਕੋਈ ਖ਼ਾਸ ਉੱਨਤੀ ਨਹੀਂ ਹੋਈ ਸੀ । ਮੁਸਲਮਾਨਾਂ ਨੂੰ ਸਿੱਖਿਆ ਦੇਣ ਦਾ ਕੰਮ ਉਲਮਾ, ਮੁੱਲਾਂ ਤੇ ਮੌਲਵੀ ਕਰਦੇ ਸਨ । ਉਹ ਮਸਜਿਦਾਂ, ਮਕਤਬਿਆਂ ਅਤੇ ਮਦਰੱਸਿਆਂ ਵਿੱਚ ਸਿੱਖਿਆ ਦਿੰਦੇ ਸਨ । ਰਾਜ ਸਰਕਾਰ ਉਨ੍ਹਾਂ ਨੂੰ ਅਨੁਦਾਨ ਦਿੰਦੀ ਸੀ । ਮਸਜਿਦਾਂ ਅਤੇ ਮਕਤਬਿਆਂ ਵਿੱਚ ਮੁੱਢਲੀ ਸਿੱਖਿਆ ਦਿੱਤੀ ਜਾਂਦੀ ਸੀ ਜਦਕਿ ਮਦਰੱਸਿਆਂ ਵਿੱਚ ਉਚੇਰੀ । ਮਦਰੱਸੇ ਆਮ ਤੌਰ ‘ਤੇ ਸ਼ਹਿਰਾਂ ਵਿੱਚ ਹੀ ਹੁੰਦੇ ਸਨ । ਉਸ ਸਮੇਂ ਮੁਸਲਮਾਨਾਂ ਦੇ ਪੰਜਾਬ ਵਿੱਚ ਸਭ ਤੋਂ ਪ੍ਰਸਿੱਧ ਸਿੱਖਿਆ ਕੇਂਦਰ ਲਾਹੌਰ ਅਤੇ ਮੁਲਤਾਨ ਵਿੱਚ ਸਨ । ਇਨ੍ਹਾਂ ਤੋਂ ਇਲਾਵਾ ਜਲੰਧਰ, ਸੁਲਤਾਨਪੁਰ, ਸਮਾਣਾ, ਨਾਰਨੌਲ, ਬਠਿੰਡਾ, ਸਰਹਿੰਦ, ਸਿਆਲਕੋਟ ਅਤੇ ਕਾਂਗੜਾ ਵੀ ਸਿੱਖਿਆ ਦੇ ਪ੍ਰਸਿੱਧ ਕੇਂਦਰ ਸਨ । ਹਿੰਦੂ ਲੋਕ ਬ੍ਰਾਹਮਣਾਂ ਤੋਂ ਮੰਦਰਾਂ ਅਤੇ ਪਾਠਸ਼ਾਲਾਵਾਂ ਵਿੱਚ ਸਿੱਖਿਆ ਪ੍ਰਾਪਤ ਕਰਦੇ ਸਨ । ਇਨ੍ਹਾਂ ਵਿੱਚ ਮੁੱਢਲੀ ਸਿੱਖਿਆ ਸੰਬੰਧੀ ਜਾਣਕਾਰੀ ਦਿੱਤੀ ਜਾਂਦੀ ਸੀ । ਪੰਜਾਬ ਵਿੱਚ ਉਚੇਰੀ ਸਿੱਖਿਆ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ ਹਿੰਦੂਆਂ ਦਾ ਕੋਈ ਕੇਂਦਰ ਨਹੀਂ ਸੀ | ਅਮੀਰ ਵਰਗ ਦੇ ਹਿੰਦੂ ਆਪਣੇ ਬੱਚਿਆਂ ਨੂੰ ਉਚੇਰੀ ਸਿੱਖਿਆ ਲਈ ਮੁਸਲਮਾਨਾਂ ਦੇ ਮਦਰੱਸਿਆਂ ਵਿੱਚ ਭੇਜ ਦਿੰਦੇ ਸਨ । ਉਨ੍ਹਾਂ ਦੀ ਗਿਣਤੀ ਨਾਂਹ ਦੇ ਬਰਾਬਰ ਸੀ ਕਿਉਂਕਿ ਮੁਸਲਮਾਨ ਹਿੰਦੂਆਂ ਨੂੰ ਨਫ਼ਰਤ ਦੀ ਨਜ਼ਰ ਨਾਲ ਵੇਖਦੇ ਸਨ ।
ਪ੍ਰਸ਼ਨ 14.
16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਲੋਕਾਂ ਦੇ ਮਨੋਰੰਜਨ ਦੇ ਸਾਧਨ ਕੀ ਸਨ ? (What were the means of entertainment of the people of Punjab in the beginning of the 16th century ?)
ਉੱਤਰ-
16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਮੁਸਲਮਾਨ ਆਪਣਾ ਮਨੋਰੰਜਨ ਕਈ ਢੰਗਾਂ ਨਾਲ ਕਰਦੇ ਸਨ । ਉਹ ਸ਼ਿਕਾਰ ਕਰਨ, ਚੌਗਾਨ ਖੇਡਣ, ਜਾਨਵਰਾਂ ਦੀਆਂ ਲੜਾਈਆਂ ਵੇਖਣ ਅਤੇ ਘੋੜ-ਦੌੜ ਵਿੱਚ ਹਿੱਸਾ ਲੈਣ ਦੇ ਬਹੁਤ ਸ਼ੌਕੀਨ ਸਨ । ਉਹ ਜਸ਼ਨਾਂ ਅਤੇ ਮਹਿਫਲਾਂ ਵਿੱਚ ਵੱਧ ਚੜ੍ਹ ਕੇ ਹਿੱਸਾ ਲੈਂਦੇ ਸਨ । ਇਨ੍ਹਾਂ ਵਿੱਚ ਸੰਗੀਤਕਾਰ ਅਤੇ ਨਰਤਕੀਆਂ ਉਨ੍ਹਾਂ ਦਾ ਮਨੋਰੰਜਨ ਕਰਦੀਆਂ ਸਨ ਉਹ ਸ਼ਤਰੰਜ ਅਤੇ ਚੌਪੜ ਖੇਡ ਕੇ ਵੀ ਆਪਣਾ ਮਨੋਰੰਜਨ ਕਰਦੇ ਸਨ । ਮੁਸਲਮਾਨ ਈਦ, ਨੌਰੋਜ ਅਤੇ ਸ਼ਬ-ਏ-ਬਰਾਤ ਆਦਿ ਦੇ ਤਿਉਹਾਰਾਂ ਨੂੰ ਬੜੀ ਧੂਮਧਾਮ ਨਾਲ ਮਨਾਉਂਦੇ ਸਨ । 16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਹਿੰਦੂ ਨਾਚ, ਗਾਣੇ ਅਤੇ ਸੰਗੀਤ ਦੇ ਬਹੁਤ ਸ਼ੌਕੀਨ ਸਨ ।ਉਹ ਤਾਸ਼ ਅਤੇ ਸ਼ਤਰੰਜ ਵੀ ਖੇਡਦੇ ਸਨ । ਪਿੰਡਾਂ ਦੇ ਲੋਕ ਜਾਨਵਰਾਂ ਦੀਆਂ ਲੜਾਈਆਂ ਵੇਖ ਕੇ ਅਤੇ ਘੋਲ ਵੇਖ ਕੇ ਆਪਣਾ ਮਨੋਰੰਜਨ ਕਰਦੇ ਸਨ । ਇਨ੍ਹਾਂ ਤੋਂ ਇਲਾਵਾ ਹਿੰਦੂ ਆਪਣੇ ਤਿਉਹਾਰਾਂ ਵਿੱਚ ਵੀ ਹਿੱਸਾ ਲੈਂਦੇ ਸਨ ।
![]()
ਪ੍ਰਸ਼ਨ 15.
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦੀ ਮਾਲੀ ਹਾਲਤ ਦਾ ਸੰਖੇਪ ਵੇਰਵਾ ਦਿਓ । (Give a brief account of the economic condition of the Punjab in the beginning of the 16th century.)
ਜਾਂ
16ਵੀਂ ਸਦੀ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਲੋਕਾਂ ਦੀ ਆਰਥਿਕ ਸਥਿਤੀ ਦਾ ਵਰਣਨ ਕਰੋ । (Explain the economic condition of Punjab during the 16th century.)
ਜਾਂ
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦੀ ਆਰਥਿਕ ਦਸ਼ਾ ਦਾ ਵਰਣਨ ਕਰੋ ।
(Briefly mention the economic condition of the Punjab in the beginning of the 16th century.)
ਉੱਤਰ-
16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਲੋਕਾਂ ਦੀ ਆਰਥਿਕ ਦਸ਼ਾ ਬਹੁਤ ਚੰਗੀ ਸੀ । ਇਸ ਕਾਲ ਦੇ ਪੰਜਾਬ ਦੇ ਲੋਕਾਂ ਦੇ ਆਰਥਿਕ ਜੀਵਨ ਦਾ ਸੰਖੇਪ ਵੇਰਵਾ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਹੈ-
- ਖੇਤੀਬਾੜੀ – 16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਲੋਕਾਂ ਦਾ ਮੁੱਖ ਕਿੱਤਾ ਖੇਤੀਬਾੜੀ ਸੀ । ਪੰਜਾਬ ਦੀ ਜ਼ਮੀਨ ਬਹੁਤ ਉਪਜਾਉ ਸੀ । ਸਿੰਜਾਈ ਲਈ ਕਿਸਾਨ ਭਾਵੇਂ ਮੁੱਖ ਤੌਰ ‘ਤੇ ਵਰਖਾ ‘ਤੇ ਨਿਰਭਰ ਕਰਦੇ ਸਨ । ਇੱਥੋਂ ਦੀਆਂ ਮੁੱਖ ਫ਼ਸਲਾਂ ਕਣਕ, ਕਪਾਹ, ਜੌ, ਮੱਕੀ, ਚੌਲ ਅਤੇ ਗੰਨਾ ਸਨ । ਫ਼ਸਲਾਂ ਦੀ ਭਰਪੂਰ ਪੈਦਾਵਾਰ ਹੋਣ ਕਾਰਨ ਪੰਜਾਬ ਨੂੰ ਭਾਰਤ ਦਾ ਅੰਨ ਭੰਡਾਰ ਕਿਹਾ ਜਾਂਦਾ ਸੀ ।
- ਉਦਯੋਗ – ਖੇਤੀਬਾੜੀ ਤੋਂ ਬਾਅਦ ਪੰਜਾਬ ਦੇ ਲੋਕਾਂ ਦਾ ਦੂਜਾ ਮੁੱਖ ਧੰਦਾ ਉਦਯੋਗ ਸੀ । ਇਹ ਉਦਯੋਗ ਸਰਕਾਰੀ ਵੀ ਸਨ ਅਤੇ ਗੈਰ-ਸਰਕਾਰੀ ਵੀ । ਪੰਜਾਬ ਦੇ ਉਦਯੋਗਾਂ ਵਿੱਚ ਕੱਪੜਾ ਉਦਯੋਗ ਸਭ ਤੋਂ ਵੱਧ ਪ੍ਰਸਿੱਧ ਸੀ । ਇੱਥੇ ਸੁਤੀ, ਊਨੀ ਅਤੇ ਰੇਸ਼ਮੀ ਤਿੰਨਾਂ ਤਰ੍ਹਾਂ ਦੇ ਕੱਪੜੇ ਬਣਾਏ ਜਾਂਦੇ ਸਨ । ਕੱਪੜਾ ਉਦਯੋਗ ਤੋਂ ਇਲਾਵਾ ਉਸ ਸਮੇਂ ਪੰਜਾਬ ਵਿੱਚ ਚਮੜਾ, ਸ਼ਸਤਰ, ਭਾਂਡੇ, ਹਾਥੀ ਦੰਦ ਅਤੇ ਖਿਡੌਣੇ ਆਦਿ ਬਣਾਉਣ ਦੇ ਉਦਯੋਗ ਵੀ ਪ੍ਰਚਲਿਤ ਸਨ ।
- ਪਸ਼ੂ ਪਾਲਣ – ਪੰਜਾਬ ਦੇ ਕੁਝ ਲੋਕ ਪਸ਼ੂ ਪਾਲਣ ਦਾ ਕਿੱਤਾ ਕਰਦੇ ਸਨ । ਪੰਜਾਬ ਵਿੱਚ ਪਾਲੇ ਜਾਣ ਵਾਲੇ ਮੁੱਖ ਪਸ਼ੂ ਗਊਆਂ, ਬਲਦ, ਮੱਝਾਂ, ਘੋੜੇ, ਖੱਚਰ, ਊਠ, ਭੇਡਾਂ ਅਤੇ ਬੱਕਰੀਆਂ ਆਦਿ ਸਨ । ਇਨ੍ਹਾਂ ਪਸ਼ੂਆਂ ਤੋਂ ਦੁੱਧ, ਉੱਨ ਅਤੇ ਭਾਰ ਢੋਣ ਦਾ ਕੰਮ ਲਿਆ ਜਾਂਦਾ ਸੀ ।
- ਵਪਾਰ – ਪੰਜਾਬ ਦਾ ਵਪਾਰ ਕਾਫ਼ੀ ਵਿਕਸਿਤ ਸੀ । ਵਪਾਰ ਦਾ ਕੰਮ ਕੁਝ ਖ਼ਾਸ ਸ਼੍ਰੇਣੀਆਂ ਦੇ ਹੱਥ ਵਿੱਚ ਹੁੰਦਾ ਸੀ । ਪੰਜਾਬ ਦਾ ਵਿਦੇਸ਼ੀ ਵਪਾਰ ਮੁੱਖ ਰੂਪ ਨਾਲ ਅਫ਼ਗਾਨਿਸਤਾਨ, ਈਰਾਨ, ਅਰਬ, ਸੀਰੀਆ, ਤਿੱਬਤ, ਭੂਟਾਨ ਅਤੇ ਚੀਨ ਆਦਿ ਦੇਸ਼ਾਂ ਨਾਲ ਹੁੰਦਾ ਸੀ । ਪੰਜਾਬ ਤੋਂ ਇਨ੍ਹਾਂ ਦੇਸ਼ਾਂ ਨੂੰ ਅਨਾਜ, ਕੱਪੜੇ, ਕਪਾਹ, ਰੇਸ਼ਮ ਅਤੇ ਖੰਡ ਨਿਰਯਾਤ ਕੀਤੀ ਜਾਂਦੀ ਸੀ । ਇਨ੍ਹਾਂ ਦੇਸ਼ਾਂ ਤੋਂ ਪੰਜਾਬ ਘੋੜੇ, ਸ਼ਸਤਰ, ਫਰ, ਕਸਤੂਰੀ ਅਤੇ ਮੇਵੇ ਆਦਿ ਆਯਾਤ ਕਰਦਾ ਸੀ ।
- ਵਪਾਰਿਕ ਨਗਰ-16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਲਾਹੌਰ ਅਤੇ ਮੁਲਤਾਨ ਪੰਜਾਬ ਦੇ ਦੋ ਸਭ ਤੋਂ ਪ੍ਰਸਿੱਧ ਵਪਾਰਿਕ ਨਗਰ ਸਨ । ਇਨ੍ਹਾਂ ਦੇ ਇਲਾਵਾ ਪਿਸ਼ਾਵਰ, ਜਲੰਧਰ, ਅੰਮ੍ਰਿਤਸਰ ਅਤੇ ਲੁਧਿਆਣਾ ਪੰਜਾਬ ਦੇ ਹੋਰ ਪ੍ਰਸਿੱਧ ਵਪਾਰਿਕ ਨਗਰ ਸਨ ।
- ਜੀਵਨ ਪੱਧਰ-ਉਸ ਸਮੇਂ ਪੰਜਾਬ ਦੇ ਲੋਕਾਂ ਦੇ ਜੀਵਨ ਪੱਧਰ ਵਿੱਚ ਬਹੁਤ ਅੰਤਰ ਸੀ । ਮੁਸਲਮਾਨਾਂ ਦੀਆਂ ਉੱਚ ਸ਼੍ਰੇਣੀਆਂ ਦੇ ਲੋਕਾਂ ਕੋਲ ਬਹੁਤ ਧਨ ਸੀ । ਹਿੰਦੂਆਂ ਦੀਆਂ ਉੱਚ ਸ਼੍ਰੇਣੀਆਂ ਦੇ ਕੋਲ ਧਨ ਤਾਂ ਬਹੁਤ ਸੀ ਪਰ ਮੁਸਲਮਾਨ ਉਨ੍ਹਾਂ ਤੋਂ ਇਹ ਧਨ ਲੁੱਟ ਕੇ ਲੈ ਜਾਂਦੇ ਸਨ । ਸਮਾਜ ਵਿੱਚ ਮੱਧ ਸ਼੍ਰੇਣੀ ਦੇ ਮੁਸਲਮਾਨਾਂ ਦਾ ਜੀਵਨ ਪੱਧਰ ਤਾਂ ਚੰਗਾ ਸੀ ਪਰ ਹਿੰਦੁ ਆਪਣਾ ਗੁਜ਼ਾਰਾ ਬੜੀ ਮੁਸ਼ਕਿਲ ਨਾਲ ਕਰਦੇ ਸਨ । ਸਮਾਜ ਵਿੱਚ ਗ਼ਰੀਬਾਂ ਅਤੇ ਕਿਸਾਨਾਂ ਦਾ ਜੀਵਨ ਪੱਧਰ ਬਹੁਤ ਨੀਵਾਂ ਸੀ ।
ਪ੍ਰਸ਼ਨ 16.
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦੀ ਖੇਤੀਬਾੜੀ ਸੰਬੰਧੀ ਸੰਖੇਪ ਜਾਣਕਾਰੀ ਦਿਓ । (Give a brief account of the agriculture of Punjab in the beginning of the 16th century.)
ਉੱਤਰ-
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਲੋਕਾਂ ਦਾ ਮੁੱਖ ਕਿੱਤਾ ਖੇਤੀਬਾੜੀ ਸੀ । ਪੰਜਾਬ ਦੀ ਜ਼ਮੀਨ ਬਹੁਤ ਉਪਜਾਊ ਸੀ । ਵਾਹੀ ਅਧੀਨ ਹੋਰ ਜ਼ਮੀਨ ਲਿਆਉਣ ਲਈ ਰਾਜ ਸਰਕਾਰ ਵੱਲੋਂ ਕਿਸਾਨਾਂ ਨੂੰ ਵਿਸ਼ੇਸ਼ ਸਹੂਲਤਾਂ ਦਿੱਤੀਆਂ ਜਾਂਦੀਆਂ ਸਨ । ਇੱਥੋਂ ਦੇ ਲੋਕ ਵੀ ਬੜੇ ਮਿਹਨਤੀ ਸਨ । ਸਿੰਜਾਈ ਲਈ ਨਹਿਰਾਂ, ਤਲਾਬਾਂ ਅਤੇ ਖੁਹਾਂ ਦੀ ਵਰਤੋਂ ਕੀਤੀ ਜਾਂਦੀ ਸੀ । ਇਨ੍ਹਾਂ ਕਾਰਨਾਂ ਕਰ ਕੇ ਭਾਵੇਂ ਪੰਜਾਬ ਦੇ ਕਿਸਾਨ ਪੁਰਾਣੇ ਢੰਗ ਨਾਲ ਹੀ ਖੇਤੀ ਕਰਦੇ ਸਨ ਤਾਂ ਵੀ ਇੱਥੇ ਫ਼ਸਲਾਂ ਦੀ ਭਰਪੂਰ ਪੈਦਾਵਾਰ ਹੁੰਦੀ ਸੀ । ਪੰਜਾਬ ਦੀਆਂ ਪ੍ਰਮੁੱਖ ਫ਼ਸਲਾਂ ਕਣਕ, ਜੌ, ਮੱਕੀ, ਚੌਲ ਅਤੇ ਗੰਨਾ ਸਨ । ਇਨ੍ਹਾਂ ਤੋਂ ਇਲਾਵਾ ਪੰਜਾਬ ਵਿੱਚ ਕਪਾਹ, ਬਾਜਰਾ, ਜੁਆਰ, ਸਰੋਂ ਅਤੇ ਕਈ ਕਿਸਮਾਂ ਦੀਆਂ ਦਾਲਾਂ ਵੀ ਪੈਦਾ ਕੀਤੀਆਂ ਜਾਂਦੀਆਂ ਸਨ । ਫ਼ਸਲਾਂ ਦੀ ਭਰਪੂਰ ਪੈਦਾਵਾਰ ਹੋਣ ਕਾਰਨ ਪੰਜਾਬ ਨੂੰ ਭਾਰਤ ਦਾ ਅੰਨ ਭੰਡਾਰ ਕਿਹਾ ਜਾਂਦਾ ਸੀ ।
ਪ੍ਰਸ਼ਨ 17.
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਉਦਯੋਗਾਂ ਬਾਰੇ ਤੁਸੀਂ ਕੀ ਜਾਣਦੇ ਹੋ ? (What do you know about the Punjab’s Industries in the beginning of the 16th century ?)
ਜਾਂ
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਪ੍ਰਮੁੱਖ ਉਦਯੋਗਾਂ ਦਾ ਵੇਰਵਾ ਦਿਓ ।
(Give an account of the main industries of Punjab in the beginning of the 16th century.)
ਉੱਤਰ-
ਖੇਤੀਬਾੜੀ ਤੋਂ ਬਾਅਦ ਪੰਜਾਬ ਦੇ ਲੋਕਾਂ ਦਾ ਦੂਜਾ ਮੁੱਖ ਧੰਦਾ ਉਦਯੋਗ ਸੀ । ਇਹ ਉਦਯੋਗ ਸਰਕਾਰੀ ਸਨ ਅਤੇ ਗੈਰ-ਸਰਕਾਰੀ ਵੀ । ਸਰਕਾਰੀ ਉਦਯੋਗ ਵੱਡੇ-ਵੱਡੇ ਸ਼ਹਿਰਾਂ ਵਿੱਚ ਸਥਾਪਿਤ ਸਨ ਜਦ ਕਿ ਗੈਰ-ਸਰਕਾਰੀ ਪਿੰਡਾਂ ਵਿੱਚ । ਪੰਜਾਬ ਦੇ ਉਦਯੋਗਾਂ ਵਿੱਚ ਕੱਪੜਾ ਉਦਯੋਗ ਸਭ ਤੋਂ ਵੱਧ ਪ੍ਰਸਿੱਧ ਸੀ। ਇੱਥੇ ਸੂਤੀ, ਊਨੀ ਅਤੇ ਰੇਸ਼ਮੀ ਤਿੰਨਾਂ ਤਰ੍ਹਾਂ ਦੇ ਕੱਪੜੇ ਬਣਾਏ ਜਾਂਦੇ ਸਨ ਕਿਉਂਕਿ ਪੰਜਾਬ ਦੀ ਉੱਚ ਸ਼੍ਰੇਣੀ ਦੇ ਲੋਕਾਂ ਵਿੱਚ ਰੇਸ਼ਮੀ ਕੱਪੜੇ ਦੀ ਬਹੁਤ ਮੰਗ ਸੀ ਇਸ ਲਈ ਪੰਜਾਬ ਵਿੱਚ ਇਹ ਕੱਪੜਾ ਵਧੇਰੇ ਮਾਤਰਾ ਵਿੱਚ ਤਿਆਰ ਕੀਤਾ ਜਾਂਦਾ ਸੀ । ਸਮਾਣਾ, ਸੁਨਾਮ, ਸਰਹਿੰਦ, ਦੀਪਾਲਪੁਰ, ਜਲੰਧਰ, ਲਾਹੌਰ ਅਤੇ ਮੁਲਤਾਨ ਇਸ ਉਦਯੋਗ ਦੇ ਪ੍ਰਸਿੱਧ ਕੇਂਦਰ ਸਨ । ਗੁਜਰਾਤ ਅਤੇ ਸਿਆਲਕੋਟ ਵਿੱਚ ਚਿਕਨ ਦੇ ਕੱਪੜੇ ਤਿਆਰ ਕੀਤੇ ਜਾਂਦੇ ਸਨ । ਮੁਲਤਾਨ ਅਤੇ ਸੁਲਤਾਨਪੁਰ ਸ਼ੀਟ ਦੇ ਕੱਪੜਿਆਂ ਲਈ ਪ੍ਰਸਿੱਧ ਸਨ । ਸਿਆਲਕੋਟ ਵਿੱਚ ਧੋਤੀਆਂ, ਸਾੜੀਆਂ, ਪੱਗਾਂ ਅਤੇ ਵਧੀਆ ਕਢਾਈ ਵਾਲੀਆਂ ਲੂੰਗੀਆਂ ਤਿਆਰ ਕੀਤੀਆਂ ਜਾਂਦੀਆਂ ਸਨ । ਅੰਮ੍ਰਿਤਸਰ, ਕਾਂਗੜਾ ਅਤੇ ਕਸ਼ਮੀਰ ਵਿੱਚ ਗਰਮ ਕੱਪੜੇ ਤਿਆਰ ਕਰਨ ਦੇ ਪ੍ਰਸਿੱਧ ਕੇਂਦਰ ਸਨ । ਕੱਪੜਾ ਉਦਯੋਗ ਤੋਂ ਇਲਾਵਾ ਉਸ ਸਮੇਂ ਪੰਜਾਬ ਵਿੱਚ ਚਮੜਾ, ਸ਼ਸਤਰ, ਭਾਂਡੇ, ਹਾਥੀ ਦੰਦ ਅਤੇ ਖਿਡੌਣੇ ਆਦਿ ਬਣਾਉਣ ਦੇ ਉਦਯੋਗ ਵੀ ਪ੍ਰਚਲਿਤ ਸਨ ।
ਪ੍ਰਸ਼ਨ 18.
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਵਪਾਰ ਦਾ ਸੰਖੇਪ ਵਰਣਨ ਕਰੋ । (Give a brief account of the Trade of Punjab in the beginning of the 16th century.)
ਉੱਤਰ-
ਪੰਜਾਬ ਦਾ ਵਪਾਰ ਕਾਫ਼ੀ ਵਿਕਸਿਤ ਸੀ ।ਵਪਾਰ ਦਾ ਕੰਮ ਕੁਝ ਖ਼ਾਸ ਸ਼੍ਰੇਣੀਆਂ ਦੇ ਹੱਥ ਵਿੱਚ ਹੁੰਦਾ ਸੀ ।ਹਿੰਦੂਆਂ ਦੀਆਂ ਜਾਤੀਆਂ ਵਪਾਰ ਦਾ ਕੰਮ ਕਰਦੀਆਂ ਸਨ |ਮਾਲ ਦੀ ਢੋਆ-ਢੁਆਈ ਦਾ ਕੰਮ ਵਣਜਾਰੇ ਕਰਦੇ ਸਨ । ਵਪਾਰੀ ਚੋਰਾਂਡਾਕੂਆਂ ਦੇ ਡਰ ਕਾਰਨ ਕਾਫ਼ਲਿਆਂ ਦੀ ਸ਼ਕਲ ਵਿੱਚ ਚਲਦੇ ਸਨ । ਉਸ ਸਮੇਂ ਹੁੰਡੀ ਬਣਾਉਣ ਦਾ ਵੀ ਰਿਵਾਜ ਸੀ । ਸ਼ਾਹੂਕਾਰ ਵਿਆਜ ਉੱਤੇ ਪੈਸਾ ਦਿੰਦੇ ਸਨ । ਮੇਲਿਆਂ ਅਤੇ ਤਿਉਹਾਰਾਂ ਸਮੇਂ ਵਿਸ਼ੇਸ਼ ਮੰਡੀਆਂ ਲਗਾਈਆਂ ਜਾਂਦੀਆਂ ਸਨ । ਪੰਜਾਬ ਵਿੱਚ ਅਜਿਹੀਆਂ ਮੰਡੀਆਂ ਮੁਲਤਾਨ, ਲਾਹੌਰ, ਜਲੰਧਰ, ਦੀਪਾਲਪੁਰ, ਸਰਹਿੰਦ, ਸੁਨਾਮ ਅਤੇ ਸਮਾਣਾ ਆਦਿ ਥਾਂਵਾਂ ‘ਤੇ ਲਗਾਈਆਂ ਜਾਂਦੀਆਂ ਸਨ । ਇਨ੍ਹਾਂ ਮੰਡੀਆਂ ਤੋਂ ਵੱਡੀ ਗਿਣਤੀ ਵਿੱਚ ਲੋਕ ਆਪਣੀ ਜ਼ਰੂਰਤ ਦੀਆਂ ਚੀਜ਼ਾਂ ਖਰੀਦਦੇ ਸਨ । ਪਸ਼ੂਆਂ ਦੇ ਵਪਾਰ ਲਈ ਵੀ ਪੰਜਾਬ ਵਿੱਚ ਵਿਸ਼ੇਸ਼ ਮੰਡੀਆਂ ਲਗਦੀਆਂ ਸਨ । ਉਸ ਸਮੇਂ ਪੰਜਾਬ ਦਾ ਵਿਦੇਸ਼ੀ ਵਪਾਰ ਮੁੱਖ ਰੂਪ ਵਿੱਚ ਅਫ਼ਗਾਨਿਸਤਾਨ, ਈਰਾਨ, ਅਰਬ, ਸੀਰੀਆ, ਤਿੱਬਤ, ਭੂਟਾਨ ਅਤੇ ਚੀਨ ਆਦਿ ਦੇਸ਼ਾਂ ਨਾਲ ਹੁੰਦਾ ਸੀ । ਪੰਜਾਬ ਤੋਂ ਇਨ੍ਹਾਂ ਦੇਸ਼ਾਂ ਨੂੰ ਅਨਾਜ, ਕੱਪੜੇ, ਕਪਾਹ, ਰੇਸ਼ਮ ਅਤੇ ਖੰਡ ਨਿਰਯਾਤ ਕੀਤੀ ਜਾਂਦੀ ਸੀ । ਇਨ੍ਹਾਂ ਦੇਸ਼ਾਂ ਤੋਂ ਪੰਜਾਬ ਘੋੜੇ, ਸ਼ਸਤਰ, ਫਰ, ਕਸਤੂਰੀ ਅਤੇ ਮੇਵੇ ਆਦਿ ਆਯਾਤ ਕਰਦਾ ਸੀ ।
ਪ੍ਰਸ਼ਨ 19.
16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਲੋਕਾਂ ਦਾ ਜੀਵਨ ਪੱਧਰ ਕਿਹੋ ਜਿਹਾ ਸੀ ? (What was the living standard of people in the beginning of the 16th century ?)
ਉੱਤਰ-
16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਲੋਕਾਂ ਦਾ ਜੀਵਨ ਪੱਧਰ ਇੱਕੋ ਜਿਹਾ ਨਹੀਂ ਸੀ । ਮੁਸਲਮਾਨਾਂ ਦੀਆਂ ਉੱਚ ਸ਼੍ਰੇਣੀਆਂ ਦੇ ਲੋਕਾਂ ਕੋਲ ਬਹੁਤ ਧਨ ਸੀ ਅਤੇ ਉਹ ਐਸ਼ਪ੍ਰਸਤੀ ਦਾ ਜੀਵਨ ਬਤੀਤ ਕਰਦੇ ਸਨ । ਉਹ ਬੜੇ ਸ਼ਾਨਦਾਰ ਮਹੱਲਾਂ ਵਿੱਚ ਰਹਿੰਦੇ ਸਨ ।ਉਨ੍ਹਾਂ ਦੀਆਂ ਪੁਸ਼ਾਕਾਂ ਬਹੁਤ ਕੀਮਤੀ ਹੁੰਦੀਆਂ ਸਨ ਅਤੇ ਉਹ ਵਿਭਿੰਨ ਤਰ੍ਹਾਂ ਦੇ ਸੁਆਦਲੇ ਭੋਜਨ ਖਾਂਦੇ ਸਨ | ਸੂਰਾ ਅਤੇ ਸੁੰਦਰੀ ਉਨ੍ਹਾਂ ਦੇ ਜੀਵਨ ਦਾ ਇੱਕ ਅਨਿੱਖੜਵਾਂ ਅੰਗ ਬਣ ਚੁੱਕਿਆ ਸੀ ।ਉਨ੍ਹਾਂ ਦੀ ਸੇਵਾ ਲਈ ਵੱਡੀ ਗਿਣਤੀ ਵਿੱਚ ਨੌਕਰ, ਦਾਸ ਅਤੇ ਦਾਸੀਆਂ ਹੁੰਦੀਆਂ ਸਨ । ਹਿੰਦੂਆਂ ਦੀਆਂ ਉੱਚ-ਸ਼ੇਣੀਆਂ ਦੇ ਕੋਲ ਧਨ ਤਾਂ ਬਹੁਤ ਸੀ ਪਰ ਮੁਸਲਮਾਨ ਉਨ੍ਹਾਂ ਤੋਂ ਇਹ ਧਨ ਲੁੱਟ ਕੇ ਲੈ ਜਾਂਦੇ ਸਨ । ਇਸ ਲਈ ਉਹ ਆਪਣਾ ਧਨ ਚੋਰੀ ਛਿਪੇ ਖ਼ਰਚ ਕਰਦੇ ਸਨ । ਸਮਾਜ ਵਿੱਚ ਮੱਧ ਸ਼੍ਰੇਣੀ ਦੇ ਮੁਸਲਮਾਨਾਂ ਦਾ ਜੀਵਨ ਪੱਧਰ ਤਾਂ ਚੰਗਾ ਸੀ ਪਰ ਹਿੰਦੁਆਂ ਦਾ ਜੀਵਨ ਪੱਧਰ ਚੰਗਾ ਨਹੀਂ ਸੀ । ਹਿੰਦੇ ਆਪਣਾ ਗੁਜ਼ਾਰਾ ਬੜੀ ਮੁਸ਼ਕਿਲ ਨਾਲ ਕਰਦੇ ਸਨ | ਸਮਾਜ ਵਿੱਚ ਗਰੀਬਾਂ ਅਤੇ ਕਿਸਾਨਾਂ ਦਾ ਜੀਵਨ ਪੱਧਰ ਬਹੁਤ ਨੀਵਾਂ ਸੀ ।ਉਹ ਨਾ ਤਾਂ ਚੰਗੇ ਕੱਪੜੇ ਪਾ ਸਕਦੇ ਸਨ ਅਤੇ ਨਾ ਹੀ ਚੰਗਾ ਭੋਜਨ ਖਾ ਸਕਦੇ ਸਨ ।
![]()
ਪ੍ਰਸਤਾਵ ਰੂਪੀ ਪ੍ਰਸ਼ਨ (Essay Type Questions)
ਰਾਜਨੀਤਿਕ ਦਸ਼ਾ (Political Condition)
ਪ੍ਰਸ਼ਨ 1.
ਗੁਰੂ ਨਾਨਕ ਦੇਵ ਜੀ ਦੇ ਜਨਮ ਸਮੇਂ (16ਵੀਂ ਸ਼ਤਾਬਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ) ਪੰਜਾਬ ਦੀ ਰਾਜਨੀਤਿਕ ਦਸ਼ਾ ਦਾ ਵਰਣਨ ਕਰੋ । [Describe the political condition of the Punjab at the time (In the beginning of the 16th century) of Guru Nanak Dev Ji’s birth.]
ਜਾਂ
ਬਾਬਰ ਦੇ ਪੰਜਾਬ ਉੱਤੇ ਕੀਤੇ ਗਏ ਹਮਲਿਆਂ ਦੀ ਸੰਖੇਪ ਜਾਣਕਾਰੀ ਦਿੰਦੇ ਹੋਏ ਉਸ ਦੀ ਸਫਲਤਾ ਦੇ ਕਾਰਨ ਦੱਸੋ । (While describing briefly the invasions of Babur over the Punjab, explain the causes of his success.)
ਜਾਂ
16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦੀ ਰਾਜਨੀਤਿਕ ਅਵਸਥਾ ਦਾ ਵਰਣਨ ਕਰੋ । (Describe the Political Condition of the Punjab in the beginning of 16th Century.)
ਉੱਤਰ-
16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦੀ ਰਾਜਨੀਤਿਕ ਦਸ਼ਾ ਬਹੁਤ ਮਾੜੀ ਸੀ । ਪੰਜਾਬ ਸਾਜ਼ਸ਼ਾਂ ਦਾ ਅਖਾੜਾ ਬਣਿਆ ਹੋਇਆ ਸੀ । ਉਸ ਸਮੇਂ ਪੰਜਾਬ ਦਿੱਲੀ ਸਲਤਨਤ ਦੇ ਅਧੀਨ ਸੀ । ਇਸ ਉੱਤੇ ਲੋਧੀ ਵੰਸ਼ ਦੇ ਸੁਲਤਾਨਾਂ ਦਾ ਸ਼ਾਸਨ ਸੀ । 16ਵੀਂ ਸ਼ਤਾਬਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦੀ ਰਾਜਨੀਤਿਕ ਦਸ਼ਾ ਦਾ ਸੰਖੇਪ ਵਰਣਨ ਅੱਗੇ ਲਿਖੇ ਅਨੁਸਾਰ ਹੈ-
ਲੋਧੀਆਂ ਦੇ ਅਧੀਨ ਪੰਜਾਬ (The Punjab under the Lodhis)
1. ਤਤਾਰ ਖਾਂ ਲੋਧੀ (Tatar Khan Lodhi) – 1469 ਈ. ਵਿੱਚ ਦਿੱਲੀ ਦੇ ਸੁਲਤਾਨ ਬਹਿਲੋਲ ਲੋਧੀ ਨੇ ਤਤਾਰ ਖ਼ਾਂ ਲੋਧੀ ਨੂੰ ਪੰਜਾਬ ਦਾ ਗਵਰਨਰ ਨਿਯੁਕਤ ਕੀਤਾ । ਉਹ ਇਸ ਅਹੁਦੇ ‘ਤੇ 1485 ਈ. ਤਕ ਰਿਹਾ। ਉਸ ਨੇ ਬੜੀ ਸਖ਼ਤੀ ਨਾਲ ਪੰਜਾਬ ‘ਤੇ 1485 ਈ. ਤਕ ਸ਼ਾਸਨ ਕੀਤਾ । 1485 ਈ. ਵਿੱਚ ਤਤਾਰ ਖਾਂ ਲੋਧੀ ਨੇ ਸੁਲਤਾਨ ਬਹਿਲੋਲ ਲੋਧੀ ਦੇ ਵਿਰੁੱਧ ਵਿਦਰੋਹ ਕਰ ਦਿੱਤਾ । ਸੁਲਤਾਨ ਨੇ ਆਪਣੇ ਸ਼ਹਿਜ਼ਾਦੇ ਨਿਜ਼ਾਮ ਖ਼ਾਂ ਨੂੰ ਤਤਾਰ ਖਾਂ ਦੇ ਵਿਦਰੋਹ ਨੂੰ ਕੁਚਲਣ ਲਈ ਭੇਜਿਆ । ਤਤਾਰ ਖਾਂ ਲੋਧੀ ਨਿਜ਼ਾਮ ਖ਼ਾਂ ਨਾਲ ਲੜਦਾ ਹੋਇਆ ਮਾਰਿਆ ਗਿਆ ।
2. ਦੌਲਤ ਖਾਂ ਲੋਧੀ (Daulat Khan Lodhi) – ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਤਤਾਰ ਖਾਂ ਲੋਧੀ ਦਾ ਪੁੱਤਰ ਸੀ । ਉਸ ਨੂੰ 1500 ਈ. ਵਿੱਚ ਨਵੇਂ ਸੁਲਤਾਨ ਸਿਕੰਦਰ ਲੋਧੀ ਨੇ ਪੰਜਾਬ ਦਾ ਗਵਰਨਰ ਨਿਯੁਕਤ ਕੀਤਾ । ਉਹ ਸਿਕੰਦਰ ਲੋਧੀ ਦੇ ਸ਼ਾਸਨ ਕਾਲ ਵਿੱਚ ਤਾਂ ਪੂਰਨ ਰੂਪ ਵਿੱਚ ਵਫ਼ਾਦਾਰ ਰਿਹਾ । ਪਰ ਸੁਲਤਾਨ ਇਬਰਾਹੀਮ ਲੋਧੀ ਦੇ ਸ਼ਾਸਨ ਕਾਲ ਵਿੱਚ ਉਹ ਸੁਤੰਤਰ ਹੋਣ ਦੇ ਸੁਪਨੇ ਵੇਖਣ ਲੱਗਾ। ਇਸ ਸੰਬੰਧੀ ਉਸ ਨੇ ਆਲਮ ਖਾਂ ਲੋਧੀ, ਜੋ ਕਿ ਇਬਰਾਹੀਮ ਲੋਧੀ ਦਾ ਚਾਚਾ ਸੀ, ਨਾਲ ਮਿਲ ਕੇ ਸਾਜ਼ਸ਼ਾਂ ਕਰਨੀਆਂ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤੀਆਂ । ਜਦੋਂ ਇਨ੍ਹਾਂ ਸਾਜ਼ਸ਼ਾਂ ਸੰਬੰਧੀ ਇਬਰਾਹੀਮ ਲੋਧੀ ਨੂੰ ਪਤਾ ਚਲਿਆ, ਤਾਂ ਉਸ ਨੇ ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਦੇ ਪੁੱਤਰ ਦਿਲਾਵਰ ਖਾਂ ਨੂੰ ਕੈਦ ਕਰ ਲਿਆ । ਛੇਤੀ ਹੀ ਦਿਲਾਵਰ ਖਾਂ ਵਾਪਸ ਪੰਜਾਬ ਪਹੁੰਚਣ ਵਿੱਚ ਕਾਮਯਾਬ ਹੋ ਗਿਆ । ਇੱਥੇ ਪਹੁੰਚ ਕੇ ਉਸ ਨੇ ਆਪਣੇ ਪਿਤਾ ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਨੂੰ ਦਿੱਲੀ ਵਿੱਚ ਉਸ ਨਾਲ ਕੀਤੇ ਗਏ ਮਾੜੇ ਸਲੂਕ ਬਾਰੇ ਦੱਸਿਆ । ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਨੇ ਇਸ ਅਪਮਾਨ ਦਾ ਬਦਲਾ ਲੈਣ ਲਈ ਬਾਬਰ ਨੂੰ ਭਾਰਤ ਉੱਤੇ ਹਮਲਾ ਕਰਨ ਦਾ ਸੱਦਾ ਦਿੱਤਾ ।
3. ਪਰਜਾ ਦੀ ਹਾਲਤ (Condition of Subject) – 16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਵਿੱਚ ਪਰਜਾ ਦੀ ਹਾਲਤ ਬਹੁਤ ਤਰਸਯੋਗ ਸੀ । ਸ਼ਾਸਕ ਵਰਗ ਦਾ ਪਰਜਾ ਵੱਲ ਧਿਆਨ ਹੀ ਨਹੀਂ ਸੀ | ਸਰਕਾਰੀ ਕਰਮਚਾਰੀ ਕੁਸ਼ਟ ਹੋ ਚੁੱਕੇ ਸਨ । ਹਰ ਪਾਸੇ ਰਿਸ਼ਵਤ ਦਾ ਬੋਲਬਾਲਾ ਸੀ । ਹਿੰਦੁਆਂ ‘ਤੇ ਅੱਤਿਆਚਾਰ ਬਹੁਤ ਜ਼ਿਆਦਾ ਵੱਧ ਗਏ ਸਨ । ਉਨ੍ਹਾਂ ਨੂੰ ਤਲਵਾਰ ਦੀ ਨੋਕ ‘ਤੇ ਜ਼ਬਰਦਸਤੀ ਇਸਲਾਮ ਧਰਮ ਵਿੱਚ ਸ਼ਾਮਲ ਕੀਤਾ ਜਾਂਦਾ ਸੀ । ਸੰਖੇਪ ਵਿੱਚ ਉਸ ਸਮੇਂ ਹਰ ਪਾਸੇ ਅੱਤਿਆਚਾਰ, ਫਰੇਬ, ਧੋਖਾ ਤੇ ਭ੍ਰਿਸ਼ਟਾਚਾਰ ਫੈਲਿਆ ਹੋਇਆ ਸੀ । ਗੁਰੂ ਨਾਨਕ ਦੇਵ ਜੀ ਨੇ ਵਾਰ ਮਾਝ ਵਿੱਚ ਇਸ ਤਰ੍ਹਾਂ ਲਿਖਿਆ ਹੈ,
ਕਲ ਕਾਤੀ ਰਾਜੇ ਕਸਾਈ ਧਰਮ ਪੰਖ ਕਰ ਉਡਰਿਆ ॥
ਕੂੜ ਅਮਾਵਸ ਸਚ ਚੰਦਰਮਾ ਦੀਸੈ ਨਾਹੀ ਕਹ ਚੜਿਆ ॥
ਬਾਬਰ ਦੇ ਹਮਲੇ (Invasions of Babur)
1519 ਈ. ਤੋਂ 1526 ਈ. ਦੇ ਸਮੇਂ ਦੌਰਾਨ ਪੰਜਾਬ ਨੂੰ ਆਪਣੇ ਅਧੀਨ ਕਰਨ ਲਈ ਇੱਕ ਤਿਕੋਣਾ ਸੰਘਰਸ਼ ਸ਼ੁਰੂ ਹੋ ਗਿਆ । ਇਹ ਸੰਘਰਸ਼ ਇਬਰਾਹੀਮ ਲੋਧੀ, ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਅਤੇ ਬਾਬਰ ਵਿਚਾਲੇ ਸ਼ੁਰੂ ਹੋਇਆ ਇਸ ਸੰਘਰਸ਼ ਦੇ ਅੰਤ ਵਿੱਚ ਬਾਬਰ ਜੇਤੂ ਰਿਹਾ । ਬਾਬਰ ਦਾ ਜਨਮ ਮੱਧ ਏਸ਼ੀਆ ਵਿੱਚ ਸਥਿਤ ਫਰਗਨਾ ਦੀ ਰਾਜਧਾਨੀ ਅੰਦੀਜਾਨ ਵਿਖੇ 14 ਫ਼ਰਵਰੀ, 1483 ਈ. ਨੂੰ ਹੋਇਆ ਸੀ । ਉਹ ਤੈਮੁਰ ਵੰਸ਼ ਨਾਲ ਸੰਬੰਧ ਰੱਖਦਾ ਸੀ ।
1. ਬਾਬਰ ਦੇ ਪਹਿਲੇ ਦੋ ਹਮਲੇ (First two Invasions of Babur) – ਬਾਬਰ ਨੇ 1519 ਈ. ਵਿੱਚ ਪੰਜਾਬ ‘ਤੇ ਦੋ ਵਾਰ ਹਮਲੇ ਕੀਤੇ । ਕਿਉਂਕਿ ਇਹ ਹਮਲੇ ਪੰਜਾਬ ਦੇ ਸੀਮਾਂਵਰਤੀ ਇਲਾਕਿਆਂ ‘ਤੇ ਹੀ ਕੀਤੇ ਗਏ ਸਨ, ਇਸ ਲਈ ਇਨ੍ਹਾਂ ਦਾ ਕੋਈ ਵਿਸ਼ੇਸ਼ ਮਹੱਤਵ ਨਹੀਂ ਹੈ ।
2. ਬਾਬਰ ਦਾ ਤੀਸਰਾ ਹਮਲਾ 1520 ਈ. (Third Invasion of Babur 1520 A.D.) – ਬਾਬਰ ਨੇ 1520 ਈ. ਵਿੱਚ ਪੰਜਾਬ ਉੱਤੇ ਤੀਸਰੀ ਵਾਰ ਹਮਲਾ ਕੀਤਾ । ਇਸ ਹਮਲੇ ਦੇ ਦੌਰਾਨ ਬਾਬਰ ਨੇ ਪਹਿਲਾਂ ਸੈਦਪੁਰ ‘ਤੇ ਹਮਲਾ ਕੀਤਾ । ਵੱਡੀ ਗਿਣਤੀ ਵਿੱਚ ਨਿਰਦੋਸ਼ ਲੋਕਾਂ ਨੂੰ ਕਤਲ ਕਰ ਦਿੱਤਾ ਗਿਆ ਅਤੇ ਉਨ੍ਹਾਂ ਨੂੰ ਬੇਰਹਿਮੀ ਨਾਲ ਲੁੱਟਿਆ ਗਿਆ । ਹਜ਼ਾਰਾਂ ਲੋਕਾਂ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰ ਲਿਆ ਗਿਆ । ਗੁਰੂ ਨਾਨਕ ਦੇਵ ਜੀ ਜੋ ਇਸ ਸਮੇਂ ਸੈਦਪੁਰ ਵਿੱਚ ਹੀ ਸਨ, ਨੇ ਬਾਬਰ ਦੇ ਇਸ ਹਮਲੇ ਦੀ ਤੁਲਨਾ ਪਾਪਾਂ ਦੀ ਜੰਝ ਨਾਲ ਕੀਤੀ ਹੈ । ਉਨ੍ਹਾਂ ਨੇ ਬਾਬਰ ਦੇ ਅੱਤਿਆਚਾਰਾਂ ਦਾ ਵਰਣਨ ‘ਬਾਬਰ ਵਾਣੀ ਵਿੱਚ ਇਸ ਤਰ੍ਹਾਂ ਕੀਤਾ,
ਖੁਰਾਸਾਨ ਖਸਮਾਨਾ ਕੀਆ ਹਿੰਦੁਸਤਾਨ ਡਰਾਇਆ ॥
ਆਪੇ ਦੋਸੁ ਨ ਦੇਈ ਕਰਤਾ, ਜਮੁ ਕਰਿ ਮੁਗਲੁ ਚੜਾਇਆ ॥
ਏਤੀ ਮਾਰ ਪਈ ਕੁਰਲਾਣੈ, ਤੈਂ ਕੀ ਦਰਦ ਨਾ ਆਇਆ ॥
ਬਾਬਰ ਦੀਆਂ ਫ਼ੌਜਾਂ ਨੇ ਗੁਰੂ ਨਾਨਕ ਸਾਹਿਬ ਜੀ ਨੂੰ ਵੀ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰ ਲਿਆ ਸੀ । ਬਾਅਦ ਵਿੱਚ ਜਦੋਂ ਬਾਬਰ ਨੂੰ ਇਸ ਬਾਰੇ ਪਤਾ ਲੱਗਿਆ ਕਿ ਉਸ ਦੀਆਂ ਫ਼ੌਜਾਂ ਨੇ ਕਿਸੇ ਸੰਤ-ਮਹਾਂਪੁਰਸ਼ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕੀਤਾ ਹੈ, ਤਾਂ ਉਸ ਨੇ ਫੌਰਨ ਉਨ੍ਹਾਂ ਦੀ ਰਿਹਾਈ ਦਾ ਹੁਕਮ ਦਿੱਤਾ ।
3. ਬਾਬਰ ਦਾ ਚੌਥਾ ਹਮਲਾ 1524 ਈ. (Fourth Invasion of Babur 1524 A.D.) – ਪੰਜਾਬ ਦੇ ਗਵਰਨਰ ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਦੇ ਸੱਦੇ ‘ਤੇ ਬਾਬਰ ਨੇ 1524 ਈ. ਵਿੱਚ ਪੰਜਾਬ ਉੱਤੇ ਚੌਥਾ ਹਮਲਾ ਕੀਤਾ । ਉਹ ਬਿਨਾਂ ਕਿਸੇ ਖ਼ਾਸ ਵਿਰੋਧ ਦੇ ਲਾਹੌਰ ਤਕ ਪਹੁੰਚ ਗਿਆ ਸੀ । ਉਸ ਨੇ ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਦੇ ਸਹਿਯੋਗ ਨਾਲ ਦੀਪਾਲਪੁਰ ’ਤੇ ਕਬਜ਼ਾ ਕਰ ਲਿਆ । ਇਸ ਤੋਂ ਬਾਅਦ ਬਾਬਰ ਨੇ ਜਲੰਧਰ ਦੁਆਬ ਨੂੰ ਆਪਣੇ ਅਧੀਨ ਕਰ ਲਿਆ ਬਾਬਰ ਨੇ ਜਲੰਧਰ ਦੁਆਬ ਅਤੇ ਸੁਲਤਾਨਪੁਰ ਦੇ ਦੇਸ਼ਾਂ ਦਾ ਸ਼ਾਸਨ ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਨੂੰ ਸੌਂਪਿਆ । ਕਿਉਂਕਿ ਇਹ ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਦੀਆਂ ਉਮੀਦਾਂ ਤੋਂ ਬਹੁਤ ਘੱਟ ਸੀ ਇਸ ਲਈ ਉਸ ਨੇ ਬਾਬਰ ਵਿਰੁੱਧ ਵਿਦਰੋਹ ਕਰ ਦਿੱਤਾ | ਬਾਬਰ ਨੇ ਉਸ ਨੂੰ ਹਰਾ ਦਿੱਤਾ ਅਤੇ ਉਹ ਸ਼ਿਵਾਲਿਕ ਦੀਆਂ ਪਹਾੜੀਆਂ ਵੱਲ ਦੌੜ ਗਿਆ । ਬਾਬਰ ਦੇ ਵਾਪਸ ਕਾਬਲ ਜਾਣ ਪਿੱਛੋਂ ਛੇਤੀ ਹੀ ਦੌਲਤ ਖ਼ਾਂ ਲੋਧੀ ਨੇ ਮੁੜ ਪੰਜਾਬ ‘ਤੇ ਕਬਜ਼ਾ ਕਰ ਲਿਆ ।
4. ਬਾਬਰ ਦਾ ਪੰਜਵਾਂ ਹਮਲਾ 1525-26 ਈ. (Fifth Invasion of Babur 1525-26 A.D.) – ਬਾਬਰ ਨੇ ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਨੂੰ ਸਬਕ ਸਿਖਾਉਣ ਲਈ ਨਵੰਬਰ, 1525 ਈ. ਵਿੱਚ ਭਾਰਤ ਉੱਤੇ ਪੰਜਵੀਂ ਵਾਰ ਹਮਲਾ ਕੀਤਾ | ਬਾਬਰ ਦੇ ਆਉਣ ਦੀ ਖ਼ਬਰ ਸੁਣ ਕੇ ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਜ਼ਿਲਾ ਹੁਸ਼ਿਆਰਪੁਰ ਵਿੱਚ ਸਥਿਤ ਮਲੋਟ ਦੇ ਕਿਲੇ ਵਿੱਚ ਜਾ ਛੁਪਿਆ । ਬਾਬਰ ਨੇ ਕਿਲ੍ਹੇ ਨੂੰ ਘੇਰਾ ਪਾ ਲਿਆ । ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਨੇ ਕੁਝ ਚਿਰ ਮੁਕਾਬਲਾ ਕਰਨ ਮਗਰੋਂ ਆਪਣੇ ਹਥਿਆਰ ਸੁੱਟ ਦਿੱਤੇ । ਇਸ ਤਰ੍ਹਾਂ ਬਾਬਰ ਨੇ ਇੱਕ ਵਾਰ ਫਿਰ ਪੂਰੇ ਪੰਜਾਬ ਨੂੰ ਆਪਣੇ ਅਧੀਨ ਕਰ ਲਿਆ । ਪੰਜਾਬ ਦੀ ਜਿੱਤ ਤੋਂ ਉੱਤਸਾਹਿਤ ਹੋ ਕੇ ਬਾਬਰ ਨੇ ਆਪਣੀਆਂ ਫ਼ੌਜਾਂ ਨੂੰ ਦਿੱਲੀ ਵੱਲ ਵਧਣ ਦਾ ਹੁਕਮ ਦਿੱਤਾ । ਜਦੋਂ ਇਬਰਾਹੀਮ ਲੋਧੀ ਨੂੰ ਇਸ ਬਾਰੇ ਖ਼ਬਰ ਮਿਲੀ ਤਾਂ ਉਹ ਬਾਬਰ ਦਾ ਮੁਕਾਬਲਾ ਕਰਨ ਲਈ ਪੰਜਾਬ ਵੱਲ ਤੁਰ ਪਿਆ । 21 ਅਪਰੈਲ, 1526 ਈ. ਨੂੰ ਦੋਹਾਂ ਫ਼ੌਜਾਂ ਵਿਚਾਲੇ ਪਾਨੀਪਤ ਦੀ ਪਹਿਲੀ ਲੜਾਈ ਹੋਈ । ਇਸ ਲੜਾਈ ਵਿੱਚ ਇਬਰਾਹੀਮ ਲੋਧੀ ਦੀ ਹਾਰ ਹੋਈ । ਇਸ ਤਰ੍ਹਾਂ ਭਾਰਤ ਵਿੱਚ ਲੋਧੀ ਵੰਸ਼ ਦਾ ਅੰਤ ਹੋ ਗਿਆ ਅਤੇ ਮੁਗ਼ਲ ਵੰਸ਼ ਦੀ ਸਥਾਪਨਾ ਹੋਈ ।
5. ਬਾਬਰ ਦੀ ਜਿੱਤ ਦੇ ਕਾਰਨ (Causes of Babur’s Success) – ਬਾਬਰ ਦੀ ਜਿੱਤ ਲਈ ਕਈ ਕਾਰਨ ਜ਼ਿੰਮੇਵਾਰ ਸਨ । ਪਹਿਲਾਂ, ਇਬਰਾਹੀਮ ਲੋਧੀ ਆਪਣੀ ਪਰਜਾ ਵਿੱਚ ਬਹੁਤ ਬਦਨਾਮ ਸੀ । ਇਸ ਲਈ ਪਰਜਾ ਨੇ ਸੁਲਤਾਨ ਦਾ ਸਾਥ ਨਾ ਦਿੱਤਾ । ਦੂਜਾ, ਉਸ ਦੀ ਫ਼ੌਜ ਬੜੀ ਕਮਜ਼ੋਰ ਸੀ ਅਤੇ ਵਧੇਰੇ ਕਰਕੇ ਲੁੱਟਮਾਰ ਕਰਦੀ ਸੀ । ਤੀਜਾ, ਬਾਬਰ ਇੱਕ ਯੋਗ ਸੈਨਾਪਤੀ ਸੀ । ਉਸ ਦੀ ਸੈਨਾ ਨੂੰ ਕਈ ਲੜਾਈਆਂ ਦਾ ਤਜਰਬਾ ਸੀ । ਚੌਥਾ, ਬਾਬਰ ਕੋਲ ਤੋਪਖ਼ਾਨਾ ਸੀ ਅਤੇ ਇਬਰਾਹੀਮ ਦੇ ਸੈਨਿਕ ਤੀਰ ਕਮਾਨਾਂ ਅਤੇ ਤਲਵਾਰਾਂ ਨਾਲ ਉਸ ਦਾ ਮੁਕਾਬਲਾ ਨਾ ਕਰ ਸਕੇ । ਇਨ੍ਹਾਂ ਕਾਰਨਾਂ ਕਰਕੇ ਅਫ਼ਗਾਨਾਂ ਦੀ ਹਾਰ ਹੋਈ ਅਤੇ ਬਾਬਰ ਨੂੰ ਜਿੱਤ ਪ੍ਰਾਪਤ ਹੋਈ ।
![]()
ਸਮਾਜਿਕ ਦਸ਼ਾ (Social Condition)
ਪ੍ਰਸ਼ਨ 2.
16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਸਮਾਜ ਦੀਆਂ ਮੁੱਖ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਬਿਆਨ ਕਰੋ । (Discuss the main features of the society of the Punjab in the beginning of the 16th century.)
ਜਾਂ
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦੀ ਸਮਾਜਿਕ ਅਵਸਥਾ ਦਾ ਵਰਣਨ ਕਰੋ । (Describe the social condition of the Punjab. in the beginning of the 16th century.)
ਉੱਤਰ-
16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦੀ ਸਮਾਜਿਕ ਦਸ਼ਾ ਬਹੁਤ ਖ਼ਰਾਬ ਸੀ । ਉਸ ਸਮੇਂ ਸਮਾਜ ਹਿੰਦੂ ਤੇ ਮੁਸਲਮਾਨ ਨਾਂ ਦੇ ਦੋ ਮੁੱਖ ਵਰਗਾਂ ਵਿੱਚ ਵੰਡਿਆ ਹੋਇਆ ਸੀ । ਮੁਸਲਮਾਨ ਸ਼ਾਸਕ ਵਰਗ ਨਾਲ ਸੰਬੰਧ ਰੱਖਦੇ ਸਨ । ਇਸ ਲਈ ਉਨ੍ਹਾਂ ਨੂੰ ਸਮਾਜ ਵਿੱਚ ਵਿਸ਼ੇਸ਼ ਅਧਿਕਾਰ ਪ੍ਰਾਪਤ ਸਨ | ਦੂਜੇ ਪਾਸੇ ਹਿੰਦੂਆਂ ਨੂੰ ਬਹੁ-ਗਿਣਤੀ ਵਿੱਚ ਹੁੰਦੇ ਹੋਏ ਵੀ ਲਗਭਗ ਸਾਰੇ ਅਧਿਕਾਰਾਂ ਤੋਂ ਵਾਂਝਿਆ ਰੱਖਿਆ ਗਿਆ ਸੀ । ਉਨ੍ਹਾਂ ਨੂੰ ਕਾਫ਼ਰ ਅਤੇ ਜਿੰਮੀ ਕਹਿ ਕੇ ਸੱਦਿਆ ਜਾਂਦਾ ਸੀ । ਸਮਾਜ ਵਿੱਚ ਇਸਤਰੀਆਂ ਦੀ ਹਾਲਤ ਬਹੁਤ ਤਰਸਯੋਗ ਸੀ । ਉਨ੍ਹਾਂ ਨੂੰ ਮਰਦਾਂ ਦੀ ਜੁੱਤੀ ਸਮਝਿਆ ਜਾਂਦਾ ਸੀ । ਡਾਕਟਰ ਜਸਬੀਰ ਸਿੰਘ ਆਹਲੂਵਾਲੀਆ ਦੇ ਅਨੁਸਾਰ,
“ਜਿਸ ਸਮੇਂ ਗੁਰੂ ਨਾਨਕ ਜੀ ਨੇ ਅਵਤਾਰ ਧਾਰਨ ਕੀਤਾ, ਤਾਂ ਉਸ ਸਮੇਂ ਤੋਂ ਪਹਿਲਾਂ ਹੀ ਭਾਰਤੀ ਸਮਾਜ ਗਤੀਹੀਨ ਅਤੇ ਪਤਿਤ ਹੋ ਚੁੱਕਾ ਸੀ ।”
I. ਮੁਸਲਿਮ ਸਮਾਜ ਦੀਆਂ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ (Features of the Muslim Society)
16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਮੁਸਲਿਮ ਸਮਾਜ ਦੀਆਂ ਮੁੱਖ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਹੇਠ ਲਿਖੀਆਂ ਸਨ-
1. ਸਮਾਜ ਤਿੰਨ ਸ਼੍ਰੇਣੀਆਂ ਵਿੱਚ ਵੰਡਿਆ ਹੋਇਆ ਸੀ (Society was divided into three Classes) – 16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦਾ ਮੁਸਲਿਮ ਸਮਾਜ ਉੱਚ ਸ਼੍ਰੇਣੀ, ਮੱਧ ਸ਼੍ਰੇਣੀ ਅਤੇ ਨੀਵੀਂ ਸ਼੍ਰੇਣੀ ਵਿੱਚ ਵੰਡਿਆ ਹੋਇਆ ਸੀ ।
(ੳ) ਉੱਚ ਸ਼੍ਰੇਣੀ (The Upper Class) – ਇਸ ਸ਼੍ਰੇਣੀ ਵਿੱਚ ਅਮੀਰ, ਖ਼ਾਨ, ਸ਼ੇਖ਼, ਮਲਿਕ, ਇਕਤਾਦਾਰ, ਉਲਮਾ ਅਤੇ ਕਾਜ਼ੀ ਆਦਿ ਸ਼ਾਮਲ ਸਨ । ਇਸ ਸ਼੍ਰੇਣੀ ਦੇ ਲੋਕ ਬੜੇ ਐਸ਼ੋ-ਆਰਾਮ ਦਾ ਜੀਵਨ ਬਤੀਤ ਕਰਦੇ ਸਨ । ਉਹ ਬੜੇ ਸ਼ਾਨਦਾਰ ਮਹੱਲਾਂ ਵਿੱਚ ਰਹਿੰਦੇ ਸਨ । ਉੱਚ ਸ਼੍ਰੇਣੀ ਦੇ ਲੋਕਾਂ ਦੀ ਸੇਵਾ ਲਈ ਵੱਡੀ ਗਿਣਤੀ ਵਿੱਚ ਨੌਕਰ ਹੁੰਦੇ ਸਨ ।
(ਅ) ਮੱਧ ਸ਼੍ਰੇਣੀ (The Middle Class) – ਇਸ ਸ਼੍ਰੇਣੀ ਵਿੱਚ ਸੈਨਿਕ, ਵਪਾਰੀ, ਕਿਸਾਨ ਅਤੇ ਰਾਜ ਦੇ ਛੋਟੇ ਕਰਮਚਾਰੀ ਸ਼ਾਮਲ ਸਨ । ਉਨ੍ਹਾਂ ਦੇ ਜੀਵਨ ਅਤੇ ਉੱਚ ਸ਼੍ਰੇਣੀ ਦੇ ਲੋਕਾਂ ਦੇ ਜੀਵਨ ਪੱਧਰ ਵਿੱਚ ਬੜਾ ਅੰਤਰ ਸੀ । ਉਹ ਹਿੰਦੂਆਂ ਦੇ ਮੁਕਾਬਲੇ ਬਹੁਤ ਚੰਗਾ ਜੀਵਨ ਬਤੀਤ ਕਰਦੇ ਸਨ ।
(ੲ) ਨੀਵੀਂ ਸ਼੍ਰੇਣੀ (The Lower Class-ਇਸ ਸ਼੍ਰੇਣੀ ਵਿੱਚ ਦਾਸ-ਦਾਸੀਆਂ, ਨੌਕਰ ਅਤੇ ਕਾਮੇ ਸ਼ਾਮਲ ਸਨ · । ਇਨ੍ਹਾਂ ਦੀ ਗਿਣਤੀ ਬਹੁਤ ਜ਼ਿਆਦਾ ਸੀ । ਉਨ੍ਹਾਂ ਦਾ ਜੀਵਨ ਚੰਗਾ ਨਹੀਂ ਸੀ । ਉਨ੍ਹਾਂ ਦੇ ਸੁਆਮੀ ਉਨ੍ਹਾਂ ‘ਤੇ ਬੜੇ ਅੱਤਿਆਚਾਰ ਕਰਦੇ ਸਨ ।
2. ਇਸਤਰੀਆਂ ਦੀ ਸਥਿਤੀ (Position of Women-ਮੁਸਲਿਮ ਸਮਾਜ ਵਿੱਚ ਇਸਤਰੀਆਂ ਦੀ ਸਥਿਤੀ ਚੰਗੀ ਨਹੀਂ ਸੀ। ਉਹ ਬਹੁਤ ਘੱਟ ਪੜ੍ਹੀਆਂ-ਲਿਖੀਆਂ ਹੁੰਦੀਆਂ ਸਨ । ਬਹੁ-ਵਿਆਹ ਅਤੇ ਤਲਾਕ-ਪ੍ਰਥਾ ਨੇ ਉਨ੍ਹਾਂ ਦੀ ਹਾਲਤ ਹੋਰ ਤਰਸਯੋਗ ਬਣਾ ਦਿੱਤੀ ਸੀ ।
3. ਖਾਣ-ਪੀਣ (Diet) – ਉੱਚ ਸ਼੍ਰੇਣੀ ਦੇ ਮੁਸਲਮਾਨ ਕਈ ਤਰ੍ਹਾਂ ਦੇ ਸੁਆਦਲੇ ਖਾਣੇ ਖਾਂਦੇ ਸਨ । ਉਹ ਆਪਣੇ ਜਸ਼ਨਾਂ ਵਿੱਚ ਮੀਟ, ਹਲਵਾ, ਪੂੜੀ ਅਤੇ ਮੱਖਣ ਆਦਿ ਦੀ ਬਹੁਤ ਵਰਤੋਂ ਕਰਦੇ ਸਨ । ਉਨ੍ਹਾਂ ਵਿੱਚ ਸ਼ਰਾਬ ਪੀਣ ਦੀ ਪ੍ਰਥਾ ਆਮ ਹੋ ਗਈ ਸੀ । ਸ਼ਰਾਬ ਤੋਂ ਇਲਾਵਾ ਉਹ ਅਫ਼ੀਮ ਅਤੇ ਭੰਗ ਦੀ ਵੀ ਵਰਤੋਂ ਕਰਦੇ ਸਨ । ਨੀਵੀਂ ਸ਼੍ਰੇਣੀ ਨਾਲ ਸੰਬੰਧਿਤ ਲੋਕਾਂ ਦਾ ਖਾਣਾ ਸਾਧਾਰਨ ਹੁੰਦਾ ਸੀ ।
4. ਪਹਿਰਾਵਾ (Dress) – ਉੱਚ ਸ਼੍ਰੇਣੀ ਦੇ ਮੁਸਲਮਾਨਾਂ ਦੀਆਂ ਪੁਸ਼ਾਕਾਂ ਬਹੁਤ ਕੀਮਤੀ ਹੁੰਦੀਆਂ ਸਨ । ਇਹ ਪੁਸ਼ਾਕਾਂ ਰੇਸ਼ਮ ਅਤੇ ਮਖਮਲ ਦੀਆਂ ਬਣੀਆਂ ਹੁੰਦੀਆਂ ਸਨ । ਨੀਵੀਂ ਸ਼੍ਰੇਣੀ ਦੇ ਲੋਕ ਸੂਤੀ ਕੱਪੜੇ ਪਹਿਨਦੇ ਸਨ । ਪੁਰਸ਼ਾਂ ਵਿੱਚ ਕੁੜਤਾ ਅਤੇ ਪਜਾਮਾ ਪਾਉਣ ਦਾ ਰਿਵਾਜ ਸੀ, ਜਦ ਕਿ ਇਸਤਰੀਆਂ ਲੰਬਾ ਬੁਰਕਾ ਪਾਉਂਦੀਆਂ ਸਨ ।
5. ਸਿੱਖਿਆ (Education) – 16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਮੁਸਲਮਾਨਾਂ ਨੂੰ ਸਿੱਖਿਆ ਦੇਣ ਦਾ ਕੰਮ ਉਲਮਾ, ਮੁੱਲਾਂ ਤੇ ਮੌਲਵੀ ਕਰਦੇ ਸਨ । ਉਹ ਮਸਜਿਦਾਂ, ਮਕਤਬਿਆਂ ਅਤੇ ਮਦਰੱਸਿਆਂ ਵਿੱਚ ਸਿੱਖਿਆ ਦਿੰਦੇ ਸਨ | ਮਸਜਿਦਾਂ ਅਤੇ ਮਕਤਬਿਆਂ ਵਿੱਚ ਮੁੱਢਲੀ ਸਿੱਖਿਆ ਦਿੱਤੀ ਜਾਂਦੀ ਸੀ ਜਦਕਿ ਮਦਰੱਸਿਆਂ ਵਿੱਚ ਉਚੇਰੀ । ਉਸ ਸਮੇਂ ਮੁਸਲਮਾਨਾਂ ਦੇ ਪੰਜਾਬ ਵਿੱਚ ਸਭ ਤੋਂ ਪ੍ਰਸਿੱਧ ਸਿੱਖਿਆ ਕੇਂਦਰ ਲਾਹੌਰ ਅਤੇ ਮੁਲਤਾਨ ਵਿੱਚ ਸਨ ।
6. ਮਨੋਰੰਜਨ ਦੇ ਸਾਧਨ (Means of Entertainment) – ਮੁਸਲਮਾਨ ਆਪਣਾ ਮਨੋਰੰਜਨ ਕਈ ਢੰਗਾਂ ਨਾਲ ਕਰਦੇ ਸਨ । ਉਹ ਸ਼ਿਕਾਰ ਕਰਨ, ਚੌਗਾਨ ਖੇਡਣ, ਜਾਨਵਰਾਂ ਦੀਆਂ ਲੜਾਈਆਂ ਵੇਖਣ ਅਤੇ ਘੋੜਦੌੜ ਵਿੱਚ ਹਿੱਸਾ ਲੈਣ ਦੇ ਬਹੁਤ ਸ਼ੌਕੀਨ ਸਨ । ਉਹ ਸ਼ਤਰੰਜ ਅਤੇ ਚੌਪੜ ਖੇਡ ਕੇ ਵੀ ਆਪਣਾ ਮਨੋਰੰਜਨ ਕਰਦੇ ਸਨ ।
II. ਹਿੰਦੂ ਸਮਾਜ ਦੀਆਂ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ (Features of the Hindu Society)
16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਹਿੰਦੂ ਸਮਾਜ ਦੀਆਂ ਮੁੱਖ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਹੇਠ ਲਿਖੀਆਂ ਸਨ-
1. ਜਾਤੀ ਪ੍ਰਥਾ (Caste System) – ਹਿੰਦੂ ਸਮਾਜ ਕਈ ਜਾਤਾਂ ਅਤੇ ਉਪ-ਜਾਤਾਂ ਵਿੱਚ ਵੰਡਿਆ ਹੋਇਆ ਸੀ । ਸਮਾਜ ਵਿੱਚ ਸਭ ਤੋਂ ਉੱਚਾ ਸਥਾਨ ਬ੍ਰਾਹਮਣਾਂ ਨੂੰ ਪ੍ਰਾਪਤ ਸੀ । ਮੁਸਲਿਮ ਸ਼ਾਸਨ ਦੀ ਸਥਾਪਨਾ ਕਾਰਨ ਬ੍ਰਾਹਮਣਾਂ ਦੇ ਪ੍ਰਭਾਵ ਵਿੱਚ ਕਾਫੀ ਕਮੀ ਆ ਗਈ ਸੀ । ਇਸੇ ਕਾਰਨ ਭਾਵ ਮੁਸਲਿਮ ਸ਼ਾਸਨ ਕਾਰਨ ਹੀ ਕਸ਼ੱਤਰੀਆਂ ਨੇ ਨਵੇਂ ਕਿੱਤੇ ਜਿਵੇਂ ਦੁਕਾਨਦਾਰੀ, ਖੇਤੀ-ਬਾੜੀ ਆਦਿ ਅਪਣਾ ਲਏ ਸਨ । ਵੈਸ਼ ਵਪਾਰ ਅਤੇ ਖੇਤੀਬਾੜੀ ਦਾ ਹੀ ਧੰਦਾ ਕਰਦੇ ਰਹੇ । ਸ਼ੂਦਰਾਂ ਨਾਲ ਇਸ ਕਾਲ ਵਿੱਚ ਵੀ ਮਾੜਾ ਸਲੂਕ ਕੀਤਾ ਜਾਂਦਾ ਰਿਹਾ । ਇਨ੍ਹਾਂ ਜਾਤਾਂ ਤੋਂ ਇਲਾਵਾ ਸਮਾਜ ਵਿੱਚ ਬਹੁਤ ਸਾਰੀਆਂ ਹੋਰ ਜਾਤਾਂ ਤੇ ਉਪ-ਜਾਤਾਂ ਪ੍ਰਚਲਿਤ ਸਨ । ਇਹ ਜਾਤਾਂ ਇੱਕ ਦੂਜੇ ਨਾਲ ਬਹੁਤ ਨਫ਼ਰਤ ਕਰਦੀਆਂ ਸਨ ।
2. ਇਸਤਰੀਆਂ ਦੀ ਸਥਿਤੀ Position of Women) – ਹਿੰਦੂ ਸਮਾਜ ਵਿੱਚ ਇਸਤਰੀਆਂ ਦੀ ਦਸ਼ਾ ਬੜੀ ਤਰਸਯੋਗ ਸੀ । ਸਮਾਜ ਵਿੱਚ ਉਨ੍ਹਾਂ ਦਾ ਦਰਜਾ ਪੁਰਸ਼ਾਂ ਦੇ ਬਰਾਬਰ ਨਹੀਂ ਸੀ । ਲੜਕੀਆਂ ਦੀ ਸਿੱਖਿਆ ਵੱਲ ਕੋਈ ਧਿਆਨ ਨਹੀਂ ਦਿੱਤਾ ਜਾਂਦਾ ਸੀ । ਉਨ੍ਹਾਂ ਦਾ ਛੋਟੀ ਉਮਰ ਵਿੱਚ ਹੀ ਵਿਆਹ ਕਰ ਦਿੱਤਾ ਜਾਂਦਾ ਸੀ । ਇਸ ਕਾਲ ਵਿੱਚ ਸਤੀ ਪ੍ਰਥਾ ਬੜੀ ਜ਼ੋਰਾਂ ‘ਤੇ ਸੀ । ਵਿਧਵਾ ਨੂੰ ਦੁਬਾਰਾ ਵਿਆਹ ਕਰਨ ਦੀ ਇਜਾਜ਼ਤ ਨਹੀਂ ਸੀ ।
3. ਖਾਣ-ਪੀਣ (Diet) – ਹਿੰਦੂਆਂ ਦਾ ਭੋਜਨ ਸਾਦਾ ਹੁੰਦਾ ਸੀ । ਜ਼ਿਆਦਾਤਰ ਹਿੰਦੂ ਸ਼ਾਕਾਹਾਰੀ ਹੁੰਦੇ ਸਨ । ਉਨ੍ਹਾਂ ਦਾ ਭੋਜਨ ਕਣਕ, ਚੌਲ, ਸਬਜ਼ੀਆਂ, ਘਿਉ ਅਤੇ ਦੁੱਧ ਆਦਿ ਤੋਂ ਤਿਆਰ ਕੀਤਾ ਜਾਂਦਾ ਸੀ । ਉਹ ਮਾਸ, ਲਸਣ ਅਤੇ ਪਿਆਜ਼ ਦੀ ਵਰਤੋਂ ਨਹੀਂ ਕਰਦੇ ਸਨ । ਗ਼ਰੀਬ ਲੋਕਾਂ ਦਾ ਭੋਜਨ ਬਹੁਤ ਸਾਧਾਰਨ ਹੁੰਦਾ ਸੀ ।
4. ਪਹਿਰਾਵਾ (Dress) – ਹਿੰਦੂਆਂ ਦਾ ਪਹਿਰਾਵਾ ਬੜਾ ਸਾਦਾ ਹੁੰਦਾ ਸੀ । ਉਹ ਆਮ ਤੌਰ ‘ਤੇ ਸੂਤੀ ਕੱਪੜੇ ਪਾਉਂਦੇ ਸਨ । ਪੁਰਸ਼ ਧੋਤੀ ਅਤੇ ਕੁੜਤਾ ਪਾਉਂਦੇ ਸਨ । ਉਹ ਸਿਰ ‘ਤੇ ਪਗੜੀ ਵੀ ਬੰਦੇ ਸਨ । ਇਸਤਰੀਆਂ ਸਾੜ੍ਹੀ, ਚੋਲੀ ਅਤੇ ਲਹਿੰਗਾ ਪਾਉਂਦੀਆਂ ਸਨ । ਗ਼ਰੀਬ ਲੋਕ ਚਾਦਰ ਨਾਲ ਹੀ ਆਪਣਾ ਸਰੀਰ ਢੱਕ ਲੈਂਦੇ ਸਨ ।
5. ਮਨੋਰੰਜਨ ਦੇ ਸਾਧਨ (Means of Entertainment) – ਹਿੰਦੂ ਨਾਚ, ਗਾਣੇ ਅਤੇ ਸੰਗੀਤ ਦੇ ਬਹੁਤ ਸ਼ੌਕੀਨ ਸਨ । ਉਹ ਤਾਸ਼ ਅਤੇ ਸ਼ਤਰੰਜ ਵੀ ਖੇਡਦੇ ਸਨ । ਪਿੰਡਾਂ ਦੇ ਲੋਕ ਜਾਨਵਰਾਂ ਦੀਆਂ ਲੜਾਈਆਂ ਵੇਖ ਕੇ ਅਤੇ ਘੋਲ ਵੇਖ ਕੇ ਆਪਣਾ ਮਨੋਰੰਜਨ ਕਰਦੇ ਸਨ । ਇਨ੍ਹਾਂ ਤੋਂ ਇਲਾਵਾ ਹਿੰਦੂ ਆਪਣੇ ਤਿਉਹਾਰਾਂ ਦੁਸਹਿਰਾ, ਦੀਵਾਲੀ, ਹੋਲੀ ਆਦਿ ਵਿੱਚ ਵੀ ਹਿੱਸਾ ਲੈਂਦੇ ਸਨ ।
6. ਸਿੱਖਿਆ (Education) – ਹਿੰਦੂ ਲੋਕ ਬ੍ਰਾਹਮਣਾਂ ਤੋਂ ਮੰਦਰਾਂ ਅਤੇ ਪਾਠਸ਼ਾਲਾਵਾਂ ਵਿੱਚ ਸਿੱਖਿਆ ਪ੍ਰਾਪਤ ਕਰਦੇ ਸਨ । ਇਨ੍ਹਾਂ ਵਿੱਚ ਮੁੱਢਲੀ ਸਿੱਖਿਆ ਸੰਬੰਧੀ ਜਾਣਕਾਰੀ ਦਿੱਤੀ ਜਾਂਦੀ ਸੀ । ਪੰਜਾਬ ਵਿੱਚ ਉਚੇਰੀ ਸਿੱਖਿਆ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ ਹਿੰਦੂਆਂ ਦਾ ਕੋਈ ਕੇਂਦਰ ਨਹੀਂ ਸੀ ।
ਉੱਪਰ ਲਿਖਿਤ ਵੇਰਵੇ ਤੋਂ ਸਪੱਸ਼ਟ ਹੈ ਕਿ 16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਮੁਸਲਿਮ ਅਤੇ ਹਿੰਦੂ ਸਮਾਜ ਵਿੱਚ ਅਣਗਿਣਤ ਕੁਰੀਤੀਆਂ ਪ੍ਰਚਲਿਤ ਸਨ । ਸਮਾਜ ਵਿੱਚ ਝੂਠ, ਫ਼ਰੇਬ, ਧੋਖਾ ਅਤੇ ਠੱਗੀ ਆਦਿ ਦਾ ਬੋਲਬਾਲਾ ਸੀ । ਲੋਕਾਂ ਦਾ ਚਰਿੱਤਰ ਬਹੁਤ ਡਿੱਗ ਚੁੱਕਿਆ ਸੀ । ਉਨ੍ਹਾਂ ਵਿੱਚ ਇਨਸਾਨੀਅਤ ਨਾਂ ਦੀ ਕੋਈ ਚੀਜ਼ ਨਹੀਂ ਸੀ ਰਹੀ । ਡਾਕਟਰ ਏ. ਸੀ. ਬੈਨਰਜੀ ਦਾ ਇਹ ਕਹਿਣਾ ਬਿਲਕੁਲ ਠੀਕ ਹੈ,
“ਇਹ ਅਨਿਸ਼ਚਿਤਤਾ ਅਤੇ ਹਲਚਲ ਦਾ ਲੰਬਾ ਹਨ੍ਹੇਰਾ ਕਾਲ ਸੀ ਜਿਸ ਨੇ ਲੋਕਾਂ ਦੇ ਜੀਵਨ ਦੇ ਵੱਖ-ਵੱਖ ਪਹਿਲੂਆਂ ‘ ਤੇ ਆਪਣੇ ਭੈੜੇ ਦਾਗ ਛੱਡੇ । ”
![]()
ਪ੍ਰਸ਼ਨ 3.
ਗੁਰੂ ਨਾਨਕ ਦੇਵ ਜੀ ਦੇ ਜਨਮ ਸਮੇਂ ਪੰਜਾਬ ਦੀ ਰਾਜਨੀਤਿਕ ਅਤੇ ਸਮਾਜਿਕ ਦਸ਼ਾ ਦਾ ਵਰਣਨ ਕਰੋ । (Explain the political and social conditions of the Punjab at the time of the birth of Guru Nanak Dev Ji.)
ਜਾਂ
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦੀ ਰਾਜਨੀਤਿਕ ਅਤੇ ਸਮਾਜਿਕ ਹਾਲਤ ਦਾ ਸੰਖੇਪ ਵਰਣਨ ਕਰੋ । (Give a brief account of the political and social conditions of the Punjab in the beginning of the 16th century.)
ਉੱਤਰ-
ਇਸ ਪ੍ਰਸ਼ਨ ਦੇ ਉੱਤਰ ਲਈ ਵਿਦਿਆਰਥੀ ਕਿਰਪਾ ਕਰਕੇ ਪ੍ਰਸ਼ਨ ਨੰ: 1 ਅਤੇ 2 ਦਾ ਉੱਤਰ ਸਾਂਝੇ ਰੂਪ ਵਿੱਚ ਲਿਖਣ ।
ਆਰਥਿਕ ਸਥਿਤੀ (Economic Condition)
ਪ੍ਰਸ਼ਨ 4.
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦੀ ਖੇਤੀਬਾੜੀ, ਵਪਾਰ ਅਤੇ ਉਦਯੋਗਾਂ ਸੰਬੰਧੀ ਤੁਸੀਂ ਕੀ ਜਾਣਦੇ ਹੋ ?
(What do you know about agriculture, trade and industries of Punjab in the beginning of the sixteenth century ?)
ਜਾਂ
16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦੀ ਆਰਥਿਕ ਦਸ਼ਾ ਦੀਆਂ ਮੁੱਖ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਬਿਆਨ ਕਰੋ ।
(Describe the main features of the economic condition of the Punjab in the beginning of the sixteenth century.)
ਉੱਤਰ-
16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਲੋਕਾਂ ਦੀ ਆਰਥਿਕ ਦਸ਼ਾ ਬਹੁਤ ਚੰਗੀ ਸੀ । ਇਸ ਕਾਲ ਦੇ ਪੰਜਾਬ ਦੇ ਲੋਕਾਂ ਦੇ ਆਰਥਿਕ ਜੀਵਨ ਦਾ ਸੰਖੇਪ ਵੇਰਵਾ ਇਸ ਤਰਾਂ ਹੈ-
1. ਖੇਤੀਬਾੜੀ (Agriculture) – 16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਲੋਕਾਂ ਦਾ ਮੁੱਖ ਕਿੱਤਾ ਖੇਤੀਬਾੜੀ ਸੀ । ਪੰਜਾਬ ਦੀ ਜ਼ਮੀਨ ਬਹੁਤ ਉਪਜਾਉ ਸੀ । ਸਿੰਜਾਈ ਲਈ ਕਿਸਾਨ ਭਾਵੇਂ ਮੁੱਖ ਤੌਰ ‘ਤੇ ਵਰਖਾ ‘ਤੇ ਨਿਰਭਰ ਕਰਦੇ ਸਨ । ਪਰ ਨਹਿਰਾਂ, ਤਲਾਬਾਂ ਅਤੇ ਖੁਹਾਂ ਦੀ ਵੀ ਵਰਤੋਂ ਕੀਤੀ ਜਾਂਦੀ ਸੀ । ਇੱਥੋਂ ਦੀਆਂ ਮੁੱਖ ਫ਼ਸਲਾਂ ਕਣਕ, ਕਪਾਹ, ਸੌਂ, ਮੱਕੀ, ਚੌਲ ਅਤੇ ਗੰਨਾ ਸਨ । ਫ਼ਸਲਾਂ ਦੀ ਭਰਪੂਰ ਪੈਦਾਵਾਰ ਹੋਣ ਕਾਰਨ ਪੰਜਾਬ ਨੂੰ ਭਾਰਤ ਦਾ ਅੰਨ ਭੰਡਾਰ ਕਿਹਾ ਜਾਂਦਾ ਸੀ ।
2. ਉਦਯੋਗ (Industries) – ਖੇਤੀਬਾੜੀ ਤੋਂ ਬਾਅਦ ਪੰਜਾਬ ਦੇ ਲੋਕਾਂ ਦਾ ਦੂਜਾ ਮੁੱਖ ਧੰਦਾ ਉਦਯੋਗ ਸੀ । ਇਹ ਉਦਯੋਗ ਸਰਕਾਰੀ ਵੀ ਸਨ ਅਤੇ ਗੈਰ-ਸਰਕਾਰੀ ਵੀ । ਪੰਜਾਬ ਦੇ ਉਦਯੋਗਾਂ ਵਿੱਚ ਕੱਪੜਾ ਉਦਯੋਗ ਸਭ ਤੋਂ ਵੱਧ ਪ੍ਰਸਿੱਧ ਸੀ । ਇੱਥੇ ਸੂਤੀ, ਊਨੀ ਅਤੇ ਰੇਸ਼ਮੀ ਤਿੰਨਾਂ ਤਰ੍ਹਾਂ ਦੇ ਕੱਪੜੇ ਬਣਾਏ ਜਾਂਦੇ ਸਨ । ਸਮਾਣਾ, ਸੁਨਾਮ, ਸਰਹਿੰਦ, ਦੀਪਾਲਪੁਰ, ਜਲੰਧਰ, ਲਾਹੌਰ ਅਤੇ ਮੁਲਤਾਨ ਇਸ ਉਦਯੋਗ ਦੇ ਪ੍ਰਸਿੱਧ ਕੇਂਦਰ ਸਨ । ਕੱਪੜਾ ਉਦਯੋਗ ਤੋਂ ਇਲਾਵਾ ਉਸ ਸਮੇਂ ਪੰਜਾਬ ਵਿੱਚ ਚਮੜਾ, ਸ਼ਸਤਰ, ਭਾਂਡੇ, ਹਾਥੀ ਦੰਦ ਅਤੇ ਖਿਡੌਣੇ ਆਦਿ ਬਣਾਉਣ ਦੇ ਉਦਯੋਗ ਵੀ ਪ੍ਰਚਲਿਤ ਸਨ ।
3. ਪਸ਼ੂ ਪਾਲਣ (Animal Rearing) – ਪੰਜਾਬ ਦੇ ਕੁਝ ਲੋਕ ਪਸ਼ੂ ਪਾਲਣ ਦਾ ਕਿੱਤਾ ਕਰਦੇ ਸਨ । ਪੰਜਾਬ ਵਿੱਚ ਪਾਲੇ ਜਾਣ ਵਾਲੇ ਮੁੱਖ ਪਸ਼ੂ ਗਊਆਂ, ਬਲਦ, ਮੱਝਾਂ, ਘੋੜੇ, ਖੱਚਰ, ਊਠ, ਭੇਡਾਂ ਅਤੇ ਬੱਕਰੀਆਂ ਆਦਿ ਸਨ । ਇਨ੍ਹਾਂ ਪਸ਼ੂਆਂ ਤੋਂ ਦੁੱਧ, ਉੱਨ ਅਤੇ ਭਾਰ ਢੋਣ ਦਾ ਕੰਮ ਲਿਆ ਜਾਂਦਾ ਸੀ ।
4. ਵਪਾਰ (Trade) – ਪੰਜਾਬ ਦਾ ਵਪਾਰ ਕਾਫ਼ੀ ਵਿਕਸਿਤ ਸੀ । ਵਪਾਰ ਦਾ ਕੰਮ ਕੁਝ ਖ਼ਾਸ ਸ਼੍ਰੇਣੀਆਂ ਦੇ ਹੱਥ ਵਿੱਚ ਹੁੰਦਾ ਹੈ । ਹਿੰਦੂਆਂ ਦੀਆਂ ਖੱਤਰੀ, ਬਾਣੀਏ, ਮਹਾਜਨ, ਸੂਦ ਅਤੇ ਅਰੋੜੇ ਨਾਂ ਦੀਆਂ ਜਾਤੀਆਂ ਅਤੇ ਮੁਸਲਮਾਨਾਂ ਵਿੱਚ ਬੋਹਰਾ ਤੇ ਖੋਜਾ ਨਾਂ ਦੀਆਂ ਜਾਤੀਆਂ ਵਪਾਰ ਦਾ ਕੰਮ ਕਰਦੀਆਂ ਸਨ । ਮਾਲ ਦੀ ਢੋਆ-ਢੁਆਈ ਦਾ ਕੰਮ ਵਣਜਾਰੇ ਕਰਦੇ ਸਨ । ਪੰਜਾਬ ਦਾ ਵਿਦੇਸ਼ੀ ਵਪਾਰ ਮੁੱਖ ਰੂਪ ਨਾਲ ਅਫ਼ਗਾਨਿਸਤਾਨ, ਈਰਾਨ, ਅਰਬ, ਸੀਰੀਆ, ਤਿੱਬਤ, ਭੂਟਾਨ ਅਤੇ ਚੀਨ ਆਦਿ ਦੇਸ਼ਾਂ ਨਾਲ ਹੁੰਦਾ ਸੀ । ਪੰਜਾਬ ਤੋਂ ਇਨ੍ਹਾਂ ਦੇਸ਼ਾਂ ਨੂੰ ਅਨਾਜ, ਕੱਪੜੇ, ਕਪਾਹ, ਰੇਸ਼ਮ ਅਤੇ ਖੰਡ ਨਿਰਯਾਤ ਕੀਤੀ ਜਾਂਦੀ ਸੀ । ਇਨ੍ਹਾਂ ਦੇਸ਼ਾਂ ਤੋਂ ਪੰਜਾਬ ਘੋੜੇ, ਸ਼ਸਤਰ, ਫਰ, ਕਸਤੂਰੀ ਅਤੇ ਮੇਵੇ ਆਦਿ ਆਯਾਤ ਕਰਦਾ ਸੀ ।
5. ਵਪਾਰਿਕ ਨਗਰ (Commercial Towns) – 16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਲਾਹੌਰ ਅਤੇ ਮੁਲਤਾਨ ਪੰਜਾਬ ਦੇ ਦੋ ਸਭ ਤੋਂ ਵੱਧ ਪ੍ਰਸਿੱਧ ਵਪਾਰਿਕ ਨਗਰ ਸਨ । ਇਨ੍ਹਾਂ ਤੋਂ ਇਲਾਵਾ ਪਿਸ਼ਾਵਰ, ਜਲੰਧਰ, ਅੰਮ੍ਰਿਤਸਰ, ਲੁਧਿਆਣਾ, ਫ਼ਿਰੋਜ਼ਪੁਰ, ਸੁਲਤਾਨਪੁਰ, ਸਰਹਿੰਦ, ਸਿਆਲਕੋਟ, ਕੁੱਲੂ, ਚੰਬਾ ਅਤੇ ਕਾਂਗੜਾ ਵੀ ਵਪਾਰਿਕ ਪੱਖ ਤੋਂ ਪੰਜਾਬ ਦੇ ਪ੍ਰਸਿੱਧ ਨਗਰ ਸਨ ।
6. ਜੀਵਨ ਪੱਧਰ (Standard of Living) – ਉਸ ਸਮੇਂ ਪੰਜਾਬ ਦੇ ਲੋਕਾਂ ਦੇ ਜੀਵਨ ਪੱਧਰ ਵਿੱਚ ਬਹੁਤ ਅੰਤਰ ਸੀ । ਮੁਸਲਮਾਨਾਂ ਦੀਆਂ ਉੱਚ ਸ਼੍ਰੇਣੀਆਂ ਦੇ ਲੋਕਾਂ ਕੋਲ ਬਹੁਤ ਧਨ ਸੀ । ਹਿੰਦੂਆਂ ਦੀਆਂ ਉੱਚ ਸ਼੍ਰੇਣੀਆਂ ਦੇ ਕੋਲ ਧਨ ਤਾਂ ਬਹੁਤ ਸੀ ਪਰ ਮੁਸਲਮਾਨ ਉਨ੍ਹਾਂ ਤੋਂ ਇਹ ਧਨ ਲੁੱਟ ਕੇ ਲੈ ਜਾਂਦੇ ਸਨ । ਸਮਾਜ ਵਿੱਚ ਮੱਧ ਸ਼੍ਰੇਣੀ ਦੇ ਮੁਸਲਮਾਨਾਂ ਦਾ ਜੀਵਨ ਪੱਧਰ ਤਾਂ ਚੰਗਾ ਸੀ ਪਰ ਹਿੰਦੂ ਆਪਣਾ ਗੁਜ਼ਾਰਾ ਬੜੀ ਮੁਸ਼ਕਿਲ ਨਾਲ ਕਰਦੇ ਸਨ । ਸਮਾਜ ਵਿੱਚ ਗ਼ਰੀਬਾਂ ਅਤੇ ਕਿਸਾਨਾਂ ਦਾ ਜੀਵਨ ਪੱਧਰ ਬਹੁਤ ਨੀਵਾਂ ਸੀ ।
ਪ੍ਰਸ਼ਨ 5.
ਸੋਲ੍ਹਵੀਂ ਸਦੀ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਲੋਕਾਂ ਦੀ ਸਮਾਜਿਕ ਤੇ ਆਰਥਿਕ ਦਸ਼ਾ ਕਿਹੋ ਜਿਹੀ ਸੀ ? (What were the social and economic condition of people of the Punjab in the 16th century ?)
ਜਾਂ
ਸੋਲ੍ਹਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦੀ ਸਮਾਜਿਕ ਤੇ ਆਰਥਿਕ ਹਾਲਤ ਬਾਰੇ ਵਰਣਨ ਕਰੋ । (What were the social and economic condition of Punjab in the beginning of 16th century ? Discuss it.).
ਉੱਤਰ-
ਇਸ ਪ੍ਰਸ਼ਨ ਦੇ ਉੱਤਰ ਲਈ ਵਿਦਿਆਰਥੀ ਕਿਰਪਾ ਕਰਕੇ ਪ੍ਰਸ਼ਨ ਨੰ: 2 ਅਤੇ 4 ਦਾ ਉੱਤਰ ਸੰਯੁਕਤ ਰੂਪ ਵਿੱਚ ਲਿਖਣ ।
ਧਾਰਮਿਕ ਸਥਿਤੀ (Religious Condition)
ਪ੍ਰਸ਼ਨ 6.
16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਲੋਕਾਂ ਦੀ ਧਾਰਮਿਕ ਦਸ਼ਾ ਦਾ ਸੰਖੇਪ ਵਰਣਨ ਕਰੋ । (Give a brief account of the religious condition of the people of Punjab in the beginning of the 16th century.)
ਉੱਤਰ-
16ਵੀਂ ਸਦੀ ਦੇ ਸੂਰ ਵਿੱਚ ਪੰਜਾਬ ਵਿੱਚ ਦੋ ਮੁੱਖ ਧਰਮ, ਹਿੰਦੂ ਧਰਮ ਅਤੇ ਇਸਲਾਮ ਪ੍ਰਚਲਿਤ ਸਨ । ਇਹ ਦੋਵੇਂ ਧਰਮ ਅੱਗੇ ਕਈ ਸੰਪਰਦਾਵਾਂ ਵਿੱਚ ਵੰਡੇ ਹੋਏ ਸਨ । ਇਨ੍ਹਾਂ ਤੋਂ ਇਲਾਵਾ ਪੰਜਾਬ ਵਿੱਚ ਬੁੱਧ ਧਰਮ ਅਤੇ ਜੈਨ ਧਰਮ ਵੀ ਪ੍ਰਚਲਿਤ ਸਨ । ਇਨ੍ਹਾਂ ਧਰਮਾਂ ਦਾ ਸੰਖੇਪ ਵੇਰਵਾ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਹੈ-
1. ਹਿੰਦੂ ਧਰਮ (Hinduism-16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਲੋਕਾਂ ਦਾ ਸਭ ਤੋਂ ਪ੍ਰਮੁੱਖ ਧਰਮ, ਹਿੰਦੁ ਧਰਮ ਸੀ । ਹਿੰਦੂ ਧਰਮ ਵੇਦਾਂ ਵਿੱਚ ਵਿਸ਼ਵਾਸ ਰੱਖਦਾ ਸੀ । 16ਵੀਂ ਸਦੀ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਲੋਕਾਂ ਵਿੱਚ ਰਾਮਾਇਣ ਅਤੇ ਮਹਾਂਭਾਰਤ ਬਹੁਤ ਹਰਮਨ-ਪਿਆਰੇ ਸਨ । ਇਸ ਕਾਲ ਦੇ ਸਮਾਜ ਵਿੱਚ ਬਾਹਮਣਾਂ ਦਾ ਪ੍ਰਭਾਵ ਸੀ । ਜਨਮ ਤੋਂ ਲੈ ਕੇ ਮੌਤ ਤਕ ਦੇ ਸਾਰੇ ਸੰਸਕਾਰ ਬ੍ਰਾਹਮਣਾਂ ਤੋਂ ਬਿਨਾਂ ਅਧੂਰੇ ਸਮਝੇ ਜਾਂਦੇ ਸਨ । ਉਸ ਸਮੇਂ ਪੰਜਾਬ ਵਿੱਚ ਹਿੰਦੂ ਧਰਮ ਦੀਆਂ ਹੇਠ ਲਿਖੀਆਂ ਸੰਪਰਦਾਵਾਂ ਪ੍ਰਚਲਿਤ ਸਨ-
(ਉ) ਸ਼ੈਵ ਮਤ (Shaivism) – 16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਵਿੱਚ ਸ਼ੈਵ ਮਤ ਕਾਫ਼ੀ ਹਰਮਨ-ਪਿਆਰਾ ਸੀ । ਇੱਥੋਂ ਦੇ ਲੋਕ ਸ਼ਿਵ ਦੇ ਵਧੇਰੇ ਪੁਜਾਰੀ ਸਨ । ਉਨ੍ਹਾਂ ਨੇ ਥਾਂ-ਥਾਂ ਸ਼ਿਵਾਲੇ ਸਥਾਪਿਤ ਕੀਤੇ ਸਨ ਜਿੱਥੇ ਸ਼ੈਵ ਮਤ ਦੀ ਸਿੱਖਿਆ ਦਿੱਤੀ ਜਾਂਦੀ ਸੀ । ਸ਼ੈਵ ਮਤ ਨੂੰ ਮੰਨਣ ਵਾਲੇ ਜੋਗੀ ਅਖਵਾਉਂਦੇ ਸਨ । ਜੋਗੀਆਂ ਦੀ ਮੁੱਖ ਸ਼ਾਖਾ ਨੂੰ ਨਾਥਪੰਥੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਇਸ ਦੀ ਸਥਾਪਨਾ ਗੋਰਖਨਾਥ ਨੇ ਕੀਤੀ ਸੀ । ਕਿਉਂਕਿ ਜੋਗੀ ਕੰਨਾਂ ਵਿੱਚ ਛੇਕ ਕਰਵਾ ਕੇ ਵੱਡੀਆਂ-ਵੱਡੀਆਂ ਮੁੰਦਰਾਂ ਪਾਉਂਦੇ ਸਨ ਇਸ ਲਈ ਉਨ੍ਹਾਂ ਨੂੰ ਕਨਫਟੇ ਜੋਗੀ ਵੀ ਕਿਹਾ ਜਾਂਦਾ ਸੀ । ਪੰਜਾਬ ਵਿੱਚ ਜੋਗੀਆਂ ਦਾ ਮੁੱਖ ਕੇਂਦਰ ਜੇਹਲਮ ਵਿਖੇ ਗੋਰਖਨਾਥ ਦਾ ਟਿੱਲਾ ਸੀ । ਜੋਗੀਆਂ ਨੇ ਬ੍ਰਾਹਮਣਾਂ ਦੀਆਂ ਰਸਮਾਂ ਅਤੇ ਜਾਤੀ ਪ੍ਰਥਾ ਦੇ ਵਿਰੁੱਧ ਪ੍ਰਚਾਰ ਕੀਤਾ ।
(ਅ) ਵੈਸ਼ਨਵ ਮਤ (Vaishnavismਵੈਸ਼ਨਵ ਮਤ ਵੀ ਪੰਜਾਬ ਵਿੱਚ ਕਾਫ਼ੀ ਲੋਕਪ੍ਰਿਅ ਸੀ । ਇਸ ਮਤ ਦੇ ਲੋਕ ਵਿਸ਼ਣੂ ਅਤੇ ਉਸ ਦੇ ਅਵਤਾਰਾਂ ਦੀ ਪੂਜਾ ਕਰਦੇ ਸਨ । ਇਸ ਕਾਲ ਵਿੱਚ ਸ੍ਰੀ ਰਾਮ ਅਤੇ ਸ੍ਰੀ ਕ੍ਰਿਸ਼ਨ ਨੂੰ ਵਿਸ਼ਣੂ ਦੇ ਅਵਤਾਰ ਮੰਨ ਕੇ ਉਨ੍ਹਾਂ ਦੀ ਪੂਜਾ ਕੀਤੀ ਜਾਂਦੀ ਸੀ । ਇਨ੍ਹਾਂ ਦੀ ਯਾਦ ਵਿੱਚ ਪੰਜਾਬ ਵਿੱਚ ਅਨੇਕਾਂ ਥਾਂਵਾਂ ‘ਤੇ ਵਿਸ਼ਾਲ ਅਤੇ ਸੁੰਦਰ ਮੰਦਰਾਂ ਦੀ ਉਸਾਰੀ ਕੀਤੀ ਗਈ । ਇਸ ਮਤ ਦੇ ਪੈਰੋਕਾਰ ਸ਼ਰਾਬ ਅਤੇ ਮੀਟ ਆਦਿ ਦੀ ਵਰਤੋਂ ਨਹੀਂ ਕਰਦੇ ਸਨ ।
(ਸ) ਸ਼ਕਤੀ ਮਤ (Shaktism) – 16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਲੋਕਾਂ ਵਿੱਚ ਸ਼ਕਤੀ ਮਤ ਵੀ ਪ੍ਰਚਲਿਤ ਸੀ । ਇਸ ਮਤ ਨੂੰ ਮੰਨਣ ਵਾਲੇ ਲੋਕ ਦੁਰਗਾ, ਕਾਲੀ ਅਤੇ ਹੋਰ ਦੇਵੀਆਂ ਦੀ ਪੂਜਾ ਕਰਦੇ ਸਨ । ਉਹ ਇਨ੍ਹਾਂ ਦੇਵੀਆਂ ਨੂੰ ਸ਼ਕਤੀ ਦਾ ਪ੍ਰਤੀਕ ਸਮਝਦੇ ਸਨ । ਇਨ੍ਹਾਂ ਦੇਵੀਆਂ ਨੂੰ ਖ਼ੁਸ਼ ਕਰਨ ਲਈ ਪਸ਼ੂਆਂ ਦੀ ਬਲੀ ਚੜਾਈ ਜਾਂਦੀ ਸੀ । ਇਨ੍ਹਾਂ ਦੇਵੀਆਂ ਦੀ ਯਾਦ ਵਿੱਚ ਅਨੇਕਾਂ ਮੰਦਰਾਂ ਦੀ ਉਸਾਰੀ ਕੀਤੀ ਗਈ ਸੀ । ਇਨ੍ਹਾਂ ਵਿੱਚੋਂ ਜਵਾਲਾਮੁਖੀ, ਚਿੰਤਪੁਰਨੀ, ਚਾਮੁੰਡਾ ਦੇਵੀ ਅਤੇ ਨੈਣਾ ਦੇਵੀ ਦੇ ਮੰਦਰ ਬਹੁਤ ਪ੍ਰਸਿੱਧ ਸਨ ।
2. ਇਸਲਾਮ (Islam) – ਇਸਲਾਮ ਦੀ ਸਥਾਪਨਾ ਹਜ਼ਰਤ ਮੁਹੰਮਦ ਸਾਹਿਬ ਨੇ ਸੱਤਵੀਂ ਸਦੀ ਵਿੱਚ ਮੱਕਾ ਵਿੱਚ ਕੀਤੀ ਸੀ । ਉਨ੍ਹਾਂ ਨੇ ਸਮਾਜ ਵਿੱਚ ਪ੍ਰਚਲਿਤ ਸਮਾਜਿਕ-ਧਾਰਮਿਕ ਕੁਰੀਤੀਆਂ ਦਾ ਖੰਡਨ ਕੀਤਾ । ਉਨ੍ਹਾਂ ਨੇ ਇੱਕ ਪਰਮਾਤਮਾ ਅਤੇ ਆਪਸੀ ਭਾਈਚਾਰੇ ਦਾ ਸੰਦੇਸ਼ ਦਿੱਤਾ । 16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਇਸਲਾਮ ਧਰਮ ਦਾ ਪ੍ਰਚਾਰ ਬੜੀ ਤੇਜ਼ੀ ਨਾਲ ਹੋ ਰਿਹਾ ਸੀ । ਇਸ ਦੇ ਦੋ ਪ੍ਰਮੁੱਖ ਕਾਰਨ ਸਨ । ਹਿਲਾ, ਭਾਰਤ ‘ਤੇ ਸ਼ਾਸਨ ਕਰਨ ਵਾਲੇ ਸਾਰੇ ਸੁਲਤਾਨ ਮੁਸਲਮਾਨ ਸਨ । ਦੂਸਰਾ, ਉਨ੍ਹਾਂ ਨੇ ਤਲਵਾਰ ਦੀ ਨੋਕ ‘ਤੇ ਲੋਕਾਂ ਨੂੰ ਜ਼ਬਰਦਸਤੀ ਮੁਸਲਮਾਨ ਬਣਾਇਆ । ਇਸਲਾਮ ਦੇ ਅਨੁਯਾਈ ਸੰਨੀ ਅਤੇ ਸ਼ੀਆ ਨਾਂ ਦੇ ਦੋ ਸੰਪਰਦਾਵਾਂ ਵਿੱਚ ਵੰਡੇ ਹੋਏ ਸਨ । ਸੰਨੀ ਮੁਸਲਮਾਨਾਂ ਦੀ ਗਿਣਤੀ ਵਧੇਰੇ ਸੀ ਅਤੇ ਉਹ ਕੱਟੜ ਵਿਚਾਰਾਂ ਦੇ ਸਨ । ਮੁਸਲਮਾਨਾਂ ਦੇ ਧਾਰਮਿਕ ਨੇਤਾਵਾਂ ਨੂੰ ਉਲਮਾ ਕਿਹਾ ਜਾਂਦਾ ਸੀ । ਉਹ ਇਸਲਾਮੀ ਕਾਨੂੰਨਾਂ ਦੀ ਵਿਆਖਿਆ ਕਰਦੇ ਸਨ ਅਤੇ ਲੋਕਾਂ ਨੂੰ ਪਵਿੱਤਰ ਜੀਵਨ ਬਤੀਤ ਕਰਨ ਦੀ ਪ੍ਰੇਰਣਾ ਦਿੰਦੇ ਸਨ । ਉਹ ਹੋਰਨਾਂ ਧਰਮਾਂ ਨੂੰ ਨਫ਼ਰਤ ਦੀ ਨਜ਼ਰ ਨਾਲ ਵੇਖਦੇ ਸਨ ।
3. ਸੂਫ਼ੀ ਮਤ (Sufism) – ਸੂਫ਼ੀ ਮਤ ਇਸਲਾਮ ਨਾਲ ਸੰਬੰਧਿਤ ਇੱਕ ਸੰਪਰਦਾ ਸੀ । ਇਹ ਮਤ ਪੰਜਾਬ ਵਿੱਚ ਬਹੁਤ ਹਰਮਨ-ਪਿਆਰਾ ਹੋਇਆ । ਇਹ ਮਤ 12 ਸਿਲਸਿਲਿਆਂ ਵਿੱਚ ਵੰਡਿਆ ਹੋਇਆ ਸੀ । ਇਨ੍ਹਾਂ ਵਿੱਚੋਂ ਚਿਸਤੀ ਅਤੇ ਸੁਹਰਾਵਰਦੀ ਸਿਲਸਿਲੇ ਪੰਜਾਬ ਵਿੱਚ ਵਧੇਰੇ ਪ੍ਰਸਿੱਧ ਸਨ । ਪੰਜਾਬ ਵਿੱਚ ਥਾਨੇਸਰ, ਹਾਂਸੀ, ਨਾਰਨੌਲ ਅਤੇ ਪਾਨੀਪਤ ਸੂਫ਼ੀਆਂ ਦੇ ਪ੍ਰਸਿੱਧ ਕੇਂਦਰ ਸਨ । ਇਸ ਮਤ ਦੇ ਲੋਕ ਕੇਵਲ ਇੱਕ ਅੱਲਾਹ ਵਿੱਚ ਵਿਸ਼ਵਾਸ ਰੱਖਦੇ ਸਨ । ਉਹ ਸਾਰੇ ਧਰਮਾਂ ਦਾ ਸਤਿਕਾਰ ਕਰਦੇ ਸਨ । ਉਹ ਮਨੁੱਖ ਦੀ ਸੇਵਾ ਕਰਨਾ ਆਪਣਾ ਸਭ ਤੋਂ ਵੱਡਾ ਕਰਤੱਵ ਸਮਝਦੇ ਸਨ । ਉਹ ਸੰਗੀਤ ਵਿੱਚ ਵਿਸ਼ਵਾਸ ਰੱਖਦੇ ਸਨ । ਸੂਫ਼ੀਆਂ ਨੇ ਹਿੰਦੂਆਂ ਅਤੇ ਮੁਸਲਮਾਨਾਂ ਵਿੱਚ ਆਪਸੀ ਮੇਲ-ਜੋਲ ਰੱਖਣ, ਸੁਲਤਾਨਾਂ ਨੂੰ ਕੱਟੜ ਨੀਤੀ ਦਾ ਤਿਆਗ ਕਰਨ ਲਈ ਪ੍ਰੇਰਿਤ ਕਰਨ, ਸਾਹਿਤ ਅਤੇ ਸੰਗੀਤ ਦੀ ਉੱਨਤੀ ਲਈ ਸ਼ਲਾਘਾਯੋਗ ਯੋਗਦਾਨ ਦਿੱਤਾ ।
4. ਜੈਨ ਮਤ (Jainism) – ਜੈਨ ਮਤ ਪੰਜਾਬ ਦੇ ਵਪਾਰੀ ਵਰਗ ਵਿੱਚ ਪ੍ਰਚਲਿਤ ਸੀ । ਇਸ ਮਤ ਦੇ ਲੋਕ 24 ਤੀਰਥੰਕਰਾਂ, ਤਿੰਨ ਰਤਨਾਂ, ਅਹਿੰਸਾ, ਕਰਮ ਸਿਧਾਂਤ ਅਤੇ ਨਿਰਵਾਣ ਵਿੱਚ ਵਿਸ਼ਵਾਸ ਰੱਖਦੇ ਸਨ । ਉਹ ਈਸ਼ਵਰ ਦੀ ਹੋਂਦ ਵਿੱਚ ਵਿਸ਼ਵਾਸ ਨਹੀਂ ਰੱਖਦੇ ਸਨ ।
5. ਬੁੱਧ ਮਤ (Buddhism) – 16ਵੀਂ ਸਦੀ ਵਿੱਚ ਪੰਜਾਬ ਵਿੱਚ ਬੁੱਧ ਮਤ ਨੂੰ ਹਿੰਦੂ ਮਤ ਦਾ ਹੀ ਇੱਕ ਹਿੱਸਾ ਸਮਝਿਆ ਜਾਂਦਾ ਸੀ । ਮਹਾਤਮਾ ਬੁੱਧ ਨੂੰ ਵਿਸ਼ਣੁ ਦਾ ਹੀ ਇੱਕ ਅਵਤਾਰ ਮੰਨਿਆ ਜਾਣ ਲੱਗਾ । ਪੰਜਾਬ ਦੇ ਬਹੁਤ ਘੱਟ ਲੋਕ ਇਸ ਮਤ ਵਿੱਚ ਸ਼ਾਮਲ ਸਨ ।
ਗੁਰੂ ਨਾਨਕ ਦੇਵ ਜੀ ਨੇ ਆਪਣੀਆਂ ਰਚਨਾਵਾਂ ਵਿੱਚ ਅਨੇਕਾਂ ਥਾਂਵਾਂ ‘ਤੇ 16ਵੀਂ ਸਦੀ ਦੇ ਪੰਜਾਬ ਦੇ ਲੋਕਾਂ ਦੀ ਧਾਰਮਿਕ ਦਸ਼ਾ ਦਾ ਵਰਣਨ ਕੀਤਾ ਹੈ ।ਉਨ੍ਹਾਂ ਦੇ ਅਨੁਸਾਰ ਹਿੰਦੂ ਅਤੇ ਮੁਸਲਮਾਨ ਦੋਨੋਂ ਧਰਮ ਦੇ ਬਾਹਰੀ ਦਿਖਾਵਿਆਂ ਜਿਵੇਂ ਸਰੀਰ ‘ਤੇ ਭਸਮ ਮਲਣੀ, ਮੱਥੇ ‘ਤੇ ਤਿਲਕ ਲਗਾਉਣਾ, ਕੰਨਾਂ ਵਿੱਚ ਮੁੰਦਰਾਂ ਪਾਉਣੀਆਂ, ਨਦੀ ਵਿੱਚ ਇਸ਼ਨਾਨ ਕਰਨਾ, ਰੋਜ਼ੇ ਰੱਖਣਾ ਅਤੇ ਕਬਰਾਂ ਆਦਿ ਦੀ ਪੂਜਾ ‘ਤੇ ਵਧੇਰੇ ਜ਼ੋਰ ਦਿੰਦੇ ਸਨ | ਧਰਮ ਦੀ ਅਸਲੀਅਤ ਨੂੰ ਲੋਕ ਪੂਰੀ ਤਰ੍ਹਾਂ ਭੁਲਾ ਬੈਠੇ ਸਨ । ਅੰਤ ਵਿੱਚ ਅਸੀਂ ਡਾਕਟਰ ਹਰੀ ਰਾਮ ਗੁਪਤਾ ਦੇ ਇਨ੍ਹਾਂ ਸ਼ਬਦਾਂ ਨਾਲ ਸਹਿਮਤ ਹਾਂ,
‘‘ਸੰਖੇਪ ਵਿੱਚ ਗੁਰੂ ਨਾਨਕ ਸਾਹਿਬ ਦੇ ਆਗਮਨ ਸਮੇਂ ਭਾਰਤ ਦੇ ਦੋਨੋਂ ਧਰਮ-ਹਿੰਦੂ ਧਰਮ ਅਤੇ ਇਸਲਾਮ ਭ੍ਰਿਸ਼ਟਾਚਾਰੀ ਅਤੇ ਪਤਿਤ ਹੋ ਚੁੱਕੇ ਸਨ । ਉਹ ਆਪਣੀ ਪਵਿੱਤਰਤਾ ਅਤੇ ਗੌਰਵ ਨੂੰ ਗੁਆ ਚੁੱਕੇ ਸਨ ।’’
![]()
ਪ੍ਰਸ਼ਨ 7.
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦੀ ਸਮਾਜਿਕ ਅਤੇ ਧਾਰਮਿਕ ਅਵਸਥਾ ਦਾ ਵਰਣਨ ਕਰੋ । (Describe the social and religious condition of the Punjab in the beginning of the 16th century.)
ਉੱਤਰ-
ਇਸ ਪ੍ਰਸ਼ਨ ਦੇ ਉੱਤਰ ਲਈ ਵਿਦਿਆਰਥੀ ਕਿਰਪਾ ਕਰਕੇ ਪ੍ਰਸ਼ਨ ਨੰ: 2 ਅਤੇ ਪ੍ਰਸ਼ਨ ਨੰ: 6 ਦਾ ਉੱਤਰ ਸਾਂਝੇ ਤੌਰ ‘ਤੇ ਲਿਖਣ ।
ਸੰਖੇਪ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ (Short Answer Type Questions)
ਪ੍ਰਸ਼ਨ 1.
16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦੀ ਰਾਜਨੀਤਿਕ ਦਸ਼ਾ ਕਿਹੋ ਜਿਹੀ ਸੀ ? (What was the political condition of Punjab in the beginning of the 16th century ?)
ਜਾਂ
16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦੀ ਰਾਜਨੀਤਿਕ ਦਸ਼ਾ ਦਾ ਵਰਣਨ ਕਰੋ । (Explain the political condition of the Punjab in the beginning of the 16th century.) |
ਉੱਤਰ-
16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦੀ ਰਾਜਨੀਤਿਕ ਦਸ਼ਾ ਬੜੀ ਖ਼ਰਾਬ ਸੀ । ਲੋਧੀ ਸੁਲਤਾਨਾਂ ਦੀਆਂ ਗ਼ਲਤ ਨੀਤੀਆਂ ਦੇ ਸਿੱਟੇ ਵਜੋਂ ਇੱਥੇ ਬਦਅਮਨੀ ਫੈਲੀ ਹੋਈ ਸੀ । ਸ਼ਾਸਕ ਵਰਗ ਭੋਗ-ਵਿਲਾਸ ਵਿੱਚ ਡੁੱਬਿਆ ਰਹਿੰਦਾ ਸੀ । ਸਰਕਾਰੀ ਕਰਮਚਾਰੀ, ਕਾਜ਼ੀ ਅਤੇ ਮੁੱਲਾਂ ਭ੍ਰਿਸ਼ਟ ਅਤੇ ਰਿਸ਼ਵਤਖੋਰ ਹੋ ਗਏ ਸਨ । ਮੁਸਲਮਾਨ ਹਿੰਦੂਆਂ ‘ਤੇ ਬਹੁਤ ਅੱਤਿਆਚਾਰ ਕਰਦੇ ਸਨ । ਉਨ੍ਹਾਂ ਨੂੰ ਜ਼ਬਰਦਸਤੀ ਇਸਲਾਮ ਧਰਮ ਵਿੱਚ ਸ਼ਾਮਲ ਕੀਤਾ ਜਾਂਦਾ ਸੀ । ਰਾਜ ਦੀ ਸ਼ਾਸਨ ਵਿਵਸਥਾ ਖੇਰੂੰ-ਖੇਰੂੰ ਹੋ ਕੇ ਰਹਿ ਗਈ ਸੀ ।
ਪ੍ਰਸ਼ਨ 2.
“16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਤਿਕੋਣੇ ਸੰਘਰਸ਼ ਦਾ ਅਖਾੜਾ ਸੀ ” ਵਿਆਖਿਆ ਕਰੋ । (“In the beginning of the 16th century, the Punjab was a cockpit of triangular struggle.” Explain.)
ਜਾਂ
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਵਿੱਚ ਤਿਕੋਣੇ ਸੰਘਰਸ਼ ਦਾ ਵਰਣਨ ਕਰੋ । (Explain the triangular struggle of the Punjab in the beginning of the 16th century.)
ਜਾਂ
ਪੰਜਾਬ ਵਿੱਚ ਤਿਕੋਣੇ ਸੰਘਰਸ਼ ਬਾਰੇ ਤੁਸੀਂ ਕੀ ਜਾਣਦੇ ਹੋ ? (What do you know about the triangular struggle in Punjab ?)
ਜਾਂ
ਪੰਜਾਬ ਵਿੱਚ 16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਹੋਏ ਤਿਕੋਣੇ ਸੰਘਰਸ਼ ਬਾਰੇ ਸੰਖੇਪ ਰੂਪ ਵਿੱਚ ਲਿਖੋ । (Write in brief about the triangular struggle of the Punjab in the beginning of the 16th Century.)
ਉੱਤਰ-
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਤਿਕੋਣੇ ਸੰਘਰਸ਼ ਦਾ ਅਖਾੜਾ ਸੀ । ਇਹ ਤਿਕੋਣਾ ਸੰਘਰਸ਼ ਕਾਬਲ ਦੇ ਸ਼ਾਸਕ ਬਾਬਰ, ਦਿੱਲੀ ਦੇ ਸ਼ਾਸਕ ਇਬਰਾਹੀਮ ਲੋਧੀ ਅਤੇ ਪੰਜਾਬ ਦੇ ਸੂਬੇਦਾਰ ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਵਿਚਾਲੇ ਚਲ ਰਿਹਾ ਸੀ । ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਪੰਜਾਬ ਦਾ ਸੁਤੰਤਰ ਸ਼ਾਸਕ ਬਣਨਾ ਚਾਹੁੰਦਾ ਸੀ । ਇਸ ਸੰਬੰਧੀ ਜਦੋਂ ਇਬਰਾਹੀਮ ਲੋਧੀ ਨੂੰ ਪਤਾ ਚਲਿਆ ਤਾਂ ਉਸ ਨੇ ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਦੇ ਪੁੱਤਰ ਦਿਲਾਵਰ ਖਾਂ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰਕੇ ਕੈਦਖ਼ਾਨੇ ਵਿੱਚ ਸੁੱਟ ਦਿੱਤਾ । ਦਿਲਾਵਰ ਖਾਂ ਕਿਸੇ ਤਰ੍ਹਾਂ ਕੈਦਖ਼ਾਨੇ ਵਿੱਚੋਂ ਭੱਜ ਨਿਕਲਣ ਵਿੱਚ ਕਾਮਯਾਬ ਹੋ ਗਿਆ । ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਨੇ ਇਸ ਅਪਮਾਨ ਦਾ ਬਦਲਾ ਲੈਣ ਲਈ ਬਾਬਰ ਨੂੰ ਭਾਰਤ ਉੱਤੇ ਹਮਲਾ ਕਰਨ ਦਾ ਸੱਦਾ ਦਿੱਤਾ । ਇਸ ਤਿਕੋਣੇ ਸੰਘਰਸ਼ ਦੇ ਅੰਤ ਵਿੱਚ ਬਾਬਰ ਦੀ ਜਿੱਤ ਹੋਈ ।
ਪ੍ਰਸ਼ਨ 3.
ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਕੌਣ ਸੀ ? (Who was Daulat Khan Lodhi ?
ਜਾਂ
ਦੌਲਤ ਖਾਂ ਲੋਧੀ ‘ ਤੇ ਇੱਕ ਸੰਖੇਪ ਨੋਟ ਲਿਖੋ । (Write a short note on Daulat Khan Lodhi.)
ਉੱਤਰ-
ਦੌਲਤ ਖਾਂ ਲੋਧੀ 1500 ਈ. ਵਿੱਚ ਪੰਜਾਬ ਦਾ ਸੂਬੇਦਾਰ ਨਿਯੁਕਤ ਹੋਇਆ ਸੀ ।ਉਹ ਪੰਜਾਬ ਵਿੱਚ ਸੁਤੰਤਰ ਰਾਜ ਦੀ ਸਥਾਪਨਾ ਕਰਨ ਦੇ ਸੁਪਨੇ ਵੇਖ ਰਿਹਾ ਸੀ । ਇਸ ਸੰਬੰਧੀ ਜਦੋਂ ਇਬਰਾਹੀਮ ਲੋਧੀ ਨੂੰ ਪਤਾ ਚਲਿਆ ਤਾਂ ਉਸ ਨੇ ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਨੂੰ ਸ਼ਾਹੀ ਦਰਬਾਰ ਵਿੱਚ ਹਾਜ਼ਰ ਹੋਣ ਲਈ ਕਿਹਾ | ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਨੇ ਆਪਣੇ ਛੋਟੇ ਪੁੱਤਰ ਦਿਲਾਵਰ ਖਾਂ ਨੂੰ ਦਿੱਲੀ ਭੇਜ ਦਿੱਤਾ । ਦਿਲਾਵਰ ਖਾਂ ਨੂੰ ਦਿੱਲੀ ਪਹੁੰਚਦਿਆਂ ਹੀ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰ ਲਿਆ ਗਿਆ । ਛੇਤੀ ਹੀ ਉਹ ਕਿਸੇ ਤਰ੍ਹਾਂ ਜੇਲ੍ਹ ਵਿੱਚੋਂ ਭੱਜਣ ਅਤੇ ਵਾਪਸ ਪੰਜਾਬ ਪਹੁੰਚਣ ਵਿੱਚ ਕਾਮਯਾਬ ਹੋ ਗਿਆ । ਇਸ ਅਪਮਾਨ ਦਾ ਬਦਲਾ ਲੈਣ ਲਈ ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਨੇ ਬਾਬਰ ਨੂੰ ਭਾਰਤ ਉੱਤੇ ਹਮਲਾ ਕਰਨ ਦਾ ਸੱਦਾ ਦਿੱਤਾ ।
ਪ੍ਰਸ਼ਨ 4.
ਬਾਬਰ ਦੇ ਭਾਰਤ ਉੱਤੇ ਹਮਲੇ ਦੇ ਕੋਈ ਤਿੰਨ ਕਾਰਨ ਲਿਖੋ । (Write any three causes of the invasions of Babur over India.)
ਉੱਤਰ-
- ਉਹ ਆਪਣੇ ਸਾਮਰਾਜ ਦਾ ਵਿਸਥਾਰ ਕਰਨਾ ਚਾਹੁੰਦਾ ਸੀ ।
- ਉਹ ਭਾਰਤ ਤੋਂ ਅਪਾਰ ਧਨ ਲੁੱਟਣਾ ਚਾਹੁੰਦਾ ਸੀ ।
- ਉਹ ਭਾਰਤ ਵਿੱਚ ਇਸਲਾਮ ਦਾ ਪ੍ਰਸਾਰ ਕਰਨਾ ਚਾਹੁੰਦਾ ਸੀ ।
ਪ੍ਰਸ਼ਨ 5.
ਬਾਬਰ ਨੇ ਸੈਦਪੁਰ ’ਤੇ ਕਦੋਂ ਹਮਲਾ ਕੀਤਾ ? ਸਿੱਖ ਇਤਿਹਾਸ ਵਿੱਚ ਇਸ ਹਮਲੇ ਦਾ ਕੀ ਮਹੱਤਵ ਹੈ ? (When did Babur invade Saidpur ? What is its importance in the Sikh History ?)
ਜਾਂ
ਬਾਬਰ ਦੇ ਪੰਜਾਬ ‘ਤੇ ਤੀਸਰੇ ਹਮਲੇ ਦਾ ਸੰਖੇਪ ਵਰਣਨ ਕਰੋ । (Give a brief account of Babur’s third invasion over Punjab.)
ਉੱਤਰ-
ਬਾਬਰ ਨੇ ਸੈਦਪੁਰ ‘ਤੇ 1520 ਈ. ਵਿੱਚ ਹਮਲਾ ਕੀਤਾ । ਇੱਥੋਂ ਦੇ ਲੋਕਾਂ ਨੇ ਬਾਬਰ ਦਾ ਮੁਕਾਬਲਾ ਕੀਤਾ । ਸਿੱਟੇ ਵਜੋਂ ਬਾਬਰ ਨੇ ਗੁੱਸੇ ਵਿੱਚ ਆ ਕੇ ਵੱਡੀ ਗਿਣਤੀ ਵਿੱਚ ਲੋਕਾਂ ਨੂੰ ਕਤਲ ਕਰ ਦਿੱਤਾ ਅਤੇ ਲੁੱਟਮਾਰ ਕਰਨ ਮਗਰੋਂ ਉਨ੍ਹਾਂ ਦੇ ਮਕਾਨਾਂ ਅਤੇ ਮਹੱਲਾਂ ਨੂੰ ਅੱਗ ਲਗਾ ਦਿੱਤੀ । ਹਜ਼ਾਰਾਂ ਇਸਤਰੀਆਂ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰ ਲਿਆ ਗਿਆ ਅਤੇ ਉਨ੍ਹਾਂ ਨਾਲ ਬਦਸਲੂਕੀ ਕੀਤੀ ਗਈ । ਗੁਰੂ ਨਾਨਕ ਦੇਵ ਜੀ ਜੋ ਇਸ ਸਮੇਂ ਸੈਦਪੁਰ ਵਿੱਚ ਹੀ ਸਨ, ਨੇ ਬਾਬਰ ਦੀਆਂ ਫ਼ੌਜਾਂ ਵੱਲੋਂ ਲੋਕਾਂ ‘ਤੇ ਕੀਤੇ ਗਏ ਅੱਤਿਆਚਾਰਾਂ ਦਾ ਵਰਣਨ ‘ਬਾਬਰ ਬਾਣੀ ਵਿੱਚ ਕੀਤਾ ਹੈ । ਬਾਅਦ ਵਿੱਚ ਬਾਬਰ ਦੀਆਂ ਫ਼ੌਜਾਂ ਨੇ ਗੁਰੂ ਨਾਨਕ ਸਾਹਿਬ ਜੀ ਨੂੰ ਰਿਹਾਅ ਕਰ ਦਿੱਤਾ ।
![]()
ਪ੍ਰਸ਼ਨ 6.
ਬਾਬਰ ਅਤੇ ਇਬਰਾਹੀਮ ਲੋਧੀ ਵਿਚਕਾਰ ਯੁੱਧ ਕਿੱਥੇ ਤੇ ਕਿਉਂ ਹੋਇਆ ? (Why and where did the battle take place between Babur and Ibrahim Lodhi ?)
ਜਾਂ
ਪਾਨੀਪਤ ਦੀ ਪਹਿਲੀ ਲੜਾਈ ਦਾ ਸੰਖੇਪ ਵਰਣਨ ਕਰੋ । (Give a brief account of the First Battle of Panipat.)
ਜਾਂ
ਪਾਨੀਪਤ ਦੀ ਪਹਿਲੀ ਲੜਾਈ ਅਤੇ ਉਸ ਦੇ ਮਹੱਤਵ ਦਾ ਸੰਖੇਪ ਵਰਣਨ ਕਰੋ । (Explain in brief the First Battle of Panipat and its significance.)
ਉੱਤਰ-
ਬਾਬਰ ਨੇ ਪੰਜਾਬ ਦੀ ਜਿੱਤ ਤੋਂ ਉਤਸਾਹਿਤ ਹੋ ਕੇ ਦਿੱਲੀ ਦੇ ਸੁਲਤਾਨ ਇਬਰਾਹੀਮ ਲੋਧੀ ਵੱਲ ਰੁਖ ਕੀਤਾ । ਇਸ ਉਦੇਸ਼ ਨਾਲ ਉਸ ਨੇ ਆਪਣੀਆਂ ਫ਼ੌਜਾਂ ਨੂੰ ਦਿੱਲੀ ਵੱਲ ਵਧਣ ਦਾ ਹੁਕਮ ਦਿੱਤਾ । 21 ਅਪਰੈਲ, 1526 ਈ. ਨੂੰ ਦੋਹਾਂ ਫ਼ੌਜਾਂ ਵਿਚਾਲੇ ਪਾਨੀਪਤ ਦੀ ਪਹਿਲੀ ਲੜਾਈ ਹੋਈ । ਇਸ ਲੜਾਈ ਵਿੱਚ ਇਬਰਾਹੀਮ ਲੋਧੀ ਦੀ ਹਾਰ ਹੋਈ ਅਤੇ ਉਹ ਲੜਾਈ ਦੇ ਮੈਦਾਨ ਵਿੱਚ ਮਾਰਿਆ ਗਿਆ । ਪਾਨੀਪਤ ਦੀ ਇਸ ਨਿਰਣਾਇਕ ਜਿੱਤ ਕਾਰਨ ਪੰਜਾਬ ਵਿੱਚੋਂ ਲੋਧੀ ਵੰਸ਼ ਦੇ ਸ਼ਾਸਨ ਦਾ ਹਮੇਸ਼ਾਂ ਲਈ ਖ਼ਾਤਮਾ ਹੋ ਗਿਆ ਅਤੇ ਭਾਰਤ ਵਿੱਚ ਮੁਗ਼ਲ ਵੰਸ਼ ਦੀ ਸਥਾਪਨਾ ਹੋਈ ।
ਪ੍ਰਸ਼ਨ 7.
ਪਾਨੀਪਤ ਦੀ ਪਹਿਲੀ ਲੜਾਈ ਵਿੱਚ ਬਾਬਰ ਕਿਉਂ ਜੇਤੂ ਰਿਹਾ ? ਕੋਈ ਤਿੰਨ ਕਾਰਨ ਦੱਸੋ । (What led to the victory of Babur in the First Battle of Panipat ? Write any three causes.)
ਜਾਂ
ਭਾਰਤ ਵਿੱਚ ਬਾਬਰ ਦੀ ਜਿੱਤ ਅਤੇ ਅਫ਼ਗਾਨਾਂ ਦੀ ਹਾਰ ਦੇ ਕਾਰਨਾਂ ਦਾ ਸੰਖੇਪ ਵਰਣਨ ਕਰੋ ।
(Give a brief account of the causes of victory of Babur and defeat of the Afghans in India.)
ਉੱਤਰ-
- ਦਿੱਲੀ ਦਾ ਸੁਲਤਾਨ ਇਬਰਾਹੀਮ ਲੋਧੀ ਆਪਣੇ ਬੁਰੇ ਵਤੀਰੇ ਅਤੇ ਅੱਤਿਆਚਾਰਾਂ ਕਾਰਨ ਬੜਾ ਬਦਨਾਮ ਸੀ ।
- ਇਬਰਾਹੀਮ ਲੋਧੀ ਦੀ ਫ਼ੌਜ ਵੀ ਬੜੀ ਕਮਜ਼ੋਰ ਸੀ ।
- ਬਾਬਰ ਇੱਕ ਯੋਗ ਸੈਨਾਪਤੀ ਸੀ । ਉਸ ਨੂੰ ਲੜਾਈਆਂ ਦਾ ਬਹੁਤ ਤਜਰਬਾ ਸੀ ।
- ਬਾਬਰ ਦੁਆਰਾ ਤੋਪਖ਼ਾਨੇ ਦੀ ਵਰਤੋਂ ਨੇ ਭਾਰੀ ਤਬਾਹੀ ਮਚਾਈ ।
ਪ੍ਰਸ਼ਨ 8.
ਪਾਨੀਪਤ ਦੀ ਪਹਿਲੀ ਲੜਾਈ ਦੇ ਤਿੰਨ ਮੁੱਖ ਸਿੱਟੇ ਲਿਖੋ । (Write the three main results of the First Battle of Panipat.)
ਉੱਤਰ-
- ਲੋਧੀ ਵੰਸ਼ ਦਾ ਅੰਤ ਹੋ ਗਿਆ ।
- ਮੁਗਲ ਸਾਮਰਾਜ ਦੀ ਸਥਾਪਨਾ ਹੋ ਗਈ ।
- ਨਵੀਂ ਯੁੱਧ ਪ੍ਰਣਾਲੀ ਦਾ ਆਰੰਭ ਹੋਇਆ ।
ਪ੍ਰਸ਼ਨ 9.
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦੀ ਸਮਾਜਿਕ ਅਵਸਥਾ ਕਿਹੋ ਜਿਹੀ ਸੀ ? (What was the social condition of the Punjab in the beginning of the 16th century ?)
ਜਾਂ
ਗੁਰੂ ਨਾਨਕ ਦੇਵ ਜੀ ਦੇ ਜਨਮ ਸਮੇਂ ਪੰਜਾਬ ਦੀ ਸਮਾਜਿਕ ਦਸ਼ਾ ਦੇ ਬਾਰੇ ਤੁਸੀਂ ਕੀ ਜਾਣਦੇ ਹੋ ? (What do you know about the social condition of the Punjab at the time of birth of Guru Nanak Dev ji ?)
ਉੱਤਰ-
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦਾ ਸਮਾਜ ਮੁਸਲਮਾਨਾਂ ਅਤੇ ਹਿੰਦੂਆਂ ਵਿੱਚ ਵੰਡਿਆ ਹੋਇਆ ਸੀ । ਮੁਸਲਮਾਨਾਂ ਨੂੰ ਖ਼ਾਸ ਅਧਿਕਾਰ ਪ੍ਰਾਪਤ ਸਨ ਕਿਉਂਕਿ ਉਹ ਸ਼ਾਸਕ ਵਰਗ ਨਾਲ ਸੰਬੰਧਿਤ ਸਨ । ਉਨ੍ਹਾਂ ਨੂੰ ਰਾਜ ਦੇ ਉੱਚ ਅਹੁਦਿਆਂ ‘ਤੇ ਨਿਯੁਕਤ ਕੀਤਾ ਜਾਂਦਾ ਸੀ । ਦੂਜੇ ਪਾਸੇ ਹਿੰਦੂਆਂ ਨੂੰ ਲਗਭਗ ਸਾਰੇ ਅਧਿਕਾਰਾਂ ਤੋਂ ਵਾਂਝਿਆਂ ਰੱਖਿਆ ਗਿਆ ਸੀ । ਮੁਸਲਮਾਨ ਉਨ੍ਹਾਂ ਨੂੰ ਕਾਫ਼ਰ ਕਹਿੰਦੇ ਸਨ । ਮੁਸਲਮਾਨ ਹਿੰਦੂਆਂ ‘ਤੇ ਬਹੁਤ ਅੱਤਿਆਚਾਰ ਕਰਦੇ ਸਨ । ਉਸ ਸਮੇਂ ਸਮਾਜ ਵਿੱਚ ਇਸਤਰੀਆਂ ਦੀ ਹਾਲਤ ਬਹੁਤ ਤਰਸਯੋਗ ਸੀ ।
ਪ੍ਰਸ਼ਨ 10.
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦੀਆਂ ਇਸਤਰੀਆਂ ਦੀ ਸਥਿਤੀ ਕਿਹੋ ਜਿਹੀ ਸੀ ? (What was the social condition of women in the Punjab in the beginning of the the 16th century ?)
ਜਾਂ
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਵਿੱਚ ਔਰਤਾਂ ਦੀ ਹਾਲਤ ਦੇ ਬਾਰੇ ਵਿੱਚ ਵਰਣਨ ਕਰੋ । (Describe about the condition of women in the Punjab in the beginning of 16th century.)
ਉੱਤਰ-
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦੀਆਂ ਇਸਤਰੀਆਂ ਦੀ ਸਮਾਜਿਕ ਦਸ਼ਾ ਬਹੁਤ ਤਰਸਯੋਗ ਸੀ । ਹਿੰਦੂ ਸਮਾਜ ਵਿੱਚ ਇਸਤਰੀਆਂ ਨੂੰ ਪੁਰਸ਼ਾਂ ਦੇ ਬਰਾਬਰ ਨਹੀਂ ਸਮਝਿਆ ਜਾਂਦਾ ਸੀ । ਉਸ ਸਮੇਂ ਬਹੁਤ ਸਾਰੀਆਂ ਲੜਕੀਆਂ ਨੂੰ ਜੰਮਦੇ ਸਾਰ ਹੀ ਮਾਰ ਦਿੱਤਾ ਜਾਂਦਾ ਸੀ । ਉਨ੍ਹਾਂ ਦਾ ਛੋਟੀ ਉਮਰ ਵਿੱਚ ਹੀ ਵਿਆਹ ਕਰ ਦਿੱਤਾ ਜਾਂਦਾ ਸੀ । ਉਨ੍ਹਾਂ ਦੀ ਸਿੱਖਿਆ ਵੱਲ ਕੋਈ ਧਿਆਨ ਨਹੀਂ ਦਿੱਤਾ ਜਾਂਦਾ ਸੀ । ਉਸ ਸਮੇਂ ਸਤੀ ਪ੍ਰਥਾ ਵੀ ਪੂਰੇ ਜ਼ੋਰਾਂ ‘ਤੇ ਸੀ । ਵਿਧਵਾ ‘ਤੇ ਅਨੇਕਾਂ ਪਾਬੰਦੀਆਂ ਲਗਾਈਆਂ ਗਈਆਂ ਸਨ । ਮੁਸਲਿਮ ਸਮਾਜ ਵਿੱਚ ਵੀ ਇਸਤਰੀਆਂ ਦੀ ਹਾਲਤ ਚੰਗੀ ਨਹੀਂ ਸੀ । ਸਮਾਜ ਵੱਲੋਂ ਉਨ੍ਹਾਂ ‘ਤੇ ਕਈ ਤਰ੍ਹਾਂ ਦੀਆਂ ਪਾਬੰਦੀਆਂ ਲਗਾਈਆਂ ਗਈਆਂ ਸਨ ।
ਪ੍ਰਸ਼ਨ 11.
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਸਮਾਜ ਵਿੱਚ ਮੁਸਲਮਾਨਾਂ ਦੀਆਂ ਸ਼੍ਰੇਣੀਆਂ ਦਾ ਵੇਰਵਾ ਦਿਓ । (Give an account of the Muslim classes of the Punjab in the beginning of the 16th century.)
ਉੱਤਰ-
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਮੁਸਲਿਮ ਸਮਾਜ ਇਨ੍ਹਾਂ ਤਿੰਨ ਸ਼੍ਰੇਣੀਆਂ ਵਿੱਚ ਵੰਡਿਆ ਹੋਇਆ ਸੀ-
- ਉੱਚ ਸ਼੍ਰੇਣੀ – ਉੱਚ ਸ਼੍ਰੇਣੀ ਵਿੱਚ ਅਮੀਰ, ਖ਼ਾਨ, ਸ਼ੇਖ਼, ਕਾਜ਼ੀ ਅਤੇ ਉਲਮਾ ਸ਼ਾਮਲ ਸਨ । ਇਸ ਸ਼੍ਰੇਣੀ ਦੇ ਲੋਕ ਬੜੇ ਐਸ਼ੋ-ਆਰਾਮ ਦਾ ਜੀਵਨ ਬਤੀਤ ਕਰਦੇ ਸਨ ।
- ਮੱਧ ਸ਼੍ਰੇਣੀ – ਮੱਧ ਸ਼੍ਰੇਣੀ ਵਿੱਚ ਵਪਾਰੀ, ਸੈਨਿਕ, ਕਿਸਾਨ ਅਤੇ ਰਾਜ ਦੇ ਛੋਟੇ ਕਰਮਚਾਰੀ ਸ਼ਾਮਲ ਸਨ । ਉਨ੍ਹਾਂ ਦੇ ਜੀਵਨ ਅਤੇ ਉੱਚ ਸ਼੍ਰੇਣੀ ਦੇ ਲੋਕਾਂ ਦੇ ਜੀਵਨ ਵਿੱਚ ਕਾਫ਼ੀ ਅੰਤਰ ਸੀ ।
- ਨੀਵੀਂ ਸ਼੍ਰੇਣੀ – ਇਸ ਸ਼੍ਰੇਣੀ ਵਿੱਚ ਜ਼ਿਆਦਾਤਰ ਦਾਸ, ਕਾਮੇ ਅਤੇ ਮਜ਼ਦੂਰ ਸ਼ਾਮਲ ਸਨ। ਉਨ੍ਹਾਂ ਨੂੰ ਆਪਣੇ ਜੀਵਨ ਨਿਰਬਾਹ ਲਈ ਸਖ਼ਤ ਮਿਹਨਤ ਕਰਨੀ ਪੈਂਦੀ ਸੀ ।
![]()
ਪ੍ਰਸ਼ਨ 12.
16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਸਮਾਜ ਵਿੱਚ ਮੁਸਲਮਾਨਾਂ ਦੀ ਸਮਾਜਿਕ ਹਾਲਤ ਕਿਹੋ ਜਿਹੀ ਸੀ ? (What was the condition of the Muslims in the society of the Punjab in the beginning of the 16th century ?)
ਜਾਂ
ਗੁਰੂ ਨਾਨਕ ਦੇਵ ਜੀ ਦੇ ਜਨਮ ਸਮੇਂ ਪੰਜਾਬ ਦੇ ਮੁਸਲਮਾਨ ਸਮਾਜ ਦੀ ਦਸ਼ਾ ਤੇ ਚਾਨਣਾ ਪਾਓ । (Throw light on the condition of Muslim society of Punjab on the eve of Guru Nanak Dev Ji’s birth.)
ਉੱਤਰ-
ਸ਼ਾਸਕ ਵਰਗ ਨਾਲ ਸੰਬੰਧਿਤ ਹੋਣ ਕਾਰਨ 16ਵੀਂ ਸਦੀ ਦੇ ਮੁਸਲਮਾਨਾਂ ਦੀ ਸਥਿਤੀ ਹਿੰਦੂਆਂ ਦੇ ਮੁਕਾਬਲੇ ਬਹੁਤ ਚੰਗੀ ਸੀ । ਉਸ ਸਮੇਂ ਮੁਸਲਿਮ ਸਮਾਜ ਉੱਚ ਸ਼੍ਰੇਣੀ, ਮੱਧ ਸ਼ੇਣੀ ਅਤੇ ਨੀਵੀਂ ਸ਼੍ਰੇਣੀ ਵਿੱਚ ਵੰਡਿਆ ਹੋਇਆ ਸੀ । ਉੱਚ ਸ਼੍ਰੇਣੀ ਵਿੱਚ ਅਮੀਰ, ਖ਼ਾਨ, ਸ਼ੇਖ਼ ਅਤੇ ਮਲਿਕ ਆਦਿ ਸ਼ਾਮਲ ਸਨ । ਇਹ ਬੜੇ ਐਸ਼ੋ-ਆਰਾਮ ਦਾ ਜੀਵਨ ਬਤੀਤ ਕਰਦੇ ਸਨ । ਮੱਧ ਸ਼੍ਰੇਣੀ ਵਿੱਚ ਸੈਨਿਕ, ਵਪਾਰੀ, ਕਿਸਾਨ ਅਤੇ ਰਾਜ ਦੇ ਛੋਟੇ ਕਰਮਚਾਰੀ ਸ਼ਾਮਲ ਸਨ । ਇਹ ਵੀ ਚੰਗਾ ਜੀਵਨ ਨਿਰਬਾਹ ਕਰਦੇ ਸਨ । ਨੀਵੀਂ ਸ਼੍ਰੇਣੀ ਵਿੱਚ ਦਾਸ-ਦਾਸੀਆਂ ਅਤੇ ਮਜ਼ਦੂਰ ਸ਼ਾਮਲ ਸਨ । ਉਨ੍ਹਾਂ ਨੂੰ ਆਪਣੀ ਰੋਜ਼ੀ ਕਮਾਉਣ ਲਈ ਸਖ਼ਤ ਮਿਹਨਤ ਕਰਨੀ ਪੈਂਦੀ ਸੀ ।
ਪ੍ਰਸ਼ਨ 13.
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਵਿੱਚ ਹਿੰਦੂਆਂ ਦੀ ਸਮਾਜਿਕ ਸਥਿਤੀ ਕਿਹੋ ਜਿਹੀ ਸੀ ? (What was the social condition of the Hindus of the Punjab in the beginning of the 16th century ?)
ਉੱਤਰ-
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਸਮਾਜ ਵਿੱਚ ਹਿੰਦੂਆਂ ਦੀ ਹਾਲਤ ਬਹੁਤ ਤਰਸਯੋਗ ਸੀ । ਸਮਾਜ ਦਾ ਬਹੁ ਵਰਗ ਹੁੰਦੇ ਹੋਏ ਵੀ ਉਨ੍ਹਾਂ ਨੂੰ ਲਗਭਗ ਸਾਰੇ ਅਧਿਕਾਰਾਂ ਤੋਂ ਵਾਂਝਿਆਂ ਰੱਖਿਆ ਗਿਆ ਸੀ । ਉਨ੍ਹਾਂ ਨੂੰ ਕਾਫ਼ਰ ਅਤੇ ਜਿੰਮੀ ਕਹਿ ਕੇ ਸੱਦਿਆ ਜਾਂਦਾ ਸੀ । ਉਨ੍ਹਾਂ ਨੂੰ ਜਜ਼ੀਆ ਅਤੇ ਯਾਤਰਾ ਕਰ ਆਦਿ ਦੇਣੇ ਪੈਂਦੇ ਸਨ । ਮੁਸਲਮਾਨ ਹਿੰਦੂਆਂ ਨੂੰ ਜ਼ਬਰਦਸਤੀ ਇਸਲਾਮ ਧਰਮ ਸਵੀਕਾਰ ਕਰਨ ਲਈ ਮਜਬੂਰ ਕਰਦੇ ਸਨ । ਉਸ ਸਮੇਂ ਹਿੰਦੂ ਸਮਾਜ ਕਈ ਜਾਤਾਂ ਅਤੇ ਉਪਜਾਤਾਂ ਵਿੱਚ ਵੰਡਿਆ ਹੋਇਆ ਸੀ । ਉੱਚ ਜਾਤੀ ਦੇ ਲੋਕ ਨੀਵੀਂ ਜਾਤੀ ਦੇ ਲੋਕਾਂ ਨਾਲ ਬਹੁਤ ਨਫ਼ਰਤ ਕਰਦੇ ਸਨ । ਹਿੰਦੂ ਸਮਾਜ ਵਿੱਚ ਇਸਤਰੀਆਂ ਦੀ ਦਸ਼ਾ ਬਹੁਤ ਤਰਸਯੋਗ ਸੀ ।
ਪ੍ਰਸ਼ਨ 14.
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਵਿੱਚ ਪ੍ਰਚਲਿਤ ਸਿੱਖਿਆ ਪ੍ਰਣਾਲੀ ਦੇ ਬਾਰੇ ਸੰਖੇਪ ਜਾਣਕਾਰੀ ਦਿਓ । (Give a brief account of the prevalent education in the Punjab in the beginning of the 16th century.)
ਉੱਤਰ-
16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਸਿੱਖਿਆ ਦੇ ਖੇਤਰ ਵਿੱਚ ਕੋਈ ਖ਼ਾਸ ਉੱਨਤੀ ਨਹੀਂ ਹੋਈ ਸੀ । ਮੁਸਲਮਾਨਾਂ ਨੂੰ ਸਿੱਖਿਆ ਦੇਣ ਦਾ ਕੰਮ ਉਲ, ਮੁੱਲਾਂ ਤੇ ਮੌਲਵੀ ਕਰਦੇ ਸਨ । ਉਹ ਮਸਜਿਦਾਂ, ਮਕਤਬਿਆਂ ਅਤੇ ਮਦਰੱਸਿਆਂ ਵਿੱਚ ਸਿੱਖਿਆ ਦਿੰਦੇ ਸਨ | ਰਾਜ ਸਰਕਾਰ ਉਨ੍ਹਾਂ ਨੂੰ ਅਨੁਦਾਨ ਦਿੰਦੀ ਸੀ । ਉਸ ਸਮੇਂ ਮੁਸਲਮਾਨਾਂ ਦੇ ਪੰਜਾਬ ਵਿੱਚ ਸਭ ਤੋਂ ਪ੍ਰਸਿੱਧ ਸਿੱਖਿਆ ਕੇਂਦਰ ਲਾਹੌਰ ਅਤੇ ਮੁਲਤਾਨ ਵਿੱਚ ਸਨ ।ਹਿੰਦੂ ਲੋਕ ਬ੍ਰਾਹਮਣਾਂ ਤੋਂ ਮੰਦਰਾਂ ਅਤੇ ਪਾਠਸ਼ਾਲਾਵਾਂ ਵਿੱਚ ਸਿੱਖਿਆ ਪ੍ਰਾਪਤ ਕਰਦੇ ਸਨ । ਇੱਥੇ ਮੁੱਢਲੀ ਸਿੱਖਿਆ ਸੰਬੰਧੀ ਜਾਣਕਾਰੀ ਦਿੱਤੀ ਜਾਂਦੀ ਸੀ ।
ਪ੍ਰਸ਼ਨ 15.
16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਲੋਕਾਂ ਦੇ ਮਨੋਰੰਜਨ ਦੇ ਸਾਧਨਾਂ ‘ਤੇ ਨੋਟ ਲਿਖੋ । (Write a note on the means of entertainment of the people of the Punjab in the beginning of the 16th century.)
ਉੱਤਰ-
16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਮੁਸਲਮਾਨ ਆਪਣਾ ਮਨੋਰੰਜਨ ਕਈ ਢੰਗਾਂ ਨਾਲ ਕਰਦੇ ਸਨ । ਉਹ ਸ਼ਿਕਾਰ ਕਰਨ, ਚੌਗਾਨ ਖੇਡਣ, ਜਾਨਵਰਾਂ ਦੀਆਂ ਲੜਾਈਆਂ ਵੇਖਣ ਅਤੇ ਘੋੜ-ਦੌੜ ਵਿੱਚ ਹਿੱਸਾ ਲੈਣ ਦੇ ਬਹੁਤ ਸ਼ੌਕੀਨ ਸਨ । ਉਹ ਜਸ਼ਨਾਂ ਅਤੇ ਮਹਿਫ਼ਲਾਂ ਵਿੱਚ ਵੱਧ-ਚੜ੍ਹ ਕੇ ਹਿੱਸਾ ਲੈਂਦੇ ਸਨ । ਉਸ ਸ਼ਤਰੰਜ ਅਤੇ ਚੌਪੜ ਖੇਡ ਕੇ ਵੀ ਆਪਣਾ ਮਨੋਰੰਜਨ ਕਰਦੇ ਸਨ । ਮੁਸਲਮਾਨ ਈਦ, ਨੌਰੋਜ ਅਤੇ ਸ਼ਬ-ਏ-ਬਰਾਤ ਆਦਿ ਤਿਉਹਾਰਾਂ ਨੂੰ ਬੜੀ ਧੂਮਧਾਮ ਨਾਲ ਮਨਾਉਂਦੇ ਸਨ । 16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਹਿੰਦੂ ਨਾਚ, ਗਾਣੇ ਅਤੇ ਸੰਗੀਤ ਦੇ ਬਹੁਤ ਸ਼ੌਕੀਨ ਸਨ । ਉਹ ਤਾਸ਼ ਅਤੇ ਸ਼ਤਰੰਜ ਵੀ ਖੇਡਦੇ ਸਨ ।
ਪ੍ਰਸ਼ਨ 16.
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦੀ ਮਾਲੀ ਹਾਲਤ ਦਾ ਸੰਖੇਪ ਵੇਰਵਾ ਦਿਓ । (Give a brief account of the economic condition of the Punjab in the beginning of the 16th century.)
ਜਾ
16ਵੀਂ ਸਦੀ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਲੋਕਾਂ ਦੀ ਆਰਥਿਕ ਸਥਿਤੀ ਦਾ ਸੰਖੇਪ ਵਰਣਨ ਕਰੋ । (Briefly explain the economic condition of the Punjab during the 16th century.)
ਜਾਂ
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦੀ ਆਰਥਿਕ ਹਾਲਤ ਦਾ ਵਰਣਨ ਕਰੋ । (Briefly mention the economic condition of the Punjab in the beginning of the 16th century.)
ਜਾਂ
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦੀ ਆਰਥਿਕ ਸਥਿਤੀ ਕਿਹੋ ਜਿਹੀ ਸੀ ? (What was the economic condition of the Punjab in the beginning of the 16th century ?)
ਉੱਤਰ-
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਲੋਕ ਆਰਥਿਕ ਤੌਰ ‘ਤੇ ਖ਼ੁਸ਼ਹਾਲ ਸਨ । ਪੰਜਾਬ ਦੇ ਲੋਕਾਂ ਦਾ ਮੁੱਖ ਕਿੱਤਾ ਖੇਤੀਬਾੜੀ ਸੀ । ਪੰਜਾਬ ਦੀ ਜ਼ਮੀਨ ਦੇ ਉਪਜਾਊ ਹੋਣ ਕਾਰਨ, ਸਿੰਜਾਈ ਸਹੁਲਤਾਂ ਕਾਰਨ ਅਤੇ ਲੋਕਾਂ ਦੇ ਮਿਹਨਤੀ ਹੋਣ ਕਾਰਨ ਪੰਜਾਬ ਵਿੱਚ ਫ਼ਸਲਾਂ ਦੀ ਭਰਪੂਰ ਪੈਦਾਵਾਰ ਹੁੰਦੀ ਸੀ । ਇਸੇ ਕਾਰਨ ਪੰਜਾਬ ਨੂੰ ਭਾਰਤ ਦਾ ਅੰਨ ਭੰਡਾਰ ਕਿਹਾ ਜਾਂਦਾ ਸੀ | ਪੰਜਾਬ ਦੀਆਂ ਪ੍ਰਮੁੱਖ ਫ਼ਸਲਾਂ ਕਣਕ, ਚੌਲ, ਮੱਕੀ, ਗੰਨਾ ਅਤੇ ਸੌਂ ਸਨ । ਪੰਜਾਬ ਦੇ ਲੋਕਾਂ ਦਾ ਦੂਜਾ ਮੁੱਖ ਧੰਦਾ ਉਦਯੋਗ ਸੀ । ਉਸ ਸਮੇਂ ਪੰਜਾਬ ਵਿੱਚ ਕੱਪੜਾ ਉਦਯੋਗ, ਚਮੜਾ ਉਦਯੋਗ, ਸ਼ਸਤਰ ਉਦਯੋਗ ਅਤੇ ਲੱਕੜ ਉਦਯੋਗ ਬਹੁਤ ਪ੍ਰਸਿੱਧ ਸਨ । ਉਸ ਸਮੇਂ ਪੰਜਾਬ ਦਾ ਵਪਾਰ ਬਹੁਤ ਵਿਕਸਿਤ ਸੀ ।
![]()
ਪ੍ਰਸ਼ਨ 17.
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦੀ ਖੇਤੀਬਾੜੀ ਸੰਬੰਧੀ ਸੰਖੇਪ ਜਾਣਕਾਰੀ ਦਿਓ । (Give a brief account of the agriculture of Punjab in the beginning of the 16th century.)
ਉੱਤਰ-
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਲੋਕਾਂ ਦਾ ਮੁੱਖ ਕਿੱਤਾ ਖੇਤੀਬਾੜੀ ਸੀ । ਪੰਜਾਬ ਦੀ ਜ਼ਮੀਨ ਬਹੁਤ ਉਪਜਾਊ ਸੀ ! ਵਾਹੀ ਅਧੀਨ ਹੋਰ ਜ਼ਮੀਨ ਲਿਆਉਣ ਲਈ ਰਾਜ ਸਰਕਾਰ ਵੱਲੋਂ ਕਿਸਾਨਾਂ ਨੂੰ ਵਿਸ਼ੇਸ਼ ਸਹੂਲਤਾਂ ਦਿੱਤੀਆਂ ਜਾਂਦੀਆਂ ਸਨ । ਇੱਥੋਂ ਦੇ ਲੋਕ ਵੀ ਬੜੇ ਮਿਹਨਤੀ ਸਨ । ਸਿੰਜਾਈ ਲਈ ਨਹਿਰਾਂ, ਤਲਾਬਾਂ ਅਤੇ ਖੂਹਾਂ ਦੀ ਵਰਤੋਂ ਕੀਤੀ ਜਾਂਦੀ ਸੀ । ਪੰਜਾਬ ਦੀਆਂ ਪ੍ਰਮੁੱਖ ਫ਼ਸਲਾਂ ਕਣਕ, ਜੌ, ਮੱਕੀ, ਚੌਲ ਅਤੇ ਗੰਨਾ ਸਨ । ਫ਼ਸਲਾਂ ਦੀ ਭਰਪੂਰ ਪੈਦਾਵਾਰ ਹੋਣ ਕਾਰਨ ਪੰਜਾਬ ਨੂੰ ਭਾਰਤ ਦਾ ਅੰਨ ਭੰਡਾਰ ਕਿਹਾ ਜਾਂਦਾ ਸੀ ।
ਪ੍ਰਸ਼ਨ 18.
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਉਦਯੋਗਾਂ ਬਾਰੇ ਤੁਸੀਂ ਕੀ ਜਾਣਦੇ ਹੋ ? (What do you know about the Punjab’s industries in the beginning of the 16th century ?)
ਜਾਂ
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਪ੍ਰਮੁੱਖ ਉਦਯੋਗਾਂ ਦਾ ਵੇਰਵਾ ਦਿਓ । (Give an account of the main industries of the Punjab in the beginning of 16th century.)
ਉੱਤਰ-
ਖੇਤੀਬਾੜੀ ਤੋਂ ਬਾਅਦ ਪੰਜਾਬ ਦੇ ਲੋਕਾਂ ਦਾ ਦੂਜਾ ਮੁੱਖ ਧੰਦਾ ਉਦਯੋਗ ਸੀ । ਇਹ ਉਦਯੋਗ ਸਰਕਾਰੀ ਵੀ ਸਨ ਅਤੇ ਗੈਰ-ਸਰਕਾਰੀ ਵੀ | ਸਰਕਾਰੀ ਉਦਯੋਗ ਵੱਡੇ-ਵੱਡੇ ਸ਼ਹਿਰਾਂ ਵਿੱਚ ਸਥਾਪਿਤ ਸਨ ਜਦ ਕਿ ਗੈਰ-ਸਰਕਾਰੀ ਪਿੰਡਾਂ ਵਿੱਚ ਹੀ ਪੰਜਾਬ ਦੇ ਉਦਯੋਗਾਂ ਵਿੱਚ ਕੱਪੜਾ ਉਦਯੋਗ ਸਭ ਤੋਂ ਵੱਧ ਪ੍ਰਸਿੱਧ ਸੀ । ਇੱਥੇ ਸੂਤੀ, ਊਨੀ ਅਤੇ ਰੇਸ਼ਮੀ ਤਿੰਨਾਂ ਤਰ੍ਹਾਂ ਦੇ ਕੱਪੜੇ ਬਣਾਏ ਜਾਂਦੇ ਸਨ । ਕੱਪੜਾ ਉਦਯੋਗ ਤੋਂ ਇਲਾਵਾ ਉਸ ਸਮੇਂ ਪੰਜਾਬ ਵਿੱਚ ਚਮੜਾ, ਸ਼ਸਤਰ, ਭਾਂਡੇ, ਹਾਥੀ ਦੰਦ ਅਤੇ ਖਿਡੌਣੇ ਆਦਿ ਬਣਾਉਣ ਦੇ ਉਦਯੋਗ ਵੀ ਪ੍ਰਚਲਿਤ ਸਨ ।
ਪ੍ਰਸ਼ਨ 19.
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਵਪਾਰ ਦਾ ਸੰਖੇਪ ਵਰਣਨ ਕਰੋ । (Give a brief account of the trade of Punjab in the beginning of the 16th century.)
ਉੱਤਰ-
ਪੰਜਾਬ ਦਾ ਵਪਾਰ ਕਾਫ਼ੀ ਵਿਕਸਿਤ ਸੀ । ਮਾਲ ਦੀ ਢੋਆ-ਢੁਆਈ ਦਾ ਕੰਮ ਵਣਜਾਰੇ ਕਰਦੇ ਸਨ । ਮੇਲਿਆਂ ਅਤੇ ਤਿਉਹਾਰਾਂ ਸਮੇਂ ਵਿਸ਼ੇਸ਼ ਮੰਡੀਆਂ ਲਗਾਈਆਂ ਜਾਂਦੀਆਂ ਸਨ । ਉਸ ਸਮੇਂ ਪੰਜਾਬ ਦਾ ਵਿਦੇਸ਼ੀ ਵਪਾਰ ਮੁੱਖ ਰੂਪ ਵਿੱਚ ਅਫ਼ਗਾਨਿਸਤਾਨ, ਈਰਾਨ, ਅਰਬ, ਸੀਰੀਆ, ਤਿੱਬਤ, ਭੂਟਾਨ ਅਤੇ ਚੀਨ ਆਦਿ ਦੇਸ਼ਾਂ ਨਾਲ ਹੁੰਦਾ ਸੀ । ਪੰਜਾਬ ਤੋਂ ਇਨ੍ਹਾਂ ਦੇਸ਼ਾਂ ਨੂੰ ਅਨਾਜ, ਕੱਪੜੇ, ਕਪਾਹ, ਰੇਸ਼ਮ ਅਤੇ ਖੰਡ ਨਿਰਯਾਤ ਕੀਤੀ ਜਾਂਦੀ ਸੀ । ਇਨ੍ਹਾਂ ਦੇਸ਼ਾਂ ਤੋਂ ਪੰਜਾਬ ਘੋੜੇ, ਸ਼ਸਤਰ, ਫਰ, ਕਸਤੂਰੀ ਅਤੇ ਮੇਵੇ ਆਦਿ ਆਯਾਤ ਕਰਦਾ ਸੀ ।
ਪ੍ਰਸ਼ਨ 20.
16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਲੋਕਾਂ ਦਾ ਜੀਵਨ ਪੱਧਰ ਕਿਹੋ ਜਿਹਾ ਸੀ ? (What was the living standard of the people in the beginning of the 16th century ?)
ਉੱਤਰ-
ਉਸ ਸਮੇਂ ਪੰਜਾਬ ਦੇ ਲੋਕਾਂ ਦਾ ਜੀਵਨ ਪੱਧਰ ਇੱਕੋ ਜਿਹਾ ਨਹੀਂ ਸੀ । ਮੁਸਲਮਾਨਾਂ ਦੀਆਂ ਉੱਚ ਸ਼੍ਰੇਣੀਆਂ ਦੇ ਲੋਕਾਂ ਕੋਲ ਬਹੁਤ ਧਨ ਸੀ ਅਤੇ ਉਹ ਐਸ਼ਪ੍ਰਸਤੀ ਦਾ ਜੀਵਨ ਬਤੀਤ ਕਰਦੇ ਸਨ । ਉਹ ਬੜੇ ਸ਼ਾਨਦਾਰ ਮਹੱਲਾਂ ਵਿੱਚ ਰਹਿੰਦੇ ਸਨ । ਹਿੰਦੂਆਂ ਦੀਆਂ ਉੱਚ ਸ਼੍ਰੇਣੀਆਂ ਦੇ ਕੋਲ ਧਨ ਤਾਂ ਬਹੁਤ ਸੀ ਪਰ ਮੁਸਲਮਾਨ ਉਨ੍ਹਾਂ ਤੋਂ ਇਹ ਧਨ ਲੱਟ ਕੇ ਲੈ ਜਾਂਦੇ ਸਨ । ਸਮਾਜ ਵਿੱਚ ਮੱਧ ਸ਼੍ਰੇਣੀ ਦੇ ਮੁਸਲਮਾਨਾਂ ਦਾ ਜੀਵਨ ਪੱਧਰ ਤਾਂ ਚੰਗਾ ਸੀ ਪਰ ਹਿੰਦੁਆਂ ਦਾ ਜੀਵਨ ਪੱਧਰ ਚੰਗਾ ਨਹੀਂ ਸੀ । ਸਮਾਜ ਵਿੱਚ ਨੀਵੀਂ ਸ਼੍ਰੇਣੀ ਦੇ ਲੋਕ ਨਾ ਤਾਂ ਚੰਗੇ ਕੱਪੜੇ ਪਾ ਸਕਦੇ ਸਨ ਅਤੇ ਨਾ ਹੀ ਚੰਗਾ ਭੋਜਨ ਖਾ ਸਕਦੇ ਸਨ ।
ਪ੍ਰਸ਼ਨ 21.
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਹਿੰਦੂਆਂ ਦੀ ਧਾਰਮਿਕ ਸਥਿਤੀ ਕਿਹੋ ਜਿਹੀ ਸੀ ? (What was the religious condition of Hinduism in the beginning of the 16th century ?)
ਉੱਤਰ-
16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਲੋਕਾਂ ਦਾ ਪ੍ਰਮੁੱਖ ਧਰਮ ਹਿੰਦੂ ਧਰਮ ਸੀ । ਇਹ ਧਰਮ ਭਾਰਤ ਦਾ ਸਭ ਤੋਂ ਪ੍ਰਾਚੀਨ ਧਰਮ ਸੀ । ਇਸ ਧਰਮ ਦੇ ਲੋਕ ਵੇਦਾਂ ਵਿੱਚ ਵਿਸ਼ਵਾਸ ਰੱਖਦੇ ਸਨ । 16ਵੀਂ ਸਦੀ ਦੇ ਪੰਜਾਬ ਵਿੱਚ ਰਾਮਾਇਣ ਅਤੇ ਮਹਾਂਭਾਰਤ ਬਹੁਤ ਹਰਮਨ-ਪਿਆਰੇ ਸਨ । ਉਹ ਅਨੇਕ ਦੇਵੀ-ਦੇਵਤਿਆਂ ਦੀ ਪੂਜਾ, ਤੀਰਥ ਯਾਤਰਾਵਾਂ, ਨਦੀਆਂ ਵਿੱਚ ਇਸ਼ਨਾਨ ਕਰਨ ਨੂੰ ਬਹੁਤ ਪਵਿੱਤਰ ਸਮਝਦੇ ਸਨ । ਉਹ ਬਾਹਮਣਾਂ ਦਾ ਬਹੁਤ ਸਤਿਕਾਰ ਕਰਦੇ ਸਨ । ਬਾਹਮਣਾਂ ਦੇ ਸਹਿਯੋਗ ਤੋਂ ਬਿਨਾਂ ਕੋਈ ਵੀ ਧਾਰਮਿਕ ਕਾਰਜ ਅਧੂਰਾ ਸਮਝਿਆ ਜਾਂਦਾ ਸੀ ।
![]()
ਪ੍ਰਸ਼ਨ 22.
ਇਸਲਾਮ ਬਾਰੇ ਇੱਕ ਸੰਖੇਪ ਨੋਟ ਲਿਖੋ । (Write a short notë on Islam.)
ਜਾਂ
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਵਿੱਚ ਇਸਲਾਮ ਦੀ ਦਸ਼ਾ ਕਿਹੋ ਜਿਹੀ ਸੀ ? (What was the condition of Islam in the beginning of the 16th century ?)
ਉੱਤਰ-
ਹਿੰਦੂ ਧਰਮ ਤੋਂ ਬਾਅਦ ਪੰਜਾਬ ਦਾ ਦੂਸਰਾ ਮੁੱਖ ਧਰਮ ਇਸਲਾਮ ਸੀ । ਇਸ ਦੀ ਸਥਾਪਨਾ ਸੱਤਵੀਂ ਸਦੀ ਵਿੱਚ ਹਜ਼ਰਤ ਮੁਹੰਮਦ ਸਾਹਿਬ ਦੁਆਰਾ ਮੱਕਾ ਵਿੱਚ ਕੀਤੀ ਗਈ ਸੀ । ਉਨ੍ਹਾਂ ਨੇ ਅਰਬ ਸਮਾਜ ਵਿੱਚ ਪ੍ਰਚਲਿਤ ਸਮਾਜਿਕ-ਧਾਰਮਿਕ ਕੁਰੀਤੀਆਂ ਦਾ ਖੰਡਨ ਕੀਤਾ । ਉਨ੍ਹਾਂ ਨੇ ਇੱਕ ਪਰਮਾਤਮਾ ਅਤੇ ਆਪਸੀ ਭਾਈਚਾਰੇ ਦਾ ਪ੍ਰਚਾਰ ਕੀਤਾ । ਉਨ੍ਹਾਂ ਦੇ ਅਨੁਸਾਰ ਹਰ ਮੁਸਲਮਾਨ ਨੂੰ ਪੰਜ ਸਿਧਾਂਤਾਂ ‘ਤੇ ਚਲਣਾ ਚਾਹੀਦਾ ਹੈ । ਇਨ੍ਹਾਂ ਸਿਧਾਂਤਾਂ ਨੂੰ ਜੀਵਨ ਦੇ ਪੰਜ ਥੰਮ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 23.
ਉਲਮਾ ਕੌਣ ਸਨ ? ਉਨ੍ਹਾਂ ਦੇ ਮੁੱਖ ਕੰਮ ਕੀ ਸਨ ? (Who were Ulemas ? What were their main functions ?)
ਉੱਤਰ-
- ਉਲਮਾ ਇਸਲਾਮ ਦੇ ਵਿਦਵਾਨ ਸਨ ।
- ਉਲਮਾ ਦੇ ਮੁੱਖ ਕੰਮ ਹੇਠ ਲਿਖੇ ਸਨ-
- ਉਹ ਇਸਲਾਮੀ ਕਾਨੂੰਨ (ਸ਼ਰੀਅਤ ਦੀ ਵਿਆਖਿਆ ਕਰਦੇ ਸਨ ।
- ਉਹ ਸੁਲਤਾਨ ਨੂੰ ਹਿੰਦੂਆਂ ਵਿਰੁੱਧ ਜ਼ਿਹਾਦ ਲਈ ਪ੍ਰੇਰਿਤ ਕਰਦੇ ਸਨ ।
- ਉਹ ਇਸਲਾਮ ਦੇ ਪਸਾਰ ਲਈ ਯੋਜਨਾਵਾਂ ਤਿਆਰ ਕਰਦੇ ਸਨ ।
ਪ੍ਰਸ਼ਨ 24.
ਸੁੰਨੀਆਂ ਬਾਰੇ ਇੱਕ ਸੰਖੇਪ ਨੋਟ ਲਿਖੋ । (Write a short note on the Sunnis.)
ਜਾਂ
ਸੁੰਨੀ ਮੁਸਲਮਾਨ । (The Sunni Musalman.)
ਉੱਤਰ-
ਪੰਜਾਬ ਦੇ ਮੁਸਲਮਾਨਾਂ ਦੀ ਬਹੁ-ਗਿਣਤੀ ਸੁੰਨੀਆਂ ਦੀ ਸੀ । ਦਿੱਲੀ ਸਲਤਨਤ ਦੇ ਸਾਰੇ ਸੁਲਤਾਨ ਅਤੇ ਮੁਗ਼ਲ ਬਾਦਸ਼ਾਹ ਸੁੰਨੀ ਸਨ । ਇਸ ਲਈ ਉਨ੍ਹਾਂ ਨੇ ਸੁੰਨੀਆਂ ਨੂੰ ਪ੍ਰੋਤਸਾਹਿਤ ਕੀਤਾ ਅਤੇ ਉਨ੍ਹਾਂ ਨੂੰ ਵਿਸ਼ੇਸ਼-ਸਹੂਲਤਾਂ ਦਿੱਤੀਆਂ । ਉਸ ਸਮੇਂ ਨਿਯੁਕਤ ਕੀਤੇ ਜਾਣ ਵਾਲੇ ਸਾਰੇ ਕਾਜ਼ੀ ਮੁਫਤੀ ਅਤੇ ਉਲੇਮਾ ਜੋ ਨਿਆਂ ਅਤੇ ਸਿੱਖਿਆ ਦੇਣ ਦਾ ਕੰਮ ਕਰਦੇ ਸਨ ਉਹ ਸੁੰਨੀ ਸੰਪਰਦਾ ਨਾਲ ਸੰਬੰਧਿਤ ਸਨ । ਸੁੰਨੀ ਹਜ਼ਰਤ ਮੁਹੰਮਦ ਸਾਹਿਬ ਨੂੰ ਆਪਣਾ ਪੈਗੰਬਰ ਸਮਝਦੇ ਸਨ । ਉਹ ਕੁਰਾਨ ਨੂੰ ਆਪਣਾ ਸਭ ਤੋਂ ਪਵਿੱਤਰ ਗ੍ਰੰਥ ਸਮਝਦੇ ਸਨ । ਉਹ ਇੱਕ ਅੱਲ੍ਹਾ ਵਿੱਚ ਵਿਸ਼ਵਾਸ ਰੱਖਦੇ ਸਨ । ਉਹ ਇਸਲਾਮ ਤੋਂ ਬਿਨਾਂ ਕਿਸੇ ਹੋਰ ਧਰਮ ਦੀ ਹੋਂਦ ਨੂੰ ਸਹਿਣ ਕਰਨ ਲਈ ਤਿਆਰ ਨਹੀਂ ਸਨ । ਉਹ ਹਿੰਦੂਆਂ ਦੇ ਕੱਟੜ ਦੁਸ਼ਮਣ ਸਨ ਅਤੇ ਉਨ੍ਹਾਂ ਨੂੰ ਕਾਫ਼ਰ ਸਮਝਦੇ ਸਨ ।
ਪ੍ਰਸ਼ਨ 25.
ਸ਼ੀਆ ਕੌਣ ਸਨ ? ਵਰਣਨ ਕਰੋ । (Who were the Shias ? Explain.)
ਜਾਂ
ਸ਼ੀਆ । (The Shias.)
ਉੱਤਰ-
ਸੁੰਨੀਆਂ ਤੋਂ ਬਾਅਦ ਪੰਜਾਬ ਦੇ ਮੁਸਲਮਾਨਾਂ ਵਿੱਚ ਦੂਸਰਾ ਮਹੱਤਵਪੂਰਨ ਸਥਾਨ ਸ਼ੀਆ ਨੂੰ ਪ੍ਰਾਪਤ ਸੀ । ਉਹ ਵੀ ਸੁੰਨੀਆਂ ਵਾਂਗ ਹਜ਼ਰਤ ਮੁਹੰਮਦ ਸਾਹਿਬ ਨੂੰ ਆਪਣਾ ਪੈਗੰਬਰ ਮੰਨਦੇ ਸਨ ।ਉਹ ਕੁਰਾਨ ਨੂੰ ਆਪਣਾ ਪਵਿੱਤਰ ਗ੍ਰੰਥ ਸਵੀਕਾਰ ਕਰਦੇ ਸਨ । ਉਹ ਇੱਕ ਅੱਲਾ ਵਿੱਚ ਵਿਸ਼ਵਾਸ ਰੱਖਦੇ ਸਨ । ਉਹ ਵੀ ਰੋਜ਼ਾਨਾ ਪੰਜ ਨਮਾਜ਼ਾਂ ਪੜ੍ਹਦੇ ਸਨ । ਉਹ ਵੀ ਰਮਜ਼ਾਨ ਦੇ ਮਹੀਨੇ ਰੋਜ਼ੇ ਰੱਖਦੇ ਸਨ । ਉਹ ਵੀ ਮੱਕੇ ਦੀ ਯਾਤਰਾ ਕਰਨਾ ਜ਼ਰੂਰੀ ਸਮਝਦੇ ਸਨ । ਸ਼ੀਆ ਅਤੇ ਸੁੰਨੀਆਂ ਵਿਚਾਲੇ ਕੁਝ ਅੰਤਰ ਪਾਏ ਗਏ ਸਨ । ਇਨ੍ਹਾਂ ਮਤਭੇਦਾਂ ਕਾਰਨ ਸੁੰਨੀ ਅਤੇ ਸ਼ੀਆ ਇੱਕ-ਦੂਜੇ ਦੇ ਵਿਰੋਧੀ ਹੋ ਗਏ ।
ਪ੍ਰਸ਼ਨ 26.
ਸੂਫ਼ੀ ਮਤ ਦੀਆਂ ਮੁੱਖ ਸਿੱਖਿਆਵਾਂ ਲਿਖੋ । (Write the main teachings of Sufism.)
ਉੱਤਰ-
ਸੂਫ਼ੀ ਮਤ ਇੱਕ ਅੱਲਾ ਵਿੱਚ ਵਿਸ਼ਵਾਸ ਰੱਖਦਾ ਸੀ । ਉਹ ਅੱਲ੍ਹਾ ਨੂੰ ਛੱਡ ਕੇ ਕਿਸੇ ਹੋਰ ਦੀ ਪੂਜਾ ਵਿੱਚ ਵਿਸ਼ਵਾਸ ਨਹੀਂ ਰੱਖਦਾ ਸੀ । ਉਸ ਅਨੁਸਾਰ ਅੱਲ੍ਹਾ ਸਰਵ-ਸ਼ਕਤੀਮਾਨ ਹੈ ਤੇ ਉਹ ਹਰ ਜਗ੍ਹਾ ਮੌਜੂਦ ਹੈ । ਅੱਲ੍ਹਾ ਨੂੰ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ ਉਹ ਪੀਰ ਜਾਂ ਗੁਰੂ ਦਾ ਹੋਣਾ ਬਹੁਤ ਜ਼ਰੂਰੀ ਸਮਝਦਾ ਸੀ । ਉਹ ਸੰਗੀਤ ਵਿੱਚ ਵੀ ਵਿਸ਼ਵਾਸ ਰੱਖਦਾ ਸੀ । ਸੂਫ਼ੀ ਮਤ ਨੇ ਕੱਵਾਲੀ ਗਾਉਣ ਦੀ ਪ੍ਰਥਾ ਚਲਾਈ । ਉਹ ਮਨੁੱਖਾਂ ਦੀ ਸੇਵਾ ਕਰਨੀ ਆਪਣਾ ਜ਼ਰੂਰੀ ਕਰਤੱਵ ਸਮਝਦਾ ਸੀ । ਉਹ ਦੂਸਰੇ ਧਰਮਾਂ ਦਾ ਸਤਿਕਾਰ ਕਰਦਾ ਸੀ ।
![]()
ਵਸਤੁਨਿਸ਼ਠ ਪ੍ਰਸ਼ਨ (Objective Type Questions)
ਇੱਕ ਸ਼ਬਦ ਤੋਂ ਇੱਕ ਵਾਕ ਵਿੱਚ ਉੱਤਰ | (Answer in one Word to one sentence)
ਪ੍ਰਸ਼ਨ 1.
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦੀ ਰਾਜਨੀਤਿਕ ਦਸ਼ਾ ਕਿਹੋ ਜਿਹੀ ਸੀ ?
ਜਾਂ
ਬਾਬਰ ਦੇ ਹਮਲੇ ਸਮੇਂ ਪੰਜਾਬ ਦੀ ਰਾਜਨੀਤਿਕ ਸਥਿਤੀ ਕਿਹੋ ਜਿਹੀ ਸੀ ?
ਉੱਤਰ-
ਬਹੁਤ ਤਰਸਯੋਗ ।
ਪ੍ਰਸ਼ਨ 2.
ਪੰਜਾਬ ਦੀ ਰਾਜਨੀਤਿਕ ਦਸ਼ਾ ਦੇ ਸੰਬੰਧ ਵਿੱਚ ਗੁਰੂ ਨਾਨਕ ਦੇਵ ਜੀ ਕੀ ਫ਼ਰਮਾਉਂਦੇ ਹਨ ?
ਉੱਤਰ-
ਹਰ ਪਾਸੇ ਝੂਠ ਅਤੇ ਰਿਸ਼ਵਤ ਦਾ ਬੋਲਬਾਲਾ ਸੀ ।
ਪ੍ਰਸ਼ਨ 3.
ਗੁਰੁ ਨਾਨਕ ਦੇਵ ਜੀ ਦੇ ਜਨਮ ਸਮੇਂ ਦਿੱਲੀ ਉੱਤੇ ਕਿਹੜੇ ਸੁਲਤਾਨ ਦਾ ਸ਼ਾਸਨ ਸੀ ?
ਜਾਂ
ਲੋਧੀ ਵੰਸ਼ ਦਾ ਮੋਢੀ ਕੌਣ ਸੀ ?
ਉੱਤਰ-
ਬਹਿਲੋਲ ਲੋਧੀ ।
ਪ੍ਰਸ਼ਨ 4.
ਬਹਿਲੋਲ ਲੋਧੀ ਦਾ ਉੱਤਰਾਧਿਕਾਰੀ ਕੌਣ ਬਣਿਆ ?
ਉੱਤਰ-
ਸਿਕੰਦਰ ਲੋਧੀ ।
ਪ੍ਰਸ਼ਨ 5.
ਸਿਕੰਦਰ ਲੋਧੀ ਕੌਣ ਸੀ ?
ਉੱਤਰ-
ਉਹ 1489 ਈ. ਤੋਂ 1517 ਈ. ਤੱਕ ਭਾਰਤ ਦਾ ਸੁਲਤਾਨ ਰਿਹਾ ।
ਪ੍ਰਸ਼ਨ 6.
ਸਿਕੰਦਰ ਲੋਧੀ ਕਦੋਂ ਸਿੰਘਾਸਨ ‘ਤੇ ਬੈਠਿਆ ਸੀ ?
ਉੱਤਰ-
1489 ਈ. ।
![]()
ਪ੍ਰਸ਼ਨ 7.
ਇਬਰਾਹੀਮ ਲੋਧੀ ਕਦੋਂ ਸਿੰਘਾਸਨ ‘ਤੇ ਬੈਠਿਆ ਸੀ ?
ਉੱਤਰ-
1517 ਈ. ਵਿੱਚ ।
ਪ੍ਰਸ਼ਨ 8.
ਲੋਧੀ ਵੰਸ਼ ਦਾ ਅੰਤਿਮ ਸੁਲਤਾਨ ਕੌਣ ਸੀ ?
ਉੱਤਰ-
ਇਬਰਾਹੀਮ ਲੋਧੀ ।
ਪ੍ਰਸ਼ਨ 9.
ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਕੌਣ ਸੀ ?
ਉੱਤਰ-
ਦੌਲਤ ਖਾਂ ਲੋਧੀ 1500 ਈ. ਤੋਂ ਲੈ ਕੇ 1525 ਈ. ਤਕ ਪੰਜਾਬ ਦਾ ਸੂਬੇਦਾਰ ਸੀ ।
ਪ੍ਰਸ਼ਨ 10.
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦਾ ਸ਼ਾਸਕ ਕੌਣ ਸੀ ?
ਉੱਤਰ-
ਦੌਲਤ ਖਾਂ ਲੋਧੀ ।
ਪ੍ਰਸ਼ਨ 11.
ਪੰਜਾਬ ਦੇ ਤਿਕੋਣੇ ਸੰਘਰਸ਼ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ?
ਉੱਤਰ-
16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਇਬਰਾਹੀਮ ਲੋਧੀ, ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਅਤੇ ਬਾਬਰ ਵਿਚਕਾਰ ਚੱਲੇ ਸੰਘਰਸ਼ ਸੀ ।
ਪ੍ਰਸ਼ਨ 12.
ਬਾਬਰ ਕਿੱਥੋਂ ਦਾ ਸ਼ਾਸਕ ਸੀ ?
ਜਾਂ
ਬਾਬਰ ਕੌਣ ਸੀ ?
ਉੱਤਰ-
ਕਾਬਲ ਦਾ ਸ਼ਾਸਕ ।
![]()
ਪ੍ਰਸ਼ਨ 13.
ਬਾਬਰ ਨੇ ਪੰਜਾਬ ਉੱਤੇ ਆਪਣਾ ਪਹਿਲਾ ਹਮਲਾ ਕਦੋਂ ਕੀਤਾ ?
ਉੱਤਰ-
1519 ਈ. ।
ਪ੍ਰਸ਼ਨ 14.
ਬਾਬਰ ਨੇ ਭਾਰਤ ‘ਤੇ ਹਮਲਾ ਕਿਉਂ ਕੀਤਾ ? ਕੋਈ ਇੱਕ ਕਾਰਨ ਲਿਖੋ ।
ਉੱਤਰ-
ਉਹ ਆਪਣੇ ਰਾਜ ਦਾ ਵਿਸਥਾਰ ਕਰਨਾ ਚਾਹੁੰਦਾ ਸੀ ।
ਪ੍ਰਸ਼ਨ 15.
ਗੁਰੂ ਨਾਨਕ ਦੇਵ ਜੀ ਨੇ ਬਾਬਰ ਦੇ ਕਿਹੜੇ ਹਮਲੇ ਦੀ ਤੁਲਨਾ ਪਾਪ ਦੀ ਜੰਝ ਬਰਾਤ) ਨਾਲ ਕੀਤੀ ਹੈ ?
ਉੱਤਰ-
ਸੈਦਪੁਰ ਹਮਲੇ ਦੀ ।
ਪ੍ਰਸ਼ਨ 16.
ਬਾਬਰ ਨੇ ਸੈਦਪੁਰ ‘ ਤੇ ਕਦੋਂ ਹਮਲਾ ਕੀਤਾ ਸੀ ?
ਉੱਤਰ-
1520 ਈ. ਨੂੰ ।
ਪ੍ਰਸ਼ਨ 17.
ਬਾਬਰ ਨੇ ਸੈਦਪੁਰ ‘ਤੇ ਹਮਲੇ ਸਮੇਂ ਸਿੱਖਾਂ ਦੇ ਕਿਹੜੇ ਗੁਰੂ ਸਾਹਿਬਾਨ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕੀਤਾ ਸੀ ?
ਉੱਤਰ-
ਗੁਰੂ ਨਾਨਕ ਸਾਹਿਬ ।
ਪ੍ਰਸ਼ਨ 18.
ਗੁਰੂ ਨਾਨਕ ਦੇਵ ਜੀ ਨੂੰ ਕਿਸ ਮੁਗ਼ਲ ਬਾਦਸ਼ਾਹ ਨੇ ਗ੍ਰਿਫ਼ਤਾਰ ਕੀਤਾ ਸੀ ?
ਉੱਤਰ-
ਬਾਬਰ ਨੇ ।
![]()
ਪ੍ਰਸ਼ਨ 19.
ਪਾਨੀਪਤ ਦੀ ਪਹਿਲੀ ਲੜਾਈ ਕਦੋਂ ਹੋਈ ? ਉੱਤਰ-21 ਅਪਰੈਲ, 1526 ਈ. ।
ਪ੍ਰਸ਼ਨ 20.
ਪਾਨੀਪਤ ਦੀ ਪਹਿਲੀ ਲੜਾਈ ਕਿੰਨ੍ਹਾਂ ਵਿਚਕਾਰ ਹੋਈ ?
ਉੱਤਰ-
ਇਬਰਾਹੀਮ ਲੋਧੀ ਅਤੇ ਬਾਬਰ ।
ਪ੍ਰਸ਼ਨ 21.
ਭਾਰਤ ਵਿੱਚ ਪਾਨੀਪਤ ਦੀ ਪਹਿਲੀ ਲੜਾਈ ਦਾ ਕੋਈ ਇੱਕ ਮਹੱਤਵਪੂਰਨ ਸਿੱਟਾ ਦੱਸੋ ।
ਉੱਤਰ-
ਭਾਰਤ ਵਿੱਚ ਮੁਗ਼ਲ ਵੰਸ਼ ਦੀ ਸਥਾਪਨਾ ਹੋ ਗਈ ।
ਪ੍ਰਸ਼ਨ 22.
ਪਾਨੀਪਤ ਦੀ ਪਹਿਲੀ ਲੜਾਈ ਦੇ ਬਾਅਦ ਭਾਰਤ ਵਿੱਚ ਕਿਸ ਵੰਸ਼ ਦੀ ਸਥਾਪਨਾ ਹੋਈ ?
ਉੱਤਰ-
ਮੁਗ਼ਲ ਵੰਸ਼ ।
ਪ੍ਰਸ਼ਨ 23.
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦਾ ਸਮਾਜ ਕਿਹੜੇ ਦੋ ਮੁੱਖ ਵਰਗਾਂ ਵਿੱਚ ਵੰਡਿਆ ਹੋਇਆ ਸੀ ?
ਉੱਤਰ-
ਮੁਸਲਿਮ ਅਤੇ ਹਿੰਦੁ ।
ਪ੍ਰਸ਼ਨ 24.
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦਾ ਮੁਸਲਿਮ ਸਮਾਜ ਕਿੰਨੇ ਵਰਗਾਂ ਵਿੱਚ ਵੰਡਿਆ ਹੋਇਆ ਸੀ ?
ਉੱਤਰ-
ਤਿੰਨ ।
![]()
ਪ੍ਰਸ਼ਨ 25.
16ਵੀਂ ਸਦੀ ਪੰਜਾਬ ਦੇ ਮੁਸਲਿਮ ਸਮਾਜ ਦੀ ਉੱਚ ਸ਼੍ਰੇਣੀ ਦੀ ਕੋਈ ਇੱਕ ਵਿਸ਼ੇਸ਼ਤਾ ਲਿਖੋ ।
ਉੱਤਰ-
ਉਹ ਬਹੁਤ ਐਸ਼ ਦਾ ਜੀਵਨ ਗੁਜ਼ਾਰਦੇ ਸਨ ।
ਪ੍ਰਸ਼ਨ 26.
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦਾ ਹਿੰਦੂ ਸਮਾਜ ਕਿੰਨੀਆਂ ਜਾਤਾਂ ਵਿੱਚ ਵੰਡਿਆ ਹੋਇਆ ਸੀ ?
ਉੱਤਰ-
ਚਾਰ ।
ਪ੍ਰਸ਼ਨ 27.
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਵਿੱਚ ਇਸਤਰੀਆਂ ਦੀ ਸਥਿਤੀ ਕਿਹੋ ਜਿਹੀ ਸੀ ?
ਉੱਤਰ-
ਬਹੁਤੀ ਚੰਗੀ ਨਹੀਂ ।
ਪ੍ਰਸ਼ਨ 28.
16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਵਿੱਚ ਮੁਸਲਿਮ ਸਿੱਖਿਆ ਦੇ ਕਿਸੇ ਇੱਕ ਪ੍ਰਸਿੱਧ ਕੇਂਦਰ ਦਾ ਨਾਂ ਲਿਖੋ ।
ਉੱਤਰ-
ਲਾਹੌਰ ।
ਪ੍ਰਸ਼ਨ 29.
16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਲੋਕਾਂ ਦਾ ਮੁੱਖ ਕਿੱਤਾ ਕਿਹੜਾ ਸੀ ?
ਉੱਤਰ-
ਖੇਤੀਬਾੜੀ ।
ਪ੍ਰਸ਼ਨ 30.
16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦੀ ਕਿਸੇ ਇੱਕ ਪ੍ਰਮੁੱਖ ਫ਼ਸਲ ਦਾ ਨਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਕਣਕ ।
![]()
ਪ੍ਰਸ਼ਨ 31.
16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦਾ ਸਭ ਤੋਂ ਪ੍ਰਸਿੱਧ ਉਦਯੋਗ ਕਿਹੜਾ ਸੀ ?
ਉੱਤਰ-
ਕੱਪੜਾ ਉਦਯੋਗ ।
ਪ੍ਰਸ਼ਨ 32.
16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਕਿਸੇ ਇੱਕ ਪ੍ਰਸਿੱਧ ਕੇਂਦਰ ਦਾ ਨਾਂ ਦੱਸੋ ਜਿੱਥੇ ਗਰਮ ਕੱਪੜਾ ਤਿਆਰ ਕੀਤਾ ਜਾਂਦਾ ਸੀ ।
ਉੱਤਰ-
ਅੰਮ੍ਰਿਤਸਰ ।
ਪ੍ਰਸ਼ਨ 33.
16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਵਿੱਚੋਂ ਨਿਰਯਾਤ ਕੀਤੀਆਂ ਜਾਣ ਵਾਲੀਆਂ ਦੋ ਪ੍ਰਮੁੱਖ ਵਸਤਾਂ ਦੇ ਨਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਕੱਪੜਾ ਅਤੇ ਅਨਾਜ ।
ਪ੍ਰਸ਼ਨ 34.
16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦੀ ਕਿਸੇ ਇੱਕ ਵਪਾਰਿਕ ਸ਼੍ਰੇਣੀ ਦਾ ਨਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਮਹਾਜਨ ।
ਪ੍ਰਸ਼ਨ 35.
16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਜੋਗੀਆਂ ਦੀ ਮੁੱਖ ਸ਼ਾਖਾ ਨੂੰ ਕੀ ਕਿਹਾ ਜਾਂਦਾ ਸੀ ?
ਉੱਤਰ-
ਨਾਥ ਪੰਥੀ ਜਾਂ ਗੋਰਖ ਪੰਥੀ ।
ਪ੍ਰਸ਼ਨ 36.
ਜੋਗੀ ਕਿਸ ਦੀ ਪੂਜਾ ਕਰਦੇ ਸਨ ?
ਉੱਤਰ-
ਸ਼ਿਵ ਜੀ ।
![]()
ਪ੍ਰਸ਼ਨ 37.
ਜੋਗੀਆਂ ਨੂੰ ਕਨਫਟੇ ਜੋਗੀ ਕਿਉਂ ਕਿਹਾ ਜਾਂਦਾ ਸੀ ?
ਉੱਤਰ-
ਕਿਉਂਕਿ ਜੋਗੀ ਕੰਨਾਂ ਵਿੱਚ ਵੱਡੇ-ਵੱਡੇ ਕੁੰਡਲ ਪਾਉਂਦੇ ਸਨ ।
ਪ੍ਰਸ਼ਨ 38.
ਸ਼ੈਵ ਮਤ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ?
ਉੱਤਰ-
ਇਸ ਮਤ ਦੇ ਲੋਕ ਸ਼ਿਵ ਜੀ ਦੇ ਪੁਜਾਰੀ ਸਨ ।
ਪ੍ਰਸ਼ਨ 39.
ਵੈਸ਼ਨਵ ਮਤ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ?
ਉੱਤਰ-
ਇਸ ਮਤ ਦੇ ਲੋਕ ਵਿਸ਼ਨੂੰ ਅਤੇ ਉਸ ਦੇ ਅਵਤਾਰਾਂ ਦੀ ਪੂਜਾ ਕਰਦੇ ਸਨ ।
ਪ੍ਰਸ਼ਨ 40.
ਸ਼ਕਤੀ ਮਤ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ?
ਉੱਤਰ-
ਇਸ ਮਤ ਦੇ ਲੋਕ ਦੁਰਗਾ, ਕਾਲੀ ਆਦਿ ਦੇਵੀਆਂ ਦੀ ਪੂਜਾ ਕਰਦੇ ਸਨ ।
ਪ੍ਰਸ਼ਨ 41.
ਇਸਲਾਮ ਦੀ ਸਥਾਪਨਾ ਕਿਸ ਨੇ ਕੀਤੀ ਸੀ ?
ਉੱਤਰ-
ਹਜ਼ਰਤ ਮੁਹੰਮਦ ਸਾਹਿਬ ।
ਪ੍ਰਸ਼ਨ 42.
ਇਸਲਾਮ ਕਿੰਨੇ ਥੰਮਾਂ ਵਿੱਚ ਵਿਸ਼ਵਾਸ ਰੱਖਦਾ ਹੈ ?
ਉੱਤਰ-
ਪੰਜ ।
![]()
ਪ੍ਰਸ਼ਨ 43.
ਭਾਰਤ ਵਿੱਚ ਚਿਸ਼ਤੀ ਸਿਲਸਿਲੇ ਦੀ ਨੀਂਹ ਕਿਸ ਨੇ ਰੱਖੀ ਸੀ ?
ਉੱਤਰ-
ਸ਼ੇਖ਼ ਮੁਈਨਉੱਦੀਨ ਚਿਸ਼ਤੀ ।
ਪ੍ਰਸ਼ਨ 44.
ਸ਼ੇਖ਼ ਮੁਈਨਉੱਦੀਨ ਚਿਸ਼ਤੀ ਨੇ ਚਿਸ਼ਤੀ ਸਿਲਸਿਲੇ ਦੀ ਸਥਾਪਨਾ ਕਿੱਥੇ ਕੀਤੀ ਸੀ ?
ਉੱਤਰ-
ਅਜਮੇਰ ।
ਪ੍ਰਸ਼ਨ 45.
ਪੰਜਾਬ ਵਿੱਚ ਚਿਸ਼ਤੀ ਸਿਲਸਿਲੇ ਦਾ ਸਭ ਤੋਂ ਪ੍ਰਸਿੱਧ ਨੇਤਾ ਕੌਣ ਸੀ ?
ਉੱਤਰ-
ਸ਼ੇਖ਼ ਫ਼ਰੀਦ ਜੀ ।
ਪ੍ਰਸ਼ਨ 46.
ਸੁਹਰਾਵਰਦੀ ਸਿਲਸਿਲੇ ਦੀ ਸਥਾਪਨਾ ਕਿਸ ਨੇ ਕੀਤੀ ਸੀ ?
ਉੱਤਰ-
ਸ਼ੇਖ਼ ਬਹਾਉੱਦੀਨ ਜ਼ਕਰੀਆ ।
ਪ੍ਰਸ਼ਨ 47.
ਸ਼ੇਖ਼ ਬਹਾਉੱਦੀਨ ਜ਼ਕਰੀਆ ਨੇ ਸੁਹਰਾਵਰਦੀ ਸਿਲਸਿਲੇ ਦੀ ਸਥਾਪਨਾ ਕਿੱਥੇ ਕੀਤੀ ਸੀ ?
ਉੱਤਰ-
ਮੁਲਤਾਨ ।
ਪ੍ਰਸ਼ਨ 48.
ਸੂਫ਼ੀਆਂ ਦਾ ਕੋਈ ਇੱਕ ਮੁੱਖ ਸਿਧਾਂਤ ਦੱਸੋ ।
ਉੱਤਰ-
ਉਹ ਕੇਵਲ ਅੱਲਾ ਵਿੱਚ ਵਿਸ਼ਵਾਸ ਰੱਖਦੇ ਸਨ ।
![]()
ਪ੍ਰਸ਼ਨ 49.
ਉਲਮਾ ਕੌਣ ਹੁੰਦੇ ਸਨ ?
ਉੱਤਰ-
ਮੁਸਲਮਾਨਾਂ ਦੇ ਧਾਰਮਿਕ ਨੇਤਾ ।
ਪ੍ਰਸ਼ਨ 50.
ਜਜ਼ੀਆ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ?
ਉੱਤਰ-
ਗੈਰ-ਮੁਸਲਮਾਨਾਂ ਤੋਂ ਵਸੂਲ ਕੀਤਾ ਜਾਣ ਵਾਲਾ ਇੱਕ ਧਾਰਮਿਕ ਕਰ ।
ਪ੍ਰਸ਼ਨ 51.
ਭਗਤੀ ਲਹਿਰ ਦਾ ਕੋਈ ਇੱਕ ਮੁੱਖ ਸਿਧਾਂਤ ਲਿਖੋ ।
ਉੱਤਰ-
ਉਹ ਇੱਕ ਪਰਮਾਤਮਾ ਵਿੱਚ ਵਿਸ਼ਵਾਸ ਰੱਖਦੇ ਸਨ ।
ਪ੍ਰਸ਼ਨ 52.
ਪੰਜਾਬ ਵਿੱਚ ਭਗਤੀ ਲਹਿਰ ਦਾ ਮੋਢੀ ਕੌਣ ਸੀ ?
ਉੱਤਰ-
ਗੁਰੂ ਨਾਨਕ ਦੇਵ ਜੀ ।
ਪ੍ਰਸ਼ਨ 53.
ਪੰਜਾਬ ਵਿੱਚ ਕਿਸ ਧਰਮ ਦਾ ਜਨਮ ਹੋਇਆ ?
ਉੱਤਰ-
ਸਿੱਖ ਧਰਮ ਦਾ ।
ਖ਼ਾਲੀ ਥਾਂਵਾਂ ਭਰੋ (Fill in the Blanks)
ਨੋਟ :-ਖ਼ਾਲੀ ਥਾਂਵਾਂ ਭਰੋ :
1. 16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦੀ ਰਾਜਨੀਤਿਕ ਦਸ਼ਾ ਬਹੁਤ ………………………. ਸੀ ।
ਉੱਤਰ-
(ਮਾੜੀ)
![]()
2. ਬਹਿਲੋਲ ਲੋਧੀ ਨੇ ……………………………………… ਵਿੱਚ ਲੋਧੀ ਵੰਸ਼ ਦੀ ਸਥਾਪਨਾ ਕੀਤੀ ਸੀ ।
ਉੱਤਰ-
(1451 ਈ.)
3. 1469 ਈ. ਵਿੱਚ ਗੁਰੂ ਨਾਨਕ ਜੀ ਦੇ ਜਨਮ ਸਮੇਂ ਦਿੱਲੀ ਦਾ ਸੁਲਤਾਨ ………………….. ਸੀ ।
ਉੱਤਰ-
(ਬਹਿਲੋਲ ਲੋਧੀ)
4. ਇਬਰਾਹੀਮ ਲੋਧੀ …………………………………. ਵਿੱਚ ਦਿੱਲੀ ਦੇ ਸਿੰਘਾਸਨ ‘ਤੇ ਬੈਠਿਆ ।
ਉੱਤਰ-
(1517 ਈ.)
5. ਦੌਲਤ ਖਾਂ ਲੋਧੀ ……………………………….. ਈ. ਵਿੱਚ ਪੰਜਾਬ ਦਾ ਸੂਬੇਦਾਰ ਨਿਯੁਕਤ ਹੋਇਆ ।
ਉੱਤਰ-
(1500)
6. 1519 ਈ. ਤੋਂ 1526 ਈ. ਦੇ ਸਮੇਂ ਦੌਰਾਨ ਪੰਜਾਬ ਨੂੰ ਆਪਣੇ ਅਧੀਨ ਕਰਨ ਲਈ ………………………….. ਸੰਘਰਸ਼ ਸ਼ੁਰੂ ਹੋ ਗਿਆ ।
ਉੱਤਰ-
(ਤਿਕੋਣਾ)
7. 1504 ਈ. ਵਿੱਚ ਬਾਬਰ ………………………………. ਦਾ ਸ਼ਾਸਕ ਬਣਿਆ ।
ਉੱਤਰ-
(ਕਾਬਲ)
8. 1519 ਈ. ਤੋਂ 1526 ਈ. ਦੇ ਦੌਰਾਨ ਬਾਬਰ ਨੇ ਪੰਜਾਬ ‘ਤੇ …………………………… ਹਮਲੇ ਕੀਤੇ ।
ਉੱਤਰ-
(ਪੰਜ)
![]()
9. ਬਾਬਰ ਨੇ ਪੰਜਾਬ ‘ਤੇ ਪਹਿਲਾ ਹਮਲਾ ………………………… ਕੀਤਾ ।
ਉੱਤਰ-
(1519 ਈ.)
10. ਬਾਬਰ ਨੇ …………………………… ਹਮਲੇ ਦੇ ਦੌਰਾਨ ਗੁਰੂ ਨਾਨਕ ਦੇਵ ਜੀ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕੀਤਾ ਸੀ ।
ਉੱਤਰ-
(ਸੈਦਪੁਰ)
11. ਪਾਨੀਪਤ ਦੀ ਪਹਿਲੀ ਲੜਾਈ ………………….. ਨੂੰ ਹੋਈ ।
ਉੱਤਰ-
(21 ਅਪਰੈਲ, 1526 ਈ.)
12. 16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦਾ ਮੁਸਲਿਮ ਸਮਾਜ ………………………… ਸ਼੍ਰੇਣੀਆਂ ਵਿੱਚ ਵੰਡਿਆ ਹੋਇਆ ਸੀ।
ਉੱਤਰ-
(ਤਿੰਨ)
13. ਪੰਜਾਬ ਵਿੱਚ ਮੁਸਲਮਾਨਾਂ ਦੇ ਉੱਚ ਸਿੱਖਿਆ ਦੇ ਪ੍ਰਸਿੱਧ ਕੇਂਦਰ ……………………. ਅਤੇ ……………………….. ਸਨ ।
ਉੱਤਰ-
(ਲਾਹੌਰ, ਮੁਲਤਾਨ)
14. 16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਹਿੰਦੂ ਸਮਾਜ ਵਿੱਚ ………………………. ਨੂੰ ਪ੍ਰਮੁੱਖਤਾ ਪ੍ਰਾਪਤ ਸੀ ।
ਉੱਤਰ-
(ਬ੍ਰਾਹਮਣਾਂ)
15. 16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਇਸਤਰੀਆਂ ਦੀ ਦਸ਼ਾ ਚੰਗੀ ………………… ਸੀ ।
ਉੱਤਰ-
(ਨਹੀਂ)
![]()
16. 16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਜ਼ਿਆਦਾਤਰ ਹਿੰਦੂ ……………………… ਭੋਜਨ ਖਾਂਦੇ ਸਨ ।
ਉੱਤਰ-
(ਸ਼ਾਕਾਹਾਰੀ)
17. 16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਲੋਕਾਂ ਦਾ ਮੁੱਖ ਕਿੱਤਾ …………………….. ਸੀ ।
ਉੱਤਰ-
(ਖੇਤੀਬਾੜੀ)
18. 16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦਾ ਸਭ ਤੋਂ ਪ੍ਰਸਿੱਧ ਉਦਯੋਗ …………………………. ਸੀ ।
ਉੱਤਰ-
(ਕੱਪੜਾ ਉਦਯੋਗ)
19. 16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਵਿੱਚ ਗਰਮ ਕੱਪੜਾ ਤਿਆਰ ਕਰਨ ਦੇ ਪ੍ਰਸਿੱਧ ਕੇਂਦਰ …………………. ਅਤੇ …………………. ਸਨ ।
ਉੱਤਰ-
(ਅੰਮ੍ਰਿਤਸਰ, ਕਸ਼ਮੀਰ)
20. 16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ………………………. ਅਤੇ ………………………. ਪੰਜਾਬ ਦੇ ਸਭ ਤੋਂ ਪ੍ਰਸਿੱਧ ਵਪਾਰਿਕ ਕੇਂਦਰ ਸਨ ।
ਉੱਤਰ-
(ਲਾਹੌਰ, ਮੁਲਤਾਨ)
21. ……………………….. ਭਗਤੀ ਲਹਿਰ ਦਾ ਮੌਢੀ ਸੀ
ਉੱਤਰ-
(ਗੁਰੂ ਨਾਨਕ ਦੇਵ ਜੀ)
22. ਜੋਗੀ ਮਤ ਦੀ ਸਥਾਪਨਾ …………………………….. ਨੇ ਕੀਤੀ ਸੀ ।
ਉੱਤਰ-
(ਗੋਰਖਨਾਥ)
![]()
23. ਇਸਲਾਮ ਦਾ ਸੰਸਥਾਪਕ ……………………… ਸੀ ।
ਉੱਤਰ-
(ਹਜ਼ਰਤ ਮੁਹੰਮਦ)
24. ਪੰਜਾਬ ਵਿੱਚ ਚਿਸ਼ਤੀ ਸਿਲਸਿਲੇ ਦਾ ਸਭ ਤੋਂ ਪ੍ਰਸਿੱਧ ਪ੍ਰਚਾਰਕ ………………….. ਸੀ ।
ਉੱਤਰ-
(ਸ਼ੇਖ਼ ਫ਼ਰੀਦ)
ਠੀਕ ਜਾਂ ਗਲਤ (True or False)
ਨੋਟ :-ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚੋਂ ਠੀਕ ਜਾਂ ਗਲਤ ਦੀ ਚੋਣ ਕਰੋ-
1. 16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦੀ ਰਾਜਨੀਤਿਕ ਦਸ਼ਾ ਬਹੁਤ ਚੰਗੀ ਸੀ ।
ਉੱਤਰ-
ਗ਼ਲਤ
2. ਲੋਧੀ ਵੰਸ਼ ਦਾ ਸੰਸਥਾਪਕ ਸਿਕੰਦਰ ਲੋਧੀ ਸੀ ।
ਉੱਤਰ-
ਗ਼ਲਤ
3. ਬਹਿਲੋਲ ਲੋਧੀ 1451 ਈ. ਵਿੱਚ ਸਿੰਘਾਸਨ ‘ਤੇ ਬੈਠਿਆ ਸੀ ।
ਉੱਤਰ-
ਠੀਕ
4. ਸਿਕੰਦਰ ਲੋਧੀ 1489 ਈ. ਵਿੱਚ ਦਿੱਲੀ ਦੇ ਸਿੰਘਾਸਨ ‘ਤੇ ਬੈਠਿਆ ।
ਉੱਤਰ-
ਠੀਕ
5. ਇਬਰਾਹੀਮ ਲੋਧੀ 1517 ਈ. ਵਿੱਚ ਲੋਧੀ ਵੰਸ਼ ਦਾ ਨਵਾਂ ਸੁਲਤਾਨ ਬਣਿਆ ਸੀ ।
ਉੱਤਰ-
ਠੀਕ
6. ਦੌਲਤ ਖਾਂ ਲੋਧੀ 1469 ਈ. ਵਿੱਚ ਪੰਜਾਬ ਦਾ ਸੂਬੇਦਾਰ ਨਿਯੁਕਤ ਹੋਇਆ ਸੀ ।
ਉੱਤਰ-
ਗ਼ਲਤ
![]()
7. ਬਾਬਰ ਦਾ ਜਨਮ 1494 ਈ. ਵਿੱਚ ਹੋਇਆ ਸੀ ।
ਉੱਤਰ-
ਗਲਤ
8. ਬਾਬਰ ਨੇ 1504 ਈ. ਵਿੱਚ ਕਾਬਲ ‘ਤੇ ਕਬਜ਼ਾ ਕਰ ਲਿਆ ਸੀ ।
ਉੱਤਰ-
ਠੀਕ
9. ਬਾਬਰ ਨੇ ਭਾਰਤ ‘ਤੇ ਪਹਿਲਾ ਹਮਲਾ 1519 ਈ. ਵਿੱਚ ਕੀਤਾ ।
ਉੱਤਰ-
ਠੀਕ
10. ਬਾਬਰ ਨੇ ਸੈਦਪੁਰ ’ਤੇ 1524 ਈ. ਵਿੱਚ ਹਮਲਾ ਕੀਤਾ ।
ਉੱਤਰ-
ਗ਼ਲਤ
11. ਗੁਰੂ ਨਾਨਕ ਦੇਵ ਜੀ ਨੇ ਬਾਬਰ ਦੇ ਸੈਦਪੁਰ ਦੇ ਹਮਲੇ ਦੀ ਤੁਲਨਾ ਪਾਪ ਦੀ ਜੰਵ ਨਾਲ , ਕੀਤੀ ਸੀ ।
ਉੱਤਰ-
ਠੀਕ
12. ਬਾਬਰ ਅਤੇ ਇਬਰਾਹੀਮ ਲੋਧੀ ਵਿਚਾਲੇ ਪਾਨੀਪਤ ਦੀ ਪਹਿਲੀ ਲੜਾਈ 21 ਅਪਰੈਲ, 1526 ਈ. ਨੂੰ ਹੋਈ ।
ਉੱਤਰ-
ਠੀਕ
![]()
13. 16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦਾ ਮੁਸਲਿਮ ਸਮਾਜ ਦੋ ਸ਼੍ਰੇਣੀਆਂ ਵਿੱਚ ਵੰਡਿਆ ਹੋਇਆ ਸੀ ।
ਉੱਤਰ-
ਗ਼ਲਤ
14. ਮੁਸਲਿਮ ਸਮਾਜ ਦੀ ਨੀਵੀਂ ਸ਼੍ਰੇਣੀ ਵਿੱਚ ਸਭ ਤੋਂ ਵਧੇਰੇ ਗਿਣਤੀ ਕਿਸਾਨਾਂ ਦੀ ਸੀ ।
ਉੱਤਰ-
ਗ਼ਲਤ
15. 16ਵੀਂ ਸਦੀ ਦੇ ਮੁਸਲਿਮ ਸਮਾਜ ਵਿੱਚ ਇਸਤਰੀਆਂ ਦਾ ਬਹੁਤ ਸਨਮਾਨ ਕੀਤਾ ਜਾਂਦਾ ਸੀ ।
ਉੱਤਰ-
ਗ਼ਲਤ
16. 16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਵਿੱਚ ਮੁਸਲਿਮ ਸਿੱਖਿਆ ਦੇ ਦੋ ਪ੍ਰਸਿੱਧ ਕੇਂਦਰ ਲਾਹੌਰ ਅਤੇ ਮੁਲਤਾਨ ਸਨ ।
ਉੱਤਰ-
ਠੀਕ
17. 16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਹਿੰਦੂ ਸਮਾਜ ਵਿੱਚ ਬ੍ਰਾਹਮਣਾਂ ਨੂੰ ਪ੍ਰਮੁੱਖਤਾ ਪ੍ਰਾਪਤ ਸੀ ।
ਉੱਤਰ-
ਠੀਕ
18. 16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਕਸ਼ੱਤਰੀਆਂ ਦਾ ਮੁੱਖ ਪੇਸ਼ਾ ਖੇਤੀਬਾੜੀ ਕਰਨਾ ਸੀ ।
ਉੱਤਰ-
ਗ਼ਲਤ
19. 16ਵੀਂ ਸਦੀ ਵਿੱਚ ਹਿੰਦੂ ਸਮਾਜ ਵਿੱਚ ਇਸਤਰੀਆਂ ਦੀ ਦਸ਼ਾ ਬੜੀ ਤਰਸਯੋਗ ਸੀ ।
ਉੱਤਰ-
ਠੀਕ
![]()
20. 16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਲੋਕਾਂ ਦਾ ਮੁੱਖ ਕਿੱਤਾ ਪਸ਼ੂ ਪਾਲਣ ਸੀ ।
ਉੱਤਰ-
ਗ਼ਲਤ
21. 16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਵਿੱਚ ਸਭ ਤੋਂ ਵੱਧ ਕਣਕ ਦੀ ਪੈਦਾਵਾਰ ਕੀਤੀ ਜਾਂਦੀ ਸੀ ।
ਉੱਤਰ-
ਠੀਕ
22. 16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦਾ ਸਭ ਤੋਂ ਪ੍ਰਸਿੱਧ ਉਦਯੋਗ ਕੱਪੜਾ ਉਦਯੋਗ ਸੀ ।
ਉੱਤਰ-
ਠੀਕ
23. 16ਵੀਂ ਸਦੀ ਵਿੱਚ ਕਸ਼ਮੀਰ ਸ਼ਾਲਾਂ ਦੇ ਉਦਯੋਗ ਲਈ ਬੜਾ ਪ੍ਰਸਿੱਧ ਸੀ ।
ਉੱਤਰ-
ਠੀਕ
24. ਗੋਰਖਨਾਥ ਨੇ ਜੋਗੀਆਂ ਦੀ ਨਾਥਪੰਥੀ ਦੀ ਸਥਾਪਨਾ ਕੀਤੀ ਸੀ ।
ਉੱਤਰ-
ਠੀਕ
25. ਇਸਲਾਮ ਦੀ ਸਥਾਪਨਾ ਹਜ਼ਰਤ ਮੁਹੰਮਦ ਸਾਹਿਬ ਨੇ ਕੀਤੀ ਸੀ ।
ਉੱਤਰ-
ਠੀਕ
26. ਚਿਸ਼ਤੀ ਸਿਲਸਿਲੇ ਦੀ ਨੀਂਹ ਖ਼ਵਾਜਾ ਮੁਈਨਉੱਦੀਨ ਚਿਸ਼ਤੀ ਨੇ ਰੱਖੀ ਸੀ ।
ਉੱਤਰ-
ਠੀਕ
![]()
27. ਪੰਜਾਬ ਵਿੱਚ ਚਿਸ਼ਤੀ ਸਿਲਸਿਲੇ ਦਾ ਪ੍ਰਮੁੱਖ ਪ੍ਰਚਾਰਕ ਸ਼ੇਖ਼ ਫ਼ਰੀਦ ਸੀ ।
ਉੱਤਰ-
ਠੀਕ
28. ਸੁਹਰਾਵਰਦੀ ਸਿਲਸਿਲੇ ਦਾ ਸੰਸਥਾਪਕ ਸ਼ੇਖ਼ ਬਹਾਉੱਦੀਨ ਜ਼ਕਰੀਆ ਸੀ ।
ਉੱਤਰ-
ਠੀਕ
ਬਹੁਪੱਖੀ ਪ੍ਰਸ਼ਨ (Multiple Choice Questions)
ਨੋਟ :-ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚੋਂ ਠੀਕ ਉੱਤਰ ਦੀ ਚੋਣ ਕਰੋ-
ਪ੍ਰਸ਼ਨ 1.
ਲੋਧੀ ਵੰਸ਼ ਦਾ ਸੰਸਥਾਪਕ ਕੌਣ ਸੀ ?
(i) ਬਹਿਲੋਲ ਲੋਧੀ
(ii) ਦੌਲਤ ਖਾਂ ਲੋਧੀ
(iii) ਸਿਕੰਦਰ ਲੋਧੀ
(iv) ਇਬਰਾਹੀਮ ਲੋਧੀ ।
ਉੱਤਰ-
(i) ਬਹਿਲੋਲ ਲੋਧੀ ।
ਪ੍ਰਸ਼ਨ 2.
ਬਹਿਲੋਲ ਲੋਧੀ ਕਦੋਂ ਦਿੱਲੀ ਦੇ ਸਿੰਘਾਸਨ ‘ਤੇ ਬੈਠਿਆ ਸੀ ?
(i) 1437 ਈ. ਵਿੱਚ
(ii) 1451 ਈ. ਵਿੱਚ
(iii) 1489 ਈ. ਵਿੱਚ
(iv) 1517 ਈ. ਵਿੱਚ ।
ਉੱਤਰ-
(ii) 1451 ਈ. ਵਿੱਚ ।
ਪ੍ਰਸ਼ਨ 3.
ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚੋਂ ਕਿਹੜੇ ਸ਼ਾਸਕ ਦਾ ਪਹਿਲਾ ਨਾਂ ਨਿਜ਼ਾਮ ਖਾਂ ਸੀ ?
(i) ਬਹਿਲੋਲ ਲੋਧੀ
(ii) ਸਿਕੰਦਰ ਲੋਧੀ
(iii) ਇਬਰਾਹਿਮ ਲੋਧੀ
(iv) ਦੌਲਤ ਖਾਂ ਲੋਧੀ ।
ਉੱਤਰ-
(ii) ਸਿਕੰਦਰ ਲੋਧੀ ।
ਪ੍ਰਸ਼ਨ 4.
ਇਬਰਾਹੀਮ ਲੋਧੀ ਕਦੋਂ ਦਿੱਲੀ ਦੇ ਸਿੰਘਾਸਨ ‘ਤੇ ਬੈਠਿਆ ਸੀ ?
(i) 1489 ਈ. ਵਿੱਚ
(ii) 1516 ਈ. ਵਿੱਚ
(iii) 1517 ਈ. ਵਿੱਚ
(iv) 1526 ਈ. ਵਿੱਚ ।
ਉੱਤਰ-
(iii) 1517 ਈ. ਵਿੱਚ ।
ਪ੍ਰਸ਼ਨ 5.
ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਕੌਣ ਸੀ ?
(i) ਪੰਜਾਬ ਦਾ ਸੂਬੇਦਾਰ
(ii) ਦਿੱਲੀ ਦਾ ਸੂਬੇਦਾਰ
(iii) ਅਵਧ ਦਾ ਸੂਬੇਦਾਰ
(iv) ਇਨ੍ਹਾਂ ਵਿੱਚੋਂ ਕੋਈ ਨਹੀਂ ।
ਉੱਤਰ-
(i) ਪੰਜਾਬ ਦਾ ਸੂਬੇਦਾਰ ।
![]()
ਪ੍ਰਸ਼ਨ 6.
ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਕਿਸ ਰਾਜ ਦਾ ਸੁਤੰਤਰ ਸ਼ਾਸਕ ਬਣਨਾ ਚਾਹੁੰਦਾ ਸੀ ?
(i) ਮਗਧ
(ii) ਦਿੱਲੀ
(iii) ਪੰਜਾਬ
(iv) ਗੁਜਰਾਤ ।
ਉੱਤਰ-
(iii) ਪੰਜਾਬ ।
ਪ੍ਰਸ਼ਨ 7.
ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਪੰਜਾਬ ਦਾ ਸੂਬੇਦਾਰ ਕਦੋਂ ਨਿਯੁਕਤ ਹੋਇਆ ਸੀ ?
(i) 1489 ਈ. ਵਿੱਚ
(ii) 1500 ਈ. ਵਿੱਚ
(iii) 1517 ਈ. ਵਿੱਚ
(iv) 1526 ਈ. ਵਿੱਚ ।
ਉੱਤਰ-
(ii) 1500 ਈ. ਵਿੱਚ ।
ਪ੍ਰਸ਼ਨ 8.
ਪੰਜਾਬ ਦੇ ਤਿਕੋਣੇ ਸੰਘਰਸ਼ ਵਿੱਚ ਕੌਣ ਸ਼ਾਮਲ ਨਹੀਂ ਸੀ ?
(i) ਬਾਬਰ
(i) ਦੌਲਤ ਖਾਂ ਲੋਧੀ
(iii) ਇਬਰਾਹੀਮ ਲੋਧੀ
(iv) ਆਲਮ ਖਾਂ ਲੋਧੀ ।
ਉੱਤਰ-
(iv) ਆਲਮ ਖਾਂ ਲੋਧੀ ।
ਪ੍ਰਸ਼ਨ 9.
ਬਾਬਰ ਨੇ ਭਾਰਤ ਉੱਤੇ ਕਿੰਨੇ ਹਮਲੇ ਕੀਤੇ ?
(i) 11
(ii) 5
(iii) 6
(iv) 17.
ਉੱਤਰ-
(ii) 5 .
ਪ੍ਰਸ਼ਨ 10.
ਬਾਬਰ ਨੇ ਪੰਜਾਬ ’ਤੇ ਪਹਿਲਾ ਹਮਲਾ ਕਦੋਂ ਕੀਤਾ ?
(i) 1509 ਈ. ਵਿੱਚ
(ii) 1519 ਈ. ਵਿੱਚ
(iii) 1520 ਈ. ਵਿੱਚ
(iv) 1524 ਈ. ਵਿੱਚ ।
ਉੱਤਰ-
(ii) 1519 ਈ. ਵਿੱਚ ।
ਪ੍ਰਸ਼ਨ 11.
ਬਾਬਰ ਨੇ ਸੈਦਪੁਰ ’ਤੇ ਹਮਲਾ ਕਦੋਂ ਕੀਤਾ ਸੀ ?
(i) 1519 ਈ. ਵਿੱਚ
(ii) 1520 ਈ. ਵਿੱਚ
(iii) 1524 ਈ. ਵਿੱਚ
(iv) 1526 ਈ. ਵਿੱਚ ।
ਉੱਤਰ-
(ii) 1520 ਈ. ਵਿੱਚ ।
![]()
ਪ੍ਰਸ਼ਨ 12.
ਬਾਬਰ ਨੇ ਸੈਦਪੁਰ ‘ਤੇ ਹਮਲੇ ਸਮੇਂ ਕਿਹੜੇ ਸਿੱਖ ਗੁਰੂ ਸਾਹਿਬ ਨੂੰ ਗ੍ਰਿਫ਼ਤਾਰ ਕਰ ਲਿਆ ਸੀ ?
(i) ਗੁਰੂ ਨਾਨਕ ਦੇਵ ਜੀ
(ii) ਗੁਰੂ ਅੰਗਦ ਦੇਵ ਜੀ
(iii) ਗੁਰੂ ਹਰਿਗੋਬਿੰਦ ਜੀ
(iv) ਗੁਰੂ ਤੇਗ਼ ਬਹਾਦਰ ਜੀ ।
ਉੱਤਰ-
(i) ਗੁਰੂ ਨਾਨਕ ਦੇਵ ਜੀ ।
ਪ੍ਰਸ਼ਨ 13.
ਬਾਬਰ ਅਤੇ ਇਬਰਾਹੀਮ ਲੋਧੀ ਵਿਚਾਲੇ ਪਾਨੀਪਤ ਦੀ ਪਹਿਲੀ ਲੜਾਈ ਕਦੋਂ ਹੋਈ ?
(i) 1519 ਈ. ਵਿੱਚ
(ii) 1525 ਈ. ਵਿੱਚ
(iii) 1526 ਈ. ਵਿੱਚ
(iv) 1556 ਈ. ਵਿੱਚ ।
ਉੱਤਰ-
(iii) 1526 ਈ. ਵਿੱਚ ।
ਪ੍ਰਸ਼ਨ 14.
ਪਾਨੀਪਤ ਦੀ ਪਹਿਲੀ ਲੜਾਈ ਵਿੱਚ ਕਿਸਦੀ ਹਾਰ ਹੋਈ ?
(i) ਬਾਬਰ ਦੀ
(ii) ਮਹਾਰਾਣਾ ਪ੍ਰਤਾਪ ਦੀ
(iii) ਇਬਰਾਹੀਮ ਲੋਧੀ ਦੀ
(iv) ਦੌਲਤ ਖਾਂ ਲੋਧੀ ਦੀ ।
ਉੱਤਰ-
(iii) ਇਬਰਾਹੀਮ ਲੋਧੀ ਦੀ ।
ਪ੍ਰਸ਼ਨ 15.
ਆਲਮ ਖਾਂ ਲੋਧੀ ਕਿਸ ਦਾ ਪੁੱਤਰ ਸੀ ?
(i) ਸਿਕੰਦਰ ਲੋਧੀ
(ii) ਇਬਰਾਹੀਮ ਲੋਧੀ
(iii) ਦੌਲਤ ਖਾਂ ਲੋਧੀ
(iv) ਕੋਈ ਨਹੀਂ ।
ਉੱਤਰ-
(i) ਸਿਕੰਦਰ ਲੋਧੀ ।
ਪ੍ਰਸ਼ਨ 16.
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦਾ ਮੁਸਲਿਮ ਸਮਾਜ ਕਿੰਨੇ ਵਰਗਾਂ ਵਿੱਚ ਵੰਡਿਆ ਹੋਇਆ ਸੀ ?
(i) ਦੋ
(ii) ਤਿੰਨ
(iii) ਚਾਰ
(iv) ਪੰਜ
ਉੱਤਰ-
(ii) ਤਿੰਨ ।
ਪ੍ਰਸ਼ਨ 17.
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਮੁਸਲਿਮ ਸਮਾਜ ਦੀ ਉੱਚ ਸ਼੍ਰੇਣੀ ਵਿੱਚ ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚੋਂ ਕੌਣ ਸ਼ਾਮਲ
ਨਹੀਂ ਸੀ ?
(i) ਮਲਿਕ
(ii) ਸ਼ੇਖ਼
(iii) ਇਕਤਾਰ
(iv) ਵਪਾਰੀ ।
ਉੱਤਰ-
(iv) ਵਪਾਰੀ ।
![]()
ਪ੍ਰਸ਼ਨ 18.
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਮੁਸਲਿਮ ਸਮਾਜ ਦੀ ਮੱਧ ਸ਼੍ਰੇਣੀ ਵਿੱਚ ਕੌਣ ਸ਼ਾਮਲ ਸੀ ?
(i) ਵਪਾਰੀ
(ii) ਸੈਨਿਕ
(iii) ਕਿਸਾਨ
(iv) ਉੱਪਰ ਲਿਖੇ ਸਾਰੇ ।
ਉੱਤਰ-
(iv) ਉੱਪਰ ਲਿਖੇ ਸਾਰੇ ।
ਪ੍ਰਸ਼ਨ 19.
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਮੁਸਲਿਮ ਸਮਾਜ ਦੀ ਨੀਵੀਂ ਸ਼੍ਰੇਣੀ ਵਿੱਚ ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚੋਂ ਕੌਣ ਸ਼ਾਮਲ ਨਹੀਂ ਸੀ ?
(i) ਕਾਜ਼ੀ
(ii) ਨੌਕਰ
(iii) ਦਾਸ
(iv) ਮਜ਼ਦੂਰ ।
ਉੱਤਰ-
(i) ਕਾਜ਼ੀ ।
ਪ੍ਰਸ਼ਨ 20.
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਮੁਸਲਮਾਨਾਂ ਦਾ ਸਭ ਤੋਂ ਪ੍ਰਸਿੱਧ ਸਿੱਖਿਆ ਦਾ ਕੇਂਦਰ ਕਿਹੜਾ ਸੀ ?
(i) ਸਰਹਿੰਦ
(ii) ਜਲੰਧਰ
(iii) ਪੇਸ਼ਾਵਰ
(iv) ਲਾਹੌਰ ।
ਉੱਤਰ-
(iv) ਲਾਹੌਰ ।
ਪ੍ਰਸ਼ਨ 21.
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਲੋਕਾਂ ਦਾ ਮੁੱਖ ਕਿੱਤਾ ਕੀ ਸੀ ?
(i) ਵਪਾਰ
(ii) ਖੇਤੀਬਾੜੀ
(iii) ਉਦਯੋਗ
(iv) ਪਸ਼ੂ-ਪਾਲਣ ।
ਉੱਤਰ-
(ii) ਖੇਤੀਬਾੜੀ ।
ਪ੍ਰਸ਼ਨ 22.
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦੀ ਸਭ ਤੋਂ ਪ੍ਰਸਿੱਧ ਫ਼ਸਲ ਕਿਹੜੀ ਸੀ ?
(i) ਕਣਕ
(ii) ਚੌਲ
(iii) ਰੀਨਾ
(iv) ਉੱਪਰ ਲਿਖੀਆਂ ਸਾਰੀਆਂ ।
ਉੱਤਰ-
(iv) ਉੱਪਰ ਲਿਖੀਆਂ ਸਾਰੀਆਂ ।
ਪ੍ਰਸ਼ਨ 23.
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦਾ ਸਭ ਤੋਂ ਪ੍ਰਸਿੱਧ ਉਦਯੋਗ ਕਿਹੜਾ ਸੀ ?
(i) ਚਮੜਾ ਉਦਯੋਗ
(ii) ਕੱਪੜਾ ਉਦਯੋਗ
(iii) ਸ਼ਸਤਰ ਉਦਯੋਗ
(iv) ਹਾਥੀ ਦੰਦ ਉਦਯੋਗ ।
ਉੱਤਰ-
(ii) ਕੱਪੜਾ ਉਦਯੋਗ ।
ਪ੍ਰਸ਼ਨ 24.
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚੋਂ ਕਿਹੜਾ ਗਰਮ ਕੱਪੜਾ ਉਦਯੋਗ ਦਾ ਕੇਂਦਰ ਨਹੀਂ ਸੀ ?
(i) ਜਲੰਧਰ
(ii) ਅੰਮ੍ਰਿਤਸਰ
(iii) ਕਸ਼ਮੀਰ
(iv) ਕਾਂਗੜਾ ।
ਉੱਤਰ-
(i) ਜਲੰਧਰ ।
![]()
ਪ੍ਰਸ਼ਨ 25.
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦਾ ਸਭ ਤੋਂ ਪ੍ਰਸਿੱਧ ਵਪਾਰਿਕ ਕੇਂਦਰ ਕਿਹੜਾ ਸੀ ?
(i) ਲਾਹੌਰ
(ii) ਲੁਧਿਆਣਾ
(iii) ਜਲੰਧਰ
(iv) ਅੰਮ੍ਰਿਤਸਰ ।
ਉੱਤਰ-
(i) ਲਾਹੌਰ ।
ਪ੍ਰਸ਼ਨ 26.
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦੇ ਲੋਕਾਂ ਦਾ ਪ੍ਰਮੁੱਖ ਧਰਮ ਕਿਹੜਾ ਸੀ ?
(i) ਇਸਲਾਮ
(ii) ਹਿੰਦੁ
(iii) ਈਸਾਈ
(iv) ਸਿੱਖ ।
ਉੱਤਰ-
(ii) ਹਿੰਦੁ ।
ਪ੍ਰਸ਼ਨ 27.
ਜੋਗੀਆਂ ਦੀ ਨਾਥਪੰਥੀ ਸ਼ਾਖਾ ਦੀ ਸਥਾਪਨਾ ਕਿਸਨੇ ਕੀਤੀ ਸੀ ?
(i) ਗੋਰਖਨਾਥ
(ii) ਸ਼ਿਵਨਾਥ
(iii) ਮਹਾਤਮਾ ਬੁੱਧ
(iv) ਸਵਾਮੀ ਮਹਾਂਵੀਰ ।
ਉੱਤਰ-
(i) ਗੋਰਖਨਾਥ ।
ਪ੍ਰਸ਼ਨ 28.
ਪੁਰਾਣਾਂ ਵਿੱਚ ਵਿਸ਼ਨੂੰ ਦੇ ਕਿੰਨੇ ਅਵਤਾਰਾਂ ਦਾ ਵਰਣਨ ਕੀਤਾ ਗਿਆ ਹੈ ?
(i) 5
(ii) 10
(iii) 24
(iv) 25.
ਉੱਤਰ-
(iii) 24.
ਪ੍ਰਸ਼ਨ 29.
16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿਚ ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚੋਂ ਕਿਹੜਾ ਮਤ ਹਿੰਦੂ ਧਰਮ ਨਾਲ ਸੰਬੰਧਿਤ ਨਹੀਂ ਸੀ ?
(i) ਸ਼ੈਵ ਮਤ
(ii) ਵੈਸ਼ਨਵ ਮਤ
(iii) ਸ਼ਕਤੀ ਮਤ
(iv) ਸੂਫ਼ੀ ਮਤ ।
ਉੱਤਰ-
(iv) ਸੂਫ਼ੀ ਮਤ ।
ਪ੍ਰਸ਼ਨ 30.
ਇਸਲਾਮ ਦਾ ਸੰਸਥਾਪਕ ਕੌਣ ਸੀ ?
(i) ਅਬੂ ਬਕਰ
(ii) ਉਮਰ
(iii) ਹਜ਼ਰਤ ਮੁਹੰਮਦ ਸਾਹਿਬ
(iv) ਅਲੀ ।
ਉੱਤਰ-
(iii) ਹਜ਼ਰਤ ਮੁਹੰਮਦ ਸਾਹਿਬ ।
![]()
ਪ੍ਰਸ਼ਨ 31.
ਇਸਲਾਮ ਦੀ ਸਥਾਪਨਾ ਕਦੋਂ ਕੀਤੀ ਗਈ ਸੀ ?
(i) ਪੰਜਵੀਂ ਸਦੀ ਵਿੱਚ
(ii) ਛੇਵੀਂ ਸਦੀ ਵਿੱਚ
(iii) ਸੱਤਵੀਂ ਸਦੀ ਵਿੱਚ
(iv) ਅੱਠਵੀਂ ਸਦੀ ਵਿੱਚ
ਉੱਤਰ-
(iii) ਸੱਤਵੀਂ ਸਦੀ ਵਿੱਚ ।
ਪ੍ਰਸ਼ਨ 32.
ਇਸਲਾਮ ਦਾ ਪਹਿਲਾ ਖਲੀਫ਼ਾ ਕੌਣ ਸੀ ?
(i) ਅਲੀ
(ii) ਅਬੂ ਬਕਰ
(iii) ਉਮਰ
(iv) ਉਥਮਾਨ ।
ਉੱਤਰ-
(ii) ਅਬੂ ਬਕਰ ।
ਪ੍ਰਸ਼ਨ 33.
ਸੂਫ਼ੀ ਸ਼ੇਖਾਂ ਦੀ ਵਿਚਾਰਧਾਰਾ ਨੂੰ ਕੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ?
(i) ਪੀਰ
(ii) ਦਰਗਾਹ
(iii) ਤਸਵੁਫ਼
(iv) ਸਿਲਸਿਲਾ ।
ਉੱਤਰ-
(iii) ਤਸਵੁਫ਼ ।
ਪ੍ਰਸ਼ਨ 34.
ਚਿਸ਼ਤੀ ਸਿਲਸਿਲੇ ਦਾ ਸੰਸਥਾਪਕ ਕੌਣ ਸੀ ?
(i) ਖ਼ਵਾਜ਼ਾ ਮੁਈਨਉੱਦੀਨ ਚਿਸ਼ਤੀ
(ii) ਸ਼ੇਖ਼ ਬਹਾਉੱਦੀਨ ਜ਼ਕਰੀਆ
(iii) ਸ਼ੇਖ਼ ਫ਼ਰੀਦ ਜੀ .
(iv) ਸ਼ੇਖ਼ ਨਿਜ਼ਾਮਉੱਦੀਨ ਔਲੀਆ
ਉੱਤਰ-
(i) ਖ਼ਵਾਜ਼ਾ ਮੁਈਨਉੱਦੀਨ ਚਿਸ਼ਤੀ ।
ਪ੍ਰਸ਼ਨ 35.
ਪੰਜਾਬ ਵਿਚ ਚਿਸ਼ਤੀ ਸਿਲਸਿਲੇ ਦਾ ਸਭ ਤੋਂ ਪ੍ਰਸਿੱਧ ਪ੍ਰਚਾਰਕ ਕੌਣ ਸੀ ?
(i) ਸ਼ੇਖ਼ ਨਿਜ਼ਾਮਉੱਦੀਨ ਔਲੀਆ
(ii) ਸ਼ੇਖ਼ ਫ਼ਰੀਦ
(iii) ਸ਼ੇਖ਼ ਕੁਤਬਉੱਦੀਨ ਬਖਤਿਆਰ ਕਾਕੀ
(iv) ਖਵਾਜ਼ਾ ਮੁਈਨਉੱਦੀਨ ਚਿਸ਼ਤੀ ।
ਉੱਤਰ-
(ii) ਸ਼ੇਖ਼ ਫ਼ਰੀਦ ।
ਪ੍ਰਸ਼ਨ 36.
ਸੂਫ਼ੀਆਂ ਦੇ ਸੁਹਰਾਵਰਦੀ ਸਿਲਸਿਲੇ ਦੀ ਸਥਾਪਨਾ ਕਿੱਥੇ ਹੋਈ ?
(i) ਲਾਹੌਰ
(ii) ਅਜਮੇਰ
(iii) ਆਗਰਾਂ
(iv) ਮੁਲਤਾਨ ।
ਉੱਤਰ-
(iv) ਮੁਲਤਾਨ ।
![]()
ਪ੍ਰਸ਼ਨ 37.
ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚੋਂ ਕਿਸਨੇ ਕੱਵਾਲੀ ਗਾਉਣ ਦੀ ਪ੍ਰਥਾ ਨੂੰ ਸ਼ੁਰੂ ਕੀਤਾ ?
(i) ਇਸਲਾਮ ਨੇ
(ii) ਸੂਫ਼ੀਆਂ ਨੇ
(iii) ਹਿੰਦੂਆਂ ਨੇ
(iv) ਸਿੱਖਾਂ ਨੇ ।
ਉੱਤਰ-
(ii) ਸੂਫ਼ੀਆਂ ਨੇ ।
Source Based Questions
ਨੋਟ-ਹੇਠ ਲਿਖੇ ਪੈਰਿਆਂ ਨੂੰ ਧਿਆਨ ਨਾਲ ਪੜ੍ਹੋ ਅਤੇ ਉਨ੍ਹਾਂ ਦੇ ਅੰਤ ਵਿੱਚ ਦਿੱਤੇ ਗਏ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਉੱਤਰ ਦਿਓ-
1. ਬਹਿਲੋਲ ਲੋਧੀ ਦੀ ਮੌਤ ਤੋਂ ਬਾਅਦ ਉਸ ਦਾ ਪੁੱਤਰ ਸਿਕੰਦਰ ਲੋਧੀ 1489 ਈ. ਵਿੱਚ ਦਿੱਲੀ ਦੇ ਤਖ਼ਤ ਉੱਤੇ ਬੈਠਿਆ । ਉਸ ਨੇ 1517 ਈ. ਤਕ ਸ਼ਾਸਨ ਕੀਤਾ । ਮੁਸਲਿਮ ਇਤਿਹਾਸਕਾਰਾਂ ਦੀ ਨਜ਼ਰ ਵਿੱਚ ਉਹ ਇੱਕ ਬਹੁਤ ਹੀ ਨਿਆਂ-ਪਸੰਦ ਅਤੇ ਦਿਆਲੂ ਸੁਲਤਾਨ ਸੀ | ਪਰ ਉਸ ਦੀ ਨਿਆਂ-ਪ੍ਰਿਯਤਾ ਅਤੇ ਦਿਆਲਤਾ ਸਿਰਫ ਮੁਸਲਮਾਨਾਂ ਤਕ ਹੀ ਸੀਮਿਤ ਸੀ । ਉਹ ਫ਼ਿਰੋਜ਼ਸ਼ਾਹ ਤੁਗਲਕ ਅਤੇ ਔਰੰਗਜ਼ੇਬ ਵਾਂਗ ਇੱਕ ਕੱਟੜ ਮੁਸਲਮਾਨ ਸੀ ! ਉਹ ਹਿੰਦੂਆਂ ਨੂੰ ਬੜੀ ਨਫ਼ਰਤ ਦੀ ਨਜ਼ਰ ਨਾਲ ਵੇਖਦਾ ਸੀ । ਉਸ ਨੇ ਹਿੰਦੂਆਂ ਪ੍ਰਤੀ ਬੜੀ ਕਠੋਰ ਅਤੇ ਜ਼ਾਲਮਾਨਾ ਨੀਤੀ ਅਪਣਾਈ । ਉਸ ਨੇ ਹਿੰਦੂਆਂ ਦੇ ਕਈ ਪ੍ਰਸਿੱਧ ਮੰਦਰਾਂ ਨੂੰ ਤਹਿਸ-ਨਹਿਸ ਕਰ ਦਿੱਤਾ ਸੀ ਅਤੇ ਉਨ੍ਹਾਂ ਦੀ ਥਾਂ ਮਸਜਿਦਾਂ ਦੀ ਉਸਾਰੀ ਕਰਵਾਈ । ਉਸ ਨੇ ਹਿੰਦੂਆਂ ਨੂੰ ਜਮਨਾ ਵਿੱਚ ਇਸ਼ਨਾਨ ਕਰਨ ਦੀ ਮਨਾਹੀ ਕਰ ਦਿੱਤੀ । ਉਸ ਨੇ ਹਿੰਦੂਆਂ ਨੂੰ ਜ਼ਬਰਦਸਤੀ ਇਸਲਾਮ ਧਰਮ ਵਿੱਚ ਸ਼ਾਮਲ ਕਰਨਾ ਸ਼ੁਰੂ ਕਰ ਦਿੱਤਾ । ਉਸ ਨੇ ਬੋਧਨ ਨਾਂ ਦੇ ਇੱਕ ਬ੍ਰਾਹਮਣ ਨੂੰ ਇਸ ਲਈ ਮੌਤ ਦੇ ਘਾਟ ਉਤਾਰ ਦਿੱਤਾ ।
1. ਸਿਕੰਦਰ ਲੋਧੀ ਕੌਣ ਸੀ?
2. ਸਿਕੰਦਰ ਲੋਧੀ ਕਦੋਂ ਸਿੰਘਾਸਨ ‘ਤੇ ਬੈਠਿਆ ਸੀ ?
(i) 1485 ਈ.
(ii) 1486 ਈ.
(iii) 1487 ਈ.
(iv) 1489 ਈ. ।
3. ਮੁਸਲਿਮ ਇਤਿਹਾਸਕਾਰ ਸਿਕੰਦਰ ਲੋਧੀ ਨੂੰ ਕਿਹੋ ਜਿਹਾ ਸੁਲਤਾਨ ਦੱਸਦੇ ਹਨ ?
4. ਸਿਕੰਦਰ ਲੋਧੀ ਨੇ ਹਿੰਦੂਆਂ ਪ੍ਰਤੀ ਕਿਹੜਾ ਕਦਮ ਚੁੱਕਿਆ ?
5. ਸਿਕੰਦਰ ਲੋਧੀ ਨੇ ਬੋਧਨ ਬਾਹਮਣ ਨੂੰ ਕਿਉਂ ਮੌਤ ਦੇ ਘਾਟ ਉਤਾਰ ਦਿੱਤਾ ਸੀ ?
ਉੱਤਰ-
1. ਸਿਕੰਦਰ ਲੋਧੀ ਦਿੱਲੀ ਦਾ ਸੁਲਤਾਨ ਸੀ ।
2. 1489 ਈ. ।
3. ਇੱਕ ਬਹੁਤ ਹੀ ਨਿਆਂ ਪਸੰਦ ਅਤੇ ਦਿਆਲੂ ਸੁਲਤਾਨ ।
4. ਉਸ ਨੇ ਹਿੰਦੂਆਂ ਨੂੰ ਜ਼ਬਰਦਸਤੀ ਇਸਲਾਮ ਵਿੱਚ ਸ਼ਾਮਲ ਕੀਤਾ ।
5. ਉਸ ਨੇ ਹਿੰਦੂ ਧਰਮ ਨੂੰ ਇਸਲਾਮ ਧਰਮ ਦੇ ਬਰਾਬਰ ਚੰਗਾ ਕਿਹਾ ਸੀ ।
2. 16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਵਿੱਚ ਪਰਜਾ ਦੀ ਹਾਲਤ ਬਹੁਤ ਤਰਸਯੋਗ ਸੀ । ਸ਼ਾਸਕ ਵਰਗ ਜਸ਼ਨਾਂ ਵਿੱਚ ਆਪਣਾਂ ਸਮਾਂ ਬਤੀਤ ਕਰਦਾ ਸੀ । ਅਜਿਹੀ ਹਾਲਤ ਵਿੱਚ ਪਰਜਾ ਵੱਲ ਕਿਸੇ ਦਾ ਧਿਆਨ ਹੀ ਨਹੀਂ ਸੀ । ਸਰਕਾਰੀ ਕਰਮਚਾਰੀ ਭ੍ਰਿਸ਼ਟ ਹੋ ਚੁੱਕੇ ਸਨ । ਹਰ ਪਾਸੇ ਰਿਸ਼ਵਤ ਦਾ ਬੋਲਬਾਲਾ ਸੀ । ਸੁਲਤਾਨ ਤਾਂ ਸੁਲਤਾਨ, ਕਾਜ਼ੀ ਅਤੇ ਉਲਮਾ ਵੀ ਰਿਸ਼ਵਤ ਲੈ ਕੇ ਨਿਆਂ ਕਰਦੇ ਸਨ । ਹਿੰਦੂਆਂ ‘ਤੇ ਅੱਤਿਆਚਾਰ ਬਹੁਤ ਜ਼ਿਆਦਾ ਵੱਧ ਗਏ ਸਨ । ਉਨ੍ਹਾਂ ਨੂੰ ਤਲਵਾਰ ਦੀ ਨੋਕ ‘ਤੇ ਜ਼ਬਰਦਸਤੀ ਇਸਲਾਮ ਧਰਮ ਵਿੱਚ ਸ਼ਾਮਲ ਕੀਤਾ ਜਾਂਦਾ ਸੀ ।
1. 16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪਰਜਾ ਦੀ ਹਾਲਤ ਕਿਹੋ ਜਿਹੀ ਸੀ ?
2. 16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਸਰਕਾਰੀ ਕਰਮਚਾਰੀਆਂ ਦਾ ਆਚਰਨ ਕਿਹੋ ਜਿਹਾ ਸੀ ?
3. 16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਸੁਲਤਾਨ, ਕਾਜ਼ੀ ਅਤੇ ਉਲਮਾਂ ਨਿਆਂ ਕਿਵੇਂ ਕਰਦੇ ਸਨ ?
4. 16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਰਾਜ ਵੱਲੋਂ ਹਿੰਦੂਆਂ ਪ੍ਰਤੀ ਕੀ ਨੀਤੀ ਅਪਣਾਈ ਜਾਂਦੀ ਸੀ ?
5. 16ਵੀਂ ਸਦੀ ਵਿੱਚ ਸ਼ਾਸਕ ਵਰਗ ……………………. ਵਿੱਚ ਆਪਣਾ ਸਮਾਂ ਬਤੀਤ ਕਰਦਾ ਸੀ ।
ਉੱਤਰ-
1. 16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ, ਪਰਜਾ ਦੀ ਹਾਲਤ ਬਹੁਤ ਤਰਸਯੋਗ ਸੀ ।
2. ਉਸ ਸਮੇਂ ਸਰਕਾਰੀ ਕਰਮਚਾਰੀ ਬਹੁਤ ਭਿਸ਼ਟ ਹੋ ਚੁੱਕੇ ਸਨ ।
3. ਉਸ ਸਮੇਂ ਸੁਲਤਾਨੀ, ਕਾਜ਼ੀ ਅਤੇ ਉਲਮਾ ਰਿਸ਼ਵਤ ਲੈ ਕੇ ਨਿਆਂ ਕਰਦੇ ਸਨ ।
4. ਉਸ ਸਮੇਂ ਰਾਜ ਵੱਲੋਂ ਹਿੰਦੂਆਂ ਤੇ ਬਹੁਤ ਅੱਤਿਆਚਾਰ ਕੀਤੇ ਜਾਂਦੇ ਸਨ ।
5. ਜਸ਼ਨਾਂ ।
3. 16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਦੀ ਸਮਾਜਿਕ ਦਸ਼ਾ ਵੀ ਬਹੁਤ ਖ਼ਰਾਬ ਸੀ । ਉਸ ਸਮੇਂ ਸਮਾਜ ਹਿੰਦੂ ਤੇ ਮੁਸਲਮਾਨ ਨਾਂ ਦੇ ਦੋ ਮੁੱਖ ਵਰਗਾਂ ਵਿੱਚ ਵੰਡਿਆ ਹੋਇਆ ਸੀ । ਕਿਉਂਕਿ ਮੁਸਲਮਾਨ ਸ਼ਾਸਕ ਵਰਗ ਨਾਲ ਸੰਬੰਧ ਰੱਖਦੇ ਸਨ ਇਸ ਲਈ ਉਨ੍ਹਾਂ ਨੂੰ ਸਮਾਜ ਵਿੱਚ ਵਿਸ਼ੇਸ਼ ਅਧਿਕਾਰ ਪ੍ਰਾਪਤ ਸਨ । ਉਨ੍ਹਾਂ ਨੂੰ ਰਾਜ ਦੇ ਉੱਚ ਅਹੁਦਿਆਂ ‘ਤੇ ਲਗਾਇਆ ਜਾਂਦਾ ਸੀ । ਦੂਜੇ ਪਾਸੇ ਹਿੰਦੂ ਜੋ ਕਿ ਵੱਸੋਂ ਦੇ ਵਧੇਰੇ ਭਾਗ ਨਾਲ ਸੰਬੰਧਿਤ ਸਨ, ਨੂੰ ਲਗਭਗ ਸਾਰੇ ਅਧਿਕਾਰਾਂ ਤੋਂ ਵਾਂਝਿਆਂ ਰੱਖਿਆ ਗਿਆ ਸੀ । ਉਨ੍ਹਾਂ ਨੂੰ ਕਾਫ਼ਰ ਅਤੇ ਜਿੰਮੀ ਕਹਿ ਕੇ ਸੱਦਿਆ ਜਾਂਦਾ ਸੀ । ਉਨ੍ਹਾਂ ਤੋਂ ਜਜ਼ੀਆ ਅਤੇ ਯਾਤਰਾ ਕਰ ਆਦਿ ਬੜੀ ਸਖ਼ਤੀ ਨਾਲ ਵਸੂਲ ਕੀਤੇ ਜਾਂਦੇ ਸਨ । ਮੁਸਲਮਾਨ ਹਿੰਦੂਆਂ ‘ਤੇ ਏਨੇ ਅੱਤਿਆਚਾਰ ਕਰਦੇ ਸਨ ਕਿ ਅਨੇਕਾਂ ਹਿੰਦੂ ਮੁਸਲਮਾਨ ਬਣਨ ਲਈ ਮਜਬੂਰ ਹੋ ਗਏ ਸਨ ।
1. 16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਪੰਜਾਬ ਦੀ ਸਮਾਜਿਕ ਦਸ਼ਾ ਨੂੰ ਬਹੁਤ ਖ਼ਰਾਬ ਕਿਉਂ ਕਿਹਾ ਜਾਂਦਾ ਸੀ ? 1
2. 16ਵੀਂ ਸਦੀ ਦੇ ਸ਼ੁਰੂ ਵਿੱਚ ਕਿਨ੍ਹਾਂ ਨੂੰ ਅਧਿਕਾਰਾਂ ਤੋਂ ਵਾਂਝਿਆ ਰੱਖਿਆ ਗਿਆ ਸੀ ?
3. ਕਾਫ਼ਰ ਕੌਣ ਸਨ?
4. ਜਜ਼ੀਆ ਕੀ ਸੀ?
5. ਮੁਸਲਮਾਨ …………………….. ਵਰਗ ਨਾਲ ਸੰਬੰਧ ਰੱਖਦੇ ਸਨ ।
ਉੱਤਰ-
1. ਕਿਉਂਕਿ ਸਮਾਜ ਵਿੱਚ ਇਸਤਰੀਆਂ ਦੀ ਹਾਲਤ ਬਹੁਤ ਤਰਸਯੋਗ ਸੀ ।
2. ਹਿੰਦੂਆਂ ਨੂੰ ।
3. ਗੈਰ-ਮੁਸਲਮਾਨਾਂ ਨੂੰ ਕਾਫ਼ਰ ਕਿਹਾ ਜਾਂਦਾ ਸੀ ।
4. ਜਜ਼ੀਆ ਹਿੰਦੁਆਂ ਤੋਂ ਲਿਆ ਜਾਣ ਵਾਲਾ ਇੱਕ ਕਰ ਸੀ ।
5. ਸ਼ਾਸਕ ।
![]()
4. 16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਸਿੱਖਿਆ ਦੇ ਖੇਤਰ ਵਿੱਚ ਕੋਈ ਖ਼ਾਸ ਉੱਨਤੀ ਨਹੀਂ ਹੋਈ ਸੀ । ਮੁਸਲਮਾਨਾਂ ਨੂੰ ਸਿੱਖਿਆ ਦੇਣ ਦਾ ਕੰਮ ਉਮਾ, ਮੁੱਲਾਂ ਤੇ ਮੌਲਵੀ ਕਰਦੇ ਸਨ । ਉਹ ਮਸਜਿਦਾਂ, ਮਕਤਬਿਆਂ ਅਤੇ ਮਦਰੱਸਿਆਂ ਵਿੱਚ ਸਿੱਖਿਆ ਦਿੰਦੇ ਸਨ । ਰਾਜ ਸਰਕਾਰ ਉਨ੍ਹਾਂ ਨੂੰ ਅਨੁਦਾਨ ਦਿੰਦੀ ਸੀ । ਮਸਜਿਦਾਂ ਅਤੇ ਮਕਤਬਿਆਂ ਵਿੱਚ ਮੁੱਢਲੀ ਸਿੱਖਿਆ ਦਿੱਤੀ ਜਾਂਦੀ ਸੀ ਜਦਕਿ ਮਦਰੱਸਿਆਂ ਵਿੱਚ ਉਚੇਰੀ । ਮਦਰੱਸੇ ਆਮ ਤੌਰ ‘ਤੇ ਸ਼ਹਿਰਾਂ ਵਿੱਚ ਹੀ ਹੁੰਦੇ ਸਨ । ਉਸ ਸਮੇਂ ਮੁਸਲਮਾਨਾਂ ਦੇ ਪੰਜਾਬ ਵਿੱਚ ਸਭ ਤੋਂ ਪ੍ਰਸਿੱਧ ਸਿੱਖਿਆਂ ਕੇਂਦਰ ਲਾਹੌਰ ਅਤੇ ਮੁਲਤਾਨ ਵਿੱਚ ਸਨ ।
1. 16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਸਿੱਖਿਆ ਦੇ ਖੇਤਰ ਵਿੱਚ ਉੱਨਤੀ ਕਿਉਂ ਨਹੀਂ ਹੋਈ ਸੀ ?
2. ਕੀ ਮੌਲਵੀ ਮੁਸਲਮਾਨਾਂ ਨੂੰ ਸਿੱਖਿਆ ਦੇਣ ਦਾ ਕੰਮ ਕਰਦੇ ਸਨ ?
3. ਮੁਸਲਮਾਨਾਂ ਨੂੰ ਮੁੱਢਲੀ ਸਿੱਖਿਆ ਕਿੱਥੇ ਦਿੱਤੀ ਜਾਂਦੀ ਸੀ ?
4. 16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਮੁਸਲਮਾਨਾਂ ਦੀ ਸਿੱਖਿਆ ਲਈ ਪ੍ਰਸਿੱਧ ਇੱਕ ਕੇਂਦਰ ਦਾ ਨਾਂ ਲਿਖੋ ।
5. ਮਦਰੱਸੇ ਆਮ ਤੌਰ ‘ਤੇ ……………………….. ਵਿੱਚ ਹੁੰਦੇ ਸਨ ।
ਉੱਤਰ-
1. ਕਿਉਂਕਿ ਉਸ ਸਮੇਂ ਲੋਕਾਂ ਨੂੰ ਸਿੱਖਿਆ ਦੇਣ ਦੀ ਜਿੰਮੇਵਾਰੀ ਸਰਕਾਰ ਦੀ ਨਹੀਂ ਹੁੰਦੀ ਸੀ ।
2. ਹਾਂ, ਮੌਲਵੀ ਮੁਸਲਮਾਨਾਂ ਨੂੰ ਸਿੱਖਿਆ ਦੇਣ ਦਾ ਕੰਮ ਕਰਦੇ ਸਨ ।
3. ਮੁਸਲਮਾਨਾਂ ਨੂੰ ਮੁੱਢਲੀ ਸਿੱਖਿਆ ਮਸਜਿਦਾਂ ਅਤੇ ਮਕਤਬਿਆਂ ਵਿੱਚ ਦਿੱਤੀ ਜਾਂਦੀ ਸੀ ।
4. 16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਮੁਸਲਮਾਨਾਂ ਦੀ ਸਿੱਖਿਆ ਦਾ ਇੱਕ ਪ੍ਰਸਿੱਧ ਕੇਂਦਰ ਲਾਹੌਰ ਸੀ ।
5. ਸ਼ਹਿਰਾਂ ।
5. ਸੂਫ਼ੀ ਮਤ 16ਵੀਂ ਸਦੀ ਦੇ ਆਰੰਭ ਵਿੱਚ ਪੰਜਾਬ ਵਿੱਚ ਬਹੁਤ ਹਰਮਨ-ਪਿਆਰਾ ਸੀ । ਸੂਫ਼ੀ ਨੇਤਾ ਸ਼ੇਖ਼ ਜਾਂ ਪੀਰ ਦੇ ਨਾਂ ਨਾਲ ਜਾਣੇ ਜਾਂਦੇ ਸਨ । ਉਹ ਇੱਕ ਅੱਲਾ ਵਿੱਚ ਵਿਸ਼ਵਾਸ ਰੱਖਦੇ ਸਨ । ਉਹ ਅੱਲਾਂ ਨੂੰ ਛੱਡ ਕੇ ਕਿਸੇ ਹੋਰ ਦੀ ਪੂਜਾ ਵਿੱਚ ਵਿਸ਼ਵਾਸ ਨਹੀਂ ਰੱਖਦੇ ਸਨ । ਉਨ੍ਹਾਂ ਅਨੁਸਾਰ ਅੱਲ੍ਹਾ ਸਰਬ ਸ਼ਕਤੀਮਾਨ ਹੈ ਤੇ ਉਹ ਹਰ ਜਗ੍ਹਾ ਮੌਜੂਦ ਹੈ । ਅੱਲ੍ਹਾ ਨੂੰ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ ਉਹ ਪ੍ਰੇਮ ਭਾਵਨਾ ਉੱਤੇ ਜ਼ੋਰ ਦਿੰਦੇ ਸਨ । ਉਹ ਧਰਮ ਦੇ ਬਾਹਰੀ ਦਿਖਾਵਿਆਂ ਵਿੱਚ ਵਿਸ਼ਵਾਸ ਨਹੀਂ ਰੱਖਦੇ ਸਨ । ਅੱਲਾ ਨੂੰ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ ਉਹ ਪੀਰ ਜਾਂ ਗੁਰੂ ਦਾ ਹੋਣਾ ਬਹੁਤ ਜ਼ਰੂਰੀ ਸਮਝਦੇ ਸਨ ।ਉਹ ਸੰਗੀਤ ਵਿੱਚ ਵੀ ਵਿਸ਼ਵਾਸ ਰੱਖਦੇ ਸਨ । ਉਨ੍ਹਾਂ ਨੇ ਕੱਵਾਲੀ ਗਾਉਣ ਦੀ ਪ੍ਰਥਾ ਚਲਾਈ । ਉਹ ਮਨੁੱਖਾਂ ਦੀ ਸੇਵਾ ਕਰਨੀ ਆਪਣਾ ਜ਼ਰੂਰੀ ਕਰਤੱਵ ਸਮਝਦੇ ਸਨ । ਉਨ੍ਹਾਂ ਦਾ ਜਾਤ-ਪਾਤ ਵਿੱਚ ਕੋਈ ਵਿਸ਼ਵਾਸ ਨਹੀਂ ਸੀ । ਉਹ ਦੂਸਰੇ ਧਰਮਾਂ ਦਾ ਸਤਿਕਾਰ ਕਰਦੇ ਸਨ ।
1. ਸੂਫ਼ੀ ਮਤ ਕਿਸ ਧਰਮ ਨਾਲ ਸੰਬੰਧਿਤ ਸੀ ?
2. ਸੂਫ਼ੀ ਸ਼ੇਖ ਹੋਰ ਕਿਸ ਨਾਂ ਨਾਲ ਜਾਣੇ ਜਾਂਦੇ ਸਨ ?
3. ਸੂਫ਼ੀ ਸ਼ੇਖਾਂ ਦੀ ਵਿਚਾਰਧਾਰਾ ਨੂੰ ਕੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ?
4. ਸੂਫ਼ੀ ਮਤ ਦਾ ਕੋਈ ਇੱਕ ਸਿਧਾਤ ਲਿਖੋ ।
5. ਅੱਲਾ ਨੂੰ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ ਸੁਫ਼ੀ ਕਿਸ ਦਾ ਹੋਣਾ ਜ਼ਰੂਰੀ ਸਮਝਦੇ ਸਨ ?
(i) ਪੀਰ
(ii) ਕੱਵਾਲੀ
(iii) ਦਰਗਾਹ
(iv) ਉੱਪਰ ਲਿਖੇ ਸਾਰੇ ।
ਉੱਤਰ-
1. ਸੂਫ਼ੀ ਮਤ ਇਸਲਾਮ ਧਰਮ ਨਾਲ ਸੰਬੰਧਿਤ ਸੀ ।
2. ਸੂਫ਼ੀ ਸ਼ੇਖ ‘ਪੀਰ’ ਦੇ ਨਾਂ ਨਾਲ ਵੀ ਜਾਣੇ ਜਾਂਦੇ ਸਨ ।
3. ਸੂਫ਼ੀ ਸ਼ੇਖਾਂ ਦੀ ਵਿਚਾਰਧਾਰਾ ਨੂੰ ਤਸਵੁਫ਼ ਕਿਹਾ ਜਾਂਦਾ ਸੀ ।
4. ਉਹ ਇੱਕ ਅੱਲ੍ਹਾ ਵਿੱਚ ਵਿਸ਼ਵਾਸ ਰੱਖਦੇ ਹਨ ।
5. ਪੀਰ ।













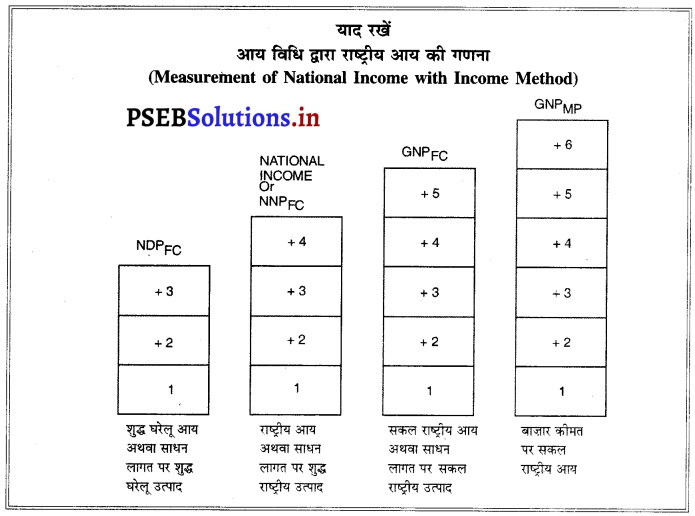









 उत्तर-
उत्तर-