Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 12 Algebraic Expressions Ex 12.2 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 7 Maths Chapter 12 Algebraic Expressions Ex 12.2
1. Fill in the blanks :
(i) 5y + 7y = ……………..
(ii) 3xy + 2xy = ……………..
(iii) 12a2 – 7a2 = ……………..
(iv) 8mn2 – 3mn2 = ……………..
Solution:
(i) 12y
(ii) 5xy
(iii) 5a2
(iv) 5mn2
2. Add the following algebraic expressions
(a) 3xy2, 7xy2
Solution:
Given terms are like terms. Their coefficients are 3 and 7.
Required sum is given as :
3xy2 + 7xy2 = (3 + 7) xy2
= 10xy2
(b) 7x, – 3x, 2x
Solution:
7x + (- 3x) + 2x = (7 – 3 + 2) x
= 6x
(c) 12p2q, 3p2q, – 5p2q
Solution:
(12p2q) + (3p2q) + (- 5p2q)
= (12 + 3 – 5) p2q
= 10p2q
(d) 3x2, – 8x2, – 5x2, 13x2
Solution:
3x2 + (- 8x)2 + (- 5x)2 + 13x2
= (3 – 8 – 5 + 13) x2
= 3x2
![]()
3. Add the following algebraic expressions.
(a) x + y and 2x – 3y
Solution:
(a) Horizontal method:
(x + y) + (2x – 3y)
= x + 2x + y – 3y
= 3x – 2y
Column method:
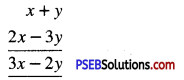
(b) 5a + 7b and 3a – 2b
Solution:
Horizontal method:
(5a + 7b) + (3a – 2b)
= 5a + 3a + 7a – 2b
= 8a + 5b.
Column method:

(c) 3m + 2n, 7m – 8n, 2m – n
Solution:
Horizontal method:
(3m + 2n) + (7m – 8n) + (2m – n)
= 3m + 7m + 2m + 2n – 8n – n
= 12m – 7n
Column method:

(d) 3x2 + 2x – 7 and 5x2 – 7x + 8
Solution:
Horizontal method:
(3x2 + 2x – 7) + (5x2 – 7x + 8)
= 3x2 + 5x2 + 2x – 7x – 1 + 8
= 8x2 – 5x + 1
Column method:
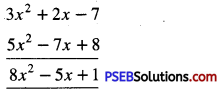
(e) m2 + 2n2 – p2, – 3m2 + n2 + 2p2 and 4m2 – 3n2 + 5p2
Solution:
Horizontal method:
(m2 + 2n2 – p2) + (- 3m2 + n2 + 2p2) + (4m2 – 3n2 + 5p2)
= m2 – 3m2 + 4m2 + 2n2 + n2 – 3n2 – p2 + 2p2 + 5p2
= 2m2 + 0n2 + 6p2
Column method:
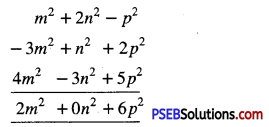
(f) 3xy + 7x2 – 2y2, 2xy + y2 and 2x2 + y2
Solution:
Horizontal method:
(3xy + 7x2 – 2y2) + (2xy + y2) + (2x2 + y2)
= 3xy + 2xy + 7x2 + 2x2 – 2y2 + y2 + y2
= 5xy + 9x2 + 0y2
Column method:
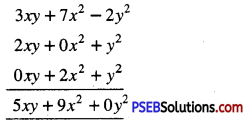
![]()
4. Simplify the following algebraic expressions by combining like terms.
(a) -5ax + 3xy + 2xy – 8ax
Solution:
– 5ax + 3xy + 2xy – 8ax
= – 5ax – 8ax + 3xy + 2xy
= – 13ax + 5xy.
(b) 3m – 2n + 5m – 3m + 8n
Solution:
3m – 2n + 5m – 3m + 8n
= 3m + 5m – 3m – 2n + 8n
= 5m + 6 n.
(c) 3pq – 15r2 – 3l2m2 + 2r2 + 2l2m2 – 5pq
Solution:
3pq – 15r2 – 3l2m2 + 2r2 + 2l2m2 – 5pq
= 3pq – 5pq – 15r2 + 2r2 – 3l2m2 + 2l2m2
= – 2pq – 13r2 – 2l2m2.
(d) 4x3 + 7x2 – 3x + 2 – 2x3 – 2x2 + 7x – 3
Solution:
4x3 + 7x2 – 3x + 2 – 2x3 – 2x2 + 7x – 3
= 4x3 – 2x3 + 7x2 – 2x2 – 3x + 7x + 2 – 3
= 2x3 + 5x2 + 4x – 1.
5. Subtract the algebraic expressions.
(a) – 3x2 from 7x2
Solution:
7x2 – (- 3x2) = 7x2 + 3x2 = 10x2
(b) – 3ab from 10ab
Solution:
10ab – (- 3ab) = 10ab + 3ab = 13 ab
![]()
(c) a + b from a – b
Solution:
(a – b) – (a+ b)
= a – b – a – b
= -2b
(d) 15m + 10n from 2m – 16n
Solution:
2m – 6n – (15m + 10n)
= 2m – 15m – 6n – 10n
= – 13m – 16n
(e) 2x + 8y – 3z from – 3x + 2y + z
Solution:
– 3x + 2y + z – (2x + 8y – 3z)
= – 3x + 2y + z – 2x – 8y + 3z
= – 5x – 6y + 4z
(f) 18m2 + 3n2 – 2mn – 7 from 3m2 – 2n2 + 8mn – 8m + 4
Solution:
(3m2 – 2n2 + 8mn – 8m + 4) – (18m2 + 3n2 – 2mn – 7)
= 3m2 – 2n2 + 8mn – 8m + 4 – 18m2 – 3n2 + 2mn + 7
= 3m2 – 18m2 – 2n2 – 3n2 + 8mn + 2mn – 8m + 4 + 7
= – 15m2 – 5n2 + 10mn – 8m + 11
6. What should be subtracted from l – 2m + 5n to get 2l – 3m + 4n ?
Solution:
(l – 2m + 5n) – (2l – 3m + 4n)
= l – 2l – 2m + 3m + 5n – 4n
= -l + m + n.
Hence, -l + m + n should be subtracted.
7. What should be added to 3x2 + 2xy – y2 to obtain x2 – 7xy + 3y2 ?
Solution:
(x2 – 7xy + 3y2) – (3x2 + 2xy – y2)
= x2 – 3x2 – 7xy – 2xy + 3y2 + y2
= – 2x2 – 9xy + 4y2.
![]()
8. Subtract 3a2 + 2b2 – 8ab + 8 from the sum of a2 – b2 + 7ab + 3 and 2a2 + 4b2 – 18ab + 7
Solution:
First add a2 – b2 + 7ab + 3 and 2a2 + 4b2 – 18ab + 7
(a2 – b2 + 7ab + 3) + (2a2 + 4b2 – 18ab + 7)
= a2 + 2a2 – b2 + 4b2 + 7ab – 18ab + 3 + 7
= 3a2 + 3b2 – 11ab + 10 …… (1)
Now we subtract 3a2 + 2b2 – 8ab + 8 from (1)
3a2 + 3b2 – 11ab + 10 – (3a2 + 2b2 – 8ab + 8)
= 3a2 – 3a2 + 3b2 – 2b2 – 11ab + 8ab + 10 – 8
= 0a2 + b2 – 3ab + 2
= b2 – 3ab + 2
9. How much x2 + 3xy + y2 is less than 2x2 + 5xy – y2 ?
Solution:
(2x2 + 5xy – y2) – (x2 + 3xy + y2)
= 2x2 – x2 + 5xy – 3xy – y2 – y2
= x2 + 2xy – 0y2
Hence, x2 + 3xy + y2 is less than 2x2 + 5xy – y2 by x2 + 2xy – 2y2.
10. Multiple Choice Questions :
Question (i).
The algebraic expression for “Number 5 added to three times the product of numbers m and n” is.
(a) 5 + 3mn
(b) 3 + 5mn
(c) (5 + 3) mn
Answer:
(a) 5 + 3mn
![]()
Question (ii).
The sum of algebraic expressions 3x + 11 and 2x – 7 is
(a) 5x + 4
(b) x + 4
(c) 5x – 18
Answer:
(a) 5x + 4
Question (iii).
Subtraction of a + b from 2a + 3b.
(a) a + 2b
(b) – a – 2b
(c) 3a + 4b
(d) a + b
Answer:
(a) a + 2b
