Class 8

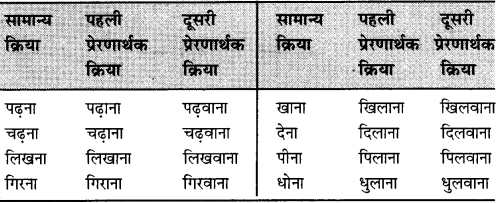
Punjab State Board PSEB 8th Class Hindi Book Solutions Hindi Rachana Patra Lekhan पत्र लेखन Exercise Questions and Answers, Notes.

PSEB 8th Class Hindi Rachana पत्र लेखन (2nd Language)

प्रश्न-ज्ञान परीक्षा प्रश्न-पत्र में दो पत्र दिए जाएंगे, जिनमें से एक अवश्य प्रार्थना-पत्र होगा। इन दोनों में से कोई एक करना होगा।

आवश्यक निर्देश पत्र या प्रार्थना-पत्र का आरम्भ तथा अन्त उचित ढंग से करना चाहिए। तिथि अवश्य लिखनी चाहिए। प्रश्न में दिए गए नाम एवं पते का ही उपयोग करना चाहिए।

पत्र की परिभाषा-प्रत्येक आदमी अपने विचारों को दूसरों तक पहुँचाने की कोशिश करता है। पास के आदमी से साधारण बातचीत द्वारा विचारों का आदान-प्रदान होता है। परन्तु जिसके माध्यम से हम दूर गए व्यक्ति के साथ विचारों का आदान-प्रदान करते हैं, उसे पत्र कहा जाता है।

पत्र के प्रकार-पत्र चार प्रकार के हैं-

• व्यक्तिगत पत्र
• व्यावहारिक पत्र
• समाचारात्मक पत्र
• आवेदन या प्रार्थना-पत्र।

पत्र के छ: अंग होते हैं-

1. स्थान तथा तिथि-यह प्रायः पत्र के ऊपर दाएं कोने में लिखी जाती है। यदि हो सके तो भेजने वाले का पूरा पता ऊपर की दो पंक्तियों में होना चाहिए। अन्तिम पंक्ति में तिथि। आजकल पूरा पता न लिख कर केवल स्थान ही लिख दिया जाता है।
2. प्रशस्ति-प्रेष्य को (जिस व्यक्ति को पत्र लिखा जाता है) जिन शब्दों से सम्बोधित व प्रणाम आदि किया जाता है उसे प्रशस्ति कहते हैं। इसमें प्रेष्य की अवस्था, पदवी आदि के अनुसार परिवर्तन हो जाता है।
3. विषय-यह पत्र का मुख्य अंग है। इसी को प्रकट करने के लिए पत्र लिखा जाता है। इस विषय में अनेक बातें लिखी जा सकती हैं।
4. विषय का स्पष्टीकरण- इसमें विषय को स्पष्ट करने के लिए उसे कई भागों में बाँटा जा सकता है।
5. प्रेषक का परिचय-इसमें केवल प्रेषक का नाम ही लिखा होना चाहिए।
6. पता-पता कार्ड के पिछले भाग पर दायीं ओर लिखते सेवा में हैं। इसमें क्रमशः पाने वाले का नाम, ग्राम या शहर, पोस्ट ऑफिस का नाम और ज़िला लिखते हैं। लिफाफे पर बायीं ओर प्रेषक का नाम और पता लिखा जाता है।

पत्र सम्बन्धी कुछ ज्ञातव्य बातें –

1. बड़ों की प्रशस्ति में पूज्य, पूजनीय, श्रद्धेय, आदरणीय, मान्यवर आदि कोई शब्द लिख कर अन्त में ‘जी’ अवश्य जोड़ना चाहिए।
2. दूसरी पंक्ति में बड़ों के लिए नमस्कार वाचक कोई शब्द (सादर प्रणाम, नमस्कार, चरण वन्दना आदि) तथा छोटों के लिए आशीर्वाद वाचक कोई शब्द (चिरंजीव, स्नेह, प्यार आदि) लिखना उचित है।
3. लगभग समान अवस्था वाले भाई-बहिन, भावज, मित्र आदि के लिए प्रिय, प्रियवर, स्नेही, स्नेहमयी आदि शब्द प्रयुक्त करने चाहिए। इसके साथ दूसरी पंक्ति में नमस्ते, नमस्कार आदि शब्द लिखने चाहिए।
4. छोटों के लिए अथवा जहाँ परस्पर प्रेम बहुत अधिक हो वहाँ प्रिय के पश्चात् भाई मित्र आदि के स्थान पर पूरा अथवा अधूरा नाम लिखा जा सकता है। जैसे प्रिय सुषमा, प्रिय राजन।
5. पति के लिए प्राणनाथ, प्राणेश्वर तथा पत्नी के लिए प्राणप्रिय, प्यारी आदि का प्रयोग होता है। आजकल पत्नी के लिए उसका संक्षिप्त नाम ही लिखा जाता है।
6. बड़ों को लिखा गया पत्र हो तो अन्त में आपका आज्ञापालक, कृपापात्र, विनीत आदि कोई शब्द लिखा होना चाहिए।
7. समान अवस्था वाले सम्बन्धियों और मित्रों के लिए तुम्हारा मित्र, भाई, अभिन्न हृदय आदि कोई शब्द लिखा जा सकता है।

अनौपचारिक (पारिवारिक या सामाजिक) पत्र की रूप-रेखा

अपने से बड़ों को पत्र-पिता को पत्र 18 लाजपतराय नगर जी० टी० रोड़, जालन्धर। दिसम्बर 18, ……….. पूज्य पिता जी, सादर प्रणाम। आपका कृपा पत्र मिला, समाचार ज्ञात हुआ। निवेदन है कि ………………………………………………………………………… ………………………………………………………………………………………………………………………………………………………………….. ………………………………………………………………………………………………………………………………………………………………….. ………………………………………………………………………………………………………………………………………………………………….. पूज्य माता जी को मेरा प्रणाम कहना। आपका आज्ञाकारी, …………………… ……………………

प्रशासनिक पत्र की रूप-रेखा

उच्च अधिकारियों को लिखा जाने वाला पत्र सेवा में उपायुक्त महोदय, ज़िला …………………… पंजाब। विषय-लाउडस्पीकर के प्रयोग पर पाबन्दी लगाये जाने बारे। श्रीमान जी, सविनय निवेदन है कि …………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………… …………. धन्यवाद सहित, आपका आज्ञाकारी, (हस्ताक्षर) नाम और पता ………… ………….. दिनांक……

आपके पाठ्यक्रम में केवल दो ही प्रकार के पत्र रखे गये हैं। जैसे-
(क) प्रार्थना पत्र या आवेदन पत्र तथा
(ख) व्यक्तिगत पत्र या पारिवारिक पत्र।।

(क) प्रार्थना पत्र/आवेदन पत्र प्रशासनिक पत्रों की कोटि में आते हैं-इसमें मुख्याध्यापक/ मुख्याध्यापिका को लिखे जाने वाले पत्र, उच्च अधिकारियों को लिखे जाने वाले शिकायत या सुझाव सम्बन्धी पत्र आते हैं। इन्हें अनौपचारिक पत्रों की कोटि में रखा जाता है।

हाथ से लिखे बधाई पत्र, निमन्त्रण पत्र, सांत्वना पत्र आदि भी अनौपचारिक पत्रों की कोटि में आते हैं। इनमें और व्यक्तिगत पत्रों में अन्तर यह होता है कि ये बहुत लम्बे नहीं लिखे जाते अर्थात् ऐसे पत्र संक्षेप में ही लिखने चाहिएं –

निमन्त्रण पत्र या शोक पत्र छपे हुए भेजे जाते हैं उन्हें औपचारिक पत्रों की कोटि में रखा जाता है। जैसे किसी बड़े नेता को उसके जन्म दिवस पर या चुनाव में जीत प्राप्त करने पर लिखे जाने वाले पत्र दो चार पंक्तियों में ही होते हैं-इसी कारण इन्हें औपचारिक पत्र कहते हैं-

विशेष रूप से ध्यान देने योग्य बात

ऊपर दी गई रूप रेखा के अनुसार ही पत्र लिखने चाहिएं, चाहे वे व्यक्तिगत पत्र हों या प्रशासनिक (प्रार्थना पत्र आदि) प्रायः देखने में आता है कि लोग इन नियमों का पालन नहीं करते हैं। हालांकि इस छोटी-सी बात को दफ़्तरों का साधारण कर्मचारी जानता है। वह ऊपर दिये गए नियमों के अनुसार ही पत्र लिखता अथवा टाइप करता है। आगे चल कर इन नियमों का पालन करते हुए लिखे गये पत्र को ही अच्छे अंक दिये जाते हैं। आशा है आप पत्र लिखते समय इन नियमों का पूरी तरह पालन करेंगे।

आवश्यक प्रार्थना-पत्र एवं अन्य पत्र

प्रश्न 1.
मान लो आपका नाम सिमरन है और आप सरकारी हाई स्कूल, तरनतारन में पढ़ती हैं। अपने स्कूल के मुख्याध्यापक को (घर में जरूरी काम है) छुट्टी के लिए प्रार्थना-पत्र लिखें।
उत्तर :
सेवा में
मुख्याध्यापक,
राजकीय उच्च विद्यालय,
तरनतारन।
महोदय,
सविनय निवेदन यह है कि मेरी माता जी कल से सख्त बीमार हैं। पिता जी बाहर गए हुए हैं। माता जी की देखभाल के लिए मेरा घर पर रहना बहुत आवश्यक है। इसलिए मैं स्कूल नहीं आ सकती। कृपया मुझे दो दिन का अवकाश दीजिए।

धन्यवाद,
आपकी आज्ञाकारी शिष्या,
सिमरन।
आठवीं कक्षा
रोल नं0 21
तिथि : 15 फरवरी, 20…..

प्रश्न 2.
मान लो आपका नाम सतवन्त कौर है और आप कन्या खालसा हाई स्कूल, अमृतसर में पढ़ती हैं। अपने स्कूल की मुख्याध्यापिका को एक प्रार्थना-पत्र लिखो, जिसमें बीमारी के कारण छुट्टी के लिए प्रार्थना की गई हो।
उत्तर :
सेवा में
मुख्याध्यापिका,
खालसा कन्या हाई स्कूल,
अमृतसर।
महोदया,
सविनय निवेदन है कि मुझे कल रात से ज्वर आ रहा है। तबीयत खराब होने के कारण कमज़ोरी हो गई है। इसलिए मैं स्कूल में उपस्थित नहीं हो सकती। कृपया मुझे दो दिन का अवकाश प्रदान कीजिए।
धन्यवाद,
आपकी आज्ञाकारी शिष्या,
सतवन्त कौर।
कक्षा आठवीं ‘ए’।
19 अप्रैल, 20……

प्रश्न 3.
मान लो आपका नाम परमजीत है। आप अपने स्कूल के मुख्याध्यापक को एक प्रार्थना-पत्र लिखो जिसमें भाई या बहन के विवाह के कारण अवकाश के लिए प्रार्थना की गई हो।
उत्तर :
सेवा में
मुख्याध्यापक,
सरकारी हाई स्कूल,
फरीदकोट।
महोदय,
सविनय प्रार्थना है कि मेरे बड़े भाई का शुभ विवाह 12 अक्तूबर को होना निश्चित हुआ है। मेरा इसमें सम्मिलित होना बहुत आवश्यक है। इसलिए इन दिनों मैं स्कूल में उपस्थित नहीं हो सकता। कृपया मुझे दो दिन का अवकाश देकर अनुगृहीत करें।
धन्यवाद सहित,
आपका आज्ञाकारी शिष्य,
परमजीत।
कक्षा आठवीं ‘बी’
11 अक्तूबर, 20….

प्रश्न 4.
मान लो आपका नाम विजय है और आप सरकारी हाई स्कूल, वेरका में पढ़ते हैं। अपने स्कूल के मुख्याध्यापक को एक प्रार्थना-पत्र लिखो जिसमें जुर्माना माफी के लिए प्रार्थना करो।
उत्तर :
सेवा में
मुख्याध्यापक,
सरकारी हाई स्कूल,
वेरका।
महोदय,
सविनय निवेदन है कि कल हमारे इंग्लिश के अध्यापक महोदय ने हमारी मासिक परीक्षा लेनी थी, किन्तु प्रातः स्कूल आते समय रास्ते में मेरी साइकिल पंक्चर हो गई। इस कारण मैं स्कूल देर से पहुँचा और परीक्षा में भाग न ले सका। अध्यापक महोदय ने मेरी इस सच्ची बात का विश्वास न किया और मुझे बीस रुपये जुर्माना कर दिया। मैं यह जुर्माना नहीं दे सकता क्योंकि मेरे पिता जी बड़े ग़रीब हैं। वैसे मैं इंग्लिश में बहुत अच्छा हूँ। इस बार त्रैमासिक परीक्षा में मेरे 100 में से 80 अंक आए थे। मैं आज तक स्कूल में अकारण अनुपस्थित नहीं रहा।

कृपया मेरा जुर्माना माफ कर दें। मैं आपका अत्यन्त आभारी रहूँगा।
आपका आज्ञाकारी शिष्य,
विजय।
कक्षा आठवीं ‘ए’
27 अगस्त, 20…

प्रश्न 5.
आप अपने विद्यालय के मुख्याध्यापक को अपने घर की आर्थिक स्थिति बताते हुए फीस माफी के लिए प्रार्थना-पत्र लिखें।
उत्तर :
सेवा में
मुख्याध्यापक,
डी० ए० वी० हाई स्कूल,
नकोदर।
महोदय,

सविनय प्रार्थना यह है कि मैं आपके स्कूल की आठवीं कक्षा का विद्यार्थी हूँ। मेरे पिता जी एक डाकखाने में क्लर्क हैं। उनकी मासिक आय केवल पच्चीस सौ रुपये है। हम घर के सात सदस्य हैं। इस महंगाई के जमाने में निर्वाह होना बहुत मुश्किल हो गया है। अतः मेरे पिता जी मेरी स्कूल की फीस देने में असमर्थ हैं।

मेरी पढ़ाई में विशेष रुचि है। मैं हमेशा अपनी कक्षा में प्रथम स्थान पर रहता आया हूँ। मैं स्कूल की जूनियर हॉकी टीम का कैप्टन भी हूँ। मेरे सभी अध्यापक मुझ से प्रसन्न हैं।

अतः आपसे मेरी नम्र प्रार्थना है कि आप मेरी पूरी फीस माफ करें। ताकि में अपनी पढ़ाई जारी रख सकूँ।

मैं आपका आभारी रहूँगा।
आपका आज्ञाकारी शिष्य,
जसदेव सिंह।
कक्षा आठवीं ‘ए’
रोल नं० 11
10 मई, 20…

प्रश्न 6.
आप अपने स्कूल के मुख्याध्यापक को एक प्रार्थना-पत्र लिखो जिसमें स्कूल छोड़ने का प्रमाण-पत्र देने की प्रार्थना की गई हो।
उत्तर :
सेवा में
मुख्याध्यापक,
राजकीय उच्च विद्यालय,
अबोहर।
महोदय,

सविनय निवेदन है कि मेरे पिता जी की तबदीली यहाँ से फिरोजपुर की हो गई है। इसलिए हमारा सारा परिवार फिरोजपुर जा रहा है। ऐसी हालत में मेरा यहाँ अकेला रहना कठिन है। कृपया मुझे स्कूल छोड़ने का प्रमाण-पत्र देकर कृतार्थ करें जिससे मैं अपनी आगे की पढ़ाई वहाँ जाकर जारी रख सकू।

मैं इस कृपया के लिए आपका आभारी रहूँगा।

आपका आज्ञाकारी शिष्य,
दर्शन सिंह।
कक्षा आठवीं ‘बी’
रोल नं0 22
15 मार्च, 20…

प्रश्न 7.
मान लो आपका नाम मनोहर लाल है और आप एस० डी० हाई स्कूल, नवांशहर में पढ़ते हैं। अपने स्कूल के मुख्याध्यापक को एक प्रार्थना-पत्र लिखो जिसमें उचित कारण बताते हुए सैक्शन बदलने की प्रार्थना की गई हो।
उत्तर :
सेवा में
मुख्याध्यापक,
एस० डी० हाई स्कूल,
नवांशहर।
महोदय,
सविनय निवेदन है कि मैं आपके स्कूल में आठवीं श्रेणी ‘बी’ सैक्शन (रोल नम्बर 40) में पढ़ रहा हूँ। मैं अपना सैक्शन बदलना चाहता हूँ। मेरे सैक्शन ‘बी’ में अधिकतर छात्र ड्राइंग विषय के हैं, जबकि मैंने संस्कृत विषय ले रखा है। पढ़ाई की सुविधा के विचार से मैं ‘ए’ सैक्शन में जाना चाहता हूँ। इसी सैक्शन में मेरे मुहल्ले के सभी छात्र पढ़ते हैं। सैक्शन अलग-अलग होने से मेरे लिए पढ़ाई में कुछ रुकावट पड़ जाती है क्योंकि मैं उनसे पूर्ण सहयोग प्राप्त नहीं कर पा रहा।

इसके अतिरिक्त ‘ए’ सैक्शन में पढ़ने वाले छात्रों को योग्यता के आधार पर रखा जाता है। मैं इस त्रैमासिक परीक्षा में अपनी श्रेणी में प्रथम आया हूँ। इस कारण मुझे ‘ए’ सैक्शन के उन योग्य छात्रों में बैठकर पढ़ने की अनुमति दी जाए, जिससे मेरा उचित विकास हो सके।

मेरी प्रार्थना है कि मुझे आठवीं ‘बी’ सैक्शन से ‘ए’ सैक्शन में जाने की अनुमति प्रदान की जाए। मैं आपको विश्वास दिलाता हूँ कि पढ़ाई में मैं किसी भी छात्र से पीछे नहीं रहूँगा।

आपका आज्ञाकारी शिष्य,
मनोहर लाल।
कक्षा आठवीं ‘बी’,
रोल नं0-40
5 मई, 20….

प्रश्न 8.
मान लो आपका नाम सुरिन्द्र है और आप एस० डी० हायर सैकण्डरी स्कूल, जालन्धर में पढ़ते हैं। अपने स्कूल के मुख्याध्यापक को पत्र लिखो जिसमें किसी स्कूल फण्ड से पुस्तकें लेकर देने की प्रार्थना की गई हो।
उत्तर :
सेवा में
मुख्याध्यापक
एस० डी० हायर सैकण्डरी स्कूल,
जालन्धर।
महोदय,
सविनय निवेदन यह है कि मैं आपके स्कूल में कक्षा आठवीं ‘ए’ में पढ़ता हूँ। मेरे पिता जी एक छोटे से दुकानदार हैं। उनकी मासिक आय केवल पच्चीस सौ रुपये है। हम घर के 6 सदस्य हैं। आजकल इस महंगाई के समय में निर्वाह होना बहुत मुश्किल है। ऐसी दशा में मेरे पिता जी मुझे पुस्तकें खरीद कर देने में असमर्थ हैं।

मुझे पढ़ाई का बहुत शौक है। मैं हमेशा अपनी कक्षा में प्रथम रहता आया हूँ। मेरे सभी अध्यापक मुझ से पूरी तरह सन्तुष्ट हैं। अतः आपसे मेरी नम्र प्रार्थना है कि आप मुझे स्कूल के ‘विद्यार्थी सहायता कोष’ (फण्ड) से सभी विषयों की पुस्तकें लेकर देने की कृपा करें, ताकि मैं अपनी पढ़ाई आगे जारी रख सकूँ।

मैं आपका आभारी रहूँगा।
आपका आज्ञाकारी शिष्य,
सुरिन्द्र कुमार
कक्षा आठवीं ‘ए’
रोल नं0 10
8 मई, 20…

प्रश्न 9.
मान लो आपका नाम बलदेव प्रकाश है और आप एस० डी० हाई स्कूल, कपूरथला में पढ़ते हैं। अपने स्कूल के मुख्याध्यापक को एक प्रार्थना-पत्र लिखो जिसमें अपनी आर्थिक कठिनाइयों का उल्लेख करते हुए छात्रवृत्ति देने की प्रार्थना की गई हो।
उत्तर :
सेवा में
मुख्याध्यापक,
एस० डी० हाई स्कूल,
कपूरथला।
मान्यवर,

सविनय निवेदन है कि मैं आपके स्कूल में कक्षा आठवीं ‘ए’ में पढ़ता हूँ। मेरे पिता जी एक छोटे से दुकानदार हैं। उनकी मासिक आमदनी केवल पन्द्रह सौ रुपये है। हम घर के सात सदस्य हैं। इस महँगाई के ज़माने में उन्हें अकेले ही सारे परिवार का पालन-पोषण करना पड़ता है। जिस कारण वे मुझे आगे पढ़ाने से इन्कार कर रहे हैं।

मेरी पढ़ाई में विशेष रुचि है। मैं सदा अपनी कक्षा में प्रथम रहता आया हूँ। सभी अध्यापक मेरे आचरण से प्रसन्न हैं। मेरी आपसे विनम्र प्रार्थना है कि आप मुझे स्कूल के ‘निर्धन विद्यार्थी सहायता कोष’ से छात्रवृत्ति प्रदान करने की कृपा करें, ताकि मैं अपनी पढ़ाई भली-भांति जारी रख सकूँ।

मैं आपका सदा आभारी रहूँगा।
आपका आज्ञाकारी शिष्य,
बलदेव प्रकाश।
कक्षा आठवीं ‘ए’
रोल नं० 11
5 अप्रैल, 20…

प्रश्न 10.
मान लो आपका नाम महेन्द्र है और आप गवर्नमैंट हाई स्कूल, आदमपुर में पढ़ते हैं। अपने स्कूल के मुख्याध्यापक को एक प्रार्थना-पत्र लिखो जिसमें अपने द्वारा हुई गलती/कसूर के लिए क्षमा याचना की गई हो।
उत्तर :
सेवा में
मुख्याध्यापक,
गवर्नमैंट हाई स्कूल,
आदमपुर।
महोदय,
सविनय प्रार्थना है कि कल श्रेणी के कमरे में जो झगड़ा हुआ है, उसके लिए मैं अपने आपको दोषी मानता हूँ। मैंने गुस्से में आकर करतार सिंह को चाँटा मार दिया था। यह मेरी गलती थी। चाहे उसने मुझे गाली दी थी पर मुझे उस पर हाथ नहीं उठाना चाहिए था। अच्छा तरीका तो यह था कि मैं आपसे करतार सिंह की शिकायत करता। परन्तु मुझ पर गुस्से का भूत सवार हो गया और मैंने श्रेणी के कमरे में ऐसी बुरी हरकत कर डाली।

अब मैं आपको विश्वास दिलाता हूँ कि आगे के लिए कभी ऐसी गलती नहीं करूँगा। कृपया इस बार मुझे क्षमा कर दें। मैं आपका सदा आभारी रहूँगा।

आपका आज्ञाकारी शिष्य, महेन्द्र,
आठवीं ‘ए’
रोल नं0 20
2 जनवरी, 20……

प्रश्न 11.
मान लीजिए आपका नाम मनजिन्दर है और आप प्रेमसभा हाई स्कूल, बरनाला में पढ़ते हैं। अपने स्कूल में साइकिल स्टैंड बनवाने के लिए अपने स्कूल के मुख्याध्यापक को एक प्रार्थना-पत्र लिखिए।
उत्तर :
सेवा में
मुख्याध्यापक,
प्रेमसभा हाई स्कूल,
बरनाला।
महोदय,

सविनय प्रार्थना है कि हमारे स्कूल में साइकिल खड़ी करने की उचित व्यवस्था नहीं है। भवन के पिछले भाग में साइकिल स्टैंड के लिए जो स्थान छोड़ा गया है, वह तीसचालीस साइकिलों के लिए भी अपर्याप्त है। सुबह ज्यादातर विद्यार्थी स्कूल के मुख्य गेट के सामने ही अपनी साइकिल खड़ी कर देते हैं। छुट्टी के समय वहाँ इतनी धक्कम-पेल होती है कि साइकिलें एक-दूसरे के ऊपर गिर जाती हैं जिससे विद्यार्थियों को बड़ी असुविधा का सामना करना पड़ता है। अतः आप से नम्र निवेदन है कि स्कूल के मैदान के एक कोने में साइकिल स्टैंड का निर्माण करवाया जाए तथा सभी विद्यार्थियों को अपनी साइकिल वहाँ खड़ी करने का आदेश दिया जाए।

धन्यवाद सहित,
आपका आज्ञाकारी शिष्य,
मनजिन्दर।
कक्षा आठवीं ‘ए’
रोल नं0 20
दिनांक : 10 अगस्त, 20…

प्रश्न 12.
मान लो आपका नाम मदन मोहन है और आप सरकारी हाई स्कूल, रोपड़ में पढ़ते हैं। अपने मुख्याध्यापक को एक प्रार्थना-पत्र लिखें जिसमें विद्यालय की सफ़ाई के बारे में कुछ सुझाव दिए गए हों।
उत्तर :
सेवा में
मुख्याध्यापक,
राजकीय उच्च विद्यालय,
रोपड़।
महोदय,
मैं आपका ध्यान पिछले कुछ मास से विद्यालय में सफ़ाई की बिगड़ती हालत की ओर दिलाना चाहता हूँ। अकसर विद्यालय लगने के समय देखा गया है कि कई श्रेणी-कक्षाओं के सामने कूड़े के ढेर लगे रहते हैं। नल के निकट हमेशा कीचड़ बना रहता है।

मेरा विनम्र सुझाव है कि सफाई कर्मचारियों को चेतावनी दी जाए ताकि वह किसी भी कक्षा के सामने कूड़े के ढेर न लगाएं। वह सारा कूड़ा स्कूल लगने से एक घण्टा पूर्व बाहर ले जाकर किसी गड़े में फेंके।

इसके अतिरिक्त सभी छात्रों को भी हिदायत की जाय कि फलों, मूंगफली आदि के छिलके कूड़दानों में ही फेंकें, इधर-उधर न बिखेरें। साथ ही और कूड़ादानों की व्यवस्था की जाये। प्रत्येक श्रेणी-कक्ष के सामने एक कूड़ादान अवश्य होना चाहिए।

नल के निकट का स्थान चूंकि कच्चा है, इसलिए वहाँ पक्की ईंटों का फर्श लगाना चाहिए ताकि जो भी छात्र पानी पीने के लिए आएं, उन्हें असुविधा न हो। कइयों का वहाँ पाँव फिसलते देखा है। आशा है कि आप मेरे इन सुझावों को अवश्य ध्यान में रखते हुए आवश्यक कार्यवाही करेंगे।

धन्यवाद सहित।
आपका शिष्य, मदन मोहन
8वीं कक्षा।
तिथि : 15 फरवरी, 20….

प्रश्न 13.
मान लो आपका नाम अनिल है और आप अमृतसर में रहते हैं। वहाँ के सरकारी हाई स्कूल के मुख्याध्यापक को एक प्रार्थना-पत्र लिखो, जिसमें अपना नाम आठवीं श्रेणी में प्रवेश देने की प्रार्थना की गई हो।
उत्तर :
सेवा में
मुख्याध्यापक,
राजकीय उच्च विद्यालय,
अमृतसर।
महोदय,

सविनय निवेदन है कि मेरे पिता जी की पटियाला से अमृतसर में स्थानांतरण हो गया है। इससे पहले मैं पटियाला के गवर्नमैंट हाई स्कूल में पढ़ता था। पिता जी के स्थानांतरण के साथ ही हमारा सारा परिवार भी अमृतसर आ गया है। अब मैं आपके स्कूल में आठवीं श्रेणी में प्रवेश प्राप्त करना चाहता हूँ। मेरा पटियाला का स्कूल छोड़ने का प्रमाण-पत्र प्रार्थना-पत्र के साथ संलग्न है। कृपया मुझे अपने स्कूल में दाखिला देकर कृतार्थ करें।

भवदीय,
अनिल।
तिथि : 17 फरवरी, 20….

प्रश्न 14.
मान लो आपका नाम राजबीर है और आप गाँव गढ़दीवाला, जिला होशियारपुर के निवासी हैं। अपने जिले के लिए मुख्य-स्वास्थ्य अधिकारी को एक प्रार्थना-पत्र लिखो जिसमें अपने गाँव में एक अस्पताल खोलने की प्रार्थना की गई हो।
उत्तर :
सेवा में
मुख्य-स्वास्थ्य अधिकारी,
होशियारपुर।
महोदय,

निवेदन है कि हमारा गाँव गढ़दीवाला, होशियारपुर से 20 किलोमीटर की दूरी पर स्थित है। इसकी जनसंख्या लगभग सात हज़ार है। परन्तु बड़े खेद की बात है कि इस गाँव में कोई अस्पताल नहीं है। गाँववासियों को छोटी-छोटी बीमारियों के इलाज के लिए शहर भागना पड़ता है। इसमें उन्हें काफ़ी परेशानी का सामना करना पड़ता है। सर्दी के मौसम में छोटे बच्चों और बूढ़ों को बीमारी की हालत में शहर ले जाना बहुत ही कठिन है।

इस गाँव में अस्पताल की बहुत आवश्यकता है। हमारा आपसे निवेदन है कि इस पिछड़े क्षेत्र के लोगों के स्वास्थ्य की ओर भी ध्यान दिया जाए। हमारे गाँव में यदि अस्पताल खुल जाता है तो इससे आसपास के गाँवों को भी लाभ पहुँच सकता है। आशा है कि आप हमारी इस प्रार्थना की ओर तुरन्त ध्यान देकर अस्पताल खोलने के लिए शीघ्र उचित कदम उठाएंगे।

निवेदक,
राजबीर।
तिथि : 8 अगस्त, 20…

प्रश्न 15.
मान लो आपका नाम दिनेश है और आप 45-आदर्श नगर, फिरोजपुर में रहते हैं। अपने पिता जी को एक पत्र लिखें जिसमें अपनी परीक्षा में उत्तीर्ण (पास) होने की सूचना देते हुए खर्चे के लिए रुपये मंगवाओ।
उत्तर :
45, आदर्श नगर,
फिरोजपुर।
27 अप्रैल, 20….
आदरणीय पिता जी,
सादर प्रणाम !

आपको यह जानकर हर्ष होगा कि हमारा परीक्षा-परिणाम निकल आया है। मैं 540 अंक लेकर प्रथम श्रेणी में उत्तीर्ण हो गया हूँ। अपनी कक्षा में मेरा दूसरा स्थान है। मुझे स्वयं इस बात का दुःख है कि मैं प्रथम स्थान प्राप्त न कर सका। इसका कारण यह है कि मैं दिसम्बर मास में बीमार हो गया था और लगभग 20-25 दिन स्कूल न जा सका। यदि मैं बीमार न हुआ होता तो सम्भवतः छात्रवृत्ति (वज़ीफा) प्राप्त करता। अब मैं मैट्रिक में अधिक अंक प्राप्त करने का यत्न करूँगा।

अब मुझे नई कक्षा के लिए नई पुस्तकें आदि खरीदनी हैं। इधर कुछ दिनों में मेरे पास अच्छे वस्त्र भी नहीं हैं। कुछ मित्र मेरी इस सफलता पर पार्टी भी माँग रहे हैं। इसलिए आप मुझे 1000 रुपये शीघ्र ही भेजने की कृपा करें ताकि मैं अगली कक्षा की पुस्तकें खरीद सकूँ और मित्रों को भी पार्टी दे सकूँ।

आपका आज्ञाकारी पुत्र,
दिनेश।

प्रश्न 16.
मान लो आपका नाम निर्मल कौर है और आप गुप्ता कॉलोनी, तरनतारन में रहती हैं। अपनी सहेली यशवन्त को एक पत्र लिखो जिसमें यह वर्णन करो कि आपके स्कूल में 15 अगस्त का दिन कैसे मनाया गया।
उत्तर :
गुप्ता कॉलोनी,
तरनतारन।
18 अगस्त, 20….
प्यारी सहेली यशवन्त,
सत् श्री अकाल।
कई दिन से तुम्हारा पत्र नहीं मिला। क्या कारण है। मैं तुम्हें दो पत्र डाल चुकी हूँ पर उत्तर एक का भी नहीं मिला। कोई नाराज़गी तो नहीं ? अगर ऐसी-वैसी कोई बात हो तो क्षमा कर दें।

हाँ, इस बार हमारे स्कूल में 15 अगस्त का दिन बड़ी ही धूमधाम से मनाया गया। इसकी थोड़ी-सी झलक मैं पत्र द्वारा पेश कर रही हूँ। 15 अगस्त मनाने की तैयारियां एक महीना पहले शुरू कर दी गई थीं। स्कूल में सफेदी कर दी गई थी। लड़कियों को लेजियम की ट्रेनिंग देनी कई दिन पहले ही शुरू हो गई थी। हमारे अमर शहीद’ एकांकी नाटक की रिहर्सल भी कई बार करवाई गई। निश्चित दिन को ठीक-सुबह सात बजे 15 अगस्त का समारोह शुरू हो गया। सबसे पहले तिरंगा झण्डा फहराने की रस्म क्षेत्र के जाने-माने समाज सेवक सरदार महासिंह जी ने अदा की। इसके बाद स्कूल की छात्राओं ने रंगारंग कार्यक्रम पेश करने शुरू कर दिए। गिद्धा नाच ने सबका मन मोह लिया। इसके बाद देश-प्रेम के गीत गाए गए। मैंने भी एक गीत गया था। मैंने लेजियम की टीम में भी भाग लिया।

इसके बाद एकांकी ‘हमारे अमर शहीद’ का अभिनय हुआ। इसके हर सीन पर तालियाँ बजती थीं। समारोह के अन्त में प्रधान महोदय और हमारी बड़ी बहन जी ने भाषण दिये, जिनमें देश भक्ति की प्रेरणा थी।

15 अगस्त का यह समारोह मुझे हमेशा याद रहेगा। क्योंकि मुझे इसमें दो खूबसूरत इनाम मिले हैं। पूज्य माता जी और भाभी को सत् श्री अकाल। अक्षत और गुड्डी को प्यार देना। इस बार पत्र का उत्तर ज़रूर देना।

तुम्हारी सहेली,
निर्मल कौर।

प्रश्न 17.
मान लो आपका नाम प्रेम सिंह है और आप 405 वसन्त विहार, कादियां में रहते हैं। अपने चाचा जी को एक पत्र लिखिए जिसमें जन्म-दिवस की भेंट पर धन्यवाद प्रकट किया गया हो।
उत्तर :
405, वसन्त निवास,
कादियां।
11 जुलाई, 20…
पूज्य चाचा जी,
सादर प्रणाम!

मेरे जन्म दिन पर आपके द्वारा भेजा हुआ पार्सल प्राप्त हुआ। जब मैंने इस पार्सल को खोला तो उसमें एक सुन्दर घड़ी देखकर बहुत प्रसन्न हुआ। कई वर्षों से इसका अभाव मुझे खटक रहा था।

कई बार विद्यालय जाने में भी विलम्ब (देर) हो जाता था। निःसन्देह अब मैं अपने आपको नियमित बनाने का प्रयत्न करूँगा। इसको पाकर मुझे असीम प्रसन्नता हुई। इसके लिए आपका बहुत-बहुत धन्यवाद।

पूज्य चाची जी को चरण वन्दना। रमेश को नमस्ते। मुझे शैली बहुत याद आती है। उसे मेरी प्यार भरी चपत लगाइए। सबको यथा योग्य।

आपका भतीजा,
प्रेम सिंह।

प्रश्न 18.
मान लो आपका नाम रमन है और आप सत्य निवास, फगवाड़ा में रहते हैं। अपने पिता जी को एक पत्र लिखो जिसमें आपके स्कूल का सुन्दर वर्णन हो।
उत्तर :
सत्य निवास,
फगवाड़ा।
17 मई, 20….
पूज्य पिता जी,
सादर प्रमाण
मैं परमात्मा की दया और आपके आशीर्वाद से पास हो गया हूँ। मेरे स्कूल का वातावरण मेरे बड़ा अनुकूल (ठीक) है। यहाँ पर विद्यार्थियों की गिनती बहुत है। लगभग एक हजार विद्यार्थी हमारे स्कूल में पढ़ते हैं। प्रत्येक श्रेणी के चार-चार विभाग हैं। स्कूल का भवन बड़ा सुन्दर और हवादार है। इसके अगले भाग में बड़ी सुन्दर फुलवाड़ी है।

हमारे स्कूल के कमरे साफ़-सुथरे तथा विशाल हैं। उनमें बिजली के पंखों का प्रबन्ध और सफ़ाई का खास ध्यान रखा जाता है। यहाँ के अध्यापकों का चरित्र बड़ा ऊंचा है। ये अपने-अपने विषय में विद्वान् हैं। मुख्याध्यापक जी बड़े परिश्रमी तथा छात्रों के साथ सहानुभूति (हमदर्दी) रखने वाले हैं। विद्यार्थियों के खेलने के लिए एक खेल का बड़ा मैदान है, जिसमें शाम को विद्यार्थी खेलते हैं। हमारे स्कूल में एक पुस्तकालय (लाइब्रेरी) भी है, जिसमें अलग-अलग विषयों पर हज़ारों पुस्तकें हैं। इसके अतिरिक्त एक विज्ञानशाला है, जिसमें विज्ञान का सारा सामान है।

इस प्रकार मेरा स्कूल पढ़ाई, खेलों तथा अन्य विषयों में अपने शहर में सबसे बढ़िया स्कूल है। इसका परिणाम हर वर्ष बहुत बढ़िया रहता है। मैं सब प्रकार से ठीक हूँ। कुशल समाचार लिखते रहा करें। माता जी को प्रणाम।

आपका सपुत्र
रमन।

प्रश्न 19.
मान लो आपका नाम रणवीर है। आप डी० ए० वी० हाई स्कूल, अमृतसर में पढ़ते हैं और छात्रावास (होस्टल) में रहते हैं। अपने पिता जी को एक पत्र लिखो जिसमें ‘मेरे जीवन का उद्देश्य’ विषय पर विचार प्रकट करो।
उत्तर :
छात्रावास,
डी० ए० वी० हाई स्कूल,
अमृतसर।
20 अप्रैल, 20…
पूज्य पिता जी,
सादर प्रणाम !

आज मैं अपने स्कूल की परीक्षा से निपट चुका हूँ। अब आगे मुझे क्या करना चाहिए ? मेरे जीवन का उद्देश्य क्या होगा-मैं अपने जीवन में क्या बन पाऊँगा, इसका उत्तर कठिन है। फिर भी मैं अपने मन के विचार लिखता हूँ।

पिता जी आप मेरी स्वाभाविक रुचियों से परिचित ही हैं। उन्हीं के अनुसार मैं अपने जीवन का उद्देश्य निश्चित करना चाहता हूँ। मेरा विचार एक अच्छा डॉक्टर बनने का है। आप जानते हैं कि हमारा देश सेहत के विचार से पिछड़ा हुआ है। हर साल लाखों लोग विभिन्न रोगों का शिकार हो जाते हैं। चिकित्सा (इलाज) के अभाव में बेमौके ही मौत के मुँह में चले जाते हैं। सरकार ने रोगों को दूर करने के लिए अनेक कदम उठाए हैं। फिर भी इतने बड़े देश के लिए वे ऊँट के मुँह में जीरा के समान हैं। हमारे देश में डॉक्टरों और वैद्यों की कमी तो नहीं, फिर भी निर्धन लोग धन न होने के कारण उनकी सेवा से वंचित रह जाते हैं। कस्बों और ग्रामों के अस्पतालों में ख़तरनाक रोगों की दवाएँ ही नहीं मिलती। इसलिए ग्रामीण भाई इलाज के अभाव में तड़प-तड़प कर जीवन का सफर पूरा करते हैं।

पिता जी की ऐसी बुरी हालत देखकर मेरा विचार डॉक्टर बनने का है। इससे देश सेवा होगी और जीवन का उद्देश्य भी पूरा होगा।

आशा है आप मेरे विचारों से सहमत होंगे। माता जी को चरण वन्दना।

आपका आज्ञाकारी पुत्र,
रणवीर।

प्रश्न 20.
मान लो आपका नाम बलदेव है और आप मल्होत्रा निवास जी० टी० रोड, करतारपुर में रहते हैं। अपने छोटे भाई कृष्ण को एक पत्र लिखो कि वह किताबी कीड़ा न बनकर खेलों में भाग लिया करे।
अथवा
अपने छोटे भाई को खेलों का महत्त्व बताते हुए एक पत्र लिखें।
उत्तर :
मल्होत्रा निवास,
जी० टी० रोड,
करतारपुर।
17 मार्च, 20….
प्रिय कृष्ण,
चिरंजीव रहो !

परीक्षा में तुम्हारी शानदार सफलता ने मेरा मन प्रसन्नता से भर दिया। पर यह जानकर मुझे दुःख भी हुआ कि यह सफलता तुझे सेहत गँवा कर मिली है। मुझे पता लगा है कि तुम आगे से भी अधिक किताबी कीड़ा बन गए हो। न तुम खेलों में भाग लेते हो और न तुम बाहर भ्रमण के लिए ही जाते हो। यह मेरी अभिलाषा है कि तुम बड़े विद्वान् बनो। पर साथ ही मैं यह भी चाहता हूँ कि तुम शरीर से भी पूर्ण स्वस्थ रहो। व्यक्ति पर जब संकट आता है तब बलवान् व्यक्ति ही उसका मुकाबला करने में समर्थ होते हैं।

यह ठीक है कि काम भगवान् है, पर रात-दिन काम में जुटे रहना भी अभिशाप ही है। मस्तिष्क (दिमाग) भी अवकाश माँगता है। स्मरण रखो कि स्वस्थ शरीर में ही स्वस्थ आत्मा निवास करती है। केवल पढ़ना व्यर्थ है। उसका मनन भी करना चाहिए। उसके लिए समय पर मस्तिष्क को विश्राम देना अनिवार्य है। मैं तुम्हें अच्छी सलाह देता हूँ कि तुम खेलों में भाग लिया करो।

खेलों का विद्यार्थी जीवन में बड़ा महत्त्व है। खेलों का सर्वप्रथम लाभ है-शरीर की पुष्टि। खेलने-कूदने और दौड़ने से शरीर के प्रत्येक अवयव (अंग) की कसरत हो जाती है। शरीर के रोमकूप पसीने के निकलने से स्वच्छ हो जाते हैं। खेलों से मनोरंजन के साथसाथ शारीरिक शक्ति भी बढ़ती है और मानसिक विकास भी होता है। खेलों से आपसी सहयोग, संगठन, अनुशासन, सहनशीलता आदि गुणों का विकास अपने आप हो जाता है। अत: तुम्हें मेरा परामर्श है कि तुम खेलों में भाग लेने के लिए कुछ समय अवश्य निकाल लिया करो।

तुम्हारा बड़ा भाई,
बलदेव।

प्रश्न 21.
मान लें आपका नाम मीना है। आप 2, एकता नगर, पटियाला में रहती हैं। अपनी सखी अंजु को अपनी ऐतिहासिक यात्रा का वर्णन देते हुए पत्र लिखें।
उत्तर :
2, एकता नगर,
पटियाला।
15 अगस्त, 20….
प्रिय सखी अंजु,
सप्रेम नमस्ते।

अब की बार तुम्हें पत्र लिखने में देरी हो गई है क्योंकि मैं एक मास के लिए दिल्ली गई हई थी। वहाँ मेरे चाचा जी रहते हैं और उन्होंने हमें छुट्टियाँ बिताने के लिए बुलाया था। इस ऐतिहासिक नगर की यात्रा अत्यन्त आनन्ददायक रही, इसलिए उसका कुछ अनुभव तुम्हें लिख रही हूँ।

भारत की राजधानी दिल्ली एक ऐतिहासिक नगर है। पुराना किला, लाल किला, कुतुबमीनार, हुमायूं का मकबरा, जन्तर मन्तर आदि दिल्ली के प्राचीन इतिहास के स्मारक हैं। हिन्दुओं का “बिड़ला मन्दिर’, मुसलमानों की विशाल जामा मस्जिद’ एवं सिक्खों का गुरुद्वारा ‘सीस गंज’ धार्मिक दृष्टि से महत्त्वपूर्ण हैं। चिड़िया घर, बुद्धा गार्डन, ओखला और बाल-भवन प्रमुख विहार केन्द्र हैं। यहीं पर ही दिल्ली गेट के बाहर राष्ट्रपिता बापू, चाचा नेहरू और शास्त्री जी की समाधियां हैं जहाँ देश-विदेश के लोग श्रद्धा के पुष्प चढ़ाने आते हैं।

दिल्ली का नया रूप नई दिल्ली में देखने को मिलता है। दिन को नई दिल्ली के दफ्तरों की भीड़-भाड़ और रात को कनाट प्लेस की शोभा देखते ही बनती है। गोलाकार संसद् भवन, राष्ट्रपति भवन, रेल भवन, विज्ञान भवन, कृषि भवन, आकाशवाणी केन्द्र जैसे बड़ेबड़े भवन दिल्ली की शोभा हैं। जहाँ नई दिल्ली में विशाल भवन और खुली-चौड़ी सड़कें हैं, तो वहाँ पुरानी दिल्ली में तंग गलियाँ और भीड़-भाड़ वाले बाजार हैं। पुरानी दिल्ली उत्तर भारत में व्यापार का मुख्य केन्द्र है।

मुझे विश्वास है कि शीघ्र ही तुम्हें दिल्ली देखने का अवसर मिलेगा। पूज्य माता जी की सेवा में चरण वन्दना।

तुम्हारी प्रिय सखी,
मीना।

प्रश्न 22.
मान लो आपका नाम प्रेम पाल है और आप 27 सी० 208, चण्डीगढ़ में रहते हैं। अपने मित्र हरजीत को एक पत्र लिखो जिसमें पर्वतीय यात्रा का वर्णन किया गया हो।
उत्तर :
27 सी० 208,
चण्डीगढ़।
16 जून, 20…
प्रिय हरजीत,
सप्रेम नमस्ते।
अब की बार तुम्हें पत्र लिखने में देरी हो गई है क्योंकि मैं एक मास के लिए शिमला गया हुआ था। वहाँ मेरे चाचा जी रहते हैं और उन्होंने हमें छुट्टियाँ बिताने के लिए बुलाया था। यह यात्रा अत्यन्त आनन्ददायक रही, इसलिए उसका कुछ अनुभव तुम्हें लिख रहा हूँ।

अवकाश होते ही हम 15 मई की रात्रि को रेल द्वारा कालका जा पहुँचे। कालका से शिमला तक छोटी पहाड़ी रेल जाती है। टैक्सियाँ भी जाती हैं। हमने शिमला के लिए टैक्सी ली। कालका से शिमला तक सड़क पहाड़ काट कर बनाई गई है। स्थान-स्थान पर ऊँचाईनिचाई तथा असंख्य मोड़ हैं। केवल 15 या 20 फुट की सड़क है। उसके दोनों ओर खाइयाँ तथा गड्डे हैं जिन्हें देखने से डर लगता है। ड्राइवर की ज़रा-सी आँख चूक जाए तो मोटर पाँचछ: सौ फुट नीचे गड्ढे में गिर सकती है। इसलिए बड़ी चौकसी रखनी पड़ती है।

हम कालका से सोलन और वहाँ से शिमला पहुँचे। पर्वतीय स्थलों में पैदल चलने और स्केटिंग करने में आनन्द आता है। वहाँ की मनोहारी छटा देखकर हमारी सारी थकान दूर हो गई। शिमला के लोअर बाज़ार और माल रोड की सैर हम हर रोज़ करते थे।

वापसी यात्रा हमने रेल से की। रेलयात्रा का दृश्य तो और भी मनोरम था। रेल की पटरी के दोनों ओर 200-300 फुट तक गड्ढे ही गड्डे। रेल की पटरी चक्कराकार थी। गाड़ी में बैठे नीचे की पटरियाँ बड़ी दिखाई देती थीं। सुरंगों में घुसने पर तो अन्धेरा ही अन्धेरा होता था।

इस प्रकार कुदरत की खूबसूरती के दर्शन करते हुए हम परसों ही वापस आए हैं। अपनी माता जी को मेरा सादर प्रणाम कहिए।

आपका मित्र, प्रेम पाल।

प्रश्न 23.
मान लो आपका नाम गणेश है। आप 15, पटेल नगर, दिल्ली में रहते हैं।
अपने मित्र, जिसका नाम हरीश है, को गर्मी की छुट्टियाँ किसी पर्वत पर बिताने के लिए निमन्त्रण-पत्र लिखें।
अथवा
अपने मित्र को एक पत्र लिखें, जिसमें उसे गर्मी की छुट्टियाँ शिमला में बिताने के लिए कहा गया हो।
उत्तर :
15, पटेल नगर,
दिल्ली।
20 मार्च, 20…
प्रिय मित्र हरीश,
सप्रेम नमस्ते।

तुम्हारा पत्र मिला। तुमने ग्रीष्मावकाश में मेरा कार्यक्रम जानने की इच्छा प्रकट की। तम्हें याद होगा कि मैंने गत गर्मियों की छुट्टियाँ तुम्हारे साथ जयपुर में बिताई थीं। इस समय तुमने वायदा किया था कि अगली गर्मी की छुट्टियाँ किसी पर्वतीय स्थान पर बिताएंगे। इस बार मेरा विचार शिमला जाने का है। अपने वचन के अनुसार तुम्हें भी मेरे साथ चलना है। मेरे मामा जी वहाँ अध्यापक हैं। अत: वहाँ मनोरंजन के साथ-साथ पढ़ाई भी हो सकेगी। इस प्रकार शिमला में गर्मियों की छुट्टियाँ बिताने में एक पंथ और दो काज होंगे।

तुम तो जानते ही होगे कि शिमला को पहाड़ों की रानी कहा जाता है। गर्मियों में वहाँ का मौसम बहुत ही सुहावना होता है। वहाँ का प्राकृतिक सौन्दर्य तो अद्भुत है। चीड़ और देवदार के ऊँचे-घने पेड़ उसकी शोभा को चार चाँद लगाते हैं। वहाँ जब शाम के समय हम रिज और माल रोड पर घूमेंगे तो मज़ा आ जाएगा।

आशा है कि तुम मेरा शिमला चलने का सुझाव अवश्य स्वीकार करोगे। तुम्हारी स्वीकृति आने पर मैं मामा जी को पत्र लिखूगा। पूज्य माता-पिता जी को मेरी चरण वन्दना कहना। आपके पत्र की प्रतीक्षा रहेगी।

तुम्हारा अभिन्न मित्र,
गणेश।

प्रश्न 24.
मान लो आपका नाम चाँद कौर है और आप मकान नं० 264, विजय नगर, जालन्धर में रहती हैं। अपनी सखी उर्मिला को एक पत्र लिखकर अपने स्कूल में हुए वार्षिक पारितोषिक वितरण उत्सव का विवरण दो।
उत्तर :
मकान नं० 264,
विजय नगर,
जालन्धर।
25 नवम्बर, 20…
प्रिय सखी उर्मिला,
सप्रेम नमस्ते।

तीन-चार दिन हुए मुझे तुम्हारा पत्र मिला। पत्र का उत्तर देने में मुझे इसलिए देरी हो गई क्योंकि 22 नवम्बर को हमारे स्कूल का पारितोषिक वितरण उत्सव मनाया गया। इसके लिए कई दिन पहले ही तैयारियाँ आरम्भ हो गई थीं।

उत्सव के दिन सारा स्कूल नववधू की तरह सजाया गया। राज्य के शिक्षा मन्त्री इस अवसर पर प्रधान अतिथि थे। ज्योंही उनकी कार स्कूल के मुख्य द्वार पर आकर रुकी, स्कूल के बैंड ने उनके स्वागत में सुरीली धुन बजाई। स्कूल की गर्ल्स स्काउटों ने उनको सलामी दी। फिर मुख्याध्यापक महोदय ने कुछ विशेष सज्जनों सहित उनका स्वागत किया और उनके गले में फूल मालाएँ डालीं। शिक्षा मन्त्री जी के पण्डाल में पधारते ही सभी छात्राओं और उपस्थित लोगों ने खड़े होकर उनका स्वागत किया। तत्पश्चात् छात्राओं ने गीत, कविताएँ, नाटक और अन्य मनोरंजक कार्यक्रम प्रस्तुत किये। मुख्याध्यापक महोदय ने स्कूल की वार्षिक रिपोर्ट पढ़ कर सुनाई। इसके बाद शिक्षा मन्त्री जी ने अपने कर-कमलों से छात्राओं में पारितोषिक बांटे और भाषण दिया। उन्होंने अपने भाषण से स्कूल की बहुत प्रशंसा की।

मुझे भी अपनी कक्षा में प्रथम आने के कारण ईनाम मिला। अपने माता-पिता को मेरा प्रणाम कहना। ज्योति को प्यार। तुम्हारी सखी चाँद कौर।

प्रश्न 25.
मान लो आपका नाम सुमीता है, आप 212 ‘ए’ मॉडल कालोनी, जालन्धर में रहती हैं। अपने भाई मोहन को, जो छात्रावास में रहता है, बुरी संगति से बचने के लिए प्रेरणा-पत्र लिखें।
अथवा
कुसंगति से बचने के लिए अपने छोटे भाई को एक पत्र लिखिए।
उत्तर :
212 ‘ए’ मॉडल कालोनी,
जालन्धर।
2 फरवरी, 20…..
प्रिय मोहन,
प्रसन्न रहो।

हमें पूर्ण विश्वास है कि तुम सदा मेहनत करते हो और मिडल परीक्षा में कोई अच्छा रस्थान लेकर उत्तीर्ण होंगे। तुम्हारी नियमितता और अनुशासन-पालन को देख कर हमें यह विश्वास हो गया है कि तुम्हारा भविष्य उज्ज्वल है। लेकिन एक बात का ध्यान अवश्य रखना कि कुसंगति में फँस कर अपने को दूषित न कर लेना। यदि तुम बुरे लड़कों के जाल से न बचोगे तो तुम्हारा भविष्य अन्धकारमय बन जाएगा और तुम अपने रास्ते से भटक जाओगे। तुम्हें जीवन भर कष्ट उठाने पड़ेंगे और तुम अपने उद्देश्य में सफल हो सकोगे।

कुसंगति छात्र का सबसे बड़ा शत्रु है। दुराचारी बच्चे होनहार बच्चों को भी भ्रष्ट कर देते हैं। प्रारम्भ में बुरे बच्चों की संगति बड़ी मनोरम लगा करती है, लेकिन यह भविष्य धूमिल कर देती है। दूसरी ओर अच्छे बच्चों की संगति करने से चरित्र ऊँचा होता है, कई अच्छे गुण आते हैं। अच्छे बालक की सभी प्रशंसा करते हैं।

आशा है कि तुम कुसंगति के पास तक नहीं फटकोगे। फिर भी तुम्हें सचेत कर देना मैं अपना कर्त्तव्य समझती हूँ। माता और पिता जी का आशीर्वाद तुम्हारे साथ है। किसी वस्तु की ज़रूरत हो तो लिखना।

तुम्हारी बड़ी बहन,
सुमीता।

प्रश्न 26.
मान लो आप का नाम वरुण है, आप 15, आदर्श नगर, लुधियाना में रहते हैं। अपनी छोटी बहन रमा को जीवन में अनुशासन का महत्त्व बताते हुए पत्र लिखें।
उत्तर :
15, आदर्श नगर,
लुधियाना।
15 मार्च, 20…..
प्रिय बहन रमा,
प्यार भरी नमस्ते।

मुझे कल माता जी का पत्र मिला। उन्होंने पत्र में तुम्हारी शिकायत करते हुए लिखा है कि तुम न तो प्रातः जल्दी उठती हो और न ही समय पर विद्यालय जाती हो। पत्र पढ़ कर मेरे हृदय को बड़ी ठेस लगी है।

प्रिय बहन, अनुशासन जीवन का मुख्य आधार है। यह उस सदाचार की नींव है जो जीवन का गौरव है। यह बड़प्पन और गौरव की कुंजी है। यह जीवन की वह प्राणवायु है, जिसके बिना न मानव और न समाज कभी भी जीवित रह सकता है। अनुशासनहीन जीवन वैसा ही है, जैसे पतवार के बिना नाव। यह हमारे उन भावों पर अंकुश रखता है जो हमारे विनाश के निमित्त हो सकते हैं। विद्यार्थी काल में ही हम इसका शिक्षण सुचारु ढंग से प्राप्त कर सकते हैं।

वैसे तो जीवन के प्रत्येक क्षेत्र में अनुशासन का महत्त्व है, पर विद्यालय में इसका महत्त्व सबसे ज्यादा है। विद्यालय के प्रत्येक विद्यार्थी को अनुशासन का पालन करना चाहिए क्योंकि यही जीवन में उन्नति का प्रतीक है। कक्षा में, क्रीडा क्षेत्र में और अन्यत्र भी अनुशासन की आवश्यकता है। अनुशासन का पालन करना आरम्भ में कुछ अखरता अवश्य है, पर इसका फल मधुर होता है। अनुशासनप्रिय छात्र ही अपने देश के गौरव को बढा सकता है।

आशा है, तुम इस पत्र को पढ़ने के बाद अनुशासनप्रिय बन जाओगी। ऐसा करने पर ही तुम एक अच्छी नागरिक बन कर देश की सेवा कर सकोगी। इसी से तुम्हारी सफलता का मार्ग है।

प्रशस्त होगा।
तुम्हारा भाई
वरुण

प्रश्न 27.
मान लो आपका नाम प्रमोद है। आप 208, कृष्ण नगर, लुधियाना में रहते हैं। अपने छोटे भाई अनिल को एक पत्र लिखिए जिसमें व्यायाम (कसरत) के लाभ बताए गए हों।
उत्तर :
208, कृष्ण नगर,
लुधियाना। 11 जुलाई, 20….
प्रिय अनिल,
चिरंजीव।

कुछ दिनों से तुम्हारा कोई पत्र प्राप्त नहीं हुआ। मुझे तुम्हारे स्वास्थ्य (सेहत) की बहुत चिन्ता है। व्यक्ति का स्वास्थ्य उसकी पूंजी होता है। स्वस्थ शरीर में ही स्वस्थ आत्मा निवास करती है। गत वर्ष के टाइफाइड का प्रभाव अभी तक तुम्हारे ऊपर बना हुआ है। मेरा एक ही सुझाव है कि तुम हर रोज़ व्यायाम (कसरत) अवश्य किया करो। यह स्वास्थ्य सुधार के लिए अनिवार्य है। इससे मनुष्य को अनेक लाभ प्राप्त होते हैं।

व्यायाम से शरीर चुस्त रहता है। कोई बीमारी पास नहीं फटकती। व्यायाम से नए रक्त का संचार होता है। मन खिल उठता है। मांसपेशियाँ बलवान् बनती हैं। स्मरण शक्ति बढ़ती है। प्रात:कालीन खेतों की हरियाली से आँखें ताज़ा हो जाती हैं।

मुझे पूर्ण आशा है कि तुम मेरे आदेश का पालन करोगे। नित्य प्रात: उठ कर सैर के लिए जाया करोगे।

तुम्हारा अग्रज,
प्रमोद कुमार

प्रश्न 28.
मान लो आपका नाम विजय है और आप 121, गान्धी नगर, जालन्धर में रहते हैं। अपने मित्र राज को एक पत्र लिखो जिसमें उसे नव वर्ष पर बधाई दी गई हो।
उत्तर :
121, गान्धी नगर,
जालन्धर।
31 दिसम्बर, 20…
प्रिय राज,
सप्रेम नमस्ते।
कल नव वर्ष का पहला शुभ दिन है। इस शुभ अवसर पर मैं आपको बहुत-बहुत बधाई देता हूँ। कामना करता हूँ कि यह नूतन वर्ष आपको सुख और समृद्धि देने वाला हो। परिवार में सुख और शान्ति का प्रसार हो। शारीरिक आरोग्यता के साथ-साथ लक्ष्मी अपनी कृपा की वर्षा करती रहे।

अन्त में पुनः-पुनः मंगल कामना।
आपका अपना,
विजय।

प्रश्न 29.
मान लो आपका नाम राजेश है और आप मकान नं0 534, गली 3C, मोहाली में रहते हैं। अपने मित्र मनोहर को एक पत्र लिखो जिसमें उसे परीक्षा में उत्तीर्ण (सफल) होने पर बधाई दी गई हो।
अथवा
आपका मित्र आठवीं कक्षा में 90% अंक लेकर जिले भर में प्रथम रहा है। उसे उसकी सफलता पर बधाई देते हुए पत्र लिखिए।
उत्तर :
मकान नं0 534, गली 3C,
मोहाली।
9 मई, 20….
प्रिय मित्र मनोहर,
सप्रेम नमस्ते।
पूज्य माता जी का पत्र मिला। यह शुभ समाचार पाकर कि तुम आठवीं की परीक्षा में प्रथम श्रेणी में उत्तीर्ण हो गए हो, मन गद्-गद् हो उठा! मुझे तुम से ऐसी ही आशा थी। इस शुभ अवसर पर मेरी हार्दिक बधाई हो। मैं कामना करता हूँ कि तुम जीवन में इसी प्रकार उन्नति के शिखर पर चढ़ते जाओगे। अपने माता-पिता और वंश का नाम चमकाओ।

मैं एक सप्ताह में तुम्हारे पास आऊँगा। उसी दिन मित्रों से जलपान कार्यक्रम की तिथि निश्चित कर लेना। इस बार मैं अच्छा खासा मुँह मीठा करूँगा। तुम्हारी इस सफलता पर मेरे माता-पिता जी भी बहुत प्रसन्न हुए हैं! उन्होंने बहुत-बहुत बधाई दी है।

पूज्य माता जी को चरण वन्दना।

तुम्हारा मित्र,
राजेश

प्रश्न 30.
मान लो आपका नाम विजय है और आप मकान नं० 628, गली 4A, जालन्धर में रहते हैं। अपने मित्र मोहन को एक पत्र लिखो, जिसमें उसे अपने भाई के विवाह पर बुलाया गया हो।
उत्तर :
मकान नं० 628,
गली 4A,
जालन्धर।
12 मार्च, 20…
प्रिय मित्र मोहन,

सप्रेम नमस्ते।
तुम्हें यह जान कर अत्यन्त प्रसन्नता होगी कि मेरे बड़े भाई संजीव का शुभ विवाह दिल्ली में श्री राम लाल जी की सुपुत्री सुनीता से इसी मास की 24 तारीख को होना निश्चित हआ है। इस विवाह में आप जैसे सभी इष्ट-मित्र तथा बन्धुओं का शामिल होना बहुत ज़रूरी है। अतः आप को भाई साहब की बारात में भी चलना पड़ेगा। विवाहोत्सव का प्रोग्राम नीचे दिया जा रहा है –

23 तारीख दोपहर – 1 बजे प्रीतिभोज
23 तारीख सायं – 6 बजे घुड़चढ़ी
24 तारीख बारात का दिल्ली प्रस्थान – प्रात: 5 बजे

आशा है कि तुम 22 तारीख को पहुँच जाओगे। राकेश और सुरेश भी 22 तारीख को यहाँ पहुँच जाएंगे।

तुम्हारा मित्र,
विजय।

प्रश्न 31.
मान लो आप का नाम हर्ष देव है और आप मकान नं0 203 ‘ए’, शिवालय रोड, पटियाला में रहते हैं। आपके मित्र दर्शन के भाई का विवाह हुआ है। अपने मित्र दर्शन को बधाई पत्र लिखें।
उत्तर :
203 ‘ए’
शिवालय रोड,
पटियाला।
10 मार्च, 20….
प्रिय मित्र दर्शन।
प्यार भरी नमस्ते।
पन्द्रह दिन पूर्व तुमने अपने बड़े भाई के विवाह के शुभ अवसर पर मुझे आमन्त्रण पत्र भेजा था। उन दिनों मैं ‘टाइफाइड’ रोग से ग्रस्त था। लगभग दस दिन मैं उपचाराधीन रहा। बीमारी हटने का नाम नहीं ले रही थी। विवाह की निश्चित तिथि तक मैं रोग-शय्या पर ही पड़ा था। अतः विवाह के शुभ अवसर पर उपस्थित न हो सका। विधि का विधान है कि कई बार मनुष्य चाहते हुए भी कुछ करने में विवश रहता है। विवाह में शामिल होने में भी भाग्य ने रुकावट डाल दी।

पूज्य भाई साहिब का विवाह बड़ी धूमधाम से सम्पन्न हुआ होगा, इसमें दो मत नहीं हो सकते। बारात का जाना और खूब चहल-पहल की मैं कल्पना ही कर सकता हूँ। ऐसे शुभ अवसर यदा-कदा ही आते हैं। मेरी ओर से इस शुभ अवसर की आप को बहुत-बहुत बधाई हो।

पूज्य माता जी को चरण वन्दना। बहन स्नेहलता को नमस्ते।

आपका मित्र,
हर्ष देव।

प्रश्न 32.
मान लो आपका नाम सुखदेव है और आप 201, मॉडल टाऊन, लुधियाना में रहते हैं। आपके मित्र युद्धवीर की माता जी का अचानक निधन हो गया है। उसको एक पत्र लिखो जिसमें उनकी मृत्यु पर शोक प्रकट किया गया हो।
उत्तर :
201, मॉडल टाऊन,
लुधियाना।
20 मई, 20…..
प्रिय युद्धवीर,

अभी-अभी तुम्हारा पत्र मिला। पूज्य माता जी की मृत्यु की दुःखदायी खबर पाकर आँखों के आगे अन्धेरा-सा छा गया। पैरों तले से ज़मीन खिसक गई। बार-बार सोचता हूँ-कहीं यह स्वप्न तो नहीं। अभी कुछ दिन की तो बात है, जब मैं उन्हें कोलकाता मेल पर चढ़ा कर आया तो न कोई दुःख था न कष्ट। उनका हँसता हुआ चेहरा अभी तक मेरे सामने मंडरा रहा है। उनके आशीर्वाद कानों में गूंज रहे हैं। उनकी मधुर वाणी, समुद्र के समान गम्भीर और शान्त स्वभाव, सबके साथ स्नेहपूर्ण व्यवहार सदा स्मरण रहेगा।

प्रिय मित्र, भाग्य रेखा मिटाई नहीं जा सकती। मनुष्य सोचता कुछ है, होता कुछ और ही है। ईश्वरीय कार्यों में कौन दखल दे सकता है। इसलिए धैर्य के सिवा और कोई चारा नहीं है। मेरी प्रार्थना है कि अब शोक को छोड़कर कर्त्तव्य की चिन्ता करो। रोने-धोने से कुछ नहीं बनेगा। इससे तो स्वास्थ्य ही बिगड़ता है। अनिल और नलिनी को सांत्वना दो। अन्त में मेरी ईश्वर से प्रार्थना है कि वह दिवंगत आत्मा को शान्ति प्रदान करे।

तुम्हारा अपना,
सुखदेव।

प्रश्न 33.
मान लो आप 101, मुहल्ला चरणजीत पुरा, जालन्धर के निवासी हैं। आपके मुहल्ले का डाकिया सुन्दर सिंह बहुत लापरवाह है। इसकी शिकायत पोस्टमास्टर को एक पत्र द्वारा करो।
उत्तर :
सेवा में,
पोस्टमास्टर,
मुख्य डाकघर,
जालन्धर।
महोदय,
निवेदन है कि हमारे मुहल्ले का डाकिया सुन्दर सिंह बहुत आलसी और लापरवाह है। वह ठीक समय पर पत्र नहीं पहुँचाता। कभी-कभी तो हमें पत्रों का उत्तर देने से भी वंचित रहना पड़ता है। इसके अतिरिक्त वह बच्चों के हाथ पत्र देकर चला जाता है। उसे वे इधरउधर फेंक देते हैं। कल ही रामनाथ का पत्र नाली में गिरा हुआ पाया गया। हमने उसे कई बार सावधान किया है पर वह आदत से मजबूर है।

अतः आप से विनम्र प्रार्थना है कि या तो उसे आगे के लिए समझा दें या कोई और डाकिया नियुक्त कर दें जिससे हमें और हानि न उठानी पड़े।

भवदीय,
दिनेश सिंह,
101, चरणजीत पुरा,
जालन्धर।
दिनांक : 15 फरवरी, 20….

प्रश्न 34.
मान लो आप 20, मुहल्ला बेदियां, बंगा के निवासी हैं। आप नगरपालिका के स्वास्थ्य अधिकारी को एक पत्र लिखो जिसमें ठीक से सफ़ाई न करने के कारण अपने क्षेत्र के सफाई सेवादार की शिकायत करो।
उत्तर :
सेवा में,
स्वास्थ्य अधिकारी,
नगरपालिका,
बंगा।
महोदय,
हम आपका ध्यान एक आवश्यक बात की ओर दिलवाना अपना कर्त्तव्य समझते हैं। मेन रोड के दाहिने मोड़ के साथ लगे हुए बेदियां मुहल्ला का सफाई सेवादार मोहन लाल अपने कर्तव्य का पूरी तरह से पालन नहीं कर रहा है। बार-बार रोकने पर भी वह बाहर से लाई हुई गन्दगी को मकान नं0 70 की नुक्कड़ पर डाल देता है। सारे मुहल्ले का कूड़ाकर्कट भी वहीं फेंकता है, कई-कई दिन तक वहाँ कूड़ा-कर्कट पड़ा रहता है जिससे सड़ांध उत्पन्न हो जाती है। चलने-फिरने वालों को नाक बन्द करके जाना पड़ता है। दुर्गन्ध के अतिरिक्त (अलावा) 24 घण्टे मक्खी-मच्छरों के झुंड उस पर मंडराते हैं। नालियों का पानी खड़ा हो जाता है और चलने-फिरने में बाधा पड़ती है। रात के समय अन्धेरे में तो यह स्थान नरक बन जाता है। गन्दी वायु के कारण रोग फूटने का भय बना रहता है। हमने उसे कई बार समझाया, किन्तु उसके कानों पर जॅ तक नहीं रेंगती। उलटे गाली-गलोच पर उतर आता है। कृपा करके इस विषय में कोई पग उठायें।

भवदीय,
जसदेव सिंह,
20, मुहल्ला बेदियां,
बंगा।
दिनांक : 12 मार्च, 20….

प्रश्न 35.
मान लो आपका नाम रमा है। आप अपनी छोटी बहन पूजा को विद्या (पढ़ाई) के लाभ बताते हुए एक पत्र लिखिए।
उत्तर :
20, माल रोड,
अमृतसर।
प्रिय बहन पूजा,
प्रेम भरी नमस्ते।
तीन दिन पहले मुझे माता जी का पत्र मिला, जिसमें लिखा था कि तुम्हारा मन पढ़ाई से उचट हो गया है। तुमने स्कूल जाना भी छोड़ दिया है। मुझे यह जानकर बहुत दुःख हुआ है। व्यक्ति को विद्या ही ज्ञान प्रदान करती है। यही उसकी उन्नति का मार्ग प्रशस्त करती है। संक्षेप में मैं तुम्हें विद्या के कुछ लाभ लिख रही हूँ, इन्हें अपने दिल में उतार लेना।

1. दुनिया की हर घटना की जानकारी पढ़ा-लिखा व्यक्ति ही प्राप्त कर सकता है। अनपढ़ तो कुएँ का मेंढक होता है।
2. विद्या ही व्यक्ति की उन्नति के सभी मार्ग खोलती है। अनपढ़ तो जीवन भर भटकता रहता है। उसे कोई मार्ग नहीं सूझता।
3. पढ़-लिखकर ही व्यक्ति समाज और देश की सेवा कर सकता है, क्योंकि समाज में फैली हुई कुरीतियाँ पढ़ा-लिखा ही दूर कर सकता है। देश की समस्याओं का समाधान अनपढ़ व्यक्ति नहीं कर सकता।
4. फिर नारी जाति की जागृति के लिए आज की नारी का पढ़ा-लिखा होना परमावश्यक है। तभी वह देश की उन्नति में पुरुषों के साथ कन्धे से कन्धा मिलाकर चल सकती है।

संक्षेप में अनपढ़ता अभिशाप है। विद्या ही ज्ञान का प्रकाश फैलाकर उसे सच्चा इन्सान बनाती है। अतः पक्का निश्चय करके पढ़ाई के लिए पूरी तरह डट जाओ। माता जी और पिता जी को चरण वन्दना। कुक्कू को प्यार। तुम्हारी बहन रमा।

प्रश्न 36.
अपने मित्र को पत्र लिखिए जिसमें नव-वर्ष (नए साल) की बधाई दी गई हो।
उत्तर :
20, गांधी नगर,
पटियाला।
27 दिसम्बर, 20…
प्रिय बहन दीपा,
प्यार भरी नमस्ते।
परसों पुराना साल विदाई ले रहा है। दो दिन बाद नया वर्ष आरम्भ हो रहा है। नव वर्ष तुम्हारे लिए मंगलमय और शुभ हो, मैं यह हार्दिक कामना करता हूँ। प्रसन्नताओं से तुम्हारी झोली भरी रहे। उन्नति एवं सफलता तुम्हारा हर कदम चूमती रहे। सुख-शान्ति, समृद्धि तथा आरोग्यता के फूल हमेशा आपकी झोली में महकते रहें। यह मेरी नव वर्ष पर शुभ कामना है। माता जी और पिता जी को नमस्कार। मोहन और मीना को प्यार।

तुम्हारा प्रिय मित्र
अक्षय।

प्रश्न 37.
अपनी भूल के लिए क्षमा-याचना करते हुए अपने पिताजी को एक पत्र लिखें।
उत्तर :
छात्रावास
पंजाबी विश्वविद्यालय,
पटियाला
14 अगस्त, 20……….
आदरणीय पिताजी
सादर प्रणाम !
कल ही आपका कृपा-पत्र मिला। आपने प्रश्न किया है कि मेरे वार्षिक परीक्षा में इतने कम अंक आने का कारण क्या है ? पिता जी इस बार मेरी संगति कुछ बुरे लड़कों से हो गई थी। मुझे अध्यापक महोदय ने भी एक-दो बार चेतावनी दी पर मैंने ध्यान नहीं दिया। आपके पत्र ने मुझे सचेत कर दिया है।

मैं अपनी इस भूल के लिए आपसे क्षमा-याचना करता हूँ और आपको आश्वासन दिलाता हूँ कि भविष्य में ऐसी भूल कभी न करूँगा। अभी से परिश्रम में जुट जाऊँगा। आप कृपा कर मुझे कुछ परीक्षोपयोगी पुस्तकें अवश्य भेज दें।

आशा है कि आप मुझे क्षमा कर देंगे। मैं पुनः आपको वचन देता हूँ कि मैं आपकी इच्छानुसार अध्ययन करूँगा और परीक्षा में शानदार सफलता प्राप्त करूँगा।

आपका आज्ञाकारी पुत्र
ललित कपूर।

प्रश्न 38.
मान लीजिए आपका नाम मनजीत है और आप आर्य कन्या हाई स्कूल, धूरी की छात्रा हैं। अपने स्कूल की मुख्याध्यापिका को एक प्रार्थना-पत्र लिखिए जिसमें अपने द्वारा हुई गलती के लिए क्षमा याचना की गई हो।
उत्तर :
सेवा में,
मुख्याध्यापिका,
आर्य कन्या हाई स्कूल,
धूरी।
महोदया,

सविनय निवेदन यह है कि मैं आपके स्कूल की आठवीं कक्षा की विद्यार्थी हूँ। कल मध्यावकाश के समय हम कुछ लड़कियाँ कक्षा में ही खेल रही थीं कि अचानक मेरे हाथ से गेंद छूटने पर कक्षा की खिड़की की काँच में जा लगी और उससे दो काँच टूट गए। कक्षा-अध्यापक ने इस गलती के लिए मुझे डाँटा व अपने माता-पिता को बुला कर लाने के लिए कहा है। मेरी आपसे विनम्र प्रार्थना है कि कृपया आप इस बार मेरी गलती को माफ कर दें। मैं आपको विश्वास दिलाती हूँ कि आगे से भविष्य में ऐसी गलती दुबारा नहीं करूँगी।

आपकी आज्ञाकारिणी,
मनजीत।
कक्षा आठवीं-बी
रोल नं० 27.
तिथि 16 अप्रैल, 20…..

प्रश्न 39.
मान लीजिए आपका नाम पंकज है। आप प्रेम सभा हाई स्कूल के छात्र हैं। स्कूल में पीने के पानी की कमी की ओर ध्यान दिलाते हुए अपने स्कूल में मुख्याध्यापक को एक प्रार्थना-पत्र लिखिए।
उत्तर :
सेवा में
मुख्याध्यापक,
प्रेम सभा हाई स्कूल,
अमृतसर।
महोदय,

सविनय प्रार्थना है कि स्कूल में पीने के पानी की उचित व्यवस्था नहीं है। एक ही नल है, जो स्कूल के चार सौ विद्यार्थियों के लिए काफ़ी नहीं है। जब दोपहर के समय आधी छुट्टी होती है तो प्यास के कारण विद्यार्थी नल की ओर लपकते हैं। वहाँ इतनी भीड़ हो जाती है कि आधी छुट्टी का सारा समय पानी पीने की धक्कम-पेल में ही बीत जाता है। बहुत से विद्यार्थी फिर भी पानी प्राप्त करने से वंचित रह जाते हैं।

नये नल लगवाने की कृपा करें। गर्मियों के मौसम में तो हर विद्यार्थी पानी पीने की इच्छा रखता है।

आपका आज्ञाकारी शिष्य,
पंकज।
आठवीं-बी
रोल नं0 28
1 मार्च, 20….

प्रश्न 40.
अपने मित्र को पत्र लिखिए जिसमें किसी आँखों देखे मेले का वर्णन हो।
उत्तर :
परीक्षा भवन,
….. नगर,
15 अप्रैल, 20…..
प्रिय मित्र रमेश,
सप्रेम नमस्ते।
मुझे पिछले बुधवार को आपके पास आना था। पर मालूम हुआ कि वीरवार को अमृतसर में वैशाखी का मेला लगेगा, इसलिए मैंने अपने चार सहपाठियों के साथ मेला देखने का कार्यक्रम बना लिया। हम सभी साथी बुधवार को सवेरे ही घर से चलकर पहली बस में बैठकर अमृतसर पहुँच गए। वहाँ जाकर देखा कि जैसे पुरुषों और स्त्रियों का समूह-सा उमड़ आया हो। ज्यों-ज्यों दिन बढ़ता गया, मेले में आने वालों की संख्या बढ़ती गई। दरबार साहब में तो तिल धरने की भी जगह नहीं थी। चाहे पुलिस ने इस सम्बन्ध में कड़े प्रबन्ध कर रखे थे। फिर भी भीड़ के इस सैलाब को रोक पाना मुश्किल कार्य था।

मेले में एक स्थान पर नौजवानों की टोली ‘जट्टा आई वैशाखी’ की तान के साथ भंगड़ा डाल रही थी तो कहीं स्त्रियों का ‘गिद्दा’ चल रहा था। किसी दुकान पर गर्म-गर्म पकौड़े तले जा रहे थे तो कहीं पर गर्मागर्म जलेबियाँ तली जा रही थीं। कहीं झूले झूले जा रहे थे तो कहीं मदारी अपना खेल दिखाने में जुटे थे। अतः यह एक यादगारी मेला था जिसकी स्मृतियाँ मेरे मानस-पटल पर सदा बनी रहेंगी।

माता व पिता जी को मेरा प्रणाम कहना,
तुम्हारा मित्र,
हर्षदेव।

प्रश्न 41.
मान लो आपका नाम निर्मल कौर है और आप गुरु नानक कालोनी, तरनतारन में रहती हैं। अपनी सहेली यशवन्त को एक पत्र लिखो जिसमें यह वर्णन करो कि आपके स्कूल में 26 जनवरी का दिन कैसे मनाया गया।
उत्तर :
गुरु नानक कालोनी,
तरनतारन।
29 जनवरी, 20……..
प्यारी सहेली यशवन्त,
सत् श्री अकाल।
कई दिन से तुम्हारा पत्र नहीं मिला। क्या कारण है। मैं तुम्हें दो पत्र डाल चुकी हूँ पर उत्तर एक का भी नहीं मिला। कोई नाराज़गी तो नहीं ? अगर ऐसी-वैसी कोई बात हो तो क्षमा कर दें।

हाँ, इस बार हमारे स्कूल में 26 जनवरी/गणतंत्र दिवस का दिन बड़ी ही धूमधाम से मनाया गया। इसकी थोड़ी-सी झलक मैं पत्र द्वारा पेश कर रही हूँ। 26 जनवरी मनाने की तैयारियां एक महीना पहले शुरू कर दी गई थीं। स्कूल में सफेदी कर दी गई थी। लड़कियों को लेजियम की ट्रेनिंग देनी कई दिन पहले ही शुरू हो गई थी। ‘हमारे अमर शहीद’ एकांकी नाटक की रिहर्सल भी कई बार करवाई गई। निश्चित दिन को ठीक-सुबह सात बजे गणतंत्र दिवस का समारोह शुरू हो गया। सबसे पहले तिरंगा झण्डा फहराने की रस्म क्षेत्र के जाने-माने समाज सेवक सरदार महासिंह जी ने अदा की। इसके बाद स्कूल की छात्राओं ने रंगारंग कार्यक्रम पेश करने शुरू कर दिए। गिद्धा नाच ने सबका मन मोह लिया। इसके बाद देश-प्रेम के गीत गाए गए। मैंने भी एक गीत गाया था। मैंने लेजियम की टीम में भी भाग लिया।

इसके बाद एकांकी ‘हमारे अमर शहीद’ का अभिनय हुआ। इसके हर सीन पर तालियाँ बजती थीं। समारोह के अन्त में प्रधान महोदय और हमारी बड़ी बहन जी ने भाषण दिये, जिनमें देश भक्ति की प्रेरणा थी।

गणतंत्र दिवस का यह समारोह मुझे हमेशा याद रहेगा। क्योंकि मुझे इसमें दो खूबसूरत इनाम मिले हैं। पूज्य माता जी और भाभी को सत् श्री अकाल। अक्षत और गुड्डी को प्यार देना। इस बार पत्र का उत्तर ज़रूर देना।

तुम्हारी सहेली
निर्मल कौर।

प्रश्न 42.
खोई हुई वस्तु लौटाने के लिए आभार प्रदर्शित करते हुए अपरिचित को पत्र लिखें।
उत्तर :
436, परेड ग्राउंड,
लुधियाना।
24 मार्च, 20…
आदरणीय श्री मेहता जी
सादर नमस्कार!
कल मुझे डाक द्वारा अपनी खोई हुई पुस्तक प्राप्त कर बड़ी प्रसन्नता का अनुभव हुआ। यह पुस्तक मैं बस में भूल गया था। आपने यह पुस्तक लौटाकर बड़ा उपकार किया। यदि इस पुस्तक के ऊपर मेरा पता न लिखा होता तो इसे प्राप्त करना संभव न होता। यह पुस्तक मेरे लिए बड़ी उपयोगी है। यह पुस्तक मुझे इसलिए भी प्रिय है, क्योंकि यह मुझे जन्मदिवस पर एक मित्र द्वारा भेंट के रूप में दी गई थी।

आपने इस पुस्तक को भेजने के लिए जो कष्ट किया है, उसके लिए मैं आपके प्रति आभार प्रदर्शित करता हूँ। पुस्तक भेजने के लिए आपने जो डाक-व्यय किया है, उसने मुझे और भी उपकृत कर दिया है।

मेरे योग्य कोई सेवा हो तो लिखें।
भवदीय
आकाश चौधरी।

प्रश्न 43.
मित्र के जन्मदिन पर उसे बधाई देते हुए पत्र लिखें।
उत्तर :
208, प्रेमनगर,
पटियाला।
25, अगस्त, 20……,
प्रिय राज,
सप्रेम नमस्ते।
कल आपका जन्मदिन है। मैं इस शुभ अवसर पर आपको हार्दिक बधाई देता हूँ। कामना करता हूँ कि यह नूतन वर्ष आपको सुख और समृद्धि देने वाला हो। शारीरिक आरोग्यता के साथ-साथ लक्ष्मी आप पर अपनी कृपा की वर्षा करती रहे।

अन्त में पुनः-पुन: मंगल कामना।
आपका अपना
राजेश।

प्रश्न 44.
छुट्टी वाले दिन स्कूल के क्रीडाक्षेत्र (खेल के मैदान) में क्रिकेट मैच खेलने की अनुमति लेने के लिए प्रिंसिपल को प्रार्थना-पत्र लिखें।
उत्तर :
सेवा में,
मुख्याध्यापक,
आर्य उच्च विद्यालय,
राजपुरा।
विषय-क्रिकेट मैच खेलने की अनुमति हेतु।
महोदय,
हमारे विद्यालय, आर्य उच्च विद्यालय की क्रिकेट टीम का मैच, गुरुकुल विद्यालय, राजपुरा की क्रिकेट टीम के साथ रविवार, मई 2000 को होना निश्चित हुआ। हमारा प्रस्ताव है कि यह मैच हमारे विद्यालय के खेल मैदान में ही खेला जाए क्योंकि इससे हमारे विद्यालय का ही नाम होगा। हम यह विश्वास दिलाते हैं कि मैच के दौरान विद्यालय के किसी भी सामान को क्षति नहीं पहुंचेगी।

आशा है कि आप हमारी प्रार्थना स्वीकार करेंगे और शीघ्र स्वीकृति-पत्र देंगे।
भवदीय
मनोहर शर्मा,
कप्तान, क्रिकेट टीम।

प्रश्न 45.
अपने गाँव के सरपंच को अपने स्कूल के विकास में योगदान देने के लिए पत्र लिखें।
उत्तर :
सेवा में,
ग्राम पंचायत सरपंच महोदय,
गांव धनौला,
जिला संगरूर।
विषय-स्कूल के विकास में योगदान हेतु।
मान्यवर महोदय,
हमारे विद्यालय का ज़िले में ही नहीं बल्कि सारे प्रदेश में नाम है, परंतु यह बड़े दुःख की बात है कि विद्यालय में पहले जैसी वह सुंदरता नहीं रही, जो इसकी शान समझी जाती थी। इस संबंध में मेरे कुछ सुझाव हैं, जो मैं आपकी सेवा में निवेदन करना चाहता हूँ।

सबसे पहले विद्यालय की फुलवाड़ी और वाटिका की ओर ध्यान देना चाहिए, जो बिना माली के मुरझा गई है। फूल-पौधे डंठल बन गए हैं। इसके लिए एक अच्छे माली का होना अत्यंत आवश्यक है। दूसरे मुख्य द्वार से लेकर विद्यालय के हॉल तक मार्ग के दोनों ओर सुंदर रंग-बिरंगे फूल लगाए जाएँ।

इसके अतिरिक्त विद्यालय के समस्त भवनों में हर छः मास के पश्चात् सफ़ेदी कराई जानी चाहिए। प्रत्येक कमरे की हर रोज़ सफ़ाई होनी चाहिए। विद्यालय का सफाई कर्मचारी इधर-उधर कूड़े के ढेर लगाए रखता है। ये बहुत ही बुरे लगते हैं। सफाई कर्मचारी को कड़ी चेतावनी दी जाए कि वह विद्यालय का सारा कूड़ा-कर्कट बाहर ले जाकर फेंकें। छात्रों को भी निर्देश हो कि वे फलों आदि के छिलके और रद्दी कागज़ कूड़ादानों में ही फैंकें।

विद्यालय का क्रीडा क्षेत्र सुधारा जाए। इसके चारों ओर दीवार खींची जानी चाहिए ताकि कोई पशु या बाहर के लोग उसमें न आ सकें। इसके अतिरिक्त विद्यालय के नलों पर पक्की ईंटों के फर्श लगाए जाएँ, जिससे वहाँ कीचड़ आदि न हो सके।

भवदीय
मोहन लाल।
धनौला गांव,
जिला संगरूर।
2 मई, 20……।

Punjab State Board PSEB 8th Class Hindi Book Solutions Hindi Grammar Viram Chinh विराम चिह्न Exercise Questions and Answers, Notes.

PSEB 8th Class Hindi Grammar विराम चिह्न (2nd Language)

विराम चिह्न – बोलते समय हम सब कुछ एक ही गति से नहीं बोलते जाते। एक वाक्य के मध्य में कहीं – कहीं कुछ क्षणों के लिए रुकते हैं और इसी प्रकार वाक्य के समाप्त होने पर भी रुकना पड़ता है। इसी रुकने को ‘विराम’ कहते हैं। इसी विराम को प्रकट करने के लिए हम जिन चिह्नों को लिखते हैं, उन्हें विराम चिह्न कहते हैं।

विराम चिहन निम्नलिखित हैं –

1. पूर्ण विराम ( । ) – वाक्य की पूर्ति की सूचना देने वाले चिह्न को पूर्ण विराम कहते हैं। जैसे – भारत एक शान्तिप्रिय देश है।
2. अर्द्ध विराम ( ; ) – वाक्य की पूर्ण समाप्ति न होने पर भी जहाँ बीच में समाप्ति – सी लगे। अगले वाक्य से जोड़ने वाले अव्यय का अभाव हो, तब इसका प्रयोग होता है। जैसे – आजकल शिक्षा का उद्देश्य नौकरी है; इसलिए उसका वास्तविक महत्त्व जाता रहा है।
3. अल्प विराम ( , ) – पढ़ते समय जहाँ थोड़ी देर ठहरना हो, वहाँ अल्प विराम ( , ) लगाते हैं। जैसे – लोकमान्य तिलक, मालवीय, महात्मा गाँधी आदि महान् नेता थे।
4. अपूर्ण विराम ( – ) – आगे जाने वाली बात के लिए पहले वाक्य से संकेत करना हो तो इसका निर्देशक वाक्य के साथ प्रयोग होता है। जैसे – निम्नलिखित प्रश्नों में से किन्हीं चार का उत्तर दीजिए :
5. प्रश्न सूचक ( ? ) – वाक्य को प्रश्नवाचक सूचित करने के लिए इसका प्रयोग होता है। जैसे – क्या मूर्ख को समझाना सरल है ?
6. विस्मयादिबोधक ( ! ) – मानसिक आवेगों को प्रकट करने के लिए इसका प्रयोग होता है। जैसे – हाय ! मैं मारा गया। उफ! इतनी पीड़ा।
7. निर्देशक ( – ) – किसी शब्द के भाव को साफ – साफ स्पष्ट करने के लिए उसके आगे लगाया जाता है। जैसे – लाला लाजपतराय – पंजाब केसरी ने अंग्रेजी साम्राज्य की जड़ें हिला दी थीं। यथा, जैसे आदि शब्द के बाद भी इसका प्रयोग होता है।
8. संयोजक ( – ) – यह समस्त पदों के बीच लगकर समास की सूचना देता है। जैसे – माता – पिता, सुख – दुःख।।
9. कोष्ठक चिह्न ( ) – किसी बात के स्पष्टीकरण के लिए उसका अर्थ वाक्य का अंग न बनाते हुए उसे कोष्ठक ( ) लिखा जाता है। जैसे – 30 जनवरी हमारे राष्ट्रपिता (महात्मा गांधी) की बलिदान तिथि है।
10. उद्धरण चिह्न ( “” ) – जब किसी वक्ता या लेख की उक्ति को ज्यों का त्यों उद्धत करना हो। जैसे – लाला लाजपत राय ने कहा था, “मेरे शरीर पर पड़ी एक – एक लाठी ब्रिटिश साम्राज्य के कफ़न में कील का काम देगी।”
11. लाघव चिहन ( ० ) – किसी शब्द को संक्षेप में लिखने के लिए इसका प्रयोग होता है। जैसे – पं० नेहरू। ला० लाजपत राय। डॉ० राजेन्द्र प्रसाद।
12. सम्बोधन चिह्न ( ! ) – किसी को बुलाने या पुकारने में इसका प्रयोग होता है। जैसे – हे ईश्वर! हम पर दया करो।

उदाहरण

प्रश्न 1.
विराम चिह्न लगाकर लिखो:

प्रश्न 1.
बुढ़िया बोली महाराज मैंने सुना है कि आप पारस हैं
उत्तर :
बुढ़िया बोली, “महाराज ! मैंने सुना है कि आप पारस हैं।”

प्रश्न 2.
सड़कों पर इधर – उधर कूड़ा कर्कट न फेंकें एक तरफ रखे हुए कूड़ेदानों में डालें
उत्तर :
सड़कों पर इधर – उधर कूड़ा कर्कट न फेंकें; एक तरफ रखे हुए कूड़ेदानों में डालें।

प्रश्न 3.
बेटी क्या बात है इतनी अधीर क्यों हो
उत्तर :
‘बेटी ! क्या बात है इतनी अधीर क्यों हो ?’

प्रश्न 4.
वाह क्या मोतियों से अक्षर हैं कलम तोड़ दी है
उत्तर :
वाह ! क्या मोतियों से अक्षर हैं, कलम तोड़ दी है।

प्रश्न 5.
तम भी शिवाजी की तरह बद्ध हो उसने उत्तर दिया
उत्तर :
“तुम भी शिवाजी की तरह बुद्ध हो,” उसने उत्तर दिया।

प्रश्न 6.
अजी आप तो बात ऐसे कर रहे हैं जैसे हम बिना टिकट सफ़र कर रहे हैं
उत्तर :
अजी ! आप तो बात ऐसे कर रहे हैं, जैसे हम बिना टिकट सफ़र कर रहे हैं।

प्रश्न 7.
विजय ने पूछा रामू चिन्ता में क्यों डूबे हो
उत्तर :
विजय ने पूछा, “रामू ! चिंता में क्यों डूबे हो ?”

प्रश्न 8.
राजदूत ने कहा महाराज हमारे सम्राट ने एक उपहार और भी आपके लिए भेजा है
उत्तर :
राजदूत ने कहा, “महाराज ! हमारे सम्राट ने एक उपहार और भी आपके लिए भेजा है।”

प्रश्न 9.
मैंने उसे इकन्नी दी बालक ने उत्साह से कहा अहा इकन्नी
उत्तर :
मैंने उसे इकन्नी दी। बालक ने उत्साह से कहा, “अहा ! इकन्नी !”

प्रश्न 10.
मैंने घृणा और आश्चर्य से देखा सचमुच उसके पैरों में बेड़ी थी
उत्तर :
मैंने घृणा और आश्चर्य से देखा, सचमुच उसके पैरों में बेड़ी थी।

प्रश्न 11.
मैंने मन ही मन में कहा हे भगवान् पेट के लिए बाप भीख मँगवाने के लिए बेटे के पैरों में बेड़ी भी डाल सकता है
उत्तर :
मैंने मन – ही – मन में कहा, “हे भगवान् ! पेट के लिए, बाप भीख मंगवाने के लिए बेटे के पैरों में बेड़ी भी डाल सकता है।”

प्रश्न 12.
बूढ़े ने कहा दाता जुग जुग जियो
उत्तर :
बूढ़े ने कहा, “दाता जुग जुग जियो।”

प्रश्न 13.
मैंने पूछा उसका पता नहीं लगा कितने दिन हुए
उत्तर :
मैंने पूछा, “उसका पता नहीं लगा। कितने दिन हुए।”

प्रश्न 14.
गाड़ी मोटर तांगे भागे जा रहे थे
उत्तर :
गाड़ी, मोटर, तांगे भागे जा रहे थे।

प्रश्न 15.
उसने पुस्तकें कापियाँ तथा कुछ अन्य सामान खरीदा सामान को थैले में डालकर दुकानदार से पूछा कितने पैसे दूँ
उत्तर :
उसने पुस्तकें, कापियाँ तथा कुछ अन्य सामान खरीदा; सामान को थैले में डालकर दुकानदार से पूछा “कितने पैसे दूँ ?”

प्रश्न 16.
घुड़सवार ने कहा वह राही शिवा जी ही थे
उत्तर :
घुड़सवार ने कहा, “वह राही शिवा जी ही थे।”

प्रश्न 17.
रास्ते में उस्ताद साहब बोले मैं एक गिलास लस्सी पी लें।
उत्तर :
रास्ते में उस्ताद साहब बोले, “मैं एक गिलास लस्सी पी लूँ।”

प्रश्न 18.
उसकी पत्नी बोल उठी भैया अंदर आ जाओ बहुत भीग गए हो
उत्तर :
उसकी पत्नी बोल उठी, “भैया ! अंदर आ जाओ। बहुत भीग गए हो।”

प्रश्न 19.
दूत ने अपने शाह का आग्रह प्रकट किया उसको हर हालात में इसी पल जाना होगा
उत्तर :
दूत ने अपने शाह का आग्रह प्रकट किया, “उसको हर हालात में इसी पल जाना होगा।”

प्रश्न 20.
अच्छा अबकी ज़रूर देंगे हामिद अल्ला कसम ले जा
उत्तर :
“अच्छा अबकी ज़रूर देंगे। हामिद, अल्ला कसम ले जा।”

प्रश्न 21.
रखे रहो क्या मेरे पास पैसे नहीं हैं
उत्तर :
“रखे रहो, क्या मेरे पास पैसे नहीं हैं ?”

प्रश्न 22.
मिट्टी ही के तो हैं गिरे तो चकनाचूर हो जाएँ
उत्तर :
“मिट्टी ही के तो हैं। गिरे तो चकनाचूर हो जाएँ।”

प्रश्न 23.
मिठाई क्या बड़ी चीज़ है किताब में इसकी कितनी बुराइयाँ लिखी हैं
उत्तर :
“मिठाई क्या बड़ी चीज़ है ? किताब में इसकी कितनी बुराइयाँ लिखी हैं।”

प्रश्न 24.
हम से गुलाब जामुन ले जा हामिद
उत्तर :
“हम से गुलाब – जामुन ले जा, हामिद।”

प्रश्न 25.
बाद में बापू ने अपने साथियों से कहा यह बच्चा मेरा गुरु है
उत्तर :
बाद में बापू ने अपने साथियों से कहा, “यह बच्चा मेरा गुरु है।”

प्रश्न 26.
कुश ने कहा अयोध्या नरेश किस चिंता में डूबे हो
उत्तर :
कुश ने कहा, “अयोध्या नरेश ! किस चिंता में डूबे हो ?”

प्रश्न 27.
राजन ने कहा मनुष्य इतना बेसमझ क्यों हो रहा है पिता जी
उत्तर :
राजन ने कहा, “मनुष्य इतना बेसमझ क्यों हो रहा है ?” पिता जी।

प्रश्न 28.
राही ने परेशान होकर पछा आप क्यों हँस रहे हैं
उत्तर :
राही ने परेशान होकर पूछा, “आप क्यों हँस रहे हैं ?”

प्रश्न 29.
नहीं बेटा मैंने जो पढ़ाया है वह झूठ नहीं है अधूरा अवश्य है
उत्तर :
नहीं बेटा, मैंने जो पढ़ाया है, वह झूठ नहीं है। अधूरा अवश्य है।

प्रश्न 30.
अहमदशाह का चेहरा क्रोध से तमतमा उठा वह बोला क्यों कुफ्र बकता है
उत्तर :
अहमदशाह का चेहरा क्रोध से तमतमा उठा। वह बोला, “क्यों कुफ्र बकता

प्रश्न 31.
उसने कहा बाबू जी यह मेरा लड़का है
उत्तर :
उसने कहा, “बाबू जी ! यह मेरा लड़का है।”

प्रश्न 32.
मैंने कहा सूरदास यह तुमको कहाँ से मिल गया
उत्तर :
मैंने कहा, “सूरदास ! यह तुम को कहाँ से मिल गया ?”

प्रश्न 33.
वह मुस्कुराता हुआ बोला बाबू जी नौकरी खोजने गया था
उत्तर :
वह मुस्कुराता हुआ बोला, “बाबू जी ! नौकरी खोजने गया था।”

प्रश्न 34.
तिवारी बोले तो क्या जो साइकिल चलाते हैं वे किसी की बात नहीं सुनते हैं बड़ी ज़रूरी बात है ज़रा उतर जाओ
उत्तर :
तिवारी बोले, “तो क्या जो साइकिल चलाते हैं, वे किसी की बात सुनते हैं ? बड़ी ज़रूरी बात है, ज़रा उतर जाओ।”

प्रश्न 35.
राजन ने पूछा पिताजी इस प्रदूषण को दूर करने के लिए हमें क्या करना चाहिए
उत्तर :
राजन ने पूछा, “पिता जी, इस प्रदूषण को दूर करने के लिए हमें क्या करना चाहिए ?”

प्रश्न 36.
ओ शरारती वहां इस तरह की फिल्में नहीं होती
उत्तर :
ओ, शरारती! वहां इस तरह की फिल्में नहीं होती।

Punjab State Board PSEB 8th Class Hindi Book Solutions Hindi Grammar Avikari Shabd Avyay अविकारी शब्द (अव्यय) Exercise Questions and Answers, Notes.

PSEB 8th Class Hindi Grammar अविकारी शब्द (अव्यय) (2nd Language)

प्रश्न 1.
अव्यय किसे कहते हैं ? ये कितने प्रकार के होते हैं ?
उत्तर :
जिन शब्दों का लिंग, वचन, कारक, काल आदि के कारण रूप में कोई परिवर्तन नहीं होता, उसे अविकारी या अव्यय कहते हैं।
अव्यय चार प्रकार के होते हैं –

• क्रिया विशेषण
• सम्बन्ध बोधक
• समुच्चय बोधक
• विस्मयादि बोधक।

1. क्रिया विशेषण

प्रश्न 2.
क्रिया विशेषण का लक्षण लिखकर उसके भेदों का वर्णन करो।
उत्तर :
वे शब्द जो क्रिया की विशेषता प्रकट करें, उन्हें क्रिया विशेषण कहते हैं। जैसे – धीरे – धीरे, यहाँ से, कल, आज, ऊँचे, ऊँचाई। क्रिया विशेषण के चार भेद हैं –

1. कालवाचक – जो क्रिया विशेषण शब्द क्रिया के होने का समय सूचित करते हैं, उन्हें कालवाचक क्रिया विशेषण कहते हैं। जैसे – आज, कल, परसों, जब, तब, कब, सायं, प्रातः।

उदाहरण –

• मैं प्रात: व्यायाम करता हूँ।
• आजकल वर्षा हो रही है।
• परसों मेला देखने चलेंगे।

2. स्थानवाचक – जो क्रिया विशेषण क्रिया के स्थान या दिशा के विषय में बोध कराएँ, उन्हें स्थानवाचक क्रिया विशेषण कहते हैं। जैसे-यहाँ, वहाँ, आगे, पीछे, मध्य, ऊपर, नीचे, इधर, उधर, दाहिने, बाएँ, सामने।

उदाहरण –

• इधर – इधर मत देखो।
• भीतर जा कर पढ़ो।
• यहाँ बैठो।

3. परिमाणवाचक – जो क्रिया विशेषण क्रिया के परिमाण को प्रकट करें, उन्हें परिमाणवाचक क्रिया विशेषण कहते हैं। जैसे – अधिक, जितना, थोड़ा, बहुत, कम।

उदाहरण –

• कम बोलो, अधिक सोचो।
• तनिक हँसो भी।
• चाय में दूध काफ़ी है, चीनी थोड़ी है।

4. रीतिवाचक – जो क्रिया विशेषण क्रिया की रीति या विधि का बोध कराएँ, उन्हें रीतिवाचक क्रिया विशेषण कहते हैं। जैसे – धीरे – धीरे, जल्दी, शीघ्र, तेज़।
ऐम० बी० डी० हिन्दी गाइड (द्वितीय भाषा) (VIII PB.)

उदाहरण –

• दिन जल्दी – जल्दी ढलता है।
• मैं तो ठीक पढ़ रहा था।
• क्या तुम पैदल चलोगे ?

अभ्यास – प्रश्न

प्रश्न 1.
नीचे लिखे वाक्यों में से क्रिया – विशेषण शब्द की पहचान करके उसको रेखांकित करो
(क) वह सवेरे चला जाएगा।
(ख) चुपचाप काम करते रहो।
(ग) हमें प्रतिदिन व्यायाम करना चाहिए।
(घ) इधर – उधर क्यों घूम रहे हो ?
(ङ) यह पुस्तक हाथों – हाथ बिक गई।
उत्तर :
(क) सवेरे
(ख) चुपचाप
(ग) प्रतिदिन
(घ) इधर – उधर
(ङ) हाथों – हाथ।

प्रश्न 2.
नीचे लिखे वाक्यों में रेखांकित शब्द क्रिया – विशेषण हैं। प्रत्येक वाक्य के आगे दिए गए कोष्ठक में उसके भेद का नाम लिखें :
(क) समय जल्दी – जल्दी बीत रहा है।
(ख) उसका काम लगभग समाप्त हो गया है।
(ग) सभी बारी – बारी आकर अपना वेतन ले जाओ।
(घ) जितना परिश्रम करोगे, उतनी ही सफलता पाओगे।
(ङ) जिधर भी जाते हैं, आपके नाम की चर्चा है।
उत्तर :
(क) रीतिवाचक
(ख) परिमाणवाचक
(ग) रीतिवाचक
(घ) परिमाणवाचक
(ङ) स्थानवाचक।

प्रश्न 3.
नीचे लिखे वाक्य में प्रयुक्त क्रिया – विशेषण शब्द की पहचान करके उसके भेद का नाम बताओ
(क) मोहन प्रतिदिन घूमने जाता है।
(ख) बाहर झाँककर देखो।
(ग) बैठे बिठाये यह मुसीबत कहाँ से आ गई।
(घ) जैसा करोगे वैसा भरोगे।
(ङ) मैंने पेट भर खाना खा लिया है।
उत्तर :
(क) प्रतिदिन – कालवाचक
(ख) बाहर – स्थानवाचक
(ग) कहाँ से – स्थानवाचक
(घ) जैसा – वैसा – रीतिवाचक
(ङ) पेटभर – परिमाणवाचक

अन्य प्रश्न

प्रश्न 1.
नीचे लिखे वाक्यों में से क्रिया विशेषण शब्द चुनो
(क) वह सवेरे चला जाएगा।
(ख) चुपचाप काम करते रहो।
(ग) हमें प्रतिदिन व्यायाम करना चाहिए।
(घ) इधर – उधर क्यों घूम रहे हो ?
(ङ) यह पुस्तक हाथों – हाथ बिक गई।
(च) उसका काम लगभग समाप्त हो गया है।
(छ) जिधर भी जाते हैं, आपके नाम की चर्चा है।
(ज) बैठे बिठाये यह मुसीबत कहाँ से आ गई ?
(झ) ये लोग क्यों ………. चल रहे हैं ? (कल/धीरे – धीरे)
उत्तर :
(क) सवेरे
(ख) चुपचाप
(ग) प्रतिदिन
(घ) इधर – उधर
(ङ) हाथों – हाथ
(च) लगभग
(छ) जिधर
(ज) बैठे बिठाये
(झ) धीरे – धीरे।

प्रश्न 2.
नीचे लिखे वाक्यों में से क्रिया – विशेषण शब्द की पहचान करके उसको रेखांकित करें

1. चारों ओर धूम मची है।
2. तम दिन भर क्या कर रहे थे ?
3. जितना परिश्रम करोगे, उतनी ही सफलता पाओगे।
4. घर के भीतर चले जाओ।
5. हमेशा सच बोलो।
6. मैं प्रतिदिन सैर करता हूँ।
7. दूर से आएं हो, बैठ जाओ।
8. एक ओर हट जाओ।
9. मैंने पेट भर खाना खा लिया है।
10. धीरे – धीरे चलो, नहीं तो थक जाओगे।
11. समय जल्दी – जल्दी बीत रहा है।
12. यह पुस्तक हाथों हाथ बिक गई।
13. सभी बारी – बारी आकर अपना वेतन ले जाएँ।
14. वह अभी आया है।
15. प्रदूषण उसे प्रतिदिन विनाश के निकट ले जा रहा है।
16. बाहर झाँककर देखो।
17. कभी – कभी मसूड़ों में भी खून बहने लगता है।

उत्तर :
ऊपर के सभी मोटे काले रेखांकित शब्द क्रिया विशेषण हैं।

2. सम्बन्धबोधक

प्रश्न 3.
सम्बन्धबोधक अव्यय किसे कहते हैं ? उदाहरण देकर स्पष्ट करो।
उत्तर :
जो संज्ञा और सर्वनाम के आगे – पीछे आ कर वाक्यों के दूसरे शब्दों से उसका सम्बन्ध बताते हैं, उन्हें सम्बन्धबोधक अव्यय कहा जाता है। जैसे – ऊपर, भीतर, पीछे, तक और सहित आदि।
उदाहरण –

• डर के मारे उसका चेहरा पीला पड़ गया।
• मेरा घर विद्यालय के पीछे है।
• विद्या के बिना मनुष्य पशु है।

प्रश्न 1.
नीचे लिखे वाक्यों में से सम्बन्धबोधक शब्द चुनकर उनको रेखांकित करें
(क) राम के साथ लक्ष्मण भी वन को गए।
(ख) उसके निकट कौन खड़ा है ?
(ग) कमरे के बाहर बैठ जाओ।
(घ) मेरे सामने से दूर हट कर बैठो।
(ङ) उसके समान कक्षा में कोई लायक नहीं है।
उत्तर :
(क) साथ,
(ख) निकट,
(ग) बाहर,
(घ) सामने,
(ङ) समान।

प्रश्न 2.
नीचे लिखे शब्दों को सम्बन्धबोधक के रूप में प्रयोग करके वाक्य बनाओ
आगे, पीछे, भीतर, अनुसार, तरह।
उत्तर :
आगे – पीछे – सीता के आगे राम थे और उसके पीछे लक्ष्मण थे। भीतर – गाड़ी के भीतर बैठ जाओ। अनुसार – जवान अधिकारी की आज्ञा के अनुसार चलता है। तरह – महात्मा गाँधी की तरह अन्याय का विरोध करो।

अन्य प्रश्न

निम्नलिखित वाक्यों में से सम्बन्धबोधक शब्द चुनो :

1. मोहन और सोहन साथ जा रहे हैं।
2. कमरे के बाहर बैठ जाओ।
3. राम के निकट कौन खड़ा है ?
4. कमरे के अन्दर चले जाओ।
5. बंदर पेड़ के नीचे बैठे हैं।
6. बच्चे छत के ऊपर उछल – कूद कर रहे हैं।
7. राम के साथ लक्ष्मण भी वन को गए।
8. मेरे सामने से दूर हट कर बैठो।
9. वह बाज़ार की ओर अभी गया है।
10. बच्चा घर से दूर पहुँच गया था।
11. नीतू राम के समान बुद्धिमान है।
12. आपके सामने कौन बोल सकता है ?
13. उसके समान कक्षा में कोई लायक नहीं है।
14. भगवान का नाम लिया ………………..आगे बढ़े।
15. चार्ली और मेधावी अपने माता – पिता …………… धर्मशाला घूमने गई।

उत्तर :

1. साथ
2. बाहर
3. निकट
4. अन्दर
5. नीचे
6. ऊपर
7. साथ
8. दूर
9. ओर
10. दूर
11. समान
12. सामने
13. समान
14. और
15. के साथ।

3. समुच्चयबोधक/योजक

प्रश्न 1.
समुच्चयबोधक अथवा योजक अव्यय किसे कहते हैं ?
उत्तर :
जो दो शब्दों, वाक्यांशों या वाक्यों को मिलाते हैं, उन्हें समुच्चयबोधक या योजक अव्यय कहते हैं। जैसे – और, भी, तथा, कि, अर्थात्, इसलिए, मानो।

उदाहरण –

• मोहन ने कहा कि मैं आपकी प्रतीक्षा करूँगा।
• मैंने तो बहुत कहा किन्तु वह नहीं माना।
• राम और लक्ष्मण भाई थे।

अभ्यास – प्रश्न

प्रश्न 1.
नीचे लिखे वाक्यों में योजक शब्द की पहचान करके उसे रेखांकित करो
(क) लव और कुश भगवान् राम के पुत्र थे।
(ख) यद्यपि वह परिश्रमी थे, तथापि वह बुद्धिमान् नहीं है।
(ग) वह बेबस तथा असहाय था।
(घ) तुम व्यायाम नहीं करते, इसीलिए बीमार रहते हो।
(ङ) यदि काम न करोगे तो वेतन कैसे पाओगे ?
उत्तर :
(क) और
(ख) यद्यपि, तथापि
(ग) तथा
(घ) इसलिए
(ङ) यदि, तो।

प्रश्न 2.
निम्नलिखित योजक शब्दों का प्रयोग करके वाक्य बनाएँ
(क) यद्यपि ……………………….. तथापि
(ख) जो ……………………….. सो
(ग) चाहे ……………………….. फिर भी
(ग) अगर ……………………….. तो
(ङ) जैसा ……………………….. वैसा
(च) क्योंकि ……………………….. इसलिए
उत्तर :
विद्यार्थी स्वयं करें।

प्रश्न 3.
निम्नलिखित शब्दों को योजक के रूप में अपने वाक्य में प्रयुक्त करो – और, अथवा, पर, एवं, या, बल्कि, अर्थात्।
उत्तर :

• और – मोहन और कमल पढ़ रहे हैं।
• अथवा – भारतेन्दु अथवा जयशंकर प्रसाद का परिचय लिखो।
• पर – यह पार्क छोटा है, पर सुंदर है।
• एवं – शक्ति एवं ज्ञान दोनों अनिवार्य है।
• या – वह सुबह या शाम दोनों समय आ सकता है।।
• बल्कि – हमें बड़ों का अपमान नहीं, बल्कि मान करना चाहिए।
• अर्थात् – पराधीन सपनेहुँ सुख नाहिं अर्थात् पराधीन सपने में सुख नहीं पाता।

प्रश्न 4.
निम्नलिखित योजक शब्दों का प्रयोग करके वाक्य बनाएँ – यद्यपि – तथापि, जो – सो, चाहे – फिर भी, अगर – तो, जैसा – वैसा, क्योंकि – इसलिए।
उत्तर :

• यद्यपि मोहन यहाँ नहीं है तथापि तुम आ सकते हो।
• जो चलेगा सो पहुँचेगा।
• चाहे वह अनपढ़ है फिर भी समझदार है।
• अगर पढ़ोगे तो पास हो जाओगे।
• जैसा करोगे वैसा भरोगे।
• क्योंकि वह देश भक्त है इसलिए उसमें गर्व की भावना है।

अन्य प्रश्न

प्रश्न 1.
निम्नलिखित वाक्यों में से योजक शब्द चुनो :

1. मोहन और सोहन इकट्ठे खेल रहे हैं।
2. चुपचाप बैठो (रहो) अन्यथा बाहर चले जाओ।
3. राम, लक्ष्मण और सीता वन को गए।
4. जो करेगा, सो भरेगा।
5. अगर वह पढ़ता तो पास हो जाता।
6. सुरेश और नरेश मित्र हैं।
7. यद्यपि वह परिश्रमी है तथापि वह बुद्धिमान् नहीं है।
8. मैंने उसे बहुत समझाया किन्तु वह नहीं माना।
9. तुम सुबह या शाम दोनों समय आ सकते हो।
10.  वह इतना कमज़ोर है कि चल – फिर नहीं सकता।
11. वह बेबस तथा असहाय था।
12. लव और कुश भगवान् राम के पुत्र थे।
13. सभी खिलाड़ियों का योगदान महत्त्वपूर्ण था ……………. ध्यानचंद की बात निराली थी।
14. मोहसिन इतना उदार नहीं है …………….. यह जानकर भी वह उसके पास जाता है।

उत्तर :

1. और
2. अन्यथा
3. और
4. जो – सो
5. अगर – तो
6. और
7. यद्यपि – तथापि
8. किन्तु
9. या
10. कि
11. तथा
12. और
13. लेकिन
14. लेकिन।

4. विस्मयादिबोधक

प्रश्न 1.
विस्मयादिबोधक किसे कहते हैं ?
उत्तर :
जो शब्द आश्चर्य, दुःख, प्रसन्नता, घृणा, लज्जा, शोक आदि भावों को प्रकट करते हैं, उन्हें विस्मयादिबोधक कहते हैं। जैसे – ओहो, आह, हाय, बाप रे, खूब, वाह वाह, धन्य, अरे, अजी।

उदाहरण –

• हाय ! मैं मारा गया।
• छिः छिः! कितनी बुरी बात है।
• शाबाश ! तुमने तो कमाल कर दिया।

अभ्यास – प्रश्न

प्रश्न 1.
नीचे लिखे वाक्यों में से विस्मयादिबोधक शब्द चुनो
(क) हाय ! मैं लुट गया।
(ख) वाह ! कितना सुन्दर दृश्य है।
(ग) उफ ! बहुत दर्द होता है।
(घ) शाबाश ! क्या गोल किया है।
(ङ) अहा ! मज़ा आ गया।
उत्तर :
(क) हाय !
(ख) वाह !
(ग) उफ !
(घ) शाबाश !
(ङ) अहा !

प्रश्न 2.
नीचे लिखे विस्मयादिबोधक शब्दों को अपने वाक्यों में प्रयोग करो हाय, वाह, छिः छिः, अहा, वाह – वाह, काश, खबरदार।
उत्तर :

• हाय ! यह क्या हो गया।
• वाह ! कैसा मनोहर दृश्य है।
• छिः छिः! मोहिनी ! तुम कितनी गंदी हो।
• अहा ! आम खाकर मज़ा आ गया।
• वाह – वाह ! हमारी टीम जीत गई।
• काश ! मैं खिलाड़ी होता।
• खबरदार ! अगर एक कदम भी आगे बढ़ाया।

प्रश्न 3.
नीचे लिखे वाक्यों में दिए गए रिक्त स्थान में उचित विस्मयादिबोधक शब्द भरो
(क) …………………………. कैसा सुन्दर दृश्य है।
(ख) …………………………. मैं एक वैज्ञानिक होता।
(ग) …………………………. इतना कठिन प्रश्न।
(घ) …………………………. तुमने तो कमाल कर दिया।
(ङ) …………………………. जरा पीछे हट कर चलो।
उत्तर :
(क) वाह !
(ख) काश !,
(ग) उफ़ !,
(घ) शाबाश !,
(ङ) छि: – छि: !

अन्य प्रश्न

प्रश्न 1.
नीचे लिखे वाक्यों में उचित विस्मयादिबोधक शब्द लिख कर रिक्त स्थान भरो
(1) …………………………. ! मैं लुट गई।
(2) ………………………….! दूध पीकर मज़ा आ गया।
(3) ………………………….! कैसी दुर्गंध है।
(4) …………………………. ! क्या गोल किया है।
(5) ………………………….! क्या मधुर आवाज़ है।
(6) …………………………. ! है उसकी बुद्धि पर।
(7) …………………………. ! तुमने ठीक पहचाना।
उत्तर :
(1) हाय
(2) अहा
(3) छिः छिः
(4) शाबाश
(5) वाह
(6) धिक्कार
(7) अरे वाह।

Punjab State Board PSEB 8th Class Hindi Book Solutions Hindi Grammar Kriya क्रिया Exercise Questions and Answers, Notes.

PSEB 8th Class Hindi Grammar क्रिया (2nd Language)

प्रश्न 1.
क्रिया किसे कहते हैं ? नीचे के वाक्यों में से क्रिया चुनिए
(1) मोहन पढ़ता है।
(2) कमला लिखती है।
उत्तर :
जिस शब्द से किसी काम का करना, होना, सहना आदि पाया जाए, उसे क्रिया कहते हैं। जैसे – मोहन पढ़ता है। कमला लिखती है। इसमें मोटे (काले) शब्द क्रियाएँ हैं।

प्रश्न 2.
कर्म के अनुसार क्रिया के कितने भेद हैं ?
उत्तर :
कर्म के अनुसार क्रिया के दो भेद हैं –
(1) अकर्मक और
(2) सकर्मक।

1. अकर्मक – जिसके व्यापार और फल दोनों का भार कर्त्ता पर ही पड़े (कर्म न हो), उसे अकर्मक क्रिया कहते हैं। जैसे – कृष्ण रोता है। मोहन भागता है।

कुछ अकर्मक क्रियाएँ – मरना, जीना, हँसना, रोना, उठना, बैठना, दौड़ना, भागना, चलना, सोना, डरना।

2. सकर्मक – जिस क्रिया में व्यापार का फल कर्ता को छोड़कर कर्म पर पड़े, उसे सकर्मक क्रिया कहते हैं। जैसे – श्याम पुस्तक पढ़ता है। मोहन पेंसिल देता है।

कुछ सकर्मक क्रियाएँ – लेना, देना, पढ़ना, लिखना, कहना, देखना, सीना, छूना, रोकना, सुनना, भागना, खाना।

प्रश्न 3.
रचना की दृष्टि से क्रिया के भेद लिखो।
उत्तर :
रचना की दृष्टि से क्रिया के निम्नलिखित भेद हैं

1. सामान्य क्रिया – जहाँ केवल एक क्रिया का प्रयोग किया जाए, वह सामान्य क्रिया कहलाती है। जैसे – अनिल आया। सोहन ने पढ़ा। मैंने खाया।
2. संयुक्त क्रिया – दो या दो से अधिक धातुओं से मिलकर बनने वाली क्रियाएँ संयुक्त क्रियाएँ कहलाती हैं। जैसे – लिखना चाहता है, पढ़ सकता है, जा सकता है।
3. नाम धातु क्रिया – संज्ञा, सर्वनाम, विशेषण से बनने वाली क्रियाओं को नाम धातु क्रिया कहते हैं। जैसे – हथियाना, बतियाना, लतियाना।
4. प्रेरणार्थक क्रिया – जिस क्रिया का कर्ता स्वयं क्रिया न करके किसी अन्य को क्रिया करने की प्रेरणा देता है, उस क्रिया को प्रेरणार्थक क्रिया कहते हैं। जैसे – सुनाना, लिखाना, पढ़ाना, कराना।

प्रेरणार्थक क्रियाएँ
मूल धातु

5. पूर्वकालिक क्रिया – जब कोई क्रिया मुख्य क्रिया से पूर्व ही समाप्त हो जाए तो उसे पूर्वकालिक क्रिया कहते हैं। जैसे – सीता खाना खा कर स्कूल जाएगी। यहाँ पर ‘जाएगी’ मुख्य क्रिया है और ‘खा कर’ पूर्वकालिक क्रिया है।

अभ्यास प्रश्न

प्रश्न 1.
नीचे लिखे शब्दों में से क्रिया – शब्दों का चयन करो
(क) पढ़ना, पढ़ाई।
(ख) मेल, मिलावट, मिलना, मिलन।
(ग) बुनाई, बुनावट, बुनना।
(घ) हम, था, वह, कैसे।
(ङ) खेलना, खेल, खिलाड़ी।
उत्तर :
(क) पढ़ना
(ख) मिलना
(ग) बुनना
(घ) था
(ङ) खेलना।

प्रश्न 2.
नीचे लिखे वाक्यों में क्रिया शब्दों को रेखांकित करो
(क) अर्जुन ने अकेले ही चक्रव्यूह का भेदन किया।
(ख) लोहड़ी का त्योहार सारे देश में धूम – धाम से मनाया जाता है।
(ग) हमने भी रात को यहीं विश्राम किया।
(घ) अंगुलिमाल ने महात्मा बुद्ध का रास्ता रोक लिया।
(ङ) तुमने फिरंगी जुबान भी पढ़ी है।
उत्तर :
(क) भेदन
(ख) मनाया
(ग) किया
(घ) रोक लिया
(ङ) पढ़ी है।

प्रश्न 3.
नीचे लिखे वाक्यों में आए क्रिया शब्द को रेखांकित किया गया है। बताइए यह क्रिया अकर्मक है या सकर्मक ?
(क) उस समय पंजाब छोटे – छोटे राज्यों में बँटा हुआ था।
(ख) पठानों की सेना अधिक थी।
(ग) पक्षी का रक्षक कौन था ?
(घ) समाज के अभाव में मनुष्य निरा पशु ही रहता है।
(ङ) मैं उसकी आवाज़ सुन कर चौंक पड़ा।
उत्तर :
(क) अकर्मक
(ख) अकर्मक
(ग) अकर्मक
(घ) अकर्मक
(ङ) सकर्मक।

अन्य प्रश्न

निम्नलिखित शब्दों/वाक्यों में से क्रिया शब्द चुनिए :

प्रश्न 1.
वे, गया, यहाँ।
उत्तर :
गया

प्रश्न 2.
खेलना, खेल, खिलाड़ी।
उत्तर :
खेलना

प्रश्न 3.
पढ़ना, पढ़ाई, पाठ।
उत्तर :
पढ़ना

प्रश्न 4.
बुनाई, बुनावट, बुनना।
उत्तर :
बुनना

प्रश्न 5.
हम, था, कैसे, मोहन, पढ़ना।
उत्तर :
था, पढ़ना

प्रश्न 6.
प्रतिदिन पढ़ाई करो।
उत्तर :
करो

प्रश्न 7.
प्रतिदिन व्यायाम करना चाहिए।
उत्तर :
करना चाहिए

प्रश्न 8.
मैं उसकी आवाज़ सुनकर चौंक पड़ा।
उत्तर :
सुनकर चौंक पड़ा

प्रश्न 9.
तुमने फिरंगी जुबान पढ़ी है।
उत्तर :
पढ़ी है

प्रश्न 10.
समय जल्दी – जल्दी जा रहा है।
उत्तर :
जा रहा है

प्रश्न 11.
समाज के अभाव में मनुष्य पशु ही रहता है।
उत्तर :
रहता है

प्रश्न 12.
प्रतिदिन स्नान करना चाहिए।
उत्तर :
करना चाहिए

प्रश्न 13.
बलराम दूध पीता है।
उत्तर :
पीता है

प्रश्न 14.
मेल, मिलावट, मिलाना, मिलन।
उत्तर :
मिलाना

प्रश्न 15.
अर्जुन ने अकेले ही चक्रव्यूह का भेदन किया।
उत्तर :
भेदन किया

प्रश्न 16.
हम सब मुस्कुराएँगे।
उत्तर :
मुस्कुराएँगे

प्रश्न 17.
धीरे – धीरे हॉकी खेलने के नियम बनने लगे।
उत्तर :
बनने लगे

प्रश्न 18.
सुरेश पत्र लिखता है।
उत्तर :
लिखता

बहुविकल्पीय प्रश्न

निम्नलिखित प्रश्नों के उत्तर सही विकल्प चुनकर लिखें :

प्रश्न 1.
क्रिया के कितने भेद हैं ?
(क) एक
(ख) दो
(ग) तीन
(घ) चार।
उत्तर :
दो।

प्रश्न 2.
क्रिया पद छाँट कर लिखें
(क) राम
(ख) रोज़
(ग) पुस्तक
(घ) पढ़ता है।
उत्तर :
पढ़ता है।

प्रश्न 3.
क्रिया शब्द छाँट कर लिखें
(क) मोहन
(ख) गया
(ग) कल
(घ) रोपड़।
उत्तर :
गया।

प्रश्न 4.
क्रिया शब्द छाँट कर लिखें
(क) रजत
(ख) गाय का
(ग) दूध
(घ) पीता है।
उत्तर :
पीता है।

प्रश्न 5.
क्रिया शब्द छाँट कर लिखें
(क) हम
(ख) सब
(ग) मिलकर’
(घ) गाएँगे।
उत्तर :
गाएँगे।

प्रश्न 6.
निम्नलिखित में सही क्रिया शब्द की पहचान करके लिखें
(क) हामिद
(ख) हाथ
(ग) फैलाता है
(घ) दोस्त।
उत्तर :
फैलाता है।

प्रश्न 7.
निम्नलिखित में सही क्रिया शब्द की पहचान करके लिखें : फिर बाबा ने घोड़े को रोका
(क) फिर
(ख) बाबा
(ग) घोड़े को
(घ) रोका।
उत्तर :
रोका।

Punjab State Board PSEB 8th Class Hindi Book Solutions Hindi Grammar Visheshan विशेषण Exercise Questions and Answers, Notes.

PSEB 8th Class Hindi Grammar विशेषण (2nd Language)

प्रश्न 1.
विशेषण किसे कहते हैं ? इसके भेद लिखो।
उत्तर :
जो शब्द संज्ञा या सर्वनाम की विशेषता प्रकट करे, विशेषण कहलाता है। जैसे – वीर पुरुष। इसमें ‘वीर’ शब्द पुरुष की विशेषता प्रकट करता है। इसलिए यह विशेषण है। विशेषण के चार भेद हैं
(1) गुणवाचक
(2) परिमाणवाचक
(3) संख्यावाचक
(4) सार्वनामिक विशेषण।

1. गुणवाचक – जो विशेषण किसी पदार्थ के गुण, दोष, आकार, रंग, अवस्था, समय आदि का बोध कराए, उसे ‘गुणवाचक विशेषण’ कहते हैं। जैसे – भला मनुष्य, काला घोड़ा, निचला कमरा।
2. परिमाणवाचक – जो विशेषण संज्ञा या सर्वनाम की माप या तोल सम्बन्धी विशेषता को प्रकट करें, उन्हें ‘परिमाणवाचक विशेषण’ कहते हैं। जैसे – दो मीटर कपड़ा, चार किलो मिठाई। इसके दो भेद हैं –
   • निश्चित परिमाणवाचक – जिस विशेषण से संज्ञा या सर्वनाम के निश्चित परिमाण का बोध हो – जैसे – दो क्विटल, चार लीटर।
   • अनिश्चित परिमाणवाचक – जिस विशेषण से संज्ञा या सर्वनाम के निश्चित परिमाण का बोध न हो – जैसे – कुछ दूध, थोड़ा घी, बहुत मिठाई।
3. संख्यावाचक – जो विशेषण किसी संज्ञा या सर्वनाम की संख्या (गिनती) का ज्ञान कराए, उसे ‘संख्यावाचक विशेषण’ कहते हैं। जैसे – एक पुस्तक, दस लड़के। इसके भी दो भेद हैं-
   • निश्चित संख्यावाचक – जो निश्चित संख्या का ज्ञान कराए। जैसे – पाँच लड़कियां, दुगुना बोझ।
   • अनिश्चित संख्यावाचक – जो निश्चित संख्या का ज्ञान न कराए। जैसे – सभी छात्र, कुछ लोग, कई दिन।
4. सार्वनामिक विशेषण – जो सर्वनाम संज्ञा की विशेषता प्रकट करे, उसे सार्वनामिक विशेषण कहते हैं। जैसे – यह घोड़ा, वह पुस्तक।

इसे निर्देशवाचक, संकेतवाचक और सांकेतिक विशेषण भी कहा जाता है।

प्रश्न 2.
सर्वनाम और सार्वनामिक विशेषण में क्या अन्तर है ? उदाहरण देकर समझाइए।
उत्तर :
संज्ञा के स्थान पर प्रयुक्त होने वाले शब्द ‘सर्वनाम’ कहलाते हैं। परन्तु यदि वाक्य में वे किसी संज्ञा से पहले प्रयुक्त होकर उसकी विशेषता बताते हैं तो वे सर्वनाम न रह कर विशेषण बन जाते हैं। जैसे – यह चुप बैठा है। वह रोटी खाता है। (यह, वह सर्वनाम)। ये कपड़े मेरे हैं। वह पुस्तक किसकी है ? (ये, वह-सार्वनामिक विशेषण)।

प्रश्न 3.
विशेषणों की तुलना से क्या अभिप्राय है ? तुलना के विचार से विशेषण की कितनी अवस्थाएँ होती हैं ?
उत्तर :
संज्ञाओं के गुण – दोषों की न्यूनता – अधिकता का बोध कराए जाने को विशेषण की तुलना कहा जाता है। तुलना के विचार से विशेषण की तीन अवस्थाएँ हैं
(1) मूलावस्था
(2) उत्तरावस्था
(3) उत्तमावस्था।

1. मूलावस्था-इसमें विशेष्य की किसी से तुलना नहीं की जाती। जैसे-मोहन सुन्दर है।
2. उत्तरावस्था – इसमें दो पदार्थों की तुलना की जाती है और एक की अधिकता या न्यूनता दिखाई जाती है। जैसे – राम श्याम से अधिक चतुर है।
3. उत्तमावस्था – इसमें एक की तुलना दो से अधिक वस्तुओं से की जाती है और उसे सबसे ऊँचा या सबसे नीचा दर्शाया जाता है। जैसे – राम अपनी श्रेणी में सबसे चतुर है।

आवश्यक जानकारी – विशेषण की पहली अवस्था (मलावस्था) में विशेषण शब्द के साथ कोई प्रत्यय नहीं लगता, जबकि उत्तरावस्था में ‘तर’ और उत्तमावस्था में ‘तम’ प्रत्यय लगते हैं।

उदाहरण :

मूलावस्था	उत्तरावस्था	उत्तमावस्था
योग्य	योग्यतर	योग्यतम
प्रिय	प्रियतर	प्रियतम
अधिक	अधिकतर	अधिकतम
निकट	निकटतर	निकटतम
कठिन	कठिनतर	कठिनतम
गुरु	गुरुतर	गुरुतम
लघु	लघुतर	लघुतम
सुन्दर	सुन्दरतर	सुन्दरतम
महान्	महत्तर	महत्तम

अभ्यास प्रश्न

प्रश्न 1.
नीचे लिखे शब्दों में से विशेषण शब्द चुनो
(क) मीठा, मिठाई, मिठास।
(ख) हरा, हरियाली।
(ग) डरना, डरपोक, डर।
उत्तर :
(क) मीठा,
(ख) हरा,
(ग) डरपोक।

प्रश्न 2.
नीचे लिखे वाक्यों में रेखांकित शब्द विशेषण हैं या सर्वनाम ?
(क) वह बालक बहुत चतुर है।
(ख) हमारा स्कूल बहुत सुंदर है।
(ग) वह किधर जा रहा है ?
(घ) यह पुस्तक मेरी है।
(ङ) तुम कहाँ जा रहे हो ?
उत्तर :
(क) वह – विशेषण
(ख) हमारा – सर्वनाम
(ग) वह – सर्वनाम
(घ) यह – विशेषण
(ङ) तुम – सर्वनाम

प्रश्न 3. नीचे लिखे वाक्यों में रेखांकित शब्द विशेषण के किस भेद से सम्बन्धित हैं ? उस भेद का नाम सामने दिए गए कोष्ठक में लिखो
(क) महात्मा गाँधी बच्चों से बहुत प्रेम करते थे। (  )
(ख) भारतीय वैज्ञानिकों ने अंतरिक्ष – विज्ञान में बहुत उन्नति कर ली है। (  )
(ग) लव और कुश राम को अन्यायी क्यों मानते हैं ? (  )
(घ) डूबते सूर्य के धीमे प्रकाश में बाघ दिखाई न पड़ा। (  )
(ङ) क्रिकेट टीम में ग्यारह सदस्य होते हैं। (  )
उत्तर :
(क) परिमाणवाचक,
(ख) गुणवाचक,
(3) गुणवाचक,
(4) गुणवाचक,
(5) संख्यावाचक।

अन्य प्रश्न

प्रश्न 1.
निम्नलिखित वाक्यों में रेखांकित शब्द (मोटे काले) सर्वनाम हैं या विशेषण

1. वह बालक बहुत सुन्दर है।
2. आम मीठा है।
3. लव और कुश राम को अन्यायी क्यों मानते हैं ?
4. कौन लड़का गा रहा है ?
5. क्रिकेट टीम में ग्यारह सदस्य होते हैं।
6. डूबते सूर्य के धीमे प्रकाश में बाघ दिखाई न पड़ा।
7. दो मीटर कपड़ा दे दो।
8. दोनों बालक भले हैं।
9. मेरा भारत महान् है।
10. हरी घास पर ओस, मोती की तरह चमक रहा है।
11. वह गाय बहुत दूध देती है।
12. बाघ की मोटी – मोटी आँखें थीं।
13. हमारे वीर हृदय का साहस देखिए।
14. बाल्यकाल में मोहनदास संकोची बालक था।

उत्तर :
ऊपर दिए वाक्यों में सभी रेखांकित (मोटे काले) शब्द विशेषण हैं।

प्रश्न 2.
निम्नलिखित वाक्यों में विशेषण चुनें
(1) शीला बहुत अच्छी लड़की है।
(2) यह कोट काला है।
(3) गिलास में थोड़ा दूध है।
(4) कक्षा में तीस विद्यार्थी हैं।
(5) वह लड़का ग़रीब है।
उत्तर :
(1) अच्छी
(2) काला
(3) थोड़ा
(4) तीस
(5) वह।

बहुविकल्पीय प्रश्न

सही उत्तर छांट कर लिखें

प्रश्न 1.
विशेषण कितने हैं ?
(क) एक
(ख) दो
(ग) तीन
(घ) चार।
उत्तर :
चार।

प्रश्न 2.
कुछ लोग अनशन कर रहे हैं रेखांकित विशेषण है
(क) गुणवाचक
(ख) संख्यावाचक।
(ग) परिणामवाचक
(घ) सार्वनामिक।
उत्तर :
परिणामवाचक।

प्रश्न 3.
विशेषण बनाइए
(क) राष्ट्र
(ख) स्वदेश
(ग) विज्ञान
(घ) भारत
(ङ) शरीर।
उत्तर :
राष्ट्रीयता, स्वदेशी, वैज्ञानिक, भारतीय, शारीरिक।

प्रश्न 4.
विशेषण छाँट कर लिखें
(क) कक्षा
(ख) में
(ग) पाँच
(घ) विद्यार्थी हैं।
उत्तर :
पाँच।

प्रश्न 5.
विशेषण छाँटकर लिखें
(क) गिलास में
(ख) थोड़ा
(ग) दूध
(घ) लाओ।
उत्तर :
थोड़ा।

प्रश्न 6.
निम्नलिखित में से सही विशेषण शब्द पहचान कर लिखें
(क) अनिल शर्मा
(ख) प्रसिद्ध
(ग) प्रशिक्षण
(घ) दिखाया।
उत्तर :
प्रसिद्ध।

प्रश्न 7.
निम्नलिखित में से सही विशेषण शब्द की पहचान करके लिखें
(क) पेड़
(ख) स्कूल
(ग) हालत
(घ) रंग – बिरंगे।
उत्तर :
रंग – बिरंगे।’

Punjab State Board PSEB 8th Class Hindi Book Solutions Hindi Grammar Sarvanam सर्वनाम Exercise Questions and Answers, Notes.

PSEB 8th Class Hindi Grammar सर्वनाम (2nd Language)

प्रश्न 1.
सर्वनाम की परिभाषा लिखो और उसके भेद भी बताओ।
उत्तर :
वाक्य में संज्ञा के स्थान पर प्रयुक्त होने वाले विकारी शब्दों को सर्वनाम कहते हैं।
जैसे – सोहन, मोहन के साथ उसके घर गया। इस वाक्य में ‘उसके’ सर्वनाम मोहन के स्थान पर प्रयुक्त हुआ है।

सर्वनाम के छः भेद हैं जो निम्नलिखित हैं –

1. पुरुषवाचक – जिसके वक्ता (बोलने वाला), श्रोता (सुनने वाला) और जिसके सम्बन्ध में चर्चा हो रही हो, उसका ज्ञान प्राप्त हो। जैसे –
   • अन्य पुरुष – वह, वे
   • मध्यम पुरुष – तू, तुम
   • उत्तम पुरुष – मैं, हम
2. निश्चयवाचक – इस सर्वनाम से वक्ता के समीप या दूर की वस्तु का निश्चय होता है। जैसे-यह, ये, वह, वे।
3. अनिश्चयवाचक – इस सर्वनाम से किसी पुरुष एवं वस्तु का निश्चित ज्ञान नहीं होता है। जैसे – कोई, कुछ।
4. सम्बन्धवाचक – इस सर्वनाम से दो संज्ञाओं में परस्पर सम्बन्ध का ज्ञान होता है। जैसे – जो, सो। जो करेगा, सो भरेगा।
5. प्रश्नवाचक – इस सर्वनाम का प्रयोग प्रश्न पूछने और कुछ जानने के लिए होता है। जैसे – कौन, क्या। आप कौन हैं ? मैं क्या करूँगा ?
6. निजवाचक सर्वनाम – जिन वाक्यों में सर्वनाम शब्दों का प्रयोग कर्ता स्वयं अपने लिए करता है, उसे निजवाचक सर्वनाम कहते हैं। जैसे –

मैं अपने विद्यालय गया। यह अपनी पुत्री है। मोहन ने अपना पाठ याद किया।

यहाँ पर ‘अपने’, ‘अपनी’ और ‘अपना’ शब्द निज वाचक सर्वनाम के रूप में प्रयोग किए गए हैं। इसलिए ये शब्द निजवाचक सर्वनाम कहलाएँगे।

अभ्यास – प्रश्न

प्रश्न 1.
नीचे लिखे वाक्यों में कौन – से शब्द सर्वनाम हैं ?
(क) यह मेरी कक्षा है।
(ख) मैं आठवीं कक्षा का छात्र हूँ।
(ग) जैसा बोओगे, वैसा ही पाओगे।
(घ) शेर के दाँत कौन गिन सकता है ?
(ङ) आ बैल मुझे मार।
उत्तर :
(क) यह, मेरी
(ख) मैं,
(ग) जैसा, वैसा,
(घ) कौन,
(ङ) मुझे।

प्रश्न 2.
नीचे दिए गए शब्दों में से सर्वनाम शब्द चनकर उसका भेद लिखो घर, सपेरा, मेरा, कोई, माता, हमारा, उसे, भाई, कक्षा, मेरी, पुस्तक।
उत्तर :

• मेरा – उत्तम पुरुषवाचक सर्वनाम
• कोई – अनिश्चयवाचक सर्वनाम
• हमारा – उत्तम पुरुषवाचक सर्वनाम
• उसे – अन्य पुरुषवाचक सर्वनाम
• मेरी – उत्तम पुरुषवाचक सर्वनाम

प्रश्न 3.
नीचे दिए वाक्यों में रेखांकित शब्द प्रश्नवाचक सर्वनाम हैं या अनिश्चयवाचक सर्वनाम ?
(क) कौन गा रहा है ?
(ख) आप क्या देख रहे हैं ?
(ग) आज कुछ होने वाला है।
(घ) जज ने किसे सजा सुनवाई ?
(ङ) कोई तो डूबते को बचाओ।
उत्तर :
(क) कौन – प्रश्नवाचक सर्वनाम
(ख) क्या – प्रश्नवाचक सर्वनाम
(ग) कुछ – अनिश्चयवाचक सर्वनाम
(घ) किसे – प्रश्नवाचक सर्वनाम।
(ङ) कोई – अनिश्चयवाचक सर्वनाम।

प्रश्न 4.
नीचे लिखे शब्दों में से पुरुषवाचक सर्वनाम चुनो
मेरा, कोई, कौन, जो, हमारा, तुम्हारा, किसका, तुम, मैं, मेरा, कैसा, जैसा, क्या।
उत्तर :
पुरुषवाचक सर्वनाम – मेरा, हमारा, तुम्हारा, तुम, मैं, मेरा।

अन्य प्रश्न

नीचे लिखे वाक्यों में से सर्वनाम चुनो :

प्रश्न 1.
मैं आठवीं कक्षा का छात्र हूँ।
उत्तर :
मैं

प्रश्न 2.
आप क्या देख रहे हैं ?
उत्तर :
आप

प्रश्न 3.
कोई तो डूबते को बचाओ।
उत्तर :
कोई

प्रश्न 4.
वह तो मेरा भाई है।
उत्तर :
वह, मेरा

प्रश्न 5.
कौन नाच रहा है ?
उत्तर :
कौन

प्रश्न 6.
यह मेरी कक्षा है।
उत्तर :
यह, मेरी

प्रश्न 7.
पहले कौन दौड़ेगा ?
उत्तर :
कौन

प्रश्न 8.
तुम क्या कर रहे हो ?
उत्तर :
तम

प्रश्न 9.
यह मेरी पुस्तक है।
उत्तर :
यह, मेरी

प्रश्न 10.
आ बैल, मुझे मार।
उत्तर :
मझे

प्रश्न 11.
शेर के दाँत कौन गिन सकता है ?
उत्तर :
कौन

प्रश्न 12.
कोई तो डूबते को बचाओ।
उत्तर :
कोई

प्रश्न 13.
आज कुछ होने वाला है।
उत्तर :
कुछ

प्रश्न 14.
कौन गा रहा है ?।
उत्तर :
कौन

प्रश्न 15.
मैं स्कूल जा रहा था।
उत्तर :
मैं

प्रश्न 16.
तुम कहाँ से आए हो ?
उत्तर :
तुम

प्रश्न 17.
उसने बन्दूक चलाना बचपन में ही सीख लिया था।
उत्तर :
उसने
वे

प्रश्न 18.
वे जंगल में नहीं जाते थे।
उत्तर :
वह

प्रश्न 19.
वह किधर जा रहा है ?
उत्तर :
हमारा

प्रश्न 20.
हमारा स्कूल बहुत सुन्दर है।
उत्तर :
आपके

बहुविकल्पीय प्रश्न
सही विकल्प चुनकर उत्तर लिखें

प्रश्न 1.
सर्वनाम के कितने भेद हैं ?
(क) दो
(ख) तीन
(ग) चार
(घ) छः।
उत्तर :
(घ) छः।

प्रश्न 2.
कौन जा रहा है – रेखांकित में सर्वनाम है
(क) निजवाचक
(ख) प्रश्नवाचक
(ग) संबंधवाचक
(घ) निश्चयवाचक।
उत्तर :
(ख) प्रश्नवाचक

प्रश्न 3.
कुछ खाने के लिए दो – रेखांकित में सर्वनाम है
(क) निजवाचक
(ख) प्रश्नवाचक
(ग) निश्चयवाचक
(घ) अनिश्चयवाचक।
उत्तर :
(घ) अनिश्चयवाचक।

प्रश्न 4.
मैं कक्षा आठ में पढ़ता हूँ, रेखांकित में सर्वनाम है
(क) पुरुषवाचक
(ख) संबंधवाचक
(ग) निजवाचक
(घ) निश्चयवाचक।
उत्तर :
(क) पुरुषवाचक

प्रश्न 5.
जो, सो, किस सर्वनाम में प्रयोग होते हैं ?
(क) निजवाचक
(ख) संबंधवाचक
(ग) निश्चयवाचक
(घ) प्रश्नवाचक।
उत्तर :
(ख) संबंधवाचक

प्रश्न 6.
‘हम लाल किला देखने जाएंगे’ में से सर्वनाम शब्द को चुनकर लिखें
(क) हम
(ख) लालकिला
(ग) देखने
(घ) जाएंगे।
उत्तर :
(क) हम

प्रश्न 7.
निम्नलिखित में से सर्वनाम शब्द को चुनकर लिखें
(क) गाड़ी
(ख) आया
(ग) बिठाकर
(घ) मैं।
उत्तर :
(घ) मैं।

Punjab State Board PSEB 8th Class Hindi Book Solutions Hindi Grammar Sangya ke Vikar संज्ञा के विकार Exercise Questions and Answers, Notes.

PSEB 8th Class Hindi Grammar संज्ञा के विकार (2nd Language)

प्रश्न 1.
संज्ञा शब्दों में विकार किनके कारण होता है ?
उत्तर :
लिंग, वचन और कारक के कारण संज्ञा शब्दों में विकार होता है। इनको विकारक तत्व भी कहते हैं।

(अ) लिंग

प्रश्न 2.
लिंग किसे कहते हैं ? उसके भेद बताओ।
उत्तर :
संज्ञा के जिस रूप से स्त्री या पुरुष जाति का बोध हो, उसे लिंग कहते हैं। हिन्दी में दो लिंग हैं –
(1) पुल्लिग
(2) स्त्रीलिंग।

1. पुल्लिग – संज्ञा के जिस रूप से पुरुष जाति का बोध हो, उसे पुल्लिग कहते हैं।
   जैसे – लड़का, शेर।
2. स्त्रीलिंग – संज्ञा के जिस रूप से स्त्री जाति का बोध हो, उसे स्त्रीलिंग कहते हैं।
   जैसे – लड़की, शेरनी।

(आ) वचन

प्रश्न 3.
वचन किसे कहते हैं और वचन कितने प्रकार के होते हैं ?
उत्तर :
संज्ञा के जिस रूप में किसी वस्तु के एक अथवा अनेक होने का बोध हो, उसे वचन कहते हैं।
हिन्दी में दो वचन हैं –
(1) एकवचन
(2) बहुवचन।

1. एकवचन – संज्ञा का जो रूप एक ही वस्तु का बोध कराए, उसे एकवचन कहते हैं। जैसे – लकड़ी, घोड़ा, बहन।
2. बहुवचन – संज्ञा का जो रूप एक से अधिक वस्तुओं का बोध कराए, उसे बहुवचन कहते हैं। जैसे – लड़कियाँ, घोड़े, बहनें।

(इ) कारक

प्रश्न 4.
कारक किसे कहते हैं ? इसके कितने भेद हैं ?
उत्तर :
संज्ञा या सर्वनाम के जिस रूप में उस वाक्य का दूसरे शब्दों से सम्बन्ध जाना जाए, उस रूप को कारक कहते हैं। जैसे – मोहन ने पुस्तक को मेज पर रख दिया।।

विभक्ति – कारक प्रकट करने के लिए संज्ञा अथवा सर्वनाम के साथ ‘ने’, ‘को’, ‘से’ आदि जो चिह्न लगाए जाते हैं, उन्हें विभक्ति कहा जाता है।

हिन्दी में आठ कारक हैं। इनके नाम और विभक्ति चिह्न इस प्रकार हैं –

कारक	विभक्ति चिहन
1. कर्ता	ने
2. कर्म	को
3. करण	से, के द्वारा, के साथ
4. सम्प्रदान	को, के लिए, वास्ते
5. अपादान	से (अलगाव बोधक)
6. सम्बन्ध	का, के, की
7. अधिकरण	में, पर
8. सम्बोधन	हे, अरे, रे

कर्ता – संज्ञा या सर्वनाम के जिस रूप से क्रिया के करने वाले का बोध होता है, उसे कर्ता कारक कहा जाता है। जैसे –
1. • मोहन पुस्तक पढ़ता है।
   • सोहन ने दूध पीया।

1. कर्म – संज्ञा या सर्वनाम के जिस रूप पर क्रिया के व्यापार का फल पड़ता हो, उसे कर्म कारक कहते हैं। जैसे – श्याम पाठशाला जाता है।
2. करण – संज्ञा या सर्वनाम के जिस रूप से कर्ता के काम करने के साधन का बोध हो, उसे करण कारक कहा जाता है। जैसे – राम ने बाण से बालि को मारा।
3. सम्प्रदान – संज्ञा या सर्वनाम के जिस रूप के लिए क्रिया की जाए, उसे सम्प्रदान कारक कहा जाता है। जैसे – अध्यापक विद्यार्थियों के लिए पुस्तकें लाया।
4. अपादान – संज्ञा या सर्वनाम के जिस रूप से पृथक्कता, आरम्भ, भिन्नता आदि का बोध होता हो, उसे अपादान कारक कहा जाता है। जैसे – वृक्ष से पत्ते गिरते हैं।
5. सम्बन्ध – संज्ञा या सर्वनाम का जो रूप एक वस्तु का दूसरी वस्तु के साथ सम्बन्ध प्रकट करे, उसे सम्बन्ध कारक कहते हैं। जैसे – यह मोहन का घर है।
6. अधिकरण – संज्ञा या सर्वनाम के जिस रूप से क्रिया के आधार का बोध हो, उसे अधिकरण कारक कहते हैं। जैसे – वीर सैनिक युद्ध – भूमि में मारा गया।
7. सम्बोधन – संज्ञा का जो रूप चेतावनी या किसी को पुकारने का सूचक हो। जैसे हे ईश्वर ! हमारी रक्षा करो।

प्रश्न 5.
नीचे लिखे कारकों में क्या भेद हैं ? स्पष्ट कीजिए।
(क) कतों और कर्म।
(ख) करण और अपादान
(ग) सम्बन्ध और सम्प्रदान।
उत्तर :
(क) कर्ता और कर्म

कर्ता	कर्म।
1. कर्ता कारक में संज्ञा या सर्वनाम के जिस रूप से क्रिया को करने वाले का बोध कराया जाता है। जैसे- देव ने कविता पढ़ी।	1. कर्म कारक में किसी वस्तु या व्यक्ति पर क्रिया के व्यापार का फल पड़ता है। जैसे – अध्यापक छात्र को पढ़ाता है।
2. कर्ता कारक का सामान्य विभक्ति चिह्न ‘ने’ होता है।	2. कर्म कारक का विभक्ति चिह्न ‘को’ होता है।

(ख) करण और अपादान

करण	अपादान म
(1) करण कारक क्रिया के साधन का बोध कराने वाले संज्ञा के रूप को कहते हैं। जैसे – सुनील कलम से लिखता है।	(1) अपादान कारक संज्ञा के किसी रूप से किसी वस्तु के दूसरे वस्तु को अलग होने का बोध कराता है जैसे – वृक्ष से पत्ता गिरता है।
(2) इसके विभक्ति चिह्न ‘से’, ‘के साथ ‘के द्वारा’ होते हैं।	(2) इसका विभक्ति चिह्न ‘से’ है।

(ग) सम्बन्ध और सम्प्रदान

सम्बन्ध	सम्प्रदान
(1) सम्बन्ध कारक में संज्ञा के किसी रूप का किसी दूसरी वस्तु से सम्बन्ध सूचित किया जाता है। जैसे – रामचरित मानस तुलसी कृत महाकाव्य है।	(1) सम्प्रदान कारक में किसी वस्तु के लिए कोई क्रिया की जाती है। जैसे- वह स्नान के लिए नदी पर जाता है।
(2) इसके विभक्ति चिह्न ‘का’, ‘के’, ‘की’, ‘रा’, ‘रे’, ‘री’, ‘ना’, ‘ने’, ‘नी’ हैं।।	(2) इसके विभक्ति चिह्न ‘को’ तथा ‘के लिए’ हैं।
(3) सम्बन्ध कारक का रूप लिंग और वचन आदि के कारण बदल जाता है।	(3) सम्प्रदान कारक का रूप लिंग और वचन आदि के कारण नहीं बदलता है।

प्रश्न 6.
नीचे लिखे वाक्यों में उपयुक्त कारक चिह्न भरें
(1) दूसरों …………………….. टिकट बार – बार पूछते थे, खुद बिना टिकट …………………….. चल रहे हो!
(2) आप लाला माधो राम …………………….. जानते हैं।
(3) दरवाजे …………………….. ज़ोर …………………….. दस्तक देता है।
उत्तर :
(क) का, के
(2) को
(3) पर, से।

बहुविकल्पीय प्रश्न

निम्नलिखित प्रश्नों के उत्तर सही विकल्प चुनकर लिखें :

प्रश्न 1.
लिंग कितने होते हैं ?
(क) एक
(ख) दो
(ग) तीन
(घ) चार।
उत्तर :
(ख) दो

प्रश्न 2.
वचन कितने होते हैं ?
(क) एक
(ख) दो
(ग) तीन
(घ) चार।
उत्तर :
(ख) दो

प्रश्न 3.
कारक कितने होते हैं ?
(क) दो
(ख) चार
(ग) सात
(घ) आठ।
उत्तर :
(घ) आठ।

प्रश्न 4.
वृक्ष से पत्ता गिरता है – रेखांकित में कारक है –
(क) अपादान
(ख) करण
(ग) संबंध
(घ) संप्रदान।
उत्तर :
(क) अपादान

प्रश्न 5.
राम कलम से पत्र लिखता है, रेखांकित में कारक है
(क) करण
(ख) अपादान
(ग) संबंध
(घ) कर्ता।
उत्तर :
(क) करण

प्रश्न 6.
‘गुरु जी ने बच्चों को बड़े प्यार से समझाया – ‘ वाक्य में रेखांकित पद में सही कारक की पहचान करके लिखें –
(क) सम्प्रदान कारक
(ख) कर्म कारक
(ग) कर्ता कारक
(घ) अपादान कारक।
उत्तर :
(ग) कर्ता कारक

प्रश्न 7.
‘भास्कर रेलगाड़ी देखने के लिए प्लेटफार्म के किनारे पर जा पहुंचा’ वाक्य में रेखांकित पद में सही कारक की पहचान करके लिखें :
(क) सम्बन्ध कारक
(ख) कर्म कारक
(ग) कर्ता कारक
(घ) सम्प्रदान कारक।
उत्तर :
(घ) सम्प्रदान कारक।

Punjab State Board PSEB 8th Class Hindi Book Solutions Hindi Grammar Sangya संज्ञा Exercise Questions and Answers, Notes.

PSEB 8th Class Hindi Grammar संज्ञा (2nd Language)

प्रश्न 1.
संज्ञा की परिभाषा लिखो और इसके भेद बताओ।
उत्तर :
किसी व्यक्ति, वस्तु, स्थान आदि के नाम को संज्ञा कहते हैं। जैसे – सुमन, गन्ना, दिल्ली, मिठास।
संज्ञा के तीन भेद हैं –

1. व्यक्तिवाचक
2. जातिवाचक
3. भाववाचक।

1. व्यक्तिवाचक – जो शब्द किसी व्यक्ति, स्थान, वस्तु आदि का बोध कराए। जैसे – कृष्ण, दिल्ली, गंगा।
2. जातिवाचक – जो शब्द किसी जाति का बोध कराए। जैसे – स्त्री, पुरुष, पशु, नगर आदि।
3. भाववाचक – जो शब्द किसी धर्म, अवस्था, भाव, गुण, दोष आदि को प्रकट करें। जैसे – मिठास, मानवता, सत्यता।

भाववाचक संज्ञाएँ बनाने के नियम :

भाववाचक संज्ञा जातिवाचक संज्ञा, सर्वनाम, विशेषण, क्रिया, क्रिया – विशेषण और निरर्थक शब्दों से बनती है।

• जातिवाचक संज्ञा से – सज्जन से सज्जनता, मूर्ख से मूर्खता, मित्र से मित्रता, युवा से यौवन।
• सर्वनाम से – आप से आपा, मम से ममता, अपना से अपनापन।
• विशेषण से – लघु से लघुता, कठिन से कठिनाई, अच्छा से अच्छाई, सफल से सफलता।
• क्रिया से – दौड़ना से दौड़, हँसना से हँसी, लड़ना से लड़ाई, पुकारना से पुकार, सजाना से सजावट।
• क्रिया – विशेषण से – दूर से दूरी, समीप से समीपता, शीघ्र से शीघ्रता।
• निरर्थक शब्दों से – चरचराहट, सरसराहट, भिनभिनाहट।

अभ्यास प्रश्न

प्रश्न 1.
नीचे लिखे वाक्यों में से संज्ञा शब्दों की पहचान करके उनको रेखांकित करो।
(क) राम मेरा पड़ोसी है।
(ख) पंजाब की राजधानी कहाँ है ?
(ग) सूर्य पूर्व में उदय होता है।
(घ) सच्चाई की सदा जीत होती है।
(ङ) नेकी कर, कुएँ में डाल।
उत्तर :
(क) राम,
(ख) पंजाब,
(ग) सूर्य, पूर्व,
(घ) सच्चाई,
(ङ) नेकी, कुएँ।

प्रश्न 2.
नीचे लिखे संज्ञा शब्दों में से भाव – वाचक संज्ञा शब्द चुनकर लिखो चंडीगढ़, भलाई, शेर।
उत्तर :
भलाई।

प्रश्न 3. नीचे लिखे वाक्यों में रेखांकित शब्द जाति – वाचक संज्ञा है या व्यक्तिवाचक संज्ञा।
(क) हाथी पानी पी रहा है।
(ख) शेर पानी पी रहा है।
(ग) शेर के दाँत कौन गिन सकता है ?
उत्तर :
(क) हाथी – जातिवाचक
(ख) शेर – जातिवाचक
(ग) दाँत – जातिवाचक।

प्रश्न 4.
नीचे कुछ संज्ञा – शब्द दिए गए हैं। इनमें से व्यक्तिवाचक, जातिवाचक और भाववाचक शब्द छाँट कर नीचे दी गई सारणी में लिखो :
घर, भलाई, अमृतसर, भारत, हिमालय, चतुराई, शहर, बचपन, दीवाली, भाई, मुसलमान, गंगा, हाथी, स्कूल, मित्रता, मित्र।।
उत्तर :
व्यक्तिवाचक संज्ञा – अमृतसर, भारत, हिमालय, गंगा, दीवाली।
जातिवाचक संज्ञा – घर, शहर, भाई, मुसलमान, हाथी, स्कूल, मित्र।
भाववाचक संज्ञा – भलाई, चतुराई, बचपन, मित्रता।

अन्य प्रश्न

प्रश्न 1.
नीचे लिखे वाक्यों में रेखांकित शब्द किस प्रकार की संज्ञा हैं

1. सभी मनुष्य उस डाकू से डरते थे।
2. अमृतसर पंजाब का प्रसिद्ध नगर है।
3. राम स्कूल जाता है।
4. भलाई करने से आनन्द मिलता है।
5. दिल्ली एक विशाल नगर है।
6. ताजमहल सफेद पत्थर का बना है।
7. गाँधी जी को राष्ट्रपिता भी कहते हैं।
8. मोहन अच्छा लड़का है।
9. इस दीवार की ऊँचाई कितनी है ?
10. घोड़ा एक उपयोगी पशु है।
11. शेर के दाँत कौन गिन सकता है ?
12. प्रसेनजित उनका शिष्य था।
13. देखो हाथी की चाल देखो।
14. उन्होंने साहस नहीं छोड़ा।
15. तुम्हारी इतनी अवस्था हो गई मगर ओछापन नहीं गया।

उत्तर :

1. जातिवाचक संज्ञा
2. व्यक्तिवाचक संज्ञा
3. जातिवाचक संज्ञा
4. भाववाचक संज्ञा
5. व्यक्तिवाचक संज्ञा
6. व्यक्तिवाचक संज्ञा
7. व्यक्तिवाचक संज्ञा
8. व्यक्तिवाचक संज्ञा
9. भाववाचक संज्ञा
10. जातिवाचक संज्ञा
11. जातिवाचक संज्ञा
12. व्यक्तिवाचक संज्ञा
13. जातिवाचक संज्ञा
14. भाववाचक संज्ञा
15. भाववाचक संज्ञा।

प्रश्न 2.
नीचे लिखे वाक्यों में रेखांकित (मोटे काले)शब्द किस प्रकार की संज्ञा हैं

1. भलाई कर कुएँ में डाल।
2. बचपन भुलाये नहीं भूलता।
3. सच्चाई की सदा जीत होती है।
4. कुछ आमों में मिठास नहीं होती।
5. चोरी करना पाप है।
6. पढ़ने से अज्ञानता दूर होती है।
7. सब से मित्रता का व्यवहार करो।
8. नीचता की भी कोई हद होती है।
9. आलस्य मनुष्य का दुश्मन है।
10. खटाई से गला खराब होता है।
11. भूमि की लम्बाई माप कर बताओ।
12. होनी बड़ी बलवान् होती है।
13. घबराहट से काम बिगड़ता है।
14. मिलावट करना अपराध है।
15. बहुत प्यास लगी है, पानी लाओ।
16. सरलता विद्यार्थी का अच्छा गुण है।
17. पर हरियाली तो बाग जैसी थी।
18. भलाई करने से आनन्द मिलता है।
19. शरीर की पूर्णता अंगों के सहयोग से मिलती है।
20. अब तो महँगाई का ज़माना है।
21. अपनी वीरता से अपने अधिकार को स्थिर रखा।

उत्तर :
ऊपर के सभी रेखांकित (काले) शब्द भाववाचक संज्ञा शब्द हैं।

प्रश्न 3.
निम्नलिखित शब्दों में से उचित शब्द छाँटकर तालिका पूरी करो मिठास, कुरान, छात्र, गीता, पक्षी, चौड़ाई, नारी, कोमलता, बहन, राम, अध्यापिका, नयापन, वन।
उत्तर :
व्यक्तिवाचक संज्ञाएँ – जातिवाचक संज्ञाएँ – भाववाचक संज्ञाएँ।
कुरान, गीता, राम – छात्र, पक्षी, नारी, बहन, अध्यापिका, वन – मिठास, चौड़ाई, कोमलता, नयापन

प्रश्न 4.
जातिवाचक संज्ञा और व्यक्तिवाचक संज्ञा में मुख्य अन्तर बताओ तथा इनके दो – दो उदाहरण लिखो।
उत्तर :
जो शब्द किसी जाति का बोध कराएँ, उन्हें जातिवाचक संज्ञा कहते हैं। जैसे – पुरुष, नदी। व्यक्तिवाचक संज्ञा किसी विशेष व्यक्ति, वस्तु अथवा स्थान का बोध कराती है। जैसे – लाल किला, महात्मा गाँधी।

प्रश्न 5.
भाववाचक संज्ञा और जातिवाचक संज्ञा में मुख्य अन्तर बताओ और इनके दो – दो उदाहरण भी लिखो।
उत्तर :
भाववाचक संज्ञा से किसी वस्तु अथवा जाति के भाव या गुण का बोध होता है। जैसे – सुन्दरता, मिठास। जो शब्द किसी पूरी जाति का बोध कराएँ, उन्हें जातिवाचक संज्ञाएँ कहते हैं। जैसे – गाय, पर्वत।

प्रश्न 6.
निम्नलिखित वाक्यों में रिक्त स्थान निर्देशानुसार भरो –

1. (व्यक्तिवाचक संज्ञा) …………………… हमारे देश के प्रथम प्रधानमन्त्री थे।
2. (जातिवाचक संज्ञा) …………………… सब प्राणियों में बुद्धिमान है।
3. (भाववाचक संज्ञा) …………………… हमें …………………… सिखाती है। …………………… मनुष्य का सबसे बड़ा गुण है।

उत्तर :

1. व्यक्तिवाचक संज्ञा – पं० जवाहर लाल नेहरू हमारे देश के प्रथम प्रधानमन्त्री थे।
2. जातिवाचक संज्ञा – मनुष्य सब प्राणियों में बुद्धिमान है।
3. भाववाचक संज्ञा – शिक्षा हमें सभ्यता सिखाती है।- नम्रता मनुष्य का सबसे बड़ा गुण है।

प्रश्न 7.
नीचे दिए गए गद्यांश में से संज्ञा शब्द चुनो –
महाराजा रणजीत सिंह का जन्म शुकरचकिया मिसल के मुखिया सरदार महा सिंह के घर गुजरांवाला में हुआ। आपकी माता राज कौर जींद की फुलकियां मिसल के सरदार की बेटी थी। आपका बचपन का नाम बुध सिंह था।
उत्तर :
संज्ञा शब्द – महाराजा रणजीत सिंह, शुकरचकिया, मिसल, सरदार, महा सिंह, घर, गुजरांवाला, माता राज कौर, जींद, फुलकियां, बुध सिंह।

निम्नलिखित प्रश्नों के उत्तर सही विकल्प चुनकर लिखें –

प्रश्न 1.
संज्ञा के कितने भेद हैं ?
(क) एक
(ख) दो
(ग) तीन
(घ) चार।
उत्तर :
तीन।

प्रश्न 2.
निम्नलिखित में से संज्ञा शब्द को चुनकर लिखें –
(क) बुरा
(ख) शेर
(ग) अनेक
(घ) जब।
उत्तर :
(ख) शेर।

प्रश्न 3.
निम्नलिखित में से संज्ञा शब्द को चुनकर लिखें –
(क) चढ़ना
(ख) असफल
(ग) मन्दिर
(घ) विशाल।
उत्तर :
(ग) मन्दिर।

प्रश्न 4.
निम्नलिखित वाक्यों से संज्ञा शब्द छाँट कर लिखें

(i) (क) विजय,
(ख) मेरा,
(ग) पड़ोसी,
(घ) है।
उत्तर :
(क) विजय।

(ii) (क) नेकी,
(ख) कर,
(ग) कुएँ में,
(घ) डाल।
उत्तर :
(क) नेकी।

(iii) (क) देखो,
(ख) कुत्ता,
(ग) भौंक,
(घ) रहा है।
उत्तर :
(ख) कुत्ता।

(iv) (क) जालंधर,
(ख) प्रसिद्ध,
(ग) नगर,
(घ) है।
उत्तर :
(क) जालंधर।

प्रश्न 5.
भाववाचक संज्ञा बनाइए-सुन्दर, मीठा।
उत्तर :
सुन्दरता, मिठास।

प्रश्न 6.
छात्र जा रहे हैं : रेखांकित कौन – सी संज्ञा है ?
उत्तर :
जातिवाचक संज्ञा।

प्रश्न 7.
नम्रता मानव का श्रेष्ठ गुण है, रेखांकित कौन – सी संज्ञा है ?
उत्तर :
भाववाचक संज्ञा।

Punjab State Board PSEB 8th Class Home Science Book Solutions Practical ਸਲਾਦ ਅਤੇ ਸੂਪ (ਭਾਗ-II) Notes.

PSEB 8th Class Home Science Practical ਸਲਾਦ ਅਤੇ ਸੂਪ (ਭਾਗ-II)

ਪਨੀਰ ਬਣਾਉਣਾ

ਸਾਮਾਨ-
ਦਹੀਂ – 1 ਲਿਟਰ
ਦੁੱਧ – 100 ਗਰਾਮ
ਨਿੰਬੂ ਦਾ ਰਸ – 2 ਵੱਡੇ ਚਮਚ

ਵਿਧੀ – ਦੁੱਧ ਨੂੰ ਅੱਗ ਤੇ ਰੱਖ ਕੇ ਉਬਾਲੋ । ਜਦੋਂ ਦੁੱਧ ਉਬਲ ਜਾਏ ਤਾਂ ਉਸ ਵਿਚ ਫੈਂਟਿਆ ਹੋਇਆ ਦਹੀਂ ਜਾਂ ਨਿੰਬੂ ਦਾ ਰਸ ਥੋੜ੍ਹਾ-ਥੋੜ੍ਹਾ ਕਰਕੇ ਪਾਓ । ਜਦੋਂ ਦੁੱਧ ਅਤੇ ਪਾਣੀ ਵੱਖ-ਵੱਖ ਹੋ ਜਾਣ ਤਾਂ ਪਤੀਲਾ ਅੱਗ ਤੋਂ ਉਤਾਰ ਦਿਓ । 10-15 ਮਿੰਟ ਤੋਂ ਬਾਅਦ ਇਸ ਨੂੰ ਇਕ ਸਾਫ਼ ਮਲਮਲ ਦੇ ਕੱਪੜੇ ਵਿਚ ਪਾ ਕੇ ਕੁੱਝ ਦੇਰ ਲਈ ਲਟਕਾ ਕੇ ਪਾਣੀ ਨੂੰ ਨਿਕਲਣ ਦਿਓ । ਜੇਕਰ ਪਨੀਰ ਦੀਆਂ ਟੁਕੜੀਆਂ ਕੱਟਣੀਆਂ ਹੋਣ ਤਾਂ ਪਨੀਰ ਵਾਲੇ ਕੱਪੜੇ ਨੂੰ ਚਕਲੇ ਤੇ ਰੱਖੋ ਅਤੇ ਉੱਪਰ ਕੋਈ ਭਾਰੀ ਚੀਜ਼ ਰੱਖੋ ਤਾਂ ਕਿ ਪਨੀਰ ਦਾ ਸਾਰਾ ਪਾਣੀ ਨਿਕਲ ਜਾਏ ਅਤੇ ਇਹ ਪ੍ਰੈੱਸ ਹੋ ਜਾਏ । ਇਸ ਤੋਂ ਬਾਅਦ ਪਨੀਰ ਦੇ ਟੁਕੜੇ ਕੱਟ ਲਓ ।

ਸ਼ਾਕਾਹਾਰੀ ਲੋਕਾਂ ਦੇ ਭੋਜਨ ਵਿਚ ਪਨੀਰ ਦੀ ਬਹੁਤ ਮਹੱਤਤਾ ਹੈ ਕਿਉਂਕਿ ਇਸ ਵਿਚ ਚੰਗੀ ਕਿਸਮ ਦੀ ਪ੍ਰੋਟੀਨ ਅਤੇ ਕੈਲਸ਼ੀਅਮ ਕਾਫ਼ੀ ਮਾਤਰਾ ਵਿਚ ਹੁੰਦੀ ਹੈ । ਪਨੀਰ ਨੂੰ ਖਾਣੇ ਨਾਲ ਤਾਂ ਵਰਤਿਆ ਹੀ ਜਾਂਦਾ ਹੈ ਪਰ ਇਸ ਤੋਂ ਇਲਾਵਾ ਭਾਰਤੀ ਲੋਕ ਪਨੀਰ ਤੋਂ ਕਈ ਤਰ੍ਹਾਂ ਦੀਆਂ ਮਿਠਾਈਆਂ ਵੀ ਬਣਾਉਂਦੇ ਹਨ ਜਿਵੇਂ ਕਿ ਰਸਗੁੱਲੇ ।

ਖੱਟਾ ਮਿੱਠਾ ਪਨੀਰ

ਸਾਮਾਨ-
ਪਨੀਰ – 200 ਗਰਾਮ
ਟਮਾਟਰ – 400 ਗਰਾਮ
ਟਮਾਟਰਾਂ ਦੀ ਸਾਸ – 1/2 ਕੱਪ
ਗਾਜਰ – 1
ਸ਼ਿਮਲਾ ਮਿਰਚ – 1
ਫਰਾਂਸ ਬੀਨ – 50 ਗਰਾਮ
ਨਮਕ ਅਤੇ ਕਾਲੀ ਮਿਰਚ – ਸਵਾਦ ਅਨੁਸਾਰ
ਪਿਆਜ – 1
ਖੰਡ – 1 ਚਮਚ
ਘਿਓ – ਵੱਡਾ 1 ਚਮਚ

ਵਿਧੀ – ਟਮਾਟਰਾਂ ਨੂੰ ਧੋ ਕੇ ਬਰੀਕ ਕੱਟ ਲਓ ਅਤੇ ਥੋੜ੍ਹੇ ਜਿਹੇ ਪਾਣੀ ਵਿਚ ਚੰਗੀ ਤਰ੍ਹਾਂ ਪਕਾਓ । ਛਾਣਨੀ ਵਿਚੋਂ ਛਾਣੋ ਅਤੇ ਫੋਕ ਸੁੱਟ ਦਿਓ | ਗਾਜਰ, ਸ਼ਿਮਲਾ ਮਿਰਚ, ਫਰਾਂਸ ਬੀਨ ਅਤੇ ਪਿਆਜ਼ ਨੂੰ ਲੰਬੇ ਅਤੇ ਪਤਲੇ ਕੱਟੋ । ਘਿਓ ਵਿਚ ਸਬਜ਼ੀਆਂ ਨੂੰ ਥੋੜ੍ਹਾ ਜਿਹਾ ਤਲੋ ਅਤੇ ਟਮਾਟਰਾਂ ਦਾ ਗੁੱਦਾ ਪਾ ਕੇ ਕੁੱਝ ਦੇਰ ਪਕਾਓ ਤਾਂ ਕਿ ਸਬਜ਼ੀਆਂ ਗਲ ਜਾਣ | ਪਨੀਰ ਦੇ ਟੁਕੜੇ ਕੱਟ ਕੇ ਪਾਉ । ਨਮਕ, ਮਿਰਚ ਅਤੇ ਖੰਡ ਪਾ ਦਿਓ ਅਤੇ ਉਤਾਰਨ ਤੋਂ ਪਹਿਲਾਂ ਟਮਾਟਰਾਂ ਦੀ ਸਾਸ ਪਾ ਦਿਓ ।

ਪਨੀਰ ਦੇ ਪਕੌੜੇ

ਸਾਮਾਨ-
ਪਨੀਰ – 100 ਗਰਾਮ
ਵੇਸਣ – 50 ਗਰਾਮ
ਸੁੱਕਾ ਧਨੀਆਂ – 1/2 ਚਮਚ
ਦਹੀਂ – 1 ਚਮਚ
ਨਮਕ ਅਤੇ ਲਾਲ ਚਮਚ – 1
ਘਿਓ – ਤਲਣ ਲਈ

ਵਿਧੀ – ਪਨੀਰ ਦੇ ਟੁਕੜੇ ਕੱਟ ਲਓ । ਵੇਸਣ ਵਿਚ ਨਮਕ, ਮਿਰਚ, ਸੁੱਕਾ ਧਨੀਆ ਤੇ ਮਿੱਠਾ ਸੋਡਾ ਮਿਲਾ ਕੇ ਪਾਣੀ ਨਾਲ ਘੋਲੋ । ਕੜਾਹੀ ਵਿਚ ਘਿਓ ਪਾ ਕੇ ਗਰਮ ਕਰਨਾ ਰੱਖੋ । ਜਦੋਂ ਘਿਓ ਵਿਚੋਂ ਧੂੰਆਂ ਨਿਕਲਣ ਲੱਗੇ ਤਾਂ ਸੇਕ ਥੋੜ੍ਹਾ ਜਿਹਾ ਹਲਕਾ ਕਰਕੇ, ਪਨੀਰ ਦੇ ਟੁਕੜਿਆਂ ਨੂੰ ਵੇਸਣ ਲਗਾ ਕੇ ਤਲੋ । ਪਕੌੜਿਆਂ ਨੂੰ ਤਲ ਕੇ ਕਿਸੇ ਸਾਫ਼ ਕਾਗ਼ਜ਼ ਤੇ ਰੱਖੋ ਤਾਂ ਕਿ ਫ਼ਾਲਤੂ ਘਿਓ ਨੁਚੜ ਜਾਏ ਟਮਾਟਰਾਂ ਦੀ ਸਾਸ ਨਾਲ ਪਰੋਸੋ ।

ਵੇਸਣ ਦਾ ਪੂੜਾ

ਸਾਮਾਨ-
ਵੇਸਣ – 100 ਗ੍ਰਾਮ
ਪਿਆਜ਼ – 2 ਛੋਟੇ
ਹਰੀ ਮਿਰਚ – 1-2
ਘਿਓ – ਤਲਣ ਲਈ
ਨਮਕ, ਮਿਰਚ – ਸੁਆਦ ਅਨੁਸਾਰ

ਵਿਧੀ – ਪਿਆਜ਼ ਅਤੇ ਹਰੀ ਮਿਰਚ ਨੂੰ ਬਰੀਕ-ਬਰੀਕ ਕੱਟ ਲਓ । ਵੇਸਣ ਨੂੰ ਛਾਣ ਲਓ ਅਤੇ ਕਿਸੇ ਡੂੰਘੀ ਪਲੇਟ ਵਿਚ ਵੇਸਣ ਪਾ ਕੇ ਪਿਆਜ਼, ਹਰੀ ਮਿਰਚ ਅਤੇ ਨਮਕ ਮਿਲਾ ਲਓ ਅਤੇ ਥੋੜ੍ਹਾ ਜਿਹਾ ਪਾਣੀ ਮਿਲਾ ਕੇ ਚੰਗੀ ਤਰ੍ਹਾਂ ਫੈਂਟੋ 1 ਤਵੇ ਨੂੰ ਗਰਮ ਕਰਕੇ ਉੱਪਰ ਓ ਪਾਓ ਅਤੇ ਆਮਲੇਟ ਦੀ ਤਰ੍ਹਾਂ ਪੂੜੇ ਨੂੰ ਦੋਨੋਂ ਪਾਸਿਓਂ ਪੱਕ ਜਾਣ ਦਿਓ । ਆਮਲੇਟ ਨਾਲੋਂ ਪੂੜੇ ਨੂੰ ਵਧੇਰੇ ਦੇਰ ਲੱਗਦੀ ਹੈ । ਜਦੋਂ ਦੋਨੋਂ ਪਾਸੇ ਚੰਗੀ ਤਰ੍ਹਾਂ ਪੱਕ ਜਾਣ ਤਾਂ ਪਰੋਸੋ ।

ਪਨੀਰ ਵਾਲੇ ਟੋਸਟ

ਸਾਮਾਨ-
ਡਬਲਰੋਟੀ ਦੇ ਟੁਕੜੇ – 4
ਕੱਦੂਕਸ ਕੀਤਾ ਪਨੀਰ – 3/4 ਪਿਆਲਾ
ਦਹੀਂ – 1 ਚਮਚ
ਵੇਸਣ – 2 ਵੱਡੇ ਚਮਚ
ਪੀਸੀ ਹੋਈ ਰਾਈ – 1/4 ਚਮਚ
ਕਾਲੀ ਮਿਰਚ – 1/2 ਚਮਚ
ਮੈਦਾ – 2 ਚਮਚ
ਘਿਓ – ਤਲਣ ਲਈ
ਨਮਕ – ਸੁਆਦ ਅਨੁਸਾਰ

ਵਿਧੀ – ਪਨੀਰ, ਰਾਈ, ਕਾਲੀ ਮਿਰਚ, ਦਹੀਂ, ਮੈਦਾ, ਵੇਸਣ ਅਤੇ ਨਮਕ ਨੂੰ ਥੋੜ੍ਹਾ ਪਾਣੀ ਪਾ ਕੇ ਮਿਲਾ ਲਓ ਤਾਂ ਕਿ ਗਾੜਾ ਜਿਹਾ ਘੋਲ ਬਣ ਜਾਏ । ਜੇਕਰ ਜ਼ਰੂਰਤ ਹੋਵੇ ਤਾਂ ਥੋੜਾ ਜਿਹਾ ਪਾਣੀ ਜਾਂ ਦੁੱਧ ਪਾ ਲਓ । ਚੰਗੀ ਤਰ੍ਹਾਂ ਫੈਂਟੋ ਡਬਲਰੋਟੀ ਦੇ ਟੁਕੜਿਆਂ ਨੂੰ ਇਸ ਘੋਲ ਵਿਚ ਦੋਨਾਂ ਪਾਸਿਆਂ ਤੋਂ ਲਬੇੜੋ ਫਰਾਇੰਗ ਪੈਨ ਵਿਚ ਘਿਓ ਪਾ ਕੇ ਗਰਮ ਕਰੋ ਅਤੇ ਟੋਸਟਾਂ ਨੂੰ ਦੋਨਾਂ ਪਾਸੇ ਤਲ ਕੇ ਪਰੋਸੋ ।
ਨੋਟ – ਜੋ ਲੋਕ ਅੰਡਾ ਖਾਂਦੇ ਹਨ ਉਨ੍ਹਾਂ ਲਈ ਵੇਸਣ ਦੀ ਥਾਂ ਅੰਡਾ ਵੀ ਇਸਤੇਮਾਲ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ।

ਦਹੀਂ ਜਮਾਉਣਾ

ਸਾਮਾਨ-
ਦੁੱਧ – 1/2 ਲਿਟਰ
ਦਹੀਂ – 1/2 ਤੋਂ 1 ਚਮਚ

ਵਿਧੀ – ਦੁੱਧ ਨੂੰ ਉਬਾਲ ਕੇ ਠੰਢਾ ਕਰੋ । ਗਰਮੀਆਂ ਵਿਚ ਦੁੱਧ ਜਮਾਉਣ ਸਮੇਂ ਬਿਲਕੁਲ ਕੋਸਾ ਹੀ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ । ਇਸ ਨੂੰ ਕਿਸੇ ਮਿੱਟੀ ਜਾਂ ਸਟੀਲ ਦੇ ਬਰਤਨ ਵਿਚ ਪਾ ਕੇ 1/2 ਚਮਚ ਦਹੀਂ ਮਿਲਾ ਕੇ ਢੱਕ ਕੇ ਰੱਖ ਦਿਓ । 3-4 ਘੰਟੇ ਬਾਅਦ ਦਹੀਂ ਜੰਮ ਜਾਏਗਾ ।

ਸਰਦੀਆਂ ਵਿਚ ਦੁੱਧ ਥੋੜਾ ਜ਼ਿਆਦਾ ਗਰਮ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ । ਇਸ ਵਿਚ 1 ਚਮਚ ਦਹੀਂ ਘੋਲ ਕੇ, ਬਰਤਨ ਨੂੰ ਢੱਕ ਕੇ ਰੱਖ ਲਓ । ਜ਼ਿਆਦਾ ਸਰਦੀ ਦੇ ਮੌਸਮ ਵਿਚ ਦਹੀਂ ਵਾਲੇ ਬਰਤਨ ਨੂੰ ਕਿਸੇ ਗਰਮ ਥਾਂ ਤੇ ਰੱਖੋ ਜਾਂ ਫਿਰ ਇਸ ਨੂੰ ਕਿਸੇ ਕੰਬਲ ਜਾਂ ਪੁਰਾਣੀ ਸ਼ਾਲ ਵਿਚ ਲਪੇਟ ਕੇ ਰੱਖੋ ।ਇਸ ਨੂੰ ਆਟੇ ਵਾਲੇ ਟੀਨ ਵਿਚ ਵੀ ਰੱਖਿਆ ਜਾ ਸਕਦਾ ਹੈ । ਸਰਦੀਆਂ ਵਿਚ ਦਹੀਂ ਜੰਮਣ ਵਿਚ 5-6 ਘੰਟੇ ਲੱਗਦੇ ਹਨ ।

ਆਲੂ ਦਾ ਰਾਇਤਾ

ਸਾਮਾਨ-
ਆਲੂ – 150 ਗਰਾਮ
ਨਮਕ – ਲੋੜ ਅਨੁਸਾਰ

ਜੀਰਾ (ਭੁੰਨਿਆ ਹੋਇਆ) – 11/2 ਚਮਚ
ਦਹੀਂ – 750 ਗਰਾਮ
ਮਿਰਚ – 11/2 ਚਮਚ
ਪੁਦੀਨਾ – 11/2 ਚਮਚ

ਵਿਧੀ – ਆਲੂ ਉਬਾਲ ਕੇ ਛਿੱਲ ਲਉ ਅਤੇ ਬਰੀਕ ਕੱਟ ਲਉ ਦਹੀਂ ਨੂੰ ਫੈਂਟ ਕੇ ਉਸ ਵਿਚ ਕੱਟੇ ਹੋਏ ਆਲੂ ਪਾਓ, ਉੱਪਰੋਂ ਸਭ ਮਸਾਲੇ ਮਿਲਾ ਦਿਉ । ਫਿਰ ਇਸ ਨੂੰ ਠੰਢਾ ਕਰੋ ।
ਠੰਢਾ ਹੋਣ ਤੇ ਪਰੋਸੋ। ਕੁੱਲ ਮਾਤਰਾ- 4 ਵਿਅਕਤੀਆਂ ਲਈ ।

ਖੀਰੇ ਦਾ ਰਾਇਤਾ

ਸਾਮਾਨ-
ਦਹੀਂ – 250 ਗਰਾਮ
ਨਮਕ – ਲੋੜ ਅਨੁਸਾਰ
ਜੀਰਾ – 1/2 ਚਮਚ
ਖੀਰਾ – 150 ਗਰਾਮ
ਮਿਰਚ – 1/2 ਚਮਚ
ਪੁਦੀਨਾ – 1/2 ਚਮਚ

ਵਿਧੀ – ਖੀਰੇ ਨੂੰ ਛਿੱਲ ਕੇ ਕੱਦੂਕਸ ਕਰ ਲਉ ਹੁਣ ਦਹੀਂ ਨੂੰ ਫੈਂਟ ਲਉ ।ਇਸ ਵਿਚ ਮਸਾਲੇ ਪਾ ਕੇ ਮਿਲਾਓ | ਇਸ ਵਿਚ ਕੱਦੂਕਸ ਕੀਤਾ ਹੋਇਆ ਖੀਰਾ ਪਾ ਕੇ ਮਿਲਾ ਲਓ ਛਰਿਜ ਵਿਚ ਰੱਖ ਕੇ ਠੰਢਾ ਕਰੋ । ਠੰਢਾ ਹੋਣ ਤੇ ਖਾਣੇ ਦੇ ਨਾਲ ਪਰੋਸੋ ।
ਕੁੱਲ ਮਾਤਰਾ- 4 ਵਿਅਕਤੀਆਂ ਲਈ ।

ਪਿਆਜ਼ ਦਾ ਰਾਇਤਾ

ਸਾਮਾਨ-
ਪਿਆਜ਼ – 250 ਗਰਾਮ
ਨਮਕ – ਲੋੜ ਅਨੁਸਾਰ
ਭੁੰਨਿਆ ਹੋਇਆ ਜੀਰਾ – 1 ਚਮਚ
ਸੁਕਾਇਆ ਹੋਇਆ ਪੁਦੀਨਾ – 1 ਚਮਚ
ਦਹੀਂ – 500 ਗਰਾਮ
ਮਿਰਚ – 1/2 ਚਮਚ
ਕਾਲੀ ਮਿਰਚ – 1/2 ਚਮਚ

ਵਿਧੀ – ਪਿਆਜ਼ ਨੂੰ ਛਿੱਲ ਕੇ ਕੱਦੂ ਕਸ ਕਰ ਲਓ । ਦਹੀਂ ਨੂੰ ਮਥ ਕੇ ਉਸ ਵਿਚ ਕੱਦੂਕਸ ਕੀਤਾ ਹੋਇਆ ਪਿਆਜ਼ ਪਾ ਦਿਓ । ਹੁਣ ਇਸ ਵਿਚ ਨਮਕ, ਮਿਰਚ, ਜੀਰਾ, ਪੁਦੀਨਾ ਅਤੇ ਕਾਲੀ ਮਿਰਚ ਪਾ ਕੇ ਮਿਲਾ ਲਓ ।
ਠੰਢਾ ਕਰਕੇ ਖਾਣੇ ਦੇ ਨਾਲ ਪਰੋਸੋ।

ਪਾਲਕ ਗਾਜਰ ਦਾ ਰਾਇਤਾ

ਸਾਮਾਨ-
ਦਹੀਂ – 250 ਗਰਾਮ
ਗਾਜਰ – 50 ਗਰਾਮ
ਪਾਲਕ – 100 ਗਰਾਮ
ਨਮਕ-ਮਿਰਚ – ਸੁਆਦ ਅਨੁਸਾਰ

ਵਿਧੀ – ਪਾਲਕ ਨੂੰ ਧੋ ਕੇ, ਬਾਰੀਕ ਕੱਟ ਕੇ, ਹਲਕੀ ਅੱਗ ਤੇ ਪਕਾਓ ਤਾਂ ਜੋ ਇਹ ਗਲ ਜਾਵੇ । ਗਾਜਰ ਨੂੰ ਧੋ ਕੇ, ਛਿੱਲ ਕੇ ਕੱਦੂਕਸ ਕਰ ਲਓ । ਦਹੀਂ ਨੂੰ ਚੰਗੀ ਤਰ੍ਹਾਂ ਫੈਂਟ ਕੇ ਪਾਲਕ ਅਤੇ ਗਾਜਰ ਮਿਲਾ ਦਿਓ । ਨਮਕ ਅਤੇ ਮਿਰਚ ਪਾ ਕੇ ਪਰੋਸੋ।
ਕੁੱਲ ਮਾਤਰਾ- 2-3 ਵਿਅਕਤੀਆਂ ਲਈ ।

ਘੀਏ ਦਾ ਰਾਇਤਾ

ਸਾਮਾਨ-
ਦਹੀਂ – 500 ਗਰਾਮ
ਘੀਆ – 100 ਗਰਾਮ
ਨਮਕ, ਕਾਲੀ ਮਿਰਚ – ਸੁਆਦ ਅਨੁਸਾਰ

ਵਿਧੀ – ਘੀਏ ਨੂੰ ਕੱਦੂਕਸ ਕਰਕੇ ਉਬਾਲ ਲਓ । ਠੰਢਾ ਕਰਕੇ ਨਿਚੋੜ ਲਓ । ਦਹੀਂ ਨੂੰ ਚੰਗੀ ਤਰ੍ਹਾਂ ਫੈਂਟੋ ਅਤੇ ਘੀਆ, ਨਮਕ ਅਤੇ ਮਿਰਚ ਪਾ ਦਿਓ । ਉੱਪਰੋਂ ਲਾਲ ਮਿਰਚ ਅਤੇ ਪੀਸਿਆ ਹੋਇਆ ਜੀਰਾ ਛਿੜਕ ਦਿਓ । ਠੰਢਾ ਕਰਕੇ ਖਾਣੇ ਨਾਲ ਪਰੋਸੋ।

ਪੁਦੀਨੇ ਦਾ ਰਾਇਤਾ

ਸਾਮਾਨ-
ਦਹੀਂ – 1/2 ਕਿਲੋ
ਪਿਆਜ਼ – 1
ਪੁਦੀਨਾ – ਕੁੱਝ ਪੱਤੇ
ਨਮਕ, ਹਰੀ ਮਿਰਚ – ਸੁਆਦ ਅਨੁਸਾਰ

ਵਿਧੀ – ਦਹੀਂ ਨੂੰ ਮਧਾਣੀ ਨਾਲ ਚੰਗੀ ਤਰ੍ਹਾਂ ਫੈਂਟ ਕੇ ਨਮਕ ਮਿਲਾ ਲਓ। ਪਿਆਜ਼ ਨੂੰ ਛਿੱਲ ਕੇ ਬਰੀਕ ਕੱਟ ਲਓ । ਪੁਦੀਨੇ ਦੇ ਪੱਤੇ ਕੱਟ ਕੇ ਧੋ ਲਓ ਅਤੇ ਬਰੀਕ ਪੀਸ ਲਓ । ਹਰੀ ਮਿਰਚ ਕੱਟ ਲਓ । ਸਾਰੀਆਂ ਚੀਜ਼ਾਂ ਦਹੀਂ ਵਿਚ ਮਿਲਾ ਕੇ ਪਰੋਸੋ।

ਕੇਲੇ ਦਾ ਰਾਇਤਾ

ਸਾਮਾਨ-
ਦਹੀਂ – 1/2 ਕਿਲੋ
ਕੇਲੇ – 3-4
ਚੀਨੀ – 2 ਵੱਡੇ ਚਮਚ
ਕਿਸ਼ਮਿਸ਼ – ਥੋੜ੍ਹੀ ਜਿਹੀ

ਵਿਧੀ – ਕਿਸ਼ਮਿਸ਼ ਨੂੰ ਕੋਸੇ ਪਾਣੀ ਵਿਚ ਧੋ ਕੇ ਸਾਫ਼ ਕਰ ਲਓ । ਦਹੀਂ ਵਿਚ ਚੀਨੀ ਮਿਲਾ ਕੇ ਮਧਾਣੀ ਨਾਲ ਚੰਗੀ ਤਰ੍ਹਾਂ ਫੈਂਟੋ ਤਾਂ ਕਿ ਚੀਨੀ ਚੰਗੀ ਤਰ੍ਹਾਂ ਘੁਲ ਜਾਵੇ । ਕੇਲੇ ਛਿੱਲ ਕੇ ਕੱਟ ਲਓ ਅਤੇ ਕੇਲੇ ਤੇ ਕਿਸ਼ਮਿਸ਼ ਦਹੀਂ ਵਿਚ ਮਿਲਾ ਦਿਓ ।

ਕਸਟਰਡ

ਸਾਮਾਨ-
ਦੁੱਧ – 1/2 ਲਿਟਰ
ਚੀਨੀ – 1\(\frac {1}{2}\) ਵੱਡਾ ਚਮਚ
ਕਸਟਰਡ ਪਾਊਡਰ – 2 ਚਾਹ ਦੇ ਚਮਚ

ਵਿਧੀ – ਅੱਧਾ ਕੱਪ ਦੁੱਧ ਬਚਾ ਕੇ ਬਾਕੀ ਦੇ ਦੁੱਧ ਨੂੰ ਉਬਾਲਣਾ ਰੱਖੋ | ਗਰਮ ਦੁੱਧ ਵਿਚ ਚੀਨੀ ਮਿਲਾ ਲਓ ਅਤੇ ਕੱਪ ਵਾਲੇ ਦੁੱਧ ਵਿਚ ਕਸਟਰਡ ਪਾਊਡਰ ਪਾ ਕੇ ਚੰਗੀ ਤਰ੍ਹਾਂ ਘੋਲੋ । ਜਦੋਂ ਦੁੱਧ ਉਬਲਣ ਲੱਗੇ ਤਾਂ ਇਸ ਵਿਚ ਕਸਟਰਡ ਵਾਲਾ ਦੁੱਧ ਹੌਲੀ-ਹੌਲੀ ਕਰਕੇ ਪਾਓ ਅਤੇ ਦੂਜੇ ਹੱਥ ਨਾਲ ਚਮਚ ਨਾਲ ਦੁੱਧ ਨੂੰ ਚੰਗੀ ਤਰ੍ਹਾਂ ਹਿਲਾਓ ਤਾਂ ਕਿ ਗਿਲਟੀਆਂ ਨਾ ਬਣ ਜਾਣ । ਉਬਾਲਾ ਆਉਣ ਤੇ ਉਤਾਰ ਲਓ । ਇਸ ਨੂੰ ਗਰਮ ਜਾਂ ਠੰਢਾ ਕਰਕੇ ਪਰੋਸਿਆ ਜਾ ਸਕਦਾ ਹੈ ।

ਕਸਟਰਡ ਵਿਚ ਰੁੱਤ ਅਨੁਸਾਰ ਫਲ ਜਿਵੇਂ-ਅੰਬ, ਕੇਲਾ, ਸੇਬ, ਅੰਗੂਰ ਆਦਿ ਪਾਏ ਜਾ ਸਕਦੇ ਹਨ । ਜੇਕਰ ਫਲ ਪਾਉਣੇ ਹੋਣ ਤਾਂ ਕਸਟਰਡ ਨੂੰ ਪਹਿਲਾਂ ਚੰਗੀ ਤਰ੍ਹਾਂ ਠੰਢਾ ਹੋਣ ਦਿਓ । ਫਰਿਜ਼ ਵਿਚ ਜਾਂ ਬਰਫ਼ ਵਿਚ ਰੱਖ ਕੇ ਠੰਢਾ ਕਰਕੇ ਪਰੋਸੋ । ਠੰਢੇ ਕਸਟਰਡ ਨੂੰ ਜੈਲੀ ਨਾਲ ਵੀ ਪਰੋਸਿਆ ਜਾ ਸਕਦਾ ਹੈ ।

ਬੇਕ ਕੀਤਾ ਹੋਇਆ ਕਸਟਰਡ

ਸਾਮਾਨ

ਆਂਡਾ – 1 ਛੋਟਾ
ਦੁੱਧ – 1 ਕੱਪ
ਚੀਨੀ – 2 ਛੋਟੇ ਚਮਚ

ਵਿਧੀ – ਆਂਡਾ ਤੇ ਚੀਨੀ ਖੂਬ ਫੈਂਟ ਲਓ । ਫਿਰ ਇਸ ਨੂੰ ਦੁੱਧ ਵਿਚ ਮਿਲਾਓ । ਹੁਣ ਇਸ ਮਿਸ਼ਰਨ ਨੂੰ ਦਰਮਿਆਨੀ ਭਖਦੀ ਭੱਠੀ (oven) ਵਿਚ ਪਕਾਓ । ਦਰਮਿਆਨੀ ਤੋਂ ਭਾਵ ਹੈ ਕਿ ਭੱਠੀ ਨਾ ਬਹੁਤ ਤੇਜ਼ ਗਰਮ ਤੇ ਨਾ ਹੀ ਠੰਢੀ ਹੋਵੇ । ਕਸਟਰਡ ਠੰਢਾ ਹੋ ਜਾਵੇ ਤਾਂ ਪਰੋਸ ਦਿਓ ।

Punjab State Board PSEB 8th Class Home Science Book Solutions Practical ਬਟਨ ਲਗਾਉਣਾ ਅਤੇ ਕਾਜ ਬਣਾਉਣਾ Notes.

PSEB 8th Class Home Science Practical ਬਟਨ ਲਗਾਉਣਾ ਅਤੇ ਕਾਜ ਬਣਾਉਣਾ

ਬਹੁਤ ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ

ਪ੍ਰਸ਼ਨ 1.
ਬਟਨ ਹਮੇਸ਼ਾ ਕਿਸ ਕੱਪੜੇ ‘ਤੇ ਲਗਣਾ ਚਾਹੀਦਾ ਹੈ ?
ਉੱਤਰ-
ਬਟਨ ਹਮੇਸ਼ਾ ਦੋਹਰੇ ਕੱਪੜੇ ‘ਤੇ ਲਗਾਉਣਾ ਚਾਹੀਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਕਮੀਜ਼ ਵਾਲੇ ਬਟਨਾਂ ਵਿਚ ਕਿੰਨੇ ਛੇਕ ਹੁੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਕਮੀਜ਼ ਵਾਲੇ ਬਟਨਾਂ ਵਿਚ ਦੋ ਜਾਂ ਚਾਰ ਛੇਕ ਹੁੰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 3.
ਕਾਜ ਕਿਸ ਪ੍ਰਕਾਰ ਦੇ ਕੱਪੜਿਆਂ ‘ਤੇ ਬਣਾਉਣਾ ਚਾਹੀਦਾ ਹੈ ?
ਉੱਤਰ-
ਕਾਜ ਹਮੇਸ਼ਾ ਦੋਹਰੇ ਕੱਪੜੇ ‘ਤੇ ਬਣਾਉਣਾ ਚਾਹੀਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 4.
ਧਾਗਾ ਕਿੱਥੇ ਲਪੇਟਣਾ ਚਾਹੀਦਾ ਹੈ ?
ਉੱਤਰ-
ਧਾਗਾ ਝੰਡੀ ਦੇ ਕੋਲ-ਕੋਲ ਲਪੇਟਣਾ ਚਾਹੀਦਾ ਹੈ ।

ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ

ਪ੍ਰਸ਼ਨ 1.
ਬਟਨ ਲਾਉਂਦੇ ਸਮੇਂ ਕਿਹੜੀਆਂ-ਕਿਹੜੀਆਂ ਗੱਲਾਂ ਦਾ ਧਿਆਨ ਰੱਖਣਾ ਚਾਹੀਦਾ ਹੈ ?
ਉੱਤਰ-
ਬਟਨ ਲਗਾਉਣ ਸਮੇਂ ਹੇਠ ਲਿਖੀਆਂ ਗੱਲਾਂ ਦਾ ਧਿਆਨ ਰੱਖਣਾ ਚਾਹੀਦਾ ਹੈ

• ਸਾਰੇ ਬਟਨਾਂ ਦੀ ਡੰਡੀ ਬਣਾਉਣੀ ਜ਼ਰੂਰੀ ਹੈ । ਡੰਡੀ ਨਾਲ ਬਟਨ ਕੱਪੜੇ ਤੋਂ ਉੱਚਾ ਰਹਿੰਦਾ ਹੈ । ਇਸ ਲਈ ਬਟਨ ਬੰਦ ਕਰਨਾ ਅਸਾਨ ਰਹਿੰਦਾ ਹੈ ਅਤੇ ਬਟਨ ਦੇ ਹੇਠਾਂ ਦਾ ਕੱਪੜਾ ਨਹੀਂ ਘਸਦਾ ।
• ਡੰਡੀ ਦੇ ਆਸ ਪਾਸ ਵੀ ਧਾਗਾ ਲਪੇਟਣਾ ਚਾਹੀਦਾ ਹੈ ਤਾਂ ਕਿ ਕਾਜ ਨਾਲ ਰਗੜ ਖਾ ਕੇ ਜਲਦੀ ਟੁੱਟ ਨਾ ਜਾਵੇ ।
• ਜਿੱਥੋਂ ਤਕ ਹੋ ਸਕੇ ਟਾਂਕੇ ਬਟਨ ਦੇ ਛੇਕ ਦੀ ਸੇਧ ਵਿਚ ਹੀ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ ।
• ਬਟਨ ਸਫ਼ਾਈ ਅਤੇ ਮਜ਼ਬੂਤੀ ਨਾਲ ਲਗਾਏ ਜਾਣੇ ਚਾਹੀਦੇ ਹਨ ।
• ਬਟਨ ਹਮੇਸ਼ਾ ਦੋਹਰੇ ਕੱਪੜੇ ‘ਤੇ ਲਗਾਉਣੇ ਚਾਹੀਦੇ ਹਨ |ਜੇਕਰ ਇਕਹਿਰੇ ਕੱਪੜੇ ‘ਤੇ ਲਗਾਇਆ ਜਾਏ ਤਾਂ ਬਟਨ ਦੇ ਹੇਠਲੇ ਪਾਸੇ ਛੋਟਾ ਜਿਹਾ ਚੌਰਸ ਕੱਪੜਾ ਲਗਾ ਲਉ !

ਪ੍ਰਸ਼ਨ 2.
ਕਮੀਜ਼ ਵਿਚ ਛੇਕਾਂ ਵਾਲੇ ਬਟਨ ਕਿਵੇਂ ਲਾਉਂਦੇ ਹਨ ?
ਉੱਤਰ-
ਬਟਨ ਲਗਾਉਣ ਲਈ ਬਟਨ ਨੂੰ ਆਪਣੀ ਜਗ੍ਹਾ ‘ਤੇ ਰੱਖੋ ।ਇਕ ਮੋਰੀ ਵਿਚੋਂ ਸੂਈ ਕੱਪੜੇ ਦੇ ਹੇਠਾਂ ਦੀ ਕੱਢੋ ਅਤੇ ਦੁਸਰੀ ਵਿਚ ਪਾ ਕੇ ਹੇਠਾਂ ਲੈ ਜਾਉ । ਤਿੰਨ ਚਾਰ ਜਾਂ ਪੰਜ ਟਾਂਕੇ ਬਣਾਉਣ ਮਗਰੋਂ ਡੰਡੀ ਬਣਾਓ ।

ਪ੍ਰਸ਼ਨ 3.
ਕਮੀਜ਼ ਵਿਚ ਚਾਰ ਛੇਕਾਂ ਵਾਲੇ ਬਟਨ ਕਿਵੇਂ ਲਾਉਂਦੇ ਹਨ ?
ਉੱਤਰ-
ਕਮੀਜ਼ ਵਿਚ ਚਾਰ ਮੋਰੀਆਂ ਦੇ ਬਟਨਾਂ ਨੂੰ ਕਾਸ (x) ਬਣਾ ਕੇ ਜਾਂ ਸਿੱਧੀਆਂ ਲਾਈਨਾਂ ਵਿਚ ਜਾਂ ਚੌਰਸ ਸ਼ਕਲ ਦੇ ਟਾਂਕੇ ਲਗਾ ਕੇ ਬਣਾਇਆ ਜਾ ਸਕਦਾ ਹੈ ।ਧਾਗੇ ਨੂੰ ਮੋਰੀਆਂ ਵਿਚੋਂ ਇੰਨੀ ਵਾਰੀ ਕੱਢੋ ਕਿ ਮੋਰੀਆਂ ਭਰ ਜਾਣ ਤੋਂ ਮਗਰੋਂ ਡੰਡੀ ਬਣਾ ਕੇ ਧਾਗਾ ਹੇਠਾਂ ਨੂੰ ਲੈ ਜਾਉ ਅਤੇ ਇਕ ਬਖੀਏ ਦਾ ਟਾਂਕਾ ਲੈ ਕੇ ਕੱਪੜੇ ਦੀਆਂ ਦੋ ਤਹਿਆਂ ਵਿਚੋਂ ਸੁਈ ਲੰਘਾ ਕੇ ਧਾਗਾ ਪੱਕਾ ਕਰਕੇ ਤੋੜ ਦਿਓ ।

ਵੱਡੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ

ਪ੍ਰਸ਼ਨ 1.
ਕਾਜ ਬਣਾਉਣ ਦੀ ਵਿਧੀ ਦਾ ਚਿਤਰ ਸਹਿਤ ਵਰਣਨ ਕਰੋ ।
ਉੱਤਰ-
1. ਕਾਜ ਹਮੇਸ਼ਾ ਦੋਹਰੇ ਕੱਪੜੇ ‘ਤੇ ਬਣਾਉਣਾ ਚਾਹੀਦਾ ਹੈ । ਜਿਸ ਥਾਂ ‘ਤੇ ਕਾਜ ਬਣਾਉਣਾ ਹੋਵੇ ਉੱਥੇ ਬਟਨ ਦੇ ਆਕਾਰ ਦੇ ਅਨੁਸਾਰ ਪੈਨਸਿਲ ਨਾਲ ਨਿਸ਼ਾਨ ਲਗਾ ਲਓ ਅਤੇ ਫਿਰ ਬਲੇਡ ਨਾਲ ਜਾਂ ਛੋਟੀ ਕੈਂਚੀ ਨਾਲ ਉੱਤੋਂ ਚੀਰੋ | ਚੀਰ ਓਨਾ ਹੀ ਦਿਓ ਜਿਸ ਵਿਚ ਬਟਨ ਜ਼ਰਾ ਮੁਸ਼ਕਿਲ ਨਾਲ ਨਿਕਲ ਸਕੇ । ਵਧੇਰੇ ਖੁੱਲ੍ਹੇ ਕਾਜ ਵਿਚੋਂ ਆਪਣੇ ਆਪ ਬਟਨ ਨਿਕਲ ਜਾਂਦੇ ਹਨ ।
2. ਪਤਲੀ ਲੰਬੀ ਸੂਈ ਵਿਚ ਧਾਗਾ ਪਾਓ । ਧਾਗੇ ਨੂੰ ਗੰਢ ਨਾ ਲਗਾਓ।

3. ਸੂਈ ਨੂੰ ਕਾਜ ਦੇ ਖੱਬੇ ਕਿਨਾਰੇ ਤੋਂ ਲਿਜਾ ਕੇ ਕੱਪੜੇ ਦੀ ਉੱਪਰਲੀ ਤਹਿ ਦੇ ਵਿਚੋਂ ਦੋ ਤਿੰਨ ਤੰਦਾਂ ਅੱਗੇ ਨੂੰ ਲੈ ਕੇ ਸੂਈ ਲੰਘਾਉ ਧਾਗੇ ਦਾ \(\frac{1}{4}\) ” ਕਿਨਾਰਾ ਛੱਡ ਕੇ ਧਾਗਾ ਖਿੱਚ ਲਓ, ਇਸ \(\frac{1}{4}\)” ਧਾਗੇ ਨੂੰ ਪਹਿਲੇ ਕੁੱਝ ਟਾਂਕਿਆਂ ਵਿਚ ਹੀ ਦਬਾ ਦਿਓ ।

4. ਚੀਰ ਦੇ ਇਸ ਕਿਨਾਰੇ ਦੇ ਕਾਜ ਟਾਂਕਾ ਬਣਾਓ ।
5. ਕਾਜ ਦਾ ਗੋਲ ਕਿਨਾਰਾ ਬਣਾਉਣ ਲਈ ਕਿਨਾਰੇ ਦੇ ਨਾਲ-ਨਾਲ 9 ਜਾਂ 7 ਸਿੱਧੇ ਟਾਂਕੇ

(Straight Stiches) ਲਾਓ । ਵਿਚਕਾਰਲਾ ਟਾਂਕਾ ਚੀਰ ਦੇ ਬਿਲਕੁਲ ਦਰਮਿਆਨ ਵਿਚ ਆਉਣਾ ਚਾਹੀਦਾ ਹੈ । ਟਾਂਕਿਆਂ ਦੀ ਲੰਬਾਈ ਬਰਾਬਰ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ਅਤੇ ਕਿਨਾਰਾ ਗੋਲ ਬਣਾਉਣਾ ਚਾਹੀਦਾ ਹੈ।
6. ਚੀਰ ਦੇ ਦੂਸਰੇ ਕਿਨਾਰੇ ਦੇ ਕਾਜ ਕਾਂਟੇ ਬਣਾਉ ।
7. ਕਿਨਾਰੇ ‘ਤੇ ਪਹੁੰਚ ਕੇ ਸੂਈ ਨੂੰ ਪਹਿਲੇ ਟਾਂਕੇ ਦੀ ਗੰਢ ਵਿਚ ਪਾਉ ਅਤੇ ਆਖਰੀ ਟਾਂਕੇ ਦੇ ਸਿਰੇ ਤੋਂ ਕੱਢ ਲਓ । ਪਹਿਲੇ ਅਤੇ ਆਖਰੀ ਟਾਂਕੇ ਦੇ ਇਕ ਸਿਰੇ ਤੋਂ ਦੂਸਰੇ ਸਿਰੇ ਤਕ 9 ਜਾਂ 7 ਟਾਂਕੇ ਕਾਜ ਟਾਂਕੇ ਦੇ ਸਿੱਧੀ ਰੇਖਾ ਵਿਚ ਬਣਾਉ । ਇਹਨਾਂ ਟਾਂਕਿਆਂ ਦੀ ਗਿਣਤੀ ਗਲਾਈ ਵਾਲੇ ਟਾਂਕਿਆਂ ਦੇ ਬਰਾਬਰ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ।

8. ਸੁਈ ਨੂੰ ਪੁੱਠੇ ਪਾਸੇ ਲੈ ਜਾਓ ਅਤੇ ਪਿਛਲੇ ਪਾਸੇ ਦੇ ਟਾਂਕਿਆਂ ਵਿਚੋਂ ਧਾਗਾ ਲੰਘਾਉ ਅਤੇ ਤੋੜ ਦਿਉ । ਪਿਛਲੇ ਪਾਸੇ ਦੇ ਟਾਂਕੇ ਵੀ ਸਾਹਮਣੇ ਪਾਸੇ ਦੀ ਤਰ੍ਹਾਂ ਇਕਸਾਰ ਅਤੇ ਇਕ ਲਾਈਨ ਵਿਚ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ ।

ਬਟਨ ਲਗਾਉਣਾ ਅਤੇ ਕਾਜ ਬਣਾਉਣਾ PSEB 8th Class Home Science Notes

ਸੰਖੇਪ ਜਾਣਕਾਰੀ

• ਬਟਨ ਹਮੇਸ਼ਾ ਦੋਹਰੇ ਕੱਪੜਿਆਂ ‘ਤੇ ਲਾਉਣਾ ਚਾਹੀਦਾ ਹੈ ।
• ਕਮੀਜ਼ ਵਾਲੇ ਬਟਨਾਂ ਵਿਚ ਦੋ ਜਾਂ ਚਾਰ ਛੇਕ ਹੁੰਦੇ ਹਨ ।
• ਕਾਜ ਹਮੇਸ਼ਾ ਦੋਹਰੇ ਕੱਪੜੇ ਤੇ ਬਣਾਉਣਾ ਚਾਹੀਦਾ ਹੈ ।
• ਕੱਪੜੇ ਵਿਚ ਕਟਾਅ ਉਨਾ ਹੀ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ਜਿਸ ਵਿਚੋਂ ਬਟਨ ਜ਼ਰਾ ਮੁਸ਼ਕਿਲ ਨਾਲ ਨਿਕਲ ਸਕੇ ।
• ਕਾਜ ਦਾ ਗੋਲ ਕਿਨਾਰਾ ਬਣਾਉਣ ਲਈ ਕਿਨਾਰੇ ਦੇ ਨਾਲ ਨਾਲ 9 ਜਾਂ 7 ਸਿੱਧੇ ਟਾਂਕੇ ਲਾਉਂਦੇ ਹਨ ।