Class 8

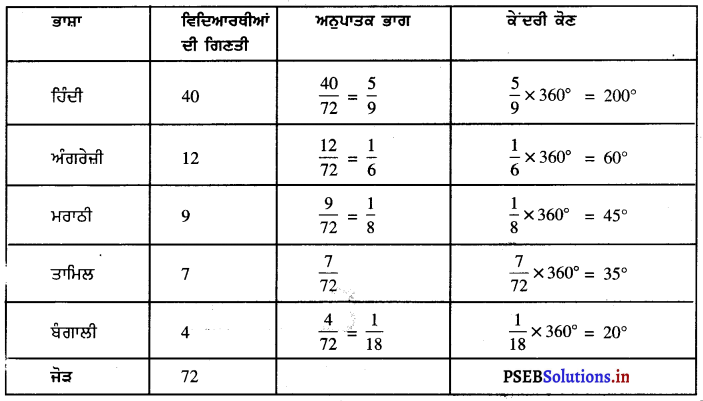
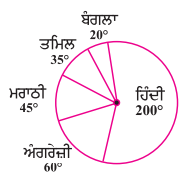
Punjab State Board PSEB 8th Class Computer Book Solutions Chapter 7 कम्प्यूटर जनरेशन्स Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Computer Chapter 7 कम्प्यूटर जनरेशन्स

Computer Guide for Class 8 PSEB कम्प्यूटर जनरेशन्स Textbook Questions and Answers

1. रिक्त स्थान भरो

1. दूसरी जनरेशन के कम्प्यूटर में ………………………………… को आधारभूत प्रोसेसिंग भाग के तौर पर प्रयोग किया जाता था
(क) वैक्यूम ट्यूब
(ख) VLSI
(ग) ULSI
(घ) ट्रांजिस्टर।
उत्तर-
(घ) ट्रांजिस्टर।

2. कम्प्यूटर की …………… जनरेशन में VLSI का प्रयोग किया जाता था।
(क) पहली
(ख) दूसरी
(ग) तीसरी
(घ) चौथी।
उत्तर-
(घ) चौथी।

3. तीसरी जनरेशन कम्प्यूटर में ट्रांसफर के स्थान पर ………… प्रयोग किए जाते थे।
(क) इंटीग्रेटेड सर्किट
(ख) वैक्यूम ट्यूब
(ग) ULSI सर्किट
(घ) VLSI सर्किट।
उत्तर-
(क) इंटीग्रेटेड सर्किट

4. ………….. कम्प्यूटर साइंस की एक नई ब्रांच है। जो कम्प्यूटर को मनुष्य की तरह सोचने तथा कार्य करने के समर्थ बनाती है।
(क) रोबोटिक
(ख) ULSI सर्किट
(ग) आर्टिफिशियल इंटेलिजेंस
(घ) इंटीग्रेटेड सर्किट।
उत्तर-
(ग) आर्टिफिशियल इंटेलिजेंस

5. ULSI टैक्नोलॉजी का प्रयोग …………………………… जनरेशन के कम्प्यूटर में किया जाता है।
(क) दूसरी
(ख) तीसरी
(ग) चौथी
(घ) पांचवीं।
उत्तर-
(घ) पांचवीं।

2. पूरा नाम लिखो

1. ENIAC
2. IBM
3. IC
4. VLSI
5. ULSI
6. AI
उत्तर-
1. ENIAC-Electronic Numerical Integrator and Computer.
2. IBM-International Business Machine
3. IC-Integrated Circuit/Chip
4. VLSI-Very Large Scale Integration
5. ULSI-Ultra Large Scale Integration
6. AI-Artificial Intelligence

3. छोटे उत्तर वाले प्रश्न

प्रश्न 1.
पहली जनरेशन के कम्प्यूटर की विशेषताएं लिखो।
उत्तर-
पहली जनरेशन के कम्प्यूटर के निम्नलिखित विशेषताएं हैं।

1. वैक्यूम टयूब अकेले विकल्प थे।
2. मशीन तथा असैंबली भाषा का प्रयोग होता था।
3. ये आकार में काफ़ी बड़े थे।
4. ये भरोसे योग्य नहीं थे।
5. इनका प्रयोग व्यापारिक कार्यों में नहीं हो सकता था।
6. ये बहुत महंगे तथा प्रयोग में मुश्किल थे।

प्रश्न 2.
दूसरी जनरेशन के कम्प्यूटर के लिए कौन सी टैकनॉलोजी का प्रयोग किया जाता था ?
उत्तर-
कम्प्यूटर की दूसरी जनरेशन पहली जनरेशन खत्म होने के बाद शुरू हुई। इसका समय 1955 से 1964 तक का था। इस जनरेशन में ट्रांजिस्टर का प्रयोग किया जाता था। यह ट्रांजिस्टर सबसे सस्ते, कम बिजली खप्त करने वाले, आकार में छोटे तथा भरोसे लायक थे। इनमें प्राइमरी मैमरी के लिए मैग्नेटिक कोर तथा सेकेंडरी मैमरी के लिए मैग्नेटिक टेप तथा मेग्नेटिक डिस्क का प्रयोग किया जाता था।

प्रश्न 3.
IC क्या होते हैं ?
उत्तर-
आई सी एक इंटीग्रेटेड इलेक्ट्रॉनिक सर्किट होता है। जिसमें कई ट्रांजिस्टर, रजिस्टर तथा कैपेसिटर लगे होते हैं। इनके प्रयोग से कम्प्यूटर का आकार काफी छोटा हो गया।

प्रश्न 4.
चौथी जनरेशन के कम्प्यूटर संबंधी लिखो।
उत्तर-
चौथी जनरेशन का समय 1975 से लेकर 1981 तक था। इसमें वेरी लार्ज स्केल इंटीग्रेटेड सर्किट का प्रयोग किया जाता था। इसमें एक छोटी चिप पर 5000 तक ट्रांजिस्टर तथा अन्य पुर्जे लगे होते हैं। इस जनरेशन के कम्प्यूटर बहुत शक्तिशाली, छोटे, भरोसे वाले तथा सस्ते थे। इस जनरेशन के कम्प्यूटर में टाइम शेयरिंग, रीयल टाइम नेटवर्क तथा डिस्ट्रीब्यूटर ऑपरेटिंग सिस्टम का प्रयोग होता था। इसमें हाई लेवल भाषाएं जैसे c, c++, DBMS आदि का प्रयोग किया जाने लगा।

प्रश्न 5.
AI क्या है ? AI के महत्त्वपूर्ण क्षेत्रों का नाम लिखो।
उत्तर-
AI का पूरा नाम आर्टिफिशियल इंटेलिजेंस है। यह कम्प्यूटर के क्षेत्र में नया क्षेत्र है। इसका मुख्य उद्देश्य मशीनों को सोचने की शक्ति प्रदान करना है। आर्टिफशियल इंटेलिजेंस के महत्त्वपूर्ण क्षेत्र निम्नानुसार हैं :

1. रोबोटिक्स
2. गेम प्लेइंग
3. एक्सपर्ट सिस्टम
4. मान व्यवस्थाओं को समझना

प्रश्न 6.
पहले जनरेशन के कम्प्यूटरों के नाम लिखो।
उत्तर-
पहली जनरेशन के कम्प्यूटर के नाम निम्नानुसार हैं-
1. ENIAC
2. EDVAC
3. EDSAC
4. UNIVAC-I
5. IBM 701

4. बड़े उत्तर वाले प्रश्न

प्रश्न 1.
कम्प्यूटर की जनरेशन से आपका क्या अभिप्राय है ? इनको किस प्रकार विभाजित किया गया है ?
उत्तर-
कम्प्यूटर की तकनीकी शब्दावली में जनरेशन से अभिप्राय कम्प्यूटर की टैकनोलॉजी में बदलाव से है। पहले जनरेशन से भाव सिर्फ हार्डवेयर बदलाव से ही माना जाता था परंतु अब इसमें हार्डवेयर तथा सॉफ्टवेयर दोनों प्रकार के बदलाव शामिल हैं-
कम्प्यूटर को निम्नलिखित जनरेशन के अनुसार विभाजित किया गया है-
1. पहली जनरेशन (1942-1955)-पहली जनरेशन का समय 1942 से 1955 तक का था। इस जनरेशन – के कम्प्यूटर में वैक्यूम ट्यूब का प्रयोग किया जाता था।

2. दूसरी जनरेशन (1955-1964) दूसरी जनरेशन पहली जनरेशन के खत्म होने के बाद शुरू होती है। इसका समय 1955 से 1964 तक का था। इस जनरेशन के कम्प्यूटर में ट्रांजिस्टर का प्रयोग किया जाता था।

3. तीसरी जनरेशन (1964-1975)-तीसरी जनरेशन का समय 1964 से 1975 तक था। इस जनरेशन के कम्प्यूटर में आई सी का प्रयोग किया जाता था।

4. चौथी जनरेशन (1975-1989)–चौथी जनरेशन के कम्प्यूटर का समय 1975 से लेकर 1989 तक था। इस जनरेशन के कम्प्यूटर में VSLI का प्रयोग किया जाता था।

5. 5वीं जेनरेशन (1989 से अब तक)-कम्प्यूटर की 5वीं जेनरेशन 1989 से शुरू मानी जाती है। इस जनरेशन के कम्प्यूटर में ULSI तकनीक का प्रयोग होता है। इस जनरेशन के कम्प्यूटर में माइक्रोप्रोसेसर चिप का प्रयोग किया जाता है।

प्रश्न 2.
5वीं जेनरेशन के कम्प्यूटर की व्याख्या करो।
उत्तर-
कम्प्यूटर की पांचवीं जनरेशन 1989 से शुरू होती है तथा आज तक चलती है। इसमें VLSI से टैक्नोलोजी ULSI में बदल गई। इसमें माइक्रोप्रोसैसर चिप का प्रयोग होता है जिसमें दस मिलियन मतलब एक करोड़ तक पुर्जे लगे होते हैं। कम्प्यूटर जनरेशज़ यह जनरेशन समांतर प्रोसैसिंग हार्डवेयर तथा आर्टीफिशियल इंटेलिजेंस के आधार पर कार्य करती है।

AI में शामिल है-

1. रोवोटिक
2. गेम प्लेईंग
3. एक्सपर्ट सिस्टम
4. मानवी भाषाओं को समझना तथा बोलना इसमें हाई लेबल भाषाएं जैसे C, C++, Java आदि का प्रयोग होता है।

पांचवीं जनरेशन कम्प्यूटर के नाम-

1. IBM नोटबुक
2. पेंटियम पीसी
3. Sun वर्क स्टेशन
4. IBM SP/2
5. परम 10000

पांचवीं जनरेशन कम्प्यूटर की निम्न विशेषताएं हैं –

1. ULSI तकनीक का प्रयोग होता है।
2. ऑप्टीकल डिस्क का प्रयोग होता है।
3. नोटबुक, डेस्कटॉप, वर्क स्टेशन, सरवर तथा सुपर कम्प्यूटर प्रयोग होते हैं।
4. इंटरनैट तथा कलस्टर कम्प्यूटिंग का प्रयोग होता है।
5. कठिन एप्लीकेशनज़ का प्रयोग होता है।
6. इनकी उत्पादकता तथा अपग्रेड करना आसान है।
7. रैपिड साफ्टवेयर डिवैल्पमैंट संभव है। 1BM नोट बुक, पैंटीयम PC, सन वर्क स्टेशन, 1BM sp/2 तथा परम 10000 इसकी उदाहरण हैं।

PSEB 8th Class Computer Guide कम्प्यूटर जनरेशन्स Important Questions and Answers

रिक्त स्थान भरो-

1. पहली जनरल के कम्प्यूटर में ………… प्रयोग की जाती थी।
(क) ट्रांजिस्टर
(ख) वैक्यूम ट्यूब
(ग) चिप
(घ) रजिस्टर।
उत्तर-
(ख) वैक्यूम ट्यूब

2. IBM 1030 ………… जनरेशन के कम्प्यूटर के उदाहरण है।
(क) पहली
(ख) दूसरी
(ग) तीसरी
(घ) चौथी।
उत्तर-
(ख) दूसरी

छोटे उत्तर वाले प्रश्न

प्रश्न 1.
पहली जनरेशन के कम्प्यूटर के नाम लिखो।
उत्तर-
ENIAC, ADVAC, EDSAC, UNIVAC-I, IBM 701.

प्रश्न 2.
दूसरी जनरेशन के कम्प्यूटर के नाम लिखो।
उत्तर-
IBM 3070, UNIVAC, LARC.

प्रश्न 3.
तीसरी जनरेशन के कम्प्यूटर में कौन सी भाषाएं प्रयोग की जाती थी ?
उत्तर-
FORTRAN II to IV, COBOL, PASCAL, PLI1, BASIC, ALGOL 68.

प्रश्न 4.
चौथी जनरेशन के कम्प्यूटर के नाम लिखो।
उत्तर-
IBM PC, APPLE II, CRAY I, II X/MP.

प्रश्न 5.
तीसरी जनरेशन के कम्प्यूटर के नाम लिखो।
उत्तर-
IB 360/370, PDP-8, PDP-II, CDC-6600.

प्रश्न 6.
चौथी जनरेशन के कम्प्यूटर में प्रयोग होने वाली भाषाओं के नाम लिखो।
उत्तर-
C, C++, DBMS.

प्रश्न 7.
AI का पूरा नाम लिखो।
उत्तर-
AI का पूरा नाम है Artificial Intelligence.

पूरे नाम लिखो-

1. EDVAC
2. EDSAC
3. UNIVAC
4. LARC
5. SSI
6. MSI
7. PDP
8. CDC
उत्तर-
1. EDVAC-Electronic Discrete Variable Automatic Computer.
2. EDSAC—Electronic Storage Automatic Calculator.
3. UNIVAC-Universal Automatic Computer.
4. LARC-Livermore Advanced Research Computer.
5. SSI-Small Scale Integration.
6. MSI-Medium Scale Integration.
7. PDP-Personal Data Processor.
8. CDC-Control Data Corporation.

Punjab State Board PSEB 8th Class Computer Book Solutions Chapter 6 माइक्रोसॉफ्ट पावर पवाइंट (भाग-3) Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Computer Chapter 6 माइक्रोसॉफ्ट पावर पवाइंट (भाग-3)

Computer Guide for Class 8 PSEB माइक्रोसॉफ्ट पावर पवाइंट (भाग-3) Textbook Questions and Answers

1. रिक्त स्थान भरें

1.. ……………………….. एक विजुअल तथा गति वाले प्रभाव होते हैं जो उस समय दिखाई देते हैं। जब हम प्रेजेंटेशन के स्लाइड शो के दौरान एक स्लाइड से अगली स्लाइड पर जाते हैं।
(a) स्लाइड ट्रांजिशन
(b) एनिमेशन
(c) एनिमेशन स्कीम
(d) स्लाइड शो।
उत्तर-
(a) स्लाइड ट्रांजिशन

2. पावर प्वाइंट ………………………… किस्म की एनिमेशन प्रदान करता है।
(a) दो
(b) तीन
(c) चार
(d) पांच
उत्तर-
(c) चार

3. पावरप्वाइंट पहले से परिभाषित एनीमेशन इफैक्ट्स का समूह प्रदान करता है जिनको ………………….. कहा जाता है।
(a) स्लाइड ट्रांजिशन
(b) एनीमेशन
(c) एनिमेशन स्कीम
(d) स्लाइड शो।
उत्तर-
(c) एनिमेशन स्कीम

4. PDF का पूरा नाम …………………….. है।
(a) पोर्टेबल डाटा फॉरमैट
(b) पोर्टेबल डाक्युमेंट फोरम
(c) पोर्टेबल डाटा फॉर्म
(d) पोर्टेबल डॉक्युमेंट फॉरमैट।
उत्तर-
(d) पोर्टेबल डॉक्युमेंट फॉरमैट।

5. हम पावरप्वाइंट प्रेजेंटेशन पावरप्वाइंट शो की तरह ……………. एक्सटेंशन के साथ सेव कर सकते
(a) .ppsx
(b) .ppt
(c) .pptx
(d) .pdf
उत्तर-
(a) .ppsx

2. पूरे नाम लिखो

1. JPEG
2. GIF
3. BMP
4. WMV
5. PNG
उत्तर
1. JPEG-Joint Photographic Expert Group
2. GIF-Graphical Interchange Format
3. BMP-BitMap Picture
4. WMV-Windows Media Video
5. PNG-Portable Network Graphics

3. छोटे उत्तर वाले प्रश्न

प्रश्न 1.
स्लाइड ट्रांजिशन क्या है ?
उत्तर-
स्लाइड ट्रांजिशन विजुअल तथा गति से संबंधित इफेक्ट्स होते हैं जो उस समय दिखाई देते हैं जब हम प्रेजेंटेशन को स्लाइड शो के दौरान एक स्लाइड से अगली स्लाइड पर ले जाते हैं। हम ट्रांजिशन इफेक्ट की गति को नियंत्रित कर सकते हैं। हम उस में आवाज भी दाखिल कर सकते हैं।

प्रश्न 2.
एनिमेशन क्या होती है ?
उत्तर-
एनिमेशन विजुअल इफेक्ट्स होते हैं जो प्रेजेंटेशन में ऑब्जैक्ट के ऊपर लगाए जाते हैं तथा जिन का मुख्य उद्देश्य ऑब्जैक्ट को गति प्रदान करना होता है। ये किसी भी प्रकार के हो सकते हैं जैसे कि टेक्सट, तस्वीरें, स्मार्ट आर्ट, ग्राफिक शेप्स, वीडियो क्लिप आदि। एनिमेशन हमारी प्रेजेंटेशन को गतिमान बनाने में सहायता करती है। जिससे हमारी प्रेजेंटेशन बहुत प्रभावशाली बन जाती है।

प्रश्न 3.
पावरप्वाइंट में एनिमेशन स्कीम क्या होती है ?
उत्तर-
पावरप्वाइंट में पहले से ही प्रभावित एनीमेशन इफेक्ट का एक संग्रह होता है। एनिमेशन इफेक्ट के इस संग्रह को एनिमेशन स्कीम कहा जाता है।

प्रश्न 4.
आप पावरप्वाइंट में एनिमेशन का प्रयोग कैसे देखोगे ?
उत्तर-
पावरप्वाइंट में स्लाइड ऑब्जैक्ट के ऊपर एनिमेशन लागू करने के लिए निम्न पग प्रयोग किए जाते-

1. एनिमेशन टैब के ऊपर क्लिक करो।
2. उस ऑब्जैक्ट का चुनाव करो जिस पर एनिमेशन लागू करनी है।
3. एनिमेशन ग्रुप में मोर एरो बटन के ऊपर क्लिक करके हम मौजूद सारी एनिमेशन की किस्मों को देख सकते हैं।
4. एनिमेशन गैलरी में अपनी आवश्यकतानुसार किसी भी एनीमेशन इफेक्ट का चुनाव करो।

यह चुनाव ऊपर दी गई चार प्रकार की एनिमेशन में से किसी भी प्रकार के लिए किया जा सकता है। आमतौर पर हम किसी भी ऑब्जैक्ट पर तीन प्रकार की एनिमेशन लगाते हैं। पहले उसकी एंट्री के लिए, दूसरी उसको प्रभावशाली बनाने के लिए तथा तीसरी उसके एग्जिट के लिए।

प्रश्न 5.
पावरप्वाइंट में मौजूद 4 किस्मों की एनिमेशन के नाम लिखो।
उत्तर-
पावरप्वाइंट में निम्नलिखित चार प्रकार की एनिमेशन मौजूद होती हैं

1. एंट्रेस
2. प्रभाव
3. एग्जिट
4. मोशन पाथ।

4. बड़े उत्तर वाले प्रश्न

प्रश्न 1.
एनिमेशन क्या है ? पावरप्वाइंट में यह कितनी किस्म की होती है ?
उत्तर-
एनिमेशन विजुअल इफेक्ट्स होते हैं। ये प्रेजेंटेशन में ऑब्जैक्ट के ऊपर लगाए जाते हैं तथा जिन का मुख्य उद्देश्य ऑब्जैक्ट को गति प्रदान करना होता है। ये किसी भी प्रकार के हो सकते हैं जैसे कि टेक्सट, तस्वीरें, स्मार्ट ऑर्ट ग्राफिक, शेप्स, वीडियो क्लिप आदि। एनिमेशन हमारी प्रेजेंटेशन को गतिमान बनाने में सहायता करती है। जिससे हमारी प्रेजेंटेशन बहुत प्रभावशाली बन जाती है।

पावरप्वाइंट में चार प्रकार के एनिमेशन उपलब्ध होते हैं-
1. एंट्रेंस (Entrance)-प्रेजेंटेशन के दौरान जब कोई ऑब्जैक्ट स्क्रीन के ऊपर दिखाई देना शुरू होता है उस समय अप्लाई की जाने वाले एनिमेशन को एंटेंस किस्म की एनिमेशन कहा जाता है। इसका मुख्य उद्देश्य ऑब्जेक्ट को गतिमान रूप से स्लाइड पर लाना होता है। उदाहरण के तौर पर किसी भी ऑब्जैक्ट का स्लाइड पर मूव करते हुए दाखिल होना।

2. प्रभाव (Emphasis)-एनिमेशन का प्रयोग किसी भी ऑब्जैक्ट और दर्शकों का ध्यान खींचने के लिए किया जाता है। यह एनिमेशन किसी भी ऑब्जैक्ट के स्लाइड में दाखिल होने के बाद दिखाई देती है। उदाहरण के तौर पर ऑब्जैक्ट के ऊपर दर्शकों का ध्यान खींचने के लिए उसका आकार बड़ा करना, उसका रंग बदलना या उसमें कोई अन्य गति प्रदान करना।

3. एग्जिट (Exit) एनिमेशन का प्रयोग ऑब्जैक्ट के स्लाइड से बाहर जाते समय किया जाता है। जब यूज़र चाहता है कि उसका ऑब्जैक्ट दर्शकों को दिखना बंद हो जाए तो उसको एक गतिमान रूप से स्लाइड से बाहर किया जा सकता है। उदाहरण के लिए ऑब्जैक्ट का स्लाइड से बाहर जाते समय Zoom होते हुए या Fade होते हुए गायब हो जाना।

4. मोशन पाथ (Motion Path)-मोशन पाथ एनिमेशन किसी भी ऑब्जेक्ट को स्लाइड पर अपने अनुसार घुमाने के लिए प्रयोग किया जाता है। इसमें ऑब्जैक्ट के लिए एक रास्ता निर्धारित कर दिया जाता है और वह ऑब्जैक्ट पर घूमते हुए ही स्लाइड में दिखाई पड़ता है। उदाहरण के तौर पर एक ऑब्जैक्ट का दाएं से बाएं की ओर चले जाना।

प्रश्न 2.
पावरप्वाइंट प्रेजेंटेशन को पीडीएफ में कैसे सेव करोगे ?
उत्तर-
किसी भी प्रेजेंटेशन को पीडीएफ के रूप में सेव करने के निम्नलिखित पग होते हैं-

1. File के ऊपर क्लिक करो।
2. Save As… विकल्प के ऊपर क्लिक करो। (Save AS डायलॉग बॉक्स दिखाई देगा।)
3. इस डायलॉग बॉक्स में फाइल का नाम तथा उसको सेव करने की लोकेशन का चुनाव करो।
4. Save As Type ड्रॉप डाउन लिस्ट में से .PDF विकल्प का चुनाव करो।
5. Save बटन पर क्लिक करो। (पावरप्वाइंट प्रेजेंटेशन को .pdf रूप में सेव कर देगा।)

प्रश्न 3.
पावरप्वाइंट में स्लाइड ट्रांजिशन कैसे लागू की जाती है ?
उत्तर-
प्रेजेंटेशन में ट्रांजिशन इफेक्ट लागू करने के निम्नलिखित स्टेप प्रयोग किए जाते हैं-

1. स्लाइड पर क्लिक करो या सिलेक्ट करो जिस पर ट्रांजिशन लागू करनी है। .
2. ट्रांजिशन टैब के ऊपर Transition to This Slide ग्रुप में अपनी इच्छा अनुसार ट्रांजिशन इफेक्ट का चुनाव करो।
3. आवश्यकतानुसार अन्य विकास जैसे कि इफेक्ट ऑप्शन, साउंड तथा समय अवधि का भी चुनाव करो।
4. ट्रांजिशन की दिखावट को देखने के लिए Preview बटन पर क्लिक करो।
5. अगर आप प्रेजेंटेशन की सारी स्लाइड्स पर ट्रांजिशन लगाना चाहते हैं तो Timing ग्रुप में से Apply to All पर क्लिक करो।

PSEB 8th Class Computer Guide माइक्रोसॉफ्ट पावर पवाइंट (भाग-3) Important Questions and Answers

रिक्त स्थान भरें

1. टाइमिंग इफेक्ट में कौन-कौन से इफेक्ट होते हैं ?
(a) अवधि
(b) देरी का समय
(c) दोनों ही
(d) कोई भी नहीं।
उत्तर-
(c) दोनों ही

2. प्रेजेंटेशन को किसकी फॉर्मेट में सेव किया जा सकता है ?
(a) PDF
(b) वीडियो
(c) स्लाइड शो
(d) उपरोक्त सभी।
उत्तर-
(d) उपरोक्त सभी।

पूरे नाम लिखो

1. WMF
2. EMF.
उत्तर-
1. Windows Meta File,
2. Enhanced Windows Meta File.

छोटे उत्तर वाले प्रश्न

प्रश्न 1.
पावरप्वाइंट प्रेजेंटेशन को किन रूपों में सेव किया जा सकता है ?
उत्तर-
पावरप्वाइंट प्रेजेंटेशन को निम्नलिखित रूप में सेव किया जा सकता है-

1. पीडीएफ
2. वीडियो
3. तस्वीरें
4. पावरप्वाइंट शो।

प्रश्न 2.
पावरप्वाइंट प्रेजेंटेशन को कौन-कौन से पिक्चर फॉर्मेट में सेव किया जा सकता है ?
उत्तर-
पावरप्वाइंट प्रेजेंटेशन को GIF, JPEG, PNG, TIFF, BMP, WMF तथा EMF पिक्चर फॉर्मेट में सेव किया जा सकता है।

Punjab State Board PSEB 8th Class Computer Book Solutions Chapter 5 माइक्रोसॉफ्ट पावर पवाइंट (भाग-2) Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Computer Chapter 5 माइक्रोसॉफ्ट पावर पवाइंट (भाग-2)

Computer Guide for Class 8 PSEB माइक्रोसॉफ्ट पावर पवाइंट (भाग-2) Textbook Questions and Answers

1. रिक्त स्थान भरें

1. ………………………… स्लाइड के ऊपर विभिन्न तत्वों के डिजाइन तथा प्लेसमेंट को परिभाषित करता है।
(क) बैकग्राउंड स्टाइल
(ख) प्लेसहोल्डर
(ग) स्टाइल लेआउट
(घ) पैटर्न
उत्तर-
(ग) स्टाइल लेआउट

2. एक ………………………. दो या दो से ज्यादा रंगों का मिश्रण होता है जो एक दूसरे में मर्ज हो जाते हैं।
(क) थीम
(ख) पैटर्न
(ग) बैकग्राउंड स्टाइल
(घ) ग्रेडियंट
उत्तर-
(घ) ग्रेडियंट

3. ……………….. डिफॉल्ट वियू है जहां हम अपनी स्लाइड बनाते, एडिट करते तथा डिजाइन करते हैं।
(क) नॉरमल वियू
(ख) स्लाइड शो
(ग) स्लाइड सोर्टर वियू
(घ) रीडिंग वियू।
उत्तर-
(क) नॉरमल वियू

4. Power point 2010 में …………………….. डिफॉल्ट स्लाइड बैकग्राउंड स्टाइल में उपलब्ध होते हैं।
(क) 48
(ख) 4
(ग) 12
(घ) 3.
उत्तर-
(ख) 4

5. ………………………. कंट्रोल स्लाइड कंटेंट को नज़दीक से देखने के लिए जूम इन करने की आज्ञा देता है।
(क) जूम
(ख) स्लाइड
(ग) नॉर्मल वियू
(घ) ग्रेडियंट।
उत्तर-
(क) जूम

2. बहुत छोटे उत्तर वाले प्रश्न

प्रश्न 1.
एक नई स्लाइड दाखिल करने की शॉर्टकट कीअ क्या है ?
उत्तर-
Ctrl + M.

प्रश्न 2.
एक नई प्रेजेंटेशन फाइल बनाने की शॉर्टकट कीअ क्या है ?
उत्तर-
Ctrl + N.

प्रश्न 3.
स्लाइड के ऊपर टैक्सट को फॉर्मेट करने के लिए किसका प्रयोग किया जाता है ?
उत्तर-
Design.

प्रश्न 4.
कौन-सा पावर प्वाइंट वियू दर्शकों के आगे प्रेजेंटेशन पेश करने की आज्ञा देता है ?
उत्तर-
स्लाइड शो।

प्रश्न 5.
पावर प्वाइंट में कौन-सी बार पर वियू बटन तथा जूम स्लाइडर मौजूद होते हैं ?
उत्तर-
स्टेटस बार।

3. छोटे उत्तर वाले प्रश्न

प्रश्न 1.
पावर प्वाइंट में फाइल टैब की मदद से नई प्रेजेंटेशन बनाने के स्टेप लिखो।
उत्तर-
पावर प्वाइंट में फाइल टैब की मदद से नई प्रेजेंटेशन बनाने के स्टेप्स निम्नानुसार हैं।

1. File मैन्यू पर क्लिक करो।
2. New पर क्लिक करो।
3. उपलब्ध टेंप्लेट तथा थीमस मे ब्लैंक प्रेजेंटेशन का चुनाव करो।
4. ब्लैंक प्रेजेंटेशन पर क्लिक करो।

प्रश्न 2.
प्लेसहोल्डर क्या होते हैं ?
उत्तर-
प्लेसहोल्डर स्लाइड लेआउट के ऊपर डॉटेड लाइन वाले कंटेनर होते हैं जिनमें हर प्रकार का कंटेंट रखा जाता है। इन प्लेसहोल्डर के अंदर ही टाइटल, सबटाइटल, टेबल, चार्ट, तस्वीरों आदि को रखा जाता है।

प्रश्न 3.
थीम क्या होते हैं ?
उत्तर-
थीम पहले से ही तैयार बैकग्राउंड डिजाइन टैक्सट, स्टाइल, कलर आदि होते हैं। इनका प्रयोग एक या ज्यादा स्लाइडो पर किया जा सकता है।

प्रश्न 4.
पावर प्वाइंट विंडो के स्टेटस बार में मौजूद वियू बटन के नाम लिखो।
उत्तर–
पावर प्वाइंट विंडो के स्टेटस बार में निम्नलिखित वियू बटन मौजूद होते हैं। नॉर्मल स्लाइड सोर्टर, रीडिंग तथा स्लाइड शो।

प्रश्न 5.
ग्रेडियंट फिल क्या होता है ?
उत्तर-
ग्रेडियंट दो या दो से ज्यादा रंगों का मिश्रण होता है जो एक दूसरे में मर्ज हो रहे होते हैं। इनका प्रयोग स्लाइड बैकग्राउंड के तौर पर किया जा सकता है।

प्रश्न 6.
फॉर्मेट बैकग्राउंड डायलॉग बॉक्स के फिल पेन में कौन-कौन से विकल्प मौजूद होते हैं ?
उत्तर-
फॉर्मेट बैकग्राउंड डायलॉग बॉक्स के पेन में निम्नलिखित विकल्प मौजूद होते हैं

1. Solid Fill
2. Gradient Fill
3. Picture or Texture Fill
4. Pattern Fill.

4. बड़े उत्तर वाले प्रश्न

प्रश्न 1.
स्लाइड की दिखावट को बदलने के विभिन्न तरीकों का विस्तार से वर्णन करो।
उत्तर-
स्लाइड की दिखावट बदलने के निम्नलिखित तरीके हैं-

1. थीम का प्रयोग करके-एक थीम कलर फोंट तथा विजुअल इफेक्ट का पहले से ही परिभाषित समूह होता है जो हम अपनी स्लाइड के ऊपर एक जैसा तथा पेशेवर दिख वाला सेट लागू कर सकते हैं।
2. बैकग्राउंड स्लाइड का प्रयोग करके-प्रेजेंटेशन स्लाइड के ऊपर बैकग्राउंड स्टाइल सेट किया जा सकता है। यह स्टाइल थीम कलर के आधार पर बने होते हैं। जब हम एक अलग थीम को सिलेक्ट करते हैं तो बैकग्राउंड स्टाइलस नए सिलेक्ट किए गए थीम के रंगों के आधार पर थीम अपने आप अपडेट हो जाते हैं।
3. फॉर्मेट बैकग्राउंड करके-बैकग्राउंड को एक ठोस रंग ग्रेडियंट पिक्चर तथा टेक्सचर या एक पैटर्न के रूप में बदला जा सकता है।

प्रश्न 2.
स्लाइड लेआउट क्या होती है ? आप पावर प्वाइंट में स्लाइड लेआउट को कैसे बदल सकते हो ?
उत्तर-
स्लाइड लेआउट स्लाइड के ऊपर विभिन्न तत्त्वों के डिज़ाइन तथा प्लेसमेंट को परिभाषित करता है। प्रेजेंटेशन में एक नई स्लाइड दाखिल करते समय स्लाइड लेआउट का चयन किया जा सकता है। प्रेजेंटेशन में स्लाइड दाखिल करने में बाद स्लाइड का लेआउट बदला जा सकता है। स्लाइड लेआउट बदलने के लिए निम्नलिखित पगों का प्रयोग किया जाता है।

1. उस स्लाइड को सिलेक्ट करो जिसका लेआउट बदलना है।
2. Home टैब Slide ग्रुप में मौजूद Layout ड्रॉप डाउन मैन्यू पर क्लिक करों।
3. अपनी आवश्यकतानुसार लेआउट का चुनाव करो।

प्रश्न 3.
पावर प्वाइंट में स्लाइड वियू विकल्प का वर्णन करो।
उत्तर-
पावर प्वाइंट में निम्नलिखित स्लाइड वियू उपलब्ध होते हैं –
1. नॉर्मल वियू-यह पावरप्वाइंट का डिफॉल्ट तथा मुख्य वियू हैं। इसमें हम स्लाइड बना सकते हैं तथा उसके कंटेंट को एडिट भी कर सकते हैं। इस वियू में बाएँ तरफ स्लाइड तथा दाईं तरफ एडिट करने के लिए एक स्लाइड नज़र आती है।

2. स्लाइड सोर्टर वियू-इसमें सारी स्लाइड थंबनेल के रूप में दिखाई देती हैं। इस वियू का प्रयोग स्लाइड का क्रम बदलने के लिए किया जाता है। इसमें हम किसी भी स्लाइड का कंटेंट नहीं बदल सकते।

3. नोट्स वियू-इस वियू का प्रयोग स्लाइड के बारे में जानकारी लिखने के लिए किया जाता है लिखी गई जानकारी को नोट कहते हैं तथा यह स्लाइड के नीचे बने एक बॉक्स में टाइप की जाती है।

4. रीडिंग वियू-इस को प्रूफरीडिंग के लिए प्रयोग किया जाता है। इसका प्रयोग प्रेजेंटेशन को कंप्यूटर पर देखने के लिए भी किया जाता है। 5. मास्टर वियू-इस को हैंग आउट नोट भी कहा जाता है। इस ग्रुप में सारा कंटेंट प्लेस किया जाता है जो यूज़र चाहता है कि सारी स्लाइडो पर दिखाई दे।

PSEB 8th Class Computer Guide माइक्रोसॉफ्ट पावर पवाइंट (भाग-2) Important Questions and Answers

रिक्त स्थान भरें

1. ग्रेडीएंट ऑप्शन …………………… डायलाग बॉक्स में होती है।
(क) फॉर्मेट शेप
(ख) फॉर्मेट बैकग्राऊंड
(ग) पैराग्राफ
(घ) फोंट।
उत्तर-
(ख) फॉर्मेट बैकग्राऊंड

2. विडियो को ………. तरीकों से शामिल किया जा सकता है।
(क) एक
(ख) दो
(ग) तीन
(घ) चार।
उत्तर-
(ग) तीन

3. क्लिप आर्ट विडियो, विडियो फ्राम वैबसाइट तथा …………………. तीन तरीके हैं, जिनके द्वारा विडियो दाखिल की जा सकती है।
(क) विडियो फ्राम फाइल
(ख) इमेज द्वारा
(ग) एनीमेशन द्वारा
(घ) सारे।
उत्तर-
(क) विडियो फ्राम फाइल

4. वर्ड डाक्यूमैंट, विटमैप, वर्कशीट को ……. ऑप्शन से दाखिल किया जाता है।
(क) इन्सर्ट टैब
(ख) वियू टैब
(ग) होम टैब
(घ) कोई नहीं।
उत्तर-
(क) इन्सर्ट टैब

5. बैकग्राऊंड स्टाइल बटन ………. रिबन पर उपलब्ध होता है।
(क) एनीमेशन
(ख) डिज़ाइन
(ग) होम
(घ) इन्सर्ट।
उत्तर-
(ख) डिज़ाइन

बहुत छोटे उत्तर वाले प्रश्न

प्रश्न 1.
बैकग्राउंड में क्या-क्या लगाया जा सकता है ?
उत्तर-
बैकग्राउंड में रंग, पिक्चर, टेक्सचर, ग्रेडियंट, आदि लगाया जा सकता है।

प्रश्न 2.
क्लिप ऑर्गेनाज़र किस लिए प्रयोग किया जाता है ?
उत्तर-
क्लिप ऑर्गेनाज़र एनीमेटेड क्लिप को स्टोर करने के लिए प्रयोग किया जाता है।

छोटे उत्तर वाले प्रश्न

प्रश्न 1.
स्लाइड की दिखावट बदलने के विभिन्न तरीकों के नाम बताओ।
उत्तर-
स्लाइड की दिखावट बदलने के लिए डिज़ाइन थीम, कलर थीम, बैकग्राउंड स्टाइल आदि तरीकों का प्रयोग किया जाता है।

प्रश्न 2.
कलर स्कीम के प्रयोग के बारे में बताएं।
उत्तर-
कलर स्कीम का प्रयोग टैक्सट, लाइन, टाइटल तथा किसी भी प्रकार के ऑबजेक्ट का रंग बदलने के लिए किया जाता है। इसके द्वारा स्लाइड के अगले भाग तथा बैकग्राउंड का रंग भी बदला जा सकता है।

प्रश्न 3.
क्लिप ऑर्गेनाइज़र के बारे में बताओ।
उत्तर-
क्लिप ऑर्गेनाइज़र का प्रयोग एनीमेटेड क्लिप्स, वीडियोस, तस्वीरें तथा अन्य प्रकार की मीडिया स्टोर करने के लिए किया जाता है।

प्रश्न 4.
थीम क्या होती है ?
उत्तर-
थीम पहले से ही तैयार बैकग्राउंड डिज़ाइन, टैक्सट स्टाइल, कलर आदि होते हैं। इनका प्रयोग एक . या एक से अधिक स्लाइड के ऊपर किया जा सकता है।

Punjab State Board PSEB 8th Class Computer Book Solutions Chapter 4 माइक्रोसॉफ्ट पावर पवाइंट (भाग-1) Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Computer Chapter 4 माइक्रोसॉफ्ट पावर पवाइंट (भाग-1)

Computer Guide for Class 8 PSEB माइक्रोसॉफ्ट पावर पवाइंट (भाग-1) Textbook Questions and Answers

1. रिक्त स्थान भरें-

1. …………………… एक प्रेजेंटेशन ग्राफिक सॉफ्टवेयर है।
(क) पावर प्वाइंट
(ख) वर्ड
(ग) एक्सेल
(घ) पेंट।
उत्तर-
(क) पावर प्वाइंट

2. …………………… किसी भी विषय को रोचक तरीके से दर्शकों के सामने पेश करने की प्रक्रिया है।
(क) वर्ड प्रोसेसर
(ख) लाइट
(ग) प्रेजेंटेशन
(घ) ट्रांजिशन।
उत्तर-
(ग) प्रेजेंटेशन

3. एक ……………….. प्रेजेंटेशन का एक पेज होता है।
(क) स्लाइड
(ख) डॉक्यूमेंट
(ग) शीट
(घ) इनमें से कोई भी नहीं।
उत्तर-
(क) स्लाइड

4. ………………………. हमारी प्रेजेंटेशन के मौजूदा स्लाइड को दर्शाता है।
(क) आउटलाइन पेन
(ख) कंटेंट पेन
(ग) रिबन
(घ) स्लाइड पेन।
उत्तर-
(ख) कंटेंट पेन।

2. बहुत छोटे उत्तर वाले प्रश्न

प्रश्न 1.
पावर प्वाइंट को आप कैसे ओपन करोगे ?
उत्तर-
Start-Programs→Microsoft PowerPoint पर क्लिक करके।

प्रश्न 2.
पावर प्वाइंट प्रेजेंटेशन को सेव करने की शॉर्टकट कीअ क्या है ?
उत्तर-
Ctrl + S.

प्रश्न 3.
पावर प्वाइंट को बंद करने की शॉर्टकट कीअ लिखो।
उत्तर-
Ctrl + F4.

प्रश्न 4.
पहली स्लाइड से स्लाइड शो स्टार्ट करने की शॉर्टकट कीअ क्या है ?
उत्तर-
F5.

प्रश्न 5.
पावर प्वाइंट प्रेजेंटेशन फाइल की एक्सटेंशन क्या होती है ?
उत्तर-.
ppt, .pptx

प्रश्न 6.
Run बॉक्स से पावर प्वाइंट ओपन करने के लिए किस शब्द का प्रयोग किया जाता है।
उत्तर-
Powerpnt.

3. छोटे उत्तर वाले प्रश्न

प्रश्न 1.
पावर प्वाइंट क्या है ?
उत्तर-
पावर प्वाइंट एक एप्लीकेशन सॉफ्टवेयर है जिसका प्रयोग प्रभावशाली प्रेजेंटेशन तैयार करने के लिए किया जाता है। यह माइक्रोसॉफ्ट कंपनी का उत्पाद है तथा एम०एस० ऑफिस का हिस्सा है।

प्रश्न 2.
प्रेजेंटेशन पर एक नोट लिखो।
उत्तर-
प्रेजेंटेशन कई स्लाइडों का समूह होता है जो किसी विशेष विषय पर बनी होती हैं। प्रेजेंटेशन में पिक्चर टैक्सट, ग्राफ चार्ट, एनिमेशन आदि हो सकता है। इसको पावर प्वाइंट की एक फाइल के रूप में सेव किया जाता है।

प्रश्न 3.
स्लाइड क्या होती है ?
उत्तर-
स्लाइड पावर प्वाइंट के एक पेज को कहते हैं। इस एक पेज पर कई प्रकार के ऑब्जेक्ट दिखाए जा सकते हैं। प्रेजेंटेशन दिखाते वक्त एक समय पर एक स्लाइड दिखाई देती है। बहुत सारी स्लाइड के मिलने से एक प्रेजेंटेशन बनती है।

प्रश्न 4.
पावर प्वाइंट विंडो के मुख्य भाग के नाम लिखो।
उत्तर-
पावर प्वाइंट विंडो में टाइटल बार, क्विक एक्सेस टूलबर, फाइल टाइप रिबन, लाइट पेन स्टेटस बार, वर्क एरिया आदि होते हैं।

प्रश्न 5.
आप पावर प्वाइंट में दर्शकों के लिए प्रेजेंटेशन किस प्रकार प्ले करोगे ?
उत्तर-
दर्शकों के लिए प्रेजेंटेशन प्ले करने के लिए प्रेजेंटेशन शो कहा जाता है। पावर प्वाइंट में प्रेजेंटेशन शो F5 शॉर्टकट की दबाकर चलाया जा सकता है।

प्रश्न 6.
पावर प्वाइंट में स्लाइड पेन तथा नोट्स पेन संबंधित जानकारी दो।
उत्तर-
स्लाइड पेन-स्लाइड पेन वह क्षेत्र होता है जिसमें स्लाइड को बनाया जाता है तथा एडिट किया जाता है। नोट्स पेन-स्टेटस बार के ऊपर होती है तथा इसका प्रयोग नोट्स तैयार करने के लिए किया जाता है।

4. बड़े उत्तर वाले प्रश्न

प्रश्न 1.
पावर प्वाइंट विंडो के कोई तीन मुख्य भागों का वर्णन करो।
उत्तर-
पावर प्वाइंट विंडो में निम्नलिखित भाग होते हैं –

1. फाइल मैन्यू- यह मैन्यू होम टैब के बाई तरफ होता है। इसमें काफी सारी कमांड होती हैं।
2. क्विक एक्सेस टूलबार-यह टूल बार फाइल मैन्यू के ऊपरी तरफ मौजूद होता है। इसमें तीन बटन होते हैं-सेव, अनडू तथा रीडू। इनको अपनी आवश्यकतानुसार बदला भी जा सकता है।
3. मैन्यू बार-इसमें विभिन्न प्रकार की टैब होती हैं जो क्लिक करने पर आगे रिबन को दिखाती हैं।
4. रिबन-पावर प्वाइंट विंडो में रिबन के साथ विभिन्न टूल तथा कमांड को दिखाता है। पावर प्वाइंट में होम डिज़ाइन, इंसर्ट, ट्रांजिशन, एनीमेशन, स्लाइड शो रिव्यू तथा युटूब होते हैं।
5. होम-इसमें शॉर्ट पैराग्राफ तथा एडिट जैसे ऑप्शन होते हैं।
6. इंसर्ट-इसमें इंसर्टेबल टैक्सट बॉक्स, क्लिपआर्ट, स्मार्ट आर्ट सिंबल, वीडियो चैट तथा फोटो एल्बम जैसे ऑप्शन होते हैं।

प्रश्न 2.
आप पावर प्वाइंट में फोटो एल्बम प्रेजेंटेशन कैसे तैयार करोगे ?
उत्तर-
पावर प्वाइंट में फोटो एल्बम तैयार करने के निम्नलिखित पग होते हैं –

1. Insert टैब पर क्लिक करो।
2. Images ग्रुप में से Photo Album विकल्प पर क्लिक करो तथा फिर New Photo Album विकल्प पर क्लिक करो।
3. Photo Album डायलॉग बॉक्स दिखाई देगा।
4. File/Disk पर क्लिक करो Insert New Pictures डायलॉग बॉक्स नज़र आएगा ज़रूरत के अनुसार अपनी इमेज फाइलों को सिलेक्ट करो। तस्वीरें सिलेक्ट करने के बाद Insert बटन पर क्लिक करो तथा वापस Photo Album डायलॉग बॉक्स पर आ जाओ।
5. Photo Album डायलॉग बॉक्स तस्वीरों को रोटेशन संबंधी ब्राइटनेस तथा कंट्रास्ट संबंधी तस्वीरों की लेआउट बदलने संबंधी उनको क्रमवार करने संबंधी या उनको हटाने संबंधी कई विकल्प प्रदान करता है। इन सेटिंग्स में अपनी आवश्यकतानुसार बदलाव करो तथा फिर Create बटन पर क्लिक करो।
6. अब फोटो एल्बम के लिए नई प्रेजेंटेशन तैयार हो जाएगी। इस प्रेजेंटेशन में एक टाइटल पेज होगा तथा प्रत्येक तस्वीर के लिए एक अलग स्लाइड अपने आप बनी होगी।

PSEB 8th Class Computer Guide माइक्रोसॉफ्ट पावर पवाइंट (भाग-1) Important Questions and Answers

रिक्त स्थान भरें

1. ……………………. एक प्रेजेंटेशन सॉफ्टवेयर है।
(क) पावर प्वाइंट
(ख) एक्सल
(ग) वर्ड
(घ) पेंट।
उत्तर-
(क) पावर प्वाइंट

2. पावर प्वाइंट के ………. वियू हैं।
(क) 3
(ख) 4
(ग) 5
(घ) 6.
उत्तर-
(ग) 5

3. स्लाइड …….. वियू में हम अपनी स्लाइड में सामग्री की कांट-छांट नहीं कर सकते ।
(क) स्लाइड शो
(ख) नारमल
(ग) सार्टर
(घ) कोई नहीं।
उत्तर-
(ग) सार्टर

4. प्रेजेंटेशन को ………… तरीकों से बनाया जा सकता है।
(क) 5
(ख) 6
(ग) 7
(घ) 8.
उत्तर-
(ख) 6

5. स्मार्ट आर्ट की …….. श्रेणियां होती हैं।
(क) 5
(ख) 6
(ग) 7
(घ) 8.
उत्तर-
(घ) 8.

सही या गलत बताएं

1. Ctrl + M कीअ का प्रयोग अपनी प्रेजेंटेशन में नई स्लाइड दाखिल करने के लिए की जाती है।
उत्तर-
सही

2. वर्ड आर्ट पहले से बने रंग, फोंट तथा इफैक्ट होते हैं।
उत्तर-
सही

3. स्लाइड टैब/पेन में स्लाइड का छोटा थंवनेल मिलता है।
उत्तर-
सही

4. प्रेजेंटेशन क सेब करने के लिए Ctrl + S दवाओ।
उत्तर-
सही

5. प्रेजेंटेशन कई स्लाइडों से मिल कर बनती है।
उत्तर-
सही।

बहुत छोटे उत्तर वाले प्रश्न

प्रश्न 1.
पावर प्वाइंट को किन-किन तरीकों से शुरू किया जा सकता है ?
उत्तर–
पावर प्वाइंट को निम्नलिखित तीन तरीकों से शुरू किया जा सकता है।

1. स्टार्ट बटन द्वारा
2. सर्च बाक्स द्वारा
3. डेस्कटॉप शॉर्टकट द्वारा।

प्रश्न 2.
नई स्लाइड किसके के साथ एंटर की जा सकती है ?
उत्तर-
कीबोर्ड से Ctrl + M कीअ दवाकर।

प्रश्न 3.
प्रैजेंटेशन को सेव करने की शार्टकट कीअ बताओ।
उत्तर-
Ctrl + S.

छोटे उत्तर वाले प्रश्न

प्रश्न 1.
पावर प्वाइंट क्या है ?
उत्तर–
पावर प्वाइंट एक प्रेजेंटेशन साफ्टवेयर है जो माइक्रोसॉफ्ट कम्पनी का उत्पाद है। इसका प्रयोग प्रभावशाली प्रेजेंटेशन तैयार करने में होता है। यह एम एम ऑफिस का भाग है।

प्रश्न 2.
प्रेजेंटेशन पर एक नोट लिखो।
उत्तर-
स्लाइडों के समूह को प्रेजेंटेशन कहते हैं। यह किसी खास विषय पर बनी होती है। प्रेजेंटेशन में पिक्चर, टैक्सट, ग्राफ, चार्ट एनीमेशन आदि हो सकते हैं। यह पावर प्वाइंट की एक फाइल की तरह सेब होती

प्रश्न 3.
प्रेजेंटेशन तैयार करने के अलग-अलग तरीकों के नाम लिखो।
उत्तर-
प्रेजेंटेशन निम्न तरीकों से तैयार की जाती है

1. ब्लैंक प्रेजेंटेशन
2. रीसेंट प्रेजेंटेशन
3. सैंपल टैंपलेट
4. थीमज
5. माई टैंपलेट
6. न्यू फ्राम एगजिस्टिंग।

प्रश्न 4.
एनीमेशन क्या है ?
उत्तर-
किसी भी वस्तु को गतिमान करने की क्षमता को एनीमेशन कहते हैं।

प्रश्न 5.
स्लाइड पर नोट लिखो।
उत्तर–
पावर प्वाइंट प्रेजेंटेशन के एक पेज़ को स्लाइड कहते हैं। प्रेजेंटेशन के समय स्क्रीन पर एक स्लाइड एक समय दिखाई देती है।

Punjab State Board PSEB 8th Class Computer Book Solutions Chapter 3 सूचना टैकनॉलोजी से जान पहचान Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Computer Chapter 3 सूचना टैकनॉलोजी से जान पहचान

Computer Guide for Class 8 PSEB सूचना टैकनॉलोजी से जान पहचान Textbook Questions and Answers

1. रिक्त स्थान भरें

1. …………………………….. का अर्थ है कम्प्यूटर इंटरनेट से डाटा प्राप्त कर रहा है।
(क) अपलोडिंग
(ख) डाऊनलोडिंग
(ग) सर्किंग
(घ) कोई नहीं।
उत्तर-
(ख) डाऊनलोडिंग

2. वैबसाइट का जो पेज खुलता है उसे ……………………… कहते हैं।
(क) होम पेज़
(ख) वैब पेज
(ग) मेन पेज
(घ) कोई नहीं।
उत्तर-
(क) होम पेज़

3. ………………………………. का अर्थ है इंटरनेट से जुड़े होना।
(क) ऑफलाइन
(ख) ऑनलाइन
(ग) इन लाइन
(घ) कोई नहीं।
उत्तर-
(ख) ऑनलाइन

4. ……………………………………….. का अर्थ है एक वैबसाइट से दूसरी पर जाना।
(क) सर्किंग
(ख) सचिंग
(ग) डाऊनलोडिंग
(ग) सारे ही।
उत्तर-
(क) सर्किंग

5. ……………………………….. एक प्रकार का इलैक्ट्रॉनिक कॉमर्स है जो उपभोक्ताओं को सीधा ही इंटरनैट से वस्तुएं खरीदने की आज्ञा देता है।
(क) मोडम
(ख) ई-मेल
(ग) ई-कॉमर्स
(ग) मोबाइल।
उत्तर-
(ग) ई-कॉमर्स

2. सही या गलत बताएँ

1. किसी भी बोर्ड या यूनिवर्सिटी का ऑनलाइन देखा जा सकता है।
उत्तर-
सही

2. हम अगर ऑफ लाइन हो तो सर्किंग कर सकते हैं।
उत्तर-
गलत

3. वैबसाइट में एक ही पेज होता है।
उत्तर-
गलत

4. वैब सर्च के साथ हम अपने पेज देख सकते हैं।
उत्तर-
गलत

5. हर पेज का अपना वैबसाइट एडरैस होता है।
उत्तर-
सही।

3. छोटे उत्तर वाले प्रश्न

प्रश्न 1.
इन्फारमेशन (सूचना) टैकनॉलोजी क्या है ?
उत्तर-
इसमें टैलीफोन और कम्प्यूटर टैकनॉलोजी दोनों ही शामिल हैं। सूचना टैकनॉलोजी की मदद से हम एक कम्प्यूटर से अलग-अलग प्रकार का डाटा दूसरे कम्प्यूटर पर भेज सकते हैं। डाटा किसी भी प्रकार का हो सकता है। जैसे-लिखति, ध्वनि वाला, वीडियो, ग्राफिकल आदि।

प्रश्न 2.
वैबसाइट क्या है ?
उत्तर-
एक या एक से ज्यादा वैब पेजों के समूह को वैबसाइट कहा जाता है।

प्रश्न 3.
सचिंग क्या होती है ?
उत्तर-
सचिंग का अर्थ है कुछ ढूंढना। वेब सर्च वेब पेजों को ढूंढने की एक प्रक्रिया होती है। इसका प्रयोग तब किया जाता है जब यूजर को यह मालूम नहीं होता कि कोई वस्तु इंटरनेट पर कहां पर मिलेगी इसके लिए वेब सर्च इंजन का प्रयोग किया जाता है। Google, Yahoo तथा Bing कुछ आम प्रयोग होने वाले सर्च इंजन हैं।

प्रश्न 4.
ऑनलाइन तथा ऑफ लाइन के बारे में बताओ।
उत्तर-
ऑफलाइन-ऑफलाइन का अर्थ है इंटरनेट से जुड़े न होने की अवस्था। इस स्थिति में इंटरनेट का प्रयोग नहीं कर सकते। ऑनलाइन-इंटरनेट के साथ जुड़े होने की अवस्था को ऑनलाइन कहा जाता है। इसमें हम इंटरनेट पर कई कार्य कर सकते हैं।

4. बड़े उत्तर वाले प्रश्न

प्रश्न 1.
इन्फारमेशन टैकनॉलोजी की आवश्यकता की व्याख्या करो।
उत्तर-
इन्फारमेशन टैकनॉलोजी की आवश्यकता निम्नलिखित कारणों से है –

1. सरकारी संस्थानों के बिलों का भुगतान का प्रिंट निकलाने के लिए
2. व्यापार तथा उद्योगों में काम करवाने तथा उत्पादन को बढ़ाने के लिए
3. ई-मेल तथा चैटिंग द्वारा दूसरे लोगों तक संदेश पहुँचाने के लिए
4. शिक्षा संबंधी तथा ज्ञान विज्ञान की जानकारी प्राप्त करने के लिए
5. ऑडियो तथा वीडियो फिल्में देखने के लिए।

प्रश्न 2.
ऑनलाइन रिजल्ट देखने का तरीका बताओ।
उत्तर-
ऑनलाइन रिजल्ट निम्न ढंग से देखा जाता है

1. अपने कम्प्यूटर पर वैब ब्राओजर जैसे कि इंटरनेट एक्सप्लोरर या मोजिला फायरफॉक्स आदि खोलो।
2. एडरैस बार में, जिस बोर्ड या यूनिवर्सिटी का रिजल्ट देखना है, उसका पता टाइप करो, जैसे-www.pseb.ac.in

प्रश्न 3.
मोबाइल टैकनॉलोजी पर एक नोट लिखो।
उत्तर-
मोबाइल टैकनॉलोजी का अर्थ मोबाइल की सहायता से टैकनॉलोजी का प्रयोग करने से है। इस टैकनॉलोजी ने संसार के दूरवर्ती क्षेत्रों का संचार के क्षेत्र में चेहरा पूरी तरह बदल दिया है। मोबाइल टैकनॉलोजी के कुछ प्रयोग क्षेत्र निम्न अनुसार हैं।

1. शिक्षा
2. निरीक्षण तथा पोलिंग
3. बैंकिंग
4. डाटा एनालिसिस

प्रश्न 4.
ऑनलाइन शॉपिंग की व्याख्या कीजिए।
उत्तर-
ऑनलाइन शॉपिंग व्यापार का तरीका है जो उपभोक्ता को इंटरनेट का प्रयोग करके वस्तुओं तथा सेवाओं को खरीदने की सहूलत प्रदान करता है। दुकानदार वस्तुओं को इंटरनेट पर उपलब्ध करवाते हैं। खरीददार इंटरनेट का प्रयोग करके उस वस्तु का ऑर्डर देता है। दुकानदार उस वस्तु को खरीददार के घर तक पहुंचा देता है। ऑनलाइन शॉपिंग में खरीददारी का बिल नेट बैंकिंग या क्रेडिट कार्ड आदि द्वारा किया जा सकता है। ऑनलाइन शॉपिंग द्वारा हमें किसी भी दुकान पर जाने की आवश्यकता नहीं होती।

प्रश्न 5.
नेट बैंकिंग क्या है व्याख्या करो।
उत्तर-
नेट बैंकिंग, बैकिंग की वह सहूलियत है जिसकी मदद से ग्राहक इंटरनेट का प्रयोग करके अपने अकाउंट की जानकारी प्राप्त कर सकता है तथा पैसे ट्रांसफर कर सकता है। इंटरनेट की सहायता से बैंक की सहूलतें प्राप्त करना तथा बैंक वाले कार्य करना ही नेट बैंकिंग है। इसके द्वारा हम कई कार्य कर सकते हैं जैसे कि-

1. पैसे ट्रांसफर करना
2. बिल भरना
3. अकाउंट चेक करना
4. फीस भरनी।

एक्टिविटी निम्नलिखित कार्यों में से बताओ कौन-से ऑनलाइन किए जा सकते हैं तथा कौन-से ऑफलाइन किए जा सकते हैं-

1. प्रेजेंटेशन बनाना – ऑनलाइन तथा ऑफलाइन दोनों ही
2. शॉपिंग करना – ऑनलाइन
3. डॉक्यूमेंट बनाना – ऑनलाइन तथा ऑफलाइन दोनों ही
4. बिल भरना – ऑनलाइन
5. बैलेंस शीट बनाना – ऑनलाइन तथा ऑफलाइन दोनों ही
6. वीडियो डाउनलोड करना – ऑनलाइन
7. एग्जाम का रिजल्ट देखना – ऑनलाइन।

PSEB 8th Class Computer Guide सूचना टैकनॉलोजी से जान पहचान Important Questions and Answers

रिक्त स्थान भरो

1. वेबसाइट के एड्रेस को ……. कहा जाता है।
(क) पेज
(ख) URL
(ग) LOC
(घ) www
उत्तर-
(ख) URL

2. हम वेब सर्च इंजन जैसे ……… या …………….. को किसी विषय से संबंधित वेब पेज सर्च करने के लिए प्रयोग करते हैं।
(क) Google
(ख) Facebook
(ग) Bing
(घ) Twitter
उत्तर-
(क) Google

3. URL से अभिप्राय है………………………
(क) Universal Resource Locator
(ख) Uniform Resource Locator
(ग) Unitech Resource Locator
(घ) Unified Resource Locator
उत्तर-
(ख) Uniform Resource Locator

4. मोबाइल टैकनॉलोजी ने संचार का तरीका ………………… दिया है।
(क) शुरू
(ख) खत्म
(ग) बदल
(घ) कोई नहीं।
उत्तर-
(ग) बदल

सही या गलत बताओ-

1. इन्फार्मेशन टैकनॉलोजी कंप्यूटर हार्डवेयर से संबंधित है।
उत्तर-
गलत

2. सचिंग सिर्फ गूगल के लिए प्रयोग किया जाता है।
उत्तर-
गलत

3. डाउनलोडिंग ऑफलाइन भी की जा सकती है।
उत्तर-
गलत

4. नेट बैंकिंग से पैसे ट्रांसफर किए जा सकते हैं।
उत्तर-
सही

5. वेब सर्च का अर्थ है वैब पेजों को देखना।।
उत्तर-
सही।

छोटे उत्तर वाले प्रश्न

प्रश्न 1.
सर्च इंजन के नाम बताओ।
उत्तर-
Google, Yahoo तथा Bing.

प्रश्न 2.
ऑनलाइन शॉपिंग कौन-सी साइट पर होती है ?
उत्तर-
ई-कॉमर्स।

प्रश्न 3.
ऑफलाइन का क्या अर्थ है ?
उत्तर-
ऑफलाइन का अर्थ है इंटरनैट से जुड़े न होना।

प्रश्न 4.
मोबाइल टैकनॉलोजी के मुख्य प्रयोग क्षेत्र कौन-से हैं ?
उत्तर-
शिक्षा, निरीक्षण तथा पोलिंग, बैंकिंग, डाटा एनालिसिस।

प्रश्न 5.
घरों में इंटरनैट टैकनॉलोजी का क्या प्रयोग हो रहा है ?
उत्तर-
ऑडियो वीडियो बनाने के लिए, मनोरंजन के लिए, संचार के लिए, शिक्षा प्राप्त करने के लिए।

प्रश्न 6.
डाउनलोडिंग का क्या अर्थ है ?
उत्तर-
डाउनलोडिंग का अर्थ है इंटरनैट सरवर से कोई फाइल अपने कंप्यूटर पर सेव करना।

प्रश्न 7.
नेट बैंकिंग क्या होती है ?
उत्तर-
नैट बैंकिंग का अर्थ है इंटरनैट का प्रयोग करके बैंक वाले कार्य करना।

प्रश्न 8.
ऑनलाइन शॉपिंग क्या है ?
उत्तर-
ऑनलाइन शॉपिंग का अर्थ है इंटरनैट का प्रयोग करके खरीददारी करना।

प्रश्न 9.
इन्फारमेशन टैकनॉलोजी क्या है ?
उत्तर-
इन्फारमेशन टैकनॉलोजी का अर्थ है तकनीक का प्रयोग करके जानकारी प्राप्त करना तथा भेजना।

प्रश्न 10.
वेबसाइट क्या होती है ?
उत्तर-
वेब पेजों के समूह को वेबसाइट कहा जाता है।

प्रश्न 11.
मोबाइल टैकनॉलोजी का क्या अर्थ है ?
उत्तर-
मोबाइल टैकनॉलोजी का अर्थ है मोबाइल फोन की मदद से इंटरनेट के माध्यम से संचार तथा अन्य ऑनलाइन कार्यों के लिए टैकनॉलोजी का प्रयोग करना।

प्रश्न 12.
आनलाइन शापिंग का क्या लाभ है ?
उत्तर-
आनलाइन शापिंग से उपभोक्ता घर बैठ कर ही सारी खरीददारी कर सकती है।

प्रश्न 13.
नेट बैंकिंग क्या है ?
उत्तर-
नैट बैंकिंग, बैंकिंग का वह सिस्टम है जिसमें ग्राहक इंटरनैट की मदद से अपने अकाऊंट की जानकारी प्राप्त कर सकता है, बिल अदा कर सकता है तथा पैसे ट्रांसफर कर सकता है।

प्रश्न 14.
डाऊनलोडिंग से आप क्या समझते हो ?
उत्तर-
डाऊनलोडिंग का अर्थ है कि हमारा कम्प्यूटर इंटरनैट से डाटा प्राप्त कर रहा है।

प्रश्न 15.
वैब सर्किंग क्या होती है ?
उत्तर-
वैब सर्किंग का अर्थ है इंटरनैट पर एक वैबसाइट से दूसरी वैबसाइट पर कुछ विषय वस्तु ढूंढ़ते हुए जाना।

Punjab State Board PSEB 8th Class Computer Book Solutions Chapter 2 इंटरनैट फंडामैंटल्स Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Computer Chapter 2 इंटरनैट फंडामैंटल्स

Computer Guide for Class 8 PSEB इंटरनैट फंडामैंटल्स Textbook Questions and Answers

1. रिक्त स्थान भरें

1. इंटरनैशनल नैटवर्क ऑफ कम्प्यूटर को ……….. कहा जाता है।
(क) अपरानैट
(ख) इंटरनेट
(ग) इंटरानैट
(घ) इथरनैट।
उत्तर-
(ख) इंटरनेट

2. www का मतलब है ……………।
(क) वर्ल्ड वाइड वैब
(ख) वाइड वैब वर्ल्ड
(ग) वाइड वर्ल्ड वैब
(घ) वैब वर्ल्ड वाइड।
उत्तर-
(क) वर्ल्ड वाइड वैब

3. …………. द्वारा आनलाइन इंटरनैट से बातचीत की जाती है।
(क) ई-कामर्स
(ख) चैटिंग
(ग) www
(घ) कोई नहीं।
उत्तर-
(ख) चैटिंग

4. …………. मेल भेजने का सबसे तेज़ तरीका है।
(क) टैलीग्राम
(ख) लैटरज़
(ग) आई० एस ० पी०
(घ) ई-मेल।
उत्तर-
(घ) ई-मेल।

5. ………. एक यंत्र है जो कम्प्यूटर को टैलीफोन से जोड़ता है।
(क) मोडम
(ख) टैलीफोन तार
(ग) माऊस
(घ) मोबाइल।
उत्तर-
(क) मोडम

2. पूरे नाम लिखो

1. www
2. Email
3. MODEM
4. ARPANET
5. ISDN
6. DSL
Answer:
1. WWW-World Wide Web
2. Email-Electronic Mail
3. MODEM–Modulator Demodulator
4. ARPANET-Advanced Research Project Agency Network
5. ISDN-Integrated Service Digital Network
6. DSL-Digital Subscriber Line

3. छोटे उत्तर वाले प्रश्न

प्रश्न 1.
इंटरनैट क्या है?
उत्तर-
दुनिया में फैले अलग-अलग तरह के नैटवर्कों को आपस में जोड़कर इंटरनैट बनता है। इससे सूचना का आदान-प्रदान करवाया जा सकता है। इंटरनेट का इस्तेमाल नीचे लिखे कामों के लिए किया जाता है-

1. व्यापार और उद्योगों के लिए
2. संचार के लिए
3. शिक्षा के लिए
4. मनोरंजन के लिए
5. विज्ञान के लिए
6. सिखलाई के लिए।

प्रश्न 2.
इंटरनेट सर्विस प्रोवाइडर (ISP) की उदाहरण दें।
उत्तर-
इंटरनैट सर्विस प्रोवाइडर्ज यूज़र को इंटरनेट की सुविधा प्रदान करवाता है। वह यूज़र से फीस प्राप्त करता है। यह फीस इंटरनैट इस्तेमाल करने के हिसाब से होती है।
इंटरनेट की अलग-अलग सेवाओं के लिए आपको अपने ISP (इंटरनेट सर्विस प्रोवाइडर) में खाता खोलना पड़ेगा। BSNL एक ISP का उदाहरण है।

प्रश्न 3.
ई-कॉमर्स से आप क्या समझते हैं ?
उत्तर-
इंटरनेट का उपयोग करके व्यापार करने तथा शापिंग करने वाली सुविधा को ई-कॉमर्स कहते हैं।

प्रश्न 4.
वैब ब्राऊजिंग क्या है ?
उत्तर-
इंटरनैट पर ब्राऊजर की मदद से विभिन्न वैब साईट को देखने की प्रक्रिया वैब ब्राऊजिंग कहलाती है। इस से हम सूचना देख सकते हैं, ढूंढ सकते हैं तथा लोगों को भी ढूंढ सकते हैं।

4. बड़े उत्तर वाले प्रश्न

प्रश्न 1.
MODEM क्या है? मोडम की किस्में तथा रफ्तार बताओ।
उत्तर-
डिजीटल से एनालॉग सिग्नल और एनालोग से डिजीटल सिग्नल में बदलने वाले उपकरण को मोडम कहा जाता है। मोडम दो प्रकार के होते हैं

1. अन्दरूनी मोडम
2. बाहरी मोडम बाहरी मोडम एक डिब्बे के रूप में कम्प्यूटर से बाहरी तरफ से केबल से जोड़े जाते हैं।

अन्दरूनी मोडम कम्प्यूटर के बीच ही लगे होते हैं। मोडम की रफ़्तार भी अलग-अलग होती है। धीमे मोडम सन्देश को भेजते समय अधिक समय लगाते हैं। केबल या टेलीफोन की तार दीवार से लगे प्लग के द्वारा मोडम में जाती है। आजकल तो बेतार मॉडम भी आ गए हैं जो मोबाइल फोन की तरह हवा में ही काम करते हैं।

मोडम की रफ़्तार अलग-अलग होती है। धीमे मोडम सन्देश भेजते या प्राप्त करते समय अधिक समय लगाते हैं। यह इंटरनेट से फाइलों की नकल करने पर भी अधिक समय लगाते हैं। अगर संचार वाले दोनों कम्प्यूटरों में अलग-अलग रफ़्तार वाले मोडम हों तो संचार कम रफ्तार वाले मोडम की रफ्तार के साथ होता है। तेज़ संचार करवाने के लिए अधिक रफ़्तार वाले मोडम ही प्रयोग करने चाहिए। आमतौर पर 28.8 Kbps रफ़्तार वाला मोडम प्रयोग किया जाता है। सर्किंग के लिए कम-से-कम 56 Kbps वाले मोडम की सिफारिश की जाती है।

प्रश्न 2.
इंटरनेट द्वारा प्रदान की जाने वाली सुविधाओं का वर्णन करो।
उत्तर-
इंटरनेट द्वारा निम्नलिखित सुविधाएं मिलती हैं-
1. ख़बर तथा जानकारी प्राप्त करना-इंटरनेट से हम ऑनलाइन अख़बार से ख़बरें पढ़ सकते हैं। इससे हम देश-विदेश की किसी भी प्रकार की जानकारी प्राप्त कर सकते हैं।

2. कला तथा मनोरंजन-इंटरनेट पर हम गेम खेल सकते हैं, गाने सुन सकते हैं, फिल्में देख सकते हैं, चुटकुले कहानियां आदि पढ़ सकते हैं। इंटरनेट की सहायता से इन सभी के द्वारा हम अपना मनोरंजन कर सकते हैं।

3. खरीदारी-इंटरनेट की सहायता से हम दुनिया में कहीं से भी कपड़े, किताबें, गिफ्ट या अन्य ज़रूरी सामान आदि खरीद सकते हैं। इस प्रक्रिया को ऑनलाइन शॉपिंग कहा जाता है।

4. पत्र भेजना-इंटरनेट पर पत्र भेजने की सर्विस को ईमेल कहते हैं। इंटरनेट की सहायता से हम दुनिया । में किसी भी व्यक्ति को ईमेल भेज सकते हैं तथा किसी से भी ईमेल प्राप्त कर सकते हैं। ईमेल के जरिए हम तस्वीरें, फिल्में, आवाज़ आदि दूसरों को भेज सकते हैं।

5. सेहत तथा तंदुरुस्ती-इंटरनेट के द्वारा हम अपने स्वास्थ्य से संबंधित किसी भी प्रकार की जानकारी प्राप्त कर सकते हैं। इसके द्वारा हम किसी भी डॉक्टर से ज़रूरी सलाह भी कर सकते हैं।

6. सैर सपाटा-इंटरनेट पर दुनिया भर के सैर सपाटे से संबंधित जानकारी रेल टिकट, हवाई टिकट तथा विभिन्न होटलों के बारे में जानकारी प्राप्त की जा सकती है।

7. चैटिंग-इंटरनेट के द्वारा हम दुनिया में किसी भी व्यक्ति के साथ टैक्सट, ऑडियो या वीडियो चैट कर सकते हैं।

8. बैंकिंग-इंटरनेट की सहायता से हम अपने बैंक के कार्य भी कर सकते हैं। ऑनलाइन बैंकिंग के द्वारा बैंक से संबंधित लगभग सभी कार्य किए जा सकते हैं।

9. वीडियो कॉन्फ्रेंसिंग-वीडियो कॉन्फ्रेंसिंग में दो या दो से ज्यादा व्यक्ति एक-दूसरे को देख कर बात करते हैं। इसके लिए वेब कैमरे का प्रयोग किया जाता है।

प्रश्न 3.
ई-मेल क्या है ? इसके प्रयोग के लाभ लिखो।
उत्तर-
ई-मेल एक इलैक्ट्रॉनिक मेल है जिसके द्वारा कम्प्यूटर से पत्र भेजे जाते हैं। इसके द्वारा दुनिया भर में कहीं भी एक ही समय सन्देश पहुँचाया जा सकता है। इंटरनेट इस्तेमाल करने के समय आपके पास विलक्षण ई-मेल पता होना चाहिए। ई-मेल के पते को दो हिस्सों में बांटा जा सकता है, यूज़र नेम और होस्ट नेम। ई-मेल में @ संकेत होता है जिसको ‘ऐट दा रेट ऑफ’ कहा जाता है। [email protected] ई-मेल के पते की एक उदाहरण है।

ई-मेल के लाभ-ई-मेल के बहुत सारे लाभ हैं जो कि नीचे लिखे अनुसार हैं-
1. खर्च (Cost)-इंटरनैट के प्रयोग के लिए दी जाने वाली रकम के बिना अन्य कुछ नहीं लगता। यूज़र को डाक टिकटों के पैसे नहीं पड़ते। यह फैक्स से भी सस्ती पड़ती है। फैक्स पर कागज़ और टैलीफोन के खर्चे पड़ते हैं। ई-मेल करते समय ऐसा कोई खर्चा नहीं पड़ता। लम्बे सन्देश का खर्च छोटे सन्देश जितना होता है। उदाहरण के लिए स्विट्ज़रलैंड और अपने शहर में सन्देश का खर्च बराबर होता है।

2. रफ़्तार (Speed)-ई-मेल की रफ्तार हमारे दूसरे चिट्ठी-पत्र से अधिक होती है। ई-मेल सन्देश अपनी मंजिल पर कुछ मिनटों-सैकिण्डों में पहुंच जाते हैं। एक दिन में कई बार पत्र-व्यवहार किया जा सकता है।

3. आराम (Convenience)-कम्प्यूटर का इस्तेमाल करने वाले सन्देश को अपने कम्प्यूटर पर टाइप करते हैं और फिर ई-मेल कर देते हैं। इसके साथ न कागज़ का प्रयोग होता है, न कोई डाक खर्चा आता है और न ही कोई अन्य समस्या आती है।

प्रश्न 4.
वर्ल्ड वाइड वेब पर एक नोट लिखो।
उत्तर-
वर्ल्ड वाइड वेब एक बहुत बड़ा कंप्यूटर नेटवर्क है जिसे हम इंटरनेट एक्सप्लोरर या गूगल क्रोम जैसे ब्राउज़र का प्रयोग करके सर्च कर सकते हैं। इससे हम आवश्यकता अनुसार जानकारी तथा सूचना प्राप्त कर सकते हैं। यह बहुत सारी पब्लिक वेबसाइट का समूह है जो आपस में हाइपरलिंक की सहायता से जुड़े हुए हैं। इसमें वेबसाइट के साथ क्लाइंट उपकरण जैसे कि कंप्यूटर मोबाइल फोन आदि भी शामिल होते हैं जो पूरी दुनिया में इंटरनेट से जुड़े होते हैं।

वर्ल्ड वाइड वेब तथा इंटरनेट इकट्ठे ही कार्य करते हैं, पर यह दोनों एक समान नहीं हैं। असल में वर्ल्ड वाइड वेब इंटरनेट पर फैला हुआ वैब पेजों का एक जाल है। यह सारे वेब पेज एचटीएमएल में बने होते हैं तथा आपस में हाइपरलिंक द्वारा जुड़े होते हैं। हाइपरलिंक द्वारा आपस में जुड़े होने के कारण इनका एक जाल बन जाता है जो पूरी दुनिया में फैला होता है। इसी कारण इसे वर्ल्ड वाइड वेब कहा जाता है।

प्रश्न 5.
इंटरनेट द्वारा प्रदान की जाने वाली मुख्य सेवाओं का वर्णन करो।
उत्तर-
1. वर्ड वाइड वैब-वर्ड वाइड वैब इंटरनैट पर वैब पेज का एक जाल है। ये पेज आपस में लिंकड होते हैं। इस को किसी खास एडरैस द्वारा पाया जाता है। इसको कम्प्यूटर, लैपटाप, मोबाइल, आदि पर असैस किया जा सकता है। वर्ल्ड वाइड वैब Www इंटरनैट की बहुत बड़ी सेवा है। इसके द्वारा पूरी दुनिया की सूचना प्राप्त की जा सकती है। इसमें व्यापार, शिक्षा स्रोत, सेहत और सरकारी अदारों आदि से सम्बन्धित सूचना शामिल होती है। यह हर एक स्थान पर यूज़र की सोच, विचारों और पसंद के मुताबिक सेवाएं देती हैं।

2. ई-मेल-ई-मेल एक इलैक्ट्रॉनिक मेल है जिसके द्वारा कम्प्यूटर से पत्र भेजे जाते हैं। इसके द्वारा दुनिया भर में कहीं भी एक ही समय सन्देश पहुँचाया जा सकता है। इंटरनेट इस्तेमाल करने के समय आपके पास विलक्षण ई-मेल पता होना चाहिए। ई-मेल के पते को दो हिस्सों में बांटा जा सकता है, यूजर नेम और होस्ट नेम। ई-मेल में @ संकेत होता है जिसको ‘ऐट दा रेट ऑफ’ कहा जाता है। [email protected] ई-मेल के पते की एक उदाहरण है।

3. ई-कामर्स-ई-कामर्स इंटरनैट पर व्यापार को करते हैं। इससे हम अपनी ज़रूरत की वस्तुएं 24 घंटे खरीद, बेच सकते हैं।

4. सोशल नेटवर्किंग साइट-यह इंटरनैट पर सोशल ग्रुप की साइट होती है। इसमें यूज़र अपना प्रोफाइल बना कर दूसरों से वार्तालाप तथा अपने अनुसार शेयर कर सकता है।

5. विडीयो कानसिंग-यह कैमरे का उपयोग करती है। इसमें हम तस्वीरों तथा आवाज़ द्वारा अपने विचार दूसरों से साझा कर सकते हैं। हम दूसरों को देख भी सकते हैं। इसमें समय की बहुत बचत होती है।

6. चैटिंग-यह फोन पर की जाने वाली बातचीत की तरह ही होती है। फर्क सिर्फ इतना है कि इसमें बातचीत के लिए शब्दों का इस्तेमाल किया जाता है। अगर आप इंटरनेट से जुड़े हो तो आप टैलीफोन में बोलने के स्थान पर कम्प्यूटर में टाइप करोगे। आजकल व्याँस चैट (जुबान के द्वारा चर्चा) करनी भी सम्भव हो गई है। व्यॉस चैट में आप बोल और सुन सकते हो।

7. वैबसाइट को सर्च करना-वैबसाइट पर पन्नों की गिनती निश्चित नहीं होती। यह अनगिनत होते हैं। यह बढ़ते ही रहते हैं। बड़ी कम्पनियां अपने वैब पन्नों को डाटाबेस में सम्भाल के रखती हैं। जानकारी ढूँढ़ने के लिए सर्च इंजन का प्रयोग किया जाता है। यह बहुत ही शक्तिशाली प्रोग्राम होता है। ढूँढ़ी जाने वाली जानकारी को टाइप करके सर्च (खोज) की जाती है। यह उस शब्द से सम्बन्धित अनेकों वैबसाइटों की सूची जारी करता है।

PSEB 8th Class Computer Guide इंटरनैट फंडामैंटल्स Important Questions and Answers

रिक्त स्थान भरो

1. मोडम ……….. को एनालॉग सिग्नल में बदलता है।
(क) एनालॉग
(ख) डिजिटल
(ग) दोनों ही
(घ) कोई भी नहीं।
उत्तर-
(ख) डिजिटल

2. ……… ऑनलाइन बातचीत का तरीका है।
(क) चैटिंग
(ख) ईमेल
(ग) सचिंग
(घ) कोई भी नहीं।
उत्तर-
(क) चैटिंगग।

2. पूरा नाम लिखो
1. DOD
2. TCP/IP
3. IAP
4. URL
5. ISP
Answer:
1. DOD – Department of Defence
2. TCP/IP-Transmission Control Protocol/Internet Protocol
3. IAP-Internet Access Providers
4. URL-Uniform Resource Locator
5. ISP-Internet Service Provider

छोटे उत्तर वाले प्रश्न

प्रश्न 1.
सोशल नेटवर्किंग साइट क्या होती है ?
उत्तर-
सोशल नेटवर्किंग साइट वह होती है जो हमें ऑनलाइन सामाजिक समूह बनाने में मदद करती है। facebook.com एक सोशल नेटवर्किंग साइट है।

प्रश्न 2.
कुछ सोशल नेटवर्किंग साइट के नाम बताओ।
उत्तर-
Facebook, Twitter, Orkut, Linkedin, Fickr

प्रश्न 3.
वीडियो कॉन्फ्रेंसिंग क्या होती है ?
उत्तर-
वीडियो कॉन्फ्रेंसिंग वह सहूलियत है जिसके द्वारा हम किसी भी दूसरे व्यक्ति की वीडियो देख कर उसके साथ बातचीत कर सकते हैं।

प्रश्न 4.
ब्राउजिंग क्या होती है ?
उत्तर-
इंटरनेट पर वेब साइट देखने की प्रक्रिया को ब्राउजिंग कहते हैं।

प्रश्न 5.
इंटरनेट कनेक्शनों के नाम बताओ।
उत्तर-
डायल अप, ब्रॉडबैंड, वायरलेस, डी० एस० एल०, आई० एस० डी० एन०।

प्रश्न 6.
मोडम का पूरा नाम बताओ।
उत्तर-
मोडूलेटर-डीमोडूलेटर।

प्रश्न 7.
मोडम की किस्में बताओ।
उत्तर-
मोडम की निम्नलिखित किस्में हैं –

1. अंदरूनी मॉडल
2. बाहरी मॉडल

प्रश्न 8.
ISP का पूरा नाम बताओ।
उत्तर-
ISP का पूरा नाम है-Internet Service Provider.

प्रश्न 9.
URL का पूरा नाम बताओ।
उत्तर-
URL का पूरा नाम है-Uniform Resource Locator.

प्रश्न 10.
www क्या है ? बताओ।
उत्तर-
www का अर्थ है-वर्ल्ड वाइड वैब। यह इंटरनैट पर फैला हुआ वैबसाइटों का एक जाल है।

प्रश्न 11.
इंटरनैट कुनैक्शनों की किस्में बताएं।
उत्तर-
इंटरनैट कुनैक्शन इस प्रकार के होते हैं-

1. डायल-अप कुनैक्शन
2. ब्रॉड बैंड
3. वायरलैस
4. डी० एस० एल०
5. आई० एस० डी० एन० ।

प्रश्न 12.
ई-मेल के बारे में बताओ।
उत्तर-
ई-मेल इंटरनैट की एक वह सुविधा है जिसके द्वारा दुनिया में किसी भी कम्प्यूटर, जो इंटरनैट से जुड़ा हो, तक संदेश भेज सकते हैं।

प्रश्न 13.
वैब सचिंग क्या है?
उत्तर-
इंटरनैट पर किसी भी वस्तु को ढूंढ़ने की प्रक्रिया को वैब सचिंग कहते हैं।

प्रश्न 14.
इंटरनेट के लिए कौन-कौन से हार्डवेयर ज़रूरी हैं ?
उत्तर-
इंटरनैट के लिए निम्न हार्डवेयर ज़रूरी है-

1. एक पर्सनल कम्प्यूटर जिसकी स्पीड 800 Mz या ज्यादा हो।
2. 128 MB या ज्यादा RAM
3. टैलीफोन कुनैक्शन लाइन
4. मोडम।

Punjab State Board PSEB 8th Class Computer Book Solutions Chapter 1 टाइपिंग ट्यूटर Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Computer Chapter 1 टाइपिंग ट्यूटर

Computer Guide for Class 8 PSEB टाइपिंग ट्यूटर Textbook Questions and Answers

1. रिक्त स्थान भरो

1. ………. फोंट का प्रयोग पंजाबी में टाइप करने के लिए किया जाता है।
(क) अनमोल लिपि
(ख) रावी
(ग) जोआए
(घ) उपरोक्त सभी।
उत्तर-
(घ) उपरोक्त सभी।

2. अनमोल लिपि के साथ टाइप करते समय बाएं हाथ की छोटी उंगली से होम रोअ की ………………………… कीअ दबाई जाती है |
(क) θ/ਅ
(ख) म/म
(ग) र/प
(घ) ਢ/ह
उत्तर-
(क) θ/ਅ

3. अनमोल लिपि को टाइप करते समय बाएं हाथ की रिंग उंगली के साथ दूसरी रोअ की ………………………. .
कीअ दवाई जाती है।
(क) उ/ਬ
(ख) \(\mathrm{T} / \dot{\mathrm{T}}\)
(ग) ट/6
(घ) ਰ/;
उत्तर-
(ख) \(\mathrm{T} / \dot{\mathrm{T}}\).

4. अनमोल लिपि टाइप करते समय दाएं हाथ की इंडेक्स उंगली के साथ तीसरी रोअ की ………………. कीअ दवाई जाती है |
(क) घ/उ
(ख) ਨ/ \(\dot{\mathrm{T}}\)
(ग) ਮ/”
(घ) ਮ/ ਨ/
उत्तर-
(ख) ਨ/ \(\dot{\mathrm{T}}\)

5. नंबर पैड का प्रयोग करने के लिए ……………………….. कीअ ON रखनी चाहिए।
(क) Num Lock
(ख) Caps Lock
(ग) Scroll Lock
(घ) इनमें से कोई भी नहीं।
उत्तर-
(क) Num Lock

2. सही या गलत बताओ-

1. टाइपिंग करने के लिए कीबोर्ड को दो हिस्सों में बांटा गया है एक बाएं हाथ के लिए तथा एक दाएं हाथ के लिए।
उत्तर-
सही

2. टच टाइपिंग एक ऐसी तकनीक है जिसके द्वारा हम कीबोर्ड को देखते हुए तेज़ रफ़्तार से टाइपिंग करना सीख सकते हैं।
उत्तर-
गलत

3. अनमोल लिपि फोंट हमें पंजाबी में टाइप करने में मदद करता है।
उत्तर-
सही

4. स्पेस बार कीअ दबाने के लिए हम छोटी उंगली का प्रयोग करते हैं।
उत्तर-
गलत

5. Shift कीअ का प्रयोग अगली लाइन में जाने के लिए किया जाता है।
उत्तर-
गलत।

3. छोटे उत्तर वाले प्रश्न

प्रश्न 1.
टच टाइपिंग क्या होती है ?
उत्तर-
टच टाइपिंग एक ऐसी तकनीक है जिसके द्वारा हम बिना कीबोर्ड को देखें अपनी सारी उंगलियों का प्रयोग करके तेज़ रफ्तार से टाइपिंग करनी सीख सकते हैं अगर हम कीबोर्ड देखकर एक एक कीअ ढूंढ कर टाइपिंग करते हैं तो हमारी स्पीड बहुत कम हो जाती है।

प्रश्न 2.
होम रोअ पर हमारी उंगलियों की स्थिति का वर्णन करो।
उत्तर-
होम रोअ पर हमारी उंगलियों की स्थिति निम्न अनुसार होती है-
सबसे पहले हमारे बाएं हाथ की चौथी उंगली (लिटिल फिंगर) A कीअ ऊपर, तीसरी उंगली S कीअ के ऊपर, दूसरी उंगली D कीअ के ऊपर तथा पहली उंगली F कीअ के ऊपर तथा साथ ही G कीअ के ऊपर होनी चाहिए। दाएं हाथ की चौथी तीसरी दूसरी तथा पहली उंगली क्रमवार ; L, K, J, H पर होनी चाहिए।

प्रश्न 3.
पंजाबी भाषा में टाइपिंग किस प्रकार की जाती है ?
उत्तर-
अनमोल लिपि फोंट द्वारा हम आसानी से पंजाबी में टाइपिंग कर सकते हैं। हम अंग्रेजी भाषा की टाइपिंग में प्रयोग होने वाली उंगलियों की स्थिति के अनुसार पंजाबी भाषा में भी टाइपिंग का अभ्यास कर सकते हैं। टाइप करने से पहले हमें अनमोल लिपि फोंट का चुनाव करना पड़ता है।

प्रश्न 4.
पंजाबी भाषा में टाइप करने के लिए कोई तीन फोंट का नाम लिखो ?
उत्तर-
पंजाबी भाषा में टाइप करने के लिए 3 फोंट निम्नानुसार हैं-

1. अनमोल,
2. रावी,
3. जोआए।

4. बड़े उत्तर वाले प्रश्न

प्रश्न 1.
हम अपनी टाइपिंग की स्पीड कैसे बढ़ा सकते हैं ?
उत्तर-
टाइपिंग स्पीड को निम्न हिदायतों का प्रयोग कर बढ़ाया जा सकता है-

1. हमारे हाथ की उंगलियां होम रोअ पर होनी चाहिए।
2. हमें हमेशा यहीं से शुरू कर वापिस आना चाहिए।
3. होम रोअ की पोजीशन से बाकी कीज़ तक पहुंचो।
4. अपना ध्यान सही कीअ दबाने पर रखो।।
5. कीअ-बोर्ड को मत देखो।
6. लगातार, आराम से तथा सही टाइप करने की तरफ ध्यान रखें।
7. जिस भी कीअ को दबाओ उसको मन में दोहराओ।

प्रश्न 2.
अनमोल लिपि का कीअ मैप बनाएं।
उत्तर-

PSEB 8th Class Computer Guide टाइपिंग ट्यूटर Important Questions and Answers

रिक्त स्थान भरें

1. टाइप मास्टर …………. सिखाने के लिए प्रयोग होता है।
(क) प्रोग्रामिंग
(ख) कम्प्यू टर
(ग) प्रिंटिंग
(घ) टाइपिंग।
उत्तर-
(घ) टाइपिंग।

2. कीअ-बोर्ड ………… भागों में बांटा जाता है।
(क) तीन
(ख) चार
(ग) दो
(घ) पांच।
उत्तर-
(ग) दो

3. न्यूमैरिक पैड …………. तरफ होते हैं।
(क) दायें
(ख) वायें
(ग) ऊपर
(घ) नीचे।
उत्तर-
(क) दायें

4. …………… की, कीअ-बोर्ड के दोनों तरफ होती है।
(क) फंक्श न
(ख) स्पैशल
(ग) ऐरो
(घ) शिफ्ट।
उत्तर-
(घ) शिफ्ट।

सही या ग़लत बताएँ

1. टाइप मास्टर टाइप की गति में सुधार करने में मदद करता है।
उत्तर-
सही

2. टच टाइपिंग में हम कीअ-बोर्ड को बगैर छुए टाइप कर सकते हैं।
उत्तर-
ग़लत

3. न्यूमैरिक पैड कीअ-बोर्ड के दाईं तरफ होता है।
उत्तर-
सही

4. न्यूमैरिक पैड की सहायता से टैक्सट टाइप किया जाता है।
उत्तर-
ग़लत

5. शिफ्ट कीअ सिर्फ एक होती है।
उत्तर-
ग़लत।

छोटे उत्तर वाले प्रश्न

प्रश्न 1.
कीअ-बोर्ड के प्रयोग के लिए निर्देश लिखें।
उत्तर-

1. कीज़ को जल्दी-जल्दी न दबाएं।
2. कीज़ को बराबर तथा सही ढंग से दबाएं।
3. कीज़ को हल्का दबाने की आदत डालें।
4. प्रत्येक शब्द टाइप करने के बाद दायें अँगूठे से स्पेस बार दबाएं।
5. टाइप के दौरान आपकी आँखों, हाथों तथा दिमाग़ का सही तालमेल होना चाहिए।

प्रश्न 2.
टाइप मास्टर क्या है ?
उत्तर-
टाइप मास्टर एक प्रोग्राम है जो हमें सही तथा तीव्र गति से टाइप करना सीखने में मदद करता है। इसकी सहायता से हम बगैर कीअ-बोर्ड देखे टाइप कर सकते हैं।

प्रश्न 3.
न्यूमैरिक की पैड क्या होता है ?
उत्तर-
यह कीअ बोर्ड के दाईं तरफ न्यूमैरिक कीज़ का ग्रुप होता है। इसका प्रयोग अंक टाइप करने में होता है।

प्रश्न 4.
शिफ्ट-कीअ की परिभाषा दो।
उत्तर-
शिफ्ट-कीअ वह कीअ है जिसका प्रयोग ऊपर वाले चिन्ह तथा बड़े अक्षर टाइप करने के लिए किया जाता है।

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 5 ਅੰਕੜਿਆਂ ਦਾ ਪ੍ਰਬੰਧਨ Ex 5.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 5 ਅੰਕੜਿਆਂ ਦਾ ਪ੍ਰਬੰਧਨ Exercise 5.3

ਪ੍ਰਸ਼ਨ 1.
ਇਹਨਾਂ ਪ੍ਰਯੋਗਾਂ ਵਿਚ ਤੁਸੀਂ ਜੋ ਨਤੀਜਾ ਦੇਖ ਸਕਦੇ ਹੋ ਉਹ ਲਿਖੋ :
(a) ਪਹੀਏ ਨੂੰ ਘੁੰਮਾਉਣਾ ।
(b) ਦੋ ਸਿੱਕਿਆਂ ਨੂੰ ਇੱਕੋ ਵੇਲੇ ਸੁੱਟਣਾ ।
ਹੱਲ:
(a) ਪਹੀਏ ਨੂੰ ਘੁੰਮਾਉਣਾ :
ਸੂਚਕ ਪਹੀਏ ਦੇ ਕਿਸੇ ਵੀ ਭਾਗ ਉੱਤੇ ਜਾ ਸਕਦਾ ਹੈ ।
∴ ਸੰਭਵ ਨਤੀਜੇ A, A, B, C ਅਤੇ D ਹਨ ।

(b) ਦੋ ਸਿੱਕਿਆਂ ਨੂੰ ਇਕ ਵਾਰੀ ਉਛਾਲਣ ਦਾ ਸੰਭਵ ਨਤੀਜਾ ਹੈ :
{HT, HH, TH, TT}
ਇੱਥੇ HT ਦਾ ਅਰਥ ਹੈ ਕਿ ਪਹਿਲੇ ਸਿੱਕੇ ਉੱਤੇ ਚਿਤ (Head) ਅਤੇ ਦੂਸਰੇ ਸਿੱਕੇ ਉੱਤੇ ਪਟ (Tail) ਆਦਿ ।

2. ਜਦੋਂ ਇਕ ਪਾਸੇ ਨੂੰ ਸੁੱਟਿਆ ਜਾਂਦਾ ਹੈ, ਤਦ ਹੇਠ ਲਿਖੀ ਹਰੇਕ ਘਟਨਾ ਨਾਲ ਪ੍ਰਾਪਤ ਹੋਣ ਵਾਲੇ ਨਤੀਜਿਆਂ ਨੂੰ ਲਿਖੋ :

ਪ੍ਰਸ਼ਨ (i).
(a) ਇਕ ਅਭਾਜ ਸੰਖਿਆ
(b) ਇਕ ਅਭਾਜ ਸੰਖਿਆ ਨਹੀਂ
ਹੱਲ:
(a) ਇਕ ਅਭਾਜ ਸੰਖਿਆ :
ਇਕ ਅਭਾਜ ਸੰਖਿਆ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਘਟਨਾ ਦੇ ਨਤੀਜੇ = {1, 3, 5}
(b) ਇਕ ਅਭਾਜ ਸੰਖਿਆ ਨਹੀਂ :
ਇਕ ਅਭਾਜ ਸੰਖਿਆ ਨਹੀਂ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਘਟਨਾ ਦੇ ਨਤੀਜੇ = {2, 4, 6}

ਪ੍ਰਸ਼ਨ (ii).
(a) 5 ਤੋਂ ਵੱਡੀ ਇਕ ਸੰਖਿਆ
(b) 5 ਤੋਂ ਵੱਡੀ ਸੰਖਿਆ ਨਹੀਂ ।
ਹੱਲ:
(a) 5 ਤੋਂ ਵੱਡੀ ਇਕ ਸੰਖਿਆ :
5 ਤੋਂ ਵੱਡੀ ਇਕ ਸੰਖਿਆ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਘਟਨਾ ਦੇ ਨਤੀਜੇ = {6}
(b) 5 ਤੋਂ ਵੱਡੀ ਸੰਖਿਆ ਨਹੀਂ :
5 ਤੋਂ ਵੱਡੀ ਸੰਖਿਆ ਨਹੀਂ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਘਟਨਾ ਦੇ ਨਤੀਜੇ = {1, 2, 3, 4, 5}

ਪ੍ਰਸ਼ਨ 3.
ਪਤਾ ਕਰੋ : (a) ਪ੍ਰਸ਼ਨ 1 (a) ਵਿਚ ਸੂਚਕ ਦੇ D ‘ਤੇ ਰੁੱਕਣ ਦੀ ਸੰਭਾਵਨਾ ।
(b) ਚੰਗੀ ਤਰ੍ਹਾਂ ਫੈਂਟ ਕੇ ਸੁੱਟੀ ਹੋਈ (ਨੇ 52 ਪੱਤਿਆਂ ਦੀ ਇਕ ਤਾਸ਼ ਵਿਚੋਂ 1 ਇੱਕਾ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ ।
(c) ਇਕ ਲਾਲ ਸੇਬ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ । ( ਦਿੱਤੇ ਹੋਏ ਚਿੱਤਰ ਵਿਚ ਦੇਖੋ ) ।

ਹੱਲ:
(a) ਪ੍ਰਸ਼ਨ 1 (a) ਵਿਚ ਸੰਭਵ ਕੁੱਲ ਨਤੀਜੇ = {A, A, B, C, D}
ਸੰਭਵ ਨਤੀਜਿਆਂ ਦੀ ਕੁੱਲ ਸੰਖਿਆ = 5
ਅਨੁਕੂਲ ਨਤੀਜਿਆਂ ਦੀ ਸੰਖਿਆ = 1
ਇਸ ਲਈ, ਸੂਚਕ D ਦੇ ਰੁਕਣ ਦੀ ਸੰਭਾਵਨਾ

(b) ਇੱਕਾ ਪ੍ਰਾਪਤ ਕਰਨ ਦੇ ਅਨੁਕੂਲ ਨਤੀਜਿਆਂ ਦੀ ਗਿਣਤੀ ਨੂੰ = 4
52 ਪੱਤਿਆਂ ਵਿਚੋਂ ਇਕ ਪੱਤਾ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਿਤ ਨਤੀਜਿਆਂ ਦੀ ਗਿਣਤੀ = 52.
ਇਸ ਲਈ, ਪੂਰੀ ਤਾਸ਼ ਵਿਚੋਂ 1. ਇੱਕਾ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ

(c) ਇਕ ਲਾਲ ਸੇਬ ਪ੍ਰਾਪਤ ਕਰਨ ਦੇ ਅਨੁਕੂਲ ਨਤੀਜਿਆਂ ਦੀ ਗਿਣਤੀ = 4
ਸੰਭਵ ਨਤੀਜਿਆਂ ਦੀ ਕੁੱਲ ਗਿਣਤੀ = 7
ਇਸ ਲਈ, ਇਕ ਲਾਲ ਸੇਬ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ

ਪ੍ਰਸ਼ਨ 4.
10 ਵੱਖ-ਵੱਖ ਪਰਚੀਆਂ ‘ਤੇ 1ਤੋਂ 10 ਤਕ ਸੰਖਿਆਵਾਂ ਲਿਖੀਆਂ ਹੋਈਆਂ ਹਨ । ( ਇਕ ਪਰਚੀ ‘ਤੇ ਇਕ ਸੰਖਿਆ ), ਉਸਨੂੰ ਇਕ ਬਕਸੇ ਵਿਚ ਰੱਖ ਕੇ ਚੰਗੀ ਤਰ੍ਹਾਂ ਮਿਲਾ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ । ਬਕਸੇ ਦੇ ਅੰਦਰ ਦੇਖੇ ਬਿਨ੍ਹਾਂ ਇਕ ਪਰਚੀ ਕੱਢੀ ਜਾਂਦੀ ਹੈ । ਹੇਠਾਂ ਲਿਖਿਆਂ ਦੀ ਸੰਭਾਵਨਾ ਕੀ ਹੈ ?
(i) ਸੰਖਿਆ 6 ਪ੍ਰਾਪਤ ਕਰਨਾ
(ii) 6 ਤੋਂ ਛੋਟੀ ਇਕ ਸੰਖਿਆ ਪ੍ਰਾਪਤ ਕਰਨਾ ।
(iii) 6 ਤੋਂ ਵੱਡੀ ਇਕ ਸੰਖਿਆ ਪ੍ਰਾਪਤ ਕਰਨਾ ।
(iv) 1 ਅੰਕ ਦੀ ਇਕ ਸੰਖਿਆ ਪ੍ਰਾਪਤ ਕਰਨਾ ।
ਹੱਲ:
10 ਵੱਖ-ਵੱਖ ਪਰਚੀਆਂ ਉੱਤੇ 1 ਤੋਂ 10 ਤੱਕ ਦੀ ਸੰਖਿਆ ਹੈ :
{1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
ਇਸ ਲਈ, ਸੰਭਵ ਨਤੀਜਿਆਂ ਦੀ ਕੁੱਲ ਗਿਣਤੀ = 10.
(i) ਸੰਖਿਆ 6 ਪ੍ਰਾਪਤ ਕਰਨ ਦੇ ਅਨੁਕੂਲ ਨਤੀਜਿਆਂ ਦੀ ਗਿਣਤੀ = 1
ਇਸ ਲਈ ਸੰਖਿਆ 6 ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ

(ii) 6 ਤੋਂ ਛੋਟੀਆਂ ਸੰਖਿਆਵਾਂ ਹਨ : {1, 2, 3, 4, 5}
ਇਸ ਲਈ, ਅਨੁਕੂਲ ਨਤੀਜਿਆਂ ਦੀ ਗਿਣਤੀ = 5
ਇਸ ਲਈ, 6 ਤੋਂ ਛੋਟੀ ਇਕ ਸੰਖਿਆ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ

(iii) 6 ਤੋਂ ਵੱਡੀਆਂ ਸੰਖਿਆਵਾਂ ਹਨ : {7, 8, 9, 10}
ਇਸ ਲਈ, 6 ਤੋਂ ਵੱਡੀ ਸੰਖਿਆ ਪ੍ਰਾਪਤ ਕਰਨ ਦੇ ਅਨੁਕੂਲ ਨਤੀਜਿਆਂ ਦੀ ਗਿਣਤੀ = 4
ਇਸ ਲਈ: 6 ਤੋਂ ਵੱਡੀ ਸੰਖਿਆ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ

(iv) 1 ਅੰਕ ਦੀਆਂ ਸੰਖਿਆਵਾਂ ਹਨ : {1, 2, 3, 4, 5, 6, 7, 8, 9}
ਇਸ ਲਈ, 1 ਅੰਕ ਦੀ ਸੰਖਿਆ ਪ੍ਰਾਪਤ ਕਰਨ ਦੇ ਅਨੁਕੂਲ ਨਤੀਜਿਆਂ ਦੀ ਗਿਣਤੀ = 9
ਇਸ ਲਈ 1 ਅੰਕ ਦੀ ਇਕ ਸੰਖਿਆ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ

ਪ੍ਰਸ਼ਨ 5.
ਜੇਕਰ ਤੁਹਾਡੇ ਕੋਲ 3 ਹਰੇ ਚੱਕਰਖੰਡ, 1 ਨੀਲਾ ਚੱਕਰਖੰਡ ਅਤੇ 1 ਲਾਲ ਚੱਕਰਖੰਡ ਵਾਲਾ ਇਕ ਘੁੰਮਣ ਵਾਲਾ ਪਹੀਆ ਹੈ ਤਾਂ ਇਕ ਚੱਕਰਖੰਡ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ ਕੀ ਹੈ ? ਇਸ ਤਰ੍ਹਾਂ ਦਾ ਚੱਕਰਖੰਡ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ ਕੀ ਹੈ, ਜੋ ਨੀਲਾ ਨਾ ਹੋਵੇ ?
ਹੱਲ:
ਘੁੰਮਣ ਵਾਲੇ ਪਹੀਏ ਵਿਚ 3 ਹਰੇ ਚੱਕਰਖੰਡ, 1 ਨੀਲਾ ਚੱਕਰਖੰਡ ਅਤੇ 1 ਲਾਲ ਚੱਕਰਖੰਡ ਹੈ ।
∴ ਸੰਭਵ ਨਤੀਜਿਆਂ ਦੀ ਕੁੱਲ ਗਿਣਤੀ
= 3 + 1 + 1 = 5

ਹਰਾ ਚੱਕਰਖੰਡ ਪ੍ਰਾਪਤ ਕਰਨ ਦੇ ਲਈ ਅਨੁਕੂਲ ਨਤੀਜਿਆਂ ਦੀ ਗਿਣਤੀ = 3
ਹਰਾ ਚੱਕਰਖੰਡ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ

ਇਕ ਇਸ ਤਰ੍ਹਾਂ ਦਾ ਚੱਕਰਖੰਡ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ ਜੋ ਨੀਲਾ ਨਹੀਂ ਹੈ = \(\frac{4}{5}\)

ਪ੍ਰਸ਼ਨ 6.
ਪ੍ਰਸ਼ਨ 2. ਵਿਚ ਦਿੱਤੀਆਂ ਗਈਆਂ ਘਟਨਾਵਾਂ ਦੀ ਸੰਭਾਵਨਾ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਇਕ ਪਾਸਾ ਸੁੱਟਣ ਤੇ ਸੰਭਵ ਨਤੀਜਿਆਂ ਦੀ ਕੁੱਲ ਸੰਖਿਆ = 6
(i) (a) ਇਕ ਅਭਾਜ ਸੰਖਿਆ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ ਅਨੁਕੂਲ ਨਤੀਜਿਆਂ ਦੀ ਗਿਣਤੀ = 3
∴ ਇਕ ਅਭਾਜ ਸੰਖਿਆ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ

(b) ਇਕ ਅਜਿਹੀ ਸੰਖਿਆ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ ਜੋ ਅਭਾਜ ਨਹੀਂ ਹੈ।
= \(\frac{3}{6}\) = \(\frac{1}{2}\)

(ii) (a) 5 ਤੋਂ ਵੱਡੀ ਸੰਖਿਆ ਪ੍ਰਾਪਤ ਕਰਨ ਦੇ ਲਈ ਅਨੁਕੂਲ ਨਤੀਜਿਆਂ ਦੀ ਗਿਣਤੀ = 1
∴ 5 ਤੋਂ ਵੱਡੀ ਸੰਖਿਆ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ = \(\frac{1}{6}\)
(b) 5 ਤੋਂ ਵੱਡੀ ਸੰਖਿਆ ਪ੍ਰਾਪਤ ਨਹੀਂ ਕਰਨ ਦੀ ਸੰਭਾਵਨਾ = \(\frac{5}{6}\)

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 5 ਅੰਕੜਿਆਂ ਦਾ ਪ੍ਰਬੰਧਨ Ex 5.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 5 ਅੰਕੜਿਆਂ ਦਾ ਪ੍ਰਬੰਧਨ Exercise 5.2

ਪ੍ਰਸ਼ਨ 1.
ਕਿਸੇ ਸ਼ਹਿਰ ਦੇ ਜਵਾਨ ਵਿਅਕਤੀਆਂ ਦੇ ਇਕ ਗੁੱਟ ਦਾ ਇਹ ਜਾਣਨ ਲਈ ਸਰਵੇ ਕੀਤਾ ਗਿਆ ਕਿ ਉਹ ਕਿਸ ਪ੍ਰਕਾਰ ਦਾ ਸੰਗੀਤ ਪਸੰਦ ਕਰਦੇ ਹਨ । ਇਸ ਤੋਂ ਪ੍ਰਾਪਤ ਅੰਕੜਿਆਂ ਨੂੰ ਨਾਲ ਦਿੱਤੇ ਪਾਈ ਚਾਰਟ ਵਿਚ ਦਰਸਾਇਆ ਗਿਆ ਹੈ । ਇਸ ਪਾਈ ਚਾਰਟ ਵਿੱਚ ਹੇਠਾਂ ਲਿਖੇ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਉੱਤਰ ਦਿਓ :

(i) ਜੇ 20 ਵਿਅਕਤੀ ਸ਼ਾਸਤਰੀ ਸੰਗੀਤ ਪਸੰਦ ਕਰਦੇ ਹਨ, ਤਾਂ ਕੁੱਲ ਕਿੰਨੇ ਜਵਾਨ ਵਿਅਕਤੀਆਂ ਦਾ ਸਰਵੇ ਕੀਤਾ ਗਿਆ ਹੈ ?
(ii) ਕਿਸ ਤਰ੍ਹਾਂ ਦਾ ਸੰਗੀਤ ਸਭ ਤੋਂ ਜ਼ਿਆਦਾ ਵਿਅਕਤੀਆਂ ਦੁਆਰਾ ਪਸੰਦ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ?
(iii) ਜੇ ਕੋਈ ਕੈਸਟ ਕੰਪਨੀ 10 ਸੀ. ਡੀ. (C.D.) ਬਣਾਏ, ਤਾਂ ਉਹ ਹਰੇਕ ਤਰ੍ਹਾਂ ਦੀਆਂ ਕਿੰਨੀਆਂ ਸੀ. ਡੀ. ਬਣਾਵੇਗੀ ?
ਹੱਲ:
(i) ਸ਼ਾਸਤਰੀ ਸੰਗੀਤ ਪਸੰਦ ਕਰਨ ਵਾਲੇ ਵਿਅਕਤੀਆਂ ਦੀ ਗਿਣਤੀ = 20
ਸ਼ਾਸਤਰੀ ਸੰਗੀਤ ਪਸੰਦ ਕਰਨ ਵਾਲੇ ਵਿਅਕਤੀਆਂ ਦਾ ਪ੍ਰਤੀਸ਼ਤ = 10%
ਮੰਨ ਲਉ ਸਰਵੇ ਕੀਤੇ ਗਏ ਜਵਾਨ ਵਿਅਕਤੀਆਂ ਦੀ ਕੁੱਲ ਗਿਣਤੀ = x
∴ x ਦਾ 10% = 20
\(\frac{10}{100}\) × x = 20
⇒ x = \(\frac{20×100}{10}\)
⇒ x = 200
∴ ਸਰਵੇ ਕੀਤੇ ਗਏ ਜਵਾਨ ਵਿਅਕਤੀਆਂ ਦੀ ਕੁੱਲ ਗਿਣਤੀ = 200.

(ii) ਮਨੋਰੰਜਨ ਸੰਗੀਤ ਸਭ ਤੋਂ ਜ਼ਿਆਦਾ ਸੰਖਿਆ ਵਿਚ ਵਿਅਕਤੀਆਂ ਦੁਆਰਾ ਪਸੰਦ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।
= 40%
= 200 ਦਾ 40%
= \(\frac{40}{100}\) × 200 = 80 ਵਿਅਕਤੀ

(iii) ਬਣਾਈ ਗਈ ਸੀ. ਡੀ. ਦੀ ਕੁੱਲ ਗਿਣਤੀ = 1000
∴ ਸ਼ਾਸਤਰੀ ਸੰਗੀਤ ਦੀ ਸੀ.ਡੀ. ਦੀ ਗਿਣਤੀ
= 1000 ਦਾ 10%
= \(\frac{10}{100}\) × 1000
= 100 ਸੀ.ਡੀ.
ਉਪ-ਸ਼ਾਸਤਰੀ ਸੰਗੀਤ ਦੀ ਸੀ.ਡੀ. ਦੀ ਗਿਣਤੀ
= 1000 ਦਾ 20%
= \(\frac{20}{100}\) × 1000
= 200 ਸੀ.ਡੀ.
ਲੋਕ ਸੰਗੀਤ ਦੀ ਸੀ.ਡੀ. ਦੀ ਗਿਣਤੀ
= 1000 ਦਾ 30%
= \(\frac{30}{100}\) × 1000
= 300 ਸੀ.ਡੀ.
ਮਨੋਰੰਜਨ ਸੰਗੀਤ ਦੀ ਸੀ.ਡੀ. ਦੀ ਗਿਣਤੀ
= 1000 ਦਾ 40%
= \(\frac{40}{100}\) × 1000
= 400 ਸੀ.ਡੀ. ॥

ਪ੍ਰਸ਼ਨ 2.
360 ਵਿਅਕਤੀਆਂ ਦੇ ਇਕ ਗੁੱਟ ਵਿਚ ਤਿੰਨ ਰੁੱਤਾਂਵਰਖਾ, ਸਰਦੀ ਅਤੇ ਗਰਮੀ ਵਿਚ ਆਪਣੀ ਮਨਪਸੰਦ ਰੁੱਤ ਦੇ ਲਈ ਵੋਟਾਂ ਕਰਨ ਨੂੰ ਕਿਹਾ ਗਿਆ । ਇਸ ਨਾਲ ਪ੍ਰਾਪਤ ਅੰਕੜਿਆਂ ਨੂੰ ਨਾਲ ਦਿੱਤੇ ਚਿੱਤਰ ਵਿਚ ਦਰਸਾਇਆ ਗਿਆ ਹੈ :


(i) ਕਿਸ ਰੁੱਤ ਨੂੰ ਸਭ ਤੋਂ ਜ਼ਿਆਦਾ ਵੋਟ ਮਿਲੇ ?
(ii) ਹਰੇਕ ਚੱਕਰਖੰਡ ਦਾ ਕੇਂਦਰੀ ਕੋਣ ਪਤਾ ਕਰੋ ।
(iii) ਇਸ ਸੂਚਨਾ ਨੂੰ ਦਰਸਾਉਣ ਦੇ ਲਈ, ਇਕ ਪਾਈ ਚਾਰਟ ਬਣਾਉ ।
ਹੱਲ:
(i) ਸਰਦ ਰੁੱਤ = 150 ਵੋਟ
(ii)

(iii) ਪਾਈ ਚਾਰਟ ਬਣਾਉਣ ਲਈ ਸਾਨੂੰ ਸੰਗਤ ਕੋਣ ਜਾਣਨ ਦੀ ਜ਼ਰੂਰਤ ਹੈ, ਅਰਥਾਤ

∴ ਕੋਣਾਂ ਦੇ ਅਨੁਸਾਰ ਲੋੜੀਂਦਾ ਪਾਈ ਚਾਰਟ ਹੇਠਾਂ ਦਿੱਤੇ ਗਏ ਅਨੁਸਾਰ ਹੈ :

ਪ੍ਰਸ਼ਨ 3.
ਹੇਠਾਂ ਲਿਖੀ ਸੂਚਨਾ ਨੂੰ ਦਰਸਾਉਣ ਵਾਲਾ ਇਕ ਪਾਈ ਚਾਰਟ ਬਣਾਉ । ਇਹ ਸਾਰਈਂ ਵਿਅਕਤੀਆਂ ਲਈ ਇਕ ਗੁੱਟ ਦੁਆਰਾ ਪਸੰਦ ਕੀਤੇ ਜਾਣ ਵਾਲੇ ਰੰਗਾਂ ਨੂੰ ਦਰਸਾਉਂਦੀ ਹੈ ?

ਹੱਲ:
ਪਾਈ ਚਾਰਟ ਬਣਾਉਣ ਦੇ ਲਈ ਸਾਨੂੰ ਉਨ੍ਹਾਂ ਦੇ ਸੰਗਤ ਕੋਣ ਜਾਣਨ ਦੀ ਜ਼ਰੂਰਤ ਹੈ :

∴ ਉੱਪਰ ਦਿੱਤੀ ਸੂਚਨਾ ਦਾ ਪਾਈ ਚਾਰਟ, ਸਾਰਣੀ ਵਿਚ ਦਿੱਤੇ ਗਏ ਸੰਗਤ ਕੋਣਾਂ ਦੇ ਅਨੁਸਾਰ ਦਰਸਾਇਆ ਗਿਆ ਹੈ ।

ਪ੍ਰਸ਼ਨ 4.
ਨਾਲ ਦਿੱਤਾ ਪਾਈ ਚਾਰਟ ਇਕ ਵਿਦਿਆਰਥੀ ਦੁਆਰਾ ਕਿਸੇ ਪ੍ਰੀਖਿਆ ਵਿਚ ਹਿੰਦੀ, ਅੰਗਰੇਜ਼ੀ, ਗਣਿਤ, ਸਮਾਜਿਕ ਵਿਗਿਆਨ ਅਤੇ ਵਿਗਿਆਨ ਵਿਚ ਪ੍ਰਾਪਤ ਕੀਤੇ ਗਏ ਅੰਕਾਂ ਨੂੰ ਦਰਸਾਉਂਦਾ ਹੈ । ਜੇ ਉਸ ਵਿਦਿਆਰਥੀ ਦੁਆਰਾ ਪ੍ਰਾਪਤ ਕੀਤੇ ਗਏ ਕੁੱਲ ਅੰਕ 540 ਹਨ, ਤਾਂ ਹੇਠਾਂ ਲਿਖੇ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਉੱਤਰ ਦਿਓ :

(i) ਕਿਸ ਵਿਸ਼ੇ ਵਿਚ ਉਸ ਵਿਦਿਆਰਥੀ ਨੇ 105 ਅੰਕ ਪ੍ਰਾਪਤ ਕੀਤੇ ?
(ii) ਉਸ ਵਿਦਿਆਰਥੀ ਨੇ ਗਣਿਤ ਵਿਚ ਹਿੰਦੀ ਨਾਲੋਂ ਕਿੰਨੇ ਅੰਕ ਵੱਧ ਪ੍ਰਾਪਤ ਕੀਤੇ ?
(iii) ਪੜਤਾਲ ਕਰੋ ਕਿ ਸਮਾਜਿਕ ਵਿਗਿਆਨ ਅਤੇ ਗਣਿਤ ਵਿਚ ਪ੍ਰਾਪਤ ਕੀਤੇ ਗਏ ਅੰਕਾਂ ਦਾ ਜੋੜ ਵਿਗਿਆਨ ਅਤੇ ਹਿੰਦੀ ਵਿਚ ਪ੍ਰਾਪਤ ਕੀਤੇ ਗਏ ਅੰਕਾਂ ਦੇ ਜੋੜ ਤੋਂ ਜ਼ਿਆਦਾ ਹੈ ।
ਹੱਲ:
(i) 540 ਅੰਕਾਂ ਦੇ ਲਈ ਕੇਂਦਰੀ ਕੋਣ = 360°
105 ਅੰਕਾਂ ਦੇ ਲਈ ਕੇਂਦਰੀ ਕੋਣ
= \(\frac{360^{\circ}}{540}\) × 105 = 70°
ਇਸ ਲਈ, ਉਸਨੇ ਹਿੰਦੀ ਵਿਚ 105 ਅੰਕ ਪ੍ਰਾਪਤ ਕੀਤੇ ।

(ii) ਹਿੰਦੀ ਦਾ ਕੇਂਦਰੀ ਕੋਣ = 70°
ਗਣਿਤ ਦਾ ਕੇਂਦਰੀ ਕੋਣ = 90°
ਗਣਿਤ ਦਾ ਕੇਂਦਰੀ ਕੋਣ, ਹਿੰਦੀ ਦੇ ਕੇਂਦਰੀ ਕੋਣ ਤੋਂ ਜਿੰਨਾ ਜ਼ਿਆਦਾ ਹੈ।
= 90° – 70° = 20°
ਜੇਕਰ ਕੇਂਦਰੀ ਕੋਣ 360° ਹੋਵੇ ਤਾਂ ਕੁੱਲ ਅੰਕ = 540
ਜੇਕਰ ਕੇਂਦਰੀ ਕੋਣ 20° ਹੈ ਤਾਂ ਕੁੱਲ ਅੰਕ
= \(\frac{540}{360}\) × 20
= 30 ਅੰਕ
ਇਸ ਲਈ, ਉਸਨੇ ਗਣਿਤ ਵਿਚ ਹਿੰਦੀ ਨਾਲੋਂ 30 ਅੰਕ ਦੇ ਜ਼ਿਆਦਾ ਪ੍ਰਾਪਤ ਕੀਤੇ ।

(iii) ਸਮਾਜਿਕ ਵਿਗਿਆਨ ਅਤੇ ਗਣਿਤ ਵਿਚ ਪ੍ਰਾਪਤ ਅੰਕਾਂ ਦਾ ਕੇਂਦਰੀ ਕੋਣ
= 90° + 650
= 155°
ਵਿਗਿਆਨ ਅਤੇ ਹਿੰਦੀ ਵਿਚ ਪ੍ਰਾਪਤ ਅੰਕਾਂ ਦਾ ਕੇਂਦਰੀ | ਕੋਣ
= 80° + 70°
= 150°
ਇਸ ਲਈ ਸਮਾਜਿਕ ਵਿਗਿਆਨ ਅਤੇ ਗਣਿਤ ਵਿਚ ਪ੍ਰਾਪਤ ਕੀਤੇ ਗਏ ਅੰਕਾਂ ਦਾ ਜੋੜ ਵਿਗਿਆਨ ਅਤੇ ਹਿੰਦੀ ਵਿਚ ਪ੍ਰਾਪਤ ਕੀਤੇ ਗਏ ਅੰਕਾਂ ਦੇ ਜੋੜ ਤੋਂ ਜ਼ਿਆਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 5.
ਕਿਸੇ ਹੋਸਟਲ ਵਿਚ, ਵੱਖ-ਵੱਖ ਭਾਸ਼ਾਵਾਂ ਬੋਲਣ ਵਾਲੇ ਵਿਦਿਆਰਥੀਆਂ ਦੀ ਗਿਣਤੀ ਹੇਠਾਂ ਦਿੱਤੀ ਗਈ ਹੈ । ਇਹਨਾਂ ਅੰਕੜਿਆਂ ਨੂੰ ਇਕ ਪਾਈ ਚਾਰਟ ਦੁਆਰਾ ਦਰਸਾਓ ।

ਹੱਲ:

∴ ਉੱਪਰ ਦਿਤੀ ਸੂਚਨਾ ਦਾ ਪਾਈ ਚਾਰਟ, ਸਾਰਣੀ ਵਿੱਚ ਦਿੱਤੇ ਗਏ ਸੰਗਤ ਕੋਣਾਂ ਦੇ ਅਨੁਸਾਰ ਦਰਸ਼ਾਇਆ ਗਿਆ ਹੈ ।

Punjab State Board PSEB 8th Class Punjabi Book Solutions Punjabi Grammar Pranava, Vyakarana ਪੜਨਾਂਵ Textbook Exercise Questions and Answers.

PSEB 8th Class Punjabi Grammar ਪੜਨਾਂਵ (1st Language)

ਪ੍ਰਸ਼ਨ 1.
ਪੜਨਾਂਵ ਕਿਸ ਨੂੰ ਆਖਦੇ ਹਨ? ਇਸ ਦੇ ਕਿੰਨੇ ਭੇਦ ਹਨ? ਉਦਾਹਰਨਾਂ ਦੇ ਕੇ ਸਮਝਾਓ।
ਜਾਂ
ਪੜਨਾਂਵ ਦੀ ਪਰਿਭਾਸ਼ਾ ਲਿਖੋ।ਇਸਦੀਆਂ ਕਿਸਮਾਂ ਕਿਹੜੀਆਂ – ਕਿਹੜੀਆਂ ਹਨ? ਉਦਾਹਰਨਾਂ ਦੇ ਕੇ ਦੱਸੋ।
ਉੱਤਰ :
ਨੋਟ – ਇਸ ਪ੍ਰਸ਼ਨ ਦੇ ਉੱਤਰ ਲਈ ਦੇਖੋ ਇਸ ਗਾਈਡ ਵਿਚ “ਪੰਜਾਬੀ ਪੁਸਤਕ’ ਵਾਲਾ ਭਾਗ, ਸਫ਼ਾ 73 ਅਤੇ 90)

ਪ੍ਰਸ਼ਨ 2.
ਹੇਠ ਲਿਖੇ ਪੜਨਾਂਵਾਂ ਦੇ ਸਾਹਮਣੇ ਉਨ੍ਹਾਂ ਦੀ ਕਿਸਮ ਲਿਖੋ
(ਉ) ਮੈਂ, ਅਸੀਂ
(ਅ) ਕਿਸ ਨੇ, ਕਿਹੜਾ
(ਈ) ਉਹ, ਇਹ
(ਸ) ਤੁਹਾਡਾ, ਤੁਹਾਨੂੰ
(ਗ) ਜਿਹੜੇ
(ਕ) ਆਪ, ਆਪਸ
(ਖ) ਜੋ, ਸੋ
(ਹ) ਕੌਣ, ਕਿਹੜਾ
(ਘ) ਕਈ, ਬਹੁਤ ਸਾਰੇ
(ਝ) ਅਹੁ, ਆਹ
ਉੱਤਰ :
(ਉ) ਪੁਰਖਵਾਚਕ ਪੜਨਾਂਵ,
(ਅ) ਪ੍ਰਸ਼ਨਵਾਚਕ ਪੜਨਾਂਵ,
(ਇ) ਪੁਰਖਵਾਚਕ ਪੜਨਾਂਵ,
(ਸ) ਪੁਰਖਵਾਚਕ ਪੜਨਾਂਵ,
(ਹ) ਪ੍ਰਸ਼ਨਵਾਚਕ ਪੜਨਾਂਵ,
(ਕ) ਨਿੱਜਵਾਚਕ ਪੜਨਾਂਵ,
(ਖ) ਸੰਬੰਧਵਾਚਕ ਪੜਨਾਂਵ,
(ਗ) ਸੰਬੰਧਵਾਚਕ ਪੜਨਾਂਵ,
(ਘ) ਅਨਿਸ਼ਚੇਵਾਚਕ ਪੜਨਾਂਵ,
(ਝ) ਨਿਸ਼ਚੇਵਾਚਕ ਪੜਨਾਂਵ

ਪ੍ਰਸ਼ਨ 3.
ਹੇਠ ਲਿਖਿਆਂ ਵਿੱਚੋਂ ਪੜਨਾਂਵ ਚੁਣੋ ਤੇ ਸਾਹਮਣੇ ਲਿਖੋ
(ਉ) ਮਿਰਚ, ਫੁੱਲ, ਦਿੱਲੀ, ਆਪ
(ਅ) ਕੌਣ, ਲੜਕੀ, ਕੱਪੜਾ, ਸਾਡੇ
(ਏ) ਜਲੰਧਰ, ਜਿਹੜਾ, ਮੈਂ, ਅਸੀਂ
(ਸ) ਕਿਸ ਨੇ, ਗੀਤ, ਵਿਸ਼ਾਲ, ਹੈ
(ਹ) ਘਰ, ਮੇਰਾ, ਉਹ, ਗਿਆ।
ਉੱਤਰ :
(ੳ) ਆਪ,
(ਅ) ਕੌਣ, ਸਾਡੇ,
(ਏ) ਮੈਂ, ਅਸੀਂ,
(ਸ) ਕਿਸਨੇ,
(ਹ) ਮੇਰਾ।

ਪ੍ਰਸ਼ਨ 4.
ਹੇਠ ਲਿਖੇ ਵਾਕਾਂ ਵਿਚੋਂ ਪੜਨਾਂਵ ਚੁਣੋ ਤੇ ਸਾਹਮਣੇ ਲਿਖੋ
(ਉ) ਉਸ ਦਾ ਭਰਾ ਬੜਾ ਬੇਈਮਾਨ ਹੈ।
(ਅ) ਤੁਹਾਨੂੰ ਆਪ ਇਹ ਕੰਮ ਕਰਨਾ ਚਾਹੀਦਾ ਸੀ।
(ਈ) ਕੌਣ – ਕੌਣ ਜਮਾਤ ਵਿਚ ਹਾਜ਼ਰ ਨਹੀਂ ਸਨ।
(ਸ) ਕਈ ਲੋਕ ਘਰ ਨੂੰ ਜਾ ਰਹੇ ਸਨ।
(ਹ) ਜੋ ਕਰੇਗਾ ਸੋ ਭਰੇਗਾ।
(ਕ) ਤੁਹਾਡੇ ਪਿਤਾ ਜੀ ਕੀ ਕਰਦੇ ਸਨ?
(ਖ) ਆਹ ਕਿਸ ਦਾ ਪੈਂਨ ਹੈ?
(ਗ) ਗ਼ਰੀਬ ਨਾਲ ਕੋਈ – ਕੋਈ ਹਮਦਰਦੀ ਕਰਦਾ ਹੈ।
ਉੱਤਰ :
(ੳ) ਉਸ,
(ਅ) ਤੁਹਾਨੂੰ, ਆਪ,
(ਈ) ਕੌਣ – ਕੌਣ,
(ਸ) ਕਈ ਨੋਟ – ਇਹ ਪੜਨਾਂਵ ਨਹੀਂ, ਸਗੋਂ ਪੜਨਾਂਵੀਂ ਵਿਸ਼ੇਸ਼ਣ ਹੈ,
(ਹ) ਜੋ, ਸੋ,
(ਕ) ਕੀ,
(ਖ) ਆਹ, ਕਿਸ,
(ਗ) ਕੋਈ ਕੋਈ

ਪ੍ਰਸ਼ਨ 5.
ਖਾਲੀ ਥਾਂਵਾਂ ਭਰੋ
(ਉ) ਜਿਹੜੇ ਪੁਰਖ ਨਾਲ ਗੱਲ ਕੀਤੀ ਜਾਵੇ ……………………………….. ਪੁਰਖ ਹੁੰਦਾ ਹੈ।
(ਅ) ਜਿਸ ਪੁਰਖ ਬਾਰੇ ਗੱਲ ਕੀਤੀ ਜਾਵੇ ……………………………….. ਪੁਰਖ ਹੁੰਦਾ ਹੈ।
(ਈ) ਨਾਂਵ ਦੀ ਥਾਂ ਵਰਤੇ ਜਾਣ ਵਾਲੇ ਸ਼ਬਦ ……………………………….. ਕਹਾਉਂਦੇ ਹਨ।
(ਸ) ਜਿਹੜੇ ਸ਼ਬਦ ਯੋਜਕਾਂ ਵਾਂਗ ਦੋ ਵਾਕਾਂ ਨੂੰ ਜੋੜਨ ……………………………….. ਪੜਨਾਂਵ ਹੁੰਦੇ ਹਨ।
ਉੱਤਰ :
(ੳ) ਮੱਧਮ,
(ਅ) ਅਨਯ,
(ਇ) ਪੜਨਾਂਵ,
(ਸ) ਸੰਬੰਧਵਾਚਕ।

ਪ੍ਰਸ਼ਨ 6.
ਹੇਠ ਲਿਖੇ ਵਾਕਾਂ ਵਿਚੋਂ ਠੀਕ ਵਾਕਾਂ ਦੇ ਸਾਹਮਣੇ ਤੋਂ ਗ਼ਲਤ ਵਾਕਾਂ ਦੇ ਸਾਹਮਣੇ ਦਾ ਨਿਸ਼ਾਨ ਲਗਾਓ
(ਉ) ਗੱਲ ਕਰਨ ਵਾਲਾ ਪੁਰਖ ਉੱਤਮ ਪੁਰਖ ਹੁੰਦਾ ਹੈ।
(ਅ) ਜੋ ਸ਼ਬਦ ਕਿਸੇ ਵਿਅਕਤੀ, ਵਸਤੂ, ਜਗ੍ਹਾ ਦਾ ਨਾਂ ਦੱਸਣ, ਪੜਨਾਂਵ ਕਹਾਉਂਦੇ ਹਨ।
(ਈ) ਜਿਹੜੇ ਸ਼ਬਦ ਨਾਂਵ ਦੀ ਥਾਂ ਆ ਕੇ ਕੋਈ ਪ੍ਰਸ਼ਨ ਪੁੱਛਣ, ਉਨ੍ਹਾਂ ਨੂੰ ਪ੍ਰਸ਼ਨਵਾਚਕ ਪੜਨਾਂਵ ਕਹਿੰਦੇ ਹਨ।
(ਸ) ਪੜਨਾਂਵ ਪੰਜ ਪ੍ਰਕਾਰ ਦੇ ਹੁੰਦੇ ਹਨ।
(ਹ) ਜਿਹੜੇ ਸ਼ਬਦ ਯੋਜਕ ਵਾਂਗ ਵਾਕਾਂ ਨੂੰ ਜੋੜਨ ਉਹ ਪ੍ਰਸ਼ਨਵਾਚਕ ਪੜਨਾਂਵ ਹੁੰਦੇ ਹਨ।
ਉੱਤਰ :
(ੳ) (✓)
(ਅ) (✗)
(ਇ) (✓)
(ਸ) (✗)
(ਹ) (✗)

ਪ੍ਰਸ਼ਨ 7.
ਹੇਠ ਲਿਖਿਆਂ ਵਿਚੋਂ ਪੁਰਖਵਾਚਕ, ਨਿੱਜਵਾਚਕ, ਸੰਬੰਧਵਾਚਕ, ਪ੍ਰਸ਼ਨਵਾਚਕ, ਨਿਸਚੇਵਾਚਕ ਅਤੇ ਨਿਸਚਿਤ ਪੜਨਾਂਵ ਚੁਣੋ :
ਮੈਂ, ਆਪ, ਜੋ, ਮੈਥੋਂ, ਜਿਹੜਾ, ਕੋਈ, ਮੇਰਾ, ਕਿਸ, ਅਸੀਂ, ਕੌਣ, ਸਾਨੂੰ, ਬਾਜ਼ੇ, ਸਾਡਾ, ਕਿਸੇ, ਸਾਥੋਂ, ਜਿਹੜੇ, ਔਹ, ਸਾਡੀਆਂ, ਆਪਸ, ਆਹ, ਤੁਹਾਥੋਂ, ਸਰਬੱਤ, ਆਪੇ, ਤੁਸੀਂ, ਕਿਨ੍ਹਾਂ, ਤੂੰ, ਸਾਰੇ, ਤੁਹਾਡਾ, ਕੀ, ਇਹ, ਕਈ, ਤੈਨੂੰ, ਹਾਹ, ਉਸ, ਤੇਰਾ, ਕਿਹੜਾ, ਇਹੋ, ਆਪਣਾ, ਉਨ੍ਹਾਂ।
ਉੱਤਰ :

1. ਪੁਰਖਵਾਚਕ ਪੜਨਾਂਵ – ਮੈਂ, ਮੈਥੋਂ, ਮੇਰਾ, ਅਸੀਂ, ਸਾਨੂੰ, ਸਾਡਾ, ਸਾਥੋਂ, ਸਾਡੀਆਂ, ਤੁਹਾਥੋਂ, ਤੁਸੀਂ, ਤੂੰ, ਤੁਹਾਡਾ, ਇਹ, ਤੈਨੂੰ, ਉਸ, ਤੇਰਾ, ਉਨ੍ਹਾਂ।
2. ਨਿੱਜਵਾਚਕ ਪੜਨਾਂਵ – ਆਪ, ਆਪਸ, ਆਪੇ, ਆਪਣਾ :
3. ਸੰਬੰਧਵਾਚਕ ਪੜਨਾਂਵ – ਜੋ, ਜਿਹੜਾ, ਜਿਹੜੇ।
4. ਪ੍ਰਸ਼ਨਵਾਚਕ ਪੜਨਾਂਵ – ਕਿਸ, ਕੌਣ, ਕਿਨਾਂ, ਕੀ, ਕਿਹੜਾ
5. ਨਿਸਚੇਵਾਚਕ ਪੜਨਾਂਵ – ਔਹ, ਆਹ, ਹਾਹ, ਇਹੋ।
6. ਅਨਿਸਚਿਤ ਪੜਨਾਂਵ – ਕੋਈ, ਬਾਜ਼ੇ, ਕਿਸੇ, ਸਰਬੱਤ, ਸਾਰੇ।

ਪ੍ਰਸ਼ਨ 8.
ਹੇਠ ਲਿਖੇ ਸ਼ਬਦਾਂ ਵਿਚੋਂ ਨਿੱਜਵਾਚਕ ਪੜਨਾਂਵ ਦੇ ਇਕ – ਵਚਨ, ਸਾਧਾਰਨ ਰੂਪ ਅਤੇ ਪ੍ਰਸ਼ਨਵਾਚਕ ਪੜਨਾਂਵ ਦੇ ਬਹੁ – ਵਚਨ ਸੰਬੰਧਕੀ ਪੁਲਿੰਗ ਰੂਪ ਚੁਣੋ –
ਆਪਣਿਆਂ, ਉਨ੍ਹਾਂ, ਸਾਡੇ, ਆਪ, ਕਿਹੜਾ, ਕਿਨ੍ਹਾਂ, ਜਿਨ੍ਹਾਂ, ਕਿਹੜੇ, ਕਿਹੜਾ, ਤਿਨ੍ਹਾਂ, ਕਿਹੜੀਆਂ।
ਉੱਤਰ :
ਨਿੱਜਵਾਚਕ ਪੜਨਾਂਵ ਇਕ – ਵਚਨ ਸਾਧਾਰਨ ਰੂਪ – ਆਪ।
ਪ੍ਰਸ਼ਨਵਾਚਕ ਪੜਨਾਂਵ, ਬਹੁ – ਵਚਨ, ਪੁਲਿੰਗ, ਸੰਬੰਧਕੀ ਰੂਪ – ਕਿਨ੍ਹਾਂ, ਕਿਹੜੇ, ਕਿਹੜੀਆਂ।