Punjab State Board PSEB 10th Class Social Science Book Solutions History Chapter 5 फ्रांसीसी क्रांति Textbook Exercise Questions and Answers.
PSEB Solutions for Class 9 Social Science History Chapter 5 फ्रांसीसी क्रांति
SST Guide for Class 9 PSEB फ्रांसीसी क्रांति Textbook Questions and Answers
(क) बहुविकल्पीय प्रश्न :
प्रश्न 1.
पुराने राज्य के दौरान आर्थिक गतिविधियों का भार किस द्वारा चुकाया जाता था ?
(क) चर्च
(ख) केवल अमीर
(ग) तीसरा वर्ग
(घ) केवल राजा।
उत्तर-
(ग) तीसरा वर्ग
प्रश्न 2.
आस्ट्रियन राजकुमारी मैरी एंटोनिटी फ्रांस के किस राजा की रानी थी ?
(क) लुइस तीसरा
(ख) लुइस 14वां
(ग) लुइस 15वां
(घ) लुइस 16वां।
उत्तर-
(घ) लुइस 16वां।
![]()
प्रश्न 3.
नेपोलियन ने स्वयं को फ्रांस का राजा कब बनाया ?
(क) 1805 ई०
(ख) 1804 ई०
(ग) 1803 ई०
(घ) 1806 ई०
उत्तर-
(ख) 1804 ई०
प्रश्न 4.
फ्रांस में टेनिस कोर्ट शपथ कब ली गई ?
(क) 4 जुलाई, 1789 ई०
(ख) 20 जून, 1789 ई०
(ग) 4 अगस्त, 1789 ई०
(घ) 5 मई, 1789 ई०।
उत्तर-
(ख) 20 जून, 1789 ई०
प्रश्न 5.
फ्रांस संदर्भ में कन्वेंशन से क्या अभिप्राय है ?
(क) एक फ्रांसीसी स्कूल
(ख) नई चुनी परिषद्
(ग) क्लब
(घ) एक महिला संगठन।
उत्तर-
(ख) नई चुनी परिषद्
प्रश्न 6.
मांटेस्क्यू ने कौन-से विचार का प्रचार किया ?
(क) दैवी अधिकार
(ख) सामाजिक समझौता
(ग) शक्तियों की विकेंद्रीकरण
(घ) शक्ति का संतुलन।
उत्तर-
(ग) शक्तियों की विकेंद्रीकरण
प्रश्न 7.
फ्रांसीसी इतिहास में किस समय को आतंक का दौर के नाम से जाना जाता है ?
(क) 1792 ई०-93 ई०
(ख) 1774 ई०-76 ई०
(ग) 1793 ई०-94 ई०
(घ) 1804 ई०-1815 ई०
उत्तर-
(ग) 1793 ई०-94 ई०
(ख) रिक्त स्थान भरो :
- एक सिर काटने वाला यंत्र था जिसका प्रयोग फ्रांसीसियों ने किया था ……………
- बेस्टाइल का हमला ………….. में हुआ था।
- 815 ई० में वाटरलू के युद्ध में …………. पराजित हुआ।
- जैकोबिन क्लब का प्रतिनिधि …………….. था।
- …………. ने सोशल कांट्रेक्ट नाम पुस्तक की रचना की।
- मारसेइस (Marseillaise) की रचना ………….. ने की ।
उत्तर-
- गुलुटाइन,
- 14 जुलाई, 1789 ई०
- नेपोलियन बोनापार्ट
- मेक्सीमिलान रोबसपायरी (Maximilian Robespierie),
- रूसो
- रोजर डी लाइसले (Roger de LTsle)THEMAHI
(ग) मिलान करो :
(क) – (ख)
1. किलेनुमा जेल – (अ) गुलूटाइन
2. चर्च द्वारा प्राप्त कर – (आ) जैकोबिन
3. आदमी का सिर काटना – (इ) रूसो
4. फ्रांस की मध्य श्रेणी का क्लब – (ई) बेस्टाइल
5. द सोशल कांट्रैक्ट – (उ) टित्थे।
उत्तर-
- बेस्टाइल
- टित्थे,
- गुलटाइन
- जैकोबिन
- रूसो।
![]()
(घ) अंतर बताओ :
प्रश्न 1.
1. पहला वर्ग और तीसरा वर्ग
2. टित्थे और टाइले।
उत्तर-
1. पहला वर्ग-समाज के पहले वर्ग में पादरी शामिल थे। पादरी वर्ग दो हिस्सों में विभाजित था-उच्च पादरी, साधारण पादरी। उच्च पादरियों में प्रधान पादरी , धर्माध्यक्ष और महंत शामिल थे। वे गिरिजाघरों का प्रबन्ध चलाते थे। उनको लोगों से कर (Tithe) इकट्ठा करने का अधिकार प्राप्त था।
तीसरा वर्ग-समाज के तीसरे वर्ग में कुल जनसंख्या के 97 प्रतिशत लोग आते थे। यह वर्ग असमानता और सामाजिक एवं आर्थिक पिछड़ेपन का शिकार था। इस श्रेणी में धनी व्यापारी, अदालती व कानूनी अधिकारी, साहूकार, किसान, कारीगर, छोटे काश्तकार, आदि आते थे। तीसरे वर्ग के लोग ही सबसे अधिक कर देते थे।
2. टित्थे (Tithe)—यह गिरिजाघर को दिया जाने वाला कर था। किसानों को अपनी वार्षिक आय का दसवां भाग भूमि कर के रूप में देना पड़ता था। यह भूमि पर लगाया जाने वाला कर था जो पहले किसान अपनी इच्छा से देते थे, परंतु बाद में इसे अनिवार्य कर दिया गया।
टाइले (Taille) यह राज्य को दिया जाने वाला कर था जो कि साधारण लोगों पर लगाया जाता था। प्रायः राजा अपनी प्रजा की भूमि और सम्पत्ति पर यह कर लगाता था। यह कर रोज़ की आवश्यकताओं जैसे कि नमक व तम्बाकू पर लगाया जाता था। इसका प्रतिशत हर वर्ष राजा की मर्जी से निश्चित किया जाता था।
अति लघु उत्तरों वाले प्रश्न
प्रश्न 1.
फ्रांस की क्रांति कब हुई ?
उत्तर-
1789 ई०।
प्रश्न 2.
जैकोबिन क्लब का नेता कौन था ?
उत्तर-
मेक्सीमिलान रोबसपायरी।
प्रश्न 3.
डायरैक्टरी क्या थी ?
उत्तर-
पांच सदस्यों की कौंसिल।
प्रश्न 4.
फ्रांस के समाज में कौन कर देता था ?
उत्तर-
तीसरा वर्ग।
प्रश्न 5.
राज्य को प्रत्यक्ष दिये जाने वाले कर को क्या कहते थे ?
उत्तर-
टैले (Taille)।
प्रश्न 6.
किन वर्गों को कर से छूट प्राप्त थी ?
उत्तर-
पहला वर्ग अथवा पादरी वर्ग तथा दूसरा वर्ग अथवा कुलीन वर्ग।
प्रश्न 7.
किसानों को कितने प्रकार के करों का भुगतान करना पड़ता था ?
उत्तर-
किसानों को दोनों प्रकार के कर देने पड़ते थे-टित्थे (Tithe) तथा टाइले (Taille)।
प्रश्न 8.
फ्रांस के राष्ट्रीय गान का नाम लिखो।
उत्तर-
‘मारसेइस’ (Marseillaise)
![]()
लघु उत्तरों वाले प्रश्न
प्रश्न 1.
फ्रांसीसी क्रांति से पूर्व समाज किस प्रकार विभाजित था ?
उत्तर-
फ्रांसीसी क्रांति से पूर्व समाज तीन वर्गों (एस्टेट) में बंट था-पहला वर्ग तथा पादरी वर्ग, दूसरा वर्ग अथवा कुलीन वर्ग, तीसरा वर्ग अथवा साधारण वर्ग।
- पहला वर्ग अथवा पादरी वर्ग-पहला वर्ग में अधिकार युक्त बड़े-बड़े सामंत, पादरी आदि सम्मिलित थे। इन लोगों को कोई कर नहीं देना पड़ता था। योग्य न होने पर भी वे राज्य के बड़े-बड़े पदों पर आसीन थे।
- दूसरा वर्ग अथवा कुलीन वर्ग-दूसरे एस्टेट में कुलीन वर्ग के लोग सम्मिलित थे।
- तीसरे वर्ग अथवा साधारण वर्ग-तीसरे एस्टेट में अर्थात् वकील, डॉक्टर तथा शिक्षक वर्ग के लोग सम्मिलित थे। योग्यता होने पर भी ये लोग राज्य के उच्च पदों से वंचित थे। जनसाधारण भी इसी वर्ग में सम्मिलित थे। उन्हें राज्य को भी कर देना पड़ता था और चर्च को भी। इनसे बेगार ली जाती थी और वर्षों से इनका शोषण हो रहा था।
प्रश्न 2.
फ्रांसीसी क्रांति में महिलाओं के योगदान पर टिप्पणी लिखें।
उत्तर-
फ्रांसीसी क्रांति के समय किसी भी सरकार ने महिलाओं को सक्रिय नागरिक नहीं माना, परंतु क्रांति के समय उनकी भूमिका बहुत महत्त्वपूर्ण थी।
तीसरे एस्टेट की अधिकतर महिलाएं जीवन निर्वाह के लिए काम करती थीं। वे सिलाई-बुनाई तथा कपड़ों की धुलाई करती थीं और बाजारों में फल-फूल तथा सब्जियां बेचती थीं। कुछ महिलाएं संपन्न घरों में घरेलू काम करती थीं। बहुतसी महिलाएं वेश्यावृत्ति भी करती थीं। अधिकांश महिलाओं के पास पढ़ाई-लिखाई तथा व्यावसायिक प्रशिक्षण के अवसर नहीं थे। कामकाजी महिलाओं को अपने परिवार की देखभाल भी करनी पड़ती थी। महिलाओं ने अपने अधिकारों के लिए निरंतर आंदोलन चलाया। फ्रांसीसी क्रांति के समय ओलंपे दे गाजस एक सक्रिय राजनीतिक महिमा प्रतिनिधि थी। उसने संविधान के मनुष्य व नागरिकों के अधिकारों के घोषणा-पत्र का विरोध किया। इसलिए उसे मृत्यु दंड दे दिया गया। ऐसी अन्य कई महिला प्रतिनिधियों को आतंक के दौर में मौत के घाट उतार दिया गया। लगभग 150 वर्षों के बाद 1946 ई० में महिलाओं के जीवन में सुधार लाने वाले कुछ कानून लागू किए। एक कानून के अनुसार सरकारी विद्यालयों की स्थापना की गई और सभी लड़कियों के लिए स्कूली शिक्षा को अनिवार्य बना दिया गया।
प्रश्न 3.
फ्रांसीसी क्रांति की प्रभावित करने वाले तीन प्रमुख लेखकों, दार्शनिकों के विषय में संक्षेप में लिखो।
उत्तर-
- जॉन लॉक ने अपनी कृति ‘टू ट्रीटाइज़ेज ऑफ़ गवर्नमैंट’ में राजा के दैवी तथा निरंकुश अधिकारों के सिद्धांत का खंडन किया।
- रूसो ने इसी विचार को आगे बढ़ाया। उसने जनता और उसके प्रतिनिधियों के बीच एक सामाजिक अनुबंध पर आधारित सरकार का प्रस्ताव रखा।
- मॉटेस्क्यू ने अपनी रचना ‘द स्पिरिट ऑफ़ द लॉज़’ में सरकार के अंदर विधायिका, कार्यपालिका तथा न्यायपालिका के बीच सत्ता विभाजन की बात कही।
दार्शनिकों के इन विचारों से फ्रांस में क्रांति के विचारों को और अधिक बल मिला।
प्रश्न 4.
राजतंत्र से आप क्या समझते हैं ?
उत्तर-
राजतंत्र ऐसी शासनतंत्र प्रणाली होती है जिसमें राजा ही सबसे बड़ा अधिकारी होता है। वह प्रायः तानाशाह होता है और राजा के दैवीय अधिकारों में विश्वास रखता है। फ्रांस में भी राजतंत्र था और वहां का शासक लुईस 16वां सभी अधिकारों का स्वामी था। उसके अधिकारों को कोई भी चुनौती नहीं दे सकता था उसे न तो देश के संविधान की चिंता थी और न ही जनता के हितों का ध्यान था। वर्षों तक उसने देश की संसद् भी नहीं बुलाई थी। जब उसने संसद् बुलाई तो उसका उद्देश्य भी कर लगाना था। यही घटना क्रांति के विस्फोट का कारण बनी।
प्रश्न 5.
‘राष्ट्रीय संवैधानिक परिषद्’ का संक्षिप्त वर्णन करें।
उत्तर-
फ्रांस का सम्राट् लुई (XVI) अपनी विद्रोही प्रजा की शक्ति को देखकर सहम गया था। अतः उसने नेशनल असेंबली को मान्यता दे दी और यह भी मान लिया कि अब से उसकी सत्ता पर संविधान का अंकुश होगा। 1791 में नेशनल असेंबली ने संविधान का प्रारूप तैयार कर लिया। इसका मुख्य उद्देश्य सम्राट की शक्तियों को सीमित करना था। अब शक्तियों को विधायिका, कार्यपालिका तथा न्यायपालिका में विभाजित कर दिया गया। इस प्रकार शक्तियां एक हाथ में केंद्रित न रह कर तीन विभिन्न संस्थाओं को हस्तांतरित कर दी गईं। इसी के फलस्वरूप फ्रांस में संवैधानिक राजतंत्र की स्थापना हुई।
दीर्घ उत्तरों वाले प्रश्न
प्रश्न 1.
उन स्थितियों का वर्णन करें जिनके कारण फ्रांसीसी क्रांति का उदय हुआ ?
उत्तर-
फ्रांसीसी क्रांति आधुनिक यूरोप के इतिहास की महानतम घटना थी। इसका आरंभ भले ही 1789 ई० में हुआ हो, परंतु इसकी पृष्ठभूमि बहुत पहले से तैयार हो रही थी। फ्रांस में राजा, उसके दरबारी, सेना के अधिकारी तथा चर्च के पादरी जन-साधारण का खून चूस रहे थे। इन्हें कोई कर नहीं देना पड़ता था। करों का सारा बोझ जनता पर था। आम आदमी राज्य की सेवा करता था, परंतु योग्यता होने पर भी वह उच्च पद प्राप्त नहीं कर सकता था। किसान तो दासता में पैदा होता था और दासता में ही मर जाता था। 1789 ई० में स्थिति और भी गंभीर हो गई और क्रांति की ज्वाला भड़क उठी। संक्षेप में, फ्रांस में क्रांति की शुरुआत निम्नलिखित परिस्थितियों में हुई
1. राजनीतिक परिस्थितियां
- फ्रांस के राजा स्वेच्छाचारी थे और वे राजा के दैवीय अधिकारों में विश्वास रखते थे। सम्राट की इच्छा ही कानून थी। वह अपनी इच्छा से युद्ध अथवा संधि करता था। सम्राट् लुई 14वां तो यहां तक कहता था-“मैं ही राज्य हूं।”
- कर बहुत अधिक थे जो मुख्यतः जनसाधारण को ही देने पड़ते थे। दरबारी और सामंत करों से मुक्त थे।
- राज्य में सैनिक तथा अन्य पद पैतृक थे और उन्हें बेचा भी जा सकता था।
- सेना में असंतोष था।
- शासन में व्यापक भ्रष्टाचार फैला हुआ था।
![]()
2. सामाजिक परिस्थितियां
- फ्रांस में मुख्य तीन श्रेणियां (एस्टेट्स) थीं-उच्च, मध्यम तथा निम्न। उच्च श्रेणी में अधिकार युक्त बड़े-बड़े सामंत, पादरी आदि सम्मिलित थे। इन लोगों को कोई कर नहीं देना पड़ता था। योग्य न होने पर भी वे राज्य के बड़ेबड़े पदों पर आसीन थे।
- दूसरे एस्टेट में कुलीन वर्ग के लोग सम्मिलित थे।
3. आर्थिक परिस्थितियां-
- फ्रांस के राजा धन का दुरुपयोग करते थे और उन्होंने व्यक्तिगत ऐश्वर्य के लिए खज़ाना खाली कर दिया।
- करों का विभाजन दोषपूर्ण था। धनी लोग कर से मुक्त थे जबकि जनसाधारण को कर चुकाने पड़ते थे। कर एकत्रित करने की विधि भी दोषपूर्ण थी।
- फांस में औद्योगिक क्रांति के कारण अनेक कारीगर बेकार हो गए और उनमें असंतोष फैल गया।
- फ्रांस ऋण के बोझ से दबा हुआ था।
- दोषपूर्ण कर-प्रणाली के कारण व्यापार अवनति की ओर बढ़ रहा था।
- फ्रांस ने अमेरिका के लोगों को वित्तीय सहायता दी जिससे राजकोष पर ऋण का बोझ बढ़ गया।
4. दार्शनिकों का योगदान-फ्रांस की स्थिति बहुत ही खराब थी, जिसे दर्शाने में दार्शनिकों ने बड़ा योगदान दिया। उन्होंने जनता को यह समझाने का प्रयास किया कि उनके दुःखों का वास्तविक कारण राजतंत्र है।
- रूसो ने अपनी पुस्तक ‘सामाजिक समझौता’ में राजा के दैवीय अधिकारों पर प्रहार किया।
- वाल्तेयर ने चर्च के धार्मिक आडंबरों और पादरियों के भ्रष्टाचार को अपना निशाना बनाया।
- मांतेस्क्यू ने अपनी पुस्तक ‘The Spirit of the Laws’ में राजा के दैवीय अधिकारों और उसकी निरंकुशता की कड़ी आलोचना की।
इस प्रकार, दार्शनिकों के प्रयत्नों से नवीन विचारधारा का प्रादुर्भाव हुआ। इसी नवीन विचारधारा के कारण फ्रांस में क्रांति हुई।
5. एस्टेट्स जेनराल का अधिवेशन बुलाया जाना तथा क्रांति की शरुआत-फ्रांसीसी क्रांति का तात्कालिक कारण एस्टेट्स जेनराल का अधिवेशन बुलाया जाना था। अधिवेशन बुलाए जाने के बाद जनसाधारण के प्रतिनिधियों ने राजा के सामने यह मांग रखी कि एस्टेट्स जेनराल के तीनों सदनों की संयुक्त बैठक बुलाई जाए। राजा के इन्कार करने
पर जनसाधारण के प्रतिनिधि टैनिस कोर्ट में एकत्रित हुए और उन्होंने नवीन संविधान बनाने की घोषणा की। इसी बीच राजा ने जनता के प्रतिनिधियों की मांग स्वीकार कर ली जिन्होंने एस्टेट्स जेनराल के प्रथम अधिवेशन में ही क्रांति का बिगुल बजा दिया।

प्रश्न 2.
फ्रांस की क्रांति के पड़ावों के बारे में विस्तारपूर्वक लिखो।
उत्तर-
फ्रांसीसी क्रांति आधुनिक काल की सबसे महान् घटना थी। यह केवल फ्रांस की ही आंतरिक घटना नहीं थी, बल्कि यह विश्व क्रांति थी। इसने केवल फ्रांसीसी समाज को ही नहीं, बल्कि पूरी मानव-जाति को प्रभावित किया। शताब्दियों के पश्चात् मानवीय मूल्यों का आदर किया जाने लगा, मध्यकालीन सामंती ढांचा जड़ से हिल गया और राजतंत्र का स्थान प्रजातंत्र ने लेना आरंभ किया। समानता, स्वतंत्रता और बंधुत्व के सिद्धांतों की गूंज विश्व के अनेक देशों में सुनी गई। फ्रांस की क्रांति के 1789 ई० से आरंभ होकर नेपोलियन के पतन तक चली इसके विभिन्न पड़ावों का वर्णन इस प्रकार है-
1. टैनिस कोट और बेस्टील का पतन-14 जुलाई, 1789 को क्रुद्ध भीड़ से पेरिस नगर में बेस्टील के किले पर धावा बोला। यह किला फ्रांस के सम्राट् की निरंकुश शक्तियों का प्रतीक था। उस दिन सम्राट ने सेना को नगर में प्रवेश करने का आदेश दे दिया था। अफ़वाह थी कि वह सेना को नागरिकों पर गोलियां चलाने का आदेश देने वाला है। अतः लगभग 7000 पुरुष तथा स्त्रियां टाऊन हॉल के सामने एकत्र हुए और उन्होंने एक जन-सेना का गठन किया। हथियारों की खोज में वे अनेक सरकारी भवनों में जबरन प्रवेश कर गए। अंततः सैंकड़ों लोगों के एक समूह ने पेरिस नगर में स्थित बेस्टील (Bastile) के किले की जेल को तोड़ डाला जहां उन्हें भारी मात्रा में गोला-बारूद मिलने की आशा थी। हथियारों पर कब्जे के इस संघर्ष में बेस्टील का कमांडर मारा गया और कैदी छुड़ा लिए गए, यद्यपि उनकी संख्या केवल सात थी। किले को ध्वस्त कर दिया गया और उसके अवशेष बाज़ार में उन लोगों को बेच दिए गए जो इस ध्वंस को स्मृति-चिह्न के रूप में संजो कर रखना चाहते थे।
2. फ्रांस में संवैधानिक राजतंत्र (राष्ट्रीय महासभा)-फ्रांस का सम्राट् लुई (XVI) अपनी विद्रोही प्रजा की शक्ति को देखकर सहम गया था। अत: उसने नेशनल असेंबली को मान्यता दे दी और यह भी मान लिया कि अब से उसकी सत्ता पर संविधान का अंकुश होगा। 1791 में नेशनल असेंबली ने संविधान का प्रारूप तैयार कर लिया। इसका मुख्य उद्देश्य सम्राट की शक्तियों को सीमित करना था। अब शक्तियों को विधायिका, कार्यपालिका तथा न्यायपालिका में विभाजित कर दिया गया। इस प्रकार शक्तियां एक हाथ में केंद्रित न रह कर तीन विभिन्न संस्थाओं को हस्तांतरित कर दी गईं। इसी के फलस्वरूप फ्रांस में संवैधानिक राजतंत्र की स्थापना हुई।
3. आतंक का राज्य जैकोबिन क्लब-जैकोबिन क्लब के सदस्य मुख्यतः समाज के हम समृद्ध वर्गों से संबंधित थे। इनमें छोटे दुकानदार और कारीगर जैसे जूता बनाने वाले, पेस्ट्री बनाने वाले, घड़ीसाज़, छपाई करने वाले और नौकर व दैनिक मज़दूर शामिल थे। उनका नेता मैक्समिलियन रोबेस्प्येर था। रोबेस्प्येर ने 1793 से 1794 तक फ्रांस पर शासन किया। उसने बहुत ही कठोर एवं क्रूर नीतियां अपनाईं। वह जिन्हें गणतंत्र का शत्रु मानता था अथवा उसकी पार्टी का जो कोई सदस्य उससे असहमति जताता था, उन्हें जेल में डाल देता था। उन पर एक क्रांतिकारी न्यायालय द्वारा मुकद्दमा चलाया जाता था। जो कोई भी दोषी पाया जाता था, उसे गुलोटाइन पर चढ़ा कर उसका सिर धड़ से अलग कर दिया जाता था।
रोबेस्प्येर ने अपनी नीतियों को इतनी कठोरता एवं क्रूरता से लागू किया कि उसके समर्थक भी त्राहि-त्राहि कर उठे। इसी कारण उसके राज्य की ‘आतंक का राज्य’ कहा जाता है।
4. डायरेक्टरी का शासन-जैकोबिन सरकार के पतन के बाद नेशनल कन्वेंशन ने 1795 ई० में फ्रांस के लिए एक संविधान तैयार किया था। इस संविधान के अनुसार देश के शासन की बागडोर डायरेक्टरी के हाथ में सौंप दी गई। 26 अक्तूबर, 1795 ई० को डायरेक्टरी का पहला अधिवेशन बुलाया गया और इसके साथ ही नेशनल कन्वेंशन भंग हो गई। डायरेक्टरी ने चार वर्ष (1795-1799 ई०) तक फ्रांस पर शासन किया। इन चार वर्षों में इसे अनेकों कठिनाइयों का सामना करना पड़ा। डायरेक्टरी की राजनीतिक असफलता ने सैनिक तानाशाह नेपोलियन बोनापार्ट के उदय का मार्ग प्रशस्त किया।
5. नेपोलियन का काल-1799 में डिरेक्ट्री के शासन का तख्तापलट कर नेपोलियन प्रथम काउंसिल (First Council) बन गया। उसने तानाशाही शक्तियां प्राप्त कर ली। उसने जनमत-संग्रह करवाया। 99.9 प्रतिशत मतदाताओं ने उसकी नई शासन व्यवस्था के पक्ष में मत दिया। विजयों की एक श्रृंखला के बाद वह फ्रांस के शत्रुओं के साथ भी शांति संधि स्थापित करने में सफल रहा। संधि तथा शांति स्थापना के इन कार्यों ने सिद्ध कर दिया कि वह एक योग्य प्रशासक है। 1799 से 1804 तक, उसने अनेक सुधार लागू किए।
- उसने वित्तीय उपायों द्वारा बढ़ती हुई मुद्रास्फीति (मूल्य वृद्धि) पर रोक लगाई।
- इसके बाद बैंक ऑफ फ्रांस की स्थापना की गई।
- उसने पोप के साथ काफ़ी समय से चले आ रहे उस विवाद को भी सुलझा लिया, जो 1789 में चर्च की भूमि को जब्त किए जाने के कारण शुरू हुआ था। इसके लिए उसने घोषित कर दिया कि कैथोलिकवाद ही बहुसंख्यक फ्रांसीसियों का धर्म है।
- तत्पश्चात् उसने फ्रांसीसी कानून को संहिताबद्ध करने का काम पूरा किया। इसीलिए उस संहिता को नेपोलियन कोड (संहिता) के नाम से पुकारा जाता है। यही संहिता भविष्य में फ्रांसीसी कानून प्रणाली का आधार बनी रही।
- नेपोलियन सम्राट् बना-1804 तक आते-आते नेपोलियन प्रथम काउंसिल के पद से संतुष्ट नहीं रहा। उसने एक बार फिर जनमत-संग्रह करवाया और उसे वह सब बनने व करने का अधिकार मिला जो वह चाहता था। दिसंबर

1804 में उसने पोप पिअस सप्तम की उपस्थिति में स्वयं अपने हाथों से अपने सिर पर राजमुकुट धारण किया। इस प्रकार उसने स्वयं को सम्राट् घोषित कर दिया।
![]()
प्रश्न 3.
फ्रांस की क्रांति के क्या प्रभाव पड़े ?
उत्तर-
फ्रांसीसी क्रांति (1789 ई०) से न केवल फ्रांस, बल्कि संसार के समस्त देश स्थायी रूप से प्रभावित हुए। वास्तव में इस क्रांति के कारण एक नये युग का उदय हुआ। इसके तीन प्रमुख सिद्धांत-समानता, स्वतंत्रता और भ्रातृत्व की भावना पूरे विश्व के लिए अमर वरदान सिद्ध हुए। इन्हीं के आधार पर संसार के अनेक देशों में एक नये समाज की स्थापना का प्रयत्न किया गया। इस क्रांति की विरासत का वर्णन इस प्रकार है-
1. स्वतंत्रता-स्वतंत्रता फ्रांसीसी क्रांति का एक मूल सिद्धांत था। इस सिद्धांत से यूरोप के लगभग सभी देश प्रभावित हुए। फ्रांस में मानव-अधिकारों के घोषणा-पत्र (Declaration of the Rights of Man) द्वारा सभी लोगों को उनके अधिकारों से परिचित कराया गया। देश में अर्द्धदास प्रथा (Serfdom) का अंत कर दिया गया और निर्धन किसानों को सामंतों के चंगुल से छुटकारा दिलाया गया। फ्रांसीसी क्रांति के परिणामस्वरूप अनेक देशों में निरंकुश शासन के विरुद्ध आंदोलन आरंभ हो गए। लोगों ने धार्मिक, सामाजिक तथा राजनीतिक स्वतंत्रता के लिए संघर्ष करना आरंभ कर दिया।
2. समानता-क्रांति के कारण निरंकुश शासन का अंत हुआ और इसके साथ ही समाज में फैली असमानता का भी अंत हो गया। समानता क्रांति का एक महत्त्वपूर्ण सिद्धांत था। इसका प्रचार लगभग सभी देशों में हुआ। इसके फलस्वरूप सभी लोग कानून की दृष्टि में एक समान समझे जाने लगे। सभी लोगों को उन्नति के समान अवसर प्राप्त होने लगे। सरकार अब सभी लोगों से एक समान व्यवहार करने लगी। वर्ग भेद सदा के लिए समाप्त हो गया।
3. लोकतंत्र-फ्रांस के क्रांतिकारियों ने राष्ट्रीय सम्मेलन द्वारा निरंकुश तथा स्वेच्छाचारी शासन का अंत कर दिया और इसके स्थान पर लोकतंत्र की स्थापना की। लोगों को बताया गया कि राज्य की सारी शक्ति जनता में निहित है और राजा के दैवी अधिकारों का सिद्धांत बिल्कुल गलत है। लोगों को यह अधिकार है कि वे अपने चुने हुए प्रतिनिधियों द्वारा सरकार चलायें। फ्रांस को क्रांति ने यह स्पष्ट कर दिया था कि सरकार केवल जनता के लिए ही नहीं बल्कि जनता के द्वारा बनाई जाए। आरंभ में लोकतंत्र के सिद्धांत के विरुद्ध यूरोप में प्रतिक्रिया हुआ, परंतु कुछ समय पश्चात् यूरोप तथा संसार के अन्य देशों ने इस सिद्धांत के महत्त्व को समझा और उन देशों में लोकतंत्र का जन्म हुआ।
4. राष्ट्रीयता की भावना-फ्रांसीसी क्रांति के कारण फ्रांस तथा यूरोप के अन्य देशों में राष्ट्रीयता की भावना का जन्म हुआ। क्रांति के समय जब आस्ट्रिया तथा प्रशा ने फ्रांस पर आक्रमण किया था तो फ्रांस के सभी लोग, कंधे से कंधा मिलाकर उनके विरुद्ध लड़े थे। यह उनकी राष्ट्रीय भावना का ही परिणाम था। फ्रांसीसी होने के नाते वे एक-दूसरे से जुड़े हुए थे और देश के शत्रु को अपना साझा शत्रु मानते थे। राष्ट्रीयता की इसी भावना से प्रेरित हो कर नेपोलियन के सैनिकों ने अनेक देशों पर विजय प्राप्त की। यह भावना केवल फ्रांस तक ही सीमित न रहकर जर्मनी, स्पेन, पुर्तगाल आदि देशों में भी पहुंची।
5. सामंतवाद से प्रजातंत्र की ओर-फ्रांसीसी क्रांति ने सामंतवाद का अंत कर दिया। सामंतों को उनके विशेषाधिकारों से वंचित कर दिया गया। अब उन्हें भी अन्य लोगों की भांति कर देने पड़ते थे। अर्द्धदास प्रथा (Serfdom) का अंत कर दिया गया और वर्ग-भेद मिटा दिये गये। समाज का गठन समानता के आधार पर किया गया। धीरे-धीरे ये परिवर्तन यूरोप तथा संसार के अन्य देशों में भी किये गए। इस प्रकार सामंतवाद का स्थान प्रजातंत्र ने लेना आरंभ कर दिया।
6. सार्वजनिक कल्याण-फ्रांस की राज्य-क्रांति ने सार्वजनिक कल्याण की भावना को विकसित किया। इस भावना से प्रेरित होकर दयालु लोगों तथा उन्नत सरकारों ने धन तथा कानूनों द्वारा लोगों के सामाजिक जीवन को सुधारने के प्रयास किए। जेलों की व्यवस्था को सुधारा गया तथा दासता का अंत कर दिया गया। कारखानों, खानों तथा खेतों में काम करने वाले मजदूरों की अवस्था में भी काफी सुधार किए गए। अशिक्षितों की शिक्षा के लिए स्कूलों की स्थापना की गई तथा रोगियों के लिए अस्पताल खोले गए। पिछड़े हुए लोगों को आर्थिक सहायता प्रदान की गई। इस प्रकार क्रांति के कारण सार्वजनिक भलाई की भावना का काफ़ी विकास हुआ। तो यह है कि क्रांति ने प्रचलित कानूनों का रूप बदल दिया, सामाजिक मान्यताएं बदल डालीं और आर्थिक ढांचे में आश्चर्यजनक परिवर्तन किए। राजनीतिक दल नवीन आदर्शों से प्रेरित हुए। सुधार आंदोलन तीव्र गति से चलने लगे। साहित्यकारों ने नवीन वाणी पाई। फ्रांसीसी क्रांति के तीन स्तंभ-समानता, स्वतंत्रता तथा बंधुत्व प्रत्येक देश के लिए पथ-प्रदर्शक बने। मानवता के लिए अंधकार का युग समाप्त हुआ और एक आशा भरी प्रातः का उदय हुआ।
प्रश्न 4.
फ्रांसीसी क्रांति के कारणों का विस्तारपूर्वक वर्णन करें।
नोट-इसके लिए दीर्घ उत्तरों वाले प्रश्नों का प्रश्न नंबर 1 पढ़ें।
प्रश्न 5.
1789 ई० से पूर्व तीसरे वर्ग की महिलाओं की क्या स्थिति थी ?
उत्तर-
फ्रांस में तीसरे एस्टेट (वर्ग) की अधिकतर महिलाएं जीवन निर्वाह के लिए काम करती थीं। वे सिलाईबुनाई तथा कपड़ों की धुलाई करती थीं और बाजारों में फल-फूल तथा सब्जियां बेचती थीं। कुछ महिलाएं संपन्न घरों में घरेलू काम करती थीं। बहुत-सी महिलाएं वेश्यावृत्ति भी करती थीं। अधिकांश महिलाओं के पास पढ़ाई-लिखाई तथा व्यावसायिक प्रशिक्षण के अवसर नहीं थे। केवल कुलीनों की लड़कियां अथवा तीसरे एस्टेट के धनी परिवारों की लड़कियां ही कॉन्वेंट में पढ़ पाती थीं। इसके बाद उनकी शादी कर दी जाती थी। कामकाजी महिलाओं को अपने परिवार की देखभाल भी करनी पड़ती थी।
प्रारंभिक वर्षों में क्रांतिकारी सरकार ने महिलाओं के जीवन में सुधार लाने वाले कुछ कानून लागू किए। एक कानून के अनुसार सरकारी विद्यालयों की स्थापना की गई और सभी लड़कियों के लिए स्कूली शिक्षा को अनिवार्य बना दिया गया।
PSEB 9th Class Social Science Guide फ्रांसीसी क्रांति Important Questions and Answers
I. बहुविकल्पीय प्रश्न :
प्रश्न 1.
फ्रांस की राज्य क्रांति कब हुई ?
(क) 1917 ई० में
(ख) 1905 ई० में
(ग) 1789 ई० में
(घ) 1688 ई० में।
उत्तर-
(ग) 1789 ई० में
प्रश्न 2.
फ्रांसीसी क्रांति के समय फ्रांस पर किसका शासन था ?
(क) लुई फिलिप का
(ख) लुई सोलहवें का
(ग) लुई चौदहवें का
(घ) लुई अमरहवें का।
उत्तर-
(ख) लुई सोलहवें का
प्रश्न 3.
फ्रांसीसी क्रांति के समय किसानों की गणना किस वर्ग में की जाती थी ?
(क) कुलीन वर्ग में
(ख) मध्य वर्ग में
(ग) निम्न वर्ग में
(घ) उपरोक्त में से कोई नहीं।
उत्तर-
(ग) निम्न वर्ग में
![]()
प्रश्न 4.
रोमन कैथोलिक चर्च का सबसे बड़ा अधिकारी था
(क) रोमन सम्राट
(ख) रोमन प्रधानमंत्री।
(ग) पोप
(घ) मैटर्निख।
उत्तर-
(ग) पोप
प्रश्न 5.
फ्रांसीसी क्रांति के समय यूरोप में भूमि के स्वामी थे
(क) जागीरदार
(ख) किसान
(ग) दास-कृषक
(घ) उपरोक्त सभी।
उत्तर-
(क) जागीरदार
प्रश्न 6.
इनमें से किसका संदर्भ राजकीय शक्ति के प्रतीक से है ?
(क) राजदंड
(ख) कानूनी टेबल
(ग) लिवर (लिव्रे)
(घ) राजस्व।
उत्तर-
(क) राजदंड
प्रश्न 7.
इनमें से कौन-सा दासों की आजादी का प्रतीक है ?
(क) राजदंड
(ख) छड़ों का बींदार गट्ठर
(ग) अपनी पूंछ मुंह में लिए सांप
(घ) टूटी हुई जंजीर/हथकड़ी।
उत्तर-
(घ) टूटी हुई जंजीर/हथकड़ी।
प्रश्न 8.
विधि पट किस बात का प्रतीक है ? .
(क) कानून की नज़र में सब बराबर हैं।
(ख) कानून सबके लिए समान हैं।
(ग) सामंत विशेष सुविधाओं के अधिकारी हैं।
(घ) (क) तथा (ख)।
उत्तर-
(घ) (क) तथा (ख)।
प्रश्न 9.
फ्रांस के राष्ट्रीय रंगों का समूह निम्न में से कौन-सा है?
(क) नीला-पीला-लाल
(ख) पीला-सफ़ेद-नीला
(ग) नीला-सफ़ेद-लाल
(घ) केसरी-सफ़ेद-हरा।
उत्तर-
(ग) नीला-सफ़ेद-लाल
प्रश्न 10.
निम्न में से किसका संदर्भ ‘एकता में ही बल है’ के प्रतीक से है ?
(क) त्रिभुज के अंदर रोशनी बिखेरती आँख
(ख) छड़ों का बींदार गट्ठर
(ग) लाल फ्राइजियन टोपी
(घ) टिथे।
उत्तर-
(ख) छड़ों का बींदार गट्ठर
प्रश्न 11.
लाल-फ्राइजियन टोपी का संबंध निम्न में से किससे है ?
(क) स्वतंत्र दासों से
(ख) समानता से
(ग) कानून के मानवीय रूप से
(घ) इनमें से कोई नहीं।
उत्तर-
(क) स्वतंत्र दासों से
प्रश्न 12.
निम्न में से कानून के मानवीय रूप का प्रतीक कौन-सा है ?
(क) विधि पट
(ख) लाल-फ्राइजियन टोपी
(ग) डैनों वाली स्त्री
(घ) अपनी पूंछ मुंह में लिए सांप।
उत्तर-
(ग) डैनों वाली स्त्री
![]()
प्रश्न 13.
निम्नलिखित में से ज्ञात का प्रतीक कौन-सा है ?
(क) राजदंड
(ख) टूटी हुई जंजीर
(ग) डैनों वालो स्त्री
(घ) त्रिभुज के अंदर रोशनी बिखेरती आंख।
उत्तर-
(घ) त्रिभुज के अंदर रोशनी बिखेरती आंख।
प्रश्न 14.
तीसरे एस्टेट (फ्रांस) द्वारा राज्य को दिए जाने वाले प्रत्यक्ष कर का नाम इनमें से क्या था ?
(क) टाइद
(ख) टेली (टाइल)
(ग) लिवर (लिव्रे)
(घ) राजस्व।
उत्तर-
(ख) टेली (टाइल)
प्रश्न 15.
चर्च द्वारा किसानों (फ्रांस) से वसूला जाने वाला धार्मिक कर निम्न में से कौन-सा था ?
(क) लिने
(ख) टाइद
(ग) टिले
(घ) उपरोक्त सभी।
उत्तर-
(ख) टाइद
प्रश्न 16.
फ्रांस के संदर्भ में लिने क्या था ?
(क) फ्रांस की मुद्रा
(ख) कारागार
(ग) एक प्रकार का कर
(घ) उच्च पद्र।
उत्तर-
(क) फ्रांस की मुद्रा
प्रश्न 17.
लुई 16वां फ्रांस का सम्राट् कब बना था ?
(क) 1747 ई० में
(ख) 1789 ई० में
(ग) 1774 ई० में
(घ) 1791 ई० में।
उत्तर-
(ग) 1774 ई० में
प्रश्न 18.
फ्रांस के शासक लुई 16वें ने किस प्रकार की सरकार को अपनाया ?
(क) निरंकुश
(ख) साम्यवादी
(ग) समाजवादी
(घ) उदारवादी।
उत्तर-
(क) निरंकुश
प्रश्न 19.
कौन-सा कारक फ्रांसीसी क्रांति के लिए उत्तरदायी था ?
(क) प्रजातंत्रात्मक शासन प्रणाली
(ख) सामंतों की शोचनीय दशा
(ग) भ्रष्ट शासन
(घ) उपरोक्त सभी।
उत्तर-
(ग) भ्रष्ट शासन
प्रश्न 20.
लुई 16वें का संबंध किस राजवंश से था ?
(क) हेप्सबर्ग
(ख) हिंडेनबर्ग
(ग) नार्डिक
(घ) बूबों।
उत्तर-
(घ) बूबों।
![]()
प्रश्न 21.
रूसो ने ग्रंथ लिखा
(क) ट्रीटाइड ऑन टालरेंस
(ख) द सोशल कंट्रेक्ट/सामाजिक समझौता।
(ग) विश्वकोष
(घ) फिलीसिफिकल डिक्शनरी।
उत्तर-
(ख) द सोशल कंट्रेक्ट/सामाजिक समझौता।
प्रश्न 22.
एस्टेट्स जेनराल का अधिवेशन हुआ
(क) पेरिस में
(ख) वर्सेय में
(ग) वियाना में
(घ) बर्लिन में।
उत्तर-
(ख) वर्सेय में
प्रश्न 23.
ऐंटोनिटी कौन थी ?
(क) लुई 14वें की पत्नी
(ख) लुई 15वें की पत्नी
(ग) लुई 16वें की पत्नी
(घ) लुई 16वें की पत्नी।
उत्तर-
(ग) लुई 16वें की पत्नी
प्रश्न 24.
मेरी ऐंटोनिटी कहां की राजकुमारी थी ?
(क) जर्मनी
(ख) फ्रांस
(ग) इंग्लैंड
(घ) आस्ट्रिया।
उत्तर-
(घ) आस्ट्रिया।
प्रश्न 25.
क्रांति (1789) के समय फ्रांस पर कितना विदेशी ऋण था ?
(क) 2 अरब लिने
(ख) 12 अरब लिने
(ग) 10 अरब लिवे
(घ) 2.8 अरब लिने।
उत्तर-
(ख) 12 अरब लिने
प्रश्न 26.
फ्रांस में एस्टेट्स जेनराल का अधिवेशन हुआ था
(क) 1788 ई० में
(ख) 1801 ई० में
(ग) 1791 ई० में
(घ) 1789 ई० में।
उत्तर-
(घ) 1789 ई० में।
प्रश्न 27.
किस पुस्तक को ‘क्रांति का बाइबल’ कहा जाता है ?
(क) दि प्रिंसिपल ऑफ पोलिटकल राइट्स
(ख) एडिसकोर्स ऑन एंड साईंसिस ।
(ग) लॉ नैवेल
(घ) द सोशल कांट्रेक्ट/सामाजिक समझौता।
उत्तर-
(घ) द सोशल कांट्रेक्ट/सामाजिक समझौता।
प्रश्न 28.
कौन-सा सिद्धांत फ्रांसीसी क्रांति का नहीं है ?
(क) समानता
(ख) स्वतंत्रता
(ग) बंधुत्व
(घ) साम्राज्यवाद।
उत्तर-
(घ) साम्राज्यवाद।
![]()
प्रश्न 29.
” मैं फ्रांस हूँ। मेरी इच्छा ही कानून है।” ये शब्द किसके हैं ?
(क) बिस्मार्क
(ख) मांटेस्क्यू
(ग) लुई 16वें
(घ) नेपोलियन।
उत्तर-
(ग) लुई 16वें
प्रश्न 30.
राष्ट्रीय सभा बुलाने का उद्देश्य क्या था ?
(क) राजा को दंड देना
(ख) कर लगाना
(ग) कर हटाना
(घ) दार्शनिकों को पुरस्कृत करना।
उत्तर-
(ख) कर लगाना
प्रश्न 31.
राजा से झगड़े के पश्चात् राष्ट्रीय सभा किस स्थान पर एकत्रित हुई ?
(क) राजा के महल में
(ख) राजमहल के सामने
(ग) टेनिस कोर्ट में
(घ) बर्लिन में।
उत्तर-
(ग) टेनिस कोर्ट में
प्रश्न 32.
टेनिस कोर्ट में जनसाधारण के प्रतिनिधियों ने क्या शपथ ली ?
(क) संविधान बनाने की
(ख) राजा को हटाने की
(ग) चर्च की संपत्ति लूटने की
(घ) सामंत वर्ग का विनाश करने की।
उत्तर-
(क) संविधान बनाने की
प्रश्न 33.
राष्ट्रीय महासभा का अधिवेशन कब आरंभ हुआ ?
(क) 15 अगस्त, 1789 को
(ख) 9 जुलाई, 1789 को
(ग) 14 अगस्त, 1789 को
(घ) 4 अगस्त, 1789 को।
उत्तर-
(घ) 4 अगस्त, 1789 को।
प्रश्न 34.
राष्ट्रीय सभा ने मानवीय अधिकारों की घोषणा कब की ?
(क) 1790 को
(ख) 1791 को
(ग) 27 अगस्त, 1789
(घ) 1792 को।
उत्तर-
(ग) 27 अगस्त, 1789
प्रश्न 35.
फ्रांस में मानव एवं नागरिक अधिकारों की घोषणा किसने की ?
(क) विधानसभा ने
(ख) राष्ट्रीय महासभा ने
(ग) राष्ट्रीय सम्मेलन ने
(घ) किसी ने भी नहीं।
उत्तर-
(ख) राष्ट्रीय महासभा ने
प्रश्न 36.
बेस्टील का पतन कब हुआ ?
(क) 12 जुलाई, 1789 को
(ख) 10 जुलाई, 1789 को
(ग) 11 जुलाई, 1789 को
(घ) 14 जुलाई, 1789 को।
उत्तर-
(घ) 14 जुलाई, 1789 को।
![]()
प्रश्न 37.
बेस्टील का किला किस बात का प्रतीक था ?
(क) स्वतंत्रता का
(ख) समानता का
(ग) बंधुत्व का
(घ) निरंकुश शक्तियों का।
उत्तर-
(घ) निरंकुश शक्तियों का।
प्रश्न 38.
फ्रांसीसी क्रांति का आरंभ किस ऐतिहासिक घटना से माना जाता है ?
(क) एस्टेट्स जेनराल का भंग होना
(ख) बेस्टील का पतन
(ग) राजा का फ्रांस से भागना
(घ) रानी का जिद्दी स्वभाव।
उत्तर-
(ख) बेस्टील का पतन
प्रश्न 39.
‘राष्ट्रीय स्वयं सेवक सेना’ के गठन का क्या उद्देश्य था ?
(क) राजा पर नियंत्रण रखना
(ख) राष्ट्रीय सभा पर नियंत्रण रखना
(ग) फ्रांस का नेतृत्व करना
(घ) अराजकता को रोकना।
उत्तर-
(घ) अराजकता को रोकना।
प्रश्न 40.
राष्ट्रीय सभा ने संविधान तैयार किया
(क) 1789 में
(ख) 1799 में
(ग) 1791 में
(घ) 1792 में।
उत्तर-
(ग) 1791 में
प्रश्न 41.
1791 ई० के फ्रांसीसी संविधान के अनुसार फ्रांस की सरकार का स्वरूप कैसा था ?
(क) गणतंत्रीय
(ख) राजतंत्रीय
(ग) अल्पतंत्रीय
(घ) सामंतशाही।
उत्तर-
(क) गणतंत्रीय
प्रश्न 42.
10 अगस्त, 1792 से लेकर 20 सितंबर, 1792 तक फ्रांस का शासन किसके हाथ में रहा ?
(क) लुई 16वां
(ख) लफायेत
(ग) फ्रांसीसी सेना
(घ) पेरिस कम्यून।
उत्तर-
(घ) पेरिस कम्यून।
प्रश्न 43.
राष्ट्रीय सम्मेलन में लुई 16वें के लिए क्या दंड निश्चित किया गया ?
(क) मृत्यु दंड
(ख) निर्वासन
(ग) आजीवन कारावास
(घ) क्षमादान।
उत्तर-
(क) मृत्यु दंड
प्रश्न 44.
लुई 16वें को मृत्यु दंड कब दिया गया ?
(क) 1791 ई० में
(ख) 1792 ई० में
(ग) 1789 ई० में
(घ) 1793 ई० में।
उत्तर-
(घ) 1793 ई० में।
![]()
प्रश्न 45.
राष्ट्रीय सम्मेलन ने किस अमानवीय प्रथा का अंत किया ?
(क) सती प्रथा
(ख) बेगार प्रथा
(ग) दास प्रथा
(घ) सामंत प्रथा।
उत्तर-
(ग) दास प्रथा
प्रश्न 46.
रोबेस्प्येर को गिलोटिन पर कब चढ़ाया गया ?
(क) जुलाई, 1794 ई० में
(ख) जुलाई, 1791 ई० में
(ग) जुलाई, 1789 ई० में
(घ) जुलाई, 1795 ई० में।
उत्तर-
(क) जुलाई, 1794 ई० में
प्रश्न 47.
फ्रांस में ‘आतंक का राज्य’ निम्नलिखित राजनीतिक दल ने स्थापित किया
(क) जिरोंदिस्त दल
(ख) राजतंत्रवादी दल
(ग) जैकोबिन दल
(घ) उपरोक्त सभी ने सामूहिक रूप से।
उत्तर-
(ग) जैकोबिन दल
प्रश्न 48.
आतंक के शासन में मृत्युदंड प्राप्त व्यक्ति को मारा जाता था
(क) फांसी देकर
(ख) गिलोटिन द्वारा
(ग) बिजली का झटका देकर
(घ) विष देकर।
उत्तर-
(ख) गिलोटिन द्वारा
प्रश्न 49.
जिरोंदिस्त दल ने देश की आर्थिक दशा सुधारने के लिए कौन-सी नई मुद्रा चलाई ?
(क) चांदी के सिक्के
(ख) सोने के सिक्के
(ग) तांबे के सिक्के
(घ) कागज़ के नोट।
उत्तर-
(घ) कागज़ के नोट।
प्रश्न 50.
‘पैट्रियाट’ नामक पत्र के प्रकाशन का कार्य फ्रांसीसी क्रांति के किस नेता ने आरंभ किया ?
(क) रूसो
(ख) रोबेस्प्येर
(ग) दांते
(घ) ब्रीसो।
उत्तर-
(घ) ब्रीसो।
प्रश्न 51.
डायरेक्टरी की राजनीतिक अस्थिरता जिस सैनिक तानाशाह के उदय का आधार बनी
(क) नेपोलियन बोनापार्ट
(ख) लुई 16वां
(ग) रोबेस्प्येर
(घ) रूसो।
उत्तर-
(क) नेपोलियन बोनापार्ट
प्रश्न 52.
फ्रांस में महिलाओं को मत देने का अधिकार मिला
(क) 1792
(ख) 1794
(ग) 1904
(घ) 1946.
उत्तर-
(घ) 1946
![]()
प्रश्न 53.
क्रांतिकारी फ्रांस से आने वाले विचारों का समर्थन किया
(क) टीपू सुल्तान तथा राजा राममोहन राय
(ख) हैदरअली तथा स्वामी दयानंद
(ग) बहादुरशाह ज़फ़र तथा स्वामी विवेकानंद
(घ) उपरोक्त सभी।
उत्तर-
(क) टीपू सुल्तान तथा राजा राममोहन राय
II. रिक्त स्थान भरो:
- फ्रांसीसी क्रांति के समय ………………….. यूरोप में भूमि के स्वामी थे।
- फ्रांस के राष्ट्रीय रंगों का समूह ………………………. है।
- …………….. तीसरे वर्ग (एस्टेट) द्वारा फ्रांस राज्य को दिया जाने वाला प्रत्यक्ष कर था।
- फ्रांस में एस्टेट्स जेनराल का अधिवेशन ……….. ………. ई० में हुआ।
- बेस्टील का किला …. ……………….. का प्रतीक था।
- फ्रांस के ‘आतंक का राज्य’ …………………….. ने स्थापित किया।
उत्तर-
- जमींदार
- नीला सफेद लाल
- टेली (टाइले)
- 1789
- निरंकुश शक्तियों
- जैकोरि
III. सही मिलान करो :
(क) – (ख)
1. फ्रांसीसी क्रांति – (i) स्वतंत्र दास
2. किसान – (ii) जैकोबिन दल
3. लाल फ्रीजियन टोपी – (iii) लुई सोलहवां
4. क्रांति का बाइबल – (iv) द सोशल कांट्रेक्ट
5. आतंक का राज्य – (v) निम्न वर्ग
उत्तर-
- लुई सोलहवां
- निम्न वर्ग
- स्वतंत्र दास
- द सोशल कांट्रेक्ट
- जैकोबिन दल। जिला
अति लघु उत्तरों वाले प्रश्न
उत्तर एक लाइन अथवा एक शब्द में :
प्रश्न 1.
फ्रांस की राज्य क्रांति कब हुई ?
उत्तर-
1789 ई० में।
प्रश्न 2.
फ्रांसीसी क्रांति से पूर्व फ्रांस में किस वर्ग को विशेषाधिकार प्राप्त थे ?
उत्तर-
सामंत वर्ग को।
प्रश्न 3.
फ्रांसीसी क्रांति के समय फ्रांस का शासक कौन था ? उसका संबंध किस राजवंश से था ?
उत्तर-
लुई सोलहवां, बूढे राजवंश।
प्रश्न 4.
फ्रांसीसी क्रांति के समय फ्रांस के समाज में सबसे अधिक शक्तिशाली थे ?
उत्तर-
सामंत, चर्च।
प्रश्न 5.
रोमन कैथोलिक चर्च का सबसे बड़ा अधिकारी कौन था ?
उत्तर-
पोप।
प्रश्न 6.
फ्रांसीसी क्रांति के समय फ्रांस की संसद् किस नाम से प्रसिद्ध थी ?
उत्तर-
एस्टेट्स जेनराल।
प्रश्न 7.
लुई सोलहवें का निवास स्थान कहां था ?
उत्तर-
वर्सेय में।
प्रश्न 8.
फ्रांसीसी क्रांति के समय फ्रांस में किस प्रकार का शासन तंत्र था ?
उत्तर-
निरंकुश राजतंत्र।
प्रश्न 9.
फ्रांसीसी क्रांति को जन्म देने वाले दो प्रमुख दार्शनिकों के नाम बताओ।
उत्तर-
मांटेस्क्यू, रूसो।
प्रश्न 10.
रूसो ने किस बात पर अधिक बल दिया ?
उत्तर-
मनुष्यों की समानता पर।
प्रश्न 11.
रूसो द्वारा लिखित ग्रंथ का नाम लिखो।
उत्तर-
द सोशल कंट्रेक्ट (सामाजिक समझौता)।
प्रश्न 12.
मांतेस्क्यू ने किस ग्रंथ की रचना की थी ?
उत्तर-
‘The Spirit of The Laws’ (कानून की आत्मा)।
![]()
प्रश्न 13.
मेरी ऐंटोनिटी कौन थी ?
उत्तर-
लुई सोलहवें की पत्नी।
प्रश्न 14.
फ्रांस की भूमि पर कितना भाग चर्च की संपत्ति थी ?
उत्तर-
1/5 भाग।
प्रश्न 15.
फ्रांसीसी क्रांति से पूर्व फ्रांस में राज्य तथा सेना के महत्त्वपूर्ण पदों पर किसका अधिकार था ?
उत्तर-
सामंतों का।
प्रश्न 16.
फ्रांस के किस दार्शनिक को दार्शनिकों का सम्राट् कहा जाता है ?
उत्तर-
वाल्तेयर को।
प्रश्न 17.
फ्रांसीसी क्रांति का फ्रांस पर कोई एक प्रभाव बताओ।
उत्तर-
निरंकुश राजतंत्र का पतन।
प्रश्न 18.
फ्रांसीसी क्रांति के तीन प्रमुख सिद्धांत कौन-कौन से थे ?
उत्तर-
समानता, स्वतंत्रता, बंधुत्व।
प्रश्न 19.
राष्ट्रीय सभा का नाम संविधान सभा कब रखा गया ?
उत्तर-
9 जुलाई, 1789.
प्रश्न 20.
राष्ट्रीय सभा बुलाने का क्या उद्देश्य था?
उत्तर-
कर लगाना।
प्रश्न 21.
तुर्गों द्वारा किया गया एक वित्तीय सुधार लिखो।
उत्तर-
कर्मचारियों की संख्या में कमी।
प्रश्न 22.
एस्टेट्स जेनराल का अधिवेशन बुलाने से पूर्व लुई 16वें ने कौन-सी सभा बुलाई ?
उत्तर-
पैरिस की पार्लियामेंट।
प्रश्न 23.
पैरिस की पार्लियामेंट क्यों बुलाई गई ?
उत्तर-
कर लगाने के लिए।
प्रश्न 24.
एस्टेट्स जेनराल का अधिवेशन कब हुआ ?
उत्तर-
17 जुलाई, 1789.
प्रश्न 25.
टैनिस कोर्ट (फ्रांस) में जनसाधारण के प्रतिनिधियों ने किस विषय में शपथ ली ?
उत्तर-
संविधान बनाने की।
प्रश्न 26.
फ्रांस में मानव एवं नागरिक अधिकारों की घोषणा किसने की ?
उत्तर-
राष्ट्रीय महासभा ने।
प्रश्न 27.
बेस्टील का पतन कब हुआ ?
उत्तर-
14 जुलाई, 1789.
प्रश्न 28.
फ्रांसीसी क्रांति का आरंभ किस घटना से माना जाता है ?
उत्तर-
बेस्टील के पतन से।
![]()
प्रश्न 29.
फ्रांस की ‘राष्ट्रीय स्वयं सेवक सेना’ का मुखिया कौन था ?
उत्तर-
लफायेत।
प्रश्न 30.
राजा को वर्सेय से पेरिस कौन लाया ?
उत्तर-
स्त्रियों का जलस।
प्रश्न 31.
राष्ट्रीय संविधान सभा ने संविधान कब तैयार किया ?
उत्तर-
1791 ई० में।
प्रश्न 32.
जिरोंदिस्त क्लब के सदस्य किस विचारधारा के पक्षपाती थे ?
उत्तर-
गणतंत्रवादी विचारधारा।
प्रश्न 33.
पहली बार फ्रांस की जनता ने किस दिन राजमहल को घेरा ?
उत्तर-
20 जून, 1792 ई०।
प्रश्न 34.
पेरिस की भीड़ ने दूसरी बार राजा के महल को कब घेरा ?
उत्तर-
10 अगस्त, 1792 ई०।
प्रश्न 35.
फ्रांस के राजा को किसके शासन द्वारा बंदी बनाया गया ?
उत्तर-
विधानसभा के शासन द्वारा।
प्रश्न 36.
फ्रांसीसी विधान सभा का सबसे प्रमुख कार्य क्या था ?
उत्तर-
राजतंत्र की समाप्ति।
प्रश्न 37.
विधानसभा द्वारा राजतंत्रवादियों की हत्या की घटना को किस नाम से पुकारा जाता है ?
उत्तर-
सितंबर हत्याकांड।
प्रश्न 38.
राष्ट्रीय सम्मेलन ने फ्रांस में कैसी शासन प्रणाली स्थापित की ?
उत्तर-
गणतंत्रात्मक।
प्रश्न 39.
राष्ट्रीय सम्मेलन द्वारा जारी नये कैलेंडर की प्रथम तिथि कब से आरंभ हुई ?
उत्तर-
22 सितंबर, 1979 से।
प्रश्न 40.
राष्ट्रीय सम्मेलन ने लुई 16वें के लिए क्या दंड निश्चित किया ?
उत्तर-
मृत्यु दंड।
प्रश्न 41.
लुई 16वें को मृत्यु दंड कब दिया गया ?
उत्तर-
1793 ई० में।
प्रश्न 42.
राष्ट्रीय सम्मेलन के शासन काल में फ्रांस के दो प्रमुख राजनीतिक दल कौन-कौन से थे ?
उत्तर-
जिरोंदिस्त तथा जैकोबिन।
प्रश्न 43.
फ्रांस के राष्ट्रीय सम्मेलन ने भीतरी शत्रुओं का सामना करने के लिए किस समिति की स्थापना की ?
उत्तर-
सार्वजनिक रक्षा समिति।
प्रश्न 44.
राष्ट्रीय सम्मेलन ने नाप-तोल की कौन-सी नई विधि अपनाई ?
उत्तर-
दशमलव विधि।
प्रश्न 45.
फ्रांस में ‘आतंक का राज्य’ लगभग कितने वर्ष चला ?
उत्तर-
एक वर्ष।
प्रश्न 46.
फ्रांस में ‘आतंक का राज्य’ किस राजनीतिक दल ने स्थापित किया ?
उत्तर-
जैकोबिन दल।
प्रश्न 47.
सामान्य सुरक्षा समिति (आतंक का राज्य) की स्थापना कब हुई ?
उत्तर-
1792 ई० में।
![]()
प्रश्न 48.
क्रांतिकारी न्यायालय (आतंक का राज्य) की स्थापना कब हुई ?
उत्तर-
1793 ई० में।
प्रश्न 49.
वह चौक किस नाम से प्रसिद्ध था जहां आतंक के राज्य में लोगों को मौत के घाट उतारा जाता था ?
उत्तर-
क्रांति चौक।
प्रश्न 50.
राष्ट्रीय सम्मेलन ने पेरिस में क्रांति के विरोधियों का अंत करने के लिए कौन-सा महत्त्वपूर्ण अधिनियम बनाया ?
उत्तर-
लॉ ऑफ़ सस्पैक्ट।
प्रश्न 51.
दांते को मृत्यु दंड कब दिया गया ?
उत्तर-
अप्रैल, 1774.
प्रश्न 52.
कौन-सा युद्ध जिरोंदिस्त दल के पतन का कारण बना ?
उत्तर-
आस्ट्रिया-फ्रांस युद्ध।
प्रश्न 53.
पेरिस कम्यून पर किस राजनीतिक दल का प्रभाव था ?
उत्तर-
जैकोबिन दल।
लघु उत्तरों वाले प्रश्न
प्रश्न 1.
फ्रांसीसी समाज के किन तबकों (वर्गों) को क्रांति का फायदा (लाभ) मिला ? कौन-से समूह सत्ता छोड़ने के लिए मजबूर हो गए ? क्रांति के नतीजों से समाज के किन समूहों को निराशा हुई होगी?
उत्तर-
- फ्रांसीसी क्रांति से श्रमिक वर्ग तथा कृषक वर्ग को लाभ पहुंचा। इसका कारण यह था कि ये समाज के सबसे शोषित वर्ग थे। करों के बोझ से दबी आम जनता को भी राहत मिली। स्वतंत्रता एवं समानता की कामना करने वाले लोग भी प्रसन्न थे।
- क्रांति से अभिजात वर्ग को सत्ता त्यागनी पड़ी। राजतंत्र का अंत हो गया। जागीरदारों, सामंतों तथा चर्च को अपने विशेषाधिकारों से हाथ धोना पड़ा।
- क्रांति से अभिजात वर्ग को ही निराशा हुई होगी। इसके अतिरिक्त राजतंत्र के समर्थकों को भी क्रांति ने निराश ही किया होगा।
प्रश्न 2.
लुई 16वां (XVI) फ्रांस का सम्राट् कब बना ? उस समय फ्रांस की आर्थिक दशा कैसी थी ?
अथवा
लुई 16वें के राजगद्दी पर बैठते समय फ्रांस आर्थिक संकट में फंसा हुआ था। इसे स्पष्ट करने के लिए कोई तीन बिंदु लिखिए।
उत्तर-
लुई XVI 1774 ई० में फ्रांस का सम्राट् बना। उस समय उसकी आयु केवल 20 वर्ष की थी। उसके राज्यारोहण के समय फ्रांस का राजकोष खाली था जिसके कारण फ्रांस आर्थिक संकट में फंसा हुआ था। इस आर्थिक संकट के लिए मुख्य रूप से निम्नलिखित कारक उत्तरदायी थे
- लंबे समय तक चले युद्धों के कारण फ्रांस के वित्तीय संसाधन नष्ट हो चुके थे।
- वर्साय (Versailles) के विशाल महल और राजदरबार की शानो-शौकत बनाए रखने के लिए धन पानी की तरह बहाया जा रहा था।
- फ्रांस ने अमेरिका के 13 उपनिवेशों को अपने सांझा शत्रु ब्रिटेन से स्वतंत्र कराने में सहायता दी थी। इस युद्ध के चलते फ्रांस पर दस अरब लिने से भी अधिक का कर्ज और बढ़ गया, जबकि उस पर पहले से ही दो अरब लिने के ऋण का बोझ था। सरकार से ऋणदाता अब 10 प्रतिशत ब्याज की मांग करने लगे थे। फलस्वरूप फ्रांसीसी सरकार अपने बजट का बहुत बड़ा भाग लगातार बढ़ते जा रहे कर्ज को चुकाने पर मजबूर थी।
प्रश्न 3.
1789 से पहले फ्रांसीसी समाज किस प्रकार व्यवस्थित था ? तीसरे एस्टेट की भूमिका का वर्णन कीजिए।
उत्तर-
1789 से पहले फ्रांसीसी समाज तीन वर्गों में बंटा हुआ था जिन्हें एस्टेट कहते थे। तीन एस्टेट थे-प्रथम एस्टेट, द्वितीय एस्टेट तथा तृतीय एस्टेट। पहले एस्टेट में कुलीन वर्ग (पादरी आदि) के लोग तथा दूसरे वर्ग में सामंत शामिल थे। तीसरे एस्टेट में बड़े-बड़े व्यवसायी, व्यापारी, सौदागर, वकील, किसान, शिल्पकार, श्रमिक आदि आते थे। पहले दो एस्टेट के लोगों को कई विशेषाधिकार प्राप्त थे जिनमें से करों से मुक्ति का अधिकार सबसे महत्त्वपूर्ण था। करों का सारा बोझ तीसरे एस्टेट पर था, जबकि सभी आर्थिक कार्य इन्हीं लोगों द्वारा किये जाते थे। किसान तथा खेतिहर अनाज उगाते थे, श्रमिक वस्तुओं का उत्पादन करते थे और सौदागर व्यापार का संचालन करते थे। परंतु वे अपनी स्थिति में सुधार नहीं ला सकते थे।
प्रश्न 4.
रोबेस्प्येर कौन था ? उसके राज्य को ‘आतंक का राज्य’ क्यों कहा जाता है ?
उत्तर-
रोबेस्प्येर ने 1793 से 1794 तक फ्रांस पर शासन किया। उसने बहुत ही कठोर एवं क्रूर नीतियां अपनाईं। वह जिन्हें गणतंत्र का शत्रु मानता था अथवा उसकी पार्टी का जो कोई सदस्य उससे असहमति जताता था, उन्हें जेल में डाल देता था। उन पर एक क्रांतिकारी न्यायालय द्वारा मुकद्दमा चलाया जाता था। जो कोई भी दोषी पाया जाता था, उसे गिलोटिन पर चढ़ा कर उसका सिर धड़ से अलग कर दिया जाता था।
रोबेस्प्येर ने अपनी नीतियों को इतनी कठोरता एवं क्रूरता से लागू किया कि उसके समर्थक भी त्राहि-त्राहि कर उठे। इसी कारण उसके राज्य को ‘आतंक का राज्य’ कहा जाता है।
प्रश्न 5.
फ्रांसीसी क्रांति के राजनीतिक कारण क्या थे?
उत्तर-
फ्रांसीसी क्रांति के राजनीतिक कारण निम्नलिखित थे-
- फ्रांस के राजा स्वेच्छाचारी थे और वे राजा के दैवीय अधिकारों में विश्वास करते थे। वे जनता के प्रति अपना कोई कर्त्तव्य नहीं समझते थे। सारे देश में भ्रष्टाचार का बोलबाला था।
- कर बहुत अधिक थे और. वे मुख्यतः जनसाधारण को ही देने पड़ते थे। दरबारी और सामंत करों से मुक्त थे।
- शासन में एकरूपता का अभाव था। सारे देश में एक जैसे कानून नहीं थे। यदि देश के एक भाग में रोमन कानून लागू थे, तो दूसरे भाग में जर्मन कानून प्रचलित थे।
- राज्य में सैनिक तथा अन्य पद पैतृक थे और उन्हें बेचा भी जा सकता था। जनसाधारण के लिए उन्नति का कोई मार्ग नहीं था।
- राज्य का धन फ्रांस की रानी मेरी एंतोएनेत पर पानी की तरह बहाया जा रहा था। जनता पर बड़े अत्याचार हो रहे थे। किसी भी व्यक्ति को बिना दोष बंदी बना लिया जाता था।
- सेना में असंतोष था। सैनिकों के वेतन बहुत कम थे तथा उन्हें पर्याप्त सुख-सुविधा उपलब्ध नहीं थी।
प्रश्न 6.
14 जुलाई, 1789 को क्रुद्ध लोगों ने पेरिस के किस भवन पर धावा बोला ? यह भवन जनता का निशाना क्यों बना ?
अथवा
बेस्टील का पतन किन कारणों से हुआ तथा इसके क्या परिणाम हुए?
उत्तर-
14 जुलाई, 1789 को क्रुद्ध भीड़ ने पेरिस नगर में बेस्टील के किले पर धावा बोला। यह किला फ्रांस के सम्राट की निरंकुश शक्तियों का प्रतीक था। उस दिन सम्राट ने सेना को नगर में प्रवेश करने का आदेश दे दिया था। अफ़वाह थी कि वह सेना को नागरिकों पर गोलियां चलाने का आदेश देने वाला है। अतः लगभग 7000 पुरुष तथा स्त्रियां टाऊन हॉल के सामने एकत्र हुए और उन्होंने एक जन-सेना का गठन किया। हथियारों की खोज में वे अनेक सरकारी भवनों में जबरन प्रवेश कर गए। अंततः सैकड़ों लोगों के एक समूह ने पेरिस नगर में स्थित बेस्टील (Bastille) के किले की जेल को तोड़ डाला जहां उन्हें भारी मात्रा में गोला-बारूद मिलने की आशा थी। हथियारों पर कब्जे के इस संघर्ष में बेस्टील का कमांडर मारा गया और कैदी छुड़ा लिए गए, यद्यपि उनकी संख्या केवल सात थी। किले को ध्वस्त कर दिया गया और उसके अवशेष बाज़ार में उन लोगों को बेच दिए गए जो इस ध्वंस को स्मृति-चिह्न के रूप में संजो कर रखना चाहते थे।
![]()
प्रश्न 7.
नेशनल असेंबली के अस्तित्व में आने के तुरंत पश्चात् क्रांति की ज्वाला किस प्रकार पूरे फ्रांस में फैल गई ?
उत्तर-
जिस समय नेशनल असेंबली संविधान का प्रारूप तैयार करने में व्यस्त थी, पूरा फ्रांस आंदोलित हो रहा था। कड़ाके की ठंड के कारण फ़सल नष्ट हो गई थी और पावरोटी की कीमतें आसमान को छू रही थीं। बेकरी मालिक स्थिति का लाभ उठा कर जमाखोरी में जुटे थे। बेकरी की दुकानों पर घंटों के इंतजार के बाद क्रोधित औरतों की भीड़ ने दुकान पर धावा बोल दिया। दूसरी ओर सम्राट ने सेना को पेरिस में प्रवेश करने का आदेश दे दिया था। अतः क्रुद्ध भीड़ ने 14 जुलाई को बेस्टील पर धावा बोलकर उसे ध्वस्त कर दिया।
शीघ्र ही गांव-गांव यह अफ़वाह फैल गई कि जागीरों के मालिकों ने भाड़े पर लठैतों-लुटेरों के दल बुला लिए हैं जो पकी फ़सलों को नष्ट कर रहे हैं। कई जिलों में भययीत किसानों ने कुदालों तथा बेलचों से ग्रामीण किलों (chateau) पर आक्रमण कर दिए। उन्होंने अन्न भंडार लूट लिये और लगान संबंधी दस्तावेजों को जलाकर राख कर दिया। कुलीन बड़ी संख्या में अपनी जागीरें छोड़कर भाग गए। उनमें से अधिकांश ने पड़ोसी देशों में जाकर शरण ली। इस प्रकार क्रांति की ज्वाला चारों ओर फैल गई।
प्रश्न 8.
4 अगस्त, 1789 की रात को फ्रांस की नेशनल असेंबली द्वारा किये गए किन्हीं तीन प्रशासनिक परिवर्तनों का वर्णन कीजिए।
उत्तर-
लुई XVI से मान्यता मिलने के बाद नेशनल असेंबली ने 4 अगस्त, 1789 की रात को निम्नलिखित प्रशासनिक परिवर्तन किए
- करों, कर्त्तव्यों और बंधनों वाली सामंती व्यवस्था के उन्मूलन का आदेश पारित कर दिया गया।
- पादरी वर्ग के लोगों को अपने विशेषाधिकारों को छोड़ देने के लिए विवश किया गया।
- धार्मिक कर समाप्त कर दिया गया और चर्च के स्वामित्व वाली भूमि ज़ब्त कर ली गई। इस प्रकार लगभग 20 अरब लिने की संपत्ति सरकार के हाथ में आ गई।
प्रश्न 9.
फ्रांस में दास-व्यापार के आरंभ तथा महत्त्व का संक्षिप्त वर्णन कीजिए।
उत्तर-
फ्रांस में दास-व्यापार सत्रहवीं शताब्दी में आरंभ हुआ। फ्रांसीसी सौदागर बोर्दे या नाते बंदरगाह से अफ्रीका तट पर जहाज़ ले जाते थे। वहां वे स्थानीय सरदारों से दास खरीदते थे। दासों को दाग कर तथा हथकड़ियां डाल कर अटलांटिक महासागर के पार कैरिबिआई देशों तक ले जाने के लिए जहाज़ों में ढूंस दिया जाता था। वहां उन्हें बागानमालिकों को बेच दिया जाता था।
महत्त्व-
- दास-श्रम के बल पर यूरोपीय बाजारों में चीनी, कॉफी तथा नील की बढ़ती मांग को पूरा करना संभव हो सका।
- बोर्दे और नाते जैसे बंदरगाह फलते-फूलते दास-व्यापार के कारण समृद्ध नगर बन गए।
प्रश्न 10.
18वीं और 19वीं शताब्दी में फ्रांस की दासता के विषय में क्या स्थिति थी ? किन्हीं तीन स्थितियों को स्पष्ट कीजिए।
उत्तर-
- 18वीं शताब्दी में फ्रांस में दास प्रथा की अधिक निंदा नहीं हुई। नेशनल असेंबली में लंबी बहस हई कि व्यक्ति के मूलभूत अधिकार उपनिवेशों में रहने वाली प्रजा सहित समस्त फ्रांसीसी प्रजा को दिए जाएं या नहीं। परंतु दास-व्यापार पर निर्भर व्यापारियों के विरोध के भय के कारण नेशनल असेंबली में कोई कानून पारित नहीं किया गया।
- अंततः सन् 1794 के कन्वेंशन ने फ्रांसीसी उपनिवेशों में सभी दासों की मुक्ति का कानून पारित कर दिया। परंतु यह कानून एक छोटी-सी अवधि तक ही लागू रहा। दस वर्ष बाद नेपोलियन ने दास-प्रथा फिर से शुरू कर दी। बागान-मालिकों को अपने आर्थिक हित साधने के लिए अफ्रीकी नीग्रो लोगों को दास बनाने की स्वतंत्रता दे दी गई।
- फ्रांसीसी उपनिवेशों से अंतिम रूप से दास-प्रथा का उन्मूलन 1848 में किया गया।
प्रश्न 11.
नेपोलियन बोनापार्ट कौन था ? उसने किन सुधारों को लागू किया ?
उत्तर-
नेपोलियन बोनापार्ट फ्रांस का सम्राट् था। उसने 1804 में अपने आपको फ्रांस का सम्राट घोषित किया था। इससे पहले वह डिरेक्ट्री में प्रथम डिरेक्टर था।
सुधार-नेपोलियन स्वयं को यूरोप के आधुनिकीकरण का अग्रदूत मानता था। उसने निम्नलिखित सुधार लागू किए1. उसने निजी संपत्ति की सुरक्षा के लिए कानून बनाए। 2. उसने दशमलव पद्धति पर आधारित नाप-तौल की एक समान प्रणाली चलायी।
प्रश्न 12.
फ्रांस के 1791 के संविधान से महिलाएं क्यों निराश थीं ? महिलाओं के जीवन में सुधार लाने के लिए क्रांतिकारी सरकार ने कौन-से कानून लागू किए ?
उत्तर-
फ्रांस में महिलाएं 1791 के संविधान से इसलिए निराश थीं क्योंकि इसमें उन्हें निष्क्रिय नागरिक का दर्जा दिया गया था। परंतु महिलाओं ने मताधिकार, असेंबली के लिए चुने जाने तथा राजनीतिक पदों की मांग रखी। उनका मानना था कि तभी नई सरकार में उनका प्रतिनिधित्व हो पायेगा। क्रांतिकारी सरकार के कानून-महिलाओं के जीवन में सुधार लाने के लिए क्रांतिकारी सरकार ने निम्नलिखित कानून लागू किए
- सभी लड़कियों के लिए स्कूली शिक्षा अनिवार्य कर दी गई।
- अब पिता उन्हें उनकी इच्छा के विरुद्ध शादी के लिए बाध्य नहीं कर सकता था। शादी को स्वैच्छिक अनुबंध माना गया और नागरिक कानूनों के अनुसार उनका पंजीकरण किया जाने लगा।
- तलाक को कानूनी रूप दे दिया गया और स्त्री-पुरुष दोनों को ही इसकी अर्जी देने का अधिकार दिया गया।
- अब महिलाएं व्यावसायिक प्रशिक्षण ले सकती थीं, कलाकार बन सकती थीं और छोटे-मोटे व्यवसाय चला सकती थीं।
प्रश्न 13.
जैकोबिन कौन थे ? उन्हें ‘सौं कुलॉत’ के नाम से क्यों जाना गया ?
उत्तर-
जैकोबिन क्लब के सदस्य मुख्यतः समाज के कम समृद्ध वर्गों से संबंधित थे। इनमें छोटे दुकानदार और कारीगर-जैसे जूता बनाने वाले, पेस्ट्री बनाने वाले, घड़ीसाज़, छपाई करने वाले और नौकर व दैनिक मजदूर शामिल थे। उनका नेता मैक्समिलियन रोबेस्प्येर था। जैकोबिनों के एक बड़े वर्ग ने गोदी कामगारों की तरह लंबी धारीदार पतलून पहनने का निर्णय किया। ऐसा उन्होंने समाज के फ़ैशनपरस्त वर्ग, विशेषकर स्वयं को घुटने तक पहने जाने वाले ब्रीचेस (घुटन्ना) पहनने वाले कुलीनों से अलग करने के लिए किया। यह उनका ब्रीचेस पहनने वाले कुलीनों की सत्ता समाप्ति को दर्शाने का तरीका था। इसलिए जैकोबिनों को ‘सौं कुलॉत’ के नाम से जाना गया जिसका शाब्दिक अर्थ है-बिना घुटन्ने वाले। सौं कुलॉत पुरुष लाल रंग की टोपी भी पहनते थे जो स्वतंत्रता की प्रतीक थी। महिलाओं को यह टोपी पहनने की अनुमति नहीं थी।
![]()
प्रश्न 14.
फ्रांस में संवैधानिक राजतंत्र के स्थान पर गणतंत्र की स्थापना कैसे हुई ?
उत्तर-
1792 ई० की गर्मियों में जैकोबिनों ने खाद्य पदार्थों की महंगाई एवं अभाव से क्रुद्ध पेरिसवासियों को लेकर एक विशाल हिंसक विद्रोह की योजना बनायी। 10 अगस्त की प्रातः उन्होंने ट्यूलेरिए के महल पर धावा बोल दिया। उन्होंने राजा के रक्षकों को मार डाला और राजा को कई घंटों तक बंधक बनाये रखा। बाद में नेशनल असेंबली ने शाही परिवार को जेल में डाल देने का प्रस्ताव पारित किया। नये चुनाव कराये गए। 21 वर्ष से अधिक उम्र वाले सभी पुरुषोंचाहे उनके पास संपत्ति थी या नहीं-को मतदान का अधिकार दिया गया।
नवनिर्वाचित असेंबली को कन्वेंशन का नाम दिया गया। 21 सितंबर, 1792 को कन्वेंशन ने राजतंत्र का अंत करके फ्रांस को एक गणतंत्र घोषित कर दिया।
प्रश्न 15.
फ्रांस के इतिहास पर फ्रांसीसी क्रांति के प्रभाव का वर्णन कीजिए।
उत्तर-
- 1789 से बाद के वर्षों में फ्रांस के लोगों के पहनावे, बोलचाल तथा पुस्तकों आदि में अनेक महत्त्वपूर्ण परिवर्तन आए।
- क्रांतिकारी सरकारों ने कानून बना कर स्वतंत्रता तथा समानता के आदर्शों को दैनिक जीवन में उतारने का प्रयास किया।
- सेंसरशिप को समाप्त कर दिया। अधिकारों के घोषणा-पत्र ने भाषण एवं अभिव्यक्ति की स्वतंत्रता को नैसर्गिक अधिकार घोषित कर दिया।
प्रश्न 16.
1791 का फ्रांसीसी संविधान किस महत्त्वपूर्ण प्रावधान से शुरू होता था ? इसमें क्या कहा गया था?
उत्तर-
1791 का फ्रांसीसी संविधान ‘पुरुष एवं नागरिक अधिकार घोषणा-पत्र’ के साथ शुरू हुआ था। इसके अनुसार जीवन के अधिकार, अभिव्यक्ति की स्वतंत्रता के अधिकार और कानूनी समानता के अधिकार को ‘नैसर्गिक एवं अहरणीय’ अधिकार के रूप में स्थापित किया गया। प्रत्येक व्यक्ति को ये अधिकार जन्म से प्राप्त थे। अतः इन अधिकारों को छीना नहीं जा सकता था। राज्य का यह कर्त्तव्य माना गया कि वह प्रत्येक नागरिक के नैसर्गिक अधिकारों की रक्षा करे।
दीर्घ उत्तरों वाले प्रश्न
प्रश्न 1.
उन जनवादी अधिकारों की सूची बनाएं जो आज हमें मिले हुए हैं और जिनका उद्गम फ्रांसीसी क्रांति में है ?
अथवा
उन लोकतांत्रिक अधिकारों की सूची बनाओ जिनका आज हम उपभोग करते हैं और जो फ्रांसीसी क्रांति की उपज होंगे।
उत्तर-
आज के मानव को निम्नलिखित लोकतांत्रिक (जनवादी) अधिकार फ्रांसीसी क्रांति की देन हैं। इनकी घोषणा 27 अगस्त, 1789 को राष्ट्रीय महासभा में की गई थी।
- मनुष्य स्वतंत्र पैदा हुआ है और उसके अधिकार अन्य मनुष्यों के समान होंगे।
- प्रत्येक राजनीतिक संगठन का उद्देश्य मनुष्य के सभी अधिकारों की रक्षा करना है।
- प्रत्येक मनुष्य को पूर्ण स्वतंत्रता का अधिकार है, परंतु वह दूसरों की स्वतंत्रता को हानि न पहुंचाए।
- राज्य की शक्ति का मुख्य स्रोत राज्य के नागरिक हैं । अतः कोई भी व्यक्ति अथवा कोई भी संगठन ऐसा निर्णय लागू नहीं कर सकता जो देश के लोगों की इच्छा के विरुद्ध हो।
- कानून केवल उन्हीं कार्यों को रोकता है जिनसे समाज को हानि पहुंचती हो।
- न्याय की दृष्टि में सभी नागरिक समान हैं। कानूनी कार्यवाही के बिना किसी भी व्यक्ति को बंदी नहीं बनाया जा सकता। दोष सिद्ध होने पर ही किसी को दंड दिया जा सकता है।
- कानून देश के सभी लोगों की इच्छा की अभिव्यक्ति हैं। अतः सभी नागरिकों को व्यक्तिगत रूप से अथवा अपने प्रतिनिधियों द्वारा कानून के निर्माण में भाग लेने का अधिकार है। .
- सभी व्यक्तियों को धार्मिक स्वतंत्रता प्राप्त है।
- प्रत्येक व्यक्ति को अपने विचार प्रकट करने की स्वतंत्रता है। परंतु उससे समाज या देश को हानि न पहुंचे।
- बिना क्षति-पूर्ति (Compensation) के किसी भी व्यक्ति की संपत्ति नहीं ली जा सकती।
- कोई भी व्यक्ति किसी दूसरे व्यक्ति का शोषण नहीं कर सकता।
प्रश्न 2.
क्या आप इस तर्क से सहमत हैं कि सार्वभौमिक अधिकारों के संदेश में नाना अंतर्विरोध थे ?
उत्तर-
सार्वभौमिक अधिकारों के संदेश निश्चित रूप से विरोधाभासों से ग्रस्त थे। इनमें निम्नलिखित कई दोष थे-
- इसमें सभा आयोजित करने तथा संघ आदि बनाने की स्वतंत्रता के विषय में कुछ नहीं कहा गया था।
- इसमें सार्वजनिक शिक्षा के विषय में कुछ नहीं कहा गया था।
- इसमें व्यापार तथा व्यवसाय की स्वतंत्रता का अधिकार नहीं दिया गया था।
- इसमें नागरिकों को संपत्ति रखने का सीमित अधिकार प्रदान किया गया था। अतः राज्य सार्वजनिक हित का बहाना बनाकर किसी की भी संपत्ति छीन सकता था।
- फ्रांस के उपनिवेशों (Colonies) में काम करने वाले हब्शी दासों के विषय में इसमें कोई उल्लेख न था।
- इन अधिकारों की सबसे बड़ी त्रुटि यह थी कि इनके साथ मानव के कर्त्तव्य निश्चित नहीं किए गए थे। कर्त्तव्यों के बिना अधिकार प्रायः महत्त्वहीन ही समझे जाते हैं। इस विषय में मिराब्यो ने भी लिखा है कि नागरिकों को अधिकार देने की उतनी आवश्यकता न थी जितनी कि उन्हें अपने कर्तव्यों से अवगत कराने की थी।
प्रश्न 3.
फ्रांस में नेशनल असेंबली किस प्रकार अस्तित्व में आई ?
उत्तर-
फ्रांस में नेशनल असेंबली टेनिस कोर्ट की शपथ के फलस्वरूप अस्तित्व में आई। तीसरे एस्टेट के प्रतिनिधि स्वयं को संपूर्ण फ्रांसीसी राष्ट्र का प्रवक्ता मानते थे। 20 जून को ये प्रतिनिधि वर्साय के इंडोर टेनिस कोर्ट में एकत्र हुए। उन्होंने अपने आप को नेशनल असेंबली घोषित कर दिया और शपथ ली कि जब तक सम्राट की शक्तियों को कम करने वाला संविधान तैयार नहीं हो जाता तब तक असेंबली भंग नहीं होगी। उनका नेतृत्व मिराब्यो और आबे सिए ने किया। मिराब्यो का जन्म कुलीन परिवार में हुआ था, परंतु वह सामंती विशेषाधिकारों वाले समाज को समाप्त करने के पक्ष में था। उसने एक पत्रिका निकाली और वर्साय में जमा भीड़ के सामने जोरदार भाषण भी दिए। आबे सिए मूलतः पादरी था और उसने ‘तीसरा एस्टेट क्या है ?’ शीर्षक से एक अत्यंत प्रभावशाली प्रचार-पुस्तिका (पैंफ़्लेट) लिखी।
अपनी विद्रोही प्रजा के तेवर देखकर लुई XVI ने अंततः नेशनल असेंबली को मान्यता दे दी और यह भी मान लिया कि उसकी सत्ता पर अब से संविधान का अंकुश होगा।
प्रश्न 4.
रोबेस्प्येर ने किस प्रकार फ्रांसीसी समाज में समानता लाने के प्रयास किए ?
उत्तर-
रोबेस्प्येर ने निम्नलिखित सुधारों द्वारा फ्रांसीसी समाज में समानता लाने का प्रयास किया-
- रोबेस्प्येर ने कानून द्वारा मज़दूरी तथा कीमतों की अधिकतम सीमा निश्चित कर दी।
- गोश्त तथा पावरोटी की राशनिंग कर दी गई।
- किसानों को अपना अनाज शहरों में जाकर सरकार द्वारा निश्चित मूल्यों पर बेचने के लिए विवश कर दिया गया।
- अपेक्षाकृत महंगे सफ़ेद आटे के प्रयोग पर रोक लगा दी गई। अब सभी नागरिकों के लिए साबुत गेहूँ से बनी और समानता का प्रतीक मानी जाने वाली ‘समता रोटी’ खाना अनिवार्य कर दिया गया।
- बोलचाल और संबोधन में भी समानता का आचार-व्यवहार लागू करने का प्रयास किया गया। परंपरागत मॉन्स्यूर (महाशय) एवं मदाम (महोदया) के स्थान पर अब सभी फ्रांसीसी पुरुषों एवं महिलाओं को सितोयेन (नागरिक) एवं सितोयीन (नागरिका) के नाम से संबोधित किया जाने लगा।
- चर्चों को बंद कर दिया गया और उनके भवनों को बैरक या दफ़्तर बना दिया गया।
प्रश्न 5.
फ्रांसीसी क्रांति के इतिहास में 1791 के संविधान का क्या महत्त्व हैं ?
उत्तर-
1791 के संविधान में सम्राट की शक्तियों को सीमित करके फ्रांस में संवैधानिक राजतंत्र की स्थापना की गई। इस संविधान के मुख्य प्रावधान निम्नलिखित थे
- शासन की शक्तियों को विभिन्न संस्थाओं अर्थात् विधायिका, कार्यपालिका एवं न्यायपालिका में विभाजित एवं हस्तांतरित कर दिया गया।
- कानून बनाने का अधिकार नेशनल असेंबली को सौंप दिया गया।
- नेशनल असेंबली का अप्रत्यक्ष रूप से चुनाव होता था। पहले नागरिक एवं निर्वाचक समूह का चुनाव करते थे जो असेंबली के सदस्यों को चुनते थे।
- मत देने का अधिकार केवल 25 वर्ष या उससे अधिक आयु के ऐसे पुरुषों को प्राप्त था जो कम-से-कम तीन दिन की मजदूरी के बराबर कर चुकाते थे। इन्हें सक्रिय नागरिक का दर्जा दिया गया था। शेष पुरुषों और महिलाओं को निष्क्रिय नागरिक के रूप में वर्गीकृत किया गया था। निर्वाचक की योग्यता प्राप्त करने तथा असेंबली का सदस्य बनने के लिए लोगों का करदाताओं की उच्चतम श्रेणी में होना आवश्यक था।
प्रश्न 6.
नेपोलियन का सम्राट के रूप में उदय किस प्रकार हुआ था ? उसके शासनकाल की मुख्य विशेषताएं बताओ।
उत्तर-
जैकोबिन सरकार के पतन के बाद फ्रांस की सत्ता मध्य वर्ग के संपन्न लोगों के हाथ में आ गई। नए संविधान के अनुसार संपत्तिहीन वर्ग को मताधिकार से वंचित कर दिया गया। इस संविधान में चुनी गई दो विधान परिषदों की व्यवस्था थी। इन परिषदों ने पांच सदस्यों वाली एक कार्यपालिका-डायरेक्टरी को नियुक्त किया। नई व्यवस्था में
जैकोबिनों के शासनकाल वाली एक व्यक्ति-केंद्रित कार्यपालिका से बचने का प्रयास किया गया, परंतु विधान परिषदों में डायरेक्टरों का झगड़ा होता रहता था। तब परिषद् उन्हें हटाने की चेष्टा करती थी। डायरेक्टरी की राजनीतिक अस्थिरता ने सैनिक तानाशाह-नेपोलियन बोनापार्ट के उदय का मार्ग प्रशस्त कर दिया। 1804 ई० में नेपोलियन ने अपने आप को फ्रांस का सम्राट घोषित कर दिया।
शासनकाल-
- नेपोलियन ने यूरोपीय देशों की विजय यात्रा आरंभ की। पुराने राजवंशों को हटा कर उसने नए साम्राज्य बनाए और उनकी बागडोर अपने खानदान के लोगों के हाथ में दे दी ।
- नेपोलियन अपने आप को आधुनिकीकरण का दूत मानता था। उसने निजी संपत्ति की सुरक्षा के लिए कानून बनाए और दशमलव पद्धति पर आधारित नाप-तौल की एक समान प्रणाली आरंभ की।
- आरंभ में बहुत-से लोगों को नेपोलियन मुक्तिदाता लगता था और उससे जनता को स्वतंत्रता दिलाने की आशा थी। परंतु जल्दी ही उसकी सेनाओं को लोग आक्रमणकारी मानने लगे। आखिरकार 1815 में वॉटरलू में उसकी पराजय हुई
यूरोप के अन्य भागों में उसके मुक्ति और आधुनिक कानूनों को फैलाने वाले क्रांतिकारी उपायों का प्रभाव उसकी मृत्यु के काफ़ी समय बाद सामने आया।
![]()
प्रश्न 7.
बेस्टील के पतन के बाद फ्रांस में पारित सबसे महत्त्वपूर्ण कानून कौन-सा था ? इसका क्या महत्त्व था ?
अथवा
फ्रांस में भाषण एवं अभिव्यक्ति की स्वतंत्रता’ को नैसर्गिक अधिकार घोषित किए जाने का फ्रांसीसी जनता के लिए क्या महत्त्व था ?
उत्तर-
बेस्टील के पतन के बाद 1789 की गर्मियों में जो सबसे महत्त्वपूर्ण कानून अस्तित्व में आया, वह था सेंसरशिप की समाप्ति। प्राचीन राजतंत्र के अंतर्गत समस्त लिखित सामग्री तथा सांस्कृतिक गतिविधियों-पुस्तकों, अखबारों, नाटक आदि को राजा के सेंसर अधिकारियों द्वारा पास किए जाने के बाद ही प्रकाशित या मंचित किया जा सकता था। परंतु अब अधिकारों के घोषणापत्र के अनुसार भाषण एवं अभिव्यक्ति की स्वतंत्रता को नैसर्गिक अधिकार घोषित कर दिया। परिणामस्वरूप फ्रांस के नगरों में अखबारों, पर्यों, पुस्तकों तथा चित्रों की बाढ़-सी आ गई, जो तेज़ी से गांव-देहात तक जा पहुंची। उनमें फ्रांस में हो रही घटनाओं एवं परिवर्तनों का ब्यौरा और उन पर टिप्पणी होती थी। प्रेस की स्वतंत्रता का अर्थ यह था कि किसी भी घटना पर परस्पर विरोधी विचार भी व्यक्त किए जा सकते थे। प्रिंट माध्यम का उपयोग करके एक पक्ष ने दूसरे पक्ष को अपने दृष्टिकोण से सहमत कराने के प्रयास किए। अब नाटक, संगीत और उत्सवी जुलूसों में असंख्य लोग जाने लगे। स्वतंत्रता और न्याय के बारे में राजनीतिज्ञों एवं दार्शनिकों के पांडित्यपूर्ण लेखन को समझने और उससे जुड़ने का यह एक लोकप्रिय तरीका था क्योंकि किताबों को केवल मुट्ठी भर शिक्षित लोग ही पढ़ सकते थे।
प्रश्न 8.
फ्रांसीसी सम्राट् लुई XVI ने एस्टेट्स जनरल (जेनराल) की बैठक क्यों बुलाई ? इसमें विभिन्न एस्टेट्स की क्या स्थिति थी ?
उत्तर-
फ्रांस पर ऋण के बढ़ते बोझ के कारण फ्रांस के सम्राट को धन की आवश्यकता थी। इसके लिए उसने नए कर लगाने का निर्णय किया। प्राचीन राजतंत्र के अंतर्गत फ्रांसीसी सम्राट अपनी मर्जी से कर नहीं लगा सकता था। इसके लिए उसे एस्टेट्स जेनराल (प्रतिनिधि सभा) की बैठक बुला कर नए करों के अपने प्रस्तावों पर मंजूरी लेनी पड़ती थी। एस्टेट्स जेनराल एक राजनीतिक संस्था थी जिसमें तीनों एस्टेट्स अपने-अपने प्रतिनिधि भेजते थे। परंतु सम्राट् ही यह निर्णय करता था कि इस संस्था की बैठक कब बुलाई जाए। इसकी अंतिम बैठक 1614 में बुलाई गई थी।
इसके बाद लुई XVI ने 5 मई, 1789 को नये करों के प्रस्ताव पर मंजूरी के लिए एस्टेट्स जेनराल की बैठक बुलाई। प्रतिनिधियों की मेजबानी के लिए वर्साय के एक भव्य भवन को सजाया गया। पहले और दूसरे एस्टेट ने इस बैठक में अपने 300-300 प्रतिनिधि भेजे जिन्हें आमने-सामने की पंक्तियों में बिठाया गया। तीसरे एस्टेट के 600 प्रतिनिधियों को उनके पीछे खड़ा किया गया। तीसरे एस्टेट का प्रतिनिधित्व इसके अपेक्षाकृत समृद्ध एवं शिक्षित वर्ग के लोग कर रहे थे। किसानों, औरतों एवं कारीगरों को सभा में प्रवेश की अनुमति नहीं थी। फिर भी लगभग 40,000 पत्रों के माध्यम से उनकी शिकायतों तथा मांगों की सूची बनाई गई थी जिसे प्रतिनिधि अपने साथ लेकर आए थे।
प्रश्न 9.
फ्रांस में जेनराल नेशनल असेंबली किस प्रकार अस्तित्व में आई? इसमें मिराब्यो और आबे सिए की क्या भूमिका रही ?
उत्तर-
एस्टेट्स जेनराल के नियमों के अनुसार प्रत्येक एस्टेट (सामाजिक वर्ग) को एक मत देने का अधिकार था। इस बार भी लुई XVI का इसी प्रथा का पालन करने के लिए दृढ़ संकल्प था। परंतु तीसरे एस्टेट के प्रतिनिधियों ने मांग रखी कि अबकी बार पूरी सभा द्वारा मतदान कराया जाना चाहिए, जिसमें प्रत्येक सदस्य को एक मत देने का अधिकार हो। यह नि:संदेह एक लोकतांत्रिक सिद्धांत था, जिसे अपनी पुस्तक ‘द सोशल कॉन्ट्रैक्ट’ में रूसो ने भी प्रस्तुत किया था। परंतु सम्राट ने इस प्रस्ताव को मानने से इंकार कर दिया। इस विरोध में तीसरे एस्टेट के प्रतिनिधि सभा से बाहर चले गए। वे स्वयं को संपूर्ण फ्रांसीसी राष्ट्र का प्रवक्ता मानते थे। 20 जून को वे वर्साय के इनडोर टेनिस कोर्ट में जमा हुए। उन्होंने स्वयं को नेशनल असेंबली घोषित कर दिया और शपथ ली कि जब तक सम्राट की शक्तियों को कम करने वाला संविधान तैयार नहीं हो जाता तब तक असेंबली भंग नहीं होगी। उनका नेतृत्व मिराब्यो और आबे सिए ने किया। मिराब्यो का जन्म कुलीन परिवार में हुआ था, लेकिन वह सामंती विशेषाधिकारों वाले समाज को समाप्त करने की ज़रूरत से सहमत था। उसने एक पत्रिका निकाली और वर्साय में जुटी भीड़ के सामने ज़ोरदार भाषण भी दिए। आबे सिए मूलतः पादरी था और उसने ‘तीसरा एस्टेट क्या है ?’ शीर्षक से एक अत्यंत प्रभावशाली प्रचार-पुस्तिका (पैंफ्लेट) लिखी।
प्रश्न 10.
फ्रांसीसी नेशनल असेंबली के अधीन क्रांतिकारी युद्धों का संक्षिप्त वर्णन कीजिए। इनके क्या परिणाम निकले ?
उत्तर-
लुई XVI ने 1791 के संविधान पर हस्ताक्षर कर दिए थे, परंतु प्रजा के राजा से उसकी गुप्त वार्ता भी चल रही थी। फ्रांस की घटनाओं से अन्य पड़ोसी देशों के शासक भी चिंतित थे। इन शासकों ने फ्रांस की नेशनल असेंबली की सरकार के विरुद्ध सेना भेजने की योजना बना ली थी। परंतु, आक्रमण होने से पहले ही, अप्रैल, 1792 में नेशनल असेंबली ने प्रशा तथा ऑस्ट्रिया के विरुद्ध युद्ध की घोषणा का प्रस्ताव पारित कर दिया। प्रांतों से हज़ारों स्वयं सेवी सेना में भर्ती होने के लिए आने लगे। उन्होंने इस युद्ध को यूरोपीय राजाओं एवं कुलीनों के विरुद्ध जनता के युद्ध के रूप में लिया। उनके होठों पर देशभक्ति के जो गीत थे उनमें कवि रॉजेट दि लाइल द्वारा रचित मार्सिले भी था। यह गीत पहली बार मार्सिलेस के स्वयंसेवियों ने पेरिस की ओर कूच करते हुए गाया था। इसलिए इस गीत का नाम मार्सिले हो गया जो अब फ्रांस का राष्ट्रगान है।
क्रांतिकारी युद्धों के परिणाम-
- क्रांतिकारी युद्धों ने जनता को भारी क्षति पहुंचाई। लोगों को अनेक आर्थिक कठिनाइयां झेलनी पड़ी। पुरुषों के मोर्चे पर चले जाने के बाद घर-परिवार और रोजी-रोटी की ज़िम्मेवारी औरतों पर आ पड़ी।
- देश की आबादी के एक बड़े भाग को ऐसा लगता था कि क्रांति के घटनाक्रम को आगे बढ़ाने की ज़रूरत है क्योंकि 1791 के संविधान से केवल धनी लोगों को ही राजनीतिक अधिकार प्राप्त हुए थे। लोग राजनीतिक क्लबों में अड्डे जमा कर सरकारी नीतियों और अपनी कार्ययोजना पर बहस करते थे। इनमें से जैकोबिन क्लब सबसे आगे था, जिसका नाम पेरिस के भूतपूर्व कॉन्वेंट ऑफ़ सेंट जेकब के नाम पर पड़ा।
प्रश्न 11.
जैकोबिन सरकार के पतन के बाद फ्रांस में हुए किन्हीं चार परिवर्तनों का वर्णन कीजिए।
अथवा
डायरेक्टरी शासित फ्रांस की कोई चार विशेषताएं बताइए।
उत्तर-
- जैकोबिन सरकार के पतन के बाद वहां की सत्ता मध्य वर्ग के संपन्न लोगों के हाथों में आ गईं।
- नए संविधान के अनुसार संपत्तिहीन वर्ग को मताधिकार से वंचित कर दिया गया।
- इस संविधान में दो निवर्चित विधान परिषदों की व्यवस्था की गई थी । इन परिषदों ने पांच सदस्यों वाली एक कार्यपालिका को नियुक्त किया। इसे डायरेक्टरी कहा जाता था। इस प्रावधान के माध्यम से जैकोबिनों के शासनकाल वाली एक व्यक्ति-केंद्रित कार्यपालिका से बचने का प्रयास किया गया, परंतु डायरेक्टरी का प्रायः विधान परिषदों से झगड़ा होता रहता था। ऐसे अवसरों पर परिषद् उन्हें पद से हटाने की चेष्टा करती थी।
- डायरेक्टरी की राजनीतिक अस्थिरता ने सैनिक तानाशाह-नेपोलियन बोनापार्ट के उदय का मार्ग प्रशस्त किया।
मानचित्र संबंधी प्रश्न (Map Work Questions)
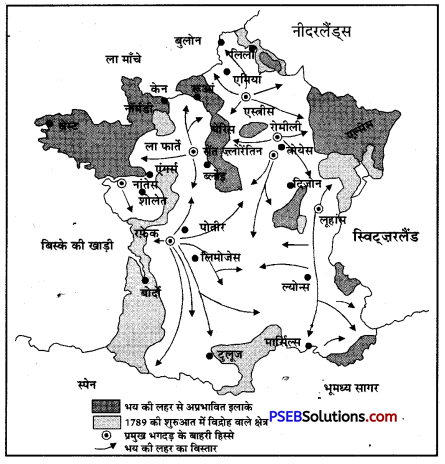
नोट- दिये गए मानचित्र में दिखाए गये तथ्यों का अध्ययन करें तथा उन्हें रिक्त मानचित्र में भरने का अभ्यास करें।
महत्त्वपूर्ण राजनीतिक प्रतीक
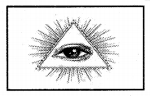
त्रिकोण में आँख ज्ञान का प्रतीक है और सूर्य की किरणें अज्ञानता दूर करने के लिए हैं।

एक सांप अपनी पूंछ को खा रहा है। इसका अर्थ है कि प्रत्येक प्रक्रिया का अंत होता है।

टूटी हुई जंजीर का अर्थ है दासता से आज़ादी।

एक फ्रीजियन टोपी (Phrygian Cap) दासों की आज़ादी का प्रतीक है।

कुल्हाड़ी सहित दंड की गांठ एकता में बल को दर्शाती है।

राजदंड राज्य की शाही ताकत का प्रतीक है।

कानून की पट्टी का अर्थ है कि कानून की नज़रों में सभी नागरिक समान हैं।

पंखों वाली औरत कानून की सर्वोच्चता को दर्शाती है।

नीला, सफेद तथा लाल रंग फ्रांस के राष्ट्रीय रंग हैं।