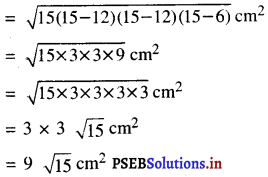Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन MCQ Questions with Answers.
PSEB 9th Class Maths Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन MCQ Questions
बहुविकल्पीय प्रश्न:
दिये गए चार विकल्पों में से सही उत्तर का चयन करें।
प्रश्न 1.
घनाभ का पृष्ठीय क्षेत्रफल होता है :
(A) 2 (lb + bh + hl)
(B) 3 (lb + bh + hl)
(C) 2 (lb + bh – hl)
(D) 3 (lb – bh – hl).
हल :
(A) 2 (lb + bh + hl)
प्रश्न 2.
गरम पानी द्वारा गरम रखने वाले एक संयंत्र में 28 m लंबाई और 5 cm व्यास वाला एक बेलनाकार पाइप है। इस संयंत्र में गरमी देने वाला कुल ष्ठ है :
(A) 6.6 m2
(B) 5.5 m2
(C) 4.4 m2
(D) 3.4 m2
हल :
(C) 4.4 m2
प्रश्न 3.
एक लंब वृत्तीय शंकु की तिर्यक ऊँचाई 10 cm और आधार की त्रिज्या 7 cm हो तो : इसका वक्र पृष्ठीय क्षेत्रफल होगा :
(A) 120 cm2
(B) 220 cm2
(C) 240 cm2
(D) 140 cm2.
हल :
(B) 220 cm2
प्रश्न 4.
एक शंकु की ऊँचाई 16 cm है और आधार की त्रिज्या 12 cm है। इसकी तिर्यक ऊँचाई होगी :
(A) 10 cm
(B) 15 cm
(C) 20 cm
(D) 8 cm.
हल :
(C) 20 cm
प्रश्न 5.
एक शंकु की ऊँचाई 16 cm और आधार की त्रिज्या 12 cm है। इसका वक्र पृष्ठीय क्षेत्रफल होगा :
(A) 753.6 cm2
(B) 1205.76 cm2
(C) 863.8 cm2
(D) 907.8 cm2
हल :
(C) 863.8 cm2

प्रश्न 6.
एक शंकु के आधार का व्यास 10.5 cm है और इसकी तिर्यक ऊँचाई 10 cm है। इसका ऊँचाई वक्र पृष्ठीय क्षेत्रफल होगा :
(A) 185 cm
(B) 160 cm2
(C) 165 cm
(D) 195 cm2.
हल :
(C) 165 cm
प्रश्न 7.
एक शंकु की तिर्यक ऊंचाई 26 m है और इसके आधार का व्यास 20 m है। इसकी ऊँचाई होगी :
(A) 24 m
(B) 25 m
(C) 23 m
(D) 35 m.
हल :
(A) 24 m
प्रश्न 8.
एक शंकु का वक्र पृष्ठीय क्षेत्रफल 308 cm2 है और इसकी तिर्यक ऊँचाई 14 cm है। इसके आधार की त्रिज्या होगी :
(A) 8 m
(B) 7 cm
(C) 9 m
(D) 12 m.
हल :
(B) 7 cm
प्रश्न 9.
शंकु के आकार का एक तंबू 10 m ऊँचा है और उसके आधार की त्रिज्या 24 m है। तंबू की तिर्यक ऊँचाई होगी :
(A) 26 m
(B) 28 m
(C) 25 m
(D) 27 m.
हल :
(A) 26 m
प्रश्न 10.
शंकु के आधार की एक गुंबज की तिर्यक ऊँचाई और आधार के व्यास क्रमश: 25 m और 14 m हैं। इसकी वक्र पृष्ठ 210 रुपए प्रति 100 m2 की दर से सफेदी कराने का व्यय होगा :
(A) 1233 रु०
(B) 1155 रु०
(C) 1388 रु०
(D) 1432 रु०।
हल :
(B) 1155 रु०

प्रश्न 11.
एक जोकर की टोपी एक शंकु के आकार की है, जिसके आधार की त्रिज्या 7 cm और ऊँचाई 24 cm है। इस प्रकार की 10 टोपियां बनाने के लिए आवश्यक गत्ते का क्षेत्रफल होगा :
(A) 5500 cm2
(B) 6500 cm2
(C) 8500 cm2
(D) 3500 cm2.
हल :
(A) 5500 cm2
प्रश्न 12.
एव अर्धगोला जिसकी त्रिज्या r है, का पृष्ठीय क्षेत्र फल होगा :
(A) 2πr2
(B) 4πr2
(C) 3πr2
(D) 5πr2.
हल :
(A) 2πr2
प्रश्न 13.
अर्धगोला जिसकी त्रिज्या r है, का पृष्ठीय क्षेत्रफल होगा :
(A) 4πr2
(B) 3πr2
(C) 2πr2
(D) 51πr2.
हल :
(B) 3πr2
प्रश्न 14.
7 cm त्रिज्या वाले गोले का पृष्ठीय क्षेत्रफल होगा :
(A) 516 cm2
(B) 616 cm2
(C) 716 cm2
(D) 880 cm2.
हल :
(B) 616 cm2
प्रश्न 15.
त्रिज्या 21 cm वाले अर्धगोले का वक्र पृष्ठीय क्षेत्रफल होगा :
(A) 2772 cm2
(B) 2564 cm
(C) 3772 cm2
(D) 4772 cm.
हल :
(A) 2772 cm2

प्रश्न 16.
14 cm त्रिज्या वाले गोले का वक्र पृष्ठीय क्षेत्रफल होगा :
(A) 2464 cm2
(B) 2428 cm2
(C) 2464 cm3
(D) 2428 cm3.
हल :
(A) 2464 cm2
प्रश्न 17.
14 cm व्यास वाले गोले का वक्र पृष्ठीय क्षेत्रफल होगा :
(A) 616 cm2
(B) 676 cm2
(C) 616 cm3
(D) 676 cm3.
हल :
(A) 616 cm2
प्रश्न 18.
10 cm त्रिज्या वाले एक अर्धगोले का कुल पृष्ठीय क्षेत्रफल होगा :
(A) 942 cm2
(B) 942 cm3
(C) 842 cm2
(D) 842 cm3.
हल :
(A) 942 cm2
प्रश्न 19.
एक गोलाकार गुब्बारे में हवा भरने पर, उसकी त्रिज्या 7 cm से 14 cm हो जाती है। दोनों स्थितियों में गुब्बारे के पृष्ठीय क्षेत्रफलों का अनुपात होगा :
(A) 4 : 1
(B) 1 : 4
(C) 3 : 1
(D) 1 : 3.
हल :
(B) 1 : 4
प्रश्न 20.
माचिस की एक डिब्बी के माप 4 cm × 2.5 cm × 1.5 cm हैं। ऐसी 12 डिब्बियों के एक पैकेट का आयतन होगा :
(A) 160 cm3
(B) 180 cm3
(C) 160 cm2
(D) 180 cm2.
हल :
(B) 180 cm3

प्रश्न 21.
एक घनाभाकार पानी की टंकी 6 m लंबी, 5 m चौड़ी और 4.5 m गहरी है। इसमें पानी आ सकता है :
(A) 1350 लिटर
(B) 13500 लिटर
(C) 135000 लिटर
(D) 135 लिटर।
हल :
(C) 135000 लिटर
प्रश्न 22.
एक घनाभाकार बर्तन 10 m लंबा और 8 m चौड़ा है। इसको कितना ऊँचा बनाया जाए कि इसमें 380 घन मीटर द्रव आ सके।
(A) 4.75 m
(B) 4.85 m
(C) 4.75 m
(D) 4.85 cm.
हल :
(A) 4.75 m
प्रश्न 23.
एक घनाभाकार टंकी की धारिता 50000 लीटर पानी की है। यदि इस टंकी की लंबाई और गहराई क्रमश: 2.5 m और 10 m है, तो इसकी चौड़ाई होगी :
(A) 4 m
(B) 3 m
(C) 2 m
(D) 5 m
हल :
(C) 2 m
प्रश्न 24.
किसी गोदाम की माप 40 m × 25 m × 10 m है। इस गोदाम में 1.5 m × 1.25 m × 0.5 m की माप वाले लकड़ी के कितने अधिकतम क्रेट रखे जा सकते हैं ?
(A) 18000
(B) 16000
(C) 15000
(D) 14000
हल :
(B) 16000
प्रश्न 25.
3 m मी० गहरी और 40 m चौड़ी एक नदी 2 km प्रति घंटा की चाल से बहकर समुद्र में गिरती है। एक मिनट में समुद्र में कितना पानी गिरेगा?
(A) 4000 m3
(B) 40 m3
(C) 400 m3
(D) 40000 m3
हल :
(A) 4000 m3

प्रश्न 26.
एक बेलनाकार बर्तन के आधार की परिधि 132 cm और उसकी ऊँचाई 25 cm है। इस बर्तन में कितने लीटर पानी आ सकता है ?
(A) 33.75 लीटर
(B) 34.65 लीटर
(C) 35.75 लीटर
(D) 38.75 लीटर।
हल :
(B) 34.65 लीटर
प्रश्न 27.
एक बेलन का पार्श्व पृष्ठीय क्षेत्रफल 94.2 cm2 है और उसकी ऊँचाई 5 cm है, इसकी आधार की त्रिज्या होगी :
(A) 3 cm
(B) 4 cm
(C) 5 cm
(D) 6 cm
हल :
(A) 3 cm
प्रश्न 28.
10 cm गहरे एक बेलनाकार बर्तन के आंतरिक वक्र पृष्ठ को पेंट कराने का व्यय 2200 रुपए हैं। यदि पेंट कराने की दर 20 रु० प्रति m2 हो तो इसके आधार की त्रिज्या होगी :
(A) 1.75 m
(B) 1.85 m
(C) 1.95 m
(D) 1.65 m
हल :
(A) 1.75 m
प्रश्न 29.
किसी शंकु की ऊँचाई और तिर्यक ऊँचाई क्रमशः 21 cm और 28 cm है। इसका आयतन होगा :
(A) 5546 cm2
(B) 7546 cm3
(C) 5564 cm3
(D) 8546 cm2
हल :
(B) 7546 cm3
प्रश्न 30.
लंब वृत्तीय शंकु जिसकी त्रिज्या 6 cm और ऊँचाई 7 cm है। इसका आयतन होगा :
(A) 254 cm3
(B) 264 cm3
(C) 274 cm2
(D) 284 cm2
हल :
(B) 264 cm3

प्रश्न 31.
शंकु के आकार के उस बर्तन की लीटरों में धारिता होगी जिसकी त्रिज्या 7 cm और ऊँचाई 25 cm है :
(A) 1.232 l
(B) 1.5 l
(C) 1.35 l
(D) 1.6 l
हल :
(A) 1.232 l
प्रश्न 32.
एक शंकु की ऊँचाई 15 cm है। यदि इसका आयतन 1570 cm3 हो तो इसके आधार की त्रिज्या होगी :
(A) 12 cm
(B) 10 cm
(C) 15 cm
(D) 18 cm
हल :
(A) 1.232 l
प्रश्न 33.
यदि 9 cm ऊंचाई वाले एक लंब वृत्तीय शंकु का आयतन 487 cm3 है तो इसके आधार का व्यास होगा :
(A) 10 cm
(B) 12 cm
(C) 8 cm
(D) 6 cm.
हल :
(C) 8 cm
प्रश्न 34.
ऊपरी व्यास 3.5 m वाले शंकु के आकार का एक गड्ढा 12 m गहरा है। इसकी धारिता किलोलीटरों में होगी :
(A) 38.5k
(B) 48.5 kl
(C) 39.5 kl
(D) 47.5 kl
हल :
(A) 38.5k
प्रश्न 35.
एक शंकु की ऊँचाई 15 cm है। इसकी आयतन 1570 cm3 है, इसकी आधार की त्रिज्या होगी :
(A) 5 cm
(B) 8 cm
(C) 10 cm
(D) 12 cm
हल :
(C) 10 cm

प्रश्न 36.
चंद्रमा का व्यास पृथ्वी के व्यास का लगभग एक चौथाई है। चंद्रमा का आयतन पृथ्वी के आयतन की कौन-सी भिन्न है ?
(A) \(\frac{1}{64}\)
(B) \(\frac{1}{32}\)
(C) \(\frac{1}{16}\)
(D) \(\frac{1}{48}\)
हल :
(A) \(\frac{1}{64}\)
प्रश्न 37.
जिस घन की विमाएं 50 cm × 40 cr × 10 cm हैं इसका आयतन लीटरों में होगा :
(A) 10 लीटर
(B) 12 लीटर
(C) 20 लीटर
(D) 25 लीटर.
हल :
(C) 20 लीटर
प्रश्न 38.
एक टंकी का आयतन 250 m3 है और इसके आधार का क्षेत्रफल 50 m2 है। इसके अंदर पानी की गहराई होगी :
(A) 5 m
(B) 200 m
(C) 300 m
(D) 12500 m
हल :
(A) 5 m
प्रश्न 39.
एय आयताकार ठोस की लंबाई, चौड़ाई और ऊँचाई क्रमश: 4 cm, 3 cm और 2 cm है। इसका आयतन होगा :
(A) (4 + 3 + 2) cm3
(B) 2 (4 + 3 + 2) cm3
(C) 4 × 3 × 2 cm3
(D) 2 (4 + 3) × 2 cm3
हल :
(C) 4 × 3 × 2 cm3
प्रश्न 40.
एक आयताकार ठोस का आयतन 200 m3 है। यह 8 m लंबा और 5 m चौड़ा है। इसकी ऊँचाई होगी :
(A) 5 m
(B) 15 m
(C) 6 m
(D) 18 m
हल :
(A) 5 m

प्रश्न 41.
एक गोलाकार गोले का पृष्ठीय क्षेत्रफल 616 cm2 है। इस गोले की त्रिज्या होगी :
(A) 6 cm
(B) 8 cm
(C) 7 cm
(D) 5 cm
हल :
(C) 7 cm
प्रश्न 42.
यदि एक गोले की त्रिज्या \(\frac{2 d}{3}\) हो तो इसका आयतन होगा :
(A) \(\frac{32}{81}\) πd3
(B) \(\frac{23}{4}\) πd3
(C) \(\frac{32}{3}\) πd3
(D) \(\frac{34}{3}\) πd3
हल :
(A) \(\frac{32}{81}\) πd3
प्रश्न 43.
एक बेलनाकार टंकी की धारिता 6160 cm3 है। यदि इसके आधार का व्यास 28 m हो तो टंकी की गहराई होगी :
(A) 5 m
(B) 8 m
(C) 10 m
(D) 15 m
हल :
(C) 10 m
प्रश्न 44.
बेलन का आयतन है :
(A) 2πrh
(B) πr2h
(C) \(\frac{4}{3}\) = πr2h
(D) 2πr2h
हल :
(B) πr2h
प्रश्न 45.
दोबेलनों की त्रिज्यों में 2 : 3 के अनुपात है और उनकी ऊँचाइयों में 5 : 3 का अनुपात है। उनके आर तनों में अनुपात होगा :
(A ) 27 : 20
(B) 25 : 24
(C) 20 : 27
(D) 15 : 20
हल :
(C) 20 : 27

प्रश्न 46.
एकलंब वृत्ताकार बेलन का आधार 7 सेमी और ऊचाई 1 सेमी है। बेलन का आयतन क्या है ?
(A) 216 सेमी3
(B) 136 सेमी3
(C) 172 सेमी3
(D) 154 सेमी3।
हल :
(D) 154 सेमी3।
प्रश्न 47.
एक गोले का व्यास 14 m है। इस गोले का आयतन होगा :
(A) 1437 \(\frac{1}{3}\)m3
(B) 1357 \(\frac{1}{3}\)m3
(C) 1437\(\frac{2}{3}\)m3
(D) 1337\(\frac{2}{3}\)m3
हल :
(A) 1437 \(\frac{1}{3}\)m3
प्रश्न 48.
एक गोले का आयतन 524 cm3 है। इस गोले का व्यास होगा :
(A) 4 cm
(B) 5 cm
(C) 3 cm
(D) 6 cm
हल :
(B) 5 cm
प्रश्न 49.
एक बेलन का कुल पृष्ठीय क्षेत्रफल 40 cm2 है। यदि बेलन की ऊँचाई 5.5 cm हो तो इसके आधार की त्रिज्या होगी :
(A) 5 cm
(B) 2.5 cm
(C) 1.5 cm
(D) 10 cm
हल :
(B) 2.5 cm
प्रश्न 50.
एक लम्ब वृत्तीय शंकु के आधार का क्षेत्रफल 78.5 cm2 है। यदि इसकी ऊँचाई 12 cm हो तो इसकी आयतन होगा :
(A) 31.4 cm3
(B) 3.14 cm3
(C) 314 cm3
(D) इनमें से कोई नहीं।
हल :
(C) 314 cm3

प्रश्न 51.
एक लंबवृत्तीय शंकु के आधार की त्रिज्या 11.3 cm है और इसकी वक्र पृष्ठ 355 cm2 है। इस शंकु की ऊँचाई होगी :
(π = \(\frac{355}{113}\) लीजिए)
(A) 11 cm
(C) 5 cm
(B) 9 cm
(D) 10 cm
हल :
(D) 10 cm
![]()