Class 9

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 5 युक्लिड के ज्यामिति का परिचय MCQ Questions with Answers

PSEB Solutions for Class 9 Maths Chapter 5 युक्लिड के ज्यामिति का परिचय MCQ Questions

बहुविकल्पीय प्रश्न :

नीचे प्रत्येक प्रश्न के चार उत्तर दिए गए हैं। सही उत्तर का चयन कीजिए।

प्रश्न 1.
दिए हुए दो भिन्न बिन्दुओं से होकर
(A) एक अद्वितीय रेखा खींची जा सकती है।
(B) अनेक रेखाएं खींची जा सकती है।
(C) दो रेखाएं खींची जा सकती है।
(D) पांच रेखाएं खींची जा सकती हैं।
उत्तर-
(A) एक अद्वितीय रेखा खींची जा सकती है।

प्रश्न 2.
दिए हुए एक बिन्दु से
(A) एक अद्वितीय रेखा खींची जा सकती है।
(B) असंख्य रेखाएं खींची जा सकती हैं।
(C) कोई रेखा नहीं खींची जा सकती।
(D) इनमें से कोई नहीं।
उत्तर-
(B) असंख्य रेखाएं खींची जा सकती हैं।

प्रश्न 3.
एक समकोण सम्पूर्ण कोण का
(A) एक आधा होता है
(B) एक तिहाई होता है।
(C) एक चौथाई होता है।
(D) दो तिहाई होता है।
उत्तर-
(C) एक चौथाई होता है।

प्रश्न 4. समभुज की
(A) दो भुजाएं बराबर होती हैं।
(B) सभी भुजाएं बराबर होती हैं
(C) एक भुजा बराबर होती हैं।
(D) इनमें से कोई नहीं।
उत्तर-
(B) सभी भुजाएं बराबर होती हैं

प्रश्न 5.
न्यून कोण
(A) समकोण से बड़ा होता है।
(B) समकोण के बराबर होता है।
(C) समकोण से छोटा है।
(D) इनमें से कोई नहीं।
उत्तर-
(C) समकोण से छोटा है।

प्रश्न 6.
लम्ब रेखाओं में
(A) प्रत्येक बराबर कोण समकोण होता है।
(B) प्रत्येक बराबर कोण अधिक कोण होता है।
(C) प्रत्येक बराबर कोण न्यून कोण होता है।
(D) इनमें से कोई नहीं।
उत्तर-
(A) प्रत्येक बराबर कोण समकोण होता है।

प्रश्न 7. समबाहु त्रिभुज की
(A) तीनों भुजाएं बराबर होती हैं।
(B) दो भुजाएं बराबर होती हैं।
(C) कोई भुजा बराबर नहीं होती।
(D) इनमें से कोई नहीं।
उत्तर-
(A) तीनों भुजाएं बराबर होती हैं।

प्रश्न 8.
समद्विबाहु त्रिभुज की
(A) सभी भुजाएं बराबर होती हैं।
(B) दो भुजाएं बराबर होती हैं।
(C) कोई भुजा बराबर नहीं होती।
(D) इनमें से कोई नहीं।
उत्तर-
(B) दो भुजाएं बराबर होती हैं।

प्रश्न 9.
समकोण त्रिभुज में
(A) एक कोण समकोण होता है।
(B) दो कोण समकोण होते हैं।
(C) तीन कोण समकोण होते हैं
(D) इनमें से कोई नहीं।
उत्तर-
(A) एक कोण समकोण होता है।

प्रश्न 10.
वर्ग
(A) समभुज और समकोणिक होता है।
(B) दो भुजाएं और दो कोण बराबर होते हैं।
(C) सम्मुख भुजाएं और कोण बराबर होते हैं।
(D) इनमें से कोई नहीं।
उत्तर-
(A) समभुज और समकोणिक होता है।

प्रश्न 11.
समचतुर्भुज के
(A) सभी कोण और भुजाएं बराबर होती है।
(B) सम्मुख कोण और सम्मुख भुजाएं समान होती हैं।
(C) a और b दोनों
(D) इनमें से कोई नहीं।
उत्तर-
(B) सम्मुख कोण और सम्मुख भुजाएं समान होती हैं।

 

प्रश्न 12.
एक समकोण त्रिभुज में एक कोण होता है
(A) 180°
(B) 90°
(C) 30°
(D) 60°
उत्तर-
(B) 90°

प्रश्न 13.
एक अधिक कोण त्रिभुज में
(A) एक अधिक कोण होता है।
(B) दो अधिक कोण होते हैं।
(C) कोई अधिक कोण नहीं होता।
(D) इनमें से कोई नहीं।
उत्तर-
(A) एक अधिक कोण होता है।

प्रश्न 14.
दो रेखाएं तभी समान्तर कही जाती हैं जब उनका प्रतिच्छेदी बिन्दु
(A) एक बिन्दु हो
(B) एक रेखा हो
(C) कोई न हो
(D) इनमें से कोई नहीं।
उत्तर-
(C) कोई न हो

प्रश्न 15.
समान्तर चतुर्भुज में सम्मुख कोण
(A) असमान होते हैं।
(B) समान होते हैं।
(C) 90° से कम होते हैं।
(D) इनमें से कोई नहीं।
उत्तर-
(B) समान होते हैं।

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 5 युक्लिड के ज्यामिति का परिचय Ex 5.2 Textbook Exercise Questions and Answers

PSEB Solutions for Class 9 Maths Chapter 5 युक्लिड के ज्यामिति का परिचय Ex 5.2

प्रश्न 1.
यूक्लिड की पाँचवी अभिधारणा को किस प्रकार लिखेंगे ताकि वह सरलता से समझी जा सके ?
हल :
यूक्लिड की अभिधारणा पाँच के अनेक समतुल्य रूपांतरण हैं। इनमें से एक प्लेफेयर का अभिगृहीत है जो कि सरलता से समझा जा सकता है। इसके अनुसार : – प्रत्येक रेखा और उस पर न स्थित प्रत्येक बिंदु P के लिए, एक अद्वितीय रेखा m ऐसी होती है जो P से होकर जाती है और l के समांतर है।

स्पष्टतया P से होकर जाने वाली सभी रेखाओं में केवल m ही रेखा के समांतर है।

प्रश्न 2.
क्या यूक्लिड की पाँचवी अभिधारणा से समांतर रेखाओं के अस्तित्व का औचित्य निर्धारित होता है ? स्पष्ट कीजिए।
हल :
हां, यूक्लिड की पाँचवी अभिधारणा समांतर रेखाओं के अस्तित्व का औचित्य निर्धारित करती हैं, क्योंकि

यदि कोई रेखा ! दो सरल रेखाओं m और n पर पड़ती हो कि l की एक ओर के अंत: कोणों का योग दो समकोण हो, तो यूक्लिड के पाँचवें अभिगृहीत के अनुसार यह रेखा l के इस ओर नहीं मिलेगी। अब आप जानते हैं कि रेखा । की दूसरी ओर के अंत: कोणों का योग भी दो समकोण होगा। अतः दूसरी ओर भी ये नहीं मिलेंगे। अतः रेखाएँ 1 l और n कभी भी नहीं मिलेंगे और इसलिए ये समांतर हैं।

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 5 युक्लिड के ज्यामिति का परिचय Ex 5.1 Textbook Exercise Questions and Answers

PSEB Solutions for Class 9 Maths Chapter 5 युक्लिड के ज्यामिति का परिचय Ex 5.1

प्रश्न 1.
निम्नलिखित कथनों में से कौन-से कथन सत्य हैं और कौन-से असत्य हैं ? अपने उत्तरों के लिए कारण दीजिए।
(i) एक बिंदु से होकर केवल एक ही रेखा खींची जा सकती है।
(ii) दो भिन्न बिंदुओं से होकर जाने वाली असंख्य रेखाएँ हैं।
(iii) एक सांत रेखा दोनों ओर अनिश्चित रूप से बढ़ाई जा सकती है।
(iv) यदि दो वृत्त बराबर हैं, तो उनकी त्रिज्याएँ बराबर होती हैं।
(v) आकृति में यदि AB = PQ और PQ = XY है, तो AB = XY होगा।

हल :
(i) असत्य :
सही कथन :
एक बिंदु से होकर असीमित रूप से अनेक रेखाएँ खींची जा सकती हैं। यह स्वयं सिद्ध है और इसे छात्र अपने आँखों से देख सकते हैं जैसा कि नीचे आकृति दी है :

(ii) असत्य :
क्योंकि दिया गया कथन यूक्लिड के अभिगृहित 1 का अंतर्विरोध करता है जिसके अनुसार दिए हुए दो भिन्न बिंदुओं से होकर एक अद्वितीय रेखा खींची जा सकती है।
दो बिंदुओं P और Q में से एक अद्वितीय रेखा खींची जा सकती है।

(iii) सत्य
यूक्ल्डि की अभिधारणा 2 के अनुसार एक सांत रेखा (terminated line) को अनिश्चित रूप से बढ़ाया जा सकता है।

(iv) सत्य
प्रमाण :
यूक्लिड के अभिगृहीत 4 के अनुसार वे वस्तुएँ जो परस्पर संपाती हों एक-दूसरे के बराबर होती हैं। यदि एक वृत्त से परिबद्ध प्रदेश को दूसरे प्रदेश पर अध्यारोपित करें, तो वे संपाती होंगे। अत: इनके केंद्र और परिसीमाएँ संपाती होती हैं। अतः इनकी त्रिज्या संपाती होती है।

(v) सत्य
प्रमाण :
यूक्लिड की अभिगृहीत 1 का कथन है कि वे वस्तुएँ जो एक ही वस्तु के बराबर हो। एक दूसरे के बराबर होती हैं।

प्रश्न 2.
निम्नलिखित पदों में से प्रत्येक की परिभाषा दीजिए। क्या इनके लिए कुछ ऐसे पद हैं, जिन्हें परिभाषित करने की आवश्यकता है? वे क्या हैं और आप इन्हें कैसे परिभाषित कर पाएँगे?
(i) समांतर रेखाएँ
(ii) लंब रेखाएँ
(iii) रेखाखंड
(iv) वृत्त की त्रिज्या
(v) वर्ग
हल :
(i) समांतर रेखाएँ : समांतर रेखाएँ वे सीधी रेखाएँ हैं जोकि एक तल पर होती हैं और दोनों दिशाओं में असीमित रूप से बढ़ाने पर एक-दूसरे को किसी भी दिशा में नहीं मिलती। अन्य पद जो इसमें आता है, वह है समतल, हम समतल को एक अपरिभाषित पद लेते हैं। इसे हम केवल अन्तः प्रेरणा से स्पष्ट कर सकते हैं या भौतिक माडल की सहायता से इसकी व्याख्या कर सकते हैं। _

(ii) लंब रेखाएँ : जब एक सीधी रेखा, किसी अन्य सीधी रेखा पर इस प्रकार खड़ी हो कि आसन्न कोण एकदूसरे के बराबर बने, तो प्रत्येक समान कोण समकोण होता है और सीधी रेखा जो दूसरी पर खड़ी है, उस पर लंब (perpendicular) कहलाती है जिस पर यह खड़ी है। अन्य पद जिन्हें पहले परिभाषित करने की आवश्यकता है, वे हैं (1) कोण, (2) आसन्न कोण, (3) समकोण। आइए हम इन्हें परिभाषित करें :
(1) कोण (Angle) : एक समतल कोण (plane angle) समतल में मिलने वाली दो रेखाओं का एक-दूसरे के साथ झुकाव है जो एक-दूसरे को मिलती हैं और एक | सीधी रेखा में स्थित नहीं होती।

(2) आसन्न कोण (Adjacent angles) : दो कोण, जिनका एक ही शीर्ष होता है, एक भुजा उभयनिष्ठ होती है और दूसरी भुजा उभनिष्ठ भुजा के विपरीत दिशाओं में होती हैं, आसन्न कोण कहलाते हैं।

(3) समकोण (Right angle) : यह कोण जो कि संपूर्ण कोण का एक चौथाई होता है, समकोण कहलाता

(iii) रेखाखंड (Line segment) : एक रेखाखंड जो दोनों दिशाओं में असीमित रूप से बढ़ाने पर रेखा देती है। एक अन्य पद रेखा है। हम रेखा को अपरिभाषित पद रहने देते हैं। हम इसे केवल अन्तः प्रेरणा से स्पष्ट कर सकते हैं या भौतिक माडल की सहायता से इसकी व्याख्या कर सकते हैं।

(iv) वृत्त की त्रिज्या (Radius) : एक रेखाखंड जो वृत्त के किसी बिंदु को केंद्र से मिलाता है, वृत्त की त्रिज्या कहलाता हैं।
अन्य पद जिन्हें पहले परिभाषित करने की आवश्यकता हैं।
(1) वृत्त (Circle),
(2) केंद्र (Centre)
आइए इन्हें परिभाषित करें
(1) वृत्त (Circle). वृत्त तल में बनी वह बंद आकृति है, जिसके तल में स्थित सभी बिंदु एक निश्चित बिंदु से समान दूरी पर होते हैं।
(2) वृत्त का केंद्र (Centre of circle) : वह स्थिर बिंदु जिससे वृत्त पर स्थित सभी बिंदु एक समान दूरी पर हो, वृत्त का केंद्र कहलाता है।

(v) वर्ग (Square). वर्ग वह चतुभुर्जी आकृति है, जो समभुज और समकोणिक दोनों ही हों। अन्य पद जिनको परिभाषित करने की आवश्यकता है : (1) समभुज, (2)
समकोण
(1) समभुज (Equilateral) : एक आकृति जिसकी सभी भुजाएँ बराबर हों समभुज या समबाहु कहलाती हैं।
(2) समकोण (Right angle) : एक कोण जो संपूर्ण कोण का एक चौथाई होता है, वह समकोण कहलाता है।

प्रश्न 3.
इस प्रकार नीचे दी हुई दो अभिधारणाओं पर विचार कीजिए :
(i) दो भिन्न बिंदु A और B दिए रहने पर, एक तीसरा बिंदु C ऐसा विद्यमान है जो A और B के बीच स्थित होता है।
(ii) यहाँ कम से कम ऐसे तीन बिंदु विद्यमान हैं कि वे एक रेखा पर स्थित नहीं हैं।
क्या इन अभिधारणाओं में कोई अपरिभाषित शब्द हैं? क्या ये अभिधारणाएँ अविरोधी हैं ? क्या ये यूक्लिड की अभिधारणाओं से प्राप्त होती हैं ? स्पष्ट कीजिए।
हल :
ऐसे अनेक अपरिभाषित शब्द हैं जिनकी जानकारी छात्र को होनी चाहिए। ये दो अभिधारणाएँ (i) और (ii) संगत हैं क्योंकि इनमें दो अलग-अलग स्थितियों का
अध्ययन किया जाता है। अभिधारणा (i) का कथन है कि यदि दो बिंदु A और B दिए हुए हों, तो उनके बीच में स्थित एक बिंदु C होता है।

अभिधारणा (ii) का कथन है कि दो दिए हुए बिंदुओं A और B के लिए हम एक बिंदु C ले सकते हैं। जो A और B से होकर जाने वाली रेखा पर स्थित नहीं होता।

अतः हम देखते हैं कि ये अभिगृहीत यूक्लिड के अभिगृहीतों का अनुसरण नहीं करते। फिर भी ये अभिगृहीत (1) का अनुसरण करते हैं जिसके अनुसार दिए गए दो बिंदुओं के लिए भिन्न एक अद्वितीय रेखा होती है जो उनमें से होकर जाती है।

प्रश्न 4.
यदि दो बिंदुओं A और B के बीच एक बिंदु C ऐसा स्थित है कि AC = BC है, तो सिद्ध कीजिए कि AC = \(\frac{1}{2}\) AB है। एक आकृति खींच कर इसे स्पष्ट कीजिए।
हल:

दिया है कि C, A और B के बीच स्थित है।
और AC = BC
इसलिए AC + AC = BC + AC
यूक्लिड की परिभाषा के अनुसार बराबरों को बराबरों में जोड़ा गया है।
अर्थात् 2AC = AB
[BC + AC, AB के संपाती है।]
अत: AC = \(\frac{1}{2}\) AB

प्रश्न 5.
प्रश्न 4 में, C रेखाखंड AB का एक मध्य बिंदु कहलाता है। सिद्ध कीजिए कि एक रेखाखंड का एक और केवल एक ही मध्य-बिंदु होता है।
हल:
मान लीजिए कि AB के दो मध्य-बिंदु C और D हैं।
इसलिए, यूक्लिड की अभिगृहीत (4) के अनुसार जब रेखा को बिंदु C पर मोड़ा जाता है तो हम देखते हैं कि भाग BC भाग AC पर अध्यारोपित होता है।
⇒ AC = BC ……………(i)
इसी प्रकार D, AB का मध्य बिंदु है।
⇒ AD = BD …………….(ii)
हमें प्राप्त है AB = AB
या AC + BC = AD + BD
AC + AC = AD + AD
[(i) और (ii) का प्रयोग करने पर]
2AC = 2AD
AC = AD ……………(iii)

जब हम AD को AC पर और BD को BC पर अध्यारोपित करते हैं तो हम देखते हैं कि D पूरी तरह CB के ऊपर आता है। इससे परिणाम निकलता है कि D और C दो भिन्न बिंदु नहीं हैं परंतु एक ही हैं। अतः, हम इस निष्कर्ष पर पहुंचते हैं कि एक रेखा-खंड का एक ही मध्य-बिंदु होता है।

प्रश्न 6.
आकृति में यदि AC = BD है, तो सिद्ध कीजिए कि AB = CD है।

हल :
दिया है कि AC = BD …………..(1)
AC = AB + BC
[बिंदु B, A और C के बीच स्थित है] …………..(2)
BD = BC + CD [बिंदु C, B और D के बीच स्थित है] ………………..(3)
(2) और (3) को (1) में प्रतिस्थापित करने पर हम प्राप्त करते हैं
AB + BC = BC + CD
दोनों ओर से BC घटाने पर हम प्राप्त करते हैं।
AB + BC – BC = BC + CD – BC
= BC – BC + CD
इसलिए AB = CD
[∵ बराबरों में से बराबरों को घटाने पर शेषफल भी बराबर होता है।]

प्रश्न 7.
यूक्लिड की अभिगृहीतों की सूची में दिया हुआ अभिगृहीत 5 एक सर्वव्यापी सत्य क्यों माना जाता है ?
हल :
यूक्लिड अभिगृहीत 5 का कथन है कि ‘एक पूर्ण अपने भाग से बड़ा होता है’ क्योंकि विश्व के किसी भाग में किसी भी वस्तु के लिए यह सत्य होता है, इसलिए इसे सार्वभौमिक सत्य माना जाता है।

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 4 दो चरों वाले रैखिक समीकरण MCQ Questions with Answers

PSEB Solutions for Class 9 Maths Chapter 4 दो चरों वाले रैखिक समीकरण MCQ Questions

बहुविकल्पीय प्रश्न

दिये गए चार विकल्पों में से सही उत्तर का चयन कीजिए।

प्रश्न 1.
समीकरण x – 2y = 4 का हल है :
(A) (0, 2)
(B) (4, 0)
(C) (1, 1)
(D) (2, 0).
उत्तर:
(B) (4, 0)

प्रश्न 2.
y = – 4 के आलेखीय रूप में रेखा :
(A) x-अक्ष के समांतर है
(B) y-अक्ष के समांतर है
(C) मूल बिंदु में से गुजरती है
(D) कुछ भी नहीं।
उत्तर:
(A) x-अक्ष के समांतर है

प्रश्न 3.
समीकरण 2x + 1 = x + 3 का हल है :
(A) 3
(B) 4
(C) 2
(D) 1
उत्तर:
(C) 2

प्रश्न 4.
समीकरण x – y = 0 आलेख किस बिंदु में से गुजरता है :
(A) (2, 3)
(B) (3, 4)
(C) (5, 6)
(D) (0, 0)
उत्तर:
(D) (0, 0)

प्रश्न 5.
समीकरण x + y = 7 का आलेख x-अक्ष को किस बिंदु पर काटता है ?
(A) (7, 0)
(B) (0, 7)
(C) (- 7, 0)
(D) (0, – 7)
उत्तर:
(A) (7, 0)

प्रश्न 6.
बिंदु (4, 1) किस रेखा के समीकरण को संतुष्ट
करता है ?
(A) x + 2y = 5
(B) x + 2y = – 6
(C) x + 2y = 6
(D) x + 2y = 16
उत्तर:
(C) x + 2y = 6

प्रश्न 7.
x = 2 का आलेख निरूपण :
(A) x-अक्ष के समांतर है
(B) y-अक्ष के समांतर है
(C) मूल बिंदु में से गुजरता है
(D) कुछ नहीं।
उत्तर:
(B) y-अक्ष के समांतर है

प्रश्न 8.
रैखिक समीकरण 2x – 5y = 7
(A) का एक अद्वितीय हल है
(B) के दो हल हैं
(C) के अपरिमित रूप से अनेक हल हैं
(D) का कोई हल नहीं है।
उत्तर:
(C) के अपरिमित रूप से अनेक हल हैं

प्रश्न 9.
रैखिक समीकरण 2x + 5y = 7 का एक अद्वितीय हल है, यदि x, y है
(A) प्राकृत संख्याएँ
(B) धनात्मक वास्तविक संख्याएँ
(C) वास्तविक संख्याएँ
(D) परिमेय संख्याएँ।
उत्तर:
(A) प्राकृत संख्याएँ

प्रश्न 10.
यदि (2, 0) रैखिक समीकरण 2x + 3y = k का एक हल है, तो k का मान है
(A) 4
(B) 6
(C) 5
(D) 2
उत्तर:
(A) 4

प्रश्न 11.
दो चरों वाली रैखिक समीकरण 2x + 0y + 9 = 0 के किसी भी हल का रूप होता है
(A) (- \(\frac{9}{2}\), m)
(B) (n, – \(\frac{9}{2}\))
(C) (0, – \(\frac{9}{2}\))
(D) (- 9, 0)
उत्तर:
(A) (- \(\frac{9}{2}\), m)

प्रश्न 12.
रैखिक समीकरण 2x + 3y = 6 का आलेख y अक्ष को निम्नलिखित में से किस बिंदु पर काटता
(A) (2, 0)
(B) (0, 3)
(C) (3, 0)
(D) (0, 2)
उत्तर:
(D) (0, 2)

प्रश्न 13.
समीकरण x = 7 को दो चरों में इस प्रकार लिखा जा सकता है
(A) 1.x + 1.y = 7
(B) 1.x + 0.y = 7
(C) 0.x + 1.y = 7
(D) 0.x + 0.y = 7
उत्तर:
(B) 1.x + 0.y = 7

प्रश्न 14.
x-अक्ष पर स्थित किसी बिंदु का रूप होता है
(A) (x, y)
(B) (0, y)
(C) (x, 0)
(D) (x, x)
उत्तर:
(C) (x, 0)

प्रश्न 15.
रेखा y = x पर स्थित किसी बिंदु का रूप होता
(A) (a, a)
(B) (0, a)
(C) (a, 0)
(D) (a, – a)
उत्तर:
(A) (a, a)

प्रश्न 16.
x-अक्ष की समीकरण का रूप है
(A) x = 0
(B) y = 0
(C) x + y = 0
(D) x = y.
उत्तर:
(B) y = 0

प्रश्न 17.
y = 6 का आलेख एक रेखा है, जो
(A) x-अक्ष के समांतर है और मूलबिंदु से 6 मात्रक की दूरी पर है
(B) y-अक्ष के समांतर है और मूलबिंदु से 6 मात्रक की दूरी पर है
(C) x-अक्ष पर अंत:खंड 6 काटती है
(D) दोनों अक्षों पर अंत-खंड 6 काटती है।
उत्तर:
(A) x-अक्ष के समांतर है और मूलबिंदु से 6 मात्रक की दूरी पर है

प्रश्न 18.
x = 5, y = 2 निम्नलिखित रैखिक समीकरण का एक हल है
(A) x + 2y = 7
(B) 5x + 2y = 7
(C) x + y = 7
(D) 5x + y = 7
उत्तर:
(C) x + y = 7

प्रश्न 19.
यदि किसी रैखिक समीकरण के हल (- 2, 2), (0, 0) और (2, – 2) हैं, तो इसका रूप होता है
(A) y – x = 0
(B) x + y = 0
(C) – 2x + y = 0
(D) – x + 2y = 0
उत्तर:
(B) x + y = 0

प्रश्न 20.
समीकरण ax + by +c = 0 के धनात्मक हल सदैव निम्नलिखित में स्थित होते हैं
(A) प्रथम चतुर्थांश
(B) द्वितीय चतुर्थंश
(C) तृतीया चतुर्थांश
(D) चतुर्थ चतुर्थांश।
उत्तर:
(A) प्रथम चतुर्थांश

प्रश्न 21.
रैखिक समीकरण 2x + 3y = 6 का आलेख . एक रेखा है जो x-अक्ष को निम्नलिखित बिंदु पर मिलती है
(A) (0, 2)
(B) (2, 0)
(C) (3, 0)
(D) (0, 3)
उत्तर:
(C) (3, 0)

प्रश्न 22.
रैखिक समीकरण y = x का आलेख निम्नलिखित बिंदु से होकर जाता है
(A) (\(\frac{3}{2}\), – \(\frac{3}{2}\))
(B) (0, \(\frac{3}{2}\))
(C) (1, 1)
(D) (- \(\frac{1}{2}\), \(\frac{1}{2}\))
उत्तर:
(C) (1, 1)

प्रश्न 23.
यदि हम किसी रैखिक समीकरण को एक शून्येतर संख्या से गुणा करें या भाग दें तो उस रैखिक समीकरण का हल
(A) बदल जाता है
(B) वही रहता है
(C) हकेवल गुणा की स्थिति में बदल जाता है
(D) केवल भाग की स्थिति में बदल जाता है।
उत्तर:
(B) वही रहता है

प्रश्न 24.
x = 1 और y = 2 द्वारा x और y में कितनी रैखिक समीकरण संतुष्ट होती हैं ?
(A) केवल एक
(B) दो
(C) अपरिमित रूप से अनेक
(D) तीन।
उत्तर:
(C) अपरिमित रूप से अनेक

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 4 दो चरों वाले रैखिक समीकरण Ex 4.4 Textbook Exercise Questions and Answers

PSEB Solutions for Class 9 Maths Chapter 4 दो चरों वाले रैखिक समीकरण Ex 4.4

प्रश्न 1.
(i) एक चर वाले
(ii) दो चर वाले
समीकरण के रूप में y = 3 का ज्यामितीय निरूपण कीजिए।
हल :
(i) एक चर वाले समीकरण के रूप में y = 3 को संख्या रेखा पर निरूपित किया गया है।

(ii) दो चर वाले समीकरण के रूप में y = 3 को कार्तीय निर्देशांक पद्धति से निरूपण इस प्रकार है :

प्रश्न 2.
(i) एक चर वाले
(ii) दो चर वाले
समीकरण के रूप में 2x + 9 = 0 का ज्यामितीय निरूपण कीजिए।
हल :
(i) एक चर वाले समीकरण के रूप में 2x + 9 = 0 को संख्या रेखा पर निरूपण किया जाता है।
2x + 9 = 0
2x = – 9
x = – \(\frac{9}{2}\)

(ii) 2x + 9 = 0 अर्थात् x = – \(\frac{9}{2}\) को दो चर वाले समीकरण के रूप में कार्तीय निर्देशांक पद्धति में निरूपित किया जाता है।

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 4 दो चरों वाले रैखिक समीकरण Ex 4.3 Textbook Exercise Questions and Answers

PSEB Solutions for Class 9 Maths Chapter 4 दो चरों वाले रैखिक समीकरण Ex 4.3

प्रश्न 1.
दो चरों वाले निम्नलिखित रैखिक समीकरणों में से प्रत्येक का आलेख खींचिएँ :
(i) x + y = 4
(ii) x – y = 2
(ii) y = 3x
(iv) 3 = 2x + y
हल :
(i) x + y = 4
⇒ y = 4 – x
x के मानों के संगत y के मानों को दर्शाती सारणी इस प्रकार है|

बिंदुओं A (0, 4), B (2, 2) और C (4, 0) को आलेख कागज़ पर आलेखित कीजिए। इन बिंदुओं को मिलाइए और रेखा प्राप्त कीजिए।

पैमाना (Scale chosen) :
X-अक्ष (X-axis) पर 5 भाग = 1 एकक
Y-अक्ष (Y-axis) पर 5 भाग = 1 एकक

(ii) x – y = 2
⇒ – y = 2 – x
या y = x – 2
x के मानों के संगत y के मानों को दर्शाती सारणी इस प्रकार है. :

बिंदुओं P (0, – 2), Q (1, – 1) और R (2, 0) आलेख कागज़ पर आलेखित कीजिए। इन बिंदुओं को मिलाइए और रेखा प्राप्त कीजिए।
पैमाना (Scale chosen) :
X-अक्ष (X-axis) पर :
5 भाग = 1 एकक
Y-अक्ष (Y-axis) पर :
5 भाग = 1 एकक

(iii) y = 3x
xके मानों के संगत । के मानों को दर्शाती सारणी इस प्रकार है

बिंदुओं P (- 1, – 3), Q (0, 0) और R (1, 3) को आलेख कागज़ पर आलेखित कीजिए।
इन बिंदुओं को मिलाइए और रेखा प्राप्त कीजिए।

पैमाना (Scale chosen) :
X-अक्ष (X-axis) पर :
5 भाग = 1 एकक
Y-अक्ष (Y-axis) पर :
5 भाग = 1 एकक

(iv) 3 = 2x + y
⇒ 3 – 2x = y
या y = 3 – 2x
x के मानों के संगत y के मानों को दर्शाती सारणी इस प्रकार है :

बिंदुओं L (0, 3), M (1, 1) और N (2, – 1) को आलेख कागज़ पर आलेखित कीजिए। इन बिंदुओं को मिलाइए और रेखा प्राप्त कीजिए।

पैमाना (Scale chosen) :
X-अक्ष (X-axis) पर :
5 भाग = 1 एकक
Y-अक्ष (Y-axis) पर :
5 भाग = 1 एकक

प्रश्न 2.
बिंदु (2, 14) से होकर जाने वाली दो रेखाओं के समीकरण लिखिए। इस प्रकार की और कितनी रेखाएं हो सकती हैं, और क्यों ?
हल :
हम जानते हैं कि एक बिंदु में से असीमित रूप से अनेक रेखाएँ खींची जा सकती हैं। इनमें से कोई दो रैखिक समीकरण जो बिंदु (2, 14) द्वारा संतुष्ट होते हैं। निम्न अनुसार हैं :
मान लीजिए x और y में रैखिक समीकरण में ax + by = c बिंदु (2, 14) द्वारा संतुष्ट होता हैं।
अतः, बिंदु (2, 14) इस पर स्थित हैं।
∴ 2a + 14b = c
समीकरण में c का मान भरने पर, हमें प्राप्त होता है
ax + by = 2a + 14b
⇒ a(x – 2) + b (y – 14) = D
⇒ b (y – 14) = – a (x – 2)
⇒ \(\frac{y-14}{x-2}=-\frac{a}{b}\)
a और b के विभिन्न मानों का प्रयोग करके हम अभीष्ट अनेक समीकरण प्राप्त कर सकते हैं।
यदि a = 2, b = 1
तो \(\frac{y-14}{x-2}=\frac{-2}{1}\)
⇒ y – 14 = – 2x + 4
⇒ 2x + y = 18
यदि a = 7, b = – 1
तो \(\frac{y-14}{x-2}=-\left(\frac{7}{-1}\right)\)
⇒ y – 14 = 7x – 14
⇒ 7x – y = 0

प्रश्न 3.
यदि बिंदु (3, 4) समीकरण 3y = ax + 7 के आलेख पर स्थित है, तो a का मान ज्ञात कीजिए।
हल :
यह दिया है कि बिंदु (3, 4) निम्नलिखित आलेख पर स्थित हैं :
3y = ax + 7
अतः, बिंदु (3, 4) इस समीकरण को संतुष्ट करता
∴ 3 × 4 = a × 3 + 7
⇒ 12 = 3a + 7
⇒ 12 – 7 = 3a
⇒ 5 = 3a
⇒ 3a = 5
⇒ a = \(\frac{3}{5}\)
अतः, a का अभीष्ट \(\frac{3}{5}\) है

स्पष्टीकरण :
दिए गए समीकरण में a = \(\frac{3}{5}\) प्रतिस्थापित करने पर हमें प्राप्त होता है :
⇒ 3y = \(\frac{3}{5}\) x + 7
9y = 5x + 21
⇒ y = \(\frac{5 x+21}{9}\)
x के मानों के संगत y के मानों को दर्शाती सारणी निम्न अनुसार है :

बिंदुओं P(- 6, – 1) और Q (12, 9) को आलेख पेपर पर आलेखित कीजिए। इन बिंदुओं को मिलाइए और एक रेखा प्राप्त कीजिए।
आलेख से हम देखते हैं कि बिंदु (3, 4) रेखा पर स्थित हैं।
अतः, यह समीकरण 3y = \(\frac{5}{3}\) x + 7 को संतुष्ट करता है।
अतः, a का प्राप्त किया गया मान सही है।

पैमाना x-अक्ष पर
5 भाग = 2 एकक
y-अक्ष पर
5 भाग = 1 एकक

प्रश्न 4.
एक नगर में टैक्सी का किराया निम्नलिखित पहले किलोमीटर का किराया 8 रु है और उसके बाद की दूरी के लिए प्रति किलोमीटर का किराया 5 रु है। यदि तय की गई दूरी x किलोमीटर हो, और कुल किरायाy रु हो, तो इसका एक रैखिक समीकरण लिखिए और उसका आलेख खींचिए।
हल :

तय की गई कुल दूरी x लेने पर पहले किलोमीटर का किराया = 8 रु
पहले किलोमीटर के बाद के प्रत्येक किमी का किराया = 5 रु
कुल किराया = y रु
∴ 8 रु + 5 (x – 1) रु = y रु
⇒ 8 + 5 (x – 1) = y
⇒ 8 + 5x – 5 = y
⇒ 5x + 3 = y
⇒ 5x – y + 3 = 0 …………..(1)
यह दी गई सूचना का एक रैखिक समीकरण है।
समीकरण (1) का आलेख खींचने के लिए x के मानों के संगत y के मानों की दर्शाती समीकरण निम्न अनुसार है :

बिंदुओं P(1.8) और 0 (2, 13) को ग्राफ पेपर पर आलेखित कीजिए। इन बिंदुओं को मिलाइए और रेखा प्राप्त कीजिए।

पैमाना
x-अक्ष पर 5 भाग = 1 किमी
y-अक्ष पर 5 भाग = 1 रु

प्रश्न 5.
निम्नलिखित आलेखों में से प्रत्येक के लिए दिए गए विकल्पों से सही समीकरण का चयन कीजिए :
आकृति (क) के लिए आकृति (ख) के लिए
(i) y = x
(ii) x + y = 0
(iii) y = 2r
(iv) 2 + 3y = 7x

(i) y = x + 2
(ii) y = x -2
(ii) y = -x + 2
(iv) x + 2y = 6

हल :
आलेख (क) पर स्थित प्रत्येक बिंदु समीकरण (ii) x + y = 0 को संतुष्ट करता है।
अतः, आलेख (क) के लिए चारों समीकरणों में से सही समीकरण है :
x + y = 0
∵ x + y = 0
y = – x
x = 0 के लिए y = 0
x = 1 के लिए y = – 1.
x = – 1 के लिए y = 1 .
अब आलेख (ख) का प्रत्येक बिंदु समीकरण

(iii) y = – x + 2 में संतुष्ट है।
अतः, आलेख (ख) के लिए चारों समीकरणों में से सही समीकरण है :
y = – x + 2
∵ y = – x + 2 में
x = 2 के लिए y = – 2 + 2
⇒ y = 0
x = 0 के लिए y = – 0 = 2
⇒ y = 2
x = – 1 के लिए y = – (-1) + 2
⇒ y = 1 + 2
⇒ y = 3

प्रश्न 6.
एक अचर बल लगाने पर एक पिंड द्वारा किया गया कार्य पिंड द्वारा तय की गई दूरी के अनुक्रमानुपाती होता है। इस कथन को दो चरों वाले एक समीकरण के रूप में व्यक्त कीजिए और अचर बल 5 मात्रक लेकर इसका आलेख खींचिए। यदि पिंड द्वारा तय की गई दूरी
(i) 2 मात्रक
(ii) 0 मात्रक
हो, तो आलेख से किया हुआ कार्य ज्ञात कीजिए।
हल :
मान लीजिए स्थिर बल (माना k मात्रक) द्वारा किया गया कार्य y मात्रक है और पिंड द्वारा तय की गई दूरी x मात्रक है।
हम जानते हैं कि बल द्वारा किया गया कार्य पिंड द्वारा तय की गई दूरी के अनुक्रमानुपाती होता है।
अनुपात और समानुपात से, हम इस तथ्य को इस प्रकार व्यक्त कर सकते हैं :
y = kx
k = 5 मात्रक लेने पर
y = 5x …………(1)
जो कि दो चलों में रैखिक समीकरण है।
समीकरण (1) का आलेख खींचने के लिए ; x के मानों के संगत y के मानों को दर्शाती सारणी निम्न अनुसार है :

बिंदुओं P(1/2, 5/2) , Q (1, 5) और R(3, 15) को ग्राफ पेपर पर आलेखित कीजिए। इन बिंदुओं को मिलाइए और रेखा प्राप्त कीजिए।
पैमाना
x-अक्ष पर
5 भाग = 1 मात्रक तय की गई दूरी
y-अक्ष पर
5 भाग = 1 मात्रक किया गया कार्य।
आलेख से हम देखते हैं कि
(i) जब x = 2 मात्रक, तो y = 10 मात्रक
अतः जब पिंड द्वारा तय की गई दूरी 2 मात्रक हो, तो किया गया कार्य 10 मात्रक है।

(ii) जब x = 0 मात्रक
तब y = 0 मात्रक
अतः, जब कोई दूरी तय न की गई हो तब कोई कार्य नहीं होता।

प्रश्न 7.
एक विद्यालय की कक्षा IX की छात्राएँ यामिनी और फातिमा ने मिलकर भूकंप पीड़ित व्यक्तियों की सहायता के लिए प्रधानमंत्री राहत कोष में 100 रु अंशदान दिया। एक रैखिक समीकरण लिखिए जो इन आंकड़ों को संतुष्ट करती हो। (आप उनका अंशदान : रु और y रु मान सकते हैं)। इस समीकरण का आलेख खींचिए।
हल :
मान लीजिए दामिनी ने x रु और फातिमा ने y रु प्रधानमंत्री राहत कोष में अंशदान दिया
दोनों का कुल अंशदान = 100 रु
⇒ x + y = 100 …………(1)
जो कि दो चरों में एक रैखिक समीकरण है।
समीकरण (1) का आलेख खींचने के लिए हम x के मानों के संगत y के मानों को दर्शाती सारणी खींचते हैं।

बिंदुओं P (40, 60), Q(50, 50) और P(70, 30) को ग्राफ पेपर पर आलेखित कीजिए। इन बिंदुओं को मिलाइए और रेखा प्राप्त कीजिए।

प्रश्न 8.
अमरीका और कनाडा जैसे देशों में तापमान फारेनहाइट में मापा जाता है, जबकि भारत जैसे देशों में तापमान सेल्सियस में मापा जाता है। यहाँ फारेनहाइट को सेल्सियस में रूपांतरित करने वाला एक रैखिक समीकरण दिया गया है :
F = (\(\frac{9}{5}\)) C + 32
(i) सेल्सियस को -अक्ष और फारेनहाइट को yअक्ष मानकर ऊपर दिए गए रैखिक समीकरण का आलेख खींचिए।।
(ii) यदि तापमान 30°C है, तो फारेनहाइट में तापमान क्या होगा?
(iii) यदि तापमान 95°F है, तो सेल्सियस में तापमान क्या होगा ?
(iv) यदि तापमान 0°C है, तो फारेनहाइट में तापमान क्या होगा और यदि तापमान 0°F है, तो सेल्सियस में तापमान क्या होगा ?
(v) क्या ऐसा भी कोई तापमान है जो फारेनहाइट और सेल्सियस दोनों के लिए संख्यात्मकतः समान है। यदि हाँ, तो उसे ज्ञात कीजिए।
हल :
दो चरों °F और °C में रैखिक समीकरण है :
F = (\(\frac{9}{5}\)) C + 32 ……………..(1)
समीकरण (1) का आलेख खींचने के लिए हम C के संगत F के मानों को दर्शाती सारणी खींचते हैं।

बिंदुओं (0, 32) और (- 20, – 4) को ग्राफ पेपर पर आलेखित कीजिए। इन बिंदुओं को मिलाइए और रेखा प्राप्त कीजिए।
(ii)आलेख से, यदि तापमान 30°C है तो फारेनहाइट में तापमान 86°F है।
(iii)आलेख से, यदि तापमान 95°F है, तो सेल्सियस में यह 35°C है।
(iv)आलेख से, यदि तापमान 0°C हो तो फारेनाहाइट में 32°F है।
यदि तापमान 0°F हो, तो सेल्सियस में यह तापमान – 17.8°C (लगभग) है।
(v) हाँ, ऐसा भी तापमान है जो फारेनहाइट और सेल्सियस दोनों के लिए संख्यात्मकतः समान है। आलेख से हम देखते हैं कि बिंदु (-40, – 40) रेखा पर स्थित
अतः, – 40 (दोनों F और C पर) संख्यात्मकतः समान तापमान है।

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 4 दो चरों वाले रैखिक समीकरण Ex 4.2 Textbook Exercise Questions and Answers

PSEB Solutions for Class 9 Maths Chapter 4 दो चरों वाले रैखिक समीकरण Ex 4.2

प्रश्न 1.
निम्नलिखित विकल्पों में कौन-सा विकल्प सत्य है, और क्यों ? y = 3x + 5 का
(i) एक अद्वितीय हल है
(ii) केवल दो हल हैं।
(iii) अपरिमित रूप से अनेक हल हैं
हल :
कथन (iii) सत्य है। क्योंकि x, के प्रत्येक मान के लिए, y का एक संगत मान होता है और विलोमतः भी।
(ii) जाँच-पड़ताल :
मान लीजिए कि
(i) x = 0 तो y = 3 × 0 + 5
⇒ y = 0 + 5
⇒ y = 5
इसलिए x = 0, y = 5 एक हल है।

(ii) x = 1; तो y = 3 x 1 + 5
⇒ y = 3 + 5
⇒ y = 8
इसलिए x = 1, y = 8 भी एक हल है।

(iii) x = – 2 तो y = 3 ( – 2) + 5
⇒ y = – 6 + 5
⇒ y = – 1
इसलिए x = – 2, y = – 1 भी एक हल है।
इसी प्रकार x (या y) के मान प्रतिस्थापित करके उसके संगत y (या x) का मान ज्ञात करके हम दी गई समीकरण के अपरिमित रूप से अनेक हल प्राप्त कर सकते हैं जितने हम चाहते हैं।

प्रश्न 2.
निम्नलिखित समीकरणों में से प्रत्येक समीकरण के चार हल लिखिए:
(i) 2x + y = 7
(ii) πx + y = 9
(iii) x = 4y
हल :
(i) 2x + y = 7
हम समीकरण को इस प्रकार लिख सकते हैं :
y = 7 – 2x
जब x = 0; y = 7 – 2 × 0
⇒ y = 7 – 0
⇒ y = 7

जब x = 1;
y = 7 – 2 × 1
⇒ y = 7 – 2
⇒ y = 5

जब x = 2;
⇒ y = 7 – 2
⇒ y = 7 – 2
⇒ y = 3

जब x = – 1;
y = 7 – 2 ( – 1)
⇒ y = 7 + 2
⇒ y = 9
अतः, समीकरण 2x + y = 7 के अपरिमित रूप से अनेक हलों में चार हल ये हैं
(0, 7), (1, 5), (2, 3) और (- 1, 9)

(ii) x + y = 9 हम इस समीकरण को इस प्रकार लिख सकते हैं :
y = 9 – πx

जब x = 0;
y = 9 – 0
0 = y = 9

जब x = 2,
y = 9 – 2π

जब x = \(\frac{9}{\pi}\)
y = 9 – 9
⇒ y = 0

जब x = – 1;
y = 9 – ( – 1) 1
⇒ y = 9 + π
अत: समीकरण x + y = 9 को अपरिमित रूप से अनेक हलों में से चार हल ये हैं :
(0, 9), (2, 9 – 2π), (\(\frac{9}{\pi}\), 0) और (- 1, 9 + π).

(iii) x = 4y हम इस समीकरण को इस प्रकार लिख सकते हैं
जब y = \(\frac{x}{4}\)
जब x = 0, y = \(\frac{0}{4}\)
⇒ y = 0

जब x = 1
y = 4

जब x = 4, y = \(\frac{4}{4}\) = 1
जब x = – 4, y = – \(\frac{4}{4}\), y = – 1
अतः, समीकरण x = 4y के अपरिमित रूप से अनेक हलों में से चार हल ये हैं :
(0, 0), (1, \(\frac{1}{4}\)), (4, 1) (- 4, – 1)

प्रश्न 3.
बताइए कि निम्नलिखित हलों में कौन-कौन समीकरण x – 2y = 4 के हल हैं और कौन-कौन हल नहीं हैं :
(i) (0, 2)
(ii) (2, 0)
(iii) (4, 0)
(iv) (√2, 4√2)
(v) (1, 1)
हल :
(i) समीकरण x – 2y = 4 में x = 0 और y = 2 प्रतिस्थापित कीजिए।
L.H.S. = x – 2y
= 0 – 2×2
= 0 – 4 = – 4
R.H.S. = 4
स्पष्टतया L.H.S.≠ R.H.S.
∴ x = 0 और y = 2 समीकरण x – 2y = 4 का हल नहीं है।

(ii) समीकरण x – 2y = 4 में x = 2 और y = 0 प्रतिस्थापित कीजिए।
L.H.S. = x – 2y
= 2 – 2 (0)
= 2 + 0
R.H.S. = 4
स्पष्टतया L.H.S. ≠ R.H.S.
∴ x = 2 और y = 0 समीकरण x – 2y = 4 का हल नहीं है।

(iii) x – 2y = 4 में x = 4 और y = 0 प्रतिस्थापित कीजिए।
L.H.S., = x – 2y
= 4 – 2 × 0
= 4 – 0 = 4
R.H.S. = 4
स्पष्टतया L.H.S. = R.H.S.
∴ x = 4 और y = 0 समीकरण x – 2y =4.का हल है।

(iv) समीकरण x – 2y = 4 में x = √2 और y = 4√2 को प्रतिस्थापित कीजिए।
L.H.S,= x – 2y = √2 – 2 × 4√2
= √2 – 8√2
= – 7√2
R.H.S. = 4
∴ L.H.S. ≠ R.H.S.
∴ x = √2, y = 4√2 समीकरण x – 2y = 4 का हल नहीं है।

(v) समीकरण x – 2y = 4 में x = 1, y = 1 प्रतिस्थापित कीजिए
L.H.S. = x – 2y = 1 – 2 ≠ 1
= 1 – 2
= – 1
R.H.S. = 4
स्पष्टतया L.H.S. ≠ R.H.S.
∴ x = 1, y = 1 समीकरण x – 2y = 4 का हल नहीं है।

प्रश्न 4.
k का मान ज्ञात कीजिए जबकि x = 2, y = 1 समीकरण 2x + 3y = k का एक हल हो।
हल :
यदि x = 2, y = 1 समीकरण 2x + 3y = k, का हल हो, तो यह निश्चय ही समीकरण को संतुष्ट करता है।
∴ 2 × 2 + 3 × 1 = k
(x = 2, y = 1 को समीकरण में प्रतिस्थापित करने पर)
⇒ 4 + 3 = k
⇒ 7 = k
k = 7
अतः k का अभीष्ट मान 7 है।

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 4 दो चरों वाले रैखिक समीकरण Ex 4.1 Textbook Exercise Questions and Answers

PSEB Solutions for Class 9 Maths Chapter 4 दो चरों वाले रैखिक समीकरण Ex 4.1

प्रश्न 1.
एक नोट बुक की कीमत एक कलम की कीमत से दो गुनी है। इस कथन को निरूपित करने के लिए दो चरों वाला एक रैखिक समीकरण लिखिए।
हल :
मान लीजिए, नोट बुक की कीमत x रु० है और कलम की कीमत y रु० है।
अतः दो चरों वाला एक रैखिक समीकरण जो दिए गए कथन को निरूपित करे, हैं x = 2y. या x – 2y = 0.

प्रश्न 2.
निम्नलिखित रैखिक समीकरणों को ax + by + c = 0 के रूप में व्यक्त कीजिए और प्रत्येक स्थिति में a, b और c के मान बताइए :
(i) 2x + 3y = \(9 .3 \overline{5}\)
(ii) x – \(\frac{y}{5}\) – 10 = 0
(iii) – 2x + 3y = 6
(iv) x = 3y
(v) 2x = – 5y
(vi) 3x + 2 = 0
(vii) y – 2 = 0
(viii) 5 = 2x.
हल :
(i) 2x + 3y = 9 को ax + by + c = 0 के रूप में इस प्रकार लिखा जा सकता है :
2x + 3y – \(9 .3 \overline{5}\) = 0
[\(9 .3 \overline{5}\) को L.H.S. में पक्षांतरण करने पर]
⇒ 2x + 3y + ( – \(9 .3 \overline{5}\)) = 0
x और y के गुणों की अचर पदों की तुलना करने पर हम देखते हैं कि a = 2, b = 3 और c = – \(9 .3 \overline{5}\)

(ii) x – \(\frac{y}{5}\) – 10 = 0 को
ax + by + c = 0 के रूप में इस प्रकार लिखा जा सकता है :
⇒ 1. x + (- \(\frac{1}{5}\))y + ( – 10) = 0
x और y के गुणांकों और अचर पदों की तुलना करने पर हम देखते हैं कि a = 1, b = – \(\frac{1}{5}\) और c = – 10

(iii) – 2x + 3y = 6 को
ax + by + c = 0 के रूप में इस प्रकार लिखा जा सकता है .
– 2x + 3y – 6 = 0
[6 को L.H.S. में पक्षांतरित करने पर]
⇒ – 2x + 3y + (- 6) = 0
x और y के गुणांकों और अचर पदों की तुलना करने पर हम देखते हैं कि a = – 2, b = 3 और c = – 6

(iv) x = 3y को ar + by + c = 0 के रूप में इस प्रकार लिखा जा सकता है :
x – 3y = 0
⇒ 1. x + (- 3)y + 0 = 0
x और y के गुणांकों और अचर पदों की तुलना करने पर हम देखते हैं क a = 1, b = – 3 और c = 0.

(v) 2x = – 5y को ax + by + c = 0 के रूप में इस प्रकार लिखा जा सकता है :
2x + 5y = 0
[- 5y को L.H.S. में पक्षांतरित करने पर]
⇒ 2x + 5y + 0 = 0
x और y के गुणांकों और अचर पदों की तुलना करने पर हम देखते हैं कि a = 2, b = 5 और c = 0

(vi) 3x + 2 = 0 को ax + by + c = 0 के रूप में इस प्रकार लिखा जा सकता है :
3x + 0.y + 2 = 0
x और y के गुणांकों और अचर पदों की तुलना करने पर हम देखते हैं कि a = 3, b = 0 and c = 2.

(vii)y-2=0 को ax + by+c = 0 के रूप में इस प्रकार लिखा जा सकता है :
⇒ 0.x + 1. y + ( – 2) = 0
x और y के गुणांकों और अचर पदों की तुलना करने पर हम देखते हैं कि
a = 0, b = 1 और c = – 2.

(viii) 5 = 2x को ax + by + c = 0 के रूप में इस प्रकार लिखा जा सकता है :
5 – 2x = 0
⇒ – 2x + 0.y + 5 = 0
x और y के गुणांकों और अचर पदों की तुलना करने पर हम देखते हैं कि
a = – 2, b = 0 और c = 5

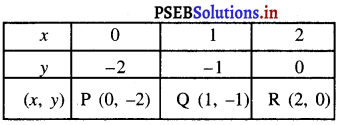
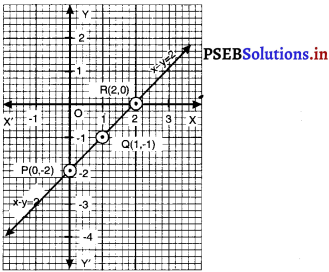
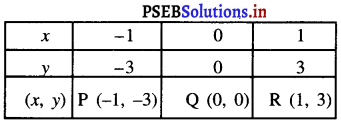
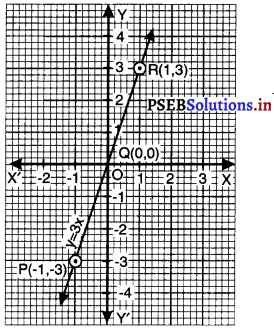
Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 2 बहुपद MCQ Questions with Answers

PSEB 9th Class Maths Chapter 2 बहुपद MCQ Questions

बहुविकल्पीय प्रश्न :

नीचे प्रत्येक प्रश्न के चार उत्तर दिए हैं। इनमें से सही उत्तर का चयन कीजिए।

प्रश्न 1.
निम्न में से कौन-सी बहुपद नहीं है ?
(A) 3z³ – √5z +9
(B) 3√z + 4x + 5z²
(C) √ax + x² – x³
(D) y² + 6y – 5.
उत्तर-
(B) 3√z + 4x + 5z²

प्रश्न 2.
बहुपद 2y² – 4y + 3 की प्रकार है
(A) एक पदी
(B) द्विपदी
(C) त्रिपदी
(D) इनमें से कोई नहीं।
उत्तर-
(C) त्रिपदी

प्रश्न 3.
बहुपद t² – 4 की प्रकार है- .
(A) द्विपदी
(B) एक पदी
(C) त्रिपदी
(D) इनमें से कोई नहीं।
उत्तर-
(A) द्विपदी

प्रश्न 4.
बहुपद x की प्रकार है
(A) एक पदी
(B) द्विपदी
(C) त्रिपदी
(D) इनमें से कोई नहीं।
उत्तर-
(A) एक पदी

प्रश्न 5.
2 + x² + x में x का गुणांक है
(A) 2
(B) 1
(C) – 1
(D) – 2.
उत्तर-
(B) 1

प्रश्न 6.
2 – x² + x³ में x² का गुणांक है
(A) 1
(B) – 1
(C) 2
(D) – 2.
उत्तर-
(B) – 1

प्रश्न 7.
\(\frac{\pi \mathbf{r}^{2}}{2}\) + x में ४ का गुणांक है
(A) 1
(B) \(\frac{\pi}{2}\)
(C) – \(\frac{\pi}{2}\)
(D) – 1.
उत्तर-
(B) \(\frac{\pi}{2}\)

प्रश्न 8.
√2x – 1 में x का गुणांक है
(A) √2
(B) – 1
(C) 0
(D) – √2
उत्तर-
(A) 2

प्रश्न 9.
√2x – 1 में x का गुणांक है
(A) 2
(B) – 1
(C) 0
(D) – 12.
उत्तर-
(C) 0

प्रश्न 10.
5x³ + 4x² + 7x की घात है
(A) 1
(B) 2
(C) 3
(D) 4
उत्तर-
(C) 3

प्रश्न 11.
4 – y² की घात है
(A) 1
(B) 2
(C) 0
(D) 3
उत्तर-
(B) 2

प्रश्न 12.
5t – √7 की घात है
(A) 1
(B) √7
(C) 5
(D) – 1.
उत्तर-
(A) 1

प्रश्न 13.
3 की घात है
(A) 0
(B) 3
(C) 1
(D) – 1.
उत्तर-
(C) 1

प्रश्न 14.
निम्नलिखित बहुपदों में से कौन-सी रैखिक बहुपद है ?
(A) 1 + x
(B) x² + x
(C) x + x² + 4
(D) 7x³²
उत्तर-
(A) 1 + x

प्रश्न 15.
निम्नलिखित में से कौन-सी द्विघाती बहुपद
(A) x + x³ + 4
(B) 5x²
(C) x – x³
(D) 3x.
उत्तर-
(B) 5x²

प्रश्न 16.
p (x) = 5x – 4x² + 3 का x = 1 के लिए मान
(A) 5
(B) 1
(C) 4
(D) 2.
उत्तर-
(C) 4

प्रश्न 17.
p (x) = 5x – 4x² + 3 का x = 0 के लिए मान
(A) 3
(B) 2
(C) – 3
(D) – 2
उत्तर-
(A) 3

प्रश्न 18.
p (x) = 5x – 4x² + 3 का x = – 1 के लिए मान है
(A) 6
(B) – 6
(C) 3
(D) – 3
उत्तर-
(B) – 6

प्रश्न 19.
P (x) = 5x – 4x² + 3 का x = 2 के लिए मान है
(A) 3
(B) 2
(C) – 2
(D) – 3.
उत्तर-
(D) – 3

प्रश्न 20.
p (t) = 2 + t + 2t² – t³ का p (0) के लिए मान है
(A) 1
(B) 2
(C) – 1
(D) 3.
उत्तर-
(B) 2

प्रश्न 21.
P (x) = (x – 1) (x + 1) का p (1) के लिए मान है
(A) 1
(B) 2
(C) 0
(D) – 2
उत्तर-
(C) 0

प्रश्न 22.
p (t) = 2 + t + 2t² – t³ का p (2) के लिए मान है
(A) 4
(B) – 4
(C) 6
(D) 7.
उत्तर-
(A) 4

प्रश्न 23.
p (y) = y² – y +1 का p (0) के लिए मान
(A) – 1
(B) 3
(C) 1
(D) – 2.
उत्तर-
(C) 1

प्रश्न 24.
P (x) = 3 + x का p (2) के लिए मान है
(A) 0
(B) 5
(C) – 5
(D) 3
उत्तर-
(B) 5

प्रश्न 25.
p (x) = 3x + 1 का निम्न में से कौन-सा शून्यक है ?
(A) \(\frac{1}{3}\)
(B) \(-\frac{1}{3}\)
(C) \(\frac{2}{3}\)
(D) \(-\frac{2}{3}\)
उत्तर-
(B) \(-\frac{1}{3}\)

प्रश्न 26.
p (x) = x² – 1 के निम्न में से कौन-से शून्यक हैं ?
(A) 1, – 1
(B) – 1, 2
(C) – 2, 2
(D) – 3, 3.
उत्तर-
(A) 1, – 1

प्रश्न 27.
P (x) = (x – 1) (x – 2) के निम्न में से कौन से शून्यक हैं.
(A) – 2, 3
(B) 2, – 2
(C) – 1, 2
(D) 3, – 3.
उत्तर-
(A) – 2, 3

प्रश्न 28.
p (x) = lx + m का निम्न में से कौन-सा शून्यक है
(A) \(\frac{m}{l}\)
(B) \(-\frac{l}{m}\)
(C) \(-\frac{m}{l}\)
(D) \(\frac{l}{m}\)
उत्तर-
(C) \(-\frac{m}{l}\)

प्रश्न 29.
P (x) = 5x – 7 का निम्न में से कौन-सा शून्यक है ?
(A) – \(\frac{4}{5}\) π
(B) \(\frac{1}{5}\) π
(C) \(\frac{4}{5}\) π
(D) – \(\frac{5}{4}\) π
उत्तर-
(B) \(\frac{1}{5}\) π

प्रश्न 30.
P (x) = 2x – 7 का शून्यक है
(A) \(\frac{2}{7}\)
(B) \(\frac{7}{2}\)
(C) \(-\frac{2}{7}\)
(D) – \(\frac{7}{2}\)
उत्तर-
(B) \(\frac{7}{2}\)

प्रश्न 31.
P (x) = 9x + 4 का शून्यक है
(A) \(\frac{4}{9}\)
(B) \(\frac{9}{4}\)
(C) \(-\frac{9}{4}\)
(D) \(-\frac{4}{9}\)
उत्तर-
(D) \(-\frac{4}{9}\)

प्रश्न 32.
x³ + 3x² + 3x + 1 को x + 1 से भाग देने पर शेषफल प्राप्त होता है
(A) 1
(B) 3x – 1
(C) 0
(D) – 1.
उत्तर-
(C) 0

प्रश्न 33.
x³ + 3x² + 3x + 1 को x – 1 से भाग देने पर शेषफल प्राप्त होता है
(A) \(\frac{8}{27}\)
(B) \(\frac{27}{8}\)
(C) \(-\frac{8}{27}\)
(D) – \(\frac{27}{8}\)
उत्तर-
(B) \(\frac{27}{8}\)

प्रश्न 34.
x³ + 3x² + 3x + 1 को x से भाग देने पर शेषफल प्राप्त होता है
(A) 1
(B) 0
(C) – 1
(D) 2.
उत्तर-
(B) 0

प्रश्न 35.
x³ + 3x² + 3x + 1 को x + 1 से भाग देने पर शेषफल प्राप्त होता है
(A) – π + 3π² – 3π + 1
(B) π – 3π² + 3π + 1
(C) – π + 3π² – 3π – 1
(D) – π + 3π² – 3π – 1
उत्तर-
(A) – π + 3π² – 3π + 1

प्रश्न 36.
x³ + 3x² + 3x + 1 को 5 + 2x से भाग देने पर शेषफल प्राप्त होता है-
(A) \(\frac{8}{27}\)
(B) \(-\frac{8}{27}\)
(C) \(-\frac{27}{8}\)
(D) \(\frac{27}{8}\)
उत्तर-
(C) \(-\frac{27}{8}\)

प्रश्न 37.
x³ + ax² + 6x – a को x-a से भाग देने पर शेषपल प्राप्त होता है
(A) 2a
(B) 3a
(C) 5a
(D) 6a.
उत्तर-
(C) 5a

प्रश्न 38.
यदि x – 2, x² – 3x + 5a का एक गुणनखण्ड हो तो a का मान होगा
(A) 1
(B) – 1
(C) \(\frac{2}{5}\)
(D) – \(\frac{2}{5}\)
उत्तर-
(C) \(\frac{2}{5}\)

प्रश्न 39.
यदि x – 2, x³ – 2ax² + ax – 1 का एक गुणनखण्ड हो तो a का मान होगा
(A) \(\frac{7}{6}\)
(B) \(-\frac{7}{6}\)
(C) \(\frac{6}{7}\)
(D) \(-\frac{6}{7}\)
उत्तर-
(A) \(\frac{7}{6}\)

प्रश्न 40.
यदि x – 2, x³ – 2ax² + ax – 1 का एक गुणनखण्ड हो तो a का मान होगा
(A) \(\frac{2}{3}\)
(B) \(\frac{3}{5}\)
(C) \(\frac{3}{2}\)
(D) \(\frac{1}{2}\)
उत्तर-
(C) \(\frac{3}{2}\)

प्रश्न 41.
यदि x + a, x³ + ax² – 2x + a + 4 का एक गुणनखण्ड हो तो a का मान होगा
(A) – \(\frac{4}{3}\)
(B) \(\frac{4}{3}\)
(C) \(\frac{3}{4}\)
(D) – \(\frac{3}{4}\)
उत्तर-
(A) \(\frac{4}{3}\)

प्रश्न 42.
यदि x + a, x⁴ + a²x² + 3x – 6a का एक गुणनखण्ड हो तो a का मान होगा
(A) 1
(B) – 1
(C) 2
(D) 0
उत्तर-
(D) 0

प्रश्न 3.
यदि x – a, x⁶ – ax⁵ + x⁴ – ax² + 3x – a + 2 का एक गुणनखण्ड हो तो a का मान होगा
(A) – 1
(B) 2
(C) – 1
(D) – 2
उत्तर-
(C) – 1

प्रश्न 44.
यदि x – a, x⁵ – ax³ + 2x + a + 1 का गुणनखण्ड है तो a का मान होगा
(A) \(\frac{1}{3}\)
(B) \(-\frac{1}{3}\)
(C) \(\frac{2}{3}\)
(D) \(-\frac{2}{3}\)
उत्तर-
(B) \(-\frac{1}{3}\)

प्रश्न 45.
2y³ – 5y² – 19y + 42 का गुणनखण्ड होगा
(A) (y – 2) (y + 3) (2y – 7)
(B) (y + 2) (y + 3) (2y + 7)
(C) (y + 2) (y – 3) (2y + 7)
(D) (y – 2) (y – 3) (2y – 7).
उत्तर-
(A) (y – 2) (y + 3) (2y – 7)

प्रश्न 46.
निम्नलिखित बहुपदों में से किस बहुपद का एक गुणनखण्ड x + 1 है
(A) x³ + x² + x + 1
(B) x⁴ + x³ + x² + 1
(C) x⁴ + 3x³ + 3x² + x + 1
(D) x⁴ – x² – (2 + √2) x + √2
उत्तर-
(A) x³ + x² + x + 1

प्रश्न 47.
यदि x – 1, p (x) = x² + x + k का एक गुणनखण्ड हो तो k का मान होगा
(A) 1
(B) – 1
(C) 2
(D) – 2.
उत्तर-
(D) – 2

प्रश्न 48.
यदि x – 1, P (x) = 2x² + kx + √2 का एक गुणनखण्ड हो तो k का मान होगा
(A) 2 + √2
(B) – (2 + √2)
(C) 1 + √2
(D) – (1 + √2)
उत्तर-
(B) – (2 + √2)

प्रश्न 49.
यदि x – 1, p (x) kx² – 2x +1 का एक गुणनखण्ड हो तो k का मान होगा
(A) √2 + 1
(B) – 1 + √2
(C) √2 – 1
(D) – √2 – 1
उत्तर-
(C) √2 – 1

प्रश्न 50.
यदि x – 1, p (x) = kx² – 3x + k का एक गुणनखण्ड हो तो k का मान होगा
(A) \(\frac{3}{2}\)
(B) – \(\frac{2}{3}\)
(C) \(-\frac{1}{2}\)
(D) \(\frac{1}{2}\)
उत्तर-
(A) \(\frac{3}{2}\)

प्रश्न 51.
12x² – 7x + 1 के गुणनखण्ड हैं
(A) (4x – 1) (3x – 1)
(B) (4x + 1) (3x – 1)
(C) (4x – 1) (3x + 1)
(D) (3x + 2) (4x – 1).
उत्तर-
(A) (4x – 1) (3x – 1)

प्रश्न 52.
2x² – 7x + 3 के गुणनखण्ड हैं
(A) (x – 3) (2x – 1)
(B) (x + 3) (2x + 1)
(C) (x + 3) (2x – 1)
(D) (x – 3) (2x + 1).
[उत्तर-
(B) (x + 3) (2x + 1)

प्रश्न 53.
6x² + 5x – 6 के गुणनखण्ड हैं
(A) (2x – 3) (3x – 2)
(B) (2x + 3) (3x – 2)
(C) (2x – 3) (3x + 2)
(D) (2x – 3) (3x – 1)
उत्तर-
(B) (2x + 3) (3x – 2)

प्रश्न 54.
3x² – x – 4 के गुणनखण्ड हैं
(A) (3x – 4) (x + 1)
(B) (3x + 4) (x – 1)
(C) (3x – 4) (x – 1)
(D) (3x + 2) (x + 1)
उत्तर-
(A) (3x – 4) (x + 1)

प्रश्न 55.
x³ – 2x² – x + 2 के गुणनखण्ड हैं
(A) (x + 1) (x – 1) (x – 2)
(B) (x + 1) (x – 1) (x + 2)
(C) (x – 1) (x – 2) (x + 2)
(D) (x + 2) (x – 1) (x + 1).
उत्तर-
(A) (x + 1) (x – 1) (x – 2)

प्रश्न 56.
x³ – 3x² – 9x – 5 के गुणनखण्ड हैं
(A) (x + 1) (x – 1) (x + 5)
(B) (x + 1) (x + 1) (x – 5)
(C) (x – 1) (x – 1) (x – 5)
(D) (x + 1) (x + 1) (x + 5).
उत्तर-
(B) (x + 1) (x + 1) (x – 5)

प्रश्न 57.
(x + 4) (x + 10) का गुणनफल है
(A) x² + 4x + 10
(B) x² + 10x + 40
(C) x² + 14x + 40
(D) x² – 14x + 40.
उत्तर-
(C) x² + 14x + 40

प्रश्न 58.
(x + 8) (x – 10) का गुणनफल है
(A) x² – 8x – 80
(B) x² – 2x – 80
(C) x² + 2x + 80
(D) x² – 2x + 80.
उत्तर-
(B) x² – 2x – 80

प्रश्न 59.
(3x + 4) (3x – 5) का गुणनफल है
(A) 9x² – 3x – 20
(B) 9x² – x – 20
(C) 9x² – 7x – 20
(D) 9x² – 4x – 40
उत्तर-
(A) 9x² – 3x – 20

प्रश्न 60.
(3 – 2x) (3 + 2x) का गुणनफल है
(A) 9 – 2x²
(B) 9 – 4x²
(C) 6 – 4x²
(D) 3 – 4x²
उत्तर-
(B) 9 – 4x²

प्रश्न 61.
104 × 96 का मान है
(A) 9984
(B) 9624
(C) 9980
(D) 9986.
उत्तर-
(A) 9984

प्रश्न 62.
95 × 96 का मान है
(A) 9020
(B) 9120
(C) 9320
(D) 9340
उत्तर-
(B) 9120

प्रश्न 63.
9x² + 6xy + y का गुणनखण्डन है- .
(A) (3x – y)²
(B) (3x + y)²
(C) (2x – y)²
(D) (2x + y)²
उत्तर-
(B) (3x + y)²

प्रश्न 64.
4y² – 4y + 1 का गुणनखण्डन हैं
(A) (2y + 1)²
(B) (4y – 1)²
(C) (2y – 1)²
(D) (2y – 2)²
उत्तर-
(C) (2y – 1)²

प्रश्न 65.
x² – \(\frac{y^{2}}{100}\) का गुणनखण्डन है
(A) \(\left(x+\frac{y}{10}\right)\left(x+\frac{y}{10}\right)\)
(B) \(\left(x+\frac{y}{10}\right)\left(x-\frac{y}{10}\right)\)
(C) \(\left(x-\frac{y}{5}\right)\left(x-\frac{y}{5}\right)\)
(D) \(\left(x+\frac{y}{5}\right)\left(x-\frac{y}{5}\right)\)
उत्तर-
(B) \(\left(x+\frac{y}{10}\right)\left(x-\frac{y}{10}\right)\)

प्रश्न 66.
(2x – y + z)² का प्रसार है
(A) 4x² + y² + z² + 4xy – 4yz + 2zx
(B) 4x² + y² + z² – 4xy – 2yz + 4zx
(C) 4x² – y² – z² – 4xy + 4yz – 2zx
(D) 4x² + y² – z² + 4xy – 2yz + 2zx.
उत्तर-
(B) 4x² + y² + z² – 4xy – 2yz + 4zx

प्रश्न 67.
(- 2x – 3y + 2z)² का प्रसार है
(A) 4x² + 9y² + 4z² + 12xy – 12yz – 8zx
(B) 4x² – 9y² – 4z² + 12xy – 12yz + 8zx
(C) 4x² – 9y² + 4z² – 12xy + 12yz – 8zx
(D) 4x² – 9y² – 4z² + 12xy – 12yz + 8zx.
उत्तर-
(A) 4x² + 9y² + 4z² + 12xy – 12yz – 8zx

प्रश्न 68.
\(\left[\frac{1}{4} a-\frac{1}{2} b+1\right]^{2}\) का प्रसार है
(A) \(\frac{1}{16} a^{2}-\frac{1}{4} b^{2}+1-\frac{1}{4} a b-b+\frac{1}{2} a\)
(B) \(\frac{1}{16} a^{2}-\frac{1}{4} b^{2}-1+\frac{1}{4} a b+b-\frac{1}{2} a\)
(C) \(\frac{1}{16} a^{2}+\frac{1}{4} b^{2}-1-\frac{1}{4} a b-b+\frac{1}{2} a\)
(D) \(-\frac{1}{16} a^{2}-\frac{1}{4} b^{2}+1+\frac{1}{4} a b+b-\frac{1}{2} a\)
उत्तर-
(A) \(\frac{1}{16} a^{2}-\frac{1}{4} b^{2}+1-\frac{1}{4} a b-b+\frac{1}{2} a\)

प्रश्न 69.
(2a – 3b)³ का प्रसार है
(A) 8a³ – 27b³ – 36a²b + 54ab²
(B) 8a³ + 27b³ + 36a²b + 54ab²
(C) 8a³ + 27b³ – 36a²b + 54ab²
(D) – 8a³ – 27b³ + 36a²b – 54ab²
उत्तर-
(A) 8a³ – 27b³ – 36a²b + 54ab²

प्रश्न 70.
(x – \(\frac{2}{3}\)y) का प्रसार है
(A) x³ – 2x²y + \(\frac{4}{3} x y^{2}-\frac{8}{27} y^{3}\)
(B) x³ + 2x²y – \(\frac{4}{3} x y^{2}+\frac{8}{27} y^{3}\)
(C) x³ – 2x²y + \(\frac{4}{3} x y^{2}+\frac{8}{27} y^{3}\)
(D) x³ + 2x²y – \(\frac{4}{3} x y^{2}-\frac{8}{27} y^{3}\)
उत्तर-
(A) x³ – 2x²y + \(\frac{4}{3} x y^{2}-\frac{8}{27} y^{3}\)

प्रश्न 71.
(99)³ का मान है
(A) 970289
(B) 970299
(C) 970389
(D) 970489.
उत्तर-
(B) 970299

प्रश्न 72.
यदि x – 2, x² – 3kx + 8 को भाग करें तो k
का मान होगा
(A) 3
(B) – 2
(C) 2
(D) – 3.
उत्तर-
(C) 2

प्रश्न 73.
यदि x + 1, x² – 4kx + 9 को भाग करें तो k का मान होगा
(A) 2
(B) – 2
(C) 3
(D) – 3.
उत्तर-
(B) – 2

प्रश्न 74.
यदि x + 3, x³ – 7x² – 7kx + 9x का एक गुणनखण्ड हो तो k का मान होगा
(A) 6
(B) 2
(C) 3
(D) – 3.
उत्तर-
(D) – 3

प्रश्न 75.
x² + xa – xb – ab के गुणनखण्ड हैं
(A) (x – a) (x – b)
(B) (x + a) (x – b)
(C) (x + a) (x + b)
(D) (x – a) (x + b)
उत्तर-
(C) (x + a) (x + b)

प्रश्न 76.
6x² – 25x – 14 के गुणनखंड हैं
(A) (2x – 1) (3x + 14)
(B) (2x + 1) (3x – 14)
(C) (2x – 1) (3x – 14)
(D) इनमें से कोई नहीं।
उत्तर-
(B) (2x + 1) (3x – 14)

प्रश्न 77.
(x + 1) के गुणनखण्ड है
(A) (x + 1) (x² + 1)
(B) (x + 1) (x² – x + 1)
(C) (x + 1) (x² + x + 1)
(D) इनमें से कोई नहीं।
उत्तर-
(B) (x + 1) (x² – x + 1)

प्रश्न 78.
(x³ – 1) के गुणनखंड है
(A) (x – 1) (x² – x + 1)
(B) (x – 1) (x² + x + 1)
(C) (x – 1) (x² – 1)
(D) इनमें से कोई नहीं।
उत्तर-
(B) (x – 1) (x² + x + 1)

प्रश्न 79.
8a³ – b³ + 12a² b + 6ab² का गुणनखंड
(A) (2a – b)³
(B) (2a + b)³
(C) (8a – b)³
(D) (8a + b)³
उत्तर-
(B) (2a + b)³

प्रश्न 80.
8a³ – b³ – 12a² b + 6ab² के गुणनखण्ड हैं
(A) (2a – b)³
(B) (2a + b)³
(C) (8a + b)³
(D) (8a + b)³
उत्तर-
(A) (2a – b)³

प्रश्न 81.
27 – 125a³ – 135a + 225a² के गुणनखण्ड हैं
(A) (3 + 5a)²
(B) (3a + 5)³
(C) (3a – 5)²
(D) (3 – 5a)³
उत्तर-
(D) (3 – 5a)³

प्रश्न 82.
64a³ – 27b³ – 144a² b + 108ab² के
गुणनखण्ड हैं
(A) (4a + 3b)²
(B) (4a – 3b)³
(C) (4a + 3b)³
(D) (4a – 3b)²
उत्तर-
(B) (4a – 3b)³

प्रश्न 83.
27p³ – \(\frac{1}{216}-\frac{9}{2} p^{2}+\frac{1}{4} p\) के गुणनखण्ड
(A) \(\left[3 p-\frac{1}{6}\right]^{3}\)
(B) \(\left[3 p+\frac{1}{6}\right]^{3}\)
(C) \(\left[3-\frac{1}{6} p\right]^{3}\)
(D) \(\left[3+\frac{1}{6} p\right]^{3}\)
उत्तर-
(A) \(\left[3 p-\frac{1}{6}\right]^{3}\)

प्रश्न 84.
27y³ + 125z³ के गुणनखण्ड हैं
(A) (3y – 5) (9y² – 5yz + 25z²)
(B) (3y + 5) (9y² + 25yz + 5z²)
(C) (3y + 5z) (9y² – 15yz + 25z²)
(D) (3y – 5z) (9y² + 15yz + 25z²)
उत्तर-
(C) (3y + 5z) (9y² – 15yz + 25z²)

प्रश्न 85.
64z³ – 343m³ के गुणनखण्ड हैं
(A) (4z – 7m) (16z² + 28zm + 49m²)
(B) (4z + 7m) (16z² – 28zm – 49m²)
(C) (4z – 7m) (16z² – 28zm – 49m²)
(D) (4z – 7m) (16z² + 28zm – 49m²)
उत्तर-
(A) (4z – 7m) (16z² + 28zm + 49m²)

प्रश्न 86.
27x³ + y + z³ – 9xyz के गुणनखण्ड हैं
(A) (3x + y + z) (9x² + y² + z² – 3xy – yz – 3xz)
(B) (3x – y – z) (9x² – y² – z² + 3xy + yz – 3xz)
(C) (- 3x – y + z) (9x² + y² + z² – 3xy – yz + 3xz)
(D) इनमें से कोई नहीं।
उत्तर-
(A) (3x + y + z) (9x² + y² + z² – 3xy – yz – 3xz)

प्रश्न 87.
8x³ + 16x – 9 का एक गुणनखण्ड है
(A) (x – 1)
(B) (2x – 1)
(C) (x – 3)
(D) (x – 2).
उत्तर-
(B) (2x – 1)

प्रश्न 88.
x³ + 7x² + 14x + 8 का एक गुणनखण्ड है
(A) (x + 1)
(B) (x – 1)
(C) (x + 3)
(D) (x – 5).
उत्तर-
(A) (x + 1)

प्रश्न 89.
जब x² + px + q को x – a से भाग दिया जाता है तो शेषफल होगा
(A) a² + pa + q
(B) a² – pa + q
(C) pa + q + 1
(D) pa – q + 1.
उत्तर-
(B) a² – pa + q

प्रश्न 90.
जब 3x³ + 8x² – 6x + 1 को x + 3 से भाग दिया जाता है तो शेषपल होगा
(A) 8
(B) 10
(C) – 10
(D) – 8.
उत्तर-
(B) 10

प्रश्न 91.
जब x + 3x² – kx + 4 को x – 2 से भाग दिया जाता है तो शेषपल k आता है। तो k का मान होगा
(A) 4
(B) – 12
(C) 8
(D) – 4.
उत्तर-
(C) 8

प्रश्न 92.
यदि x + y + z = 0 तो x – y + 7 बराबर होगा
(A) 3xyz
(B) – 3xyz
(C) xy
(D) – 2xy
उत्तर-
(A) 3xyz

प्रश्न 93.
वास्तवक में घनों का परिकलन किए बिना (- 12)³ + (7)³ + (5)³ का मान होगा
(A) 84
(B) 35
(C) 7260
(D) – 1260
उत्तर-
(D) – 1260

प्रश्न 94.
वास्तव में घनों का परिकलन किए बिना (28)³ + (- 15)³ + (- 13)³ का मान होगा
(A) 16380
(B) – 16380
(C) 15380
(D) – 15380.
उत्तर-
(A) 16380

प्रश्न 95.
यदि किसी आयत का क्षेत्रफल 25a³ – 35a + 12 हो तो इसकी लम्बई और चौड़ाई के सम्भव व्यंजक होंगे
(A) (5a – 3), (5a – 4), (5a – 3), (5a – 4)
(B) (5a + 3), (5a – 4), (5a + 3), (5a – 4)
(C) (5a -3), (5a + 4), (5a – 3), (5a + 4)
(D) इनमें से कोई नहीं।
उत्तर-
(D) इनमें से कोई नहीं।

प्रश्न 96.
यदि किसी घन का आयतन 3x² – 12x है तो इसकी विभाओं के लिए सम्भव व्यंजक होंगे
(A) 3, x, x +4
(B) 3, x – 4, x
(C) – 3, – x, – x – 4
(D) इनमें से कोई नहीं।
उत्तर-
(B)3, x – 4, x

प्रश्न 97.
a⁴ – b⁴ के गुणनखण्ड हैं
(A) (a² + b²) (a² + b²)
(B) (a² + b²) (a + b) (a – b)
(C) (a² – b²) (a² – b²)
(D) इनमें से कोई नहीं।
उत्तर-
(B) (a² + b²) (a + b) (a – b)

प्रश्न 98.
निम्न में से कौन 8x³ – 125y³ को पूर्णतया
विभाजित करता है ?
(A) 8x – 125y
(B) 2x – 5y
(C) 2x + 5y
(D) 8x + 125y.
उत्तर-
(B) 2x – 5y

 

प्रश्न 99.
यदि x – \(\frac{1}{x}\) = m हो तो \(x^{3}-\frac{1}{x^{3}}\) का मान होगा
(A) m²
(B) 3m
(C) m² + 3m
(D) m³ + 3m.
उत्तर-
(C) m² + 3m

प्रश्न 100.
यदि p + \(\frac{1}{p}\) = 2 हो तो \(p^{2}-\frac{1}{p^{2}}\) का मान होगा
(A) 4
(B) 2
(C) – 4
(D) इनमें से को नहीं।
उत्तर-
(B) 2

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 3 निर्देशांक ज्यामिति MCQ Questions with Answers

PSEB Solutions for Class 9 Maths Chapter 3 निर्देशांक ज्यामिति MCQ Questions

बहुविकल्पीय प्रश्न:

दिये गए चार विकल्पों में से सही उत्तर का चयन कीजिए।

प्रश्न 1.
बिंदु (- 3, – 2) कौन से चतुर्थांश में हैं :
(A) I
(B) II
(C) IV
(D) III
उत्तर:
(D) III

प्रश्न 2.
बिंदुओं (0, 0), (0, 2), (2, 2) तथा (2, 0) को मिलाने पर कौन-सी आकृति प्राप्त होती है ?
(A) वर्ग
(B) आयत
(C) समचतुर्भुज
(D) समांतर चतुर्भुज।
उत्तर:
(A) वर्ग

प्रश्न 3.
बिंदु (5, – 7) कौन से चतुर्थांश में है :
(A) III
(B) II
(C) IV
(D) I.
उत्तर:
(C) IV

प्रश्न 4.
बिंदु (- 4, – 3) का भुज और कोटि क्या है ?
(A) x = – 4, y = – 3
(B) x = – 3, y = – 4
(C) x = 4, y = 3
(D) कुछ नहीं।
उत्तर:
(A) x = – 4, y = – 3

प्रश्न 5.
बिंदु (0, 0) जहाँ x-अक्ष और y-अक्ष परस्पर प्रतिच्छेद करते हैं उसे क्या कहते हैं ?
(A) भुज
(B) कोटि
(C) मूल
(D) कुछ नहीं।
उत्तर:
(C) मूल

प्रश्न 6.
बिंदु (1, 4) कौन से चतुर्थांश में है :
(A) I
(B) IV
(C) II
(D) III.
उत्तर:
(A) I

प्रश्न 7.
बिंदु (0, – 3) स्थित है :
(A) x-अक्ष पर
(B) y-अक्ष पर
(C) पहले चतुर्थांश में
(D) दूसरे चतुर्थांश में।
उत्तर:
(B) y-अक्ष पर

प्रश्न 8.
बिंदु (- 3, 5) स्थित है :
(A) प्रथम चतुर्थांश में
(B) द्वितीय चतुर्थांश में
(C) तीसरे चतुर्थांश में
(D) चौथे चतुर्थांश।
उत्तर:
(B) द्वितीय चतुर्थांश में

प्रश्न 9.
द्वितीय चतुर्थांश में स्थित किसी बिंदु के भुज और कोटि के क्रमश: चिन्ह हैं :
(A) +, +
(B) -, –
(C) -, +
(D) +, -.
उत्तर:
(C) -, +

प्रश्न 10.
बिंदु (0, – 7) स्थित हैं :
(A) x-अक्ष पर
(B) द्वितीय चतुर्थांश में
(C) y-अक्ष पर
(D) चौथे चतुर्थांश में।
उत्तर:
(C) y-अक्ष पर

प्रश्न 11.
बिंदु (- 10, 0) स्थित हैं :
(A) x-अक्ष की ऋणात्मक दिशा में
(B) y-अक्ष की ऋणात्मक दिशा में
(C) तीसरे चतुर्थांश में
(D) चौथे चतुर्थांश में।
उत्तर:
(A) x-अक्ष की ऋणात्मक दिशा में

प्रश्न 12.
x-अक्ष पर स्थित सभी बिंदुओं का भुज है :
(A) 0
(B) 1
(C) 2
(D) कोई भी संख्या।
उत्तर:
(D) कोई भी संख्या।

प्रश्न 13.
x-अक्ष पर स्थित सभी बिंदुओं की कोटि है :
(A) 0
(B) 1
(C) – 1
(D) कोई भी संख्या।
उत्तर:
(A) 0

प्रश्न 14.
वह बिंदु, जहां दोनों निर्देशांक अक्ष मिलते हैं, कहलाता है :
(A) भुज
(B) कोटि
(C) मूलबिंदु
(D) चतुर्थांश।
उत्तर:
(C) मूलबिंदु

प्रश्न 15.
वह बिंदु जिसके दोनों निर्देशांक ऋणात्मक है स्थित होगा :
(A) चतुर्थांश I
(B) चतुर्थांश II
(C) चतुर्थांश III
(D) चतुर्थांश IV
उत्तर:
(C) चतुर्थांश III

प्रश्न 16.
बिंदु (1, – 1) (2, – 2) (4, – 5), (- 3, – 4)
(A) चतुर्थांश II में
(B) चतुर्थांश III में
(C) चतुर्थांश IV में
(D) एक ही चतुर्थांश में स्थित नहीं है।
उत्तर:
(D) एक ही चतुर्थांश में स्थित नहीं है।

प्रश्न 17.
यदि किसी बिंदु का y निर्देशांक शून्य है, तो वह बिंदु सदैव स्थित है :
(A) चतुर्थांश I में
(B) चतुर्थांश II में
(C) x-अक्ष
(D) y-अक्ष पर।
उत्तर:
(C) x-अक्ष

प्रश्न 18.
बिंदु (- 5, 2) और (2, – 5) स्थित हैं :
(A) एक ही चतुर्थांश में
(B) क्रमशः चतुर्थांश II और III में
(C) क्रमशः चतुर्थांश II और IV में
(D) क्रमशः चतुर्थांश IV और II में।
उत्तर:
(C) क्रमशः चतुर्थांश II और IV में

प्रश्न 19.
यदि किसी बिंदु P की x-अक्ष से लांबिक दूरी 5 मात्रक हो तथा इस लंब का पाद x-अक्ष की ऋणात्मक दिशा पर स्थित हो, तो बिंदु P का
(A) x-निर्देशांक = – 5 है
(B) y-निर्देशांक = 5 केवल
(C) y-निर्देशांक = – 5 केवल
(D) y-निर्देशांक = 5 या – 5.
उत्तर:
(D) y-निर्देशांक = 5 या – 5.

प्रश्न 20.
बिंदुओं 0 (0, 0), A (3, 0), B (3, 4), C (0, 4) को आलेखित करके तथा OA, AB, BC और CO को मिलाने पर, निम्नलिखित में से कौन-सी आकृति प्राप्त होगी ?
(A) वर्ग
(B) आयत
(C) समलंब
(D) समचतुर्भुज
उत्तर:
(B) आयत

प्रश्न 21.
यदि बिंदुओं P (- 1, 1), Q (3, – 4), R (1, – 1), S (- 2, – 3) और (- 4, 4) को आलेख कागज पर आलेखित किया जाए, तो चौथे चतुर्थांश के बिंदु हैं :
(A) P और T
(B) Q और R
(C) केवल S
(D) P और R.
उत्तर:
(B) Q और R

प्रश्न 22.
यदि दो बिंदुओं P और Q के निर्दशांक क्रमश: (- 2, 3) और (- 3, 5) हैं तो (P का भुज) – (Q का भुज) बराबर है :
(A) – 5
(B) 1
(C) – 1
(D) – 2
उत्तर:
(B) 1

प्रश्न 23.
यदि P (5, 1), Q (8, 0), R (0, 4), S (0, 5) और 0 (0, 0) को एक आलेख कागज पर आलेखित किया जाए तो x-अक्ष पर स्थित बिंदु है :
(A) P और R
(B) R और S
(C) केवल Q
(D) Q और O
उत्तर:
(D) Q और O

प्रश्न 24.
किसी बिंदु का भुज धनात्मक होता है :
(A) चतुर्थांश I और II में
(B) चतुर्थांश I और IV में
(C) केवल चतुर्थांश I में
(D) केवल चतुर्थांश II में।
उत्तर:
(B) चतुर्थांश I और IV में

प्रश्न 25.
वे बिंदु जिनके भुज और कोटि विभिन्न चिन्हों के होते हैं स्थित होंगे :
(A) चतुर्थांश I और II में
(B) चतुर्थांश II और III में
(C) चतुर्थांश I और III में
(D) चतुर्थांश II और IV में।

उत्तर:
(D) चतुर्थांश II और IV में।

प्रश्न 26.
आकृति में, P के निर्देशांक है :
(A) (- 4, 2)
(B) (- 2, 4)
(C) (4, – 2)
(D) (2, – 4)
उत्तर:
(B) (- 2, 4)

प्रश्न 27.
आकृति में, निर्देशांक (- 5, 3) वाला बिंदु है :
(A) T
(B) R
(C) L
(D) S
उत्तर:
(C) L

प्रश्न 28.
वह बिंदु जिसकी कोटि 4 है और जो y-अक्ष पर
(A) (4, 0)
(B) (0, 4)
(C) (1, 4)
(D) (4, 2)
उत्तर:
(B) (0, 4)

प्रश्न 29.
बिंदुओं P (0, 3), Q (1, 0), R (0, – 1), S (- 5, 0) और T (1, 2) में से कौन-कौन से बिंदु x-अक्ष पर स्थित नहीं है ?
(A) केवल P और R
(B) Q और s
(C) P, R और T
(D) Q, S और T.

उत्तर:
(C) P, R और T

प्रश्न 30.
वह बिंदु जो y-अक्ष की ऋणात्मक दिशा में y-अक्ष पर 5 मात्रक की दूरी पर स्थित है, होगा :
(A) (0, 5)
(B) (5, 0)
(C) (0, – 5)
(D) (- 5, 0)
उत्तर:
(C) (0, – 5)

प्रश्न 31.
y-अक्ष से बिंदु P (3, 4) की लांबिक दूरी है :
(A) 3
(B) 4
(C) 5
(D) 7
उत्तर:
(A) 3