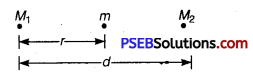Important Questions

Punjab State Board PSEB 11th Class Physics Important Questions Chapter 1 Physical World Important Questions and Answers.

PSEB 11th Class Physics Important Questions Chapter 1 Physical World

Very short answer type questions

Question 1.
Why do we call Physics an exact Science?
Answer:
Most of measurement in Physics are made with high precise and accuracy, so it is called an exact Science.

Question 2.
Give two approaches to study physics.
Answer:
Two approaches to study physics are unification and reduction.

Question 3.
Name the scientific principle behind the technology of steam engine.
Answer:
Laws of thermodynamics is the scientific principle behind the technology of steam engine.

Question 4.
Give one major discovery resulted due to basic laws of electricity and magnetism.
Answer:
Wireless communication technology was a major discovery due to laws of electricity and magnetism.

Question 5.
What is the range of weak nuclear force?
Answer:
The range of a weak nuclear force is of the order of 10^-16 m.

Question 6.
Give an example of achievement in unification.
Answer:
Unified celestial and terrestrial mechanics showed that the same laws of motion and the law of gravitation apply to both the domains.

Question 7.
Give an example for conservation law of energy.
Answer:
A freely falling body under gravity is an example of conservation law of energy.

Short answer type questions

Question 1.
Give the salient features of Einstein’s theory.
Answer:
According to Einstein

• Mass and energy are interconvertible.
• Space and time are interconnected.

Question 2.
Name the phenomena/fields with which microscopic domain of physics deals. Which theory explains these phenomena?
Answer:
The microscopic domain of physics deals with the constitution and structure of matter at atomic and nuclear scale.
The Questionuantum theory is currently accepted, as the proper framework for explaining microscopic phenomena.

Question 3.
Name three important discoveries of physics, which have revolutionised modem chemistry.
Answer:
Three important discoveries of physics, which have revolutionised modem chemistry are :

1. study of radioactivity,
2. quantum theory
3. study of isotopes and determination of their masses by mass spectrographs.

Question 4.
Name four fundamental forces in nature.
Answer:
Four fundamental forces present in nature are:

• Gravitational force
• Electromagnetic force
• Weak nuclear force
• Strong nuclear force.

Question 5.
Name three important discoveries of physics, which have contributed a lot in development of biological sciences.
Answer:
The most important discoveries of physics, which have contributed a lot in development of biological sciences are :

• Ultrasonic waves.
• X-rays and neutron diffraction technique.
• Electron microscope.
• Radio isotopes.

Question 6.
Briefly explain how physics is related to technology?
Answer:
Progress in the field of science and technology is interrelated. Sometimes technology gives rise to new physics and at other times physics generates new technology. The discipline of thermodynamics arose mainly to understand and improve the working of heat engines. Similarly discovery of basic laws of electricity and magnetism led to development of wireless communication technology. Therefore, we can conclude that physics and technology are closely related.

Long answer type questions

Question 1.
How Physics is related to other sciences?
Answer:
Physics is so important branch of science that without the knowledge of Physics, other branches of science cannot make any progress. This can be seen from the following:

(a) Physics in relation to Mathematics: The theories and concepts of Physics lead to the development of various mathematical tools like differential equations, equations of motion etc.

(b) Physics in relation to Chemistry: The concept of interaction between various particles lead to understand the bonding and the chemical structure of a substance. The concept of X-ray diffraction and radioactivity had helped to distinguish between the various solids and to modify the periodic table.

(c) Physics in relation to Biology: The concept of pressure and its measurement has helped us to know the blood pressure of a human being, which in turn is helpful to know the working of heart. The discovery of X-rays has made it possible to diagonose the various diseases in the body and fracture in bones. The optical and electron microscopes are helpful in the studies of various organisms. Skin diseases and cancer can be cured with the help of high energy radiations like X-rays, ultraviolet rays.

(d) Physics in relation to Geology: The internal structure of various rocks can be known with the study of crystal structure. Age of rocks and fossils can be known easily with the help of radioactivity i. e., with the help of carbon dating.

(e) Physics in relation to Astronomy: Optical telescope has made it possible to study the motion of various planets and satellites in our solar system.
Radio telescope has helped to study the structure of our galaxy and to discover pulsars and quasars (heavenly bodies having star like structure). Pulsars are rapidly rotating neutron stars. Doppler’s effect predicted the expAnswer:ion of universe. Kepler’s laws are responsible to understand the nature of orbits of the planets around the sun.

(f) Physics in relation of Meterology: The variation of pressure with temperature leads to forecast the weather.

(g) Physics in relation to Seismology: The movement of earth’s crust and the types of waves produced help us in studying the earthquake and its effect.

Question 2.
Write short note on origin and Fundamental forces in nature.
Answer:
These are the. following four basic forces in nature:
(a) Gravitational forces
(b) Electromagnetic forces
(c) Strong force or nuclear forces
(d) Weak forces.
Some of the important features of these forces are discussed below:

(a) Gravitational forces: These are the forces of attraction between any two bodies in the universe due to their masses separated by a definite distance. These are governed by Newton’s law of gravitation given by

where, m₁, m₂ are the masses of two bodies
r = distance between them
G = Universal gravitational constant
= 6.67 × 10¹¹ Nm²kg²

Characteristics of Gravitational Forces

• They are always attractive. They are never repulsive. They exist between macroscopic as well as microscopic bodies.
• They are the weakest forces in nature.
• They are central forces in nature i. e., they set along the line joining the centres of two bodies.
• They are conservative forces.
• They obey inverse square law i.e.,F ∝ \(\frac{I}{r^{2}}\) they vary inversely as the
  square of the distance between the two bodies.
• They are long range forces i.e., gravitational forces between any two bodies exist even when their distance of separatioji is quite large.
• The field particles of gravitational forces are called gravions. The concept of exchange of field particles between two bodies explains how the two bodies interact from a distance.

(b) Electromagnetic forces: They include the electrostatic and magnetic forces. The electrostatic forces are the forces between two static charges while magnetic forces are the forces between two magnetic poles. The moving charges give rise to the magnetic firce. The combined action of these forces are called electromagnetic forces.
Characteristics of Electromagnetic Forces

• These forces are both attractive as well as repulsive.
• They are central forces in anture.
• They obey inverse sQuestionuare law.
• They are conservative forces in nature.
• These forces are due to the exchange of particles known as photons which carry no charge and have zero rest mass.
• They are 10 times stronger as compared to gravitational forces and 1011 times stronger than the weak forces.

(c) Strong forces: They are the forces of nuclear origin. The particles inside the nucleus are charged particles (protons) and neutral particles (neutrons) which are bonded to each other by a strong interaction called nuclear force or strong force.
Hence they may be defined as the forces binding the nucleons (protons and neutrons) together in a nucleus. They are responsible for the stability of the atomic nucleus. They are of three types :

1. n-n forces are the forces of attraction between two neutrons.
2. p-p forces are the forces of attraction between two protons.
3. n-p forces are the forces of attraction between a proton and a neutron.

Characteristics of Strong Forces

• They are basically attractive in nature and become repulsive when the distance between nucleons is less than 0.7 fermi.
• They obey inverse square law.

(d) Weak forces: They are defined as the interactions which take place between elementary particles during radioactive decay of a radioactive substance. In β – decay, the nucleus changes into a proton, an electron and a particle called anti-neutrino (which is uncharged). The interaction between the electron and the anti-neutrino is known as weak interaction or weak force.

Characteristics of Weak Forces

• They are 10²⁵ times stronger than the gravitational forces.
• They exist between leptons and leptons, leptons and mesons etc.
  (a) and (b) types are the forces that we encouncer in macroscopic world while (c) and (d) types are the forces that we encountered in microscopic world.

Punjab State Board PSEB 11th Class Physics Important Questions Chapter 2 Units and Measurements Important Questions and Answers.

PSEB 11th Class Physics Important Questions Chapter 2 Units and Measurements

Very short answer type questions

Question 1.
Is it possible to have length and velocity both as fundamental quantities? Why?
Answer:
No, since length is fundamental quantity and velocity is the derived quantity.

Question 2.
Which of these is largest: astronomical unit, light year and par sec?
Answer:
Par sec is larger than light year which in turn is larger than an astronomical unit.

Question 3.
Define one Bam. How it is related with metre?
Answer:
One bam is a small unit of area used to measure area of nuclear cross-section.
∴ 1 barn = 10^-28 m²

Question 4.
What is meant by angular diameter of moon?
Answer:
Angular diameter of moon is the angle subtended at a point on the earth, by two diameterically opposite ends of the moon. Its value is about 0.5°.

Question 5.
Name the device used for measuring the mass of atoms and molecules. (NCERT Exemplar)
Answer:
Spectrograph.

Question 6.
Write the dimensional formula of wavelength and frequency of a wave.
Answer:
Wavelength [λ] = [L]
Frequency [v] = [T^-1]

Question 7.
Obtain the dimensional formula for coefficient of viscosity.
Answer:
Coefficient of viscosity (η) = \(\frac{F d x}{A \cdot d v}\)
= \(\frac{\left[\mathrm{MLT}^{-2}\right][\mathrm{L}]}{\left[\mathrm{L}^{2}\right]\left[\mathrm{LT}^{-1}\right]}\) = [M¹L^-1T^-1]

Question 8.
Write three pairs of physical quantities, which have same dimensional formula.
Answer:

• Work and energy
• Energy and torque
• Pressure and stress

Short answer type questions

Question 1.
Does AU and Å represent the same unit of length?
Answer:
No, AU and Å represent two different units of length.
1 AU = 1 astronomical unit = 1.496 x 10¹¹ m
1Å = 1 angstrom = 10^-10 m

Question 2.
What is common between bar and torr?
Solution:
Both bar and torr are the units of pressure.
1 bar =1 atmospheric pressure = 760 mm of Hg column .
= 10⁵ N/m²
1 torr = 1 mm of Hg column
bar 760 torr

Question 3.
Why has second been defined in term of periods of radiations from cesium-133?
Answer:
Second has been defined in terms of periods of radiation, because

• this period is accurately defined.
• this period is not affeced by change of physical conditions like temperature, pressure and volume etc.
• the unit is easily reproducible in any good laboratoty.

Question 4.
Why parallax method cannot be used for measuring distances of stars more than 100 light ýears away?
Answer:
When a star is more than loo light years away, then the parallax angle is so small that it cannot be measured accurately.

Question 5.
What is the technique used for measuring large time intervals?
Answer:
For measuring large time intervals, we use the technique of radioactive dating. Large time intervals are measured by studying the ratio of number of radioactive atoms decayed to the number of surviving atoms in the
specimen.

Question 6.
Using the relation E = hv, obtain the dimensions of Planck’s constant.
Answer:
We know that dimensional formula of energy E of photon is [M¹L²T^-2
and dimensional formula of frequency is y is [T^-1].
The given relation is E = hv
[h] = \(\frac{[E]}{[v]}=\frac{\left[M^{1} \mathrm{~L}^{2} \mathrm{~T}^{-2}\right]}{\left[\mathrm{T}^{-1}\right]}\) = M¹L²T^-1

Question 7.
The rotational kinetic energy of a body is given by E = \(\frac {1}{2}\)Iω², where ω is the angular velocity of the body. Use the equation to obtain dimensional formula for moment of inertia I. Also write
its SI unit.
Solution:
The given relation is E = \(\frac {1}{2}\)Iω²

Its SI unit is Joule.

Question 8.
Distinguish between dimensional variables and dimensional constants. Give example too.
Answer:
Dimensional variables are those quantities which have dimensions and whose numerical value may change. Speed, velocity, acceleration etc. are dimensional variables.

Dimensional constants are quantities having dimensions but having a constant value, e.g., gravitation constant (G), Planck’s constant (H), Stefan’s constant (σ) etc.

Question 9.
Dow will you convert a physical quantity from one unit system to another by method of dimensions?
Solution:
If a given quantity is measured in two different unit system, then Q = n₁u₁ = n₂u₂.
Let the dimensional formula of the quantity be [M^aL^bT^c], then we have n₁ [M₁^aL₁^bT₁^c ] = n₂ [M₂^aL₂^bT₂^c]
Here M₁, L₁, T₁ are the fundamental units of mass, length and time in
first unit system and M₂, L₂, T₂

This relation helps us to convert a physical quantity from one unit system to another.

Question 10.
The displacement of a progressive wave is represented by y = A sin (ωt – kx), where x is distance, and t is time. Write the dimensional formula of (i) ω and (ii) k. (NCERT Exemplar)
Solution:
Now, by the principle of homogeneity, i. e., dimensions of LHS and RHS should be equal, hence
[LHS] = [RHS]
⇒ [L] = [A] = L
As ωt – kx should be dimensionless,
[ωt] [kx] = 1
⇒ [ω]T = [k]L= 1
⇒ [ω] = T^-1 and [k] = L^-1

Question 11.
Which of the following time measuring devices is most precise?
(a) A wall clock
(b) A stop watch
(c) A digital watch
(d) An atomic clock
Give reason for your answer. (NCERT Exemplar)
Solution:
A wall clock can measure time correctly upto one second. A stop watch can measure time correctly upto a fraction of a second. A digital watch can measure time up to a fraction of second. An atomic clock can measure time most precisely as its precision is 1 s in 10¹³ s.

Long answer type questions

Question 1.
A large fluid star oscillates in shape under the influence of its own gravitational field. Using dimensional analysis, find the expression for period of oscillation (T) in terms of radius of star (R), Mean density of fluid (ρ) and universal gravitational constant (G).
Solution:
Suppose period of oscillation T depends on radius of star R, mean density of fluid p and universal gravitational constant (G) as
T = kR^a ρ^b G^c,where kis a dimensionless constant
Writing dimentions on both sides of the equation, we have
[M⁰L⁰T¹]=[L]^a[ML^-3]^b[M^-1L³T^-2]^c
= M^{b – c}L^{a – 3b + 3c}T^-2c
Comparing powers of M, L and T, we have
b – c = 0;
a – 3b + 3c = 0 and -2c = 1
On simplifying these equations, we get
c = -1/2,b = -1/2, a = 0
Thus, we have T = kρ^-1/2G^-1/2 = \(\frac{k}{\sqrt{\rho G}}\)

Question 2.
Find an expression for viscous force F acting on a tiny steel ball of radius,r,moving in a viscous liquid of viscosity q with a constant speed υ by the niethod of dimensional analysis.
Solution:
It is given that viscous force F depends on (i) radius r of steel ball, (ii) coefficient of viscosity η of viscous liquid (iii), Speed υ of the ball i.e.,F = kr^aη^bυ^c,where kis dimensionless constant
Writing dimensions on both sides of equation, we have
[MLT^-2] = [L]^a[M¹L^-1T^-1]^b[LT^-1]^c
= [M^aL^{a – b + c}T^{-b -c}]
Comparing powers of M, L and T on two sides of equation, we get
a = 1
a – b + c = 1
-b -c =-2
On solving, these above equations, we get ,
a = 1, b = 1 and c = 1
Hence, the relation becomes
F = krηυ

Punjab State Board PSEB 11th Class Physics Important Questions Chapter 13 Kinetic Theory Important Questions and Answers.

PSEB 11th Class Physics Important Questions Chapter 13 Kinetic Theory

Very Short Answer Type Questions

Question 1.
Under what conditions, real gases behave as an ideal gas?
Answer:
At low pressure and high temperature, real gases behave as an ideal gas.

Question 2.
When air is pumped into a cycle tyre, the volume and pressure of the air in the tyre, both are increased. What about Boyle’s law in this case? (NCERT Exemplar]
Answer:
When air is pumped, more molecules are pumped in Boyle’s law is stated for situation where number of molecules remain constant.

Question 3.
What is the minimum possible temperature on the basis of Charles’ law?
Answer:
The minimum possible temperature on the basis of Charles’ law is -273.15°C.

Question 4.
If a vehicle runs on the road for a long time, then the air pressure in the tyres increases. Explain.
Answer:
Due to the presence of friction between the road and tyres, the tyres get heated as a result of which temperature of air inside the tyre increases and hence pressure in tyre also increases.

Question 5.
What is the number of degree of freedom of a bee flying in a room?
Answer:
Three, because bee is free to move along x-direction or y-direction or z-direction.

Question 6.
How degree of freedom of a gas molecule is related with the temperature?
Answer:
Degree of freedom will increase when temperature is very high because at high temperature, vibrational motion of the gas will contribute to the kinetic energy. Hence, there is an additional kinetic energy associated with the gas, as a result of increased degree of freedom.

Question 7.
Is molar specific heat of a solid a constant quantity?
Answer:
Yes, the molar specific heat of a solid is a constant quantity and its value is 3 cal/mol-K.

Question 8.
Name experimental evidence in support of random motion of gas molecules.
Answer:
Brownian motion and diffusion of gases provide experimental evidence in support of random motion of gas molecules.

Question 9.
What is mean free path of a gas?
Answer:
The average distance travelled by a molecule between two successive collisions is known as mean free path of the molecule.

Short Answer Type Questions

Question 1.
State ideal gas equation. Draw a graph to check whether a real gas obeys this equation. What is the conclusion drawn?
Answer:
According to the ideal gas equation, we have PV = µRT
Thus, according to this equation \(\frac{P V}{\mu T}\) = R i.e., value of \( \frac{P V}{\mu T}\) must be a constant having a value 8.31 J mol^-1 K^-1. Experimentally value of \(\frac{P V}{\mu T}\) for real gases was calculated by altering the pressure of gas at different temperatures. The graphs obtained have been shown in the figure.

Here, for the purpose of comparison, graph for an ideal gas has also been drawn, which is a straight line parallel to pressure axis. From the graph it is clear that behaviour of real gases differ from an ideal gas. However, at high temperatures and low pressures behaviour is nearly same as that of an ideal gas.

Question 2.
Explain, why
(i) there is no atmosphere on Moon.
(ii) there is fall in temperature with altitude. (NCERT Exemplar)
Answer:
(i) The Moon has small gravitational force and hence the escape velocity is small. As the Moon is in the proximity of the Earth as seen from the Sun, the Moon has the same amount of heat per unit area as that of the Earth. The air molecules have large range of speeds.

Even though the rms speed of the air molecules is smaller than escape velocity on the Moon, a significant number of molecules have speed greater than escape velocity and they escape. Now, rest of the molecules arrange the speed distribution for the equilibrium temperature. Again, a significant number of molecules escape as their speeds exceed escape speed. Hence, over a long time, the Moon has lost most of its atmosphere.

(ii) As the molecules move higher, their potential energy increases and hence kinetic energy decreases and temperature reduces. At greater height, more volume is available and gas expands. Hence, some cooling takes place.

Question 3.
Two perfect gases at absolute temperatures T₁ and T₂ are mixed. There is no loss of energy. Find the temperature of the mixture if the masses of the molecules are m₁ and m₂ and the number of the molecules in the gases are n₁ and n₂ respectively.
Solution:
According to kinetic theory, the average kinetic energy per molecule of a
gas = \(\frac{3}{2} \) K_BT
Before mixing the two gases,the average K.E. of all the molecules of two gases
= \(\frac{3}{2} \)K_Bn₁T₁ + \(\frac{3}{2} \)K_Bn₁T₂
After mixing, the average K.E. of both the gases
= \(\frac{3}{2} \)k_B (n₁ +n₂)T
where, T is the temperature of mixture.
Since there is no loss of energy,
Hence, \(\frac{3}{2} \)k_B (n₁ +n₂)T = \(\frac{3}{2} k_{B} n_{1} T_{1}+\frac{3}{2} k_{B} n_{2} T_{2}\)
or T = \(\frac{n_{1} T_{1}+n_{2} T_{2}}{\left(n_{1}+n_{2}\right)}\).

Question 4.
At room temperature, diatomic gas molecule has five degrees of freedom. At high temperatures, it has seven degrees of freedom. Explain.
Answer:
At low temperatures, diatomic gas has three translational and two rotational degrees of freedom, so total number of degrees of freedom is 5. But at high temperature, gas molecule starts to vibrate which give two additional degrees of freedom. So the total numbers of degrees of freedom is 7.

Question 5.
What is basic law followed by equipartition of energy?
Answer:
The law of equipartiüon of energy for any dynamical system in thermal equilibrium, the total energy is distributed equally amongst all the degrees of freedom. The energy associated with each molecule per degree of freedom is \(\frac{1}{2}\) k_BT, where kB is Boltzmann’s constant and T is temperature of the system.

Question 6.
On what parameters does the λ (mean free path) depends?
Solution:
We know that,
λ = \(\frac{k T}{\sqrt{2} \pi d^{2} P}=\frac{m}{\sqrt{2} \pi d^{2} \rho}=\frac{1}{\sqrt{2} \pi n d^{2}}\)
Therefore, A depends upon:
(i) diameter (d) of the molecule, smaller the ‘d’, larger is the mean free path λ .
(ii) λ ∝ T i. e., higher the temperature larger is the λ.
(iii) λ ∝ \(\frac{1}{P}\) i.e., smaller the pressure larger is the λ.
(iv) λ ∝ \(\frac{1}{\rho}\) i.e., smaller the density (ρ), larger will be the λ.
(v) λ ∝ \(\frac{1}{n}\) i. e., smaller the number of molecules per unit volume of the gas, larger is the λ.

Question 7.
Although velocity of air molecules is very fast but fragrance of a perfume spreads at a much slower rate. Explain?
Answer:
This is because perfume vapour molecules do not travel uninterrupted, they undergo a number of collisions and trace a zig-zag path, due to which their effective displacement per unit time is small, so spreading is at a much slower rate.

Long Answer Type Questions

Question 1.
Consider an ideal gas with following distribution of speeds:

Speed (m/s)	% of molecules
200	10
400	20
600	40
800	20
1000	10

(i) Calculate υ_rms and hence T(m = 3.0 x 10^-26 kg)
(ii) If all the molecules with speed 1000 m/s escape from the system, calculate newvma and hence T.(NCERTExemplar)
Solution:
This problem is designed to give an idea about cooling by evaporation.
(i) υ²_rms = \(\frac{\sum n_{i} v_{i}^{2}}{\sum n_{i}}\)

(ii)

Question 2.
A box of 1.00 m³ is filled with nitrogen at 1.50 atm at 300 K. The box has a hole of an area Is 0.010 mm². How much time is required for the pressure to reduce by 0.10 atm., if the pressure outside is 1 atm.
Solution:
Given, the volume of the box, V 1.00 m³
Area of hole, a = 0.010 mm³ = 0.01 x 10^-6 m²
Temperature outside = Temperature inside
Initial pressure inside the box = 1.50 atm
Final pressure inside the box = 0.10 atm

Assuming,
υ_ix= Speed of nitrogen molecule inside the box along x-direction.
n₁ = Number of molecules per unit volume in a time interval of Δt, all the particles at a distance (υ_ixΔt) will collide the hole and the wall, the particle colliding along the hole will escape out reducing the pressure in the box.

Let the area of the wall is A, Number of particles colliding in time, Δt = \(\frac{1}{3}\) n₁(υ_ixΔt)A \(\frac{1}{2}\) is the factor because all the particles along x-direction are behaving randomly. Hence, half of these are colliding against the walls on either side.
Inside the box, υ²_ix + υ²_iy + υ²_iz = υ²_rms
⇒ υ²_ix = \(\frac{v_{r m s}^{2}}{3}\) [∵ υ_ix = υ_iy= υ_iz]

If particles collide along hole, they move out. Similarly, outer particles colliding along hole will move in.
Ifa = area of hole
Then, net particle flow in time,
Δt = \(\frac{1}{2}\left(n_{1}-n_{2}\right) \frac{k_{B} T}{m} \Delta t a\) [∵υ_rms = \(\sqrt{\frac{3 k_{B} T}{m}} \)]

[Temperature inside and outside the box are equal]
Let n = number of density of nitrogen
n = \(\frac{\mu N_{A}}{V}=\frac{p N_{A}}{R T}\) [∵ \(\frac{\mu}{V}=\frac{p}{R T}\)]
where, N_A = Avogadro’s number
If after time Δt, pressure inside changes from p₁ to p₂
n’₁ = \(\frac{p_{1}^{\prime} N_{A}}{R T}\)
Now, number of molecules gone out = n₁V -n’₁V

Punjab State Board PSEB 11th Class Physics Important Questions Chapter 3 Motion in a Straight Line Important Questions and Answers.

PSEB 11th Class Physics Important Questions Chapter 3 Motion in a Straight Line

Very short answer type questions

Question 1.
What is the condition for an object to be considered as a point object?
Answer:
An object can be considered as a point object if the distance travelled by it is very large than its size.

Question 2.
For which condition, the distance and the magnitude of displacement of an object have the same values?
Answer:
The distance and the magnitude of displacement of an object have the same values, when the body is moving along a straight line path in a fixed direction.

Question 3.
Speed of a particle cannot be negative. Why?
Answer:
Speed is the distance travelled in unit time and distance cannot be negative.

Question 4.
Is it possible that a body could have constant speed but varying velocity?
Answer:
Yes, a body could have constant speed but varying velocity if only the direction of motion changes.

Question 5.
For which condition, the average velocity will be equal to the instantaneous velocity?
Answer:
When a body moves with a uniform velocity, then
υ_av = υ_inst

Question 6.
Give an example of uniformly accelerated linear motion.
Answer:
Motion of a body under gravity.

Question 7.
Give example of motion where x > 0, υ < 0, a > 0 at a particular instant. (NCERT Exemplar)
Solution:
Let the motion is represented by
x(t) = A + Be^-γt ……………. (i)
Let A>B and γ > 0
Now velocity x(t) = \(\frac{d x}{d t}\) = -Bγe^-γt
Acceleration a(t) = \(\frac{d x}{d t}\) = Bγ²e^-γt
Suppose we are considering any instant t, then from Eq. (i) we can say that
x(t)>0,υ(t)< 0 and a>0

Short answer type questions

Question 1.
Explain how an object could have zero average velocity but non-zero average speed?
Solution:
υ = \(=\frac{\text { Net displacement }}{\text { Total time taken }}\)
and average speed,

If an object moves along a straight line starting from origin and then returns back to origin.
Average velocity = 0
and Average speed = \(\frac{2 s}{t}\)

Question 2.
If the displacement of a body is zero, is distance necessarily zero? Answer with one example.
Answer:
No, because the distance covered by an object is the path length of the path covered by the object. The displacement of an object is given by the change in position between the initial position and final position.

Question 3.
Is earth inertial or non-inertial frame of reference?
Answer:
Since, earth revolves around the sun and also spins about its own axis, so it is an accelerated frame of reference. Hence, earth is a non-inertial frame of reference.
However, if we do not take large scale motion such as wind and ocean currents into consideration, we can say that approximation the earth is an inertial frame.

Question 4.
A person travels along a straight road for the first half with a velocity υ ₁ and the second half with velocity υ ₂. What is the mean velocity of the person?
Solution:

Question 5.
The displacement of a particle is given by at² What is dependency of acceleration on time?
Solution:
Let x be the displacement. Then, x = at²
∴ Velocity of the object, υ = \(\frac{d x}{d t}\) = 2 at
Acceleration of the object, a = \(\frac{d v}{d t}\) = 2 a
It means that a is constant.

Question 6.
What are uses of a velocity-time graph?
Solution:
From a velocity-time graph, we can find out
(i) The velocity of a body at any instant.
(ii) The acceleration of the body and
(iii) The net displacement of the body in a given time-interval.

Question 7.
Draw displacement-time graph for a uniformly accelerated motion. What is its shape?
Solution:
Displacement-time graph for a uniformly accelerated motion has been shown in adjoining fig. The graph is parabolic in shape.

Question 8.
The distance travelled by a body is proportional to the square of time. What type of motion this body has?
Solution:
Let x be the distance travelled in time t. Then,
x ∝ t² [given]
x = kt² [here, k = constant of proportionality]
We know that velocity is given
υ = \(\frac{d x}{d t}\) = 2kt
and acceleration is given by
a = \(\frac{d v}{d t}\) = 2 k [constant]
Thus, the body has uniform accelerated motion.

Long answer type questions

Question 1.
It is a common observation that rain clouds can be at about a kilometre altitude above the ground.
(i) If a rain drop falls from such a height freely under gravity, what will be its speed? Also, calculate in km/h (g = 10m/s²).
(ii) A typical rain drop is about 4 mm diameter. Momentum is mass × speed in magnitude. Estimate its momentum when it hits ground.
(iii) Estimate time required to flatten the drop.
(iv) Rate of change of momentum is force. Estimate how much force such a drop would exert on you?
(v) Estimate the order of magnitude force on umbrella. Typical lateral separation between two rain drops is 5 cm.
(Assume that umbrella is circular and has a diameter of 1 m and cloth is not pierced through it.) (NCERT Exemplar)
Solution:
Here, height (h) = 1 km = 1000 m, g = 10 m/²
(i) Velocity attained by the rain drop in freely falling through a height h.
υ = \(\sqrt{2 g h}=\sqrt{2 \times 10 \times 1000}\)
= 100√2 m/s
= 100√2 \(\frac{60 \times 60}{1000}\) km/h
= 360√2 km/h ≈ 510 km/h

(ii) Diameter of the drop (d) = 2 r = 4 mm
∴ Radius of the drop (r) = 2 mm = 2 × 10^-3 m
Mass of a rain drop (m) = V × ρ
= \(\frac{4}{3}\) πr³ρ = \(\frac{4}{3} \times \frac{22}{7}\) x (2 × 10^-3)³ × 10³
[ v density of water = 10³ kg/m³ ]
≈ 3.4 × 10^-5 kg
Momentum of the rain drop (p) = mυ
= 3.4 × 10^-5 × 100√2
≈ 4.7 × 10^-3 kg-m/s

(iii) Time required to flatten the drop = time taken by the drop to travel the distance equal to the diameter of the drop near the ground
t = \(\frac{d}{v} \times \frac{4 \times 10^{-3}}{100 \sqrt{2}}\) = 0.028 × 10^-3 s
= 2.8 × 10^-5 s

(iv) Force exerted by a rain drop

= \(\frac{p-0}{t}=\frac{4.7 \times 10^{-3}}{2.8 \times 10^{-5}}\) ≈ 168 N

(v) Radius of the umbrella (R) = \(\frac{1}{2}\) m
∴ Area of the umbrella (A) = πR² = \(\frac{22}{7}\) x (\(\frac{1}{2}\))² = \(\frac{22}{28}=\frac{11}{14}\) ≈ 0.8M²
Number of drops striking the umbrella
simultaneously with average separation of 5 cm or 5 × 10^-2 m
= \(\frac{0.8}{\left(5 \times 10^{-2}\right)^{2}}\) = 320
∴ Net force exerted on umbrella = 320 × 168 = 53760 N

Question 2.
If a body moving with uniform acceleration in straight line describes successive equal distance in time interval t₁, t₂ and t₃, then show that
\(\frac{1}{t_{1}}-\frac{1}{t_{2}}+\frac{1}{t_{3}}=\frac{3}{t_{1}+t_{2}+t_{3}}\)
Solution:
As shown in figure, let three successive equal distances be represented by AB, BC and CD

Let each distance berm. Let υ_A,υ_B,υ_C and υ_D be the velocities at points A, B, C and D respectively.
Average velocity between A and B = \(\frac{v_{A}+v_{B}}{2}\)

Punjab State Board PSEB 11th Class Physics Important Questions Chapter 15 Waves Important Questions and Answers.

PSEB 11th Class Physics Important Questions Chapter 15 Waves

very Short Answer Type Questions

Question 1.
Why should the difference between the frequencies be less than 10 to produce beats?
Answer:
Human ear cannot identify any change in intensity is less than \(\left(\frac{1}{10}\right)^{\mathrm{th}} \)‘ of a second. So, difference should be less than 10.

Question 2.
Does a vibrating source always produce sound?
Answer:
A vibrating source produces sound when it vibrates in a medium and frequency of vibration lies within the audible range (10 Hz to 20 kHz).

Question 3.
What is the nature of water waves produced by a motorboat sailing in water? (NCERT Exemplar)
Answer:
Water waves produced by a motorboat sailing in water are both longitudinal and transverse.

Question 4.
In a hot summer day, pitch of an organ pipe will be higher or lower?
Solution:
The speed of sound in air is more at higher temperatures, as υ ∝ \(\sqrt{T}\) if. As we know frequency υ = \(\frac{v}{\lambda}\) as y is more, hence y will be more and accordingly pitch will be more.

Question 5.
When two waves of almost equal frequencies n₁ and n₂ reach at a point simultaneously. What is the time interval between successive maxima? (NCERT Exemplar)
Solution:
Number of beats/sec = (n₁ – n₂)
Hence, time interval between two successive beats time interval between two successive maxima = \(\frac{1}{n_{1}-n_{2}}\)

Short Answer Type Questions

Question 1.
Transverse waves are generated in two uniform steel wires A and B of diameters 10^-3 m and 0.5 x 10^-3 m respectively, by attaching their free end to a vibrating source of frequency 500 Hz. Find the ratio of the wavelengths if they are stretched with the same tension.
Solution:
The density ρ of a wire of mass M, length L and diameter ‘d’ is given by
ρ = \(\frac{4 M}{\pi d^{2} L}=\frac{4 m}{\pi d^{2}}\)
Now υ_A = \(\sqrt{\frac{T}{m_{A}}}\)
and
υ_B = \(\sqrt{\frac{T}{m_{B}}}\)
∴ \(\frac{v_{A}}{v_{B}}=\sqrt{\frac{m_{B}}{m_{A}}}=\frac{d_{B}}{d_{A}} \)
but υ_A = νλ_A and ν_B = νλ_B, n being the frequency of the source.
Hence, \(\frac{\lambda_{A}}{\lambda_{B}}=\frac{v_{A}}{v_{B}}=\frac{d_{B}}{d_{A}}=\frac{0.5 \times 10^{-3}}{10^{-3}} \) = 0.5

Question 2.
What are the uses of ultrasonic waves?
Answer:
Ultrasonic waves are used for the following purposes

• They are used in SONAR for finding the range and direction of submarines.
• They are used for detecting the presence of cracks and other inhomogeneities in solids.
• They are used to kill the bacteria and hence for sterilising milk.
• They are used for cleaning the surface of solid.

Question 3.
A progressive and a stationary wave have frequency 300 Hz and the same wave velocity 360 in/s. Calculate
(i) the phase difference between two points on the progressive wave which are 0.4 m apart,
(ii) the equation of motion of progressive wave if its amplitude is 0.02 m,
(iii) the equation of the stationary wave if its amplitude is 0.01 m and
(iv) the distance between consecutive nodes in the stationary wave.
Solution:
Wave velocity υ = 360 rn/s
Frequency,f= 300 Hz
∴ Wavelength, λ = \(\frac{v}{f}=\frac{360}{300}\) = 1.2 m

(i) The phase difference between two points at a distance one wavelength apart is 2π. Phase difference between points 0.4 m apart is given by
\(\frac{2 \pi}{\lambda} \times 0.4\) = \(\frac{2 \pi}{1.2} \times 0.4=\frac{2 \pi}{3}\) rad

(ii) The equation of motion of a progressive wave is
y=A sin 2π \(\left(\frac{t}{T}-\frac{x}{\lambda}\right)\)
In the case given
y=0.02sin2π\(\left(300 t-\frac{x}{1.2}\right)\)

(iii) The equation of the stationary wave is
y=2Acos\(\frac{2 \pi x}{\lambda} \sin \frac{2 \pi t}{T}\)
Here, 2A=2×0.01=0.02m
λ =1.2m
\(\frac{1}{T}\) =300Hz

∴ y=0.02 cos \(\frac{2 \pi x}{1.2} \sin 600 \pi t\)

(iv) The distance between the two consecutive nodes in the stationary wave is given by
\(\frac{\lambda}{2}=\frac{1.2}{2}\)m = 0.6m

Question 4.
Write basic conditions for formation õf stationary waves.
Answer:
The basic conditions for formation of stationary waves are listed below:

• The direct and reflected waves must be traveling along the same line.
• For stationary wave formation, the superposing waves should either be longitudinal or transverse. A longitudinal and a transverse wave cannot superposition.
• For formation of stationary waves, there should not be any relative motion between the medium and oppositely traveling waves.
• Amplitude and period of the superposing waves should be same.

Question 5.
The intensity of sound in a normal conversation at home is about 3 x 10^-6 w m^-2 and the frequency of normal human voice Is about 1000 Hz. Find the amplitude of waves, assuming that the air is at standard conditions.
Solution:
At standard conditions (STP)
density (ρ) of air = 129 kg m^-3
velocity of sound,
v=332.5ms^-1
Now, I= 2π²ρn²A²υ
where, n =1000 Hz,
I=3 x 10^-6 Wm^-2
∴ A= \(\frac{1}{\pi n} \sqrt{\frac{I}{2 \rho v}}\)
= \(\frac{1}{3.142 \times 1000} \times \sqrt{\frac{3 \times 10^{-6}}{2 \times 1.29 \times 332.5}}\)
= \(\frac{5.91 \times 10^{-5}}{3.142 \times 10^{3}}\)
=1.88 x 10^-8 m
Note that the amplitude of sound waves in normal conversation is extremely small.

Question 6.
The Intensities due to two sources of sound are I₀ and 4I₀. What is the intensity at a point where the phase difference between two waves is (i) 0⁰ (ii) \(\frac{\pi}{2}\) (iii) π?
Solution:
If a₁ and a₂ are the amplitudes of two waves, then the resultant amplitude is given by
A = \(\sqrt{a_{1}^{2}+a_{2}^{2}+2 a_{1} a_{2} \cos \phi}\)
where Φ is the phase difference between two waves.

Now, A²=a₁² +a₂² +2a₁a₂cos θ
Expressing this equation in terms of intensity.
I= I₁+4I₂+2\(\sqrt{I_{1}} \sqrt{I_{2}} \cos \phi\)
(j) I = I₀ + 4I₀ + 2 \(\sqrt{I_{1}} \sqrt{I_{2}}\) cos 0° = 9I₀
(ii) I = I₀ + 4I₀ + 2\(\sqrt{I_{0}} \sqrt{4 I_{0}} \cos \frac{\pi}{2}\) = 5I₀
(iii) I = I₀ + 4I₀ + 2 \(\sqrt{I_{0}} \sqrt{4 I_{0}} \cos \pi \) = I₀

Question 7.
Compare the velocities of sound In hydrogen (H₂) and carbon dioxide (CO₂) The ratio (γ) of specific beats of H₂ and CO₂ are respectively 1.4 and 1.3.
Solution:

Since density of a gas is proportional to its molecular weight.

Question 8.
Two loudspeakers have been installed in an open space to listen to a speech. When both the loudspeakers are in operation, a listener sitting at a particular place receives a very feeble sound. Why? What will happen if one loudspeaker is kept off?
Solution:
When the distance between two loudspeakers from the position of listener is an odd multiple of \(\frac{\lambda}{2} \) then due to destructive interference between sound waves from two loudspeakers, a feeble sound is heard by the listener. When one loudspeaker is kept off, no interference will take place and the listener will hear the full sound of the operating loudspeaker.

Question 9.
The second overtone of an open pipe has the same frequency as the first overtone of a closed pipe 2m long. What is the length of the open pipe?
Solution:
Let L₀ be the length of the open pipe. The fundamental frequency of the pipe is given by
ν₀ = \(\frac{v}{\lambda_{f}}=\frac{v}{2 L_{0}}\)
where, ν = velocity of sound in air
The second overtone of the open pipe has a frequency
3ν₀ = \(\frac{3 v}{2 L_{0}} \) Hz

The length of the closed pipe
L_c = 2m
The frequency of the fundamental omitted by the closed pipe
v_c = \(\frac{v}{\lambda}=\frac{v}{4 L_{C}} \)
The first overtone of the closed pipe has a frequency
3v_c=\(\frac{3 v}{4 L_{c}}=\frac{3 v}{4 \times 2}=\frac{3 v}{8}\) Hz
Now, 3v₀ = 3v_c
or 2L₀=8 or L₀=4m

Question 10.
Calculate the number of beata heard per second is there are three sources of sound of frequencies 400, 401, and 402 of equal Intensity sounded together.
Solution:
Let us consider the case of three disturbances each of amplitude a and frequencies (n -1), and (n + 1)respectìvely. The resultant displacement is given by
y=a sin 2π(n-1)t +asin2πnt +asin2π(n +1)x
=2a sin 2πnrcos2πt +asin2π(n+1)t
=a(1 +2cos2πt)sin 2πtnt
So the resultant amplitude is a (1 + 2 cos 2πt)
which is maximum when cos2πt = + 1
∴ 2πt=2k where k=0,1,2,3 ………………..
t =0, 1,2, 3 ……………………

Thus the time interval between two consecutive maxima is one. This shows that the frequency of maxima is one.
Similarly, the amplitude is minimum when
1 +2 cos 2πt = 0
or
cos2πt= – \(\frac{1}{2}\)
or
2πt = 2kπ +\(\frac{2 \pi}{3}\)
(Where k 0,1,2 )
or
t= \(\left(k+\frac{1}{3}\right)=\frac{1}{3}, \frac{4}{3}, \frac{7}{3}, \frac{10}{3}\)
Thus the minima occurs after an interval of one second, i.e., the frequency of minima is also one. Hence, the frequency of beats is also one.
Thus, one beat is heard per second.

Long Answer Type Quèstions

Question 1.
Derive expressions for apparent frequency when
(i) source Is moving towards an observer at rest.
(ii) observer Is moving towards source at rest.
(iii) both source and observer are in motion.
Solution:
Let S and O be the positions of source and observer respectively.
ν = frequency of sound waves emitted by the source.
υ = velocity of sound waves.

Case (i) Source (S) ¡n motion and observer at rest: When S is at rest, it will emit waves in one second and these will occupy a space of length ν in one second.
If λ = wavelength of these waves, then
λ = \(\frac{v}{v}\)
Let υ_s = velocity of a source moving towards O at rest and let S reaches to S’ in one second. Thus the sound waves wifi be crowded in length (υ – υ_s).
So if λ’ be the new wavelength,
Then ,
λ’ = \(\frac{v-v_{S}}{v}\)
if v’ be the apparent frequency, then
v’ = \(\frac{v}{\lambda^{\prime}}=\frac{v}{v-v_{s}} v\)

∴ v’ > v i. e., when S moves towards O, the apparent frequency of sound waves is greater than the actual frequency.

(ii) If the observer moves towards the source at rest:

Let v₀ = velocity of observer moving towards S at rest.
As the observer moves towards S at rest, so the velocity of sound waves w.r.t. the observer is v + v₀.
If v’ = apparent frequency, then
v’ = \(\frac{v+v_{o}}{\lambda}=\frac{v+v_{o}}{v} v\)
Clearly v’ > v

(iii) If both S and O are moving
(a) towards each other : We know that when S moves towards stationary observer,

then v’ = \(\frac{v}{v-v_{s}}\)
When O moves towards S, then
v”= \(\left(\frac{v+v_{o}}{v}\right) \mathrm{v}^{\prime}=\left(\frac{v+v_{o}}{v-v_{S}}\right) \mathrm{v} \)

(b) If both S and O move in the direction of sound waves:
Then the apparent frequency is given by

(c) When both S and O are moving away from each other:
When source moves away from O at rest, then apparent frequency is given by

When observer is also moving away from the source, the frequency v’ will change to v” and is given by

Question 2.
Give the analytical treatment of beats.
Solution:
Consider two simple harmonic progressive waves traveling simultaneously in the same direction and in the same medium. Let
(i) A be the amplitude of each wave.
(ii) There is no initial phase difference between them.
(iii) Let v₁ and v₂ be their frequencies.
If y₁ and y₂ be displacements of the two waves, then
y₁ =Asin2πv₁t
and Y₁ =Asin2πv₂t
If y be the result and displacement at any instant, then
y = y₁ + y₂
= A (sin2πv₂t) + Asin (2πv₂t)

where R = 2Acos π (v₁ – v₂)t ……………………………… (ii)
is the amplitude of the resultant displacement and depends upon t. The following cases arise
(a) If R is maximum, then
cos π (v₁ — v₂ )t = max. = ± 1 = cos nπ
∴ π (v₁ — v₂ )t = n π
or t= \(\frac{n}{v_{1}-v_{2}}\) …………………………. (iii)

where, n =0,1,2, …
∴ Amplitude becomes maximum at times given by
t=0, \(\frac{1}{v_{1}-v_{2}}, \frac{2}{v_{1}-v_{2}}, \frac{3}{v_{1}-v_{2}}, \ldots \)
∴ Time interval between two consecutive maxima is
= \(\frac{1}{v_{1}-v_{2}} \)
∴ Beat period = \(\frac{1}{v_{1}-v_{2}}\)
∴ Beat frequency = v₁ — v₂
∴ no. of beasts formed per sec = v₁ — v₂

(b) If R is minimum, then
cosπ (v₁ – v₂)t = min. = O = cos (2n +1) \(\frac{\pi}{2}\)

where, n 0,1, 2, …
∴ Amplitude becomes minimum at times given by
t = \(\frac{1}{2\left(v_{1}-v_{2}\right)}, \frac{3}{2\left(v_{1}-v_{2}\right)}, \frac{5}{2\left(v_{1}-v_{2}\right)}, \ldots \)

∴ Time interval between two consecutive minima is = \(\frac{1}{v_{1}-v_{2}}\)
∴ Beatperiod = \(\frac{1}{v_{1}-v_{2}}\)
∴ Beat frequency = v₁ – v₂
∴ No. of beats formed per sec = v₁ – v₂
Hence the number of beats formed per second is equal to the difference between the frequencies of two-component waves.

Punjab State Board PSEB 11th Class Physics Important Questions Chapter 9 Mechanical Properties of Solids Important Questions and Answers.

PSEB 11th Class Physics Important Questions Chapter 9 Mechanical Properties of Solids

Very Short Answer Type Questions

Question 1.
Two identical solid balls, one of ivory and the other of wet clay, are dropped from the same height on the floor. Which will rise to a greater height after striking the floor and why?
Answer:
The ball of ivory will rise to a greater height because ivory is more elastic than wet-clay.

Question 2.
Is it possible to double the length of a metallic wire by applying a force over it?
Answer:
No, it is not possible because, within elastic limit, strain is only order of 10^-3, wires actually break much before it is stretched to double the length.

Question 3.
Is stress a vector quantity? (NCERT Exemplar)
Stress = \(\frac{\text { Magnitude of internal reaction force }}{\text { Area of cross – section }}\)
Therefore, stress is a scalar quantity, not a vector quantity.

Question 4.
What does the slope of stress versus strain graph indicate?
Answer:
The slope of stress (on y-axis) and strain (on x-axis) gives modulus of elasticity.
The slope of stress (on x-axis) and strain (on y-axis) gives the reciprocal of modulus of elasticity.

Question 5.
Stress and pressure are both forces per unit area. Then in what respect does stress differ from pressure?
Answer:
Pressure is an external force per unit area, while stress is the internal restoring force which comes into play in a deformed body acting transversely per unit area of a body.

Question 6.
What is the Young’s modulus for a perfect rigid body?
Solution:
Young’s modulus (Y) = \(\frac{F}{A} \times \frac{l}{\Delta l}\)
For a perfectly rigid body, change in length Δl = 0
∴ Y = \(\frac{F}{A} \times \frac{l}{0}\) = ∞
Therefore, Young’s modulus for a perfectly rigid body is ∞.

Question 7.
What is Bulk modulus for a perfectly rigid body?
Solution:
Bulk modulus (B) = \(\frac{p}{\Delta V / V}=\frac{p V}{\Delta V}\)
For perfectly rigid body, change in volume ΔV = 0
∴ B = \(\frac{p V}{0}\) = ∞
Therefore, Bulk modulus for a perfectly rigid body is ∞.

Short Answer Type Questions

Question 1.
Explain why steel is more elastic than rubber?
Solution:
Consider two pieces of wires, one of steel and the other of rubber. Suppose both are of equal length (L) and of equal area of cross-section (a). Let each be stretched by equal forces, each being equal to F. We find that the change in length of the rubber wire (l_r) is more than that of the steel (l_s)i.e.,l_r>l_s.
If Y_s and Y_r are the Young’s moduli of steel and rubber respectively, then from the definition of Young’s modulus,

i. e,, the Young’s modulus of steel is more than that of rubber. Hence steel is more elastic than rubber.
Or
Any material which offers more opposition to the deforming force to change its configuration is more elastic.

Question 2.
Elasticity is said to be internal property of matter. Explain.
Answer:
When a deforming force acts on a body, the atoms of the substance get displaced from their original positions. Due to this, the configuration of the body (substance) changes. The moment, the deforming force is removed, the atoms return to their original positions and hence, the substance or body regains its original configuration. That is why, elasticity is said to be internal property of matter.

Question 3.
A wire elongates by l mm when a load W is hanged from it. If the wire goes over a pulley and two weights W each are hung at the two ends, then what will be the elongation of the wire in mm?
Solution:
According to Hooke’s law,
Modulus of elasticity, E = \(\frac{W}{A} \times \frac{L}{l}\)
where, L = original length of the wire
A- cross-sectional area of the wire
Elongation, l = \(\frac{W L}{A E}\) ………………………… (i)
On either side of the wire, tension is W and length is L/2.
Δl = \(\frac{W L / 2}{A E}=\frac{W L}{2 A E}=\frac{l}{2}\) [from eq.(i)]
Total elongation in the wire = \(\frac{l}{2}+\frac{l}{2}\) = l

Question 4.
A bar of cross-section A is subjected to equal and opposite tensile forces at its, ends. Consider a plane section of the bar whose normal makes an angle θ with the axis of the bar.
(i) What is the tensile stress on this plane?
(ii) What is the shearing stress on this plane?
(iii) For what value of θ is the tensile stress maximum?
(iv) For what value of θ is the shearing stress maximum?

Solution:
(i) The resolved part of F along the normal is the tensile force on this plane and the resolved part parallel to the plane is the shearing force on the plane.
∵ Area of MO plane section = A sec θ
Tensile stress = \(\frac{\text { Force }}{\text { Area }}=\frac{F \cos \theta}{A \sec \theta}=\frac{F}{A} \cos ^{2} \theta\)
= [ ∵ sec θ = \(\frac{1}{\cos \theta}\)]

(ii) Shearing stress applied on the top face
So, F = F sinθ
Shearing stress = \(\frac{\text { Force }}{\text { Area }}=\frac{F \sin \theta}{A \sec \theta}\)
= \(\frac{F}{A}\) sinθcosθ
= \(\frac{F}{2 A} \sin 2 \theta\) [∵ sin 2θ = 2sinθcosθ]

(iii) Tensile stress will be maximum when cos²θ is maximum i.e., cosθ = 1 or θ=0°.

(iv) Shearing stress will be maximum when sin20 is maximum i.e., sin2θ = 1 or 2θ = 90° or θ = 45°.

Question 5.
What is an elastomer? What are their special features?
Answer:
Elastomers are those substances which can be stretched to cause large strains.Substances like tissue of aorta, rubber etc., are elastomers.

The stress-strain curve for an elastomer is shown in figure. Although elastic region is very large but the materials does not obey Hooke’s law over most of the region. Moreover, there is no well-defined plastic region.

Question 6.
The Young’s modulus for steel is much more than that for rubber. For the same longitudinal strain, which one will have greater tensile stress? (NCERT Exemplar)
Solution:
Young’s modulus (Y) = \( \frac{\text { Stress }}{\text { Longitudinal strain }}\)
For same longitudinal strain, Y ∝ stress

Question 7.
Why are the springs made of steel and not of copper?
Answer:
A spring will be better one if a large restoring force is set up in it on being deformed, which in turn depends upon the elasticity of the material of the spring. Since the Young’s modulus of elasticity of steel is more than that of copper, hence, steel is preferred in making the springs.

Question 8.
Identical springs of steel and copper are equally stretched. On which, more work will have to be done? (NCERT Exemplar)
Solution:
Work done in stretching a wire is given by
W =- \(\frac{1}{2}\) F x Δl
As springs of steel and copper are equally stretched.
Therefore, for same force (F).
W ∝ Δl …………………………………… (i)

Young’s modulus (Y) = \(\frac{F}{A} \times \frac{l}{\Delta l}\)
or Δl = \(\frac{F}{A} \times \frac{l}{Y}\)
As both spring are identical,
∴ Δl ∝ \(\frac{1}{Y}\) …………………………………. (ii)
From eqs. (i) and (ii), we get W ∝ \(\frac{1}{Y}\) .
∴ \(\frac{W_{\text {steel }}}{W_{\text {copper }}}=\frac{Y_{\text {copper }}}{Y_{\text {steel }}}<1\)
[as Y_steel > Y_copper]
or W_steel < W_Copper
Therefore, more work will be done for stretching copper spring.

Long Answer Type Questions

Question 1.
A steel wire of length 21 and cross-sectional area A is stretched within elastic limit as shown in figure. Calculate the strain and stress in the wire.

Solution:
Total length L =21. Increase in length of the wire, when it is stretched from its mid-point.

From Pythagoras theorem, BC² =l² + x²
BC= \(\sqrt{l^{2}+x^{2}}\)
Similarly, AC = \(\sqrt{l^{2}+x^{2}}\)

Since x<< l, so using Binomial expansion, we have
\(\left(1+\frac{x^{2}}{l^{2}}\right)^{1 / 2}=\left(1+\frac{x^{2}}{2 l^{2}}\right)\)
[Neglecting terms containing higher powers of x]
∴ ΔL = 2l\(\left(1+\frac{x^{2}}{2 l^{2}}\right)-2 l=\frac{x^{2}}{l}\)
Hence Strain = \(\frac{\Delta L}{L}=\frac{x^{2}}{l \times 2 l}=\frac{x^{2}}{2 l^{2}}\)

Stress = \(\frac{F}{A}=\frac{\text { Tension }}{\text { Area }} \)
So, area of cross section of wire having radius r is πr²
Stress = \(\frac{T}{\pi r^{2}}\)

Question 2.
Consider a long steel bar unde a tensile stress due to forces F acting at the edges along the length of the bar (figure). Consider a plane making an angle θ with the length. What are the tensile and shearing stresses on this plane?

(a) For what angle is the tensile stress a maximum?
(b) For what angle is the shearing stress a maximum? (NCERT Exemplar)
Solution:
Consider the adjacent diagram.
Let the cross-sectional area of the bar be A. Consider the equilibrium of the plane aa’.
A force F must be acting on this plane making an angle \(\frac{\pi}{2}\) – θ with the normal ON. Resolving F into components, along the plane (FP) and normal to the plane.

F_P = F cosθ
F_N = Fsinθ
Let the area of the face aa’ be A’, then
\(\frac{A}{A^{\prime}}\) = sinθ’
∴ A’= \(\frac{A}{\sin \theta}\)

(a) For tensile stress to be maximum, sin²θ =1
⇒ sinθ = 1
⇒ θ = \(\frac{\pi}{2}\)
(b) For shearing stress to be maximum,
sin 2θ = 1
⇒ 2θ = \(\frac{\pi}{2}\)
⇒ θ = \(\frac{\pi}{4}\)

Punjab State Board PSEB 11th Class Physics Important Questions Chapter 7 System of Particles and Rotational Motion Important Questions and Answers.

PSEB 11th Class Physics Important Questions Chapter 7 System of Particles and Rotational Motion

very short answer type questions

Question 1.
(n – 1) equal point masses each of mass m are placed at the vertices of a regular n-polygon. The vacant vertex has a position vector \(\vec{a}\) with respect to the centre of the polygon. Find the position vector of centre of mass. (NCERT Exemplar)
Solution
Suppose, \(\vec{b}\) be the position vector of centre of mass of regular n-polygon. As (n – 1) equal point masses each of mass m are placed at (n – 1) vertices of regular polygon, therefore
\(\frac{(n-1) m b+m a}{(n-1+1) m}\) = 0
⇒ (n – 1)mb + ma = 0
⇒ b = \(\frac{-a}{(n-1)}\)

Question 2.
If net torque on a rigid body is zero, does it linear momentum necessary remain conserved?
Answer:
The linear momentum remain conserved if the net force on the system is zero.

Question 3.
When is a body lying in a gravitation field in stable equilibrium?
Answer:
A body in a gravitation field will be in stable equilibrium, if the vertical line through its centre of gravity passes through the base of the body.

Question 4.
Is centre of mass and centre of gravity body always coincide?
Ans.
No, if the body is large such that g varies from one point to another, then centre of gravity is offset from centre of mass.
But for small bodies, centre of mass and centre of gravity lies at their geometrical centres.

Question 5.
Why is moment of inertia also called rotational inertia?
Answer:
The moment of inertia gives a measure of inertia in rotational motion. So, it is also called rotational inertia.

Question 6.
In a flywheel, most of the mass is concentrated at the rim. Explain why?
Answer:
Concentration of mass at the rim increases the moment of inertia and thereby brings uniform motion.

Question 7.
Does the radius of gyration depend upon the speed of rotation of the body?
Answer:
No, it depends only on the distribution of mass of the body.

Question 8.
Can the mass of body be taken to be concentrated at its centre of mass for the purpose of calculating its rotational inertia?
Answer:
No, the moment of inertia greatly depends on the distribution of mass about the axis of rotation.

Short answer type questions

Question 1.
Does angular momentum of a body in translatory motion is zero?
Solution:
Angular momentum of a body is measured with respect to certain origin.

So, a body in translatory motion can have angular momentum.
It will be zero, if origin lies on the line of motion of particle.

Question 2.
Figure shows momentum versus time graph for a particle moving along x – axis. In which region, force on the particle is large. Why?

Solution:
Net force is given by F = \(\frac{d p}{d t}\)
Also, rate of change of momentum = slope of graph.
As from graph, slope AB = slope CD
And slope (BC) = slope (DE) = 0
So, force acting on the particle is equal in regions AB and CD and in regions BC and DE (which is zero).

Question 3.
Two cylindrical hollow drums of radii R and 2J2, and of a common height h, are rotating with angular velocities ω (anti-clockwise) and ω (clockwise), respectively.
Their axes, fixed are parallel and in a horizontal plane separated by (3R + δ). They are now brought in contact (δ → 0).
(i) Show the frictional forces just after contact.
(ii) Identify forces and torques external to the system just after contact.
(iii) What would be the ratio of final angular velocities when friction ceases? (NCERT Exemplar)
Solution:

(ii) F’ = F = F” where F and F” are external forces through support.
F_net = 0
External torque = F x 3 R, anti-clockwise.

(iii) Let ω₁ and ω₂ be final angular velocities (anti-clockwise and clockwise respectively).
Finally, there will be no friction.
Hence, Rω₁ = 2Rω₂ ⇒ \(\frac{\omega_{1}}{\omega_{2}}\) = 2

Question 4.
Angular momentum of a system is conserved if its M.I. is changed. Is its rotational K. E. also conserved?
Solution:
Kinetic energy of rotation = \(\frac{1}{2}\)Iω² = \(\frac{1}{2}\) (Iω)ω = \(\frac{1}{2}\)Lω

L = Iω is constant, if moment of inertia (I) of the system changes. It means as I changes, then ω also changes.
Hence K.E. of rotation also changes with the change in I. In other words, rotational K.E. is not conserved.

Question 5.
How much fraction of the kinetic energy of rolling is purely
(i) translational, (ii) rotational.
Solution:

Question 6.
Listening to the discussion on causes of pollution and due to which temperature on earth is rising, increase in temperature leads to melting of polar ice, Meenu realised that if each one of us contributed to create pollution free environment, then even small efforts can lead to big results. So, she decided to lead the step and instead of going to school by her car, she joined school bus and also asked her father to go to office using car pool.
(i) What do you think is mainly responsible for global warming?
(ii) If the ice on polar caps of the earth melts due to pollution, how will it affect the duration of the day?
Explain.
(iii) What values does Meenu show?
Answer:
(i) Pollution created by the people of world is the main cause of global warming.
(ii) Earth rotates about its polar axis. When ice of polar caps of earth melts, mass concentrated near the axis of rotation spreads out, therefore moment of inertia, I increases.
As no external torque acts,
∴ L = I = Iω = (\(\frac{2 \pi}{T}\)) = Constant
With increase of I, T will increase i.e., length of day will also increase,
(iii) Meenu is considerate towards environment and her thought of leading the steps to reduce pollution is commendable.

Question 7.
Explain how a cat is able to land on its feet after a fall taking the advantage of principle of conservation of angular momentum?
Answer:
When a cat falls to ground from a height, it stretches its body alongwith the tail so that its moment of inertia becomes high. Since, la is to remain constant, the value of angular speed a decreases and therefore the cat is able to’ land on the ground gently.

Question 8.
A uniform disc of radius R is resting on a table on its rim. The coefficient of friction between disc and table is μ (figure). Now, the disc is pulled with a force \(\overrightarrow{\boldsymbol{F}}\) as shown in the figure. What is the maximum value of \(\overrightarrow{\boldsymbol{F}}\) for which the disc rolls without slipping? (NCERT Exemplar)

Solution:
Let the acceleration of the centre of mass of disc be a, then
Ma = F – f
The angular acceleration of the disc is a = a/R (if there is no sliding).
Then, (\(\frac{1}{2}\)MR²)α = Rf
⇒ Ma = 2f
Thus, f =F/3. Since, there is no sliding.
⇒ f ≤ μ mg ⇒ F ≤ 3μ Mg

Question 9.
Two equal and opposite forces act on a rigid body. Under what condition will the body (i) rotate (ii) not rotate?
Answer:
(i) Two equal and opposite forces acting on a rigid body such that their lines of action do not coincide, constitute a couple. This couple produces the turning effect on the body. Hence, the rigid body will rotate.

(ii) If two equal and opposite forces act in such a way that their lines of action coincide, then these forces cancel out the effect of each other. Hence, the body will not rotate.

Long answer type questions

Question 1.
Find position of centre of mass of a semicircular disc of radius r. (NCERT Exemplar)
Solution:
As semicircular disc is symmetrical about its one of diameter, we take axes as shown. So, now we only have to calculate Y_CM (As X_CM is zero by symmetry and choice of origin).

Now, for a small element OAB, as element is small and it can be treated as a triangle so,
Area of sector OAB = \(\frac{1}{2}\) x r x rdθ
Height of triangle = r
Base of triangle = AB = rdθ
So, its mass dm = \(\frac{1}{2}\)r² dθ.ρ [∵ ρ = \(\frac{\text { mass }}{\text { area }}\)]
As centre of mass of a triangle is at a distance of \(\frac{2}{3}\) from its vertex (at centroid, intersection of medians). So, y = \(\frac{2}{3}\)rsinθ (location of CM of small sector AOB).


So, CM of disc is at a distance of \(\frac{4 r}{3 \pi}\)from its centre on its axis of symmetry.

Question 2.
Obtain an expression for linear acceleration of a cylinder rolling down an inclined plane and hence find the condition for the cylinder to roll down the inclined plane without slipping.
Solution:
When a cylinder rolls down on an inclind plane, then forces involved are (i) Weight mg (ii) Normal reaction N (iii) Friction f
From free body diagam,

From free body diagram,
N – mg cos θ = 0
or N = mg cosθ
Also, if a = acceleration of centre of mass down the plane, then
F_net = ma = mgsin θ – f …………… (i)
As friction produces torque necessary for rotation,
τ = Iα = f R

Punjab State Board PSEB 11th Class Physics Important Questions Chapter 8 Gravitation Important Questions and Answers.

PSEB 11th Class Physics Important Questions Chapter 8 Gravitation

Very Short Answer Type Questions

Question 1.
By which law is the Kepler’s law of areas identical?
Answer:
The law of conservation of angular momentum.

Question 2.
Draw areal velocity versus time graph for mars. (NCERT Exemplar)
Answer:
Areal velocity of planet revolving around the Sun is constant with time (Kepler’s second law).

Question 3.
At what factor between the two particles gravitational force does not depend?
Answer:
Gravitational force does not depend upon the medium between the two particles.

Question 4.
Two particles of masses m₁ and m₂ attract each other gravitationally and are set in motion under the influence of the gravitational force? Will the centre of mass move?
Answer:
Since the gravitational force is an internal force, therefore the centre of mass would not move.

Question 5.
Work done in moving a particle round a closed path under the action of gravitation force is zero. Why?
Answer:
Gravitational force is a conservative force which means that work done by it, is independent of path followed.

Question 6.
What would happen if the force of gravity were to disappear suddenly?
Answer:
The universe would collapse. We would be thrown away because of the centrifugal force. Eating, drinking and in fact all activities would become impossible.

Question 7.
Why a body weighs more at poles and less at equator?
Answer:
The value of g is more at poles than at the equator. Therefore, a body weighs more at poles than at equator.

Question 8.
Give a method for the determination of the mass of the moon.
Solution:
Soli By making use of the relation, gm = \(\frac{G M_{m}}{R_{m}^{2}} \)

Short Answer Type Questions

Question 1.
A planet moving along an elliptical orbit is closest to the Sim at a distance r₁ and farthest away at a distance of r₂.
If v₁ and v₂ are the linear velocities at these points respectively, then find the ratio \(\frac{v_{1}}{v_{2}}\).
Solution:
From the law of conservation of angular momentum
mr₁v₁ = mr₂v₂
⇒ r₁v₁ = r₂v₂ or
\(\frac{v_{1}}{v_{2}}=\frac{r_{2}}{r_{1}}\)

Question 2.
A mass M is broken into two parts, m and (M – m). How is m related to M so that the gravitational force between two parts is maximum?
Solution:
Let =m,m₂ =M – m
F = G\(\frac{m(M-m)}{r^{2}}=\frac{G}{r^{2}}\left(M m-m^{2}\right)\)
Differentiating w.r:t. m, \(\frac{d F}{d m}=\frac{G}{r^{2}}(M-2 m)\)
For F to be maximum, \(\frac{d F}{d m}\) = 0

m₁ = m₂ = M/2

Question 3.
Two stationary particles of masses M₁ and M₂ are a distance d apart. A third particle lying on the line joining the particles, experiences no resultant gravitational force. What is the distance of this particle from M₁?
Solution:
The force on m towards Mi is F =G \(\frac{M_{1} m}{r^{2}}\)
The force on m towards Mi is F = G \(\frac{M_{2} m}{(d-r)^{2}} \)

Equating two forces, we have

So, distance of an particle from m is . r = d
r = d \(\left(\frac{\sqrt{M_{1}}}{\sqrt{M_{1}}+\sqrt{M_{2}}}\right)\).

Question 4.
Aspherical planet has mass M_p and clinometer D_p. A particle of mass m falling freely near the surface of this planet will experience an acceleration due to gravity, equal to whom?
Solution:
Force is given by
F = \(-\frac{G M m}{R^{2}}=\frac{G M_{p} m}{\left(D_{P} / 2\right)^{2}}=\frac{4 G M_{P} m}{D_{P}^{2}}\)
\(\frac{F}{m}=\frac{4 G M_{P}}{D_{P}^{2}}\)

Question 5.
What is the gravitational potential energy of a body at height h from the Earth surface?
Solution:
Gravitational potential energy, i. e.,
U_h = \(-\frac{G M m}{R+h}=-\frac{g R^{2} m}{R+h}\)
[where g = \(\frac{G M}{R^{2}}\) ]
= – \(\frac{g R^{2} m}{R\left(1+\frac{h}{R}\right)}=-\frac{m g R}{1+\frac{h}{R}}\)
.
Question 6.
An artificial satellite is moving in a circular orbit around the Earth with a speed equal to half the magnitude of escape velocity from Earth.
Determine
(i) the height of satellite above Earth’s surface.
(ii) if the satellite is suddenly stopped, find the speed with
which the satellite will hit the Earth’s surface after falling down.
Solution:
Escape velocity = \(\sqrt{2 g R}\), where g is acceleration due to gravity on surface of Earth and R the radius of Earth.
Orbital velocity = \(\frac{1}{2} v_{e}=\frac{1}{2} \sqrt{2 g R}=\sqrt{\frac{g R}{2}} \) …………………. (i)

(i) If h is the height of satellite above Earth

h=R
(ii) If the satellite is stopped in orbit, the kinetic energy is zero and its
potential energy is – \(\frac{G M m}{2 R}\)
Total energy =-\(\frac{G M m}{2 R}\)

Let v be its velocity when it reaches the Earth.
Hence the kinetic energy = \(\frac{1}{2} m v^{2}\)
Potential energy = – \(\frac{G M m}{2 R}\)

Question 7.
Why do different planets have different escape velocities?
Solution:
Escape velocity, v = \(\sqrt{2 g R}=\sqrt{\frac{2 G M}{R}}\)
Thus escape velocity of a planet depends upon (i) its mass (M) and
(ii) its size (R).
As different planets have different masses and sizes, so they have different escape velocities.

Question 8.
Under what circumstances would your weight become zero?
Answer:
The weight will become zero under the following circumstances
(i) during free fall
(ii) at the centre of the Earth
(iii) in an artificial satellite
(iv) at a point where gravitational pull of Earth is equal to the gravitational pull of the Moon.

Long Answer Type Questions

Question 1.
A mass m is placed at P, a distance h along the normal through the centre O of a thin circular ring of mass M and radius r. If the mass is removed further away such that OP becomes 2h, by what factor the force of gravitation will decrease, if h = r? (NCERT Exemplar)

Solution:
Consider a small element of the ring of mass dM, gravitational force between dM and m, distance x apart in figure i.e.,
dF = \(\frac{G(d m) m}{x^{2}}\)

dF can be resolved into two rectangular components.
(i) dF cos θ along PO and
(ii) dF sinθ perpendicular to PO (given figure)
The total force (F) between the ring and mass (m) can be obtained by integrating the effects of all the elements forming the ring, whereas all the components perpendicular to PO cancel out i.e., ∫dFsinθ=O, the component along PO add together to give F i.e.,

Question 2.
A satellite is to be placed in equatorial geostationary orbit around the Earth for communication.
(i) Calculate height of such a satellite.
(ii) Find out the minimum number of satellites that are needed to cover entire Earth so that at least one of satellite is visible from any point on the equator.
[M = 6 x 10 ²⁴ kg, R = 6400 km, T = 24 h, G = 6.67 x 10^-11SI (NCERT Exemplar)
Solution:
(i) As, according co Kepler’s third law, we get
T² = \(\frac{4 \pi^{2} r^{3}}{G M}\)
⇒ r = \( \left(\frac{G M T^{2}}{4 \pi^{2}}\right)^{1 / 3}\)

As we known =R +h
h=r-R
h=4.23 x 10⁷ m – 6.4 x 10⁶ m
h = 3.59 x 10⁷ m

(ii) In ΔOES,cos θ = \(\frac{O A}{O S}=\frac{R}{R+h}\)
= \(\frac{1}{\left(1+\frac{h}{R}\right)}\)
= \(\frac{1}{(1+5.609)}\)
=0.1513
(as,\(\frac{h}{R}=\frac{3.59 \times 10^{7} \mathrm{~m}}{6.4 \times 10^{6} \mathrm{~m}}\) = 5.609)
where, θ ≈ 81° or 2θ = 162°
Number of satellites required to cover entire the Earth.
= \(\frac{360^{\circ}}{162^{\circ}}=2.2\) ≈ 3.

Punjab State Board PSEB 11th Class Biology Important Questions Chapter 1 The Living World Important Questions and Answers.

PSEB 11th Class Biology Important Questions Chapter 1 The Living World

Very short answer type questions

Question 1.
Define living things.
Answer:
The organisms exhibiting growth, development, metabolism, response to stimuli, reproduction and other characteristics such as movement, etc., are called living things.

Question 2.
In which organisms reproduction is synonymous with growth?
Answer:
In unicellular organisms like Amoeba, bacteria and unicellular algae, reproduction is synonymous with growth, i. e., increase in number of cells.

Question 3.
Amoeba multiplies by mitotic cell division. Is this phenomenon growth or reproduction? Explain. [NCERT Exemplar]
Answer:
The phenomenon is reproduction in which unicellular organisms like Amoeba, cell division is a means of multiplication, while in multicellular organisms, it is a means of growth.

Question 4.
Can we relate metabolism with growth of the body?
Answer:
Metabolism occurs due to two phenomena, i.e., anabolism and catabolism. While growth of living things occur when quantity of anabolic reactions exceeds quantity of catabolic reactions.

Question 5.
Linnaeus is considered as father of taxonomy. Name two other botanists known for their contribution to the field of taxonomy. [NCERT Exemplar]
Answer:
John Ray and Bentham and Hooker.

Question 6.
What does ICZN stand for? [NCERT Exemplar]
Answer:
ICZN: International Code of Zoological Nomenclature

Question 7.
How is diversity in living world related to taxonomy?
Answer:
The spectrum of diversity in the living world can be known only through the study of taxonomy.

Question 8.
Which is the largest botanical garden in the world? Name a few well known botanical gardens in India. [NCERT Exemplar]
Answer:
Largest botanical garden in the world is Royal Botanical Garden, Kew
(London). Some well known botanical gardens in India are as follows:

• National Botanical Garden, Lucknow
• Lloyed Botanical Garden, Darjeeling
• Indian Botanical Garden Sibpur, Kolkata

Question 9.
The concept of new systematics was developed by which scientist?
Answer:
Julian Huxley (1940)

Question 10.
How correlated characters help in defining genus?
Answer:
Correlated characters are those common features, which are used in delimitation of a taxon above the rank of species.

Short answer type questions

Question 1.
What do you know about herbarium?
Answer:
Herbarium is a store house of collected plant specimens that are dried, pressed and preserved on sheets. Further, these sheets are arranged according to k universally accepted system of classification. These specimens, along with their descriptions on herbarium sheets, become a store house or repository for future use. The herbarium sheets also carry a label providing information about date and place of collection, English, local and botanical names, family, collector’s name, etc. Herbaria also serve as quick referral systems in taxonomical studies.

Question 2.
How is botanical garden useful for scientists?
Answer:
In a botanical garden various plant species are reared. Special artificial climate is created for a plant’s specific needs. The purpose of botanical garden is to maintain a rich flora of diverse species. Since, they are live specimens so they help scientists in studying physiology and anatomy over a long duration. Imagine if Mendel were given a botanical garden full of variety of species. He could have done experiment on so many plants and may have come with more insights.

Question 3.
Write a short note on museum.
Answer:
Museums are those places which have collections of preserved animals and plants for taxonomic studies. The organisms are exhibited in the following manners:

• The plant and animal specimens are kept in chemical solutions and are preserved for longer duration.
• Plant and animal specimens may also be preserved as dry specimens.
• Insects are preserved in insect boxes; the collected insects are dried and pinned in these boxes.
• Larger animals like birds and mammals are usually preserved as stuffed specimens.
• Skeletons of animals are also collected in the museums.

Question 4.
How is a zoological park helpful to scientists?
Answer:
It is difficult and dangerous to study ferocious animals in their natural habitats. Further, it is cruel to study them in captivity. So zoological park is a better option. Scientists can study different behavioural patterns, like feeding habits, mating rituals. This can help in a better understanding about them.

Long answer type questions

Question 1.
A student of taxonomy was puzzled when told by his professor to look for a key to identify a plant. He went to his friend to clarify what key the professor was referring to? What would the friend explain to him? [NCERT Exemplar]
Answer:
The key for identification of plants is a taxonomic key. It is a important taxonomic aid. Key can be defined as a set of alternate characters arranged in such a manner that by selection and elimination one can quickly find out the name of an organism. Depending upon the category, a key may be class key, order key, family key, genus key and species key.

Taxonomic keys can be of following two types:
(i) Indented or Yolked key
(ii) Bracketed key
Indented key, provides a sequence of two or more alternate characters from which selection and elimination are carried out. In bracketed key, the alternate characters are given numbers in brackets. For example, take four genera of family – Ranunculaceae to explain this,
(i) Ranunculus: Leaves alternate or radical, flowers not subtended by involucre, carpels ovuled, fruit achenes.
(ii) Clematis: Leaves opposite, compound petals absent, sepals 4, carpels uniovulated and fruit achenes.
(iii) Nigella: Flowers regular, carpels united at base, many ovulated, fruit follicles.
(iv) Anemone: Leaves alternate or radical, flowers subtended by involucre, carpels 1-ovulated, fruit achenes.

Question 2.
Some of the properties of tissues are not the properties of constituents of its cells. Give three examples to support the statement. [NCERT Exemplar]
Answer:
A living thing has multiple level of organisation. Each level of organisaton i has its own properties, which are not found in its constituents.
Examples of three tissues supporting the statements are
(i) Cardiac muscle tissue: It is a contractile tissue present only in heart. Cell junctions fuse the plasma membrane of cardiac muscle cells and make them stick together. When one cell receives a signal to contract, its neighbours also starts to contract. It means a single cell cannot contract, while there are some fusion points, which allow the cells to contract as a unit.

(ii) Blood: It is a fluid connective tissue. The individual components of blood, i.e., RBCs, WBCs and platelets have different properties but as a unit they make the blood, a tissue serving many functions.

(iii) Bone: It is a hard connective tissue that forms the framework of the body. The individual cells inside the bone do not have this property.

Punjab State Board PSEB 11th Class Physics Important Questions Chapter 11 Thermal Properties of Matter Important Questions and Answers.

PSEB 11th Class Physics Important Questions Chapter 11 Thermal Properties of Matter

Very Short Answer Type Questions

Question 1.
Is it correct to call heat as the energy in transit?
Answer:
Yes, it is perfect correct to call heat as the energy in transit because it is continuously flowing on account of temperature differences between bodies or parts of a system.

Question 2.
Why should a thermometer bulb have a small heat capacity?
Answer:
The thermometer bulb having small heat capacity will absorb less heat from the body whose temperature is to be measured. Hence, the temperature of that body will practically remain unchanged.

Question 3.
Why is a gap left between the ends of two railway lines in a railway track?
Answer:
It is done to accommodate the linear expansion of railway line during summer. If the gap is not left in summer, the lines will bend causing a threat of derailment.

Question 4.
Why water is used as an coolant in the radiator of cars?
Answer:
Because specific heat of water is very high due to this it absorbs a large amount of heat. This helps in maintaining the temperature of the engine low.

Question 5.
Black body radiation is white. Comment.
Answer:
The statement is true. A black body absorbs radiations of all wavelengths. When heated to a suitable temperature, it emits radiations of all wavelengths. Hence, a black body radiation is white.

Question 6.
White clothes are more comfortable in summer while colourful clothes are more comfortable in winter. Why?
Answer:
White clothes absorb very little heat radiation and hence they are comfortable in summer. Coloured clothes absorb almost whole of the incident radiation and keep the body warm in winter.

Question 7.
Can we boil water inside in the earth satellite?
Answer:
No, the process of transfer of heat by convection is based on the fact that a liquid becomes lighter on becoming hot and rise up. In condition of weightlessness, this is not possible. So, transfer of heat by convection is not possible in the earth satellite.

Question 8.
What is the difference between the specific heat and the molar specific heat?
Answer:
The specific heat is the heat capacity per unit mass whereas the molar specific heat is the heat capacity per mole.

Question 9.
Calorimeters are made of metals not glass. Why?
Answer:
This is because metals are good conductors of heat and have low specific heat capacity.

Question 10.
Calculate the temperature which has numeral value of Celsius and Fahrenheit scale. (NCERT Exemplar)
Answer:
Let Q be the value of temperature having same value an Celsius and Fahrenheit scale.
\(\frac{{ }^{\circ} F-32}{180}=\frac{{ }^{\circ} C}{100}\)
⇒ Let F = C = Q
⇒ \(\frac{Q-32}{180}=\frac{Q}{100}\) = Q= 40°C or -40°F

Short Answer Type Questions

Question 1.
In what ways are the gas thermometers superior to mercury thermometers?
Answer:
A gas thermometer is more superior to a mercury thermometer, as its working is independent of the nature of gas (working substance) used. As the variation of pressure (or volume) with temperature is uniform, the range, in which temperature can be measured with a gas thermometer is quite large. Further, a gas thermometer is more sensitive than mercury thermometer.

Question 2.
The difference between length of a certain brass rod and that of a steel rod is claimed to be constant at all temperatures. Is this possible?
Solution:
Yes, it is possible to describe the difference of length to remain constant. So, the change in length of each rod must be equal at all temperature. Let α_b and α_s be the length of the brass and the steel rod and a band as be the coefficients of linear expansion of the two metals. Let there is change in temperature be ΔT.
Then, α_bL_bΔT = α_sL_sΔT
or α_bL_b=α_sL_s => L_b/L_s=α_s/α_b
Hence, the lengths of the rods must be in the inverse ratio of the coefficient of linear expansion of their materials.

Question 3.
Two identical rectangular strips-one of copper and the other of steel are riveted to form a bimetallic strip. What will happen on heating?
Solution:
The coefficient of linear expansion of copper is more than steel. On heating, the expansion in copper strip is more than the steel strip. The bimetallic strip will bend with steel strip on inner (concave) side.

Question 4.
What kind of thermal conductivity and specific heat requirements would you specify for cooking utensils?
Solution:
A cooking utensil should have (i) high conductivity, so that it can conduct heat through itself and transfer it to the contents quickly, (ii) low specific heat, so that it immediately attains the temperature of the source.

Question 5.
Woollen clothes are warm in winter. Why?
Solution:
Woollen fibres enclose a large amount of air in them. Both wool and air are bad conductors of heat. The small coefficient of thermal conductivity prevents the loss of heat from our body due to conduction. So, we feel warm in woollen clothes.

Question 6.
Why rooms are provided with the ventilators near the roof?
Solution:
It is done so to remove the harmful impure air and to replace it by the cool fresh air. The air we breathe out is warm and so it is lighter. It rises upwards and can go out through the ventilator provided near the roof. The cold fresh air from outside enters the room through the doors and windows. Thus, the convection current is set up in the air.

Question 7.
Why it is much hotter above a fire than by its side?
Solution:
Heat carried away from a fire sideways mainly by radiation. Above the fire, heat is carried by both radiation and convection of air but convection carries much more heat than radiation. So, it is much hotter above a fire than by its sides.

Question 8.
How does tea in a Thermo flask remain hot for a long time?
Solution:
The air between the two walls of the Thermo flask is evacuated. This prevents heat loss due to conduction and convection. The loss of heat due to radiation is minimised by silvering the inside surface of the double wall. As the loss of heat due to the three prócesses is minimised and the tea remains hot for a long time.

Question 9.
100 g of water is supercooled to -10°C. At this point, due to some disturbance mechanised or otherwise, some of it suddenly freezes to ice. What will be the temperature of the resultant mixture and how much mass would freeze? [S_w = 1 cal/g/°C and L^w_fusion =80 cal/g/°C] (NCERT Exemplar)
Answer:
Gwen, mass of water (m) = 100
Change in temperature, ΔT =0 – (-10) = 10°C
Specific heat of water (S_w) =1 cal/g/°C
Latent heat of fusion of water L^w_fusion = 80 cal/g
Heat required to bring water in supercooling from —10° C to 0°C.
Q = ms_wΔT
=100 x 1 x 10 = 1000cal
Let m gram of ice be melted.
∴ Q = mL
or m= \(\frac{Q}{L}\) = \(\frac{1000}{80}\) =12.5g
As small mass of ice is melted, therefore the temperature of the mixture will remain 0°C.

Long Answer Type Questions

Question 1.
Show that the coefficient of volume expansion for a solid substance is three times its coefficient of linear expansion.
Solution:
Consider a solid in the form of a rectangular parallelopiped of sides a, b and c respectively so that its volume V = abc.
If the solid is heated so that its temperature rises by ΔT, then increase in its sides will be
Δa=a.αΔT, Δb=b.α.ΔT and Δc=c. α . ΔT
or a’ =a+Δa =a(1 +α ΔT)
b’=b+Δb = b(l +α ΔT)
and c’ =c + Δc=c (1 +a.ΔT)
∵ New volume, V’ = V + ΔV = a’ b’ c’ = abc (1+ α . Δ T)³
∴ Increase in volume,
ΔV=V’ -V=[abc(1+α ΔT)³ -abc]
∴ Coefficient of volume expansion,

However, as a has an extremely small value for solids, hence terms containing higher powers of a may be neglected. Therefore, we obtain the relation γ =3 α i. e., coefficient of volume expansion of a solid is three times of its coefficient of linear expansion.

Question 2.
Distinguish between conduction, convection and radiation.
Solution:

Conduction	Convection	Radiation
1. It is the transfer of heat by direct physical contact.	1. It is the transfer of heat by the motion of a fluid.	1. It is the transfer of heat by electromagnetic waves.
2. It is due to temperature differences. Heat flows from high-temperature region to low temperature region.	2. It is due to difference in density. Heat flows from low-density region to high-density region.	2. It occurs from all bodies at temperatures above 0 K.
3. It occurs in solids through molecular collisions, without actual flow of matter.	3. It occurs in fluids by actual flow of matter.	3. It can take place at large distances and does not heat the intervening medium.
4. It is a slow process.	4. It is also a slow process.	4. It propagates at the speed of light.
5. It does not obey the laws of reflection and refraction.	5. It does not obey the laws of reflection and refraction.	5. It obeys the laws of reflection and refraction.