Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 1 Real Numbers Ex 1.1 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 10 Maths Chapter 1 Real Numbers Ex 1.2
Question 1.
Express each number as a product of its prime factors :
(i) 140 (Pb, 2019)
(ii) 156
(iii) 3825
(iv) 5005 (Pb. 2019, Set-1, II, III)
(v) 7429.
Solution:
(i) Prime factorisation of 140 = (2)2 (35) = (2)2 (5) (7)
(ii) Prime factorisation of 156 = (2)2 (39) = (2)2 (3) (13)
(iii) Prime factorisation of 3825 = (3)2 (425)
= (3)2 (5) (85)
= (3)2 (5)2 (17)
(iv) Prime factorisation of 5005
= (5) (1001)
= (5) (7) (143)
= (5) (7) (11) (13)
(v) Prime factorisation of 7429
= (17) (437)
= (17) (19) (23)
![]()
Question 2.
Find the LCM and HCF of the following pairs of integers and verify that LCM × HCF = Product of the two numbers.
(i) 26 and 91 [Pb. 2017 Set-C]
(ii) 510 and 92
(iii) 336 and 54.
Solution:
(i) Given numbers are 26 and 91 Prime factorisation of 26 and 91 are
26 = (2) (13) and
91 = (7) (13)
HCF (26, 91)
Product of least powers of common factors
∴ HCF (26, 91) = 13
and LCM (26, 91) = Product of highest powers of all the factors
= (2) (7) (13) = 182
Verification :
LCM (26, 91) × HCF (26, 91)
= (13) × (182) = (13) × (2) × (91)
= (26) × (91)
= Product of given numbers.
(ii) Given numbers are 510 and 92 Prime factorisation of 510 and 92 are
510 = (2) (255)
= (2) (3) (85)
= (2) (3) (5) (17)
and 92 = (2) (46) = (2)2 (23)
HCF (510, 92) = Product of least powers of common factors = 2
LCM (510, 92) = Product of highest Powers of all the factors
= (2)2 (3) (5) (17) (23) = 23460
Verification:
LCM (510, 92) × HCF (510, 92)
= (2) (23460)
= (2) × (2)2 (3) (5) (17) (23)
= (2) (3) (5) (17) × (2)2 (23)
= 510 × 92 = Product of given numbers.
![]()
(iii) Given numbers are 336 and 54
Prime factorisation of 336 and 54 are
336 = (2) (168)
= (2) (2) (84)
= (2) (2) (2) (42)
= (2) (2) (2) (2) (21)
= (2)4 (3) (7)
and 54 = (2) (27)
= (2) (3) (9)
= (2) (3) (3) (3)
= (2) (3)3
HCF (336, 54) = Product of least powers of common factors = (2) (3) = (6)
LCM (336, 54) = Product of highest powers of all the factors
= (2)4 (3)3 (7) = 3024
Verification :
LCM (336, 54) × H.C.F. (336, 54)
= 6 × 3024
= (2) (3) × (2)4 (3)3 (7)
= (2)4 (3) (7) × (2) (3)3
= 336 × 54
= Product of given numbers.
Question 3.
Find the LCM and HCF of the following integers by applying the prime factorisation method.
(i) 12, 15 and 21 [MQP 2015, Pb. 2015 Set A, Set B, Set C]
(ii) 17, 23 and 29
(iii) 8, 9 and 25
Solution:
(i) Given numbers are 12, 15 and 21
Prime factorisation of 12, 15 and 21 are
12 = (2) (6)
= (2) (2) (3)
= (2)2 (3)
15 = (3) (5)
21 = (3) (7)
HCF (12, 15 and 21) = 3
LCM (12, 15 and 21) = (2)2 (3) (5) (7) = 420
![]()
(ii) Given numbers are 17, 23 and 29
Prime factorisation of 17, 23 and 29 are
17 = (17) (1)
23 = (23) (1)
29 = (29) (1)
HCF (17, 23 and 29) = 1
LCM (17, 23 and 29)
= 17 × 23 × 29 = 11339
(iii) Given numbers are 8, 9 and 25
Prime factorisation of 8, 9 and 25 are
8 = (2) (4)
= (2) (2) (2)
= (2)3 (1)
9 = (3) (3) = (3)2 (1)
25 = (5) (5) = (5)2 (1)
HCF (8, 9 and 25) = 1
LCM (8, 9 and 25) = (2)3 (3)2 (5)2 = 1800
Question 4.
Prove that HCF (306,657) = 9, find LCM (306,657). [Pb. 2016 Set-B, 2017 Set-B]
Solution:
Given numbers are 306 and 657 Prime factorisation of 306 and 657 are
306 = (2) (153)
= (2) (3) (51)
= (2) (3) (3) (17)
= (2) (3)2 (17)
657 = (3) (219)
= (3) (3) (73)
= (3)2 (73)
HCF (306, 657) = (3)2 = 9
∵HCF × LCM = Product of given number
∵9 × LCM (306, 657) = 306 × 657
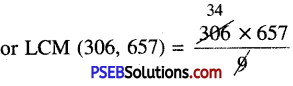
= 34 × 657 = 22338
![]()
Question 5.
Check whether 6n can end with the digit 0 for any natural number n:
Solution:
Let us suppose that 6n ends with the digit 0 for some n ∈ N.
6n is divisible by 5.
But, prime factor of 6 are 2 and 3 Prime factor of (6)n are (2 × 3)n
⇒ It is clear that in prime factorisation of 6n there is no place for 5.
∵ By Fundamental Theorem of Arithmetic, Every composite number can be expressed as a product of primes and this factorisation is unique, apart from the order in which the prime factors occur.
∴ Our supposition is wrong.
Hence, there exists no natural number n for which 6n ends with the digit zero.
Question 6.
Explain why 7 × 11 × 13 + 13 and 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 are composite numbers.
Solution:
Consider, 7 × 11 × 13 + 13 = 13 [7 × 11 + 1]
which is not a prime number because it has a factor 13. So, it is a composite number.
Also, 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5
= 5[7 × 6 × 5 × 4 × 3 × 2 × 1 + 1], which is not a prime number because it has a factor 5. So it is a composite number.
![]()
Question 7.
There is a circular path around a sports field. Sonia takes 18 minutes to drive one round of the field, while Ravi takes 12 minutes for die same. Suppose they both start at the same point and at file same time, and go in the same direction. After how many minutes will they meet again at the starting point?
Solution:
Time taken by Sonia to drive one round of the field =18 minutes
Time taken by Ravi to drive one round of same field = 12 minutes
They meet again at the starting point = LCM (18, 12)
Now, Prime factorisation of 18 and 12 are 18 = (2) (9)
= (2) (3) (3)
= (2) (3)2
12 = (2) (6)
= (2) (2) (3)
= (2)2 (3)
LCM (18, 12) = (2)2 (3)2 = 4 × 9 = 36
Hence, After 36 minutes Sonia and Ravi will meet again at the starting point.
