PSEB 10th Class Maths Solutions Chapter 12 ਚੱਕਰ ਨਾਲ ਸੰਬੰਧਿਤ ਖੇਤਰਫਲ Ex 12.2

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 12 ਚੱਕਰ ਨਾਲ ਸੰਬੰਧਿਤ ਖੇਤਰਫਲ Ex 12.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 12 ਚੱਕਰ ਨਾਲ ਸੰਬੰਧਿਤ ਖੇਤਰਫਲ Exercise 12.2

(ਜਦੋਂ ਤੱਕ ਨਾ ਕਿਹਾ ਜਾਵੇ, π = \(\frac{22}{7}\) ਦਾ ਪ੍ਰਯੋਗ ਕਰੋ ।)

ਪ੍ਰਸ਼ਨ 1.
6 cm ਅਰਧ ਵਿਆਸ ਵਾਲੇ ਇੱਕ ਚੱਕਰ ਦੇ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ, ਜਿਸਦਾ ਕੋਣ 60° ਹੈ ।
ਹੱਲ:
ਚੱਕਰ ਦੇ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 6 cm

ਕੇਂਦਰ ਦਾ ਕੋਣ (θ) = 60°
∴ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ = \(\frac{\pi R^{2} \theta}{360}\)
= \(\frac{22}{7}\) × \(\frac{6×6×60}{360}\) cm²
= \(\frac{132}{7}\) cm²
∴ ਚੱਕਰ ਦੇ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ = 18.86 cm²

ਪ੍ਰਸ਼ਨ 2.
ਇੱਕ ਚੱਕਰ ਦੇ ਚੌਥੇ ਭਾਗ (quadrant) ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ, ਜਿਸਦਾ ਘੇਰਾ 22 cm ਹੈ ।
ਹੱਲ:
ਚੱਕਰ ਦਾ ਘੇਰਾ = 22 cm
2πR = 22
R = \(\frac{22×7}{2×22}\) = \(\frac{7}{2}\) cm
R = \(\frac{7}{2}\)
ਕੇਂਦਰ ਦਾ ਕੋਣ (θ) = 90°
∴ ਚੱਕਰ ਦੇ ਚੌਥੇ ਭਾਗ ਦਾ ਖੇਤਰਫਲ
= \(\frac{\pi R^{2} \theta}{360}\) = \(\frac{\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2} \times 90}{360}\) cm²
= \(\frac{77}{8}\) cm²
= 9.625 cm²

ਪ੍ਰਸ਼ਨ 3.
ਇੱਕ ਘੜੀ ਦੀ ਮਿੰਟਾਂ ਵਾਲੀ ਸੂਈ ਦੀ ਲੰਬਾਈ 14 cm ਹੈ । ਇਸ ਸੂਈ ਦੁਆਰਾ 5 ਮਿੰਟ ਵਿੱਚ ਤੈਅ ਕੀਤੇ ਖੇਤਰ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮਿੰਟਾਂ ਵਾਲੀ ਸੂਈ ਦੀ ਲੰਬਾਈ
= ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 14 cm

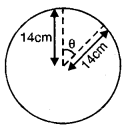
ਸਾਨੂੰ ਪਤਾ ਹੈ
60′ = 360°
1′ = \(\frac{360}{60}\) = 6°
5′ = 6° × 5 = 30°
ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਕੋਣ (θ) = 30°
∴ ਸੂਈ ਦੁਆਰਾ 5 ਮਿੰਟਾਂ ਵਿਚ ਬਣਾਏ ਗਏ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ

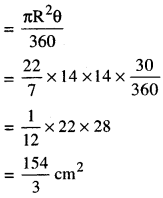
∴ ਸੂਈ ਦੁਆਰਾ 5 ਮਿੰਟਾਂ ਵਿਚ ਤੈਅ ਕੀਤੇ ਖੇਤਰ ਦਾ ਖੇਤਰਫਲ
= 51∙33 cm²

ਪ੍ਰਸ਼ਨ 4.
10 cm ਅਰਧ ਵਿਆਸ ਵਾਲੇ ਇੱਕ ਚੱਕਰ ਦੀ ਕੋਈ ਜੀਵਾ ਕੇਂਦਰ ‘ਤੇ ਇੱਕ ਸਮਕੋਣ ਬਣਾਉਂਦੀ ਹੈ । ਹੇਠਾਂ ਦਿੱਤਿਆਂ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ :
(i) ਸੰਗਤ ਲਘੂ ਚੱਕਰ ਖੰਡ
(ii) ਸੰਗਤ ਦੀਰਘ ਅਰਧ ਵਿਆਸੀ ਖੰਡ (π = 3.14 ਦਾ ਪ੍ਰਯੋਗ ਕਰੋ)
ਹੱਲ:
ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 10 cm
ਕੇਂਦਰ ਤੇ ਬਣਿਆ ਕੋਣ (θ) = 90°
∴ ਲਘੂ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ = \(\frac{\pi \mathrm{R}^{2} \theta}{360}\)
= 3∙14 × 10 × 10 × \(\frac{90}{360}\) = \(\frac{314}{4}\)
ਲਘੂ ਖੰਡ ਦਾ ਖੇਤਰਫਲ = \(\frac{314}{4}\) = 78.5 cm²
ਲਘੁ ਚੱਕਰ ਖੰਡ ਦਾ ਖੇਤਰਫਲ
= ਲਘੁ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ – △AOB ਦਾ ਖੇਤਰਫਲ
= 78.5 – \(\frac{1}{2}\) × ਆਧਾਰ × ਉਚਾਈ
= (78.5 – \(\frac{1}{2}\) × 10 × 10) cm²
= (78.5 – 50) cm²
= 28.5 cm²
∴ ਲਘੂ ਚੱਕਰ ਖੰਡ ਦਾ ਖੇਤਰਫਲ
= 28.5 cm²
ਵੱਡੇ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ

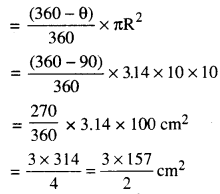
∴ ਵੱਡੇ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ
= 235.5 cm²

ਪ੍ਰਸ਼ਨ 5.
ਅਰਧ ਵਿਆਸ 21 cm ਵਾਲੇ ਚੱਕਰ ਦਾ ਇੱਕ ਚਾਪ ਕੇਂਦਰ ’ਤੇ 60° ਦਾ ਕੋਣ ਬਣਾਉਂਦਾ ਹੈ । ਪਤਾ ਕਰੋ :
(i) ਚਾਪ ਦੀ ਲੰਬਾਈ
(ii) ਚਾਪ ਦੁਆਰਾ ਬਣਾਏ ਗਏ ਅਰਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ
(iii) ਸੰਗਤ ਜੀਵਾ ਦੁਆਰਾ ਬਣਾਏ ਗਏ ਚੱਕਰ ਖੰਡ ਦਾ ਖੇਤਰਫਲ ।
ਹੱਲ:
(i) ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 21 cm

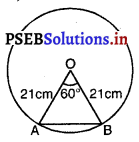
ਕੇਂਦਰ ਤੇ ਬਣਿਆ ਕੋਣ (θ) = 60°
ਚਾਪ ਦੀ ਲੰਬਾਈ = \(\frac{θ}{360}\) × 2πR
= \(\frac{60}{360}\) × 2 × \(\frac{22}{7}\) × 21
∴ ਚਾਪ ਦੀ ਲੰਬਾਈ = 22 cm

(ii) ਚਾਪ ਦੁਆਰਾ ਬਣਾਏ ਗਏ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ
= \(\frac{\pi R^{2} \theta}{360}\)
= \(\frac{22}{7}\) × \(\frac{21×21×60}{360}\)
= 231 cm²
ਕਿਉਂਕਿ △OAB ਸਮਭੁਜੀ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸ ਵਿਚ θ = 60°.

(iii) ਚੱਕਰ ਖੰਡ ਦਾ ਖੇਤਰਫਲ = ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ – vAOB ਦਾ ਖੇਤਰਫਲ
= \(\frac{\pi R^{2} \theta}{360}\) – \(\frac{\sqrt{3}}{4}\) (ਭੁਜਾ)²
= 231 – \(\frac{1∙73}{4}\) × 21 × 21 cm²
= 231 – 0.4325 × 441 cm²
= 231 – 190.7325 cm²
=4026 cm²
∴ ਚੱਕਰ ਖੰਡ ਦਾ = 40.26 cm²

ਪ੍ਰਸ਼ਨ 6.
15 cm ਅਰਧ ਵਿਆਸ ਵਾਲੇ ਇਕ ਚੱਕਰ ਦੀ ਕੋਈ ਜੀਵਾ ਕੇਂਦਰ ‘ਤੇ 60° ਦਾ ਕੋਣ ਬਣਾਉਂਦੀ ਹੈ। ਸੰਗਤ ਲਘੂ ਅਤੇ ਦੀਰਘ ਚੱਕਰ ਖੰਡਾਂ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।
(π = 3.14 ਅਤੇ \(\sqrt {3}\) = 1.73 ਦਾ ਪ੍ਰਯੋਗ ਕਰੋ ॥)
ਹੱਲ:
ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ = (R) = 15 cm
ਕੇਂਦਰ ਦਾ ਕੋਣ (θ) = 60°

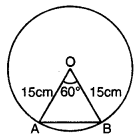
△OAB ਵਿੱਚ ਕੇਂਦਰੀ ਕੋਣ θ = 60°
OA = OB = 15 cm
∴ ∠AZB = 60°
∴ △OAB ਸਮਭੁਜੀ ਤ੍ਰਿਭੁਜ ਹੈ ।
ਲਘੂ ਚੱਕਰ ਖੰਡ ਦਾ ਖੇਤਰਫਲ = (ਲਘੂ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ) – ਸਮਭੁਜੀ ਤਿਭੁਜ ਦਾ ਖੇਤਰਫਲ

∴ ਲਘੂ ਚੱਕਰ ਖੰਡ ਦਾ ਖੇਤਰਫਲ =20.43 cm²
ਦੀਰਘ ਚੱਕਰ ਖੰਡ ਦਾ ਖੇਤਰਫਲ = ਚੱਕਰ ਦਾ ਖੇਤਰਫਲ – ਲਘੂ ਚੱਕਰ ਖੰਡ ਦਾ ਖੇਤਰਫਲ
= πR² – 20.43
= 3.14 × 15 × 15 – 20.43
= (706.5 – 20.43) cm²
= 686.07 cm²
∴ ਦੀਰਘ ਚੱਕਰ ਖੰਡ ਦਾ ਖੇਤਰਫਲ = 686.07 cm²

ਪ੍ਰਸ਼ਨ 7.
12 cm ਅਰਧ ਵਿਆਸ ਵਾਲੇ ਇੱਕ ਚੱਕਰ ਦੀ ਕੋਈ ਜੀਵਾ ਕੇਂਦਰ ‘ ਤੇ 120° ਦਾ ਕੋਣ ਬਣਾਉਂਦੀ ਹੈ । ਸੰਗਤ ਚੱਕਰ ਖੰਡ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।
(π = 3.14 ਅਤੇ \(\sqrt {3}\) = 1.73 ਦਾ ਪ੍ਰਯੋਗ ਕਰੋ)
ਹੱਲ:
ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 12 cm
ਕੇਂਦਰ ਦਾ ਕੋਣ (θ) = 120°
△OAM ਵਿੱਚ, OM ⊥ AB
∴ AM = MB = \(\frac{1}{2}\) AB

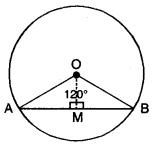
∴ ∠OAM = 30° = ∠OBM

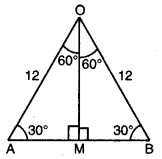
AB = 2AM
= 2\(\left(\frac{\mathrm{AM}}{\mathrm{OA}}\right)\)OA
= 2 (sin 60°) 12
AB = 2 × \(\frac{\sqrt{3}}{2}\) × 12 = 12\(\sqrt {3}\) cm
OM = OA\(\left(\frac{\mathrm{OM}}{\mathrm{OA}}\right)\) = 12 (cos 60°)
= 12 × \(\frac{1}{2}\) = 6 cm
∴ ਚੱਕਰ ਖੰਡ ਦਾ ਖੇਤਰਫਲ = ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ – △OAB ਦਾ ਖੇਤਰਫਲ
ਚੱਕਰ ਖੰਡ ਦਾ ਖੇਤਰਫਲ

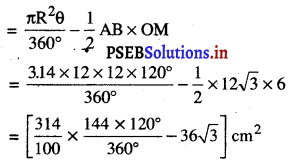
= (150.72 – 36 × 1.73) cm²
= (150.72 – 62.28) cm²
= 8844 cm²
∴ ਚੱਕਰ, ਖੰਡ ਦਾ ਖੇਤਰਫਲ = 88.44 cm²

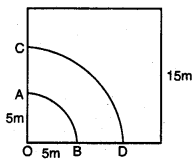
8. 15 m ਪੂਜਾ ਵਾਲੇ ਇੱਕ ਵਰਗਾਕਾਰ ਘਾਹ ਦੇ ਮੈਦਾਨ ਦੇ ਇੱਕ ਕੋਨੇ ‘ਤੇ ਲੱਗੇ ਕਿੱਲੇ ਨਾਲ ਘੋੜੇ ਨੂੰ 5 m ਲੰਬੀ ਰੱਸੀ ਨਾਲ ਬੰਨ੍ਹਿਆ ਹੋਇਆ ਹੈ । (ਦੇਖੋ ਚਿੱਤਰ ਪਤਾ ਕਰੋ ।

ਪ੍ਰਸ਼ਨ (i).
ਮੈਦਾਨ ਦੇ ਉਸ ਭਾਗ ਦਾ ਖੇਤਰਫਲ ਜਿੱਥੇ ਘੋੜਾ ਘਾਹ ਚਰ ਸਕਦਾ ਹੈ ।
ਹੱਲ:
ਵਰਗ ਦੀ ਭੁਜਾ = 15 m
ਕਿੱਲੇ ਨਾਲ ਬੰਨੀ ਰੱਸੀ ਦੀ ਲੰਬਾਈ = ਅਰਧ ਵਿਆਸੀ ਖੰਡ OAB ਦਾ ਅਰਧ ਵਿਆਸ (R) = 5 m
ਕੇਂਦਰੀ ਕੋਣ (θ) = 90°
[ਵਰਗ ਦਾ ਹਰੇਕ ਕੋਣ 90°]

ਅਰਧ ਵਿਆਸੀ ਖੰਡ OAB ਦਾ ਖੇਤਰਫਲ = \(\frac{\pi \mathrm{R}^{2} \theta}{360^{\circ}}\)
= \(\frac{3.14 \times 5 \times 5 \times 90^{\circ}}{360^{\circ}}\)
= \(\frac{3.14 \times 25}{4}\) = \(\frac{78.5}{4}\) m²
= 19.625 m²

ਪ੍ਰਸ਼ਨ (ii).
ਚਰੇ ਜਾਣ ਵਾਲੇ ਖੇਤਰਫਲ ਵਿੱਚ ਵਾਧਾ ਜੇਕਰ ਘੋੜੇ ਨੂੰ 5 m ਲੰਬੀ ਰੱਸੀ ਦੇ ਸਥਾਨ ‘ਤੇ 10 m ਲੰਬੀ ਰੱਸੀ ਨਾਲ ਬੰਨ ਦਿੱਤਾ ਜਾਵੇ। (π = 3.14 ਦਾ ਪ੍ਰਯੋਗ ਕਰੋ) !

ਹੱਲ:
ਜਦੋਂ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਅਰਧਵਿਆਸ ਵੱਧ ਕੇ 10 m ਹੋ ਜਾਂਦਾ ਹੈ ।
∴ ਅਰਧ ਵਿਆਸੀ ਖੰਡ OCD ਦਾ ਅਰਧ ਵਿਆਸ | (R₁) = 10 m
ਕੇਂਦਰੀ ਕੋਣ (θ) = 90°
∴ ਅਰਧ ਵਿਆਸੀ ਖੰਡ OCDP ਖੇਤਰਫਲ = \(\frac{\pi \mathrm{R}_{1}^{2} \theta}{360^{\circ}}\)

∴ ਚਰੇ ਜਾ ਸਕਣ ਵਾਲੇ ਖੇਤਰ ਦੇ ਖੇਤਰਫਲ ਵਿੱਚ ਵਾਧਾ
= ਅਰਧ ਵਿਆਸੀ ਖੰਡ OCD ਦਾ ਖੇਤਰਫਲ – ਅਰਧ ਵਿਆਸੀ ਖੰਡ OAB ਦਾ ਖੇਤਰਫਲ
= (78.5 – 19.625) cm²
= 58.875 m²
∴ ਚਰੇ ਜਾ ਸਕਣ ਵਾਲੇ ਖੇਤਰ ਦੇ ਖੇਤਰਫਲ ਵਿੱਚ ਵਾਧਾ
= 58.875 m²

ਪ੍ਰਸ਼ਨ 9.
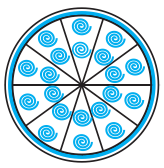
ਇੱਕ ਚੱਕਰਾਕਾਰ ਬਰੂਚ (brooch) ਨੂੰ ਚਾਂਦੀ ਦੇ ਤਾਰ । ਨਾਲ ਬਣਾਇਆ ਜਾਣਾ ਹੈ ਜਿਸ ਦਾ ਵਿਆਸ 35 mm ਹੈ । ਤਾਰ ਨੂੰ ਚੱਕਰ ਦੇ 5 ਵਿਆਸਾਂ ਨੂੰ ਬਣਾਉਣ ਵਿੱਚ ਵਰਤਿਆ ਗਿਆ ਹੈ ਜੋ ਉਸ ਨੂੰ 10 ਬਰਾਬਰ ਅਰਧ ਵਿਆਸੀ ਖੰਡਾਂ ਵਿੱਚ ਵੰਡਦੀ ਹੈ ਜਿਵੇਂ ਕਿ ਚਿੱਤਰ ਵਿੱਚ ਦਰਸ਼ਾਇਆ ਗਿਆ ਹੈ । ਤਾਂ ਪਤਾ ਕਰੋ :
(i) ਕੁੱਲ ਲੋੜੀਂਦੀ ਚਾਂਦੀ ਦੇ ਤਾਰ ਦੀ ਲੰਬਾਈ
(ii) ਬਰੂਚ ਦੇ ਹਰੇਕ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ

ਹੱਲ:
ਚੱਕਰ ਦਾ ਵਿਆਸ (D) = 35 mm
ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ (R) = \(\frac{35}{2}\) mm
ਵਿਆਸਾਂ ਦੀ ਸੰਖਿਆ = 5
ਬਰਾਬਰ ਅਰਧ ਵਿਆਸੀ ਖੰਡਾਂ ਦੀ ਸੰਖਿਆ = 10
(i) ਪ੍ਰਯੋਗ ਕੀਤੀ ਗਈ ਤਾਰ ਦੀ ਲੰਬਾਈ = 5 ਵਿਆਸਾਂ ਦੀ ਲੰਬਾਈ + ਚੱਕਰ (ਬਚ) ਦਾ ਪਰਿਮਾਪ
= 5(35) + 2πR
= [175 + 2 × \(\frac{22}{7}\) × \(\frac{35}{2}\)] mm
= [175 + 110] mm
= 285 mm

(ii) ਬਰੂਚ ਦੇ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਕੋਣ

ਹਰੇਕ ਬਰੂਚ ਦਾ ਖੇਤਰਫਲ (ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ)
= \(\frac{\pi R^{2} \theta}{360}\)
= \(\frac{36}{360}\) × \(\frac{22}{7}\) × \(\frac{35}{2}\) × \(\frac{35}{2}\)
= \(\frac{1135}{4}\) = \(\frac{385}{4}\) mm²
= 96.25 mm²
∴ ਬਰੂਚ ਦੇ ਹਰੇਕ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ
= 96.25 mm²

ਪ੍ਰਸ਼ਨ 10.
ਇੱਕ ਛੱਤਰੀ ਵਿੱਚ ਅੱਠ ਤਾਰਾਂ ਹਨ, ਜੋ ਬਰਾਬਰ ਦੂਰੀ ‘ਤੇ ਲੱਗੀਆਂ ਹੋਈਆਂ ਹਨ (ਦੇਖੋ ਚਿੱਤਰ । ਛੱਤਰੀ ਨੂੰ 45 cm ਅਰਧ ਵਿਆਸ ਵਾਲਾ ਇੱਕ ਸਪਾਟ ਚੱਕਰ ਮੰਨਦੇ ਹੋਏ ਇਸ ਦੀਆਂ ਦੋ ਲਗਾਤਾਰ ਤਾਰਾਂ ਦੇ ਵਿਚਕਾਰ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ।

ਹੱਲ:
ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ = 45 cm
ਤਾਰਾਂ ਦੀ ਸੰਖਿਆ = 8
ਕੇਂਦਰੀ ਕੋਣ (ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਕੋਣ) = \(\frac{360^{\circ}}{8}\)
= 45°
ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ = \(\frac{\pi R^{2} \theta}{360^{\circ}}\)
= \(\frac{45}{360^{\circ}}\) × \(\frac{22}{7}\) × 45 × 45 cm²
= \(\frac{1}{8}\) × \(\frac{22}{7}\) × 45 × 45 cm²
= \(\frac{22275}{28}\) cm²
= 795:53 cm²
∴ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ =795.53 cm²
∴ ਛੱਤਰੀ ਦੇ ਦੋ ਲਗਾਤਾਰ ਤਾਰਾਂ ਵਿਚਕਾਰ ਦਾ ਖੇਤਰਫਲ
= 795.53 cm²

ਪ੍ਰਸ਼ਨ 11.
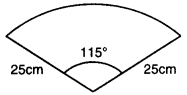
ਕਿਸੇ ਕਾਰ ਦੇ ਦੋ ਵਾਇਪਰ (wipers) ਹਨ, ਆਪਸ ਵਿੱਚ ਕਦੇ ਵੀ ਇੱਕ ਦੂਸਰੇ ਨੂੰ ਛੂਹਦੇ ਨਹੀਂ । ਹਰੇਕ ਵਾਇਪਰ, ਜਿਸਦੀ ਪੱਤੀ ਦੀ ਲੰਬਾਈ 25 cm ਹੈ ਅਤੇ 115° ਦੇ ਕੋਣ ਤੱਕ ਘੁੰਮ ਕੇ ਸਫਾਈ ਕਰ ਸਕਦਾ ਹੈ । ਵਾਇਪਰਾਂ ਦੇ ਹਰੇਕ ਗੇੜੇ ਨਾਲ ਜਿੰਨਾ ਖੇਤਰਫਲ ਸਾਫ਼ ਹੋ ਜਾਂਦਾ ਹੈ, ਉਹ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਪੱਤੀ ਦੀ ਲੰਬਾਈ (R) = 25 cm
ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਕੋਣ (θ) = 115°
ਵਾਇਪਰ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦੇ ਰੂਪ ਵਿਚ ਘੁੰਮਦਾ ਹੈ ।

ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ = ਇਕ ਪੱਤੀ ਦੁਆਰਾ ਘੁੰਮਿਆ ਗਿਆ ਖੇਤਰਫਲ
= \(\frac{\pi \mathrm{R}^{2} \theta}{360^{\circ}}\)
= \(\frac{22}{7}\) × \(\frac{115}{360}\) × 25 × 25 cm²
= 27.48 cm²
ਵਾਇਪਰ ਦੀਆਂ ਦੋ ਪੱਤੀਆਂ ਦੁਆਰਾ ਘੁੰਮਿਆ ਗਿਆ ਖੇਤਰਫਲ = 2 ਖੰਡਾਂ ਦਾ ਖੇਤਰਫਲ
= 2 × 627.48 cm²
= 1254.96 cm²

ਪ੍ਰਸ਼ਨ 12.
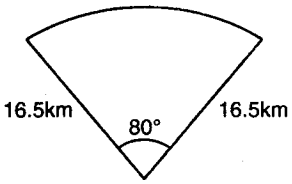
ਜਹਾਜ਼ਾਂ ਨੂੰ ਸਮੁੰਦਰ ਜਲ ਸੜਾ ਦੇ ਹੇਠਾਂ ਸਥਿਤ ਚੱਟਾਨਾਂ ਦੀ ਚੇਤਾਵਨੀ ਦੇਣ ਦੇ ਲਈ, ਇੱਕ ਲਾਈਟ ਹਾਉਸ (light house) 80° ਕੋਣ ਵਾਲੇ ਇੱਕ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਵਿੱਚ 6.5 km ਦੀ ਦੂਰੀ ਤੱਕ ਲਾਲ ਰੰਗ ਦਾ ਪ੍ਰਕਾਸ਼ ਫੈਲਾਉਂਦਾ ਹੈ । ਸਮੁੰਦਰ ਦੇ ਉਸ ਭਾਗ ਦਾ ਖੇਤਰਫਲ ਪਤਾ ਕਰੋ ਜਿਸ ਨਾਲ ਜਹਾਜ਼ਾਂ ਨੂੰ ਚੇਤਾਵਨੀ ਦਿੱਤੀ ਜਾ ਸਕੇ । (π = 3.14 ਦਾ ਪ੍ਰਯੋਗ ਕਰੋ ।)
ਹੱਲ:
ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਕੋਣ (θ) = 80°
ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਅਰਥਵਿਆਸ (R) = 16.5 km

ਸਮੁੰਦਰ ਦੇ ਉਸ ਭਾਗ ਦਾ ਖੇਤਰਫਲ ਜਿਥੋਂ ਤੱਕ ਜਹਾਜਾਂ ਨੂੰ ਚੇਤਾਵਨੀ ਦਿੱਤੀ ਜਾ ਸਕੇ
ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ = \(\frac{\pi \mathrm{R}^{2} \theta}{360^{\circ}}\)
= \(\frac{3.14 \times 16.5 \times 16.5 \times 80}{360}\) km²
= 189.97 km²
ਉਹ ਖੇਤਰ ਜਿੱਥੋਂ ਤੱਕ ਚੇਤਾਵਨੀ ਦਿੱਤੀ ਜਾ ਸਕੇ
= 189.97 km²

ਪ੍ਰਸ਼ਨ 13.
ਇੱਕ ਗੋਲ ਮੇਜਪੋਸ਼ ‘ਤੇ ਛੇ ਇੱਕੋ ਜਿਹੇ ਸਮਾਨ ਡਿਜਾਈਨ ਬਣੇ ਹੋਏ ਹਨ ਜਿਵੇਂ ਕਿ ਚਿੱਤਰ ਵਿੱਚ ਦਰਸਾਇਆ ਗਿਆ ਹੈ । ਜੇਕਰ ਮੇਜਪੋਸ਼ ਦਾ ਅਰਧ ਵਿਆਸ 28 cm ਹੈ ਤਾਂ ਤੋਂ 0.35 ਪ੍ਰਤੀ ਵਰਗ ਸੈਂਟੀਮੀਟਰ ਦੀ ਦਰ ਨਾਲ ਇਨ੍ਹਾਂ | ਡਿਜਾਈਨਾਂ ਨੂੰ ਬਣਾਉਣ ਦੀ ਲਾਗਤ ਪਤਾ ਕਰੋ ।
(\(\sqrt {3}\) = 1.7 ਲਓ)

ਹੱਲ:
ਸਮਾਨ ਡਿਜਾਈਨਾਂ ਦੀ ਸੰਖਿਆ = 6
ਡਿਜਾਈਨਾਂ ਦਾ ਅਰਧ ਵਿਆਸ (R) = 28 cm
ਹਰੇਕ ਡਿਜਾਇਨ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦੇ ਆਕਾਰ ਦਾ ਹੈ, ਕੇਂਦਰੀ ਕੋਣ (θ) = \(\frac{360^{\circ}}{6}\) = 60°
ਕਿਉਂਕਿ ਕੇਂਦਰੀ ਕੋਣ 60° ਹੈ ਅਤੇ OA = OB ਹੈ ।
∴ △OAB ਇਕ ਸਮਭੁਜੀ ਤ੍ਰਿਭੁਜ ਹੈ ਜਿਸਦੀ ਭੂਜਾ 28 cm ਹੈ ।

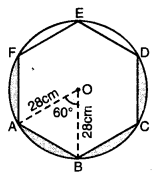
ਇੱਕ ਛਾਇਆ ਅੰਕਿਤ ਡਿਜਾਇਨ ਵਾਲੇ ਭਾਗ ਦਾ ਖੇਤਰਫਲ = ਚੱਕਰ ਖੰਡ ਦਾ ਖੇਤਰਫਲ = ਅਰਧ ਵਿਆਸੀ ‘ ਖੰਡ OAB ਦਾ ਖੇਤਰਫਲ – △OAB ਦਾ ਖੇਤਰਫਲ
= \(\frac{\pi \mathrm{R}^{2} \theta}{360^{\circ}}\) – \(\frac{\sqrt{3}}{4}\) (ਭੂਜਾ)²
= (\(\frac{22}{7}\) × \(\frac{2828}{360}\) × 60 – \(\frac{1.7}{4}\) × 28 × 28) cm²
= (410.66 – 333.2) cm²
= 77.46 cm²
∴ ਇਕ ਛਾਇਆ ਅੰਕਿਤ ਡਿਜਾਇਨ ਵਾਲੇ ਭਾਗ ਦਾ ਖੇਤਰਫਲ
= 77.46 cm²
ਛੇ ਡਿਜਾਈਨ ਭਾਗਾਂ ਦਾ ਖੇਤਰਫਲ = 6 [ਇਕ ਡਿਜਾਈਨ ਭਾਗ ਦਾ ਖੇਤਰਫਲ]
= 6 [77.46]
= 464.76 cm²
1 cm² ਡਿਜਾਈਨ ਬਣਾਉਣ ਦਾ ਖ਼ਰਚ = ₹ 0.35
464.76 cm² ਡਿਜਾਈਨ ਬਣਾਉਣ ਦਾ ਖ਼ਰਚ
= ₹0.35 × 464.76
= ₹ 162.67

ਪ੍ਰਸ਼ਨ 14.
ਹੇਠਾਂ ਦਿੱਤਿਆਂ ਵਿੱਚੋਂ ਸਹੀ ਉੱਤਰ ਚੁਣੋ :
ਅਰਧ ਵਿਆਸ Rਵਾਲੇ ਚੱਕਰ ਦੇ ਉਸ ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ ਜਿਸਦਾ ਕੋਣ p° ਹੈ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਹੈ :
(A) \(\frac{p}{180}\) × 2πR
(B) \(\frac{p}{180}\) × πR²
(C) \(\frac{p}{360}\) × 2πR
(D) \(\frac{p}{720}\) × 2πR²
ਹੱਲ:
ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਕੋਣ (θ) = p°
ਚੱਕਰ ਦਾ ਅਰਧ ਵਿਆਸ = R
ਅਰਧ ਵਿਆਸੀ ਖੰਡ ਦਾ ਖੇਤਰਫਲ = \(\frac{\pi R^{2} \theta}{360}\)
= \(\frac{\pi \mathrm{R}^{2} \times p}{360}\)
∴ ਸਹੀ ਵਿਕਲਪ (D) ਹੈ ।